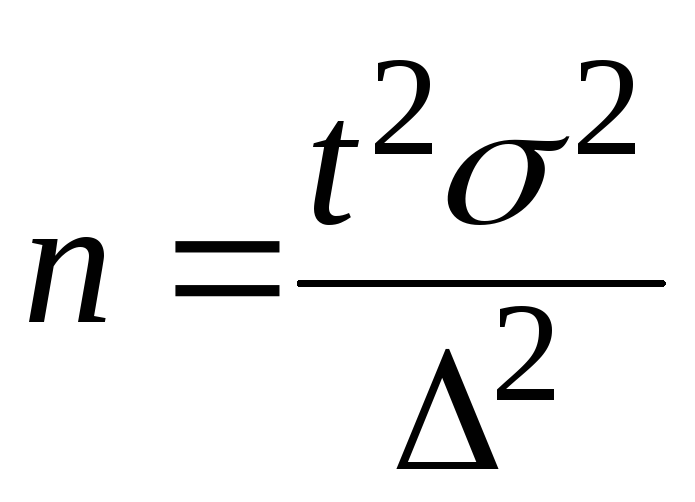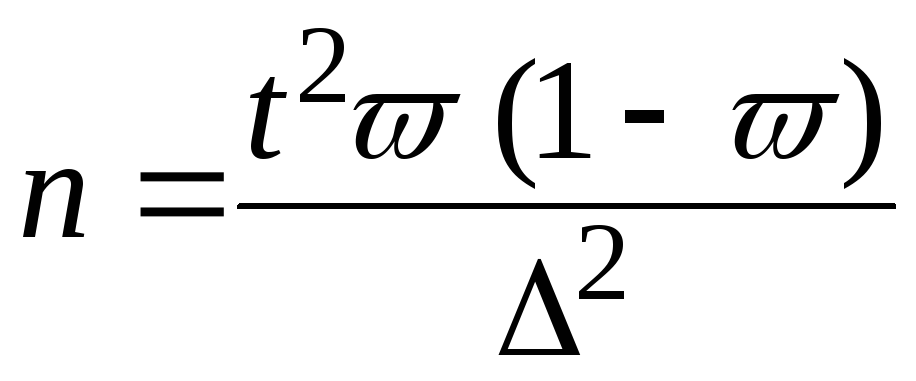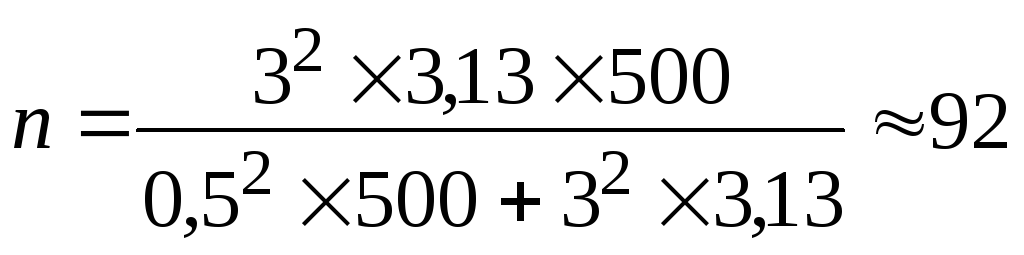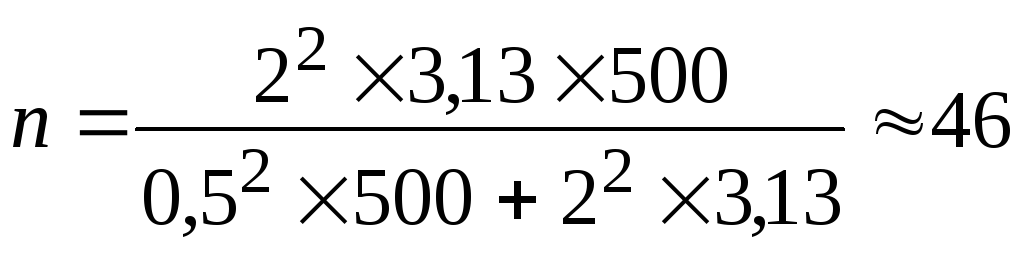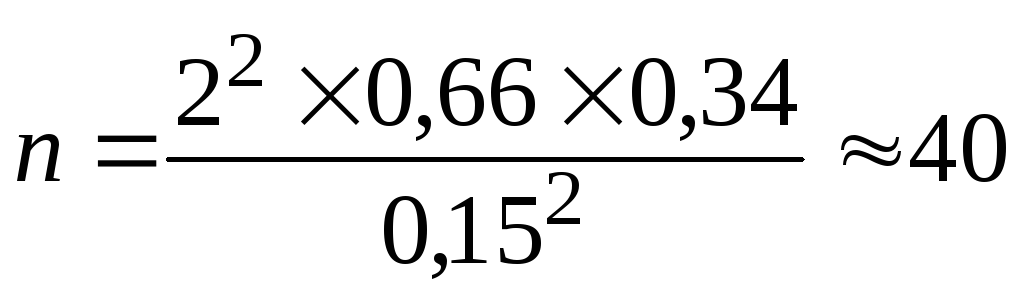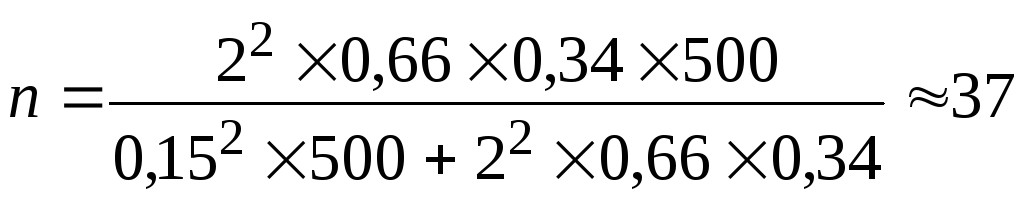Задачи по статистике с решением — Выборочное наблюдение
Решения задач по выборочному наблюдению
Задача 1 по статистике
При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.
Решение.
В данном примере – случайный повторный отбор.
n=200


p=0,997, тогда t=3
Формула средней ошибки для случайного повторного отбора:


Определяем величину средней ошибки.

Ответ: пределы в которых находится средний вес изделий:
Задача 2
В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:
P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.
|
Число детей в семье, xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кол-во детей в семье |
1000 |
2000 |
1200 |
400 |
200 |
200 |
Решение
2%-я выборка означает:
n=250000*0,02= 5000 семей было исследовано.
Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:
Найдем среднее число детей в выборочной совокупности:

Определим дисперсию

Т.к p = 0,954, то t = 2


Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.
Задача 3
С целью определения средней фактической продолжительности рабочего дня в гос. учреждении с численностью служащих 480 человек была проведена 25%-ная механическая выборка. По результатам наблюдения оказалось, что у 10% обследованных потери рабочего времени достигали более 45 мин.в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности: n=480*0.25=120 чел.
Выборочная доля w по условию 10%.Учитывая, что показатели точности механической и собственно случайной бесповторной выборки определяются одинаково, а также то, что при P=0,683 t=1, предельная ошибка выборочной доли: 
Ответ: пределы в которых находится средняя доля 

Т.о., с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6 до 12,4 %.
Задача 4 по статистике
В АО 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что дисперсия доли бесповторной выборки равна 225. с вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Численность выборки для бесповторного отбора:

Решение типовых задач
Пример
1.
Для изучения оснащения заводов основными
производственными фондами было
проведено 10%-ное выборочное обследование,
в результате которого получены следующие
данные о распределении заводов по
стоимости основных производственных
фондов:
|
Среднегодовая |
До |
2 |
4 |
Свыше |
Итого |
|
Число |
5 |
12 |
23 |
10 |
50 |
Требуется
определить: 1) с вероятностью 0,997 предельную
ошибку выборочной средней и границы, в
которых будет находиться среднегодовая
стоимость основных производственных
фондов всех заводов генеральной
совокупности; 2) с вероятностью 0,954
предельную ошибку выборки при определении
доли и границы, в которых будет находиться
удельный вес заводов со стоимостью
основных производственных фондов
свыше 4 млн. руб.
Решение.
Предельная
ошибка выборки (ошибка репрезентативности)
исчисляется по формуле:
,
где
μ
– средняя ошибка репрезентативности;
t
–
коэффициент кратности ошибки, показывающий,
сколько средних ошибок содержится в
предельной ошибке.
Пределы
возможной ошибки (∆) определяются с
вероятностью. Значение t
найдем
по таблице интеграла вероятностей.
Для Соответствует
вероятность
t
= 1 Р
=0,683;
t
= 2 Р
=0,954;
t
= 3 Р
=0,997
и т. д.
Конкретное
количественное выражение предельная
ошибка принимает после определения
средней ошибки выборки. Для нахождения
ошибки репрезентативности собственно
чайной и механической выборок имеются
нижеследующие формулы.
Повторная
выборка при
определении:
среднего
размера ошибки признака (1)
средней
ошибки доли признака (2)
Бесповторная
выборка
при определении:
среднего
размера ошибки признака 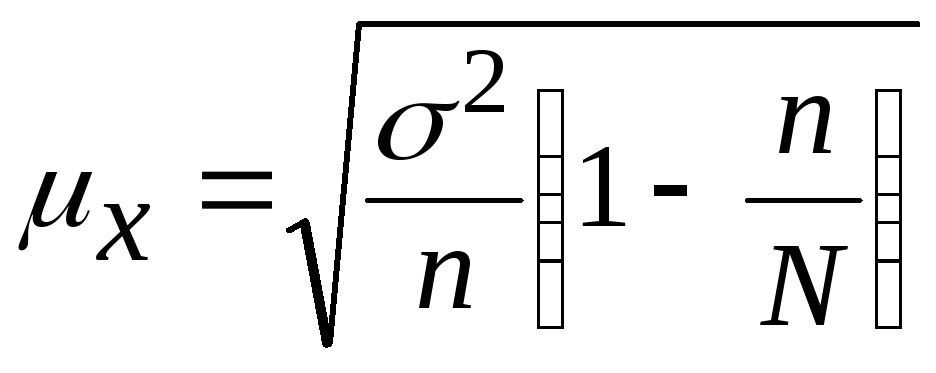
средней
ошибки доли признака (4)
N
– численность генеральной совокупности;
п
– численность выборочной совокупности;
2
– дисперсия варьирующего (осредняемого)
признака в выборочной совокупности;
ω
– доля данного признака в выборке;
(1
– ω) – доля противоположного признака
в выборке.
1.
Для определения границ генеральной
средней необходимо исчислить среднюю
выборочную ()и
дисперсию (2),
техника расчета которых приведена в
таблице:
|
Среднегодовая |
Число |
Середина |
х |
х |
(х |
(х |
|
До |
5 |
1 |
5 |
-3,52 |
12,39 |
61,95 |
|
2 |
12 |
3 |
36 |
-1,52 |
2,31 |
27,72 |
|
4 |
23 |
5 |
115 |
0,48 |
0,23 |
5,29 |
|
Свыше |
10 |
7 |
70 |
2,48 |
6,15 |
61,50 |
|
50 |
226 |
156,46 |
Тогда
млн.
руб.;
.
Для
упрощения расчетов средней и дисперсии
можно использовать способ моментов.
Техника расчетов
и
2
по способу моментов изложена в первой
части брошюры «Практикум по общей
теории статистики».
Итак
имеются данные: N
= 500, п
= 50 заводов; 2
= 3,13.
Средняя
ошибка выборки при определении
среднегодовой .стоимости основных
фондов составит:
а)
при повторном отборе (по формуле 1) –
≈
±
0,25 млн. руб.;
б)
при бесповторном отборе (по формуле 3)
–
≈ ±
0,24 млн. руб.;
Следовательно,
при определении среднегодовой стоимости
основных производственных фондов в
среднем мы могли допустить среднюю
ошибку репрезентативности в 0,25 млн.
руб. при повторном и 0,24 млн. руб. при
бесповторном отборе в ту или иную
сторону от среднегодовой стоимости
основных производственных фондов,
приходящейся на один завод в выборочной
совокупности. Исчисленные данные
показывают, что при бесповторной
выборке средняя ошибка репрезентативности
(0,24) меньше, чем при тех же условиях при
повторном отборе (0,25).
В
нашем примере Р
=
0,997, следовательно, t
= 3.
Исчислим
предельную ошибку выборочной средней
(∆х):
∆х
= ±3μ; т. е. ∆х
= = ±3 × 0,25 = ±0,75 млн. руб. (при повторном
отборе); ∆х
= ±3 × 0,24 = ±0,72 млн. руб. (при бесповторном
отборе).
Порядок
установления пределов, в которых
находится средняя величина изучаемого
показателя в генеральной совокупности
в общем виде, может быть представлен
следующим образом:
;
Для
нашего примера среднегодовая стоимость
основных производственных фондов в
среднем на один завод генеральной
совокупности будет находиться в следующих
пределах.
а)
при повторном отборе –
=
4,52 ± 0,25 или 4,27 млн. руб. ≤
≤
4,77
млн.
руб.;
б)
при бесповторном отборе –
=
4,52 ± 0,24 или 4,28 млн. руб. ≤
≤
4,76 млн. руб.
Эти
границы можно гарантировать е вероятностью
0,997.
2.
Вычисление пределов при установлении
доли осуществляется аналогично
нахождению пределов для средней величины.
В общем виде расчет можно представить
следующим образом:
;
,
где
р
–
доля единиц, обладающих данным признаком
в генеральной совокупности.
Доля
заводов в выборочной совокупности со
стоимость основных производственных
фондов свыше 4 млн. руб. составляет:
,
или 66%.
Определяем
предельную ошибку для дели. По условию
задачи известно, что N
= 500; n
= 5; ω = 0,66; Р
= 0,954; t
= 2.
Исчислим
предельную ошибку доли:
при
повторном отборе (по формуле 2) –
,
или 13,4%;
при
бесповторном отборе (по формуле 4) –
,
или 12,7%.
Следовательно,
с вероятностью 0,954 доля заведен се
стоимостью основных производственных
фондов свыше 4 млн. руб. в генеральной
совокупности будет находиться в пределах:
р
= 66% ± 13,4%, или 52,6% ≤ р ≤ 79,4% при повторном
отборе;
р
= 66%
± 12,7%, или 53,3% ≤ р ≤ 78,7% при бесповторном
отборе.
Расчеты
убеждают в том, что при бесповторном
отборе ошибка выборки меньше, чем при
тех же условиях при повторной выборке.
Пример
2.
Используя данные предыдущей задачи,
требуется ответить, каким должен быть
объем выборочной совокупности при
условии, что: 1) предельная ошибка выборки
при определении среднегодовой стоимости
основных производственных фондов
(с вероятностью 0,997) была бы не более 0,5
млн. руб.; 2) то же при вероятности 0,954; 3)
предельная ошибка доли (с вероятностью
0,954) была бы не более 15%.
Решение.
Для нахождения численности случайной
и механической выборок имеются следующие
четыре формулы:
Повторный
отбор Бесповторный
отбор
При
определении
среднего
размера
ошибки
признака
(5); 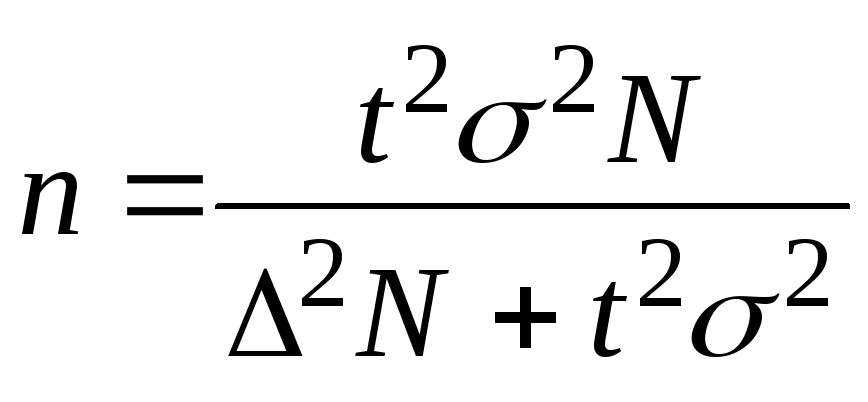
При
определении
ошибки
доли признака
(7); 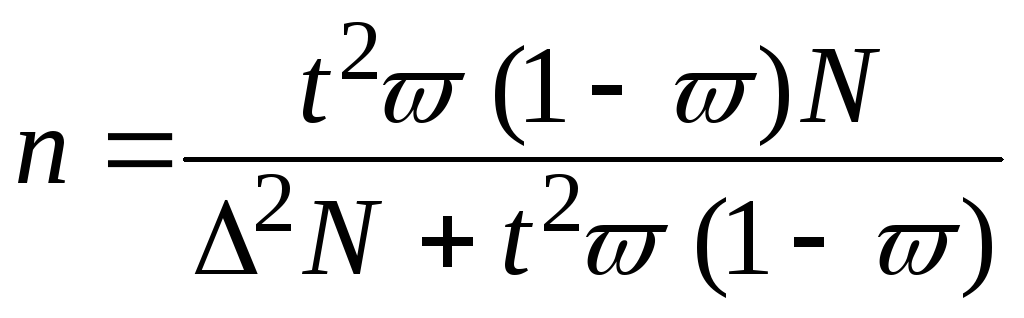
1)
Известно, что N
= 500;
= 0,5 млн. руб.; 2
= 3,13; Р
= 0,997; t
= 3.
Найдем
объем выборки для расчета ошибки средней:
при
повторном отборе (по формуле 5) –
заводов;
при
бесповторном отборе (по формуле 6) –
завода.
2)
Известно, что N
= 500;
= 0,5 млн. руб.; 2
= 3,13; Р
= 0,954; t
= 2.
Определим
объем выборки при бесповторном отборе
(по формуле 6):
завода.
3)
Известно, что N
= 500;
= 0,5 млн. руб.; ω =
0,66; Р
= 0,954; t
= 2.
Объем
выборки для расчета ошибки доли будет:
при повторном отборе (по формуле 7) –
заводов;
при
бесповторном отборе (по формуле 
заводов.
Выводы:
1) численность выборки увеличится, если
при прочих равных условиях уменьшить
предельную ошибку; 2) численность выборки
уменьшится, если при прочих равных
условиях уменьшить вероятность, с
которой требуется гарантировать
результат выборочного обследования;
3) численность выборки уменьшится, если
при прочих равных условиях увеличить
предельную ошибку.
Пример
3.
На заводе 1000 рабочих вырабатывают
одноименную продукцию. Из них со стажем
работы до пяти лет трудятся 400 чел., а
более пяти лет – 600 чел. Для изучения
среднегодовой выработки и установления
доли квалифицированных рабочих проведена
10%-ная типическая выборка с отбором
единиц пропорционально численности
рабочих по указанным группам (внутри
групп применялся случайный метод
отбора).
На
основе обследования получены следующие
данные:
|
Группы |
Общая |
Число |
Среднедневная |
Дисперсия |
Число |
Доля |
|
До |
400 |
40 |
25 |
81 |
32 |
0,8 |
|
Свыше |
600 |
60 |
30 |
64 |
54 |
0,9 |
|
Итого |
1000 |
100 |
Определим:
1) с вероятностью 0,954 предельную ошибку
выработки и границы, в которых будут
находиться среднедневная выработка
всех рабочих завода; 2) с той же вероятностью
пределы удельного веса квалифицированных
рабочих в общей численности рабочих
завода.
Решение.
1) Средняя ошибка типической выборки
определяется по формуле:

где
–
средняя
из внутригрупповых дисперсий.
Она
исчисляется по формуле:

Тогда
.
Определим
среднюю ошибку выборки при бесповторном
отборе (по формуле 9) :
шт.
Техника
расчета предельной ошибки при типической
выборке аналогична вышеизложенному
расчету предельной ошибки при случайном
отборе:
или
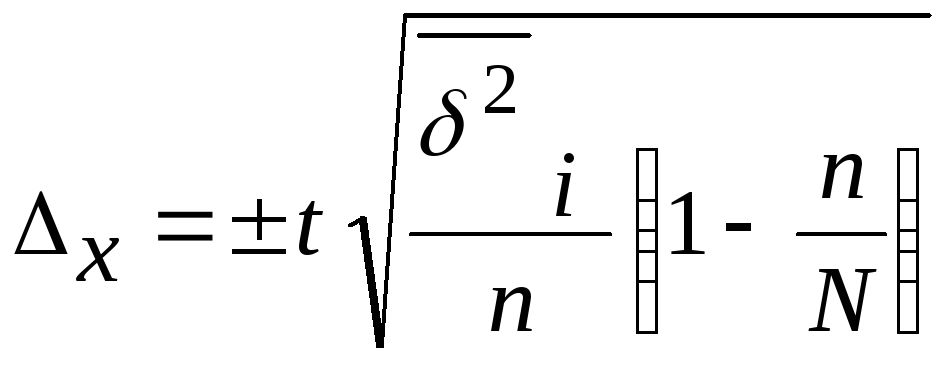
Подставив
данные, получим:
= ± 2 × 0,83 = ± 1,6 шт.
Для
определения возможных пределов
среднедневной выработки всех рабочих
завода первоначально нужно исчислить
среднедневную выработку в выборочной
совокупности по средней арифметической
взвешенной:

Пределы
среднедневной выработки всех рабочих
завода:
= 28 ± 1,6 шт.
С
вероятностью 0,954 можно утверждать, что
среднедневная выработка всех рабочих
завода находится в пределах 26,4 шт. ≤
≤
29,6 шт.
2)
Средняя ошибка репрезентативности для
доли исчисляется по формуле:
(10)
где
– дисперсия доли ()
является средней из внутри групповых
дисперсий.
Эта
величина исчисляется по формуле:
Технику
расчета покажем в таблице:
|
Группы |
Численность |
Доля |
Доля
|
Дисперсия
|
Взвешенный
|
|
До |
40 |
0,8 |
0,2 |
0,16 |
6,4 |
|
Свыше |
60 |
0,9 |
0,1 |
0,09 |
5,4 |
|
Итого |
100 |
11,8 |
Тогда
.
Определим
среднюю ошибку репрезентативности для
доли (по формуле 10):
,
или ± 3,2%.
Исчислим
среднюю ошибку выборочной доли с
вероятностью 0,954:
,
или 6,4%.
Расчет
предела при установлении доли в общем
виде представляется следующим образом:
.
Определим
среднюю долю для выборочной совокупности:
,
или 86%.
Отсюда:
р
= 86% ± 6,4%.
Вывод:
с вероятностью 0,954 можно утверждать,
что доля квалифицированных рабочих на
заводе будет находиться в пределах
79,6% ≤ р
≤ 92,4%.
Пример
4.
С целью определения среднего
эксплуатационного пробега 10000 шин
легковых автомобилей, распределенных,
на партии по 100 шт., проводится серийная
4%-ная бесповторная выборка. Результаты
испытания отобранных шин характеризуются
следующими данными:
|
Показатели |
Партии |
|||
|
1 |
2 |
3 |
4 |
|
|
Средний |
40 |
42 |
45 |
48 |
|
Доля |
0,80 |
0,85 |
0,90 |
0,95 |
Определите:
1) средние ошибки репрезентативности:
а) эксплуатационного пробега шин; б)
удельного веса шин с пробегом не менее
42 тыс. км; 2) с вероятностью 0,954 пределы,
в которых будет находиться: а) средний
эксплуатационный пробег всех
обследуемых шин; б) доля шин, пробег
которых не менее 42 тыс. км в генеральной
совокупности.
Решение.
1) При бесповторном отборе серий средняя
ошибка репрезентативности определяется
по формулам:
для
средней –

для
доли –
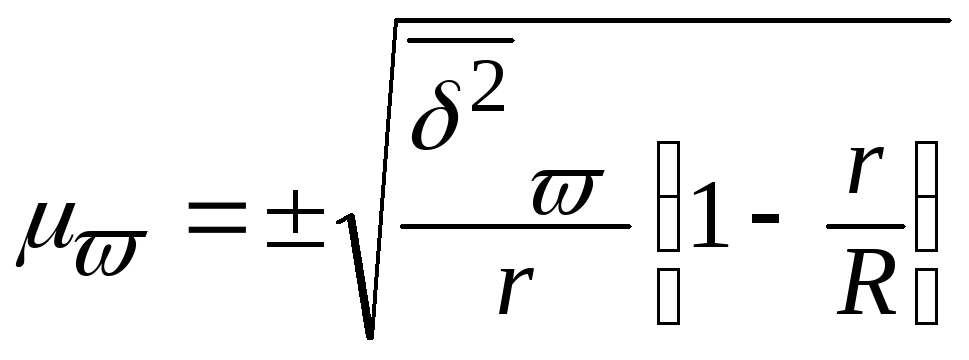
где
R
– число серий в генеральной совокупности;
r
– число отобранных серий;
– межсерийная
дисперсия средних;
–
межсерийная
дисперсия доли.
Сначала
исчислим обобщающие показатели.
Средний
эксплуатационный пробег шин:
тыс.
км.
Средний
удельный вес шин с пробегом не менее 42
тыс. км равен:
(или
87,5%)
Межсерийная
дисперсия определяется по формулам:
для средней –
для
средней –
;
для
доли –
.
Для
ее расчета построим вспомогательную
расчетную таблицу:
|
№ партии |
Средний |
|
|
Доля |
|
|
|
1 |
40 |
-3,75 |
14,06 |
0,8 |
-0,075 |
0,005625 |
|
2 |
42 |
-1,76 |
3,06 |
0,85 |
-0,025 |
0,000625 |
|
3 |
45 |
1,25 |
1,56 |
0,90 |
0,025 |
0,000625 |
|
4 |
48 |
4,25 |
18,06 |
0,95 |
0,075 |
0,005625 |
|
Итого |
36,74 |
0,012500 |
Тогда
;
.
Определим
средние ошибки репрезентативности:
для
средней (по формуле 11) –
тыс.
км.;
для
доли (по формуле 12) –
,
или ± 2,74%.
2)
Определим с вероятностью 0,954 предельные
ошибки репрезентативности для средней
и для доли:
тыс.
км.;
%.
Отсюда
средний эксплуатационный пробег
всех обследуемых шин будет находиться
в пределах:
=
±
= 43,75 ± 3,0, или 40,75 тыс. км ≤ х
≤ 46,75 тыс. км.
Средний
удельный вес шин с пробегом не менее 42
тыс. км в генеральной совокупности будет
находиться в пределах:
p
=
±
=
87,5% ± 5,5%, или 82,0% ≤ р
≤
93,0%.
Пример
5.
Используя условие и решение предыдущей
задачи, определите вероятность того,
что: а) предельная ошибка выборки при
установлении среднего эксплуатационного
пробега шин не превышает 4,0 тыс. км;
б) доля шин с пробегом не менее 42 тыс. км
будет находиться в пределах от 83% До
92%.
Решение.
При определении вероятности используется
формула предельной ошибки:
.
В
нашем примере следует использовать
формулу предельной ошибки серийного
отбора.
а)
Дано: R
= 100; r
= 4;
= 43,75 тыс. км;
= 9,185;
= 4,0 тыс. км.
Требуется
определить вероятность того, что разница
средних величин эксплуатационного
пробега шин в выборочной и генеральной
совокупности не превысит ± 4,0 тыс. км,
т. е.
р
|
–
|
≤ 4,0 тыс. км.
Подставляем
данные в формулу:


.
По
таблице значений вероятностей находим,
что при t
= 2,67
вероятность будет 0,992.
Следовательно,
с вероятностью 0,992 можно гарантировать,
что средний эксплуатационный пробег
шин легковых автомобилей в генеральной
совокупности будет находиться в пределах
39,75 тыс. км ≤
≤ 47,75 тыс. км;
б)
Дано: R
= 100; r
= 4;
= 87,5%;
= 0,003125;
= 4,5%.
Требуется
определить: p
|
–р
| ≤ 4,5%, т. е. вероятность того, что доля
шин с пробегом не менее 42 тыс. км в
выборочной совокупности не будет
отклоняться от доли генеральной
совокупности более чем на 4,5%.
Подставив
данные в формулу
(см.
решение выше), получим 4,5% = t
× 2,74%;
,
тогда Р
= 0,899.
Следовательно,
вероятность того, что удельный вес шин
с пробегом не менее 42 тыс. км будет
находиться в пределах от 83% до 92%,
равна 0,899.
Соседние файлы в папке статистика
- #
- #
- #
- #
- #
- #
Выборочное наблюдение
Задача №32. Расчёт предела, в котором находится средний возраст рабочих
На заводе, где число рабочих составляет 1000 человек, было проведено выборочное обследование возраста рабочих. Методом случайного бесповторного отбора было отобрано 50 человек. Результаты обследования следующие:
| Возраст рабочих (лет) | до 30 | 30 – 40 | 40 – 50 | 50 – 60 | свыше 60 |
|---|---|---|---|---|---|
| Число рабочих | 8 | 22 | 10 | 6 | 4 |
С вероятностью 0,997 определите предел, в котором находится средний возраст рабочих завода.
Решение
Задача №34. Расчёт пределов доли признака в генеральной совокупности
Для изучения мнения студентов о проведении определенных мероприятий из совокупности, состоящей из 10 тыс. человек, методом случайного бесповторного отбора опрошено 600 студентов. Из них 240 одобрили план мероприятий. С вероятностью 0,954 определите предел, в котором находится доля студентов, одобривших мероприятия, во всей совокупности.
Решение
Задача №35. Расчёт предела доли признака в генеральной совокупности
В порядке случайной повторной выборки было обследовано 80 предприятий отрасли промышленности, из которых 20 предприятий имели долю нестандартной продукции выше 0,5%.
С вероятностью 0,997 определите предел, в котором находится доля предприятий, выпускающих более 0,5% нестандартной продукции промышленности данной отрасли.
Решение
Задача №36. Расчёт необходимой численности выборки при механическом отборе
Для определения среднего размера вклада определенной категории вкладчиков в сберегательных кассах города, где число вкладчиков равно 5000, необходимо провести выборку лицевых счетов методом механического отбора. Предварительно установлено, что среднее квадратическое отклонение размера вкладов составляет 120 тыс. руб.
Определите необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит 10 тыс. руб.
Решение
Рента
Совершенная конкуренция
Задача №37. Расчёт необходимой численности выборки
В городе Н предполагается определить число детей в семье методом случайного повторного отбора.
Какова должна быть численность выборки, чтобы с вероятностью 0,997 ошибка выборки не превышала 1,0 человека, если на основе предыдущих обследований известно, что дисперсия равна 9,0?
Решение
Задача №38. Расчет необходимой численности выборки для определения доли
На заводе с числом рабочих 12 тыс. необходимо установить долю рабочих, обучающихся в высших учебных заведениях, методом механического отбора.
1) Какова должна быть численность выборки, чтобы с вероятностью 0,997 ошибка выборки не превышала 0,08, если на основе предыдущих обследований известно, что дисперсия равна 0,16?
2) определить численность выборки при условии, что метод отбора повторный.
Решение
Задача №39. Расчёт предела, в котором находятся средние затраты времени
Для выявления затрат времени на обработку деталей рабочими разных квалификаций на заводе была произведена 10%-ная типическая выборка пропорционально численности выделенных групп (внутри типичных по специальности групп произведен случайный бесповторный отбор данных о затратах времени на обработку одной детали). Результаты обследования представлены в таблице:
| Группы рабочих по квалификации | Число рабочих в выборке | Средние затраты времени на обработку одной детали (минут) | Среднее квадратическое отклонение |
|---|---|---|---|
| I | 60 | 10 | 1 |
| II | 120 | 14 | 4 |
| III | 80 | 20 | 2 |
| IV | 40 | 25 | 6 |
С вероятностью 0,954 определите предел, в котором находятся средние затраты времени на обработку деталей рабочими завода.
Решение
Задача №51. Расчёт ошибки выборочной доли
При обследовании 500 образцов изделий, отобранных из партии готовой продукции предприятия в случайном порядке, 40 оказались нестандартными.
С вероятностью 0,954 определите пределы, в которых находится доля нестандартной продукции, выпускаемой заводом.
Решение
Задача №52. Расчёт минимальной численности генеральной совокупности
На основе случайной бесповторной выборки планируется 10%-ное обследование доли различных признаков, характеризующих население области. Какова должна быть минимальная численность населения области, чтобы предельная ошибка выборки с вероятностью 0,997 при определении доли всех подлежащих регистрации признаков не превышала 0,5%?
Решение
Совершенная конкуренция
Темп роста
Средняя арифметическая
Издержки
Экономическая прибыль
Есть график!
Счёт операций с капиталом
Повторный и бесповторный отбор.
Ошибка выборки
Краткая теория
На основании выборочных данных дается оценка статистических
показателей по всей (генеральной) совокупности. Подобное возможно, если выборка
основывается на принципах случайности отбора и репрезентативности
(представительности) выборочных данных. Каждая единица генеральной совокупности
должна иметь равную возможность (вероятность) попасть в выборку.
При формировании выборочной совокупности используются следующие
способы отбора: а) собственно-случайный отбор; б) механическая выборка; в)
типический (районированный) отбор; г) многоступенчатая (комбинированная)
выборка; д) моментно-выборочное наблюдение.
Выборка может осуществляться по схеме повторного и бесповторного
отбора.
В первом случае единицы совокупности, попавшие в выборку, снова
возвращаются в генеральную, а во втором случае – единицы совокупности, попавшие
в выборку, в генеральную совокупность уже не возвращаются.
Выборка может осуществляться отдельными единицами или сериями
(гнездами).
Собственно-случайная выборка
Отбор в этом случае производится либо по жребию, либо по таблицам
случайных чисел.
На основании приемов классической выборки решаются следующие
задачи:
а) определяются границы среднего значения показателя по генеральной
совокупности;
б) определяются границы доли признака по генеральной совокупности.
Предельная ошибка средней при собственно-случайном отборе
исчисляется по формулам:
а) при повторном отборе:
б) при бесповторном отборе:
где
– численность выборочной совокупности;
– численность генеральной совокупности;
– дисперсия признака;
– критерий кратности ошибки: при
;
при
;
при
.
Значения
определяются
по таблице функции Лапласа.
Границы (пределы) среднего значения признака по генеральной
совокупности определяются следующим неравенством:
где
– среднее значение признака по выборочной
совокупности.
Предельная ошибка доли при собственно-случайном отборе определяется
по формулам:
а) при повторном отборе:
при бесповторном отборе:
где
– доля единиц совокупности с заданным
значением признака в обзей численности выборки,
– дисперсия доли признака.
Границы (пределы) доли признака по всей (генеральной) совокупности
определяются неравенством:
где
– доля признака по генеральной совокупности.
Типическая (районированная) выборка
Особенность этого вида
выборки заключается в том, что предварительно генеральная совокупность по
признаку типизации разбивается на частные группы (типы, районы), а затем в
пределах этих групп производится выборка.
Предельная ошибка средней
при типическом бесповторном отборе определяется по формуле:
где
– средняя из внутригрупповых дисперсий
по каждой типичной группе.
При пропорциональном отборе из групп генеральной совокупности
средняя из внутригрупповых дисперсий определяется по формуле:
где
– численности единиц совокупности групп по выборке.
Границы (пределы) средней по генеральной совокупности на основании
данных типической выборки определяются по тому же неравенству, что при
собственно-случайной выборке. Только предварительно необходимо вычислить общую
выборочную среднюю
из частных выборочных средних
.
Для случая пропорционального отбора это определяется по формуле:
При непропорциональном отборе средняя из внутригрупповых дисперсий вычисляется по
формуле:
где
– численность единиц групп по генеральной
совокупности.
Общая выборочная средняя в этом случае определяется по формуле:
Предельная ошибка доли
признака при типическом бесповторном отборе определяется формулой:
Средняя дисперсия доли
признака из групповых дисперсий доли
при
типической пропорциональной выборке вычисляется по формуле:
Средняя доля признака по
выборке из показателей групповых долей рассчитывается формуле:
Средняя дисперсия доли при
непропорциональном типическом отборе определяется следующим образом:
а средняя доля признака:
Формулы ошибок выборки при типическом повторном отборе будут те же,
то и для случая бесповторного отбора. Отличие заключается только в том, что в
них будет отсутствовать по корнем сомножитель
.
Серийная выборка
Серийная ошибка выборки
может применяться в двух вариантах:
а) объем серий различный
б) все серии имеют
одинаковое число единиц (равновеликие серии).
Наиболее распространенной
в практике статистических исследований является серийная выборка с
равновеликими сериями. Генеральная совокупность делится на одинаковые по объему
группы-серии
и
производится отбор не единиц совокупности, а серий
. Группы (серии) для обследования отбирают в
случайном порядке или путем механической выборки как повторным, так и
бесповторными способами. Внутри каждой отобранной серии осуществляется сплошное
наблюдение. Предельные ошибки выборки
при
серийном отборе исчисляются по формулам:
а) при повторном отборе
б) при бесповторном отборе
где
– число
серий в генеральной совокупности;
– число
отобранных серий;
– межсерийная дисперсия, исчисляемая для случая равновеликих
серий по формуле:
где
–
среднее значение признака в каждой из отобранных серий;
– межсерийная
средняя, исчисляемая для случая равновеликих серий по формуле:
Определение численности выборочной совокупности
При проектировании
выборочного наблюдения важно наряду с организационными вопросами решить одну из
основных постановочных задач: какова должна быть необходимая численность
выборки с тем, чтобы с заданной степенью точности (вероятности) заранее
установленная ошибка выборки не была бы превзойдена.
Примеры решения задач
Задача 1
На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:
| Группы рабочих по размеру заработной платы, тыс.р. | до 200 | 200-240 | 240-280 | 280-320 | 320 и выше | Итого |
| Число рабочих | 33 | 35 | 47 | 45 | 40 | 200 |
На основании приведенных данных определите:
1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);
2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.
2) Выборочная дисперсия:
Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:
где
—
аргумент функции Лапласа.
Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:
Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:
Доля рабочих с з/п от 320 тыс.р.:
Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:
Задача 2
В
городе 23560 семей. В порядке механической выборки предполагается определить
количество семей в городе с числом детей трое и более. Какова должна быть
численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала
0,02 человека. На основе предыдущих обследований известно, что дисперсия равна
0,3.
Решение
Численность
выборки можно найти по формуле:
В нашем случае:
Вывод к задаче
Таким образом численность
выборки должна составить 2661 чел.
Задача 3
С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:
| Номер филиала |
Средняя месячная заработная плата, руб. |
Среднее квадратическое отклонение, руб. |
Число сотрудников, чел. |
| 1 | 870 | 40 | 30 |
| 2 | 1040 | 160 | 80 |
| 3 | 1260 | 190 | 140 |
| 4 | 1530 | 215 | 190 |
С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.
Решение
Предельная
ошибка выборочной средней:
Средняя
из внутригрупповых дисперсий:
Получаем:
Средняя
месячная заработная плата по всей совокупности филиалов:
Искомые
пределы средней месячной заработной платы:
Вывод к задаче
Таким
образом с вероятностью 0,954 средняя месячная заработная плата всех сотрудников
гостиниц находится в пределах от 1294,3 руб. до 1325,7 руб.
Пример 5.1. При выборочном обследовании (отбор случайный бесповторный) 25 деталей из общей партии в 400 деталей было обнаружено две бракованных детали.
Найдите доверительный интервал с доверительной вероятностью 0,95 для доли бракованных деталей. Укажите доверительный интервал для числа бракованных деталей в партии.
Решение.
Выборочная доля бракованных деталей
Средняя ошибка выборки
Коэффициент доверия T при доверительной вероятности A=0,95 и объеме выборки N=25 равен 2,0595 (см. приложение).
Предельная ошибка выборки
Доверительный интервал для генеральной доли
Доверительный интервал для числа бракованных деталей в партии
По смыслу задачи отрицательные значения нижней границы недопустимы, поэтому откорректируем их с учетом имеющихся данных.
Доверительный интервал для числа бракованных деталей
Доверительный интервал для генеральной доли
E Этот парадоксальный результат (отрицательные значения нижней границы доверительного интервала) связан с тем, что в условиях малых выборок используемые формулы не в полной мере отражают особенности распределения выборочных значений.
Пример 5.2.
При выборочном обследовании выполнения рабочими норм времени были получены следующие данные:
|
Выполнение норм времени, % |
До 96 |
96–98 |
98–100 |
100–102 |
102 и более |
|
Число рабочих |
2 |
5 |
11 |
17 |
5 |
Определите доверительный интервал для среднего процента выполнения норм времени (доверительная вероятность 0,99). Всего на предприятии работает 1000 рабочих.
Решение.
|
Выполнение норм времени, % |
Число рабочих, Fi |
Середина интервала, Xi |
Xi× fi |
|
|
|
До 96 |
2 |
95 |
190 |
24,01 |
48,02 |
|
96–98 |
5 |
97 |
485 |
8,41 |
42,05 |
|
98–100 |
11 |
99 |
1089 |
0,81 |
8,91 |
|
100–102 |
17 |
101 |
1717 |
1,21 |
20,57 |
|
102 и более |
5 |
103 |
515 |
9,61 |
48,05 |
|
Итого |
40 |
3996 |
167,6 |
Выборочная средняя =3996/40=99,9%.
Выборочная дисперсия S2=167,6/40=4,19.
Средняя ошибка выборки
Коэффициент доверия T при доверительной вероятности A=0,99 и объеме выборки N=40 равен 2,7045 (см. приложение).
Предельная ошибка выборки
Доверительный интервал для генеральной средней
Пример 5.3.
При обследовании месторождения золота было взято 100 проб. Среднее содержание золота составило 2,4 г/куб. м при среднем квадратическом отклонении 0,4 г/куб. м. Найти доверительный интервал для среднего содержания золота в породах месторождения (доверительная вероятность 0,9). Спрогнозировать потенциальные запасы золота на месторождении, если объем золотосодержащих пород оценивается в 20 млн. куб. м.
Решение.
Так как выборка является гипотетической, то объем генеральной совокупности N=¥. Отсюда средняя ошибка выборки
Коэффициент доверия T при доверительной вероятности A=0,9 и объеме выборки N=100 равен 1,6602 (см. приложение).
Предельная ошибка выборки
Г/куб. м.
Доверительный интервал для генеральной средней
Прогноз запасов золота на месторождении (в тоннах)
Пример 5.4. С целью определения средних затрат времени при поездках на работу планируется провести опрос сотрудников предприятия на основе случайного бесповторного отбора. Оцените необходимый объем выборочной совокупности, чтобы с вероятностью 0,95 ошибка выборочной средней не превышала 1 минуты. На предприятии работает 2000 человек.
Решение. Так как нам неизвестна выборочная дисперсия изучаемого признака, попробуем приблизительно оценить ее. Выскажем предположение, что в среднем работники затрачивают на одну поездку 30 минут. Используем одну из приближенных формул для оценки выборочной дисперсии
Положим коэффициент доверия T при доверительной вероятности A=0,95 равным 1,96, так как объем выборки N нам неизвестен..
Тогда необходимый объем выборочной совокупности

| < Предыдущая | Следующая > |
|---|