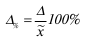Ошибка
наблюдения
– это расхождение между расчетным и
действительным значениями изучаемых
величин. Следует иметь в виду, что ошибки
наблюдения могут возникнуть при любых
статистических исследованиях (сплошных
и выборочных). Эти ошибки бывают двух
видов: регистрации
и репрезентативности.
Ошибка
регистрации
– это отклонение между значением
показателя, полученного в ходе
статистического наблюдения (как
сплошного,
так и несплошного),
и фактическим, действительным его
значением. Ошибки регистрации бывают
случайные
(непреднамеренные) и систематические
(тенденциозные). Случайные
ошибки регистрации
– это результат действия различных
случайных факторов (например, цифры
переставлены местами, перепутаны
соседние графы или графы при заполнении
статистического формуляра). При достаточно
большой обследуемой совокупности в
результате действия закона больших
чисел эти ошибки взаимно погашаются,
так как они обычно уравновешивают друг
друга, поскольку не имеют преимущественного
направления в сторону преувеличения
или преуменьшения значения изучаемого
показателя. Систематические
ошибки регистрации направлены
в одну сторону вследствие преднамеренного
нарушения правил отбора (предвзятые
цели) (например, многие опрашиваемые
вместо 48-49 лет и 51-52 года говорят, что им
50 лет, т.е. округляют возраст на цифрах,
оканчивающихся на цифре 0 (при
соответствующих случаях – на 5))
Ошибка
репрезентативности
возникает потому, что отобранная и
обследованная совокупность недостаточно
точно воспроизводит (репрезентирует)
всю исходную совокупность в целом
(характерна только для несплошного
наблюдения), другими словами, ошибка
репрезентативности
есть отклонение значения показателя
обследованной совокупности от его
величины по исходной совокупности.
Случайные
ошибки репрезентативности
возникают, если отобранная совокупность
неполно воспроизводит всю совокупность
в целом (ее
величина может быть оценена).
Систематическая
ошибка репрезентативности
появляются вследствие нарушения
принципов отбора единиц из исходной
совокупности, которые должны быть
подвергнуты наблюдению. Для каждого
конкретного выборочного наблюдения
значение ошибки репрезентативности
может быть определено по соответствующим
формулам, которые зависят от вида,
метода
и способа
формирования выборочной совокупности.
2. Формирование выборочной совокупности.
I)
По виду
отбора
различают
индивидуальный,
групповой
и комбинированный
отбор.
Индивидуальный
отбор –
в выборочную совокупность отбираются
отдельные единицы генеральной
совокупности.
Групповой
отбор
– в выборочную
совокупность отбираются качественно
однородные или серии изучаемых единиц.
Комбинированный
отбор –
сочетание группового
и индивидуального
видов отбора.
II).
По методу
отбора
различают повторную
и бесповторную
выборки.
Повторная
выборка
– общая численность генеральной
совокупности в процессе выборки остается
неизменной, т.е. ту или иную единицу,
попавшую в выборку, возвращают в
генеральную совокупность, и она сохраняет
равную возможность со всеми прочими
единицами при повторном отборе единиц
вновь попасть в выборку (в
социально-экономической жизни встречается
редко).
Бесповторная
выборка
– единица
совокупности, попавшая в выборку, в
генеральную совокупность не возвращается
и в дальнейшем в выборке не участвует,
т.е. последующую выборку делают из
генеральной совокупности уже без
отобранных ранее единиц; т.о, при
бесповторной
выборке численность
единиц генеральной совокупности
сокращается в процессе исследования.
III)
Способ
отбора
определяет конкретный механизм или
процедуру выборки единиц из генеральной
совокупности, что основывается на
алгоритме
(методе) отбора единиц выборочной
совокупности,
то есть реализуется принцип случайности
в процессе формирования выборочной
совокупности.
Метод
жеребьевки
– требуемое в соответствии с установленным
процентом отбора число жребиев (фишек,
карточек) извлекается из общей совокупности
в случайном порядке (количество жребиев
соответствует объему генеральной
совокупности). Недостаток
данного способа заключается в том, что
жеребьевка является в большей степени
теоретическим методом формирования
выборки, так как ее техническая реализация
при большом объеме генеральной
совокупности затруднительна.
Метод
случайной сортировки:
1)
каждой единице генеральной совокупности
присваивается случайное число u,
полученное с помощью процессора случайных
чисел в интервале от 0 до 1;
2)
единицы генеральной совокупности
ранжируются в соответствии с полученным
значением u;
3)
отбираются n
первых единиц.
Достоинства
данного способа заключаются в простом
алгоритме отбора единиц, а также в
возможности формирования нескольких
выборок без перекрытия. К недостатку
относят наличие процедуры сортировки
единиц генеральной совокупности, которая
при достаточно большом ее объеме
нежелательна.
Метод
прямой реализации:
1)
все единицы генеральной совокупности,
расположенные в случайном порядке или
ранжированные по какому-либо признаку,
нумеруются от 1 до N;
2)
с помощью процессора случайных чисел
получают n
значений в интервале от 1 до N;
3) из сформированного
списка единиц генеральной совокупности
отбираются единицы, соответствующие
по номеру полученным случайным числам.
Отбор
по таблице случайных чисел
(упрощенный вариант метода
прямой реализации)
– при отборе используются цифры любого
столбца таблицы случайных чисел с учетом
объема генеральной совокупности. При
проведении бесповторного
отбора повторяющиеся номера следует
учитывать только один
раз. При повторном
отборе, если тот или иной номер случайно
встретится один или более раз,
соответствующая этому номеру единица
в каждом
случае
повторно
включается в выборочную совокупность.
Метод
отбора-отказа:
1)
последовательно образуют случайные
числа
,
,
… в соответствии с законом равномерного
распределения в интервале от 0 до 1;
2)
первая единица генеральной совокупности
включается в выборку при выполнении
для нее неравенства
;
3)
из оставшихся единиц
-я
включается в выборку при выполнении
для нее неравенства(
— число отобранных в выборку единиц
среди первыхk
просмотренных);
4)
когда
,
т.е. выборка необходимого объема
сформирована, процедура заканчивается
(этот момент может наступить и до
завершения просмотра всех единиц
генеральной совокупности).
К
достоинствам
метод отбора-отказа можно отнести то,
что данный способ основан на алгоритме
последовательного извлечения единиц,
не требующем ни предварительной
сортировки единиц генеральной совокупности
или образования случайных чисел, ни
многократного считывания исходного
файла.
По
степени
охвата единиц совокупности
различают большие
(n>30)
и малые
(n
< 30) выборки.
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.
Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.
Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.
Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.
Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.
Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.
Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.
Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностей. Предельной ошибкой выборки принято считать максимально возможное расхождение, т. е. максимум ошибки при заданной вероятности ее появления.
В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П. Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле:
где µx– стандартная ошибка.
Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина µx зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).
Академик А. М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:
В математической статистике употребляют коэффициент доверия t, и значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности.
Коэффициент доверия позволяет вычислить предельную ошибку выборки, вычисляемую по формуле:
Из формулы вытекает, что предельная ошибка выборки равна -кратному числу средних ошибок выборки.
Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности x и величину предельной ошибки этой средней ?x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна
Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.
Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.
Данный текст является ознакомительным фрагментом.
Читайте также
Наблюдения за объемом
Наблюдения за объемом
Имеет значение не сам объем, а его соотношения в различные периоды рыночного движения. Соотношения объемов – очень важный, но и наименее объективный из технических инструментов, так как здесь нет никаких непреложных правил. Вместо этого есть набор
Закономерности и наблюдения
Закономерности и наблюдения
Я верю в существование закономерностей на рынке и считаю, что отношусь к числу людей, которые способны их улавливать. Но я также хорошо помню и о том, что все закономерности нечеткие. Нечеткие они потому, что в них присутствует фактор
Ошибки в инвестициях – это ошибки инвесторов
Ошибки в инвестициях – это ошибки инвесторов
Сейчас я больше, чем когда бы то ни было, убежден в том, что все ошибки в инвестициях на самом деле ошибки инвесторов.Инвестиции не совершают ошибок. В отличие от инвесторов.Инвестирование – это выбор. Именно об этой
8. Способы статистического наблюдения
8. Способы статистического наблюдения
Способами получения статистической информа–ции являются документальный способ наблюдения; способ непосредственного наблюдения: опрос.Документальное наблюдение основано на исполь–зовании в качестве источника информации данных
9. Формы статистического наблюдения
9. Формы статистического наблюдения
В теории статистики рассматриваются и формы статистического наблюдения: отчетность; специально организованное статистическое наблюдение; реги–стры.Статистическая отчетность – основная форма статистического наблюдения, которая
2. Ошибки выборочного наблюдения
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но
19. Наблюдения
19. Наблюдения
Наблюдение представляет собой сбор первичной информации об объекте наблюдения для построения гипотез, проверки исходных данных и т. д.К способам проведения наблюдения относят:1) прямой, который предполагает непосредственное наблюдение за объектом
6. Организация статистического наблюдения
6. Организация статистического наблюдения
Начальным этапом статистического исследования является статистическое наблюдение.В процессе статистического наблюдения формируется оснавная информация, которая является основной для статистического
11. Ошибки статистического наблюдения и контроль материалов наблюдения
11. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Любое статистическое наблюдение предполагает получение данных, которые будут
34. Определение выборочного наблюдения
34. Определение выборочного наблюдения
Так как сплошное наблюдение дорого и трудоемко, то его заменили выборочным.Выборочное наблюдение – это способ несплошного наблюдения, при котором лишь часть совокупности, отобранная по определенным правилам выборки и
Часть 5 Наблюдения
Часть 5
Наблюдения
За свою тридцатипятилетнюю карьеру в бизнесе я смотрел на мир с разных точек зрения. Я был свидетелем взлетов и падений в экономике и отрасли, появления на рынке новых продуктов и их исчезновения. Я представлял новые товары, возрождал старые, закрывал
Введение процедуры наблюдения
Введение процедуры наблюдения
Наблюдение вводится с целью сохранения активов должника, проведения оценки его финансового состояния, изучения объективной возможности восстановления платежеспособности и продолжения функционирования организации.С момента введения
1. Организация статистического наблюдения
1. Организация статистического наблюдения
Статистическое наблюдение – это организованная работа по сбору первичных сведений об изучаемых массовых явлениях и процессах общественной жизни. Статистическое наблюдение проводится организованно и по заранее разработанным
5. Ошибки статистического наблюдения и контроль материалов наблюдения
5. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Точность – это уровень соответствия значения какого–либо признака или
1. Определение выборочного наблюдения
1. Определение выборочного наблюдения
Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным.Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности
Общие наблюдения и впечатления
Общие наблюдения и впечатления
Члены команды систематически выполняли требования восьми этапов цикла кайдзен и обнаружили, что с их помощью смогли построить процесс решения проблем в правильной последовательности. Использование таких инструментов, как «рыбий скелет»
Ошибки выборочного наблюдения
Информация, получаемая в результате
любого статистического наблюдения,
имеет расхождение с реальной
действительностью. Такое расхождение
получило название ошибок статистического
наблюдения. При массовом наблюдении
ошибки неизбежны, но возникают они
в результате действия различных причин
(см. гл. 4).
В данной главе рассматривается только
ошибка репрезентативности и причины
ее возникновения. Под ошибкой
репрезентативности (представительства)
понимают расхождение между выборочной
характеристикой и предполагаемой
характеристикой генеральной
совокупности. Причиной образования
этой ошибки является то обстоятельство,
что обследуются не все единицы генеральной
совокупности, а лишь их некоторая часть,
и различия между единицами, попавшими
в выборку, не соответствуют различиям
единиц, не попавших в выборку. Вследствие
этого выборочная совокупность становится
непредставительной по отношению к
генеральной совокупности. Ошибка
репрезентативности может возникнуть
по двум причинам: из-за нарушения научных
принципов отбора —систематическая
ошибка — и в результате случайности
отбора —случайная ошибка. В результате
первой причины выборка легко может
оказаться смещенной, так как при отборе
каждой единицы допускается ошибка,
всегда направленная в одну и ту же
сторону. Эта ошибка получила названиеошибки смещения. Ее размер может
превышать величину случайной ошибки.
Особенность ошибки смещения состоит
в том, что, представляя собой постоянную
часть ошибки репрезентативности, она
увеличивается с увеличением объема
выборки. Случайная же ошибка с увеличением
объема выборки уменьшается. Кроме того,
величину случайной ошибки можно
определить (см. ниже), тогда как размер
ошибки смещения непосредственно
практически определить очень сложно,
а иногда — невозможно. Поэтому необходимо
знать причины, вызывающие ошибку смещения
и меры, способствующие её устранению.
Ошибки смещения бывают преднамеренные
и непреднамеренные. Причиной
возникновения преднамеренной ошибки
является тенденциозный подход к
выбору единиц из генеральной совокупности.
Мерой устранения этой ошибки может быть
только исключение тенденциозности.
Выявить эту ошибку можно только путем
проведения повторного отбора с
обязательным соблюдением принципа
случайности.
Непреднамеренные ошибки могут
возникать на стадии подготовки
выборочного наблюдения, формирования
выборочной совокупности и анализа ее
данных. Чаще всего создаются условия
для возникновения ошибок смещения на
стадии подготовки выборочного наблюдения.
Недостаточно хорошо продуманные и четко
сформулированные взаимоувязанные
вопросы плана организации и проведения
выборочного обследования могут дать
информацию, не соответствующую цели
исследования или, что еще хуже, вводящую
в заблуждение. Если при сплошном
наблюдении это возможно только при
преднамеренном искажении фактов, то
при выборочном это связано с
непреднамеренными ошибками смещения.
При разработке плана организации и
проведения выборочного наблюдения
особое внимание следует уделятьединице
отбора, т. е. такой единице изучаемой
совокупности, которая является
основанием самого процесса отбора.
Единицей отбора могут служить естественные
единицы изучаемого явления, например
предприятие, рабочий, покупатель, семья
и т. д. В некоторых случаях необходимо
создать искусственные единицы, не
соответствующие естественному делению
изучаемой совокупности. Удачное
установление единицы отбора уменьшает
вероятность получить смещенную выборку.
Сокращению опасности возникновения
ошибок смещения во многом способствует
хорошая основа выборки, т. е. та
генеральная совокупность, из которой
предполагается производить отбор,
например список единиц отбора. Поэтому
при подготовке выборочного наблюдения
необходимо особенно тщательно
ознакомиться с тем, какова основа
выборки, пригодна ли она для производства
отбора, позволит ли она образовать
несмещенную выборку. Если готовой основы
выборки нет, то ее необходимо построить.
Основа выборки должна быть достоверной,
полной и соответствовать цели
исследования, а единицы отбора и их
характеристики должны соответствовать
действительному их состоянию на
момент подготовки выборочного наблюдения.
Если основа выборки не отвечает
перечисленным требованиям, ее
необходимо либо существенно улучшить,
внеся соответствующие изменения,
уточнения, дополнения, либо создать
заново.
На стадиях формирования выборочной
совокупности и производства наблюдения
ошибки смещения особенно опасны, так
как их трудно заметить и исправить. При
формировании выборочной совокупности
ошибку смещения чаще всего дает неточное
соблюдение установленного порядка
отбора, предусматривающего отбор
вполне определенных единиц. Иногда
может показаться, что выборочная
совокупность «не пострадает», если,
например, вместо предусмотренной десятой
единицы по списку взять одиннадцатую
или двенадцатую; в действительности же
такое нарушение установленного порядка
отбора нередко приводит к смещенной
выборке. Ошибки смещения при анализе
данных могут возникнуть из-за неправильных
приемов распространения выборочных
характеристик на генеральную
совокупность (см. 11.4).
Случайная ошибка выборки возникает
в результате случайных различий
между единицами, попавшими в выборку,
и единицами генеральной совокупности,
т. е. она связана со случайным отбором.
Теоретическим обоснованием появления
случайных ошибок выборки является
теория вероятностей и ее предельные
теоремы.
Сущность предельных теорем состоит в
том, что в массовых явлениях совокупное
влияние различных случайных причин на
формирование закономерностей и обобщающих
характеристик будет сколь угодно малой
величиной или практически не зависит
от случая. Так как случайная ошибка
выборки возникает в результате случайных
различий между единицами выборочной
и генеральной совокупностей, то при
достаточно большом объеме выборки она
будет сколь угодно мала. Этот вывод,
опирающийся на доказательства предельных
теорем, позволяет предполагать, что
характеристики выборочного наблюдения
могут достаточно хорошо представлять
характеристики генеральной
совокупности.
Предельные теоремы исходят из закона
нормального распределения, согласно
которому большая часть выборочных
средних сосредоточивается около
генеральной средней
.
Следовательно, закон нормального
распределения теоретически позволяет
установить, в какой мере изменяется
размер случайной ошибки выборки с
изменением вероятности ее появления.
Так как многие массовые явления
подчиняются закону нормального
распределения, то он служит основой при
оценке вероятности тех или иных
результатов выборочного наблюдения.
Предельные теоремы теории вероятностей
позволяют определять размер случайных
ошибок выборки. Различают среднюю
(стандартную) и предельную ошибку
выборки. Под средней (стандартной)
ошибкой выборки понимают расхождение
между средней выборочной и генеральной
совокупностей,не
превышающее.
Предельной ошибкой выборки принято
считать максимально возможное расхождение,
т. е. максимум ошибки при заданной
вероятности ее появления. На основании
теоремы, доказанной П. Л. Чебышевым,
величину стандартной ошибки так
называемого собственно-случайного
отбора при достаточно большом объёме
выборки можно определить по формуле:
,
где
— стандартная ошибка.
Величина стандартной ошибки прямо
пропорциональна колеблемости признака
в генеральной совокупности и обратно
пропорциональна квадратному корню
объёма выборки. Величина
зависит также от способа и вида отбора.
Академик А.М.Ляпунов, продолжив разработки
П.Л.Чебышева, доказал, что вероятность
появления случайной ошибки выборки при
её достаточно большом объёме подчиняется
закону нормального распределения. Эта
вероятность определяется по формуле:
Значения функции
табулированы
при различных значенияхt.
Предельная ошибка выборки определяется
по формуле
,
где
-предельная
ошибка,t– заданный
коэффициент доверия.
Так, при t=1 величина
предельной ошибки составит,
гарантированную с вероятностью 0,683. Это
означает, что в 683 выборках из тысячи
подобных максимальная ошибка выборки
(предельная) не превысит.
Приt=2 с вероятностью
0,954 она не выйдет за пределыи
т.д. В практике выборочных наблюдений
массовых общественных явлений максимальный
предел ошибок, как правило, вполне
достаточен в пределах.
Однако приведённые формулы нахождения
ошибок выборки практически непригодны,
т.к. в них σ – это показатель колеблемости
признака в генеральной совокупности,
который неизвестен, как неизвестна и
генеральная средняя. Но в теории
вероятностей доказывается, что
.
Так как
при
достаточно большомn– величина, близкая к единице, то условно
принимается, что.
На основании этого утверждения в
вышеприведённых формулах вместо
генеральной дисперсии принимают значение
выборочной дисперсии.
Предельная ошибка выборки позволяет
определять предельные значения
характеристик генеральной совокупности
при заданной вероятности и их доверительные
интервалы:
.
Это означает следующее: с заданной
вероятностью можно утверждать, что
значение генеральной средней ожидается
в пределах от
до
.
Наряду с абсолютной величиной предельной
ошибки выборки рассчитывают и относительную
ошибку, определяемую как процентное
отношение предельной ошибки выборки к
соответствующей характеристике
выборочной совокупности:
,
,
Если при выборочном наблюдении изучению
подлежит альтернативный признак, то
случайная ошибка выборки для доли
определяется в соответствии с теоремой
Я.Бернулли. так
как вероятность расхождения между
частостью и долей тоже подчиняется
закону нормального распределения, то
стандартная ошибка выборки альтернативного
признака определяется по формуле:
,
где pq– дисперсия
доли альтернативного признака в
генеральной совокупности.
Так как pqнеизвестно,
то на практике её заменяют дисперсией
выборочной совокупностиw(1-w)
и формула принимает вид:
Соседние файлы в папке 14-05-2013_10-41-11
- #
- #
- #
- #
- #
- #
- #
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.
Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.
Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.
Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.
Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.
Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.
Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.
Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностей. Предельной ошибкой выборки принято считать максимально возможное расхождение, т. е. максимум ошибки при заданной вероятности ее появления.
В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П. Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле:
где µx– стандартная ошибка.
Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина µx зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).
Академик А. М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:
В математической статистике употребляют коэффициент доверия t, и значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности.
Коэффициент доверия позволяет вычислить предельную ошибку выборки, вычисляемую по формуле:
Из формулы вытекает, что предельная ошибка выборки равна -кратному числу средних ошибок выборки.
Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности x и величину предельной ошибки этой средней ?x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна
Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.
Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.
Данный текст является ознакомительным фрагментом.
Читайте также
Наблюдения за объемом
Наблюдения за объемом
Имеет значение не сам объем, а его соотношения в различные периоды рыночного движения. Соотношения объемов – очень важный, но и наименее объективный из технических инструментов, так как здесь нет никаких непреложных правил. Вместо этого есть набор
Закономерности и наблюдения
Закономерности и наблюдения
Я верю в существование закономерностей на рынке и считаю, что отношусь к числу людей, которые способны их улавливать. Но я также хорошо помню и о том, что все закономерности нечеткие. Нечеткие они потому, что в них присутствует фактор
Ошибки в инвестициях – это ошибки инвесторов
Ошибки в инвестициях – это ошибки инвесторов
Сейчас я больше, чем когда бы то ни было, убежден в том, что все ошибки в инвестициях на самом деле ошибки инвесторов.Инвестиции не совершают ошибок. В отличие от инвесторов.Инвестирование – это выбор. Именно об этой
8. Способы статистического наблюдения
8. Способы статистического наблюдения
Способами получения статистической информа–ции являются документальный способ наблюдения; способ непосредственного наблюдения: опрос.Документальное наблюдение основано на исполь–зовании в качестве источника информации данных
9. Формы статистического наблюдения
9. Формы статистического наблюдения
В теории статистики рассматриваются и формы статистического наблюдения: отчетность; специально организованное статистическое наблюдение; реги–стры.Статистическая отчетность – основная форма статистического наблюдения, которая
2. Ошибки выборочного наблюдения
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но
19. Наблюдения
19. Наблюдения
Наблюдение представляет собой сбор первичной информации об объекте наблюдения для построения гипотез, проверки исходных данных и т. д.К способам проведения наблюдения относят:1) прямой, который предполагает непосредственное наблюдение за объектом
6. Организация статистического наблюдения
6. Организация статистического наблюдения
Начальным этапом статистического исследования является статистическое наблюдение.В процессе статистического наблюдения формируется оснавная информация, которая является основной для статистического
11. Ошибки статистического наблюдения и контроль материалов наблюдения
11. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Любое статистическое наблюдение предполагает получение данных, которые будут
34. Определение выборочного наблюдения
34. Определение выборочного наблюдения
Так как сплошное наблюдение дорого и трудоемко, то его заменили выборочным.Выборочное наблюдение – это способ несплошного наблюдения, при котором лишь часть совокупности, отобранная по определенным правилам выборки и
Часть 5 Наблюдения
Часть 5
Наблюдения
За свою тридцатипятилетнюю карьеру в бизнесе я смотрел на мир с разных точек зрения. Я был свидетелем взлетов и падений в экономике и отрасли, появления на рынке новых продуктов и их исчезновения. Я представлял новые товары, возрождал старые, закрывал
Введение процедуры наблюдения
Введение процедуры наблюдения
Наблюдение вводится с целью сохранения активов должника, проведения оценки его финансового состояния, изучения объективной возможности восстановления платежеспособности и продолжения функционирования организации.С момента введения
1. Организация статистического наблюдения
1. Организация статистического наблюдения
Статистическое наблюдение – это организованная работа по сбору первичных сведений об изучаемых массовых явлениях и процессах общественной жизни. Статистическое наблюдение проводится организованно и по заранее разработанным
5. Ошибки статистического наблюдения и контроль материалов наблюдения
5. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Точность – это уровень соответствия значения какого–либо признака или
1. Определение выборочного наблюдения
1. Определение выборочного наблюдения
Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным.Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности
Общие наблюдения и впечатления
Общие наблюдения и впечатления
Члены команды систематически выполняли требования восьми этапов цикла кайдзен и обнаружили, что с их помощью смогли построить процесс решения проблем в правильной последовательности. Использование таких инструментов, как «рыбий скелет»
Главная / Математика /
Статистика — подробные проблемы / Тест 2
Упражнение 1:
Номер 1
Что такое единица наблюдения?
Ответ:
(1) отдельно взятый признак или их совокупность
(2) составной элемент объекта, являющийся носителем информации о признаках, изучение которых является целью исследования
(3) общая черта отдельных объектов, изучаемых исследователем
Номер 2
Что из перечисленного ниже не относится к основным этапам статистического наблюдения?
Ответ:
(1) контроль собранной первичной статистической информации
(2) сводка и группировка первичной информации
(3) определение статистической совокупности
(4) сбор первичной статистической информации
Номер 3
Что такое критический момент наблюдения?
Ответ:
(1) время, в течение которого собираются сведения
(2) сроки приведения наблюдения
(3) момент времени, по отношению к которому собираются сведения
Упражнение 2:
Номер 1
Для повышения точности наблюдения необходимо
Ответ:
(1) провести логический анализ данных после сбора формуляров наблюдения
(2) правильно разработать формуляр статистического наблюдения
(3) иметь хорошо обученный персонал для проведения обследования
(4) Верны все вышеперечисленные варианты
Номер 2
Укажите, какому виду обследования присущи ошибки репрезентативности
Ответ:
(1) монографическому обследованию
(2) статистической отчетности
(3) выборочному наблюдению
(4) сплошному обследованию
Номер 3
Точность статистического наблюдения — это
Ответ:
(1) расчет показателя с определенной точностью (например, до 0,01)
(2) степень соответствия значения наблюдаемого показателя, вычисленного по материалам обследования, его действительной величине
(3) полнота охвата наблюдением генеральной совокупности
Упражнение 3:
Номер 1
В чем заключается особенность метода ведения дневников?
Ответ:
(1) в том, что счетчик ежедневно следит за правильностью заполнения формуляров
(2) в том, что сведения сообщаются в органы, проводящие статистическое наблюдение, ежедневно
(3) в том, что события регистрируются в «дневниках» респондентами сразу же по мере их наступления
Номер 2
Что из перечисленного относится к способам статистического наблюдения?
Ответ:
(1) саморегистрация
(2) устный опрос
(3) корреспондентский способ сбора информации
(4) Верны все вышеперечисленные варианты
Номер 3
Что из перечисленного относится к видам несплошного наблюдения?
Ответ:
(1) наблюдение основного массива
(2) выборочное наблюдение
(3) бизнес-обследование
(4) Верны все вышеперечисленные варианты
Упражнение 4:
Номер 1
По каким направлениям расходов идет оценка затрат на проведение статистического наблюдения?
Ответ:
(1) обучение персонала, принимающего участие в обследовании
(2) получение предварительной информации об изучаемой совокупности
(3) получение предварительной информации об изучаемой совокупности
(4) Верны все вышеперечисленные варианты
Номер 2
Статистический формуляр — это
Ответ:
(1) программа статистического наблюдения
(2) таблица статистических данных
(3) статистический документ, содержащий программу наблюдения, в который заносятся данные о единице наблюдения
Номер 3
Срок проведения наблюдения — это
Ответ:
(1) момент времени, по отношению к которому собираются статистические сведения
(2) интервал времени, в течение которого происходит сбор статистической информации
Упражнение 5:
Номер 1
Единица наблюдения — это
Ответ:
(1) субъект, от которого непосредственно получают статистические сведения о единице наблюдения
(2) единичный элемент, как непосредственный носитель информации о тех признаках, изучение которых является целью обследования
Номер 2
Что из перечисленного относится к программно-методологическим вопросам проведения статистического наблюдения?
Ответ:
(1) определение объекта наблюдения
(2) указание единицы наблюдения и отчетной единицы
(3) постановка цели и задач конкретного наблюдения
(4) Верны все вышеперечисленные варианты
Номер 3
Что из перечисленного относится к основным этапам проведения статистического наблюдения?
Ответ:
(1) контроль собранной информации
(2) непосредственно сбор первичных данных
(3) проведение мероприятий по подготовке наблюдения
(4) Верны все вышеперечисленные варианты
Упражнение 6:
Номер 1
Что такое статистический формуляр?
Ответ:
(1) совокупность единиц наблюдения
(2) документ единого образца, содержащий программу наблюдения
(3) перечень признаков, подлежащий регистрации в процессе наблюдения
Номер 2
По охвату наблюдением единиц совокупности различают
Ответ:
(1) специально организованное и сплошное наблюдения
(2) сплошное и несплошное наблюдения
(3) периодическое и специально организованное наблюдения
Номер 3
Что относится к способам статистического наблюдения (в зависимости от источника сведений)?
Ответ:
(1) регистр, отчетность, текущее статистическое наблюдение
(2) специально организационное наблюдение
(3) прерывное наблюдение
(4) непосредственное наблюдение, опрос, документальное наблюдение
Упражнение 7:
Номер 1
Каковы виды несплошного статистического наблюдения?
Ответ:
(1) текущее статистическое наблюдение, монографическое обследование
(2) специально организационное наблюдение, обследование основного массива
(3) выборочные наблюдения, монографическое обследование, обследование основного массива, анкетное
(4) непрерывное наблюдение, единовременное наблюдение
Номер 2
Каковы организационные формы статистического наблюдения?
Ответ:
(1) группировка материалов
(2) отчетность, специально организационное наблюдение, регистр
(3) монографическое обследование, отчетность
(4) регистр, монографическое обследование
Номер 3
Какие ошибки присущи только выборочному наблюдению?
Ответ:
(1) случайные ошибки регистрации
(2) ошибки репрезентативности
(3) систематические ошибки регистрации
Упражнение 8:
Номер 1
С какого года ведется в нашей стране Единый государственный регистр предприятий — ЕГРПО?
Ответ:
(1) с 1997 г.
(2) с 1993 г.
(3) с 2003 г.
(4) с 1991 г.
Номер 2
Что из перечисленного является отличительными признаками регистрового наблюдения?
Ответ:
(1) стадия развития
(2) фиксированное начало
(3) фиксированное окончание
(4) Верны все вышеперечисленные варианты
Номер 3
Что из перечисленного относится к формам проведения статистического наблюдения?
Ответ:
(1) регистры
(2) статистическая отчетность
(3) специально организованное статистическое наблюдение
(4) Верны все вышеперечисленные варианты
Упражнение 9:
Номер 1
Какие ошибки присущи сплошному статистическому наблюдению?
Ответ:
(1) систематические ошибки репрезентативности
(2) случайные ошибки регистрации, систематические ошибки регистрации
(3) случайные ошибки репрезентативности
Номер 2
Местом наблюдения является
Ответ:
(1) территория Российской Федерации
(2) территория, по отношению к которой собираются сведения
(3) Москва
Номер 3
Что из перечисленного включает в себя организационная подготовка статистического наблюдения?
Ответ:
(1) выбор формы, вида и способа наблюдения
(2) выбор места и времени проведения наблюдения
(3) оценка затрат на проведение обследования
(4) Верны все вышеперечисленные варианты