Диагностика — это
исследование причин как отдельной,
индивидуальной ошибки, так и определенного
типа ошибок, допускаемых многими
учениками или даже большинством. В
процессе анализа ошибок и их причин
учитель опирается на признанные типологии
и использует свои, новые критерии. В
результате анализа строится методика
исправления и предупреждения ошибок,
прогнозируется дальнейшее обучение,
делаются определенные акценты в обучении,
выделяются приоритетные темы курса,
методы и приемы.
В диагностике
ошибок используются методы статистики,
накапливаются картотеки ошибок,
вычисляется частотность их по типам.
На основе анализа
и статистических обобщений установлено,
что в начальных классах самыми частотными
оказываются:
· Ошибки на
безударные гласные, преимущественно в
корне слова, на употребление звонких и
глухих согласных;
Ошибки на правописание
гласных и согласных в непроверяемых
словах (слабые позиции фонем);
· Ошибки от слабой
орфографической зоркости, от неумения
увидеть орфограмму.
Много ошибок на
жи, ши, ча, ща, чу, щу: у детей сильна
тенденция писать по произношению.
Нередки ошибки в написании безударных
падежных и личных окончаний имен
существительных, прилагательных и
глаголов, в слитном или раздельном
написании предлогов, приставок. Бывают
и такие случаи, когда статистика
показывает неожиданные «скачки»:
например, ошибки в употреблении заглавной
буквы.
Следующий этап
диагностики — выяснение причин массовых
ошибок. Так, в результате анализа
выясняется, что причины ошибок
квалифицируются так: первое место-
бедность или пассивность словаря,
мешающая быстро и правильно находить
проверочные слова; вторая — слабая
зоркость: ученик не видит орфограмму,
не слышит безударного гласного; третья
причина: ученик плохо разбирается в
морфемном составе слова, не обнаруживает
границ корня в слове.
У каждого типа
ошибок — свои причины, и очень важно,
чтобы сам ученик, допустивший ошибку,
понял ее причину. Это существенно
повышает осознание познавательного
процесса самим учеником.
2.4.3. Исправление и предупреждение ошибок
Согласно школьной
традиции, все допущенные учениками
ошибки должны быть исправлены. И не
только в тетради ученика, но и в его
сознании, в его памяти.
Наилучший способ
исправления — индивидуальная работа,
ибо сами ошибки носят личностный,
индивидуальный характер. Ученик и
учитель вместе проверяют написанное,
находят ошибку: учитель создает такую
ситуацию, в которой ученик сам находит
ошибку, определяет ее тип, анализирует
причины. Вместе они выясняют способы
проверки и исправления. К сожалению,
такая методика отнимает много времени.
Второй вариант:
учитель проверяет тетради, находит
ошибки, отмечает их, но сам исправляет
лишь в трудных случаях. В остальных —
ограничивается отметкой на полях
условными знаками, чтобы ученик сам
нашел и исправил ошибку. Операция
исправления завершается в индивидуальной
работе, помощь учителя — эпизодическая.
Известны приемы самостоятельного
письменного объяснения ошибки и ее
исправления. Оно завершается составлением
и записью предложения, в котором
употреблено слово, уже безошибочно
написанное.
Третий способ —
фронтальная проверка написанного общего
текста с устным комментированием всех
или выбранных (учителем) орфограмм. При
этом каждый ученик, прослушивая
комментарий, находит свои ошибки и
исправляет их при общем наблюдении
учителя. Метод удобен для такого класса,
где достигнут высокий уровень
самостоятельности и сознательности
учащихся.
Система исправления
ошибок предполагает ведение каждым
учеником (кроме безупречно пишущих)
своего личного учета ошибок в удобной
для него форме.
Для работы над
ошибками, свойственными большинство,
на одном из уроков выделяется фрагмент
продолжительностью в 20 минут на единую
тему: повторение грамматико-орфографической
темы, выполнение нескольких упражнений,
обсуждение конкретных ошибок, составление
примеров и задач самими учащимися и
т.п. Такой фрагмент урока проводится
обычно после контрольной работы или в
конце изучаемой темы по совокупности
накопившихся ошибок.
Уместны также
орфографические минутки в начале урока:
отчетливое проговаривание 5 — 10 слов, в
которых ранее многими допускались
ошибки. Практикуется также включение
таких слов в упражнения, выполняемые
устно или письменно на уроке. Также
ученику задаются вопросы по его прежним
ошибкам, когда он вызван отвечать к
столу учителя или к доске.
Полезна для
предупреждения ошибок работа с
орфографическим словарями, пользоваться
которыми учитель разрешает на всех
уроках; словари находятся в классе в
достаточном количестве.
Для слабых в
орфографии учащихся организуются
дополнительные групповые и индивидуальные
занятия во внеурочное время: письмо
дополнительных упражнений, диктантов,
повторение плохо усвоенных тем, приучение
детей к приемам самопроверки написанного.
К таким занятиям нередко привлекаются
хорошо успевающие дети.
Способы
предупредительной работы:
· На основе
диагностики допущенных ошибок выделение
«опасных» правил, слов, их сочетаний,
типов орфограмм;
· Соответствующие
акценты в процессе изучения курса:
усиление внимания к тем темам, вопросам,
которые труднее усваиваются;
· Отчетливое
выделение перечня трудных слов для
каждого класса, включение их в упражнения,
вывешивание плакатов с этими словами
и пр.;
· Поощрение тех
учащихся, которые сами преодолевают
свои ошибки;
· Одобрение каждого,
даже малого, успеха ученика, стремление
придать уверенности тем детям, которых
преследуют ошибки;
· Воспитание
орфографического оптимизма, создание
повышенной мотивации;
· Воспитание
уверенности учащихся в возможности
достижения высокого уровня грамотного
письма.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ошибка прогнозирования: виды, формулы, примеры
Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.
В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):
Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!
MPE — Mean Percent Error
MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.
- Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
- Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
- Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error
MAPE — Mean Absolute Percent Error
MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
- Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
- Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error
Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.
WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error
WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:
- Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
- Находится сумма всех фактов по всем позициям (общий фактический объем)
- Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE
Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.
Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.
RMSE (as %) / nRMSE — Root Mean Square Error
RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.
- Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
- Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
- Извлекаем корень из полученного результат — RMSE
- Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
- Разделить на разницу между максимальным и минимальным значением показателей
- Разделить на разницу между третьим и первым квартилем значений показателей
- Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)
MASE — Mean Absolute Scaled Error
MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.
Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.
Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:
Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.
Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.
Об авторе
HeinzBr
Автор статей и создатель сайта SHTEM.RU
Прогнозирование ошибок программного обеспечения. Обнаружение ошибок
1
Источниками ошибок в программном обеспечении являются специалисты — конкретные люди с их индивидуальными особенностями, квалификацией, талантом и опытом.
В большинстве случаев поток программных ошибок может быть описан негомогенным процессом Пуассона. Это означает, что программные ошибки проявляются в статистически независимые моменты времени, наработки подчиняются экспоненциальному распределению, а интенсивность проявления ошибок изменяется во времени. Обычно используют убывающую интенсивность проявления ошибок. Т. е. ошибки, как только они выявлены, эффективно устраняются без введения новых ошибок.
Применительно к надежности программного обеспечения ошибка это погрешность или искажение кода программы, неумышленно внесенные в нее в процессе разработки, которые в ходе функционирования этой программы могут вызвать отказ или снижение эффективности функционирования. Под отказом в общем случае понимают событие, заключающееся в нарушении работоспособности объекта. При этом критерии отказов, как признак или совокупность признаков нарушения работоспособного состояния программного обеспечения, должны определяться исходя из его предназначения в нормативно — технической документации.
В общем случае отказ программного обеспечения можно определить как:
- прекращение функционирования программы (искажения нормального хода ее выполнения, зацикливание) на время превышающее заданный порог;
- прекращение функционирования программы (искажения нормального хода ее выполнения, зацикливание) на время не превышающее заданный порог, но с потерей всех или части обрабатываемых данных;
- прекращение функционирования программы (искажения нормального хода ее выполнения, зацикливание) потребовавшее перезагрузки ЭВМ, на которой функционирует программное обеспечение.
Из данного определения программной ошибки следует, что ошибки могут по разному влиять на надежность программного обеспечения и можно определить тяжесть ошибки, как количественную или качественную оценку последствий этой ошибки. При этом категорией тяжести последствий ошибки будет являться классификационная группа ошибок по тяжести их последствий. Ниже представлены возможные категории тяжести ошибок в программном обеспечении общего применения в соответствии с ГОСТ 51901.12 — 2007 «Менеджмент риска. Метод анализа видов и последствий отказов».
|
Описание последствий проявления ошибки |
||
|
Критическая |
проявление ошибки с высокой вероятностью влечет за собой прекращение функционирования программного обеспечения (его отказ) |
|
|
Существенная |
проявление ошибки влечет за собой снижение эффективности функционирования программного обеспечения и может вызвать прекращение функционирования программного обеспечения (его отказ) |
|
|
Несущественная |
проявление ошибки может повлечь за собой снижение эффективности функционирования программного обеспечения и практически не приводит к возникновению отказа в нем (вероятность возникновения отказа очень низкая) |
В качестве показателя степени тяжести ошибки, позволяющего дать количественную оценку тяжести проявления последствий ошибки можно использовать условную вероятность отказа программного обеспечения при проявлении ошибки. Оценку степени тяжести ошибки как условной вероятности возникновения отказа, можно производить согласно ГОСТ 28195 — 89 «Оценка качества программных средств. Общие положения», используя метрики и оценочные элементы, характеризующие устойчивость программного обеспечения. При этом оценку необходимо производить для каждой ошибки в отдельности, а не для всего программного обеспечения.
Библиографическая ссылка
Дроботун Е.Б. КРИТИЧНОСТЬ ОШИБОК В ПРОГРАММНОМ ОБЕСПЕЧЕНИИ И АНАЛИЗ ИХ ПОСЛЕДСТВИЙ // Фундаментальные исследования. – 2009. – № 4. – С. 73-74;
URL: http://fundamental-research.ru/ru/article/view?id=4467 (дата обращения: 06.04.2019).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
1. Анализ особенностей программной надежности АСОИУ и методов прогнозирования программных отказов
1.1 Основные понятия надежности программного обеспечения
Автоматизация процессов управления является главным направлением развитие систем управления войсками, в ходе которого осуществляется разработка, создание и использование в процессах управления войсками электронно-вычислительной техники, сопряженных с ней технических средств, информационного и математического обеспечения, что позволяет значительно повысить оперативность управления, улучшить качество обработки информации и производительность систем управления. Для этих целей создаются автоматизированные системы управления войсками.
Основным элементом автоматизированной системы управления войсками является комплекс средств автоматизации КП различных уровней, которые представляют собой совокупность технических средств (передачи, обработки, отображения информации) и программного обеспечения.
Одними из самых серьезных недостатков программного обеспечения АСОИУ является дороговизна и низкая надежность. Многие специалисты считают первый из этих недостатков продолжением второго. Поскольку программное обеспечение по самой своей природе ненадежно, его тестирование и сопровождение требует постоянных существенных расходов.
Перед тем как анализировать надежность программного обеспечения уточним фундаментальные основные понятия теории надежности.
Надежность программного обеспечения — это свойство обеспечивать получение в соответствии с заданным алгоритмом правильных результатов в течении определенного интервала времени.
Отказпрограммного обеспечения — состояние комплекса программ связанное с нарушением работоспособности комплекса программ и прекращением дальнейшего функционирования из-за ошибок.
Под ошибкойв программном обеспечении будем понимать такое сочетание команд в программе, при исполнении которых при правильных исходных данных получают результат, не соответствующий эталонным значениям, заданные в технической документации.
Надежность программного обеспечения АСОИУ определяется его безотказностью, восстанавлиемостью и устойчивостью.
Безотказность программного обеспечения есть его свойство сохранять способность правильно выполнять задание функции и решать задачи, возложенные на вычислительные средства АСУ в процессе обработки информации на ЭВМ в течение заданного времени. При этом состояние программного обеспечения, при котором задачи по обработке информации на ЭВМ решаются правильно (корректно), называется работоспособным состоянием. В противном случае состояние носит название неработоспособным.
Переход из работоспособного состояния в неработоспособное происходит под воздействием программных отказов. Особенностью программного отказа является то, что его устранение осуществляется путем исправления программы или входных данных.
Важным свойством программного обеспечения является его восстанавлиемость, под ним понимается свойство, заключающее в приспособленности программного обеспечения к обнаружению причин возникновения программных отказов и устранению их. Восстановление после отказа в программе может заключатся в корректировке и восстановлении текста программы, исправления данных, внесении изменений в организацию вычислительного процесса (что часто оказывается необходимым при работе вычислительных средств в реальном масштабе времени).
Известно, что сбой в теории надежности определяется как самоустраняющийся отказ, не требующий вмешательства из вне для его устранения. Другим словом — сбой есть автоматически устраняющийся отказ, имеющий достаточно малое время восстановления. Поэтому применительно к надежности программного обеспечения АСУ следует конкретно указывать критерий, позволяющий отнести потерю работоспособности комплекса программ к отказу или сбою. В качестве такого критерия возьмем некоторое пороговое значение времени восстановления (? в пор).
Таким образом на устранение сбоя затрачивается меньше времени и ресурсов чем на устранение отказа. В формализованном виде определение сбоя и отказа программного обеспечения могут быть представлены как:
В с < ? в пор
В с — время восстановления после сбоя.
В о — время восстановления после отказа.
Устойчивость функционирования программного обеспечения — это способность ограничивать последствия внутренних ошибок в программах и неблагоприятных воздействий внешней среды (к которым относится неисправности аппаратуры, некорректность входных данных, ошибки оператора и другие) и противостояние им.
В проведенном анализе основных понятий надежности программного обеспечения даны определения, отказа, ошибки и надежности программного обеспечения. Выяснилось, что переход из работоспособного состояния в неработоспособное происходит под воздействием программных отказов. Из временных показателей видно, что на устранение сбоя затрачивается меньше времени и ресурсов чем на устранение отказа.
1.2 Основные причины и признаки выявления ошибок программного обеспечения
Основными причинами ошибок программного обеспечения являются:
Большая сложность программного обеспечения, например, по сравнению с аппаратурой ЭВМ.
Неправильный перевод информации из одного представления в другое на макро и микро уровнях. На макро уровне, уровне проекта, осуществляется передача и преобразование различных видов информации между организациями, подразделениями и конкретными исполнителями на всех этапах жизненного цикла ПО. На микро уровне, уровне исполнителя, производится преобразование информации по схеме: получить информацию, запомнить, выбрать из памяти, воспроизвести информацию.
Источниками ошибок программного обеспечения являются:
Внутренние: ошибки проектирования, ошибки алгоритмизации, ошибки программирования, недостаточное качество средств защиты, ошибки в документации.
Внешние: ошибки пользователей, сбои и отказы аппаратуры ЭВМ, искажение информации в каналах связи, изменения конфигурации системы.
Признаками выявления ошибок являются:
1. Преждевременное окончание программы.
2. Увеличение времени выполнения программы.
3. Нарушение последовательности вызова отдельных подпрограмм.
4. Ошибки выхода информации, поступающей от внешних источников, между входной информацией возникает не соответствие из-за: искажение данных на первичных носителях, сбои и отказы в аппаратуре, шумы и сбои в каналах связи, ошибки в документации.
Ошибки скрытые в самой программе: ошибка вычислений, ошибка ввода-вывода, логические ошибки, ошибка манипулирования данными, ошибка совместимости, ошибка сопряжения.
Искажения входной информации подлежащей обработке: искажения данных на первичных носителях информации; сбои и отказы в аппаратуре ввода данных с первичных носителей информации; шумы и сбои в каналах связи при передачи сообщений по линиям связи; сбои и отказы в аппаратуре передачи или приема информации; потери или искажения сообщений в буферных накопителях вычислительных систем; ошибки в документировании; используемой для подготовки ввода данных; ошибки пользователей при подготовки исходной информации.
Неверные действия пользователя:
1. Неправильная интерпретация сообщений.
2. Неправильные действия пользователя в процессе диалога с программным обеспечением.
3. Неверные действия пользователя или по-другому, их можно назвать ошибками пользователя, которые возникают вследствие некачественной программной документации: неверные описания возможности программ; неверные описания режимов работы; неверные описания форматов входной и выходной информации; неверные описания диагностических сообщений.
Неисправности аппаратуры установки: приводят к нарушениям нормального хода вычислительного процесса; приводят к искажениям данных и текстов программ в основной и внешней памяти.
Итак, при рассмотрение основных причин возникновения отказа и сбоев программного обеспечения можно сказать, что эти знания позволяют своевременно принимать необходимые меры по недопущению отказов и сбоев программного обеспечения.
1.3 Основные параметры и показатели надежности программ АСОИУ
Термин модели надежности программного обеспечения, как правило относится к математической модели, построенной для оценки зависимости программного обеспечения от некоторых определенных параметров.
Параметр — количественные величины, в функции или математической модели выбираемая или оцениваемая в конкретных условиях.
Значение таких параметров либо предлагаются известными, либо могут быть измерены в ходе наблюдений или экспериментального исследования процесса функционирования программного обеспечения.
Усложнение алгоритмов функционирования автоматизированных систем приводит к значительному объему и сложности программного обеспечения. Увеличение же объема (до 10 5 и более машинных команд) и сложности программного обеспечения делает невозможной разработку полностью бездефектных составляющих программного обеспечения программ. В результате программное обеспечение сдается в эксплуатацию с ошибками, являющимися причинами отказа программного обеспечения. Процесс отладки программного обеспечения по выявлению и устранению ошибок в программах можно представить графиком изменения интенсивности отказов программного обеспечения о.
Рис. 1.3.1. — время жизни программы.
Участок 1 соответствует этапам отладки, испытания и опытной эксплуатации программного обеспечения. На участке 2 остаточные после проектирования ошибки программного обеспечения, соответствующие достаточно редкому сочетанию входных данных, и отладка ошибок. На участке 3 появляются новые ошибки и после нескольких доработок комплекса программ наступает моральное устаревание программного обеспечения. После этого программное обеспечение подлежит полной замене как отработавший свой срок и не соответствующий новым условиям.
1.4 Методы прогнозирования программных отказов и тестирование программ
Предупреждение ошибок — лучший путь повышения надёжности программного обеспечения. Для его реализации была разработана методика проектирования систем управления, соответствующая спиральной модели жизненного цикла программного обеспечения. Методика предусматривает последовательное понижение сложности на всех этапах анализа объекта. При декомпозиции АСОИУ были выделены уровни управления системы, затем подсистемы, комплексы задач и так далее, вплоть до отдельных автоматизируемых функций и процедур.
Методы прогнозирования и тестирования программного обеспечения позволяют предупредить, минимизировать или исключить появление ошибок.
Методы прогнозирования и тестирования программного обеспечения включают в себя:
1. Методы, позволяющие справиться со сложностью системы.
Сложность системы является одной из главных причин низкой надежности программного обеспечения. В общем случае, сложность объекта является функцией взаимодействия между его компонентами. В борьбе со сложностью программного обеспечения используются две концепции: [Л.1]
Иерархическая структура. Иерархия позволяет разбить систему по уровням понимания. Концепция уровней позволяет анализировать систему, скрывая несущественные для данного уровня детали реализации других уровней. Иерархия позволяет понимать, проектировать и описывать сложные системы.
Независимость. В соответствии с этой концепцией, для минимизации сложности, необходимо максимально усилить независимость элементов системы.
2. Методы достижения большей точности при переводе информации.
Методы улучшения обмена информацией базируются на введении в программное обеспечение системы различных видов избыточности:
Временная избыточность. Использование части производительности ЭВМ для контроля исполнения и восстановления работоспособности программного обеспечения после сбоя.
Информационная избыточность. Дублирование части данных информационной системы для обеспечения надёжности и контроля достоверности данных.
Программная избыточность включает в себя:
взаимное недоверие — компоненты системы проектируются, исходя из предположения, что другие компоненты и исходные данные содержат ошибки, и должны пытаться их обнаружить;
немедленное обнаружение и регистрацию ошибок;
выполнение одинаковых функций разными модулями системы и сопоставление результатов обработки;
контроль и восстановление данных с использованием других видов избыточности.
Каждый из методов позволяет повысить надежность программного обеспечения и устойчивость к ошибкам. Какой из данных методов лучше определить нельзя, так как каждый метод основан на своих принципах и концепциях. Поэтому можно использовать оба метода.
Важным этапом жизненного цикла программного обеспечения, определяющим качество и надёжность системы, является тестирование. Тестирование — процесс выполнения программ с намерением найти ошибки. Этапы тестирования: контроль отдельного программного модуля отдельно от других модулей системы; контроль сопряжений (связей) между частями системы (модулями, компонентами, подсистемами); контроль выполнения системой автоматизируемых функций; проверка соответствия системы требованиям пользователей, и корректности документации, выполнение программы в строгом соответствии с инструкциями.
Существуют две стратегии при проектировании тестов: тестирование по отношению к спецификациям (документации), не заботясь о тексте программы, и тестирование по отношению к тексту программы, не заботясь о спецификациях. Разумный компромисс лежит где-то посередине, смещаясь в ту или иную сторону в зависимости от функций, выполняемых конкретным модулем, комплексом или подсистемой.
Качество подготовки исходных данных для проведения тестирования серьёзно влияет на эффективность процесса в целом и включает в себя:
1. Техническое задание.
2. Описание системы.
3. Руководство пользователя.
4. Исходный текст.
5. Правила построения (стандарты) программ и интерфейсов.
6. Критерии качества тестирования.
7. Эталонные значения исходных и результирующих данных.
8. Выделенные ресурсы, определяемые доступными финансовыми средствами.
Однако, исчерпывающее тестирование всех веток алгоритма любой программы для всех вариантов входных данных практически неосуществимо. Следовательно, продолжительность этапа тестирования является вопросом чисто временным. Учитывая, что реальные ресурсы любого проекта ограничены бюджетом и временным показателем, можно утверждать, что искусство тестирования заключается в отборе тестов с максимальной отдачей.
Ошибки в программах и данных могут проявиться на любой стадии тестирования, а также в период эксплуатации системы. Зарегистрированные и обработанные сведения должны использоваться для выявления отклонений от требований заказчика или технического задания. Для решения этой задачи используется система конфигурационного управления версиями программных компонент, база документирования тестов, результатов тестирования и выполненных корректировок программ. Средства накопления сообщений об отказах, ошибках, предложениях на изменения, выполненных корректировках и характеристиках версий являются основной для управления развитием и сопровождением комплекса программного обеспечения и состоят из журналов:
Предлагаемых изменений.
Найденных дефектов.
Утвержденных корректировок.
Реализованных изменений.
Пользовательских версий.
В данной главе анализируются основные причины и признаки ошибок, вводятся основные параметры и показатели надежности программного обеспечения. Также рассмотрены методы прогнозирования программных отказов и тестирование программ с целью повышения надежности. Для оценки надежности программного обеспечения используются специальные модели на основание параметров и показателей приведенных выше.
2. Анализ моделей оценки программной надежности
Существующие математические модели должны оценивать характеристики ошибок в программах и прогнозировать их надежность при эксплуатации. Модели имеют вероятностный характер, и достоверность прогнозов зависит от точности исходных данных и глубины прогнозирования по времени.
Эти математические модели предназначены для оценки:
1. Показателей надежности комплекса программ в процессе отладки;
2. Количества ошибок оставшиеся не выявленными;
3. Времени, необходимого для обнаружения следующей ошибки в функционирующей программе;
4. Времени, необходимого для выявления всех ошибок с заданной вероятностью.
Существуют ряд математических моделей:
Экспоненциальная модель изменения ошибок в зависимости от времени отладки.
Дискретно-меняющаяся модель, учитывающая дискретно-повышающую времени наработки на отказ, как линейную функцию времени тестирования и испытания.
Модель Шумана. Исходные данные для модели Шумана собираются в процессе тестирования программного обеспечения в течение фиксированных или случайных временных интервалов.
Модель La Padula. По этой модели выполнение последовательности тестов в m этапов. Каждый этап заканчивается внесением исправлений в программное обеспечение.
Модель Джелинского — Моранды. Исходные данные собираются в процессе тестирования программного обеспечения. При этом фиксируется время до очередного отказа.
Модель Шика — Волвертона. Модификация модели Джелинского — Моранды для случая возникновения на рассматриваемом интервале более одной ошибки.
Модель Муса. В процессе тестирования фиксируется время выполнения программы (тестового прогона) до очередного отказа.
Модель переходных вероятностей. Эта модель основана на марковском процессе, протекающем в дискретной системе с непрерывным временем.
Модель Миллса. Использование этой модели предполагает необходимость перед началом тестирования искусственно вносить в программу некоторое количество известных ошибок.
Модель Липова. Модификация модели Миллса, рассматривающая вероятность обнаружения ошибки при использовании различного числа тестов.
Простая интуитивная модель. Использование этой модели предполагает проведения тестирования двумя группами программистов независимо друг от друга, использующими независимые тестовые наборы.
Модель Коркорэна. Модель использует изменяющиеся вероятности отказов для различных типов ошибок.
Модель Нельсона. Данная модель при расчете надежности программного обеспечения учитывает вероятность выбора определенного тестового набора для очередного выполнения программы.
При таком большом количестве моделей все-таки основными из них являютсяэкспоненциальная и дискретно-меняющаяся модели.
2.1 Дискретно-меняющая модель
В данной работе под дискретно-меняющей моделью подразумевается модель, которая основывается на дискретном увеличении времени наработки на отказ. Такая модель базируется на следующих предположениях:
1. Устранение ошибок в программе приводит к увеличению времени наработки на отказ T на одну и ту же величину, равную:
T (1) =T (2) =…=T (i) = const (2.1.1)
T (i) = T (i) — T (i-1) (2.2.2)
2. Время между двумя последовательными отказами:
i = t i — t i -1 (2.1.3)
является случайной величиной, которую можно представить в виде суммы двух случайных величин:
i = i -1 + I (2.1.4)
где i — независимые случайные величины, которые имеют одинаковые математические ожидания M{} и среднеквадратические отклонения.
3. Начальный интервал времени 0 сравним со случайной величиной 0 , т.е. 0 0 , поскольку в начальный период эксплуатации программ отказы в них возникают весьма часто.
На основании второго предположения величину интервала между i-м (i-1) — м отказами можно определить соотношением:
i = i -1 + i = 0 + j (2.1.5)
из которого можно получить соотношение для определения времени наступления m-го отказа в программе:
t m = i = (0 + j) (2.1.6)
исходя из третьего предположения полученные соотношения примут вид:
i = 0 + j = j (2.1.7)
t m = (0 + j) = i j (2.1.8)
При этих предположениях средняя наработка между (m-1) — м и m-м отказами программы равна:
T 0 (m) = M{ m -1 } = M{ j } = i j = m M{}. (2.1.9)
Средняя наработка до возникновения m-го отказа может быть определена по соотношению:
T m = M{t m } = i jk) = M{}. (2.1.10)
2.2 Экспоненциальное распределение
Теперь непосредственно перейдем к анализу собственно экспоненциального распределения.
Рассматриваемое распределение характеризуется рядом свойств, такими как:
1. Ошибки в комплексе программ являются независимыми и проявляются в случайные моменты времени. Данное свойство характеризует неизменность во времени интенсивности проявления и обнаружения ошибок (т.е. ош =const) в течение всего времени выполнения программы (=t н -t 0).
2. Интенсивность проявления и обнаружения ошибок ош (интенсивность отказов) пропорционально числу оставшихся в ней ошибок:
()= Kn 0 () (2.2.1)
где K — коэффициент пропорциональности, учитывающий реальное быстродействию ЭВМ и число команд в программе.
3. В процессе исправления ошибок программы новые ошибки не порождаются. Это означает, что интенсивность исправления ошибок dn/dt будет равна интенсивности их обнаружения:
Тогда n 0 ()= N 0 — n(). (2.2.3)
Основываясь на предположениях, введенных выше, получим:
n()=N 0 (1-e — K); (2.5)
Если принять, что, получим:
2.3 Методика оценки надежности программ по числу исправленных ошибок
Пусть N 0 — число ошибок, имеющихся в программе перед началом испытаний.
n() — количество ошибок, устраненных в ходе испытаний (тестирования) программы;
n 0 () — число оставшихся в программе ошибок на момент окончания испытаний.
Тогда n 0 ()= N 0 — n().
Основываясь на предположениях введенных в пункте 2.2.1, а именно: и ()= Kn 0 () то получим:
K — коэффициент, учитывающий быстродействие компьютера.
Решением этого дифференциального уравнения при начальных условиях t=0 и =0 является:
n()=N 0 (1-e -K); (2.3.2)
n 0 ()=N 0 — n()=N 0 e -K . (2.3.3)
Надежность программы по результатам испытаний в течении времени можно охарактеризовать средним временим наработки на отказ, равным:
Если ввести исходное значение среднего времени наработки на отказ перед испытанием, равного, то получим:
откуда видно, что среднее время наработки на отказ увеличивается по мере выявления и исправления ошибок.
На практике в процессе корректировки программы все же могут появляться новые ошибки. Пусть В-коэффициент уменьшения ошибок, определяемый как отношение интенсивности уменьшения ошибок к интенсивности их проявления, или к интенсивности отказов, то есть:
Если обозначить за m — число обнаруженных отказов, а M 0 — число отказов, которое должно произойти, чтобы можно было выявить и устранить n соответствующих ошибок, то есть:
то среднее время наработки на отказ и число обнаруженных отказов определяется следующими соотношениями:
Если принять, что, получим:
Для практического использования представляет интерес число ошибок m, которое должно быть обнаружено и исправлено для того, чтобы добиться увеличения среднего времени наработки на отказ от T 01 до T 02 . Этот показатель может быть получен из следующих соотношений:
Итак, оценка надежности программ по числу исправленных ошибок определяется по формуле:
2.4 Методика оценки надежности программ по времени испытания
Дополнительное время испытаний, необходимое для обеспечения увеличения среднего времени наработки на отказ с T 01 до T 02 определяется из соотношений:
где T 01 и T 02 определяются согласно формуле (2.3.9):
Оценка надежности программ по времени испытаний определяется согласно формуле:
2.5 Методика оценки безотказности программ по наработке
Наработку между очередными отказами — случайную величину T (i) можно представить в виде суммы двух случайных величин:
T (i) = T (i -1) + T (i) (2.5.1)
Последовательно применяя (3.3.1) ко всем периодам наработки между отказами, получаем:
T (i) = T (0) + T (?) (2.5.2)
Случайная величина Т n — наработка до возникновения n-го отказа программы — равна:
T n = T (i) = (2.5.3)
Введем следующие допущения:
1) все случайные величины T () независимы и имеют одинаковые математические ожидания m ? t и среднеквадратические отклонения? ? t ;
2) случайная величина T (0) пренебрежимо мала по сравнению с суммой T (?)
Основанием для второго допущения могут служить следующие соображения: в самый начальный период эксплуатации программы ошибки возникают очень часто, то есть время T (0) мало. Сумма (2.5.3) быстро растет с увеличением n, и доля T (0) быстро падает. Будем считать что T (0) ? T (0) .
В соответствии со вторым допущением имеем:
T (n) =T (?) . (2.5.4)
При одинаковых T (?) наработка между (n-1) и n отказами — случайная величина T (n) — имеет математическое ожидание:
m t (n) =M=nm ? t (2.5.6)
T (n) = ? ? t ; (2.5.7)
Для случайной величины T n математическое ожидание равно:
M ? t ; (2.5.8)
и среднеквадратическое отклонение:
T ; (2.5.9)
Чтобы вычислить значения, и, необходимо по данным об отказах программы в течение периода наблюдения t н найти статистические оценки числовых характеристик случайной разности T (i) :
n н — число отказов программы за наработку (0, t н).
Учитывая, что при t >t н число отказов n н >> 1, из (2.5.8) и (2.5.9) имеем:
m t (n) ? m ? t , (2.5.12)
T (n) = ? ? t n ; (2.5.13)
Поскольку случайные величины T (n) и T n согласно (2.5.4) и (2.5.5) равны суммам многих случайных величин, T (n) и T n можно считать распределенными нормально с математическими ожиданиями и дисперсиями, определенными по (2.5.6) — (2.5.9), (2.5.12) и (2.5.13). Так как наработка положительна, на практике используется усеченное на интервале (0, ?) нормальное распределение. Обычно нормирующий множитель с?1.
При n>n н плотность распределения наработки между очередными (n-1) и n отказами:
f (n) (?) = , (2.5.14)
где? отсчитывается с момента последнего, (n-1) отказа.
Заключение
В работе было показано, что надежность программного обеспечения, в десятки раз ниже чем аппаратурная надежность. Требования к программной надежности это определение необходимого выполнения боевых задач в течении не менее чем 1872 часов.
Из анализа видно, что наибольшее влияние на надежность программного обеспечения оказывают внутренние ошибки и ошибки которые находятся при начале эксплуатации программ. Исходя из этого был проведен анализ моделей надежности, методов расчета и оценки программной надежности. С помощью этого анализа, на основе дискретного и экспоненциального метода рассчитали время необходимое на тестирование программного обеспечения, для повышения времени жизни программы.
Список литературы
программный безотказность надежность прогнозирование
1. В.В. Липаев Проектирование математического обеспечения АСУ. (системотехника, архитектура, технология). М., «Сов. радио», 1977.
2. Р.С. Захарова Основные вопросы теории и практики надежности.
3. В.А. Благодатских, В.А. Волнин, К.Ф. ПоскакаловСтандартизация разработки программных средств.
4. А.А. ВороновТеоретические основы построения автоматизированных систем управления. Разработка технического задания.-М.: Наука, 1997.
5. Основы прикладной теории надежности АСУ. Учебное пособие, Тверь, ВА ПВО, 1995, н/с 32. 965,0-75. В.М. Ионов и др., инв. №8856.
6. Б.Н. Горевич. Расчет показателей надежности систем вооружения и резервированных элементов. Конспект лекций, ВА ПВО, 1998, н/с 68.501.4, Г68, инв. №9100
Размещено на Allbest.ru
Подобные документы
Анализ методов оценки надежности программных средств на всех этапах жизненного цикла, их классификация и типы, предъявляемые требования. Мультиверсионное программное обеспечение. Современные модели и алгоритмы анализа надежности программных средств.
дипломная работа , добавлен 03.11.2013
Действия, которые выполняются при проектировании АИС. Кластерные технологии, их виды. Методы расчета надежности на разных этапах проектирования информационных систем. Расчет надежности с резервированием. Испытания программного обеспечения на надежность.
курсовая работа , добавлен 02.07.2013
Программное обеспечение как продукт. Основные характеристик качества программного средства. Основные понятия и показатели надежности программных средств. Дестабилизирующие факторы и методы обеспечения надежности функционирования программных средств.
лекция , добавлен 22.03.2014
Модель надежности программного средства как математическая модель для оценки зависимости надежности программного обеспечения от некоторых определенных параметров, анализ видов. Общая характеристика простой интуитивной модели, анализ сфер использования.
презентация , добавлен 22.03.2014
Запросы клиента по области возможных запросов к серверу. Программа для прогнозирования поведения надежности программного обеспечения на основе метода Монте-Карло. Влияние количества программ-клиентов на поведение программной системы клиент-сервера.
контрольная работа , добавлен 03.12.2010
Особенности аналитической и эмпирической моделей надежности программных средств. Проектирование алгоритма тестирования и разработка программы для определения надежности ПО моделями Шумана, Миллса, Липова, с использованием языка C# и VisualStudio 2013.
курсовая работа , добавлен 29.06.2014
Надежность системы управления как совокупность надежности технических средств, вычислительной машины, программного обеспечения и персонала. Расчет надежности технических систем, виды отказов САУ и ТСА, повышение надежности и причины отказов САУ.
курс лекций , добавлен 27.05.2008
Точные и приближенные методы анализа структурной надежности. Критерии оценки структурной надежности методом статистического моделирования. Разработка алгоритма и программы расчета структурной надежности. Методические указания по работе с программой.
дипломная работа , добавлен 17.11.2010
Постановка проблемы надежности программного обеспечения и причины ее возникновения. Характеристики надежности аппаратуры. Компьютерная программа как объект исследования, ее надежность и правильность. Модель последовательности испытаний Бернулли.
реферат , добавлен 21.12.2010
Надежность как характеристика качества программного обеспечения (ПО). Методика расчета характеристик надежности ПО (таких как, время наработки до отказа, коэффициент готовности, вероятность отказа), особенности прогнозирования их изменений во времени.
В области информатики и управления проектами в настоящее время
нет моделей, которые могут точно прогнозировать ошибки программного
обеспечения. Существуют различные теории и модели, но ни один из
них не обеспечит вас гарантированными результатами. См. циклическая сложность как один из примеров, когда
есть несогласие с мерой корреляция с дефектами .
В вашем случае вы пытаетесь выполнить статистический анализ без
достаточных соображений, даваемых либо тестовой конструкции, либо
контролируемым переменным, либо нулевая гипотеза . Вы также вводите в заблуждение
причинность и корреляция . Даже если у вас есть
корректно сконструированный тест с адекватным контролем, и даже
если вы сможете отклонить нулевую гипотезу, вам будет крайне сложно
использовать любой из этих проектов в качестве прямого
доказательства причины и эффекта.
Просматривайте свои проекты
Лучшее использование вашего времени — это внимательно изучить
проект 2, чтобы понять, почему у вас такой высокий уровень
дефектов. Осмотрите свои процессы, сформируйте гипотезу, а затем
попытайтесь адаптировать свои процессы, чтобы уменьшить
дефекты.
Хороший руководитель проекта не будет тратить время на создание
«универсальной теории всего» на основе экстраполяции из двух
проектов. Вместо этого опытный руководитель проекта потратил на это
время fixing
Project 2, чтобы улучшить свои шансы на
успех, или сообщив о вероятности неудачи менеджера портфеля, чтобы
можно было принять стратегическое решение о том, проект должен быть
прекращен в качестве меры контроля затрат или качества.
Представьте себе, что вы определяете стоимость автомобиля,
исходя из того, как часто он был вымыт.
Разработчики, которые оставили файл
Я понятия не имею, что вы пытаетесь сделать из этого показателя.
Похоже, что пытаться предсказать популярность быстрого питания,
основанного на том, сколько кварталов они дали в качестве
изменения.
The rules
about bugs is to test from early
stages of development, and to keep a 1:1 or 2:1 ratio of
programmers to testers. Then you can safely assume the
testing-debugging stage will take as long as the time originally
estimated to write the code.
Чем позже вы начнете тестирование, тем меньше тестировщиков у
вас есть, тогда больше ошибок будет жить и начнет расти в
программном обеспечении, а этап отладки займет больше времени.
Затем вы можете удвоить или утроить время тестирования/отладки.
Поскольку код исправления, который был написан недавно
(сегодня), проще, чем исправление кода, написанного некоторое время
назад (дни, недели или месяцы). Код, который не является свежим в
голове программиста, нуждается в повторном чтении и понимании.
Более новый код часто основывается на более раннем коде,
поэтому, если раньше была ошибка, он может полностью упасть и
повредить проблемы.
Наконец: Количество ошибок
не является хорошим
показателем чего-либо, если вы не учитываете их серьезность,
важность и влияние. Важными ошибками являются и опечатка, и
прерывистая система. Один займет немного минут, чтобы исправить,
другой может занять очень много времени, так как прерывистые сбои
почти невозможно воссоздать и найти.
Значительная часть производственного процесса опирается на тестирование программ. Что это такое и как осуществляется подобная деятельность обсудим в данной статье.
Что называют тестированием?
Под этим понимают процесс, во время которого выполняется программное обеспечение с целью обнаружения мест некорректного функционирования кода. Для достижения наилучшего результата намеренно конструируются трудные наборы входных данных. Главная цель проверяющего заключается в том, чтобы создать оптимальные возможности для отказа Хотя иногда тестирование разработанной программы может быть упрощено до обычной проверки работоспособности и выполнения функций. Это позволяет сэкономить время, но часто сопровождается ненадежностью программного обеспечения, недовольством пользователей и так далее.
Эффективность
То, насколько хорошо и быстро находятся ошибки, существенным образом влияет на стоимость и длительность разработки программного обеспечения необходимого качества. Так, несмотря на то, что тестеры получают заработную плату в несколько раз меньшую, чем программисты, стоимость их услуг обычно достигает 30 — 40 % от стоимости всего проекта. Это происходит из-за численности личного состава, поскольку искать ошибку — это необычный и довольно трудный процесс. Но даже если программное обеспечение прошло солидное количество тестов, то нет 100 % гарантии, что ошибок не будет. Просто неизвестно, когда они проявятся. Чтобы стимулировать тестеров выбирать типы проверки, которые с большей вероятностью найдут ошибку, применяются различные средства мотивации: как моральные, так и материальные.
Подход к работе
Оптимальной является ситуация, когда реализовываются различные механизмы, направленные на то, чтобы ошибок в программном обеспечении не было с самого начала. Для этого необходимо позаботится о грамотном проектировании архитектуры, четком техническом задании, а также важно не вносить коррективы в связи, когда работа над проектом уже начата. В таком случае перед тестером стоит задача нахождения и определения небольшого количества ошибок, которые остаются в конечном результате. Это сэкономит и время, и деньги.
Что такое тест?
Это немаловажный аспект деятельности проверяющего, который необходим для успешного выявления недочетов программного кода. Они необходимы для того, чтобы контролировать правильность приложения. Что входит в тест? Он состоит их начальных данных и значений, которые должны получиться как результирующие (или промежуточные). Для того чтобы успешнее выявлять проблемы и несоответствия, тесты необходимо составлять после того, как был разработан алгоритм, но не началось программирование. Причем желательно использовать несколько подходов при расчете необходимых данных. В таком случае растёт вероятность обнаружения ошибки благодаря тому, что можно исследовать код с другой точки зрения. Комплексно тесты должны обеспечивать проверку внешних эффектов готового программного изделия, а также его алгоритмов работы. Особенный интерес предоставляют предельные и вырожденные случаи. Так, в практике деятельности с ошибками часто можно выявить, что цикл работает на один раз меньше или больше, чем было запланировано. Также важным является тестирование компьютера, благодаря которому можно проверить соответствие желаемому результату на различных машинах. Это необходимо для того, чтобы удостовериться, что программное обеспечение сможет работать на всех ЭВМ. Кроме того, тестирование компьютера, на котором будет выполняться разработка, является важным при создании мультиплатформенных разработок.
Искусство поиска ошибок
Программы часто нацелены на работу с огромным массивом данных. Неужели его необходимо создавать полностью? Нет. Широкое распространение приобрела практика «миниатюризации» программы. В данном случае происходит разумное сокращение объема данных по сравнению с тем, что должно использоваться. Давайте рассмотрим такой пример: есть программа, в которой создаётся матрица размером 50×50. Иными словами — необходимо вручную ввести 2500 тысячи значений. Это, конечно, возможно, но займёт очень много времени. Но чтобы проверить работоспособность, программный продукт получает матрицу, размерность которой составляет 5×5. Для этого нужно будет ввести уже 25 значений. Если в данном случае наблюдается нормальная, безошибочная работа, то это значит, что всё в порядке. Хотя и здесь существуют подводные камни, которые заключаются в том, что при миниатюризации происходит ситуация, в результате которой изменения становятся неявными и временно исчезают. Также очень редко, но всё же случается и такое, что появляются новые ошибки.
Преследуемые цели
Тестирование ПО не является легким делом из-за того, что данный процесс не поддаётся формализации в полном объеме. Большие программы почти никогда не обладают необходимым точным эталоном. Поэтому в качестве ориентира используют ряд косвенных данных, которые, правда, не могут полностью отражать характеристики и функции программных разработок, что отлаживаются. Причем они должны быть подобраны таким образом, чтобы правильный результат вычислялся ещё до того, как программный продукт будет тестирован. Если этого не сделать заранее, то возникает соблазн считать всё приблизительно, и если машинный результат попадёт в предполагаемый диапазон, то будет принято ошибочное решение, что всё правильно.
Проверка в различных условиях
Как правило, тестирование программ происходит в объемах, которые необходимы для минимальной проверки функциональности в ограниченных пределах. Деятельность ведётся с изменением параметров, а также условий их работы. Процесс тестирования можно поделить на три этапа:
- Проверка в обычных условиях. В данном случае тестируется основной функционал разработанного программного обеспечения. Полученный результат должен соответствовать ожидаемому.
- Проверка в чрезвычайных условиях. В этих случаях подразумевается получение граничных данных, которые могут негативно повлиять на работоспособность созданного программного обеспечения. В качестве примера можно привести работу с чрезвычайно большими или малыми числами, или вообще, полное отсутствие получаемой информации.
- Проверка при исключительных ситуациях. Она предполагает использование данных, которые лежат за гранью обработки. В таких ситуациях очень плохо, когда программное обеспечение воспринимает их как пригодные к расчету и выдаёт правдоподобный результат. Необходимо позаботиться, чтобы в подобных случаях происходило отвержение любых данных, которые не могут быть корректно обработаны. Также необходимо предусмотреть информирование об этом пользователя
Тестирование ПО: виды
Создавать программное обеспечение без ошибок весьма трудно. Это требует значительного количества времени. Чтобы получить хороший продукт часто применяются два вида тестирования: «Альфа» и «Бета». Что они собой представляют? Когда говорят об альфа-тестировании, то под ним подразумевают проверку, которую проводит сам штат разработчиков в «лабораторных» условиях. Это последний этап проверки перед тем, как программа будет передана конечным пользователям. Поэтому разработчики стараются развернуться по максимуму. Для легкости работы данные могут протоколироваться, чтобы создавать хронологию проблем и их устранения. Под бета-тестированием понимают поставку программного обеспечения ограниченному кругу пользователей, чтобы они смогли поэксплуатировать программу и выявить пропущенные ошибки. Особенностью в данном случае является то, что часто ПО используется не по своему целевому назначению. Благодаря этому неисправности будут выявляться там, где ранее ничего не было замечено. Это вполне нормально и переживать по этому поводу не нужно.
Завершение тестирования
Если предыдущие этапы были успешно завершены, то остаётся провести приемочный тест. Он в данном случае становиться простой формальностью. Во время данной проверки происходит подтверждение, что никаких дополнительных проблем не найдено и программное обеспечение можно выпускать на рынок. Чем большую важность будет иметь конечный результат, тем внимательней должна проводиться проверка. Необходимо следить за тем, чтобы все этапы были пройдены успешно. Вот так выглядит процесс тестирования в целом. А теперь давайте углубимся в технические детали и поговорим о таких полезных инструментах, как тестовые программы. Что они собой представляют и в каких случаях используются?
Автоматизированное тестирование
Ранее считалось, что динамический анализ разработанного ПО — это слишком тяжелый подход, который неэффективно использовать для обнаружения дефектов. Но из-за увеличения сложности и объема программ появился противоположный взгляд. Автоматическое тестирование применяется там, где самыми важными приоритетами является работоспособность и безопасность. И они должны быть при любых входных данных. В качестве примера программ, для которых целесообразным является такое тестирование, можно привести следующие: сетевые протоколы, веб-сервер, sandboxing. Мы далее рассмотрим несколько образцов, которые можно использовать для такой деятельности. Если интересуют бесплатные программы тестирования, то среди них качественные найти довольно сложно. Но существуют взломанные «пиратские» версии хорошо зарекомендовавших себя проектов, поэтому можно обратиться к их услугам.
Avalanche
Этот инструмент помогает обнаружить дефекты, проходя тестирование программ в режиме динамического анализа. Он собирает данные и анализирует трассу выполнения разработанного объекта. Тестеру же предоставляется набор входных данных, которые вызывают ошибку или обходят набор имеющихся ограничений. Благодаря наличию хорошего алгоритма проверки разрабатывается большое количество возможных ситуаций. Программа получает различные наборы входных данных, которые позволяют смоделировать значительное число ситуаций и создать такие условия, когда наиболее вероятным является возникновение сбоя. Важным преимуществом программы считается применение эвристической метрики. Если есть проблема, то ошибка приложения находится с высокой вероятностью. Но эта программа имеет ограничения вроде проверки только одного помеченного входного сокета или файла. При проведении такой операции, как тестирование программ, будет содержаться детальная информация о наличие проблем с нулевыми указателями, бесконечными циклами, некорректными адресами или неисправностями из-за использования библиотек. Конечно, это не полный список обнаруживаемых ошибок, а только их распространённые примеры. Исправлять недочеты, увы, придётся разработчикам — автоматические средства для этих целей не подходят.
KLEE
Это хорошая программа для тестирования памяти. Она может перехватывать примерно 50 системных вызовов и большое количество виртуальных процессов, таким образом, выполняется параллельно и отдельно. Но в целом программа не ищет отдельные подозрительные места, а обрабатывает максимально возможное количество кода и проводит анализ используемых путей передачи данных. Из-за этого время тестирования программы зависит от размера объекта. При проверке ставка сделана на символические процессы. Они являются одним из возможных путей выполнения задач в программе, которая проверяется. Благодаря параллельной работе можно анализировать большое количество вариантов работы исследуемого приложения. Для каждого пути после окончания его тестирования сохраняются наборы входных данных, с которых начиналась проверка. Следует отметить, что тестирование программ с помощью KLEE помогает выявлять большое количество отклонений, которых не должно быть. Она может найти проблемы даже в приложениях, которые разрабатываются десятилетиями.
Если предполагать, что в программном обеспечении какие-то ошибки все же будут, то лучшая (после предупреждения ошибок) стратегия — включить средства обнаружения ошибок в само про-граммное обеспечение.
Большинство методов направлено по возможности на неза-медлительное обнаружение сбоев. Немедленное обнаружение имеет два преимущества: можно минимизировать влияние ошиб-ки и последующие затруднения для человека, которому придется извлекать информацию о ней, находить ее и исправлять.
{SITELINK-S405}Меры по обнаружению ошибок {/SITELINK}можно разбить на две под-группы: пассивные
попытки обнаружить симптомы ошибки в про-цессе «обычной» работы программного обеспечения и активные
попытки программной системы периодически обследовать свое состояние в поисках признаков ошибок.
Пассивное обнаружение
.
Меры по обнаружению ошибок могут быть приняты на нескольких структурных уровнях программной системы. Здесь мы будем рассматривать уровень подсистем, или ком-понентов, т.е. нас будут интересовать меры по обнаружению симп-томов ошибок, предпринимаемые при переходе от одного компо-нента к другому, а также внутри компонента. Все это, конечно, при-менимо также к отдельным модулям внутри компонента.
Разрабатывая эти меры, мы будем опираться на следующее.
1. Взаимное недоверие.
Каждый из компонентов должен пред-полагать, что все другие содержат ошибки. Когда он получает какие-нибудь данные от другого компонента или из источника вне системы, он должен предполагать, что данные могут быть неправильными, и пытаться найти в них ошибки.
2.
Немедленное обнаружение.
Ошибки необходимо обнаружить как можно раньше. Это не только ограничивает наносимый ими ущерб, но и значительно упрощает задачу отладки.
3. Избыточность.
Все средства обнаружения ошибок основаны на некоторой форме избыточности (явной или неявной).
Когда разрабатываются {SITELINK-S405}меры по обнаружению ошибок{/SITELINK}, важ-но принять согласованную стратегию для всей системы. Действия, предпринимаемые после обнаружения ошибки в программном обеспечении, должны быть единообразными для всех компонен-тов системы. Это ставит вопрос о том, какие именно действия следует предпринять, когда ошибка обнаружена. Наилучшее решение — немедленно завершить выполнение программы или (в случае операционной системы) перевести центральный про-цессор в состояние ожидания. С точки зрения предоставления че-ловеку, отлаживающему программу, например системному про-граммисту, самых благоприятных условий для диагностики оши-бок немедленное завершение представляется наилучшей стратегией. Конечно, во многих системах подобная стратегия бывает нецелесообразной (например, может оказаться, что при-останавливать работу системы нельзя). В таком случае использу-ется метод регистрации ошибок.
Описание симптомов ошибки и «моментальный снимок» состояния системы сохраняются во внеш-нем файле, после чего система может продолжать работу. Этот файл позднее будет изучен обслуживающим персоналом.
Всегда, когда это возможно, лучше приостановить выполне-ние программы, чем регистрировать ошибки (либо обеспечить как дополнительную возможность работу системы в любом из этих режимов). Различие между этими методами проиллюстриру-ем на способах выявления причин возникающего иногда скреже-та вашего автомобиля. Если автомеханик находится на заднем сиденье, то он может обследовать состояние машины в тот мо-мент, когда скрежет возникает. Если вы выбираете метод регист-рации ошибок, задача диагностики станет сложнее.
Активное обнаружение ошибок.
Не все ошибки можно выя-вить пассивными методами, поскольку эти методы обнаружива-ют ошибку лишь тогда, когда ее симптомы подвергаются соот-ветствующей проверке. Можно делать и дополнительные провер-ки, если спроектировать специальные программные средства для активного поиска признаков ошибок в системе. Такие средства называются средствами активного обнаружения ошибок.
Активные средства обнаружения ошибок обычно объединя-ются в диагностический монитор:
параллельный процесс, кото-рый периодически анализирует состояние системы с целью обна-ружить ошибку. Большие программные системы, управляющие ресурсами, часто содержат ошибки, приводящие к потере ресур-сов на длительное время. Например, управление памятью опера-ционной системы сдает блоки памяти «в аренду» программам пользователей и другим частям операционной системы. Ошибка в этих самых «других частях» системы может иногда вести к не-правильной работе блока управления памятью, занимающегося возвратом сданной ранее в аренду памяти, что вызывает медлен-ное вырождение системы.
Диагностический монитор можно реализовать как периоди-чески выполняемую задачу (например, она планируется на каж-дый час) либо как задачу с низким приоритетом, которая плани-руется для выполнения в то время, когда система переходит в со-стояние ожидания. Как и прежде, выполняемые монитором конкретные проверки зависят от специфики системы, но некото-рые идеи будут понятны из примеров. Монитор может обследо-вать основную память, чтобы обнаружить блоки памяти, не вы-деленные ни одной из выполняемых задач и не включенные в си-стемный список свободной памяти. Он может проверять также необычные ситуации: например, процесс не планировался для выполнения в течение некоторого разумного интервала времени. Монитор может осуществлять поиск «затерявшихся» внутри си-стемы сообщений или операций ввода-вывода, которые необыч-но долгое время остаются незавершенными, участков памяти на диске, которые не помечены как выделенные и не включены в спи-сок свободной памяти, а также различного рода странностей в файлах данных.
Иногда желательно, чтобы в чрезвычайных обстоятельствах монитор выполнял диагностические тесты системы. Он может вы-зывать определенные системные функции, сравнивая их результат с заранее определенным и проверяя, насколько разумно время вы-полнения. Монитор может также периодически предъявлять сис-теме «пустые» или «легкие» задания, чтобы убедиться, что система функционирует хотя бы самым примитивным образом.
Вариант 1
Задание 1. Модель парной линейной регрессии.
Имеются данные о размере среднемесячных доходов в разных группах семей
|
Номер группы |
Среднедушевой денежный доход в месяц, руб., X |
Доля оплаты труда в структуре доходов семьи, %, Y |
|
1 |
79,8 |
64,2 |
|
2 |
152,1 |
66,1 |
|
3 |
199,3 |
69,0 |
|
4 |
240,8 |
70,6 |
|
5 |
282,4 |
72,4 |
|
6 |
301,8 |
74,3 |
|
7 |
385,3 |
76,0 |
|
8 |
457,8 |
77,1 |
|
9 |
577,4 |
78,4 |
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы
2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.
4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.
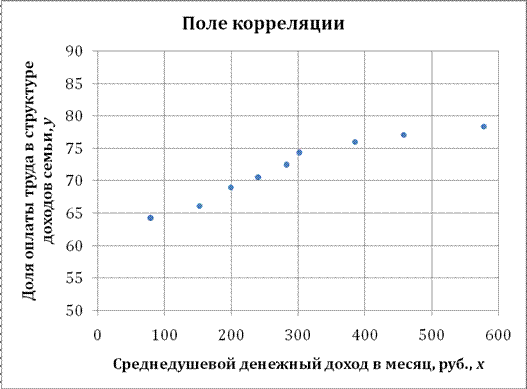
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.
Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .
Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
X×Y |
X2 |
Y2 |
|
1 |
79,8 |
64,2 |
5123,16 |
6368,04 |
4121,64 |
|
2 |
152,1 |
66,1 |
10053,81 |
23134,41 |
4369,21 |
|
3 |
199,3 |
69,0 |
13751,70 |
39720,49 |
4761,00 |
|
4 |
240,8 |
70,6 |
17000,48 |
57984,64 |
4984,36 |
|
5 |
282,4 |
72,4 |
20445,76 |
79749,76 |
5241,76 |
|
6 |
301,8 |
74,3 |
22423,74 |
91083,24 |
5520,49 |
|
7 |
385,3 |
76,0 |
29282,80 |
148456,09 |
5776,00 |
|
8 |
457,8 |
77,1 |
35296,38 |
209580,84 |
5944,41 |
|
9 |
577,4 |
78,4 |
45268,16 |
333390,76 |
6146,56 |
|
S |
2676,7 |
648,1 |
198645,99 |
989468,27 |
46865,43 |
|
Среднее |
297,41 |
72,01 |
22071,78 |
109940,92 |
5207,27 |
Вычислим коэффициент корреляции. Используем следующую формулу:
= 0,9568.
Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.
Среднюю ошибку коэффициента корреляции определим по формуле:
= 0,032.
Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.
TТабл(0,05; 7) = 2,36.
Запишем доверительный интервал для коэффициента корреляции.
Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.
Вычислим параметры уравнения регрессии.
= 0,03.
= 72,01 – 0,03×297,41 = 63,09.
Получим следующее уравнение: .
Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.
Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.
Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:
Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
|
|
|
|
1 |
79,8 |
64,2 |
65,48 |
1,6384 |
47354,1 |
|
2 |
152,1 |
66,1 |
67,65 |
2,4025 |
21115,0 |
|
3 |
199,3 |
69,0 |
69,07 |
0,0049 |
9625,6 |
|
4 |
240,8 |
70,6 |
70,31 |
0,0841 |
3204,7 |
|
5 |
282,4 |
72,4 |
71,56 |
0,7056 |
225,3 |
|
6 |
301,8 |
74,3 |
72,14 |
4,6656 |
19,3 |
|
7 |
385,3 |
76,0 |
74,65 |
1,8225 |
7724,7 |
|
8 |
457,8 |
77,1 |
76,82 |
0,0784 |
25725,0 |
|
9 |
577,4 |
78,4 |
80,41 |
4,0401 |
78394,4 |
|
S |
2676,7 |
648,1 |
648,09 |
15,4421 |
193388,1 |
Вычислим стандартные ошибки коэффициентов уравнения.


Вычислим T-статистики.
Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и
, т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.
Сделаем рисунок.
Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.
Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.
Fтабл(0,05; 1; 7) = 5,59.
Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.
Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.
XP = 297,41 × 1,11 = 330,1.
Вычислим прогнозное значение Yp с помощью уравнения регрессии.
» 73%.
Доверительный интервал прогноза имеет вид
(УP – Tкр×My, УP + Tкр×My),
Где 

Запишем доверительный интервал прогноза:
Þ
Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.
Задание 2. Модель парной нелинейной регрессии.
По территориям Центрального района известны данные за 1995 г.
|
Район |
Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X |
Средний размер назначенных ежемесячных пенсий, тыс. руб., Y |
|
Брянская обл. |
178 |
240 |
|
Владимирская обл. |
202 |
226 |
|
Ивановская обл. |
197 |
221 |
|
Калужская обл. |
201 |
226 |
|
Костромская обл. |
189 |
220 |
|
Орловская обл. |
166 |
232 |
|
Рязанская обл. |
199 |
215 |
|
Смоленская обл. |
180 |
220 |
|
Тверская обл. |
181 |
222 |
|
Тульская обл. |
186 |
231 |
|
Ярославская обл. |
250 |
229 |
Задания:
1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной (
) парной регрессии. Сделать рисунки.
2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.
3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии
4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.
Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.
Получим следующий рисунок.
По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.
Построение полулогарифмической модели регрессии.
Уравнение логарифмической кривой: .
Обозначим:
Получим линейное уравнение регрессии:
Y = A + B×X.
Произведем линеаризацию модели путем замены . В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Xy |
X2 |
Y2 |
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
1243,63 |
26,85 |
57600 |
226,40 |
206,314 |
184,904 |
6,006 |
|
2 |
202 |
226 |
5,3083 |
1199,67 |
28,18 |
51076 |
225,17 |
0,132 |
0,694 |
0,370 |
|
3 |
197 |
221 |
5,2832 |
1167,59 |
27,91 |
48841 |
225,41 |
21,496 |
19,464 |
1,957 |
|
4 |
201 |
226 |
5,3033 |
1198,55 |
28,13 |
51076 |
225,22 |
0,132 |
0,615 |
0,348 |
|
5 |
189 |
220 |
5,2417 |
1153,18 |
27,48 |
48400 |
225,82 |
31,769 |
33,833 |
2,576 |
|
6 |
166 |
232 |
5,1120 |
1185,98 |
26,13 |
53824 |
227,08 |
40,496 |
24,172 |
2,165 |
|
7 |
199 |
215 |
5,2933 |
1138,06 |
28,02 |
46225 |
225,31 |
113,132 |
106,362 |
4,577 |
|
8 |
180 |
220 |
5,1930 |
1142,45 |
26,97 |
48400 |
226,29 |
31,769 |
39,601 |
2,781 |
|
9 |
181 |
222 |
5,1985 |
1154,07 |
27,02 |
49284 |
226,24 |
13,223 |
17,968 |
1,874 |
|
10 |
186 |
231 |
5,2257 |
1207,15 |
27,31 |
53361 |
225,97 |
28,769 |
25,273 |
2,225 |
|
11 |
250 |
229 |
5,5215 |
1264,41 |
30,49 |
52441 |
223,09 |
11,314 |
34,980 |
2,651 |
|
Итого |
2129 |
2482 |
57,862 |
13054,74 |
304,48 |
560528 |
2482,00 |
498,545 |
487,867 |
27,530 |
|
Среднее |
193,5 |
225,6 |
5,260 |
1186,79 |
27,68 |
50957,091 |
225,636 |
45,322 |
44,352 |
2,503 |
= -9,76.
= 225,6 – (-9,76)×5,26 = 276,99.
Уравнение модели имеет вид:
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Рассчитаем средний коэффициент эластичности по формуле:
= -0,04%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Построение степенной модели парной регрессии.
Уравнение степенной модели имеет вид: .
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
.
Произведем линеаризацию модели путем замены и
. В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Y = ln(Y) |
XY |
X2 |
Y2 |
|
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
5,4806 |
28,3995 |
26,851 |
30,037 |
226,3 |
206,3 |
188,391 |
241,661 |
6,07 |
|
2 |
202 |
226 |
5,3083 |
5,4205 |
28,7737 |
28,178 |
29,382 |
225,1 |
0,132 |
0,835 |
71,479 |
0,406 |
|
3 |
197 |
221 |
5,2832 |
5,3982 |
28,5196 |
27,912 |
29,140 |
225,3 |
21,496 |
18,671 |
11,934 |
1,918 |
|
4 |
201 |
226 |
5,3033 |
5,4205 |
28,7467 |
28,125 |
29,382 |
225,1 |
0,132 |
0,753 |
55,570 |
0,385 |
|
5 |
189 |
220 |
5,2417 |
5,3936 |
28,2720 |
27,476 |
29,091 |
225,7 |
31,769 |
32,607 |
20,661 |
2,530 |
|
6 |
166 |
232 |
5,1120 |
5,4467 |
27,8437 |
26,132 |
29,667 |
226,9 |
40,496 |
25,675 |
758,752 |
2,233 |
|
7 |
199 |
215 |
5,2933 |
5,3706 |
28,4284 |
28,019 |
28,844 |
225,2 |
113,132 |
104,576 |
29,752 |
4,540 |
|
8 |
180 |
220 |
5,1930 |
5,3936 |
28,0089 |
26,967 |
29,091 |
226,2 |
31,769 |
38,059 |
183,479 |
2,728 |
|
9 |
181 |
222 |
5,1985 |
5,4027 |
28,0858 |
27,024 |
29,189 |
226,1 |
13,223 |
16,950 |
157,388 |
1,821 |
|
10 |
186 |
231 |
5,2257 |
5,4424 |
28,4407 |
27,308 |
29,620 |
225,9 |
28,769 |
26,413 |
56,934 |
2,275 |
|
11 |
250 |
229 |
5,5215 |
5,4337 |
30,0021 |
30,487 |
29,525 |
223,1 |
11,314 |
34,846 |
3187,116 |
2,646 |
|
Итого |
2129 |
2482 |
57,862 |
59,603 |
313,521 |
304,479 |
322,969 |
2480,927 |
498,545 |
487,777 |
4774,727 |
27,548 |
|
Среднее |
193,5 |
225,6 |
5,260 |
5,418 |
28,502 |
27,680 |
29,361 |
225,539 |
45,322 |
44,343 |
434,066 |
2,504 |
С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.
= -0,042.
= 5,418 – 0,959×5,26 = 5,637.
Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.
A = eA = e5,637 = 280,76
Получим уравнение степенной модели регрессии: .
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Для степенной модели средний коэффициент эластичности равен коэффициенту B.
= -0,042%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Сводная таблица вычислений
|
Параметры |
Модель |
|
|
Полулогарифмическая |
Степенная |
|
|
Уравнение связи |
|
|
|
Индекс корреляции |
0,1464 |
0,147 |
|
Коэффициент детерминации |
0,021 |
0,021 |
|
Средняя ошибка аппроксимации, % |
2,5 |
2,5 |
Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.
Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.
Прогнозное значение составит:
= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:
= 224,6 тыс. р.
Определим доверительный интервал прогноза для уровня значимости a = 0,05.
Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

Получаем: 
Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.
= 14,8.
Запишем доверительный интервал прогноза.
= 224,6 – 14,8 = 209,8 тыс. р.
= 224,6 + 14,8 = 239,4 тыс. р.
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.
Задание 3. Моделирование временных рядов
Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.
|
Номер квартала |
Товарооборот % к предыдущему периоду |
Номер квартала |
Товарооборот % к предыдущему периоду |
|
1 |
100 |
11 |
98,8 |
|
2 |
93,9 |
12 |
101,9 |
|
3 |
96,5 |
13 |
113,1 |
|
4 |
101,8 |
14 |
98,4 |
|
5 |
107,8 |
15 |
97,3 |
|
6 |
96,3 |
16 |
112,1 |
|
7 |
95,7 |
17 |
97,6 |
|
8 |
98,2 |
18 |
93,7 |
|
9 |
104 |
19 |
114,3 |
|
10 |
99 |
20 |
108,4 |
Задания:
1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.
2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.
3. Рассчитать трендовую компоненту временного ряда и построить его график
4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.
Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.
Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.
Построим мультипликативную модель временного ряда.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.
Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты S.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.
4) Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений T×E.
6) Расчет абсолютных и/или относительных ошибок.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).
Таблица 2.1
|
№ месяца, T |
Товарооборот, Yi |
Итого за четыре месяца |
Скользящая средняя за четыре месяца |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
100,0 |
– |
– |
– |
– |
|
2 |
93,9 |
392 |
98 |
– |
– |
|
3 |
96,5 |
400 |
100 |
99 |
0,975 |
|
4 |
101,8 |
402 |
100,5 |
100,25 |
1,015 |
|
5 |
107,8 |
402 |
100,5 |
100,5 |
1,073 |
|
6 |
96,3 |
398 |
99,5 |
100 |
0,963 |
|
7 |
95,7 |
394 |
98,5 |
99 |
0,967 |
|
8 |
98,2 |
397 |
99,25 |
98,875 |
0,993 |
|
9 |
104,0 |
400 |
100 |
99,625 |
1,044 |
|
10 |
99,0 |
404 |
101 |
100,5 |
0,985 |
|
11 |
98,8 |
413 |
103,25 |
102,125 |
0,967 |
|
12 |
101,9 |
412 |
103 |
103,125 |
0,988 |
|
13 |
113,1 |
411 |
102,75 |
102,875 |
1,099 |
|
14 |
98,4 |
309 |
77,25 |
90 |
1,093 |
|
15 |
97,3 |
196 |
49 |
63,125 |
1,541 |
|
16 |
112,1 |
303 |
75,75 |
62,375 |
1,797 |
|
17 |
97,6 |
418 |
104,5 |
90,125 |
1,083 |
|
18 |
93,7 |
414 |
103,5 |
104 |
0,901 |
|
19 |
114,3 |
– |
– |
– |
– |
|
20 |
108,4 |
– |
– |
– |
– |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Таблица 2.2
|
Показатели |
Год |
№ квартала, I |
|||
|
I |
II |
III |
IV |
||
|
1 |
– |
– |
0,975 |
1,015 |
|
|
2 |
1,073 |
0,963 |
0,967 |
0,993 |
|
|
3 |
1,044 |
0,985 |
0,967 |
0,988 |
|
|
4 |
1,099 |
1,093 |
1,541 |
1,797 |
|
|
5 |
1,083 |
0,901 |
– |
– |
|
|
Всего за I-й квартал |
4,299 |
3,942 |
4,45 |
4,793 |
|
|
Средняя оценка сезонной компоненты для I-го квартала, |
0,860 |
0,788 |
0,890 |
0,959 |
|
|
Скорректированная сезонная компонента, |
0,984 |
0,901 |
1,018 |
1,097 |
Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.
Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.
Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки
на корректирующий коэффициент K.
Проверяем условие: равенство 4 суммы значений сезонной компоненты:
0,984 + 0,901 + 1,018 + 1,097 = 4.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.
Таблица 2.3
|
T |
Yt |
St |
|
T |
T×S |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
100,0 |
0,984 |
101,6 |
100,02 |
98,42 |
1,016 |
|
2 |
93,9 |
0,901 |
104,2 |
100,19 |
90,27 |
1,040 |
|
3 |
96,5 |
1,018 |
94,8 |
100,36 |
102,17 |
0,945 |
|
4 |
101,8 |
1,097 |
92,8 |
100,53 |
110,28 |
0,923 |
|
5 |
107,8 |
0,984 |
109,6 |
100,7 |
99,09 |
1,088 |
|
6 |
96,3 |
0,901 |
106,9 |
100,87 |
90,88 |
1,060 |
|
7 |
95,7 |
1,018 |
94,0 |
101,04 |
102,86 |
0,930 |
|
8 |
98,2 |
1,097 |
89,5 |
101,21 |
111,03 |
0,884 |
|
9 |
104,0 |
0,984 |
105,7 |
101,38 |
99,76 |
1,043 |
|
10 |
99,0 |
0,901 |
109,9 |
101,55 |
91,50 |
1,082 |
|
11 |
98,8 |
1,018 |
97,1 |
101,72 |
103,55 |
0,954 |
|
12 |
101,9 |
1,097 |
92,9 |
101,89 |
111,77 |
0,912 |
|
13 |
113,1 |
0,984 |
114,9 |
102,06 |
100,43 |
1,126 |
|
14 |
98,4 |
0,901 |
109,2 |
102,23 |
92,11 |
1,068 |
|
15 |
97,3 |
1,018 |
95,6 |
102,4 |
104,24 |
0,933 |
|
16 |
112,1 |
1,097 |
102,2 |
102,57 |
112,52 |
0,996 |
|
17 |
97,6 |
0,984 |
99,2 |
102,74 |
101,10 |
0,965 |
|
18 |
93,7 |
0,901 |
104,0 |
102,91 |
92,72 |
1,011 |
|
19 |
114,3 |
1,018 |
112,3 |
103,08 |
104,94 |
1,089 |
|
20 |
108,4 |
1,097 |
98,8 |
103,25 |
113,27 |
0,957 |
|
Среднее |
101,4 |
1,0011 |
Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.
Таблица 2.4
|
T |
|
T2 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
101,6 |
1 |
101,6 |
2,5 |
1,58 |
2,0 |
|
|
2 |
104,2 |
4 |
208,4 |
13,2 |
3,87 |
56,3 |
|
|
3 |
94,8 |
9 |
284,4 |
32,1 |
5,88 |
24,0 |
|
|
4 |
92,8 |
16 |
371,2 |
71,9 |
8,33 |
0,2 |
|
|
5 |
109,6 |
25 |
548 |
75,9 |
8,08 |
41,0 |
|
|
6 |
106,9 |
36 |
641,4 |
29,4 |
5,63 |
26,0 |
|
|
7 |
94,0 |
49 |
658 |
51,3 |
7,48 |
32,5 |
|
|
8 |
89,5 |
64 |
716 |
164,6 |
13,07 |
10,2 |
|
|
9 |
105,7 |
81 |
951,3 |
18,0 |
4,08 |
6,8 |
|
|
10 |
109,9 |
100 |
1099 |
56,3 |
7,58 |
5,8 |
|
|
11 |
97,1 |
121 |
1068,1 |
22,6 |
4,81 |
6,8 |
|
|
12 |
92,9 |
144 |
1114,8 |
97,4 |
9,69 |
0,3 |
|
|
13 |
114,9 |
169 |
1493,7 |
160,5 |
11,20 |
136,9 |
|
|
14 |
109,2 |
196 |
1528,8 |
39,6 |
6,39 |
9,0 |
|
|
15 |
95,6 |
225 |
1434 |
48,2 |
7,13 |
16,8 |
|
|
20 |
102,2 |
400 |
2044 |
0,2 |
0,37 |
114,5 |
|
|
21 |
99,2 |
441 |
2083,2 |
12,3 |
3,59 |
14,4 |
|
|
22 |
104,0 |
484 |
2288 |
1,0 |
1,05 |
59,3 |
|
|
23 |
112,3 |
529 |
2582,9 |
87,6 |
8,19 |
166,4 |
|
|
24 |
98,8 |
576 |
2371,2 |
23,7 |
4,49 |
49,0 |
|
|
Сумма |
230 |
2035,2 |
3670 |
23588 |
1008,3 |
122,49 |
778,2 |
|
Среднее |
11,5 |
101,8 |
183,5 |
1179,4 |
50,4 |
6,12 |
38,91 |
Вычислим параметры уравнения тренда.

= 99,85.
В результате получим уравнение тренда:
T = 99,85 + 0,17×T.
Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).
Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
Расчет ошибки в мультипликативной модели произведем по формуле:
Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).
Рассчитаем сумму квадратов абсолютных ошибок .
Используя 5-й столбец таблицы 2.4, получим:

Рассчитаем среднюю относительную ошибку: .
Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.
| < Предыдущая | Следующая > |
|---|
УДК 004
Прогнозирование ошибок при помощи нейросетей как способ увеличения точности прогноза погоды
Литвинов Антон Андреевич – магистрант МИРЭА – Российского технологического университета
Аннотация: В статье рассматривается метод увеличения точности прогноза полей осадков посредством прогнозирования ошибок при помощи искусственных нейронных сетей.
Ключевые слова: наукастинг, поля осадков, нейронные сети, прогнозирование ошибок, многослойный персептрон.
Введение
В настоящее время, существуют различные методы прогнозирования полей осадков, применяемые по всему миру. В частности, во ФГБУ «Гидрометцентр России», одна из систем представляет собой комбинацию системы ансамблевого краткосрочного прогноза (STEPS) и прогноза мезомасштабной модели COSMO-RU [1].
Однако, данная система обладает ошибками прогнозирования, которые увеличиваются по мере увеличения срока прогноза [2].
Одним из способов увеличения точности прогноза, может стать прогнозирование отклонений, которые возникают в комплексных прогнозах. Одним из методов прогнозирования может быть применение различных моделей искусственных нейронных сетей.
Описание метода
Исходные данные представляют из себя матрицу числовых значений, которые в дальнейшем переводятся в графическое изображение при помощи специализированного ПО [1]. Для решения задачи можно обозначить две возможные архитектуры:
- сверточные нейронные сети [3];
- многослойные персептроны [4].
Первый тип нейросетей целесообразно применять в том случае, если мы используем данные большого размера в изначальном, матричном виде, так как сверточные нейронные сети предназначены для обработки данных, имеющих топологию в виде сетки
Второй тип подойдет в том случае, если мы используем данные небольшой размерности. Например, это может быть, когда размерность была сознательно уменьшена в целях облегчения данных для тестирования новых моделей и проверки гипотез. Для использования данного метода будет необходимо использовать данные в виде одномерного массива.
Задача нейронной сети – спрогнозировать значения ошибок на основе входных данных радарных наблюдений.
Рассмотрим применение второго типа нейронных сетей.
Работа с данными
В качестве исходных данных имеем следующее:
- Input – Объединенные поля радиолокационных наблюдений. 17424 файла;
- Output – 180-ти минутный прогноз на основе STEPS и COSMO-RU. 16943 файлов.
Регион: Центральный федеральный округ.
Период испытаний: июнь – сентябрь 2020 г. («теплый период года»),
В каждом файле содержится матрица 5х5 числовых значений интенсивности осадков, которые в дальнейшем могут быть преобразованы в графическую карту осадков (рисунок 1).
Рисунок 1. Содержание файлов.
Предварительная обработка файлов заключает в себя следующие этапы:
- Преобразование данных в виде матрицы в одномерные массивы длинной в 25 элементов
- Имена файлов преобразуются в формат (ДД.ММ.ГГГГ ЧЧ.ММ)
- Для файлов из папки output к дате прибавляется три часа
- Далее из папки input удаляются все файлы, имен которых нет в папке output (так как некоторые прогнозы отсутствуют).
- Предыдущий шаг повторяется для output
- После этого создаются файлы в папке error, значения которых равны input – output. Значения берутся по модулю.
Далее, данные из папок input и error соотносятся друг с другом по времени и все значения объединяются в одну структуру при помощи библиотеки Pandas языка Python
Данные разбиваются на обучающую и тестовую выборки в соотношении 80/20 процентов.
Создание тестовой модели
В качестве оптимизатора был использован Adamax
Количество эпох: 200
В качестве функции потерь и валидации использовалась среднеквадратичная ошибка (MSE)
В структуре сети применяется слой нормализации данных и Dropaut – слои [5].
Архитектура нейронной сети изображена на рисунке 2.
Рисунок 2. Архитектура нейронной сети.
График функции обучения и валидации изображен на рисунке 3.
Рисунок 3. Значения функций обучения и валидации.
Из графика на Рисунке 3 видно, что переобучение наступает примерно после 75 эпохи. Значение функции валидации, которого удалось достигнуть – 0,0123
Распределение ошибок в изначальных данных является следующим:
- минимальная ошибка – 0;
- максимальная ошибка – 5,7608;
- средняя величина ошибки – 0,065.
Заключение
В результате, был описан метод, который позволит увеличить точность прогноза либо путем автоматической коррекции прогнозируемых значений, либо путем ручного контроля за слишком большими возникающими ошибками.
Так же была приведена тестовая архитектура нейронной сети, которая способна решать данную задачу и приведены результаты ее работы.
Список литературы
- Наукастинг метеорологических параметров и опасных явлений: опыт реализации и перспективы развития // Гидрометеорологические исследования и прогнозы. 2019 № 4 (374). С. 92-111.
- Муравьев А.В., Киктев Д.Б., Смирнов А.В. Сравнительная верификация усовершенствованной системы радарного наукастинга осадков с учетом пропусков и при различных методах формирования выборок (по результатам испытаний в теплый период года май-сентябрь 2017 и 2020 гг.) // Результаты испытаний новых усовершенствованных технологий, моделей и методов гидрометеорологических прогнозов. 2022. С. 3-56.
- Сверточная нейронная сеть (CNN) // Электронный ресурс https://www.helenkapatsa.ru/sviortochnaia-nieironnaia-siet / Дата обращения: 25.05.2023
- Глава 4. Персептроны // Электронный ресурс https://neural.radkopeter.ru/chapter/персептроны/ Дата обращения: 25.05.2023
- Dropaut – метод решения проблемы переобучения в нейронных сетях // Электронный ресурс https://habr.com/ru/companies/wunderfund/articles/330814/ Дата обращения: 25.05.2023.
Интересная статья? Поделись ей с другими: