Лабораторная
работа №4
Нелинейные ИНС в задачах
прогнозирования.
Цель работы: Изучить обучение и
функционирование нелинейной ИНС при
решении задач прогнозирования.
1. Математические
основы алгоритма обратного распространения
ошибки
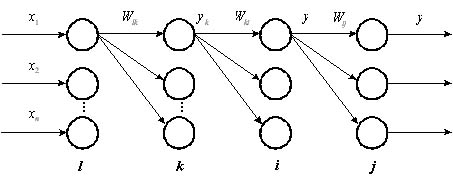
Рис. 1.
Четырехслойная нейронная сеть.
Алгоритм обратного распространения
ошибки был предложен в и является
эффективным средством для обучения
многослойных нейронных сетей.
Рассмотрим нейронную сеть, состоящую
из четырех слоев (рис 1). Обозначим слои
нейронных элементов от входа к выходу
соответственно через
.
Тогда выходное значение j-го нейрона
последнего слоя равняется:
(1)
,
(2)
где
—
взвешенная сумма j-го нейрона
выходного слоя;
—
выходное
значение i-го нейрона
предпоследнего слоя;
и
—
соответственно весовой коэффициент и
порог j-го нейрона выходного слоя.
Аналогичным образом выходное значение
i-го нейрона предпоследнего слоя
определяется, как:
(3)
.
(4)
Соответственно для k-го слоя:
(5)
.
(6)
Алгоритм обратного распространения
ошибки минимизирует среднеквадратичную
ошибку нейронной сети. Для этого с целью
настройки синаптических связей
используется метод градиентного спуска
в пространстве весовых коэффициентов
и порогов нейронной сети. Согласно
методу градиентного спуска изменение
весовых коэффициентов и порогов нейронной
сети происходит по следующему правилу:
,
(7)
,
(8)
где
—
среднеквадратичная ошибка нейронной
сети для одного образа.
Она определяется, как
,
(9)
где
—
эталонное выходное значение j-го
нейрона.
Ошибка j-го нейрона выходного слоя
равняется:
.
(10)
Теорема 2.2. Для любого скрытого слоя
ошибка
-го
нейронного элемента определяется
рекурсивным образом через ошибки
нейронов следующего слоя
:
(11)
где
—
количество нейронов следующего слоя
по отношению к слою
;
—
синаптическая связь между
-м
и
-м
нейроном различных слоев;
—
взвешенная сумма
-го
нейрона.
Теорема 2.3. Производные среднеквадратичной
ошибки по весовым коэффициентам и
порогам нейронных элементов для любых
двух слоев
и
многослойной
сети определяются следующим образом:
(12)
(13)
Следствие 2.1: Для минимизации
среднеквадратичной ошибки сети весовые
коэффициенты и пороги нейронных элементов
должны изменяться с течением времени
следующим образом:
(14)
(15)
где—
скорость обучения.
Данное следствие является очевидным.
Оно определяет правило обучения
многослойных нейронных сетей в общем
виде, которое называется обобщенным
дельта правилом .
2. Обобщенное дельта
правило для различных функций активации
нейронных элементов
Определим выражения (14) и (15) для различных
функций активации нейронных элементов.
2.1. Сигмоидная функция
Выходное значение j-го нейронного
элемента определяется следующим
образом:
,
(16)
.
(17)
Тогда
(18)
В результате обобщенное дельта правило
для сигмоидной функции активации можно
представить в следующем виде:
(19)
(20)
Ошибка для j-го нейрона выходного
слоя определяется, как
.
(21)
Для j-го нейронного элемента скрытого
слоя:
(22)
где m— количество нейронных
элементов следующего слоя по отношению
к слою i(рис. 2).
Рис.
2. Определение ошибки j-го
нейронного элемента.
2.2. Биполярная сигмоидная
функция
Выходное значение j-го нейрона
определяется, как
(23)
Тогда
(24)
Отсюда получаем следующие выражения
для обучения нейронной сети с биполярной
сигмоидной функцией активации:
(25)
(26)
Ошибка для j-го нейрона выходного и
скрытого слоев определяется соответственно,
как:
(27)
.
(28)
2.3. Гиперболический
тангенс
Для данной функции активации выходное
значение j-го нейрона определяется
следующим образом:
.
(29)
Определим производную функции
гиперболический тангенс:
.
(30)
Тогда правило обучения можно представить
в виде следующих выражений:
(31)
(32)
Ошибка для j-го нейрона выходного и
скрытого слоев соответственно равняется:
,
(33)
.
(34)
Используя полученные в данном разделе
выражения можно определить алгоритм
обратного распространения ошибки для
различных функций активации нейронных
элементов.
3. Алгоритм обратного
распространения ошибки
Как уже отмечалось, алгоритм обратного
распространения ошибки был предложен
в 1986 г. рядом авторов независимо друг
от друга. Он является эффективным
средством обучения нейронных сетей и
представляет собой следующую
последовательность шагов:
1. Задается шаг обучения
и
желаемая среднеквадратичная ошибка
нейронной сети
.
2. Случайным образом инициализируются
весовые коэффициенты и пороговые
значения нейронной сети.
3. Последовательно подаются образы из
обучающей выборки на вход нейронной
сети. При этом для каждого входного
образа выполняются следующие действия:
a) производится фаза прямого распространения
входного образа по нейронной сети. При
этом вычисляется выходная активность
всех нейронных элементов сети:
,
где индекс j характеризует нейроны
следующего слоя по отношению к слою i.
b) производится фаза обратного
распространения сигнала, в результате
которой определяется ошибка
нейронных
элементов для всех слоев сети. При этом
соответственно для выходного и скрытого
слоев:
,
.
В последнем выражении индекс i
характеризует нейронные элементы
следующего слоя по отношению к слою
.
c) для каждого слоя нейронной сети
происходит изменение весовых коэффициентов
и порогов нейронных элементов:
.
4. Вычисляется суммарная среднеквадратичная
ошибка нейронной сети:
где
—
размерность обучающей выборки.
5. Если
то
происходит переход к шагу 3 алгоритма.
В противном случае алгоритм обратного
распространения ошибки заканчивается.
Таким образом, данный алгоритм
функционирует до тех пор, пока суммарная
среднеквадратичная ошибка сети не
станет меньше заданной, т. е.
.
Задание.
1. Написать на любом ЯВУ программу
моделирования прогнозирующей нелинейной
ИНС. Для тестирования использовать
функцию
.
Варианты заданий приведены в следующей
таблице:
|
№ варианта |
a |
b |
с |
d |
Кол-во входов |
Кол-во НЭ в |
|
1 |
0.1 |
0.1 |
0.05 |
0.1 |
6 |
2 |
|
2 |
0.2 |
0.2 |
0.06 |
0.2 |
8 |
3 |
|
3 |
0.3 |
0.3 |
0.07 |
0.3 |
10 |
4 |
|
4 |
0.4 |
0.4 |
0.08 |
0.4 |
6 |
2 |
|
5 |
0.1 |
0.5 |
0.09 |
0.5 |
8 |
3 |
|
6 |
0.2 |
0.6 |
0.05 |
0.6 |
10 |
4 |
|
7 |
0.3 |
0.1 |
0.06 |
0.1 |
6 |
2 |
|
8 |
0.4 |
0.2 |
0.07 |
0.2 |
8 |
3 |
|
9 |
0.1 |
0.3 |
0.08 |
0.3 |
10 |
4 |
|
10 |
0.2 |
0.4 |
0.09 |
0.4 |
6 |
2 |
|
11 |
0.3 |
0.5 |
0.05 |
0.5 |
8 |
3 |
Для прогнозирования использовать
многослойную ИНС с одним скрытым слоем.
В качестве функций активации для скрытого
слоя использовать сигмоидную функцию,
для выходного — линейную.
2. Результаты представить в виде отчета
содержащего:
-
Титульный лист,
-
Цель работы,
-
Задание,
-
График прогнозируемой функции на
участке обучения, -
Результаты обучения: таблицу со
столбцами: эталонное значение, полученное
значение, отклонение; график изменения
ошибки в зависимости от итерации. -
Результаты прогнозирования: таблицу
со столбцами: эталонное значение,
полученное значение, отклонение. -
Выводы по лабораторной работе.
Результаты для пунктов 3 и 4 приводятся
для значения , при
котором достигается минимальная ошибка.
В выводах анализируются все полученные
результаты.
Контрольные вопросы.
-
ИНС какой архитектуры Вы использовали
в данной работе? Опишите принцип
построения этой ИНС. -
Как функционирует используема Вами
ИНС? -
Опишите (в общих чертах) алгоритм
обучения Вашей ИНС. -
Как формируется обучающая выборка для
решения задачи прогнозирования? -
Как выполняется многошаговое
прогнозирование временного ряда? -
Предложите критерий оценки качества
результатов прогноза.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
$begingroup$
I’m studying with a book and I’m at the Linear Regression part. The author is showing that we have to calculate the derivative of each part of the equation that leads to the loss.
But he’s using the MSE to calculate the loss and so, I tried to calculate the derivative of MSE:
the derivative of $ (y-p)^2 $ with respect to y (the target) is equal to $2(y-p)$ but in the book it is written $-1*(2(y-p))$ which is simplified as $-2(y-p)$. Why do I have different values ? Where is this $-1$ coming from?
asked Jun 10, 2020 at 10:30
$endgroup$
2
$begingroup$
Since you take derivative with respect to $p$, you first take the derivative of $(y−p)^2$ and then $−p$. Finally multiply them.
So first part is $2(y−p)$ and the second part is simply $−1$.
Therefore the derivative is $-1 times2times(y-p) =−2(y−p)$
answered Dec 17, 2020 at 10:39
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Постановка задачи регрессии
Задача регрессии — это один из основных типов моделей машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные в математике модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, датасеты для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.
Задача регрессии в машинном обучении — это задача предсказания какой-то численной характеристики объекта предметной области по определенному набору его параметров (атрибутов).
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Зачастую говорят именно о “моделировании” значения целевой переменной. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (independent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
Датасет, набор данных — совокупность информации в определенной структурированной форме, которая используется для построения модели машинного обучения для решения определенной задачи. Датасет обычно представляется в табличной форме. Датасет описывает некоторое множество объектов предметной области — точек данных.
С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.
Регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
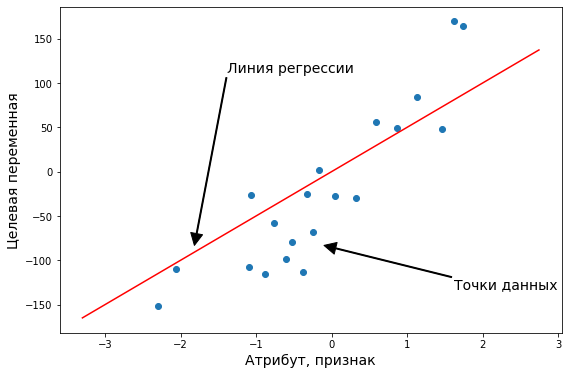
Парная линейная регрессия
Функция гипотезы
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Функция гипотезы — преобразование, которое принимает на вход набор значений признаков определенного объекта и выдает оценку значения целевой переменной данного объекта. Она лежит в основе модели машинного обучения.
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной — линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
[hat{y} = h_b (x) = b_0 + b_1 x]
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y. Допустим, мы имеем следующий обучающий набор данных:
| входная переменная x | выходная переменная y |
| 0 | 4 |
| 1 | 7 |
| 2 | 7 |
| 3 | 8 |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$, которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных — эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно (чтобы теоретические значения были как можно ближе к эмпирическим), или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения — это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия — одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
Функция ошибки
Как мы уже говорили, разные значения параметров дают разные конкретные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, или если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
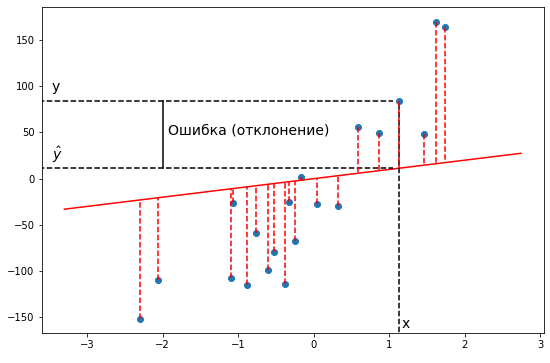
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений. Казалось бы, что это довольно произвольный выбор. Но он вполне обоснован и логичен. Давайте порассуждаем. Чтобы оценить, насколько хороша модель, мы должны оценить, насколько отклоняются эмпирические значения, то есть (y_i) от теоретических, предсказанных моделью, то есть (h_b(x_i)). Проще всего это отклонение выразить в виде разницы между этими двумя значениями. Но эта разница будет характеризовать отклонение только в одной точке данных, а в датасете может быть их произвольное количество. Поэтому имеет смысл взять сумму этих разностей для всех точек данных:
[J = sum_{i=1}^{m} (h_b(x_i) — y_i)]
Но с этим подходом есть одна проблема. Дело в том, что отклонения реальных значений от предсказанных могут быть как положительные, так и отрицательные. И если мы просто их все сложим, то положительные как бы скомпенсируют отрицательные. И в итоге даже очень плохие модели могут выглядеть, как имеющие маленькие ошибки. Фактически, для любого набора данных, если модель проходит через геометрический центр распределения, то такая ошибка будет равна нулю. То есть для достижения нулевой ошибки линии регрессии достаточно проходить через одну определенную точку. Таких моделей, очевидно, бесконечное количество, и все они будут иметь нулевую сумму отклонений. Конечно, так не пойдет и нужно придумать такую формулу, чтобы положительные и отрицательные отклонения не взаимоуничтожались, а складывались без учета знака.
Можно было бы взять отклонения по модулю. Но у такого подхода есть один большой недостаток: Функция абсолютного значения не везде дифференцируема. В одной точке у нее не существует производной. А чуть позже нам очень понадобится брать производную от функции ошибки. Поэтому модуль нам не подходит. Но в математике есть и другие функции, которые позволяют “избавиться” от знака числа. Например, возведение в квадрат. Его как раз и применяют в функции ошибки:
[J = sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
У этого подхода есть еще одно неочевидное достоинство. Квадратичная функция дополнительно сильно увеличивает размер больших чисел. То есть, если среди наших отклонений будет какое-то очень большое, то после возведения в квадрат оно станет еще непропорционально больше. Таким образом квадратичная функция ошибки как бы сильнее “штрафует” сильные отклонения предсказанных значений от реальных.
Но есть еще одна проблема. Дело в том, что в разных наборах данных может быть разное количество точек. Если мы просто будем считать сумму отклонений, то чем больше точек будем суммировать, тем больше итоговое отклонение будет только из-за количества слагаемых. Поэтому модели, обученные на маленьких объемах данных будут иметь преимущество. Это тоже неправильно и поэтому берут не сумму, а среднее из отклонений. Для этого достаточно лишь поделить эту сумму на количество точек данных:
[J = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
В итоге мы как раз получаем среднеквадратичное отклонение реальных значений от предсказанных. Эта функция дает хорошее представление о том, какая конкретная модель хорошо соответствует имеющимся данным, а какая — хуже или еще лучше.
[J(b_0, b_1)
= frac{1}{2m} sum_{i=1}^{m} (hat{y_i} — y_i)^2
= frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то — высокую ошибку, они подходят нам меньше.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
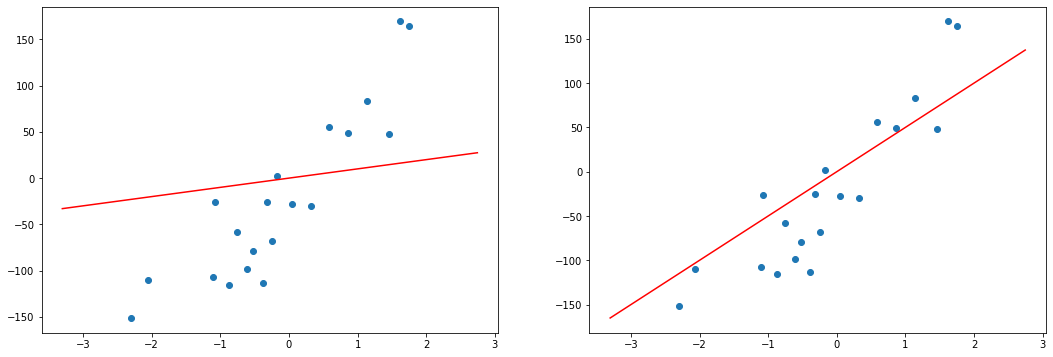
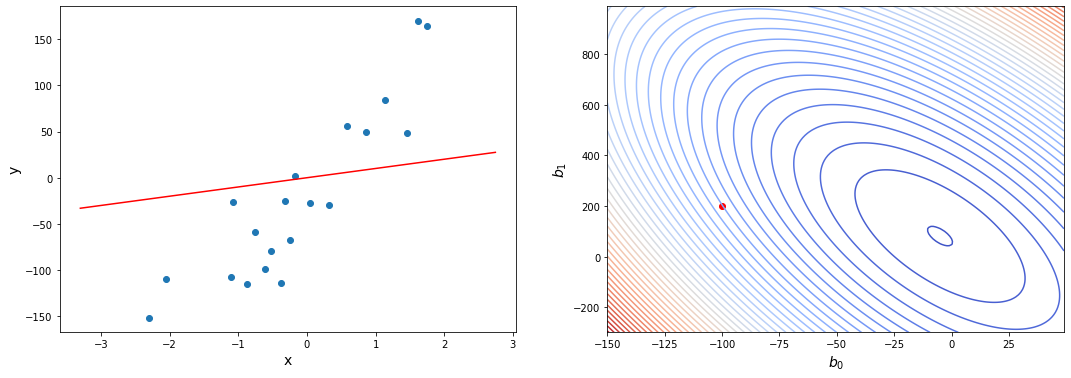
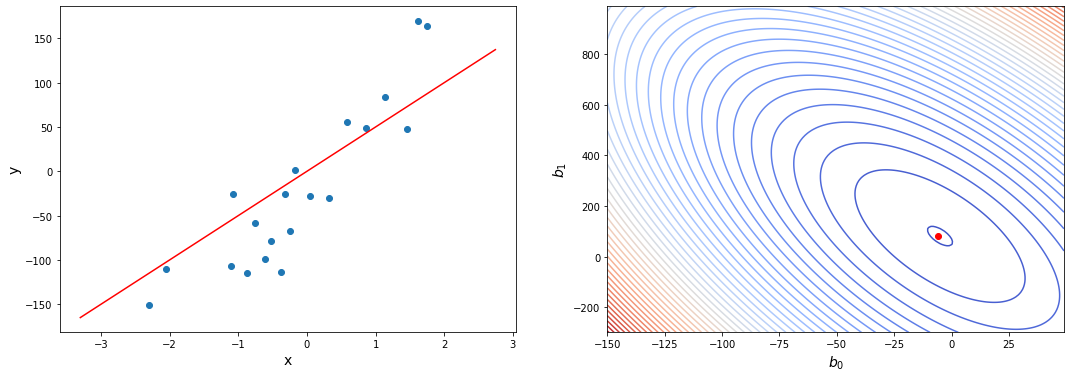
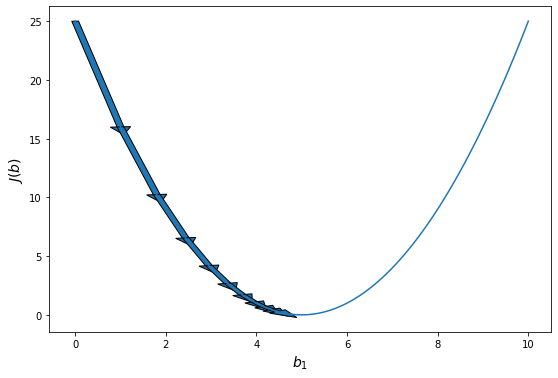
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели — прямую пропорциональность. Она выражается формулой:
[hat{y} = h_b (x) = b_1 x]
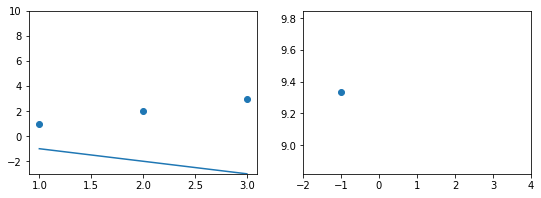
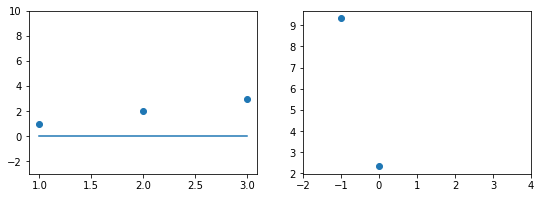
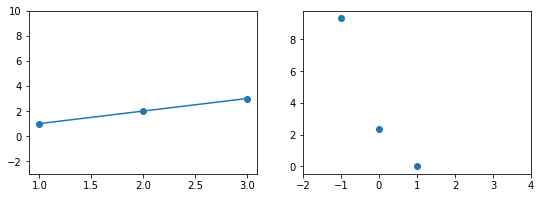
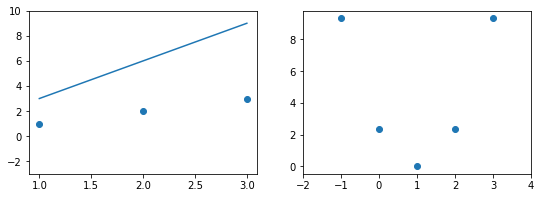
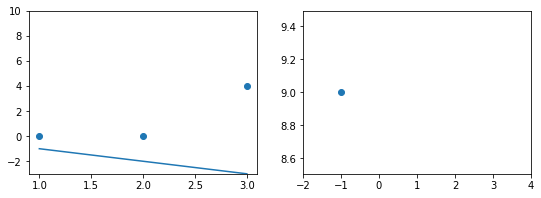
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
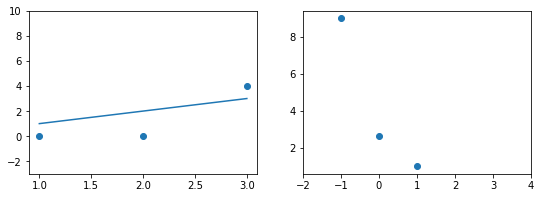
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
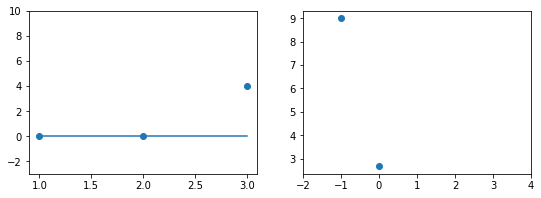
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
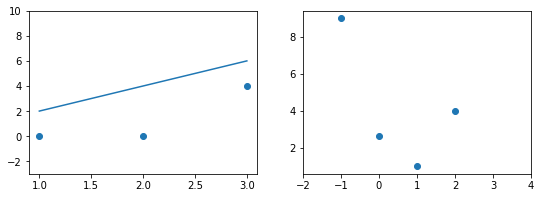
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
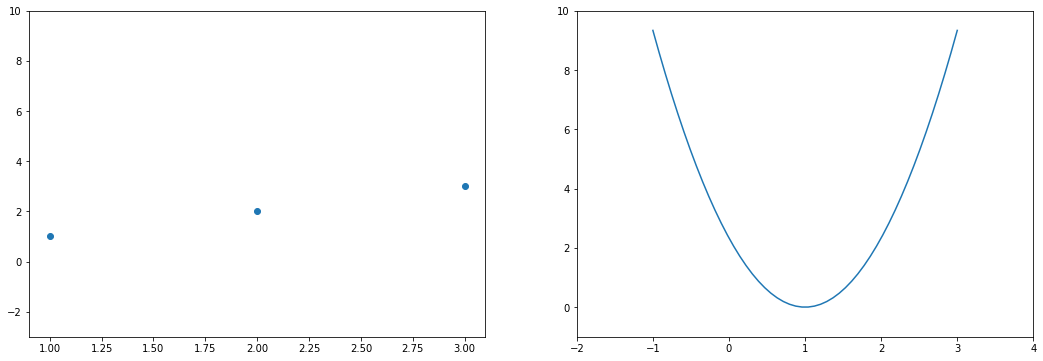
На этом примере мы видим еще одно преимущество возведения в квадрат — это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
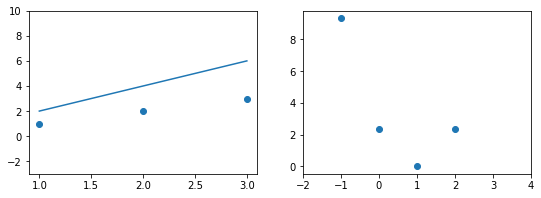
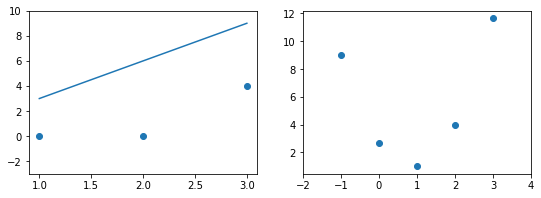
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
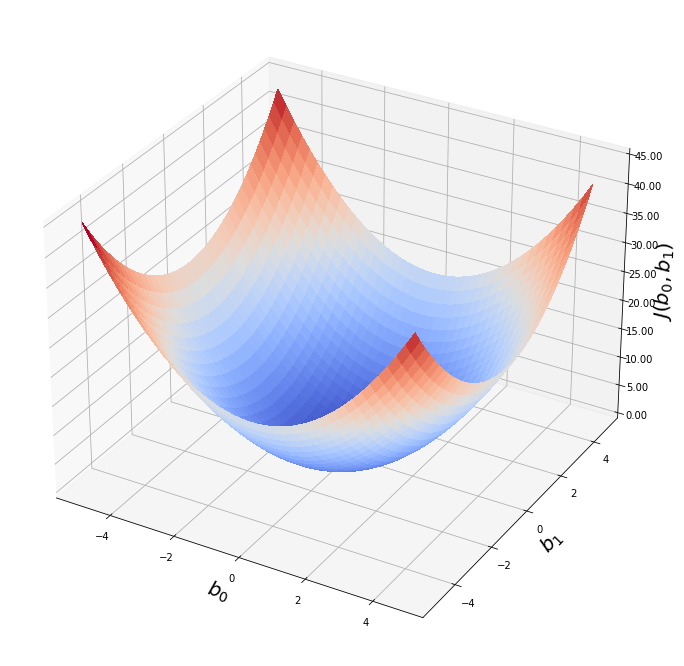
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска. Идея этого метода достаточно проста, но потребует для детального знакомства вспомнить основы математического анализа и дифференциального исчисления.
Несмотря на то, что мы настоятельно советуем разобраться в основах функционирования метода градиентного спуска шаг за шагом для более полного понимания того, как модели машинного обучения подбирают свои параметры, если читатель совсем не владеет матанализом, данные объяснения можно пропустить, они не являются критичными для повседневного понимания сути моделей машинного обучения.
Это происходит при помощи производной функции ошибки. Напомним, что производная функции показывает направление роста этой функции с ростом аргумента. Необходимое условие минимума функции — обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум — минимум, то наша задача очень проста — вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки. Так как эта функция зависит от двух аргументов — (b_0) и (b_1), то нам понадобится взять частные производные этой функции по всем ее аргументам. Для начала вспомним формулу самой функции ошибки:
[J(b_0, b_1) = frac{1}{2 m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Частная производная обозначается (frac{partial f}{partial x}) или (frac{partial}{partial x} f) и является обобщением обычной (полной) производной для функций нескольких аргументов. Частая производная показывает наклон функции в направлении изменения определенного аргумента, то есть как бы “в разрезе” этого аргумента. Градиент — это вектор частных производных функции по всем ее аргументам. Вектор градиента показывает направление максимального роста функции.
Что бы посчитать производную по какому-то из аргументов нам понадобятся обычные правила вычисления производной. Во-первых, общий множитель можно вынести из-под производной, Во-вторых, производная суммы равна сумме производных, поэтому знак суммы тоже можно вынести из-под производной. Поэтому получаем:
[frac{partial}{partial b_i} J =
frac{1}{2 m} sum_{i=1}^{m} frac{partial}{partial b_i} (h_b(x_i) — y^{(i)})^2]
Теперь самое сложное — производная сложной функции. По правилу она равна производной внешней функции, умноженной на производную внутренней. Внешняя функция — это квадратическая, ее производная равна удвоенному подквадратному выражению ((frac{d}{dt} t^2 = 2 t)). Подставляем (t = h_b(x_i) — y^{(i)}) и получаем:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i)]
Обратите внимание, что эта самая двойка прекрасно сократилась со знаменателем в постоянном множителе функции ошибки. Именно за этим он и был нужен.
Чтобы продолжить вычисление производной дальше, нужно представить функцию гипотезы как линейную функцию:
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (b_0 + b_1 x_i — y_i)^2]
И теперь мы уже не можем говорить о какой-то частной производной в общем, нужно отдельно посчитать производные по разным значениям параметров. Но тут все как раз очень просто, так как нам осталось посчитать производные линейной функции. Они равны просто коэффициентам при соответствующих аргументах. Для свободного коэффициента аргумент равен, очевидно, 1:
[frac{partial J}{partial b_0} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) =
frac{1}{m} sum (h_b(x_i) — y_i)]
А для коэффициента при $x_i$ производная равна самому значению $x_i$:
[frac{partial J}{partial b_1} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) cdot x_i =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i]
Теперь для нахождения минимального значения функции ошибки нам нужно только приравнять эти производные к нулю, то есть решить для $b_0, b_1$ следующую систему уравнений:
[frac{partial J}{partial b_0} =
frac{1}{m} sum (h_b(x_i) — y_i) = 0]
[frac{partial J}{partial b_1} =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i = 0]
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции — это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот — функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
[b_j := b_j — alpha frac{partial}{partial b_j} J(b_0, b_1)]
где j=0,1 — представляет собой индекс номера признака.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр — скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.
Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)} )- y^{(i)})]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x^{(i)}]
На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки.
На практике эту проблему решают методом семплирования — запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм — это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
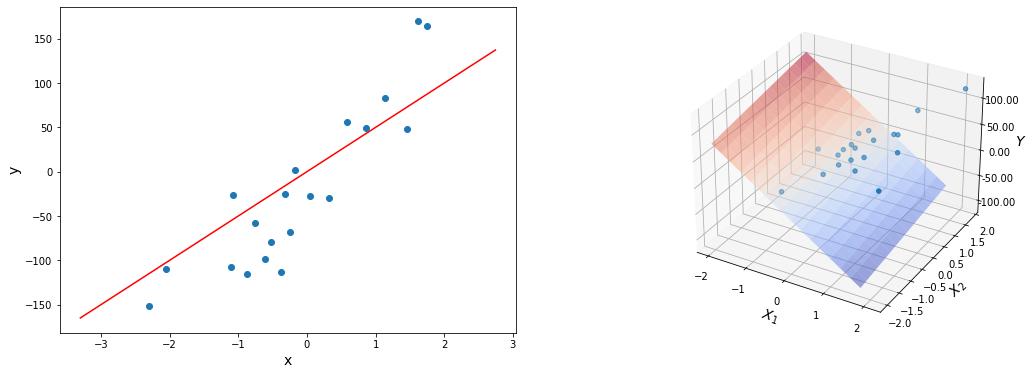
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ — значение j-го признака i-го обучающего примера;
$ x_j $ — вектор j-го признака всех обучающих примеров;
m — количество примеров в обучающей выборке;
n — количество признаков;
X — матрица признаков;
b — вектор параметров регрессии.
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
Вообще, уравнения для алгоритмов машинного обучения, зависящие от нескольких параметров часто записываются в матричной форме. Это лишь способ сделать запись уравнений более компактной, а не какое-то новое знание. Если вы не владеете линейной алгеброй, то можете просто безболезненно пропустить эти формы записи уравнений. Однако, лучше, конечно, разобраться. Особенно это пригодится при изучении нейронных сетей.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
[h_b(x) = b_0 + b_1 x_1 + b_2 x_2 + … + b_n x_n]
Или в матричной форме:
[h_b(x) = X cdot vec{b}]
Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
[J(b) = frac{1}{2m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)})^2]
Или в матричной форме:
[J(b) = frac{1}{2m} (X b — vec{y})^T (X b — vec{y})]
Обратите внимание, что мы специально не раскрываем выражение (h_b(x^{(i)})). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x^{(i)})]
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_0^{(i)}]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_1^{(i)}]
[b_2 := b_2 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_2^{(i)}]
[…]
Или в матричной форме:
[b := b — frac{alpha}{m} X^T (X b — vec{y})]
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных — приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ — в долях единицы.
В таком случае форма функции ошибки будет очень вытянутой. Это не проблема для математической формализации градиентного спуска — при достаточно малых $alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых — минимаксная нормализация и стандартизация или z-оценки.
Минимаксная нормализация — это изменение входных данных по следующей формуле:
[x’ = frac{x — x_{min}}{x_{max} — x_{min}}]
После преобразования все значения будут лежать в диапазоне $x in [0; 1]$.
Z-оценки или стандартизация производится по формуле:
[x’ = frac{x — M[x]}{sigma_x}]
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия — 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной — минимальное и максимальное значение признака. У стандартизации — выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Про использование обучающей и тестовой выборок мы будем говорить значительно позже, при рассмотрении диагностики моделей машинного обучения.
Целевая переменная не нормируется. Это просто не нужно, а если ее нормировать, это сильно усложнит все математические расчеты и преобразования.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации — минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Полиномиальная регрессия
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае — линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы
$ hat{y} = h_b (x) = b_0 + b_1 x $,
то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2]
или кубическую функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2 + b_3 x^3]
В кубической функции мы по сути ввели два новых признака:
$ x_2 = x^2, x_3 = x^3 $.
Точно таким же образом, мы можем создать, например, такую функцию:
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 sqrt{x}]
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек — ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
[h_b (x) = b_0 + b_1 x_1 + b_2 x_2]
Квадратичная модель (полином степени 2):
[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2]
Кубическая модель (полином степени 3):
[hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]
При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак — это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Практическое построение регрессии
В данной главе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данной главы предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного — объектно-ориентированного программирования, немного — использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами — датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов — x, а в другом — значения целевой переменной — y.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
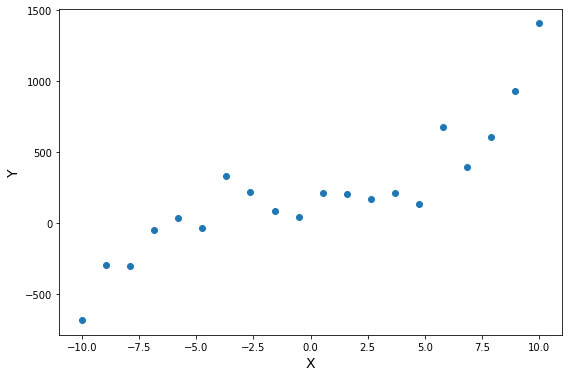
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов — DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
Это код генерирует вот такой вот график:
Как работает метод машинного обучения “на пальцах”?
Для того, чтобы более полно понимать, как работает метод градиентного спуска для линейной регрессии, давайте реализуем его самостоятельно, не обращаясь к библиотечным методам. На этом примере мы проследим все шаги обучения модели.
Мы будем использовать объектно-ориентированный подход, так как именно он используется в современных библиотеках. Начнем строить класс, который будет реализовывать метод парной линейной регрессии:
1
2
3
4
5
class hypothesis(object):
"""Модель парной линейной регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
Здесь мы определили конструктор класса, который запоминает в полях экземпляра параметры регрессии. Начальные значения этих параметров не очень важны, так как градиентный спуск сойдется из любой точки. В данном случае мы выбрали нулевые, но можно задать любые другие начальные значения.
Реализуем метод, который принимает значение входной переменной и возвращает теоретическое значение выходной — это прямое действие нашей регрессии — метод предсказания результата по факторам (в случае парной регрессии — по одному фактору):
1
2
def predict(self, x):
return self.b0 + self.b1 * x
Название выбрано не случайно, именно так этот метод называется и работает в большинстве библиотечных классов.
Теперь зададим функцию ошибки:
1
2
def error(self, X, Y):
return sum((self.predict(X) - Y)**2) / (2 * len(X))
В данном случае мы используем простую функцию ошибки — среднеквадратическое отклонение (mean squared error, MSE). Можно использовать и другие функции ошибки. Именно вид функции ошибки будет определять то, какой вид регрессии мы реализуем. Существует много разных вариаций простого алгоритма регрессии. О большинстве распространенных методах регрессии можно почитать в официальной документации sklearn.
Теперь реализуем метод градиентного спуска. Он должен принимать массив X и массив Y и обновлять параметры регрессии в соответствии в формулами градиентного спуска:
1
2
3
4
5
6
def BGD(self, X, Y):
alpha = 0.5
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
О выборе конкретного значения alpha мы говорить пока не будем,на практике его довольно просто подбирают, мы же возьмем нейтральное значение.
Давайте создадим объект регрессии и проверим начальное значение ошибки. В примерах приведены значения на модельном наборе данных, но этот метод можно использовать на любых данных, которые подходят по формату — x и y должны быть одномерными массивами чисел.
1
2
3
4
5
6
7
8
hyp = hypothesis()
print(hyp.predict(0))
print(hyp.predict(100))
J = hyp.error(x, y)
print("initial error:", J)
0
0
initial error: 36271.58344889084
Как мы видим, для начала оба параметра регрессии равны нулю. Конечно, такая модель не дает надежных предсказаний, но в этом и состоит суть метода градиентного спуска: начиная с любого решения мы постепенно его улучшаем и приходим к оптимальному решению.
Теперь все готово к запуску градиентного спуска.
1
2
3
4
5
6
7
8
9
10
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 6734.135540194945
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Как мы видим, численное значение ошибки значительно уменьшилось. Да и линия на графике существенно приблизилась к точкам. Конечно, наша модель еще далека от совершенства. Мы прошли всего лишь одну итерацию градиентного спуска. Модифицируем метод так, чтобы он запускался в цикле пока ошибка не перестанет меняться существенно:
1
2
3
4
5
6
7
8
9
10
11
12
13
def BGD(self, X, Y, alpha=0.5, accuracy=0.01, max_steps=5000):
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y)
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
Заодно мы проверяем, насколько изменилось значение функции ошибки. Если оно изменилось на величину, меньшую, чем заранее заданная точность, мы завершаем спуск. Таким образом, мы реализовали два стоп-механизма — по количеству итераций и по стабилизации ошибки. Вы можете выбрать любой или использовать оба в связке.
Запустим наш градиентный спуск:
1
2
3
4
5
hyp = hypothesis()
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 298.76881676471504
Как мы видим, теперь ошибка снизилась гораздо больше. Однако, она все еще не достигла нуля. Заметим, что нулевая ошибка не всегда возможна в принципе из-за того, что точки данных не всегда будут располагаться на одной линии. Нужно стремиться не к нулевой, а к минимально возможной ошибке.
Посмотрим, как теперь наша регрессия выглядит на графике:
1
2
3
4
5
6
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Уже значительно лучше. Линия регрессии довольно похожа на оптимальную. Так ли это на самом деле, глядя на график, сказать сложно, для этого нужно проанализировать, как ошибка регрессии менялась со временем:
Как оценить качество регрессионной модели?
В простых случаях качество модели можно оценить визуально на графике. Но если у вас многомерная задача, это уже не представляется возможным. Кроме того, если ошибка и сама модель меняется незначительно, то очень сложно определить, стало хуже или лучше. Поэтому для диагностики моделей машинного обучения используют кривые.
Самая простая кривая обучения — зависимость ошибки от времени (итерации градиентного спуска). Для того, чтобы построить эту кривую, нам нужно немного модифицировать наш метод обучения так, чтобы он возвращал нужную нам информацию:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def BGD(self, X, Y, alpha=0.1, accuracy=0.01, max_steps=1000):
steps, errors = [], []
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y) - 1
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
step += 1
steps.append(step)
errors.append(new_err)
return steps, errors
Мы просто запоминаем в массивах на номер шаа и ошибку на каждом шаге. Получив эти данные можно легко построить их на графике:
1
2
3
4
5
6
hyp = hypothesis()
steps, errors = hyp.BGD(x, y)
plt.figure()
plt.plot(steps, errors, 'g')
plt.show()
На этом графике наглядно видно, что в начале обучения ошибка падала быстро, но в ходе градиентного спуска она вышла на плато. Учитывая, что мы используем гладкую функцию ошибки второго порядка, это свидетельствует о том, что мы достигли локального оптимума и дальнейшее повторение алгоритма не принесет улучшения модели.
Если бы мы наблюдали на графике обучения ситуацию, когда по достижении конца обучения ошибка все еще заметно снижалась, это значит, что мы рано прекратили обучение, и нужно продолжить его еще на какое-то количество итераций.
При анализе графиков с библиотечными моделями не получится таких гладких графиков, они больше напоминают случайные колебания. Это из-за того, что в готовых реализациях используется очень оптимизированный вариант метода градиентного спуска. А он может работать с произвольными флуктуациями. В любом случае, нас интересует общий вид этой кривой.
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр — скорость обучения — который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ alpha $ близкое к 1, скажем, $ alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача — на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных — двумерный, а массивы целевых переменных — одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
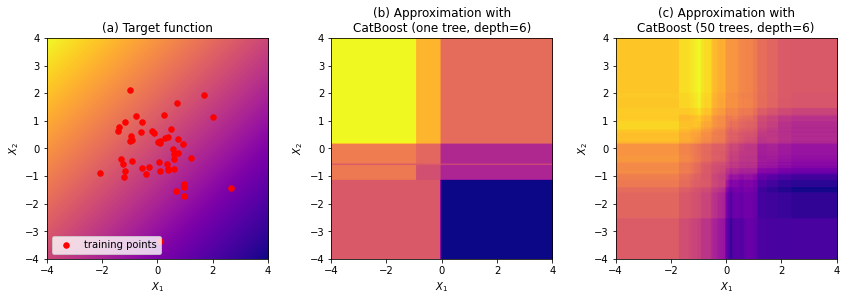
Сейчас существенная часть машинного обучения основана на решающих деревьях и их ансамблях, таких как CatBoost и XGBoost, но при этом не все имеют представление о том, как устроены эти алгоритмы «изнутри».
Данный обзор охватывает сразу несколько тем. Мы начнем с устройства решающего дерева и градиентного бустинга, затем подробно поговорим об XGBoost и CatBoost. Среди основных особенностей алгоритма CatBoost:
-
Упорядоченное target-кодирование категориальных признаков с большим числом значений (параметр
one_hot_max_size) -
Использование решающих таблиц (параметр по умолчанию
grow_policy='SymmetricTree') -
Разделение ветвей не только по отдельным признакам, но и по их комбинациям (параметр
max_ctr_complexity) -
Упорядоченный бустинг (параметр
boosting_type='Ordered') для датасетов небольшого размера -
Возможность работы с текстовыми признаками (параметр
text_featuresметодаfit) с помощью bag-of-words -
Возможность обучения на GPU (параметр
task_type='GPU'в методеfit), хотя это может сказаться на качестве
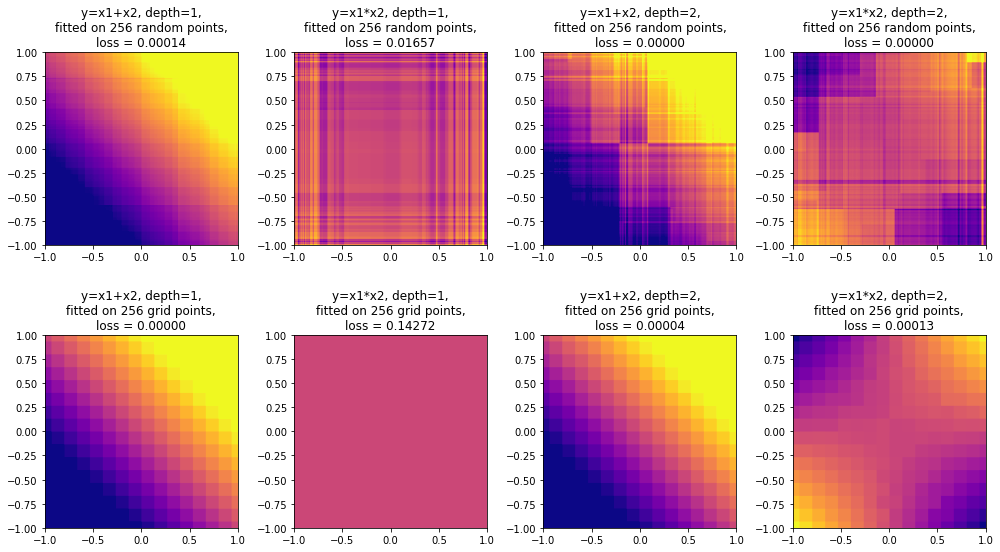
В конце обзора поговорим о методах интерпретации решающих деревьев (MDI, SHAP) и о выразительной способности решающих деревьев. Удивительно, но ансамбли деревьев ограниченной глубины, в том числе CatBoost, не являются универсальными аппроксиматорами: в данном обзоре приведено собственное исследование этого вопроса с доказательством (и экспериментальным подтверждением) того, что ансамбль деревьев глубины N не способен сколь угодно точно аппроксимировать функцию . Поговорим также о выводах, которые можно из этого сделать.
Содержание
Структура решающих деревьев
Обучение решающих деревьев
Построение решающего дерева
Оптимальное разделение в задаче регрессии
Оптимальное разделение в задаче классификации
Критерий остановки и обрезка дерева
Работа с категориальными признаками
Другие особенности решающих деревьев
Ансамблирование решающих деревьев
Бэггинг
Бустинг
Ранний вариант бустинга: AdaBoost
Градиентный бустинг
Алгоритм градиентного бустинга
Регуляризация градиентного бустинга
Особенности градиентного бустинга
Связь с градиентным спуском
XGBoost
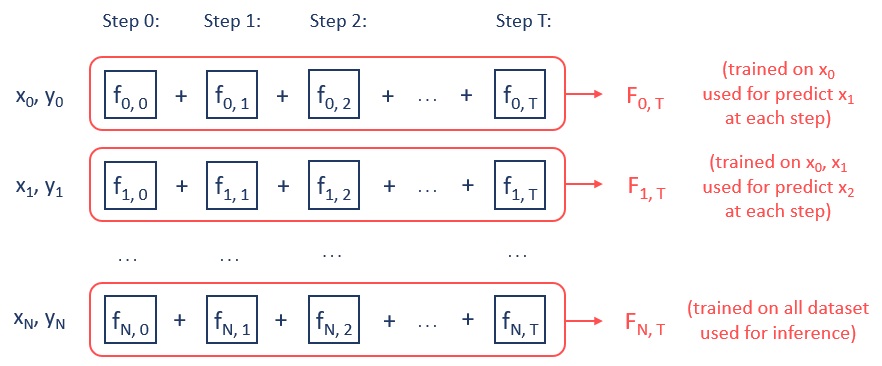
CatBoost: несмещённый упорядоченный бустинг
Упорядоченное target-кодирование
Использование решающих таблиц
Проблема смещённости бустинга
Упорядоченный бустинг
Алгоритм CatBoost
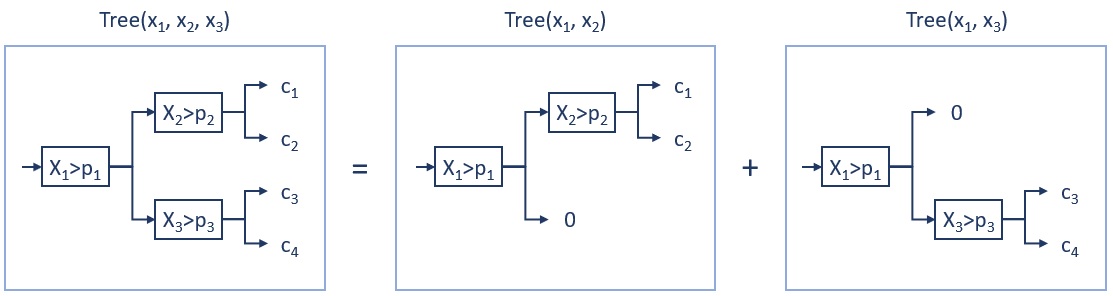
Комбинирование признаков в CatBoost
Обзор некоторых параметров CatBoost
Интерпретация ансамблей решающих деревьев
Оценка важности признаков в решающих деревьях
SHAP values
Выразительная способность ансамблей решающих деревьев
Понятие выразительной способности
Выразительная способность решающего дерева
Выразительная способность ансамбля решающих деревьев
Выводы и эксперименты
Список источников
Структура решающих деревьев
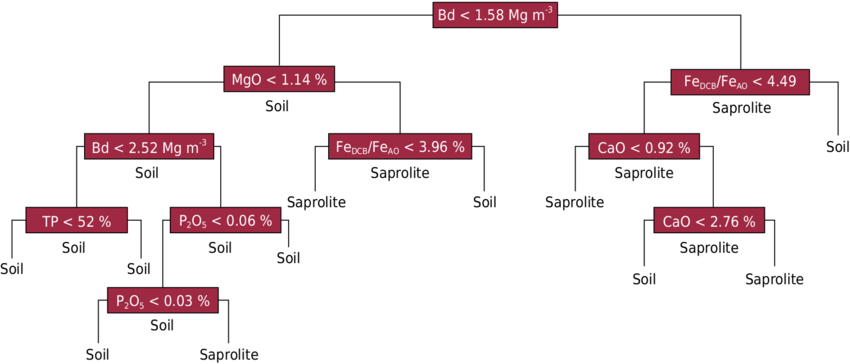
Решающие деревья применяются в основном в задачах классификации и регрессии в машинном обучении на табличных данных (хотя могут быть и другие применения). В общем виде решающее дерево — это иерархическая схема принятия решений в виде графа. В промежуточных вершинах (звеньях) проверяются некие условия, и в зависимости от результатов выбирается путь в графе, который приводит к одной из конечных вершин (листьев).
В общем случае звенья и листья могут быть сложными функциями. Однако в большинстве практических реализаций каждый лист соответстствует константному ответу, а в каждом звене проверяется значение лишь одного признака (рис. 1). Если в звене проверяется количественный признак, то все значения больше некоего порога отправляются по одному пути, меньше порога — по другому пути. Если это категориальный признак, то одна или несколько категорий отправляется по одному пути, остальные категории по другому пути (категориальные признаки иногда преобразуются в количественные, более подробно рассмотрим позже).
Модели такого вида появились больше полувека назад (Morgan and Sonquist, 1963), и с тех пор практически не изменились. В наши дни одни из наиболее эффективных моделей машинного обучения для работы с табличными данными (scikit-learn, XGBoost, LightGBM, CatBoost) основаны на суммировании предсказаний множества решающих деревьев.
С первого взгляда кажется, что такой подход хорошо подходит для одних задач, но очень плохо подходит для других задач.
Позитивный пример. Многие способы принятия решений выглядят как блок-схема. Например при постановке диагноза врач сначала может измерить температуру. Если температура выше определенного порога, то может заподозрить простуду и посмотреть горло, послушать легкие и так далее. Листьями решающего дерева окажутся конкретные диагнозы. В целом, решающее дерево хорошо следует идее о том, что на некоторые признаки нужно обращать внимание только при условии определенных значений других признаков.
Негативный пример. Попробуем аппроксимировать функцию (рис. 2a) решающим деревом (рис. 2b). Решающее дерево разбивает все пространство признаков на прямоугольные области, в каждой из которых ответом является константа. В данной задаче такой подход явно неоптимален. Во-первых, если решающее дерево представить в виде функции
, то эта функция будет разрывной (кусочно-постоянной), тогда как целевая функция
непрерывна. Во-вторых, на ответ влияет разность
, а в каждом звене дерева проверяется либо
, либо
, что тоже неоптимально. Для достижения хорошей точности потребуется большое и сложное дерево, хотя сама задача определения
очень проста. И наконец, поскольку решающее дерево обучается на данных (о способе обучения мы поговорим далее), то в тех областях, где мало данных или они вовсе отсутствуют, функция
будет продолжена неправильно (проблема экстраполяции).
Проблему разрывности функции и негладкости границ между листьями можно смягчить, если обучать не одно решающее дерево, а много деревьев, и усреднять их ответы (рис. 2c). При этом деревья либо должны обучаться на разных подвыборках данных, либо сам процесс обучения должен содержать элемент случайности, чтобы деревья получились неодинаковыми. Поэтому на практике обучают так называемый «случайный лес» из множества деревьев с помощью алгоритмов бэггинга или бустинга, которые мы расмотрим позже. Проблема экстраполяции при этом все же остается — например, случайный лес не может предсказывать значения, большие или меньшие всех тех, что встречались при обучении.
На нашей модельной задаче (рис. 2) решающие деревья дают не впечатляющий результат, тогда как, например, нейронная сеть в этой же задаче обучается почти точно аппроксимировать целевую функцию. Но на реальных задачах, наоборот, ансамбли решающих деревьев сейчас являются одними из самых эффективных моделей.
While deep learning models are more appropriate in fields like image recognition, speech recognition, and natural language processing, tree-based models consistently outperform standard deep models on tabular-style datasets where features are individually meaningful and do not have strong multi-scale temporal or spatial structures. (Lundberg et al., 2019)
Обучение решающих деревьев
Допустим мы имеем обучающую выборку из пар и хотим построить по нему решающее дерево. Можно без труда построить сколько угодно деревьев, дающих на обучающей выборке 100%-ю точность (если в ней нет примеров с одинаковыми
, но разными
). Для этого достаточно в каждой вершине выбирать для разделения любой признак и любой порог, и тогда рано или поздно все примеры попадут в разные листья. Но нам важна не точность на обучающей выборке, а степень обобщения — то есть точность на всем порождающем распределении, из которого взята обучающая выборка.
Можно воспользоваться принципом бритвы Оккама, который говорит, что простые гипотезы предпочтительнее сложных, и попробовать построить как можно более простое дерево. Однако задача нахождения наиболее простого решающего дерева для данного датасета (по суммрному количеству листьев или по средней длине пути в графе) является NP-полной (Hancock et al., 1996; Hyafil and Rivest, 1976), то есть (если ) экспоненциально сложной.
Вообще многие задачи являются экспоненциально сложными, если искать лучшее решение из всех возможных, то есть выполнять исчерпывающий поиск (exhaustive search). Но это не мешает находить хорошие приближенные решения, выполняя либо жадный поиск (greedy search), либо лучевой поиск (beam search). Жадный поиск означает, что на каждом шаге мы ищем локально оптимальное решение, то есть решение, приводящее к наибольшему «сиюминутному» выигрышу. Например, знакомясь с девушкой, которая вам нравится, вы не можете перебрать все возможные варианты развития диалога и заранее выбрать наилучший (т. е. выполнить исчерпывающий поиск), но можете после каждой фразы искать оптимальное продолжение диалога (жадный поиск).
Примечание: пока работаем с количественными признаками, работу с категориальными признаками рассмотрим позднее.
Построение решающего дерева
Применительно к решающим деревьям жадный поиск означает, что мы строим дерево пошагово, на каждом шаге заменяя один из листьев на разделяющее правило, ведущее к двум листьям. На каждом шаге мы должны выбрать:
-
Лист
, который заменяем решающим правилом
-
Способ разделения (признак и порог)
-
Значения
и
на двух новых листьях
Этот выбор мы должны сделать так, чтобы функция потерь всего дерева на обучающей выборке уменьшилась как можно сильнее. Для этого достаточно рассмотреть функцию потерь на примерах из обучающей выборки, которые относятся к листу .
Шаг алгоритма выглядит следующим образом: мы перебираем все возможные листья, признаки и пороги (если обучающая выборка имеет размер , то каждый признак принимает не более
различных значений, поэтому для каждого признака имеет смысл перебирать не более
порогов). Для каждого листа, признака и порога определяем значения
и
на листьях и считаем функцию потерь получившегося дерева. В итоге мы выбираем тот лист, признак и порог, для которых значение функции потерь наименьшее, и дополняем дерево новым разделяющим правилом.
Осталось ответить на вопрос: как именно определяются значения и
на двух новых листьях?
Пусть после добавления разделяющего правила в один лист попало примеров со значениями целевого признака
, в другой лист попало
примеров со значениями целевого признака
. Запишем суммарную функцию потерь после разделения, и минимизируем ее по
и
:
Первое слагаемое зависит только от , второе только от
, поэтому их можно минимизировать независимо по
и
, если известны примеры, попавшие в один и в другой лист.
Оптимальное разделение в задаче регрессии
В качестве функции потерь выберем среднеквадратичную ошибку. Исходя из формулы , на первом листе нужно выбрать такое значение
на первом листе, что:
Поскольку — константы, то задача означает поиск минимума функции от одной переменной. Взяв производную и приравняв ее к нулю мы найдем, что
— среднее арифметическое значений
. Аналогично,
— среднее арифметическое значений
.
Если бы мы минимизировали не среднеквадратичную ошибку (MSE), а среднюю абсолютную ошибку (MAE), тогда оптимальным значением была бы медиана значений
.
Оптимальное разделение в задаче классификации
Мы можем пойти стандартным путем: пусть каждый лист выдает вероятности классов, а в качестве функции потерь используем категориальную перекрестную энтропию (logloss). Пусть количество классов равно . Введем следующие обозначения:
-
— доля объектов
-го класса в первом листе
-
— доля объектов
-го класса во втором листе
-
— предсказываемая вероятность
-го класса в первом листе
-
— предсказываемая вероятность
-го класса во втором листе
Минимизируем суммарную ошибку на первом листе. Количество примеров в первом листе, для которых верным ответом является класс , равно
. Суммируем ошибку по всем классам и будем искать минимум по
:
Из данной формулы можно исключить , и тогда задача нахождения оптимального распределения
сводится к минимизации перекрестной энтропии между распределениями
и
. Это эквивалентно минимизации расхождения Кульбака-Лейблера между
и
и достигается при
для всех
. Полученный результат интуитивно понятен: если, например, в листе 10% примеров класса 0 и 90% примеров класса 1, то предсказывая ответ для неизвестного примера оптимальным вариантом будет назначить классам вероятности 10% и 90%.
Таким образом, мы нашли, что оптимальное равно
. Суммарная функция потерь на обоих листьях будет равна:
Здесь — энтропия распределения
(ее более корректно записывать как
). Иными словами, нам нужно искать такой признак и порог, чтобы минимизировать взвешенную сумму энтропий распределений классов в обоих листьях. Энтропию можно интерпретировать как степень неопределенности, или «загрязненности» (impurity) распределения, и энтропия достигает минимума в том случае, если распределение вероятностей назначает вероятность 1 одному из классов.
Минимизация взвешенной суммы энтропий называется энтропийным критерием разделения (рис. 3). Интересно, что если мы будем минимизировать не кроссэнтропию, а среднюю абсолютную ошибку (MAE) между предсказанным распределением и истинным (эмпирическим) распределением, которое назначает вероятность 1 верному классу, то придем к критерию Джини:
На практике чаще используется энтропийный критерий, потому что он соответствует перекрестной энтропии, которая чаще других применяется в задачах классификации.
Критерий остановки и обрезка дерева
Мы рассмотрели шаг роста дерева, но остается еще один вопрос: до какой степени нужно растить дерево? На рис. 3 показаны шаги роста дерева для классификации по энтропийному критерию. На первых шагах дерево находит явные закономерности в распределении классов, но затем начинает переобучаться на случайном шуме. Говоря в терминах так называемой дилеммы смещения-дисперсии, дерево неограниченной глубины имеет высокую дисперсию, то есть получаемый результат сильно зависит от случайных изменений в обучающей выборке (например, мы удалили часть примеров или добавили новые).
Если мы соберем ансамбль из деревьев, то проблема переобучения ослабнет. Однако чем больше дерево, тем больше вычислительных ресурсов требуется для его обучения, поэтому размер дерева в ансамбле все же имеет смысл ограничивать.
На практике чаще ограничивают не суммарное количество листьев, а максимальную глубину дерева, то есть максимальную длину пути от корня к листу. Можно также воспользоваться следующим критерием: прекращать рост дерева, если после добавления нового разделяющего правила функция потерь упала на величину, меньшую некоего порога. Однако такой подход тоже имеет свои проблемы.
На рис. 4а показана ситуация, когда добавление первого оптимального разделяющего правила не приведет к значимому снижению ошибки классификации, тогда как следующие два разделяющих правила ведут к радикальному снижению функции потерь. Более того, оптимальное значение порога для первого разделяющего правила сильно зависит от случайных факторов и может быть выбрано не равным нулю. На этом примере мы видим ситуацию «отложенного выигрыша», когда жадный алгоритм построения дерева может сработать не лучшим образом (см. также Biau et al., 2008, раздел 6).
Обрезкой решающего дерева (pruning) называется процесс удаления из него отдельных ветвей, которые не приводят к существенному падению функции потерь. Имеел ли смысл сначала строить, а затем удалять ветви? Как мы увидели на рис. 4, при построении ветви мы не можем точно сказать, насколько сильно эта ветвь и дочерние к ней ветви помогут снизить функцию потерь. Это станет понятно только тогда, когда мы построим дочерние ветви, затем дочерние к дочерним и так далее. Если даже после этого функцию потерь на данной ветви не удалось сушественно снизить, тогда всю ветвь можно удалить, упростив дерево. См. также Соколов, 2018, раздел 5.
Работа с категориальными признаками
До сих пор мы рассматривали работу только с количественными признаками. Если в обучающей выборке примеров, то в количественном признаке имеет смысл перебирать не более
значений порога. Теперь рассмотрим категориальный признак с
категориями. Можно разделить все категории на два подмножества, и отправить эти подмножества в разные ветви. Но количество возможных делений всех категорий на два подмножества растет экспоненциально с ростом количества категорий
, что делает невозможным полный перебор при большом
.
Есть два достаточно простых пути. Мы можем закодировать категориальный признак one-hot кодированием. Тогда если по этому признаку произойдет деление, то одна категория отправится в одву ветвь, все остальные в другую, то есть мы ищем только деления вида «одина категория против всех». Также мы можем оставить признаки в label-кодировании и рассматривать их как количественный признак, тогда в одну из ветвей отправятся все категории, индексы которых меньше определенного числа. Такие деления получаются менее осмысленными, но из этого напрямую не следует, что эффективность такого подхода будет ниже. Могут быть и другие подходы, например мы можем перебрать какое-то количество случайных делений всех категорий на два подмножества или упорядочить категории по среднему значению целевой переменной и искать разбиение как для количественного признака (см. Соколов, 2018, раздел 7).
На практике установлено, что для категориальных признаков небольшой размерности (т. е. с небольшим количеством категорий) лучше работает one-hot кодирование (см. Prokhorenkova et al., 2017). Для признаков большой размерности можно тоже применять one-hot кодирование, хотя если сделать это в явном виде, то получившаяся матрица признаков будет занимать очень много места в памяти. Более эффективным подходом к работе с категориальными признаками большой размерности считается target-кодирование.
При target-кодировании мы заменяем каждую категорию некой статистикой (обычно средним значением) целевой переменной, рассчитанной по объектам данной категории. Например, если категориальной переменной является модель автомобиля, а целевым признаком является цена, то мы рассчитываем среднюю цену по каждой модели, и используем полученные данные вместо модели автомобиля.
Данный подход имеет два недостатка. Во-первых, представим, что в каждой категории только один объект. Тогда после target-кодирования признак будет содержать готовые ответы. Модели, обучаемой на этом датасете, будет достаточно извлекать ответ из этого признака, не используя никакие другие признаки. Очевидно, такой подход приведет к переобучению. Как вариант, можно использовать две обучающие выборки: на первой рассчитывать статистику по целевой переменной, а на второй с помощью этой статистики делать target-кодирование и обучать модель.
Вторая проблема в том, что категориальные признаки могут влиять на целевой признак не независимо друг от друга. Например, пусть мы имеем два категориальных признака в label-кодировани, принимающие значения 0 или 1: если они не равны друг другу, то целевой признак равен 1, в противном случае целевой признак равен 0. Если мы выполним target-кодирование, то эта информация будет полностью утеряна.
Несмотря на эти недостатки, target-кодирование и его различные варианты остается одним из самых эффективных способов работы с категориальными признаками высокой размерности. Авторы библиотеки CatBoost разработали метод упорядоченного target-кодирования, при котором на обучающих примерах задается некий порядок, и для каждого -го примера статистика по целевой переменной рассчитывается только на основе примеров с индексами меньше
(см. далее в разделе «CatBoost: несмещённый упорядоченный бустинг»). Обзор различных способов target-кодирования также можно найти в Pargent et al., 2021.
Другие особенности решающих деревьев
Одним из преимуществ решающих деревьев является отсутствие необходимости нормализации данных и в целом почти полная нечувствительность к монотонным преобразованиям количественных признаков (например, логарифмированию).
Еще одним преимуществом является простота работы с пропущенными значениями. При вычислении суммарной функции потерь мы можем игнорировать те объекты, для которых значение признака не указано. Далее при построении дерева эти объекты можно отправять одновременно в обе ветви. При инференсе (то есть получении предсказаний с помощью уже построенного дерева) можно также отправлять объекты с неизвестным значением признака одновременно в обе ветви, и в обоих ветвях рассчитывать целевую переменную. После этого мы усредняем оба значения с весами, равными количеству обучающих примеров, прошедших через обе ветви (подробнее см. Соколов, 2018).
Ансамблирование решающих деревьев
Выше мы видели (рис. 2, 3), что одно решающее дерево имеет достаточно грубые границы между листьями, и при этом либо существенно недообучается (при малом количестве листьев), либо сильно переобучается (при большом количестве листьев). Эту проблему можно исправить, обучая сразу много разных решающих деревьев.
В целом ансамблированием называется комбинация нескольких моделей машинного обучения в одну модель. Ансамблирование решающих деревьев как правило осуществляется «одноуровнево», то есть при инференсе все деревья работают параллельно и независимо выдают ответ, а затем их предсказания складываются или усредняются. Процесс обучения при этом может выполняться параллельно (бэггинг) или последовательно (бустинг).
Существует также стекинг, при котором предсказания одной модели используются в качестве входных данных для другой модели. Однако распространенные алгоритмы ансамблирования решающих деревьев (random forest, XGBoost, LightGBM, CatBoost) не включают в себя стекинг. Стекинг может выполняться поверх этих моделей, так же как и поверх любых других (нейронных сетей и пр.).
Бэггинг
Алгоритм бэггинга достаточно прост: каждое дерево обучается на своей подвыборке данных, взятой из обучающей выборки. Подвыборка делается с возвращением, то есть один пример может быть выбран более одного раза. Если при этом в каждом дереве мы также будем использовать случайную подвыборку признаков, то получим алгоритм построения случайного леса, реализованный, например, в sklearn. Можно внести еще больше случайности в процесс ансамблирования, если процесс построения дерева также будет содержать элементы случайности (см. Extremely Randomized Trees).
Бустинг
Более распространенным методом ансаблирования решающих деревьев является бустинг. Бустинг — это способ построения ансамбля, в котором обучается много копий более слабой модели («weak learner»), то есть такой модели, которая не может достичь высокой точности на обучающем датасете, переобучившись на нем. Как правило такой моделью является решающее дерево небольшой глубины. На каждом шаге новый weak learner концентрируется на исправлении ошибок, допущенных предыдущими weak learner’ами. В итоге предсказания всех weak learner’ов суммируются с определенными весами. Бустинг чем-то похож на бэггинг, но в бэггинге модели обучаются совершенно независимо и параллельно, а в бустинге последовательно, с оглядкой на предыдущие.
Ранний вариант бустинга: AdaBoost
Итак, в бустинге каждый следующий weak learner стремится скорректировать предсказания предыдущих. Это можно сделать разными способами. Одной из первых эффективных реализаций бустинга был AdaBoost — в нем каждый следующий weak learner фокусировал внимание на тех примерах, на которых предыдущие weak learner’ы дали неверные ответы. При этом он не знал, какие именно ответы даны предыдущими weak learner’ами — было лишь известно, что ответы неверны или неточны. Задачей нового weak learner’а было дать верные ответы преимущественно на этих примерах.
Заметим, что при этом не используется никакого валидационного датасета. Используется только обучающий датасет, на нем же оценивается точность предыдущих weak learner’ов. Это означает, что если очередной weak learner после обучения дал верные ответы на все примеры, то бустинг продолжить будет невозможно. Например, если в качестве weak learner’а мы используем решающее дерево неограниченной глубины, то так и произойдет. Нужно использовать решающие деревья небольшой глубины: weak learner должен быть действительно «слабым», не переобучаясь слишком сильно.
Градиентный бустинг
В градиентном бустинге (Friedman, 2001) целевыми данными для следующего weak learner’а является градиент (со знаком минус) функции потерь по предсказаниям предыдущих алгоритмов. Таким образом следующий weak learner корректирует предсказания предыдущих.
Например, производная среднеквадратичной ошибки по
равна
, а значит предсказывая градиент weak learner как раз и предсказывает разность предсказания и правильного ответа. Но можно использовать и другие функции потерь.
Далее рассмотрим алгоритм градиентного бустинга более формально. Для дальнейшего изложения введем необходимые обозначения:
Алгоритм градиентного бустинга
Пусть мы имеем обучающую выборку, обучаемый алгоритм (weak learner) и функцию потерь. В качестве исходного приближения выберем константу так, чтобы сумма
была минимальна. К начальному приближению мы будем прибавлять предсказания weak learner’ов.
Заранее выберем число шагов .
for k = 0, …, N-1:
-
На
-м шаге мы уже обучили
weak learner’ов. Мы получаем предсказания с помощью их взвешенной суммы для всех примеров из обучающего датасета:
-
Считаем производную функции потерь со знаком минус по каждому предсказанию:
. Таким образом мы получаем информацию о том, как нам нужно изменить каждое предсказание, чтобы функция потерь уменьшилась (исходя из смысла понятия производной).
-
Обучаем новый weak learner предсказывать
по
. Обозначим параметры нового weak learner’а за
.
-
Осталось выбрать вес для нового weak learner’а. Для этого получаем предсказания нового weak learner’а на всей обучающей выборке:
. Затем подбираем такой вес
, чтобы значение
было минимально.
В итоге мы получаем ансамбль из weak learner’ов. Алгоритм инференса (то есть предсказания на произвольных данных) выглядит аналогично:
Про градиентный бустинг см. также в этом посте на Хабре.
Регуляризация градиентного бустинга
Для того, чтобы ослабить переобучение градиентного бустинга, применяются следующие техники:
Subsampling. Мы обучаем каждый следующий weak learner не на всей обучающей выборке, а на случайной подвыборке. В этом случае градиентный бустинг называется стохастическим.
Shrinkage. После того, как мы расчитали вес нового weak learner’а , мы умножаем его на некоторое число меньше 1 (learning rate). Таким образом мы укорачиваем шаг в направлении градиента.
Регуляризация weak learner’а. Например, в sklearn можно использовать параметр max_features, который определяет, сколько случайно выбранных признаков будет использоваться при поиске оптимального разбиения в каждом узле дерева.
Особенности градиентного бустинга
В случае выбора функции потерь ее производная пропорциональна разности предсказания и верного ответа, поэтому градиентный бустинг сводится к тому, что каждый следующий weak learner пытается предсказать величину ошибки, допущенную предыдущим. Но при этом сам допускает ошибки, и их пытается предсказать уже следующий weak learner, и так далее.
Важно, чтобы weak learner не был способен слишком сильно переобучиться, иначе следующим weak learner’ам будет не на чем учиться. Поэтому в качестве weak learner’а обычно выбирают деревья небольшой глубины. Линейная регрессия не подходит в качестве weak learner’а, поскольку взвешенная сумма линейных моделей линейна, поэтому и весь ансамбль получится линейным.
Интересно, что если мы выберем в градиентном бустинге специальную «экспоненциальную» функцию потерь, то мы получаем алгоритм, эквивалентный AdaBoost. Конечно с вычистельной точки зрения эти алгоритмы получатся все равно разные, но было доказано, что они эквивалентны в плане получаемого результата. Таким образом, алгоритм AdaBoost эквивалентен частному случаю градиентного бустинга.
Связь с градиентным спуском
Идея как градиентного спуска, так и градиентного бустинга состоит в том, что мы рассчитываем градиент функции потерь по предсказаниям, а затем ходим сдвинуть предсказания в направлении, противоположном градиенту, и таким образом сделать их более точными.
Но в градиентном спуске это достигается с помощью распространения градиента на веса и обновления весов, а в градиентном бустинге с помощью прибавления предсказаний нового weak learner’а, который аппроксимирует градиент со знаком минус. Таким образом, в градиентном спуске используется фиксированное число параметров, а в градиентном бустинге — переменное (каждый новый weak learner содержит новые параметры).
Иногда градиентный бустинг рассматривают как покоординатный градиентный спуск в пространстве функций.
XGBoost
Теперь рассмотрим современные алгоритмы бустинга над решающими деревьями, и начнем с XGBoost.
Библиотека XGBoost (Chen and Guestrin, 2016) является вычислительно эффективной реализацией градиентного бустинга над решающими деревьями. Помимо оптимизированного программного кода, авторы предлагают различные улучшения алгоритма.
Рассмотрим для примера задачу регрессии и введем следующие обозначения:
-
— обучающая выборка
-
— количество деревьев в ансамбле
-
— k-e дерево ансамбля как функция
-
— весь ансамбль как функция
-
— выбранная пользователем основная функция потерь
-
— количество листьев в
-м дереве ансамбля
-
— вектор, составленный из выходных значений на всех листьях
-го дерева
В XGBoost ответы суммируются по всем деревьям ансамбля:
Суммарная функция потерь в XGBoost выглядит следующим образом:
Здесь ,
— гиперпараметры. Первое слагаемое — это основная функция потерь, второе слагаемое штрафует деревья за слишком большое количество листьев, третье слагаемое за слишком большие предсказания. Третье слагаемое является нетипичным в машинном обучении. Оно обеспечивает то, что каждое дерево вносит минимальный вклад в результат. Функция потерь используется при построении каждого следующего дерева, то есть функция потерь оптимизируется по параметрам лишь последнего дерева, не затрагивая предыдущие. Для минимизации
используется метод второго порядка, то есть рассчитываются не только производные, но и вторые производные функции потерь по предсказаниям предыдущих деревьев (подробнее см. Chen and Guestrin, 2016, раздел 2.2).
При поиске каждого нового разделяющего правила, для каждого признака перебираются не все возможные значения порога, а значения с определенным шагом. Для этого на признаке рассчитывается набор персентилей, используя статистику из обучающего датасета. Поиск оптимального порога выполняется только среди этих персентилей. Это позволяет существенно сократить время перебора и ускорить обучение. Для работы с пропущенными значениями в каждом решающем правиле определяется ветвь, в которую будут отправлены объекты с пропущенным значением данного признака.
Однако основной ценностью библиотеки XGBoost является эффективная программная реализация. За счет разных оптимизаций, таких как эффективная работа с пропущенными значениями, поиск порога только среди персентилей, оптимизация работа с кэшем и распределенное обучение, достигается выигрыш в десятки или даже сотни раз по сравнению с наивной реализацией.
CatBoost: несмещённый упорядоченный бустинг
Библиотека CatBoost (Prokhorenkova et al., 2017; Dorogush et al, 2018) — еще одна эффективная реализация градиентного бустинга над решающими деревьями. Основные особенности алгоритма следующие (не в порядке важности):
-
Использование решающих таблиц (разновидности решающих деревьев)
-
Упорядоченное target-кодирование на категориальных признаках высокой размерности
-
Бустинг с упорядочиванием обучающих примеров
Упорядоченное target-кодирование
Упорядоченное target-кодирование мы уже кратко рассматривали в разделе «Работа с категориальными признаками». Рассмотрим некий категориальный признак . Все обучающие примеры случайным образом упорядочиваются. Пусть
-й пример имеет категорию
. Для данного примера рассчитывается выбранная статистика целевой переменной для всех примеров с индексами строго меньше
, имеющими ту же категорию
. Полученное значение является новым признаком, который используется вместо исходного признака
. О том, какие статистики можно использовать, см. документацию CatBoost (1, 2).
В таком подходе есть одна проблема: статистика целевой переменной на первых примерах будет рассчитана слишком неточно (будет иметь высокую дисперсию). Поэтому в CatBoost target-кодирование выполняется несколько раз, каждый раз с новым случайным упорядочиванием обучающей выборки.
Использование решающих таблиц
Решающая таблица является частным случаем забывчивого решающего дерева (oblivious decision tree). В таком дереве все решающие правила одного уровня (то есть на одном и том же расстоянии от корня) проверяют один и тот же признак (Kohavi, 1994; Rokach and Maimon, 2005). Забывчивые решающие деревья разрабатывались для задач с большим количеством нерелевантных признаков.
В варианте, реализованном в CatBoost, на каждом уровне решающего дерева используется не только общий признак, но и общий порог разделения (аналогично Modrý and Ferov, 2016). Благодаря этому порядок следования разделяющих правил становится не важен: можно переставить уровни дерева, и его функционирование от этого не изменится. Такое дерево более естественно представлять в виде таблицы, в которой решающее правило соответствует колонке, в которой может быть значение 0 или 1. Если в дереве уровней , то в таблице
колонок и
строк, содержащих все возможные сочетания значений колонок. Каждой строке сопоставляется константное значение целевого признака. Как можно видеть, такая модель имеет достаточно слабое сходство с обычным решающим деревом, хотя и строится по тем же правилам.
На рис. 5 показана работа CatBoost на примере задачи регрессии (сравните с рис. 2).
Несколько решающих таблиц можно объединить в одну, поэтому весь ансамбль CatBoost можно представить в виде одной решающей таблицы, что видно из рис. 5. При этом не любая сложная решающая таблица может быть разложена в сумму многих простых таблиц.
Впрочем, CatBoost поддерживает не только решающие таблицы, но и обычные решающие деревья (см. параметр grow_policy). Возможно, мотивацией использовать именно решающие таблицы была скорость инференса. Как говорит один из разрабочиков библиотеки Станислав Кириллов:
Мы изначально создавали его [CatBoost] как библиотеку для применения в сервисах Яндекса, отсюда характерные для большой компании требования. К примеру, у наших сервисов всегда высокие нагрузки, поэтому скорость инференса модели критична для CatBoost. (habr)
В чем профит наших oblivious-деревьев? Они быстро учатся, быстро применяются и помогают обучению быть более устойчивым к изменению параметров с точки зрения изменений итогового качества модели, что сильно уменьшает необходимость в подборе параметров. (habr)
Проблема смещённости бустинга
Алгоритм бустинга имеет одну достаточно очевидную проблему. Выполняя шаг бустинга, мы хотим скорректировать предсказания алгоритма , обучив новый алгоритм
, то есть алгоритм
должен выявить и исправить систематические ошибки, допущенные алгоритмом
. При этом для обучения
мы используем те же обучающие данные
, что использовали для обучения
. Это означает, что мы оцениваем работу алгоритма
(точнее, производные функции потерь по его предсказаниям) на тех же данных, на которых этот алгоритм обучался. Однако алгоритм
переобучился на данных
, и его работа на этих данных уже не показательна.
Gradients used at each step are estimated using the same data points the current model was built on. This leads to a shift of the distribution of estimated gradients in any domain of feature space in comparison with the true distribution of gradients in this domain, which leads to overfitting. The idea of biased gradients was discussed in previous literature [1] [9]. (Dorogush et al, 2018, раздел 3)
Рассмотрим эту проблему более формально. Обозначим на порождающее распределение, из которого взята обучающая выборка. Совместное распределение
в обучающей выборке можно обозначить за
(эмпирическое распределение). Алгоритм
моделирует условное распределение
, алгоритм
обучается моделировать условное распределение производных:
Целью является моделирование
для всего порождающего распределения, то есть при
, однако мы имеем выборку из
только для обучающих данных, то есть при
. Проблема заключается в том, что распределение производных на обучающей выборке
является смещённым (biased), проще говоря искаженным, относительно распределения производных на всем порождающем распределении
:
В качестве примера, если максимально переобучился на
, то
. Из-за этого
получается не оптимальным, так как обучается на выборке не из того распределения, которое в идеале должен моделировать. В идеале хотелось бы использовать для оценки градиента данные, на которых алгоритм
не обучался, но тогда нам нужно использовать новые данные на каждом шаге бустинга, что невозможно при большом числе шагов.
Можно привести еще такой пример. Представим, что ученик обучается решать математические задачи из класса
(например, упрощение дробей), имея выборку из этих задач
, и у нас есть также тестовая выборка задач
. Часть примеров из
ученик
не понял и просто запомнил, но не идеально. Если после обучения ученика
дать ему задачи из
, которые он никогда не видел, то часть задач он решит, на на других сделает на них какие-то осмысленные ошибки. Если же дать ученику
снова решать задачи из
, то он будет пытаться вспомнить решение, и сделает во-первых меньше ошибок, во-вторых уже ошибки другого рода (неправильно вспомнит и напишет что-то бессмысленное, что сойдется с ответом). Это означает, что распределение ошибок может быть совсем разным на обучающих и тестовых данных, по причине переобучения и так называемой утечки данных (target leakage).
Несмотря на то, что градиентный бустинг содержит такую проблему, он все равно хорошо работает на практике, поэтому на эту проблему долгое время закрывали глаза. Авторы библиотеки CatBoost нашли способ ее решения, названный упорядоченным бустингом.
Упорядоченный бустинг
В Prokhorenkova et al., 2017 (раздел 4) упорядоченный бустинг описывается в двух вариантах. В первом варианте на каждом шаге бустинга обучается сразу много деревьев (подробнее рассмотрим далее), но тогда вычислительная сложность алгоритма многократно растет. Во втором варианте на каждом шаге обучается только одно дерево, как и в обычном бустинге. В обоих случаях авторы доказывают несмещенность получаемой оценки градиента.
Рассмотрим сначала первый вариант упорядоченного бустинга. Введем на обучающих примерах некий порядок (так же, как в упорядоченном target-кодировании) и пронумеруем их согласно этому порядку: . На каждом шаге бустинга
мы будем обучать не одно решающее дерево, а набор решающих деревьев для каждого номера обучающего примера:
. При этом последовательность деревьев для каждого
рассматривается как модель градентного бустинга, то есть ответы деревьев суммируются по
:
(рис. 6). Таким образом, мы обучаем столько моделей градиентного бустинга, сколько у нас обучающих примеров. При этом
-е дерево обучается на примерах с 1-го по
-й включительно и на каждом шаге используется для получения предсказания на
-м примере.
Например, чтобы на 100-м шаге обучить 10-е дерево, нам нужны предсказания для первых 10 примеров. Предсказание для 10-го примера мы получаем 9-й моделью градиентного бустинга (то есть суммируя все деревья, которые обучались на первых 9 примерах), предсказание для 9-го примера мы получаем 8-й моделью градиентного бустинга и так далее. Что делать с первым примером при этом, правда, не уточняется — возможно, ответом на нем всегда является константа.
После шагов бустинга финальным результатом является модель
, то есть та, что обучалась на всех примерах. Эта модель в дальнейшем используется для тестирования и инференса. Те деревья, которые обучались не на всех примерах, после обучения отбрасываются.
В таком алгоритме оценка градиента получается несмещенной, так как деревья не используются для предсказания на тех же примерах, на которых обучались. Однако такой подход не реализуем на практике из-за большого объема вычислений. Можно было бы объединять примеры в группы, и обучать по одному дереву для каждой группы, но все равно на каждом шаге пришлось бы обучать много деревьев. Авторы CatBoost предлагают иной подход, также обладающий свойством несмещенности.
Алгоритм CatBoost
Общая идея алгоритма CatBoost в том, что во-первых мы выполняем упорядоченное target-кодирование, а во-вторых при расчете предсказаний на листьях мы используем примеры с индексами меньше, чем тот пример, на котором хотим получить предсказание.
На каждом шаге бустинга обучается одна решающая таблица (дерево). Глубина дерева является гиперпараметром, то есть задается заранее. Если глубина равна , то дерево представляет собой последовательность из
признаков и порогов разделения и имеет
листьев.
Далее рассмотрим алгоритм в том виде, в каком он дан в Prokhorenkova et al., 2017, appendix B. Алгоритм CatBoost имеет два режима: plain (бустинг без упорядочивания) и ordered (упорядоченный бустинг), мы рассмотрим только режим ordered.
Примечание. В CatBoost по умолчанию не всегда используется упорядоченный бустинг, см. параметр boosting_type. Также есть возможность использовать разные виды решающих деревьев (см. далее). В данном разделе мы будем рассматривать только использование решающих таблиц.
В качестве входных данных алгоритм принимает обучающую выборку, пронумерованную от до
, количество шагов
, функцию потерь
и два гиперпараметра:
, используемый как learning rate (см. раздел «Регуляризация градиентного бустинга») и
— количество перестановок минус единица.
Сначала (строка 1) создаются случайных перестановок, то есть упорядочиваний обучающей выборки (например, см.
np.random.permutation). Позицию -го элемента обучающей выборке в перестановке
будем обозначать как
. Эти перестановки используются как для упорядоченного бустинга, так и для упорядоченного target-кодирования. Перестановки
будут использоваться для обучения, перестановка
будет использоваться для создания финальной модели для инференса.
В обычном градиентном бустинге мы обучаем последовательность деревьев, и на каждом шаге прибавляем предсказания нового дерева к результату. Таким образом, на каждом шаге результатом является новое дерево и предсказаний (для каждого обучающего примера). В CatBoost на каждом шаге тоже обучается одно дерево, но при этом имитируется обучение сразу многих «виртуальных» моделей градиентного бустинга, поэтому на каждом шаге результатом является сразу несколько предсказаний для каждого примера. Эти предсказания хранятся в массиве
.
Запись означает предсказание (в случае регрессии — число), сделанное на
-м примере «виртуальной» моделью с индексами
. Индекс
соответствуют номеру перестановки (при этом
— особный случай, когда индекс
отсутствует). Идея упорядоченного бустинга в том, что на выборке и на моделях вводится некий порядок (см. раздел «Упорядоченный бустинг»), и индекс
соответствует этому порядку. В простом варианте мы использовали столько моделей, сколько есть обучающих примеров (рис. 6). Но из соображений производительности хотелось бы уменьшить количество моделей, поэтому в CatBoost при
обучающих примерах используется
моделей (это и есть диапазон значений для индекса
). Символ
означает округление до целого в большую сторону.
Чтобы лучше понять, почему используется именно моделей, представим, что мы имеем 70 обучающих примеров. Мы раскладываем их по мешкам, и в каждый следующий мешок кладем в 2 раза больше примеров, чем в предыдущий. Тогда в мешках окажется 1, 2, 4, 8, 16, 32 и 7 примеров (последний мешок заполнен не полностью). Каждому
-му мешку соответствует «виртуальная» модель градиентного бустинга, которая обучается на примерах из мешков с номерами
и используется для предсказания на примерах из
-го мешка.
Таким образом, — это массив чисел. Подмассив
имеет размерность
, подмассив
при
имеет размерность
. Последний индекс, соответствующий номеру обучающего примера, записывается в круглых скобках. Например, в задаче регрессии
и
— это числа. В строках 2-4 алгоритма массив
инициализируется нулями.
Далее начинается основной цикл из шагов бустинга. В строке 6 строится новое дерево (функцию
рассмотрим далее), при этом используется массив предыдущих предсказаний
и перестановки
, то есть
и
на этом шаге не используются. Дерево
, построенное на шаге
, представляет собой последовательность разделяющих правил, каждое из которых состоит из признака и порога. При этом значения на листьях в
не указаны (идея в том, что они разные для разных виртуальных моделей).
Функция (строка 7) используется для получения номера листа в дереве. Запись
означает следующее: используя перестановку
, мы выполняем target-кодирование обучающей выборки, и таким образом мы получаем значения всех признаков для примера
. С помощью этих значений можно выбрать путь в дереве
и определить номер листа. Таким образом, в строке 7 мы определяем номер листа для каждого обучающего примера, используя перестановку
. В итоге все обучающие примеры распределяются по листьям дерева
.
В строке 8 мы рассчитываем градиент функции потерь по предсказаниями . Обозначение
означает градиент по
-му примеру. Индекс 0 здесь означает, что градиенты рассчитаны по
. Далее для каждого листа
дерева
мы рассчитываем значение
на этом листе, усредняя градиенты (со знаком минус) всех примеров, попавших в каждый лист. Далее (строка 12) мы обновляем
, добавляя в него предсказания из нового дерева. В выражении
нижним индексом является номер листа для
-го примера, соответственно все выражение означает значение, предсказываемое на
-м примере, используя значения
на листьях дерева
.
В итоге, результатом шага является дерево
со значениями
на листьях. Также на каждом шаге обновляется массив
, который используется в следующих шагах, и после обучения отбрасывается.
Алгоритм инференса CatBoost показан в строке 13. Мы суммируем предсказания по всем деревьям (с множителем , как и при обучении). Чтобы получить предсказание для тестового примера, нужно выполнить target-кодирование на его категориальных признаках, для этого используется статистика, рассчитанная по всем обучающим примерам (что означает символ
, подставленный вместо перестановки). Запись
судя по всему означает то же самое, что
, но записанное в виде скалярного произведения.
Теперь рассмотрим функцию . Эта функция принимает на вход обучающую выборку, массив промежуточных предсказаний
(кроме
), массив перестановок (кроме
), функцию потерь и коэффициент
. Функция возвращает новое дерево
и обновленный массив промежуточных предсказаний.
В функции выбираем случайную перестановку
и далее работаем только с ней. Этой перестановке соответствует массив предсказаний
, который имеет размерность
. По этому массиву мы рассчитываем градиент
, который имеет такую же размерность.
Второй индекс () массива M соответствует порядку в упорядоченном бустинге. Каждому
-му примеру из обучающей выборки можно сопоставить значение
по этому индексу. В приведенной выше аналогии с мешками это номер мешка, в который попадает
-й пример.
Массив (строка 3) имеет размерность
(для задачи регрессии) и содержит производные для всех
примеров обучающей выборки, то есть целевые данные для обучения следующего дерева. При этом производные по каждому примеру рассчитаны с помощью «виртуальной модели», ответственной за этот пример (вспомним, что модель, обучающаяся на первых
мешках, используется для рассчета производных на
-м мешке).
На каждом шаге роста дерева мы перебираем все возможные разделяющие правила (строка 6), то есть признаки и пороги разделения. Зафиксировав
, мы хотим оценить качество, с которым полученное дерево
предсказывает градиент
. Для этого мы определяем листья, в которые попали примеры из обучающей выборки, используя перестановку
для target-кодирования (строка 8). Далее нужно определить значения на каждом листе, но делается это нетривиальным образом (строка 10). Глобальные, общие для всей выборки значения на листьях не рассчитываются. Вместо этого для
-го обучающего примера предсказанием
считается среднее значение градиента
по всем примерам
, попавшим в этот же лист (
) и имеющим меньший индекс в выбранной перестановке (
). При этом глобальные значения на листьях дерева будут рассчитаны уже тогда, когда дерево будет полностью построено (строка 10 в алгоритме CatBoost).
Далее качество предсказания оценивается с помощью cosine similarity между ним и
(строка 11), и на основании качества выбирается наилучшее решающее правило.
После того, как дерево построено, требуется обновить все промежуточные предсказания (строки 13-17), добавив слагаемое, предсказанное деревом на текущей итерации. Здесь в целом все аналогично.
Комбинирование признаков в CatBoost
Еще одной интересной особенностью CatBoost является комбинирование признаков при поиске оптимальных разделяющих правил. Ранее мы уже говорили о том, что категориальные признаки могут влиять на ответ не независимо друг от друга, и при target-кодировании эта информация будет утеряна (см. раздел «Работа с категориальными признаками»). Чтобы уменьшить влияние этой проблемы, в CatBoost применяется следующая стратегия (см. Dorogush et al, 2018, раздел «Feature combinations»).
Пусть мы уже построили уровней дерева, использовав для разделения признаки
, и на
-м уровне рассматриваем возможность деления по некоему категориальному признаку
. Мы комбинируем признак
с признаками
, то есть в качестве значений нового (комбинированного) признака рассматриваем все возможные сочетания значений признаков
, и работаем с полученным признаком.
Впрочем, в статье этот механизм описан очень кратко, из-за чего остается не до конца понятным, как конкретно он реализован. В библиотеке CatBoost за комбинирование признаков отвечает параметр max_ctr_complexity.
Обзор некоторых параметров CatBoost
Выше мы рассмотрели алгоритм в том виде, в каком он приведен в научной статье. Программная реализация отличается тем, что в ней больше возможностей и гиперпараметров. Важно упомянуть, что CatBoost может использовать для обучения как CPU, так и GPU (параметр task_type метода fit). Многие значения гиперпараметры доступны либо только для CPU, либо только для GPU, из-за этого результаты обучения и метрика качества может отличаться.
Параметр grow_policy определяет тип деревьев и может принимать следующие значения:
-
grow_policy=SymmetricTree(по умолчанию) — использование решающих таблиц: одинаковая глубина всех листьев, общее разделяющее правило на каждом уровне дерева -
grow_policy=Depthwise— одинаковая глубина всех листьев, но разделяющие правила могут быть разными в разных ветвях -
grow_policy=Lossguide— обычное решающее дерево, глубина листьев могут быть разной
Параметр boosting_type задает тип бустинга: упорядоченный или неупорядоченный. Согласно документации, упорядоченный бустинг обучается медленнее, но обычно показывает лучшее качество на небольших датасетах. На CPU значение по умолчанию boosting_type='Plain', а на GPU значение по умолчанию выбирается в зависимости от размера обучающего датасета: если в нем меньше 50 тысяч примеров, то используется boosting_type='Ordered', за исключением отдельных частных случаев (см. документацию).
Также в CatBoost используется bootstrap aggregation (параметр bootstrap_type, подробнее см. в документации). Он может быть релализован в разных вариантах, например следующих:
-
При построении каждого следующего дерева оно обучается не на всей обучающей выборке, а на случайной подвыборке (
bootstrap_type='Bernoulli'). Такой способ мы рассматривали в разделе «Регуляризация градиентного бустинга». При этом не только накладывается регуляризации, но и обучение выполняется быстрее. -
При построении каждого следующего дерева обучающим примерам присваиваются случайные веса (
bootstrap_type='Bayesian'), и при поиске оптимального разделения в основном учитываются примеры с большими весами.
Для поиска оптимальных разделяющих правил в CatBoost, конечно, перебираются не все возможные значения порога, которых очень много для больших датасетов, а значения с некоторым шагом (как и в других библиотеках — XGBoost, LightGBM). Подробнее см. Dorogush et al, 2018, раздел «Dense numerical features».
CatBoost также может работать с текстовыми признаками (для этого неявно используется модель bag-of-words). Это позволяет создавать на основе CatBoost отличные бейзлайны для задач табличного ML, в которых есть тестовые признаки. В методе fit нужно не забывать указывать параметры cat_features и text_features, чтобы алгоритм мог распознать типы признаков и корректно с ними работать.
Интерпретация ансамблей решающих деревьев
Одно дерево небольшой глубины полностью интерпретируемо, то есть процесс принятия решения уже представлен в понятной человеку форме. При ансамблировании большого числа деревьев часть интерпретируемости теряется, но тем не менее ансамбль деревьев интерпретируем лучше, чем, скажем, нейронная сеть. Начнем с оценки важности признаков.
Оценка важности признаков в решающих деревьях
В машинном обучении важностью признака (feature importance) неформально называется степень влияния этого признака на целевой признак. Оценка важности признаков имеет несомненную практическую пользу. При правильном применении она помогает отсеять нерелевантные признаки и в целом лучше понять данные. Кроме того, если мы сумеем найти признаки с явно завышенной важностью, то так мы можем распознать переобучение модели и утечку данных (подробнее см. здесь).
Понятие «степени влияния признака на ответ модели» можно формализовать по-разному.
Рассмотрим способ mean decrease impurity (MDI), который часто используется в решающих деревьях. В процессе построения решающего дерева добавление каждого решающего правила можно описать как шаг роста дерева, превращающий дерево в дерево
(дерево
имеет на один лист больше). Обозначим суммарную функцию потерь обоих деревьев за
и
. При этом новое решающее правило выбиралось таким образом, чтобы минимизировать
(см. раздел «Построение решающего дерева»).
Мы можем посчитать падение функции потерь от добавления правила: , и считать полученное значение важностью этого правила. Далее можно найти все правила во всех деревьях, использующих данный признак, и взять сумму важности эти правил по каждому дереву и среднее по всем деревьям.
Рассмотрим частный случай, когда функцией потерь является среднеквадратичная ошибка. Если до разделения на листе было значение , а после разделения появилось два листа со значениями
и
(см. раздел «Оптимальное разделение в задаче регрессии»), и количество примеров в листьях равно
и
, то получим следующую формулу для важности данного правила:
Такой способ расчета используется, например, в CatBoost (см. PredictionValuesChange).
Другой способ оценки важности некоего признака, называемый permutation importance, заключается в следующем: мы измеряем точность предсказания ансамбля деревьев на тестовой выборке, затем случайным образом переставляем значения этого признака и снова измеряем точность предсказания. Падение точности после перестановки и принимается за важность признака.
В оценке важности признаков таким способом кроется много подводных камней. Например, признак присутствует лишь в небольшой доле объектов, но сильно влияет на результат, тогда как признак
оказывает лишь небольшое влияние на результат, но во всех объектах. Оба этих признака важны, но эта важность разного рода, и в стандартных методах оценки важности признаков не будет видно этого различия.
Более того, важность пропорциональна доле связанных с ним объектов в выборке, а эта доля может варьироваться в зависимости от способа сбора данных. Иными словами, важность признаков может сильно зависеть от особенностей распределения данных, а это распределение может отличаться при обучении и инференсе. Эта особенность добавляет неоднозначности понятию важности признака.
Переобученная модель может давать в целом неверную важность признаков. Если релевантность признаков заранее известна, то это может помочь распознать переобучение, но если релевантность заранее неизвестна, то отбор признаков на основе важности может в этом случае только усилить переобучение.
SHAP values
Еще одним, более современным способом оценки важности признаков являются SHAP values, основанные на теории игр. SHAP values позволяют оценить важность признаков на конкретном тестовом примере. SHAP values имеют некоторые проблемы. SHAP values, как и mean decrease impurity, зависит от распределения данных, то есть является характеристикой не только модели, но объединенной системы «модель + распределение данных». При этом можно получить ненулевые SHAP values для тех признаков, которые никак не используются моделью.
Перед использованием SHAP values полезно подробно ознакомиться с принципом работы этого метода, его преимуществами и недостатками. Подробнее см. в обзоре Интерпретация моделей и диагностика сдвига данных: LIME, SHAP и Shapley Flow.
Выразительная способность ансамблей решающих деревьев
Понятие выразительной способности
Любая модель машинного обучения — это некое параметризованное семейство функций . При обучении, как правило, мы выбираем одну из этих функций, которая хорошо приближает исследуемую зависимость
. Под выразительной способностью (expressivity) модели машинного обучения понимается то, насколько широкий класс функций представляет собой модель
. Таким образом модели можно сравнивать друг с другом: модель
имеет большую выразительную способность, чем модель
, если
. При этом функции в
и
могут быть параметризованы по разному.
Даже если какая-то функция отсутствует в модели
, то возможно в
найдутся функции, близкие к
— это называется аппроксимацией функции
моделью
. Модель
называется универсальным аппроксиматором, если с ее помощью можно со сколь угодно высокой точностью аппроксимировать любую функцию из достаточно широкого класса (например, любую непрерывную функцию или любую интегрируемую функцию; пример математически строгой формулировки см., например, здесь).
Прежде, чем переходить к решающим деревьям, вспомним нейронные сети. Нейронная сеть с одним скрытым слоем без функции активации имеет ту же выразительную способность, что и нейронная сеть без скрытых слоев (если размерность скрытого слоя не меньше, чем размерность входа и выхода). То есть эти модели равны как семейство функций, хотя параметризованы по-разному. Нейронная сеть с одним скрытым слоем и многими неполиномиальными функциями активации (например, ReLU или tanh) имеет выразительную способность намного больше, чем сеть без скрытых слоев, и при этом является универсальным аппроксиматором. Например, если мы используем функцию активации ReLU, то при конечном размере скрытого слоя не существует таких весов сети, чтобы сеть в точности реализовывала функцию , но подбирая веса и размер скрытого слоя можно создать сколь угодно точное приближение для этой функции на любом конечном интервале
.
Если модель является универсальным аппроксиматором — это хорошо или плохо? Вопрос неоднозначный. Наличие факта универсальной аппроксимации ничего не говорит об обобщающей способности алгоритма, который будет осуществлять поиск решения. С одной стороны, отсутствие универсальной аппроксимации в модели может привести к тому, что обучиться некоторым типам зависимостей модель в принципе не способна. С другой стороны, наличие универсальной аппроксимации означает очень широкое пространство поиска и потенциальную возможность переобучиться на любом шуме (это будет еще зависеть от алгоритма обучения).
Итак, являются ли решающие деревья универсальными аппроксиматорами?
Выразительная способность решающего дерева
Решающие деревья (в том числе решающие таблицы, используемые в CatBoost), является универсальными аппроксиматорами при условии неограниченной глубины. С помощью дерева неограниченной глубины пространство можно разбить на сколь угодно маленькие участки, введя на каждом участке константное значение
. Такое приближение напоминает сумму Римана (см. также Royden and Fitzpatrick «Real Analysis», The Simple Approximation Theorem).
Однако на практике глубину деревьев часто ограничивают, и более интересным является вопрос о том, являются ли универсальными аппроксиматорами ансамбли решающих деревьев ограниченной глубины. Я не смог найти в научной литературе исследования вопроса о том, являются ли ансамбли деревьев ограниченной глубины универсальными аппроксиматорами.
В этом разделе я приведу собственное доказательство того, что ансамбль деревьев фиксированной глубины не является универсальным аппроксиматором и способен аппроксимировать с произвольной точностью лишь те функции, которые представимы в виде суммы функций от
признаков. Например, функция
не может быть аппроксимирована с произвольной точностью ансамблем деревьев глубины
.
Выразительная способность ансамбля решающих деревьев
Рассмотрим сначала ансамбль (т. е. сумму) деревьев, в котором все деревья имеют глубину 1, затем ансамбль деревьев глубины 2, и затем случай произвольной глубины .
Ансамбль деревьев глубины 1
При глубине 1 каждое дерево состоит из одного решающего правила и двух листьев. Каждое такое дерево может быть представлено как кусочно-постоянная функция от одного признака: . Сгруппировав все деревья в ансамбле по номеру признака, можно записать ансамбль в таком виде:
Здесь — любые кусочно-постоянные функции, представимые как сумма функцией вида
.
Отсюда, ансамблем деревьев глубины 1 можно представить любую функцию, представимую в виде , где
— любая функция из очень широкого класса (интегрируемых по Риману) функций, которые можно сколь угодно точно приблизить кусочно-постоянной функцией.
Таким образом, с помощью ансамбля деревьев глубины 1 можно сколь угодно точно приблизить любую функцию, в которой зависимость представима в форме , где
— произвольные функции. Если предсказывать не само значение
, а его экспоненту, тогда суммирование в
можно заменить произведением.
Ансамбль деревьев глубины 2
Дерево глубины 2 может иметь до трех решающих правил, а значит быть функцией от трех признаков. Однако такое дерево можно представить как сумму двух деревьев, в каждом из которых проверяется лишь два признака (рис. 7). Поэтому ансамбль из деревьев глубины 2 можно представить в виде суммы функций, каждая из которых использует 1 или 2 признака.
Если ансамбль решающих деревьев как функцию можно разложить на слагаемые, каждое из которых использует по два признака, то такой ансамбль можно представить в виде функции:
При этом любую функцию от двух переменных можно аппроксимировать суммой деревьев глубины 2. Доказать это можно следующим образом: любую функцию (из очень широкого класса) можно сколь угодно точно аппроксимировать «кирпичиками» вида:
, и такой «кирпичик» можно построить, используя не более четырех деревьев глубины 2:
Отсюда можно сделать вывод о том, ансамблем решающих деревьев можно сколь угодно близко приблизить любую (интегрируемую по Риману) функцию, представимую в виде , где
могут быть любыми.
Ансамбль деревьев глубины
Докажем, что ни при каком фиксированном ансамбль деревьев глубины
не является универсальным аппроксиматором. Для этого достаточно показать, что произведение
входных признаков не может быть сколь угодно точно аппроксимировано суммой деревьев глубины
.
Введем запись , которая означает, что
. По умолчанию будем считать, что области определения функций равны и максимум берется по всей области определения. Будем говорить, что функции из множества
«сколь угодно точно аппроксимируют» функцию
, если для любого
существует такое
, что
. Иначе говоря, это означает, что существует последовательность функций из
, равномерно сходящаяся к
. Для упрощения в дальнейшем будем считать, что все переменные принимают значения в замкнутом промежутке
. Введем также следующие обозначения:
-
— множество всех функций, представимых в виде суммы конечного числа решающих деревьев глубины
.
-
— множество всех функций, представимых в виде суммы конечного числа функций от
переменных.
Покажем, что . Каждое решающее дерево глубины
можно представить как сумму деревьев, в которых лишь один лист содержит ненулевое значение, а значит решающее дерево глубины
можно представить как сумму функций от
переменных (для случая
см. рис. 7).
Таким образом, осталось доказать, что функциями из множества нельзя сколь угодно точно аппроксимировать функцию
. Чтобы упростить математическую нотацию, докажем для случая
. Полученное доказательство обобщается на случай произвольного
.
Теорема. Функцию нельзя сколь угодно точно аппроксимировать функциями из множества
(а следовательно и функциями из множества
).
Доказательство. Докажем от противного. Зафиксируем произвольное . Пусть существует искомая аппроксимация:
Рассмотрим случаи и
:
Вычтем второе выражение из первого, при этом последнее слагаемое сократится:
Мы пришли к тому, что функцию можно сколь угодно точно аппроксимировать сумой функций от двух переменных. Говоря более формально, имея ряд функций из
, равномерно сходящийся к функции
, можно построить ряд функций из
, равномерно сходящийся к функции
.
Повторив такой шаг, придем к тому, что функцию можно сколь угодно точно аппроксимировать сумой функций от одной переменной. Еще раз повторив такой шаг, придем к тому, что функцию
можно сколь угодно точно аппроксимировать константой, что очевидно неверно. ■
Выводы и эксперименты
Как мы выяснили, суммой решающих деревьев ограниченной глубины нельзя аппроксимировать некоторые типы функций. Однако это не означает, что модель не сможет обучиться на конечной выборке, взятой из аргументов и значений таких функций. Просто такое обучение будет сопряжено с сильным переобучением.
Например, ансамбль деревьев глубины 1 не может аппроксимировать с произвольной точностью функцию . Возьмем выборку из 4 значений аргумента:
. Поскольку ансамбль деревьев глубины 1 всегда можно представить как сумму функций от одной переменной (см. формулу
), то для любого ансамбля
из деревьев глубины 1 будет верно следующее:
.
При этом для функции это равенство не выполняется, поэтому обучая ансамбль деревьев глубины 1 мы всегда будем видеть высокое значение функции потерь. Но если к исходным признакам добавить случайный шум, тогда, наоборот, функция потерь на обучающей выборке может стремиться к нулю, но получаемое решение будет некорректным и не будет обобщаться на тестовую выборку.
В качестве эксперимента попробуем обучить модель градиентного бустинга аппроксимировать функции и
, с помощью обучающей выборки 256 точек, при этом точки могут быть распределены либо случайно, либюо по равномерной сетке. Будем использовать 1000 деревьев глубиной 1 или 2. Результаты эксперимента показаны на рис. 8. Каждое изображение представляет собой функцию
, реализуемую обученной моделью.
Как можно видеть, ансамбль деревьев глубины 1 может обучиться функции , но не может обучиться функции
(второй столбец): при равномерном расположении точек обучения вообще не происходит, а при случайном расположении точек происходит лишь переобучение. Ансамбль деревьев глубины 2 при этом без труда обучается функции
(четвертый столбец).
Что интересно, деревья глубины 1 лучше обучаются функции на случайных точках, чем деревья глубины 2. По-видимому, маленькую глубину дерева можно рассматривать как способ регуляризации, если известно, что искомая зависимость достаточно проста, например, имеет вид
или
.
Такие выводы, судя по всему, обобщаются и на случай большей размерности. В машинном обучении могут встречаться датасеты, где искомая зависимость имеет сложный вид и не представима как сумма функций от небольшого числа переменных. При этом библиотеки градиентного бустинга, такие как CatBoost, по умолчанию имеют не очень большую глубину дерева, из-за чего модель не сможет обучиться такой зависимости (недообучится либо переобучится, в зависимости от степени регуляризации).
Например, положительный ответ о выдаче кредита можно давать лишь тогда, когда одновременно строго соблюдено много условий. Если каждое условие представлено в виде бинарного признака, то искомая зависимость может иметь вид произведения многих признаков . Хотя, с другой стороны, подобную зависимость можно описать в другом виде:
. Поэтому вопрос о том, является ли отсутствие возможности универсальной аппроксимации существенным ограничением, остается открытым. Вполне возможно, что практически все зависимости на табличных данных, которые встречаются на практике, могут быть представлены как сумма функций от небольшого числа переменных.
Список источников
Biau et al., 2008. Consistency of Random Forests and Other Averaging Classifiers.
Breiman, 2001. Random Forests.
Chen and Guestrin, 2016. XGBoost: A Scalable Tree Boosting System.
Criminisi et al., 2011. Decision forests: A unified framework for classification, regression, density estimation, manifold learning and semi-supervised learning.
Dorogush et al., 2018. CatBoost: gradient boosting with categorical features support.
Freund and Schapire, 1997. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting.
Friedman, 2001. Greedy Function Approximation: A Gradient Boosting Machine.
Hancock et al., 1996. Lower Bounds on Learning Decision Lists and Trees.
Hyafil and Rivest, 1976. Constructing optimal binary decision trees is NP-complete.
Ke et al., 2017. LightGBM: A Highly Efficient Gradient Boosting Decision Tree.
Kohavi, 1994. Bottom-Up Induction of Oblivious Read-Once Decision Graphs.
Lundberg et al., 2019. Explainable AI for Trees: From Local Explanations to Global Understanding.
Modrý and Ferov, 2016. Enhancing LambdaMART Using Oblivious Trees.
Morgan and Sonquist, 1963. Problems in the Analysis of Survey Data, and a Proposal.
Pargent et al., 2021. Regularized target encoding outperforms traditional methods in supervised machine learning with high cardinality features.
Prokhorenkova et al., 2017. CatBoost: unbiased boosting with categorical features.
Rokach and Maimon, 2005. Decision Trees.
Royden and Fitzpatrick. Real Analysis.
Weinberger, 2018. Lecture 12: Bias-Variance Tradeoff.
Соколов, 2018. Решающие деревья.
Подробный вывод алгоритма обратного распространения ошибки
Обратное распространение (английский: Backpropagation, сокращенно BP) — это сокращение от «обратного распространения ошибки», который является распространенным методом, используемым для обучения искусственных нейронных сетей в сочетании с методами оптимизации (такими как градиентный спуск). Этот метод вычисляет градиент функции потерь для всех весов в сети. Этот градиент возвращается в метод оптимизации для обновления весов, чтобы минимизировать функцию потерь. Основной алгоритм метода градиентного спуска реализован на нейронной сети. Алгоритм сначала вычисляет (и кэширует) выходное значение каждого узла в соответствии с методом прямого распространения, а затем вычисляет частную производную значения функции потерь по каждому параметру в графе обхода обратного распространения.
Мы будем использовать полностью связанный слой и функцию активации, чтобы принятьSigmoid Функция, функция ошибкиSoftmax+MSE Возьмите нейронную сеть функции потерь в качестве примера, чтобы получить ее метод распространения градиента.
Готов к работе
1. Производная сигмоидной функции
Обзорsigmoid Выражение функции:
σ
(
x
)
=
1
1
+
e
−
x
sigma(x) = frac{1}{1+e^{-x}}
Его производная:
d
d
x
σ
(
x
)
=
d
d
x
(
1
1
+
e
−
x
)
frac{d}{dx}sigma(x) = frac{d}{dx} left(frac{1}{1+e^{-x}} right)
=
e
−
x
(
1
+
e
−
x
)
2
= frac{e^{-x}}{(1+e^{-x})^2}
=
(
1
+
e
−
x
)
−
1
(
1
+
e
−
x
)
2
= frac{(1 + e^{-x})-1}{(1+e^{-x})^2}
=
1
+
e
−
x
(
1
+
e
−
x
)
2
−
(
1
1
+
e
−
x
)
2
=frac{1+e^{-x}}{(1+e^{-x})^2} — left(frac{1}{1+e^{-x}}right)^2
=
σ
(
x
)
−
σ
(
x
)
2
= sigma(x) — sigma(x)^2
=
σ
(
1
−
σ
)
= sigma(1-sigma)
можно увидеть,Sigmoid В конечном итоге производное выражение функции можно выразить как простую операцию с выходным значением функции активации.
С помощью этого свойства при вычислении градиента нейронной сети путем кэширования выходного значения сигмоидной функции каждого слоя можно
При необходимости вычислить производную. Реализация производной сигмовидной функции:
import numpy as np # Импортировать numpy
def sigmoid(x): # сигмовидная функция
return 1 / (1 + np.exp(-x))
def derivative(x): # sigmoid Расчет производной
return sigmoid(x)*(1-sigmoid(x))
2. Градиент функции среднеквадратичной ошибки.
Выражение функции потерь среднеквадратичной ошибки:
L
=
1
2
∑
k
=
1
K
(
y
k
−
o
k
)
2
L = frac{1}{2}sum_{k=1}^{K}(y_k-o_k)^2
где
y
k
y_k
Истинная ценность,
o
k
o_k
Выходное значение. Его частная производная
∂
L
∂
o
i
frac{partial L}{partial o_i}
Может быть расширен до:
∂
L
∂
o
i
=
1
2
∑
k
=
1
K
∂
∂
o
i
(
y
k
−
o
k
)
2
frac{partial L}{partial o_i} = frac{1}{2}sum_{k=1}^{K}frac{partial}{partial o_i}(y_k — o_k)^2
использует правило цепочки для разложения на
∂
L
∂
o
i
=
1
2
∑
k
=
1
K
⋅
2
⋅
(
y
k
−
o
k
)
⋅
∂
(
y
k
−
o
k
)
∂
o
i
frac{partial L}{partial o_i} = frac{1}{2}sum_{k=1}^{K}cdot2cdot(y_k-o_k)cdotfrac{partial(y_k-o_k)}{partial o_i}
∂
L
∂
o
i
=
∑
k
=
1
K
(
y
k
−
o
k
)
⋅
(
−
1
)
⋅
∂
o
k
∂
o
i
frac{partial L}{partial o_i} = sum_{k=1}^{K}(y_k-o_k)cdot(-1)cdotfrac{partial o_k}{partial o_i}
∂
o
k
∂
o
i
frac{partial o_k}{partial o_i}
Только еслиk = i Только тогда, когда1, Остальные точки0, То есть
∂
o
k
∂
o
i
frac{partial o_k}{partial o_i}
Только сiУзел числа связан и не имеет ничего общего с другими узлами, поэтому знак суммы в приведенной выше формуле можно удалить, а производную среднеквадратичной ошибки можно получить как
∂
L
∂
o
i
=
(
o
i
−
y
i
)
frac{partial L}{partial o_i} = (o_i — y_i)
Градиент одиночного нейрона
Для принятияSigmoid Нейронную модель функции активации, ее математическую модель можно записать в виде
o
1
=
σ
(
w
1
x
+
b
1
)
o^1 = sigma(w^1x+b^1)
где
- Верхний индекс переменной указывает количество слоев, например
o
1
o^1
Представляет вывод первого скрытого слоя xПредставляет вход сети
Модель одиночного нейрона показана на рисунке ниже.
- Количество входных узлов
J- Где войти
j
j
Узлы для выводаo
1
o^1
Связь веса записывается какw
j
1
1
w^1_{j1}
- Где войти
- Верхний индекс указывает количество уровней, которым принадлежит вес, а нижний индекс указывает номер начального узла и номер конечного узла текущего соединения
- Следующим образом
j
1
j1
Представляет собой первыйj
j
Номер узла к узлу номер 1 текущего слоя
- Следующим образом
- Выходная переменная без функции активации:
z
1
1
z_1^1
, Выход после активации функцииo
1
1
o_1^1
- Поскольку есть только один выходной узел,
o
1
1
=
o
1
o_1^1 = o^1
Рассчитаем среднеквадратичную ошибку как градиент функции
Поскольку один нейрон имеет только один выход, функцию потерь можно выразить как
L
=
1
2
(
o
1
1
−
t
)
2
L = frac{1}{2}(o_1^1 — t)^2
добавить
1
2
frac{1}{2}
Для удобства расчета подключаем первые
j
∈
[
1
,
J
]
jin[1,J]
Вес номера узла
w
j
1
w_{j1}
В качестве примера рассмотрим функцию потерь
L
L
Частная производная
∂
L
∂
w
j
1
frac{partial L}{partial w_{j1}}
∂
L
∂
w
j
1
=
(
o
1
−
t
)
∂
o
1
∂
w
j
1
frac{partial L}{partial w_{j1}} = (o_1 — t)frac{partial o_1}{partial w_{j1}}
, потому что
o
1
=
σ
(
z
1
)
o_1 = sigma(z_1)
, Производная сигмоидной функции может быть известна из приведенного выше вывода
σ
′
=
σ
(
1
−
σ
)
sigma’ = sigma(1-sigma)
∂
L
∂
w
j
1
=
(
o
1
−
t
)
∂
σ
(
z
1
)
∂
w
j
1
frac{partial L}{partial w_{j1}} = (o_1 — t)frac{partial sigma(z_1)}{partial w_{j1}}
=
(
o
1
−
t
)
σ
(
z
1
)
(
1
−
σ
(
z
1
)
)
∂
z
1
∂
w
j
1
= (o_1-t)sigma(z_1)(1-sigma(z_1))frac{partial z_1}{partial w_{j1}}
Ставить
σ
(
z
1
)
sigma(z_1)
Написано как
o
1
o_1
=
(
o
1
−
t
)
o
1
(
1
−
o
1
)
∂
z
1
∂
w
j
1
= (o_1-t)o_1(1-o_1)frac{partial z_1}{partial w_{j1}}
, потому что
∂
z
1
∂
w
j
1
=
x
j
frac{partial z_1}{partial w_{j1}} = x_j
∂
L
∂
w
j
1
=
(
o
1
−
t
)
o
1
(
1
−
o
1
)
x
j
frac{partial L}{partial w_{j1}} = (o_1-t)o_1(1-o_1)x_j
Из приведенной выше формулы видно, что ошибка
w
j
1
w_{j1}
Частная производная связана только с выходным значением
o
1
o_1
,реальная стоимость t И текущее весовое соединение
x
j
x_j
Связанный
Полный градиент канального уровня
Мы расширяем модель одного нейрона до однослойной полностью связанной многоуровневой сети, как показано на рисунке ниже. Входной слой получает выходной вектор через полностью связанный слой.
o
1
o^1
, И истинный вектор меткиt Рассчитайте среднеквадратичную ошибку. Количество входных узлов
J
J
, Количество выходных узлов равноK 。
В отличие от одиночного нейрона, полностью связанный слой имеет несколько выходных узлов.
o
1
1
,
o
2
1
,
o
3
1
,
.
.
.
,
o
K
1
o_1^1, o_2^1, o_3^1,…,o_K^1
, Каждый выходной узел соответствует разной истинной метке
t
1
,
t
2
,
t
3
,
.
.
.
,
t
K
t_1, t_2, t_3,…, t_K
, Среднеквадратичная ошибка может быть выражена как
L
=
1
2
∑
i
=
1
K
(
o
i
1
−
t
i
)
2
L = frac{1}{2}sum_{i=1}^K(o_i^1-t_i)^2
, потому что
∂
L
∂
w
j
k
frac{partial L}{partial w_{jk}}
Только с
o
k
1
o_k^1
Связано, символ суммы в приведенной выше формуле можно удалить, а именно
i
=
k
i = k
∂
L
∂
w
j
k
=
(
o
k
−
t
k
)
∂
o
k
∂
w
j
k
frac{partial L}{partial w_{jk}} = (o_k-t_k)frac{partial o_k}{partial w_{jk}}
будет
o
k
=
σ
(
z
k
)
o_k=sigma(z_k)
Принести в
∂
L
∂
w
j
k
=
(
o
k
−
t
k
)
∂
σ
(
z
k
)
∂
w
j
k
frac{partial L}{partial w_{jk}} = (o_k-t_k)frac{partial sigma(z_k)}{partial w_{jk}}
рассмотрите
S
i
g
m
o
i
d
Sigmoid
Производная функции
σ
′
=
σ
(
1
−
σ
)
sigma’ = sigma(1-sigma)
∂
L
∂
w
j
k
=
(
o
k
−
t
k
)
σ
(
z
k
)
(
1
−
σ
(
z
k
)
)
∂
z
k
1
∂
w
j
k
frac{partial L}{partial w_{jk}} = (o_k-t_k)sigma(z_k)(1-sigma(z_k))frac{partial z_k^1}{partial w_{jk}}
будет
σ
(
z
k
)
sigma(z_k)
Помечено как
o
k
o_k
∂
L
∂
w
j
k
=
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
∂
z
k
1
∂
w
j
k
frac{partial L}{partial w_{jk}} = (o_k-t_k)o_k(1-o_k)frac{partial z_k^1}{partial w_{jk}}
наконец-то доступен
∂
L
∂
w
j
k
=
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
⋅
x
j
frac{partial L}{partial w_{jk}} = (o_k-t_k)o_k(1-o_k)cdot x_j
Отсюда видно, что определенное соединение
w
j
k
w_{jk}
Вышеуказанное соединение только с текущим подключенным выходным узлом
o
k
1
o_k^1
, Метка соответствующего узла истинного значения
t
k
1
t_k^1
, И соответствующий входной узелx Связанный.
Мы делаем
δ
k
=
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
delta_k = (o_k-t_k)o_k(1-o_k)
, Затем
∂
L
∂
w
j
k
frac{partial L}{partial w_{jk}}
Может быть выражено как
∂
L
∂
w
j
k
=
δ
k
⋅
x
j
frac{partial L}{partial w_{jk}}=delta_kcdot x_j
где
δ
k
delta _k
Переменная представляет собой некоторую характеристику распространения градиента конечного узла соединительной линии, используя
δ
k
delta_k
После показа,
∂
L
∂
w
j
k
frac{partial L}{partial w_{jk}}
Частная производная связана только с начальным узлом текущего соединения.
x
j
x_j
, В конечном узле
δ
k
delta_k
Это более интуитивно понятно.
Алгоритм обратного распространения ошибки
Здесь не всем легко увидеть, ведь формул столько хахаха, но момент азарта настал
Сначала просмотрите формулу частной производной выходного слоя.
∂
L
∂
w
j
k
=
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
⋅
x
j
=
δ
k
⋅
x
j
frac{partial L}{partial w_{jk}} = (o_k-t_k)o_k(1-o_k)cdot x_j = delta_k cdot x_j
Многослойный полностью связанный слой показан ниже.
- Количество выходных узлов
K, Выводo
k
=
[
o
1
k
,
o
2
k
,
o
3
k
,
.
.
.
,
o
k
k
]
o^k = [o_1^k, o_2^k, o_3^k,…, o_k^k]
- Количество узлов в двух нижних слоях равно
J, Выводo
J
=
[
o
1
J
,
o
2
J
,
.
.
.
,
o
J
J
]
o^J=[o_1^J, o_2^J,…, o_J^J]
- Количество узлов в предпоследнем слое равно
I, Выводo
I
=
[
o
1
I
,
o
2
I
,
.
.
.
,
o
I
I
]
o^I = [o_1^I, o_2^I,…, o_I^I]
Функция среднеквадратичной ошибки
∂
L
∂
w
i
j
=
∂
∂
w
i
j
1
2
∑
k
(
o
k
−
t
k
)
2
frac{partial L}{partial w_{ij}}=frac{partial}{partial w_{ij}}frac{1}{2}sum_{k}(o_k-t_k)2
, потому что
L
L
Через каждый выходной узел
o
k
o_k
против
w
i
w_i
Связано, поэтому здесь нельзя удалить символ суммы
∂
L
∂
w
i
j
=
∑
k
(
o
k
−
t
k
)
∂
o
k
∂
w
i
j
frac{partial L}{partial w_{ij}}=sum_k(o_k-t_k)frac{partial o_k}{partial w_{ij}}
будет
o
k
=
σ
(
z
k
)
o_k=sigma(z_k)
Принести в
∂
L
∂
w
i
j
=
∑
k
(
o
k
−
t
k
)
∂
σ
(
z
k
)
∂
w
i
j
frac{partial L}{partial w_{ij}}=sum_k(o_k-t_k)frac{partial sigma(z_k)}{partial w_{ij}}
S
i
g
m
o
i
d
Sigmoid
Производная функции
σ
′
=
σ
(
1
−
σ
)
sigma’ = sigma(1-sigma)
, Продолжайте искать производные и
σ
(
z
k
)
sigma(z_k)
Напишите ответ
o
k
o_k
∂
L
∂
w
i
j
=
∑
k
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
∂
z
k
∂
w
i
j
frac{partial L}{partial w_{ij}}=sum_k(o_k-t_k)o_k(1-o_k)frac{partial z_k}{partial w_{ij}}
для
∂
z
k
∂
w
i
j
frac{partial z_k}{partial w_{ij}}
Его можно разложить на
∂
z
k
∂
w
i
j
=
∂
z
k
o
j
⋅
∂
o
j
∂
w
i
j
frac{partial z_k}{partial w_{ij}} = frac{partial z_k}{o_j}cdot frac{partial o_j}{partial w_{ij}}
видно на картинке
(
z
k
=
o
j
⋅
w
j
k
+
b
k
)
left(z_k = o_j cdot w_{jk} + b_kright)
, Итак, есть
∂
z
k
o
j
=
w
j
k
frac{partial z_k}{o_j} = w_{jk}
Итак
∂
L
∂
w
i
j
=
∑
k
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
w
j
k
⋅
∂
o
j
∂
w
i
j
frac{partial L}{partial w_{ij}}=sum_k(o_k-t_k)o_k(1-o_k)w_{jk}cdotfrac{partial o_j}{partial w_{ij}}
учитывая
∂
o
j
∂
w
i
j
frac{partial o_j}{partial w_{ij}}
против k Неактуально, можно извлечь
∂
L
∂
w
i
j
=
∂
o
j
∂
w
i
j
⋅
∑
k
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
w
j
k
frac{partial L}{partial w_{ij}}=frac{partial o_j}{partial w_{ij}}cdotsum_k(o_k-t_k)o_k(1-o_k)w_{jk}
еще раз
o
k
=
σ
(
z
k
)
o_k=sigma(z_k)
И использовать
S
i
g
m
o
i
d
Sigmoid
Производная функции
σ
′
=
σ
(
1
−
σ
)
sigma’ = sigma(1-sigma)
Есть
∂
L
∂
w
i
j
=
o
j
(
1
−
o
j
)
∂
z
j
∂
w
i
j
⋅
∑
k
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
w
j
k
frac{partial L}{partial w_{ij}}= o_j(1-o_j)frac{partial z_j}{partial w_{ij}} cdotsum_k(o_k-t_k)o_k(1-o_k)w_{jk}
, потому что
∂
z
j
∂
w
i
j
=
o
i
(
z
j
=
o
i
⋅
w
i
j
+
b
j
)
frac{partial z_j}{partial w_{ij}} = o_i left(z_j = o_icdot w_{ij} + b_jright)
∂
L
∂
w
i
j
=
o
j
(
1
−
o
j
)
o
i
⋅
∑
k
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
w
j
k
frac{partial L}{partial w_{ij}}= o_j(1-o_j)o_i cdotsum_k(o_k-t_k)o_k(1-o_k)w_{jk}
где
δ
k
K
=
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
delta _k^K = (o_k-t_k)o_k(1-o_k)
,затем
∂
L
∂
w
i
j
=
o
j
(
1
−
o
j
)
o
i
⋅
∑
k
δ
k
K
⋅
w
j
k
frac{partial L}{partial w_{ij}}= o_j(1-o_j)o_i cdotsum_kdelta _k^Kcdot w_{jk}
имитируя метод записи выходного слоя, определите
δ
j
J
=
o
j
(
1
−
o
j
)
⋅
∑
k
δ
k
K
⋅
w
j
k
delta_j^J = o_j(1-o_j) cdot sum_k delta _k^Kcdot w_{jk}
На этом этапе
∂
L
∂
w
i
j
frac{partial L}{partial w_{ij}}
Может быть записано как выходное значение начального узла текущего соединения
o
i
o_i
И конечный узел
j
j
Информация о градиенте
δ
j
J
delta _j^J
Простая операция умножения:
∂
L
∂
w
i
j
=
δ
j
J
⋅
o
i
I
frac{partial L}{partial w_{ij}} = delta_j^Jcdot o_i^I
по определению
δ
delta
Переменные, выражение градиента каждого слоя становится более ясным и кратким, где $ delta $ можно просто понимать как текущее соединение
w
i
j
w_{ij}
Вклад в функцию ошибок.
подводить итоги
Выходной слой:
∂
L
∂
w
j
k
=
δ
k
K
⋅
o
j
frac{partial L}{partial w_{jk}} = delta _k^Kcdot o_j
δ
k
K
=
(
o
k
−
t
k
)
o
k
(
1
−
o
k
)
delta _k^K = (o_k-t_k)o_k(1-o_k)
Предпоследний слой:
∂
L
∂
w
i
j
=
δ
j
J
⋅
o
i
frac{partial L}{partial w_{ij}} = delta _j^Jcdot o_i
δ
j
J
=
o
j
(
1
−
o
j
)
⋅
∑
k
δ
k
K
⋅
w
j
k
delta_j^J = o_j(1-o_j) cdot sum_k delta _k^Kcdot w_{jk}
Третий нижний слой:
∂
L
∂
w
n
i
=
δ
i
I
⋅
o
n
frac{partial L}{partial w_{ni}} = delta _i^Icdot o_n
δ
i
I
=
o
i
(
1
−
o
i
)
⋅
∑
j
δ
j
J
⋅
w
i
j
delta _i^I = o_i(1-o_i)cdot sum_jdelta_j^Jcdot w_{ij}
среди них
o
n
o_n
Является ли входом предпоследнего слоя, то есть выходом предпоследнего слоя.
Согласно этому правилу, нужно только итеративно выполнять цикл, чтобы вычислить
δ
k
K
,
δ
j
J
,
δ
i
I
,
.
.
.
delta _k^K, delta_j^J, delta_i^I,…
Частную производную текущего слоя можно получить равным значением, тем самым получая матрицу весов каждого слоя
W
W
Затем параметры сети можно итеративно оптимизировать с помощью алгоритма градиентного спуска.
Хорошо, алгоритм обратного распространения выведен, и реализация кода может ссылаться на другой блогПрактическая реализация алгоритма обратного распространения (BP) нейронной сети