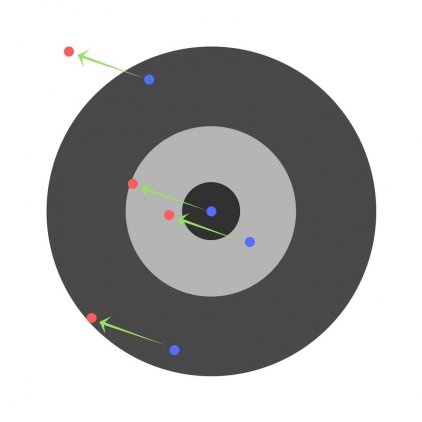
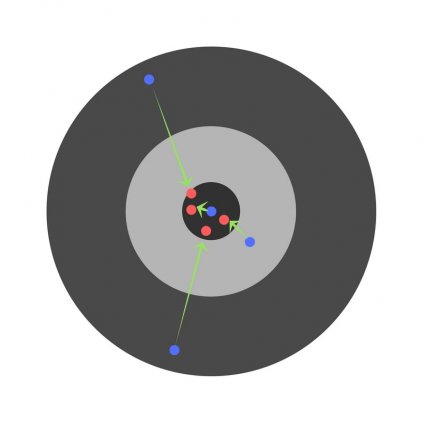
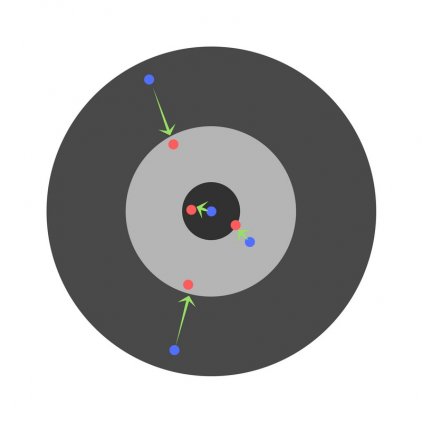
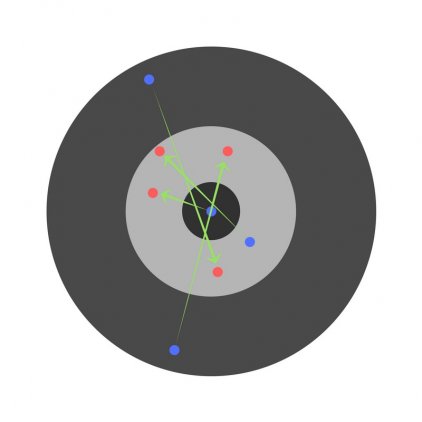
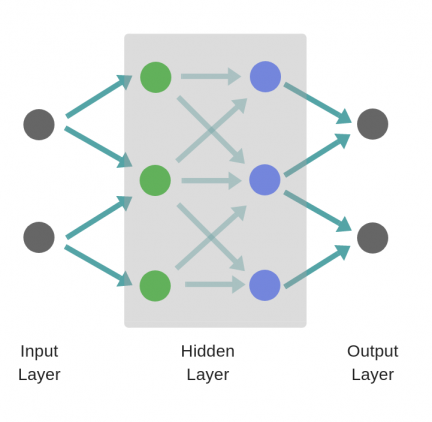
Подробно рассматриваем обратное распространение ошибки для простой нейронной сети. Численный пример
Уровень сложности
Средний
Время на прочтение
6 мин
Количество просмотров 4.6K
В данной статье мы рассмотрим прямое распространение сигнала и обратное распространение ошибки в полносвязной нейронной сети прямого распространения. В результате получим весь набор формул, необходимых для программной реализации нейронной сети. В завершении статьи рассмотрим численный пример.
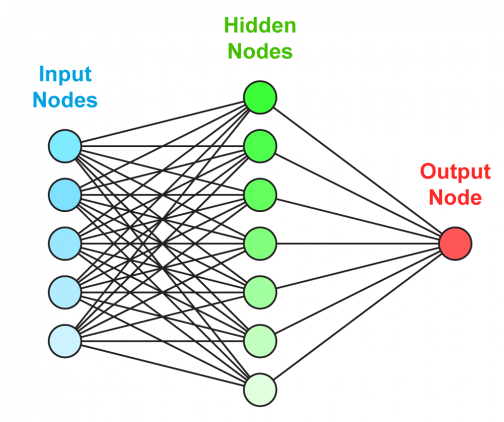
«Полносвязная» (fully connected) — означает, что каждый нейрон предыдущего слоя соединён с каждым нейроном следующего слоя. «Прямого распространения» (feedforward) — означает, что сигнал проходит через нейронную сеть в одном направлении от входного к выходному слою.
Полносвязная нейронная сеть прямого распространения («перцептрон») — это простейший и наиболее типичный пример искусственной нейронной сети.
Содержание
-
Нейронная сеть как функция
-
Дизайн нейронной сети
-
Прямое распространение сигнала
-
Обратное распространение ошибки и обновление
4.1. Вычисление новых весов матрицы W^3
4.2. Вычисление новых смещений вектора b^3
4.3. Вычисление новых весов матрицы W^2
4.4. Вычисление новых смещений вектора b^2
-
Численный пример
-
Обобщение для произвольного числа слоёв
Нейронная сеть как функция
Искусственная нейронная сеть является математической функцией, а точнее — композицией (суперпозицией) функций.
Было доказано (George Cybenko, 1989), что полносвязная нейронная сеть прямого распространения с хотя бы одним скрытым слоем и достаточным количеством нейронов потенциально может аппроксимировать любую непрерывную функцию, т.е. по своей сути она — универсальный аппроксиматор.
«Свойства универсальной аппроксимации встречаются в математике чаще, чем можно было бы ожидать. Например, теорема Вейерштрасса — Стоуна доказывает, что любая непрерывная функция на замкнутом интервале может быть приближена многочленной функцией. Если ослабить наши критерии далее, можно использовать ряды Тейлора и ряды Фурье, предлагающие некоторые возможности универсальной аппроксимации (в пределах их областей схождения). Тот факт, что универсальная сходимость — довольно обычное явление в математике, дает частичное обоснование эмпирического наблюдения, что существует много малых вариантов полносвязных сетей, которые, судя по всему, дают свойство универсальной аппроксимации».
— Рамсундар Б., Заде Р.Б. TensorFlow для глубокого обучения. Спб., 2019. С. 101.
Запишем нейронную сеть, которую мы будем рассматривать в данной статье, в виде функции:
где — вектор входных значений — первый слой,
— второй, скрытый и
— третий слои нейронной сети,
,
— векторы смещений и
,
— матрицы весов второго и третьего слоёв соответственно,
— вектор-функция активации второго слоя,
— вектор-функция активации третьего, последнего слоя и, соответственно, вектор выходных значений нейронной сети.
Мы будем использовать принятую в литературе по нейронам сетям запись , где
— вектор-столбец (в литературе по математике под вектором стандартно (по умолчанию) понимается вектор-столбец). Произведение матриц
определено, если число столбцов
равно числу строк
. Таким образом число столбцов
матрицы
равно числу строк
векторов
и
.
Для комфортного чтения статьи необходимо обладать некоторым знанием линейной алгебры (обязательный минимум — операции над матрицами), производной сложной функции и частных производных.
Дизайн нейронной сети
Нейронная сеть имеет три слоя с тремя нейронами в каждом из них. Нелинейное изменение проходящего через сеть сигнала обеспечивает функция активации сигмоид (sigmoid) на скрытом и выходном слоях:
Поскольку на практике большинство реальных данных имеют нелинейный характер, используются нелинейные функции активации, позволяющие извлекать нелинейные зависимости в данных.
Перепишем уравнение рассматриваемой сети для заданных параметров:
Функция активации поэлементно применяется к каждому элементу соответствующего вектора .
Прямое распространение сигнала
Запишем уравнения для прямого прохождения сигнала через нейронную сеть:
и функцию стоимости (cost function)
где — номер соответствующего целевого
(вектора
) и выходного
значений,
— число выходных значений.
Таким образом, функция стоимости для нашей нейронной сети в развёрнутом виде:
Функция стоимости показывает нам насколько сильно отличаются текущие значения нейронной сети от целевых.
Обратное распространение ошибки и обновление
В сущности, для реализации алгоритма обратного распространения ошибки используется довольно простая идея.
Градиент (в общем случае) — вектор, определяющий направление наискорейшего роста функции нескольких переменных. Вычитая из текущих значений весов и смещений соответствующие значения частных производных как элементов градиента функции стоимости , мы будем приближаться к одному из ближайших (относительно начальной точки) минимумов функции стоимости и, таким образом, уменьшать величину ошибки. Согласно необходимому условию экстремума, в точках экстремума функции многих переменных её градиент равен нулю,
.
Этот подход называется алгоритмом градиентного спуска. Иногда может возникать путаница или отождествление этих двух алгоритмов, поскольку они тесно взаимосвязаны и один используется для реализации другого.
Несмотря на простоту и эффективность, алгоритм градиентного спуска в общем случае имеет свои ограничения, например, седловая точка, локальный минимум, перетренировка (overtraining) (попадание в глобальный минимум).
Найдём частные производные по всем элементам матрицы :
поскольку — константа, то
,
Преобразуем функцию активации сигмоид и найдём её производную:
В производной по матрице мы находим производную по каждому из её элементов.
Раскроем сумму для переменной матрицы
:
Найдём частную производную по переменной . Поскольку
Преобразуем сигмоид и получим окончательную форму выражения для :
Обратное распространение ошибки является частным случаем автоматического дифференцирования, для реализации которого нам и необходимо привести все вычислительные выражения к определённому виду.
Таким же образом для переменных и
получим:
Найдём новые значения (обновлённые веса) для переменных ,
и
:
где (и́та) — буква греческого алфавита, обычно используемая для обозначения скорости обучения (learning rate), её значение должно быть установлено на промежутке от 0 до 1; * — новое значение переменной.
Найдём остальные частные производные для матрицы . Раскроем сумму для
:
Найдём частную производную по переменной :
Преобразуем сигмоид и получим окончательную форму выражения для :
Таким же образом для переменных и
получим:
Найдём новые значения (обновлённые веса) для переменных ,
и
:
Раскроем сумму для :
Найдём частную производную по переменной :
Преобразуем сигмоид и получим окончательную форму выражения для :
Таким же образом для переменных и
получим:
Найдём новые значения (обновлённые веса) для переменных ,
и
:
Теперь найдём частные производные по всем элементам вектора :
Найдём частную производную по :
Преобразуем сигмоид и получим окончательную форму выражения для :
Найдём новое значение для смещения :
Вычислим частные производные по и
:
Найдём новые значения для и
:
Найдём частные производные по всем элементам матрицы . Раскроем сумму для переменной
матрицы
. Поскольку
в свою очередь,
тогда сумма для переменной матрицы
:
Найдём новое значение (обновлённый вес) для переменной :
Найдём остальные частные производные и их новые значения для матрицы .
Теперь найдём частные производные по всем элементам вектора . Раскроем сумму для переменной
:
Найдём новое значение для :
Найдём остальные частные производные для вектора :
Найдём новые значения для переменных и
:
Численный пример
Задача обучения нейронной сети состоит в аппроксимации некоторой неизвестной функции, которая отображает в
.
Другими словами, существует некоторая неизвестная нам функция , которая для набора значений независимых переменных
выдаёт результат, соответствующий набору значений зависимых переменных
. Задача нейронной сети в результате обучения «заменить», приблизить, т.е. аппроксимировать неизвестную функцию
. В случае успешного решения задачи, значения нашей нейронной сети на выходном слое
будут приблизительно равны значениям вектора
аппроксимируемой функции.
Выберем случайным образом следующие начальные значения для нашей нейронной сети:
А также входные и целевые значения:
После первого прямого прохождения сигнала значения скрытого и выходного слоёв:
Для скорости обучения установим значение .
Вычислим для первой эпохи (epoch) обучения нейронной сети обновлённые значения весов и
:
Новые значения других весов и смещений находятся аналогичным образом, в соответствии с полученными ранее формулами.
После 10 000 эпох обучения матрицы весов и выходной слой имеют следующие значения:
Обобщение для произвольного числа слоёв
Мы рассмотрели частный случай алгоритма обратного распространения ошибки для нейронной сети с одним скрытым слоем. Запишем формулы для реализации нейронной сети с произвольным числом скрытых слоёв.
где — номер выходного слоя,
— индекс строки матрицы весов,
— число выходных значений.
— обобщённое дельта-правило (delta rule).
Надеемся, что статья будет интересной и полезной для всех, кто приступает к изучению глубинного обучения и нейронных сетей!
Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.
Искусственная нейронная сеть обычно обучается с учителем. Это означает наличие обучающего набора (датасета), который содержит примеры с истинными значениями: тегами, классами, показателями.
Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.
Например, если вы хотите создать нейросеть для оценки тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.
Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.
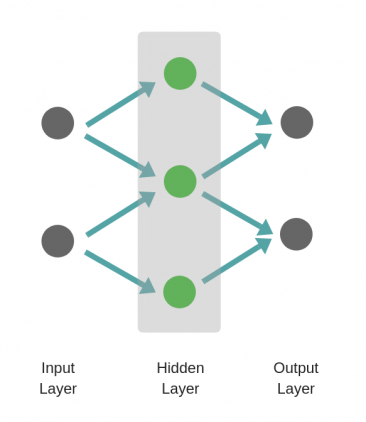
Искусственная нейронная сеть состоит из трех компонентов:
- Входной слой;
- Скрытые (вычислительные) слои;
- Выходной слой.
Обучение нейросетей происходит в два этапа:
- Прямое распространение ошибки;
- Обратное распространение ошибки.
Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.
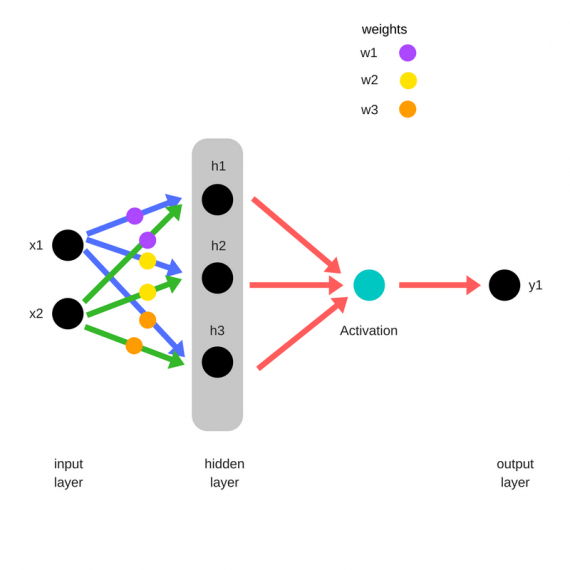
Прямое распространение ошибки
Зададим начальные веса случайным образом:
- w1
- w2
- w3
Умножим входные данные на веса для формирования скрытого слоя:
- h1 = (x1 * w1) + (x2 * w1)
- h2 = (x1 * w2) + (x2 * w2)
- h3 = (x1 * w3) + (x2 * w3)
Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:
- y_ = fn(h1 , h2, h3)
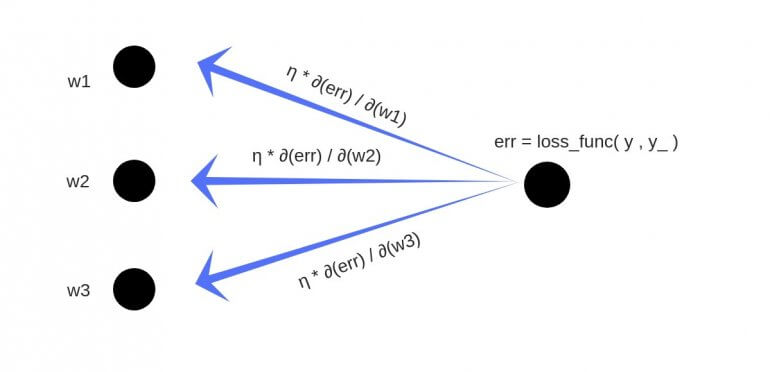
Обратное распространение
- Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
- Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
- Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).
Полученный результат затем вычитается из соответствующих весов.
В результате получатся следующие обновленные веса:
- w1 = w1 — (η * ∂(err) / ∂(w1))
- w2 = w2 — (η * ∂(err) / ∂(w2))
- w3 = w3 — (η * ∂(err) / ∂(w3))
То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.
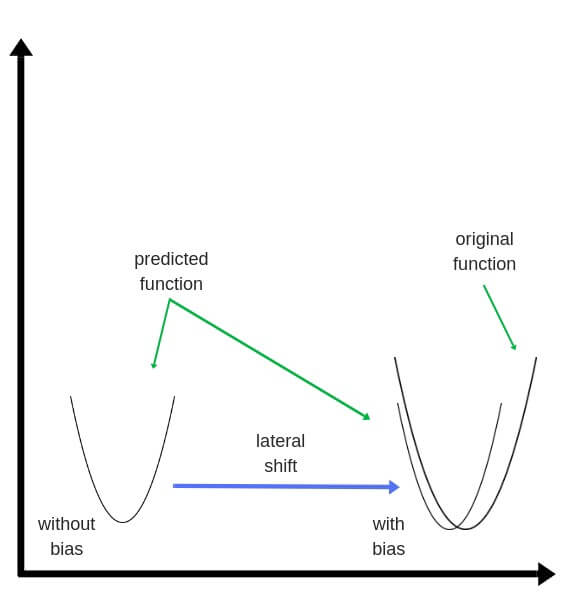
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.
Частные производные
Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.
Разберем необходимость частных производных на примере.
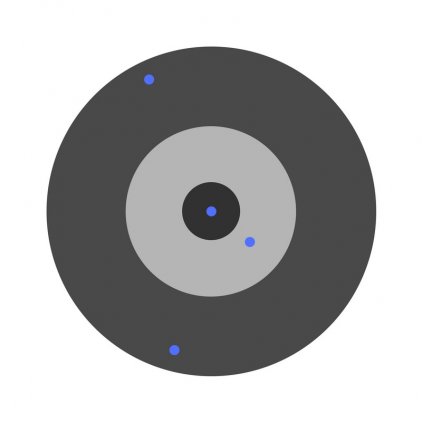
Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:
Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.
Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:
Гиперпараметры
Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.
Скорость обучения (learning rate)
Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:
С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:
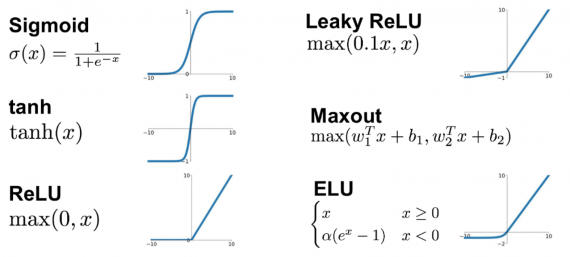
Функция активации (activation function)
Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.
Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:
Функция потери (loss function)
Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.
Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.
Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.
Некоторые известные функции потерь:
- Квадратичная (среднеквадратичное отклонение);
- Кросс-энтропия;
- Экспоненциальная (AdaBoost);
- Расстояние Кульбака — Лейблера или прирост информации.
Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:
Функция потерь в нейронной сети должна удовлетворять двум условиям:
- Функция потерь должна быть записана как среднее;
- Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.
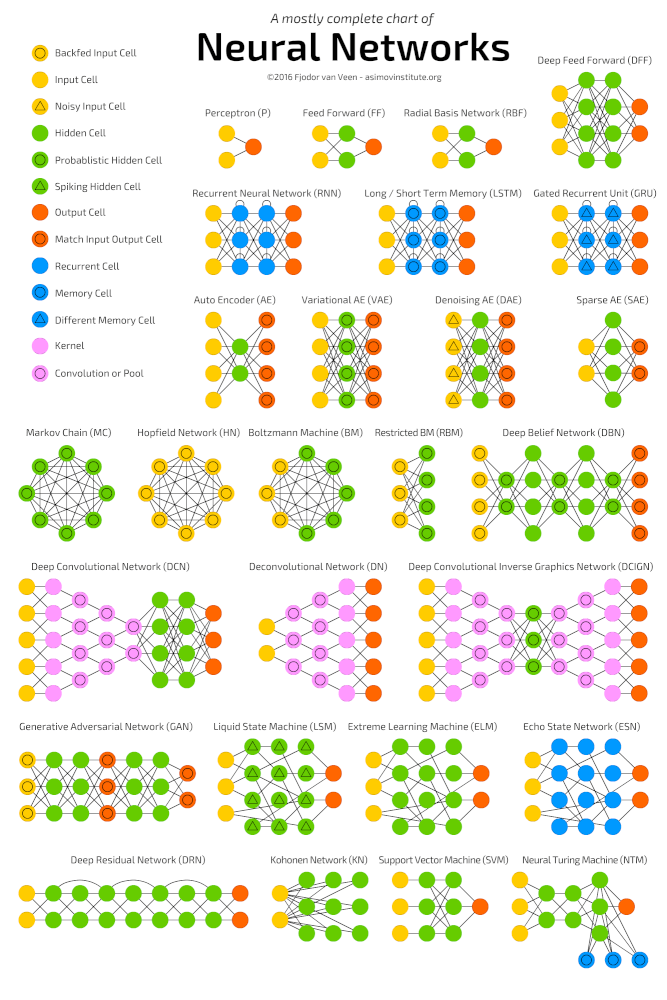
Глубокие нейронные сети
Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.
Более формально в deep learning:
- Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
- Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
- Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.
Пример
Рассмотрим однослойную нейронную сеть:
Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.
В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:
Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.
Не следует путать с широкой нейронной сетью.
В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.
Пример:
Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.
Но
В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.
Главное — баланс
Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:
- Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
- Обе имеют экспоненциальную сложность;
- Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
- Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.
Проклятье размерности
Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.
Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:
- Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
- От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.
Компромисс
На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.
В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.
Действительно,
алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.
Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.
Сейчас есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
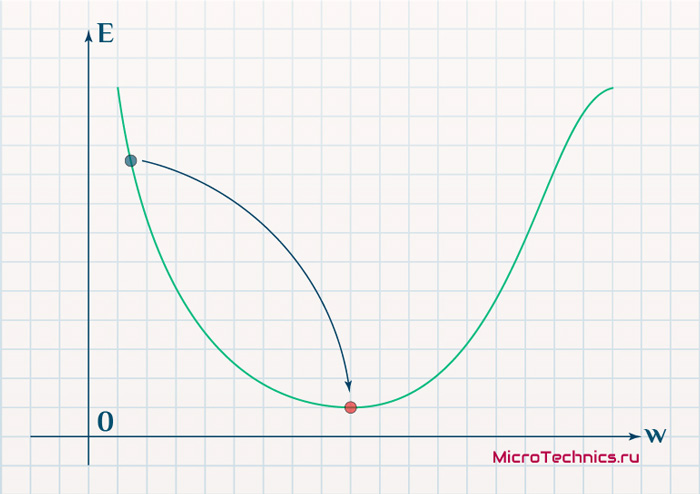
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
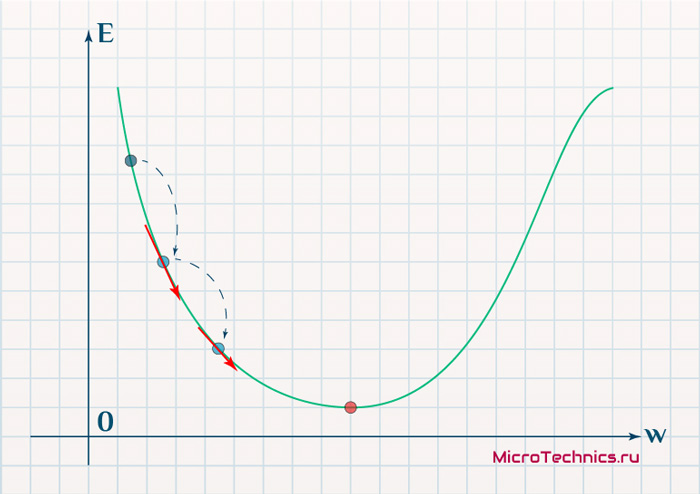
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
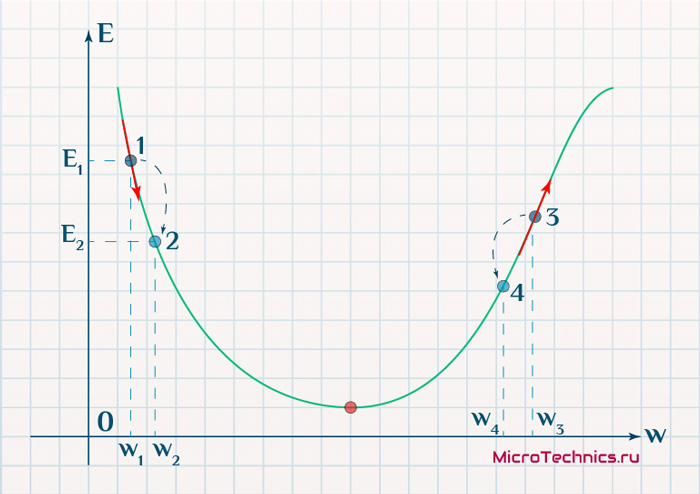
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
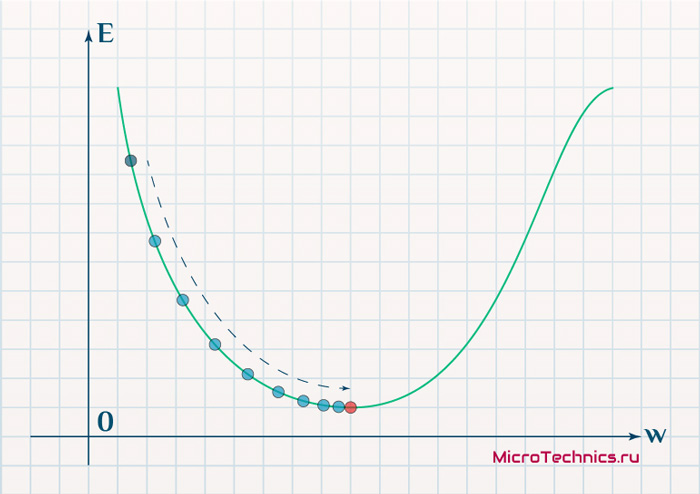
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
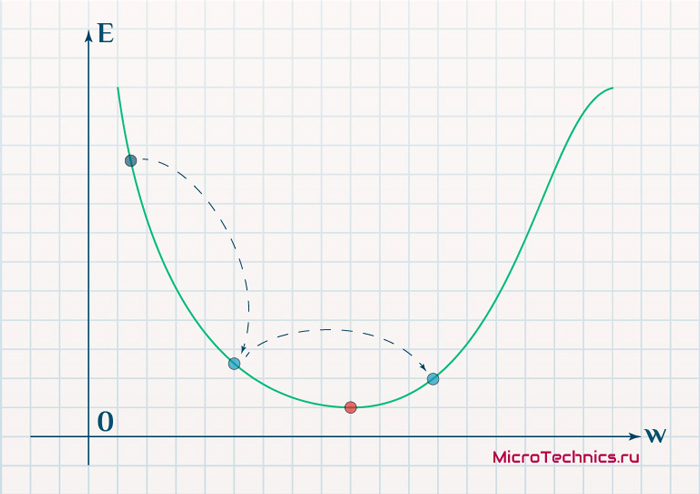
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
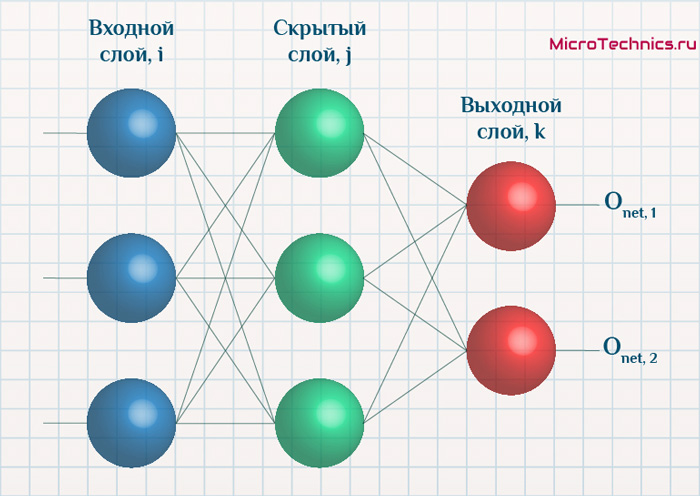
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
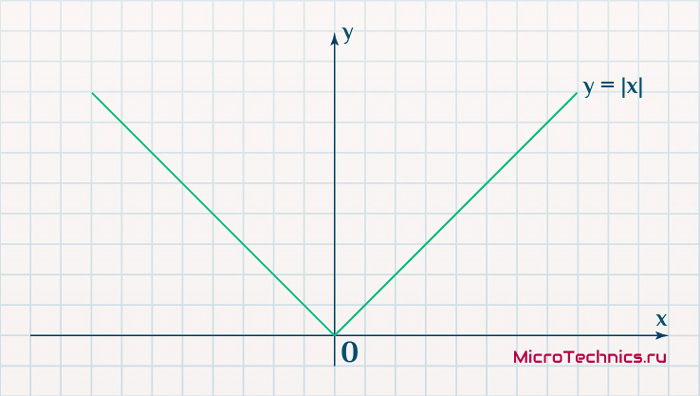
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
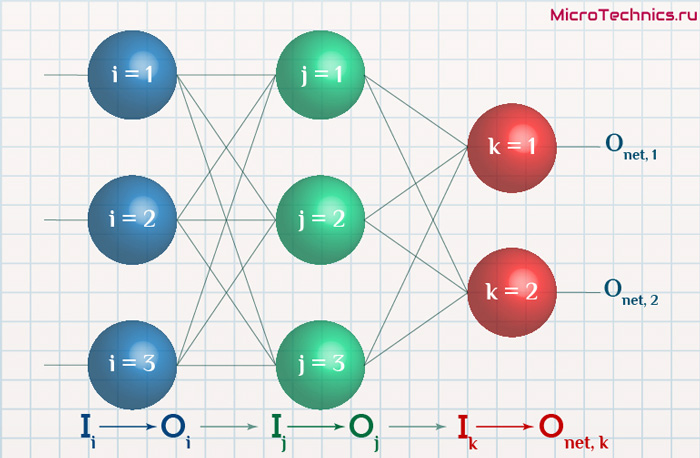
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
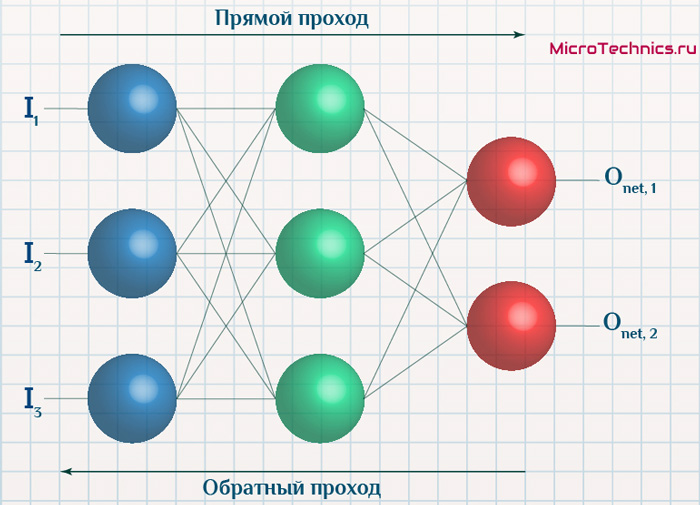
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
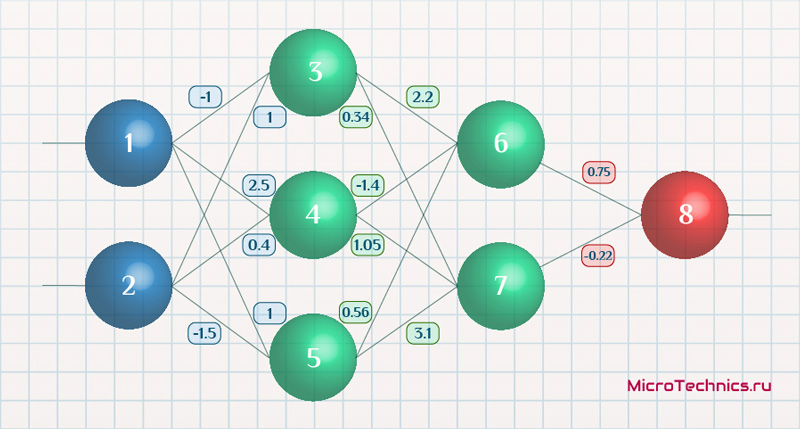
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Все курсы > Оптимизация > Занятие 6
В рамках вводного курса мы начали изучать нейросети. Кроме того, нам знаком важный элемент алгоритма нейронной сети — умножение матриц.
На сегодняшнем занятии мы более подробно поговорим про то, почему нейросеть может оказаться более эффективным алгоритмом, чем рассмотренные ранее линейная и логистическая регрессия.
Кроме того, обладая знаниями о производной и градиенте, мы разберем до сих пор неизученный компонент, а именно процесс оптимизации, который в терминологии нейросетей называется обратным распространением, и построим несколько алгоритмов с нуля.
Зачем нужна нейронная сеть
Нелинейная гипотеза
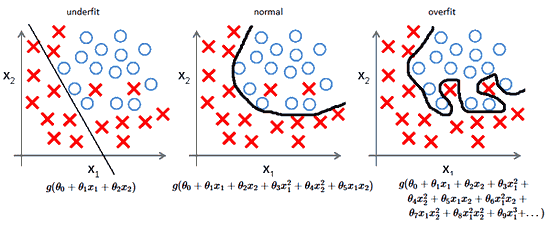
Мы уже знаем, что некоторые гипотезы нелинейны. В случае задачи классификации и алгоритма логистической регрессии это означает, что, как видно на графике ниже, два класса нельзя разделить прямой линией (еще говорят, что они линейно неразделимы).
Можно обучить полиномиальную логистическую регрессию, однако с ростом количества признаков и степени полинома итоговое количество признаков, а значит и «затратность» алгоритма с точки зрения вычислительных ресурсов будет расти.
Для полинома n-ой степени (с одним признаком!) формула выглядит следующим образом.
$$ y = sum{}^n_{j=0} theta_j x^j $$
Например, полином второй степени будет иметь три коэффициента.
$$ y = theta_0 + theta_{1}x + theta_{2}x^2 $$
Полином второй степени с двумя признаками уже будет иметь шесть коэффициентов.
$$ y = theta_{0} + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
В целом, количество полиномиальных коэффициентов (N) можно рассчитать по формуле.
$$ N(n, d) = C(n+d, d), text{где} $$
- n — количество линейных признаков
- d — степень полинома
- C — количество возможных сочетаний
Используя пример выше, получим
$$ N(2, 2) = C(4, 2) = 6 $$
Полином третьей степени на основе десяти линейных признаков уже потребует создать 286 коэффициентов.
$$ N(10, 3) = C(13, 10) = 286 $$
Если речь идет о картинках 28 х 28 пикселей, то после «вытягивания» каждой картинки у нас появится датасет с 784 признаками. Значит, количество членов полинома второй степени составит
$$ N(784, 2) = C(786, 2) = 308 505 $$
Замечу, что примерное количество признаков полинома второй степени также можно посчитать по формуле $ frac{(n)^2}{2} $, то есть $ frac{(784)^2}{2} = 307 328 $
Такое количество признаков потребует очень больших вычислительных ресурсов. Посмотрим, как нейросеть может помочь справиться с этой сложностью.
Работа нейронной сети
Рассмотрим работу нейронных сетей с трех различных углов зрения.
Нейрон как дополнительный признак
Возьмем упрощенную модель нейронной сети с двумя скрытыми слоями.
Каждый нейрон каждого из скрытых слоев можно рассматривать как новый, дополнительный признак, зачастую нелинейный, способный уловить то, что не могут уловить линейные признаки. При этом умножение матриц, лежащее в основе работы нейронной сети, и векторизация операций позволяют сделать этот алгоритм достаточно быстрым.
Слой как модель логистической регрессии
Одновременно, если считать, что каждый скрытый слой проходит через функцию активации (activation function), зачастую сигмоиду, то каждый слой, кроме выходного, можно представить как, например, модель логистический регрессии.
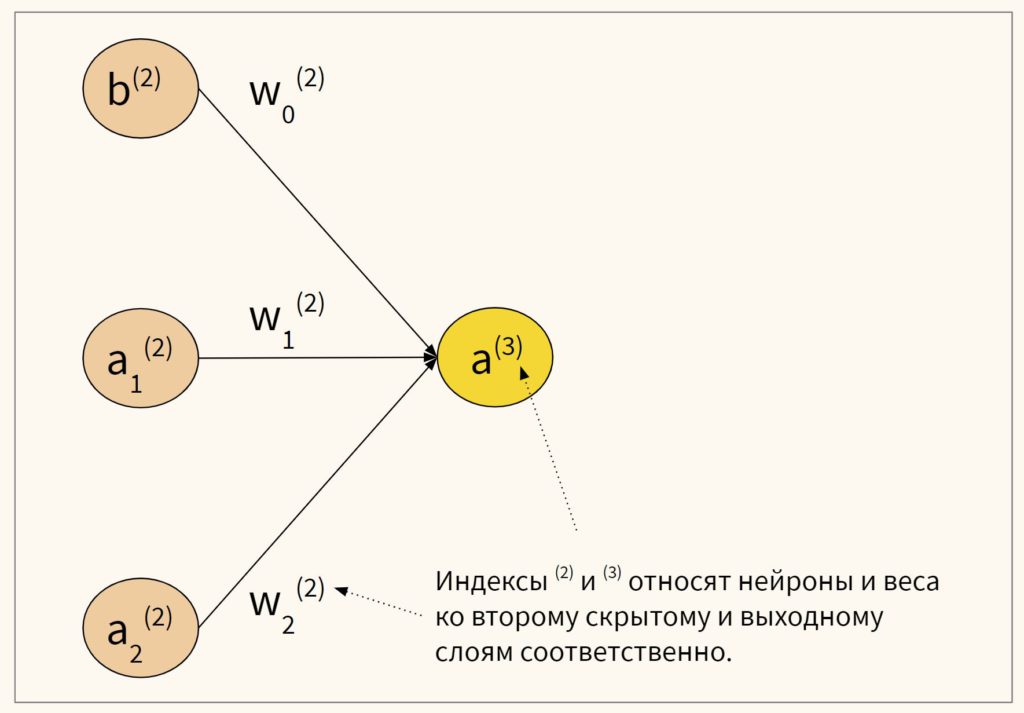
Для модели представленной выше рассмотрим как из второго скрытого слоя получается значение выходного слоя.
- На основе первого скрытого слоя мы получили некоторые значения нейронов второго скрытого слоя ($a_1^{(2)}$ и $a_2^{(2)}$)
- У нас есть вектор весов ($w_1^{(2)}$ и $w_2^{(2)}$)
- Кроме того, мы добавим смещение (b^{(2))
Замечу, что для удобства матричных операций мы можем добавить еще один нейрон скрытого слоя ($w_0^{(2)}$) со значением 1 так, как мы это делали, например, в модели линейной регрессии.
Результат умножения двух векторов мы пропустим через сигмодиду или функцию активации (отсюда выбор буквы a для обозначения этих нейронов) и таким образом получим значение выходного слоя ($a^{(3)}$). Уверен, вы распознали уравнение логистической регрессии.
$$ a^{(3)} = g(w_0^{(2)} cdot b^{(2)} + w_1^{(2)} cdot a_1^{(2)} + w_2^{(2)} cdot a_2^{(2)}) $$
Соответственно, имея два скрытых слоя, мы строим две связанные между собой логистические регрессии. И вдвоем они могут запомнить более сложные зависимости, чем смогла бы одна такая модель, одновременно преодолевая проблему роста количества признаков полиномиальной модели.
Нейросеть и таблица истинности
Продемонстрируем, как нейросеть обучается на нелинейной гипотезе с помощью таблиц истинности.
Этот пример взят из курса по машинному обучению Эндрю Ына⧉ (Andrew Ng).
Рассмотрим линейно неразделимые данные двух классов (на рисунке слева) и упростим их до четырех наблюдений, которые могут принимать только значения 0 и 1 (на рисунке справа).
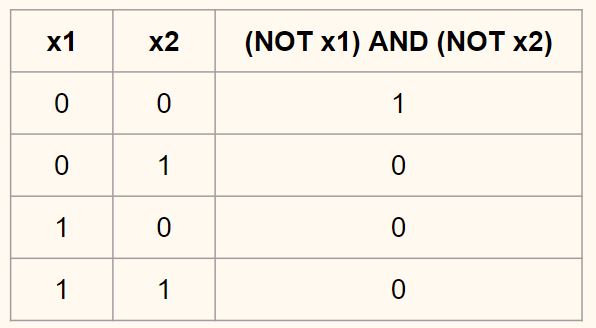
Логически такая схема соответствует условию $x_1 XNOR x_2$ или $ NOT x_1 XNOR x_2 $. В таблице истинности это условие выглядит так.
Другими словами, когда наблюдение по обоим признакам $x_1$ и $x_2$ имеет значение 0, то результатом будет класс 1, когда хотя бы один из признаков равен единице, то класс 0.
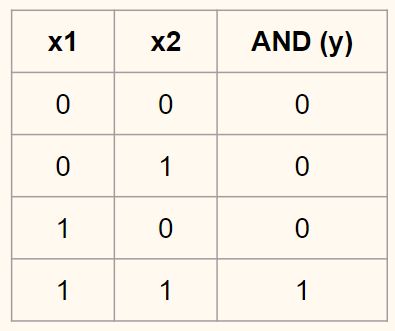
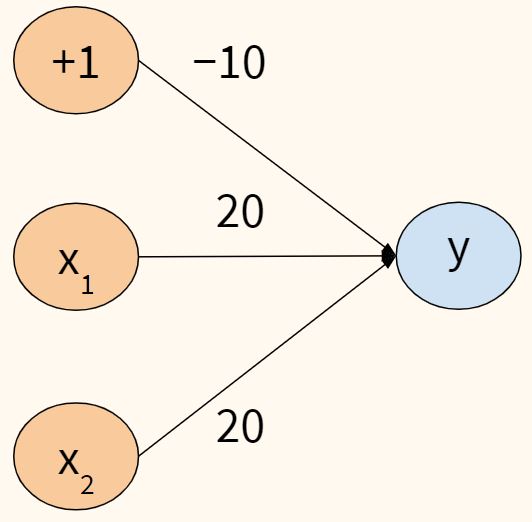
Построим нейросеть, которая будет предсказывать именно такую зависимость. Начнем с более простого компонента, а именно нейросети, которая делает прогноз в соответствии с логическим И (AND).
Итак, $x_1. x_2 in {0, 1} $ и $y = x_1 AND x_2 $. В нейросети будет два нейрона для признаков + смещение. Одновременно сразу пропишем веса модели.
Тогда выражение будет иметь вид, $y_{AND} = sigmoid(-30 + 20x_1 + 20x_2)$. Вспомним, как выглядит график сигмоиды.
Рассмотрим четыре варианта значений $x_1, x_2$ применительно к такой гипотезе.
- Если оба признака будут равны нулю, то результат линейного выражения будет равен $-30$. Если «пропустить» это значение через сигмоиду, то результат будет близок к нулю.
- Если один из них будет равен нулю, а второй единице, то результат будет равен $-10$. Сигмоида опять выдаст близкое к нулю значение.
- И только если оба признака равны единице, то результат будет равен 10 и сигмоида выдаст значение близкое к единице.
Это и есть условие логического И. Аналогичным образом можно подобрать веса для логического ИЛИ (OR).
Соответственно $y_{OR} = sigmoid(-10 + 20x_1 + 20x_2)$. Создадим еще более простую сеть для логического НЕ (NOT).
Как следствие, $y_{NOT} = sigmoid(10-20x_1)$. Создадим нейросеть, которая будет предсказывать NOT($x1$) AND NOT($x2$).
Объединим эти сети в одну.
Рассчитаем таблицу истинности.
Таким образом, мы видим, что на каждом последующем слое нейросеть строит все более сложную зависимость. Первый скрытый слой обучился достаточно простым зависимостям ($x_1$ AND $x_2$ и NOT($x_1$) AND NOT($x_2$)), второй слой дополнил это знание новым ($x1$ OR $x2$), и вместе они обучились выдавать достаточно сложный результат ($x_1$ XNOR $x_2$).
Подготовка данных
Давайте вновь возьмем данные о вине, построим вначале бинарный, а затем мультиклассовый классификатор и посмотрим, сможет ли нейросеть улучшить показатели логистической регрессии.
Откроем ноутбук к этому занятию⧉
Импортируем датасет о вине, удалим класс 2, из признаков оставим спирт и пролин, масштабируем данные.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# импортируем датасет from sklearn import datasets data = datasets.load_wine() # сформируем датафрейм и добавим целевую переменную df = pd.DataFrame(data.data, columns = data.feature_names) df[‘target’] = data.target # удалим класс 2 df = df[df.target != 2] # оставим только спирт и пролин X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # масштабируем признаки X = (X — X.mean()) / X.std() # посмотрим на размерность и оставшиеся классы df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Дополнительно преобразуем датафрейм признаков X в массив Numpy с размерность 2 x 130 и сделаем целевую переменную y двумерным массивом.
|
# каждый столбец — это одно наблюдение X = X.to_numpy().T X.shape |
|
y = y.to_numpy().reshape(1, —1) y.shape |
Нейросеть без смещения
Архитектура сети
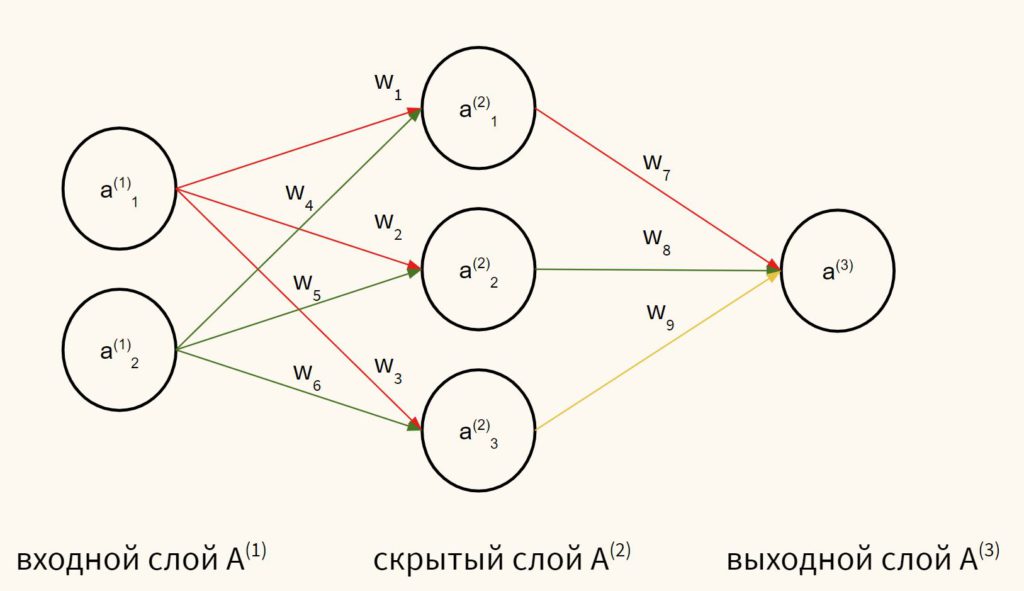
Предлагаю идти от простого к сложному и на первом этапе создать алгоритм для бинарной классификации без смещения (bias) с приведенной ниже архитектурой.
Итак, сеть будет состоять из следующих слоев:
- входной слой $A^{(1)}$ из двух нейронов $a^{(1)}_1$ и $a^{(1)}_2$ т.е. двух признаков, на основе которых мы будем предсказывать класс вина;
- один скрытый слой $A^{(2)}$, состоящий из трех нейронов: $a^{(2)}_1$, $a^{(2)}_2$ и $a^{(2)}_3$; и
- выходной слой из одного нейрона $a^{(3)}$, т.е. вероятности принадлежности к одному из двух классов
Заглавной буквой, например, $A^{(1)}$ обозначаются сразу все нейроны, в данном случае, входного слоя, строчной с соответствющим индексом $a^{(1)}_1$ — отдельный нейрон этого слоя.
Также напомню, что у нас последовательная (sequential) архитектура сети, при которой каждый слой получает один тензор на вход и выдает также только один тензор. Кроме этого, мы используем полносвязные (дословно, «плотно связанные», dense, densely connected) слои, где каждый нейрон одного слоя связан с каждым нейроном последующего (обратите внимание на красные и зеленые стрелки между входным и скрытым слоями).
Размерность матриц
Алгоритм нейронной сети, в конечном счете, не более чем умножение матриц или, в общем случае, тензоров (отсюда, в частности, название библиотеки Tensorflow⧉, которой мы пользовались, изучая основы нейронных сетей) и после выбора архитектуры модели нам важно определиться с размерностью используемых нами матриц.
Первая матрица весов
Начнем со входного слоя, в который мы одновременно (за счет умножения матриц и векторизации кода) подадим матрицу из 130 наблюдений и двух признаков (после транспонирования размерность напомню была 2 x 130).
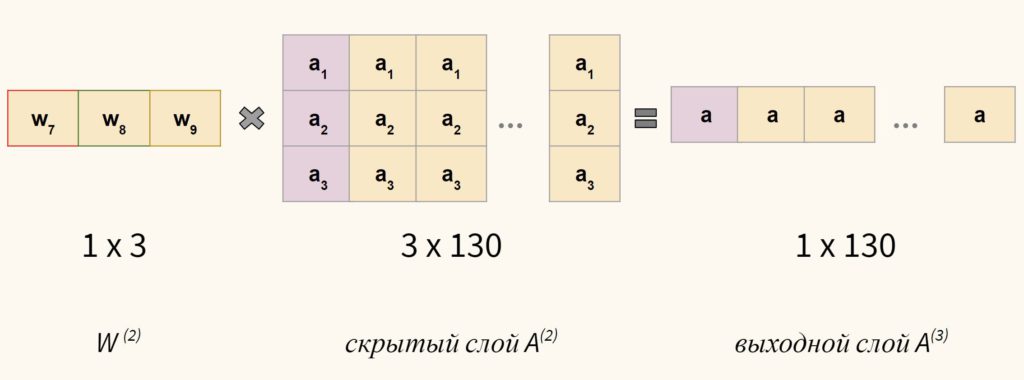
На нее мы будем умножать матрицу весов ($W^{(1)} cdot X$ или в терминологии слоев $W^{(1)} cdot A^{(1)}$). Как определить размерность матрицы весов? Очень просто, нужно взглянуть на количество нейронов скрытого слоя. Их три. Значит размерность первой матрицы весов составит 3 х 2.
Практический совет. Для того чтобы быстро найти размерность матрицы весов вспомним про две особенности умножения матриц:
- внутренние размеры, т.е. количество столбцов первой и строк второй, должны совпадать, в нашем случае 2 = 2.
- размерность результирующей матрицы будет равна внешним размерам умножаемых матриц, 3 и 130.
Итак, в скрытом слое у нас будет матрица 3 х 130, где каждый столбец — это три (активационных) нейрона для каждого из наблюдений.
Полносвязный слой
Убедимся, что такое умножение матриц обеспечивает умножение каждого нейрона входного слоя на каждый нейрон скрытого слоя (т.е. полносвязность, density, слоев). Для простоты, предположим, что у нас только четыре наблюдения, я не 130.
Рассмотрим первую операцию. Здесь веса $w_1$ и $w_4$ умножаются на нейроны входного слоя $a_1$ и $a_2$ и, таким образом, обеспечивают их «участие» в значении нейрона $a_1$ скрытого слоя. Аналогично, при второй операции за это отвечают $w_2$ и $w_5$. Наконец третий нейрон скрытого слоя рассчитывается благодаря весам $w_3$ и $w_6$ и опять же обоим нейронам входного слоя.
Эти же операции можно посмотреть на стрелках на схеме архитектуры сети.
Вторая матрица весов
Теперь, чтобы получить один единственный нейрон выходного слоя (вернее вектор-строку из 130 таких нейронов, 1 х 130), нам нужно новую матрицу весов умножить на результат скрытого слоя на $W^{(2)} cdot A^{(2)}$.
Очевидно, это должна быть матрица 1 х 3, потому что только она даст нам нужную итоговую размерность 1 x 130.
Важная деталь. Как нейроны скрытого слоя, так и нейрон выходного слоя проходят через функцию активации (activation function), в нашем случае сигмоиду (на схемах выше не показана).
В целом мы только что рассмотрели прямое распространение. Давайте напишем соответствующий код.
Код прямого распространения
Вначале объявим знакомые нам функции сигмоиды (функция активации) и логистической ошибки (функция потерь). Их место в архитектуре сети можно увидеть на схеме ниже.
Дополнительно замечу, что в нашей терминологии $z^(1)$ и $z^(2)$ — это результат умножения матрицы весов на матрицу нейронов соответствующего слоя, который мы «пропускаем» через сигмоиду (g). Т.е., например, для скрытого слоя
$$ Z^{(1)} = W^{(1)} cdot A^{(1)} $$
$$ A^{(2)} = g(Z^{(1)}) $$
|
# функция активации def sigmoid(z): s = 1 / (1 + np.exp(—z)) return s # функция потерь def objective(y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) |
Теперь объявим веса и поместим признаки в нейроны скрытого слоя (исключительно ради единнобразия терминологии).
|
# зададим точку отсчета np.random.seed(33) # инициализируем случайные веса, # взятые из стандартного нормального распределения W1 = np.random.randn(3, 2) W2 = np.random.randn(1, 3) # найдем количество наблюдений n = X.shape[1] # поместим признаки в нейроны входного слоя A1 = X |
Последовательно выполним операции умножения весов на нейроны и пропустим результаты через две сигмоиды.
|
# выполним умножение матриц W1 и A1 и «пропустим» результат через сигмоиду # в скобках указана итоговая размерность операции Z1 = np.dot(W1, A1) # (3 x 130) A2 = sigmoid(Z1) # (3 x 130) # поступим аналогично с матрицами W2 и A2 Z2 = np.dot(W2, A2) # (1 x 130) A3 = sigmoid(Z2) # (1 x 130) # посмотрим, какую вероятность модель выдала для первого наблюдения A3[:,0] |
Найдем ошибку при текущих весах.
|
loss = objective(A3, y) loss |
Обратное распространение
Теперь главный вопрос. Как обновить веса так, чтобы уменьшить ошибку?
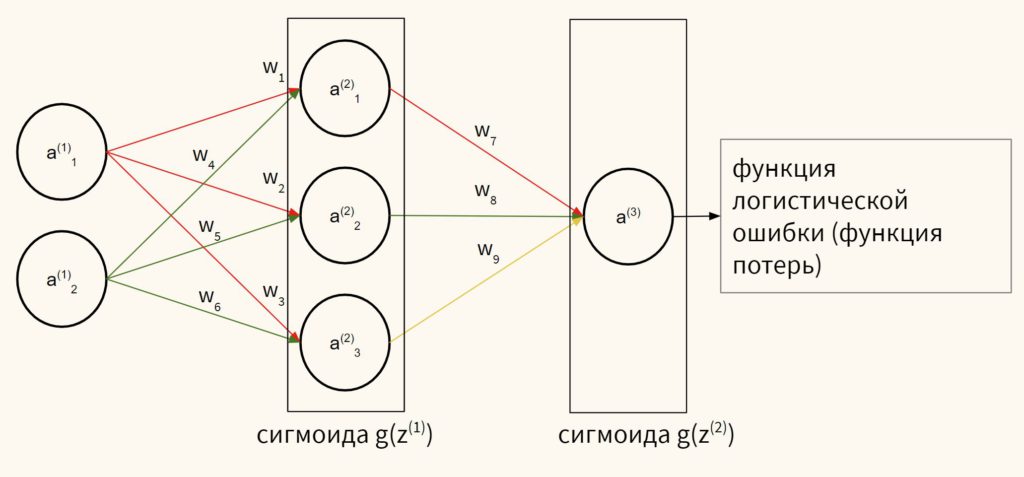
По большому счету нам нужно рассчитать частную производную функции логистической ошибки ($L$) относительно каждого веса ($w_1, w_2, w_3, …, w_9$), ведь именно их мы и будем обновлять. Начнем с весов второго слоя, а именно, $w_7, w_8, w_9$ (все вместе мы будем обозначать их как $W^{(2)}$).
Частные производные весов $W^{(2)}$
Согласно chain rule градиент (т.е. совокупность частных производных) весов второго слоя будет иметь вид
$$ frac{partial L}{partial w^{(2)}} = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial w^{(2)} } $$
Что нам нужно сделать?
- Вначале найти производную функции логистической ошибки $ frac{partial L}{partial a^{(3)}} $
- После этого производную сигмоиды $frac{partial a^{(3)} }{partial z^{(2)}}$
- И наконец линейной функции $frac{ partial z^{(2)} }{partial w^{(2)} }$
- Перемножить эти производные
Возможно вы заметили, что выше использовались индексы (3) и (2), индекс (3) относит активационную функцию $a^{(3)}$ к третьему выходному слою, а линейную функцию $z^{(2)}$ и веса линейной функции $ w^{(2)} $ ко второму. В такой нотации нам будет удобнее в дальнейшем рассчитывать градиенты и писать код.
На всякий случай также уточню, что это будет поэлементное умножение или произведение Адамара (Hadamard product), которое мы будем обозначать через оператор $circ$.
Далее, уверен, вы обратили внимание на то, что мы выполняем операции в обратном от прямого распространения порядке: сначала производная ошибки, потом сигмоиды третьего слоя, затем линейной функции второго. Именно поэтому процесс называется обратным распространением ошибки (error back propagation).
Производная функции логистической ошибки
$$ frac{partial L}{partial a^{(3)}} = frac{partial}{partial a^{(3)}} left( -y log(a^{(3)})-(1-y) log(1-a^{(3)}) right) $$
Применим правило производной разности и вынесем константы.
$$ -y frac{partial}{partial a^{(3)}} log(a^{(3)})-(1-y) frac{partial}{partial a^{(3)}} log(1-a^{(3)}) $$
Найдем производную натурального логарифма, вынесем минус за скобку и вычтем одну дробь из другой.
$$ -left( frac{y}{a^{(3)}}-frac{(1-y) }{1-a^{(3)}} right) = frac{a^{(3)}-y}{a^{(3)}(1-a^{(3)})} $$
Производная сигмоиды
Производную сигмоиды мы уже находили.
$$ frac{partial a^{(3)} }{partial z^{(2)}} = g(z^{(2)}) (1-g(z^{(2)})) $$
При этом так как результат сигмоиды $ g(z^{(2)}) $ — это нейрон выходного слоя $ a^{(3)} $, то
$$ frac{partial a^{(3)} }{partial z^{(2)}} = a^{(3)} (1-a^{(3)}) $$
Производная линейной функции
Найдем производную линейной функции, расписав умножение для каждого веса и для каждого нейрона.
$$ frac{ partial }{partial w^{(2)} } left( w_7 times a^{(2)}_1 + w_8 times a^{(2)}_2 + w_9 times a^{(2)}_3 right) $$
Для того чтобы найти производную относительно, например, веса $w_7$, мы «замораживаем» (считаем константами, производная которых равна нулю) все веса кроме первого и тогда
$$ w_7^{1-1} times a^{(2)}_1 + 0 times a^{(2)}_2 + 0 times a^{(2)}_3 = $$
$$ 1 times a^{(2)}_1 + 0 times a^{(2)}_2 + 0 times a^{(2)}_3 = a^{(2)}_1 $$
Аналогичный результат мы получим, продифференцировав относительно других весов. Тогда,
$$ frac{ partial z^{(2)} }{partial w^{(2)}} = a^{(2)} $$
Наконец перемножим найденные производные и упростим выражение.
$$ frac{partial L}{partial w^{(2)}} = frac{a^{(3)}-y}{a^{(3)}(1-a^{(3)})} circ a^{(3)} (1-a^{(3)}) circ a^{(2)} = $$
$$ (a^{(3)}-y) circ a^{(2)} $$
В векторной нотации (и матричном умножении) получим
$$ frac{partial L}{partial W^{(2)}} = (A^{(3)}-y) cdot A^{(2)}.T times frac{1}{n} $$
Множитель $ frac{1}{n} $ усредняет градиент на количество наблюдений.
Дельта-правило ($ delta_2 $)
Замечу, что $frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}}$ также обозначают через греческую букву «дельта» (в нашем случае $delta_2$), и тогда градиент для обновления весов $W^{(2)}$, с учетом векторизованного кода, приобретет вид (опять же в векторной нотации)
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
В дальнейшем использование так называемого «дельта-правила» (delta rule) упростит наш код.
Обновление весов $W^{(2)}$
Остается только обновить веса $W^{(2)}$ в направлении антиградиента, умноженного на коэффициент скорости обучения.
$$ W^{(2)} := W^{(2)}-alpha times frac{partial L}{partial W^{(2)}}$$
Частные производные весов $W^{(1)}$
Теперь нужно найти производные относительно весов ($w_1, …, w_6$) или $W^{(1)}$. И мы снова должны «раскручивать» chain rule от функции логистической ошибки. На этот раз цепь будет более длинной.
$$ frac{partial L}{partial w^{(1)}} = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } circ frac{ partial a^{(2)} }{partial z^{(1)} } circ frac{ partial z^{(1)} }{partial w^{(1)} } $$
Нахождение производных
Вспомним, что первые два множителя $frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}}$ мы обозначили через $delta_2$.
Обратим внимание на третий множитель $ frac{ partial z^{(2)} }{partial a^{(2)} } $. В отличие от градиента весов $W^{(2)}$, где мы, напомню, искали производную линейной функции относительно весов $frac{ partial z^{(2)} }{partial w^{(2)} }$, здесь нас интересует частная производная относительно нейронов активационного слоя $a^{(2)}$.
Тогда в данном случае мы «замораживаем» (считаем константами) не веса, а нейроны $ a^{(2)} $ (считая веса просто числами) и, например, частная производная относительно $a^{(2)}_1$ будет равна
$$ frac{ partial }{partial a^{(2)}_1 } left( w_7 times a^{(2)}_1 + w_8 times a^{(2)}_2 + w_9 times a^{(2)}_3 right) $$
$$ w_7 times 1 + w_8 times 0 + w_9 times 0 = w_7 $$
Аналогично находим производные относительно других нейронов. В векторной нотации,
$$ frac{ partial z^{(2)} }{partial a^{(2)} } = W^{(2)}$$
Интересно, что ошибкой скрытого слоя $E_2$ (ошибкой $E_1$ была бы общая ошибка, которую мы рассчитали с помощью функции логистической ошибки) называют произведение
$$ E_2 = frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } $$
Это утверждение более понятно, если переписать (в векторной нотации) выражение выше как,
$$ E_2 = W^{(2)}.T cdot delta_2 $$
То есть, мы по сути распространяем «ошибку» $ delta_2 $ (число, скаляр) на каждый из трех весов $W^{(2)}$.
Перейдем к четвертому множителю $ frac{ partial a^{(2)} }{partial z^{(1)} }$. Это снова производная сигмоиды, только уже «на слой раньше»,
$$ frac{ partial a^{(2)} }{partial z^{(1)} } = g(z^{(1)}) (1-g(z^{(1)})) = a^{(2)} (1-a^{(2)}) $$
И наконец пятый компонент,
$$ frac{ partial z^{(1)} }{partial w^{(1)} } = a^{(1)} $$
Дельта-правило ($ delta_1 $)
Аналогично предыдущему слою мы можем обозначить $ frac{partial L}{partial a^{(3)}} circ frac{partial a^{(3)} }{partial z^{(2)}} circ frac{ partial z^{(2)} }{partial a^{(2)} } circ frac{ partial a^{(2)} }{partial z^{(1)} } $ как $ delta_1 $ (то есть мы опять взяли все множители, кроме последнего).
Градиент относительно $W^{(1)}$
В итоге градиент относительно весов $W^{(1)}$ имел бы вид,
$$ frac{partial L}{partial W^{(1)}} = left( E_2 circ A^{(2)} circ (1-A^{(2)}) right) cdot A^{(1)}.T times frac{1}{n} $$
Или, раскрыв $E_2$,
$$ frac{partial L}{partial W^{(1)}} = left( ( W^{(2)}.T cdot delta_2) circ A^{(2)} circ (1-A^{(2)}) right) cdot A^{(1)}.T times frac{1}{n} $$
Или через $ delta_1 $
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Обратите внимание на паттерн, градиент каждого слоя представляет собой произведение дельты на соответствующие нейроны активационного слоя, усредненное на количество наблюдений.
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Разумеется, это правило справедливо и для большего количества скрытых слоев.
Обновление весов $W^{(1)}$
Обновление весов $W^{(1)}$ аналогично предыдущему слою.
$$ W^{(1)} := W^{(1)}-alpha times frac{partial L}{partial W^{(1)}}$$
Перейдем к коду.
Код обратного распространения
Продолжим писать код, которые мы начали, изучая прямое распространение.
|
# найдем дельту весов между слоями 3 и 2 W2_delta = A3 — y # (1 x 130) |
|
# обратите внимание, это одно число, как и результат # третьего слоя A3 (мы выводим первый столбец из 130) W2_delta[:, 0] |
|
# найдем дельту весов между слоями 1 и 2 W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) |
|
# дельта 1 состоит уже из трех чисел, как и скрытый слой нейросети W1_delta[:, 0] |
|
array([-0.0099838 , 0.06300821, -0.01243332]) |
|
# напомню, что умножение дельты 2 на веса скрытого слоя W2 можно # считать «промежуточной ошибкой» сети или ошибкой скрытого слоя E2 = np.dot(W2.T, W2_delta) # то есть одно число W2_delta мы «распространили» на весь скрытый слой, # поэтому ошибка состоит из трех чисел E2[:, 0] |
|
array([-0.07704936, 1.03666489, -0.04989736]) |
|
# наконец найдем частную производную относительно весов W2 W2_derivative = np.dot(W2_delta, A2.T) / n # (1 x 3) W2_derivative |
|
array([[-0.16738339, -0.23720379, 2.99973404]]) |
|
# и весов W1 # (размерность опять же должна совпадать с размерностью матриц весов) W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 3) W1_derivative |
|
array([[-0.14145948, -0.12624909], [ 1.41742921, 1.87529043], [-0.19429558, -0.21266884]]) |
|
# обновим веса (скорость обучения возьмем равной единице) W2 = W2 — 1 * W2_derivative W1 = W1 — 1 * W1_derivative |
Обучение модели
Теперь соединим прямое и обратное распространение и с помощью цикла произведем обучение нейронной сети.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
np.random.seed(33) W1 = np.random.randn(3, 2) W2 = np.random.randn(1, 3) epochs = 100000 learning_rate = 1 n = X.shape[1] A1 = X for i in range(epochs): # рассчитываем прямое распространение Z1 = np.dot(W1, A1) # (3 x 130) A2 = sigmoid(Z1) # (3 x 130) Z2 = np.dot(W2, A2) # (1 x 130) A3 = sigmoid(Z2) # (1 x 130) # рассчитываем ошибку loss = objective(A3, y) # находим дельту весов между слоями 3 и 2 W2_delta = A3 — y # (1 x 130) # находим дельту весов между слоями 2 и 1 W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # находим частные производные W2_derivative = np.dot(W2_delta, A2.T)/n # (1 x 3) W1_derivative = np.dot(W1_delta, A1.T)/n # (3 x 3) # обновляем веса W2 = W2 — learning_rate * W2_derivative W1 = W1 — learning_rate * W1_derivative # периодически выводим количество итераций и текущую ошибку if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) # можем добавить паузу для более аккуратного вывода time.sleep(0.5) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 7.522291935047792 ———————— Эпоха: 20000 Ошибка: 0.7636370744482613 ———————— Эпоха: 40000 Ошибка: 0.7137144818217118 ———————— Эпоха: 60000 Ошибка: 0.6981278394758277 ———————— Эпоха: 80000 Ошибка: 0.6901729606032463 ———————— Итоговая ошибка 0.6847941294287265 Нейросеть успешно обучена |
Прогноз и оценка качества
Сделаем прогноз и оценим качество.
|
A1 = X Z1 = np.matmul(W1, A1) A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) A3 = sigmoid(Z2) # A3.flatten() делает массив одномерным, # условие выводит True или False (1 или 0) y_pred, y_true = A3.flatten() >= 0.5, y.flatten() |
|
(array([[ 1.59357193e-03, -1.11510787e+00], [-2.70942468e+01, 1.10767378e+01], [-1.78982169e-03, 1.11459111e+00]]), array([[ 14.76831281, 8.70860599, -21.63309402]])) |
|
from sklearn.metrics import accuracy_score accuracy_score(y_true, y_pred) |
Инициализация весов
В моделях линейной и логистической регрессии в качестве начальных значений коэффициентов мы использовали нули, в алгоритме нейронной сети — случайные значения, почему так?
Если веса изначально равны нулю, то произойдет несколько нежелательных событий:
- значения активационных слоев $a_1^(2) = a_2^(2) = a_3^(2) $ будут одинаковыми, то есть запоминать одну и ту же зависимость
- более того, так как веса между вторым и третьим (выходным) слоем будут одинаковыми, то и значения матрицы $ delta_2 $ будут одинаковыми,
- а значит и частные производные, относящиеся к весам одного входного нейрона (например, $w_1, w_2, w_3$) будут одинаковыми
Таким образом, после, например, одного обновления весов, хотя значения весов $w_1, w_2, w_3$ не будут нулевыми, они будут одинаковыми. То же можно сказать про веса $w_4, w_5, w_6$. И снова $a_1^(2) = a_2^(2) = a_3^(2) $.
Как следствие, мы существенно ограничиваем возможности (гибкость) нейронной сети запоминать сложные зависимости.
Масштабирование целевой переменной
Как мы только что убедились, градиент нейронной сети зависит от целевой переменной. Если эта переменная имеет большой диапазон, то это может создать большую ошибку при вычислении градиента, что, в свою очередь, вызовет существенное изменение весов и дестабилизирует процесс обучения.
Очевидно после обучения и прогноза целевую переменную нужно вернуть к прежнему масштабу.
Модель в Tensorflow и Keras
Библиотека Keras представляет собой «надстройку«⧉ (интерфейс, API), через которую удобно создавать нейросети в библиотеке Tensorflow. Реализуем созданную выше несложную нейросеть в библиотеке Keras.
|
# в Google Colab уже установлена вторая версия библиотеки Tensorflow, # которая существенно отличается от первой версии import tensorflow as tf tf.__version__ |
В нейросеть мы будем подавать признаки и целевую переменную таким образом, чтобы объекты были строками.
Перейдем к созданию и обучению нейросети.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# зададим две точки отсчета, одну в библиотеке Numpy np.random.seed(42) # вторую непосредственно в Tensorflow tf.random.set_seed(42) # зададим архитектуру: последовательная модель model = tf.keras.models.Sequential([ # с полносвязными слоями # также укажем нейроны скрытого и выходного слоев # откажемся от смещения tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = False), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = False) ]) # зададим особенности стохастического градиентного спуска (SGD) # в частности, откажемся от импульса # (подробнее об этом на последующих занятиях) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) # соберем все вместе, дополнительно укажем тип функции потерь и метрику качества model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) # зададим количество эпох, # размер batch, после которой мы обновляем веса, равен объему данных (fullbatch) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) |
|
<keras.callbacks.History at 0x7f5f49c0aa90> |
|
Model: «sequential_3» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_6 (Dense) (130, 3) 6 dense_7 (Dense) (130, 1) 3 ================================================================= Total params: 9 Trainable params: 9 Non—trainable params: 0 _________________________________________________________________ |
Оценим качество.
|
model.history.history[‘accuracy’][—1] |
Нейросеть со смещением
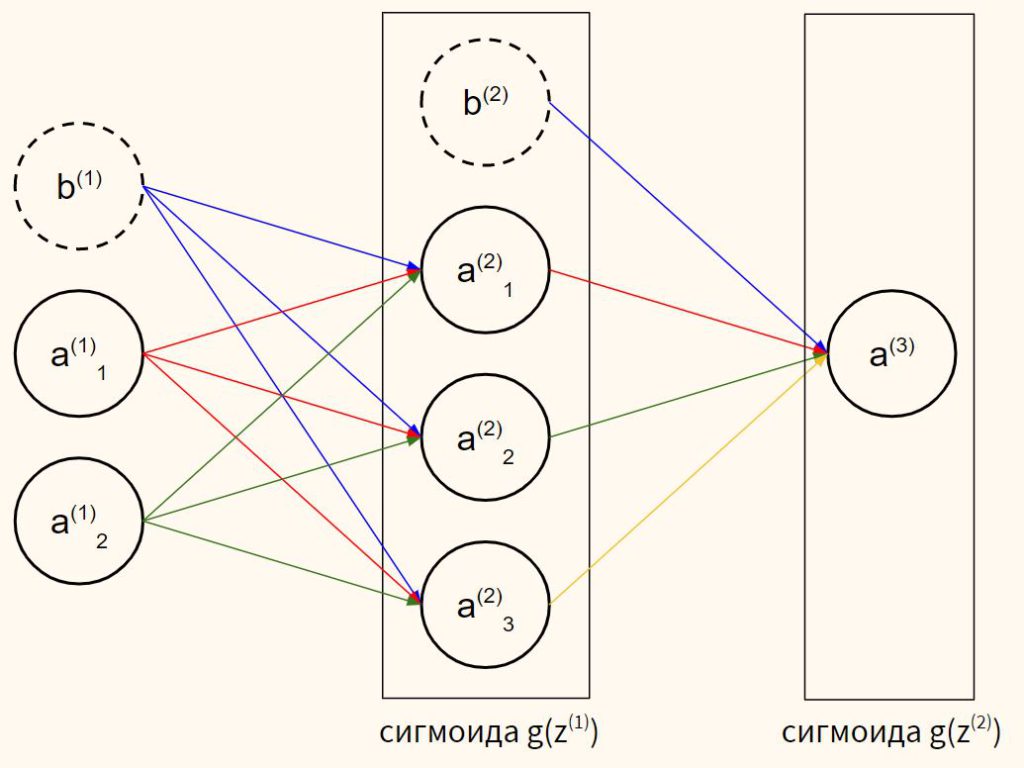
Добавим смещение, это должно сделать нашу модель более гибкой.
В отличие от линейных моделей, мы не будем использовать одну и ту же производную и для $b$, и для $W$ (с добавлением столбца из единиц в X). Это связано с тем, что в нейросетях при обратном распространении ошибку на смещение мы не распространяем.
Найдем производные смещения относительно сигмоиды (последний компонент в цепи производных).
$$ frac{ partial z^{(2)} }{partial b^{(2)}} = 1 $$
$$ frac{ partial z^{(2)} }{partial b^{(1)}} = 1 $$
Тогда в целом, используя дельта-правило, частные производные относительно $b^{(2)}$ и $b^{(1)}$ будут равны
$$ frac{partial L}{partial b^{(2)}} = sum delta_2 times frac{1}{n} $$
$$ frac{partial L}{partial b^{(1)}} = sum delta_1 times frac{1}{n} $$
Перейдем к коду.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
np.random.seed(33) # инициализируем веса W1 = np.random.randn(3, 2) # b1 будет иметь размерность 3 х 1, # потому что распространяется на три нейрона скрытого слоя b1 = np.random.randn(3, 1) W2 = np.random.randn(1, 3) b2 = np.random.randn(1, 1) n = X.shape[1] epochs = 100000 learning_rate = 1 A1 = X for i in range(epochs): # 3 х 2 на 2 х 130 Z1 = np.dot(W1, A1) + b1 A2 = sigmoid(Z1) # (3 x 130) # 1 х 3 на 3 х 130 Z2 = np.dot(W2, A2) + b2 A3 = sigmoid(Z2) # (1 x 130) loss = objective(A3, y) W2_delta = A3 — y # (1 x 130) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # keepdims сохраняет исходную размерность # 1 х 130 на 130 х 3 W2_derivative = np.dot(W2_delta, A2.T) / n # (1 x 3) b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) # 3 х 130 на 130 х 2 W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 2) b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) time.sleep(0.5) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 10.080172158274355 ———————————— Эпоха: 20000 Ошибка: 0.5460931772435075 ———————————— Эпоха: 40000 Ошибка: 0.5235933834724054 ———————————— Эпоха: 60000 Ошибка: 0.5153108060799304 ———————————— Эпоха: 80000 Ошибка: 0.5104559107317911 ———————————— Итоговая ошибка 0.5070018571750416 Нейросеть успешно обучена |
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) y_pred, y_true = A3.flatten() > 0.5, y.flatten() accuracy_score(y_true, y_pred) |
TF / Keras. Добавим смещение в нашу модель в библиотеке Keras.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
np.random.seed(42) tf.random.set_seed(42) model = tf.keras.models.Sequential([ tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = True) ]) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) model.summary() |
|
Model: «sequential_6» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_12 (Dense) (130, 3) 9 dense_13 (Dense) (130, 1) 4 ================================================================= Total params: 13 Trainable params: 13 Non-trainable params: 0 _________________________________________________________________ |
|
model.history.history[‘accuracy’][—1] |
|
(array([[ 6.12093182, -12.02342998], [-22.00510547, -9.19535995], [ 14.35718419, 9.69417827]]), array([[ 12.32118926, 15.26008905, -10.91093576]])) |
Два скрытых слоя
Добавим второй скрытый слой.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
np.random.seed(33) W1 = np.random.randn(3, 2) b1 = np.random.randn(3, 1) W2 = np.random.randn(3, 3) b2 = np.random.randn(3, 1) W3 = np.random.randn(1, 3) b3 = np.random.randn(1, 1) n = X.shape[1] epochs = 10000 learning_rate = 1 A1 = X for i in range(epochs): Z1 = np.dot(W1, A1) + b1 # (3 x 130) A2 = sigmoid(Z1) Z2 = np.dot(W2, A2) + b2 # (3 x 130) A3 = sigmoid(Z2) Z3 = np.dot(W3, A3) + b3 # (1 x 130) A4 = sigmoid(Z3) loss = objective(A4, y) W3_delta = A4 — y # (1 x 130) W2_delta = np.dot(W3.T, W3_delta) * A3 * (1 — A3) # (3 x 130) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (3 x 130) # 3 х 130 на 130 х 3 W3_derivative = np.dot(W3_delta, A3.T) / n # (3 x 3) b3_derivative = np.sum(W3_delta, keepdims = True) / n # (1 x 1) # 3 х 130 на 130 х 3 W2_derivative = np.dot(W2_delta, A2.T) / n # (3 x 3) b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) W1_derivative = np.dot(W1_delta, A1.T) / n # (3 x 2) b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W3 = W3 — learning_rate * W3_derivative b3 = b3 — learning_rate * b3_derivative W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) time.sleep(1) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 11.483275165239569 ———————— Эпоха: 2000 Ошибка: 0.7137240298878413 ———————— Эпоха: 4000 Ошибка: 0.683999037922229 ———————— Эпоха: 6000 Ошибка: 0.6718618481850791 ———————— Эпоха: 8000 Ошибка: 0.6640320570961954 ———————— Итоговая ошибка 0.6583025695728971 Нейросеть успешно обучена |
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = sigmoid(Z3) y_pred, y_true = A4.flatten() > 0.5, y.flatten() accuracy_score(y_true, y_pred) |
Сравним с моделью в Keras.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
np.random.seed(42) tf.random.set_seed(42) model = tf.keras.models.Sequential([ tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(3, activation = ‘sigmoid’, use_bias = True), tf.keras.layers.Dense(1, activation = ‘sigmoid’, use_bias = True) ]) sgd = tf.keras.optimizers.SGD(learning_rate = 1, momentum = 0, nesterov = False) model.compile(optimizer = sgd, loss = ‘binary_crossentropy’, metrics = [‘accuracy’]) model.fit(X.T, y.T, epochs = 10000, batch_size = 130, verbose = 0) model.summary() |
|
Model: «sequential_2» _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_4 (Dense) (130, 3) 9 dense_5 (Dense) (130, 3) 12 dense_6 (Dense) (130, 1) 4 ================================================================= Total params: 25 Trainable params: 25 Non-trainable params: 0 |
|
model.history.history[‘accuracy’][—1] |
Многоклассовая классификация
Создадим нейросеть, которая будет предсказывать вероятности нескольких классов. Во многом, идея алгоритма совпадает с softmax логистической регрессией.
Постановка задачи и архитектура
Возьмемся за ту же задачу, которую мы решили в рамках вводного курса с помощью библиотеки Keras, а именно создадим нейросеть, которая будет распознавать рукописные цифры из датасета MNIST.
Архитектуру модели сохраним прежней.

Функции активации
Как видно на графике, мы будем использовать сигмоиду для промежуточных слоев и softmax для выходного слоя.
|
def sigmoid(z): s = 1 / (1 + np.exp(—z)) return s |
|
def softmax(z): # на выходном слое тензор будет иметь размерность 10 х 60000, # поэтому складывать мы будем по столбцам z = z — np.max(z, axis = 0, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = 0, keepdims = True) softmax = numerator / denominator return softmax |
Функция потерь
Функцией потерь будет категориальная кросс-энтропия.
|
def cross_entropy(probs, y_enc, epsilon = 1e—9): # опять же, так как softmax выдаст тензор 10 х 60000 # количество наблюдений содержится в атрибуте shape[1] n = probs.shape[1] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Обратное распространение
Очевидно, так как изменилась функция потерь и функция активации выходного слоя (softmax) необходимо заново рассчитать производные. Напомню, для весов $W^{(3)}$ цепное правило будет работать следующим образом.
$$ frac{partial L}{partial w^{(3)}} = frac{partial L}{partial a^{(4)}} circ frac{partial a^{(4)} }{partial z^{(3)}} circ frac{ partial z^{(3)} }{partial w^{(3)} } $$
При этом, оказывается, что производная первых двух компонентов $frac{partial L}{partial a^{(4)}} circ frac{partial a^{(4)} }{partial z^{(3)}}$ (т.е. кросс-энтропии и softmax) сводится к $a^{(4)}-y$ (она аналогична бинарной кросс-энтропии и сигмоиде, но находится⧉, разумеется, иначе).
Одновременно этот компонент производной представляет собой $delta_3$, которую для нахождения градиента необходимо умножить на $A^{(3)}.T$.
$$ frac{partial L}{partial W^{(3)}} = delta_3 cdot A^{(3)}.T times frac{1}{n} $$
Остальные производные находятся аналогично предыдущим моделям.
$$ frac{partial L}{partial W^{(2)}} = delta_2 cdot A^{(2)}.T times frac{1}{n} $$
$$ frac{partial L}{partial W^{(1)}} = delta_1 cdot A^{(1)}.T times frac{1}{n} $$
Подготовка данных
|
import mnist from tensorflow import keras |
|
def ohe(y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
X_train = mnist.train_images() y_train = mnist.train_labels() X_test = mnist.test_images() y_test = mnist.test_labels() X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 X_train = X_train.reshape((—1, 784)).T X_test = X_test.reshape((—1, 784)).T y_train_enc, y_test_enc = ohe(y_train).T, ohe(y_test).T X_train.shape, y_train_enc.shape |
|
((784, 60000), (10, 60000)) |
Обучение модели
Код ниже исполняется в Google Colab около 10 минут.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
np.random.seed(33) W1 = np.random.randn(64, 784) b1 = np.random.randn(64, 1) W2 = np.random.randn(64, 64) b2 = np.random.randn(64, 1) W3 = np.random.randn(10, 64) b3 = np.random.randn(10, 1) n = X_train.shape[1] epochs = 500 learning_rate = 1 A1 = X_train for i in range(epochs): # 64 x 784 на 784 x 60000 —> 64 x 60000 Z1 = np.dot(W1, A1) + b1 A2 = sigmoid(Z1) # 64 x 64 на 64 x 60000 —> 64 x 60000 Z2 = np.dot(W2, A2) + b2 A3 = sigmoid(Z2) # 10 x 64 на 64 x 60000 —> 10 x 60000 Z3 = np.dot(W3, A3) + b3 A4 = softmax(Z3) loss = cross_entropy(A4, y_train_enc) W3_delta = A4 — y_train_enc # (10 x 60000) W2_delta = np.dot(W3.T, W3_delta) * A3 * (1 — A3) # (64 x 60000) W1_delta = np.dot(W2.T, W2_delta) * A2 * (1 — A2) # (64 x 60000) # 10 x 60000 на 60000 x 64 —> 10 x 64 W3_derivative = np.dot(W3_delta, A3.T) / n b3_derivative = np.sum(W3_delta, keepdims = True) / n # (1 x 1) # 64 x 60000 на 60000 x 64 —> 64 x 64 W2_derivative = np.dot(W2_delta, A2.T) / n b2_derivative = np.sum(W2_delta, keepdims = True) / n # (1 x 1) # 64 x 60000 на 60000 x 784 —> 64 x 784 W1_derivative = np.dot(W1_delta, A1.T) / n b1_derivative = np.sum(W1_delta, keepdims = True) / n # (1 x 1) W3 = W3 — learning_rate * W3_derivative b3 = b3 — learning_rate * b3_derivative W2 = W2 — learning_rate * W2_derivative b2 = b2 — learning_rate * b2_derivative W1 = W1 — learning_rate * W1_derivative b1 = b1 — learning_rate * b1_derivative if i % (epochs / 5) == 0: print(‘Эпоха:’, i) print(‘Ошибка:’, loss) print(‘————————‘) print(‘Итоговая ошибка’, loss) print(‘Нейросеть успешно обучена’) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Эпоха: 0 Ошибка: 6.215969648082527 ———————— Эпоха: 100 Ошибка: 0.9316990279468341 ———————— Эпоха: 200 Ошибка: 0.7055264357349225 ———————— Эпоха: 300 Ошибка: 0.5950572560699322 ———————— Эпоха: 400 Ошибка: 0.5276765625306427 ———————— Итоговая ошибка 0.4813698685793663 Нейросеть успешно обучена |
Прогноз и оценка качества
Сделаем прогноз и оценим качество на обучающей выборке.
|
Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = softmax(Z3) |
|
y_pred = np.argmax(A4, axis = 0) y_pred[:4] |
|
from sklearn.metrics import accuracy_score accuracy_score(y_train, y_pred) |
Теперь на тестовых данных.
|
A1 = X_test Z1 = np.matmul(W1, A1) + b1 A2 = sigmoid(Z1) Z2 = np.matmul(W2, A2) + b2 A3 = sigmoid(Z2) Z3 = np.matmul(W3, A3) + b3 A4 = softmax(Z3) y_pred = np.argmax(A4, axis = 0) accuracy_score(y_test, y_pred) |
Алгоритм показал достаточно высокую точность и при увеличении количества эпох и настройке скорости обучения мог бы показать более высокий результат.
При этом очевидно, что модель, которую мы создали в рамках вводного курса в библиотеке Keras обучилась гораздо быстрее. На занятии по градиентному спуску мы посмотрим, как можно ускорить работу нашего алгоритма.
Подведем итог
На сегодняшнем занятии мы в деталях посмотрели на математику обратного распространения, а также с нуля построили несколько алгоритмов нейронных сетей.
На следующем занятии мы вернемся к теме качества алгоритмов, а также рассмотрим один из инструментов повышения этого качества, который называется регуляризацией.
Ответы на вопросы
Вопрос. Чем отличается умножение матриц от векторизации?
Ответ. Принцип умножения матриц относится к математике и описывает правила, по которым мы умножаем два двумерных тензора. Векторизация кода — термин из программирования, который позволяет избежать использования циклов в процессе выполнения кода.

В прошлой статье мы рассказывали о том, как устроена свёрточная нейронная сеть. В этой статье мы подробно разберём алгоритмы работы свёрточного слоя, напишем прямое распространение сигнала, обратное распространение ошибки с вычислением градиентов функции потерь по весам и по входам и научимся обновлять коэффициенты фильтров с помощью метода градиентного спуска.
В основном мы будем использовать код, написанный на С++, или псевдокод, однако это никак не должно помешать созданию аналогичных структур и алгоритмов на любом другом языке программирования.
Этап 0. Подготовительный
Прежде чем переходить к созданию свёрточного слоя, необходимо создать структуру для тензора. Тензор, как было сказано в прошлой статье, представляет из себя 3D массив. У тензора имеются три размерности, а значит нам потребуется структура для хранения размера тензора, мы назовём её TensorSize:
// размерность тензора
struct TensorSize {
int depth; // глубина
int height; // высота
int width; // ширина
};
Создав размерность, можно создавать и сам тензор. В нём нам потребуется хранить depth·height·width вещественных чисел, которые мы будем хранить в одномерном векторе для уменьшения количества обращений к элементам по индексам. Для того, чтобы можно было работать с тензором, получать и изменять числа, необходима индексация. Индексация будет производиться по трём индексам в следующем порядке: глубина, высота, ширина. Поскольку в качестве хранения мы выбрали одномерный вектор, то потребуется применить несколько умножений и сложений.
// тензор
class Tensor {
TensorSize size; // размерность тензора
std::vector<double> values; // значения тензора
int dw; // произведение глубины на ширину для индексации
void Init(int width, int height, int depth);
public:
Tensor(int width, int height, int depth); // создание из размеров
Tensor(const TensorSize &size); // создание из размера
double& operator()(int d, int i, int j); // индексация
double operator()(int d, int i, int j) const; // индексация
TensorSize GetSize() const; // получение размера
friend std::ostream& operator<<(std::ostream& os, const Tensor &tensor); // вывод тензора
};
// инициализация по размерам
void Tensor::Init(int width, int height, int depth) {
size.width = width; // запоминаем ширину
size.height = height; // запоминаем высоту
size.depth = depth; // запоминаем глубину
dw = depth * width; // запоминаем произведение глубины на ширину для индексации
values = std::vector<double>(width * height * depth, 0); // создаём вектор из width * height * depth нулей
}
// создание из размеров
Tensor::Tensor(int width, int height, int depth) {
Init(width, height, depth);
}
// создание из размера
Tensor::Tensor(const TensorSize &size) {
Init(size.width, size.height, size.depth);
}
// индексация
double& Tensor::operator()(int d, int i, int j) {
return values[i * dw + j * size.depth + d];
}
// индексация
double Tensor::operator()(int d, int i, int j) const {
return values[i * dw + j * size.depth + d];
}
// получение размера
TensorSize Tensor::GetSize() const {
return size;
}
// вывод тензора
std::ostream& operator<<(std::ostream& os, const Tensor &tensor) {
for (int d = 0; d < tensor.size.depth; d++) {
for (int i = 0; i < tensor.size.height; i++) {
for (int j = 0; j < tensor.size.width; j++)
os << tensor.values[i * tensor.dw + j * tensor.size.depth + d] << " ";
os << std::endl;
}
os << std::endl;
}
return os;
}
Теперь, когда у нас в распоряжении есть тензор, можно приступать к созданию свёрточного слоя.
Этап 1. Свёрточный слой
Из прошлой статьи мы узнали, что свёрточный слой содержит в себе набор фильтров и смещений. Также для создания слоя необохдимо задать несколько гиперпараметров, а именно: fs — размер фильтров, fc — количество фильтров, S — шаг свёртки и P — дополнение нулями. Поскольку фильтры являются тензорами, а смещения всего лишь числами, то добавим фильтры в виде вектора тензоров и назовём W, а смещения добавим в виде векторов вещественных чисел и назовём их b. Поскольку эти веса являются обучаемыми, нам потребуется аналогичные наборы векторов для хранения градиентов.
Весовые коэффициенты должны заполняться случайными числами, так что добавим в класс генератор случайных чисел с нормальным распределением и метод инициализации весов. Для работы слоя также необходимо определить метод прямого распространения сигнала, метод обратного распространения ошибки и метод для обновления весовых коэффициентов:
class ConvLayer {
std::default_random_engine generator; // генератор случайных чисел
std::normal_distribution<double> distribution; // с нормальным распределением
TensorSize inputSize; // размер входа
TensorSize outputSize; // размер выхода
std::vector<Tensor> W; // фильтры
std::vector<double> b; // смещения
std::vector<Tensor> dW; // градиенты фильтров
std::vector<double> db; // градиенты смещений
int P; // дополнение нулями
int S; // шаг свёртки
int fc; // количество фильтров
int fs; // размер фильтров
int fd; // глубина фильтров
void InitWeights(); // инициализация весовых коэффициентов
public:
ConvLayer(TensorSize size, int fc, int fs, int P, int S); // создание слоя
Tensor Forward(const Tensor &X); // прямое распространение сигнала
Tensor Backward(const Tensor &dout, const Tensor &X); // обратное распространение ошибки
void UpdateWeights(double learningRate); // обновление весовых коэффициентов
};
Само создание слоя довольно простое: необходимо запомнить переданные параметры в полях класса и инициализировать весовые коэффициенты фильтров и смещений:
// создание свёрточного слоя
ConvLayer::ConvLayer(TensorSize size, int fc, int fs, int P, int S) : distribution(0.0, sqrt(2.0 / (fs*fs*size.depth))) {
// запоминаем входной размер
inputSize.width = size.width;
inputSize.height = size.height;
inputSize.depth = size.depth;
// вычисляем выходной размер
outputSize.width = (size.width - fs + 2 * P) / S + 1;
outputSize.height = (size.height - fs + 2 * P) / S + 1;
outputSize.depth = fc;
this->P = P; // сохраняем дополнение нулями
this->S = S; // сохраняем шаг свёртки
this->fc = fc; // сохраняем число фильтров
this->fs = fs; // сохраняем размер фильтров
this->fd = size.depth; // сохраняем глубину фильтров
// добавляем fc тензоров для весов фильтров и их градиентов
W = std::vector<Tensor>(fc, Tensor(fs, fs, fd));
dW = std::vector<Tensor>(fc, Tensor(fs, fs, fd));
// добавляем fc нулей для весов смещения и их градиентов
b = std::vector<double>(fc, 0);
db = std::vector<double>(fc, 0);
InitWeights(); // инициализируем весовые коэффициенты
}
Для заполнения весовых коэффициентов случайными числами просто проходимся по всем тензорам и присваиваем каждому элементу очередное случайное число:
// инициализация весовых коэффициентов
void ConvLayer::InitWeights() {
// проходимся по каждому из фильтров
for (int index = 0; index < fc; index++) {
for (int i = 0; i < fs; i++)
for (int j = 0; j < fs; j++)
for (int k = 0; k < fd; k++)
W[index](k, i, j) = distribution(generator); // генерируем случайное число и записываем его в элемент фильтра
b[index] = 0.01; // все смещения устанавливаем в 0.01
}
}
Этап 2. Прямое распространение сигнала
При прямом распространении сигнала нам необходимо выполнить свёртку входного тензора с каждым из фильтров, а значит примерный алгоритм должен быть следующим:
for index = 0 to fc - 1 do
output[index] = Convolve(X, W[index]) + b[index]
Теперь необходимо реализовать саму свёртку. Нам известно, что необходимо пройтись по всем возможным элементам на входном тензоре с заданным шагом, однако давайте сначала разберёмся, как действовать, когда параметр дополнения нулями отличен от нуля.
Дополнение нулями, padding
Самым простым решением дополнения нулями было бы создание тензора с высотой и шириной на 2P больше и последующим копированием во внутреннюю часть исходного тензора. Увы, подобные копирования сильно замедлят программу, так как требуют постоянных копирований памяти. Мы, конечно, хотим написать простую свёрточную сеть, однако всё-таки постараемся описать её наиболее эффективным способом.
Поскольку входные тензоры дополняются нулями, то элементы, выходящие за границу тензора, можно просто игнорировать. Для проверки на выход за границу потребуется всего навсего один if, что не идёт ни в какое сравнение с полным копированием исходного тензора в другой, дополненный нулями. Теперь же, когда дополнение нулями нам больше не помеха, можем написать прямое распространение:
// прямое распространение
Tensor ConvLayer::Forward(const Tensor &X) {
Tensor output(outputSize); // создаём выходной тензор
// проходимся по каждому из фильтров
for (int f = 0; f < fc; f++) {
for (int y = 0; y < outputSize.height; y++) {
for (int x = 0; x < outputSize.width; x++) {
double sum = b[f]; // сразу прибавляем смещение
// проходимся по фильтрам
for (int i = 0; i < fs; i++) {
for (int j = 0; j < fs; j++) {
int i0 = S * y + i - P;
int j0 = S * x + j - P;
// поскольку вне границ входного тензора элементы нулевые, то просто игнорируем их
if (i0 < 0 || i0 >= inputSize.height || j0 < 0 || j0 >= inputSize.width)
continue;
// проходимся по всей глубине тензора и считаем сумму
for (int c = 0; c < fd; c++)
sum += X(c, i0, j0) * W[f](c, i, j);
}
}
output(f, y, x) = sum; // записываем результат свёртки в выходной тензор
}
}
}
return output; // возвращаем выходной тензор
}
Этап 3. Обратное распространение ошибки
Цель обратного распространения ошибки заключается в том, что от следующего слоя нам приходят градиенты некоторой функции потерь L. Исходя из этих градиентов, нам нужно расчитать градиенты по входному тензору (
) и градиенты весовых коэффициентов (
и
).
Это становится вполне логичным, если рассматривать нейросеть как обыкновенную функцию с огромным количеством параметров, которую мы хотим минимизировать. А чтобы найти её минимум, нам нужно найти производные по каждому из весовых коэффициентов, чтобы затем шагнуть в направлении антиградиента (направление, в котором функция уменьшается). Поскольку нейросеть состоит из большого числа блоков, сходу тяжело предрассчитать производные, а потому на помощь приходит расчёт производной сложной функции: пусть у нас есть некоторая функция y = f(x) и функция g(y), и нам требуется найти производную по x функции z = g(f(x)). Для этого сначала нужно найти производную функции g, а затем умножить её на производную функции f: z’ = g'(f(x)) * f'(x).
В нейросети в качестве функций выступают слои. Каждый из слоёв умеет вычислять производную по своему аргументу (входному тензору), основываясь на градиентах следующего слоя (или градиентах функции ошибки, если слой является выходным). Некоторые слои не имеют обучаемых параметров, поэтому они вычисляют только градиенты по своему аргументу. Свёрточный слой является обучаемым, а потому помимо входных градиентов ему необходимо вычислять и градиенты по весам, чтобы затем их можно было обновить и уменьшить ошибку.
Вычисление градиента по весовым коэффициентам
Вычисление градиента по весовым коэффициентам можно разбить на две части: по весам фильтров и по коэффициентам смещения. Проще всего вычисляются градиенты по весам смещения: это всего лишь сумма всех градиентов, которые относятся к данному весу смещения:
for (int f = 0; f < fc; f++)
for (int y = 0; y < size.height; y++)
for (int x = 0; x < size.width; x++)
db[f] += deltas(f, y, x);
Для вычисления же градиентов по весам фильтров, необходимо выполнить слегка модифицированную свёртку входного тензора и тензора градиентов:
for (int f = 0; f < fc; f++) {
for (int y = 0; y < size.height; y++) {
for (int x = 0; x < size.width; x++) {
double delta = deltas(f, y, x); // запоминаем значение градиента
for (int i = 0; i < fs; i++) {
for (int j = 0; j < fs; j++) {
int i0 = i + y - P;
int j0 = j + x - P;
// игнорируем выходящие за границы элементы
if (i0 < 0 || i0 >= inputSize.height || j0 < 0 || j0 >= inputSize.width)
continue;
// наращиваем градиент фильтра
for (int c = 0; c < fd; c++)
dW[f](c, i, j) += delta * X(c, i0, j0);
}
}
}
}
}
Вычисление градиента по входному тензору
Градиент по входному тензору считается обыкновенной свёрткой тензора дельт и весов с небольшим отличием: для вычисления фильтры поворачиваются на 180 градусов, а дополнение нулями заменяется на величину fs — 1 — P. Данную операцию называют транспонированной свёрткой или кросскорелляцией.
Tensor dX(inputSize);
int pad = fs - 1 - P;
for (int y = 0; y < inputSize.height; y++) {
for (int x = 0; x < inputSize.width; x++) {
for (int c = 0; c < fd; c++) {
double sum = 0; // сумма для градиента
// идём по всем весовым коэффициентам фильтров
for (int i = 0; i < fs; i++) {
for (int j = 0; j < fs; j++) {
int i0 = y + i - pad;
int j0 = x + j - pad;
// игнорируем выходящие за границы элементы
if (i0 < 0 || i0 >= size.height || j0 < 0 || j0 >= size.width)
continue;
// суммируем по всем фильтрам
for (int f = 0; f < fc; f++)
sum += W[f](c, fs - 1 - i, fs - 1 - j) * deltas(f, i0, j0); // добавляем произведение повёрнутых фильтров на дельты
}
}
dX(c, y, x) = sum; // записываем результат в тензор градиента
}
}
}
Внимательный читаель мог заметить, что в заголовке метода использовался параметр dout, а в приведённом выше коде используется параметр deltas, а также неизвестный размер size. Действительно, deltas и dout не совсем одно и то же. Если шаг свёртки равен 1, то они совпадают, при другом шаге size и deltas вычисляются следующим образом:
TensorSize size; // размер дельт
// расчитываем размер для дельт
size.height = S * (outputSize.height - 1) + 1;
size.width = S * (outputSize.width - 1) + 1;
size.depth = outputSize.depth;
Tensor deltas(size); // создаём тензор для дельт
// расчитываем значения дельт
for (int d = 0; d < size.depth; d++)
for (int i = 0; i < outputSize.height; i++)
for (int j = 0; j < outputSize.width; j++)
deltas(d, i * S, j * S) = dout(d, i, j);
Итоговый код для расчёта градиентов будет таким:
// обратное распространение
Tensor ConvLayer::Backward(const Tensor &dout, const Tensor &X) {
TensorSize size; // размер дельт
// расчитываем размер для дельт
size.height = S * (outputSize.height - 1) + 1;
size.width = S * (outputSize.width - 1) + 1;
size.depth = outputSize.depth;
Tensor deltas(size); // создаём тензор для дельт
// расчитываем значения дельт
for (int d = 0; d < size.depth; d++)
for (int i = 0; i < outputSize.height; i++)
for (int j = 0; j < outputSize.width; j++)
deltas(d, i * S, j * S) = dout(d, i, j);
// расчитываем градиенты весов фильтров и смещений
for (int f = 0; f < fc; f++) {
for (int y = 0; y < size.height; y++) {
for (int x = 0; x < size.width; x++) {
double delta = deltas(f, y, x); // запоминаем значение градиента
for (int i = 0; i < fs; i++) {
for (int j = 0; j < fs; j++) {
int i0 = i + y - P;
int j0 = j + x - P;
// игнорируем выходящие за границы элементы
if (i0 < 0 || i0 >= inputSize.height || j0 < 0 || j0 >= inputSize.width)
continue;
// наращиваем градиент фильтра
for (int c = 0; c < fd; c++)
dW[f](c, i, j) += delta * X(c, i0, j0);
}
}
db[f] += delta; // наращиваем градиент смещения
}
}
}
int pad = fs - 1 - P; // заменяем величину дополнения
Tensor dX(inputSize); // создаём тензор градиентов по входу
// расчитываем значения градиента
for (int y = 0; y < inputSize.height; y++) {
for (int x = 0; x < inputSize.width; x++) {
for (int c = 0; c < fd; c++) {
double sum = 0; // сумма для градиента
// идём по всем весовым коэффициентам фильтров
for (int i = 0; i < fs; i++) {
for (int j = 0; j < fs; j++) {
int i0 = y + i - pad;
int j0 = x + j - pad;
// игнорируем выходящие за границы элементы
if (i0 < 0 || i0 >= size.height || j0 < 0 || j0 >= size.width)
continue;
// суммируем по всем фильтрам
for (int f = 0; f < fc; f++)
sum += W[f](c, fs - 1 - i, fs - 1 - j) * deltas(f, i0, j0); // добавляем произведение повёрнутых фильтров на дельты
}
}
dX(c, y, x) = sum; // записываем результат в тензор градиента
}
}
}
return dX; // возвращаем тензор градиентов
}
Этап 4. Обновление весовых коэффициентов
После того, как градиенты вычислены, необходимо обновить весовые коэффициенты, чтобы уменьшить ошибку на текущем обучающем примере. Для этого из каждого веса вычитается значение градиента, умноженное на скорость обучения — вещественное число, гиперпараметр метода градиентного спуска. Данный алгоритм является наиболее простым и довольно медленным с точки зрения сходимости методом оптимизации, однако ничего не мешает реализовать более быстрые алгоритмы, как, например, Adam, Adagrad, RMSprop и другие. В одной из статей мы обязательно расскажем, как их реализовать и добавить к создаваемой нами сети, а пока посмотрим на код обновления параметров:
// обновление весовых коэффициентов
void ConvLayer::UpdateWeights(double learningRate) {
for (int index = 0; index < fc; index++) {
for (int i = 0; i < fs; i++) {
for (int j = 0; j < fs; j++) {
for (int d = 0; d < fd; d++) {
W[index](d, i, j) -= learningRate * dW[index](d, i, j); // вычитаем градиент, умноженный на скорость обучения
dW[index](d, i, j) = 0; // обнуляем градиент фильтра
}
}
}
b[index] -= learningRate * db[index]; // вычитаем градиент, умноженный на скорость обучения
db[index] = 0; // обнуляем градиент веса смещения
}
}
Этап 5. Проверка
После написания всех методов хотелось бы удостовериться, что они работают корректно. Логичнее всего было бы написать небольшую процедуру для тестирования слоя, однако на данный момент у нас нет возможности задавать свои собственные параметры для весовых коэффициентов, а проверять работу слоя на случайных числах крайне неприятно. Поэтому мы создадим два метода для задания значений весовых коэффициентов фильтров и смещений соответственно:
// установка веса фильтра по индексу
void ConvLayer::SetWeight(int index, int i, int j, int k, double weight) {
W[index](i, j, k) = weight;
}
// установка веса смещения по индексу
void ConvLayer::SetBias(int index, double bias) {
b[index] = bias;
}
После этого напишем небольшую тестирующую функцию, которая проверит значения после применения прямого распространения и обратного распространения. Мы не будем приводить её код ввиду простоты и большого объёма проверок, но покажем значения, на которых будет производиться проверка.
Для начала создадим свёрточный слой, который будет принимать на вход тензор размером 5x5x3 (три канала 5×5), содержать 2 фильтра размером 3×3, шаг смещения 2 и единичное дополнение нулями. На выходе мы ожидаем тензор размером (5-3+2*1)/2+1 x (5-3+2*1)/2+1 x 2 = 3x3x2. Возьмём следующие фильтры и входной тензор для проверки:
|-1 1 1 | | 0 -1 1 | | 1 -1 0 |
W[0]: |-1 1 1 | | -1 0 -1 | | -1 0 -1 |
| 0 0 1 | | 1 0 0 | | 0 1 -1 |
| 0 0 -1 | | 1 -1 0 | | 1 0 1 |
W[1]: | 1 0 0 | | -1 1 0 | | 1 -1 1 |
| 0 -1 0 | | -1 1 1 | | -1 0 0 |
b[0]: 1
b[1]: 0
| 1 2 0 1 0 | | 1 2 2 1 2 | | 0 2 0 1 1 |
| 2 0 0 0 1 | | 0 2 2 0 2 | | 2 0 2 1 1 |
X: | 1 2 2 0 2 | | 1 2 2 1 1 | | 2 0 1 2 1 |
| 2 2 2 0 1 | | 2 2 0 1 0 | | 0 1 0 1 2 |
| 2 0 1 0 1 | | 2 2 1 0 0 | | 1 0 1 2 1 |
Если всё сделано правильно, то на выходе должен получиться следующий тензор:
| 2 -3 1 | | 3 5 2 |
Y: | 5 -7 2 | | 1 0 -3 |
| 5 0 0 | |-2 4 3 |
Пусть теперь слой принимает тензоры размером 4x4x1 и содержит 1 фильтр 3х3 с единичным шагом без дополнения нулями.
| 1 4 1 |
W[0]: | 1 4 3 |
| 3 3 1 |
b[0]: 0
| 4 5 8 7 |
X: | 1 8 8 8 |
| 3 6 6 4 |
| 6 5 7 8 |
Результат прямого распространения должен быть таким:
Y: | 122 148 | | 126 134 |
Запустим же теперь обратное распространение с такими дельтами:
dout: | 2 1 |
| 4 4 |
В результате должны получить такой тензор:
| 2 9 6 1 |
dX: | 6 29 30 7 |
| 10 29 33 13 |
| 12 24 16 4 |
Интерактивный пример
Чтобы операция свёртки стала ещё более понятной, мы добавили интерактивный пример ниже. В нём вы можете задать гиперпараметры слоя и увидеть анимацию прохода фильтра по тензорам.
Размер:
Глубина:
Число фильтров:
Размер фильтров:
Шаг свёртки:
Дополнение нулями:
Итоги
В результате мы получили класс для работы с тензорами, и, что самое главное, описали класс для работы свёрточного слоя с различными гиперпараметрами, а также проверили корректность работы методов прямого и обратного распространения. В следующей части мы расскажем вам о том, как создать слои подвыборки (пулинга) различного типа (максимума, среднего или суммы).
Следующая часть: Свёрточная нейронная сеть с нуля. Часть 2. Слой подвыборки