Стандартная ошибка среднего — это способ измерить, насколько разбросаны значения в наборе данных. Он рассчитывается как:
Стандартная ошибка среднего = s / √n
куда:
- s : стандартное отклонение выборки
- n : размер выборки
В этом руководстве объясняются два метода, которые вы можете использовать для вычисления стандартной ошибки среднего значения для набора данных в Python. Обратите внимание, что оба метода дают одинаковые результаты.
Способ 1: используйте SciPy
Первый способ вычислить стандартную ошибку среднего — использовать функцию sem() из библиотеки SciPy Stats.
Следующий код показывает, как использовать эту функцию:
from scipy. stats import sem
#define dataset
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29]
#calculate standard error of the mean
sem(data)
2.001447
Стандартная ошибка среднего оказывается равной 2,001447 .
Способ 2: использовать NumPy
Другой способ вычислить стандартную ошибку среднего для набора данных — использовать функцию std() из NumPy.
Обратите внимание, что мы должны указать ddof=1 в аргументе этой функции, чтобы вычислить стандартное отклонение выборки, а не стандартное отклонение генеральной совокупности.
Следующий код показывает, как это сделать:
import numpy as np
#define dataset
data = np.array([3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29])
#calculate standard error of the mean
np.std(data, ddof= 1 ) / np.sqrt (np.size (data))
2.001447
И снова стандартная ошибка среднего оказывается равной 2,001447 .
Как интерпретировать стандартную ошибку среднего
Стандартная ошибка среднего — это просто мера того, насколько разбросаны значения вокруг среднего. При интерпретации стандартной ошибки среднего следует помнить о двух вещах:
1. Чем больше стандартная ошибка среднего, тем более разбросаны значения вокруг среднего в наборе данных.
Чтобы проиллюстрировать это, рассмотрим, изменим ли мы последнее значение в предыдущем наборе данных на гораздо большее число:
from scipy. stats import sem
#define dataset
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 150 ]
#calculate standard error of the mean
sem(data)
6.978265
Обратите внимание на скачок стандартной ошибки с 2,001447 до 6,978265.Это указывает на то, что значения в этом наборе данных более разбросаны вокруг среднего значения по сравнению с предыдущим набором данных.
2. По мере увеличения размера выборки стандартная ошибка среднего имеет тенденцию к уменьшению.
Чтобы проиллюстрировать это, рассмотрим стандартную ошибку среднего для следующих двух наборов данных:
from scipy.stats import sem
#define first dataset and find SEM
data1 = [1, 2, 3, 4, 5]
sem(data1)
0.7071068
#define second dataset and find SEM
data2 = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]
sem(data2)
0.4714045
Второй набор данных — это просто первый набор данных, повторенный дважды. Таким образом, два набора данных имеют одинаковое среднее значение, но второй набор данных имеет больший размер выборки, поэтому стандартная ошибка меньше.
Дополнительные ресурсы
Как рассчитать стандартную ошибку среднего в R
Как рассчитать стандартную ошибку среднего в Excel
Как рассчитать стандартную ошибку среднего в Google Sheets
— Я ничего в ней не вижу, — сказал я, возвращая шляпу Шерлоку Холмсу.
— Нет, Уотсон, видите, но не даете себе труда поразмыслить над тем, что видите.
Артур Конан Дойл. Голубой карбункул
В предыдущей серии постов для начинающих (первый пост тут) из ремикса книги Генри Гарнера «Clojure для исследования данных» (Clojure for Data Science) на языке Python было представлено несколько численных и визуальных подходов, чтобы понять, что из себя представляет нормальное распределение. Мы обсудили несколько описательных статистик, таких как среднее значение и стандартное отклонение, и то, как они могут использоваться для краткого резюмирования больших объемов данных.
Набор данных обычно представляет собой выборку из некой более крупной популяции, или генеральной совокупности. Иногда эта популяция слишком большая, чтобы быть измеренной полностью. Иногда она неизмерима по своей природе, потому что она бесконечна по размеру либо потому что к ней нельзя получить непосредственный доступ. В любом случае мы вынуждены делать вывод, исходя из данных, которыми мы располагаем.
В этой серии из 4-х постов мы рассмотрим статистический вывод: каким образом можно выйти за пределы простого описания выборок и вместо этого описать популяцию, из которой они были отобраны. Мы подробно рассмотрим степени нашей уверенности в выводах, которые мы делаем из выборочных данных. Мы раскроем суть робастного подхода к решению задач в области исследования данных, каким является проверка статистических гипотез, которая как раз и привносит научность в исcледование данных.
Кроме того, по ходу изложения будут выделены болевые точки, связанные с терминологическим дрейфом в отечественной статистике, иногда затуманивающим смысл и подменяющим понятия. В конце заключительного поста можно будет проголосовать за или против размещения следующей серии постов. А пока же…
В целях иллюстрации принципов статистического вывода, мы создадим вымышленную компанию под названием AcmeContent, которая недавно наняла нас в качестве исследователей данных.
Представляем AcmeContent
Для оказания помощи в иллюстрировании понятий, представленных в этой серии постов, предположим, что в компанию AcmeContent нас недавно назначили в качестве исследователей данных. Компания заведует веб-сайтом, предлагающим своим посетителям возможность делиться между собой понравившимися им видеоклипами по Интернет.
Одна из метрик, которая отслеживается в AcmeContent посредством веб-аналитики — это время пребывания. Указанная метрика служит мерой количества времени, в течение которого посетитель остается на веб-сайте. Безусловно, посетителям, которые проводят на веб-сайте продолжительное время, веб-сайт нравится, и в AcmeContent хотели бы, чтобы посетители оставались на нем максимально долго.
Время пребывания (dwell time)— это отрезок времени между временем, прибытия посетителя на веб-сайт и временем, когда он сделал последний запрос.
Отскок (bounce) — это посетитель, который выполняет всего один запрос — его время пребывания равно нулю.
На вас, как новом исследователе данных, лежит в компании обязанность анализировать время пребывания посетителей на веб-сайте — этот показатель фигурирует в аналитических отчетах посещаемости веб-страниц и разделов веб-сайта — и измерять успех веб-сайта AcmeContent.
Загрузка и обследование данных
Здесь мы будем пользоваться теми же самыми библиотеками, что и ранее: scipy, pandas и matplotlib. В предыдущей серии постов мы использовали библиотеку pandas для загрузки электронных таблиц Excel, задействуя ее функцию read_excel. Здесь мы будем загружать набор данных из текстового файла с разделением значений символом табуляции. Для этого мы воспользуемся функцией pandas read_csv, которая на входе ожидает URL-адрес либо путь к файлу в строковом формате.
Файл был любезно переформатирован веб-командой AcmeContent и содержит всего два столбца — дату запроса и время пребывания на веб-сайте в секундах. Заголовки столбцов расположены в первой строке файла:
Названия приводимых примеров имеют формат ex_N_M, где ex — example (пример), N — номер серии постов и M — порядковый номер в посте. Примеры оформлены в виде функций без аргументов и возвращаемых значений. Это сделано намеренно, т.к. задачно-ориентированный стиль изложения требует кратких и четких примеров без отвлекающей внимание информации. К тому же, в таком виде примеры могут быть собраны вместе и исполняться независимо в рамках программной оболочки.
def load_data( fname ):
return pd.read_csv('data/ch02/' + fname, 't')
def ex_2_1():
return load_data('dwell-times.tsv').head()Если выполнить этот пример (в консоли интерпретатора Python либо в блокноте Jupyter), то можно увидеть результат, который показан ниже:
|
date |
dwell-time |
|
|
0 |
2015-01-01T00:03:43Z |
74 |
|
1 |
2015-01-01T00:32:12Z |
109 |
|
2 |
2015-01-01T01:52:18Z |
88 |
|
3 |
2015-01-01T01:54:30Z |
17 |
|
4 |
2015-01-01T02:09:24Z |
11 |
|
… |
… |
… |
Посмотрим, как выглядит время пребывания на гистограмме.
Визуализация времени пребывания
Мы можем построить гистограмму времени пребывания, выбрав столбец dwell-time и применив к нему функцию hist:
def ex_2_2():
load_data('dwell-times.tsv')['dwell-time'].hist(bins=50)
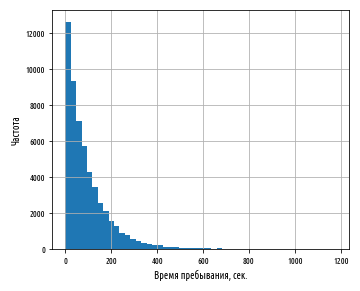
plt.xlabel('Время пребывания, сек.')
plt.ylabel('Частота')
plt.show() Приведенный выше пример сгенерирует следующую ниже гистограмму:
Очевидно, что эти данные не являются нормально распределенными; они даже не представляют собой сильно смещенное нормальное распределение. Слева от пика нет никакого хвоста (посетитель явно не может быть на веб-сайте менее 0 сек.). Сначала данные круто убывают вправо и потом тянутся вдоль оси X намного дольше, чем можно было бы ожидать от данных, которые нормально распределены.
Когда встречаются подобные распределения, где большинство значений малы, и иногда случаются предельные значения, может оказаться полезным изобразить ось Y в виде логарифмической шкалы. Логарифмические шкалы используются для того, чтобы представлять события, которые меняются в очень широких пределах. Оси графика обычно линейны, и они делят диапазон на равноразмерные шаги подобно «числовой оси», которую мы изучали в школе. В отличие от них, логарифмические шкалы делят диапазон на шаги, которые становятся все длиннее и длиннее по мере удаления от источника.
Некоторые системы измерения природных явлений, которые изменяются в очень широких пределах, представлены в логарифмической шкале. Например, шкала Рихтера для измерения интенсивности землетрясений является логарифмической шкалой по основанию 10, что означает, что землетрясение магнитудой 5 баллов по шкале Рихтера в 10 раз интенсивнее землетрясения магнитудой 4 балла. Децибельная шкала громкости тоже имеет логарифмическую шкалу, но с другим основанием — звуковая волна магнитудой 30 децибелов в 10 раз больше звуковой волны в 20 децибелов. В каждом случае принцип один и тот же — использование логарифмической шкалы позволяет сжать очень широкий предел значений в диапазон гораздо меньшего размера.
Изобразить на графике ось Y с логарифмической шкалой достаточно легко при помощи именованного аргумента logy=True функции pandas plot.hist:
def ex_2_3():
load_data('dwell-times.tsv')['dwell-time'].plot.hist(bins=20, logy=True)
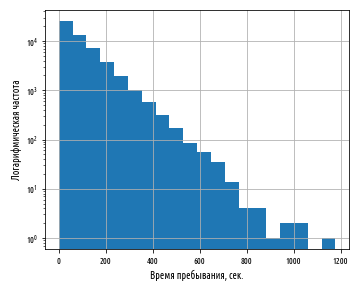
plt.xlabel('Время пребывания, сек.')
plt.ylabel('Логарифмическая частота')
plt.show() В библиотеке pandas по умолчанию используется десятичная логарифмическая шкала, каждое деление на оси которой представляет собой интервал в 10 раз шире относительно предыдущего. График, в котором только одна ось имеет логарифмическую шкалу, называется полулогарифмическим или лог-линейным. Неудивительно, что график с двумя логарифмическими осями называется просто логарифмическим или логлог-линейным графиком (иногда также двойным логарифмическим, loglog=True).
Нанесение данных времени пребывания на полулогарифмический график показывает, что они обладают скрытой связностью — имеется линейная связь между временем пребывания и логарифмом частоты. На графике ясность связи ухудшается справа, где число посетителей меньше 10, но, помимо этого, связь удивительно постоянная.
Прямая линия на полулогарифмическом графике — это явный индикатор экспоненциального распределения.
Экспоненциальное распределение
Экспоненциальное (или показательное) распределение часто встречается в ситуациях, когда имеется много малых положительных значений и намного меньше более крупных. С учетом того, что мы узнали о шкале Рихтера, не будет никаким секретом, что магнитуда землетрясений подчинена экспоненциальному распределению.
Кроме того, это распределение часто встречается в период ожидания — время до наступления следующего землетрясения любой магнитуды тоже приближенно подчиняется экспоненциальному распределению. Это распределение часто используется для имитационного моделирования интенсивности отказов, которые по существу являются временем ожидания события, когда механизм выйдет из строя. Наше экспоненциальное распределение моделирует процесс, аналогичный поломке — время ожидания события, когда посетитель заскучает и покинет веб-сайт.
Экспоненциальное распределение характерно многими интересными свойствами. Одно из них имеет отношение к среднему значению и стандартному отклонению:
def ex_2_4():
ts = load_data('dwell-times.tsv')['dwell-time']
print('Среднее: ', ts.mean())
print('Медиана: ', ts.median())
print('Стандартное отклонение:', ts.std())Среднее: 93.2014074074074
Медиана: 64.0
Стандартное отклонение: 93.96972402519819Среднее значение и стандартное отклонение очень похожи. Фактически, для идеального экспоненциального распределения они абсолютно одинаковые. Это свойство сохраняется для всех экспоненциальных распределений — при увеличении средних увеличиваются и стандартные отклонения.
Для экспоненциальных распределений средние значения и стандартные отклонения эквивалентны.
Вторым свойством экспоненциального распределения является отсутствие памяти (или последействия). Это противоречащее интуитивному пониманию свойство лучше всего проиллюстрировать на примере. Мы ожидаем, что пока посетитель продолжает просматривать наш веб-сайт, вероятность, что ему надоест, и он покинет веб-сайт, увеличивается. Поскольку среднее время пребывания составляет 93 сек., то может создаться впечатление, что за пределами этих 93 сек., он будет продолжать просмотр веб-сайта все в меньшей степени.
Свойство отсутствия памяти экспоненциальных распределений говорит о том, что вероятность, что посетитель останется на нашем веб-сайте в течение следующих 93 сек. совершенно одинаковая, независимо от того, находится он на веб-сайте уже 93 сек., 5 мин. или целый час, либо только что на него зашел.
Для распределения без памяти количество истекшего времени не влияет на вероятность продолжения события в течение дополнительных x минут.
Свойство отсутствия памяти экспоненциальных распределений частично объясняет причину, почему очень трудно предсказывать время следующего землетрясения. Нам приходится опираться не на истекшее время, а на другие подтверждающие данные (такие как отклонения в геомагнетизме).
Поскольку медианное время пребывания составляет 64 сек., то примерно половина наших посетителей остаются на веб-сайте в течение примерно всего одной минуты. Среднее значение в 93 сек. показывает, что некоторые посетители остаются намного дольше медианы. Эти статистики были вычислены по всем посетителям за последние 6 месяцев. Было бы интересно узнать, каким образом эти статистики варьируются в расчете на один день. Давайте их вычислим.
Распределение среднесуточных значений
Предоставленный веб-командой файл включает метку даты посещения. В целях агрегирования данных по дням, необходимо удалить ту часть метки даты, которая соответствует времени. Хотя мы можем проделать это при помощи нативных средств Python, более гибкий подход состоит в использовании функционала pandas для обработки даты и времени — функции to_datetime.
На входе она принимает строковое значение, значение с типом date-time, список, кортеж, 1-мерный массив либо числовой ряд Series библиотеки pandas как в нашем случае, а также набор именованных аргументов. Например, именованный аргумент errors='ignore' позволяет проигнорировать даты, которые неправильно отформатированы либо выходят за допустимые пределы. Отметим также, что в функции mean_dwell_times_by_date использован вспомогательный метод resample для частотных преобразований и перестановки временного ряда. Он выполняет группировку по дате-времени, а после него следует метод свертки по каждой группе. В данном случае аргумент 'D' группирует по будним дням, и затем каждая группа агрегируется методом mean. Таким образом, выражение dt.resample('D').mean() берет средние значения по будним дням:
def with_parsed_date(df):
'''Привести поле date к типу date-time'''
df['date'] = pd.to_datetime(df['date'], errors='ignore')
return df
def filter_weekdays(df):
'''Отфильтровать по будним дням'''
return df[df['date'].index.dayofweek < 5] # понедельник..пятница
def mean_dwell_times_by_date(df):
'''Среднесуточные времена пребывания'''
df.index = with_parsed_date(df)['date']
return df.resample('D').mean() # перегруппировать
def daily_mean_dwell_times(df):
'''Средние времена пребывания с фильтрацией - только по будним дням'''
df.index = with_parsed_date(df)['date']
df = filter_weekdays(df)
return df.resample('D').mean()Сочетание приведенных выше функций позволяет вычислить среднее, медиану и стандартное отклонение для времен пребывания по будним дням:
def ex_2_5():
df = load_data('dwell-times.tsv')
mus = daily_mean_dwell_times(df)
print('Среднее: ', float(means.mean()))
print('Медиана: ', float(means.median()))
print('Стандартное отклонение: ', float(means.std()))Среднее: 90.21042865056198
Медиана: 90.13661202185793
Стандартное отклонение: 3.7223429053200348По будним дням среднее значение составляет 90.2 сек. Оно близко к среднему значению, которое мы вычислили ранее по всему набору данных, включая выходные дни. А вот стандартное отклонение намного ниже, всего 3.7 сек. Другими словами, распределение значений по будним дням имеет стандартные отклонения намного ниже, чем по всему набору данных. Давайте построим гистограмму значений времен пребывания по будним дням:
def ex_2_6():
df = load_data('dwell-times.tsv')
daily_mean_dwell_times(df)['dwell-time'].hist(bins=20)
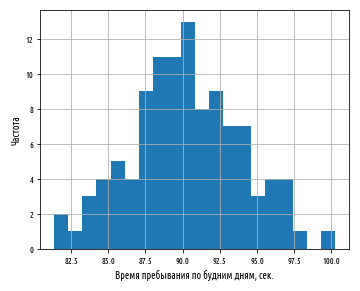
plt.xlabel('Время пребывания по будним дням, сек.')
plt.ylabel('Частота')
plt.show()Этот пример сгенерирует следующую ниже гистограмму:
Распределение средних значений в выборках расположено симметрично вокруг общего популяционного среднего значения, равного 90 сек. со стандартным отклонением 3.7 сек. В отличие от распределения, из которого эти средние были отобраны, т.е. экспоненциального распределения, распределение выборочных средних нормально распределено.
Центральная предельная теорема
Мы встречались с центральной предельной теоремой в предыдущей серии постов, когда делали выборки из равномерного распределения и их усредняли. На самом деле, центральная предельная теорема работает для любого распределения значений при условии, что это распределение имеет конечное стандартное отклонение.
Согласно центральной предельной теореме, распределение выборочных средних нормально распределено независимо от распределения, из которого они были вычислены.
То, что опорное распределение — экспоненциальное, не играет никакой роли — центральная предельная теорема показывает, что средние значения случайных выборок, взятых из любого распределения, близко аппроксимируют нормальное распределение. Теперь давайте построим график нормальной кривой поверх нашей гистограммы, чтобы посмотреть, насколько близко она совпадает.
В целях выведения нормальной кривой поверх гистограммы последняя должна быть построена как гистограмма плотностей распределения. Она изображает не частоту, а долю всех точек, помещенных в каждую корзину. После чего мы сможем наложить нормальную плотность вероятности с тем же средним значением и стандартным отклонением (Обратите внимание на применение функции dropna, которая удаляет строки, где есть пропущенные значения):
def ex_2_7():
'''Подгонка нормальной кривой поверх гистограммы'''
df = load_data('dwell-times.tsv')
means = daily_mean_dwell_times(df)['dwell-time'].dropna()
ax = means.hist(bins=20, density=True)
xs = sorted(means) # корзины
df = pd.DataFrame()
df[0] = xs
df[1] = stats.norm.pdf(xs, means.mean(), means.std())
df.plot(0, 1, linewidth=2, color='r', legend=None, ax=ax)
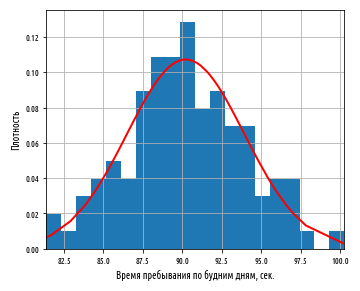
plt.xlabel('Время пребывания по будним дням, сек.')
plt.ylabel('Плотность')
plt.show()Этот пример сгенерирует следующий ниже график:
Нормальная кривая, изображенная поверх гистограммы, имеет стандартное отклонение, равное примерно 3.7 сек. Другими словами, она количественно определяет изменчивость каждого значения в будние дни относительно общего среднего значения, равного 90 сек. Можно представить среднее каждого дня как выборку из общей популяции, где изображенная выше кривая показывает распределение средних по выборкам. Поскольку 3.7 сек. — это величина, на которую среднее значение выборки отличается от популяционного среднего, она называется стандартной ошибкой.
Стандартная ошибка
В то время как стандартное отклонение измеряет величину изменчивости внутри выборки, стандартная ошибка (Standard Error, аббр. SE) среднего, измеряет величину изменчивости между средними значениями выборок, взятыми из той же самой популяции.
Стандартная ошибка среднего — это стандартное отклонение распределения средних по выборкам.
Мы вычислили стандартную ошибку времени пребывания эмпирически, глядя на данные за предыдущие 6 месяцев. Однако существует уравнение, которое позволяет ее вычислять, исходя из одной единственной выборки:
Здесь σx — это стандартное отклонение, подсчитанное по выборке x, и n — размер выборки. Эта формула не похожа на описательные статистики, которые мы встречали в предыдущей серии постов. Они описывали одиночную выборку. В отличие от них, стандартная ошибка пытается описать свойство выборок в целом — величину изменчивости в средних значениях выборок, которую можно ожидать для выборок заданного размера:
def variance(xs):
'''Несмещенная дисперсия (варианс) при n <= 30'''
x_hat = xs.mean()
n = len(xs)
n = n-1 if n in range(1, 30) else n
square_deviation = lambda x : (x – x_hat) ** 2
return sum( map(square_deviation, xs) ) / n
def standard_deviation(xs):
return sp.sqrt(variance(xs))
def standard_error(xs):
return standard_deviation(xs) / sp.sqrt(len(xs))Стандартная ошибка среднего таким образом связана с двумя факторами:
-
Размером выборки
-
Популяционным стандартным отклонением
Размер выборки оказывает самое большое влияние на стандартную ошибку. Для того, чтобы уменьшить размер стандартной ошибки вдвое, мы должны увеличить его в четыре раза, поскольку мы берем квадратный корень размера выборки.
Может показаться странным, что доля популяции, из которой отбирается выборка, никак не влияет на размер стандартной ошибки. Но это именно так, поскольку некоторые популяции могут иметь бесконечные размеры.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Темой следующего поста, поста №2, будет разница между выборками и популяцией, а также интервал уверенности. Да-да, именно интервал уверенности, а не доверительный интервал.
Python
Импорт библиотек
import pandas as pd
импортирует библиотеку для работы с таблицами и данными в виде датафреймов
import numpy as np
импортирует библиотеку для работы с числами
import seaborn as sns
импортирует библиотеку для создания графиков и визуализации данных
import matplotlib.pyplot as plt
импортирует библиотеку для создания графиков и визуализации данных
import plotly.express as px
импортирует библиотеку для создания интерактивных графиков
import datetime
импортирует модуль для работы с датами и временем
import matplotlib.dates as mdates
импортирует модуль для работы с датами и временем в библиотеке matplotlib
import random
импортирует модуль для генерации случайных чисел
import re
импортирует модуль для работы с регулярными выражениями
import vk_ip
импортирует модуль для работы с IP-адресами ВКонтакте
import os
импортирует модуль для работы с операционной системой
import json as json
импортирует модуль для работы с JSON-данными
import requests
импортирует модуль для работы с HTTP-запросами
import gspread
импортирует библиотеку для работы с Google Sheets
import zipfile
импортирует модуль, который предоставляет функции для работы с архивами ZIP в Python
from io import BytesIO
импортирует модуль для работы с бинарными данными в памяти
import pandahouse as ph
импортирует библиотеку для работы с ClickHouse
from scipy import stats
импортирует модуль для статистических вычислений
from scipy.stats import zscore
импортирует функцию для вычисления z-оценки
import pingouin as pg
предоставляет различные функции для статистического анализа данных, включая ANOVA, корреляцию, регрессию и др.
from scipy.special import comb
функция comb из библиотеки scipy.special, которая используется для вычисления комбинаторных коэффициентов
import statistics
библиотека, которая содержит набор функций для выполнения статистических расчетов
from statsmodels.formula.api import ols
интерфейс для моделирования линейной регрессии с помощью формул
from statsmodels.stats.anova import anova_lm
используется для проведения анализа дисперсии (ANOVA) в статистическом анализе данных
import statsmodels.formula.api as smf
работа с формулами и моделями
import statsmodels.api as sm
предоставляет классы и функции для моделирования и статистического анализа данных
from sklearn.cluster import AgglomerativeClustering
используется для кластеризации данных с помощью иерархической кластеризации
import bootstrapped.bootstrap as bsimport bootstrapped.stats_functions as bs_stats
позволяют оценить распределение статистических показателей, таких как среднее значение, медиана, стандартное отклонение и т.д.
from statsmodels.stats.contingency_tables import StratifiedTable
используется для анализа таблиц сопряженности
from scipy.stats import chi2_contingency
используется для расчета критерия хи-квадрат для таблиц сопряженности
from df2gspread import df2gspread as d2g
функция используется для экспорта данных из pandas DataFrame в Google Sheets
from oauth2client.service_account import ServiceAccountCredentials
используется для аутентификации в Google API с помощью учетных данных службы
from my_module import my_function
содержит функцию или библиотеку функций, специфичных для проекта, над которым работает конкретный автор
Файловая система, импорт/экспорт данных
Файловая система
[x[0] for x in os.walk('my_directory')]
выводит список всех папок внутри папки ‘my_directory’ (включая подпапки)
Импорт данных
df = pd.read_csv('C:\temp\example.csv')
df2 = pd.read_csv('C:\temp\example2.csv', parse_dates=['date'], sep=';', dayfirst=True)
импорт с локального диска и сохранение файла в датафрейм, во втором примере указан парсинг дат, указан разделитель и формат времени dd/mm/yyyy
connection_default = {'host': 'link',
'database':'default',
'user':'******',
'password':'******'
}
q =
'''
SELECT *
FROM
{db}.table
WHERE
id != 'none'
'''
df = ph.read_clickhouse(query=q, connection=connection_default)
SQL запрос в Python через CLICKHOUSE в пандас (нужно подставить link, заменить звездочки учетными данными, верно указать базу данных и написать корректный запрос)
df = pd.read_csv('C:\temp\data.csv.zip', compression='zip')
with zipfile.ZipFile('C:\temp\data2.csv.zip') as myzip:
with myzip.open('data2.csv') as myfile:
df2 = pd.read_csv(myfile, encoding='ISO-8859-1')
импорт в датасет csv файла, а во втором случае импорт конкретного csv файла в архиве
df = np.genfromtxt('C:\temp\data.txt', dtype=None)
pd.DataFrame(df)
загружает данные из txt файла в виде массива numpy и создает датасет с этими данными
df = pd.read_excel('C:\temp\data.xls')
загружает данные из excel файла и создает датасет с этими данными (загружается первый лист по умолчанию)
df = pd.read_excel('C:\temp\data.xls', sheet_name = 'Лист3')
загружает данные из excel файла c указанного листа
df = pd.read_csv('link', sep=";")
загружает файл csv по ссылке
def download(link, df):
base_url = 'link'
final_url = base_url + urlencode(dict(public_key=link))
response = requests.get(final_url)
download_url_file = response.json()['href']
file_df = pd.read_csv(download_url_file)
pattern = r'[;,|t]'
pattern_test = re.search(pattern, file_df.columns[0])
if pattern_test is not None:
sep = pattern_test[0]
file_df = pd.read_csv(download_url_file, delimiter=None, sep=sep, parse_dates=True)
globals()[df] = file_df
функция для загрузки файлов с ЯндексДиска (заполнить link)
Экспорт данных
filename = 'C:\temp\data.csv'<br> df.to_csv(filename)`
сохраняет датасет в csv файл
Работа со строками
S1 + S2
сложение строк
S * 3
повторение строки три раза
S[i]
обращение по индексу символа в строке
S[i:j:step]
позволяет выбрать срез последовательности элементов начиная с индекса i и заканчивая индексом j-1 с заданным шагом step
len(S)
выводит длину строки
S.find(str, [start],[end])
возвращает индекс первого символа первого вхождения str в S или -1, если подстрока не найдена.
start является необязательным и указывает индекс, с которого нужно начать поиск подстроки. Если start не указан, поиск начинается с начала строки
end также является необязательным и указывает индекс, до которого нужно искать подстроку. Если end не указан, поиск производится до конца строки
S.rfind(str, [start],[end])
то же что и предыдущее, но возвращает номер последнего вхождения или -1
S.index(str, [start],[end])
аналогично S.find, отличие в том, что если подстрока не найдена, S.index() генерирует исключение ValueError
S.rindex(str, [start],[end])
то же что и предыдущее, но возвращает номер последнего вхождения или ValueError
S.replace(шаблон, замена)
замена символов в строке по шаблону
S.split(символ)
разбиение строки по разделителю, указанному в скобках
S.isdigit()
cостоит ли строка из цифр — возвращает true или false
S.isalpha()
cостоит ли строка из букв — возвращает true или false
S.isalnum()
cостоит ли строка из цифр или букв — возвращает true или false
S.islower()
cостоит ли строка из символов в нижнем регистре — возвращает true или false
S.isupper()
cостоит ли строка из символов в верхнем регистре — возвращает true или false
S.isspace()
cостоит ли строка из неотображаемых символов: пробел, перевод страницы новая строка и т.д. — возвращает true или false
S.istitle()
начинаются ли слова в строке с заглавной буквы — возвращает true или false
S.upper()
преобразовывает строку к верхнему регистру
S.lower()
преобразовывает строку к нижнему регистру
S.startswith(шаблон)
начинается ли строка с шаблона — возвращает true или false
S.endswith(шаблон)
заканчивается ли строка шаблоном — возвращает true или false
S.join(список)
объединяет элементы списка в одну строку S, используя строку S в качестве разделителя между элементами списка
ord(символ)
возвращает код символа в таблице символов ASCII
chr(число)
возвращает символ, соответствующий переданному числу в кодировке Unicode
S.capitalize()
переводит первый символ строки в верхний регистр, а все остальные в нижний
S.center(width, [fill])
выравнивает строку S по центру, путем добавления символов fill (если указано) слева и справа от строки до достижения заданной ширины (width)
S.count(str, [start],[end])
возвращает количество непересекающихся вхождений подстроки в диапазоне [start, end]
S.expandtabs([tabsize])
возвращает копию строки, в которой все символы табуляции заменяются одним или несколькими пробелами. Если TabSize не указан, табуляция полагается равным 8 пробелам
S.lstrip([chars])
удаление пробельных символов в начале строки
S.rstrip([chars])
удаление пробельных символов в конце строки
S.strip([chars])
удаление пробельных символов в начале и в конце строки
S.partition(шаблон)
возвращает кортеж из трех элементов: 1й будет содержать часть строки S, которая находится перед первым вхождением шаблона; 2й элемент будет содержать сам шаблон; 3й элемент будет содержать часть строки S, которая находится после первого вхождения шаблона
S.rpartition(sep)
то же самое, что и предыдущая команда, но выполняется в обратном направлении
S.swapcase()
переводит символы нижнего регистра в верхний, а верхнего – в нижний
S.title()
первую букву каждого слова переводит в верхний регистр, а все остальные в нижний
S.zfill(width)
используется для добавления ведущих нулей в строку S до заданной ширины width
S.ljust(width, fillchar=" ")
то же самое, что и предыдущая команда, но заполняет символом fillchar
S.rjust(width, fillchar=" ")
то же самое, что и предыдущая команда, но заполняет символом fillchar и выполняется в обратном направлении
Работа со списками
append()
добавляет в конец списка один новый элемент
extend()
расширяет список другим списком
insert(index, value)
позволяет вставлять значение в список в заданной позиции
index()
возвращает индекс первого элемента, значение которого равняется переданному в метод значению
remove()
удаляет первый элемент, значение которого равняется переданному в метод значению
pop(index)
удаляет элемент по указанному индексу и возвращает его
reverse()
меняет на противоположный порядок следования значений в списке
len(list)
выводит количество элементов списка
sum(list)
выводит сумму элементов в списке
count()
возвращает количество элементов в списке, значения которых равны переданному в метод значению
clear()
удаляет все элементы из списка
copy()
создает поверхностную копию списка
sort()
сортирует список, для обратного порядка указать reverse
Списочные выражения
Дано:
word = 'test'
numbers = [1, 5, 10, 25, 50]
words = ['house', 'worm', 'sex']
str_numbers = ‘12345’<br> mix = [1, ‘house’, 3.45]`
тогда:
| Выражение | Суть | Результат |
|---|---|---|
| [0 for i in range(10)] | создает список, содержащий определенное количество заданных элементов | [0, 0, 0, 0, 0] |
| [int(i) for i in str_numbers] | преобразует список строк из чисел в список целых чисел | [1, 2, 3, 4, 5] |
| [i ** 3 for i in range(1, 5)] | list comprehension, которое в данном случае генерит список кубов чисел in range | [1, 8, 27, 64] |
| [i for i in numbers if i != 10] | удаляет элементы из списка по условию | [1, 5, 25, 50] |
| [i * 2 for i in numbers] | создаст список, в котором каждый элемент «numbers» будет умножен на 2 | [2, 10, 20, 50, 100] |
| len([item for item in numbers if item > 5]) | вычисляет количество элементов списка numbers, которые больше 5 | 3 |
| [w * 2 for w in word] | создаст список с удвоенными значениями элементов word | [‘tt’, ‘ee’, ‘ss’, ‘tt’] |
| [l[0] for l in words] | создаст список, содержащий первый элемент от каждого элемента списка words | [‘h’, ‘w’, ‘s’] |
| all(numbers[i] <= numbers[i+1] for i in range(len(numbers)-1)) | проверяет условие, что каждый последующий элемент списка «numbers» не меньше предыдущего элемента | True |
| [i for i in numbers if i < 15] | вернет список с элементами списка «numbers», которые меньше 15 | [1, 5, 10] |
| [l[0] for l in words if len(l) == 3] | вернет список из первых элементов каждого элемента списка words, длина которого равна 3 | [‘s’] |
Работа со временем
df['column'] = pd.to_datetime(df.column)
преобразует столбец в формат даты и времени
df['column'] = df['column'].dt.strftime('%m/%d/%Y')
преобразует значения столбца из формата datetime в строковый формат
Прочие методы
Дано:
word = 'test'
numbers = [1, 5, 10, 25, 50]
words = ['house', 'worm', 'sex']
str_numbers = ‘12345’<br> mix = [1, ‘house’, 3.45]`
for num, word in zip(numbers, words):
print(f"{num} {word}")
1 house
5 worm
10 sex
использована функция zip() для создания итератора, который позволяет проходить по двум спискам одновременно
result = 1
for i in range(0,len(numbers)):
result = result * numbers[i]
print(result)
62500
перемножает все числа в списке «numbers» по очереди и сохраняет результат в переменной «result»
print(list(map(type, mix)))
[<class 'int'>, <class 'str'>, <class 'float'>]
выведет список, содержащий тип каждого элемента списка
if len(set(numbers)) == 1:
print('YES')
else:
print('NO')
NO
код проверяет, все ли элементы списка numbers равны между собой
n = int(input())
counter = []
while n != 0:
last_digit = n % 10
n = n // 10
counter.append(last_digit)
counter.reverse()
print(counter)
выводит список цифр введенного пользователем числа в порядке от первой цифры до последней, и для числа 456 результатом будет [4, 5, 6]
Работа с датафреймами (Pandas / NumPy)
pd.Series(['One','Two','Three'])
cоздает Series из списка
df = pd.DataFrame()
cоздает пустой датафрейм
df = df.reset_index()
возвращает датафрейм с новым индексом, начинающимся с 0, и старым индексом, сохраненным в виде нового столбца
df['Column'].to_frame()
возвращает столбец из датафрейма в виде датафрейма
df.isna().sum()
возвращает количество пропущенных значений в каждом столбце
df.columns = [x.lower() for x in df.columns]
приводит все названия столбцов к нижнему регистру
df = df.rename(columns={'x': 'name', 'y': 'new_name'})
переименовывает столбец в датасете
df = df.rename(columns={df.columns[0]:"new_column_name"})
переименовывает столбец в датасете по индексу
df.columns = df.columns.str.replace('[.]', '_').str.replace('[ ]', '').lower()
переименовывает столбец в датасете, удаляя «лишние» символы и переводит к нижнему регистру
df[['One', 'Two', 'Three']]
выводит три столбца датафрейма df в виде датафрейма
df = df.drop(['column_1','column_2'], axis=1)
df = df.loc[:,('column_1', 'column_4', 'column_7')]
df = df.drop(columns=df.columns[0])
удаление столбцов в датасете:
первый — удаляет указанные столбцы;
второй — удаляет все столбцы, кроме указанных;
третий — удаляет столбцы по индексу
df['numbers'] = df['numbers'].astype(int)
df = df.apply(lambda x: pd.to_numeric(x, errors='coerce')).dropna()
первый код переводит текстовые значения в целые числа,
второй код позволяет также удалить все строки с некорректными или отсутствующими значениями — оставить только строки с числовыми значениями
len(df.loc[df.assign_type != df.reserved_type])
позволяет вывести количество строк не соответствующих строкам другого столбца
df.groupby('year').month.agg(pd.Series.mode)
группирует строки по году и для каждой группы найдет моду (самое часто встречающееся значение), в данном случае, месяца
df = df.astype({"a": int, "b": complex})
меняет типы данных в столбцах
df['column'].tolist()
переводит cтолбец колонки в список
df = df['column'] + '\' + df['column_2']
делает из содержимого двух колонок третью
df = df.assign(new_column = df.column_1 * df.column_2)
cоздает столбец на основании математической операции между двумя столбцами
orders.isna().sum()
выводит информацию по пропущенным значениям в датасете
df.groupby('column_1').agg({'success': 'sum'})
группирует датафрейм по количество успешных операций для столбца column_1
df = df.unstack('column_1')
преобразует иерархически индексированный датасет, добавляя колонки из уровня, соответствующего указанной колонке, на новый уровень колонок
df2 = pd.wide_to_long(df, ['column_1', 'column_2'], i=['type', 'name'], j='year', sep='_')
создает новый датасет, в котором идентификаторы (в данном случае, type, name) хранятся в отдельных столбцах, а значения из исходных столбцов с годами (year) и значениями (column_1, column_2) хранятся в отдельных строках
df2 = df.explode('Column_1')
создает новый датасет, в котором каждый элемент списка в столбце ‘Column_1’ разбивается на отдельную строку, а значения в остальных столбцах дублируются соответственно
df.groupby('column_1').agg({'column_2': 'sum'})
группирует строки в датасете df по уникальным значениям в столбце «column_1» и для каждой группы вычисляет сумму значений в столбце «column_2». Результатом будет новый датасет с одним индексом «column_1» и одним столбцом «column_2», содержащим сумму значений «column_2» для каждого уникального значения «column_1»
df.sort_values('column_2', ascending=False)
сортирует датасет df по столбцу column_2 в порядке убывания (от наибольшего значения к наименьшему)
df.sort_values(['Column_1','Column_2'], ascending = [True, False])
сортитует датасет сразу по двум колонкам, одну по убыванию, другую по возрастанию
df['name'].value_counts()
используется для подсчета количества уникальных значений в столбце «name» датасета df и создания объекта типа Series с количеством вхождений каждого уникального значения
Фильтрация данных в датасетах
df.query("name == 'John' and surname == 'Doe'")
выбирает в датасете df все строки, где значение столбца «name» равно «John» и значение столбца «surname» равно «Doe»
df[df['price']>500]
выводит строки датасета, где значение столбца «price» больше 500
df[~(df['price']>500)]
выводит строки датасета, где значение столбца «price» меньше 500
df[df['price']>500][['product_id', 'weight']]
выводит после фильтрации только два указанных столбца в отфильтрованном датасете
df[df['price'].between(10,20)]
выводит строки датасета, где значение столбца «price» между 10 и 20 (включительно)
можно добавить параметр inclusive со следующими значениями: ‘neither’ — не захватывает границы диапазона;’left’ — захватывает левую границу диапазона; ‘right’ — захватывает правую границу диапазона
df[df['Title'].isin(['Sales Agent','Sales Manager','Assistant Sales Agent'])]
выводит строки датасета, в которых по столбцу Title указаны только значения из списка
df[(df['price']>500)&(df['OrderDate'].between('1997-01-01', '1997-12-31'))]
пример объединения нескольких фильтров с оператором and. Объединять можно также с оператором or, который прописывается таким символом: |
df[df['Column'].str.startswith('A')]
выводит датасет со строками начинающимися с символа A. В методе можно применять иные команды работы со строками: contains, endswith и т.д.
Описательная статистика датасетов
df.info()
позволяет получить общую информацию о датасете, такую как количество строк, количество столбцов, их имена и типы данных, количество ненулевых значений в каждом столбце и использованную память
df.dtypes
позволяет получить информацию о типах данных столбцов
df.groupby(['name', 'age']).agg({'income': 'describe'})
вычисляет основные статистические показатели для каждой группы значений столбца income, включая количество наблюдений (count), среднее значение (mean), стандартное отклонение (std), минимальное и максимальное значения (min и max) и квартили (25%, 50%, 75%)
df.describe(include='object')
df.describe(include='datetime')
первый используется для получения статистической информации о колонках в объекте Pandas DataFrame, содержащих данные типа «object», второй для для колонок даты и времени
Математические методы в Python
Для исполнения кодов раздела необходимо импортировать библиотеки/модули:
math;
Логарифмы
Натуральный логарифм
ln_x = math.log(x)
Десятичный логарифм
ln_10_x = math.log10(x)
Экспонента
exp_x = math.exp(x)
Логарифмирование значений столбца датасета:
df = np.log(df.view)
Среднее
df_mean = df.mean()
Скользящее среднее
df_rolling_mean = df.rolling(window=2).mean()
Экспоненциальное скользящее среднее:
df_ewm_rolling_mean = df.ewm(span=2).mean()
Исчисление процентов
Процентное отношение значений ячеек столбца к общему значению
df["percent"] = (df["users"] / df["users"].sum()) * 100
Статистические методы в Python
Содержание:
- Меры центральной тенденции
- Меры изменчивости
- Меры статистической связи между переменными
- Z-преобразование
- Проверка распределения на нормальность
- Проверка гомогенности дисперсий
- Определение доверительных интервалов
- Статистические тесты (критерии)
Для исполнения кодов раздела необходимо импортировать библиотеки/модули:
statistics, numpy;
stats from scipy;
normaltest, shapiro, normaltest, levene, bartlett, norm, ttest_ind, chi2, chi2_contingency from scipy.stats;
math;
pingouin;
Меры центральной тенденции
Мода
data = [1, 2, 2, 3, 4, 4, 4]
print("Мода: ", statistics.mode(data))
Мода: 4
Мода — это значение в наборе данных, которое встречается наиболее часто
Среднее
data = [1, 2, 2, 3, 4, 4, 4]
print("Среднее: ", statistics.mean(data))
Среднее: 2.857142857142857
Среднее значение, также известное как среднее арифметическое, вычисляется путем сложения всех значений в наборе данных и деления полученной суммы на количество значений в наборе
$$bar{x} = frac{1}{n}sum_{i=1}^{n} x_i$$
где $bar{x}$ обозначает среднее значение, $n$ — количество элементов в выборке, а $x_1, x_2, …, x_n$ — значения элементов выборки. Формула использует знак суммы $sum$, который означает суммирование всех значений $x$ в выборке.
Медиана
data = [1, 2, 2, 3, 4, 4, 4]
print("Медиана: ", statistics.median(data))
Медиана: 3
Значение, которое разделяет упорядоченный набор данных на две равные половины
Формула для расчета с четным числом элементов выборки:
$$median=frac{x_{frac{n}{2}} + x_{frac{n}{2}+1}}{2}$$
где где $n$ — количество элементов в выборке, $x_{frac{n}{2}}$ — значение элемента с индексом $frac{n}{2}$ и $x_{frac{n}{2}+1}$ — значение элемента с индексом $frac{n}{2}+1$
Формула для расчета с нечетным числом элементов выборки:
$$median = x_{frac{n+1}{2}}$$
где $x$ — массив элементов, а $n$ — число элементов в массиве
Межквартильный размах
data = np.array([12, 15, 16, 18, 19, 20, 22, 25, 28, 31, 35])
Q1 = np.percentile(data, 25, interpolation='midpoint')
Q3 = np.percentile(data, 75, interpolation='midpoint')
IQR = Q3 - Q1
print("Межквартильный размах:", IQR)
Межквартильный размах: 9.5
Межквартильный размах — определяется как разница между верхним и нижним квартилями в наборе данных.
Квартили — это значения, которые разделяют упорядоченный набор данных на четыре равные части. Верхний квартиль (Q3) — это значение, которое делит верхние 25% данных от нижних 75%, а нижний квартиль (Q1) — это значение, которое делит нижние 25% данных от верхних 75%.
Таким образом, межквартильный размах (IQR) — это разница между Q3 и Q1. Он представляет собой интерквартильный диапазон, который содержит 50% данных и позволяет оценить разброс значений в наборе данных, игнорируя выбросы
Меры изменчивости
Дисперсия
data = [1, 5, 2, 7, 1, 9, 3, 8, 5, 9]
print("Дисперсия: ", statistics.variance(data))
Дисперсия: 10
Дисперсия — это среднее арифметическое квадратов отклонений каждого элемента выборки от ее среднего значения. Она измеряет, насколько значения в выборке отклоняются от ее среднего значения и показывает, как распределены значения вокруг среднего значения. Дисперсия выражается в квадратных единицах измерения выборки
$$s^2 = frac{1}{n-1}sum_{i=1}^{n}(x_i — bar{x})^2$$
где $s^2$ — выборочная дисперсия, $n$ — размер выборки, $x_i$ — i-й элемент выборки, $bar{x}$ — выборочное среднее.
Стандартное отклонение
data = [1, 5, 2, 7, 1, 9, 3, 8, 5, 9]
print("Стандартное отклонение: ", statistics.stdev(data))
Стандартное отклонение: 3.1622776601683795
Стандартное отклонение — это квадратный корень из дисперсии выборки. Оно измеряет степень разброса данных относительно их среднего значения и представляет собой стандартную меру распределения выборки. Стандартное отклонение может быть выражено в тех же единицах измерения, что и сама выборка.
Таким образом, стандартное отклонение и дисперсия оба показывают, насколько значения в выборке отклоняются от ее среднего значения, но стандартное отклонение также показывает, как распределены значения вокруг среднего значения.
$$sigma = sqrt{frac{1}{N} sum_{i=1}^{N} (x_i — bar{x})^2}$$
где $N$ — количество значений, $x_i$ — i-е значение, а $bar{x}$ — среднее значение
Среднеквадратическое отклонение
data = [1, 5, 2, 7, 1, 9, 3, 8, 5, 9]
mean_value = statistics.mean(data)
print("Среднеквадратическое отклонение: ", statistics.stdev(data, xbar=mean_value))
Среднеквадратическое отклонение: 3.1622776601683795
Среднеквадратическое отклонение — это корень из среднего арифметического квадратов отклонений каждого элемента выборки от ее среднего значения. Оно также измеряет степень разброса данных относительно их среднего значения и представляет собой стандартную меру распределения выборки. Среднеквадратическое отклонение может быть выражено в тех же единицах измерения, что и сама выборка.
$$sigma = sqrt{frac{1}{N}sum_{i=1}^{N}(x_i — mu)^2}$$
где $N$ — количество элементов в выборке, $x_i$ — i-й элемент выборки, а $mu$ — среднее значение выборки
Стандартная ошибка среднего
variance = 4
n = 100
SEM = math.sqrt(variance/n)
print("SEM:", SEM)
SEM: 0.2
Стандартная ошибка среднего — мера разброса среднего значения в выборке относительно среднего значения в генеральной совокупности, это среднеквадратическое отклонение распределения выборочных средних
$$SE = frac{s}{sqrt{n}}$$
где $s$ — стандартное отклонение выборки, $n$ — размер выборки
Меры статистической связи между переменными
Коэффициент корреляции
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 7, 9, 11, 13])
corr_coef = np.corrcoef(x, y)[0, 1]
print("Коэффициент корреляции между x и y:", corr_coef)
Коэффициент корреляции между x и y: 0.9999999999999999
Это мера статистической связи между двумя переменными, которая показывает, насколько сильно связаны эти переменные между собой. Положительный коэффициент корреляции указывает на прямую связь между переменными. Отрицательный коэффициент корреляции указывает на обратную связь между переменными. Коэффициент корреляции, равный (или близкий) нулю, означает отсутствие связи между переменными
$$r = frac{nsum_{i=1}^{n}x_iy_i — sum_{i=1}^{n}x_isum_{i=1}^{n}y_i}{sqrt{left[nsum_{i=1}^{n}x_i^2 — left(sum_{i=1}^{n}x_iright)^2right]left[nsum_{i=1}^{n}y_i^2 — left(sum_{i=1}^{n}y_iright)^2right]}}$$
где $n$ — размер выборки, $x_i$ и $y_i$ — соответствующие значения в выборках X и Y
Коэффициент детерминации
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 7, 9, 11, 13])
# оценка параметров линейной регрессии
slope, intercept = np.polyfit(x, y, 1)
# расчет коэффициента детерминации
y_predicted = slope * x + intercept
r_squared = 1 - (np.sum((y - y_predicted) ** 2) / ((len(y) - 1) * np.var(y, ddof=1)))
print("Коэффициент детерминации:", r_squared)
Коэффициент детерминации: 1.0
(R-квадрат) — это мера, которая показывает, какую долю изменчивости одной переменной можно объяснить вариацией другой переменной. Значение R-квадрат находится в диапазоне от 0 до 1, где 0 означает, что модель не объясняет никакой изменчивости, а 1 означает, что модель объясняет всю изменчивость
$$R^2 = 1 — frac{SS_{res}}{SS_{tot}}$$
где $SS_{res}$ — остаточная сумма квадратов, а $SS_{tot}$ — общая сумма квадратов
Z-преобразование (стандартизация)
z-оценка
zscore(df.column)
мера того, насколько значение точки данных отклоняется от среднего значения в единицах стандартного отклонения,
это позволяет сравнивать данные, измеренные в разных единицах или имеющие разные масштабы
$$z = frac{X — mu}{sigma}$$
где $z$ — z-оценка, $X$ — одно необработанное значение данных, $mu$ — среднее значение набора данных, $sigma$ — стандартное отклонение набора данных
Для генеральной совокупности
data = np.array([12, 15, 16, 18, 19, 20, 22, 25, 28, 31, 35])
mean = np.mean(data)
std = np.std(data)
z_data = stats.zscore(data)
print('Z-преобразованные данные:', z_data)
Z-преобразованные данные: [-1.45683394 -1.01577412 -0.86875418 -0.57471431 -0.42769437 -0.28067443 0.01336545 0.45442527 0.89548508 1.3365449 1.92462466]
Z-преобразование — это процесс стандартизации набора данных путем вычитания среднего значения и деления на стандартное отклонение. Если результат z-преобразования равен 0, то это означает, что значение переменной равно ее среднему значению. Если результат равен 1, то это означает, что значение переменной отклоняется от ее среднего значения на одно стандартное отклонение
$$Z = frac{x — mu}{sigma}$$
где — $x$ — наблюдаемое значение, $mu$ — среднее значение распределения, $sigma$ — стандартное отклонение распределения
Для выборки из генеральной совокупности
all_data = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
sample = np.random.choice(all_data, size=5, replace=False)
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1)
z_sample = (sample - sample_mean) / sample_std
print('Z-преобразованная выборка:', z_sample)
Z-преобразованная выборка: [-1.19571306 -0.15596257 1.14372554 0.88378792 -0.67583782]
для применения z-преобразования к выборке необходимо вычислить выборочное среднее значение и выборочное стандартное отклонение
$$Z = frac{bar{x} — mu}{frac{sigma}{sqrt{n}}}$$
где $bar{x}$ — выборочное среднее, $mu$ — среднее значение генеральной совокупности, $sigma$ — стандартное отклонение генеральной совокупности, а $n$ — размер выборки
Для отдельного наблюдения из выборки
sample = np.array([4, 5, 6, 7, 8, 9, 10])
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1)
z_sample = (sample[4] - sample_mean) / sample_std
print('Отдельно взятое наблюдение выборки:', sample[4])
print('Z-значение для отдельно взятого наблюдения:', z_sample)
Отдельно взятое наблюдение выборки: 8
Z-значение для отдельно взятого наблюдения: 0.4629100498862757
$$z = frac{x — mu}{sigma}$$
где $x$ — значение в выборке, $mu$ — среднее значение выборки, $sigma$ — стандартное отклонение выборки
Проверка распределения на нормальность
ни один из этих тестов не гарантирует, что данные точно имеют нормальное распределение. Они только дают представление о том, насколько близки данные к нормальному распределению
Тест Шапиро-Уилка
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
stat, p = shapiro(data)
print('Statistics=%.3f, p=%.3f' % (stat, p))
alpha = 0.05
if p > alpha:
print('Распределение похоже на нормальное (не отвергаем H0)')
else:
print('Распределение не похоже на нормальное (отвергаем H0)')
Statistics=0.970, p=0.892
Распределение похоже на нормальное (не отвергаем H0)
Тест Шапиро-Уилка является более чувствительным к отклонениям от нормальности, особенно в случаях, когда данные имеют ярко выраженные выбросы. Он также более точен при малых выборках. Однако, он может оказаться менее мощным в случае, когда выборка слишком большая
Тест хи-квадрат
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
stat, p = normaltest(data)
print('Statistics=%.3f, p=%.3f' % (stat, p))
alpha = 0.05
if p > alpha:
print('Распределение похоже на нормальное (не отвергаем H0)')
else:
print('Распределение не похоже на нормальное (отвергаем H0)')
Statistics=2.027, p=0.363
Распределение похоже на нормальное (не отвергаем H0)
Тест хи-квадрат может быть более устойчивым в случае, когда данные более-менее нормальные, но не слишком точны. Также, он может быть полезен, когда нам интересно не только проверить, нормальные ли данные, но и определить, насколько сильно они отклоняются от нормальности
qq-plot
pg.qqplot(df, dist='norm')
график используется для сравнения распределения выборки данных df с теоретическим нормальным распределением
Проверка гомогенности дисперсий
Тесты Левена и Бартлетта применяются для проверки равенства дисперсий в нескольких выборках
Тест Левена
data = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
statistic, pvalue = levene(*data)
if pvalue > 0.05:
print(f"p-value = {pvalue}. Гомогенность дисперсий присутствует")
else:
print(f"p-value = {pvalue}. Гомогенность дисперсий отсутствует")
p-value = 1.0. Гомогенность дисперсий присутствует
Тест основан на сравнении среднеквадратических отклонений (MSE) в группах. Он менее чувствителен к выбросам, чем тест Бартлетта, так как MSE рассчитывается на основе медианы, а не на основе среднего значения. Он предполагает нормальность распределения в каждой группе. Если распределение не является нормальным, то тест Левена может давать неправильные результаты
$$W=frac{(N-k) sum_{i=1}^{k}left(n_{i}left(Z_{i}-overline{Z}right)^{2}right)}{(k-1) sum_{i=1}^{N}left(Y_{i}-overline{Y}right)^{2}}$$
где $W$ — статистика теста Левена, $N$ — общее число наблюдений, $k$ — количество групп, $n_i$ — размер $i$-й группы, $Z_i$ — среднее значение $i$-й группы, $overline{Z}$ — общее среднее значение всех групп, $Y_i$ — каждое наблюдение в $i$-й группе, $overline{Y}$ — общее среднее значение всех наблюдений
или можно сделать тоже самое иным способом:
pg.homoscedasticity(df, dv='events', group='group')
‘df’ — аргумент, датасет, в котором должны содержаться данные для анализа на гомоскедастичность;
«dv=’events'» — переменная (колонка), c зависимой переменной (в данном случае ‘events’);
«group=’group'» — переменная (колонка), c независимой переменной и разделяет данные на группы (в данном случае ‘group’)
Тест Бартлетта
group1 = [1, 2, 3, 4, 5]
group2 = [2, 4, 6, 8, 10]
stat, p = bartlett(group1, group2)
if p < 0.05:
result = 'Отвергаем гипотезу о гомогенности дисперсий'
else:
result = 'Не отвергаем гипотезу о гомогенности дисперсий'
print(f'Тест Бартлетта: статистика = {stat:.3f}, p-значение = {p:.3f}. {result}')
Тест Бартлетта: статистика = 1.587, p-значение = 0.208. Не отвергаем гипотезу о гомогенности дисперсий
Тест основан на сравнении дисперсий в группах. Он более чувствителен к выбросам, чем тест Левена, так как рассчитывает статистику на основе среднего значения, а не на основе медианы. Он предполагает нормальность распределения в каждой группе. Если распределение не является нормальным, то тест Бартлетта может давать неправильные результаты
$$B = frac{(N-1)sum_{i=1}^k n_i ln(s_i^2) — N ln(s_p^2)}{1 + frac{1}{3(k-1)}left(sum_{i=1}^k frac{1}{n_i} — frac{1}{N}right)}$$
где $N$ — общее количество наблюдений, $k$ — количество групп, $n_i$ — количество наблюдений в $i$-й группе, $s_i^2$ — выборочная дисперсия $i$-й группы, $s_p^2$ — средняя выборочная дисперсия всех групп
или можно сделать тоже самое иным способом:
pg.homoscedasticity(df, dv='weight', group='group', method='bartlett')
‘df’ — аргумент, датасет, в котором должны содержаться данные для анализа на гомоскедастичность;
«dv=’weight'» — зависимая переменная, которую нужно проверить на гомоскедастичность;
«group=’group'» — независимая переменная, определяющая группы, между которыми сравниваются дисперсии;
«method=’bartlett'» — метод, который будет использоваться для проверки гомоскедастичности
Определение доверительных интервалов
n = 30 # размер выборки
x_bar = 7.5 # выборочное среднее
alpha = 0.05 # уровень доверия
# известное стандартное отклонение генеральной совокупности
sigma = 2.5
# находим значение квантиля распределения
z = norm.ppf(1 - alpha/2)
# вычисляем границы доверительного интервала
lower = x_bar - z * sigma / math.sqrt(n)
upper = x_bar + z * sigma / math.sqrt(n)
print(f'Доверительный интервал: [{lower:.3f}, {upper:.3f}]')
Доверительный интервал: [6.605, 8.395]
Доверительный интервал — это диапазон значений, в котором находится неизвестный параметр генеральной совокупности с известным уровнем доверия
$$bar{x} pm z_{alpha/2} cdot frac{sigma}{sqrt{n}}$$
где $bar{x}$ — выборочное среднее, $z_{alpha/2}$ — критическое значение стандартного нормального распределения, соответствующее уровню доверия $alpha$, $sigma$ — известное стандартное отклонение, $n$ — размер выборки
Основываясь на знании t — распределения
# устанавливаем уровень доверия
confidence_level = 0.95
# задаем количество степеней свободы
degrees_of_freedom = 19
# вычисляем критическое значение t-статистики
t_critical = stats.t.ppf((1 + confidence_level) / 2, degrees_of_freedom)
# задаем значения стандартного отклонения, размера выборки и стандартной ошибки среднего
sd = 11.3
n = 20
standard_error = sd / np.sqrt(n)
# задаем выборочное среднее и предельную ошибку
sample_mean = 89.9
margin_of_error = t_critical * standard_error
# рассчитываем доверительный интервал
confidence_interval = (sample_mean - margin_of_error, sample_mean + margin_of_error)
print("Доверительный интервал для t - распределения: ", confidence_interval)
Доверительный интервал для t - распределения: (84.61143720745503, 95.18856279254499)
$$CI = bar{x} pm t_{frac{alpha}{2},n-1}frac{s}{sqrt{n}}$$
где $bar{x}$ — среднее значение выборки, $t_{frac{alpha}{2},n-1}$ — критическое значение t-распределения с $frac{alpha}{2}$ уровнем значимости и $n-1$ степенями свободы (где $alpha$ — уровень значимости), $s$ — стандартное отклонение выборки, $n$ — размер выборки
Статистические тесты (критерии)
Двухвыборочный t-критерий Стьюдента
group1 = [3, 5, 7, 9, 11]
group2 = [2, 4, 6, 8, 10]
# вычисляем средние значения
mean1 = sum(group1) / len(group1)
mean2 = sum(group2) / len(group2)
# вычисляем стандартные отклонения
std1 = stats.tstd(group1)
std2 = stats.tstd(group2)
# вычисляем t-статистику
t = (mean1 - mean2) / ((std1 ** 2 / len(group1)) + (std2 ** 2 / len(group2))) ** 0.5
# определяем степени свободы
df = len(group1) + len(group2) - 2
# определяем p-уровень значимости
p = stats.t.sf(abs(t), df) * 2
# задаем уровень значимости
alpha = 0.05
if p < alpha:
print(f"Различия статистически значимы: p={p}")
else:
print(f"Различия не являются статистически значимыми:p={p}")
Различия не являются статистически значимыми:p=0.6305360755569764
тест, используемый для проверки значимости различий между двумя выборками. В основе t-критерия лежит понятие t-статистики, которая представляет собой отношение разности между средними значениями двух выборок к их стандартной ошибке. Важным условием применения t-критерия является то, что данные должны быть распределены нормально или близко к нормальному распределению. Если это условие не выполняется, то использование t-критерия может привести к неверным результатам
$$t = frac{overline{X_1} — overline{X_2}}{s_p sqrt{frac{1}{n_1} + frac{1}{n_2}}}$$
где $overline{X_1}$ и $overline{X_2}$ — выборочные средние первой и второй выборок, $s_p$ — выборочное стандартное отклонение, рассчитанное по объединенным выборкам, $n_1$ и $n_2$ — размерности первой и второй выборок соответственно
Распределение Хи-квадрат (Chi-squared) Пирсона для одной номинативной переменной
# Наблюдаемые частоты
observed = np.array([10, 10, 10, 5, 10, 15])
# Ожидаемые частоты (равномерное распределение)
expected_uniform = np.array([10, 10, 10, 10, 10, 10])
# Вычисляем статистику Хи-квадрат
chi2_stat = np.sum((observed - expected_uniform)**2 / expected_uniform)
dof = len(observed) - 1
# Вычисляем P-значение
p_value = 1 - chi2.cdf(chi2_stat, dof)
# Задаем пороговый уровень значимости
alpha = 0.05
print("Статистика Хи-квадрат:", chi2_stat)
print("P-значение:", p_value)
print("Степени свободы:", dof)
print("nГипотезы:")
print("H0: эмпирическое распределение частот не отличается от равномерного")
print("H1: эмпирическое распределение частот отличается от равномерного")
print("nРезультат:")
if p_value < alpha:
print(f"Отвергаем H0 на уровне значимости {alpha}. Эмпирическое распределение частот отличается от равномерного.")
else:
print(f"Не можем отвергнуть H0 на уровне значимости {alpha}. Эмпирическое распределение частот не отличается от равномерного.")
Вывод:
Статистика Хи-квадрат: 5.0 P-значение: 0.415880186995508 Степени свободы: 5 Гипотезы: H0: эмпирическое распределение частот не отличается от равномерного H1: эмпирическое распределение частот отличается от равномерного Результат: Не можем отвергнуть H0 на уровне значимости 0.05. Эмпирическое распределение частот не отличается от равномерного.
Это статистический тест, который позволяет оценить, есть ли значимая связь между двумя категориальными переменными на основе наблюдаемых частот в таблице сопряженности
Критерий Хи-квадрат Пирсона сравнивает наблюдаемые частоты с частотами, которые ожидались бы при условии независимости переменных (то есть, при отсутствии связи между ними). Статистика Хи-квадрат Пирсона (χ²) является мерой расхождения между наблюдаемыми и ожидаемыми частотами и имеет распределение Хи-квадрат с определенным числом степеней свободы
$$chi^2 = sum_{i=1}^{r} sum_{j=1}^{c} frac{(O_{ij} — E_{ij})^2}{E_{ij}}$$
где $sum_{i=1}^{r}$ и $sum_{j=1}^{c}$ — сумма по всем строкам, а $O_{ij}$ — наблюдаемые частоты в ячейках таблицы, $E_{ij}$ — ожидаемые частоты в ячейках, $r$ — количество строк таблицы сопряженности, $c$ — количество столбцов таблицы сопряженности
Распределение Хи-квадрат (Chi-squared) Пирсона для связи между двумя номинативными переменными
Примечание по использованию критерия! При анализе четырехпольных таблиц ожидаемые значения в каждой из ячеек должны быть не менее 10. В том случае, если хотя бы в одной ячейке ожидаемое явление принимает значение от 5 до 9, критерий хи-квадрат должен рассчитываться с поправкой Йейтса. Если хотя бы в одной ячейке ожидаемое явление меньше 5, то для анализа должен использоваться точный критерий Фишера. В случае анализа многопольных таблиц ожидаемое число наблюдений не должно принимать значения менее 5 более чем в 20% ячеек.
# Создаем таблицу сопряженности (contingency table) для двух номинативных переменных
contingency_table = np.array([
[10, 6],
[5, 15]
])
# Вычисляем статистику Хи-квадрат, p-значение и степени свободы
chi2_stat, p_value, dof, expected_freq = chi2_contingency(contingency_table)
# Задаем пороговый уровень значимости
alpha = 0.05
print("Статистика Хи-квадрат:", chi2_stat)
print("P-значение:", p_value)
print("Степени свободы:", dof)
print("nГипотезы:")
print("H0: нет связи между двумя номинативными переменными")
print("H1: есть связь между двумя номинативными переменными")
print("nРезультат:")
if p_value < alpha:
print(f"Отвергаем H0 на уровне значимости {alpha}. Есть связь между двумя номинативными переменными.")
else:
print(f"Не можем отвергнуть H0 на уровне значимости {alpha}. Нет связи между двумя номинативными переменными.")
Вывод:
Статистика Хи-квадрат: 3.715714285714286 P-значение: 0.053902557169387154 Степени свободы: 1 Гипотезы: H0: нет связи между двумя номинативными переменными H1: есть связь между двумя номинативными переменными Результат: Не можем отвергнуть H0 на уровне значимости 0.05. Нет связи между двумя номинативными переменными.
Критерий использует таблицу сопряженности для определения, есть ли статистически значимая связь между двумя категориальными переменными. В этом случае, вы сравниваете наблюдаемые частоты с частотами, ожидаемыми при условии независимости переменных. Формула расчета та же, что и для одной номинативной переменной
The mean squared error is a common way to measure the prediction accuracy of a model. In this tutorial, you’ll learn how to calculate the mean squared error in Python. You’ll start off by learning what the mean squared error represents. Then you’ll learn how to do this using Scikit-Learn (sklean), Numpy, as well as from scratch.
What is the Mean Squared Error
The mean squared error measures the average of the squares of the errors. What this means, is that it returns the average of the sums of the square of each difference between the estimated value and the true value.
The MSE is always positive, though it can be 0 if the predictions are completely accurate. It incorporates the variance of the estimator (how widely spread the estimates are) and its bias (how different the estimated values are from their true values).
The formula looks like below:

Now that you have an understanding of how to calculate the MSE, let’s take a look at how it can be calculated using Python.
Interpreting the Mean Squared Error
The mean squared error is always 0 or positive. When a MSE is larger, this is an indication that the linear regression model doesn’t accurately predict the model.
An important piece to note is that the MSE is sensitive to outliers. This is because it calculates the average of every data point’s error. Because of this, a larger error on outliers will amplify the MSE.
There is no “target” value for the MSE. The MSE can, however, be a good indicator of how well a model fits your data. It can also give you an indicator of choosing one model over another.
Loading a Sample Pandas DataFrame
Let’s start off by loading a sample Pandas DataFrame. If you want to follow along with this tutorial line-by-line, simply copy the code below and paste it into your favorite code editor.
# Importing a sample Pandas DataFrame
import pandas as pd
df = pd.DataFrame.from_dict({
'x': [1,2,3,4,5,6,7,8,9,10],
'y': [1,2,2,4,4,5,6,7,9,10]})
print(df.head())
# x y
# 0 1 1
# 1 2 2
# 2 3 2
# 3 4 4
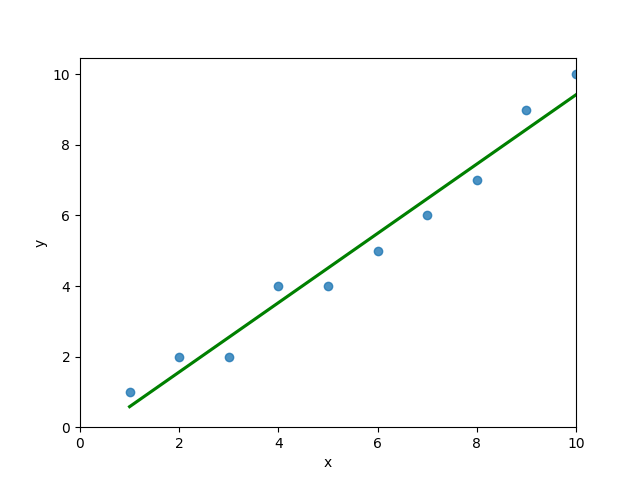
# 4 5 4You can see that the editor has loaded a DataFrame containing values for variables x and y. We can plot this data out, including the line of best fit using Seaborn’s .regplot() function:
# Plotting a line of best fit
import seaborn as sns
import matplotlib.pyplot as plt
sns.regplot(data=df, x='x', y='y', ci=None)
plt.ylim(bottom=0)
plt.xlim(left=0)
plt.show()This returns the following visualization:
The mean squared error calculates the average of the sum of the squared differences between a data point and the line of best fit. By virtue of this, the lower a mean sqared error, the more better the line represents the relationship.
We can calculate this line of best using Scikit-Learn. You can learn about this in this in-depth tutorial on linear regression in sklearn. The code below predicts values for each x value using the linear model:
# Calculating prediction y values in sklearn
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(df[['x']], df['y'])
y_2 = model.predict(df[['x']])
df['y_predicted'] = y_2
print(df.head())
# Returns:
# x y y_predicted
# 0 1 1 0.581818
# 1 2 2 1.563636
# 2 3 2 2.545455
# 3 4 4 3.527273
# 4 5 4 4.509091Calculating the Mean Squared Error with Scikit-Learn
The simplest way to calculate a mean squared error is to use Scikit-Learn (sklearn). The metrics module comes with a function, mean_squared_error() which allows you to pass in true and predicted values.
Let’s see how to calculate the MSE with sklearn:
# Calculating the MSE with sklearn
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(df['y'], df['y_predicted'])
print(mse)
# Returns: 0.24727272727272714This approach works very well when you’re already importing Scikit-Learn. That said, the function works easily on a Pandas DataFrame, as shown above.
In the next section, you’ll learn how to calculate the MSE with Numpy using a custom function.
Calculating the Mean Squared Error from Scratch using Numpy
Numpy itself doesn’t come with a function to calculate the mean squared error, but you can easily define a custom function to do this. We can make use of the subtract() function to subtract arrays element-wise.
# Definiting a custom function to calculate the MSE
import numpy as np
def mse(actual, predicted):
actual = np.array(actual)
predicted = np.array(predicted)
differences = np.subtract(actual, predicted)
squared_differences = np.square(differences)
return squared_differences.mean()
print(mse(df['y'], df['y_predicted']))
# Returns: 0.24727272727272714The code above is a bit verbose, but it shows how the function operates. We can cut down the code significantly, as shown below:
# A shorter version of the code above
import numpy as np
def mse(actual, predicted):
return np.square(np.subtract(np.array(actual), np.array(predicted))).mean()
print(mse(df['y'], df['y_predicted']))
# Returns: 0.24727272727272714Conclusion
In this tutorial, you learned what the mean squared error is and how it can be calculated using Python. First, you learned how to use Scikit-Learn’s mean_squared_error() function and then you built a custom function using Numpy.
The MSE is an important metric to use in evaluating the performance of your machine learning models. While Scikit-Learn abstracts the way in which the metric is calculated, understanding how it can be implemented from scratch can be a helpful tool.
Additional Resources
To learn more about related topics, check out the tutorials below:
- Pandas Variance: Calculating Variance of a Pandas Dataframe Column
- Calculate the Pearson Correlation Coefficient in Python
- How to Calculate a Z-Score in Python (4 Ways)
- Official Documentation from Scikit-Learn
The standard error of the mean is a way to measure how spread out values are in a dataset. It is calculated as:
Standard error of the mean = s / √n
where:
- s: sample standard deviation
- n: sample size
This tutorial explains two methods you can use to calculate the standard error of the mean for a dataset in Python. Note that both methods produce the exact same results.
Method 1: Use SciPy
The first way to calculate the standard error of the mean is to use the sem() function from the SciPy Stats library.
The following code shows how to use this function:
from scipy.stats import sem #define dataset data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29] #calculate standard error of the mean sem(data) 2.001447
The standard error of the mean turns out to be 2.001447.
Method 2: Use NumPy
Another way to calculate the standard error of the mean for a dataset is to use the std() function from NumPy.
Note that we must specify ddof=1 in the argument for this function to calculate the sample standard deviation as opposed to the population standard deviation.
The following code shows how to do so:
import numpy as np #define dataset data = np.array([3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29]) #calculate standard error of the mean np.std(data, ddof=1) / np.sqrt(np.size(data)) 2.001447
Once again, the standard error of the mean turns out to be 2.001447.
How to Interpret the Standard Error of the Mean
The standard error of the mean is simply a measure of how spread out values are around the mean. There are two things to keep in mind when interpreting the standard error of the mean:
1. The larger the standard error of the mean, the more spread out values are around the mean in a dataset.
To illustrate this, consider if we change the last value in the previous dataset to a much larger number:
from scipy.stats import sem #define dataset data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 150] #calculate standard error of the mean sem(data) 6.978265
Notice how the standard error jumps from 2.001447 to 6.978265. This is an indication that the values in this dataset are more spread out around the mean compared to the previous dataset.
2. As the sample size increases, the standard error of the mean tends to decrease.
To illustrate this, consider the standard error of the mean for the following two datasets:
from scipy.stats import sem #define first dataset and find SEM data1 = [1, 2, 3, 4, 5] sem(data1) 0.7071068 #define second dataset and find SEM data2 = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5] sem(data2) 0.4714045
The second dataset is simply the first dataset repeated twice. Thus, the two datasets have the same mean but the second dataset has a larger sample size so it has a smaller standard error.
Additional Resources
How to Calculate the Standard Error of the Mean in R
How to Calculate the Standard Error of the Mean in Excel
How to Calculate Standard Error of the Mean in Google Sheets
Стандартная ошибка среднего — это способ измерить, насколько разбросаны значения в наборе данных. Он рассчитывается как:
Стандартная ошибка среднего = s / √n
куда:
- s : стандартное отклонение выборки
- n : размер выборки
В этом руководстве объясняются два метода, которые вы можете использовать для вычисления стандартной ошибки среднего значения для набора данных в Python. Обратите внимание, что оба метода дают одинаковые результаты.
Способ 1: используйте SciPy
Первый способ вычислить стандартную ошибку среднего — использовать функцию sem() из библиотеки SciPy Stats.
Следующий код показывает, как использовать эту функцию:
from scipy. stats import sem
#define dataset
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29]
#calculate standard error of the mean
sem(data)
2.001447
Стандартная ошибка среднего оказывается равной 2,001447 .
Способ 2: использовать NumPy
Другой способ вычислить стандартную ошибку среднего для набора данных — использовать функцию std() из NumPy.
Обратите внимание, что мы должны указать ddof=1 в аргументе этой функции, чтобы вычислить стандартное отклонение выборки, а не стандартное отклонение генеральной совокупности.
Следующий код показывает, как это сделать:
import numpy as np
#define dataset
data = np.array([3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 29])
#calculate standard error of the mean
np.std(data, ddof= 1 ) / np.sqrt (np.size (data))
2.001447
И снова стандартная ошибка среднего оказывается равной 2,001447 .
Как интерпретировать стандартную ошибку среднего
Стандартная ошибка среднего — это просто мера того, насколько разбросаны значения вокруг среднего. При интерпретации стандартной ошибки среднего следует помнить о двух вещах:
1. Чем больше стандартная ошибка среднего, тем более разбросаны значения вокруг среднего в наборе данных.
Чтобы проиллюстрировать это, рассмотрим, изменим ли мы последнее значение в предыдущем наборе данных на гораздо большее число:
from scipy. stats import sem
#define dataset
data = [3, 4, 4, 5, 7, 8, 12, 14, 14, 15, 17, 19, 22, 24, 24, 24, 25, 28, 28, 150 ]
#calculate standard error of the mean
sem(data)
6.978265
Обратите внимание на скачок стандартной ошибки с 2,001447 до 6,978265.Это указывает на то, что значения в этом наборе данных более разбросаны вокруг среднего значения по сравнению с предыдущим набором данных.
2. По мере увеличения размера выборки стандартная ошибка среднего имеет тенденцию к уменьшению.
Чтобы проиллюстрировать это, рассмотрим стандартную ошибку среднего для следующих двух наборов данных:
from scipy.stats import sem
#define first dataset and find SEM
data1 = [1, 2, 3, 4, 5]
sem(data1)
0.7071068
#define second dataset and find SEM
data2 = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5]
sem(data2)
0.4714045
Второй набор данных — это просто первый набор данных, повторенный дважды. Таким образом, два набора данных имеют одинаковое среднее значение, но второй набор данных имеет больший размер выборки, поэтому стандартная ошибка меньше.
Дополнительные ресурсы
Как рассчитать стандартную ошибку среднего в R
Как рассчитать стандартную ошибку среднего в Excel
Как рассчитать стандартную ошибку среднего в Google Sheets
To calculate the standard error of the mean (SEM) in Python, use scipy library’s sem() function.
For instance, let’s calculate the SEM for a group of numbers:
from scipy.stats import sem # Create a dataset data = [19, 2, 12, 3, 100, 2, 3, 2, 111, 82, 4] # Calculate the standard error of mean s = sem(data) print(s)
Output:
13.172598656753378
If you do not have scipy installed, run:
pip install scipy
That was the quick answer. But make sure to read along to learn about the standard error and how to implement the function yourself.
What Is the Standard Error of Mean (SEM)
The standard error of the mean (SEM) is an estimate of the standard deviation.
The SEM is used to measure how close sample means are likely to be to the true population mean. This gives a good indication as to where a given sample actually lies in relation to its corresponding population.
The standard error of the mean follows the following formula:
Where σ is the standard deviation and n is the number of samples.
How to Implement Standard Error of Mean Function in Python
To write a function that calculates the standard error of the mean in Python, you first need to implement a function that calculates the standard deviation of the data.
What Is Standard Deviation
Standard deviation is a measure of how far numbers lie from the average.
For example, if we look at a group of men we find that most of them are between 5’8” and 6’2” tall. Those who lie outside this range make up only a small percentage of the group. The standard deviation identifies the percentage by which the numbers tend to vary from the average.
The standard deviation follows the formula:
Where:
= sample standard deviation
= the size of the population
= each value from the population
= the sample mean (average)
How to Calculate Standard Deviation in Python
Assuming you do not use a built-in standard deviation function, you need to implement the above formula as a Python function to calculate the standard deviation.
Here is the implementation of standard deviation in Python:
from math import sqrt
def stddev(data):
N = len(data)
mu = float(sum(data) / len(data))
s = [(x_i - mu) ** 2 for x_i in data]
return sqrt(float(sum(s) / (N - 1)))
The Standard Error of Mean in Python
Now that you have set up a function to calculate the standard deviation, you can write the function that calculates the standard error of the mean.
Here is the code:
def sem(data):
return stddev(data) / sqrt(len(data))
Now you can use this function.
For example:
data = [19, 2, 12, 3, 100, 2, 3, 2, 111, 82, 4] sem_data = sem(data) print(sem_data)
Output:
13.172598656753378
To verify that this really is the SEM, use a built-in SEM function to double-check. Let’s use the one you already saw in the introduction:
from scipy.stats import sem # Create a dataset data = [19, 2, 12, 3, 100, 2, 3, 2, 111, 82, 4] # Calculate the standard error of mean s = sem(data) print(s)
As a result, you get the same output as the custom implementation yielded.
13.172598656753378
This completes our example of building the functionality for calculating the standard error of the mean in Python.
Here is the full code used in this example for your convenience:
from math import sqrt
def stddev(data):
N = len(data)
mu = float(sum(data) / len(data))
s = [(x_i - mu) ** 2 for x_i in data]
return sqrt(float(sum(s) / (N - 1)))
def sem(data):
return stddev(data) / sqrt(len(data))
data = [19, 2, 12, 3, 100, 2, 3, 2, 111, 82, 4]
sem_data = sem(data)
print(sem_data)
This is the hard way to obtain the standard error of the mean in Python.
Usually, when you have a common problem, you should rely on using existing functionality as much as possible.
Let’s next take a look at the two ways to find the standard error of mean in Python using built-in functionality.
How to Use Existing Functionality to Calculate the Standard Error of Mean in Python
Standard Error of Mean Using Scipy
You have seen this approach already twice in this guide.
The scipy module comes in with a built-in sem() function. This directly calculates the standard mean of error for a given dataset.
For instance:
from scipy.stats import sem # Create a dataset data = [19, 2, 12, 3, 100, 2, 3, 2, 111, 82, 4] # Calculate the standard error of mean s = sem(data) print(s)
Output:
13.172598656753378
Standard Error of Mean Using Numpy
You can also use NumPy module to calculate the standard error of the mean in Python.
However, there is no dedicated sem() function in numpy. But there is a function called std() that calculates the standard deviation.
So, to calculate the SEM with NumPy, calculate the standard deviation and divide it by the square root of the data size.
For example:
import numpy as np data = [19, 2, 12, 3, 100, 2, 3, 2, 111, 82, 4] sem_data = np.std(data, ddof=1) / np.sqrt(np.size(data)) print(sem_data)
Output:
13.172598656753378
Conclusion
Today you learned how to calculate the standard error of the mean in Python.
To recap, the standard error of the mean is an estimate of the standard deviation of all samples that could be drawn from a particular population.
To calculate the SEM in Python, you can use scipy‘s sem() function.
Another way to calculate SEM in Python is by using the NumPy module. But there is no direct sem() function there. Thus you need to use the standard deviation and the equation of SEM.
The laborious approach to find the SEM is to implement the sem() function yourself. To do this, you need to implement the functionality to calculate the standard deviation first. Then the rest is simple.
Thanks for reading. Happy coding!
Further Reading
Python Tricks
How to Write to a File in Python
The with Statement in Python
About the Author
- I’m an entrepreneur and a blogger from Finland. My goal is to make coding and tech easier for you with comprehensive guides and reviews.
Recent Posts
The Standard Error of the Mean (SEM) describes how far a sample mean varies from the actual population mean.
It is used to estimate the approximate confidence intervals for the mean.
In this tutorial, we will discuss two methods you can use to calculate the Standard Error of the Mean in python with step-by-step examples.
The Standard error of the mean for a sample is calculated using below formula:
Standard error of the mean (SEM) = s / √n
where:
s : sample standard deviation
n : sample size
Method 1: Use Numpy
We will be using the numpy available in python, it provides std() function to calculate the standard error of the mean.
If you don’t have numpy package installed, use the below command on windows command prompt for numpy library installation.
pip install numpy
Example 1: How to calculate SEM in Python
Let’s understand, how to calculate the standard error of mean (SEM) with the given below python code.
#import modules
import numpy as np
#define dataset
data = np.array([4,7,3,9,12,8,14,10,12,12])
#calculate standard error of the mean
result = np.std(data, ddof=1) / np.sqrt(np.size(data))
#Print the result
print("The Standard error of the mean : %.3f"%result)
In the above code, we import numpy library to define the dataset.
Using std() function we calculated the standard error of the mean.
Note that we must specify ddof=1 in the argument for std() function to calculate the sample standard deviation instead of population standard deviation.
The Output of the above code is shown below.
#Output The Standard error of the mean : 1.149
The Standard error of the mean is 1.149.
Method 2: Use Scipy
We will be using Scipy library available in python, it provides sem() function to calculate the standard error of the mean.
If you don’t have the scipy library installed then use the below command on windows command prompt for scipy library installation.
pip install scipy
Example 2: How to calculate SEM in Python
Lets assume we have dataset as below
data = [4,7,3,9,12,8,14,10,12,12]
Lets calculate the standard error of mean by using below python code.
#import modules
import scipy.stats as stat
#define dataset
data = [4,7,3,9,12,8,14,10,12,12]
#calculate standard error of the mean
result = stat.sem(data)
#Print the result
print("The Standard error of the mean : %.3f"%result)
In the above code, we import numpy library to define the dataset.
Using sem() function we calculated the standard error of the mean.
The Output of the above code is shown below.
#Output The Standard error of the mean : 1.149
How to Interpret the Standard Error of the Mean
The two important factors to keep in mind while interpreting the SEM are as follows:-
1 Sample Size:- With the increase in sample size, the standard error of mean tends to decrease.
Let’s see this with below example:-
#import modules
import scipy.stats as stat
#define dataset 1
data1 = [4,7,3,9,12,8,14,10,12,12]
#define dataset 2 by repeated the first dataset twice
data2 = [4,7,3,9,12,8,14,10,12,12,4,7,3,9,12,8,14,10,12,12]
#calculate standard error of the mean
result1 = stat.sem(data1)
result2 = stat.sem(data2)
#Print the result
print("The Standard error of the mean for the original dataset: %.3f"%result1)
print("The Standard error of the mean for the repeated dataset : %.3f"%result2)
In the above example, we created the two datasets i.e. data1 & data2 where data2 is just the twice of data1.
The Output of the above code is shown below:-
# Output The Standard error of the mean for the original dataset: 1.149 The Standard error of the mean for the repeated dataset : 0.791
We seen that for data1 the SEM is 1.149 and for data2 SEM is 0.791.
It clearly shows that with an increase in size the SEM decreases.
Values of data2 are less spread out around the mean as compared to data1, although both have the same mean value.
2 The Value of SEM : The larger value of the SEM indicates that the values are more spread around the mean .
Let’s discuss this with below example:-
#import modules
import scipy.stats as stat
#define dataset 1
data1 = [4,7,3,9,12,8,14,10,12,12]
#define dataset 2 by replace last value with 120
data2 = [4,7,3,9,12,8,14,10,12,120]
#calculate standard error of the mean
result1 = stat.sem(data1)
result2 = stat.sem(data2)
#Print the result
print("The Standard error of the mean for the original dataset: %.3f"%result1)
print("The Standard error of the mean for the repeated dataset : %.3f"%result2)
In the above example, we created the two datasets i.e. data1 & data2 where data2 is created by replacing the last value with 120.
The Output of the above code is shown below:-
#Output The Standard error of the mean for the original dataset: 1.149 The Standard error of the mean for the repeated dataset : 11.177
We seen that for data1 the SEM is 1.149 and for data2 SEM is 11.177.
It clearly shows that SEM for data2 is larger as compared to data1.
It means the values of data2 are more spread out around the mean as compared to data1.
Conclusion
I hope, you may find how to calculate the Standard Error of the Mean in the python tutorial with a step-by-step illustration of examples educational and helpful.
Python is a great language for doing data analysis, primarily because of the fantastic ecosystem of data-centric python packages. Pandas is one of those packages and makes importing and analyzing data much easier.
Pandas dataframe.sem() function return unbiased standard error of the mean over requested axis. The standard error (SE) of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution[1] or an estimate of that standard deviation. If the parameter or the statistic is the mean, it is called the standard error of the mean (SEM).
Syntax : DataFrame.sem(axis=None, skipna=None, level=None, ddof=1, numeric_only=None, **kwargs)
Parameters :
axis : {index (0), columns (1)}
skipna : Exclude NA/null values. If an entire row/column is NA, the result will be NA
level : If the axis is a MultiIndex (hierarchical), count along a particular level, collapsing into a Series
ddof : Delta Degrees of Freedom. The divisor used in calculations is N – ddof, where N represents the number of elements.
numeric_only : Include only float, int, boolean columns. If None, will attempt to use everything, then use only numeric data. Not implemented for SeriesReturn : sem : Series or DataFrame (if level specified)
For link to the CSV file used in the code, click here
Example #1: Use sem() function to find the standard error of the mean of the given dataframe over the index axis.
import pandas as pd
df = pd.read_csv("nba.csv")
df
Let’s use the dataframe.sem() function to find the standard error of the mean over the index axis.
Output :
Notice, all the non-numeric columns and values are automatically not included in the calculation of the dataframe. We did not have to specifically input the numeric columns for the calculation of the standard error of the mean.
Example #2: Use sem() function to find the standard error of the mean over the column axis. Also do not skip the NaN values in the calculation of the dataframe.
import pandas as pd
df = pd.read_csv("nba.csv")
df.sem(axis = 1, skipna = False)
Output :
When we include the NaN values then it will cause that particular row or column to be NaN
14. Comparing Two Means¶
In the previous chapter we covered the situation when your outcome variable is nominal scale and your predictor variable1 is also nominal scale. Lots of real world situations have that character, and so you’ll find that chi-square tests in particular are quite widely used. However, you’re much more likely to find yourself in a situation where your outcome variable is interval scale or higher, and what you’re interested in is whether the average value of the outcome variable is higher in one group or another. For instance, a psychologist might want to know if anxiety levels are higher among parents than non-parents, or if working memory capacity is reduced by listening to music (relative to not listening to music). In a medical context, we might want to know if a new drug increases or decreases blood pressure. An agricultural scientist might want to know whether adding phosphorus to Australian native plants will kill them.2 In all these situations, our outcome variable is a fairly continuous, interval or ratio scale variable; and our predictor is a binary “grouping” variable. In other words, we want to compare the means of the two groups.
The standard answer to the problem of comparing means is to use a (t)-test, of which there are several varieties depending on exactly what question you want to solve. As a consequence, the majority of this chapter focuses on different types of (t)-test: one sample (t)-tests, student’s and welch’s, and paired samples (t)-tests. After that, we’ll talk a bit about Cohen’s (d), which is the standard measure of effect size for a (t)-test. The later sections of the chapter focus on the assumptions of the (t)-tests, and possible remedies if they are violated. However, before discussing any of these useful things, we’ll start with a discussion of the (z)-test.
14.1. The one-sample (z)-test¶
In this section I’ll describe one of the most useless tests in all of statistics: the (z)-test. Seriously – this test is almost never used in real life. Its only real purpose is that, when teaching statistics, it’s a very convenient stepping stone along the way towards the (t)-test, which is probably the most (over)used tool in all statistics.
14.1.1. The inference problem that the test addresses¶
To introduce the idea behind the (z)-test, let’s use a simple example. A friend of mine, Dr Zeppo, grades his introductory statistics class on a curve. Let’s suppose that the average grade in his class is 67.5, and the standard deviation is 9.5. Of his many hundreds of students, it turns out that 20 of them also take psychology classes. Out of curiosity, I find myself wondering: do the psychology students tend to get the same grades as everyone else (i.e., mean 67.5) or do they tend to score higher or lower? He emails me the zeppo.csv file, which I use to pull up the grades of those students,
import pandas as pd df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/zeppo.csv") df.head()
| grades | |
|---|---|
| 0 | 50 |
| 1 | 60 |
| 2 | 60 |
| 3 | 64 |
| 4 | 66 |
and calculate the mean:
import statistics statistics.mean(df['grades'])
Hm. It might be that the psychology students are scoring a bit higher than normal: that sample mean of (bar{X} = 72.3) is a fair bit higher than the hypothesised population mean of (mu = 67.5), but on the other hand, a sample size of (N = 20) isn’t all that big. Maybe it’s pure chance.
To answer the question, it helps to be able to write down what it is that I think I know. Firstly, I know that the sample mean is (bar{X} = 72.3). If I’m willing to assume that the psychology students have the same standard deviation as the rest of the class, then I can say that the population standard deviation is (sigma = 9.5). I’ll also assume that since Dr Zeppo is grading to a curve, the psychology student grades are normally distributed.
Next, it helps to be clear about what I want to learn from the data. In this case, my research hypothesis relates to the population mean (mu) for the psychology student grades, which is unknown. Specifically, I want to know if (mu = 67.5) or not. Given that this is what I know, can we devise a hypothesis test to solve our problem? The data, along with the hypothesised distribution from which they are thought to arise, are shown in Fig. 14.1. Not entirely obvious what the right answer is, is it? For this, we are going to need some statistics.
from myst_nb import glue import matplotlib.pyplot as plt import numpy as np import seaborn as sns import scipy.stats as stats mu = 67.5 sigma = 9.5 x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) y = 100* stats.norm.pdf(x, mu, sigma) fig, ax = plt.subplots() ax1 = sns.histplot(df['grades']) ax2 = sns.lineplot(x=x,y=y, color='black') plt.ylim(bottom=-1) ax1.set_frame_on(False) ax1.axes.get_yaxis().set_visible(False) glue("zeppo-fig", ax, display=False)
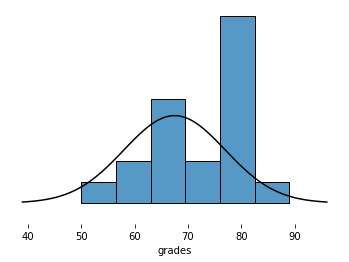
<AxesSubplot:xlabel='grades', ylabel='Count'>
Fig. 14.1 The theoretical distribution (solid line) from which the psychology student grades (blue bars) are supposed to have been generated.¶
14.1.2. Constructing the hypothesis test¶
The first step in constructing a hypothesis test is to be clear about what the null and alternative hypotheses are. This isn’t too hard to do. Our null hypothesis, (H_0), is that the true population mean (mu) for psychology student grades is 67.5%; and our alternative hypothesis is that the population mean isn’t 67.5%. If we write this in mathematical notation, these hypotheses become,
[begin{split}
begin{array}{ll}
H_0: & mu = 67.5
H_1: & mu neq 67.5
end{array}
end{split}]
though to be honest this notation doesn’t add much to our understanding of the problem, it’s just a compact way of writing down what we’re trying to learn from the data. The null hypotheses (H_0) and the alternative hypothesis (H_1) for our test are both illustrated in Fig. 14.2. In addition to providing us with these hypotheses, the scenario outlined above provides us with a fair amount of background knowledge that might be useful. Specifically, there are two special pieces of information that we can add:
-
The psychology grades are normally distributed.
-
The true standard deviation of these scores (sigma) is known to be 9.5.
For the moment, we’ll act as if these are absolutely trustworthy facts. In real life, this kind of absolutely trustworthy background knowledge doesn’t exist, and so if we want to rely on these facts we’ll just have make the assumption that these things are true. However, since these assumptions may or may not be warranted, we might need to check them. For now though, we’ll keep things simple.
import numpy as np import seaborn as sns from scipy import stats from matplotlib import pyplot as plt mu = 0 sigma = 1 x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) y = 100* stats.norm.pdf(x, mu, sigma) fig, axes = plt.subplots(1, 2, figsize=(15, 5)) sns.lineplot(x=x,y=y, color='black', ax=axes[0]) sns.lineplot(x=x,y=y, color='black', ax=axes[1]) axes[0].set_frame_on(False) axes[1].set_frame_on(False) axes[0].get_yaxis().set_visible(False) axes[1].get_yaxis().set_visible(False) axes[0].get_xaxis().set_visible(False) axes[1].get_xaxis().set_visible(False) axes[0].axhline(y=0, color='black') axes[0].axvline(x=mu, color='black', linestyle='--') axes[1].axhline(y=0, color='black') axes[1].axvline(x=mu + sigma, color='black', linestyle='--') axes[0].hlines(y=23.6, xmin = mu-sigma, xmax = mu, color='black') axes[1].hlines(y=23.6, xmin = mu-sigma, xmax = mu, color='black') axes[0].text(mu,42, r'$mu = mu_0$', size=20, ha="center") axes[1].text(mu + sigma, 42, r'$mu neq mu_0$', size=20, ha="center") axes[0].text(mu-sigma - 0.2, 23.6, r'$sigma = sigma_0$', size=20, ha="right") axes[1].text(mu-sigma - 0.2, 23.6, r'$sigma = sigma_0$', size=20, ha="right") glue("ztesthyp-fig", ax, display=False)
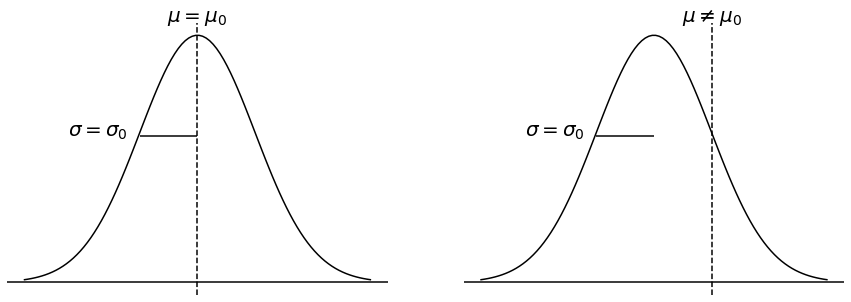
<AxesSubplot:xlabel='grades', ylabel='Count'>
Fig. 14.2 Graphical illustration of the null and alternative hypotheses assumed by the one sample (z)-test (the two sided version, that is). The null and alternative hypotheses both assume that the population distribution is normal, and additionally assumes that the population standard deviation is known (fixed at some value (sigma_0)). The null hypothesis (left) is that the population mean (mu) is equal to some specified value (mu_0). The alternative hypothesis is that the population mean differs from this value, (mu neq mu_0).¶
The next step is to figure out what we would be a good choice for a diagnostic test statistic; something that would help us discriminate between (H_0) and (H_1). Given that the hypotheses all refer to the population mean (mu), you’d feel pretty confident that the sample mean (bar{X}) would be a pretty useful place to start. What we could do, is look at the difference between the sample mean (bar{X}) and the value that the null hypothesis predicts for the population mean. In our example, that would mean we calculate (bar{X} — 67.5). More generally, if we let (mu_0) refer to the value that the null hypothesis claims is our population mean, then we’d want to calculate
[
bar{X} — mu_0
]
If this quantity equals or is very close to 0, things are looking good for the null hypothesis. If this quantity is a long way away from 0, then it’s looking less likely that the null hypothesis is worth retaining. But how far away from zero should it be for us to reject (H_0)?
To figure that out, we need to be a bit more sneaky, and we’ll need to rely on those two pieces of background knowledge that I wrote down previously, namely that the raw data are normally distributed, and we know the value of the population standard deviation (sigma). If the null hypothesis is actually true, and the true mean is (mu_0), then these facts together mean that we know the complete population distribution of the data: a normal distribution with mean (mu_0) and standard deviation (sigma). Adopting the notation from Section @ref(normal), a statistician might write this as:
[
X sim mbox{Normal}(mu_0,sigma^2)
]
Okay, if that’s true, then what can we say about the distribution of (bar{X})? Well, as we discussed earlier, the sampling distribution of the mean (bar{X}) is also normal, and has mean (mu). But the standard deviation of this sampling distribution (mbox{SE}({bar{X}})), which is called the standard error of the mean, is
[
mbox{SE}({bar{X}}) = frac{sigma}{sqrt{N}}
]
In other words, if the null hypothesis is true then the sampling distribution of the mean can be written as follows:
[
bar{X} sim mbox{Normal}(mu_0,mbox{SE}({bar{X}}))
]
Now comes the trick. What we can do is convert the sample mean (bar{X}) into a standard score. This is conventionally written as (z), but for now I’m going to refer to it as (z_{bar{X}}). (The reason for using this expanded notation is to help you remember that we’re calculating standardised version of a sample mean, not a standardised version of a single observation, which is what a (z)-score usually refers to). When we do so, the (z)-score for our sample mean is
[
z_{bar{X}} = frac{bar{X} — mu_0}{mbox{SE}({bar{X}})}
]
or, equivalently
[
z_{bar{X}} = frac{bar{X} — mu_0}{sigma / sqrt{N}}
]
This (z)-score is our test statistic. The nice thing about using this as our test statistic is that like all (z)-scores, it has a standard normal distribution:
[
z_{bar{X}} sim mbox{Normal}(0,1)
]
(again, see the section on z-scores) if you’ve forgotten why this is true). In other words, regardless of what scale the original data are on, the (z)-statistic iteself always has the same interpretation: it’s equal to the number of standard errors that separate the observed sample mean (bar{X}) from the population mean (mu_0) predicted by the null hypothesis. Better yet, regardless of what the population parameters for the raw scores actually are, the 5% critical regions for (z)-test are always the same, as illustrated in Figures @ref(fig:ztest1) and @ref(fig:ztest2).
mu = 0 sigma = 1 x = np.arange(-3,3,0.001) y = stats.norm.pdf(x, mu, sigma) fig, (ax0, ax1) = plt.subplots(1, 2, sharey = True, figsize=(15, 5)) # Two-sided test crit = 1.96 p_lower = x[x<crit*-1] p_upper = x[x>crit] ax0.plot(x, y) ax0.fill_between(p_lower, 0, stats.norm.pdf(p_lower, mu, sigma),color="none",hatch="///",edgecolor="b") ax0.fill_between(p_upper, 0, stats.norm.pdf(p_upper, mu, sigma), color="none",hatch="///",edgecolor="b") ax0.set_title("Two sided test", size = 20) ax0.text(-1.96,-.03, '-1.96', size=18, ha="right") ax0.text(1.96,-.03, '1.96', size=18, ha="left") # One-sided test crit = 1.64 p_upper = x[x>crit] ax1.plot(x, y) ax1.set_title("One sided test", size = 20) ax1.text(1.64,-.03, '1.64', size=18, ha="left") ax1.fill_between(p_upper, 0, stats.norm.pdf(p_upper, mu, sigma), color="none",hatch="///",edgecolor="b") ax0.set_frame_on(False) ax1.set_frame_on(False) ax0.get_yaxis().set_visible(False) ax1.get_yaxis().set_visible(False) ax0.get_xaxis().set_visible(False) ax1.get_xaxis().set_visible(False) glue("ztest-fig", ax, display=False)

<AxesSubplot:xlabel='grades', ylabel='Count'>
Fig. 14.3 Rejection regions for the two-sided z-test (left) and the one-sided z-test (right).¶
And what this meant, way back in the days where people did all their statistics by hand, is that someone could publish a table like this:
|
critical z value |
||
|---|---|---|
|
desired a level |
two-sided test |
one-sided test |
|
.1 |
1.644854 |
1.281552 |
|
.05 |
1.959964 |
1.644854 |
|
.01 |
2.575829 |
2.326348 |
|
.001 |
3.290527 |
3.090232 |
which in turn meant that researchers could calculate their (z)-statistic by hand, and then look up the critical value in a text book. That was an incredibly handy thing to be able to do back then, but it’s kind of unnecessary these days, since it’s trivially easy to do it with software like Python.
14.1.3. A worked example using Python¶
Now, as I mentioned earlier, the (z)-test is almost never used in practice. However, the test is so incredibly simple that it’s really easy to do one manually. Let’s go back to the data from Dr Zeppo’s class. Having loaded the grades data, the first thing I need to do is calculate the sample mean:
grades = df['grades'] sample_mean = statistics.mean(grades) sample_mean
Then, I create variables corresponding to known population standard deviation ((sigma = 9.5)), and the value of the population mean that the null hypothesis specifies ((mu_0 = 67.5)):
sd_true = 9.5 mu_null = 67.5
Let’s also create a variable for the sample size. We could count up the number of observations ourselves, and type N = 20 at the command prompt, but counting is tedious and repetitive. Let’s get Python to do the tedious repetitive bit by using the len() function, which tells us how many elements there are in a vector:
Next, let’s calculate the (true) standard error of the mean:
import math sem_true = sd_true / math.sqrt(N) sem_true
And finally, we calculate our (z)-score:
z_score = (sample_mean - mu_null) / sem_true z_score
At this point, we would traditionally look up the value 2.26 in our table of critical values. Our original hypothesis was two-sided (we didn’t really have any theory about whether psych students would be better or worse at statistics than other students) so our hypothesis test is two-sided (or two-tailed) also. Looking at the little table that I showed earlier, we can see that 2.26 is bigger than the critical value of 1.96 that would be required to be significant at (alpha = .05), but smaller than the value of 2.58 that would be required to be significant at a level of (alpha = .01). Therefore, we can conclude that we have a significant effect, which we might write up by saying something like this:
With a mean grade of 73.2 in the sample of psychology students, and assuming a true population standard deviation of 9.5, we can conclude that the psychology students have significantly different statistics scores to the class average ((z = 2.26), (N=20), (p<.05)).
However, what if want an exact (p)-value? Well, back in the day, the tables of critical values were huge, and so you could look up your actual (z)-value, and find the smallest value of (alpha) for which your data would be significant (which, as discussed earlier, is the very definition of a (p)-value). However, looking things up in books is tedious, and typing things into computers is awesome. So let’s do it using Python instead. Now, notice that the (alpha) level of a (z)-test (or any other test, for that matter) defines the total area “under the curve” for the critical region, right? That is, if we set (alpha = .05) for a two-sided test, then the critical region is set up such that the area under the curve for the critical region is (.05). And, for the (z)-test, the critical value of 1.96 is chosen that way because the area in the lower tail (i.e., below (-1.96)) is exactly (.025) and the area under the upper tail (i.e., above (1.96)) is exactly (.025). So, since our observed (z)-statistic is (2.26), why not calculate the area under the curve below (-2.26) or above (2.26)? In Python we can calculate this using the NormalDist().cdf() method. For the lower tail:
from statistics import NormalDist lower_area = NormalDist().cdf(-z_score) lower_area
NormalDist().cdf() calculates the “cumulative density function” for a normal distribution. Translated to something slightly less opaque, this means that NormalDist().cdf() gives us the probability that a random variable X will be less than or equal to a given value. In our case, the given value for the lower tail of the distribution was our z-score, (2.259). So NormalDist().cdf(-z_score) gives us the probability that a random value draw from a normal distribution would be less than or equal to (-2.259).
Of course, becauwe we didn’t have any particular theory about whether psychology students would do better worse than other students, our test should be two-tailed, that is, we are interested not only in the probability that a random value would be less than or equal to (-2.259), but also whether it might fall in the upper tail, that is be greater than or equal to (-2.259).
Since the normal distribution is symmetrical, the upper area under the curve is identical to the lower area, and we can simply add them together to find our exact (p)-value:
lower_area = NormalDist().cdf(-z_score) upper_area = lower_area p_value = lower_area + upper_area p_value
14.1.4. Assumptions of the (z)-test¶
As I’ve said before, all statistical tests make assumptions. Some tests make reasonable assumptions, while other tests do not. The test I’ve just described – the one sample (z)-test – makes three basic assumptions. These are:
-
Normality. As usually described, the (z)-test assumes that the true population distribution is normal.3 is often pretty reasonable, and not only that, it’s an assumption that we can check if we feel worried about it (see Section @ref(shapiro)).
-
Independence. The second assumption of the test is that the observations in your data set are not correlated with each other, or related to each other in some funny way. This isn’t as easy to check statistically: it relies a bit on good experimetal design. An obvious (and stupid) example of something that violates this assumption is a data set where you “copy” the same observation over and over again in your data file: so you end up with a massive “sample size”, consisting of only one genuine observation. More realistically, you have to ask yourself if it’s really plausible to imagine that each observation is a completely random sample from the population that you’re interested in. In practice, this assumption is never met; but we try our best to design studies that minimise the problems of correlated data.
-
Known standard deviation. The third assumption of the (z)-test is that the true standard deviation of the population is known to the researcher. This is just stupid. In no real world data analysis problem do you know the standard deviation (sigma) of some population, but are completely ignorant about the mean (mu). In other words, this assumption is always wrong.
In view of the stupidity of assuming that (sigma) is known, let’s see if we can live without it. This takes us out of the dreary domain of the (z)-test, and into the magical kingdom of the (t)-test, with unicorns and fairies and leprechauns, and um…
14.2. The one-sample (t)-test¶
After some thought, I decided that it might not be safe to assume that the psychology student grades necessarily have the same standard deviation as the other students in Dr Zeppo’s class. After all, if I’m entertaining the hypothesis that they don’t have the same mean, then why should I believe that they absolutely have the same standard deviation? In view of this, I should really stop assuming that I know the true value of (sigma). This violates the assumptions of my (z)-test, so in one sense I’m back to square one. However, it’s not like I’m completely bereft of options. After all, I’ve still got my raw data, and those raw data give me an estimate of the population standard deviation:
import statistics statistics.stdev(grades)
In other words, while I can’t say that I know that (sigma = 9.5), I can say that (hatsigma = 9.52).
Okay, cool. The obvious thing that you might think to do is run a (z)-test, but using the estimated standard deviation of 9.52 instead of relying on my assumption that the true standard deviation is 9.5. So, we could just type this new number into Python and out would come the answer. And you probably wouldn’t be surprised to hear that this would still give us a significant result. This approach is close, but it’s not quite correct. Because we are now relying on an estimate of the population standard deviation, we need to make some adjustment for the fact that we have some uncertainty about what the true population standard deviation actually is. Maybe our data are just a fluke … maybe the true population standard deviation is 11, for instance. But if that were actually true, and we ran the (z)-test assuming (sigma=11), then the result would end up being non-significant. That’s a problem, and it’s one we’re going to have to address.
mu = 0 sigma = 1 x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100) y = 100* stats.norm.pdf(x, mu, sigma) fig, axes = plt.subplots(1, 2, figsize=(15, 5)) sns.lineplot(x=x,y=y, color='black', ax=axes[0]) sns.lineplot(x=x,y=y, color='black', ax=axes[1]) axes[0].set_frame_on(False) axes[1].set_frame_on(False) axes[0].get_yaxis().set_visible(False) axes[1].get_yaxis().set_visible(False) axes[0].get_xaxis().set_visible(False) axes[1].get_xaxis().set_visible(False) axes[0].axhline(y=0, color='black') axes[0].axvline(x=mu, color='black', linestyle='--') axes[1].axhline(y=0, color='black') axes[1].axvline(x=mu + sigma, color='black', linestyle='--') axes[0].hlines(y=23.6, xmin = mu-sigma, xmax = mu, color='black') axes[1].hlines(y=23.6, xmin = mu-sigma, xmax = mu, color='black') axes[0].text(mu,42, r'$mu = mu_0$', size=20, ha="center") axes[1].text(mu + sigma, 42, r'$mu neq mu_0$', size=20, ha="center") axes[0].text(mu-sigma - 0.2, 23.6, r'$sigma = ??$', size=20, ha="right") axes[1].text(mu-sigma - 0.2, 23.6, r'$sigma = ??$', size=20, ha="right") glue("ttesthyp_onesample-fig", ax, display=False)
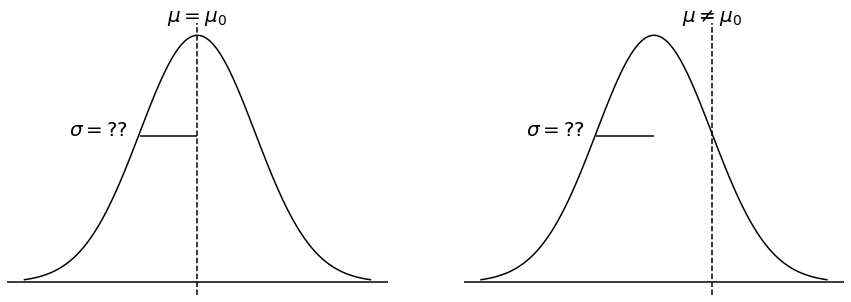
<AxesSubplot:xlabel='grades', ylabel='Count'>
Fig. 14.4 Graphical illustration of the null and alternative hypotheses assumed by the (two sided) one sample (t)-test. Note the similarity to the (z)-test. The null hypothesis is that the population mean (mu) is equal to some specified value (mu_0), and the alternative hypothesis is that it is not. Like the (z)-test, we assume that the data are normally distributed; but we do not assume that the population standard deviation (sigma) is known in advance.¶
14.2.1. Introducing the (t)-test¶
This ambiguity is annoying, and it was resolved in 1908 by a guy called William Sealy Gosset [@Student1908], who was working as a chemist for the Guinness brewery at the time [see @Box1987]. Because Guinness took a dim view of its employees publishing statistical analysis (apparently they felt it was a trade secret), he published the work under the pseudonym “A Student”, and to this day, the full name of the (t)-test is actually Student’s (t)-test. The key thing that Gosset figured out is how we should accommodate the fact that we aren’t completely sure what the true standard deviation is.4 The answer is that it subtly changes the sampling distribution. In the (t)-test, our test statistic (now called a (t)-statistic) is calculated in exactly the same way I mentioned above. If our null hypothesis is that the true mean is (mu), but our sample has mean (bar{X}) and our estimate of the population standard deviation is (hat{sigma}), then our (t) statistic is:
[
t = frac{bar{X} — mu}{hat{sigma}/sqrt{N} }
]
The only thing that has changed in the equation is that instead of using the known true value (sigma), we use the estimate (hat{sigma}). And if this estimate has been constructed from (N) observations, then the sampling distribution turns into a (t)-distribution with (N-1) degrees of freedom (df). The (t) distribution is very similar to the normal distribution, but has “heavier” tails, as discussed earlier and illustrated in Fig. 14.5. Notice, though, that as df gets larger, the (t)-distribution starts to look identical to the standard normal distribution. This is as it should be: if you have a sample size of (N = 70,000,000) then your “estimate” of the standard deviation would be pretty much perfect, right? So, you should expect that for large (N), the (t)-test would behave exactly the same way as a (z)-test. And that’s exactly what happens!
mu = 0 variance = 1 sigma = np.sqrt(variance) x = np.linspace(-4, 4, 100) y_norm = stats.norm.pdf(x, mu, sigma) fig, axes = plt.subplots(1, 2, figsize=(15, 5)) # t-distribution with 2 degrees of freedom y_t = stats.t.pdf(x, 2) sns.lineplot(x = x, y = y_norm, color = 'black', linestyle='--', ax = axes[0]) sns.lineplot(x = x, y = y_t, color = 'black', ax = axes[0]) # t-distribution with 10 degrees of freedom y_t = stats.t.pdf(x, 10) sns.lineplot(x = x, y = y_norm, color = 'black', linestyle='--', ax = axes[1]) sns.lineplot(x = x, y = y_t, color = 'black', ax = axes[1]) axes[0].text(0, 0.42, r'$df = 2$', size=20, ha="center") axes[1].text(0, 0.42, r'$df = 10$', size=20, ha="center") #sns.despine() axes[0].get_yaxis().set_visible(False) axes[1].get_yaxis().set_visible(False) axes[0].set_frame_on(False) axes[1].set_frame_on(False)
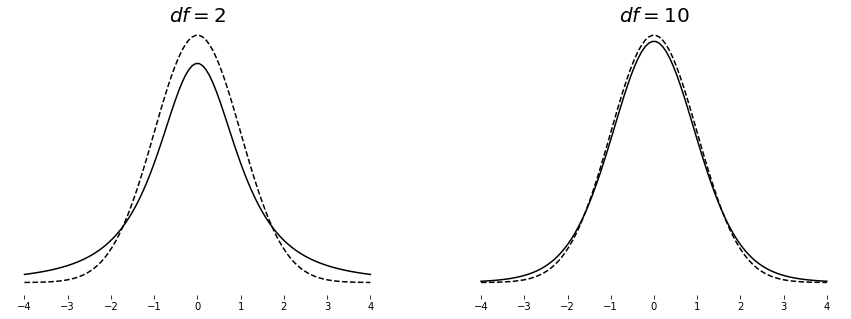
Fig. 14.5 The (t) distribution with 2 degrees of freedom (left) and 10 degrees of freedom (right), with a standard normal distribution (i.e., mean 0 and std dev 1) plotted as dotted lines for comparison purposes. Notice that the (t) distribution has heavier tails (higher kurtosis) than the normal distribution; this effect is quite exaggerated when the degrees of freedom are very small, but negligible for larger values. In other words, for large (df) the (t) distribution is essentially identical to a normal distribution.¶
14.2.2. Doing the test in Python¶
As you might expect, the mechanics of the (t)-test are almost identical to the mechanics of the (z)-test. So there’s not much point in going through the tedious exercise of showing you how to do the calculations using low level commands: it’s pretty much identical to the calculations that we did earlier, except that we use the estimated standard deviation (i.e., something like se_est = statistics.stdev(grades)), and then we test our hypothesis using the (t) distribution rather than the normal distribution. And so instead of going through the calculations in tedious detail for a second time, I’ll jump straight to showing you how (t)-tests are actually done in practice.
The situation with (t)-tests is very similar to the one we encountered with chi-squared tests. scipy.stats includes a variety of methods for running different kinds of (t)-tests, but the pingouin package makes wraps these up and makes them easier (to my mind) to deal with. We’ll start with the scipy version for the one-sample (t)-test, so you can get a flavor for how scipy deals with (t)-tests, and then use the pingouin alternatives for the rest.
To run a one-sample (t)-test with scipy, use the ttest_1samp method. It’s pretty straightforward to use: all you need to do is specify a, the variable containing the data, and popmean, the true population mean according to the null hypothesis. All you need to type is this:
from scipy.stats import ttest_1samp t, p = ttest_1samp(a = grades, popmean = 67.5) t, p
(2.25471286700693, 0.03614521878144544)
So that seems straightforward enough. Our calculation resulted in a (t)-statistic of 2.54, and a (p)-value of 0.36. Now what do we do with this output? Well, since we’re pretending that we actually care about my toy example, we’re overjoyed to discover that the result is statistically significant (i.e. (p) value below .05), and we will probably want to report our result. We could report the result by saying something like this:
With a mean grade of 72.3, the psychology students scored slightly higher than the average grade of 67.5 ((t(19) = 2.25), (p<.05)); the 95% confidence interval is [67.8, 76.8].
where (t(19)) is shorthand notation for a (t)-statistic that has 19 degrees of freedom.
As you will have already noticed, ttest_1samp() does not give us all the information included in the report above. A (t)-statistic, yes, and a (p)-value as well. But what about 95% confidence intervals? Where can we find those, and what about the degrees of freedom? In a better, simpler, kinder world, ttest_1samp() would provide all this information for us, and it’s honestly a bit shocking that it doesn’t. But sadly that is not the world we live in, and we have a bit more work to do.
First, off: degrees of freedom. In this case, that is not so difficult, because the degrees of freedom for a one-sample t-test is just (N-1), so we can easily find that ourselves. We also already know how to find the sample mean of our data:
N = len(grades) degfree = N-1 sample_mean = statistics.mean(grades) print('Sample mean:', sample_mean) print('Degrees of freedom:', degfree)
Sample mean: 72.3 Degrees of freedom: 19
Now at least we have the bare minimum of what is necessary to report our results. Still, it would be sweet if we could get those confidence intervals as well. scipy actually has all the tools we need, and why these are not just built into the ttest_1samp() method is beyond me. To find the confidence interval, we need to:
-
To set a confidence level
-
To know the sample mean
-
To know the degrees of freedom for the test
-
To know the standard error of the sample
We discussed confidence intervals earlier, and now is not the time to go into detail on this, so for now I’m just going to give you some code that you can use to find 95% confidence intervals for a one-sample t-test, so that we can get on with reporting our data:
from scipy import stats confidence_level = 0.95 degrees_freedom = len(grades)-1 sample_mean = statistics.mean(grades) sample_standard_error = stats.sem(grades) confidence_interval = stats.t.interval(confidence_level, degrees_freedom, sample_mean, sample_standard_error) confidence_interval
(67.84421513791415, 76.75578486208585)
Whew. Now at least we have everything we need for a full report of our results.
That said, it’s often the case that people don’t report the confidence interval, or do so using a much more compressed form than I’ve done here. For instance, it’s not uncommon to see the confidence interval included as part of the stat block, like this:
(t(19) = 2.25), (p<.05), CI(_{95} = [67.8, 76.8])
With that much jargon crammed into half a line, you know it must be really smart. 5
Having gone through all that, let’s take a look at the pingouin command to achieve the same thing.
from pingouin import ttest ttest(grades, 67.5)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.254713 | 19 | two-sided | 0.036145 | [67.84, 76.76] | 0.504169 | 1.795 | 0.571446 |
Well. That was easy! All we need to do is feed the ttest() function from pingouin with the data and the population mean under the null hypothesis, and pinguoin does the rest. We get a nice table with the (t)-value, the degrees of freedom, the (p)-value, 95% confidence interval, effect size (Cohen’s (d)), and a power estimate. BF10 refers to the “bayes factor”, which we will meet (briefly) in the section on Bayesian statistics.
14.2.3. Assumptions of the one sample (t)-test¶
Okay, so what assumptions does the one-sample (t)-test make? Well, since the (t)-test is basically a (z)-test with the assumption of known standard deviation removed, you shouldn’t be surprised to see that it makes the same assumptions as the (z)-test, minus the one about the known standard deviation. That is
-
Normality. We’re still assuming that the the population distribution is normal6.
-
Independence. Once again, we have to assume that the observations in our sample are generated independently of one another. See the earlier discussion about the (z)-test for specifics.
Overall, these two assumptions aren’t terribly unreasonable, and as a consequence the one-sample (t)-test is pretty widely used in practice as a way of comparing a sample mean against a hypothesised population mean.
14.3. The independent samples (t)-test (Student test)¶
Although the one sample (t)-test has its uses, it’s not the most typical example of a (t)-test7. A much more common situation arises when you’ve got two different groups of observations. In psychology, this tends to correspond to two different groups of participants, where each group corresponds to a different condition in your study. For each person in the study, you measure some outcome variable of interest, and the research question that you’re asking is whether or not the two groups have the same population mean. This is the situation that the independent samples (t)-test is designed for.
14.3.1. The data¶
Suppose we have 33 students taking Dr Harpo’s statistics lectures, and Dr Harpo doesn’t grade to a curve. Actually, Dr Harpo’s grading is a bit of a mystery, so we don’t really know anything about what the average grade is for the class as a whole. There are two tutors for the class, Anastasia and Bernadette. There are (N_1 = 15) students in Anastasia’s tutorials, and (N_2 = 18) in Bernadette’s tutorials. The research question I’m interested in is whether Anastasia or Bernadette is a better tutor, or if it doesn’t make much of a difference. Dr Harpo emails me the course grades, in the harpo.csv file. As usual, I’ll load the file and have a look at what variables it contains:
import pandas as pd df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/harpo.csv") df.head()
| grade | tutor | |
|---|---|---|
| 0 | 65 | Anastasia |
| 1 | 72 | Bernadette |
| 2 | 66 | Bernadette |
| 3 | 74 | Anastasia |
| 4 | 73 | Anastasia |
As we can see, there’s a single data frame with two variables, grade and tutor. The grade variable is a numeric vector, containing the grades for all (N = 33) students taking Dr Harpo’s class; the tutor variable is a factor that indicates who each student’s tutor was. The first five observations in this data set are shown above, and below is a nice little table with some summary statistics:
harpo_summary = pd.DataFrame( {'students': ['Anastasia's students','Bernadette's students'], 'mean': [statistics.mean(df.loc[df['tutor'] == 'Anastasia']['grade']), statistics.mean(df.loc[df['tutor'] == 'Bernadette']['grade'])], 'std dev': [statistics.stdev(df.loc[df['tutor'] == 'Anastasia']['grade']), statistics.stdev(df.loc[df['tutor'] == 'Bernadette']['grade'])], 'N': [len(df.loc[df['tutor'] == 'Anastasia']), len(df.loc[df['tutor'] == 'Bernadette'])] }) harpo_summary
| students | mean | std dev | N | |
|---|---|---|---|---|
| 0 | Anastasia’s students | 74.533333 | 8.998942 | 15 |
| 1 | Bernadette’s students | 69.055556 | 5.774918 | 18 |
To give you a more detailed sense of what’s going on here, I’ve plotted histograms showing the distribution of grades for both tutors Fig. 14.6. Inspection of these histograms suggests that the students in Anastasia’s class may be getting slightly better grades on average, though they also seem a little more variable.
fig, axes = plt.subplots(1, 2, figsize=(15, 5)) Anastasia = pd.DataFrame(df.loc[df['tutor'] == 'Anastasia']['grade']) Bernadette = pd.DataFrame(df.loc[df['tutor'] == 'Bernadette']['grade']) sns.histplot(Anastasia['grade'], ax = axes[0], binwidth = 5) sns.histplot(Bernadette['grade'], ax = axes[1], binwidth = 5) axes[0].set_xlim(50,100) axes[1].set_xlim(50,100) axes[0].set_ylim(0,7) axes[1].set_ylim(0,7) axes[0].set_title('Anastasia') axes[1].set_title('Bernadette') sns.despine()
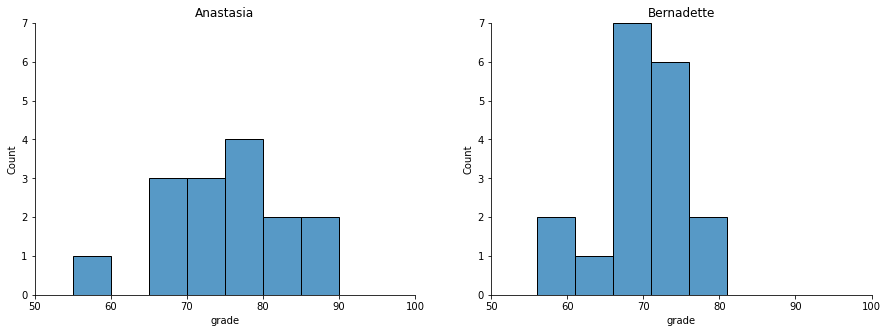
Fig. 14.6 Histogram showing the overall distribution of grades for students in Anastasia and Bernadette’s classes¶
Fig. 14.7 is a simpler plot showing the means and corresponding confidence intervals for both groups of students.
sns.pointplot(x = 'tutor', y = 'grade', data = df) sns.despine()
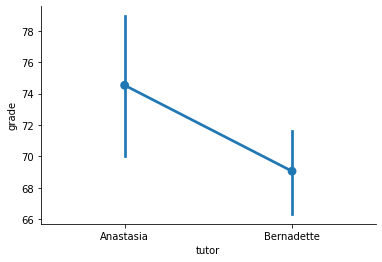
Fig. 14.7 Plot showing the mean grade for the students in Anastasia’s and Bernadette’s tutorials. Error bars depict 95% confidence intervals around the mean. On the basis of visual inspection, it does look like there’s a real difference between the groups, though it’s hard to say for sure.¶
14.3.2. Introducing the test¶
The independent samples (t)-test comes in two different forms, Student’s and Welch’s. The original Student (t)-test – which is the one I’ll describe in this section – is the simpler of the two, but relies on much more restrictive assumptions than the Welch (t)-test. Assuming for the moment that you want to run a two-sided test, the goal is to determine whether two “independent samples” of data are drawn from populations with the same mean (the null hypothesis) or different means (the alternative hypothesis). When we say “independent” samples, what we really mean here is that there’s no special relationship between observations in the two samples. This probably doesn’t make a lot of sense right now, but it will be clearer when we come to talk about the paired samples (t)-test later on. For now, let’s just point out that if we have an experimental design where participants are randomly allocated to one of two groups, and we want to compare the two groups’ mean performance on some outcome measure, then an independent samples (t)-test (rather than a paired samples (t)-test) is what we’re after.
Okay, so let’s let (mu_1) denote the true population mean for group 1 (e.g., Anastasia’s students), and (mu_2) will be the true population mean for group 2 (e.g., Bernadette’s students),8 and as usual we’ll let (bar{X}_1) and (bar{X}_2) denote the observed sample means for both of these groups. Our null hypothesis states that the two population means are identical ((mu_1 = mu_2)) and the alternative to this is that they are not ((mu_1 neq mu_2)). Written in mathematical-ese, this is…
[begin{split}
begin{array}{ll}
H_0: & mu_1 = mu_2
H_1: & mu_1 neq mu_2
end{array}
end{split}]
mu1 = 0 sigma1 = 1 mu2 = 2 x1 = np.linspace(mu1 - 4*sigma, mu1 + 4*sigma, 100) y1 = 100* stats.norm.pdf(x1, mu1, sigma) x2 = np.linspace(mu2 - 4*sigma, mu2 + 4*sigma, 100) y2 = 100* stats.norm.pdf(x2, mu2, sigma) fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5)) sns.lineplot(x=x1,y=y, color='black', ax = ax1) sns.lineplot(x=x1,y=y, color='black', ax = ax2) sns.lineplot(x=x2,y=y2, color='black', ax = ax2) ax1.text(0, 43, 'null hypothesis', size=20, ha="center") ax2.text(0, 43, 'alternative hypothesis', size=20, ha="center") ax1.set_frame_on(False) ax2.set_frame_on(False) ax1.get_yaxis().set_visible(False) ax2.get_yaxis().set_visible(False) ax1.get_xaxis().set_visible(False) ax2.get_xaxis().set_visible(False) ax1.axhline(y=0, color='black') ax2.axhline(y=0, color='black')
<matplotlib.lines.Line2D at 0x17d73d120>
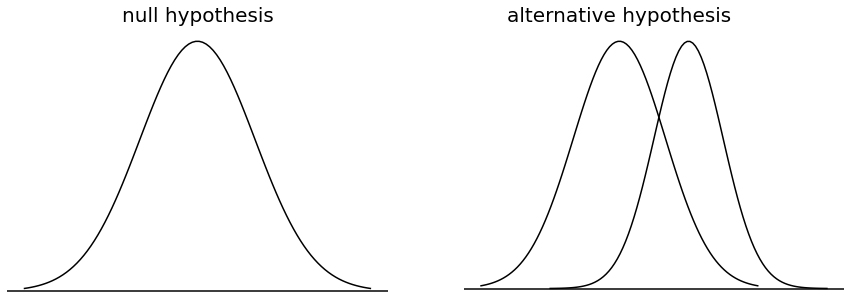
Fig. 14.8 Graphical illustration of the null and alternative hypotheses assumed by the Student (t)-test. The null hypothesis assumes that both groups have the same mean (mu), whereas the alternative assumes that they have different means (mu_1) and (mu_2). Notice that it is assumed that the population distributions are normal, and that, although the alternative hypothesis allows the group to have different means, it assumes they have the same standard deviation¶
To construct a hypothesis test that handles this scenario, we start by noting that if the null hypothesis is true, then the difference between the population means is exactly zero,
(mu_1 — mu_2 = 0)
As a consequence, a diagnostic test statistic will be based on the difference between the two sample means. Because if the null hypothesis is true, then we’d expect
[
bar{X}_1 — bar{X}_2
]
to be pretty close to zero. However, just like we saw with our one-sample tests (i.e., the one-sample (z)-test and the one-sample (t)-test) we have to be precise about exactly how close to zero this difference should be. And the solution to the problem is more or less the same one: we calculate a standard error estimate (SE), just like last time, and then divide the difference between means by this estimate. So our (t)-statistic will be of the form
[
t = frac{bar{X}_1 — bar{X}_2}{mbox{SE}}
]
We just need to figure out what this standard error estimate actually is. This is a bit trickier than was the case for either of the two tests we’ve looked at so far, so we need to go through it a lot more carefully to understand how it works.
14.3.3. A “pooled estimate” of the standard deviation¶
In the original “Student (t)-test”, we make the assumption that the two groups have the same population standard deviation: that is, regardless of whether the population means are the same, we assume that the population standard deviations are identical, (sigma_1 = sigma_2). Since we’re assuming that the two standard deviations are the same, we drop the subscripts and refer to both of them as (sigma). How should we estimate this? How should we construct a single estimate of a standard deviation when we have two samples? The answer is, basically, we average them. Well, sort of. Actually, what we do is take a weighed average of the variance estimates, which we use as our pooled estimate of the variance. The weight assigned to each sample is equal to the number of observations in that sample, minus 1. Mathematically, we can write this as
[begin{split}
begin{array}{rcl}
w_1 &=& N_1 — 1
w_2 &=& N_2 — 1
end{array}
end{split}]
Now that we’ve assigned weights to each sample, we calculate the pooled estimate of the variance by taking the weighted average of the two variance estimates, ({hatsigma_1}^2) and ({hatsigma_2}^2)
[
hatsigma^2_p = frac{w_1 {hatsigma_1}^2 + w_2 {hatsigma_2}^2}{w_1 + w_2}
]
Finally, we convert the pooled variance estimate to a pooled standard deviation estimate, by taking the square root. This gives us the following formula for (hatsigma_p),
[
hatsigma_p = sqrt{frac{w_1 {hatsigma_1}^2 + w_2 {hatsigma_2}^2}{w_1 + w_2}}
]
And if you mentally substitute (w_1 = N_1 -1) and (w_2 = N_2 -1) into this equation you get a very ugly looking formula; a very ugly formula that actually seems to be the “standard” way of describing the pooled standard deviation estimate. It’s not my favourite way of thinking about pooled standard deviations, however.9
14.3.4. The same pooled estimate, described differently¶
I prefer to think about it like this. Our data set actually corresponds to a set of (N) observations, which are sorted into two groups. So let’s use the notation (X_{ik}) to refer to the grade received by the (i)-th student in the (k)-th tutorial group: that is, (X_{11}) is the grade received by the first student in Anastasia’s class, (X_{21}) is her second student, and so on. And we have two separate group means (bar{X}_1) and (bar{X}_2), which we could “generically” refer to using the notation (bar{X}_k), i.e., the mean grade for the (k)-th tutorial group. So far, so good. Now, since every single student falls into one of the two tutorials, then we can describe their deviation from the group mean as the difference
[
X_{ik} — bar{X}_k
]
So why not just use these deviations (i.e., the extent to which each student’s grade differs from the mean grade in their tutorial?) Remember, a variance is just the average of a bunch of squared deviations, so let’s do that. Mathematically, we could write it like this:
[
frac{sum_{ik} left( X_{ik} — bar{X}_k right)^2}{N}
]
where the notation “(sum_{ik})” is a lazy way of saying “calculate a sum by looking at all students in all tutorials”, since each “(ik)” corresponds to one student.^[A more correct notation will be introduced in chapter on ANOVA(anova).] But, as we saw in the chapter on estimation, calculating the variance by dividing by (N) produces a biased estimate of the population variance. And previously, we needed to divide by (N-1) to fix this. However, as I mentioned at the time, the reason why this bias exists is because the variance estimate relies on the sample mean; and to the extent that the sample mean isn’t equal to the population mean, it can systematically bias our estimate of the variance. But this time we’re relying on two sample means! Does this mean that we’ve got more bias? Yes, yes it does. And does this mean we now need to divide by (N-2) instead of (N-1), in order to calculate our pooled variance estimate? Why, yes…
[
hatsigma^2_p = frac{sum_{ik} left( X_{ik} — bar{X}_k right)^2}{N -2}
]
Oh, and if you take the square root of this then you get (hat{sigma}_p), the pooled standard deviation estimate. In other words, the pooled standard deviation calculation is nothing special: it’s not terribly different to the regular standard deviation calculation.
14.3.5. Completing the test¶
Regardless of which way you want to think about it, we now have our pooled estimate of the standard deviation. From now on, I’ll drop the silly (p) subscript, and just refer to this estimate as (hatsigma). Great. Let’s now go back to thinking about the bloody hypothesis test, shall we? Our whole reason for calculating this pooled estimate was that we knew it would be helpful when calculating our standard error estimate. But, standard error of what? In the one-sample (t)-test, it was the standard error of the sample mean, (mbox{SE}({bar{X}})), and since (mbox{SE}({bar{X}}) = sigma / sqrt{N}) that’s what the denominator of our (t)-statistic looked like. This time around, however, we have two sample means. And what we’re interested in, specifically, is the the difference between the two (bar{X}_1 — bar{X}_2). As a consequence, the standard error that we need to divide by is in fact the standard error of the difference between means. As long as the two variables really do have the same standard deviation, then our estimate for the standard error is
[
mbox{SE}({bar{X}_1 — bar{X}_2}) = hatsigma sqrt{frac{1}{N_1} + frac{1}{N_2}}
]
and our (t)-statistic is therefore
[
t = frac{bar{X}_1 — bar{X}_2}{mbox{SE}({bar{X}_1 — bar{X}_2})}
]
Just as we saw with our one-sample test, the sampling distribution of this (t)-statistic is a (t)-distribution (shocking, isn’t it?) as long as the null hypothesis is true, and all of the assumptions of the test are met. The degrees of freedom, however, is slightly different. As usual, we can think of the degrees of freedom to be equal to the number of data points minus the number of constraints. In this case, we have (N) observations ((N_1) in sample 1, and (N_2) in sample 2), and 2 constraints (the sample means). So the total degrees of freedom for this test are (N-2).
14.3.6. Doing the test in Python¶
Now, you can run an independent samples (t)-test with a method from scipy, and since the method for a one-sample (t)-test was ttest_1samp, it may come as no big surprise to you that the method for an independent-samples (t)-test is called ttest_ind. But from here on out, I think it will be easier for everyone (certainly easier for me!) if we use pingouin to ease the process of running these tests. How will it make it easier, you ask? Well, for one thing, remember how we just used the ttest() function from pingouin to run a one-sample (t)-test? Well we can use the exact same function to run all of the (t)-tests in this chapter. How’s that for making things easier? Also, pingouin unifies the output format, so we get the same familiar table for each one of the tests.
So let’s give it a try. An important point here, and one that can cause a lot of frustration if you don’t realize what is going on, is that ttest() wants the data from the two groups served up as two separate variables (this is true of the scipy version as well, by the way). Since Dr Harpo sent the data to us in long format, that is, with all the grades in one column, and a second column telling us who the tutor was for each student, we will need to do something to break the grade data into two. So step one will be creating a new dataframe, with one column per tutor (“wide” format):
Harpo_wide = pd.DataFrame( {'Anastasia': df.loc[df['tutor'] == 'Anastasia']['grade'], 'Bernadette': df.loc[df['tutor'] == 'Bernadette']['grade']}) Harpo_wide.head()
| Anastasia | Bernadette | |
|---|---|---|
| 0 | 65.0 | NaN |
| 1 | NaN | 72.0 |
| 2 | NaN | 66.0 |
| 3 | 74.0 | NaN |
| 4 | 73.0 | NaN |
Now, you will have noticed right away that this new dataframe has a bunch of things that aren’t numbers in it. In fact, “NaN” stands for “Not a Number”. But after a moment’s reflection, this makes perfect sense: the students were divided up between Anastasia and Bernadette, and so of course now that we have a row for each student, if a student has Anastasia as a tutor, they can’t also have Bernadette as a tutor. Luckily, ttest() is smart enough to see what is going on, and deal with it appropriately. So, now that we have all of our ducks in order, let’s do the test:
from pingouin import ttest ttest(Harpo_wide['Anastasia'], Harpo_wide['Bernadette'], correction = False)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.115432 | 31 | two-sided | 0.042529 | [0.2, 10.76] | 0.739561 | 1.755 | 0.53577 |
You probably noticed that in addition to telling ttest() which means I wanted to compare, I also added the argument correction = False to the command. This wasn’t strictly necessary in this case, because by default this argument is set to True. By saying correction = False, what we’re really doing is telling Python to use the Student independent samples (t)-test, and not the Welch independent samples (t)-test. More on this later, when we get to Welch. For now, let’s just get the descriptive statistics for Anastasia and Bernadette’s students so we can report our results:
| Anastasia | Bernadette | |
|---|---|---|
| count | 15.000000 | 18.000000 |
| mean | 74.533333 | 69.055556 |
| std | 8.998942 | 5.774918 |
| min | 55.000000 | 56.000000 |
| 25% | 69.000000 | 66.250000 |
| 50% | 76.000000 | 69.000000 |
| 75% | 79.000000 | 73.000000 |
| max | 90.000000 | 79.000000 |
The difference between the two groups is significant (just barely), so we might write up the result using text like this:
The mean grade in Anastasia’s class was 74.5% (std dev = 9.0), whereas the mean in Bernadette’s class was 69.1% (std dev = 5.8). A Student’s independent samples (t)-test showed that this 5.4% difference was significant ((t(31) = 2.1), (p<.05)), suggesting that a genuine difference in learning outcomes has occurred.
14.3.7. Positive and negative (t) values¶
Before moving on to talk about the assumptions of the (t)-test, there’s one additional point I want to make about the use of (t)-tests in practice. The first one relates to the sign of the (t)-statistic (that is, whether it is a positive number or a negative one). One very common worry that students have when they start running their first (t)-test is that they often end up with negative values for the (t)-statistic, and don’t know how to interpret it. In fact, it’s not at all uncommon for two people working independently to end up with Python outputs that are almost identical, except that one person has a negative (t) values and the other one has a positive (t) value. Assuming that you’re running a two-sided test, then the (p)-values will be identical. On closer inspection, the students will notice that the confidence intervals also have the opposite signs. This is perfectly okay: whenever this happens, what you’ll find is that the two versions of the Python output arise from slightly different ways of running the (t)-test. What’s happening here is very simple. The (t)-statistic that Python is calculating here is always of the form
[
t = frac{mbox{(mean 1)} -mbox{(mean 2)}}{ mbox{(SE)}}
]
If “mean 1” is larger than “mean 2” the (t) statistic will be positive, whereas if “mean 2” is larger then the (t) statistic will be negative. Similarly, the confidence interval that R reports is the confidence interval for the difference “(mean 1) minus (mean 2)”, which will be the reverse of what you’d get if you were calculating the confidence interval for the difference “(mean 2) minus (mean 1)”.
Okay, that’s pretty straightforward when you think about it, but now consider our (t)-test comparing Anastasia’s class to Bernadette’s class. Which one should we call “mean 1” and which one should we call “mean 2”. It’s arbitrary. However, you really do need to designate one of them as “mean 1” and the other one as “mean 2”. Not surprisingly, the way that Python handles this is also pretty arbitrary. In earlier versions of the book I used to try to explain it, but after a while I gave up, because it’s not really all that important, and to be honest I can never remember myself. Whenever I get a significant (t)-test result, and I want to figure out which mean is the larger one, I don’t try to figure it out by looking at the (t)-statistic. Why would I bother doing that? It’s foolish. It’s easier just look at the actual group means!
Here’s the important thing. Because it really doesn’t matter what Python printed out, I usually try to report the (t)-statistic in such a way that the numbers match up with the text. Here’s what I mean… suppose that what I want to write in my report is “Anastasia’s class had higher grades than Bernadette’s class”. The phrasing here implies that Anastasia’s group comes first, so it makes sense to report the (t)-statistic as if Anastasia’s class corresponded to group 1. If so, I would write
Anastasia’s class had higher grades than Bernadette’s class ((t(31)= 2.1, p=.04)).
(I wouldn’t actually emphasise the word “higher” in real life, I’m just doing it to emphasise the point that “higher” corresponds to positive (t) values). On the other hand, suppose the phrasing I wanted to use has Bernadette’s class listed first. If so, it makes more sense to treat her class as group 1, and if so, the write up looks like this:
Bernadette’s class had lower grades than Anastasia’s class ((t(31)= -2.1, p=.04)).
Because I’m talking about one group having “lower” scores this time around, it is more sensible to use the negative form of the (t)-statistic. It just makes it read more cleanly.
One last thing: please note that you can’t do this for other types of test statistics. It works for (t)-tests, but it wouldn’t be meaningful for chi-square testsm (F)-tests or indeed for most of the tests I talk about in this book. So don’t overgeneralise this advice! I’m really just talking about (t)-tests here and nothing else!
14.3.8. Assumptions of the test¶
As always, our hypothesis test relies on some assumptions. So what are they? For the Student t-test there are three assumptions, some of which we saw previously in the context of the one sample (t)-test (see Section @ref(ttestoneassumptions)):
-
Normality. Like the one-sample (t)-test, it is assumed that the data are normally distributed. Specifically, we assume that both groups are normally distributed. In Section @ref(shapiro) we’ll discuss how to test for normality, and in Section @ref(wilcox) we’ll discuss possible solutions.
-
Independence. Once again, it is assumed that the observations are independently sampled. In the context of the Student test this has two aspects to it. Firstly, we assume that the observations within each sample are independent of one another (exactly the same as for the one-sample test). However, we also assume that there are no cross-sample dependencies. If, for instance, it turns out that you included some participants in both experimental conditions of your study (e.g., by accidentally allowing the same person to sign up to different conditions), then there are some cross sample dependencies that you’d need to take into account.
-
Homogeneity of variance (also called “homoscedasticity”). The third assumption is that the population standard deviation is the same in both groups. You can test this assumption using the Levene test, which I’ll talk about later on in the book (Section @ref(levene)). However, there’s a very simple remedy for this assumption, which I’ll talk about in the next section.
14.4. The independent samples (t)-test (Welch test)¶
The biggest problem with using the Student test in practice is the third assumption listed in the previous section: it assumes that both groups have the same standard deviation. This is rarely true in real life: if two samples don’t have the same means, why should we expect them to have the same standard deviation? There’s really no reason to expect this assumption to be true. We’ll talk a little bit about how you can check this assumption later on because it does crop up in a few different places, not just the (t)-test. But right now I’ll talk about a different form of the (t)-test [Welch, 1947] that does not rely on this assumption. A graphical illustration of what the Welch (t) test assumes about the data is shown in Figure Fig. 14.9, to provide a contrast with the Student test version in Fig. 14.8. I’ll admit it’s a bit odd to talk about the cure before talking about the diagnosis, but as it happens the Welch test is often the default (t)-test, so this is probably the best place to discuss it.
The Welch test is very similar to the Student test. For example, the (t)-statistic that we use in the Welch test is calculated in much the same way as it is for the Student test. That is, we take the difference between the sample means, and then divide it by some estimate of the standard error of that difference:
[
t = frac{bar{X}_1 — bar{X}_2}{mbox{SE}({bar{X}_1 — bar{X}_2})}
]
The main difference is that the standard error calculations are different. If the two populations have different standard deviations, then it’s a complete nonsense to try to calculate a pooled standard deviation estimate, because you’re averaging apples and oranges.10 But you can still estimate the standard error of the difference between sample means; it just ends up looking different:
[
mbox{SE}({bar{X}_1 — bar{X}_2}) = sqrt{ frac{{hat{sigma}_1}^2}{N_1} + frac{{hat{sigma}_2}^2}{N_2} }
]
The reason why it’s calculated this way is beyond the scope of this book. What matters for our purposes is that the (t)-statistic that comes out of the Welch test is actually somewhat different to the one that comes from the Student test.
The second difference between Welch and Student is that the degrees of freedom are calculated in a very different way. In the Welch test, the “degrees of freedom ” doesn’t have to be a whole number any more, and it doesn’t correspond all that closely to the “number of data points minus the number of constraints” heuristic that I’ve been using up to this point. The degrees of freedom are, in fact…
[
mbox{df} = frac{ ({hat{sigma}_1}^2 / N_1 + {hat{sigma}_2}^2 / N_2)^2 }{ ({hat{sigma}_1}^2 / N_1)^2 / (N_1 -1 ) + ({hat{sigma}_2}^2 / N_2)^2 / (N_2 -1 ) }
]
… which is all pretty straightforward and obvious, right? Well, perhaps not. It doesn’t really matter for our purposes. What matters is that you’ll see that the “df” value that pops out of a Welch test tends to be a little bit smaller than the one used for the Student test, and it doesn’t have to be a whole number.
mu1 = 0 sigma1 = 1 mu2 = 2 sigma2 = 1.45 x1 = np.linspace(mu1 - 4*sigma, mu1 + 4*sigma1, 100) y1 = 100* stats.norm.pdf(x1, mu1, sigma1) x2 = np.linspace(mu2 - 4*sigma, mu2 + 4*sigma2, 100) y2 = 100* stats.norm.pdf(x2, mu2, sigma2) fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5)) sns.lineplot(x=x,y=y, color='black', ax = ax1) sns.lineplot(x=x,y=y, color='black', ax = ax2) sns.lineplot(x=x2,y=y2, color='black', ax = ax2) ax1.text(0, 47, 'null hypothesis', size=20, ha="center") ax2.text(0, 47, 'alternative hypothesis', size=20, ha="center") ax1.text(0, 41, r'$mu$', size=20, ha="center") ax2.text(0, 41, r'$mu_1$', size=20, ha="center") ax2.text(1.50, 30, r'$mu_2$', size=20, ha="left") ax1.set_frame_on(False) ax2.set_frame_on(False) ax1.get_yaxis().set_visible(False) ax2.get_yaxis().set_visible(False) ax1.get_xaxis().set_visible(False) ax2.get_xaxis().set_visible(False) ax1.axhline(y=0, color='black') ax2.axhline(y=0, color='black')
<matplotlib.lines.Line2D at 0x17d80d2a0>
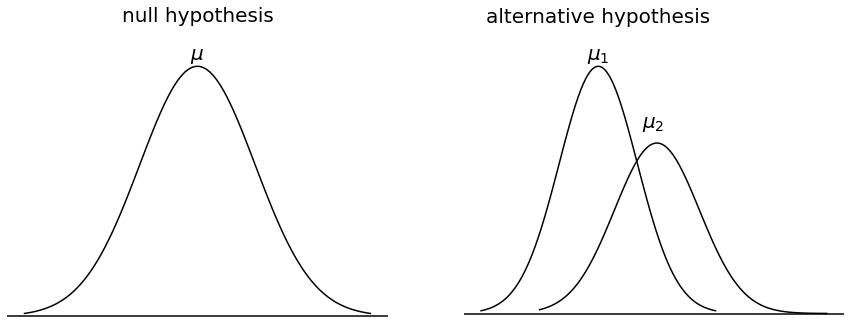
Fig. 14.9 Graphical illustration of the null and alternative hypotheses assumed by the Welch (t)-test. Like the Student test we assume that both samples are drawn from a normal population; but the alternative hypothesis no longer requires the two populations to have equal variance.¶
14.4.1. Doing the test in Python¶
To run a Welch test in Python is pretty easy. All you have to do is not bother telling Python to assume equal variances. That is, the command is exactly the same as for the Student test, but where correction = True. In fact, in this case, you could just leave the correction argument off entirely, because Anasatasia and Bernadette had different numbers of students, and in cases where the (t)-test is comparing two unequal-sized samples, pingouin assumes unequal variance and does a Welch test by default, which is why we had to force it to do a Student test above by setting correction to False.
from pingouin import ttest ttest(Harpo_wide['Anastasia'], Harpo_wide['Bernadette'], correction = True)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.034187 | 23.024806 | two-sided | 0.05361 | [-0.09, 11.05] | 0.739561 | 1.556 | 0.53577 |
Not too difficult, right? Not surprisingly, the output has exactly the same format as it did last time too: a test statistic (t), and a (p)-value. So that’s all pretty easy.
Except, except… our result isn’t significant anymore. When we ran the Student test, we did get a significant effect; but the Welch test on the same data set is not ((t(23.03) = 2.03), (p = .054)). What does this mean? Should we panic? Is the sky burning? Probably not. The fact that one test is significant and the other isn’t doesn’t itself mean very much, especially since I kind of rigged the data so that this would happen. As a general rule, it’s not a good idea to go out of your way to try to interpret or explain the difference between a (p)-value of .049 and a (p)-value of .051. If this sort of thing happens in real life, the difference in these (p)-values is almost certainly due to chance. What does matter is that you take a little bit of care in thinking about what test you use. The Student test and the Welch test have different strengths and weaknesses. If the two populations really do have equal variances, then the Student test is slightly more powerful (lower Type II error rate) than the Welch test. However, if they don’t have the same variances, then the assumptions of the Student test are violated and you may not be able to trust it: you might end up with a higher Type I error rate. So it’s a trade off. However, in real life, I tend to prefer the Welch test; because almost no-one actually believes that the population variances are identical.
14.4.2. Assumptions of the test¶
The assumptions of the Welch test are very similar to those made by the Student (t)-test, except that the Welch test does not assume homogeneity of variance. This leaves only the assumption of normality, and the assumption of independence. The specifics of these assumptions are the same for the Welch test as for the Student test.
14.5. The paired-samples (t)-test¶
Regardless of whether we’re talking about the Student test or the Welch test, an independent samples (t)-test is intended to be used in a situation where you have two samples that are, well, independent of one another. This situation arises naturally when participants are assigned randomly to one of two experimental conditions, but it provides a very poor approximation to other sorts of research designs. In particular, a repeated measures design – in which each participant is measured (with respect to the same outcome variable) in both experimental conditions – is not suited for analysis using independent samples (t)-tests. For example, we might be interested in whether listening to music reduces people’s working memory capacity. To that end, we could measure each person’s working memory capacity in two conditions: with music, and without music. In an experimental design such as this one,11 each participant appears in both groups. This requires us to approach the problem in a different way; by using the paired samples (t)-test.
14.5.1. The data¶
The data set that we’ll use this time comes from Dr Chico’s class.12 In her class, students take two major tests, one early in the semester and one later in the semester. To hear her tell it, she runs a very hard class, one that most students find very challenging; but she argues that by setting hard assessments, students are encouraged to work harder. Her theory is that the first test is a bit of a “wake up call” for students: when they realise how hard her class really is, they’ll work harder for the second test and get a better mark. Is she right? To test this, let’s have a look at the chico.csv file:
import pandas as pd df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/chico.csv")
The data frame chico contains three variables: an id variable that identifies each student in the class, the grade_test1 variable that records the student grade for the first test, and the grade_test2 variable that has the grades for the second test. Here’s the first five students:
| id | grade_test1 | grade_test2 | |
|---|---|---|---|
| 0 | student1 | 42.9 | 44.6 |
| 1 | student2 | 51.8 | 54.0 |
| 2 | student3 | 71.7 | 72.3 |
| 3 | student4 | 51.6 | 53.4 |
| 4 | student5 | 63.5 | 63.8 |
At a glance, it does seem like the class is a hard one (most grades are between 50% and 60%), but it does look like there’s an improvement from the first test to the second one. If we take a quick look at the descriptive statistics
| grade_test1 | grade_test2 | |
|---|---|---|
| count | 20.000000 | 20.000000 |
| mean | 56.980000 | 58.385000 |
| std | 6.616137 | 6.405612 |
| min | 42.900000 | 44.600000 |
| 25% | 51.750000 | 53.100000 |
| 50% | 57.700000 | 59.700000 |
| 75% | 62.050000 | 63.050000 |
| max | 71.700000 | 72.300000 |
we see that this impression seems to be supported. Across all 20 students13 the mean grade for the first test is 57%, but this rises to 58% for the second test. Although, given that the standard deviations are 6.6% and 6.4% respectively, it’s starting to feel like maybe the improvement is just illusory; maybe just random variation. This impression is reinforced when you see the means and confidence intervals plotted in pairedta panel A. If we were to rely on this plot alone, we’d come to the same conclusion that we got from looking at the descriptive statistics that the describe() method produced. Looking at how wide those confidence intervals are, we’d be tempted to think that the apparent improvement in student performance is pure chance.
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5)) df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/chico.csv") sns.pointplot(data=df, ax = ax1) sns.scatterplot(data = df, x='grade_test1', y='grade_test2', ax = ax2) ax2.plot(ax2.get_xlim(), ax2.get_ylim(), ls="--", c=".3") #ax1.set_ylim(40,80) #ax1.set_xlim(40,80) #ax1.set_ylim(40,80) df2 = df df2['improvement'] = df2['grade_test2']-df2['grade_test1'] sns.histplot(data = df2, x='improvement') ax1.title.set_text('A') ax2.title.set_text('B') ax3.title.set_text('C') sns.despine()
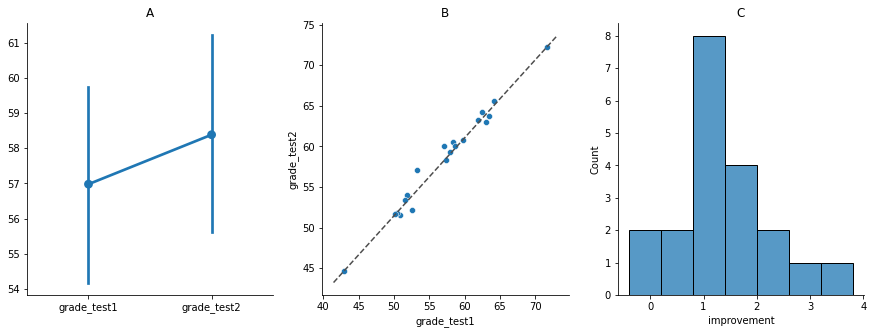
Fig. 14.10 Mean grade for test 1 and test 2, with associated 95% confidence intervals (panel a). Scat- terplot showing the individual grades for test 1 and test 2 (panel b). Histogram showing the improvement made by each student in Dr Chico’s class (panel c). In panel c, notice that almost the entire distribution is above zero: the vast majority of students did improve their performance from the first test to the second one¶
Nevertheless, this impression is wrong. To see why, take a look at the scatterplot of the grades for test 1 against the grades for test 2. shown in Fig. 14.10 panel B.
In this plot, each dot corresponds to the two grades for a given student: if their grade for test 1 ((x) co-ordinate) equals their grade for test 2 ((y) co-ordinate), then the dot falls on the line. Points falling above the line are the students that performed better on the second test. Critically, almost all of the data points fall above the diagonal line: almost all of the students do seem to have improved their grade, if only by a small amount. This suggests that we should be looking at the improvement made by each student from one test to the next, and treating that as our raw data. To do this, we’ll need to create a new variable for the improvement that each student makes, and add it to the data frame containing the chico.csv data. The easiest way to do this is as follows:
df['improvement'] = df['grade_test2']-df['grade_test1']
Notice that I assigned the output to a variable called df['improvement]. That has the effect of creating a new column called improvement inside the chico data frame. Now that we’ve created and stored this improvement variable, we can draw a histogram showing the distribution of these improvement scores, shown in Fig. 14.10 panel C.
When we look at histogram, it’s very clear that there is a real improvement here. The vast majority of the students scored higher on the test 2 than on test 1, reflected in the fact that almost the entire histogram is above zero. In fact, if we use scipy.stats.t.interval() to compute a confidence interval for the population mean of this new variable,
import numpy as np from scipy import stats data = df['improvement'] stats.t.interval(alpha=0.95, df=len(data)-1, loc=np.mean(data), scale=stats.sem(data))
(0.9508686092602991, 1.8591313907397005)
we see that it is 95% certain that the true (population-wide) average improvement would lie between 0.95% and 1.86%. So you can see, qualitatively, what’s going on: there is a real “within student” improvement (everyone improves by about 1%), but it is very small when set against the quite large “between student” differences (student grades vary by about 20% or so).
14.5.2. What is the paired samples (t)-test?¶
In light of the previous exploration, let’s think about how to construct an appropriate (t) test. One possibility would be to try to run an independent samples (t)-test using grade_test1 and grade_test2 as the variables of interest. However, this is clearly the wrong thing to do: the independent samples (t)-test assumes that there is no particular relationship between the two samples. Yet clearly that’s not true in this case, because of the repeated measures structure to the data. To use the language that I introduced in the last section, if we were to try to do an independent samples (t)-test, we would be conflating the within subject differences (which is what we’re interested in testing) with the between subject variability (which we are not).
The solution to the problem is obvious, I hope, since we already did all the hard work in the previous section. Instead of running an independent samples (t)-test on grade_test1 and grade_test2, we run a one-sample (t)-test on the within-subject difference variable, improvement. To formalise this slightly, if (X_{i1}) is the score that the (i)-th participant obtained on the first variable, and (X_{i2}) is the score that the same person obtained on the second one, then the difference score is:
[
D_{i} = X_{i1} — X_{i2}
]
Notice that the difference scores is variable 1 minus variable 2 and not the other way around, so if we want improvement to correspond to a positive valued difference, we actually want “test 2” to be our “variable 1”. Equally, we would say that (mu_D = mu_1 — mu_2) is the population mean for this difference variable. So, to convert this to a hypothesis test, our null hypothesis is that this mean difference is zero; the alternative hypothesis is that it is not:
[begin{split}
begin{array}{ll}
H_0: & mu_D = 0
H_1: & mu_D neq 0
end{array}
end{split}]
(this is assuming we’re talking about a two-sided test here). This is more or less identical to the way we described the hypotheses for the one-sample (t)-test: the only difference is that the specific value that the null hypothesis predicts is 0. And so our (t)-statistic is defined in more or less the same way too. If we let (bar{D}) denote the mean of the difference scores, then
[
t = frac{bar{D}}{mbox{SE}({bar{D}})}
]
which is
[
t = frac{bar{D}}{hatsigma_D / sqrt{N}}
]
where (hatsigma_D) is the standard deviation of the difference scores. Since this is just an ordinary, one-sample (t)-test, with nothing special about it, the degrees of freedom are still (N-1). And that’s it: the paired samples (t)-test really isn’t a new test at all: it’s a one-sample (t)-test, but applied to the difference between two variables. It’s actually very simple; the only reason it merits a discussion as long as the one we’ve just gone through is that you need to be able to recognise when a paired samples test is appropriate, and to understand why it’s better than an independent samples (t) test.
14.5.3. Doing the test in Python¶
How do you do a paired samples (t)-test in Python? One possibility is to follow the process I outlined above: create a “difference” variable and then run a one sample (t)-test on that, setting the population mean argument popmean to zero. Since we’ve already created a variable called improvement, let’s do that:
from pingouin import ttest ttest(df['improvement'], 0)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 6.475436 | 19 | two-sided | 0.000003 | [0.95, 1.86] | 1.447952 | 5991.577 | 0.999984 |
However, suppose you’re lazy and you don’t want to go to all the effort of creating a new variable. Or perhaps you just want to keep the difference between one-sample and paired-samples tests clear in your head. In that case, you can do:
from pingouin import ttest ttest(df['grade_test2'], df['grade_test1'], paired=True)
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 6.475436 | 19 | two-sided | 0.000003 | [0.95, 1.86] | 0.215765 | 5991.577 | 0.150446 |
Either way, you’ll get the same (t)-value, and the same (p)-value, which is strangely comforting, actually. Not only that, but the result confirms our intuition. There’s an average improvement of 1.4% from test 1 to test 2, and this is significantly different from 0 ((t)(19) = 6.48, (p) < .001). In fact, (p) is quite a bit less than one, since the (p)-value has been given in scientific notation. The exact (p)-value is (3.32^{-06}), that is, (p) = 0.0000032.
14.6. One sided tests¶
When introducing the theory of null hypothesis tests, I mentioned that there are some situations when it’s appropriate to specify a one-sided test. So far, all of the (t)-tests have been two-sided tests. For instance, when we specified a one sample (t)-test for the grades in Dr Zeppo’s class, the null hypothesis was that the true mean was 67.5%. The alternative hypothesis was that the true mean was greater than or less than 67.5%. Suppose we were only interested in finding out if the true mean is greater than 67.5%, and have no interest whatsoever in testing to find out if the true mean is lower than 67.5%. If so, our null hypothesis would be that the true mean is 67.5% or less, and the alternative hypothesis would be that the true mean is greater than 67.5%. The ttest() function lets you do this, by specifying the alternative argument. If you set alternative = 'greater', it means that you’re testing to see if the true mean is larger than mu. If you set alternative = 'less', then you’re testing to see if the true mean is smaller than mu. To see how it would work for Dr Zeppo’s class, let’s compare the results of the two-sided test we did before with the results of a one-sided test, where the alternative hypothesis is set to “greater”:
from pingouin import ttest df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/zeppo.csv") # two-sided test ttest(df['grades'], 67.5, alternative = 'two-sided')
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.254713 | 19 | two-sided | 0.036145 | [67.84, 76.76] | 0.504169 | 1.795 | 0.571446 |
# one-sided test ttest(df['grades'], 67.5, alternative = 'greater')
| T | dof | alternative | p-val | CI95% | cohen-d | BF10 | power | |
|---|---|---|---|---|---|---|---|---|
| T-test | 2.254713 | 19 | greater | 0.018073 | [68.62, inf] | 0.504169 | 3.59 | 0.701407 |
The (t)-statistics are exactly the same, which makes sense, if you think about it, because the calculation of the (t) is based on the mean and standard deviation, and these do not change. The (p)-value, on the other hand, is lower for the one-sided test. The only thing that changes between the two tests is the expectation that we bring to data. The way that the (p)-value is calculated depends on those expectations, and they are the reason for choosing one test over the other. It should go without saying, but maybe is worth saying anyway, that our reasons for choosing one test over the other should be theoretical, and not based on which test is more likely to give us the (p)-value we want!
So that’s how to do a one-sided one sample (t)-test. However, all versions of the (t)-test can be one-sided. For an independent samples (t) test, you could have a one-sided test if you’re only interestd in testing to see if group A has higher scores than group B, but have no interest in finding out if group B has higher scores than group A. Let’s suppose that, for Dr Harpo’s class, you wanted to see if Anastasia’s students had higher grades than Bernadette’s. The ttest_ind function lets you do this, again by specifying the alternative argument. However, this time around the order that we enter the variables in the test makes a difference. If we expect that Anastasia’s students have higher grades, and we want to conduct a one-sided test, we need to the data for Anastasia’s students first. Otherwise, we end up testing the hypothesis that Bernadette’s students had the higher grade, which is the opposite of what we intended:
df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/harpo.csv") # create two new variables for the grades from each tutor's students Anastasia = pd.DataFrame(df.loc[df['tutor'] == 'Anastasia']['grade']) Bernadette = pd.DataFrame(df.loc[df['tutor'] == 'Bernadette']['grade']) # run an independent samples t-test from scipy import stats print('Two-sided:', stats.ttest_ind(Anastasia, Bernadette, equal_var = True)) print('') print('One-sided, Anastasia first:', stats.ttest_ind(Anastasia, Bernadette, equal_var = True, alternative = 'greater')) print('') print('One-sided, Bernadette first:', stats.ttest_ind(Bernadette, Anastasia, equal_var = True, alternative = 'greater'))
Two-sided: Ttest_indResult(statistic=array([2.11543239]), pvalue=array([0.04252949])) One-sided, Anastasia first: Ttest_indResult(statistic=array([2.11543239]), pvalue=array([0.02126474])) One-sided, Bernadette first: Ttest_indResult(statistic=array([-2.11543239]), pvalue=array([0.97873526]))
What about the paired samples (t)-test? Suppose we wanted to test the hypothesis that grades go up from test 1 to test 2 in Dr. Chico’s class, and are not prepared to consider the idea that the grades go down. Again, we can use the alternative argument to specify the one-sided test, and it works the same way it does for the independent samples (t)-test. Since we are comparing test 1 to test 2 by substracting one from the other, it makes a difference whether we subract test 1 from test 2, or test 2 from test 1. So, to test the hypothesis that grades for test 2 are higher than test 2, we will need to enter the grades from test 2 first; otherwise we are testing the opposite hypothesis:
import pandas as pd from scipy.stats import ttest_rel df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/chico.csv") print('test 2 - test 1:', ttest_rel(df['grade_test2'], df['grade_test1'], alternative = 'greater')) print('') print('test 1 - test 2:', ttest_rel(df['grade_test1'], df['grade_test2'], alternative = 'greater'))
test 2 - test 1: Ttest_relResult(statistic=6.475436088339379, pvalue=1.660335028063474e-06) test 1 - test 2: Ttest_relResult(statistic=-6.475436088339379, pvalue=0.9999983396649719)
14.7. Effect size¶
The most commonly used measure of effect size for a (t)-test is Cohen’s (d) [@Cohen1988]. It’s a very simple measure in principle, with quite a few wrinkles when you start digging into the details. Cohen himself defined it primarily in the context of an independent samples (t)-test, specifically the Student test. In that context, a natural way of defining the effect size is to divide the difference between the means by an estimate of the standard deviation. In other words, we’re looking to calculate something along the lines of this:
[
d = frac{mbox{(mean 1)} — mbox{(mean 2)}}{mbox{std dev}}
]
and he suggested a rough guide for interpreting (d) in the table below. You’d think that this would be pretty unambiguous, but it’s not; largely because Cohen wasn’t too specific on what he thought should be used as the measure of the standard deviation (in his defence, he was trying to make a broader point in his book, not nitpick about tiny details). As discussed by @McGrath2006, there are several different version in common usage, and each author tends to adopt slightly different notation. For the sake of simplicity (as opposed to accuracy) I’ll use (d) to refer to any statistic that you calculate from the sample, and use (delta) to refer to a theoretical population effect. Obviously, that does mean that there are several different things all called (d).
Although Cohen’s (d) is a very commonly-reported measure of effect size, there are not currently any modules that provide built-in tools to calculate it. At least, not any that I am aware of. Luckily, it isn’t too hard to calculate “by hand”.
The table below gives a (very) rough guide to interpreting Cohen’s (d). My personal recommendation is to not use these blindly. The (d) statistic has a natural interpretation in and of itself: it redescribes the different in means as the number of standard deviations that separates those means. So it’s generally a good idea to think about what that means in practical terms. In some contexts a “small” effect could be of big practical importance. In other situations a “large” effect may not be all that interesting.
|
d-value |
rough interpretation |
|---|---|
|
about 0.2 |
“small” effect |
|
about 0.5 |
“moderate” effect |
|
about 0.8 |
“large” effect |
14.7.1. Cohen’s (d) from one sample¶
The simplest situation to consider is the one corresponding to a one-sample (t)-test. In this case, the one sample mean (bar{X}) and one (hypothesised) population mean (mu_o) to compare it to. Not only that, there’s really only one sensible way to estimate the population standard deviation: we just use our usual estimate (hat{sigma}). Therefore, we end up with the following as the only way to calculate (d),
[
d = frac{bar{X} — mu_0}{hat{sigma}}
]
import pandas as pd import statistics # load Zeppo data df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/zeppo.csv") # subract the population mean from the sample mean, and divide by #the estimated population standard deviation d = (statistics.mean(df['grades']) - 67.5) / statistics.stdev(df['grades']) print('Cohen's d:', d)
Cohen's d: 0.5041691240370938
What does this effect size mean? Overall, then, the psychology students in Dr Zeppo’s class are achieving grades (mean = 72.3%) that are about .5 standard deviations higher than the level that you’d expect (67.5%) if they were performing at the same level as other students. Judged against Cohen’s rough guide, this is a moderate effect size.
14.7.2. Cohen’s (d) from a Student (t) test¶
The majority of discussions of Cohen’s (d) focus on a situation that is analogous to Student’s independent samples (t) test, and it’s in this context that the story becomes messier, since there are several different versions of (d) that you might want to use in this situation. To understand why there are multiple versions of (d), it helps to take the time to write down a formula that corresponds to the true population effect size (delta). It’s pretty straightforward,
[
delta = frac{mu_1 — mu_2}{sigma}
]
where, as usual, (mu_1) and (mu_2) are the population means corresponding to group 1 and group 2 respectively, and (sigma) is the standard deviation (the same for both populations). The obvious way to estimate (delta) is to do exactly the same thing that we did in the (t)-test itself: use the sample means as the top line, and a pooled standard deviation estimate for the bottom line:
[
d = frac{bar{X}_1 — bar{X}_2}{hat{sigma}_p}
]
where (hatsigma_p) is the exact same pooled standard deviation measure that appears in the (t)-test. This is the most commonly used version of Cohen’s (d) when applied to the outcome of a Student (t)-test ,and is sometimes referred to as Hedges’ (g) statistic [@Hedges1981].
However, there are other possibilities, which I’ll briefly describe. Firstly, you may have reason to want to use only one of the two groups as the basis for calculating the standard deviation. This approach (often called Glass’ (Delta)) only makes most sense when you have good reason to treat one of the two groups as a purer reflection of “natural variation” than the other. This can happen if, for instance, one of the two groups is a control group. Secondly, recall that in the usual calculation of the pooled standard deviation we divide by (N-2) to correct for the bias in the sample variance; in one version of Cohen’s (d) this correction is omitted. Instead, we divide by (N). This version makes sense primarily when you’re trying to calculate the effect size in the sample; rather than estimating an effect size in the population. Finally, there is a version based on @Hedges1985, who point out there is a small bias in the usual (pooled) estimation for Cohen’s (d). Thus they introduce a small correction, by multiplying the usual value of (d) by ((N-3)/(N-2.25)).
In any case, ignoring all those variations that you could make use of if you wanted, let’s have a look at how to calculate the default version. In particular, suppose we look at the data from Dr Harpo’s class.
import pandas as pd import statistics from numpy import sqrt, mean, std df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/harpo.csv") # create two new variables for the grades from each tutor's students tutor1 = pd.DataFrame(df.loc[df['tutor'] == 'Anastasia']['grade']) tutor2 = pd.DataFrame(df.loc[df['tutor'] == 'Bernadette']['grade']) # find number of student grades for each tutor n1 = len(tutor1) n2 = len(tutor2) # find mean student grade for each tutor u1 = mean(tutor1['grade']) u2 = mean(tutor2['grade']) # find variance in students' grades for each tutor s1 = var(tutor1['grade']) s2 = var(tutor2['grade']) # find pooled standard deviation (square root of weighted variation, # divided by total N, with a correction for bias of -2) s = sqrt(((n1) * s1 + (n2) * s2) / (n1 + n2 - 2)) # calculate Cohen's d d = (u1 - u2) / s d
--------------------------------------------------------------------------- NameError Traceback (most recent call last) Input In [43], in <cell line: 20>() 17 u2 = mean(tutor2['grade']) 19 # find variance in students' grades for each tutor ---> 20 s1 = var(tutor1['grade']) 21 s2 = var(tutor2['grade']) 24 # find pooled standard deviation (square root of weighted variation, 25 # divided by total N, with a correction for bias of -2) NameError: name 'var' is not defined
14.7.3. Cohen’s (d) from a Welch test¶
Suppose the situation you’re in is more like the Welch test: you still have two independent samples, but you no longer believe that the corresponding populations have equal variances. When this happens, we have to redefine what we mean by the population effect size. I’ll refer to this new measure as (delta^prime), so as to keep it distinct from the measure (delta) which we defined previously. What @Cohen1988 suggests is that we could define our new population effect size by averaging the two population variances. What this means is that we get:
[
delta^prime = frac{mu_1 — mu_2}{sigma^prime}
]
where
[
sigma^prime = sqrt{displaystyle{frac{ {sigma_1}^2 + {sigma_2}^2}{2}}}
]
This seems quite reasonable, but notice that none of the measures that we’ve discussed so far are attempting to estimate this new quantity. It might just be my own ignorance of the topic, but I’m only aware of one version of Cohen’s (d) that actually estimates the unequal-variance effect size (delta^prime) rather than the equal-variance effect size (delta).
All we do to calculate (d) for this version is substitute the sample means (bar{X}_1) and (bar{X}_2) and the corrected sample standard deviations (hat{sigma}_1) and (hat{sigma}_2) into the equation for (delta^prime). This gives us the following equation for (d),
[
d = frac{bar{X}_1 — bar{X}_2}{sqrt{displaystyle{frac{ {hatsigma_1}^2 + {hatsigma_2}^2}{2}}}}
]
as our estimate of the effect size.
# find mean student grade for each tutor u1 = mean(tutor1['grade']) u2 = mean(tutor2['grade']) # find variance in students' grades for each tutor s1 = var(tutor1['grade']) s2 = var(tutor2['grade']) # find the mean variance of the two samples s = sqrt((s1 + s2)/2) # calculate Cohen's d d = (u1 - u2) / s d
14.7.4. Cohen’s (d) from a paired-samples test¶
Finally, what should we do for a paired samples (t)-test? In this case, the answer depends on what it is you’re trying to do. If you want to measure your effect sizes relative to the distribution of difference scores, the measure of (d) that you calculate is just
[
d = frac{bar{D}}{hat{sigma}_D}
]
where (hat{sigma}_D) is the estimate of the standard deviation of the differences. The calculation here is pretty straightforward
from numpy import mean, std df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/chico.csv") difference = df['grade_test2'] - df['grade_test1'] mean_diff = mean(difference) sd_diff = std(difference) d = mean_diff/sd_diff d
The only wrinkle is figuring out whether this is the measure you want or not. To the extent that you care about the practical consequences of your research, you often want to measure the effect size relative to the original variables, not the difference scores (e.g., the 1% improvement in Dr Chico’s class is pretty small when measured against the amount of between-student variation in grades), in which case you use the same versions of Cohen’s (d) that you would use for a Student or Welch test. For instance, when we do that for Dr Chico’s class,
# find mean student grade for each tutor u1 = mean(df['grade_test1']) u2 = mean(df['grade_test2']) # find variance in students' grades for each tutor s1 = var(df['grade_test1']) s2 = var(df['grade_test2']) # find the mean variance of the two samples s = sqrt((s1 + s2)/2) # calculate Cohen's d d = (u2 - u1) / s d
what we see is that the overall effect size is quite small, when assessed on the scale of the original variables.
14.8. Checking the normality of a sample¶
All of the tests that we have discussed so far in this chapter have assumed that the data are normally distributed. This assumption is often quite reasonable, because the central limit theorem (Section @ref(clt)) does tend to ensure that many real world quantities are normally distributed: any time that you suspect that your variable is actually an average of lots of different things, there’s a pretty good chance that it will be normally distributed; or at least close enough to normal that you can get away with using (t)-tests. However, life doesn’t come with guarantees; and besides, there are lots of ways in which you can end up with variables that are highly non-normal. For example, any time you think that your variable is actually the minimum of lots of different things, there’s a very good chance it will end up quite skewed. In psychology, response time (RT) data is a good example of this. If you suppose that there are lots of things that could trigger a response from a human participant, then the actual response will occur the first time one of these trigger events occurs.14 This means that RT data are systematically non-normal. Okay, so if normality is assumed by all the tests, and is mostly but not always satisfied (at least approximately) by real world data, how can we check the normality of a sample? In this section I discuss two methods: QQ plots, and the Shapiro-Wilk test.
14.8.1. QQ plots¶
One way to check whether a sample violates the normality assumption is to draw a “quantile-quantile” plot (QQ plot). This allows you to visually check whether you’re seeing any systematic violations. In a QQ plot, each observation is plotted as a single dot. The x co-ordinate is the theoretical quantile that the observation should fall in, if the data were normally distributed (with mean and variance estimated from the sample) and on the y co-ordinate is the actual quantile of the data within the sample. If the data are normal, the dots should form a straight line. For instance, lets see what happens if we generate data by sampling from a normal distribution, and then drawing a QQ plot, using probplot from scipy. We can compare this with a histogram of the data as well:
import numpy as np import seaborn as sns from scipy.stats import probplot np.random.seed(42) normal_data = np.random.normal(size=100) fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5)) qq = probplot(normal_data, dist="norm", plot = ax1) hist = sns.histplot(normal_data, axes=ax2) glue("qq_fig", ax, display=False)
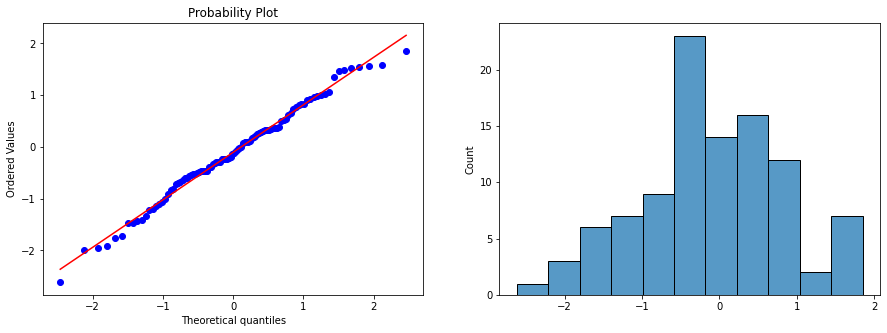
<AxesSubplot:xlabel='grades', ylabel='Count'>
Fig. 14.11 QQ plot (left) and histogram (right) of normal_data, a normally distributed sample with 100 observations. The Shapiro-Wilk statistic associated with these data is (W = .99), indicating that no significant departures from normality were detected ((p = .73)).¶
And the results are shown in {numref}(fig-qq), above.
As you can see, these data form a pretty straight line; which is no surprise given that we sampled them from a normal distribution! In contrast, have a look at the data shown in {numref}(qqskew) and {numref}(qqheavy), which show the histogram and a QQ plot for a data sets that are highly skewed and have a heavy tail (i.e., high kurtosis), respectively.
df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/skewed_data.csv") fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5)) qq = probplot(df['data'], dist="norm", plot = ax1) hist = sns.histplot(df['data'], axes=ax2) glue("qqskew_fig", ax, display=False)
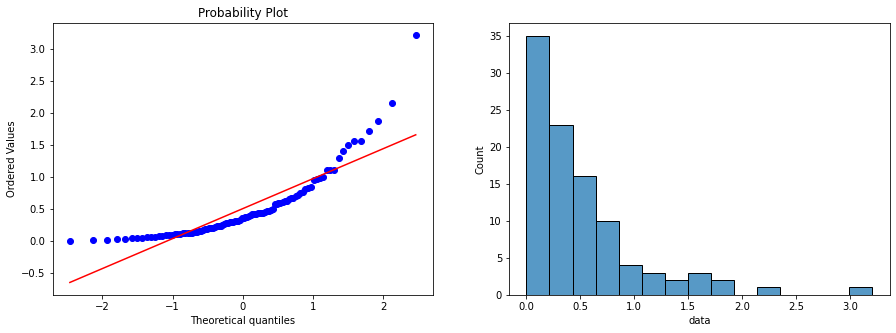
Fig. 14.12 The skewness of these data of 100 observations is 1.94, and is reflected in a QQ plot that curves upwards. As a consequence, the Shapiro-Wilk statistic is (W=.80), reflecting a significant departure from normality ((p<.001)).¶
df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/heavy_tailed_data.csv") fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 5)) qq = probplot(df['data'], dist="norm", plot = ax1) hist = sns.histplot(df['data'], axes=ax2) glue("qqheavy_fig", ax, display=False)
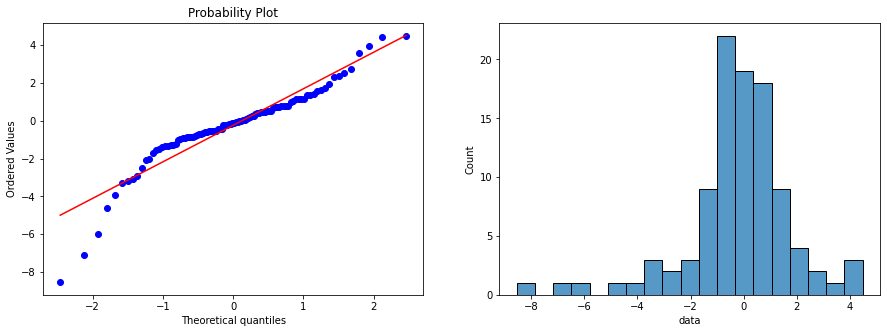
<AxesSubplot:xlabel='grades', ylabel='Count'>
Fig. 14.13 Plots for a heavy tailed data set, again consisting of 100 observations. In this case, the heavy tails in the data produce a high kurtosis (2.80), and cause the QQ plot to flatten in the middle, and curve away sharply on either side. The resulting Shapiro-Wilk statistic is (W = .93), again reflecting significant non-normality ((p < .001)).¶
14.8.2. Shapiro-Wilk tests¶
Although QQ plots provide a nice way to informally check the normality of your data, sometimes you’ll want to do something a bit more formal. And when that moment comes, the Shapiro-Wilk test [@Shapiro1965] is probably what you’re looking for.15 As you’d expect, the null hypothesis being tested is that a set of (N) observations is normally distributed. The test statistic that it calculates is conventionally denoted as (W), and it’s calculated as follows. First, we sort the observations in order of increasing size, and let (X_1) be the smallest value in the sample, (X_2) be the second smallest and so on. Then the value of (W) is given by
[
W = frac{ left( sum_{i = 1}^N a_i X_i right)^2 }{ sum_{i = 1}^N (X_i — bar{X})^2}
]
where (bar{X}) is the mean of the observations, and the (a_i) values are … mumble, mumble … something complicated that is a bit beyond the scope of an introductory text.
Because it’s a little hard to explain the maths behind the (W) statistic, a better idea is to give a broad brush description of how it behaves. Unlike most of the test statistics that we’ll encounter in this book, it’s actually small values of (W) that indicated departure from normality. The (W) statistic has a maximum value of 1, which arises when the data look “perfectly normal”. The smaller the value of (W), the less normal the data are. However, the sampling distribution for (W) – which is not one of the standard ones that I discussed in Chapter @ref(probability) and is in fact a complete pain in the arse to work with – does depend on the sample size (N). To give you a feel for what these sampling distributions look like, I’ve plotted three of them in Figure @ref(fig:swdist). Notice that, as the sample size starts to get large, the sampling distribution becomes very tightly clumped up near (W=1), and as a consequence, for larger samples (W) doesn’t have to be very much smaller than 1 in order for the test to be significant.
Fig. 14.14 Sampling distribution of the Shapiro-Wilk (W) statistic, under the null hypothesis that the data are normally distributed, for samples of size 10, 20 and 50. Note that small values of (W) indicate departure from normality.¶
To run the test in Python, we use the scipy.stats.shapiro method. It has only a single argument x, which is a numeric vector containing the data whose normality needs to be tested. For example, when we apply this function to our normal_data, we get the following:
from scipy.stats import shapiro shapiro(normal_data)
ShapiroResult(statistic=0.9898834228515625, pvalue=0.6551706790924072)
So, not surprisingly, we have no evidence that these data depart from normality. When reporting the results for a Shapiro-Wilk test, you should (as usual) make sure to include the test statistic (W) and the (p) value, though given that the sampling distribution depends so heavily on (N) it would probably be a politeness to include (N) as well.
14.9. Testing non-normal data with Wilcoxon tests¶
Okay, suppose your data turn out to be pretty substantially non-normal, but you still want to run something like a (t)-test? This situation occurs a lot in real life: for the AFL winning margins data, for instance, the Shapiro-Wilk test made it very clear that the normality assumption is violated. This is the situation where you want to use Wilcoxon tests.
Like the (t)-test, the Wilcoxon test comes in two forms, one-sample and two-sample, and they’re used in more or less the exact same situations as the corresponding (t)-tests. Unlike the (t)-test, the Wilcoxon test doesn’t assume normality, which is nice. In fact, they don’t make any assumptions about what kind of distribution is involved: in statistical jargon, this makes them nonparametric tests. While avoiding the normality assumption is nice, there’s a drawback: the Wilcoxon test is usually less powerful than the (t)-test (i.e., higher Type II error rate). I won’t discuss the Wilcoxon tests in as much detail as the (t)-tests, but I’ll give you a brief overview.
14.9.1. Two sample Wilcoxon test¶
I’ll start by describing the two sample Wilcoxon test (also known as the Mann-Whitney test), since it’s actually simpler than the one sample version. Suppose we’re looking at the scores of 10 people on some test. Since my imagination has now failed me completely, let’s pretend it’s a “test of awesomeness”, and there are two groups of people, “A” and “B”. I’m curious to know which group is more awesome. The data are included in the file awesome.Rdata, and like many of the data sets I’ve been using, it contains only a single data frame, in this case called awesome. Here’s the data:
df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/awesome2.csv") df
| score_A | score_B | |
|---|---|---|
| 0 | 6.4 | 14.5 |
| 1 | 10.7 | 10.4 |
| 2 | 11.9 | 12.9 |
| 3 | 7.3 | 11.7 |
| 4 | 10.0 | 13.0 |
As long as there are no ties (i.e., people with the exact same awesomeness score), then the test that we want to do is surprisingly simple. All we have to do is construct a table that compares every observation in group (A) against every observation in group (B). Whenever the group (A) datum is larger, we place a check mark in the table:
|
group B |
||||||
|---|---|---|---|---|---|---|
|
14.5 |
10.4 |
12.4 |
11.7 |
13 |
||
|
6.4 |
. |
. |
. |
. |
. |
|
|
group A |
10.7 |
. |
✓ |
. |
. |
. |
|
11.9 |
. |
✓ |
. |
✓ |
. |
|
|
7.3 |
. |
. |
. |
. |
. |
|
|
10 |
. |
. |
. |
. |
. |
We then count up the number of checkmarks. This is our test statistic, (W).16 The actual sampling distribution for (W) is somewhat complicated, and I’ll skip the details. For our purposes, it’s sufficient to note that the interpretation of (W) is qualitatively the same as the interpretation of (t) or (z). That is, if we want a two-sided test, then we reject the null hypothesis when (W) is very large or very small; but if we have a directional (i.e., one-sided) hypothesis, then we only use one or the other.
from scipy.stats import wilcoxon w,p = wilcoxon(df['score_A'], df['score_B'] ) w,p
14.9.2. One sample Wilcoxon test¶
What about the one sample Wilcoxon test (or equivalently, the paired samples Wilcoxon test)? Suppose I’m interested in finding out whether taking a statistics class has any effect on the happiness of students. Here’s my data:
df = pd.read_csv("https://raw.githubusercontent.com/ethanweed/pythonbook/main/Data/happiness.csv") df
| before | after | change | |
|---|---|---|---|
| 0 | 30 | 6 | -24 |
| 1 | 43 | 29 | -14 |
| 2 | 21 | 11 | -10 |
| 3 | 24 | 31 | 7 |
| 4 | 23 | 17 | -6 |
| 5 | 40 | 2 | -38 |
| 6 | 29 | 31 | 2 |
| 7 | 56 | 21 | -35 |
| 8 | 38 | 8 | -30 |
| 9 | 16 | 21 | 5 |
What I’ve measured here is the happiness of each student before taking the class and after taking the class; the change score is the difference between the two. Just like we saw with the (t)-test, there’s no fundamental difference between doing a paired-samples test using before and after, versus doing a one-sample test using the change scores. As before, the simplest way to think about the test is to construct a tabulation. The way to do it this time is to take those change scores that are positive valued, and tabulate them against all the complete sample. What you end up with is a table that looks like this:
|
all differences |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
-24 |
-14 |
-10 |
7 |
-6 |
-38 |
2 |
-35 |
-30 |
5 |
||
|
positive differences |
7 |
. |
. |
. |
✓ |
✓ |
. |
✓ |
. |
✓ |
|
|
2 |
. |
. |
. |
. |
. |
. |
✓ |
. |
. |
||
|
5 |
. |
. |
. |
. |
. |
. |
✓ |
. |
. |
✓ |
Counting up the tick marks this time, we get a test statistic of (V = 7). As before, if our test is two sided, then we reject the null hypothesis when (V) is very large or very small. As far of running it with Python goes, it’s pretty much what you’d expect. For the one-sample version, the command you would use is
w,p = wilcoxon(df['change']) w,p
As this shows, we have a significant effect. Evidently, taking a statistics class does have an effect on your happiness.
14.10. Summary¶
-
A one sample (t)-test is used to compare a single sample mean against a hypothesised value for the population mean.
-
An independent samples (t)-test is used to compare the means of two groups, and tests the null hypothesis that they have the same mean. It comes in two forms: the Student test (Section @ref(studentttest) assumes that the groups have the same standard deviation, the Welch test does not.
-
A paired samples (t)-test is used when you have two scores from each person, and you want to test the null hypothesis that the two scores have the same mean. It is equivalent to taking the difference between the two scores for each person, and then running a one sample (t)-test on the difference scores.
-
Effect size calculations for the difference between means can be calculated via the Cohen’s (d) statistic..
-
You can check the normality of a sample using QQ plots and the Shapiro-Wilk test.
-
If your data are non-normal, you can use Wilcoxon tests instead of (t)-tests.
- 1
-
We won’t cover multiple predictors until the chapter on regression.
- 2
-
Informal experimentation in my garden suggests that yes, it does. Australian natives are adapted to low phosphorus levels relative to everywhere else on Earth, apparently, so if you’ve bought a house with a bunch of exotics and you want to plant natives, don’t follow my example: keep them separate. Nutrients to European plants are poison to Australian ones. There’s probably a joke in that, but I can’t figure out what it is.
- 3
-
Actually this is too strong. Strictly speaking the (z) test only requires that the sampling distribution of the mean be normally distributed; if the population is normal then it necessarily follows that the sampling distribution of the mean is also normal. However, as we saw when talking about the central limit theorem, it’s quite possible (even commonplace) for the sampling distribution to be normal even if the population distribution itself is non-normal. However, in light of the sheer ridiculousness of the assumption that the true standard deviation is known, there really isn’t much point in going into details on this front!
- 4
-
Well, sort of. As I understand the history, Gosset only provided a partial solution: the general solution to the problem was provided by Sir Ronald Fisher.
- 5
-
More seriously, I tend to think the reverse is true: I get very suspicious of technical reports that fill their results sections with nothing except the numbers. It might just be that I’m an arrogant jerk, but I often feel like an author that makes no attempt to explain and interpret their analysis to the reader either doesn’t understand it themselves, or is being a bit lazy. Your readers are smart, but not infinitely patient. Don’t annoy them if you can help it.
- 6
-
A technical comment… in the same way that we can weaken the assumptions of the (z)-test so that we’re only talking about the sampling distribution, we can weaken the (t) test assumptions so that we don’t have to assume normality of the population. However, for the (t)-test, it’s trickier to do this. As before, we can replace the assumption of population normality with an assumption that the sampling distribution of (bar{X}) is normal. However, remember that we’re also relying on a sample estimate of the standard deviation; and so we also require the sampling distribution of (hat{sigma}) to be chi-square. That makes things nastier, and this version is rarely used in practice: fortunately, if the population is normal, then both of these two assumptions are met., and as noted earlier, there are standard tools that you can use to check to see if this assumption is met, and other tests you can do in it’s place if this assumption is violated.
- 7
-
Although it is the simplest, which is why I started with it.
- 8
-
A funny question almost always pops up at this point: what the heck is the population being referred to in this case? Is it the set of students actually taking Dr Harpo’s class (all 33 of them)? The set of people who might take the class (an unknown number) of them? Or something else? Does it matter which of these we pick? It’s traditional in an introductory behavioural stats class to mumble a lot at this point, but since I get asked this question every year by my students, I’ll give a brief answer. Technically yes, it does matter: if you change your definition of what the “real world” population actually is, then the sampling distribution of your observed mean (bar{X}) changes too. The (t)-test relies on an assumption that the observations are sampled at random from an infinitely large population; and to the extent that real life isn’t like that, then the (t)-test can be wrong. In practice, however, this isn’t usually a big deal: even though the assumption is almost always wrong, it doesn’t lead to a lot of pathological behaviour from the test, so we tend to just ignore it.
- 9
-
Yes, I have a “favourite” way of thinking about pooled standard deviation estimates. So what?
- 10
-
Well, I guess you can average apples and oranges, and what you end up with is a delicious fruit smoothie. But no one really thinks that a fruit smoothie is a very good way to describe the original fruits, do they?
- 11
-
This design is very similar to the one in Categorical data analysis that motivated the McNemar test. This should be no surprise. Both are standard repeated measures designs involving two measurements. The only difference is that this time our outcome variable is interval scale (working memory capacity) rather than a binary, nominal scale variable (a yes-or-no question).
- 12
-
At this point we have Drs Harpo, Chico and Zeppo. No prizes for guessing who Dr Groucho is.
- 13
-
This is obviously a class being taught at a very small or very expensive university, or else is a postgraduate class. I’ve never taught an intro stats class with less than 350 students.
- 14
-
This is a massive oversimplification.
- 15
-
Either that, or the Kolmogorov-Smirnov test, which is probably more traditional than the Shapiro-Wilk, though most things I’ve read seem to suggest Shapiro-Wilk is the better test of normality, although Kolomogorov-Smirnov is a general purpose test of distributional equivalence, so it can be adapted to handle other kinds of distribution tests.
- 16
-
Actually, there are two different versions of the test statistic; they differ from each other by a constant value. I’ll just describe one of them here.