Python вывести матрицу ошибок

В компьютерном зрении обнаружение объекта — это проблема определения местоположения одного или нескольких объектов на изображении. Помимо традиционных методов обнаружения, продвинутые модели глубокого обучения, такие как R-CNN и YOLO, могут обеспечить впечатляющие результаты при различных типах объектов. Эти модели принимают изображение в качестве входных данных и возвращают координаты прямоугольника, ограничивающего пространство вокруг каждого найденного объекта.

В этом руководстве обсуждается матрица ошибок и то, как рассчитываются precision, recall и accuracy метрики.

Здесь мы рассмотрим:

• Матрицу ошибок для двоичной классификации.
• Матрицу ошибок для мультиклассовой классификации.
• Расчет матрицы ошибок с помощью Scikit-learn.
• Accuracy, Precision и Recall.
• Precision или Recall?

Матрица ошибок для бинарной классификации

В бинарной классификации каждая выборка относится к одному из двух классов. Обычно им присваиваются такие метки, как 1 и 0, или положительный и отрицательный (Positive и Negative). Также могут использоваться более конкретные обозначения для классов: злокачественный или доброкачественный (например, если проблема связана с классификацией рака), успех или неудача (если речь идет о классификации результатов тестов учащихся).

Предположим, что существует проблема бинарной классификации с классами positive и negative. Вот пример достоверных или эталонных меток для семи выборок, используемых для обучения модели.

positive, negative, negative, positive, positive, positive, negative

Такие наименования нужны в первую очередь для того, чтобы нам, людям, было проще различать классы. Для модели более важна числовая оценка. Обычно при передаче очередного набора данных на выходе вы получите не метку класса, а числовой результат. Например, когда эти семь семплов вводятся в модель, каждому классу будут назначены следующие значения:

0.6, 0.2, 0.55, 0.9, 0.4, 0.8, 0.5

На основании полученных оценок каждой выборке присваивается соответствующий класс. Такое преобразование числовых результатов в метки происходит с помощью порогового значения. Данное граничное условие является гиперпараметром модели и может быть определено пользователем. Например, если порог равен 0.5, тогда любая оценка, которая больше или равна 0.5, получает положительную метку. В противном случае — отрицательную. Вот предсказанные алгоритмом классы:

positive (0.6), negative (0.2), positive (0.55), positive (0.9), negative (0.4), positive (0.8), positive (0.5)

Сравните достоверные и полученные метки — мы имеем 4 верных и 3 неверных предсказания. Стоит добавить, что изменение граничного условия отражается на результатах. Например, установка порога, равного 0.6, оставляет только два неверных прогноза.

Реальность: positive, negative, negative, positive, positive, positive, negative 
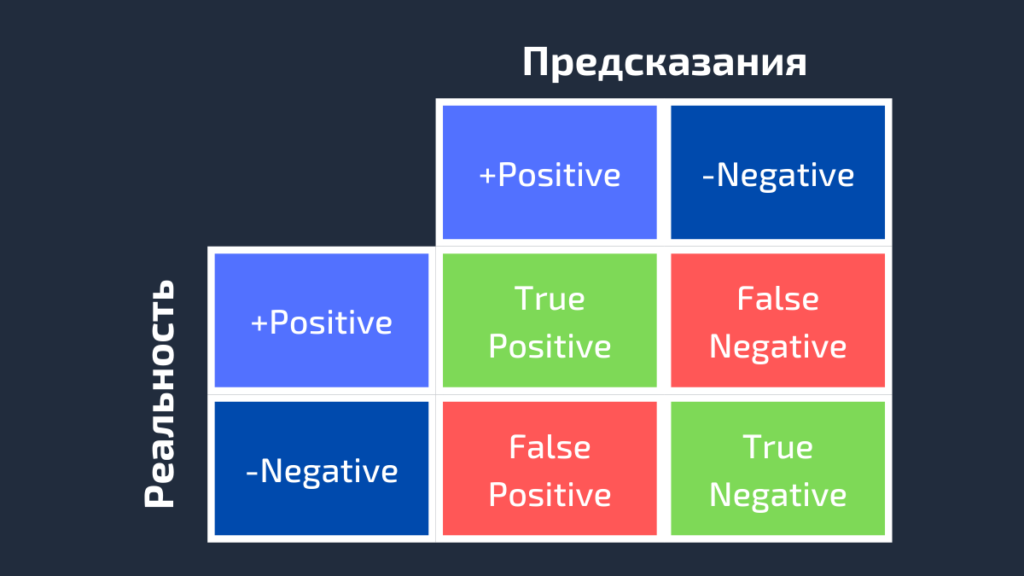
Предсказания: positive, negative, positive, positive, negative, positive, positive

Для получения дополнительной информации о характеристиках модели используется матрица ошибок (confusion matrix). Матрица ошибок помогает нам визуализировать, «ошиблась» ли модель при различении двух классов. Как видно на следующем рисунке, это матрица 2х2. Названия строк представляют собой эталонные метки, а названия столбцов — предсказанные.

Четыре элемента матрицы (клетки красного и зеленого цвета) представляют собой четыре метрики, которые подсчитывают количество правильных и неправильных прогнозов, сделанных моделью. Каждому элементу дается метка, состоящая из двух слов:

1. True или False.
2. Positive или Negative.

True, если получено верное предсказание, то есть эталонные и предсказанные метки классов совпадают, и False, когда они не совпадают. Positive или Negative — названия предсказанных меток.

Таким образом, всякий раз, когда прогноз неверен, первое слово в ячейке False, когда верен — True. Наша цель состоит в том, чтобы максимизировать показатели со словом «True» (True Positive и True Negative) и минимизировать два других (False Positive и False Negative). Четыре метрики в матрице ошибок представляют собой следующее:

1. Верхний левый элемент (True Positive): сколько раз модель правильно классифицировала Positive как Positive?
2. Верхний правый (False Negative): сколько раз модель неправильно классифицировала Positive как Negative?
3. Нижний левый (False Positive): сколько раз модель неправильно классифицировала Negative как Positive?
4. Нижний правый (True Negative): сколько раз модель правильно классифицировала Negative как Negative?

Мы можем рассчитать эти четыре показателя для семи предсказаний, использованных нами ранее. Полученная матрица ошибок представлена на следующем рисунке.

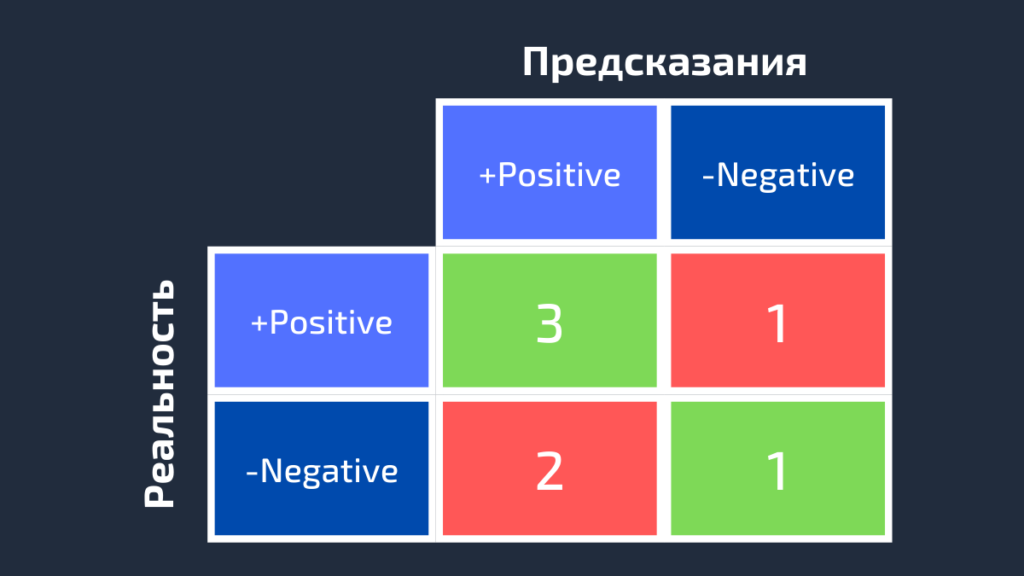
Вот так вычисляется матрица ошибок для задачи двоичной классификации. Теперь посмотрим, как решить данную проблему для большего числа классов.

Матрица ошибок для мультиклассовой классификации

Что, если у нас более двух классов? Как вычислить эти четыре метрики в матрице ошибок для задачи мультиклассовой классификации? Очень просто!

Предположим, имеется 9 семплов, каждый из которых относится к одному из трех классов: White, Black или Red. Вот достоверные метки для 9 выборок:

Red, Black, Red, White, White, Red, Black, Red, White

После загрузки данных модель делает следующее предсказание:

Red, White, Black, White, Red, Red, Black, White, Red

Для удобства сравнения здесь они расположены рядом.

Реальность: Red, Black, Red, White, White, Red, Black, Red, White Предсказания: Red, White, Black, White, Red, Red, Black, White, Red

Перед вычислением матрицы ошибок необходимо выбрать целевой класс. Давайте назначим на эту роль класс Red. Он будет отмечен как Positive, а все остальные отмечены как Negative.

Positive, Negative, Positive, Negative, Negative, Positive, Negative, Positive, Negative Positive, Negative, Negative, Negative, Positive, Positive, Negative, Negative, Positive

11111111111111111111111После замены остались только два класса (Positive и Negative), что позволяет нам рассчитать матрицу ошибок, как было показано в предыдущем разделе. Стоит заметить, что полученная матрица предназначена только для класса Red.

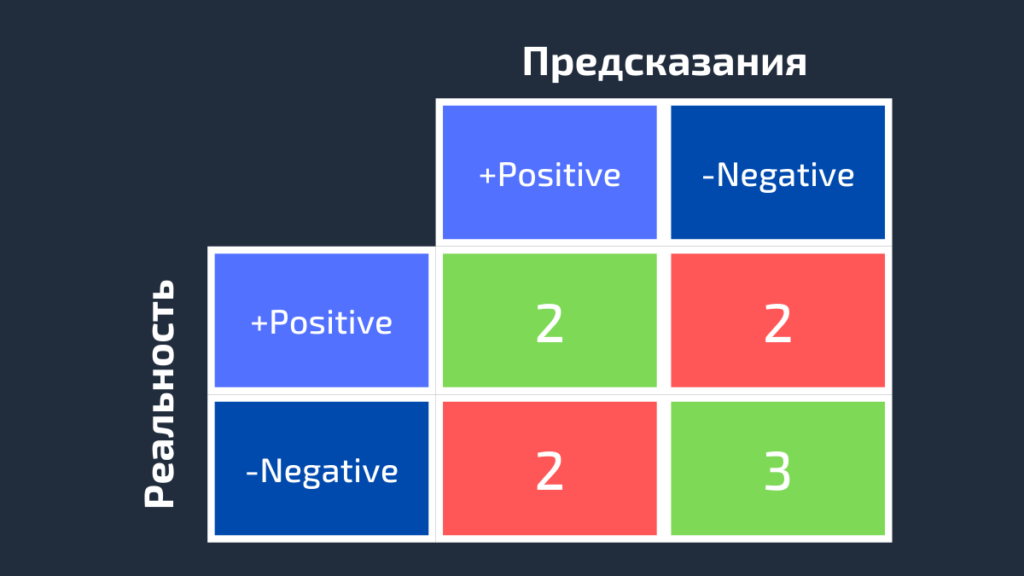
Далее для класса White заменим каждое его вхождение на Positive, а метки всех остальных классов на Negative. Мы получим такие достоверные и предсказанные метки:

Negative, Negative, Negative, Positive, Positive, Negative, Negative, Negative, Positive Negative, Positive, Negative, Positive, Negative, Negative, Negative, Positive, Negative

На следующей схеме показана матрица ошибок для класса White.

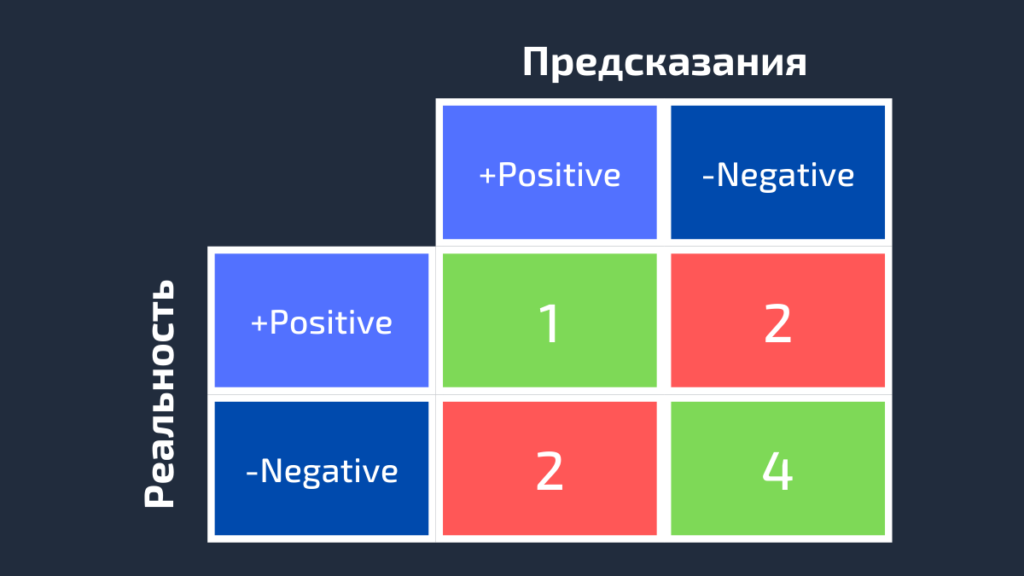
Точно так же может быть получена матрица ошибок для Black.

Расчет матрицы ошибок с помощью Scikit-Learn

В популярной Python-библиотеке Scikit-learn есть модуль metrics, который можно использовать для вычисления метрик в матрице ошибок.

Для задач с двумя классами используется функция confusion_matrix(). Мы передадим в функцию следующие параметры:

1. y_true: эталонные метки.
2. y_pred: предсказанные метки.

Следующий код вычисляет матрицу ошибок для примера двоичной классификации, который мы обсуждали ранее.

import sklearn.metrics

y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative"]
y_pred = ["positive", "negative", "positive", "positive", "negative", "positive", "positive"]

r = sklearn.metrics.confusion_matrix(y_true, y_pred)
print(r)

array([[1, 2],
       [1, 3]], dtype=int64)

Обратите внимание, что порядок метрик отличается от описанного выше. Например, показатель True Positive находится в правом нижнем углу, а True Negative — в верхнем левом углу. Чтобы исправить это, мы можем перевернуть матрицу.

import numpy

r = numpy.flip(r)
print(r)

array([[3, 1],
       [2, 1]], dtype=int64)

Чтобы вычислить матрицу ошибок для задачи с большим числом классов, используется функция multilabel_confusion_matrix(), как показано ниже. В дополнение к параметрам y_true и y_pred третий параметр labels принимает список классовых меток.

import sklearn.metrics
import numpy

y_true = ["Red", "Black", "Red",   "White", "White", "Red", "Black", "Red",   "White"]
y_pred = ["Red", "White", "Black", "White", "Red",   "Red", "Black", "White", "Red"]

r = sklearn.metrics.multilabel_confusion_matrix(y_true, y_pred, labels=["White", "Black", "Red"])
print(r)

array([
    [[4 2]
     [2 1]]

    [[6 1]
     [1 1]]
    
    [[3 2]
     [2 2]]], dtype=int64)

Функция вычисляет матрицу ошибок для каждого класса и возвращает все матрицы. Их порядок соответствует порядку меток в параметре labels. Чтобы изменить последовательность метрик в матрицах, мы будем снова использовать функцию numpy.flip().

print(numpy.flip(r[0]))  # матрица ошибок для класса White
print(numpy.flip(r[1]))  # матрица ошибок для класса Black
print(numpy.flip(r[2]))  # матрица ошибок для класса Red

# матрица ошибок для класса White
[[1 2]
 [2 4]]

# матрица ошибок для класса Black
[[1 1]
 [1 6]]

# матрица ошибок для класса Red
[[2 2]
 [2 3]]

В оставшейся части этого текста мы сосредоточимся только на двух классах. В следующем разделе обсуждаются три ключевых показателя, которые рассчитываются на основе матрицы ошибок.

Как мы уже видели, матрица ошибок предлагает четыре индивидуальных показателя. На их основе можно рассчитать другие метрики, которые предоставляют дополнительную информацию о поведении модели:

1. Accuracy
2. Precision
3. Recall

В следующих подразделах обсуждается каждый из этих трех показателей.

Метрика Accuracy

Accuracy — это показатель, который описывает общую точность предсказания модели по всем классам. Это особенно полезно, когда каждый класс одинаково важен. Он рассчитывается как отношение количества правильных прогнозов к их общему количеству.

Рассчитаем accuracy с помощью Scikit-learn на основе ранее полученной матрицы ошибок. Переменная acc содержит результат деления суммы True Positive и True Negative метрик на сумму всех значений матрицы. Таким образом, accuracy, равная 0.5714, означает, что модель с точностью 57,14% делает верный прогноз.

import numpy
import sklearn.metrics

y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative"]
y_pred = ["positive", "negative", "positive", "positive", "negative", "positive", "positive"]

r = sklearn.metrics.confusion_matrix(y_true, y_pred)
r = numpy.flip(r)

acc = (r[0][0] + r[-1][-1]) / numpy.sum(r)
print(acc)
# вывод будет 0.571

В модуле sklearn.metrics есть функция precision_score(), которая также может вычислять accuracy. Она принимает в качестве аргументов достоверные и предсказанные метки.

acc = sklearn.metrics.accuracy_score(y_true, y_pred)

Стоит учесть, что метрика accuracy может быть обманчивой. Один из таких случаев — это несбалансированные данные. Предположим, у нас есть всего 600 единиц данных, из которых 550 относятся к классу Positive и только 50 — к Negative. Поскольку большинство семплов принадлежит к одному классу, accuracy для этого класса будет выше, чем для другого.

Если модель сделала 530 правильных прогнозов из 550 для класса Positive, по сравнению с 5 из 50 для Negative, то общая accuracy равна (530 + 5) / 600 = 0.8917. Это означает, что точность модели составляет 89.17%. Полагаясь на это значение, вы можете подумать, что для любой выборки (независимо от ее класса) модель сделает правильный прогноз в 89.17% случаев. Это неверно, так как для класса Negative модель работает очень плохо.

Precision

Precision представляет собой отношение числа семплов, верно классифицированных как Positive, к общему числу выборок с меткой Positive (распознанных правильно и неправильно). Precision измеряет точность модели при определении класса Positive.

Когда модель делает много неверных Positive классификаций, это увеличивает знаменатель и снижает precision. С другой стороны, precision высока, когда:

1. Модель делает много корректных предсказаний класса Positive (максимизирует True Positive метрику).
2. Модель делает меньше неверных Positive классификаций (минимизирует False Positive).

Представьте себе человека, который пользуется всеобщим доверием; когда он что-то предсказывает, окружающие ему верят. Метрика precision похожа на такого персонажа. Если она высока, вы можете доверять решению модели по определению очередной выборки как Positive. Таким образом, precision помогает узнать, насколько точна модель, когда она говорит, что семпл имеет класс Positive.

Основываясь на предыдущем обсуждении, вот определение precision:

Precision отражает, насколько надежна модель при классификации Positive-меток.

На следующем изображении зеленая метка означает, что зеленый семпл классифицирован как Positive, а красный крест – как Negative. Модель корректно распознала две Positive выборки, но неверно классифицировала один Negative семпл как Positive. Из этого следует, что метрика True Positive равна 2, когда False Positive имеет значение 1, а precision составляет 2 / (2 + 1) = 0.667. Другими словами, процент доверия к решению модели, что выборка относится к классу Positive, составляет 66.7%.

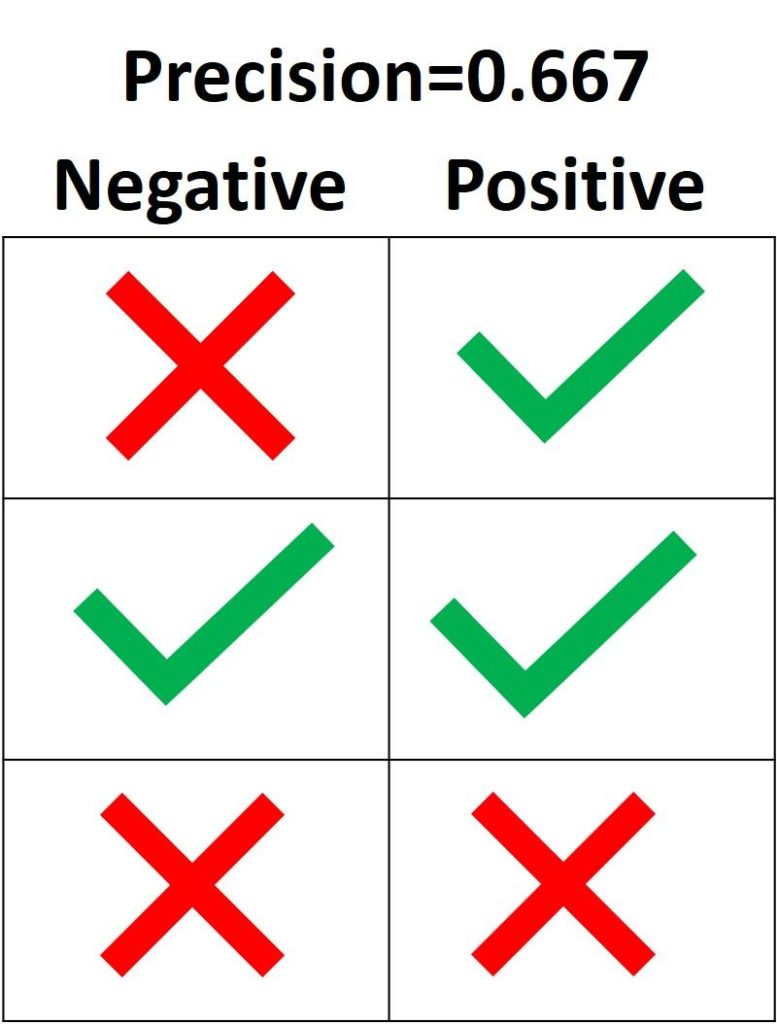
Цель precision – классифицировать все Positive семплы как Positive, не допуская ложных определений Negative как Positive. Согласно следующему рисунку, если все три Positive выборки предсказаны правильно, но один Negative семпл классифицирован неверно, precision составляет 3 / (3 + 1) = 0.75. Таким образом, утверждения модели о том, что выборка относится к классу Positive, корректны с точностью 75%.

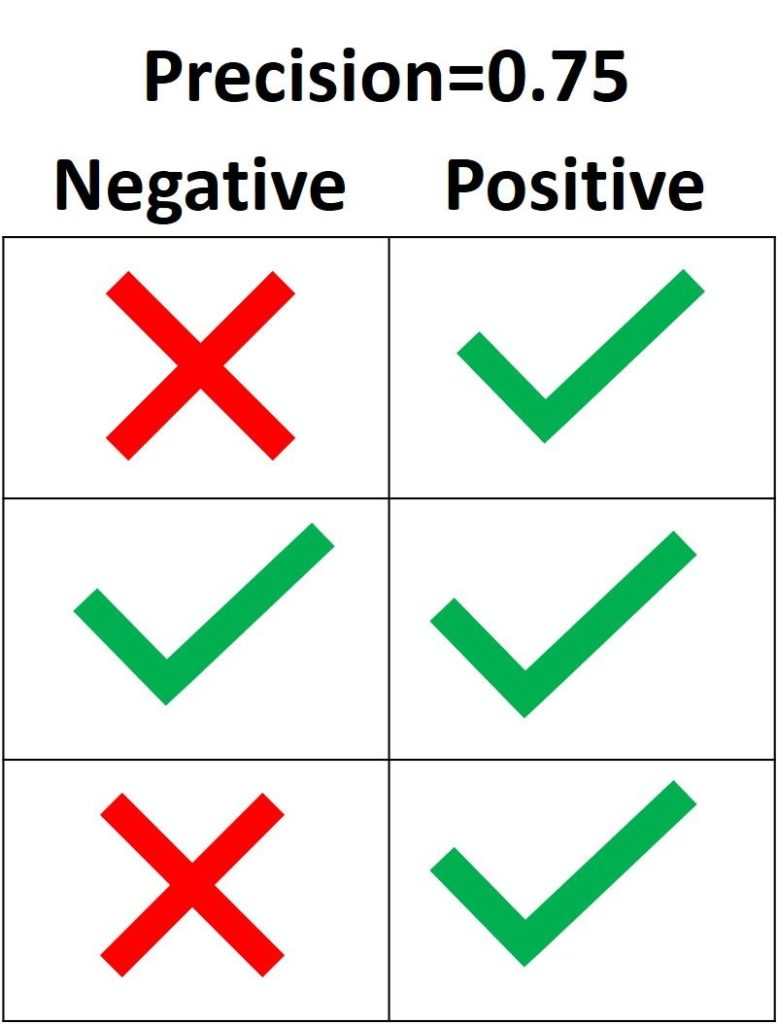
Единственный способ получить 100% precision — это классифицировать все Positive выборки как Positive без классификации Negative как Positive.

В Scikit-learn модуль sklearn.metrics имеет функцию precision_score(), которая получает в качестве аргументов эталонные и предсказанные метки и возвращает precision. Параметр pos_label принимает метку класса Positive (по умолчанию 1).

import sklearn.metrics

y_true = ["positive", "positive", "positive", "negative", "negative", "negative"]
y_pred = ["positive", "positive", "negative", "positive", "negative", "negative"]

precision = sklearn.metrics.precision_score(y_true, y_pred, pos_label="positive")
print(precision)

Вывод: 0.6666666666666666.

Recall

Recall рассчитывается как отношение числа Positive выборок, корректно классифицированных как Positive, к общему количеству Positive семплов. Recall измеряет способность модели обнаруживать выборки, относящиеся к классу Positive. Чем выше recall, тем больше Positive семплов было найдено.

Recall заботится только о том, как классифицируются Positive выборки. Эта метрика не зависит от того, как предсказываются Negative семплы, в отличие от precision. Когда модель верно классифицирует все Positive выборки, recall будет 100%, даже если все представители класса Negative были ошибочно определены как Positive. Давайте посмотрим на несколько примеров.

На следующем изображении представлены 4 разных случая (от A до D), и все они имеют одинаковый recall, равный 0.667. Представленные примеры отличаются только тем, как классифицируются Negative семплы. Например, в случае A все Negative выборки корректно определены, а в случае D – наоборот. Независимо от того, как модель предсказывает класс Negative, recall касается только семплов относящихся к Positive.

Из 4 случаев, показанных выше, только 2 Positive выборки определены верно. Таким образом, метрика True Positive равна 2. False Negative имеет значение 1, потому что только один Positive семпл классифицируется как Negative. В результате recall будет равен 2 / (2 + 1) = 2/3 = 0.667.
Поскольку не имеет значения, как предсказываются объекты класса Negative, лучше их просто игнорировать, как показано на следующей схеме. При расчете recall необходимо учитывать только Positive выборки.

Что означает, когда recall высокий или низкий? Если recall имеет большое значение, все Positive семплы классифицируются верно. Следовательно, модели можно доверять в ее способности обнаруживать представителей класса Positive.

На следующем изображении recall равен 1.0, потому что все Positive семплы были правильно классифицированы. Показатель True Positive равен 3, а False Negative – 0. Таким образом, recall вычисляется как 3 / (3 + 0) = 1. Это означает, что модель обнаружила все Positive выборки. Поскольку recall не учитывает, как предсказываются представители класса Negative, могут присутствовать множество неверно определенных Negative семплов (высокая False Positive метрика).

С другой стороны, recall равен 0.0, если не удается обнаружить ни одной Positive выборки. Это означает, что модель обнаружила 0% представителей класса Positive. Показатель True Positive равен 0, а False Negative имеет значение 3. Recall будет равен 0 / (0 + 3) = 0.

Когда recall имеет значение от 0.0 до 1.0, это число отражает процент Positive семплов, которые модель верно классифицировала. Например, если имеется 10 экземпляров Positive и recall равен 0.6, получается, что модель корректно определила 60% объектов класса Positive (т.е. 0.6 * 10 = 6).

Подобно precision_score(), функция repl_score() из модуля sklearn.metrics вычисляет recall. В следующем блоке кода показан пример ее использования.

import sklearn.metrics

y_true = ["positive", "positive", "positive", "negative", "negative", "negative"]
y_pred = ["positive", "positive", "negative", "positive", "negative", "negative"]

recall = sklearn.metrics.recall_score(y_true, y_pred, pos_label="positive")
print(recall)

Вывод: 0.6666666666666666.

После определения precision и recall давайте кратко подведем итоги:

• Precision измеряет надежность модели при классификации Positive семплов, а recall определяет, сколько Positive выборок было корректно предсказано моделью.
• Precision учитывает классификацию как Positive, так и Negative семплов. Recall же использует при расчете только представителей класса Positive. Другими словами, precision зависит как от Negative, так и от Positive-выборок, но recall — только от Positive.
• Precision принимает во внимание, когда семпл определяется как Positive, но не заботится о верной классификации всех объектов класса Positive. Recall в свою очередь учитывает корректность предсказания всех Positive выборок, но не заботится об ошибочной классификации представителей Negative как Positive.
• Когда модель имеет высокий уровень recall метрики, но низкую precision, такая модель правильно определяет большинство Positive семплов, но имеет много ложных срабатываний (классификаций Negative выборок как Positive). Если модель имеет большую precision, но низкий recall, то она делает высокоточные предсказания, определяя класс Positive, но производит всего несколько таких прогнозов.

Некоторые вопросы для проверки понимания:

• Если recall равен 1.0, а в датасете имеются 5 объектов класса Positive, сколько Positive семплов было правильно классифицировано моделью?
• Учитывая, что recall составляет 0.3, когда в наборе данных 30 Positive семплов, сколько представителей класса Positive будет предсказано верно?
• Если recall равен 0.0 и в датасете14 Positive-семплов, сколько корректных предсказаний класса Positive было сделано моделью?

Precision или Recall?

Решение о том, следует ли использовать precision или recall, зависит от типа вашей проблемы. Если цель состоит в том, чтобы обнаружить все positive выборки (не заботясь о том, будут ли negative семплы классифицированы как positive), используйте recall. Используйте precision, если ваша задача связана с комплексным предсказанием класса Positive, то есть учитывая Negative семплы, которые были ошибочно классифицированы как Positive.

Представьте, что вам дали изображение и попросили определить все автомобили внутри него. Какой показатель вы используете? Поскольку цель состоит в том, чтобы обнаружить все автомобили, используйте recall. Такой подход может ошибочно классифицировать некоторые объекты как целевые, но в конечном итоге сработает для предсказания всех автомобилей.

Теперь предположим, что вам дали снимок с результатами маммографии, и вас попросили определить наличие рака. Какой показатель вы используете? Поскольку он обязан быть чувствителен к неверной идентификации изображения как злокачественного, мы должны быть уверены, когда классифицируем снимок как Positive (то есть с раком). Таким образом, предпочтительным показателем в данном случае является precision.

Вывод

В этом руководстве обсуждалась матрица ошибок, вычисление ее 4 метрик (true/false positive/negative) для задач бинарной и мультиклассовой классификации. Используя модуль metrics библиотеки Scikit-learn, мы увидели, как получить матрицу ошибок в Python.

Основываясь на этих 4 показателях, мы перешли к обсуждению accuracy, precision и recall метрик. Каждая из них была определена и использована в нескольких примерах. Модуль sklearn.metrics применяется для расчета каждого вышеперечисленного показателя.

Visualizations play an essential role in the exploratory data analysis activity of machine learning.

You can plot confusion matrix using the confusion_matrix() method from sklearn.metrics package.

Why Confusion Matrix?

After creating a machine learning model, accuracy is a metric used to evaluate the machine learning model. On the other hand, you cannot use accuracy in every case as it’ll be misleading. Because the accuracy of 99% may look good as a percentage, but consider a machine learning model used for Fraud Detection or Drug consumption detection.

In such critical scenarios, the 1% percentage failure can create a significant impact.

For example, if a model predicted a fraud transaction of 10000$ as Not Fraud, then it is not a good model and cannot be used in production.

In the drug consumption model, consider if the model predicted that the person had consumed the drug but actually has not. But due to the False prediction of the model, the person may be imprisoned for a crime that is not committed actually.

In such scenarios, you need a better metric than accuracy to validate the machine learning model.
This is where the confusion matrix comes into the picture.

In this tutorial, you’ll learn what a confusion matrix is, how to plot confusion matrix for the binary classification model and the multivariate classification model.

What is Confusion Matrix?

Confusion matrix is a matrix that allows you to visualize the performance of the classification machine learning models. With this visualization, you can get a better idea of how your machine learning model is performing.

Creating Binary Class Classification Model

In this section, you’ll create a classification model that will predict whether a patient has breast cancer or not, denoted by output classes True or False.

The breast cancer dataset is available in the sklearn dataset library.

It contains a total number of 569 data rows. Each row includes 30 numeric features and one output class. If you want to manipulate or visualize the sklearn dataset, you can convert it into pandas dataframe and play around with the pandas dataframe functionalities.

To create the model, you’ll load the sklearn dataset, split it into train and testing set and fit the train data into the KNeighborsClassifier model.

After creating the model, you can use the test data to predict the values and check how the model is performing.

You can use the actual output classes from your test data and the predicted output returned by the predict() method to plot the confusion matrix and evaluate the model accuracy.

Use the below snippet to create the model.

Snippet

import numpy as np

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier as KNN

breastCancer = load_breast_cancer()

X = breastCancer.data
y = breastCancer.target

# Split the dataset into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4, random_state = 42)

knn = KNN(n_neighbors = 3)

# train the model
knn.fit(X_train, y_train)

print('Model is Created')

The KNeighborsClassifier model is created for the breast cancer training data.

Output

    Model is Created

To test the model created, you can use the test data obtained from the train test split and predict the output. Then, you’ll have the predicted values.

Snippet

y_pred = knn.predict(X_test)

y_pred

Output

    array([0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1,
           0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1,
           1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1,
           0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0,
           1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1,
           0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0,
           0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1,
           1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1,
           0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1,
           0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1,
           0, 1, 0, 0, 1, 1, 0, 1])

Now use the predicted classes and the actual output classes from the test data to visualize the confusion matrix.

You’ll learn how to plot the confusion matrix for the binary classification model in the next section.

Plot Confusion Matrix for Binary Classes

You can create the confusion matrix using the confusion_matrix() method from sklearn.metrics package. The confusion_matrix() method will give you an array that depicts the True Positives, False Positives, False Negatives, and True negatives.

** Snippet**

from sklearn.metrics import confusion_matrix

#Generate the confusion matrix
cf_matrix = confusion_matrix(y_test, y_pred)

print(cf_matrix)

Output

    [[ 73   7]
     [  7 141]]

Once you have the confusion matrix created, you can use the heatmap() method available in the seaborn library to plot the confusion matrix.

Seaborn heatmap() method accepts one mandatory parameter and few other optional parameters.

• data – A rectangular dataset that can be coerced into a 2d array. Here, you can pass the confusion matrix you already have
• annot=True – To write the data value in the cell of the printed matrix. By default, this is False.
• cmap=Blues – This is to denote the matplotlib color map names. Here, we’ve created the plot using the blue color shades.

The heatmap() method returns the matplotlib axes that can be stored in a variable. Here, you’ll store in variable ax. Now, you can set title, x-axis and y-axis labels and tick labels for x-axis and y-axis.

• Title – Used to label the complete image. Use the set_title() method to set the title.
• Axes-labels – Used to name the x axis or y axis. Use the set_xlabel() to set the x-axis label and set_ylabel() to set the y-axis label.
• Tick labels – Used to denote the datapoints on the axes. You can pass the tick labels in an array, and it must be in ascending order. Because the confusion matrix contains the values in the ascending order format. Use the xaxis.set_ticklabels() to set the tick labels for x-axis and yaxis.set_ticklabels() to set the tick labels for y-axis.

Finally, use the plot.show() method to plot the confusion matrix.

Use the below snippet to create a confusion matrix, set title and labels for the axis, and set the tick labels, and plot it.

Snippet

import seaborn as sns

ax = sns.heatmap(cf_matrix, annot=True, cmap='Blues')

ax.set_title('Seaborn Confusion Matrix with labelsnn');
ax.set_xlabel('nPredicted Values')
ax.set_ylabel('Actual Values ');

## Ticket labels - List must be in alphabetical order
ax.xaxis.set_ticklabels(['False','True'])
ax.yaxis.set_ticklabels(['False','True'])

## Display the visualization of the Confusion Matrix.
plt.show()

Output

Alternatively, you can also plot the confusion matrix using the ConfusionMatrixDisplay.from_predictions() method available in the sklearn library itself if you want to avoid using the seaborn.

Next, you’ll learn how to plot a confusion matrix with percentages.

Plot Confusion Matrix for Binary Classes With Percentage

The objective of creating and plotting the confusion matrix is to check the accuracy of the machine learning model. It’ll be good to visualize the accuracy with percentages rather than using just the number. In this section, you’ll learn how to plot a confusion matrix for binary classes with percentages.

To plot the confusion matrix with percentages, first, you need to calculate the percentage of True Positives, False Positives, False Negatives, and True negatives. You can calculate the percentage of these values by dividing the value by the sum of all values.

Using the np.sum() method, you can sum all values in the confusion matrix.

Then pass the percentage of each value as data to the heatmap() method by using the statement cf_matrix/np.sum(cf_matrix).

Use the below snippet to plot the confusion matrix with percentages.

Snippet

ax = sns.heatmap(cf_matrix/np.sum(cf_matrix), annot=True, 
            fmt='.2%', cmap='Blues')

ax.set_title('Seaborn Confusion Matrix with labelsnn');
ax.set_xlabel('nPredicted Values')
ax.set_ylabel('Actual Values ');

## Ticket labels - List must be in alphabetical order
ax.xaxis.set_ticklabels(['False','True'])
ax.yaxis.set_ticklabels(['False','True'])

## Display the visualization of the Confusion Matrix.
plt.show()

Output

Plot Confusion Matrix for Binary Classes With Labels

In this section, you’ll plot a confusion matrix for Binary classes with labels True Positives, False Positives, False Negatives, and True negatives.

You need to create a list of the labels and convert it into an array using the np.asarray() method with shape 2,2. Then, this array of labels must be passed to the attribute annot. This will plot the confusion matrix with the labels annotation.

Use the below snippet to plot the confusion matrix with labels.

Snippet

labels = ['True Neg','False Pos','False Neg','True Pos']

labels = np.asarray(labels).reshape(2,2)

ax = sns.heatmap(cf_matrix, annot=labels, fmt='', cmap='Blues')

ax.set_title('Seaborn Confusion Matrix with labelsnn');
ax.set_xlabel('nPredicted Values')
ax.set_ylabel('Actual Values ');

## Ticket labels - List must be in alphabetical order
ax.xaxis.set_ticklabels(['False','True'])
ax.yaxis.set_ticklabels(['False','True'])

## Display the visualization of the Confusion Matrix.
plt.show()

Output

Plot Confusion Matrix for Binary Classes With Labels And Percentages

In this section, you’ll learn how to plot a confusion matrix with labels, counts, and percentages.

You can use this to measure the percentage of each label. For example, how much percentage of the predictions are True Positives, False Positives, False Negatives, and True negatives

For this, first, you need to create a list of labels, then count each label in one list and measure the percentage of the labels in another list.

Then you can zip these different lists to create labels. Zipping means concatenating an item from each list and create one list. Then, this list must be converted into an array using the np.asarray() method.

Then pass the final array to annot attribute. This will create a confusion matrix with the label, count, and percentage information for each class.

Use the below snippet to visualize the confusion matrix with all the details.

Snippet

group_names = ['True Neg','False Pos','False Neg','True Pos']

group_counts = ["{0:0.0f}".format(value) for value in
                cf_matrix.flatten()]

group_percentages = ["{0:.2%}".format(value) for value in
                     cf_matrix.flatten()/np.sum(cf_matrix)]

labels = [f"{v1}n{v2}n{v3}" for v1, v2, v3 in
          zip(group_names,group_counts,group_percentages)]

labels = np.asarray(labels).reshape(2,2)

ax = sns.heatmap(cf_matrix, annot=labels, fmt='', cmap='Blues')

ax.set_title('Seaborn Confusion Matrix with labelsnn');
ax.set_xlabel('nPredicted Values')
ax.set_ylabel('Actual Values ');

## Ticket labels - List must be in alphabetical order
ax.xaxis.set_ticklabels(['False','True'])
ax.yaxis.set_ticklabels(['False','True'])

## Display the visualization of the Confusion Matrix.
plt.show()

Output

This is how you can create a confusion matrix for the binary classification machine learning model.

Next, you’ll learn about creating a confusion matrix for a classification model with multiple output classes.

Creating Classification Model For Multiple Classes

In this section, you’ll create a classification model for multiple output classes. In other words, it’s also called multivariate classes.

You’ll be using the iris dataset available in the sklearn dataset library.

It contains a total number of 150 data rows. Each row includes four numeric features and one output class. Output class can be any of one Iris flower type. Namely, Iris Setosa, Iris Versicolour, Iris Virginica.

To create the model, you’ll load the sklearn dataset, split it into train and testing set and fit the train data into the KNeighborsClassifier model.

After creating the model, you can use the test data to predict the values and check how the model is performing.

You can use the actual output classes from your test data and the predicted output returned by the predict() method to plot the confusion matrix and evaluate the model accuracy.

Use the below snippet to create the model.

Snippet

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier as KNN
iris = load_iris()
X = iris.data
y = iris.target
# Split dataset into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4, random_state = 42)
knn = KNN(n_neighbors = 3)
# train th model
knn.fit(X_train, y_train)
print('Model is Created')

Output

    Model is Created

Now the model is created.

Use the test data from the train test split and predict the output value using the predict() method as shown below.

Snippet

y_pred = knn.predict(X_test)

y_pred

You’ll have the predicted output as an array. The value 0, 1, 2 shows the predicted category of the test data.

Output

    array([1, 0, 2, 1, 1, 0, 1, 2, 1, 1, 2, 0, 0, 0, 0, 1, 2, 1, 1, 2, 0, 2,
           0, 2, 2, 2, 2, 2, 0, 0, 0, 0, 1, 0, 0, 2, 1, 0, 0, 0, 2, 1, 1, 0,
           0, 1, 1, 2, 1, 2, 1, 2, 1, 0, 2, 1, 0, 0, 0, 1])

Now, you can use the predicted data available in y_pred to create a confusion matrix for multiple classes.

Plot Confusion matrix for Multiple Classes

In this section, you’ll learn how to plot a confusion matrix for multiple classes.

You can use the confusion_matrix() method available in the sklearn library to create a confusion matrix. It’ll contain three rows and columns representing the actual flower category and the predicted flower category in ascending order.

Snippet

from sklearn.metrics import confusion_matrix

#Get the confusion matrix
cf_matrix = confusion_matrix(y_test, y_pred)

print(cf_matrix)

Output

    [[23  0  0]
     [ 0 19  0]
     [ 0  1 17]]

The below output shows the confusion matrix for actual and predicted flower category counts.

You can use this matrix to plot the confusion matrix using the seaborn library, as shown below.

Snippet

import seaborn as sns
import matplotlib.pyplot as plt

ax = sns.heatmap(cf_matrix, annot=True, cmap='Blues')

ax.set_title('Seaborn Confusion Matrix with labelsnn');
ax.set_xlabel('nPredicted Flower Category')
ax.set_ylabel('Actual Flower Category ');

## Ticket labels - List must be in alphabetical order
ax.xaxis.set_ticklabels(['Setosa','Versicolor', 'Virginia'])
ax.yaxis.set_ticklabels(['Setosa','Versicolor', 'Virginia'])

## Display the visualization of the Confusion Matrix.
plt.show()

Output

Plot Confusion Matrix for Multiple Classes With Percentage

In this section, you’ll plot the confusion matrix for multiple classes with the percentage of each output class. You can calculate the percentage by dividing the values in the confusion matrix by the sum of all values.

Use the below snippet to plot the confusion matrix for multiple classes with percentages.

Snippet

ax = sns.heatmap(cf_matrix/np.sum(cf_matrix), annot=True, 
            fmt='.2%', cmap='Blues')

ax.set_title('Seaborn Confusion Matrix with labelsnn');
ax.set_xlabel('nPredicted Flower Category')
ax.set_ylabel('Actual Flower Category ');

## Ticket labels - List must be in alphabetical order
ax.xaxis.set_ticklabels(['Setosa','Versicolor', 'Virginia'])
ax.yaxis.set_ticklabels(['Setosa','Versicolor', 'Virginia'])

## Display the visualization of the Confusion Matrix.
plt.show()

Output

Plot Confusion Matrix for Multiple Classes With Numbers And Percentages

In this section, you’ll learn how to plot a confusion matrix with labels, counts, and percentages for the multiple classes.

You can use this to measure the percentage of each label. For example, how much percentage of the predictions belong to each category of flowers.

For this, first, you need to create a list of labels, then count each label in one list and measure the percentage of the labels in another list.

Then you can zip these different lists to create concatenated labels. Zipping means concatenating an item from each list and create one list. Then, this list must be converted into an array using the np.asarray() method.

This final array must be passed to annot attribute. This will create a confusion matrix with the label, count, and percentage information for each category of flowers.

Use the below snippet to visualize the confusion matrix with all the details.

Snippet

#group_names = ['True Neg','False Pos','False Neg','True Pos','True Pos','True Pos','True Pos','True Pos','True Pos']

group_counts = ["{0:0.0f}".format(value) for value in
                cf_matrix.flatten()]

group_percentages = ["{0:.2%}".format(value) for value in
                     cf_matrix.flatten()/np.sum(cf_matrix)]

labels = [f"{v1}n{v2}n" for v1, v2 in
          zip(group_counts,group_percentages)]

labels = np.asarray(labels).reshape(3,3)

ax = sns.heatmap(cf_matrix, annot=labels, fmt='', cmap='Blues')

ax.set_title('Seaborn Confusion Matrix with labelsnn');
ax.set_xlabel('nPredicted Flower Category')
ax.set_ylabel('Actual Flower Category ');

## Ticket labels - List must be in alphabetical order
ax.xaxis.set_ticklabels(['Setosa','Versicolor', 'Virginia'])
ax.yaxis.set_ticklabels(['Setosa','Versicolor', 'Virginia'])

## Display the visualization of the Confusion Matrix.
plt.show()

Output

This is how you can plot a confusion matrix for multiple classes with percentages and numbers.

Plot Confusion Matrix Without Classifier

To plot the confusion matrix without a classifier model, refer to this StackOverflow answer.

Conclusion

To summarize, you’ve learned how to plot a confusion matrix for the machine learning model with binary output classes and multiple output classes.

You’ve also learned how to annotate the confusion matrix with more details such as labels, count of each label, and percentage of each label for better visualization.

If you’ve any questions, comment below.

You May Also Like

• How to Save and Load Machine Learning Models in python
• How to Plot Correlation Matrix in Python

A Dependency Free Multiclass Confusion Matrix

# A Simple Confusion Matrix Implementation
def confusionmatrix(actual, predicted, normalize = False):
    """
    Generate a confusion matrix for multiple classification
    @params:
        actual      - a list of integers or strings for known classes
        predicted   - a list of integers or strings for predicted classes
        normalize   - optional boolean for matrix normalization
    @return:
        matrix      - a 2-dimensional list of pairwise counts
    """
    unique = sorted(set(actual))
    matrix = [[0 for _ in unique] for _ in unique]
    imap   = {key: i for i, key in enumerate(unique)}
    # Generate Confusion Matrix
    for p, a in zip(predicted, actual):
        matrix[imap[p]][imap[a]] += 1
    # Matrix Normalization
    if normalize:
        sigma = sum([sum(matrix[imap[i]]) for i in unique])
        matrix = [row for row in map(lambda i: list(map(lambda j: j / sigma, i)), matrix)]
    return matrix

The approach here is to pair up the unique classes found in the actual vector into a 2-dimensional list. From there, we simply iterate through the zipped actual and predicted vectors and populate the counts using the indices to access the matrix positions.

Usage

cm = confusionmatrix(
    [1, 1, 2, 0, 1, 1, 2, 0, 0, 1], # actual
    [0, 1, 1, 0, 2, 1, 2, 2, 0, 2]  # predicted
)

# And The Output
print(cm)
[[2, 1, 0], [0, 2, 1], [1, 2, 1]]

Note: the actual classes are along the columns and the predicted classes are along the rows.

# Actual
# 0  1  2
  #  #  #   
[[2, 1, 0], # 0
 [0, 2, 1], # 1  Predicted
 [1, 2, 1]] # 2

Class Names Can be Strings or Integers

cm = confusionmatrix(
    ["B", "B", "C", "A", "B", "B", "C", "A", "A", "B"], # actual
    ["A", "B", "B", "A", "C", "B", "C", "C", "A", "C"]  # predicted
)

# And The Output
print(cm)
[[2, 1, 0], [0, 2, 1], [1, 2, 1]]

You Can Also Return The Matrix With Proportions (Normalization)

cm = confusionmatrix(
    ["B", "B", "C", "A", "B", "B", "C", "A", "A", "B"], # actual
    ["A", "B", "B", "A", "C", "B", "C", "C", "A", "C"], # predicted
    normalize = True
)

# And The Output
print(cm)
[[0.2, 0.1, 0.0], [0.0, 0.2, 0.1], [0.1, 0.2, 0.1]]

A More Robust Solution

Since writing this post, I’ve updated my library implementation to be a class that uses a confusion matrix representation internally to compute statistics, in addition to pretty printing the confusion matrix itself. See this Gist.

Example Usage

# Actual & Predicted Classes
actual      = ["A", "B", "C", "C", "B", "C", "C", "B", "A", "A", "B", "A", "B", "C", "A", "B", "C"]
predicted   = ["A", "B", "B", "C", "A", "C", "A", "B", "C", "A", "B", "B", "B", "C", "A", "A", "C"]

# Initialize Performance Class
performance = Performance(actual, predicted)

# Print Confusion Matrix
performance.tabulate()

With the output:

===================================
        Aᴬ      Bᴬ      Cᴬ

Aᴾ      3       2       1

Bᴾ      1       4       1

Cᴾ      1       0       4

Note: classᴾ = Predicted, classᴬ = Actual
===================================

And for the normalized matrix:

# Print Normalized Confusion Matrix
performance.tabulate(normalized = True)

With the normalized output:

===================================
        Aᴬ      Bᴬ      Cᴬ

Aᴾ      17.65%  11.76%  5.88%

Bᴾ      5.88%   23.53%  5.88%

Cᴾ      5.88%   0.00%   23.53%

Note: classᴾ = Predicted, classᴬ = Actual
===================================