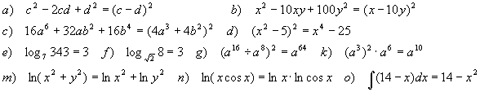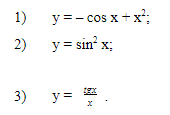Работа над ошибками матем

Работа над ошибками

По математике

1. Ошибки в ходе решения задачи:

а) прочитай задачу;

б) составь и сделай краткую запись;

в) реши по действиям с пояснениями и ответом.

2. Ошибки в ходе решения уравнения:

а) запиши уравнение;

б) назови компоненты;

в) вспомни правило нахождения неизвестного компонента;

г) реши уравнение верно;

д) придумай и реши похожее уравнение.

3. Сложение и вычитание в пределах 10 и 20:

а) запиши пример верно;

б) повтори таблицу сложения и вычитания в пределах 10 или 20;

в) реши пример по образцу:

1) 3 + 5 = 8                10 – 4 = 6

5 + 3 = 8                10 – 6 = 4

8 – 3 = 5                4 + 6 = 10

8 – 5 = 3                6 + 4 = 10

2) 8 + 7 = 8 + (2 + 5) = (8 + 2) + 5 = 10 + 5 = 15

16 – 9 = 16 – (6 + 3) = (16 – 6) = 10 – 3 = 7

4. Сложение и вычитание многозначных чисел:

а) повтори таблицу разрядов и классов;

б) запиши пример правильно (разряд под разрядом);

в) повтори таблицы сложения в пределах 10 и 20;

г) реши пример правильно;

д) проверь сложение вычитанием или вычитание сложением.

Образец:   48                Проверка:    82

     34                                48

     82                                34

5. Таблица умножения и деления:

а) повтори таблицу умножения;

б) запиши пример и реши его верно;

в) запиши все случаи умножения и деления с этими числами;

г) придумай различные примеры на умножение и деление с данным ответом:

1) 18 : 3 = 6                2) 2 × 3 = 6

18 : 6 = 3                42 : 7 = 6

6 × 3 = 18                30 : 6 = 5

3 × 6 = 18                54 : 9 = 6

6. Внетабличное умножение и деление:

а) запиши пример;

б) разложи одно из чисел на сумму удобных или разрядных слагаемых;

в) реши пример с объяснением;

г) проверь умножение делением или деление умножением.

Образец: 84 : 6 = (60 + 24): 6 = 60 : 6 + 24 : 6 = 10 + 4 = 14

Проверка: 14 × 6 = (10 + 4) × 6 = 10 × 6 + 4 × 6 = 60 + 24 = 84

Образец: 16 × 5 = (10 + 6) × 5 + 10 × 5 + 6 × 5 = 50 + 30 = 80

Проверка: 80 : 5 = (50 + 30) : 5 = 50 : 5 + 30 : 5 = 10 + 6 = 16

7. Деление вида 96 :16:

а) вспомни правило подбора частного;

б) запиши пример и реши его верно;

в) проверь умножением.

Образец: 96 : 16 = 6

Проверка: 16 × 6 = (10 + 6) × 6 = 10 × 6 + 6 × 6 = 60 + 36 = 96

8. Внетабличное умножение и деление:

а) запиши пример верно;

б) вспомни правило умножения или деления в столбик;

в) реши пример;

г) проверь умножение делением или деление умножением.

Образец:

425                        Проверка: 315775‌│425

743                                        2975         743

          1275                                        1827

          1700                                        1700     

          2975            1275

      315775                                             1275

              0

9. Ошибки на порядок действий в выражениях со скобками и без скобок:

1) запиши выражение верно;

2) вспомни порядок выполнения действий в выражениях со скобками или без скобок:

а) выполни действия в скобках;

б) выполни действия по порядку: умножение и (или) деление, а потом сложение и (или) вычитание;

в) запиши ответ.

По русскому языку

1. Точка в конце предложения.

Выпиши предложение правильно. Поставь в конце точку. Делай так: Птицы улетели.

2. Слоги жи-ши, ча-ща, чу-щу.

Выпиши слово. Запиши еще два слова на это правило. Делай так: жил, жизнь, машина.

3. Перенос слова.

Раздели слово на слоги для переноса. Делай так: ру-чей-ки.

4. Пропуск буквы.

Выпиши слово, раздели его на слоги. Делай так: при-леж-ный, при-леж-
ные.

5. Большая буква в именах людей, кличках животных.

Выпиши слово. Придумай и запиши еще два слова на это правило. Делай так: Саша, Алеша, Миша.

6. Слова из словаря.

Напиши слово три раза.

Делай так: карандаш, карандаш, карандаш.

7. Ь на конце и в середине слова.

Выпиши слово верно. Придумай и запиши еще два слова на это правило. Делай так: огонь, учитель, морковь.

8. Разделительные ъ и ь знаки.

Выпиши слово. Запиши еще два слова на это правило. Делай так: вьет, лью, семья; подъезд, объяснил, съемка.

Запомни! Разделительный ь знак пишется после согласных перед гласными буквами: е, ё, ю, я, и.

Разделительный ъ знак пишется после приставок, которые оканчиваются на согласный перед гласными: е, ё, ю, я.

9. Приставки в словах.

Напиши слово верно. Придумай и запиши еще два слова с приставками. Делай так: приехал, заехал, уехал.

Запомни! Приставка – часть слова. Она пишется слитно.

10. Предлоги со словами.

Напиши слово вместе с предлогом. Докажи раздельное написание предлога со словом. Делай так: у дома, (какого?) дома, у большого дома.

Запомни! Предлог – это отдельное слово. Это часть речи. Предлог со словом пишется раздельно.

11. Безударная проверяемая гласная в корне слова.

Выпиши слово, поставь ударение, выдели корень, подчеркни проверяемую гласную, напиши проверочное слово.
 

Вспомни правило проверки безударного гласного в корне слова.

12. Звонкие и глухие согласные в корне слова.

Выпиши слово грамотно. Выдели в нем корень. Подчеркни букву, в которой допущена ошибка. Напиши проверочное слово.

Вспомни правило проверки парных согласных в корне.

13. Непроизносимые согласные в корне.

Выпиши слово. Выдели корень. Подчеркни непроизносимый согласный. Напиши проверочное слово.

Вспомни правило проверки непроизносимых согласных.

14. Ь после шипящих. .

Выпиши слово. Запиши еще два слова на это правило.

Делай так: дочь, ночь, речь (сущ., ж. р.);

жечь, печь, стеречь (гл., неопр. ф.);

пишешь, читаешь, решаешь (гл., 2 л.).

• Запомни! В существительных женского рода, в глаголах неопределенной формы и 2-го лица после шипящих пишется ь.

15. Правописание слов с шипящим на конце.

Выпиши слово. Запиши еще два слова на это правило.

Делай так: шалаш, сторож, камыш (сущ., м. р.);

с крыш, много задач, из-за туч (сущ., мн. ч., Род. п.);

кипуч, могуч, скрипуч (кратк. прилаг.).

• Запомни! У существительных мужского рода в родительном падеже множественного числа и у имен прилагательных в краткой форме после шипящих ь не пишется.

16. Гласные е – и в окончаниях имен существительных.

Выпиши слово, в котором  допущена ошибка.  Докажи  написание  букв е – и в окончаниях. Делай так: на дороге – дорога – сущ., 1 скл., Предл.п.

• Запомни! Для определения окончания существительного нужно знать склонение и падеж.

17. Гласные е –  и в окончаниях имен прилагательных.

Выпиши прилагательное вместе с тем существительным, к которому оно  относится.  Докажи  окончание  имени  прилагательного.  Делай так: к дальнему лесу, к лесу (какому?) дальнему (м. р., Дат. п.).

• Запомни! Для определения окончания прилагательного надо знать его род и падеж. Это определи по существительному. Кроме того, окончание прилагательного можно определить по вопросу, который задается от существительного. В этом случае надо хорошо знать родовые окончания имен прилагательных.

18. Гласные е – и в окончаниях глаголов.

Выпиши глагол, в котором допущена ошибка. Обоснуй окончание глагола.

Делай так: пишет – писать (I спр.) – е; смотрит – смотреть (II спр.) – и (искл.).

• Запомни! Гласные е – и в окончании глагола следует устанавливать по неопределенной форме.

19. Однородные члены предложения.

Выпиши предложение. Правильно расставь знаки. Подчеркни однородные члены предложения. Делай так: Грачи, скворцы и жаворонки улетели в тёплые края.

20. Разбор слова по составу.

Выпиши слово. Разбери его по составу.

21. Фонетический разбор слов.

Выпиши слово. Разбери его фонетически грамотно, пользуясь памяткой.

22. Разбор предложения по частям речи.

Выпиши предложение. Над словами сокращенно обозначь названия частей речи.

 предл.  сущ.            глаг.                 прилаг.             сущ.

Делай так: С   гор   побежали  звонкие   ручейки.

23. Разбор по членам предложения.

Выпиши предложение.

Делай так: С гор побежали звонкие ручейки.

ручейки (какие?) звонкие;

побежали (откуда?) с гор.

Требования к ведению тетрадей

1. Писать аккуратным, разборчивым почерком.

2. Единообразно выполнять надписи на обложке тетради:

Образец надписи:

      Тетрадь

для творческих работ

по русскому языку

ученика____ класса

средней школы______

г. _________________

___________________

Тетради для учащихся 1 класса подписываются только учителем.

3. Соблюдать поля с внешней стороны (4 клеточки, отчеркиваются простым карандашом).

4. В 1 классе в первом полугодии дата работ по русскому языку и математике не пишется. Со второго полугодия в 1 классе, а также во 2–4 классах обозначается время выполнения работы: число – арабской цифрой, название месяца – прописью. В 3–4 классах в тетрадях по русскому языку число записывается прописью.

5. Обозначить номер упражнения, задачи; указывать, где выполняется работа (классная или домашняя).

6. Соблюдать красную строку.

7. Для учащихся 1–4 классов текст каждой новой работы начинать с красной строки на той же странице тетради, на которой написаны дата и наименование работы.

8. Между датой и заголовком, наименованием вида работы и заголовком, а также между заголовком в тетрадях по русскому языку строку не пропускать. В тетрадях по математике во всех этих случаях пропускать только две клеточки. Между заключительной частью текста одной письменной работы и датой или заголовком (наименованием вида) следующей работы в тетрадях по русскому языку пропускать две линейки, а в тетрадях по математике – четыре клеточки (для отделения одной работы от другой и для выставления отметки за работу).

9. Исправлять ошибки следующим образом: неверно написанную букву или пунктуационный знак зачеркивать ручкой косой линией, часть слова, предложение зачеркивать тонкой горизонтальной линией; вместо зачеркнутого надписывать нужные буквы, слова, предложения; не заключать неверные написания в скобки.

10. Подчеркивания выполнять аккуратно карандашом, с применением линейки. Тетради, в которых выполняются обучающие классные и домашние работы по русскому языку и математике, проверяют после каждого урока у всех учеников.

Все дети пишут шариковой ручкой школьного образца. Паста заправки должна быть только синего цвета.

Для обучения письму в 1 классе введена тетрадь, разлинованная в две линейки. Для 2–4 классов рекомендована тетрадь в одну линейку.

Упражнения по чистописанию выполняются учащимися в рабочих тетрадях. Образцы букв в 1 классе прописывает учитель, во 2–4 классах они прописываются выборочно с учетом индивидуальных особенностей каждого ребенка. Объем работы – 2 строки в 1 классе во втором полугодии, 2–3 строки во 2 классе, 3–4 строки в 3–4 классах.

В классном журнале на странице «Русский язык» фиксируется содержание работы по чистописанию. При выставлении отметок за работы по русскому языку принимается во внимание каллиграфия ученика.

Оформление работы над ошибками по
математике во 2-4 классе

o    Пропускаю
4 клеточки после работы.

o    На
5 клеточке пишу посередине с большой буквы:

                              
Работа над ошибками

o    Начинаю
с ошибок в оформлении задачи, используя памятку.

o    Далее
нахожу ошибки, допущенные в работе и выполняю   задания, следуя инструкциям в памятке.

Памятка
работы над ошибками по математике

1.      
Сложение
и вычитание в пределах 10:

  — запиши пример верно

— повтори таблицу
сложения и вычитания в пределах 10
— реши пример по образцу

Образец: 

3 + 5 = 8           10
– 4 = 6 

5 + 3 = 8  
        10 – 6 = 4 

8 – 5 =
3            4 + 6 = 10

8 – 3 =
5            6 + 4 = 10

2.       Сложение и вычитание в пределах
20:
— запиши пример
верно
— повтори таблицу сложения и вычитания в пределах 20
— реши пример по образцу

Образец: 

8 + 7 = 8 + (2 + 5) = (8 + 2) +
5 = 10 + 5 = 15

16 – 9 = 16 – (6 + 3) = (16 – 6)
– 3 = 10 – 3 = 7

3.     Ошибки в задаче:

а) в краткой записи:

— снова прочитай задачу, выполни
краткую запись верно.

б) в решении:

— прочитай задачу и представь себе,
о чём говорится в задаче;
— запиши задачу кратко, можно выполнить рисунок или чертеж;
— поясни, что показывает каждое число, повтори вопрос задачи;

— подумай, можно ли сразу ответить
на вопрос задачи. Если нет, то почему?

— что нужно узнать сначала, что
потом?

— составь план решения;

-реши по действиям с пояснениями;
— проверь решение;

— запиши ответ задачи.

4.  
Ошибки в задаче с отрезками:

— внимательно прочитай задание и
снова выполни решение

Образец:

5 + 3 = 8 (см)

Ответ: 8 см равен второй
отрезок.

5.   Ошибки в сравнении числовых
выражений:

— выпиши выражения

-посчитай результат решения

-запиши и поставь знак сравнения

Образец:

5 + 10 › 12 – 9

15 › 3

(Будь внимателен! Не во всех
выражениях нужно доказывать своё решение, например: 5 + 3 = 3 + 5)

6.   Ошибки в сравнении
именованных чисел:

— выпиши выражения

-докажи своё решение

-запиши и поставь знак сравнения

Образец: 2 дм 5 см ‹ 29 см

25     м ‹ 29 см

7.
Таблица умножения и деления:

а)
повтори таблицу умножения;

б)
запиши пример и реши его верно;

в)
запиши все случаи умножения и деления с этими числами;

г)
придумай различные примеры на умножение и деление с данным ответом:

14 : 7= 2 14 : 2= 7 2 · 7= 14 7 · 2= 14

18 : 9= 2 18 : 2= 9 2 · 9= 18 9 · 2= 18

8. Ошибки в ходе решения уравнения:

           
а) запиши уравнение;

б)
назови компоненты;

в)
вспомни правило нахождения неизвестного компонента;

г)
реши уравнение верно;

д)
придумай и реши похожее уравнение.

Работа над ошибками – одна из основных
форм преодоления пробелов в знаниях и
умениях учащихся. Эта работа приносит
пользу только тогда, когда она находится
постоянно в центре внимания учителя.

Разбор ошибок полезен ещё потому, что,
ознакомившись с какой-нибудь ошибкой и
проанализировав её, ученик в какой-то
степени застраховывает себя от повторения
таких ошибок в будущем. Кроме того, работа
над ошибками может служить хорошим
средством для достижения точности
определений, точности формулировок теорем.
Разбирая ошибки, которые появляются в
процессе учёбы, ученики учатся шлифовать
каждое слово в своём ответе. А это имеет
немаловажное значение.

О значении своевременного реагирования
на ошибки известный чешский педагог Ян Амос
Коменский писал: “Любая ошибка
превращается из маленького “снежка” в
большой “снежный ком” неуспеваемости,
если на эту ошибку сразу же не реагировал
учитель при непременном привлечении самого
учащегося к её осознанию и последующему
труду, направленному на её полное
преодоление”.

На каждом уроке учитель сталкивается с
различными видами ошибок, с необходимостью
их исправления. Учитель поступает
правильно, если не торопится сам исправить
ошибку, а привлекает для этого учащихся.
Нужно дать понять ученику, к чему может
привести его ошибка.

Например: Учитель задаёт вопрос: “Почему
два данных треугольника равны?”. Ученик
отвечает: “Если сторона и два угла одного
треугольника равны стороне и двум углам
другого треугольника, то такие
треугольники равны”.

Чтобы отвечающий ученик и ученики,
которые не заметили ошибки, лучше осознали
неправильность формулировки, нужно
предложить им построить АВС
(где С
— тупой), а затем.
Треугольники АВС и
удовлетворяют формулировке, которую дал
ученик, но они не равны. После выяснения
ошибки ученик как правило даёт правильный
ответ. Конечно же, такое исправление ошибок
способствует повышению качества знаний
учащихся, активизирует их мышление и служит
целям развивающего обучения.

Целенаправленная работа над ошибками
требует их систематизации. При этом главную
роль должны сыграть группы ошибок, которые
объединены общими причинами их появления,
общей методикой работы над ними. Такая
систематизация ошибок позволяет наметить
пути их исправления и предупреждения этих
ошибок в дальнейшем.

Какие же наиболее характерные ошибки
допускают учащиеся при работе:

1. Ошибки и недочёты, которые обусловлены
невниманием к формированию теоретико-множественных
представлений учащихся:

• ошибки, связанные с недостаточно чётким
  владением понятиями множества, элемента
  множества, отношения принадлежности,
  равенства множеств;
• ошибки, которые возникают в результате
  недостаточно чёткого владения
  операциями пересечения и объединения
  множеств.

2. Ошибки, которые связаны с недостаточной
логической подготовкой учащихся:

• ошибки, связанные с непониманием
  структуры теоремы;
• ошибки, которые обусловлены
  непониманием зависимости между прямой и
  обратной теоремами;
• ошибки, связанные с непониманием метода
  доказательства от противного.

3. Ошибки, которые допускают учащиеся из-за
отсутствия и неустойчивости самоконтроля.

Рассмотренные ошибки и недочёты типичны
на всех ступенях обучения.

Для осуществления целенаправленных мер
по исправлению и предупреждению ошибок
учителю необходимо систематически изучать
ошибки учащихся, выявлять наиболее
устойчивые и типичные из них, вести учёт
распространённых и индивидуальных ошибок
учащихся. Знание учителем типичных
ученических ошибок, а также причин их
возникновения и форм проявления даёт ему
возможность предвидеть и предупреждать их
появление. Достичь этого можно путём
подбора таких упражнений, которые
препятствуют образованию односторонних
ассоциаций и неправильных обобщений.

Ошибки учащихся, которые регистрирует и
учитывает учитель, помогают ему установить,
что не понимают учащиеся, что ими плохо
усвоено; это даёт возможность учителю
своевременно ликвидировать пробелы в
знаниях учащихся и внести соответствующие
коррективы в дальнейшее преподавание с
целью предупреждения повторения
аналогичных ошибок.

Чтобы определить сущность допускаемых
учащимися ошибок, необходимо проследить
ход рассуждений, который приводит к такому
ошибочному решению, установить этап, на
котором зарождаются такие ошибки. Как
показывает опыт, часто учащемуся непонятен
не весь материал, а лишь какая-то его часть.
Выявив, что именно непонятно ученику, можно
сосредоточить на этом материале всё
внимание, не отвлекаясь на те моменты,
которые уже усвоены.

Допускаемые учеником ошибки
свидетельствуют не только о недостатках
его знаний, но и о потенциальных
возможностях. Ошибки служат также
показателем проблем, которые могут быть
поставлены перед учеником, а иногда они
приводят к созданию проблемных ситуаций,
которые необходимы в данный момент для
развития действий.

Ни в коем случае нельзя снижать оценок
ученикам за ошибки в процессе поиска. Очень
важно приучить их не бояться допускаемых
ошибок. Ошибки, допускаемые учениками, надо
исправлять тактично, обоснованно,
привлекая к этой работе самих учащихся.

Боязнь допустить ошибку сковывает
инициативу ученика. Боясь ошибиться, он не
будет сам решать поставленную проблему, а
станет ждать помощи от учителя. Он будет
решать только лёгкие проблемы. Но без
такого самостоятельного решения задач с
последовательно нарастающей сложностью не
может происходить интеллектуальное
развитие. Во многих случаях по этой причине
учащиеся проявляют робость и
интеллектуальную пассивность, что в
дальнейшем приводит к неуспеваемости.

Очень оживлённо воспринимаются учащимися
“Задачи на выявление ошибки”. Речь идёт не
только о софизмах, но и об ошибках, которые
допускают сами школьники. Не нужно
специально исправлять каждое ошибочное
утверждение школьника. Лучше поставить это
утверждение на обсуждение всего класса и
добиться осознанного исправления ошибки.
Если они и не допускают ошибок, то всё же
нередко целесообразно проверить, насколько
они “устойчивы” против типичных ошибок.

Например: Найти ошибки:

Процесс отыскания и исправления ошибок
самими учащимися под руководством учителя
можно сделать поучительным для учащихся, в
результате чего изучение и анализ ошибок
становится эффективным средством в
развитии познавательного интереса к
изучению математики.

Для исправления и предупреждения многих
ошибок важно сформировать у школьников
навыки самоконтроля. Эти навыки состоят из
двух частей: а) умения обнаружить ошибку; в)
умения её объяснить и исправить.

В процессе обучения применяются
несколько приёмов самоконтроля, которые
помогают обнаружить допущенные ошибки и
своевременно их исправить. К ним относятся:

• проверка вычисления и тождественного
  преобразования путём выполнения
  обратного действия или преобразования;
• проверка правильности решения задач
  путём составления и решения задач,
  обратных к данной;
• оценка результата решения задачи с
  точки зрения здравого смысла;
• проверка аналитического решения
  графическим .

Выработке навыков самоконтроля помогает
и приём приближённой оценки ожидаемого
результата. Установление возможных
пределов ожидаемого ответа предупреждает
недочёты типа описок, пропуска цифр.

Например, рассмотрим задачу: “За неделю
завод выпустил 130 холодильников, выполнив
месячный план на 25%. Сколько холодильников
должен выпустить завод за месяц по плану”.

Пусть решение ученика выглядит так: .
Ошибка становится очевидной, если перед
решением ученик прикинет в уме: “За неделю
завод выпустил 130 холодильников.
Следовательно, за месяц он выпустит больше.
Значит, ответ должен быть больше, чем 130”.
Такая прикидка в уме полезна при решении
задач с дробными числами и процентами.

В жизненной практике в чертежах, схемах,
расчётах, с которыми ребята будут
встречаться, могут быть и ошибки. Если не
научить их критически относиться к данным,
то могут быть и аварии, и брак, и серьёзные
упущения в работе. Чтобы этого избежать,
необходимо формировать у учащихся умение
анализировать данные, способность
обнаруживать встречающиеся ошибки и
обосновывать ошибочность положения.

Польский математик Г. Штейнгауз, отмечая
большое значение работы над
математическими ошибками для активизации
мыслительной деятельности учащихся, пишет:
“Если учащегося заверить, что в
предложенном ему доказательстве есть
ошибка, то можно быть уверенным даже без
специальной проверки, что материал будет
изучен полностью и очень тщательно”.
Поэтому составление списка математических
ошибок и использование его в учебных целях
является одним из важных факторов
повышения эффективности обучения.

Таким образом, важную роль в
предупреждении ошибок играет продуманная
организация изучения нового материала.
Изучение нового материала надо строить так,
чтобы ученик был активным участником этого
процесса. Не надо бояться, если при первом
изложении материала им будут допускаться
ошибки, высказываться необоснованные
выводы. Важно, чтобы те или иные ошибки в
понимании материала исправлялись в
зародыше, чтобы ученики воспринимали
материал осознанно.

Такому подходу к изучению нового
материала способствует создание
проблемной ситуации и решение её учащимися
под руководством учителя. На таких уроках
ученики проходят через следующие стадии:
поиск нового, возможное появление ошибок в
процессе поиска нового, обоснованное
опровержение этих ошибок, снова поиски, в
результате которых приходят к правильной
догадке, и, наконец, доказательство
составленного в поисках предложения. Всё
это способствует развитию математического
мышления.

Работа над ошибками

По математике

1. Ошибки в ходе решения задачи:

а) прочитай задачу;

б) составь и сделай краткую запись;

в) реши по действиям с пояснениями и ответом.

2. Ошибки в ходе решения уравнения:

а) запиши уравнение;

б) назови компоненты;

в) вспомни правило нахождения неизвестного компонента;

г) реши уравнение верно;

д) придумай и реши похожее уравнение.

3. Сложение и вычитание в пределах 10 и 20:

а) запиши пример верно;

б) повтори таблицу сложения и вычитания в пределах 10 или 20;

в) реши пример по образцу:

1) 3 + 5 = 8 10 – 4 = 6

5 + 3 = 8 10 – 6 = 4

8 – 3 = 5 4 + 6 = 10

8 – 5 = 3 6 + 4 = 10

2) 8 + 7 = 8 + (2 + 5) = (8 + 2) + 5 = 10 + 5 = 15

16 – 9 = 16 – (6 + 3) = (16 – 6) = 10 – 3 = 7

4. Сложение и вычитание многозначных чисел:

а) повтори таблицу разрядов и классов;

б) запиши пример правильно (разряд под разрядом);

в) повтори таблицы сложения в пределах 10 и 20;

г) реши пример правильно;

д) проверь сложение вычитанием или вычитание сложением.

Образец: 48 Проверка: 82

34 48

82 34

5. Таблица умножения и деления:

а) повтори таблицу умножения;

б) запиши пример и реши его верно;

в) запиши все случаи умножения и деления с этими числами;

г) придумай различные примеры на умножение и деление с данным ответом:

1) 18 : 3 = 6 2) 2 × 3 = 6

18 : 6 = 3 42 : 7 = 6

6 × 3 = 18 30 : 6 = 5

3 × 6 = 18 54 : 9 = 6

6. Внетабличное умножение и деление:

а) запиши пример;

б) разложи одно из чисел на сумму удобных или разрядных слагаемых;

в) реши пример с объяснением;

г) проверь умножение делением или деление умножением.

Образец: 84 : 6 = (60 + 24): 6 = 60 : 6 + 24 : 6 = 10 + 4 = 14

Проверка: 14 × 6 = (10 + 4) × 6 = 10 × 6 + 4 × 6 = 60 + 24 = 84

Образец: 16 × 5 = (10 + 6) × 5 + 10 × 5 + 6 × 5 = 50 + 30 = 80

Проверка: 80 : 5 = (50 + 30) : 5 = 50 : 5 + 30 : 5 = 10 + 6 = 16

7. Деление вида 96 :16:

а) вспомни правило подбора частного;

б) запиши пример и реши его верно;

в) проверь умножением.

Образец: 96 : 16 = 6

Проверка: 16 × 6 = (10 + 6) × 6 = 10 × 6 + 6 × 6 = 60 + 36 = 96

8. Внетабличное умножение и деление:

а) запиши пример верно;

б) вспомни правило умножения или деления в столбик;

в) реши пример;

г) проверь умножение делением или деление умножением.

Образец:

425 Проверка: 315775‌│425

743 2975 743

1275 1827

1700 1700

2975 1275

315775 1275

0

9. Ошибки на порядок действий в выражениях со скобками и без скобок:

1) запиши выражение верно;

2) вспомни порядок выполнения действий в выражениях со скобками или без скобок:

а) выполни действия в скобках;

б) выполни действия по порядку: умножение и (или) деление, а потом сложение и (или) вычитание;

в) запиши ответ.

По русскому языку

1. Точка в конце предложения.

Выпиши предложение правильно. Поставь в конце точку. Делай так: Птицы улетели.

2. Слоги жи-ши, ча-ща, чу-щу.

Выпиши слово. Запиши еще два слова на это правило. Делай так: жил, жизнь, машина.

3. Перенос слова.

Раздели слово на слоги для переноса. Делай так: ру-чей-ки.

4. Пропуск буквы.

Выпиши слово, раздели его на слоги. Делай так: при-леж-ный, при-леж-
ные.

5. Большая буква в именах людей, кличках животных.

Выпиши слово. Придумай и запиши еще два слова на это правило. Делай так: Саша, Алеша, Миша.

6. Слова из словаря.

Напиши слово три раза.

Делай так: карандаш, карандаш, карандаш.

7. Ь на конце и в середине слова.

Выпиши слово верно. Придумай и запиши еще два слова на это правило. Делай так: огонь, учитель, морковь.

8. Разделительные ъ и ь знаки.

Выпиши слово. Запиши еще два слова на это правило. Делай так: вьет, лью, семья; подъезд, объяснил, съемка.

Запомни! Разделительный ь знак пишется после согласных перед гласными буквами: е, ё, ю, я, и.

Разделительный ъ знак пишется после приставок, которые оканчиваются на согласный перед гласными: е, ё, ю, я.

9. Приставки в словах.

Напиши слово верно. Придумай и запиши еще два слова с приставками. Делай так: приехал, заехал, уехал.

Запомни! Приставка – часть слова. Она пишется слитно.

10. Предлоги со словами.

Напиши слово вместе с предлогом. Докажи раздельное написание предлога со словом. Делай так: у дома, (какого?) дома, у большого дома.

Запомни! Предлог – это отдельное слово. Это часть речи. Предлог со словом пишется раздельно.

11. Безударная проверяемая гласная в корне слова.

Выпиши слово, поставь ударение, выдели корень, подчеркни проверяемую гласную, напиши проверочное слово.

Вспомни правило проверки безударного гласного в корне слова.

12. Звонкие и глухие согласные в корне слова.

Выпиши слово грамотно. Выдели в нем корень. Подчеркни букву, в которой допущена ошибка. Напиши проверочное слово.

Вспомни правило проверки парных согласных в корне.

13. Непроизносимые согласные в корне.

Выпиши слово. Выдели корень. Подчеркни непроизносимый согласный. Напиши проверочное слово.

Вспомни правило проверки непроизносимых согласных.

14. Ь после шипящих. .

Выпиши слово. Запиши еще два слова на это правило.

Делай так: дочь, ночь, речь (сущ., ж. р.);

жечь, печь, стеречь (гл., неопр. ф.);

пишешь, читаешь, решаешь (гл., 2 л.).

• Запомни! В существительных женского рода, в глаголах неопределенной формы и 2-го лица после шипящих пишется ь.

15. Правописание слов с шипящим на конце.

Выпиши слово. Запиши еще два слова на это правило.

Делай так: шалаш, сторож, камыш (сущ., м. р.);

с крыш, много задач, из-за туч (сущ., мн. ч., Род. п.);

кипуч, могуч, скрипуч (кратк. прилаг.).

• Запомни! У существительных мужского рода в родительном падеже множественного числа и у имен прилагательных в краткой форме после шипящих ь не пишется.

16. Гласные е – и в окончаниях имен существительных.

Выпиши слово, в котором допущена ошибка. Докажи написание букв е – и в окончаниях. Делай так: на дороге – дорога – сущ., 1 скл., Предл.п.

• Запомни! Для определения окончания существительного нужно знать склонение и падеж.

17. Гласные е – и в окончаниях имен прилагательных.

Выпиши прилагательное вместе с тем существительным, к которому оно относится. Докажи окончание имени прилагательного. Делай так: к дальнему лесу, к лесу (какому?) дальнему (м. р., Дат. п.).

• Запомни! Для определения окончания прилагательного надо знать его род и падеж. Это определи по существительному. Кроме того, окончание прилагательного можно определить по вопросу, который задается от существительного. В этом случае надо хорошо знать родовые окончания имен прилагательных.

18. Гласные е – и в окончаниях глаголов.

Выпиши глагол, в котором допущена ошибка. Обоснуй окончание глагола.

Делай так: пишет – писать (I спр.) – е; смотрит – смотреть (II спр.) – и (искл.).

• Запомни! Гласные е – и в окончании глагола следует устанавливать по неопределенной форме.

19. Однородные члены предложения.

Выпиши предложение. Правильно расставь знаки. Подчеркни однородные члены предложения. Делай так: Грачи, скворцы и жаворонки улетели в тёплые края.

20. Разбор слова по составу.

Выпиши слово. Разбери его по составу.

21. Фонетический разбор слов.

Выпиши слово. Разбери его фонетически грамотно, пользуясь памяткой.

22. Разбор предложения по частям речи.

Выпиши предложение. Над словами сокращенно обозначь названия частей речи.

предл. сущ. глаг. прилаг. сущ.

Делай так: С гор побежали звонкие ручейки.

23. Разбор по членам предложения.

Выпиши предложение.

Делай так: С гор побежали звонкие ручейки.

ручейки (какие?) звонкие;

побежали (откуда?) с гор.

Требования к ведению тетрадей

1. Писать аккуратным, разборчивым почерком.

2. Единообразно выполнять надписи на обложке тетради:

Образец надписи:

Тетрадь

для творческих работ

по русскому языку

ученика____ класса

средней школы______

г. _________________

___________________

Тетради для учащихся 1 класса подписываются только учителем.

3. Соблюдать поля с внешней стороны (4 клеточки, отчеркиваются простым карандашом).

4. В 1 классе в первом полугодии дата работ по русскому языку и математике не пишется. Со второго полугодия в 1 классе, а также во 2–4 классах обозначается время выполнения работы: число – арабской цифрой, название месяца – прописью. В 3–4 классах в тетрадях по русскому языку число записывается прописью.

5. Обозначить номер упражнения, задачи; указывать, где выполняется работа (классная или домашняя).

6. Соблюдать красную строку.

7. Для учащихся 1–4 классов текст каждой новой работы начинать с красной строки на той же странице тетради, на которой написаны дата и наименование работы.

8. Между датой и заголовком, наименованием вида работы и заголовком, а также между заголовком в тетрадях по русскому языку строку не пропускать. В тетрадях по математике во всех этих случаях пропускать только две клеточки. Между заключительной частью текста одной письменной работы и датой или заголовком (наименованием вида) следующей работы в тетрадях по русскому языку пропускать две линейки, а в тетрадях по математике – четыре клеточки (для отделения одной работы от другой и для выставления отметки за работу).

9. Исправлять ошибки следующим образом: неверно написанную букву или пунктуационный знак зачеркивать ручкой косой линией, часть слова, предложение зачеркивать тонкой горизонтальной линией; вместо зачеркнутого надписывать нужные буквы, слова, предложения; не заключать неверные написания в скобки.

10. Подчеркивания выполнять аккуратно карандашом, с применением линейки. Тетради, в которых выполняются обучающие классные и домашние работы по русскому языку и математике, проверяют после каждого урока у всех учеников.

Все дети пишут шариковой ручкой школьного образца. Паста заправки должна быть только синего цвета.

Для обучения письму в 1 классе введена тетрадь, разлинованная в две линейки. Для 2–4 классов рекомендована тетрадь в одну линейку.

Упражнения по чистописанию выполняются учащимися в рабочих тетрадях. Образцы букв в 1 классе прописывает учитель, во 2–4 классах они прописываются выборочно с учетом индивидуальных особенностей каждого ребенка. Объем работы – 2 строки в 1 классе во втором полугодии, 2–3 строки во 2 классе, 3–4 строки в 3–4 классах.

В классном журнале на странице «Русский язык» фиксируется содержание работы по чистописанию. При выставлении отметок за работы по русскому языку принимается во внимание каллиграфия ученика.

Для математики популярная поговорка «умные люди учатся на чужих ошибках» практически не работает, так как ошибка в большинстве случаев является необходимой и полезной, ведь она позволяет определить пробелы в знаниях школьника и своевременно их устранить. Главное – правильно относится к ошибке и ее правильно ее использовать.

Тем более обидно получать глупые ошибки, которые вызваны невнимательностью обучающихся, пропусками переменных, случайными потерями знаков, скобок и другими различными ляпами.

Для того чтобы снизить вероятность ошибок, необходимо использовать различные методики предупреждения типичных ошибок, что будет в итоге способствовать повышению уровня математической подготовки школьников.

Разбор, анализ и проработка ошибок и неточностей, допущенных при выполнении задания

Организация работы обучающихся, направленной на анализ и исправление допущенных недочетов называется работой над ошибками. Ее основной целью является разбор, анализ и проработка ошибок и неточностей, допущенных при выполнении задания. Правильно организованная работа обучающихся обеспечивает:

• дифференцированный подход к обучению;

• является профилактикой будущих ошибок;

• позволяет своевременно ликвидировать пробелы в знаниях и навыках детей;

• формирует умение систематизировать и обобщать, закреплять полученные знания.

Грамотный, творческий подход учителя к организации работы над ошибками создает условия для развития адекватного отношения обучающегося к ошибкам, умение работать с ними.

Можно говорить о том, что, после проведения работы над ошибками итоговая оценка отражает действительный уровень усвоения знаний и умений обучающихся. Существует практика, когда некоторые учителя практикуют выставление оценок за каждую проведенную работу. При этом, часто бывает, что после работы над ошибками, отметка за проверяемую работу повышается (как правило на один бал).

Обычно, работа над ошибками проводится в классе, под руководством учителя, но может проводиться и дома, возможно, под контролем родителей. Если учитель считает возможным дать выполнение работы над ошибками в качестве домашнего задания, он должен убедиться, что все обучающиеся знают и помнят основной алгоритм действий по выполнению работы. Целесообразно, каждому ребенку выдать памятку с порядком выполнения действий. Кроме этого, необходимо предварительно, на уроке провести общий анализ допущенных ошибок.

В классе, работу над ошибками проводят, как правило, после контрольных, самостоятельных или творческих работ. Работе над ошибками может быть посвящен, как весь урок, так и его часть. Это зависит от характера и количества видов ошибок, от уровня самостоятельности обучающихся и т.п. По усмотрению учителя возможны: фронтальная, групповая, парная, индивидуальная работа.

Основные этапы и формы организации работы над ошибками на уроке

При работе на уроке выделяют несколько основных этапов:

• консультация;

• коррекция знаний и умений;

• диагностика результатов;

• оценочная деятельность.

По усмотрению учителя возможны: фронтальная, групповая, индивидуальная работа.

Рассмотрим несколько вариантов проведения работы над ошибками

В начале урока, после проведения общего анализа проверенной работы, учитель просит поднять руку тех обучающихся, которые допустили ошибки при выполнении первого задания. К доске приглашается один из обучающихся, который будет выполнять и комментировать аналогичное задание у доски. Обучающийся определяется либо по его желанию, либо по решению учителя. Остальные обучающиеся выполняют работу у себя в тетрадях. Затем все самостоятельно решают задание проверочной работы. Таким образом, дети прорешивая аналогичное задание, прорабатывают ошибки, допущенные не только ими самими, но и остальными обучающимися. Такой подход целесообразен, когда в данном задании большинство обучающихся допустили ошибки.

Следующая форма работы используется, когда один, или несколько обучающихся допустили ошибки в задании, которое большинство обучающихся выполнили правильно. При данной форме организации урока один обучающийся выполняет работу над своими ошибками у доски, остальные обучающиеся исправляют свои недочеты в тетрадях или выполняют индивидуальные задания. С одной стороны, этот метод позволяет экономить время, затрачиваемое на данную деятельность, с другой — учитель не может контролировать деятельность других детей. Для исправления возникшей ситуации, нужно обеспечить каждому обучающемуся возможность обратиться к учителю за помощью, за консультацией.

Бывают ситуации, когда часть обучающихся выполнила проверочную работу на «отлично», т.е. возникает необходимость организовать деятельность этих обучающихся, и, одновременно организовать выполнение работы над ошибками остальными обучающимися. В этом случае, есть несколько вариантов организации работы на уроке.

Во-первых, «отличникам» можно предложить выполнение индивидуальных заданий повышенного или углубленного уровней, творческие задания, работу по подготовке, например, информационного сообщения к следующему уроку. С остальными обучающимися проводится работа над ошибками.

Во-вторых, обучающихся, показавших высокий уровень усвоения учебного материала, можно привлечь к консультированию других детей. В этом случае возможна организация групповой и (или) парной работы.

Имеют место случаи, когда педагог, в целях экономии времени, выделяет только типичные ошибки, допущенные обучающимися при выполнении проверочной работы, и на уроке проводят работу только таким видом ошибок. В этом случае работа организовывается фронтально, анализ и исправление типичных ошибок и недочетов выполняет весь класс вместе. При этом у доски работают обучающиеся по желанию, по очереди или по решению учителя, в зависимости от того, кто какие ошибки допустил.

Алгоритм действий по выполнению работы над ошибками

Алгоритм действий по проведению работы над ошибками определяется учителем самостоятельно, исходя из особенностей класса, общего уровня обученности и т.д.

Например, алгоритм действий обучающегося может выглядеть следующим образом:

1. просмотреть всю работу, обратить внимание на исправления учителя;
2. найти ошибку, выписать задание, в котором она допущена, проанализировать причину ее возникновения:

• ошибка в вычислении – перерешать;

• ошибка в применении формулы (правила, закона) — вспомнить нужную формулу (правило, закон) по данной теме, применить при решении;

• ошибка в построении рисунка – повторить материал в учебнике и выполнить рисунок правильно;

1. решить аналогичное задание

Памятка-помощник

В практике работы некоторых учителей встречается использование памяток, которые изготавливаются педагогом и раздаются каждому обучающемуся. Памятки могут быть индивидуальными. Работа с памятками выполняется под контролем педагога.

В памятке пронумерованы и записаны основные группы ошибок в виде:

Тема «….».

Примеры.

1.  
2.  
3. …

Если учитель планирует проводить работу над ошибками, с использованием памяток, то при проверке работы на полях тетради, напротив задания, в котором допущена ошибка, ставится номер, соответствующего задания в памятке. Это не только облегчает работу обучающихся, но и совершенствует систему обучения. Обучающийся неоднократно обращается к данной памятке, что способствует лучшему запоминанию учебного материала.

Проверка и подведение итогов работы над ошибками

В конце работы над ошибками необходимо провести проверку. Существует несколько форм ее организации.

• самопроверка;

• парная работа;

• групповая работа, когда «сильные» обучающиеся выступают в роли консультантов;

• фронтальная работа со всем классом.

Во всех случаях, необходимо обеспечить возможность каждому обучающемуся консультирования и помощи учителя, если возникают трудности.

В конце работы над ошибками, как и в конце любого урока, необходимо провести рефлексию. Дети анализируют свои ошибки, отмечают, как изменились собственные умения, отмечают моменты, которые остались не понятны, говорят о том, что вызвало трудности и высказывают свои предложения.

Следует отметить, что проведение работы над ошибками является обязательным и систематическим действием после каждой контрольной и проверочной работы. При этом необходимо обращать внимание и прорабатывать все ошибки, допущенные обучающимися, тщательно проводить отбор задач и примеров для отработки знаний и умений, для закрепления пройденного материала.

Превентивная деятельность учителя по предупреждению ошибок

Большая часть ошибок, допускаемых обучающимися, не связана с отсутствием или наличием знаний, хотя, конечно, доведение до уровня автоматизма ряда вычислительных операций позволяет существенно снизить вероятность появления ошибок. Однако при этом необходимо, чтобы обучающийся все равно руководствовался нужными правилами и постоянно сохранял концентрацию внимания.

Знание определенных правил нужно и для того, чтобы обучающийся мог проверить правильность решения и дать его обоснование. В тоже время многие школьники воспринимают курс алгебры в качестве набора правил, которые абсолютно не связаны между собой, поэтому они заучиваются исключительно для решения какой-то конкретной задачи, а по истечению незначительного промежутка времени просто забываются. В этой связи требуется организовывать процесс обучения правилам с использованием приемов, которые активизируют рефлексивную деятельность школьников по предупреждению и исправлению ошибок, возникающих при формальном усвоении правил.

Если процесс поиска и исправления ошибок сделать максимально поучительным для обучающихся, то анализ ошибок может стать эффективным средством для развития познавательного интереса к математике.

Наиболее распространенными ошибками являются:

• незнание или непонимание правил, формул и определений;

• неправильное применение формул или неумение правильно применять определения и правила;

• совершение вычислительных ошибок;

• невнимательное чтение условий задачи;

• отказ от использования свойств фигур при решении геометрических задач;

• неправильное раскрытие скобок;

• совершение логических ошибок при решении текстовых задач;

• применение формул сокращенного умножения.

К основным причинам совершения ошибок по математике относят:

• пропуски уроков, в результате чего появляются пробелы в знаниях;

• поверхностное изучение нового материала;

• повышенная усталость, вызванная чрезмерной нагрузкой или недостаточным сном, в результате чего понижается скорость мышления и снижается уровень внимания;

• неаккуратный почерк, из-за чего учитель часто не понимает, что написал обучающийся;

• скорость работы. При этом на появление ошибок влияет как высокая скорость работы, из-за которой обучающийся просто не стремиться вникнуть в суть задания, так и медленная. В последнем случае замедленная скорость мыслительных операций не позволяет обучающемуся в полной мере контролировать себя, а из-за «зависания» нужная информация просто удаляется из «оперативной памяти»;

• полное либо кратковременное переключение внимания с одной деятельности на другую;

• низкая мотивация, в результате которой теряется внимание и появляются ошибки.

Объяснение и предупреждение ошибок

Для предупреждения ошибок и сведения их к минимуму используются следующие профилактические мероприятия и действия:

• постоянный разбор наиболее распространенных ошибок в классе;

• предлагаемые обучающимся письменные задания должны быть максимально удобны для восприятия, то есть грамотно сформулированными и понятными;

• подбор заданий и упражнений, которые будут вызывать у детей интерес и повышенное внимание;

• учитель должен при объяснении нового материала стараться предугадать возможные ошибки обучающихся и разработать систему заданий, которые позволят правильно усвоить новые понятия;

• использование правил удобных для запоминания и исключающих двойную их трактовку.

Кроме того, учитель математики должен помнить, что систематическое и планомерное повторение является основным инструментом для ликвидации пробелов знаний.

Также рекомендуется при объяснении нового материала активно применять определения и теоремы, которые изучались ранее. Так, при изучении темы «Теоремы сложения» целесообразно организовать повторение ряда теоретических вопросов:

1. Изменение тригонометрических функций при возрастании и убывании аргумента.

2. Четные и нечетные функции.

3. Таблицы значений тригонометрических функций.

4. Знаки тригонометрических функций.

Дополнительно выполняются следующие задания:

1. Необходимо определить четность и нечестность тригонометрических функций:

1. Найдите область определения функции y = x2 – 6x + 10.

2. Определите, при каких значениях x, функции y = sin x и y = cos x принимают одинаковые значения?

Перед тем как приступить к изучению темы «Первообразная и интеграл», следует повторить все формулы дифференцирования. После этого обучающиеся выполняют самостоятельную работу (время решения – 10-15 минут), во время которой школьникам предлагаются карточки-задания, где «опущены» один-два компонента из формулы дифференцирования, а также приведены две функции, производные которых необходимо найти.

Затем проводиться проверка работы и анализ совершенных ошибок, что необходимо для выявления пробелов в знаниях и проведения работы по их устранению.

Список литературы:

1. Азиев И.К. Индивидуальные задания для устранения ошибок. // Журнал «Математика в школе» – 1993 г. – №5, с. 9.
2. Амонашвили Ш.А. Воспитательная и образовательная функции оценки обучения школьников: Экспериментальное педагогическое исследование. – М.: Педагогика, 1984. – 296 с.
3. Бабанский Ю.К. Педагогика. М.: Просвещение, 1983.
4. Волович И.Б. Наука обучать: Технология преподавания математики. – М.: LINKA-PRESS. 1995. – 280 с.
5. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990. – 224 с.
6. Груденов Я.И. Психолого-дидактические основы методике обучения математики. – газета «Математика», 1987 г. с. 91-96.
7. Гуцанович С.А. Дидактические основы математического развития учащихся: Монография. – Минск: БГПУ им. М. Танка, 1999. – 301 с.
8. Давыдов В. В. Проблемы развивающего обучения. Опыт теоретического и экспериментального исследования / В. В. Давыдов. – М.: Педагогика, 1986. – 239 с.
9. Далингер В.А. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя. – М.: Просвещение, 1991. – 80 с.
10. Далингер В.А. Обучение учащихся доказательству теорем: Учебное пособие. – Омск: Омский пед. ин-т, 1990. – 127 с.
11. Действующие учебники и учебные пособия по математике для средней школы.
12. Журналы «Математика в школе» за 1970-1990 гг.
13. Колягин Ю.М. Задачи в обучении математике: Математические задачи как средство обучения и развития учащихся: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
14. Колягин Ю.М. Задачи в обучении математике: Обучение математике через задачи и обучение решению задач: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
15. Метельский Н.В. Дидактика математики. – Минск: Изд-во БГУ, 1982–254с.
16. Методика преподавания математики в средней школе: Общая методика: учеб. пособие; сост. Р. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – 336 с.
17. Новик И.А. Формирование методической культуры учителя математики в педвузе. – Мн.: БГПУ им. М. Танка, 2002. – 193 с.
18. Новик, И. А. Практикум по методике преподавания математики / И. А. Новик. – Минск: Выш. шк., 1984. – 175 с.
19. Оганесян В.А. Принципы отбора основного содержания обучения математике в средней школе. – Ереван: Луис, 1984. – 215 с.
20. Рогановский, Н. М. Методика преподавания математики в средней школе: учеб. пособие / Н. М. Рогановский. – Минск: Выш. шк., 1990. – 267 с.
21. Селевко, Г. К. Современные образовательные технологии: учеб. пособие / Г. К. Селевко. – М.: Народное образование, 1998. – 256 с.
22. Столяр, А. А. Педагогика математики: учеб. пособие / А. А. Столяр. – Минск: Выш. шк., 1986. – 414 с.
23. Темербекова, А. А. Методика преподавания математики: учеб. пособие / А. А. Темербекова. – М.: ВЛАДОС, 2003. – 176 с.
24. Фридман, Л. М. Психолого-педагогические основы обучения математике в школе / Л. М. Фридман. – М.: Просвещение, 1983. – 160 с.
25. Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов // Журнал «Математика в школе» – 1999 г. – №6, с. 21.
26. Эрдниев, П. М. Обучение математике в школе. Укрупнение дидактических единиц / П. М. Эрдниев, Б. Л. Эрдниев. – М.: Столетие, 1996. – 320 с.
27. Якиманская И.С. Личностно-ориентированное обучение в современной школе – М., 1996. – 347 с.
28. Якиманская И.С. Психологические основы математического образования. – М.: Acadiia, 2004.
29. Ярский А.С. Что делать с ошибками // Журнал «Математика в школе» – 1998 г. – №2, с. 8-14.