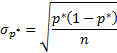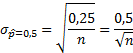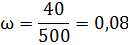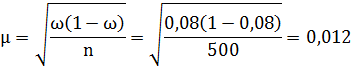Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
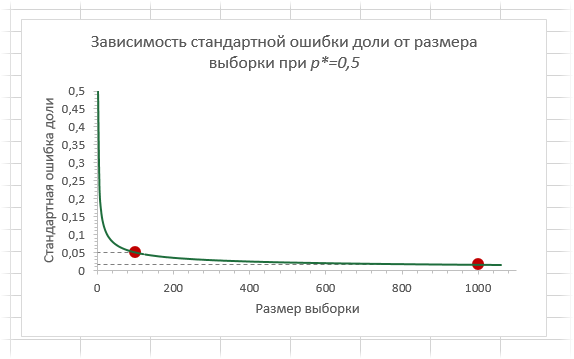
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.
Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.
Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:
Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы
Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.
Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.
Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:
Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы
Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
При обследовании 500 образцов изделий, отобранных из партии готовой продукции предприятия в случайном порядке, 40 оказались нестандартными.
С вероятностью 0,954 определите пределы, в которых находится доля нестандартной продукции, выпускаемой заводом.
Решение:
Рассчитаем долю нестандартной продукции в выборочной совокупности:
Средняя ошибка выборочной доли при повторном отборе рассчитывается по формуле:
где n – численность выборки.
С вероятностью 0,954 рассчитаем предельную ошибку выборочной доли по формуле:
Δ = μ × t
где
t – коэффициент доверия.
Значение коэффициента доверия t определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного наблюдения и берётся из готовых таблиц.
При Р = 0,954, t = 2.
Δ = t * μ = 2 * 0,012 = 0,024
С вероятностью 0,954 можно утверждать, что доля нестандартной продукции в партии товара колеблется:
ω – Δ ˂ р ˂ ω + Δ
0,08 – 0,02 ˂ р ˂ 0,08+0,02
0,06 ˂ р ˂ 0,10
или
6% ˂ р ˂ 10%
Расчет средней ошибки
|
Способ отбора |
Средняя |
|
|
для средней |
для доли |
|
|
Повторный (формула |
|
– дисперсия доли |
|
Бесповторный |
|
|
Порядок расчета ошибок выборки для средней:
1. По данным
выборочного наблюдения устанавливается
величина выборочной средней (
).
2. Определяется
средняя ошибка выборки:
а) для повторного
отбора:
;
(8.4)
б) для бесповторного
отбора (согласно исходным данным):
.
(8.5)
3. С заданной
вероятностью P(t)
находится предельная
ошибка
выборки – это максимально возможное
расхождение (
),
т.е. максимум ошибки при заданной
вероятности ее появления:
,
(8.6)
где t
– заданный коэффициент доверия (критерий
кратности ошибки выборки);
– предельная ошибка выборки.
Множитель t
определяется в зависимости от того, с
какой доверительной вероятностью P(t)
надо гарантировать результаты выборочного
наблюдения. На практике пользуются
готовыми таблицами значений (табл. 8.2).
Таблица 8.2
Доверительная
вероятность и коэффициент доверия
|
Коэффициент |
Вероятность |
|
0,0 |
0,000 |
|
0,5 |
0,383 |
|
1,0 |
0,683 |
|
1,5 |
0,866 |
|
2,0 |
0,954 |
|
3,0 |
0,997 |
4. Доверительные
пределы, в которых следует ожидать
генеральную среднюю, составляют:
.
(8.7)
Порядок расчета ошибок для доли:
1. По данным
выборочного наблюдения рассчитывается
величина выборочной доли:
,
где m
– численность единиц выборочной
совокупности, обладающих данным
признаком; n
– численность выборочной совокупности.
2. Находится средняя
ошибка для доли:
а) при повторном
отборе:
;
(8.8)
б) при бесповторном
отборе:
.
(8.9)
3. С заданной
вероятностью P(t)
находится предельная ошибка выборки
для доли:
.
(8.10)
4. Расчет предельной
границы, в которой следует ожидать
генеральную долю, составляет:
.
(8.11)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- →
- →
Калькулятор ошибки выборки
Рассчитать статистическую ошибку и размер выборки
Введены некорректные данные
Доля признака
Ожидаемая доля признака, для которого рассчитывается ошибка. В случае, если данные о доле признака отсутствуют, необходимо использовать значение равное 50, при котором достигается максимальная ошибка.
Объем выборки
Количество людей, которых опросили для оценки доли.
Уровень значимости
Вероятность того, что реальная доля признака лежит в границах полученного доверительного интервала. Уровень значимости выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно 95%.
125315, г. Москва, Ленинградский проспект 68, стр. 2, 3 этаж
+7 (495) 648 78 20
client@tiburon-research.ru