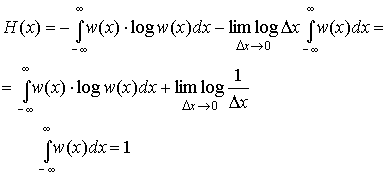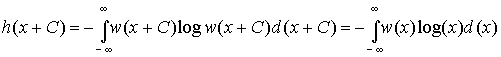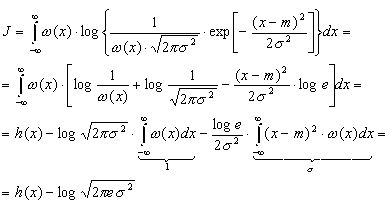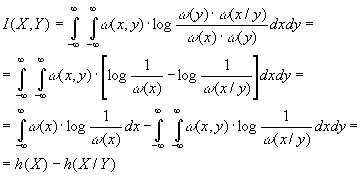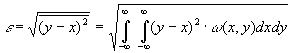Ошибки квантования
В реальных
устройствах цифровой обработки сигналов
необходимо учитывать
эффекты, обусловленные квантованием
входных сигналов
и конечной разрядностью всех регистров.
Источниками ошибок
в процессах обработки сигналов являются
округление (усечение)
результатов арифметических операций,
шум аналого-цифрового квантования
входных аналоговых сигналов, неточность
реализации характеристик цифровых
фильтров из-за округления их коэффициентов
(параметров). В дальнейшем с целью
упрощения анализа предполагается, что
вес источники ошибок независимы и не
коррелируют с входным сигналом (хотя
мы и рассмотрим явление предельных
циклов, обусловленных коррелированным
шумом округления).
Эффект квантования
приводят в конечном итоге к погрешностями выходных сигналах цифровых фильтров
(ЦФ), а в некоторыхслучаяхи к неустойчивым
режимам. Выходную ошибку ЦФ будем
рассчитыватькаксуперпозицию ошибок, обусловленных
каждым независимымисточником.
Квантование
чисел– нелинейная операция;m-разрядное
двоичное числоА
представляетсяb-разрядным
двоичнымчислом
B=F(A),
причем b
< m. В
результате квантования число А
представляется
с ошибкой
е
=B–А= F(А)
–А.
Шаг квантования
Q
=
2–b
определяется весом младшего
числовогоразряда.
При квантовании
используется усечение или округление.
Усечение
числаА
состоит в отбрасываниит
– b
младших разрядов числа, при этом
ошибка усечения
eус=
Fус(А) –А.
Оценим величину
ошибки в предположении m
» b.
Для положительных чисел при любом
способе кодирования –2–b
<еус
0. Для
отрицательных чисел при использовании
прямого и обратного кодов ошибка усечения
неотрицательна: 0еус
< 2–b,
а в дополнительном коде эта ошибка
неположительна: 0еус
> –2–b.
Таким образом, во всех случаях
абсолютное значение ошибки усечения
не превосходит шага квантования:maxeус
< 2–b
=Q.
Округление
m-разрядного
числаA
доb
разрядов (b «
m)b-й
разряд остается неизменным или
увеличивается на единицув
зависимости от соотношения (больше –
меньше) между отбрасываемой дробью
0,аb+1…ат
и величиной
,
гдеаi–i-й
разряд числаA;
i =
b+1,
…,m.
Округление можно практически выполнить
путемприбавления
единицы к (b+1)-му
разряду и усечения полученного числа
до b разрядов.
В таком случае ошибка округления еoк
=
fок(А)–
А
при всех способах кодирования лежит в
пределах
–2–(b+1)
<
еoк
< 2–(b+1)
(1.11)
и, следовательно,
max<2–b
= Q/2.
(1.12)
В задачах ЦОС
ошибки квантования чисел рассматриваются
как стационарный
шумоподобный процесс с равномерным
распределением
вероятности по диапазону распределения
ошибок квантования.
(nT)
x(nT)
e(nT)
Рис. 3. Линейная модель квантования
сигналов:
(nT) —дискретный
или m-разрядный
цифровой сигнал (m
> b);
x(nT) —квантованный
b-разрядный
цифровой сигнал;
e(nT)
= x(nT)
–f(nT)
— ошибка
квантования.
Квантование
дискретных сигналов состоит в
представлении отсчета
(выборки сигнала) числамиx(nT),
содержащими b
числовых разрядов. Квантование сигналов,
как и квантование
чисел – нелинейная операция. Однако
при анализе процессов в ЦФ целесообразно
использовать линейную модель квантования
сигналов – рис. 3.
Верхнее значение ошибки квантования
определяетсясоотношением
(1.11) или (1.12).
Вероятностные
оценки ошибок квантования основаны на
предположениях о том, что
последовательностье(пТ)являетсястационарным
случайным процессом с равномерным
распределением вероятности по
диапазону ошибок квантования ие(пТ)
не коррелирован
с f(nT).
Математическое
ожидание (среднее значение) e
и дисперсия
ошибки квантованияе
определяются
по формулам:
=E(е)
=,
=
=
=E(е2)
–,
где ре
— плотность вероятности ошибки. По
этим формуламвычисляются
математическое ожидание и дисперсия
для ошибок
округления и усечения:
=
=
В логарифмическоммасштабе
=
Лекция 2
Вычислите ошибку квантования
В этом примере показано, как вычислить и сравнить статистику ошибки квантования сигнала при использовании различных методов округления.
Во-первых, случайный сигнал создается, который порождает линейную оболочку столбцов квантизатора.
Затем сигнал квантуется, соответственно, с округлением методов ‘фиксируют’, ‘ставят в тупик’, ‘перекрывают’, ‘самый близкий’, и ‘конвергентный’, и статистические данные сигнала оцениваются.
Теоретическая функция плотности вероятности ошибки квантования будет вычислена с ERRPDF, теоретическое среднее значение ошибки квантования будет вычислено с ERRMEAN, и теоретическое отклонение ошибки квантования будет вычислено с ERRVAR.
Равномерно распределенный случайный сигнал
Сначала мы создаем равномерно распределенный случайный сигнал, который охватывает область-1 к 1 из квантизаторов фиксированной точки, на которые мы посмотрим.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Фиксация: вокруг по направлению к нулю.
Заметьте, что с округлением ‘фиксации’, функция плотности вероятности вдвое более широка, чем другие. Поэтому отклонение в четыре раза больше чем это других.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Пол: вокруг к минус бесконечность.
Пол, округляющийся, часто называется усечением, когда используется с целыми числами и числами фиксированной точки, которые представлены в дополнении two. Это — наиболее распространенный режим округления процессоров DSP, потому что это требует, чтобы никакое оборудование не реализовало. Пол не производит квантованные значения, которые являются как близко к истинным значениям, когда ROUND будет, но это имеет то же отклонение, и маленькие сигналы, которые варьируются по знаку, будут обнаружены, тогда как в ROUND они будут потеряны.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Потолок: вокруг к плюс бесконечность.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.
Вокруг более точно, чем пол, но все значения, меньшие, чем eps (q), округлены, чтобы обнулить и потеряны — также.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.
Конвергентное округление устраняет смещение, введенное обычным «раундом», вызванным, всегда округляя связь в том же направлении.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Сравнение самых близких по сравнению с конвергентным
Функция плотности вероятности появления ошибки для конвергентного округления затрудняет, чтобы различать от того из раунда-к-самому-близкому путем рассмотрения графика.
Ошибка p.d.f. из конвергентных
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
в то время как ошибка p.d.f. из раунда
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Обратите внимание на то, что ошибка p.d.f. из конвергентных симметрично, в то время как вокруг немного склоняется к положительному.
Единственной разницей является направление округления вничью.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Постройте функцию помощника
Функция помощника, которая использовалась, чтобы сгенерировать графики в этом примере, описана ниже.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.
Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.
Чем отличается цифровой аудиосигнал от аналогового?
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).
рис. 1
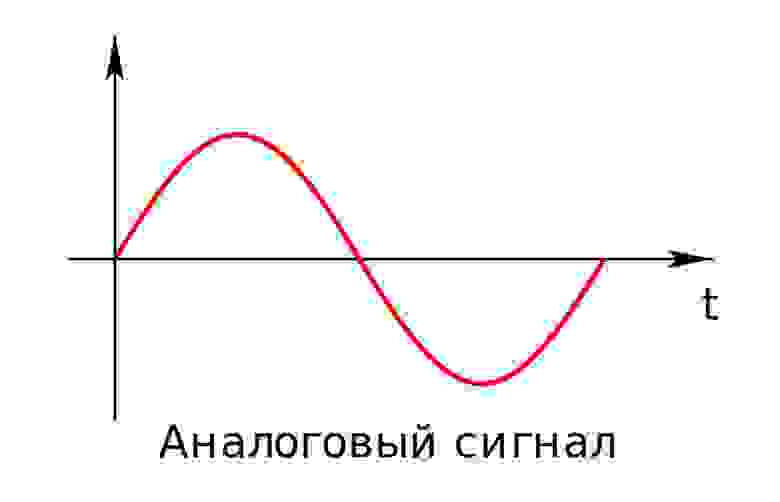
Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).
рис. 2
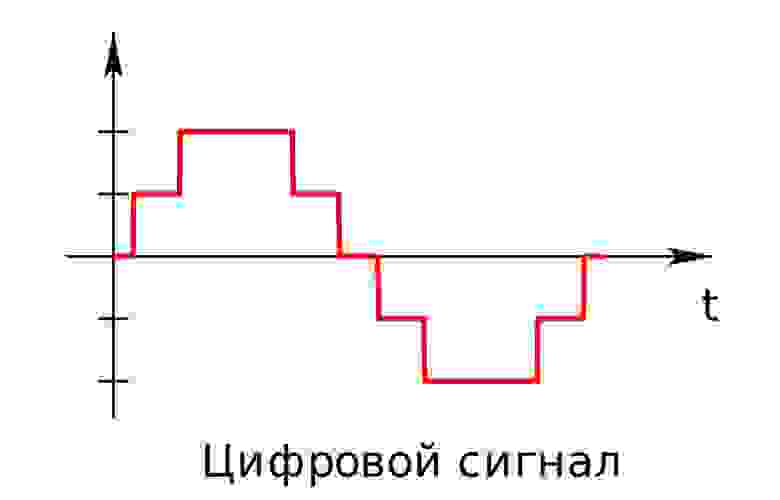
Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).
рис. 3
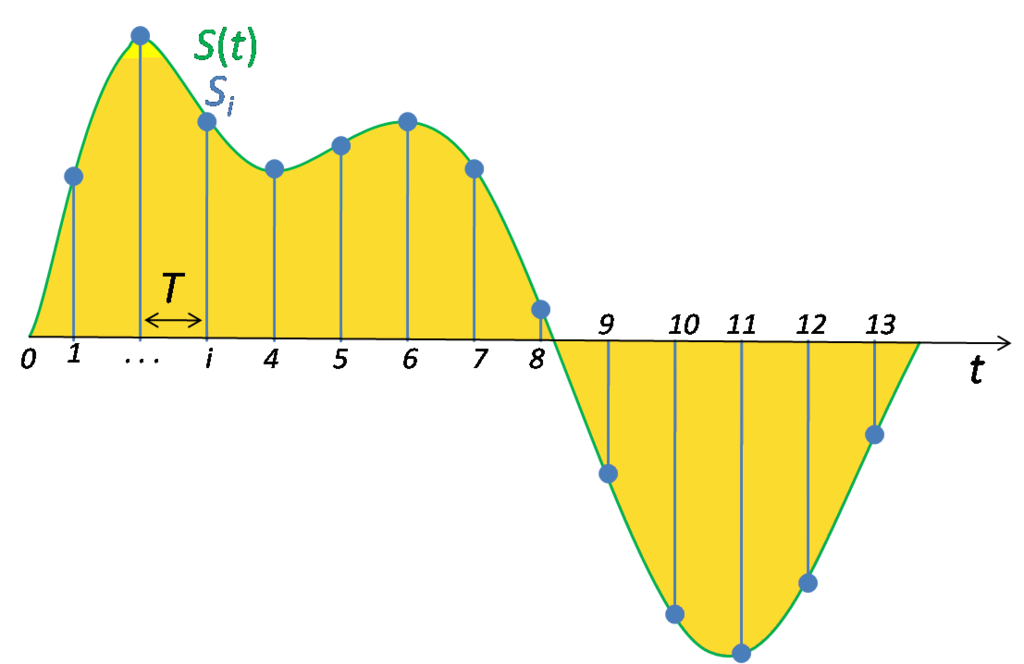
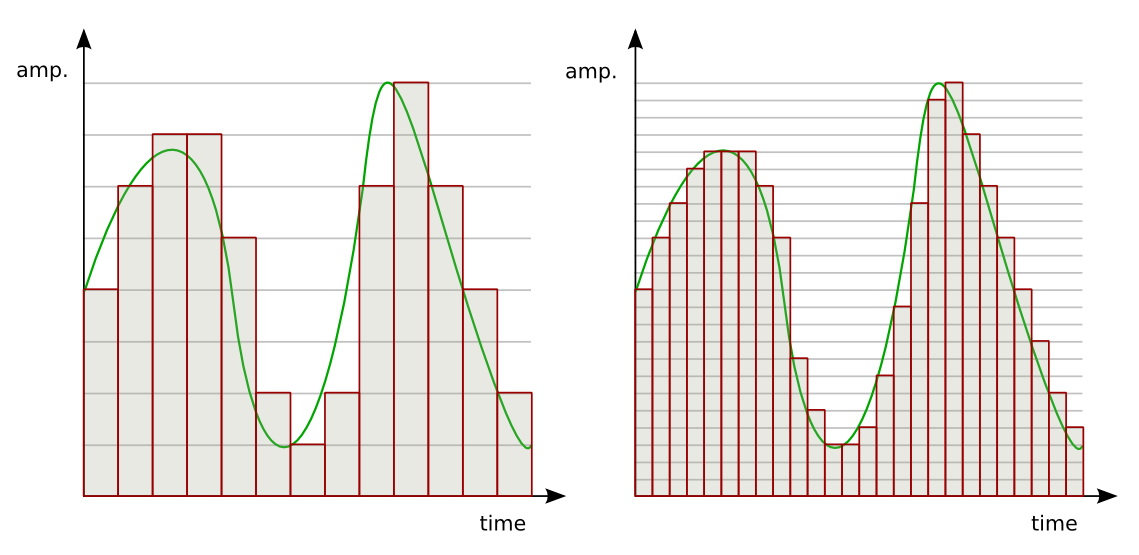
Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).
рис. 4
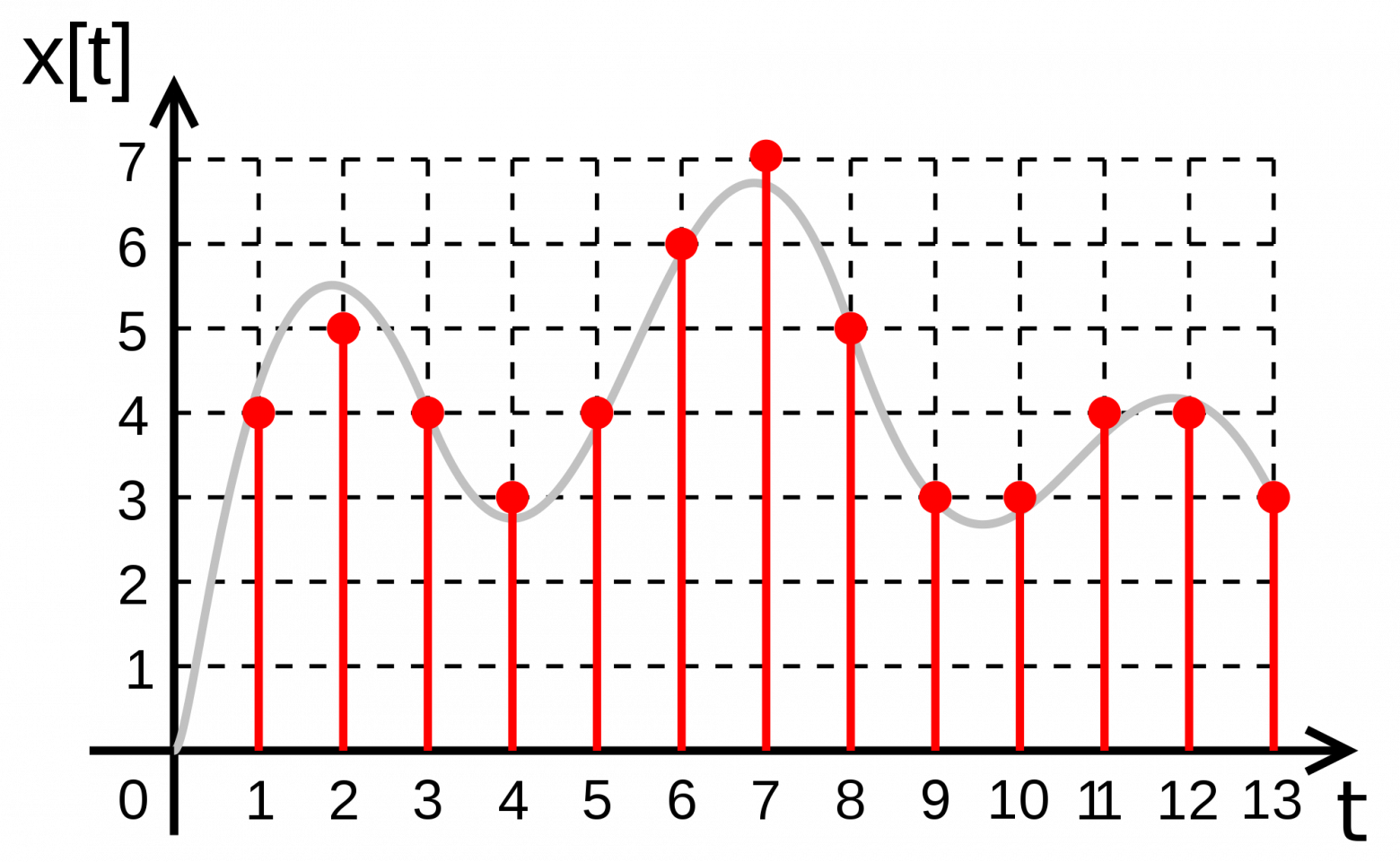
Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).
рис. 5
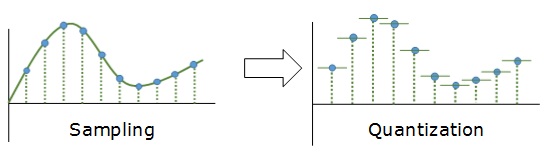
Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).
рис. 6
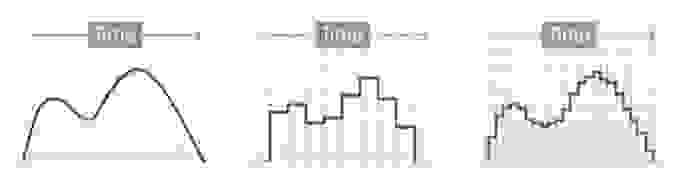
Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)
рис. 7
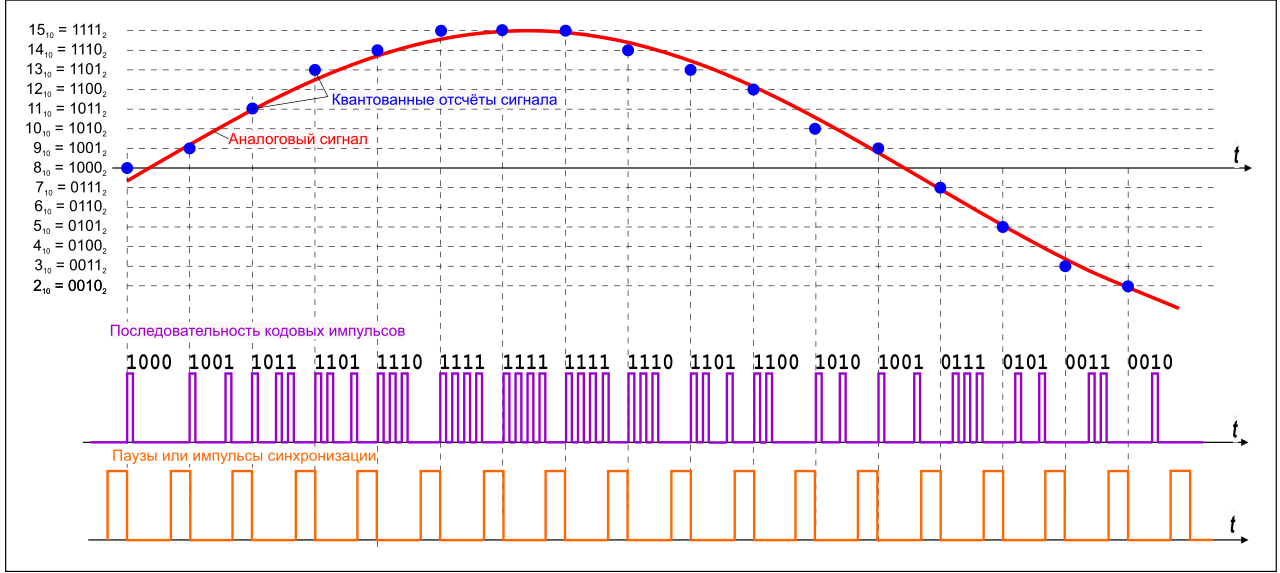
Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).
рис. 8.
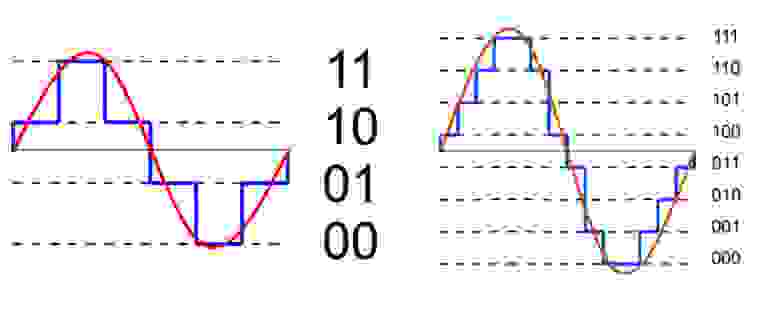
Данная формула позволяет вычислить количество уровней квантования:
Если N — количество уровней квантования,
n — разрядность, то
Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.
При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.
Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением и квантованным значением
(
)
Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).
Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).
рис. 9
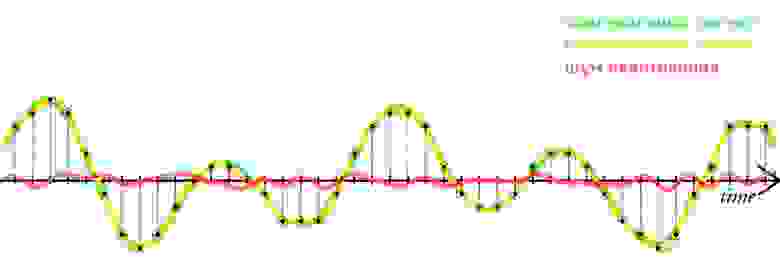
Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).
рис. 10. Интенсивность шумов при разрядности 6 бит и 8 бит
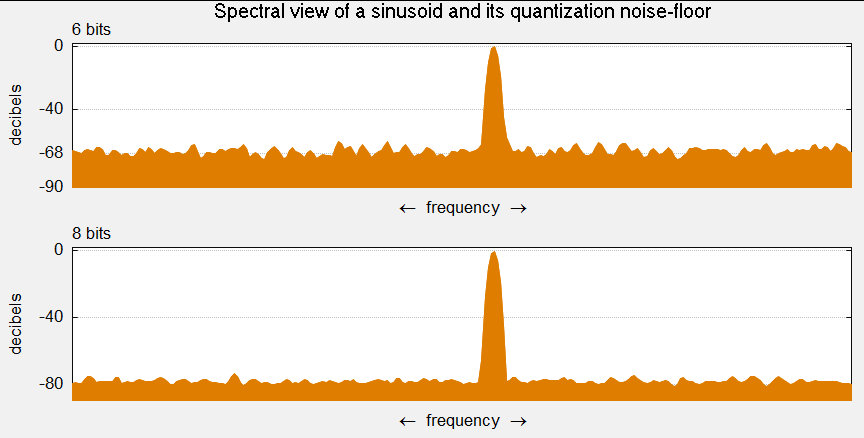
Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.
шум квантования
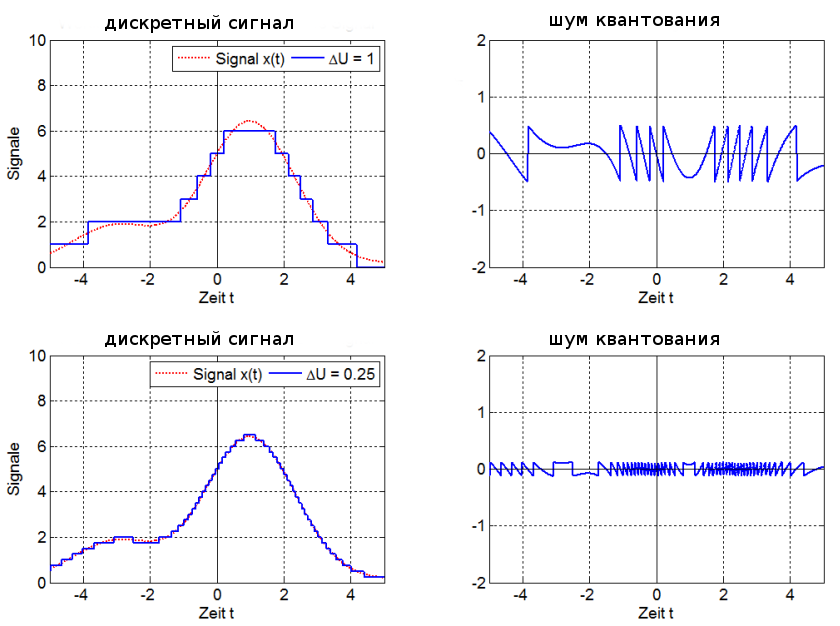
амплитуда сигнала при разрядности 1 бит (сверху) и 4 бит
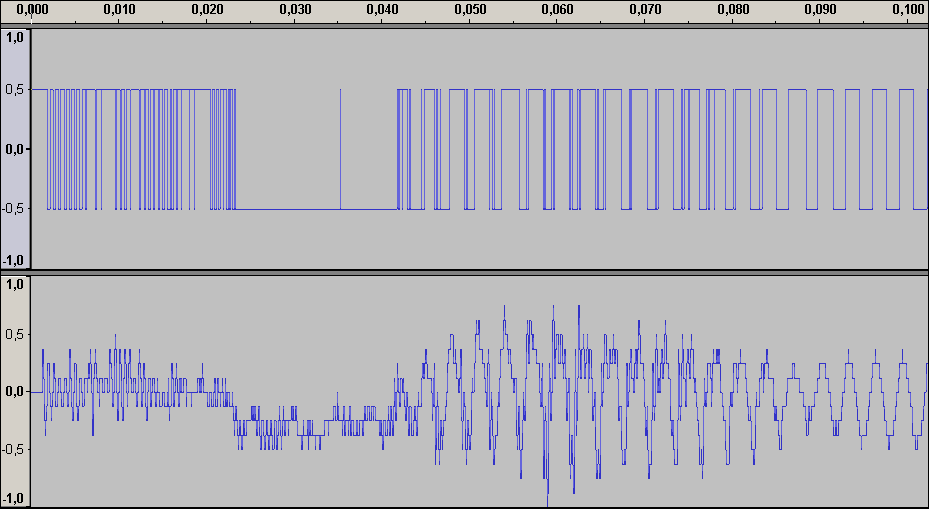
Аудиопример 1: 8bit/44.1kHz, ~50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.
Аудиопример 1
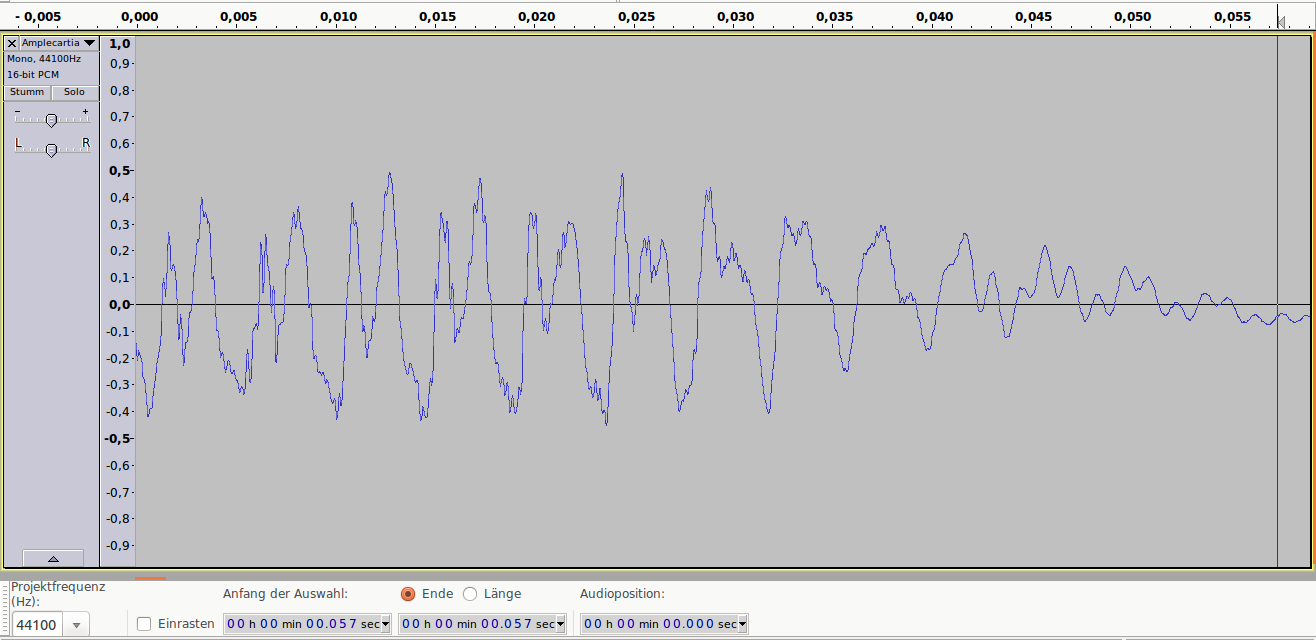
Аудиопример 2: 4bit/48kHz, ~25dB SNR
Аудиопример 2
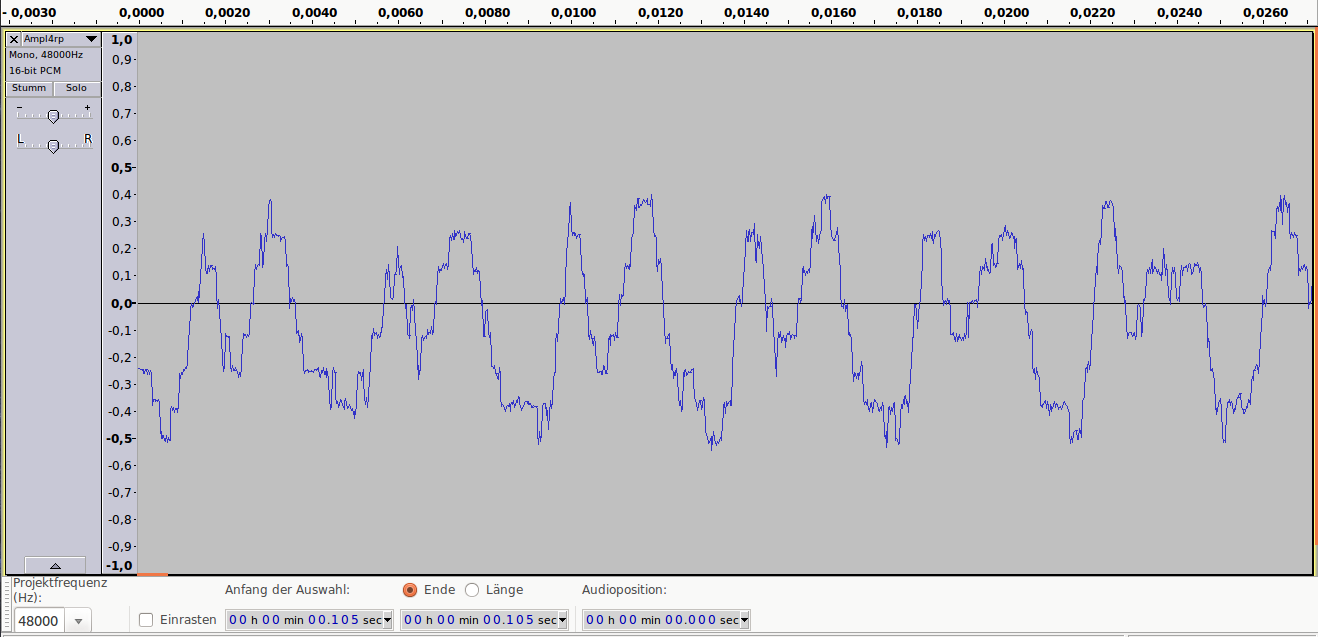
Аудиопример 3: 1bit/48kHz, ~8dB SNR
Аудиопример 3
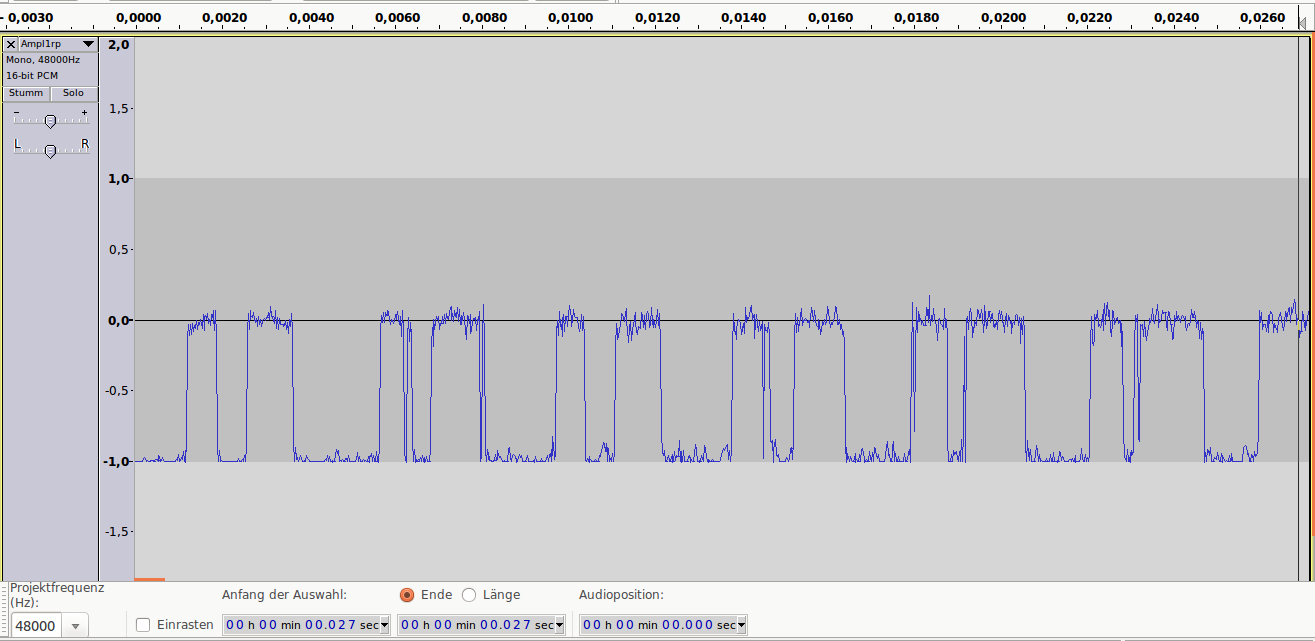
Теперь о дискретизации.
Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то
Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).
Теорема Котельникова гласит:
Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.
Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.
Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.
Алиасинг
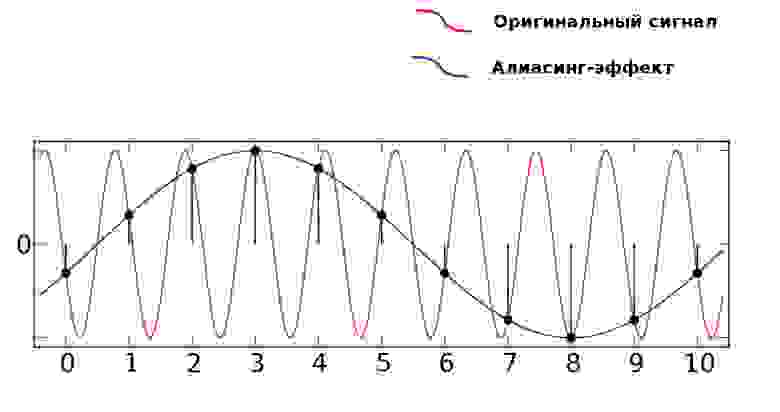
Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.
Аудиопример 4: Линейно возрастающая частота от ~100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.
Спектральный анализ
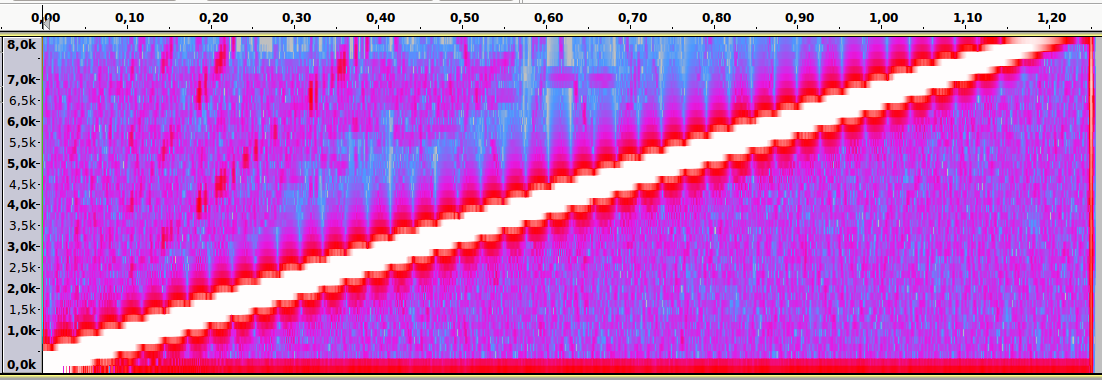
Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг
Спектральный анализ
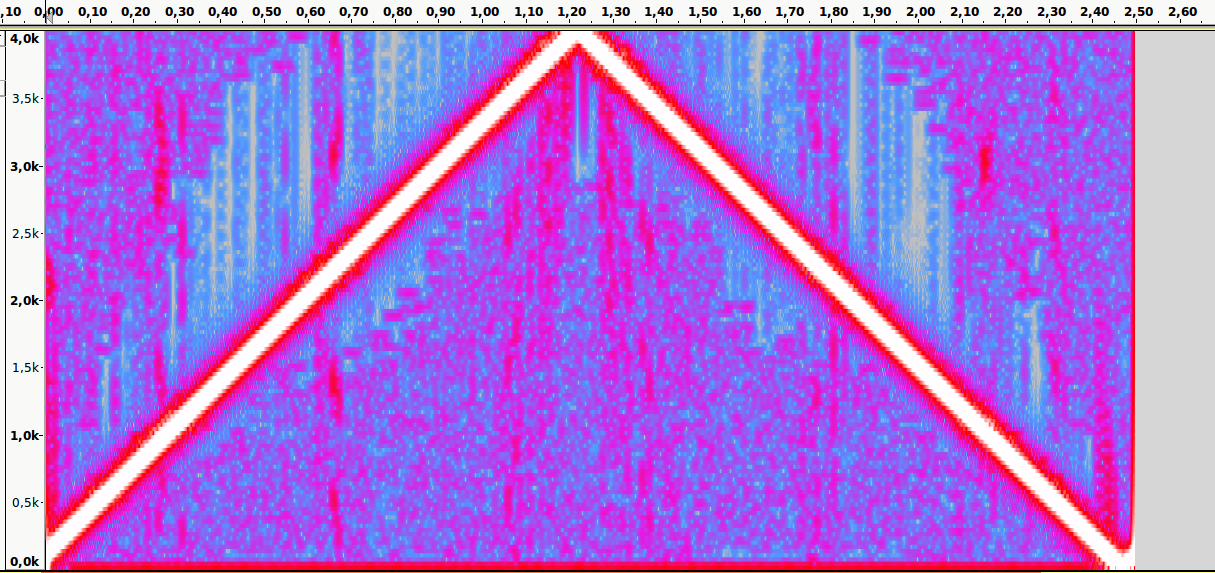
Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.
Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.
Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):
Битрейт = Частота дискретизации * Разрядность * Количество каналов
Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s
При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.
При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.
Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.
При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.
ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.
Существуют 3 метода хранения цифрового аудиоматериала:
- Несжатые («сырые») данные
- Данные, сжатые без потерь
- Данные, сжатые с потерями
Несжатый (RAW) формат данных
содержит просто последовательность бинарных значений.
Именно в таком формате хранится аудиоматериал в Аудио-CD. Несжатый аудиофайл можно открыть, например, в программе Audacity. Они имеют расширение .raw, .pcm, .sam, или же вообще не имеют расширения. RAW не содержит заголовка файла (метаданных).
Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.
Аудиоформаты с сжатием без потерь
Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.
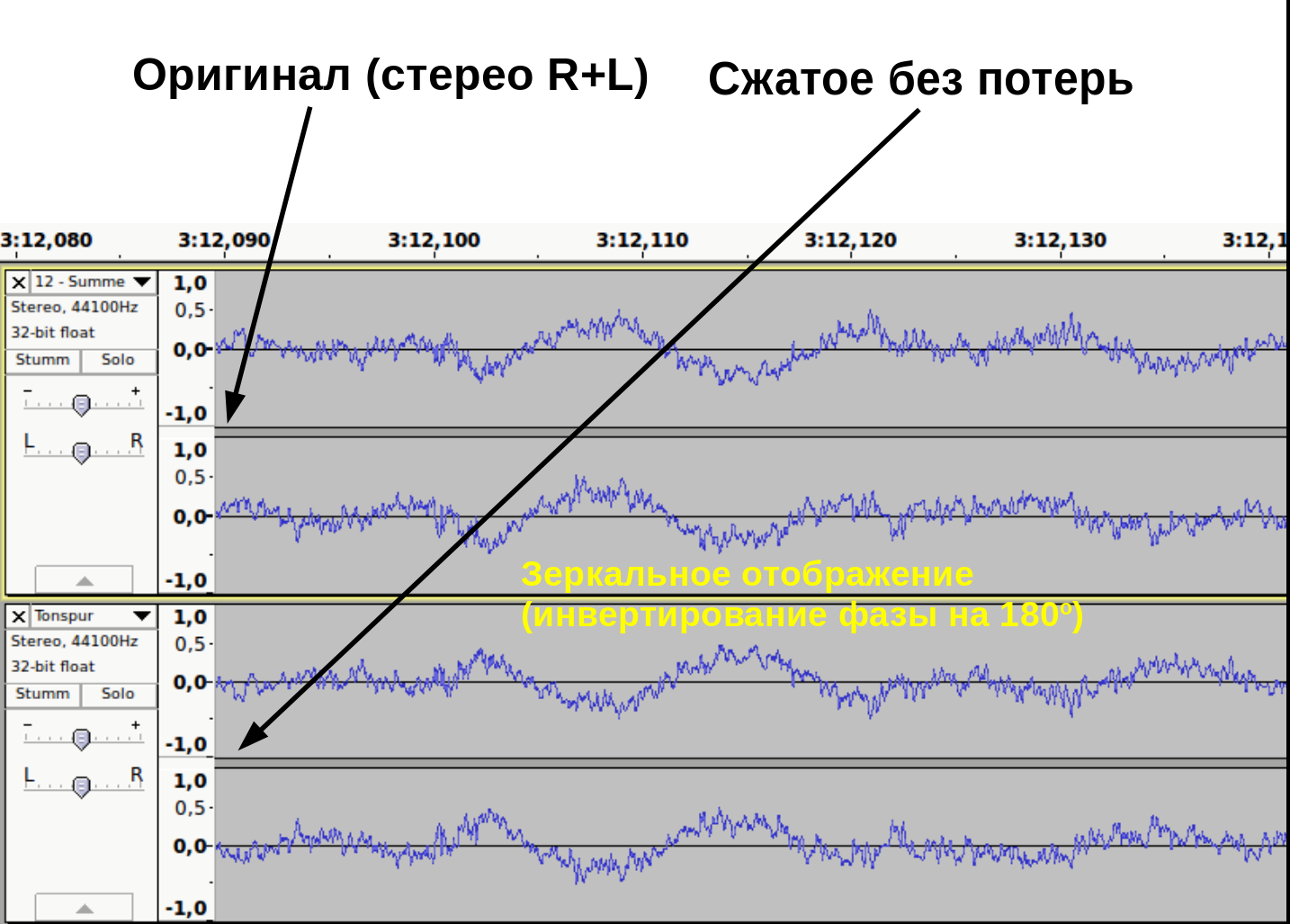
Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.
Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).
рис. 11
Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…
При сжатии с потерями
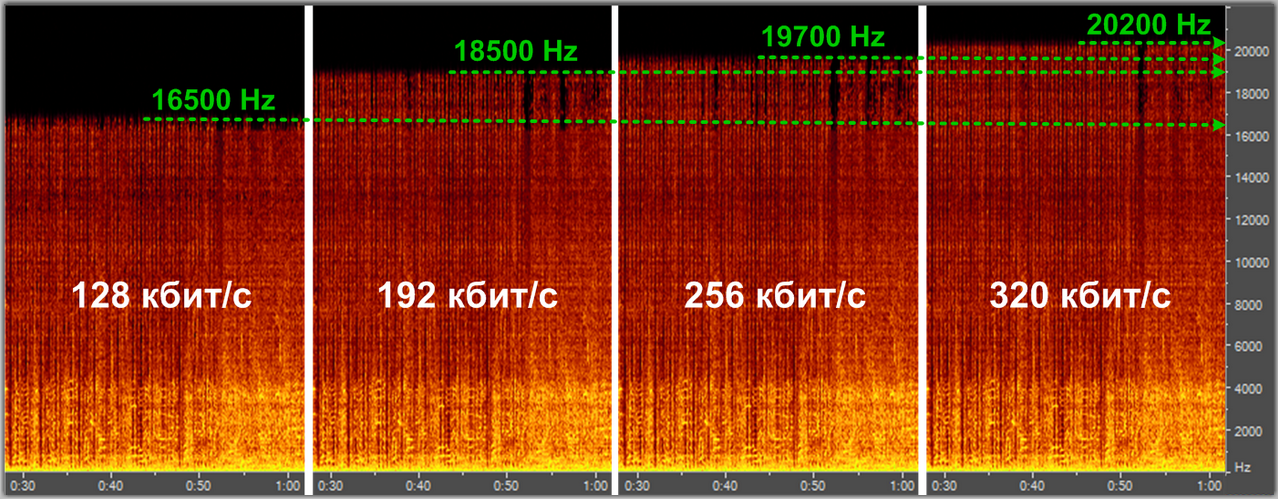
акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».
Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.
Этим и пользуется кодек: 2kHz-звук можно убрать.
Спектральный анализ кодека mp3 с разными уровнями компрессии
Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…
Спасибо за внимание.
UPD:
Если по каким-либо причинам аудиофайлы не загружаются, можете их скачать здесь: cloud.mail.ru/public/HbzU/YEsT34i4c
This example shows how to compute and compare the statistics of the signal quantization error when using various rounding methods. Quantization occurs when a data type cannot represent a value exactly. In these cases, the value must be rounded to the nearest value that can be represented by the data type.
First, a random signal is created that spans the range of the quantizer object. Next, the signal is quantized, respectively, with rounding methods 'fix', 'floor', 'ceil', 'nearest', and 'convergent', and the statistics of the signal are estimated.
The theoretical probability density function of the quantization error is computed with the errpdf function, the theoretical mean of the quantization error is computed with the errmean function, and the theoretical variance of the quantization error is computed with the errvar function.
Create Uniformly Distributed Random Signal
Create a uniformly distributed random signal that spans the domain -1 to 1 of the fixed-point quantizer object q.
q = quantizer([8 7]); r = realmax(q); u = r*(2*rand(50000,1) - 1); xi = linspace(-2*eps(q),2*eps(q),256);
Fix: Round Towards Zero
With 'fix' rounding, the probability density function is twice as wide as the others. For this reason, the variance is four times that of the others.
q = quantizer('fix',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
The theoretical variance is eps(q)^2/3 and the theoretical mean is 0.
Floor: Round Towards Negative Infinity
'floor' rounding is often called truncation when used with integers and fixed-point numbers that are represented using two’s complement notation. It is the most common rounding mode of DSP processors because it requires no hardware to implement. 'floor' does not produce quantized values that are as close to the true values as 'round' will, but it has the same variance. Using 'floor', small signals that vary in sign will be detected, whereas in 'round' they will be lost.
q = quantizer('floor',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
The theoretical variance is eps(q)^2/12 and the theoretical mean is -eps(q)/2.
Ceil: Round Towards Positive Infinity
q = quantizer('ceil',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
The theoretical variance is eps(q)^2/12 and the theoretical mean is eps(q)/2.
Round: Round to Nearest; In a Tie Round to Largest Magnitude
'round' is more accurate than 'floor', but all values smaller than eps(q) get rounded to zero and are lost.
q = quantizer('nearest',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
The theoretical variance is eps(q)^2/12 and the theoretical mean is 0.
Convergent: Round to Nearest; In a Tie Round to Even
'convergent' rounding eliminates the bias introduced by ordinary 'round' caused by always rounding the tie in the same direction.
q = quantizer('convergent',[8 7]);
err = quantize(q,u) - u;
f_t = errpdf(q,xi);
mu_t = errmean(q);
v_t = errvar(q);
qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
The theoretical variance is eps(q)^2/12 and the theoretical mean is 0.
Compare Nearest and Convergent Rounding
The error probability density function for convergent rounding is difficult to distinguish from that of round-to-nearest by looking at the plot.
The error probability density function of convergent is
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
while the error probability density function of round is
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
The error probability density function of convergent is symmetric, while round is slightly biased towards the positive.
The only difference is the direction of rounding in a tie.
x = (-3.5:3.5)'; [x convergent(x) nearest(x)]
ans = 8×3
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
See Also
quantizer | quantize | Rounding
Будем
рассматривать квантование
с равномерным шагом x=const, т.е. равномерное
квантование.
Как было отмечено в §
3.1.1. в процессе квантования неизбежно
возникает ошибка квантования .
Последовательность ошибок квантования
(kt), возникающая при квантовании
процесса с дискретным временем, называется
шумом квантования. Обычно шум квантования
предполагают стационарным эргодическим
случайным процессом.
Чаще всего
интерес представляют максимальное
значение ошибки квантования, ее среднее
значение , равное математическому
ожиданию шума и среднеквадратическое
отклонение ,
равное квадратному корню из дисперсии
шума
(она характеризует мощность шума
квантования). Все эти величины зависят
от способа округления, применяемого
при квантовании, кроме того
и
зависят от закона распределения w()
мгновенных значений сигнала в пределах
шага квантования.
Считая шаг квантования
x малым по сравнению с диапазоном
изменения сигнала, плотность w(x) в
пределах этого шага можно принять
равномерной, т.е.
.
Различают
квантование с округлением, с усечением
и с усечением модуля.
При квантовании
с округлением истинному значению отсчета
приписывает ближайший разрешенный
уровень квантования независимо от того,
находится он сверху или снизу. Очевидно,
что при этом
|
max=0.5x; |
(3.31а) |
Квантование
с округлением требует определенной
сложности в реализации. Проще выполняется
квантование с усечением, при котором
истинному значению отсчета приписывается
ближайший нижний уровень. При
этом
|
max=x; |
т.е.
максимальное значение погрешности в 2
раза больше, а
,
что приводит к накоплению погрешности
квантования при дальнейшей обработке
квантованной последовательности.
Промежуточное
положение по точности и сложности
реализации занимает квантование с
усечением модуля, которое для положительных
отсчетов является таким же, как и
квантование с усечением. Отрицательным
отсчетам приписывается ближайший
верхний уровень. При этом
то
есть накопление погрешностей не
происходит, но в 2 раза увеличивается
максимальная погрешность, и в 2 раза —
мощность шума квантования
.
Выбирая достаточно большее число уровней
квантования N, шаг квантования.
,
а следовательно и все рассмотренные
погрешности можно сделать необходимо
малыми. При неравномерном законе
распределения мгновенных значений
сигнала квантования с постоянным шагом
не
является оптимальным по критерию
минимума среднеквадратической ошибки
.
Квантуя участки с менее вероятными
значениями сигнала с большим шагом
значение
можно
уменьшить, при этом же количестве уровней
квантования.
3.3. Информация в непрерывных сообщениях
Для
того, чтобы оценить потенциальные
возможности передачи сообщений
по непрерывным каналам, необходимо
вести количественные информационные
характеристики непрерывных сообщений
и каналов.
Обобщим с этой целью понятие энтропии
и взаимной
информации
на ансамбли непрерывных сигналов.
Пусть
Х — случайная величина (сечение или
отсчет случайного процесса), определенная
в некоторой непрерывной области и ее
распределение вероятностей характеризуется
плотностью w(х).
Разобьем область
значений Х на небольшие интервалы
протяженностью x. Вероятность Рк
того, что хк<x<xк+
x, приблизительно равна w(хк)
x т.е.
|
Рк=Р( |
(3.32) |
причем
приближение тем точнее, чем меньше
интервал x. Степень положительности
такого события.
Если
заменить истинные значения Х в пределах
интервала x значениями хк
в начале интервала, то непрерывный
ансамбль заменится дискретным и его
энтропия в соответствии с (1.4)
определится, как
или
с учетом (3.32)
|
|
(3.33) |
Будем
теперь увеличивать точность определения
значения х, уменьшения интервал x. В
пределе при x0 получим
энтропию непрерывной случайной величины.
|
|
(3.34) |
Второй
член в полученном выражении стремится
к
и
совершенно не зависит от распределения
вероятностей Х. Это означает, что
собственная информация любой непрерывной
случайной величины бесконечно велика.
Физический смысл такого результата
становиться понятным, если учесть, что
в конечном диапазоне непрерывная
величина может принимать бесконечное
множество значений, поэтому вероятность
того, что ее реализация будет точно
равна какому-то наперед заданному
конкретному значению является бесконечно
малой величиной 0. В результате энтропия,
определенная в соответствии с (1.4),
характеризующая среднюю степень
неожиданности появления возможных
реализаций для любой непрерывной
случайной величины не зависит от ее
закона распределения и всегда равна
бесконечности. Поэтому для описания
информационных свойств непрерывных
величин необходимо ввести другие
характеристики. Это можно сделать, если
обратить внимание на то, что первое
слагаемое выражении (3.34) является
конечным и однозначно определяется
плотностью распределения вероятности
w(x). Его называют дифференциальной
энтропией и обозначают h(x):
|
|
(3.35) |
Дифференциальная
энтропия обладает следующими свойствами.
1.
Дифференциальная энтропия в отличии
от обычной энтропии дискретного источника
не является мерой собственной информации,
содержащейся в ансамбле значений
случайной величины Х. Она зависит от
масштаба Х и может принимать отрицательные
значения. Информационный смысл имеет
не сама дифференциальная энтропия, а
разность двух дифференциальных энтропий,
чем и объясняется ее название.
2.
Дифференциальная энтропия не меняется
при изменении всех возможных значений
случайной величины Х на постоянную
величину. Действительно, масштаб Х при
этом не меняется и
справедливо равенство
|
|
(3.36) |
Из
этого следует, что h(x) не зависит от
математического ожидания случайной
величины, т.к. изменяя все значения Х на
С мы тем самым изменяем на С и ее среднее,
то есть математическое ожидание.
3.
Дифференциальная энтропия аддитивна,
то есть для объединения ХY независимых
случайный величин Х и Y справедливо:
h(XY)=
h(X)+ h(Y).
Доказательство этого свойства
аналогично доказательству (1.8) аддитивности
обычной энтропии.
4. Из всех
непрерывных величин Х с фиксированной
дисперсией 2
наибольшую дифференциальную энтропию
имеет
величина с гауссовским распределением,
т.е.
|
|
(3.37) |
Доказательство
свойства проведем в два этапа: сначала
вычислим h(x) для гауссовского распределения,
задаваемого плотностью.
где
м — математическое ожидание,
а затем
докажем неравенство (3.37).
Подставив
(3.38) в (3.35) найдем<
Для
доказательства неравенства (3.37) зададимся
произвольным распределением (х) с
дисперсией 2
и математическим ожиданием m и вычислим
интеграл J вида
|
|
Но
в силу неравенства (1.7)
с учетом правила изменения основания
логарифмов (log t = log e ln t)
имеем:
|
|
|
|
так |
Таким
образом
,
откуда
.
Но
как только что было показано,
—
это дифференциальная энтропия гауссовского
распределения. Доказанное неравенство
и означает, что энтропия
гауссовского распределения
максимальна.
Попытаемся теперь
определить с помощью предельного
перехода взаимную
информацию между двумя непрерывными
случайными величинами X и Y. Разбив
области определения Х и Y соответственно
на небольшие интервалы x и y, заменим
эти величины дискретными так же, как
это делалось при выводе формулы
(3.34).
Исходя из выражения
(1.14) можно определить взаимную информацию
между величинами Х и Y .
|
|
(3.39) |
При
этом предельном переходе никаких явных
бесконечностей не появилось, т.е. взаимная
информация оказывается величиной
конечной, имеющей тот же смысл, что и
для дискретных сообщений.
С
учетом того, что
|
(x,y)= (y) |
равенство
(3.39) можно представить в виде
|
|
(3.40) |
Здесь
h(X) — определенная выражением (3.35)
дифференциальная энтропия Х, а
|
|
(3.41) |
h(X/Y)
— условная дифференциальная энтропия.
Можно показать, что во всех случаях
h(X/Y)h(X).
Формула
(3.40) имеет ту же форму, что и (1.13), а
отличается лишь заменой энтропии
дифференциальной энтропией. Легко
убедиться, что основные свойства 1 и 2
(см. пункт 1.3) взаимной информации,
описываемые равенствами (1.15)(1.17),
остаются справедливыми и в этом случае.
3.4 -энтропия
и -производительность
источника непрерывных сообщений
Как
было показано в § 3.3, в одном отсчете
любого непрерывного сообщения содержится
бесконечное количество собственной
информации. И тем не менее, непрерывные
сообщения (телефонные разговоры,
телепередачи) успешно передаются по
каналам связи. Это объясняется тем, что
на практике никогда не требуется
абсолютно точного воспроизведения
переданного сообщения, а для передачи
даже с очень высокой, но ограниченной
точностью, требуется конечное количество
информации, также как и при передаче
дискретных сообщений. Данное обстоятельство
и положено в основу определения
количественной меры собственной
информации, источников непрерывных
сообщений. В качестве такой меры,
принимается минимальное количество
информации, необходимое для воспроизведения
непрерывного сообщения с заданной
точностью. Очевидно, что при таком
подходе собственная информация зависит
не только от свойств источника сообщений,
но и от выбора параметра , характеризующего
точность воспроизведения. Возможны
различные подходы к определению в
зависимости от вида и назначения
передаваемой информации. Наиболее часто
в информационной технике в качестве
используют среднеквадратическое
отклонение между принятым у и переданным
х сигналами, отражающими непрерывные
сообщения, т.е.
|
|
(3.42) |
где
Х и Y – ансамбли сигналов, отражающих
исходное и воспроизведенное сообщения.
Два
варианта сообщения или сигнала,
различающиеся не более, чем на заданное
значение 0,
называются эквивалентными. Взаимная
информация
I(X,Y) между двумя эквивалентными процессами
X(t) и Y(t) может быть определена в соответствии
с (3.40) как
|
I(X,Y)=h(X)-h(X/Y), |
где
h(X) и h(X/Y) – соответственно дифференциальная
и условная дифференциальная энтропии.
Из приведенного выражения видно,
что величина I(X,Y) зависит не только от
собственного распределения (х) ансамбля
Х (см. (3.35)), но и от условного распределения
(x/y) (см. (3.41)), которое определяется
способом преобразования процесса X в
Y. Для характеристики собственной
информации, содержащейся в одном отсчете
процесса Х, нужно устранить ее зависимость
от способа преобразования сообщения Х
в эквивалентное ему сообщение Y. Этого
можно добиться, если под количеством
собственной информации или — энтропией
H(Х)
процесса Х понимать минимизированную
по всем распределениям (X/Y) величину
I(X,Y), при которой сообщения Х
и Y еще эквивалентны, т.е.
|
|
(3.43) |
Таким
образом,
— энтропия
определяет минимальное количество
информации, содержащейся в одном отсчете
непрерывного
сообщения,
необходимое для воспроизведения его с
заданной верностью.
Если ансамбль
сообщений Х представляет собой процесс
с дискретным
временем
с непрерывными отсчетами, то под
— производительностью источника понимают
величину
|
|
(3.44) |
где
с
– количество отсчетов сообщения,
выдаваемых в единицу времени.
В том
случае, когда Х — непрерывный случайный
процесс с ограниченным спектром, вся
информация, содержащаяся в его значениях,
эквивалентна информации, содержащейся
в отсчетах процесса, следующих друг за
другом с интервалом
,
(fm-граничная
частота спектра), т.е. со
скоростью
|
c=2 |
(3.45) |
При
этом
— производительность
источника или процесса по-прежнему
определяется выражением (3.44), где величина
с
рассчитывается из условия (3.45).
В том
случае, если следующие друг за другом
отсчеты процесса коррелированны
(взаимозависимы), величина Н(Х)
в (3.43) должна вычисляться с учетом
вероятностных связей между отсчетами.
Итак,
— производительность источника
непрерывных сообщений представляет
собой минимальное количество информации,
которое нужно создать источнику в
единицу времени, для воспроизведения
его сообщений с заданной верностью.
— производительность называют также
скоростью создания информации при
заданном критерии верности.
Максимально
возможная — производительность
непрерывного
источника Х обеспечивается при гауссовском
распределении Х с дисперсией
(при
этом условии h(X) максимальна (см. (3.37)).
Оценим значение
.
Рассмотрим случай, когда непрерывное
сообщение X(t) представляет собой
стационарный гауссовский процесс с
равномерным энергетическим спектром,
ограниченным частотой Fc,
и с заданной мощностью (дисперсией) Рх,
а критерий эквивалентности задан в
виде (3.42).
Будем считать, что заданная верность
воспроизведения обусловлена действием
аддитивной статистически не связанной
с сигналом помехи (t) с математическим
ожиданием М[]=0 и дисперсией (мощностью)
.
Исходный сигнал Х рассматриваем
как сумму воспроизводящего сигнала Y и
помехи:
|
X=Y+. |
При
этом, поскольку (x/y)= (y+/y)= (/y)=
(), то h(X/Y) полностью определяется
шумом воспроизведения (t). Поэтому max
h(X/Y)=max h(). Так как шум воспроизведения
имеет фиксированную дисперсию
,
то дифференциальная энтропия имеет
максимум (3.37) при гауссовском
распределении шума
|
|
В
свою очередь дифференциальная энтропия
гауссовского источника с дисперсией
.
|
|
Следовательно,
— энтропия на один отсчет
сообщения
|
|
(3.46) |
Величина
характеризует
минимальное отношение сигнал-шум, при
котором сообщения X(t) и Y(t) еще
эквивалентны.
Согласно теореме
Котельникова
шаг
дискретизации
,
а c=2
Fc.
При этом равномерность спектра сообщения
обеспечивает некоррелированность
отстоящих на t друг от друга отсчетов,
а гауссовский характер распределения
X(t) — их независимость. Следовательно,
в соответствии с (3.44)
|
|
или с учетом (3.46)
|
|
(3.47) |
Количество
информации,
выданное таким источником за время Тс
|
|
(3.48) |
Интересно
отметить, что правая часть выражения
(3.48) совпадает с наиболее общей
характеристикой сигнала, называемой
его объемом, если принять динамический
диапазон сигнала D=log
0.
Это означает, что объем сигнала равен
максимальному количеству информации,
которое может содержаться в сигнале
длительностью Тс.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление ошибки квантования
Этот пример показывает, как вычислить и сравнить статистику ошибки квантования сигнала при использовании различных методов округления.
Сначала создается случайный сигнал, который охватывает область значений квантователя.
Затем квантуют сигнал, соответственно, с помощью методов округления ‘fix’, ‘floor’, ‘ceil’, ‘near’ и ‘convergent’, и оценивают статистику сигнала.
Теоретическая функция плотности вероятностей ошибки квантования будет вычисляться с помощью ERRPDF, теоретическое среднее значение ошибки квантования будет вычисляться с помощью ERRMEAN, а теоретическое отклонение ошибки квантования будет вычисляться с помощью ERRVAR.
Равномерно распределенный случайный сигнал
Сначала мы создадим равномерно распределенный случайный сигнал, который охватывает область от -1 до 1 квантователей с фиксированной точкой, которые мы рассмотрим.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Исправление: Округлить к нулю.
Заметьте, что с ‘fix’ округлением, функция плотности вероятностей в два раза шире, чем другие. По этой причине отклонение в четыре раза больше, чем у остальных.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Пол: Круглый к минусовой бесконечности.
Округление пола часто называется усечением при использовании с целыми числами и числами с фиксированной точкой, которые представлены в дополнении двойки. Это наиболее распространенный режим округления процессоров DSP, поскольку для его реализации не требуется никакого оборудования. Floor не приводит к квантованным значениям, которые так близки к истинным значениям, как ROUND will, но имеет то же отклонение, и будут обнаружены небольшие сигналы, которые варьируются в знаке, тогда как в ROUND они будут потеряны.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Ceil: Round To Plus Infinity.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Раунд: Круглый до ближайшего. В связи, скругление к наибольшей величине.
Раунд более точен, чем этаж, но все значения, меньшие, чем eps (q), округляются до нуля, и поэтому теряются.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Сходимость: раунд к ближайшему. В галстуке, Round to Even.
Сходящееся округление устраняет смещение, вызванное обычным «округлением», вызванным всегда округлением галстука в том же направлении.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Сравнение ближайшего и сходимого
Функцию плотности вероятности ошибки для сходимого округления трудно отличить от функции округления к ближайшему, глядя на график.
Ошибка p.d.f. сходящимся является
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
в то время как ошибка p.d.f. round есть
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Обратите внимание, что ошибка p.d.f. сходимость симметрична, а округлость слегка смещена к положительной.
Единственное различие — это направление округления в галстуке.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Функция Plot Helper
Функция helper, которая использовалась для генерации графиков в этом примере, приведена ниже.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
4Δ-8Δ=-4Δ<0, присваиваем
0; ε2=4Δ.
UВЫХ2=11000010;
5 сегмент, 2 уровень.
Разница: 148-(128+16)=4
UВХ1/UMAX=0,94; UBX2/UMAX=0,062.
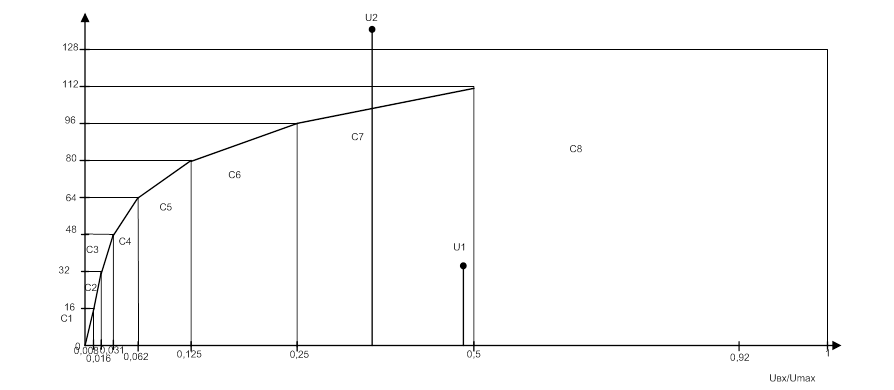
B; UВЫХ2=
B; Степень сжатия высокого уровня=0,92 дБ; Степень
сжатия низкого уровня=24,02 дБ; ε1=0,162 В; ε2=0,024 В;
При декодировании искажения
уменьшаются путем применения нелинейного кодера и уменьшения шага квантования.
6.
Отсчеты группового ИКМ сигнала
закодированы с помощью нелинейного кодера 8-разрядной кодовой комбинацией кк.
Определить амплитуду (в у. е.), полярность и номер уровня квантования отсчетов
АИМ сигнала.
Кк1=01101101, кк2=01101100, кк3=11001100.
Решение:
1). Кк1=01101101.
Старший разряд=0, значит,
число отрицательное, 110 – 7 сегмент, 1101 – 13 уровень, N1=13.
U1=-(512+256+128+32)=-928 у.е.
2). Кк2=01101100.
Старший разряд = 0, значит,
число отрицательное, 110 – 7 сегмент, 1100 – 12 уровень. N2=12.
U2=-(512+256+128)=-896 у.е.
3). Кк3=11001100.
Старший разряд =1, значит
число положительное, 100 – 5 сегмент, 1100 – 12 уровень. N3=12.
U3=128+64+32=224 у.е.
Ответ: U1=-928 y.e., N1=13, U2=-896 y.e., N2=12, U3=224 y.e.,N3=12.
7.
Закодировать с помощью
симметричного кода номера уровней квантования дискретных отсчетов АИМ сигнала UАИМ1, мВ и UАИМ2, мВ,
если шаг квантования равен Δ мВ, а разрядность кода равна m.
UАИМ1=20,4 мВ; UАИМ2=-7,2 мВ; m=8; Δ=6 мВ.
Решение:
1). UАИМ1=20,4
мВ; N1
N1=10000011;
2). UАИМ2=-7,2
мВ; N2
N2=00000001;
Ответ: N1=10000011;
N2=00000001.
8.
Определить амплитуду и знак
отсчета аналогового сигнала, переданного с системы передачи с ИКМ с помощью
симметричного кода в виде кодовой комбинации кк, если ошибка квантования равна ξкв,
мВ, шаг квантования равен Δ, мВ.
Кк=1.001101; ξкв=-2,2мВ; Δ=2,9 мВ.
Решение:
U КВ=128+64+32+8=232Δ=672,8
мВ;
UАИМ=UКВ+ ξкв=672,8+(-2,2)=670,6 мВ.
Ответ: U=670,6
мВ.
9.
На вход компаратора линейного
кодера взвешивающего типа подается положительный/отрицательный отсчет с
амплитудой Uc Δ,
мВ.
1). Определить состояние компаратора и логического
устройства в конце каждого этапа кодирования.
2). Определить ИКМ сигнал на выходе преобразователя
кода.
Uc1=17;
Uc2=-58;
Решение:
Uc=17.
1). Вых1 логического устройства=1, остальные равны 0.
Так как отсчет положительный, то на выходе компаратора будет 0. Состояние «1»
первого ключа на выходе ЛУ сохраняется и ключ «+» замыкается.
2). Появляется 1 на вых2 ЛУ. Идет на 2 вход
компаратора. В компараторе происходит сравнение.
17<64. Состояние компаратора =1 (к=1). 0 идет на ЛУ
17<32; K=1, ЛУ=0.
17>16; К=0,ЛУ=1
17<16+8; К=1,ЛУ=0
17<16+4; К=1,ЛУ=0
17<16+2; К=1,ЛУ=0
17=16+1; K=0,ЛУ=1
U1икм=10010001.
Uc=-58.
1). Вых1 ЛУ=1, остальные =0. Так как отсчет
отрицательный, К=1, ЛУ=0 и ключ «-» замыкается.
2). Вых2 ЛУ=1, 58<64, K=1, ЛУ=0.
3). Вых3 ЛУ=1, 58>32, К=0, ЛУ=1.
4). Вых4 ЛУ=1, 58>32+16, K=0, ЛУ=1.
5). Вых5 ЛУ=1, 58>32+16+8, К=0, ЛУ=1.
6). Вых6 ЛУ=1, 58<32+16+8+4, К=1, ЛУ=0.
7). Вых7 ЛУ=1, 58=32+16+8+2, К=0, ЛУ=1.
8). Вых8 ЛУ=1, 58<32+16+8+2+1, К=1, ЛУ=0.
U2икм=00111010.
10.
Определить количество символов
ПСП на выходе генератора ПСП, построенного на 5-разрядном регистре сдвига.
Составить таблицу состояний такого генератора.
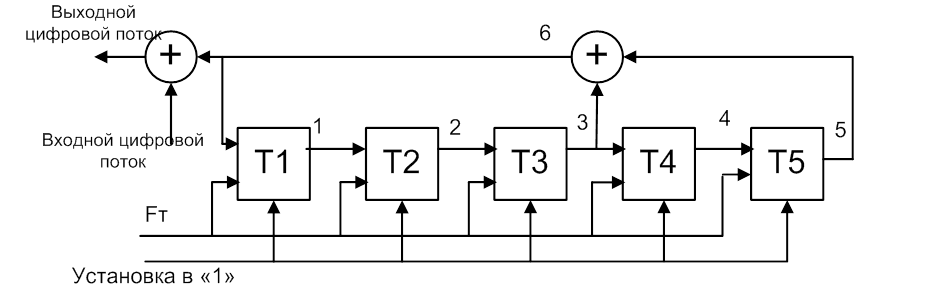
n=5; N=25-1=31;
|
N такта |
N выхода |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
2 |
0 |
1 |
1 |
1 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
1 |
0 |
|
4 |
0 |
0 |
0 |
1 |
1 |
1 |
|
5 |
1 |
0 |
0 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
0 |
0 |
0 |
|
7 |
0 |
1 |
1 |
0 |
0 |
1 |
|
8 |
1 |
0 |
1 |
1 |
0 |
1 |
|
9 |
1 |
1 |
0 |
1 |
1 |
1 |
|
10 |
1 |
1 |
1 |
0 |
1 |
0 |
|
11 |
0 |
1 |
1 |
1 |
0 |
1 |
|
12 |
1 |
0 |
1 |
1 |
1 |
0 |
|
13 |
0 |
1 |
0 |
1 |
1 |
1 |
|
14 |
1 |
0 |
1 |
0 |
1 |
0 |
|
15 |
0 |
1 |
0 |
1 |
0 |
0 |
|
16 |
0 |
0 |
1 |
0 |
1 |
0 |
|
17 |
0 |
0 |
0 |
1 |
0 |
0 |
|
18 |
0 |
0 |
0 |
0 |
1 |
1 |
|
19 |
1 |
0 |
0 |
0 |
0 |
0 |
|
20 |
0 |
1 |
0 |
0 |
0 |
0 |
|
21 |
0 |
0 |
1 |
0 |
0 |
1 |
|
22 |
1 |
0 |
0 |
1 |
0 |
0 |
|
23 |
0 |
1 |
0 |
0 |
1 |
1 |
|
24 |
1 |
0 |
1 |
0 |
0 |
1 |
|
25 |
1 |
1 |
0 |
1 |
0 |
0 |
|
26 |
0 |
1 |
1 |
0 |
1 |
0 |
|
27 |
0 |
0 |
1 |
1 |
0 |
1 |
|
28 |
1 |
0 |
0 |
1 |
1 |
1 |
|
29 |
1 |
1 |
0 |
0 |
1 |
1 |
|
30 |
1 |
1 |
1 |
0 |
0 |
1 |
|
31 |
1 |
1 |
1 |
1 |
0 |
1 |