Расчет средней относительной ошибки пример

При
выборе единиц наблюдения возможны
ошибки смещения, т.е. такие события,
появление которых не может быть точно
предсказуемым. Эти ошибки являются
объектив­ными и закономерными. При
определении степени точности выборочно­го
исследования оценивается величина
ошибки, которая может прои­зойти в
процессе выборки. Такие ошибки носят
название случайных ошибок
репрезентативности
(m),
На практике для определения средней
ошибки выборки при проведении
статистических исследований, используются
следующие Формулы:

для
расчета средней ошибки (m_Р)
относительной величины (Р):

,
где Ρ
— соответствующая относительная величина
(рассчитанная, например, в процентах
(%));

q
— 100 — Ρ;

n
— численность выборки.

96 Определение доверительных границ относительных показателей. Понятие о вероятности безошибочного прогноза.

Для
оп­ред точности, с которой исследователь
желает получить ре­зультат, в статистике
исп-ся такое понятие, как вероят­ность
безошибочного прогноза,
кот является характеристикой надежности
результатов выборочных мед-биолог стат
исс-ий. Обычно, при проведении мед-биолог
стат исс-ий использ вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%

Определенной
степени вероятности безошибочного
прогноза соот­ветствует определенная
величина предельной ошибки случайной
выборки (Δ)
Определяется эта величина по формуле:

Δ=t
* m
,

где
t
— доверительный коэффициент, который
при вероятности безо­шибочного
прогноза 95% равен 2. при вероятности
безоши­бочного прогноза 99% — 3,. и при
вероятности безошибочно­го прогноза
99,7% — 3,3.

Используя
предельную ошибку выборки (Δ),
можно определить до­верительные
границы, в которых с опред вероятностью
безо­шиб прогноза заключено
действительное значение стат величины,
характериз
всю ген. совокупность (сред­ней или
относительной).

Для опред доверительных
границ использ следующие Формулы:

,
где
— доверительные границы относ величины
в ген совокупности;

—
относ величина, полученная при проведении
исслед-я на выбороч совокупности;

t
— доверит коэффициент;

m_P
— ошибка репрезентативности относ
величины.

При
малом числе наблюдений (n<30), для
вычисления довери­тельных границ
значение коэффициента t
находят по спец табл Стьюдента (Значения
t
расположены в таблице на пересечении
с избранной вероятностью безошибочного
прогноза и строки,
указывающей
на имеющееся число степеней свободы
(n`),
которое
равно n-1.

97 Оценка достоверности разности относительных величин. Критерий “t” (Стьюдента).

При
проведении медико-биологических
исследований на двух срав­ниваемых
совокупностях возникает необходимость
определить не только их различие, но и
его достоверность.

Для
оценки достоверности различия сравниваемых
относительных величин:
,

где,
P₁
и P₂
— относительные величины, полученные
при проведении выборочных исследований:
m₁
и m₂
— их ошибки репрезен­тативности; t
— коэффициент достоверности. Различие
достоверно при t>2.
что соответствует вероятности
безошибочного прогноза равной или более
95%. При величине коэффициента достоверности
t<2
степень вероятности безошибочного
прогноза менее 95%. При такой степени
вероятности мы не можем утверждать, что
полученная раз­ность показателей
достоверна с достаточной степенью
вероятности. В этом случае необходимо
получить дополнительные данные, увели­чив
число наблюдений. Если после увеличения
численности выборки, и. соответственно,
уменьшения
ошибки репрезентативности, разли­чие
продолжает оставаться недостоверным,
можно считать доказан­ным, что между
сравниваемыми совокупностями не
обнаружено разли­чий по изучаемому
признаку.

Соседние файлы в папке Шпора к госкзамену

• #
• #

Вариант 1

Задание 1. Модель парной линейной регрессии.

Имеются данные о размере среднемесячных доходов в разных группах семей

Номер группы	Среднедушевой денежный доход в месяц, руб., X	Доля оплаты труда в структуре доходов семьи, %, Y
1	79,8	64,2
2	152,1	66,1
3	199,3	69,0
4	240,8	70,6
5	282,4	72,4
6	301,8	74,3
7	385,3	76,0
8	457,8	77,1
9	577,4	78,4

Задания:

1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы

2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.

3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.

4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.

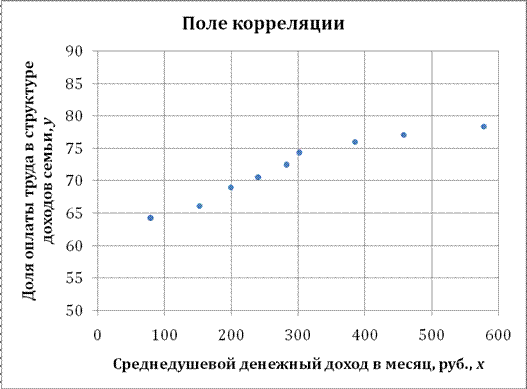
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.

Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .

Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.

№ п/п	X	Y	X×Y	X2	Y2
1	79,8	64,2	5123,16	6368,04	4121,64
2	152,1	66,1	10053,81	23134,41	4369,21
3	199,3	69,0	13751,70	39720,49	4761,00
4	240,8	70,6	17000,48	57984,64	4984,36
5	282,4	72,4	20445,76	79749,76	5241,76
6	301,8	74,3	22423,74	91083,24	5520,49
7	385,3	76,0	29282,80	148456,09	5776,00
8	457,8	77,1	35296,38	209580,84	5944,41
9	577,4	78,4	45268,16	333390,76	6146,56
S	2676,7	648,1	198645,99	989468,27	46865,43
Среднее	297,41	72,01	22071,78	109940,92	5207,27

Вычислим коэффициент корреляции. Используем следующую формулу:

= 0,9568.

Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.

Среднюю ошибку коэффициента корреляции определим по формуле:

= 0,032.

Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.

TТабл(0,05; 7) = 2,36.

Запишем доверительный интервал для коэффициента корреляции.

Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.

Вычислим параметры уравнения регрессии.

= 0,03.

= 72,01 – 0,03×297,41 = 63,09.

Получим следующее уравнение: .

Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

= 23,04.

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.

Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.

Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:

Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.

№ п/п	X	Y
1	79,8	64,2	65,48	1,6384	47354,1
2	152,1	66,1	67,65	2,4025	21115,0
3	199,3	69,0	69,07	0,0049	9625,6
4	240,8	70,6	70,31	0,0841	3204,7
5	282,4	72,4	71,56	0,7056	225,3
6	301,8	74,3	72,14	4,6656	19,3
7	385,3	76,0	74,65	1,8225	7724,7
8	457,8	77,1	76,82	0,0784	25725,0
9	577,4	78,4	80,41	4,0401	78394,4
S	2676,7	648,1	648,09	15,4421	193388,1

Вычислим стандартные ошибки коэффициентов уравнения.

= 1,2.

= 0,003.

Вычислим T-статистики.

Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и , т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.

Сделаем рисунок.

Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.

Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

= 75,81.

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.

Fтабл(0,05; 1; 7) = 5,59.

Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.

Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.

XP = 297,41 × 1,11 = 330,1.

Вычислим прогнозное значение Yp с помощью уравнения регрессии.

» 73%.

Доверительный интервал прогноза имеет вид

(УP – Tкр×My, УP + Tкр×My),

Где , M = 2 – число параметров уравнения.

= 1,695 » 1,7.

Запишем доверительный интервал прогноза:

Þ

Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.

Задание 2. Модель парной нелинейной регрессии.

По территориям Центрального района известны данные за 1995 г.

Район	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y
Брянская обл.	178	240
Владимирская обл.	202	226
Ивановская обл.	197	221
Калужская обл.	201	226
Костромская обл.	189	220
Орловская обл.	166	232
Рязанская обл.	199	215
Смоленская обл.	180	220
Тверская обл.	181	222
Тульская обл.	186	231
Ярославская обл.	250	229

Задания:

1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной () парной регрессии. Сделать рисунки.

2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.

3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии

4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.

Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.

Получим следующий рисунок.

По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.

Построение полулогарифмической модели регрессии.

Уравнение логарифмической кривой: .

Обозначим:

Получим линейное уравнение регрессии:

Y = A + B×X.

Произведем линеаризацию модели путем замены . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Xy	X2	Y2				Ai
1	178	240	5,1818	1243,63	26,85	57600	226,40	206,314	184,904	6,006
2	202	226	5,3083	1199,67	28,18	51076	225,17	0,132	0,694	0,370
3	197	221	5,2832	1167,59	27,91	48841	225,41	21,496	19,464	1,957
4	201	226	5,3033	1198,55	28,13	51076	225,22	0,132	0,615	0,348
5	189	220	5,2417	1153,18	27,48	48400	225,82	31,769	33,833	2,576
6	166	232	5,1120	1185,98	26,13	53824	227,08	40,496	24,172	2,165
7	199	215	5,2933	1138,06	28,02	46225	225,31	113,132	106,362	4,577
8	180	220	5,1930	1142,45	26,97	48400	226,29	31,769	39,601	2,781
9	181	222	5,1985	1154,07	27,02	49284	226,24	13,223	17,968	1,874
10	186	231	5,2257	1207,15	27,31	53361	225,97	28,769	25,273	2,225
11	250	229	5,5215	1264,41	30,49	52441	223,09	11,314	34,980	2,651
Итого	2129	2482	57,862	13054,74	304,48	560528	2482,00	498,545	487,867	27,530
Среднее	193,5	225,6	5,260	1186,79	27,68	50957,091	225,636	45,322	44,352	2,503

= -9,76.

= 225,6 – (-9,76)×5,26 = 276,99.

Уравнение модели имеет вид:

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Рассчитаем средний коэффициент эластичности по формуле:

= -0,04%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид: .

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

.

Произведем линеаризацию модели путем замены и . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Y = ln(Y)	XY	X2	Y2					Ai
1	178	240	5,1818	5,4806	28,3995	26,851	30,037	226,3	206,3	188,391	241,661	6,07
2	202	226	5,3083	5,4205	28,7737	28,178	29,382	225,1	0,132	0,835	71,479	0,406
3	197	221	5,2832	5,3982	28,5196	27,912	29,140	225,3	21,496	18,671	11,934	1,918
4	201	226	5,3033	5,4205	28,7467	28,125	29,382	225,1	0,132	0,753	55,570	0,385
5	189	220	5,2417	5,3936	28,2720	27,476	29,091	225,7	31,769	32,607	20,661	2,530
6	166	232	5,1120	5,4467	27,8437	26,132	29,667	226,9	40,496	25,675	758,752	2,233
7	199	215	5,2933	5,3706	28,4284	28,019	28,844	225,2	113,132	104,576	29,752	4,540
8	180	220	5,1930	5,3936	28,0089	26,967	29,091	226,2	31,769	38,059	183,479	2,728
9	181	222	5,1985	5,4027	28,0858	27,024	29,189	226,1	13,223	16,950	157,388	1,821
10	186	231	5,2257	5,4424	28,4407	27,308	29,620	225,9	28,769	26,413	56,934	2,275
11	250	229	5,5215	5,4337	30,0021	30,487	29,525	223,1	11,314	34,846	3187,116	2,646
Итого	2129	2482	57,862	59,603	313,521	304,479	322,969	2480,927	498,545	487,777	4774,727	27,548
Среднее	193,5	225,6	5,260	5,418	28,502	27,680	29,361	225,539	45,322	44,343	434,066	2,504

С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.

= -0,042.

= 5,418 – 0,959×5,26 = 5,637.

Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.

A = eA = e5,637 = 280,76

Получим уравнение степенной модели регрессии: .

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Для степенной модели средний коэффициент эластичности равен коэффициенту B.

= -0,042%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Сводная таблица вычислений

Параметры	Модель
Полулогарифмическая	Степенная
Уравнение связи
Индекс корреляции	0,1464	0,147
Коэффициент детерминации	0,021	0,021
Средняя ошибка аппроксимации, %	2,5	2,5

Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.

Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.

Прогнозное значение составит:

= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:

= 224,6 тыс. р.

Определим доверительный интервал прогноза для уровня значимости a = 0,05.

Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

, где

Получаем: = 7,55.

Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.

= 14,8.

Запишем доверительный интервал прогноза.

= 224,6 – 14,8 = 209,8 тыс. р.

= 224,6 + 14,8 = 239,4 тыс. р.

Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.

Задание 3. Моделирование временных рядов

Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.

Номер квартала	Товарооборот % к предыдущему периоду	Номер квартала	Товарооборот % к предыдущему периоду
1	100	11	98,8
2	93,9	12	101,9
3	96,5	13	113,1
4	101,8	14	98,4
5	107,8	15	97,3
6	96,3	16	112,1
7	95,7	17	97,6
8	98,2	18	93,7
9	104	19	114,3
10	99	20	108,4

Задания:

1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.

2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.

3. Рассчитать трендовую компоненту временного ряда и построить его график

4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.

Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.

Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.

Построим мультипликативную модель временного ряда.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.

Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1)  Выравнивание исходного ряда методом скользящей средней.

2)  Расчет значений сезонной компоненты S.

3)  Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.

4)  Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.

5)  Расчет полученных по модели значений T×E.

6)  Расчет абсолютных и/или относительных ошибок.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).

Таблица 2.1

№ месяца, T	Товарооборот, Yi	Итого за четыре месяца	Скользящая средняя за четыре месяца	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	100,0	–	–	–	–
2	93,9	392	98	–	–
3	96,5	400	100	99	0,975
4	101,8	402	100,5	100,25	1,015
5	107,8	402	100,5	100,5	1,073
6	96,3	398	99,5	100	0,963
7	95,7	394	98,5	99	0,967
8	98,2	397	99,25	98,875	0,993
9	104,0	400	100	99,625	1,044
10	99,0	404	101	100,5	0,985
11	98,8	413	103,25	102,125	0,967
12	101,9	412	103	103,125	0,988
13	113,1	411	102,75	102,875	1,099
14	98,4	309	77,25	90	1,093
15	97,3	196	49	63,125	1,541
16	112,1	303	75,75	62,375	1,797
17	97,6	418	104,5	90,125	1,083
18	93,7	414	103,5	104	0,901
19	114,3	–	–	–	–
20	108,4	–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.

Таблица 2.2

Показатели	Год	№ квартала, I
I	II	III	IV
	1	–	–	0,975	1,015
	2	1,073	0,963	0,967	0,993
	3	1,044	0,985	0,967	0,988
	4	1,099	1,093	1,541	1,797
	5	1,083	0,901	–	–
Всего за I-й квартал		4,299	3,942	4,45	4,793
Средняя оценка сезонной компоненты для I-го квартала,		0,860	0,788	0,890	0,959
Скорректированная сезонная компонента,		0,984	0,901	1,018	1,097

Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.

Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.

Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки на корректирующий коэффициент K.

Проверяем условие: равенство 4 суммы значений сезонной компоненты:

0,984 + 0,901 + 1,018 + 1,097 = 4.

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.

Таблица 2.3

T	Yt	St		T	T×S
1	2	3	4	5	6	7
1	100,0	0,984	101,6	100,02	98,42	1,016
2	93,9	0,901	104,2	100,19	90,27	1,040
3	96,5	1,018	94,8	100,36	102,17	0,945
4	101,8	1,097	92,8	100,53	110,28	0,923
5	107,8	0,984	109,6	100,7	99,09	1,088
6	96,3	0,901	106,9	100,87	90,88	1,060
7	95,7	1,018	94,0	101,04	102,86	0,930
8	98,2	1,097	89,5	101,21	111,03	0,884
9	104,0	0,984	105,7	101,38	99,76	1,043
10	99,0	0,901	109,9	101,55	91,50	1,082
11	98,8	1,018	97,1	101,72	103,55	0,954
12	101,9	1,097	92,9	101,89	111,77	0,912
13	113,1	0,984	114,9	102,06	100,43	1,126
14	98,4	0,901	109,2	102,23	92,11	1,068
15	97,3	1,018	95,6	102,4	104,24	0,933
16	112,1	1,097	102,2	102,57	112,52	0,996
17	97,6	0,984	99,2	102,74	101,10	0,965
18	93,7	0,901	104,0	102,91	92,72	1,011
19	114,3	1,018	112,3	103,08	104,94	1,089
20	108,4	1,097	98,8	103,25	113,27	0,957
Среднее	101,4					1,0011

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.

Таблица 2.4

	T		T2
	1	2	3	4	5	6	7
	1	101,6	1	101,6	2,5	1,58	2,0
	2	104,2	4	208,4	13,2	3,87	56,3
	3	94,8	9	284,4	32,1	5,88	24,0
	4	92,8	16	371,2	71,9	8,33	0,2
	5	109,6	25	548	75,9	8,08	41,0
	6	106,9	36	641,4	29,4	5,63	26,0
	7	94,0	49	658	51,3	7,48	32,5
	8	89,5	64	716	164,6	13,07	10,2
	9	105,7	81	951,3	18,0	4,08	6,8
	10	109,9	100	1099	56,3	7,58	5,8
	11	97,1	121	1068,1	22,6	4,81	6,8
	12	92,9	144	1114,8	97,4	9,69	0,3
	13	114,9	169	1493,7	160,5	11,20	136,9
	14	109,2	196	1528,8	39,6	6,39	9,0
	15	95,6	225	1434	48,2	7,13	16,8
	20	102,2	400	2044	0,2	0,37	114,5
	21	99,2	441	2083,2	12,3	3,59	14,4
	22	104,0	484	2288	1,0	1,05	59,3
	23	112,3	529	2582,9	87,6	8,19	166,4
	24	98,8	576	2371,2	23,7	4,49	49,0
Сумма	230	2035,2	3670	23588	1008,3	122,49	778,2
Среднее	11,5	101,8	183,5	1179,4	50,4	6,12	38,91

Вычислим параметры уравнения тренда.

= 0,17.

= 99,85.

В результате получим уравнение тренда:

T = 99,85 + 0,17×T.

Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).

Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.

Расчет ошибки в мультипликативной модели произведем по формуле:

Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).

Рассчитаем сумму квадратов абсолютных ошибок .

Используя 5-й столбец таблицы 2.4, получим:

= 7,099.

Рассчитаем среднюю относительную ошибку: .

Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.

< Предыдущая		Следующая >