17 авг. 2022 г.
читать 2 мин
Всякий раз, когда мы подбираем модель линейной регрессии , модель принимает следующую форму:
Y = β 0 + β 1 X + … + β i X +ϵ
где ϵ — член ошибки, не зависящий от X.
Независимо от того, насколько хорошо можно использовать X для предсказания значений Y, в модели всегда будет какая-то случайная ошибка.
Одним из способов измерения дисперсии этой случайной ошибки является использование стандартной ошибки регрессионной модели , которая представляет собой способ измерения стандартного отклонения остатков ϵ.
В этом руководстве представлен пошаговый пример расчета стандартной ошибки регрессионной модели в Excel.
Шаг 1: Создайте данные
В этом примере мы создадим набор данных, содержащий следующие переменные для 12 разных учащихся:
- Оценка экзамена
- Часы, потраченные на учебу
- Текущая оценка
Шаг 2: Подгонка регрессионной модели
Далее мы подгоним модель множественной линейной регрессии , используя экзаменационный балл в качестве переменной ответа и часы обучения и текущую оценку в качестве переменных-предикторов.
Для этого щелкните вкладку « Данные » на верхней ленте, а затем щелкните « Анализ данных» :
Если вы не видите эту опцию доступной, вам нужно сначала загрузить Data Analysis ToolPak .
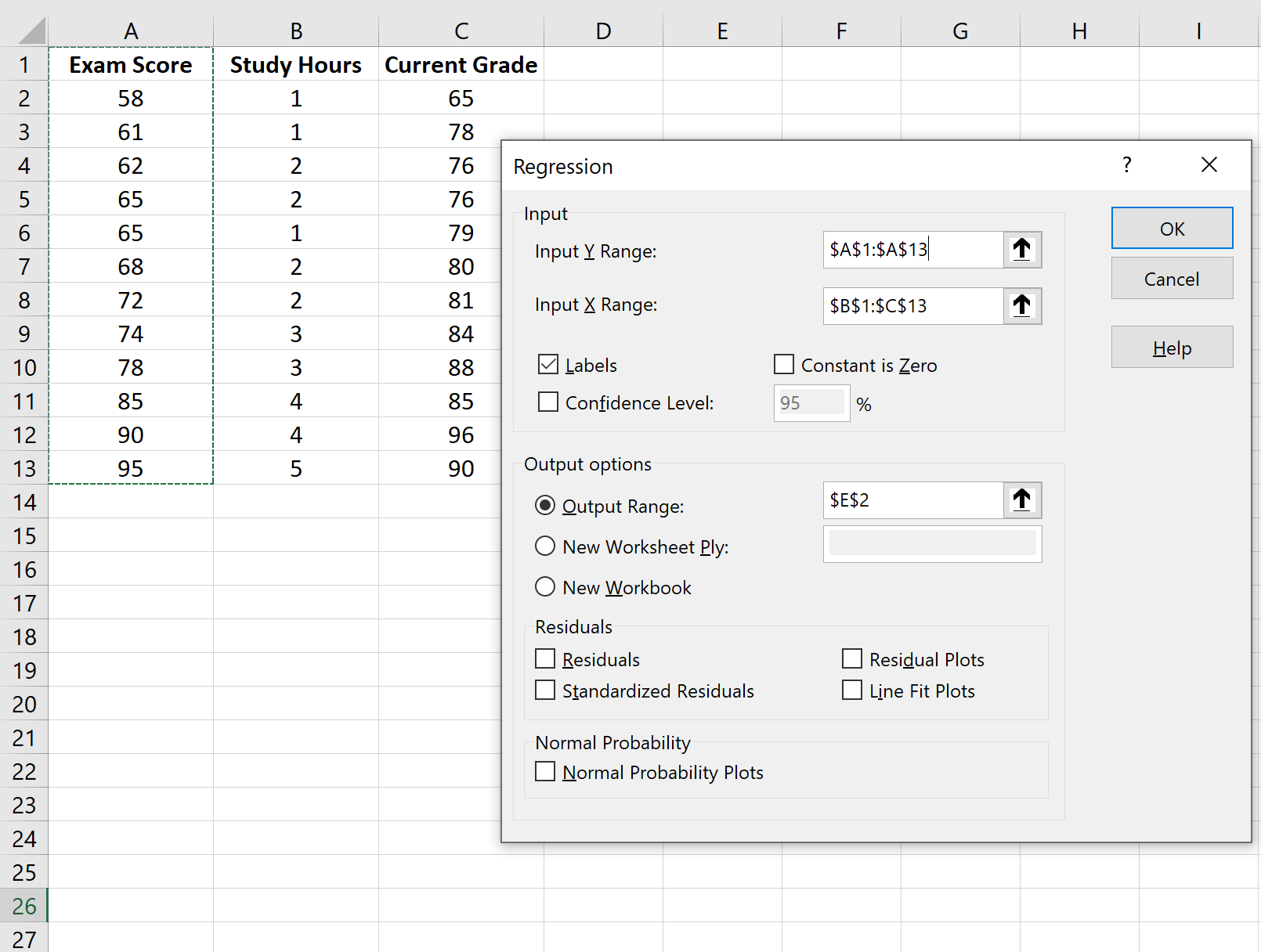
В появившемся окне выберите Регрессия.В появившемся новом окне заполните следующую информацию:
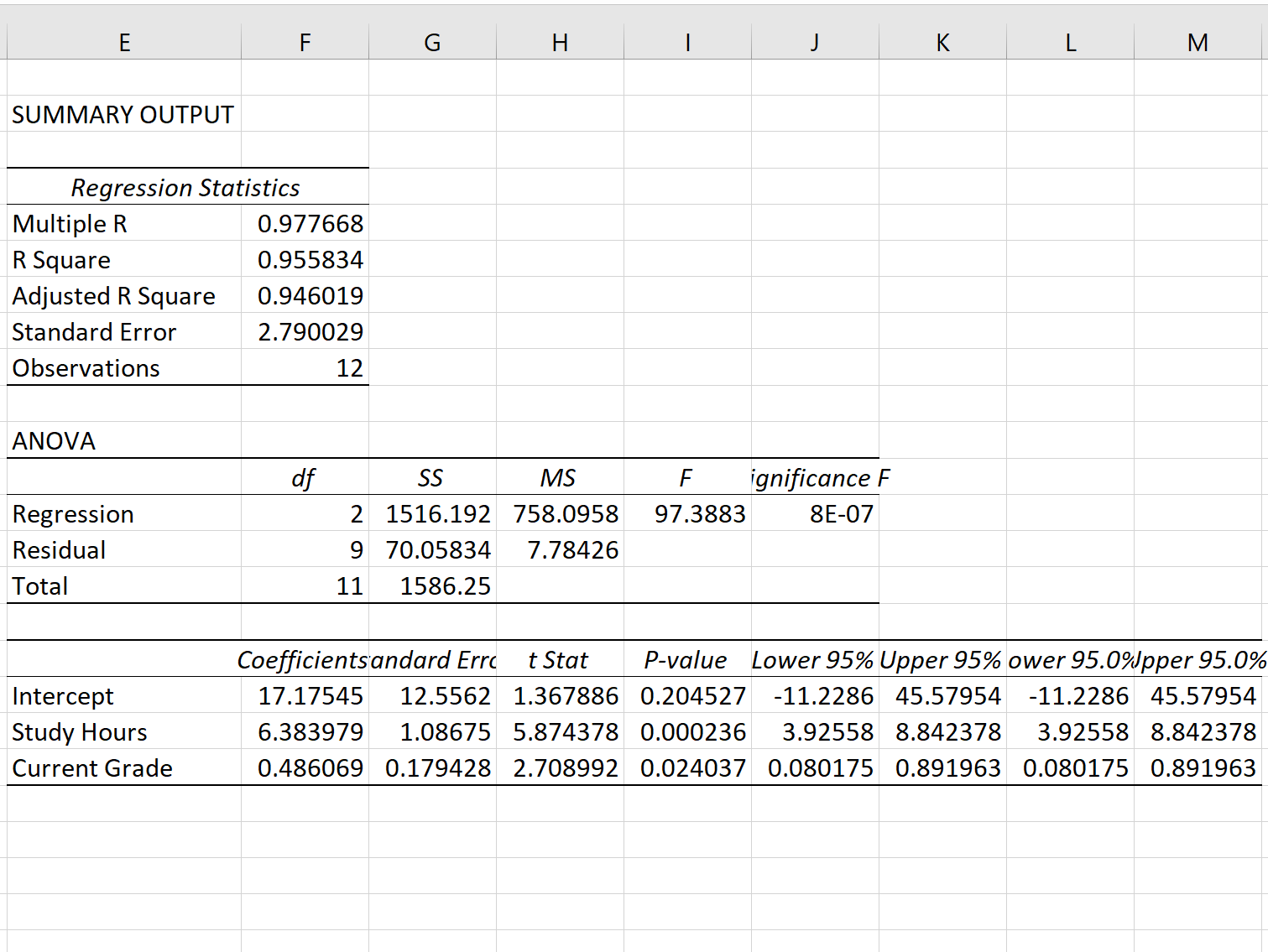
Как только вы нажмете OK , появится результат регрессионной модели:
Шаг 3: Интерпретируйте стандартную ошибку регрессии
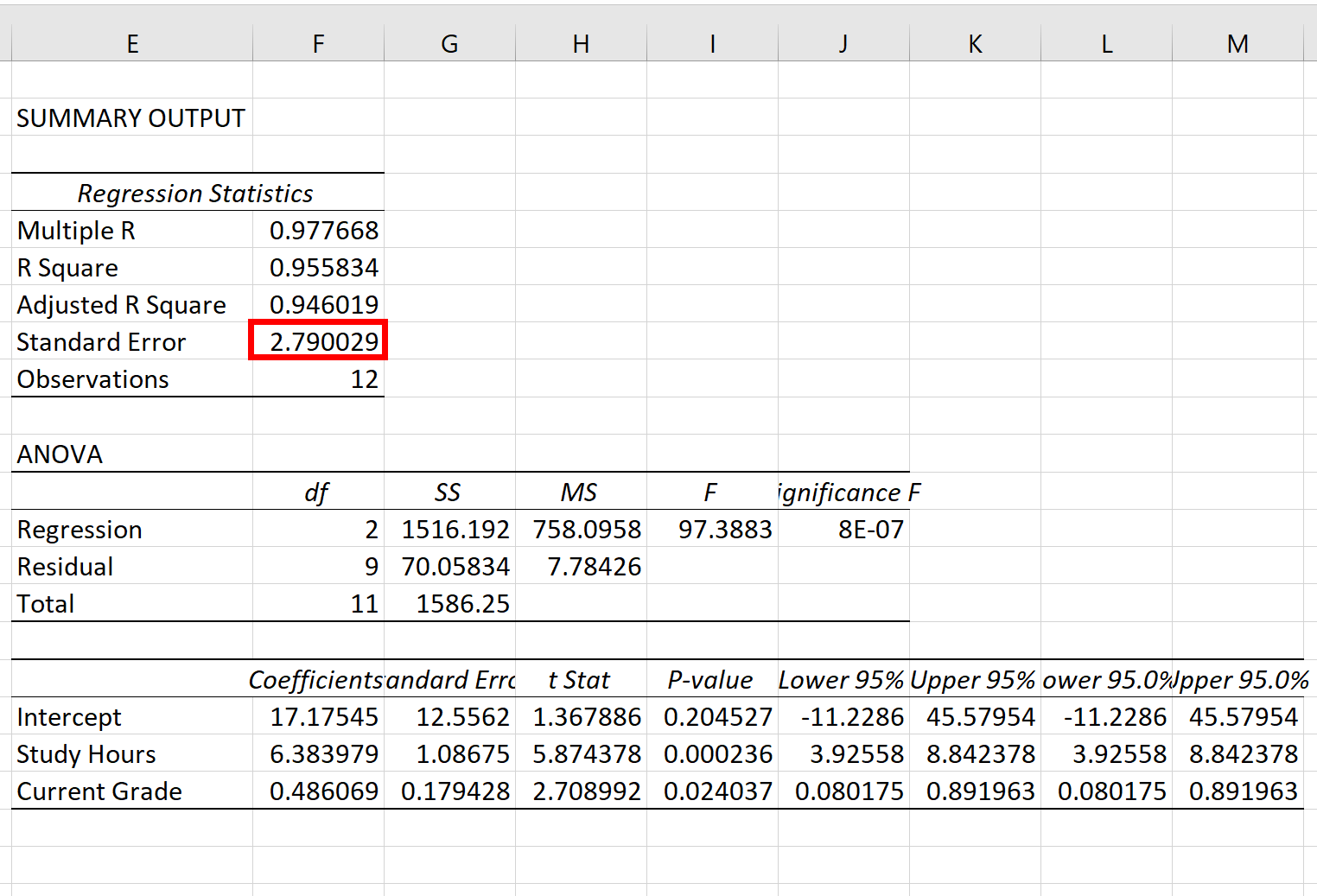
Стандартная ошибка модели регрессии — это число рядом со стандартной ошибкой :
Стандартная ошибка этой конкретной модели регрессии оказывается равной 2,790029 .
Это число представляет собой среднее расстояние между фактическими результатами экзаменов и оценками экзаменов, предсказанными моделью.
Обратите внимание, что некоторые экзаменационные баллы будут отличаться от прогнозируемого более чем на 2,79 единицы, в то время как некоторые будут ближе. Но в среднем расстояние между реальными экзаменационными баллами и прогнозируемыми составляет 2,790029 .
Также обратите внимание, что меньшая стандартная ошибка регрессии указывает на то, что модель регрессии более точно соответствует набору данных.
Таким образом, если мы подгоним новую регрессионную модель к набору данных и получим стандартную ошибку, скажем, 4,53 , эта новая модель будет хуже предсказывать результаты экзаменов, чем предыдущая модель.
Дополнительные ресурсы
Другим распространенным способом измерения точности регрессионной модели является использование R-квадрата. Прочтите эту статью , чтобы получить хорошее объяснение преимуществ использования стандартной ошибки регрессии для измерения точности по сравнению с R-квадратом.
Имея
прямую регрессии, необходимо оценить
насколько сильно точки исходных данных
отклоняются от прямой регрессии. Можно
выполнить оценку разброса, аналогичную
стандартному отклонению выборки. Этот
показатель, называемый стандартной
ошибкой оценки, демонстрирует величину
отклонения точек исходных данных от
прямой регрессии в направлении оси Y.
Стандартная ошибка оценки ()
вычисляется по следующей формуле.
Стандартная
ошибка оценки измеряет степень отличия
реальных значений Y от оцененной величины.
Для сравнительно больших выборок следует
ожидать, что около 67% разностей по модулю
не будет превышать
и около 95% модулей разностей будет не
больше 2.
Стандартная
ошибка оценки подобна стандартному
отклонению. Ее можно использовать для
оценки стандартного отклонения
совокупности. Фактически
оценивает стандартное отклонение
слагаемого ошибки
в статистической модели простой линейной
регрессии. Другими словами,
оценивает общее стандартное отклонение
нормального распределения значений Y,
имеющих математические ожидания
для каждого X.
Малая
стандартная ошибка оценки, полученная
при регрессионном анализе, свидетельствует,
что все точки данных находятся очень
близко к прямой регрессии. Если стандартная
ошибка оценки велика, точки данных могут
значительно удаляться от прямой.
2.3 Прогнозирование величины y
Регрессионную
прямую можно использовать для оценки
величины переменной Y
при данных значениях переменной X. Чтобы
получить точечный прогноз, или предсказание
для данного значения X, просто вычисляется
значение найденной функции регрессии
в точке X.
Конечно
реальные значения величины Y,
соответствующие рассматриваемым
значениям величины X, к сожалению, не
лежат в точности на регрессионной
прямой. Фактически они разбросаны
относительно прямой в соответствии с
величиной
.
Более того, выборочная регрессионная
прямая является оценкой регрессионной
прямой генеральной совокупности,
основанной на выборке из определенных
пар данных. Другая случайная выборка
даст иную выборочную прямую регрессии;
это аналогично ситуации, когда различные
выборки из одной и той же генеральной
совокупности дают различные значения
выборочного среднего.
Есть
два источника неопределенности в
точечном прогнозе, использующем уравнение
регрессии.
-
Неопределенность,
обусловленная отклонением точек данных
от выборочной прямой регрессии. -
Неопределенность,
обусловленная отклонением выборочной
прямой регрессии от регрессионной
прямой генеральной совокупности.
Интервальный
прогноз значений переменной Y
можно построить так, что при этом будут
учтены оба источника неопределенности.
Стандартная
ошибка прогноза
дает меру вариативности предсказанного
значения Y
около истинной величины Y
для данного значения X.
Стандартная ошибка прогноза равна:
Стандартная
ошибка прогноза зависит от значения X,
для которого прогнозируется величина
Y.
минимально, когда
,
поскольку тогда числитель в третьем
слагаемом под корнем в уравнении будет
0. При прочих неизменных величинах
большему отличию соответствует большее
значение стандартной ошибки прогноза.
Если
статистическая модель простой линейной
регрессии соответствует действительности,
границы интервала прогноза величины Y
равны:
где
— квантиль распределения Стьюдента с
n-2 степенями свободы ().
Если выборка велика (),
этот квантиль можно заменить соответствующим
квантилем нормального распределения.
Например, для большой выборки 95%-ный
интервал прогноза задается следующими
значениями:
Завершим
раздел обзором предположений, положенных
в основу статистической модели линейной
регрессии.
-
Для
заданного значения X генеральная
совокупность значений Y имеет нормальное
распределение относительно регрессионной
прямой совокупности. На практике
приемлемые результаты получаются
и
тогда, когда значения Y имеют
нормальное распределение лишь
приблизительно. -
Разброс
генеральной совокупности точек данных
относительно регрессионной прямой
совокупности остается постоянным всюду
вдоль этой прямой. Иными словами, при
возрастании значений X в точках данных
дисперсия генеральной совокупности
не увеличивается и не уменьшается.
Нарушение этого предположения называется
гетероскедастичностью. -
Слагаемые
ошибок
независимы между собой. Это предположение
определяет случайность выборки точек
Х-Y.
Если точки данных X-Y
записывались в течение некоторого
времени, данное предположение часто
нарушается. Вместо независимых данных,
такие последовательные наблюдения
будут давать серийно коррелированные
значения. -
В
генеральной совокупности существует
линейная зависимость между X и Y.
По аналогии с простой линейной регрессией
может рассматриваться и нелинейная
зависимость между X и У. Некоторые такие
случаи будут обсуждаться ниже.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вариант 1
Задание 1. Модель парной линейной регрессии.
Имеются данные о размере среднемесячных доходов в разных группах семей
|
Номер группы |
Среднедушевой денежный доход в месяц, руб., X |
Доля оплаты труда в структуре доходов семьи, %, Y |
|
1 |
79,8 |
64,2 |
|
2 |
152,1 |
66,1 |
|
3 |
199,3 |
69,0 |
|
4 |
240,8 |
70,6 |
|
5 |
282,4 |
72,4 |
|
6 |
301,8 |
74,3 |
|
7 |
385,3 |
76,0 |
|
8 |
457,8 |
77,1 |
|
9 |
577,4 |
78,4 |
Задания:
1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы
2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.
3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.
4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.
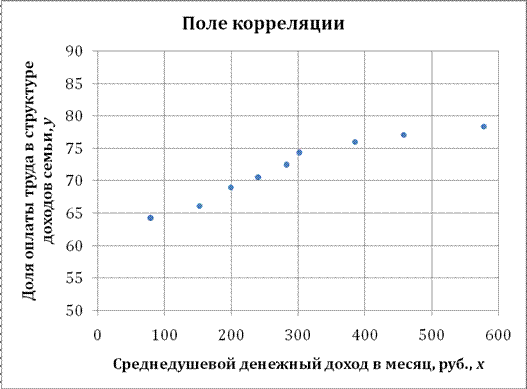
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.
Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .
Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
X×Y |
X2 |
Y2 |
|
1 |
79,8 |
64,2 |
5123,16 |
6368,04 |
4121,64 |
|
2 |
152,1 |
66,1 |
10053,81 |
23134,41 |
4369,21 |
|
3 |
199,3 |
69,0 |
13751,70 |
39720,49 |
4761,00 |
|
4 |
240,8 |
70,6 |
17000,48 |
57984,64 |
4984,36 |
|
5 |
282,4 |
72,4 |
20445,76 |
79749,76 |
5241,76 |
|
6 |
301,8 |
74,3 |
22423,74 |
91083,24 |
5520,49 |
|
7 |
385,3 |
76,0 |
29282,80 |
148456,09 |
5776,00 |
|
8 |
457,8 |
77,1 |
35296,38 |
209580,84 |
5944,41 |
|
9 |
577,4 |
78,4 |
45268,16 |
333390,76 |
6146,56 |
|
S |
2676,7 |
648,1 |
198645,99 |
989468,27 |
46865,43 |
|
Среднее |
297,41 |
72,01 |
22071,78 |
109940,92 |
5207,27 |
Вычислим коэффициент корреляции. Используем следующую формулу:
= 0,9568.
Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.
Среднюю ошибку коэффициента корреляции определим по формуле:
= 0,032.
Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.
TТабл(0,05; 7) = 2,36.
Запишем доверительный интервал для коэффициента корреляции.
Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.
Вычислим параметры уравнения регрессии.
= 0,03.
= 72,01 – 0,03×297,41 = 63,09.
Получим следующее уравнение: .
Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.
Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.
Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:
Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.
|
№ п/п |
X |
Y |
|
|
|
|
1 |
79,8 |
64,2 |
65,48 |
1,6384 |
47354,1 |
|
2 |
152,1 |
66,1 |
67,65 |
2,4025 |
21115,0 |
|
3 |
199,3 |
69,0 |
69,07 |
0,0049 |
9625,6 |
|
4 |
240,8 |
70,6 |
70,31 |
0,0841 |
3204,7 |
|
5 |
282,4 |
72,4 |
71,56 |
0,7056 |
225,3 |
|
6 |
301,8 |
74,3 |
72,14 |
4,6656 |
19,3 |
|
7 |
385,3 |
76,0 |
74,65 |
1,8225 |
7724,7 |
|
8 |
457,8 |
77,1 |
76,82 |
0,0784 |
25725,0 |
|
9 |
577,4 |
78,4 |
80,41 |
4,0401 |
78394,4 |
|
S |
2676,7 |
648,1 |
648,09 |
15,4421 |
193388,1 |
Вычислим стандартные ошибки коэффициентов уравнения.


Вычислим T-статистики.
Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и
, т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.
Сделаем рисунок.
Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.
Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.
Fтабл(0,05; 1; 7) = 5,59.
Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.
Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.
XP = 297,41 × 1,11 = 330,1.
Вычислим прогнозное значение Yp с помощью уравнения регрессии.
» 73%.
Доверительный интервал прогноза имеет вид
(УP – Tкр×My, УP + Tкр×My),
Где 

Запишем доверительный интервал прогноза:
Þ
Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.
Задание 2. Модель парной нелинейной регрессии.
По территориям Центрального района известны данные за 1995 г.
|
Район |
Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X |
Средний размер назначенных ежемесячных пенсий, тыс. руб., Y |
|
Брянская обл. |
178 |
240 |
|
Владимирская обл. |
202 |
226 |
|
Ивановская обл. |
197 |
221 |
|
Калужская обл. |
201 |
226 |
|
Костромская обл. |
189 |
220 |
|
Орловская обл. |
166 |
232 |
|
Рязанская обл. |
199 |
215 |
|
Смоленская обл. |
180 |
220 |
|
Тверская обл. |
181 |
222 |
|
Тульская обл. |
186 |
231 |
|
Ярославская обл. |
250 |
229 |
Задания:
1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной (
) парной регрессии. Сделать рисунки.
2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.
3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии
4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.
Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.
Получим следующий рисунок.
По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.
Построение полулогарифмической модели регрессии.
Уравнение логарифмической кривой: .
Обозначим:
Получим линейное уравнение регрессии:
Y = A + B×X.
Произведем линеаризацию модели путем замены . В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Xy |
X2 |
Y2 |
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
1243,63 |
26,85 |
57600 |
226,40 |
206,314 |
184,904 |
6,006 |
|
2 |
202 |
226 |
5,3083 |
1199,67 |
28,18 |
51076 |
225,17 |
0,132 |
0,694 |
0,370 |
|
3 |
197 |
221 |
5,2832 |
1167,59 |
27,91 |
48841 |
225,41 |
21,496 |
19,464 |
1,957 |
|
4 |
201 |
226 |
5,3033 |
1198,55 |
28,13 |
51076 |
225,22 |
0,132 |
0,615 |
0,348 |
|
5 |
189 |
220 |
5,2417 |
1153,18 |
27,48 |
48400 |
225,82 |
31,769 |
33,833 |
2,576 |
|
6 |
166 |
232 |
5,1120 |
1185,98 |
26,13 |
53824 |
227,08 |
40,496 |
24,172 |
2,165 |
|
7 |
199 |
215 |
5,2933 |
1138,06 |
28,02 |
46225 |
225,31 |
113,132 |
106,362 |
4,577 |
|
8 |
180 |
220 |
5,1930 |
1142,45 |
26,97 |
48400 |
226,29 |
31,769 |
39,601 |
2,781 |
|
9 |
181 |
222 |
5,1985 |
1154,07 |
27,02 |
49284 |
226,24 |
13,223 |
17,968 |
1,874 |
|
10 |
186 |
231 |
5,2257 |
1207,15 |
27,31 |
53361 |
225,97 |
28,769 |
25,273 |
2,225 |
|
11 |
250 |
229 |
5,5215 |
1264,41 |
30,49 |
52441 |
223,09 |
11,314 |
34,980 |
2,651 |
|
Итого |
2129 |
2482 |
57,862 |
13054,74 |
304,48 |
560528 |
2482,00 |
498,545 |
487,867 |
27,530 |
|
Среднее |
193,5 |
225,6 |
5,260 |
1186,79 |
27,68 |
50957,091 |
225,636 |
45,322 |
44,352 |
2,503 |
= -9,76.
= 225,6 – (-9,76)×5,26 = 276,99.
Уравнение модели имеет вид:
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Рассчитаем средний коэффициент эластичности по формуле:
= -0,04%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Построение степенной модели парной регрессии.
Уравнение степенной модели имеет вид: .
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
.
Произведем линеаризацию модели путем замены и
. В результате получим линейное уравнение
.
Рассчитаем его параметры, используя данные таблицы.
|
№ п/п |
X |
Y |
X = ln(X) |
Y = ln(Y) |
XY |
X2 |
Y2 |
|
|
|
|
Ai |
|
1 |
178 |
240 |
5,1818 |
5,4806 |
28,3995 |
26,851 |
30,037 |
226,3 |
206,3 |
188,391 |
241,661 |
6,07 |
|
2 |
202 |
226 |
5,3083 |
5,4205 |
28,7737 |
28,178 |
29,382 |
225,1 |
0,132 |
0,835 |
71,479 |
0,406 |
|
3 |
197 |
221 |
5,2832 |
5,3982 |
28,5196 |
27,912 |
29,140 |
225,3 |
21,496 |
18,671 |
11,934 |
1,918 |
|
4 |
201 |
226 |
5,3033 |
5,4205 |
28,7467 |
28,125 |
29,382 |
225,1 |
0,132 |
0,753 |
55,570 |
0,385 |
|
5 |
189 |
220 |
5,2417 |
5,3936 |
28,2720 |
27,476 |
29,091 |
225,7 |
31,769 |
32,607 |
20,661 |
2,530 |
|
6 |
166 |
232 |
5,1120 |
5,4467 |
27,8437 |
26,132 |
29,667 |
226,9 |
40,496 |
25,675 |
758,752 |
2,233 |
|
7 |
199 |
215 |
5,2933 |
5,3706 |
28,4284 |
28,019 |
28,844 |
225,2 |
113,132 |
104,576 |
29,752 |
4,540 |
|
8 |
180 |
220 |
5,1930 |
5,3936 |
28,0089 |
26,967 |
29,091 |
226,2 |
31,769 |
38,059 |
183,479 |
2,728 |
|
9 |
181 |
222 |
5,1985 |
5,4027 |
28,0858 |
27,024 |
29,189 |
226,1 |
13,223 |
16,950 |
157,388 |
1,821 |
|
10 |
186 |
231 |
5,2257 |
5,4424 |
28,4407 |
27,308 |
29,620 |
225,9 |
28,769 |
26,413 |
56,934 |
2,275 |
|
11 |
250 |
229 |
5,5215 |
5,4337 |
30,0021 |
30,487 |
29,525 |
223,1 |
11,314 |
34,846 |
3187,116 |
2,646 |
|
Итого |
2129 |
2482 |
57,862 |
59,603 |
313,521 |
304,479 |
322,969 |
2480,927 |
498,545 |
487,777 |
4774,727 |
27,548 |
|
Среднее |
193,5 |
225,6 |
5,260 |
5,418 |
28,502 |
27,680 |
29,361 |
225,539 |
45,322 |
44,343 |
434,066 |
2,504 |
С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.
= -0,042.
= 5,418 – 0,959×5,26 = 5,637.
Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.
A = eA = e5,637 = 280,76
Получим уравнение степенной модели регрессии: .
Определим индекс корреляции
Используя данные таблицы, получим:

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.
Вариация результата Y всего на 2,1% объясняется вариацией фактора X.
Сделаем рисунок.
Для степенной модели средний коэффициент эластичности равен коэффициенту B.
= -0,042%.
Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.
Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:
= 2,5%.
Сводная таблица вычислений
|
Параметры |
Модель |
|
|
Полулогарифмическая |
Степенная |
|
|
Уравнение связи |
|
|
|
Индекс корреляции |
0,1464 |
0,147 |
|
Коэффициент детерминации |
0,021 |
0,021 |
|
Средняя ошибка аппроксимации, % |
2,5 |
2,5 |
Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.
Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.
Прогнозное значение составит:
= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:
= 224,6 тыс. р.
Определим доверительный интервал прогноза для уровня значимости a = 0,05.
Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

Получаем: 
Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.
= 14,8.
Запишем доверительный интервал прогноза.
= 224,6 – 14,8 = 209,8 тыс. р.
= 224,6 + 14,8 = 239,4 тыс. р.
Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.
Задание 3. Моделирование временных рядов
Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.
|
Номер квартала |
Товарооборот % к предыдущему периоду |
Номер квартала |
Товарооборот % к предыдущему периоду |
|
1 |
100 |
11 |
98,8 |
|
2 |
93,9 |
12 |
101,9 |
|
3 |
96,5 |
13 |
113,1 |
|
4 |
101,8 |
14 |
98,4 |
|
5 |
107,8 |
15 |
97,3 |
|
6 |
96,3 |
16 |
112,1 |
|
7 |
95,7 |
17 |
97,6 |
|
8 |
98,2 |
18 |
93,7 |
|
9 |
104 |
19 |
114,3 |
|
10 |
99 |
20 |
108,4 |
Задания:
1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.
2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.
3. Рассчитать трендовую компоненту временного ряда и построить его график
4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.
Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.
Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.
Построим мультипликативную модель временного ряда.
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.
Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1) Выравнивание исходного ряда методом скользящей средней.
2) Расчет значений сезонной компоненты S.
3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.
4) Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.
5) Расчет полученных по модели значений T×E.
6) Расчет абсолютных и/или относительных ошибок.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).
1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).
Таблица 2.1
|
№ месяца, T |
Товарооборот, Yi |
Итого за четыре месяца |
Скользящая средняя за четыре месяца |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
100,0 |
– |
– |
– |
– |
|
2 |
93,9 |
392 |
98 |
– |
– |
|
3 |
96,5 |
400 |
100 |
99 |
0,975 |
|
4 |
101,8 |
402 |
100,5 |
100,25 |
1,015 |
|
5 |
107,8 |
402 |
100,5 |
100,5 |
1,073 |
|
6 |
96,3 |
398 |
99,5 |
100 |
0,963 |
|
7 |
95,7 |
394 |
98,5 |
99 |
0,967 |
|
8 |
98,2 |
397 |
99,25 |
98,875 |
0,993 |
|
9 |
104,0 |
400 |
100 |
99,625 |
1,044 |
|
10 |
99,0 |
404 |
101 |
100,5 |
0,985 |
|
11 |
98,8 |
413 |
103,25 |
102,125 |
0,967 |
|
12 |
101,9 |
412 |
103 |
103,125 |
0,988 |
|
13 |
113,1 |
411 |
102,75 |
102,875 |
1,099 |
|
14 |
98,4 |
309 |
77,25 |
90 |
1,093 |
|
15 |
97,3 |
196 |
49 |
63,125 |
1,541 |
|
16 |
112,1 |
303 |
75,75 |
62,375 |
1,797 |
|
17 |
97,6 |
418 |
104,5 |
90,125 |
1,083 |
|
18 |
93,7 |
414 |
103,5 |
104 |
0,901 |
|
19 |
114,3 |
– |
– |
– |
– |
|
20 |
108,4 |
– |
– |
– |
– |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
Таблица 2.2
|
Показатели |
Год |
№ квартала, I |
|||
|
I |
II |
III |
IV |
||
|
1 |
– |
– |
0,975 |
1,015 |
|
|
2 |
1,073 |
0,963 |
0,967 |
0,993 |
|
|
3 |
1,044 |
0,985 |
0,967 |
0,988 |
|
|
4 |
1,099 |
1,093 |
1,541 |
1,797 |
|
|
5 |
1,083 |
0,901 |
– |
– |
|
|
Всего за I-й квартал |
4,299 |
3,942 |
4,45 |
4,793 |
|
|
Средняя оценка сезонной компоненты для I-го квартала, |
0,860 |
0,788 |
0,890 |
0,959 |
|
|
Скорректированная сезонная компонента, |
0,984 |
0,901 |
1,018 |
1,097 |
Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.
Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.
Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки
на корректирующий коэффициент K.
Проверяем условие: равенство 4 суммы значений сезонной компоненты:
0,984 + 0,901 + 1,018 + 1,097 = 4.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.
Таблица 2.3
|
T |
Yt |
St |
|
T |
T×S |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
100,0 |
0,984 |
101,6 |
100,02 |
98,42 |
1,016 |
|
2 |
93,9 |
0,901 |
104,2 |
100,19 |
90,27 |
1,040 |
|
3 |
96,5 |
1,018 |
94,8 |
100,36 |
102,17 |
0,945 |
|
4 |
101,8 |
1,097 |
92,8 |
100,53 |
110,28 |
0,923 |
|
5 |
107,8 |
0,984 |
109,6 |
100,7 |
99,09 |
1,088 |
|
6 |
96,3 |
0,901 |
106,9 |
100,87 |
90,88 |
1,060 |
|
7 |
95,7 |
1,018 |
94,0 |
101,04 |
102,86 |
0,930 |
|
8 |
98,2 |
1,097 |
89,5 |
101,21 |
111,03 |
0,884 |
|
9 |
104,0 |
0,984 |
105,7 |
101,38 |
99,76 |
1,043 |
|
10 |
99,0 |
0,901 |
109,9 |
101,55 |
91,50 |
1,082 |
|
11 |
98,8 |
1,018 |
97,1 |
101,72 |
103,55 |
0,954 |
|
12 |
101,9 |
1,097 |
92,9 |
101,89 |
111,77 |
0,912 |
|
13 |
113,1 |
0,984 |
114,9 |
102,06 |
100,43 |
1,126 |
|
14 |
98,4 |
0,901 |
109,2 |
102,23 |
92,11 |
1,068 |
|
15 |
97,3 |
1,018 |
95,6 |
102,4 |
104,24 |
0,933 |
|
16 |
112,1 |
1,097 |
102,2 |
102,57 |
112,52 |
0,996 |
|
17 |
97,6 |
0,984 |
99,2 |
102,74 |
101,10 |
0,965 |
|
18 |
93,7 |
0,901 |
104,0 |
102,91 |
92,72 |
1,011 |
|
19 |
114,3 |
1,018 |
112,3 |
103,08 |
104,94 |
1,089 |
|
20 |
108,4 |
1,097 |
98,8 |
103,25 |
113,27 |
0,957 |
|
Среднее |
101,4 |
1,0011 |
Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.
Таблица 2.4
|
T |
|
T2 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
101,6 |
1 |
101,6 |
2,5 |
1,58 |
2,0 |
|
|
2 |
104,2 |
4 |
208,4 |
13,2 |
3,87 |
56,3 |
|
|
3 |
94,8 |
9 |
284,4 |
32,1 |
5,88 |
24,0 |
|
|
4 |
92,8 |
16 |
371,2 |
71,9 |
8,33 |
0,2 |
|
|
5 |
109,6 |
25 |
548 |
75,9 |
8,08 |
41,0 |
|
|
6 |
106,9 |
36 |
641,4 |
29,4 |
5,63 |
26,0 |
|
|
7 |
94,0 |
49 |
658 |
51,3 |
7,48 |
32,5 |
|
|
8 |
89,5 |
64 |
716 |
164,6 |
13,07 |
10,2 |
|
|
9 |
105,7 |
81 |
951,3 |
18,0 |
4,08 |
6,8 |
|
|
10 |
109,9 |
100 |
1099 |
56,3 |
7,58 |
5,8 |
|
|
11 |
97,1 |
121 |
1068,1 |
22,6 |
4,81 |
6,8 |
|
|
12 |
92,9 |
144 |
1114,8 |
97,4 |
9,69 |
0,3 |
|
|
13 |
114,9 |
169 |
1493,7 |
160,5 |
11,20 |
136,9 |
|
|
14 |
109,2 |
196 |
1528,8 |
39,6 |
6,39 |
9,0 |
|
|
15 |
95,6 |
225 |
1434 |
48,2 |
7,13 |
16,8 |
|
|
20 |
102,2 |
400 |
2044 |
0,2 |
0,37 |
114,5 |
|
|
21 |
99,2 |
441 |
2083,2 |
12,3 |
3,59 |
14,4 |
|
|
22 |
104,0 |
484 |
2288 |
1,0 |
1,05 |
59,3 |
|
|
23 |
112,3 |
529 |
2582,9 |
87,6 |
8,19 |
166,4 |
|
|
24 |
98,8 |
576 |
2371,2 |
23,7 |
4,49 |
49,0 |
|
|
Сумма |
230 |
2035,2 |
3670 |
23588 |
1008,3 |
122,49 |
778,2 |
|
Среднее |
11,5 |
101,8 |
183,5 |
1179,4 |
50,4 |
6,12 |
38,91 |
Вычислим параметры уравнения тренда.

= 99,85.
В результате получим уравнение тренда:
T = 99,85 + 0,17×T.
Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).
Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
Расчет ошибки в мультипликативной модели произведем по формуле:
Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).
Рассчитаем сумму квадратов абсолютных ошибок .
Используя 5-й столбец таблицы 2.4, получим:

Рассчитаем среднюю относительную ошибку: .
Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.
| < Предыдущая | Следующая > |
|---|
Для множественной регрессии формула несмещенной оценки дисперсии случайной ошибки имеет вид
begin{equation*} widehat {sigma ^2}=S^2=frac 1{n-k}{ast}sum _{i=1}^ne_i^2 end{equation*}
Она почти такая же, как для парной регрессии за тем исключением, что в знаменателе вместо выражения (left(n-2right)) стоит (left(n-kright)). Если извлечь корень из этой величины, то можно получить стандартную ошибку регрессии
begin{equation*} mathit{SEE}=sqrt{S^2}=sqrt{frac 1{n-k}{ast}sum _{i=1}^ne_i^2} end{equation*}
Расчет стандартной ошибки регрессии — это один из способов оценить точность вашей модели в целом. То есть оценить, насколько хорошо она соответствует данным. Чем меньше стандартная ошибка регрессии, тем лучше ваша модель соответствует доступным вам наблюдениям.
Следующая характеристика качества подгонки — это коэффициент детерминации (R^2).
Для множественной регрессии с константой так же, как и для парной, верно, что общая сумма квадратов может быть представлена как сумма квадратов остатков и объясненная сумма квадратов:
begin{equation*} sum _{i=1}^nleft(y_i-overline yright)^2=sum _{i=1}^ne_i^2+sum _{i=1}^nleft(widehat y_i-overline yright)^2 end{equation*}
Поэтому и (R^2) может быть рассчитан в точности таким же образом, как и для модели парной регрессии:
begin{equation*} R^2=1-frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=frac{sum _{i=1}^nleft(widehat y_i-overline yright)^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=frac{widehat {mathit{Var}}left(widehat yright)}{widehat {mathit{Var}}left(yright)} end{equation*}
И точно так же, как и в случае парной регрессии, он будет лежать между нулем и единицей. Если ваша модель хорошо соответствует данным, то (R^2) будет близок к единице, если нет, то к нулю. Ещё раз подчеркнем, что условие (sum _{i=1}^nleft(y_i-overline yright)^2=sum _{i=1}^ne_i^2+sum _{i=1}^nleft(widehat y_i-overline yright)^2) выполняется только тогда, когда в модели есть константа. Если же ее нет, то указанное равенство, вообще говоря, неверно, и (R^2) не обязан лежать между нулем и единицей, и интерпретировать стандартным образом его нельзя.
Некоторые эконометристы старой школы придают важное значение величине коэффициента (R^2). Действительно, если он близок к единице, то это, как правило, приятная новость. Однако не стоит переоценивать эту характеристику качества модели потому, что у коэффициента (R^2) есть существенные ограничения:
- Высокий (R^2) характеризует наличие множественной корреляции между регрессорами и зависимой переменной, но ничего не говорит о наличии или отсутствии причинно-следственной связи между анализируемыми переменными. Вспомните примеры из первой главы, где мы обсуждали, что высокая корреляция не гарантирует причинно-следственной связи.
- (R^2) не может быть использован для принятия решения о том, стоит ли добавлять в модель новые переменные или нет. Дело в том, что, когда вы добавляете новые переменные в ваше уравнение, качество подгонки данных не может стать хуже, следовательно, и сумма квадратов остатков не может увеличиться. В теории она может остаться неизменной, но на практике она всегда будет уменьшаться. А в этом случае, как видно из расчетной формулы, (R^2) будет увеличиваться. Получается, что какие бы дурацкие новые переменные вы ни добавляли в модель, коэффициент (R^2) будет увеличиваться (или, в крайнем случае, оставаться неизменным).
Последний из указанных недостатков легко можно преодолеть. Для этого есть усовершенствованная версия (R^2), которую называют скорректированным (или нормированным) коэффициентом (R^2) ( (R^2) adjusted):
begin{equation*} R_{mathit{adj}}^2=R^2-frac{k-1}{n-k}{ast}left(1-R^2right) end{equation*}
(R_{mathit{adj}}^2) меньше, чем обычный (R^2), на величину (frac{k-1}{n-k}{ast}left(1-R^2right)), которая представляет собой штраф за добавление избыточных переменных. Обратите внимание, что при прочих равных этот штраф растет по мере увеличения параметра (k), характеризующего число коэффициентов в вашей модели. Если вы будете добавлять в модель много регрессоров, которые не вносят существенного вклада в объяснение зависимой переменной, то (R^2_{mathit{adj}}) будет снижаться.
Поэтому, если вы хотите сравнить межу собой модели с разным числом объясняющих переменных, то лучше использовать (R^2_{mathit{adj}}), чем обычный (R^2). А ещё лучше обращать внимание не только на этот коэффициент, но и на прочие характеристики адекватности вашей модели, которые мы обсудим в этой книге.
Чтобы понять, откуда берется формула для скорректированного R-квадрата, запишем обычный R-квадрат следующим образом:
begin{equation*} R^2=1-frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=1-frac{frac{sum _{i=1}^ne_i^2} n}{frac{sum _{i=1}^nleft(y_i-overline yright)^2} n}. end{equation*}
В числителе дроби стоит выборочная дисперсия остатков, а в знаменателе — выборочная дисперсия зависимой переменной. Если и ту, и другую дисперсии заменить их несмещенными аналогами, то получим следующее выражение:
begin{equation*} 1-frac{S^2}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}=1-frac{frac{sum _{i=1}^ne_i^2}{n-k}}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}. end{equation*}
Легко проверить, что это и есть скорректированный R-квадрат:
begin{equation*} 1-frac{frac{sum _{i=1}^ne_i^2}{n-k}}{frac{sum _{i=1}^nleft(y_i-overline yright)^2}{n-1}}=1-frac{n-1}{n-k}frac{sum _{i=1}^ne_i^2}{sum _{i=1}^nleft(y_i-overline yright)^2}=1-frac{n-1}{n-k}left(1-R^2right)= end{equation*}
begin{equation*} R^2-frac{k-1}{n-k}{ast}left(1-R^2right)=R_{mathit{adj}}^2. end{equation*}
Загрузить PDF
Загрузить PDF
Стандартная ошибка оценки служит для того, чтобы выяснить, как линия регрессии соответствует набору данных. Если у вас есть набор данных, полученных в результате измерения, эксперимента, опроса или из другого источника, создайте линию регрессии, чтобы оценить дополнительные данные. Стандартная ошибка оценки характеризует, насколько верна линия регрессии.
-
1
Создайте таблицу с данными. Таблица должна состоять из пяти столбцов, и призвана облегчить вашу работу с данными. Чтобы вычислить стандартную ошибку оценки, понадобятся пять величин. Поэтому разделите таблицу на пять столбцов. Обозначьте эти столбцы так:[1]
-
2
Введите данные в таблицу. Когда вы проведете эксперимент или опрос, вы получите пары данных — независимую переменную обозначим как
, а зависимую или конечную переменную как
. Введите эти значения в первые два столбца таблицы.
- Не перепутайте данные. Помните, что определенному значению независимой переменной должно соответствовать конкретное значение зависимой переменной.
- Например, рассмотрим следующий набор пар данных:
- (1,2)
- (2,4)
- (3,5)
- (4,4)
- (5,5)
-
3
Вычислите линию регрессии. Сделайте это на основе представленных данных. Эта линия также называется линией наилучшего соответствия или линией наименьших квадратов. Расчет можно сделать вручную, но это довольно утомительно. Поэтому рекомендуем воспользоваться графическим калькулятором или онлайн-сервисом, которые быстро вычислят линию регрессии по вашим данным.[2]
- В этой статье предполагается, что уравнение линии регрессии дано (известно).
- В нашем примере линия регрессии описывается уравнением
.
-
4
Вычислите прогнозируемые значения по линии регрессии. С помощью уравнения линии регрессии можно вычислить прогнозируемые значения «y» для значений «x», которые есть и которых нет в наборе данных.
Реклама
-
1
Вычислите ошибку каждого прогнозируемого значения. В четвертом столбце таблицы запишите ошибку каждого прогнозируемого значения. В частности, вычтите прогнозируемое значение (
) из фактического (наблюдаемого) значения (
).[3]
- В нашем примере вычисления будут выглядеть так:
-
2
Вычислите квадраты ошибок. Возведите в квадрат каждое значение четвертого столбца, а результаты запишите в последнем (пятом) столбце таблицы.
- В нашем примере вычисления будут выглядеть так:
-
3
Найдите сумму квадратов ошибок. Она пригодится для вычисления стандартного отклонения, дисперсии и других величин. Чтобы найти сумму квадратов ошибок, сложите все значения пятого столбца. [4]
- В нашем примере вычисления будут выглядеть так:
- В нашем примере вычисления будут выглядеть так:
-
4
Завершите расчеты. Стандартная ошибка оценки — это квадратный корень из среднего значения суммы квадратов ошибок. Обычно ошибка оценки обозначается греческой буквой
. Поэтому сначала разделите сумму квадратов ошибок на число пар данных. А потом из полученного значения извлеките квадратный корень.[5]
- Если рассматриваемые данные представляют всю совокупность, среднее значение находится так: сумму нужно разделить на N (количество пар данных). Если же рассматриваемые данные представляют некоторую выборку, вместо N подставьте N-2.
- В нашем примере, скорее всего, имеет место выборка, потому что мы рассматриваем всего 5 пар данных. Поэтому стандартную ошибку оценки вычислите следующим образом:
-
5
Интерпретируйте полученный результат. Стандартная ошибка оценки — это статистический показатель, которые оценивает, насколько близко измеренные данные лежат к линии регрессии. Ошибка оценка «0» означает, что каждая точка лежит непосредственно на линии. Чем выше ошибка оценки, тем дальше от линии регрессии лежат точки.[6]
- В нашем примере выборка достаточно маленькая, поэтому стандартная оценка ошибки 0,894 является довольно низкой и характеризует близко расположенные данные.
Реклама
Об этой статье
Эту страницу просматривали 4719 раз.