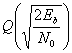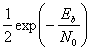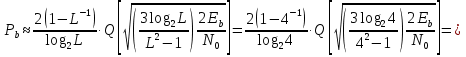Расчет вероятности битовой ошибки

(матрице переходных вероятностей)

(т. е. в канале с независимыми

14

… О П П П П П О О П П П …

Цель нашего повествования — вычислить вероятность ошибки на выходе дифференциального декодера, которая в рамках принятых обозначений

соответствует событию «О» и обозначается	как PО	. Эта вероятность будет
зависеть от вероятностей перехода PX/X ,	которых,	по сути, всего две, т. к.
оставшиеся две являются дополнениями до единицы.

Всякая вероятность есть предельная величина, определяемая по бесконечному количеству событий, поэтому чтобы определить PО требуется выписать всю «линию жизни» автомата и подсчитать долю букв «О» относительно общего количества букв; практически это сделать невозможно, а вот в уме — возможно, чем мы и займемся.

Предположим, что автомат начал жить, и его жизнь кратна дням, т. е. каждый день выпадает буква, «О» или «П». Какова вероятность того, что в первый день жизни произойдет ошибочный прием «О»? Эту вероятность логично приравнять к вероятности ошибки в канале без памяти

ошибками), PО 1 =p . Во второй день могут выпасть буквы либо «О», либо «П». Соответствующие вероятности вычисляются вполне однозначно по матрице канала

(PPПО)2 =(PPП/ПО/П PPП/ОО/О)(PPПО)1 ,

и так далее. Логика данного уравнения основана на формуле умножения и сложения вероятностей.

Упражнение: распишите матричное уравнение в виде системы линейных алгебраических уравнений, и поразмыслите над смыслом умножения и сложения вероятностей.

Пусть теперь уже прошло очень много дней жизни автомата… В этом случае вероятности PО n и PП n должны сходиться к искомым безусловным вероятностям PО и PП

PП n+1 ≈ PП n	,	lim	PП n = PП	.	(10)
(PО)	(PО)		n→∞	(PО) (PО)

Тогда справедливо предельное равенство

16

IV.Правильный прием в предыдущем и ошибочный — в текущем, PО/П : 0 0 1, декодируем как 0 1, (0 + 0 = 0, 0 + 1 = 1), 1 1 0, декодируем как 0 1, (1 + 1 = 0, 1 + 0 = 1).

Вероятность этого события равна	PО/П=p(1−p)+(1− p) p=2 p(1−p) .
Подставим найденные переходные вероятности в (11) и получим
окончательный результат
PО=2 p(1−p) ,	PП= p2 +(1−p)2 .	(12)
Таким образом, вероятность ошибки на выходе дифференциального
декодера почти в два раза превышает канальную вероятность ошибки p	; этот
результат тем точнее, чем лучше	канал,	т. е. чем меньше p . Данный	факт

объясняется достаточно просто: при малых p ошибки происходят изредка и, в основном, по одиночке, а из логики дифференциального декодирования следует, что одна одиночная ошибка после декодирования трансформируется в две.

Любопытно также отметить, что если в канале вероятность ошибки равна ½, то после дифференциального декодирования вероятность ошибки остается той же!

From Wikipedia, the free encyclopedia

In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.

The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.^[1]

The bit error probability p_e is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.

Example[edit]

As an example, assume this transmitted bit sequence:

1 1 0 0 0 1 0 1 1

and the following received bit sequence:

0 1 0 1 0 1 0 0 1,

The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.

Packet error ratio[edit]

The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability p_p, which for a data packet length of N bits can be expressed as

,

assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately

Similar measurements can be carried out for the transmission of frames, blocks, or symbols.

The above expression can be rearranged to express the corresponding BER (p_e) as a function of the PER (p_p) and the data packet length N in bits:

Factors affecting the BER[edit]

In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.

The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.

The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.

Analysis of the BER[edit]

The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.

Examples of simple channel models used in information theory are:

• Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
• Additive white Gaussian noise (AWGN) channel without fading.

A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).

In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).

For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:
.^[2]

People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.

Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.

A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.^[3]

Mathematical draft[edit]

The BER is the likelihood of a bit misinterpretation due to electrical noise . Considering a bipolar NRZ transmission, we have

for a «1» and for a «0». Each of and has a period of .

Knowing that the noise has a bilateral spectral density ,

is

and is .

Returning to BER, we have the likelihood of a bit misinterpretation .

and

where is the threshold of decision, set to 0 when .

We can use the average energy of the signal to find the final expression :

±§

Bit error rate test[edit]

BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.

A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.

Common types of BERT stress patterns[edit]

• PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
• QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
• 3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
• 1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
• Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
• All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
• All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
• Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
• 2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
• Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
• Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
• T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.

Bit error rate tester[edit]

A bit error rate tester (BERT), also known as a «bit error ratio tester»^[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.

The main building blocks of a BERT are:

• Pattern generator, which transmits a defined test pattern to the DUT or test system
• Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
• Clock signal generator to synchronize the pattern generator and the error detector
• Digital communication analyser is optional to display the transmitted or received signal
• Electrical-optical converter and optical-electrical converter for testing optical communication signals

See also[edit]

• Burst error
• Error correction code
• Errored second
• Pseudo bit error ratio
• Viterbi Error Rate

References[edit]

 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).

External links[edit]

• QPSK BER for AWGN channel – online experiment

4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK

4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK

4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK

4.7.6. Вероятность ошибки для различных модуляций

4.7.1. Вероятность появления ошибочного бита при когерентном обнаружении сигнала BPSK

Важной мерой производительности, используемой для сравнения цифровых схем модуляции, является вероятность ошибки, РЕ Для коррелятора или согласованного фильтра вычисление РЕ можно представить геометрически (см. рис. 4.6). Расчет РЕ включает нахождение вероятности того, что при данном векторе переданного сигнала, скажем si вектор шума n выведет сигнал из области 1. Вероятность принятия детектором неверного решения называется вероятностью символьной ошибки, рE. Несмотря на то что решения принимаются на символьном уровне, производительность системы часто удобнее задавать через вероятность битовой ошибки (Ps). Связь РВ и РЕ рассмотрена в разделе 4.9.3 для ортогональной передачи сигналов и в разделе 4.9.4 для многофазной передачи сигналов.

Для удобства изложения в данном разделе мы ограничимся когерентным обнаружением сигналов BPSK. В этом случае вероятность символьной ошибки — это то же самое, что и вероятность битовой ошибки. Предположим, что сигналы равновероятны. Допустим также, что при передаче сигнала принятый сигнал r(t) равен , где n(t) — процесс AWGN; кроме того, мы пренебрегаем ухудшением качества вследствие введенной каналом или схемой межсимвольной интерференции. Как показывалось в разделе 4.4.1, антиподные сигналы и можно описать в одномерном сигнальном пространстве, где

(4.74)

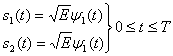
Детектор выбирает с наибольшим выходом коррелятора ; или, в нашем случае антиподных сигналов с равными энергиями, детектор, используя формулу (4.20), принимает решение следующего вида.

(4.74)

Как видно из рис. 4.9, возможны ошибки двух типов: шум так искажает переданный сигнал , что измерения в детекторе дают отрицательную величину z(T), и детектор выбирает гипотезу H2, что был послан сигнал s2(t). Возможна также обратная ситуация: шум искажает переданный сигнал , измерения в детекторе дают положительную величину z(T), и детектор выбирает гипотезу Н1, соответствующую предположению о передаче сигнала .

В разделе 3.2.1.1 была выведена формула (3.42), описывающая вероятность битовой ошибки РB для детектора, работающего по принципу минимальной вероятности ошибки.

(4.76)

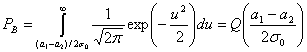
Здесь σ0 — среднеквадратическое отклонение шума вне коррелятора. Функция Q(x), называемая гауссовым интегралом ошибок, определяется следующим образом.

(4.77)

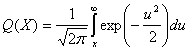
Эта функция подробно описывается в разделах 3.2 и Б.3.2.

Для передачи антиподных сигналов с равными энергиями, таких как сигналы в формате BPSK, приведенные в выражении (4.74), на выход приемника поступают следующие компоненты: , при переданном сигнале , и , при переданном сигнале s2(t), где Еь — энергия сигнала, приходящаяся на двоичный символ. Для процесса AWGN дисперсию шума вне коррелятора можно заменить N0/2 (см. приложение В), так что формулу (4.76) можно переписать следующим образом.

(4.78)

(4.79)

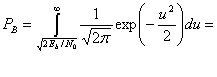
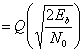
Данный результат для полосовой передачи антиподных сигналов BPSK совпадает с полученными ранее формулами для обнаружения антиподных сигналов с использованием согласованного фильтра (формула (3.70)) и обнаружения узкополосных антиподных сигналов с применением согласованного фильтра (формула (3.76)). Это является примером описанной ранее теоремы эквивалентности. Для линейных систем теорема эквивалентности утверждает, что на математическое описание процесса обнаружения не влияет сдвиг частоты. Как следствие, использование согласованных фильтров или корреляторов для обнаружения полосовых сигналов (рассмотренное в данной главе) дает те же соотношения, что были выведены ранее для сопоставимых узкополосных сигналов.

4.7.2. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в дифференциальной модуляции BPSK

Сигналы в канале иногда инвертируются; например, при использовании когерентного опорного сигнала, генерируемого контуром ФАПЧ, фаза может быть неоднозначной. Если фаза несущей была инвертирована при использовании схемы DPSK, как это скажется на сообщении? Поскольку информация сообщения кодируется подобием или отличием соседних символов, единственным следствием может быть ошибка в бите, который инвертируется, или в бите, непосредственно следующим за инвертированным. Точность определения подобия или отличия символов не меняется при инвертировании несущей. Иногда сообщения (и кодирующие их сигналы) дифференциально кодируются и когерентно обнаруживаются, чтобы просто избежать неопределенности в определении фазы.

Вероятность появления ошибочного бита при когерентном обнаружении сигналов в дифференциальной модуляции PSK (DPSK) дается выражением [5].

(4.80)

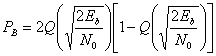
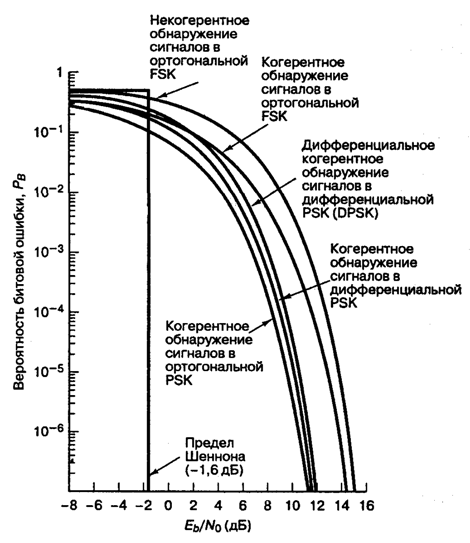
Это соотношение изображено на рис. 4.25. Отметим, что существует незначительное ухудшение достоверности обнаружения по сравнению с когерентным обнаружением сигналов в модуляции PSK. Это вызвано дифференциальным кодированием, поскольку любая отдельная ошибка обнаружения обычно приводит к принятию двух ошибочных решений. Подробно вероятность ошибки при использовании наиболее популярной схемы — когерентного обнаружения сигналов в модуляции DPSK — рассмотрена в разделе 4.7.5.

Рис. 4.25. Вероятность появления ошибочного бита для бинарных систем нескольких типов

4.7.3. Вероятность появления ошибочного бита при когерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

Формулы (4.78) и (4.79) описывают вероятность появления ошибочного бита для когерентного обнаружения антиподных сигналов. Более общую трактовку для когерентного обнаружения бинарных сигналов (не ограничивающихся антиподными сигналами) дает следующее выражение для РВ [6].

(4.81)

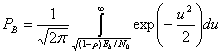
Из формулы (3.64,б) — временной коэффициент взаимной корреляций между и , где θ — угол между векторами сигналов и s2 (см. рис. 4.6). Для антиподных сигналов, таких как сигналы BPSK, θ = π, поэтому ρ = -1.

Для ортогональных сигналов, таких как сигналы бинарной FSK (BFSK), θ = π/2, поскольку векторы и s2 перпендикулярны; следовательно, ρ = 0, что можно доказать с помощью формулы (3.64,а), поэтому выражение (4.81) можно переписать следующим образом.

(4.82)

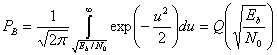
Здесь Q(x) — дополнительная функция ошибок, подробно описанная в разделах 3.2 и Б.3.2. Зависимость (4.82) для когерентного обнаружения ортогональных сигналов BFSK, показанная на рис. 4.25, аналогична зависимости, полученной для обнаружения ортогональных сигналов с помощью согласованного фильтра (формула (3.71)) и узкополосных ортогональных сигналов (униполярных импульсов) с использованием согласованного фильтра (формула (3.73)). В данной книге мы не рассматриваем амплитудную манипуляцию ООК (on-off keying), но соотношение (4.82 применимо к обнаружению с помощью согласованного фильтра сигналов ООК, так же как и к когерентному обнаружению любых ортогональных сигналов.

Справедливость соотношения (4.82) подтверждает и то, что разность энергий между ортогональными векторами сигналов и s2 с амплитудой , как показано на рис. 3.10, б, равна квадрату расстояния между концами ортогональных векторов Ed = 2Eb. Подстановка этого результата в формулу (3.63) также дает формулу (4.82). Сравнивая формулы (4.82) и (4.79), видим, что, по сравнению со схемой BPSK, схема BFSK требует на 3 дБ большего отношения E/N0 для обеспечения аналогичной достоверности передачи. Этот результат не должен быть неожиданным, поскольку при данной мощности сигнала квадрат расстояния между ортогональными векторами вдвое (на 3 дБ) больше квадрата расстояния между антиподными векторами.

4.7.4. Вероятность появления ошибочного бита при некогерентном обнаружении сигнала в бинарной ортогональной модуляции FSK

Рассмотрим бинарное ортогональное множество равновероятных сигналов FSK , определенное формулой (4.8).

Фаза φ неизвестна и предполагается постоянной. Детектор описывается М = 2 каналами, состоящими, как показано на рис. 4.19, из полосовых фильтров и детекторов огибающей. На вход детектора поступает принятый сигнал r(t) = si(t) + n(t), где n(i) — гауссов шум с двусторонней спектральной плотностью мощности No/2. Предположим, что и достаточно разнесены по частоте, чтобы их перекрытием можно было пренебречь. Вычисление вероятности появления ошибочного бита для равновероятных сигналов и начнем, как и в случае узкополосной передачи, с уравнения (3.38).

(4.83)

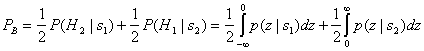
Для бинарного случая тестовая статистика z(T) определена как . Предположим, что полоса фильтра Wf равна 1/T, так что огибающая сигнала FSK (приблизительно) сохраняется на выходе фильтра. При отсутствии шума в приемнике значение z(T) равно при передаче s1(t) и — — при передаче s2(t). Вследствие такой симметрии оптимальный порог γ0=0. Плотность вероятности подобна плотности вероятности .

(4.84)

Таким образом, можем записать

(4.85)

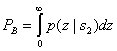
или

(4.86)

где z1 и z2 обозначают выходы z1(T) и z2(T) детекторов огибающей, показанных на рис.4.19. При передаче тона , т.е. когда r(t) = s2(t) + n(t), выход z1(T) состоит исключительно из случайной переменной гауссового шума; он не содержит сигнального компонента. Распределение Гаусса в нелинейном детекторе огибающей дает распределение Релея на выходе [6], так что

(4.87)

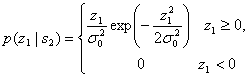
где — шум на выходе фильтра. С другой стороны, z2(T) имеет распределение Раиса, поскольку на вход нижнего детектора огибающей подается синусоида плюс шум [6]. Плотность вероятности p(z2s2) записывается как

(4.88)

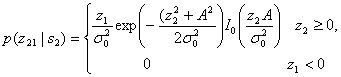
где и, как и ранее, — шум на выходе фильтра. Функция 10(х), известная как модифицированная функция Бесселя первого рода нулевого порядка [7], определяется следующим образом.

(4.89)

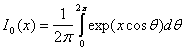
Ошибка при передаче s2(t) происходит, если выборка огибающей z1(T), полученная из верхнего канала (по которому проходит шум), больше выборки огибающей z2(T), полученной из нижнего канала (по которому проходит сигнал и шум). Таким образом, вероятность этой ошибки можно получить, проинтегрировав до бесконечности с последующим усреднением результата по всем возможным z2.

(4.91)

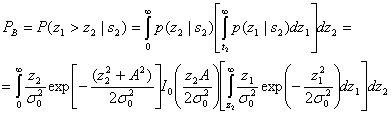
Здесь , внутренний интеграл — условная вероятность ошибки, при фиксированном значении z2, если был передан сигнал s2(1), а внешний интеграл усредняет условную вероятность по всем возможным значениям z2. Данный интеграл можно вычислить аналитически [8], и его значение равно следующему.

(4.92)

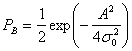
С помощью формулы (1.19) шум на выходе фильтра можно выразить как

(4.93)

где a Wf — ширина полосы фильтра. Таким образом, формула (4.92) приобретает следующий вид.

(4.94)

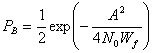
Выражение (4.94) показывает, что вероятность ошибки зависит от ширины полосы полосового фильтра и РB уменьшается при снижении Wf. Результат справедлив только при пренебрежении межсимвольной интерференцией (intersymbol interference — ISI). Минимальная разрешенная Wf (т.е. не дающая межсимвольной интерференции) получается из уравнения (3.81) при коэффициенте сглаживания г = 0. Следовательно, Wf= R бит/с =1/T, и выражение (4.94) можно переписать следующим образом.

(4.95)

(4.96)

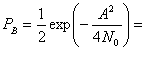
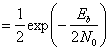
Здесь Еь= (1/2)А²Т — энергия одного бита. Если сравнить вероятность ошибки схем некогерентной и когерентной FSK (см. рис. 4.25), можно заметить, что при равных РB некогерентная FSK требует приблизительно на 1 дБ большего отношения Eb/N0, чем когерентная FSK (для РB < 10^-4). При этом некогерентный приемник легче реализуется, поскольку не требуется генерировать когерентные опорные сигналы. По этой причине практически все приемники FSK используют некогерентное обнаружение. В следующем разделе будет показано, что при сравнении когерентной ортогональной схемы FSK с нёкогерентной схемой DPSK имеет место та же разница в 3 дБ, что и при сравнении когерентной ортогональной FSK и когерентной PSK. Как указывалось ранее, в данной книге не рассматривается амплитудная манипуляция ООК (on-off keying). Все же отметим, что вероятность появления ошибочного бита РB, выраженная в формуле (4.96), идентична РB для некогерентного обнаружения сигналов ООК.

4.7.5. Вероятность появления ошибочного бита для бинарной модуляции DPSK

Определим набор сигналов BPSK следующим образом.

(4.97)

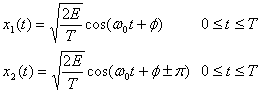
Особенностью схемы DPSK является отсутствие в сигнальном пространстве четко определенных областей решений. В данном случае решение основывается на разности фаз между принятыми сигналами. Таким образом, при передаче сигналов DPSK каждый бит в действительности передается парой двоичных сигналов.

(4.98)

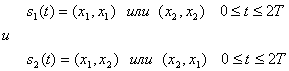
Здесь обозначает сигнал , за которым следует сигнал . Первые Т секунд каждого сигнала — это в действительности последние Т секунд предыдущего. Отметим, что оба сигнала s1(t) и s2(t) могут принимать любую из возможных форм и что и — это антиподные сигналы. Таким образом, корреляцию между и s2(t) для любой комбинации сигналов можно записать следующим образом.

(4.99)

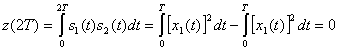
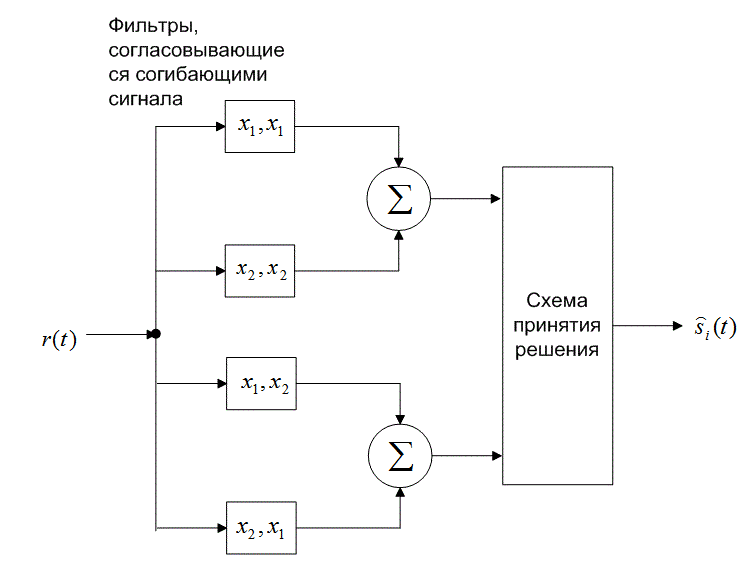
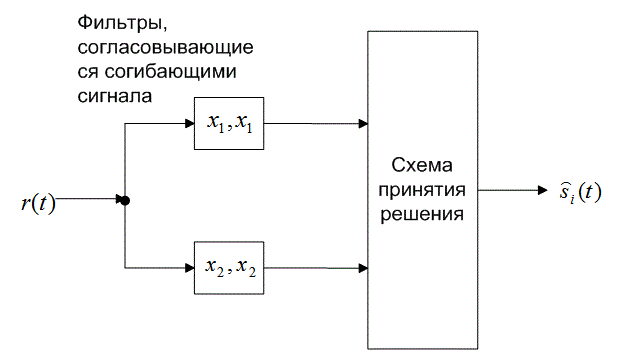
Следовательно, каждую пару сигналов DPSK можно представить как ортогональный сигнал длительностью 2Т секунд. Обнаружение может соответствовать некогерентному обнаружению огибающей с помощью четырех каналов, согласованных с каждым возможным выходом огибающей, как показано на рис. 4.26. Поскольку два детектора огибающей, представляющих каждый символ, обратны друг другу, выборки их огибающих будут совпадать. Значит, мы можем реализовать детектор как один канал для , согласовывающегося с или , и один канал для , согласовывающегося с или , как показано на рис. 4.26. Следовательно, детектор DPSK сокращается до стандартного двухканального некогерентного детектора. В действительности фильтр может согласовываться с разностным сигналом; так что необходимым является всего один канал. На рис. 4.26 показаны фильтры, которые согласовываются с огибающими сигнала (в течение двух периодов передачи символа). Что это означает, если вспомнить, что DPSK — это схема передачи сигналов с постоянной огибающей? Это означает, что нам требуется реализовать детектор энергии, подобный квадратурному приемнику на рис. 4.18, где каждый сигнал в течение периода представляется синфазным и квадратурным опорными сигналами.

синфазный опорный сигнал квадратурный опорный сигнал синфазный опорный сигнал квадратурный опорный сигнал

Поскольку пары сигналов DPSK ортогональны, вероятность ошибки при подобном некогерентном обнаружении дается выражением (4.96). Впрочем, поскольку сигналы DPSK длятся 2Т секунд, энергия сигналов , определенных в формуле (4.98), равна удвоенной энергии сигнала, определенного в течение одного периода передачи символа.

а)

б)

Рис. 4.26. Обнаружение в схеме DPSK: а) четырехканальное дифференциально-когерентное обнаружение сигналов в бинарной модуляции DPSK; б) эквивалентный двухканальный детектор сигналов в бинарной модуляции DPSK

Таким образом, РВможно записать в следующем виде.

(4.100)

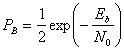
Зависимость (4.100), изображенная на рис. 4.25, представляет собой дифференциальное когерентное обнаружение сигналов в дифференциальной модуляции PSK, или просто DPSK. Выражение справедливо для оптимального детектора DPSK (рис. 4.17, в). Для детектора, показанного на рис. 4.17, б, вероятность ошибки будет несколько выше приведенной в выражении (4.100) [3]. Если сравнить вероятность ошибки, приведенную в формуле (4.100), с вероятностью ошибки когерентной схемы PSK (см. рис. 4.25), видно, что при равных РB схема DPSK требует приблизительно на 1 дБ большего отношения E^N0, чем схема BPSK (для ). Систему DPSK реализовать легче, чем систему PSK, поскольку приемник DPSK не требует фазовой синхронизации. По этой причине иногда предпочтительнее использовать менее эффективную схему DPSK, чем более сложную схему PSK.

4.7.6. Вероятность ошибки для различных модуляций

В табл. 4.1 и на рис. 4.25 приведены аналитические выражения и графики Р_B для наиболее распространенных схем модуляции, описанных выше. Для Р_B = 10^-4 можно видеть, что разница между лучшей (когерентной PSK) и худшей (некогерентной ортогональной FSK) из рассмотренных схем равна приблизительно 4 дБ. В некоторых случаях 4 дБ — это небольшая цена за простоту реализации, увеличивающуюся от когерентной схемы PSK до некогерентной FSK (рис. 4.25); впрочем, в других случаях ценным является даже выигрыш в 1 дБ. Помимо сложности реализации и вероятности Р_B существуют и другие факторы, влияющие на выбор модуляции; например, в некоторых случаях (в каналах со случайным затуханием) желательными являются некогерентные системы, поскольку иногда когерентные опорные сигналы затруднительно определять и использовать. В военных и космических приложениях весьма желательны сигналы, которые могут противостоять значительному ухудшению качества, сохраняя возможность обнаружения.

Таблица 4.1. Вероятность ошибки для различных бинарных модуляций

В цифровая передача, количество битовые ошибки это количество полученных биты из поток данных через канал связи которые были изменены из-за шум, вмешательство, искажение или же битовая синхронизация ошибки.

В частота ошибок по битам (BER) — количество битовых ошибок в единицу времени. В коэффициент битовых ошибок (также BER) — количество битовых ошибок, деленное на общее количество переданных битов за исследуемый интервал времени. Коэффициент битовых ошибок — это безразмерная мера производительности, часто выражаемая как процент.^[1]

В вероятность битовой ошибки п_е это ожидаемое значение коэффициента ошибок по битам. Коэффициент битовых ошибок можно рассматривать как приблизительную оценку вероятности битовых ошибок. Эта оценка верна для длительного интервала времени и большого количества битовых ошибок.

Пример

В качестве примера предположим, что эта переданная битовая последовательность:

0 1 1 0 0 0 1 0 1 1

и следующая полученная битовая последовательность:

0 0 1 0 1 0 1 0 0 1,

Количество битовых ошибок (подчеркнутые биты) в данном случае равно 3. BER — это 3 неверных бита, разделенных на 10 переданных битов, в результате чего BER составляет 0,3 или 30%.

Коэффициент ошибок пакета

В коэффициент ошибок пакета (PER) — это количество неправильно полученных пакеты данных деленное на общее количество полученных пакетов. Пакет объявляется некорректным, если хотя бы один бит ошибочен. Ожидаемое значение PER обозначается вероятность ошибки пакета п_п, что для длины пакета данных N биты могут быть выражены как

,

предполагая, что битовые ошибки не зависят друг от друга. Для небольших вероятностей битовых ошибок и больших пакетов данных это примерно

Аналогичные измерения могут быть выполнены для передачи кадры, блоки, или же символы.

Факторы, влияющие на BER

В системе связи на BER на стороне приемника может влиять канал передачи. шум, вмешательство, искажение, битовая синхронизация проблемы, затухание, беспроводной многолучевость угасание, так далее.

BER может быть улучшен путем выбора сильного сигнала (если это не вызывает перекрестных помех и большего количества битовых ошибок), путем выбора медленного и надежного модуляция схема или линейное кодирование схему, и применяя кодирование каналов такие схемы как избыточные упреждающее исправление ошибок коды.

В передача BER — число обнаруженных неверных битов до исправления ошибок, деленное на общее количество переданных битов (включая избыточные коды ошибок). В информация BER, примерно равное вероятность ошибки декодирования, — количество декодированных битов, которые остаются некорректными после исправления ошибок, деленное на общее количество декодированных битов (полезная информация). Обычно BER передачи больше, чем BER информации. На информационный BER влияет сила кода прямого исправления ошибок.

Анализ BER

BER можно оценить с помощью стохастического (Монте-Карло ) компьютерное моделирование. Если простая передача модель канала и источник данных Предполагается, что BER можно рассчитать аналитически. Примером такой модели источника данных является Бернулли источник.

Примеры простых моделей каналов, используемых в теория информации находятся:

• Бинарный симметричный канал (используется при анализе вероятности ошибки декодирования в случае непиковые битовые ошибки на канале передачи)
• Аддитивный белый гауссовский шум (AWGN) канал без замирания.

Наихудший сценарий — это полностью случайный канал, в котором шум полностью преобладает над полезным сигналом. В результате BER передачи составляет 50% (при условии, что Бернулли предполагается источник двоичных данных и двоичный симметричный канал, см. ниже).

В шумном канале BER часто выражается как функция нормализованного отношение несущая / шум мера обозначена Eb / N0, (отношение энергии на бит к спектральной плотности мощности шума), или Es / N0 (энергия на символ модуляции к спектральной плотности шума).

Например, в случае QPSK модуляции и канала AWGN, BER как функция Eb / N0 определяется как:.^[2]

Люди обычно строят кривые BER для описания производительности цифровой системы связи. В оптической связи обычно используется зависимость BER (дБ) от принимаемой мощности (дБм); в то время как в беспроводной связи используется BER (дБ) по сравнению с SNR (дБ).

Измерение коэффициента битовых ошибок помогает людям выбрать подходящий упреждающее исправление ошибок коды. Поскольку большинство таких кодов исправляют только перевороты битов, но не вставки или удаления битов, Расстояние Хэмминга метрика — это подходящий способ измерения количества битовых ошибок. Многие кодеры FEC также непрерывно измеряют текущий BER.

Более общий способ измерения количества битовых ошибок — это Расстояние Левенштейна.Измерение расстояния Левенштейна больше подходит для измерения характеристик сырого канала перед кадровая синхронизация, а также при использовании кодов исправления ошибок, предназначенных для исправления вставки и удаления битов, таких как коды маркеров и коды водяных знаков.^[3]

Математический проект

BER — это вероятность неправильной интерпретации из-за электрического шума. . Рассматривая биполярную передачу NRZ, мы имеем

для «1» и за «0». Каждый из и имеет период .

Зная, что шум имеет двустороннюю спектральную плотность ,

является

и является .

Возвращаясь к BER, у нас есть вероятность некоторой неверной интерпретации .

и

куда это порог принятия решения, установленный в 0, когда .

Мы можем использовать среднюю энергию сигнала чтобы найти окончательное выражение:

±§

Проверка коэффициента битовых ошибок

БЕРТ или же проверка коэффициента битовых ошибок это метод тестирования для схемы цифровой связи который использует заранее определенные шаблоны напряжения, состоящие из последовательности логических единиц и нулей, сгенерированные генератором тестовых шаблонов.

BERT обычно состоит из генератора тестовых шаблонов и приемника, который может быть настроен на один и тот же шаблон. Их можно использовать парами, по одному на любом конце линии передачи, или по отдельности на одном конце с петля на удаленном конце. BERT обычно представляют собой отдельные специализированные инструменты, но могут быть персональный компьютер -основан. При использовании количество ошибок, если таковые имеются, подсчитывается и представляется в виде отношения, например 1 на 1 000 000 или 1 на 1e06.

Распространенные типы моделей стресса BERT

• PRBS (псевдослучайная двоичная последовательность ) — псевдослучайный двоичный секвенсор из N бит. Эти последовательности шаблонов используются для измерения дрожь и глаз-маска TX-данных в электрических и оптических каналах передачи данных.
• QRSS (источник квазислучайного сигнала) — псевдослучайный двоичный секвенсор, который генерирует каждую комбинацию 20-битного слова, повторяет каждые 1048 575 слов и подавляет последовательные нули до не более 14. Он содержит последовательности с высокой плотностью, последовательности с низкой плотностью и последовательности, которые меняются от низкого к высокому и наоборот. Этот шаблон также является стандартным шаблоном, используемым для измерения джиттера.
• 3 в 24 — Шаблон содержит самую длинную строку последовательных нулей (15) с самой низкой плотностью (12,5%). Этот образец одновременно подчеркивает минимальную плотность единиц и максимальное количество последовательных нулей. В D4 формат кадра 3 из 24 может вызвать D4 желтый сигнал тревоги для схем кадра в зависимости от выравнивания одного бит кадра.
• 1:7 — Также упоминается как 1 из 8. Он имеет только один в восьмибитовой повторяющейся последовательности. Этот образец подчеркивает минимальную плотность 12,5% и должен использоваться при испытании оборудования для B8ZS кодирование в виде шаблона 3 из 24 увеличивается до 29,5% при преобразовании в B8ZS.
• Мин Макс — Последовательность рисунка быстро меняется с низкой плотности на высокую. Наиболее полезно при нагрузке ретранслятора ALBO особенность.
• Все (или отметки) — Выкройка, состоящая только из единиц. Этот шаблон заставляет повторитель потреблять максимальное количество энергии. Если постоянный ток к ретранслятору отрегулирован должным образом, ретранслятор не будет иметь проблем с передачей длинной последовательности. Этот образец следует использовать при измерении регулирования мощности диапазона. Шаблон без рамки используется для обозначения АИС (также известный как синяя сигнализация).
• Все нули — Шаблон, состоящий только из нулей. Это эффективно при поиске оборудования, не подходящего для AMI, например, низкоскоростные входы мультиплексного волокна / радио.
• Чередование нулей и единиц — Шаблон, состоящий из чередующихся единиц и нулей.
• 2 в 8 — Шаблон содержит максимум четыре последовательных нуля. Он не вызовет последовательность B8ZS, потому что для подстановки B8ZS требуется восемь последовательных нулей. Эта схема эффективна при поиске оборудования, не использованного для B8ZS.
• Bridgetap — Мостовые краны в пределах диапазона могут быть обнаружены с помощью ряда тестовых шаблонов с различными плотностями единиц и нулей. Этот тест генерирует 21 тестовую таблицу и длится 15 минут. Если возникает ошибка сигнала, на участке может быть один или несколько ответвлений моста. Этот шаблон эффективен только для участков T1, которые передают необработанный сигнал. Модуляция, используемая в HDSL пролетов сводит на нет способность образцов мостов выявлять мостовые переходы.
• Мультипат — Этот тест генерирует пять часто используемых тестовых шаблонов, позволяющих DS1 тестирование диапазона без необходимости выбирать каждый тестовый образец индивидуально. Шаблоны: все единицы, 1: 7, 2 из 8, 3 из 24 и QRSS.
• T1-DALY и 55 октетов — Каждый из этих шаблонов содержит пятьдесят пять (55) восьмибитовых октетов данных в последовательности, которая быстро изменяется между низкой и высокой плотностью. Эти паттерны используются в основном для нагрузки на схему ALBO и эквалайзера, но они также усиливают восстановление синхронизации. 55 OCTET имеет пятнадцать (15) последовательных нулей и может использоваться только без рамки без нарушения требований к плотности. Для сигналов с фреймами следует использовать шаблон T1-DALY. Оба шаблона вызовут код B8ZS в схемах с опцией для B8ZS.

Тестер коэффициента битовых ошибок

Тестер коэффициента ошибок по битам (BERT), также известный как «тестер коэффициента ошибок по битам»^[4] или же решение для проверки коэффициента битовых ошибок (BERT) — это электронное испытательное оборудование, используемое для проверки качества передачи сигнала отдельных компонентов или целых систем.

Основные строительные блоки BERT:

• Генератор паттернов, который передает заданный тестовый шаблон на DUT или тестовая система
• Детектор ошибок, подключенный к DUT или тестовой системе, для подсчета ошибок, генерируемых DUT или тестовой системой
• Генератор тактовых сигналов для синхронизации генератора шаблонов и детектора ошибок
• Анализатор цифровой связи не является обязательным для отображения переданного или принятого сигнала.
• Электрооптический преобразователь и оптико-электрический преобразователь для проверки сигналов оптической связи.

Смотрите также

• Ошибка пакета
• Код исправления ошибок
• Секунда с ошибками
• Частота ошибок Витерби

Рекомендации

Эта статья включаетматериалы общественного достояния от Администрация общих служб документ: «Федеральный стандарт 1037С». (в поддержку MIL-STD-188 )

внешняя ссылка

• QPSK BER для канала AWGN — онлайн-эксперимент

---

Подборка по базе: Каковы особенности информации в системах социального управления., Письменная работа №1 — Оценка стоимости бизнеса.docx, к.р Контроль и оценка результатов образования.docx, В организационном плане оценка портфолио может проходитьввп.docx, ПР Экономика и оценка недвижимости.docx, логические уловки в передаче информации.pptx, 56 тема Яременко Е.А. Бухгалтерский финансовый баланс как источн, Лабораторная работа 5 — Обработка символьной информации.docx, Вкр Влияние ОФП на качества футболистов.pdf, контроль качества жлф.pdf

---

Глава 3. РАСЧЁТНАЯ ЧАСТЬ

3.1 Показатели качества цифровых каналов связи

Основным назначением каналов связи является передача информации. Исследуемые в данной работе широкополосные каналы связи предназначены для передачи данных, в частности мобильных, аудио- и видеосигналов. На качество передаваемого сигнала влияет множество факторов. К основным, наиболее широко изучаемым причинам снижения качества сигнала, относятся: искажение сигнала и снижение значения отношения сигнал/шум (SNR — Signal Noise Ratio). В теории связи к понятию сигнал относят видеоимпульс, информационный сигнал, или модулированную несущую. На снижение достоверности передачи аналоговых сигналов влияют так называемые интермодуляционные искажения (например, канальные искажения). Применительно к цифровым системам связи в основном используют понятие межсимвольной интерференции. В данной работе произведён расчёт вероятности появления битовой ошибки (BER — Bit Error Rate) в зависимости от заданного значения SNR [11].
По отношению к аналоговым сигналам критерием качества является показатель S/N (Signalto Noise), который определяет отношение средней мощности сигнала (S) к средней мощности шума (N). Для цифрового сигнала данный критерий обозначается как E_b/N_o (формула (1)). Здесь E_b — энергия бита, определяемая как произведение мощности сигнала S и времени передачи одного бита T_b; N_o — спектральная плотность мощности шума, которую можно выразить как отношение мощности шума N к ширине полосы пропускания W.
 (1)
Время передачи одного бита можно представить как 1/R, гдеR-битовая скорость, т.к. время и скорость передачи бита взаимно обратны:
 (2)
Для более наглядного выделения отношения сигнал/шум представим формулу (2) в следующем виде (формула (3)):
 (3)

3.2 Расчёт показателей качества для многопозиционной модуляции

Введём понятие метрики качества системы цифровой связи, которая представляет собой график зависимости вероятности появления ошибочного бита BEP (Bit Error Probability) от отношения E_b/N_o. В цифровых системах связи передача символов осуществляется в течение времени передачи одного символа — Ts. По отношению к одному информационному символу мощность находится в прямой зависимости от скорости передачи. Наиболее удобным параметром для описания цифрового сигнала является энергия, которую можно представить как мощность, проинтегрированную по времени. Поэтому для цифровых систем связи таким параметром является нормированный параметр E_b/N_o.

На рисунке 19 представлен «водопадоподобный» вид большей части таких кривых при условии, что E_b/N_o≥Х₀, Р_В≤Р₀, где Х₀ — некоторый критерий отношения сигнал/шум для обеспечения удовлетворительной связи. Т.е. с увеличением значения требуемого отношения E_b/N_o повышается эффективность процесса детектирования при данной вероятности ошибки.

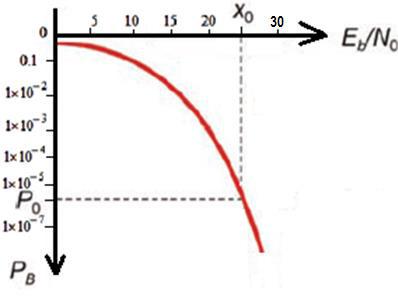
Рисунок 19 — Общий вид кривых зависимости вероятности ошибочно переданного бита к уровню E_b/N_o [12]
Сравнение одной цифровой системы с другой должно производиться с помощью критерия качества на битовом уровне. Поэтому в цифровых системах наиболее удобно использовать параметр E_b/N_o, а не S/N, который незаменим для аналоговых систем связи.

Поскольку понятие спектральной плотности мощности шума N_o описывает нормированный параметр E_b/N_o, подробнее опишем понятие мощности шума. В теории связи для описания модели случайного (хаотического) процесса чаще всего используется шум, который описывается гауссовским (нормальным) распределением. Шум возникает как результат одновременного воздействия нескольких независимых друг от друга случайных источников. Одним из примеров равномерного шума является тепловой шум, который обусловлен броуновским движением электронов в проводнике. Такой шум называется белым.

Поскольку на входе приёмного устройства канала цифровой системы связи стоят фильтры, примем, что реальный белый шум соответствует идеальному. Шум ограничен по спектру, а значит, его мощность также конечна. Рассчитывая мощность N реального белого шума в полосе частот W (Гц), используется абсолютная температура источника шума Т, измеряемая в Кельвинах (К⁰ = С⁰ + 273) и спектральная плотность мощности шума, измеряемая в Вт/Гц:

No = N/W

(4)

Наибольшая мощность шума от теплового источника:

N = kTW,	(5)
где k = 1,38∙10-23 (Дж/К) — постоянная Больцмана.
Для расчётов наиболее удобным является применение формул (6),
(7), преобразованных из формулы (5) в децибельном виде:
N = –228,6 + 10lg(T) + 10lg(W),дБ·Вт	(6)
N0 = –228,6 + 10lg(T),дБ·Вт/Гц	(7)

Зная, что энергия сигнала E = ST_o, а мощность шума N = N_оW, где Т_о — время передачи сигнала, получаю формулу (8):
 (8)
Величина WT_o представляет коэффициент пересчёта отношения энергий сигнала и шума в отношение их средних мощностей.
Число уровней амплитуд L при передаче цифрового сигнала с форматом модуляции M-КAM (QAM), где M представляет разрядность модуляции, определяется из формулы (9):
 (9)
Энергия символа сигнала определяется по формуле (10):
 (10)
В случае передачи в основной полосе частот многоуровневых импульсов, которые совпадают с полосой Найквиста, где W_N = 1/2T_b, мощность символа и мощность шума определяются по формулам (11) и (12) соответственно:
 (11)
 (12)
Таким образом, отношение сигнал/шум принимает вид:
 (13)
Формулу (13) можно преобразовать в вид:
, (14)
где m = 2(log₂L) =log₂M — коэффициент мапинга (число бит на символ информации).

Таким образом, для сигналов с типом модуляции 16QAM разница между отношениями S/N и Eb/N0 составляет 6 дБ.

Ещё одним показателем, характеризующим отношение мощностей, является отношение несущая/шум (C/N). Он определят, во сколько раз мощность С принимаемой модулированной ВЧ несущей на выходе приёмного фильтра больше мощности шума N.

Ниже в формуле (15) указана зависимость:
, дБ , (15)
где   — символьная скорость.
При определении защитного отношения учитываются следующие параметры: шум, полоса частот, метод кодирования, а также значение коэффициента скругления, обозначенный на рисунке 20 (безразмерная величина, принимающая значения от 0,15 до 1) [12].

Рисунок 20 — Зависимость формы сигнала от коэффициента скругления
Кроме того, для более точного расчёта отношения сигнал/шум в реальных условиях выведена корректирующая формула:
, (16)
где а – коэффициент скругления спектра.
Формула пересчёта (16) выведена из расчёта, что реальная полоса шума для идеальной цифровой системы занимает полосу частот:
, (17)
а мощность несущей определяется как:
 (18)
Свёрточный код также оказывает влияние на канал связи. Коэффициент, корректирующий ошибки FEC (Forward Error Correction) принимает значения от 1/2 до 7/8. Чем он ниже, тем ниже скорость передачи данных. При значении FEC = 1/2, E_b/N₀ снизится в 2 раза, т.е. на 3 дБ. Физический смысл данного примера заключается в том, что половина мощности сигнала уходит на FEC. Следовательно, значение Eb/No увеличивают на величину, равную 10lg(1/FEC) по отношению к C/N. Например, при скорости кодирования RC = 1/2 уровень FEC составит 3 дБ, при RC = 7/8 — 0,58 дБ. Однако, при RC = 1, FEC равен нулю.

Для определения качества канала связи вводится два схожих понятия: вероятность появления битовой ошибки (BEP) и скорость появления битовой ошибки (BER). На практике удобнее использовать понятие BER, т.к. есть возможность физического измерения данной величины.

4.3 Расчёт вероятности битовой ошибки в канале связи технологии LTE

При распространении в радиоэфире сигнал претерпевает различного рода изменения: искажения, снижение отношения сигнал/шум (SNR — Signal Noise Ratio). В цифровых системах радиосвязи используется обозначение E_b/N₀ — отношение энергии одного бита к спектральной плотности шума, согласно формуле (14.14).
Используя формулу пересчёта (17), можно легко вычислить показатель BER при заранее известном уровне SNR:
 , дБ, (19)
где CR — скорость кодирования.
Вероятность битовой ошибки в Гауссовском канале распространения имеет вид: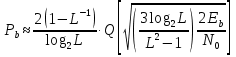
 , (20)
где Q(x) является табличной величиной, которая напрямую не рассчитывается.
Однако, для х<3 значение параметра Q(x) можно рассчитать по формуле

(14.12):

 (21)
Для минимизации расчётов на практике пользуются кривыми зависимости BER от SNR (E_b/N₀), представленными в логарифмическом масштабе (рисунок 21).

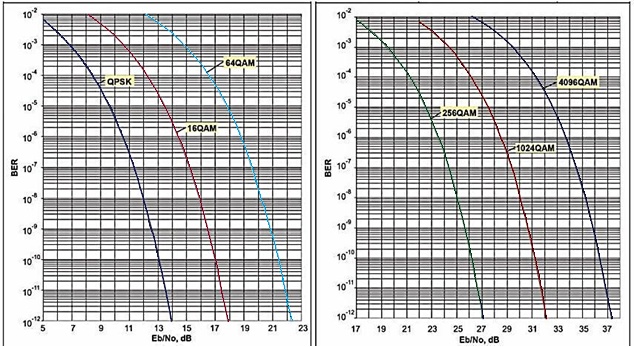
Рисунок 21 — Зависимости BER от E_b/N₀ в логарифмическом масштабе
Для подтверждения проведённого эксперимента рассчитываю вероятность появления битовых ошибок при заданном уровне отношения сигнал/шум.

Необходимо подтвердить, что при использовании типа модуляции 64QAM при заданном значении SNR=18,9 дБ уровень BER не превышает 10^-6.

Для расчётов использую формулы (20) и (21):

 (22)
Отсюда х=2/7

Перевожу значение отношения сигнал/шум в единицы:
18, 9дБ 10^1.89 78
Подставляю значение Q(x) и SNR для расчёта уровня BER:
 (23)

 (24)

Таким образом, из расчётов видно, что при данном значении SNR=18,9 дБ уровень BER соответствует требованиям качества к каналу связи технологии LTE.
Аналогичный расчёт произведём для типа модуляции 16QAM при заданном SNR=13,5 дБ

 (25)
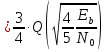
Отсюда х=4/5

Перевожу значение отношения сигнал/шум в единицы:
13, 5дБ 10^1.35 22, 4
Подставляю значение Q(x) и SNR для расчёта уровня BER: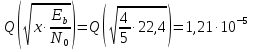
 (26)
 (27)
Таким образом, из расчётов видно, что при заданном значении SNR=13,5 дБ уровень BER также соответствует требованиям качества к каналу связи технологии LTE.
Произведу сравнение результатов расчётов и результатов экспериментального моделирования, приведённых в таблице 5 (рисунки 22а, 22б).
Таблица 5 — Зависимость BER от SNR по результат эксперимента и расчётов

Тип модуляции	Значение	SNR по		Значение	SNR по
	результатам расчётов, дБ		результатам
				эксперимента, дБ
16QAM	12,9			13,5
64QAM	19			18,9

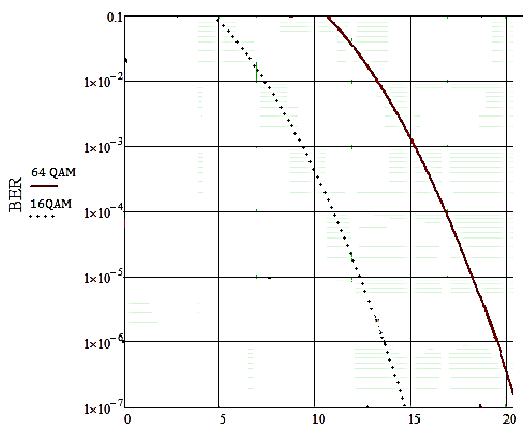
Рисунок 22а — Кривые зависимости BER от SNR, полученные в результате эксперимента

Рисунок 22б — Кривые зависимости BER от SNR, полученные в результате расчётов
Погрешность результатов экспериментальных и расчётных данных составляет:
 для 64QAM (28)

 для 16QAM (29)
Расхождение значений в 3-5% является допустимым.