Вместо введения
Системы автоматического управления (САУ) предназначены для автоматического изменения одного или нескольких параметров объекта управления с целью установления требуемого режима его работы. САУ обеспечивает поддержание постоянства заданных значений регулируемых параметров или их изменение по заданному закону либо оптимизирует определенные критерии качества управления. Например, к таким системам относятся:
- системы стабилизации,
- системы программного управления,
- следящие системы
Это достаточно широкий класс систем, которые можно найти где угодно. Но какое это отношение имеет к Unity3D и вероятно к играм в частности? В принципе прямое: в любой игре так или иначе использующей симуляцию как элемент геймплея реализуются САУ, к таким играм относятся, например, Kerbal Space Programm, Digital Combat Simulator (бывший Lock On), Strike Suit Zero и т.д. (кто знает еще примеры — пишите в комментариях). В принципе любая игра, моделирующая реальные физические процессы, в том числе и просто кинематику с динамикой движения, может реализовывать те или иные САУ — этот подход проще, естественнее, а у разработчика уже есть есть набор готовых инструментов, предоставленных всякими Вышнеградскими, Ляпуновыми, Калманами, Чебышевами и прочими Коломогоровами, поэтому можно обойтись без изобретения велосипеда, т.к. его уже изобрели, да так, что получилась отдельная наука: Теория автоматического управления. Главное тут не переусердствовать. Одна тут только проблема: рассказывают про ТАУ не везде, не всем, зачастую мало и не очень понятно.
Немножко теории
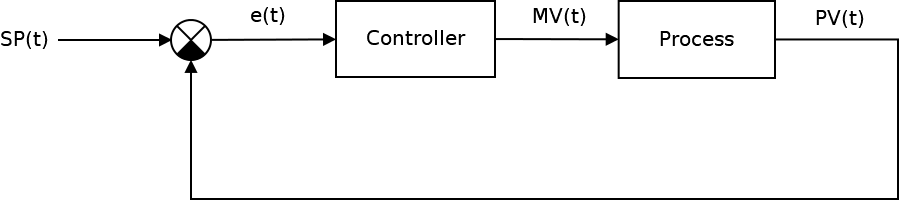
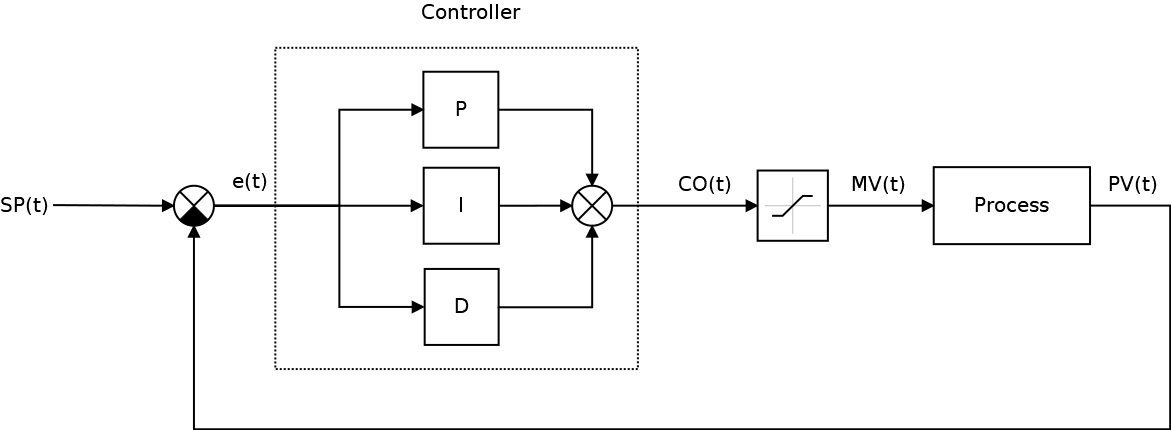
Классическая система автоматического управления представленная на следующем рисунке:
Ключевым элементом любой САУ является регулятор представляющий из себя устройство, которое следит за состоянием объекта управления и обеспечивает требуемый закон управления. Процесс управления включает в себя: вычисление ошибки управления или сигнала рассогласования e(t) как разницы между желаемой уставкой (set point или SP) и текущей величиной процесса (process value или PV), после чего регулятор вырабатывает управляющие сигналы (manipulated value или MV).
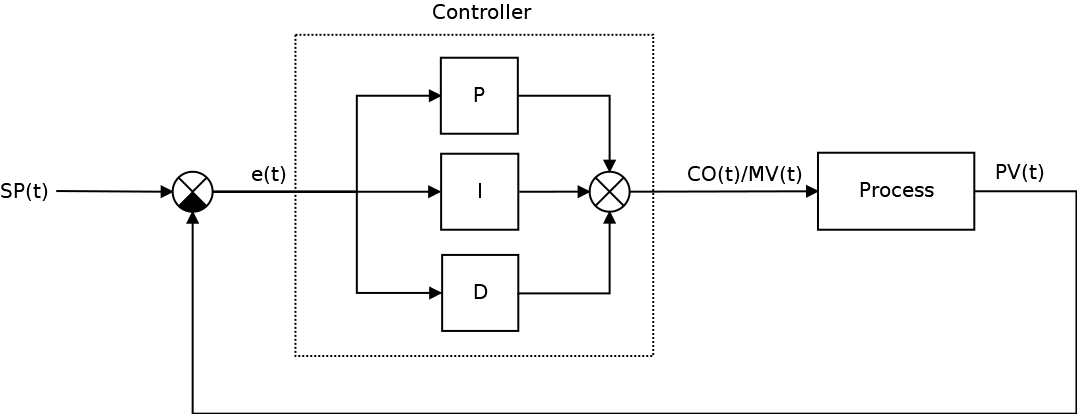
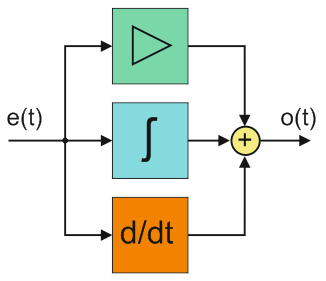
Одной из разновидностью регуляторов является пропорционально-интегрально-дифференцирующий (ПИД) регулятор, который формирует управляющий сигнал, являющийся суммой трёх слагаемых: пропорционального, интегрального и дифференциального.
Где, ошибка рассогласования, а также,
— пропорциональная,
— интегральная,
— дифференциальная составляющие (термы) закона управления, который в итоговом виде описывается следующими формулами
Пропорциональная составляющая P — отвечает за т.н. пропорциональное управление, смысл которого в том, что выходной сигнал регулятора, противодействует отклонению регулируемой величины (ошибки рассогласования или еще это называют невязкой) от заданного значения. Чем больше ошибка рассогласования, тем больше командное отклонение регулятора. Это самый простой и очевидный закон управления. Недостаток пропорционального закона управления заключается в том, что регулятор никогда не стабилизируется в заданном значении, а увеличение коэффициента пропорциональности всегда приводит к автоколебаниям. Именно поэтому в довесок к пропорциональному закону управления приходиться использовать интегральный и дифференциальный.
Интегральная составляющая I накапливает (интегрирует) ошибку регулирования, что позволяет ПИД-регулятору устранять статическую ошибку (установившуюся ошибку, остаточное рассогласование). Или другими словами: интегральное звено всегда вносит некоторое смещение и если система подвержена некоторыми постоянным ошибкам, то оно их компенсирует (за счет своего смещения). А вот если же этих ошибок нет или они пренебрежительно малы, то эффект будет обратным — интегральная составляющая сама будет вносить ошибку смещения. Именно по этой причине её не используют, например, в задачах сверхточного позиционирования. Ключевым недостатком интегрального закона управления является эффект насыщения интегратора (Integrator windup).
Дифференциальная составляющая D пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Примечательно то, что дифференциальная компонента устраняет затухающие колебания. Дифференциальное регулирование особенно эффективно для процессов, которые имеют большие запаздывания. Недостатком дифференциального закона управления является его неустойчивость к воздействую шумов (Differentiation noise).
Таким образом, в зависимости от ситуации могут применятся П-, ПД-, ПИ- и ПИД-регуляторы, но основным законом управления в основном является пропорциональный (хотя в некоторых специфических задачах и могут использоваться исключительно только звенья дифференциаторов и интеграторов).
Казалось бы, вопрос реализации ПИД-регуляторов уже давно избит и здесь на Хабре есть парочка неплохих статей на эту тему в том числе и на Unity3D, также есть неплохая статья PID Without a PhD (перевод) и цикл статей в журнале «Современные технологии автоматизации» в двух частях: первая и вторая. Также к вашим услугам статья на Википедии (наиболее полную читайте в английском варианте). А на форумах коммьюнити Unity3D нет-нет, да и всплывет PID controller как и на gamedev.stackexchange
При вопрос по реализации ПИД-регуляторов несколько глубже чем и кажется. Настолько, что юных самоделкиных, решивших, реализовать такую схему регулирования ждет немало открытий чудных, а тема актуальная. Так что надеюсь сей опус, кому-нибудь да пригодиться, поэтому приступим.
Попытка номер раз
В качестве примера попытаемся реализовать схему регулирования на примере управления поворотом в простенькой космической 2D-аркаде, по шагам, начиная с самого начала (не забыли, что это туториал?).
Почему не 3D? Потому что реализация не измениться, за исключением того, что придется воротить ПИД-регулятор для контроля тангажа, рысканья и крена. Хотя вопрос корректного применения ПИД-регулирования вместе с кватернионами действительно интересный, возможно в будущем его и освящу, но даже в NASA предпочитают углы Эйлера вместо кватернионов, так что обойдемся простенькой моделью на двухмерной плоскости.
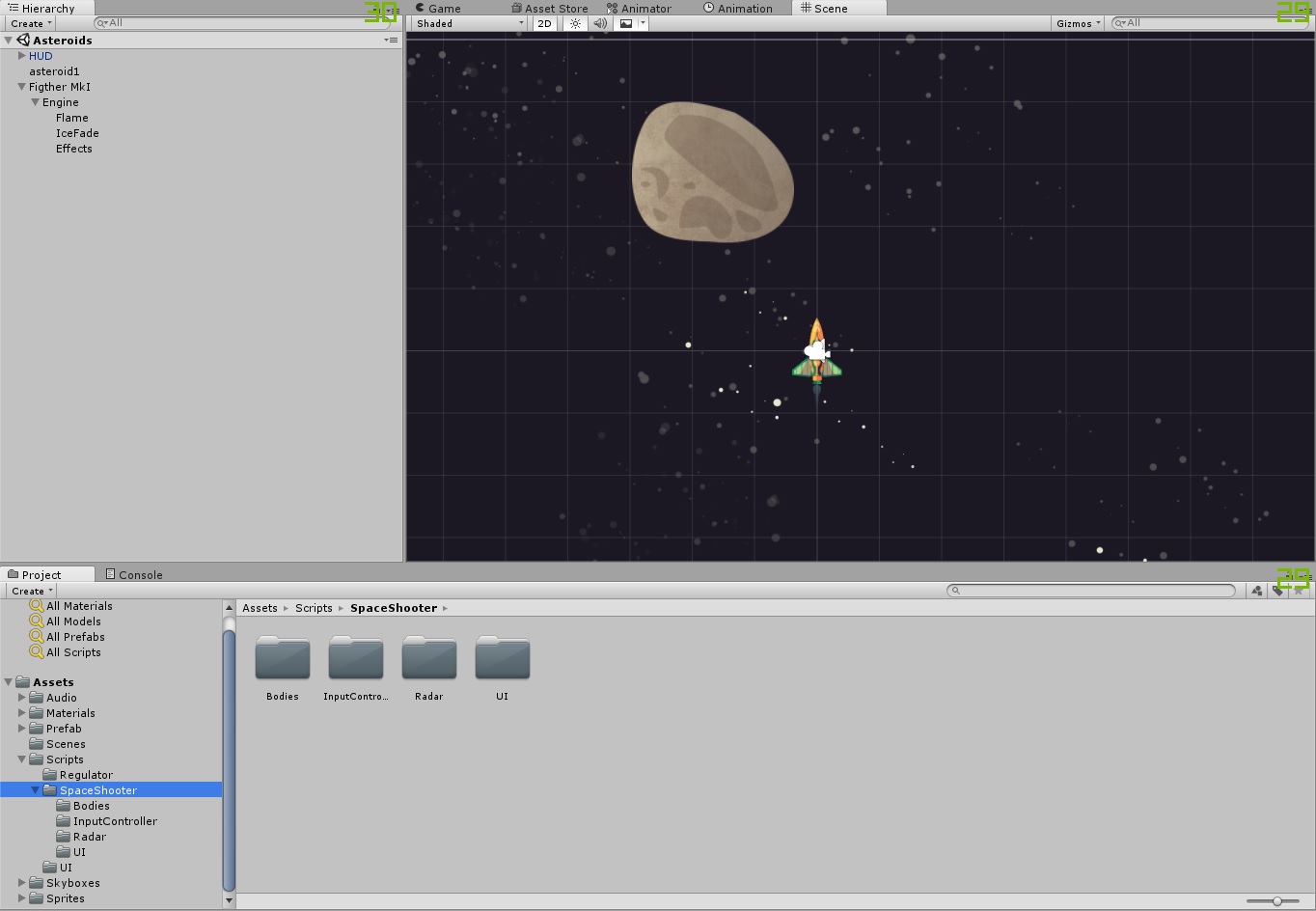
Для начала создадим сам объект игровой объект космического корабля, который будет состоять из собственно самого объекта корабля на верхнем уровне иерархии, прикрепим к нему дочерний объект Engine (чисто спецэффектов ради). Вот как это выглядит у меня:
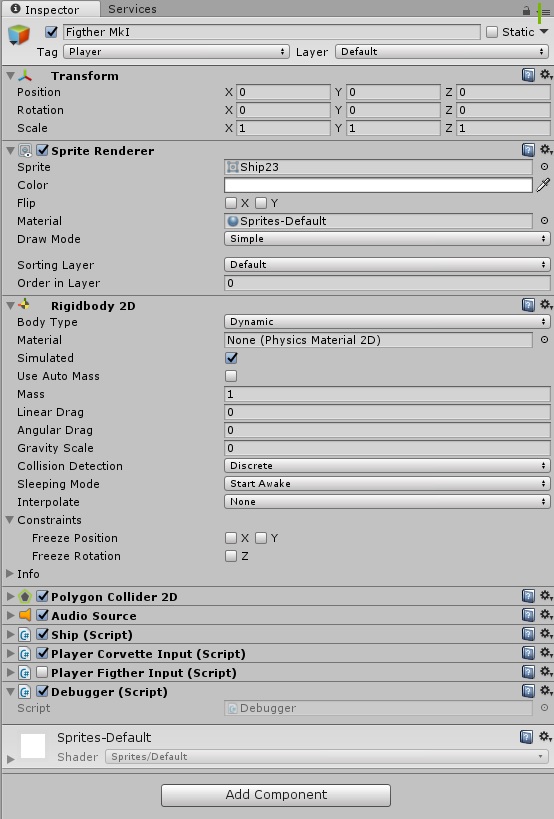
А на сам объект космического корабля накидаем в инспекторе всяческих компонент. Забегая вперед, приведу скрин того, как он будет выглядеть в конце:
Но это потом, а пока в нем еще нет никаких скриптов, только стандартный джентльменский набор: Sprite Render, RigidBody2D, Polygon Collider, Audio Source (зачем?).
Собственно физика у нас сейчас самое главное и управление будет осуществляться исключительно через неё, в противном случае, применение ПИД-регулятора потеряло бы смысл. Масса нашего космического корабля оставим также в 1 кг, а все коэффициенты трения и гравитации равны нулю — в космосе же.
Т.к. помимо самого космического корабля есть куча других, менее умных космических объектов, то сначала опишем родительский класс BaseBody, который в себе будет содержать ссылки на на наши компоненты, методы инициализации и уничтожения, а также ряд дополнительных полей и методов, например для реализации небесной механики:
BaseBody.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
[RequireComponent(typeof(SpriteRenderer))]
[RequireComponent(typeof(AudioSource))]
[RequireComponent(typeof(Rigidbody2D))]
[RequireComponent(typeof(Collider2D))]
public class BaseBody : MonoBehaviour
{
readonly float _deafultTimeDelay = 0.05f;
[HideInInspector]
public static List<BaseBody> _bodies = new List<BaseBody>();
#region RigidBody
[HideInInspector]
public Rigidbody2D _rb2d;
[HideInInspector]
public Collider2D[] _c2d;
#endregion
#region References
[HideInInspector]
public Transform _myTransform;
[HideInInspector]
public GameObject _myObject;
/// <summary>
/// Объект, который появляется при уничтожении
/// </summary>
public GameObject _explodePrefab;
#endregion
#region Audio
public AudioSource _audioSource;
/// <summary>
/// Звуки, которые проигрываются при получении повреждения
/// </summary>
public AudioClip[] _hitSounds;
/// <summary>
/// Звуки, которые проигрываются при появлении объекта
/// </summary>
public AudioClip[] _awakeSounds;
/// <summary>
/// Звуки, которые воспроизводятся перед смертью
/// </summary>
public AudioClip[] _deadSounds;
#endregion
#region External Force Variables
/// <summary>
/// Внешние силы воздйствующие на объект
/// </summary>
[HideInInspector]
public Vector2 _ExternalForces = new Vector2();
/// <summary>
/// Текущий вектор скорости
/// </summary>
[HideInInspector]
public Vector2 _V = new Vector2();
/// <summary>
/// Текущий вектор силы гравитации
/// </summary>
[HideInInspector]
public Vector2 _G = new Vector2();
#endregion
public virtual void Awake()
{
Init();
}
public virtual void Start()
{
}
public virtual void Init()
{
_myTransform = this.transform;
_myObject = gameObject;
_rb2d = GetComponent<Rigidbody2D>();
_c2d = GetComponentsInChildren<Collider2D>();
_audioSource = GetComponent<AudioSource>();
PlayRandomSound(_awakeSounds);
BaseBody bb = GetComponent<BaseBody>();
_bodies.Add(bb);
}
/// <summary>
/// Уничтожение персонажа
/// </summary>
public virtual void Destroy()
{
_bodies.Remove(this);
for (int i = 0; i < _c2d.Length; i++)
{
_c2d[i].enabled = false;
}
float _t = PlayRandomSound(_deadSounds);
StartCoroutine(WaitAndDestroy(_t));
}
/// <summary>
/// Ждем некоторое время перед уничтожением
/// </summary>
/// <param name="waitTime">Время ожидания</param>
/// <returns></returns>
public IEnumerator WaitAndDestroy(float waitTime)
{
yield return new WaitForSeconds(waitTime);
if (_explodePrefab)
{
Instantiate(_explodePrefab, transform.position, Quaternion.identity);
}
Destroy(gameObject, _deafultTimeDelay);
}
/// <summary>
/// Проигрывание случайного звука
/// </summary>
/// <param name="audioClip">Массив звуков</param>
/// <returns>Длительность проигрываемого звука</returns>
public float PlayRandomSound(AudioClip[] audioClip)
{
float _t = 0;
if (audioClip.Length > 0)
{
int _i = UnityEngine.Random.Range(0, audioClip.Length - 1);
AudioClip _audioClip = audioClip[_i];
_t = _audioClip.length;
_audioSource.PlayOneShot(_audioClip);
}
return _t;
}
/// <summary>
/// Получение урона
/// </summary>
/// <param name="damage">Уровень урона</param>
public virtual void Damage(float damage)
{
PlayRandomSound(_hitSounds);
}
}
}Вроде описали все что надо, даже больше чем нужно (в рамках этой статьи). Теперь отнаследуем от него класс корабля Ship, который должен уметь двигаться и поворачивать:
SpaceShip.cs
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _rotation = 0f;
public void FixedUpdate()
{
float torque = ControlRotate(_rotation);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(Vector2 rotate)
{
float result = 0f;
return result;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 result = new Vector2();
return result;
}
}
}Пока в нем нет ничего интересно, на текущий момент это просто класс-заглушка.
Также опишем базовый(абстрактный) класс для всех контроллеров ввода BaseInputController:
BaseInputController.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public enum eSpriteRotation
{
Rigth = 0,
Up = -90,
Left = -180,
Down = -270
}
public abstract class BaseInputController : MonoBehaviour
{
public GameObject _agentObject;
public Ship _agentBody; // Ссылка на компонент логики корабля
public eSpriteRotation _spriteOrientation = eSpriteRotation.Up; //Это связано с нестандартной
// ориентации спрайта "вверх" вместо "вправо"
public abstract void ControlRotate(float dt);
public abstract void ControlForce(float dt);
public virtual void Start()
{
_agentObject = gameObject;
_agentBody = gameObject.GetComponent<Ship>();
}
public virtual void FixedUpdate()
{
float dt = Time.fixedDeltaTime;
ControlRotate(dt);
ControlForce(dt);
}
public virtual void Update()
{
//TO DO
}
}
}И наконец, класс контроллера игрока PlayerFigtherInput:
PlayerInput.cs
using UnityEngine;
using Assets.Scripts.SpaceShooter.Bodies;
namespace Assets.Scripts.SpaceShooter.InputController
{
public class PlayerFigtherInput : BaseInputController
{
public override void ControlRotate(float dt)
{
// Определяем позицию мыши относительно игрока
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
float targetAngle = Mathf.Atan2(dy, dx) * Mathf.Rad2Deg;
_agentBody._targetAngle = targetAngle + (float)_spriteOrientation;
}
public override void ControlForce(float dt)
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up
+ Input.GetAxis("Horizontal") * Vector2.right;
}
}
}Вроде бы закончили, теперь наконец можно перейти к тому, ради чего все это затевалось, т.е. ПИД-регуляторам (не забыли надеюсь?). Его реализация кажется простой до безобразия:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable] // Этот атрибут необходим для того что бы поля регулятора
// отображались в инспекторе и сериализовывались
public class SimplePID
{
public float Kp, Ki, Kd;
private float lastError;
private float P, I, D;
public SimplePID()
{
Kp = 1f;
Ki = 0;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float dt)
{
P = error;
I += error * dt;
D = (error - lastError) / dt;
lastError = error;
float CO = P * Kp + I * Ki + D * Kd;
return CO;
}
}
}Значения коэффициентов по умолчанию возьмем с потолка: это будет тривиальный единичный коэффициент пропорционального закона управления Kp = 1, небольшое значение коэффициента для дифференциального закона управления Kd = 0.2, который должен устранить ожидаемые колебания и нулевое значение для Ki, которое выбрано потому, что в нашей программной модели нет никаких статичных ошибок (но вы всегда можете их внести, а потом героически побороться с помощью интегратора).
Теперь вернемся к нашему классу SpaceShip и попробуем заюзать наше творение в качестве регулятора поворота космического корабля в методе ControlRotate:
public float ControlRotate(Vector2 rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}ПИД-регулятор будет осуществлять точное угловое позиционировая космического корабля только за счет крутящего момента. Все честно, физика и САУ, почти как в реальной жизни.
И без этих ваших Quaternion.Lerp
if (!_rb2d.freezeRotation)
rb2d.freezeRotation = true;
float deltaAngle = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
float T = dt * Mathf.Abs( _rotationSpeed / deltaAngle);
// Трансформируем угол в вектор
Quaternion rot = Quaternion.Lerp(
_myTransform.rotation,
Quaternion.Euler(new Vector3(0, 0, targetAngle)),
T);
// Изменяем поворот объекта
_myTransform.rotation = rot;Получившейся исходный код Ship.cs под спойлером
using UnityEngine;
using Assets.Scripts.Regulator;
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
[Header("PID")]
public SimplePID _angleController = new SimplePID();
public void FixedUpdate()
{
float torque = ControlRotate(_targetAngle);
Vector2 force = ControlForce(_movement);
_rb2d.AddTorque(torque);
_rb2d.AddRelativeForce(force);
}
public float ControlRotate(float rotate)
{
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_angle, rotate);
//Получаем корректирующее ускорение
MV = _angleController.Update(angleError, dt);
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
//Кусок кода спецэффекта работающего двигателя ради
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement;
return MV;
}
}
}
Все? Расходимся по домам?
WTF! Что происходит? Почему корабль поворачивается как-то странно? И почему он так резко отскакивает от других объектов? Неужели этот глупый ПИД-регулятор не работает?
Без паники! Давайте попробуем разобраться что происходит.
В момент получения нового значения SP, происходит резкий (ступенчатый) скачок рассогласования ошибки, которая, как мы помним, вычисляется вот так: соответственно происходит резкий скачок производной ошибки
, которую мы вычисляем в этой строчке кода:
D = (error - lastError) / dt;Можно, конечно, попробовать другие схемы дифференцирования, например, трехточечную, или пятиточечную, или… но все равно это не поможет. Ну вот не любят производные резких скачков — в таких точках функция не является дифференцируемой. Однако поэкспериментировать с разными схемами дифференцирования и интегрирования стоит, но потом и не в этой статье.
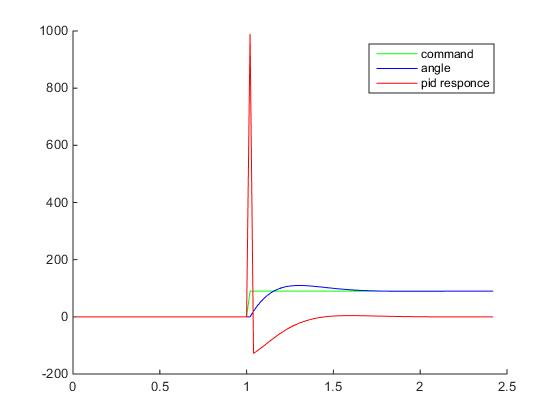
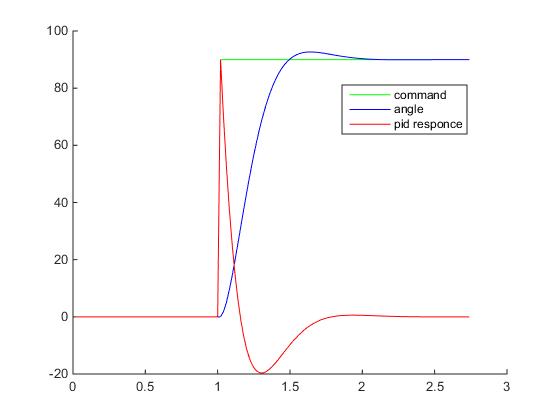
Думаю что настал момент построить графики переходного процесса: ступенчатое воздействие от S(t) = 0 в SP(t) = 90 градусов для тела массой в 1 кг, длинной плеча силы в 1 метр и шагом сетки дифференцирования 0.02 с — прям как в нашем примере на Unity3D (на самом деле не совсем, при построении этих графиков не учитывалось, что момент инерции зависит от геометрии твердого тела, поэтому переходный процесс будет немножко другой, но все же достаточно похожий для демонстрации). Все величены на грифике приведены в абсолютных значениях:
Хм, что здесь происходит? Куда улетел отклик ПИД-регулятора?
Поздравляю, мы только что столкнулись с таким явлением как «удар» (kick). Очевидно, что в момент времени, когда процесс еще PV = 0, а уставка уже SP = 90, то при численном дифференцировании получим значение производной порядка 4500, которое умножится на Kd=0.2 и сложится с пропорциональным теромом, так что на выходе мы получим значение углового ускорения 990, а это уже форменное надругательство над физической моделью Unity3D (угловые скорости будут достигать 18000 град/с… я думаю это предельное значение угловой скорости для RigidBody2D).
- Может стоит подобрать коэффициенты ручками, так чтобы скачок был не таким сильным?
- Нет! Самое лучше чего мы таким образом сможем добиться — небольшая амплитуда скачка производной, однако сам скачок как был так и останется, при этом можно докрутиться до полной неэффективности дифференциальной составляющей.
Впрочем можете поэкспериментировать.
Попытка номер два. Сатурация
Логично, что привод (в нашем случае виртуальные маневровые двигатели SpaceShip), не может отрабатывать сколько угодно большие значения которые может выдать наш безумный регулятор. Так что первое что мы сделаем — сатурируем выход регулятора:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}А очередной раз переписанный класс Ship полностью выглядит так
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, dt);
//Сатурируем
MV = CO;
if (MV > thrust) MV = thrust;
if (MV< -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * _thrust;
return MV;
}
public void Update()
{
}
}
}Итоговая схема нашего САУ тогда станет уже вот такой
При этом уже становится понятно, что выход контроллера CO(t) немного не одно и тоже, что управляемая величина процесса MV(t).
Собственно с этого места можно уже добавлять новую игровую сущность — привод, через которую и будет осуществляться управление процессом, логика работы которой может быть более сложной, чем просто Mathf.Clamp(), например, можно ввести дискретизацию значений (дабы не перегружать игровую физику величинами идущими шестыми после запятой), мертвую зону (опять таки не имеет смысл перегружать физику сверхмалыми реакциями), ввести задержку в упраление и нелинейность (например, сигмоиду) привода, после чего посмотреть, что из этого получится.
Запустив игру, мы обнаружим, что космический корабль стал наконец управляемым:
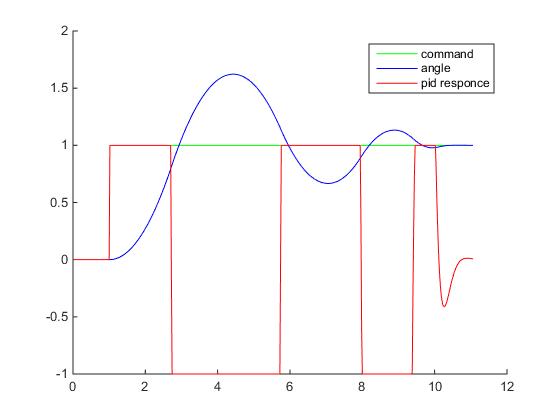
Если построить графики, то можно увидеть, что реакция контроллера стала уже вот такой:
Здесь уже используются нормированные величены, углы поделены на значение SP, а выход контроллера отнормирован относительно максимального значения на котором уже происходит сатурация.
Теперь на графике видно наличие ошибки перерегулирования (overshooting) и затухающие колебания. Уменьшая Kp и увеличивая Kd можно добиться уменьшения колебаний, но зато увеличится время реакции контроллера (скорость поворота корабля). И наоборот, увеличивая Kp и уменьшая Kd — можно добиться увеличения скорости реакции контроллера, но появятся паразитные колебания, которые при определенных (критических) значениях, перестанут быть затухающими.
Ниже приведена известна таблица влияния увеличения параметров ПИД-регулятора (как уменьшить шрифт, а то таблица безе переносов не лезет?):
А общий алгоритм ручной настройки ПИД-регулятора следующий:
- Подбираем пропорциональный коэффициенты при отключенных дифференциальных и интегральных звеньях до тех пор пока не начнутся автоколебания.
- Постепенно увеличивая дифференциальную составляющую избавляемся от автоколебаний
- Если наблюдается остаточная ошибка регулирования (смещение), то устраняем её за счет интегральной составляющей.
Каких-то общих значений параметров ПИД-регулятора нет: конкретные значения зависят исключительно от параметров процесса (его передаточной характеристики): ПИД-регулятор отлично работающий с одним объектом управления окажется неработоспособным с другим. Более того, коэффициенты при пропорциональной, интегральной и дифференциальной составляющих еще и взаимозависимы.
В общем не будем о грустном, дальше нас ждет самое интересное…
Попытка номер три. Еще раз производные
Приделав костыль в виде ограничения значений выхода контроллера мы так и не решили самую главную проблему нашего регулятора — дифференциальная составляющая плохо себя чувствует при ступенчатом изменении ошибки на входе регуляторе. На самом деле есть множество других костылей, например, в момент скачкообразного изменения SP «отключать» дифференциальную составляющую или же поставить фильтры нижних частот между SP(t) и операцией за счет которого будет происходить плавное нарастание ошибки, а можно совсем развернуться и впендюрить самый настоящий фильтр Калмана для сглаживания входных данных. В общем костылей много, и добавить наблюдателя конечно хотелось бы, но не в этот раз.
Поэтому снова вернемся к производной ошибки рассогласования и внимательно на неё посмотрим:
Ничего не заметили? Если хорошенько присмотреться, то можно обнаружить, что вообще-то SP(t), не меняется во времени (за исключением моментов ступенчатого изменения, когда регулятор получает новую команду), т.е. её производная равна нулю:
тогда
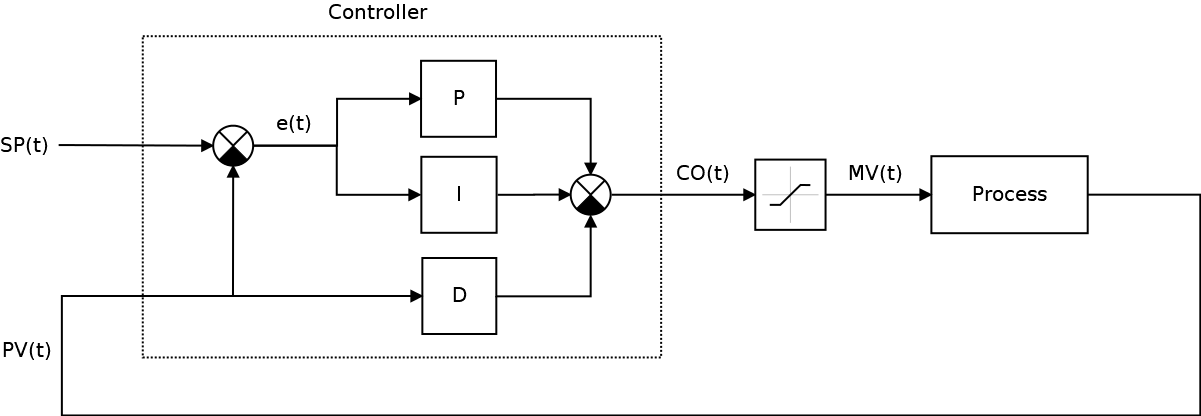
Иными словами, вместо производной ошибки, которая дифференцируема не везде мы можем использовать производную от процесса, который в мире классической механики как правило непрерывен и дифференцируем везде, а схема нашей САУ уже приобретет следующий вид:
Модифицируем код регулятора:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class SimplePID
{
public float Kp, Ki, Kd;
private float P, I, D;
private float lastPV = 0f;
public SimplePID()
{
Kp = 1f;
Ki = 0f;
Kd = 0.2f;
}
public SimplePID(float pFactor, float iFactor, float dFactor)
{
this.Kp = pFactor;
this.Ki = iFactor;
this.Kd = dFactor;
}
public float Update(float error, float PV, float dt)
{
P = error;
I += error * dt;
D = -(PV - lastPV) / dt;
lastPV = PV;
float CO = Kp * P + Ki * I + Kd * D;
return CO;
}
}
}И немного изменим метод ControlRotate:
public float ControlRotate(Vector2 rotate, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
//Вычисляем ошибку
float angleError = Mathf.DeltaAngle(_myTransform.eulerAngles.z, targetAngle);
//Получаем корректирующее ускорение
CO = _angleController.Update(angleError, _myTransform.eulerAngles.z, dt);
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}И-и-и-и… если запустить игру, то обнаружиться, что на самом деле ничего ничего не изменилось с последней попытки, что и требовалось доказать. Однако, если убрать сатурацию, то график реакции регулятора будет выглядеть вот так:
Скачок CO(t) по прежнему присутствует, однако он уже не такой большой как был в самом начале, а самое главное — он стал предсказуемым, т.к. обеспечивается исключительно пропорциональной составляющей, и ограничен максимально возможной ошибкой рассогласования и пропорциональным коэффициентом ПИД-регулятора (а это уже намекает на то, что Kp имеет смысл выбрать все же меньше единицы, например, 1/90f), но не зависит от шага сетки дифференцирования (т.е. dt). В общем, я настоятельно рекомендую использовать именно производную процесса, а не ошибки.
Думаю теперь никого не удивит, но таким же макаром можно заменить на
, однако останавливаться на этом мы не будем, можете сами поэкспериментировать и рассказать в комментариях, что из этого получилось (самому интересно)
Попытка номер четыре. Альтернативные реализации ПИД-регулятор
Помимо описанного выше идеального представления ПИД-регулятора, на практике часто применяется стандартная форма, без коэффициентов Ki и Kd, вместо которых используются временные постоянные.
Такой подход связан с тем, что ряд методик настройки ПИД-регулятора основан на частотных характеристиках ПИД-регулятора и процесса. Собственно вся ТАУ и крутится вокруг частотных характеристик процессов, поэтому для желающих углубиться, и, внезапно, столкнувшихся с альтернативной номенклатурой, приведу пример т.н. стандартной формы ПИД-регулятора:
где, — постоянная дифференцирования, влияющая на прогнозирование состояния системы регулятором,
— постоянная интегрирования, влияющая на интервал усреднения ошибки интегральным звеном.
Основные принципы настройки ПИД-регулятора в стандартной форме аналогичны идеализированному ПИД-регулятору:
- увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;
- с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;
- уменьшение постоянной интегрирования уменьшает запас устойчивости;
- увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие
Исходный код стандартной формы, вы можете найти под спойлером
namespace Assets.Scripts.Regulator
{
[System.Serializable]
public class StandartPID
{
public float Kp, Ti, Td;
public float error, CO;
public float P, I, D;
private float lastPV = 0f;
public StandartPID()
{
Kp = 0.1f;
Ti = 10000f;
Td = 0.5f;
bias = 0f;
}
public StandartPID(float Kp, float Ti, float Td)
{
this.Kp = Kp;
this.Ti = Ti;
this.Td = Td;
}
public float Update(float error, float PV, float dt)
{
this.error = error;
P = error;
I += (1 / Ti) * error * dt;
D = -Td * (PV - lastPV) / dt;
CO = Kp * (P + I + D);
lastPV = PV;
return CO;
}
}
}В качестве значений по умолчанию, выбраны Kp = 0.01, Ti = 10000, Td = 0.5 — при таких значениях корабль поворачивается достаточно быстро и обладает некоторым запасом устойчивости.
Помимо такой формы ПИД-регулятора, часто используется т.н. реккурентная форма:
Не будем на ней останавливаться, т.к. она актуальна прежде всего для хардверных программистов, работающих с FPGA и микроконтроллерами, где такая реализация значительно удобнее и эффективнее. В нашем же случае — давайте что-нибудь сваям на Unity3D — это просто еще одна реализация ПИД-контроллера, которая ни чем не лучше других и даже менее понятная, так что еще раз дружно порадуемся как хорошо программировать в уютненьком C#, а не в жутком и страшном VHDL, например.
Вместо заключения. Куда бы еще присобачить ПИД-регулятор
Теперь попробуем немного усложнить управление корабля используя двухконтурное управление: один ПИД-регулятор, уже знакомый нам _angleController, отвечает по прежнему за угловое позиционирование, а вот второй — новый, _angularVelocityController — контролирует скорость поворота:
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}Назначение второго регулятора — гашение избыточных угловых скоростей, за счет изменения крутящего момента — это сродни наличию углового трения, которое мы отключили еще при создании игрового объекта. Такая схема управления [возможно] позволит получить более стабильное поведение корабля, и даже обойтись только пропорциональными коэффициентами управления — второй регулятор будет гасить все колебания, выполняя функцию, аналогичную дифференциальной составляющей первого регулятора.
Помимо этого, добавим новый класс ввода игрока — PlayerInputCorvette, в котором повороты буду осуществляться уже за счет нажатия клавиш «вправо-влево», а целеуказание с помощью мыши мы оставим для чего-нибудь более полезного, например, для управления турелью. Заодно у нас теперь появился такой параметр как _turnRate — отвечающий за скорость/отзывчивость поворота (не понятно только куда его поместить лучше в InputCOntroller или все же Ship).
public class PlayerCorvetteInput : BaseInputController
{
public float _turnSpeed = 90f;
public override void ControlRotate()
{
// Находим указатель мыши
Vector3 worldPos = Input.mousePosition;
worldPos = Camera.main.ScreenToWorldPoint(worldPos);
// Сохраняем относительные координаты указателя мыши
float dx = -this.transform.position.x + worldPos.x;
float dy = -this.transform.position.y + worldPos.y;
//Передаем направление указателя мыши
Vector2 target = new Vector2(dx, dy);
_agentBody._target = target;
//Вычисляем поворот в соответствии с нажатием клавиш
_agentBody._rotation -= Input.GetAxis("Horizontal") * _turnSpeed * Time.deltaTime;
}
public override void ControlForce()
{
//Передаем movement
_agentBody._movement = Input.GetAxis("Vertical") * Vector2.up;
}
}Также для наглядности накидаем на коленках скрипт для отображения отладочной информации
namespace Assets.Scripts.SpaceShooter.UI
{
[RequireComponent(typeof(Ship))]
[RequireComponent(typeof(BaseInputController))]
public class Debugger : MonoBehaviour
{
Ship _ship;
BaseInputController _controller;
List<SimplePID> _pids = new List<SimplePID>();
List<string> _names = new List<string>();
Vector2 _orientation = new Vector2();
// Use this for initialization
void Start()
{
_ship = GetComponent<Ship>();
_controller = GetComponent<BaseInputController>();
_pids.Add(_ship._angleController);
_names.Add("Angle controller");
_pids.Add(_ship._angularVelocityController);
_names.Add("Angular velocity controller");
}
// Update is called once per frame
void Update()
{
DrawDebug();
}
Vector3 GetDiretion(eSpriteRotation spriteRotation)
{
switch (_controller._spriteOrientation)
{
case eSpriteRotation.Rigth:
return transform.right;
case eSpriteRotation.Up:
return transform.up;
case eSpriteRotation.Left:
return -transform.right;
case eSpriteRotation.Down:
return -transform.up;
}
return Vector3.zero;
}
void DrawDebug()
{
//Направление поворота
Vector3 vectorToTarget = transform.position
+ 5f * new Vector3(-Mathf.Sin(_ship._targetAngle * Mathf.Deg2Rad),
Mathf.Cos(_ship._targetAngle * Mathf.Deg2Rad), 0f);
// Текущее направление
Vector3 heading = transform.position + 4f * GetDiretion(_controller._spriteOrientation);
//Угловое ускорение
Vector3 torque = heading - transform.right * _ship._Torque;
Debug.DrawLine(transform.position, vectorToTarget, Color.white);
Debug.DrawLine(transform.position, heading, Color.green);
Debug.DrawLine(heading, torque, Color.red);
}
void OnGUI()
{
float x0 = 10;
float y0 = 100;
float dx = 200;
float dy = 40;
float SliderKpMax = 1;
float SliderKpMin = 0;
float SliderKiMax = .5f;
float SliderKiMin = -.5f;
float SliderKdMax = .5f;
float SliderKdMin = 0;
int i = 0;
foreach (SimplePID pid in _pids)
{
y0 += 2 * dy;
GUI.Box(new Rect(25 + x0, 5 + y0, dx, dy), "");
pid.Kp = GUI.HorizontalSlider(new Rect(25 + x0, 5 + y0, 200, 10),
pid.Kp,
SliderKpMin,
SliderKpMax);
pid.Ki = GUI.HorizontalSlider(new Rect(25 + x0, 20 + y0, 200, 10),
pid.Ki,
SliderKiMin,
SliderKiMax);
pid.Kd = GUI.HorizontalSlider(new Rect(25 + x0, 35 + y0, 200, 10),
pid.Kd,
SliderKdMin,
SliderKdMax);
GUIStyle style1 = new GUIStyle();
style1.alignment = TextAnchor.MiddleRight;
style1.fontStyle = FontStyle.Bold;
style1.normal.textColor = Color.yellow;
style1.fontSize = 9;
GUI.Label(new Rect(0 + x0, 5 + y0, 20, 10), "Kp", style1);
GUI.Label(new Rect(0 + x0, 20 + y0, 20, 10), "Ki", style1);
GUI.Label(new Rect(0 + x0, 35 + y0, 20, 10), "Kd", style1);
GUIStyle style2 = new GUIStyle();
style2.alignment = TextAnchor.MiddleLeft;
style2.fontStyle = FontStyle.Bold;
style2.normal.textColor = Color.yellow;
style2.fontSize = 9;
GUI.TextField(new Rect(235 + x0, 5 + y0, 60, 10), pid.Kp.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 20 + y0, 60, 10), pid.Ki.ToString(), style2);
GUI.TextField(new Rect(235 + x0, 35 + y0, 60, 10), pid.Kd.ToString(), style2);
GUI.Label(new Rect(0 + x0, -8 + y0, 200, 10), _names[i++], style2);
}
}
}
}Класс Ship также претерпел необратимые мутации и теперь должен выглядеть вот так:
namespace Assets.Scripts.SpaceShooter.Bodies
{
public class Ship : BaseBody
{
public GameObject _flame;
public Vector2 _movement = new Vector2();
public Vector2 _target = new Vector2();
public float _targetAngle = 0f;
public float _angle = 0f;
public float _thrust = 1f;
[Header("PID")]
public SimplePID _angleController = new SimplePID(0.1f,0f,0.05f);
public SimplePID _angularVelocityController = new SimplePID(0f,0f,0f);
private float _torque = 0f;
public float _Torque
{
get
{
return _torque;
}
}
private Vector2 _force = new Vector2();
public Vector2 _Force
{
get
{
return _force;
}
}
public void FixedUpdate()
{
_torque = ControlRotate(_targetAngle, _thrust);
_force = ControlForce(_movement, _thrust);
_rb2d.AddTorque(_torque);
_rb2d.AddRelativeForce(_force);
}
public float ControlRotate(float targetAngle, float thrust)
{
float CO = 0f;
float MV = 0f;
float dt = Time.fixedDeltaTime;
_angle = _myTransform.eulerAngles.z;
//Контроллер угла поворота
float angleError = Mathf.DeltaAngle(_angle, targetAngle);
float torqueCorrectionForAngle =
_angleController.Update(angleError, _angle, dt);
//Контроллер стабилизации скорости
float angularVelocityError = -_rb2d.angularVelocity;
float torqueCorrectionForAngularVelocity =
_angularVelocityController.Update(angularVelocityError, -angularVelocityError, dt);
//Суммарный выход контроллера
CO = torqueCorrectionForAngle + torqueCorrectionForAngularVelocity;
//Дискретизируем с шагом 100
CO = Mathf.Round(100f * CO) / 100f;
//Сатурируем
MV = CO;
if (CO > thrust) MV = thrust;
if (CO < -thrust) MV = -thrust;
return MV;
}
public Vector2 ControlForce(Vector2 movement, float thrust)
{
Vector2 MV = new Vector2();
if (movement != Vector2.zero)
{
if (_flame != null)
{
_flame.SetActive(true);
}
}
else
{
if (_flame != null)
{
_flame.SetActive(false);
}
}
MV = movement * thrust;
return MV;
}
public void Update()
{
}
}
}А вот, собственно заключительное видео того, что должно получиться:
К сожалению получилось охватить не все, что хотелось бы, в частности почти не затронут вопрос настройки ПИД-регулятора и практически не освящена интегральная составляющая — фактически приведен пример только для ПД-регулятора. Собственно изначально планировалось несколько больше примеров (круиз-контроль, вращение турели и компенсация вращательного момента), но статья итак уже разбухла, да и вообще:
Немного ссылок
- Годная статья на английской вики
- PID tutorial
- ПИД-регуляторы: вопросы реализации. Часть 1
- ПИД-регуляторы: вопросы реализации. Часть 2
- PID Without a PhD
- PID Without a PhD. Перевод
- Derivative Action and PID Control
- Control System Lab: PID
- ПИД-регулятор своими руками
- Корректная реализация разностной схемы ПИД регулятора
- Программируем квадрокоптер на Arduino (часть 1)
- Виртуальный квадрокоптер на Unity + OpenCV (Часть 1)
- Поляков К.Ю. Теория автоматического управления для чайников
- PID control system analysis, design, and technology
- Aidan O’Dwyer. Handbook of PI and PID Controller Tuning Rules (3rd ed.)
- PID process control, a “Cruise Control” example
- https://www.mathworks.com/discovery/pid-control.html
- http://scilab.ninja/study-modules/scilab-control-engineering-basics/module-4-pid-control/
- https://sourceforge.net/p/octave/control/ci/default/tree/inst/optiPID.m
Еще немного ссылок на другие примеры
http://luminaryapps.com/blog/use-a-pid-loop-to-control-unity-game-objects/
http://www.habrador.com/tutorials/pid-controller/3-stabilize-quadcopter/
https://www.gamedev.net/articles/programming/math-and-physics/pid-control-of-physics-bodies-r3885/
https://ksp-kos.github.io/KOS/tutorials/pidloops.html
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Хлеба и зрелищ
31.01%
Таки давайте попробуем прикрутить нейросеть к Unity3D
40
24.81%
Алгоритмы самонаведения ракет в Unity3D
32
19.38%
Так как же настраивать этот ПИД-регулятор? Желательно автоматически пока я ем зефирки с кофе
25
10.85%
Мы хотим больше всяких разных регуляторов, например, линейно-квадратичный
14
3.1%
МНК, градиентный спуск, квази-ньютоновские методы. Куда это можно впихнуть в Unity3D?
4
1.55%
Может в Unity3D найдется место для цифровой фильтрации?
2
3.1%
Изложение не достаточно формальное. Больше математики богу математики!
4
6.2%
Кинуть в автора куриным яйцом
8
Проголосовали 129 пользователей.
Воздержались 23 пользователя.
Главная
»
Самолетостроение
»
Основы теории управления
»
Основные понятия и общие принципы построения автоматических систем. Дать определения и пояснить термины система автоматического управления (САУ), разомкнутые и замнкнутые САУ, сигнал ошибки (рассогласования).
Основные понятия и общие принципы построения автоматических систем. Дать определения и пояснить термины система автоматического управления (САУ), разомкнутые и замнкнутые САУ, сигнал ошибки (рассогласования).
Теория автоматического управления— это дисциплина, изучающая процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию.
Основные понятия:
-Автоматика
-Управление
-Цель
-Объекты:
-Система автоматического управления.
-Устройство
-Объект управления
-Регулирование
-Регулятор
-Задающее воздействие g(t)
-Ошибка регулирования ε(t) = g(t) — y(t),
-Возмущающее воздействие f(t)
САУ- система состоящая из объекта управления и устройства управления, в которой автоматически выполняется заданный процесс.
Разомкнутые САУ
Сущность принципа разомкнутого управления заключается в жестко заданной программе управления. То есть управление осуществляется «вслепую», без контроля результата, основываясь лишь на заложенной в САУ модели управляемого объекта. Примеры таких систем : таймер, блок управления светофора, автоматическая система полива газона, автоматическая стиральная машина и т. п.
В свою очередь различают:
Разомкнутые по задающему воздействию
Разомкнутые по возмущающему воздействию
Замкнутые САУ
В замкнутых системах автоматического регулирования управляющее воздействие формируется в непосредственной зависимости от управляемой величины. Связь входа системы с его выходом называется обратной связью. Сигнал обратной связи вычитается из задающего воздействия. Такая обратная связь называется отрицательной.
Сигнал ошибки ε(t) = g(t) — y(t), разность между требуемым значением регулируемой величины и текущим её значением. Если ε(t) отлична от нуля, то этот сигнал поступает на вход регулятора, который формирует такое регулирующее воздействие, чтобы в итоге с течением времени ε(t) = 0.
2. Классификация динамических звеньев САУ. Обыкновенные и типовые динамические звенья (ДТЗ) САУ.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Управление
– это совокупность действий, направленных
на достижение объектом управления
(сварочный процесс) заданного состояния
(требуемых качества шва, скорости сварки,
глубины проплавления, размеров литого
ядра и т. п.). Формирование управляющего
воздействия и само воздействие на объект
управления осуществляется управляющим
устройством.
Система управления
(СУ) – это
совокупность объекта управления и
управляющего устройства, взаимодействующих
между собой.
Воздействие
управляющего устройства (УУ) на объект
управления осуществляется по каналу
прямой связи, а воздействие объекта
управления на управляющее устройство
– по каналу обратной связи.
X y Прямаясвязь
X
Обратная
связь
x
— управляемая величина,
y
— задающее воздействие.
СУ, в которой
присутствует только прямая связь
называется разомкнутой.
X
Y
Прямая связь
Обратная
связь
СУ, в которой наряду
с прямой связью существует обратная
связь называется замкнутой.
Под обратной
связью в
теории управления понимают передачу
сигнала (информации) с выхода объекта
управления (ОУ) на вход управляющего
устройства (УУ). Обратная связь передаёт
результат изменения выходной величины
на вход системы.
Эта выходная
величина представляет собой реальную
физич. величину (длина дуги, глубина
проплавления, ширина свароч. ванны,
длина и диаметр обратного валика),
подлежащую управлению.
Теория
автоматического управления
– это наука, которая изучает процессы
управления и основы проектирования
автоматич. систем, работающих по
замкнутому циклу в любой области науки
и техники. Иначе говоря, она изучает
процессы управления и задачи создания
любых систем управления с обратной
связью.
Главная обратная
связь – это
связь между выходом и входом системы
управления.
Местная обратная
связь – это
связь между входом и выходом каких-либо
элементов внутри системы управления.
Обобщённая функциональная схема сау
Эта блок-схема
является инвариантной (общей), для всех
систем автоматического управления.
Зу – задающее устройство — формирует сигнал задающего воздействия g(t) пропорциональный заданному значению управляемой величиныx(t).
СС – система
сравнения (схема сравнения),
ИУ – измерительное
устройство,
(T) – сигнал рассогласования (сигнал ошибки),
(t)
= g(t)
– y(t),
где у(t)=
k·x(t),
ε(t)
→ 0 – главная
идея ТАУ.
ОУ – объект
управления,
УПУ –
усилительно-преобразоват. устройство
(регулятор) – решает основную
интеллектуальную функцию СУ.
ИО – исполнительный
орган (привод подачи проволоки):
гидравлический, пневматический, зубчатые,
планетарные передачи. ИО может быть
источник питания.
X1(t)
– сигнал с
выхода регулятора (УПУ),
X2(t)
— управляющее
воздействие ИО на ОУ.
КУ – корректирующее
устройство
Z(t)
– выходной сигнал КУ (местн. обр. связь)
Если задающее
воздействие g(t)
= const,
то это соответствует случаю автоматич.
регулирования, основанному на поддержании
постоянного значения управляемой
величины. Такие системы называются
системами автоматического регулирования
САР.
Лекция №3 Основные элементы сау:
1) ИУ
– чувствительный элемент или датчик,
который измеряет текущие значения
управляемой величины Х
и преобразует их с коэффициентом усиления
k
к сигналу Y
удобному для дальнейшего использования
в системе;
2) ЗУ
– формирует сигнал задающего воздействия
g(t)
в удобном для сравнения с виде;
3) CC
– измеряет сигнал ошибки (t)
пропорциональный отклонению управляемой
величины X(t)
от заданного значения g(t);
4) УПУ
(регулятор)
– усиливает и преобразует в соответствии
с заданным законом управления сигнал
ошибки (t)
необходимый для управления исполнительным
органом ИО;
5) ИО
– преобразует сигнал x1(t)
в управляющее воздействие x2(t),
которое не обязательно может быть
электрич. природы;
6) КУ
(корректирующее устройство) – включаются
последовательно или параллельно ИО.
Назначение КУ: улучшить качество
процессов управления внутри системы с
помощью дополнительного воздействия
z(t).
Классификация
САУ по виду функциональных схем и
принципу действия системы:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Продолжение разработки проекта контроллера модуля Пельтье, начатой в уроке 36. Узнаем, что такое ПИД регулятор.
Предыдущий урок Список уроков Следующий урок
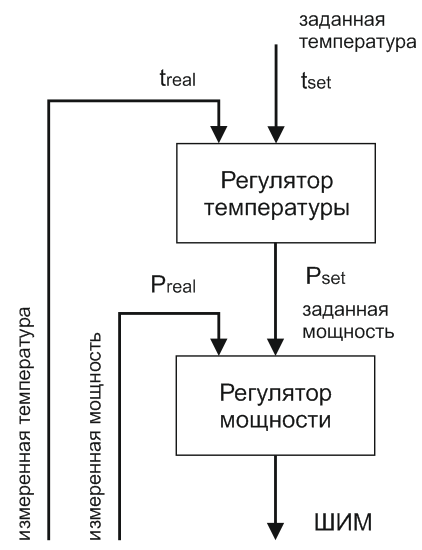
Основная задача контроллера холодильника – поддержание в камере заданной температуры. Делать это будет регулятор температуры за счет изменения электрической мощности на модуле Пельтье.
В предыдущем уроке мы разработали регулятор мощности. Связь регуляторов мощности и температуры выглядит так.
- Регулятор температуры получает измеренную температуру, сравнивает ее с заданной температурой и вычисляет значение заданной мощности для регулятора мощности.
- Регулятор мощности формирует ШИМ, соответствующий заданной мощности.
Регулятор мощности мы построили по интегральному закону регулирования. Для стабилизации температуры будем использовать более сложный алгоритм управления – пропорционально-интегрально-дифференцирующий (ПИД) регулятор.
ПИД регулятор.
В предыдущем уроке я подробно рассказал об интегральном регуляторе. Подчеркнул его достоинства и недостатки.
Регулятор, работающий по такому принципу, обладает высокой точностью. Остальные критерии качества регулирования – быстродействие и устойчивость — у него не на высоте.
Для того чтобы добиться высоких показателей для всех критериев необходимо использовать регулятор, объединяющий в себе разные законы регулирования.
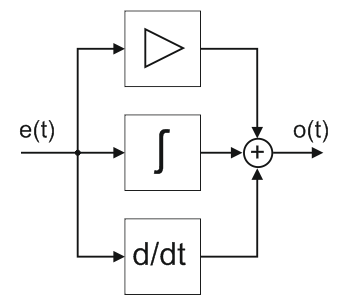
Именно таким устройством является пропорционально-интегрально-дифференцирующий (ПИД) регулятор. Он формирует выходной сигнал, являющийся суммой трех составляющих с разными передаточными характеристиками. Благодаря этому ПИД регулятор обеспечивает высокое качество регулирования и позволяет оптимизировать управление по отдельным критериям.
В формировании выходного сигнала ПИД регулятора участвуют:
- Пропорциональная составляющая – значение пропорционально ошибке рассогласования (разности заданного и реального значений регулируемого параметра).
- Интегрирующая составляющая – интеграл ошибки рассогласования.
- Дифференцирующая составляющая – производная ошибки рассогласования.
Математическая форма записи закона ПИД регулятора имеет вид:
o(t) = P + I + D = Kp e(t) + Ki ∫e(t)dt + Kd de(t)/dt
- o(t) – выходной сигнал;
- P – пропорциональная составляющая;
- I – интегрирующая составляющая;
- D – дифференцирующая составляющая;
- Kp, Ki, Kd – коэффициенты пропорционального, интегрирующего, дифференцирующего звеньев;
- e(t) – ошибка рассогласования.
В схематичном виде ПИД регулятор можно представить так.
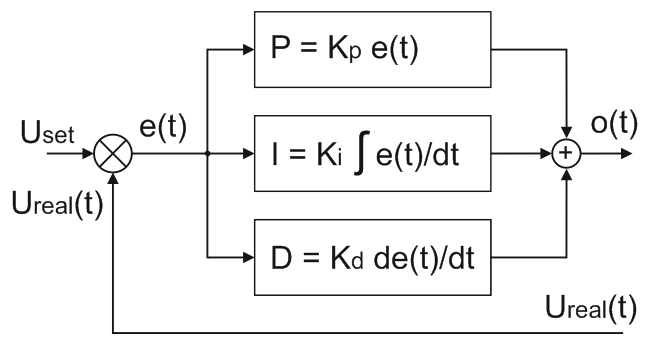
Структурная схема ПИД регулятора напряжения U выглядит так.
- Измеренное напряжение Ureal(t) вычитается из заданного Uset.
- Полученная ошибка рассогласования e(t) поступает на пропорциональное, интегрирующее и дифференцирующее звенья.
- В результате суммы составляющих получается управляющее воздействие o(t), которое подается на регулирующий элемент.
При программной реализации ПИД регулятора вычисления выходного сигнала происходят через равные промежутки времени. Т.е. регулятор является дискретным по времени. Поэтому, далее я буду употреблять выражения: предыдущее состояние сигнала, предыдущее значение и т.п. Речь идет о состоянии системы в предыдущей точке временной дискретизации.
Составляющие ПИД регулятора.
Еще раз. Выходной сигнал ПИД регулятора это сумма трех составляющих:
- пропорциональной;
- интегрирующей;
- дифференцирующей.
Пропорциональная составляющая.
P(t) = Kp * e(t)
Не имеет памяти, т.е. значение выходного сигнала не зависит от предыдущего состояния системы. Просто ошибка рассогласования, умноженная на коэффициент, передается на выход. Выходной сигнал компенсирует отклонение регулируемого параметра. Сигнал тем больше, чем больше ошибка рассогласования. При ошибке равной 0, сигнал на выходе тоже равен 0.
Пропорциональная составляющая не способна компенсировать ошибку полностью. Это видно из формулы. Выходной сигнал в Kp раз больше ошибки. Если ошибка рассогласования равна 0, то и выходной сигнал регулятора равен 0. А тогда и компенсировать нечем.
Поэтому в пропорциональных регуляторах всегда существует так называемая статическая ошибка. Уменьшить ее можно за счет увеличения коэффициента Kp, но это может привести к снижению устойчивости системы и даже к автоколебаниям.
К недостаткам пропорциональных регуляторов следует отнести:
- наличие статической ошибки регулирования;
- невысокая устойчивость при увеличении коэффициента.
Есть весомое преимущество:
- Высокая скорость регулирования. Реакция пропорционального регулятора на ошибку рассогласования ограничена только временем дискретизации системы.
Регуляторы, работающие только по пропорциональному закону, применяют редко.
Главная задача пропорциональной составляющей в ПИД регуляторе – повысить быстродействие.
Интегрирующая составляющая.
I(t) = Ki ∫e(t)dt
Пропорциональна интегралу ошибки рассогласования. С учетом временной дискретности регулятора можно написать так:
I(t) = I(t-1) + Ki * e(t)
- I(t-1) – значение I в предыдущей точке временной дискретизации.
Ошибка рассогласования умножается на коэффициент и прибавляется к предыдущему значению интегрирующего звена. Т.е. выходной сигнал все время накапливается и со временем увеличивает свое воздействие на объект. Таким образом, ошибка рассогласования полностью компенсируется даже при малых значениях ошибки и коэффициента Ki. В установившемся состоянии выходной сигнал регулятора полностью обеспечивается интегрирующей составляющей.
К недостаткам интегрального регулятора следует отнести:
- низкое быстродействие;
- посредственная устойчивость.
Достоинство:
- Способность полностью компенсировать ошибку рассогласования при любом коэффициенте усиления.
На практике часто используют интегрирующие регуляторы (только интегрирующая составляющая) и пропорционально-интегрирующие (интегрирующая и пропорциональная составляющие).
Главная задача интегрирующего звена в ПИД регуляторе – компенсация статической ошибки, обеспечение высокой точности регулирования.
Дифференцирующая составляющая.
D(t) = Kd de(t)/dt
Пропорциональна скорости изменения ошибки рассогласования. Своеобразный показатель ускорения ошибки рассогласования. Дифференцирующая составляющая предсказывает отклонения регулируемого параметра в будущем и противодействует этому отклонению. Как правило, она компенсирует запаздывания воздействия регулятора на объект и повышает устойчивость системы.
С учетом временной дискретности регулятора дифференцирующую составляющую можно вычислить так:
D(t) = Kd * ( e(t) — e(t-1) )
Она показывает, насколько изменилось значение ошибки рассогласования за одну временную единицу дискретности регулятора.
Регуляторов, состоящих из единственного дифференцирующего звена, не бывает.
Главная задача дифференцирующего звена в ПИД регуляторе – повышение устойчивости.
Настройка ПИД регулятора.
Качество регулирования ПИД регуляторов в значительной мере зависит от того, насколько оптимально выбраны коэффициенты. Коэффициенты ПИД регулятора определяются на практике в системе с реальным объектом путем подбора. Существуют разные методики настройки. Я расскажу только об общих принципах.
О качестве регулирования судят по переходной характеристике регулятора. Т.е. по графику изменения регулируемого параметра во времени.
К традиционным пунктам последовательности настройки ПИД регулятора я бы добавил, что, прежде всего, надо определиться какие критерии качества регулирования предпочтительнее.
В предыдущем уроке при разработке регулятора мощности нас в первую очередь интересовали точность и устойчивость. А быстродействие мы даже искусственно снизили. Какие-то регуляторы работают в условиях значительных помех и им важнее устойчивость, от других требуется высокое быстродействие даже в ущерб точности. Критерии оптимизации могут быть разными. В общем случае ПИД регуляторы настраивают для обеспечения всех критериев качества регулирования на высоком уровне.
Составляющие ПИД регулятора настраиваются отдельно.
- Отключается интегрирующее и дифференцирующее звенья и выбирается коэффициент пропорционального звена. Если регулятор пропорционально-интегрирующий (отсутствует дифференцирующее звено), то добиваются полного отсутствия колебаний на переходной характеристике. При настройке регулятора на высокое быстродействие колебания могут остаться. Их попытается скомпенсировать дифференцирующее звено.
- Подключается дифференцирующее звено. Его коэффициентом стремятся убрать колебания параметра регулирования. Если не удается, то уменьшают пропорциональный коэффициент.
- За счет интегрирующего звена убирают остаточную ошибку рассогласования.
Настройка ПИД регулятора носит итерационный характер. Т.е. пункты подбора коэффициентов могут многократно повторяться до тех пор, пока не будет достигнут приемлемый результат.
Благодаря высоким характеристикам и универсальности ПИД регуляторы широко применяются в системах автоматизации производства.
В следующем уроке будем разрабатывать ПИД регулятор температуры.
Предыдущий урок Список уроков Следующий урок
Автор публикации
270
Комментарии: 1908Публикации: 195Регистрация: 13-12-2015
ОБОРУДОВАНИЕ ТЕХНОЛОГИИ РАЗРАБОТКИ
Продолжение разработки проекта контроллера модуля Пельтье, начатой в уроке 36. Узнаем, что такое ПИД регулятор.
Предыдущий урок Список уроков Следующий урок
Основная задача контроллера холодильника – поддержание в камере заданной температуры. Делать это будет регулятор температуры за счет изменения электрической мощности на модуле Пельтье.
В предыдущем уроке мы разработали регулятор мощности. Связь регуляторов мощности и температуры выглядит так.
- Регулятор температуры получает измеренную температуру, сравнивает ее с заданной температурой и вычисляет значение заданной мощности для регулятора мощности.
- Регулятор мощности формирует ШИМ, соответствующий заданной мощности.
Регулятор мощности мы построили по интегральному закону регулирования. Для стабилизации температуры будем использовать более сложный алгоритм управления – пропорционально-интегрально-дифференцирующий (ПИД) регулятор.
ПИД регулятор.
В предыдущем уроке я подробно рассказал об интегральном регуляторе. Подчеркнул его достоинства и недостатки.
Регулятор, работающий по такому принципу, обладает высокой точностью. Остальные критерии качества регулирования – быстродействие и устойчивость — у него не на высоте.
Для того чтобы добиться высоких показателей для всех критериев необходимо использовать регулятор, объединяющий в себе разные законы регулирования.
Именно таким устройством является пропорционально-интегрально-дифференцирующий (ПИД) регулятор. Он формирует выходной сигнал, являющийся суммой трех составляющих с разными передаточными характеристиками. Благодаря этому ПИД регулятор обеспечивает высокое качество регулирования и позволяет оптимизировать управление по отдельным критериям.
В формировании выходного сигнала ПИД регулятора участвуют:
- Пропорциональная составляющая – значение пропорционально ошибке рассогласования (разности заданного и реального значений регулируемого параметра).
- Интегрирующая составляющая – интеграл ошибки рассогласования.
- Дифференцирующая составляющая – производная ошибки рассогласования.
Математическая форма записи закона ПИД регулятора имеет вид:
o(t) = P + I + D = Kp e(t) + Ki ∫e(t)dt + Kd de(t)/dt
- o(t) – выходной сигнал;
- P – пропорциональная составляющая;
- I – интегрирующая составляющая;
- D – дифференцирующая составляющая;
- Kp, Ki, Kd – коэффициенты пропорционального, интегрирующего, дифференцирующего звеньев;
- e(t) – ошибка рассогласования.
В схематичном виде ПИД регулятор можно представить так.
Структурная схема ПИД регулятора напряжения U выглядит так.
- Измеренное напряжение Ureal(t) вычитается из заданного Uset.
- Полученная ошибка рассогласования e(t) поступает на пропорциональное, интегрирующее и дифференцирующее звенья.
- В результате суммы составляющих получается управляющее воздействие o(t), которое подается на регулирующий элемент.
При программной реализации ПИД регулятора вычисления выходного сигнала происходят через равные промежутки времени. Т.е. регулятор является дискретным по времени. Поэтому, далее я буду употреблять выражения: предыдущее состояние сигнала, предыдущее значение и т.п. Речь идет о состоянии системы в предыдущей точке временной дискретизации.
Составляющие ПИД регулятора.
Еще раз. Выходной сигнал ПИД регулятора это сумма трех составляющих:
- пропорциональной;
- интегрирующей;
- дифференцирующей.
Пропорциональная составляющая.
P(t) = Kp * e(t)
Не имеет памяти, т.е. значение выходного сигнала не зависит от предыдущего состояния системы. Просто ошибка рассогласования, умноженная на коэффициент, передается на выход. Выходной сигнал компенсирует отклонение регулируемого параметра. Сигнал тем больше, чем больше ошибка рассогласования. При ошибке равной 0, сигнал на выходе тоже равен 0.
Пропорциональная составляющая не способна компенсировать ошибку полностью. Это видно из формулы. Выходной сигнал в Kp раз больше ошибки. Если ошибка рассогласования равна 0, то и выходной сигнал регулятора равен 0. А тогда и компенсировать нечем.
Поэтому в пропорциональных регуляторах всегда существует так называемая статическая ошибка. Уменьшить ее можно за счет увеличения коэффициента Kp, но это может привести к снижению устойчивости системы и даже к автоколебаниям.
К недостаткам пропорциональных регуляторов следует отнести:
- наличие статической ошибки регулирования;
- невысокая устойчивость при увеличении коэффициента.
Есть весомое преимущество:
- Высокая скорость регулирования. Реакция пропорционального регулятора на ошибку рассогласования ограничена только временем дискретизации системы.
Регуляторы, работающие только по пропорциональному закону, применяют редко.
Главная задача пропорциональной составляющей в ПИД регуляторе – повысить быстродействие.
Интегрирующая составляющая.
I(t) = Ki ∫e(t)dt
Пропорциональна интегралу ошибки рассогласования. С учетом временной дискретности регулятора можно написать так:
I(t) = I(t-1) + Ki * e(t)
- I(t-1) – значение I в предыдущей точке временной дискретизации.
Ошибка рассогласования умножается на коэффициент и прибавляется к предыдущему значению интегрирующего звена. Т.е. выходной сигнал все время накапливается и со временем увеличивает свое воздействие на объект. Таким образом, ошибка рассогласования полностью компенсируется даже при малых значениях ошибки и коэффициента Ki. В установившемся состоянии выходной сигнал регулятора полностью обеспечивается интегрирующей составляющей.
К недостаткам интегрального регулятора следует отнести:
- низкое быстродействие;
- посредственная устойчивость.
Достоинство:
- Способность полностью компенсировать ошибку рассогласования при любом коэффициенте усиления.
На практике часто используют интегрирующие регуляторы (только интегрирующая составляющая) и пропорционально-интегрирующие (интегрирующая и пропорциональная составляющие).
Главная задача интегрирующего звена в ПИД регуляторе – компенсация статической ошибки, обеспечение высокой точности регулирования.
Дифференцирующая составляющая.
D(t) = Kd de(t)/dt
Пропорциональна скорости изменения ошибки рассогласования. Своеобразный показатель ускорения ошибки рассогласования. Дифференцирующая составляющая предсказывает отклонения регулируемого параметра в будущем и противодействует этому отклонению. Как правило, она компенсирует запаздывания воздействия регулятора на объект и повышает устойчивость системы.
С учетом временной дискретности регулятора дифференцирующую составляющую можно вычислить так:
D(t) = Kd * ( e(t) — e(t-1) )
Она показывает, насколько изменилось значение ошибки рассогласования за одну временную единицу дискретности регулятора.
Регуляторов, состоящих из единственного дифференцирующего звена, не бывает.
Главная задача дифференцирующего звена в ПИД регуляторе – повышение устойчивости.
Настройка ПИД регулятора.
Качество регулирования ПИД регуляторов в значительной мере зависит от того, насколько оптимально выбраны коэффициенты. Коэффициенты ПИД регулятора определяются на практике в системе с реальным объектом путем подбора. Существуют разные методики настройки. Я расскажу только об общих принципах.
О качестве регулирования судят по переходной характеристике регулятора. Т.е. по графику изменения регулируемого параметра во времени.
К традиционным пунктам последовательности настройки ПИД регулятора я бы добавил, что, прежде всего, надо определиться какие критерии качества регулирования предпочтительнее.
В предыдущем уроке при разработке регулятора мощности нас в первую очередь интересовали точность и устойчивость. А быстродействие мы даже искусственно снизили. Какие-то регуляторы работают в условиях значительных помех и им важнее устойчивость, от других требуется высокое быстродействие даже в ущерб точности. Критерии оптимизации могут быть разными. В общем случае ПИД регуляторы настраивают для обеспечения всех критериев качества регулирования на высоком уровне.
Составляющие ПИД регулятора настраиваются отдельно.
- Отключается интегрирующее и дифференцирующее звенья и выбирается коэффициент пропорционального звена. Если регулятор пропорционально-интегрирующий (отсутствует дифференцирующее звено), то добиваются полного отсутствия колебаний на переходной характеристике. При настройке регулятора на высокое быстродействие колебания могут остаться. Их попытается скомпенсировать дифференцирующее звено.
- Подключается дифференцирующее звено. Его коэффициентом стремятся убрать колебания параметра регулирования. Если не удается, то уменьшают пропорциональный коэффициент.
- За счет интегрирующего звена убирают остаточную ошибку рассогласования.
Настройка ПИД регулятора носит итерационный характер. Т.е. пункты подбора коэффициентов могут многократно повторяться до тех пор, пока не будет достигнут приемлемый результат.
Благодаря высоким характеристикам и универсальности ПИД регуляторы широко применяются в системах автоматизации производства.
В следующем уроке будем разрабатывать ПИД регулятор температуры.
Предыдущий урок Список уроков Следующий урок
Поддержать проект
1
Автор публикации
не в сети 1 день
Эдуард
206
Комментарии: 1699Публикации: 173Регистрация: 13-12-2015
Преобразователи частоты ABB серии ACS355
Преобразователи частоты ABB серии ACS355 – оптимальный выбор по соотношению «цена-качество» для решения задач с ПИД-регулированием. Общий вид приводов ACS355 показан на рис.4.
Частотные приводы ACS355 обладают широким набором параметров и возможностей. Настроить необходимый режим работы возможно как с панели управления преобразователем, так и при помощи персонального компьютера, посредством специализированного программного обеспечения DriveWindow Light.
Рис.4. Преобразователи частоты ABB серии ACS355 с базовой панелью управления.
В данной статье, для примера, рассмотрен вариант настройки ПИД-регулятора преобразователя ACS355 при помощи панели управления.
Панель управления к частотному приводу ACS355 предлагается в двух вариантах исполнения: базовая панель и интеллектуальная панель управления (см. рис.5).
Рис.5. Варианты панелей управления к преобразователям частоты ABB серии ACS355.
Интеллектуальная панель управления частотным приводом ACS355 имеет встроенный мастер запуска (настройки) и интерактивную справку. С помощью этих инструментов настройку преобразователя частоты ACS355 на режим ПИД-регулирования можно выполнить без особых временных затрат и не пользуясь руководством по эксплуатации.
При использовании базовой панели управления встроенных удобных инструментов, указанных выше, нет.
VII. Измерение входных данных
Я пропускаю этот вопрос, потому как он достоен отдельной большой статьи. О том, как я решал вопрос с термосопротивлением, можно найти в архиве почившего в бозе моего блога.
Главное что нам надо знать, это что мы измеряем данные с нужной нам частотой (в данном случае — 25Гц), и нужной точностью (на выходе — число от 0 до 2048 градусов кельвина через 1/32 градуса). Данные предполагаются уже нормализованные для всех дальнейших расчетов.
Если будет кому интересно — пишите в комментах, распишу в следующий раз как это делается для термопар.
Методика настройки ПИД-регулятора
Выбор алгоритма управления и его настройка является основной задачей в процессе проектирования и последующего удовлетворительного запуска агрегата в промышленную или иную эксплуатацию.
В основе методики лежит закон Циглера-Никольса, являющийся эмпирическим и основанным на использовании данных, полученных экспериментально на реальном объекте.
В результате ознакомления с методикой, а также при близком рассмотрении объектов регулирования, были выбраны формулы и коэффициенты ближе всего подходящие к реальному объекту регулирования.
Объект регулирования – камерная электрическая печь. Число зон регулирования от 24 до 40. Каждая зона есть набор электронагревателей. Материал нагревателей нихром. Тип — проволочные, навитые на керамические трубки.
Требования: поддержание температуры по зонам печи +/- 5С.
МЕТОДИКА:
Настройка пропорциональной компоненты (Xp)
- Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются:
- Постоянная интегрирования устанавливается минимально возможной (Ти =0),
- Постоянная дифференцирования минимально возможной (Тд = 0).
Тο — начальная температура в системе; Тsp — заданная температура (уставка); ∆T — размах колебаний температуры; ∆t — период колебаний температуры.
- Меняем значение пропорциональной составляющей Xp от минимума (0) до момента, пока не появятся устойчивые колебания системы с периодом ∆t.
Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, где ∆T– характеристика колебания равная значению величины рассогласования (±10С, или как по заданию). Колебания должны быть одинаковы от Тsp.
После получения данной кривой на нашем объекте, засекаем время периода колебаний ʌt – полный период. Данное время есть характеристика системы, оборудования.
3. Используя полученные параметры рассчитываем Ти и Тд.
| Зона пропорциональности | Коэффициент передачи | Постоянная времени интегрирования | Постоянная времени дифференцирования | |
| П-регулятор | 2*PBs | 0.5*Xp | ||
| ПИ-регулятор | 2.2*PBs | 0.45*Xp | 0.83*ʌТ | |
| ПИД-регулятор | 1.67*PBs | 0.6*Xp | 0.5*ʌТ | 0.125*ʌТ |
Цифры в формулах для расчета коэффициентов ПИД-регулирования скорректированы на основе запуска камерной электрической печи в опытно-промышленную эксплуатацию. И конечно в зависимости от типа объекта регулирования могут незначительно меняться.
Сравнение ПИД –регулятора с позиционным регулированием
В системах АСУ ТП наибольшее распространение получили два типа регуляторов – двухпозиционный и ПИД.
Двухпозиционный регулятор наиболее простой в использовании и широко распространенный.
Данный тип регулятора сравнивает значение входной величины с заданным параметром уставки. Если значение измеренной величины ниже заданного значения уставки, регулятор включает исполнительное устройство, при превышении заданного значения, исполнительное устройство выключается. Для предотвращения слишком частого срабатывания устройства, в следствии колебаний системы и следовательно изменении значений, задается минимальный и максимальный порог срабатывания — гистерезис, или по другому зона нечувствительности, мертвая зона, дифференциал. Например, нам необходимо поддерживать температуру в 15°С. Если гистерезис задан 2°, то регулятор будет включать нагрев при 14°С и отключать соответственно при 16°С.
Чем меньше значение гистерезиса, тем точнее будет процесс регулирования, но увеличивается частота срабатывания ,что в конечном итоге приводит к износу коммутационных аппаратов. Увеличение гистерезиса уменьшит частоту переключений, но при этом увеличивается амплитуда колебаний регулируемого параметра, что приведет к ухудшению точности регулирования.
Так или иначе, при таком типе регулирования происходят незатухающие колебания, частота и амплитуда которых зависит от параметров системы. Поэтому данный метод обеспечивает хороший результат в системах, обладающих инерционностью и малым запаздыванием. В частности, такой метод широко применяется при регулировании температуры в нагревательных печах.
В отличии от двухпозиционного с помощью ПИД-регулятора удается свести колебания системы к минимуму, благодаря тому, что при таком методе регулирования учитываются различные значения системы — фактическая величина, заданное значение, разность, скорость. Это позволяет стабилизировать систему и добиться повышения точности в десятки раз по сравнению с двухпозиционным методом. Конечно, здесь многое зависит от правильно подобранных коэффициентов ПИД регулятора.
Для того, чтобы правильно выбрать необходимый тип регулятора необходимо хотя бы приблизительно знать характеристики управляемого объекта , требования к точности регулирования, характер возмущений, воздействующих на объект регулирования.
Задачи ПИД-регулятора в системах АСУ ТП
Основная задача ПИД регулятора состоит в поддержании определенного значения параметра технологического процесса на заданном уровне. То есть говоря простым языком, задача ПИД-регулятора заключается в том, чтобы учитывая полученные значения с датчиков (обратная связь) воздействовать на объект управления, плавно подводя регулируемое значение к заданным уставкам. Применение ПИД регуляторов целесообразно, а зачастую и единственно возможно в процессах, где необходима высокая точность переходных процессов, непрерывный контроль и регулирование заданных параметров, недопустимы значительные колебания в системе.