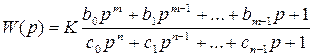ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
— в общем случае это функционалы, характеризующие отклонение показателя качества работы (Ф) системы автоматического управления (САУ) от его заданного или экстремального значения 





с. а. у. могут оцениваться по значениям, взятым в определенные моменты времени (напр., максимум ошибки в процессе управления), либо по интегральным критериям (напр., среднеквадратичная ошибка 
О. в с. а. у. зависят прежде всего от структуры систем, а также от возмущений, действующих на объект управления, от ограниченности управляющего воздействия по величине и мощности, погрешностей в измерительных цепях и т. п. В связи с этим в линейных САУ выделяют вынужденную составляющую ошибки, определяемую действием возмущения на объект управления или задания, и свободную составляющую, определяемую начальным отклонением показателя качества работы САУ. Кроме того, рассматривают О. в с. а. у., связанные с действием случайных сигналов на объект управления и соответствующие оценки этих ошибок (например, математическое ожидание и дисперсия). В следящих САР вынужденная составляющая ошибки определяется изменением задания во времени 


где 


где 



С помощью методов автоматического управления теории структура САУ может быть выбрана таким образом, чтобы минимизировать О. в с. а. у. при принятой ее оценке или минимизировать некоторый показатель, связанный с изменением ошибки во времени (напр., время переходного процесса). Путем рационального выбора структуры некоторые виды ошибок САУ могут быть сведены к нулю, напр., установившиеся ошибки в САР при интегральном регулирования законе или динамические ошибки, связанные с действием возмущений на объект управления в некоторых случаях инвариантных систем управления. См. также Астатизм 
Лит.: Современные методы проектирования систем автоматического управления. М., 1967; Ивахненко А. Г. Электроавтоматика. К., 1957 [библиогр. с. 440—442]; Воронов А. А. Основы теории автоматического управления, ч. 1. М. Л., 1965 [библиогр. с. 382—392]. Л. М. Бойчук.
-
Виды ошибок регулирования и методы их снижения.
Прямые показатели качества подразделяются
на показатели качества динамического
и установившегося режимов.
Показателями качества динамических
режимов определяются из графика
переходного процесса и основными из
них являются (рис.1.42):
—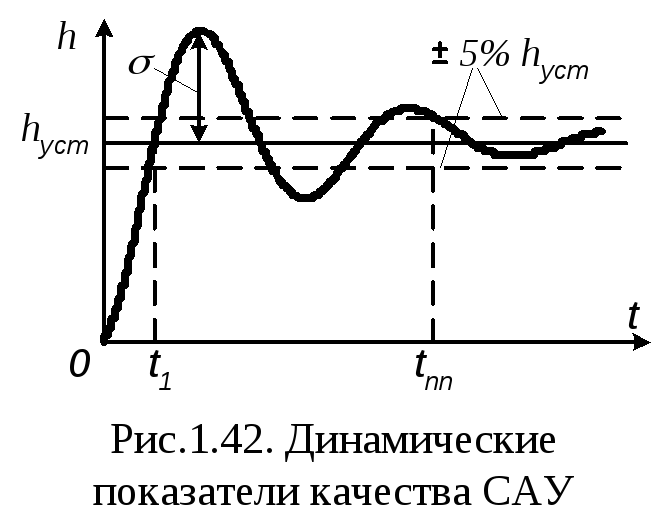
равный максимуму отклонения значения
переходного процесса относительно
установившегося значения процессаhycm;
— время первой установки t1,
определяемое моментом первого пересечения
графиком переходного процесса
установившегося значенияhycm;
— время переходного процесса tПП,
определяемое момент окончательного
входа графика переходного процесса в
зону допуска, равную±5%от
установившегося значения процессаhycm.
Для всех названных динамических
показателей качества невозможно в общем
случае получить формулы для их расчета.
Это является существенным препятствием
для решения задач анализа и синтеза
САУ.
Показателями качества установившихся
режимов являются ошибки регулирования,
равные абсолютной величине разности
между заданным и фактическим значениями
сигналов САУ и которые в зависимости
от вида входного сигнала САУ подразделяются
на статические (εСТ) и
скоростные ошибки (εСК) и
ошибки (εm)
при отработке гармонического входного
сигнала.
Д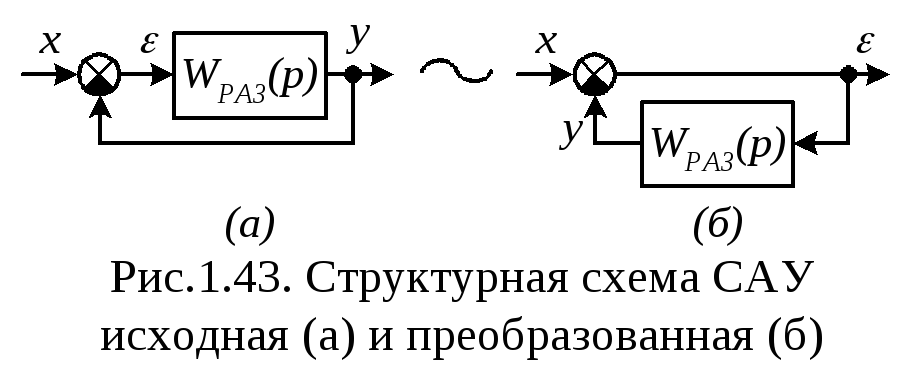
всех названных ошибок регулирования
можно в общем случае получить формулы
их расчета.
Из структурной схемы замкнутой САУ
(рис.1.43) следуют выражения передаточной
функции САУ Wε(p)по ошибке и изображенияε(р)ошибки
регулирования:
Расчет ошибки εmотработки гармонического входного
сигналаx=Xmsinωt
производится по формуле
где
— модуль комплексного числа
.
Статическая (εСТ) и
скоростная (εСК) ошибки
равны установившимся значениям оригиналаи
,
или в общем виде, по формуле.
Значениевычисляют через изображениеε(р)
по доказываемой в теории операционного
исчисления формуле предельного перехода,
(1.54)
Выражение передаточной функции
разомкнутой САУ в общем случае может
быть приведено к виду:
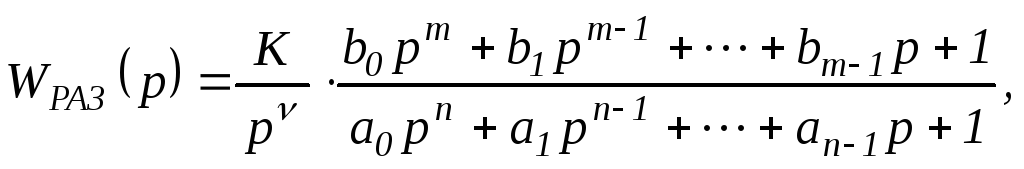
где К– общий коэффициент усиления
разомкнутой САУ:
ν— порядок астатизма САУ, причемνявляется целым неотрицательным
числом.
Для удобства вычислений по формуле
(1.54) подставим в нее выражение WРАЗ(р)из (1.55) и выполним предельный переход:
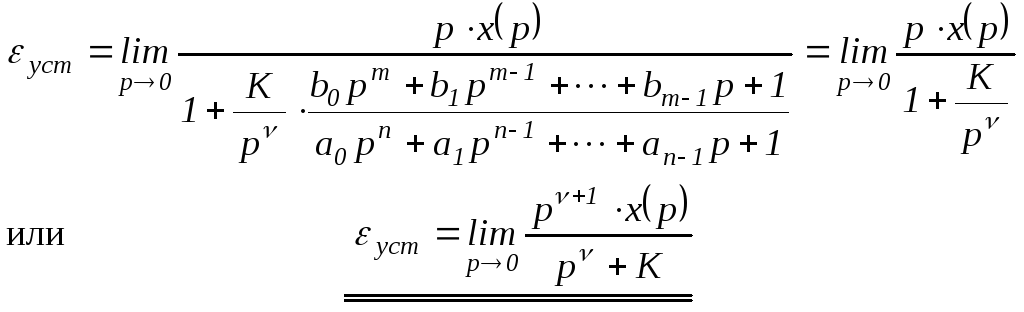
Статическая ошибка регулирования εСТрассчитывается при постоянном входном
сигналеx(t)=X=const,
а скоростнаяεСК— при
входном сигналеx=Vt,
изменяющемуся во времени с постоянной
скоростьюV=const.
Далее расчеты статической (εСТ)
и скоростной (εСК) ошибок
выполним раздельно.
Расчеты статической ошибки εСт регулирования
Входной сигнал x(t)=X=constи изображением его является.
В соответствии с (1.56) статическую ошибкуεСТследует вычислять по
формуле
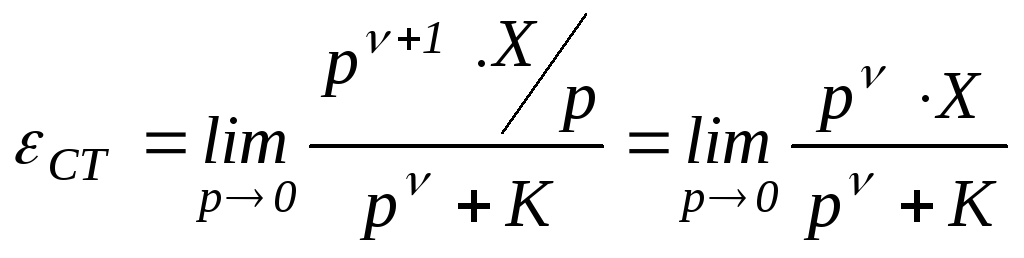
1). Пусть в (1.57) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
статическая ошибкаεСТбудет равна
В статической САУ имеется статическая
ошибка εСТ, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияКразомкнутой САУ, но обратить в ноль ее
нельзя.
2). Пусть в (1.57) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаεСТбудет равна
В астатической САУ 1-го порядка статическая
ошибка εСТравна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1, статическая ошибка регулирования
всегда будет нулевой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Качество управления. Ошибка системы. Система автоматической стабилизации скорости вращения электродвигателя
Страницы работы
Фрагмент текста работы
6 Качество управления
Ошибка системы
Любая автоматическая система должна быть не
только устойчивой, но и достаточно точной в работе. В любой реальной системе
невозможно точное равенство задающего воздействия g
и управляемой величины y во всё время процесса управления. Возникает
ошибка системы x=g—y. Её можно представить в виде X=Xп+Хуст.,
где Xп – переходная ошибка, а Хуст. – это ошибка
системы по окончанию переходного процесса. Для определения Xп приходится
либо находить корни характеристического уравнения, либо использовать критерии
качества, не требующие нахождения ошибки Xп (частотный критерий качества, интегральный
критерий качества).
6.2 Ошибки САУ в установившемся режиме
Рассмотрим неподвижное состояние, когда g=const ,или f=const. Имеются 2 вида систем: статические и
астатические. Статической системой автоматического управления называется
система, переходная функция которой в разомкнутом состоянии при размыкании по
ошибке имеет вид:
В статических САУ интегрирующие звенья или отсутствуют.
или охвачены обратной связью, т.е. нет множителя p
в знаменателе.
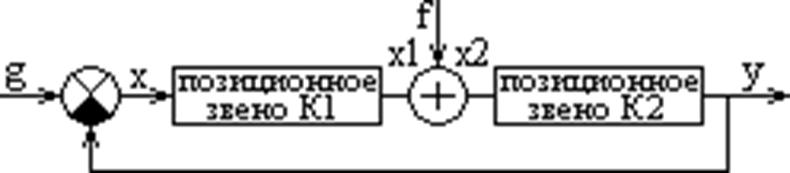 |
Определим ошибку Хуст., если g=g0, f=f0,
тогда Хуст.=g0—yуст. (а),
Но yуст.=Х2уст.К2
= (Х1уст.+f0)К2= (Хуст.К1+f0)K2
(в).
Подставим (в) в (а): Хуст.= g0-К1К2
Хуст.-К2f0. Хуст.(1+K1K2)= g0—K2f0.
Пусть К1К2=К, тогда Хуст.=
(g0/1+К)-( К2f0/1+К).
Из выражения (в) следует, что для
уменьшения ошибки от задающего воздействия g
необходимо увеличивать общий коэффициент передачи звеньев, стоящих до
возмущения (К1) и уменьшать для стоящих после возмущения(K2). В
статических САУ ошибку от задающего воздействия легко ликвидировать
масштабированием. Этот метод рассмотрим позднее. Исследуем ошибку от
возмущающего воздействия.
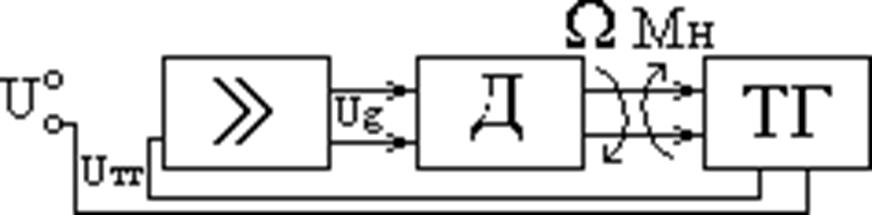
Пример: Система автоматической стабилизации скорости вращения
электродвигателя.
Мн – момент нагрузки.
При изменении Мн меняется скорость вращения
ω, что приводит к изменению Uтг (напряжения, вырабатываемого тахогенератором). При
правильном выборе знака обратной связи скорость вращения будет меняться
значительно меньше, чем при отсутствии обратной связи. Покажем, что в системе
будет установившаяся ошибка. При изменении момента нагрузки Мн
изменится и момент двигателя, потому что в установившемся режиме Mдв = Мн.
Mдв меняется при изменении ω или Uдвиг., но Uдвиг. (Uд) при постоянном U может измениться
лишь при изменении Uтг, т.е. Uд = U— Uтг. Поэтому при изменении Мн обязательно
меняется ω, т.е. появляется ошибка.
6.3 Оценка динамических
свойств САУ по переходной характеристике
1) Качество оценивается по перерегулированию
σ %= (ym-yуст.)/ yуст.·100%
.
σ %= |10-50|%.

переходного процесса от момента подачи скачка до момента tп, начиная с
которого для всех t ≥ tп: |y(t)- yуст. | ≤ Δyуст., Δyуст.=1-5%.
6.4 Корневые оценки
динамических свойств САУ
О динамических свойствах САУ можно судить по
расположению полюсов и нулей замкнутой системы управления.
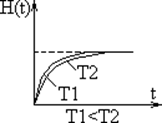
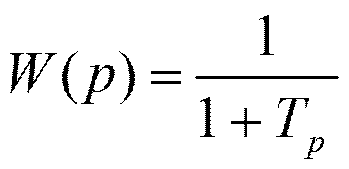
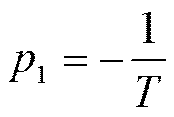
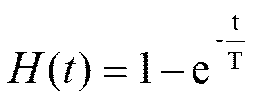
Чем меньше Т, тем быстрее растёт сигнал на выходе.
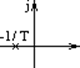
быстродействие уменьшается.
2-й вариант: два комплексно сопряжённых полюса.
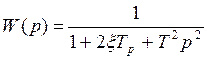
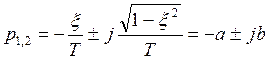
Можно показать, что. Перерегулирование зависит от
параметра 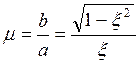
этот параметр называется колебательностью. При равном удалении полюсов
от мнимой оси σ % больше в той системе, в которой полюсы дальше отстоят от
вещественной оси. Увеличение μ приводит к возрастанию перерегулирования, чтобы
колебательность системы не превышала заданной величины, полюса должны быть
расположены внутри области, в которой tgφ=μ.

(корень числителя) – это эквивалентно действию дифференцирующего звена и
колебательность возрастает с приближением нуля к мнимой оси. Добавление
вещественного полюса уменьшает перерегулирование и увеличивает время
переходного процесса. Если имеется несколько полюсов и нулей, но они достаточно
удалены от мнимой оси, то их влиянием можно пренебречь.
Улучшение качества
правления
Способы уменьшения ошибки
Общими методами уменьшения ошибки
(повышения точности) САР являются:
1.
Увеличение
коэффициента усиления K
разомкнутой цепи
2.
Повышение порядка
астатизма r
3.
Применение
регулирования по производным
4.
Включение
масштабирующих устройств на входе или выходе
6.5.1.1 Повышение
точности систем увеличением коэффициента усиления
Метод эффективен, широко применяется, но обычно
увеличение K приводит к
уменьшению запаса устойчивости
Повышение точности
систем увеличением порядка астатизма
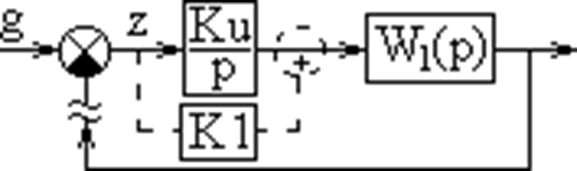
Астатическими называются системы, переходная функция которых в
разомкнутом виде имеет вид: 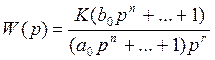
называется порядком астатизма.
В астатической системе обязательно имеются
интегрирующие звенья.
Кu/p– интегрирующее звено.
Рассмотрим установившееся состояние системы при g=g0, f1=f10, f2=f20. После
окончания переходного процесса y=yуст. Это может быть только если Х2=0,
иначе интегратор вырабатывал бы возрастающий сигнал Х3. Х2=К1Хуст.+
f10=0. Найдём отсюда Хуст.=- f10/ К1.
В выражение не входит f2 и К2.
Ошибка астатической системы в режиме неподвижного состояния зависит лишь от
возмущающего воздействия, приложенного до интегрирующего звена. Поэтому
надо создавать системы в которых возмущение приложено после интегрирующего
звена, тогда ошибка равна нулю.
 |
Статическую систему ,не имеющую интегрирующих звеньев,
будем называть
Похожие материалы
- Компенсация инерционности САУ. Методы повышения качества САУ с помощью программы МВТУ
- Самонастраивающиеся САУ. Виды самонастраивающихся САУ. Самонастраивающиеся системы с моделью
- Устойчивость линейных САУ. Основные понятия устойчивости. Решение линейного дифференциального уравнения для переходного процесса
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
3.1.
Дайте характеристику принципам построения
современных систем автоматики: структурные
схемы, достоинства и недостатки принципов
управления, примеры применения на судах
Классификация САУ. Принципы автоматического
управления
Теория автоматического управления
(ТАУ) — это наука о принципах построения
и методах расчётов систем автоматического
управления (САУ). САУ в самом общем виде
имеют следующую обобщенную структурную
схему:
Задатчиком (ЗД)задается желаемый
закон изменения сигналаxж
. Все остальные элементы САУ должны
работать так, что бы фактический сигналхф, который пропорционален
выходному сигналуyобъекта
управления(ОУ)повторял закон
изменения входного сигналаxжс заданными показателями качества,
такими какошибка, время регулированияи т.д.
Чувствительный элемент (ЧЭ)преобразует
выходной сигналy объекта управления
к видухф, в котором
представлен сигналxж,
например, при электрическом сигналехжсигналхфтакже электрический.
Элемент сравнения (ЭС) служит для
формирования сигнала ошибки регулированияε, равного разности желаемогохжи фактическогохфзначений
сигналов САУ.
Регулятор (Рег)— ключевой элемент
САУ, который выполняет такие преобразования
сигнала, при которых обеспечиваются
требуемые показатели качества
регулирования.
В САУ также обычно используются:
усилитель мощности (УМ), исполнительный
механизм (ИМ), и регулирующий орган (РО),предназначенные для того, чтобы
преобразовывать маломощный сигнал
регулятора в мощный сигнал, действующий
наОУ.
Классификация САУ
Системы автоматического управления
(САУ) достаточно разнообразны, однако
они поддаются четкой классификации по
следующим признакам:
1. По виду уравнений статики и динамики,
описывающих процессы управления:
линейные и нелинейные.
2. По закону изменения входного сигнала
x:
— системы автоматической стабилизации(x=const);примеры: САР частоты вращения
дизеля; система автоматической
стабилизации напряжения судовой сети
САУ курсом судна в режиме «Автомат»;
— системы программного управления(закон измененияxзаранее известен);
пример: САР стерилизации консервов в
автоклаве;
— следящие системы(xизменяется
по произвольному закону); пример: САУ
курсом судна в режиме «Следящий».
3. По виду используемого регулятора:
— линейные, нелинейные, импульсные и
цифровые САУ.
4. По общему алгоритму функционирования:
— обычные САУ; оптимальные и адаптивные
САУ.
Принципы автоматического управления
О
понятиями САУ являются:
— структурная схема САУ и динамические
характеристики звеньев САУ;
— состав и характеристики входных
сигналов, которые подразделяются на
сигналы управления и сигналы возмущения;
— совокупность показателей качества
регулирования выходного сигнала.
Все
многообразие САУ может быть сведено к
3-м элементарным схемам управления,
называемыми также принципами управления:
прямое управление, управление по
возмущению, управление по отклонению.
САУ с прямым управлением содержит ОУ(на рис.В.2 под объектом управления
понимается совокупностьУМ+ИМ+РО+ОУ+ЧЭиз элементов рис.В.1) и регулятор. НаОУиРегдействуют возмущающие сигналыg1,…,g6,
изменяющие произвольным образом и
которые ведут к непредсказуемым
изменениям их выходных сигналовииу. За выходным сигналомyследит
человек-оператор, который вручную
изменяет сигналxтак, чтобы достичь
заданных значений сигналаy. Сигналы
возмущенияg1..g6
человеком не контролируются.
Данная САУ называется также САУ
разомкнутого типа, чем подчеркивается
то обстоятельство, что выходной сигналуне используется техническими
средствами автоматизацииУМ, ИМ, РО,
ОУ, ЧЭ и Регв формировании сигнала
заданиях и управления объектом.
Достоинства: Предельная простота
регулятора.
Недостатки:1. Обязательное присутствие
человека- оператора, который является
наиболее ненадежным звеном САУ.
2. Малая точность регулирования, особенно
в динамике, когда сигналы х,g1,
…, g6 быстро изменяются.
3. Невысокое быстродействие, обусловленное
медленной реакцией человека на изменения
сигнала у.
Пример: Электропривод якорно-швартового
устройства. Оператор с помощью
соответствующих органов управления
задаёт одну из фиксированных скоростей
вращения двигателя. Сигналами возмущенияg1..g6 являются:
натяжение якорной цепи, напряжение
питания электродвигателя, температура
обмоток двигателя и др.
1.2.2. Принцип управления по возмущению (рис.В.3)
В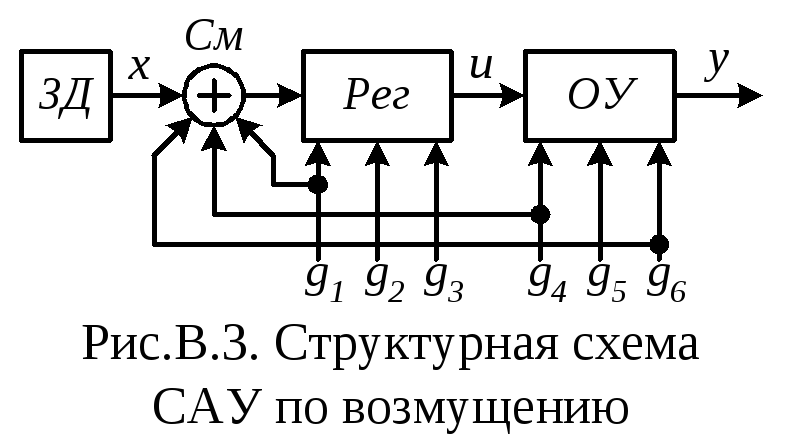
напримерg1, g4
иg6 , которые можно
измерить и преобразовать в электрический
сигнал (принимаем регулятор электрическим),
заводятся на вход регулятора через
сумматорСм.Это приводит к такому
изменению выходного сигнала регулятораu, при котором компенсируется действие
на систему измеренных сигналов возмущения.
Достоинства:1. Наивысшее быстродействие
в сравнении быстродействием с другими
типов САУ.
2. Выше точность регулирования в сравнении
с прямым управлением.
3. Выше надежность регулирования, так
как человек не участвует непосредственно
в управлении объектом.
Недостатки:1. Сложность выделения
всех возмущений, действующих на элементы
САУ.
2. Сложность их классификации на основные
и второстепенные.
3. Сложность измерения и преобразования
сигналов возмущения в электрический
сигнал. Например, чрезвычайно сложной
на практике является задача измерения
механического момента в валах вращающихся
механизмов.
П
токового компаундирования). Регулируемый
сигнал – напряжение на выводах генератора.
Возмущающий сигнал – ток нагрузки
генератора, который измеряется просто
трансформатором тока.
1.2.3. Принцип управления по отклонению (рис.В.4)
Вводится цепь отрицательной обратной
связи ООСи элемент сравненияЭС,
на котором вычитаются заданное значениеxи фактическое значениеyрегулируемого сигнала. ВЭС
формируется ошибка регулирования.
РегуляторРегвырабатывает такой
сигналu, который уменьшает ошибку
регулирования.
Достоинства:1. Нет необходимости в
выяснении того, какие сигналы возмущения
действуют на САУ, и, следовательно, не
нужно их измерять.
2. Самая высокая точность регулирования
в сравнении с другими схемами САУ.
Недостатки: Меньше в сравнении с
управлением по возмущению быстродействие,
т.к. регулирующий сигналuначинает
изменяться не в момент появления
возмущений, а только после измененияy.
Примеры:
1. Авторулевой, удерживающий судно на
заданном курсе с требуемой точностью
в условиях волнения моря и других
возмущающих сигналах.
2 .Электропривод траловой лебедки,
обеспечивающий требуемые усилия и
скорость выборки трала в условиях
переменной нагрузки на ваерах, волнения
моря, действия течений.
3. Холодильная автоматика, обеспечивающая
поддержание заданной температуры в
камерах в условиях изменяющегося притока
тепла.
Достоинства схемы управления по
отклонению настолько велики, что САУ в
подавляющем числе случаев выполняются
работающими именно по этой схеме.
На практике применяют также комбинированные
САУ, сочетающие регулирование как по
возмущению (рис.В.3), так и по отклонению
(рис.В.4), которые обладают достоинствами
обоих типов САУ.
3.2. Какие прямые и косвенные
показатели качества процесса управления
определяются по временным и частотным
характеристикам и каким образом ?
Требования согласно Регистра флота по
показателям качества для судовых систем
автоматического управления. За счет
настройки каких параметров в авторулевых
можно изменить показатели качества при
изменении загрузки судна ?
Прямые показатели качества подразделяются
на показатели качества динамического
и установившегося режимов.
П
качества динамических режимов определяются
из графика переходного процесса и
основными из них являются (рис.1.42):
— перерегулирование или заброс σ,
равный максимуму отклонения значения
переходного процесса относительно
установившегося значения процессаhycm;
— время первой установки t1,
определяемое моментом первого пересечения
графиком переходного процесса
установившегося значенияhycm;
— время переходного процесса tПП,
определяемое момент окончательного
входа графика переходного процесса в
зону допуска, равную±5%от
установившегося значения процессаhycm.
Для всех названных динамических
показателей качества невозможно в общем
случае получить формулы для их расчета.
Это является существенным препятствием
для решения задач анализа и синтеза
САУ.
Показателями качества установившихся
режимов являются ошибки регулирования,
равные абсолютной величине разности
между заданным и фактическим значениями
сигналов САУ и которые в зависимости
от вида входного сигнала САУ подразделяются
на статические (εСТ) и
скоростные ошибки (εСК) и
ошибки (εm)
при отработке гармонического входного
сигнала.
Д
всех названных ошибок регулирования
можно в общем случае получить формулы
их расчета.
Из структурной схемы замкнутой САУ
(рис.1.43) следуют выражения передаточной
функции САУ Wε(p)по ошибке и изображенияε(р)ошибки
регулирования:
Расчет ошибки εmотработки гармонического входного
сигналаx=Xmsinωt
производится по формуле
где
— модуль комплексного числа
.
Статическая (εСТ) и
скоростная (εСК) ошибки
равны установившимся значениям оригиналаи
,
или в общем виде, по формуле.
Значениевычисляют через изображениеε(р)
по доказываемой в теории операционного
исчисления формуле предельного перехода,
(1.54)
Выражение передаточной функции
разомкнутой САУ в общем случае может
быть приведено к виду:

где К– общий коэффициент усиления
разомкнутой САУ:
ν— порядок астатизма САУ, причемνявляется целым неотрицательным
числом.
Для удобства вычислений по формуле
(1.54) подставим в нее выражение WРАЗ(р)из (1.55) и выполним предельный переход:

Статическая ошибка регулирования εСТрассчитывается при постоянном входном
сигналеx(t)=X=const,
а скоростнаяεСК— при
входном сигналеx=Vt,
изменяющемуся во времени с постоянной
скоростьюV=const.
Далее расчеты статической (εСТ)
и скоростной (εСК) ошибок
выполним раздельно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главная
»
Самолетостроение
»
Основы теории управления
»
Основные понятия и общие принципы построения автоматических систем. Дать определения и пояснить термины система автоматического управления (САУ), разомкнутые и замнкнутые САУ, сигнал ошибки (рассогласования).
Основные понятия и общие принципы построения автоматических систем. Дать определения и пояснить термины система автоматического управления (САУ), разомкнутые и замнкнутые САУ, сигнал ошибки (рассогласования).
Теория автоматического управления— это дисциплина, изучающая процессы автоматического управления объектами разной физической природы. При этом при помощи математических средств выявляются свойства систем автоматического управления и разрабатываются рекомендации по их проектированию.
Основные понятия:
-Автоматика
-Управление
-Цель
-Объекты:
-Система автоматического управления.
-Устройство
-Объект управления
-Регулирование
-Регулятор
-Задающее воздействие g(t)
-Ошибка регулирования ε(t) = g(t) — y(t),
-Возмущающее воздействие f(t)
САУ- система состоящая из объекта управления и устройства управления, в которой автоматически выполняется заданный процесс.
Разомкнутые САУ
Сущность принципа разомкнутого управления заключается в жестко заданной программе управления. То есть управление осуществляется «вслепую», без контроля результата, основываясь лишь на заложенной в САУ модели управляемого объекта. Примеры таких систем : таймер, блок управления светофора, автоматическая система полива газона, автоматическая стиральная машина и т. п.
В свою очередь различают:
Разомкнутые по задающему воздействию
Разомкнутые по возмущающему воздействию
Замкнутые САУ
В замкнутых системах автоматического регулирования управляющее воздействие формируется в непосредственной зависимости от управляемой величины. Связь входа системы с его выходом называется обратной связью. Сигнал обратной связи вычитается из задающего воздействия. Такая обратная связь называется отрицательной.
Сигнал ошибки ε(t) = g(t) — y(t), разность между требуемым значением регулируемой величины и текущим её значением. Если ε(t) отлична от нуля, то этот сигнал поступает на вход регулятора, который формирует такое регулирующее воздействие, чтобы в итоге с течением времени ε(t) = 0.
2. Классификация динамических звеньев САУ. Обыкновенные и типовые динамические звенья (ДТЗ) САУ.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
1. Точность САУ
2. План
1 Общие положения
2 Понятие о типовых режимах САУ
3 Теорема о предельном значении оригинала и
методика определения установившихся
ошибок
4 Ошибки статических и астатических САУ в
типовых режимах
5 Ошибки САУ при произвольных входных
сигналах (коэффициенты ошибок)
6 Методы повышения точности САУ
3. 1 Общие положения
Точность является важнейшим критерием
качества систем. В настоящее время
практически все многочисленные
элементы любых технических систем
изготавливаются автоматически т.е. с
помощью САУ. Таким образом точность
САУ определяет качество продукции,
товаров, их надежность,
энергопотребление, долговечность и т.д.
и т.п.
4. 2 Понятие о типовых режимах САУ
Точность САУ принято оценивать по величине
ошибок в типовых режимах. Типовыми
называются режимы просто описываемые
математически и имеющие четкий
физический смысл. К ним относятся:
— режим покоя, когда х(t)=const;
— режим линейно-нарастающих сигналов, когда
х(t)=a*t, где а=const;
— режим гармонических входных сигналов,
когда х(t)=A*sinωt.
5.
ε
Итак, нам необходимо вычислить
установившуюся ошибку ε(t) при t→∞,
при типовых режимах и по ней можно
будет судить о точности САУ.
6. 3 Теорема о предельном значении оригинала и методика определения установившихся ошибок
Сформулируем для этого теорему о
предельном значении оригинала:
limX(t)=limX(s),
t→ ∞
s→ 0
т.е. предел оригинала при t→∞ равен
пределу изображения по Лапласу при
s→0.
7.
Передаточная функция САУ по ошибке:
( s)
1
F (s)
x( s ) 1 w p ( s )
Итак, чтобы определить установившуюся (при t→ ∞)
ошибку САУ нужно:
— Найти x(s) зная x(t)
— Определить Fε(s)
— Найти ε(s)= X(s) * Fε (s)
— Определить εуст= lim ε(s)
S→0
8. 4 Ошибки статических и астатических САУ в типовых режимах
Рассмотрим ошибки САУ в типовых режимах:
1. Ошибка САУ в покое (статическая ошибка)
X(t)=X0=const X(s)=X0
K
Пусть W p ( s )
— статическая
(T1S 1)(T2 S 1)
САУ, поскольку в знаменателе нет
множителя S, т.е. интегрирующего элемента
в системе
9.
По теореме о предельном значении аргумента
1
ст lim (t ) lim (s) (s) * F (s) (s) *
t
s 0
1 Wp ( s)
Подставляя Wp(s) в (1) получим:
X 0 (T1S 1)(T2 S 1)
X0
ст lim
s 0 (T S 1)(T S 1) K
1 K
1
2
(1)
10.
Статическая ошибка в
статической САУ в
(1+К) раз меньше
входной величины.
y(t)
X0
εст
t
11.
Пусть теперь
— астатическая САУ (есть
интегратор, т.е.
множитель S в знаменателе передаточной
функции)
K
W p ( s)
S (T1S 1)
ст
X 0 *1
X 0 S (TS 1)
lim (s) lim
lim
0
s 0
s 0 1 W ( s )
s 0 K S (TS 1)
p
12.
Таким образом,
статическая ошибка
в астатической САУ
равна 0
y(t)
X0
εст=0
t
13.
2. Второй типовой режим — движение с постоянной
скоростью (скоростная ошибка)
x(t)=at
a=cost
x( s)
a
s
Пусть:
K
W p ( s)
— статическая САУ
(T1S 1)(T2 S 1)
Тогда:
a (T1S 1)(T2 S 1)
(
t
)
lim
t a s 0 s K (T1S 1)(T2 S 1)
14.
x(t)=at
εα→∞
y(t)
α
t
tgα=a
Ошибка в статической
САУ при линейнонарастающем входном
сигнале x(t)=at
возрастает до ∞.
Т.о. статические САУ в
таком режиме не
работоспособны.
15.
Пусть теперь
K
Wp ( s)
S (TS 1)
— астатическая САУ
Тогда
S ( ST 1)
a
a
*
t a ( t ) lims 0(s) lim
s 0 s
K S (TS 1) K
16.
a
a
K
x(t)
y(t)
t
Т.о. в астатических
САУ при x(t)=at
a=const
устанавливается
ошибка в “К” раз
меньше чем “a”, т.е.
они работоспособны
в таких режимах.
17. 3. Третий режим — гармонических входных сигналов.
Пусть x(t)=xmsinωkt
xm,ωk – амплитуда и
частота “качки”.
x(s)
ε(s)
Wp(S)
y(s)
18. Определим амплитуду εm ошибки САУ в этом режиме.
Для этого найдем:
1
( s)
F ( s)
1 W p ( s ) x( s )
— ПФ САУ по ошибке
Подставим S=jωk
X ( j k )
( j k )
1 Wp ( j k )
(1)
19. Выражение (1) справедливо и для амплитуд, т.е.
m
xm
Xm
1 W p ( j k ) W p ( j k )
Откуда следует:
W p ( j k )
Ак
20 lg
xm
xm
(2)
m
Прологарифмируем (2):
L(ω)
m
ω
ω=ωk
Ак – контрольная точка
20 lg W p ( j k ) 20 lg
xm
m
(3)
20.
Из (3) следует, что САУ будет иметь амплитуду
ошибки не более допустимой εдоп, если
20 lg W p ( j k ) L( k ) 20 lg
xm
доп
21. Т.о. чтобы ошибка САУ в гармоническом режиме не превышала допустимой εдоп необходимо:
1. Определить положение контрольной точки
Ак с координатами:
xm
ω=ωк и 20 lg
доп
2. Обеспечить прохождение L(ω) выше
контрольной точки Ак
22. 5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок)
Пусть на вход САУ действует сигнал x(t)
произвольной формы. Чтобы определить
ошибку ε(t) в этом случае найдем вначале ее
изображение.
x(s)
ε(s)
Wp(S)
y(s)
23.
( s)
Поскольку:
1
F ( s)
x( s ) 1 W p ( s )
(1)
То:
x( s )
( s)
1 Wp ( s)
(2)
Разложим далее Fε(s) по возрастающим
степеням S в ряд, тогда (2) можно записать в
виде:
C2 2 C3 3
( s ) C0 C1S S S x( s )
2!
3!
(3)
24.
При нулевых начальных условиях
S p
d
dt
и переходя в (3) к оригиналам можно записать
2
dx(t ) C2 d x(t )
(t ) C0 x(t ) C1 *
*
2
dt 2! dt
Величины С0, С1, С2 … называются
коэффициентами ошибок САУ.
(4)
25. Чтобы определить ошибку САУ при произвольной форме входного сигнала x(t) необходимо:
1. Определить передаточную функцию
САУ по ошибке Fε(s);
2. Разложить в ряд Fε(s) путем деления
ее числителя на знаменатель и найти
коэффициенты С0, С1, С2 …;
3. Подставить коэффициенты ошибок в
(4) и найти установившуюся ошибку
ε(t).
26. Пример
Найти ошибку в САУ при:
Если:
bt 2
x(t ) x0 at
2
K
W p (s)
S (T1S 1)(T2 S 1)
27. Решение:
1.Найдем
1
F (s)
1 Wp ( s)
1
S (T1S 1)(T2 S 1)
T1T2 S 3 (T1 T2 ) S 2 S
F ( s)
1 W p ( s) K S (T1S 1)(T2 S 1) T1T2 S 3 (T1 T2 ) S 2 S K
28. 2. Разложим (1) в степенной ряд путем деления числителя на знаменатель
S (T1 T2 ) S T1T2 S
2
—
—
3
1
1
S S 2 * (T1 T2 ) S 3 …
K
K
1 2
T T 3
T1 T2 S T1T2 1 2 S …
K
K
1 2
T1 T2 S …
K
K S (T1 T2 )S 2 T1T2 S 3
1 2
1 1
S * T1 T2 S
K
K K
29.
Ограничимся первыми тремя членами
ряда, т.к. входной сигнал X(t) имеет
лишь три не нулевых первых
производных.
30.
3. Итак:
1
1 2
T1T2
F ( s ) S
2 S
K
K
K
(5)
Сопоставляя (5) и (4) имеем коэффициенты
ошибок:
T1T2
1
1
С0=0
C2 2
2 (6)
C1
K
K
K
31.
4. Определим далее производные от X(t):
bt 2
x(t ) x0 at
2
dx(t )
a bt
dt
d 2 x(t )
b
dt
(7)
32.
5. Подставляя коэффициенты С0, С1, С2… и
производные (7) в (4) получим:
1
1
T1T2
(t ) * (a bt )
2 *b
K
K
K
Т.е. ошибка с течением времени будет
нарастать до ∞ из-за члена “bt”.
33. 6 Методы повышения точности САУ
Анализируя выражения для
коэффициентов ошибок отметим, что:
1. Все коэффициенты обратнопропорциональны коэффициенту К –
усиления системы;
2. Чем выше порядок астатизма “v” тем
большее количество первых
коэффициентов ошибок равны 0
34. ВНИМАНИЕ
Порядок астатизма “v” определяется числом
интегрирующих звеньев в контуре системы.
Формально “v” равно показателю степени
множителя S в знаменателе передаточной
функции wp.
N ( s)
wp v
S M ( s)
35. 1. Первый способ повышения точности САУ – увеличение К
Т.о. самым универсальным способом
повышения точности САУ являются
увеличение коэффициента К усиления
системы. При этом все коэффициенты
ошибок уменьшаются, а это означает, что
система во всех режимах работы будет иметь
меньшие ошибки. Однако этот способ
снижает запасы устойчивости системы и рано
или поздно приводит к полной потере
устойчивости. Это можно показать на
примере критерия Найквиста.
36.
Im
K2>K1
К1
К2
-1;j0
wp(jω)
Re
37. 2. Способ повышения точности САУ – путем увеличения астатизма “v”
Этот способ исключает первые коэффициенты в
ряду ошибок. Действительно:
v=0 (статическая САУ)
Все коэффициенты не
равны 0, т.е. с0≠0 с1≠0
с2≠0 …, т.е. статическая
система в любых
режимах работы, в т.ч. и
в покое будет иметь
ошибки
38.
v=1 (астатическая САУ
с астатизмом
первого порядка)
с0=0 с1≠0 с2≠0 …, т.е.
такая система не
будет иметь ошибки
в режиме покоя.
v=2 (астатическая САУ
с астатизмом
второго порядка)
с0=0 с1=0 с2≠0 с3≠0 …,
такая система не
будет иметь ошибок
не только в режиме
покоя, но и при
линейнонарастающем
сигнале
39.
К сожалению, этот способ также снижает
запасы устойчивости САУ. Действительно:
Im
v=2
Re
-1;j0
v=0
v=1
По критерию Найквиста системы при v=0, v=1
могут быть как устойчивыми так и не
устойчивыми, но при v=2 они становятся не
устойчивыми при любых коэффициентах К.
40. 3. Повышение точности САУ с использованием принципов комбинированного управления.
Принцип комбинированного управления
состоит в том, что в дополнение к принципу
обратной связи реализуется принцип
управления по возмущению. V(t)
Измеритель
x(t)
y(t)
Регулятор
Объект
41.
Здесь сочетается (комбинируются) оба
названных принципа:
— Управление по возмущению (за счет
измерения возмущения v(t) и выработки
дополнительного управляющего сигнала
компенсирующего действия возмущения);
— Управление по отклонению или принцип
обратной связи реализуется за счет главной
отрицательной обратной связи и сигнала
рассогласования и регулятора.
42.
Рассмотрим следящую систему с
комбинированным управлением и найдем
передаточную функцию обычной системы
эквивалентной по точности.
W3(S)
y(s)
x(s)
W1(s)
W2(S)
≡
Wэ(S)
43.
Для этого приравняем их передаточные функции.
wэ (s)
y(s) w1 (s)w2 (s)
w2 (s)
F (s)
w3 (s)
x(s) 1 w1 (s)w2 (s)
1 w1 (s)w2 (s) 1 wэ (s)
(1)
44.
Из (1) после некоторых преобразований можно
получить:
w1 ( s) w3 ( s)
wэ ( s) w2 ( s) *
1 w3 ( s) w2 ( s)
(2)
Как видно из последнего выражения, при:
1
w3 ( s )
w2 ( s )
wэ(s)=∞
Условие (3) называется условием полной
инвариантности.
(3)
45.
Это означает, что ошибка рассматриваемой
комбинированной следящей системы будет
равна 0 в любых режимах работы поскольку:
( s)
1
F ( s )
0
x( s ) 1 wэ ( s )
46.
Достоинство принципа комбинированного
управления в том, что он не изменяет
(не ухудшает) устойчивости и качества
переходных процессов. Однако,
реализовать точно условие полной
инвариантности практически
невозможно.
47. ПРИМЕР
Пусть:
K
w2 ( s)
S (T1S 1)(T2 S 1)
Найдем:
1
S (T1S 1)(T2 S 1) 1
T1 T2 2 T1T2 3
w3 ( s)
S
S
S
w2 ( s)
K
K
K
K
48.
Структурная схема такой комбинированной
следящей системы имеет вид:
III
II
I
T1T2
S3
K
T1 T2 2
S
K
1
S
K
x(s)
w1(s)
K
S (T1S 1)(T2 S 1)
y(s)
49.
Итак, чтобы точно реализовать условие полной
инвариантности в нашем примере необходимо:
• реализовать канал I (тахогенератор)
• реализовать канал II (это 2-ая производная от угла)
• реализовать канал III (это 3-ая производная от угла)
Точно это сделать практически нельзя. Кроме того, в
реальных САУ имеется множество нелинейностей,
которые мы не учитывали при выводе условия
полной инвариантности.
Поэтому часто используют частично-инвариантные
САУ, т.е. САУ не имеющие ошибок лишь в некоторых
режимах.