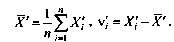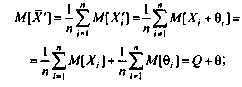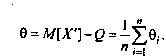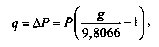Систематическая ошибка отклонения отсутствует

Глава восемнадцатая.

СБОР ДАННЫХ:
РЕАЛЬНЫЕ ПРОЦЕДУРЫ И СИСТЕМАТИЧЕСКИЕ
ОШИБКИ

Одна из основных
проблем, с которой мы сталкиваемся при
маркетинговых исследованиях, — это
проблема сбора данных. На этой стадии
исследования используется персонал,
занятый полевым, телефонным или почтовым
опросом. В этой главе речь будет идти
главным образом о возможных ошибках
при проведении опросов и об их причинах.
Если вы будете осознавать потенциальные
источники ошибок, возникающих при сборе
данных, вы сможете надлежащим образом
оценивать исследовательскую информацию,
на основе которой должны приниматься
те или иные решения.

Влияние
и значение систематических ошибок

ОШИБКА
В ВЫБОРКЕ

Разность
между наблюдаемыми значениями
количественного признака и их долгосрочным
средним значением при повторении
измерений.

СИСТЕМАТИЧЕСКАЯ
ОШИБКА

Ошибка
исследования, не связанная с выборкой;
может быть вызвана концептуальными или
логическими ошибками, неправильной
интерпретацией ответов, а также
статистическими, арифметическими,
табуляционными, кодовыми или отчетными
ошибками.

Ошибки, возникающие
при обследовании, можно разделить на
два основных типа: ошибки
в выборке и
систематические
ошибки.
Концепция
ошибки в выборке
широко использовалась в главах 15, 16 и
17. Основой для ее рассмотрения была
концепция выборочного распределения
некой статистики, например выборочного
среднего, выборочной доли и тому подобное.
Само понятие выборочного распределения
неразрывно связано с понятием ошибки
в выборке. Названное распределение
существует благодаря тому, что различные
выборки, сформированные в соответствии
с принятым планом обследования, дают
разные оценки параметра. Статистика
меняется от выборки к выборке в силу
того, что в каждом случае выборочному
отбору подвергается лишь часть генеральной
совокупности. Соответственно мы можем
определить ошибку в выборке как «разность
между наблюдаемыми значениями
количественное» признака и их долгосрочным
средним значением при повторении
измерений». Как мы видели, ошибка в
выборке может быть уменьшена путем
увеличения объема выборки. Концентрация
распределения выборочной статистики
возле долгосрочного среднего значения
возрастает, а выборочная статистика
выравнивается при увеличении количества
наблюдений.

Систематические
ошибки
являются отражением ошибок иного рода,
которые, вообще говоря, могут возникать
и не при выборочных обследованиях. Они
подразделяются на случайные
и неслучайные.
Неслучайные систематические ошибки
имеют более тяжкие последствия. Случайные
ошибки дают оценки, отличные от истинного
значения; они могут приводить к отклонениям
и в большую, и в меньшую сторону и имеют
при этом случайный характер. Неслучайные
же систематические ошибки приводят к
односторонним отклонениям. Соответственно
для них характерна тенденция к смещению
выборочного значения относительно
параметра совокупности. Систематические
ошибки могут являться следствием
концептуальных или логических ошибок,
неправильной интерпретации ответов, а
также статистических, арифметических,
табуляционных, кодовых или отчетных
ошибок. Они столь вездесущи, что один
из авторов не смог сдержать своих чувств
и написал:

«Перечень
возможных бед и напастей с увеличением
наших познаний только расширяется.
Многолетняя работа в определенной
области позволяет приобрести известный
методологический опыт, который, к
сожалению, практически никогда не
становится доступным другим. Подлинной
уверенности в правильности выработанных
подходов нет и быть не может (выделено
нами)».

Систематические
ошибки не только вездесущи, но они и не
столь подконтрольны, как ошибки в
выборке. При увеличении объема выборки
ошибки в выборке уменьшаются. Сказать
то же самое о систематических ошибках
нельзя. В этом случае они могут как
уменьшаться, так и возрастать. Помимо
прочего, ошибки в выборке при использовании
вероятностных методов могут быть
оценены. В случае же систематических
ошибок, как направление, так, тем более,
и величина ошибки могут оказаться
совершенно непредсказуемыми.

Систематические
ошибки приводят к смещению выборочного
значения относительно параметра
совокупности, но в ряде случаев мы не
можем судить даже о том, к чему именно
они приведут, — к переоценке или к
недооценке параметра. Систематические
ошибки влияют и на достоверность
выборочных оценок. Вызванное ими смещение
может увеличить ошибку оценки определенных
статистик до такой степени, что оценка
доверительного интервала окажется
ошибочной.

Одно из обследований,
призванное оценить уровень накоплений
потребителей, проведенное Иллинойским
университетом, может служить наглядным
свидетельством сказанного. В ходе этого
обследования исследователи сравнивали
полученные от потребителей сведения
об их финансовых средствах и долгах с
известной информацией.

«Опытное
обследование неожиданно показало, что
систематические ошибки существуют не
только в теории, оказалось, что именно
они являются основной причиной замеченной
тенденции к занижению агрегированных
показателей…

Эта ошибка не
просто присутствовала в данных
обследования, в ряде случаев роль
систематических ошибок была столь
велика, что
определение доверительных интервалов
по известным формулам статистики теряло
всяческий смысл… Следует
особо отметить, что
при увеличении объема выборки величина
этой ошибки только возрастала (выделено
нами)».

В некоторых
ситуациях даже самые изощренные выборки
не могут избавить нас от систематических
ошибок.

«Значимость
полученных в ходе этого обследования
данных весьма специфична, они лишний
раз говорят о том, что исследователь
постоянно должен стремиться к выявлению
и устранению систематических ошибок.
Особенно критичными они становятся при
работе с широкомасштабными, хорошо
продуманными вероятностными выборками,
поскольку при увеличении эффективности
проектирования выборки и уменьшении
выборочной дисперсии, эффект систематических
ошибок усиливается. Поскольку
систематические отклонения практически
не зависят от объема выборки, мы
сталкиваемся с парадоксальной ситуацией:
чем эффективнее составлена выборка,
тем большую роль играют систематические
ошибки и тем меньшим смыслом обладают
вычисления по определению доверительного
интервала, в основе которых лежат обычные
формулы».

В случае обследования,
проведенного Иллинойским университетом,
мы могли определить систематическую
ошибку, поскольку в распоряжении
исследователей находились не только
результаты опроса, но и реальные данные,
отражающие финансовое положение
потребителей. Предположим, что мы не
обладаем подобными данными. Исследователи
смогут предположить, что полученные
ими ответы не совсем точны, но как они
смогут определить хотя бы направление
вызванного такими ошибками смещения?
То ли респонденты сознательно завышали
уровень своих сбережений, желая впечатлить
интервьюера, то ли занижали их, боясь,
что реальные цифры могут вызвать
повышенный интерес у сотрудников
Налогового управления. Предположим,
что сам факт неточности приведенных
сведений не вызывает у нас сомнений.
Возникает еще один вопрос: какова
величина этой «неточности»? Завышение
реальной суммы на 10000 долларов или ее
занижение на 2000? Или наоборот?

Как вы, вероятно,
уже начинаете осознавать, зачастую
проблема систематических ошибок
оказывается

центральной. Два
типа систематических ошибок, отсутствие
ответов одних и некорректные ответы
других участников обследования, могут
обратить результаты обследования
буквально в ничто. Наглядной иллюстрацией
этого является исследовательское окно
18.1. В результате специальных исследований,
проведенных Бюро переписей, выяснилось,
что такие систематические ошибки могут
в десять раз превышать ошибку выборки.
В этом результате нет ничего неожиданного.
Помимо прочего, оказалось, что
систематическая ошибка составляет
большую часть ошибки обследования, в
то время как случайная ошибка выборки
сведена к минимуму. Систематические
ошибки могут быть уменьшены, но уменьшение
их связано не столько с увеличением
объема выборки, сколько с использованием
специальных методов. Для того чтобы
исследователь имел такую возможность,
ему необходимо прежде всего осознавать
их причины.

ОШИБКА
НЕНАБЛЮДЕНИЯ

Систематическая
ошибка, возникающая вследствие неполучения
данных от ряда элементов, входящих в
обследуемую выборку.

Типы систематических ошибок

На рис. 18.1 представлены
основные типы систематических ошибок.
Они делятся на два основных типа:

ошибки, связанные
с неполучением данных, и ошибки наблюдения.
Ошибки ненаблюдения
возникают вследствие невозможности
получения данных от части элементов
обследуемой совокупности. Ошибки
ненаблюдения могут быть вызваны тем,
что часть обследуемой совокупности не
была представлена в выборке, или же
элементы, отобранные для включения в
выборку, не представили данных.
Ошибки наблюдений
возникают вследствие некорректной
информации, полученной от элементов
выборки, они могут возникнуть и на стадии
обработки данных или формулирования
итогового вывода. По ряду характеристик
они представляются еще более неприятными,
чем ошибки ненаблюдения. В случае
последних мы по крайней мере знаем, что
ошибки этого вида обусловлены неполным
охватом или неполучением данных. О
существовании же ошибок наблюдения мы
даже и не подозреваем. Само понятие
ошибки наблюдения основывается на
предположении о том, что для количественного
признака или признаков существует некое
«истинное» значение. Соответственно
ошибка наблюдения является разностью
объявленного и «истинного» значения.
Вы уже понимаете, что определение Ошибки
наблюдения ставит исследователя в
ужасно неудобное положение, поскольку
при этом он задается той самой величиной,
определение которой является целью
обследования.

ОШИБКА
НАБЛЮДЕНИЯ

Систематическая
ошибка, либо возникающая при обработке
данных или формулировании заключений,
либо являющаяся следствием некорректности
информации, получаемой от элементов
выборки.

ОШИБКИ НЕНАБЛЮДЕНИЯ

Как вы видите на
рис. 18.1, существуют два типа ошибок
ненаблюдения: ошибки неохвата и ошибки
неполучения данных. Любая из этих ошибок
может привести к существенным неточностям,
однако аналитик, знакомый с сутью
проблемы, может существенно уменьшить
возможную ошибку.

ОШИБКА
НЕОХВАТА

Систематическая
ошибка, являющаяся следствием того, что
определенные части или целые блоки
генеральной совокупности не были
включены в основу выборки.

Ошибки неохвата.
Неохват может стать источником серьезных
неточностей, при этом
ошибка неохвата относится
только к ошибочно выпавшим из рассмотрения
частям совокупности, но никак не к
частям, исключенным намеренно. Таким
образом, проблема неохвата имеет
отношение к основе выборки.

Например, при общем
обследовании ошибка неохвата может
возникнуть при использовании телефонного
справочника в качестве основы выборки.
Телефоны есть далеко не у всех семей, и
не все номера телефонов включены в
справочник. Помимо прочего, существует
целый ряд демографических отличий между
лицами, имеющими телефоны и не имеющими
их.

При почтовом
опросе, где основой выборки служит
рассылочная ведомость, ошибка неохвата
может быть следствием того, что рассылочная
ведомость не дает адекватного представления
о различных группах популяции. Опытные
исследователи знают, сколь редко подобные
ведомости бывают удачными, пусть даже
речь идет о весьма специфичных группах
населения (смотри табл. 18.1).

В тех случаях,
когда данные должны собираться методом
обхода квартир, респондентов сводят в
своеобразную территориальную выборку.
В этом случае основой выборки становится
скорее не список респондентов, а
определенные районы, кварталы или дома.
Тем не менее это не снимает проблемы
неполноты основы выборки. Городские
карты могут устареть, вследствие чего
районы новой застройки полностью выпадут
из рассмотрения. Помимо прочего,
инструкции, данные интервьюерам, могут
оказаться недостаточно детальными.
Указание «начните обследование с
северо-западной оконечности означенного
района, избрав начальный пункт случайным
образом и подвергая обследованию каждый
пятый жилой дом» может оказаться
неполным, если в этом районе существуют
многоквартирные дома. Практика показывает,
что при проведении обследования
интервьюеры предпочитают обходить
стороной ветхие или запущенные строения.
Вместе с тем интервьюеры предпочитают
общаться с максимально доступными
членами семей, что противоречит положению
инструкции о случайном характере опроса.
Все это приводит к недостаточному
представлению определенной части
популяции при одновременном избыточном
представлении другой, наиболее доступной
ее части.

Проблемы с основой
выборки существуют и при проведении
опросов в торговых центрах. С одной
стороны, здесь отсутствует список
элементов совокупности. С другой стороны,
попасть в число обследуемых могут только
те люди, которые привыкли совершать
здесь покупки, при этом чем чаще они это
делают, тем выше вероятность того, что
они станут респондентами. Именно по
этой причине при обследованиях такого
рода часто используются пропорциональные
выборки.

Тем не менее
использование пропорциональных выборок
не снимает проблем, связанных с ошибками
неохвата. Свобода же выбора респондентов
интервьюером буквально распахивает
двери для таких ошибок. «Недобор»
характерен как для лиц с самыми низкими,
так и для лиц с самыми высокими доходами.
Руководитель проекта может не осознавать
этого, поскольку исполнители зачастую
склонны к фальсификации результатов,
позволяющей скрыть это обстоятельство.
Чем более сложной и развитой будет такая
пропорциональная выборка, тем более
критичным становится названный момент.
Если некоторые элементы выборки будут
задаваться набором, состоящим из трех
или четырех признаков, интервьюер,
испытывающий в этой связи определенные
затруднения, может «немного слукавить»,
приписав требуемые характеристики тем,
кто ими не обладает.

Ошибка перебора
может возникать вследствие возникновения
повторов в сводке элементов выборки.
Единицы с множественными входами в
основу выборки, например семьи, имеющие
несколько телефонных номеров, имеют
более высокую вероятность включения в
выборку, чем единицы, соответствующие
только одной позиции списка. Впрочем,
для большинства обследований ошибки
неохвата представляют куда большую
опасность.

ОШИБКА
ПЕРЕБОРА

Систематическая
ошибка, возникающая вследствие повтора
позиций в сводке элементов выборки.

Ошибка неохвата
представляет проблему далеко не для
любого обследования. В ряде случаев
исследователь имеет в своем распоряжении
четкую, ясную и полную основу выборки.
Скажем, если администрация универмага
решит провести обследование покупателей,
приобретающих товары в кредит, проблем
с определением основы выборки у нее не
будет. Основа выборки, очевидно, будет
совпадать со списком таких кредитов по
открытым счетам. Возможны разве что
какие-то затруднения при распознавании
активных и неактивных счетов, но указанная
проблема может быть разрешена уже на
подготовительном этапе обследования.

—

Таблица
18.1

Количество		Цена (долл.)	Количество		Цена (долл.)
12900	Розничная продажа детской одежды	45/1000	135	Книжные клубы	85
800	Торговля баранками	85	6300	Издательства	45/1000
30200	Розничная продажа хлеба	45/1000	1725	Издательства (крупнейшие)	45/1000
2400	Хлебопеки	45/1000	850	Оптовые торговцы книгами	85
600	Балетные труппы	85	24000	Бухгалтерский учет	45/1000
2450	Владельцы воздушных шаров	45/1000	20100	Книжные магазины	45/1000
10500	Руководители оркестров	45/1000	588	Книжные магазины, сети	85
16100	Ипотеки, руководство	45/1000	3100	Книжные магазины, учебная литература	45/1000
4100	Ипотеки, фирмы	45/1000	3300	Книжные магазины, религ. литература	45/1000
13790	Банки главные офисы	45/1000	132	Ботанические сады	85
324	Банки с капиталом свыше 1 млрд.	85	2700	Ботаники	45/1000
538	Банки с капиталом свыше 500 млн.	85	2600	Розлив безалк. напитков	45/1000
1278	Банки с капиталом свыше 200 млн.	85	4600	Магазины женской одежды	45/1000
3582	Банки с капиталом свыше 75 млн.	45/1000	7500	Кегельбаны	45/1000
8835	Банки с капиталом свыше 25 млн.	45/1000	6000	Производство тары	45/1000
12400	Банки с капиталом свыше 10 млн.	45/1000	530	Советы бой-скаутов	85
13245	Банки с капиталом свыше 5 млн.	45/1000	2400	Производство хлебопекарной продукции	45/1000
200	Банки с капиталом менее 5 млн.	85	14500	Каменщики	45/1000
40100	Отделения банков	45/1000	8290	Магазины для новобрачных	45/1000
20000	Банковские кассиры	45/1000	30100	Работники радиовещания	45/1000
209600	Банковские служащие	45/1000	4798	Радиостанции СВ-диапазона	45/1000
66700	Банковские служащие, женщины	45/1000	4428	Радиостанции FM-диапазон	45/1000
3490	Сбербанки, кредитование	45/1000	1050	Телевизионные станции	85
16800	Сбербанки, кредитование, филиалы	45/1000	211000	Брокеры и агенты, страхование	45/1000
6000	Работники траст-отдела банков	45/1000	207200	Брокеры и агенты, страхование (офисы)	45/1000
11030	Работники отдела кредитования	45/1000	3600	Брокеры (бизнес)	45/1000
243	Судьи по делам о несостоятельности	85	300000	Брокеры и агенты недв., инд.	45/1000
8400	Поставщики продукции для салонов красоты	45/1000	170000	Брокеры и агенты недв. (офисы)	45/1000
64200	Парикмахерские	45/1000	47000	Брокеры, ценные бумаги, оф. представ.	45/1000
81900	Бары, закусочные	45/1000	28400	Брокеры, ценные бумаги, офисы	45/1000
2800	Школы моделей	45/1000	17000	Брокеры, ценные бумаги, оф. представ.	85/1000
200000	Салоны красоты	45/1000	276000	Строительные подрядчики	45/1000
315	Пчеловоды	85	53900	Стройматериалы, дилеры	45/1000
90	Пивовары	85	46600	Стройматериалы, оптовики	45/1000
11900	Поставщики пива	45/1000	31300	Уборка помещений и офисов	45/1000
37000	Ученые-бихевиористы	45/1000	13600	Установка противоуг. систем	45/1000
170	Бюро консультаций в сфере бизнеса	85	19000	Печи (жидкое и тв.), дилеры	45/1000
4000	Розлив и постановка прохлад. напитков	45/1000	9000	Автобусные компании (все)	45/1000
26000	Производство прохлад. напитков	45/1000	5200	Автобусные компании (заказы)	45/1000
11700	Продажа и ремонт велосипедов	45/1000	3550	Автобусные компании (междугор.)	45/1000
2500	Бильярдные и залы для игр в пул	45/1000	4700	Автобусные компании (админ.)	45/1000
1380	Компании Billion Dollar	85	3600	Профессиональные брокеры	45/1000
5700	Биохимики	45/1000	3100	Профессиональные экономисты	45/1000
23700	Биологи	45/1000	2000000	Профессиональные администраторы	договорная
3900	Центры контроля за рождаемостью	45/1000	200000	Проф. администр. (дом. адреса)	договорная
6400000	Семьи афро-американцев	договорная	60000	Проф. адм., макс. окл. (адреса)	50/1000
4600	Банки крови	45/1000	4600	Производство коммер. бланков	45/1000
3000000	Производственные рабочие	договорная	9300	Конторские машины, дилеры	45/1000
5250	Гавани (морские)	45/1000	1000000	Бизнесмены (адреса)	договорная
12350	Торговцы судами	45/1000	2000000	Бизнесмены (мелкий бизнес)	договорная
21 000	Снабжение судов	45/1000	525	Школы бизнеса (академические)	85
567400	Владельцы судов (тип, длина, мощность)	50/1000	2000	Школы секретарей	45/1000
10000	Верфи, строительство и ремонт судов	45/1000	3700	Торговые организации	45/1000
14000	Отделы образования	45/1000	4530	Публикации на тему торговли	45/1000
67700	Ремонт кузовов автомобилей	45/1000	20400	Мясные лавки	45/1000
5000	Паровое оборудование	45/1000	8900	Мясо, оптовые поставки	45/1000

Подобным же образом
общество взаимного кредита в некой
фирме вряд ли столкнется с ошибкой
неохвата при обследовании потенциальных
клиентов. Здесь целевой совокупностью
будут сотрудники фирмы; список же их,
по всей вероятности, не будет нуждаться
в уточнении, поскольку он лежит в основе
платежной ведомости.

Ошибки неохвата
ставят перед исследователем два вопроса:
(1) насколько они серьезны? (2) каким
образом возможно их уменьшить? Основная
проблема состоит в том, что их величина
может быть оценена только при сравнении
результатов выборочного обследования
с некими независимыми внешними
показателями. Внешний же показатель в
свою очередь может быть либо определен,
посредством дополнительной проверки
качества части результатов, либо получен
в ходе другого надежного обследования,
результаты которого не утратили своей
актуальности, например, последней
переписи населения. Возможность сравнения
результатов с результатами переписи
или обследования выборки большого
объема предполагает общность операционных
определений элементов выборки. Если
исследователь планирует проведение
таких сравнений, он должен учитывать
это обстоятельство при выборе обследуемых
объектов (например, квартир или индивидов).

Предположим, ошибка
неохвата весьма велика. Что должен
делать исследователь для того, чтобы
уменьшить ее влияние? Разумеется, самый
очевидный шаг состоит в улучшении
качества основы выборки. Улучшение это
может заключаться в обновлении карт, в
выборочной проверке качества и
репрезентативности ведомости и т. д.
Проблема отсутствия ряда элементов,
характерная для телефонных обследований,
может решаться путем набора случайных
цифр или дополнительными звонками, хотя
такой способ не дает адекватного
представления о лицах, не имеющих
телефона:

Несовершенная
основа выборки может быть улучшена лишь
до определенного предела. Когда этот
предел будет достигнут, исследователь
может попытаться уменьшить ошибку
неохвата посредством отбора элементов
выборки или уточнением результатов.
Скажем, при формировании выборки по
списку аналитики часто сталкиваются с
тем, что в нем содержатся повторы,
неподходящие элементы и пропуски. Первым
шагом, направленным на исправление
ситуации, должно стать обновление и
уточнение списка, для чего могут
использоваться дополнительные источники.
Впрочем, подобные меры могут привести
разве что к сокращению количества
пропусков, но никак не к выявлению
повторов или неприемлемых элементов.
При отборе элементов выборки неприемлемые
элементы должны исключаться из
рассмотрения. Не поддайтесь искушению
заменить неприемлемый элемент элементом,
следующим в списке за ним, поскольку
использование подобного приема может
оказать серьезное влияние на характер
выборки. Если отбор осуществляется
случайным образом, следует просто-напросто
перейти к следующему отобранному
случайным образом элементу. Если же
отбор производится систематически, при
появлении неприемлемых элементов
следует прежде всего отрегулировать
выборочный интервал.

Проблема повторов
обычно решается методом корректировки.
Обычно результаты получают вес обратный
вероятности попадания элемента в
выборку. При обследовании, базирующемся
на регистрационной ведомости автомобилей,
каждому респонденту будет задан вопрос:
«Сколько у вас машин?» Обладатель двух
машин получит весовой коэффициент 1/2,
обладатель трех машин соответственно
1/2 .

Выбор надлежащих
процедур отбора элементов корректировки
и отстройки, компенсирующей неадекватность
основы выборки, при проведении серьезных
выборочных обследований имеет особую
значимость и во многом определяется
квалификацией исследователя. Мы не
станем вдаваться в детали, отметим лишь
то, что ошибки неохвата:

1) относятся к
разряду систематических ошибок и потому
не входят в стандартные статистические
зависимости;

2) как правило, не
могут быть устранены посредством
увеличения объема выборки;

3) могут иметь
существенный размер;

4) могут быть
уменьшены (но не обязательно устранены)
при осознании их наличия посредством
улучшения основы выборки и принятия
ряда специальных мер, позволяющих до
определенной степени компенсировать
остаточное несовершенство основы.

Ошибки неполучения
данных. Другой возможный источник
систематического отклонения ненаблюдения
— ошибка
неполучения данных.
Она порождается отсутствием информации
о некоторых элементах, которые должны
были войти в состав выборки. Попытка
контакта с выделенным респондентом
может оказаться неудачной, — об этом
никогда нельзя забывать. Например, на
рис. 18.2 представлены различные исходы
предполагаемого телефонного контакта.
Количество этих исходов столь велико,
что даже условная оценка серьезности
проблемы неполучения данных может
оказаться весьма и весьма затруднительной.

ОШИБКА
НЕПОЛУЧЕНИЯ ДАННЫХ

Систематическая
ошибка, порождаемая отсутствием
информации о некоторых элементах,
которые должны были войти в состав
выборки.

ДОЛЯ
ОТВЕТИВШИХ

Отношение
количества проведенных с респондентами
интервью к количеству приемлемых
респондентов в выборке.

В конце семидесятых
несколько исследователей осознали, что
в практике маркетинговых исследова­ний
не существует стандартной процедуры
для определения соотношения полученных
и неполученных ответов. Поскольку
различные исследовательские организации
использовали при определении показателя
неполучения данных разные определения
и методики, эта проблема не получала
точного и однозначного разрешения.
Пытаясь найти выход из этой ситуации,

аналитики провели
исследование, в котором участвовали
представители Совета исследовательских
организации Америки с (CASRO)
и ведущих заказчиков. Каждому участнику
обследования был выслан опросный лист,
на котором были представлены данные
трех реальных телефонных опросов по
контактам и ответам — выборки по
телефонному справочнику, выборки по
методу случайных чисел и списочной
выборки. Респондентов просили определить
долю ответивших, контактов, выполненных
работ и отказов для каждого из трех
обследований. (Ниже будут даны определения
для каждой из этих долей). Отличие
результатов друг от друга оказалось
разительным. В верхней части табл. 18.2
представлены необработанные данные
для выборки, основанной на телефонном
справочнике. Используя эти данные, одна
организация пришла к выводу, что
доля ответивших
(отношение количества интервью к
количеству контактов) составляет 12%, в
то время как другая организация нашла
ее равной 90%. Ответы других участников
опроса были столь же разноречивыми.
Всего 3 фирмы из 40 пришли к одному и тому
же ответу, но при этом они пользовались
различными определениями. В нижней
части табл. 18.2 представлены три наиболее
часто используемых определения, а также
определения, дающие минимальные и
максимальные значения доли ответивших.

Разнообразие
определений не только приводило к
множественности значений доли
неответивших, но и осложняло разрешение
проблемы, связанной с ошибкой неполучения
данных. Последняя могла зависеть как
от эффективности используемых методов,
так и от того, насколько удачно были
выбраны определения. Пытаясь оптимизировать
и стандартизировать практику обследований,
CASRO
предложил следующее стандартное
определение доли ответивших:

Главное условие
для правильного определения доли
ответивших — надлежащее использование
критерия приемлемости. В табл. 18.3 показан
порядок определения доли ответивших
при наличии и при отсутствии требования
приемлемости.

Неполучение данных
представляет проблему для любого
обследования, при котором оно возникает,
поскольку возникает закономерный
вопрос: не существует ли серьезных
отличий между ответившими и неответившими?
Естественно, мы не можем однозначно
ответить на этот вопрос, пусть даже
предыдущие обследования свидетельствуют
о том, что между представителями двух
этих групп не существует особой разницы.

Две главные причины
ошибки неполучения данных — это
отсутствие и отказ от интервью. Ошибки
неполучения данных могут возникать при
обследованиях, использующих личный,
телефонный или почтовый опросы. При
проведении почтовых опросов проблема
отсутствия подменяется проблемой
неполучения опросного листа. Опросный
лист может просто-напросто затеряться
на почте, и в этом случае систематическую
ошибку можно считать случайной (если
только этой потере не подлежат некие
фундаментальные причины, такие как
выбытие или смерть адресата; последние
приведут к появлению систематической
ошибки.

Отсутствие.
Данные о некоторых элементах выборки
могут отсутствовать, поскольку в момент
звонка интервьюера респондентов может
не оказаться дома. Опытные данные
показывают, что процент
отсутствия
растет со временем. Очевидно, многое
зависит от респондента и времени суток,
в которое совершается звонок. Замужние
женщины с маленькими детьми в течение
дня (речь не идет о выходных) оказываются
дома чаще, чем мужчины или бездетные и
незамужние женщины. Вероятность того,
что вам ответят, выше для семей с низким
достатком или для сельских семей. Этот
показатель подвержен сезонным и недельным
(рабочие дни/выходные) колебаниям. Мало
того, куда проще застать дома «ответственного
подростка», нежели нужного вам респондента,
соответственно проблема отсутствия
может оказаться действительно серьезной.

ОТСУТСТВИЕ

Систематическая
ошибка, возникающая вследствие неполучения
ответов от заранее определенных
респондентов, отсутствующих дома в
момент звонка регистратора.

Для
снижения эффекта отсутствия может быть
принят ряд мер. Например, при некоторых
обследованиях интервьюер может заранее
договориться с респондентом о времени
своего звонка. Этот подход будет особенно
эффективным при обследовании
административных работников, но может
оказаться неоправданным при обследовании
обычных потребителей. В последнем случае
принято использовать повторный звонок
(или повторные звонки), который должен
производиться в другой час. На деле
неполучение данных, обусловленное
отсутствием респондентов, имеет очень
большое влияние на точность большинства
обследований. Один ведущий эксперт
пришел к заключению, что небольшие
выборки с 4-6 повторными звонками
оказываются более эффективными, чем
большие выборки без повторных звонков,
если только процентное значение доли
ответивших существенно не превышает
нормальный уровень. Некоторые данные
свидетельствуют о том, что для осуществления
контакта с тремя четвертями выборки
семей необходимо совершить от 4 до 5
звонков (смотри табл. 18.3).

Альтернативой
прямому
повторному звонку
может являться модифицированная
попытка контакта.
Если после первой попытки контакта и
нескольких повторных звонков интервьюеру
так и не удастся вступить в контакт с
нужным лицом, он может послать ему
опросный лист с конвертом или оставить
этот лист у его двери. Если же отсутствие
обусловлено «отсутствием нужного лица»,
а не «отсутствием кого-либо дома»,
регистратор может узнать у домашних
время, когда респондент обычно бывает
дома.

Неопытные
исследователи наивно пытаются решить
проблему отсутствия посещением соседней
квартиры или звонком по номеру, следующему
в списке за нужным. Подобную тактику
следует признать крайне неудачной.

Интервьюер подменяет
«присутствующими» (которые могут
существенно отличаться от отсутствующих
по ряду характеристик) часть обследуемого
сегмента популяции. При этом доля
«присутствующих» увеличивается, но
проблема не разрешается, а лишь
усугубляется.

Доля отсутствующих
зависит как от искусности интервьюера,
так и от принятой процедуры первичных
контактов и повторных попыток контакта.
Соответственно ошибка отсутствия может
быть уменьшена до некоторой степени
надлежащим обучением персонала, при
котором особенное внимание должно
обращаться на повышение эффективности
повторных попыток контакта.

Указанная зависимость
доли отсутствующих от профессионализма
интервьюера позволяет ввести меру для
оценки и сравнения самих интервьюеров:
для этого определяется
доля контактов (К)

ДОЛЯ
КОНТАКТОВ

Мера,
используемая для оценки и сравнения
работы интервьюеров при установлении
ими контакта с избранными респондентами;
К
= отношению установленных контактов к
общему количеству приемлемых элементов
выборки, с которыми надлежит вступить
в контакт.

Доля контактов
может служить мерилом настойчивости
интервьюера. Сравнение работы интервьюеров
и принятие корректирующих мер может
производиться по соответствующим
контактным уровням.

Контролера может
заинтересовать причина низких контактных
уровней у тех или иных интервьюеров.
Возможно, интервьюер работает в зоне с
традиционно высокой долей отсутствующих,
например в районе, где проживают люди
с высоким уровнем доходов. При анализе
отчетов, в которых приводится время
попыток контакта, может быть выявлена
и обусловленность низких результатов
неадекватностью дополнительных процедур.
В любом случае организаторам обследования
имеет смысл провести дополнительное
обучение персонала (этим может заняться
и сам контролер). Доля контактов может
использоваться и для оценки потенциальной
ошибки неполучения данных, обусловленной
отсутствием респондентов.

Ошибка неполучения
данных, обусловленная отсутствием
респондентов, может быть учтена и в
схеме статистической корректировки
результатов Политца-Симмонса. Эта схема
строится не на повторных, а на единичных
попытках контакта с каждым членом
выборки в момент времени, определенный
случайным образом. При этом контакте
респонденту задается вопрос, находился
ли он (или она) дома в это же время в
течение пяти предыдущих дней. Пять
соответствующих ответов и время самого
интервью дают информацию о том, когда
же респондент бывал дома в течение шести
последних дней. Ответам каждого информанта
присваивается соответствующий
(вероятность нахождения дома может
сообщаться интервьюеру и самим
респондентом) обратный весовой
коэффициент: например, для информанта,
присутствовавшего дома в это время
только один раз, весовой коэффициент
будет равен 6. Идея, подлежащая этой
схеме, состоит в том, что люди, редко
бывающие дома, не получают при обследовании
должного представления. Соответственно
чем реже респондент бывает дома, тем
выше должен быть соответствующий ему
весовой коэффициент.

Отказы от интервью.
Почти всегда при проведении обследования
находятся люди, которые отказываются
принять в нем участие. В одном из самых
массированных исследований серьезности
этой проблемы «Ваш голос» принимали
участие 46 исследовательских фирм,
проведших почти 1,4 миллиона телефонных
и персональных интервью. Обследование
показало, что около 38% опрошенных
отказались от участия в опросе, причем,
количество людей, отказавшихся участвовать
в нем до проведения или в ходе
предварительного собеседования
составляло 86%. Остальные отказались от
участия непосредственно в ходе
обследования. Исследовательское окно
18.2 дает представление о динамике и
специ­фике отказов от участия в
обследовании.

ОТКАЗЫ
ОТ ИНТЕРВЬЮ

Систематическая
ошибка, возникающая вследствие того,
что часть респондентов отказывается
принимать участие в обследовании.

Доля
отказов
зависит, помимо прочего, от особенностей
респондентов, организаций, осуществляющих
финансовое обеспечение обследования,
обстоятельств контакта, темы обследования
и искусства интервьюера. На долю отказов
может повлиять даже культура данной
территории. Скажем, в некоторых
государствах, таких как Саудовская
Аравия, обследовать женщин практически
невозможно.

Имеет значение и
метод сбора информации. Опытные данные
свидетельствуют о том, что наиболее
эффективными являются персональные, а
наименее эффективными — почтовые методы
опроса. Телефонные интервью занимают
промежуточное положение.

Хотя существуют
особые техники, позволяющие вовлекать
в обследование отдельные группы
населения, в общем случае наименее
«отзывчивыми» оказываются женщины,
представители цветного населения и
лица с невысоким уровнем образования
и низким уровнем доходов.

На количество
отказов может повлиять и характер
организации, производящей обследование.
Многие люди определяют свое участие
или неучастие в опросе именно этим
обстоятельством»

Порой к отказу
приводят какие-то внешние обстоятельства.
Респондент может быть занят, может
испытывать усталость или чувствовать
себя не лучшим образом. На долю отказов
влияет и предмет исследования. Лица,
интересующиеся данным предметом, охотнее
принимают участие в опросе. В общем
случае действует следующий закон: более
щекотливые темы вызывают большее
количество отказов.

И наконец, сама
личность интервьюера может оказать
существенное влияние на количество
отказов. Его подход, манеры и даже
демографические характеристики могут
повлиять на решение потенциального
респондента.

Каким образом
возможно скорректировать такую ошибку?
Рекомендуется использование трех
стратегий:

1. Увеличение доли
первичных ответов.

2. Повторные попытки.

3. Экстраполяция
полученной информации.

Увеличение доли
первичных ответов.
Улучшение условий проведения интервью
и углубленное обучение интервьюеров —
очевидные пути увеличения доли ответивших;
однако особенности респондента могут
оказаться фактором, неподвластным
контролю исследователя. Целевая популяция
определяется поставленной задачей, и
популяция эта может содержать семьи с
различным образовательным уровнем и
уровнем доходов, культурой и профессиональной
принадлежностью и т. д. Тем не менее
поставленная нами цель вполне достижима.
Как будет показано далее, при рассмотрении
нами взаимодействия интервьюера—интервьюируемого
можно заранее задать «нужный» тип
интервьюера.

Надлежащему
сотрудничества может способствовать
и убеждение респондентов в ценности
проводимого обследования и важности
их участия в нем. Может сыграть свою
роль и предварительное уведомление.

Если идентификация
организации, финансирующей обследование,
может привести к уменьшению количества
ответивших, исследователям надлежит
либо скрыть эту информацию, либо
обратиться к профессиональной организации,
занимающейся проведением подобных
обследований. Именно по этой причине
некоторые компании, имеющие в своем
составе исследовательские департаменты,
пользуются услугами специализированных
исследовательских фирм.

Чем больше информации
о сути и цели обследования сообщают
интервьюеры потенциальным респондентам,
тем большей становится доля ответивших
как при персональном, так и при телефонном
обследовании. Гарантия конфиденциальности
также способствует увеличению доли
ответивших, так как многие участники
опроса не хотят, чтобы их ответы
ассоциировались с их именами. При
проведении почтовых обследований
позитивную роль может сыграть и
материальный стимул. Интересен тот
факт, что подобный же стимул не эффективен
при персональных опросах, если только
они не проводятся в торговых центрах.

Использование
одной и той же техники повышения уровня
сотрудничества может давать для различных
обследований существенно отличающиеся
друг от друга результаты. Просмотр
результатов различных обследований
проясняет картину, пусть роль побудительного
стимулирования и разнится от случая к
случаю. Это может быть отчасти обусловлено
как самим предметом обследования, так
и соответствующим ему временным периодом.
На рис. 18.3 показаны результаты одного
из самых массовых недавних исследований
техник стимулирования участия в
корреспондентских опросах. Средний
эффект от применения соответствующих
техник представлен взвешенным
коэффициентом корреляции для обследования,
где веса отражают объем различных
выборок, на которых основываются
отдельные корреляции. Чем выше корреляция
взвешенного среднего, тем более
эффективной является данная техника.
Приведенные на рис. 18.3 результаты
свидетельствуют о том, что самыми
успешными техниками повышения
эффективности почтовых опросов являются
использование поощрений, уведомление
о предстоящем опросе и повторные почтовые
отправления.

Повышение доли
ответивших путем повтора попытки
контакта. В
некоторых случаях причиной отказа
участвовать в обследовании могут стать
некие обстоятельства. Поскольку последние
могут оказаться изменчивыми или
временными, повторная попытка установления
контакта может привести к успешному
исходу и позитивно повлиять на общий
показатель доли ответивших. Если
респондент отказался от участия в
обследовании, сославшись на болезнь
или на усталость, вы вправе надеяться
на успешный исход повторной (аналогичной
или несколько видоизмененной) попытки.
При почтовом опросе эта попытка выразится
в отправке повторного почтового
отправления. Успех подобных мероприятий
во многом зависит от уровня компетентности
персонала.

Если же источником
ошибки, обусловленной неполучением
данных, является сам предмет исследования,
ситуация становится куда более сложной.
Обследование, не представляющее для
респондентов особого интереса или же
представляющееся им сомнительным,
скорее всего, будет сопровождаться
большим количеством отказов. Соответственно
исследователь должен использовать все
возможности для того, чтобы заинтересовать
респондента,— например, он может ввести
в опросный лист не относящиеся к делу
вопросы.

Если респондент
отказался от участия в персональном
или телефонном опросе не в силу неких
сложившихся в данный момент обстоятельств,
а по каким-то иным причинам, повторные
попытки окажутся не столь успешными.
Почтовый опрос в этом смысле является
исключением. Многие люди склонны отвечать
только на второй или даже третий запрос.
Разумеется, в таком случае необходимо
провести идентификацию лиц, не ответивших
на предыдущие запросы, или, что то же
самое, ответивших на них, нежелание же
подвергнуться таковой идентификации,
как уже отмечалось, заставляет многих
людей отвечать отказом. Таким образом,
идентификация респондентов, призванная
уменьшить одну составляющую ошибки
неполучения данных, может привести к
увеличению другой ее составляющей.
Альтернативный же подход, при котором
повторные почтовые отправления будут
разосланы всем участникам обследования,
будет раздражать иных респондентов и
может оказаться излишне дорогостоящим
для организации, проводящей обследование.

Коррекция
результатов, призванная учитывать
эффект неполучения данных.
Третья стратегия состоит в оценке
возможного эффекта, обусловленного
неполучением данных, и в соответствующей
коррекции результатов обследования.
Предположим, что при определении среднего
уровня доходов для некой популяции
регистратору удалось получить ответы
только части лиц, входящих в обследуемую
выборку
.
Долю неответивших обозначим.
Если
,
— средний
уровень доходов ответивших, а

— средний
уровень дохода не ответивших, общий
средний уровень будет равен

Разумеется, при
этом предполагается, что значение

известно или по крайней мере может быть
оценено. В ряде случаев для оценки этой
величины предпринимаются интенсивные
повторные попытки контакта с выборкой
нереспондентов. Указанные попытки могут
иметь форму видоизмененного повтора,
о котором говорилось ранее. Поскольку
же ситуация, при которой в ходе повторного
обследования будут получены ответы
всех респондентов, достаточно редка,
можно говорить только о приблизительной
оценке. Игнорирование первичного
неполучения информации эквивалентно
принятию того, что

равно
,
что обычно неверно.

Второй метод
корректировки результатов состоит в
отслеживании количества ответивших на
первичный запрос, на первый повтор,
второй повтор и т. д. По этим данным
определяется среднее значение
количественного признака (или другая
приемлемая статистика), после чего
производится сравнение подмножеств,
призванное ответить на вопрос, приводит
ли проблема неполучения ответа к
статистически значимым последствиям.
Если нет, среднее значение количественного
признака для нереспондентов принимается
равным аналогичному значению для
ответивших. Если же выявляется определенный
тренд, то возникает необходимость в
соответствующей экстраполяции
результатов. Данный метод особенно
ценен при проведении почтовых опросов,
при которых идентификация лиц, ответивших
на первый запрос, второй запрос и т. д.,
не вызывает особых трудностей.

Опыт, накопленный
в ходе предыдущих опросов, также может
служить основой для уменьшения эффекта
неполучения данных. Организации, часто
проводящие однотипные выборочные
обследования, сочтут этот подход наиболее
действенным. Ни один из названных методов
оптимизации не может быть назван
совершенным, однако лучше воспользоваться
любым из них, чем не использовать никакого
и уравнять характеристики нереспондентов
и респондентов. Именно это и происходит
в тех случаях, когда мы не пытаемся
ослабить эффект неполучения данных.

Частичное
неполучение данных.
До сих пор мы говорили о полном
неполучении данных. Частичное неполучение
данных,
которое также может приводить к
возникновению серьезных проблем, состоит
в том, что респондент, согласившийся
принять участие в опросе, не хочет или
не может ответить на некоторые вопросы
вследствие специфики их формы или
содержания или вследствие нежелания
обременять себя поиском нужной информации.
Как уже говорилось ранее, при разработке
опросных листов исследователи пытаются
сделать все возможное для того, чтобы
подобных проблем не возникало. Тем не
менее полностью исключить появление
таких вопросов невозможно.

Возможность
исправления ситуации во многом зависит
от размера частичного неполучения
данных. Здесь мы должны различать
катастрофическое или случайное, частичное
неполучение данных. Если слишком большое
количество вопросов остается без
ответов, последние теряют смысл, и мы
приходим к ситуации полного неполучения
данных от ряда респондентов. Если же
количество таких вопросов относительно
невелико, ответ остается осмысленным.
В любом случае при обработке результатов
варианты «не знаю» и «отсутствие ответа»
должны идти отдельными позициями. Этот
подход представляется оптимальным,
поскольку явлению частичного неполучения
данных в этом случае может быть дана
должная оценка. В некоторых случаях
недостающая информация по какому-то
пункту или пунктам может быть восполнена
путем анализа иных пунктов заполненного
опросного листа. Это относится прежде
всего к тем

случаям, когда
одной теме или предмету посвящено сразу
несколько вопросов. Полученные ответы
анализируются, и на этой основе заполняется
пропущенная позиция. Если подобная
согласованность отсутствует, возможно
прибегнуть к регрессивному
анализу,
посредством которого устанавливается
взаимосвязь нескольких показателей.
Отсутствующий пункт рассматривается
как целевой количественный показатель.
С помощью регрессивного анализа
устанавливается его априорная
функциональная зависимость от других
показателей (по результатам обследований,
в которых были получены ответы на все
вопросы). Установленная зависимость
позволяет неким образом оценить
недостающие ответы опросных листов.

Последний, третий
способ восполнения частичного неполучения
информации состоит в подстановке
среднего значения, определенного для
полученных ответов. Разумеется, при
этом мы исходим из предположения, что
лица, не ответившие на вопросы, ничем
не отличаются от лиц, ответивших на них.
Подобная подстановка среднего весьма
рискованна, — ею следует пользоваться
с большой осторожностью.

ДОЛЯ
ПОЛНЫХ ОТВЕТОВ

Мера
оценки и сравнения работы интервьюеров
по их умению получать от респондентов
всю требуемую информацию.

Доля ответивших
и доля полных ответов.
Подобно тому, как доля контактов может
использоваться для оценки и сравнения
работы регистраторов по количеству
отсутствующих респондентов, для сравнения
их работы по количеству отказов могут
использоваться два показателя: доля
ответивших R,
и доля полных
ответов С.
Как уже объяснялось ранее, доля ответивших
равна отношению количества ответивших
к общему количеству приемлемых
респондентов в выборке. Доля ответивших
может использоваться для оценки
определенных аспектов работы интервьюера.

Доля полных ответов
имеет существенно иное значение. Обычно
этот показатель используется для оценки
способности интервьюеров получать
ответы на ключевые вопросы обследования,
такие как уровень доходов респондента,
наличие у него долгов и тому подобное,
хотя его можно использовать и для оценки
всего обследования. Доля полных ответов
позволяет судить о полноте представленного
ответа.

ОШИБКИ НАБЛЮДЕНИЯ

Ошибки наблюдения,
определенные ранее, могут быть менее
очевидными, чем ошибки ненаблюдения,
вследствие чего наблюдатель может даже
не догадываться об их существовании.

ОШИБКИ
СБОРА

Систематическая
ошибка, возникающая при сборе данных.

Ошибки сбора.
Наиболее распространенной ошибкой
наблюдений является
ошибка сбора,
которая возникает уже после того, как
нужный индивид согласится принять
участие в обследовании. Вместо того
чтобы идти на полное сотрудничество,
он отказывается отвечать на одни и дает
неправильные ответы на другие вопросы
интервьюера. Такие ошибки принято
именовать соответственно ошибками
пропуска и
ошибками
свидетельства.
В предыдущей части мы рассматривали
ошибки пропуска и неполного получения
информации. Теперь мы хотим привлечь
ваше внимание к ошибкам свидетельства,
которые принято относить к ошибкам в
ответах.

При рассмотрении
ошибок в ответах следует понимать смысл
процедуры опроса. Во-первых, респонденту
надлежит понять суть вопроса. Во-вторых,
ему необходимо обдумать свой ответ.
Респондент пытается найти требуемую
информацию и восстанавливает в сознании
соответствующие факты, события и
ощущения. Он или она пытается неким
образом организовать свой ответ исходя
из этой информации. В-третьих, респондент
понимает, что его ответ должен быть
точным. В-четвертых, он должен
руководствоваться и иными соображениями:
стремлением произвести на интервьюера
должное впечатление и тому подобное. И
наконец, он должен вербализовать
результаты представленного ментального
процесса. Целью опроса является реализация
последней стадии. Нарушить же этот
процесс возможно на любом этапе,
следствием чего будет неточный ответ
или, что то же самое, ошибка в ответе.

Рис.
18.4.
Опрос — модель возникновения ошибок

Факторы, способные
вызвать ошибки в ответах, столь
многочисленны, что практически не
поддаются классификации. Тем не менее
при работе с ошибками сбора данных можно
воспользоваться схемой Кана— Кэннела
(рис. 18.4). Данная модель исходит из
нескольких предположений. Во-первых,
каждая личность имеет свойственные ей
характеристики и психологические
предпочтения, которые могут повлиять
на отношение к опросу. Некоторые
характеристики (такие, как возраст и
пол) очевидны, другие (такие, как
психологическое состояние) могут
оставаться неизвестными интервьюеру.
В любом случае интервьюер и респондент
вступают в определенную систему
взаимоотношении, обусловленных как
названными факторами, так и данными
непосредственного чувственного
восприятия. Во-вторых, интервью является
интерактивным процессом, детерминантами
которого являются как интервьюер, так
и респондент. Каждая из сторон отрабатывает
специфическое поведение другой стороны.
Заметьте, однако, что между поведенческими
блоками нет непосредственной связи.
Эта связь имеет более сложный характер.
«Поведение интервьюера и респондента
определяется восприятием поведения
противной стороны, когнитивной или
социально обусловленной реакцией и,
наконец, результирующим стимулом,
подлежащим той или иной модели поведения.
Только на этой стадии поведенческий
акт принимает свойственную ему
определенность, которая воспринимается
и отрабатывается вторым участником
взаимодействия».

Восприятие поведения
может быть неадекватным, точно так же
как неадекватным может быть само
восприятие сторон. И интервьюер, и
респондент должны сделать определенные
усилия, для того чтобы стало возможным
их полноценное общение в ситуации
опроса. На его результат влияет не только
специфика поведения участников интервью,
но и их характеристики, и психологические
особенности.

Модель взаимодействия
интервьюера-респондента имеет ряд
привлекательных особенностей. Во-первых,
она соответствует эмпирическим данным.
Во-вторых, она позволяет судить о том,
как можно было бы свести к минимуму
ошибки в ответах (а также ошибки
неполучения данных, вызванные отказами).
Данная модель приложима не только к
персональному, но и к телефонному и
почтовому методам опроса, что еще больше
повышает ее ценность. Приведем пример.
Специфическое восприятие данным
респондентом характеристик и модели
поведения телефонного интервьюера, вне
всяких сомнений повлияет на его,
респондента, ответы. Это касается как
личности самого интервьюера, так и
возможных подозрений респондента,
считающего истинные цели обследования
иными, сомневающегося в конфиденциальности
беседы и т. п. Факторы такого рода могут
свести все попытки интервьюера на нет,
причем ложность ответов будет уже
неслучайной.

Личные особенности
(характеристики).
Опытные данные свидетельствуют о том,
что личные особенности могут серьезно
повлиять на ответы. Если интервьюер и
респондент имеют много общего, их
взаимодействие становится куда более
легким и успешным. В первую очередь это
относится к таким очевидным характеристикам,
как национальность, возраст и пол, но
это же правило приложимо и к менее
очевидным особенностям: принадлежности
к определенному классу или группе
населения. Имеет смысл подбирать
интервьюера таким образом, чтобы он как
можно меньше отличался от респондента,
в этом случае вероятность позитивного
исхода интервью существенно возрастает.

К сожалению,
использовать этот принцип на практике
крайне сложно. В роли интервьюеров в
большинстве случаев выступают домохозяйки,
пытающиеся повысить доходы семьи.
Сказать, что в деятельности такого рода
принимают участи представители различных
групп и слоев населения, можно было бы
только с очень большой натяжкой. Каким
же образом исследователь может повлиять
на соответственные ошибки? Можно
определить степень изменчивости
интервьюеров, можно поменять график и
стиль их работы, но самым эффективным
способом, как уже было отмечено выше,
является подбор интервьюеров, принадлежащих
к различным социальным группам.

Психологические
факторы.
Опытные данные говорят о том, что
результаты работы интервьюеров имеют
явную обусловленность их взглядами,
позициями и стремлениями. Естественно,
подобную психологическую обусловленность
имеет любой человек. Возможно ли вообще
как-то контролировать эти факторы, и
если да, то как это сделать? Прежде всего
следует обратить особое внимание на
обучение персонала. Сами психологические
склонности интервьюеров некритичны,
поскольку этот психологический фактор
остается скрытым от респондента. Главное,
чтобы они не влияли на ход интервью и
соответственно не искажали бы ответов.

Именно по этой
причине большинство обследова­ний
проводится по жесткой фиксированной
схеме, которой должны неукоснительно
придерживаться все интервьюеры.
Необходимо наличие ясной письменной
инструкции. Она должна четко определять
цель обследования и содержать описание
используемых материалов: опросных
листов, карт, нормативов и т. п. Должно
даваться развернутое описание процедуры
опроса, типы приемлемых формулировок,
способы и нормы проверок (если таковые
производятся). В инструкциях должны
задаваться количество и тип респондентов,
с которыми интервьюеру следует вступить
в контакт, а также временные рамки
обследования. Инструкции должны быть
упорядоченными и однозначными.

Важно, чтобы
содержание и язык инструкций были
доступны каждому интервьюеру. Эта цель
может быть достигнута в ходе занятий с
ними. В некоторых случаях имеет смысл
экзаменовать потенциальных интервьюеров
на предмет понимания ими цели обследования
:

и владения методами,
позволяющими получать объективные, не
обусловленные позицией самого интервьюера
ответы.

Поведенческие
факторы.
Биографические данные, мнения, позиции,
намерения респондента также могут
являться источником ошибок. Их наличие
или отсутствие зависит от характера
взаимодействия интервьюер—респондент.
Иными словами, ошибки такого рода
возникают непосредственно в ходе этого
взаимодействия.

К сожалению, опытные
данные говорят о том, что даже при
относительной простоте опросных листов
и жесткости правил проведения опроса
интервьюеры зачастую не соблюдают
требований инструкции, что влечет за
собой ошибки. В одном классическом
обследовании 15 интервьюеров, окончивших
колледж, производили опрос одного и
того же респондента, которому была дана
инструкция дать одинаковые ответы всем
пятнадцати интервьюерам. Все интервью
были записаны и впоследствии
проанализированы. Самой большой
неожиданностью стало количество
допущенных ошибок. Было сделано 66
неудачных попыток прояснить суть явно
неадекватных ответов дополнительными
вопросами; общее же количество ошибок
в расчете на одного респондента колебалось
между 12 и 36. При другом обследовании
было установлено, что «треть интервьюеров…
часто допускает ошибки и пренебрегает
требованиями действующей инструкции,
не умея ясно выразить суть основных
понятий, искажая их, сокращая вопросы
или не понимая ответов».

Три модели поведения
интервьюеров приводят к появлению
ошибок: (1) ошибки при формулировке
вопросов и неумение задавать уточняющие
вопросы, (2) ошибки при записи ответов,
(3) подтасовка данных.

Ошибки при
формулировке вопросов могут сопутствовать
вопросам любого типа, наиболее же острой
эта проблема становится при работе с
вопросами, допускающими различные
толкования, предполагающими продолжение
опроса. Разные интервьюеры будут задавать
разные уточняющие вопросы. Могут
отличаться как смысл, так и продолжительность
дополнительного опроса. Соответственно
различие ответов может вызываться как
«истинным» отличием позиций респондентов,
так и различием подходов при проведении
дополнительного опроса.

Немаловажное
значение имеет и то, как будет сформулирован
исходный вопрос. Интервьюеры склонны
перефразировать его, дабы сделать суть
вопроса более понятной для респондента.
При этом они могут «вчитывать» в него
собственное понимание или собственную
позицию, тем самым предрасполагая
респондента к тому или к иному ответу.

Как ни странно,
альтернативные вопросы сопряжены с
высокой вероятностью появления ошибки.
Эта ошибка может возникать, например,
вследствие того, что при постановке
вопроса интервьюер может сделать особый
акцент на одной из альтернатив. Небольшого
изменения тона достаточно для того,
чтобы изменить смысл всего вопроса. В
одном из недавних исследований,
посвященных проблеме ошибок интервьюеров
при формулировке вопросов, было
установлено, что в зависимости от типа
среднее количество ошибок, приходящихся
на один вопрос, составляет

• ошибки чтения
0,293;

• варианты
вербализации 0,116;

• уточняющие
вопросы 0,140;

• обратная связь
0,161.

Одна из главных
задач интервьюера — удержание внимания
и интереса респондента. Одновременно
интервьюер должен фиксировать
неоднозначные ответы респондента или
перепроверять их соответствие друг
другу. Одновременное решение двух этих
задач в ряде случаев может приводить к
ошибкам. Занятый своим делом интервьюер
может «не услышать» респондента. Причиной
этого может стать как неразборчивость
сказанного, так и сосредоточенность
интервьюера на чем-то ином. Последний
может услышать именно то, что он хотел
услышать, и воспринять именно то, что
он хотел воспринять. К ошибкам такого
рода склонен любой человек, их может
совершить каждый. Если же мы будем
слишком требовательными, работа может
показаться интервьюерам непосильной,
вследствие чего они откажутся от ее
исполнения.

Подтасовка данных
также может стать источником ошибки.
Эта подтасовка может относиться как ко
всему опросному листу, так и к отдельным
его пунктам. Фонд рекламных исследований
(АКР) порой проводит проверочные повторные
обследования выборок, уже подвергавшихся
обследованию. Сотрудники фонда хотят
убедиться в том, что опрос действительно
имел место, и что были заданы все нужные
вопросы. При проведении одного из таких
обследований оказалось, что 5,4% опросных
листов 33 различных обследований не
находят подтверждения, а 7,9% имеют не
менее двух серьезных противоречий. Даже
Бюро переписей, которое можно было бы
назвать самым скрупулезным и аккуратным
сборщиком информации в мире, постоянно
сталкивается со сфабрикованными
опросными листами. Исследовательское
окно 18.3 может служить иллюстрацией к
сказанному.

Большинство
коммерческих исследовательских фирм
проверяет достоверность 10-20 % опросных
листов путем проведения контрольного
почтового или телефонного опроса. При
этом проверяется следующее:

1. Метод опроса —
проверяется соответствие использованного
метода заданному (например, действительно
ли проводился персональный, а не
телефонный опрос).

2. Поставленные
вопросы — проверка того, не были ли
выпущены из рассмотрения важные вопросы
(демографического или классификационного
характера).

3. Демонстрация
продукции — проверка того, действительно
ли была произведена потребная для
проведения опроса демонстрация продукта
или информационного листа.

4. Знакомство
респондента с интервьюером — проверка
того, не занимался ли интервьюер опросом
своих знакомых или друзей.

5. Реакция на
проведение опроса — проверка «качества»
работы интервьюера.

Другой разновидностью
обмана, не являющейся ошибкой в ответах,
но серьезно влияющей на все систематические
ошибки, могут быть раздутые счета.
Интервьюер может указать завышенное
расстояние или завышенную продолжительность
обследования. Проблема эта имеет весьма
широкое распространение вследствие
специфики работы интервьюера. Прямой
контроль над интервьюером отсутствует,
оплачивается же его труд весьма скромно.
Оплата труда инспектора обычно зависит
от зарплаты интервьюера, чем выше
последняя, тем больше первая. Раздутые
счета отвлекают средства от других
статей обследования и снижают его
эффективность, поскольку стоимость
информации возрастает.

Как уже говорилось
ранее, ошибки в ответах сложнее поддаются
коррекции, чем ошибки неполучения
информации. Их знак и их величина
неизвестны, поскольку их невозможно
определить, не зная истинного значения.
Исследователю надлежит стремиться к
их недопущению, ибо они не поддаются
устранению. Источники ошибок могут быть
различными, соответственно различными
могут быть и меры их предотвращения.
Скажем, обучение позволяет сократить
количество ошибок при формулировании
вопросов и записи ответов. Подобным же
образом с подтасовкой данных можно
бороться надлежащим отбором персонала
и определением уровня оплаты интервьюеров
и системы контроля. Квалификация
интервьюера может оцениваться по
качеству его работы, ее стоимости, типам
ошибок, способности следовать инструкциям
и т. п. Мы не будем останавливаться на
этом вопросе, поскольку это потребовало
бы написания отдельной книги. Нам
достаточно помнить о существовании
ошибок в ответах, о причинах, их
порождающих, и об их деструктивном
характере. Модель взаимодействия
интервьюер—респондент способствует
наглядному представлению этих причин
и нахождению методов их предотвращения.

Офисные ошибки.
Систематические ошибки могут возникать
не только при сборе информации. Они
могут появляться при редактировании,
кодировании, составлении таблиц и
анализе данных. В большинстве случаев
эти ошибки могут быть устранены частично
или полностью введением надлежащего
контроля над процессом обработки данных.
Эти вопросы обсуждаются в главах,
посвященных анализу полученных
результатов.

Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалом, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.

Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.

В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей.

1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.

Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества -вообще.

К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекаюших процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и т.д.

2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений.. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств.

3.   Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и т.д.

4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.

По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.

Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.

Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.

Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и

удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.

Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.

Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.

В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.

Способы обнаружения систематических погрешностей. Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например, Х1, Х₂ и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,

Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого /-го наблюдения будем обозначать через 8., то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 0, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,

Если систематические погрешности постоянны, т.е. 0_/ = 0, /=1,2, …, п, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:

q = -Oi.

Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.

Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.

Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.

Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.

Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.

Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью.

Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения

где Р — измеряемое давление.

Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.

Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся погрешности:

•   определения поправок;

•   зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;

•   связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).

Перечисленные погрешности малы, и поправки на них не вводятся.

faruk писал(а):

Очень кратко, непонятно и с опечатками.

Пусть случайная величина (ошибка измерения высоты) имеет нормальное распределение с математическим ожиданием и средним квадратичным отклонением . Тогда функцию распределения можно записать в виде , где — функция Лапласа.

Имеют место формулы и .

В данном случае заданы (систематическая ошибка отсутствует) и , поэтому получаем условие , откуда . Из таблиц функции Лапласа (или с помощью программы, умеющей вычислять функцию, обратную функции Лапласа) находим , откуда , так что можно взять .

Дискретная СВ Х имеет геометрическое распределение, принимает значения 0, 1, … , ∞ с вероятностями

p( X = i) = pi = qi p ,

где p – параметр распределения (0 ≤ p ≤ 1), q = 1 – p.

Числовые характеристики геометрического распределения:

Дискретная значения 0, 1, … ,

m X = q / p , D X = q / p 2 .

СВ X имеет биномиальное распределение, если она принимает n со следующими вероятностями:

p(X =i) = p =	n!	piqn−i	(7.2)
i	i!(n −i)!	,

где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p. Числовые характеристики биномиального распределения:

m X = n p , D X = n q p .

Дискретная СВ Х имеет распределение Пуассона, если она принимает значения 0, 1, … , ∞ со следующими вероятностями:

p(X =i) = p = ai	e−a	(7.3)
i	i!	,
где a – параметр распределения (a > 0).
Числовые характеристики пуассоновской СВ:
m X = a , D X	= a .

Непрерывная СВ Х имеет равномерное распределение, если ее плотность вероятности в некотором интервале [а; b] постоянна, т.е. если все значения X в этом интервале равновероятны:

0, x <

f ( x ) = 1

b − a

0, x >

a ,	0 , x	< a ,
		− a
, a ≤ x ≤ b , F ( x ) =	x	, a	≤	x ≤	b ,
				(7.4)
		a
b.	b	−
1, x	> b .

Числовые характеристики равномерно распределенной СВ:

	m X =	a + b	, D X	=	( b − a ) 2	.
	2	1 2

Непрерывная СВ T, принимающая только положительные значения, имеет экспоненциальное распределение, если ее плотность вероятности и функция распределения равны

		λ e	− λ t	, t	≥ 0 ,		− e	−λt	, t ≥ 0,
f (t ) =		1		(7.5)
	0 , t < 0 ,	F(t) =	0, t < 0,

где λ – параметр распределения (λ > 0).

Числовые характеристики экспоненциальной СВ:

m T = 1 / λ , D T = 1 / λ 2 .

Непрерывная СВ Х имеет нормальное распределение, если ее плотность вероятности и функция распределения равны

f (x ) =

1

exp −

(x − m)2

F ( x ) =

0 .5 + Φ

x − m

,

2

,

(7.6)

σ 2π

2σ

σ

где m, σ – параметры распределения ( σ >0),

1

x

t2

Φ(x) =

∫e−

dt — функция Лапласа.

2

2π

0

Значения функции Лапласа приведены в приложении. При использовании таблицы значений функции Лапласа следует учитывать, что Φ(–x) = –Φ(x),

Φ(0) = 0, Φ(∞) = 0,5.

Числовые характеристики нормальной СВ:

m X = m , D X = σ 2 ,

I [ k / 2 ]

m

k −2 i

(σ

/ 2)

i

αk ( x) = k ! ∑

,

(k − 2i)!i !

i =0

0 , k − нечетное,

µ

( x ) =

2 k / 2

k

k !

σ

, k − четное.

( k / 2 ) !

2

Пример 7.1. Время безотказной работы аппаратуры является случайной величиной Х, распределенной по экспоненциальному закону. Среднее время безотказной работы 100 ч. Найти вероятность того, что аппаратура проработает больше среднего времени.

Решение. Так как среднее время безотказной работы, т.е. математическое ожидание, равно 100 ч, то параметр λ экспоненциального закона будет равен λ = 1 / m X = 1 / 100 = 0, 01 . Искомая вероятность

p(X > mX ) = p(100 < X < ∞) =1− F(100) = e−1 ≈ 0,368.

Пример 7.2. Для замера напряжения используются специальные датчики. Определить среднюю квадратическую ошибку датчика, если он не имеет систематических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2.

Решение. Из условия задачи следует, что p(-0,2<X<0,2) = 0,8. Так как распределение ошибок нормальное, а математическое ожидание m равно 0 (систематические ошибки отсутствуют), то

р{–0,2 < X < 0,2} = Ф(–0,2 / σ) – Ф(0,2 / σ) = 2Ф(0,2 / σ) = 0,8.

По таблице функции Лапласа находим аргумент 0,2/ σ =1,28, откуда

σ = 0,2 / 1,28 = 1,0156.

ЗАДАЧИ

7.1. По каналу связи пересылается пакет информации до тех пор, пока он не будет передан без ошибок. Вероятность искажения пакета равна 0,1, найти среднее количество попыток передать пакет.

Ответ: 1,11.

7.2. При работе прибора в случайные моменты времени возникают неисправности. Количество неисправностей, возникающих за определенный промежуток времени, подчиняется закону Пуассона. Среднее число неисправностей за сутки равно двум. Определить вероятность того, что: а) за двое суток не будет ни одной неисправности; б) в течение суток возникнет хотя бы одна неисправность; в) за неделю работы прибора возникнет не более трех неисправностей.

Ответ: а) 0,018; б) 0,865; в) 0,004.

7.3. Шкала рычажных весов имеет цену деления 1 г. При измерении массы отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность того, что абсолютная ошибка определения массы: а) не превысит величины среднего квадратического отклонения возможных ошибок определения массы; б) будет заключена между

значениями σX и2σX .

	Ответ: а)	1	; б) 1 −	1	.
	3	3

7.4. Среднее время работы электронного модуля равно 700 ч. Определить время безотказной работы модуля с надежностью 0,8.

Ответ: 140 ч.

7.5. Сообщение передается последовательностью амплитудномодулированных импульсов с заданным шагом квантования ∆ (∆ – наименьшая разность амплитуд импульсов). На сообщение накладываются шумы, распределенные по нормальному закону N(0, σ). Если мгновенное значение шума превышает половину шага квантования, то при передаче сообщения возникает ошибка. Определить, при каком минимально допустимом шаге квантования ∆ вероятность ошибки из-за шумов не превысит 0,1.

Ответ: 3,4 σ.

7.6. СВ X – ошибка измерительного прибора – распределена нормально с дисперсией 16 мВ2. Систематическая ошибка прибора отсутствует. Вычислить вероятность того, что в пяти независимых измерениях ошибка: а) превысит по модулю 6 мВ не более трех раз; б) хотя бы один раз окажется в интервале

(0,5; 3,5) мВ.

Ответ: а) 0,999; б) 0,776.

8. ФУНКЦИИ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА

Рассмотрим функцию одного случайного аргумента Y = ϕ(X). Если X – непрерывная случайная величина, то плотность вероятности g(y) величины Y определяется по формуле

k
g( y) = ∑ f (ψ j ( y))		ψ′j ( y)		,	(8.1)
j=1

где f(х) – плотность вероятности величины X; ψj(y) – функции, обратные функции ϕ(x);

k – число обратных функций для данного y.

Весь диапазон значений Y необходимо разбить на интервалы, в которых число k обратных функций постоянно, и определить вид g(y) по формуле (8.1) для каждого интервала.

Если X – дискретная случайная величина, принимающая значения xi, то величина Y будет принимать дискретные значения yi = ϕ(xi) с вероятностями

p(yi) = p(xi).

Числовые характеристики функции Y = ϕ(X) одного случайного аргумента

Xопределяются по формулам:

–начальные моменты

		∑n	ϕ k ( xi ) pi	для ДСВ
	i =1		;	(8.2)
α k ( y ) = M [Y k ] = M [ϕ k ( x)] =	∞
		∫ ϕ k ( x) f ( x)dx для НСВ
– математическое ожидание		−∞
m y = M [Y ] = M [ϕ (x )] = α1 ( x ) ;	(8.3)
– центральные моменты
	n
∑(ϕ( xi ) − m y )k pi	для ДСВ
i=1			;	(8.4)
µk ( y) = M[(Y − mY )k ] =	∞
	∫ (ϕ( x) − my )k f ( x)dx для НСВ
	−∞
– дисперсия
DY =µ2(y) =M[(Y −mY )2]=α2(y)−mY2 .	(8.5)

Пример 8.1. Определить плотность вероятности величины Y = X2, если X – случайная величина, равномерно распределенная на интервале [–1, 2].

Решение. Так как Х равномерно распределена в интервале [–1, 2], то ее

плотность вероятности равна (7.4):	−1≤ x ≤ 2,
1/3,
f (x) =	x < −1, x > 2.
0,

Построим график величины Y = X2 для x в интервале [–1, 2] и в зависимости от числа k обратных функций выделим следующие интервалы для

Y (рис. 8.1):

k = 0,

[–∞, 0[

[0, 1]

k = 2,

]1, 4]

k = 1,

]4, +∞]

k = 0.

Так как на интервалах [–∞, 0[ и ]4, +∞]

обратная функция не существует, то для этих

интервалов g(y) = 0.

В интервале [0, 1] две обратные функции:

ψ1(y) = + y и ψ2(y) = – y .

По формуле (8.1) получим

g( y) = fx (ψ1( y))

ψ1′( y)

+ fx (ψ2( y))

ψ2′ ( y)

=

= fx ( y )

1

+ fx

(− y )

1

=

1

.

2

y

2

y

3

y

В интервале ]1, 4] одна обратная функция

ψ1(y) = +

y , следовательно,

g( y) = fx (ψ1( y))

ψ1′( y)

= fx (

y )

1

=

1

.

Рис. 8.1

2

y

6

y

Таким образом, плотность вероятности величины Y равна

0,

y < 0,

1

0 ≤ y ≤1,

y

,

3

g ( y) =

1

,

1 < y ≤ 4,

6

y

y > 4.

0,

Пример 8.2 Случайная величина X равномерно распределена от –1 до +1. Определить математическое ожидание и дисперсию величины Y = X2.

Решение. Плотность вероятности СВ X равна

0,5, −1 ≤ x ≤1, f (x) =

0 , x < −1, x >1.

Вычислим математическое ожидание Y по формуле (8.3):

m y = M [X 2 ] = ∫1	x 2 0, 5dx =	1 .
−1		3

Дисперсию Dy рассчитаем по формуле (8.5):

	Dy = M[( X 2 )2 ] − mY2 = ∫1	(x2 )2 0,5dx − my2 =	4	.
	45
	−1

ЗАДАЧИ

8.1. Определить плотность вероятности величины Y = lnX, если X – случайная величина, равномерно распределенная на интервале (1, 3).

		0, 5e	y	, 0	≤ y < ln 3,
Ответ:	g ( y ) =
		0 , y < 0, y > ln 3 .

8.2. Определить плотность вероятности величины Y = |X|, если X – случайная равномерно распределенная величина со следующими характеристиками mx = 1, Dx = 1, и вычислить вероятность того, что р{1 ≤ Y < 2}.

	0, y < 0, y > 2, 73,
		1
	Ответ: g( y) =		, 0	≤ y < 0, 73,
	3
		1		, 0, 73 ≤ y ≤ 2, 73.
	2 3

р{1 ≤ Y < 2} = 0,445.

8.3. Случайная величина X равномерно распределена от 0 до 1. Определить математическое ожидание и дисперсию величины Y = X – 0,2 .

Ответ: mY = 0,34; DY = 0,0574.

8.4. Точка U, изображающая объект на круглом экране радиолокатора, распределена равномерно в пределах круга единичного радиуса. Найти дисперсию расстояния Y от точки U до центра экрана.

Ответ: DY = 1/18.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Тема: Задача по теор веру, определить СКО  (Прочитано 2222 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Ребята, помогите срочно решить задачу по теор веру…
Итоговая работа на сессии

Ошибка Х измерительного прибора распределена нормально. Систематической ошибки прибор не имеет (mx=0). Каким должно быть среднее квадратическое отклонение Qx ( сигма), чтобы с вероятностью не меньшей 0,9 ошибка измерения не превышала 20 микрометров по модулю?

« Последнее редактирование: 20 Января 2012, 10:36:38 от Asix »

---

Всегда пожалуйста, только Вы забыли сообщить, какая помощь нужна. Видимо, кусок сообщения, где Вы рассказываете, как решали задачу и что не получается, куда-то потерялся.

---

К сожалению, я не могу написать ход решения, т к не понимаю, как можно сделать
Поэтому и обращаюсь за помощью к вам.
Знаю только что ответ должен получиться : Qx<12.2(мкм)
натолкните на умные мысли пожалуйста.

---

Всё просто: изучаете по учебнику, что такое нормальное распределение, как считаются вероятности для него, и задачка сразу решается.

---

Измерительный прибор работает без систематических ошибок.doc

Зарегистрируйся в два клика и получи неограниченный доступ к материалам, а также
промокод

на новый заказ в Автор24. Это бесплатно.

Условие

Измерительный прибор работает без систематических ошибок (работа измерительного прибора без систематических ошибок означает, что mx=0). Известно, что вероятность ошибки измерения, превышающей по абсолютной величине 7, равна 0,08. Пусть случайная величина X- это величина ошибки измерения. Предполагается, что случайная величина X нормально распределена, найти:
а) приближенное значение дисперсии;
б) вероятность того, что ошибка измерения не превысит ε=4;
в) вероятность того, что ошибка измерения изменяется от α=-4 до β=6.

Решение

А) Для случайной величины Х имеещей нормальный закон распределения с параметрами mx и  σx справедливо:
Px-mx≤ε=Фε σx, где Фt=12π-∞xe- t22dt-функция Лапласа.
По условию задачи вероятность ошибки измерения, превышающей по абсолютной величине 7, равна 0,08
. Тогда вероятность противоположного события (вероятность того, что случайная величина Х не превышает по абсолютной величине 7, равна 1-0,08=0,92. Имеем:
Px-0≤7=Ф7 σx=0,92⇒7 σx≈5⇒ σx≈7 5=1,4.
Тогда искомая дисперсия приближенно равна: Dx=σx2≈1,96.
б) вероятность того, что ошибка измерения не превысит ε=4:
Px-0≤4=Ф4 1,4≈Ф2,857≈0,4979..
в) вероятность того, что ошибка измерения изменяется от α=-4 до β=6 найдем по формуле:
Pα≤Х≤β=Фβ-mxσx-Фα-mxσx.
P-4≤Х≤6=Ф61,4-Ф-41,4≈Ф4,286-Ф-2,857=
≈0,499997+0,4979≈0,998.
Ответ

50% решения задач недоступно для прочтения

Закажи персональное решение задач. Эксперты

напишут качественную работу за 30 минут! ⏱️

Макеты страниц

Ошибки измерений и способ наименьших квадратов

9.1.21. Ошибки измерений и нормальный закон распределения.

Измерения всегда сопровождаются ошибками. Различают ошибки двух основных видов: систематические и случайные. Систематические ошибки имеют определенные причины, которые искажают измерение всегда в одном направлении и часто на постоянную величину. Они возникают за счет неисправности или плохой регулировки приборов, за счет ошибок в эталонах, из-за плохого выполнения технологии и т. д. Во многих случаях можно найти причины таких ошибок и устранить их.

Случайные ошибки неопределенны, и причина их неизвестна. Свое незнание причины ошибок мы обычно маскируем, говоря, что их порождает случай. А это просто означает, что их можно приписать большому количеству причин, действующих в любом направлении и создающих каждая свою погрешность. Такие случайные ошибки можно учитывать статистическими методами.

Существует еще одна категория ошибок, о которой будет кратко сказано в п. 9.1.27; это категория отдельных промахов, происходящих по однократной вине экспериментатора, например, если он по рассеянности один раз неправильно считает показания со шкалы измерительного прибора. В этом случае мы имеем дело с анормальным результатом измерения. Существует простое правилу, позволяющее исключить из таблицы результатов измерений ошибки этой категории.

Мы займемся в основном категорией случайных ошибок. Допустим, что имеется несколько в одинаковой степени надежных измерений физической величины, истинное значение которой равно Ошибки, соответствующие измерениям будут равны

Это чисто случайные ошибки.

Мы не знаем точного значения величины X и не можем определить ее на опыте, так как всякое измерение, сделанное для ее определения, искажается ошибкой. Обозначим через X наиболее вероятное значение величины

Рассмотрим величины

Величины называются отклонениями. Так как речь здесь идет только о случайных ошибках, то величины х и у могут быть а положительными, и отрицательными, а малые значения будут встречаться чаще, чем большие. Примем допущение, что эти величины, следуют нормальному закону распределения

Положим

как известно, называется мерой точности. При этом примет вид

где относительное число ошибок, равных х.

Вычертим кривые Гаусса при двух различных значениях мерь; точности Легко заметить, что чем больше тем кривые острее, тем круче их склоны. Это означает, что чем больше параметр тем реже встречаются большие ошибки. Поэтому величину и называют мерой точности.

Вероятность того, что ошибка будет заключаться между равна

Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с

Измерительный прибор не имеет систематической ошибки. Случайные ошибки распределены по нормальному закону, и с вероятностью 0,8 они не превосходят по абсолютной величине 12 мм. Найти среднюю квадратическую ошибку.

Используем нормальный закон и следующую формулу, таблицу значений функции Лапласа Ф(х):
px-a<δ=2Фδσ;
0.8=2Ф12σ;1.62=12σ;σ=7.407 мм.
Ответ: 7,407 мм.

• Измерительный прибор работает без систематических ошибок (работа измерительного прибора без систематических ошибок означает, что
• Измерить и записать результат измерения активной мощности Р = U·I·cosφ, рассеиваемой на нагрузке Zнагр.;
  —
• Измеряется мощность трехфазного тока двумя ваттметрами. Какова наибольшая погрешность измерения, если стрелка первого ваттметра
• Измеряется напряжение в виде периодической последовательности прямоугольных импульсов с параметрами: длительность импульсов τ, период
• Измеряется напряжение переменного тока.
  Дано.
  Цифровой вольтметр:
  — предел измерения Uк = 200 B;
  — измеренное
• Измеряется размер некоторой детали, затем из генеральной совокупности берется выборка объемом n=8. Зная, что
• Измеряется электрическое сопротивление постоянному току (рисунок).
  Получено:
  UV =(5,00±0,50) мВ; Р=1
  IA=(2,60±0,25) мА; Р=1
  RV=
  Записать результат измерения сопротивления
• Измерительный канал включает в себя термометр сопротивления типа 150М и вторичный прибор со шкалой
• Измерительный механизм (ИМ) магнитоэлектрической системы расситан на ток и Iии напряжение Uи и имеет
• Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=15 мA и напряжение Uи=75 мB
• Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=25 мA и напряжение Uи=100 мB
• Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=25 мA и напряжение Uи=75 мB
• Измерительный механизм (ИМ) магнитоэлектрической системы рассчитан на ток Iи=7,5 мA и напряжение Uи=75 мB
• Измерительный прибор (ИП) магнитоэлектрической системы рассчитан на ток IП и напряжение UП и имеет