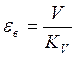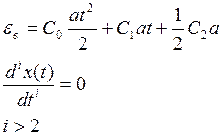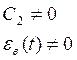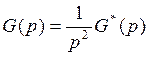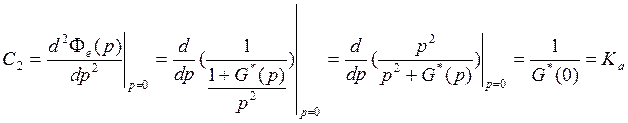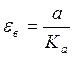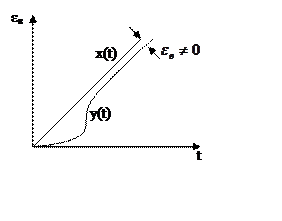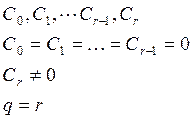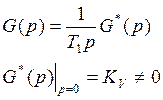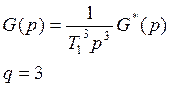Скоростная ошибка тау это

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В предыдущих сериях:
1. Введение в теорию автоматического управления
2. Математическое описание систем автоматического управления 2.1 — 2.3

В это части будут рассмотрены:
2.4 Основные виды входных воздействий
2.5. Основные положения и свойства интегральных преобразований Лапласа
2.6. Основные свойства преобразований Лапласа
2.7. Способы нахождения обратных преобразований Лапласа
2.8 Некоторые способы нахождения оригинала по известному изображению

Будет интересно познавательно и жестко.


На рисунке 3D график функции косеканс куба, к теме лекции отношения не имеет, но чертовски красив.

2.4 Основные виды входных воздействий

Для того, что бы определить свойства системы нужно осуществить воздействие и посмотреть на реакцию.

В теории управления техническими системами принят ряд стандартных входных воздействий, по реакции на которые определяются динамические свойства (характеристики) системы управления (звена). К таким воздействиям относятся: единичное импульсное воздействие, единичное ступенчатое воздействие, единичное гармоническое воздействие, линейное воздействие и др. Рассмотрим их более подробно…

2.4.1. Единичное ступенчатое воздействие

Данное воздействие является одним из наиболее «жестких» (неблагоприятных) воздействий, по реакции на которое сравниваются переходные свойства (переходной процесс) идентичных или близко идентичных систем.

Реакция системы (звена) на такое воздействие называется переходной функцией.

Единичное ступенчатое воздействие обозначается 1(t) и бывает 3-х видов: два асимметричных и одно симметричное.

$1(y) Rightarrow left[ begin{gathered} 1_+(t) 1(t) 1_-(t) end{gathered} right. mathbf{(2.4.1)}$

Рассмотрим каждый из этих видов воздействий:

$1(t)=left { begin{gathered} 1, если t>0 frac{1}{2}, если t=0 0, если t<0 end{gathered} right. 1_-(t) = left { begin{gathered} 1, если tgeq 0 0, если t<0 end{gathered} right. 1_+(t) = left { begin{gathered} 1, если t> 0 0, если tleq0 end{gathered} right. $

Рисунок 2.4.1 – Графики единичных ступенчатых воздействий

В теории управления наибольшее распространение имеет асимметричное воздействие 1+ (t), поскольку часто в анализе удобно рассматривать процесс, когда при t$leq$0 САР находится в равновесии, и анализ переходных процессов ведется только при t > 0.

Для удобства представления будем в дальнейшем записывать воздействие 1+(t), опуская индекс. 1+ (t) ≡ 1(t).

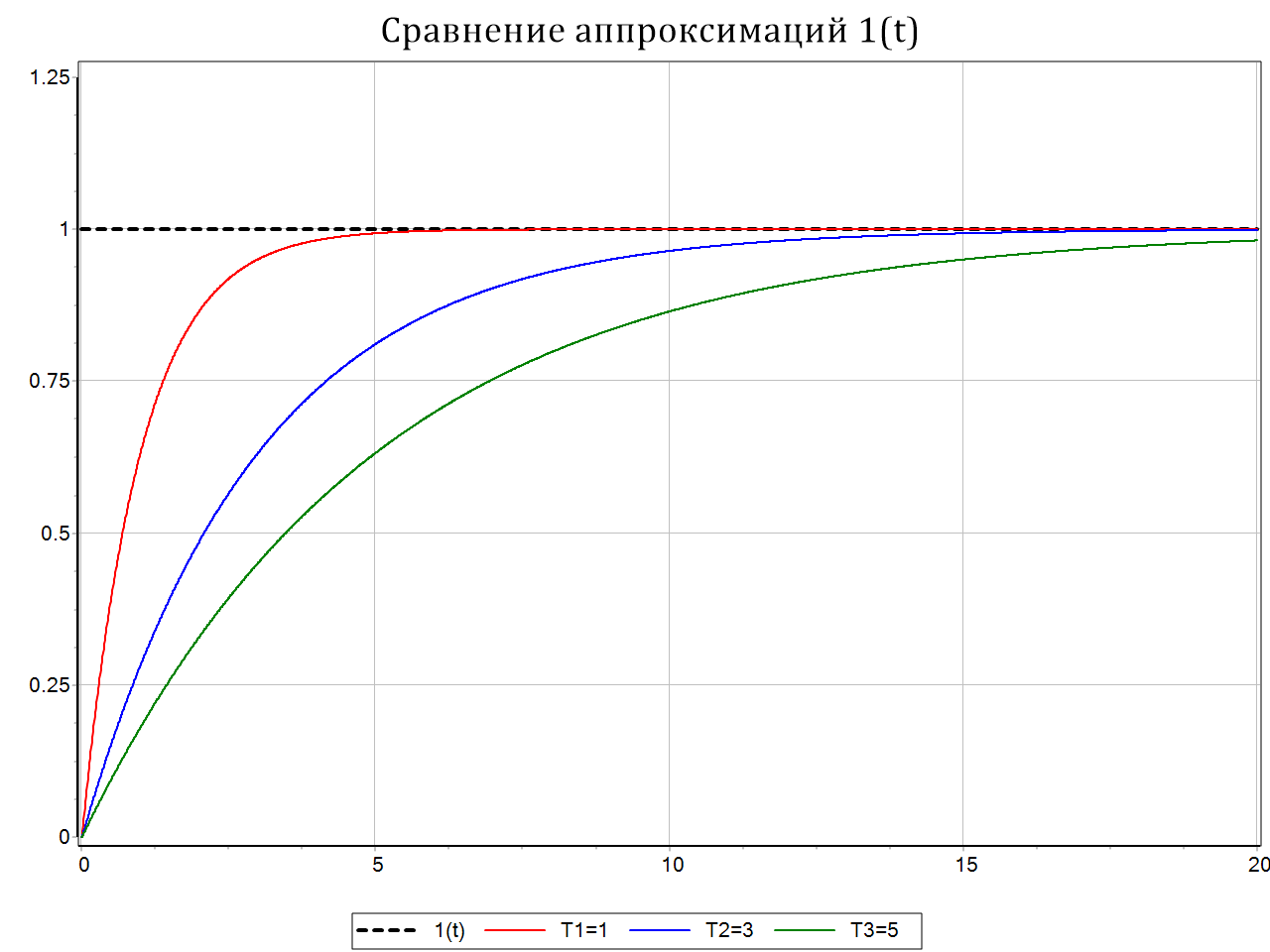
Поскольку рассматриваемое входное воздействие имеет разрыв при t = 0 (что часто нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать единичное ступенчатое воздействие, в виде неразрывной функции:

$1(t) = lim_{Tto0}(1 -e^{-frac{t}{T}}) mathbf{(2.4.2)}$

где Т – постоянная времени, а текущее время $t geq 0$

На рисунке 2.4.2 представлена графическая иллюстрация аппроксимации 1(t) по формуле (2.4.2).

Рисунок 2.4.1 – Графики единичных ступенчатых воздействий

2.4.2. Единичное импульсное воздействие: δ — функция Дирака

В математике различают три вида данного воздействия: одно симметричное и два асимметричных

$delta (t) Rightarrow left[ begin{gathered} delta_+(t) delta(t) delta_-(t) end{gathered} right. $

Рассмотрим все эти воздействия:
Симметричное единичное импульсное воздействие δ (t) определено как:

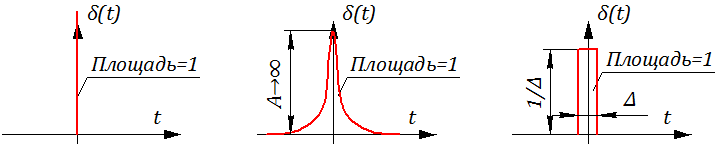
$delta (t) = left{ begin{gathered} 0, если t >0 infty, если t =0 0, если t <0 end{gathered} int_{-infty}^{+infty} delta(t) dt = 1; right.$

Графическая иллюстрация симметричного единичного импульсного воздействия представлена на рисунке 2.4.3. Фактически δ (t) – импульс (с длительностью стремящейся к нулю и амплитудой, равной бесконечности), площадь которого равна 1.

Рисунок 2.4.3 – Варианты представления симметричного импульсного воздействия

Для симметричного единичного импульсного воздействия δ(t) существует аналитическая форма представления:

$int_{-infty}^{+infty} delta(t)dt = int_{-infty}^{+infty} lim_{h to infty}frac{h}{sqrt{pi}}e^{-h^2t^2} = lim_{h to infty}frac{1}{sqrt{pi}}int_{-infty}^{+infty}e^{-(ht)^2} d(ht)$

Введем новую переменную $u = h cdot t$, тогда:

$frac{1}{sqrt{pi}} lim_{u to infty}int_{-infty}^{+infty}e^{-(u)^2} d(u) = frac{1}{sqrt{pi}} cdot sqrt{pi} = 1, поскольку lim_{u to infty}int_{-infty}^{+infty}e^{-(u)^2} d(u) = sqrt{pi}$

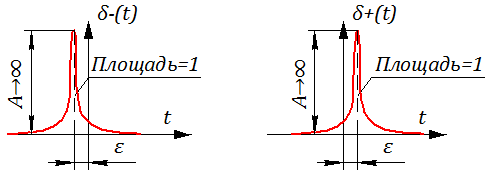
Смещенные (асимметричные) единичные импульсные воздействия определяются как:

$delta_- (t) = left{ begin{gathered} 0, если t leq 0 infty, если t =-epsilon 0, если t < epsilon end{gathered} right. delta_+ (t) = left{ begin{gathered} 0, если t > epsilon leq 0 infty, если t =epsilon 0, если t leq 0 end{gathered} right. int_{-infty}^{+infty} delta(t) dt = 1;$

где $epsilon -$сколь угодно малое положительное число (ε → 0)

Графическая иллюстрация смещенных единичных импульсных воздействий представлена на рисунке 2.4.4

Рисунок 2.4.4 – Смещенные единичные импульсные воздействия.

В дальнейшем в нашем курсе будет использоваться только δ+ (t). ==> Индекс «+» опускается… ==> δ+ (t) ≡ δ(t).

Поскольку смещенное единичное импульсное воздействие фактически имеет разрыва при t = 0 (что иногда нежелательно в численных алгоритмах, использующих конечно-разностную схему), имеется формула, позволяющая приближенно описать смещенное единичное импульсное воздействие:

$delta(t) = lim_{T to 0} frac{1}{T} e^{frac{-t}{T}} mathbf{(2.4.3)}$

где Т – постоянная времени, а текущее время t>0!!!
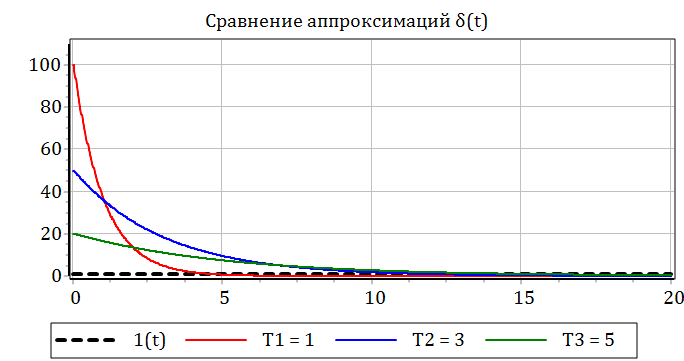
На рисунке 2.4.5 представлена графическая иллюстрация аппроксимации δ(t) по формуле (2.4.3).

Рисунок 2.4.5 – Графики аппроксимаций единичного импульсного воздействия

Реакция САУ (звена) на воздействие δ (t) называется весовой функцией.

2.4.3. Единичное гармоническое воздействие

Данное воздействие используется для анализа частотных характеристик САУ (звена) в установившемся режиме колебаний в системе, т.е. свойства САУ (звена) исследуются при больших значениях t (времени), когда влияние начальных условий пренебрежимо мало и движение (колебания) системы определяются только входным внешним воздействием.

$x(t) = sin (omega cdot t) mathbf{(2.4.4)} $

где ω — круговая частота, [1/с]; $ omega = 2 cdot picdot f$, где $f$ — частота в Герцах.

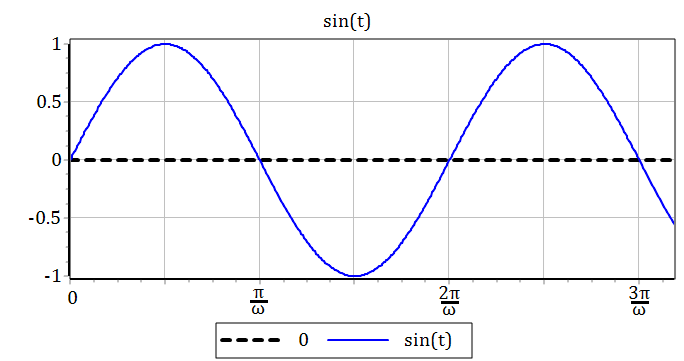
На рисунке 2.4.6 представлен график единичного гармонического воздействия.

Рисунок 2.4.6 – Гармоничное воздействие

Поскольку при анализе частотных характеристик САУ рассматривается режим установившихся вынужденных колебаний САУ (при больших значениях времени t, когда собственная составляющая переходного процесса пренебрежимо мала), то удобнее представить x(t) в показательной форме.

$x(t) = e^{omega cdot i cdot t} mathbf{(2.4.5)}$

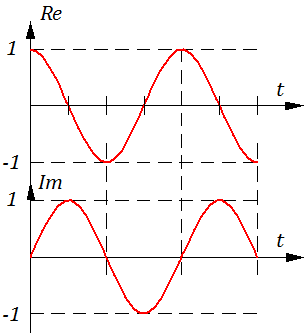
Необходимо отметить, что показательная форма – «комплексное» воздействие, и оно выглядит так (действительная и мнимая части условно показаны на рисунке 2.4.7):

$x(t)=e^{icdot omega cdot t} = underbrace{cos (omega cdot t)}_{Re}+ underbrace{i cdot sin(omega cdot t)}_{Im} mathbf{(2.4.6)} $

Рисунок 2.4.7 – Гармоничное воздействие действительна и менимая часть

Действительная часть «комплексного» воздействия (Re) – на самом деле косинусоидальное воздействие. Но так как частотные характеристики САУ определяются в режиме установившихся гармонических колебаний (т.е. при «очень-очень» больших значениях t), то не важно, по какому закону вводилось единичное гармоническое воздействие – по «синусу» или по «косинусу».

2.4.4. Линейное воздействие

Данный вид входного воздействия используется для оценки точности систем управления, а именно, для определения скоростных ошибок.

$x(t)= a cdot t mathbf{(2.4.7)}$

где t ≥ 0, а при t < 0 входное воздействие всегда равно нулю.

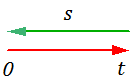
На рисунке 2.4.8 представлен график линейного входного воздействия

Рисунок 2.4.8 – Линейное входное воздействие

2.5. Основные положения и свойства интегральных преобразований Лапласа

Решение однородного обыкновенного дифференциального уравнения (ОДУ) усоб(t) записывается в виде (если нет повторяющихся корней):

$y_{соб.}(t) = sum_{j=0}^nc_je^{lambda_i}t$

т.е. все члены уравнения имеют одну и ту же форму. Этот результат наводит на мысль: «а нельзя ли ввести какое-то преобразование, в результате которого уравнение динамики (дифференциальное) можно привести к чисто алгебраическому, решение которого не представляет проблем.» А если затем сделать соответствующее обратное преобразование, то получим усоб (t), то есть получим цепочку:

Обыкновенное дифференциальное уравнение (ОДУ) $Rightarrow$ Алгебраическое уравнение $Rightarrow$ Решение $Rightarrow$ Обратное преобразование $Rightarrow$ Результат.

Именно такими соображениями руководствовался Лаплас, предлагая такое преобразование, называемое в настоящее время преобразованием Лапласа.

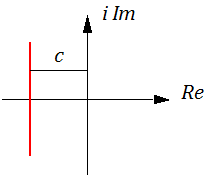
Предположим, что имеется нестационарный процесс f(t). Лаплас предложил ввести интегральное преобразование, которое отображает f(t) на комплексную плоскость согласно соотношению:

$F(s) = int_0^{infty}f(t) cdot e^{-st}dt mathbf{(2.5.1)}$

Рисунок 2.5.1

где s = c+i⋅ω: ω ∈ ] -∞; +∞ [; с – абсцисса абсолютной сходимости
(обычно в курсе «УТС» с = 0); f(t) – прообраз (оригинал); F(s) – изображение (образ);

Символическое обозначение преобразования Лапласа:

$f(t) Longrightarrow F(s) mathbf{(2.5.2)}$

Преобразование Лапласа существует, если при t<0 f(t ) = 0 и выполняется условия сходимости:

$int_0^infty mid f(t) mid cdot e^{-ct} dt < infty mathbf{(2.5.3)}$

В соответствии с соотношением (2.5.1) переходной процесс f(t) отображается на комплексную плоскость, где каждому значению оператора Лапласа «s» соответствует свой вектор. Линия, соединяющая концы векторов называется годографом.

Обратное преобразование Лапласа определяется следующим соотношением:

$f(t) = lim_{omega to infty} frac{1}{2pi cdot i} int_{c-icdot omega}^{c+i cdotomega} F(s) cdot e^{st}ds mathbf{(2.5.4)}$

Необходимо подчеркнуть, что если условие сходимости выполняется, то любому оригиналу соответствует изображение. Обратное преобразование Лапласа не всегда существует, т.е. если известно F(s), это не означает, что ему соответствует оригинал f(t)!

Прямое преобразование Лапласа символически обозначается:

$f(t) longrightarrow F(s) или L[f(t)] equiv F(s) mathbf{(2.5.5)}$

Обратное преобразование Лапласа обозначается:

$F(s) longrightarrow f(t) или L^{-1}[F(s)] equiv f(t) mathbf{(2.5.6)}$

Существует двухстороннее преобразование Лапласа $L_B [f(t)]$, частным случаем которого является обычное преобразование Лапласа

$L_B[f(t)] = int_{-infty}^{+infty}f(t) cdot e^{- s t} dt mathbf{(2.5.7)}$

Если при t ≤ 0 функция f(t) = 0, то $L_B [f(t)] ≡ L[f(t)]$

Частным случаем двухстороннего преобразования Лапласа (при с = 0, т.е. s = i⋅ω) является преобразование Фурье, определяемое соотношениями:

$Psi(i cdot omega) equiv L_B[f(t)]_{s=i cdot omega} = int_{ - infty}^{+infty}f(t) cdot e^{-i cdot omega cdot t} dt f(t) = frac{1}{2 pi}int_{ - infty}^{+infty}Psi(i cdot omega) cdot e^{-i cdot omega cdot t} d omega mathbf{(2.5.8)}$

2.5.1. Использование преобразования Лапласа для операции дифференцирования

Пусть известно $f(t)$ и его изображение по Лапласу: $f(t) longrightarrow F(s), $ выведем выражение для $ L[f(t)’ ]$.

Воспользуемся соотношением (2.5.1): $F(s) = int_0^{infty}f(t) cdot e^{-st}dt$, тогда получаем:

$L[f'(t)] = int_0^{infty}[f(t)'] cdot e^{-st}dtRightarrow left { begin{array} по частям u = e^{-st}; Rightarrow du = -s cdot e^{-st} ; d nu = f'(t)dt; Rightarrow nu = f(t). end{array} right. Rightarrow u cdot v mid_0^{infty}-int_0^{infty} v cdot dv Rightarrow$

$Rightarrow f(t) cdot e^{-st} mid_0^{infty}+ int_0^{infty}f(t)s cdot e^{-st} dt=[f(infty) cdot underbrace{e^{-scdot infty}}_{0}-f(0) cdot e^0]+s underbrace{int_0^{infty}f(t) cdot e^{-st}}_{F(s)}=$

$=s cdot F(s) - f(0) Rightarrow L[f'(t)] = s cdot F(s) - f(0), mathbf{(2.5.9)}$

где: $f(0) $ — начальное условия.
Если начальные условия равны нулю, то $f(0)=0$;

$L[f'(t)] = s cdot F(s); mathbf{(2.5.9.a)}$

Аналогичным способом найдем изображение 2-ой производной:

$L[f''(t)] = int_0^{infty}[f''(t)] cdot e^{-st}dtRightarrow left { begin{array} cu = e^{-st}; Rightarrow du = -s cdot e^{-st} ; d nu = f''(t)dt; Rightarrow nu = f'(t). end{array} right. Rightarrow Rightarrow f'(t) cdot e^{-st} mid_0^{infty}+s cdot underbrace{int_0^{infty} f'(t) cdot e^{-st} dt}_{L[f'(t)]} = -f'(0)+s cdot F[f'(t)] Rightarrow$

$ L[f''(t)] = s^2 cdot F(s) -s cdot f(0) - f'(0), mathbf{(2.5.10)}$

Если при $t=0, f(t) и f'(0)$ равны нулю (нулевые начальные условия), то:

$L[f''(t)] = s^2 cdot F(s) mathbf{(2.5.10.a)}$

Обобщая на производную n-го порядка при нулевых начальных условиях, имеем:

$L[f^{(n)}(t)] = s^n cdot F(s) mathbf{(2.5.11)}$

2.5.2. Использование преобразования Лапласа для операции интегрирования

Пусть известно $f(t)$ и его изображение по Лапласу: $f(t) longrightarrow F(s), $ выведем выражение для $ L[int f(t) ]$.

$L[int f(t)dt] = int_0^{infty}[f(t)dt] cdot e^{-st}dt Rrightarrow left { begin{array} e^{-st}dt = dv; Rightarrow v = - frac{1}{s}e^{-st}; int f(t)dt = u; Rightarrow du =f(t)dt; end{array} right. Rightarrow$

$[-1 frac{1}{s}e^{-st} cdot int f(t) dt] mid_0^{infty} + frac{1}{s} underbrace{int_0^{infty}f(t) cdot e^{-st} dt}_{F(s)} = frac {1}{s}F(s)+frac {1}{s}[int f(t) dt ] mid_0$

Окончательно:

$L[int f(t)dt] =frac {1}{s}F(s)+underbrace{frac {1}{s}[int f(t) dt ] mid_0}_{добавка н.у} mathbf{(2.5.12)}$

Если начальные условия равные нулю, то:

$L[underbrace{ intintint}_{n-раз} f(t)dt] =frac {1}{s^n}F(s) mathbf{(2.5.13)}$

Таким образом, операция интегрирования в оригинале функции приводит появлению в её изображении “добавке”, равной 1/s.

2.6. Основные свойства преобразований Лапласа

2.6.1. Свойство линейности

Пусть есть процессы описываемые функциями $f_1(t)$ и $f_2(t)$, каждый из которых имеет свое изображение по Лапласу: $f_1(t) longrightarrow F_1(s); f_2(t) longrightarrow F_2(s);$. Если $f(t) = f_1(t) pm f_2(t) $ то:

$L[f(t)]=L[f_1(t) pm f_2(t)] = F_1(s) pm F_2(s) mathbf{(2.6.1)}$

Если $f(t)= a cdot f_1(t)$, то:

$L[f(t)] = L[a cdot f_1(t)] = a cdot L[f_1(t)]= a cdot F_1(s) mathbf{(2.6.2)}$

2.6.2. Свойство подобия (свойство изменения масштаба)

Пусть $f(t) longrightarrow F(s)$ — известно, необходимо найти $L[f(a cdot t)]$

$L[f(a cdot t)] = frac{1}{a} int_0^{infty} f(a cdot t) cdot e^{-st cdot frac{a}{a}}d(at) = frac{1}{a} int_0^{infty} f(a cdot t) cdot e^{-frac{s}{a} cdot at}d(at) Rightarrow$

$L[f(at)]= frac{1}{a} F(frac{s}{a}) mathbf{(2.6.3)}$

2.6.3. Свойство запаздывания (теорема запаздывания)

Пусть $f(t) longrightarrow F(s)$ — известно, необходимо найти $L[f(t - tau )]$

Рисунок 2.6.1 – Иллюстрация переходного процесса с запаздыванием

$L[f(t - tau)] = int_0^ infty f(t -tau)e^{-s[t- tau+ tau]}d(t- tau) = e^{-s cdot tau} underbrace{int_0^infty f(t -tau)e^{-s[t- tau]}d(t- tau)}_{F(s)} $

$L[f(t pm tau)] = F(s) cdot e^{pm scdot tau} mathbf{(2.6.4)}$

2.6.4. Свойство смещения в комплексной плоскости

$L[f(t) cdot e^{pm s_0 cdot t}]= F(s pm s_0) mathbf{(2.6.5)} $

2.6.5. Первая предельная теорема

Если $f(t) longrightarrow F(s)$ — известно, а так же существует $lim_{s to infty}f(t)$, то:

$ lim_{t to infty}f(t) = lim_{s to 0}s cdot F(s) mathbf{(2.6.6)} $

Рисунок 2.6.2 – Иллюстрация первой предельной теоремы

Это означает, что оси «t» и «s» формально направлены в противоположные стороны, т.е. чем больше t, тем меньше s и наоборот.

2.6.6.Вторая предельная теорема

$lim_{t to 0}f(t)= lim_{s to infty}s cdot F(s) mathbf{(2.6.7)}$

2.7. Способы нахождения обратных преобразований Лапласа по известному изображению

Вычисление оригиналов по известному (данному) изображению можно выполнить:
— по соответствующим таблицам преобразований Лапласа;
— по формулам Хэвисайда;
— разложением на элементарные дроби;
— другими способами.

В математических справочниках приводятся обширные таблицы, по которым можно найти оригиналы большинства изображений. Приведем основыные преобразования:

Таблица основных преобразований Лапласа

Однако, нередко бывают и случаи, когда необходимое преобразование отсутствует в таблицах. В этом случае используются различные специальные способы.

Например, если изображение F(s) можно представить в виде отношения полиномов по степеням «s», то наиболее общим и эффективным способом поиска оригинала является формула Хэвисайда.

Если $F(s) = frac{D_1(s)}{D_0(s)}$, где $D_1(s)$ и $D_0(s)$ – полиномы по степеням «s», то:

$ f(t)=sum_{j=1} frac{1}{(k_j-1)!} cdot lim_{s to s_j} frac{d^{k_j-1}}{ds^{k_j-1}}[(s-s_j)^{k_j} cdot F(s) cdot e^{st}], mathbf{(2.7.1)}$

где $s_j$ – полюса изображения, т.е. те значения «s» при которых полином $D_0(s)$ обращается в ноль;
$k_j$ – кратность j – го полюса.

Если уравнение $D_0(s)=0$ имеет n различных корней, то это означает что полюса F(s) имеют кратность, равную единице, т.е. нет повторяющихся полюсов.

Необходимо отметить, что использование формулы (2.7.1) будет корректно только в том случае, когда степень полинома $D_0(s)$ выше степени полинома $D_1(s)$. Если степени равны, то необходимо выделить целую часть (разделив «в столбик» полиномы) и чисто дробную часть, после чего для чисто дробной части корректна формула (2.7.1).

2.8 Некоторые способы нахождения оригинала по известному изображению

В качестве иллюстрации возможностей формулы Хэвисайда рассмотрим следующий пример:

Пример 1. Предположим, что изображение F(s) некоторого неизвестного процесса f(t) равно:

$F(s) = frac{A}{S^2(T cdot S+1)}; F(s) to f(t)=?$

$D_1(s) = A; D_0(s) = s^2(Ts+1)$

Найдем полюса:

$D_0(s) = s^2(Ts+1) Rightarrow S_1 =-frac{1}{T}; S_2=S_3=0; $

$ f(t) = S_1+S_2 для j=1; S_1=- frac{1}{T} Rightarrow lim_{s to -frac{1}{T}}[(s+frac{1}{T})cdot frac{A}{S^2(T cdot S+1)} cdot e^{st}] Rightarrow frac{1}{T}cdot frac{A}{frac{1}{T^2}} cdot e^{-frac{t}{T}}=A cdot T cdot e^{-frac{t}{T}}; для j =2,3 frac{1}{(2-1)!}lim_{s to 0} frac{d}{ds}[(s-0)^2 cdot frac{A}{S^2(T cdot S+1)} cdot e^{st}] = lim_{s to 0}[-frac{A}{(TS+1)^2} cdot T cdot e^{st}+t cdot e^{st} frac{A}{TS+1}] = =[-AT +At] Rightarrow f(t) =A cdot T cdot e^{-frac{t}{T}} - A cdot T+A cdot t = A[t - T(1 -e^{-frac{t}{T}})]; $

Рисунок 2.8.1 – График процесса построенный по изображению: $F(s) = frac{A}{S^2(T cdot S+1)}$.

Разложение на элементарные дроби.

$f(t) = ? F(s) = frac{D_1(s)}{D_0(s)}$

Если корни уравнение уравнения $D_0(s) = 0$ различны, т.е. нет совпадающих, то:

$F(s) = frac{D_1(s)}{D_0(s)}=frac{a_1}{s -s_1}+frac{a_2}{s -s_2}+ ..+frac{a_k}{s -s_k} +R(s)$

где $S_i$ — корни уравнения; $R(s)$ — остаточный член (не разлагается на действительные дроби);

$s_1,s_2,...,s_k in R s_{k+1},s_{k+2},...,s_n in C$

Используя свойства линейности преобразований Лапласа, мы можем представить $f(t) $ как сумму преобразований:

$f(t) = f_1(t)+f_2(t)+...+f_k(t)+f_{ост}(t)$

Пример 2

Имеем известное изображение:

$F(s)=frac{s+3}{s^2+3s+2}$

$f(t)$ — оригинал, при нулевых начальных условиях: $t =0, f(0)=0.$

Разложение на элементарные дроби:

$left | begin{gathered} s_1 = -1; s_2 = -2; end{gathered} right. Rightarrow F(s)=frac{a_1}{s+1}+frac{a_2}{s+2}.$

Используя метод неопределенных коэффициентов, приведем полученное выражение к общему знаменателю:

$a_1(s+2)+a_2(s+1) = s+3 left { begin{gathered} a_1+a_2 =1 2 cdot a_1+a_2 = 3 end{gathered} right. Rightarrow left { begin{gathered} a_1 =2 a_2 = -1 end{gathered} right. $

Тогда изображение разложенное на элементарные дроби принимает такой вид, что его решение можно получить из таблиц:

$F(s) = frac{2}{s+1} - frac{1}{s+2} и L^{-1} left[frac{2}{s+1}right] = 2 cdot L^{-1} left[frac{1}{s+1}right] = 2 cdot e^{-t} cdot 1(t) L^{-1} left[frac{1}{s+2}right] = e^{-2t} cdot 1(t) f(t) = f_1+f_2 =(2 cdot e^{-t} -e^{-2t})cdot 1(t) $

Рисунок 2.8.2 – График процесса построенный по изображению:$F(s)=frac{s+3}{s^2+3s+2}$.

Продолжение лекций: 2. Математическое описание систем автоматического управления ч. 2.9 — 2.13

В заключение несколько полезных ссылок теме описанной в этой лекции:

  • Нижегородский государственный университет им. Н.И. Лобачевского. Учебно-методическое пособие ПРЕОБРАЗОВАНИЕ ЛАПЛАСА — www.lib.unn.ru/students/src/Laplace%20transform.pdf
  • Калькулятор Интегралов — www.integral-calculator.ru
  • СФУ Институт Космических и Информационых технологий Лекция ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ К РАСЧЕТУ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ (МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД) — ikit.edu.sfu-kras.ru/files/3/L_10.pdf
  • Понятие полюсов и нулей в передаточных функциях — radioprog.ru/post/765
Источник

1. Понятие об
управлении. Управлением
называется любое действие, вносящее
желаемые изменения в процесс, подлежащий
управлению. Под процессом
понимается нечто, изменяющееся качественно
или количественно во времени. Процессы
протекают в объектах различного вида.
Объекты бывают технические, экономические,
биологические, человеческие коллективы
и т.д. Нас интересуют технические объекты
и технологические процессы, протекающие
в этих объектах.

Желаемое
изменение процесса, имеющего место в
объекте, определяется целью
управления.
Цели управления весьма разнообразны.

Объектом
управления
или управляемой
системой
называется техническое устройство,
выходные параметры которого необходимо
изменять по желаемому закону. Выходные
параметры объекта управления называются
выходными
величинами или управляемыми величинами.

Все внешние
воздействия, оказывающие влияние на
ход управляемого процесса, другими
словами, на объект управления, можно
разделить на полезные и «вредные».

Полезные внешние
воздействия, которые дают возможность
обеспечить протекание процесса в нужном
русле, называются управляющими
воздействиями.
Это контролируемые воздействия,
приложенные к объекту управления,
позволяет изменять ход процесса в
желаемом направлении. За их счет
реализуется цель управления.

Обычно другие
«вредные» внешние как контролируемые,
так и неконтролируемые воздействия,
изменяющие состояние объекта нежелательным
образом, называются возмущающими
воздействиями.
Почему происходят нежелательные
отклонения, причем неопределенные?

В случае корабля
положение руля и мощность сигналов,
поступающих на двигатели, являются
управляющими воздействиями. Их изменение
приводит к желаемым значениям некоторых
выходных сигналов, например курса и
скорости движения. Ветер, волны и течение
являются возмущающими воздействиями,
т.к. они стремятся нежелательным образом
повлиять на управляемые величины:
местоположение, курс и скорость корабля.
Кроме того, возмущения вызывают усиление
таких движений корабля как бортовая и
килевая качки, вертикальное перемещение.

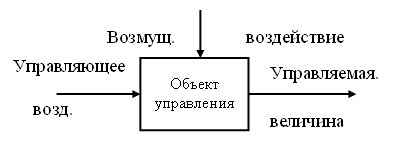
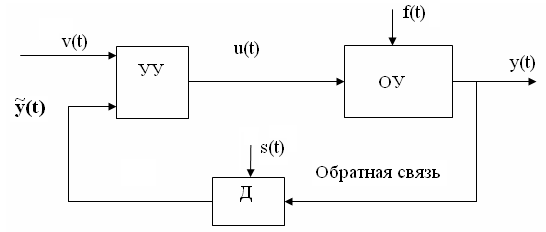
В общем случае
связь между управляющими воздействиями,
возмущающими воздействиями, объектом
управления и управляемыми величинами
показана на рисунке ниже.

В

зависимости от способа формирования
управляющего воздействия различают:

1. Ручное
управление.
Осуществляется оператором, недостатки:
низкая точность, малое быстродействие.

2. Автоматизированное
управление.
Осуществляется оператором с помощью
ЦВМ. При этом оператор принимает решения,
анализируя результаты, получаемые от
ЦВМ, ЦВМ выступает как советник. Другое
название — супервизорное управление.

3. Автоматическое
управление.
Осуществляется техническими средствами
без непосредственного участия человека.
Самодействующее управление.

Техническое
устройство, с помощью которого
осуществляется автоматическое управление,
т.е. вырабатывается управляющее
воздействие, называется управляющим
устройством.
(УУ) или регулятором.

При автоматическом
управлении УУ соединяется с объектом
управления. Совокупность взаимосвязанных
между собой объекта управления (ОУ) и
управляющего устройства (УУ) называется
системой
автоматического управления (САУ).

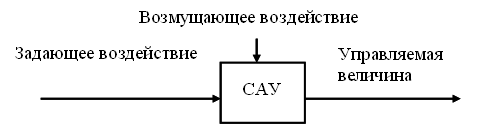
Информация о цели
управления вводится в САУ с помощью
задающего
воздействия.

В общем случае все
эти воздействия и САУ связаны между
собой, как показано на рис. выше, и
являются векторными сигналами.

Пример.

Пусть объект
управления: помещение. Управляемая
величина: температура.

Нужно обеспечить
стабилизацию температуры, чтобы она
была постоянной. Возмущающие воздействия
– окружающая среда оказывает влияние
через окна и стены (температура горячей
воды, температура окружающего воздуха,
направление и скорость ветра).

  1. Ручное управление.

Управляющее
воздействие – изменение расхода горячей
воды с помощью вентиля (управляющего
органа), степень открытия вентиля.

2. Автоматическое
управление.
Первое требование для управления
(регулирования) температурой в помещении
иметь устройство (датчик), которое
определяет или «чувствет» изменения
температуры. Второе требование – надо
иметь устройство (управляющее устройство),
которое изменяет подводимую в помещение
теплоту (тепловую энергию).

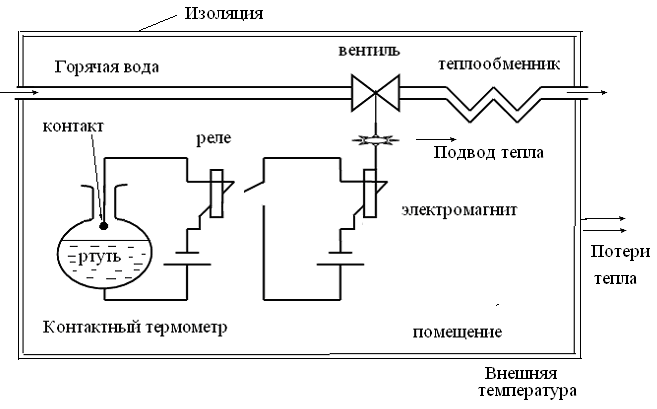
П
рерывистое
управление. Физическая реализация
системы автоматического регулирования
температуры показана на рис. ниже.

Система работает
следующим образом. Если температура в
помещении повысилась относительно
желаемого значения, столбик ртути в
термометре (датчике) поднимается,
достигает контакта, замыкается токовая
цепь, включается реле, затем срабатывает
электромагнит, вентиль закрывается,
отопление отключается. Через некоторое
время температура в помещении падает,
столбик ртути опускается, отключается
реле, вентиль открывается. Такая система
работает только на охлаждение температуры.

Вопрос №2.
Определение порядка астатизма по
передаточной функции разомкнутой
системы.

Рассмотрим замкнутую систему с единичной
обратной связью и с порядком астатизма,
равным ν, которая в разомкнутом
состоянии имеет передаточную функцию


.

Действительно, передаточная функция
по ошибке


,

где


.

Следовательно, коэффициент статической
ошибки согласно

будет равен:

Полагая ν≥1, разложим

в ряд Маклорена в окрестности точки
р=0:

Так как

,
то


Приравнивая коэффициенты при одинаковых
степенях р у двух последних выражений,
получаем

Следовательно, для системы с единичной
обратной связью, содержащей ν
интегрирующих звеньев, первые ν
коэффициентов ошибок обращаются в нуль,
т.е. такая система имеет ν-ый порядок
астатизма.

Определение астатической системы
порядка ν как системы, у которой
первые ν коэффициентов ошибок равны
нулю, является более общим, чем ее
определение как системы, имеющей ν
интегрирующих звеньев.

Ненулевые коэффициенты ошибок Сi
обязательно включают в себя в качестве
делителя коэффициент усиления системы.
Поэтому с увеличением коэффициента
усиления величина ненулевых коэффициентов
ошибок уменьшается.

Нужно отметить, что для системы с
единичной обратной связью основное
значение в вопросе обеспечения заданной
точности имеют коэффициент усиления и
порядок астатизма. Однако, стремление
увеличить коэффициент усиления и (или)
порядок астатизма может повлечь за
собой дестабилизацию системы.

Вопрос №3 Основные принципы управления.

Применяют два основных принципа
управления: один из них приводит к
разомкнутой системе, второй – к замкнутой
системе.

2. Замкнутые системы (системы с обратной
связью (ОС))

Остановимся на двух законах управления,
используемых в замкнутых системах.

а) Управление с прямой и обратной
связью.

Функциональная схема замкнутой системы:

В данной системе используется
информация о результатах управления.
Она заключена в ОС. Информацию содержит

.

Закон управления с прямой и обратной
связью:


.

Используется только информация прошлая
и текущая (в настоящий момент времени).
Замкнутые системы обладают более высоким
качеством и большей точностью, чем
разомкнутые, т.к.:

  1. Уменьшает влияние неопределенности и
    изменчивости свойств ОУ на управляемую
    величину (обеспечивают робастность).

  2. Снижают эффект, обусловленный возмущающим
    воздействием.

  3. Позволяют изменять реакцию системы на
    задающее воздействие.

  4. Дают возможность управлять неустойчивыми
    ОУ.

К недостаткам замкнутых систем следует
отнести проблемы, порождаемые обратной
связью, а именно, обеспечение устойчивости
(обратная связь может дестабилизировать
систему) и помехоустойчивости (возникает
проблема уменьшения влияния шума
измерения).

Управляющее устройство проектируется
так, чтобы обеспечить компромисс между
требованиями, предъявляемыми к
робастности, точности воспроизведения
задающего воздействия, виду реакции на
внешние воздействия, и устойчивостью
системы.

б) Принцип управления по ошибке (по
отклонению)

Этот принцип называют принципом
Ползунова-Уатта.

Пусть

и ошибка

.

Тогда закон управления по ошибке
имеет вид:

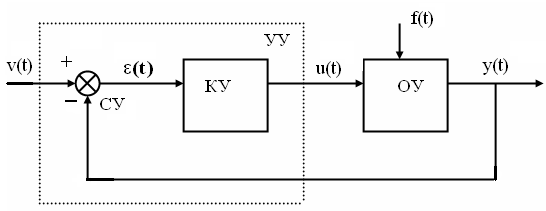
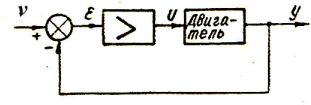
Функциональная схема системы, в которой
используется закон управления по ошибке:

Управляющее устройство (УУ) состоит из
сравнивающего устройства (СУ), определяющего
ошибку управления, и корректирующего
устройства (КУ), вырабатывающего
управляющее воздействие.

Философия таких систем весьма прозрачна:

Независимо от причины возникновения
ошибки УУ система стремится свести эту
ошибку к нулю. В сущности управляющее
устройство работает, используя
лингвистические правила:

Если ошибка больше нуля, то управление
положительное, Если ошибка меньше нуля,
то управление отрицательное, Если ошибка
равна нулю, то управление равно нулю.

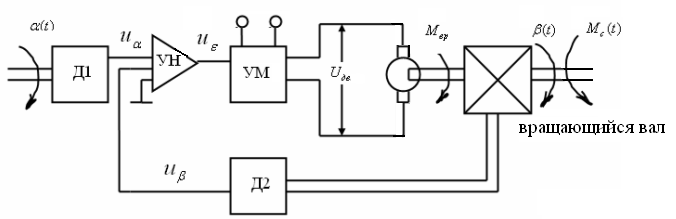
Пример. Электромеханическая следящая
система.

Здесь

(t)
— момент сопротивления,

(t)
— момент вращения.

Двигатель с вращающим валом является
ОУ. Цель управления состоит в обеспечении
примерного равенства углов поворота
задающей оси и следящего (вращающегося)
вала, т.е.

,
причем угол

изменяется случайным образом. С помощью
датчика Д1 в систему вводится информация
о цели управления. Задающий сигнал

,
где

— коэффициент пропорциональности. За
счет датчика Д2 система получает
информацию о результатах управления.
Его выходная величина

пропорциональна управляемой величине

и является сигналом ОС.

Дифференциальный усилитель напряжения
(УН) служит для вычисления разности
напряжений

и

,
и ее последующего усиления, так что его
выход

.

С учетом выражений для

и

сигнал рассогласования

оказывается пропорциональным отклонению
(ошибке, рассогласованию)
.

К двигателю подводится управляющее
воздействие


,представляющее
собой преобразованный усилителем
мощности (УМ) сигнал рассогласования.
Как видим, управляющее воздействие
пропорционально ошибке. Следовательно,
в системе используется принцип управления
по ошибке.

Система работает следующим образом.

Если

>0,
то

>
,
при этом сигнал рассогласования

>0,
усиленный УН и УМ, поступает на двигатель,
как

>0,
создается момент, ускоряющий вращение
вала в необходимую сторону, и вал начинает
«догонять» задающую ось; если ошибка
отрицательна

<0,

>
,
при этом

<0,
то

<0,
то к валу двигателя прикладывается
момент противоположного знака, и следящий
вал тормозится.

Для данной системы возмущающим
воздействием является момент сопротивления
(нагрузки) на валу двигателя.

В описанной простейшей системе
функции управляющего устройства сводятся
к вычитанию сигналов двух датчиков и
умножению разности (сигнала ошибки) на
постоянный коэффициент, равный
произведению коэффициентов усиления
усилителей напряжения и мощности. Как
мы убедимся в дальнейшем, для высокого
качества управления (малости ошибки)
приходится усложнять эти функции, вводя
в закон управления производные и
интегралы от ошибки.

Установившееся
значение ошибки воспроизведения в ряде
случаев определяется с помощью известной
в операционном исчислении теоремы о
конечном значении, которая применительно
к данному случаю может быть записана в
видеεуст=
(8)

Преобразование
Лапласа ε(р) ошибки легко найти, если
известны преобразование Лапласа v(р)
входного сигнала и передаточная функция
для ошибки Фε(р),
связанная с передаточной функцией Ф(р)
замкнутой системы соотношением

Фε(р)=1-Ф(р) (9)Действительно,
согласно (4)ε(р)=Фε(р)v(p)(10)

Принимая
во внимание существующую связь между
передаточными функциями замкнутой Ф(р)
и разомкнутой W(р)
системФ(р)=W(p)/(1+W(p)),а
также, что
,на
основании (9) имеемФε(р)=

Передаточная
функция по ошибке называется также
функцией чувствительности.

Следовательно,
(11)

Учитывая,
что W0(p)
обладает свойством W0(0)=1
получаем
(12)

Выражение
(12) имеет смысл, если ε(t)
стремится к определенному пределу при
t→∞.
В противном случае выражение (8)
неприменимо. Рассмотрим от каких факторов
зависит ошибка εуст
при типовых входных сигналах, для которых
вышеуказанное требование соблюдается.

Входной
сигнал – ступенчатая функция v(t)=a01(t).

Операторное
выражение такой функции v(p)=a0/p.
При этом

(13)

Если
ν=0 (система не содержит интегрирующих
звеньев), то

(14)

Следовательно,
в такой системе, даже при постоянном
входном сигнале, имеет место ошибка,
называемая ошибкой по положению или
статической ошибкой. Ошибка

при известном а0
определяется статизмом системы
(15)

и
она тем меньше, чем больше коэффициент
усиления k.

Системы,
обладающие статической ошибкой,
называются статическими системами.
Коэффициент усиления k
статических систем является безразмерной
величиной, так как величины а0
и εуст
имеют одинаковую размерность.

Отметим,
что статическая ошибка, определяемая
выражением (14), является принципиальной
(методической) ошибкой и обусловлена
принципом действия системы.

Если
ν>1 (система содержит одно или несколько
интегрирующих звеньев), то, как это видно
из выражения (13), статическая ошибка
равна нулю. Системы, обладающие нулевой
статической ошибкой, называются
астатическими системами. При этом
величина ν, как говорят, определяет
порядок астатизма системы.

Астатическую
систему можно рассматривать как
статическую систему с бесконечно большим
коэффициентом усиления k.
Действительно, наличие интегрирующих
звеньев приводит к тому, что при постоянном
входе сигнал на выходе разомкнутой
системы с течением времени растет до
бесконечности.

Входной
сигнал v(t)=a1t,
изменяющийся с постоянной скоростью
a1.

В
этом случае v(p)=a1/p2,
а установившаяся ошибка


(16)

Если
ν=0 (статическая система), то εуст=∞.
Полученному результату легко дать
объяснение, если учесть, что в установившемся
режиме, т.е. при t→∞,
на входе системы имеется бесконечно
большой сигнал и поэтому при конечном
коэффициенте усиления k,
согласно (14), ошибка εуст
равна бесконечности. Другими словами,
данный случай можно рассматривать как
предыдущий при v(t)=a0,
если положить a0=∞.

Если
ν=1 (система с астатизмом первого порядка),
то


(17)

При
этом ошибка εуст
обратно пропорциональна коэффициенту
усиления и носит название скоростной
ошибки. Так как входной сигнал v
и ошибка ε имеют одинаковую размерность,
то коэффициент усиления системы с
астатизмом первого порядка имеет
размерность [сек-1]
и характеризует установившуюся скорость
изменения выходной величины разомкнутой
системы при постоянном входном сигнале.

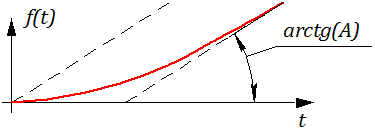
Физический
смысл полученного результата виден на
примере простейшей следящей системы
(рис. 1). Если на входе имеем сигнал v,
изменяющийся с постоянной линейной
скоростью a1,
то установившийся режим будет иметь
место лишь в случае, когда выходная
величина у будет изменяться с той же
скоростью а1.

Р
ис.
1

Но
для этого необходимо подвести к двигателю
определенное напряжение U=a1/Kдв,
зависящее от коэффициента усиления
двигателя Кдв.
Это напряжение может появиться только
при наличии сигнала ошибки εуст.
Чем больше коэффициент усиления усилителя
Кус,
а следовательно, и всей системы –
К=КусКдв,
тем меньшее значение εуст=а1/Кус
требуется для вращения двигателя со
скоростью, равной скорости изменения
входного сигнала.

Используя
выражение (17), по заданным значениям
скорости а10
и скоростной ошибки (εск)доп
можно найти величину коэффициента
усиления


(18)обеспечивающую
требуемую точность воспроизведения
сигнала v(t)=a10t.

Если
ν≥2 (система с порядком астатизма выше
первого), то скоростная ошибка равна
нулю.

Входной
сигнал

,
изменяющийся с постоянным ускорением
а2.

Так
как

,
то ошибка с учетом (12)


(19)

Если
ν=0, 1, то установившаяся ошибка равна
бесконечности. Если ν=2 (система с
астатизмом второго порядка), то ошибка
определяется выражением


(20)

и
носит название ошибки по ускорению. Как
видно их этого выражения, коэффициент
усиления системы с астатизмом второго
порядка имеет размерность [сек-2].

Если
ν≥3, то установившаяся ошибка равна
нулю.

Таким
образом, точность работы САУ при входных
сигналах вида степенной функции


(20а)
зависит только от порядка астатизма ν
и коэффициента усиления k
системы, причем, чем больше значения ν
и k,
тем меньше величина ошибки воспроизведения.

Формулу
(12) для определения ошибки εуст
удобно использовать, если входное
воздействие представляет собой степенную
функцию вида (20а). Однако на практике
часто встречаются входные сигналы,
которые меняются достаточно медленно
по известному, а порой и неизвестному,
законам. Обычно такие сигналы на некотором
текущем интервале времени можно
представить в виде ряда Тейлора. В этом
случае удобно ввести понятие о
коэффициентах ошибок, с помощью которых
нетрудно найти установившуюся ошибку
воспроизведения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #

    15.04.2015104.96 Кб27ТБ.doc

  • #
  • #
  • #
  • #
Источник

C1V –
скоростная ошибка, ошибка от скорости.

С1
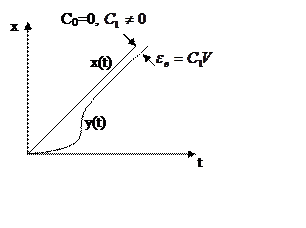
– коэффициент скоростной ошибки.

 

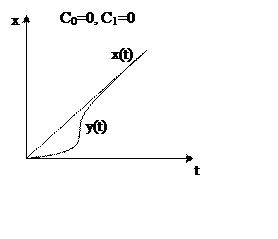q=1, I
порядок астатизма                            Данная система называется системой
с астатизмом второго порядка и она содержит в разомкнутой системе 2 и более
интеграторов.

Определим коэффициент С1 для системы с
первым порядком астатизма

KV – Добротность
системы по скорости.

— статический
коэффициент усиления позиционной части

разомкнутой системы.

Можно сказать, что общее значение

5.2.3 Режим изменения задающей величины с постоянным
ускорением.

Пусть

— ускорение

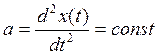
Чтобы система имела  необходимо,
чтоб С0, С1=0, иначе ошибка будет неограниченно расти.

Установившееся значение ошибки

С2 – коэффициент ошибки от ускорения

Система с ошибкой от ускорения

 

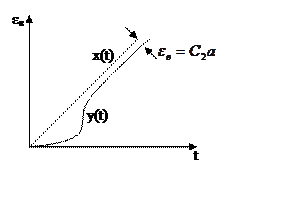Система
с астатизмом второго порядка (q=2), содержит в разомкнутом виде два интегрирующих
звена.

 — позиционная часть разомкнутой
системы.

Система без ошибки от ускорения

Если в системе С2=0, εв=0, то
это система без ошибки от ускорения.

 

                                                      Система
с астатизмом выше второго порядка

                                                      q>2

         Свяжем С2 с передаточной функцией
разомкнутой системы

— коэффициент
усиления позиционной части разомкнутой системы, добротность системы по
ускорению.

5.2.4 Связь астатизма системы с ЛАЧХ разомкнутой
системы.

Порядок астатизма – целое число q, которое равно
порядку в описании входного сигнала , при котором
установившаяся ошибка постоянна и отлична от нуля.

1.

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                  

 

2.

3.

 

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   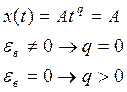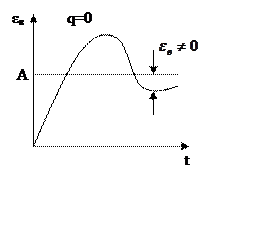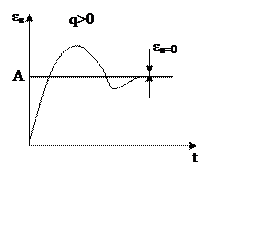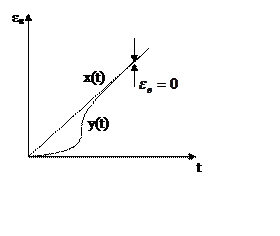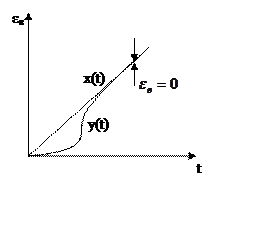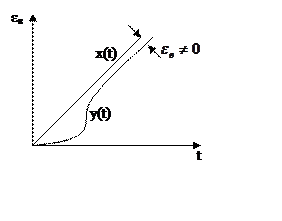q=2                                                                   
q>2

На практике астатизм выше второго порядка (q>2)
не применяется, поэтому мы их не рассматриваем.

5.2.5 Способы определения порядка астатизма

1. По коэффициентам ошибок

2. По количеству интегрирующих звеньев в передаточной
функции разомкнутой системы.

 — позиционная
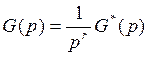
часть системы

Система имеет r интеграторов и q=r

3.По наклону ЛАЧХ в низкочастотной области.

Предположим, что передаточная функция разомкнутой
системы имеет вид

Тогда
ЛАЧХ будет иметь следующий вид.

Пусть 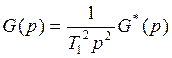, где

 — позиционная
часть

 

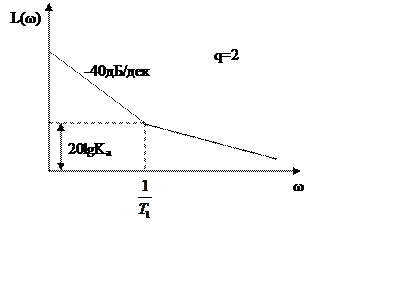Этот случай в жизни практически не встречается

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                    

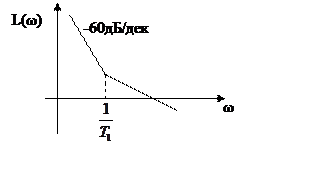
В итоге, астатизм системы определяется по ЛАЧХ
следующим образом

 

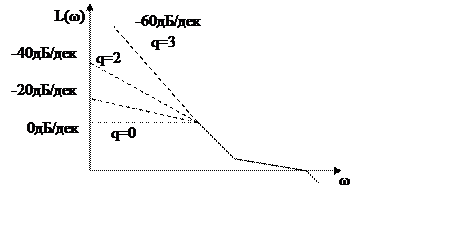5.2.6 Исследование точности в условиях действия
управляющих и возмущающих сигналов

В общем случае на систему действуют как управляющие
(задающие), так и возмущающие сигналы.

Источник

Понравилась статья? Поделить с друзьями:
  • Скоростная ошибка системы
  • Скоростемер кпд ошибки
  • Скоропостижный ответ студента привел к досадной ошибке
  • Скоропостижные выводы речевая ошибка
  • Скорее всего ошибка