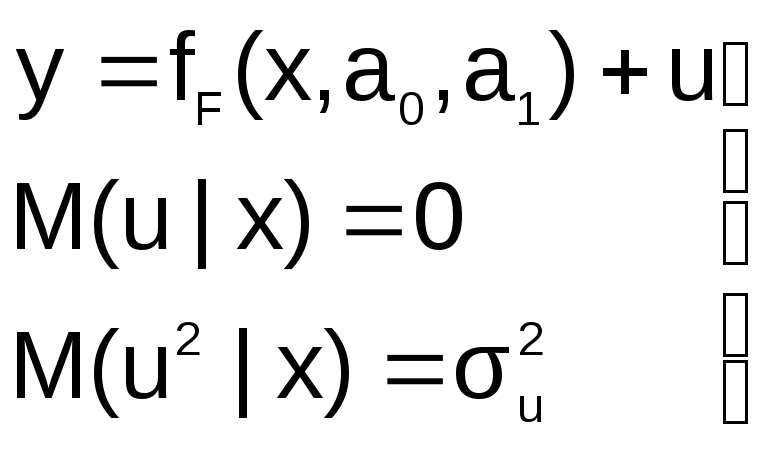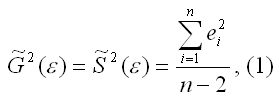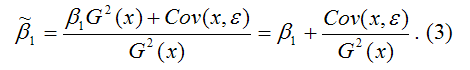Случайная ошибка
Предмет
Статистика
Разместил
🤓 DyArn
👍 Проверено Автор24
неточность, возникшая в процессе статистического наблюдения при установлении или регистрации фактов по чисто случайным причинам.
Научные статьи на тему «Случайная ошибка»
Регрессия в эконометрике
ошибки должны быть равны нулю;
Дисперсия случайной ошибки для всех наблюдений должна быть постоянной…
;
Случайные ошибки не должны иметь между собой статической зависимости;
Объясняющая переменная x должна…
Согласно первому условию, случайная ошибка не должна систематически смещаться….
Второе условие – это наличие в каждом наблюдении только одного значения дисперсии случайной ошибки….
Дисперсия – это возможное изменение случайной ошибки до проведения выборки.

Статья от экспертов
Исследование составляющих ошибки для решения обратной задачи с использованием случайных проекций
Проведен сравнительный анализ решений дискретных некорректных обратных задач, полученных в результате оцифровки интегрального уравнения (задача Carasso, Delves, Phillips). Использовались методы псевдообращения и регуляризации Тихонова и эти же методы с использованием дополнительного проецирования случайной матрицей. Исследована зависимость составляющих ошибки решение (смещение и дисперсия) от размерности матрицы проектора. При использовании проецирования метод псевдообращения продемонстрировал точность на уровне регуляризации Тихонова
Статистические методы определения ожидаемой ошибки в аудите
, содержащиеся в генеральной совокупности, равновозможные и распределяются случайным образом….
берется нормальное распределение вероятностей случайной величины — размера ошибки элементов выборки….
Согласно теории вероятности известна информация о случайной величине….
величину, то случайная величина считается распределенной по нормальному закону….
Но для того чтобы определить ожидаемую ошибку потребуется большое количество расчетов.

Статья от экспертов
Применение фильтра Калмана для решения задачи численного дифференцирования при случайных ошибках измерений
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек
Возможные ошибки спецификации модели:
1. Неправильный выбор вида уравнения
регрессии
2. В уравнение регрессии включена лишняя
(незначимая) переменная
3. В уравнении регрессии пропущена
значимая переменная
-
Неправильный выбор вида функции в
уравнении
Пусть на первом этапе была сделана
спецификация модели в виде:
в
которой функция fF(x,a0,a1)
выбрана не верно. Предположим, что
yT=fT(x,a0,a1)+v
– правильный вид функции регрессии.
Тогда справедливо выражение:
И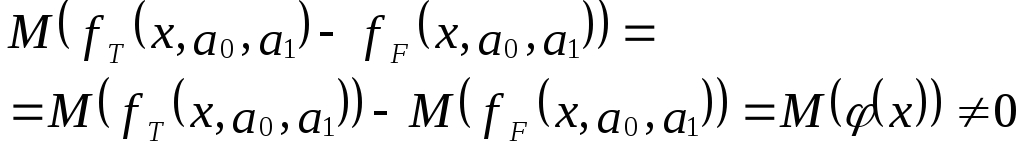
выражения следует:
Иными словами, математические ожидания
эндогенной переменной, полученные с
помощью функций fT
и fF
не совпадают, т.е. первая предпосылка
теоремы Гаусса-Маркова M(ulx)=0
не выполняется
Следовательно, в результате оценивания
такой модели параметры а0 и а1
будут смещенными
Симптомы наличия ошибки спецификации
первого типа:
1. Несоответствие диаграммы рассеяния,
построенной по имеющейся выборке виду
функции, принятой в спецификации
2. В динамических моделях длительно
сохраняется знак значений оценок
случайных возмущений у смежных (по
номеру t ) уравнений
наблюдений
Именно этот симптом и улавливается
статистикой DW Дарбина–Уотсона!
В силу данного обстоятельства тесту
Дарбина–Уотсона в эконометрике придается
большое значение.
Способ устранения: выбор другой формы
спецификации модели. Например, нелинейная
вместо линейной и т.д.
2. В уравнение регрессии включена
лишняя переменная
П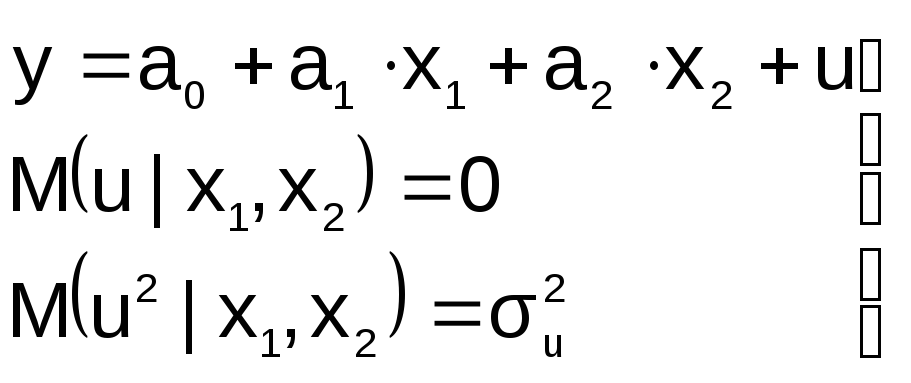
на этапе спецификации в модель включена
«лишняя» переменная, например, X2
«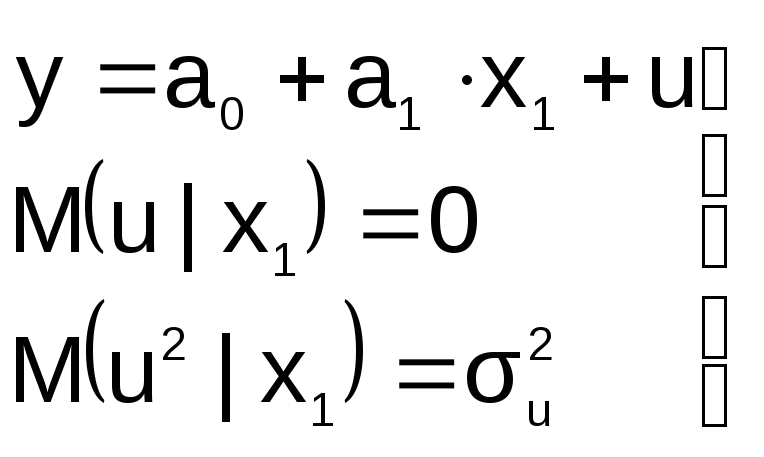
спецификация должна иметь вид:
Последствия:
1.
Оценки параметров а0, а1, а2
останутся несмещенными, но потеряют
свою эффективность (точность)
2. Увеличивается ошибка прогноза по
модели
как за счет ошибок оценок коэффициентов
и σu,
так и за счет последнего слагаемого.
Это особенно опасно при больших абсолютных
значениях регрессора
Диагностика:
В моделях множественной регрессии
необходимо для каждого коэффициента
уравнения проверять статистическую
гипотезу H0: ai=0.
Вспомним, что для этого достаточно
оценить дробь Стьюдента и сравнить ее
значение с критическим значением
распределения Стьюдента, которое
вычисляется по значению доверительной
вероятности и значению степени свободы
n2 = n – (k+1)
3.
В модели не достает важной переменной
Последствия такие же, как и в первом
случае: получаем смещенные оценки
параметров модели
Для устранения необходимо вернуться к
изучению особенностей поведения
экономического объекта, выявить опущенные
переменные и дополнить ими модель
29. Фиктивные переменные и особенности их использования в моделях.
На практике приходится учитывать в
моделях факторы, носящие качественный
характер, значения которых в наблюдениях
не возможно измерить с помощью числовой
шкалы.
Примеры.
Моделирование влияния пола специалистов
на уровень зарплаты.
Моделирование доходов граждан от типа
учебного заведения, в котором он получил
образование (государственное, частное,
специализированное,…)
Модель инфляции с учетом различных
видов регулирования со стороны государства
Возможны два подхода к решению задачи:
— построить несколько моделей отдельно
для каждого значения (градации)
качественной переменной
— учесть влияние качественного фактора
в одной модели
Второй способ представляется более
прогрессивным, т.к в этом случае появляется
возможность оценить статистическую
значимость влияния данного фактора на
поведение эндогенной переменной на
фоне других факторов, внесенных в
спецификацию модели
Пример. Изучается зависимость
расходов на образование «С» в «обычных»
и «специализированных» школах в
зависимости от числа учащихся N
Предположим:
-
Зависимость затрат на обучение от
количества учащихся N в
обоих типах школ одинакова
2. Разница в затратах объясняется
необходимостью приобретения
специализированного оборудования для
обучения специальным дисциплинам
Тогда если строить различные модели
для каждого типа школ, то спецификацию
моделей можно записать в виде:
Yo
= a0 +
a1N +u
Ys
= b0 +
a1N +
v
О
модели можно объединить, если ввести
переменную d, область
определения которой два целых числа :
0 и 1. При этом:
Спецификация такой модели имеет вид:
Y = a0
+ a1N
+ δd + u
Тогда при d=0 получим Yo
= a0 + a1N
+ u
при d=1 получим Ys
= (a0+δ)
+a1N +
v
d – фиктивная переменная
сдвига
Фиктивные переменные часто применяются
при построении динамических моделей,
когда с определенного момента времени
начинает действовать какой-либо
качественный фактор
Пусть некоторый качественный фактор
имеет несколько градаций (более 2-х)
Введение в модель фиктивных переменных
с несколькими градациями рассмотрим
на примере шанхайских школ, где имеются
4 категории школ: общеобразовательные,
технические, ПТУ и специализированные
Казалось достаточно ввести фиктивную
переменную сдвига d, придав
ей четыре различных значения и проблема
будет решена
Такой подход мало эффективен, т.к не
удается оценить статистическую значимость
влияния каждой градации на значения
эндогенной переменной
В этом случае имеет смысл ввести отдельную
переменную для каждой градации фактора
Н
Однако, если взять спецификацию модели
в виде:
Y=a0
+ a1d1+a2d2+a3d3+a4d4+a5N+u
при этом всегда верно тождество
d1+d2+d3+d4=1
Это означает, что матрица Х коэффициентов
системы уравнений наблюдений будет
коллинеарной т.к в ней присутствует
столбец из 1, и как следствие отсутствует
возможность применения МНК для оценки
параметров модели.
Предлагается в спецификацию ввести
(к-1) фиктивную переменную (к- кол-во
градаций), сделав одну из градаций
базовой, относительно которой изучать
влияние остальных градаций. Проблемы
мультиколинеарности в этом случае не
возникает
Для учета возможного изменения наклона
графика модели при изменении градации
качественного фактора предлагается
ввести в спецификацию модели еще одно
слагаемое вида «d умноженное
на x»
Вернемся к примеру изучения зависимости
расходов на образование в различных
школах. Для простоты ограничимся лишь
двумя градациями фактора «тип школы»:
d=0 – обычная школа;
d=1 – профессиональная
школа
Спецификацию модели следует записать
в виде:
Y = a0
+ a1N
+ a2*d
+ a3dN
+U
50
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
анастасия александровна янченко
Эксперт по предмету «Эконометрика»
Задать вопрос автору статьи
Проблема спецификации эконометрической модели
Проблема спецификации эконометрической модели предполагает определение:
- конечной цели моделирования;
- набора эндогенных и экзогенных переменных;
- состава и структуры системы уравнений, набора переменных;
- первоначальных ограничений стохастических составляющих.
Спецификация в эконометрике является важнейшим этапом исследования, эффективность решения влияет на успех исследования в целом. В основе спецификации — имеющиеся теории, интуиция и специальные знания.
Проблема идентифицируемости
В эконометрике проблема идентифицируемости сводится к следующему: нас интересует такие эндогенные переменные, которые относятся к случайным величинам.
Уравнение структурной формы является точно идентифицируемым тогда, когда каждый участвующий неизвестный коэффициент однозначно восстанавливается по коэффициентам приведенной формы, не ограничивая значения последних.

Учим создавать игры
Создавай 3D-графику и концепты, придумывай персонажей, учись программировать с нуля
Записаться на курс
Определение 1
Эконометрическую модель можно назвать точно идентифицируемой, если каждое уравнение ее структурной формы является точно идентифицируемым.
Если какой-либо коэффициент не может быть восстановлен, не идентифицируемо и уравнение, и модель. Проблемы идентификации сводятся к «настройкам» модели по реальным статистическим данным.
Проблема верификации
Замечание 1
Проблема верификации применительно к эконометрическим моделям заключается в разрешении вопросов относительно возможностей использования модели.
Иными словами эта проблема сводится к точности имитационных и прогнозных расчетов. Верификация подразумевает статистическую проверку гипотез и анализ параметров точности оценки. Зачастую применяется ретроспективный расчет: исходные данные делятся на части: обучающая выборка и экзаменующая выборка.
«Проблемы эконометрики» 👇
Обучающая выборка позволяет определить значения неизвестных параметров и получить модельные значения для экзаменующей выборки, которые затем подлежат сравнению с реальными значениями.
Недостаточный набор данных
Замечание 2
Проблема недостаточности данных заключается в том, что имеющиеся данные могут быть недостаточны для определения функциональной связи между переменными, или они мало варьируются для выявления отличий влияния одних факторов от влияния других.
Последнюю проблему в эконометрическом моделировании часто называют «мультиколлинеарностью».
В отличие от экспериментальной науки, отдельный исследователь, изучающий экономические процессы обычно не имеет возможности заметно повлиять на них.
Для восполнения недостатка данных, исследователь должен принимать определенные априорные допущения, которые часто могут быть недостаточно обоснованными.
Обычно функциональная форма эконометрической модели неизвестна заранее. В таком случае целесообразно использовать непараметрические методы оценивания. Но применение подобных методов требует достаточно значительного набора данных. На практике поэтому, как правило, предполагается, что зависимость двумя переменных линейна. Это связано с тем, что линейная зависимость подразумевает хороший уровень аппроксимации гладкой зависимости в определенной окрестности. Однако нет никаких гарантий, что истинная зависимость не будет нелинейной в интервале, к которому отнесены данные.
В случае применении методов эконометрики следует понимать, что обычно постулируемые свойства имеют асимптотический характер, или проявляются при стремлении числа наблюдений к бесконечности. Например, если линейная регрессия подразумевает использование в качестве регрессоров лагов (запаздывания) зависимых переменных, то, даже при выполнении стандартных предположений регрессионного анализа, итоговые оценки будут смещенными, но состоятельными.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Шпоры по эконометрике.
№ 1. СПЕЦИФИКАЦИЯ МОДЕЛИ
Простая регрессия представляет собой регрессию между двумя переменными у и х, т.е. модель вида , где у результативный признак; х — признак-фактор.
Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида
Спецификация модели — формулировка вида модели, исходя из соответствующей теории связи между переменными. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. где yj фактическое значение результативного признака;
yxj -теоретическое значение результативного признака.
случайная величина, характеризующая отклонения реального значения результативного признака от теоретического.
Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным у.
К ошибкам спецификации относятся неправильный выбор той или иной математической функции для, и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной.
Ошибки выборки — исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками.
Ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
В парной регрессии выбор вида математической функции может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным.
Графический метод основан на поле корреляции. Аналитический метод основан на изучении материальной природы связи исследуемых признаков.
Экспериментальный метод осуществляется путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях. Если фактические значения результативного признака совпадают с теоретическими у =, то Docm =0. Если имеют место отклонения фактических данных от теоретических (у ) то .
Чем меньше величина остаточной дисперсии, тем лучше уравнение регрессии подходит к исходным данным. Число наблюдений должно в 6 7 раз превышать число рассчитываемых параметров при переменной х.
№ 2 ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ.
Линейная регрессия сводится к нахождению уравнения вида или .
Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.
Построение линейной регрессии сводится к оценке ее параметров а и в.
Оценки параметров линейной регрессии могут быть найдены разными методами.
1.
2.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Формально а значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а < 0.
Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэффициента корреляции.
Линейный коэффициент корреляции находится и границах: -1≤.rxy ≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и наоборот при b<0 -1≤.rxy ≤0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
№ 3. МНК.
МНК позволяет получить такие оценки параметров а и b, которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) минимальна:
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. Решается система нормальных уравнений
№ 4. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от средне го значения у на две части — «объясненную» и «необъясненную»:
— общая сумма квадратов отклонений
— сумма квадратов отклонения объясненная регрессией — остаточная сумма квадратов отклонения.
Любая сумма квадратов отклонений связана с числом степеней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из п возможных требуется для образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
F-отношения (F-критерий):
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.
Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.
Стандартная ошибка коэффициента регрессии
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое
затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).
Стандартная ошибка параметра а:
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции тr:
Общая дисперсия признака х:
Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.
Ошибка аппроксимации:
№ 5. ИНТЕРВАЛЫ ПРОГНОЗА ПО ЛИНЕЙНОМУ УРАВНЕНИЮ
РЕГРЕССИИ
Оценка стат. значимости параметров регрессии проводится с помощью t статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t критерия Стьюдента.
Определяется стат. значимость параметров.
ta ›Tтабл — a стат. значим
tb ›Tтабл — b стат. значим
Находятся границы доверительных интервалов.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что п
При проведении регрессионного анализа
основная трудность заключается в том,
что генеральная дисперсия случайной
ошибки является неизвестной величиной,
что вызывает необходимость в расчёте
её несмещённой выборочной оценки.
Несмещённой оценкой дисперсии(или
исправленной дисперсией) случайной
ошибки линейной модели парной регрессии
называется величина, рассчитываемая
по формуле:
где n
– это объём выборочной совокупности;
еi– остатки регрессионной модели:
Для линейной модели множественной
регрессии несмещённая оценка дисперсии
случайной ошибки рассчитывается по
формуле:
где k
– число оцениваемых параметров модели
регрессии.
Оценка матрицы ковариаций случайных
ошибок Cov(ε) будет являться оценочная
матрица ковариаций:
где In
– единичная матрица.
Оценка дисперсии случайной
ошибки модели регрессии распределена
по ε2(хи-квадрат)
закону распределения с (n-k-1)
степенями свободы.
Для доказательства несмещённости оценки
дисперсии случайной ошибки модели
регрессии необходимо доказать
справедливость равенства
Доказательство. Примем без
доказательства справедливость следующих
равенств:
где G2(ε)
– генеральная дисперсия случайной
ошибки;
S2(ε)– выборочная дисперсия случайной
ошибки;
– выборочная оценка дисперсии
случайной ошибки.
Тогда:
т. е.
что и требовалось доказать.
Следовательно, выборочная оценка
дисперсии случайной ошибки
является несмещённой оценкой
генеральной дисперсии случайной ошибки
модели регрессии G2(ε).
При условии извлечения из
генеральной совокупности нескольких
выборок одинакового объёма n
и при одинаковых значениях объясняющих
переменных х,
наблюдаемые значения зависимой переменной
у будут случайным образом колебаться
за счёт случайного характера случайной
компоненты β.
Отсюда можно сделать вывод, что будут
варьироваться и зависеть от значений
переменной у значения оценок коэффициентов
регрессии и оценка дисперсии случайной
ошибки модели регрессии.
Для иллюстрации данного утверждения
докажем зависимость значения МНК-оценки
от величины случайной ошибки
ε.
МНК-оценка коэффициента β1 модели
регрессии определяется по формуле:
В связи с тем, что переменная
у зависит от случайной компоненты ε
(yi=β0+β1xi+εi), то ковариация
между зависимой переменной у
и независимой переменной х
может быть представлена следующим
образом:
Для дальнейших преобразования используются
свойства ковариации:
1) ковариация между переменной
х и
константой С
равна нулю: Cov(x,C)=0,
C=const;
2) ковариация
переменной х
с самой собой равна дисперсии этой
переменной: Cov(x,x)=G2(x).
Исходя из указанных свойств ковариации,
справедливы следующие равенства:
Cov(x,β0)=0
(β0=const);
Cov(x, β1x)=
β1*Cov(x,x)=
β1*G2(x).
Следовательно, ковариация
между зависимой и независимой переменными
Cov(x,y)
может быть записана как:
Cov(x,y)=
β1G2(x)+Cov(x,ε).
В результате МНК-оценка коэффициента
β1 модели регрессии примет вид:
Таким образом, МНК-оценка
может быть представлена как сумма двух
компонент:
1) константы β1,
т. е. истинного значения коэффициента;
2) случайной ошибки Cov(x,ε),
вызывающей вариацию коэффициента модели
регрессии.
Однако на практике подобное разложение
МНК-оценки невозможно, потому что
истинные значения коэффициентов модели
регрессии и значения случайной ошибки
являются неизвестными. Теоретически
данное разложение можно использовать
при изучении статистических свойств
МНК-оценок.
Аналогично доказывается, что МНК-оценка
коэффициента модели регрессии и
несмещённая оценка дисперсии случайной
ошибки
могут быть представлены как сумма
постоянной составляющей (константы) и
случайной компоненты, зависящей от
ошибки модели регрессии ε.
В предыдущем параграфе мы выяснили, что дисперсия оценки (widehat {beta _2}) равна:
begin{equation*} mathit{var}left(widehat {beta _2}right)=frac{sigma ^2}{Sigma left(x_i-overline xright)^2}. end{equation*}
Это полезная информация, так как дисперсия (widehat {beta _2}) характеризует точность результатов оценивания соответствующего параметра (чем меньше дисперсия, тем точнее наша оценка). Проблема в том, что непосредственно величину (mathit{var}left(widehat {beta _2}right)) мы вычислить не можем: хотя мы наблюдаем значения (x_i,) (i=1,2,{dots},n), но мы не наблюдаем величину (sigma ^2). Этот параметр является неизвестным параметром классической линейной модели подобно величинам (beta _1) и (beta _2). Впрочем, как и в случае с (beta _1) и (beta _2), мы можем получить оценку неизвестного параметра (sigma ^2). Несмещенная оценка дисперсии случайной ошибки (sigma ^2) имеет вид:
begin{equation*} S^2=frac 1{n-2}{ast}sum _{i=1}^ne_i^2 end{equation*}
Чтобы доказать её несмещенность, достаточно осуществить выкладки, аналогичные преобразованиям из предыдущего параграфа, и убедиться, что (Eleft(S^2right)=sigma ^2).
Если в формуле для (mathit{var}left(widehat {beta _2}right)) вместо дисперсии случайной ошибки (sigma ^2) подставить её оценку (S^2), мы получим несмещенную оценку дисперсии МНК-оценки (widehat {beta _2}), которая будет иметь вид:
begin{equation*} widehat {mathit{var}}left(widehat {beta _2}right)=frac{S^2}{Sigma left(x_i-overline xright)^2} end{equation*}
Корень из этой величины называется стандартной ошибкой оценки коэффициента (widehat {beta _2}):
begin{equation*} mathit{se}left(widehat {beta _2}right)=sqrt{widehat {mathit{var}}left(widehat {beta _2}right)}=sqrt{frac{S^2}{Sigma left(x_i-overline xright)^2}} end{equation*}
Аналогичным образом вычисляется стандартная ошибка оценки коэффициента (widehat {beta _1}) (здесь мы опираемся на равенство 2.4, заменяя в нем дисперсию случайной ошибки её оценкой).
begin{equation*} mathit{se}left(widehat {beta _1}right)=sqrt{widehat {mathit{var}}left(widehat {beta _1}right)}=sqrt{frac{frac{S^2} n{ast}sum x_i^2}{sum left(x_i-overline xright)^2}} end{equation*}
Стандартные ошибки оценок коэффициентов пригодятся нам для тестирования гипотез.
Представим, что мы хотим выяснить, влияет ли уровень образования (переменная x) на заработную плату работника в некоторой отрасли (переменная y)? Ответы на такого сорта вопросы, как мы обсудили в первой главе, и есть одна из главных задач эконометрики.
Представим также, что все предпосылки классической линейной модели парной регрессии выполнены. Тогда в терминах нашей модели вопрос «Верно ли, что образование не влияет на заработную плату?» эквивалентен вопросу «Верно ли, что в регрессии (y_i=beta _1+beta _2x_i+varepsilon _i) коэффициент (beta _2) равен нулю?».
Как мы могли бы ответить на этот вопрос?
Естественная идея состоит в том, чтобы посмотреть оценки коэффициентов (widehat {beta _1}) и (widehat {beta _2}) и увидеть, равен ли коэффициент (widehat {beta _2}) нулю. Однако при этом возникает следующая проблема: (widehat {beta _1}) и (widehat {beta _2}) — оценки, полученные при помощи МНК на основе случайной выборки. Следовательно, они сами являются случайными величинами, которые могут принимать значения лишь «приблизительно» равные истинным. Поэтому, даже если истинное значение коэффициента (beta _2) равно нулю, его оценка (widehat {beta _2}), скорее всего, будет отклоняться от нуля.
Следовательно, нужно уметь определять, достаточно ли сильно (widehat {beta _2}) отличается от нуля для того, чтобы можно было с уверенностью утверждать, что и истинное значение коэффициента (beta _2) также не равно нулю. Опишем процедуру, которая позволяет это сделать.
Процедура тестирования незначимости коэффициента:
Формулируем тестируемую гипотезу (H_0:beta _2=0) («переменная x не влияет на переменную y») и альтернативную гипотезу (H_1:beta _2{neq}0) («переменная x влияет на переменную y»)
Находим расчетное значение тестовой статистки по формуле
(frac{widehat {beta _2}}{mathit{se}left(widehat {beta }_2right)}.)
Выбираем уровень значимости (alpha ). Уровнем значимости в математической статистике называется вероятность ошибки первого рода, то есть вероятность отклонить тестируемую гипотезу при условии, что в действительности эта гипотеза верна. Разумеется, нам хотелось бы ошибаться не слишком часто, поэтому данную вероятность обычно выбирают маленькой. Чаще всего в эконометрике используются уровни значимости 1% и 5%.
Из таблиц распределения Стьюдента находим критическое значение тестовой статистки (t_{n-2}^{alpha }) для выбранного уровня значимости и так называемого числа степеней свободы, которое в нашем случае равно (left(n-2right)).
Если (left|frac{widehat {beta _2}}{mathit{se}left(widehat {beta }_2right)}right|>t_{n-2}^{alpha }), то есть (widehat {beta _2}) достаточно велик по абсолютной величине, следует отвергнуть гипотезу (H_0:beta _2=0) и сделать вывод в пользу альтернативной гипотезы, то есть заключить, что переменная x влияет на переменную y. В этом случае переменную x называют статистически значимой при уровне значимости (alpha ). В противном случае, соответственно, гипотеза (H_0) не может быть отвергнута, и переменную x называют статистически незначимой при уровне значимости (alpha ).
Здесь и далее во всех тестах, если явно не указано иное, мы подразумеваем альтернативную гипотезу «(beta _2) не равно c» , а не (beta _2<c) или (beta _2>c). Поэтому под критическими значениями из таблиц распределения Стьюдента по умолчанию подразумеваются критические значения для двусторонних (а не односторонних) тестов. Все стандартные эконометрические пакеты используют такой же подход.}
Замечание 1. В этой процедуре мы опираемся на тот факт, что тестовая статистика имеет t-распределение Стьюдента. Чтобы это было верно, как раз и нужна предпосылка №6 КЛМПР, которую мы до этого никак не использовали.
В соответствии с этой предпосылкой случайные ошибки имеют нормальное распределение. Мы показали (см. равенство (2.2)), что (widehat {beta _2}) — это линейная комбинация случайных ошибок, то есть независимых, одинаково и нормально распределенных случайных величин.
Из математической статистики известно, что отсюда следуют два утверждения:
Во-первых, (widehat {beta _2}) имеет нормальное распределение (так как линейная комбинация нормальных случайных величин является нормальной случайной величиной), дисперсию и математическое ожидание которого мы вычислили в предыдущем параграфе. Иными словами (widehat {beta _2}) имеет вот такое распределение:
begin{equation*} Nleft(beta _2,frac{sigma ^2}{Sigma left(x_i-overline xright)^2}right) end{equation*}
Во-вторых, случайная величина (frac{widehat {beta _2}-beta _2}{mathit{se}left(widehat {beta _2}right)}) имеет t-распределение Стьюдента. В нашем случае это будет распределение с (n-2) степенями свободы: (frac{widehat {beta _2}-beta _2}{mathit{se}left(widehat {beta _2}right)})~(t_{n-2})
В частности, если верна сформулированная нами гипотеза (beta _2=0), то распределение Стьюдента имеет дробь (frac{widehat {beta }_2}{mathit{se}left(widehat {beta }_2right)}), которую мы используем в нашей процедуре. В этом случае критическое значение определяется из вот такого условия (его геометрическая интерпретация представлена в примере 2.3):
begin{equation*} Pleft(left|frac{widehat {beta }_2}{mathit{se}left(widehat {beta }_2right)}right|<t_{n-2}^{alpha }right)=1-alpha . end{equation*}
Замечание 2. Аналогичным образом можно тестировать гипотезу (H_0:beta _2=c) (против альтернативной гипотезы (H_0:beta _2{neq}c)), где c — это некоторая константа. В этом случае процедура тестирования остается такой же с одним исключением: расчетное значение тестовой статистики будет иметь вид (frac{widehat {beta }_2-c}{mathit{se}left(widehat {beta }_2right)}).
Замечание 3. Раньше для определения величины критического значения (t_{n-2}^{alpha }) было необходимо использовать таблицы распределения Стьюдента. Сейчас этот способ тоже доступен (например, соответствующая таблица представлена в Приложении 3.А в конце третьей главы), однако теперь это значение можно рассчитать непосредственно в эконометрическом пакете или, например, в MS Excel (см. пример ниже).
Альтернативным способом является использование для тестирования гипотезы так называемого p-значения. P-значением называют такой уровень значимости, при котором тестируемая гипотеза находится на грани между отвержением и принятием.
Поэтому использовать p-значение при принятии решения очень просто: если оно меньше заранее выбранного уровня значимости (alpha ), то тестируемая гипотеза отвергается при уровне значимости (alpha ). Например, если при тестировании незначимости коэффициента вы используете пятипроцентный уровень значимости ( (alpha =0,05)), а p-значение оказалось равно 0,0002, следует заключить, что соответствующий коэффициент является значимым. Удобство использования p-значения состоит в том, что эта величина автоматически рассчитывается всеми стандартными эконометрическими пакетами, поэтому для принятия решения о значимости или незначимости того или иного коэффициента (а также для проведения любых других тестов, которые мы обсудим далее) вам не требуется никаких таблиц распределения и никаких дополнительных расчетов.
Рассмотрим для большей наглядности еще один пример.
Пример 2.3. Тестирование незначимости коэффициента и графическая иллюстрация
Представим, что у нас 10 наблюдений ( (n=10)), оценка коэффициента оказалась равна (widehat {beta _2})= 8,0, а ее стандартная ошибка (mathit{se}left(widehat {beta }_2right))= 4,0. Если использовать подход, связанный с критическими значениями, нужно открыть таблицу распределения Стьюдента (см. Приложение 3.А), и найти критическое значение для пятипроцентного уровня значимости и (left(n-2right)=8) степеней свободы2. Это критическое значение (t_{mathit{text{к}text{р}}}=t_8^{0,05}{approx}2,3). Расчетное значение t-статистики здесь тоже посчитать несложно
begin{equation*} t_{mathit{text{р}text{а}text{с}text{ч}}}=frac{widehat {beta }_2}{mathit{se}left(widehat {beta }_2right)}=frac 8 4=2 end{equation*}
Если мы нанесем все указанные значения на картинку, у нас получится рисунок 2.4а. Критическое значение отсекает по 2,5% слева и справа (всего 5%). Следовательно, вероятность попасть между (-t_{mathit{text{к}text{р}}}) и (t_{mathit{text{к}text{р}}}) будет 95%. Нанесем также (-t_{mathit{text{р}text{а}text{с}text{ч}}}) и (t_{mathit{text{р}text{а}text{с}text{ч}}}). Эти значения отсекают по 3% справа и слева, как это показано на рисунке 2.4б.
Обозначим (xi ) — случайную величину, имеющую распредление стьюдента с (left(n-2right)=8) степенями свободы. Тогда формально P-значение в нашем случае — это вот такая вероятность:
p-значение (Pleft(left|xi right|>2right)).
То есть в нашем примере p-значение — это вероятность такого события, что случайная величина, имеющая t-распределение Стьюдента с 8 степенями свободы, по модулю превысит (t_{mathit{text{р}text{а}text{с}text{ч}}}=2). Как видно из рисунка, в нашем случае эта вероятность равна 0,03+0,03=0,06.
Рисунок 2.4а. Расчетное и критическое значения тестовой статистики для примера 2.3.
Рисунок 2.4б. P-значение для примера 2.3.
Как видно из нашего примера, P-значение больше заранее выбранного уровня значимости только тогда, когда (left|t_{mathit{text{р}text{а}text{с}text{ч}}}right|<t_{mathit{text{к}text{р}}}), что подтверждает сформулированное нами правило принятия решения при помощи P-значения: если P-значение больше уровня значимости, то нулевая гипотеза не отвергается. Если P-значение меньше уровня значимости, то нулевая гипотеза отвергается.
***
Решив неравенство (left|frac{widehat {beta }_2-beta _2}{mathit{se}left(widehat {beta }_2right)}right|<t_{n-2}^{alpha }) относительно (beta _2), получим:
begin{equation*} widehat {beta }_2-mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha }<beta _2<widehat {beta }_2+mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha } end{equation*}
Иными словами, с вероятностью (1-alpha ) интервал (left(widehat {beta }_2-mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha },widehat {beta }_2+mathit{se}left(widehat {beta }_2right){ast}t_{n-2}^{alpha }right)) содержит истинное значение оцениваемого параметра. Например, если (alpha =0,05) и, следовательно, (1-alpha =0,95), этот интервал и называют 95-процентным доверительным интервалом для параметра (beta _2).
Возможность построения доверительных интервалов важна с практической точки зрения. Дело в том, что, так как (widehat {beta }_2) является лишь приблизительной оценкой параметра (beta _2), эта точечная оценка сама по себе несет гораздо меньше информации, чем интервал. Ведь без доверительного интервала невозможно понять, насколько она эта оценка на самом деле (не)точная. Например, утверждение « (widehat {beta }_2) равно 23,4» куда менее информативно, чем утверждение «истинное значение оцениваемого параметра с вероятностью 95 процентов содержится в пределах от 23,1 до 23,7».
Завершим раздел еще двумя примерами. В первом из них все расчеты проделаны вручную, чтобы, проследив их, можно было еще раз разобраться во взаимосвязях между введенными нами понятиями. Во втором примере используется эконометрический пакет, что позволяет продемонстрировать, как подобные вычисления осуществляются в реальных прикладных исследованиях.
Пример 2.4. Доходы индивидов и потребление риса
Исследователь анализирует зависимость потребления риса от уровня дохода (кривую Энгеля) для однородной группы из 20 потребителей. Все потребители из этой группы сталкиваются с одинаковыми ценами на рис и другие товары, и только уровни дохода у них различны, поэтому исследователь использует модель парной регрессии.
Обозначим:
(x_i) — ежемесячный располагаемый доход i-го потребителя (в тысячах денежных единиц),
(y_i) — ежемесячное потребление риса i-м потребителем (в килограммах).
Имеются следующие данные о переменных x и y:
begin{equation*} sum _{i=1}^{20}x_i=20,sum _{i=1}^{20}x_i^2=40,sum _{i=1}^{20}y_i=42,sum _{i=1}^{20}y_i^2=108, end{equation*}
begin{equation*} sum _{i=1}^{20}x_i{ast}y_i=60 end{equation*}
(а) Вычислите МНК-оценки коэффициентов в регрессии
begin{equation*} y_i=beta _1+beta _2{ast}x_i+varepsilon _i. end{equation*}
Выпишите полученное уравнение регрессии и коэффициент (R^2).
(б) При уровне значимости 5% проверьте значимость переменной x.
(в) Дайте содержательную интерпретацию коэффициента при переменной x.
(г) Вспомнив соответствующие определения из курса микроэкономики и вычислив необходимую эластичность, определите: является ли рис для этой группы потребителей низкокачественным товаром, товаром первой необходимости или предметом роскоши?
(д) При уровне значимости 5% проверьте гипотезу о том, что коэффициент (beta _2) равен единице.
(е) Постройте 95-процентный доверительный интервал для коэффициента (beta _2).
Решение:
(а) Вычислим средние значения:
begin{equation*} overline x=1,overline{x^2}=2,overline y=2,1,overline{y^2}=5,4,overline{mathit{xy}}=3 end{equation*}
Найдем оценки коэффициентов:
begin{equation*} widehat {beta _2}=frac{overline{mathit{xy}}-overline x{ast}overline y}{overline{x^2}-overline x^2}=frac{3-1{ast}2,1}{2-1}=0,9 end{equation*}
begin{equation*} widehat {beta _1}=overline y-widehat {beta _2}{ast}overline x=2,1-1{ast}0,9=1,2 end{equation*}
Таким образом, (widehat y_i=1,2+0,9{ast}x_i).
Теперь вычислим (R^2). Для этого воспользуемся тем, что по определению он равен отношению объясненной суммы квадратов к общей сумме квадратов:
begin{equation*} R^2=frac{sum _{i=1}^{20}left(widehat y_i-overline yright)^2}{sum _{i=1}^{20}left(y_i-overline yright)^2}. end{equation*}
Вычислим каждую из этих сумм по отдельности. Сначала найдем общую сумму квадратов:
begin{equation*} mathit{TSS}=sum _{i=1}^{20}left(y_i-overline yright)^2=sum _{i=1}^{20}y_i^2-2{ast}sum _{i=1}^{20}y_i{ast}overline y+sum _{i=1}^{20}overline y^2= end{equation*}
begin{equation*} sum _{i=1}^{20}y_i^2-2{ast}overline y{ast}sum _{i=1}^{20}y_i+20{ast}overline y^2=108-2{ast}2,1{ast}42+20{ast}2,1^2=19,8 end{equation*}
Теперь найдем объясненную сумму квадратов:
begin{equation*} sum _{i=1}^{20}left(widehat y_i-overline yright)^2=sum _{i=1}^{20}left(1,2+0,9{ast}x_i-2,1right)^2=sum _{i=1}^{20}left(0,9{ast}x_i-0,9right)^2= end{equation*}
begin{equation*} 0,9^2sum _{i=1}^{20}left(x_i-1right)^2=0,81{ast}left(sum _{i=1}^{20}x_i^2-2{ast}sum _{i=1}^{20}x_i+20right)=16,2 end{equation*}
Теперь можно вычислить коэффициент детерминации:
begin{equation*} R^2=frac{sum _{i=1}^{20}left(widehat y_i-overline yright)^2}{sum _{i=1}^{20}left(y_i-overline yright)^2}=frac{16,2}{19,8}=0,82 end{equation*}
Ответ на пункт (а): (widehat y_i=1,2+0,9{ast}x_i,R^2=0,82)
(б) Тестируемая гипотеза (H_0:beta _2=0). Альтернативная гипотеза (H_1:beta _2{neq}0).
Чтобы проверить значимость, нам понадобится стандартная ошибка оценки коэффициента. Для этого нам придется оценить сумму квадратов остатков. Воспользуемся тем фактом, что для регрессии с константой верно равенство:
begin{equation*} sum _{i=1}^{20}left(y_i-overline yright)^2=sum _{i=1}^{20}left(widehat y_i-overline yright)^2+sum _{i=1}^{20}e_i^2 end{equation*}
В этой формуле мы вычислили все элементы, кроме суммы квадратов остатков:
begin{equation*} 19,8=16,2+sum _{i=1}^{20}e_i^2 end{equation*}
Следовательно, (sum _{i=1}^{20}e_i^2=19,8-16,2=3,6).
Вычислим оценку дисперсии случайной ошибки:
begin{equation*} S^2=frac{sum _{i=1}^{20}e_i^2}{n-2}=frac{3,6}{20-2}=0,2 end{equation*}
Теперь вычислим стандартную ошибку оценки коэффициента:
begin{equation*} mathit{se}left(widehat {beta _2}right)=sqrt{frac{S^2}{sum _{i=1}^{20}left(x_i-overline xright)^2}}=end{equation*}
begin{equation*} =sqrt{frac{0,2}{sum _{i=1}^{20}x_i^2-n{ast}left(overline xright)^2}}=sqrt{frac{0,2}{40-20}}=0,1 end{equation*}
Расчетное значение t-статистики равно (frac{widehat {beta _2}}{mathit{se}left(widehat {beta _2}right)}=frac{0,9}{0,1}=9).
Критическое значение t-статистки из таблицы распределения Стьюдента при уровне значимости 5% и (20–2)=18 степенях свободы составляет 2,101. Расчетное значение больше критического, следовательно, мы отклоняем нулевую гипотезу и делаем вывод о том, что уровень дохода индивида значимо влияет на его спрос на рис.
Ответ на пункт (б): Переменная значима.
Ответ на пункт (в): При увеличении располагаемого дохода потребителя на одну тысячу денежных единиц его спрос на рис увеличивается в среднем на 0,9 кг.
(г) Вычислим эластичность спроса на рис по доходу. По определению эластичность равна:
begin{equation*} frac{frac{dwidehat y}{mathit{dx}}{ast}x}{widehat y}=frac{0,9{ast}x}{1,2+0,9{ast}x} end{equation*}
Легко видеть, что при любых положительных значениях (x) эластичность спроса по доходу лежит между нулем и единицей, следовательно, для рассматриваемой группы потребителей рис является товаром первой необходимости. Что, в общем-то, неудивительно.
Ответ на пункт (г): Товар первой необходимости.
(д) Тестируемая гипотеза (H_0:beta _2=1). Альтернативная гипотеза (H_1:beta _2{neq}1).
Для проверки значимости нам понадобится стандартная ошибка оценки коэффициента.
Расчетное значение t-статистики равно (frac{widehat {beta _2}-1}{mathit{se}left(widehat {beta _2}right)}=frac{0,9-1}{0,1}=-1).
Критическое значение t-статистки из таблицы распределения Стьюдента при уровне значимости 5% и (20–2)=18 степенях свободы составляет 2,101. Расчетное значение по модулю меньше критического, следовательно, мы принимаем (не отклоняем) нулевую гипотезу.
Ответ на пункт (д): Гипотеза не отклоняется.
(е) В рамках предпосылок классической линейной модели парной регрессии доверительный интервал может быть посчитан следующим образом:
begin{equation*} left(widehat {beta _2}-mathit{se}left(widehat {beta _2}right){ast}t_{n-2},widehat {beta _2}+mathit{se}left(widehat {beta _2}right){ast}t_{n-2}right) end{equation*}
begin{equation*} left(0,9-0,1{ast}2,101,0,9+0,1{ast}2,101right) end{equation*}
Таким образом, c вероятностью 95% интервал (left(0,69,1,11right)) содержит истинное значение коэффициента (beta _2).
Ответ на пункт (е): (left(0,69,1,11right)).
***
Пример 2.5. Площадь однокомнатной квартиры и её цена
В этом задании вам предлагается проанализировать взаимосвязь между площадью квартиры и ее ценой. Вам доступны следующие данные о московском рынке недвижимости в 2012 году (файл Price2012):
Price — рыночная цена однокомнатной квартиры в Москве (в тысячах руб.), выкуп которой был осуществлен с 10.01.2012 по 28.09.2012
TotalArea — общая площадь квартиры (кв. м)
(а) Оцените регрессию переменной Price на переменную TotalArea. Запишите оцененное уравнение регрессии, указав коэффициент детерминации и (в скобках под соответствующими коэффициентами) стандартные ошибки. Постройте диаграмму рассеяния с линией регрессии.
(б) Является ли коэффициент при переменной TotalArea статистически значимым при уровне значимости 1%? Дайте содержательную интерпретацию для этого коэффициента.
Решение:
(а) Ниже представлена распечатка результатов оценивания уравнения в эконометрическом пакете Gretl3. (Любой стандартный эконометрический пакет, например R, Stata или Econometric Views, выдаст аналогичную табличку. Пользуйтесь тем из них, который вам больше нравится. Ну или тем, который есть под рукой.)
Модель 1: МНК, использованы наблюдения 1-121
Зависимая переменная: Price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | 786,456 | 583,051 | 1,349 | 0,1799 | |
| TotalArea | 135,317 | 16,5144 | 8,194 | 0,0001 | *** |
| Среднее зав. перемен | 5540,335 | Ст. откл. зав. перемен | 792,7127 | |
| Сумма кв. остатков | 48208118 | Ст. ошибка модели | 636,4827 | |
| R-квадрат | 0,360696 | Испр. R-квадрат | 0,355324 | |
| F(1, 119) | 67,14000 | Р-значение (F) | 3,30e-13 | |
| Лог. правдоподобие | $-$951,8540 | Крит. Акаике | 1907,708 | |
| Крит. Шварца | 1913,300 | Крит. Хеннана-Куинна | 1909,979 |
В столбце «Коэффициент» указаны оценки коэффициентов, а в столбце «Ст. ошибка» — их стандартные ошибки. В нижней части таблицы среди прочих показателей можно найти и коэффициент R-квадрат.
Общепринятый формат записи полученных результатов имеет следующий вид (в скобках под оценками коэффициентов указаны соответствующие стандартные ошибки):
begin{equation*} widehat {mathit{Price}}_i=underset{left(583,051right)}{786,456}+underset{left(16,514right)}{135,317}mathit{TotalArea}_i,R^2=0,36 end{equation*}
Обратите внимание, что в скобках под оценками коэффициентов мы указали их стандартные ошибки. Такой формат является хорошим тоном при записи результатов эконометрического моделирования, так как позволяет читателю оценить точность ваших результатов и прикинуть доверительные интервалы для коэффициентов.
(б) В столбце «P-значение» указано, что P-значение для оценки коэффициента при переменной TotalArea меньше, чем 0,0001 (и тем более меньше, чем 0,01). Следовательно, этот коэффициент является статистически значимым при уровне значимости 1%.
Содержательная интерпретация: при увеличении общей площади квартиры на один квадратный метр ее цена в среднем при прочих равных условиях увеличивается на 135 тысяч рублей.
Отметим, что свободное слагаемое в данном случае отличается от нуля статистически незначимо, так как соответствующее P-значение равно 0,18, что больше любого разумного уровня значимости. Да и если бы даже эта константа была значима, все равно отдельно интерпретировать её смысла не было бы, ведь константа показывает значение зависимой переменной при условии, что регрессор TotalArea равен нулю (то есть при условии, что анализируемая квартира имеет нулевую площадь). Вряд ли кто-то всерьез интересуется ценой квартиры площадью 0 квадратных метров.
- Вместо использования готовых таблиц распределения можно, например, ввести в MS Excel формулу =СТЬЮДЕНТ.ОБР( 1 — 0,05 / 2; 10 — 2) ↵
- Для получения этого результата достаточно запустить Gretl; используя пункт меню «Импорт», импортировать данные из файла MS Excel (или просто мышкой «перетащить» нужный файл в рабочую область эконометрического пакета); выбрать в меню «Модель» пункт «Метод наименьших квадратов» и указать в качестве зависимой переменной переменную Price, а в качестве объясняющей — переменную TotalArea. ↵