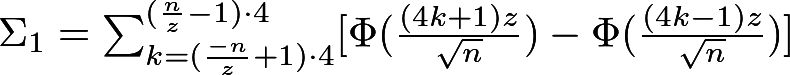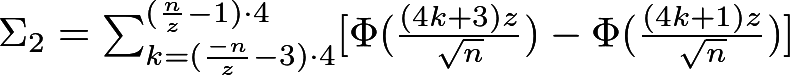Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Проверка корректности А/Б тестов
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
Ошибки, встроенные в систему: их роль в статистике
В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.
Ошибка и некорректное применение: в чем разница?
В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.
И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.
То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.
Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.
Ошибки первого и второго рода
Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.
Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:
До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.
Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.
Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.
Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?
ROC-анализ
ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.
Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):
Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:
Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):
А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.
С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.
Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.
С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.
Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Радиолокация
- 4.2 Компьютеры
- 4.2.1 Компьютерная безопасность
- 4.2.2 Фильтрация спама
- 4.2.3 Вредоносное программное обеспечение
- 4.2.4 Поиск в компьютерных базах данных
- 4.2.5 Оптическое распознавание текстов (OCR)
- 4.2.6 Досмотр пассажиров и багажа
- 4.2.7 Биометрия
- 4.3 Массовая медицинская диагностика (скрининг)
- 4.4 Медицинское тестирование
- 4.5 Исследования сверхъестественных явлений
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 

где 

,
сопоставляющий каждой реализации выборки 
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе
, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. [1][2]
| Верная гипотеза | |||
|---|---|---|---|
 |
 |
||
| Результат применения критерия |
 |
 верно принята верно принята |
 неверно принята неверно принята (Ошибка второго рода) |
 |
 неверно отвергнута неверно отвергнута (Ошибка первого рода) |
 верно отвергнута верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы 



С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.
В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.
Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.
Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.
Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.
В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.
Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.
Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой 

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой 


Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Радиолокация
В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда нарушители классифицируются как авторизованные пользователи (ошибки первого рода)
- когда авторизованные пользователи классифицируются как нарушители (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.
Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.
Вредоносное программное обеспечение
Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.
Поиск в компьютерных базах данных
При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[3]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[4]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.[5] Самый низкий уровень наблюдается в Нидерландах, 1%.[6]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[7]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.[8]
См. также
- Статистическая значимость
- Ложноположительный
- Атака второго рода
- Случаи ложного срабатывания систем предупреждения о ракетном нападении
- Receiver_operating_characteristic
Примечания
- ↑ ГОСТ Р 50779.10-2000. «Статистические методы. Вероятность и основы статистики. Термины и определения.». Стр. 26
- ↑ Valerie J. Easton, John H. McColl. Statistics Glossary: Hypothesis Testing.
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95% женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ1>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
This article is about erroneous outcomes of statistical tests. For closely related concepts in binary classification and testing generally, see false positives and false negatives.
In statistical hypothesis testing, a type I error is the mistaken rejection of an actually true null hypothesis (also known as a «false positive» finding or conclusion; example: «an innocent person is convicted»), while a type II error is the failure to reject a null hypothesis that is actually false (also known as a «false negative» finding or conclusion; example: «a guilty person is not convicted»).[1] Much of statistical theory revolves around the minimization of one or both of these errors, though the complete elimination of either is a statistical impossibility if the outcome is not determined by a known, observable causal process.
By selecting a low threshold (cut-off) value and modifying the alpha (α) level, the quality of the hypothesis test can be increased.[2] The knowledge of type I errors and type II errors is widely used in medical science, biometrics and computer science.[clarification needed]
Intuitively, type I errors can be thought of as errors of commission, i.e. the researcher unluckily concludes that something is the fact. For instance, consider a study where researchers compare a drug with a placebo. If the patients who are given the drug get better than the patients given the placebo by chance, it may appear that the drug is effective, but in fact the conclusion is incorrect.
In reverse, type II errors are errors of omission. In the example above, if the patients who got the drug did not get better at a higher rate than the ones who got the placebo, but this was a random fluke, that would be a type II error. The consequence of a type II error depends on the size and direction of the missed determination and the circumstances. An expensive cure for one in a million patients may be inconsequential even if it truly is a cure.
Definition[edit]
Statistical background[edit]
In statistical test theory, the notion of a statistical error is an integral part of hypothesis testing. The test goes about choosing about two competing propositions called null hypothesis, denoted by H0 and alternative hypothesis, denoted by H1. This is conceptually similar to the judgement in a court trial. The null hypothesis corresponds to the position of the defendant: just as he is presumed to be innocent until proven guilty, so is the null hypothesis presumed to be true until the data provide convincing evidence against it. The alternative hypothesis corresponds to the position against the defendant. Specifically, the null hypothesis also involves the absence of a difference or the absence of an association. Thus, the null hypothesis can never be that there is a difference or an association.
If the result of the test corresponds with reality, then a correct decision has been made. However, if the result of the test does not correspond with reality, then an error has occurred. There are two situations in which the decision is wrong. The null hypothesis may be true, whereas we reject H0. On the other hand, the alternative hypothesis H1 may be true, whereas we do not reject H0. Two types of error are distinguished: type I error and type II error.[3]
Type I error[edit]
The first kind of error is the mistaken rejection of a null hypothesis as the result of a test procedure. This kind of error is called a type I error (false positive) and is sometimes called an error of the first kind. In terms of the courtroom example, a type I error corresponds to convicting an innocent defendant.
Type II error[edit]
The second kind of error is the mistaken failure to reject the null hypothesis as the result of a test procedure. This sort of error is called a type II error (false negative) and is also referred to as an error of the second kind. In terms of the courtroom example, a type II error corresponds to acquitting a criminal.[4]
Crossover error rate[edit]
The crossover error rate (CER) is the point at which type I errors and type II errors are equal. A system with a lower CER value provides more accuracy than a system with a higher CER value.
False positive and false negative[edit]
In terms of false positives and false negatives, a positive result corresponds to rejecting the null hypothesis, while a negative result corresponds to failing to reject the null hypothesis; «false» means the conclusion drawn is incorrect. Thus, a type I error is equivalent to a false positive, and a type II error is equivalent to a false negative.
Table of error types[edit]
Tabularised relations between truth/falseness of the null hypothesis and outcomes of the test:[5]
| Table of error types | Null hypothesis (H0) is |
||
|---|---|---|---|
| True | False | ||
| Decision about null hypothesis (H0) |
Don’t reject |
Correct inference (true negative) (probability = 1−α) |
Type II error (false negative) (probability = β) |
| Reject | Type I error (false positive) (probability = α) |
Correct inference (true positive) (probability = 1−β) |
Error rate[edit]
The results obtained from negative sample (left curve) overlap with the results obtained from positive samples (right curve). By moving the result cutoff value (vertical bar), the rate of false positives (FP) can be decreased, at the cost of raising the number of false negatives (FN), or vice versa (TP = True Positives, TPR = True Positive Rate, FPR = False Positive Rate, TN = True Negatives).
A perfect test would have zero false positives and zero false negatives. However, statistical methods are probabilistic, and it cannot be known for certain whether statistical conclusions are correct. Whenever there is uncertainty, there is the possibility of making an error. Considering this nature of statistics science, all statistical hypothesis tests have a probability of making type I and type II errors.[6]
- The type I error rate is the probability of rejecting the null hypothesis given that it is true. The test is designed to keep the type I error rate below a prespecified bound called the significance level, usually denoted by the Greek letter α (alpha) and is also called the alpha level. Usually, the significance level is set to 0.05 (5%), implying that it is acceptable to have a 5% probability of incorrectly rejecting the true null hypothesis.[7]
- The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test, which equals 1−β.[8]
These two types of error rates are traded off against each other: for any given sample set, the effort to reduce one type of error generally results in increasing the other type of error.[9]
The quality of hypothesis test[edit]
The same idea can be expressed in terms of the rate of correct results and therefore used to minimize error rates and improve the quality of hypothesis test. To reduce the probability of committing a type I error, making the alpha value more stringent is quite simple and efficient. To decrease the probability of committing a type II error, which is closely associated with analyses’ power, either increasing the test’s sample size or relaxing the alpha level could increase the analyses’ power.[10] A test statistic is robust if the type I error rate is controlled.
Varying different threshold (cut-off) value could also be used to make the test either more specific or more sensitive, which in turn elevates the test quality. For example, imagine a medical test, in which an experimenter might measure the concentration of a certain protein in the blood sample. The experimenter could adjust the threshold (black vertical line in the figure) and people would be diagnosed as having diseases if any number is detected above this certain threshold. According to the image, changing the threshold would result in changes in false positives and false negatives, corresponding to movement on the curve.[11]
Example[edit]
Since in a real experiment it is impossible to avoid all type I and type II errors, it is important to consider the amount of risk one is willing to take to falsely reject H0 or accept H0. The solution to this question would be to report the p-value or significance level α of the statistic. For example, if the p-value of a test statistic result is estimated at 0.0596, then there is a probability of 5.96% that we falsely reject H0. Or, if we say, the statistic is performed at level α, like 0.05, then we allow to falsely reject H0 at 5%. A significance level α of 0.05 is relatively common, but there is no general rule that fits all scenarios.
Vehicle speed measuring[edit]
The speed limit of a freeway in the United States is 120 kilometers per hour. A device is set to measure the speed of passing vehicles. Suppose that the device will conduct three measurements of the speed of a passing vehicle, recording as a random sample X1, X2, X3. The traffic police will or will not fine the drivers depending on the average speed 

In addition, we suppose that the measurements X1, X2, X3 are modeled as normal distribution N(μ,4). Then, T should follow N(μ,4/3) and the parameter μ represents the true speed of passing vehicle. In this experiment, the null hypothesis H0 and the alternative hypothesis H1 should be
H0: μ=120 against H1: μ1>120.
If we perform the statistic level at α=0.05, then a critical value c should be calculated to solve

According to change-of-units rule for the normal distribution. Referring to Z-table, we can get

Here, the critical region. That is to say, if the recorded speed of a vehicle is greater than critical value 121.9, the driver will be fined. However, there are still 5% of the drivers are falsely fined since the recorded average speed is greater than 121.9 but the true speed does not pass 120, which we say, a type I error.
The type II error corresponds to the case that the true speed of a vehicle is over 120 kilometers per hour but the driver is not fined. For example, if the true speed of a vehicle μ=125, the probability that the driver is not fined can be calculated as

which means, if the true speed of a vehicle is 125, the driver has the probability of 0.36% to avoid the fine when the statistic is performed at level 125 since the recorded average speed is lower than 121.9. If the true speed is closer to 121.9 than 125, then the probability of avoiding the fine will also be higher.
The tradeoffs between type I error and type II error should also be considered. That is, in this case, if the traffic police do not want to falsely fine innocent drivers, the level α can be set to a smaller value, like 0.01. However, if that is the case, more drivers whose true speed is over 120 kilometers per hour, like 125, would be more likely to avoid the fine.
Etymology[edit]
In 1928, Jerzy Neyman (1894–1981) and Egon Pearson (1895–1980), both eminent statisticians, discussed the problems associated with «deciding whether or not a particular sample may be judged as likely to have been randomly drawn from a certain population»:[12] and, as Florence Nightingale David remarked, «it is necessary to remember the adjective ‘random’ [in the term ‘random sample’] should apply to the method of drawing the sample and not to the sample itself».[13]
They identified «two sources of error», namely:
- (a) the error of rejecting a hypothesis that should have not been rejected, and
- (b) the error of failing to reject a hypothesis that should have been rejected.
In 1930, they elaborated on these two sources of error, remarking that:
…in testing hypotheses two considerations must be kept in view, we must be able to reduce the chance of rejecting a true hypothesis to as low a value as desired; the test must be so devised that it will reject the hypothesis tested when it is likely to be false.
In 1933, they observed that these «problems are rarely presented in such a form that we can discriminate with certainty between the true and false hypothesis» . They also noted that, in deciding whether to fail to reject, or reject a particular hypothesis amongst a «set of alternative hypotheses», H1, H2…, it was easy to make an error:
…[and] these errors will be of two kinds:
- (I) we reject H0 [i.e., the hypothesis to be tested] when it is true,[14]
- (II) we fail to reject H0 when some alternative hypothesis HA or H1 is true. (There are various notations for the alternative).
In all of the papers co-written by Neyman and Pearson the expression H0 always signifies «the hypothesis to be tested».
In the same paper they call these two sources of error, errors of type I and errors of type II respectively.[15]
[edit]
Null hypothesis[edit]
It is standard practice for statisticians to conduct tests in order to determine whether or not a «speculative hypothesis» concerning the observed phenomena of the world (or its inhabitants) can be supported. The results of such testing determine whether a particular set of results agrees reasonably (or does not agree) with the speculated hypothesis.
On the basis that it is always assumed, by statistical convention, that the speculated hypothesis is wrong, and the so-called «null hypothesis» that the observed phenomena simply occur by chance (and that, as a consequence, the speculated agent has no effect) – the test will determine whether this hypothesis is right or wrong. This is why the hypothesis under test is often called the null hypothesis (most likely, coined by Fisher (1935, p. 19)), because it is this hypothesis that is to be either nullified or not nullified by the test. When the null hypothesis is nullified, it is possible to conclude that data support the «alternative hypothesis» (which is the original speculated one).
The consistent application by statisticians of Neyman and Pearson’s convention of representing «the hypothesis to be tested» (or «the hypothesis to be nullified») with the expression H0 has led to circumstances where many understand the term «the null hypothesis» as meaning «the nil hypothesis» – a statement that the results in question have arisen through chance. This is not necessarily the case – the key restriction, as per Fisher (1966), is that «the null hypothesis must be exact, that is free from vagueness and ambiguity, because it must supply the basis of the ‘problem of distribution,’ of which the test of significance is the solution.»[16] As a consequence of this, in experimental science the null hypothesis is generally a statement that a particular treatment has no effect; in observational science, it is that there is no difference between the value of a particular measured variable, and that of an experimental prediction.[citation needed]
Statistical significance[edit]
If the probability of obtaining a result as extreme as the one obtained, supposing that the null hypothesis were true, is lower than a pre-specified cut-off probability (for example, 5%), then the result is said to be statistically significant and the null hypothesis is rejected.
British statistician Sir Ronald Aylmer Fisher (1890–1962) stressed that the «null hypothesis»:
… is never proved or established, but is possibly disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
— Fisher, 1935, p.19
Application domains[edit]
Medicine[edit]
In the practice of medicine, the differences between the applications of screening and testing are considerable.
Medical screening[edit]
Screening involves relatively cheap tests that are given to large populations, none of whom manifest any clinical indication of disease (e.g., Pap smears).
Testing involves far more expensive, often invasive, procedures that are given only to those who manifest some clinical indication of disease, and are most often applied to confirm a suspected diagnosis.
For example, most states in the USA require newborns to be screened for phenylketonuria and hypothyroidism, among other congenital disorders.
Hypothesis: «The newborns have phenylketonuria and hypothyroidism»
Null Hypothesis (H0): «The newborns do not have phenylketonuria and hypothyroidism»,
Type I error (false positive): The true fact is that the newborns do not have phenylketonuria and hypothyroidism but we consider they have the disorders according to the data.
Type II error (false negative): The true fact is that the newborns have phenylketonuria and hypothyroidism but we consider they do not have the disorders according to the data.
Although they display a high rate of false positives, the screening tests are considered valuable because they greatly increase the likelihood of detecting these disorders at a far earlier stage.
The simple blood tests used to screen possible blood donors for HIV and hepatitis have a significant rate of false positives; however, physicians use much more expensive and far more precise tests to determine whether a person is actually infected with either of these viruses.
Perhaps the most widely discussed false positives in medical screening come from the breast cancer screening procedure mammography. The US rate of false positive mammograms is up to 15%, the highest in world. One consequence of the high false positive rate in the US is that, in any 10-year period, half of the American women screened receive a false positive mammogram. False positive mammograms are costly, with over $100 million spent annually in the U.S. on follow-up testing and treatment. They also cause women unneeded anxiety. As a result of the high false positive rate in the US, as many as 90–95% of women who get a positive mammogram do not have the condition. The lowest rate in the world is in the Netherlands, 1%. The lowest rates are generally in Northern Europe where mammography films are read twice and a high threshold for additional testing is set (the high threshold decreases the power of the test).
The ideal population screening test would be cheap, easy to administer, and produce zero false-negatives, if possible. Such tests usually produce more false-positives, which can subsequently be sorted out by more sophisticated (and expensive) testing.
Medical testing[edit]
False negatives and false positives are significant issues in medical testing.
Hypothesis: «The patients have the specific disease».
Null hypothesis (H0): «The patients do not have the specific disease».
Type I error (false positive): «The true fact is that the patients do not have a specific disease but the physicians judges the patients was ill according to the test reports».
False positives can also produce serious and counter-intuitive problems when the condition being searched for is rare, as in screening. If a test has a false positive rate of one in ten thousand, but only one in a million samples (or people) is a true positive, most of the positives detected by that test will be false. The probability that an observed positive result is a false positive may be calculated using Bayes’ theorem.
Type II error (false negative): «The true fact is that the disease is actually present but the test reports provide a falsely reassuring message to patients and physicians that the disease is absent».
False negatives produce serious and counter-intuitive problems, especially when the condition being searched for is common. If a test with a false negative rate of only 10% is used to test a population with a true occurrence rate of 70%, many of the negatives detected by the test will be false.
This sometimes leads to inappropriate or inadequate treatment of both the patient and their disease. A common example is relying on cardiac stress tests to detect coronary atherosclerosis, even though cardiac stress tests are known to only detect limitations of coronary artery blood flow due to advanced stenosis.
Biometrics[edit]
Biometric matching, such as for fingerprint recognition, facial recognition or iris recognition, is susceptible to type I and type II errors.
Hypothesis: «The input does not identify someone in the searched list of people»
Null hypothesis: «The input does identify someone in the searched list of people»
Type I error (false reject rate): «The true fact is that the person is someone in the searched list but the system concludes that the person is not according to the data».
Type II error (false match rate): «The true fact is that the person is not someone in the searched list but the system concludes that the person is someone whom we are looking for according to the data».
The probability of type I errors is called the «false reject rate» (FRR) or false non-match rate (FNMR), while the probability of type II errors is called the «false accept rate» (FAR) or false match rate (FMR).
If the system is designed to rarely match suspects then the probability of type II errors can be called the «false alarm rate». On the other hand, if the system is used for validation (and acceptance is the norm) then the FAR is a measure of system security, while the FRR measures user inconvenience level.
Security screening[edit]
False positives are routinely found every day in airport security screening, which are ultimately visual inspection systems. The installed security alarms are intended to prevent weapons being brought onto aircraft; yet they are often set to such high sensitivity that they alarm many times a day for minor items, such as keys, belt buckles, loose change, mobile phones, and tacks in shoes.
Here, the null hypothesis is that the item is not a weapon, while the alternative hypothesis is that the item is a weapon.
A type I error (false positive): «The true fact is that the item is not a weapon but the system still alarms».
Type II error (false negative) «The true fact is that the item is a weapon but the system keeps silent at this time».
The ratio of false positives (identifying an innocent traveler as a terrorist) to true positives (detecting a would-be terrorist) is, therefore, very high; and because almost every alarm is a false positive, the positive predictive value of these screening tests is very low.
The relative cost of false results determines the likelihood that test creators allow these events to occur. As the cost of a false negative in this scenario is extremely high (not detecting a bomb being brought onto a plane could result in hundreds of deaths) whilst the cost of a false positive is relatively low (a reasonably simple further inspection) the most appropriate test is one with a low statistical specificity but high statistical sensitivity (one that allows a high rate of false positives in return for minimal false negatives).
Computers[edit]
The notions of false positives and false negatives have a wide currency in the realm of computers and computer applications, including computer security, spam filtering, Malware, Optical character recognition and many others.
For example, in the case of spam filtering the hypothesis here is that the message is a spam.
Thus, null hypothesis: «The message is not a spam».
Type I error (false positive): «Spam filtering or spam blocking techniques wrongly classify a legitimate email message as spam and, as a result, interferes with its delivery».
While most anti-spam tactics can block or filter a high percentage of unwanted emails, doing so without creating significant false-positive results is a much more demanding task.
Type II error (false negative): «Spam email is not detected as spam, but is classified as non-spam». A low number of false negatives is an indicator of the efficiency of spam filtering.
See also[edit]
- Binary classification
- Detection theory
- Egon Pearson
- Ethics in mathematics
- False positive paradox
- False discovery rate
- Family-wise error rate
- Information retrieval performance measures
- Neyman–Pearson lemma
- Null hypothesis
- Probability of a hypothesis for Bayesian inference
- Precision and recall
- Prosecutor’s fallacy
- Prozone phenomenon
- Receiver operating characteristic
- Sensitivity and specificity
- Statisticians’ and engineers’ cross-reference of statistical terms
- Testing hypotheses suggested by the data
- Type III error
References[edit]
- ^ «Type I Error and Type II Error». explorable.com. Retrieved 14 December 2019.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Sheskin, David (2004). Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press. p. 54. ISBN 1584884401.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Lindenmayer, David. (2005). Practical conservation biology. Burgman, Mark A. Collingwood, Vic.: CSIRO Pub. ISBN 0-643-09310-9. OCLC 65216357.
- ^ Chow, Y. W.; Pietranico, R.; Mukerji, A. (27 October 1975). «Studies of oxygen binding energy to hemoglobin molecule». Biochemical and Biophysical Research Communications. 66 (4): 1424–1431. doi:10.1016/0006-291x(75)90518-5. ISSN 0006-291X. PMID 6.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Smith, R. J.; Bryant, R. G. (27 October 1975). «Metal substitutions incarbonic anhydrase: a halide ion probe study». Biochemical and Biophysical Research Communications. 66 (4): 1281–1286. doi:10.1016/0006-291x(75)90498-2. ISSN 0006-291X. PMC 9650581. PMID 3.
- ^ Moroi, K.; Sato, T. (15 August 1975). «Comparison between procaine and isocarboxazid metabolism in vitro by a liver microsomal amidase-esterase». Biochemical Pharmacology. 24 (16): 1517–1521. doi:10.1016/0006-2952(75)90029-5. ISSN 1873-2968. PMID 8.
- ^ NEYMAN, J.; PEARSON, E. S. (1928). «On the Use and Interpretation of Certain Test Criteria for Purposes of Statistical Inference Part I». Biometrika. 20A (1–2): 175–240. doi:10.1093/biomet/20a.1-2.175. ISSN 0006-3444.
- ^ C.I.K.F. (July 1951). «Probability Theory for Statistical Methods. By F. N. David. [Pp. ix + 230. Cambridge University Press. 1949. Price 155.]». Journal of the Staple Inn Actuarial Society. 10 (3): 243–244. doi:10.1017/s0020269x00004564. ISSN 0020-269X.
- ^ Note that the subscript in the expression H0 is a zero (indicating null), and is not an «O» (indicating original).
- ^ Neyman, J.; Pearson, E. S. (30 October 1933). «The testing of statistical hypotheses in relation to probabilities a priori». Mathematical Proceedings of the Cambridge Philosophical Society. 29 (4): 492–510. Bibcode:1933PCPS…29..492N. doi:10.1017/s030500410001152x. ISSN 0305-0041. S2CID 119855116.
- ^ Fisher, R.A. (1966). The design of experiments. 8th edition. Hafner:Edinburgh.
Bibliography[edit]
- Betz, M.A. & Gabriel, K.R., «Type IV Errors and Analysis of Simple Effects», Journal of Educational Statistics, Vol.3, No.2, (Summer 1978), pp. 121–144.
- David, F.N., «A Power Function for Tests of Randomness in a Sequence of Alternatives», Biometrika, Vol.34, Nos.3/4, (December 1947), pp. 335–339.
- Fisher, R.A., The Design of Experiments, Oliver & Boyd (Edinburgh), 1935.
- Gambrill, W., «False Positives on Newborns’ Disease Tests Worry Parents», Health Day, (5 June 2006). [1] Archived 17 May 2018 at the Wayback Machine
- Kaiser, H.F., «Directional Statistical Decisions», Psychological Review, Vol.67, No.3, (May 1960), pp. 160–167.
- Kimball, A.W., «Errors of the Third Kind in Statistical Consulting», Journal of the American Statistical Association, Vol.52, No.278, (June 1957), pp. 133–142.
- Lubin, A., «The Interpretation of Significant Interaction», Educational and Psychological Measurement, Vol.21, No.4, (Winter 1961), pp. 807–817.
- Marascuilo, L.A. & Levin, J.R., «Appropriate Post Hoc Comparisons for Interaction and nested Hypotheses in Analysis of Variance Designs: The Elimination of Type-IV Errors», American Educational Research Journal, Vol.7., No.3, (May 1970), pp. 397–421.
- Mitroff, I.I. & Featheringham, T.R., «On Systemic Problem Solving and the Error of the Third Kind», Behavioral Science, Vol.19, No.6, (November 1974), pp. 383–393.
- Mosteller, F., «A k-Sample Slippage Test for an Extreme Population», The Annals of Mathematical Statistics, Vol.19, No.1, (March 1948), pp. 58–65.
- Moulton, R.T., «Network Security», Datamation, Vol.29, No.7, (July 1983), pp. 121–127.
- Raiffa, H., Decision Analysis: Introductory Lectures on Choices Under Uncertainty, Addison–Wesley, (Reading), 1968.
External links[edit]
- Bias and Confounding – presentation by Nigel Paneth, Graduate School of Public Health, University of Pittsburgh
Любой, кто, так или иначе, сталкивался с криптографией, знает, что без генераторов случайных чисел в этом деле не обойтись. Одно из возможных применений таких генераторов, например, – генерация ключей. Но не каждый при этом задумывается, а насколько «хорош» тот или иной генератор. А если и задумывался, то сталкивался с тем фактом, что в мире не существует какого-либо единственного «официального» набора критериев, который бы оценивал, насколько данные случайные числа применимы именно для данной области криптографии. Если последовательность случайных чисел предсказуема, то даже самый стойкий алгоритм шифрования, в котором данная последовательность будет использоваться, оказывается, уязвим — например, резко уменьшается пространство возможных ключей, которые необходимо «перебрать» злоумышленнику для получения некоторой информации, с помощью которой он сможет «взломать» всю систему. К счастью, разные организации все же пытаются навести здесь порядок, в частности, американский институт по стандартам NIST разработал набор тестов для оценки случайности последовательности чисел. О них и пойдет речь в данной статье. Но сначала — немного теории (постараюсь изложить не нудно).
Случайные двоичные последовательности
Во-первых, под генерацией случайных чисел подразумевается получение последовательности из двоичных знаков 0 и 1, а не байтами, как бы ни хотелось программистам. Идеальным подобным генератором является подбрасывание «идеальной» монеты (ровная монета, у которой вероятности выпадения каждой из сторон одинаковы), которую бы подбрасывали столько раз, сколько нужно, но проблема в том, ничего идеального не сущ ествует, а производительность такого генератора оставляла бы желать лучшего (один подрос монеты = одному биту). Тем не менее, все тесты, описываемые ниже, оценивают, насколько исследуемый генератор случайных чисел «похож» или «не похож» на воображаемую идеальную монету (не по скорости получения «случайных» знаков, а их «качества»).
Во-вторых, все генераторы случайных чисел делятся на 2 типа —истинно случайные — физические генераторы/датчики случайных чисел (ДСЧ/ФДСЧ) и псевдослучайные – программные датчики/генераторы случайных чисел (ПДСЧ). Первые принимают на вход некий случайный бесконечный процесс, а на выходе дают бесконечную (зависит от времени наблюдения) последовательность 0 и 1. Вторые представляют собой заданную разработчиком детерминированную функцию, которая инициализируется т. н. зерном, после чего также на выходе выдает последовательность 0 и 1. Зная это зерно, можно предсказать всю последовательность. Хороший ПДСЧ — этот тот, для которого невозможно предсказать последующие значения, имея всю историю предыдущих значений, не имея зерна. Это свойство называется прямой непредсказуемостью. Есть еще обратная непредсказуемость — невозможность вычислить зерно, зная любое количество генерируемых значений.
Казалось бы, проще всего взять истинно случайные/физические ДСЧ и не думать ни о какой предсказуемости. Однако тут есть проблемы:
- Случайное явление/процесс, которое берется за основу, может быть не способно выдавать числа с нужной скоростью. Если вы вспоминаете, когда последний раз генерировали пару 2048битных ключей, то не обольщайтесь. Это происходит очень редко? Тогда вообразите себя сервером, принимающим сотни запросов на SSL-соединения в секунду (SSL handshake предполагает генерацию пары случайных чисел).
- С виду случайные явления могут быть не такими случайными, как казалось бы. Например, электромагнитный шум может быть суперпозицией нескольких более-менее однообразных периодических сигналов.
Каждый из тестов, предлагаемых NIST, получает на вход конечную последовательность. Далее вычисляется статистика, характеризующая некое свойство данной последовательности — это может быть и единичное значение, и множество значений. После чего эта статистика сравнивается с эталонной статистикой, которую даст идеально случайная последовательность. Эталонная статистика выводится математически, этому посвящено множество теорем и научных трудов. В конце статьи будут даны все ссылки на источники, где выводятся нужные формулы.
Нулевая и альтернативная гипотезы
В основе тестов лежит понятие нулевой гипотезы. Попробую объяснить, что это. Допустим, мы набрали некую статистическую информацию. Например, пусть это будет количество людей, заболевших раком легких в группе из 1000 человек. И пусть известно, что некоторые люди из этой группы являются курильщиками, а другие нет, причем известно, какие конкретно. Стоит следующая задача: понять, есть ли взаимосвязь между курением и заболеванием. Нулевая гипотеза — это предположение, что между двумя фактами отсутствует какая-либо взаимосвязь. В нашем примере это предположение, что курение
не вызывает
рак легких. Существует также альтернативная гипотеза, которая опровергает нулевую гипотезу: т.е. между явлениями взаимосвязь существует (курение
вызывает
рак легких). Если переходить к терминам случайных чисел, то за нулевую гипотезу принимается предположение, что последовательность является истинно случайной (знаки которой появляются равновероятно и независимо друг от друга). Следовательно, если нулевая гипотеза верна, то наш генератор производит достаточно «хорошие» случайные числа.
Как проверяется гипотеза? С одной стороны, мы имеем статистику, подсчитанную на основе фактически собранных данных (т.е. по измеряемой последовательности). С другой стороны, есть эталонная статистика, получаемая математическими методами (теоретически вычисленная), которую
бы
имела истинно случайная последовательность. Очевидно, что собранная статистика не может сравняться с эталонной — насколько бы ни был хорошо наш генератор, он все равно не идеален. Поэтому вводят некую погрешность, например 5%. Она означает, что если, например, собранная статистика отклоняется от эталонной больше чем на 5%, то делается вывод о том, что нулевая гипотеза не верна с большой надежностью.
Так как мы имеем дело с гипотезами, то существует 4 варианта развития событий:
- Сделан вывод о том, что последовательность случайна, и это верный вывод
- Сделан вывод о том, что последовательность не случайна, хотя она была на самом деле случайна. Такие ошибки называют ошибками первого рода
- Последовательность признана случайной, хотя на самом деле таковой не является. Такие ошибки называют ошибками второго рода
- Последовательность справедливо отбракована
Вероятность ошибки первого рода называют уровнем статистической значимости и обозначают как α. Т.е. α — это вероятность отбраковать «хорошую» случайную последовательность. Это значение определяется областью применения. В криптографии принято α брать от 0.001 до 0.01.
В каждом тесте вычисляется т.н. P-значение: это вероятность того, что подопытный генератор произведет последовательность не хуже, чем гипотетический истинный. Если Pзначение = 1, то наша последовательность идеально случайна, а если оно = 0, то последовательность полностью предсказуема. В дальнейшем P-значение сравнивается с α, и если она больше α, то нулевая гипотеза принимается и последовательность признается случайной. В противном случае — отбраковывается.
В тестах берется α = 0.01. Из этого следует, что:
- Если P-значение ≥ 0.01, то последовательность признается случайной с уровнем доверия 99%
- Если P-значение < 0.01, то последовательность отбраковывается с уровнем доверия 99%
Итак, перейдем непосредственно к тестам.
Частотный побитовый тест
Очевидно, что чем более случайна последовательность, тем ближе это соотношение к 1. Данный тест оценивает, насколько это соотношение близко к 1.
Принимаем каждую «1» за +1, а каждый «0» за -1 и считаем сумму по всей последовательности. Это можно записать так:
Sn = X1 + X2 +… + Xn, где Xi = 2xi — 1.
Кстати, говорят, что распределение количества «успехов» в серии экспериментов, где в каждом эксперименте возможен успех или неуспех с заданной вероятностью, имеет биномиальное распределение.
Возьмем такую последовательность: 1011010101
Тогда S = 1 + (-1) + 1 + 1 + (-1) + 1 + (-1) + 1 + (-1) + 1 = 2
Вычисляем статистику:
Вычисляем P-значение через дополнительную функцию ошибок:
Дополнительная функция ошибок (complementary error function) определяется так:
Видим, что результат > 0.01, а значит наша последовательность прошла тест. Рекомендуется тестировать последовательности длиной не менее 100 бит.
Частотный блочный тест
Этот тест делается на основе предыдущего, только теперь значения пропорции «1»/«0» для каждого блока анализируются методом Хи-квадрат. Ясно, что это соотношение должно быть приблизительно равным 1.
Например, пусть дана последовательность 0110011010. Разобъем ее на блоки по 3 бита («бесхозный» 0 на конце отброшен):
011 001 101
Посчитаем пропорции πi для каждого блока: π1 = 2/3, π2 = 1/3, π3 = 1/3. Далее вычисляем статистику по методу Хи-квадрат c N степенями свободы (здесь N — количество блоков):
Вычислим P-значение через специальную функцию Q:
Q — это т.н. неполная верхняя гамма-функция, определяемая как:
При этом функция Г — стандартная гамма-функция:
Последовательность считается случайной, если P-значение > 0.01. Рекомендуется анализировать последовательности длиной не менее 100 бит, а также должны выполняться соотношения M >= 20, M > 0.01n и N < 100.
Тест на одинаковые идущие подряд биты
В тесте ищутся все последовательности одинаковых битов, а затем анализируется, насколько количество и размеры этих последовательностей соответствуют количеству и размерам истинно случайной последовательности. Смысл в том, что если смена 0 на 1 (и обратно) происходит слишом редко, то такая последовательность «не тянет» на случайную.
Пусть дана последовательность 1001101011. Сначала вычисляем долю единиц в общей массе:
Дальше проверяется условие:
Если оно не удовлетворяется, то весь тест считается неуспешным и на этом все заканчивается. В нашем случае 0.63246 > 0.1, а значит идем дальше.
Вычисляем суммарное число знакоперемен V:
где если
, или
в противном случае.
Вычисляем P-значение через функцию ошибок:
Если результат >= 0.01 (как в нашем примере), то последовательность признается случайной.
Тест на самую длинную последовательность из единиц в блоке
Исходная последовательность из n битов разбивается на N блоков, каждый по M бит, после чего в каждом блоке ищется самая длинная последовательность единиц, а затем оценивается, насколько показатель близок к такому же показателю для истинно случайной последовательности. Очевидно, что аналогичного теста на нули не требуется, так как если единицы распределены хорошо, то нули также будут распределены хорошо.
Какую взять длину блока? NIST рекомендует несколько опорных значений, как разбивать на блоки:
| Общая длина, n | Длина блока, M |
|---|---|
| 128 | 8 |
| 6272 | 128 |
| 750000 | 10000 |
Пусть дана последовательность:
11001100 00010101 01101100 01001100 11100000 00000010
01001101 01010001 00010011 11010110 10000000 11010111
11001100 11100110 11011000 10110010
Разобьем ее на блоки по 8 бит (M=8), после чего посчитаем максимальную последовательность из единиц для каждого блока:
| Блок | Длина единиц |
|---|---|
| 11001100 | 2 |
| 00010101 | 1 |
| 01101100 | 2 |
| 01001100 | 2 |
| 11100000 | 3 |
| 00000010 | 1 |
| 01001101 | 2 |
| 01010001 | 1 |
| 00010011 | 2 |
| 11010110 | 2 |
| 10000000 | 1 |
| 11010111 | 3 |
| 11001100 | 2 |
| 11100110 | 3 |
| 11011000 | 2 |
| 10110010 | 2 |
Далее считаем статистику по разным длинам на основе следующей таблицы:
| vi | M = 8 | M = 128 | M = 10000 |
|---|---|---|---|
| v0 | ≤1 | &le4 | &le10 |
| v1 | 2 | 5 | 11 |
| v2 | 3 | 6 | 12 |
| v3 | ≥4 | 7 | 13 |
| v4 | 8 | 14 | |
| v5 | ≥9 | 15 | |
| v6 | ≥16 |
Как пользоваться этой таблицей: у нас M = 8, поэтому смотрим только один соответствующий столбец. Считаем vi:
v0 = { кол-во блоков с макс. длиной ≤ 1 } = 4
v1 = { кол-во блоков с макс. длиной = 2 } = 9
v2 = { кол-во блоков с макс. длиной = 3 } = 3
v3 = { кол-во блоков с макс. длиной ≥ 4 } = 0
Вычисляем Хи-квадрат:
Где значения K и R берутся исходя из такой таблицы:
| M | K | R |
|---|---|---|
| 8 | 3 | 16 |
| 128 | 5 | 49 |
| 10000 | 6 | 75 |
Теоретические вероятности πi задаются константами. Например, для K=3 и M=8 рекомендуется взять π0 = 0.2148, π1 = 0.3672, π2 = 0.2305, π3 = 0.1875. (Значения для других K и M приведены в [2]).
Далее вычисляем P-значение:
Если оно > 0.01, как в нашем примере, то последовательность считается достаточно случайной.
Тест рангов бинарных матриц
Тест анализирует матрицы, которые составлены из исходной последовательности, а именно — рассчитывает ранги непересекающихся подматриц, построенных из исходной двоичной последовательности. В основе тест лежат исследования Коваленко [6], где ученый исследовал случайные матрицы, состоящие из 0 и 1. Он показал, что можно спрогнозировать вероятности того, что матрица M x Q будем иметь ранг R, где R = 0,1,2,…min(M,Q). Эти вероятности равны:
NIST рекомендует брать M = Q = 32, а также, чтобы длина последовательности n = M^2 * N. Но мы для примера возьмем M = Q = 3. Далее нужны вероятности PM, PM-1 и PM-2. С небольшой долей погрешности формулу можно упростить, и тогда эти вероятности равны:
Итак, пусть дана последовательность 01011001001010101101. «Раскладываем» ее по матрицам — хватило на 2 матрицы:
Определяем ранг матриц: получается R1 = 2, R2 = 3. Для теста нужно 3 числа:
- FM = {кол-во матриц с рангом M} = {кол-во матриц с рангом 3} = 1
- FM-1 = 1 (аналогично)
- N — FM — FM-1 = 2 — 1 — 1 = 0
Вычисляем Хи-квадрат:
Вычисляем P-значение:
Если результат > 0.01, то последовательность признается случайной. NIST рекомендует, чтобы общая длина последовательности была >= 38MQ.
Спектральный тест
Подопытная последовательность рассматривается как дискретный сигнал, для которого делается спектральное разложение с целью выявить частотные пики. Очевидно, что такие пики будут свидетельствовать о наличии периодических составляющих, что не есть гут. Если вкратце, то тест выявляет пики, превышающие 95%-й барьер, после чего проверяет, не превышает ли доля этих пиков 5%.
Как нетрудно догадаться, для представления последовательности в виде суммы периодических составляющих будем использовать дискретное преобразование Фурье. Оно выглядит так:
Здесь xk — исходная последовательность, в которой единице соответствует +1, а нулю -1, Xj — полученные значения комплексных амплитуд (комплексные означает, что в них содержится как вещественное значение амплитуды, так и фаза).
Вы спросите, а где же здесь периодичности? Ответ — экспоненту можно выразить через тригонометрические функции:
Для нашего теста интересны не фазы, а абсолютные значения амплитуд. И если мы вычислим эти абсолютные значения, то окажется, что они симметричны (это общеизвестный факт при переходе от комплексных значений к вещественным), поэтому для дальнейшего рассмотрения мы возьмём только половину этих значений (от 0 до n/2) — остальные не несут дополнительной информации.
Покажем все это на примере. Пусть задана последовательность 1001010011.
Тогда x = { 1, -1, -1, 1, -1, 1, -1, -1, 1, 1 }.
Вот как разложение Фурье можно сделать, например, в программе GNU Octave:
octave:1> x = [1, -1, -1, 1, -1, 1, -1, -1, 1, 1]
x =
1 -1 -1 1 -1 1 -1 -1 1 1
octave:2> abs(fft(x))
ans =
0.0000 2.0000 4.4721 2.0000 4.4721 2.0000 4.4721 2.0000 4.4721 2.0000 Видим, что наблюдается симметрия. Поэтому нам хватит и пять значений: 0, 2, 4.4721, 2, 4.4721.
Далее вычисляем граничное значение по формуле
Оно означает, что если последовательность истинно случайная, то 95% пиков не должны превышать эту границу.
Вычислим предельное число пиков, которых должно быть меньше, чем T:
Далее смотрим на результат разложения и видим, что все наши 4 пика меньше граничного значения. Далее оцениваем эту разницу:
Вычисляем P-значение:
Оно получилось >0.01, поэтому гипотеза о случайности принимается. И да, для теста рекомендуется брать не менее 1000 бит.
Тест на встречающиеся непересекающиеся шаблоны
Подопытная последовательность разбивается на блоки одинаковой длины. Например:
1010010010 1110010110
В каждом блоке будем искать какой-нибудь шаблон, например «001». Слово непересекающиеся означает, что в случае нахождения шаблона внутри последовательности, следующее сравнение не будет захватывать ни одного бита найденного шаблона. В результате поиска для каждого i-го блока будет найдено число Wi, равное кол-ву найденных случаев.
Итак, для наших блоков W1 = 2 и W2 = 1:
101 001 001 0
111 001 0110
Вычислим математические ожидание и дисперсию, как если бы наша последовательность была подлинно случайна. Ниже приведены формулы. Здесь N = 2 (кол-во блоков), M = 10 (длина блока), m = 3 (длина образца).
Вычислим Хи-квадрат:
Вычислим итоговое P-значение через неполную гамма-функцию:
Видим, что P-значение > 0.1, а значит, последовательность достаточно случайна.
Мы оценили только один шаблон. На самом деле нужно проверить все комбинации шаблонов, да и ещё к тому же для разной длины этих шаблонов. Сколько того и другого нужно, определяется исходя из конкретных требований, но обычно m берут 9 или 10. Чтобы получить осмысленные результаты, следует брать N < 100 и M > 0.01 * n.
Тест на встречающиеся пересекающиеся шаблоны
Этот тест отличается от предыдущего тем, что при нахождении шаблона «окно» поиска сдвигается не на длину шаблона, а только на 1 бит. Чтобы не загромождать статью, мы не станем приводить пример расчета по этому методу. Он полностью аналогичен.
Универсальный тест Мауэра
Тест оценивает, насколько «далеко» друг от друга отстоят шаблоны внутри последовательности. Смысл теста в том, чтобы понять, насколько последовательность сжимаема (конечно, имеется в виду сжатие без потерь). Чем более сжимаема последовательность, тем она менее случайна. Алгоритм этого теста весьма громоздкий для Хабра-формата, поэтому опустим его.
Тест на линейную сложность
В основе теста лежит предположение, что подопытная последовательность была получена через регистр сдвига с линейной обратной связью (или LFSR, Linear feedback shift register). Это общеизвестный метод получения бесконечной последовательности: тут каждый следующий бит получается как некая функция бит, «сидящих» в регистре. Минус LFSR в том, что он всегда имеет конечный период, т.е. последовательность обязательно будет рано или поздно повторяться. Чем больше длина LFSR, тем лучше случайная последовательность.
Исходная последовательность разбивается на равные блоки длиной M. Далее для каждого блока с помощью алгоритма Берлекэмпа — Мэсси [10] находится его линейная сложность (Li), т.е. длина LFSR. Затем для всех найденных Li оценивается распределение Хи-квадрат со 6 степенями свободы. Покажем на примере.
Пусть дан блок 1101011110001 (M=13), для которого алгоритм Берлекэмпа — Мэсси выдал L = 4. Убедимся, что это так. Действительно, нетрудно догадаться, что для этого блока каждый следующий бит получается как сумма (по модулю 2) 1-го и 2-го бита (нумерация с 1):
x5 = x1 + x2 = 1 + 1 = 0
x6 = x2 + x3 = 1 + 0 = 1
x7 = x3 + x4 = 1 + 0 = 1
и.т.д.
Вычисляем математическое ожидание по формуле
Для каждого блока вычисляем значение Ti:
Далее на основе множества T вычисляем набор v0,…,v6 таким образом:
- если Ti <= -2.5, то v0++
- если -2.5 < Ti <= -1.5, то v1++
- если -1.5 < Ti <= -0.5, то v2++
- если -0.5 < Ti <= 0.5, то v3++
- если 0.5 < Ti <= 1.5, то v4++
- если 1.5 < Ti <= 2.5, то v5++
- если Ti > 2.5, то v6++
Имеем 7 возможных исходов, а значит вычисляем Хи-квадрат с числом степеней свободы 7 — 1 = 6:
Вероятности πi в тесте жестко заданы и равны соответственно: 0.010417, 0.03125, 0.125, 0.5, 0.25, 0.0625, 0.020833. (πi для большего числа степеней свободы можно вычислить по формулам, данным в [2]).
Вычислить P-значение:
Если результат получился > 0.01, то последовательность признается случайной. Для реальных тестов рекомендуется брать n >= 10^6 и М в пределах от 500 до 5000.
Тест на подпоследовательности
Анализируется частота нахождения всевозможных последовательностей длиной «m» бит внутри исходной последовательности. При этом каждый образец ищется независимо, т.е. возможно как бы «наложение» одного найденного образца на другой. Очевидно, что количество всевозможных образцов будет 2m. Если последовательность достаточно велика и случайна, то вероятности нахождения каждого из этих образцов одинакова. (Кстати, если m = 1, то этот тест «вырождается» в уже описанный ранее тест на соотношение «0» или «1»).
В основе теста лежат работы [8] и [11]. Там описываются 2 показателя (∇ψ2m и ∇2ψ2m), которые характеризуют, насколько частоты появления образцов соответствуют этим же частотам для истинно случайной последовательности. Покажем алгоритм на примере.
Пусть дана последовательность 0011011101 длиной n = 10, а также m = 3.
Сначала формируется 3 новых последовательности, каждая из которых получается добавлением m-1 первых битов последовательности к её концу. Получается:
- Для m = 3: 0011011101 00 (добавили 2 бита к концу)
- Для m-1 = 2: 0011011101 0 (добавили 1 бит к концу)
- Для m-2 = 1: 0011011101 (исходная последовательность)
Далее найдем частоты появления всех блоков длиной m, m-1 и m-2 соответственно:
- v000 = 0, v001 = 1, v010 = 1, v011 = 2, v100 = 1, v101 = 2, v110 = 2, v111 = 0
- v00 = 1, v01 = 3, v10 = 3, v11 = 3
- v0 = 4, v1 = 6
Вычисляем нужные статистики по формулам:
Подставляем:
Тогда:
Итоговые значения:
Итак, оба P-значения > 0.01, а значит последовательность признается случайной.
Приблизительная энтропия
Метод приблизительной энтропии (Approximate Entropy) изначально проявил себя в медицине, особенно в кардиологии. Вообще, согласно классическому определению, энтропия является мерой хаоса: чем она выше, тем более непредсказуемые явления. Хорошо это или плохо, зависит от контекста. Для случайных последовательностей, используемых в криптографии, важно иметь высокую энтропию — это значит, что будет сложно предсказать последующие случайные биты на основе того, что уже имеем. А вот, например, если за случайную величину взять сердечный ритм, измеряемый с заданным периодом, то ситуация иная: есть множество исследований (например, [12]), доказывающих, что чем ниже вариабельность сердечных ритмов, тем реже вероятность инфарктов и прочих неприятных явлений. Очевидно, что сердце человека не может биться с постоянной частотой. Однако одни умирают от инфарктов, а другие нет. Поэтому метод приблизительной энтропии позволяет оценить, насколько с виду случайные явления действительно случайны.
Конкретно, тест вычисляет частоты появления всевозможных образцов заданной длины (m), а затем аналогичные частоты, но уже для образцов длиной m+1. Затем распределение частот сравнивается с эталонным распределением Хи-квадрат. Как и в предыдущем тесте, образцы могут перекрываться.
Покажем на примере. Пусть дана последовательность 0100110101 (длина n = 10), и возьмём m = 3.
Для начала дополним последовательность первыми m-1 битами. Получится 0100110101 01.
Посчитаем встречаемость каждого из 8 всевозможных блоков. Получится:
k000 = 0, k001 = 1, k010 = 3, k011 = 1, k100 = 1, k101 = 3, k110 = 1, k111 = 0.
Посчитаем соответствующие частоты по формуле Cim = ki / n:
C0003 = 0, C0013 = 0.1, C0103 = 0.3, C0113 = 0.1, C1003 = 0.1, C1013 = 0.3, C1103 = 0.1, C1113 = 0.
Аналогичным образом считаем частоты появления подблоков длиной m+1=4. Их уже 24=16:
С00114 = С01004 = С01104 = С10014 = С11014 = 0.1, С01014 = 0.2, С10104 = 0.3. Остальные частоты = 0.
Вычисляем φ3 и φ4 (заметьте, что здесь натуральный логарифм):
Вычисляем Хи-квадрат:
P-значение:
Получившееся значение > 0.01, а значит последовательность признается случайной.
Тест кумулятивных сумм
Примем каждый нулевой бит исходной последовательности за -1, а каждый единичный — за +1, после чего посчитаем сумму. Интуитивно понятно, что чем более случайна последовательность, тем быстрее эта сумма будет стремиться к нулю. С другой стороны, представим, что дана последовательность, состоящая из 100 нулей и 100 единиц, идущих подряд: 00000…001111…11. Здесь сумма получится равной 0, однако очевидно, что назвать такую последовательность случайной «рука не поднимется». Следовательно, нужен более глубокий критерий. И этим критерием являются частичные суммы. Будем постепенно считать суммы, начиная от первого элемента:
S1 = x1
S2 = x1 + x2 S3 = x1 + x2 + x3…
Sn = x1 + x2 + x3 +… + xn
Далее находится число z = максимум среди этих сумм.
Наконец, считается P-значение по следующей формуле (её вывод см. в [9]):
Где:
Здесь Φ — функция распределения стандартной нормальной случайной величины. Напоминаем, что стандартное нормальное распределение — это всем известное гауссово распределение (в форме колокола), у которого математическое ожидание 0 и дисперсия 1. Выглядит так:
Если получившееся P-значение > 0.01, то последовательность признается случайной.
Кстати, у этого теста есть 2 режима: первый мы только что рассмотрели, а во втором суммы считаются начиная с последнего элемента.
Тест на произвольные отклонения
Этот тест похож на предыдущий: аналогичным образом считаются частичные суммы нормализованной последовательности (т.е. состоящей из -1 и 1). Пусть дана последовательность 0110110101 и пусть S(i) — это частичная сумма с 1 по i-й элемент. Нанесем эти точки на график, предварительно прибавив «0» к началу и концу последовательности S(i) — это нужно для целостности дальнейших рассчетов:
Отметим точки, где график пересекает горизонтальную ось — эти точки будут делить последовательность на т.н. циклы. Здесь мы имеем 3 цикла: {0, -1, 0}, {0, 1, 0} и {0, 1, 2, 1, 2, 1, 2, 0}. Далее, говорят, что каждый из этих циклов последовательно принимает различные состояния. Например, первый цикл 2 раза принимает состояние «0» и 1 раз состояние «-1». Для данного теста интересуют состояния от -4 до 4. Занесем все нахождения в этих состояниях в такую таблицу:
| Состояние (x) | Цикл №1 | Цикл №2 | Цикл №3 |
|---|---|---|---|
| -4 | 0 | 0 | 0 |
| -3 | 0 | 0 | 0 |
| -2 | 0 | 0 | 0 |
| -1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 3 |
| 2 | 0 | 0 | 3 |
| 3 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 |
На основе этой таблицы формируем другую таблицу: в ней по горизонтали пойдут
количества
циклов, принимающих заданное состояние:
| Состояние (x) | Ни разу | 1 раз | 2 раза | 3 раза | 4 раза | 5 раз |
|---|---|---|---|---|---|---|
| -4 | 3 | 0 | 0 | 0 | 0 | 0 |
| -3 | 3 | 0 | 0 | 0 | 0 | 0 |
| -2 | 3 | 0 | 0 | 0 | 0 | 0 |
| -1 | 2 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 2 | 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 0 | 0 |
| 4 | 3 | 0 | 0 | 0 | 0 | 0 |
Далее для каждого из восьми состояний вычисляется Хи-квадрат статистики по формуле
Где vk(x) — значения в таблице для данного состояния, J — количество циклов (у нас 3), πk(x) — вероятности того, что состояние «x» возникнет k раз в подлинно случайном распределении (они известны).
Например, для x=1 получается:
Значения π для остальных x смотрите в [2].
Вычисляем P-значение:
Если оно > 0.01, то делается вывод о случайности. В итоге необходимо вычислить 8 P-значений. Какие-то могут оказаться больше 0.01, какие-то — меньше. В таком случае финальное решение о последовательности делается на основе других тестов.
Разновидность теста на произвольные отклонения
Практически похож на предыдущий тест, но берется более широкий набор состояний: -9, -8, -7, -6, -5, -4, -3, -2, -1, +1, +2, +3, +4, +5, +6, +7, +8, +9. Но главное отличие в том, что здесь Р-значение вычисляется не через гамма-функцию (igamc) и Хи-квадрат, а через функцию ошибок (erfc). За точными формулами читатель может обратиться к исходному документу.
Ниже привожу список источников, которые можно посмотреть, если хочется углубиться в тему:
- csrc.nist.gov/groups/ST/toolkit/rng/stats_tests.html
- csrc.nist.gov/groups/ST/toolkit/rng/documents/SP800-22rev1a.pdf
- Центральная предельная теорема
- Anant P. Godbole and Stavros G. Papastavridis, (ed), Runs and patterns in probability: Selected papers. Dordrecht: Kluwer Academic, 1994
- Pal Revesz, Random Walk in Random and Non-Random Environments. Singapore: World Scientific, 1990
- И. Н. Коваленко, Теория вероятностей и её применения, 1972
- O. Chrysaphinou, S. Papastavridis, “A Limit Theorem on the Number of Overlapping Appearances of a Pattern in a Sequence of Independent Trials.” Probability Theory and Related Fields, Vol. 79, 1988
- I. J. Good, “The serial test for sampling numbers and other tests for randomness,” Cambridge, 1953
- A. Rukhin, “Approximate entropy for testing randomness,” Journal of Applied Probability, 2000
- Алгоритм Берлекэмпа — Мэсси
- D. E. Knuth, The Art of Computer Programming. Vol. 2 & 3, 1998
- www.ncbi.nlm.nih.gov/pubmed/8466069
Терминология ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа:
2.3. (генеральная) совокупность
Множество всех рассматриваемых единиц.
Примечание — Для случайной величины распределение вероятностей рассматривают как определение совокупности этой случайной величины
3.1. (измеримая) величина; физическая величина
Признак явления, материала или вещества, который можно различить качественно и определить количественно [п. 1].
Примечания
1. Термин «величина» может относиться к количеству в общем смысле, например длина, время, масса, температура, электрическое сопротивление, или к определенным установленным величинам, например длина определенного стержня, электрическое сопротивление определенной проволоки.
2. Величины, которые взаимно сравнимы, можно объединять в количественные категории, например:
— работа, тепло, энергия;
— толщина, периметр, длина волны.
3. Символы для величин приведены в ИСО 31.0 — ИСО 31.13.
4. Измеримые величины можно определить количественно
2.86. c2-критерий
Критерий, в котором в нулевой гипотезе используемая статистика имеет по предположению распределение c2.
Примечание — Его применяют, например, при решении следующих задач:
— проверка равенства дисперсии нормальной совокупности и заданного значения дисперсии, оцениваемой на основе статистики критерия по выборке, взятой из этой совокупности;
— сравнение наблюдаемых частот с теоретическими частотами
Определения термина из разных документов: c2-критерий
2.88. F -критерий , критерий Фишера
Статистический критерий, в котором в нулевой гипотезе используемая статистика имеет по предположению F-распределение.
Примечание — Этот критерий применяют, например, при решении следующих задач:
— проверка равенства дисперсий двух нормальных совокупностей на основе выборочных дисперсий, оцениваемых по двум независимым выборкам;
— проверка математических ожиданий равенства нескольких (например, К) нормальных совокупностей с одинаковыми дисперсиями на основе средних арифметических и выборочных дисперсий независимых выборок
Определения термина из разных документов: F -критерий
1.41. F -распределение
Распределение вероятностей непрерывной случайной величины, принимающей значения от 0 до +∞, плотность распределения вероятностей которой
где F ³ 0 с параметрами n1 = 1, 2, …; n2 = 1, 2, …;
Г — гамма-функция.
Примечание — Это распределение отношения двух независимых случайных величин с распределениями c2, в котором делимое и делитель разделены на свои числа степеней свободы. Число степеней свободы числителя равно n1, а знаменателя — n2. В таком порядке и записывают числа степеней свободы случайной величины с распределением F
2.87. t -критерий; критерий Стьюдента
Статистический критерий, в котором в нулевой гипотезе используемая статистика соответствует t-распределению.
Примечание — Этот критерий применяют, например, при решении следующих задач:
— проверка равенства математического ожидания нормальной совокупности заданному значению с помощью критерия, основанного на выборочном среднем и выборочной дисперсии;
— проверка равенства математических ожиданий из двух нормальных совокупностей с одинаковой дисперсией на основе двух выборочных средних и двух выборочных дисперсий из двух независимых выборок, взятых из этих совокупностей;
— критерий, применяемый к значению линейной регрессии или коэффициента корреляции
Определения термина из разных документов: t -критерий
1.40. t -распределение; распределение Стьюдента
Распределение вероятностей непрерывной случайной величины, плотность распределения вероятностей которой
где -¥ < t < +¥ с параметром n = 1, 2, …;
Г — гамма-функция.
Примечание — Отношение двух независимых случайных величин, числитель которого — стандартизованная нормальная случайная величина, а знаменатель — положительное значение квадратного корня из частного от деления случайной величины c2 на ее число степеней свободы n — это распределение Стьюдента с v степенями свободы
1.45. бета-распределение
Распределение вероятностей непрерывной случайной величины X, которая может принимать любые значения от 0 до 1, включая границы, и плотность распределения которой
при 0 £ x £ 1 и параметрах m1 > 0, m2 > 0,
где Г — гамма-функция.
Примечание — При m1 = m2 = 1 бета-распределение переходит в равномерное распределение с параметрами a = 0 и b = 1
1.49. биномиальное распределение
Распределение вероятностей дискретной случайной величины X, принимающей любые целые значения от 0 до n, такое что
при х = 0, 1, 2, …, n
и параметрах n = 1, 2, … и 0 < p < 1, где
1.1 вероятность
Действительное число в интервале от 0 до 1, относящееся к случайному событию.
Примечания
1. Число может отражать относительную частоту в серии наблюдений или степень уверенности в том, что некоторое событие произойдет. Для высокой степени уверенности вероятность близка к единице.
2. Вероятность события А обозначают Рr (А) или Р (А)
Определения термина из разных документов: вероятность
2.78. вероятность ошибки второго рода
Вероятность допустить ошибку второго рода.
Примечание — Вероятность ошибки второго рода, обычно обозначаемая b, зависит от реальной ситуации и может быть вычислена лишь в том случае, если альтернативная гипотеза задана адекватно
2.76. вероятность ошибки первого рода
Вероятность допустить ошибку первого рода.
Примечания
1. Она всегда меньше уровня значимости критерия или равна ему.
2. В примечании 2 к п. 2.71 ошибка первого рода состоит в отбрасывании H0 (m < m0), потому что меньше А, в то время как на самом деле m равно или превышает m0. Вероятность такой ошибки равна a при m = m0 и уменьшается с увеличением m
2.27. взвешенное среднее арифметическое
Сумма произведений каждого значения на его вес, деленная на сумму весов, где веса — неотрицательные коэффициенты, связанные с каждым значением
3.20. воспроизводимость (результатов проверки)
Прецизионность в условиях воспроизводимости (по ИСО 5725.1)
4.22. вторичная выборка [проба]
Выборка [проба], получаемая из первичной выборки [пробы] на второй стадии многостадийного отбора.
Примечание — Это можно распространить на k-ю стадию при k > 2
4.2. выборка [проба]
Одна или несколько выборочных единиц, взятых из генеральной совокупности и предназначенных для получения информации о ней.
Примечание — Выборка [проба] может служить основой для принятия решения о генеральной совокупности или о процессе, который ее формирует
Определения термина из разных документов: выборка
4.7. выборка без возвращения
Выборка, в которую единицы отбирают из совокупности только один раз или последовательно и не возвращают в нее
4.6. выборка с возвращением
Выборка, из которой каждую отобранную и наблюдаемую единицу возвращают в совокупность перед отбором следующей единицы.
Примечание — Одна и та же единица может многократно появляться в выборке
2.33. выборочная дисперсия
Одна из мер рассеяния, представляющая собой сумму квадратов отклонений наблюдений от их среднего арифметического, деленная на число наблюдений минус единица.
Примечания
1. Для серии из n наблюдений х1, x2, …, хn со средним арифметическим
выборочная дисперсия
2. Выборочная дисперсия — это несмещенная оценка дисперсии совокупности.
3. Выборочная дисперсия — это центральный момент второго порядка, кратный n/(n — 1) (п. 2.39, примечание)
4.24. выборочная доля
а) Отношение объема выборки к общему числу выборочных единиц.
b) Когда отбирают нештучную или непрерывно производимую продукцию, выборочную долю определяют отношением количества пробы к количеству совокупности или подсовокупности.
Примечание — Под количеством пробы или совокупности понимают массу, объем, площадь и т.д.
4.1. выборочная единица
а) Одна из конкретных единиц, из которых состоит генеральная совокупность.
b) Определенное количество продукции, материала или услуг, образующее единство и взятое из одного места, в одно время для формирования части выборки.
Примечания
1. Выборочная единица может содержать более одного изделия, допускающего испытание, например пачка сигарет, но при этом получают один результат испытания или наблюдения.
2. Единицей продукции может быть одно изделие, пара или набор изделий, или ею может быть определенное количество материала, такое как отрезок латунного прутка определенной длины, определенный объем жидкой краски или заданная масса угля. Она необязательно должна быть такой же, как единица закупки, поставки, производства или отгрузки
2.40. выборочная ковариация
Сумма произведений отклонений х и у от их соответствующих средних арифметических, деленная на число наблюдаемых пар без единицы:
где n — число наблюдаемых пар.
Примечание — Выборочная ковариация — это несмещенная оценка ковариации совокупности
2.28. выборочная медиана
Если n случайных значений упорядочены по возрастанию и пронумерованы от 1 до n, то, если n нечетно, выборочная медиана принимает значение с номером ; если n четно, медиана лежит между
-м и
-м значениями и не может быть однозначно определена.
Примечание — При отсутствии других указаний и четном n за выборочную медиану можно принять среднее арифметическое этих двух значений
2.34. выборочное стандартное отклонение
Положительный квадратный корень из выборочной дисперсии.
Примечание — Выборочное стандартное отклонение — это смещенная оценка стандартного отклонения совокупности
2.35. выборочный коэффициент вариации (Ндп. относительное стандартное отклонение)
Отношение выборочного стандартного отклонения к среднему арифметическому для неотрицательных признаков.
Примечание — Это отношение можно выразить в процентах
2.41. выборочный коэффициент корреляции
Частное от деления выборочной ковариации двух показателей на произведение их выборочных стандартных отклонений:
где Sxy — выборочная ковариация Х и Y;
Sx и Sy — выборочные стандартные отклонения Х и Y соответственно.
Примечания
1. Этот коэффициент часто используют как цифровое выражение взаимной зависимости между Х и Y в серии парных наблюдений. Для проверки линейности можно строить диаграмму разброса.
2. Его значения всегда лежат между минус 1 и плюс 1. Когда выборочный коэффициент корреляции равен одному из указанных пределов, это означает, что существует точная линейная зависимость в серии парных наблюдений.
3. Этот выборочный коэффициент корреляции применяют для измеряемых признаков; для ранговых данных используют другие коэффициенты корреляции, такие как коэффициенты Спирмена и Кендалла
2.44. выборочный коэффициент регрессии
Коэффициент при переменной в уравнении кривой или поверхности регрессии
2.36. выборочный момент порядка q относительно начала отсчета
Среднее арифметическое наблюдаемых значений в степени q в распределении единственного признака:
где n — общее число наблюдений.
Примечание — Момент первого порядка — это среднее арифметическое наблюдаемых значений
2.38. выборочный совместный момент порядков q и s относительно начала отсчета
В совместном распределении двух показателей — среднее арифметическое произведений xi в степени q и yi в степени s для всех наблюдаемых пар значений (xi, уi)
где n — число наблюдаемых пар.
Примечания
1. Выборочный совместный момент порядков q и s — это один из моментов порядка (q + s).
2. Выборочный момент порядков 1 и 0 — это среднее арифметическое маргинального распределения частот X, а момент порядков 0 и 1 — среднее арифметическое маргинального распределения частот Y
2.39. выборочный совместный центральный момент порядков q и s
В совместном распределении двух признаков — среднее арифметическое произведений разности между xi и его средним арифметическим значением в степени q и разности между уi и его средним арифметическим значением
в степени s для всех наблюдаемых пар (xi, уi):
где n — число наблюдаемых пар.
Примечание — Выборочный центральный момент порядков 2 и 0 — это выборочная дисперсия маргинального распределения частот X, умноженная на (n — 1)/n, а выборочный центральный момент порядков 0 и 2 — выборочная дисперсия маргинального распределения частот Y, умноженная на (n — 1)/n
2.37. выборочный центральный момент порядка q
Среднее арифметическое разностей между наблюдаемыми значениями хi и их средним арифметическим в степени q в распределении единственного признака:
где n — число наблюдений.
Примечание — Выборочный центральный момент первого порядка равен нулю
2.64. выбросы
Наблюдения в выборке, отличающиеся от остальных по величине настолько, что возникает предположение, что они принадлежат другой совокупности или получены в результате ошибки измерения
Определения термина из разных документов: выбросы
1.44. гамма-распределение
Распределение вероятностей непрерывной случайной величины X, которая может принимать любые значения от 0 до +¥ и плотность вероятности которой
при х ³ 0 и параметрах m > 0, a > 0;
где Г — гамма-функция
Примечания
1. При m целом имеем:
Г (m) = (m — 1)!
2. Параметр m определяет форму распределения. При m = 1 гамма-распределение превращается в экспоненциальное распределение.
3. Сумма m независимых случайных величин, подчиняющихся экспоненциальному закону распределения с параметром — это гамма-распределение с параметрами m и a
1.52. гипергеометрическое распределение
Дискретное распределение вероятностей с функцией распределения:
где х = max (0, М — N + n), …, max (0, М — N + n) + 1, …, min (М, n); параметры N = 1, 2, …;
М = 0, 1, 2, …, N;
n = 1, 2, …, N
и
и т.п.
Примечание — Это распределение возникает как распределение вероятностей числа успехов в выборке объема n, взятой без возвращения из генеральной совокупности объема N, содержащий М успехов
2.17. гистограмма
Графическое представление распределения частот для количественного признака, образуемое соприкасающимися прямоугольниками, основаниями которых служат интервалы классов, а площади пропорциональны частотам этих классов
Определения термина из разных документов: гистограмма
2.8. границы класса; пределы класса
Значения, определяющие верхнюю и нижнюю границы класса.
Примечания
1. Следует уточнить, какую из двух границ считают принадлежащей классу.
2. Если возможно, надо чтобы граница класса не совпадала с возможным значением
1.7. двумерная функция распределения
Функция, дающая для любой пары значений х, у вероятность того, что случайная величина X будет меньше или равна х, а случайная величина Y — меньше или равна y:
Примечание — Выражение в квадратных скобках означает пересечение событий Х £ х и Y £ у
1.53. двумерное нормальное распределение ; двумерное распределение Лапласа—Гаусса
Распределение вероятностей двух непрерывных случайных величин Х и Y такое, что плотность распределения вероятностей
при -¥ < x < +¥ и -¥ < у < +¥,
где mx и my — математические ожидания;
sx и sy — стандартные отклонения маргинальных распределений Х и Y, которые нормальны;
r — коэффициент корреляции Х и Y.
Примечание — Это понятие можно распространить на многомерное распределение более двух случайных величин таких, что маргинальное распределение любой их пары может быть представлено в той форме, что приведена выше
2.20. двумерное распределение частот
Эмпирическое отношение между парами значений или классами признаков с одной стороны, и их частотами с другой — для двух признаков, рассматриваемых одновременно
2.57. двусторонний доверительный интервал
Если T1 и T2 — две функции от наблюдаемых значений таких, что для оценки параметра распределения совокупности q вероятность равна (1 — a), где (1 — a) — константа, положительная и меньше 1, то интервал между T1 и T2 — это двусторонний доверительный интервал для q при доверительной вероятности (1 — a).
Примечания
1. Границы T1 и T2 доверительного интервала — это статистики (2.45), которые в общих предположениях принимают различные значения от выборки к выборке.
2. В длинном ряду выборок относительная частота случаев, когда доверительный интервал накрывает истинное значение параметра совокупности q, больше или равна (1 — a)
2.74. двусторонний критерий
Критерий, в котором используемая статистика одномерна, а критическая область состоит из множества значений, меньших первого критического значения, и множества значений, больших второго критического значения.
Примечание — Выбор между односторонним и двусторонним критериями определяется альтернативной гипотезой. В примечании, приведенном в п. 2.71, критерий односторонний, а критическое значение равно А
3.3. действительное значение (величины)
Значение величины, которое для данной цели можно рассматривать как истинное [п. 1], [п. 2].
Примечания
1. Действительное значение в общем смысле рассматривают как достаточно близкое к истинному значению, поскольку разница не имеет большого значения для данной цели.
2. Значение, приписанное в организации некоторому эталону, можно рассматривать как действительное значение величины, воспроизводимой этим эталоном
4.11. деление пробы
Процесс отбора одной или нескольких проб из пробы нештучной продукции таким способом, как нарезание, механическое деление или квартование
Определения термина из разных документов: деление пробы
2.21. диаграмма разброса [рассеяния]
Графическое представление множества точек, координаты которых х и у в обычной прямоугольной системе координат — это значения признаков Х и Y.
Примечания
1. Множество из n элементов таким образом дает n точек, которые наглядно показывают зависимость между Х и Y.
2. Концепцию диаграммы разброса можно распространить на более чем два признака
1.22. дисперсия (случайной величины)
Математическое ожидание квадрата центрированной случайной величины
2.59. доверительная вероятность; уровень доверия
Величина (1 — a) — вероятность, связанная с доверительным интервалом или со статистически накрывающим интервалом.
Примечание — Величину (1 — a) часто выражают в процентах
2.60. доверительная граница
Каждая из границ, нижняя T1, верхняя T2 для двустороннего доверительного интервала или граница Т для одностороннего интервала
4.12. дублирующая выборка [проба]
Одна из двух или более выборок [проб] или подвыборок [проб], полученных одновременно, одним методом ее отбора или делением выборки [пробы]
2.1. единица [объект]
То, что можно рассмотреть и описать индивидуально.
Примечание — Единицей может, например, быть:
— изделие;
— определенное количество материала;
— услуга, действие или процесс;
— организация или человек;
— некоторая их комбинация.
Определения термина из разных документов: единица
2.51. значение оценки
Значение параметра, полученное в результате оценивания
2.84. значимый результат (на выбранном уровне значимости a)
Результат статистической проверки, который приводит к отбрасыванию нулевой гипотезы, в противном случае — результат незначим.
Примечания
1. Когда результат проверки называют статистически значимым, это показывает, что результат выходит за тот диапазон значений, в который укладываются случайные воздействия, когда нулевая гипотеза верна.
2. Для примера, приведенного в п. 2.71, при , меньшем А, где
считают, что
значимо меньше m0 на уровне значимости 1 — a
3.5. измеряемая величина
Величина, подвергаемая измерению [1], [2].
Примечание — По обстоятельствам это может быть величина, измеряемая количественно или качественно
2.10. интервал класса
Разница между верхней и нижней границами класса для количественного признака
3.2. истинное значение (величины)
Значение, которое идеальным образом определяет величину при тех условиях, при которых эту величину рассматривают [п. 1].
Примечание — Истинное значение — теоретическое понятие, которое нельзя определить точно
1.14. квантиль (случайной величины)
Значение случайной величины хp, для которого функция распределения принимает значение p (0 £ p £ 1) или ее значение изменяется скачком от меньшего p до превышающего р.
Примечания
1. Если значение функции распределения равно p во всем интервале между двумя последовательными значениями случайной величины, то любое значение в этом интервале можно рассматривать как p-квантиль.
2. Величина хp будет p-квантилем, если
3. Для непрерывной величины p-квантиль — это то значение переменной, ниже которого лежит р-я доля распределения.
4. Процентиль — это квантиль, выраженный в процентах
1.16. квартиль
Квантиль порядка p = 0,25 или p = 0,75
Определения термина из разных документов: квартиль
2.7. класс
а) Для качественного признака — Определенные группы объектов, каждые из которых имеют отдельные общие признаки, взаимно исключают друг друга, исчерпывая все объекты.
b) Для количественного признака — Каждый из последовательных взаимоисключающих интервалов, на которые разделен весь интервал варьирования.
Определения термина из разных документов: класс
4.18. кластерный отбор; отбор методом группировки
Способ отбора, при котором совокупность разделяют на взаимоисключающие и исчерпывающие группы или кластеры, в которых выборочные единицы объединены определенным образом, и выборку из этих кластеров берут случайно, причем все выборочные единицы включают в общую выборку
1.32. ковариация; корреляционный момент
Совместный центральный момент порядков 1 и 1:
Определения термина из разных документов: ковариация
4.23. конечная выборка
Выборка, получаемая на последней стадии многостадийного отбора
1.13. корреляция
Взаимозависимость двух или нескольких случайных величин в распределении двух или нескольких случайных величин.
Примечание — Большинство статистических мер корреляции измеряют только степень линейной зависимости
Определения термина из разных документов: корреляция
1.24. коэффициент вариации (случайной величины)
Отношение стандартного отклонения к абсолютному значению математического ожидания случайной величины
1.33. коэффициент корреляции
Отношение ковариации двух случайных величин к произведению их стандартных отклонений:
Примечания
1. Эта величина всегда будет принимать значения от минус 1 до плюс 1, включая крайние значения.
2. Если две случайные величины независимы, коэффициент корреляции между ними равен нулю только в случае двумерного нормального распределения
2.81. кривая мощности (критерия)
Графическое представление функции мощности критерия.
Примечания
1. На рисунке 1 представлена кривая мощности для проверки гипотезы H0 (m ³ m0) против альтернативной гипотезы H1 (m < m0) в зависимости от математического ожидания совокупности m и уровня значимости критерия a.
1 — Pa — вероятность отклонения гипотезы H0; m — математическое ожидание совокупности
Рисунок 1 — Кривая мощности
2. На рисунке 2 представлена кривая мощности критерия для гипотезы H0 (p £ p0) против H1 (p > p0) в зависимости от р0 — доли несоответствующих единиц в партии, проходящей контроль.
1 — Pa — вероятность отклонения гипотезы H0; p — доля несоответствующих единиц в партии
Рисунок 2 — Кривая мощности
2.83. кривая оперативной характеристики; кривая ОХ
Графическое представление оперативной характеристики.
Примечания
1. На рисунке 3 представлена кривая оперативной характеристики для проверки гипотезы H0 (m ³ m0) против H1 (m < m0) в зависимости от математического ожидания генеральной совокупности m и уровня значимости критерия a
Pa — вероятность принятия гипотезы H0; m — математическое ожидание совокупности
Рисунок 3 — Кривая оперативной характеристики
2. На рисунке 4 представлена кривая оперативной характеристики для проверки гипотезы H0 (p < p0) против H1 (p ³ p0) в зависимости от р — доли несоответствующих единиц в партии, проходящей контроль.
Pa — вероятность принятия гипотезы H0; p — доля несоответствующих единиц в партии
Рисунок 4 — Кривая оперативной характеристики
1.34. кривая регрессии ( Y по X)
Для двух случайных величин Х и Y кривая, отображающая зависимость условного математического ожидания случайной величины Y при условии Х = х для каждой переменной х.
Примечание — Если кривая регрессии Y по X представляет собой прямую линию, то регрессию называют «простой линейной». В этом случае коэффициент линейной регрессии Y по Х — это коэффициент наклона перед х в уравнении линии регрессии
2.42. кривая регрессии (Y по Х для выборки)
Для выборки n пар наблюдений двух показателей Х и Y — кривая регрессии Y от X отображает зависимость функции Y от X
2.63. критерий согласия распределения
Мера соответствия между наблюдаемым распределением и теоретическим распределением, выбранным априори либо подобранным по результатам наблюдений
2.71. критическая область
Множество возможных значений статистики, лежащей в основе критерия, для которого отвергают нулевую гипотезу.
Примечания
1. Критические области определяют таким образом, что если нулевая гипотеза верна, вероятность ее отбрасывания равна заданному значению a, обычно малому, например 5 % или 1 %.
2. Классический способ проверки нулевой гипотезы, относящийся к математическому ожиданию нормального распределения с известным стандартным отклонением s, H0 (m ³ m0) против альтернативы H1 (m < m0), — использование статистики выборочного среднего арифметического.
Критическая область — это множество значений статистики, меньших чем
где n — объем выборки;
m1-a — это квантиль уровня (1 — a) стандартизованной нормальной случайной величины.
Если рассчитанное значение меньше А, гипотезу Н0 отвергают. В противном случае — Н0 не отвергают (принимают)
3.24. критическая разность воспроизводимости
Значение, меньшее или равное абсолютной разности между двумя конечными значениями, каждое из которых представляет собой ряды результатов проверок, полученных в условиях воспроизводимости, ожидаемое с заданной вероятностью (по ИСО 5725.1).
Примечание — Примерами конечных результатов служат среднее арифметическое и выборочная медиана рядов результатов проверок; ряды могут содержать только по одному результату проверки
3.19. критическая разность повторяемости
Значение, меньшее или равное абсолютной разности между двумя конечными значениями, каждое из которых представляет собой ряды результатов проверок, полученных в условиях повторяемости, ожидаемое с заданной вероятностью (по ИСО 5725.1).
Примечания
1. Примерами конечных результатов служат среднее арифметическое и выборочная медиана рядов результатов проверок; сами ряды могут содержать только по одному результату проверки.
2. Предел повторяемости r — это критическая разность повторяемости для двух единичных результатов проверки при вероятности 95 %
2.72. критическое значение
Значение, ограничивающее критическую область
2.14. кумулятивная относительная частота
Кумулятивная частота, деленная на общее число наблюдений
4.31. лабораторная проба
Проба, предназначенная для лабораторных исследований или испытаний
1.42 логарифмически нормальное распределение
Распределение вероятностей непрерывной случайной величины X, которая может принимать любые значения от а до +¥ и плотность распределения вероятности которой
где x > a;
m и s — соответственно математическое ожидание и стандартное отклонение случайной величины loge(X — a).
Примечания
1. Распределение вероятностей случайной величины loge(X — a) — это нормальное распределение; m и s — соответственно математическое ожидание и стандартное отклонение этой случайной величины.
2. Параметры m и s — это не логарифмы математического ожидания и стандартного отклонения X.
3. Часто вместо обозначения loge (или ln) используют log10. В этом случае
где m и s — соответственно математическое ожидание и стандартное отклонение log10(X — a);
1.19. маргинальное математическое ожидание
Математическое ожидание маргинального распределения случайной величины
1.9. маргинальное распределение (вероятностей)
Распределение вероятностей подмножества k1 из множества k случайных величин, при этом остальные (k — k1) случайные величины принимают любые значения в соответствующих множествах возможных значений.
Примечание — Для распределения вероятностей трех случайных величин X, Y, Z существуют:
— три двумерных маргинальных распределения, т.е. распределения пар (X, Y), (X, Z), (Y, Z);
— три одномерных маргинальных распределения, т.е. распределения X, Y и Z
2.24. маргинальное распределение частот
Распределение частот подмножества k1 < k признаков из многомерного распределения частот k признаков, когда остальные (k — k1) переменных принимают любые значения из своих областей значений.
Примечания
1. Для k = 2 признаков маргинальное распределение частот можно получить, добавляя к каждому значению или классу значений рассматриваемого признака соответствующие частоты или относительные частоты остальных признаков.
2. В распределении частот трех признаков X, Y и Z существуют:
— три двумерных маргинальных распределения частот, то есть распределения пар (X, Y), (X, Z), (Y, Z);
— три одномерных маргинальных распределения частот, то есть распределения X, Y и Z
1.18. математическое ожидание (случайной величины)
а) Для дискретной случайной величины X, принимающей значения xi с вероятностями pi, математическое ожидание, если оно существует, определяют формулой
где суммируют все значения xi, которые может принимать случайная величина X;
b) Для непрерывной случайной величины X, имеющей плотность f (x), математическое ожидание, если оно существует, определяют формулой
где интеграл берут по всему интервалу (интервалам) изменения Х
4.25. мгновенная проба
Количество нештучной продукции, взятое единовременно за один прием из большего объема этой же продукции
1.15. медиана
Квантиль порядка p = 0,5
Определения термина из разных документов: медиана
1.8. многомерная функция распределения
Функция, дающая для любого набора значений х, у,… вероятность того, что несколько случайных величин X, Y,… будут меньше или равны соответствующим значениям х, у,…:
2.23. многомерное распределение частот
Эмпирическое отношение между совместными наборами значений или классов признаков с одной стороны и их частотами с другой — для нескольких признаков, рассматриваемых одновременно
4.20. многостадийный кластерный отбор
Кластерный отбор, проведенный в две или более стадии, при котором каждый отбор делают из кластеров, которые уже получены из разделения предшествующей выборки
4.19. многостадийный отбор
Отбор, при котором выборку берут в несколько стадий, выборочные единицы на каждой стадии отбирают из больших выборочных единиц, отобранных на предыдущей стадии
1.17. мода
Значение случайной величины, при котором функция распределения вероятностей масс или плотность распределения вероятностей имеет максимум.
Примечание — Если имеется единственная мода, то распределение вероятностей случайной величины называется унимодальным; если имеется более чем одна мода, оно называется многомодальным, в случае двух мод — бимодальным
Определения термина из разных документов: мода
1.27. момент1) порядка q относительно а
Математическое ожидание величины (X — а) в степени q для одномерного распределения
1.26. момент1) порядка q относительно начала отсчета
Математическое ожидание случайной величины в степени q для одномерного распределения
Примечание — Момент первого порядка — математическое ожидание случайной величины Х
2.79. мощность критерия
Вероятность недопущения ошибки второго рода.
Примечания
1. Это вероятность отбрасывания нулевой гипотезы, когда она не верна. Ее обычно обозначают (1 — β).
2. В примечании 2 к п. 2.71 ошибка второго рода состоит в принятии гипотезы H0 (m ³ m0), поскольку превышает А, в то время как на самом деле m меньше m0. Вероятность b такой ошибки зависит от фактического значения m: чем ближе m к m0, тем ближе мощность к 1.
3. В примечании 4 к п. 2.66 проверка нулевой гипотезы H0 (нормально распределенная совокупность) против альтернативы H1 (совокупность с ненормальным распределением) невозможно выразить b как функцию от альтернативной гипотезы, поскольку она не определена
3.6. наблюдаемое значение
Значение данного признака, полученное в результате единичного наблюдения (по ИСО 5725.1)
2.12. накопленная кумулятивная частота
Число наблюдений из множества, имеющих значения, которые меньше заданного значения или равны ему.
Примечание — Для данных, объединенных в классы, кумулятивную частоту можно указать только в границах класса
1.11. независимость (случайных величин)
Две случайные величины Х и Y независимы, если их функции распределения представлены как
где F (х, ¥) = G (х) и F (¥, у) = Н (у) — маргинальные функции распределения X и Y, соответственно, для всех пар (х, у).
Примечания:
1. Для непрерывной независимой случайной величины ее плотность распределения, если она существует, выражают как
где g (x) и h (у) — маргинальные плотности распределения Х и Y, соответственно, для всех пар (х, у).
Для дискретной независимой случайной величины ее вероятности выражают как
для всех пар (xi, уj).
2. Два события независимы, если вероятность того, что они оба произойдут, равна произведению вероятностей этих двух событий
3.25. неопределенность (результата проверки)
Оценка, относящаяся к результату проверки, которая характеризует область значений, внутри которой лежит истинное значение.
Примечания
1. Неопределенность измеряет совокупность многих компонентов. Некоторые из них можно оценить на основе статистического распределения результатов в рядах измерений и охарактеризовать стандартными отклонениями. Оценки других компонентов возможны только на основе опыта или из других источников информации.
2. Неопределенность следует отличать от оценки, связанной с результатом проверки, которая характеризуется значениями интервалов, внутри которых лежит математическое ожидание. Эта последняя оценка — мера прецизионности, а не правильности, и ее надо использовать, только если истинное значение не определено. Когда математическое ожидание используют вместо истинного значения, надо употреблять выражение «случайный компонент неопределенности»
2.55. несмещенная оценка
Оценка со смещением, равным нулю
1.37. нормальное распределение ; распределение Лапласа—Гаусса
Распределение вероятностей непрерывной случайной величины Х такое, что плотность распределения вероятностей при — ¥ < х < + ¥ принимает действительное значение
Примечание — m — математическое ожидание; s — стандартное отклонение нормального распределения
2.66. нулевая гипотеза и альтернативная гипотеза
Утверждения относительно одного или нескольких параметров или о распределении, которые проверяют с помощью статистического критерия.
Примечания
1. Нулевая гипотеза (Н0) — предположение, обычно сложное, относят к утверждению, подвергаемому проверке, в то время как альтернативную гипотезу (Н1) относят к утверждению, которое будет принято, если нулевую гипотезу отвергают.
2. Проверка гипотезы о том, что математическое ожидание m случайной величины Х в совокупности не меньше, чем заданное значение m0:
3. Проверка гипотезы о том, что доли несоответствующих деталей в двух партиях р1 и p2 одинаковы (неодинаковы):
4. Проверка гипотезы о том, что случайная величина X имеет нормальное распределение с неизвестными параметрами. Альтернативная гипотеза — распределение не нормально
4.26. образец (для испытаний)
Часть выборочной единицы, требуемая для целей испытания
4.29. объединенная выборка [проба]
Выборка [проба] из совокупности, получаемая объединением всех выборочных единиц, взятых из этой совокупности
4.3. объем выборки
Число выборочных единиц в выборке
Определения термина из разных документов: объем выборки
2.16. одномерное распределение частот
Распределение частот для единственного признака
2.58. односторонний доверительный интервал
Если Т — функция от наблюдаемых значений такая, что для оценки параметра распределения совокупности q вероятность или вероятность
равна (1 — a), где (1 — a) — константа, положительная и меньше 1, то интервал от наименьшего возможного значения q до Т или интервал от T до наибольшего возможного значения q — это односторонний доверительный интервал для q при доверительной вероятности (1 — a).
Примечания
1. Граница T доверительного интервала — это статистика, которая в общих предположениях принимает различные значения от выборки к выборке.
2. См. п. 2.57, примечание 2
2.73. односторонний критерий
Критерий, в котором используемая статистика одномерна, а критическая область включает в себя множество значений, меньших критического значения, или множество значений, больших критического значения
2.82. оперативная характеристика
Функция, которая определяет вероятность принятия нулевой гипотезы относительно значений скалярного параметра, обычно обозначаемая Ра.
Примечание — Оперативная характеристика всегда равна единице минус значение критерия мощности
4.4. отбор выборки
Процесс извлечения или составления выборки
Определения термина из разных документов: отбор выборки
4.27. отбор проб
Отбор из партий нештучной продукции, где выборочные единицы изначально трудноразличимы.
Примечание — Примерами могут служить отбор проб из больших куч угля для анализа на содержание золы или теплоты сгорания, или табака на содержание влаги
Определения термина из разных документов: отбор проб
2.13. относительная частота
Частота, деленная на общее число событий или наблюдений
1.50. отрицательное биномиальное распределение
Распределение вероятностей дискретной случайной величины Х такое, что
при x = 0, 1, 2, …
и параметрах c > 0 (целое положительное число), 0 < p < 1,
где
Примечания
1. Название «отрицательное биномиальное распределение» связано с тем, что последовательные вероятности при х = 0, 1, 2, … получают при разложении бинома с отрицательным показателем степени (-с):
последовательных положительных целых степеней величины (1 — р).
2. Когда параметр с равен 1, распределение называют геометрическим распределением
2.49. оценивание (параметра)
Операция определения на основе выборочных данных числовых значений параметров распределения, принятого в качестве статистической модели генеральной совокупности, из которой извлечена выборка.
Примечание — Результат этой операции может быть выражен как одним числовым значением, так и доверительным интервалом
2.50. оценка
Статистика, используемая для оценивания параметра совокупности
Определения термина из разных документов: оценка
2.77. ошибка второго рода
Ошибка принять нулевую гипотезу, поскольку статистика принимает значение, не принадлежащее критической области, в то время как нулевая гипотеза не верна
2.75. ошибка первого рода
Ошибка, состоящая в отбрасывании нулевой гипотезы, поскольку статистика принимает значение, принадлежащее критической области, в то время как эта нулевая гипотеза верна
3.8. ошибка результата (проверки)
Результат проверки минус принятое нормальное значение величины (по ИСО 5725.1).
Примечание — Ошибка — это сумма случайных ошибок и систематических ошибок
1.12. параметр
Величина, используемая в описании распределения вероятностей некоторой случайной величины
Определения термина из разных документов: параметр
4.21. первичная выборка [проба]
Выборка [проба], получаемая из совокупности на первой стадии многостадийного отбора
4.17. период отбора (выборки)
Интервал времени, в течение которого берут очередную выборочную единицу при периодическом систематическом отборе.
Примечание — Период отбора может быть постоянным или зависеть от выхода или от скорости процесса, то есть зависеть от количества материала, изготовленного в производственном процессе или загруженного в процессе погрузки
4.16. периодический систематический отбор
Отбор n выборочных единиц с порядковыми номерами:
h, h + k, h + 2k, …, h + (n — 1)k,
где h и k — целые числа, удовлетворяющие соотношениям
и h обычно выбирают случайно из k первых целых чисел, если N объектов совокупности расположены по определенной системе и если они пронумерованы от 1 до N.
Примечание — Периодический систематический отбор обычно применяют для получения выборки, которая случайна по отношению к некоторым признакам, о которых известно, что они не зависят от систематического смещения
1.5. плотность распределения (вероятностей)
Первая производная, если она существует, функции распределения непрерывной случайной величины
Примечание — f(x)dx называется элементом вероятности
2.43. поверхность регрессии (Z по Х и Y для выборки)
Для выборки n наблюдений каждого из трех показателей X, Y и Z — поверхность регрессии Z от Х и Y отображает зависимость функции Z от X и Y.
Примечание — Вышеуказанные определения можно распространить также на случай более трех показателей
1.35. поверхность регрессии (Z по Х и Y)
Для трех случайных величин X, Y, Z поверхность, отображающая зависимость условного математического ожидания случайной величины Z при условии Х = х и Y = y для каждой пары переменных (х, у).
Примечания
1. Если поверхность регрессии представляет собой плоскость, то регрессию называют «линейной». В этом случае коэффициент линейной регрессии Z по Х — это коэффициент перед х в уравнении регрессии.
2. Определение можно распространить на число случайных величин более трех
2.89. повторение
Термин, обозначающий выполнение статистического исследования несколько раз одним и тем же методом на одной и той же совокупности при одинаковых условиях
Определения термина из разных документов: повторение
3.15. повторяемость (результата проверки); сходимость
Прецизионность в условиях повторяемости (по ИСО 5725.1)
2.53. погрешность выборочного метода
Часть погрешности при оценивании, обусловленная только тем, что объем выборки меньше, чем объем генеральной совокупности
2.52. погрешность оценки
Разность (Т — q) при оценивании параметра, где T обозначает результат оценки, а q — оцениваемый параметр.
Примечание — Погрешность при оценивании может включать в себя один или несколько из следующих компонентов:
— погрешность выборочного метода;
— погрешность измерения;
— округление значений или разделение на классы;
— другие погрешности
4.10. подвыборка
Выборка [проба], взятая из выборки [пробы] генеральной совокупности.
Примечания
1. Ее можно отбирать тем же методом, что и при отборе исходной выборки [пробы], но это необязательно.
2. При отборе пробы из нештучной продукции подвыборки часто получают делением пробы
Определения термина из разных документов: подвыборка
4.30. подготовка пробы
Для нештучной продукции — система операций, таких как измельчение, смешивание, деление и т.д., необходимых для превращения отобранной пробы материала в лабораторную пробу или пробу для испытаний.
Примечание — Подготовка пробы не должна, насколько это возможно, изменять репрезентативность совокупности, из которой она изготовлена
2.5. подсовокупность
Определенная часть генеральной совокупности
2.19. полигон кумулятивных частот
Ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам классов, а ординаты — либо кумулятивным абсолютным частотам, либо кумулятивным относительным частотам
2.46. порядковая статистика
Каждое из упорядоченных выборочных значений, расположенных в неубывающем порядке.
Примечания
1. В более общем выражении всякую статистику, основанную на порядковых статистиках в этом узком смысле, также называют порядковой статистикой.
2. k-e значение в неубывающей последовательности наблюдений x|k| — это значение случайной величины X|k|, называемое k-й порядковой статистикой. В выборке объема n наименьшее наблюдаемое значение x|1| и наибольшее значение x|n| — это значения случайных величин X|1| и X|n| — первая и n-я порядковые статистики соответственно. Размах x|n| — x|1| — это значение порядковой статистики X|n| — X|1|
3.12. правильность (результата проверки)
Близость среднего значения, полученного в длинном ряду результатов проверок, к принятому нормальному значению величины (по ИСО 5725.1).
Примечание — Меру правильности обычно выражают в терминах смещения
3.23. предел воспроизводимости
Значение, меньшее или равное абсолютной разности между двумя результатами проверки, полученными в условиях воспроизводимости, ожидаемое с вероятностью 95 % (по ИСО 5725.1).
Примечания
1. Используют обозначение R.
2. В настоящее время в нормативных документах принято обозначение D
3.18. предел повторяемости
Значение, которое меньше или равно абсолютной разности между двумя результатами проверок, получаемыми в условиях повторяемости, ожидаемое с вероятностью 95 % (по ИСО 5725.1).
Примечания
1. Используют обозначение r.
2. В настоящее время в нормативных документах принято обозначение d
3.14. прецизионность (результата проверки)
Близость между независимыми результатами проверки, полученными при определенных принятых условиях (по ИСО 5725.1).
Примечания
1. Прецизионность зависит от распределения случайных ошибок и не связана ни с истинным значением, ни с заданным значением.
2. Меру прецизионности обычно выражают в терминах рассеяния и вычисляют как стандартное отклонение результатов проверки. Малой прецизионности соответствует большое стандартное отклонение.
3. Независимые результаты проверки означают результаты, полученные таким образом, что отсутствует влияние предыдущих результатов на том же самом или аналогичном объекте проверки. Количественные меры прецизионности решающим образом зависят от принятых условий. Условия повторяемости и воспроизводимости являются разными степенями принятых условий
2.2. признак
Свойство, которое помогает идентифицировать или различать единицы данной генеральной совокупности.
Примечание — Признак может быть количественным или качественным (альтернативным)
Определения термина из разных документов: признак
3.4. принятое нормальное значение
Значение величины, служащее согласованным эталоном для сравнения и определяемое как:
а) теоретическое или установленное значение, основанное на научных принципах;
b) принятое или сертифицированное значение, основанное на экспериментальных данных некоторых национальных или международных организаций;
с) согласованное (на основе консенсуса) или сертифицированное значение, основанное на совместной экспериментальной работе, проводимой научным или инженерным коллективом;
d) когда а), b) и с) не подходят, математическое ожидание измеримой величины, то есть среднее арифметическое измерений конкретной совокупности
4.32. проба для анализа
Проба, подготовленная для проведения испытаний или анализа, которую полностью и единовременно используют для проведения испытания или анализа
2.67. простая гипотеза
Гипотеза, которая полностью задает распределение совокупности
4.9. простая случайная выборка
Выборка n выборочных единиц, взятых из совокупности таким образом, что все возможные комбинации из n единиц имеют одинаковую вероятность быть отобранными
4.5. процедура выборочного контроля
Пооперационные требования и (или) инструкции, связанные с реализацией конкретного плана выборочного контроля, то есть запланированный метод отбора, извлечения и подготовки выборки (выборок) из партий для получения информации о признаке (признаках) в партии
1.36. равномерное распределение; прямоугольное распределение
а) Распределение вероятностей непрерывной случайной величины, плотность распределения вероятности которой постоянна на конечном интервале [а, b] и равна нулю вне его.
b) Распределение вероятностей дискретной случайной величины такое, что
для i = 1, 2,…, n.
Примечание — Равномерное распределение дискретной случайной величины имеет равные вероятности для каждого из п значений, то есть
для j = 1, 2,…, n
2.30. размах (выборки)
Разность между наибольшим и наименьшим наблюденными значениями количественного признака в выборке
2.4. рамки отбора
Список, заполняемый для выборочных целей, в котором отмечают те единицы, которые надо отобрать и исследовать
Определения термина из разных документов: рамки отбора
2.91. рандомизация
Процесс, с помощью которого множество объектов устанавливают в случайном порядке.
Примечание — Если из совокупности, состоящей из натуральных чисел от 1 до n, извлекать числа случайно (то есть таким образом, чтобы все числа имели одинаковые шансы быть выбранными) одно за другим без возвращения, пока совокупность не исчерпается, то порядок отбора чисел называют случайным. Если эти n чисел ассоциировать с n различными объектами или с n разными обработками (по 1.4, ИСО 3534.3), которые, таким образом, переупорядочиваются в том порядке, в котором были вытянуты числа, порядок объектов или обработок называют случайным (по 1.12, ИСО 3534.3)
Определения термина из разных документов: рандомизация
1.3. распределение (вероятностей)
Функция, определяющая вероятность того, что случайная величина примет какое-либо заданное значение или будет принадлежать заданному множеству значений.
Примечание — Вероятность того, что случайная величина находится в области ее изменения, равна единице
1.39. распределение c2
Распределение вероятностей непрерывной случайной величины, принимающей значения от 0 до +¥, плотность распределения вероятностей которой
где c2 ³ 0 при значении параметра n = 1, 2, …;
Г — гамма-функция.
Примечания
1. Сумма квадратов n независимых стандартизованных нормальных случайных величин образует случайную величину c2 с параметром n; n называют степенью свободы случайной величины c2.
2. Распределение вероятностей случайной величины c2/2 — это гамма-распределение с параметром m = n/2
Определения термина из разных документов: распределение c2
1.48. распределение Вейбулла; распределение экстремальных значений типа III
Распределение вероятностей непрерывной случайной величины Х с функцией распределения:
где х ³ а; y = (x — a)/b;
а параметры -¥ < a < +¥, k > 0, b > 0.
Примечание — Параметр k определяет форму распределения
1.46. распределение Гумбеля; распределение экстремальных значений типа I
Распределение вероятностей непрерывной случайной величины Х с функцией распределения:
где -¥ < х < +¥;
а параметры -¥ < a < +¥, b > 0
1.55. распределение многомерной случайной величины; мультиномиальное распределение
Распределение вероятностей k дискретных случайных величин Х1, Х2, …, Хk такое, что
где x1, x2, …, xk — целые числа, такие что x1 + x2 +… + xk = n,
с параметрами pi ³ 0 (i = 1, 2, …, k) и ,
где k = 2, 3, …
Примечание — Распределение многомерной случайной величины — обобщение биномиального распределения (п. 1.49) на распределение k > 2 случайных величин
1.51. распределение Пуассона
Распределение вероятностей дискретной случайной величины Х такое, что
при х = 0, 1, 2, … и параметре m > 0.
Примечания
1. Математическое ожидание и дисперсия распределения Пуассона оба равны параметру m.
2. Распределение Пуассона можно использовать для аппроксимации биномиального распределения, когда n — велико, p — мало, а произведение пр = m
1.47. распределение Фрешэ; распределение экстремальных значений типа II
Распределение вероятностей непрерывной случайной величины Х с функцией распределения:
где х ³ а;
а параметры -¥ < a < +¥, k > 0, b > 0.
Примечание — Параметр k определяет форму распределения
2.15. распределение частот
Эмпирическое отношение между значениями признака и его частотами или его относительными частотами.
Примечание — Это распределение можно представить графически в виде гистограммы, столбиковой диаграммы, полигона кумулятивных частот или как таблицу сопряженности двух признаков
4.13. расслоение
Разделение совокупности на взаимоисключающие и исчерпывающие подсовокупности, называемые слоями, которые должны быть более однородными относительно исследуемых показателей, чем вся совокупность
Определения термина из разных документов: расслоение
4.14. расслоенная выборка [проба]
В совокупности, которую можно разделить на различные взаимно исключающие и исчерпывающие подсовокупности, называемые слоями, отбор, проводимый таким образом, что в выборку [пробу] отбирают определенные доли от разных слоев и каждый слой представляют хотя бы одной выборочной единицей
3.7. результат проверки
Значение некоторого признака, полученное применением определенного метода проверки.
Примечания
1. Под проверкой можно понимать такие процедуры, как измерение, испытание, контроль и т.д.
2. В методе проверки должно быть уточнено, что будут выполнять одно или несколько индивидуальных наблюдений, что будут регистрировать в качестве результата проверки — их среднее арифметическое или иную подходящую функцию, такую как медиана или стандартное отклонение. Может также потребоваться применить стандартный метод корректировки, например поправку на объем газа при стандартных температуре и давлении таким образом, что результат проверки может быть результатом, вычисленным по нескольким наблюдаемым значениям. В простом случае результат проверки — это само наблюдаемое значение
2.90. реплика; повторное проведение эксперимента
Определение значений более чем один раз в ходе эксперимента или исследования.
Примечание — Реплики отличаются от повторений тем, что предполагают повторные проверки в разных местах и (или) в разное время в соответствии с планом (по 1.10, ИСО 3534.3)
Определения термина из разных документов: реплика
2.69. свободный от распределения критерий
Критерий, в котором функция распределения статистики, лежащей в основе критерия, не зависит от функции распределения наблюдений
2.9. середина класса
Среднее арифметическое верхней и нижней границ класса для количественного признака
2.29. середина размаха (выборки)
Среднее арифметическое между наибольшим и наименьшим наблюденными значениями количественного признака
2.48. серия
а) Появление в рядах наблюдений по качественному признаку непрерывающихся рядов одного и того же значения признака.
b) Последовательный набор монотонно возрастающих или монотонно убывающих значений в рядах наблюдений по количественному признаку.
Примечание — Последовательный набор монотонно возрастающих значений называют возрастающей серией, а монотонно убывающих значений — убывающей серией
Определения термина из разных документов: серия
3.10. систематическая ошибка результата (проверки)
Компонент ошибки результата, который остается постоянным или закономерно изменяется в ходе получения результатов проверки для одного признака.
Примечание — Систематические ошибки и их причины могут быть известны или неизвестны
4.15. систематический отбор
Отбор выборки каким-либо систематическим методом
2.68. сложная гипотеза
Гипотеза, которая не полностью задает распределение совокупности.
Примечания
1. Это обычно гипотеза, которая включает в себя бесконечную систему простых гипотез.
2. В предположении нормального распределения гипотеза m = m0 будет простой, если стандартное отклонение совокупности известно, но она будет сложной, если оно неизвестно.
3. Все гипотезы из примечаний, приведенных в п. 2.66, сложные
1.2. случайная величина
Переменная, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей.
Примечание — Случайную величину, которая может принимать только отдельные значения, называют дискретной. Случайную величину, которая может принимать любые значения из конечного или бесконечного интервала, называют непрерывной
4.8. случайная выборка
Выборка n выборочных единиц, взятых из совокупности таким образом, что каждая возможная комбинация из n единиц имеет определенную вероятность быть отобранной
3.9. случайная ошибка результата (проверки)
Компонент ошибки, который изменяется непредвиденным образом в ходе получения результатов проверки одного признака (по ИСО 5725.1).
Примечание — Случайную ошибку результата проверки нельзя скорректировать
2.92. случайные причины
Факторы, каждый из которых играет относительно малую роль, но создают вариацию, которую нельзя идентифицировать (по ГОСТ Р 50779.11)
3.13. смещение (результата проверки)
Разность между математическим ожиданием результатов проверки и принятым нормальным значением (по ИСО 5725.1).
Примечание — Смещение — это общая систематическая ошибка в противоположность случайной ошибке. Может быть один или несколько компонентов, образующих систематическую ошибку. Большее систематическое смещение от принятого значения соответствует большому значению смещения
2.54. смещение оценки
Разность между математическим ожиданием оценки и значением оцениваемого параметра
1.29. совместный момент1) порядков q и s относительно начала отсчета
Математическое ожидание произведения случайной величины Х в степени q и случайной величины Y в степени s для двумерного распределения
Примечание — Совместный момент порядков 1 и 0 — маргинальное математическое ожидание случайной величины X.
Совместный момент порядков 0 и 1 — маргинальное математическое ожидание случайной величины Y
1.30. совместный момент1) порядков q и s относительно точки (а, b )
Математическое ожидание произведения случайной величины (X — а) в степени q и случайной величины (Y — b) в степени s для двумерного распределения:
1.31. совместный центральный момент1) порядков q и s
Математическое ожидание произведения центрированной случайной величины (X — mx) в степени q и центрированной случайной величины (Y — my)в степени s для двумерного распределения:
Примечание — Совместный центральный момент порядков 2 и 0 — дисперсия маргинального распределения X.
Совместный центральный момент порядков 0 и 2 — дисперсия маргинального распределения Y.
1) Если при определении моментов значения случайных величин X, X — a, Y, Y — b и т.д. заменяют на их абсолютные значения |Х|, |Х — а|, |Y|, |Y — b| и т.д., то моменты называют «абсолютными моментами»
2.26. среднее арифметическое
Сумма значений, деленная на их число.
Примечания
1. Термин «среднее» обычно используют, когда имеют в виду параметр совокупности, а термин «среднее арифметическое» — когда имеют в виду результат вычислений по данным, полученным из выборок.
2. Среднее арифметическое простой случайной выборки, взятой из совокупности, — это несмещенная оценка арифметического среднего генеральной совокупности. Однако другие формулы для оценки, такие как геометрическое или гармоническое среднее, медиана или мода, иногда тоже используют
2.32. среднее отклонение (выборки)
Среднее арифметическое отклонение от начала координат, когда все отклонения имеют положительный знак.
Примечание — Обычно выбранное начало отсчета представляет собой среднее арифметическое, хотя среднее отклонение минимизируется, когда за начало отсчета принимают медиану
2.31. средний размах (выборок)
Среднее арифметическое размахов множества выборок одинакового объема
1.25. стандартизованная случайная величина
Случайная величина, математическое ожидание которой равно нулю, а стандартное отклонение — единице.
Примечания
1. Если случайная величина X имеет математическое ожидание m и стандартное отклонение s, то соответствующая стандартизованная случайная величина равна
Распределение стандартизованной случайной величины называется стандартным распределением.
2. Понятие стандартизованной случайной величины является частным случаем «приведенной случайной величины», определяемой относительно центрального значения и параметра масштаба, отличных от математического ожидания и стандартного отклонения
1.54 стандартизованное двумерное нормальное распределение; нормированное двумерное распределение Лапласа—Гаусса
Распределение вероятностей пары стандартизованных нормальных случайных величин
с плотностью распределения
где -¥ < u < +¥ и -¥ < v < +¥;
(X, Y) — пара нормальных случайных величин с параметрами (mx, my) и (sx, sy) и r;
r — коэффициент корреляции Х и Y, а также U и V.
Примечание — Это понятие можно распространить на многомерное распределение более двух случайных величин, таких, что маргинальное распределение любой их пары может быть представлено в той же форме, что приведена выше
2.56. стандартная ошибка; среднеквадратичная ошибка
Стандартное отклонение оценки
1.38. стандартное нормальное распределение ; стандартное распределение Лапласа—Гаусса
Распределение вероятностей стандартизованной нормальной случайной величины U, плотность распределения которой
при -¥ < u < +¥ (п. 1.25, примечание 1)
1.23. стандартное отклонение (случайной величины)
Положительный квадратный корень из значения дисперсии
3.22. стандартное отклонение воспроизводимости
Стандартное отклонение результатов проверки, полученных в условиях воспроизводимости.
Примечания
1. Это мера рассеяния распределения результатов проверки в условиях воспроизводимости.
2. Аналогично «дисперсию воспроизводимости» и «коэффициент вариации воспроизводимости» надо определять как меры рассеяния результатов проверки в условиях воспроизводимости
3.17. стандартное отклонение повторяемости
Стандартное отклонение результатов проверки, полученных в условиях повторяемости (по ИСО 5725.1).
Примечания
1. Это мера рассеяния результатов проверки в условиях повторяемости.
2. Аналогично «дисперсию повторяемости» и «коэффициент вариации повторяемости» надо определять как меры рассеяния результатов проверки в условиях повторяемости
2.45. статистика
Функция от выборочных значений.
Примечание — Статистика как функция от выборочных значений — случайная величина, которая может принимать различные значения от выборки к выборке. Значение статистики, получаемое при использовании наблюдаемых значений, как их функция может быть использовано при проверке статистических гипотез или как оценка параметра совокупности, например среднего арифметического или стандартного отклонения
Определения термина из разных документов: статистика
2.65. статистический критерий
Статистический метод принятия решений о том, стоит ли отвергнуть нулевую гипотезу в пользу альтернативной или нет.
Примечания
1. Решение о нулевой гипотезе принимают исходя из значений соответствующих статистик, лежащих в основе статистических критериев или рассчитанных по результатам наблюдений. Так как статистики — случайные величины, существует некоторый риск принятия ошибочного решения (п. 2.75 и п. 2.77).
2. Критерий априори предполагает, что проверяют некоторые предположения, например предположение о независимости наблюдений, предположение о нормальности и т.д.
2.85. степень свободы
В общем случае число слагаемых минус число ограничений, налагаемых на них
2.18. столбиковая диаграмма
Графическое представление распределения частот для дискретной случайной величины, образуемое набором столбцов равной ширины, высоты которых пропорциональны частотам
4.28. суммарная проба
Объединение мгновенных проб материала, когда отбирают нештучную продукцию
2.22. таблица сопряженности двух признаков
Таблица, используемая для представления распределения двух признаков, в строках и столбцах которой указывают, соответственно, значения или классы первого и второго признаков, при этом на пересечении строки и столбца появляется частота, соответствующая данной комбинации значений или классов.
Примечание — Это понятие можно распространить на число признаков более двух
2.62. толерантные границы
Для двустороннего статистически накрывающего интервала — нижняя и верхняя границы этого интервала; для одностороннего статистически накрывающего интервала — значение статистики, ограничивающей этот интервал
2.61. толерантный интервал
Интервал, для которого можно утверждать с данным уровнем доверия, что он содержит, по крайней мере, заданную долю определенной совокупности.
Примечание — Если определены обе границы по статистическим данным, то интервал двусторонний. Если одна из двух границ представляет собой бесконечность или ограничение области определения случайной величины, то интервал односторонний
3.11. точность (результата проверки)
Близость результата проверки к принятому нормальному значению величины (по ИСО 5725.1).
Примечание — Понятие точности, когда его относят к результатам проверки, включает в себя комбинацию случайных компонентов и общего компонента систематической ошибки или смещения
2.47. тренд
Тенденция к возрастанию или убыванию наблюдаемых значений, нанесенных на график в порядке их получения после исключения случайных ошибок и циклических эффектов
Определения термина из разных документов: тренд
2.70. уровень значимости (критерия)
Заданное значение верхнего предела вероятности ошибки первого рода.
Примечание — Уровень значимости обычно обозначают α
3.21. условия воспроизводимости
Условия, при которых результаты проверки получены одним методом, на идентичных испытательных образцах, в различных лабораториях, разными операторами, с использованием различного оборудования (по ИСО 5725.1)
3.16. условия повторяемости
Условия, при которых независимые результаты проверки получены одним методом, на идентичных испытательных образцах, в одной лаборатории, одним оператором, с использованием одного оборудования и за короткий интервал времени (по ИСО 5725.1)
1.20. условное математическое ожидание
Математическое ожидание условного распределения случайной величины
1.10. условное распределение (вероятностей)
Распределение подмножества k1 < k случайных величин из распределения случайных величин, когда остальные (k — k1) случайные величины принимают постоянные значения.
Примечание — Для распределения вероятностей двух случайных величин X, Y существуют:
— условные распределения X: некоторое конкретное распределение представляют как «распределение X при Y = y»; — условные распределения Y: некоторое конкретное распределение представляют как «распределение Y при Х = х»
2.25. условное распределение частот
Распределение частот k1 < 1 признаков из многомерного распределения частот, когда остальные (k — k1) признаков фиксированы.
Примечания
1. Для k = 2 признаков условные распределения частот считывают непосредственно из строк и столбцов таблицы сопряженности двух признаков. Условное распределение относительных частот получают делением чисел в каждой строке (столбце) на общее число в соответствующей строке (столбце).
2. В распределении частот двух признаков Х и Y:
— условное распределение частот X; конкретные распределения выражают как распределение X при Y = у;
— условное распределение частот Y; конкретные распределения выражают как распределение Y при Х = х
2.80. функция мощности критерия
Функция, которая определяет мощность критерия, обычно обозначаемую (1 — β) или (1 — Pa), при проверке гипотезы относительно значений скалярного параметра.
Примечание — Эта функция, определяемая для значений тех параметров, которые относятся к соответствующим альтернативным гипотезам, представляет собой вероятность отклонения нулевой гипотезы, когда она не верна
1.4. функция распределения
Функция, задающая для любого значения х вероятность того, что случайная величина Х меньше или равна х,
1.6. функция распределения (вероятностей) масс
Функция, дающая для каждого значения xi дискретной случайной величины Х вероятность pi того, что случайная величина равна хi:
1.28. центральный момент порядка q
Математическое ожидание центрированной случайной величины для одномерного распределения
Примечание — Центральный момент второго порядка — дисперсия случайной величины Х
1.21. центрированная случайная величина
Случайная величина, математическое ожидание которой равно нулю.
Примечание — Если случайная величина Х имеет математическое ожидание m, то соответствующая центрированная случайная величина равна X — m
2.11. частота
Число наступлений события данного типа или число наблюдений, попавших в данный класс
Определения термина из разных документов: частота
1.43. экспоненциальное распределение
Распределение вероятностей непрерывной случайной величины X, которая может принимать любые значения от 0 до + ¥ и плотность распределения которой
при х ³ 0 и параметре , где b — параметр масштаба.
Примечание — Такое распределение вероятностей можно обобщить подстановкой (х — а) вместо х при х ³ а
Словарь-справочник терминов нормативно-технической документации.
.
2015.
Содержание
- Автокорреляция
- Тестирование автокорреляции
- Автокорреляционная функция
- См. также
- Полезное
- Смотреть что такое «Автокорреляция» в других словарях:
- Автокорреляция
- Что такое автокорреляция?
- Ключевые выводы
- Понимание автокорреляции
- Тестирование на автокорреляцию
- Автокорреляция в техническом анализе
- Пример автокорреляции
- АВТОКОРРЕЛЯЦИЯ
- Смотреть что такое «АВТОКОРРЕЛЯЦИЯ» в других словарях:
- Сущность и последствия автокорреляции
- Автокорреляция
- Полезное
- Смотреть что такое «Автокорреляция» в других словарях:
Автокорреляция
Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.
Данное понятие широко используется в эконометрике. Наличие автокорреляции случайных ошибок регрессионной модели приводит к ухудшению качества МНК-оценок параметров регрессии, а также к завышению тестовых статистик, по которым проверяется качество модели (то есть создается искусственное улучшение качества модели относительно её действительного уровня точности). Поэтому тестирование автокорреляции случайных ошибок является необходимой процедурой построения регрессионной модели.
Коэффициенты автокорреляции также имеют самостоятельное важное значение для моделей временных рядов ARMA.
Тестирование автокорреляции
Чаще всего тестируется наличие в случайных ошибках авторегрессионного процесса первого порядка. Для тестирования нулевой гипотезы, о равенстве коэффициента автокорреляции нулю чаще всего применяют критерий Дарбина-Уотсона. При наличии лаговой зависимой переменной в модели данный критерий неприменим, можно использовать асимптотический h-тест Дарбина. Оба эти теста предназначены для проверки автокорреляции случайных ошибок первого порядка. Для тестирования автокорреляции случайных ошибок большего порядка можно использовать более универсальный асимптотический LM-тест Бройша-Годфри. В данном тесте случайные ошибки не обязательно должны быть нормально распределены. Тест применим также и в авторегрессионных моделях (в отличие от критерия Дарбина-Уотсона).
Для тестирования совместной гипотезы о равенстве нулю всех коэффициентов автокорреляции до некоторого порядка можно использовать Q-тест Бокса — Пирса или Q-тест Льюнга-Бокса
Автокорреляционная функция
Автокорреляционная функция показывает зависимость автокорреляции от величины сдвига во времени. При этом предполагается стационарность временного ряда, означающая в том числе независимость автокорреляций от момента времени. Анализ автокорреляционной функции (вместе с частной автокорреляционной функцией) позволяет проводить идентификацию порядка ARMA-моделей.
См. также
Полезное
Смотреть что такое «Автокорреляция» в других словарях:
автокорреляция — автокорреляция … Орфографический словарь-справочник
АВТОКОРРЕЛЯЦИЯ — (autocorrelation) Измерение зависимости между значением какой либо величины из временного ряда и ее предыдущими или последующими значениями. Автокорреляцией первого порядка называют зависимость между значением данной величины и ее непосредственно … Экономический словарь
автокорреляция — сериальная корреляция Словарь русских синонимов. автокорреляция сущ., кол во синонимов: 1 • корреляция (8) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
Автокорреляция — [autocorrelation, serial correlation] — корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией … Экономико-математический словарь
автокорреляция — – это корреляция (взаимосвязь) между наблюдениями временного ряда и значениями того же ряда, отстоящими на фиксированный интервал времени. При работе с дискретизированными временными рядами проще всего считать, что вычисляется корреляция между… … Словарь социологической статистики
АВТОКОРРЕЛЯЦИЯ — (англ. autocorrelation) способ обработки сигнала, при котором сигнал задерживается и затем задержанный сигнал умножается на первоначальный. Помогает выделить периодические составляющие сигнала. Большой психологический словарь. М.: Прайм ЕВРОЗНАК … Большая психологическая энциклопедия
автокорреляция — Корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией. При анализе временных рядов автокорреляционная … Справочник технического переводчика
автокорреляция — autokoreliacija statusas T sritis fizika atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus. автокорреляция, f pranc. autocorrélation, f … Fizikos terminų žodynas
автокорреляция — autokoreliacija statusas T sritis ekologija ir aplinkotyra apibrėžtis Organizmo ląstelių, audinių, organų, sistemų sandaros ir funkcijų tarpusavio savaiminė priklausomybė. atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus.… … Ekologijos terminų aiškinamasis žodynas
АВТОКОРРЕЛЯЦИЯ — случайного процесса корреляция значений Термин употребляют (наряду с термином корреляционная функция ) в основном при изучении стационарных случайных процессов, для к рых А. зависит лишь от h(но Не от t). А. В. Прохоров … Математическая энциклопедия
Источник
Автокорреляция
Опубликовано 06.06.2021 · Обновлено 06.06.2021
Что такое автокорреляция?
Автокорреляция – это математическое представление степени сходства между заданным временным рядом и запаздывающей версией самого себя в последовательных временных интервалах. Это концептуально похоже на корреляцию между двумя разными временными рядами, но автокорреляция использует один и тот же временной ряд дважды: один раз в исходной форме и один раз с запаздыванием на один или несколько периодов времени.
Например, если сегодня дождь, данные говорят о том, что завтра будет дождь с большей вероятностью, чем если сегодня будет ясно. Когда дело доходит до инвестирования, акция может иметь сильную положительную автокорреляцию доходности, что говорит о том, что если она «растет» сегодня, то с большей вероятностью она вырастет и завтра.
Естественно, автокорреляция может быть полезным инструментом для трейдеров; особенно для технических аналитиков.
Ключевые выводы
Понимание автокорреляции
Автокорреляцию также можно называть корреляцией с задержкой или последовательной корреляцией, поскольку она измеряет взаимосвязь между текущим значением переменной и ее прошлыми значениями.
В качестве очень простого примера взгляните на пять процентных значений в таблице ниже. Мы сравниваем их с столбцом справа, который содержит тот же набор значений, только что перемещенный на одну строку вверх.
Автокорреляция +1 представляет собой идеальную положительную корреляцию (увеличение, наблюдаемое в одном временном ряду, приводит к пропорциональному увеличению в другом временном ряду).
Автокорреляция измеряет линейные отношения. Даже если автокорреляция мала, все равно может существовать нелинейная взаимосвязь между временным рядом и самой лаговой версией.
Тестирование на автокорреляцию
Наиболее распространенным методом тестовой автокорреляции является тест Дарбина-Ватсона. Не вдаваясь в технические подробности, можно сказать, что Durbin-Watson – это статистика, которая обнаруживает автокорреляцию на основе регрессионного анализа.
Метод Дарбина-Ватсона всегда дает диапазон значений теста от 0 до 4. Значения, близкие к 0, указывают на большую степень положительной корреляции, значения, близкие к 4, указывают на большую степень отрицательной автокорреляции, а значения, близкие к среднему, предполагают меньшую автокорреляцию.
Итак, почему автокорреляция важна на финансовых рынках? Простой. Автокорреляция может применяться для тщательного анализа исторических движений цен, которые инвесторы затем могут использовать для прогнозирования будущих движений цен. В частности, автокорреляция может использоваться, чтобы определить, имеет ли смысл стратегия импульсной торговли.
Автокорреляция в техническом анализе
Автокорреляция может быть полезна для технического анализа, потому что технический анализ больше всего касается тенденций и взаимосвязей между ценами на ценные бумаги с использованием методов построения графиков. Это контрастирует с фундаментальным анализом, который вместо этого фокусируется на финансовом состоянии или управлении компанией.
Технические аналитики могут использовать автокорреляцию, чтобы выяснить, насколько прошлые цены на ценные бумаги влияют на их будущую цену.
Автокорреляция может помочь определить, действует ли фактор импульса для данной акции. Если, например, акция с высокой положительной автокорреляцией демонстрирует значительный рост в течение двух дней подряд, было бы разумно ожидать, что она вырастет и в следующие два дня.
Пример автокорреляции
Предположим, Эмма хочет определить, обнаруживает ли доходность акций в ее портфеле автокорреляцию; то есть доходность акций связана с доходностью предыдущих торговых сессий.
Если доходность демонстрирует автокорреляцию, Эмма могла бы охарактеризовать ее как импульсную акцию, потому что прошлые доходности, похоже, влияют на будущую доходность. Эмма выполняет регрессию с доходностью предыдущей торговой сессии в качестве независимой переменной и текущей доходностью в качестве зависимой переменной. Она обнаружила, что доходность за день до этого имеет положительную автокорреляцию 0,8.
Поскольку 0,8 близко к +1, прошлые прибыли кажутся очень хорошим положительным предиктором будущей доходности для этой конкретной акции.
Следовательно, Эмма может скорректировать свой портфель, чтобы воспользоваться преимуществами автокорреляции или импульса, продолжая удерживать свою позицию или накапливая больше акций.
Источник
АВТОКОРРЕЛЯЦИЯ
случайного процесса 
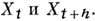
Смотреть что такое «АВТОКОРРЕЛЯЦИЯ» в других словарях:
автокорреляция — автокорреляция … Орфографический словарь-справочник
АВТОКОРРЕЛЯЦИЯ — (autocorrelation) Измерение зависимости между значением какой либо величины из временного ряда и ее предыдущими или последующими значениями. Автокорреляцией первого порядка называют зависимость между значением данной величины и ее непосредственно … Экономический словарь
автокорреляция — сериальная корреляция Словарь русских синонимов. автокорреляция сущ., кол во синонимов: 1 • корреляция (8) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
Автокорреляция — Автокорреляция статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса со сдвигом по времени. Данное понятие широко используется в эконометрике. Наличие… … Википедия
Автокорреляция — [autocorrelation, serial correlation] — корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией … Экономико-математический словарь
автокорреляция — – это корреляция (взаимосвязь) между наблюдениями временного ряда и значениями того же ряда, отстоящими на фиксированный интервал времени. При работе с дискретизированными временными рядами проще всего считать, что вычисляется корреляция между… … Словарь социологической статистики
АВТОКОРРЕЛЯЦИЯ — (англ. autocorrelation) способ обработки сигнала, при котором сигнал задерживается и затем задержанный сигнал умножается на первоначальный. Помогает выделить периодические составляющие сигнала. Большой психологический словарь. М.: Прайм ЕВРОЗНАК … Большая психологическая энциклопедия
автокорреляция — Корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией. При анализе временных рядов автокорреляционная … Справочник технического переводчика
автокорреляция — autokoreliacija statusas T sritis fizika atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus. автокорреляция, f pranc. autocorrélation, f … Fizikos terminų žodynas
автокорреляция — autokoreliacija statusas T sritis ekologija ir aplinkotyra apibrėžtis Organizmo ląstelių, audinių, organų, sistemų sandaros ir funkcijų tarpusavio savaiminė priklausomybė. atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus.… … Ekologijos terminų aiškinamasis žodynas
Источник
Сущность и последствия автокорреляции



Автокорреляция – это корреляционная зависимость между текущими значениями некоторой переменной и значениями этой же переменной, сдвинутыми на несколько периодов времени назад. Автокорреляция случайной составляющей e модели – это корреляционная зависимость текущих 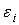
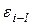
Автокорреляция случайных возмущений модели нарушает одну из предпосылок регрессионного анализа: условие
Автокорреляция может быть вызвана несколькими причинами, имеющими различную природу. Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результирующей переменной. Во-вторых, в ряде случаев причину автокорреляции следует искать в формулировке модели. Модель может не включать фактор, оказывающий существенное воздействие на результат, влияние которого отражается на возмущениях, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени t: автокорреляция обычно встречается при анализе временных рядов.
Постоянная направленность воздействия не включенных в модель переменных является наиболее частой причиной так называемой положительной автокорреляции.
Иллюстрацией положительной автокорреляции может служить следующий пример.
Пример 5.2. Пусть исследуется спрос Y на прохладительные напитки в зависимости от дохода X по ежемесячным и сезонным наблюдениям. Зависимость, отражающая увеличение спроса с ростом дохода, может быть представлена линейной функцией регрессии y = ax + b, изображенной вместе с результатами наблюдений на рис. 5.2.
Рис. 5.2. Положительная автокорреляция
На величину спроса Y оказывают влияние не только доход X (учтенный фактор), но и другие факторы, которые не учтены в модели. Одним из таких факторов является время года.
Положительная автокорреляция означает постоянное в одном направлении действие неучтенных факторов на результирующую переменную. Так спрос на прохладительные напитки всегда выше линии регрессии летом (т.е. для летних наблюдений e > 0) и ниже зимой (т.е. для зимних наблюдений e
Рис. 5.3. Отрицательная автокорреляция
Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК обычно выделяют следующие.
1. МНК-оценки параметров, оставаясь несмещенными и линейными, перестают быть эффективными. Следовательно, они перестают обладать свойствами наилучших линейных несмещенных оценок.
Вследствие вышесказанного все выводы, получаемые на основе соответствующих t— и F— статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при проверке качества оценок (параметров модели и самой модели в целом), могут быть ошибочными и приводить к неверным заключениям по построенной модели.
Источник
Автокорреляция
А. затрудняет применение ряда классических методов анализа временных рядов. В моделях регрессии, описывающих зависимости между случайными значениями взаимосвязанных величин, она снижает эффективность применения метода наименьших квадратов. Поэтому выработаны и применяются специальные статистические приемы для ее выявления (напр. критерий Дарбина — Уотсона) и ее элиминирования (напр., преобразование временного ряда в ряд значений разностей между его соседними членами), а также для модификации самого метода наименьших квадратов.
Полезное
Смотреть что такое «Автокорреляция» в других словарях:
автокорреляция — автокорреляция … Орфографический словарь-справочник
АВТОКОРРЕЛЯЦИЯ — (autocorrelation) Измерение зависимости между значением какой либо величины из временного ряда и ее предыдущими или последующими значениями. Автокорреляцией первого порядка называют зависимость между значением данной величины и ее непосредственно … Экономический словарь
автокорреляция — сериальная корреляция Словарь русских синонимов. автокорреляция сущ., кол во синонимов: 1 • корреляция (8) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
Автокорреляция — Автокорреляция статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса со сдвигом по времени. Данное понятие широко используется в эконометрике. Наличие… … Википедия
автокорреляция — – это корреляция (взаимосвязь) между наблюдениями временного ряда и значениями того же ряда, отстоящими на фиксированный интервал времени. При работе с дискретизированными временными рядами проще всего считать, что вычисляется корреляция между… … Словарь социологической статистики
АВТОКОРРЕЛЯЦИЯ — (англ. autocorrelation) способ обработки сигнала, при котором сигнал задерживается и затем задержанный сигнал умножается на первоначальный. Помогает выделить периодические составляющие сигнала. Большой психологический словарь. М.: Прайм ЕВРОЗНАК … Большая психологическая энциклопедия
автокорреляция — Корреляционная связь (см. Корреляция) между значениями одного и того же случайного процесса X(t) в моменты времени t1 и t2. Функция, характеризующая эту связь, называется автокорреляционной функцией. При анализе временных рядов автокорреляционная … Справочник технического переводчика
автокорреляция — autokoreliacija statusas T sritis fizika atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus. автокорреляция, f pranc. autocorrélation, f … Fizikos terminų žodynas
автокорреляция — autokoreliacija statusas T sritis ekologija ir aplinkotyra apibrėžtis Organizmo ląstelių, audinių, organų, sistemų sandaros ir funkcijų tarpusavio savaiminė priklausomybė. atitikmenys: angl. autocorrelation vok. Autokorrelation, f rus.… … Ekologijos terminų aiškinamasis žodynas
АВТОКОРРЕЛЯЦИЯ — случайного процесса корреляция значений Термин употребляют (наряду с термином корреляционная функция ) в основном при изучении стационарных случайных процессов, для к рых А. зависит лишь от h(но Не от t). А. В. Прохоров … Математическая энциклопедия
Источник


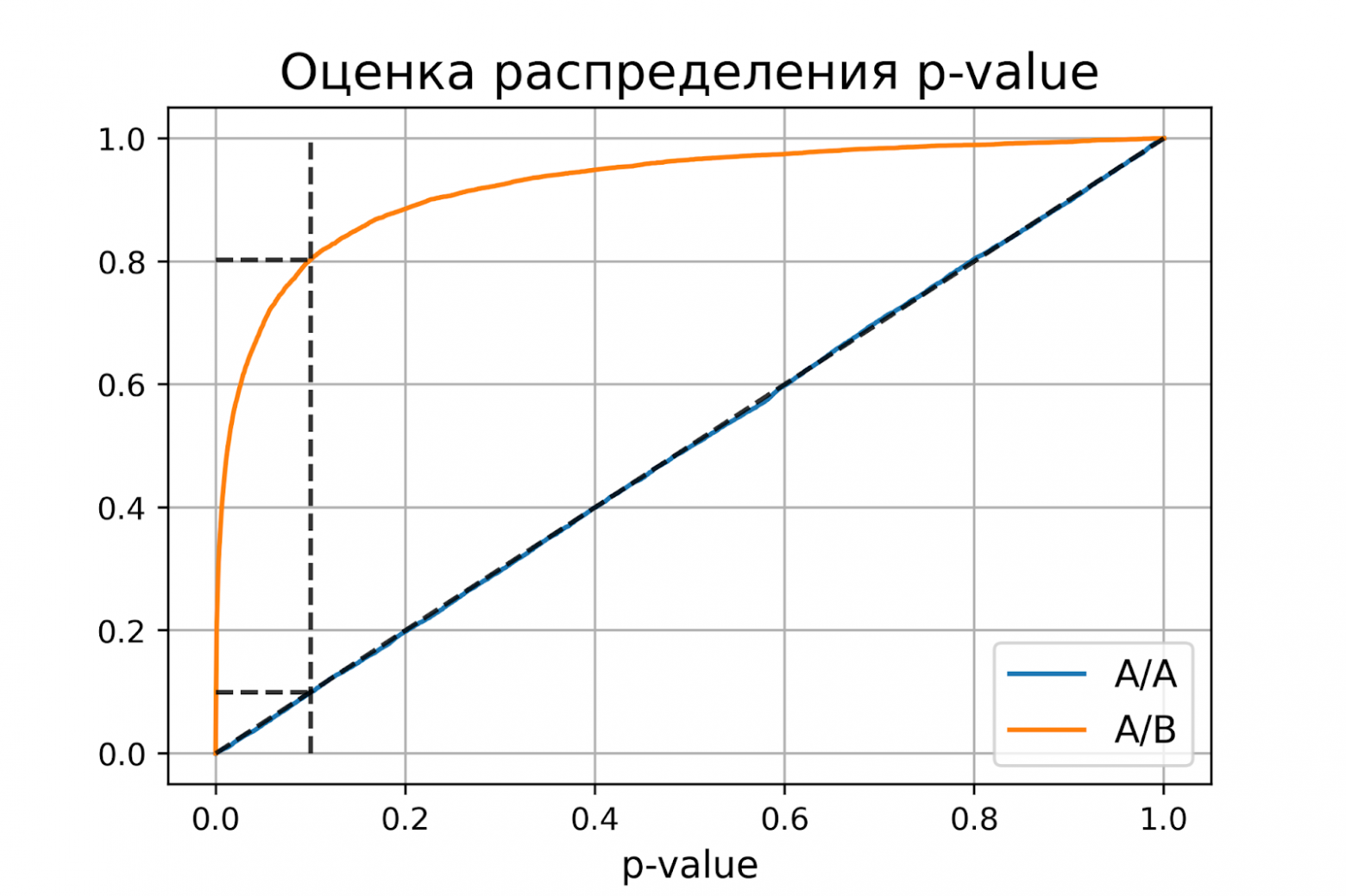
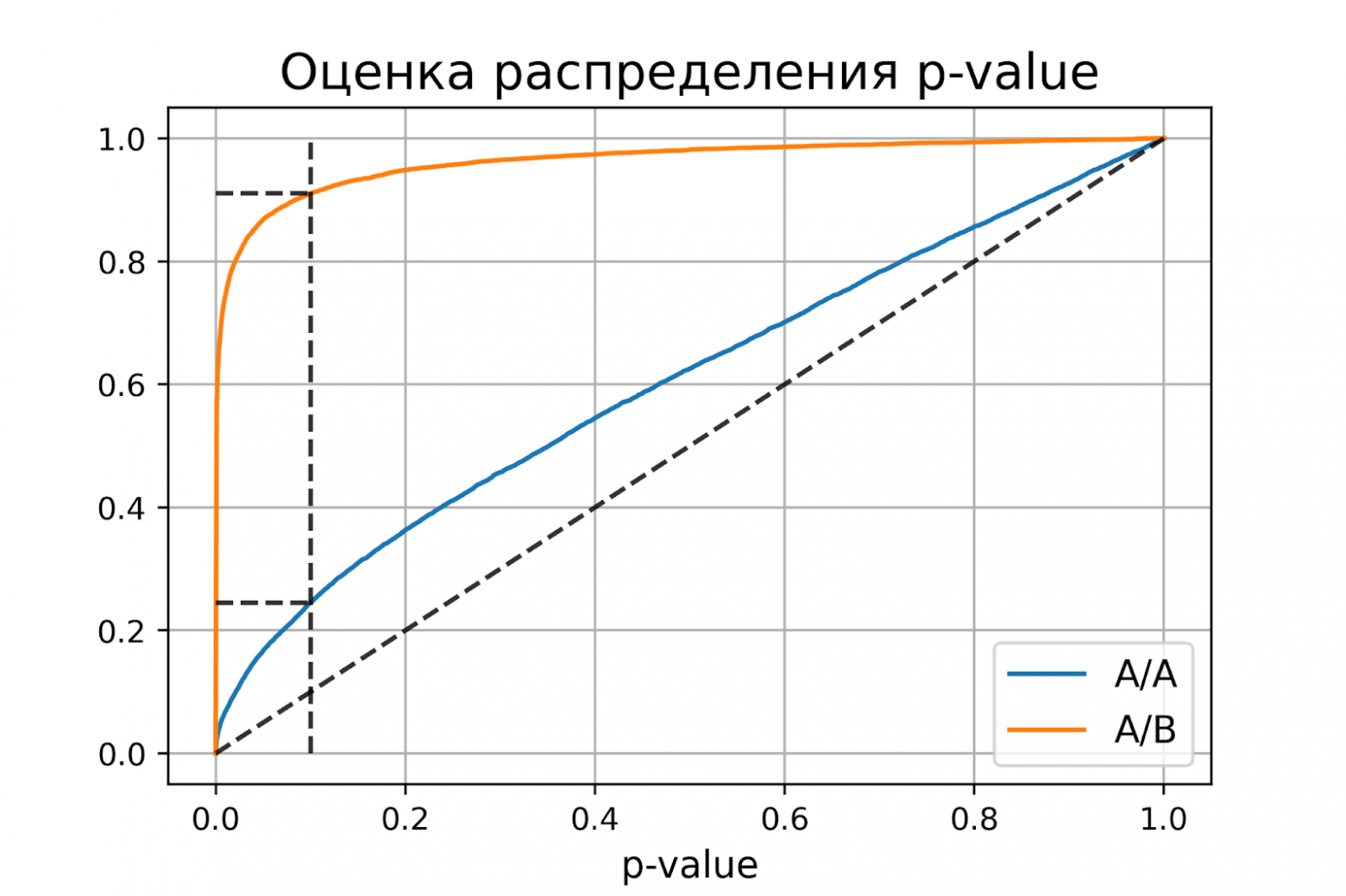


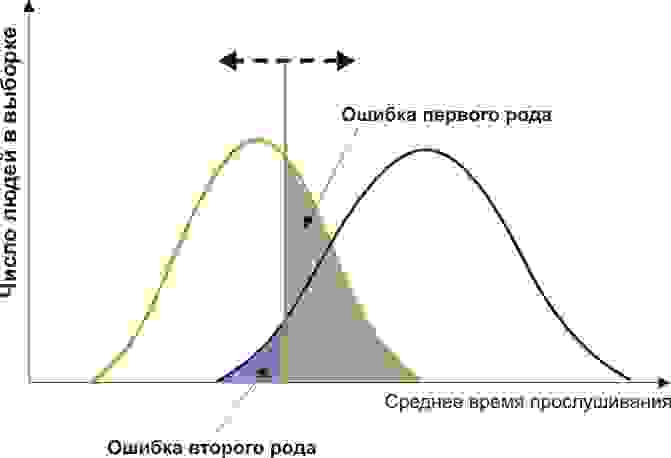
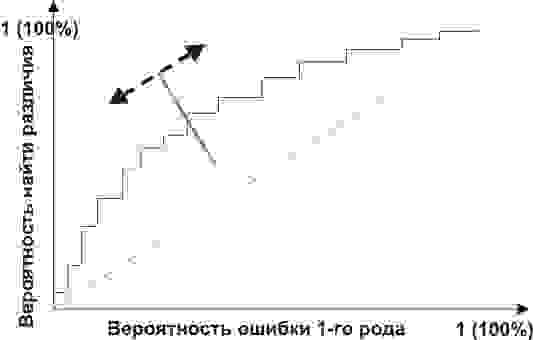

 ,
, соответствует гипотезе
соответствует гипотезе  .
. .
.