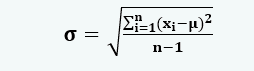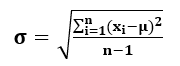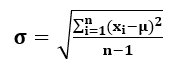Среднее
квадратическое отклонение
характеризует среднее отклонение
всех вариант вариационного ряда от
средней арифметической
величины. Поскольку отклонения вариант
от средней,
имеют значения с «+» и «-», то при
суммировании
они взаимоуничтожаются. Чтобы избежать
этого, отклонения возводятся
во вторую степень, а затем, после
определенных вычислений,
производится обратное действие —
извлечение корня квадратного. Поэтому
среднее отклонение именуется
квадратическим.
Среднее
квадратическое отклонение определяют
по формуле:
(отклонение
d
— это разность между каждой вариантой
и средней величиной, т. е. d
= V-M;
р –частота; количество вариант n
(при числе наблюдений менее 30 сумма
делится
на n-1);
При
вычислении среднеквад. отклонения по
способу
моментов используется следующая формула.
Т.о.
, формула вычисления сред. отклонения
по способу моментов будет читаться как
корень квадратный
из
разности момента второй степени и
квадрата момента первой степени.
Результаты
вычисления сред. отклонения обычным
способом и способом моментов идентичны.
Однако, как указывалось
выше, второй способ значительно убыстряет
и упрощает
расчеты. Итак,
нахождение сред. отклонения позволяет
судить о характере однородности
исследуемой группы наблюдений. Если
величина среднеквад. отклонения
небольшая, то
это свидетельствует о достаточно высокой
однородности изучаемого
явления. Среднюю арифметическую в таком
случае следует признать
вполне характерной для данного
вариационного ряда. Однако
слишком малая величина сигмы заставляет
думать об искусственном
подборе наблюдений. При очень большой
сигме средняя арифметическая в меньшей
степени характеризует вариационный
ряд,
что говорит о значительной вариабельности
изучаемого признака
или явления или о неоднородности
исследуемой группы. Значение:
Определение
среднеквад. отклонения представляет
немалую ценность для медицинской науки
и практики. При диагностике
отдельных заболеваний очень важно
оценить на основании конкретных
исследований, какие признаки проявляются
у соответствующей
группы больных относительно одинаково,
с небольшими колебаниями,
а для каких признаков характерны большие
индивидуальные
колебания. Очень широко используется
это свойство при оценке
физического развития отдельных групп
населения, при выработке
стандартов школьной меб.
Ошибка
репрезентативности (сред.
ошибка сред. арифметич.)
Чтобы
определить степень точности выборочного
наблюдения, необходимо оценить величину
ошибки, которая может
случайно произойти в процессе выборки.
Такие ошибки носят название
случайных ошибок репрезентативности
т.
Они
фактически являются разностью
между средними числами, полученными
при выборочном статистическом
наблюдении, и аналогичными величинами,
которые были бы
получены при сплошном исследовании
того же объекта (т. е. при исследовании
генеральной совокупности).
Ошибки
репрезентативности вытекают из самой
сущности выборочного
исследования. С помощью ошибок
репрезентативности числовые характеристики
выборочной совокупности распространяются
на всю генеральную совокупность, то
есть она характеризуется с учетом
определенной погрешности. Величины
ошибок репрезентативности определяются
как объемом
выборки, так и разнообразием признака.
Чем больше число наблюдений,
тем меньше ошибка, чем больше изменчив
признак, тем больше
величина статистической ошибки.
На
практике для определения средней ошибки
выборки в статистических
исследованиях пользуются следующей
формулой:
(где
m
— ошибка репрезентативности;
σ
— среднее квадратическое отклонение;
n
— число наблюдений в выборке (при числе
наблюдений менее 30
в подкоренное выражение вносится
значение п-1)).
Размер
средней ошибки прямо пропорционален
среднему квадратичному отклонению, т.
е. вариабельности изучаемого
признака, и обратно пропорционален
корню квадратному из
числа наблюдений
Билет 25
Среднее квадратичное отклонение двух, трех, четырех и более чисел. Оно же стандартное отклонение, среднеквадратическое отклонение, среднеквадратичное отклонение, средняя квадратическая, стандартный разброс — показатель рассеивания значений случайной величины относительно её математического ожидания в теории вероятностей и статистике.
Как правило перечисленные термины равны квадратному корню дисперсии.
Пример вычисления стандартного отклонения по следующим формулам:
Вычислим среднюю оценку ученика: 2; 4; 5; 6; 8.
Cредняя оценка будет равна:
Вычисляем квадраты отклонений оценок от их средней оценки:
Вычислим среднее арифметическое (дисперсию) этих значений:
Стандартное отклонение равно квадратному корню дисперсии:
Эта формула справедлива только если эти пять значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки пяти случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 5 нужно было бы поставить n − 1 = 4:
Тогда стандартное отклонение будет равняться:
Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Смотрите также
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Определение стандартного отклонения
Стандартное отклонение измеряет величину вариации или дисперсии в наборе значений данных относительно его среднего значения (среднего). Это статистический инструмент, используемый для интерпретации надежности данных. Он представлен символом «σ».
Если отклонение меньше, точки данных близки к среднему значению, и данные считаются
надежный. Напротив, если отклонение велико, точки данных разбросаны дальше от среднего значения; такие данные считаются менее надежными. Стандартное отклонение используется при анализе общего риска и доходности портфеля.
Оглавление
- Определение стандартного отклонения
- Объяснение стандартного отклонения
- Уравнение стандартного отклонения
- Расчет
- Пример
- Интерпретация
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- Стандартное отклонение — это статистический инструмент, который измеряет волатильность данных. Он указывает, в какой степени значения выборки отклоняются от средних значений. Он вычисляется как квадратный корень из дисперсии и обозначается символом «σ» (греческая буква).
- σ не может быть отрицательным значением и может быть равен 0 только в том случае, если значения в наборе данных равны и не имеют вариаций.
- В финансах этот математический инструмент применяется для определения уровня рисков, связанных с конкретными инвестициями или активами. Метод измеряет спред соответствующих цен и доходов. Более высокое отклонение отражает высокую волатильность и наоборот.
- Если символ σ обозначает стандартное отклонение, n — общее количество наблюдений в наборе данных, xi — i-е количество наблюдений, а µ — выборочное среднее, то отклонение вычисляется по следующей формуле:
В большинстве случаев минимальное стандартное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.
Этот статистический инструмент помогает исследователям и аналитикам понять распространение данных, чтобы
определить степень разброса данных. Этот математический аппарат показывает
разброс выборочных значений от среднего значения.
Стандартные ошибки подчеркивают точность среднего значения выборки по отношению к генеральной совокупности.
означает, когда данные обширны и широко распространены. На графике отклонение может лежать влево, вправо или в обе стороны — формирование колоколообразной кривойГрафик колоколообразной кривой изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол. читать далее.
Уравнение стандартного отклонения
Уравнение для определения стандартного отклонения ряда данных выглядит следующим образом:
т.е. σ=√v
Также, µ =∑x/n
Здесь,
- σ — это символ, обозначающий стандартное отклонение.
- n — количество наблюдений в наборе данных.
- xi — i-е количество наблюдений в наборе данных.
- µ — среднее значение выборки.
- V — дисперсия.
- ∑x — сумма всех значений в наборе данных.
Расчет
Основные шаги, используемые для поиска и расчета стандартного отклонения, следующие:
- Сначала определите среднее значение набора данных.
- Затем подготовьте диаграмму со значениями выборки и разницей между выборкой.
значения и средние значения. - В следующем столбце найдите квадрат разностей.
- Чтобы получить дисперсию, сложите все квадраты и разделите результат на разницу между общим количеством наблюдений и 1.
- Наконец, найдите квадратный корень из дисперсии, чтобы получить стандартное отклонение.
Пример
Давайте рассмотрим несколько примеров, чтобы понять практические последствия:
Найти отклонение цен на сырую нефть за год, когда среднемесячные цены за литр были следующими:
МесяцСредняя цена за литр в долларахЯнварь0,83Февраль0,81Март0,78Апрель0,82Май0,79Июнь0,75Июль0,76Август0,79Сентябрь0,81Октябрь0,77Ноябрь0,76Декабрь0,75
Решение:
Расчет среднего:
µ = ∑x/n
µ = 9,42/12
= 0,785 доллара за литр
С. №МесяцСредняя цена за литр в $ (x)х – 0,785 доллара США(х – 0,785 долл. США)21January0.830.0450.0020252February0.810.0250.0006253March0.78-0.0050.0000254April0.820.0350.0012255May0.790.0050.0000256June0.75-0.0350.0012257July0.76-0.0250.0006258August0.790.0050.0000259September0.810.0250.00062510October0.77-0.0150.00022511November0. 76-0.0250.00062512декабрь0.75-0.0350.00122512–9.42 0,0085
Расчет стандартного отклонения :
- σ = √ [0.0085 / (12-1)]
- σ = √ (0,00077272727)
- σ = 0,0277979724571285 долл. США
Таким образом, стандартное отклонение цен на нефть за литр для данного года равно
0,0277979724571285.
Интерпретация
Стандартное отклонение указывает на волатильность или дисперсию значений конкретного распределения. Он показывает, в какой степени значения выборки отклоняются от средних значений. Таким образом, эта мера облегчает сравнение и анализ.
Ниже приведены различные интерпретации полученного результата:
- Если σ велико, то волатильность анализируемых данных также высока.
- Точно так же, когда σ низкое, дисперсия между точками данных также незначительна.
- В распределении σ может быть равно 0 только тогда, когда разница между точками данных равна нулю. Это также наименьшее значение отклонения, которое можно получить.
- Невозможно получить отрицательное значение σ, так как числитель включает квадрат разности между выборочными значениями и средними значениями.
- Кроме того, количество наблюдений всегда больше 1; следовательно, знаменатель должен быть положительным значением.
- Стандартное отклонение измеряется в тех же единицах, что и значения распределения. Например, в приведенном выше примере σ выражается в долларах.
- Выбросы (чрезвычайно высокие или низкие значения) существенно влияют на измерения отклонения.
Часто задаваемые вопросы (FAQ)
Что такое стандартное отклонение?
Стандартное отклонение — это статистический метод, используемый для нахождения разброса данных в распределении с использованием средних значений. Обозначается символом «σ».
Как рассчитать стандартное отклонение?
Стандартное отклонение рассчитывается как квадратный корень из дисперсии. Дисперсия — это сумма квадрата разности между каждым значением в наборе данных и их средними значениями, деленная на значение, полученное путем вычитания единицы из общего числа наблюдений.
Почему стандартное отклонение важно?
Он определяет степень изменчивости значений в выборочном распределении. Это широко используемый статистический инструмент в финансах, инвестициях и бизнесе для интерпретации величины риска, связанного с ценной бумагой или активом. В большинстве случаев минимальное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.
Может ли стандартное отклонение быть равным нулю?
Единственный случай, когда он может быть равен нулю, — это когда все точки данных в распределении одинаковы. Нулевое отклонение указывает на нулевой разброс или изменчивость значений. Для реальных сценариев это практически невозможно.
Рекомендуемые статьи
Эта статья была руководством к тому, что такое стандартное отклонение в статистике и его определение. Мы объясняем его уравнение, расчеты, символы, статистику и его интерпретацию. Подробнее об этом вы можете узнать из следующих статей —
- Стандартное отклонение в ExcelСтандартное отклонение в ExcelСтандартное отклонение показывает отклонение значений данных от среднего (среднего). В Excel СТАНДОТКЛОН и СТАНДОТКЛОН.С вычисляют стандартное отклонение выборки, а СТАНДОТКЛОН и СТАНДОТКЛОН.П вычисляют стандартное отклонение совокупности. СТАНДОТКЛОН доступен в Excel 2007 и предыдущих версиях. Однако СТАНДОТКЛОН.П и СТАНДОТКЛОН.С доступны только в Excel 2010 и последующих версиях. читать далее
- Примеры стандартных отклоненийПримеры стандартных отклоненийПримеры стандартных отклонений помогут вам применить формулу стандартного отклонения для определения риска, связанного с волатильностью финансовых ценных бумаг.Подробнее
- Формула стандартного отклоненияФормула стандартного отклоненияСтандартное отклонение (SD) — популярный статистический инструмент, обозначаемый греческой буквой «σ», для измерения вариации или дисперсии набора значений данных относительно их среднего (среднего) значения, таким образом интерпретируя надежность данных.Подробнее
Эксперт по предмету «Математика»
Задать вопрос автору статьи
При рассмотрении какой-либо величины и её изменения важным является не только понятие среднего арифметического этой величины, но и её отклонение.
Для оценки отклонения и разброса измеряемой величины пользуются несколькими различными критериями, например, абсолютной погрешностью, иначе называемой отклонением от среднего каждой конкретной величины.
Но абсолютная погрешность не является критерием, показывающим разброс измеряемой величины, так как сумма всех абсолютных погрешностей равна нулю.
Поэтому для оценки погрешности вводится другая величина, называемая средним квадратическим отклонением.
Основные понятия
Для объяснения термина «среднеквадратичное отклонение» необходимо ознакомиться с используемой терминологией.
Определение 1
Средним арифметическим или средней величиной называют число, являющееся суммой всех проведённых измерений, разделённой на количество этих измерений.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 4 500 ₽
Для пяти чисел $a_1, a_2, a_3, a_4$ и $a_5$ средняя величина $M$ определяется по формуле
$M=frac{a_1+ a_2+ a_3+ a_4+ a_5}{5}$.
Со средним арифметическим также связано другое понятие — математическое ожидание.
Определение 2
Математическое ожидание — это значение среднего арифметического некоторой величины при стремлении количества измерений этой величины к бесконечности.
Математическое ожидание также могут обозначать буквой $M$, а среднее арифметическое некоторого количества измерений исследуемой величины могут называть оценкой математического ожидания.
Определение 3
Абсолютной погрешностью измеряемой единичной величины, иногда также называемой вариантой, является её разность со средним значением $M$.
Для того чтобы найти абсолютную погрешность некоторого единичного измерения $x_i$, обозначаемую греческой буквой $Δ$ (произносится как «дельта»), необходимо отнять от измеренного значения $x_i$ среднее арифметическое $M$: $Δx_i=x_i – M$.
«Среднеквадратичное отклонение» 👇
Часто для оценки единичного измерения пользуются не только абсолютной погрешностью, но и относительной погрешностью $δ$, она рассчитывается по формуле:
$δ=frac{|Δx_i|}{M} cdot 100$%.
Оценив относительную погрешность каждого измерения, можно отбросить значения, погрешность которых слишком большая и при дальнейших расчётах использовать только значения с небольшими относительными погрешностями.
Определение 4
Среднее арифметическое квадратов всех абсолютных погрешностей называют дисперсией и обозначают буквой $D$.
Дисперсия является характеристикой разброса значений некоторой измеряемой случайной величины $x$.
Что такое среднее квадратичное отклонение и как его определять
Теперь перейдём непосредственно к термину «среднеквадратическое отклонение».
Среднеквадратическим отклонением называют значение квадратного корня из дисперсии случайной величины $D$.
Обозначается среднее квадратичное отклонение греческой буквой $ϭ$ (читается как «сигма»).
Формула для среднего квадратичного отклонения для пяти измеренных значений величины $X$ выглядит так:
$ϭ=sqrt{frac{Δx_1^2 + Δx_2^2 + Δx_3^2 + Δx_4^2 + Δx_5^2}{5}}$,
где $Δx_1… Δx_5$ — абсолютные погрешности каждого конкретного измерения.
Если дисперсия и, соответственно, среднее квадратическое отклонение достаточно малы, то это значит, что величина большинства погрешностей не велика по модулю и все значения измеряемой величины достаточно близки к среднему.
В идеальном случае когда дисперсия равна нулю, наблюдается соотношение $x_1=x_2=x_3=….=x_n=M$, то есть каждое измеренное значение равно среднему арифметическому.
Покажем, как применять полученную информацию.
Пример 1
Задача:
В ходе эксперимента по физике ребята пять раз измерили напряжение и получили следующие значения: $U_1= 5,22$ В; $U_2= 5,30$ В; $U_3=5,27$ В; В $U_4=5,23$ В; $U_5=5,20$ В. Найдите абсолютные и относительные погрешности каждого измерения, дисперсию и среднее квадратичное отклонение.
Решение:
Найдём среднее арифметическое, оно равно:
$U_ср=frac{U_1+U_2+ U_3 + U_4 + U_5}{5}=frac{5,22 + 5,30+ 5,27+5,23+5,20}{5}=5,244$ В.
Теперь найдём абсолютную и относительную погрешность каждого измерения:
$ΔU_1=U_ср-U_1= 5,244-5,22 =0,024; δ_1=frac{|U_1|}{U_ср} cdot 100%=frac{0,024}{5,244}cdot 100$%$=0.50$%;
$ΔU_2=U_ср-U_2= 5,244-5,30=-0,056; δ_2=frac{|U_2|}{U_ср} cdot 100%=frac{0,056}{5,244}cdot 100$%$=1,06$%;
$ΔU_3=U_ср-U_3= 5,244-5,27=-0,026; δ_3=frac{|U_3|}{U_ср}cdot 100%=frac{0,026}{5,244}cdot 100$%$=0,50$%;
$ΔU_4=U_ср-U_4= 5,244-5,23=0,014; δ_4=frac{|U_4|}{U_ср}cdot 100%=frac{0,014}{5,244}cdot 100$%$=0,25$%;
$ΔU_5=U_ср-U_5= 5,244-5,20=0,044; δ_5=frac{|U_5|}{U_ср}cdot 100%=frac{0,044}{5,244}cdot 100$%$=0,84$%.
Сосчитаем дисперсию:
$D=frac{ΔU_1^2+ΔU_2^2+ ΔU_3^2 + ΔU_4^2 + ΔU_5^2}{5}=frac{0,024^2+ (-0,056)^2 + (-0,026)^2+ 0,014^2 + 0,044^2)}{5}=0,001304$;
И квадратичное отклонение:
$ϭ=sqrt{D}=sqrt{0,001304}=0,0361$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме


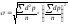
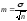
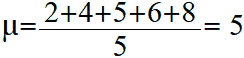
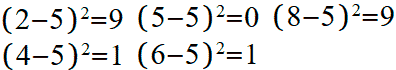
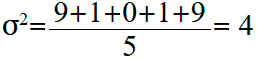
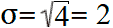
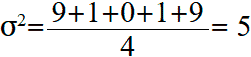
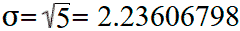



![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)