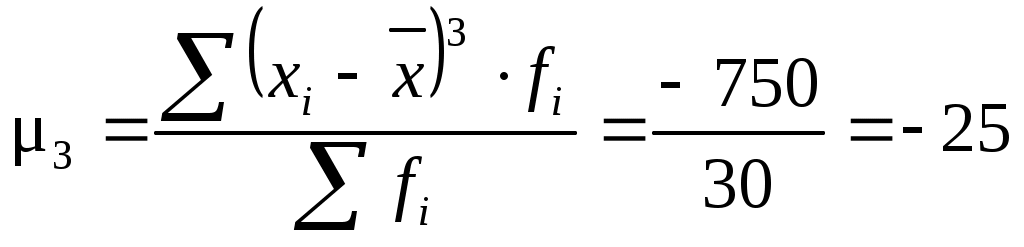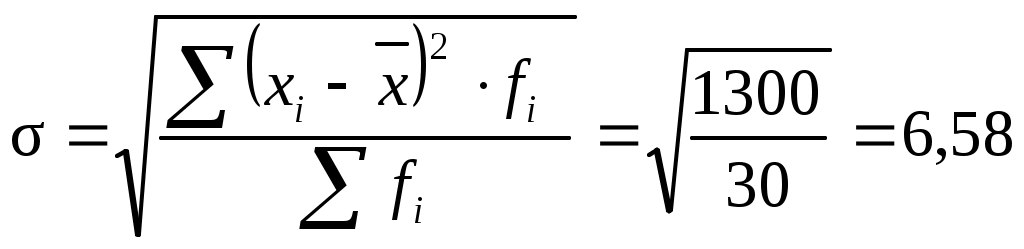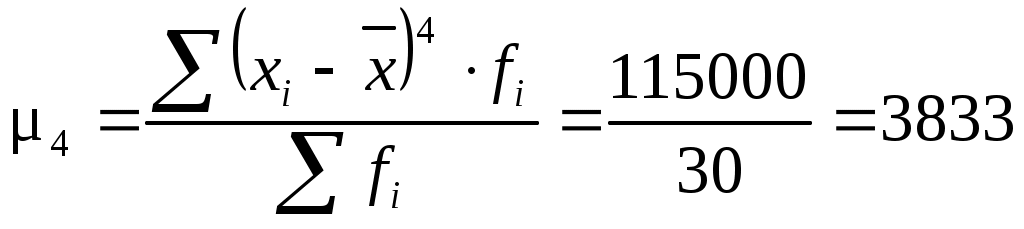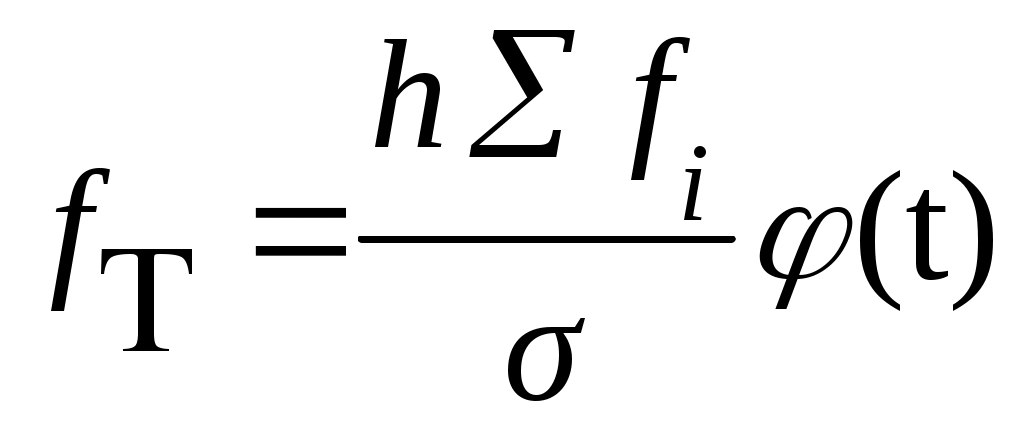Средней квадратической ошибки коэффициента асимметрии

58. Коэффициенты асимметрии и эксцесса.

Центральные
моменты распределения

Для дальнейшего изучения характера
вариации используются средние значения
разных степеней отклонений отдельных
величин признака от его средней
арифметической величины. Эти показатели
получили название центральных
моментов распределения порядка,
соответствующего степени, в которую
возводятся отклонения,
или просто моментов.

Показатели формы распределения

• Асимметрия – Коэффициент
  асимметрии
  
  характеризует асимметричность
  («скошенность») распределения признака
  в совокупности

• Эксцесс – Показатель эксцесса
  
  
  представляет собой отклонение вершины
  эмпирического распределения вверх или
  вниз («крутость») от вершины кривой
  нормального распределения

Асимметрия распределения

• При
  =0
  распределение считается нормальным.

• При
  
  > 0 правосторонняя асимметрия.

• При
  <0
  левосторонняя асимметрия.

• Если асимметрия более 0,5, то независимо
  от знака она считается значительной

• Если асимметрия меньше 0,25, то она
  считается незначительной

Асимметрия распределения рассчитанная по формулам К.Пирсона:

является приблизительной

Расчет асимметрии распределения при помощи нормированного момента третьего порядка дает наиболее точный результат

т.е. — нормированный момент третьего порядка

Показатель Пирсона зависит от степени
асимметричности в средней части ряда
распределения, а показатель асимметрии,
основанный на моменте третьего порядка,
— от крайних значений признака.

Оценка существенности асимметрии

Для оценки существенности асимметрии
вычисляют показатель средней квадратической
ошибки коэффициента асимметрии

Если отношение

имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии

Эксцесс распределения

Показатель эксцесса

представляет собой отклонение вершины
эмпирического распределения вверх или
вниз («крутость») от вершины кривой
нормального распределения, НО! График
распределения может выглядеть сколь
угодно крутым в зависимости от силы
вариации признака: чем слабее вариация,
тем круче кривая распределения при
данном масштабе. Не говоря уже о том,
что, изменяя масштабы по оси абсцисс и
по оси ординат, любое распределение
можно искусствен но сделать «крутым»
и «пологим». Чтобы показать, в чем состоит
эксцесс распределения, и правильно его
интерпретировать, нужно сравнить ряды
с одинаковой силой вариации (одной и
той же величиной σ) и разными показателями
эксцесса. Чтобы не смешать эксцесс с
асимметрией, все сравниваемые ряды
должны быть симметричными. Такое
сравнение изображено на рис.

Поскольку эксцесс нормального
распределения равен 3, показатель
эксцесса вычисляется по формуле

или

где — нормированный момент четвертого порядка

• При
  >0
  – высоковершинный эксцесс распределения

• При
  <0
  – низковершинный эксцесс распределение

• При
  
  =0 – нормальное распределение

Оценка существенности эксцесса

Для оценки существенности эксцесса
вычисляют показатель его средней
квадратической ошибки

Если отношение

имеет значение больше 3, то это
свидетельствует о существенном характере
эксцесса

Коэффициент асимметрии. Эксцесс распределения

Краткая теория

---

При изучении распределений, отличных от нормального,
возникает необходимость количественно оценить это различие. С этой целью вводят
специальные характеристики, в частности асимметрию и эксцесс. Для нормального
распределения эти характеристики равны нулю. Поэтому если для изучаемого
распределения асимметрия и эксцесс имеют небольшие значения, то можно
предположить близость этого распределения к нормальному.
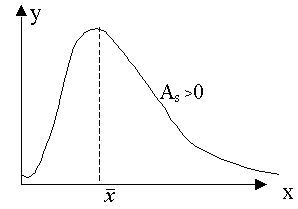
Наоборот, большие значения асимметрии и эксцесса указывают на значительное
отклонение от нормального.

Асимметрией теоретического распределения называют отношение
центрального момента третьего порядка к кубу среднего квадратического
отклонения:

Коэффициент асимметрии характеризует скошенность
распределения по отношению к математическому ожиданию. Асимметрия положительна,
если «длинная часть» кривой распределения расположена справа от математического
ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева
от математического ожидания.

На рисунке показаны две кривые распределения: I и II. Кривая I имеет
положительную (правостороннюю) асимметрию

,
а кривая II – отрицательную (левостороннюю)

.

Кроме вышеописанного коэффициента, для характеристики асимметрии
рассчитывают также показатель асимметрии Пирсона:

Коэффициент асимметрии Пирсона характеризует асимметрию только в
центральной части распределения, поэтому более распространенным и более точным
является коэффициент асимметрии, рассчитанный на основе центрального момента третьего
порядка.

Для оценки «крутости», т. е. большего или меньшего подъема кривой
теоретического распределения по сравнению с нормальной кривой, пользуются
характеристикой — эксцессом.

Эксцессом (или коэффициентом эксцесса) случайной величины
называется число:

Число 3 вычитается из отношения

 потому, что для наиболее часто встречающегося
нормального распределения отношение

.

Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные — отрицательным
эксцессом.

Примеры решения задач

---

Задача 1

Для заданного
вариационного ряда вычислить коэффициенты асимметрии и эксцесса.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим расчетную
таблицу

Средняя:

Найдем моду — варианту, которой соответствует наибольшая частота.

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии Пирсона:

Коэффициент асимметрии можно найти по формуле:

Центральный момент
3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Центральный момент
4-го порядка:

Получаем:

---

Задача 2

Для заданного
вариационного ряда (см. условие задачи 1) вычислить коэффициенты асимметрии и
эксцесса методом произведений, используя условные моменты.

Решение

Составим расчетную таблицу

Перейдем к условным вариантам

В качестве ложного нуля возьмем
3-ю варианту

0

Условные варианты вычислим по
формуле:

где

4
(разность между соседними вариантами)

Условный момент 1-го порядка:

Средняя:

Условный момент 2-го порядка:

Дисперсия:

Среднее квадратическое
отклонение:

Коэффициент асимметрии можно найти
по формуле:

Условный момент 3-го порядка:

Центральный момент 3-го порядка:

Получаем:

Эксцесс можно найти по формуле:

Условный момент 4-го порядка:

Центральный момент 4-го порядка:

Получаем:

---

Подборка по базе: Абабков В. А., Валидизация русскоязычной версии опросника«Шкала , Российский государственный социальный университет.docx, Самарский медицинский университет.docx, Қазақ Ұлттық Аграрлық Университеті.pptx, Московский финансово-промышленный университет «Синергия».pdf, Адрес университета.docx, ФГБОУ ВПО ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕ, вопрос-ответ.Московский финансово-промышленный университет «Сине, Эссе Университеты.docx, Московский финансово-промышленный университет«Синергия».pdf

---

6.4. Показатели асимметрии и эксцесса

Для обобщающей характеристики особенностей формы распределения применяются кривые распределения. Кривая распределения выражает графически (полигон, гистограмма) закономерность распределения единиц совокупности по величине варьирующего признака. Различают эмпирические и теоретические кривые распределения.

Эмпирическая кривая распределения – это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение.

Теоретическая кривая распределения – это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения. При этом теоретическое распределение играет роль некоторой идеализированной модели эмпирического распределения, а сам анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений.

Кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута – правая или левая, различают правостороннюю или левостороннюю асимметрию. Кривые распределения могут быть одно-, двух и многовершинными.

Для однородных совокупностей, как правило, характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп. Для симметричных распределений частоты двух вариант, равноотстоящих в обе стороны от центра, равны между собой. Рассчитанные для таких рядов распределений характеристики равны:
.

Если указанные соотношения нарушены, то это свидетельствует о наличии асимметрии распределения. Так, при , разности между и положительные и асимметрия правосторонняя, а при , наоборот, разности и отрицательные и асимметрия левосторонняя.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии или коэффициент асимметрии Пирсона (As):

или (6.26)

В одновершинных распределениях величина данного показателя изменяется от – 1 до + 1. В симметричных распределениях As=0.

Его величина может быть положительной и отрицательной. Если величина положительная – то асимметрия правосторонняя (рис. 17 а), если – отрицательная, то асимметрия левосторонняя (рис. 17 б).

a б

Рис. 17. a) правосторонняя асимметрия;
б) левосторонняя асимметрия

Чем ближе к 1, тем асимметрия существеннее:

Коэффициент асимметрии Пирсона характеризует асимметрию только центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка.

(6.27)

где – центральный момент третьего порядка;

– среднее квадратическое отклонение в третьей степени.

(6.28)

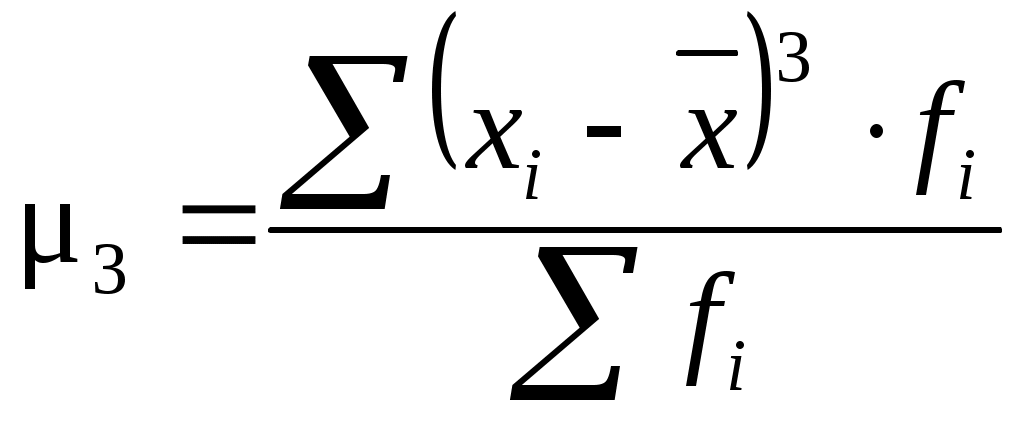
Центральным моментом называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины.

Если As> 0, то асимметрия правосторонняя, а если As< 0, то асимметрия левосторонняя. Чем числитель ближе к 0, тем асимметрия меньше.

Оценка существенности As проводится на основе средней квадратической ошибки коэффициента асимметрии , которая зависит от числа наблюдений ( ) и рассчитывается по формуле:

(6.29)

В случае >3, асимметрия является существенной и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна и ее наличие может быть вызвано случайными обстоятельствами.

Для одновершинных распределений рассчитывается еще один показатель оценки его формы – эксцесс. Эксцесс рассчитывается для симметричных распределений на основе центрального момента 4-ого порядка.

(6.30)

где – центральный момент четвертого порядка;

– среднее квадратическое отклонение в четвертой степени.

(6.31)

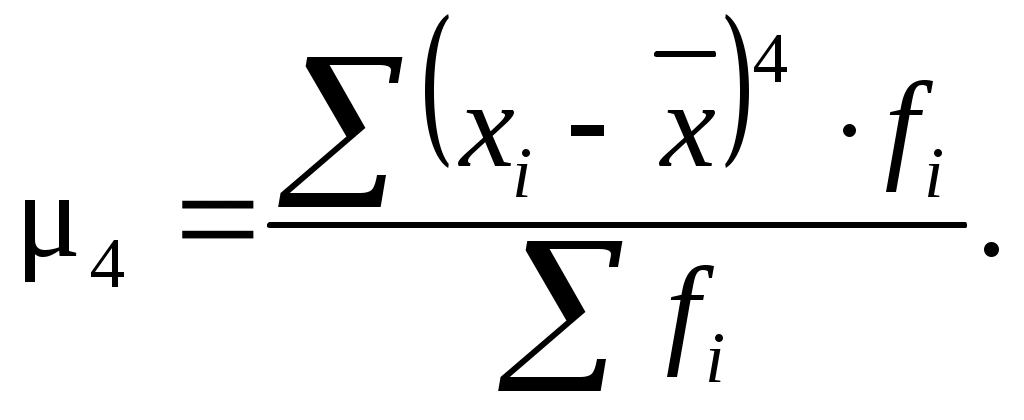
При симметричном (нормальном) распределении Ek= 0. Если
Ek> 0, то распределение считается островершинным (рис. 18 a), если Ek< 0, то распределение считается плосковершинным (рис. 18 б).

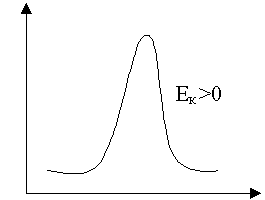
a b

Рис. 18. a) островершинное распределение;

б) плосковершинное распределение

Среднеквадратическая ошибка эксцесса рассчитывается по формуле:

(6.32)

где – число наблюдений.

Пример 7. Имеется распределение коммерческих банков РФ по размеру выданных кредитов, представленные в таблице 12 (данные условные). Определите коэффициент асимметрии и эксцесса.

Таблица 12

Распределение коммерческих банков РФ
по размеру выданных кредитов, млн. р.

Группы банков по размеру выданных кредитов, млн. р.	Число банков	Середина интервала
1 – 6	6	3,5	21	600	— 6000	60 000
6 – 11	3	8,5	25,5	75	— 375	1875
11 – 16	11	13,5	148,5	0	0	0
16 – 21	5	18,5	92,5	125	625	3125
21 – 26	5	23,5	117,5	500	5000	50 000
Итого	30		405	1300	— 750	115 000

Дополнительные расчеты произведем в табл. 12.

Рассчитаем по формуле (5.10)

млн. р.

Рассчитаем коэффициент асимметрии по центральному моменту
3-его порядка по формуле (6.27). Для этого определим центральный момент 3-его порядка (формула 6.28) и среднее квадратическое отклонение (формула 6.7):

Рассчитаем показатель эксцесса по формуле (6.30). Для этого рассчитаем центральный момент 4-ого порядка (6.31):

Полученный результат свидетельствует о том, что распределение является плосковершинным.

Вывод. Значение коэффициента асимметрии свидетельствует о незначительной левосторонней асимметрии. Полученный результат показателя эксцесса свидетельствует о том, что распределение является плосковершинным.

6.5. Теоретические кривые распределения

Анализ вариационных рядов предполагает выявление законо­мерностей распределения, определение и построение (получение) некой теоретической (вероятностной) формы распределения. Характер распределения лучше всего проявляется при большом числе наблюдений и малых интервалах. В этом случае графическое изо­бражение эмпирического вариационного ряда принимает вид плавной кривой, именуемой кривой распределения. Кривая распределения может рассматриваться как некая теоретическая (вероятностная) форма распределения, свойственная определенной совокупности в конкретных условиях.

Анализируя частоты в эмпирическом распределении, можно описать это распределение с помощью математической модели — закона распределения, установить по исходным данным параметры теоретической кривой и проверить правильность выдвинутой гипотезы о типе распределения данного ряда.

В практике статистического исследования встречаются различные распределения: нормальное, логарифмически нормальное, биномиальное, Пуассона, Шарлье и др. Каждое распределение имеет свою специфику и область применения.

Нормальное распределение

При построении статистических моделей наиболее широко при­меняется нормальное распределение (закон Гаусса – Лапласса).

В 1727 г. английский математик Абрахам де Муавр (1667-1754) открыл закон распределения, вероятностей, названный законом нормального распределения. Вначале XIX в. данными вопросами занимались Пьер Лаплас (1749-1827) и Карл Гаусс (1777-1855). Общие условия возникновения закона нормального распределения установил А.М Ляпунов (1857-1918). Распределения, близкие к нормальному распределению, были обнаружены при изучении самых различных явлений, как в природе, так и в развитии общества.

Нормальное распределение признака наблюдается в тех случаях, когда на величину вариантов, входящих в состав вариационного ряда, действует множество случайных, независимых или слабо зависимых факторов, каждый из которых играет в общей сумме незначительную роль. Нарушение нормального характера распределения часто является свидетельством неоднородности совокупности.

Закон нормального распределения выражается формулой:

(6.33)

где – ордината кривой нормального распределения;

– стандартизованная (нормированная) величина;

e– основание натурального логарифма (e=2,7183);

π– постоянное число (π= 3,1416);

x_i – варианты вариационного ряда;

– средняя величина;

 – среднее квадратическое отклонение.

Функция широко используется в экономических расчетах, а ее значение при разных tтабулированы и представлены в математических таблицах. При графическом изображении плотности распределении получим кривую нормального распределения, симметричную от­носительно вертикальной прямой х = (рис. 19), поэтому величину называют центром распределения.

Случайные величины, распределенные по нормальному закону, различаются значениями параметров и , поэтому очень важно выяснить, как эти параметры влияют на вид нормальной кривой.

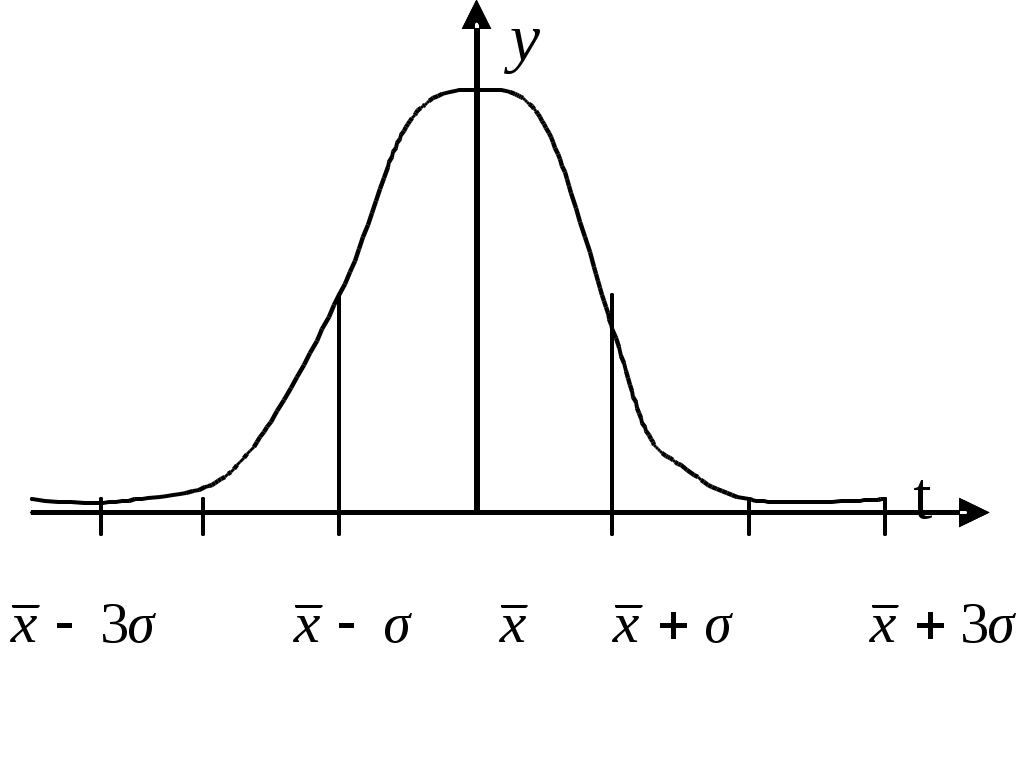
Рис. 19. Нормальное распределение с одно-, двух-, трехсигмовыми пределами

Свойства кривой нормального распределения:

1. Функция нормального распределения четная, т.е. y(-t)=y(+t). Следовательно, изображающая ее кривая распределена симметрично относительно оси ординат, т.е. .

2. Функция имеет бесконечно малые значения при t= . Это означает, что ветви кривой удалены в бесконечность и асимптотически приближаются к оси абсцисс.

3. Кривая имеет две точки перегиба на расстоянии от .

4. Коэффициенты асимметрии и эксцесса равны нулю.

5. Площадь между ординатами, проведенными на расстоянии . составляет 0,683. Это означает, что при t= 1 заключается 68,26% всех значений признаков; между  2 при t= 2 располагается 95,44% всех значений признаков; между  3 при t= 3 находится 99,73% значений признаков. На рис. 19 показано нормальное распределение с одно-, двух-, трехсигмовыми пределами.

На практике почти не встречаются отклонения, которые превышают 3. Отклонение 3 может считаться максимально возможным. Это положение называют “правилом трех сигм”

В математической статистике нормальное распределение играет роль некоторого стандарта, с которым сравнивают другие распределения.

Порядок расчета теоретических частот кривой нормального распределения следующий:

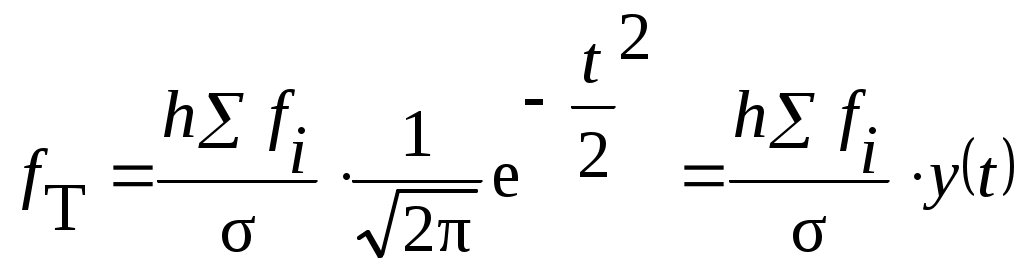
(6.34)

где h– величина интервала;

f_i– сумма всех частот, равная объему совокупности;

 – среднее квадратическое отклонение.

Если вариационный ряд имеет равные интервалы, тогда

(6.35)

6.6. Критерии согласия

Так как все предположения о характере того или иного распре­деления – это гипотезы, а не категорические утверждения, то они должны быть подвергнуты статистической проверке с помощью так называемых критериев согласия. Критерии согласия, опираясь на установленный закон распределения, дают возможность установить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными (случайными), а когда – существенными (неслучайными). Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда гипотезы о характере распределения в эмпирическом ряду и дать ответ, можно ли принять для данного эмпирического распределения модель, выраженную некоторым теоретическим законом распределения.

Существует ряд критериев согласия, среди которых наиболее чаще применяют критерии Пирсона, Романовского и Колмогорова. Рассмотрим их более подробно.

Критерий согласия Пирсона ( ) вычисляется по формуле:

(6.36)

где эмпирические и теоретические частоты соответственно.

Фактическое значение сравнивают с критическим, которое находится по специальным таблицам в зависимости от принимаемого уровня значимости и числа степеней свободы (см. Приложение 2).

Уровень значимости (α) – вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В зависимости от важности и ответственности решаемых задач в статистических исследованиях используют следующие три уровня значимости:

1. α = 0,10, P(t) = 0,90;
2. α = 0,05, P(t) = 0,95;
3. α = 0,01, P(t) = 0,99.

Например, вероятность 0,01 означает, что в одном случае из 100 может быть отвергнута правильная гипотеза. В экономических исследованиях приемлемой считается вероятность ошибки 0,05, т.е. в 5 случаях из 100 может быть отвергнута правильная гипотеза.

Число степеней свободы (ν) рассчитывается как число групп в ряду распределения минус единица и минус число параметров эмпирического распределения, использованных для нахождения теоретических частот. Так, при выравнивании по кривой нормального распределения число степеней свободы ν=n-1-2, поскольку при расчете теоретических частот используется два параметра эмпирического распределения:и т.е. ν=n-3.

Для оценки существенности расчетное значение сравнивается с табличным . При полном совпадении теоретического и эмпирического распределений =0, в противном случае >0. Если > , то при заданном уровне значимости (α) и числе степеней свободы (ν) гипотезу о несущественности (случайности) расхождений отклоняем. Если фактическое (расчетное) оказывается меньше табличного (критического), т.е. < то расхождения между эмпирическими и теоретическими частотами можно считать случайными.

Критерий Романовского (C), также используемый для проверки близости эмпирического и теоретического распределений, определяется следующим образом:

, (6.37)

где – расчетная величина критерия Пирсона;

ν– число степеней свободы, ν= n– 3,

n– число интервальных групп.

При С<3 различие несущественно, что позволяет считать эмпирическое распределение близким к нормальному.

Критерий Колмогорова () вычисляется по формуле:

, (6.38)

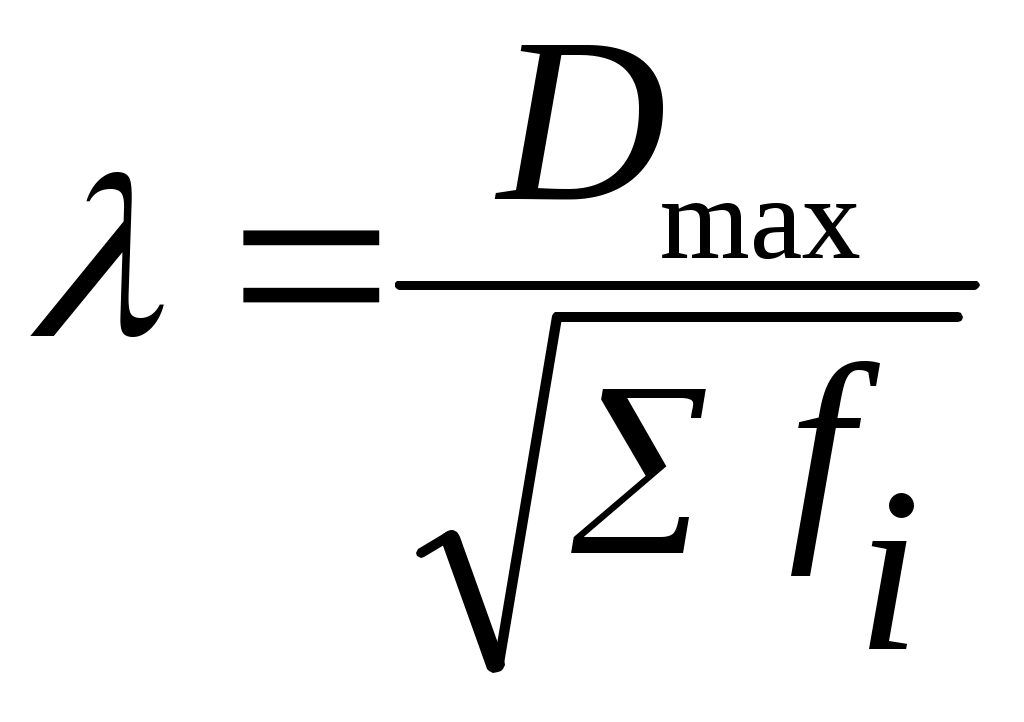
где D_max– максимальное значение разности между накопленными эмпирическими и теоретическими частотами;

– сумма эмпирических частот (объем совокупности).

Рассчитав значение λ, по таблице (см. Приложение 3) определяют вероятность Р(λ), с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны. Вероятность Р(λ) может изменяться от 0 до 1. При Р(λ)=1 происходит полное совпадение частот, при Р(λ)=0 – полное расхождение. Если λ принимает значения до 0,3, то Р(λ)=1.

Необходимым условием использования этого критерия является достаточно большое число наблюдений (не меньше 100).

Пример 8: Имеются данные по цеху о распределении рабочих по стажу работы (табл. 13). На основе приведенных данных проверить соответствие эмпирического распределения закону нормального распределения, используя критерий согласия Пирсона.

Таблица 13

Группы рабочих по стажу работы, лет	Число рабочих,	Середина интервала					Теоретические частоты
1	2	3	4	5	6	7	8	9
0-2	6	1	6	216	1,935	0,063	3	2,21
2-4	8	3	24	128	1,290	0,174	9	0,11
4-6	12	5	60	48	0,645	0,325	17	1,37
6-8	24	7	168	0	0	0,399	21	0,56
8-10	17	9	153	68	0,645	0,325	17	0,00
10-12	8	11	88	128	1,290	0,174	9	0,11
12-14	5	13	65	180	1,935	0,063	3	0,88
Итого	80		564	768			79	5,24

Выдвинув гипотезу о нормальном распределении, определим по эмпирическим данным параметры этой кривой.

Сначала рассчитаем средний уровень ряда по формуле (5.10), используя данные графы 4 табл. 13:

Затем определим среднее квадратическое отклонение по формуле 6.7, используя промежуточные расчеты графы 5 табл. 13:

года.

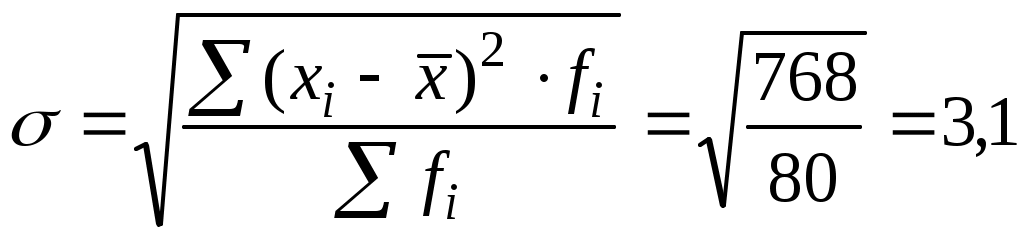
Далее определим нормированное отклонение tдля каждого варианта (см. графу 6 табл. 13), после чего по таблице распределения функции (см. Приложение 1) найдем значения функции при значениях аргумента, полученных в графе 6. При этом необходимо учитывать, что функция четная, т.е. = .

Анализируемый вариационный ряд имеет равные интервалы, следовательно, можно определить:

.

Последовательно умножив const на величину для каждого варианта, получим теоретические частоты (см. графу 8 табл.13).

Иногда за счет округлений при расчетах может быть нарушено равенство сумм эмпирических и теоретических частот, что и произошло в данном случае ( )

Сравним на графике эмпирические и теоретические частоты, полученные на основе данных табл. 13 (рис. 20).

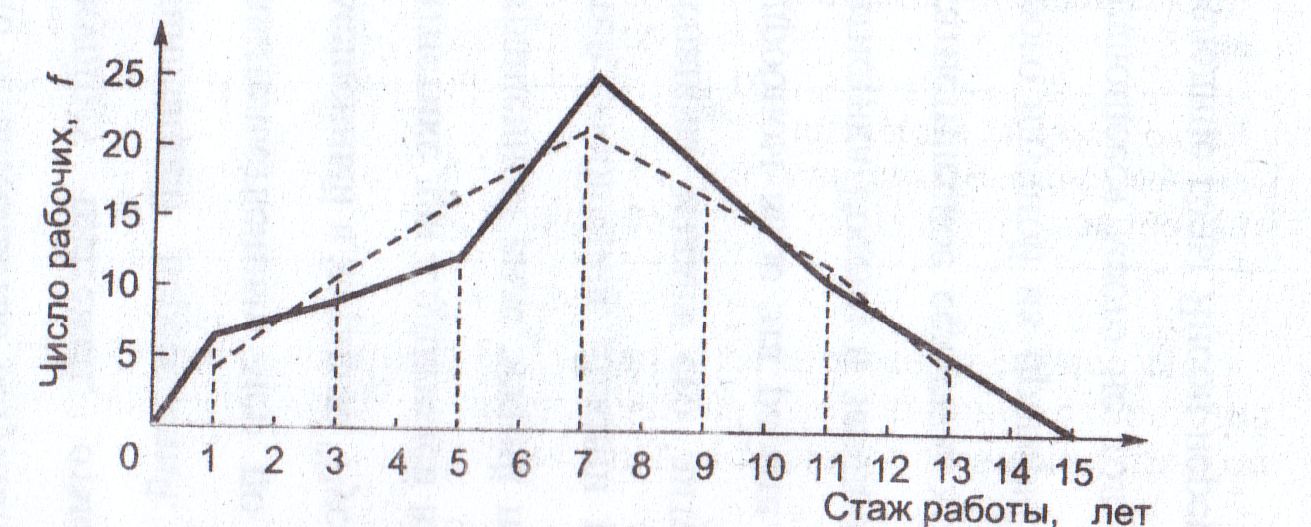
─ эмпирическое распределение;

—- теоретическая кривая нормального распределения

Рис. 20. Распределение рабочих по стажу работы

Сопоставление на графике эмпирического распределения с теоретической кривой нормального распределения свидетельствует о достаточно хорошем согласовании распределений.

Степень расхождения теоретических и эмпирических частот оценивается с помощью критерия К. Пирсона (см. графу 9 табл.13):

.

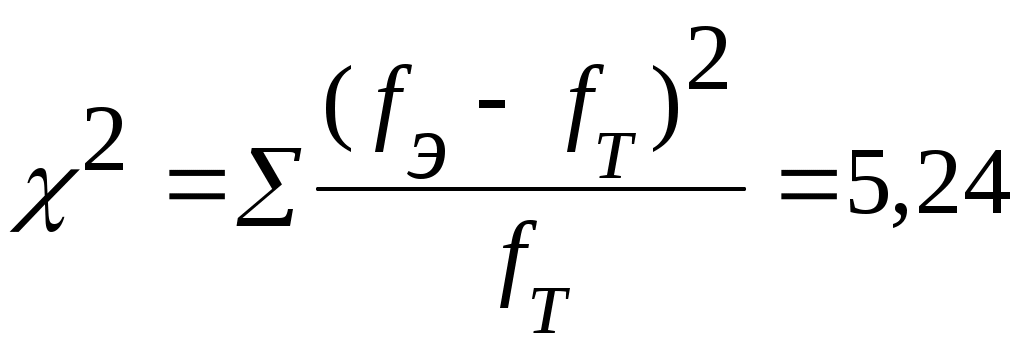
Полученное значение критерия сравнивается с табличным значение , которое определяется по таблице (см. Приложение 2).

При вероятности Р(t)=0,95 (α = 0,05) и числе степеней свободы ν=n-3=7 – 3=4 (n – число групп, в нашем примере 7 групп) получим табличное значение =9,5.

На основе проведенных расчетов получаем, что < (5,24<9,5), следовательно, гипотеза о близости эмпирического распределения к нормальному не отвергается, а расхождения объясняются случайными факторами.

Вопросы и задания для самоконтроля

1. Что представляет собой вариация признака?
2. Что называется средним квадратическим отклонением?
3. Перечислите относительные показатели вариации.
4. Что показывает коэффициент вариации?
5. Какие виды дисперсий вычисляются для совокупностей, разделенных на группы?
6. Что характеризуют коэффициент асимметрии и коэффициент эксцесса?
7. По каким критериям проходит проверка исходных данных на соответствии нормальному закону распределения?