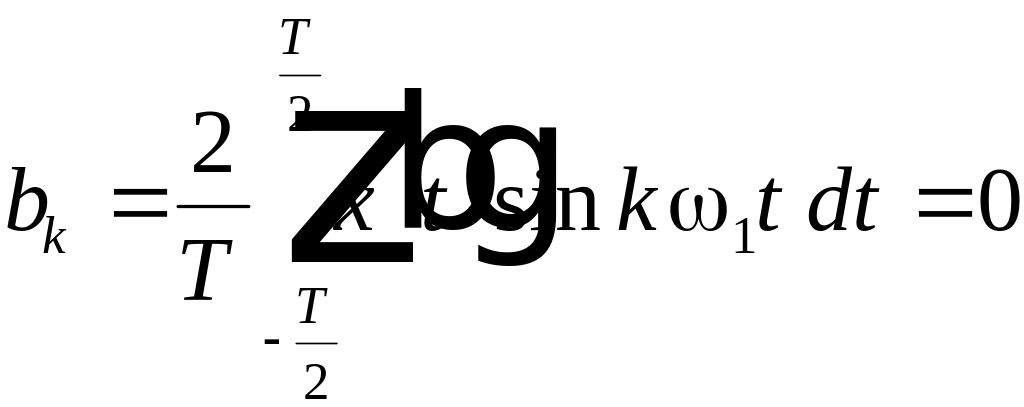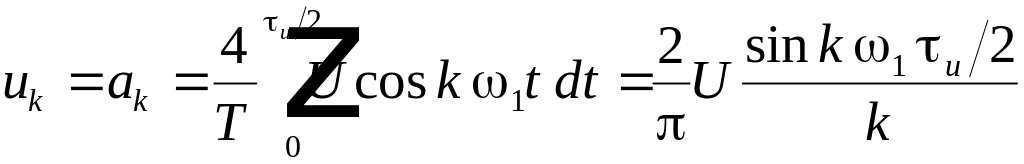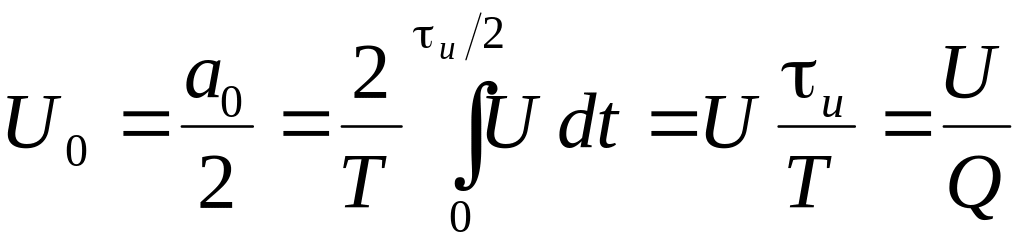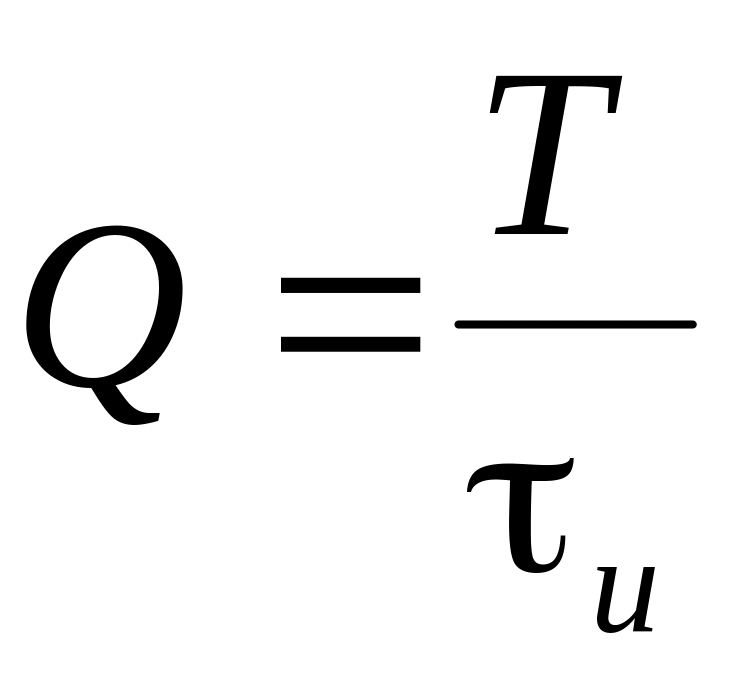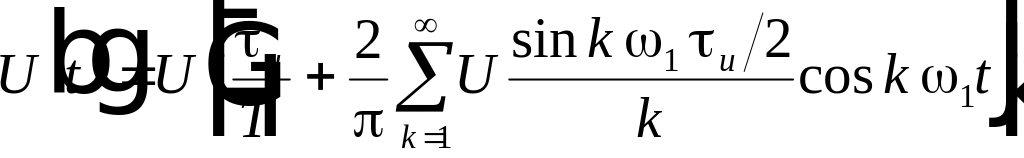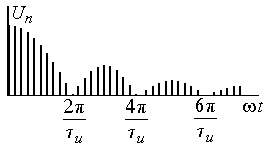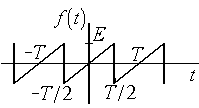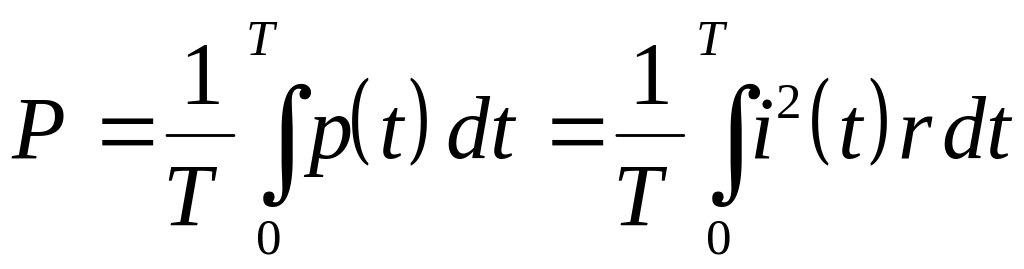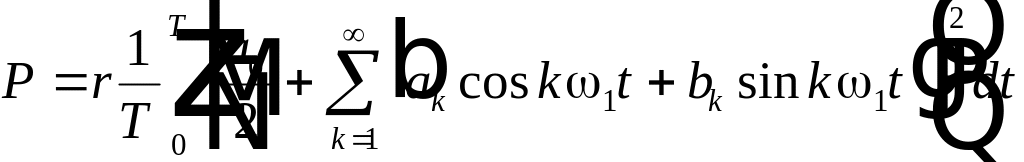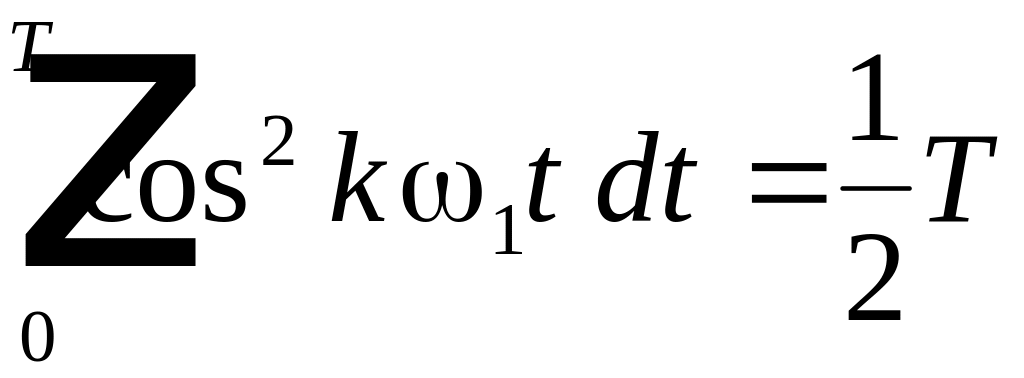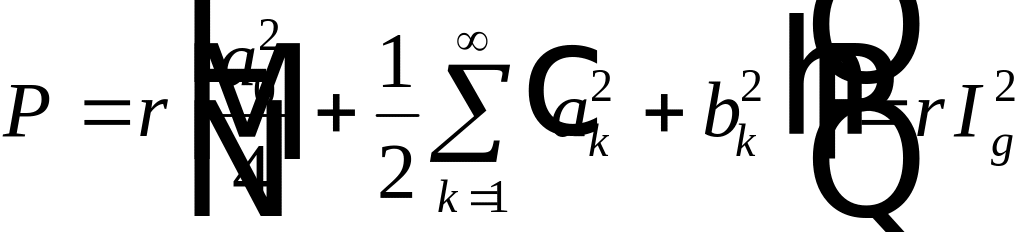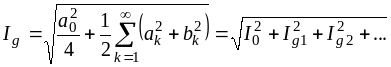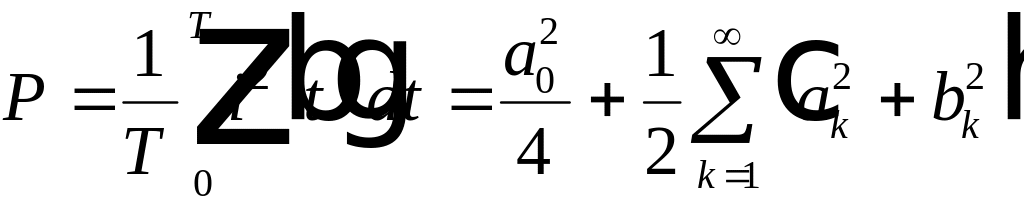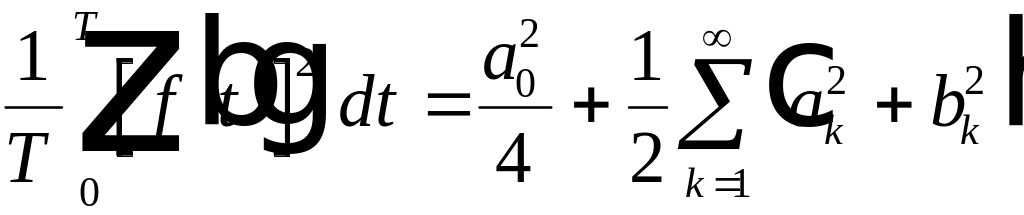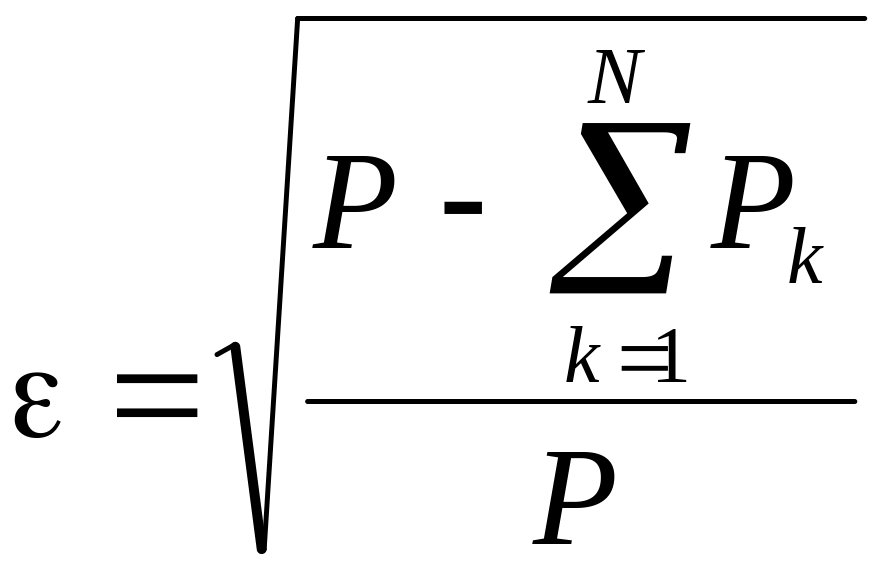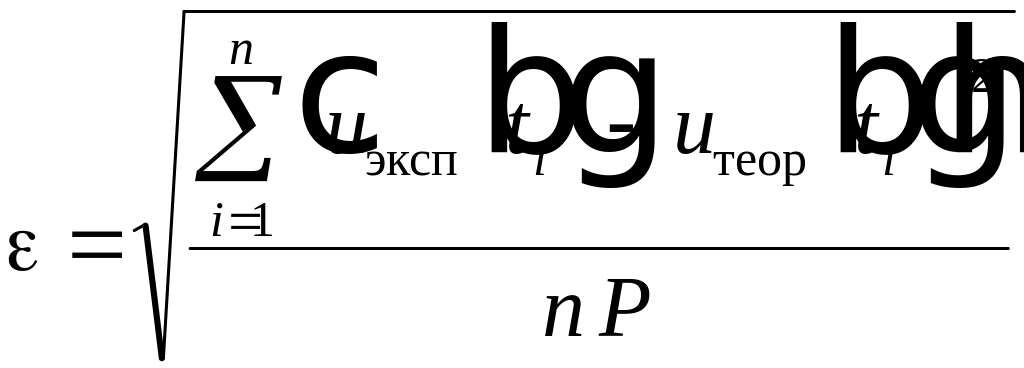Среднеквадратическая ошибка аппроксимации ряда фурье

Цель
работы. Изучить возможности синтеза
сигналов с помощью ряда Фурье по
ортогональной системе тригонометрических
функций. Синтезировать периодические
сигналы различной формы и исследовать
влияние числа ортогональных составляющих
на погрешность аппроксимации.

4.1. Разложение сигналов в обобщенный ряд фурье

4.1.1. Спектры простейших периодических функций

Если
функция

четная (симметричная относительно оси
ординат), т.е.

,
то в этом случае

;
(4.1)

.
(4.2)

Разложение
функции будет следующим

. (4.3)

Аналогично
для нечетной функции можно найти, что

. (4.4)

На
рис. 4.1 показана последовательность
прямоугольных импульсов которую можно
рассматривать как четную функцию.

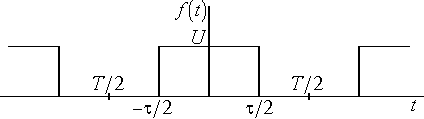
Рис.
4.1. Последовательность прямоугольных
импульсов

По
формуле (4.1) находим амплитуду

-й
гармоники:

. (4.5)

Постоянная
составляющая будет равна

;

. (4.6)

где

–
скважность импульсов. Разложение функции
запишется в виде:

. (4.7)

Графически
амплитудный и фазовый спектры прямоугольных
импульсов показаны на рис. 4.2.

Расстояния
между отдельными спектральными
составляющими обратно пропорциональны
периоду следования импульсов —

,
а положение нулей кратно

.

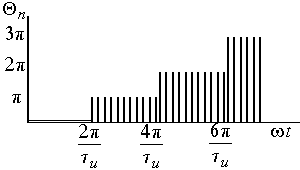
а) б)

Рис.
4.2. Амплитудный и фазовый спектры
прямоугольных импульсов

Можно
показать, что для импульсов, представленных
на рис. 4.3, разложения в ряд Фуре будут
иметь следующий вид:

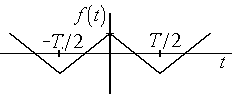
а) б)

Рис.
4.3. Пилообразное колебание и треугольные
импульсы

для
периодического пилообразного колебания
(рис 4.3,а);

; (4.8)

для
периодической последовательности
треугольных импульсов (рис.4.3,б):

. (4.9)

4.1.2. Мощность и действующее значение периодического сигнала

Пусть
несинусоидальный периодический ток

течет через активное сопротивление

.
Средняя за период мощность будет равна

. (4.10)

здесь

мгновенная мощность. Представим функцию

в виде ряда Фурье (4.6), тогда

Возводя
в квадрат и интегрируя каждое из слагаемых
можно убедиться, что только интегралы
вида:

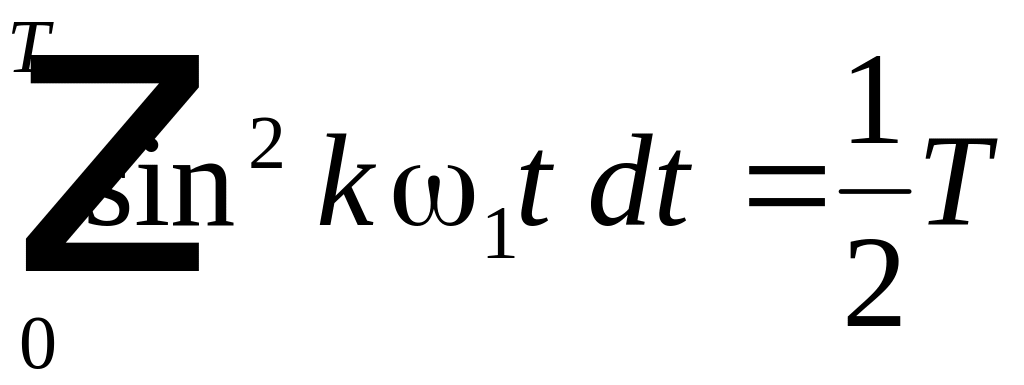
имеют
значения, не равные 0. Все остальные
интегралы равны нулю Поэтому после
интегрирования получим

где

. (4.11)

;

;

. (4.12)

Величины

,

,

,

,
… называют действующими значениями
тока. Аналогично вычисляются и
действующие значения напряжения. Если
сопротивление

Ом, то мощность равна

. (4.13)

Последнее
выражение справедливо для любой
периодической функции, т.е.

. (4.14)

В
таком виде последнее соотношение носит
название равенства Парсеваля.

4.1.3. Среднеквадратическая погрешность аппроксимации

Представим
приближенно функцию

разложением в усеченный ряд по
ортонормированным базисным функциям

(см. п. 2.1)

(4.15)

и
определим коэффициенты

так, чтобы минимизировать среднеквадратическую
погрешность:

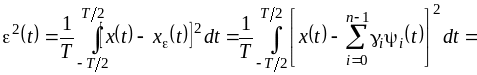
С
учетом (2.4) можно записать

. (4.16)

Погрешность

принимает минимальное значение, если

,
т.е. если коэффициенты разложения в
усеченном представлении (4.15) являются
коэффициентами обобщенного ряда Фурье.
Исходя из (4.16) можно записать

или

. (4.17)

Неравенство
(4.17) называют неравенством Бесселя.
С ростом

величина среднеквадратической погрешности
уменьшается. Если при

среднеквадратическая погрешность
стремится к нулю, то систему базисных
функций

называют полной. Эта система функций
является также замкнутой, т.к. для
любой функции

неравенство (4.17) переходит при

в равенство.

Точность
аппроксимации периодических сигналов
зависит от числа членов ряда при конечном
числе членов ряда. Относительную
среднеквадратическую погрешность
аппроксимации периодической функции
конечным числом членов ряда Фурье можно
определить по формуле :

. (4.18)

где

— средняя мощность сигнала;

— средняя мощность

-й
ортогональной составляющей сигнала.

Экспериментальное
значение погрешности аппроксимации
может быть найдено следующим образом.
Пусть имеется

экспериментально полученных точек

сигнала. Известен также теоретический
вид зависимости. Тогда погрешность
аппроксимации может быть вычислена
следующим образом

, (4.19)

где

— теоретическое значение отсчета сигнала
в момент времени

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Остаточный член ряда Фурье. Погрешности приближения функций. Численное дифференцирование

Страницы работы

Содержание работы

12.Остаточный член ряда Фурье.

Для функции f(x) Î L₂[a,b]
обобщенный ряд Фурье сходится к ней в среднеквадратичном смысле и методическая
погрешность аппроксимации может быть определена выражением (1.48)

Представим

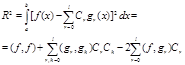Имея ввиду, что функции g_r(x), rÎ[0,l] ортогональны, а коэфиценты Фурье вычисляются по
соотношению (1.51) получим

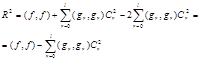oткуда

(1.54)

а если g_r(x), rÎ[0,l] ортонормированные, то

(1.55)

Если на приближаемую функцию
наложить дополнительные ограничения, то обобщенный ряд Фурье может сходиться к ней
и в равномерном смысле. Например, необходимым и достаточным условием
равномерной сходимости обобщенного ряда Фурье по полиномам Лежандра или
Чебышева к f(x) на [a,b]. Независимо от типа сходимости, иногда оказывается
необходимо оценить погрешность аппроксимации на [a,b] в
виде максимального отклонения ряда Фурье от приближаемой f(x), что
можно осущесвить дав оценку остаточного члена ряда Фурье

(1.56)

Однако в общнм случае
аппроксимации таких оценок не существует. В частности, же, например, для (l+1) раз
дифферинцируемых функций f(x), xÎ[a,b]

(1.57)

где a(x) –
значение частичной суммы ряда Фурье на [a,b].Если
более конкретизировать

задачу аппроксимации, положив
в качестве базисных функций ряда Фурье полиномы Чебышева, то

(1.58)

Оценка остаточного члена ряда
Фурье для непрерывной, преиодической, периода 2p функции f(x)

(1.59)

где K – некоторая
константа, определение которой, вообще говоря, проблематично, l
— максимальное значение скорости изменения f(x) на
интервале аппроксимации. Оценки (1.57) ¸(1.59) являются
неконструктивными, поскольку содержат в себе параметры, определение которых
практически невозможны или вызывают существенные трудности. Представляется
целесообразным в случае неоходимости оценку остаточного члена (1.56) давать по
некоторой модели аппроксимируемой функции, которая принадлежит к тому же
классу, что и f(x), но в то же время является наиболее неблагоприятной в
отношении точности аппроксимации. Учитывая наиболее вероятную с практической
точки зрения априорную информацию об аппроксимируемой функции, за такую модель
может быть принята функция вида

(1.60)

где f_min и
f_max – минимальное и максимальное значение f(x) на [a,b], W_М –
максимальное значение круговой частоты спектра аппроксимируемой функции, если
таковая информация может быть получена, или

W_М = V_М / A_М

где V_М – максимальная скорость изменения f(x) на [a,b]. При
аппроксимации модели (1.60) обобщенными рядами Фурье по полиномам Лежандра и
Чебышева первого рода были получены экспериментальные номограммы

которые позволили дать оценки остаточных членов в
следующем аналитическом виде

(1.61)

где K≈0,212(5,3125 + l) для полиномов
Лежандра и K_l=4
для полиномов Чебышевва. Следует отметить, что модельная оценка (1.61)
совпадает с оценкой (1.58), если модели положить A_М = 1,

имея в виду, что

13.Погрншности приближения функций.

Результирующая погрешноси
приближения функции f(x), xÎ[a,b] в виде некоторой F(x), xÎ[a,b]
вобщем случае складывается составляющих .

1. Методическая погрешность
используемого способа приближения, возникающая из-за отбрасывания остаточного
члена при опрнделении F(x). Данная погрешность уменьшается с увеличением числа
слагаемых в F(x), и в ряде случаев её удаётся оценить.

2. Погрешность приближенных
вычислений ЭВМ, которые, в свою очередь, можно подразделить на две группы:

Методическая погрешность,
возникающая в результате использования численных методовпри реализации
алгоритмов вычислений требуемых параметров. Данная погрешность имеет место,
например, при исппользовании квадратурных формул численного интегрирования для
определения коэфициентов Фурье. Эта погрешность может быть уменьшена за счет
использования более точного вычислительного алгоритма и оценена в виде
методической погрешности данного алгоритма.

Вычислительная погрешность,
порождаемая конечностью разрядной сетки памяти ЭВМ и зависящая (при выбранном
алгоритме) от возможностей используемой вычислительной техники.

3. Погрешность от неточного
задания исходных данных, которая носит случайный характер и может быть оценена
вероятностными характеристиками. На пример, при аппроксимации некоторой
функции f_*(x)=f(x)+ sf(x), где
sf(x) –
погрешности, искажающие истинную f(x) и
характеризуемые математическим ожиданием М{sf(x)}=0
и дисперсией D{sf(x)}=s², увеличение числа учитываемых членов ряда Фурье
приводит к тому, что математическое ожидание случайной погрешности определения
коэффициентов Фурье остаётся нулевым, а вот дисперсия возрастает.

Анализируя поведение
приведённых погрешностей в зависимости от числа слагаемых в приближающей F(x),
можно сделать вывод, что увеличение количества учитываемых членов в F(x)
приводит к тому, чтометодическая погрешность приближения уменьшается, в то
время как все остальные, связанные, как правило, свычислением коэфициентов
приближающей функции, возрастает. Таким образом, существует некое оптимальное
значение числа учитываемых членов функции F(x),
превышение которого приведёт к увеличению результирующей погрешности, поскольку
скорость нарастания вычислительной погрешности становится больше, чем скорость
уменьшения методической.

Информация о работе

Тип:

Ответы на экзаменационные билеты

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник

4.1. Разложение сигналов в обобщенный ряд фурье

4.1.1. Спектры простейших периодических функций

Если
функция

четная (симметричная относительно оси
ординат), т.е.

,
то в этом случае

;
(4.1)

.
(4.2)

Разложение
функции будет следующим

. (4.3)

Аналогично
для нечетной функции можно найти, что

. (4.4)

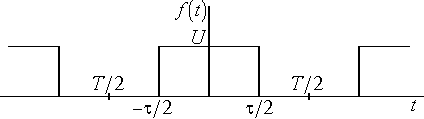
Рис.
4.1. Последовательность прямоугольных
импульсов

По
формуле (4.1) находим амплитуду

-й
гармоники:

. (4.5)

Постоянная
составляющая будет равна

;

. (4.6)

где

–
скважность импульсов. Разложение функции
запишется в виде:

. (4.7)

Графически
амплитудный и фазовый спектры прямоугольных
импульсов показаны на рис. 4.2.

а) б)

Рис.
4.2. Амплитудный и фазовый спектры
прямоугольных импульсов

Можно
показать, что для импульсов, представленных
на рис. 4.3, разложения в ряд Фуре будут
иметь следующий вид:

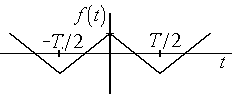
а) б)

Рис.
4.3. Пилообразное колебание и треугольные
импульсы

для
периодического пилообразного колебания
(рис 4.3,а);

; (4.8)

для
периодической последовательности
треугольных импульсов (рис.4.3,б):

. (4.9)

4.1.2. Мощность и действующее значение периодического сигнала

Пусть
несинусоидальный периодический ток

течет через активное сопротивление

.
Средняя за период мощность будет равна

. (4.10)

здесь

мгновенная мощность. Представим функцию

в виде ряда Фурье (4.6), тогда

Возводя
в квадрат и интегрируя каждое из слагаемых
можно убедиться, что только интегралы
вида:

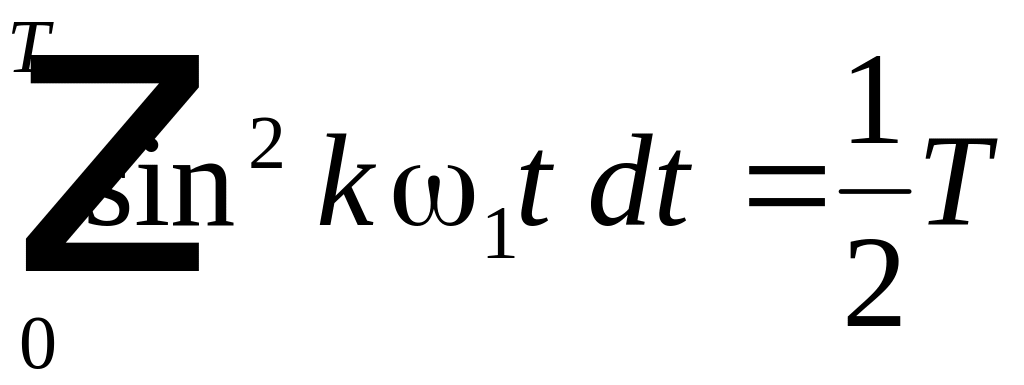
имеют
значения, не равные 0. Все остальные
интегралы равны нулю Поэтому после
интегрирования получим

где

. (4.11)

;

;

. (4.12)

Ом, то мощность равна

. (4.13)

Последнее
выражение справедливо для любой
периодической функции, т.е.

. (4.14)

В
таком виде последнее соотношение носит
название равенства Парсеваля.

4.1.3. Среднеквадратическая погрешность аппроксимации

Представим
приближенно функцию

разложением в усеченный ряд по
ортонормированным базисным функциям

(см. п. 2.1)

(4.15)

и
определим коэффициенты

так, чтобы минимизировать среднеквадратическую
погрешность:

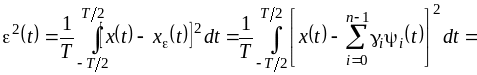
С
учетом (2.4) можно записать

. (4.16)

Погрешность

или

. (4.17)

Неравенство
(4.17) называют неравенством Бесселя.
С ростом

величина среднеквадратической погрешности
уменьшается. Если при

среднеквадратическая погрешность
стремится к нулю, то систему базисных
функций

называют полной. Эта система функций
является также замкнутой, т.к. для
любой функции

неравенство (4.17) переходит при

в равенство.

. (4.18)

где

— средняя мощность сигнала;

— средняя мощность

-й
ортогональной составляющей сигнала.

Экспериментальное
значение погрешности аппроксимации
может быть найдено следующим образом.
Пусть имеется

экспериментально полученных точек

, (4.19)

где

— теоретическое значение отсчета сигнала
в момент времени

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

Исследование влияния числа учитываемых членов ряда Фурье на точность аппроксимации

Страницы работы

Содержание работы

НГТУ

Расчетно-графическое задание

по вычислительной математике

Аппроксимация функций

Выполнил: Преподаватель:

студент Чикильдин
Г.П

группы
АП019

Малыгин Иван

Вариант №9

Новосибирск, 2002 г.

I. Цель:
Исследовать влияние числа учитываемых членов ряда Фурье на точность
аппроксимации. Определить погрешность аппроксимации.

Постановка задачи: На интервале [a,b] произвести
аппроксимацию функций f(t), заданной шагом ,
обобщённым рядом Фурье по системе ортогональных (ортонормированных) на [a,b] c весом
базисных функций

Данные:

Функция:

Интервал:

Шаг: 0,05

II. Теоретические
сведения

Система
линейно независимых функций называется
ортогональной на с весом ,
если .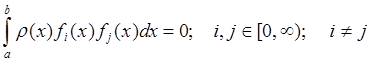

— нормирующая функция. Она неотрицательна
на и интегрируема на с
положительным результатом.

Если для
ортогональной системы выполняется условие

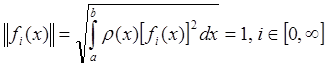
, то такая система функций называется
ортонормированной.

Пусть на задана система линейно независимых функций
и некоторая последовательность констант Ряд вида называется
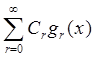
функциональным рядом. Если этот ряд сходится, то его сумму обозначают как .

Если
система функций будет ортогональна или
ортонормированна, то получаемый функциональный ряд будет называться рядом
Фурье.

Коэффициенты
, коэффициенты Фурье, в таком случает будут
определяться так:

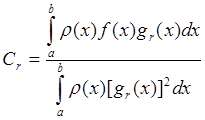
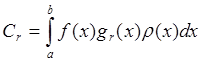
в случае ортогональной системы функций,

в случает ортонормированной системы.

Произвольную
кусочно-непрерывную функцию на [a;b]
приближённо можно представить в виде обобщённого ряда Фурье с конечным числом
членов

, (**)

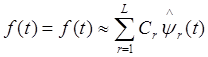
где , – система
ортогональных на [a;b] базисных функций, а

– коэффициенты Фурье . (*)

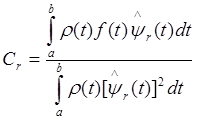
Таким
образом, чтобы решить задачу аппроксимации функции f(t) на
[a;b], необходимо при заданном базисе , , , вычислить коэффициенты Фурье согласно (*) и восстановить оценку , аппроксимируемой функции f(t) по
(**).

Полиномы
Лежандра, ортогональные на с весом

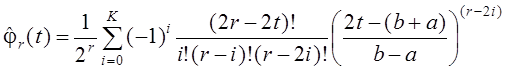
К – целая часть

Нормирующий множитель полиномов Лежандра

и ортонормированные полиномы —

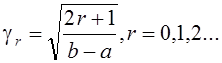
III. Листинг

program main

real f(113),t(113),ro(113),fi(7,113),f1(113),c(7),ff(113)

real a,b,dt,e(113),em,es,ep,emo,eso,epo,ff1(113)

real ff3(113),ff5(113),e1(113),e3(113),e5(113)

integer i,kon,l

open
(1,file=’data’)

write
(1,*)’Студент:Малыгин Иван’

write
(1,*)’Группа: АП-019′

write
(1,*)’Вариант №9′

write
(1,*)’Исходные данные:a=0,6;b=2,05;dt=0,025;’

write
(1,*)’аппророксимируемая функция:5+2,5*SIN(0,5*t);’

write
(1,*)’базисные функции Лежандра.’

a=0.8

b=6.4

dt=0.05

kon=(b-a)/dt+1

do 1 i=1,kon

c Вычисление реализации
аппроксимируемой

c функции f(t) на
заданном [a,b] при фиксированном dt

t(i)=0.8+0.05*(i-1)

f(i)=5+2.5*sin(0.5*t(i))

1 continue

open
(4,FILE=’graph3′)

do 2 l=1,7

c Вычисление базисных
функций полинома Лежанжра

call
n1yplg(a,b,kon,dt,l,ro,fi)

c Вычисление
коэффициентов Фурье

call
n1ykf(kon,dt,l,f,f1,fi,ro,c)

c Реализация оценки
аппроксимируемой функции f~(t)

call
n1ywst(kon,l,c,fi,ff)

c Вычисление
погрешности аппроксимации

call
n1yeee(f,ff,kon,e,em,es,ep,emo,eso,epo)

if(l.gt.2) write
(4,*)l,emo,eso

write (1,10)l

write (1,11)

write (1,16)

write (1,12)

do 4 i=1,l

write (1,13)i,c(i)

4 continue

write (1,14) l-2,l

do 3 i=1,kon

if
((l.eq.4).or.(l.eq.6)) go to 7

if (l.eq.3)
ff1(i)=ff(i)

if (l.eq.3) e1(i)=e(i)

if (l.eq.5)
ff3(i)=ff(i)

if (l.eq.5) e3(i)=e(i)

if (l.eq.7) ff5(i)=ff(i)

if (l.eq.7) e5(i)=ff(i)

7 write (1,15)
t(i),f(i),ff(i),e(i)

3 continue

2 continue

close(4)

write
(1,11)

write (1,17)

write (1,19)

c Вывод
в файл graph1 значений функции и аппроксимирующих

с полиномов

open(2,FILE=’graph1′)

do 8 i=1,kon

write (2,23)t(i),f(i),ff1(i),ff3(i),ff5(i)

8
continue

open(5,FILE=’graph4′)

c Вывод
зависимости погрешности аппроксимирующих полиномов от

с аргумента

do 9 i=1,kon

write (5,*)t(i),e1(i),e3(i),e5(i)

9 continue

open
(3,FILE=’graph2′)

c Вывод в файл graph2 реализации базисных фунций и
весовой

c функции

do 5 i=1,kon

write
(1,18)t(i),(fi(j,i),j=1,5)

write
(3,23)t(i),(fi(j,i),j=1,5),ro(i)

5 continue

close (3)

write (1,11)

write (1,20)

write (1,21)

do 6 i=1,kon

write
(1,22)t(i),ro(i)

6 continue

close (1)

close(2)

10 format (‘Количество
учитываемых членов ряда Фурье:’,I1)

11 format (1x/’__________________________________________’)

12 format
(‘Коэффициенты Фурье:’)

13 format
(‘c(‘,I1,’)=’,f6.4)

14 format (1x/’Табл.’,1x,I1/8x,’Результаты
расчетов при l=’,I1/3x, * ‘T’,9x,’F’,10x,’~F’,10x,’E’)

15 format
(F8.5,3x,F8.5,3x,F8.5,3x,F8.5,3x,F9.5)

16 format (1x)

17 format (1x/’Табл. 6’/11x,*’Реализации первых
пяти базисных функций’)

18 format
(F6.4,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5,1x,F8.5)

19 format
(3x,’T’,6x,’^T1′,6x,’^T2′,6x,’^T3′,6x,’^Т4′,6x,’^T5′)

20 format (1x/’Табл.
7’/’Реализация весовой функции’)

21 format
(6x,’T’,8x,’Po’)

22 format
(1x,F8.5,1x,F8.5)

23 format
(F6.2,1x,6(F11.8,1x))

end

IV. Результаты.

Приведены
графики функций , , , , а
также графики базисных функций и графики
относительной и абсолютной погрешностей (EMO и ESO). Т.к.
весовая функция , она на графики не выводится. Поскольку у полиномов
при l>3достаточно
высокая степень приближения, также приведены графики зависимости погрешности от
t.

V. Заключение

1.
Погрешности аппроксимации падают с
увеличением числа L учитываемых членов ряда Фурье, но если при малых L это
падение очень заметно, то при увеличении L оно начинает
уменьшаться, что связано с возрастанием числа вычислительных операций и,
следственно, накоплением вычислительной погрешности.

2.
Ряды Фурье приближают функцию
лучше в среднеквадратическом смысле, а не в равномерном, что видно из последнего
графика: е_со на порядок меньше, чем е_мо.

VI. Список литературы

4.1. Разложение сигналов в обобщенный ряд фурье

4.1.1. Спектры простейших периодических функций

4.1.2. Мощность и действующее значение периодического сигнала

4.1.3. Среднеквадратическая погрешность аппроксимации

Остаточный член ряда Фурье. Погрешности приближения функций. Численное дифференцирование

Страницы работы

Содержание работы

Похожие материалы

Информация о работе

4.1. Разложение сигналов в обобщенный ряд фурье

4.1.1. Спектры простейших периодических функций

4.1.2. Мощность и действующее значение периодического сигнала

4.1.3. Среднеквадратическая погрешность аппроксимации

Предложите, как улучшить StudyLib

Исследование влияния числа учитываемых членов ряда Фурье на точность аппроксимации

Страницы работы

Содержание работы

Расчетно-графическое задание

Аппроксимация функций

II. Теоретические
сведения

Оглавление

Похожие материалы

Информация о работе

4.1. Разложение сигналов в обобщенный ряд фурье

4.1.1. Спектры простейших периодических функций

4.1.2. Мощность и действующее значение периодического сигнала

4.1.3. Среднеквадратическая погрешность аппроксимации

Остаточный член ряда Фурье. Погрешности приближения функций. Численное дифференцирование

Страницы работы

Содержание работы

Похожие материалы

Информация о работе

4.1. Разложение сигналов в обобщенный ряд фурье

4.1.1. Спектры простейших периодических функций

4.1.2. Мощность и действующее значение периодического сигнала

4.1.3. Среднеквадратическая погрешность аппроксимации

Предложите, как улучшить StudyLib

Исследование влияния числа учитываемых членов ряда Фурье на точность аппроксимации

Страницы работы

Содержание работы

Расчетно-графическое задание

Аппроксимация функций

II. Теоретические сведения

Оглавление

Похожие материалы

Информация о работе

II. Теоретические
сведения