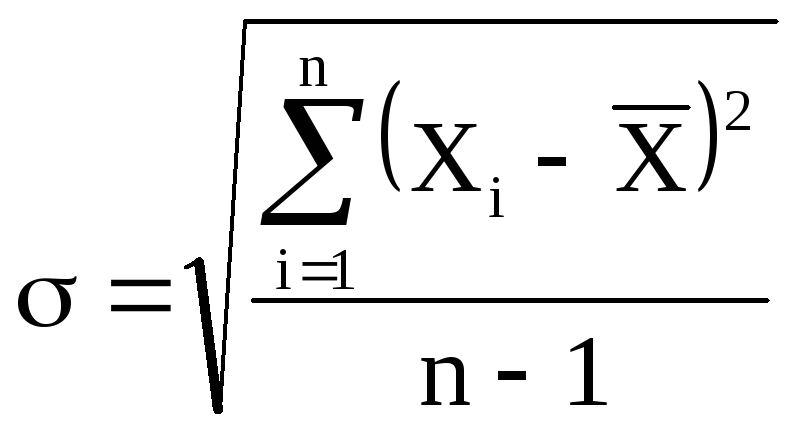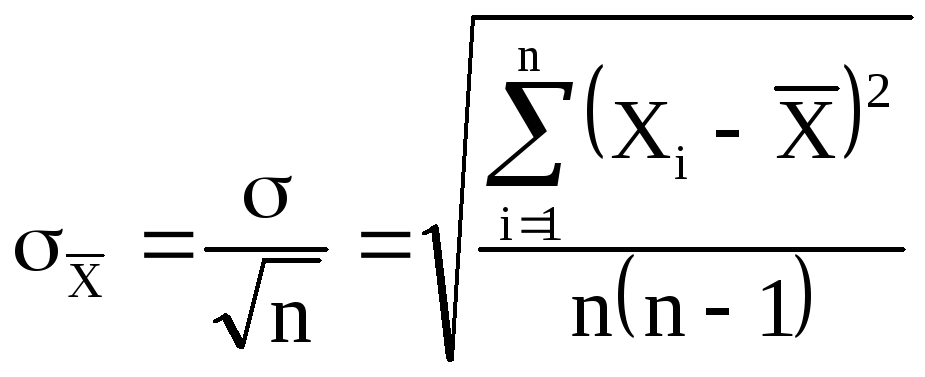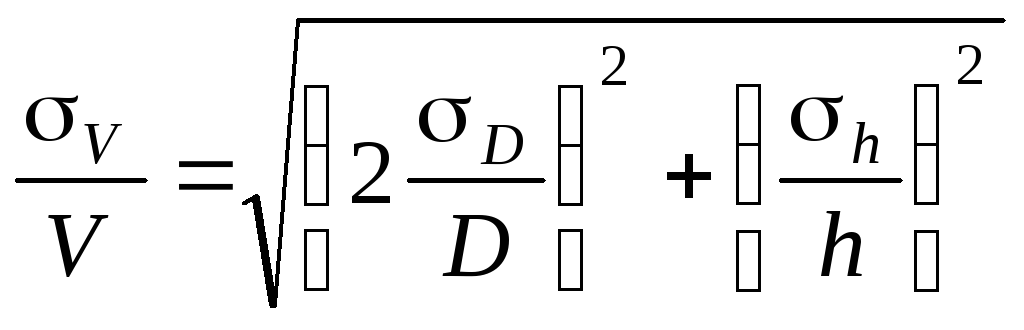Среднеквадратическая ошибка ско - Не ошибается лишь тот, кто ничего не делает!

From Wikipedia, the free encyclopedia

In statistics, the mean squared error (MSE)^[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.^[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.^[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).

The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.

The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).^{[citation needed]} For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.

Definition and basic properties[edit]

The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.

Predictor[edit]

If a vector of predictions is generated from a sample of data points on all variables, and is the vector of observed values of the variable being predicted, with hat{Y} being the predicted values (e.g. as from a least-squares fit), then the within-sample MSE of the predictor is computed as

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

In other words, the MSE is the mean ${textstyle left({frac {1}{n}}sum _{i=1}^{n}right)}$ of the squares of the errors ${textstyle left(Y_{i}-{hat {Y_{i}}}right)^{2}}$ . This is an easily computable quantity for a particular sample (and hence is sample-dependent).

In matrix notation,

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}(e_{i})^{2}={frac {1}{n}}mathbf {e} ^{mathsf {T}}mathbf {e} }$

where $e_{i}$ is ${displaystyle (Y_{i}-{hat {Y_{i}}})}$ and is the column vector.

The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,^[4] and is computed as

${displaystyle operatorname {MSE} ={frac {1}{q}}sum _{i=n+1}^{n+q}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

Estimator[edit]

The MSE of an estimator with respect to an unknown parameter theta is defined as^[1]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}$

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator is derived as a sample statistic and is used to estimate some population parameter, then the expectation is with respect to the sampling distribution of the sample statistic.

The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.^[5]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} ({hat {theta }},theta )^{2}.}$

Proof of variance and bias relationship[edit]

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}$

An even shorter proof can be achieved using the well-known formula that for a random variable , ${textstyle mathbb {E} (X^{2})=operatorname {Var} (X)+(mathbb {E} (X))^{2}}$ . By substituting with, , we have

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}$

But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.

In regression[edit]

In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,^[6] but whose limitation is related to known distribution of the data.

The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).^[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.

In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.

Examples[edit]

Mean[edit]

Suppose we have a random sample of size from a population, $X_{1},dots ,X_{n}$ . Suppose the sample units were chosen with replacement. That is, the units are selected one at a time, and previously selected units are still eligible for selection for all draws. The usual estimator for the is the sample average

$overline{X}=frac{1}{n}sum_{i=1}^n X_i$

which has an expected value equal to the true mean (so it is unbiased) and a mean squared error of

${displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}$

where $sigma ^{2}$ is the population variance.

For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.

Variance[edit]

The usual estimator for the variance is the corrected sample variance:

${displaystyle S_{n-1}^{2}={frac {1}{n-1}}sum _{i=1}^{n}left(X_{i}-{overline {X}}right)^{2}={frac {1}{n-1}}left(sum _{i=1}^{n}X_{i}^{2}-n{overline {X}}^{2}right).}$

This is unbiased (its expected value is $sigma ^{2}$ ), hence also called the unbiased sample variance, and its MSE is^[8]

${displaystyle operatorname {MSE} (S_{n-1}^{2})={frac {1}{n}}left(mu _{4}-{frac {n-3}{n-1}}sigma ^{4}right)={frac {1}{n}}left(gamma _{2}+{frac {2n}{n-1}}right)sigma ^{4},}$

where $mu _{4}$ is the fourth central moment of the distribution or population, and is the excess kurtosis.

However, one can use other estimators for $sigma ^{2}$ which are proportional to $S^2_{n-1}$ , and an appropriate choice can always give a lower mean squared error. If we define

${displaystyle S_{a}^{2}={frac {n-1}{a}}S_{n-1}^{2}={frac {1}{a}}sum _{i=1}^{n}left(X_{i}-{overline {X}},right)^{2}}$

then we calculate:

${displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}$

This is minimized when

$a=frac{(n-1)gamma_2+n^2+n}{n} = n+1+frac{n-1}{n}gamma_2.$

For a Gaussian distribution, where , this means that the MSE is minimized when dividing the sum by a=n+1 . The minimum excess kurtosis is ,^[a] which is achieved by a Bernoulli distribution with p = 1/2 (a coin flip), and the MSE is minimized for ${displaystyle a=n-1+{tfrac {2}{n}}.}$ Hence regardless of the kurtosis, we get a «better» estimate (in the sense of having a lower MSE) by scaling down the unbiased estimator a little bit; this is a simple example of a shrinkage estimator: one «shrinks» the estimator towards zero (scales down the unbiased estimator).

Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be $S^2_{n-1}.$

Gaussian distribution[edit]

The following table gives several estimators of the true parameters of the population, μ and σ², for the Gaussian case.^[9]

True value	Estimator	Mean squared error
	= the unbiased estimator of the population mean, $overline{X}=frac{1}{n}sum_{i=1}^n(X_i)$	$operatorname{MSE}(overline{X})=operatorname{E}((overline{X}-mu)^2)=left(frac{sigma}{sqrt{n}}right)^2$
${displaystyle theta =sigma ^{2}}$	= the unbiased estimator of the population variance, $S^2_{n-1} = frac{1}{n-1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n-1})=operatorname{E}((S^2_{n-1}-sigma^2)^2)=frac{2}{n - 1}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n} = frac{1}{n}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n})=operatorname{E}((S^2_{n}-sigma^2)^2)=frac{2n - 1}{n^2}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n+1} = frac{1}{n+1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n+1})=operatorname{E}((S^2_{n+1}-sigma^2)^2)=frac{2}{n + 1}sigma^4$

Interpretation[edit]

An MSE of zero, meaning that the estimator predicts observations of the parameter theta with perfect accuracy, is ideal (but typically not possible).

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).

Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.

In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.

MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.

Applications[edit]

Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.

Loss function[edit]

Squared error loss is one of the most widely used loss functions in statistics^{[citation needed]}, though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.^[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.

Criticism[edit]

The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.^[10]

Like variance, mean squared error has the disadvantage of heavily weighting outliers.^[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.

Notes[edit]

^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.

References[edit]

^ ^a ^b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20. If we use quadratic loss, our risk function is called the mean squared error (MSE) …
^ ^a ^b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)
^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.

Источник

Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

MSE как среднее дистанций между предсказаниями и реальными наблюдениями

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:

$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$

MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.

Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:

$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$

Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:

$$y = 0,5252 * x + 17,306$$

Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):

$$MSE = frac{1}{9} × 4445 = 493$$

Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.

MSE и Scikit-learn

Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:

import sklearn
from sklearn.metrics import mean_squared_error

Инициализируем крошечные списки, содержащие реальные и предсказанные координаты y:

y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]

Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:

mean_squared_error(y_true, y_pred)

Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:

496.0

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Автор оригинальной статьи: @mmoshikoo

Фото: @tobyelliott

Источник

Средняя квадратичная ошибка.

При ответственных
измерениях, когда необходимо знать
надежность полученных результатов,
используется средняя квадратичная
ошибка  (или
стандартное отклонение), которая
определяется формулой

(5)

Величина 
характеризует отклонение отдельного
единичного измерения от истинного
значения.

Если мы вычислили
по n
измерениям среднее значение

по формуле (2), то это значение будет
более точным, то есть будет меньше
отличаться от истинного, чем каждое
отдельное измерение. Средняя квадратичная
ошибка среднего значения

равна

(6)

где  — среднеквадратичная
ошибка каждого отдельного измерения,
n
– число
измерений.

Таким образом,
увеличивая число опытов, можно уменьшить
случайную ошибку в величине среднего
значения.

В настоящее время
результаты научных и технических
измерений принято представлять в виде

(7)

Как показывает
теория, при такой записи мы знаем
надежность полученного результата, а
именно, что истинная величина Х с
вероятностью 68% отличается от

не более, чем на
.

При использовании
же средней арифметической (абсолютной)
ошибки (формула 2) о надежности результата
ничего сказать нельзя. Некоторое
представление о точности проведенных
измерений в этом случае дает относительная
ошибка (формула 4).

При выполнении
лабораторных работ студенты могут
использовать как среднюю абсолютную
ошибку, так и среднюю квадратичную.
Какую из них применять указывается
непосредственно в каждой конкретной
работе (или указывается преподавателем).

Обычно если число
измерений не превышает 3 – 5, то
можно использовать среднюю абсолютную
ошибку. Если число измерений порядка
10 и более, то следует использовать более
корректную оценку с
помощью средней квадратичной ошибки
среднего (формулы 5 и 6).

Учет систематических ошибок.

Увеличением числа
измерений можно уменьшить только
случайные ошибки опыта, но не
систематические.

Максимальное
значение систематической ошибки обычно
указывается на приборе или в его паспорте.
Для измерений с помощью обычной
металлической линейки систематическая
ошибка составляет не менее 0,5 мм; для
измерений штангенциркулем –

0,1 – 0,05 мм;
микрометром – 0,01 мм.

Часто в качестве
систематической ошибки берется половина
цены деления прибора.

На шкалах
электроизмерительных приборов указывается
класс точности. Зная класс точности К,
можно вычислить систематическую ошибку
прибора ∆Х по формуле

где К – класс
точности прибора, Х_пр – предельное
значение величины, которое может быть
измерено по шкале прибора.

Так, амперметр
класса 0,5 со шкалой до 5А измеряет ток с
ошибкой не более

Среднее значение
полной погрешности складывается из
случайной и систематической
погрешностей.

Ответ с учетом
систематических и случайных ошибок
записывается в виде

Погрешности косвенных измерений

В физических
экспериментах чаще бывает так, что
искомая физическая величина сама на
опыте измерена быть не может, а является
функцией других величин, измеряемых
непосредственно. Например, чтобы
определить объём цилиндра, надо измерить
диаметр D и высоту h, а затем вычислить
объем по формуле

Величины D и h будут измерены с
некоторой ошибкой. Следовательно,
вычисленная величина
V
получится также с некоторой ошибкой.
Надо уметь выражать погрешность
вычисленной величины через погрешности
измеренных величин.

Как и при прямых
измерениях можно вычислять среднюю
абсолютную (среднюю арифметическую)
ошибку или среднюю квадратичную ошибку.

Общие правила
вычисления ошибок для обоих случаев
выводятся с помощью дифференциального
исчисления.

Пусть искомая
величина φ является функцией нескольких
переменных Х,
У, Z…

φ(Х,
У, Z…).

Путем прямых
измерений мы можем найти величины
,
а также оценить их средние абсолютные
ошибки
…
или средние квадратичные ошибки _Х,
_У,
_Z…

Тогда средняя
арифметическая погрешность 
вычисляется по формуле

где

— частные
производные от φ по
Х, У, Z. Они
вычисляются для средних значений
…

Средняя квадратичная
погрешность вычисляется по формуле

Пример.
Выведем формулы погрешности для
вычисления объёма цилиндра.

а) Средняя
арифметическая погрешность.

Величины
D и h
измеряются соответственно с ошибкой
D
и h.

Погрешность
величины объёма будет равна

б) Средняя
квадратичная погрешность.

Величины
D и h
измеряются соответственно с ошибкой
_D, _h.

Погрешность
величины объёма будет равна

Если формула
представляет выражение удобное для
логарифмирования (то есть произведение,
дробь, степень), то удобнее вначале
вычислять относительную погрешность.
Для этого (в случае средней арифметической
погрешности) надо проделать следующее.

1. Прологарифмировать
выражение.

2. Продифференцировать
его.

3. Объединить
все члены с одинаковым дифференциалом
и вынести его за скобки.

4. Взять выражение
перед различными дифференциалами по
модулю.

5. Заменить
значки дифференциалов d
на значки абсолютной погрешности .

В итоге получится
формула для относительной погрешности

Затем,
зная ,
можно вычислить абсолютную погрешность


 = 

Пример.

Аналогично можно
записать относительную среднюю
квадратичную погрешность

Правила
представления результатов измерения
следующие:

погрешность должна
округляться до одной значащей цифры:

правильно  = 0,04,

неправильно —
 = 0,0382;

последняя значащая
цифра результата должна быть того же
порядка величины, что и погрешность:

правильно
 = 9,830,03,

неправильно —
 = 9,8260,03;

если результат
имеет очень большую или очень малую
величину, необходимо использовать
показательную форму записи — одну и ту
же для результата и его погрешности,
причем запятая десятичной дроби должна
следовать за первой значащей цифрой
результата:

правильно —
 = (5,270,03)10^-5,

неправильно —
 = 0,00005270,0000003,

 = 5,2710^-50,0000003,

 =
= 0,0000527310^-7,

 = (5273)10^-7,

 = (0,5270,003)
10^-4.

Если результат
имеет размерность, ее необходимо
указать:

правильно – g=(9,820,02)
м/c²,

неправильно – g=(9,820,02).

Соседние файлы в папке Отчеты_Погрешность

Источник

Добро пожаловать!

Войдите или зарегистрируйтесь сейчас!

Войти

Страница 1 из 2

Регистрация:

5 мар 2016

Сообщения:

3

Симпатии:

1
Дорогие друзья, помогите пожалуйста разобраться со «среднеквадратической ошибкой/погрешностью». На сколько я понял это ошибка/погрешность, множества измеренных чисел, (угловые измерения). Не ясно мне, по какой формуле считать (вот тут посмотрел http://zem-kadastr.ru/blog/geodesy/203.html), так же имеется вопрос связанный с нормами на данную ошибку/погрешность. В одной умной книжке вычитал такие допуски (фотка во вложении). Вопрос вот в чем….в чем различие между суммарной среднеквадратической ошибкой и максимальной суммарной среднеквадратической ошибкой…О_о, Прошу Вашей помощи, голова кругом уже…
Вложения:
#1

89027155216 нравится это.
Форумчанин

Если вчитаться в текст документа, поставившего вас в тупик, то становится понятно, что под «суммарной СКП» понимается итоговое значение СКП суммы погрешностей нескольких (в данном случае двух) технологических подэтапов измерений, а под «максимальной СКП» понимается допуск на величину предельно допустимой СКП. Обычно это 2СКП при уровне доверительной вероятности 95%, или 3СКП при уровне 98%. Написано, конечно коряво, с претензией на наукообразие, но суть понять можно…Я, правда, опасаюсь, что мое пояснение вам понятно. Однако желаю успехов!

#2

ТАКИСКОБАРЬ нравится это.
Форумчанин

Регистрация:

20 янв 2013

Сообщения:

45

Симпатии:

9

В той книжке говорится о максимальной СКО определения отклонений от вертикали — ни кто ее не называет суммарной.

#3
Форумчанин

Регистрация:

6 мар 2016

Сообщения:

150

Симпатии:

62

Что понаписано полу- и червертьпрофессионалами, всерьез не все принимайте. Фраза «угол между осью симметрии и направлением сооружения» вообще перл. Зерна истины таковы:
1) можно работать инструментом-5-и-секундником или более точным
2) допуск на вертикальность 1мм/м или 0,7мм/м
3) допуск на погрешность измерений 5мм
Чтобы погрешность измерений выявить, нужно проделать ДВА независимых комплекса измерений. Скажем, получилось один раз +32мм (допустим, по направлению осьА – осьБ), второй раз –30мм (то есть +30мм по направлению ось Б — ось А). Это значит, погрешность измерений (32 — (-30))/2 = 31мм — очень грубо, недопустимо грубо.

Реально с четырех станций я измерял только раз. Убедился, что погрешность составила маленькие мм и больше не стал. Но с двух станций всегда измерял полным приемом и с замыканием горизонта (точней, проверял ориентировку после полуприема), а вычислял раздельно КЛ и КП. Поскольку систематические ошибки инструмента невелики и мне известны, разница между полуприемами в основном показывала погрешность измерений.

#4
Форумчанин

Регистрация:

18 июн 2007

Сообщения:

242

Симпатии:

49

Адрес:

Тюмень

Здравствуйте, Уважаемые! Уверен, в этой ветке мне помогут, вопрос тоже про СКП/СКО, но более базовый.
Для начала, покажу как я понимаю СКО, т.к. возможно путаюсь уже с этого этапа.
Итак, имеем несколько линейных (для простоты примера) измерений между двумя точками, пусть это будет ряд:
5, 2, 4, 7, 6, 8
т.к. для расчета необходимо истинное расстояние, но на практике оно почти всегда неизвестно, то под истинным будет фигурировать среднее арифметическое, оно для данного ряда равно 32/6=5,3
Дальше, нам необходимо вычислить дисперсию, она равна среднему арифметическому от квадратов изначальных величин уменьшенных на среднее арифметическое этих величин (брр….((( если на пальцах то вот так:
1)
5-5,3=[0,3]
2-5,3=[3,3]
4-5,3=[1,3]
7-5,3=[1,7]
6-5,3=[0,7]
8-5,3=[2,7]

2)
(0,3²+3,3²+1,3²+1,7²+0,7²+2,7²)/6= 23,34

А теперь уже вычисляем СКО/СКП, которое равно корню из дисперсии, т.е.
СКО=√23,34=4,83

Если всё верно, то у меня вопрос: «Зачем такие сложности и как с этим работать?»
Ведь если разбираться по-существу то максимальное удаление от истины это 2,7, что такого мне сообщает число 4,83?
Почему во всей практически нормативке используется СКО/СКП притом что никто из прикладников (изыскателей, строителей) не понимает как этим пользоваться? Мне вот за 15 лет работы не попадалось ни одного инженера или маркшейдера который понимал бы как работать с этим термином. По сути все полагаются на точность современных приборов, а допуски определяют «на глазок», самые «продвинутые» используют СКО как абсолютную ошибку, что неверно, судя из расчета.
Нет ли тут боязни покуситься на святое? Когда со времен великого Гаусса эта величина кочует из издания в издание, и каждый новый интерпретатор боится вывести из обихода основу основ?
Что вы об этом думаете? И подскажите, наконец, как работать с СКО/СКП? Вот например на картинке предельная погрешность (которая равна двум СКО О_о…. ) должна быть не больше 50 мм. Т.е. если я делаю контрольное измерение между соседними реперами и оно на 49мм в абсолютном выражении отличается то это правильный анализ или же должен 49 возвести в квадрат, чтобы получить дисперсию а потом из полученного взять корень, получить СКО равное 49 О_о… и затем увеличить его в два раза чтобы получить предельную погрешность ? О_о….. ё…
зачем они это всё?

#5
Форумчанин

Олег Сергеевич!. На ваши вопросы весьма не просто ответить коротко и конкретно(лапидарно, как сейчас любят говорить в СМИ), поскольку они, как-бы, азбучные. Азбуку пояснять трудно — ее надобно знать.

Не могу согласиться с вашей мыслью о сложности, непонятности и архаичности понятия СКП/СКО применительно к геодезии.

СКП, оно же СКО, оно же «стандартное отклонение», оно же «стандарт» весьма важное и пока незаменимое понятие, которое используется для предрасчета точности измерений, для формирования допусков на комбинацию геодезических измерений, для назначения весов измерениям, для апостериорной оценки точности скалярных и векторных величин, а также геодезических параметров и функций измеренных величин.
Не стоит отказываться от этого понятия. Может быть, лучше освежить свои знания по теории обработки геодезических измерений применительно к той области, в которой вы заняты вот уже 15 лет?

#6
Команда форума
Форумчанин

Регистрация:

10 дек 2008

Сообщения:

17.003

Симпатии:

4.779

Именно так и есть. Ваша ошибка в том, что Вы смешали «мух с котлетами»:

Когда используют СКП, никак она не может быть одного порядка с величиной измерений. Та же СКП:

отличается от расстояния между пунктами, как минимум, в тысячи раз.
Попробуйте определить СКП ряда измерений: 100.005, 100.002, 100.004, 100.007, 100.006, 100.008. Не правда ли, совсем иное представление о точности измерений?

#7
Регистрация:

12 дек 2012

Сообщения:

2

Симпатии:

1

Олег Сергеевич, в Ваших расчетах есть ошибка, которая не позволяет «почувствовать» результат. При вычислении дисперсии Вы не поделили на 6 сумму квадратов отклонений, что дало бы в результате значение дисперсии 3.89, а СКО в таком случае составит 1.97, а вовсе не 4.83. Таким образом, все Ваши измерения попадают в интервал от 3.36 до 7.31 с вероятностью 68.2% (плюс минус 1 СКО) и в интервал от 1.39 до 9.28 с вероятностью 95.4% (плюс минус 2 СКО). Придирчивые спецы возразят, что в подобных случаях нужно использовать СТО вместо СКО, оговаривать нормальное распределение вместо Пуассона и т.п., но чтобы не уйти от сути вопроса, остановимся на СКО.

#8

Олег Сергеевич нравится это.
Команда форума
Форумчанин

Регистрация:

10 дек 2008

Сообщения:

17.003

Симпатии:

4.779

И действительно возражаю, что выражение:

не имеет места быть, в принципе. Если мы будем и далее обсуждать статистическую обработку каких-то действий, а не измерений, где, соответственно, нет точности измерений, тогда не стоит, вообще, употреблять термин СКО/СКП в таком контексте.

#9
Форумчанин

Регистрация:

18 июн 2007

Сообщения:

242

Симпатии:

49

Адрес:

Тюмень

Спасибо за указание на ошибку и вообще за доброжелательность!
Однако по прежнему не «чувствую» наглядности СКО. Что такого мне сообщает число 1,97, если разброс значений равен 2,7?
Как это применить на практике, допустим при оценке точности ГРО?
Вот если есть два репера на площадке, при решении обратной задачи я получаю расстояние между ними в 100, 10 м, а при контрольном измерении тахеометром получаю ряд значений, например 100,11; 100,09; 100,12.
Дисперсия в данном случае равна (0,1²+0,1²+0,2²)/3=0,0002
СКО равно √0,02=0,014 м
И что?
Фактическое максимальное отклонение равно 0,02. Среднее отклонение равно 0,013.
Что мне сообщает значение 0,014, или 0,028, если брать двойное СКО?
Стоит ожидать с вероятностью в 95.4% что на самом деле рассматриваемое расстояние может быть не 100,10 а 100,128 или 100,072?

#10

Последнее редактирование: 23 мар 2017
Форумчанин

Дисперсия в данном случае равна (0,01²+0,01²+0,02²)/3=0,0002
СКО = 0,014 м

#11

Последнее редактирование: 23 мар 2017
Форумчанин

Регистрация:

18 июн 2007

Сообщения:

242

Симпатии:

49

Адрес:

Тюмень

[QUOTE=»Yudge, post: 699426,Дисперсия в данном случае равна (0,01²+0,01²+0,02²)/3=0,0002
СКО = 0,014 м[/QUOTE]
Блин… Спасибо… Простите за не внимательность, считал в спешке.
Но по сути вопроса можно ответить?

#12
Форумчанин

Вернее среднее значение измерений не 100,10 а 100,106
Дисперсия равна (0,016²+0,004²+0,014²)/3=0,000156
СКО = 0,012 м. По результатам контрольных измерений расстояние находится в пределах 100,082-100,130 (100,106±2 СКО) с вероятностью 95,4%

#13
Форумчанин

Регистрация:

18 июн 2007

Сообщения:

242

Симпатии:

49

Адрес:

Тюмень

Хм… Ок, вроде понял с вероятностью. Но что с контролем? Насколько плохо либо хорошо значение 100,10, полученное из огз? Если предельная допустимая погрешность равна 0,01, то в допуске ли проверяемое значение? Как определить?

#14
Форумчанин

Для контроля в приведенном примере не хватает точности измерений. Необходимо переделать контрольные измерения (как вариант поменять прибор на более точный, провести больше приемов, использовать на цели не веху, а штатив, чтобы избежать сантиметровых расхождений в длине стометровой линии) и добиться, чтобы полученная двойная СКО укладывалась в допуск (в примере 0,01, а двойная СКО при имеющихся измерениях 0,024). Если после этого значение из ОГЗ совпадет со средним значением из контрольных промеров с точностью до 2 СКО, то оно в допуске.

#15
Форумчанин

Регистрация:

18 июн 2007

Сообщения:

242

Симпатии:

49

Адрес:

Тюмень

Ок. Имеем подрядчика-изыскателя, сдающего нам съёмочное обоснование. Желаем оценить качество этого обоснования. От подрядчика имеем лишь каталог координат. Решаем что будем делать контроль по расстояниям между смежными пунктами. Промеряем расстояние тахеометром десять раз. Получаем:

Исходное расстояние горизонтальное проложение (из ОГЗ по каталогу подрядчика) = 250,123 м
Среднее расстояние горизонтальное проложение по итогам наших 10 контрольных измерений = 250,172 м
СКО наших 10 контрольных измерений = 0,025 м
Допустимая предельная погрешность (двойная СКО) по табл.1 СП 11-104-97=50мм=0,05м

Уложился ли подрядчик в допуск?
Уложился ли контролер в допуск?
Если Вам будет несложно, не могли бы Вы разложить расчет по действиям со значениями из этого примера?

#16
Форумчанин

Вопрос интересный, заставил задуматься и переосмыслить мое утверждениеПочему-то я был свято уверен, что все обстоит именно так. Но ведь если мы провели наблюдения с очень высокой точностью и сходимостью результатов, получили СКО в 1 мм, то согласно моему утверждению при отклонениях контролируемого значения от измеренного нами больше, чем на 2 мм будет уже не в допуске. Но допуск в первом примере составлял 1 см, а не 0,2 см.
Теперь я считаю, что СКО контрольных измерений мы вычисляем, чтобы понять, уложились ли мы сами по точности в требуемый допуск. При положительном результате мы должны просто сравнить среднее значение из наших измерений со значением из каталога, и если величина расхождения не превышает допуска, то качество обоснования следует признать достаточным. В Вашем примере СКО 25 мм, двойная — 50 — все в допуске, правда на пределе. Расхождения контрольных замеров с каталогом тоже на пределе, но в допуске — 49 мм. Соответственно работа выполнена с достаточным качеством.
Правда, теперь я уже не на 100% уверен в своем мнении, если неправ, пусть кто-нибудь поправит.

#17
Форумчанин

Регистрация:

18 июн 2007

Сообщения:

242

Симпатии:

49

Адрес:

Тюмень
вот мы и подошли к корню проблемы. Ведь в нормативке нет такого термина как «расхождение контрольных и контролируемых замеров», а есть лишь СКО, СКП и т.д. см. скриншот вдогонку ранее приведенному мнойпо-сути сейчас мы использовали СКО, как абсолютную ошибку. Но ведь понятно, что здесь что-то неверно. Либо СНИП, либо методика контроля…
Вложения:
#18
Форумчанин

Регистрация:

15 июл 2015

Сообщения:

60

Симпатии:

2

Здравствуйте Уважаемые Форумчатсы!
Вопрос такого характера.
При проведение наблюдений по зданиям и сооружениям (разрядное нивелирование) расчетное СКО на станции превышает допустимого значения (для первого разряда 0.08мм, для второго 0.13мм). В приборе были установлены настройки что ошибка на станции между двумя измерениями не более 0.08 мм, количество штативов между узлами не превышает 14 шт. Уравнивание проводилось через Кредо Нивелир. В чем может быть ошибка? И Почему? Невязки в полигонах получились хорошие, примерно в три раза меньше допустимых. Прямо и обратно вышло в допуске (самая большая невязка между прямо и обратно 0.35 мм, при 8 штативах).

Заранее спасибо.

#19
Форумчанин

Регистрация:

10 окт 2014

Сообщения:

1.275

Симпатии:

1.731

Дрончик1987, выложи сюда весь файл. Может кто и разберётся, где косяк.
Обратись к ЮС, он спец по Кредо.

#20

В.Шуфотинский нравится это.

Страница 1 из 2

Поделиться этой страницей

Источник

17 авг. 2022 г.
читать 2 мин

Модели регрессии используются для количественной оценки взаимосвязи между одной или несколькими переменными-предикторами и переменной отклика .

Всякий раз, когда мы подбираем регрессионную модель, мы хотим понять, насколько хорошо модель может использовать значения переменных-предикторов для прогнозирования значения переменной отклика.

Две метрики, которые мы часто используем для количественной оценки того, насколько хорошо модель соответствует набору данных, — это среднеквадратическая ошибка (MSE) и среднеквадратическая ошибка (RMSE), которые рассчитываются следующим образом:

MSE : метрика, которая сообщает нам среднеквадратичную разницу между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже MSE, тем лучше модель соответствует набору данных.

СКО = Σ(ŷ i – y i ) 2 / n

куда:

Σ — это символ, который означает «сумма»
ŷ i — прогнозируемое значение для i -го наблюдения
y i — наблюдаемое значение для i -го наблюдения
n — размер выборки

RMSE : метрика, которая сообщает нам квадратный корень из средней квадратичной разницы между прогнозируемыми значениями и фактическими значениями в наборе данных. Чем ниже RMSE, тем лучше модель соответствует набору данных.

Он рассчитывается как:

СКО = √ Σ(ŷ i – y i ) 2 / n

куда:

Σ — это символ, который означает «сумма»
ŷ i — прогнозируемое значение для i -го наблюдения
y i — наблюдаемое значение для i -го наблюдения
n — размер выборки

Обратите внимание, что формулы почти идентичны. На самом деле среднеквадратическая ошибка — это просто квадратный корень из среднеквадратичной ошибки.

RMSE против MSE: какую метрику следует использовать?

При оценке того, насколько хорошо модель соответствует набору данных, мы чаще используем RMSE , потому что он измеряется в тех же единицах, что и переменная ответа.

И наоборот, MSE измеряется в квадратах переменной отклика.

Чтобы проиллюстрировать это, предположим, что мы используем регрессионную модель для прогнозирования количества очков, которые 10 игроков наберут в баскетбольном матче.

В следующей таблице показаны прогнозируемые очки по модели и фактические очки, набранные игроками:

Мы бы рассчитали среднеквадратичную ошибку (MSE) как:

СКО = Σ(ŷ i – y i ) 2 / n
MSE = ((14-12) 2 +(15-15) 2 +(18-20) 2 +(19-16) 2 +(25-20) 2 +(18-19) 2 +(12-16) 2 +(12-20) 2 +(15-16) 2 +(22-16) 2 ) / 10
СКО = 16

Среднеквадратическая ошибка равна 16. Это говорит нам о том, что среднеквадратическая разница между предсказанными значениями, сделанными моделью, и фактическими значениями составляет 16.

Среднеквадратическая ошибка (RMSE) будет просто квадратным корнем MSE:

СКО = √ СКО
СКО = √ 16
СКО = 4

Среднеквадратическая ошибка равна 4. Это говорит нам о том, что среднее отклонение между прогнозируемыми набранными баллами и фактическими набранными баллами равно 4.

Обратите внимание, что интерпретация среднеквадратичной ошибки намного проще, чем среднеквадратическая ошибка, потому что мы говорим о «набранных очках», а не о «набранных квадратичных очках».

Как использовать RMSE на практике

На практике мы обычно подгоняем несколько моделей регрессии к набору данных и вычисляем среднеквадратичную ошибку (RMSE) каждой модели.

Затем мы выбираем модель с самым низким значением RMSE в качестве «лучшей» модели, потому что именно она делает прогнозы, наиболее близкие к фактическим значениям из набора данных.

Обратите внимание, что мы также можем сравнивать значения MSE каждой модели, но RMSE проще интерпретировать, поэтому он используется чаще.

Дополнительные ресурсы

Введение в множественную линейную регрессию
RMSE против R-Squared: какую метрику следует использовать?
Калькулятор среднеквадратичной ошибки

Источник

Definition and basic properties[edit]

Predictor[edit]

Estimator[edit]

Proof of variance and bias relationship[edit]

In regression[edit]

Examples[edit]

Mean[edit]

Variance[edit]

Gaussian distribution[edit]

Interpretation[edit]

Applications[edit]

Loss function[edit]

Criticism[edit]

See also[edit]

Notes[edit]

References[edit]

MSE и Scikit-learn

Средняя квадратичная ошибка.

Учет систематических ошибок.

Погрешности косвенных измерений

Добро пожаловать!

Вложения:

Форумчанин

Форумчанин

Форумчанин

Форумчанин

Форумчанин

Команда форума Форумчанин

Команда форума Форумчанин

Форумчанин

Форумчанин

Форумчанин

Форумчанин

Форумчанин

Форумчанин

Форумчанин

Форумчанин

Вложения:

Форумчанин

Форумчанин

Поделиться этой страницей

RMSE против MSE: какую метрику следует использовать?

Как использовать RMSE на практике

Дополнительные ресурсы

Команда форума
Форумчанин

Команда форума
Форумчанин