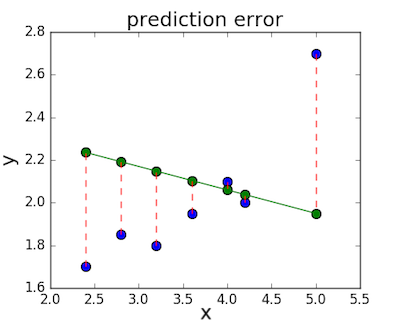
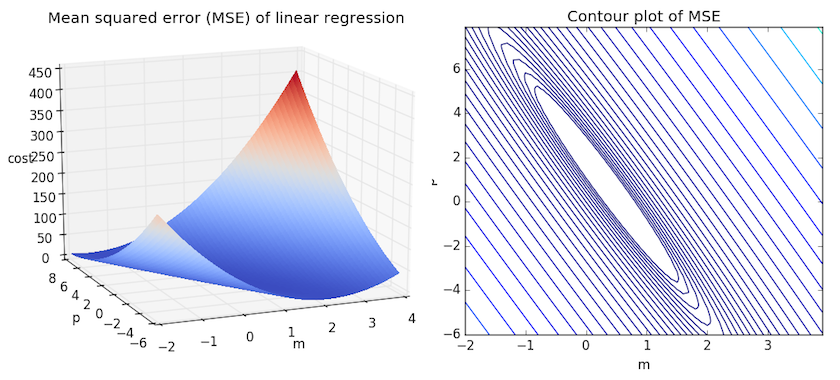
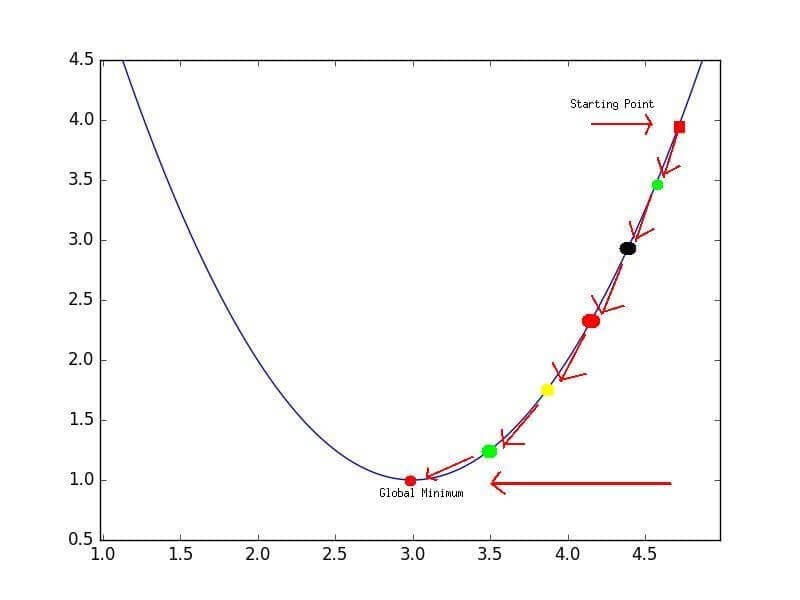
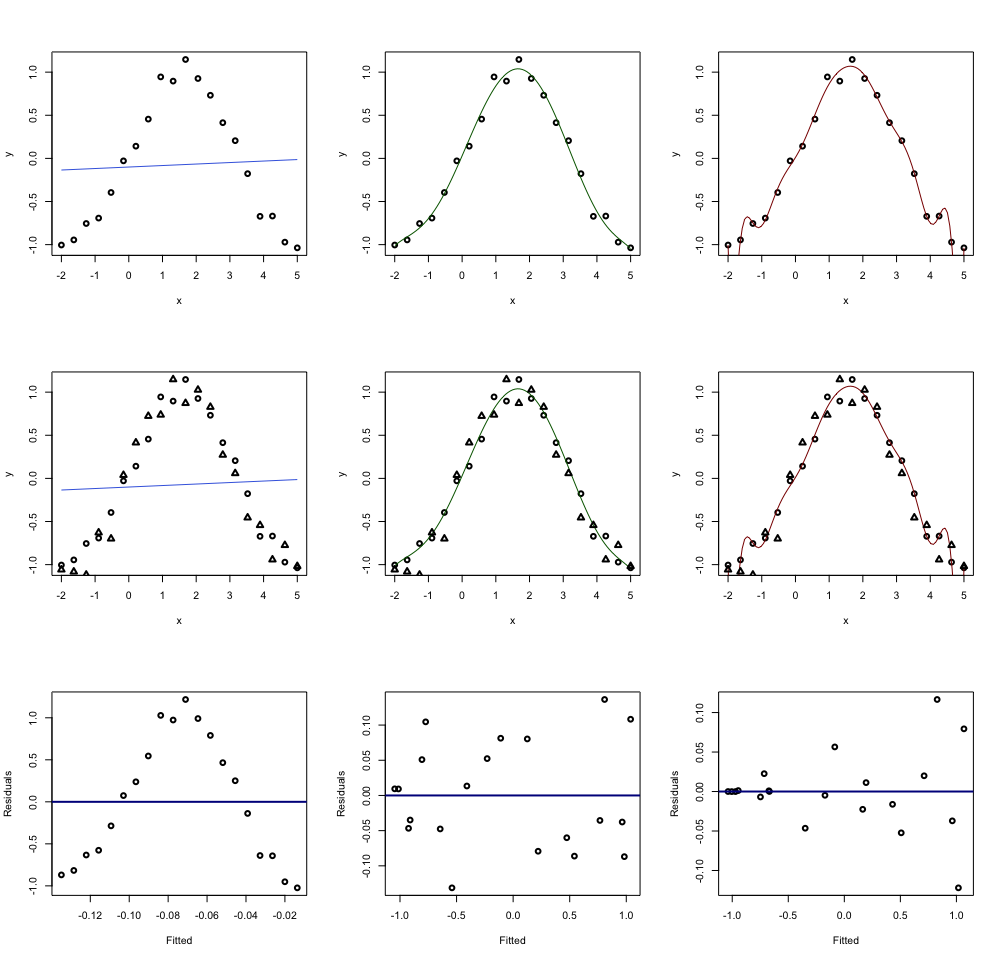
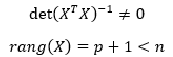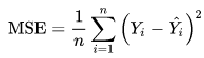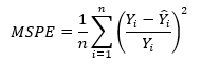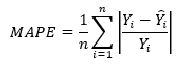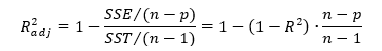Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
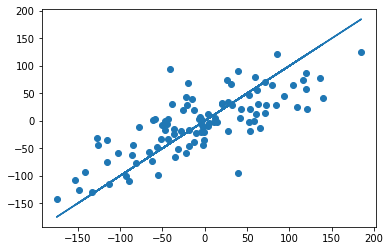
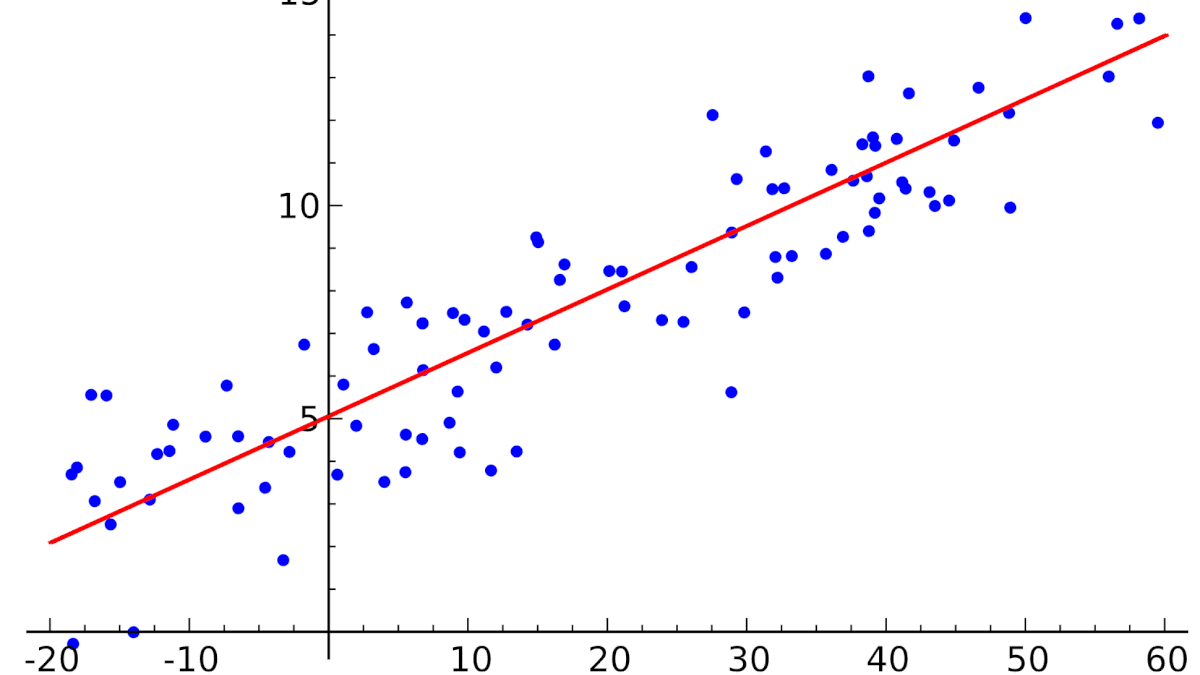
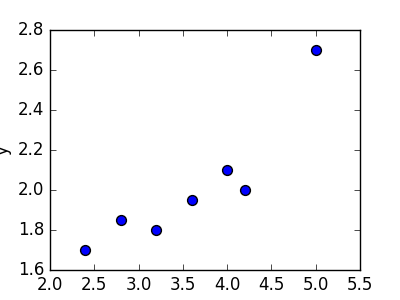
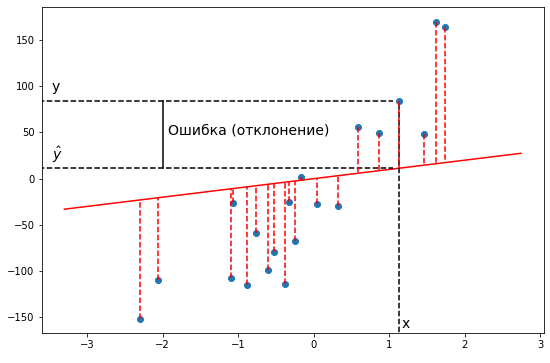
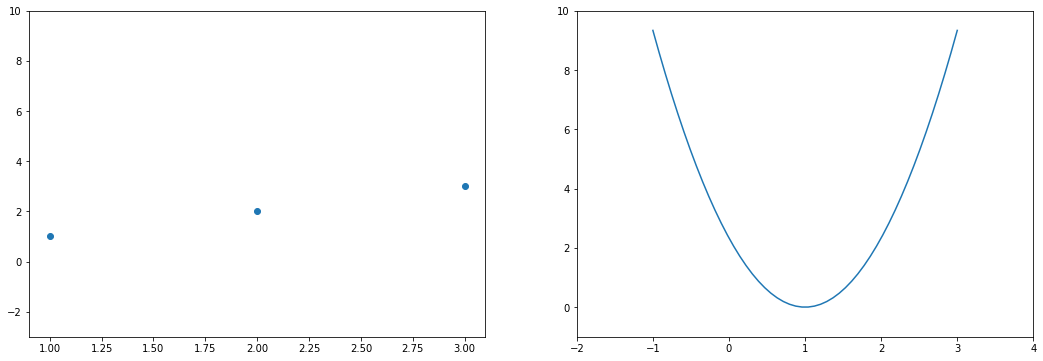
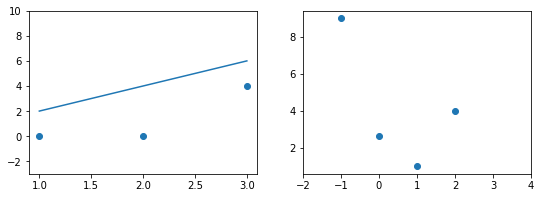
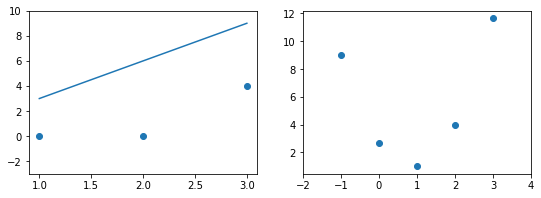
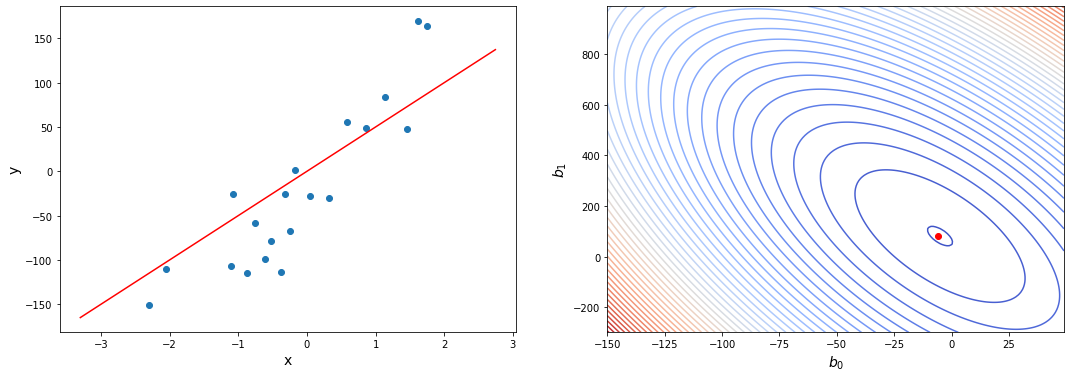
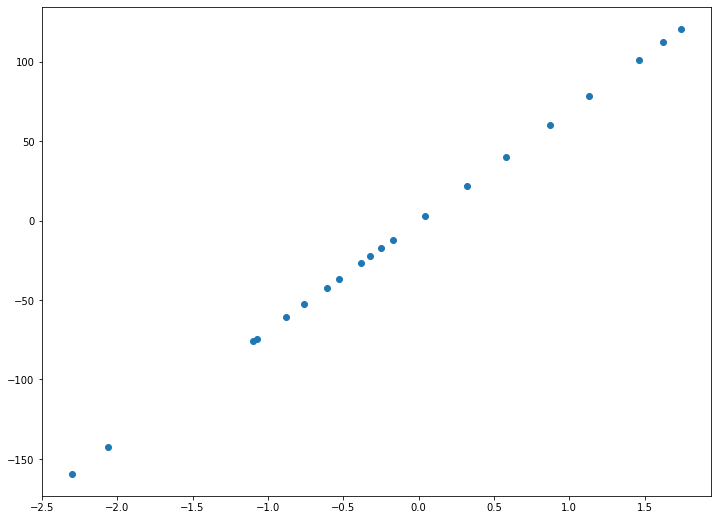
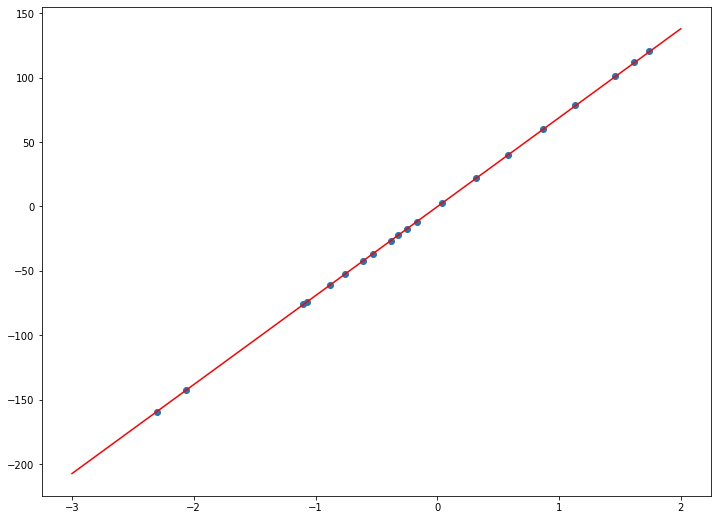
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
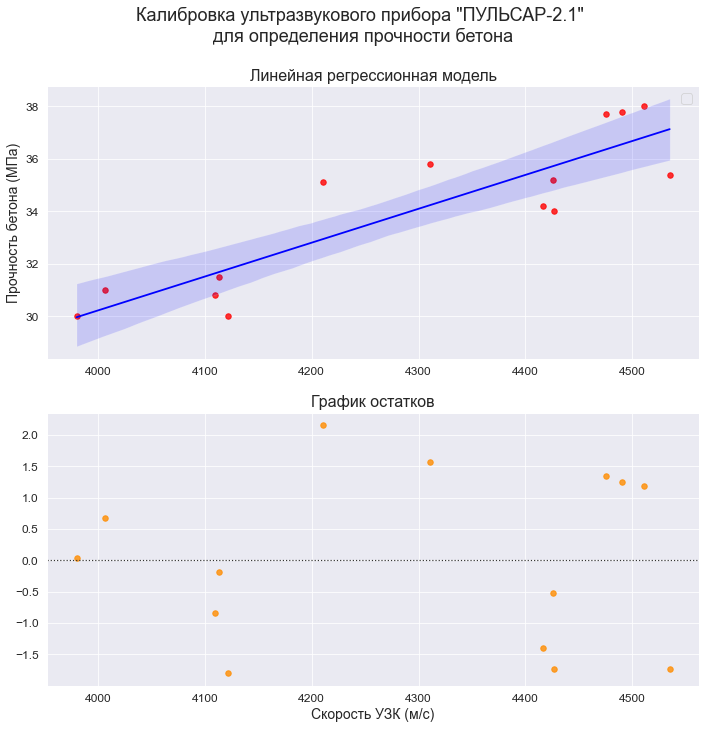
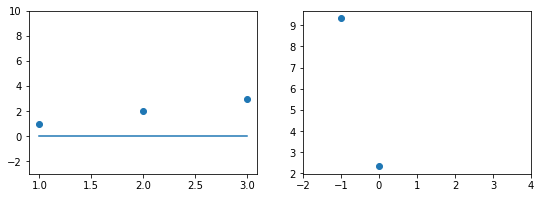
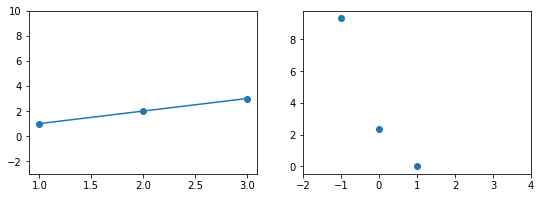
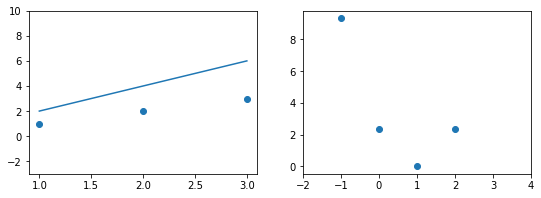
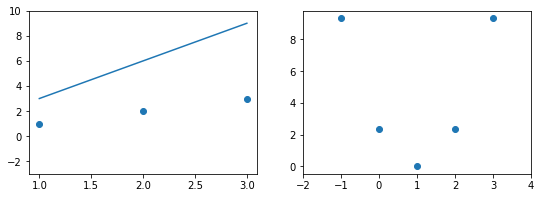
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
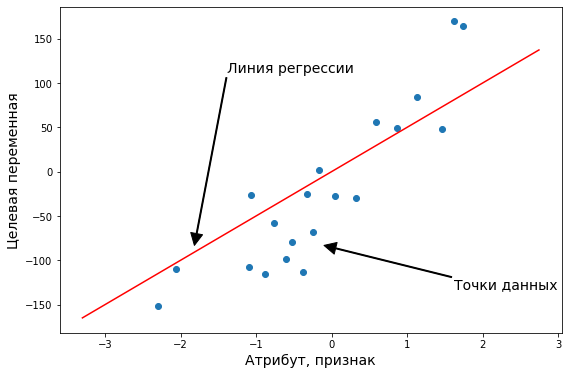
Рисунок 1. Линейная регрессия
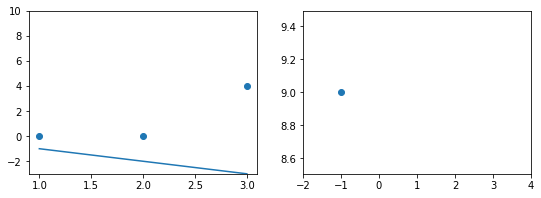
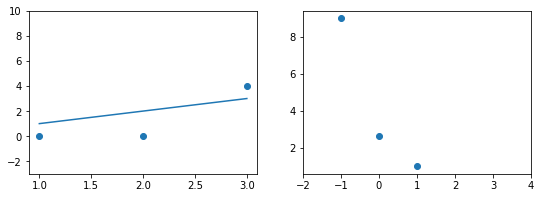
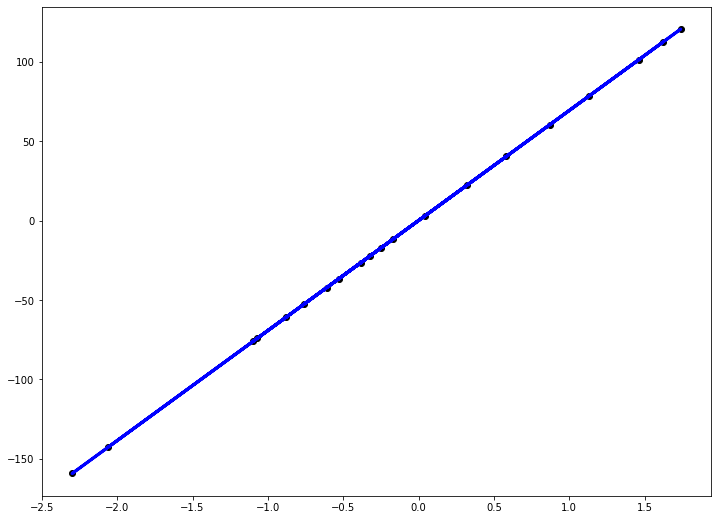
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
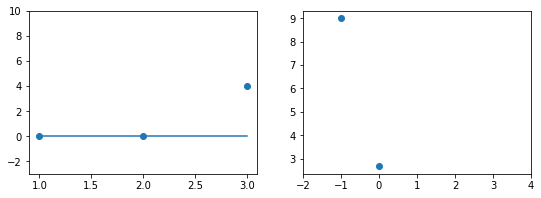
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(y_{i}-widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
frac{partial RMSE}{partial widehat{y}_{i}}=frac{1}{2sqrt{MSE}}frac{partial MSE}{partial widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=frac{100}{n}sumlimits_{i=1}^{n}left ( frac{y_{i}-widehat{y}_{i}}{y_{i}} right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=frac{1}{n}sumlimits_{i=1}^{n}left | y_{i}-widehat{y}_{i} right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{left | y_{i} right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=frac{100}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y_{i}} right |}{(left | y_{i} right |+left | widehat{y}_{i} right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=frac{1}{n}sumlimits_{i=1}^{n}frac{left | y_{i}-widehat{y}_{i}right |}{left | y_{i} right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=sqrt{frac{1}{n}sumlimits_{i=1}^{n}(log(widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-frac{sumlimits_{i=1}^{n}(widehat{y}_{i}-y_{i})^{2}/(n-k)}{sumlimits_{i=1}^{n}({overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных. [1]
Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?
Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию — статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X. В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х1, Х2, …, Xk). [2]
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Виды регрессионных моделей
В заметке Представление числовых данных в виде таблиц и диаграмм для иллюстрации зависимости между переменными X и Y использовалась диаграмма разброса. На ней значения переменной X откладывались по горизонтальной оси, а значения переменной Y — по вертикальной. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рис. 1.
Рис. 1. Положительная линейная зависимость
Простая линейная регрессия:
(1) Yi = β0 + β1Xi + εi
где β0 — сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y), β1 — наклон прямой Y, εi— случайная ошибка переменной Y в i-м наблюдении.
В этой модели наклон β1 представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной Y (положительного или отрицательного) на заданном отрезке оси X. Сдвиг β0 представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели εi является случайной ошибкой переменной Y в i-м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рис. 2.
Рис. 2. Диаграммы разброса, иллюстрирующие разные виды зависимостей
На панели А значения переменной Y почти линейно возрастают с увеличением переменной X. Этот рисунок аналогичен рис. 1, иллюстрирующему положительную зависимость между размером магазина (в квадратных футах) и годовым объемом продаж. Панель Б является примером отрицательной линейной зависимости. Если переменная X возрастает, переменная Y в целом убывает. Примером этой зависимости является связь между стоимостью конкретного товара и объемом продаж. На панели В показан набор данных, в котором переменные X и Y практически не зависят друг от друга. Каждому значению переменной X соответствуют как большие, так и малые значения переменной Y. Данные, приведенные на панели Г, демонстрируют криволинейную зависимость между переменными X и Y. Значения переменной Y возрастают при увеличении переменной X, однако скорость роста после определенных значений переменной X падает. Примером положительной криволинейной зависимости является связь между возрастом и стоимостью обслуживания автомобилей. По мере старения машины стоимость ее обслуживания сначала резко возрастает, однако после определенного уровня стабилизируется. Панель Д демонстрирует параболическую U-образную форму зависимости между переменными X и Y. По мере увеличения значений переменной X значения переменной Y сначала убывают, а затем возрастают. Примером такой зависимости является связь между количеством ошибок, совершенных за час работы, и количеством отработанных часов. Сначала работник осваивается и делает много ошибок, потом привыкает, и количество ошибок уменьшается, однако после определенного момента он начинает чувствовать усталость, и число ошибок увеличивается. На панели Е показана экспоненциальная зависимость между переменными X и Y. В этом случае переменная Y сначала очень быстро убывает при возрастании переменной X, однако скорость этого убывания постепенно падает. Например, стоимость автомобиля при перепродаже экспоненциально зависит от его возраста. Если перепродавать автомобиль в течение первого года, его цена резко падает, однако впоследствии ее падение постепенно замедляется.
Мы кратко рассмотрели основные модели, которые позволяют формализовать зависимости между двумя переменными. Несмотря на то что диаграмма разброса чрезвычайно полезна при выборе математической модели зависимости, существуют более сложные и точные статистические процедуры, позволяющие описать отношения между переменными. В дальнейшем мы будем рассматривать лишь линейную зависимость.
Вывод уравнения простой линейной регрессии
Вернемся к сценарию, изложенному в начале главы. Наша цель — предсказать объем годовых продаж для всех новых магазинов, зная их размеры. Для оценки зависимости между размером магазина (в квадратных футах) и объемом его годовых продаж создадим выборки из 14 магазинов (рис. 3).
Рис. 3. Площади и годовые объемы продаж 14 магазинов сети Sunflowers: (а) исходные данные; (б) диаграмма разброса
Анализ рис. 3 показывает, что между площадью магазина X и годовым объемом продаж Y существует положительная зависимость. Если площадь магазина увеличивается, объем продаж возрастает почти линейно. Таким образом, наиболее подходящей для исследования является линейная модель. Остается лишь определить, какая из линейных моделей точнее остальных описывает зависимость между анализируемыми переменными.
Метод наименьших квадратов
Данные, представленные на рис. 1а, получены для случайной выборки магазинов. Если верны некоторые предположения (об этом чуть позже), в качестве оценки параметров генеральной совокупности (β0 и β1) можно использовать сдвиг b0 и наклон b1 прямой Y. Таким образом, уравнение простой линейной регрессии принимает следующий вид:
где — предсказанное значение переменной Y для i-гo наблюдения, Xi — значение переменной X в i-м наблюдении.
Для того чтобы предсказать значение переменной Y, в уравнении (2) необходимо определить два коэффициента регрессии — сдвиг b0 и наклон b1 прямой Y. Вычислив эти параметры, проведем прямую на диаграмме разброса. Затем исследователь может визуально оценить, насколько близка регрессионная прямая к точкам наблюдения. Простая линейная регрессия позволяет найти прямую линию, максимально приближенную к точкам наблюдения. Критерии соответствия можно задать разными способами. Возможно, проще всего минимизировать разности между фактическими значениями Yi, и предсказанными значениями . Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов.
Поскольку = b0 + b1Xi, сумма квадратов принимает следующий вид:
Параметры b0 и b1 неизвестны. Таким образом, сумма квадратов разностей является функцией, зависящей от сдвига b0 и наклона b1 выборки Y. Для того чтобы найти значения параметров b0 и b1, минимизирующих сумму квадратов разностей, применяется метод наименьших квадратов. При любых других значениях сдвига b0 и наклона b1 сумма квадратов разностей между фактическими значениями переменной Y и ее наблюдаемыми значениями лишь увеличится.
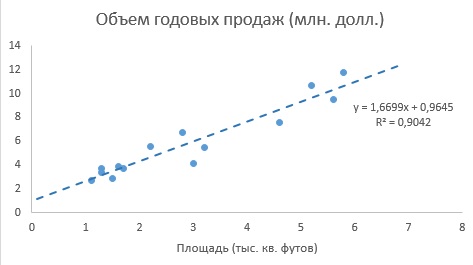
До того, как Excel взял на себя всю рутинную работу, вычисления по методу наименьших квадратов были очень трудоемкими. Excel позволяет решать подобные задачи двумя способами. Во-первых, можно воспользоваться Пакетом анализа (строка Регрессия). Результаты представлены на рис. 4. Во-вторых, можно, выделив точки на графике (как на рис. 3б), кликнуть правой кнопкой мыши и выбрать Добавить линию тренда. Далее можно выбрать вид линии тренда (в нашем случае – Линейная), отформатировать линию, показать на графике уравнение и величину достоверности аппроксимации (R2) (рис. 5).
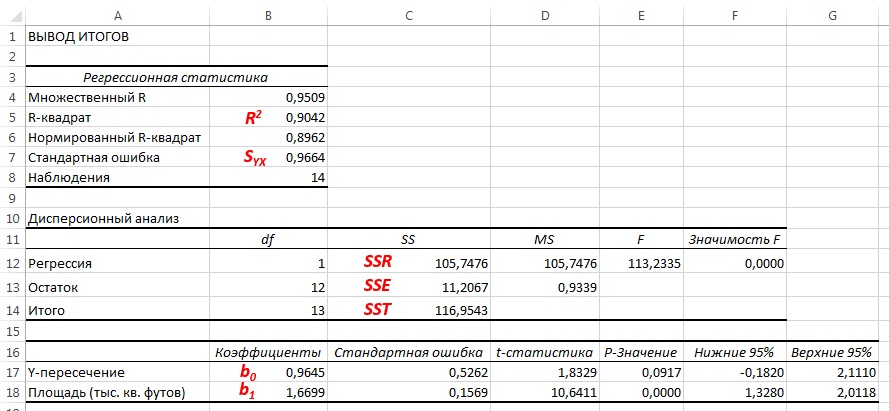
Рис. 4. Результаты решения задачи о зависимости между площадями и годовыми объемами продаж в магазинах сети Sunflower (получены с помощью Пакета анализа Excel)
Рис. 5. Диаграмма разброса и линия регрессии (тренда) в задаче о выборе магазина
Как следует из рис. 4 и 5, b0 = 0,9645, а b1 = 1,6699. Таким образом, уравнение линейной регрессии для этих данных имеет следующий вид: = 0,9645 + 1,6699Xi. Вычисленный наклон b1 = +1,6699. Это означает, что при возрастании переменной X на единицу среднее значение переменной Y возрастает на 1,6699 единиц. Иначе говоря, увеличение площади магазина на один квадратный фут приводит к увеличению годового объема продаж на 1,67 тыс. долл. Таким образом, наклон представляет собой долю годового объема продаж, зависящую от размера магазина. Вычисленный сдвиг b0 = +0,9645 (млн. долл.). Эта величина представляет собой среднее значение переменной Y при X = 0. Поскольку площадь магазина не может равняться нулю, сдвиг можно считать долей годового дохода, зависящей от других факторов. Следует отметить, однако, что сдвиг переменной Y выходит за пределы диапазона переменной X. Следовательно, к интерпретации параметра b0 необходимо относиться внимательно.
Пример 1. Один экономист решил предсказать изменение индекса 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемого агентством Standard and Poor, на основе показателей экономики США за 50 лет. В результате он получил следующее уравнение линейной регрессии: Ŷi = –5,0 + 7Хi. Какой смысл имеют параметры сдвига b0 и наклона b1.
Решение. Сдвиг регрессии b0 равен –5,0. Это значит, что если рост экономики США равен нулю, индекс акций за год снизится на 5%. Наклон b1 равен 7. Следовательно, при увеличении темпов роста экономики на 1% индекс акций возрастает на 7%.
Пример 2. Вернемся к сценарию, изложенному в начале заметки. Применим модель линейной регрессии для прогноза объема годовых продаж во всех новых магазинах в зависимости от их размеров. Предположим, что площадь магазина равна 4000 квадратных футов. Какой среднегодовой объем продаж можно прогнозировать?
Решение. Подставим значение X = 4 (тыс. кв. футов) в уравнение линейной регрессии: = 0,9645 + 1,6699Xi = 0,9645 + 1,6699*4 = 7,644 млн. долл. Итак, прогнозируемый среднегодовой объем продаж в магазине, площадь которого равна 4000 кв. футов, составляет 7 644 000 долл.
Прогнозирование в регрессионном анализе: интерполяция и экстраполяция
Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения независимой переменной. В этот диапазон входят все значения переменной X, начиная с минимальной и заканчивая максимальной. Таким образом, предсказывая значение переменной Y при конкретном значении переменной X, исследователь выполняет интерполяцию между значениями переменной X в диапазоне возможных значений. Однако экстраполяция значений за пределы этого интервала не всегда релевантна. Например, пытаясь предсказать среднегодовой объем продаж в магазине, зная его площадь (рис. 3а), мы можем вычислять значение переменной Y лишь для значений X от 1,1 до 5,8 тыс. кв. футов. Следовательно, прогнозировать среднегодовой объем продаж можно лишь для магазинов, площадь которых не выходит за пределы указанного диапазона. Любая попытка экстраполяции означает, что мы предполагаем, будто линейная регрессия сохраняет свой характер за пределами допустимого диапазона.
Оценки изменчивости
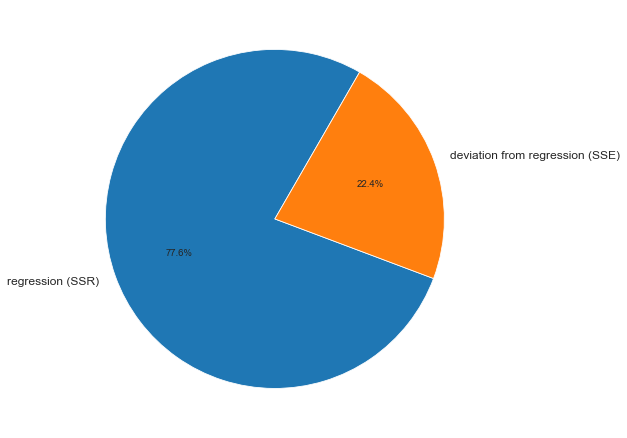
Вычисление сумм квадратов. Для того чтобы предсказать значение зависимой переменной по значениям независимой переменной в рамках избранной статистической модели, необходимо оценить изменчивость. Существует несколько способов оценки изменчивости. Первый способ использует общую сумму квадратов (total sum of squares — SST), позволяющую оценить колебания значений Yi вокруг среднего значения . В регрессионном анализе полная вариация, представляющая собой полную сумму квадратов, разделяется на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares — SSR), и необъяснимую вариацию, или сумму квадратов ошибок (error sum of squares — SSE). Объяснимая вариация характеризует взаимосвязь между переменными X и Y, а необъяснимая зависит от других факторов (рис. 6).
Рис. 6. Оценки изменчивости в модели регрессии
Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Ŷi (предсказанным значением переменной Y) и (средним значением переменной Y). Сумма квадратов ошибок (SSE) является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.
Полная сумма квадратов (SST) равна сумме квадратов регрессии плюс сумма квадратов ошибок:
(3) SST = SSR + SSE
Полная сумма квадратов (SST) равна сумме квадратов разностей между наблюдаемыми значениями переменной Y и ее средним значением:
Сумма квадратов регрессии (SSR) равна сумме квадратов разностей между предсказанными значениями переменной Y и ее средним значением:
Сумма квадратов ошибок (SSE) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями переменной Y:
Суммы квадратов, вычисленные с помощью программы Пакета анализа Excel при решении задачи о сети магазинов Sunflowers, представлены на рис. 4.
Полная сумма квадратов разностей равна SST = 116,9543. Эта величина состоит из суммы квадратов регрессии (SSR) равной 105,7476, и суммы квадратов ошибок (SSE), равной 11,2067.
Коэффициент смешанной корреляции. Величины SSR, SSE и SST не имеют очевидной интерпретации. Однако отношение суммы квадратов регрессии (SSR) к полной сумме квадратов (SST) представляет собой оценку полезности регрессионного уравнения. Это отношение называется коэффициентом смешанной корреляции r2:
Коэффициент смешанной корреляции оценивает долю вариации переменной Y, которая объясняется независимой переменной X в регрессионной модели. В задаче о сети магазинов Sunflowers SSR = 105,7476 и SST = 116,9543. Следовательно, r2 = 105,7476 / 116,9543 = 0,904. Таким образом, 90,4% вариации годового объема продаж объясняется изменчивостью площади магазинов, измеренной в квадратных футах. Данная величина r2 свидетельствует о сильной положительной линейной взаимосвязи между двумя переменными, поскольку применение регрессионной модели снижает изменчивость прогнозируемых годовых объемов продаж на 90,4%. Только 9,6% изменчивости годовых объемов продаж в выборке магазинов объясняются другими факторами, не учтенными в регрессионной модели.
Коэффициент смешанной корреляции в задаче о сети магазинов Sunflowers представлен в таблице Регрессионная статистика на рис. 4.
Среднеквадратичная ошибка оценки. Хотя метод наименьших квадратов позволяет вычислить линию, минимизирующую отклонение от наблюдаемых значений, наличие суммы квадратов ошибок (SSE) свидетельствует о том, что линейная регрессия не дает абсолютной точности прогноза, если, конечно, точки наблюдения не лежат на регрессионной прямой. Однако ожидать этого так же неестественно, как предполагать, что все выборочные значения точно равны их среднему арифметическому. Следовательно, необходима статистика, которая позволила бы оценить отклонение предсказанных значений переменной Y от ее реальных значений, аналогично тому, как стандартное отклонение, введенное ранее, позволяет оценить колебание данных вокруг их средней величины. Стандартное отклонение наблюдаемых значений переменной Y от ее регрессионной прямой называется среднеквадратичной ошибкой оценки. Отклонение реальных данных от регрессионной прямой в задаче о сети магазинов Sunflowers показано на рис. 5.
Среднеквадратичная ошибка оценки
где Yi — фактическое значение переменной Y при заданном значении Xi, Ŷi — предсказанное значение переменной Y при заданном значении Xi, SSE — сумма квадратов ошибок.
Поскольку SSE = 11,2067, по формуле (8) получаем:
Таким образом, среднеквадратичная ошибка оценки равна 0,9664 млн. долл. (т.е. 966 400 долл.). Этот параметр также рассчитывается Пакетом анализа (см. рис. 4). Среднеквадратичная ошибка оценки характеризует отклонение реальных данных от линии регрессии. Она измеряется в тех же единицах, что и переменная Y. По смыслу среднеквадратичная ошибка очень похожа на стандартное отклонение. В то время как стандартное отклонение характеризует разброс данных вокруг их среднего значения, среднеквадратичная ошибка позволяет оценить колебание точек наблюдения вокруг регрессионной прямой. Cреднеквадратичная ошибка оценки позволяет обнаружить статистически значимую зависимость, существующую между двумя переменными, и предсказать значения переменной Y.
Предположения
Обсуждая методы проверки гипотез и дисперсионного анализа, мы не раз подчеркивали важность условий, которые должны обеспечивать корректность сделанных выводов. Поскольку и регрессионный, и дисперсионный анализ используют линейную модель, условия их применения приблизительно одинаковы:
- Ошибка должна иметь нормальное распределение.
- Вариация данных вокруг линии регрессии должна быть постоянной.
- Ошибки должны быть независимыми.
Первое предположение, о нормальном распределении ошибок, требует, чтобы при каждом значении переменной X ошибки линейной регрессии имели нормальное распределение (рис. 7). Как и t— и F-критерий дисперсионного анализа, регрессионный анализ довольно устойчив к нарушениям этого условия. Если распределение ошибок относительно линии регрессии при каждом значении X не слишком сильно отличается от нормального, выводы относительно линии регрессии и коэффициентов регрессии изменяются незначительно.
Рис. 7. Предположение о нормальном распределении ошибок
Второе условие заключается в том, что вариация данных вокруг линии регрессии должна быть постоянной при любом значении переменной X. Это означает, что величина ошибки как при малых, так и при больших значениях переменной X должна изменяться в одном и том же интервале (см. рис. 7). Это свойство очень важно для метода наименьших квадратов, с помощью которого определяются коэффициенты регрессии. Если это условие нарушается, следует применять либо преобразование данных, либо метод наименьших квадратов с весами.
Третье предположение, о независимости ошибок, заключается в том, что ошибки регрессии не должны зависеть от значения переменной X. Это условие особенно важно, если данные собираются на протяжении определенного отрезка времени. В этих ситуациях ошибки, присущие конкретному отрезку времени, часто коррелируют с ошибками, характерными для предыдущего периода.
Анализ остатков
Чуть выше при решении задачи о сети магазинов Sunflowers мы использовали модель линейной регрессии. Рассмотрим теперь анализ ошибок — графический метод, позволяющий оценить точность регрессионной модели. Кроме того, с его помощью можно обнаружить потенциальные нарушения условий применения регрессионного анализа.
Оценка пригодности эмпирической модели. Остаток, или оценка ошибки еi, представляет собой разность между наблюдаемым (Yi) и предсказанным (Ŷi) значениями зависимой переменной при заданном значении Xi.
(9) ei = Yi – Ŷi
Для оценки пригодности эмпирической модели регрессии остатки откладываются по вертикальной оси, а значения Xi — по горизонтальной. Если эмпирическая модель пригодна, график не должен иметь ярко выраженной закономерности. Если же модель регрессии не пригодна, на рисунке проявится зависимость между значениями Xi и остатками еi.
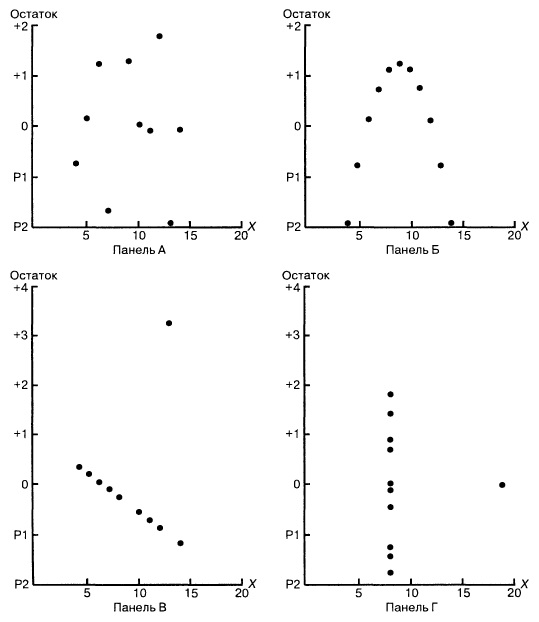
Рассмотрим примеры (рис. 8). Панель А иллюстрирует возрастание переменной Y при увеличении переменной X. Однако зависимость между этими переменными носит нелинейный характер, поскольку скорость возрастания переменной Y падает при увеличении переменной X. Таким образом, для аппроксимации зависимости между этими переменными лучше подойдет квадратичная модель. Особенно ярко квадратичная зависимость между величинами Xi и ei проявляется на панели Б. Графическое изображение остатков позволяет отфильтровать или удалить линейную зависимость между переменными X и Y и выявить недостаточную точность модели простой линейной регрессии. Таким образом, в данной ситуации вместо простой линейной модели должна применяться квадратичная модель, обладающая более высокой точностью.
Рис. 8. Исследование эмпирической модели простой линейной регрессии
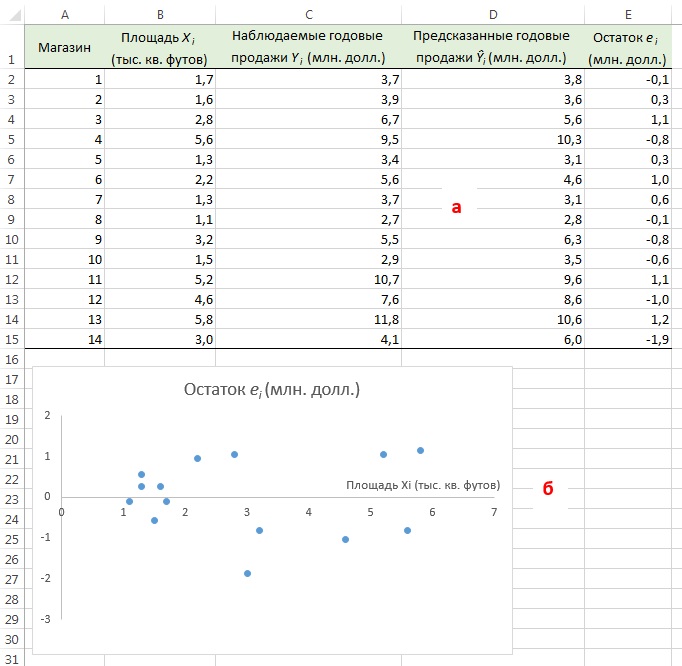
Вернемся к задаче о сети магазинов Sunflowers и посмотрим, хорошо ли подходит простая линейная регрессия для ее решения. Соответствующие данные и расчеты приведены на рис. 9а (формулы можно посмотреть в Excel-файле). Построим диаграмму разброса, откладывая по вертикальной оси остатки ei, а по горизонтальной — независимую переменную Xi (рис. 9б). Несмотря на большой разброс остатков, между ei и Хi нет ярко выраженной зависимости. Остатки одинаково часто принимают как положительные, так и отрицательные значения. Это позволяет сделать вывод, что модель линейной регрессии пригодна для решения задачи о сети магазинов Sunflowers.
Рис. 9. Остатки ei, вычисленные при решении задачи о сети магазинов Sunflowers
Значения остатков (таблица на рис. 9а) и график остатков (аналог рис. 9б) можно получить непосредственно в процедуре Регрессия Пакета анализа. Просто поставьте соответствующие галки (рис. 10).
Рис. 10. Остатки ei и график остатков полученные с помощью Пакета анализа
Проверка условий. График остатков позволяет оценить вариации ошибок. На рис. 10 нет особых различий между ошибками, соответствующими разным значениям Xi. Следовательно, вариации ошибок при разных значениях Хi приблизительно одинаковы. Рассмотрим гипотетическую ситуацию, в которой это условие не выполняется (рис. 11). На этом рисунке изображен эффект веера: при возрастании значений Хi ошибки увеличиваются. Таким образом, изменчивость значений Yi при разных значениях Хi является непостоянной.
Рис. 11. Пример нарушения условия независимости вариаций ошибок от Xi
Нормальность. Чтобы проверить предположение о нормальном распределении ошибок, построим график нормального распределения на основе точечного графика, на вертикальной оси которого отложены значения остатков, а на горизонтальной оси — соответствующие квантили стандартизованного нормального распределения (подробнее см. Проверка гипотезы о нормальном распределении). Для построения такого графика значения остатков должны быть упорядочены по возрастанию (рис. 12). График нормального распределения может быть построен одним кликом с помощью Пакета анализа Excel – просто поставьте соответствующую галочку в окне Регрессия (см. рис. 10, самый низ окна Регрессия – опция График нормальной вероятности).
Рис. 12. График нормального распределения для остатков
Без визуализации данных (с помощью гистограммы, диаграммы «ствол и листья», блочной диаграммы или графика как на рис. 12) проверить предположение о нормальном распределении ошибок очень трудно. Данные, изображенные на рис. 12, не слишком сильно отличаются от нормального распределения. Устойчивость регрессионного анализа и небольшой объем выборки позволяют утверждать, что условие о нормальном распределении ошибок нарушается незначительно.
Независимость. Предположение о независимости ошибок также проверяется с помощью графика остатков. Данные, собранные на протяжении некоторого периода времени, иногда демонстрируют эффект автокорреляции между последовательными наблюдениями. В таких ситуациях остатки зависят от значений предыдущих остатков. Подобная связь между остатками нарушает предположение о независимости ошибок. Эффект автокорреляции хорошо выявляется на графике. Кроме того, его можно измерить с помощью процедуры Дурбина-Уотсона (см. ниже). Если данные о размерах магазинов и объемах продаж собирались в течение одного и того же периода времени, гипотезу об их независимости проверять не имеет смысла.
Измерение автокорреляции: статистика Дурбина–Уотсона
Одним из основных предположений о регрессионной модели является гипотеза о независимости ее ошибок. Если данные собираются в течение определенного отрезка времени, это условие часто нарушается, поскольку остаток в определенный момент времени может оказаться приблизительно равным предыдущим остаткам. Такое поведение остатков называется автокорреляцией. Если набор данных обладает свойством автокорреляции, корректность регрессионной модели становится весьма сомнительной.
Распознавание автокорреляции с помощью графика остатков. Для выявления автокорреляции необходимо упорядочить остатки по времени и построить их график. Если данные обладают положительной автокорреляцией, на графике возникнут кластеры остатков, имеющие одинаковый знак. В случае отрицательной автокорреляции остатки будут скачкообразно принимать то положительные, то отрицательные значения. Этот вид автокорреляции очень редко встречается в регрессионном анализе, поэтому мы рассмотрим лишь положительную автокорреляцию. Проиллюстрируем ее следующим примером. Предположим, что менеджер магазина, доставляющего товары на дом, пытается предсказать объем продаж по количеству клиентов, совершивших покупки в течение 15 недель (рис. 13).
Рис. 13. Количество клиентов и объемы продаж за 15 недель
Поскольку данные собирались на протяжении 15 последовательных недель в одном и том же магазине, необходимо определить, наблюдается ли эффект автокорреляции. Построим регрессию с использованием Пакета анализа; включим вывод Остатков, но не будем включать График остатков (рис. 14).
Рис. 14. Параметры линейной регрессии, полученные с использованием Пакета анализа
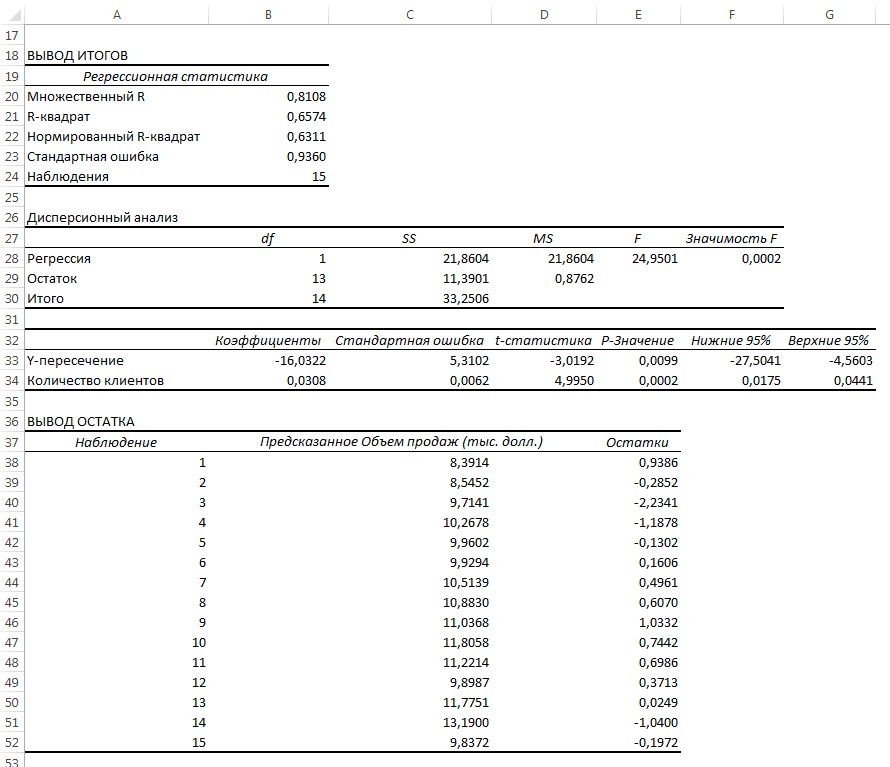
Анализ рис. 14 показывает, что r2 = 0,657. Это значит, что 65,7% вариации объемов продаж объясняется изменчивостью количества клиентов. Кроме того, сдвиг b0 переменной Y равен –16,032, а наклон b1 = 0,0308. Однако, прежде чем применять эту модель, необходимо выполнить анализ остатков. Поскольку данные собирались на протяжении 15 последовательных недель, их следует отобразить на графике в том же порядке (рис. 15).
Рис. 15. Зависимость остатков от времени
Анализ рис. 15 показывает, что остатки циклически колеблются вверх и вниз. Эта цикличность является явным признаком автокорреляции. Следовательно, гипотезу о независимости остатков следует отклонить.
Статистика Дурбина-Уотсона. Автокорреляцию можно выявить и измерить с помощью статистики Дурбина-Уотсона. Эта статистика оценивает корреляцию между соседними остатками:
где еi — остаток, соответствующий i-му периоду времени.
Чтобы лучше понять статистику Дурбина-Уотсона, рассмотрим ее составные части. Числитель представляет собой сумму квадратов разностей между соседними остатками, начиная со второго и заканчивая n-м наблюдением. Знаменатель является суммой квадратов остатков. Вот, что по этому поводу написано в Википедии:
где ρ1 – коэффициент автокорреляции; если ρ1 = 0 (нет автокорреляции), D ≈ 2; если ρ1 ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ1 = -1 (отрицательная автокорреляции), D ≈ 4.
На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями dL и dU для заданного числа наблюдений n, числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D < dL, гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > dU, гипотеза не отвергается (то есть автокорреляция отсутствует); если dL < D < dU, нет достаточных оснований для принятия решения. Когда расчётное значение D превышает 2, то с dL и dU сравнивается не сам коэффициент D, а выражение (4 – D).
Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка. Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).
Рис. 16. Формулы расчета статистики Дурбина-Уотсона
В нашем примере D = 0,883. Основной вопрос заключается в следующем — какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (dL и dU), зависящими от числа наблюдений n и уровня значимости α (рис. 17).
Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)
Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1), 15 наблюдений (n = 15) и уровень значимости α = 0,05. Следовательно, dL= 1,08 и dU = 1,36. Поскольку D = 0,883 < dL= 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.
Проверка гипотез о наклоне и коэффициенте корреляции
Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.
Применение t-критерия для наклона. Проверяя, равен ли наклон генеральной совокупности β1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X и Y. Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: β1 = 0 (нет линейной зависимости), Н1: β1 ≠ 0 (есть линейная зависимость). По определению t-статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:
(11) t = (b1 – β1) / Sb1
где b1 – наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, , а тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t-критерий выводится наряду с другими параметрами при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.
Рис. 18. Результаты применения t-критерия, полученные с помощью Пакета анализа Excel
Поскольку число магазинов n = 14 (см. рис.3), критическое значение t-статистики при уровне значимости α = 0,05 можно найти по формуле: tL =СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n – 2; tU =СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.
Поскольку t-статистика = 10,64 > tU = 2,1788 (рис. 19), нулевая гипотеза Н0 отклоняется. С другой стороны, р-значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н0 снова отклоняется. Тот факт, что р-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.
Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы
Применение F-критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F-критерия. Напомним, что F-критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. Однофакторный дисперсионный анализ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR, деленной на количество независимых переменных k), к дисперсии ошибок (MSE = SYX2).
По определению F-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR/MSE, где MSR = SSR / k, MSE = SSE/(n– k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F-распределение с k и n – k – 1 степенями свободы.
При заданном уровне значимости α решающее правило формулируется так: если F > FU, нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.
Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии
Аналогично t-критерию F-критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F-статистике – на рис. 21.
Рис. 21. Результаты применения F-критерия, полученные с помощью Пакета анализа Excel
F-статистика равна 113,23, а р-значение близко к нулю (ячейка Значимость F). Если уровень значимости α равен 0,05, определить критическое значение F-распределения с одной и 12 степенями свободы можно по формуле FU =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > FU = 4,7472, причем р-значение близко к 0 < 0,05, нулевая гипотеза Н0 отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.
Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы
Доверительный интервал, содержащий наклон β1. Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β1 и убедиться, что гипотетическое значение β1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β1, является выборочный наклон b1, а его границами — величины b1 ± tn–2Sb1
Как показано на рис. 18, b1 = +1,670, n = 14, Sb1 = 0,157. t12 =СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b1 ± tn–2Sb1 = +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.
Использование t-критерия для коэффициента корреляции. Ранее был введен коэффициент корреляции r, представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н0: ρ = 0 (нет корреляции), Н1: ρ ≠ 0 (есть корреляция). Проверка существования корреляции:
где r = +, если b1 > 0, r = –
, если b1 < 0. Тестовая статистика t имеет t-распределение с n – 2 степенями свободы.
В задаче о сети магазинов Sunflowers r2 = 0,904, а b1— +1,670 (см. рис. 4). Поскольку b1 > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t-статистику:
При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.
При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.
Оценка математического ожидания и предсказание индивидуальных значений
В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X.
Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов) регрессионное уравнение позволило предсказать значение переменной Y при заданном значении переменной X. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. Ранее для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X:
где 
= b0 + b1Xi – предсказанное значение переменное Y при X = Xi, SYX – среднеквадратичная ошибка, n – объем выборки, Xi — заданное значение переменной X, µY|X=Xi – математическое ожидание переменной Y при Х = Хi, SSX =
Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений Xi. Если значение переменной Y предсказывается для величин X, близких к среднему значению , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.
Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:
Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.
Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика YX=Xi при конкретном значении переменной Xi определяется по формуле:
Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:
Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.
Подводные камни и этические проблемы, связанные с применением регрессии
Трудности, связанные с регрессионным анализом:
- Игнорирование условий применимости метода наименьших квадратов.
- Ошибочная оценка условий применимости метода наименьших квадратов.
- Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
- Применение регрессионного анализа без глубоких знаний о предмете исследования.
- Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
- Путаница между статистической и причинно-следственной зависимостями.
Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?
Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).
Рис. 23. Четыре набора искусственных данных
Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)
Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.
Рис. 25. Диаграммы разброса для четырех наборов данных
Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х8 = 19, Y8 = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.
Рис. 26. Графики остатков для четырех наборов данных
Как избежать подводных камней при регрессионном анализе:
- Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
- Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
- Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
- Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
- Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
- Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
- Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
- Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.
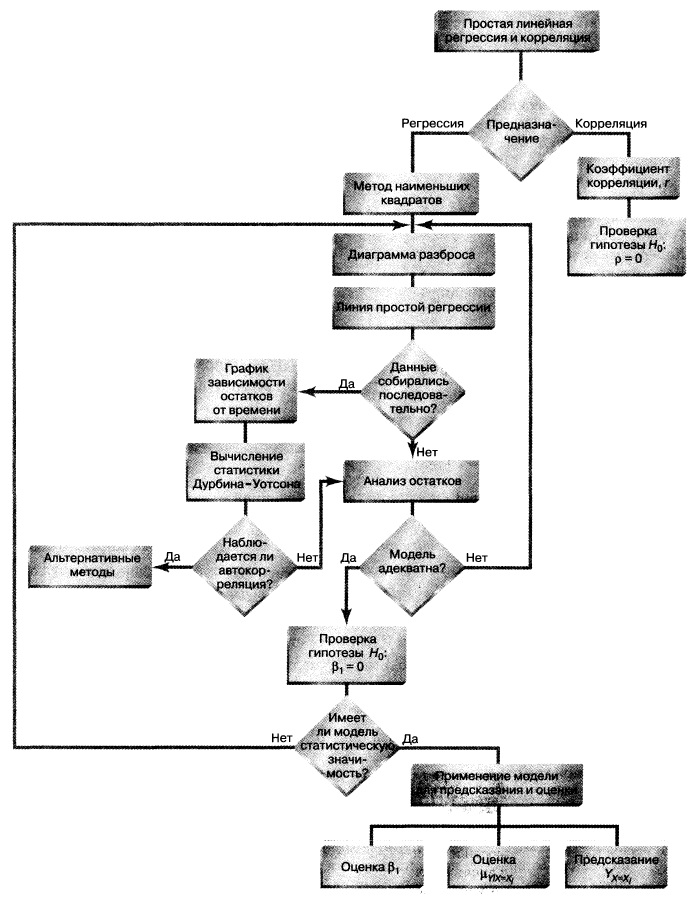
Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.
Рис. 27. Структурная схема заметки
Предыдущая заметка Критерий согласия «хи-квадрат»
Следующая заметка Введение в множественную регрессию
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872
[2] Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.
АКТУАЛЬНОСТЬ ТЕМЫ
Общие положения
Про регрессионный анализ вообще, и его применение в DataScience написано очень много. Есть множество учебников, монографий, справочников и статей по прикладной статистике, огромное количество информации в интернете, примеров расчетов. Можно найти множество кейсов, реализованных с использованием средств Python. Казалось бы — что тут еще можно добавить?
Однако, как всегда, есть нюансы:
1. Регрессионный анализ — это прежде всего процесс, набор действий исследователя по определенному алгоритму: «подготовка исходных данных — построение модели — анализ модели — прогнозирование с помощью модели». Это ключевая особенность. Не представляет особой сложности сформировать DataFrame исходных данных и построить модель, запустить процедуру из библиотеки statsmodels. Однако подготовка исходных данных и последующий анализ модели требуют гораздо больших затрат человеко-часов специалиста и строк программного кода, чем, собственно, построение модели. На этих этапах часто приходится возвращаться назад, корректировать модель или исходные данные. Этому, к сожалению, во многих источниках, не удаляется достойного внимания, а иногда — и совсем не уделяется внимания, что приводит к превратному представлению о регрессионном анализе.
2. Далеко не во всех источниках уделяется должное внимание интерпретации промежуточных и финальных результатов. Специалист должен уметь интерпретировать каждую цифру, полученную в ходе работы над моделью.
3. Далеко не все процедуры на этапах подготовки исходных данных или анализа модели в источниках разобраны подробно. Например, про проверку значимости коэффициента детерминации найти информацию не представляет труда, а вот про проверку адекватности модели, построение доверительных интервалов регрессии или про специфические процедуры (например, тест Уайта на гетероскедастичность) информации гораздо меньше.
4. Своеобразная сложность может возникнуть с проверкой статистических гипотез: для отечественной литературы по прикладной статистике больше характерно проверять гипотезы путем сравнения расчетного значения критерия с табличным, а в иностранных источниках чаще определяется расчетный уровень значимости и сравнивается с заданным (чаще всего 0.05 = 1-0.95). В разных источниках информации реализованы разные подходы. Инструменты python (прежде всего библиотеки scipy и statsmodels) также в основном оперируют с расчетным уровнем значимости.
5. Ну и, наконец, нельзя не отметить, что техническая документация библиотеки statsmodels составлена, на мой взгляд, далеко не идеально: информация излагается путано, изобилует повторами и пропусками, описание классов, функций и свойств выполнено фрагментарно и количество примеров расчетов — явно недостаточно.
Поэтому я решил написать ряд обзоров по регрессионному анализу средствами Python, в которых акцент будет сделан на практических примерах, алгоритме действий исследователя, интерпретации всех полученных результатов, конкретных методических рекомендациях. Буду стараться по возможности избегать теории (хотя совсем без нее получится) — все-таки предполагается, что специалист DataScience должен знать теорию вероятностей и математическую статистику, хотя бы в рамках курса высшей математики для технического или экономического вуза.
В данном статье остановимся на самои простом, классическом, стереотипном случае — простой линейной регрессии (simple linear regression), или как ее еще принято называть — парной линейной регрессионной модели (ПЛРМ) — в ситуации, когда исследователя не подстерегают никакие подводные камни и каверзы — исходные данные подчиняются нормальному закону, в выборке отсутствуют аномальные значения, отсутствует ложная корреляция. Более сложные случаи рассмотрим в дальнейшем.
Для построение регрессионной модели будем пользоваться библиотекой statsmodels.
В данной статье мы рассмотрим по возможности полный набор статистических процедур. Некоторые из них (например, дескриптивная статистика или дисперсионный анализ регрессионной модели) могут показаться избыточными. Все так, но эти процедуры улучшают наше представление о процессе и об исходных данных, поэтому в разбор я их включил, а каждый исследователь сам вправе для себя определить, потребуются ему эти процедуры или нет.
Краткий обзор источников
Источников информации по корреляционному и регрессионному анализу огромное количество, в них можно просто утонуть. Поэтому позволю себе просто порекомендовать ряд источников, на мой взгляд, наиболее полезных:
-
Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.
-
Львовский Е.Н. Статистические методы построения эмпирических формул. — М.: Высшая школа, 1988. — 239 с.
-
Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа / пер с нем. — М.: Финансы и статистика, 1983. — 302 с.
-
Афифи А., Эйзен С. Статистический анализ. Подход с использованием ЭВМ / пер с англ. — М.: Мир, 1982. — 488 с.
-
Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Книга 1 / пер.с англ. — М.: Финансы и статистика, 1986. — 366 с.
-
Айвазян С.А. и др. Прикладная статистика: Исследование зависимостей. — М.: Финансы и статистика, 1985. — 487 с.
-
Прикладная статистика. Основы эконометрики: В 2 т. 2-е изд., испр. — Т.2: Айвазян С.А. Основы эконометрики. — М.: ЮНИТИ-ДАНА, 2001. — 432 с.
-
Магнус Я.Р. и др. Эконометрика. Начальный курс — М.: Дело, 2004. — 576 с.
-
Носко В.П. Эконометрика. Книга 1. — М.: Издательский дом «Дело» РАНХиГС, 2011. — 672 с.
-
Брюс П. Практическая статистика для специалистов Data Science / пер. с англ. — СПб.: БХВ-Петербург, 2018. — 304 с.
-
Уатт Дж. и др. Машинное обучение: основы, алгоритмы и практика применения / пер. с англ. — СПб.: БХВ-Петербург, 2022. — 640 с.
Прежде всего следует упомянуть справочник Кобзаря А.И. [1] — это безусловно выдающийся труд. Ничего подобного даже близко не издавалось. Всем рекомендую иметь под рукой.
Есть очень хорошее практическое пособие [2] — для начинающих и практиков.>
Добротная работа немецких авторов [3]. Все разобрано подробно, обстоятельно, с примерами — очень хорошая книга. Примеры приведены из области экономики.
Еще одна добротная работа — [4], с примерами медико-биологического характера.
Работа [5] считается одним из наиболее полных изложений прикладного регрессионного анализа.
Более сложные работы — [6] (классика жанра), [7], [8], [9] — выдержаны на достаточно высоком математическом уровне, примеры из экономической области.
Свежие работы [10] (с примерами на языке R) и [11] (с примерами на python).
Cтатьи
Статей про регрессионный анализ в DataScience очень много, обращаю внимание на некоторые весьма полезные из них.
Серия статей «Python, корреляция и регрессия», охватывающая весь процесс регрессионного анализа:
-
первичная обработка данных, визуализация и корреляционный анализ;
-
регрессия;
-
теория матриц в регрессионном анализе, проверка адекватности, мультиколлинеарность;
-
прогнозирование с помощью регрессионных моделей.
Очень хороший обзор «Интерпретация summary из statsmodels для линейной регрессии». В этой статье даны очень полезные ссылки:
-
Statistical Models
-
Interpreting Linear Regression Through statsmodels .summary()
Статья «Регрессионные модели в Python».
Основные предпосылки (гипотезы) регрессионного анализа
Очень кратко — об этом написано тысячи страниц в учебниках — но все же вспомним некоторые основы теории.
Проверка исходных предпосылок является очень важным моментом при статистическом анализе регрессионной модели. Если мы рассматриваем классическую линейную регрессионную модель вида:
то основными предпосылками при использовании обычного метода наименьших квадратов (МНК) для оценки ее параметров являются:
-
Среднее значение (математическое ожидание) случайной составляющей равно нулю:
-
Дисперсия случайной составляющей является постоянной:
В случае нарушения данного условия мы сталкиваемся с явлением гетероскедастичности.
-
Значения случайной составляющей статистически независимы (некоррелированы) между собой:
В случае нарушения данного условия мы сталкиваемся с явлением автокорреляции.
-
Условие существования обратной матрицы
что эквивалентно одному из двух следующих условий:
то есть число наблюдений должно превышать число параметров.
-
Значения случайной составляющей некоррелированы со значениями независимых переменных:
-
Случайная составляющая имеет нормальный закон распределения (с математическим ожиданием равным нулю — следует из условия 1):
Более подробно — см.: [3, с.90], [4, с.147], [5, с.122], [6, с.208], [7, с.49], [8, с.68], [9, с.88].
Кроме гетероскедастичности и автокорреляции возможно возникновение и других статистических аномалий — мультиколлинеарности, ложной корреляции и т.д.
Доказано, что оценки параметров, полученные с помощью МНК, обладают наилучшими свойствами (несмещенность, состоятельность, эффективность) при соблюдении ряда условий:
-
выполнение приведенных выше исходных предпосылок регрессионного анализа;
-
число наблюдений на одну независимую переменную должно быть не менее 5-6;
-
должны отсутствовать аномальные значения (выбросы).
Кроме обычного МНК существуют и другие его разновидности (взвешенный МНК, обобщенный МНК), которые применяются при наличии статистических аномалий. Кроме МНК применяются и другие методы оценки параметров моделей. В этом обзоре мы эти вопросы рассматривать не будем.
Алгоритм проведения регрессионного анализа
Алгоритм действий исследователя при построении регрессионной модели (полевые работы мы, по понятным причинам, не рассматриваем — считаем, что исходные данные уже получены):
-
Подготовительный этап — постановка целей и задач исследования.
-
Первичная обработка исходных данных — об этом много написано в учебниках и пособиях по DataScience, сюда могут относится:
-
выявление нерелевантных признаков (признаков, которые не несут полезной информации), нетипичных данных (выбросов), неинформативных признаков (имеющих большое количество одинаковых значений) и работа с ними (удаление/преобразование);
-
выделение категориальных признаков;
-
работа с пропущенными значениями;
-
преобразование признаков-дат в формат datetime и т.д.
-
Визуализация исходных данных — предварительный графический анализ.
-
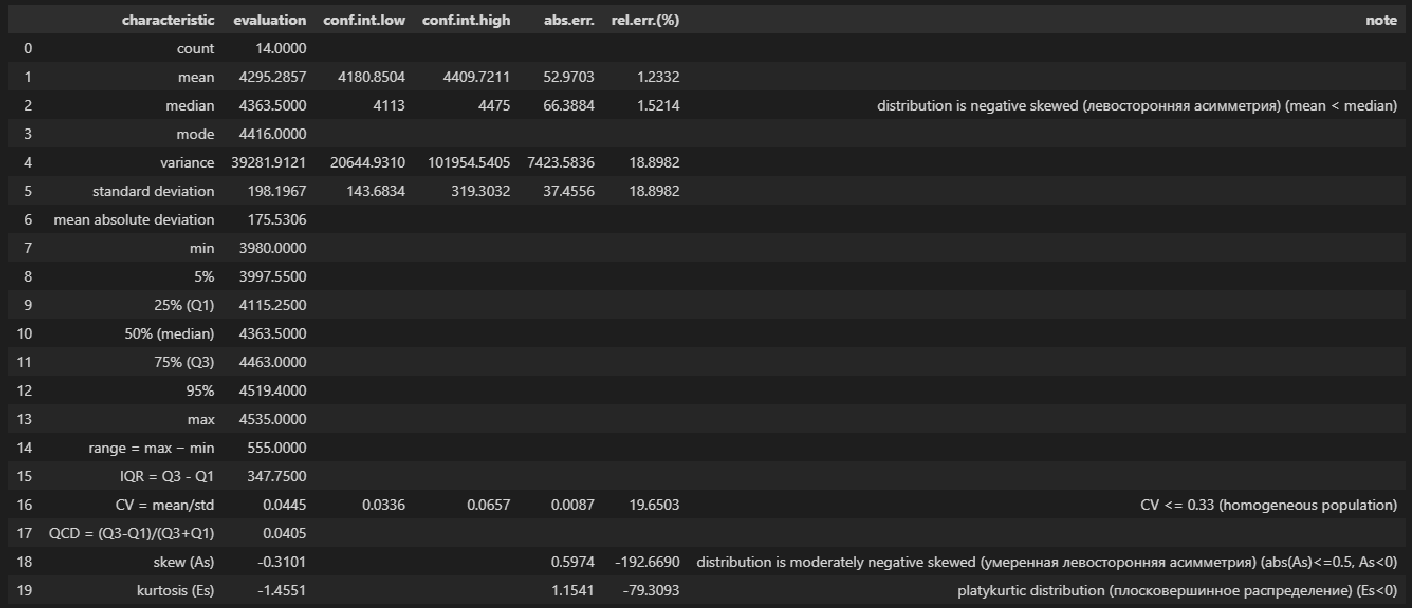
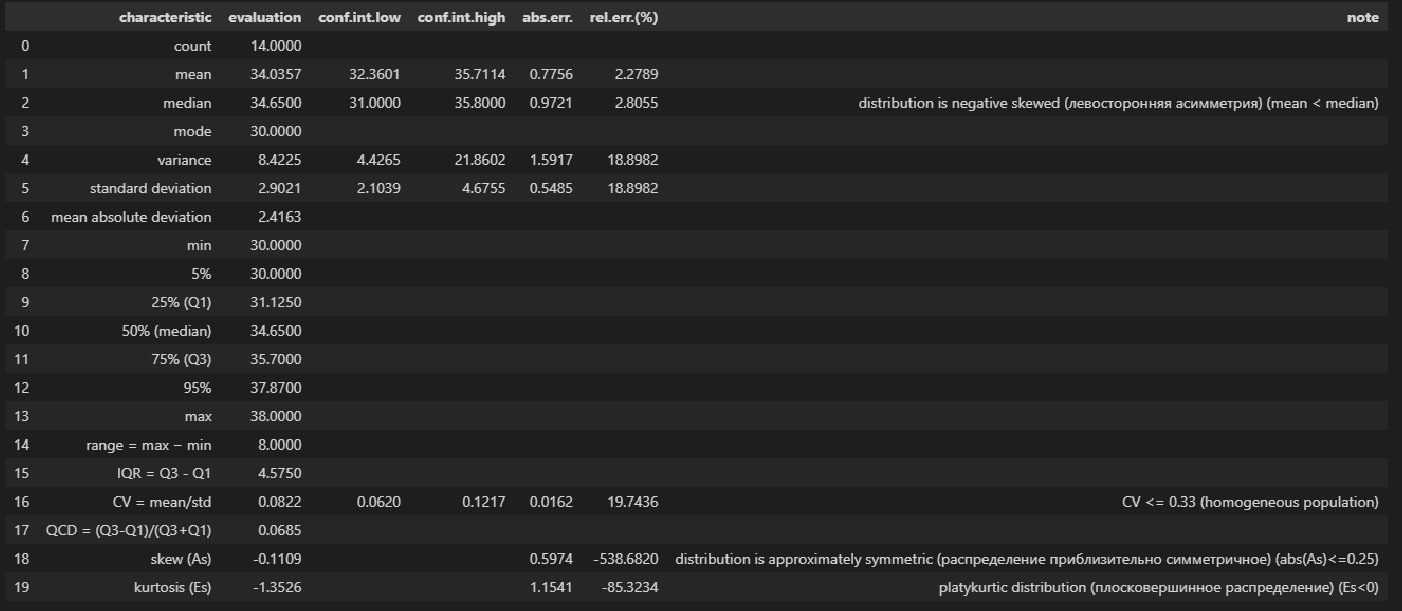
Дескриптивная (описательная) статистика — расчет выборочных характеристик и предварительные выводы о свойствах исходных данных.
-
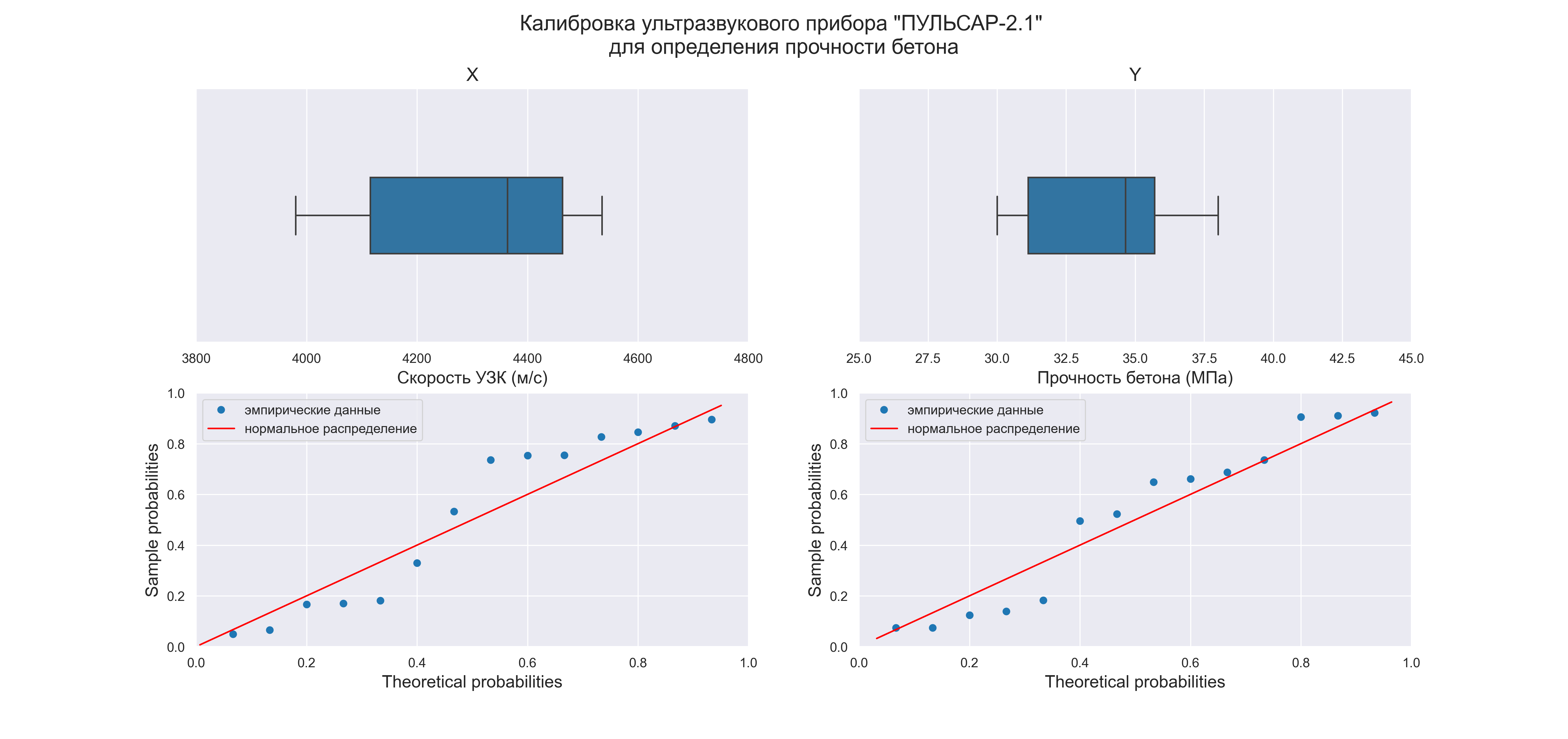
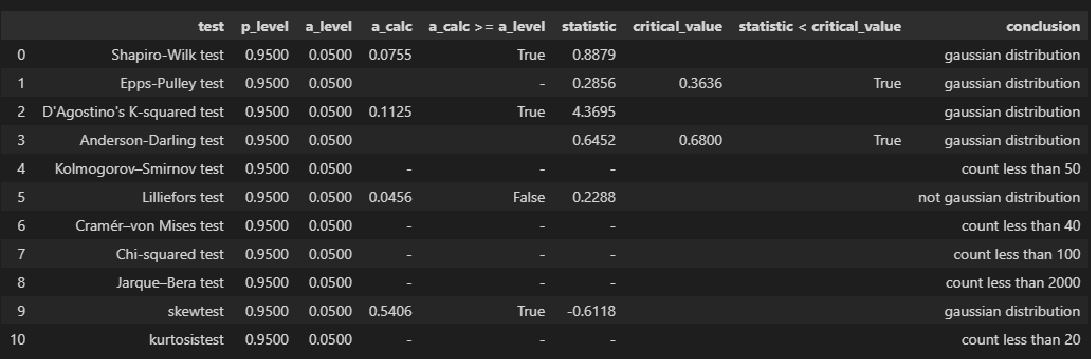
Исследование закона распределения исходных данных и, при необходимости, преобразование исходных данных к нормальному закону распределения.
-
Выявление статистически аномальных значений (выбросов), принятие решения об их исключении.
Этапы 4, 5 и 6 могут быть при необходимости объединены.
-
Корреляционный анализ — исследование корреляционных связей между исходными данными; это разведка перед проведением регрессионного анализа.
-
Построение регрессионной модели:
-
выбор моделей;
-
выбор методов;
-
оценка параметров модели.
-
Статистический анализ регрессионной модели:
-
оценка ошибок аппроксимации (error metrics);
-
анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков);
-
проверка адекватности модели;
-
проверка значимости коэффициента детерминации;
-
проверка значимости коэффициентов регрессии;
-
проверка мультиколлинеарности (для множественных регрессионных моделей; вообще мультиколлинеарные переменные выявляются еще на стадии корреляционного анализа);
-
проверка автокорреляции;
-
проверка гетероскедастичности.
Этапы 8 и 9 могут быть при необходимости повторяться несколько раз.
-
Сравнительный анализ нескольких регрессионных моделей, выбор наилучшей (при необходимости).
-
Прогнозирование с помощью регрессионной модели и оценка качества прогноза.
-
Выводы и рекомендации.
Само собой, этот алгоритм не есть истина в последней инстанции — в зависимости от особенностей исходных данных и вида модели могут возникать дополнительные задачи.
Применение пользовательских функций
Далее в обзоре мной будут использованы несколько пользовательских функций для решения разнообразных задач. Все эти функции созданы для облегчения работы и уменьшения размера программного кода. Данные функции загружается из пользовательского модуля my_module__stat.py, который доступен в моем репозитории на GitHub. Лично мне так удобнее работать, хотя каждый исследователь сам формирует себе инструменты по душе — особенно в части визуализации. Желающие могут пользоваться этими функциями, либо создать свои.
Итак, вот перечень данных функций:
-
graph_scatterplot_sns — функция позволяет построить точечную диаграмму средствами seaborn и сохранить график в виде png-файла;
-
graph_hist_boxplot_probplot_XY_sns — функция позволяет визуализировать исходные данные для простой линейной регрессии путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика (для переменных X и Y) средствами seaborn и сохранить график в виде png-файла; имеется возможность выбирать, какие графики строить (h — hist, b — boxplot, p — probplot);
-
descriptive_characteristics — функция возвращает в виде DataFrame набор статистических характеристики выборки, их ошибок и доверительных интервалов;
-
detecting_outliers_mad_test — функция выполняет проверку наличия аномальных значений (выбросов) по критерию наибольшего абсолютного отклонения (более подробно — см.[1, с.547]);
-
norm_distr_check — проверка нормальности распределения исходных данных с использованием набора из нескольких статистических тестов;
-
corr_coef_check — функция выполняет расчет коэффициента линейной корреляции Пирсона, проверку его значимости и расчет доверительных интервалов; об этой функции я писал в своей статье.
-
graph_regression_plot_sns — — функция позволяет построить график регрессионной модели.
Ряд пользовательских функций мы создаем в процессе данного обзора (они тоже включены в пользовательский модуль my_module__stat.py):
-
regression_error_metrics — расчет ошибок аппроксимации регрессионной модели;
-
ANOVA_table_regression_model — вывод таблицы дисперсионного анализа регрессионной модели;
-
regression_model_adequacy_check — проверка адекватности регрессионной модели по критерию Фишера;
-
determination_coef_check — проверка значимости коэффициента детерминации по критерию Фишера;
-
regression_coef_check — проверка значимости коэффициентов регрессии по критеирю Стьюдента;
-
Goldfeld_Quandt_test, Breush_Pagan_test, White_test — проверка гетероскедастичности с использование тестов Голдфелда-Квандта, Бриша-Пэгана и Уайта соответственно;
-
regression_pair_predict — функция для прогнозирования с помощью парной регрессионной модели: рассчитывает прогнозируемое значение переменной Y по заданной модели, а также доверительные интервалы среднего и индивидуального значения для полученного прогнозируемого значения Y;
-
graph_regression_pair_predict_plot_sns — прогнозирование: построение графика регрессионной модели (с доверительными интервалами) и вывод расчетной таблицы с данными для заданной области значений X.
ПОСТАНОВКА ЗАДАЧИ
В качестве примера рассмотрим практическую задачу из области экспертизы промышленной безопасности — калибровку ультразвукового прибора для определения прочности бетона.
Итак, суть задачи: при обследовании несущих конструкций зданий и сооружений эксперт определяет прочность бетона с использованием ультразвукового прибора «ПУЛЬСАР-2.1», для которого необходимо предварительно построить градуировочную зависимость. Заключается это в следующем — производятся замеры с фиксацией следующих показателей:
-
X — показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с)
-
Y — результаты замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03.
Предполагается, что между показателями X и Y имеется линейная регрессионная зависимость, которая позволит прогнозировать прочность бетона на основании измерений, проведенных прибором «ПУЛЬСАР-2.1».
Были выполнены замеры фактической прочности бетона конструкций для бетонов одного вида с одним типом крупного заполнителя, с единой технологией производства. Для построения были выбраны 14 участков (не менее 12), включая участки, в которых значение косвенного показателя максимальное, минимальное и имеет промежуточные значения.
Настройка заголовков отчета:
# Общий заголовок проекта
Task_Project = 'Калибровка ультразвукового прибора "ПУЛЬСАР-2.1" nдля определения прочности бетона'
# Заголовок, фиксирующий момент времени
AsOfTheDate = ""
# Заголовок раздела проекта
Task_Theme = ""
# Общий заголовок проекта для графиков
Title_String = f"{Task_Project}n{AsOfTheDate}"
# Наименования переменных
Variable_Name_X = "Скорость УЗК (м/с)"
Variable_Name_Y = "Прочность бетона (МПа)"
# Константы
INCH = 25.4 # мм/дюйм
DecPlace = 5 # number of decimal places - число знаков после запятой
# Доверительная вероятность и уровень значимости:
p_level = 0.95
a_level = 1 - p_level Подключение модулей и библиотек:
# Стандартные модули и библиотеки
import os # загрузка модуля для работы с операционной системой
import sys
import platform
print('{:<35}{:^0}'.format("Текущая версия Python: ", platform.python_version()), 'n')
import math
from math import * # подключаем все содержимое модуля math, используем без псевдонимов
import numpy as np
#print ("Текущая версия модуля numpy: ", np.__version__)
print('{:<35}{:^0}'.format("Текущая версия модуля numpy: ", np.__version__))
from numpy import nan
import scipy as sci
print('{:<35}{:^0}'.format("Текущая версия модуля scipy: ", sci.__version__))
import scipy.stats as sps
import pandas as pd
print('{:<35}{:^0}'.format("Текущая версия модуля pandas: ", pd.__version__))
import matplotlib as mpl
print('{:<35}{:^0}'.format("Текущая версия модуля matplotlib: ", mpl.__version__))
import matplotlib.pyplot as plt
import seaborn as sns
print('{:<35}{:^0}'.format("Текущая версия модуля seaborn: ", sns.__version__))
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.graphics.api as smg
import statsmodels.stats.api as sms
from statsmodels.compat import lzip
print('{:<35}{:^0}'.format("Текущая версия модуля statsmodels: ", sm.__version__))
import statistics as stat # module 'statistics' has no attribute '__version__'
import sympy as sym
print('{:<35}{:^0}'.format("Текущая версия модуля sympy: ", sym.__version__))
# Настройки numpy
np.set_printoptions(precision = 4, floatmode='fixed')
# Настройки Pandas
pd.set_option('display.max_colwidth', None) # текст в ячейке отражался полностью вне зависимости от длины
pd.set_option('display.float_format', lambda x: '%.4f' % x)
# Настройки seaborn
sns.set_style("darkgrid")
sns.set_context(context='paper', font_scale=1, rc=None) # 'paper', 'notebook', 'talk', 'poster', None
# Настройки Mathplotlib
f_size = 8 # пользовательская переменная для задания базового размера шрифта
plt.rcParams['figure.titlesize'] = f_size + 12 # шрифт заголовка
plt.rcParams['axes.titlesize'] = f_size + 10 # шрифт заголовка
plt.rcParams['axes.labelsize'] = f_size + 6 # шрифт подписей осей
plt.rcParams['xtick.labelsize'] = f_size + 4 # шрифт подписей меток
plt.rcParams['ytick.labelsize'] = f_size + 4
plt.rcParams['legend.fontsize'] = f_size + 6 # шрифт легенды
# Пользовательские модули и библиотеки
Text1 = os.getcwd() # вывод пути к текущему каталогу
#print(f"Текущий каталог: {Text1}")
sys.path.insert(1, "D:REPOSITORYMyModulePython")
from my_module__stat import *ФОРМИРОВАНИЕ ИСХОДНЫХ ДАННЫХ
Показания ультразвукового прибора «ПУЛЬСАР-2.1» (м/с):
X = np.array([
4416, 4211, 4113, 4110, 4122,
4427, 4535, 4311, 4511, 4475,
3980, 4490, 4007, 4426
])Результаты замера прочности бетона (методом отрыва со скалыванием) прибором ИПС-МГ4.03:
Y = np.array([
34.2, 35.1, 31.5, 30.8, 30.0,
34.0, 35.4, 35.8, 38.0, 37.7,
30.0, 37.8, 31.0, 35.2
])Запишем данные в DataFrame:
calibrarion_df = pd.DataFrame({
'X': X,
'Y': Y})
display(calibrarion_df)
calibrarion_df.info()Сохраняем данные в csv-файл:
calibrarion_df.to_csv(
path_or_buf='data/calibrarion_df.csv',
mode='w+',
sep=';')Cоздаем копию исходной таблицы для работы:
dataset_df = calibrarion_df.copy()ВИЗУАЛИЗАЦИЯ ДАННЫХ
Границы значений переменных (при построении графиков):
(Xmin_graph, Xmax_graph) = (3800, 4800)
(Ymin_graph, Ymax_graph) = (25, 45)# Пользовательская функция
graph_scatterplot_sns(
X, Y,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=Ymin_graph, Ymax=Ymax_graph,
color='orange',
title_figure=Task_Project,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
s=100,
file_name='graph/scatterplot_XY_sns.png')Существует универсальный набор графиков — гистограмма, коробчатая диаграмма, вероятностный график — которые позволяют исследователю сделать предварительные выводы о свойствах исходных данных.
Так как объем выборки невелик (n=14), строить гистограммы распределения переменных X и Y не имеет смысла, поэтому ограничимся построением коробчатых диаграмм и вероятностных графиков:
# Пользовательская функция
graph_hist_boxplot_probplot_XY_sns(
data_X=X, data_Y=Y,
data_X_min=Xmin_graph, data_X_max=Xmax_graph,
data_Y_min=Ymin_graph, data_Y_max=Ymax_graph,
graph_inclusion='bp', # выбираем для построения виды графиков: b - boxplot, p - probplot)
data_X_label=Variable_Name_X,
data_Y_label=Variable_Name_Y,
title_figure=Task_Project,
file_name='graph/hist_boxplot_probplot_XY_sns.png') Для сравнения характера распределений переменных X и Y возможно также построить совмещенную коробчатую диаграмму по стандартизованным данным:
# стандартизуем исходные данные
standardize_df = lambda X: ((X - np.mean(X))/np.std(X))
dataset_df_standardize = dataset_df.copy()
dataset_df_standardize = dataset_df_standardize.apply(standardize_df)
display(dataset_df_standardize)
# построим график
fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/2))
axes.set_title("Распределение стандартизованных переменных X и Y", fontsize = 16)
sns.boxplot(
data=dataset_df_standardize,
orient='h',
width=0.5,
ax=axes)
plt.show()Графический анализ позволяет сделать следующие выводы:
-
Отсутствие выбросов на коробчатых диаграммах свидетельствует об однородности распределения переменных.
-
Смещение медианы вправо на коробчатых диаграммах свидетельствует о левосторонней асимметрии распределения.
ДЕСКРИПТИВНАЯ (ОПИСАТЕЛЬНАЯ СТАТИСТИКА)
Собственно говоря, данный этап требуется проводить далеко не всегда, однако с помощью статистических характеристик выборки мы тоже можем сделать полезные выводы.
Описательная статистика исходных данных средствами библиотеки Pandas — самый простой вариант:
dataset_df.describe()Описательная статистика исходных данных средствами библиотеки statsmodels — более развернутый вариант, с большим количеством показателей:
from statsmodels.stats.descriptivestats import Description
result = Description(
dataset_df,
stats=["nobs", "missing", "mean", "std_err", "ci", "ci", "std", "iqr", "mad", "coef_var", "range", "max", "min", "skew", "kurtosis", "mode",
"median", "percentiles", "distinct", "top", "freq"],
alpha=a_level,
use_t=True)
display(result.summary())Описательная статистика исходных данных с помощью пользовательской функции descriptive_characteristics:
# Пользовательская функция
descriptive_characteristics(X)Выводы:
-
Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).
-
Значение коэффициента вариации CV = 0.0445 и доверительный интервал для него 0.0336 ≤ CV ≤ 0.0657 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).
-
Значение показателя асимметрии skew (As) = -0.3101 свидетельствует об умеренной левосторонней асимметрии распределении (т.к. |As| ≤ 0.5, As < 0).
-
Значение показателя эксцесса kurtosis (Es) = -1.4551 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).
# Пользовательская функция
descriptive_characteristics(Y)Выводы:
-
Сравнение показателей среднего арифметического (mean) и медианы (median) свидетельствует о левосторонней асимметрии (т.к.mean < median).
-
Значение коэффициента вариации CV = 0.0822 и доверительный интервал для него 0.06202 ≤ CV ≤ 0.1217 свидетельствует об однородности исходных данных (т.к. CV ≤ 0.33).
-
Значение показателя асимметрии skew (As) = -0.1109 свидетельствует о приблизительно симметричном распределении (т.к. |As| ≤ 0.25).
-
Значение показателя эксцесса kurtosis (Es) = -1.3526 свидетельствует о плосковершинном распределении (platykurtic distribution) (т.к. Es < 0).
ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ
Для проверки нормальности распределения использована пользовательская функция norm_distr_check, которая объединяет в себе набор стандартных статистических тестов проверки нормальности. Все тесты относятся к стандартному инструментарию Pyton (библиотека scipy, модуль stats), за исключением теста Эппса-Палли (Epps-Pulley test); о том, как реализовать этот тест средствами Pyton я писал в своей статье https://habr.com/ru/post/685582/.
Примечание: для использования функции norm_distr_check в каталог с ipynb-файлом необходимо поместить папку table c файлом Tep_table.csv, который содержит табличные значения статистики критерия Эппса-Палли.
# пользовательская функция
norm_distr_check(X)# Пользовательская функция
norm_distr_check (Y)Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения переменных X и Y.
ПРОВЕРКА АНОМАЛЬНЫХ ЗНАЧЕНИЙ (ВЫБРОСОВ)
Статистическую проверку аномальных значений (выбросов) не стоит путать с проверкой выбросов, которая проводится на этапе первичной обработки результатов наблюдений. Последняя проводится с целью отсеять явные ошибочные данные (например, в результате неправильно поставленной запятой величина показателя может увеличиться/уменьшиться на порядок); здесь же мы говорим о статистической проверке данных, которые уже прошли этап первичной обработки.
Имеется довольно много критериев для проверки аномальных значений (подробнее см.[1]); вообще данная процедура довольно неоднозначная:
-
критерии зависят от вида распределения;
-
мало данных о сравнительной мощности этих критериев;
-
даже в случае принятии гипотезы о нормальном распределении в выборке могут быть обнаружены аномальные значения и пр.
Кроме существует дилемма: если какие-то значения в выборке признаны выбросами — стоит или не стоит исследователю исключать их? Ведь каждое значение несет в себе информацию, причем иногда весьма ценную, а сильно отклоняющиеся от основного массива данные (которые не являются выбросами в смысле первичной обработки, но являются статистическим значимыми аномальными значениями) могут кардинально изменить статистический вывод.
В общем, о задаче выявления аномальных значений (выбросов) можно написать отдельно, а пока, в данном разборе, ограничимся проверкой аномальных значений по критерию наибольшего максимального отклонения (см.[1, с.547]) с помощью пользовательской функции detecting_outliers_mad_test. Данные функция возвращает DataFrame, которые включает список аномальных значений со следующими признаками:
-
value — проверяемое значение из выборки;
-
mad_calc и mad_table — расчетное и табличное значение статистики критерия;
-
outlier_conclusion — вывод (выброс или нет).
Обращаю внимание, что критерий наибольшего максимального отклонения можно использовать только для нормально распределенных данных.
# пользовательская функция
print("Проверка наличия выбросов переменной X:n")
result = detecting_outliers_mad_test(X)
mask = (result['outlier_conclusion'] == 'outlier')
display(result[mask])# пользовательская функция
print("Проверка наличия выбросов переменной Y:n")
result = detecting_outliers_mad_test(Y)
mask = (result['outlier_conclusion'] == 'outlier')
display(result[mask])Вывод: в случае обеих переменных X и Y список пуст, следовательно, аномальных значений (выбросов) не выявлено.
КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Корреляционный анализ — это разведка перед построением регрессионной модели.
Выполним расчет коэффициента линейной корреляции Пирсона, проверку его значимости и построение доверительных интервалов с помощью пользовательской функции corr_coef_check (про эту функцию более подробно написано в моей статье https://habr.com/ru/post/683442/):
# пользовательская функция
display(corr_coef_check(X, Y, scale='Evans'))Выводы:
-
Значение коэффициента корреляции coef_value = 0.8900 свидетельствует о весьма сильной корреляционной связи (по шкале Эванса).
-
Коэффициент корреляции значим по критерию Стьюдента: t_calc ≥ t_table, a_calc ≤ a_level.
-
Доверительный интервал для коэффициента корреляции: 0.6621 ≤ coef_value ≤ 0.9625.
РЕГРЕССИОННЫЙ АНАЛИЗ
Предварительная визуализация
python позволяет выполнить предварительную визуализацию, например, с помощью функции jointplot библиотеки seaborn:
fig = plt.figure(figsize=(297/INCH, 210/INCH))
axes = sns.jointplot(
x=X, y=Y,
kind='reg',
ci=95)
plt.show()Построение модели
Выполним оценку параметров и анализ простой линейной регрессии (simple linear regression), используя библиотеку statsmodels (https://www.statsmodels.org/) и входящий в нее модуль линейной регрессии Linear Regression (https://www.statsmodels.org/stable/regression.html).
Данный модуль включает в себя классы, реализующие различные методы оценки параметров моделей линейной регрессии, в том числе:
-
класс OLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.OLS.html#statsmodels.regression.linear_model.OLS) — Ordinary Least Squares (обычный метод наименьших квадратов).
-
класс WLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.WLS.html#statsmodels.regression.linear_model.WLS) — Weighted Least Squares (метод взвешенных наименьших квадратов) (https://en.wikipedia.org/wiki/Weighted_least_squares), применяется, если имеет место гетероскедастичность данных (https://ru.wikipedia.org/wiki/Гетероскедастичность).
-
класс GLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLS.html#statsmodels.regression.linear_model.GLS) — Generalized Least Squares (обобщенный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Generalized_least_squares), применяется, если существует определенная степень корреляции между остатками в модели регрессии.
-
класс GLSAR (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.GLSAR.html#statsmodels.regression.linear_model.GLSAR) — Generalized Least Squares with AR covariance structure (обобщенный метод наименьших квадратов, ковариационная структура с автокорреляцией — экспериментальный метод)
-
класс RecurciveLS (https://www.statsmodels.org/stable/examples/notebooks/generated/recursive_ls.html) — Recursive least squares (рекурсивный метод наименьших квадратов) (https://en.wikipedia.org/wiki/Recursive_least_squares_filter)
-
классы RollingOLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingOLS.html#statsmodels.regression.rolling.RollingOLS) и RollingWLS (https://www.statsmodels.org/stable/generated/statsmodels.regression.rolling.RollingWLS.html#statsmodels.regression.rolling.RollingWLS) — скользящая регрессия (https://www.statsmodels.org/stable/examples/notebooks/generated/rolling_ls.html, https://help.fsight.ru/ru/mergedProjects/lib/01_regression_models/rolling_regression.htm)
и т.д.
Так как исходные данные подчиняются нормальному закону распределения и аномальные значения (выбросы) отсутствуют, воспользуемся для оценки параметров обычным методом наименьших квадратов (класс OLS):
model_linear_ols = smf.ols(formula='Y ~ X', data=dataset_df)
result_linear_ols = model_linear_ols.fit()
print(result_linear_ols.summary())Альтернативная форма выдачи результатов:
print(result_linear_ols.summary2())Результаты построения модели мы получаем как класс statsmodels.regression.linear_model.RegressionResults (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults).
Экспресс-выводы, которые мы можем сразу сделать из результатов построения модели:
-
Коэффициенты регрессии модели Y = b0 + b1∙X:
-
Intercept = b0 = -21.3741
-
b1 = 0.0129
-
-
Коэффициент детерминации R-squared = 0.776, его скорректированная оценка Adj. R-squared = 0.757 — это означает, что регрессионная модуль объясняет 75.75% вариации переменной Y.
-
Проверка значимости коэффициента детерминации:
-
расчетное значение статистики критерия Фишера: F-statistic = 41.61
-
расчетный уровень значимости Prob (F-statistic) = 3.16e-05
-
так как значение Prob (F-statistic) < 0.05, то нулевая гипотеза R-squared = 0 НЕ ПРИНИМАЕТСЯ, т.е. коэффициент детерминации ЗНАЧИМ
-
-
Проверка значимости коэффициентов регрессии:
-
расчетный уровень значимости P>|t| не превышает 0.05 — это означает, что оба коэффициента регрессии значимы
-
об этом же свидетельствует то, что доверительный интервал для обоих коэффициентов регрессии ([0.025; 0.975]) не включает в себя точку 0
Также в таблице результатов содержится прочая информация по коэффициентам регрессии: стандартная ошибка Std.Err. расчетное значение статистики критерия Стьюдента t для проверки гипотезы о значимости.
-
-
Анализ остатков модели:
-
Тест Omnibus — про этот тест подробно написано в https://en.wikipedia.org/wiki/Omnibus_test, https://medium.com/swlh/interpreting-linear-regression-through-statsmodels-summary-4796d359035a, http://work.thaslwanter.at/Stats/html/statsModels.html.
Расчетное значение статистики критерия Omnibus = 3.466 — по сути расчетное значение F-критерия (см. https://en.wikipedia.org/wiki/Omnibus_test).
Prob(Omnibus) = 0.177 — показывает вероятность нормального распределения остатков (значение 1 указывает на совершенно нормальное распределение).
Учитывая, что в дальнейшем мы проверим нормальность распределения остатков по совокупности различных тестов, в том числе с достаточно высокой мощностью, и все тесты позволят принять гипотезу о нормальном распределении — в данном случае к тесту Omnibus возникают вопросы. С этим тестом нужно разбираться отдельно.
-
Skew = 0.014 и Kurtosis = 1.587 — показатели асимметрии и эксцесса остатков свидетельствуют, что распределение остатков практически симметричное, островершинное.
-
проверка нормальности распределения остатков по критерию Харке-Бера: расчетное значение статистики критерия Jarque-Bera (JB) = 1.164 и расчетный уровень значимости Prob(JB) = 0.559. К данным результатам также возникают вопросы, особенно, если учесть, что критерий Харке-Бера является асимптотическим, расчетное значение имеет распределение хи-квадрат, поэтому данный критерий рекомендуют применять только для больших выборок (см. https://en.wikipedia.org/wiki/Jarque–Bera_test). Проверку нормальности распределения остатков модели лучше проводить с использованием набора стандартных статистических тестов python (см. далее).
-
-
Проверка автокорреляции по критерию Дарбина-Уотсона: Durbin-Watson = 1.443.
Мы не будем здесь разбирать данный критерий, так как явление автокорреляции больше характерно для данных, выражаемых в виде временных рядов. Однако, для грубой оценки считается, что при расчетном значении статистики криетрия Дарбина=Уотсона а интервале [1; 2] автокорреляция отсутствует (см.https://en.wikipedia.org/wiki/Durbin–Watson_statistic).
Более подробно про критерий Дарбина-Уотсона — см. [1, с.659].
Прочая информация, которую можно извлечь из результатов построения модели:
-
Covariance Type — тип ковариации, подробнее см. https://habr.com/ru/post/681218/, https://towardsdatascience.com/simple-explanation-of-statsmodel-linear-regression-model-summary-35961919868b#:~:text=Covariance type is typically nonrobust,with respect to each other.
-
Scale — масштабный коэффициент для ковариационной матрицы (https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.scale.html#statsmodels.regression.linear_model.RegressionResults.scale), равен величине Mean squared error (MSE) (cреднеквадратической ошибке), об подробнее см. далее, в разделе про ошибки аппроксимации моделей.
-
Показатели сравнения качества различных моделей:
-
Log-Likelihood — логарифмическая функция правдоподобия, подробнее см. https://en.wikipedia.org/wiki/Likelihood_function#Log-likelihood, https://habr.com/ru/post/433804/
-
AIC — информационный критерий Акаике (Akaike information criterion), подробнее см. https://en.wikipedia.org/wiki/Akaike_information_criterion
-
BIC — информационный критерий Байеса (Bayesian information criterion), подробнее см. https://en.wikipedia.org/wiki/Bayesian_information_criterion
В данной статье мы эти показатели рассматривать не будем, так как задача выбора одной модели из нескольких перед нами не стоит.
-
-
Число обусловленности Cond. No = 96792 используется для проверки мультиколлинеарности (считается, что мультиколлинеарность есть, если значение Cond. No > 30) (см. http://work.thaslwanter.at/Stats/html/statsModels.html). В нашем случае парной регрессионной модели о мультиколлинеарности речь не идет.
Далее будем извлекать данные из стандартного набора выдачи результатов и анализировать их более подробно. Последующие этапы вовсе не обязательно проводить в полном объеме при решении задач, но здесь мы рассмотрим их подробно.
Параметры и уравнение регрессионной модели
Извлечем параметры полученной модели — как свойство params модели:
print('Параметры модели: n', result_linear_ols.params, type(result_linear_ols.params))Имея параметры модели, можем формализовать уравнение модели Y = b0 + b1*X:
b0 = result_linear_ols.params['Intercept']
b1 = result_linear_ols.params['X']
Y_calc = lambda x: b0 + b1*xГрафик регрессионной модели
Для построения графиков регрессионных моделей можно воспользоваться стандартными возможностями библиотек statsmodels, seaborn, либо создать пользовательскую функцию — на усмотрение исследователя:
1. Построение графиков регрессионных моделей с использованием библиотеки statsmodels
С помощью функции statsmodels.graphics.plot_fit (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_fit.html#statsmodels.graphics.regressionplots.plot_fit) — отображается график Y and Fitted vs.X (фактические и расчетные значения Y с доверительным интервалом для каждого значения Y):
fig, ax = plt.subplots(figsize=(297/INCH, 210/INCH))
fig = sm.graphics.plot_fit(
result_linear_ols, 'X',
vlines=True, # это параметр отвечает за отображение доверительных интервалов для Y
ax=ax)
ax.set_ylabel(Variable_Name_Y)
ax.set_xlabel(Variable_Name_X)
ax.set_title(Task_Project)
plt.show()С помощью функции statsmodels.graphics.plot_regress_exog (https://www.statsmodels.org/stable/generated/statsmodels.graphics.regressionplots.plot_regress_exog.html#statsmodels.graphics.regressionplots.plot_regress_exog) — отображается область 2х2, которая содержит:
-
предыдущий график Y and Fitted vs.X;
-
график остатков Residuals versus X;
-
график Partial regression plot — график частичной регрессии, пытается показать эффект добавления другой переменной в модель, которая уже имеет одну или несколько независимых переменных (более подробно см. https://en.wikipedia.org/wiki/Partial_regression_plot);
-
график CCPR Plot (Component-Component plus Residual Plot) — еще один способ оценить влияние одной независимой переменной на переменную отклика, принимая во внимание влияние других независимых переменных (более подробно — см. https://towardsdatascience.com/calculating-price-elasticity-of-demand-statistical-modeling-with-python-6adb2fa7824d, https://www.kirenz.com/post/2021-11-14-linear-regression-diagnostics-in-python/linear-regression-diagnostics-in-python/).
fig = plt.figure(figsize=(297/INCH, 210/INCH))
sm.graphics.plot_regress_exog(result_linear_ols, 'X', fig=fig)
plt.show()2. Построение графиков регрессионных моделей с использованием библиотеки seaborn
Воспользуемся модулем regplot библиотеки seaborn (https://seaborn.pydata.org/generated/seaborn.regplot.html). Данный модуль позволяет визуализировать различные виды регрессии:
-
линейную
-
полиномиальную
-
логистическую
-
взвешенную локальную регрессию (LOWESS — Locally Weighted Scatterplot Smoothing) (см. http://www.machinelearning.ru/wiki/index.php?title=Алгоритм_LOWESS, https://www.statsmodels.org/stable/generated/statsmodels.nonparametric.smoothers_lowess.lowess.html)
Более подробно про модуль regplot можно прочитать в статье: https://pyprog.pro/sns/sns_8_regression_models.html.
Есть более совершенный модуль lmplot (https://seaborn.pydata.org/generated/seaborn.lmplot.html), который объединяет в себе regplot и FacetGrid, но мы его здесь рассматривать не будем.
# создание рисунка (Figure) и области рисования (Axes)
fig = plt.figure(figsize=(297/INCH, 420/INCH/1.5))
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 18)
# заголовок области рисования (Axes)
title_axes_1 = 'Линейная регрессионная модель'
ax1.set_title(title_axes_1, fontsize = 16)
# график регрессионной модели
order_mod = 1 # порядок модели
#label_legend_regr_model = 'фактические данные'
sns.regplot(
#data=dataset_df,
x=X, y=Y,
#x_estimator=np.mean,
order=order_mod,
logistic=False,
lowess=False,
robust=False,
logx=False,
ci=95,
scatter_kws={'s': 30, 'color': 'red'},
line_kws={'color': 'blue'},
#label=label_legend_regr_model,
ax=ax1)
ax1.set_ylabel(Variable_Name_Y)
ax1.legend()
# график остатков
title_axes_2 = 'График остатков'
ax2.set_title(title_axes_2, fontsize = 16)
sns.residplot(
#data=dataset_df,
x=X, y=Y,
order=order_mod,
lowess=False,
robust=False,
scatter_kws={'s': 30, 'color': 'darkorange'},
ax=ax2)
ax2.set_xlabel(Variable_Name_X)
plt.show()3. Построение графиков регрессионных моделей с помощью пользовательской функции
# Пользовательская функция
graph_regression_plot_sns(
X, Y,
regression_model=Y_calc,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=Ymin_graph, Ymax=Ymax_graph,
title_figure=Task_Project,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
s=80,
file_name='graph/regression_plot_lin.png')Статистический анализ регрессионной модели
1. Расчет ошибки аппроксимации (Error Metrics)
Ошибки аппроксимации (Error Metrics) позволяют получить общее представление о качестве модели, а также позволяют сравнивать между собой различные модели.
Создадим пользовательскую функцию, которая рассчитывает основные ошибки аппроксимации для заданной модели:
-
Mean squared error (MSE) или Mean squared deviation (MSD) — среднеквадратическая ошибка (https://en.wikipedia.org/wiki/Mean_squared_error):
-
Root mean square error (RMSE) или Root mean square deviation (RMSD) — квадратный корень из MSE (https://en.wikipedia.org/wiki/Root-mean-square_deviation):
-
Mean absolute error (MAE) — средняя абсолютная ошибка (https://en.wikipedia.org/wiki/Mean_absolute_error):
-
Mean squared prediction error (MSPE) — среднеквадратическая ошибка прогноза (среднеквадратическая ошибка в процентах) (https://en.wikipedia.org/wiki/Mean_squared_prediction_error):
-
Mean absolute percentage error (MAPE) — средняя абсолютная ошибка в процентах (https://en.wikipedia.org/wiki/Mean_absolute_percentage_error):
Про выбор метрики см. также https://machinelearningmastery.ru/how-to-select-the-right-evaluation-metric-for-machine-learning-models-part-2-regression-metrics-d4a1a9ba3d74/.
# Пользовательская функция
def regression_error_metrics(model, model_name=''):
model_fit = model.fit()
Ycalc = model_fit.predict()
n_fit = model_fit.nobs
Y = model.endog
MSE = (1/n_fit) * np.sum((Y-Ycalc)**2)
RMSE = sqrt(MSE)
MAE = (1/n_fit) * np.sum(abs(Y-Ycalc))
MSPE = (1/n_fit) * np.sum(((Y-Ycalc)/Y)**2)
MAPE = (1/n_fit) * np.sum(abs((Y-Ycalc)/Y))
model_error_metrics = {
'MSE': MSE,
'RMSE': RMSE,
'MAE': MAE,
'MSPE': MSPE,
'MAPE': MAPE}
result = pd.DataFrame({
'MSE': MSE,
'RMSE': RMSE,
'MAE': MAE,
'MSPE': "{:.3%}".format(MSPE),
'MAPE': "{:.3%}".format(MAPE)},
index=[model_name])
return model_error_metrics, result
(model_error_metrics, result) = regression_error_metrics(model_linear_ols, model_name='linear_ols')
display(result)В литературе по прикладной статистике нет единого мнения о допустимом размере относительных ошибок аппроксимации: в одних источниках допустимой считается ошибка 5-7%, в других она может быть увеличена до 8-10%, и даже до 15%.
Вывод: модель хорошо аппроксимирует фактические данные (относительная ошибка аппроксимации MAPE = 3.405% < 10%).
2. Дисперсионный анализ регрессионной модели (ДАРМ)
ДАРМ не входит в стандартную форму выдачи результатов Regression Results, однако я решил написать здесь о нем по двум причинам:
-
Именно анализ дисперсии регрессионной модели, разложение этой дисперсии на составляющие дает фундаментальное представление о сути регрессии, а термины, используемые при ДАРМ, применяются на последующих этапах анализа.
-
С терминами ДАРМ в литературе по прикладной статистике имеется некоторая путаница, в разных источниках они могут именоваться по-разному (см., например, [8, с.52]), поэтому, чтобы двигаться дальше, необходимо определиться с понятиями.
При ДАРМ общую вариацию результативного признака (Y) принято разделять на две составляющие — вариация, обусловленная регрессией и вариация, обусловленная отклонениями от регрессии (остаток), при этом в разных источниках эти термины могут именоваться и обозначаться по-разному, например:
-
Вариация, обусловленная регрессией — может называться Explained sum of squares (ESS), Sum of Squared Regression (SSR) (https://en.wikipedia.org/wiki/Explained_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684), Sum of squared deviations (SSD).
-
Вариация, обусловленная отклонениями от регрессии (остаток) — может называться Residual sum of squares (RSS), Sum of squared residuals (SSR), Squared estimate of errors, Sum of Squared Error (SSE) (https://en.wikipedia.org/wiki/Residual_sum_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684); в отчественной практике также применяется термин остаточная дисперсия.
-
Общая (полная) вариация — может называться Total sum of squares (TSS), Sum of Squared Total (SST) (https://en.wikipedia.org/wiki/Partition_of_sums_of_squares, https://towardsdatascience.com/anova-for-regression-fdb49cf5d684).
Как видим, путаница знатная:
-
в разных источниках под SSR могут подразумеваться различные показатели;
-
легко перепутать показатели ESS и SSE;
-
в библиотеке statsmodel также есть смешение терминов: для показателя Explained sum of squares используется свойство ess, а для показателя Sum of squared (whitened) residuals — свойство ssr.
Мы будем пользоваться системой обозначений, принятой в большинстве источников — SSR (Sum of Squared Regression), SSE (Sum of Squared Error), SST (Sum of Squared Total). Стандартная таблица ДАРМ в этом случае имеет вид:
Примечания:
-
Здесь приведена таблица ДАРМ для множественной линейной регрессионной модели (МЛРМ), в нашем случае при ПЛРМ мы имеем частный случай p=1.
-
Показатели Fcalc-ad и Fcalc-det — расчетные значения статистики критерия Фишера при проверке адекватности модели и значимости коэффициента детерминации (об этом — см.далее).
Более подробно про дисперсионный анализ регрессионной модели — см.[4, глава 3].
Класс statsmodels.regression.linear_model.RegressionResults позволяет нам получить данные для ANOVA (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.html#statsmodels.regression.linear_model.RegressionResults) как свойства класса:
-
Сумма квадратов, обусловленная регрессией / SSR (Sum of Squared Regression) — свойство ess.
-
Сумма квадратов, обусловленная отклонением от регрессии / SSE (Sum of Squared Error) — свойство ssr.
-
Общая (полная) сумма квадратов / SST (Sum of Squared Total) — свойство centered_tss.
-
Кол-во наблюдений / Number of observations — свойство nobs.
-
Число степеней свободы модели / Model degrees of freedom — равно числу переменных модели (за исключением константы, если она присутствует — свойство df_model.
-
Среднеквадратичная ошибка модели / Mean squared error the model — сумма квадратов, объясненная регрессией, деленная на число степеней свободы регрессии — свойство mse_model.
-
Среднеквадратичная ошибка остатков / Mean squared error of the residuals — сумма квадратов остатков, деленная на остаточные степени свободы — свойство mse_resid.
-
Общая среднеквадратичная ошибка / Total mean squared error — общая сумма квадратов, деленная на количество наблюдений — свойство mse_total.
Также имеется модуль statsmodels.stats.anova.anova_lm, который позволяет получить результаты ДАРМ (нескольких типов — 1, 2, 3):
# тип 1
print('The type of Anova test: 1')
display(sm.stats.anova_lm(result_linear_ols, typ=1))
# тип 2
print('The type of Anova test: 2')
display(sm.stats.anova_lm(result_linear_ols, typ=2))
# тип 3
print('The type of Anova test: 3')
display(sm.stats.anova_lm(result_linear_ols, typ=3))На мой взгляд, форма таблица результатов statsmodels.stats.anova.anova_lm не вполне удобна, поэтому сформируем ее самостоятельно, для чего создадим пользовательскую функцию ANOVA_table_regression_model:
# Пользовательская функция
def ANOVA_table_regression_model(model_fit):
n = int(model_fit.nobs)
p = int(model_fit.df_model)
SSR = model_fit.ess
SSE = model_fit.ssr
SST = model_fit.centered_tss
result = pd.DataFrame({
'sources_of_variation': ('regression (SSR)', 'deviation from regression (SSE)', 'total (SST)'),
'sum_of_squares': (SSR, SSE, SST),
'degrees_of_freedom': (p, n-p-1, n-1)})
result['squared_error'] = result['sum_of_squares'] / result['degrees_of_freedom']
R2 = 1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']
F_calc_adequacy = result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']
F_calc_determ_check = result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']
result['F-ratio'] = (F_calc_determ_check, F_calc_adequacy, '')
return result
result = ANOVA_table_regression_model(result_linear_ols)
display(result)
print(f"R2 = 1 - SSE/SST = {1 - result.loc[1, 'sum_of_squares'] / result.loc[2, 'sum_of_squares']}")
print(f"F_calc_adequacy = MST / MSE = {result.loc[2, 'squared_error'] / result.loc[1, 'squared_error']}")
print(f"F_calc_determ_check = MSR / MSE = {result.loc[0, 'squared_error'] / result.loc[1, 'squared_error']}")ДАРМ позволяет визуализировать вариацию:
fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/1.5))
axes.pie(
(result.loc[0, 'sum_of_squares'], result.loc[1, 'sum_of_squares']),
labels=(result.loc[0, 'sources_of_variation'], result.loc[1, 'sources_of_variation']),
autopct='%.1f%%',
startangle=60)
plt.show()На основании данных ДАРМ мы рассчитали ряд показателей (R2, Fcalc-ad и Fcalc-det), которые будут использоваться в дальнейшем.
3. Анализ остатков (проверка нормальности распределения остатков и гипотезы о равенстве нулю среднего значения остатков)
Проверка нормальности распределения остатков — один их важнейших этапов анализа регрессионной модели. Требование нормальности распределения остатков не требуется для отыскания параметров модели, но необходимо в дальнейшем для проверки статистических гипотез с использованием критериев Фишера и Стьюдента (проверка адекватности модели, значимости коэффициента детерминации, значимости коэффициентов регрессии) и построения доверительных интервалов [5, с.122].
Остатки регрессионной модели:
print('Остатки регрессионной модели:n', result_linear_ols.resid, type(result_linear_ols.resid))
res_Y = np.array(result_linear_ols.resid)statsmodels может выдавать различные преобразованные виды остатков (см. https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.resid_pearson.html, https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.wresid.html).
График остатков:
# Пользовательская функция
graph_scatterplot_sns(
X, res_Y,
Xmin=Xmin_graph, Xmax=Xmax_graph,
Ymin=-3.0, Ymax=3.0,
color='red',
#title_figure=Task_Project,
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=18,
x_label=Variable_Name_X,
y_label='ΔY = Y - Ycalc',
s=75,
file_name='graph/residuals_plot_sns.png')Проверка нормальности распределения остатков:
# Пользовательская функция
graph_hist_boxplot_probplot_sns(
data=res_Y,
data_min=-2.5, data_max=2.5,
graph_inclusion='bp',
data_label='ΔY = Y - Ycalc',
#title_figure=Task_Project,
title_axes='Остатки линейной регрессионной модели', title_axes_fontsize=16,
file_name='graph/residuals_hist_boxplot_probplot_sns.png') norm_distr_check(res_Y)Вывод: большинство статистических тестов позволяют принять гипотезу о нормальности распределения остатков.
Проверка гипотезы о равенстве нулю среднего значения остатков — так как остатки имеют нормальное распределение, воспользуемся критерием Стьюдента (функция scipy.stats.ttest_1samp, https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html):
sps.ttest_1samp(res_Y, popmean=0)Вывод: так как расчетный уровень значимости превышает заданный (0.05), то нулевая гипотеза о равенстве нулю остатков ПРИНИМАЕТСЯ.
4. Проверка адекватности модели
Суть проверки адекватности регрессионной модели заключается в сравнении полной дисперсии MST и остаточной дисперсии MSE — проверяется гипотеза о равенстве этих дисперсий по критерию Фишера. Если дисперсии различаются значимо, то модель считается адекватной. Более подробно про проверку адекватности регрессионной — см.[1, с.658], [2, с.49], [4, с.154].
Для проверки адекватности регрессионной модели создадим пользовательскую функцию regression_model_adequacy_check:
def regression_model_adequacy_check(
model_fit,
p_level: float=0.95,
model_name=''):
n = int(model_fit.nobs)
p = int(model_fit.df_model) # Число степеней свободы регрессии, равно числу переменных модели (за исключением константы, если она присутствует)
SST = model_fit.centered_tss # SST (Sum of Squared Total)
dfT = n-1
MST = SST / dfT
SSE = model_fit.ssr # SSE (Sum of Squared Error)
dfE = n - p - 1
MSE = SSE / dfE
F_calc = MST / MSE
F_table = sci.stats.f.ppf(p_level, dfT, dfE, loc=0, scale=1)
a_calc = 1 - sci.stats.f.cdf(F_calc, dfT, dfE, loc=0, scale=1)
conclusion_model_adequacy_check = 'adequacy' if F_calc >= F_table else 'adequacy'
# формируем результат
result = pd.DataFrame({
'SST': (SST),
'SSE': (SSE),
'dfT': (dfT),
'dfE': (dfE),
'MST': (MST),
'MSE': (MSE),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_calc),
'F_table': (F_table),
'F_calc >= F_table': (F_calc >= F_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'adequacy_check': (conclusion_model_adequacy_check),
},
index=[model_name]
)
return result
regression_model_adequacy_check(result_linear_ols, p_level=0.95, model_name='linear_ols')Вывод: модель является АДЕКВАТНОЙ.
5. Коэффициент детерминации и проверка его значимости
Различают несколько видов коэффициента детерминации:
-
Собственно обычный коэффициент детерминации:
Его значение может быть получено как свойство rsquared модели.
-
Скорректированный (adjusted) коэффициент детерминации — используется для того, чтобы была возможность сравнивать модели с разным числом признаков так, чтобы число регрессоров (признаков) не влияло на статистику R2, при его расчете используются несмещённые оценки дисперсий:
Его значение может быть получено как свойство rsquared_adj модели.
-
Обобщённый (extended) коэффициент детерминации — используется для сравнения моделей регрессии со свободным членом и без него, а также для сравнения между собой регрессий, построенных с помощью различных методов: МНК, обобщённого метода наименьших квадратов (ОМНК), условного метода наименьших квадратов (УМНК), обобщённо-условного метода наименьших квадратов (ОУМНК). В данном разборе ПЛРМ рассматривать этот коэффициент мы не будем.
Более подробно с теорией вопроса можно ознакомиться, например: http://www.machinelearning.ru/wiki/index.php?title=Коэффициент_детерминации), а также в [7].
Значения коэффициента детерминации и скорректированного коэффициента детерминации, извлеченные с помощью свойств rsquared и rsquared_adj модели.
print('R2 =', result_linear_ols.rsquared)
print('R2_adj =', result_linear_ols.rsquared_adj)Значимость коэффициента детерминации можно проверить по критерию Фишера [3, с.201-203; 8, с.83].
Расчетное значение статистики критерия Фишера может быть получено с помощью свойства fvalue модели:
print(f"result_linear_ols.fvalue = {result_linear_ols.fvalue}")Расчетный уровень значимости при проверке гипотезы по критерию Фишера может быть получено с помощью свойства f_pvalue модели:
print(f"result_linear_ols.f_pvalue = {result_linear_ols.f_pvalue}")Можно рассчитать уровень значимости самостоятельно (так сказать, для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Фишера scipy.stats.f, свойством cdf (функция распределения):
df1 = int(result_linear_ols.df_model)
df2 = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
F_calc = result_linear_ols.fvalue
a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
print(a_calc)Как видим, результаты совпадают.
Табличное значение статистики критерия Фишера получить с помощью Regression Results нельзя. Рассчитаем его самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.f, свойством ppf (процентные точки):
F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
print(F_table)Для удобства создадим пользовательскую функцию determination_coef_check для проверки значимости коэффициента детерминации, которая объединяет все вышеперечисленные расчеты:
# Пользовательская функция
def determination_coef_check(
model_fit,
p_level: float=0.95):
a_level = 1 - p_level
R2 = model_fit.rsquared
R2_adj = model_fit.rsquared_adj
n = model_fit.nobs # объем выборки
p = model_fit.df_model # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
F_calc = R2 / (1 - R2) * (n-p-1)/p
df1 = int(p)
df2 = int(n-p-1)
F_table = sci.stats.f.ppf(p_level, df1, df2, loc=0, scale=1)
a_calc = 1 - sci.stats.f.cdf(F_calc, df1, df2, loc=0, scale=1)
conclusion_determ_coef_sign = 'significance' if F_calc >= F_table else 'not significance'
# формируем результат
result = pd.DataFrame({
'notation': ('R2'),
'coef_value (R)': (sqrt(R2)),
'coef_value_squared (R2)': (R2),
'p_level': (p_level),
'a_level': (a_level),
'F_calc': (F_calc),
'df1': (df1),
'df2': (df2),
'F_table': (F_table),
'F_calc >= F_table': (F_calc >= F_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'significance_check': (conclusion_determ_coef_sign),
'conf_int_low': (''),
'conf_int_high': ('')
},
index=['Coef. of determination'])
return result
determination_coef_check(
result_linear_ols,
p_level=0.95)Вывод: коэффициент детерминации ЗНАЧИМ.
6. Коэффициенты регрессии и проверка их значимости
Ранее мы уже извлекли коэффициенты регрессии как параметры модели b0 и b1 (как свойство params модели). Также можно получить их значения, как свойство bse модели:
print(b0, b1)
print(result_linear_ols.bse, type(result_linear_ols.bse))Значимость коэффициентов регрессии можно проверить по критерию Стьюдента [3, с.203-212; 8, с.78].
Расчетные значения статистики критерия Стьюдента могут быть получены с помощью свойства tvalues модели:
print(f"result_linear_ols.tvalues = n{result_linear_ols.tvalues}")Расчетные значения уровня значимости при проверке гипотезы по критерию Стьюдента могут быть получены с помощью свойства pvalues модели:
print(f"result_linear_ols.pvalues = n{result_linear_ols.pvalues}")Доверительные интервалы для коэффициентов регрессии могут быть получены с помощью свойства conf_int модели:
print(result_linear_ols.conf_int(), 'n')Можно рассчитать уровень значимости самостоятельно (как ранее для критерия Фишера — для лучшего понимания и общей демонстрации возможностей) — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством cdf (функция распределения):
t_calc = result_linear_ols.tvalues
df = int(result_linear_ols.nobs - result_linear_ols.df_model - 1)
a_calc = 2*(1-sci.stats.t.cdf(abs(t_calc), df, loc=0, scale=1))
print(a_calc)Как видим, результаты совпадают.
Табличные значения статистики критерия Стьюдента получить с помощью Regression Results нельзя. Рассчитаем их самостоятельно — для этого воспользуемся библиотекой scipy, модулем распределения Стьюдента scipy.stats.t, свойством ppf (процентные точки):
t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
print(t_table)Для удобства создадим пользовательскую функцию regression_coef_check для проверки значимости коэффициентов регрессии, которая объединяет все вышеперечисленные расчеты:
def regression_coef_check(
model_fit,
notation_coef: list='',
p_level: float=0.95):
a_level = 1 - p_level
# параметры модели (коэффициенты регрессии)
model_params = model_fit.params
# стандартные ошибки коэффициентов регрессии
model_bse = model_fit.bse
# проверка гипотезы о значимости регрессии
t_calc = abs(model_params) / model_bse
n = model_fit.nobs # объем выборки
p = model_fit.df_model # Model degrees of freedom. The number of regressors p. Does not include the constant if one is present.
df = int(n - p - 1)
t_table = sci.stats.t.ppf((1 + p_level)/2 , df)
a_calc = 2*(1-sci.stats.t.cdf(t_calc, df, loc=0, scale=1))
conclusion_ = ['significance' if elem else 'not significance' for elem in (t_calc >= t_table).values]
# доверительный интервал коэффициента регрессии
conf_int_low = model_params - t_table*model_bse
conf_int_high = model_params + t_table*model_bse
# формируем результат
result = pd.DataFrame({
'notation': (notation_coef),
'coef_value': (model_params),
'std_err': (model_bse),
'p_level': (p_level),
'a_level': (a_level),
't_calc': (t_calc),
'df': (df),
't_table': (t_table),
't_calc >= t_table': (t_calc >= t_table),
'a_calc': (a_calc),
'a_calc <= a_level': (a_calc <= a_level),
'significance_check': (conclusion_),
'conf_int_low': (conf_int_low),
'conf_int_high': (conf_int_high),
})
return result
regression_coef_check(
result_linear_ols,
notation_coef=['b0', 'b1'],
p_level=0.95)Вывод: коэффициенты регрессии b0 и b1 ЗНАЧИМЫ.
7. Проверка гетероскедастичности
Для проверка гетероскедастичности statsmodels предлагает нам следующие инструменты:
-
тест Голдфелда-Квандта (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_goldfeldquandt.html#statsmodels.stats.diagnostic.het_goldfeldquandt) — теорию см. [8, с.178], также https://ru.wikipedia.org/wiki/Тест_Голдфелда_—_Куандта.
-
тест Бриша-Пэгана (Breush-Pagan test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_breuschpagan.html#statsmodels.stats.diagnostic.het_breuschpagan) — теорию см.[8, с.179], также https://en.wikipedia.org/wiki/Breusch–Pagan_test.
-
тест Уайта (White test) (https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.het_white.html#statsmodels.stats.diagnostic.het_white) — теорию см.[8, с.177], а также https://ru.wikipedia.org/wiki/Тест_Уайта.
Тест Голдфелда-Квандта (Goldfeld–Quandt test)
# тест Голдфелда-Квандта (Goldfeld–Quandt test)
test = sms.het_goldfeldquandt(result_linear_ols.resid, result_linear_ols.model.exog)
test_result = lzip(['F_calc', 'p_calc'], test) # распаковка результатов теста
# расчетное значение статистики F-критерия
F_calc_tuple = test_result[0]
F_calc = F_calc_tuple[1]
print(f"Расчетное значение статистики F-критерия: F_calc = {round(F_calc, DecPlace)}")
# расчетный уровень значимости
p_calc_tuple = test_result[1]
p_calc = p_calc_tuple[1]
print(f"Расчетное значение доверительной вероятности: p_calc = {round(p_calc, DecPlace)}")
#a_calc = 1 - p_value
#print(f"Расчетное значение уровня значимости: a_calc = 1 - p_value = {round(a_calc, DecPlace)}")
# вывод
if p_calc < a_level:
conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} < a_level = {round(a_level, DecPlace)}" +
", то дисперсии в подвыборках отличаются значимо, т.е. гипотеза о наличии гетероскедастичности ПРИНИМАЕТСЯ"
else:
conclusion_GQ_test = f"Так как p_calc = {round(p_calc, DecPlace)} >= a_level = {round(a_level, DecPlace)}" +
", то дисперсии в подвыборках отличаются незначимо, т.е. гипотеза о наличии гетероскедастичности ОТВЕРГАЕТСЯ"
print(conclusion_GQ_test)Для удобства создадим пользовательскую функцию Goldfeld_Quandt_test:
def Goldfeld_Quandt_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_goldfeldquandt(model_fit.resid, model_fit.model.exog)
test_result = lzip(['F_statistic', 'p_calc'], test) # распаковка результатов теста
# расчетное значение статистики F-критерия
F_calc_tuple = test_result[0]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости
p_calc_tuple = test_result[1]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('Goldfeld–Quandt test'),
'p_level': (p_level),
'a_level': (a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Тест Бриша-Пэгана (Breush-Pagan test)
# тест Бриша-Пэгана (Breush-Pagan test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_breuschpagan(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)Для удобства создадим пользовательскую функцию Breush_Pagan_test:
def Breush_Pagan_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_breuschpagan(model_fit.resid, model_fit.model.exog)
name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
test_result = lzip(name, test) # распаковка результатов теста
# расчетное значение статистики теста множителей Лагранжа
LM_calc_tuple = test_result[0]
Lagrange_multiplier_statistic = LM_calc_tuple[1]
# расчетный уровень значимости статистики теста множителей Лагранжа
p_calc_LM_tuple = test_result[1]
p_calc_LM = p_calc_LM_tuple[1]
# расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
F_calc_tuple = test_result[2]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости F-статистики
p_calc_tuple = test_result[3]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('Breush-Pagan test'),
'p_level': (p_level),
'a_level': (a_level),
'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
'p_calc_LM': (p_calc_LM),
'p_calc_LM < a_level': (p_calc_LM < a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Тест Уайта (White test)
# тест Уайта (White test)
name = ["Lagrange multiplier statistic", "p-value", "f-value", "f p-value"]
test = sms.het_white(result_linear_ols.resid, result_linear_ols.model.exog)
lzip(name, test)Для удобства создадим пользовательскую функцию White_test:
def White_test(
model_fit,
p_level: float=0.95,
model_name=''):
a_level = 1 - p_level
# реализация теста
test = sms.het_white(model_fit.resid, model_fit.model.exog)
name = ['Lagrange_multiplier_statistic', 'p_calc_LM', 'F_statistic', 'p_calc']
test_result = lzip(name, test) # распаковка результатов теста
# расчетное значение статистики теста множителей Лагранжа
LM_calc_tuple = test_result[0]
Lagrange_multiplier_statistic = LM_calc_tuple[1]
# расчетный уровень значимости статистики теста множителей Лагранжа
p_calc_LM_tuple = test_result[1]
p_calc_LM = p_calc_LM_tuple[1]
# расчетное значение F-статистики гипотезы о том, что дисперсия ошибки не зависит от x
F_calc_tuple = test_result[2]
F_statistic = F_calc_tuple[1]
# расчетный уровень значимости F-статистики
p_calc_tuple = test_result[3]
p_calc = p_calc_tuple[1]
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
# вывод
conclusion_test = 'heteroscedasticity' if p_calc < a_level else 'not heteroscedasticity'
result = pd.DataFrame({
'test': ('White test'),
'p_level': (p_level),
'a_level': (a_level),
'Lagrange_multiplier_statistic': (Lagrange_multiplier_statistic),
'p_calc_LM': (p_calc_LM),
'p_calc_LM < a_level': (p_calc_LM < a_level),
'F_statistic': (F_statistic),
'p_calc': (p_calc),
'p_calc < a_level': (p_calc < a_level),
'heteroscedasticity_check': (conclusion_test)
},
index=[model_name])
return result
White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')Объединим результаты всех тестов гетероскедастичность в один DataFrame:
Goldfeld_Quandt_test_df = Goldfeld_Quandt_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
Breush_Pagan_test_df = Breush_Pagan_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
White_test_df = White_test(result_linear_ols, p_level=0.95, model_name='linear_ols')
heteroscedasticity_tests_df = pd.concat([Breush_Pagan_test_df, White_test_df, Goldfeld_Quandt_test_df])
display(heteroscedasticity_tests_df)Выводы
Итак, мы провели статистический анализ регрессионной модели и установили:
-
исходные данные имеют нормальное распределение;
-
между переменными имеется весьма сильная корреляционная связь;
-
регрессионная модель хорошо аппроксимирует фактические данные;
-
остатки модели имеют нормальное распределение;
-
регрессионная модель адекватна по критерию Фишера;
-
коэффициент детерминации значим по критеию Фишера;
-
коэффициенты регрессии значимы по критерию Стьюдента;
-
гетероскедастичность отсутствует.
Применительно к рассматриваемой задаче выполнять проверку автокорреляции не имеет особого смысла из-за особенностей исходных данных (результаты замеров прочности бетона на разных участках здания).
Про статистический анализ регрессионных моделей с помощью statsmodels— см. еще https://www.statsmodels.org/stable/examples/notebooks/generated/regression_diagnostics.html.
Доверительные интервалы регрессионной модели
Для регрессионных моделей определяют доверительные интервалы двух видов [3, с.184-192; 4, с.172; 8, с.205-209]:
-
Доверительный интервал средних значений переменной Y.
-
Доверительный интервал индивидуальных значений переменной Y.
При этом размер доверительного интервала для индивидуальных значений больше, чем для средних значений.
Доверительные интервалы регрессионных моделей (ДИРМ) могут быть найдены разными способами:
-
непосредственно путем расчетов по формулам (см., например, https://habr.com/ru/post/558158/);
-
с использованием инструментария библиотеки statsmodels (см., например, https://www.stackfinder.ru/questions/17559408/confidence-and-prediction-intervals-with-statsmodels).
Разбререм более подробно способ с использованием библиотеки statsmodels. Прежде всего, с помощью свойства summary_table класса statsmodels.stats.outliers_influence.OLSInfluence (https://www.statsmodels.org/stable/generated/statsmodels.stats.outliers_influence.OLSInfluence.html?highlight=olsinfluence) мы можем получить таблицу данных, содержащую необходимую нам информацию:
-
Dep Var Population — фактические значения переменной Y;
-
Predicted Value — предсказанные значения переменной Y по по регрессионной модели;
-
Std Error Mean Predict — среднеквадратическая ошибка предсказанного среднего;
-
Mean ci 95% low и Mean ci 95% upp — границы доверительного интервала средних значений переменной Y;
-
Predict ci 95% low и Predict ci 95% upp — границы доверительного интервала индивидуальных значений переменной Y;
-
Residual — остатки регрессионной модели;
-
Std Error Residual — среднеквадратическая ошибка остатков;
-
Student Residual — стьюдентизированные остатки (подробнее см. http://statistica.ru/glossary/general/studentizirovannie-ostatki/);
-
Cook’s D — Расстояние Кука (Cook’s distance) — оценивает эффект от удаления одного (рассматриваемого) наблюдения; наблюдение считается выбросом, если Di > 4/n (более подробно — см.https://translated.turbopages.org/proxy_u/en-ru.ru.f584ceb5-63296427-aded8f31-74722d776562/https/en.wikipedia.org/wiki/Cook’s_distance, http://www.machinelearning.ru/wiki/index.php?title=Расстояние_Кука).
from statsmodels.stats.outliers_influence import summary_table
st, data, ss2 = summary_table(result_linear_ols, alpha=0.05)
print(st, 'n', type(st))В нашем случае критическое значение расстояния Кука равно:
print(f'D_crit = 4/n = {4/result_linear_ols.nobs}')то есть выбросов, смещающих оценки коэффициентов регрессии, не наблюдается.
Мы получили данные как класс statsmodels.iolib.table.SimpleTable. Свойство data преобразует данные в список. Далее для удобства работы преобразуем данные в DataFrame:
st_data_df = pd.DataFrame(st.data)Будем использовать данный DataFrame в дальнейшем, несколько преобразуем его:
-
изменим наименование столбцов (с цифр на названия показателей из таблицы summary_table)
-
удалим строки с текстовыми значениями
-
изменим индекс
-
добавим новый столбец — значения переменной X
-
отсортируем по возрастанию значений переменной X (это необходимо, чтобы графики границ доверительных интервалов выглядели как линии)
st_df = st_data_df.copy()
# изменим наименования столбцов
str = st_df.iloc[0,0:] + ' ' + st_df.iloc[1,0:]
st_df = st_df.rename(str, axis='columns')
# удалим строки 0, 1
st_df = st_df.drop([0,1])
# изменим индекс
st_df = st_df.set_index(np.arange(0, result_linear_ols.nobs))
# добавим новый столбец - значения переменной X
st_df.insert(1, 'X', X)
# отсортируем по возрастанию значений переменной X
st_df = st_df.sort_values(by='X')
display(st_df)С помощью полученных данных мы можем построить график регрессионной модели с доверительными интервалами:
# создание рисунка (Figure) и области рисования (Axes)
fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
# заголовок рисунка (Figure)
title_figure = Task_Project
fig.suptitle(title_figure, fontsize = 16)
# заголовок области рисования (Axes)
title_axes = 'Линейная регрессионная модель'
axes.set_title(title_axes, fontsize = 14)
# фактические данные
sns.scatterplot(
x=st_df['X'], y=st_df['Dep Var Population'],
label='фактические данные',
s=50,
color='red',
ax=axes)
# график регрессионной модели
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X'
sns.lineplot(
x=st_df['X'], y=st_df['Predicted Value'],
label=label_legend_regr_model,
color='blue',
ax=axes)
# доверительный интервал средних значений переменной Y
Mean_ci_low = st_df['Mean ci 95% low']
plt.plot(
st_df['X'], Mean_ci_low,
color='magenta', linestyle='--', linewidth=1,
label='доверительный интервал средних значений Y')
Mean_ci_upp = st_df['Mean ci 95% upp']
plt.plot(
st_df['X'], Mean_ci_upp,
color='magenta', linestyle='--', linewidth=1)
# доверительный интервал индивидуальных значений переменной Y
Predict_ci_low = st_df['Predict ci 95% low']
plt.plot(
st_df['X'], Predict_ci_low,
color='orange', linestyle='-.', linewidth=2,
label='доверительный интервал индивидуальных значений Y')
Predict_ci_upp = st_df['Predict ci 95% upp']
plt.plot(
st_df['X'], Predict_ci_upp,
color='orange', linestyle='-.', linewidth=2)
axes.set_xlabel(Variable_Name_X)
axes.set_ylabel(Variable_Name_Y)
axes.legend(prop={'size': 12})
plt.show()Однако, мы получили данные о границах доверительных интервалов регрессионной модели только в пределах области фактических значений переменной X. Как быть, если мы хотим распространить прогноз за пределы этой области?
Прогнозирование
Под прогнозированием мы в данном случае будем понимать определение значений переменной Y и доверительных интервалов для ее средних и индивидуальных значений при заданном X. По сути, нам предстоит построить аналог рассмотренной выше таблицы summary_table, только с другими значениями X, причем эти значения могут выходить за пределы тех значений, которые использовались нами для построения регрессии.
Методика расчета доверительных интервалов регрессионных моделей разобрана в статье «Python, корреляция и регрессия: часть 4» (https://habr.com/ru/post/558158/), всем рекомендую ознакомиться.
Найти прогнозные значения Y не представляет труда, так как ранее мы уже формализовали модель в виде лямбда-функции, а вот для построения доверительных интервалов придется выполнить расчеты по формулам. Для этого создадим пользовательскую функцию regression_pair_predict, которая в случае парной регрессии (pair regression) для заданного значения X возвращает:
-
прогнозируемое по регрессионной модели значение y_calc
-
доверительный интервал [y_calc_mean_ci_low, y_calc_mean_ci_upp] средних значений переменной Y
-
доверительный интервал [y_calc_predict_ci_low, y_calc_predict_ci_upp] индивидуальных значений переменной Y
Алгоритм расчета доверительных интервалов для множественной регрессии (multiple regression) отличается и в данном обзоре не рассматривается (рассмотрим в дальнейшем).
Про прогнозирование с помощью регрессионных моделей — см.также:
-
https://www.statsmodels.org/stable/generated/statsmodels.regression.linear_model.RegressionResults.predict.html?highlight=predict#statsmodels.regression.linear_model.RegressionResults.predict
-
How to Make Predictions Using Regression Model in Statsmodels
-
https://www.statsmodels.org/stable/examples/notebooks/generated/predict.html
def regression_pair_predict(
x_in,
model_fit,
regression_model,
p_level: float=0.95):
a_level = 1 - p_level
X = pd.DataFrame(model_fit.model.exog)[1].values # найти лучшее решение
Y = model_fit.model.endog
# вспомогательные величины
n = int(result_linear_ols.nobs)
SSE = model_fit.ssr # SSE (Sum of Squared Error)
dfE = n - p - 1
MSE = SSE / dfE # остаточная дисперсия
Xmean = np.mean(X)
SST_X = np.sum([(X[i] - Xmean)**2 for i in range(0, n)])
t_table = sci.stats.t.ppf((1 + p_level)/2 , dfE)
S2_y_calc_mean = MSE * (1/n + (x_in - Xmean)**2 / SST_X)
S2_y_calc_predict = MSE * (1 + 1/n + (x_in - Xmean)**2 / SST_X)
# прогнозируемое значение переменной Y
y_calc=regression_model(x_in)
# доверительный интервал средних значений переменной Y
y_calc_mean_ci_low = y_calc - t_table*sqrt(S2_y_calc_mean)
y_calc_mean_ci_upp = y_calc + t_table*sqrt(S2_y_calc_mean)
# доверительный интервал индивидуальных значений переменной Y
y_calc_predict_ci_low = y_calc - t_table*sqrt(S2_y_calc_predict)
y_calc_predict_ci_upp = y_calc + t_table*sqrt(S2_y_calc_predict)
result = y_calc, y_calc_mean_ci_low, y_calc_mean_ci_upp, y_calc_predict_ci_low, y_calc_predict_ci_upp
return resultСравним результаты расчета доверительных интервалов разными способами — с использованием функции regression_pair_predict и средствами statsmodels, для этого сформируем DaraFrame с новыми данными:
regression_pair_predict_df = pd.DataFrame(
[regression_pair_predict(elem, result_linear_ols, regression_model=Y_calc) for elem in st_df['X'].values],
columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
regression_pair_predict_df.insert(0, 'X', st_df['X'].values)
display(regression_pair_predict_df)Видим, что результаты расчетов идентичны, следовательно мы можем использовать функцию regression_pair_predict для прогнозирования.
def graph_regression_pair_predict_plot_sns(
model_fit,
regression_model_in,
Xmin=None, Xmax=None, Nx=10,
Ymin_graph=None, Ymax_graph=None,
title_figure=None, title_figure_fontsize=18,
title_axes=None, title_axes_fontsize=16,
x_label=None,
y_label=None,
label_fontsize=14, tick_fontsize=12,
label_legend_regr_model='', label_legend_fontsize=12,
s=50, linewidth_regr_model=2,
graph_size=(297/INCH, 210/INCH),
result_output=True,
file_name=None):
# фактические данные
X = pd.DataFrame(model_fit.model.exog)[1].values # найти лучшее решение
Y = model_fit.model.endog
X = np.array(X)
Y = np.array(Y)
# границы
if not(Xmin) and not(Xmax):
Xmin=min(X)
Xmax=max(X)
Xmin_graph=min(X)*0.99
Xmax_graph=max(X)*1.01
else:
Xmin_graph=Xmin
Xmax_graph=Xmax
if not(Ymin_graph) and not(Ymax_graph):
Ymin_graph=min(Y)*0.99
Ymax_graph=max(Y)*1.01
# формируем DataFrame данных
Xcalc = np.linspace(Xmin, Xmax, num=Nx)
Ycalc = regression_model_in(Xcalc)
result_df = pd.DataFrame(
[regression_pair_predict(elem, model_fit, regression_model=regression_model_in) for elem in Xcalc],
columns=['y_calc', 'y_calc_mean_ci_low', 'y_calc_mean_ci_upp', 'y_calc_predict_ci_low', 'y_calc_predict_ci_upp'])
result_df.insert(0, 'x_calc', Xcalc)
# заголовки графика
fig, axes = plt.subplots(figsize=graph_size)
fig.suptitle(title_figure, fontsize = title_figure_fontsize)
axes.set_title(title_axes, fontsize = title_axes_fontsize)
# фактические данные
sns.scatterplot(
x=X, y=Y,
label='фактические данные',
s=s,
color='red',
ax=axes)
# график регрессионной модели
sns.lineplot(
x=Xcalc, y=Ycalc,
color='blue',
linewidth=linewidth_regr_model,
legend=True,
label=label_legend_regr_model,
ax=axes)
# доверительный интервал средних значений переменной Y
Mean_ci_low = result_df['y_calc_mean_ci_low']
plt.plot(
result_df['x_calc'], Mean_ci_low,
color='magenta', linestyle='--', linewidth=1,
label='доверительный интервал средних значений Y')
Mean_ci_upp = result_df['y_calc_mean_ci_upp']
plt.plot(
result_df['x_calc'], Mean_ci_upp,
color='magenta', linestyle='--', linewidth=1)
# доверительный интервал индивидуальных значений переменной Y
Predict_ci_low = result_df['y_calc_predict_ci_low']
plt.plot(
result_df['x_calc'], Predict_ci_low,
color='orange', linestyle='-.', linewidth=2,
label='доверительный интервал индивидуальных значений Y')
Predict_ci_upp = result_df['y_calc_predict_ci_upp']
plt.plot(
result_df['x_calc'], Predict_ci_upp,
color='orange', linestyle='-.', linewidth=2)
axes.set_xlim(Xmin_graph, Xmax_graph)
axes.set_ylim(Ymin_graph, Ymax_graph)
axes.set_xlabel(x_label, fontsize = label_fontsize)
axes.set_ylabel(y_label, fontsize = label_fontsize)
axes.tick_params(labelsize = tick_fontsize)
#axes.tick_params(labelsize = tick_fontsize)
axes.legend(prop={'size': label_legend_fontsize})
plt.show()
if file_name:
fig.savefig(file_name, orientation = "portrait", dpi = 300)
if result_output:
return result_df
else:
return
graph_regression_pair_predict_plot_sns(
model_fit=result_linear_ols,
regression_model_in=Y_calc,
Xmin=Xmin_graph-300, Xmax=Xmax_graph+200, Nx=25,
Ymin_graph=Ymin_graph-5, Ymax_graph=Ymax_graph+5,
title_figure=Task_Project, title_figure_fontsize=16,
title_axes='Линейная регрессионная модель', title_axes_fontsize=14,
x_label=Variable_Name_X,
y_label=Variable_Name_Y,
label_legend_regr_model=f'линейная регрессия Y = {b0:.3f} + {b1:.4f}*X',
s=50,
result_output=True,
file_name='graph/regression_plot_lin.png')Выводы и рекомендации
Исследована зависимость показаний ультразвукового прибора «ПУЛЬСАР-2.1» (X) и результатов замера прочности бетона (методом отрыва со скалыванием) склерометром ИПС-МГ4.03 (Y).
Между переменными имеется весьма сильная линейная корреляционная связь. Получена регрессионная модель:
Y = b0 + b1∙X = -21.3741 + 0.0129∙X
Модель хорошо аппроксимирует фактические данные, является адекватной, значимой и может использоваться для предсказания прочности бетона.
Также построен график прогноза с доверительными интервалами.
ИТОГИ
Итак, мы рассмотрели все этапы регрессионного анализа в случае простой линейной регрессии (simple linear regression) с использованием библиотеки statsmodels на конкретном практическом примере; подробно остановились на статистическом анализа модели с проверкой гипотез; также предложен ряд пользовательских функций, облегчающих работу исследователя и уменьшающих размер программного кода.
Конечно, мы разобрали далеко не все вопросы анализа регрессионных моделей и возможности библиотеки statsmodels применительно к simple linear regression, в частности статистики влияния (Influence Statistics), инструмент Leverage, анализ стьюдентизированных остатков и пр. — это темы для отдельных обзоров.
Исходный код находится в моем репозитории на GitHub.
Надеюсь, данный обзор поможет специалистам DataScience в работе.
Диагностика систем машинного обучения
86 мин на чтение
(128.303 символов)
Что такое метрики эффективности?
Для того, чтобы эффективно проводить обучение моделей необходимо иметь способ оценки, насколько хорошо та или иная модель выполняет свою работу — предсказывает значение целевой переменной. Кажется, мы уже что-то подобное изучали. У каждой модели есть функция ошибки, которая показывает, на сколько модель соответствует эмпирическим значениям. Однако, использование функции ошибки не очень удобно для оценки именно “качества” уже построенных моделей. Ведь эта функция специально создается для единственной цели — организации процесса обучения. Поэтому для оценки уже построенных моделей используется не функция ошибки, а так называемые метрики эффективности — специальные функции, которые показывают, насколько эффективна уже готовая, обученная модель.
Метрики эффективности на первый взгляд очень похожи на функции ошибки, ведь у них одна цель — отличать хорошие модели от плохих. Но делают они это по-разному, по-разному и применяются. К метрикам эффективности предъявляются совершенно другие требования, нежели к функциям ошибки. Поэтому давайте рассмотрим, для чего нужны и те и другие.
Функция ошибки нужна в первую очередь для формализации процесса обучения модели. То есть для того, чтобы подбирать параметры модели именно такими, чтобы модель как можно больше соответствовала реальным данным в обучающей выборке. Да, значение этой функции можно использовать как некоторую оценку качества модели уже после того, как она обучена, но это не удобно.
Функция ошибки нужна, чтобы формализовать отклонения предсказанных моделью значений от реальных. Например, в методе линейной регрессии функция ошибки (среднеквадратическое отклонение) используется для метода градиентного спуска. Поэтому функция ошибки обязательно должна быть везде дифференцируемой, мы это отдельно отмечали, когда говорили про метод градиентного спуска. Это требование — дифференцируемость — нужно исключительно для метода оптимизации, то есть для обучения модели.
Зато функция, которая используется для оценки качества модели совершенно не должна быть аналитической и гладкой. Ведь мы не будем вычислять ее производную, мы только вычислим ее один раз для того, чтобы понять, насколько хорошая модель получилась. Так что не любую метрику эффективности вообще физически возможно использовать как функцию ошибки — метод обучения может просто не сработать.
Кроме того, функция ошибки должна быть вычислительно простой, ведь ее придется считать много раз в процессе обучения — тысячи или миллионы раз. Это еще одно требование, которое совершенно необязательно для метрики эффективности. Она как раз может считаться довольно сложно, ведь вычислять ее приходится всего несколько раз.
Зато метрика эффективности должна быть понятной и интерпретируемой, в отличие от функции ошибки. Раньше мы подчеркивали, что само абсолютное значение функции ошибки ничего не показывает. Важно лишь, снижается ли оно в процессе обучения. И разные значения функции ошибки имеет смысл сравнивать только на одних и тех же данных. Что значит, если значение функции ошибки модели равно 35 000? Да ничего, только то, что эта модель хуже, чем та, у которой ошибка 32 000.
Для того, чтобы значение было более понятно, метрики эффективности зачастую выражаются в каких-то определенных единицах измерения — чеще всего в натуральных или в процентах. Натуральные единицы — это единицы измерения целевой переменной. Допустим, целевая переменная выражается в рублях. То есть, мы предсказываем некоторую стоимость. В таком случае будет вполне понятно, если качество этой модели мы тоже выразим в рублях. Например, так: модель в среднем ошибается на 500 рублей. И сразу становится ясно, насколько эта модель применима на практике.
Еще одно важное отличие. Как мы сказали, требования к функции ошибки определяются алгоритмом оптимизации. Который, в свою очередь зависит от типа модели. У линейной регрессии будет один алгоритм (и одна функция ошибки), а у, например, решающего дерева — другой алгоритм и совершенно другая функция ошибки. Это в частности значит, что функцию ошибки невозможно применять для сравнения нескольких разных моделей, обученных на одной и той же задаче.
И вот для этого как раз и нужны метрики эффективности. Они не зависят от типа модели, а выбираются исходя из задачи и тех вопросов, ответы на которые мы хотим получить. Например, в одной задаче качество модели лучше измерять через среднеквадратическую логарифмическую ошибку, а в другой — через медианную ошибку. Как раз в этом разделе мы посмотрим на примеры разных метрик эффективности, на их особенности и сферы применения.
Кстати, это еще означает, что в каждой конкретной задаче вы можете применять сразу несколько метрик эффективности, для более глубокого понимания работы модели. Зачастую так и поступают, ведь одна метрика не может дать полной информации о сильных и слабых сторонах модели. Тут исследователи ничем не ограничены. А вот функция ошибки обязательно должна быть только одна, ведь нельзя одновременно находить минимум сразу нескольких разных функций (на самом деле можно, но многокритериальная оптимизация — это гораздо сложнее и не используется для обучения моделей).
| Функция ошибки | Метрика эффективности |
|---|---|
| Используется для организации процесса обучения | Используется для оценки качества полученной модели |
| Используется для нахождения оптимума | Используется для сравнения моделей между собой |
| Должна быть быстро вычислимой | Должна быть понятной |
| Должна конструироваться исходя их типа модели | Должна выбираться исходя из задачи |
| Может быть только одна | Может быть несколько |
Еще раз определим, эффективность — это свойство модели машинного обучения давать предсказания значения целевой переменной, как можно ближе к реальным данным. Это самая главная характеристика модели. Но надо помнить, что исходя из задачи и ее условий, к моделям могут предъявляться и другие требования, как сказали бы в программной инженерии — нефункциональные. Типичный пример — скорость работы. Иногда маленький выигрыш в эффективности не стоит того, что модель стала работать в десять раз меньше. Другой пример — интерпретируемость модели. В некоторых областях важно не только сделать точное предсказание, но и иметь возможность обосновать его, провести анализ, выработать рекомендации по улучшению ситуации и так далее. Все эти нефункциональные требования — скорость обучения, скорость предсказания, надежность, робастность, федеративность, интерпретируемость — выходят за рамки данного пособия. Здесь мы сконцентрируемся на измерении именно эффективности модели.
Обратите внимание, что мы старательно избегаем употребления слова “точность” при описании качества работы модели. Хотя казалось бы, оно подходит как нельзя лучше. Дело в том, что “точностью” называют одну из метрик эффективности моделей классификации. Поэтому мы не хотим внести путаницу в термины.
Как мы говорили, метрики эффективности не зависят от самого типа модели. Для их вычисления обычно используется два вектора — вектор эмпирических значений целевой переменной (то есть тех, которые даны в датасете) и вектор теоретических значений (то есть тех, которые выдала модель). Естественно, эти вектора должны быть сопоставимы — на соответствующих местах должны быть значения целевой переменной, соответствующие одном у и тому же объекту. И, конечно, у них должна быть одинаковая длина. То есть метрика зависит от самих предсказаний, но не от модели, которая их выдала. Причем, большинство метрик устроены симметрично — если поменять местами эти два вектора, результат не изменится.
При рассмотрении метрик надо помнить следующее — чем выше эффективность модели, тем лучше. Но некоторые метрики устроены как измерение ошибки модели. В таком случае, конечно, тем ниже, тем лучше. Так что эффективность и ошибка модели — это по сути противоположные понятия. Так сложилось, что метрики регрессии чаще устроены именно как ошибки, а метрики классификации — как метрики именно эффективности. При использовании конкретной метрики на это надо обращать внимание.
Выводы:
- Метрики эффективности — это способ показать, насколько точно модель отражает реальный мир.
- Метрики эффективность должны выбираться исходя из задачи, которую решает модель.
- Функция ошибки и метрика эффективности — это разные вещи, к ним предъявляются разные требования.
- В задаче можно (и, зачастую, нужно) применять несколько метрик эффективности.
- Наряду с метриками эффективности есть и другие характеристики моделей — скорость обучения, скорость работы, надежность, робастность, интерпретируемость.
- Метрики эффективности вычисляются как правило из двух векторов — предсказанных (теоретических) значений целевой переменной и эмпирических (реальных) значений.
- Обычно метрики устроены таким образом, что чем выше значение, тем модель лучше.
Метрики эффективности для регрессии
Как мы говорили в предыдущем пункте, метрики зависят от конкретной задачи. А все задачи обучения с учителем разделяются на регрессию и классификацию. Совершенно естественно, что метрики для регрессии и для классификации будут разными.
Метрики эффективности для регрессии оценивают отклонение (расстояние) между предсказанными значениями и реальными. Кажется, что это очевидно, но метрики эффективности классификации устроены по-другому. Предполагается, что чем меньше каждое конкретное отклонение, тем лучше. Разница между разными метриками в том, как учитывать индивидуальные отклонения в общей метрике и в том, как агрегировать ряд значений в один интегральный показатель.
Все метрики эффективности моделей регрессии покажутся вам знакомыми, если вы изучали математическую статистику, ведь именно статистические методы легли в основу измерения эффективности моделей машинного обучения. Причем, метрики эффективности — это лишь самые простые статистические показатели, которые можно использовать для анализа качества модели. При желании можно и нужно задействовать более мощные статистические методы исследования данных. Например, можно проанализировать вид распределения отклонений, и сделать из этого вывод о необходимость корректировки моделей. Но в 99% случаев можно обойтись простым вычислением одной или двух рассматриваемых ниже метрик.
Так как метрики эффективности позволяют интерпретировать оценку качества модели, они зачастую неявно сравнивают данную модель с некоторой тривиальной. Тривиальна модель — это очень простая, даже примитивная модель, которая выдает предсказания оценки целевой переменной абсолютно без оглядки на эффективность и вообще соответствие реальным данным. Тривиальной моделью может выступать, например, предсказание для любого объекта среднего значения целевой переменной из обучающей выборки. Такие тривиальные модели нужны, чтобы оценить, насколько данная модель лучше или хуже них.
Естественно, мы хотим получить модель, которая лучше тривиальной. Причем, у нас есть некоторый идеал — модель, которая никогда не ошибается, то есть чьи предсказания всегда совпадают с реальными значениями. Поэтому реальная модель может быть лучше тривиальной только до этого предела. У такой идеальной модели, говорят, 100% эффективность или нулевая ошибка.
Но надо помнить, что в задачах регрессии модель предсказывает непрерывное значение. Это значит, что величина отклонения может быть неограниченно большой. Так что не бывает нижнего предела качества модели. Модель регрессии может быть бесконечно далекой от идеала, бесконечно хуже даже тривиальной модели. Поэтому ошибки моделей регрессии не ограничиваются сверху (или, что то же самое, эффективность моделей регрессии не ограничивается снизу).
Поэтому в задачах регрессии
Выводы:
- Метрики эффективности для регрессий обычно анализируют отклонения предсказанных значений от реальных.
- Большинство метрик пришло в машинное обучение из математической статистики.
- Результаты работы модели можно исследовать более продвинутыми статистическими методами.
- Обычно метрики сравнивают данную модель с тривиальной — моделью, которая всегда предсказывает среднее реальное значение целевой переменной.
- Модель могут быть точны на 100%, но плохи они могут быть без ограничений.
Коэффициент детерминации (r-квадрат)
Те, кто раньше хотя бы немного изучал математическую статистику, без труда узнают первую метрику эффективности моделей регрессии. Это так называемый коэффициент детерминации. Это доля дисперсии (вариации) целевой переменной, объясненная данной моделью. Данная метрика вычисляется по такой формуле:
[R^2(y, hat{y}) = 1 — frac
{sum_{i=1}^n (y_i — hat{y_i})^2}
{sum_{i=1}^n (y_i — bar{y_i})^2}]
где
$y$ — вектор эмпирических (истинных) значений целевой переменной,
$hat{y}$ — вектор теоретических (предсказанных) значений целевой переменной,
$y_i$ — эмпирическое значение целевой переменной для $i$-го объекта,
$hat{y_i}$ — теоретическое значение целевой переменной для $i$-го объекта,
$bar{y_i}$ — среднее из эмпирических значений целевой переменной для $i$-го объекта.
Если модель всегда предсказывает идеально (то есть ее предсказания всегда совпадают с реальностью, другими словами, теоретические значения — с эмпирическими), то числитель дроби в формуле будет равен 0, а значит, вся метрика будет равна 1. Если же мы рассмотрим тривиальную модель, которая всегда предсказывает среднее значение, то числитель будет равен знаменателю, дробь будет равна 1, а метрика — 0. Если модель хуже идеальной, но лучше тривиальной, то метрика будет в диапазоне от 0 до 1, причем чем ближе к 1 — тем лучше.
Если же модель предсказывает такие значения, что отклонения их от теоретических получаются больше, чем от среднего значения, то числитель будет больше знаменателя, а значит, что метрика будет принимать отрицательные значения. Запомните, что отрицательные значения коэффициента детерминации означают, что модель хуже, чем тривиальная.
В целом эта метрика показывает силу линейной связи между двумя случайными величинами. В нашем случае этими величинами выступают теоретические и эмпирические значения целевой переменной (то есть предсказанные и реальные). Если модель дает точные предсказания, то будет наблюдаться сильная связь (зависимость) между теоретическим значением и реальным, то есть высокая детерминация, близкая к 1. Если эе модель дает случайные предсказания, никак не связанные с реальными значениями, то связь будет отсутствовать.
Причем так как нас интересует, насколько значения совпадают, нам достаточно использовать именно линейную связь. Ведь когда мы оцениваем связь, например, одного из факторов в целевой переменной, то связь может быть нелинейной, и линейный коэффициент детерминации ее не покажет, то есть пропустит. Но в данному случае это не важно, так как наличие нелинейной связи означает, что предсказанные значения все-таки отклоняются от реальных. Такую линейную связь можно увидеть на графике, если построить диаграмму рассеяния между теоретическими и эмпирическими значениями, вот так:
1
2
3
4
5
6
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X, Y)
Y_ = reg.predict(X)
plt.scatter(Y, Y_)
plt.plot(Y, Y)
Здесь мы еще строим прямую $y = y$. Она нужна только для удобства. Вот как может выглядеть этот график:
Здесь мы видим, что точки немного отклоняются от центральной линии, но в целом ей следуют. Такая картина характерна для высокого коэффициента детерминации. А вот как может выглядеть менее точная модель:
И в целом, чем точки ближе к центральной линии, тем лучше модель и тем ближе коэффициент детерминации к 1.
В англоязычной литература эта метрика называется $R^2$, так как в определенных случаях она равна квадрату коэффициента корреляции. Пусть это название не вводит вас в заблуждение. Некоторые думаю, что раз метрика в квадрате, то она не может быть отрицательной. Это лишь условное название.
Пару слов об использовании метрик эффективности в библиотеке sklearn. Именно коэффициент детерминации чаще всего используется как метрика по умолчанию, которую можно посмотреть при помощи метода score() у модели регрессии. Обратите внимание, что этот метод принимает на вход саму обучающую выборку. Это сделано для единообразия с методами наподобие fit().
Но более универсально будет использовать эту метрику независимо от модели. Все метрики эффективности собраны в отдельный пакет metrics. Данная метрика называется r2_score. Обратите внимание, что при использовании этой функции ей надо передавать два вектора целевой переменной — сначала эмпирический, а вторым аргументом — теоретический.
1
2
3
4
5
6
7
8
from sklearn.metrics import r2_score
def r2(y, y_):
return 1 - ((y - y_)**2).sum() / ((y - y.mean())**2).sum()
print(reg.score(X, Y))
print(r2_score(Y, Y_))
print(r2(Y, Y_))
В данном коде мы еще реализовали самостоятельный расчет данной метрики, чтобы пояснить применение формулы выше. Можете самостоятельно убедиться, что три этих вызова напечатают одинаковые значения.
Коэффициент детерминации, или $R^2$ — это одна из немногих метрик эффективности для моделей регрессии, значение которой чем больше, тем лучше. Почти все остальные измеряют именно ошибку, что мы и увидим ниже. Еще это одна из немногих несимметричных метрик. Ведь если в формуле поменять теоретические и эмпирические значения, ее смысл и значение могут поменяться. Поэтому при использовании этой метрики нужно обязательно следить за порядком передачи аргументов.
При использовании этой метрики есть один небольшой подводный камень. Так как в знаменатели у этой формулы стоит вариация реального значения целевой переменной, важно следить, чтобы эта вариация присутствовала. Ведь если реальное значение целевой переменной будет одинаковым для всех объектов выборки, то вариация этой переменной будет равна 0. А значит, метрика будет не определена. Причем это единственная причина, почему эта метрика может быть неопределена. Надо понимать, что отсутствие вариации целевой переменной ставит под сомнение вообще целесообразность машинного обучения и моделирования в целом. Ведь что нам предсказывать если $y$ всегда один и тот же? С другой стороны, такая ситуация может случиться, например, при случайном разбиении выборки на обучающую и тестовую. Но об этом мы поговорим дальше.
Выводы:
- Коэффициент детерминации показывает силу связи между двумя случайными величинами.
- Если модель всегда предсказывает точно, метрика равна 1. Для тривиальной модели — 0.
- Значение метрики может быть отрицательно, если модель предсказывает хуже, чем тривиальная.
- Это одна из немногих несимметричных метрик эффективности.
- Эта метрика не определена, если $y=const$. Надо следить, чтобы в выборке присутствовали разные значения целевой переменной.
Средняя абсолютная ошибка (MAE)
Коэффициент детерминации — не единственная возможная характеристика эффективности моделей регрессии. Иногда полезно оценить отклонения предсказаний от истинных значений более явно. Как раз для этого служат сразу несколько метрик ошибок моделей регрессии. Самая простая из них — средняя абсолютная ошибка (mean absolute error, MAE). Она вычисляется по формуле:
[MAE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} |y_i — hat{y_i}|]
Данная метрика действительно очень проста: это средняя величина разницы между предсказанными и реальными значениями целевой переменной. Причем эта разница берется по модулю, чтобы компенсировать возможные отрицательные отклонения. Мы уже рассматривали похожую функцию, когда говорили о конструировании функции ошибки для градиентного спуска. Но тогда мы отмели использование абсолютного значения, так как эта функция не везде дифференцируема. Но вот для метрики эффективности такого требования нет и MAE вполне можно использовать.
Если модель предсказывает идеально, то, естественно, все отклонения равны 0 и MAE в целом равна нулю. Но эта метрика не учитывает явно сравнение с тривиальной моделью — она просто тем хуже, чем больше. Ниже нуля она быть, конечно, не может.
Данная метрика выражается в натуральных единицах и имеет очень простой и понятный смысл — средняя ошибка модели. Степень применимости модели в таком случае можно очень просто понять исходя из предметной области. Например, наша модель ошибается в среднем на 500 рублей. Хорошо это или плохо? Зависит от размерности исходных данных. Если мы предсказываем цены на недвижимость — то модель прекрасно справляется с задачей. Если же мы моделируем цены на спички — то такая модель скорее всего очень неэффективна.
Использование данной метрики в пакете sklearn очень похоже на любую другую метрику, меняется только название:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
Выводы:
- MAE показывает среднее абсолютное отклонение предсказанных значений от реальных.
- Чем выше значение MAE, тем модель хуже. У идеальной модели $MAE=0$
- MAE очень легко интерпретировать — на сколько в среднем ошибается модель.
Средний квадрат ошибки (MSE)
Средний квадрат ошибки (mean squared error, MSE) очень похож на предыдущую метрику, но вместо абсолютного значения (модуля) используется квадрат:
[MSE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2]
Граничные случаи у этой метрики такие же, как у предыдущей — 0 у идеальной модели, а в остальном — чем больше, тем хуже. MSE у тривиальной модели будет равна дисперсии целевой переменной. Но это не то, чтобы очень полезно на практике.
Эта метрика используется во многих моделях регрессии как функция ошибки. Но вот как метрику эффективности ее применяют довольно редко. Дело в ее интерпретируемости. Ведь она измеряется в квадратах натуральной величины. А какой физический смысл имеют, например, рубли в квадрате? На самом деле никакого. Поэтому несмотря на то, что математически MAE и MSE в общем-то эквивалентны, первая более проста и понятна, и используется гораздо чаще.
Единственное существенное отличие данной метрики от предыдущей состоит в том, что она чуть больший “вес” в общей ошибке придает большим значениям отклонений. То есть чем больше значение отклонения, тем сильнее оно будет вкладываться в значение MSE. Это иногда бывает полезно, когда исходя из задачи стоит штрафовать сильные отклонения предсказанных значений от реальных. Но с другой стороны это свойство делает эту метрику чувствительной к аномалиям.
Пример расчета метрики MSE:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred, squared=False)
0.612...
Выводы:
- MAE показывает средний квадрат отклонений предсказанных значений от реальных.
- Чем выше значение MSE, тем модель хуже. У идеальной модели $MSE=0$
- MSE больше учитывает сильные отклонения, но хуже интерпретируется, чем MAE.
Среднеквадратичная ошибка (RMSE)
Если главная проблема метрики MSE в том, что она измеряется в квадратах натуральных величин, что что будет, если мы возьмем от нее квадратный корень? Тогда мы получим среднеквадратичную ошибку (root mean squared error, RMSE):
[RMSE(y, _hat{y}) = sqrt{frac{1}{n} sum_{i=0}^{n-1} (y_i — hat{y_i})^2}]
Использование данной метрики достаточно привычно при статистическом анализе данных. Однако, для интерпретации результатов машинного обучения она имеет те же недостатки, что и MSE. Главный из них — чувствительность к аномалиям. Поэтому при интерпретации эффективности моделей регрессии чаще рекомендуется применять метрику MAE.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
Выводы:
- RMSE — это по сути корень из MSE. Выражается в тех же единицах, что и целевая переменная.
- Чаще применяется при статистическом анализа данных.
- Данная метрика очень чувствительна к аномалиям и выбросам.
Среднеквадратичная логарифмическая ошибка (MSLE)
Еще одна довольно редкая метрика — среднеквадратическая логарифмическая ошибка (mean squared logarithmic error, MSLE). Она очень похожа на MSE, но квадрат вычисляется не от самих отклонений, а от разницы логарифмов (про то, зачем там +1 поговорим позднее):
[MSLE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1} (
ln(1 + y_i) — ln(1 + hat{y_i})
)^2]
Данная материка имеет специфическую, но довольно полезную сферу применения. Она применяется в тех случаях, когда значения целевой переменной простираются на несколько порядков величины. Например, если мы анализируем доходы физических лиц, они могут измеряться от тысяч до сотен миллионов. Понятно, что при использовании более привычных метрик, таких как MSE, RMSE и даже MAE, отклонения в больших значениях, даже небольшие относительно, будут полностью доминировать над отклонениями в малых значениях.
Это приведет к тому, что оценка моделей в подобных задачах классическими метриками будет давать преимущество моделям, которые более точны в одной части выборки, но почти не будут учитывать ошибки в других частях выборки. Это может привести к несправедливой оценке моделей. А вот использование логарифма поможет сгладить это противоречие.
Чаще всего, величины с таким больших размахом, что имеет смысл использовать логарифмическую ошибку, возникают в тех задачах, которые моделируют некоторые естественные процессы, характеризующиеся экспоненциальным ростом. Например, моделирование популяций, эпидемий, финансов. Такие процессы часто порождают величины, распределенные по экспоненциальному закону. А они чаще всего имеют область значений от нуля до плюс бесконечности, то есть иногда могут обращаться в ноль.
Проблема в том, что логарифм от нуля не определен. Именно поэтому в формуле данной метрики присутствует +1. Это искусственный способ избежать неопределенности. Конечно, если вы имеете дело с величиной, которая может принимать значение -1, то у вас опять будут проблемы. Но на практике такие особые распределения не встречаются почти никогда.
Использование данной метрике в коде полностью аналогично другим:
1
2
3
4
5
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
Выводы:
- MSLE это среднее отклонение логарифмов реальных и предсказанных данных.
- Так же, идеальная модель имеет $MSLE = 0$.
- Данная метрика используется, когда целевая переменная простирается на несколько порядков величины.
- Еще эта метрика может быть полезна, если моделируется процесс в экспоненциальным ростом.
Среднее процентное отклонение (MAPE)
Все метрики, которые мы рассматривали до этого рассчитывали абсолютную величину отклонения. Но ведь отклонение в 5 единиц при истинном значении 5 и при значении в 100 — разные вещи. В первом случае мы имеем ошибку в 100%, а во втором — только в 5%. Очевидно, что первый и второй случай должны по-разному учитываться в ошибке. Для этого придумана средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE). В ней каждое отклонение оценивается в процентах от истинного значения целевой переменной:
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, |y_i|)}]
Эта метрика имеет одно критическое преимущество над остальными — с ее помощью можно сравнивать эффективность моделей на разных обучающих выборках. Ведь если мы возьмем классические метрики (например, MAE), то размер отклонений будет очевидно зависеть от самих данных. А в двух разных выборках и средняя величина скорее всего будет разная. Поэтому метрики MAE, MSE, RMSE, MSLE не сопоставимы при сравнении предсказаний, сделанных на разных выборках.
А вот по метрике MAPE можно сравнивать разные модели, которые были обучены на разных данных. Это очень полезно, например, в научных публикациях, где метрика MAPE (и ее вариации) практически обязательны для описания эффективности моделей регрессии.Ведь если одна модель ошибается в среднем на 3,9%, а другая — на 3,5%, очевидно, что вторая более точна. А вот если оперировать той же MAE, так сказать нельзя. Ведь если одна модель ошибается в среднем на 500 рублей, а вторая — на 490, очевидно ли, что вторая лучше? Может, она даже хуже, просто в исходных данных величина целевой переменной во втором случае была чуть меньше.
При этом у метрики MAPE есть пара недостатков. Во-первых, она не определена, если истинное значение целевой переменной равно 0. Именно для преодоления этого в знаменателе формулы этой метрики присутствует $max(epsilon, |y_i|)$. $epsilon$ — это некоторое очень маленькое значение. Оно нужно только для того, чтобы избежать деления на ноль. Это, конечно, настоящий математический костыль, но позволяет без опаски применять эту метрику на практике.
Во-вторых, данная метрика дает преимущество более низким предсказаниям. Ведь если предсказание ниже, чем реальное значение, процентное отклонение может быть от 0% до 100%. В это же время если предсказание выше реального, то верхней границы нет, предсказание может быть больше и на 200%, и на 1000%.
В-третьих, эта метрика несимметрична. Ведь в этой формуле $y$ и $hat{y}$ не взаимозаменяемы. Это не большая проблема и может быть исправлена использованием симметричного варианта этой метрики, который называется SMAPE (symmetric mean absolute percentage error):
[MAPE(y, _hat{y}) = frac{1}{n} sum_{i=0}^{n-1}
frac{|y_i — hat{y_i}|}{max(epsilon, (|hat{y_i}|, |y_i|) / 2)}]
В русскоязычной литературе данная метрика часто называется относительной ошибкой, так как она учитывает отклонение относительно целевого значения. В английском названии метрики она называется абсолютной. Тут нет никакого противоречия, так как “абсолютный” здесь значит просто взятие по модулю.
С точки зрения использования в коде, все полностью аналогично:
1
2
3
4
5
>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666...
Выводы:
- Идея этой метрики — это чувствительность к относительным отклонениям.
- Данная модель выражается в процентах и имеет хорошую интерпретируемость.
- Идеальная модель имеет $MAPE = 0$. Верхний предел — не ограничен.
- Данная метрика отдает предпочтение предсказанию меньших значений.
Абсолютная медианная ошибка
Практически во всех ранее рассмотренных метриках используется среднее арифметическое для агрегации частных отклонений в общую величину ошибки. Иногда это может быть не очень уместно, если в выборке присутствует очень неравномерное распределение по целевой переменной. В таких случаях может быть целесообразно использование медианной ошибки:
[MedAE(y, _hat{y}) = frac{1}{n} median_{i=0}^{n-1}
|y_i — hat{y_i}|]
Эта метрика полностью аналогична MAE за одним исключением: вместо среднего арифметического подсчитывается медианное значение. Медиана — это такое значение в выборке, больше которого и меньше которого примерно половина объектов выборки (с точностью до одного объекта).
Эта метрика чаще всего применяется при анализе демографических и экономических данных. Ее особенность в том, что она не так чувствительна к выбросам и аномальным значениям, ведь они практически не влияют на медианное значение выборки, что делает эту метрику более надежной и робастной, чем абсолютная ошибка.
Пример использования:
1
2
3
4
5
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
Выводы:
- Медианная абсолютная ошибка похожа на среднюю абсолютную, но более устойчива к аномалиям.
- Применяется в задачах, когда известно, что в данных присутствуют выбросы, аномальные , непоказательные значения.
- Эта метрика более робастная, нежели MAE.
Максимальная ошибка
Еще одна достаточно экзотическая, но очень простая метрика эффективности регрессии — максимальная ошибка:
[ME(y, _hat{y}) = max_{i=0}^{n-1}
|y_i — hat{y_i}|]
Как следует из названия, это просто величина максимального абсолютного отклонения предсказанных значений от теоретических. Особенность этой метрики в том, что она вообще не характеризует распределение отклонений в целом. Поэтому она практически никогда не применяется самостоятельно, в качестве единственной метрики.
Эта метрика именно вспомогательная. В сочетании с другими метриками, она может дополнительно охарактеризовать, насколько сильно модель может ошибаться в самом худшем случае. Опять же, в зависимости от задачи, это может быть важно. В некоторых задачах модель, которая в среднем ошибается пусть чуть больше, но при этом не допускает очень больших “промахов”, может быть предпочтительнее, чем более точная модель в среднем, но у которой встречаются сильные отклонения.
Применение этой метрики та же просто, как и других:
1
2
3
4
5
>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6
Выводы:
- Максимальная ошибка показывает наихудший случай предсказания модели.
- В некоторых задачах важно, чтобы модель не ошибалась сильно, а небольшие отклонения не критичны.
- Зачастую эта метрика используется как вспомогательная совместно с другими.
Метрики эффективности для классификации
Приступим к рассмотрению метрик эффективности, которые применяются для оценки моделей классификации. Для начала ответим на вопрос, почему для них нельзя использовать те метрики, которые мы уже рассмотрели в предыдущей части? Дело в том, что метрики эффективности регрессии так или иначе оценивают расстояние от предсказанного значения до реального. Это подразумевает, что в значениях целевой переменной существует определенный порядок. Формально говоря, предполагается, что целевая переменная измеряется по относительной шкале. Это значит, что разница между значениями имеет какой-то смысл. Например, если мы ошиблись в предполагаемой цене товара на 10 рублей, это лучше, чем ошибка на 20 рублей. Причем, можно сказать, что это в два раза лучше.
Но вот целевые переменные, которые существуют в задачах классификации обычно не обладают таким свойством. Да, метки классов часто обозначают числами (класс 0, класс 1, класс 5 и так далее). И мы используем эти числа в качестве значения переменных в программе. Но это ничего не значит. Представим объект, принадлежащий 0 классу, что бы этот класс не значил. Допустим, мы предсказали 1 класс. Было бы хуже, если бы мы предсказали 2 класс. Можно ли сказать, что во втором случае модель ошиблась в два раза сильнее? В общем случае, нельзя. Что в первом, что во втором случае модель просто ошиблась. Имеет значение только разница между правильным предсказанием и неправильным. Отклонение в задачах классификации не играет роли.
Поэтому метрики эффективности для классификации оценивают количество правильно и неправильно классифицированных (иногда еще говорят, распознанных) объектов. При этом разные метрики, как мы увидим, концентрируются на разных соотношениях этих количеств, особенно в случае, когда классов больше двух, то есть имеет место задача множественной классификации.
Причем метрики эффективности классификации тоже нельзя применять для оценки регрессионных моделей. Дело в том, что в задачах регрессии почти никогда не встречается полное совпадение предсказанного и реального значения. Так как мы работам с непрерывным континуумом значений, вероятность такого совпадения равна, буквально, нулю. Поэтому по метрикам для классификации практически любая регрессионная модель будет иметь нулевую эффективность, даже очень хорошая и точная модель. Именно потому, что для метрик классификации даже самая небольшая ошибка уже считается как промах.
Как мы говорили ранее,для оценки конкретной модели можно использовать несколько метрик одновременно. Это хорошая практика для задач регрессии, но для классификации — это практически необходимость. Дело в том, что метрики классификации гораздо легче “обмануть” с помощью тривиальных моделей, особенно в случае несбалансированных классов (об этом мы поговорим чуть позже). Тривиальной моделью в задачах классификации может выступать модель, которая предсказывает случайный класс (такая используется чаще всего), либо которая предсказывает всегда какой-то определенный класс.
Надо обратить внимание, что по многим метрикам, ожидаемая эффективность моделей классификации сильно зависит от количества классов в задаче. Чем больше классов, тем на меньшую эффективность в среднем можно рассчитывать.Поэтому метрики эффективности классификации не позволяют сопоставить задачи, состоящие из разного количества классов. Это следует помнить при анализе моделей. Если точность бинарной классификации составляет 50%, это значит, что модель работает не лучше случайного угадывания. Но в модели множественной классификации из, допустим, 10 000 классов, точность 50% — это существенно лучше случайного гадания.
Еще обратим внимание, что некоторые метрики учитывают только само предсказание, в то время, как другие — степень уверенности модели в предсказании. Вообще, все модели классификации разделяются на логические и метрические. Логические методы классификации выдают конкретное значение класса, без дополнительной информации. Типичные примеры — дерево решений, метод ближайших соседей. Метрические же методы выдают степень уверенности (принадлежности) объекта к одному или, чаще, ко всем классам. Так, например, работает метод логистической регрессии в сочетании с алгоритмом “один против всех”. Так вот, в зависимости, от того, какую модель классификации вы используете, вам могут быть доступны разные метрики. Те метрики, которые оценивают эффективность классификации в зависимости от выбранной величины порога не могут работать с логическими методами. Поэтому, например, нет смысла строить PR-кривую для метода ближайших соседей. Остальные метрики, которые не используют порог, могут работать с любыми методами классификации.
Выводы:
- Метрики эффективности классификации подсчитывают количество правильно распознанных объектов.
- В задачах классификации почти всегда надо применять несколько метрик одновременно.
- Тривиальной моделью в задачах классификации считается та, которая предсказывает случайный класс, либо самый популярный класс.
- Качество бинарной классификации при прочих равных почти всегда будет сильно выше, чем для множественной.
- Вообще, чем больше в задаче классов, тем ниже ожидаемые значения эффективности.
- Некоторые метрики работают с метрическими методами, другие — со всеми.
Доля правильных ответов (accuracy)
Если попробовать самостоятельно придумать способ оценить качество модели классификации, ничего не зная о существующих метриках, скорее всего получится именно метрика точности (accuracy). Это самая простая и естественная метрика эффективности классификации. Она подсчитывается как количество объектов в выборке, которые были классифицированы правильно (то есть, для которых теоретическое и эмпирическое значение метки класса — целевой переменной — совпадает), разделенное на общее количество объектов выборки. Вот формула для вычисления точности классификации:
[acc(y, hat{y}) = frac{1}{n} sum_{i=0}^{n} 1(hat{y_i} = y_i)]
В этой формуле используется так называемая индикаторная функция $1()$. Эта функция равна 1 тогда, когда ее аргумент — истинное выражение, и 0 — если ложное. В данном случае она равна единице для всех объектов, у которых предсказанное значение равно реальному ($hat{y_i} = y_i$). Суммируя по всем объектам мы получим количество объектов, классифицированных верно. Перед суммой стоит множитель $frac{1}{n}$, где $n$ — количество объектов в выборке. То есть в итоге мы получаем долю правильных ответов исследуемой модели.
Значение данной метрики может быть выражено в долях единицы, либо в процентах, домножив значение на 100%. Чем выше значение accuracy, тем лучше модель классифицирует выборку, то есть тем лучше ответы модели соответствуют значениям целевой переменной, присутствующим в выборке. Если модель всегда дает правильные предсказания, то ее accuracy будет равн 1 (или 100%). Худшая модель, которая всегда предсказывает неверно будет иметь accuracy, равную нулю, причем это нижняя граница, хуже быть не может.
В дальнейшем, для обозначения названий метрик эффективности я буду использовать именно английские названия — accuracy, precision, recall. У каждого из этих слов есть перевод на русский, но так случилось, что в русскоязычных терминах существует путаница. Дело в том, что и accuracy и precision чаще всего переводятся словом “точность”. А это разные метрики, имеющие разный смысл и разные формулы. Accuracy еще называют “правильность”, precision — “прецизионность”. Причем у последнего термина есть несколько другое значение в метрологии. Поэтому, пока будем обозначать эти метрики изначальными названиями.
А вот accuracy тривиальной модели будет как раз зависеть от количества классов. Если мы имеем дело с бинарной классификацией, то модель будет ошибаться примерно в половине случаев. То есть ее accuracy будет 0,5. В общем же случае, если есть $m$ классов, то тривиальная модель, которая предсказывает случайный класс будет иметь accuracy в среднем около $frac{1}{m}$.
Но это в случае, если в выборке объекты разных классов встречаются примерно поровну. В реальности же часто встречаются несбалансированные выборки, в которых распределение объектов по классам очень неравномерно. Например, может быть такое, что объектов одного класса в десять раз больше, чем другого. В таком случае, accuracy тривиальной модели может быть как выше, так и ниже $1/m$. Вообще, метрика accuracy очень чувствительна к соотношению классов в выборке. И именно поэтому мы рассматриваем другие способы оценки качества моделей классификации.
Использование метрики accuracy в библиотеке sklearn ничем принципиальным не отличается от использования других численных метрик эффективности:
1
2
3
4
5
6
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
В данном примере в задаче 4 класса (0, 1, 2, 3) и столько же объектов, по одному на каждый класс. Модель правильно классифицировала первый и третий объект, то есть половину. Поэтому ее accuracy составляет 0,5 или 50%.
Выводы:
- Точность (accuracy) — самая простая метрика качества классификации, доля правильных ответов.
- Может быть выражена в процентах и в долях единицы.
- Идеальная модель дает точность 1.0, тривиальная — 0.5, самая худшая — 0.0.
- Тривиальная модель в множественной сбалансированной задаче классификации дает точность 1/m.
- Метрика точности очень чувствительная к несбалансированности классов.
Метрики классификации для неравных классов (precision, recall, F1)
Как мы говорили ранее, метрика accuracy может быть чувствительна к несбалансированности классов. Рассмотрим типичный пример — диагностика заболевания. Допустим, в случайной выборке людей заболевание встречается один раз на 100 человек. То есть в выборке у нас может быть всего 1% объектов, принадлежащих положительному классу и 99% — отрицательному, то есть почти в 100 раз больше. Какая accuracy будет у абсолютно тривиальной модели, которая всегда предсказывает отрицательный класс? Такая модель будет права в 99% случаев и ошибаться только в 1%. То есть иметь accuracy 0,99. Естественно, ценность такой модели минимальна, несмотря на высокий показатель метрики. Поэтому в случае с сильно несбалансированными классами метрика accuracy не то, чтобы неверна, она непоказательна, то есть не дает хорошего представления о качественных характеристиках модели.
Для более полного описания модели используется ряд других метрик. Для того, чтобы понять, как они устроены и что показывают нужно разобраться с понятием ошибок первого и второго рода. Пока будем рассматривать случай бинарной классификации, а о том, как эти метрики обобщаются на множественные задачи, поговорим позднее. Итак, у нас есть задача бинарной классификации, объекты положительного и отрицательного класса. Идеальным примером для этого будет все та же медицинская диагностика.
По отношению к модели бинарной классификации все объекты выборки можно разделить на четыре непересекающихся множества. Истинноположительные (true positive, TP) — это те объекты, которые отнесены моделью к положительному классу и действительно ему принадлежат. Истинноотрицательные (true negative, TN) — соответственно те, которые правильно распознаны моделью как принадлежащие отрицательному классу. Ложноположительные объекты (FP, false positive) — это те, которые модель распознала как положительные, хотя на самом деле они отрицательные. В математической статистике такая ситуация называется ошибкой первого рода. И, наконец, ложноотрицательные значения (false negative, FN) — это те, которые ошибочно отнесены моделью к отрицательному классу, хотя на самом деле они принадлежат положительному.
В примере с медицинско диагностикой, ложноположительные объекты или ошибки первого рода — это здоровые пациенты, которых при диагностике ошибочно назвали больными. Ложноотрицательные, или ошибки второго рода, — это больные пациенты, которых диагностическая модель “пропустила”, ошибочно приняв за здоровых. Очевидно, что в этой задаче, как и во многих других, ошибки первого и второго рода не равнозначны. В медицинской диагностике, например, гораздо важнее распознать всех здоровых пациентов, то есть не допустить ложноотрицательных объектов или ошибок второго рода. Ошибки же первого рода, или ложноположительные предсказания, тоже нежелательны, но значительно меньше, чем ложноотрицательные.
Так вот, метрика accuracy учитывает и те и другие ошибки одинаково, абсолютно симметрично. В терминах наших четырех классов она может выражаться такой формулой:
[A = frac{TP + TN}{TP + TN + FP + FN}]
Обратите внимание, что если в модели переименовать положительный класс в отрицательный и наоборот, то это никак не повлияет на accuracy. Так вот, в зависимости от решаемой задачи, нам может быть необходимо воспользоваться другими метриками. Вообще, их существует большое количество, но на практике чаще других применяются метрики precision и recall.
Precision (чаще переводится как “точность”, “прецизионность”) — это доля объектов, плавильно распознанных как положительные из всех, распознанных как положительные. Считается этот показатель по следующей формуле: $P = frac{TP}{TP + FP}$. Как можно видеть, precision будет равен 1, если модель не делает ошибок первого рода, то есть не дает ложноположительных предсказаний. Причем ошибки второго рода (ложноотрицательные) вообще не влияют на величину precision, так как эта метрика рассматривает только объекты, отнесенные моделью к положительным.
Precision характеризует способность модели отличать положительный класс от отрицательного, не делать ложноположительных предсказаний. Ведь если мы будем всегда предсказывать отрицательный класс, precision будет не определен. А вот если модель будет всегда предсказывать положительный класс, то precision будет равен доли объектов этого класса в выборке. В нашем примере с медицинской диагностикой, модель, всех пациентов записывающая в больные даст precision всего 0,01.
Метрика recall (обычно переводится как “полнота” или “правильность”) — это доля положительных объектов выборки, распознанных моделью. То есть это отношение все тех же истинноположительных объектов к числу всех положительных объектов выборки: $R = frac{TP}{TP + FN}$. Recall будет равен 1 только в том случае, если модель не делает ошибок второго рода, то есть не дает ложноотрицательных предсказаний. А вот ошибки первого рода (ложноположительные) не влияют на эту метрику, так как она рассматривает только объекты, которые на самом деле принадлежат положительному классу.
Recall характеризует способность модели обнаруживать все объекты положительного класса. Если мы будем всегда предсказывать отрицательный класс, то данная метрика будет равна 0, а если всегда положительный — то 1. Метрика Recall еще называется полнотой, так как она характеризует полноту распознавания положительного класса моделью.
В примере с медицинской диагностикой нам гораздо важнее, как мы говорили, не делать ложноотрицательных предсказаний. Поэтому метрика recall будет для нас важнее, чем precision и даже accuracy. Однако, как видно из примеров, каждый из этих метрик легко можно максимизировать довольно тривиальной моделью. Если мы будет ориентироваться на recall, то наилучшей моделью будет считаться та, которая всегда предсказывает положительный класс. Если только на precision — то “выиграет” модель, которая всегда предсказывает наоборот, положительный. А если брать в расчет только accuracy, то при сильно несбалансированных классах модель, предсказывающая самый популярный класс. Поэтому эти метрики нелья использовать по отдельности, только сразу как минимум две из них.
Так как метрики precision и recall почти всегда используются совместно, часто возникает ситуация, когда есть две модели, у одной из которых выше precision, а у второй — recall. Возникает вопрос, как выбрать лучшую? Для такого случая можно посчитать среднее значение. Но для этих метрик больше подойдет среднее не арифметическое, а гармоническое, ведь оно равно 0, если хотя бы одно число равно 0. Эта метрика называется $F_1$:
[F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN}]
Эта метрика полезна, если нужно одно число, которое в себе объединяет и precision и recall. Но эта формула подразумевает, что нам одинаково важны и то и другое. А как мы заметили раньше, часто одна из этих метрик важнее. Поэтому иногда используют обобщение метрики $F_1$, так называемое семейство F-метрик:
[F_{beta} = (1 + beta^2) frac{P R}{beta^2 P + R}]
Эта метрика имеет параметр $beta > 0$, который определяет, во сколько раз recall важнее precision. Если этот параметр больше единицы, то метрика будет полагать recall более важным. А если меньше — то важнее будет precision. Если же $beta = 1$, то мы получим уже известную нам метрику $F_1$. Все метрики из F-семейства измеряются от 0 до 1, причем чем значение больше, тем модель лучше.
1
2
3
4
5
6
7
8
9
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
Выводы:
- Если классы в задаче не сбалансированы, то метрика точности не дает полного представления о качестве работы моделей.
- Для бинарной классификации подсчитывается количество истинно положительных, истинно отрицательных, ложно положительных и ложно отрицательных объектов.
- Precision — доля истинно положительных объектов во всех, распознанных как положительные.
- Precision характеризует способность модели не помечать положительные объекты как отрицательные (не делать ложно положительных прогнозов).
- Recall — для истинно положительных объектов во всех положительных.
- Recall характеризует способность модели выявлять все положительные объекты (не делать ложно отрицательных прогнозов).
- F1 — среднее гармоническое между этими двумя метриками. F1 — это частный случай. Вообще, семейство F-метрик — это взвешенное среднее гармоническое.
- Часто используют все вместе для более полной характеристики модели.
Матрица классификации
Матрица классификации — это не метрика сама по себе, но очень удобный способ “заглянуть” внутрь модели и посмотреть, насколько хорошо она классифицирует какую-то выборку объектов. Особенно удобна эта матрица в задачах множественной классификации, когда из-за большого количества классов численные метрики не всегда наглядно показывают, какие объекты к каким классам относятся.
С использованием библиотеки sklearn матрица классификации может быть сформирована всего одной строчкой кода:
1
2
3
4
5
6
7
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
В этой матрице по строкам располагаются истинные значения целевой переменной, то есть действительные значения классов. По столбцам же отмечены предсказанные классы. В самой матрице на пересечении строки и столбца отмечается число объектов, которые принадлежат данному действительному классу, но моделью были распознаны как объекты данного предсказанного класса.
Естественно, элементы, располагающиеся на главной диагонали, показывают объекты, которые были правильно распознаны моделью. Элементы же вне этой диагонали — это ошибки классификации. Поэтому чем лучше модель, тем выше должны быть значения по диагонали и тем меньше — вне ее. В идеале все элементы вне главной диагонали должны быть нулевыми.
Но гораздо удобнее представлять ее в графическом виде:
Источник: sklearn.
В таком виде матрица представляется в виде тепловой карты, в которой чем выше значение, тем насыщеннее оттенок цвета. Это позволяет при первом взгляде на матрицу понять, как часто она ошибается и в каких именно классах. В отличие от простых численных метрик, матрица классификации может дать информацию о паттернах распространенных ошибок, которые допускает данная модель.
Практически любое аномальное или тривиальное поведение модели будет иметь отражение в матрице классификации. Например, если модель чаще чем нужно предсказывает один класс, это сразу подсветит отдельный столбец в ней. Если же модель путает два класса, то есть не различает объекты этих классов, то в матрице будут подсвечены четыре элемента, располагающиеся в углах прямоугольника. Еще одно распространенное поведение модель — когда она распознает объекты одного класса, как объекты другого — подсветит один элемент вне главной диагонали.
Эта матрица очень наглядно показывает, как часто и в каких конкретно классах ошибается модель. Поэтому анализ этой матрицы может дать ценную информацию о путях увеличения эффективности моделей. Например, можно провести анализ ошибок на основе показаний данной матрицы — проанализировать объекты, на которых модель чаще всего ошибается. Может, будет выявлена какая-то закономерность, либо общая характеристика. Добавление информации о таких параметрах объектов к матрице атрибутов обычно очень сильно улучшает эффективность моделей.
Выводы:
- Матрица классификации, или матрица ошибок представляет собой количество объектов по двум осям — истинный класс и предсказанный класс.
- Обычно, истинный класс располагается по строкам, а предсказанный — по столбцам.
- Для идеальной модели матрица должна содержать ненулевые элементы только на главной диагонали.
- Матрица позволяет наглядно представить результаты классификации и увидеть, в каких случаях модель делает ошибки.
- Матрица незаменима при анализе ошибок, когда исследуется, какие объекты были неправильно классифицированы.
Метрики множественной классификации
Все метрики, о которых мы говорили выше рассчитываются в случае бинарной классификации, так как определяются через понятия ложноположительных, ложноотрицательных прогнозов. Но на практике чаще встречаются задачи множественной классификации. В них не определяется один положительный и один отрицательный класс, поэтому все рассуждения о precision и recall, казалось бы, не имеют смысла.
На самом деле, все рассмотренные метрики прекрасно обобщаются на случай множественных классов. Рассмотрим простой пример. У нас есть три класса — 0, 1 и 2. Есть пять объектов, каждый их которых принадлежит одному их этих трех классов. Истинные значения целевой переменной такие: $y = lbrace 0, 1, 2, 2, 0 rbrace$. Имеется модель, которая предсказывает классы этих объектов, соответственно так: $hat{y} = lbrace 0, 0, 2, 1, 0 rbrace$. Давайте рассчитаем известные нам метрики качества классификации.
С метрикой accuracy все просто. Модель правильно предсказала класс в трех случаях из пяти — первом, третьем и пятом. А в двух случаях — ошиблась. Поэтому метрика рассчитывается так: $A = 3 / 5 = 0.6$. То есть точность модели — 60%.
А вот precision и recall рассчитываются более сложно. В моделях множественной классификации эти метрики могут быть рассчитаны отдельно по каждому классу. Подход в этом случае очень похож на алгоритм “один против всех” — для каждого класса он предполагается положительным, а все остальные классы — отрицательными. Давайте рассчитаем эти метрики на нашем примере.
Возьмем нулевой класс. Его обозначим за 1, а все остальные — за 0. Тогда вектора эмпирических и теоретических значений целевой пременной станут выглядеть так:
$y = lbrace 1, 0, 0, 0, 1 rbrace$,
$hat{y} = lbrace 1, 1, 0, 0, 1 rbrace$.
Тогда $P = frac{TP}{TP + FP} = frac{2}{3} approx 0.67$, ведь у нас получается 2 истинноположительных предсказания (первый и пятый объекты) и одно ложноположительное (второй). $R = frac{TP}{TP + FN} = frac{2}{2} = 1$, ведь в модели нет ложноотрицательных прогнозов.
$F_1 = frac{2 P R}{P + R} = frac{2 TP}{2 TP + FP + FN} = frac{2 cdot 2}{2 cdot 2 + 1 + 0} = frac{4}{5} = 0.8$.
Аналогично рассчитываются метрики и по остальным классам. Например, для первого класса вектора целевой переменной будут такими:
$y = lbrace 0, 1, 0, 0, 0 rbrace$,
$hat{y} = lbrace 0, 0, 0, 1, 0 rbrace$. Обратите внимание, что в данном случае получается, что модель ни разу не угадала. Такое тоже бывает, и в таком случае, метрики будут нулевые. Для третьего класса попробуйте рассчитать метрики самостоятельно, а чуть ниже можно увидеть правильный ответ.
Конечно, при использовании библиотечный функций не придется рассчитывать все эти метрики вручную. В библиотеке sklearn для этого есть очень удобная функция — classification_report, отчет о классификации, которая как раз вычисляет все необходимые метрики и представляет результат в виде наглядной таблицы. Вот как будет выглядеть рассмотренный нами пример:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
Здесь мы видим несколько строк, соответствующих классам в нашей задаче. По каждому классу рассчитаны метрики precision, recall и $F_1$. Последний столбец называется support — это количество объектов данного класса в используемой выборке. Это тоже важный показатель, так как чем меньше объектов какого-то класса, тем хуже он обычно распознается.
Ниже приведены интегральные, то есть общие метрики эффективности модели. Это три последние строки таблицы. В первую очередь это accuracy — она всегда рассчитывается один раз. Обратите внимание, что в столбце support здесь везде стоит 5 — это общее число объектов выборки. Ниже приведены средние значения по метрикам precision, recall и $F_1$. Почему же строк две? Дело в том, что усреднять эти метрики можно по-разному.
Во-первых, можно взять обычное среднее арифметическое из метрик всех классов. Это называется macro average. Это самый простой способ, но у него есть одна проблема. Почему метрики очень малочисленных классов должны давать тот же вклад в итоговый результат, что и метрики очень многочисленных? Можно усреднить метрики используя в качестве весов долю каждого класса в выборке. Такое усреднение называется weighted average. Обратите внимание, что при усреднении метрика $F_1$ может получиться не между precision и recall.
Отчет о классификации — очень полезная функция, использование которой практически обязательно при анализе эффективности моделей классификации. Особенно для задач множественной классификации. Эта таблица может дать важную информацию о том, какие классы распознаются моделью лучше, какие — хуже, как это связано в численностью классов в выборке. Анализ этой таблицы может навести на необходимость определенных действий по повышению эффективности модели. Например, можно понять, какие данные полезно будет добавить в модель.
Выводы:
- Метрики для каждого класса рассчитываются, полагая данный класс положительным, а все остальные — отрицательными.
- Каждую метрику можно усреднить арифметически или взвешенно по классам. Весами выступают объемы классов.
- В модуле sklearn реализовано несколько алгоритмов усреднения они выбираются исходя их задачи.
- В случае средневзвешенного, F1-метрика может получиться не между P и R.
- Отчет о классификации содержит всю необходимую информацию в стандартной форме.
- Отчет показывает метрики для каждого класса, а так же объем каждого класса.
- Также отчет показывает средние и средневзвешенные метрики для всей модели.
- Отчет о классификации — обязательный элемент представления результатов моделирования.
- По отчету можно понять сбалансированность задачи, какие классы определяются лучше, какие — хуже.
PR-AUC
При рассмотрении разных моделей классификации мы упоминали о том, что они подразделяются на метрические и логические методы. Логические методы (дерево решений, k ближайших соседей) выдают конкретную метку класса,без какой-либо дополнительной информации. Метрические методы (логистическая регрессия, перцептрон, SVM) выдают принадлежность данного объекта к разным классам, присутствующим в задаче. При рассмотрении модели логистической регрессии мы говорили, что предсказывается положительный класс, если значение логистической функции больше 0,5.
Но это пороговое значение можно поменять. Что будет, если мы измени его на 0,6? Тогда мы для некоторых объектовы выборки изменим предсказание с положительного класса на отрицательный. То есть без изменения модели можно менять ее предсказания. Это значит, что изменятся и метрики модели, то есть ее эффективность.
Чем больше мы установим порог, тем чаще будем предсказывать отрицательный класс. Это значит, что в среднем, у модели будет меньше ложноположительных предсказаний, но может стать больше ложноотрицательных. Значит, у модели может увеличится precision, то упадет recall. В крайнем случае, если мы возьмем порог равный 1, мы всегда будем предсказывать отрицательный класс. Тогда у модели будет $P = 1, R = 0$. Если же, наоборот, возьмем в качестве порога 0, то мы всегда будем предсказывать отрицательный класс, а значит у модели будет $P = 0, R = 1$, так как она не будет давать ложноположительных прогнозов, но будут встречаться ложноотрицательные.
Это означает, что эффективность моделей метрической классификации зависит не только от того, как модель соотносится с данными, но и от значения порога. Из этого следует, кстати, что было бы не совсем правильно вообще сравнивать метрики двух разных моделей между собой. Ведь значение этих метрик будет зависеть не только от самих моделей, но и от порогов, которые они используют. Может, первая модель будет лучше, если немного изменить ее пороговое значение? Может, одна из метрик второй модели станет выше, если изменить ее порог.
Это все сильно затрудняет анализ метрических моделей классификации. Для сравнения разных моделей необходим способ “убрать” влияние порога, сравнить модели вне зависимости от его значения. И такой способ есть. Достаточно просто взять все возможные значения порога, посчитать метрики в каждом из них и затем усреднить. Для этого служит PR-кривая или кривая “precision-recall”:
Каждая точка на этом графике представляет собой значение precision и recall для конкретного значения порога. Для построения этого графика выбирают все возможные значение порога и отмечают на графике. Давайте рассмотрим простой пример из 10 точек. Истинные значения классов этих точек равны, соответственно, $y = lbrace 0, 0, 0, 0, 0, 1, 1, 1, 1, 1 rbrace$. Модель (сейчас совершенно неважно, какая) выдает следующие предсказания для этих объектов: $h(x) = lbrace 0.1, 0.2, 0.3, 0.45, 0.6, 0.4, 0.55, 0.7, 0.8, 0.9 rbrace$. Заметим, что модель немного ошибается для средних объектов, то есть она не будет достигать стопроцентной точности. Построим таблицу, в которой переберем некоторые значения порога и вычислим, к какому классу будет относиться объект при каждом значении порога:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0,1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,3 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,45 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0,6 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0,4 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,55 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0,8 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0,9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Можно сразу заметить, что чем выше порог, тем чаще предсказывается отрицательный класс. В крайних случаях модель всегда предсказывает либо положительный класс (при малых значениях порога), либо отрицательный (при больших).
Далее, для каждого значения порога рассчитаем количество истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных предсказаний. На основе этих данных легко рассчитать и метрики precision и recall. Запишем это в таблицу:
| y | h(x) | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TP | 5 | 5 | 5 | 5 | 5 | 4 | 3 | 3 | 2 | 1 | 0 | |
| TN | 0 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 5 | 5 | 5 | |
| FP | 5 | 5 | 4 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | |
| FN | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 3 | 4 | 5 | |
| P | 0,50 | 0,50 | 0,56 | 0,63 | 0,71 | 0,80 | 0,75 | 1,00 | 1,00 | 1,00 | 1,00 | |
| R | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 |
При самом низком значении порога модель всегда предсказывает отрицательный класс, метрика recall равна 1, а метрика precision равна доли отрицательного класса в выборке. Причем ниже этого значения precision уже не опускается. Можно заметить, что в целом при повышении порога precision повышается, а recall понижается. В другом крайнем случае, когда порог равен 1, модель всегда предсказывает отрицательный класс, метрика recall равна 0, а precision — 1 (на самом деле эта метрика не определена, но считается равной именно 1, так как ее значение стремится к этому при повышении порога). За счет чего это происходит?
При повышении порога может произойти один из трех случаев. Первый заключается в том, что данное изменение может не влияет ни на одно предсказание. Так происходит, например, при повышении порога с 0,1 до 0,15. Оценка ни одного объекта не попадает в данный диапазон, поэтому ни одно предсказание не меняется. И, соответственно, не изменится ни одна метрика.
Если же повышение порога все-таки затрагивает один или несколько объектов, то изменение предсказания может произойти только с положительного на отрицательное. Допустим, для простоты, что повышение порога затрагивает только один объект. То есть мы изменяем предсказание по одному объекту с 1 на 0. Второй случай заключается в том, что это изменение правильное. То есть объект в действительности принадлежит отрицательному классу. Так происходит, например, при изменении порога с 0,15 до 0,2. В данном случае первый объект из ложноположительного стал истинно отрицательным. Такое изменение не влияет на recall, но повышает precision.
Третий случай заключается в том, что изменение предсказаные было неверным. То есть объект из истинно положительного стал ложноотрицательным. Это происходит, например, при изменении порога с 0,4 до 0,5 — в данном случае шестой объект становится классифицированным ошибочно. Уменьшение количества истинно положительных объектов снижает обе метрики — и precision и recall.
Таким образом можно заключить, что recall при повышении порога может оставаться неизменным или снижаться, а precision может как повышаться, так и понижаться, но в среднем будет повышаться за счет уменьшения доли ложноположительных предсказаний. Если изобразить рассмотренный пример на графике можно получить такую кривую:
PR-кривая не всегда монотонна, обе метрики могут изменяться как однонаправленно, так и разнонаправленно при изменении порогового значения. Но главный смысл этой кривой не в этом. При таком анализе очень просто обобщить эффективность модели вне зависимости от значения порога. Для этого нужно всего лишь найти площадь под графиком этой кривой. Эта метрика называется PR-AUC (area under the curve) или average precision (AP). Чем она выше, тем качественнее модель.
Давайте порассуждаем, ка будет вести себя идеальная модель. Крайние случаи, когда порога равны 0 и 1, значения метрик будут такими же, как и всегда. Но вот при любом другом значении порога модель будет классифицировать все объекты правильно. И обе метрики у нее будут равны 1. Таким образом, PR-кривая выродится в два отрезка, один из которых проходит из точки (0, 1) в точку (1, 1). и площадь под графиком будет равна 1. У самой худшей же модели метрики будут равны 0, так как она всегда будет предсказывать неверно. И площадь тоже будет равна 0.
У случайной модели, как можно догадаться, площадь под графиком будет равна 0,5. Поэтому метрика PR-AUC может использоваться для сравнения разных моделей метрической классификации вне зависимости от значения порога. Также эта метрика показывает соотношение данной модели и случайной. Если PR-AUC модели меньше 0,5, значит она хуже предсказывает класс, чем простое угадывание.
Выводы:
- Кривая precision-recall используется для методов метрической классификации, которые выдают вероятность принадлежности объекта данному классу.
- Дискретная классификации производится при помощи порогового значения.
- Чем больше порог, тем больше объектов модель будет относить к отрицательному классу.
- Повышение порога в среднем увеличивает precision модели, но понижает recall.
- PR-кривая используется чтобы выбрать оптимальное значение порога.
- PR-кривая нужна для того, чтобы сравнивать и оценивать модели вне зависимости от выбранного уровня порога.
- PR-AUC — площадь под PR-кривой, у лучшей модели — 1.0, у тривиальной — 0.5, у худшей — 0.0.
ROC_AUC
Помимо кривой PR есть еще один довольно популярный метод оценки эффективности метрических моделей классификации. Он использует тот же подход, что и PR-кривая, но немного другие координаты. ROC-кривая (receiver operating characteristic) — это график показывающий соотношение доли истинно положительных предсказаний и ложноположительных предсказаний в модели метрической классификации для разных значений порога.
В этой кривой используются два новых термина — доля истинно положительных и доля ложноположительных предсказаний. Доля истинно положительных предсказаний (TPR, true positive rate), как можно догадаться, это отношение количества объектов выборки, правильно распознанных как положительные, ко всем положительным объектам. Другими словами, это всего лишь иное название метрики recall.
А вот доля ложноположительных предсказаний (FPR, false positive rate) считается как отношение количества отрицательных объектов, неправильно распознанных как положительные, в общем количестве отрицательных объектов выборки:
[TPR = frac{TP}{TP + FN} = R
FRP = frac{FP}{TN + FP} = 1 — S]
Обратите внимание, что FPR — мера ошибки модели. То есть, чем больше — тем хуже. У идеальной модели $FRP=0$, а у наихудшей — $FPR=1$. Для иллюстрации давайте рассчитаем эти метрики для нашего примера, который мы использовали выше (для дополнительной информации еще приведена метрика accuracy для каждого значения порога):
| y | h(x) | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TPR | 1,00 | 1,00 | 1,00 | 1,00 | 0,80 | 0,60 | 0,60 | 0,40 | 0,20 | 0,00 | |
| FPR | 1,00 | 0,80 | 0,60 | 0,40 | 0,20 | 0,20 | 0,00 | 0,00 | 0,00 | 0,00 | |
| A | 0,50 | 0,60 | 0,70 | 0,80 | 0,80 | 0,70 | 0,80 | 0,70 | 0,60 | 0,50 |
Можно заметить, что при увеличении порога обе эти метрики увеличиваются, начиная со значения 1 до нуля. Причем, движения этих двух показателей всегда однонаправленно. Давайте опять же разберемся, почему так. Если увеличение порога приводит к правильному изменению классификации, то есть изменению ложноположительного значения на истинно отрицательное, то это уменьшит FRP, но не затронет TRP. Если же изменение будет неверным, то есть истинно положительное значение поменялось на ложноотрицательное, это однозначно уменьшит TPR, при этом FRP либо уменьшится так же, либо останется неименным.
В итоге, кривая получается монотонной, причем она всегда проходит через центр координат и через точку (1, 1). В нашем примере кривая будет выглядеть так:
Более сложные данные могут выглядеть с большим количеством деталей, но общая форма и монотонность сохраняются:
Также, как и с кривой PR, важное значение имеет площадь под графиком. Эта метрика называется ROC-AUC и является одной из самых популярных метрик качества метрических моделей классификации. Ее главное преимущество перед другими метриками состоит в том, что она позволяет объективно сопоставить уровень качества разных моделей классификации, решающих одну и ту же задачу, но обученных на разных данных. Это приводит к частому использованию ROC-AUC, например, в научной литературе для представления результатов моделирования.
Существует множество споров, какая диагностическая кривая более адекватно измеряет качество классификации — ROC или PR. Считается, что PR-кривая больше ориентирована на задачи, в которых присутствует дисбаланс классов. Это задачи в которых объектов одного класса значительно больше чем другого, классы имеют разное толкование и, как следствие, ошибки первого и второго рода не равнозначны. Зачастую это модели бинарной классификации. ROC же дает более адекватную картину в задачах, где классов примерно поровну в выборке. Но для полного анализа модели все равно рекомендуется использовать оба метода.
В случае с множественной классификацией построение диагностических кривых происходит отдельно по каждому классу. Так же, как и при расчете метрик precision и recall, каждый класс поочередно полагается положительным, а остальные — отрицательными. Каждая такая частная кривая показывает качество распознавания конкретного класса. Поэтому кривые могут выглядеть примерно так:
Источник: sklearn.
На данном графике мы видим PR-кривую модели множественной классификации из 3 классов. Кроме отдельных значений precision и recall в каждой точке рассчитываются и усредненные значения. Так формируется кривая средних значений. Интегральная метрика качества модели классификации считается как площадь под кривой средних значений. Алгоритм построения ROC-кривой полностью аналогичен.
Выводы:
- ROC-кривая показывает качество бинарной классификации при разных значениях порога.
- В отличие от PR-кривой, ROC-кривая монотонна.
- Площадь под графиком ROC-кривой, ROC_AUC — одна из основных метрик качества классификационных моделей.
- ROC_AUC можно использовать для сравнения качества разных моделей, обученных на разных данных.
- ROC чаще используют для сбалансированных и множественных задач, PR — для несбалансированных.
- Кривые для множественной классификации строятся отдельно для каждого класса.
- Метрика AUC считается по кривой средних значений.
Топ k классов
Все метрики, которые мы обсуждали выше оперируют точным совпадением предсказанного класса с истинным. В некоторых особых задачах может быть полезно немного смягчить это условие. Как мы говорили, метрические методы классификации выдают больше информации — степень принадлежности объекта выборки каждому классу. Обычно, мы выбираем из них тот класс, который имеет наибольшую принадлежность. Но можно выбрать не один класс, а несколько. Таким образом можно рассматривать не единственный вариант класса для конкретного объекта, а 3, 5, 10 и так далее.
Другими словами можно говорить о том, находится ли истинный класс объекта среди 3, 5 или 10 классов, которые выбрала для него модель. Количество классов, которые мы рассматриваем, можно брать любым. В данной метрике оно обозначается k. Таким образом, можно построить метрику, которая оценивает долю объектов выборки, для которых истинный класс находится среди k лучших предсказаний модели:
[tka(y, hat{f}) = frac{1}{n} sum_{i=0}^{n-1}
sum_{j=1}^{k} 1(hat{f_{ij}} = y_i)]
где $hat{f_{ij}}$ — это j-й в порядке убывания уверенности модели класс i-го объекта.
Рассмотрим такой пример. Пусть у нас есть задача классификации из 3 классов. Мы оцениваем 4 объекта, которые имеют на самом деле такие классы:
$y = lbrace 0, 1, 2, 2 rbrace$.
1
2
3
>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
Модель предсказывает следующие вероятности для каждого объекта:
1
2
3
4
>>> y_score = np.array([[0.5, 0.2, 0.2],
... [0.4, 0.3, 0.2],
... [0.2, 0.4, 0.3],
... [0.7, 0.2, 0.1]])
То есть для первого объекта она выбирает первый класс, но немного предполагает и второй. А вот, например, последний, четвертый объект она уверенно относит тоже к первому классу. Давайте посчитаем метрику топ-2 для этой модели. Для этого для каждого объекта рассмотрим, какие 2 класса модель называет наиболее вероятными. Для первого — это 0 и 1, для второго — также 0 и 1, причем модель отдает предпочтение 0 классу, хотя на самом деле объект относится к 1 классу. Для третьего — уже 2 и 2 класс, причем класс 1 кажется модели более вероятным, для четвертого — так же наиболее вероятными модели кажутся 0 и 1 класс.
Если бы мы говорили об обычной accuracy, то для такой модели она была бы равна 0,25. Ведь только для первого объекта модель дала правильное предсказание наиболее вероятного класса. Но по метрике топ-2, для целых трех объектов истинный класс находится среди двух наиболее вероятных. Модель полностью ошибается только в последнем случае. Так что эта метрика равна 0,75. Это же подтверждают и автоматические расчеты:
1
2
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
Как мы говорили, количество классов k можно взять любым. В частном случае $k=1$ эта метрика превращается в классическую accuracy. Чем больше возьмем k, тем выше будет значение данной метрики, но слабее условие. Так что брать очень большие k нет никакого смысла. В другом крайнем случае, когда k равно количеству классов, метрика будет равна 1 для любой модели.
Эта метрика имеет не очень много практического смысла. Ведь при прикладном применении моделей машинного обучения важен все-таки итоговый результат классификации. И если модель ошиблась, то модель ошиблась. Но эта метрика может пролить свет на внутреннее устройство модели, показать, насколько сильно она ошибается. Ведь одно дело, если модель иногда называет правильный ответ может и не наиболее вероятным, но в топ, скажем, 3. Совсем другое дело, если модель не находит правильный ответ и среди топ-10. Так что эта метрика может использоваться для диагностики моделей классификации и для поиска путей их совершенствования. Еще она бывает полезна, если две модели имеют равные значения метрики accuracy, но нужно понять, какая их них адекватнее имеющимся данным.
Такие проблемы часто возникают в задачах, где классов очень много. Например, в распознавании объектов на изображениях количество объектов может быть несколько тысяч. А в задачах обработки текста количество классов может определяться количеством слов в языке — сотни тысяч и миллионы (если учитывать разные формы слов). Естественно, что эффективность моделей классификации в таких задачах, измеренная обычными способами будет очень низкой. А данная метрика позволяет эффективно сравнивать и оценивать такие модели.
Выводы:
- Эта метрика — обобщение точности для случая, когда модель выдает вероятности отнесения к каждому классу.
- Вычисляется как доля объектов, для которых правильный класс попадает в список k лучших предсказанных классов.
- Чем больше k, тем выше метрика, но бесполезнее результат.
- Эта метрика часто применяется в задачах с большим количеством классов.
- Применимость этой метрики сильно зависит от характера задачи.
Проблема пере- и недообучения
Проблема Bias/Variance
При решении задачи методами машинного обучения всегда встает задача выбора вида модели. Как мы обсуждали в предыдущих главах, существует большое количество классов модели — достаточно вспомнить линейные модели, метод опорных векторов, перцептрон и другие. Каждая их этих моделей, будучи обученной на одном и том же наборе данных может давать разные результаты. Важно понимать, что мы не говорим о степени подстройки модели к данным. Даже если обучение прошло до конца, найдены оптимальные значения параметров, все равно модели могут и, скорее всего, будут различаться.
Причем многие классы моделей представляют собой не одно, а целое множество семейств функций. Например, та же логарифмическая регрессия — это не одна функция, а бесконечное количество — квадратичные, кубические, четвертой степени и так далее. Множество функций или моделей, имеющих единую форму, но различающуюся значениями параметров составляет так называемое параметрическое семейство функций. Так, все возможные линейные функции — это одно параметрическое семейство, все возможные квадратические — другое, а, например, множество всех возможных однослойных перцептронов с 5 нейронами во входном, 3 нейронами в скрытом и одном нейроне в выходном слое — третье семейство.
Таким образом можно говорить, что перед аналитиком стоит задача выбора параметрического семейства модели, которую он будет обучать на имеющихся данных. Причем разные семейства дадут модели разного уровня качества после обучения. К сожалению, очень сложно заранее предугадать, какое семейство моделей после завершения обучения даст наилучшее качество предсказания по данной выборке.
Что является главным фактором выбора этого семейства? Как показывает практика, самое существенное влияние на эффективность оказывает уровень сложности модели. Любое параметрическое семейство моделей имеет определенное количество степеней свободы, которое определяет то, насколько сложное и изменчивое поведение может демонстрировать получившаяся функция.
Сложность модели можно определять разными способами, но в контексте нашего рассуждения сложность однозначно ассоциируется с количеством параметров в модели. Чем больше параметров, тем больше у модели степеней свободы, возможности изменять свое поведение при разных значениях входных признаков. Конечно, это не означает полной эквивалентности разных типов моделей с одинаковым количеством параметров. Например, никто не говорит, что модель, скажем, регрессии по методу опорных векторов эквивалентна модели нейронной сети с тем же самым количеством весов. Главное, что модели со сходным уровнем сложности демонстрируют сходное поведение по отношению к конкретному набору данных.
Влияние уровня сложности на поведение модели относительно данных наиболее наглядно можно проследить на примере модели полиномиальной модели. Степень полинома — это очень показательная характеристика уровня сложности модели. Давайте рассмотрим три модели регрессии — линейную (которую можно рассматривать как полином первой степени), полином четвертой и двадцатой степени. Мы обучили эти модели на одном и том же датасете и вот что получилось:
Следует отдельно заметить, что в каждом из представленных случаев модель обучалась до конца, то есть до схождения метода численной оптимизации параметров. То есть для каждой модели на графике представлены оптимальные значения параметров. Гладя на эти три графика и то, как эти линии ложатся в имеющиеся точки, можно заметить некоторое противоречие. Естественно предположить, что модель, изображенная на втором графике показывает наилучшее описание точек данных. Но по любой метрике качества третья модель будет показывать более высокий результат.
Человек, глядя на график третьей модели, сразу сделает вывод, что она “слишком” хорошо подстроилась под имеющиеся данные. Сравните это поведение с первым графиком, который демонстрирует самую низкую эффективность на имеющихся данных. Можно проследить, как именно сложность модели влияет на ее применимость. Если модель слишком простая, то она может не выявить имеющиеся сложные зависимости между признаками и целевой переменной. Говорят, что у простых моделей низкая вариативность (variance). Слишком же сложная модель имеет слишком высокую вариативность, что тоже не очень хорошо.
Те же самые рассуждения можно применить и к моделям классификации. Можно взглянуть на форму границы принятия решения для трех моделей разного уровня сложности, обученных на одних и тех же данных:
В данном случае мы видим ту же картину — слишком простая модель не может распознать сложную форму зависимости между факторами и целевой переменной. Такая ситуация называется недообучение. Обратите внимание, что недообучение не говорит о том, что модель не обучилась не до конца. Просто недостаток сложности, вариативности модели не дает ни одной возможной функции их этого параметрического семейства хорошо описывать данные.
Слишком сложные модели избыточно подстраиваются под малейшие выбросы в данных. Это увеличивает значение метрик эффективности, но снижает пригодность модели на практике, так как очевидно, что модель будет делать большие ошибки на новых данных из той же выборки. Такая ситуация называется переобучением. Переобучение — это очень коварная проблема моделей машинного обучения, ведь на “бумаге” все метрики показывают отличный результат.
Конечно, в общем случае не получится так наглядно увидеть то, как модель подстраивается под данные. Ведь в случае, когда данные имеют большую размерность, строить графики в проекции не даст представления об общей картине. Поэтому ситуацию пере- и недообучения довольно сложно обнаружить. Для этого нужно проводить отдельную диагностику.
Это происходит потому, что в практически любой выборке данных конкретное положение точек, их совместное распределение определяется как существенной зависимостью между признаками и целевой переменной, так и случайными отклонениями. Эти случайные отклонения, выбросы, аномалии не позволяют сделать однозначный вывод, что модель, которая лучше описывает имеющиеся данные, является лучшей в глобальном смысле.
Выводы:
- Прежде чем обучать модель, нужно выбрать ее вид (параметрическое семейство функций).
- Разные модели при своих оптимальных параметрах будут давать разный результат.
- Чем сложнее и вариативнее модель, тем больше у нее параметров.
- Простые модели быстрые, но им недостает вариативности, изменчивости, у них высокое смещение (bias).
- Сложные модели могут описывать больше зависимостей, но вычислительно более трудоемкие и имеют большую дисперсию (variance).
- Слишком вариативные (сложные) модели алгоритм может подстраиваться под случайный шум в данных — переобучение.
- Слишком смещенные (простые) модели алгоритм может пропустить связь признака и целевой переменной — недообучение.
- Не всегда модель, которая лучше подстраивается под данные (имеет более высокие метрики эффективности) лучше.
Обобщающая способность модели, тестовый набор
Как было показано выше, не всякая модель, которая показывает высокую эффективность на тех данных, на которых она обучалась, полезна на практике. Нужно всегда помнить, что модели машинного обучения строят не для того, чтобы точно описывать объекты из обучающего набора. На то он и обучающий набор, что мы уже знаем правильные ответы. Цель моделирования — создать модель, которая на примере этих данных формализует некоторые внутренние зависимости в данных для того, чтобы адекватно описывать новые объекты, которые модель не учитывала при обучении.
Полезность модели машинного обучения определяется именно способность описывать новые данные. Это называется обобщающей способностью модели. И как мы показали в предыдущей главе, эффективность модели на тех данных, на которых она обучается, не дает адекватного понимания этой самой обобщающей способности модели. Вместе с тем, обобщающая способность — это главный показатель качества модели машинного обучения и у нас должен быть способ ее измерять.
Конечно, мы не можем измерить эффективность модели на тех данных, которых у нас нет. Поэтому для того, чтобы иметь адекватное представление об уровне качества модели применяется следующий трюк: до начала обучения весь имеющийся датасет разбивают на две части. Первая часть носит название обучающая выборка (training set) и используется для подбора оптимальных параметров модели, то есть для ее обучения. Вторая часть — тестовый набор (test set) — используется только для оценки эффективности модели.
Такая эффективность, измеренная на “новых” данных — объектах, которые модель не видела при своем обучении — дает более объективную оценку обобщающей силы модели, то есть эффективности, которую модель будет показывать на неизвестных данных. В машинном обучении часто действует такое правило — никогда не оценивать эффективность модели на тех данных, на которых она обучалась. Не то, чтобы этого нельзя делать категорически (и в следующих главах мы это часто будем применять), просто нужно осознавать, что эффективность модели на обучающей выборки всегда будет завышенной, ведь модель подстроилась именно к этим данным, включая все их случайные колебания.
Надо помнить, что все рассуждения и выводы в этой и последующих главах носят чисто вероятностный характер. Так что в конкретном случае, тестовая эффективность вполне может оказаться даже выше, чем эффективность на обучающей выборке. Когда мы говорим о наборах данных и случайных процессах, все возможно. Но смысл в том, что распределение оценки эффективности модели, измеренное на обучающих данных имеет значимо более высокое математическое ожидание, чем “истинная” эффективность этой модели.
Для практического применения этого приема надо ответить на два вопроса: как делить выборку и сколько данных оставлять на тестовый датасет. Что касается способа деления, здесь чуть проще — практически всегда делят случайным образом. Случайное разбиение выгодно тем, что у каждого объекта датасета равная вероятность оказаться в обучающей или в тестовой выборке. Причем, эта вероятность независима для всех объектов выборки. Это делает все случайные ошибки выборки нормально распределенными, то есть их математическое ожидание равно нулю. Об этом мы еще поговорим в следующей главе.
Но этот способ не работает в случае со специальными наборами данных. Например с временными рядами. Ведь при разбиении выборки важно, чтобы сами объекты в тестовой выборке были независимы от объектов обучающей. В случае, если мы анализируем какое-то неупорядоченное множество объектов, это почти всегда выполняется. Но для временных рядов это не так. Объекты более позднего времени могут зависеть от предыдущих объектов. Так цена актива за текущий период однозначно зависит от цены актива за предыдущий. Поэтому нельзя допустить, чтобы в обучающей выборке оказались объекты более ранние, чем в обучающей. Поэтому такие временные ряды делят строго хронологически — в тестовую выборку попадает определенное количество последних по времени объектов. Но анализ временных рядов сам по себе довольно специфичен как статистическая дисциплина, и как раздел машинного обучения.
Что касается пропорции деления, то, опять же, как правило, выборку разделяют в соотношении 80/20. То есть если в исходном датасете, например, 1000 объектов, то случайно выбранные 800 из них образуют обучающую выборку, а оставшиеся 200 — тестовую. Но это соотношение “по умолчанию” в общем-то ничем не обосновано. Его можно изменять в любую сторону исходя из обстоятельств. Но для этого надо понимать, как вообще формируется эта пропорция и что на нее влияет.
Что будет, если на тестовую выборку оставить слишком много данных, скажем, 50% всего датасета? Очевидно, у нас останется мало данных для обучения. То есть модель будет обучена на всего лишь небольшой части объектов, которых может не хватить для того, чтобы модель “распознала” зависимости в данных. Вообще, чем больше данных для обучения, тем в целом лучше, так как на маленьком объеме большую роль играют те самые случайные колебания. Поэтому модель может переобучаться. И чем меньше данных, тем переобученнее и “случайнее” будет получившаяся модель. И это не проблема модели, это именно проблема нехватки данных. А чем больше точек данных, тем больше все эти случайные колебания будут усредняться и это сильно повысит качество обученной модели.
А что будет, если наоборот, слишком мало данных оставить на тестовую выборку? Скажем, всего 1% от имеющихся данных. Мы же сказали, что чем больше данных для обучения, тем лучше. Значит, но обучающую выборку надо оставить как можно большую часть датасета? Не совсем так. Да, обучение модели пройдет более полно. Но вот оценка ее эффективности будет не такой надежной. Ведь такие же случайные колебания будут присутствовать и в тестовой выборке. И если мы оценим эффективность модели на слишком маленьком количестве точек, случайные колебания этой оценки будут слишком большими. Другими словами мы получим оценку, в которой будет сильно не уверены. Истинная оценка эффективности может быть как сильно больше, так и сильно меньше получившегося уровня. То есть даже если модель обучается хорошо, мы этого никогда не узнаем с точностью.
То есть пропорция деления выборки на обучающуюся и тестовую является следствием компромисса между полнотой обучения и надежность оценки эффективности. Соотношение 80/20 является хорошим балансом — не сильно много, но и не сильно мало. Но это оптимально для среднего размера датасетов. Если у вас очень мало данных, то его можно немного увеличить в пользу тестовой выборки. Если же данных слишком много — то в пользу обучающей. Кроме того, при использовании кросс-валидации размер тестовой выборки тоже можно уменьшить.Но на практике очень редько используются соотношения больше, чем 70/30 или меньше чем 90/10 — такое значения уже считаются экстремальными.
Выводы:
- Цель разработки моделей машинного обучения — не описывать обучающий набор, а на его примере описывать другие объекты реального мира.
- Главное качество модели — описывать объекты, которых она не видела при обучении — обобщающая способность.
- Для того, чтобы оценить обобщающую способность модели нужно вычислить метрики эффективности на новых данных.
- Для этого исходный датасет разбивают на обучающую и тестовую выборки. Делить можно в любой пропорции, обычно 80-20.
- Чаще всего выборку делят случайным образом, но временные ряды — только в хронологической последовательности.
- Обучающая выборки используется для подбора параметров модели (обучения), а тестовая — для оценки ее эффективности.
- Никогда не оценивайте эффективность модели на тех же данных, на которых она училась — оценка получится слишком оптимистичная.
Кросс-валидация
Как мы говорили ранее, маленькая тестовая выборка проблемна тем, что большое влияние на результат оценки эффективности модели имеют случайные отклонения. Это становится меньше заметно при росте объема выборки, но полностью проблема не исчезает. Эта проблема состоит в том, что каждый раз разбивая датасет на две выборки, мы вносим случайные ошибки выборки. Эта случайная ошибка обоснована тем, что две получившиеся подвыборки наверняка будут демонстрировать немного разное распределение. Даже если взять простой пример. Возьмем группу людей и разделим ее случайным образом на две половины. В каждой половине посчитаем какую-нибудь статистику, например, средний рост. Будут ли в двух группах выборочные средние точно совпадать? Наверняка нет. Обосновано ли чем-то существенным такое различие? Тоже нет, это случайные отклонения, которые возникают при выборке объектов из какого-то множества.
Поэтому разбиение выборки на тестовую и обучающую вносит такие случайные колебания, из-за которых мы не можем быть полностью уверены в получившейся оценке эффективности модели. Допустим, мы получили тестовую эффективность 95% (непример, измеренную по метрике accuracy, но вообще это не важно). Можем ли мы быть уверены, что это абсолютно точный уровень эффективности? Нет, ведь как любая выборочная оценка, то есть статистика, рассчитанная на определенной выборке метрика эффективности представляет собой случайную величину с некоторым распределением. А у этого распределения есть математическое ожидание и дисперсия. Как мы говорили в предыдущей главе, случайное разделение выборки на тестовую и обучающую приводит к тому, что распределение этой величины имеет математическое ожидание, совпадающее с истинным уровнем эффективности модели. Но это именно математическое ожидание. И у этой случайной величины есть какая-то ненулевая дисперсия. Это значит, что при каждом измерении, выборочная оценка может отклоняться от матожидания, то есть быть произвольно больше или меньше.
Есть ли способ уменьшить эту дисперсию, то есть неопределенность при измерении эффективности модели? Да, очень простой. Нужно всего лишь повторить измерение несколько раз, а затем усреднить полученные значения. Так как математическое ожидание случайных отклонений всегда предполагается равным нулю, чем больше независимых оценок эффективности мы получим, тем ближе среднее этих оценок будет к математическом ожиданию распределения, то есть к истинному значению эффективности.
Проблема в том, что эти измерения должны быть независимы, то есть производиться на разных данных. Но кратное увеличение тестовой выборки имеет существенные недостатки — соответствующее уменьшение обучающей выборки. Поэтому так никогда не делают. Гораздо лучше повторить случайное разбиение датасета на обучающую и тестовую выборки еще раз и измерить метрику эффективности на другой тестовой выборки из того же изначального датасета.
К сожалению, это означает, что и обучающая выборка будет другая. То есть нам необходимо будет повторить обучение. Но зато после обучения мы получим новую, независимую оценку эффективности модели. Если мы повторим этот процесс несколько раз, мы сможем усреднить эти значения и получить гораздо более точную оценку эффективности модели.
Имейте в виду, что все, что мы говорим в этой части применимо к любой метрике эффективности или метрике ошибки модели. Чаще всего, на практике измеряют метрики accuracy для моделей классификации и $R^2$ для регрессии. Но вы можете использовать эти методики для оценки любых метрик качества моделей машинного обучения. Напомним, что они должны выбираться исходя из задачи.
Конечно, можно реализовать это случайное разбиение руками и повторить процедуру оценивания несколько раз, но на практике используют готовую схему, которая называется кросс-валидация или перекрестная проверка. Она заключается в том, что датасет заранее делят на несколько равных частей случайным образом. Затем каждая из этих частей выступает как тестовый набор, а остальные вместе взятые — как обучающий:
Источник: Towards Data Science.
На схеме части датасета изображены для наглядности непрерывными блоками, но на самом деле это именно случайные разбиения. Так что они буду в датасете “вперемешку”. Количество блоков, на которые делится выборка задает количество проходов или оценок. Это количество называется k. Обычно его берут равным 5 или трем. Это называется, 5-fold cross-validation. То есть на первом проходе блоки 1,2,3 и 4 в совокупность составляют обучающую выборку. Модель обучается на них, а затем ее эффективность измеряется на блоке 5. Во втором проходе та же модель заново обучается на данных их блоков 1,2,3 и 5, и ее эффективность измеряется на блоке 4. И таким образом мы получаем 5 независимых оценок эффективности модели. Они могут различаться из-за тех самых случайных оценок выборки. Но если посчитать их среднее, оно будет значительно ближе к истинному значению эффективности. Поэтому что статистика.
Количество проходов k еще определяет то, сколько раз будет повторяться обучение модели. Чем больше выбрать k, тем более надежными будут оценки, но вся процедура займет больше машинного времени. Это особенно актуально для моделей, которые сами по себе обучаются долго — например, глубокие нейронные сети. Надо помнить, что использование кросс-валидации сильно замедляет процесс обучения. Если же выбрать k слишком маленьким, то не будет главного эффекта кросс-валидации — усреднения индивидуальных оценок эффективности. Кроме того, чем больше k, тем меньшая часть выборки будет отводиться на тестовый набор. Поэтому k не стоит брать больше, скажем, 10, даже если у вас достаточно вычислительных мощностей.
Кросс-валидация никак не влияет на эффективность модели. Многие думают, что валидированные модели получаются более эффективными. Это не так, просто использование перекрестной проверки позволяет более точно и надежно измерить уже имеющуюся эффективность данной модели. И уж тем более кросс-валидация не может ускорить процесс обучения, совсем наоборот. Но несмотря на это, использование кросс-валидации с k равным 5 или, в крайнем случае, 3, совершенно обязательно в любом серьезном проекте по машинному обучению, ведь оценки, полученные без использования этой методики совершенно ненадежны.
В библиотеке sklearn, естественно, кросс-валидация реализована в виде готовых функций. Поэтому ее применение очень просто. В примере ниже используется кросс-валидация с количеством проходов по умолчанию для получения робастных оценок заранее выбранных метрик (precision и recall):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro','recall_macro']
>>> clf =
svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores =
cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time',
'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
Такой код просто оценивает значение метрик. Но обратите внимание, что он возвращает не просто одно значение метрики, но целый вектор. Это именно те индивидуальные оценки. Из них очень легко получить средние и выборочную дисперсию. Эта выборочная дисперсия как раз и показывает степень уверенности в данной оценке — чем она ниже, тем уверенность больше, как доверенный интервал в статистике. Кроме такого явного использования кросс-валидации для оценки метрик, она зачастую встроена в большое количество функций, которые используют ее неявно. О некоторых таких функциях, осуществляющих оптимизацию гиперпараметров модели, пойдет речь чуть позже.
Выводы:
- Разбиение выборки на обучающую и тестовую может внести случайные ошибки.
- Нужно повторить разбиение несколько раз, посчитать метрики и усреднить.
- Кросс-валидация разбивает выборку на $k$ блоков, каждый из которых используется по очереди как тестовый.
- Сколько задать $k$, столько и будет проходов. Обычно берут 3 или 5.
- Чем больше $k$ тем надежнее оценка, но дольше ее получение, так как модель каждый раз заново обучается.
- Использование кросс-валидации обязательно для получения робастных оценок.
- В библиотеке sklearn кросс-валидация (CV) встроена во многие функции.
Кривые обучения
Как мы говорили раньше, не следует ориентироваться на эффективность модели, измеренную на обучающей выборке, ведь она получается слишком оптимистичной. Но эта обучающая эффективность все равно может дать интересную информацию о работе модели. А именно с ее помощью можно оценить, переобучается модель или недообучается. В этой главе мы расскажем об одном из самых наглядных способов диагностики моделей машинного обучения — кривых обучения.
Построение кривых обучения может быть проведено после разделения датасета на обучающую и тестовую выборки. Происходит это следующим образом. Тестовый набор фиксируется и каждый раз используется один и тот же. Из обучающего набора же сначала берут малую часть, скажем 10% от общего количества точек в нем. Обучают модель на этой малой части, а затем измеряют ее эффективность на этой части и на постоянной тестовой выборке. Первая оценка называется обучающая эффективность (training score), а вторая — тестовая эффективность (test score). Затем повторяют процесс с чуть большей частью обучающей выборки, например, 20%, затем еще с большей и так, пока мы не дойдем до полной обучающей выборки.
На каждом этапе мы измеряем обучающую эффективность (измеренную именно на той части данных, на которых модель училась, не на полной обучающей выборке) и тестовую эффективность. Таким образом мы получаем зависимость эффективности модели от размера обучающей выборки. Эти данные можно построить на графике. Это график и называется кривой обучения (learning curve). Такой график может выглядеть, например, так:
В данном случае, на графике мы видим всего пять точек на каждой кривой. Верхняя кривая показывает обучающую эффективность, нижняя — тестовую. Значит, мы использовали всего пять делений обучающей выборки на подвыборки разного размера. Это размер как раз и отложен на горизонтальной оси. Сколько таких разбиений брать? Если взять слишком мало, то не будет понятна форма графика, а именно она нам важна для диагностики. Если же взять слишком много — то построение кривой обучения займет много времени, так как каждая точка на графике — это заново обученная модель.
Давайте объясним форму этого графика. Слева, когда обучающая выборка мала, обучающая эффективность довольно высока. Это вполне понятно, ведь чем меньше данных, тем проще модели к ним подстроиться. Помните, что через любые две точки можно провести линию (то есть линейную регрессию)? Это, конечно, крайний случай, но в общем, чем меньше обучающая выборка, тем большую эффективность одной и той же модели (параметрического семейства функций) можно на ней ожидать. А вот тестовая эффективность довольно маленькая. Это тоже понятно. Ведь на маленькой выборке модель не смогла обнаружить зависимости в данных так, чтобы эффективно предсказывать значение целевой переменной в новых данных. То есть она подстроилась под конкретные точки без какой-либо обобщающей способности.
Сперва отметим, что обычно кривые обучения демонстрируют некоторые общие тенденции. Например, при малых объемах обучающей выборки, обучающая эффективность модели может быть очень большой. Ведь чем меньше данных, тем проще подобрать параметры любой, пусть даже простой модели, так, чтобы эта модель ошибалась меньше. В самом предельном случае, вспомните, что через любые две точки можно провести прямую. Это значит, что линейная регрессия, обученная на двух точках, всегда будет давать нулевую ошибку или полную, 100%-ю эффективность. То же можно сказать и про квадратичную функцию, обученную на трех точках. Но и в целом, чем меньше данных, тем меньше можно ожидать суммарную ошибку любого рассматриваемого класса моделей на этих данных.
Тестовая же эффективность модели, обученной на малом объеме выборки, скорее всего будет очень невысокой. Это тоже естественно. Ведь модель видела всего малую часть примеров и не может подстроиться под какие-то глобальные зависимости в данных. Поэтому в левой части кривых обучения почти всегда будет большой зазор.
При повышении объема обучающей выборки обучающая же эффективность будет падать. Это связано в тем, что чем больше данных, тем больше пространства для ошибки для конкретной модели. Поэтому чем больше точек описывает модель, тем хуже она это делает в среднем. Это неизбежно и не страшно. Важно то, что тестовая эффективность наоборот, растет. Это происходит потому, что чем больше данных, тем больше вероятность того, что модель подстроится под существенные связи между признаками и целевой переменной, и таким образом, повысит обобщающую способность, свою предсказательную силу.
В итоге, кривая обучения показывает, как изменяется эффективность модели по сравнению к конкретному набору данных. В частности, именно с помощью кривых обучения можно предположить пере- и недообучение модели, что является главной целью диагностики моделей машинного обучения. Например, взглянув на график кривой обучения, приведенный выше, можно ответить на вопрос, хватает ли модели данных для обучения. Для этого можно спросить, улучшится ли тестовая эффективность модели, если добавить в датасет больше точек. Для этого можно мысленно продолжить кривую обучения вправо.
При построении кривых обучения обращайте внимание на деления вертикальной оси. Если вы строите графики с использованием библиотечных инструментов, то они автоматически масштабируются по осям. Имейте в виду, что одна и та же кривая обучения может выглядеть при разном масштабе совершенно по-разному. А навык сопоставления разных кривых очень важен при диагностике моделей. Лучше всего вручную задавать масштаб вертикальной оси и использовать один и тот же для всех графиков в одной задаче.
Обратите внимание, что на графике помимо самих кривых обучения присутствуют еще какие-то полосы. Что они значат? Дело в том, что при построении кривых обучения очень часто применяется кросс-валидация, о которой мы говорили в предыдущей главе. Ведь разбиение выборки на тестовую и обучающую вносит случайные ошибки. Поэтому для построения на кривых обучения более надежных оценок всех измеряемых оценок эффективности процесс повторяют несколько раз и усредняют полученные оценки. Каждая точка на графике — это не просто оценка эффективности, это среднее из всех кросс-валидированных оценок. Именно поэтому, кстати, в легенде нижняя линяя называется не test score, а cross-validation score. А ширина полосы вокруг точки определяется величиной дисперсии этих оценок. Чем шире полоса, тем больше разброс оценки на разных проходах кросс-валидации и тем меньше мы уверены в значении этой оценки. При построении кривых обучения эта неопределенность почти всегда выше при малых объемах обучающей выборки (слева на графике) и меньше — справа.
Выводы:
- Кривая обучения — это зависимость эффективности модели от размера обучающей выборки.
- Для построения кривых обучения модель обучают много раз, каждый раз с другим размером обучающей выборки (от одного элемента до всех, что есть).
- При малых объемах обучающая эффективность будет очень большой, а тестовая — очень маленькой.
- При увеличении объема обучающей выборки они будут сходиться, но обычно тестовая эффективность всегда ниже обучающей.
- Кривые обучения позволяют увидеть, как быстро модель учится, хватает ли ей данных, а также обнаруживать пере- и недообучение.
- Кривые обучения часто используют кросс-валидацию.
Обнаружение пере- и недообучения
Как мы говорили, построение кривых обучения — это исключительно диагностическая процедура. Именно они позволяют нам предполагать, к чему более склонна модель, обученная на конкретном наборе данных — к переобучению или к недообучению. Это важно, так как подходы у повышению эффективности в этих двух случаях будут совершенно противоположными. Давайте предположим, как будут вести себя на кривых обучения переобученные и недообученные модели.
Что будет, если модель слишком проста для имеющихся данных? При увеличении количества объектов в обучающей выборке, эффективность, измеренная на ней же будет вначале заметно падать по причинам, описанным выше. Но постепенно она будет выходить на плато и больше не будет уменьшаться. Это связано с тем, что начиная с какого-то объема выборки в ней будут превалировать нелинейные зависимости, слишком сложные для данной модели. С ростом объема обучающей выборки неизбежно растет тестовая эффективность, но так как модель слишком проста и не может ухватить этих сложных зависимостей в данных, то ее тестовая эффективность не будет повышаться сильно. Причем при достаточном объеме обучающей выборки тестовая и обучающая эффективности будут достаточно близкими. Другими словами, простые модели одинаково работают как на старых, так и на новых данных, но одинаково плохо.
А что будет происходить со слишком сложной моделью для существующих данных? Ее показатели в левой части графика будут аналогичны — высокая обучающая и низкая тестовая эффективности. Причины вс те же. Но вот с ростом объема обучающей выборки, разрыв между этими двумя показателями не будет сокращаться так сильно. Модель, обученная на полном датасете покажет высокую эффективность на обучающей выборке, но гораздо более низкую — на тестовой. Это же практически определение переобучения — низкая ошибка, но отсутствие обобщающей способности. Это происходит, как мы уже обсуждали, за счет того, что слишком сложная модель имеет достаточный запас вариативности, чтобы подстроиться под случайные отклонения в данных.
Таким образом, недообученные и переобученные модели демонстрируют совершенно разное поведение на кривых обучения. А значит, недообучение и переобучения можно выявить, проанализировав поведение модели на графике. Типичное переобучение характеризуется большим разрывом между тестовой и обучающей эффективность. Признак типичного недообучения — низкая эффективность как на тестовой, так и на обучающей выборке. Но на практике, конечно, диагностика моделей машинного обучения не такая простая.
Как вы могли заметить, мы нигде не говорим о четких критериях. Недо- и переобученной моделей — это вообще относительные понятия. И кривые обучения измеряют их только косвенно. Поэтому диагностика не сводится к оценке какой-либо метрики или статистики. Нам нужно оценить общую форму графика кривых обучения, что не является точной наукой. Возникает множество вопросов. Например, мы говорили, что большой зазор между тестовой и обучающей эффективностью — это признак переобучения. Но какой зазор считать большим? Это вопрос интерпретации. Точно так же, что считать низким уровнем эффективности? 50%? Может, 75%? Вообще это очень зависит от самой задачи. В некоторых задачах 80% accuracy — это выдающийся результат, а в других — даже 99% считается недостаточной точностью.
Поэтому рассматривая один график кривой обучения очень сложно понять, особенно без опыта анализа моделей машинного обучения, на что мы смотрим — на слишком простую недообученную модель, или на слишком сложную — переобученную. Вообще, строго говоря, большой зазор между эффективностями модели указывает на присутствующую в модели вариативность (variance), а низкий,не 100%-й уровень обучающей эффективности — на наличие в модели смещения (bias). А любые модели в той или иной степени обладают этими характеристиками. Вопрос в их соотношении друг к другу и к конкретному набору данных.
Чтобы облегчить задачу диагностики модели очень часто эффективность данной модели рассматривают не абстрактно, а сравнивают с аналогами. Практически всегда выбор моделей осуществляется от простого к сложному — сначала строят очень простые модели. Их тестовая эффективность может задать некоторых базовый уровень, планку, по сравнению к которой уже можно готовить об улучшении эффективности у данной, более сложной модели, насколько это улучшение существенно и так далее. Кроме того, строя кривые обучения нескольких моделей можно получить сравнительное представление о том, как эти модели соотносятся между собой, какие из них более недообученные, какие — наоборот.
Ситуация еще очень осложняется тем, что на практике вы никогда не получите таких красивых и однозначных кривых обучения, как в учебнике. Положение точек на кривых обучения зависит, в том числе и от тех самых случайных отклонений в данных, которые так портят нам жизнь. Поэтому в реальности графики могут произвольно искривляться, быть немонотонными. Тестовая эффективность вообще может быть выше обучающей. Что это начит для диагностики? Да в общем-то, ничего, это лишь свидетельствует об особом характере имеющихся данных. И, естественно, чем меньше данных, тем более явно проявляются эти случайности и тем менее показательными будут графики.
Достаточно сильно от этих случайных колебаний помогает применение кросс-валидации. Так как усреднение случайности — это и есть цель перекрестной проверки, она может быть полезна и для “сглаживания” кривых обучения. Еще надо помнить, что во многих библиотеках по умолчанию кривые обучения строятся на основе всего нескольких точек, то есть всего пяти-десяти вариантов размера обучающей выборки. Если такой график не дает достаточной информации, можно попробовать построить кривую по большему количеству точек. Но при этом и случайные колебания тоже могут проявиться сильнее.
Вообще, все факторы, которые улучшают “читаемость” кривых обучения, одновременно сильно замедляют их построение — кросс-валидация, использование большей выборки, построение большего количества точек. Помните, что это приводит к кратному увеличению количества циклов обучения модели.
Как мы говорили, поведение модели в целом не зависит от выбранной метрики, которую вы используете для построения кривых обучения. Поэтому зачастую используют не метрики эффективности, а метрики ошибок. Поэтому графики кривых обучения выглядят “перевернутыми” — тестовая ошибка больше, чем обучающая и так далее. Следует помнить, что все сказанное выше остается справедливым в этом случае, только следует помнить, где у модели высокая эффективность и малая ошибка.
Выводы:
- При недообучении тестовая и обучающая эффективности будут достаточно близкими, но недостаточными.
- При переобучении тестовая и обучающая эффективности будут сильно различаться — тестовая будет значительно ниже.
- Пере- и недообучение — это относительные понятия.
- Более простые модели склонны к недообучению, более сложные — к переобучению.
- Диагностика пере- и недообучения очень важна, так как для повышения эффективности предпринимаются противоположные меры.
- Для построения можно использовать функцию ошибки, метрику эффективности или метрику ошибки, важна только динамика этих показателей.
- Диагностика моделей машинного обучения — это не точная наука, здесь нужно принимать в расчет и задачу, и выбор признаков и многие другие факторы.
Методы повышения эффективности моделей
Регуляризация
Как мы говорили, диагностика моделей нужна для поиска путей повышения ее эффективности. И мы выяснили, что пере- и недообучение моделей напрямую связаны с уровнем сложности моделей. Сейчас самое время поговорить об одном математическом приеме, который используется для искусственного управления сложностью моделей.
Но для начала заметим небольшой факт. Можно рассмотреть гипотетический график, на котором показан уровень ошибок моделей на конкретном наборе данных в зависимости от уровня сложности этой модели. Пока мы не сталкивались с тем, как можно плавно менять уровень сложности модели в рамках одного параметрического класса. Но представим, что речь идет о полиномиальной модели, а по горизонтали отложена степень этого полинома.
Если модель слишком проста, то уровень тестовых и обучающих ошибок будет высок и достаточно близок. Мы говорили об этом (правда другими словами, в терминах эффективности) в предыдущей главе. По мере увеличения сложности разрыв между этими уровнями ошибок будет в среднем увеличиваться. Это происходит за счет более глубокой подстройки модели именно к обучающей выборке. Причем уровень ошибок на обучающей выборке будет в среднем падать за счет повышения вариативности модели. Но уровень ошибок не может опуститься ниже нуля. Поэтому либо с какого-то момента он стабилизируется, либо будет асимптотически приближаться к 0. А это значит, что уровень тестовой ошибки неизбежно рано или поздно начнет повышаться с ростом сложности модели. Таким образом, у уровня тестовой ошибки есть некоторое оптимальное значение.
Другими словами, для любого конкретного датасета существует некоторый оптимальный уровень сложности модели, который дает наименьшую ошибку на тестовой выборке. Модели, имеющие более низкую сложность будут недообучаться, а более высокую — переобучаться. Поэтому существует задача нахождения этого оптимального уровня сложности. К сожалению, это не получится сделать методом обучения, или любой другой численной оптимизации, так как изменение уровня сложности модели требует запуска ее обучения занаво. Мы не можем непрерывно менять уровень сложности, как какой-то дополнительный параметр модели.
Выводы:
- Регуляризация — это способ искусственно ограничить вариативность моделей.
- При использовании регуляризации можно применять более сложные модели и снижать склонность к переобучению.
- Регуляризация модифицирует функцию ошибки модели, добавляя в нее штрафы за повышение сложности.
- Основная идея регуляризации — отдавать предпочтение низким значениям параметров в модели.
- Регуляризация обычно не затрагивает свободный коэффициент $b_0$.
- Регуляризация обычно параметрическая, можно управлять ее степенью.
Ridge
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} b_j^2]
Выводы:
- $lambda > 0$ — параметр регуляризации.
- Чем он больше, тем сильнее штрафуются сложные модели.
- Этот прием может применяться как к классификации, так и к регрессии.
- Ridge еще называют регуляризацией по L2-норме. Она же — гребневая регрессия.
- Такая регуляризация делает параметры более робастными к мультиколлинеарности признаков.
- В классификации такая модель может обучаться заметно быстрее за счет внутренней оптимизации вычислений.
Lasso
[J(vec{b}) = sum_{i=1}^{m} (h_b(x_i) — y_i)^2 + lambda sum_{j=1}^{n} | b_j |]
Выводы:
- Lasso еще называют регуляризацией по L1-норме.
- Lasso заставляет модель использовать меньше ненулевых коэффициентов.
- Фактически, эта регуляризация уменьшает количество признаков, от которых зависит модель.
- Может использоваться для отбора признаков.
- Полезна в задачах с разреженной матрицей признаков.
Elastic net
[J(vec{b}) = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2 +
lambda_1 sum_{j=1}^{n} | b_j | + lambda_2 sum_{j=1}^{n} b_j^2]
Выводы:
- По сути, это комбинация регуляризации по L1 и L2 нормам.
- Имеет два параметра, которые определяют соотношение соответствующих норм.
- Комбинирует достоинства предыдущих двух методов.
- Недостаток в необходимости задавать сразу два параметра регуляризации.
Методы борьбы с недообучением
Выводы:
- Ввести в модель новые данные об объектах (атрибуты).
- Уменьшение степени регуляризации модели.
- Введение полиномиальных и других признаков.
- В целом, инжиниринг признаков.
- Использование более сложных моделей.
Методы борьбы с переобучением
Выводы:
- Ввести в модель данные о новых объектах, использовать большую выборку.
- Убрать признаки из модели, использовать отбор признаков.
- Увеличить степень регуляризации модели.
- Использовать более простые модели.
- Регуляризация обычно работает лучше уменьшения количества параметров.
Анализ ошибок
Выводы:
- Анализ ошибок — это ручная проверка объектов, на которых модель делает ошибки.
- Анализ характеристик таких объектов может подсказать направление инжиниринга признаков.
- Можно сравнить эти объекты с остальной выборкой. Может, это аномалии.
- В задачах регрессии в первую очередь обращать внимание на объекты с самым высоким отклонением.
- Полезно бывает проинтерпретировать модель — проанализировать ее предметный смысл.
- Для сложных моделей есть методы локальной линейной интерпретации.
Выбор модели
Выводы:
- Задача выбора класса модели для решения определенной задачи.
- Очень сложно сказать априори какой класс модели будет работать лучше на конкретных данных.
- Следует учитывать нефункциональные требования к задаче.
- Обычно начинают с самых простых моделей — они быстро считаются и дают базовый уровень эффективности.
- По результатам диагностики простых моделей принимают решение о дальнейших действиях.
- Можно провести поиск по разным классам моделей для определения самых перспективных.
- Выбор модели — это творческий и исследовательский процесс.
- Есть подходы автоматизации выбора модели (AutoML), но они пока несовершенны.
- В исследовательских задачах модели сравниваются со state-of-the-art.
Гиперпараметры модели
Выводы:
- Гиперпараметр модели — это численное значение, которое влияет на работу модели, но не подбирается в процессе обучения.
- Примеры гиперпараметров — k в kNN, параметр регуляризации, степень полиномиальной регрессии, глубина дерева решения.
- У каждой модели множество гиперпараметров, которые можно посмотреть в документации.
- Гиперпараметры модели нужно задавать до начала обучения.
- Если значение гиперпараметра изменилось, то обучение надо начинать заново.
- Существуют скрытые гиперпараметры модели — степень полинома, количество нейронов и слоев, ядерная функция.
- Оптимизация гиперпараметров и задача выбора модели — одно и то же.
Поиск по сетке
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
tuned_parameters = [
{"kernel": ["rbf"],
"gamma": [1e-3, 1e-4],
"C": [1, 10, 100, 1000]},
{"kernel": ["linear"],
"C": [1, 10, 100, 1000]},
]
scores = ["precision", "recall"]
grid_search = GridSearchCV(SVC(), tuned_parameters,
scoring=scores).fit(X_train, y_train)
Выводы:
- Поиск по сетке — полный перебор всех комбинаций значений гиперпараметров для поиска оптимальных значений.
- Для его организации надо задать список гиперпараметров и их конкретных значений.
- Непрерывные гиперпараметры надо дискретизировать.
- Поиск по сетке имеет экспоненциальную сложность.
- Чем больше параметров и значений задать, тем лучше модель, но дольше поиск.
- Можно задать критерии поиска — целевые метрики.
Случайный поиск
1
2
3
4
5
6
7
8
9
10
11
12
clf = SGDClassifier(loss="hinge", penalty="elasticnet", fit_intercept=True)
param_dist = {
"average": [True, False],
"l1_ratio": stats.uniform(0, 1),
"alpha": loguniform(1e-2, 1e0),
}
n_iter_search = 15
random_search = RandomizedSearchCV(
clf, param_distributions=param_dist, n_iter=n_iter_search
).fit(X, y)
Выводы:
- Случайный поиск позволяет задать распределение гиперпараметра, в котором будет вестись поиск.
- Случайный поиск семплирует набор значений гиперпараметров из указанных распределений.
- Можно задать количество итераций поиска независимо от количества гиперпараметров.
- Добавление параметров не влияет на продолжительность поиска.
- Результат не гарантируется. Воспроизводимость можно настроить.
Сравнение эффективности моделей (валидационный набор)
Выводы:
- При сравнении нескольких моделей между собой возникает проблема оптимистичной оценки эффективности.
- Поэтому для исследования выбранной модели нужно использовать третью часть выборки — валидационную.
- В терминах существует путаница, главное — три непересекающиеся части выборки.
- Обучающая (train) используется для оптимизации параметров (обучения) модели.
- Валидационная (validation) — для оптимизации гиперпараметров и выбора модели.
- Тестовая (test, holdout) — для итоговой оценки качества, представления результатов.
- Во многих случаях использование кросс-валидации автоматически разбивает выборку. Поэтому тестовая играет роль валидационной.
- Есть проблема глобального переобучения моделей на известных датасетах.
Линейная регрессия (Linear regression) — модель зависимости переменной x от одной или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.
Линейная регрессия относится к задаче определения «линии наилучшего соответствия» через набор точек данных и стала простым предшественником нелинейных методов, которые используют для обучения нейронных сетей. В этой статье покажем вам примеры линейной регрессии.
Где применяется линейная регрессия
Предположим, нам задан набор из 7 точек (таблица ниже).
Цель линейной регрессии — поиск линии, которая наилучшим образом соответствует этим точкам. Напомним, что общее уравнение для прямой есть f (x) = m⋅x + b, где m — наклон линии, а b — его y-сдвиг. Таким образом, решение линейной регрессии определяет значения для m и b, так что f (x) приближается как можно ближе к y. Попробуем несколько случайных кандидатов:
Довольно очевидно, что первые две линии не соответствуют нашим данным. Третья, похоже, лучше, чем две другие. Но как мы можем это проверить? Формально нам нужно выразить, насколько хорошо подходит линия, и мы можем это сделать, определив функцию потерь.
Функция потерь — метод наименьших квадратов
Функция потерь — это мера количества ошибок, которые наша линейная регрессия делает на наборе данных. Хотя есть разные функции потерь, все они вычисляют расстояние между предсказанным значением y(х) и его фактическим значением. Например, взяв строку из среднего примера выше, f(x)=−0.11⋅x+2.5, мы выделяем дистанцию ошибки между фактическими и прогнозируемыми значениями красными пунктирными линиями.
Одна очень распространенная функция потерь называется средней квадратичной ошибкой (MSE). Чтобы вычислить MSE, мы просто берем все значения ошибок, считаем их квадраты длин и усредняем.
Вычислим MSE для каждой из трех функций выше: первая функция дает MSE 0,17, вторая — 0,08, а третья — 0,02. Неудивительно, что третья функция имеет самую низкую MSE, подтверждая нашу догадку, что это линия наилучшего соответствия.
Рассмотрим приведенный ниже рисунок, который использует две визуализации средней квадратичной ошибки в диапазоне, где наклон m находится между -2 и 4, а b между -6 и 8.
Глядя на два графика, мы видим, что наш MSE имеет форму удлиненной чаши, которая, по-видимому, сглаживается в овале, грубо центрированном по окрестности (m, p) ≈ (0.5, 1.0). Если мы построим MSE линейной регрессии для другого датасета, то получим аналогичную форму. Поскольку мы пытаемся минимизировать MSE, наша цель — выяснить, где находится самая низкая точка в чаше.
Больше размерностей
Вышеприведенный пример очень простой, он имеет только одну независимую переменную x и два параметра m и b. Что происходит, когда имеется больше переменных? В общем случае, если есть n переменных, их линейная функция может быть записана как:
f(x) = b+w_1*x_1 + … + w_n*x_n
Один трюк, который применяют, чтобы упростить это — думать о нашем смещении «b», как о еще одном весе, который всегда умножается на «фиктивное» входное значение 1. Другими словами:
f(x) = b*1+w_1*x_1 + … + w_n*x_n
Добавление измерений, на первый взгляд, ужасное усложнение проблемы, но оказывается, постановка задачи остается в точности одинаковой в 2, 3 или в любом количестве измерений. Существует функция потерь, которая выглядит как чаша — гипер-чаша! И, как и прежде, наша цель — найти самую нижнюю часть этой чаши, объективно наименьшее значение, которое функция потерь может иметь в отношении выбора параметров и набора данных.
Итак, как мы вычисляем, где именно эта точка на дне? Распространенный подход — обычный метод наименьших квадратов, который решает его аналитически. Когда есть только один или два параметра для решения, это может быть сделано вручную, и его обычно преподают во вводном курсе по статистике или линейной алгебре.
Проклятие нелинейности
Увы, обычный МНК не используют для оптимизации нейронных сетей, поэтому решение линейной регрессии будет оставлено как упражнение, оставленное читателю. Причина, по которой линейную регрессию не используют, заключается в том, что нейронные сети нелинейны.
Различие между линейными уравнениями, которые мы составили, и нейронной сетью — функция активации (например, сигмоида, tanh, ReLU или других).
Эта нелинейность означает, что параметры не действуют независимо друг от друга, влияя на форму функции потерь. Вместо того, чтобы иметь форму чаши, функция потерь нейронной сети более сложна. Она ухабиста и полна холмов и впадин. Свойство быть «чашеобразной» называется выпуклостью, и это ценное свойство в многопараметрической оптимизации. Выпуклая функция потерь гарантирует, что у нас есть глобальный минимум (нижняя часть чаши), и что все дороги под гору ведут к нему.
Но, вводя нелинейность, мы теряем это удобство ради того, чтобы дать нейронным сетям гораздо большую «гибкость» при моделировании произвольных функций. Цена, которую мы платим, заключается в том, что больше нет простого способа найти минимум за один шаг аналитически. В этом случае мы вынуждены использовать многошаговый численный метод, чтобы прийти к решению. Хотя существует несколько альтернативных подходов, градиентный спуск остается самым популярным методом.
Линейная регрессия
В этой заметке мы рассмотрим простую и многомерную линейную регрессию, метод наименьших квадратов, а также рассмотрим понятия ковариации и корреляции.
Понятия ковариации и корреляции
Для примера будем использовать набор данных Animals из пакета MASS, описание которого можно получить с помощью команды ?Animals:
> head(Animals)
body brain
Mountain beaver 1.35 8.1
Cow 465.00 423.0
Grey wolf 36.33 119.5
Goat 27.66 115.0
Guinea pig 1.04 5.5
Dipliodocus 11700.00 50.0
> nrow(Animals)
[1] 28
У нас имеется n=28 наблюдений и мы хотим проверить «силу взаимосвязи» (и есть ли такая взаимосвязь вообще) между весом мозга (переменная brain) и весом тела (переменная body). Хорошим правилом считается посмотреть на данные, с которыми мы работаем, поэтому отобразим точки на диаграмме рассеяния:
plot_animals <- function(animals, xlab='', ylab='', main_label='') {
plot(animals$body, animals$brain,
xlab=xlab, ylab=ylab, main=main_label,
col='royal blue', lwd=2)
}
plot_animals(Animals, xlab='body weight', ylab='brain weight',
main='Brain and Body Weights for 28 Species')
Из полученного графика может показаться, что между наблюдениями (парами x_i и y_i) нет никакой взаимосвязи, поэтому попробуем преобразовать наши данные к log-log шкале:
animals.log <- data.frame(body=log(Animals$body), brain=log(Animals$brain))
plot_animals(animals.log, xlab='log(body weight)', ylab='log(brain weight)',
main='Brain and Body Weights for 28 Species')
Note
Иногда трудно понять какие именно преобразования нужно провести над имеющимися данными, поэтому эта задача полностью ложится на интуицию аналитика.
Теперь стало более очевидно, что имеется линейная взаимосвязь между наблюдениями. Возникает вопрос: «На сколько эта взаимосвязь сильная?» Чтобы ответить на этот вопрос мы можем посчитать так называемый коэффициент корреляции. Для этого сначала найдем выборочные средние и отобразим их соответствующими линиями на диаграмме рассеяния:
bar{y} = frac{sum_{i=1}^{n}y_{i}}{n}
bar{x} = frac{sum_{i=1}^{n}x_{i}}{n}
plot_animals(animals.log, xlab='log(body weight)', ylab='log(brain weight)',
main = 'Brain and Body Weights for 28 Species')
# Номера четвертей
text(x=10, y=8, labels="1", col="black", cex=2)
text(x=10, y=0, labels="4", col="black", cex=2)
text(x=-3, y=8, labels="2", col="black", cex=2)
text(x=-3, y=0, labels="3", col="black", cex=2)
# Знаки в четвертях
text(x=7, y=6, labels="+/+", col="dark red", cex=2)
text(x=0, y=6, labels="+/-", col="dark red", cex=2)
text(x=7, y=2, labels="-/+", col="dark red", cex=2)
text(x=0, y=2, labels="-/-", col="dark red", cex=2)
(body.mean <- mean(animals.log$body))
[1] 3.771306
(brain.mean <- mean(animals.log$brain))
[1] 4.425446
abline(v=body.mean, col="dark red", cex=2)
abline(h=brain.mean, col="dark red", cex=2)
Две линии делят диаграмму на четыре квадранта. Для каждой i-ой точки на графике вычислим следующие величины:
- y_{i} — bar{y} отклонение каждого наблюдения y_{i} от выборочного среднего;
- x_{i} — bar{x} отклонение каждого наблюдения x_{i} от выборочного среднего;
- произведение двух величин (y_{i} — bar{y})(x_{i} — bar{x}).
y_deviation <- animals.log$brain - brain.mean
x_deviation <- animals.log$body - body.mean
xy_product <- y_deviation * x_deviation
Очевидно, что величины (y_{i} — bar{y}) положительны для каждой точки в 1 и 2 квадрантах и отрицательны в 3 и 4 квадрантах. Аналогично (x_{i} — bar{x}) положительны в 1 и 4 квадрантах и отрицательны в 2 и 3 квадрантах. Если линейная связь между y и x отрицательна (с увеличением x уменьшается y), то больше точек в 2 и 4 квадрантах. И наоборот, если связь положительна (с увеличением x увеличивается y), то больше точек в 1 и 3 квадрантах. Таким образом, знак следующего выражения:
cov(y,x) = frac{sum_{i=1}^{n}(y_{i} — bar{y})(x_{i} — bar{x})}{n-1}
которое известно как коэффициент ковариации между y и x, указывает направление линейного отношения между y и x. Если cov(y,x) gt 0, то связь положительная, иначе отрицательная.
> sum(xy_product) / (nrow(animals.log) - 1)
[1] 7.051974
# Или с помощью функции cov()
> cov(x=animals.log$body, y=animals.log$brain)
[1] 7.051974
К сожалению, cov(Y,X) не может нам много сказать о силе связи, потому что она зависима от изменений в шкале измерения объектов. Для того, чтобы избежать этого недостатка ковариации необходимо нормализовать (стандартизировать) данные прежде чем вычислять ковариацию. Для нормализации Y сначала вычитается выборочное среднее из каждого наблюдения и делится на стандартное отклонение:
z_{i} = frac{y_{i} — bar{y}}{s_{y}}
где
s_{y} = sqrt{frac{sum_{i=1}^{n}(y_{i} — bar{y})^2}{n-1}}
называется выборочным среднеквадратическим отклонением Y. Легко показать, что нормализованная переменная Z имеет математическое ожидание 0 и стандартное отклонение 1. Аналогично нормализуется X. Ковариация между нормализованными X и Y называется коэффициентом корреляции между X и Y и вычисляется по следующей формуле:
cor(Y, X) = frac{1}{n-1}sum_{i=1}^{n}(frac{y_{i} — bar{y}}{s_{y}})(frac{x_{i} — bar{x}}{s_{x}}) = frac{cov(Y,X)}{s_{y}s_{x}} = frac{sum{(y_{i} — bar{y})(x_{i} — bar{x})}}{sqrt{sum{(y_{i} — bar{y})^2(x_{i} — bar{x})^2}}}
> cov(x=animals.log$body, y=animals.log$brain) / (sd(animals.log$body) * sd(animals.log$brain))
[1] 0.7794935
# Или с помощью функции cor()
> cor(animals.log$body, animals.log$brain)
[1] 0.7794935
par(mfrow=c(1, 2))
animals.log.cor <- cor(animals.log$body, animals.log$brain)
animals.cor <- cor(Animals$body, Animals$brain)
plot_animals(paste('r = ', round(animals.cor, 3)))
plot_animals(paste('r = ', round(animals.log.cor, 3)))
par(mfrow=c(1, 1))
Таким образом, Cor(Y, X) может быть интерпретирована как ковариация между стандартизированными переменными или отношение ковариации к стандартным отклонениям двух переменных. Коэффициент корреляции является симметричным, то есть: Cor(Y,X) = Cor(X,Y).
В отличии от Cov(Y,X), Cor(Y,X) инвариантна (не зависит от шкалы измеряемых величин) и удовлетворяет условию -1 leq Cor(Y,X) leq 1.
Итак, убедившись, что между y и x сущетвует линейная взаимосвязь необходимо построить модель, которая наилучшим образом позволила бы эту взаимосвязь описать, но какую модель следует выбрать?
plot_animals()
abline(lm(animals.log$brain ~ animals.log$body), col="darkred")
abline(a = 2.0, b = 0.8, col='darkred')
abline(a = 3.0, b = 0.3, col='darkred')
Мы рассмотрим разные линейные модели и начнем с простой линейной регрессии.
Todo
Рассказать про коэффициент корреляции, ближе к -1, 1 и 0. 0 не значит отсутствие зависимости, просто она может не быть линейной, например, Y = 50 — x^2. Рассказать про Anscombe датасет:
data(anscombe)
summary(anscombe)
cor(anscombe)
Простая линейная регрессия
Простая линейная регрессия (least squares regression line) это метод восстановления зависимости между двумя переменными: предсказываемой переменной Y и предиктором X:
Y = beta_{0} + beta_{1} X + epsilon
Где beta_{0} это пересечение (показывает значение Y при X = 0), beta_{1} угол наколна прямой, а epsilon случайная ошибка. Параметры beta_{0} и beta_{1} называются регрессионными коэффициентами.
Метод наименьших квадратов позволяет вычислить параметры beta_{0} и beta_{1} минимизируя сумму квадратов ошибок (вертикальных дистанций, см. рисунок ниже). Ошибки могут быть найдены по следующей формуле:
epsilon_{i} = y_{i} — beta_{0} — beta_{1}times x_{i}, i=1,2,…,n
Сумма квадратов ошибок (sum of squares errors) может быть записана как:
SSE(beta_{0}, beta_{1}) = sum_{i=1}^{n} epsilon_{i}^2 = sum_{i=1}^{n}(y_{i} — beta_{0} — beta_{1} x_{i})^2 rightarrow min
Note
В разной литературе можно встретить разные обозначения: SSE (sum of squared errors of prediction) == RSS (residual sum of squares) == SSR (sum of squared residuals).
Наша задача найти такие значения hat{beta_{0}} и hat{beta_{1}}, которые минимизируют SSE(beta_{0}, beta_{1}):
library(manipulate)
plotMininizeError <- function(beta0, beta1) {
error <- sum((beta0 + beta1 * animals.log$body - animals.log$brain)^2)
plot(animals.log$body, animals.log$brain,
xlab='log(body weight)', ylab='log(brain weight)',
main=paste(round(error, 3)))
abline(a = beta0, b = beta1, col='darkred')
}
manipulate(plotMininizeError(b0, b1),
b0=slider(0, 3, step=0.1),
b1=slider(0, 2, step = 0.1))
Чтобы найти beta_{0}, beta_{1}, которые минимизируют SSE, необходимо решить:
triangledown SSE = left (frac{partial SSE}{partial beta_0}, frac{partial SSE}{partial beta_1}right ) = (0,0)
begin{aligned}
frac{partial SSE}{partial beta_0} =& -2sum_{i=1}^{n}(y_{i} — (beta_{0} + beta_{1} x_{i})) = 0 & Rightarrow &
&nbeta_0& + Big(sum_{i=1}^{n}x_iBig)beta_1 = sum_{i=1}^{n}y_i \
frac{partial SSE}{partial beta_1} =& -2sum_{i=1}^{n}(y_{i} — (beta_{0} + beta_{1} x_{i}))x_{i} = 0 & Rightarrow &
&Big(sum_{i=1}^{n}x_iBig)beta_0& + Big(sum_{i=1}^{n}x_i^2Big)beta_1 = sum_{i=1}^{n}x_iy_i
end{aligned}
Откуда получим:
beta_1 = frac{nsum x_iy_i — (sum x_i)(sum y_i)}{n(sum x_i^2) — (sum x_i)^2} = frac{sum (x_i-bar{x})(y_i-bar{y})}{sum (x_i-bar{x})} = rfrac{s_y}{s_x} qquad
beta_0 = bar{y} — beta_1bar{x}
Note
Линейная регрессия (или как ее еще иногда называют метод наименьших квадратов) была впервые описана Гауссом в 1795 году (Гауссу было всего 18 лет) и позже опубликована в его знаменитой книге «Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium» (Теория движения небесных тел), где он изложил методы вычисления планетных орбит.
В случае простой линейной регрессии коэффициент beta_{1} можно вычислить и более простым способом. Угол наклона прямой считается как frac{dy}{dx}, откуда получим:
begin{aligned}
beta_1 = frac{dy}{dx} rightarrow \
beta_1 = frac{sum_{i=1}^{n}(y_{i} — bar{y})}{sum_{i=1}^{n}(x_{i} — bar{x})} | times sum_{i=1}^{n}(x — bar{x}) rightarrow \
beta_1 = frac{sum_{i=1}^{n}(y_{i} — bar{y})(x_{i} — bar{x})}{sum_{i=1}^{n}(x_{i} — bar{x})^2} rightarrow … \
beta_1 = rfrac{s_{y}}{s_{x}}
end{aligned}
> (beta1 <- cor(animals.log$body, animals.log$brain) * sd(animals.log$brain) / sd(animals.log$body))
[1] 0.4959947
> (beta0 <- mean(animals.log$brain) - beta1 * mean(animals.log$body))
[1] 2.554898
> plot_animals(animals.log, xlab='log(body weight)', ylab='log(brain weight)',
main = 'Brain and Body Weights for 28 Species')
> abline(a = beta0, b = beta1, col="darkred")
В R такую модель можно построить с помощью функции lm:
> model <- lm(formula = brain ~ body, data = animals.log)
> summary(model)
Call:
lm(formula = brain ~ body, data = animals.log)
Residuals:
Min 1Q Median 3Q Max
-3.2890 -0.6763 0.3316 0.8646 2.5835
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.55490 0.41314 6.184 1.53e-06 ***
body 0.49599 0.07817 6.345 1.02e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.532 on 26 degrees of freedom
Multiple R-squared: 0.6076, Adjusted R-squared: 0.5925
F-statistic: 40.26 on 1 and 26 DF, p-value: 1.017e-06
y ~ x называется формулой. Символ ~ в формуле следует читать как «описывается переменной». К объяснению вывода результатов команды summary мы еще вернемся. А пока ответим на вопрос «Как с помощью полученной модели делать прогнозы?».
Итак, наша оцененная модель в общем виде может быть записана следующим образом:
hat{y} = hat{beta_0} + hat{beta_1}x
Подставив значения для оцененных коэффициентов hat{beta_0} и hat{beta_1} получим:
Теперь мы можем использовать эту модель для прогнозов.
library(manipulate)
plotPrediction <-function(newx) {
model <- lm(brain~body, data=animals.log)
plot(animals.log$body, animals.log$brain,
xlab='log(body weight)', ylab='log(brain weight)',
main=paste('y = ', round(predict(model, newdata=data.frame(body=newx)), 3)))
abline(model, lwd=2, col='dark blue')
points(c(newx), c(min(animals.log$brain)-0.35), lwd=3, col='darkred')
points(c(newx, newx), c(min(animals.log$brain)-0.35,
model$coefficients[1] + newx*model$coefficients[2]),
type='l', lwd=2, col="darkred", lty=2)
points(c(min(animals.log$body)-0.4, newx),
c(model$coefficients[1] + newx*model$coefficients[2],
model$coefficients[1] + newx*model$coefficients[2]),
type='l', lwd=2, col="darkred", lty=2)
points(c(min(animals.log$body)-0.6),
c(model$coefficients[1] + newx*model$coefficients[2]),
lwd=3, col='darkred')
}
manipulate(plotPrediction(new_x), new_x = slider(min(animals.log$body), max(animals.log$body)))
Нам необходимо вернуться к исходной шкале измерения, чтобы делать легко интерпретируемые прогнозы:
begin{aligned}
ln(y) & = 2.555 + 0.496 times ln(x) + epsilon \
e^{ln(y)} & = e^{2.555 + 0.496 times ln(x) + epsilon} \
y & = e^{2.555}e^{ln(x)^{0.496}}e^{epsilon} \
y & = e^{2.555 + epsilon} times x^{0.496}
end{aligned}
Оценка полученной модели
Коэффициент детерминации (R-square) — это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью. Более точно — это единица минус доля необъяснённой дисперсии (дисперсии случайной ошибки модели, или условной по признакам дисперсии зависимой переменной) в дисперсии зависимой переменной:
R^{2} = 1 — frac{sum_{i=1}^{n}(y_i-hat{y_{i}})^2}{sum_{i=1}^{n}(y_i-bar{y})^2}
model <- lm(animals.log$brain ~ animals.log$body)
(r2 <- 1 - sum((animals.log$brain - predict(model))^2) / sum((animals.log$brain - mean(animals.log$brain))^2))
[1] 0.6076101
Одной из проблем коэффициента детерминации является то, что его значение только увеличивается при добавлении в модель новых переменных, поэтому при сравнении моделей с разным числом переменных может быть ошибочно принято решение, что модель с большим числом переменных лучше чем модель с меньшим числом переменных.
Скорректированный коэффициент детерминации (Adjusted R-square) — выражает долю дисперсии зависимой переменной, объясняемую регрессионной моделью с заданным набором независимых переменных, скорректированный с помощью штрафа, накладываемого на модель при увеличении числа переменных:
R{_{adj}}^{2} = 1 — frac{(1-R^2)(N-1)}{N-p-1}
(r2_adj <- 1 - ((1-r2)*(nrow(animals.log) - 1)) / (nrow(animals.log) - 1 - 1))
[1] 0.5925182
Также для оценки модели используют среднеквадратичную ошибку, которая характеризует отклонение реальных данных от линии регрессии и измеряется в тех же единицах, что и зависимая переменная (y):
RMSE = sqrt{frac{sum_{i=1}^{m}(hat{y_i} — y_i)^2}{m}}
Квартет Энскомба
Связь МНК и ММП
Рассмотрим принцип максимального правдоподобия (maximum likelihood estimation) на примере задачи подбрасывания монетки, а затем применим его к задаче линейной регрессии. Пусть у нас имеется:
- y — число решек при подбрасывании монетки n раз;
- n — число бросков;
- p — вероятность выпадания решки (неизвестна);
- hat{p} — оценка вероятности выпадания решки.
Предположим, что мы не знаем истинную вероятность выпадания решки (0.5), поэтому попробуем ее оценить. По интуиции:
hat{p} = frac{y}{n} = frac{# textit{решек}}{# textit{бросков}}
Например, если выпало 3 решки при 5 бросках, то:
hat{p} = frac{y}{n} = frac{3}{5} = 0.6
Теперь давайте попробуем подтвердить нашу интуицию математически. Эксперимент с подбрасыванием монетки может быть описан с помощью Биномиального распределения:
P(Y = y|n, p) = begin{pmatrix} n \ y end{pmatrix}p^y(1 — p)^{n — y}
Читаем как: «Вероятность того, что решка выпадет y раз при заданной вероятности p и числе бросков n».
Для y=3 и n=5 получим:
P(Y = 3|5, p) = begin{pmatrix} 5 \ 3 end{pmatrix}p^3(1 — p)^{5 — 3}
Но мы все еще не знаем p. Принцип максимального правдоподобия заключается в том, чтобы найти такое значение p для имеющихся y и n, при котором мы получим максимальное значение для P.
Итак, зафиксируем y и n, тогда функция правдоподобия (likelihood) будет выглядеть следующим образом:
L(p|y, n) = begin{pmatrix} n \ y end{pmatrix}p^y(1 — p)^{n — y} rightarrow max
Для наглядности будем перебирать значения p in [0;1] с шагом 0.1 и для каждого значения вычислим функцию правдоподобия:
library(graphics)
probs <- seq(0,1,0.1)
likelihoods <- dbinom(3, size=5, prob=probs)
plot(probs, likelihoods, type='l', xlab = 'probability', ylab = 'likelihood')
points(probs, likelihoods, col = 'royal blue')
segments(probs, rep(0, length(probs)), probs, likelihoods, lty=3, col='royal blue')
Из графика хорошо видно, что мы достигаем максимума при p = 0.6, но мы не будем каждый раз перебирать параметр p.
Иногда для упрощения расчетов берут логарифм, таким образом, максимизируя log-likelihood:
log ell (p|y, n) = log begin{pmatrix} n \ y end{pmatrix} + ylog p + (n — y)log (1 — p)
И наконец продифференцируем функцию относительно параметра p и приравняем ее нулю:
frac{partial log ell}{partial p} = frac{y}{p} — frac{n — y}{1 — p} = 0 Rightarrow y — yp — np + yp = 0 Rightarrow hat{p} = frac{y}{n}
Теперь кратко рассмотрим метод максимального правдоподобия применительно к линейной регрессии:
Y_i = beta_0 + beta_1x_i + epsilon
Предположим, что остатки имеют нормальное распределение epsilon_i sim mathcal{N}(0, sigma^2), тогда:
Y_i|X_i sim mathcal{N}(beta_0 + beta_1 x_i, sigma^2)
В случае нормального распределния функция плотности вероятности для случайной величины X выглядит следующим образом:
f_X(x; mu, sigma^2) = frac{1}{sqrt{2pisigma^2}}exp -frac{(x — mu)^2}{2sigma^2}
Тогда мы можем записать функцию плотности вероятности для каждой величины Y_i как:
f_{Y_i}(y_i; x_i, beta_0, beta_1, sigma^2) = frac{1}{sqrt{2pisigma^2}}exp -frac{(y_i — beta_0 — beta_1 x_i)^2}{2sigma^2}
Для n точек (x_i, y_i) мы можем записать функцию правдоподобия от трех параметров beta_0, beta_1, sigma^2 следующим образом:
L(beta_0, beta_1, sigma^2) = prod_{i = 1}^{n}frac{1}{sqrt{2pisigma^2}}exp -frac{(y_i — beta_0 — beta_1 x_i)^2}{2sigma^2}
Наша задача найти такие параметры beta_0, beta_1 и sigma^2, которые максимизируют L(beta_0, beta_1, sigma^2). Для простоты вычислений будем считать log-likelihood:
Note
По интуиции должно быть понятно, что log ell rightarrow max это тоже самое, что и SSE(beta_0, beta_1) rightarrow min.
begin{align}
log ell =& -sum_{i = 1}^{n}Big(frac{1}{2}log2pi + frac{1}{2}logsigma^2 + frac{1}{2sigma^2}(y_i — beta_0 — beta_1 x_i)^2Big) \
=& -frac{n}{2}log2pi -frac{n}{2}logsigma^2 — frac{1}{2sigma^2}sum_{i=1}^{n}(y_i — beta_0 — beta_1 x_i)^2
end{align}
Как и в задаче с подбрасыванием монетки возьмем частные проиводные по параметрам beta_0, beta_1 и sigma^2 и затем приравняем нулю:
frac{partial log ell}{partial beta_0} = frac{1}{sigma^2}sum_{i=1}^{n}(y_i — beta_0 — beta_1 x_i) Rightarrow sum_{i=1}^{n}(y_i — beta_0 — beta_1 x_i) = 0
frac{partial log ell}{partial beta_1} = frac{1}{sigma^2}sum_{i=1}^{n}(y_i — beta_0 — beta_1 x_i)x_i Rightarrow sum_{i=1}^{n}(y_i — beta_0 — beta_1 x_i)x_i = 0
frac{partial log ell}{partial sigma^2} = -frac{n}{2 sigma^2} + frac{1}{2 (sigma^2)^2}sum_{i=1}^{n}(y_i — beta_0 — beta_1 x_i)^2 Rightarrow -frac{n}{2 sigma^2} + frac{1}{2 (sigma^2)^2}sum_{i=1}^{n}(y_i — beta_0 — beta_1 x_i)^2 = 0
Откуда получим:
hat{beta_0} = bar{y} — beta_1bar{x}
hat{beta_1} = rfrac{s_y}{s_x}
hat{sigma}^2 = frac{1}{n}sum_{i=1}^{n}(y_i — hat{y_i})^2
Многомерная линейная регрессия
y_i = beta_1 + beta_2x_{2i} + … + beta_kx_{ki} + epsilon_i,quad (i=1,…,n)
Запишем в матричной форме:
y = begin{pmatrix} y_1 \ … \ y_n end{pmatrix},quad
X = begin{pmatrix} 1 & x_{21} & … & x_{k1} \ … & … & … & … \ 1 & x_{2n} & … & x_{kn} end{pmatrix},quad
beta = begin{pmatrix} beta_1 \ … \ beta_k end{pmatrix},quad
epsilon = begin{pmatrix} epsilon_1 \ … \ epsilon_n end{pmatrix}
Опять хотим минимизировать квадрат ошибки:
begin{align*}
L = sum_{i=1}^{n}epsilon_{i}^2 = epsilon’epsilon &= (y — Xbeta)'(y-Xbeta) \
&= y’y — y’Xbeta — X’beta’y + beta’X’b rightarrow min
end{align*}
Уже по известной схеме:
frac{partial L}{partial beta} = -2X’y + 2X’Xbeta = 0
Откуда получим:
X’Xb = X’y Rightarrow beta = (X’X)^{-1}X’y
Последнее уравнение называется нормальным уравнением (normal equation).
n <- length(y)
X <- cbind(x, rep(1,n))
B <- solve(t(X)%*%X)%*%t(X)%*%y
x.test <- seq(1,5, 0.25)
y.hat <- B[2]+B[1]*x.test
lines(x.test, y.hat,col="red")
Робастность регрессии
par(mfrow=c(1,2))
plot(brain ~ body, data=animals.log,
xlab='log(body weight)', ylab='log(brain weight)')
points(animals.log[animals.log$body > 8 & animals.log$brain < 6,],
pch=16, col="darkred")
model <- lm(brain ~ body, data = animals.log)
abline(model, lwd=2, col='dark blue')
plot(brain ~ body, data=animals.log,
xlab='log(body weight)', ylab='log(brain weight)')
points(animals.log[animals.log$body > 8 & animals.log$brain < 6,],
pch=16, col="darkred")
model <- rlm(brain ~ body, data=animals.log)
abline(model, lwd=2, col='dark blue')
par(mfrow=c(1,1))
Полиномиальная регрессия, ridge-регрессия и LASSO-регрессия
par(mfrow=c(1,2))
set.seed(123456)
x <- seq(-2, 5, length.out=20)
y <- sin(x) + runif(length(x), -0.25, 0.25)
fit <- lm(y ~ x)
plot(y ~ x, lwd=2, main="Ordinary Least Squares")
abline(fit, lwd=2, col='dark blue')
plot(resid(fit) ~ fitted(fit), lwd=2, ylab="Residuals", xlab="Fitted", main="Residuals vs Fitted values")
abline(0, 0, lwd=2, col='dark blue')
par(mfrow=c(1,1))
par(mfrow=c(3,3))
poly.1 <- lm(y ~ poly(x, 1))
poly.7 <- lm(y ~ poly(x, 7))
poly.14 <- lm(y ~ poly(x, 14))
plot(y ~ x, lwd = 2, main="")
curve(predict(poly.1, data.frame(x=x)), add=TRUE, col="royalblue")
plot(y ~ x, lwd = 2, main="")
curve(predict(poly.7, data.frame(x=x)), add=TRUE, col="darkgreen")
plot(y ~ x, lwd = 2, main="")
curve(predict(poly.14, data.frame(x=x)), add=TRUE, col="darkred")
plot(y ~ x, lwd = 2, main="")
curve(predict(poly.1, data.frame(x=x)), add=TRUE, col="royalblue")
points(x1, y1, lwd=2, pch=2)
plot(y ~ x, lwd = 2, main="")
curve(predict(poly.7, data.frame(x=x)), add=TRUE, col="darkgreen")
points(x1, y1, lwd=2, pch=2)
plot(y ~ x, lwd = 2, main="")
curve(predict(poly.14, data.frame(x=x)), add=TRUE, col="darkred")
points(x1, y1, lwd=2, pch=2)
plot(resid(poly.1) ~ fitted(poly.1), lwd=2, ylab="Residuals", xlab="Fitted")
abline(0, 0, lwd=2, col='dark blue')
plot(resid(poly.7) ~ fitted(poly.7), lwd=2, ylab="Residuals", xlab="Fitted")
abline(0, 0, lwd=2, col='dark blue')
plot(resid(poly.14) ~ fitted(poly.14), lwd=2, ylab="Residuals", xlab="Fitted")
abline(0, 0, lwd=2, col='dark blue')
par(mfrow=c(1,1))
Простая модель очень плохо описывает наши данные и это называется underfitting, полиномиальная модель же наоборот, прошла через каждую точку и в точности описала все данные, это называется overfitting.
poly.2 <- lm(y ~ poly(x, 2))
poly.3 <- lm(y ~ poly(x, 3))
poly.4 <- lm(y ~ poly(x, 4))
poly.5 <- lm(y ~ poly(x, 5))
poly.6 <- lm(y ~ poly(x, 6))
poly.8 <- lm(y ~ poly(x, 8))
poly.9 <- lm(y ~ poly(x, 9))
poly.10 <- lm(y ~ poly(x, 10))
poly.11 <- lm(y ~ poly(x, 11))
poly.12 <- lm(y ~ poly(x, 12))
poly.13 <- lm(y ~ poly(x, 13))
anova(poly.1, poly.2, poly.3, poly.4, poly.5, poly.6, poly.7, poly.8, poly.9,
poly.10, poly.11, poly.12)
Analysis of Variance Table
Model 1: y ~ poly(x, 1)
Model 2: y ~ poly(x, 2)
Model 3: y ~ poly(x, 3)
Model 4: y ~ poly(x, 4)
Model 5: y ~ poly(x, 5)
Model 6: y ~ poly(x, 6)
Model 7: y ~ poly(x, 7)
Model 8: y ~ poly(x, 8)
Model 9: y ~ poly(x, 9)
Model 10: y ~ poly(x, 10)
Model 11: y ~ poly(x, 11)
Model 12: y ~ poly(x, 12)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 13 6.7847
2 12 1.7598 1 5.0249 68.7312 0.01424 *
3 11 1.6804 1 0.0794 1.0859 0.40679
4 10 0.2022 1 1.4782 20.2190 0.04607 *
5 9 0.1992 1 0.0030 0.0416 0.85728
6 8 0.1548 1 0.0444 0.6075 0.51732
7 7 0.1542 1 0.0006 0.0079 0.93723
8 6 0.1542 1 0.0000 0.0004 0.98568
9 5 0.1473 1 0.0069 0.0937 0.78845
10 4 0.1470 1 0.0003 0.0042 0.95421
11 3 0.1469 1 0.0001 0.0017 0.97091
12 2 0.1462 1 0.0007 0.0090 0.93296
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Ridge-регрессия
Note
Регуляризация Тихонова.
Мы видели, что если в модель включить слишком много параметров, то она склонна к переобучению. В случае гребневой регрессии (ridge regression) мы включаем дополнительный параметр lambda для регулирования сложности модели. Простыми словами, чем больше значение lambda, тем проще модель мы хотим получить.
Ранее мы минимизировали:
SSE(beta) = sum_{i=1}^{n}(y_{i} — sum_{j=1}^{p}beta_{j} x_{j})^2
А теперь будем минимизировать:
SSE(beta) = sum_{i=1}^{n}(y_{i} — sum_{j=1}^{p}beta_{j} x_{j})^2 + lambdasum_{j=1}^{p}beta_{j}^2
где lambda — параметр регуляризации, который надо как-то выбрать.
L = (y — Xbeta)^{T}(y-Xbeta) + lambdabeta^{T}beta
Если взять производную, то получим:
beta = (X^{T}X + lambda I)^{-1}X^{T}y
x <- seq(-2, 5, length.out=15)
y <- sin(x) + runif(length(x), -0.25, 0.25)
plot(y ~ x, lwd = 2)
x1 <- seq(-2, 5, length.out = 20)
y <- sin(x1) + runif(length(x1), -0.25, 0.25)
points(x1, y1, col="darkred", lwd=2, pch=17)
cv.ridge <- cv.glmnet(poly(x, 7), y, alpha=0, family='gaussian')
points(x1, predict(cv.ridge, poly(x1, 7), s=cv.ridge$lambda.min), type="l", col="royalblue", lwd=2)
LASSO-регрессия
SSE(beta) = sum_{i=1}^{n}(y_{i} — sum_{j=1}^{p}beta_{j} x_{j})^2 + lambdasum_{j=1}^{p}beta_{j}^2
library(lars)
lasso.model <- lars(x = poly(x, 14), y = y, type = "lasso")
plot(lasso.model)
x1 <- seq(-2, 5, length.out = 20)
y1 <- sin(x1) + runif(20, -0.25, 0.25)
y.pred.lasso <- predict(lasso.model,
poly(x1, 14),
s=best.fraction,
type="fit",
mode="fraction")
plot(y ~ x, lwd = 2, main="")
points(x1, y.pred.lasso$fit, type="l", col="royalblue", lwd=2)
points(x1, y1, col="darkred", lwd=2, pch=17)
Последнее обновление: 4 мая 2021 г.
From Wikipedia, the free encyclopedia
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its «true value» (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals.
In econometrics, «errors» are also called disturbances.[1][2][3]
Introduction[edit]
Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the deviations of the observations from the population mean, while the residuals are the deviations of the observations from the sample mean.
A statistical error (or disturbance) is the amount by which an observation differs from its expected value, the latter being based on the whole population from which the statistical unit was chosen randomly. For example, if the mean height in a population of 21-year-old men is 1.75 meters, and one randomly chosen man is 1.80 meters tall, then the «error» is 0.05 meters; if the randomly chosen man is 1.70 meters tall, then the «error» is −0.05 meters. The expected value, being the mean of the entire population, is typically unobservable, and hence the statistical error cannot be observed either.
A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error. Consider the previous example with men’s heights and suppose we have a random sample of n people. The sample mean could serve as a good estimator of the population mean. Then we have:
- The difference between the height of each man in the sample and the unobservable population mean is a statistical error, whereas
- The difference between the height of each man in the sample and the observable sample mean is a residual.
Note that, because of the definition of the sample mean, the sum of the residuals within a random sample is necessarily zero, and thus the residuals are necessarily not independent. The statistical errors, on the other hand, are independent, and their sum within the random sample is almost surely not zero.
One can standardize statistical errors (especially of a normal distribution) in a z-score (or «standard score»), and standardize residuals in a t-statistic, or more generally studentized residuals.
In univariate distributions[edit]
If we assume a normally distributed population with mean μ and standard deviation σ, and choose individuals independently, then we have
and the sample mean
is a random variable distributed such that:
The statistical errors are then
with expected values of zero,[4] whereas the residuals are
The sum of squares of the statistical errors, divided by σ2, has a chi-squared distribution with n degrees of freedom:
However, this quantity is not observable as the population mean is unknown. The sum of squares of the residuals, on the other hand, is observable. The quotient of that sum by σ2 has a chi-squared distribution with only n − 1 degrees of freedom:
This difference between n and n − 1 degrees of freedom results in Bessel’s correction for the estimation of sample variance of a population with unknown mean and unknown variance. No correction is necessary if the population mean is known.
[edit]
It is remarkable that the sum of squares of the residuals and the sample mean can be shown to be independent of each other, using, e.g. Basu’s theorem. That fact, and the normal and chi-squared distributions given above form the basis of calculations involving the t-statistic:
where 


The probability distributions of the numerator and the denominator separately depend on the value of the unobservable population standard deviation σ, but σ appears in both the numerator and the denominator and cancels. That is fortunate because it means that even though we do not know σ, we know the probability distribution of this quotient: it has a Student’s t-distribution with n − 1 degrees of freedom. We can therefore use this quotient to find a confidence interval for μ. This t-statistic can be interpreted as «the number of standard errors away from the regression line.»[6]
Regressions[edit]
In regression analysis, the distinction between errors and residuals is subtle and important, and leads to the concept of studentized residuals. Given an unobservable function that relates the independent variable to the dependent variable – say, a line – the deviations of the dependent variable observations from this function are the unobservable errors. If one runs a regression on some data, then the deviations of the dependent variable observations from the fitted function are the residuals. If the linear model is applicable, a scatterplot of residuals plotted against the independent variable should be random about zero with no trend to the residuals.[5] If the data exhibit a trend, the regression model is likely incorrect; for example, the true function may be a quadratic or higher order polynomial. If they are random, or have no trend, but «fan out» — they exhibit a phenomenon called heteroscedasticity. If all of the residuals are equal, or do not fan out, they exhibit homoscedasticity.
However, a terminological difference arises in the expression mean squared error (MSE). The mean squared error of a regression is a number computed from the sum of squares of the computed residuals, and not of the unobservable errors. If that sum of squares is divided by n, the number of observations, the result is the mean of the squared residuals. Since this is a biased estimate of the variance of the unobserved errors, the bias is removed by dividing the sum of the squared residuals by df = n − p − 1, instead of n, where df is the number of degrees of freedom (n minus the number of parameters (excluding the intercept) p being estimated — 1). This forms an unbiased estimate of the variance of the unobserved errors, and is called the mean squared error.[7]
Another method to calculate the mean square of error when analyzing the variance of linear regression using a technique like that used in ANOVA (they are the same because ANOVA is a type of regression), the sum of squares of the residuals (aka sum of squares of the error) is divided by the degrees of freedom (where the degrees of freedom equal n − p − 1, where p is the number of parameters estimated in the model (one for each variable in the regression equation, not including the intercept)). One can then also calculate the mean square of the model by dividing the sum of squares of the model minus the degrees of freedom, which is just the number of parameters. Then the F value can be calculated by dividing the mean square of the model by the mean square of the error, and we can then determine significance (which is why you want the mean squares to begin with.).[8]
However, because of the behavior of the process of regression, the distributions of residuals at different data points (of the input variable) may vary even if the errors themselves are identically distributed. Concretely, in a linear regression where the errors are identically distributed, the variability of residuals of inputs in the middle of the domain will be higher than the variability of residuals at the ends of the domain:[9] linear regressions fit endpoints better than the middle. This is also reflected in the influence functions of various data points on the regression coefficients: endpoints have more influence.
Thus to compare residuals at different inputs, one needs to adjust the residuals by the expected variability of residuals, which is called studentizing. This is particularly important in the case of detecting outliers, where the case in question is somehow different from the others in a dataset. For example, a large residual may be expected in the middle of the domain, but considered an outlier at the end of the domain.
Other uses of the word «error» in statistics[edit]
The use of the term «error» as discussed in the sections above is in the sense of a deviation of a value from a hypothetical unobserved value. At least two other uses also occur in statistics, both referring to observable prediction errors:
The mean squared error (MSE) refers to the amount by which the values predicted by an estimator differ from the quantities being estimated (typically outside the sample from which the model was estimated).
The root mean square error (RMSE) is the square-root of MSE.
The sum of squares of errors (SSE) is the MSE multiplied by the sample size.
Sum of squares of residuals (SSR) is the sum of the squares of the deviations of the actual values from the predicted values, within the sample used for estimation. This is the basis for the least squares estimate, where the regression coefficients are chosen such that the SSR is minimal (i.e. its derivative is zero).
Likewise, the sum of absolute errors (SAE) is the sum of the absolute values of the residuals, which is minimized in the least absolute deviations approach to regression.
The mean error (ME) is the bias.
The mean residual (MR) is always zero for least-squares estimators.
See also[edit]
- Absolute deviation
- Consensus forecasts
- Error detection and correction
- Explained sum of squares
- Innovation (signal processing)
- Lack-of-fit sum of squares
- Margin of error
- Mean absolute error
- Observational error
- Propagation of error
- Probable error
- Random and systematic errors
- Reduced chi-squared statistic
- Regression dilution
- Root mean square deviation
- Sampling error
- Standard error
- Studentized residual
- Type I and type II errors
References[edit]
- ^ Kennedy, P. (2008). A Guide to Econometrics. Wiley. p. 576. ISBN 978-1-4051-8257-7. Retrieved 2022-05-13.
- ^ Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. Cengage Learning. p. 57. ISBN 978-1-337-67133-0. Retrieved 2022-05-13.
- ^ Das, P. (2019). Econometrics in Theory and Practice: Analysis of Cross Section, Time Series and Panel Data with Stata 15.1. Springer Singapore. p. 7. ISBN 978-981-329-019-8. Retrieved 2022-05-13.
- ^ Wetherill, G. Barrie. (1981). Intermediate statistical methods. London: Chapman and Hall. ISBN 0-412-16440-X. OCLC 7779780.
- ^ a b Frederik Michel Dekking; Cornelis Kraaikamp; Hendrik Paul Lopuhaä; Ludolf Erwin Meester (2005-06-15). A modern introduction to probability and statistics : understanding why and how. London: Springer London. ISBN 978-1-85233-896-1. OCLC 262680588.
- ^ Peter Bruce; Andrew Bruce (2017-05-10). Practical statistics for data scientists : 50 essential concepts (First ed.). Sebastopol, CA: O’Reilly Media Inc. ISBN 978-1-4919-5296-2. OCLC 987251007.
- ^ Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, with Special Reference to Biological Sciences. McGraw-Hill. p. 288.
- ^ Zelterman, Daniel (2010). Applied linear models with SAS ([Online-Ausg.]. ed.). Cambridge: Cambridge University Press. ISBN 9780521761598.
- ^ «7.3: Types of Outliers in Linear Regression». Statistics LibreTexts. 2013-11-21. Retrieved 2019-11-22.
- Cook, R. Dennis; Weisberg, Sanford (1982). Residuals and Influence in Regression (Repr. ed.). New York: Chapman and Hall. ISBN 041224280X. Retrieved 23 February 2013.
- Cox, David R.; Snell, E. Joyce (1968). «A general definition of residuals». Journal of the Royal Statistical Society, Series B. 30 (2): 248–275. JSTOR 2984505.
- Weisberg, Sanford (1985). Applied Linear Regression (2nd ed.). New York: Wiley. ISBN 9780471879572. Retrieved 23 February 2013.
- «Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
External links[edit]
Media related to Errors and residuals at Wikimedia Commons
Постановка задачи регрессии
Задача регрессии — это один из основных типов моделей машинного обучения. И хотя, большинство задач на практике относятся к другому типу — классификации, мы начнем знакомство с машинным обучением именно с регрессии. Регрессионные модели были известны задолго до появления машинного обучения как отрасли и активно применяются в статистике, эконометрике, математическом моделировании. Машинное обучение предлагает новый взгляд на уже известные в математике модели. И этот новый взгляд позволит строить более сложные и мощные модели, чем классические математические дисциплины.
Задача регрессии относится к категории задач обучения с учителем. Это значит, что набор данных, который используется для обучения, должен иметь определенную структуру. Обычно, датасеты для машинного обучения представляют собой таблицу, в которой по строкам перечислены разные объекты наблюдений или измерений. В столбцах — различные характеристики, или атрибуты, объектов. А на пересечении строк и столбцов — значение данной характеристики у данного объекта. Обычно один атрибут (или переменная) имеет особый характер — именно ее значение мы и хотим научиться предсказывать с помощью модели машинного обучения. Эта характеристика объекта называется целевая переменная. И если эта целевая переменная выражена числом (а точнее, некоторой непрерывной величиной) — то мы говорим о задаче регрессии.
Задача регрессии в машинном обучении — это задача предсказания какой-то численной характеристики объекта предметной области по определенному набору его параметров (атрибутов).
Задачи регрессии на практике встречаются довольно часто. Например, предсказание цены объекта недвижимости — классическая регрессионная задача. В таких проблемах атрибутами выступают разные характеристики квартир или домов — площадь, этажность, расположение, расстояние до центра города, количество комнат, год постройки. В разных наборах данных собрана разная информация И, соответственно, модели тоже должны быть разные. Другой пример — предсказание цены акций или других финансовых активов. Или предсказание температуры завтрашним днем.
Во всех таких задачах нам нужно иметь данные, которые позволят осуществить такое предсказание. Да, “предсказание” — это условный термин, не всегда мы говорим о будущих событиях. Зачастую говорят именно о “моделировании” значения целевой переменной. Регрессионные модели используют информацию об объектах в обучающем наборе данных, чтобы сделать вывод о возможном значении целевой переменной. И для этого нужно, чтобы ее значение имело какую-то зависимость от имеющихся у нас атрибутов. Если построить модель предсказания цены акции, но на вход подать информацию о футбольных матчах — ничего не получится. Мы предполагаем, что в наборе данных собраны именно те атрибуты объектов, которые имеют влияние на на значение целевой переменной. И чем больше это предположение выполняется, тем точнее будет потенциально наша модель.
Немного поговорим о терминах. Набор данных который мы используем для обучения модели называют датасетом (dataset) или обучающей выборкой (training set). Объекты, которые описываются в датасете еще называют точками данных (data points). Целевую переменную еще называют на статистический манер зависимой переменной (dependent variable) или результативной, выходной (output), а остальные атрибуты — независимыми переменными (independent variables), или признаками (features), или факторами, или входными переменными (input). Значения одного конкретного атрибута для всех объектов обучающей выборки часто представляют как вектор этого признака (feature vector). А всю таблицу всех атрибутов называют матрицей атрибутов (feature matrix). Соответственно, еще есть вектор целевой переменной, он не входит в матрицу атрибутов.
Датасет, набор данных — совокупность информации в определенной структурированной форме, которая используется для построения модели машинного обучения для решения определенной задачи. Датасет обычно представляется в табличной форме. Датасет описывает некоторое множество объектов предметной области — точек данных.
С точки зрения информатики, регрессионная модель — это функция, которая принимает на вход значения атрибутов какого-то конкретного объекта и выдает на выходе предполагаемое значение целевой переменной. В большинстве случаев мы предполагаем, что целевая переменная у нас одна. Если стоит задача предсказания нескольких характеристик, то их чаще воспринимают как несколько независимых задач регрессии на одних и тех же атрибутах.
Мы пока ничего не говорили о том, как изнутри устроена регрессионная модель. Это потому, что она может быть какой угодно. Это может быть математическое выражение, условный алгоритм, сложная программа со множеством ветвлений и циклов, нейронная сеть — все это можно представить регрессионной моделью. Единственное требование к модели машинного обучения — она должна быть параметрической. То есть иметь какие-то внутренние параметры, от которых тоже зависит результат вычисления. В простых случаях, чаще всего в качестве регрессионной модели используют аналитические функции. Таких функций бесконечное количество, но чаще всего используется самая простая функция, с которой мы и начнем изучение регрессии — линейная функция.
Регрессионные модели подразделяют на парную и множественную регрессии. Парная регрессия — это когда у нас всего один атрибут. Множественная — когда больше одного. Конечно, на практике парная регрессия не встречается, но на примере такой простой модели мы поймем основные концепции машинного обучения. Плюс, парную регрессию очень удобно и наглядно можно изобразить на графике. Когда у нас больше двух переменных, графики уже не особо построишь, и модели приходится визуализировать иначе, более косвенно.
Выводы:
- Регрессия — это задача машинного обучения с учителем, которая заключается в предсказании некоторой непрерывной величины.
- Для использования регрессионных моделей нужно, чтобы в датасете были характеристики объектов и “правильные” значения целевой переменной.
- Примеры регрессионных задач — предсказание цены акции, оценка цены объекта недвижимости.
- Задача регрессии основывается на предположении, что значение целевой переменной зависит от значения признаков.
- Регрессионная модель принимает набор значений и выдает предсказание значения целевой переменной.
- В качестве регрессионных моделей часто берут аналитические функции, например, линейную.
Парная линейная регрессия
Функция гипотезы
Напомним, что в задачах регрессии мы принимаем входные переменные и пытаемся получить более-менее достоверное значение целевой переменной. Любая функция, даже самая простая линейная может выдавать совершенно разные значения для одних и тех же входных данных, если в функции будут разные параметры. Поэтому, любая регрессионная модель — это не какая-то конкретная математическая функция, а целое семейство функций. И задача алгоритма обучения — подобрать значения параметров таким образом, чтобы для объектов обучающей выборки, для которых мы уже знаем правильные ответы, предсказанные (или теоретические, вычисленные из модели) значения были как можно ближе к тем, которые есть в датасете (эмпирические, истинные значения).
Функция гипотезы — преобразование, которое принимает на вход набор значений признаков определенного объекта и выдает оценку значения целевой переменной данного объекта. Она лежит в основе модели машинного обучения.
Парная, или одномерная (univariate) регрессия используется, когда вы хотите предсказать одно выходное значение (чаще всего обозначаемое $y$), зависящее от одного входного значения (обычно обозначается $x$). Сама функция называется функцией гипотезы или моделью. В качестве функции гипотезы для парной регрессии можно выбрать любую функцию, но мы пока потренируемся с самой простой функцией одной переменной — линейной функцией. Тогда нашу модель можно назвать парной линейной регрессией.
В случае парной линейной регрессии функция гипотезы имеет следующий общий вид:
[hat{y} = h_b (x) = b_0 + b_1 x]
Обратите внимание, что это похоже на уравнение прямой. Эта модель соответствует множеству всех возможных прямых на плоскости. Когда мы конкретизируем модель значениями параметров (в данном случае — $b_0$ и $b_1$), мы получаем конкретную прямую. И наша задача состоит в том, чтобы выбрать такую прямую, которая бы лучше всего “легла” в точки из нашей обучающей выборки.
В данном случае, мы пытаемся подобрать функцию h(x) таким образом, чтобы отобразить данные нам значения x в данные значения y. Допустим, мы имеем следующий обучающий набор данных:
| входная переменная x | выходная переменная y |
| 0 | 4 |
| 1 | 7 |
| 2 | 7 |
| 3 | 8 |
Мы можем составить случайную гипотезу с параметрами $ b_0 = 2, b_1 = 2 $. Тогда для входного значения $ x=1 $ модель выдаст предсказание, что $ y=4 $, что на 3 меньше данного. Значение $y$, которое посчитала модель будем называть теоретическим или предсказанным (predicted), а значение, которое дано в наборе данных — эмпирическим или истинным (true). Задача регрессии состоит в нахождении таких параметров функции гипотезы, чтобы она отображала входные значения в выходные как можно более точно (чтобы теоретические значения были как можно ближе к эмпирическим), или, другими словами, описывала линию, наиболее точно ложащуюся в данные точки на плоскости $(x, y)$.
Выводы:
- Модель машинного обучения — это параметрическая функция.
- Задача обучения состоит в том, чтобы подобрать параметры модели таким образом, чтобы она лучше всего описывала обучающие данные.
- Парная линейная регрессия работает, если есть всего одна входящая переменная.
- Парная линейная регрессия — одна из самых простых моделей машинного обучения.
- Парная линейная регрессия соответствует множеству всех прямых на плоскости. Из них мы выбираем одну, наиболее подходящую.
Функция ошибки
Как мы уже говорили, разные значения параметров дают разные конкретные модели. Для того, чтобы подобрать наилучшую модель, нам нужно средство измерения “точности” модели, некоторая функция, которая показывает, насколько модель хорошо или плохо соответствует имеющимся данным.
В простых случаях мы можем отличить хорошие модели от плохих, только взглянув на график. Но это затруднительно, если количество признаков очень велико, или если модели лишь немного отличаются друг от друга. Да и для автоматизации процесса нужен способ формализовать наше общее представление о том, что модель “ложится” в точки данных.
Такая функция называется функцией ошибки (cost function). Она измеряет отклонения теоретических значений (то есть тех, которые предсказывает модель) от эмпирических (то есть тех, которые есть в данных). Чем выше значение функции ошибки, тем хуже модель соответствует имеющимся данным, хуже описывает их. Если модель полностью соответствует данным, то значение функции ошибки будет нулевым.
В задачах регрессии в качестве функции ошибки чаще всего берут среднеквадратичное отклонение теоретических значений от эмпирических. То есть сумму квадратов отклонений, деленную на удвоенное количество измерений. Казалось бы, что это довольно произвольный выбор. Но он вполне обоснован и логичен. Давайте порассуждаем. Чтобы оценить, насколько хороша модель, мы должны оценить, насколько отклоняются эмпирические значения, то есть (y_i) от теоретических, предсказанных моделью, то есть (h_b(x_i)). Проще всего это отклонение выразить в виде разницы между этими двумя значениями. Но эта разница будет характеризовать отклонение только в одной точке данных, а в датасете может быть их произвольное количество. Поэтому имеет смысл взять сумму этих разностей для всех точек данных:
[J = sum_{i=1}^{m} (h_b(x_i) — y_i)]
Но с этим подходом есть одна проблема. Дело в том, что отклонения реальных значений от предсказанных могут быть как положительные, так и отрицательные. И если мы просто их все сложим, то положительные как бы скомпенсируют отрицательные. И в итоге даже очень плохие модели могут выглядеть, как имеющие маленькие ошибки. Фактически, для любого набора данных, если модель проходит через геометрический центр распределения, то такая ошибка будет равна нулю. То есть для достижения нулевой ошибки линии регрессии достаточно проходить через одну определенную точку. Таких моделей, очевидно, бесконечное количество, и все они будут иметь нулевую сумму отклонений. Конечно, так не пойдет и нужно придумать такую формулу, чтобы положительные и отрицательные отклонения не взаимоуничтожались, а складывались без учета знака.
Можно было бы взять отклонения по модулю. Но у такого подхода есть один большой недостаток: Функция абсолютного значения не везде дифференцируема. В одной точке у нее не существует производной. А чуть позже нам очень понадобится брать производную от функции ошибки. Поэтому модуль нам не подходит. Но в математике есть и другие функции, которые позволяют “избавиться” от знака числа. Например, возведение в квадрат. Его как раз и применяют в функции ошибки:
[J = sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
У этого подхода есть еще одно неочевидное достоинство. Квадратичная функция дополнительно сильно увеличивает размер больших чисел. То есть, если среди наших отклонений будет какое-то очень большое, то после возведения в квадрат оно станет еще непропорционально больше. Таким образом квадратичная функция ошибки как бы сильнее “штрафует” сильные отклонения предсказанных значений от реальных.
Но есть еще одна проблема. Дело в том, что в разных наборах данных может быть разное количество точек. Если мы просто будем считать сумму отклонений, то чем больше точек будем суммировать, тем больше итоговое отклонение будет только из-за количества слагаемых. Поэтому модели, обученные на маленьких объемах данных будут иметь преимущество. Это тоже неправильно и поэтому берут не сумму, а среднее из отклонений. Для этого достаточно лишь поделить эту сумму на количество точек данных:
[J = frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
В итоге мы как раз получаем среднеквадратичное отклонение реальных значений от предсказанных. Эта функция дает хорошее представление о том, какая конкретная модель хорошо соответствует имеющимся данным, а какая — хуже или еще лучше.
[J(b_0, b_1)
= frac{1}{2m} sum_{i=1}^{m} (hat{y_i} — y_i)^2
= frac{1}{2m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Эту функцию называют «функцией квадрата ошибки» или «среднеквадратичной ошибкой» (mean squared error, MSE). Среднее значение уменьшено вдвое для удобства вычисления градиентного спуска, так как производная квадратичной функции будет отменять множитель 1/2. Вообще, функцию ошибки можно свободно домножить или разделить на любое число (положительное), ведь нам не важна конкретная величина этой функции. Нам важно, что какие-то модели (то есть наборы значений параметров модели) имеют низкую ошибку, они нам подходят больше, а какие-то — высокую ошибку, они подходят нам меньше.
Обратите внимание, что в качестве аргументов у функции ошибки выступают параметры нашей функции гипотезы. Ведь функция ошибки оценивает отклонение конкретной функции гипотезы (то есть набора значений параметров этой функции) от эмпирических значений, то есть ставит в соответствие каждому набору параметров модели число, характеризующее ошибку этого набора.
Давайте проследим формирование функции ошибки на еще более простом примере. Возьмем упрощенную форму линейной модели — прямую пропорциональность. Она выражается формулой:
[hat{y} = h_b (x) = b_1 x]
Эта модель поможет нам, так как у нее всего один параметр. И функцию ошибки можно будет изобразить на плоскости. Возьмем фиксированный набор точек и попробуем несколько значений параметра для вычисления функции ошибки. Слева на графике изображены точки данных и текущая функция гипотезы, а на правом графике бы будем отмечать значение использованного параметра (по горизонтали) и получившуюся величину функции ошибки (по вертикали):
При значении $b_1 = -1$ линия существенно отклоняется от точек. Отметим уровень ошибки (примерно 10) на правом графике.
Если взять значение $b_1 = 0$ линия гораздо ближе к точкам, но ошибка все еще есть. Отметим новое значение на правом графике в точке 0.
При значении $b_1 = 1$ график точно ложится в точки, таким образом ошибка становится равной нулю. Отмечаем ее так же.
При дальнейшем увеличении $b_1$ линия становится выше точек. Но функция ошибки все равно будет положительной. Теперь она опять станет расти.
На этом примере мы видим еще одно преимущество возведения в квадрат — это то, что такая функция в простых случаях имеет один глобальный минимум. На правом графике формируется точка за точкой некоторая функция, которая похожа очертаниями на параболу. Но мы не знаем аналитического вида этой параболы, мы можем лишь строить ее точка за точкой.
В нашем примере, в определенной точке функция ошибки обращается в ноль. Это соответствует “идеальной” функции гипотезы. То есть такой, когда она проходит четко через все точки. В нашем примере это стало возможно благодаря тому, что точки данных и так располагаются на одной прямой. В общем случае это не выполняется и функция ошибки, вообще говоря, не обязана иметь нули. Но она должна иметь глобальный минимум. Рассмотрим такой неидеальный случай:
Какое бы значение параметра мы не использовали, линейная функция неспособна идеально пройти через такие три точки, которые не лежат на одной прямой. Эта ситуация называется “недообучение”, об этом мы еще будем говорить дальше. Это значит, что наша модель слишком простая, чтобы идеально описать данные. Но зачастую, идеальная модель и не требуется. Важно лишь найти наилучшую модель из данного класса (например, линейных функций).
Выше мы рассмотрели упрощенный пример с функцией гипотезы с одним параметром. Но у парной линейной регрессии же два параметра. В таком случае, функция ошибки будет описывать не параболу, а параболоид:
Теперь мы можем конкретно измерить точность нашей предсказывающей функции по сравнению с правильными результатами, которые мы имеем, чтобы мы могли предсказать новые результаты, которых у нас нет.
Если мы попытаемся представить это наглядно, наш набор данных обучения будет разбросан по плоскости x-y. Мы пытаемся подобрать прямую линию, которая проходит через этот разбросанный набор данных. Наша цель — получить наилучшую возможную линию. Лучшая линия будет такой, чтобы средние квадраты вертикальных расстояний точек от линии были наименьшими. В лучшем случае линия должна проходить через все точки нашего набора данных обучения. В таком случае значение J будет равно 0.
В более сложных моделях параметров может быть еще больше, но это не важно, ведь нам не нужно строить функцию ошибки, нам нужно лишь оптимизировать ее.
Выводы:
- Функция ошибки нужна для того, чтобы отличать хорошие модели от плохих.
- Функция ошибки показывает численно, насколько модель хорошо описывает данные.
- Аргументами функции ошибки являются параметры модели, ошибка зависит от них.
- Само значение функции ошибки не несет никакого смысла, оно используется только в сравнении.
- Цель алгоритма машинного обучения — минимизировать функцию ошибки, то есть найти такой набор параметров модели, при которых ошибка минимальна.
- Чаще всего используется так называемая L2-ошибка — средний квадрат отклонений теоретических значений от эмпирических (метрика MSE).
Метод градиентного спуска
Таким образом, у нас есть функция гипотезы, и способ оценить, насколько хорошо конкретная гипотеза вписывается в данные. Теперь нам нужно подобрать параметры функции гипотезы. Вот где приходит на помощь метод градиентного спуска. Идея этого метода достаточно проста, но потребует для детального знакомства вспомнить основы математического анализа и дифференциального исчисления.
Несмотря на то, что мы настоятельно советуем разобраться в основах функционирования метода градиентного спуска шаг за шагом для более полного понимания того, как модели машинного обучения подбирают свои параметры, если читатель совсем не владеет матанализом, данные объяснения можно пропустить, они не являются критичными для повседневного понимания сути моделей машинного обучения.
Это происходит при помощи производной функции ошибки. Напомним, что производная функции показывает направление роста этой функции с ростом аргумента. Необходимое условие минимума функции — обращение в ноль ее производной. А так как мы знаем, что квадратичная функция имеет один глобальный экстремум — минимум, то наша задача очень проста — вычислить производную функции ошибки и найти, где она равна нулю.
Давайте найдем производную среднеквадратической функции ошибки. Так как эта функция зависит от двух аргументов — (b_0) и (b_1), то нам понадобится взять частные производные этой функции по всем ее аргументам. Для начала вспомним формулу самой функции ошибки:
[J(b_0, b_1) = frac{1}{2 m} sum_{i=1}^{m} (h_b(x_i) — y_i)^2]
Частная производная обозначается (frac{partial f}{partial x}) или (frac{partial}{partial x} f) и является обобщением обычной (полной) производной для функций нескольких аргументов. Частая производная показывает наклон функции в направлении изменения определенного аргумента, то есть как бы “в разрезе” этого аргумента. Градиент — это вектор частных производных функции по всем ее аргументам. Вектор градиента показывает направление максимального роста функции.
Что бы посчитать производную по какому-то из аргументов нам понадобятся обычные правила вычисления производной. Во-первых, общий множитель можно вынести из-под производной, Во-вторых, производная суммы равна сумме производных, поэтому знак суммы тоже можно вынести из-под производной. Поэтому получаем:
[frac{partial}{partial b_i} J =
frac{1}{2 m} sum_{i=1}^{m} frac{partial}{partial b_i} (h_b(x_i) — y^{(i)})^2]
Теперь самое сложное — производная сложной функции. По правилу она равна производной внешней функции, умноженной на производную внутренней. Внешняя функция — это квадратическая, ее производная равна удвоенному подквадратному выражению ((frac{d}{dt} t^2 = 2 t)). Подставляем (t = h_b(x_i) — y^{(i)}) и получаем:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x_i) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x_i)]
Обратите внимание, что эта самая двойка прекрасно сократилась со знаменателем в постоянном множителе функции ошибки. Именно за этим он и был нужен.
Чтобы продолжить вычисление производной дальше, нужно представить функцию гипотезы как линейную функцию:
[J(b_0, b_1) = frac{1}{2m} sum_{i=1}^{m} (b_0 + b_1 x_i — y_i)^2]
И теперь мы уже не можем говорить о какой-то частной производной в общем, нужно отдельно посчитать производные по разным значениям параметров. Но тут все как раз очень просто, так как нам осталось посчитать производные линейной функции. Они равны просто коэффициентам при соответствующих аргументах. Для свободного коэффициента аргумент равен, очевидно, 1:
[frac{partial J}{partial b_0} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) =
frac{1}{m} sum (h_b(x_i) — y_i)]
А для коэффициента при $x_i$ производная равна самому значению $x_i$:
[frac{partial J}{partial b_1} =
frac{1}{m} sum (b_0 + b_1 x_i — y_i) cdot x_i =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i]
Теперь для нахождения минимального значения функции ошибки нам нужно только приравнять эти производные к нулю, то есть решить для $b_0, b_1$ следующую систему уравнений:
[frac{partial J}{partial b_0} =
frac{1}{m} sum (h_b(x_i) — y_i) = 0]
[frac{partial J}{partial b_1} =
frac{1}{m} sum (h_b(x_i) — y_i) cdot x_i = 0]
Проблема в том, что мы не можем просто решить эти уравнения аналитически. Ведь мы не знаем общий вид функции ошибки, не то, что ее производной. Ведь он зависит от всех точек данных. Но мы можем вычислить эту функцию (и ее производную) в любой точке. А точка на этой функции — это конкретный набор значений параметров модели. Поэтому пришлось изобрести численный алгоритм. Он работает следующим образом.
Сначала, мы выбираем произвольное значение параметров модели. То есть, произвольную точку в области определения функции. Мы не знаем, является ли эта точка оптимальной (скорее нет), не знаем, насколько она далека от оптимума. Но мы можем вычислить направление к оптимуму. Ведь мы знаем наклон касательной к графику функции ошибки.
Наклон касательной является производной в этой точке, и это даст нам направление движения в сторону самого крутого уменьшения значения функции. Если представить себе функцию одной переменной (параболу), то там все очень просто. Если производная в точке отрицательна, значит функция убывает, значит, что оптимум находится справа от данной точки. То есть, чтобы приблизиться к оптимуму надо увеличить аргумент функции. Если же производная положительна, то все наоборот — функция возрастает, оптимум находится слева и нам нужно уменьшить значение аргумента. Причем, чем дальше от оптимума, тем быстрее возрастает или убывает функция. То есть значение производной дает нам не только направление, но и величину нужного шага. Сделав шаг, пропорциональный величине производной и в направлении, противоположном ей, можно повторить процесс и еще больше приблизиться к оптимуму. С каждой итерацией мы будем приближаться к минимуму ошибки и математически доказано, что мы можем приблизиться к ней произвольно близко. То есть, данный метод сходится в пределе.
В случае с функцией нескольких переменных все немного сложнее, но принцип остается прежним. Только мы оперируем не полной производной функции, а вектором частных производных по каждому параметру. Он задает нам направление максимального увеличения функции. Чтобы получить направление максимального спада функции нужно просто домножить этот вектор на -1. После этого нужно обновить значения каждого компонента вектора параметров модели на величину, пропорциональную соответствующему компоненту вектора градиента. Таким образом мы делаем шаги вниз по функции ошибки в направлении с самым крутым спуском, а размер каждого шага пропорционален определяется параметром $alpha$, который называется скоростью обучения.
Алгоритм градиентного спуска:
повторяйте до сходимости:
[b_j := b_j — alpha frac{partial}{partial b_j} J(b_0, b_1)]
где j=0,1 — представляет собой индекс номера признака.
Это общий алгоритм градиентного спуска. Она работает для любых моделей и для любых функций ошибки. Это итеративный алгоритм, который сходится в пределе. То есть, мы никогда не придем в сам оптимум, но можем приблизиться к нему сколь угодно близко. На практике нам не так уж важно получить точное решение, достаточно решения с определенной точностью.
Алгоритм градиентного спуска имеет один параметр — скорость обучения. Он влияет на то, как быстро мы будем приближаться к оптимуму. Кажется, что чем быстрее, тем лучше, но оказывается, что если значение данного параметра слишком велико, то мы буем постоянно промахиваться и алгоритм будет расходиться.
Алгоритм градиентного спуска для парной линейной регрессии:
повторяйте до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)} )- y^{(i)})]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x^{(i)}]
На практике “повторяйте до сходимости” означает, что мы повторяем алгоритм градиентного спуска до тех пор, пока значение функции ошибки не перестанет значимо изменяться. Это будет означать, что мы уже достаточно близко к минимуму и дальнейшие шаги градиентного спуска слишком малы, чтобы быть целесообразными. Конечно, это оценочное суждение, но на практике обычно, нескольких значащих цифр достаточно для практического применения моделей машинного обучения.
Алгоритм градиентного спуска имеет одну особенность, про которую нужно помнить. Он в состоянии находить только локальный минимум функции. Он в принципе, по своей природе, локален. Поэтому, если функция ошибки будет очень сложна и иметь несколько локальных оптимумов, то результат работы градиентного спуска будет зависеть от выбора начальной точки.
На практике эту проблему решают методом семплирования — запускают градиентный спуск из множества случайных точек и выбирают то минимум, который оказался меньше по значению функции ошибки. Но этот подход понадобится нам при рассмотрении более сложных и глубоких моделей машинного обучения. Для простых линейных, полиномиальных и других моделей метод градиентного спуска работает прекрасно. В настоящее время этот алгоритм — это основная рабочая лошадка классических моделей машинного обучения.
Выводы:
- Метод градиентного спуска нужен, чтобы найти минимум функции, если мы не можем ее вычислить аналитически.
- Это численный итеративный алгоритм локальной оптимизации.
- Для запуска градиентного спуска нужно знать частную производную функции ошибки.
- Для начала мы берем произвольные значения параметров, затем обновляем их по данной формуле.
- Доказано, что этот метод сходится к локальному минимуму.
- Если функция ошибки достаточно сложная, то разные начальные точки дадут разный результат.
- Метод градиентного спуска имеет свой параметр — скорость обучения. Обычно его подстаивают автоматически.
- Метод градиентного спуска повторяют много раз до тех пор, пока функция ошибки не перестанет значимо изменяться.
Регрессия с несколькими переменными
Множественная линейная регрессия
Парная регрессия, как мы увидели выше, имеет дело с объектами, которые характеризуются одним числовым признаком ($x$). На практике, конечно, объекты характеризуются несколькими признаками, а значит в модели должна быть не одна входящая переменная, а несколько (или, что то же самое, вектор). Линейная регрессия с несколькими переменными также известна как «множественная линейная регрессия». Введем обозначения для уравнений, где мы можем иметь любое количество входных переменных:
$ x^{(i)} $- вектор-столбец всех значений признаков i-го обучающего примера;
$ x_j^{(i)} $ — значение j-го признака i-го обучающего примера;
$ x_j $ — вектор j-го признака всех обучающих примеров;
m — количество примеров в обучающей выборке;
n — количество признаков;
X — матрица признаков;
b — вектор параметров регрессии.
Задачи множественной регрессии уже очень сложно представить на графике, ведь количество параметров каждого объекта обучающей выборки соответствует измерению, в котором находятся точки данных. Плюс нужно еще одно измерение для целевой переменной. И вместо того, чтобы подбирать оптимальную прямую, мы будем подбирать оптимальную гиперплоскость. Но в целом идея линейной регрессии остается неизменной.
Для удобства примем, что $ x_0^{(i)} = 1 $ для всех $i$. Другими словами, мы ведем некий суррогатный признак, для всех объектов равный единице. Это никак не сказывается на самой функции гипотезы, это лишь условность обозначения, но это сильно упростит математические выкладки, особенно в матричной форме.
Вообще, уравнения для алгоритмов машинного обучения, зависящие от нескольких параметров часто записываются в матричной форме. Это лишь способ сделать запись уравнений более компактной, а не какое-то новое знание. Если вы не владеете линейной алгеброй, то можете просто безболезненно пропустить эти формы записи уравнений. Однако, лучше, конечно, разобраться. Особенно это пригодится при изучении нейронных сетей.
Теперь определим множественную форму функции гипотезы следующим образом, используя несколько признаков. Она очень похожа на парную, но имеет больше входных переменных и, как следствие, больше параметров.
Общий вид модели множественной линейной регрессии:
[h_b(x) = b_0 + b_1 x_1 + b_2 x_2 + … + b_n x_n]
Или в матричной форме:
[h_b(x) = X cdot vec{b}]
Используя определение матричного умножения, наша многопараметрическая функция гипотезы может быть кратко представлена в виде: $h(x) = B X$.
Обратите внимание, что в любой модели линейной регрессии количество параметров на единицу больше количества входных переменных. Это верно для любой линейной модели машинного обучения. Вообще, всегда чем больше признаков, тем больше параметров. Это будет важно для нас позже, когда мы будем говорить о сложности моделей.
Теперь, когда мы знаем виды функции гипотезы, то есть нашей модели, мы можем переходить к следующему шагу: функции ошибки. Мы построим ее по аналогии с функцией ошибки для парной модели. Для множественной регрессии функция ошибки от вектора параметров b выглядит следующим образом:
Функция ошибки для множественной линейной регрессии:
[J(b) = frac{1}{2m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)})^2]
Или в матричной форме:
[J(b) = frac{1}{2m} (X b — vec{y})^T (X b — vec{y})]
Обратите внимание, что мы специально не раскрываем выражение (h_b(x^{(i)})). Это нужно, чтобы подчеркнуть, что форма функции ошибки не зависит от функции гипотезы, она выражается через нее.
Теперь нам нужно взять производную этой функции ошибки. Здесь уже нужно знать производную самой функции гипотезы, так как:
[frac{partial}{partial b_i} J =
frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot frac{partial}{partial b_i} h_b(x^{(i)})]
В такой формулировке мы представляем частные производные функции ошибки (градиент) через частную производную функции гипотезы. Это так называемое моделенезависимое представление градиента. Ведь для этой формулы совершенно неважно, какой функцией будет наша гипотеза. Пока она является дифференцируемой, мы можем использовать градиент ее функции ошибки. Именно поэтому метод градиентного спуска работает с любыми аналитическими моделями, и нам не нужно каждый раз заново “переизобретать” математику градиентного спуска, адаптировать ее к каждой конкретной модели машинного обучения. Достаточно изучить этот метод один раз, в общей форме.
Метод градиентного спуска для множественной регрессии определяется следующими уравнениями:
повторять до сходимости:
[b_0 := b_0 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_0^{(i)}]
[b_1 := b_1 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_1^{(i)}]
[b_2 := b_2 — alpha frac{1}{m} sum_{i=1}^{m} (h_b(x^{(i)}) — y^{(i)}) cdot x_2^{(i)}]
[…]
Или в матричной форме:
[b := b — frac{alpha}{m} X^T (X b — vec{y})]
Выводы:
- Множественная регрессия очень похожа на парную, но с большим количеством признаков.
- Для удобства и однообразия, почти всегда обозначают $x_0 = 1$.
- Признаки образуют матрицу, поэтому уравнения множественной регрессии часто приводят в матричной форме, так короче.
- Алгоритм градиентного спуска для множественной регрессии точно такой же, как и для парной.
Нормализация признаков
Мы можем ускорить сходимость метода градиентного спуска, преобразовав входные данные таким образом, чтобы все атрибуты имели значения примерно в том же диапазоне. Это называется нормализация данных — приведение всех признаков к одной шкале. Это ускоряет сходимость градиентного спуска за счет эффекта масштаба. Дело в том, что зачастую значения разных признаков измеряются по шкалам с очень разным порядком величины. Например, $x_1$ измеряется в миллионах, а $x_2$ — в долях единицы.
В таком случае форма функции ошибки будет очень вытянутой. Это не проблема для математической формализации градиентного спуска — при достаточно малых $alpha$ метод все равно рано или поздно сходится. Проблема в практической реализации. Получается, что если выбрать скорость обучения выше определенного предела по самому компактному признаку, спуск разойдется. Значит, скорость обучения надо делать меньше. Но тогда в направлении второго признака спуск будет проходить слишком медленно. И получается, что градиентный спуск потребует гораздо больше итераций для завершения.
Эту проблему можно решить если изменить диапазоны входных данных, чтобы они выражались величинами примерно одного порядка. Это не позволит одному измерению численно доминировать над другим. На практике применяют несколько алгоритмов нормализации, самые распространенные из которых — минимаксная нормализация и стандартизация или z-оценки.
Минимаксная нормализация — это изменение входных данных по следующей формуле:
[x’ = frac{x — x_{min}}{x_{max} — x_{min}}]
После преобразования все значения будут лежать в диапазоне $x in [0; 1]$.
Z-оценки или стандартизация производится по формуле:
[x’ = frac{x — M[x]}{sigma_x}]
В таком случае данный признак приводится к стандартному распределению, то есть такому, у которого среднее 0, а дисперсия — 1.
У каждого из этих двух методов нормализации есть по два параметра. У минимаксной — минимальное и максимальное значение признака. У стандартизации — выборочные среднее и дисперсия. Параметры нормализации, конечно, вычисляются по каждому признаку (столбцу данных) отдельно. Причем, эти параметры надо запомнить, чтобы при использовании модели для предсказании использовать именно их (вычисленные по обучающей выборке). Даже если вы используете тестовую выборку, ее надо нормировать с использованием параметров, вычисленных по обучающей. Да, при этом может получиться, что при применении модели на данных, которых не было в обучающей выборке, могут получиться значения, например, меньше нуля или больше единицы (при использовании минимаксной нормализации). Это не страшно, главное, что будет соблюдена последовательность вычисления нормированных значений.
Про использование обучающей и тестовой выборок мы будем говорить значительно позже, при рассмотрении диагностики моделей машинного обучения.
Целевая переменная не нормируется. Это просто не нужно, а если ее нормировать, это сильно усложнит все математические расчеты и преобразования.
При использовании библиотечных моделей машинного обучения беспокоиться о нормализации входных данных вручную, как правило, не нужно. Большинство готовых реализаций моделей уже включают нормализацию как неотъемлемый этап подготовки данных. Более того, некоторые типы моделей обучения с учителем вовсе не нуждаются в нормализации. Но об этом пойдет речь в следующих главах.
Выводы:
- Нормализация нужна для ускорения метода градиентного спуска.
- Есть два основных метода нормализации — минимаксная и стандартизация.
- Параметры нормализации высчитываются по обучающей выборке.
- Нормализация встроена в большинство библиотечных методов.
- Некоторые методы более чувствительны к нормализации, чем другие.
- Нормализацию лучше сделать, чем не делать.
Полиномиальная регрессия
Функция гипотезы не обязательно должна быть линейной, если это не соответствует данным. На практике вы не всегда будете иметь данные, которые можно хорошо аппроксимировать линейной функцией. Наглядный пример вы видите на иллюстрации. Вполне очевидно, что в среднем увеличение целевой переменной замедляется с ростом входной переменной. Это значит, что данные демонстрируют нелинейную динамику. И это так же значит, что мы никак не сможем их хорошо приблизить линейной моделью.
Надо подчеркнуть, что это не свидетельствует о несовершенстве наших методов оптимизации. Мы действительно можем найти самую лучшую линейную функцию для данных точек, но проблема в том, что мы всегда выбираем лучшую функцию из некоторого класса функций, в данном случае — линейных. То есть проблема не в алгоритмах оптимизации, а в ограничении самого вида модели.
вполне логично предположить, что для описания таких нелинейных наборов данных следует использовать нелинейные же функции моделей. Но очень бы не хотелось, для каждого нового класса функций изобретать собственный метод оптимизации, поэтому мы постараемся максимально “переиспользовать” те подходы, которые описали выше. И механизм множественной регрессии в этом сильно поможет.
Мы можем изменить поведение или кривую нашей функции гипотезы, сделав ее квадратичной, кубической или любой другой формой.
Например, если наша функция гипотезы
$ hat{y} = h_b (x) = b_0 + b_1 x $,
то мы можем добавить еще один признак, основанный на $ x_1 $, получив квадратичную функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2]
или кубическую функцию
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 x^2 + b_3 x^3]
В кубической функции мы по сути ввели два новых признака:
$ x_2 = x^2, x_3 = x^3 $.
Точно таким же образом, мы можем создать, например, такую функцию:
[hat{y} = h_b (x) = b_0 + b_1 x + b_2 sqrt{x}]
В любом случае, мы из парной линейной функции сделали какую-то другую функцию. И к этой нелинейной функции можно относиться по разному. С одной стороны, это другой класс функций, который обладает нелинейным поведением, а следовательно, может описывать более сложные зависимости в данных. С другой стороны, это линейна функция от нескольких переменных. Только сами эти переменные оказываются в функциональной зависимости друг от друга. Но никто не говорил, что признаки должны быть независимы.
И вот такое представление нелинейной функции как множественной линейной позволяет нам без изменений воспользоваться алгоритмом градиентного спуска для множественной линейной регрессии. Только вместо $ x_2, x_3, … , x_n $ нам нужно будет подставить соответствующие функции от $ x_1 $.
Очевидно, что нелинейных функций можно придумать бесконечное количество. Поэтому встает вопрос, как выбрать нужный класс функций для решения конкретной задачи. В случае парной регрессии мы можем взглянув на график точек обучающей выборки сделать предположение о том, какой вид нелинейной зависимости связывает входную и целевую переменные. Но если у нас множество признаков, просто так проанализировать график нам не удастся. Поэтому по умолчанию используют полиномиальную регрессию, когда в модель добавляют входные переменные второго, третьего, четвертого и так далее порядков.
Порядок полиномиальной регрессии подбирается в качестве компромисса между качеством получаемой регрессии, и вычислительной сложностью. Ведь чем выше порядок полинома, тем более сложные зависимости он может аппроксимировать. И вообще, чем выше степень полинома, тем меньше будет ошибка при прочих равных. Если степень полинома на единицу меньше количества точек — ошибка будет нулевая. Но одновременно с этим, чем выше степень полинома, тем больше в модели параметров, тем она сложнее и занимает больше времени на обучение. Есть еще вопросы переобучения, но про это мы поговорим позднее.
А что делать, если изначально в модели было несколько признаков? Тогда обычно для определенной степени полинома берутся все возможные комбинации признаком соответствующей степени и ниже. Например:
Для регрессии с двумя признаками.
Линейная модель (полином степени 1):
[h_b (x) = b_0 + b_1 x_1 + b_2 x_2]
Квадратичная модель (полином степени 2):
[h_b (x) = b_0 + b_1 x + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2]
Кубическая модель (полином степени 3):
[hat{y} = h_b (x) = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_1^2 + b_4 x_2^2 + b_5 x_1 x_2 + b_6 x_1^3 + b_7 x_2^3 + b_7 x_1^2 x_2 + b_8 x_1 x_2^2]
При этом количество признаков и, соответственно, количество параметров растет экспоненциально с ростом степени полинома. Поэтому полиномиальные модели обычно очень затратные в обучении при больших степенях. Но полиномы высоких степеней более универсальны и могут аппроксимировать более сложные данные лучше и точнее.
Выводы:
- Данные в датасете не всегда располагаются так, что их хорошо может описывать линейная функция.
- Для описания нелинейных зависимостей нужна более сложная, нелинейная модель.
- Чтобы не изобретать алгоритм обучения заново, можно просто ввести в модель суррогатные признаки.
- Суррогатный признак — это новый признак, который считается из существующих атрибутов.
- Чаще всего используют полиномиальную регрессию — это когда в модель вводят полиномиальные признаки — степени существующих атрибутов.
- Обычно берут все комбинации факторов до какой-то определенной степени полинома.
- Полиномиальная регрессия может аппроксимировать любую функцию, нужно только подобрать степень полинома.
- Чем больше степень полиномиальной регрессии, тем она сложнее и универсальнее, но вычислительно сложнее (экспоненциально).
Практическое построение регрессии
В данной главе мы посмотрим, как можно реализовать методы линейной регрессии на практике. Сначала мы попробуем создать алгоритм регрессии с нуля, а затем воспользуемся библиотечной функцией. Это поможет нам более полно понять, как работают модели машинного обучения в целом и в библиотеке sckikit-learn (самом популярном инструменте для создания и обучения моделей на языке программирования Python) в частности.
Для понимания данной главы предполагаем, что читатель знаком с основами языка программирования Python. Нам понадобится знание его базового синтаксиса, немного — объектно-ориентированного программирования, немного — использования стандартных библиотек и модулей. Никаких продвинутых возможностей языка (типа метапрограммирования или декораторов) мы использовать не будем.
Как должны быть представлены данные для машинного обучения?
Применение любых моделей машинного обучения начинается с подготовки данных в необходимом формате. Для этого очень удобными для нас будут библиотеки numpy и pandas. Они практически всегда используются совместно с библиотекой sckikit-learn и другими инструментами машинного обучения. В первую очередь мы будем использовать numpy для создания массивов и операций с векторами и матрицами. Pandas нам понадобится для работы с табличными структурами — датасетами.
Если вы хотите самостоятельно задать в явном виде данные обучающей выборки, то нет ничего лучше использования обычных массивов ndarray. Обычно в одном массиве хранятся значения атрибутов — x, а в другом — значения целевой переменной — y.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
Если мы имеем дело с задачей множественной регрессии, то в массиве атрибутов будет уже двумерный массив, состоящий из нескольких векторов атрибутов, вот так:
1
2
3
4
5
x = np.array([
[0, 1, 2, 3, 4],
[5, 4, 9, 6, 3],
[7.8, -0.1, 0.0, -2.14, 10.7],
])
Важно следить за тем, чтобы в массиве атрибутов в каждом вложенном массиве количество элементов было одинаковым и в свою очередь совпадало с количеством элементов в массиве целевой переменной. Это называется соблюдение размерности задачи. Если размерность не соблюдается, то модели машинного обучения будут работать неправильно. А библиотечные функции чаще всего будут выдавать ошибку, связанную с формой массива (shape).
Но чаще всего вы не будете задавать исходные данные явно. Практически всегда их приходится читать из каких-либо входных файлов. Удобнее всего это сделать при помощи библиотеки pandas вот так:
1
2
3
4
import pandas as pd
x = pd.read_csv('x.csv', index_col=0)
y = pd.read_csv('y.csv', index_col=0)
Или, если данные лежат в одном файле в общей таблице (что происходит чаще всего), тогда его читают в один датафрейм, а затем выделяют целевую переменную, и факторные переменные:
1
2
3
4
5
6
7
8
import pandas as pd
data = pd.read_csv('data.csv', index_col=0)
y = data.Y
y = data["Y"]
x = data.drop(["Y"])
Обратите внимание, что матрицу атрибутов проще всего сформировать, удалив из полной таблицы целевую переменную. Но, если вы хотите выбрать только конкретные столбцы, тогда можно использовать более явный вид, через перечисление выбранных колонок.
Если вы используете pandas или numpy для формирования массивов данных, то получившиеся переменные будут разных типов — DataFrame или ndarray, соответственно. Но на дальнейшую работу это не повлияет, так как интерфейс работы с этими структурами данных очень похож. Например, неважно, какие именно массивы мы используем, их можно изобразить на графике вот так:
1
2
3
4
5
import maiplotlib.pyplot as plt
plt.figure()
plt.scatter(x, y)
plt.show()
Конечно, такая визуализация будет работать только в случае задачи парной регрессии. Если x многомерно, то простой график использовать не получится.
Давайте соберем весь наш код вместе:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
import pandas as pd
import maiplotlib.pyplot as plt
# x = pd.read_csv('x.csv', index_col=0)
x = np.array([1.46, 1.13, -2.30, 1.74, 0.04,
-0.61, 0.32, -0.76, 0.58, -1.10,
0.87, 1.62, -0.53, -0.25, -1.07,
-0.38, -0.17, -0.32, -2.06, -0.88, ])
# y = pd.read_csv('y.csv', index_col=0)
y = np.array([101.16, 78.44, -159.24, 120.72, 2.92,
-42.33, 22.07, -52.67, 40.32, -76.10,
59.88, 112.38, -36.54, -17.25, -74.24,
-26.57, -11.93, -22.31, -142.54, -60.74,])
plt.figure()
plt.scatter(x, y)
plt.show()
Это код генерирует вот такой вот график:
Как работает метод машинного обучения “на пальцах”?
Для того, чтобы более полно понимать, как работает метод градиентного спуска для линейной регрессии, давайте реализуем его самостоятельно, не обращаясь к библиотечным методам. На этом примере мы проследим все шаги обучения модели.
Мы будем использовать объектно-ориентированный подход, так как именно он используется в современных библиотеках. Начнем строить класс, который будет реализовывать метод парной линейной регрессии:
1
2
3
4
5
class hypothesis(object):
"""Модель парной линейной регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
Здесь мы определили конструктор класса, который запоминает в полях экземпляра параметры регрессии. Начальные значения этих параметров не очень важны, так как градиентный спуск сойдется из любой точки. В данном случае мы выбрали нулевые, но можно задать любые другие начальные значения.
Реализуем метод, который принимает значение входной переменной и возвращает теоретическое значение выходной — это прямое действие нашей регрессии — метод предсказания результата по факторам (в случае парной регрессии — по одному фактору):
1
2
def predict(self, x):
return self.b0 + self.b1 * x
Название выбрано не случайно, именно так этот метод называется и работает в большинстве библиотечных классов.
Теперь зададим функцию ошибки:
1
2
def error(self, X, Y):
return sum((self.predict(X) - Y)**2) / (2 * len(X))
В данном случае мы используем простую функцию ошибки — среднеквадратическое отклонение (mean squared error, MSE). Можно использовать и другие функции ошибки. Именно вид функции ошибки будет определять то, какой вид регрессии мы реализуем. Существует много разных вариаций простого алгоритма регрессии. О большинстве распространенных методах регрессии можно почитать в официальной документации sklearn.
Теперь реализуем метод градиентного спуска. Он должен принимать массив X и массив Y и обновлять параметры регрессии в соответствии в формулами градиентного спуска:
1
2
3
4
5
6
def BGD(self, X, Y):
alpha = 0.5
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
О выборе конкретного значения alpha мы говорить пока не будем,на практике его довольно просто подбирают, мы же возьмем нейтральное значение.
Давайте создадим объект регрессии и проверим начальное значение ошибки. В примерах приведены значения на модельном наборе данных, но этот метод можно использовать на любых данных, которые подходят по формату — x и y должны быть одномерными массивами чисел.
1
2
3
4
5
6
7
8
hyp = hypothesis()
print(hyp.predict(0))
print(hyp.predict(100))
J = hyp.error(x, y)
print("initial error:", J)
0
0
initial error: 36271.58344889084
Как мы видим, для начала оба параметра регрессии равны нулю. Конечно, такая модель не дает надежных предсказаний, но в этом и состоит суть метода градиентного спуска: начиная с любого решения мы постепенно его улучшаем и приходим к оптимальному решению.
Теперь все готово к запуску градиентного спуска.
1
2
3
4
5
6
7
8
9
10
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 6734.135540194945
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Как мы видим, численное значение ошибки значительно уменьшилось. Да и линия на графике существенно приблизилась к точкам. Конечно, наша модель еще далека от совершенства. Мы прошли всего лишь одну итерацию градиентного спуска. Модифицируем метод так, чтобы он запускался в цикле пока ошибка не перестанет меняться существенно:
1
2
3
4
5
6
7
8
9
10
11
12
13
def BGD(self, X, Y, alpha=0.5, accuracy=0.01, max_steps=5000):
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y)
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
Заодно мы проверяем, насколько изменилось значение функции ошибки. Если оно изменилось на величину, меньшую, чем заранее заданная точность, мы завершаем спуск. Таким образом, мы реализовали два стоп-механизма — по количеству итераций и по стабилизации ошибки. Вы можете выбрать любой или использовать оба в связке.
Запустим наш градиентный спуск:
1
2
3
4
5
hyp = hypothesis()
hyp.BGD(x, y)
J = hyp.error(x, y)
print("error after gradient descent:", J)
error after gradient descent: 298.76881676471504
Как мы видим, теперь ошибка снизилась гораздо больше. Однако, она все еще не достигла нуля. Заметим, что нулевая ошибка не всегда возможна в принципе из-за того, что точки данных не всегда будут располагаться на одной линии. Нужно стремиться не к нулевой, а к минимально возможной ошибке.
Посмотрим, как теперь наша регрессия выглядит на графике:
1
2
3
4
5
6
X0 = np.linspace(60, 180, 100)
Y0 = hyp.predict(X0)
plt.figure()
plt.scatter(x, y)
plt.plot(X0, Y0, 'r')
plt.show()
Уже значительно лучше. Линия регрессии довольно похожа на оптимальную. Так ли это на самом деле, глядя на график, сказать сложно, для этого нужно проанализировать, как ошибка регрессии менялась со временем:
Как оценить качество регрессионной модели?
В простых случаях качество модели можно оценить визуально на графике. Но если у вас многомерная задача, это уже не представляется возможным. Кроме того, если ошибка и сама модель меняется незначительно, то очень сложно определить, стало хуже или лучше. Поэтому для диагностики моделей машинного обучения используют кривые.
Самая простая кривая обучения — зависимость ошибки от времени (итерации градиентного спуска). Для того, чтобы построить эту кривую, нам нужно немного модифицировать наш метод обучения так, чтобы он возвращал нужную нам информацию:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def BGD(self, X, Y, alpha=0.1, accuracy=0.01, max_steps=1000):
steps, errors = [], []
step = 0
old_err = hyp.error(X, Y)
new_err = hyp.error(X, Y) - 1
dJ = 1
while (dJ > accuracy) and (step < max_steps):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X) /len(X)
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
old_err = new_err
new_err = hyp.error(X, Y)
dJ = abs(old_err - new_err)
step += 1
steps.append(step)
errors.append(new_err)
return steps, errors
Мы просто запоминаем в массивах на номер шаа и ошибку на каждом шаге. Получив эти данные можно легко построить их на графике:
1
2
3
4
5
6
hyp = hypothesis()
steps, errors = hyp.BGD(x, y)
plt.figure()
plt.plot(steps, errors, 'g')
plt.show()
На этом графике наглядно видно, что в начале обучения ошибка падала быстро, но в ходе градиентного спуска она вышла на плато. Учитывая, что мы используем гладкую функцию ошибки второго порядка, это свидетельствует о том, что мы достигли локального оптимума и дальнейшее повторение алгоритма не принесет улучшения модели.
Если бы мы наблюдали на графике обучения ситуацию, когда по достижении конца обучения ошибка все еще заметно снижалась, это значит, что мы рано прекратили обучение, и нужно продолжить его еще на какое-то количество итераций.
При анализе графиков с библиотечными моделями не получится таких гладких графиков, они больше напоминают случайные колебания. Это из-за того, что в готовых реализациях используется очень оптимизированный вариант метода градиентного спуска. А он может работать с произвольными флуктуациями. В любом случае, нас интересует общий вид этой кривой.
Как подбирать скорость обучения?
В нашей реализации метода градиентного спуска есть один параметр — скорость обучения — который нам приходится так же подбирать руками. Какой смысл автоматизировать подбор параметров линейной регрессии, если все равно приходится вручную подбирать какой-то другой параметр?
На самом деле подобрать скорость обучения гораздо легче. Нужно использовать тот факт, что при превышении определенного порогового значения ошибка начинает возрастать. Кроме того, мы знаем, что скорость обучения должна быть положительна, но меньше единицы. Вся проблема в этом пороговом значении, которое сильно зависит от размерности задачи. При одних данных хорошо работает $ alpha = 0.5 $, а при каких-то приходится уменьшать ее на несколько порядков, например, $ alpha = 0.00000001 $.
Мы еще не говорили о нормализации данных, которая тоже практически всегда применяется при обучении. Она “благотворно” влияет на возможный диапазон значений скорости обучения. При использовании нормализации меньше вероятность, что скорость обучения нужно будет уменьшать очень сильно.
Подбирать скорость обучения можно по следующему алгоритму. Сначала мы выбираем $ alpha $ близкое к 1, скажем, $ alpha = 0.7 $. Производим одну итерацию градиентного спуска и оцениваем, как изменилась ошибка. Если она уменьшилась, то ничего не надо менять, продолжаем спуск как обычно. Если же ошибка увеличилась, то скорость обучения нужно уменьшить. Например, раа в два. После чего мы повторяем первый шаг градиентного спуска. Таким образом мы не начинаем спуск, пока скорость обучения не снизится настолько, чтобы он начал сходиться.
Как применять регрессию с использованием scikit-learn?
Для серьезной работы, все-таки рекомендуется использовать готовые библиотечные решения. Они работаю гораздо быстрее, надежнее и гораздо проще, чем написанные самостоятельно. Мы будем использовать библиотеку scikit-learn для языка программирования Python как наш основной инструмент реализации простых моделей. Сегодня это одна их самых популярных библиотек для машинного обучения. Мы не будем повторять официальную документацию этой библиотеки, которая на редкость подробная и понятная. Наша задача — на примере этих инструментов понять, как работают и как применяются модели машинного обучения.
В библиотеке scikit-learn существует огромное количество моделей машинного обучения и других функций, которые могут понадобиться для их работы. Поэтому внутри самой библиотеки есть много разных пакетов. Все простые модели, например, модель линейной регрессии, собраны в пакете linear_models. Подключить его можно так:
1
from sklearn import linear_model
Надо помнить, что все модели машинного обучения из это библиотеки имеют одинаковый интерфейс. Это очень удобно и универсально. Но это значит, в частности, что все модели предполагают, что массив входных переменных — двумерный, а массивы целевых переменных — одномерный. Отдельного класса для парной регрессии не существует. Поэтому надо убедиться, что наш массив имеет нужную форму. Проще всего для преобразования формы массива использовать метод reshape, например, вот так:
Если вы используете DataFrame, то они обычно всегда настроены правильно, поэтому этого шага может не потребоваться. Важно запомнить, что все методы библиотечных моделей машинного обучения предполагают, что в x будет двумерный массив или DataFrame, а в y, соответственно, одномерный массив или Series.
Эта строка преобразует любой массив в вектор-столбец. Это если у вас один признак, то есть парная регрессия. Если признаков несколько, то вместо 1 следует указать число признаков. -1 на первой позиции означает, что по нулевому измерению будет столько элементов, сколько останется в массиве.
Само использование модели машинного обучения в этой библиотеке очень просто и сводится к трем действиям: создание экземпляра модели, обучение модели методом fit(), получение предсказаний методом predict(). Это общее поведение для любых моделей библиотеки. Для модели парной линейной регрессии нам понадобится класс LinearRegression.
1
2
3
4
5
6
reg = linear_model.LinearRegression()
reg.fit(x, y)
y_pred = reg.predict(x)
print(reg.score(x, y))
print("Коэффициенты: n", reg.coef_)
В этом классе кроме уже упомянутых методов fit() и predict(), которые есть в любой модели, есть большое количество методов и полей для получения дополнительной информации о моделях. Так, практически в каждой модели есть встроенный метод score(), который оценивает качество полученной модели. А поле coef_ содержит коэффициенты модели.
Обратите внимание, что в большинстве моделей коэффициентами считаются именно параметры при входящих переменных, то есть $ b_1, b_2, …, b_n $. Коэффициент $b_0$ считается особым и хранится отдельно в поле intercept_
Так как мы работаем с парной линейной регрессией, результат можно нарисовать на графике:
1
2
3
4
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()
Как мы видим, результат ничем не отличается от модели, которую мы обучили сами, вручную:
Соберем код вместе и получим пример довольно реалистичного фрагмента работы с моделью машинного обучение. Примерно такой код можно встретить и в промышленных проектах по интеллектуальному анализу данных:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.linear_model import LinearRegression
x = x.reshape((-1, 1))
reg = LinearRegression()
reg.fit(x, y)
print(reg.score(x, y))
from sklearn.metrics import mean_squared_error, r2_score
y_pred = reg.predict(x)
print("Коэффициенты: n", reg.coef_)
print("Среднеквадратичная ошибка: %.2f" % mean_squared_error(y, y_pred))
print("Коэффициент детерминации: %.2f" % r2_score(y, y_pred))
plt.figure(figsize=(12, 9))
plt.scatter(x, y, color="black")
plt.plot(x, y_pred, color="blue", linewidth=3)
plt.show()