Всем привет!
Сегодня мы детально обсудим очень важный класс моделей машинного обучения – линейных. Ключевое отличие нашей подачи материала от аналогичной в курсах эконометрики и статистики – это акцент на практическом применении линейных моделей в реальных задачах (хотя и математики тоже будет немало).
Пример такой задачи – это соревнование Kaggle Inclass по идентификации пользователя в Интернете по его последовательности переходов по сайтам.
UPD 01.2022: С февраля 2022 г. ML-курс ODS на русском возрождается под руководством Петра Ермакова couatl. Для русскоязычной аудитории это предпочтительный вариант (c этими статьями на Хабре – в подкрепление), англоговорящим рекомендуется mlcourse.ai в режиме самостоятельного прохождения.
Все материалы доступны на GitHub.
А вот видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017). В ней, в частности, рассмотрены два бенчмарка соревнования, полученные с помощью логистической регрессии.
План этой статьи:
- Линейная регрессия
- Метод наименьших квадратов
- Метод максимального правдоподобия
- Разложение ошибки на смещение и разброс (Bias-variance decomposition)
- Регуляризация линейной регрессии
- Логистическая регрессия
- Линейный классификатор
- Логистическая регрессия как линейный классификатор
- Принцип максимального правдоподобия и логистическая регрессия
- L2-регуляризация логистической функции потерь
- Наглядный пример регуляризации логистической регрессии
- Где логистическая регрессия хороша и где не очень
-Анализ отзывов IMDB к фильмам
-XOR-проблема - Кривые валидации и обучения
- Плюсы и минусы линейных моделей в задачах машинного обучения
- Домашнее задание №4
- Полезные ресурсы
1. Линейная регрессия
Метод наименьших квадратов
Рассказ про линейные модели мы начнем с линейной регрессии. В первую очередь, необходимо задать модель зависимости объясняемой переменной от объясняющих ее факторов, функция зависимости будет линейной:
. Если мы добавим фиктивную размерность
для каждого наблюдения, тогда линейную форму можно переписать чуть более компактно, записав свободный член
под сумму:
. Если рассматривать матрицу наблюдения-признаки, у которой в строках находятся примеры из набора данных, то нам необходимо добавить единичную колонку слева. Зададим модель следующим образом:
где
Можем выписать выражение для каждого конкретного наблюдения
Также на модель накладываются следующие ограничения (иначе это будет какая то другая регрессия, но точно не линейная):
Оценка весов
называется линейной, если
где зависит только от наблюдаемых данных
и почти наверняка нелинейно. Так как решением задачи поиска оптимальных весов будет именно линейная оценка, то и модель называется линейной регрессией. Введем еще одно определение. Оценка
называется несмещенной тогда, когда матожидание оценки равно реальному, но неизвестному значению оцениваемого параметра:
Один из способов вычислить значения параметров модели является метод наименьших квадратов (МНК), который минимизирует среднеквадратичную ошибку между реальным значением зависимой переменной и прогнозом, выданным моделью:
Для решения данной оптимизационной задачи необходимо вычислить производные по параметрам модели, приравнять их к нулю и решить полученные уравнения относительно (матричное дифференцирование неподготовленному читателю может показаться затруднительным, попробуйте расписать все через суммы, чтобы убедиться в ответе):
Шпаргалка по матричным производным
Итак, имея в виду все определения и условия описанные выше, мы можем утверждать, опираясь на теорему Маркова-Гаусса, что оценка МНК является лучшей оценкой параметров модели, среди всех линейных и несмещенных оценок, то есть обладающей наименьшей дисперсией.
Метод максимального правдоподобия
У читателя вполне резонно могли возникнуть вопросы: например, почему мы минимизируем среднеквадратичную ошибку, а не что-то другое. Ведь можно минимизировать среднее абсолютное значение невязки или еще что-то. Единственное, что произойдёт в случае изменения минимизируемого значения, так это то, что мы выйдем из условий теоремы Маркова-Гаусса, и наши оценки перестанут быть лучшими среди линейных и несмещенных.
Давайте перед тем как продолжить, сделаем лирическое отступление, чтобы проиллюстрировать метод максимального правдоподобия на простом примере.
Как-то после школы я заметил, что все помнят формулу этилового спирта. Тогда я решил провести эксперимент: помнят ли люди более простую формулу метилового спирта: . Мы опросили 400 человек и оказалось, что формулу помнят всего 117 человек. Разумно предположить, что вероятность того, что следующий опрошенный знает формулу метилового спирта –
. Покажем, что такая интуитивно понятная оценка не просто хороша, а еще и является оценкой максимального правдоподобия.
Разберемся, откуда берется эта оценка, а для этого вспомним определение распределения Бернулли: случайная величина имеет распределение Бернулли, если она принимает всего два значения (
и
с вероятностями
и
соответственно) и имеет следующую функцию распределения вероятности:
Похоже, это распределение – то, что нам нужно, а параметр распределения и есть та оценка вероятности того, что человек знает формулу метилового спирта. Мы проделали
независимых экспериментов, обозначим их исходы как
. Запишем правдоподобие наших данных (наблюдений), то есть вероятность наблюдать 117 реализаций случайной величины
и 283 реализации
:
Далее будем максимизировать это выражение по , и чаще всего это делают не с правдоподобием
, а с его логарифмом (применение монотонного преобразования не изменит решение, но упростит вычисления):
Теперь мы хотим найти такое значение , которое максимизирует правдоподобие, для этого мы возьмем производную по
, приравняем к нулю и решим полученное уравнение:
Получается, что наша интуитивная оценка – это и есть оценка максимального правдоподобия. Применим теперь те же рассуждения для задачи линейной регрессии и попробуем выяснить, что лежит за среднеквадратичной ошибкой. Для этого нам придется посмотреть на линейную регрессию с вероятностной точки зрения. Модель, естественно, остается такой же:
но будем теперь считать, что случайные ошибки берутся из центрированного нормального распределения:
Перепишем модель в новом свете:
Так как примеры берутся независимо (ошибки не скоррелированы – одно из условий теоремы Маркова-Гаусса), то полное правдоподобие данных будет выглядеть как произведение функций плотности . Рассмотрим логарифм правдоподобия, что позволит нам перейти от произведения к сумме:
Мы хотим найти гипотезу максимального правдоподобия, т.е. нам нужно максимизировать выражение , а это то же самое, что и максимизация его логарифма. Обратите внимание, что при максимизации функции по какому-то параметру можно выкинуть все члены, не зависящие от этого параметра:
Таким образом, мы увидели, что максимизация правдоподобия данных – это то же самое, что и минимизация среднеквадратичной ошибки (при справедливости указанных выше предположений). Получается, что именно такая функция стоимости является следствием того, что ошибка распределена нормально, а не как-то по-другому.
Разложение ошибки на смещение и разброс (Bias-variance decomposition)
Поговорим немного о свойствах ошибки прогноза линейной регрессии (в принципе эти рассуждения верны для всех алгоритмов машинного обучения). В свете предыдущего пункта мы выяснили, что:
Тогда ошибка в точке раскладывается следующим образом:
Для наглядности опустим обозначение аргумента функций. Рассмотрим каждый член в отдельности, первые два расписываются легко по формуле :
Пояснения:
И теперь последний член суммы. Мы помним, что ошибка и целевая переменная независимы друг от друга:
Наконец, собираем все вместе:
Итак, мы достигли цели всех вычислений, описанных выше, последняя формула говорит нам, что ошибка прогноза любой модели вида складывается из:
Если с последней мы ничего сделать не можем, то на первые два слагаемых мы можем как-то влиять. В идеале, конечно же, хотелось бы свести на нет оба этих слагаемых (левый верхний квадрат рисунка), но на практике часто приходится балансировать между смещенными и нестабильными оценками (высокая дисперсия).
Как правило, при увеличении сложности модели (например, при увеличении количества свободных параметров) увеличивается дисперсия (разброс) оценки, но уменьшается смещение. Из-за того что тренировочный набор данных полностью запоминается вместо обобщения, небольшие изменения приводят к неожиданным результатам (переобучение). Если же модель слабая, то она не в состоянии выучить закономерность, в результате выучивается что-то другое, смещенное относительно правильного решения.
Теорема Маркова-Гаусса как раз утверждает, что МНК-оценка параметров линейной модели является самой лучшей в классе несмещенных линейных оценок, то есть с наименьшей дисперсией. Это значит, что если существует какая-либо другая несмещенная модель тоже из класса линейных моделей, то мы можем быть уверены, что
.
Регуляризация линейной регрессии
Иногда бывают ситуации, когда мы намеренно увеличиваем смещенность модели ради ее стабильности, т.е. ради уменьшения дисперсии модели . Одним из условий теоремы Маркова-Гаусса является полный столбцовый ранг матрицы
. В противном случае решение МНК
не существует, т.к. не будет существовать обратная матрица
Другими словами, матрица
будет сингулярна, или вырожденна. Такая задача называется некорректно поставленной. Задачу нужно скорректировать, а именно, сделать матрицу
невырожденной, или регулярной (именно поэтому этот процесс называется регуляризацией). Чаще в данных мы можем наблюдать так называемую мультиколлинеарность — когда два или несколько признаков сильно коррелированы, в матрице
это проявляется в виде «почти» линейной зависимости столбцов. Например, в задаче прогнозирования цены квартиры по ее параметрам «почти» линейная зависимость будет у признаков «площадь с учетом балкона» и «площадь без учета балкона». Формально для таких данных матрица
будет обратима, но из-за мультиколлинеарности у матрицы
некоторые собственные значения будут близки к нулю, а в обратной матрице
появятся экстремально большие собственные значения, т.к. собственные значения обратной матрицы – это
. Итогом такого шатания собственных значений станет нестабильная оценка параметров модели, т.е. добавление нового наблюдения в набор тренировочных данных приведёт к совершенно другому решению. Иллюстрации роста коэффициентов вы найдете в одном из наших прошлых постов. Одним из способов регуляризации является регуляризация Тихонова, которая в общем виде выглядит как добавление нового члена к среднеквадратичной ошибке:
Часто матрица Тихонова выражается как произведение некоторого числа на единичную матрицу: . В этом случае задача минимизации среднеквадратичной ошибки становится задачей с ограничением на
норму. Если продифференцировать новую функцию стоимости по параметрам модели, приравнять полученную функцию к нулю и выразить
, то мы получим точное решение задачи.
Такая регрессия называется гребневой регрессией (ridge regression). А гребнем является как раз диагональная матрица, которую мы прибавляем к матрице , в результате получается гарантированно регулярная матрица.
Такое решение уменьшает дисперсию, но становится смещенным, т.к. минимизируется также и норма вектора параметров, что заставляет решение сдвигаться в сторону нуля. На рисунке ниже на пересечении белых пунктирных линий находится МНК-решение. Голубыми точками обозначены различные решения гребневой регрессии. Видно, что при увеличении параметра регуляризации решение сдвигается в сторону нуля.
Советуем обратиться в наш прошлый пост за примером того, как регуляризация справляется с проблемой мультиколлинеарности, а также чтобы освежить в памяти еще несколько интерпретаций регуляризации.
2. Логистическая регрессия
Линейный классификатор
Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на два полупространства, в каждом из которых прогнозируется одно из двух значений целевого класса.
Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.
Мы уже знакомы с линейной регрессией и методом наименьших квадратов. Рассмотрим задачу бинарной классификации, причем метки целевого класса обозначим «+1» (положительные примеры) и «-1» (отрицательные примеры).
Один из самых простых линейных классификаторов получается на основе регрессии вот таким образом:
где
Логистическая регрессия как линейный классификатор
Логистическая регрессия является частным случаем линейного классификатора, но она обладает хорошим «умением» – прогнозировать вероятность отнесения примера
к классу «+»:
Прогнозирование не просто ответа («+1» или «-1»), а именно вероятности отнесения к классу «+1» во многих задачах является очень важным бизнес-требованием. Например, в задаче кредитного скоринга, где традиционно применяется логистическая регрессия, часто прогнозируют вероятность невозврата кредита (). Клиентов, обратившихся за кредитом, сортируют по этой предсказанной вероятности (по убыванию), и получается скоркарта — по сути, рейтинг клиентов от плохих к хорошим. Ниже приведен игрушечный пример такой скоркарты.
Банк выбирает для себя порог предсказанной вероятности невозврата кредита (на картинке –
) и начиная с этого значения уже не выдает кредит. Более того, можно умножить предсказанную вероятность на выданную сумму и получить матожидание потерь с клиента, что тоже будет хорошей бизнес-метрикой (Далее в комментариях специалисты по скорингу могут поправить, но главная суть примерно такая).
Итак, мы хотим прогнозировать вероятность , а пока умеем строить линейный прогноз с помощью МНК:
. Каким образом преобразовать полученное значение в вероятность, пределы которой – [0, 1]? Очевидно, для этого нужна некоторая функция
В модели логистической регрессии для этого берется конкретная функция:
. И сейчас разберемся, каковы для этого предпосылки.
Обозначим вероятностью происходящего события
. Тогда отношение вероятностей
определяется из
, а это — отношение вероятностей того, произойдет ли событие или не произойдет. Очевидно, что вероятность и отношение шансов содержат одинаковую информацию. Но в то время как
находится в пределах от 0 до 1,
находится в пределах от 0 до
.
Если вычислить логарифм (то есть называется логарифм шансов, или логарифм отношения вероятностей), то легко заметить, что
. Его-то мы и будем прогнозировать с помощью МНК.
Посмотрим, как логистическая регрессия будет делать прогноз (пока считаем, что веса
мы как-то получили (т.е. обучили модель), далее разберемся, как именно).
-
Шаг 1. Вычислить значение
. (уравнение
задает гиперплоскость, разделяющую примеры на 2 класса);
-
Шаг 2. Вычислить логарифм отношения шансов:
.
-
Шаг 3. Имея прогноз шансов на отнесение к классу «+» –
, вычислить
с помощью простой зависимости:
В правой части мы получили как раз сигмоид-функцию.
Итак, логистическая регрессия прогнозирует вероятность отнесения примера к классу «+» (при условии, что мы знаем его признаки и веса модели) как сигмоид-преобразование линейной комбинации вектора весов модели и вектора признаков примера:
Следующий вопрос: как модель обучается? Тут мы опять обращаемся к принципу максимального правдоподобия.
Принцип максимального правдоподобия и логистическая регрессия
Теперь посмотрим, как из принципа максимального правдоподобия получается оптимизационная задача, которую решает логистическая регрессия, а именно, – минимизация логистической функции потерь.
Только что мы увидели, что логистическая регрессия моделирует вероятность отнесения примера к классу «+» как
Тогда для класса «-» аналогичная вероятность:
Оба этих выражения можно ловко объединить в одно (следите за моими руками – не обманывают ли вас):
Выражение называется отступом (margin) классификации на объекте
(не путать с зазором (тоже margin), про который чаще всего говорят в контексте SVM). Если он неотрицателен, модель не ошибается на объекте
, если же отрицателен – значит, класс для
спрогнозирован неправильно.
Заметим, что отступ определен для объектов именно обучающей выборки, для которых известны реальные метки целевого класса .
Чтобы понять, почему это мы сделали такие выводы, обратимся к геометрической интерпретации линейного классификатора. Подробно про это можно почитать в материалах Евгения Соколова.
Рекомендую решить почти классическую задачу из начального курса линейной алгебры: найти расстояние от точки с радиус-вектором до плоскости, которая задается уравнением
Ответ
Когда получим (или посмотрим) ответ, то поймем, что чем больше по модулю выражение , тем дальше точка
находится от плоскости
Значит, выражение – это своего рода «уверенность» модели в классификации объекта
:
- если отступ большой (по модулю) и положительный, это значит, что метка класса поставлена правильно, а объект находится далеко от разделяющей гиперплоскости (такой объект классифицируется уверенно). На рисунке –
.
- если отступ большой (по модулю) и отрицательный, значит метка класса поставлена неправильно, а объект находится далеко от разделяющей гиперплоскости (скорее всего такой объект – аномалия, например, его метка в обучающей выборке поставлена неправильно). На рисунке –
.
- если отступ малый (по модулю), то объект находится близко к разделяющей гиперплоскости, а знак отступа определяет, правильно ли объект классифицирован. На рисунке –
и
.
Теперь распишем правдоподобие выборки, а именно, вероятность наблюдать данный вектор у выборки
. Делаем сильное предположение: объекты приходят независимо, из одного распределения (i.i.d.). Тогда
где – длина выборки
(число строк).
Как водится, возьмем логарифм данного выражения (сумму оптимизировать намного проще, чем произведение):
То есть в даном случае принцип максимизации правдоподобия приводит к минимизации выражения
Это логистическая функция потерь, просуммированная по всем объектам обучающей выборки.
Посмотрим на новую фунцию как на функцию от отступа: . Нарисуем ее график, а также график 1/0 функциий потерь (zero-one loss), которая просто штрафует модель на 1 за ошибку на каждом объекте (отступ отрицательный):
.
Картинка отражает общую идею, что в задаче классификации, не умея напрямую минимизировать число ошибок (по крайней мере, градиентными методами это не сделать – производная 1/0 функциий потерь в нуле обращается в бесконечность), мы минимизируем некоторую ее верхнюю оценку. В данном случае это логистическая функция потерь (где логарифм двоичный, но это не принципиально), и справедливо
где – попросту число ошибок логистической регрессии с весами
на выборке
.
То есть уменьшая верхнюю оценку на число ошибок классификации, мы таким образом надеемся уменьшить и само число ошибок.
 -регуляризация логистических потерь
-регуляризация логистических потерь
L2-регуляризация логистической регрессии устроена почти так же, как и в случае с гребневой (Ridge регрессией). Вместо функционала минимизируется следующий:
В случае логистической регрессии принято введение обратного коэффициента регуляризации . И тогда решением задачи будет
Далее рассмотрим пример, позволяющий интуитивно понять один из смыслов регуляризации.
3. Наглядный пример регуляризации логистической регрессии
В 1 статье уже приводился пример того, как полиномиальные признаки позволяют линейным моделям строить нелинейные разделяющие поверхности. Покажем это в картинках.
Посмотрим, как регуляризация влияет на качество классификации на наборе данных по тестированию микрочипов из курса Andrew Ng по машинному обучению.
Будем использовать логистическую регрессию с полиномиальными признаками и варьировать параметр регуляризации C.
Сначала посмотрим, как регуляризация влияет на разделяющую границу классификатора, интуитивно распознаем переобучение и недообучение.
Потом численно установим близкий к оптимальному параметр регуляризации с помощью кросс-валидации (cross-validation) и перебора по сетке (GridSearch).
Подключение библиотек
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.model_selection import cross_val_score, StratifiedKFold
from sklearn.model_selection import GridSearchCVЗагружаем данные с помощью метода read_csv библиотеки pandas. В этом наборе данных для 118 микрочипов (объекты) указаны результаты двух тестов по контролю качества (два числовых признака) и сказано, пустили ли микрочип в производство. Признаки уже центрированы, то есть из всех значений вычтены средние по столбцам. Таким образом, «среднему» микрочипу соответствуют нулевые значения результатов тестов.
Загрузка данных
data = pd.read_csv('../../data/microchip_tests.txt',
header=None, names = ('test1','test2','released'))
# информация о наборе данных
data.info()<class ‘pandas.core.frame.DataFrame’>
RangeIndex: 118 entries, 0 to 117
Data columns (total 3 columns):
test1 118 non-null float64
test2 118 non-null float64
released 118 non-null int64
dtypes: float64(2), int64(1)
memory usage: 2.8 KB
Посмотрим на первые и последние 5 строк.
Сохраним обучающую выборку и метки целевого класса в отдельных массивах NumPy. Отобразим данные. Красный цвет соответствует бракованным чипам, зеленый – нормальным.
Код
X = data.ix[:,:2].values
y = data.ix[:,2].valuesplt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов')
plt.legend();Определяем функцию для отображения разделяющей кривой классификатора
Код
def plot_boundary(clf, X, y, grid_step=.01, poly_featurizer=None):
x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
xx, yy = np.meshgrid(np.arange(x_min, x_max, grid_step),
np.arange(y_min, y_max, grid_step))
# каждой точке в сетке [x_min, m_max]x[y_min, y_max]
# ставим в соответствие свой цвет
Z = clf.predict(poly_featurizer.transform(np.c_[xx.ravel(), yy.ravel()]))
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, cmap=plt.cm.Paired)Полиномиальными признаками до степени для двух переменных
и
мы называем следующие:
Например, для это будут следующие признаки:
Нарисовав треугольник Пифагора, Вы сообразите, сколько таких признаков будет для и вообще для любого
.
Попросту говоря, таких признаков экспоненциально много, и строить, скажем, для 100 признаков полиномиальные степени 10 может оказаться затратно (а более того, и не нужно).
Создадим объект sklearn, который добавит в матрицу полиномиальные признаки вплоть до степени 7 и обучим логистическую регрессию с параметром регуляризации
. Изобразим разделяющую границу.
Также проверим долю правильных ответов классификатора на обучающей выборке. Видим, что регуляризация оказалась слишком сильной, и модель «недообучилась». Доля правильных ответов классификатора на обучающей выборке оказалась равной 0.627.
Код
poly = PolynomialFeatures(degree=7)
X_poly = poly.fit_transform(X)C = 1e-2
logit = LogisticRegression(C=C, n_jobs=-1, random_state=17)
logit.fit(X_poly, y)
plot_boundary(logit, X, y, grid_step=.01, poly_featurizer=poly)
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов. Логит с C=0.01')
plt.legend();
print("Доля правильных ответов классификатора на обучающей выборке:",
round(logit.score(X_poly, y), 3))Увеличим до 1. Тем самым мы ослабляем регуляризацию, теперь в решении значения весов логистической регрессии могут оказаться больше (по модулю), чем в прошлом случае. Теперь доля правильных ответов классификатора на обучающей выборке – 0.831.
Код
C = 1
logit = LogisticRegression(C=C, n_jobs=-1, random_state=17)
logit.fit(X_poly, y)
plot_boundary(logit, X, y, grid_step=.005, poly_featurizer=poly)
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов. Логит с C=1')
plt.legend();
print("Доля правильных ответов классификатора на обучающей выборке:",
round(logit.score(X_poly, y), 3))Еще увеличим – до 10 тысяч. Теперь регуляризации явно недостаточно, и мы наблюдаем переобучение. Можно заметить, что в прошлом случае (при
=1 и «гладкой» границе) доля правильных ответов модели на обучающей выборке не намного ниже, чем в 3 случае, зато на новой выборке, можно себе представить, 2 модель сработает намного лучше.
Доля правильных ответов классификатора на обучающей выборке – 0.873.
Код
C = 1e4
logit = LogisticRegression(C=C, n_jobs=-1, random_state=17)
logit.fit(X_poly, y)
plot_boundary(logit, X, y, grid_step=.005, poly_featurizer=poly)
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов. Логит с C=10k')
plt.legend();
print("Доля правильных ответов классификатора на обучающей выборке:",
round(logit.score(X_poly, y), 3))Чтоб обсудить результаты, перепишем формулу для функционала, который оптимизируется в логистической регрессии, в таком виде:
где
Промежуточные выводы:
- чем больше параметр
, тем более сложные зависимости в данных может восстанавливать модель (интуитивно
соответствует «сложности» модели (model capacity))
- если регуляризация слишком сильная (малые значения
), то решением задачи минимизации логистической функции потерь может оказаться то, когда многие веса занулились или стали слишком малыми. Еще говорят, что модель недостаточно «штрафуется» за ошибки (то есть в функционале
«перевешивает» сумма квадратов весов, а ошибка
может быть относительно большой). В таком случае модель окажется недообученной (1 случай)
- наоборот, если регуляризация слишком слабая (большие значения
), то решением задачи оптимизации может стать вектор
с большими по модулю компонентами. В таком случае больший вклад в оптимизируемый функционал
имеет
и, вольно выражаясь, модель слишком «боится» ошибиться на объектах обучающей выборки, поэтому окажется переобученной (3 случай)
- то, какое значение
выбрать, сама логистическая регрессия «не поймет» (или еще говорят «не выучит»), то есть это не может быть определено решением оптимизационной задачи, которой является логистическая регрессия (в отличие от весов
). Так же точно, дерево решений не может «само понять», какое ограничение на глубину выбрать (за один процесс обучения). Поэтому
– это гиперпараметр модели, который настраивается на кросс-валидации, как и max_depth для дерева.
Настройка параметра регуляризации
Теперь найдем оптимальное (в данном примере) значение параметра регуляризации . Сделать это можно с помощью LogisticRegressionCV – перебора параметров по сетке с последующей кросс-валидацией. Этот класс создан специально для логистической регрессии (для нее известны эффективные алгоритмы перебора параметров), для произвольной модели мы бы использовали GridSearchCV, RandomizedSearchCV или, например, специальные алгоритмы оптимизации гиперпараметров, реализованные в hyperopt.
Код
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=17)
c_values = np.logspace(-2, 3, 500)
logit_searcher = LogisticRegressionCV(Cs=c_values, cv=skf, verbose=1, n_jobs=-1)
logit_searcher.fit(X_poly, y)Посмотрим, как качество модели (доля правильных ответов на обучающей и валидационной выборках) меняется при изменении гиперпараметра .
Выделим участок с «лучшими» значениями C.
Как мы помним, такие кривые называются валидационными, раньше мы их строили вручную, но в sklearn для них их построения есть специальные методы, которые мы тоже сейчас будем использовать.
4. Где логистическая регрессия хороша и где не очень
Анализ отзывов IMDB к фильмам
Будем решать задачу бинарной классификации отзывов IMDB к фильмам. Имеется обучающая выборка с размеченными отзывами, по 12500 отзывов известно, что они хорошие, еще про 12500 – что они плохие. Здесь уже не так просто сразу приступить к машинному обучению, потому что готовой матрицы нет – ее надо приготовить. Будем использовать самый простой подход – мешок слов («Bag of words»). При таком подходе признаками отзыва будут индикаторы наличия в нем каждого слова из всего корпуса, где корпус – это множество всех отзывов. Идея иллюстрируется картинкой
Импорт библиотек и загрузка данных
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import numpy as np
from sklearn.datasets import load_files
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer, TfidfVectorizer
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVCЗагрузим данные отсюда (краткое описание — тут). В обучающей и тестовой выборках по 12500 тысяч хороших и плохих отзывов к фильмам.
reviews_train = load_files("YOUR PATH")
text_train, y_train = reviews_train.data, reviews_train.targetprint("Number of documents in training data: %d" % len(text_train))
print(np.bincount(y_train))# поменяйте путь к файлу
reviews_test = load_files("YOUR PATH")
text_test, y_test = reviews_test.data, reviews_test.target
print("Number of documents in test data: %d" % len(text_test))
print(np.bincount(y_test))Пример плохого отзыва:
‘Words can’t describe how bad this movie is. I can’t explain it by writing only. You have too see it for yourself to get at grip of how horrible a movie really can be. Not that I recommend you to do that. There are so many clichxc3xa9s, mistakes (and all other negative things you can imagine) here that will just make you cry. To start with the technical first, there are a LOT of mistakes regarding the airplane. I won’t list them here, but just mention the coloring of the plane. They didn’t even manage to show an airliner in the colors of a fictional airline, but instead used a 747 painted in the original Boeing livery. Very bad. The plot is stupid and has been done many times before, only much, much better. There are so many ridiculous moments here that i lost count of it really early. Also, I was on the bad guys’ side all the time in the movie, because the good guys were so stupid. «Executive Decision» should without a doubt be you’re choice over this one, even the «Turbulence»-movies are better. In fact, every other movie in the world is better than this one.’
Пример хорошего отзыва:
‘Everyone plays their part pretty well in this «little nice movie». Belushi gets the chance to live part of his life differently, but ends up realizing that what he had was going to be just as good or maybe even better. The movie shows us that we ought to take advantage of the opportunities we have, not the ones we do not or cannot have. If U can get this movie on video for around $10, itxc2xb4d be an investment!’
Простой подсчет слов
Составим словарь всех слов с помощью CountVectorizer. Всего в выборке 74849 уникальных слов. Если посмотреть на примеры полученных «слов» (лучше их называть токенами), то можно увидеть, что многие важные этапы обработки текста мы тут пропустили (автоматическая обработка текстов – это могло бы быть темой отдельной серии статей).
Код
cv = CountVectorizer()
cv.fit(text_train)
print(len(cv.vocabulary_)) #74849print(cv.get_feature_names()[:50])
print(cv.get_feature_names()[50000:50050])[’00’, ‘000’, ‘0000000000001’, ‘00001’, ‘00015’, ‘000s’, ‘001’, ‘003830’, ‘006’, ‘007’, ‘0079’, ‘0080’, ‘0083’, ‘0093638’, ’00am’, ’00pm’, ’00s’, ’01’, ’01pm’, ’02’, ‘020410’, ‘029’, ’03’, ’04’, ‘041’, ’05’, ‘050’, ’06’, ’06th’, ’07’, ’08’, ‘087’, ‘089’, ’08th’, ’09’, ‘0f’, ‘0ne’, ‘0r’, ‘0s’, ’10’, ‘100’, ‘1000’, ‘1000000’, ‘10000000000000’, ‘1000lb’, ‘1000s’, ‘1001’, ‘100b’, ‘100k’, ‘100m’]
[‘pincher’, ‘pinchers’, ‘pinches’, ‘pinching’, ‘pinchot’, ‘pinciotti’, ‘pine’, ‘pineal’, ‘pineapple’, ‘pineapples’, ‘pines’, ‘pinet’, ‘pinetrees’, ‘pineyro’, ‘pinfall’, ‘pinfold’, ‘ping’, ‘pingo’, ‘pinhead’, ‘pinheads’, ‘pinho’, ‘pining’, ‘pinjar’, ‘pink’, ‘pinkerton’, ‘pinkett’, ‘pinkie’, ‘pinkins’, ‘pinkish’, ‘pinko’, ‘pinks’, ‘pinku’, ‘pinkus’, ‘pinky’, ‘pinnacle’, ‘pinnacles’, ‘pinned’, ‘pinning’, ‘pinnings’, ‘pinnochio’, ‘pinnocioesque’, ‘pino’, ‘pinocchio’, ‘pinochet’, ‘pinochets’, ‘pinoy’, ‘pinpoint’, ‘pinpoints’, ‘pins’, ‘pinsent’]
Закодируем предложения из текстов обучающей выборки индексами входящих слов. Используем разреженный формат. Преобразуем так же тестовую выборку.
X_train = cv.transform(text_train)
X_test = cv.transform(text_test)Обучим логистическую регрессию и посмотрим на доли правильных ответов на обучающей и тестовой выборках. Получается, на тестовой выборке мы правильно угадываем тональность примерно 86.7% отзывов.
Код
%%time
logit = LogisticRegression(n_jobs=-1, random_state=7)
logit.fit(X_train, y_train)
print(round(logit.score(X_train, y_train), 3), round(logit.score(X_test, y_test), 3))Коэффициенты модели можно красиво отобразить.
Код визуализации коэффициентов модели
def visualize_coefficients(classifier, feature_names, n_top_features=25):
# get coefficients with large absolute values
coef = classifier.coef_.ravel()
positive_coefficients = np.argsort(coef)[-n_top_features:]
negative_coefficients = np.argsort(coef)[:n_top_features]
interesting_coefficients = np.hstack([negative_coefficients, positive_coefficients])
# plot them
plt.figure(figsize=(15, 5))
colors = ["red" if c < 0 else "blue" for c in coef[interesting_coefficients]]
plt.bar(np.arange(2 * n_top_features), coef[interesting_coefficients], color=colors)
feature_names = np.array(feature_names)
plt.xticks(np.arange(1, 1 + 2 * n_top_features), feature_names[interesting_coefficients], rotation=60, ha="right");
def plot_grid_scores(grid, param_name):
plt.plot(grid.param_grid[param_name], grid.cv_results_['mean_train_score'],
color='green', label='train')
plt.plot(grid.param_grid[param_name], grid.cv_results_['mean_test_score'],
color='red', label='test')
plt.legend();
visualize_coefficients(logit, cv.get_feature_names())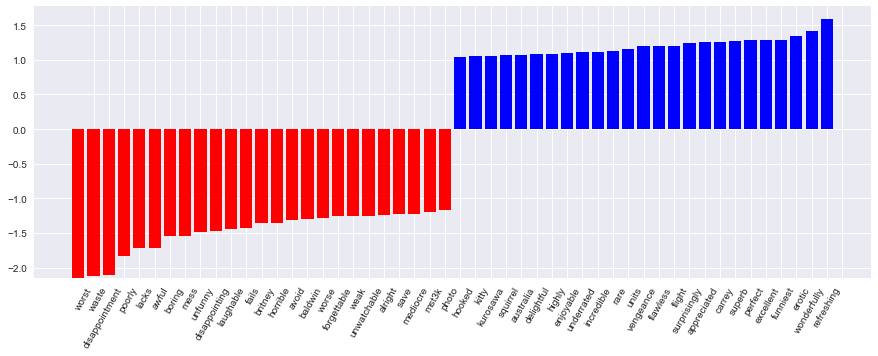
Подберем коэффициент регуляризации для логистической регрессии. Используем sklearn.pipeline, поскольку CountVectorizer правильно применять только на тех данных, на которых в текущий момент обучается модель (чтоб не «подсматривать» в тестовую выборку и не считать по ней частоты вхождения слов). В данном случае pipeline задает последовательность действий: применить CountVectorizer, затем обучить логистическую регрессию. Так мы поднимаем долю правильных ответов до 88.5% на кросс-валидации и 87.9% – на отложенной выборке.
Код
from sklearn.pipeline import make_pipeline
text_pipe_logit = make_pipeline(CountVectorizer(),
LogisticRegression(n_jobs=-1, random_state=7))
text_pipe_logit.fit(text_train, y_train)
print(text_pipe_logit.score(text_test, y_test))
from sklearn.model_selection import GridSearchCV
param_grid_logit = {'logisticregression__C': np.logspace(-5, 0, 6)}
grid_logit = GridSearchCV(text_pipe_logit, param_grid_logit, cv=3, n_jobs=-1)
grid_logit.fit(text_train, y_train)
grid_logit.best_params_, grid_logit.best_score_
plot_grid_scores(grid_logit, 'logisticregression__C')
grid_logit.score(text_test, y_test)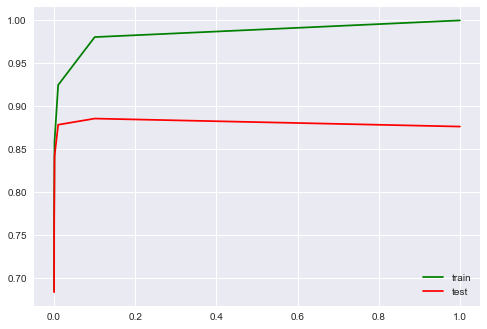
Теперь то же самое, но со случайным лесом. Видим, что с логистической регрессией мы достигаем большей доли правильных ответов меньшими усилиями. Лес работает дольше, на отложенной выборке 85.5% правильных ответов.
Код для обучения случайного леса
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators=200, n_jobs=-1, random_state=17)
forest.fit(X_train, y_train)
print(round(forest.score(X_test, y_test), 3))XOR-проблема
Теперь рассмотрим пример, где линейные модели справляются хуже.
Линейные методы классификации строят все же очень простую разделяющую поверхность – гиперплоскость. Самый известный игрушечный пример, в котором классы нельзя без ошибок поделить гиперплоскостью (то есть прямой, если это 2D), получил имя «the XOR problem».
XOR – это «исключающее ИЛИ», булева функция со следующей таблицей истинности:
XOR дал имя простой задаче бинарной классификации, в которой классы представлены вытянутыми по диагоналям и пересекающимися облаками точек.
Код, рисующий следующие 3 картинки
# порождаем данные
rng = np.random.RandomState(0)
X = rng.randn(200, 2)
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)plt.scatter(X[:, 0], X[:, 1], s=30, c=y, cmap=plt.cm.Paired);def plot_boundary(clf, X, y, plot_title):
xx, yy = np.meshgrid(np.linspace(-3, 3, 50),
np.linspace(-3, 3, 50))
clf.fit(X, y)
# plot the decision function for each datapoint on the grid
Z = clf.predict_proba(np.vstack((xx.ravel(), yy.ravel())).T)[:, 1]
Z = Z.reshape(xx.shape)
image = plt.imshow(Z, interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
aspect='auto', origin='lower', cmap=plt.cm.PuOr_r)
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2,
linetypes='--')
plt.scatter(X[:, 0], X[:, 1], s=30, c=y, cmap=plt.cm.Paired)
plt.xticks(())
plt.yticks(())
plt.xlabel(r'$<!-- math>$inline$x_1$inline$</math -->$')
plt.ylabel(r'$<!-- math>$inline$x_2$inline$</math -->$')
plt.axis([-3, 3, -3, 3])
plt.colorbar(image)
plt.title(plot_title, fontsize=12);plot_boundary(LogisticRegression(), X, y,
"Logistic Regression, XOR problem")from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipelinelogit_pipe = Pipeline([('poly', PolynomialFeatures(degree=2)),
('logit', LogisticRegression())])plot_boundary(logit_pipe, X, y,
"Logistic Regression + quadratic features. XOR problem")Очевидно, нельзя провести прямую так, чтобы без ошибок отделить один класс от другого. Поэтому логистическая регрессия плохо справляется с такой задачей.
А вот если на вход подать полиномиальные признаки, в данном случае до 2 степени, то проблема решается.
Здесь логистическая регрессия все равно строила гиперплоскость, но в 6-мерном пространстве признаков и
. В проекции на исходное пространство признаков
граница получилась нелинейной.
На практике полиномиальные признаки действительно помогают, но строить их явно – вычислительно неэффективно. Гораздо быстрее работает SVM с ядровым трюком. При таком подходе в пространстве высокой размерности считается только расстояние между объектами (задаваемое функцией-ядром), а явно плодить комбинаторно большое число признаков не приходится. Про это подробно можно почитать в курсе Евгения Соколова (математика уже серьезная).
5. Кривые валидации и обучения
Мы уже получили представление о проверке модели, кросс-валидации и регуляризации.
Теперь рассмотрим главный вопрос:
Если качество модели нас не устраивает, что делать?
- Сделать модель сложнее или упростить?
- Добавить больше признаков?
- Или нам просто нужно больше данных для обучения?
Ответы на данные вопросы не всегда лежат на поверхности. В частности, иногда использование более сложной модели приведет к ухудшению показателей. Либо добавление наблюдений не приведет к ощутимым изменениям. Способность принять правильное решение и выбрать правильный способ улучшения модели, собственно говоря, и отличает хорошего специалиста от плохого.
Будем работать со знакомыми данными по оттоку клиентов телеком-оператора.
Импорт библиотек и чтение данных
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV, SGDClassifier
from sklearn.model_selection import validation_curve
data = pd.read_csv('../../data/telecom_churn.csv').drop('State', axis=1)
data['International plan'] = data['International plan'].map({'Yes': 1, 'No': 0})
data['Voice mail plan'] = data['Voice mail plan'].map({'Yes': 1, 'No': 0})
y = data['Churn'].astype('int').values
X = data.drop('Churn', axis=1).valuesЛогистическую регрессию будем обучать стохастическим градиентным спуском. Пока объясним это тем, что так быстрее, но далее в программе у нас отдельная статья про это дело. Построим валидационные кривые, показывающие, как качество (ROC AUC) на обучающей и проверочной выборке меняется с изменением параметра регуляризации.
Код
alphas = np.logspace(-2, 0, 20)
sgd_logit = SGDClassifier(loss='log', n_jobs=-1, random_state=17)
logit_pipe = Pipeline([('scaler', StandardScaler()), ('poly', PolynomialFeatures(degree=2)),
('sgd_logit', sgd_logit)])
val_train, val_test = validation_curve(logit_pipe, X, y,
'sgd_logit__alpha', alphas, cv=5,
scoring='roc_auc')
def plot_with_err(x, data, **kwargs):
mu, std = data.mean(1), data.std(1)
lines = plt.plot(x, mu, '-', **kwargs)
plt.fill_between(x, mu - std, mu + std, edgecolor='none',
facecolor=lines[0].get_color(), alpha=0.2)
plot_with_err(alphas, val_train, label='training scores')
plot_with_err(alphas, val_test, label='validation scores')
plt.xlabel(r'$alpha$'); plt.ylabel('ROC AUC')
plt.legend();Тенденция видна сразу, и она очень часто встречается.
-
Для простых моделей тренировочная и валидационная ошибка находятся где-то рядом, и они велики. Это говорит о том, что модель недообучилась: то есть она не имеет достаточное кол-во параметров.
-
Для сильно усложненных моделей тренировочная и валидационная ошибки значительно отличаются. Это можно объяснить переобучением: когда параметров слишком много либо не хватает регуляризации, алгоритм может «отвлекаться» на шум в данных и упускать основной тренд.
Сколько нужно данных?
Известно, что чем больше данных использует модель, тем лучше. Но как нам понять в конкретной ситуации, помогут ли новые данные? Скажем, целесообразно ли нам потратить N$ на труд асессоров, чтобы увеличить выборку вдвое?
Поскольку новых данных пока может и не быть, разумно поварьировать размер имеющейся обучающей выборки и посмотреть, как качество решения задачи зависит от объема данных, на котором мы обучали модель. Так получаются кривые обучения (learning curves).
Идея простая: мы отображаем ошибку как функцию от количества примеров, используемых для обучения. При этом параметры модели фиксируются заранее.
Давайте посмотрим, что мы получим для линейной модели. Коэффициент регуляризации выставим большим.
Код
from sklearn.model_selection import learning_curve
def plot_learning_curve(degree=2, alpha=0.01):
train_sizes = np.linspace(0.05, 1, 20)
logit_pipe = Pipeline([('scaler', StandardScaler()), ('poly', PolynomialFeatures(degree=degree)),
('sgd_logit', SGDClassifier(n_jobs=-1, random_state=17, alpha=alpha))])
N_train, val_train, val_test = learning_curve(logit_pipe,
X, y, train_sizes=train_sizes, cv=5,
scoring='roc_auc')
plot_with_err(N_train, val_train, label='training scores')
plot_with_err(N_train, val_test, label='validation scores')
plt.xlabel('Training Set Size'); plt.ylabel('AUC')
plt.legend()
plot_learning_curve(degree=2, alpha=10)Типичная ситуация: для небольшого объема данных ошибки на обучающей выборке и в процессе кросс-валидации довольно сильно отличаются, что указывает на переобучение. Для той же модели, но с большим объемом данных ошибки «сходятся», что указывается на недообучение.
Если добавить еще данные, ошибка на обучающей выборке не будет расти, но с другой стороны, ошибка на тестовых данных не будет уменьшаться.
Получается, ошибки «сошлись», и добавление новых данных не поможет. Собственно, это случай – самый интересный для бизнеса. Возможна ситуация, когда мы увеличиваем выборку в 10 раз. Но если не менять сложность модели, это может и не помочь. То есть стратегия «настроил один раз – дальше использую 10 раз» может и не работать.
Что будет, если изменить коэффициент регуляризации (уменьшить до 0.05)?
Видим хорошую тенденцию – кривые постепенно сходятся, и если дальше двигаться направо (добавлять в модель данные), можно еще повысить качество на валидации.
А если усложнить модель ещё больше ()?
Проявляется переобучение – AUC падает как на обучении, так и на валидации.
Строя подобные кривые, можно понять, в какую сторону двигаться, и как правильно настроить сложность модели на новых данных.
Выводы по кривым валидации и обучения
- Ошибка на обучающей выборке сама по себе ничего не говорит о качестве модели
- Кросс-валидационная ошибка показывает, насколько хорошо модель подстраивается под данные (имеющийся тренд в данных), сохраняя при этом способность обобщения на новые данные
- Валидационная кривая представляет собой график, показывающий результат на тренировочной и валидационной выборке в зависимости от сложности модели:
- если две кривые распологаются близко, и обе ошибки велики, — это признак недообучения
- если две кривые далеко друг от друга, — это показатель переобучения
- Кривая обучения — это график, показывающий результаты на валидации и тренировочной подвыборке в зависимости от количества наблюдений:
- если кривые сошлись друг к другу, добавление новых данных не поможет – надо менять сложность модели
- если кривые еще не сошлись, добавление новых данных может улучшить результат.
6. Плюсы и минусы линейных моделей в задачах машинного обучения
Плюсы:
Минусы:
- Плохо работают в задачах, в которых зависимость ответов от признаков сложная, нелинейная
- На практике предположения теоремы Маркова-Гаусса почти никогда не выполняются, поэтому чаще линейные методы работают хуже, чем, например, SVM и ансамбли (по качеству решения задачи классификации/регрессии)
7. Домашнее задание № 4
В качестве закрепления изученного материала предлагаем следующее задание: разобраться с тем, как работает TfidfVectorizer и DictVectorizer, обучить и настроить модель линейной регрессии Ridge на данных о публикациях на Хабрахабре и воспроизвести бенчмарк в соревновании. Проверить себя можно отправив ответы в веб-форме (там же найдете и решение).
Актуальные и обновляемые версии демо-заданий – на английском на сайте курса. Также по подписке на Patreon («Bonus Assignments» tier) доступны расширенные домашние задания по каждой теме (только на англ.)
8. Полезные ресурсы
- Перевод материала этой статьи на английский – Jupyter notebooks в репозитории курса
- Видеозаписи лекций по мотивам этой статьи: классификация, регрессия
- Основательный обзор классики машинного обучения и, конечно же, линейных моделей сделан в книге «Deep Learning» (I. Goodfellow, Y. Bengio, A. Courville, 2016);
- Реализация многих алгоритмов машинного обучения с нуля – репозиторий rushter. Рекомендуем изучить реализацию логистической регрессии;
- Курс Евгения Соколова по машинному обучению (материалы на GitHub). Хорошая теория, нужна неплохая математическая подготовка;
- Курс Дмитрия Ефимова на GitHub (англ.). Тоже очень качественные материалы.
Статья написана в соавторстве с mephistopheies (Павлом Нестеровым). Он же – автор домашнего задания. Авторы домашнего задания в первой сессии курса (февраль-май 2017)– aiho (Ольга Дайховская) и das19 (Юрий Исаков). Благодарю bauchgefuehl (Анастасию Манохину) за редактирование.
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Метод наименьших квадратов
Если
некоторая физическая величина зависит
от другой величины, то эту зависимость
можно исследовать, измеряя y
при различных значениях x.
В результате измерений получается ряд
значений:
;
.
По данным такого
эксперимента можно построить график
зависимости
.
Полученная кривая дает возможность
судить о виде функции.
Однако постоянные коэффициенты, которые
входят в эту функцию, остаются неизвестными.
Оптимальный подход к решению подобных
задач возможен на основе применения
метода наименьших квадратов.
Суть метода
наименьших квадратов состоит в том, что
наивероятнейшими значениями аргументов
искомой аналитической зависимости
будут те, при которых сумма квадратов
отклонений экспериментальных значений
функции
от значений самой функцииy,
т.е.
является наименьшей.
На
практике этот метод наиболее часто (и
наиболее просто) используется в случае
линейной зависимости, т.е. когда
или
.
Линейная
зависимость очень широко распространена
в физике. И даже когда зависимость
нелинейная, обычно стараются строить
график так, чтобы получить прямую линию.
Например, если предполагают, что
показатель преломления стекла n
связан с длиной λ световой волны
соотношением
,
то на графике строят зависимостьn
от
.
Для
начала рассмотрим зависимость
(прямая, проходящая через начало
координат). Составим величину– сумму квадратов отклонений
экспериментальных точек от прямой
.
Величина
всегда положительна и оказывается тем
меньше, чем ближе к прямой лежат
экспериментальные точки. Метод наименьших
квадратов утверждает, что дляk
следует выбирать такое значение, при
котором
имеет минимум
или
|
|
(16) |
Вычисление
показывает, что среднеквадратичная
ошибка определения величины k
при этом равна
|
|
(17) |
Теперь
можно рассмотреть более трудный случай,
когда точки должны удовлетворить формуле
.
Задача
состоит в том, чтобы по имеющемуся набору
значений
найти наилучшие значенияa
и b.
Составляя
квадратичную форму
,
равную сумме квадратов отклонений точекот прямой
определяют
значения a
и b,
при которых
имеет минимум
,
.
Совместное
решение этих уравнений дает
|
|
(18) |
|
|
(19) |
Среднеквадратичные
ошибки определения a
и b
равны
|
|
(20) |
|
|
(21) |
При
обработке результатов измерения этим
методом удобно все данные сводить в
таблицу, в которой предварительно
подсчитываются все суммы, входящие в
формулы (16) – (21). Формы этих таблиц
приведены в рассматриваемых ниже
примерах.
Пример 1.
Исследовалось основное уравнение
динамики вращательного движения
(прямая, проходящая через начало
координат). При различных значениях
моментаM
измерялось угловое ускорение ε некоторого
тела. Требуется определить момент
инерции этого тела. Результаты измерений
момента силы и углового ускорения
занесены во второй и третий столбцы
таблицы 2.
Таблица 2. Результаты эксперимента
|
n |
|
|
|
|
|
|
|
1 |
1.44 |
0.52 |
2.0736 |
0.7488 |
0.039432 |
0.001555 |
|
2 |
3.12 |
1.06 |
9.7344 |
3.3072 |
0.018768 |
0.000352 |
|
3 |
4.59 |
1.45 |
21.0681 |
6.6555 |
|
0.006693 |
|
4 |
5.90 |
1.92 |
34.8100 |
11.3280 |
|
0.002401 |
|
5 |
7.45 |
2.56 |
55.5025 |
19.0720 |
0.073725 |
0.005435 |
|
|
– |
– |
123.1886 |
41.1115 |
– |
0.016436 |
Используя линейную
зависимость
,
по
формуле (16) определяем

откуда
.
Для определения
среднеквадратичной ошибки воспользуемся
формулой (17)

По формуле
(14) имеем

Задавшись надежностью
,
по таблице коэффициентов Стьюдента для,
находими определяем абсолютную ошибку
.
Относительная
погрешность
.
Окончательно
результат можно записать в виде:
при
,
.
Пример 2. Вычислить
коэффициент линейного расширения
металлического стержня по методу
наименьших квадратов. Длина металлического
стержня от температуры зависит по
линейному закону
.
Свободный
член
определяет первоначальную длину
при температуре 0° C, а угловой
коэффициент– произведение коэффициента линейного
расширенияна первоначальную длину
.
Результаты
измерений и расчетов приведены в таблице
3.
Таблица 3.Результаты эксперимента
|
n |
|
l, |
|
|
|
|
|
|
1 |
23 |
150.005 |
|
2500 |
|
0.0001429 |
2.041 |
|
2 |
43 |
150.040 |
|
900 |
|
0.0003143 |
9.878 |
|
3 |
63 |
150.074 |
|
100 |
1500.74 |
0.0002286 |
5.224 |
|
4 |
83 |
150.109 |
10 |
100 |
1501.09 |
0.0002286 |
5.226 |
|
5 |
103 |
150.143 |
30 |
900 |
4504.29 |
0.0003143 |
9.878 |
|
6 |
123 |
150.178 |
50 |
2500 |
7508.90 |
0.0001429 |
2.041 |
|
|
438 |
900.549 |
0 |
7000 |
12.09 |
– |
34.286 |
|
|
73 |
150.091 |
– |
– |
– |
– |
– |
По
формулам (18),
(19)
определяем

.
Отсюда:
.
Найдем
ошибку в определении
.
Так как
,
то по формуле (14) имеем:

Пользуясь
формулами (20),
(21)
имеем

.
Тогда
.
Задавшись
надежностью
,
по таблице коэффициентов Стьюдента для
,
находим
и определяем абсолютную ошибку
.
Тогда результат
вычисления равен
.
Относительная
погрешность
.
Окончательно
результат
можно
записать в виде:
при
,
.
Соседние файлы в папке 07-02-2013_14-00-36
- #
- #
- #
- #
- #
В статистических данных и обработки сигналов , A минимальной среднеквадратической ошибки ( MMSE ) оценки является метод оценки , который минимизирует среднеквадратичную ошибку (MSE), которая является общей мерой оценки качества, из подогнанных значений зависимой переменной . В байесовской установке термин MMSE более конкретно относится к оценке с квадратичной функцией потерь . В таком случае оценка MMSE задается апостериорным средним значением параметра, который необходимо оценить. Поскольку вычисление апостериорного среднего затруднительно, форма оценки MMSE обычно ограничивается определенным классом функций. Линейные оценщики MMSE — популярный выбор, поскольку они просты в использовании, легко вычисляются и очень универсальны. Это породило множество популярных оценок , таких как фильтр Винера-Колмогорова и фильтра Калмана .
Мотивация
Термин MMSE более конкретно относится к оценке в байесовской среде с квадратичной функцией стоимости. Основная идея байесовского подхода к оценке проистекает из практических ситуаций, когда у нас часто есть некоторая предварительная информация о параметре, который нужно оценить. Например, у нас может быть предварительная информация о диапазоне, который может принимать параметр; или у нас может быть старая оценка параметра, который мы хотим изменить, когда станет доступным новое наблюдение; или статистика фактического случайного сигнала, такого как речь. Это контрастирует с небайесовским подходом, таким как несмещенная оценка с минимальной дисперсией (MVUE), где предполагается, что о параметре заранее ничего не известно и который не учитывает такие ситуации. В байесовском подходе такая априорная информация фиксируется априорной функцией плотности вероятности параметров; и основанный непосредственно на теореме Байеса , он позволяет нам делать более точные апостериорные оценки по мере появления большего количества наблюдений. Таким образом, в отличие от небайесовского подхода, при котором представляющие интерес параметры считаются детерминированными, но неизвестными константами, байесовская оценка стремится оценить параметр, который сам по себе является случайной величиной. Кроме того, байесовская оценка также может иметь дело с ситуациями, когда последовательность наблюдений не обязательно независима. Таким образом, байесовская оценка представляет собой еще одну альтернативу MVUE. Это полезно, когда MVUE не существует или не может быть найден.
Определение
Пусть будет скрытой случайной векторной переменной, и пусть будет известной случайной векторной переменной (измерение или наблюдение), причем обе они не обязательно имеют одинаковую размерность. Оценка по какой — либо функции измерения . Вектор ошибки оценки задается выражением, а его среднеквадратическая ошибка (MSE) задается следом ковариационной матрицы ошибок.
где ожидание берется за и . Когда — скалярная переменная, выражение MSE упрощается до . Обратите внимание, что MSE может быть эквивалентно определено другими способами, поскольку
Затем оценщик MMSE определяется как оценщик, достигающий минимальной MSE:
Характеристики
- Когда средние значения и дисперсии конечны, оценка MMSE определяется однозначно и определяется следующим образом:
-
- Другими словами, оценка MMSE — это условное ожидание данного известного наблюдаемого значения измерений.
- Оценка MMSE является беспристрастной (согласно предположениям регулярности, упомянутым выше):
- Оценщик MMSE асимптотически несмещен и сходится по распределению к нормальному распределению:
-
- где есть информация Фишера из . Таким образом, оценка MMSE асимптотически эффективна .
-
- для всех в замкнутом линейном подпространстве измерений. Для случайных векторов, поскольку MSE для оценки случайного вектора является суммой MSE координат, нахождение оценки MMSE для случайного вектора разлагается на нахождение оценок MMSE для координат X по отдельности:
- для всех i и j . Говоря более кратко, взаимная корреляция между минимальной ошибкой оценки и средством оценки должна быть равна нулю,
Линейный оценщик MMSE
Во многих случаях невозможно определить аналитическое выражение оценки MMSE. Два основных численных подхода для получения оценки MMSE зависят либо от нахождения условного ожидания, либо от нахождения минимумов MSE. Прямая численная оценка условного ожидания требует больших вычислительных ресурсов, поскольку часто требует многомерного интегрирования, обычно выполняемого с помощью методов Монте-Карло . Другой вычислительный подход заключается в прямом поиске минимумов MSE с использованием таких методов, как методы стохастического градиентного спуска ; но этот метод по-прежнему требует оценки ожидания. Хотя эти численные методы оказались плодотворными, выражение в закрытой форме для оценки MMSE, тем не менее, возможно, если мы готовы пойти на некоторые компромиссы.
Одна из возможностей состоит в том, чтобы отказаться от требований полной оптимальности и найти метод минимизации MSE в рамках определенного класса оценщиков, такого как класс линейных оценщиков. Таким образом, мы постулируем , что условное математическое ожидание данности является простым линейной функцией , где измерение является случайным вектором, является матрицей и является вектором. Это можно рассматривать как приближение Тейлора первого порядка . Линейный оценщик MMSE — это оценщик, достигающий минимальной MSE среди всех оценщиков такой формы. То есть решает следующие задачи оптимизации:
Одним из преимуществ такого линейного средства оценки MMSE является то, что нет необходимости явно вычислять апостериорную функцию плотности вероятности . Такая линейная оценка зависит только от первых двух моментов и . Таким образом, хотя может быть удобно предположить, что и являются вместе гауссовыми, нет необходимости делать это предположение, пока предполагаемое распределение имеет хорошо определенные первый и второй моменты. Форма линейной оценки не зависит от типа предполагаемого базового распределения.
Выражение для оптимального и определяется выражением:
где , является кросс-ковариационная матрица между и , то есть автоматически ковариационная матрица .
Таким образом, выражение для линейной оценки MMSE, его среднего значения и автоковариации имеет вид
где — матрица кросс-ковариации между и .
Наконец, ковариация ошибки и минимальная среднеквадратичная ошибка, достижимые такой оценкой, равны
Вывод по принципу ортогональности
Пусть у нас есть оптимальная линейная оценка MMSE, заданная как , где мы должны найти выражение для и . Требуется, чтобы оценка MMSE была беспристрастной. Это означает,
Подставляя выражение для выше, мы получаем
где и . Таким образом, мы можем переписать оценку как
и выражение для ошибки оценки принимает вид
Исходя из принципа ортогональности, мы можем иметь , где возьмем . Здесь левый член
Приравнивая к нулю, мы получаем искомое выражение для as
Является кросс-ковариационная матрица между Х и Y, а это автоматически ковариационная матрица Y. Так , выражение может быть также переписана в терминах , как
Таким образом, полное выражение для линейной оценки MMSE имеет вид
Поскольку оценка сама по себе является случайной величиной с , мы также можем получить ее автоковариацию как
Подставляя выражение для и , получаем
Наконец, ковариация линейной ошибки оценки MMSE будет тогда выражена как
Первый член в третьей строке равен нулю из-за принципа ортогональности. Поскольку мы можем переписать в терминах ковариационных матриц как
Мы можем признать, что это то же самое, что и. Таким образом, минимальная среднеквадратичная ошибка, достижимая такой линейной оценкой, равна
-
.
Одномерный случай
Для особого случая, когда оба и являются скалярами, приведенные выше отношения упрощаются до
где — коэффициент корреляции Пирсона между и .
Вычисление
Стандартный метод, такой как исключение Гаусса, может использоваться для решения матричного уравнения для . Более стабильный в числовом отношении метод обеспечивается методом QR-разложения . Поскольку матрица является симметричной положительно определенной матрицей, ее можно решить в два раза быстрее с помощью разложения Холецкого , в то время как для больших разреженных систем метод сопряженных градиентов более эффективен. Рекурсия Левинсона — это быстрый метод, когда она также является матрицей Теплица . Это может произойти, когда это стационарный процесс в широком смысле . В таких стационарных случаях эти оценки также называют фильтрами Винера – Колмогорова .
Линейная оценка MMSE для процесса линейного наблюдения
Давайте далее смоделируем основной процесс наблюдения как линейный процесс:, где — известная матрица, а — вектор случайного шума со средним значением и кросс-ковариацией . Здесь искомое среднее и ковариационные матрицы будут
Таким образом, выражение для матрицы линейной оценки MMSE дополнительно изменяется на
Подставляя все в выражение для , получаем
Наконец, ковариация ошибок равна
Существенное различие между описанной выше задачей оценивания и проблемой наименьших квадратов и оценкой Гаусса-Маркова состоит в том, что количество наблюдений m (т. Е. Размерность ) не обязательно должно быть по крайней мере таким же большим, как количество неизвестных n (т. Е. размер ). Оценка для процесса линейного наблюдения существует при условии, что M матрицы с размерностью м матрица существует; это так для любого m, если, например, положительно определено. Физическая причина этого свойства заключается в том, что, поскольку теперь это случайная величина, можно сформировать значимую оценку (а именно ее среднее значение) даже без измерений. Каждое новое измерение просто предоставляет дополнительную информацию, которая может изменить нашу первоначальную оценку. Еще одна особенность этой оценки состоит в том, что при m < n погрешности измерения быть не должно. Таким образом, мы можем иметь , потому что, пока она положительно определена, оценка все еще существует. Наконец, этот метод может обрабатывать случаи, когда шум коррелирован.
Альтернативная форма
Альтернативная форма выражения может быть получена с помощью матричного тождества
что может быть установлено путем последующего умножения на и предварительного умножения на, чтобы получить
а также
Поскольку теперь можно записать в терминах as , мы получаем упрощенное выражение для as
В таком виде приведенное выше выражение легко сравнить с взвешенным методом наименьших квадратов и оценкой Гаусса – Маркова . В частности, когда , соответствующий бесконечной дисперсии априорной информации относительно , результат идентичен взвешенной линейной оценке по методу наименьших квадратов с использованием весовой матрицы. Более того, если компоненты не коррелированы и имеют одинаковую дисперсию, так что где — единичная матрица, то она идентична обычной оценке методом наименьших квадратов.
Последовательная линейная оценка MMSE
Во многих приложениях реального времени данные наблюдений недоступны в виде единого пакета. Вместо этого наблюдения производятся последовательно. Наивное применение предыдущих формул заставило бы нас отбросить старую оценку и пересчитать новую оценку по мере поступления свежих данных. Но тогда мы теряем всю информацию, предоставленную старым наблюдением. Когда наблюдения являются скалярными величинами, один из возможных способов избежать таких повторных вычислений — сначала объединить всю последовательность наблюдений, а затем применить стандартную формулу оценки, как это сделано в Примере 2. Но это может быть очень утомительно, поскольку количество наблюдений увеличивается, поэтому увеличивается размер матриц, которые необходимо инвертировать и умножать. Также этот метод трудно распространить на случай векторных наблюдений. Другой подход к оценке на основе последовательных наблюдений — просто обновить старую оценку по мере появления дополнительных данных, что приведет к более точным оценкам. Таким образом, желателен рекурсивный метод, при котором новые измерения могут изменять старые оценки. В этих обсуждениях подразумевается предположение, что статистические свойства не меняются со временем. Другими словами, стационарен.
Для последовательной оценки, если у нас есть оценка, основанная на измерениях, генерирующих пространство , то после получения другого набора измерений мы должны вычесть из этих измерений ту часть, которую можно было бы ожидать по результатам первых измерений. Другими словами, обновление должно быть основано на той части новых данных, которая ортогональна старым данным.
Предположим, что оптимальная оценка была сформирована на основе прошлых измерений и что матрица ковариации ошибок равна . Для процессов линейного наблюдения наилучшей оценкой, основанной на прошлых наблюдениях и, следовательно, старой оценке , является . Вычитая из , получаем ошибку предсказания
-
.
Новая оценка, основанная на дополнительных данных, теперь
где — кросс-ковариация между и и — автоковариация
Используя тот факт, что и , мы можем получить ковариационные матрицы в терминах ковариации ошибок как
Собирая все вместе, мы получаем новую оценку как
и новая ковариация ошибок как
Повторное использование двух вышеупомянутых уравнений по мере того, как становится доступным больше наблюдений, приводит к методам рекурсивной оценки. Более компактно выражения можно записать как
Матрицу часто называют коэффициентом усиления. Повторение этих трех шагов по мере того, как становится доступным больше данных, приводит к итерационному алгоритму оценки. Обобщение этой идеи на нестационарные случаи приводит к созданию фильтра Калмана . Три этапа обновления, описанные выше, действительно образуют этап обновления фильтра Калмана.
Частный случай: скалярные наблюдения
В качестве важного частного случая может быть получено простое в использовании рекурсивное выражение, когда в каждый t-й момент времени основной процесс линейного наблюдения выдает скаляр, такой что , где — известный вектор-столбец размером n на 1, значения которого могут изменяться со временем , представляет собой оцениваемый случайный вектор-столбец размером n на 1 и представляет собой скалярный шумовой член с дисперсией . После ( t +1) -го наблюдения прямое использование приведенных выше рекурсивных уравнений дает выражение для оценки как:
где это новое наблюдение скалярного и коэффициент усиления является п его-1 вектор — столбца задается
Является п матрицы с размерностью п ошибка ковариационная матрица задается
Здесь инверсия матрицы не требуется. Кроме того, коэффициент усиления зависит от нашей уверенности в новой выборке данных, измеренной по дисперсии шума, по сравнению с предыдущими данными. За начальные значения и принимаются среднее значение и ковариация априорной функции плотности вероятности .
Альтернативные подходы: этот важный частный случай также привел к появлению многих других итерационных методов (или адаптивных фильтров ), таких как фильтр наименьших средних квадратов и рекурсивный фильтр наименьших квадратов , которые напрямую решают исходную проблему оптимизации MSE с использованием стохастических градиентных спусков . Однако, поскольку ошибку оценки нельзя непосредственно наблюдать, эти методы пытаются минимизировать среднеквадратичную ошибку прогноза . Например, в случае скалярных наблюдений у нас есть градиент. Таким образом, уравнение обновления для фильтра наименьших квадратов имеет вид
где — размер скалярного шага, а математическое ожидание аппроксимируется мгновенным значением . Как мы видим, эти методы обходят необходимость в ковариационных матрицах.
Примеры
Пример 1
В качестве примера возьмем задачу линейного прогнозирования . Пусть линейная комбинация наблюдаемых скалярных случайных величин и будет использоваться для оценки другой будущей скалярной случайной величины, такой что . Если случайные величины являются действительными гауссовскими случайными величинами с нулевым средним и ее ковариационная матрица, заданная формулой
то наша задача — найти такие коэффициенты , чтобы получить оптимальную линейную оценку .
В терминах терминологии, разработанной в предыдущих разделах, для этой задачи у нас есть вектор наблюдения , матрица оценки как вектор-строка и оцениваемая переменная как скалярная величина. Матрица автокорреляции определяется как
Матрица взаимной корреляции определяется как
Теперь мы решаем уравнение путем инвертирования и предварительного умножения, чтобы получить
Итак, у нас есть и
в качестве оптимальных коэффициентов для . Тогда вычисление минимальной среднеквадратичной ошибки дает . Обратите внимание, что нет необходимости получать явную матрицу, обратную для вычисления значения . Матричное уравнение может быть решено с помощью хорошо известных методов, таких как метод исключения Гаусса. Более короткий нечисловой пример можно найти в принципе ортогональности .

Пример 2
Рассмотрим вектор, сформированный путем наблюдений за фиксированным, но неизвестным скалярным параметром, нарушенным белым гауссовским шумом. Мы можем описать процесс линейным уравнением , где . В зависимости от контекста будет ясно, представляет ли он скаляр или вектор. Предположим, что мы знаем, что это диапазон, в который будет попадать значение. Мы можем смоделировать нашу неопределенность с помощью априорного равномерного распределения по интервалу и, таким образом, будем иметь дисперсию . Пусть вектор шума распределен нормально, как где — единичная матрица. Также и независимы и . Легко увидеть, что
Таким образом, линейная оценка MMSE имеет вид
Мы можем упростить выражение, используя альтернативную форму для as
где у нас есть
Точно так же дисперсия оценки равна
Таким образом, MMSE этой линейной оценки
Для очень больших мы видим, что оценка MMSE скаляра с равномерным априорным распределением может быть аппроксимирована средним арифметическим всех наблюдаемых данных.
в то время как дисперсия не будет зависеть от данных, и LMMSE оценки будет стремиться к нулю.
Однако оценка является неоптимальной, поскольку ограничена линейностью. Если бы случайная величина также была гауссовой, тогда оценка была бы оптимальной. Обратите внимание, что форма оценки останется неизменной, независимо от априорного распределения , до тех пор, пока среднее и дисперсия этих распределений одинаковы.
Пример 3
Рассмотрим вариант приведенного выше примера: на выборах баллотируются два кандидата. Пусть доля голосов , что кандидат получит на день выборов будет Таким образом доля голосов, другой кандидат получит будет Примем как случайная величина с равномерным априорное распределение , так что его среднее значение и дисперсия Несколько За несколько недель до выборов два независимых опроса общественного мнения провели два независимых опроса общественного мнения. Первый опрос показал, что кандидат, скорее всего, наберет небольшую часть голосов. Так как некоторые ошибки всегда присутствует из — за конечной выборки и методологии частности опроса , принятого, первый опросчик объявляет свою оценку , чтобы иметь ошибку с нулевым средним и дисперсией Аналогично, второй опросчик объявляет свою оценку , чтобы быть с ошибкой с нулевым средним и дисперсией Обратите внимание, что, за исключением среднего значения и дисперсии ошибки, распределение ошибок не указано. Как следует объединить эти два опроса, чтобы получить прогноз голосования для данного кандидата?
Как и в предыдущем примере, у нас есть
Здесь оба файла . Таким образом, мы можем получить оценку LMMSE как линейную комбинацию и как
где веса даны как
Здесь, поскольку член знаменателя постоянен, опросу с меньшей ошибкой дается более высокий вес, чтобы предсказать результат выборов. Наконец, дисперсия прогноза определяется выражением
что делает меньше, чем
В общем, если у нас есть опросчики, то где вес для i-го опроса определяется как
Пример 4
Предположим, что музыкант играет на инструменте, и звук улавливается двумя микрофонами, каждый из которых расположен в двух разных местах. Пусть ослабление звука из-за расстояния до каждого микрофона равно и , которые считаются известными константами. Аналогично, пусть шум на каждом микрофоне будет и , каждый с нулевым средним значением и дисперсией и соответственно. Позвольте обозначить звук, издаваемый музыкантом, который является случайной величиной с нулевым средним значением и дисперсией. Как следует объединить записанную музыку с этих двух микрофонов после синхронизации друг с другом?
Мы можем смоделировать звук, получаемый каждым микрофоном, как
Здесь оба файла . Таким образом, мы можем объединить два звука как
где i-й вес задается как
Смотрите также
- Байесовская оценка
- Среднеквадратичная ошибка
- Наименьших квадратов
- Несмещенная оценка с минимальной дисперсией (MVUE)
- Принцип ортогональности
- Фильтр Винера
- Фильтр Калмана
- Линейное предсказание
- Эквалайзер с нулевым форсированием
Примечания
-
^
«Среднеквадратичная ошибка (MSE)» . www.probabilitycourse.com . Дата обращения 9 мая 2017 . - ^ Мун и Стирлинг.
дальнейшее чтение
- Джонсон, Д. «Оценщики минимальной среднеквадратичной ошибки» . Связи. Архивировано из минимальных среднеквадратичных оценщиков ошибок оригинала 25 июля 2008 года . Проверено 8 января 2013 года .
- Джейнс, ET (2003). Теория вероятностей: логика науки . Издательство Кембриджского университета. ISBN 978-0521592710.
- Bibby, J .; Тутенбург, Х. (1977). Прогнозирование и улучшенная оценка в линейных моделях . Вайли. ISBN 9780471016564.
- Lehmann, EL; Казелла, Г. (1998). «Глава 4». Теория точечного оценивания (2-е изд.). Springer. ISBN 0-387-98502-6.
- Кей, С.М. (1993). Основы статистической обработки сигналов: теория оценивания . Прентис Холл. стр. 344 -350. ISBN 0-13-042268-1.
- Люенбергер, Д.Г. (1969). «Глава 4, Оценка методом наименьших квадратов». Оптимизация методами векторного пространства (1-е изд.). Вайли. ISBN 978-0471181170.
- Луна, ТЗ; Стирлинг, WC (2000). Математические методы и алгоритмы обработки сигналов (1-е изд.). Прентис Холл. ISBN 978-0201361865.
- Ван Trees, HL (1968). Выявление, оценка и теория модуляции, часть I . Нью-Йорк: Вили. ISBN 0-471-09517-6.
- Хайкин, СО (2013). Теория адаптивного фильтра (5-е изд.). Прентис Холл. ISBN 978-0132671453.

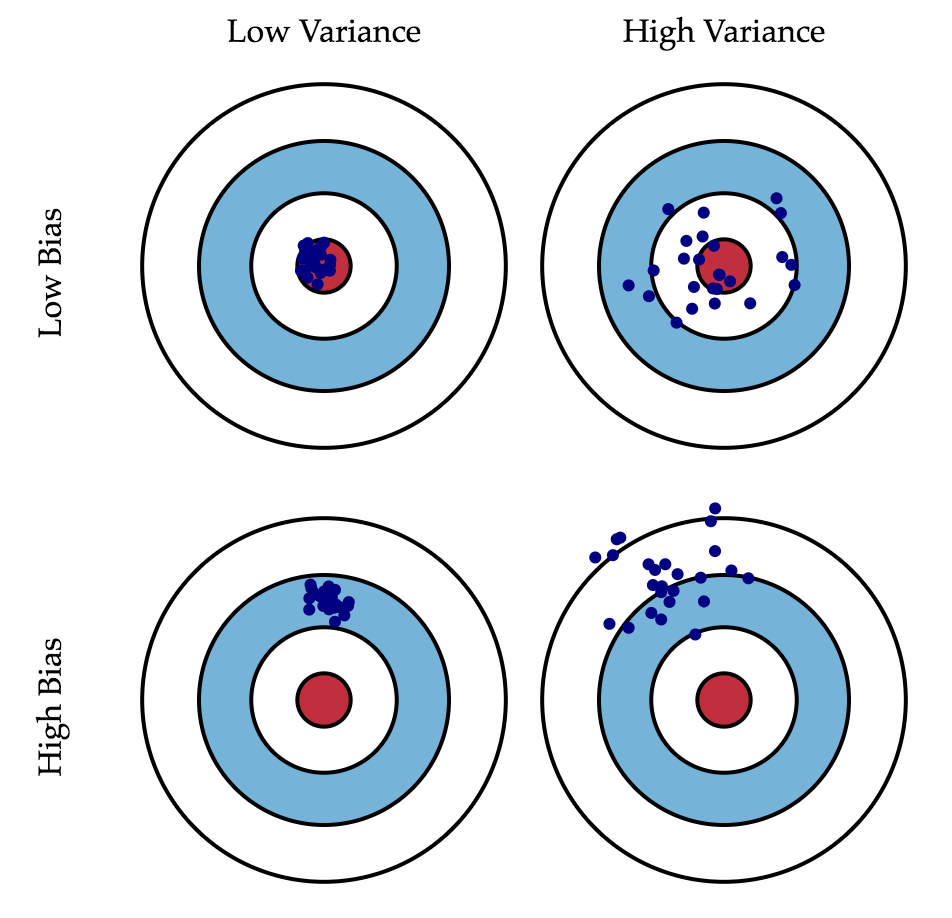


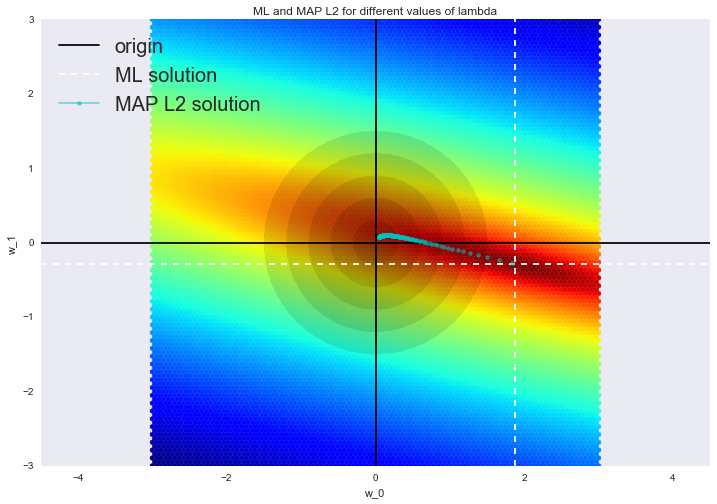






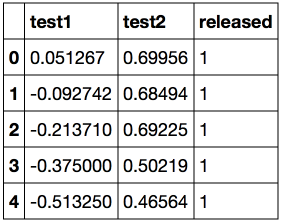
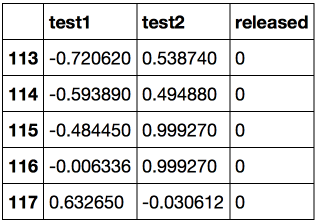

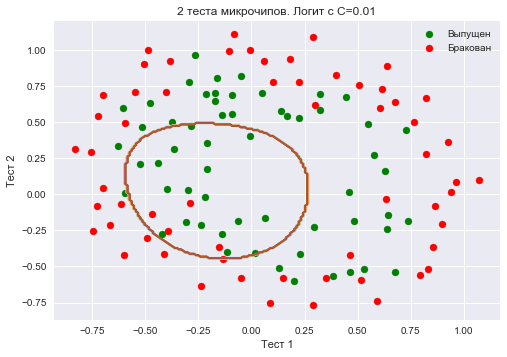

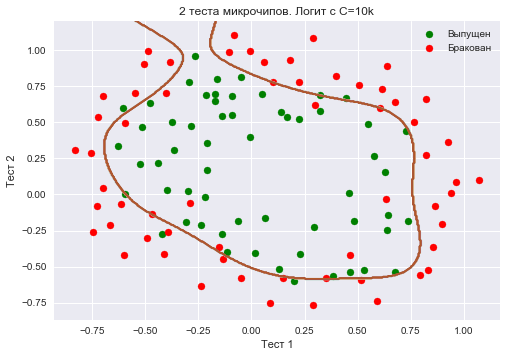



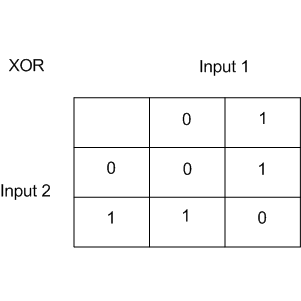

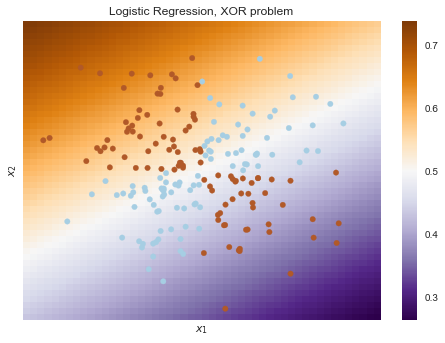
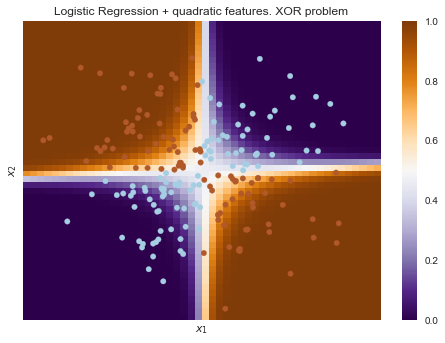
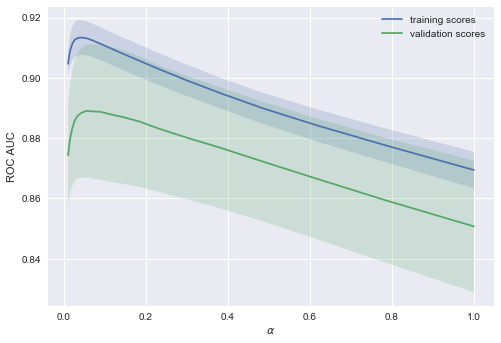
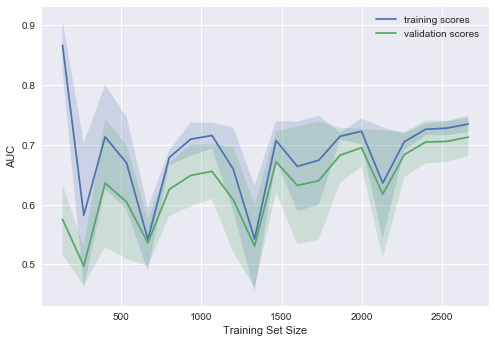

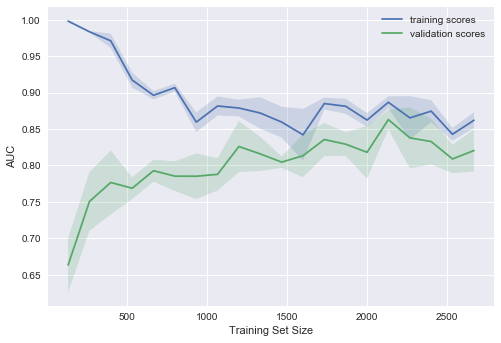







![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)

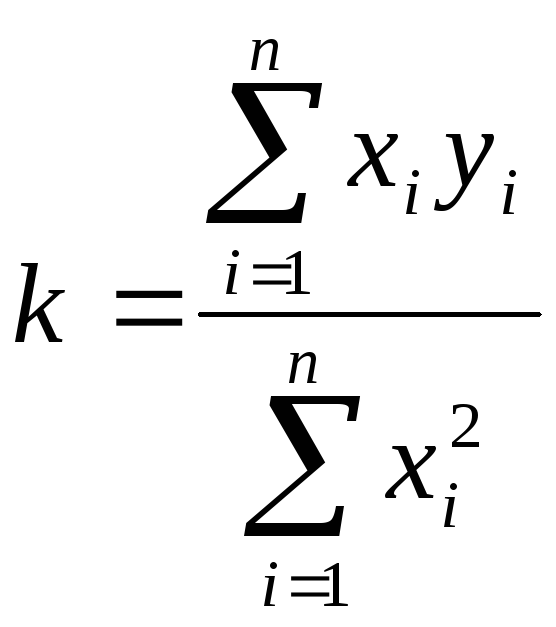 .
. .
. ,
, ,
, .
.



































































































































![{ displaystyle z = [z_ {1}, z_ {2}, z_ {3}, z_ {4}] ^ {T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45cb1f9123fdf786074088616e42dfbcc1359d07)
![{ displaystyle operatorname {cov} (Z) = operatorname {E} [zz ^ {T}] = left [{ begin {array} {cccc} 1 & 2 & 3 & 4 \ 2 & 5 & 8 & 9 \ 3 & 8 & 6 & 10 \ 4 & 9 & 10 & 15 end { массив}} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90889a9de7192d317decb8381ca25cda49892b5c)


![{ Displaystyle у = [z_ {1}, z_ {2}, z_ {3}] ^ {T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fdeb8eb600c7a066561d28e2b3f32fb5b1572b9)
![Ш = [ш_ {1}, ш_ {2}, ш_ {3}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd8e9343b228a9044dbb8208e9ceeb31270b04c1)

![{ Displaystyle C_ {Y} = left [{ begin {array} {ccc} E [z_ {1}, z_ {1}] & E [z_ {2}, z_ {1}] и E [z_ {3} , z_ {1}] \ E [z_ {1}, z_ {2}] & E [z_ {2}, z_ {2}] & E [z_ {3}, z_ {2}] \ E [z_ { 1}, z_ {3}] & E [z_ {2}, z_ {3}] & E [z_ {3}, z_ {3}] end {array}} right] = left [{ begin {array } {ccc} 1 & 2 & 3 \ 2 & 5 & 8 \ 3 & 8 & 6 end {array}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c0831c4af6cc131c13cd4da73e21ee08aac40c)
![{ Displaystyle C_ {YX} = left [{ begin {array} {c} E [z_ {4}, z_ {1}] \ E [z_ {4}, z_ {2}] \ E [ z_ {4}, z_ {3}] end {array}} right] = left [{ begin {array} {c} 4 \ 9 \ 10 end {array}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0b4e00619f85de1c0967817d68b6b154557af03)

![{ displaystyle C_ {Y} ^ {- 1} C_ {YX} = left [{ begin {array} {ccc} 4.85 & -1.71 & -0.142 \ - 1.71 & 0.428 & 0.2857 \ - 0.142 & 0 .2857 & -0,1429 end {array}} right] left [{ begin {array} {c} 4 \ 9 \ 10 end {array}} right] = left [{ begin {array } {c} 2,57 \ - 0,142 \ 0,5714 end {array}} right] = W ^ {T}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f29d9505d5f630feae8a4566c23bae8dd82fd5d)


![{ displaystyle left Vert e right Vert _ { min} ^ {2} = operatorname {E} [z_ {4} z_ {4}] - WC_ {YX} = 15-WC_ {YX} = .2857}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44558ab7a0b5ead1b9571853096d800773b38877)


![1 = [1,1, ldots, 1] ^ {T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43fec89f837a5e8d53869fb49ec95a9e56a788f0)

![[-x_ {0}, x_ {0}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e79873ca5ddfd5d6b0168f6373b33c8bc3756c69)





![y = [y_ {1}, y_ {2}, ldots, y_ {N}] ^ {T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8317c7045e5b1318cec0c4ee89727a02cdeecafc)




![х в [0,1].](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c44eb6b4643a03d3c166df0e61c4925b6d4d4f0)

![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)























