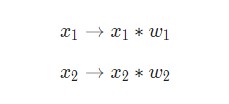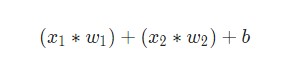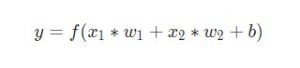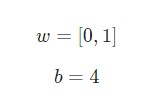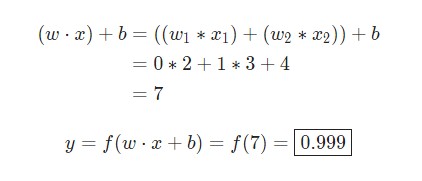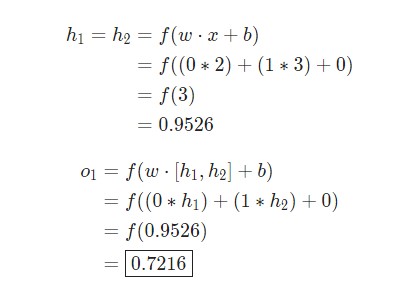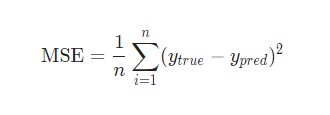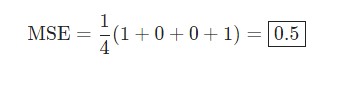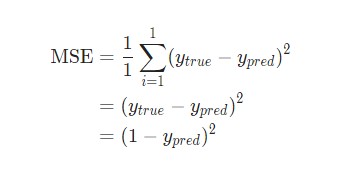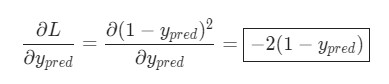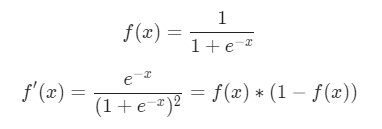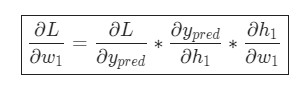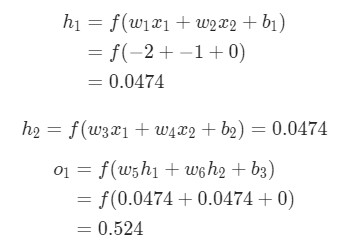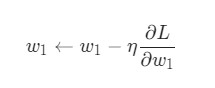Время на прочтение
6 мин
Количество просмотров 21K
Заранее хочу отметить, что тот кто знает как обучается персептрон — в этой статье вряд ли найдет что-то новое. Вы можете смело пропускать ее. Почему я решил это написать — я хотел бы написать цикл статей, связанных с нейронными сетями и применением TensorFlow.js, ввиду этого я не мог опустить общие теоретические выдержки. Поэтому прошу отнестись с большим терпением и пониманием к конечной задумке.
При классическом программировании разработчик описывает на конкретном языке программирования определённый жестко заданный набор правил, который был определен на основании его знаний в конкретной предметной области и который в первом приближении описывает процессы, происходящие в человеческом мозге при решении аналогичной задачи.
Например, может быть запрограммирована стратегия игры в крестики-нолики, шахмат и другое (рисунок 1).
Рисунок 1 – Классический подход решения задач
В то время как алгоритмы машинного обучения могут определять набор правил для решения задач без участия разработчика, а только на базе наличия тренировочного набора данных.
Тренировочный набор — это какой-то набор входных данных ассоциированный с набором ожидаемых результатов (ответами, выходными данными). На каждом шаге обучения, модель за счет изменения внутреннего состояния, будет оптимизировать и уменьшать ошибку между фактическим выходным результатом модели и ожидаемым результатом (рисунок 2).
Рисунок 2 – Машинное обучение
Нейронные сети
Долгое время учёные, вдохновляясь процессами происходящими в нашем мозге, пытались сделать реверс-инжиниринг центральной нервной системы и попробовать сымитировать работу человеческого мозга. Благодаря этому родилось целое направление в машинном обучении — нейронные сети.
На рисунке 3 вы можете увидеть сходство между устройством биологического нейрона и математическим представлением нейрона, используемого в машинном обучении.
Рисунок 3 – Математическое представление нейрона
В биологическом нейроне, нейрон получает электрические сигналы от дендритов, модулирующих электрические сигналы с разной силой, которые могут возбуждать нейрон при достижении некоторого порогового значения, что в свою очередь приведёт к передаче электрического сигнала другим нейронам через синапсы.
Персептрон
Математическая модель нейронной сети, состоящего из одного нейрона, который выполняет две последовательные операции (рисунок 4):
- вычисляет сумму входных сигналов с учетом их весов (проводимости или сопротивления) связи
- применяет активационную функцию к общей сумме воздействия входных сигналов.
Рисунок 4 – Математическая модель персептрона
В качестве активационной функции может использоваться любая дифференцируемая функция, наиболее часто используемые приведены в таблице 1. Выбор активационной функции ложиться на плечи инженера, и обычно этот выбор основан или на уже имеющемся опыте решения похожих задач, ну или просто методом подбора.
Заметка
Однако есть рекомендация – что если нужна нелинейность в нейронной сети, то в качестве активационной функции лучше всего подходит ReLU функция, которая имеет лучшие показатели сходимости модели во время процесса обучения.
Таблица 1 — Распространенные активационные функции
Процесс обучения персептрона
Процесс обучения состоит из несколько шагов. Для большей наглядности, рассмотрим некую вымышленную задачу, которую мы будем решать нейронной сетью, состоящей из одного нейрона с линейной активационной функции (это по сути персептрон без активационной функции вовсе), также для упрощения задачи – исключим в нейроне узел смещения b (рисунок 5).
Рисунок 5 – Обучающий набор данных и состояние нейронной сети на предыдущем шаге обучения
На данном этапе мы имеем нейронную сеть в некотором состоянии с определенными весами соединений, которые были вычислены на предыдущем этапе обучения модели или если это первая итерация обучения – то значения весов соединений выбраны в произвольном порядке.
Итак, представим, что мы имеем некоторый набор тренировочных данных, значения каждого элемента из набора представлены вектором входных данных (input data), содержащих 2 параметра (feature)
. Под
в модели в зависимости от рассматриваемой предметной области может подразумеваться все что угодно: количество комнат в доме, расстояние дома от моря, ну или мы просто пытаемся обучить нейронную сеть логической операции И, или ИЛИ.
Каждый вектор входных данных в тренировочном наборе сопоставлен с вектором ожидаемого результата (expected output). В данном случае вектор выходных данных содержит только один параметр, которые опять же в зависимости от выбранной предметной области может означать все что угодно – цена дома, результат выполнения логической операции И или ИЛИ.
ШАГ 1 — Прямое распространение ошибки (feedforward process)
На данном шаге мы вычисляем сумму входных сигналов с учетом веса каждой связи и применяем активационную функцию (в нашем случае активационной функции нет). Сделаем вычисления для первого элемента в обучающем наборе:
Рисунок 6 – Прямое распространение ошибки
Обратите внимание, что написанная формула выше – это упрощенное математическое уравнение для частного случая операций над тензорами.
Тензор – это по сути контейнер данных, который может иметь N осей и произвольное число элементов вдоль каждой из осей. Большинство с тензорами знакомы с математики – векторы (тензор с одной осью), матрицы (тензор с двумя осями – строки, колонки).
Формулу можно написать в следующем виде, где вы увидите знакомые матрицы (тензоры) и их перемножение, а также поймете о каком упрощении шла речь выше:
ШАГ 2 — Расчет функции ошибки
Функция ошибка – это метрика, отражающая расхождение между ожидаемыми и полученными выходными данными. Обычно используют следующие функции ошибки:
— среднеквадратичная ошибка (Mean Squared Error, MSE) – данная функция ошибки особенно чувствительна к выбросам в тренировочном наборе, так как используется квадрат от разности фактического и ожидаемого значений (выброс — значение, которое сильно удалено от других значений в наборе данных, которые могут иногда появляться в следствии ошибок данных, таких как смешивание данных с разными единицами измерения или плохие показания датчиков):
— среднеквадратичное отклонение (Root MSE) – по сути это тоже самое что, среднеквадратичная ошибка в контексте нейронных сетей, но может отражать реальную физическую единицу измерения, например, если в нейронной сети выходным параметров нейронной сети является цена дома выраженной в долларах, то единица измерения среднеквадратичной ошибки будет доллар квадратный (
), а для среднеквадратичного отклонения это доллар ($), что естественно немного упрощает задачу анализа человеком:
— среднее отклонение (Mean Absolute Error, MAE) -в отличии от двух выше указанных значений, является не столь чувствительной к выбросам:
— перекрестная энтропия (Cross entropy) – использует для задач классификации:
где
– число экземпляров в тренировочном наборе
– число классов при решении задач классификации
— ожидаемое выходное значение
– фактическое выходное значение обучаемой модели
Для нашего конкретного случая воспользуемся MSE:
ШАГ 3 — Обратное распространение ошибки (backpropagation)
Цель обучения нейронной сети проста – это минимизация функции ошибки:
Одним способом найти минимум функции – это на каждом очередном шаге обучения модифицировать веса соединений в направлении противоположным вектору-градиенту – метод градиентного спуска, и это математически выглядит так:
где
– k -ая итерация обучения нейронной сети;
– шаг обучения (learning rate) и задается инженером, обычно это может быть 0.1; 0.01 (о том как шаг обучения влияет на процесс сходимости обучения отметить чуть позже)
– градиент функции-ошибки
Для нахождения градиента, используем частные производные по настраиваемым аргументам
:
В нашем конкретном случае с учетом всех упрощений, функция ошибки принимает вид:
Памятка формул производных
Напомним некоторые формулы производных, которые пригодятся для вычисления частных производных
Найдем следующие частные производные:
Тогда процесс обратного распространения ошибки – движение по модели от выхода по направлению к входу с модификацией весов модели в направлении обратном вектору градиента. Задавая обучающий шаг 0.1 (learning rate) имеем (рисунок 7):
Рисунок 7 – Обратное распространение ошибки
Таким образом мы завершили k+1 шаг обучения, чтобы убедиться, что ошибка снизилась, а выход от модели с новыми весами стал ближе к ожидаемому выполним процесс прямого распространения ошибки по модели с новыми весами (см. ШАГ 1):
Как видим, выходное значение увеличилось на 0.2 единица в верном направлении к ожидаемому результату – единице (1). Ошибка тогда составит:
Как видим, на предыдущем шаге обучения ошибка составила 0.64, а с новыми весами – 0.36, следовательно мы настроили модель в верном направлении.
Следующая часть статьи:
Машинное обучение. Нейронные сети (часть 2): Моделирование OR; XOR с помощью TensorFlow.js
Машинное обучение. Нейронные сети (часть 3) — Convolutional Network под микроскопом. Изучение АПИ Tensorflow.js
y question is about Neural Network Training. I already searched about this but, there is no good explanation about it.
There are dozens of good explanations on the web, and in the literature, one such example may be the book by Haykin: Neural Networks and Learning machines
So for the first one, how to calculate mean square error? (I know this is silly, but I really don’t get it)
In the most simple terms, mean squared error is defined as
sum_i 1/n (desired_output(i) - model_output(i))^2
So you simply calculate the mean of the squares of the errors (differences between your output, and the desired one).
Now when should we calculate the mean square error? does it when we already take all pairs? or does we calculate it for each pair?
Both methods are used, one is called batch learning, and one is online learning. So all next questions have the answer «both are correct, depending whether you are using batch or online learning». Which one to choose? Obviously — it depends, but for a sake of simplicity I would suggest starting with batch learning (so you compute the error over all training samples and then update).
Выбор функции потерь для задач построения нейронных сетей
Время прочтения: 4 мин.
При построении нейронных сетей перед нами часто встаёт вопрос правильного выбора функции потерь, используемой для формирования соответствий между входными и выходными параметрами. Функция потерь отвечает за оценку того, насколько хорошо модель предсказывает реальное значение, и построение модели сводится к решению задачи минимизации значения этой функции на каждом этапе. И в зависимости от того, как выглядят наши данные, требуется использовать разные подходы.
В рамках данной статьи мы рассмотрим три функции потерь для нейронных сетей, решающих регрессионные задачи.
Mean Squared Error
Среднеквадратичная ошибка (MSE) — одна из основных функций расчёта отклонения. Для каждой точки вычисляется квадрат отклонения, после чего полученные значения суммируются и делятся на общее количество точек. Чем ближе полученное значение к нулю, тем точнее наша модель. Данный метод расчёта в значительной мере чувствителен к выбросам в выборке, или к выборкам где разброс значений очень большой. В основном, данная функция применяется для переменных, распределение которых близко к распределению Гаусса.
Mean Absolute Error
Средняя абсолютная ошибка (MAE) – это усреднённая сумма модулей разницы между реальным и предсказанным значениями. MAE во многом похожа на MSE, но она отличается меньшей чувствительностью к выбросам значений (так как не берётся квадрат отклонения).
Mean Squared Logarithmic Error
Среднеквадратичная логарифмическая ошибка (MSLE) – усреднённая сумма квадратов разностей между логарифмами значений. Благодаря большому гасящему эффекту логарифма она более применима к моделям, строящимся на данных, которые имеют большой разброс значений на несколько порядков.
Продемонстрируем как выбор функции потерь влияет на процесс построения нейронной сети. Для генерации данных будем использовать встроенную в scikit-learn функцию make_regression, а в качестве нейронной сети будет выступать многослойный перцептрон.
Код используемый для демонстрации:
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# формирование датасета
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# нормализация
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# разделение
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# определение для модели
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss=вид функции потерь, optimizer=opt)
# расчёт
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Оценка качества
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot Демонстрация результата
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
В данном коде мы будем заменять только указанный вид функции потерь.
Результат для MSE:
model.compile(loss='mean_squared_error', optimizer=opt)Полученное отклонение для модели:
Train: 0.000, Test: 0.001Как видно из графика, модель показывает хорошую сходимость и низкое отклонение.
Результат для MSLE:
model.compile(loss=' mean_squared_logarithmic_error', optimizer=opt)Полученное отклонение для модели:
Train: 0.165, Test: 0.184По графику видно, что для данного набора данных MSLE сходится медленней чем MSE. С одной стороны, это может привести к тому что модель будет строиться медленней и получится хуже, с другой – использование MSE может привести к переобучению. Результат для MAE:
model.compile(loss='mean_absolute_error', optimizer=opt)Полученное отклонение для модели:
Train: 0.002, Test: 0.002Здесь мы можем увидеть, что результат сходится очень эффективно, но ошибка имеет нерегулярный характер. Так как используемый нами генератор строит гауссово распределение без выбросов, использование MAE не даёт значительных преимуществ.
Очевидно, что от выбора правильной функции потерь сильно зависит точность, качество и скорость построения модели, поэтому следует внимательно подходить к выбору опираясь как на используемую модель, так и на характеристики входных данных.
Далее будет представлено максимально простое объяснение того, как работают нейронные сети, а также показаны способы их реализации в Python. Приятная новость для новичков – нейронные сети не такие уж и сложные. Термин нейронные сети зачастую используют в разговоре, ссылаясь на какой-то чрезвычайно запутанный концепт. На деле же все намного проще.
Данная статья предназначена для людей, которые ранее не работали с нейронными сетями вообще или же имеют довольно поверхностное понимание того, что это такое. Принцип работы нейронных сетей будет показан на примере их реализации через Python.
Содержание статьи
- Создание нейронных блоков
- Простой пример работы с нейронами в Python
- Создание нейрона с нуля в Python
- Пример сбор нейронов в нейросеть
- Пример прямого распространения FeedForward
- Создание нейронной сети прямое распространение FeedForward
- Пример тренировки нейронной сети — минимизация потерь, Часть 1
- Пример подсчета потерь в тренировки нейронной сети
- Python код среднеквадратической ошибки (MSE)
- Тренировка нейронной сети — многовариантные исчисления, Часть 2
- Пример подсчета частных производных
- Тренировка нейронной сети: Стохастический градиентный спуск
- Создание нейронной сети с нуля на Python
Создание нейронных блоков
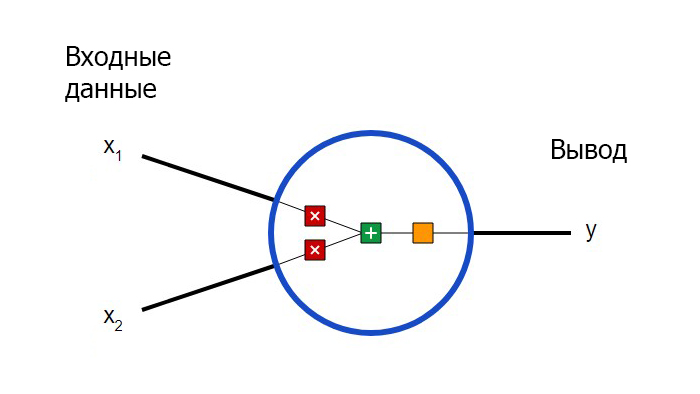
Для начала необходимо определиться с тем, что из себя представляют базовые компоненты нейронной сети – нейроны. Нейрон принимает вводные данные, выполняет с ними определенные математические операции, а затем выводит результат. Нейрон с двумя входными данными выглядит следующим образом:
Здесь происходят три вещи. Во-первых, каждый вход умножается на вес (на схеме обозначен красным):
Затем все взвешенные входы складываются вместе со смещением b (на схеме обозначен зеленым):
Наконец, сумма передается через функцию активации (на схеме обозначена желтым):
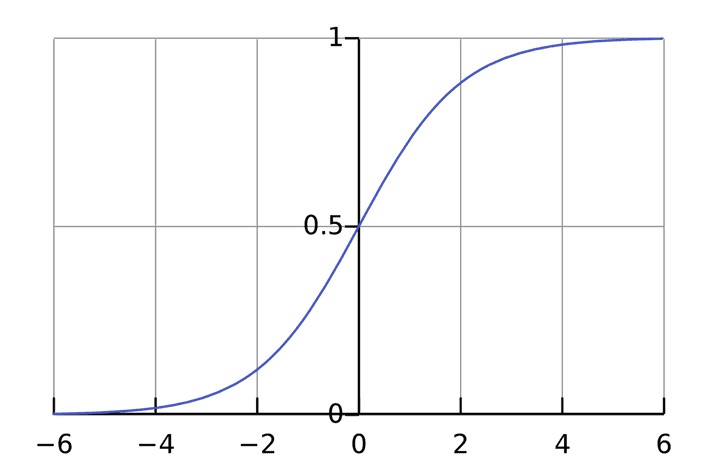
Функция активации используется для подключения несвязанных входных данных с выводом, у которого простая и предсказуемая форма. Как правило, в качестве используемой функцией активации берется функция сигмоида:
Функция сигмоида выводит только числа в диапазоне (0, 1). Вы можете воспринимать это как компрессию от (−∞, +∞) до (0, 1). Крупные отрицательные числа становятся ~0, а крупные положительные числа становятся ~1.
Предположим, у нас есть нейрон с двумя входами, который использует функцию активации сигмоида и имеет следующие параметры:
w = [0,1] — это просто один из способов написания w1 = 0, w2 = 1 в векторной форме. Присвоим нейрону вход со значением x = [2, 3]. Для более компактного представления будет использовано скалярное произведение.
С учетом, что вход был x = [2, 3], вывод будет равен 0.999. Вот и все. Такой процесс передачи входных данных для получения вывода называется прямым распространением, или feedforward.
Создание нейрона с нуля в Python
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
Приступим к имплементации нейрона. Для этого потребуется использовать NumPy. Это мощная вычислительная библиотека Python, которая задействует математические операции:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np def sigmoid(x): # Наша функция активации: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(—x)) class Neuron: def __init__(self, weights, bias): self.weights = weights self.bias = bias def feedforward(self, inputs): # Вводные данные о весе, добавление смещения # и последующее использование функции активации total = np.dot(self.weights, inputs) + self.bias return sigmoid(total) weights = np.array([0, 1]) # w1 = 0, w2 = 1 bias = 4 # b = 4 n = Neuron(weights, bias) x = np.array([2, 3]) # x1 = 2, x2 = 3 print(n.feedforward(x)) # 0.9990889488055994 |
Узнаете числа? Это тот же пример, который рассматривался ранее. Ответ полученный на этот раз также равен 0.999.
Пример сбор нейронов в нейросеть
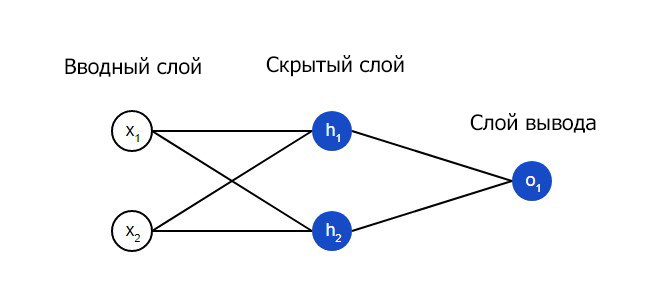
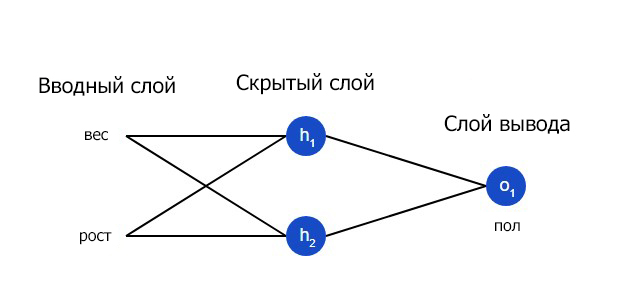
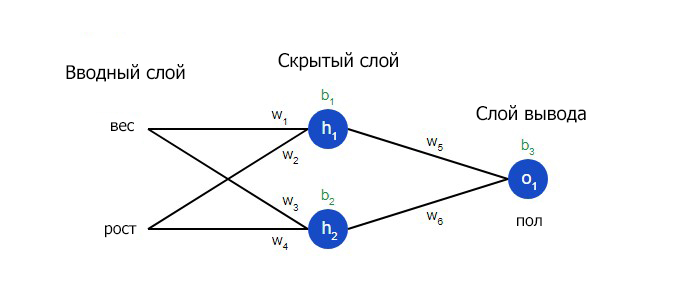
Нейронная сеть по сути представляет собой группу связанных между собой нейронов. Простая нейронная сеть выглядит следующим образом:
На вводном слое сети два входа – x1 и x2. На скрытом слое два нейтрона — h1 и h2. На слое вывода находится один нейрон – о1. Обратите внимание на то, что входные данные для о1 являются результатами вывода h1 и h2. Таким образом и строится нейросеть.
Скрытым слоем называется любой слой между вводным слоем и слоем вывода, что являются первым и последним слоями соответственно. Скрытых слоев может быть несколько.
Пример прямого распространения FeedForward
Давайте используем продемонстрированную выше сеть и представим, что все нейроны имеют одинаковый вес w = [0, 1], одинаковое смещение b = 0 и ту же самую функцию активации сигмоида. Пусть h1, h2 и o1 сами отметят результаты вывода представленных ими нейронов.
Что случится, если в качестве ввода будет использовано значение х = [2, 3]?
Результат вывода нейронной сети для входного значения х = [2, 3] составляет 0.7216. Все очень просто.
Нейронная сеть может иметь любое количество слоев с любым количеством нейронов в этих слоях.
Суть остается той же: нужно направить входные данные через нейроны в сеть для получения в итоге выходных данных. Для простоты далее в данной статье будет создан код сети, упомянутая выше.
Создание нейронной сети прямое распространение FeedForward
Далее будет показано, как реализовать прямое распространение feedforward в отношении нейронной сети. В качестве опорной точки будет использована следующая схема нейронной сети:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import numpy as np # … Здесь код из предыдущего раздела class OurNeuralNetwork: «»» Нейронная сеть, у которой: — 2 входа — 1 скрытый слой с двумя нейронами (h1, h2) — слой вывода с одним нейроном (o1) У каждого нейрона одинаковые вес и смещение: — w = [0, 1] — b = 0 «»» def __init__(self): weights = np.array([0, 1]) bias = 0 # Класс Neuron из предыдущего раздела self.h1 = Neuron(weights, bias) self.h2 = Neuron(weights, bias) self.o1 = Neuron(weights, bias) def feedforward(self, x): out_h1 = self.h1.feedforward(x) out_h2 = self.h2.feedforward(x) # Вводы для о1 являются выводами h1 и h2 out_o1 = self.o1.feedforward(np.array([out_h1, out_h2])) return out_o1 network = OurNeuralNetwork() x = np.array([2, 3]) print(network.feedforward(x)) # 0.7216325609518421 |
Мы вновь получили 0.7216. Похоже, все работает.
Пример тренировки нейронной сети — минимизация потерь, Часть 1
Предположим, у нас есть следующие параметры:
| Имя/Name | Вес/Weight (фунты) | Рост/Height (дюймы) | Пол/Gender |
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
Давайте натренируем нейронную сеть таким образом, чтобы она предсказывала пол заданного человека в зависимости от его веса и роста.
Мужчины Male будут представлены как 0, а женщины Female как 1. Для простоты представления данные также будут несколько смещены.
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
Для оптимизации здесь произведены произвольные смещения
135и66. Однако, обычно для смещения выбираются средние показатели.
Потери
Перед тренировкой нейронной сети потребуется выбрать способ оценки того, насколько хорошо сеть справляется с задачами. Это необходимо для ее последующих попыток выполнять поставленную задачу лучше. Таков принцип потери.
В данном случае будет использоваться среднеквадратическая ошибка (MSE) потери:
Давайте разберемся:
n– число рассматриваемых объектов, которое в данном случае равно 4. ЭтоAlice,Bob,CharlieиDiana;y– переменные, которые будут предсказаны. В данном случае это пол человека;ytrue– истинное значение переменной, то есть так называемый правильный ответ. Например, дляAliceзначениеytrueбудет1, то естьFemale;ypred– предполагаемое значение переменной. Это результат вывода сети.
(ytrue - ypred)2 называют квадратичной ошибкой (MSE). Здесь функция потери просто берет среднее значение по всем квадратичным ошибкам. Отсюда и название ошибки. Чем лучше предсказания, тем ниже потери.
Лучшие предсказания = Меньшие потери.
Тренировка нейронной сети = стремление к минимизации ее потерь.
Пример подсчета потерь в тренировки нейронной сети
Скажем, наша сеть всегда выдает 0. Другими словами, она уверена, что все люди — Мужчины. Какой будет потеря?
| Имя/Name | ytrue | ypred | (ytrue — ypred)2 |
| Alice | 1 | 0 | 1 |
| Bob | 0 | 0 | 0 |
| Charlie | 0 | 0 | 0 |
| Diana | 1 | 0 | 1 |
Python код среднеквадратической ошибки (MSE)
Ниже представлен код для подсчета потерь:
|
import numpy as np def mse_loss(y_true, y_pred): # y_true и y_pred являются массивами numpy с одинаковой длиной return ((y_true — y_pred) ** 2).mean() y_true = np.array([1, 0, 0, 1]) y_pred = np.array([0, 0, 0, 0]) print(mse_loss(y_true, y_pred)) # 0.5 |
При возникновении сложностей с пониманием работы кода стоит ознакомиться с quickstart в NumPy для операций с массивами.
Тренировка нейронной сети — многовариантные исчисления, Часть 2
Текущая цель понятна – это минимизация потерь нейронной сети. Теперь стало ясно, что повлиять на предсказания сети можно при помощи изменения ее веса и смещения. Однако, как минимизировать потери?
В этом разделе будут затронуты многовариантные исчисления. Если вы не знакомы с данной темой, фрагменты с математическими вычислениями можно пропускать.
Для простоты давайте представим, что в наборе данных рассматривается только Alice:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
Затем потеря среднеквадратической ошибки будет просто квадратической ошибкой для Alice:
Еще один способ понимания потери – представление ее как функции веса и смещения. Давайте обозначим каждый вес и смещение в рассматриваемой сети:
Затем можно прописать потерю как многовариантную функцию:
Представим, что нам нужно немного отредактировать w1. В таком случае, как изменится потеря L после внесения поправок в w1?
На этот вопрос может ответить частная производная . Как же ее вычислить?
Здесь математические вычисления будут намного сложнее. С первой попытки вникнуть будет непросто, но отчаиваться не стоит. Возьмите блокнот и ручку – лучше делать заметки, они помогут в будущем.
Для начала, давайте перепишем частную производную в контексте :
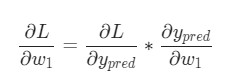
Подсчитать можно благодаря вычисленной выше
L = (1 - ypred)2:
Теперь, давайте определим, что делать с . Как и ранее, позволим
h1, h2, o1 стать результатами вывода нейронов, которые они представляют. Дальнейшие вычисления:
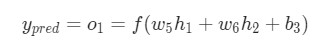
f является функцией активации сигмоида.
Так как w1 влияет только на h1, а не на h2, можно записать:
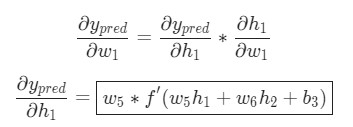
Те же самые действия проводятся для :
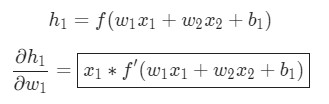
В данном случае х1 — вес, а х2 — рост. Здесь f′(x) как производная функции сигмоида встречается во второй раз. Попробуем вывести ее:
Функция f'(x) в таком виде будет использована несколько позже.
Вот и все. Теперь разбита на несколько частей, которые будут оптимальны для подсчета:
Эта система подсчета частных производных при работе в обратном порядке известна, как метод обратного распространения ошибки, или backprop.
У нас накопилось довольно много формул, в которых легко запутаться. Для лучшего понимания принципа их работы рассмотрим следующий пример.
Пример подсчета частных производных
В данном примере также будет задействована только Alice:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
Здесь вес будет представлен как 1, а смещение как 0. Если выполним прямое распространение (feedforward) через сеть, получим:
Выдачи нейронной сети ypred = 0.524. Это дает нам слабое представление о том, рассматривается мужчина Male (0), или женщина Female (1). Давайте подсчитаем :
Напоминание: мы вывели
f '(x) = f (x) * (1 - f (x))ранее для нашей функции активации сигмоида.
У нас получилось! Результат говорит о том, что если мы собираемся увеличить w1, L немного увеличивается в результате.
Тренировка нейронной сети: Стохастический градиентный спуск
У нас есть все необходимые инструменты для тренировки нейронной сети. Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (SGD), который говорит нам, как именно поменять вес и смещения для минимизации потерь. По сути, это отражается в следующем уравнении:
η является константой под названием оценка обучения, что контролирует скорость обучения. Все что мы делаем, так это вычитаем из
w1:
Если мы применим это на каждый вес и смещение в сети, потеря будет постепенно снижаться, а показатели сети сильно улучшатся.
Наш процесс тренировки будет выглядеть следующим образом:
- Выбираем один пункт из нашего набора данных. Это то, что делает его стохастическим градиентным спуском. Мы обрабатываем только один пункт за раз;
- Подсчитываем все частные производные потери по весу или смещению. Это может быть
,
и так далее;
- Используем уравнение обновления для обновления каждого веса и смещения;
- Возвращаемся к первому пункту.
Давайте посмотрим, как это работает на практике.
Создание нейронной сети с нуля на Python
Наконец, мы реализуем готовую нейронную сеть:
| Имя/Name | Вес/Weight (минус 135) | Рост/Height (минус 66) | Пол/Gender |
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
import numpy as np def sigmoid(x): # Функция активации sigmoid:: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(—x)) def deriv_sigmoid(x): # Производная от sigmoid: f'(x) = f(x) * (1 — f(x)) fx = sigmoid(x) return fx * (1 — fx) def mse_loss(y_true, y_pred): # y_true и y_pred являются массивами numpy с одинаковой длиной return ((y_true — y_pred) ** 2).mean() class OurNeuralNetwork: «»» Нейронная сеть, у которой: — 2 входа — скрытый слой с двумя нейронами (h1, h2) — слой вывода с одним нейроном (o1) *** ВАЖНО ***: Код ниже написан как простой, образовательный. НЕ оптимальный. Настоящий код нейронной сети выглядит не так. НЕ ИСПОЛЬЗУЙТЕ этот код. Вместо этого, прочитайте/запустите его, чтобы понять, как работает эта сеть. «»» def __init__(self): # Вес self.w1 = np.random.normal() self.w2 = np.random.normal() self.w3 = np.random.normal() self.w4 = np.random.normal() self.w5 = np.random.normal() self.w6 = np.random.normal() # Смещения self.b1 = np.random.normal() self.b2 = np.random.normal() self.b3 = np.random.normal() def feedforward(self, x): # x является массивом numpy с двумя элементами h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1) h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2) o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3) return o1 def train(self, data, all_y_trues): «»» — data is a (n x 2) numpy array, n = # of samples in the dataset. — all_y_trues is a numpy array with n elements. Elements in all_y_trues correspond to those in data. «»» learn_rate = 0.1 epochs = 1000 # количество циклов во всём наборе данных for epoch in range(epochs): for x, y_true in zip(data, all_y_trues): # — Выполняем обратную связь (нам понадобятся эти значения в дальнейшем) sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1 h1 = sigmoid(sum_h1) sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2 h2 = sigmoid(sum_h2) sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3 o1 = sigmoid(sum_o1) y_pred = o1 # — Подсчет частных производных # — Наименование: d_L_d_w1 представляет «частично L / частично w1» d_L_d_ypred = —2 * (y_true — y_pred) # Нейрон o1 d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1) d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1) d_ypred_d_b3 = deriv_sigmoid(sum_o1) d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1) d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1) # Нейрон h1 d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1) d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1) d_h1_d_b1 = deriv_sigmoid(sum_h1) # Нейрон h2 d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2) d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2) d_h2_d_b2 = deriv_sigmoid(sum_h2) # — Обновляем вес и смещения # Нейрон h1 self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1 self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2 self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1 # Нейрон h2 self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3 self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4 self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2 # Нейрон o1 self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5 self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6 self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3 # — Подсчитываем общую потерю в конце каждой фазы if epoch % 10 == 0: y_preds = np.apply_along_axis(self.feedforward, 1, data) loss = mse_loss(all_y_trues, y_preds) print(«Epoch %d loss: %.3f» % (epoch, loss)) # Определение набора данных data = np.array([ [—2, —1], # Alice [25, 6], # Bob [17, 4], # Charlie [—15, —6], # Diana ]) all_y_trues = np.array([ 1, # Alice 0, # Bob 0, # Charlie 1, # Diana ]) # Тренируем нашу нейронную сеть! network = OurNeuralNetwork() network.train(data, all_y_trues) |
Вы можете поэкспериментировать с этим кодом самостоятельно. Он также доступен на Github.
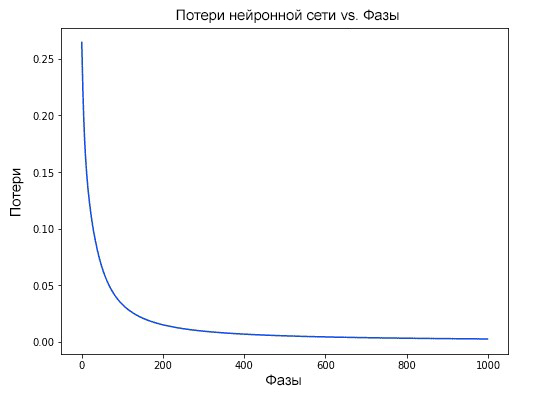
Наши потери постоянно уменьшаются по мере того, как учится нейронная сеть:
Теперь мы можем использовать нейронную сеть для предсказания полов:
|
# Делаем предсказания emily = np.array([—7, —3]) # 128 фунтов, 63 дюйма frank = np.array([20, 2]) # 155 фунтов, 68 дюймов print(«Emily: %.3f» % network.feedforward(emily)) # 0.951 — F print(«Frank: %.3f» % network.feedforward(frank)) # 0.039 — M |
Что теперь?
У вас все получилось. Вспомним, как мы это делали:
- Узнали, что такое нейроны, как создать блоки нейронных сетей;
- Использовали функцию активации сигмоида в отношении нейронов;
- Увидели, что по сути нейронные сети — это просто набор нейронов, связанных между собой;
- Создали набор данных с параметрами вес и рост в качестве входных данных (или функций), а также использовали пол в качестве вывода (или маркера);
- Узнали о функциях потерь и среднеквадратичной ошибке (MSE);
- Узнали, что тренировка нейронной сети — это минимизация ее потерь;
- Использовали обратное распространение для вычисления частных производных;
- Использовали стохастический градиентный спуск (SGD) для тренировки нейронной сети.
Подробнее о построении нейронной сети прямого распросранения Feedforward можно ознакомиться в одной из предыдущих публикаций.
Спасибо за внимание!
Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.
E-mail: vasile.buldumac@ati.utm.md
Образование
Universitatea Tehnică a Moldovei (utm.md)
- 2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
- 2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»
оглавление
1 связанные термины
2 функция потерь
2.1 Определение
2.2 Среднеквадратичная ошибка
2.3 Ошибка перекрестной энтропии
2.4 данные партии
2.5 Зачем нужна функция потерь
3 Численное дифференцирование
3.1 Производная
3.2 частные производные
4 градиента
5 реализация корпуса
5.1dataset
5.2common
5.2.1functions.py:
5.2.2gradient.py:
5.3ch04
5.3.1two_layer_net.py
5.3.2train_neuralnet.py
Эта статья представляет собой краткое изложение «Введение в теорию глубокого обучения и реализацию на основе Python», автор — [ ] Сайто Ясуи.
1 связанные термины
В нейронных сетях данные очень важны, также очень важно извлечение функций данных.
«Количество функций»Это преобразователь, который может точно извлекать важные данные (важные данные) из входных данных (входное изображение).
Сравнение нейронной сети и машинного обучения выглядит следующим образом:
В машинном обучении данные обычно делятся наДанные обученияс участиемДанные испытанийДве части для обучения и экспериментов
ОбобщениеОтносится к способности обрабатывать ненаблюдаемые данные (данные не включаются в данные обучения). Получение способности обобщения — конечная цель машинного обучения.
Состояние переобучения только на определенный набор данных называетсяПереоснащение(over fitting)
2 функция потерь
2.1 Определение
Функция потерьЭто показатель «плохой степени» производительности нейронной сети, то есть степени, в которой текущая нейронная сеть не соответствует данным наблюдения, и насколько она непоследовательна. Использование «плохой производительности» в качестве индикатора может заставить людей чувствовать себя неестественно, но если вы умножите функцию потерь на отрицательное значение, это можно интерпретировать как «насколько плохая производительность», то есть «насколько хороша производительность».
2.2 Среднеквадратичная ошибка
Формат среднеквадратичной ошибки следующий:
[Примечание]: y k — это выходной сигнал нейронной сети, t k — это данные наблюдения, а k — размер данных.
Код реализован следующим образом:
import numpy as np
def mean_squared_error(y, t):
return 0.5*np.sum((y-t)**2)
if __name__ == "__main__":
# Используйте распознавание чисел, чтобы понять, что y - это прогнозируемые данные (с точки зрения вероятности), а t - реальные данные
# Установите 2 как правильное решение
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 2 имеет самую высокую вероятность и составляет 0,6
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# 7 имеет самую высокую вероятность 0,6
y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
# Среднеквадратичная ошибка
# r1 = mean_squared_error(np.array(y), np.array(t))
# r2 = mean_squared_error(np.array(y1), np.array(t))
# print(r1) # 0.09750000000000003
# print(r2) # 0.5975
# Мы обнаружили, что значение функции потерь в первом примере меньше, и разница между
# Ошибка небольшая. Другими словами, среднеквадратичная ошибка показывает, что результат первого примера более согласуется с данными наблюдения.
2.3 Ошибка перекрестной энтропии
Формат функции потерь кросс-энтропийной ошибки следующий:
[Примечание]: log представляет собой натуральный логарифм с основанием e (log e). y k — выход нейронной сети, а t k — метка правильного решения.
Код реализован следующим образом:
import numpy as np
# Добавлена крошечная дельта значения. Это потому, что когда появляется np.log (0), np.log (0) становится отрицательным бесконечным -inf
# Это приведет к сбою последующих вычислений. В качестве защитной меры добавление небольшого значения может предотвратить возникновение отрицательной бесконечности.
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
if __name__ == "__main__":
# Установите 2 как правильное решение
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
# 2 имеет самую высокую вероятность и составляет 0,6
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
# 7 имеет самую высокую вероятность 0,6
y1 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
# Ошибка перекрестной энтропии
r1 = cross_entropy_error(np.array(y), np.array(t))
r2 = cross_entropy_error(np.array(y1), np.array(t))
print(r1) # 0.510825457099338
print(r2) # 2.302584092994546
2.4 данные партии
В приведенных выше примерах функций потерь рассматриваются все функции потерь для отдельных данных. Если требуется сумма функций потерь всех обучающих данных, взяв в качестве примера кросс-энтропийную ошибку, ее можно записать в виде следующей формулы:
[Примечание]: Предполагая, что имеется N данных, t nk представляет значение k-го элемента n-х данных (y nk — это выходной сигнал нейронной сети, t nk — это данные наблюдения).
Данные пакетной обработки, тогда как читать несколько частей данных случайным образом за раз? Вы можете использовать np.random.choice () NumPy, например, np.random.choice (60000, 10) случайным образом выберет 10 чисел от 0 до 59999.
Например:
import sys,os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# print(x_train.shape) # (60000, 784)
# print(t_train.shape) # (60000, 10)
# Произвольно рисуем 10 данных
train_size = x_train.shape[0] # 60000
batch_size = 10
# Случайно выбрать 10 чисел от 0 до 59999
batch_mask = np.random.choice (train_size, batch_size) # случайным образом выбираем желаемое число из указанных чисел
# print(batch_mask) # [40011 45133 49757 27590 11182 32214 23597 45193 56422 33356]
x_batch = x_train[batch_mask] # (10, 784)
t_batch = t_train[batch_mask] # (10, 10)
Можно добиться следующегоОдновременная обработка отдельных данных и пакетных данных(Данные вводятся централизованно) Функция двух наблюдений.
В коде реализована ошибка кросс-энтропии mini_batch:
def batch_cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7))/batch_size[Примечание]: y — выход нейронной сети, t — данные наблюдения. Когда размерность y равна 1, то есть, когда вычисляется ошибка кросс-энтропии отдельных данных, форму данных необходимо изменить. И, когда вводится мини-пакетом, нормализуйте с количеством пакетов, чтобы вычислить среднюю ошибку кросс-энтропии отдельных данных.
Когда данные мониторингаФорма этикетки(Не одна горячая, а метки типа «2» и «7»), ошибка перекрестной энтропии может быть достигнута с помощью следующего кода.
def batch_cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7))/batch_size[Примечание]: для np.log (y [np.arange (batch_size), t]). np.arange (batch_size) сгенерирует массив от 0 до batch_size-1. Например, когда batch_size равно 5, np.arange (batch_size) сгенерирует массив NumPy [0, 1, 2, 3, 4]. Поскольку метка в t хранится в форме [2, 7, 0, 9, 4], y [np.arange (batch_size), t] может извлекать выходные данные нейронной сети, соответствующие правильной маркировке каждого данных (в В этом примере y [np.arange (batch_size), t] сгенерирует массив NumPy [y [0,2], y [1,7], y [2,0], y [3,9], y [ 4,4]]).
2.5 Зачем нужна функция потерь
1. При поиске оптимальных параметров (весов и смещений) при обучении нейронных сетей,Найдите параметр, чтобы сделать значение функции потерь как можно меньше. Чтобы найти место, где значение функции потерь является как можно меньшим, необходимо вычислить производную параметра (а точнее, градиент), а затем использовать эту производную в качестве руководства для постепенного обновления значения параметра.
2. Если значение производной отрицательное, значение функции потерь может быть уменьшено путем изменения весового параметра в положительном направлении; наоборот, если значение производной положительно, весовой параметр может быть изменен в отрицательном направлении для уменьшения Значение функции малых потерь. Однако, когда значение производной равно 0, независимо от того, в каком направлении изменяется весовой параметр, значение функции потерь не изменится, и обновление весового параметра здесь остановится.
3 Численное дифференцирование
3.1 Производная
Производная означает количество изменений в определенный момент (предел коэффициента приращения) и имеет следующий формат:
[Примечание]: левая часть знака равенства представляет собой производную от значения функции, а правая часть представляет степень изменения значения функции f (x) относительно независимой переменной x (представленной пределами)
Ошибка округления: Относится к ошибке в окончательном результате вычисления, вызванной пропуском значения точной части десятичной дроби (например, значения после восьмой десятичной точки).
Например:
print(np.float32(1e-50)) # 10^-50 = 0.0[Примечание]: указанное выше значение h необходимо установить разумно, иначе это приведет к большой ошибке, вы можете изменить 1e-50 на 1e-4.
Помимо изменения значения h, вторая область, которая нуждается в улучшении, связана с различием функции f. Хотя разность между x + h и x функции f вычисляется в приведенной выше реализации, необходимо отметить, что это вычисление имеет ошибки с самого начала. «Истинная производная» соответствует наклону функции в точке x (называемой касательной), но производная, вычисленная в приведенной выше реализации, соответствует наклону между (x + h) и x.
Чтобы уменьшить эту ошибку, мы можем вычислить разницу функции f между (x + h) и (x — h). Поскольку этот метод расчета принимает x в качестве центра и вычисляет разницу между его левой и правой сторонами, его также называютЦентральная разница(Разница между (x + h) и x называется прямой разницей).
Производный код реализован следующим образом:
import numpy as np
# Плохая реализация, примерная разница
def forward_numerical_diff(f, x):
h = 10e-50
# h = 1e-4 # 0.0001
return (f(x+h) - f(x))/h
# Центральное отличие
def center_numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h))/(2*h)
def fun(x):
return 0.01*x**2 + 0.1*x
def fun2(x):
# return x[0]**2 + x[1]**2
return np.sum(x**2)
if __name__ == "__main__":
# Аппроксимация производной при x = 5
z = center_numerical_diff(fun, 5) # 0.1999999999990898
# Аппроксимация производной при x = 10
z1 = center_numerical_diff(fun, 10) # 0.2999999999986347
3.2 частные производные
Когда в функции несколько параметров, ищется частная производная функции.
Например:
Когда требуется частная производная от x0, рассматривайте x1 как константу. При поиске x1 также рассматривайте x0 как константу.
Остальные такие же, как и в предыдущем методе поиска производной.
4 градиента
Основная задача машинного обучения — найти оптимальные параметры во время обучения.Точно так же нейронная сеть должна также найти оптимальные параметры (веса и смещения) во время обучения. Упомянутый здесь оптимальный параметр относится к параметру, когда функция потерь принимает минимальное значение. Градиент представляет направление, в котором значение функции в каждой точке уменьшается в наибольшей степени.
Формат градиентного метода следующий:
Скорость обучения необходимо определить заранее до определенного значения, например 0,01 или 0,001. Приведенная выше формула обновляется один раз, и этот шаг будет повторяться. Другими словами, каждый шаг обновляет значение переменной в соответствии с приведенной выше формулой и постепенно уменьшает значение функции, повторяя этот шаг.
[Примечание]: η представляет собой количество обновлений, которое называется скоростью обучения при обучении нейронных сетей.
Код для поиска градиента реализован следующим образом:
import numpy as np
# Определить функцию
def fun2(x):
return x[0]**2 + x[1]**2
# Найдите частную производную
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like (x) # Сгенерировать тот же массив, что и x
for idx in range(x.size):
tmp_val = x[idx]
# f (x + h) вычисление
x[idx] = tmp_val + h
fxh1 = f (x) # При вычислении x! = [3, 4], но [3 + h, 4]
# f (x-h) вычисление
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2)/(2*h)
x [idx] = tmp_val # значение восстановления
return grad
# Реализация метода градиентного спуска
# f: функция для оптимизации, init_x: начальное значение, lr: скорость обучения, step_num: время повторения градиентного метода
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numeric_gradient (f, x) # Найти градиент функции
x -= lr * grad
return x
if __name__ == "__main__":
x, y = numerical_gradient(fun2, np.array([3.0, 4.0]))
# print(x) # 6.00000000000378
# print(y) # 7.999999999999119
# Установить начальное значение
init_x = np.array([-3.0, 4.0])
# m, n = gradient_descent(fun2, init_x=init_x, lr=0.1, step_num=100)
# print(m) # -6.111107928998789e-10
# print(n) # 8.148143905314271e-10
# Скорость обучения слишком велика
# m, n = gradient_descent(fun2, init_x=init_x, lr=10, step_num=100)
# print(m) # -25898374737328.363
# print(n) # -1295248616896.5398
# Скорость обучения слишком мала
m, n = gradient_descent(fun2, init_x=init_x, lr=1e-4, step_num=100)
print(m) # -2.9405901379497053
print(n) # 3.920786850599603
'''
Если скорость обучения слишком велика, она превратится в большое значение; и наоборот, если скорость обучения слишком мала, она в основном закончится без значительного обновления.
'''
5 реализация корпуса
Документы, необходимые для реализации дела:
5.1dataset
Можно найти в предыдущей главе
5.2common
5.2.1functions.py:
Этот файл играет роль функции активации и функции потери.
# coding: utf-8
import numpy as np
def identity_function(x):
return x
def step_function(x):
return np.array(x > 0, dtype=np.int)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def relu(x):
return np.maximum(0, x)
def relu_grad(x):
grad = np.zeros(x)
grad[x>=0] = 1
return grad
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) #
return np.exp(x) / np.sum(np.exp(x))
def sum_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
def softmax_loss(X, t):
y = softmax(X)
return cross_entropy_error(y, t)
5.2.2gradient.py:
Файл воспроизводит производную, градиент
# coding: utf-8
import numpy as np
# Найти одномерную частную производную
def _numerical_gradient_1d(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x [idx] = tmp_val # восстановление
return grad
# Найдите двумерную частную производную
def numerical_gradient_2d(f, X):
if X.ndim == 1:
return _numerical_gradient_1d(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_1d(f, x)
return grad
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
# flags: использовать внешние циклы, мультииндекс: каждая итерация может отслеживать один тип индекса
# У объекта nditer есть еще один необязательный параметр op_flags. По умолчанию nditer будет рассматривать массив, который будет повторяться, как объект только для чтения.
# Чтобы понять, что элементы массива стоит изменять при обходе массива, вы должны указать режим чтения-записи или только для записи.
it = np.nditer (x, flags = ['multi_index'], op_flags = ['readwrite']) # итерация
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x [idx] = tmp_val # восстановление
it.iternext()
return grad
5.3ch04
5.3.1two_layer_net.py
Этот документ создает двухуровневую сеть
# coding: utf-8
import sys, os
sys.path.append (os.pardir) # путь загрузки
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# Инициализация сети
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x: прогнозируемое значение, t: истинное значение
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
dz1 = np.dot(dy, W2.T)
da1 = sigmoid_grad(a1) * dz1
grads['W1'] = np.dot(x.T, da1)
grads['b1'] = np.sum(da1, axis=0)
return grads
5.3.2train_neuralnet.py
Используйте нейронные сети для обучения
# coding: utf-8
import sys, os
sys.path.append (os.pardir) # путь загрузки
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from ch04.two_layer_net import TwoLayerNet
# Прочитать набор данных
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
iters_num = 10000 # количество итераций 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# Расчет градиента
# grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch)
# Обновление параметров
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))
# Рисование
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
Получите окончательный результат
Создание и тренировка Нейронной Сети с нуля в Python
Создание нейронных блоков
Для начала необходимо определиться с тем, что из себя представляют базовые компоненты нейронной сети – нейроны. Нейрон принимает вводные данные, выполняет с ними определенные математические операции, а затем выводит результат. Нейрон с двумя входными данными выглядит следующим образом:
Здесь происходят три вещи. Во-первых, каждый вход умножается на вес (на схеме обозначен красным):
Затем все взвешенные входы складываются вместе со смещением b (на схеме обозначен зеленым):
Наконец, сумма передается через функцию активации (на схеме обозначена желтым):
Функция активации используется для подключения несвязанных входных данных с выводом, у которого простая и предсказуемая форма. Как правило, в качестве используемой функцией активации берется функция сигмоида:
Функция сигмоида выводит только числа в диапазоне (0, 1). Вы можете воспринимать это как компрессию от (−∞, +∞) до (0, 1). Крупные отрицательные числа становятся ~0, а крупные положительные числа становятся ~1.
Простой пример работы с нейронами в Python
Предположим, у нас есть нейрон с двумя входами, который использует функцию активации сигмоида и имеет следующие параметры:
w = [0,1] — это просто один из способов написания w1 = 0, w2 = 1 в векторной форме. Присвоим нейрону вход со значением x = [2, 3]. Для более компактного представления будет использовано скалярное произведение.
С учетом, что вход был x = [2, 3], вывод будет равен 0.999. Вот и все. Такой процесс передачи входных данных для получения вывода называется прямым распространением, или feedforward.
Создание нейрона с нуля в Python
Приступим к имплементации нейрона. Для этого потребуется использовать NumPy. Это мощная вычислительная библиотека Python, которая задействует математические операции:
import numpy as np
def sigmoid(x):
# Наша функция активации: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
class Neuron:
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
# Вводные данные о весе, добавление смещения
# и последующее использование функции активации
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4 # b = 4
n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994
Узнаете числа? Это тот же пример, который рассматривался ранее. Ответ полученный на этот раз также равен 0.999.
Пример сбор нейронов в нейросеть
Нейронная сеть по сути представляет собой группу связанных между собой нейронов. Простая нейронная сеть выглядит следующим образом:
На вводном слое сети два входа – x1 и x2. На скрытом слое два нейтрона — h1 и h2. На слое вывода находится один нейрон – о1. Обратите внимание на то, что входные данные для о1 являются результатами вывода h1 и h2. Таким образом и строится нейросеть.
Скрытым слоем называется любой слой между вводным слоем и слоем вывода, что являются первым и последним слоями соответственно. Скрытых слоев может быть несколько.
Пример прямого распространения FeedForward
Давайте используем продемонстрированную выше сеть и представим, что все нейроны имеют одинаковый вес w = [0, 1], одинаковое смещение b = 0 и ту же самую функцию активации сигмоида. Пусть h1, h2 и o1 сами отметят результаты вывода представленных ими нейронов.
Что случится, если в качестве ввода будет использовано значение х = [2, 3]?
Результат вывода нейронной сети для входного значения х = [2, 3] составляет 0.7216. Все очень просто.
Нейронная сеть может иметь любое количество слоев с любым количеством нейронов в этих слоях.
Суть остается той же: нужно направить входные данные через нейроны в сеть для получения в итоге выходных данных. Для простоты далее в данной статье будет создан код сети, упомянутая выше.
Создание нейронной сети прямое распространение FeedForward
Далее будет показано, как реализовать прямое распространение feedforward в отношении нейронной сети. В качестве опорной точки будет использована следующая схема нейронной сети:
import numpy as np
class OurNeuralNetwork:
«»»
Нейронная сеть, у которой:
— 2 входа
— 1 скрытый слой с двумя нейронами (h1, h2)
— слой вывода с одним нейроном (o1)
У каждого нейрона одинаковые вес и смещение:
— w = [0, 1]
— b = 0
«»»
def __init__(self):
weights = np.array([0, 1])
bias = 0
# Класс Neuron из предыдущего раздела
self.h1 = Neuron(weights, bias)
self.h2 = Neuron(weights, bias)
self.o1 = Neuron(weights, bias)
def feedforward(self, x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
# Вводы для о1 являются выводами h1 и h2
out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421
Мы вновь получили 0.7216. Похоже, все работает.
Пример тренировки нейронной сети — минимизация потерь, Часть 1
Предположим, у нас есть следующие параметры:
Имя/NameВес/Weight (фунты)Рост/Height (дюймы)Пол/Gender Alice13365FBob16072MCharlie15270MDiana12060FДавайте натренируем нейронную сеть таким образом, чтобы она предсказывала пол заданного человека в зависимости от его веса и роста.
Мужчины Male будут представлены как 0, а женщины Female как 1. Для простоты представления данные также будут несколько смещены.
Имя/NameВес/Weight (минус 135)Рост/Height (минус 66)Пол/Gender Alice-2-11Bob2560Charlie1740Diana-15-61Для оптимизации здесь произведены произвольные смещения
135и66. Однако, обычно для смещения выбираются средние показатели.
Потери
Перед тренировкой нейронной сети потребуется выбрать способ оценки того, насколько хорошо сеть справляется с задачами. Это необходимо для ее последующих попыток выполнять поставленную задачу лучше. Таков принцип потери.
В данном случае будет использоваться среднеквадратическая ошибка (MSE) потери:
Давайте разберемся:
n– число рассматриваемых объектов, которое в данном случае равно 4. ЭтоAlice,Bob,CharlieиDiana;y– переменные, которые будут предсказаны. В данном случае это пол человека;ytrue– истинное значение переменной, то есть так называемый правильный ответ. Например, дляAliceзначениеytrueбудет1, то естьFemale;ypred– предполагаемое значение переменной. Это результат вывода сети.
(ytrue - ypred)2 называют квадратичной ошибкой (MSE). Здесь функция потери просто берет среднее значение по всем квадратичным ошибкам. Отсюда и название ошибки. Чем лучше предсказания, тем ниже потери.
Пример подсчета потерь в тренировки нейронной сети
Скажем, наша сеть всегда выдает 0. Другими словами, она уверена, что все люди — Мужчины. Какой будет потеря?
Имя/Nameytrueypred(ytrue — ypred)2Alice101Bob000Charlie000Diana101
Python код среднеквадратической ошибки (MSE)
Ниже представлен код для подсчета потерь:
import numpy as np
def mse_loss(y_true, y_pred):
# y_true и y_pred являются массивами numpy с одинаковой длиной
return ((y_true — y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5
При возникновении сложностей с пониманием работы кода стоит ознакомиться с quickstart в NumPy для операций с массивами.
Тренировка нейронной сети — многовариантные исчисления, Часть 2
Текущая цель понятна – это минимизация потерь нейронной сети. Теперь стало ясно, что повлиять на предсказания сети можно при помощи изменения ее веса и смещения. Однако, как минимизировать потери?
В этом разделе будут затронуты многовариантные исчисления. Если вы не знакомы с данной темой, фрагменты с математическими вычислениями можно пропускать.
Для простоты давайте представим, что в наборе данных рассматривается только Alice:
Имя/NameВес/Weight (минус 135)Рост/Height (минус 66)Пол/GenderAlice-2-11Затем потеря среднеквадратической ошибки будет просто квадратической ошибкой для Alice:
Еще один способ понимания потери – представление ее как функции веса и смещения. Давайте обозначим каждый вес и смещение в рассматриваемой сети:
Затем можно прописать потерю как многовариантную функцию:
Представим, что нам нужно немного отредактировать w1. В таком случае, как изменится потеря L после внесения поправок в w1?
На этот вопрос может ответить частная производная
. Как же ее вычислить?
Здесь математические вычисления будут намного сложнее. С первой попытки вникнуть будет непросто, но отчаиваться не стоит. Возьмите блокнот и ручку – лучше делать заметки, они помогут в будущем.
Для начала, давайте перепишем частную производную в контексте
:
Данные вычисления возможны благодаря дифференцированию сложной функции.
Подсчитать
можно благодаря вычисленной выше L = (1 - ypred)2:
Теперь, давайте определим, что делать с
. Как и ранее, позволим h1, h2, o1 стать результатами вывода нейронов, которые они представляют. Дальнейшие вычисления:
Как было указано ранее, здесь f является функцией активации сигмоида.
Так как w1 влияет только на h1, а не на h2, можно записать:
Использование дифференцирования сложной функции.
Те же самые действия проводятся для
:
Еще одно использование дифференцирования сложной функции.
В данном случае х1 — вес, а х2 — рост. Здесь f′(x) как производная функции сигмоида встречается во второй раз. Попробуем вывести ее:
Функция f'(x) в таком виде будет использована несколько позже.
Вот и все. Теперь
разбита на несколько частей, которые будут оптимальны для подсчета:
Эта система подсчета частных производных при работе в обратном порядке известна, как метод обратного распространения ошибки, или backprop.
У нас накопилось довольно много формул, в которых легко запутаться. Для лучшего понимания принципа их работы рассмотрим следующий пример.
Пример подсчета частных производных
В данном примере также будет задействована только Alice:
Имя/NameВес/Weight (минус 135)Рост/Height (минус 66)Пол/GenderAlice-2-11Здесь вес будет представлен как 1, а смещение как 0. Если выполним прямое распространение (feedforward) через сеть, получим:
Выдачи нейронной сети ypred = 0.524. Это дает нам слабое представление о том, рассматривается мужчина Male (0), или женщина Female (1). Давайте подсчитаем
:
Напоминание: мы вывели f '(x) = f (x) * (1 - f (x)) ранее для нашей функции активации сигмоида.
У нас получилось! Результат говорит о том, что если мы собираемся увеличить w1, L немного увеличивается в результате.
Тренировка нейронной сети: Стохастический градиентный спуск
У нас есть все необходимые инструменты для тренировки нейронной сети. Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (SGD), который говорит нам, как именно поменять вес и смещения для минимизации потерь. По сути, это отражается в следующем уравнении:
η является константой под названием оценка обучения, что контролирует скорость обучения. Все что мы делаем, так это вычитаем
из w1:
- Если
- положительная,
w1уменьшится, что приведет к уменьшениюL. - Если
- отрицательная,
w1увеличится, что приведет к уменьшениюL.
Если мы применим это на каждый вес и смещение в сети, потеря будет постепенно снижаться, а показатели сети сильно улучшатся.
Наш процесс тренировки будет выглядеть следующим образом:
- Выбираем один пункт из нашего набора данных. Это то, что делает его стохастическим градиентным спуском. Мы обрабатываем только один пункт за раз;
- Подсчитываем все частные производные потери по весу или смещению. Это может быть
- ,
- и так далее;
- Используем уравнение обновления для обновления каждого веса и смещения;
- Возвращаемся к первому пункту.
Давайте посмотрим, как это работает на практике.
Создание нейронной сети с нуля на Python
Наконец, мы реализуем готовую нейронную сеть:
import numpy as np
def sigmoid(x):
# Функция активации sigmoid:: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Производная от sigmoid: f'(x) = f(x) * (1 — f(x))
fx = sigmoid(x)
return fx * (1 — fx)
def mse_loss(y_true, y_pred):
# y_true и y_pred являются массивами numpy с одинаковой длиной
return ((y_true — y_pred) ** 2).mean()
class OurNeuralNetwork:
«»»
Нейронная сеть, у которой:
— 2 входа
— скрытый слой с двумя нейронами (h1, h2)
— слой вывода с одним нейроном (o1)
*** ВАЖНО ***:
Код ниже написан как простой, образовательный. НЕ оптимальный.
Настоящий код нейронной сети выглядит не так. НЕ ИСПОЛЬЗУЙТЕ этот код.
Вместо этого, прочитайте/запустите его, чтобы понять, как работает эта сеть.
«»»
def __init__(self):
# Вес
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# Смещения
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self, x):
# x является массивом numpy с двумя элементами
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
«»»
— data is a (n x 2) numpy array, n = # of samples in the dataset.
— all_y_trues is a numpy array with n elements.
Elements in all_y_trues correspond to those in data.
«»»
learn_rate = 0.1
epochs = 1000 # количество циклов во всём наборе данных
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# — Выполняем обратную связь (нам понадобятся эти значения в дальнейшем)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# — Подсчет частных производных
# — Наименование: d_L_d_w1 представляет «частично L / частично w1»
d_L_d_ypred = -2 * (y_true — y_pred)
# Нейрон o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Нейрон h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Нейрон h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# — Обновляем вес и смещения
# Нейрон h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Нейрон h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# Нейрон o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# — Подсчитываем общую потерю в конце каждой фазы
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print(«Epoch %d loss: %.3f» % (epoch, loss))
# Определение набора данных
data = np.array([
[-2, -1], # Alice
[25, 6], # Bob
[17, 4], # Charlie
[-15, -6], # Diana
])
all_y_trues = np.array([
1, # Alice
0, # Bob
0, # Charlie
1, # Diana
])
# Тренируем нашу нейронную сеть!
network = OurNeuralNetwork()
network.train(data, all_y_trues)
Вы можете поэкспериментировать с этим кодом самостоятельно. Он также доступен на Github.
Наши потери постоянно уменьшаются по мере того, как учится нейронная сеть:
Теперь мы можем использовать нейронную сеть для предсказания полов:
Python
# Делаем предсказания
emily = np.array([-7, -3]) # 128 фунтов, 63 дюйма
frank = np.array([20, 2]) # 155 фунтов, 68 дюймов
print(«Emily: %.3f» % network.feedforward(emily)) # 0.951 — F
print(«Frank: %.3f» % network.feedforward(frank)) # 0.039 — M
Что теперь?
У вас все получилось. Вспомним, как мы это делали:
- Узнали, что такое нейроны, как создать блоки нейронных сетей;
- Использовали функцию активации сигмоида в отношении нейронов;
- Увидели, что по сути нейронные сети — это просто набор нейронов, связанных между собой;
- Создали набор данных с параметрами вес и рост в качестве входных данных (или функций), а также использовали пол в качестве вывода (или маркера);
- Узнали о функциях потерь и среднеквадратичной ошибке (MSE);
- Узнали, что тренировка нейронной сети — это минимизация ее потерь;
- Использовали обратное распространение для вычисления частных производных;
- Использовали стохастический градиентный спуск (SGD) для тренировки нейронной сети.
Подробнее о построении нейронной сети прямого распросранения Feedforward можно ознакомиться в одной из предыдущих публикаций.
Спасибо за внимание!