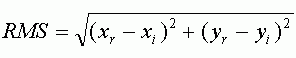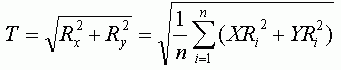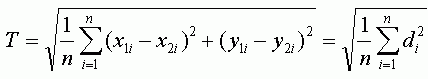Среднеквадратичная ошибка определения координат

Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:

$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$

MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.

Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:

$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$

Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:

$$y = 0,5252 * x + 17,306$$

Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):

$$MSE = frac{1}{9} × 4445 = 493$$

Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.

MSE и Scikit-learn

Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:

import sklearn
from sklearn.metrics import mean_squared_error

Инициализируем крошечные списки, содержащие реальные и предсказанные координаты y:

y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]

Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:

mean_squared_error(y_true, y_pred)

Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:

496.0

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Автор оригинальной статьи: @mmoshikoo

Фото: @tobyelliott

From Wikipedia, the free encyclopedia

In statistics, the mean squared error (MSE)^[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.^[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.^[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).

The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.

The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).^{[citation needed]} For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.

Definition and basic properties[edit]

The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.

Predictor[edit]

If a vector of predictions is generated from a sample of data points on all variables, and is the vector of observed values of the variable being predicted, with being the predicted values (e.g. as from a least-squares fit), then the within-sample MSE of the predictor is computed as

In other words, the MSE is the mean of the squares of the errors . This is an easily computable quantity for a particular sample (and hence is sample-dependent).

In matrix notation,

where is and is the column vector.

The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,^[4] and is computed as

Estimator[edit]

The MSE of an estimator with respect to an unknown parameter is defined as^[1]

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator is derived as a sample statistic and is used to estimate some population parameter, then the expectation is with respect to the sampling distribution of the sample statistic.

The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.^[5]

Proof of variance and bias relationship[edit]

An even shorter proof can be achieved using the well-known formula that for a random variable , . By substituting with, , we have

But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.

In regression[edit]

In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,^[6] but whose limitation is related to known distribution of the data.

The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).^[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.

In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.

Examples[edit]

Mean[edit]

Suppose we have a random sample of size from a population, . Suppose the sample units were chosen with replacement. That is, the units are selected one at a time, and previously selected units are still eligible for selection for all draws. The usual estimator for the is the sample average

which has an expected value equal to the true mean (so it is unbiased) and a mean squared error of

where is the population variance.

For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.

Variance[edit]

The usual estimator for the variance is the corrected sample variance:

This is unbiased (its expected value is ), hence also called the unbiased sample variance, and its MSE is^[8]

where is the fourth central moment of the distribution or population, and is the excess kurtosis.

However, one can use other estimators for which are proportional to , and an appropriate choice can always give a lower mean squared error. If we define

then we calculate:

This is minimized when

For a Gaussian distribution, where , this means that the MSE is minimized when dividing the sum by . The minimum excess kurtosis is ,^[a] which is achieved by a Bernoulli distribution with p = 1/2 (a coin flip), and the MSE is minimized for Hence regardless of the kurtosis, we get a «better» estimate (in the sense of having a lower MSE) by scaling down the unbiased estimator a little bit; this is a simple example of a shrinkage estimator: one «shrinks» the estimator towards zero (scales down the unbiased estimator).

Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be

Gaussian distribution[edit]

The following table gives several estimators of the true parameters of the population, μ and σ², for the Gaussian case.^[9]

True value	Estimator	Mean squared error
	= the unbiased estimator of the population mean,
	= the unbiased estimator of the population variance,
	= the biased estimator of the population variance,
	= the biased estimator of the population variance,

Interpretation[edit]

An MSE of zero, meaning that the estimator predicts observations of the parameter with perfect accuracy, is ideal (but typically not possible).

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).

Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.

In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.

MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.

Applications[edit]

• Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
• In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
• In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.

Loss function[edit]

Squared error loss is one of the most widely used loss functions in statistics^{[citation needed]}, though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.^[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.

Criticism[edit]

The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.^[10]

Like variance, mean squared error has the disadvantage of heavily weighting outliers.^[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.

See also[edit]

• Bias–variance tradeoff
• Hodges’ estimator
• James–Stein estimator
• Mean percentage error
• Mean square quantization error
• Mean square weighted deviation
• Mean squared displacement
• Mean squared prediction error
• Minimum mean square error
• Minimum mean squared error estimator
• Overfitting
• Peak signal-to-noise ratio

Notes[edit]

References[edit]

Большинство проводимых работ по межеванию земель заключаются в определении или уточнении местоположения границ наделов земли относительно опорных точек межевания.

Зафиксированные на бумаге координаты границ могут расходиться с измеренными кадастровым работником из-за погрешности измерений, и величины таких погрешностей должны не превышать установленные нормы.

Рассмотрим допустимые нормы и расскажем о формулах и порядке расчета по действующему законодательству.

Показать содержание

• Что такое точность определения координат?
• Законодательство
• Допустимые нормы расхождения
• От чего зависит величина отклонения?
• Как правильно рассчитать: используемые формулы

Среднеквадратичный расчет     Метод допустимой площади     Диагональный    
• Примеры вычисления
• Показатели для муниципальных и государственных земель

Что такое точность определения координат?

Границы всех земельных наделов проводятся между угловыми (характерными) точками, а положение угловых точек определяется относительно опорных межевых пунктов, разбросанных по 2-4 пункта на один кв. километр и имеющих координаты в системе GPS.

Погрешностью измерений называют разность между истинными координатами угловой точки и координатами, измеренными кадастровым инженером. Погрешность неизбежно возникает при измерениях и складывается из следующих факторов:

1. человеческий фактор;
2. неточность измерительных приборов;
3. погодные условия;
4. особенности рельефа местности.

Одной из основных величин, применяемых для расчёта погрешности, является пункт съемочного обоснования. Это точка на местности, где кадастровый инженер устанавливает измерительное оборудование, и неровности рельефа могут привести к смещению точки установки и возрастанию общей погрешности.

Любой измерительный прибор незначительно искажает измеренную им величину из-за особенностей его конструкции, а при снятии показаний с нецифровых приборов, такие показания могут расходиться у разных работников.

СПРАВКА! Величина расхождения показаний, снятых с одного и того же геодезического прибора разными кадастровыми работниками, принимается равной половине цены деления такого прибора.

Для уменьшения погрешности измерения положения одной и той же граничной точки проводят несколько раз.

Точностью определения границ называют максимальное отклонение измеренной величины от среднего значения всех измеренных величин для одного и того же поворотного пункта. Увеличение числа проведённых измерений повышает точность итоговых расчётов.

Законодательство

Согласно части 13 ст. 22 закона № 218, допустимые погрешности при измерениях координат угловых точек, а также методы проводимых измерений и формулы расчёта погрешностей отображены в приказе Минэкономразвития №90.

Определены следующие методы определения координат угловых пунктов:

• полигонометрический;
• спутниковый;
• аналитический;
• фотографический;
• картометрический.

Началом координатной системы при определении положения угловых (характерных) пунктов является специальная опорная сеть межевания, (п. 4 прил. № 1 приказа № 90).

Допустимые нормы расхождения

При проведении межевых работ по уточнению границ земельного надела или при определении места границ вновь образуемых наделов при выделе или разделе участков могут возникнуть расхождения значений площадей между отображённой в кадастровом паспорте и вновь рассчитанной.

ВНИМАНИЕ! Рассчитанная площадь надела земли с уточнёнными границами не может превышать площадь данного надела, указанную в кадастровых документах больше, чем на предельный минимальный размер земельного надела, установленный законом для данного вида земли.

Минимальные размеры устанавливаются региональными и муниципальными нормативными актами с небольшими различиями в зависимости от субъекта федерации. Для большинства субъектов нормы расхождения площади в сторону увеличения после уточнения границ определены следующим образом (в зависимости от целевого назначения земель):

• участки для индивидуального строительства – 300 кв. м;
• участки для дачного строительства – 600 кв. м;
• участки под крестьянские хозяйства – 600 кв. м;
• участки под ЛПХ – 400 кв. м;
• наделы для огородничества (без права строительства) – 400 кв. м;
• земли под гараж – 18 кв. м;
• места под уличную торговлю – 5 кв. м.

Величина допустимых норм расхождения может быть уменьшена до 2-х раз местным законодательством, в зависимости от ситуации в регионе.

От чего зависит величина отклонения?

После проведения измерений на местности кадастровый инженер производит расчёты погрешности. Значения погрешности зависят от следующих факторов:

1. количества проведённых измерений;
2. метода определения погрешности;
3. внешних условий;
4. отношения максимального расстояния S между двумя угловыми точками участка и минимального расстояния D от одной из точек участка до опорного пункта межевания.

К внешним условиям относят погоду, погрешность приборов, квалификацию кадастрового инженера и т.д. Чем большее число измерений проведено, тем точнее можно рассчитать погрешность при межевании, приближаясь к истинному значению координат границ.

Как правильно рассчитать: используемые формулы

Величина S рассчитывается путём измерения расстояния между двумя самыми отдалёнными друг от друга поворотными точками участка, а для расчёта D измеряется расстояние от опорного пункта межевых сетей до самой близкой к данному пункту поворотной точки.

ВАЖНО! Величина погрешности при межевых работах увеличивается по мере возрастания значения отношения S/D, которое растёт по мере приближения границ участка к опорным межевым сетям.

К основным методам определения погрешностей, применяемых при межевании, относят следующие:

• метод среднеквадратичной погрешности;
• метод допустимой площади;
• диагональный метод.

Среднеквадратичный расчет

Метод расчёта величины среднеквадратичной погрешности M_t описан в приказе Минэкономразвития №90.

Среднеквадратичная величина M_t является основной единицей сравнения в методах допустимой площади и диагональном методе.

Метод допустимой площади

При расчёте погрешности по методу допустимой площади необходимо вычислить значение площади участка после проведения межевых работ П_(выч) и значение площади, указное в кадастровом документе П_(кад), после чего сравнить разность вычисленных площадей с допустимой площадью П_(доп).

Разность площадей П = П_(выч) – П_(кад). Значение П по абсолютной величине должно быть меньше или равно чем величина допустимой площади, рассчитываемая по формуле П_(доп) = 3,5*M_t*(П(_кад))^1/2.

Диагональный

В диагональном методе необходимо измерить точность расстояния и определения координат между двумя характерными угловыми точками границ, установленными в результате кадастровых работ. Важно учесть, что точки, взятые для измерения, должны быть не смежными, а отстоять одна от другой как можно дальше, образуя «диагональ» участка.

Вычисленное значение S должно быть меньше или равно, чем допустимая диагональ S_доп, которая рассчитывается по формуле S_доп = 2*M_t.

Диагональный метод в качестве дополнительного уточнения применяется при межевых работах, когда требуется высокая точность измерений, например, в землях городских поселений при определении границ земель, относящихся к многоквартирным домам.

Согласно п. 6 приказа № 90, для разных категорий земли допускается разное среднеквадратичное отклонение M_t. Максимальные допустимые значения Mt приведены в таблице.

№ п/п	Категория земель и вид их разрешённого пользования	Максимальное отклонение Mt,в метрах
1	Поселения и населённые пункты	0,1
2	Земельные наделы сельскохозяйственного назначения, предназначенные для ЛПХ, дачного и индивидуального жилищного строительства, а также для занятий садоводством и огородничеством	0,2
3	Прочие сельскохозяйственные территории	2,5
4	Земли промышленности и энергетики	0,5
5	Земли транспорта, связи и информатики	0,5
6	Земли обороны и специального назначения	0,5
7	Особо охраняемые наделы	2,5
8	Территории лесного и водного фондов	5,0
9	Земли запаса	5,0
10	Прочие территории	2,5

Примеры вычисления

ПРИМЕР 1. После проведения межевых работ картографическим способом при определении границ водоёма были измерены значения среднеквадратичной погрешности положения места геодезического измерения относительно опорного пункта m₀ = 5,6 метров.

Среднеквадратичная погрешность положения угловой точки относительно места измерения m₁ при картографическом способе принимается равной 0,0005 метров, (п. 13 приложения №1 к приказу № 90).

В первую очередь необходимо вычислить среднеквадратичное отклонение Mt.

M_t = ((m₀)² + (m₁)²)^1/2 = (5,6² + 0,0005²)^1/2 = (31,36 + 2,5*10^-7)^1/2 = (31,36000025)^1/2 = 5,600000022.

Значение M_t = 5,6 больше, чем допустимое для земель водного фонда отклонение, равное 5, следовательно, при указании в межевом плане данной граничной точки кадастровому инженеру придётся обосновывать её координаты пояснительной запиской.

ПРИМЕР 2. При уточнении границ на прямоугольном дачном участке были определены новые координаты граничных точек, для которых были рассчитаны значения m₀ и m₁ следующим образом:

1. для первой точки – m₀ = 0,010; m₁ = 0,004;
2. для второй – m₀ = 0,012; m₁ = 0,004;
3. для третьей – m₀ = 0,011; m₁ = 0,005;
4. для четвёртой – m₀ = 0,009; m₁ = 0,003.

Сначала вычисляются значения Mt для каждой из четырёх точек:

• M_t1 = ((m₀)² + (m₁)²)^1/2 = ((0,01)² + (0,004)²)^1/2 = 0,01078;
• M_t2 = ((0,012)² + (0,004)²)^1/2 = 0,01265;
• M_t3 = ((0,012)² + (0,004)²)^1/2 = 0,01208;
• M_t4 = ((0,012)² + (0,004)²)^1/2 = 0,00949.

Ни одно из рассчитанных значений Mt не превысило 0,2 метра, следовательно, допущенные погрешности находятся в пределах допустимой нормы.

Показатели для муниципальных и государственных земель

Определение точности измерении при геодезических работах по уточнению границ муниципальных земель, допустимое среднеквадратичное отклонение M_t равно 0,1 метра для участков – частей генерального плана застройки, расположенных внутри красных линий границ муниципалитета, и 0,2 метра для участков под внутригородские личные подсобные хозяйства, не отнесённые к сельскохозяйственным территориям.

Государственные земли разграничиваются по решению федеральных властей и могут иметь в своём составе любые категории земель, и максимальное расхождение документально подтверждённых границ таких земель с рассчитанными при кадастровых работах определяется согласно таблице выше.

При расчёте погрешностей государственных земель любой категории, относящихся к особо ценным землям, а также землям заповедников (кроме водного фонда), максимальное среднеквадратичное отклонение составляет 2,5 метра.

Итак, при определении границ земельных наделов в рамках межевых работ неизбежно возникают погрешности, обусловленные неточностью проводимых измерений. Величины таких погрешностей не должны превышать установленные правительством значения для каждой категории земли. Для определения погрешности используются разные методы, в зависимости от требуемой точности измерений.

• Главная
• Вопросы и ответы

Среднеквадратичная ошибка (RMSE)

Краткая объяснение что такое RMSE применительно к данным ДЗЗ

Обсудить в форуме Комментариев — 1

Среднеквадратичная ошибка (Root Mean Square Error, RMS Error, RMSE) — расстояние между двумя точками.

В случае если речь идет о привязке данных, в качестве точек между которыми измеряется расстояние могут выступать:

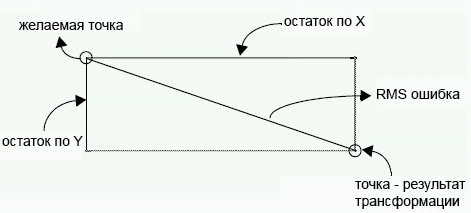
1. Исходная точка и конечная точки (например результат трансформации), в этом случае RMSE будет показателем насколько исходная точка близка к конечной — текущая ошибка.
2. Желаемое положение выходной точки (точка поставленная пользователем) и результатом ее трансформации (точка поставленная моделью). Трансформация — то или иное математическое преобразование исходных координат в конечные, примером такого преобразования может быть аффинная или полиномиальная трансформация. В данном случае RMSE показывает насколько используемая трансформация позволяет точно приблизить исходную точку к конечной, т.е. RMSE в этом случае — ошибка трансформации.

Как видно на иллюстрации ниже, выходные точки 1, 2, 3 поставленные оператором (синие) совпадают с трансформированными (расчетными) значениями (зеленые) и не видны из-за точного совпадения, а вот точка 4 поставлена не там, куда бы она попала используя ту же трансформацию, это дает возможность вычислить для нее RMSE, для точек 1, 2, 3 RMSE = 0.

Привязываемое изображение слева, изображение используемое в качестве источника координат (привязанное) справа.

Примечание: здесь и далее в статье, как и в ERDAS IMAGINE Field Guide, RMS определяется как расстояние (длина гипотенузы), что не совсем соответствует определению Root Mean Squared, так как отсутствует компонент усреднения, классический RMS должен вычисляться делением выражения под корнем на N измерений, в этом случае на 2. В данном случае удобнее называть RMS — расстоянием.

Ошибка RMS рассчитывается по следующей формуле, представляющей из себя формулу вычисления расстояния:

где x_i, y_i — исходные координаты, x_r, y_r — конечные координаты

RMSE выражается как расстояние в единицах исходной системы координат, то есть, если вы привязываете только что отсканированную карту, то RMSE будет выражаться в пикселях (или долях пикселя), если вы производите дополнительную привязку снимка, то RMSE будет показывать значения в метрах. Значение RMSE равное 2 для определенной точки будет означать, что ее исходная координата удалена на 2 пикселя или метра от конечной (расчетной) точки.

Чтобы лучше понять когда и как можно получить RMSE при привязке можно использовать следующий алгоритм, иллюстрирующую процесс привязки с помощью аффинного преобразования:

1. Получение изображения, например сканированием, изображение получает пиксельную систему координат X,Y (колонка, ряд).
2. Расстановка трех точек с начальными и конечными координатами. Эти координаты указывают:
   • Начальные координаты — положение точки на непривязанном материале (координаты конкретного пиксела по системе ряд/колонка);
   • Конечные координаты — положение точки на привязанном материале, любом источнике координат, географических или спроектированных.
3. Три точки — минимальное количество, необходимое для того, чтобы решить систему уравнений аффинного преобразования:

   x₀ = a+ b*x + c*y
   y₀ = d + e*x + f*y

   Решение уравнения заключается в нахождении всех шести коэффициентов, например решением системы уравнений:

   x1′ = a + b*x1 + c*y1
   y1′ = d + e*x1 + f*y1
   x2′ = a + b*x2 + c*y2
   y2′ = d + e*x2 + f*y2
   x3′ = a + b*x3 + c*y3
   y3′ = d + e*x3 + f*y3

   Если точек меньше чем минимально необходимо — решить систему невозможно, нельзя найти коэффициенты трансформации и соответственно невозможно произвести пересчет координат. RMSE для точек также вычислить невозможно.

4. Расстановка минимально необходимого количества точек для данного преобразования (трех) приводит к тому, что RMSE для каждой точки становится равна 0. Можно производить трансформацию. Однако в таком случае мы не можем сделать выводов о качестве точек, ведь для этого надо рассчитать RMSE, а значит….
5. Ставим дополнительные точки. Появление новых данных как правило приводит к тому, что то положение, куда мы ставим конечную точку в процессе привязки и ее расчетное положение не совпадают. Это делает возможным расчет RMS ошибки.

С примером и математикой расчета полиномиального преобразования 2-ой степени можно прочитать в статье «Полиномиальные преобразования — вычисления и практика».

Помимо RMSE часто также можно увидеть также значения ошибки по одной из осей X или Y. Эти значения являются остатками (residuals) и могут быть рассчитаны для каждой точки. Изучение значений этих ошибок может помочь понять, почему привязанный материал смещен по одной из осей. Это проблема часто возникает при привязке данных полученных при съемке под углом (не в надир).

Уравнение вычисления RMS для каждой точки можно переписать как:

где XR и YR — остаточные ошибки по X и Y соответственно.

Графически ошибки по X и Y, а также RMSE соотносятся следующим образом:

Вычислив RMSE для каждой точки, можно также определить общую ошибку по X (Rx), Y (Ry) и общую RMSE (T) используя следующие формулы:

где n — число контрольных точек, i — порядковый номер контрольной точки, d — расстояние между парой точек.

Связь со средним расстоянием

Другим, достаточно объективным, способом оценить точность привязки является среднее расстояние, которое очень похоже по формуле на RMSE, но является менее консервативным показателем, так как расстояния не возводятся в квадрат как в RMSE. Выразив расстояние через d, приведем для сравнения формулы вычисления общей RMSE (T) и среднего расстояния (MD):

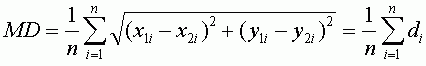
RMSE является более общеупотребимым в литературе.

Другим распространенным способом описания точности набора измерений являются квантили дробные стандартному отклонению (сигма).

Вклад точки в общую RMSE

Для того, чтобы вычислить вклад точки в общую ошибку (E_i), необходимо разделить RMSE этой точки (R_i) на общую RMSE.

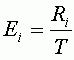
Допуск RMSE

В большинстве случаев, вместо того, чтобы усложнять тип трансформации (например переходить к более высоким порядкам полиномиальных преобразований) имеет смысл допустить некоторую ошибку. Величину допустимой RMSE можно представить как окно, окружающее точку с желаемыми координатами, положением расчетной точки внутри которого считается корректным. Например, если допуск RMSE равен 2, то расчетный пиксел может находится в двух пикселях от указанного оператором и являться допустимым. Величина допустимой ошибки зависит от типа и точности данных, задачи и точности контрольных точек.

Важно помнить, что RMSE указывается в пикселях, поэтому, если привязываются данные Landsat имеющие разрешение 30 метров и задача осуществить привязку с точностью не меньше тех же 30 метров, то RMSE не должна превышать 1.00 (пикселя).

Оценка RMSE

Если RMSE расчитана и найдена слишком высокой, есть 4 варианта решения проблемы:

1. Найти и удалить контрольные точки с большой RMSE, подразумевая, что это наименее точные точки. Это чревато еще возникновением еще больших ошибок, если отбраковываемая точка — единственная на большой участок изображения.
2. Увеличить допуск RMSE.
3. Увеличить сложность функции трансформации, которая более точно будет соответствовать введенным точкам. RMSE точек при этом уменьшится, однако использование сложных криволинейных функций может привести к нежелательным сильным искажениям растра.
4. Оставить только точки в которых Вы уверены, что они правильны.

В статье использованы материалы ERDAS IMAGINE Field Guide

Обсудить в форуме Комментариев — 1

Последнее обновление: September 09 2021

Дата создания: 27.07.2007

Автор(ы): Максим Дубинин

Средняя
квадратическая ошибка:

,при n
→
∞

Средняя квадратическая
ошибка более эффективна (чувствительна
к большим по модулю ошибкам), устойчива
(мало меняется с изменением числа
измерений).

36.Предельная ошибка. Понятие относительной ошибки.

Предельная ошибка:
результаты измерений неизбежно
сопровождаются ошибками. Максимальное
значение которых не должно превышать
определенного предела для данных условий
съемки и прибора.

Относительная
ошибка: ошибка
в измерении предмета относительно
этлона.

∆=L—X
,

где
L
это измеренная величина а X
абсолютная величина.

37. Принцип арифметической середины. Средняя квадратическая ошибка арифметической середины.

В случае равноточных
измерений арифметическое среднее
вычисляется по формуле

где [l]
– сумма результатов измерений; n
– их число.

Средняя
квадратическая ошибка
функции такого вида будет иметь вид:

,при n
→
∞

Средняя квадратическая
ошибка более эффективна (чувствительна
к большим по модулю ошибкам), устойчива
(мало меняется с изменением числа
измерений).

38. Вывод формулы Бесселя для средней квадратической ошибки.

По Гауссу :

, где ∆
— истинная случайная ошибка.

По
Бесселю:

, где υ
–
вероятная ошибка.
X
– среднее
значение измеренной величины.

По Гауссу:

По Бесселю:

39. Средняя квадратическая ошибка функции общего вида.

Средняя квадратичная
ошибка функции общего вида:

,
где a,b,c,…t
независимые переменные.

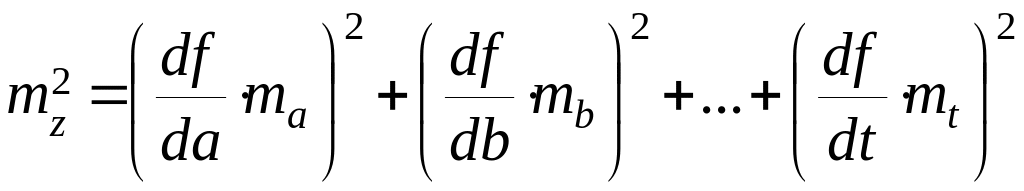
40. Оценка точности двойных равноточных измерений.

Измерение
—
это процесс сравнения некоторой
физической вели­чины
с однородной ей величиной, принятой за
единицу измерения. Результат
любого измерения q
— это число (или коэффициент), показы­вающее,
во сколько раз измеряемая величина Q
больше
или меньше единицы
измерения n:

Q=
qn

Результат
измерений неизбежно содержит ошибку.
Если обозна­чить
через l
результат
измерений, а через X
точное
значение измеряемой
величины, то ошибка результата измерений
Δ определится выра­жением

Δ=l
—
X.

Измерения
выполняют при наличии следующих условий
и факто­ров:
объект измерения, наблюдатель,
измерительный прибор, метод измерения,
внешняя среда, момент измерения.

Измерения,
выполненные в одинаковых условиях,
называют равноточными.
Вследствие
изменений, происходящих с объектом
измерений, наблюдателем, прибором и
внешней средой с течением времени,
условия измерений меняются, и результаты
измерения нельзя
в этих случаях считать равноточными. В
случае
соблюдения требований и правил при
геодезических измерениях получают
равно­точные
результаты.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Среднеквадратичная погрешность утверждена Приказом Росреестра от 23.10.2020 № П/0393 «Об утверждении требований к точности и методам определения координат характерных точек границ земельного участка, требований к точности и методам определения координат характерных точек контура здания, сооружения или объекта незавершенного строительства на земельном участке, а также требований к определению площади здания, сооружения, помещения, машино-места».

На деле, это значит, что допустимая погрешность, отступ от границ, определённых кадастровым инженером может быть не более 2,5 метров.

Погрешность зависит от категории земельного участка:

1. Земли населенных пунктов — 0,10;
2. Земли сельскохозяйственного назначения и предоставленные для ведения личного подсобного хозяйства, огородничества, садоводства, индивидуального гаражного или индивидуального жилищного строительства 0,20;
3. Земли сельскохозяйственного назначения, за исключением земельных участков, указанных в пункте 2 — 2,50;
4. Земли промышленности, энергетики, транспорта, связи, радиовещания, телевидения, информатики, землям для обеспечения космической деятельности, землям обороны, безопасности и землям иного специального назначения 0,50;
5. Земли особо охраняемых территорий и объектов — 2,50;
6. Земли лесного фонда, водного фонда и землям запаса 5,00;
7. Земельные участки, не указанные в пунктах 1 — 6 настоящих значений — 2,50.

Положение на местности характерных точек границы земельного участка и характерных точек контура здания, сооружения или объекта незавершенного строительства на земельном участке (далее — характерные точки) описывается плоскими прямоугольными координатами, вычисленными в системе координат, установленной для ведения Единого государственного реестра недвижимости.

При выполнении измерений в государственных системах координат для определения значения координат характерных точек в местных системах координат используются параметры перехода между соответствующей местной системой координат и государственными системами координат, определенные в соответствии с законодательством о геодезии и картографии.

Для оценки точности определения координат (местоположения) характерной точки рассчитывается средняя квадратическая погрешность.

Читайте также: «Выписка из ЕГРН. На что стоит обратить внимание?»

Не критическое, но все-таки важное значение в результатах межевания земельного участка имеет соблюдение нормативной точности определения координат поворотных точек границ. Для так называемых бытовых земельных участков (для индивидуального жилищного строительства, садоводства, дачного строительства, ведения личного подсобного хозяйства в черте поселения, огородничества) нормативная точность никогда не могла быть ниже 0,3 м. Однако, до сих пор не являются экзотикой выписки из ЕГРН, в которых погрешность установления координат — 0,5 м, 2,5 м и даже 7,5 м. То есть, при таком межевании допускается, чтобы углы участка «гуляли» на указанные неприемлемые для собственника величины.

Как правило, выписка из ЕГРН, в том числе об основных характеристиках земельного участка (не расширенная), содержит данные о его площади с указанием погрешности, например, 612 +/- 17 кв.м. В данном случае погрешность — 17 кв. м.

Для определения погрешности измерения площади участка ΔР кадастровые инженеры в основном используют формулу Методических рекомендаций проведения межевания, утвержденных Росземкадастром 17.02.2003 г.: ΔР= 3,5 Мt √P, где Мt — среднеквадратичная погрешность измерения координат поворотных точек границ, Р — площадь земельного участка. Отсюда легко определить Мt и сравнить ее с нормативным значением по Приказу Росреестра № П/0393 от 23.10.2020 г. « Об утверждении требований к точности и методам определения координат характерных точек границ земельного участка, требований к точности и методам определения координат характерных точек контура здания, сооружения и объекта незавершенного строительства на земельном участке, а также требований к определению площади здания, сооружения, помещения, машино-места».

В настоящее время для «бытовых» участков на землях населенных пунктов погрешность не должна быть выше 0,1 м, на землях сельхозназначения — не выше 0,2 м.

Что делать, если погрешность межевания больше нормативной? Ответ в каждом конкретном случае будет свой, но инструмент давления на продавца объекта появляется всегда.