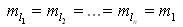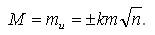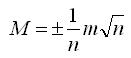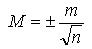Средняя квадратическая ошибка арифметической средины

Предельная
и относительная ошибки

Исходя
из четвертого свойства случайных ошибок
при геодези­ческих измерениях
одинаковой точности, за окончательный
ре­зультатпринимаютсреднее
арифметическоеиз ряда измерений.

Если
измерена одна и та же величина п
раз
и получены результаты: l₁,
l₂
,
l₃….l_n

(8)

Величина
х
называется
арифметической
срединой
или вероятнейшим
значением измеренной
величины.

Разности
между каждым измерением и арифметической
сре­диной называются вероятнейшими
ошибками измерений

(9)

Сложив
равенства (9), получим

(10)

Из
формул (8) и (10) следует, что
=
0.

Точность
результатов измерений
оценивается средней квадратической
ошибкой. Средняя
квадратическая ошибка одного
измерения вычисляется по формуле

(11)

где
[v²]—
сумма квадратов вероятнейших ошибок;
п
—
число из­мерений.

Средняя
квадратическая ошибка арифметической
срединывычисляется
по формуле

(12)

Предельная ошибка
не превышает утроенной средней
квадратической ошибки, т.е.

(13)

Пример.
Линия измерена шесть раз. Определить
ее вероятнейшую длину и оценить точность
этого результата. Вычисления приведены
в таблицу 1.

Таблица 1

№ п/п	Длина линии, м	Ν, см	ν2	Вычисления
1	225,26	+6	36	m = M=
2	225,23	+3	9
3	225,22	+2	4
4	225,14	+6	36
5	225,23	+3	9
6	225,12	+8	64
Хср=225,20	[v]=0	[V2]=158.

Относительная
ошибка вероятнейшего значения изме­ненной
линии равна

.

4.3 Средняя квадратическая ошибка функций измеренных величин

Если
мы имеем функцию суммы или разности
двух независимых величин

,

то
квадрат
средней квадратической
ошибки функции выразится формулой

m_z²=m_x²+m_y²

При

Пример.
Линия на плане масштаба 1:5000 измерена
по частям. Одна часть длиной 600,5 м, вторая
часть длиной 400,0 м. Найти средние
квадратические ошибки суммы и разности
этих длин и соответствующие им
относительные ошибки.

Ответ.
Средняя квадратическая ошибка суммы
и разности двух длин будет т_z=
т=0,5м

=
0,7 м, где m
= 0,5 м — точность масштаба. Относительные
ошибки суммы и разности длин соответственно
равны

Если функция имеет
вид

,

то

(14)

т.
е. квадрат средней квадратической
ошибки алгебраической суммы аргументов
равен сумме квадратов средних
квадратических ошибок слагаемых.

Если
m₁=m₂=m₃=…=m_n=m,то
формула(14) примет вид

т.
е. средняя квадратическая ошибка
алгебраической суммы (разности)
измеренных с одинаковой точностью
величин в
раз
больше средней квадратической ошибки
одного сла­гаемого.

Пример.
В шестиугольнике каждый угол измерен
с одина­ковой точностью 0,5′, средняя
квадратическая ошибка суммы всех
измененных углов
будет

Если функция имеет
вид

то

где
k₁,
k₂,
k_з,
…, k_п
— постоянные числа; m₁,m₂,m₃,…,
т_п
—
средние квадратические ошибки
соответствующих аргументов. Если имеем
функцию многих независимых переменных
общего вида

то

.
(15)

Из
формулы (15) следует, что квадрат средней
квадратиче­ской ошибки функции общего
вида равен сумме квадратов про­изведений
частных производных по каждому аргументу
на среднюю квадратическую ошибку
соответствующего аргумента.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Арифметическая средина результатов равноточных измерений. Пусть имеем результаты многократных равноточных измерений одной величины: l₁, l₂, …, l_n. Рассмотрим их среднее арифметическое

. (5.7)

Из (5.1) следует l_i= Х + Δ_i (i = 1, 2, … n). Поэтому напишем

= X — .

Согласно (5.2) с увеличением числа измерений сумма случайных погрешностей, деленная на их число, стремится к нулю, и, следовательно, среднее арифметическое L стремится к истинному значению Х. Поэтому значение определяемой величины принимают равным среднему арифметическому.

Средняя квадратическая погрешность арифметической средины. Пусть точность результатов измерений l₁, l₂, …, l_n характеризуется средними квадратическими погрешностями

m₁ = m₂ = ¼ = m_n = m

и требуется найти среднюю квадратическую погрешность M арифметической средины.

Представим формулу (5.7) в следующем виде:

L = .

Среднюю квадратическую погрешность арифметической средины найдем как погрешность функции измеренных величин по формуле (5.6)

или

(5.8)

Формула (5.8) показывает, что погрешность арифметической средины с ростом числа измерений убывает пропорционально квадратному корню из этого числа. Так, чтобы погрешность среднего арифметического уменьшить в 2 раза, число измерений надо увеличить в 4 раза.

Обработка результатов равноточных измерений. Математическая обработка ряда результатов l₁, l₂, …, l_n прямых равноточных измерений одной величины выполняется в следующей последовательности:

1. Вычисляют среднее арифметическое L

.

2. Вычисляют поправки к v_i результатам измерений

(i = 1, 2, …, n)

Контролем правильности вычислений служит сумма поправок, которая должна быть близка к нулю.

3. Вычисляют среднюю квадратическую погрешность одного измерения по формуле Бесселя:

.

Значение m вычисляют с двумя-тремя значащими цифрами.

4. Вычисляют среднюю квадратическую погрешность среднего арифметического

.

Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:

$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$

MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.

Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:

$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$

Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:

$$y = 0,5252 * x + 17,306$$

Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):

$$MSE = frac{1}{9} × 4445 = 493$$

Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.

MSE и Scikit-learn

Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:

import sklearn
from sklearn.metrics import mean_squared_error

Инициализируем крошечные списки, содержащие реальные и предсказанные координаты y:

y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]

Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:

mean_squared_error(y_true, y_pred)

Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:

496.0

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Автор оригинальной статьи: @mmoshikoo

Фото: @tobyelliott