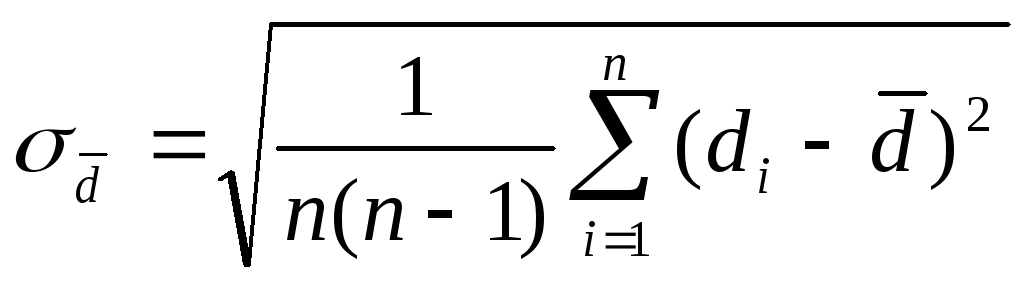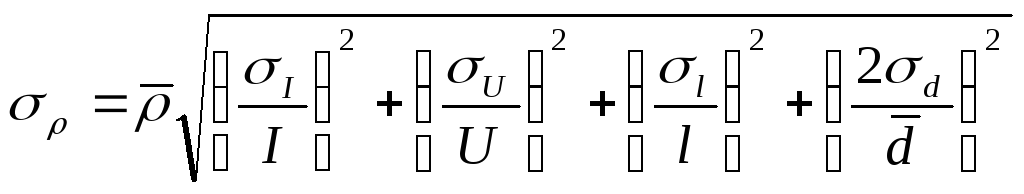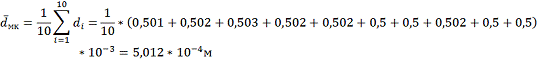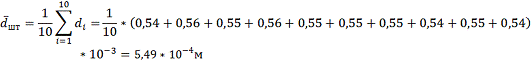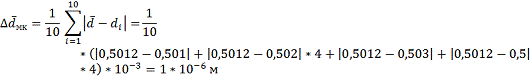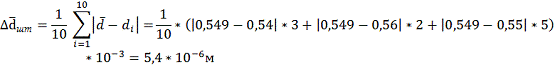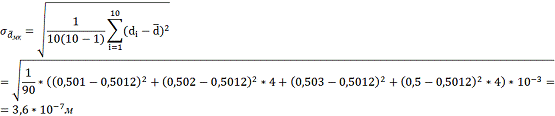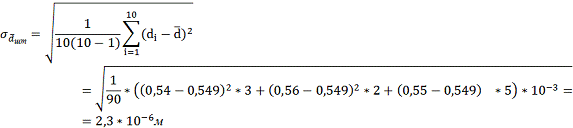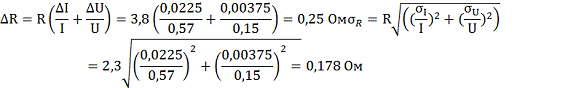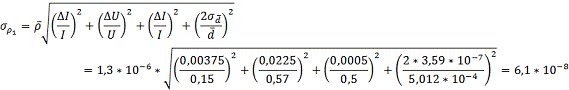Средняя квадратичная ошибка измерений диаметра

Министерство образования Российской
Федерации

Национальный минерально-сырьевой
университет «Горный»

(наименование
учебной дисциплины согласно учебному
плану)

Тема:
Оценка
точности прямых и косвенных измерений

Выполнила: студентка гр. АПН-12
_________ Малкова Ю.В.

^{(подпись)
(Ф.И.О.)}

Дата:
16.09.12

Проверил: доцент Тупицкая н.А.

^{(должность) (подпись)
(Ф.И.О.)}

Санкт-Петербург

2012

Цель работы – провести
прямые и косвенные измерения физических
величин. Сделать оценку точности
измерений.

Общие сведения:

R– величина,
характеризующая сопротивление проводника
электрическому току.

[R] = [Ом] – сопротивление
такого проводника, в котором при
напряжении 1В течет постоянный ток 1А.
Сопротивление зависит от формы, размеров
и материала проводника.

Каждую из физических величин – длина
проводника, диаметр сечения, напряжение
и сила тока(,
d, U, I)
– прямые измерения (можно измерить
непосредственно соответствующими
приборами с определенной точностью).
Величина удельного сопротивления (ρ)
– косвенные измерения (вычисляется
при помощи формул).

В общем случае результат измерения
величины Х представляют в виде:

,

где
погрешность
или ошибка измерения;
—
среднее значение величины.

Для однократных измерений за величину
ошибки принимается систематическая
погрешность, которую вносит сам прибор,
а средним считается измеренное значение
физической величины.

Измерение длины проволоки
проводится
однократно линейкой. Погрешность
измерения линейкой определяется как
половина цены наименьшего деления.

Значения тока I и напряжения
U измеряют однократно с
помощью электромагнитных приборов
(амперметра и вольтметра) для десяти
значений длины
.
Погрешность

и

этих измерений определяется по классу
точности, который указан на шкале
приборов, значению силы тока и напряжения,
которые могут быть измерены по шкале
прибора.

Диаметр проволоки измеряется многократно
штангенциркулем и микрометром. Проведя
n измерений, получим
результаты: d1,
d2,
d3,…,
dn.
Диаметр определяется как среднее
арифметическое. Если ошибка меньше
точности используемого прибора, то за
величину ошибки следует принять
последнюю.

Основные расчётные формулы:

Сила тока:

[]

Сопротивление проводника:
[],

Удельное сопротивление:
[]
= [Ом∙м]

Среднее значение диаметра:

Графическое вычисление среднего
значения удельного сопротивления:

,
где

Формулы погрешности:

При прямых измерениях:

Средняя абсолютная ошибка измерений
диаметра:

Средняя квадратичная ошибка измерений
диаметра:

Абсолютная погрешность прибора:
,
,
где К – класс точности приборов;

и

— наибольшие значения силы тока и
напряжения, которые могут быть измерены
по шкале прибора.

При косвенных измерениях:

Средняя абсолютная погрешность измерения
сопротивления:

Средняя квадратичная погрешность
измерения сопротивления:

Средняя абсолютная погрешность измерения
удельного сопротивления:

Средняя квадратичная погрешность
измерения удельного сопротивления:

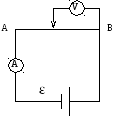
Схема установки:

АВ —
исследуемый участок

 — источник тока

V
– вольтметр

А —
амперметр

Таблица 1. Результаты измерений
диаметра проволоки штангенциркулем и
микрометром

Диаметр	Штангенциркуль	Микрометр
Размерность
мм	мм
d1	0,50	0,52
d2	0,48	0,49
d3	0,49	0,49
d4	0,51	0,52
d5	0,52	0,49
d6	0,50	0,52
d7	0,50	0,48
d8	0,48	0,48
d9	0,51	0,49
d10	0,51	0,52
	0,50	0,50
d
d	0,0042	0,0056
	0,02	0,032
	0,0084	0,0112

Таблица 2. Результаты измерений тока
и напряжения.

Номер опыта
	м	мм	A	A			Ом	Ом	Ом
1	0,50		0,065		0,29		4,46	0,805	0,5751
2	0,45		0,065		0,27		4,15	0,780	0,5610
3	0,40		0,065		0,25		3,85	0,758	0,5489
4	0,35		0,065		0,23		3,54	0,734	0,5362
5	0,30		0,065		0,20		3,08	0,699	0,5193
6	0,25		0,065		0,18		2,77	0,675	0,5086
7	0,20		0,065		0,16		2,46	0,651	0,4986
8	0,15		0,065		0,14		2,15	0,626	0,4896
9	0,10		0,065		0,12		1,85	0,604	0,4839
10	0,05		0,065		0,10		1,54	0,580	0,4770

Примеры расчетов:

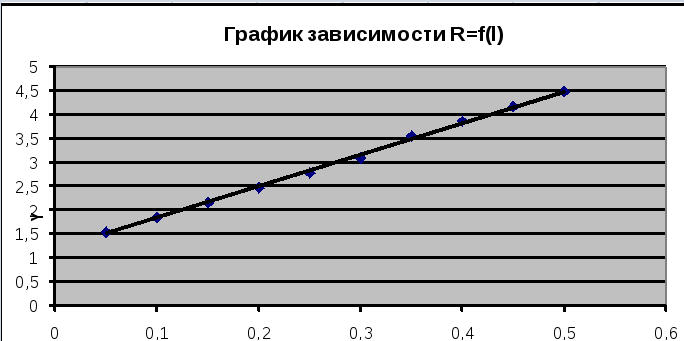
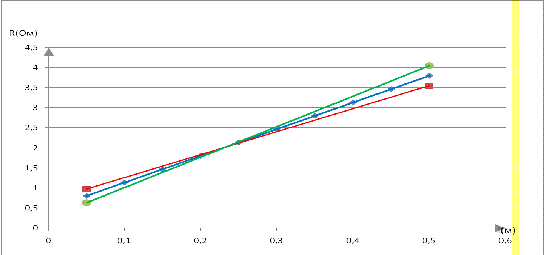
График зависимости R = f(l).

Таблица
данных для графика:

l, м	R, Ом
0,50	4,46
0,45	4,15
0,40	3,85
0,35	3,54
0,30	3,08
0,25	2,77
0,20	2,46
0,15	2,15
0,10	1,85
0,05	1,54

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики

Отчет

ЛАБОРАТОРНАЯ РАБОТА №1

“Оценка точности прямых и косвенных измерений”

Выполнил: студент группы НТС– 22 ______________ /

Адальшин Д.К. /

(подпись) (Ф.И.О.)
Дата: _________________
Проверил: _____________

/ /

(подпись) (Ф.И.О)

Санкт-Петербург

2023

Цель работы — обработать данные прямых и косвенных измерений физических величин.

Краткое теоретическое содержание

Явление, изучаемое в работе: возникновение тока на участке электрической цепи.

Определение основных физических понятий, объектов, процессов и величин:

Электрический ток – упорядоченное (направленное) движение заряженных частиц.

Напряжение – разность потенциалов в начальной и конечной точках траектории движения заряда, где потенциал – это отношение потенциальной энергии заряда в поле к этому заряду. Ток всегда направлен от большего потенциала к меньшему. [U] = 1Вольт, где 1 Дж – единица измерения работы, совершённой для перемещения заряда.

Сила тока – отношение заряда q, переносимого через поперечное сечение проводника площадью S за промежуток времени t, к этому промежутку: [I] = 1Кл/с = 1 Ампер, где (Кл) = Кулон – единица измерения заряда.

Электрическое сопротивление – физическая величина, при неизменной температуре и постоянном сечении однородного проводника прямо пропорциональная его длине l и обратно пропорциональная площади S поперечного сечения этого проводника: [R] = 1Ом

Амперметр – физический прибор, предназначенный для измерения силы тока в замкнутой цепи.

Вольтметр– физический прибор, предназначенный для измерения напряжения в замкнутой цепи.

Штангенциркуль – физический прибор, предназначенный для измерения диаметра проволоки.

Микрометр – физический прибор, предназначенный для измерения диаметра проволоки с большей точностью, чем у штангенциркуля.

Схема установки

Электрическая схема

Основные расчетные формулы

Удельное сопротивление: ,

U – разность потенциалов на концах проводника, В

I – сила тока в проводнике, А

d — диаметр проволоки, измеренный микрометром, м

l — длина проволоки, м

Среднее значение диаметра проволоки: , м

n — количество измерений

d₁, d₂, …, d_n — диаметры проволоки в разных местах, м

Сопротивление проводника: ,

Графическое вычисление:

Формулы погрешности прямых измерений

1. Величина средней абсолютной погрешности измерений диаметра:
2. Средняя квадратичная ошибка измерений диаметра:
3. Абсолютная погрешность прибора:

Формулы погрешности косвенных измерений

1. Средняя абсолютная погрешность прибора
2. Средняя квадратичная ошибка:
3. Абсолютная погрешность:
4. Средняя квадратичная ошибка:

Таблицы

№п.п.	Название прибора	Число делений	Цена деления	Класс точности	Предел измерений	Абсолютная приборная погрешность
1	Амперметр	50	5мА	1,5	250мА	3,75мА
2	Вольтметр	30	0,05В	1,5	1,5В	0,0225В
3	Штангенциркуль	3000	0,05мм	—	30см	0,05мм
4	Микрометр	31250	0,01мм	—	25мм	0,01мм

Таблица 1 Погрешности приборов

Физ. величина	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10		∆d	σd
Ед. изм. / прибор	мм	мм	мм	мм	мм	мм	мм	мм	мм	мм	мм	мм	мм	—	—
Штангенциркуль	0,50	0,50	0,50	0,50	0,50	0,50	0,50	0,50	0,50	0,50	0,50	0	0	0	0
Микрометр	0,53	0,51	0,50	0,51	0,52	0,49	0,50	0,51	0,50	0,53	0,51	0,01	0,004	0,02	0,008

Таблица 2 Результаты измерений диаметра проволоки штангенциркулем и микрометром

Физическая величина	l	∆l	I	∆I	U	∆U	R	∆R	σR
Ед. изм. / № опыта	м	м	мА	мА	В	В	Ом	Ом	Ом
1	0,500	0,001	210	3,75	0,70	0,0225	3,3	0,165	0,121
2	0,448	210	0,65	3,1	0,163	0,121
3	0,408	210	0,60	2,9	0,161	0,120
4	0,367	210	0,55	2,6	0,153	0,116
5	0,325	210	0,50	2,4	0,151	0,116
6	0,283	210	0,45	2,1	0,143	0,111
7	0,202	210	0,35	1,6	0,131	0,107
8	0,172	210	0,30	1,4	0,130	0,108
9	0,132	210	0,20	1,0	0,130	0,114
10	0,091	210	0,15	0,7	0,118	0,106

Таблица 3 Результаты измерения сопротивления

Физическая величина
Ед. изм. / № опыта	Ом*м*10-6	Ом*м*10-6	Ом*м*10-6	Ом*м*10-6
1	1,362	1,517	0,168	0,085
2	1,411
3	1,431
4	1,458
5	1,497
6	1,547
7	1,686
8	1,697
9	1,474
10	1,603

Таблица 4 Вычисление удельного сопротивления проводника

Вычисление погрешностей

Для амперметра:

Для амперметра:

Для микрометра:

1. Вычисление среднего значения диаметра проволоки d:

1. Определение средней абсолютной погрешности:

1. Определение средней квадратичной погрешности:

Для удельного сопротивления:

1. Определение средней абсолютной погрешности:

1. Определение средней квадратичной погрешности:

Для сопротивления проводника:

1. Определение средней абсолютной погрешности:

1. Определение средней квадратичной погрешности:

Пример вычислений

Для опыта №1:

Рисунок 1 Зависимость сопротивления проводника от его длины
График

По графику, среднее удельное сопротивление равно:

Результаты

1. Удельное сопротивление:

1. Значение удельного сопротивления проволоки, вычисленное графически:

Сравнение

1. Графическое и экспериментальное удельное сопротивление:

1. Экспериментальное удельное сопротивление:

1. Графическое удельное сопротивление:

Вывод

В ходе работы было вычислено удельное сопротивление проводника. Значения полученных погрешностей не велики. Разница между графическим и экспериментальным удельным сопротивлением составила 6,5%, между графическим и табличным 22,4%, а между экспериментальным и графическим 27,5. Такие расхождения свидетельствуют о том, что данный метод можно использовать для определения удельного сопротивления. Значения не столь точные, поскольку при измерении длины проводника и напряжения, приборы обладали недостаточной точностью. При измерении толщины проволоки следует использовать микрометр, так как при его использовании, измерения можно проводить на 25% точнее, о чем свидетельствует абсолютная приборная погрешность. Цель работы достигнута.

Оценка точности прямых и косвенных измерений

Министерство образования и науки
Российской Федерации

Федеральное государственное бюджетное
образовательное учреждение

высшего профессионального образования

Национальный минерально-сырьевой
университет «Горный»

Кафедра общей и технической физики

Отчёт по лабораторной работе № 1

По дисциплине: Физика

Выполнил: студент гр.ОНГ-12-2 _____________ /Митришкин Д.С./

Проверил:
профессор _____________ /Мустафаев С.А./

Санкт-Петербург

Цель работы — обработать данные прямых и косвенных измерений удельного
сопротивления проволоки.

удельное сопротивление
погрешность

Схема установки:

V-вольтметр

А-амперметр

АВ — искомый участок

Краткие теоретические сведения

Возникновение погрешностей в ходе измерений — при измерении физических
величин с помощью даже самых точных и совершенных средств и методов их
результат всегда отличается от истинного значения измеряемой физической
величины, т.е. определяется с некоторой погрешностью.

Погрешность средств измерения — это разность между результатом измерения
величины и настоящим (действительным) значением этой величины. Для рабочего
средства измерения настоящим (действительным) значением измеряемой величины
считается показание рабочего эталона более низкого разряда.

Причины возникновения погрешностей:

·        несовершенство измерительных приборов (инструментальные
погрешности),

·        несовершенство выбранного метода измерений или влияния
лабораторных приборов на измеряемую величину (методологические погрешности),

·        влияние внешних условий на одну или несколько величин,
влияющих на результат, например, температуры, влажности воздуха, внешних
электрических и магнитных полей и т.п. (внешние погрешности),

·        неправильный отсчет показаний приборов, невнимательность и
небрежность исследователя (субъективные погрешности).

Прямое измерение — измерение, проводимое прямым методом, при котором
искомое значение физической величины получают путем сравнения этой величины с
ее единицей.

Косвенное измерение — вычисление измеряемой величины по некоторой
расчетной формуле, куда входят константы и результаты прямых измерений.

Класс точности — основная метрологическая характеристика прибора,
определяющая допустимые значения основных и дополнительных погрешностей,
влияющих на точность измерения.

Сила тока — скалярная величина, численно равная заряду, протекающему в
единицу времени через сечение проводника.

Напряжение — работа электрических и сторонних сил по перемещению
единичного положительного заряда.

Сопротивление — физическая величина, характеризующая свойства проводника
и равная отношению напряжения на концах проводника к силе электрического тока,
протекающего по нему.

Удельное сопротивление — величина, характеризующая способность вещества
не проводить электрический ток.

Закон Ома для участка цепи: сила тока I, текущего по металлическому проводнику (при отсутствии
сторонних сил), пропорциональна падению напряжения U на проводнике:

I = U/R,

где I — сила тока в цепи, [I] = A (Ампер); U —
напряжение в цепи, [U] = В (вольт); R — сопротивление проводника, [R] = Ом.

R = l/S,

Где
 — удельное сопротивление, [] = ; l —
длина проводника, [l] = м (метр); S — площадь
поперечного сечения, [S] = м2

Удельное
сопротивление характеризует способность вещества проводить электрический ток и
зависит от химической природы вещества и условий в которых находится проводник.

RS/l

Площадь поперечного сечения S рассчитывается по измеренному значению диаметра d:

S =

Сопротивление R вычисляется по
измеренным значениям напряжения U и
тока I в цепи согласно закону Ома:

R = U/I

Исходя из выше указанных формул, получается выражение для нахождения
удельного сопротивления:

Измерения размеров проволоки проводим с помощью микрометра или
штангенциркуля. Силу тока измеряем амперметром, а напряжение вольтметром.

Основные расчётные формулы

Сопротивление
проводника ;

R —
сопротивление проводника, [R] = Ом; U — напряжение в цепи, [U] = В; I —
сила тока, [I] = A.

Удельное
сопротивление , ;

l- длина
проводника, [l] = м; d — диаметр проволоки, [d] = м.

Среднее
значение диаметра проволоки ;

Графическое
вычисление , где

R5 , R6-
сопротивление в 5-ом и 6-ом опытах.

L5 ,l6 —
длина проводника в 5-ом и 6-ом опытах.

— среднее
значение удельного сопротивления, [] = .

Формулы расчёта погрешностей

Погрешности прямых измерений:

Величина средней абсолютной ошибки диаметра

;

ср —
средняя абсолютная ошибка измерений диаметра, [ср] = м

— среднее
значение диаметра, [] = м

di — диаметр
того или иного опыта,

di — число
измерений

Средняя
квадратичная ошибка измерений диаметра

;

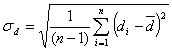
d- средняя квадратичная ошибка диаметра, [d] = м

Абсолютная
погрешность амперметра ;

—
абсолютная погрешность амперметра, [] = A

Iпр. —
наибольшее значение силы тока, которое может быть измерено по шкале прибора.

K — класс
точности прибора

Абсолютная
погрешность вольтметра

;

— наибольшее значение напряжения, которое может быть измерено по шкале
прибора.

Погрешности косвенных измерений

Средняя абсолютная погрешность

—
абсолютная погрешность косвенных измерений удельного сопротивления

— среднее
значение удельного сопротивления, [] =

U- абсолютная погрешность вольтметра

—
абсолютная погрешность амперметра

d- абсолютная ошибка измерений диаметра

— среднее
значение диаметра l- длина проводника

Средняя
квадратичная ошибка

;

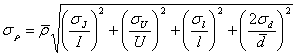
p- средняя квадратичная ошибка косвенных измерений
удельного сопротивления

— среднее
значение удельного сопротивления

J-
средняя квадратичная ошибка косвенных измерений силы тока

U- средняя квадратичная ошибка косвенных измерений
напряжения

l -средняя квадратичная ошибка косвенных измерений длинны
проводника

d-
средняя квадратичная ошибка косвенных измерений диаметра проводника

Средняя абсолютная погрешность

;

—
абсолютная погрешность косвенных измерений сопротивления

Средняя
квадратичная ошибка

;

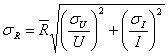
R- средняя квадратичная ошибка косвенных измерений
сопротивления

Ход работы:

)        Измерить штангенциркулем диаметр проволоки в десяти точках
проводника и определить погрешность, фиксирую результаты измерения и расчетов в
табл. 1;

Таблица 1. «Результатов измерений диаметра проволоки штангенциркулем и
микрометром»

Диаметр (мм)	Штангенциркуль, м	Микрометр, м
	0,00054	0,000501
	0,00056	0,000502
	0,00055	0,000503
	0,00056	0,000502
	0,00055	0,000502
	0,00055	0,0005
	0,00055	0,0005
	0,00054	0,000502
	0,00055	0,0005
	0,00054	0,0005
	0,000549	0,0005012
	0,0012
	0,0043	0,0007

Примеры вычислений:

)        Использую полученные данные для тока и напряжения (см. табл.2
«Результаты измерения тока и напряжений»), вычислим значения сопротивлений R:

Таблица 2. «Результаты измерения тока и напряжений»

№              l м.l,

мI AI

АU

BU

BR

ОмDR

ОмR

Oм
1	0,50	0,0005	0,15	0,00375	0,57	0,0225	3,80	0,25	0,178
2	0,45	0,0005	0,15	0,00375	0,52	0,0225	3,47	0,24	0,173
3	0,40	0,0005	0,15	0,00375	0,47	0,0225	3,13	0,23	0,169
4	0,35	0,0005	0,15	0,00375	0,42	0,0225	2,80	0,22	0,166
5	0,30	0,0005	0,15	0,00375	0,0225	2,47	0,21	0,162
6	0,25	0,0005	0,15	0,00375	0,32	0,0225	2,13	0,20	0,159
7	0,20	0,0005	0,15	0,00375	0,327	0,0225	2,18	0,20	0,160
8	0,15	0,0005	0,15	0,00375	0,22	0,0225	1,47	0,19	0,154
9	0,10	0,0005	0,15	0,00375	0,17	0,0225	1,13	0,18	0,153
10	0,05	0,0005	0,15	0,00375	0,12	0,0225	0,80	0,17	0,151

Примеры вычислений:

Построим
график зависимости

R=f(I)

где l, м — длина проводника и R, Ом — сопротивление.

l, м	R, Ом
0,5	3,8
0,45	3,47
0,4	3,13	2,8
0,3	2,47
0,25	2,13
0,2	1,8
0,15	1,47
0,1	1,13
0,05	0,8

)        Определим графически среднее значение удельного сопротивления:

Для I:

 Ом,

 Ом.

Тогда

 Ом*м

Для
II:

 Ом,

 Ом.

Тогда:

 Ом*м

Таким образом:

№ № опыта           
штангенциркуль

Ом*м*
микрометр

Ом*м*
1	1,7	1,5
2	1,9	1,5
3	1,9	1,6
4	1,9	1,6
5	1,9	1,6
6	2,0	1,7
7	2,1	1,8
8	2,2	2,0
9	2,7	2,2
10	3,7	3,1

Ом*м и

Ом*м

То
есть Ом*м

)        Вычислим
погрешности  результатов
косвенного определения удельного сопротивления для штангенциркуля:

Ом*м

 Ом*м

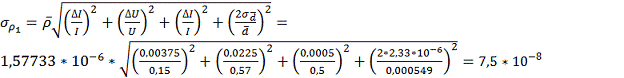
5)     

 Ом*м

Таким
образом, значения удельного сопротивления по штангенциркулю:

И
по микрометру:

Δρ штангенциркуль	Δρ микрометр	σρ штагенциркуль	σρ микрометр

Вывод:

·        при выполнении данной работы мы провели прямые и косвенные
измерения физических величин, а также выполнили оценку точности измерений;

·        выяснили, что сопротивление проволоки прямопропорционально
длине это проволоки, и эта зависимость линейна, что видно из графика, то есть,
теоретические при l=0 — R=0, но практически (из данных
графика) получим l=0 — R≠0, это противоречие
объясняется несовершенством измеретильной системы, на которой проводилась
работа, она имеет погрешности и ошибки.