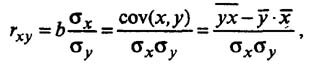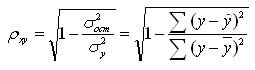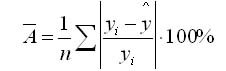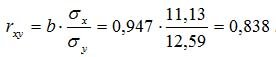2.6.1
Коэффициент детерминации.
Для оценки качества построенной модели
регрессии можно использовать коэффициент
детерминации
.
Коэффициент детерминации может быть
вычислен по формуле:

С другой стороны,
для парной линейной регрессии верно
равенство:
.
При
близости значения коэффициента
детерминации к 1 говорят, что уравнение
регрессии статистически значимо и
фактор
оказывает сильное воздействие на
результирующий признак.
При анализе модели
парной линейной регрессии по значению
коэффициента детерминации можно сделать
следующие предварительные выводы о
качестве модели:
-
Если
,
то будем считать, что использование
регрессионной модели для аппроксимации
зависимости между переменнымии
статистически необоснованно.
-
Если
,
то использование регрессионной модели
возможно, но после оценивания параметров
модель подлежит дальнейшему многостороннему
статистическому анализу. -
Если
,
то будем. считать, что у нас есть основания
для использования регрессионной модели
при анализе поведения переменной.
2.6.2 Средняя ошибка аппроксимации.
Другой
показатель качества построенной модели
–– среднее относительное отклонение
расчетных значений от фактических или
средняя
ошибка аппроксимации:
.
Построенное
уравнение регрессии считается
удовлетворительным, если значение
не превышает 10% – 12% .
3. Пример.
По
21 региону страны изучается зависимость
розничной продажи телевизоров ()
от среднедушевого денежного дохода в
месяц ().
|
Номер региона |
Среднедушевой |
Объем |
|
1 |
2 |
28 |
|
2 |
2,4 |
21,3 |
|
3 |
2,1 |
21 |
|
4 |
2,6 |
23,3 |
|
5 |
1,7 |
15,8 |
|
6 |
2,5 |
21,9 |
|
7 |
2,4 |
20 |
|
8 |
2,6 |
22 |
|
9 |
2,8 |
23,9 |
|
10 |
2,6 |
26 |
|
11 |
2,6 |
24,6 |
|
12 |
2,5 |
21 |
|
13 |
2,9 |
27 |
|
14 |
2,6 |
21 |
|
15 |
2,2 |
24 |
|
16 |
2,6 |
24 |
|
17 |
3,3 |
31,9 |
|
18 |
3,9 |
33 |
|
19 |
4 |
35,4 |
|
20 |
3,7 |
34 |
|
21 |
3,4 |
31 |
Необходимо
найти зависимость, наилучшим образом
отражающую связь между переменными
и
.
Рассмотрим вопрос
применения модели линейной регрессии
в этой задаче.
Построим
поле корреляции, т.е. нанесем исходные
данные на координатную плоскость. Для
этого воспользуемся, например,
возможностями MS
Excel
2003.
Подготовим таблицу
исходных данных.
Нанесем на
координатную плоскость исходные данные:
Характер
расположения точек на графике дает нам
основание предположить, что искомая
функция регрессии линейная:
.
Для оценки коэффициентов уравнения
регрессии необходимо составить и решить
систему нормальных уравнений ( ).
По исходным данным
рассчитываем необходимые суммы:
|
Номер региона |
|
|
|
|
|
|
1 |
2 |
28 |
56 |
4 |
784 |
|
2 |
2,4 |
21,3 |
51,12 |
5,76 |
453,69 |
|
3 |
2,1 |
21 |
44,1 |
4,41 |
441 |
|
4 |
2,6 |
23,3 |
60,58 |
6,76 |
542,89 |
|
5 |
1,7 |
15,8 |
26,86 |
2,89 |
249,64 |
|
6 |
2,5 |
21,9 |
54,75 |
6,25 |
479,61 |
|
7 |
2,4 |
20 |
48 |
5,76 |
400 |
|
8 |
2,6 |
22 |
57,2 |
6,76 |
484 |
|
9 |
2,8 |
23,9 |
66,92 |
7,84 |
571,21 |
|
10 |
2,6 |
26 |
67,6 |
6,76 |
676 |
|
11 |
2,6 |
24,6 |
63,96 |
6,76 |
605,16 |
|
12 |
2,5 |
21 |
52,5 |
6,25 |
441 |
|
13 |
2,9 |
27 |
78,3 |
8,41 |
729 |
|
14 |
2,6 |
21 |
54,6 |
6,76 |
441 |
|
15 |
2,2 |
24 |
52,8 |
4,84 |
576 |
|
16 |
2,6 |
24 |
62,4 |
6,76 |
576 |
|
17 |
3,3 |
31,9 |
105,27 |
10,89 |
1017,61 |
|
18 |
3,9 |
33 |
128,7 |
15,21 |
1089 |
|
19 |
4 |
35,4 |
141,6 |
16 |
1253,16 |
|
20 |
3,7 |
34 |
125,8 |
13,69 |
1156 |
|
21 |
3,4 |
31 |
105,4 |
11,56 |
961 |
|
Сумма |
57,4 |
530,1 |
1504,46 |
164,32 |
13926,97 |
Составляем систему
уравнений:
Имеем систему
линейных алгебраических уравнений,
которая может быть решена, например, по
формулам Крамера. Для этого вычислим
следующие определители:
Тогда, согласно
теореме Крамера,
Получаем уравнение
регрессии:
Величина
коэффициента регрессии
означает, что увеличение среднедушевого
месячного дохода на 1 тыс. руб. приведет
к увеличение объема розничной продажи
в среднем на 7 540 телевизоров. Коэффициентв данном случае не имеет содержательной
интерпретации.
Оценим тесноту
линейной связи между переменными и
качество построенной модели в целом.
Для оценки тесноты
линейной зависимости рассчитаем
коэффициент детерминации. Для этого
необходимо провести ряд дополнительных
вычислений.
Прежде
всего, найдем выборочное
среднее
по формуле:
.
Для рассматриваемого
примера имеем:
Теперь произведем
расчет остальных вспомогательных
величин:
|
Номер региона |
|
|
|
|
|
|
|
|
1 |
2 |
28 |
19,76 |
8,24 |
67,89 |
2,76 |
7,60 |
|
2 |
2,4 |
21,3 |
22,75 |
-1,45 |
2,11 |
-3,94 |
15,55 |
|
3 |
2,1 |
21 |
20,51 |
0,49 |
0,24 |
-4,24 |
18,00 |
|
4 |
2,6 |
23,3 |
24,25 |
-0,95 |
0,90 |
-1,94 |
3,77 |
|
5 |
1,7 |
15,8 |
17,52 |
-1,72 |
2,95 |
-9,44 |
89,17 |
|
6 |
2,5 |
21,9 |
23,50 |
-1,60 |
2,56 |
-3,34 |
11,17 |
|
7 |
2,4 |
20 |
22,75 |
-2,75 |
7,57 |
-5,24 |
27,49 |
|
8 |
2,6 |
22 |
24,25 |
-2,25 |
5,04 |
-3,24 |
10,52 |
|
9 |
2,8 |
23,9 |
25,74 |
-1,84 |
3,39 |
-1,34 |
1,80 |
|
10 |
2,6 |
26 |
24,25 |
1,75 |
3,08 |
0,76 |
0,57 |
|
11 |
2,6 |
24,6 |
24,25 |
0,35 |
0,13 |
-0,64 |
0,41 |
|
12 |
2,5 |
21 |
23,50 |
-2,50 |
6,24 |
-4,24 |
18,00 |
|
13 |
2,9 |
27 |
26,49 |
0,51 |
0,26 |
1,76 |
3,09 |
|
14 |
2,6 |
21 |
24,25 |
-3,25 |
10,54 |
-4,24 |
18,00 |
|
15 |
2,2 |
24 |
21,26 |
2,74 |
7,53 |
-1,24 |
1,54 |
|
16 |
2,6 |
24 |
24,25 |
-0,25 |
0,06 |
-1,24 |
1,54 |
|
17 |
3,3 |
31,9 |
29,48 |
2,42 |
5,86 |
6,66 |
44,32 |
|
18 |
3,9 |
33 |
33,96 |
-0,96 |
0,93 |
7,76 |
60,17 |
|
19 |
4 |
35,4 |
34,71 |
0,69 |
0,47 |
10,16 |
103,17 |
|
20 |
3,7 |
34 |
32,47 |
1,53 |
2,34 |
8,76 |
76,69 |
|
21 |
3,4 |
31 |
30,23 |
0,77 |
0,60 |
5,76 |
33,14 |
|
Сумма |
57,4 |
530,1 |
130,68 |
545,73 |
Здесь
столбец «»
– это значения,
рассчитанные с помощью построенного
уравнения регрессии, столбцы «»
и– это столбцы, так называемых, «остатков»:
разностей между исходными значениями,
и рассчитанными с помощью уравнения
регрессии,
а также их квадратов, а в последних двух
столбцах – разности между исходными
значениями,
выборочным средним,
а также их квадраты.
Для
вычисления коэффициента детерминации
воспользуемся формулой ( ):
Значение
коэффициента детерминации позволяет
сделать предварительный вывод о том,
что у нас имеются основания использовать
модель линейной регрессии в данной
задаче, поскольку
.
Построим
линию регрессии на корреляционном поле,
для чего добавим на координатной
плоскости точки, соответствующие
уравнению регрессии ().
Нанесем
теперь уравнение регрессии на диаграмму,
используя специальные средства Excel.
Для этого необходимо выделить правой
кнопкой мыши исходные точки и выбрать
опцию Добавить
линию тренда.
В
открывшемся меню Параметры
линии тренда
выбрать Линейную
аппроксимацию.
Далее поставить флажок напротив полей
Показывать
уравнение на диаграмме
и Поместить
на диаграмму величину достоверности
аппроксимации .
Нажав
на ОК, получаем еще одну прямую на
диаграмме, которая совпадает с построенными
ранее точками линии регрессии:
Сплошная
черная линия на диаграмме – это линия
регрессии, рассчитанная средствами
Excel.
Линия регрессии, построенная нами ранее,
совпала с данной линией регрессии.
Нетрудно убедиться, что уравнение
регрессии и коэффициент детерминации
тоже совпадают с полученными ранее
вручную.
Найдем
теперь среднюю ошибку аппроксимации
для оценки погрешности модели. Для этого
нам потребуется вычислить еще ряд
промежуточных величин:
|
Номер региона |
|
|
|
|
|
|
1 |
2 |
28 |
19,76 |
8,24 |
0,29 |
|
2 |
2,4 |
21,3 |
22,75 |
-1,45 |
0,07 |
|
3 |
2,1 |
21 |
20,51 |
0,49 |
0,02 |
|
4 |
2,6 |
23,3 |
24,25 |
-0,95 |
0,04 |
|
5 |
1,7 |
15,8 |
17,52 |
-1,72 |
0,11 |
|
6 |
2,5 |
21,9 |
23,50 |
-1,60 |
0,07 |
|
7 |
2,4 |
20 |
22,75 |
-2,75 |
0,14 |
|
8 |
2,6 |
22 |
24,25 |
-2,25 |
0,10 |
|
9 |
2,8 |
23,9 |
25,74 |
-1,84 |
0,08 |
|
10 |
2,6 |
26 |
24,25 |
1,75 |
0,07 |
|
11 |
2,6 |
24,6 |
24,25 |
0,35 |
0,01 |
|
12 |
2,5 |
21 |
23,50 |
-2,50 |
0,12 |
|
13 |
2,9 |
27 |
26,49 |
0,51 |
0,02 |
|
14 |
2,6 |
21 |
24,25 |
-3,25 |
0,15 |
|
15 |
2,2 |
24 |
21,26 |
2,74 |
0,11 |
|
16 |
2,6 |
24 |
24,25 |
-0,25 |
0,01 |
|
17 |
3,3 |
31,9 |
29,48 |
2,42 |
0,08 |
|
18 |
3,9 |
33 |
33,96 |
-0,97 |
0,03 |
|
19 |
4 |
35,4 |
34,71 |
0,69 |
0,02 |
|
20 |
3,7 |
34 |
32,47 |
1,53 |
0,05 |
|
21 |
3,4 |
31 |
30,23 |
0,77 |
0,02 |
Здесь
столбец «»
– это значения,
рассчитанные с помощью построенного
уравнения регрессии, столбец «»
– это столбец так называемых «остатков»:
разностей между исходными значениями,
и рассчитанными с помощью уравнения
регрессии,
и, наконец, последний столбец «
»
– это вспомогательный столбец для
вычисления элементов суммы по формуле
( ). Просуммируем теперь элементы
последнего столбца и разделим полученную
сумму на 21 – общее количество исходных
данных:
.
Переведем это
число в проценты и запишем окончательное
выражение для средней ошибки аппроксимации:
.
Итак,
средняя ошибка аппроксимации оказалась
около 8%, что говорит о небольшой
погрешности построенной модели. Данную
модель, с учетом неплохих характеристик
ее качества, вполне можно использовать
для прогноза – одной из основных целей
эконометрического анализа. Предположим,
что среднедушевой месячный доход в
одном из регионов составит 4,1 тыс. руб.
Оценим, каков будет уровень продаж
телевизоров в этом регионе согласно
построенной модели? Для этого необходимо
выбранное значение фактора
подставить в уравнение регрессии (
):
(тыс.
руб.),
т.е. при таком
уровне дохода, розничная продажа
телевизоров составит, в среднем, 35 480
телевизоров.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Коэффициент корреляции
Тесноту (силу) связи изучаемых показателей в предмете эконометрика оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.
Если Rxy > 0,7 — связь между изучаемыми показателями сильная, можно проводить анализ линейной модели
Если 0,3 < Rxy < 0,7 — связь между показателями умеренная, можно использовать нелинейную модель при отсутствии Rxy > 0,7
Если Rxy < 0,3 — связь слабая, модель строить нельзя
Для нелинейной регрессии используют индекс корреляции (0 < Рху < 1):
Средняя ошибка аппроксимации
Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических
Допустимая ошибка аппроксимации не должна превышать 10%.
В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.
Пример нахождения коэффициента корреляции
Исходные данные:
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., |
Среднедневная заработная плата, руб., |
|
1 |
81 |
124 |
|
2 |
77 |
131 |
|
3 |
85 |
146 |
|
4 |
79 |
139 |
|
5 |
93 |
143 |
|
6 |
100 |
159 |
|
7 |
72 |
135 |
|
8 |
90 |
152 |
|
9 |
71 |
127 |
|
10 |
89 |
154 |
|
11 |
82 |
127 |
|
12 |
111 |
162 |
Рассчитаем параметры парной линейной регрессии, составив таблицу
| x |
x2 |
y |
xy |
y2 |
|
|
1 |
81 |
6561 |
124 |
10044 |
15376 |
|
2 |
77 |
5929 |
131 |
10087 |
17161 |
|
3 |
85 |
7225 |
146 |
12410 |
21316 |
|
4 |
79 |
6241 |
139 |
10981 |
19321 |
|
5 |
93 |
8649 |
143 |
13299 |
20449 |
|
6 |
100 |
10000 |
159 |
15900 |
25281 |
|
7 |
72 |
5184 |
135 |
9720 |
18225 |
|
8 |
90 |
8100 |
152 |
13680 |
23104 |
|
9 |
71 |
5041 |
127 |
9017 |
16129 |
|
10 |
89 |
7921 |
154 |
13706 |
23716 |
|
11 |
82 |
6724 |
127 |
10414 |
16129 |
|
12 |
111 |
12321 |
162 |
17982 |
26244 |
|
Среднее |
85,8 |
7491 |
141,6 |
12270,0 |
20204,3 |
|
Сумма |
1030,0 |
89896 |
1699 |
147240 |
242451 |
| σ |
11,13 |
12,59 |
|||
| σ2 |
123,97 |
158,41 |
формула расчета дисперсии σ2 приведена здесь.
Коэффициенты уравнения y = a + bx определяются по формуле
Получаем уравнение регрессии: y = 0,947x + 60,279.
Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:
Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.
Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
Означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: 
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее , и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа . В главном меню последовательно выберите: Файл/Параметры/Надстройки .
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК .
Если Пакет анализа отсутствует в списке поля Доступные надстройки , нажмите кнопку Обзор , чтобы выполнить поиск.
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да , чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия , а затем нажмите кнопку ОК .
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y — диапазон, содержащий данные результативного признака;
Входной интервал X — диапазон, содержащий данные факторного признака;
Метки — флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа — ноль — флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист — можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК .
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 — 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н 0 о статистически незначимом отличии показателей от нуля:


На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
где 
Данные для расчёта возьмём из таблицы на Рисунке 7.
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н 0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций : в главном меню выберете Формулы / Вставить функцию .
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК .
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2003. — 192 с.: ил.
Для общей оценки качества построенной эконометрической определяются такие характеристики как коэффициент детерминации, индекс корреляции, средняя относительная ошибка аппроксимации, а также проверяется значимость уравнения регрессии с помощью F -критерия Фишера. Перечисленные характеристики являются достаточно универсальными и могут применяться как для линейных, так и для нелинейных моделей, а также моделей с двумя и более факторными переменными. Определяющее значение при вычислении всех перечисленных характеристик качества играет ряд остатков ε i , который вычисляется путем вычитания из фактических (полученных по наблюдениям) значений исследуемого признака y i значений, рассчитанных по уравнению модели y рi .
показывает, какая доля изменения исследуемого признака учтена в модели. Другими словами коэффициент детерминации показывает, какая часть изменения исследуемой переменной может быть вычислена, исходя из изменений включённых в модель факторных переменных с помощью выбранного типа функции, связывающей факторные переменные и исследуемый признак в уравнении модели.
Коэффициент детерминации R 2 может принимать значения от 0 до 1. Чем ближе коэффициент детерминации R 2 к единице, тем лучше качество модели.
Индекс корреляции можно легко вычислить, зная коэффициент детерминации:
Индекс корреляции R характеризует тесноту выбранного при построении модели типа связи между учтёнными в модели факторами и исследуемой переменной. В случае линейной парной регрессии его значение по абсолютной величине совпадает с коэффициентом парной корреляции r (x, y) , который мы рассмотрели ранее, и характеризует тесноту линейной связи между x и y . Значения индекса корреляции, очевидно, также лежат в интервале от 0 до 1. Чем ближе величина R к единице, тем теснее выбранный вид функции связывает между собой факторные переменные и исследуемый признак, тем лучше качество модели.

выражается в процентах и характеризует точность модели. Приемлимая точность модели при решении практических задач может определяться, исходя из соображений экономической целесообразности с учётом конкретной ситуации. Широко применяется критерий, в соответствии с которым точность считается удовлетворительной, если средняя относительная погрешность меньше 15%. Если E отн.ср. меньше 5%, то говорят, что модель имеет высокую точность. Не рекомендуется применять для анализа и прогноза модели с неудовлетворительной точностью, то есть, когда E отн.ср. больше 15%.
F-критерий Фишера используется для оценки значимости уравнения регрессии. Расчётное значение F-критерия определяется из соотношения:

Критическое значение F -критерия определяется по таблицам при заданном уровне значимости α и степенях свободы (можно использовать функцию FРАСПОБР в Excel). Здесь, по-прежнему, m – число факторов, учтённых в модели, n – количество наблюдений. Если расчётное значение больше критического, то уравнение модели признаётся значимым. Чем больше расчётное значение F -критерия, тем лучше качество модели.
Определим характеристики качества построенной нами линейной модели для Примера 1 . Воспользуемся данными Таблицы 2. Коэффициент детерминации :
Следовательно, в рамках линейной модели изменение объёма продаж на 90,1% объясняется изменением температуры воздуха.

Значение индекса корреляции в случае парной линейной модели как мы видим, действительно по модулю равно коэффициенту корреляции между соответствующими переменными (объём продаж и температура). Поскольку полученное значение достаточно близко к единице, то можно сделать вывод о наличии тесной линейной связи между исследуемой переменной (объём продаж) и факторной переменноё (температура).
Критическое значение F кр при α = 0,1; ν 1 =1; ν 2 =7-1-1=5 равно 4,06. Расчётное значение F -критерия больше табличного, следовательно, уравнение модели является значимым.
Средняя относительная ошибка аппроксимации
Построенная линейная модель парной регрессии имеет неудовлетворительную точность (>15%), и её не рекомендуется использовать для анализа и прогнозирования.
В итоге, несмотря на то, что большинство статистических характеристик удовлетворяют предъявляемым к ним критериям, линейная модель парной регрессии непригодна для прогнозирования объёма продаж в зависимости от температуры воздуха. Нелинейный характер зависимости между указанными переменными по данным наблюдений достаточно хорошо виден на Рис.1. Проведённый анализ это подтвердил.
Среди различных методов прогнозирования нельзя не выделить аппроксимацию. С её помощью можно производить приблизительные подсчеты и вычислять планируемые показатели, путем замены исходных объектов на более простые. В Экселе тоже существует возможность использования данного метода для прогнозирования и анализа. Давайте рассмотрим, как этот метод можно применить в указанной программе встроенными инструментами.
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Рассмотрим каждый из вариантов более подробно в отдельности.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
В конкретно нашем случае формула принимает такой вид:
Величина достоверности аппроксимации у нас равна 0,9418 , что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
Общий вид функции сглаживания при этом такой:
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
В общем виде формула сглаживания выглядит так:
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
В конкретно нашем случае она выглядит так:
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844 ), наименьший уровень достоверности у линейного метода (0,9418 ). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Контрольная работа: Парная регрессия
Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1 , Х2 , … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.
Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.
Парная регрессия – уравнение связи двух переменных у иx :
,
где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия:.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней
•равносторонняя гипербола
Регрессии, нелинейные по оцениваемым параметрам:
• степенная ;
• показательная
• экспоненциальная
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b :
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии
и индекс корреляции — для нелинейной регрессии ():
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений – не более 8 – 10%.
Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения:
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
где – общая сумма квадратов отклонений;
– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
–остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R 2 :
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F -тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F -критерия Фишера. F факт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
п – число единиц совокупности;
т – число параметров при переменных х.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл Fфакт , то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t -критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт – принимаем или отвергаем гипотезу Hо .
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
Если tтабл tфакт , то гипотеза Но не отклоняется и признается случайная природа формирования a , b или .
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза :
где
и строится доверительный интервал прогноза:
где
По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):
| Название: Парная регрессия Раздел: Рефераты по математике Тип: контрольная работа Добавлен 13:41:57 15 апреля 2011 Похожие работы Просмотров: 3780 Комментариев: 22 Оценило: 4 человек Средний балл: 4.5 Оценка: неизвестно Скачать |
| № региона | X | Y |
| 1,000 | 2,800 | 28,000 |
| 2,000 | 2,400 | 21,300 |
| 3,000 | 2,100 | 21,000 |
| 4,000 | 2,600 | 23,300 |
| 5,000 | 1,700 | 15,800 |
| 6,000 | 2,500 | 21,900 |
| 7,000 | 2,400 | 20,000 |
| 8,000 | 2,600 | 22,000 |
| 9,000 | 2,800 | 23,900 |
| 10,000 | 2,600 | 26,000 |
| 11,000 | 2,600 | 24,600 |
| 12,000 | 2,500 | 21,000 |
| 13,000 | 2,900 | 27,000 |
| 14,000 | 2,600 | 21,000 |
| 15,000 | 2,200 | 24,000 |
| 16,000 | 2,600 | 34,000 |
| 17,000 | 3,300 | 31,900 |
| 19,000 | 3,900 | 33,000 |
| 20,000 | 4,600 | 35,400 |
| 21,000 | 3,700 | 34,000 |
| 22,000 | 3,400 | 31,000 |
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
5. Качество уравнений оцените с помощью средней ошибки аппроксимации.
6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
1. Поле корреляции для:
· Линейной регрессии y=a+b*x:
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
· Степенной регрессии :
Гипотеза о форме связи : степенная функция имеет вид Y=ax b .
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
· Экспоненциальная регрессия :
· Равносторонняя гипербола :
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
· Обратная гипербола :
· Полулогарифмическая регрессия :
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x 2 , ∑y 2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с увеличением среднедушевого денежного дохода в месяц на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
· Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y .
· Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
где
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем замены:
где
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
Получим линейное уравнение: .
· Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель к линейному виду, заменив , тогда
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
Получим линейное уравнение: . Выполнив его потенцирование, получим:
Для расчета теоретических значений y подставим в уравнение значения x .
· Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы к линейному виду, заменив , тогда
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
Получим линейное уравнение: . Получим уравнение регрессии: .
3. Оценка тесноты связи с помощью показателей корреляции и детерминации :
· Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции rxy =b=7,122*, что говорит о прямой сильной связи фактора и результата. Коэффициент детерминации r²xy =(0,845)²=0,715. Это означает, что 71,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции =, что говорит о очень сильной тесной связи, но немного больше чем в линейной модели. Коэффициент детерминации r²xy =0,7175. Это означает, что 71,75% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy =0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy =0,66. Это означает, что 66% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy =0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,58% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy =0,8448 и коэффициент корреляции rxy =-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,7358. Это означает, что 73,5% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy =0,8114 и коэффициент корреляции rxy =-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy =0,6584. Это означает, что 65,84% вариации результативного признака (розничнаяпродажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy =0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
· Для уравнения прямой:y = 5,777+7,122∙x
· Для уравнениястепенноймодели :
· Для уравненияэкспоненциальноймодели :
Для уравненияполулогарифмическоймодели :
· Для уравнения обратной гиперболической модели :
· Для уравнения равносторонней гиперболической модели :
Сравнивая значения , характеризуем оценку силы связи фактора с результатом:
·
·
·
·
·
·
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :
В среднем расчетные значения отклоняются от фактических на:
· Линейная регрессия. =*100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Степенная регрессия. =*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Экспоненциальная регрессия. =*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Полулогарифмическая регрессия. =*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Гиперболическая регрессия. =*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
· Обратная регрессия. =*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в допустимых пределах.
Качество построенной модели оценивается как хорошее, так как не превышает 8 -10%.
6. Рассчитаем F-критерий:
· Линейная регрессия. = *19= 47,579
http://welom.ru/srednyaya-oshibka-approksimacii-v-excel-ocenka-kachestva-uravneniya/
http://www.bestreferat.ru/referat-268496.html