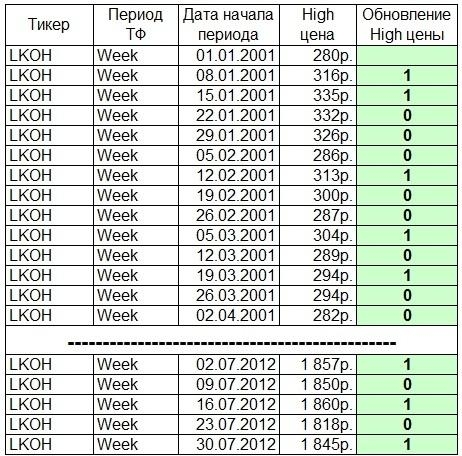
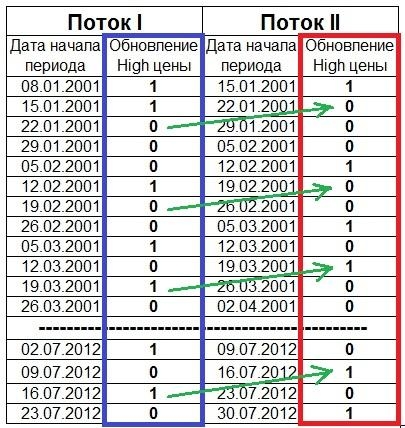
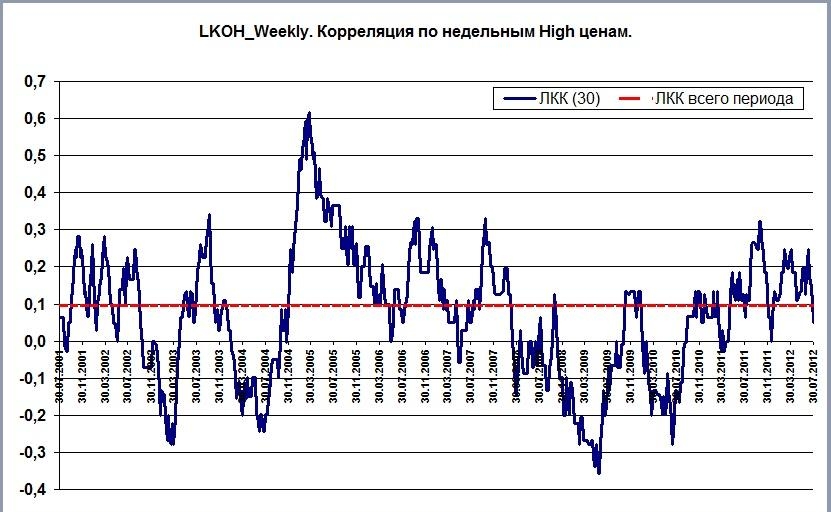
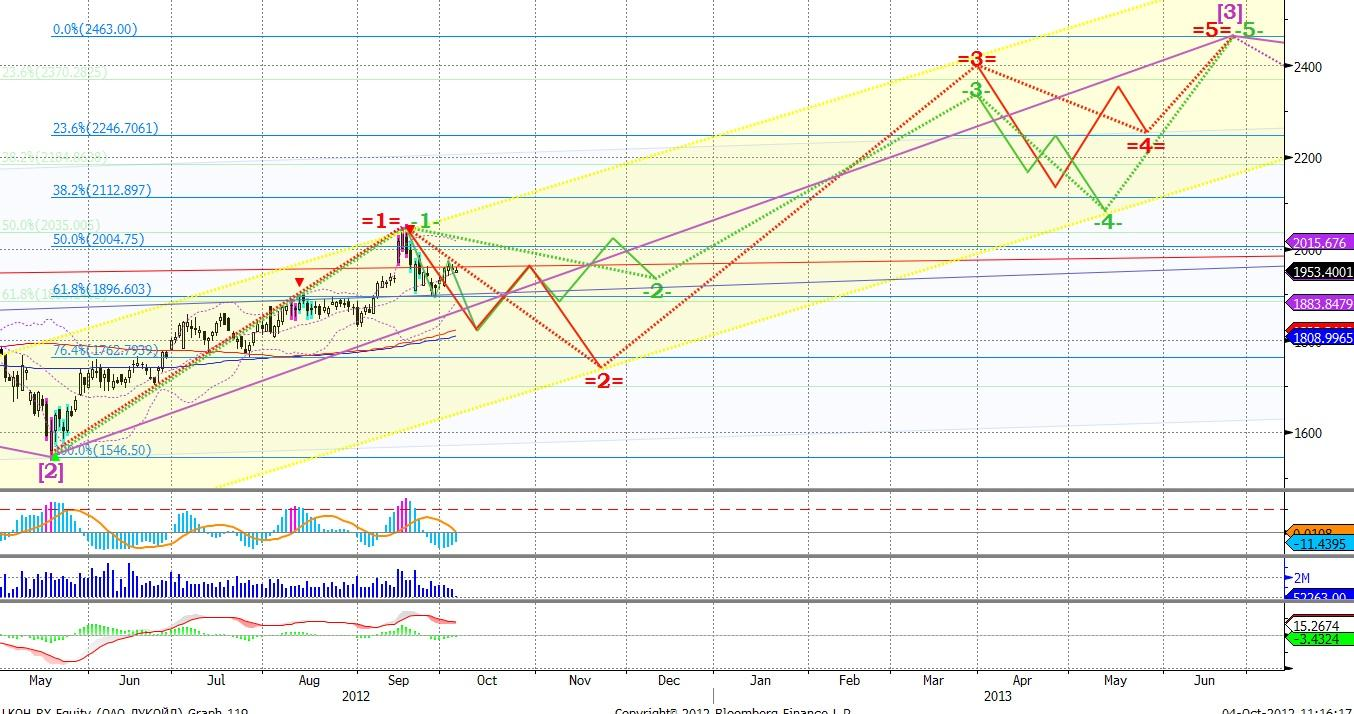
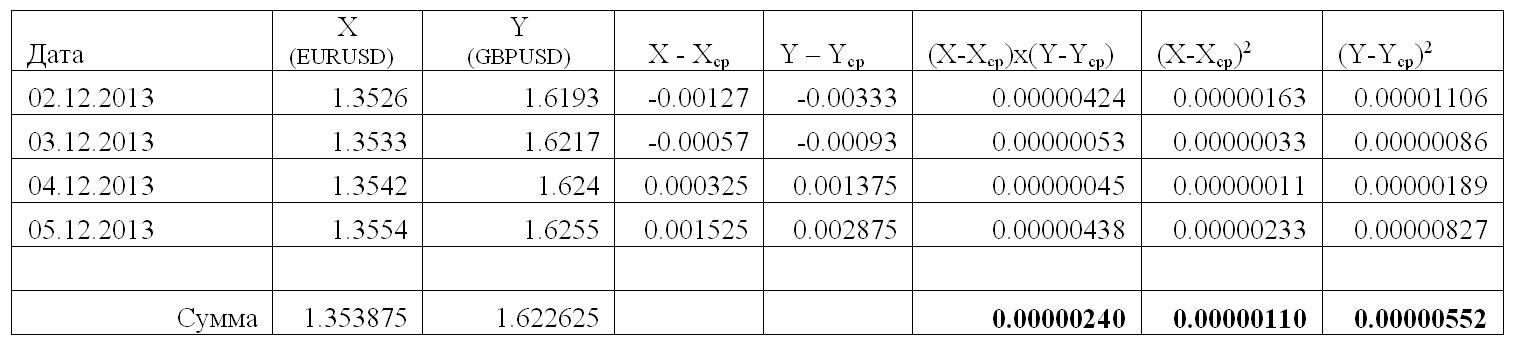
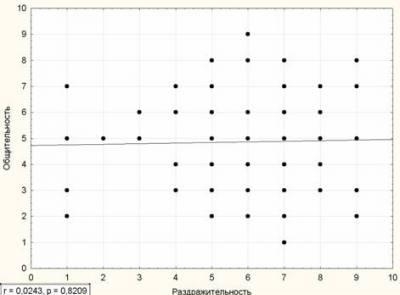
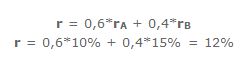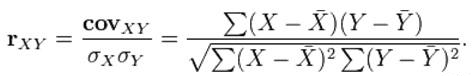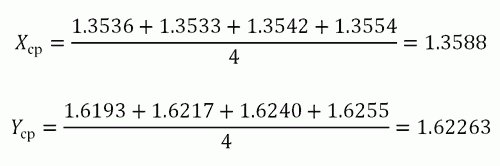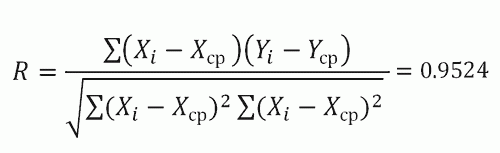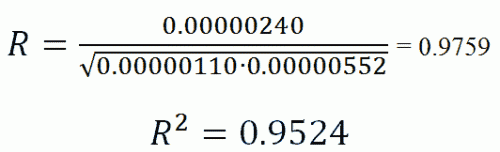Затем каждую из величин Σfxyax перемножаем на условные отклонения ряда у для данной строки (ay) и результаты записываем в графу 17. Суммируя полученные произведения, получаем величину Σ(Σfxyax)ay=417.
Теперь в нашем распоряжении имеются все необходимые величины для вычисления r по формуле:
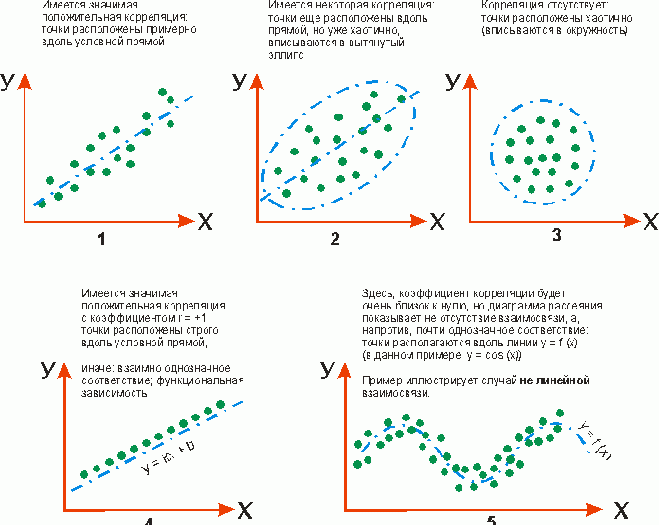
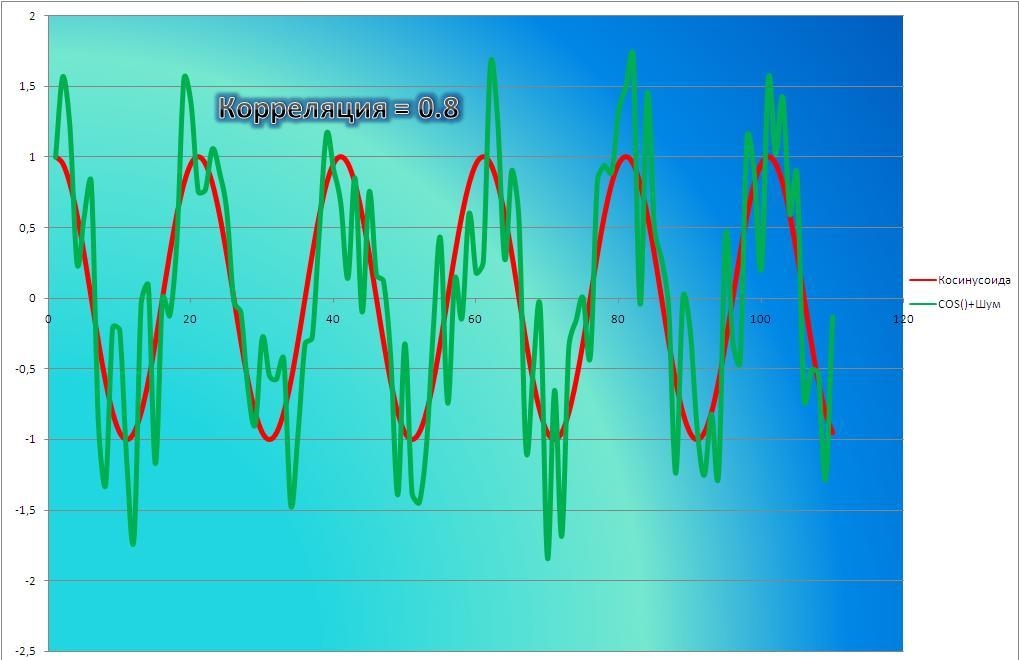
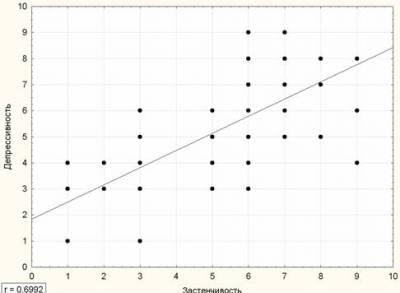
Величина полученного коэффициента корреляции говорит об умеренной тесноте связи исследованных признаков, а знак свидетельствует о прямом характере этой связи.
Иногда при наличии линейной связи можно, используя коэффициент корреляции, оценить влияние признака-фактора на результативный признак. Для этого применяется квадрат коэффициента корреляции, называемый коэффициентом детерминации (r2). Если выразить коэффициент детерминации в процентах, то он покажет долю влияния данного факториального признака на результативный. Например, коэффициент корреляции между ростом и весом детей равен +0,75, тогда коэффициент детерминации будет: rxy2=0,752=0,56. Если принять все факторы, влияющие на вес тела, за 100%, то на долю роста приходится 56%.
Поскольку коэффициент корреляции в клинических исследованиях рассчитывается обычно для ограниченного числа наблюдений, нередко возникает вопрос о надежности полученного коэффициента. С этой целью определяют сред-
нюю ошибку коэффициента корреляции. При достаточно большом числе на-
блюдений (больше 100) средняя ошибка коэффициента корреляции (тr) вычисляется по формуле:
|
1− r |
2 |
|||
|
mr |
= |
xy |
(1.37) |
|
|
n |
||||
где n — число парных наблюдений.
В том случае, если число наблюдений меньше 100, но больше 30, точнее определять среднюю ошибку коэффициента корреляции, пользуясь формулой:
|
1− r 2 |
|||
|
mr = |
xy |
(1.38) |
|
|
n −1 |
|||
66

С достаточной для медицинских исследований надежностью о наличии той или иной степени связи можно утверждать только тогда, когда величина коэффициента корреляции превышает или равняется величине трех своих ошибок (rxy>=3mr). Обычно это отношение коэффициента корреляции (rху) к его средней ошибке (тr) обозначают буквой t и называют критерием достоверности:
|
tr |
= |
rxy |
(1.39) |
|
|
mr |
||||
Если tr >= 3, то коэффициент корреляции достоверен. В рассмотренном выше примере число наблюдений 142, а коэффициент корреляции 0,68. Тогда
|
mr |
= |
1− rxy2 |
1−(0,68)2 |
||
|
n |
= |
142 |
= 0,045 |
||
|
r |
|||||
|
tr = |
= |
0,68 |
=15 , |
||
|
mr |
0,045 |
||||
т. е. коэффициент корреляции вполне достоверен.
В случае малой выборки (число наблюдений меньше 30) для оценки достоверности коэффициента корреляции, т. е. для определения соответствия коэффициента корреляции, вычисленного по выборочным данным, действительным размерам связи в генеральной совокупности, средняя ошибка коэффициента корреляции (тr) определяется по формуле:
|
1− r 2 |
|||
|
mr = |
xy |
(1.40) |
|
|
n − 2 |
|||
Значения критерия tr оцениваются по таблице t Стьюдента при числе степеней свободы v = п — 2. Если величина tr больше табличного значения t05, то коэффициент корреляции признается надежным с доверительной вероятностью больше 95%. Например, имеется коэффициент корреляции, равный +0,72 при числе наблюдений 28. Тогда
mr = 1−(0,72)2 = ±0,019 28 −2
tr = 0,0190,72 = 35,9
Полученное значение tr = 35,9 значительно больше табличного t01 = 2,779, следовательно, полученному коэффициенту корреляции можно доверять с высокой степенью вероятности (>99%).
В медицинской практике нередко возникает необходимость сравнить между собой два выборочных коэффициента корреляции и определить, существенна ли разница между ними. Ввиду того, что распределение коэффициента корреляции отличается от нормального, для оценки значимости различия между двумя коэффициентами корреляции рекомендуется использовать величину Z,
67

предложенную Р. Фишером. Величины Z, соответствующие различным значениям коэффициента корреляции, представлены в табл. 1.38.
Например, при исследовании тесноты связи между ростом и весом девочек и мальчиков было установлено, что у мальчиков коэффициент корреляции равен 0,5, а у девочек — 0,7. При этом обследовано 20 мальчиков и 30 девочек. Можно ли считать, что у девочек сильнее выражена связь между ростом и весом, чем у мальчиков? Для решения этого вопроса переведем значение наших коэффициентов корреляции (r) в величины Z. Находим по таблице, что r = 0,5 соответствует Z = 0,5493, а для r = 0,7 соответствует Z = 0,8673. Ошибка разности вычисляется по формуле:
|
mz |
= |
n1 |
1 |
+ |
1 |
= |
1 |
+ |
1 |
= 0,10 = 0,316 |
|
−3 |
n2 −3 |
20 −3 |
30 −3 |
Вычисляем критерий значимости различий:
|
tz |
= |
z1 − z2 |
= |
0,8673 −0,5493 |
= |
0,3188 |
=1,005 |
|
|
mz |
0,316 |
0,316 |
||||||
Разность признается значимой, если tz ≥ 3. В нашем примере tz < 3; следовательно, на основании полученных коэффициентов корреляции нельзя делать вывод о более выраженной связи между ростом и весом у девочек.
Таблица 1.38 — Таблица величин Z
|
r |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,90 |
1,4722 |
1,5275 |
1,5890 |
1,6584 |
1,7380 |
1,8318 |
1,9459 |
2,0923 |
2,2976 |
2,6467 |
|
0,80 |
1,0986 |
1,1270 |
1,1568 |
1,1881 |
1,2212 |
1,2562 |
1,2933 |
1,3101 |
1,3758 |
1,4219 |
|
0,70 |
0,8673 |
0,8872 |
0,9076 |
0,9287 |
0,9505 |
0,9730 |
0,9962 |
1,0203 |
1,0454 |
1,0714 |
|
0,60 |
0,6931 |
0,7089 |
0,7250 |
0,7414 |
0,7582 |
0,7753 |
0,7623 |
0,8107 |
0,8291 |
0,8480 |
|
0,50 |
0,5493 |
0,5627 |
0,5763 |
0,5901 |
0,6042 |
0,6184 |
0,6328 |
0,6475 |
0,6625 |
0,6777 |
|
0,40 |
0,4236 |
0,4356 |
0,4477 |
0,4599 |
0,4722 |
0,4847 |
0,4973 |
0,5101 |
0,5230 |
0,5361 |
|
0,30 |
0,3045 |
0,3205 |
0,3316 |
0,3428 |
0,3541 |
0,3654 |
0,3769 |
0,3884 |
0,4001 |
0,4118 |
|
0,20 |
0,2027 |
0,2132 |
0,2237 |
0,2342 |
0,2448 |
0,2554 |
0,2661 |
0,2769 |
0,2877 |
0,2986 |
|
0,10 |
0,1003 |
0,1104 |
0,1205 |
0,1307 |
0,1409 |
0,1511 |
0,1614 |
0,1717 |
0,1820 |
0,1923 |
|
0,00 |
0,0000 |
0,0100 |
0,0200 |
0,0300 |
0,0400 |
0,0501 |
0,0600 |
0,0701 |
0,0802 |
0,0902 |
1.8.5 Определение тесноты связи между качественными признаками
При изучении зависимости качественных признаков используется коэффициент сопряженности. Для определения тесноты связи в случае альтернативной изменчивости двух сопоставляемых признаков имеющиеся данные сводятся в четырехпольную таблицу, и коэффициент сопряженности вычисляется по формуле:
|
C1 = |
ad −bc |
(1.41) |
|
(a +c)(b + d)(a +b)(c + d) |
68

Если ранее по данным этой таблицы был вычислен критерий χ2, то коэффициент сопряженности вычисляется по формуле:
|
C1 = |
χ2 |
= |
χ2 |
(1.42) |
|
a +b +c + d |
n |
Например, требуется установить, имеется ли связь между степенью тяжести ревматизма и эффективностью тонзиллэктомии (табл. 1.39).
Таблица 1.39 — Эффективность тонзиллэктомии в зависимости от симптоматики ревматизма
|
Симптоматика ревматизма |
Результат лечения |
Итого |
|||
|
успешное |
неэффективное |
||||
|
Больные, имевшие изменения со |
9 |
26 |
|||
|
cтороны сердца и суставов. |
|||||
|
Больные, имевшие изменения |
8 |
16 |
|||
|
только со cтороны сердца . . |
|||||
|
Всего |
25 |
17 |
42 |
||
Коэффициент сопряженности изменяется в пределах от +1 до -1 и оценивается аналогично коэффициенту корреляции.
При сопоставлении качественных признаков, имеющих три и больше групп, для определения тесноты связи, пользуются коэффициентом средней квадратичной сопряженности Пирсона:
и коэффициентом взаимной сопряженности Чупрова:
|
K = |
φ2 |
(1.44) |
|
(k1 −1) (k2 −1) |
где k1 — число групп по столбцам;
k2 — число групп по строкам таблицы;
ϕ2 + 1 — равно о сумме отношений квадратов частот каждой клетки таблицы к произведению итогов строк и соответствующих итогов столбцов
|
2 |
||||||||
|
ϕ2 |
+ 1 = |
∑ |
mxy |
(1.45) |
||||
|
m |
m |
|||||||
|
x |
||||||||
|
y |
Пример. Вычислим коэффициент средней квадратической сопряженности Пирсона между гистологической структурой и типом роста опухоли по данным таблицы 1.40.
Находим значение ϕ2 + 1:
69

|
φ |
2 |
+1 |
= |
∑ |
mxy2 |
= |
112 |
+ |
62 |
+ |
22 |
+ |
2 |
2 |
+ |
32 |
+ |
10 |
2 |
+ |
12 |
+ |
12 |
+ |
32 |
+ |
|||||||||||||||||||||||||||||||||||
|
mx |
my |
20 |
21 |
33 21 |
14 |
21 |
6 |
21 |
20 |
15 |
33 |
15 |
14 15 |
6 |
15 |
20 |
12 |
||||||||||||||||||||||||||||||||||||||||||||
|
+ |
52 |
+ |
32 |
+ |
12 |
+ |
12 |
+ |
72 |
+ |
32 |
+ |
12 |
+ |
52 |
+ |
2 |
2 |
+ |
4 |
2 |
+ |
22 |
=1,47 |
|||||||||||||||||||||||||||||||||||||
|
33 12 |
14 12 |
6 12 |
20 12 |
33 11 |
14 11 |
33 6 |
14 6 |
20 |
8 |
33 |
6 |
6 8 |
|||||||||||||||||||||||||||||||||||||||||||||||||
Отсюда находим ϕ2 =1,47 – 1 = 0,47.
Коэффициент средней квадратичной сопряженности Пирсона:
C1 = 
Коэффициент взаимной сопряженности Чупрова равняется
|
K = |
0,47 |
= |
0,47 |
= |
0,47 |
= 0,12 = 0,348 |
|
(4 |
−1) (6 −1) |
3 5 |
15 |
Полученный коэффициент К также свидетельствует о наличии связи между рассматриваемыми признаками.
Таблица 1.40 — Зависимость между гистологической структурой опухоли и типом ее роста
|
Гистологическая |
Тип роста опухоли (х) |
Итого |
|||
|
структура (у) |
экзофит- |
язвенно- |
диффузно- |
переход- |
(my) |
|
ный |
инфиль- |
инфильтра- |
ный |
||
|
тративный |
тивный |
||||
|
Аденокарцинома |
11(mxy) |
6 |
2 |
2 |
21 |
|
Cr. simplex……… |
3 |
10 |
1 |
1 |
15 |
|
Солидный рак…… |
3 |
5 |
3 |
1 |
12 |
|
Слизистый……… |
1 |
7 |
3 |
─ |
11 |
|
Фиброзный рак… |
─ |
1 |
5 |
─ |
6 |
|
Смешанные формы |
2 |
4 |
─ |
2 |
8 |
|
Всего (mx)……… |
20 |
33 |
14 |
6 |
73 |
При применении коэффициента сопряженности С1 следует учитывать, что он всегда меньше 1 и теоретическая его величина зависит от числа строк и столбцов таблицы. Поэтому вычисление коэффициента С1 правомочно только тогда, когда каждый из сопоставляемых признаков имеет не менее 5 градаций (таблица 5×5 групп). Коэффициент Чупрова, который всегда меньше коэффициента С1 не имеет этого ограничения.
Достоверность выборочного коэффициента взаимной сопряженности оценивается с помощью критерия χ2. Полученная величина χ2=nϕ2 сопоставляется с табличными значениями χ2 при числе степеней свободы v=(k —1)(k2-1) и р = 0,05.
70
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson’s r, the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation,[1] or colloquially simply as the correlation coefficient[2] ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).
Examples of scatter diagrams with different values of correlation coefficient (ρ)
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. Note that the correlation reflects the strength and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
Naming and history[edit]
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844.[a][6][7][8][9] The naming of the coefficient is thus an example of Stigler’s Law.
Definition[edit]
Pearson’s correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The form of the definition involves a «product moment», that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier product-moment in the name.
For a population[edit]
Pearson’s correlation coefficient, when applied to a population, is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. Given a pair of random variables 
where:
The formula for 
the formula for 
where:
The formula for 
the formula for 
Peason’s correlation coefficient does not exist when either 

For a sample[edit]
Pearson’s correlation coefficient, when applied to a sample, is commonly represented by 




where:
Rearranging gives us this formula for 
where 
This formula suggests a convenient single-pass algorithm for calculating sample correlations, though depending on the numbers involved, it can sometimes be numerically unstable.
Rearranging again gives us this[10] formula for 
where 
An equivalent expression gives the formula for 
where:
Alternative formulae for 

where:
Practical issues[edit]
Under heavy noise conditions, extracting the correlation coefficient between two sets of stochastic variables is nontrivial, in particular where Canonical Correlation Analysis reports degraded correlation values due to the heavy noise contributions. A generalization of the approach is given elsewhere.[12]
In case of missing data, Garren derived the maximum likelihood estimator.[13]
Some distributions (e.g., stable distributions other than a normal distribution) do not have a defined variance.
Mathematical properties[edit]
The values of both the sample and population Pearson correlation coefficients are on or between −1 and 1. Correlations equal to +1 or −1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).
A key mathematical property of the Pearson correlation coefficient is that it is invariant under separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants with b, d > 0, without changing the correlation coefficient. (This holds for both the population and sample Pearson correlation coefficients.) Note that more general linear transformations do change the correlation: see § Decorrelation of n random variables for an application of this.
Interpretation[edit]
The correlation coefficient ranges from −1 to 1. An absolute value of exactly 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line. The correlation sign is determined by the regression slope: a value of +1 implies that all data points lie on a line for which Y increases as X increases, and vice versa for −1.[14] A value of 0 implies that there is no linear dependency between the variables.[15]
More generally, note that (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative (anti-correlation) if Xi and Yi tend to lie on opposite sides of their respective means. Moreover, the stronger either tendency is, the larger is the absolute value of the correlation coefficient.
Rodgers and Nicewander[16] cataloged thirteen ways of interpreting correlation or simple functions of it:
- Function of raw scores and means
- Standardized covariance
- Standardized slope of the regression line
- Geometric mean of the two regression slopes
- Square root of the ratio of two variances
- Mean cross-product of standardized variables
- Function of the angle between two standardized regression lines
- Function of the angle between two variable vectors
- Rescaled variance of the difference between standardized scores
- Estimated from the balloon rule
- Related to the bivariate ellipses of isoconcentration
- Function of test statistics from designed experiments
- Ratio of two means
Geometric interpretation[edit]
Regression lines for y = gX(x) [red] and x = gY(y) [blue]
For uncentered data, there is a relation between the correlation coefficient and the angle φ between the two regression lines, y = gX(x) and x = gY(y), obtained by regressing y on x and x on y respectively. (Here, φ is measured counterclockwise within the first quadrant formed around the lines’ intersection point if r > 0, or counterclockwise from the fourth to the second quadrant if r < 0.) One can show[17] that if the standard deviations are equal, then r = sec φ − tan φ, where sec and tan are trigonometric functions.
For centered data (i.e., data which have been shifted by the sample means of their respective variables so as to have an average of zero for each variable), the correlation coefficient can also be viewed as the cosine of the angle θ between the two observed vectors in N-dimensional space (for N observations of each variable)[18]
Both the uncentered (non-Pearson-compliant) and centered correlation coefficients can be determined for a dataset. As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, and y = (0.11, 0.12, 0.13, 0.15, 0.18).
By the usual procedure for finding the angle θ between two vectors (see dot product), the uncentered correlation coefficient is:
This uncentered correlation coefficient is identical with the cosine similarity.
Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by ℰ(x) = 3.8 and y by ℰ(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which
as expected.
Interpretation of the size of a correlation[edit]
This figure gives a sense of how the usefulness of a Pearson correlation for predicting values varies with its magnitude. Given jointly normal X, Y with correlation ρ, 
Several authors have offered guidelines for the interpretation of a correlation coefficient.[19][20] However, all such criteria are in some ways arbitrary.[20] The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
Inference[edit]
Statistical inference based on Pearson’s correlation coefficient often focuses on one of the following two aims:
- One aim is to test the null hypothesis that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r.
- The other aim is to derive a confidence interval that, on repeated sampling, has a given probability of containing ρ.
We discuss methods of achieving one or both of these aims below.
Using a permutation test[edit]
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson’s correlation coefficient involves the following two steps:
- Using the original paired data (xi, yi), randomly redefine the pairs to create a new data set (xi, yi′), where the i′ are a permutation of the set {1,…,n}. The permutation i′ is selected randomly, with equal probabilities placed on all n! possible permutations. This is equivalent to drawing the i′ randomly without replacement from the set {1, …, n}. In bootstrapping, a closely related approach, the i and the i′ are equal and drawn with replacement from {1, …, n};
- Construct a correlation coefficient r from the randomized data.
To perform the permutation test, repeat steps (1) and (2) a large number of times. The p-value for the permutation test is the proportion of the r values generated in step (2) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here «larger» can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.
Using a bootstrap[edit]
The bootstrap can be used to construct confidence intervals for Pearson’s correlation coefficient. In the «non-parametric» bootstrap, n pairs (xi, yi) are resampled «with replacement» from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile of the resampled r values.
Standard error[edit]
If 

where 

Testing using Student’s t-distribution[edit]
Critical values of Pearson’s correlation coefficient that must be exceeded to be considered significantly nonzero at the 0.05 level.
For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson’s correlation coefficient follows Student’s t-distribution with degrees of freedom n − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
has a student’s t-distribution in the null case (zero correlation).[23] This holds approximately in case of non-normal observed values if sample sizes are large enough.[24] For determining the critical values for r the inverse function is needed:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper[25] provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson’s correlation coefficient follows a Student’s t-distribution, but the degrees of freedom are reduced.[26]
Using the exact distribution[edit]
For data that follow a bivariate normal distribution, the exact density function f(r) for the sample correlation coefficient r of a normal bivariate is[27][28][29]
where 

In the special case when 
where 
Using the exact confidence distribution[edit]
Confidence intervals and tests can be calculated from a confidence distribution. An exact confidence density for ρ is[30]
where 

Using the Fisher transformation[edit]
In practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformation, 
F(r) approximately follows a normal distribution with
and standard error
where n is the sample size. The approximation error is lowest for a large sample size 


Using the approximation, a z-score is
under the null hypothesis that 

To obtain a confidence interval for ρ, we first compute a confidence interval for F(
The inverse Fisher transformation brings the interval back to the correlation scale.
For example, suppose we observe r = 0.7 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.8673, so the confidence interval on the transformed scale is 0.8673 ± 1.96/√47, or (0.5814, 1.1532). Converting back to the correlation scale yields (0.5237, 0.8188).
In least squares regression analysis[edit]
The square of the sample correlation coefficient is typically denoted r2 and is a special case of the coefficient of determination. In this case, it estimates the fraction of the variance in Y that is explained by X in a simple linear regression. So if we have the observed dataset 

where the 
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between 

Thus
where 
In the derivation above, the fact that
can be proved by noticing that the partial derivatives of the residual sum of squares (RSS) over β0 and β1 are equal to 0 in the least squares model, where
.
In the end, the equation can be written as:
where
The symbol 

Sensitivity to the data distribution[edit]
Existence[edit]
The population Pearson correlation coefficient is defined in terms of moments, and therefore exists for any bivariate probability distribution for which the population covariance is defined and the marginal population variances are defined and are non-zero. Some probability distributions, such as the Cauchy distribution, have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
Sample size[edit]
- If the sample size is moderate or large and the population is normal, then, in the case of the bivariate normal distribution, the sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient, and is asymptotically unbiased and efficient, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient.
- If the sample size is large and the population is not normal, then the sample correlation coefficient remains approximately unbiased, but may not be efficient.
- If the sample size is large, then the sample correlation coefficient is a consistent estimator of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers can be applied).
- If the sample size is small, then the sample correlation coefficient r is not an unbiased estimate of ρ.[10] The adjusted correlation coefficient must be used instead: see elsewhere in this article for the definition.
- Correlations can be different for imbalanced dichotomous data when there is variance error in sample.[31]
Robustness[edit]
Like many commonly used statistics, the sample statistic r is not robust,[32] so its value can be misleading if outliers are present.[33][34] Specifically, the PMCC is neither distributionally robust,[citation needed] nor outlier resistant[32] (see Robust statistics § Definition). Inspection of the scatterplot between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson’s correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap can be applied to construct confidence intervals, and permutation tests can be applied to carry out hypothesis tests. These non-parametric approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.[35]
Variants[edit]
Variations of the correlation coefficient can be calculated for different purposes. Here are some examples.
Adjusted correlation coefficient[edit]
The sample correlation coefficient r is not an unbiased estimate of ρ. For data that follows a bivariate normal distribution, the expectation E[r] for the sample correlation coefficient r of a normal bivariate is[36]
therefore r is a biased estimator of
The unique minimum variance unbiased estimator radj is given by[37]
-
(1)
where:
An approximately unbiased estimator radj can be obtained[citation needed] by truncating E[r] and solving this truncated equation:
-
(2)
An approximate solution[citation needed] to equation (2) is:
-
(3)
where in (3):
are defined as above,
- radj is a suboptimal estimator,[citation needed][clarification needed]
- radj can also be obtained by maximizing log(f(r)),
- radj has minimum variance for large values of n,
- radj has a bias of order 1⁄(n − 1).
Another proposed[10] adjusted correlation coefficient is:[citation needed]
Note that radj ≈ r for large values of n.
Weighted correlation coefficient[edit]
Suppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),[38][39]
- Weighted mean:
- Weighted covariance
- Weighted correlation
Reflective correlation coefficient[edit]
The reflective correlation is a variant of Pearson’s correlation in which the data are not centered around their mean values.[citation needed] The population reflective correlation is
The reflective correlation is symmetric, but it is not invariant under translation:
The sample reflective correlation is equivalent to cosine similarity:
The weighted version of the sample reflective correlation is
Scaled correlation coefficient[edit]
Scaled correlation is a variant of Pearson’s correlation in which the range of the data is restricted intentionally and in a controlled manner to reveal correlations between fast components in time series.[40] Scaled correlation is defined as average correlation across short segments of data.
Let 


The scaled correlation across the entire signals 
where 

By choosing the parameter 
Pearson’s distance[edit]
A distance metric for two variables X and Y known as Pearson’s distance can be defined from their correlation coefficient as[41]
Considering that the Pearson correlation coefficient falls between [−1, +1], the Pearson distance lies in [0, 2]. The Pearson distance has been used in cluster analysis and data detection for communications and storage with unknown gain and offset.[42]
The Pearson «distance» defined this way assigns distance greater than 1 to negative correlations. In reality, both strong positive correlation and negative correlations are meaningful, so care must be taken when Pearson «distance» is used for nearest neighbor algorithm as such algorithm will only include neighbors with positive correlation and exclude neighbors with negative correlation. Alternatively, an absolute valued distance: 
Circular correlation coefficient[edit]
For variables X = {x1,…,xn} and Y = {y1,…,yn} that are defined on the unit circle [0, 2π), it is possible to define a circular analog of Pearson’s coefficient.[43] This is done by transforming data points in X and Y with a sine function such that the correlation coefficient is given as:
where 

Partial correlation[edit]
If a population or data-set is characterized by more than two variables, a partial correlation coefficient measures the strength of dependence between a pair of variables that is not accounted for by the way in which they both change in response to variations in a selected subset of the other variables.
Decorrelation of n random variables[edit]
It is always possible to remove the correlations between all pairs of an arbitrary number of random variables by using a data transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.[44]
A corresponding result exists for reducing the sample correlations to zero. Suppose a vector of n random variables is observed m times. Let X be a matrix where 

where an exponent of −+1⁄2 represents the matrix square root of the inverse of a matrix. The correlation matrix of T will be the identity matrix. If a new data observation x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
This decorrelation is related to principal components analysis for multivariate data.
Software implementations[edit]
- R’s statistics base-package implements the correlation coefficient with
cor(x, y), or (with the P value also) withcor.test(x, y). - The SciPy Python library via
pearsonr(x, y). - The Pandas Python library implements Pearson correlation coefficient calculation as the default option for the method
pandas.DataFrame.corr - Wolfram Mathematica via the
Correlationfunction, or (with the P value) withCorrelationTest. - The Boost C++ library via the
correlation_coefficientfunction. - Excel has an in-built
correl(array1, array2)function for calculationg the pearson’s correlation coefficient.
See also[edit]
- Anscombe’s quartet
- Association (statistics)
- Coefficient of colligation
- Yule’s Q
- Yule’s Y
- Concordance correlation coefficient
- Correlation and dependence
- Correlation ratio
- Disattenuation
- Distance correlation
- Maximal information coefficient
- Multiple correlation
- Normally distributed and uncorrelated does not imply independent
- Odds ratio
- Partial correlation
- Polychoric correlation
- Quadrant count ratio
- RV coefficient
- Spearman’s rank correlation coefficient
Footnotes[edit]
- ^ As early as 1877, Galton was using the term «reversion» and the symbol «r» for what would become «regression».[3][4][5]
References[edit]
- ^ «SPSS Tutorials: Pearson Correlation».
- ^ «Correlation Coefficient: Simple Definition, Formula, Easy Steps». Statistics How To.
- ^ Galton, F. (5–19 April 1877). «Typical laws of heredity». Nature. 15 (388, 389, 390): 492–495, 512–514, 532–533. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. S2CID 4136393. In the «Appendix» on page 532, Galton uses the term «reversion» and the symbol r.
- ^ Galton, F. (24 September 1885). «The British Association: Section II, Anthropology: Opening address by Francis Galton, F.R.S., etc., President of the Anthropological Institute, President of the Section». Nature. 32 (830): 507–510.
- ^ Galton, F. (1886). «Regression towards mediocrity in hereditary stature». Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.
- ^ Pearson, Karl (20 June 1895). «Notes on regression and inheritance in the case of two parents». Proceedings of the Royal Society of London. 58: 240–242. Bibcode:1895RSPS…58..240P.
- ^ Stigler, Stephen M. (1989). «Francis Galton’s account of the invention of correlation». Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580. JSTOR 2245329.
- ^ «Analyse mathematique sur les probabilités des erreurs de situation d’un point». Mem. Acad. Roy. Sci. Inst. France. Sci. Math, et Phys. (in French). 9: 255–332. 1844 – via Google Books.
- ^ Wright, S. (1921). «Correlation and causation». Journal of Agricultural Research. 20 (7): 557–585.
- ^ a b c d e Real Statistics Using Excel: Correlation: Basic Concepts, retrieved 22 February 2015
- ^ Weisstein, Eric W. «Statistical Correlation». mathworld.wolfram.com. Retrieved 22 August 2020.
- ^ Moriya, N. (2008). «Noise-related multivariate optimal joint-analysis in longitudinal stochastic processes». In Yang, Fengshan (ed.). Progress in Applied Mathematical Modeling. Nova Science Publishers, Inc. pp. 223–260. ISBN 978-1-60021-976-4.
- ^ Garren, Steven T. (15 June 1998). «Maximum likelihood estimation of the correlation coefficient in a bivariate normal model, with missing data». Statistics & Probability Letters. 38 (3): 281–288. doi:10.1016/S0167-7152(98)00035-2.
- ^ «2.6 — (Pearson) Correlation Coefficient r». STAT 462. Retrieved 10 July 2021.
- ^ «Introductory Business Statistics: The Correlation Coefficient r». opentextbc.ca. Retrieved 21 August 2020.
- ^ Rodgers; Nicewander (1988). «Thirteen ways to look at the correlation coefficient» (PDF). The American Statistician. 42 (1): 59–66. doi:10.2307/2685263. JSTOR 2685263.
- ^ Schmid, John Jr. (December 1947). «The relationship between the coefficient of correlation and the angle included between regression lines». The Journal of Educational Research. 41 (4): 311–313. doi:10.1080/00220671.1947.10881608. JSTOR 27528906.
- ^ Rummel, R.J. (1976). «Understanding Correlation». ch. 5 (as illustrated for a special case in the next paragraph).
- ^ Buda, Andrzej; Jarynowski, Andrzej (December 2010). Life Time of Correlations and its Applications. Wydawnictwo Niezależne. pp. 5–21. ISBN 9788391527290.
- ^ a b Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.).
- ^ Bowley, A. L. (1928). «The Standard Deviation of the Correlation Coefficient». Journal of the American Statistical Association. 23 (161): 31–34. doi:10.2307/2277400. ISSN 0162-1459. JSTOR 2277400.
- ^ «Derivation of the standard error for Pearson’s correlation coefficient». Cross Validated. Retrieved 30 July 2021.
- ^ Rahman, N. A. (1968) A Course in Theoretical Statistics, Charles Griffin and Company, 1968
- ^ Kendall, M. G., Stuart, A. (1973) The Advanced Theory of Statistics, Volume 2: Inference and Relationship, Griffin. ISBN 0-85264-215-6 (Section 31.19)
- ^ Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. (1917). «On the distribution of the correlation coefficient in small samples. Appendix II to the papers of «Student» and R.A. Fisher. A co-operative study». Biometrika. 11 (4): 328–413. doi:10.1093/biomet/11.4.328.
- ^ Davey, Catherine E.; Grayden, David B.; Egan, Gary F.; Johnston, Leigh A. (January 2013). «Filtering induces correlation in fMRI resting state data». NeuroImage. 64: 728–740. doi:10.1016/j.neuroimage.2012.08.022. hdl:11343/44035. PMID 22939874. S2CID 207184701.
- ^ Hotelling, Harold (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Kenney, J.F.; Keeping, E.S. (1951). Mathematics of Statistics. Vol. Part 2 (2nd ed.). Princeton, NJ: Van Nostrand.
- ^ Weisstein, Eric W. «Correlation Coefficient—Bivariate Normal Distribution». mathworld.wolfram.com.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
- ^ Lai, Chun Sing; Tao, Yingshan; Xu, Fangyuan; Ng, Wing W.Y.; Jia, Youwei; Yuan, Haoliang; Huang, Chao; Lai, Loi Lei; Xu, Zhao; Locatelli, Giorgio (January 2019). «A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty» (PDF). Information Sciences. 470: 58–77. doi:10.1016/j.ins.2018.08.017. S2CID 52878443.
- ^ a b Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing. Academic Press.
- ^ Devlin, Susan J.; Gnanadesikan, R.; Kettenring J.R. (1975). «Robust estimation and outlier detection with correlation coefficients». Biometrika. 62 (3): 531–545. doi:10.1093/biomet/62.3.531. JSTOR 2335508.
- ^ Huber, Peter. J. (2004). Robust Statistics. Wiley.[page needed]
- ^ Katz., Mitchell H. (2006) Multivariable Analysis – A Practical Guide for Clinicians. 2nd Edition. Cambridge University Press. ISBN 978-0-521-54985-1. ISBN 0-521-54985-X
- ^ Hotelling, H. (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Olkin, Ingram; Pratt,John W. (March 1958). «Unbiased Estimation of Certain Correlation Coefficients». The Annals of Mathematical Statistics. 29 (1): 201–211. doi:10.1214/aoms/1177706717. JSTOR 2237306..
- ^ «Re: Compute a weighted correlation». sci.tech-archive.net.
- ^ «Weighted Correlation Matrix – File Exchange – MATLAB Central».
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram» (PDF). European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Fulekar (Ed.), M.H. (2009) Bioinformatics: Applications in Life and Environmental Sciences, Springer (pp. 110) ISBN 1-4020-8879-5
- ^ Immink, K. Schouhamer; Weber, J. (October 2010). «Minimum Pearson distance detection for multilevel channels with gain and / or offset mismatch». IEEE Transactions on Information Theory. 60 (10): 5966–5974. CiteSeerX 10.1.1.642.9971. doi:10.1109/tit.2014.2342744. S2CID 1027502. Retrieved 11 February 2018.
- ^ Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics. New Jersey: World Scientific. p. 176. ISBN 978-981-02-3778-3. Retrieved 21 September 2016.
- ^ Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall. Appendix 3. ISBN 0-412-12420-3.
External links[edit]
- «cocor». comparingcorrelations.org. – A free web interface and R package for the statistical comparison of two dependent or independent correlations with overlapping or non-overlapping variables.
- «Correlation». nagysandor.eu. – an interactive Flash simulation on the correlation of two normally distributed variables.
- «Correlation coefficient calculator». hackmath.net. Linear regression. –
- «Critical values for Pearson’s correlation coefficient» (PDF). frank.mtsu.edu/~dkfuller. – large table.
- «Guess the Correlation». – A game where players guess how correlated two variables in a scatter plot are, in order to gain a better understanding of the concept of correlation.
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson’s r, the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation,[1] or colloquially simply as the correlation coefficient[2] ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).
Examples of scatter diagrams with different values of correlation coefficient (ρ)
Several sets of (x, y) points, with the correlation coefficient of x and y for each set. Note that the correlation reflects the strength and direction of a linear relationship (top row), but not the slope of that relationship (middle), nor many aspects of nonlinear relationships (bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlation coefficient is undefined because the variance of Y is zero.
Naming and history[edit]
It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844.[a][6][7][8][9] The naming of the coefficient is thus an example of Stigler’s Law.
Definition[edit]
Pearson’s correlation coefficient is the covariance of the two variables divided by the product of their standard deviations. The form of the definition involves a «product moment», that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier product-moment in the name.
For a population[edit]
Pearson’s correlation coefficient, when applied to a population, is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. Given a pair of random variables 
where:
The formula for 
the formula for 
where:
The formula for 
the formula for 
Peason’s correlation coefficient does not exist when either 

For a sample[edit]
Pearson’s correlation coefficient, when applied to a sample, is commonly represented by 




where:
Rearranging gives us this formula for 
where 
This formula suggests a convenient single-pass algorithm for calculating sample correlations, though depending on the numbers involved, it can sometimes be numerically unstable.
Rearranging again gives us this[10] formula for 
where 
An equivalent expression gives the formula for 
where:
Alternative formulae for 

where:
Practical issues[edit]
Under heavy noise conditions, extracting the correlation coefficient between two sets of stochastic variables is nontrivial, in particular where Canonical Correlation Analysis reports degraded correlation values due to the heavy noise contributions. A generalization of the approach is given elsewhere.[12]
In case of missing data, Garren derived the maximum likelihood estimator.[13]
Some distributions (e.g., stable distributions other than a normal distribution) do not have a defined variance.
Mathematical properties[edit]
The values of both the sample and population Pearson correlation coefficients are on or between −1 and 1. Correlations equal to +1 or −1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(X,Y) = corr(Y,X).
A key mathematical property of the Pearson correlation coefficient is that it is invariant under separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY, where a, b, c, and d are constants with b, d > 0, without changing the correlation coefficient. (This holds for both the population and sample Pearson correlation coefficients.) Note that more general linear transformations do change the correlation: see § Decorrelation of n random variables for an application of this.
Interpretation[edit]
The correlation coefficient ranges from −1 to 1. An absolute value of exactly 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line. The correlation sign is determined by the regression slope: a value of +1 implies that all data points lie on a line for which Y increases as X increases, and vice versa for −1.[14] A value of 0 implies that there is no linear dependency between the variables.[15]
More generally, note that (Xi − X)(Yi − Y) is positive if and only if Xi and Yi lie on the same side of their respective means. Thus the correlation coefficient is positive if Xi and Yi tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative (anti-correlation) if Xi and Yi tend to lie on opposite sides of their respective means. Moreover, the stronger either tendency is, the larger is the absolute value of the correlation coefficient.
Rodgers and Nicewander[16] cataloged thirteen ways of interpreting correlation or simple functions of it:
- Function of raw scores and means
- Standardized covariance
- Standardized slope of the regression line
- Geometric mean of the two regression slopes
- Square root of the ratio of two variances
- Mean cross-product of standardized variables
- Function of the angle between two standardized regression lines
- Function of the angle between two variable vectors
- Rescaled variance of the difference between standardized scores
- Estimated from the balloon rule
- Related to the bivariate ellipses of isoconcentration
- Function of test statistics from designed experiments
- Ratio of two means
Geometric interpretation[edit]
Regression lines for y = gX(x) [red] and x = gY(y) [blue]
For uncentered data, there is a relation between the correlation coefficient and the angle φ between the two regression lines, y = gX(x) and x = gY(y), obtained by regressing y on x and x on y respectively. (Here, φ is measured counterclockwise within the first quadrant formed around the lines’ intersection point if r > 0, or counterclockwise from the fourth to the second quadrant if r < 0.) One can show[17] that if the standard deviations are equal, then r = sec φ − tan φ, where sec and tan are trigonometric functions.
For centered data (i.e., data which have been shifted by the sample means of their respective variables so as to have an average of zero for each variable), the correlation coefficient can also be viewed as the cosine of the angle θ between the two observed vectors in N-dimensional space (for N observations of each variable)[18]
Both the uncentered (non-Pearson-compliant) and centered correlation coefficients can be determined for a dataset. As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, and y = (0.11, 0.12, 0.13, 0.15, 0.18).
By the usual procedure for finding the angle θ between two vectors (see dot product), the uncentered correlation coefficient is:
This uncentered correlation coefficient is identical with the cosine similarity.
Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by ℰ(x) = 3.8 and y by ℰ(y) = 0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from which
as expected.
Interpretation of the size of a correlation[edit]
This figure gives a sense of how the usefulness of a Pearson correlation for predicting values varies with its magnitude. Given jointly normal X, Y with correlation ρ, 
Several authors have offered guidelines for the interpretation of a correlation coefficient.[19][20] However, all such criteria are in some ways arbitrary.[20] The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
Inference[edit]
Statistical inference based on Pearson’s correlation coefficient often focuses on one of the following two aims:
- One aim is to test the null hypothesis that the true correlation coefficient ρ is equal to 0, based on the value of the sample correlation coefficient r.
- The other aim is to derive a confidence interval that, on repeated sampling, has a given probability of containing ρ.
We discuss methods of achieving one or both of these aims below.
Using a permutation test[edit]
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson’s correlation coefficient involves the following two steps:
- Using the original paired data (xi, yi), randomly redefine the pairs to create a new data set (xi, yi′), where the i′ are a permutation of the set {1,…,n}. The permutation i′ is selected randomly, with equal probabilities placed on all n! possible permutations. This is equivalent to drawing the i′ randomly without replacement from the set {1, …, n}. In bootstrapping, a closely related approach, the i and the i′ are equal and drawn with replacement from {1, …, n};
- Construct a correlation coefficient r from the randomized data.
To perform the permutation test, repeat steps (1) and (2) a large number of times. The p-value for the permutation test is the proportion of the r values generated in step (2) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here «larger» can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.
Using a bootstrap[edit]
The bootstrap can be used to construct confidence intervals for Pearson’s correlation coefficient. In the «non-parametric» bootstrap, n pairs (xi, yi) are resampled «with replacement» from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled r values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile of the resampled r values.
Standard error[edit]
If 

where 

Testing using Student’s t-distribution[edit]
Critical values of Pearson’s correlation coefficient that must be exceeded to be considered significantly nonzero at the 0.05 level.
For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson’s correlation coefficient follows Student’s t-distribution with degrees of freedom n − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
has a student’s t-distribution in the null case (zero correlation).[23] This holds approximately in case of non-normal observed values if sample sizes are large enough.[24] For determining the critical values for r the inverse function is needed:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper[25] provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson’s correlation coefficient follows a Student’s t-distribution, but the degrees of freedom are reduced.[26]
Using the exact distribution[edit]
For data that follow a bivariate normal distribution, the exact density function f(r) for the sample correlation coefficient r of a normal bivariate is[27][28][29]
where 

In the special case when 
where 
Using the exact confidence distribution[edit]
Confidence intervals and tests can be calculated from a confidence distribution. An exact confidence density for ρ is[30]
where 

Using the Fisher transformation[edit]
In practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformation, 
F(r) approximately follows a normal distribution with
and standard error
where n is the sample size. The approximation error is lowest for a large sample size 


Using the approximation, a z-score is
under the null hypothesis that 

To obtain a confidence interval for ρ, we first compute a confidence interval for F(
The inverse Fisher transformation brings the interval back to the correlation scale.
For example, suppose we observe r = 0.7 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is arctanh(r) = 0.8673, so the confidence interval on the transformed scale is 0.8673 ± 1.96/√47, or (0.5814, 1.1532). Converting back to the correlation scale yields (0.5237, 0.8188).
In least squares regression analysis[edit]
The square of the sample correlation coefficient is typically denoted r2 and is a special case of the coefficient of determination. In this case, it estimates the fraction of the variance in Y that is explained by X in a simple linear regression. So if we have the observed dataset 

where the 
The two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).
Next, we apply a property of least square regression models, that the sample covariance between 

Thus
where 
In the derivation above, the fact that
can be proved by noticing that the partial derivatives of the residual sum of squares (RSS) over β0 and β1 are equal to 0 in the least squares model, where
.
In the end, the equation can be written as:
where
The symbol 

Sensitivity to the data distribution[edit]
Existence[edit]
The population Pearson correlation coefficient is defined in terms of moments, and therefore exists for any bivariate probability distribution for which the population covariance is defined and the marginal population variances are defined and are non-zero. Some probability distributions, such as the Cauchy distribution, have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.
Sample size[edit]
- If the sample size is moderate or large and the population is normal, then, in the case of the bivariate normal distribution, the sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient, and is asymptotically unbiased and efficient, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient.
- If the sample size is large and the population is not normal, then the sample correlation coefficient remains approximately unbiased, but may not be efficient.
- If the sample size is large, then the sample correlation coefficient is a consistent estimator of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers can be applied).
- If the sample size is small, then the sample correlation coefficient r is not an unbiased estimate of ρ.[10] The adjusted correlation coefficient must be used instead: see elsewhere in this article for the definition.
- Correlations can be different for imbalanced dichotomous data when there is variance error in sample.[31]
Robustness[edit]
Like many commonly used statistics, the sample statistic r is not robust,[32] so its value can be misleading if outliers are present.[33][34] Specifically, the PMCC is neither distributionally robust,[citation needed] nor outlier resistant[32] (see Robust statistics § Definition). Inspection of the scatterplot between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.
Statistical inference for Pearson’s correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap can be applied to construct confidence intervals, and permutation tests can be applied to carry out hypothesis tests. These non-parametric approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.
A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.[35]
Variants[edit]
Variations of the correlation coefficient can be calculated for different purposes. Here are some examples.
Adjusted correlation coefficient[edit]
The sample correlation coefficient r is not an unbiased estimate of ρ. For data that follows a bivariate normal distribution, the expectation E[r] for the sample correlation coefficient r of a normal bivariate is[36]
therefore r is a biased estimator of
The unique minimum variance unbiased estimator radj is given by[37]
-
(1)
where:
An approximately unbiased estimator radj can be obtained[citation needed] by truncating E[r] and solving this truncated equation:
-
(2)
An approximate solution[citation needed] to equation (2) is:
-
(3)
where in (3):
are defined as above,
- radj is a suboptimal estimator,[citation needed][clarification needed]
- radj can also be obtained by maximizing log(f(r)),
- radj has minimum variance for large values of n,
- radj has a bias of order 1⁄(n − 1).
Another proposed[10] adjusted correlation coefficient is:[citation needed]
Note that radj ≈ r for large values of n.
Weighted correlation coefficient[edit]
Suppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),[38][39]
- Weighted mean:
- Weighted covariance
- Weighted correlation
Reflective correlation coefficient[edit]
The reflective correlation is a variant of Pearson’s correlation in which the data are not centered around their mean values.[citation needed] The population reflective correlation is
The reflective correlation is symmetric, but it is not invariant under translation:
The sample reflective correlation is equivalent to cosine similarity:
The weighted version of the sample reflective correlation is
Scaled correlation coefficient[edit]
Scaled correlation is a variant of Pearson’s correlation in which the range of the data is restricted intentionally and in a controlled manner to reveal correlations between fast components in time series.[40] Scaled correlation is defined as average correlation across short segments of data.
Let 


The scaled correlation across the entire signals 
where 

By choosing the parameter 
Pearson’s distance[edit]
A distance metric for two variables X and Y known as Pearson’s distance can be defined from their correlation coefficient as[41]
Considering that the Pearson correlation coefficient falls between [−1, +1], the Pearson distance lies in [0, 2]. The Pearson distance has been used in cluster analysis and data detection for communications and storage with unknown gain and offset.[42]
The Pearson «distance» defined this way assigns distance greater than 1 to negative correlations. In reality, both strong positive correlation and negative correlations are meaningful, so care must be taken when Pearson «distance» is used for nearest neighbor algorithm as such algorithm will only include neighbors with positive correlation and exclude neighbors with negative correlation. Alternatively, an absolute valued distance: 
Circular correlation coefficient[edit]
For variables X = {x1,…,xn} and Y = {y1,…,yn} that are defined on the unit circle [0, 2π), it is possible to define a circular analog of Pearson’s coefficient.[43] This is done by transforming data points in X and Y with a sine function such that the correlation coefficient is given as:
where 

Partial correlation[edit]
If a population or data-set is characterized by more than two variables, a partial correlation coefficient measures the strength of dependence between a pair of variables that is not accounted for by the way in which they both change in response to variations in a selected subset of the other variables.
Decorrelation of n random variables[edit]
It is always possible to remove the correlations between all pairs of an arbitrary number of random variables by using a data transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.[44]
A corresponding result exists for reducing the sample correlations to zero. Suppose a vector of n random variables is observed m times. Let X be a matrix where 

where an exponent of −+1⁄2 represents the matrix square root of the inverse of a matrix. The correlation matrix of T will be the identity matrix. If a new data observation x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:
This decorrelation is related to principal components analysis for multivariate data.
Software implementations[edit]
- R’s statistics base-package implements the correlation coefficient with
cor(x, y), or (with the P value also) withcor.test(x, y). - The SciPy Python library via
pearsonr(x, y). - The Pandas Python library implements Pearson correlation coefficient calculation as the default option for the method
pandas.DataFrame.corr - Wolfram Mathematica via the
Correlationfunction, or (with the P value) withCorrelationTest. - The Boost C++ library via the
correlation_coefficientfunction. - Excel has an in-built
correl(array1, array2)function for calculationg the pearson’s correlation coefficient.
See also[edit]
- Anscombe’s quartet
- Association (statistics)
- Coefficient of colligation
- Yule’s Q
- Yule’s Y
- Concordance correlation coefficient
- Correlation and dependence
- Correlation ratio
- Disattenuation
- Distance correlation
- Maximal information coefficient
- Multiple correlation
- Normally distributed and uncorrelated does not imply independent
- Odds ratio
- Partial correlation
- Polychoric correlation
- Quadrant count ratio
- RV coefficient
- Spearman’s rank correlation coefficient
Footnotes[edit]
- ^ As early as 1877, Galton was using the term «reversion» and the symbol «r» for what would become «regression».[3][4][5]
References[edit]
- ^ «SPSS Tutorials: Pearson Correlation».
- ^ «Correlation Coefficient: Simple Definition, Formula, Easy Steps». Statistics How To.
- ^ Galton, F. (5–19 April 1877). «Typical laws of heredity». Nature. 15 (388, 389, 390): 492–495, 512–514, 532–533. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0. S2CID 4136393. In the «Appendix» on page 532, Galton uses the term «reversion» and the symbol r.
- ^ Galton, F. (24 September 1885). «The British Association: Section II, Anthropology: Opening address by Francis Galton, F.R.S., etc., President of the Anthropological Institute, President of the Section». Nature. 32 (830): 507–510.
- ^ Galton, F. (1886). «Regression towards mediocrity in hereditary stature». Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.
- ^ Pearson, Karl (20 June 1895). «Notes on regression and inheritance in the case of two parents». Proceedings of the Royal Society of London. 58: 240–242. Bibcode:1895RSPS…58..240P.
- ^ Stigler, Stephen M. (1989). «Francis Galton’s account of the invention of correlation». Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580. JSTOR 2245329.
- ^ «Analyse mathematique sur les probabilités des erreurs de situation d’un point». Mem. Acad. Roy. Sci. Inst. France. Sci. Math, et Phys. (in French). 9: 255–332. 1844 – via Google Books.
- ^ Wright, S. (1921). «Correlation and causation». Journal of Agricultural Research. 20 (7): 557–585.
- ^ a b c d e Real Statistics Using Excel: Correlation: Basic Concepts, retrieved 22 February 2015
- ^ Weisstein, Eric W. «Statistical Correlation». mathworld.wolfram.com. Retrieved 22 August 2020.
- ^ Moriya, N. (2008). «Noise-related multivariate optimal joint-analysis in longitudinal stochastic processes». In Yang, Fengshan (ed.). Progress in Applied Mathematical Modeling. Nova Science Publishers, Inc. pp. 223–260. ISBN 978-1-60021-976-4.
- ^ Garren, Steven T. (15 June 1998). «Maximum likelihood estimation of the correlation coefficient in a bivariate normal model, with missing data». Statistics & Probability Letters. 38 (3): 281–288. doi:10.1016/S0167-7152(98)00035-2.
- ^ «2.6 — (Pearson) Correlation Coefficient r». STAT 462. Retrieved 10 July 2021.
- ^ «Introductory Business Statistics: The Correlation Coefficient r». opentextbc.ca. Retrieved 21 August 2020.
- ^ Rodgers; Nicewander (1988). «Thirteen ways to look at the correlation coefficient» (PDF). The American Statistician. 42 (1): 59–66. doi:10.2307/2685263. JSTOR 2685263.
- ^ Schmid, John Jr. (December 1947). «The relationship between the coefficient of correlation and the angle included between regression lines». The Journal of Educational Research. 41 (4): 311–313. doi:10.1080/00220671.1947.10881608. JSTOR 27528906.
- ^ Rummel, R.J. (1976). «Understanding Correlation». ch. 5 (as illustrated for a special case in the next paragraph).
- ^ Buda, Andrzej; Jarynowski, Andrzej (December 2010). Life Time of Correlations and its Applications. Wydawnictwo Niezależne. pp. 5–21. ISBN 9788391527290.
- ^ a b Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.).
- ^ Bowley, A. L. (1928). «The Standard Deviation of the Correlation Coefficient». Journal of the American Statistical Association. 23 (161): 31–34. doi:10.2307/2277400. ISSN 0162-1459. JSTOR 2277400.
- ^ «Derivation of the standard error for Pearson’s correlation coefficient». Cross Validated. Retrieved 30 July 2021.
- ^ Rahman, N. A. (1968) A Course in Theoretical Statistics, Charles Griffin and Company, 1968
- ^ Kendall, M. G., Stuart, A. (1973) The Advanced Theory of Statistics, Volume 2: Inference and Relationship, Griffin. ISBN 0-85264-215-6 (Section 31.19)
- ^ Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. (1917). «On the distribution of the correlation coefficient in small samples. Appendix II to the papers of «Student» and R.A. Fisher. A co-operative study». Biometrika. 11 (4): 328–413. doi:10.1093/biomet/11.4.328.
- ^ Davey, Catherine E.; Grayden, David B.; Egan, Gary F.; Johnston, Leigh A. (January 2013). «Filtering induces correlation in fMRI resting state data». NeuroImage. 64: 728–740. doi:10.1016/j.neuroimage.2012.08.022. hdl:11343/44035. PMID 22939874. S2CID 207184701.
- ^ Hotelling, Harold (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Kenney, J.F.; Keeping, E.S. (1951). Mathematics of Statistics. Vol. Part 2 (2nd ed.). Princeton, NJ: Van Nostrand.
- ^ Weisstein, Eric W. «Correlation Coefficient—Bivariate Normal Distribution». mathworld.wolfram.com.
- ^ Taraldsen, Gunnar (2020). «Confidence in Correlation». doi:10.13140/RG.2.2.23673.49769.
- ^ Lai, Chun Sing; Tao, Yingshan; Xu, Fangyuan; Ng, Wing W.Y.; Jia, Youwei; Yuan, Haoliang; Huang, Chao; Lai, Loi Lei; Xu, Zhao; Locatelli, Giorgio (January 2019). «A robust correlation analysis framework for imbalanced and dichotomous data with uncertainty» (PDF). Information Sciences. 470: 58–77. doi:10.1016/j.ins.2018.08.017. S2CID 52878443.
- ^ a b Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing. Academic Press.
- ^ Devlin, Susan J.; Gnanadesikan, R.; Kettenring J.R. (1975). «Robust estimation and outlier detection with correlation coefficients». Biometrika. 62 (3): 531–545. doi:10.1093/biomet/62.3.531. JSTOR 2335508.
- ^ Huber, Peter. J. (2004). Robust Statistics. Wiley.[page needed]
- ^ Katz., Mitchell H. (2006) Multivariable Analysis – A Practical Guide for Clinicians. 2nd Edition. Cambridge University Press. ISBN 978-0-521-54985-1. ISBN 0-521-54985-X
- ^ Hotelling, H. (1953). «New Light on the Correlation Coefficient and its Transforms». Journal of the Royal Statistical Society. Series B (Methodological). 15 (2): 193–232. doi:10.1111/j.2517-6161.1953.tb00135.x. JSTOR 2983768.
- ^ Olkin, Ingram; Pratt,John W. (March 1958). «Unbiased Estimation of Certain Correlation Coefficients». The Annals of Mathematical Statistics. 29 (1): 201–211. doi:10.1214/aoms/1177706717. JSTOR 2237306..
- ^ «Re: Compute a weighted correlation». sci.tech-archive.net.
- ^ «Weighted Correlation Matrix – File Exchange – MATLAB Central».
- ^ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram» (PDF). European Journal of Neuroscience. 35 (5): 1–21. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
- ^ Fulekar (Ed.), M.H. (2009) Bioinformatics: Applications in Life and Environmental Sciences, Springer (pp. 110) ISBN 1-4020-8879-5
- ^ Immink, K. Schouhamer; Weber, J. (October 2010). «Minimum Pearson distance detection for multilevel channels with gain and / or offset mismatch». IEEE Transactions on Information Theory. 60 (10): 5966–5974. CiteSeerX 10.1.1.642.9971. doi:10.1109/tit.2014.2342744. S2CID 1027502. Retrieved 11 February 2018.
- ^ Jammalamadaka, S. Rao; SenGupta, A. (2001). Topics in circular statistics. New Jersey: World Scientific. p. 176. ISBN 978-981-02-3778-3. Retrieved 21 September 2016.
- ^ Cox, D.R.; Hinkley, D.V. (1974). Theoretical Statistics. Chapman & Hall. Appendix 3. ISBN 0-412-12420-3.
External links[edit]
- «cocor». comparingcorrelations.org. – A free web interface and R package for the statistical comparison of two dependent or independent correlations with overlapping or non-overlapping variables.
- «Correlation». nagysandor.eu. – an interactive Flash simulation on the correlation of two normally distributed variables.
- «Correlation coefficient calculator». hackmath.net. Linear regression. –
- «Critical values for Pearson’s correlation coefficient» (PDF). frank.mtsu.edu/~dkfuller. – large table.
- «Guess the Correlation». – A game where players guess how correlated two variables in a scatter plot are, in order to gain a better understanding of the concept of correlation.
Для каждого трейдера важно понимать, что мы работаем с торговыми инструментами, состоящими из пары валют. В отличие от фондового рынка, где, как правило, каждый торговый инструмент это всего лишь одна индивидуальная единица, на Форекс используется измерение стоимости одной валюты в единицах другой. При этом мы не редко можем наблюдать, визуальную схожесть в движении нескольких валютных пар. Это может быть связано с тем, что обе пары могут содержать одну и ту же валюту в обоих случаях. Например, можно говорить о корреляции валютных пар EUR/USD и USD — CHF с отрицательным значением К.
Одним из способов использования корреляции пар в торговле является устранение расхождения инструментов. Например, трейдер выбрал для своей работы две валютные пары, которые коррелируют с К = 0.8. В этом случае, при наблюдении за движением подопытных, человек заметит, что К время от времени меняется, то несколько увеличиваясь, то несколько уменьшаясь. Тем не менее, средние значения коэффициента все равно находятся в диапазоне 0.7<К<0.8.
Как только на рынке наступит ситуация, что К<0.4, например, то это будет означать наличие лишь частичного соответствия в движении обоих инструментов. То есть, при росте одной пары рост другой окажется весьма ограничен. Но, помня о том, что в целом эти инструменты коррелируют с К=0.7 или 0.8, мы можем использовать данный разрыв себе на пользу, открыв позиции в сторону сближения пар.
Нахождение подобных ситуаций и дальнейшее их использование затрудняется непостоянностью значения К. Мы можем не верно толковать новые значения коэффициента, принимая из за ожидаемый нами разрыв, но позже может оказаться, что это новое значение данного коэффициента, которое теперь станет постоянным на определенное время. Существуют специальные корреляционные индикаторы, помогающие трейдерам наблюдать за схождением и расхождением инструментов, а другими словами, за изменениями текущих значений К.
Сложно переоценить значимость коэффициента корреляции в рыночной торговле. Его использование позволяет смотреть на трейдинг более глобально, учитывая движения пар, относительно друг друга. Еще одной областью применения коэффициента стало хеджирование. Желая снизить риски в своей торговле, спекулянты могут проводить хеджирование не только на разных рынках, но и с помощью коррелирующих инструментов. Таким образом, происходит частичное хеджирование.
Для начала разберемся в самой сути такого понятия, как арбитраж. Это несколько логически связанных сделок, направленных на извлечение прибыли из разницы в ценах на одинаковые или связанные активы в одно и то же время на разных рынках (пространственный арбитраж), либо на одном и том же рынке в разные моменты времени (временно́й арбитраж, обычная биржевая спекуляция). Выделяют эквивалентный арбитраж — операции с комбинацией составных или производных активов (опционов, биржевых индексов) и обычных контрактов, когда между теоретически эквивалентными комбинациями на практике возникает разница цен.
Упрощенно арбитраж выглядит следующим образом: торгуются пары или группы инструментов, суммарная стоимость которых должна быть равна определенной величине, исходя из природы инструментов. Например: акции одной и той же компании на различных торговых площадках, группа инструментов входящих в индекс и фьючерс на индекс. При отклонении стоимости корзины от расчетной величины, совершается сделка. Трейдеры-арбитражеры сглаживают дисбаланс цен на родственных» инструментах.
Коэффициент корреляции (Correlation coefficient) — это
В первоначальном виде арбитраж возник на заре развития вторичных (региональных) бирж, когда один итот же актив торговался на разных площадках по разным ценам и с 44 каждым годом разрыв этой цены стремительно сокращался, а вместе с ним скорость арбитражных стратегий и их объем.
Сегодня существует в качестве межбиржевого варианта, когда актив торгуется на биржах разных стран, например на токийской и нью-йоркской, лондонской и франкфуртской. А также на NYSE и NASDAQ в качестве арбитража разных активов, например двух-трех акций из одного сектора.
В основе арбитража лежит такое понятие, как корреляция. корреляция, если простыми словами — это взаимосвязь двух или более событий, т.е. когда происходит одно, то вероятно (статистически подтверждено) и другое. Когда-то корреляции на рынке были невыраженными в моменте, они были растянуты во времени. Вот к примеру, как рассуждают экономисты/аналитики: «Если индекс доллара упадет, цена на нефть должна расти…» или «Если индекс SNP упадет, цена на золото должна вырасти или наоборот…», ну это как бы простые причинно-следственные связи. Однако совершенно очевидно, что если все так просто, то все бы с легкостью зарабатывали, чего, как мы все прекрасно знаем, не происходит. Пример самой жесткой корреляции — это пары типа Евро/Доллар. Они намертво связаны между собой. Малейшее изменение цены одного приводит к мгновенному изменению цены другого. Тут, понятно, корреляция обратная и речь идет о торгуемых инструментах, например, на СМЕ. И данная корреляция действительна в обе стороны. Есть же, например, бумаги, которые сами «ничего не решают», но есть у них «старший», который и скажет, куда им «идти». А есть ситуации, в которых таких «старших» два и более, вот тут совсем все интересно становится.
Когда речь заходит о корреляциях, в том смысле, в каком я их понимаю, неизбежно возникает вопрос: «а кто главный (ведущий)?». Для этого введем понятие «Поводырь» — это будет любой торгуемый инструмент, изменение цены которого приведет к какой-либо реакции того, за которым мы наблюдаем (торгуем).
Основные поводыри для Американского фондового рынка следующие (в порядке убывания силы глобального влияния):
1. Фьючерсный контракт на индекс SNP 500 — главный поводырь, самый влиятельный, нет ни одного ликвидного инструмента, на который бы не оказало влияние изменение цены фьючерсного контракта хотя бы на тик, реакция есть всегда. Вопрос о первичности (кто за кем «ходит»), индекс или фьючерс, всегда рождает много споров, но нас, спекулянтов, скальперов, волнует только одно — кто из них быстрее. Я могу ответственно заявить, что фьючерсный контракт — быстрее, изменчивее (в разы) и главнее в данном контексте.
2. Фьючерс на нефть марки Light Sweet — углеводороды, что тут еще сказать. Сильное влияние оказывает на некоторые сектора, на отдельные индустрии, связанные с нефтедобычей и нефтепереработкой, а также на те отрасли, где существенная статья издержек — топливо и ГСМ, например авиакомпании. Сам актив несколько зависим от Индекса доллара.
3. Фьючерсный контракт на золото (и другие драг. металлы) — Au рулит по-прежнему, ибо мировое «золотое плечо» уже вылезло за все допустимые рамки, не дам источник, но цитату приведу: «В мире обещания продать золото, больше в 100 раз, чем самого золота», как-то так. Т.е. это и мерило ценности некоторых валют, и надежный (однако!) для многих актив, и инструмент хеджирования рисков и еще много чего полезного делает. Также как и нефть, оказывает серьезное влияние на компании, занимающиеся золотодобычей, переработкой, реализацией и прочим. Сам по себе поводырь зависим (в моменте) от Индекса доллара.
4. Индекс доллара — с появлением евро все сильнее стал подвержен колебаниям, связанным с проблемами в Еврозоне, также изменчив за счет спекулятивных действий в торгуемой валютной паре евро/доллар. Сам зависим от макроэкономической статистики, стоимости облигаций (и наоборот тоже, тут уже сложный аналитический расклад, который данной статьи никак не касается, тем более, я не аналитик и тем более, не экономист, а спекулянт. Оказывает влияние на многие товарные фьючерсы, расчет по которым ведется в долларах Соединенных Штатов.
Поводырем вторичным (а иногда и первичным) может также являться акция, которая в данный момент самая сильная/слабая в секторе/индустрии, которая сама по себе является более весомой в индексе из всего сектора. Например, если $C (Citigroup) измениться резко в цене на полпроцента, это мгновенно скажется на остальных акциях, связанных с банковской деятельностью и с финансами, не так сильно отразиться на $JPM и $BAC, но точно «дернет» $BBT и $PNC, к примеру, а уж $FAZ и $FAS отреагируют как следует, по взрослому, с резким изменением котировок и объемом. А вот обратное не будет иметь такого влияния. Если $PNC или какой-нибудь банк Испании или Ирландии не обрушиться на пару процентов, то никто из «толстых» не заметит, однако по цепочке может привести к некоей корректировке на графике. Скажем так, $PNC также входит в состав портфеля, торгуемого в виде ETF $FAZ ($FAS), так вот сильное его ($PNC) изменение приведет к неминуемому (но небольшому) изменению цены индекса, что, закономерно, приведет к корректировке даже $C и $BAC, первого на несколько центов, а второго, возможно, ни на сколько, разве стакан уплотниться в «сильную» сторону. Это один из вариантов, комбинаций может быть очень много. На графике видно, как акции вторичные стоят в рэйндже, пока сильнейшие представители сектора «смотрят» в разные стороны, и как послушно они «идут» за всеми, если направление сильных совпадает:
На графике изображены: SPY — SPDR S&P 500 (белая линия), C — Citigroup, Inc., JPM — JP Morganand Co., BAC — Bank of America Corp Corporation, GS — The Goldman Sachs Group, Inc., BBT — BB&T Corporation, PNC — PNC Financial Services Group Inc.
Теперь давайте рассмотрим какой-нибудь самый необычный пример. Вот Авиакомпании. Например $UAL или $DAL или $LCC, не входят в состав индекса SNP 500 и тем более DJIA, однако довольно объемны, имеют высокую капитализацию, в целом привязаны к рынку, как таковому, но главное — зависят от цен на топливо. И не нужно рассказывать, что у них все поставки фьючерсные, с фиксированной ценой на пару лет вперед и прочее, это все так, но откройте их график минутный и понаблюдайте, что происходит, когда нефть очень резко изменяется в цене. А теперь добавьте сюда индекс доллара, который влияет на них самих, т.к. Цены их услуг — они в долларахи сама нефть зависит от него (доллара), ну и SNP 500, который частенько идет в противоход нефти… Вот их (акции авиакомпаний) разрывает в разные стороны. А еще помню день был, когда у $LCC отчет случился и нефть с рынком в разные стороны… Вот остальных трепало! График выглядел интересно. Вот пример за эту неделю, $LCC валится на растущей черного золота и растущем фьючерсе, и отрастает на падающей черного золота (тикер $USO):
На графике изображены: SPY — SPDR S&P 500 (белая линия), USO — United States Oil, UAL — United Continental Holdings, Inc., LCC — US Airways Group, Inc., DAL — Delta Air Lines Inc.
Также, для дальнейшего понимания написанного мною, потребуется ввести еще один термин — «Драйвер», под которым понимается некое событие, которое сильно влияет на поведение торгуемого актива, либо, что немаловажно, поводыря, за которым мы также наблюдаем, это может быть новость в компании, отчет, понижение/повышение рейтинга или новость, касающаяся сектора в целом, макроэкономическая статистика, изменение ставки вложения инвистиций и другие. Т.е. драйверы глобальные влияют на фьючерсные контракты (поводыри, описанные выше), а те, в свою очередь, на торгуемые инструменты и т.д.
Теперь вопрос: почему акции так одинаково ходят и кто за всем этим стоит? Да все, особенно скальперы, роботы-скальперы, люди-скальперы. Роботы-арбитражеры в первую очередь, а также алгоритмы, котирующие акцию (читай маркетмейеры). Ведь иначе невозможно было бы такую массу акций заставить двигаться более менее одинаково, речь, понятно, внутри дня. Потому что, если мы взглянем на большие таймфреймы, то выясниться, что многие сектора живут своей отдельной жизнью. Вот например, график месячный, с 2000 года:
На нем изображены: XLK — Technology Select Sector SPDR, XLF — Financial Select Sector SPDR, XLP — customer Staples Select Sector SPDR, XLE — energy Select Sector SPDR, XLV — Health Care Select Sector SPDR, XLI — Industrial Select Sector SPDR, XLB — Materials Select Sector SPDR, XLU — Utilities Select Sector SPDR, XLY — customer Discret Select Sector SPDR, SPY — SPDR S&P 500 (белая линия).
Ютилитис какие слабенькие. Интересно, они рванут вверх, за ростом фьючерсного контракта или на малейшем его откате шлёпнутся еще ниже? Разброс относительно $SPY приличный. А вот, что на меньших масштабах времени, дневка, за 2012 год:
Действующие лица те же. В общем есть некое понимание, что графики похожи, но одни сильнее рынка в целом, а другие слабее, в абсолютном выражении, при расчете на начало года. Это все глобально, на год, а вот на месяц:
Действующие лица те же. Меня же в торговле интересует арбитраж внутридневной, график — от пятиминутного до минутного:
Или, например, технологический сектор в пятницу (14.09.2012), смотрите, как на откатах фьючерсного контракта вниз они «валяться» и «стоят» на его росте, между прочим — это и есть входы в шорт:
На графике изображены: SPY — SPDR S&P 500 (белая линия), T — AT&T, Inc., VZ — Verizon Communications Inc., XLK — Technology Select Sector SPDR.
Это, что касательно фьючерсного контракта SNP 500 (на графиках, для моего удобства показан не сам фьючерс, а ETF на индекс SNP 500, учитывая, что график — линия, различий нет совсем). А вот пример акций нефтяной индустрии, в сравнении с черным золотом:
На графике изображены: USO — United States Oil, XOM — Exxon Mobil Corporation, SLB — Schlumberger Limited, CVX — Chevron. Или, например, «золотые» акции, в сравнении, понятно, с золотом:
На графике изображены: GLD — SPDR gold Shares, NEM — Newmont mining industry Corp., KGC — Kinross gold Corporation, ABX — Barrick gold Corporation.
Однако, график — одно, а стакан с лентой (LEVEL II + Time & sales) — совсем другое дело (кстати, именно это и позволяет торговать $SPY, опираясь на фьючерс). Показать в картинках, что происходит и какая реакция — сложно, потому распишу немного словами. Что можем видеть на ведомых, если на ведущих есть большое движение? В первую очередь — изменение котировки без сделок, оно и понятно, акции скоррелированы, а торговать-то некому, ибо акции не первого эшелона, но машинки-котировщики будут исправно двигать биды с оферами, в след за «старшим» братом, держа при этом некий спред, обычно больше 3-4 ц. Если же движение общее, не только на сильных акциях, а на всем рынке в целом, то может произойти сильное движение, с объемом, и с еще большим расширением спреда в противоположную от него (движения) сторону. Например, нефть ($USO) улетела вверх на полпроцента за секунду, в $SLB будет расширен спред в сторону оферов (ASK), чтобы продать повыше, а потом закрыться пониже, поднимая биды (BID). Это один из десятков сценариев, понятно, что всегда есть вариации, но уловить общее можно, если тщательно понаблюдать и проанализировать поведение акций и их поводырей.
Стиль торговли таким образом называется «арбитраж», торгуется, как правило, минимум два инструмента, причем часто в разные стороны, но можно торговать один, рассматривая другие инструменты, как поводырей. Стиль сегодня очень роботизирован, но и для «мануальных скальперов» еще есть место.
Сложим все варианты арбитража в одну табличку и определим четыре варианта действий (простым языком, не пинайте, но так понятно всем будет): что отросло и главное — продавать, а что недоросло — покупать; что упало и главное — покупать, а что недоупало — продавать; что отросло и главное — не трогать, а что недоросло — продавать; что упало и главное — не трогать, а что недоупало — покупать.
Имея ввиду торговлю одного инструмента, чаще поступают так, торгуя по тренду сектора (индустрии): что не главное и отросло сильно — продавать, в случае, когда главное — «стоит и смотрит» вниз (было на вебинаре, кто помнит, $TCK); что не главное и упало сильно — покупать, в случае, когда главное — «стоит и смотрит» вверх.
Еще более кратко сам процесс можно описать так: определяем глобально (по секторам), кто сильный, кто слабый — по дневке; смотрим внутри сектора (на дневках) между акциями тоже самое; смотрим внутри дня на акции (по тренду сектора), опираясь на фьючерсный контракт (+ другие поводыри).
Коэффициент корреляции (Correlation coefficient) — это
Теперь, как определить «главного» в секторе/индустрии. Те, кто первый в столбце, те и рулят, как правило. НО!!! В случае, если нет глобальных новостей по сектору или если нет отчетов у разных акций из этого сектора. Т.е. их главенство имеет место быть в самый скучный понедельник, а не в день статистики, запасов газа, безработицы да еще с отчетом старших акций.
Вычисление коэффициента корреляции портфеля
Итак, перейдем к вычислению средней доходности, дисперсии и стандартного отклонения для портфеля акций, состоящего на 60% из акций А и на 40% из акций В. Мы предполагаем, что доходность по каждой из акций А и В — это случайные величины Rа и Rв. Среднее значение доходности акции А равно 10%, со стандартным отклонением 8,66%. Среднее значение доходности акции В равно 15%, со стандартным отклонением 12%.
Коэффициент корреляции (Correlation coefficient) — это
Теперь нас интересует, каково будет среднее значение доходности портфеля и стандартное отклонение для портфеля. Вопрос средней доходности портфеля решается просто. А вот стандартное отклонение — показатель уровня изменчивости доходности портфеля, не отражает средней изменчивости доходности его компонентов (акций). Причина в том, что диверсификация снижает изменчивость, так как цены различных акций изменяются неодинаково. Во многих случаях снижение стоимости одной акции компенсируется ростом цены на другую.
Ожидаемая доходность нашего портфеля равна средневзвешенной ожидаемых значений доходностей отдельных акций:
Для того, чтобы найти дисперсию и стандартное отклонение доходности портфеля, мы должны знать значения ковариации акций А и В. Ковариация служит для измерения степени совместной изменчивости двух акций. Общая формула вычисления ковариации:
Из формулы видно, что ковариация любой акции с ней самой равна ее дисперсии. В задачах, значение ковариации двух активов будет дано. Или, вместо нее будет дано значение коэффициента корреляции — безразмерной величины, которая стандартизует ковариацию для облегчения сравнения, и принимает значения от -1 до 1. Пусть нам дано, что коэффициент корреляции акций А и В равен 0,7. Формула коэффициента корреляции:
В большинстве случаев, изменение акций происходит в одном направлении. В этом случае коэффициент корреляции и, соответственно, ковариация, положительны. Если акции изменяются соверженно не связанно, тогда коэффициент корреляции и ковариация равны нулю. Если акции изменяются в противоположных направляения — коэффициент корреляции и ковариация отрицательны. Для нахождения дисперсии портфеля, нам надо заполнить матрицу:
Эта матрица очень похожа на матрицу ковариаций. Заполнив матрицу, надо просто сложить полученные в ней величины и найдем дисперсию портфеля:
Вычислим дисперсию портфеля:
Стандартное отклонение равно квадратному корню из дисперсии, то есть:
Легко подсчитать, что только в том случае, если коэффициент корреляции двух акций равен +1, то стандартное отклонение портфеля равно средневзвешенному стандартных отклонений доходности отдельных акций:
Если же коэффициент корреляции равен -1, то стандартное отклонение портфеля равно:
и можно было бы добиться, изменяя пропорции X1 и X2 акций в портфеле, чтобы стандартное отклонение портфеля было равно нулю. К сожалению, в реальности, отрицательная корреляция акций практически не встречается.
Коэффициент корреляции (Correlation coefficient) — это
Применение линейного коэффициента корреляции в трейдинге
Коллеги, добрый день! В настоящей статье я хочу предложить вашему вниманию небольшое исследование, посвященное одному из статистических показателей — линейному коэффициенту корреляции. А также поделюсь некоторыми соображениями по его применению в трейдинге на примере акций Лукойла.
Коэффициент корреляции (Correlation coefficient) — это
Для начала позвольте небольшой экскурс в историю возникновения показателя корреляции (да возблагодарим Википедию!): Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение либо коэффициент корреляции. В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.
Впервые в научный оборот термин «корреляция» ввёл французский палеонтолог Жорж Кювье в XVIII веке. Он разработал «закон корреляции» частей и органов живых существ, с помощью которого можно восстановить облик ископаемого животного, имея в распоряжении лишь часть его останков. В статистике слово «корреляция» первым стал использовать английский биолог и статистик Фрэнсис Гальтон в конце XIX века.
Некоторые виды коэффициентов корреляции могут быть положительными или отрицательными. В первом случае предполагается, что мы можем определить только наличие или отсутствие связи, а во втором — также и ее направление. Если предполагается, что на значениях переменных задано отношение строгого порядка, то отрицательная корреляция — корреляция, при которой увеличение одной переменной связано с уменьшением другой. При этом коэффициент корреляции будет отрицательным. Положительная корреляция в таких условиях — это такая связь, при которой увеличение одной переменной связано с увеличением другой переменной. Возможна также ситуация отсутствия статистической взаимосвязи — например, для независимых случайных величин.
Линейный коэффициент корреляции (далее ЛКК) (коэффициент корреляции Пирсона), который разработали Карл Пирсон, Фрэнсис Эджуорт и Рафаэль Уэлдон в 90-х годах XIX века. Коэффициент корреляции рассчитывается по формуле:
Коэффициент корреляции изменяется в пределах [-1…+1]. Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Итак, коллеги, ЛКК определяет: во-первых, наличие связи между двумя потоками данных, во-вторых, силу этой связи (сила связи определяется приближением абсолютного значения ЛКК к единице), в-третьих, направление этой связи (прямая — ЛКК больше единицы или обратная — ЛКК меньше единицы). Важным и необходимым условием для расчета ЛКК является наличие двух одинаковых по количеству данных потоков данных. Так же в общем случае считается, что значения ЛКК можно считать достоверным, если в расчете участвует поток из более, чем 30 пар данных.
Коэффициент корреляции (Correlation coefficient) — это
В Excel расчет значения ЛКК реализован через функцию «КОРРЕЛ()». Пример наличия корреляции: Положительная корреляция: температура окружающего воздуха и продажи летней одежды. Чем теплее на улице, тем больше покупаем летних вещей. Рост температуры — рост продаж. Отрицательная корреляция: та же самая температура окружающего воздуха, но продажи уже зимней одежды. Чем холоднее на улице, тем больше покупаем зимних теплых вещей. Снижение температуры — рост продаж.
Примеры применения ЛКК в трейдинге. Области применения ЛКК в трейдинге достаточно широки. Например, долго считалось, что при падении фондовых рынков в целом растет спрос на золото. То есть между динамикой фондовых рынков и динамикой цен на золото существует обратная корреляционная зависимость. Другой пример. Рост котировок нефти и рост рынков, вес «нефтянки» в которых высок и является значимым. К таким рынкам относится и фондовый рынок России. Но в последние несколько лет, а именно в основном начиная с 2007 года, такие зависимости явно изменились. И либо сильно ослабли, либо исчезли совсем.
У приведенных выше примеров есть одна общая особенность: они построены строго на двух потоках данных, как того и требует формула расчета ЛКК. Тем не менее, в одной из книг, посвященных теории управления капиталом (а именно, Р.Винс «Математика управления капиталом») я нашел интересный подход к построению ЛКК на массиве, состоящем только из одного потока данных. Это может быть, например, непрерывный поток исходов в системных сделках или поток цен какой-то одной акции. О таком методе построения ЛКК ниже.
Коэффициент корреляции (Correlation coefficient) — это
Торговая стратегия, построенная на коэффициенте корреляции
Итак, давайте исследуем, например, поток цен на акции Лукойла (LKOH). Составим поток из недельных свечей. Мне удалось найти архив, начиная с 01.01.2001 и по сей день, то есть поток из почти 600 недельных свечей за десять с половиной лет. Исследовать будем не свечи в целом, а, например, максимальные цены в каждой свечей. Таким образом, перед нами непрерывный поток из 600 данных — максимальные цены в каждой торговой неделе, начиная с 01 января 2001 года. Кроме этих данных, пока никакие другие данные нам не нужны.
На рисунке показана динамика максимальных недельных цен в акциях LKOH. Расчет ЛКК должен дать ответы на вопросы: Есть ли зависимость между максимальными ценами двух любых соседних недель. Если зависимость есть, то какова ее направленность? Коллеги, если упростить, то вопрос можно сформулировать так: Если на истекшей неделе Лукойл обновил свой недельный максимум по сравнению с предыдущей неделей, то можем ли мы ожидать продолжения роста и на будущей неделе? Для расчета ЛКК поток данных требует некоторой трансформации. Составим таблицу:
В таблице на рисунке в последнем столбце, построенном на основе данных столбца «High цена», логика расчета следующая: если максимум текущей недели выше, чем максимум предыдущей недели, то в ячейке стоит значение 1. В противном случае значение равно 0. Таким образом, поток цен преобразован в поток единиц и нулей. Далее произведем расчет ЛКК на основе данных столбца «Обновление High цены». Поскольку для расчета ЛКК необходимо два потока данных, то сделаем следующее:
Как видно из рисунка, поток 2 «сдвинут» относительно потока 1 на один период. Таким образом, из одного потока данных получено два. И теперь смысл расчета ЛКК заключается в выяснении связи между двумя соседними значениями выборки. В нашем случае — максимальными ценами соседних недель (текущей и предыдущей). Теперь собственно по расчету ЛКК. Расчет произведем двумя способами: Охватим весь период выборки (600 недель).
Начиная с 30й недели выборки (август 2001 года) для каждой недели рассчитаем значение ЛКК по последним 30 неделям. То есть для каждой недели рассчитаем т.н. «скользящее» значение ЛКК с периодом n=30 (по аналогии со скользящей средней), поскольку при n>30 в общем случае значение ЛКК считается значимым. Результаты расчетов отражены на рисунке:
Выводы по рисунка: На протяжении всего периода выборки у акций Лукойла наблюдается неярко выраженная положительная корреляция между максимальными ценами соседних недель (красная линия графика с ЛКК = +0,1). То есть факт обновления максимальной цены на текущей неделе по сравнению с предыдущей позволяет сделать предположение о том, что на следующей неделе в сравнении с текущей вероятность обновления максимума выше вероятности НЕобновления максимума.
Коэффициент корреляции (Correlation coefficient) — это
ЛКК, построенное по последним 30 неделям (синяя линия на графике), изменяется в диапазоне от -0,35 (сильная отрицательная корреляция) до +0,6 (очень сильная положительная корреляция). Самый продолжительный период, в течение которого корреляция между недельными максимумами была положительная — это период с мая 2004 года до августа 2007 года. В этот период обновление максимумов на прошлой неделе в большинстве случаев приводило к обновлению максимумов в течение текущей недели. Именно в этот период акции Лукойла агрессивно росли.
Самый продолжительный период, в течение которого корреляция между недельными максимумами была отрицательная — это период с августа 2007 года по июль 2011 года. В этот период недельной обновление максимумов на прошлой неделе в большинстве случаев не приводило к обновлению максимумов в течение текущей недели. И наоборот, НЕобновление недельных максимумов в течение текущей недели в большинстве случае приводило к росту на следующей неделе. В этот период акции Лукойла «запилило» от максимумов весной 2008 года до низов в июле 2009 года.
В точках, где синяя линия находится выше красной, корреляция между недельными максимумами выше средней за период и имеет прямую направленность. В таких точках при обновлении недельных максимумов на текущей неделе наиболее вероятно обновление максимумов в течение следующей недели. В точках, где синяя линия находится ниже красной, корреляция между недельными максимумами ниже средней за период и имеет в основном обратную направленность. В таких точках, в отличие от ситуации п.5, наиболее вероятно обновление максимумов в течение следующей недели при НЕобновлении недельных максимумов текущей недели.
Коллеги, на основании последних двух выводов у меня сформировалась идея тестирования стратегии, построенной на принципах такого парного корреляционного эффекта.
Коэффициент корреляции (Correlation coefficient) — это
Торговля ациями по коэффициенту корреляции
Стратегия, построенная на принципах автокорреляции. Общее описание стратегии. Принципы стратегии: тестируемый инструмент — акции Лукойла (LKOH) на недельном ТФ за период с 01.01.2001 по 31.07.2012; типы совершаемых сделок — исключительно Long; время удержания позиции — вход на Open недельной свечи, выход на Close этой же свечи. Таким образом, удержание позиции строго в течение торговой недели без ухода в бумагах на выходные; внешние факторы — цены на нефть, мировые новости, динамика западных рынков и проч. — не учитываются; внутренние факторы — внутрикорпоративные новости, дивидендные отсечки и проч. — не учитываются.
Принципы формирования сигналов: Методом тестирования определяется некое критическое скользящее значение линейного коэффициента корреляции (далее — ЛККкр) по 30 периодам. Покупка Вариант 1. Если текущее значение ЛКК ВЫШЕ критического значения и на текущей неделе ПРОИЗОШЛО обновление максимума по сравнению с прошлой неделей, то на Open следующей недели происходит покупка. Срок удержания позиции — не позднее Close недели открытия позиции.
Покупка Вариант 2. Если текущее значение ЛКК НИЖЕ критического значения и на текущей неделе НЕ ПРОИЗОШЛО обновление максимума по сравнению с прошлой неделей, то на Open следующей недели происходит покупка. Срок удержания позиции — не позднее Close недели открытия позиции. Во всех остальных случаях — вне позиции (cash). Таким образом, для принятия решения о входе/невходе в позицию необходима информация о максимальных ценах последних 30ти недель. И ничего более сверх этого.
Коэффициент корреляции (Correlation coefficient) — это
Само решение принимается в промежутке между закрытием торговой недели и открытием следующей торговой недели. В случае формирования торгового сигнала трейдеру необходимо находиться в рынке утром первого дня торговой недели для открытия позиции и вечером последнего дня торговой недели для выхода из бумаг. Для тестирования такой стратегии вполне хватило возможностей Excel. У недельного Лукойла критическим значением ЛКК оказалось значение 0,15. Приведу пару примеров для иллюстрации:
Пример 1.
Сигнал от 25.06.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1855 (>0,15) и обновлен максимум предыдущей недели (1805 руб. > 1765 руб.). На основании этого на Open свечи 02.07.12 совершена покупка по 1804 руб. Позиция закрыта на Close свечи 02.07.12, то есть 06.07.12, по цене 1825 руб. Рентабельность сделки составила +1,2% при периоде удержания позиции 5 сессий.
Сигнал от 02.07.12. В данном случае так же выполнены оба условия покупки: ЛККкр=0,2472 (>0,15) и обновлен максимум предыдущей недели (1857 руб. > 1805 руб.). На основании этого на Open свечи 09.07.12 совершена покупка по 1826 руб. Позиция закрыта на Close свечи 09.07.12, то есть 13.07.12, по цене 1818 руб. Рентабельность сделки составила -0,4% при периоде удержания позиции 5 сессий.
Пример 2.
Сигнал от 07.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1098 (<0,15) и НЕ обновлен максимум предыдущей недели (1700 руб. < 1802 руб.). На основании этого на Open свечи 14.05.12 совершена покупка по 1684 руб. Позиция закрыта на Close свечи 14.05.12, то есть 18.05.12, по цене 1594 руб. Рентабельность сделки составила -5,4% при периоде удержания позиции 5 сессий.
Сигнал от 14.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1258 (<0,15) и НЕ обновлен максимум предыдущей недели (1684 руб. < 1700 руб.). На основании этого на Open свечи 21.05.12 совершена покупка по 1602 руб. Позиция закрыта на Close свечи 21.05.12, то есть 25.05.12, по цене 1639 руб. Рентабельность сделки составила +2,3% при периоде удержания позиции 5 сессий.
Коэффициент корреляции (Correlation coefficient) — это
Сигнал от 21.05.12. В данном случае выполнены оба условия покупки: ЛККкр=0,1336 (<0,15) и НЕ обновлен максимум предыдущей недели (1602 руб. < 1684 руб.). На основании этого на Open свечи 28.05.12 совершена покупка по 1647 руб. Позиция закрыта на Close свечи 28.05.12, то есть 01.06.12, по цене 1742 руб. Рентабельность сделки составила +5,8% при периоде удержания позиции 5 сессий.
Back-testing стратегии. В данном разделе приведу результаты тестирования стратегии в сравнении со стратегией «Buy&Hold» (B&H).
На рисунке показана динамика дохода тестируемой стратегии в сравнении с принципом B&H. За точку отчета (0%) принята цена акций Лукойла в начале января 2001 года (270 руб.). Как видно, принцип B&H опережал стратегию в течение 2001-2008 гг. Падение ранка в 2008 году сравняло результаты обоих стратегий до уровня примерно +200% к старту. Затем, начиная с 2009 года, обе стратегии показали примерно одинаковые результаты и на сегодня корреляционная стратегия незначительно опережает по доходности принцип B&H.
Как видно из профилей графиков, волатильность (риск) принципа B&H гораздо выше волатильности тестируемой стратегии. Размер среднегодовой доходности тестируемой стратегии составляет 20% годовых на всем периоде тестирования.
Риск-менеджмент, основанный на коэффициенте корреляции
Покупка по Варианту 1 (ЛККкр >0,15 + новый максимум)
Из 600 недель тестового периода сигналы по Варианту 1 возникли в 109 случаях (19% потока или каждая пятая неделя). Из 109 сигналов 74 отработали в плюс (68%, или два из трех сигналов). Средний результат положительного исхода равен по модулю среднему результату отрицательного исхода (38 руб./акция) Общий положительный результат потока сигналов сформирован за счет превышения в 2 раза количества положительных исходов над отрицательными исходами.
Коэффициент корреляции (Correlation coefficient) — это
С учетом частоты распределения положительных и отрицательных исходов расчет математического ожидания выглядит следующим образом: Размер ожидаемого успеха +26 руб./акция, Размер ожидаемого убытка -13 руб./акция, Общий ожидаемый результат +13 руб./акция, Размер среднеквадратичного отклонения исходов сигналов составляет 24 руб./акция. Диапазон колебаний исходов сигналов находится в пределах [-11 руб.;+38 руб.], Максимальная серия подряд убыточных сигналов составила 2 сигнала с максимальным риском не более 178 руб./акция. В нынешних ценах это около 9% торгового депозита.
Покупка по Варианту 2 (ЛККкр <0,15 + нет нового максимума)
Фактически покупки по варианту 2 — это покупки против падения рынка. Поэтому показатели риска и волатильности выше, нежели по варианту 1. Из 600 недель тестового периода сигналы по Варианту 2 возникли в 190 случаях (33% потокаили каждая третья неделя). Из 190 сигналов 91 отработали в плюс (48% или половина сигналов). Средний результат положительного исхода равен +66 руб./акция, а отрицательного исхода -50 руб./акция. Общий положительный результат потока сигналов сформирован за счет превышения размера средней прибыли над средним убытком.
Коэффициент корреляции (Correlation coefficient) — это
С учетом частоты распределения положительных и отрицательных исходов расчет математического ожидания выглядит следующим образом: Размер ожидаемого успеха +32 руб./акция, Размер ожидаемого убытка -26 руб./акция, Общий ожидаемый результат +6 руб./акция, Размер среднеквадратичного отклонения исходов сигналов составляет 49 руб./акция. Диапазон колебаний исходов сигналов находится в пределах [-44 руб.;+55 руб.], Максимальная серия подряд убыточных сигналов составила 6 сигналов с максимальным риском 187 руб./акция. В нынешних ценах это около 10% торгового депозита. Стратегия в целом:
Из 600 недель тестового периода сигналы по стратегии в целом возникли в 299 случаях (53% потока или каждая вторая неделя). Из 299 сигналов 165 отработали в плюс (55% или более половины сигналов). Средний результат положительного исхода равен +53 руб./акция, а отрицательного исхода -47 руб./акция. Общий положительный результат потока сигналов сформирован как за счет превышения количества положительных исходов над отрицательными исходами, так и за счет превышения размера средней прибыли над средним убытком.
С учетом частоты распределения положительных и отрицательных исходов расчет математического ожидания выглядит следующим образом: Размер ожидаемого успеха +29 руб./акция, Размер ожидаемого убытка -21 руб./акция, Общий ожидаемый результат +8 руб./акция, Размер среднеквадратичного отклонения исходов сигналов составляет 55 руб./акция. Диапазон колебаний исходов сигналов находится в пределах [-47 руб.;+63 руб.], Максимальная серия подряд убыточных сигналов составила 6 сигналов с максимальным риском 187 руб./акция. В нынешних ценах это около 10% торгового депозита при доходности 20% годовых.
В целом стратегия показала неплохой тренд-следящий результат, а так же оказалась достаточно устойчива в условиях падения 2008 года. Особенно, если учесть усилия трейдера по следованию сигналам. Коллеги, за сим пока все по описанию линейной корреляции и ее применении в трейдинге.
Коэффициент корреляции валютных пар
Рассмотрим такое явление, как межвалютная корреляция на Форексе. Данная методика может существенно повысить понимание рыночных процессов, а также улучшить качество ваших краткосрочных и среднесрочных прогнозов. Существует две разновидности межвалютной корреляции, которые могут помочь в работе трейдера. Рассмотрим подробнее.
Коэффициент корреляции (Correlation coefficient) — это
Корреляция — это статистический термин, означающий наличие взаимосвязанных тенденций изменений между двумя рядами данных. В нашем случае Валютная корреляция — это взаимосвязь между историческими данными курсов одной валютной пары. Или изменения курса одной пары могут быть взаимосвязанными с изменениями другой пары. Данная взаимосвязь чаще всего имеет фундаментальное экономическое обоснование и уходит корнями в особенности всемирного хозяйства. Проще говоря, есть две валютных пары: A/B и C/D. Если между ними есть корреляция, при росте курса A/B может стабильно наблюдаться или рост кусра C/D (тогда это прямая корреляция) или его падение (тогда корреляция буде обратной).
Выше мы говорили о двух разновидностях. Это скользящая и прямая корреляция. Прямая корреляция валютных пар — явление, полезное для повышения точности прогнозов. Даже торгуя на одном инструменте, вы можете повысить точность прогнозирования, применяя анализ нескольких валютных пар. Вернемся к нашим A/B и C/D, допустим, вы торгуете инструментом A/B. Известно, что эти валютные пары в прямой корреляции, то есть вверх и вниз идут синхронно. Ваш технический анализ показал, что пара A/B должна падать. Соответственно, если теханализ пары C/D говорит об обратном, есть повод усомниться в достоверности сигнала. Если же всё совпало, — вы можете с большей уверенностью открывать позицию. Получается, зная взаимосвязи, можно уменьшить количество случайных сигналов. Однако нужно помнить, что корреляционный анализ работает на относительно больших масштабах (в лучшем случае на часовых или получасовых графиках). Если ваша торговая стратегия базируется на «минутках», эти данные могут только помешать.
Следующий вид корреляции — скользящая. Суть в том, что взаимосвязь проявляется на сдвинутом по временной шкале наборе данных. То есть изменение курса пары A/B сейчас является предвестником изменения пары C/D в будущем. Если собрать информацию, достаточно детальную для формирования торговой стратегии, наличие таких корреляций может очень существенно повысить точность. Фактически, у вас появляется инструмент базового прогнозирования курса.
Как анализировать корреляцию?
Чтобы отыскать корреляционную связь, можно пользоваться существующими утилитами из Интернета (которые не сложно найти в Гугле по запросу «корреляция валют форекс») или делать всё руками, в старом добром экселе. Там есть такая замечательная функция КОРРЕЛ, которая показывает корреляцию двух выбранных множеств данных. Берем курсы нескольких инструментов, копируем исторические данные в Эксель и ищем корреляцию. Чтобы искать прямую корреляцию, необходимо выделять два совпадающих по временному промежутку набора данных. Чтобы искать скользящую взаимосвязь, сдвигаем множество вправо или влево на несколько периодов. Корреляция более 0.5 свидетельствует о прямой взаимосвязи, менее 0.5 — об обратной взаимосвязи, в пределах от -0.5 до 0.5 — об отсутствии взаимосвязи. Эти границы более чем условны, следует проверять их на практике…
Коэффициент корреляции (Correlation coefficient) — это
Для того чтобы легче было понять взаимосвязи и соотношение с числом коэффициента корреляции я подготовил рисунки, которые наглядно показывают коэффициент и визуальное сходство двух рядов. В качестве примера взяты рад косинуса и зашумлённый ряд косинусоиды, от амплитуды зашумления зависит коэффициент корреляции:
А здесь пример обратной корреляции валют. Как видим когда одна расчёт другая падает! Как EUR/USD и USD — CHF:
Текущая корреляция наиболее популярных валютных пар. Нужно понимать, что корреляция между валютами не является постоянной, рынок постоянно меняется. Приведенные здесь данные являются примерными, точную информацию нужно рассчитывать самостоятельно. Рассмотрим, как коррелирует с другими инструментами наиболее популярный среди трейдеров инструмент EUR/USD: прямая корреляция с: AUD — USD, BP/USD, NZD — USD; обратная корреляция с: USD-JPY, USD / CHF, USD — CAD.
Еще один любимый нашими трейдерами инструмент — «йенадоллар», USD/JPY. Взгялем на него: прямая: Доллар / Франк, USD / CAD; обратная: EUR/USD, AUS/USD,GBP/USD,NZD/USD. Что касается скользящей корреляции, ловить ее довольно сложно. К примеру, часто цена на золото опережает или немного отстает от GBP — USD. Но такую взаимосвязь нужно рассчитывать чуть ли не для каждого отдельного торгового дня.
Изменение коэффициента корреляции ценовых графиков
В качестве примера корреляции двух пар с положительным К, можно вспомнить о EUR/USD и EUR / JPY. В обоих случаях мы покупаем EUR и продаем вторую валюту. Некоторые пары движутся относительно друг друга, но со временем К может меняться. Например, чтобы определить для своей работы две коррелирующие между собой валютные пары, достаточно найти такую из всего ассортимента, предоставляемого ДЦ, которая бы имела очень низкую волатильность. В 2012 году в качестве такого инструмента вполне могла бы выступать EUR/CHF. Не каждый день ширина ее движения на рынке превышала бы 30 пунктов, что можно считать малой величиной, относительно аналогичных показателей других пар.
Данную валютную пару можно без труда разложить на две пары, используя для этого ту валюту, которая “разбавит” выбранный нами инструмент. Для этого мы берем USD, который позволит представить нам EUR/CHF, как EUR/USD*USD/CHF. Действительно, если перемножить две новых долларовых пары, то в результате мы вновь получаем исследуемую нами EUR/CHF. Данное преобразование говорит о том, что обе пары будут коррелировать между собой, так как их произведение будет демонстрировать значения пары EUR/CHF, а они относительно малы, о чем говорили в самом начале примера.
Коэффициент корреляции (Correlation coefficient) — это
Для уверенной торговли необходимо иметь четкое представление не только об особенностях отдельных инструментов торговли, но и об их взаимодействии друг с другом. Существуют целые торговые стратегии, построенные с использованием К. Могут применяться даже наложения одного ценового графика на другой, для выявления аналогий в движениях цены. Коэффициент может периодически рассчитываться заново, учитывая последние изменения в поведении ценовых графиков.
Коэффициент корреляции в анализе инвестиционного портфеля
Согласно Марковицу, любой инвестор должен основывать свой выбор исключительно на ожидаемой доходности и стандартном отклонении при выборе портфеля. Таким образом, осуществив оценку различных комбинаций портфелей, ондолжен выбрать «лучший», исходя из соотношения ожидаемой доходности и стандартного отклонения этих портфелей. При этом соотношение доходность-риск портфеля остается обычным: чем выше доходность, тем выше риск.
Также, прежде чем приступить к формированию портфеля, необходимо дать определение термину «эффективный портфель». Эффективный портфель — это портфель, который обеспечивает: максимальную ожидаемую доходность для некоторого уровня риска, или минимальный уровень риска для некоторой ожидаемой доходности.
В дальнейшем будем находить эффективные портфели в среде Excel в соответствии со вторым принципом — с минимальным уровнем риска для любой ожидаемой доходности. Для нахождения оптимального портфеля необходимо определить допустимое множество соотношений «риск-доход» для инвестора, которое достигается путем построения минимально-дисперсионной границы портфелей, т.е. границы, на которой лежат портфели с минимальным риском при заданной доходности.
граница src=»/pictures/investments/img1996892_Minimalno_dispersionnaya_granitsa.gif» style=»width: 600px; height: 373px;» title=»Минимально — дисперсионная граница» />
На рисунке выше жирной линией отображена «эффективная граница», а большими точками отмечены возможные комбинации портфелей.
Эффективная граница — это граница, которая определяет эффективное множество портфелей. Портфели, лежащие слева от эффективной границы применить нельзя, т.к. они не принадлежат допустимому множеству. Портфели, находящиеся справа (внутренние портфели) и ниже эффективной границы являются неэффективными, т.к. существуют портфели, которые при данном уровне риска обеспечивают более высокую доходность, либо более низкий риск для данного уровня доходности.
Коэффициент корреляции (Correlation coefficient) — это
Для построения минимально-дисперсионной границы и определения «эффективной границы» нам будут необходимы значения ожидаемых доходностей, рисков (стандартных отклонений) и ковариации активов. Имея эти данные можно приступить к нахождению «эффективных портфелей».
Начнем с расчета ожидаемой доходности портфеля по формуле:
где Хi — доля i-ой бумаги в портфеле, E(ri) — ожидаемая доходность i-ой бумаги. А затем определим дисперсию портфеля, в формуле которой используется двойное суммирование:
И как следствие найдем стандартное отклонение портфеля, которое является квадратным корнем из дисперсии. Для наглядности приведем пример построения эффективной границы при помощи Microsoft Excel, а точнее при помощи встроенного в него компонента Поиск решения.
Зададим долю каждого актива в нашем первоначальном портфеле пропорционально их количеству. Следовательно, доля каждого актива в портфеле составит 1/3, т.е. 33%. Общая доля должна равняться 1, как для портфелей,в которых разрешены «короткие» позиции, так и для тех, в которых запрещены. Сам Марковиц запрещает открывать «короткие» позиции по активам, входящим в портфель, однако современная портфельная это разрешает. Если «короткие» позиции разрешены, то доля по активу будет отображена как -0.33 и средства, вырученные от его продажи, должны быть вложены в другой актив, таким образом, доля активов в портфеле в любом случае будет равняться 1.
Рассчитаем ожидаемую доходность, дисперсию и стандартное отклонение средневзвешенного портфеля:
Как видно из таблицы, для определения дисперсии портфеля нужно просто просуммировать данные в ячейках B19-D19, а квадратный корень из значения ячейки C21 даст нам стандартное отклонение портфеля в ячейке C22. Произведение долей бумаг на их ожидаемую доходность даст нам ожидаемую доходность нашего портфеля, которая отражена в ячейке C23. Окончательный результат средневзвешенного портфеля представлен ниже.
Средняя (ожидаемая) месячная доходность средневзвешенного портфеля 0,28% при риске 6,94%. Теперь можноприменить тот самый второй принцип, о котором было написано выше, т.е. обеспечить минимальный риск при заданном уровне доходности. Для этого воспользуемся функцией «Поиск Решений» из меню «Сервис». Если нет, значит надо открыть «Сервис» выбрать «Надстройки» и установить «Поиск решений». Запускаем «Поиск решений», в пункте «Установить указанную ячейку» указываем ячейку С22, которую будем минимизировать за счет изменения долей бумаг в портфеле, т.е. варьированием значений в ячейках A16-A18. Далее надо добавить два условия, а именно:
— сумма долей должна равняться 1, т.е. ячейка A19 = 1;
— задать доходность, которая нас интересует, к примеру, доходность 0.28% (ячейка С23), которая получилась при расчете средневзвешенного портфеля.
Так как мы запрещаем наличие «коротких» позиций по бумагам в меню «Параметры» надо установить галочку «Неотрицательные значения». Вот так должно выглядеть:
В результате мы получаем:
Итак, задав «Поиск решений» найти минимальное стандартное отклонение при заданной ожидаемой доходности в 0,33% мы получили оптимальный портфель, состоящий на 83% из РАО ЕЭС, на 17% из Лукойла и на 0% из Ростелекома. Несмотря на то, что уровень доходности тот же, что и при средневзвешенном портфеле, риск снизился.
Парный трейдинг и коэффициент корреляции
Понятие корреляция лежит в основе многих прибыльных торговых стратегий валютного рынка. В качестве примера можно привести парный трейдинг, основанный на корреляции валютных пар, позволяющий получить стабильную высокую прибыль на разных коррелирующих инструментах (об этом мы писали в предыдущих статьях) и торгового робота Octopus Arbitrage, его реализующего. В этой статье мы попытаемся просто и доступно объяснить суть корреляции и показать, как это можно применить на практике для парного трейдинга.
Почему было решено посвятить этой теме отдельную статью? Дело вот в чем. Несмотря на то, что корреляция нашла широкое практическое применение, доступное объяснение найти весьма трудно.
Как говорил Альберт Эйнштейн «если ты не можешь объяснить шестилетнему ребенку, чем ты занимаешься, значит, ты шарлатан». К сожалению, математики, пишущие учебные материалы этого принципа не придерживаются. Как только открываешь их талмуды, желая понять достаточно простые вещи, например, корреляция, так на тебя злобно смотрят четырехэтажные формулы, тройные интегралы и двухстраничные доказательства с применением огромного количества матерных слов незнакомых терминов. Самые стойкие засыпают через три минуты прочтения. Менее стойкие — через пять секунд созерцания этой «математической гармонии» создают облако пыли от захлопывающегося талмуда или нажимают крестик в правом верхнем углу экрана.
Корреляция — величина, характеризующая взаимную зависимость двух случайных величин, X и Y, безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением… Итак, что такое корреляция? По сути, корреляция показывает, насколько сильно связаны между собой величины. Если взять две произвольные величины, они могут быть сильно связаны между собой, никак не связаны, или слабо связаны.
Рассмотрим пример. Насколько связаны между собой количество прибыли, которую заработал трейдер за торговую сессию от количества выпитых им чашек кофе за тот же период? Т.е. имеем две величины: количество кружек кофе и прибыль.
Простой и наглядный способ анализа корреляции — загнать эти данные в Microsoft Excel и построить график. Стандартными средствами Excel можно вывести линию тренда, а также коэффициент корреляции R2. Как определяется коэффициент корреляции, поговорим чуть позже, пока лишь скажем, что эта величина изменяется от 0 до 1. При этом 0 — показывает, что связи нет вообще, а 1 — самая сильная связь, какая может быть. Линия тренда при отсутствии связи будет направлена параллельно оси X, при максимально сильной связи — под углом 45 градусов.
Ну что ж, похоже количество выпитого кофе на получение прибыли трейдером не влияет никак. Коэфициент корреляции R2 всего лишь 0,0289, линия тренда почти горизонтальна. Почему так? Возможно, помимо выпитого кофе существует множество факторов, оказывающих куда более существенное влияния на получение прибыли: факторы рынка, работа ДЦ, особенности выбранной торговой стратегии, личные качества трейдера и т.д.
Теперь разберем другой пример. Рассмотрим связь между валютными парами EUR/USD и GBP / USD. Были взяты скользящие средние дневных цен с 2 по 5 декабря 2013 года. Было взято четыре точки для простоты дальнейшего объяснения расчетов. Как правило, для подобных расчетов, точек нужно брать больше.
Теперь, аналогично, предыдущему примеру на основании этих данных построим график в Excel.
Так, здесь видно, что зависимость гораздо сильнее, так как R2 близко к единице, а линия тренда расположена почти под 45о. Можно сказать, что величины здесь коррелируют. Теперь рассмотрим, как рассчитывается коэффициент R. Здесь, к сожалению, без формул не обойтись. Однако, на самом деле, все заумные формулы можно свести к уровню седьмого класса средней школы. Для начала определимся, что у нас есть две «случайные» величины. Обозначим EURUSD как X, а GBPUSD как Y.
Далее хочу отметить, что большинство понятий, математической статистики базируются на среднем значении выборки. Проще говоря, на среднем арифметическом, т.е. сумма всех элементов, поделенная на их число. Вычислим среднее для величин X и Y.
Далее, приведем формулу расчета R2. В ней нет ничего сложного, как может показаться на первый взгляд. Здесь просто используются вычисленные нами средние арифметические:
Подставив выделенное в формулу получаем:
Таким образом, мы получили, посчитав «вручную», то, что автоматически делает Excel. Коэффициент R2 называется еще «коэффициентом Пирсона». Корреляция по EURUSD и GBPUSD, на самом деле, достаточно сильная, на это конечно есть фундаментальные причины, рассмотрение которых находится за рамками этой статьи.
Как корреляцию можно использовать для получения прибыли? Ярким примером может послужить стратегия парного трейдинга. Стратегия подразумевает, что большую часть времени выбранные валютные пары двигаются в рынке синхронно, но расхождения в поведении курсов происходят достаточно часто и каждое значительное рассогласование можно использовать для извлечения прибыли. Когда валютные пары расходятся на определенное количество пунктов: открываются две сделки, на одной паре — продажа, на другой — покупка. Когда пары возвращаются «друг к другу», позиции закрываются и прибыль фиксируется на одной или обеих позициях.
При расхождении инструментов открываются встречные позиции, при возвращении корреляции в исходное положение, встречные ордера закрываются, прибыль фиксируется на одной или обеих позициях
Безусловно, в нашей статье, описаны только основные принципы корреляции и парного трейдинга, поняв которые можно четко уяснить суть. Однако, для того, чтобы получать прибыль на FOREX, одних этих знаний недостаточно. Необходимо использовать специальные индикаторы, понимать расхождение каждой из пар и многое другое. Сколько трейдеров уже набили себе шишек на этом пути!
Коэффициент корреляции (Correlation coefficient) — это
Кроме того, необходимо постоянно быть «в рынке», двадцать четыре часа в сутки, семь дней в неделю, чтобы «не проспать», когда разойдется или же наоборот сойдется корреляция. При этом для устойчивого получения прибыли необходимо использовать не две валютные пары, а больше. Трейдер просто физически не сможет этого сделать. Как же здесь быть?
К счастью, есть уникальный торговый советник Octopus Arbitrage. Правильно настроив его и установив на нескольких парах, от трейдера, как правило, больше ничего не требуется. Все остальное сделает робот. Уникальный алгоритм позволит получать достойную прибыль при минимальных просадках, трейдер просто наблюдает за ростом депозита. Как говорится: «Вкалывают роботы — счастлив человек».
Коэффициент корреляции в психологических исследованиях
Коэффициент корреляции является одним из самых востребованых методов математической статистики в психологических и педагогических исследованиях. Формально простой, этот метод позволяет получить массу информации и сделать такое же количество ошибок. В этой статье мы рассмотрим сущность коэффициента корреляции, его свойства и виды. Слово correlation (корреляция) состоит из приставки «co-», которая обозначает совместность происходящего (по аналогии с «координация») и корня «relation», переводится как «отношение» или «связь» (вспомним public relations — связи с общественностью). Дословно correlation переводится как взаимосвязь.
Коэффициент корреляции — это мера взаимосвязи измеренных явлений. Коэффициент корреляции (обозначается «r») рассчитывается по специальной формуле и изменяется от -1 до +1. Показатели близкие к +1 говорят о том, что при увеличении значения одной переменной увеличивается значение другой переменной. Показатели близкие к -1 свидетельствуют об обратной связи, т.е. При увеличении значений одной переменной, значения другой уменьшаются.
Пример. На большой выборке был проведён тест FPI. Проанализируем взаимосвязи шкал Общительность, Застенчивость, Депрессивность. Начнем с Застенчивости и Депрессивности. Для наглядности, задаём систему координат, на которой по X будет застенчивость, а по Y — депрессивность. Таким образом, каждый человек из выборки исследования может быть изображен точкой на этой системе координат. В результате расчетов, коэффициент корреляции между ними r=0,6992.
Как видим, точки (испытуемые) расположены не хаотично, а выстраиваются вокруг одной линии, причём, глядя на эту линию можно сказать, что чем выше у человека выражена застенчивость, тем больше депрессивность, т. е. эти явления взаимосвязаны. Построим аналогичный график для Застенчивости и Общительности.
Мы видим, что с увеличением застенчивости общительность уменьшается. Их коэффициент корреляции -0,43. Таким образом, коэффициент корреляции больший от 0 до 1 говорит о прямопропорциональной связи (чем больше… тем больше…), а коэффициент от -1 до 0 о обратнопропорциональной (чем больше… тем меньше…). Если бы точки были расположены хаотично, коэффициент корреляции приближался бы к 0.
Коэффициент корреляции отражает степень приближенности точек на графике к прямой. Приведём примеры графиков, отражающих различную степень взаимосвязи (корреляции) переменных исследования. Сильная положительная корреляция:
Слабая положительная корреляция:
Нулевая корреляция:
В подписи у каждого графика кроме значения r есть значение p. p — это вероятность ошибки, о которой будет рассказано отдельно.
Источники и ссылки
ru.wikipedia.org — свободная энциклопедия Википедия
ru.math.wikia.com — математическая энциклопедия
vocabulary.ru — национальная психологическая энциклопедия
basegroup.ru — технологии анализа данных
investpark.ru — портал инвестора ИнвестПарк
megafx.ru — сайт для начинающих на рынке Форекс
psyfactor.org — центр практической психологии
learnspss.ru — сайт профессиональной обработки даных
exceltip.ru — блог о программе Microsoft Excel
economyreview.ru — информационные системы и технологии в экономике
aup.ru — аминистративно-управленческий портал
math-pr.com — решение задач и примеров по высшей математике
neerc.ifmo.ru — Викиконспекты
exponenta.ru — образовательный математический сайт
edu.jobsmarket.ru — курсы повышения квалификации в России и за рубежом
quans.ru — анализ и исследование рынка




![{displaystyle operatorname {cov} (X,Y)=operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e88bc4ba085b98d5cca09b958ad378d50127308)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [(X-mu _{X})(Y-mu _{Y})]}{sigma _{X}sigma _{Y}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/042c646e848d2dc6e15d7b5c7a5b891941b2eab6)
![{displaystyle mu _{X}=operatorname {mathbb {E} } [,X,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1182bdcc66a113596e3ece07a0acbeda8d56d483)
![{displaystyle mu _{Y}=operatorname {mathbb {E} } [,Y,]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2f14f5eda9d726e57048a2c56889912a80a06b6)
![{displaystyle sigma _{X}^{2}=operatorname {mathbb {E} } [,left(X-operatorname {mathbb {E} } [X]right)^{2},]=operatorname {mathbb {E} } [,X^{2},]-left(operatorname {mathbb {E} } [,X,]right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf27c91550c7c82ee7e9e948673eb99da1a7378)
![{displaystyle sigma _{Y}^{2}=operatorname {mathbb {E} } [,left(Y-operatorname {mathbb {E} } [Y]right)^{2},]=operatorname {mathbb {E} } [,Y^{2},]-left(,operatorname {mathbb {E} } [,Y,]right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed498483dae15dbb86e957b5a1463f5536885902)
![{displaystyle operatorname {mathbb {E} } [,left(X-mu _{X}right)left(Y-mu _{Y}right),]=operatorname {mathbb {E} } [,left(X-operatorname {mathbb {E} } [,X,]right)left(Y-operatorname {mathbb {E} } [,Y,]right),]=operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,],,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4443378e105084380438782ebd391f8cb0e8e048)
![{displaystyle rho _{X,Y}={frac {operatorname {mathbb {E} } [,X,Y,]-operatorname {mathbb {E} } [,X,]operatorname {mathbb {E} } [,Y,]}{{sqrt {operatorname {mathbb {E} } [,X^{2},]-left(operatorname {mathbb {E} } [,X,]right)^{2}}}~{sqrt {operatorname {mathbb {E} } [,Y^{2},]-left(operatorname {mathbb {E} } [,Y,]right)^{2}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a96c914bb811b84698b4d4118794cf4c8167ca7)








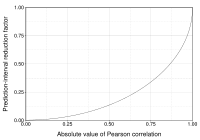

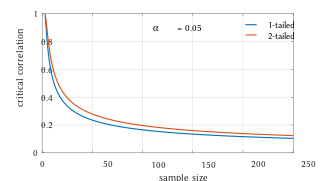








![z={frac {x-{text{mean}}}{text{SE}}}=[F(r)-F(rho _{0})]{sqrt {n-3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da7a3d54a70f9005e3bf9a2accf62cbf0fa0ea71)
![{displaystyle 100(1-alpha )%{text{CI}}:operatorname {artanh} (rho )in [operatorname {artanh} (r)pm z_{alpha /2}{text{SE}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/affc3f0ee39499c97bb851229113f49d83100bf2)
![{displaystyle 100(1-alpha )%{text{CI}}:rho in [tanh(operatorname {artanh} (r)-z_{alpha /2}{text{SE}}),tanh(operatorname {artanh} (r)+z_{alpha /2}{text{SE}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf658969d39ea848505750b5cd76db21da78dd5c)


![{displaystyle {begin{aligned}r(Y,{hat {Y}})&={frac {sum _{i}(Y_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={frac {sum _{i}(Y_{i}-{hat {Y}}_{i}+{hat {Y}}_{i}-{bar {Y}})({hat {Y}}_{i}-{bar {Y}})}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={frac {sum _{i}[(Y_{i}-{hat {Y}}_{i})({hat {Y}}_{i}-{bar {Y}})+({hat {Y}}_{i}-{bar {Y}})^{2}]}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sqrt {sum _{i}(Y_{i}-{bar {Y}})^{2}cdot sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}}}[6pt]&={sqrt {frac {sum _{i}({hat {Y}}_{i}-{bar {Y}})^{2}}{sum _{i}(Y_{i}-{bar {Y}})^{2}}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86595f3f77e8ee96952760d9176a5fa140cc562)




![{displaystyle operatorname {mathbb {E} } left[rright]=rho -{frac {rho left(1-rho ^{2}right)}{2n}}+cdots ,quad }](https://wikimedia.org/api/rest_v1/media/math/render/svg/683b838e709e3b32a3c22dfec4fa665a593f42ad)


![{displaystyle r=operatorname {mathbb {E} } [r]approx r_{text{adj}}-{frac {r_{text{adj}}(1-r_{text{adj}}^{2})}{2n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6382c40e3ad4e06d65c7d09e214ebc8daba5d30c)
![{displaystyle r_{text{adj}}approx rleft[1+{frac {1-r^{2}}{2n}}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf3f71f2cfe17f8f0d422d5ac0d482cc429a925)





![{displaystyle operatorname {corr} _{r}(X,Y)={frac {operatorname {mathbb {E} } [,X,Y,]}{sqrt {operatorname {mathbb {E} } [,X^{2},]cdot operatorname {mathbb {E} } [,Y^{2},]}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6d897e4b303a062ed14cc9f88f35f5c8ffc91f7)