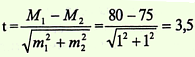Средняя ошибка опыта определяется на основании

Определение точности опыта

В
практике биометрическо­го анализа
используется относитель­ная ошибка
измерений – «показатель точности опыта»
– отношение ошибки средней к самой
средней арифметической, выраженное в
процентах:
.
Чем точ­нее определена средняя, тем
меньше будет ε,
и наоборот. Точность считается хорошей,
если ε
меньше 3%, и удовлетворительной при
3 < ε < 5%.
Иначе приходится собирать допол­нительный
материал. В примере показатель точности
составил ε = (0.11 / 9.3) ∙ 100
= 1.2%, что говорит о достаточной надежности
выборочной оценки.

Оптимальный объем выборки

В
биологических исследованиях часто
заранее требуется установить число
наблюдений, достаточное для получения
репрезентативных оценок генеральной
совокупности.

Для
непрерывных признаков метод состоит в
том, чтобы, используя известные соотношения
между средней, стандартным отклонением,
ошибкой средней, плотностью вероятности
распределения Стьюдента, найти число
степеней свободы, соответствующее
доверительному интервалу для средней
при уровне значимости α = 0.05.
Объем выборки, достаточной для получения
результата за­данной точности, находят
по формуле:

,

где п
– объем
выборки,

t – граничное
значение из таблицы распределения
Стьюдента (табл. 6П),
соответствующее принятому уровню
значимости при планируемом объеме
выборки,

CV
– приблизительное значение коэффициента
вариации (%),

ε
– плани­руемая точность оценки
(погрешности) (%).

Рассчитаем
необходимый объем условной выборки,
обеспечивающий хорошую точность ε = 3%,
для уровня значимости α = 0.05
(t = 1.98,
для df ≈ 100)
и для коэффициента вариации CV
=
12% (такова относительная изменчивость
многих размерно-весовых признаков
животных):

≈63 экз.

Если
исследуется фенотипическое (видовое)
разнообразие (дискретный признак), может
возникнуть задача определения минимального
объема выборки, в которой будет
присутствовать хотя бы один экземпляр
с определенным фенотипом (Животовский,
1991). С позиций теории вероятности задача
ставится так: определить объем выборки,
в которой с вероятностью P
можно ожидать присутствие особи с
признаком, частота которого в генеральной
совокупности составляет π.
Предлагается следующая формула:

.

В
первом приближении значение π можно
определить приблизительно по имеющимся
данным. Что же касается вероятности P,
то ее уровень довольно сильно влияет
на величину необходимого объема выборки.
Для большей надежности следует брать
P = 0.99,
но тогда возрастет объем работ; не столь
высокие требования (P = 0.95)
могут и не позволить найти искомый
фенотип. В частности, при уровне
вероятности P = 0.95
и предположительной частоте фенотипа
в популяции π = 0.05
потребуется

=
58.4 ≈ 59 экз.,

чтобы
отловить хотя бы одну особь с этим
дискретным признаком.

Оценка принадлежности варианты к выборке

Иногда
встречается ситуация, когда одна из
полученных вариант сильно отличается
от остальных. Можно ли такие резко
выде­ляющиеся значения использовать
при дальнейших расчетах? В терминах
математической статистики поставленный
вопрос звучит так: относится
ли данная варианта вместе с другими
вариантами изучаемой выборки к одной
и той же генеральной совокупности или
– к разным?
Его можно сформулировать и по-другому:
сформировано ли данное значение варианты
под действием тех же доминирующих и
случайных факторов, что и все остальные
варианты данной выборки, или это были
иные факторы? Здесь возможны два ответа.

1.
Факторы те же, т. е. все варианты взяты
из одной и той же генеральной совокупности.

2.
Факторы иные, т. е. особенная варианта
и выборка порознь взяты из разных
генеральных совокупностей.

Ответ
на этот вопрос можно получить с
использованием рассмотренных выше
свойств нормального распределения.
Так, если все варианты были взяты из
одной генеральной совокупности, значит,
они должны отличаться друг от друга
только в силу случайных причин и (с
вероятностью P = 0.95)
находиться в диапазоне M ± 2 ∙ S.
Иными словами, по случайным причинам
варианты достаточно большой выборки
будут отклоняться влево или вправо от
средней арифметической не более чем на
2 ∙ S:
x−M
< 2 ∙ S
или (x−M)/S
< 2.

Эта
величина, нормированное
отклонение,
и служит безразмерной характеристикой
отклонения отдельной варианты от средней
арифметической:

~
t_табл., 

где
t – критерий
выпада (исключения),

x – выделяющееся
значение призна­ка,

М – средняя
величина для группы вариант,

t_табл. – стандартные
значения критерия выпадов, определяемые
свойствами нормального распределения,
их можно найти по табл. 5П
для трех уровней вероятности (для больших
выборок обычно пользуются значением
t_табл.
=
2 при P = 0.95,
или α = 0.05).

Для
вариант, принадлежащих изучаемой
достаточно большой выборке, нормированное
отклонение меньше двух (с вероятностью
P = 0.95):
t < 2.
В случае действия на варианту некоего
необычного фактора, она окажется за
пределами указанного диапазона M ± 2S,
и ее нормированное отклонение будет
равно или больше двух: t  2.

Нормированное
отклонение есть простейший статистический
критерий,
который помогает определять так
называемые «выскакивающие» варианты
и решать вопрос о возможности их
отбрасывания как артефактов (исключать
из дальнейшей обработки). После такой
«чистки» параметры выборки должны быть
рассчитаны заново. К оценке чужеродности
вариант, как и к другим методам статистики,
нельзя подходить формально; цель
биометрического исследования всегда
состоит в том, чтобы понять специфику
явления. В частности, «отскакивающая»
варианта может быть следствием того,
что признак имеет иное, не-нормальное
распределение.

Рассмотрим
работу критерия на примере. При измерении
длины черепа взрослых самцов обыкно­венной
землеройки-бурозубки получены выборки
с такими па­раметрами: М = 18.8,
S = 0.3 мм.
Общее число животных n = 85.
Среди прочих вариант два больших значения
(19.2 и 21.0) вызывали сомнения. Определим
для них критерии выпада:

,

.

Согласно
таблице 5П,
критическое значение нормированного
отклонения для уровня значимости
α = 0.05
и n = 85
равно t = 2.0.
Поскольку первое полученное значение
(1.3) меньше табличного (2), первый из
сомнительных результатов исключать не
следует, а второй должен быть отброшен
– критерий выпада (7.3) превышает таб­личное
значение (2).

Понятие
нормированного отклонения позволяет
ввести важнейшее понятие статистики.
Статистика
–
безразмерная
случайная величина, которая имеет
известный закон распределения и
используется в качестве критерия для
проверки статистических гипотез.

В этом
смысле нормированное отклонение есть
статистика. Во-первых, это безразмерная
величина, поскольку единицы измерения
числителя (x_i−M)
и знаменателя (S)
взаимно уничтожаются. Во-вторых,
нормированное отклонение имеет вполне
определенное распределение (в случае
непрерывных признаков – нормальное)
со своими параметрами (рис. 9). Его средняя
равна нулю M_t
=
t_M
=
(M − M) / S = 0,
а стандартное отклонение равно единице
S_t = t_S = (S − M) / S
=
(S − 0) / S
=
S / S
=
1.

Рис.
9.
Переход от реального признака x
к нормированному отклонению t

Нормированное
отклонение – универсальная величина.
Какой бы признак (имеющий нормальное
распределение) мы ни брали, его значения
можно выразить в виде расстояния от
центра в единицах стандартного отклонения,
т. е. на сколько S
данное значение x
отклонилось от M.
При этом, как следует из свойств
нормального распределения, крайние
значения в 95% случаев не будут принимать
значения меньше −2 и больше 2.

С
помощью нормированного отклонения
можно, например, оценивать отличия
разнокачественных объектов (пород и
сортов, ви­дов, популяций, генераций
и пр.), причем даже по разным признакам.

Нормированное
отклонение можно использовать и для
срав­нительной оценки разных индивидов
по одному и тому же признаку. Например,
если сопоставляемые по относительному
весу сердца молодая и взрослая
землеройки-бурозубки демонстрируют
оди­наковые показатели (10.5 мг%), то
это, тем не менее, не озна­чает их
сходства по изучаемому признаку.
Используя известную информацию (у
молодых средний индекс сердца равен
M = 10.0
при стандартном отклонении S = 1.3,
у взрослых – M = 11.8,
S = 1.1),
рассчитаем нормированное отклонение
для молодого зверь­ка

и для взрослого
.
Налицо существенное различие: взрослый
зверек имеет относительно низкий
показатель сердеч­ного индекса, а
молодой близок по этому признаку к
ви­довой норме.

Наибольшее
развитие такой подход получает в
процедурах обработки многомерных
данных, при исследовании объектов,
охарактеризованных по многим признакам,
методом корреляций, главных компонент,
при их кластеризации и т. п. Во многих
случаях обработка многомерного массива
начинается с нормирования
данных по формуле нормированного
отклонения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Изучение всех влияющих на исследуемый объект факторов одновременно
провести невозможно, поэтому в эксперименте рассматривается их ограниченное
число. Остальные активные факторы стабилизируются, т.е. устанавливаются на
каких-то одинаковых для всех опытов уровнях.

Некоторые факторы не могут быть обеспечены системами стабилизации
(например, погодные условия, самочувствие оператора и т.д.), другие же
стабилизируются с какой-то погрешностью (например, содержание какого-либо
компонента в среде зависит от ошибки при взятии навески и приготовления
раствора). Учитывая также, что измерение параметра у осуществляется
прибором, обладающим какой-то погрешностью, зависящей от класса точности
прибора, можно прийти к выводу, что результаты повторностей одного и того же
опыта у_к будут приближенными и должны
отличаться один от другого и от истинного значения выхода процесса.
Неконтролируемое, случайное изменение и множества других влияющих на процесс
факторов вызывает случайные отклонения измеряемой величины у_к
от ее истинного значения – ошибку опыта.

Каждый эксперимент содержит элемент неопределенности вследствие
ограниченности экспериментального материала. Постановка повторных (или
параллельных) опытов не дает полностью совпадающих результатов, потому что
всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и нужно
оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в
одинаковых условиях несколько раз и затем берется среднее арифметическое всех
результатов. Среднее арифметическое у равно сумме всех n отдельных результатов, деленной на
количество параллельных опытов n:

Отклонение результата любого опыта от среднего арифметического
можно представить как разность y₂–
, где y₂ – результат отдельного
опыта. Наличие отклонения свидетельствует об изменчивости, вариации значений
повторных опытов. Для измерения этой изменчивости чаще всего используют
дисперсию.

Дисперсией называется среднее значение квадрата отклонений
величины от ее среднего значения. Дисперсия обозначается s² и
выражается формулой:

где (n-1)
– число степеней свободы, равное количеству опытов минус единица. Одна степень
свободы использована для вычисления среднего.

Корень квадратный из дисперсии, взятый с положительным знаком,
называется средним квадратическим отклонением, стандартом или квадратичной
ошибкой:

Ошибка опыта является суммарной величиной, результатом многих
ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др.
Каждую из этих ошибок можно, в свою очередь, разделить на составляющие.

Все ошибки принято разделять на два класса: систематические и
случайные (рисунок 1).

Систематические ошибки порождаются причинами, действующими
регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая ошибка – это ошибка,
которая остаётся постоянно или закономерно изменяется при повторных измерениях
одной и той же величины. Эти ошибки появляются вследствие неисправности
приборов, неточности метода измерения, какого либо упущения экспериментатора,
либо использования для вычисления неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка всех измерительных приборов и
безусловное выполнение выработанных практикой правил экспериментальных работ.
Если систематические ошибки вызваны известными причинами, то их можно
определить. Подобные погрешности можно устранить введением поправок.

Систематические ошибки находят, калибруя измерительные приборы и
сопоставляя опытные данные с изменяющимися внешними условиями (например, при
градуировке термопары по реперным точкам, при сравнении с эталонным прибором).
Если систематические ошибки вызываются внешними условиями (переменной
температуры, сырья и т.д.), следует компенсировать их влияние.

Случайными ошибками называются
те, которые появляются нерегулярно, причины, возникновения которых неизвестны и
которые невозможно учесть заранее. Случайные ошибки вызываются и объективными
причинами и субъективными. Например, несовершенством приборов, их освещением,
расположением, изменением температуры в процессе измерений, загрязнением
реактивов, изменением электрического тока в цепи. Когда случайная ошибка больше
величины погрешности прибора, необходимо многократно повторить одно и тоже
измерение. Это позволяет сделать случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше погрешности прибора, то уменьшать её нет
смысла. Такие ошибки имеют значение, которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми для измерений сделанных даже в
одинаковых условиях. Поскольку причины, приводящие к случайным ошибкам
неодинаковы в каждом эксперименте, и не могут быть учтены, поэтому исключить
случайные ошибки нельзя, можно лишь оценить их значения. При многократном
определении какого-либо показателя могут встречаться результаты, которые
значительно отличаются от других результатов той же серии. Они могут быть
следствием грубой ошибки, которая вызвана невнимательностью экспериментатора.

Систематические и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы исключать инструментальные ошибки, следует
проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта.
Ошибки при проведении самого опыта возникают вследствие неравномерного нагрева
реакционной среды, разного способа перемешивания и т.п.

При повторении опытов такие ошибки могут вызвать большой разброс
экспериментальных результатов.

Очень важно исключить из экспериментальных данных грубые ошибки,
так называемый брак при повторных опытах. Грубые ошибки легко
обнаружить. Для выявления ошибок необходимо произвести измерения в других
условиях или повторить измерения через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность в записях, тщательность в работе и
записи результатов эксперимента. Грубая ошибка должна быть исключена из
экспериментальных данных. Для отброса ошибочных данных существуют определённые
правила.

Например, используют критерий Стьюдента t (Р;
f):
Опыт считается бракованным, если экспериментальное значение критерия t по
модулю больше табличного значения t (Р; f).

Если в распоряжении исследователя имеется экспериментальная оценка
дисперсии S²(y_k)
с небольшим конечным числом степеней свободы, то доверительные ошибки
рассчитываются с помощью критерий Стьюдента t (Р;
f):

ε()
= t (Р; f)* S(y_k)/= t (Р; f)* S()

ε(y_k) = t (Р; f)* S(y_k)

В практической и научно-практической работе
врачи обобщают результаты, полученные как правило на выборочных
совокупностях.
Для более широкого распространения и применения полученных при изучении
репрезентативной выборочной совокупности данных и выводов
надо уметь по части явления судить о явлении и его закономерностях в
целом.

Учитывая, что врачи, как правило, проводят исследования на
выборочных совокупностях, теория статистики позволяет с помощью
математического аппарата (формул) переносить данные с выборочного
исследования на генеральную совокупность. При этом врач должен
уметь не только воспользоваться математической формулой, но сделать
вывод, соответствующий каждому способу оценки достоверности
полученных данных. С этой целью врач должен знать способы оценки
достоверности.

Применяя метод оценки достоверности результатов исследования для изучения общественного здоровья и деятельности учреждений
здравоохранения, а также в своей научной деятельности, исследователь должен уметь правильно выбрать способ данного метода.
Среди методов оценки достоверности различают параметрические и непараметрические.

Параметрическими называют количественные методы статистической обработки данных, применение которых требует обязательного
знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.

Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания
закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.

Как параметрические, так и непараметрические методы, используемые
для сравнения результатов исследований, т.е. для сравнения
выборочных совокупностей, заключаются в применении определенных формул и
расчете определенных показателей в соответствии с
предписанными алгоритмами. В конечном результате высчитывается
определенная числовая величина, которую сравнивают с табличными
пороговыми значениями. Критерием достоверности будет результат сравнения
полученной величины и табличного значения при данном числе
наблюдений (или степеней свободы) и при заданном уровне безошибочного
прогноза.

Таким образом, в статистической процедуре оценки основное
значение имеет полученный критерий достоверности, поэтому сам способ
оценки достоверности в целом иногда называют тем или иным критерием по
фамилии автора, предложившего его в качестве основы метода.

---

Применение параметрических методов

При проведении выборочных исследований полученный результат не обязательно совпадает с результатом, который мог бы быть получен
при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой
репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную
совокупность.

Определение доверительных границ средних
и относительных величин

Формулы определения доверительных границ представлены следующим образом:

• для средних величин (М): М_ген = М_выб ± tm
• для относительных показателей (Р): Р_ген = Р_выб ± tm
  
  где М_ген и Р_ген — соответственно, значения средней величины и относительного показателя генеральной
  совокупности;
  
  М_вы6 и Р_вы6 — значения средней величины и относительного показателя выборочной совокупности;
  
  m — ошибка репрезентативности;
  
  t — критерий достоверности (доверительный коэффициент).

Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого
явления (или признака) в генеральной совокупности.

Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов,
полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р),
показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в
генеральной совокупности.

При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам
задает определенную (необходимую) степень вероятности безошибочного прогноза (Р).

Для большинства медико-биологических исследований считается
достаточной степень вероятности безошибочного прогноза, равная 95%,
а число случаев генеральной совокупности, в котором могут наблюдаться
отклонения от закономерностей, установленных при выборочном
исследовании, не будут превышать 5%. При ряде исследований, связанных,
например, с применением высокотоксичных веществ, вакцин,
оперативного лечения и т.п., в результате чего возможны тяжелые
заболевания, осложнения, летальные исходы, применяется степень
вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной
совокупности возможны отклонения от закономерностей,
установленных в выборочной совокупности.

Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия
t, зависящее также и от числа наблюдений.

При n>30 степени вероятности безошибочного прогноза Р = 99,7% — соответствует значение t = 3, а при Р = 95,5% — значение
t = 2.

При п<30 величина t при соответствующей степени вероятности безошибочного прогноза определяется по специальной таблице
(Н.А. Плохинского).

на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (М_ген)
при числе наблюдений больше 30

Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было
установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80
ударов в 1 минуту; σ = ± 6 ударов в минуту.

Задание: определить ошибку репрезентативности (m_M) и доверительные границы средней величины генеральной
совокупности (М_ген).

Решение.

1. Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m):

   m = σ / √n =
   6 / √36 =
   ±1 удар в минуту

2. Вычисление доверительных границ средней величины генеральной совокупности (М_ген). Для этого необходимо:
   • а) задать степень вероятности безошибочного прогноза (Р = 95 %);
   • б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t,
     определяемого по таблице, равна 2 (t = 2). Тогда М_ген = М_выб ± tm = 80 ± 2×1 = 80 ± 2
     удара в минуту.

Вывод. Установлено с вероятностью безошибочного прогноза Р =
95%, что средняя частота пульса в генеральной совокупности,
т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в
аналогичных условиях будет находиться в пределах от 78 до 82
ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в
минуту возможна не более, чем у 5% случаев генеральной
совокупности.

на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности
(Р_ген)

Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18%
случаев обнаружено нарушение осанки функционального характера.

Задание: определить ошибку репрезентативности (m_p) и доверительные границы относительного показателя
генеральной совокупности (Р_ген).

Решение.

1. Вычисление ошибки репрезентативности относительного показателя:

   m = √P x q / n =
   √18 x (100 — 18) / 164 =
   ± 3%

2. Вычисление доверительных границ средней величины генеральной совокупности (Р_ген) производится следующим образом:
   • необходимо задать степень вероятности безошибочного прогноза (Р=95%);
   • при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2).
     Тогда Р_ген = Р_выб± tm = 18% ± 2 х 3 = 18% ± 6%.

Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у
детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.

---

Оценка достоверности разности результатов исследования

Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены
какой-то причиной, различия между двумя средними величинами или относительными показателями.

Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие
причинно-следственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них.

Формулы определения достоверности разности представлены следующим образом:

Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или
более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что
будет иметь место и в генеральной совокупности.

При t < 2, вероятность безошибочного прогноза Р < 95%, это означает, что разность недостоверна, случайна, т.е. не
обусловлена какой-то закономерностью (не обусловлена влиянием какого-то фактора).

Поэтому полученный критерий должен всегда оцениваться по отношению к конкретной цели исследования.

на оценку достоверности разности средних величин

Условие задачи: при изучении комбинированного воздействия шума
и низкочастотной вибрации на организм человека было
установлено, что средняя частота пульса у водителей сельскохозяйственных
машин через 1 ч после начала работы составила 80 ударов в
минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы
водителей до начала работы равнялась 75 ударам в минуту;
m = ± 1 удар в минуту.

Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч
работы.

Решение.

Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно
утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а
достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.

на оценку достоверности разности относительных показателей

Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение
осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24%
(m = ± 2,64%).

Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.

Решение.

Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в
частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено
влиянием возраста детей.

---

Типичные ошибки, допускаемые исследователями при
применении способа оценки достоверности разности результатов исследования

• При оценке достоверности разности результатов исследования по критерию t часто делается вывод о достоверности (или
  недостоверности) самих результатов исследования. В действительности же этот способ позволяет судить только о достоверности
  (существенности) или случайности различий между результатами исследования.

• При полученном значении критерия t<2 часто делается вывод о необходимости увеличения числа наблюдений. Если же
  выборочные совокупности репрезентативны, то нельзя делать вывод о необходимости увеличения числа наблюдений, т.к. в данном
  случае значение критерия t<2 свидетельствует о случайности, недостоверности различия между двумя сравниваемыми результатами
  исследования.

---

Применение методов статистического анализа для изучения общественного здоровья и здравоохранения.
Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов

1. Власов В.В. Эпидемиология. — М.: ГЭОТАР-МЕД, 2004. — 464 с.
2. Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
3. Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью
   и здравоохранению: Часть 1. Общественное здоровье. — М.: Медицина,
   2003. — 368 с.
4. Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). — СПб, 1998. -528 с.
5. Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) — Москва, 2000. — 432 с.
6. С. Гланц. Медико-биологическая статистика. Пер с англ. — М., Практика, 1998. — 459 с.

Абсолютная и относительная погрешности (ошибки).

Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x₁,
x₂,
x₃,
…, x_n

Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:

Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.

Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:

(13)

Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.

Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):

(14)

Отношения

называются относительными погрешностями
(ошибками) отдельных измерений.

Отношение средней
абсолютной погрешности результата

к среднему арифметическому значению

измеряемой величины называют относительной
ошибкой результата и выражают в процентах:

Относительная
ошибка характеризует точность измерения.

Законы распределения случайных величин.

Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.

Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.

Непрерывная
случайная величина принимает любые
значения в данном интервале.

Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.

Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.

Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.

Два события,
одновременное появление которых
невозможно, называются несовместными.

Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:

называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:

При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:

Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.

Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений х_i
на вероятность этих значений р_i:

Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:

,

где m_i
— число дискретных случайных величин,
имеющих значение х_i.

Для непрерывной
случайной величины математическим
ожиданием служит интеграл:

,

где р(х) — плотность
вероятности.

Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:

(15)

(16)

Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:

(17)

Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».

Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:

а) ряд распределения
(для дискретных величин);

б) функция
распределения;

в) кривая распределения
(для непрерывных величин).

Существует
относительно много законов распределения
случайных величин.

Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина

распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:

(18),

где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);

—
среднее квадратичное отклонение;

—
основание натурального логарифма
(неперово число);

f
(x)
– плотность вероятности (функция
распределения вероятностей).

Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.

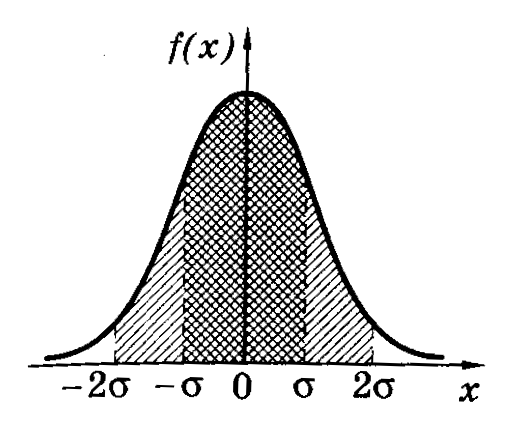
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).

Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:

(19)

Таким образом,
максимальное значение функции f_max(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом ₂>₁.
(При увеличении 
кривая распределения становится более
пологой, а при уменьшении 
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и ₃
= ₂.

Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал

теоретически была определена в 1860 году
английским физиком Максвеллом

. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т₁
< Т₂).
Закон распределения Максвелла определяется
формулой:

(20),

где m_о
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.

Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:

(21)

Где n(h)
– концентрация молекул газа на высоте
h,
n₀
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.

Распределение
Больцмана.

Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному

статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).

n

1. h

Гистограмма
распределения Больцмана.

Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов x_i
одинаковой ширины. Для каждого интервала
подсчитывают число m_i
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины

для каждого интервала x_i
и среднее значение случайной величины
<x_i
> в каждом интервале.

Затем по оси абсцисс
откладывают интервалы x_i,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой

– плотностью относительной частоты
).

Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).

Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:

(22)

Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:

(23)

Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.

Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.

Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.

Доверительной
вероятностью
(надежностью)

результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность 
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.

Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t_,n<>,
<x>
+ t_,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .

Коэффициент t_,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).

Значении коэффициента
Стьюдента t_,n
зависит от доверительной вероятности

и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.

Таблица 1

n	
0,6	0,7	0,8	0,9	0,95	0,98	0,99
2	1,38	2,0	3,1	6,3	12,7	31,8	63,7
3	1,06	1,3	1,9	2,9	4,3	7,0	9,9
4	0,98	1,3	1,6	2,4	3,2	4,5	5,8
5	0,94	1,2	1,5	2,1	2,8	3,7	4,6
6	0,92	1,2	1,5	2,0	2,6	3,4	4,0
7	0,90	1,1	1,4	1,9	2,4	3,1	3,7
8	0,90	1,1	1,4	1,9	2,4	3,0	3,5
9	0,90	1,1	1,4	1,9	2,3	2,9	3,4
10	0,88	1,1	1,4	1,9	2,3	2,8	3,3

В таблице 1 в верхней
строке заданы значения доверительной
вероятности 
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.

Окончательный
результат измерений записывается в
виде:

(25)

Где

– полуширина доверительного интервала.

Результат серии
измерений оценивается относительной
погрешностью:

(26)