Sse ошибка статистика - Не ошибается лишь тот, кто ничего не делает!

Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.

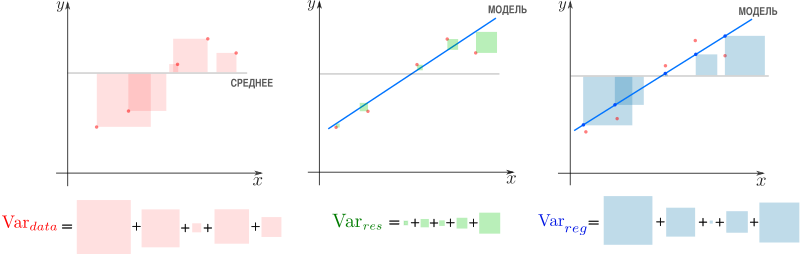
Мы часто используем три разных значения суммы квадратов , чтобы измерить, насколько хорошо линия регрессии действительно соответствует данным:

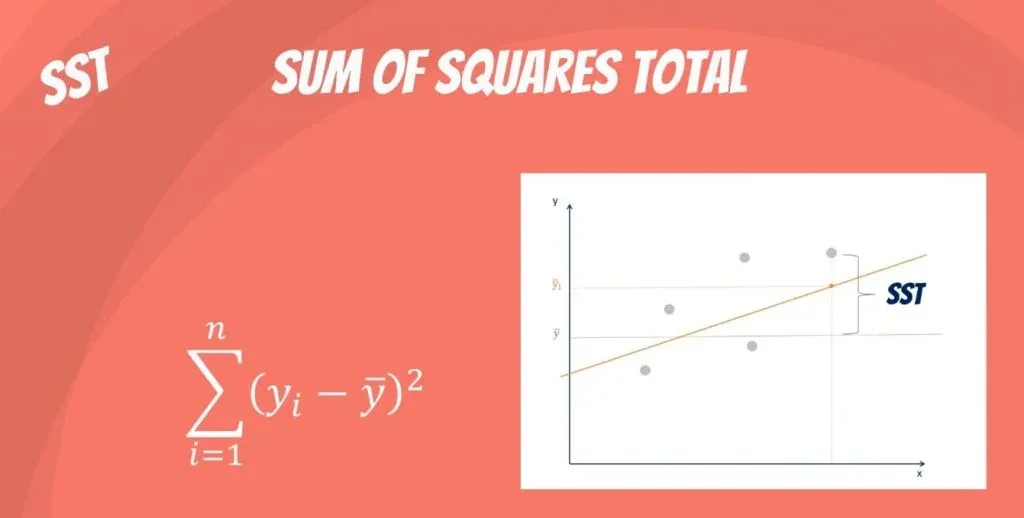
1. Общая сумма квадратов (SST) – сумма квадратов разностей между отдельными точками данных (y i ) и средним значением переменной ответа ( y ).

SST = Σ(y i – y ) 2

2. Регрессия суммы квадратов (SSR) – сумма квадратов разностей между прогнозируемыми точками данных (ŷ i ) и средним значением переменной ответа ( y ).

SSR = Σ(ŷ i – y ) 2

3. Ошибка суммы квадратов (SSE) – сумма квадратов разностей между предсказанными точками данных (ŷ i ) и наблюдаемыми точками данных (y i ).

SSE = Σ(ŷ i – y i ) 2

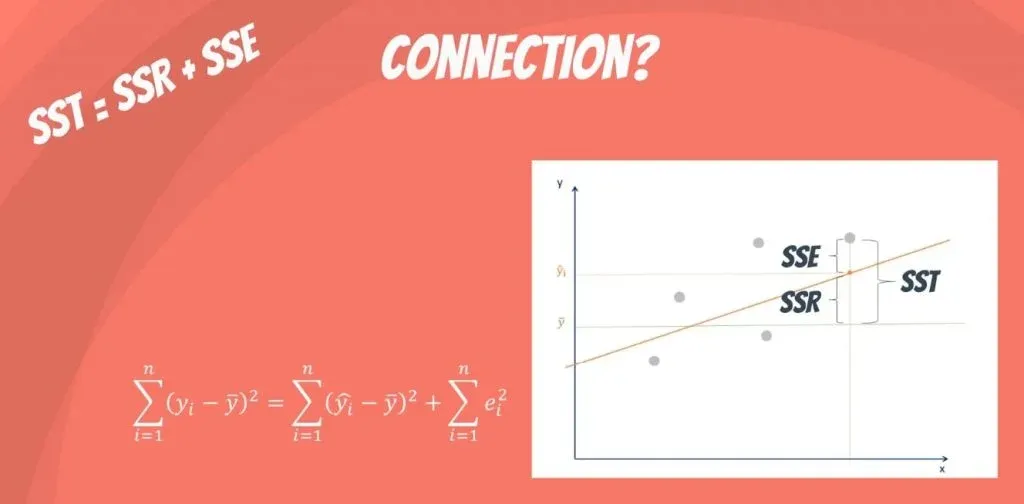
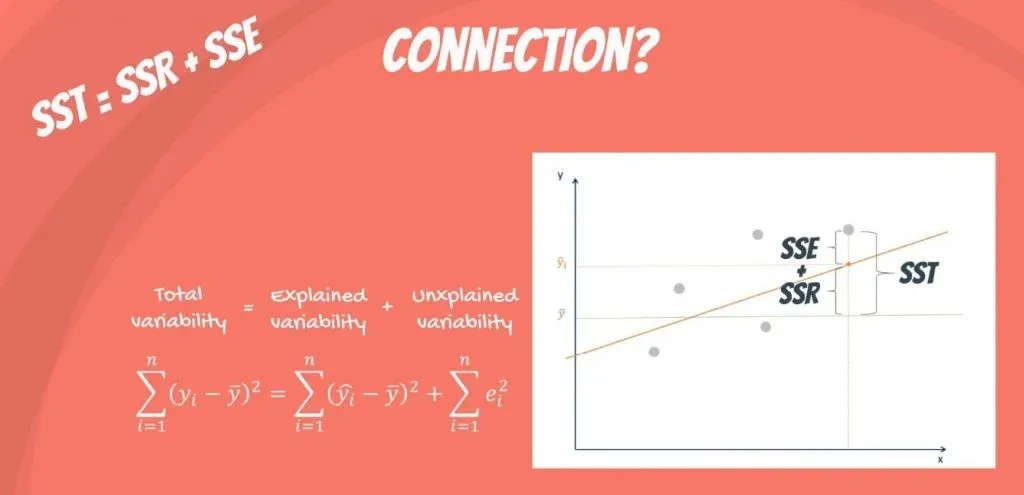
Между этими тремя показателями существует следующая зависимость:

SST = SSR + SSE

Таким образом, если мы знаем две из этих мер, мы можем использовать простую алгебру для вычисления третьей.

SSR, SST и R-квадрат

R-квадрат , иногда называемый коэффициентом детерминации, является мерой того, насколько хорошо модель линейной регрессии соответствует набору данных. Он представляет собой долю дисперсии переменной отклика , которая может быть объяснена предикторной переменной.

Значение для R-квадрата может варьироваться от 0 до 1. Значение 0 указывает, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.

Используя SSR и SST, мы можем рассчитать R-квадрат как:

R-квадрат = SSR / SST

Например, если SSR для данной модели регрессии составляет 137,5, а SST — 156, тогда мы рассчитываем R-квадрат как:

R-квадрат = 137,5/156 = 0,8814

Это говорит нам о том, что 88,14% вариации переменной отклика можно объяснить переменной-предиктором.

Расчет SST, SSR, SSE: пошаговый пример

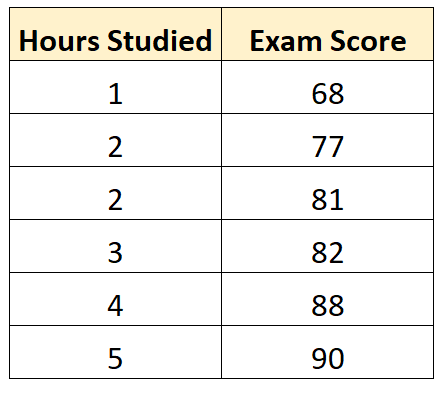
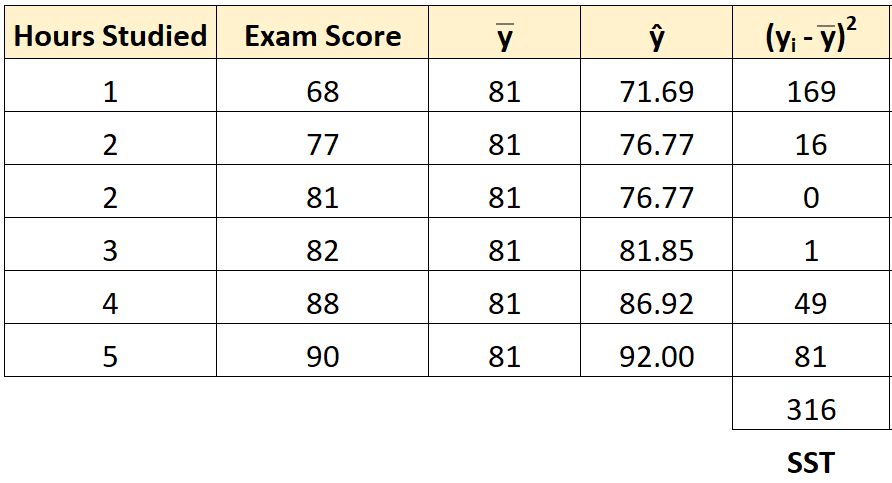
Предположим, у нас есть следующий набор данных, который показывает количество часов, отработанных шестью разными студентами, а также их итоговые оценки за экзамены:

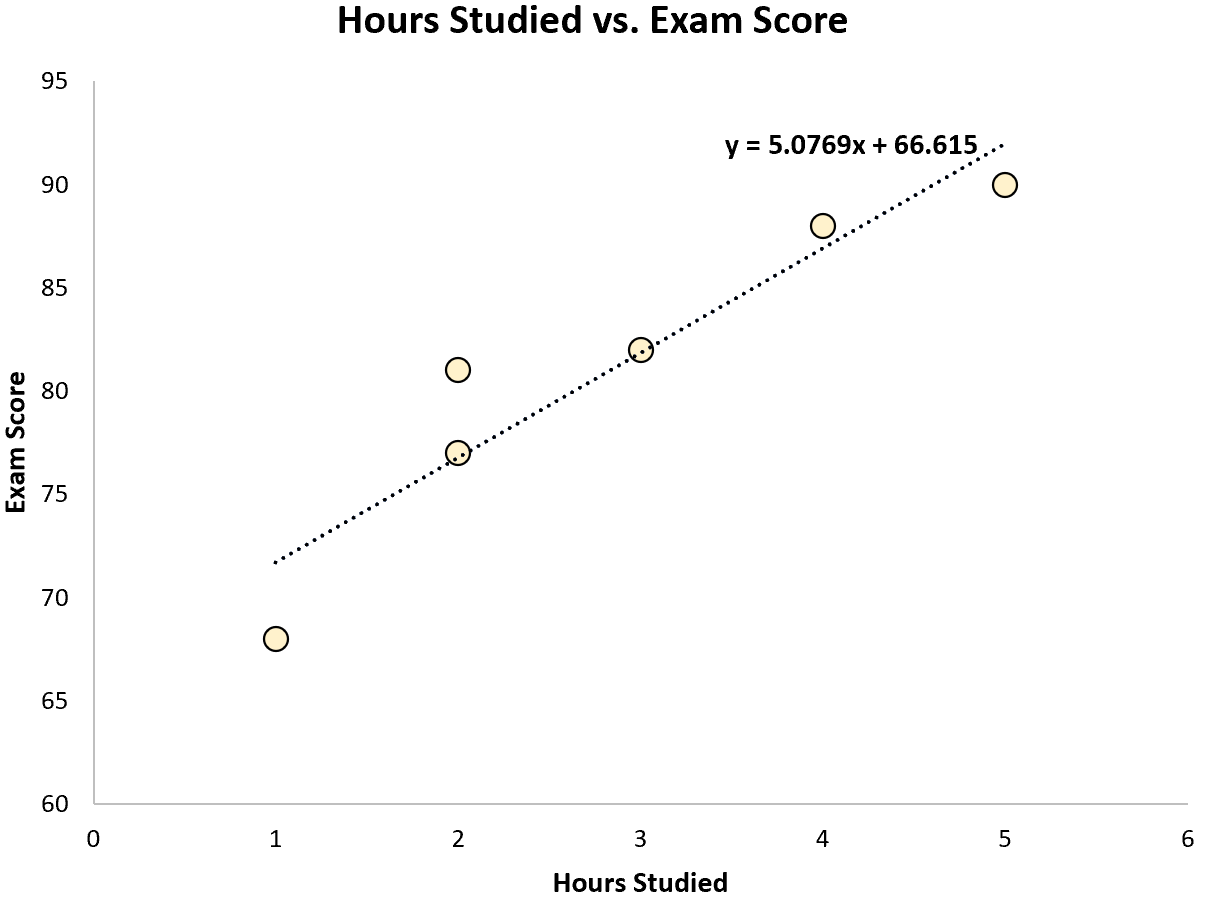
Используя некоторое статистическое программное обеспечение (например, R , Excel , Python ) или даже вручную , мы можем найти, что линия наилучшего соответствия:

Оценка = 66,615 + 5,0769 * (часы)

Как только мы узнаем строку уравнения наилучшего соответствия, мы можем использовать следующие шаги для расчета SST, SSR и SSE:

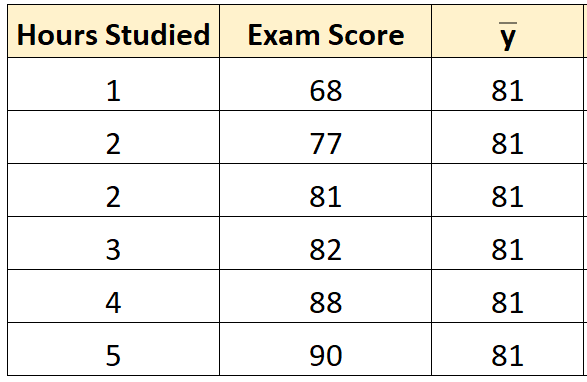
Шаг 1: Рассчитайте среднее значение переменной ответа.

Среднее значение переменной отклика ( y ) оказывается равным 81 .

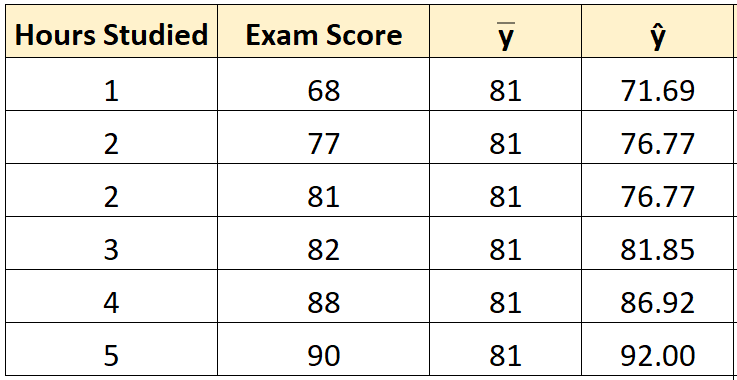
Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.

Затем мы можем использовать уравнение наилучшего соответствия для расчета прогнозируемого экзаменационного балла () для каждого учащегося.

Например, предполагаемая оценка экзамена для студента, который учился один час, такова:

Оценка = 66,615 + 5,0769*(1) = 71,69 .

Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого ученика:

Шаг 3: Рассчитайте общую сумму квадратов (SST).

Далее мы можем вычислить общую сумму квадратов.

Например, сумма квадратов для первого ученика равна:

(y i – y ) 2 = (68 – 81) 2 = 169 .

Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:

Сумма квадратов получается 316 .

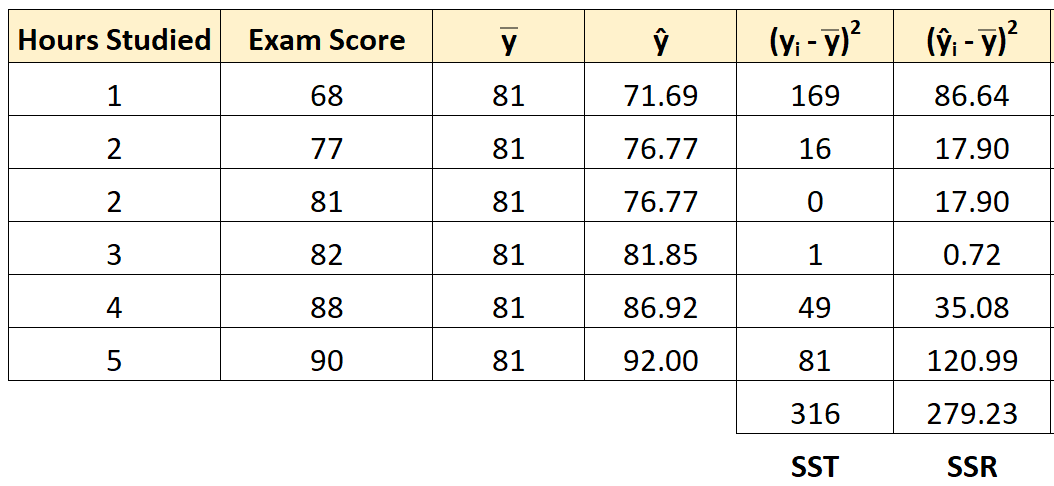
Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).

Далее мы можем вычислить сумму квадратов регрессии.

Например, сумма квадратов регрессии для первого ученика равна:

(ŷ i – y ) 2 = (71,69 – 81) 2 = 86,64 .

Мы можем использовать тот же подход, чтобы найти сумму квадратов регрессии для каждого ученика:

Сумма квадратов регрессии оказывается равной 279,23 .

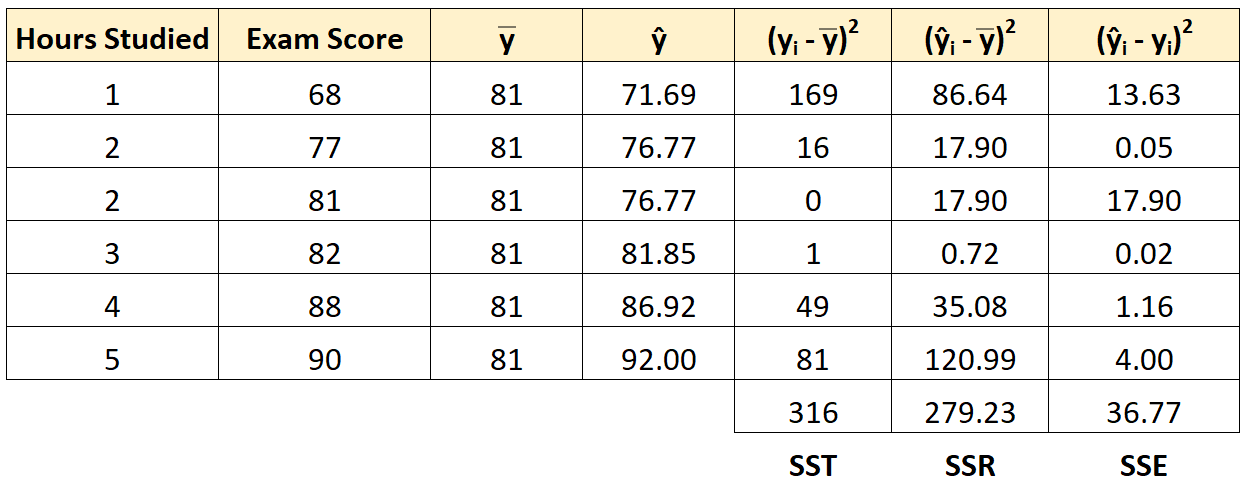
Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).

Далее мы можем вычислить сумму квадратов ошибок.

Например, ошибка суммы квадратов для первого ученика:

(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .

Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:

Мы можем проверить, что SST = SSR + SSE

SST = SSR + SSE
316 = 279,23 + 36,77

Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:

R-квадрат = SSR / SST
R-квадрат = 279,23/316
R-квадрат = 0,8836

Это говорит нам о том, что 88,36% вариаций в экзаменационных баллах можно объяснить количеством часов обучения.

Дополнительные ресурсы

Вы можете использовать следующие калькуляторы для автоматического расчета SST, SSR и SSE для любой простой линии линейной регрессии:

Калькулятор ТПН
Калькулятор ССР
Калькулятор SSE

Источник

Линейная регрессия используется для поиска линии, которая лучше всего «соответствует» набору данных.

SST = Σ(y i – y ) 2

SSR = Σ(ŷ i – y ) 2

SSE = Σ(ŷ i – y i ) 2

Между этими тремя показателями существует следующая зависимость:

SST = SSR + SSE

Таким образом, если мы знаем две из этих мер, мы можем использовать простую алгебру для вычисления третьей.

SSR, SST и R-квадрат

Используя SSR и SST, мы можем рассчитать R-квадрат как:

R-квадрат = SSR / SST

Например, если SSR для данной модели регрессии составляет 137,5, а SST — 156, тогда мы рассчитываем R-квадрат как:

R-квадрат = 137,5/156 = 0,8814

Это говорит нам о том, что 88,14% вариации переменной отклика можно объяснить переменной-предиктором.

Расчет SST, SSR, SSE: пошаговый пример

Оценка = 66,615 + 5,0769 * (часы)

Шаг 1: Рассчитайте среднее значение переменной ответа.

Среднее значение переменной отклика ( y ) оказывается равным 81 .

Шаг 2: Рассчитайте прогнозируемое значение для каждого наблюдения.

Например, предполагаемая оценка экзамена для студента, который учился один час, такова:

Оценка = 66,615 + 5,0769*(1) = 71,69 .

Мы можем использовать тот же подход, чтобы найти прогнозируемый балл для каждого ученика:

Шаг 3: Рассчитайте общую сумму квадратов (SST).

Далее мы можем вычислить общую сумму квадратов.

Например, сумма квадратов для первого ученика равна:

(y i – y ) 2 = (68 – 81) 2 = 169 .

Мы можем использовать тот же подход, чтобы найти общую сумму квадратов для каждого ученика:

Сумма квадратов получается 316 .

Шаг 4: Рассчитайте регрессию суммы квадратов (SSR).

Далее мы можем вычислить сумму квадратов регрессии.

Например, сумма квадратов регрессии для первого ученика равна:

(ŷ i – y ) 2 = (71,69 – 81) 2 = 86,64 .

Мы можем использовать тот же подход, чтобы найти сумму квадратов регрессии для каждого ученика:

Сумма квадратов регрессии оказывается равной 279,23 .

Шаг 5: Рассчитайте ошибку суммы квадратов (SSE).

Далее мы можем вычислить сумму квадратов ошибок.

Например, ошибка суммы квадратов для первого ученика:

(ŷ i – y i ) 2 = (71,69 – 68) 2 = 13,63 .

Мы можем использовать тот же подход, чтобы найти сумму ошибок квадратов для каждого ученика:

Мы можем проверить, что SST = SSR + SSE

SST = SSR + SSE
316 = 279,23 + 36,77

Мы также можем рассчитать R-квадрат регрессионной модели, используя следующее уравнение:

R-квадрат = SSR / SST
R-квадрат = 279,23/316
R-квадрат = 0,8836

Дополнительные ресурсы

Калькулятор ТПН
Калькулятор ССР
Калькулятор SSE

Все курсы > Оптимизация > Занятие 4 (часть 2)

Во второй части занятия перейдем к практике.

Продолжим работать в том же ноутбуке⧉

Сквозной пример

Данные и постановка задачи

Обратимся к хорошо знакомому нам датасету недвижимости в Бостоне.

boston = pd.read_csv(‘/content/boston.csv’)

При этом нам нужно будет решить две основные задачи:

Задача 1. Научиться оценивать качество модели не только с точки зрения метрики, но и исходя из рассмотренных ранее допущений модели. Эту задачу мы решим в три этапа.

Этап 1. Построим базовую (baseline) модель линейной регрессии с помощью класса LinearRegression библиотеки sklearn и оценим, насколько выполняются рассмотренные выше допущения.
Этап 2. Попробуем изменить данные таким образом, чтобы модель в большей степени соответствовала этим критериям.
Этап 3. Обучим еще одну модель и посмотрим как изменится результат.

Задача 2. С нуля построить модель множественной линейной регрессии и сравнить прогноз с результатом полученным при решении первой задачи. При этом обучение модели мы реализуем двумя способами, а именно, через:

Метод наименьших квадратов
Метод градиентного спуска

Разделение выборки

Мы уже не раз говорили про важность разделения выборки на обучаущую и тестовую части. Сегодня же, с учетом того, что нам предстоит изучить много нового материала, мы опустим этот этап и будем обучать и тестировать модель на одних и тех же данных.

Исследовательский анализ данных

Теперь давайте более внимательно посмотрим на имеющиеся у нас данные. Как вы вероятно заметили, признаки в этом датасете количественные, за исключением переменной CHAS.

RangeIndex: 506 entries, 0 to 505

Data columns (total 14 columns):

# Column Non-Null Count Dtype

— —— ————— ——

0 CRIM 506 non-null float64

1 ZN 506 non-null float64

2 INDUS 506 non-null float64

3 CHAS 506 non-null float64

4 NOX 506 non-null float64

5 RM 506 non-null float64

6 AGE 506 non-null float64

7 DIS 506 non-null float64

8 RAD 506 non-null float64

9 TAX 506 non-null float64

10 PTRATIO 506 non-null float64

11 B 506 non-null float64

12 LSTAT 506 non-null float64

13 MEDV 506 non-null float64

dtypes: float64(14)

memory usage: 55.5 KB

# мы видим, что переменная CHAS категориальная

boston.CHAS.value_counts()

0.0 471

1.0 35

Name: CHAS, dtype: int64

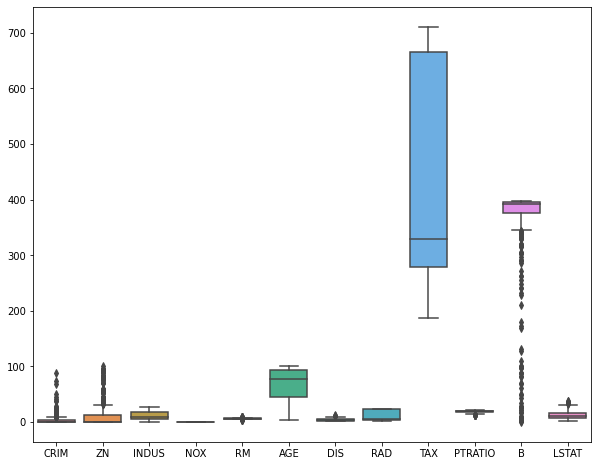
Посмотрим на распределение признаков с помощью boxplots.

plt.figure(figsize = (10, 8))

sns.boxplot(data = boston.drop(columns = [‘CHAS’, ‘MEDV’]))

plt.show()

Посмотрим на распределение целевой переменной.

def box_density(x):

# создадим два подграфика

f, (ax_box, ax_kde) = plt.subplots(nrows = 2, # из двух строк

ncols = 1, # и одного столбца

sharex = True, # оставим только нижние подписи к оси x

gridspec_kw = {‘height_ratios’: (.15, .85)}, # зададим разную высоту строк

figsize = (10,8)) # зададим размер графика

# в первом подграфике построим boxplot

sns.boxplot(x = x, ax = ax_box)

ax_box.set(xlabel = None)

# во втором — график плотности распределения

sns.kdeplot(x, fill = True)

# зададим заголовок и подписи к осям

ax_box.set_title(‘Распределение переменной’, fontsize = 17)

ax_kde.set_xlabel(‘Переменная’, fontsize = 15)

ax_kde.set_ylabel(‘Плотность распределения’, fontsize = 15)

plt.show()

box_density(boston.iloc[:, —1])

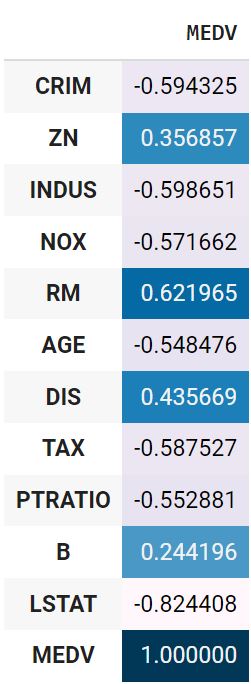
Посмотрим на корреляцию количественных признаков с целевой переменной.

boston.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

Используем точечно-бисериальную корреляцию для оценки взамосвязи переменной CHAS и целевой переменной.

def pbc(continuous, binary):

# преобразуем количественную переменную в массив Numpy

continuous_values = np.array(continuous)

# классы качественной переменной превратим в нули и единицы

binary_values = np.unique(binary, return_inverse = True)[1]

# создадим две подгруппы количественных наблюдений

# в зависимости от класса дихотомической переменной

group0 = continuous_values[np.argwhere(binary_values == 0).flatten()]

group1 = continuous_values[np.argwhere(binary_values == 1).flatten()]

# найдем средние групп,

mean0, mean1 = np.mean(group0), np.mean(group1)

# а также длины групп и всего датасета

n0, n1, n = len(group0), len(group1), len(continuous_values)

# рассчитаем СКО количественной переменной

std = continuous_values.std()

# подставим значения в формулу

return (mean1 — mean0) / std * np.sqrt( (n1 * n0) / (n * (n—1)) )

pbc(boston.MEDV, boston.CHAS)

Обработка данных

Пропущенные значения

Посмотрим, есть ли пропущенные значения.

CRIM 0

ZN 0

INDUS 0

CHAS 0

NOX 0

RM 0

AGE 0

DIS 0

RAD 0

TAX 0

PTRATIO 0

B 0

LSTAT 0

MEDV 0

dtype: int64

Выбросы

Удалим выбросы.

from sklearn.ensemble import IsolationForest

clf = IsolationForest(max_samples = 100, random_state = 42)

clf.fit(boston)

boston[‘anomaly’] = clf.predict(boston)

boston = boston[boston.anomaly == 1]

boston = boston.drop(columns = ‘anomaly’)

boston.shape

При удалении выбросов важно помнить, что полное отсутствие вариантивности в данных не позволит выявить взаимосвязи

Масштабирование признаков

Приведем признаки к одному масштабу (целевую переменную трогать не будем).

boston.iloc[:, :—1] = (boston.iloc[:, :—1] — boston.iloc[:, :—1].mean()) / boston.iloc[:, :—1].std()

Замечу, что метод наименьших квадратов не требует масштабирования признаков, градиентному спуску же напротив необходимо, чтобы все значения находились в одном диапазоне (подробнее в дополнительных материалах).

Кодирование категориальных переменных

Даже после стандартизации переменная CHAS сохранила только два значения.

boston.CHAS.value_counts()

-0.182581 389

5.463391 13

Name: CHAS, dtype: int64

Ее можно не трогать.

Построение модели

Создадим первую пробную (baseline) модель с помощью библиотеки sklearn.

baseline-модель

X = boston.drop(‘MEDV’, axis = 1)

y = boston[‘MEDV’]

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества

Диагностика модели, метрики качества и функции потерь

Вероятно, вы заметили, что мы использовали MSE и для обучения модели, и для оценки ее качества. Возникает вопрос, есть ли отличие между функцией потерь и метрикой качества модели.

Функция потерь и метрика качества могут совпадать, а могут и не совпадать. Важно понимать, что у них разное назначение.

Функция потерь — это часть алгоритма, нам важно, чтобы эта функция была дифференцируема (у нее была производная)
Производная метрики качества нас не интересует. Метрика качества должна быть адекватна решаемой задаче.

MSE, RMSE, MAE, MAPE

MSE и RMSE

Для оценки качества RMSE предпочтительнее, чем MSE, потому что показывает насколько ошибается модель в тех же единицах измерения, что и целевая переменная. Например, если диапазон целевой переменной от 80 до 100, а RMSE 20, то в среднем вы ошибаетесь на 20-25 процентов.

В качестве практики напишем собственную функцию.

# параметр squared = True возвращает MSE

# параметр squared = False возвращает RMSE

def mse(y, y_pred, squared = True):

mse = ((y — y_pred) ** 2).sum() / len(y)

if squared == True:

return mse

else:

return np.sqrt(mse)

mse(y, y_pred), mse(y, y_pred, squared = False)

(9.980044349414223, 3.1591208190593507)

Сравним с sklearn.

from sklearn.metrics import mean_squared_error

# squared = False дает RMSE

mean_squared_error(y, y_pred, squared = False)

MAE

Приведем формулу.

$$ MAE = frac{sum |y-hat{y}|}{n} $$

Средняя абсолютная ошибка представляет собой среднее арифметическое абсолютной ошибки $varepsilon = |y-hat{y}| $ и использует те же единицы измерения, что и целевая переменная.

def mae(y, y_pred):

return np.abs(y — y_pred).sum() / len(y)

from sklearn.metrics import mean_absolute_error

mean_absolute_error(y, y_pred)

MAE часто используется при оценке качества моделей временных рядов.

MAPE

Средняя абсолютная ошибка в процентах (mean absolute percentage error) по сути выражает MAE в процентах, а не в абсолютных величинах, выражая отклонение как долю от истинных ответов.

$$ MAPE = frac{1}{n} sum vert frac{y-hat{y}}{y} vert $$

Это позволяет сравнивать модели с разными единицами измерения между собой.

def mape(y, y_pred):

return 1/len(y) * np.abs((y — y_pred) / y).sum()

from sklearn.metrics import mean_absolute_percentage_error

mean_absolute_percentage_error(y, y_pred)

Коэффициент детерминации

В рамках вводного курса в ответах на вопросы к занятию по регрессии мы подробно рассмотрели коэффициент детерминации ($R^2$), его связь с RMSE, а также зачем нужен скорректированный $R^2$. Как мы знаем, если использовать, например, класс LinearRegression, то эта метрика содержится в методе .score().

Также можно использовать функцию r2_score() модуля metrics.

from sklearn.metrics import r2_score

r2_score(y, y_pred)

Для скорректированного $R^2$ напишем собственную функцию.

def r_squared(x, y, y_pred):

r2 = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum()

n, k = x.shape

r2_adj = 1 — ((y — y_pred)** 2).sum()/((y — y.mean()) ** 2).sum()

return r2, r2_adj

(0.7965234359550825, 0.7965234359550825)

Диагностика модели

Теперь проведем диагностику модели в соответствии с выдвинутыми выше допущениями.

Анализ остатков и прогнозных значений

Напишем диагностическую функцию, которая сразу выведет несколько интересующих нас графиков и метрик, касающихся остатков и прогнозных значений.

from scipy.stats import probplot

from statsmodels.graphics.tsaplots import plot_acf

from statsmodels.stats.stattools import durbin_watson

def diagnostics(y, y_pred):

residuals = y — y_pred

residuals_mean = np.round(np.mean(y — y_pred), 3)

f, ((ax_rkde, ax_prob), (ax_ry, ax_auto), (ax_yy, ax_ykde)) = plt.subplots(nrows = 3,

ncols = 2,

figsize = (12, 18))

# в первом подграфике построим график плотности

sns.kdeplot(residuals, fill = True, ax = ax_rkde)

ax_rkde.set_title(‘Residuals distribution’, fontsize = 14)

ax_rkde.set(xlabel = f‘Residuals, mean: {residuals_mean}’)

ax_rkde.set(ylabel = ‘Density’)

# во втором график нормальной вероятности остатков

probplot(residuals, dist = ‘norm’, plot = ax_prob)

ax_prob.set_title(‘Residuals probability plot’, fontsize = 14)

# в третьем график остатков относительно прогноза

ax_ry.scatter(y_pred, residuals)

ax_ry.set_title(‘Predicted vs. Residuals’, fontsize = 14)

ax_ry.set(xlabel = ‘y_pred’)

ax_ry.set(ylabel = ‘Residuals’)

# автокорреляция остатков

plot_acf(residuals, lags = 30, ax = ax_auto)

ax_auto.set_title(‘Residuals Autocorrelation’, fontsize = 14)

ax_auto.set(xlabel = f‘Lags ndurbin_watson: {durbin_watson(residuals).round(2)}’)

ax_auto.set(ylabel = ‘Autocorrelation’)

# на четвертом сравним прогнозные и фактические значения

ax_yy.scatter(y, y_pred)

ax_yy.plot([y.min(), y.max()], [y.min(), y.max()], «k—«, lw = 1)

ax_yy.set_title(‘Actual vs. Predicted’, fontsize = 14)

ax_yy.set(xlabel = ‘y_true’)

ax_yy.set(ylabel = ‘y_pred’)

sns.kdeplot(y, fill = True, ax = ax_ykde, label = ‘y_true’)

sns.kdeplot(y_pred, fill = True, ax = ax_ykde, label = ‘y_pred’)

ax_ykde.set_title(‘Actual vs. Predicted Distribution’, fontsize = 14)

ax_ykde.set(xlabel = ‘y_true and y_pred’)

ax_ykde.set(ylabel = ‘Density’)

ax_ykde.legend(loc = ‘upper right’, prop = {‘size’: 12})

plt.tight_layout()

plt.show()

Разберем полученную информацию.

В целом остатки модели распределены нормально с нулевым средним значением
Явной гетероскедастичности нет, хотя мы видим, что дисперсия не всегда равномерна
Присутствует умеренная отрицательная корреляция
График y_true vs. y_pred показывает насколько сильно прогнозные значения отклоняются от фактических. В идеальной модели (без шума, т.е. без случайных колебаний) точки должны были би стремиться находиться на диагонали, в более реалистичной модели нам бы хотелось видеть, что точки плотно сосредоточены вокруг диагонали.
Распределение прогнозных значений в целом повторяет распределение фактических.

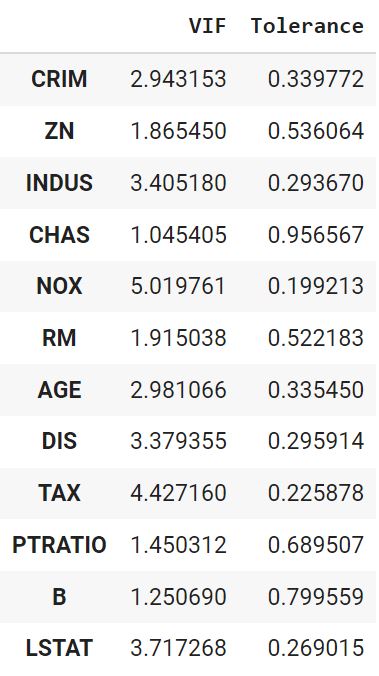
Мультиколлинеарность

Отдельно проведем анализ на мультиколлинеарность. Напишем соответствующую функцию.

def vif(df, features):

vif, tolerance = {}, {}

# пройдемся по интересующим нас признакам

for feature in features:

# составим список остальных признаков, которые будем использовать

# для построения регрессии

X = [f for f in features if f != feature]

# поместим текущие признаки и таргет в X и y

X, y = df[X], df[feature]

# найдем коэффициент детерминации

r2 = LinearRegression().fit(X, y).score(X, y)

# посчитаем tolerance

tolerance[feature] = 1 — r2

# найдем VIF

vif[feature] = 1 / (tolerance[feature])

# выведем результат в виде датафрейма

return pd.DataFrame({‘VIF’: vif, ‘Tolerance’: tolerance})

vif(df = X.drop(‘CHAS’, axis = 1), features = X.drop(‘CHAS’, axis = 1).columns)

Дополнительная обработка данных

Попробуем дополнительно улучшить некоторые из диагностических показателей.

VIF

Уберем признак с наибольшим VIF (RAD) и посмотрим, что получится.

vif(df = X, features = [‘CRIM’,

‘ZN’,

‘INDUS’,

‘CHAS’,

‘NOX’,

‘RM’,

‘AGE’,

‘DIS’,

‘TAX’,

‘PTRATIO’,

‘B’,

‘LSTAT’])

Показатели пришли в норму. Окончательно удалим RAD.

boston.drop(columns = ‘RAD’, inplace = True)

Преобразование данных

Применим преобразование Йео-Джонсона.

from sklearn.preprocessing import PowerTransformer

pt = PowerTransformer()

boston = pd.DataFrame(pt.fit_transform(boston),

columns = boston.columns)

Отбор признаков

Посмотрим на линейную корреляцию Пирсона количественных признаков и целевой переменной.

boston_t.drop(columns = ‘CHAS’).corr().MEDV.to_frame().style.background_gradient()

Также рассчитаем точечно-бисериальную корреляцию.

pbc(boston_t.MEDV, boston_t.CHAS)

Удалим признаки с наименьшей корреляцией, а именно ZN, CHAS, DIS и B.

boston.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’], inplace = True)

Повторное моделирование и диагностика

Повторное моделирование

Выполним повторное моделирование.

X = boston_t.drop(columns = [‘ZN’, ‘CHAS’, ‘DIS’, ‘B’, ‘MEDV’])

y = boston_t.MEDV

from sklearn.linear_model import LinearRegression

model = LinearRegression()

y_pred = model.fit(X, y).predict(X)

Оценка качества и диагностика

Оценим качество. Так как мы преобразовали целевую переменную, показатель RMSE не будет репрезентативен. Воспользуемся MAPE и $R^2$.

(0.7546883769637166, 0.7546883769637166)

Отклонение прогнозного значения от истинного снизилось. $R^2$ немного уменьшился, чтобы бывает, когда мы пытаемся привести модель к соответствию допущениям. Проведем диагностику.

Распределение остатков немного улучшилось, при этом незначительно усилилась их отрицательная автокорреляция. Распределение целевой переменной стало менее островершинным.

Данные можно было бы продолжить анализировать и улучшать, однако в рамках текущего занятия перейдем к механике обучения модели.

Коэффициенты

Выведем коэффициенты для того, чтобы сравнивать их с результатами построенных с нуля моделей.

model.intercept_, model.coef_

(9.574055157844797e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Обучение модели

Теперь, когда мы поближе познакомились с понятием регрессии, разобрали функции потерь и изучили допущения, при которых модель может быть удачной аппроксимацией данных, пора перейти к непосредственному созданию алгоритмов.

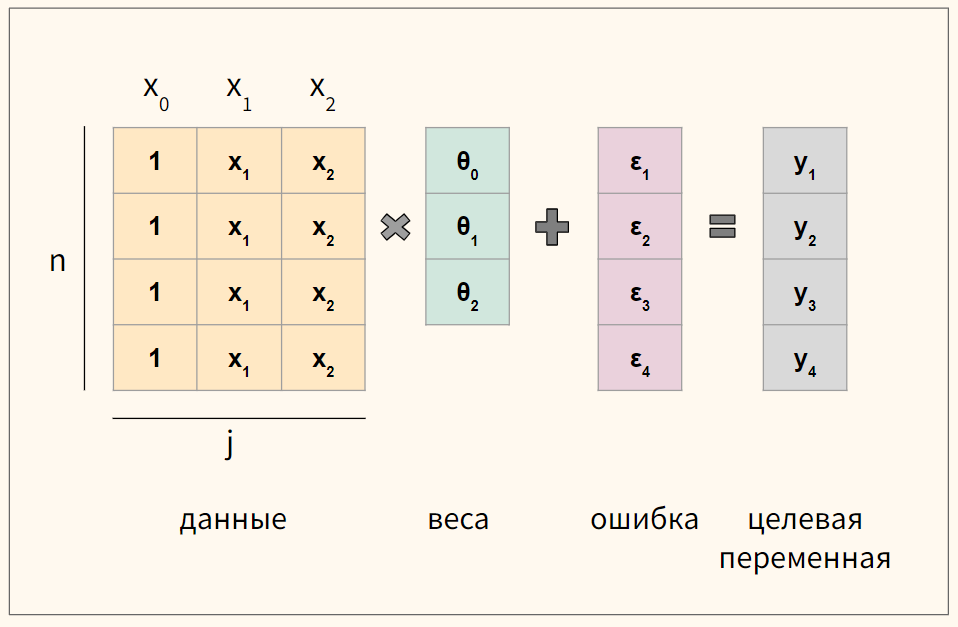
Векторизация уравнения

Для удобства векторизуем приведенное выше уравнение множественной линейной регрессии

$$ y = begin{bmatrix} y_1 y_2 vdots y_n end{bmatrix} X = begin{bmatrix} x_0 & x_1 & ldots & x_j x_0 & x_1 & ldots & x_j vdots & vdots & vdots & vdots x_{0} & x_{1} & ldots & x_{n,j} end{bmatrix}, theta = begin{bmatrix} theta_0 theta_1 vdots theta_n end{bmatrix}, varepsilon = begin{bmatrix} varepsilon_1 varepsilon_2 vdots varepsilon_n end{bmatrix} $$

где n — количество наблюдений, а j — количество признаков.

Обратите внимание, что мы создали еще один столбец данных $ x_0 $, который будем умножать на сдвиг $ theta_0 $. Его мы заполним единицами.

В результате такого несложного преобразования значение сдвига не изменится, но мы сможем записать записать уравнение через умножение матрицы на вектор.

$$ y = Xtheta + varepsilon $$

Кроме того, как мы увидим ниже, так нам не придется искать отдельную производную для коэффициента $ theta_0 $.

Схематично для модели с четырьмя наблюдениями (n = 4) и двумя признаками (j = 2) получаются вот такие матрицы.

Функция потерь

Как мы уже говорили, чтобы подобрать оптимальные коэффициенты $theta$, нам нужен критерий или функция потерь. Логично измерять отклонение прогнозного значения от истинного.

$$ varepsilon = Xtheta-y $$

При этом опять же просто складывать отклонения или ошибки мы не можем. Положительные и отрицательные значения будут взаимоудалятся. Для решения этой проблемы можно, например, использовать модуль и это приводит нас к абсолютной ошибку или L1 loss.

Абсолютная ошибка, L1 loss

При усреднении на количество наблюдений мы получаем среднюю абсолютную ошибку (mean absolute error, MAE).

$$ MAE = frac{sum{|y-Xtheta|}}{n} = frac{sum{|varepsilon|}}{n} $$

Приведем пример такой функции на Питоне.

def L1(y_true, y_pred):

return np.sum(np.abs(y_true — y_pred)) / y_true.size

Помимо модуля ошибку можно возводить в квадрат.

Квадрат ошибки, L2 loss

В этом случай говорят про сумму квадратов ошибок (sum of squared errors, SSE) или сумму квадратов остатков (sum of squared residuals, SSR или residual sum of squares, RSS).

$$ SSE = sum (y-Xtheta)^2 $$

Как мы уже говорили, на практике вместо SSE часто используется MSE, или вернее half MSE для удобства нахождения производной.

$$ MSE = frac{1}{2n} sum (y-theta X)^2 $$

Ниже код на Питоне.

def L2(y_true, y_pred):

return np.sum((y_true — y_pred) ** 2) / y_true.size

На практике у обеих функций есть сильные и слабые стороны. Рассмотрим L1 loss (MAE) и L2 loss (MSE) на графике.

# для построения графиков мы используем x вместо y_true, y_pred

# в качестве входящего значения

def mse(x):

return x ** 2

def mae(x):

return np.abs(x)

plt.figure(figsize = (10, 8))

x_vals = np.arange(—3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Как мы видим, при отклонении от точки минимума из-за возведения в квадрат L2 значительно быстрее увеличивает ошибку, поэтому если в данных есть выбросы при суммированнии они очень сильно влияют на ошибку, хотя де-факто большая часть значений такого уровня потерь не дали бы.

Функция L1 не дает такой большой ошибки на выбросах, однако ее сложно дифференцировать, в точке минимума ее производная не определена.

Функция Хьюбера

Рассмотрим функцию Хьюбера (Huber loss), которая объединяет сильные стороны вышеупомянутых функций и при этом лишена их недостатков. Посмотрим на формулу.

$$ L_{delta}= left{begin{matrix} frac{1}{2}(y-hat{y})^{2} & if | y-hat{y} | < delta delta (|y-hat{y}|-frac1 2 delta) & otherwise end{matrix}right. $$

Представим ее на графике.

plt.figure(figsize = (10, 8))

def huber(x, delta = 1.):

huber_mse = 0.5 * np.square(x)

huber_mae = delta * (np.abs(x) — 0.5 * delta)

return np.where(np.abs(x) <= delta, huber_mse, huber_mae)

x_vals = np.arange(—3, 3, 0.01)

plt.plot(x_vals, mae(x_vals), label = ‘MAE’)

plt.plot(x_vals, mse(x_vals), label = ‘MSE’)

plt.plot(x_vals, huber(x_vals, delta = 2), label = ‘Huber’)

plt.legend(loc = ‘upper center’, prop = {‘size’: 14})

plt.grid()

plt.show()

Также приведем код этой функции.

def huber(y_pred, y_true, delta = 1.0):

# пропишем обе части функции потерь

huber_mse = 0.5 * (y_true — y_pred) ** 2

huber_mae = delta * (np.abs(y_true — y_pred) — 0.5 * delta)

# выберем одну из них в зависимости от дельта

return np.where(np.abs(y_true — y_pred) <= delta, huber_mse, huber_mae)

На сегодняшнем занятии мы, как и раньше, в качестве функции потерь используем MSE.

Метод наименьших квадратов

Нормальные уравнения

Для множественной линейной регрессии коэффициенты находятся по следующей формуле

$$ theta = (X^TX)^{-1}X^Ty $$

Давайте разбираться, как мы к ней пришли. Сумма квадратов остатков (SSE) можно переписать как произведение вектора $ hat{varepsilon} $ на самого себя, то есть $ SSE = varepsilon^{T}varepsilon$. Помня, что $varepsilon = y-Xtheta $ получаем (не забывая транспонировать)

$$ (y-Xtheta)^T(y-Xtheta) $$

Раскрываем скобки

$$ y^Ty-y^T(Xtheta)-(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Заметим, что $A^TB = B^TA$, тогда

$$ y^Ty-(Xtheta)^Ty-(Xtheta)^Ty+(Xtheta)^T(Xtheta)$$

$$ y^Ty-2(Xtheta)^Ty+(Xtheta)^T(Xtheta) $$

Вспомним, что $(AB)^T = A^TB^T$, тогда

$$ y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$

Теперь нужно найти частные производные этих функций

$$ nabla_{theta} J(theta) = y^Ty-2theta^TX^Ty+theta^TX^TXtheta $$

После дифференцирования мы получаем следующую производную

$$ -2X^Ty+2X^TXtheta $$

Как мы помним, оптимум функции находится там, где производная равна нулю.

$$ -2X^Ty+2X^TXtheta = 0 $$

$$ -X^Ty+X^TXtheta = 0 $$

$$ X^TXtheta = X^Ty $$

Выражение выше называется нормальным уравнением (normal equation). Решив его для $theta$ мы найдем аналитическое решение минимизации суммы квадратов отклонений.

$$ theta = (X^TX)^{-1}X^Ty $$

Замечу только, что по теореме Гаусса-Маркова, оценка через МНК является наиболее оптимальной (обладающей наименьшей дисперсией) среди всех методов построения модели.

Код на Питоне

Перейдем к созданию класса линейной регрессии наподобие LinearRegression библиотеки sklearn. Вначале напишем функцию гипотезы (т.е. функцию самой модели), снабдив ее функцией, которая добавляет столбец из единиц к признакам.

$$ h_{theta}(x) = theta X $$

def add_ones(x):

# важно! изменяет исходный датафрейм

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def h(x, theta):

x = x.copy()

add_ones(x)

return np.dot(x, theta)

Перейдем к функции, отвечающей за обучение модели.

$$ theta = (X^TX)^{-1}X^Ty $$

# строчную `x` используем внутри функций и методов класса

# заглавную `X` вне функций и методов

def fit(x, y):

x = x.copy()

add_ones(x)

xT = x.transpose()

inversed = np.linalg.inv(np.dot(xT, x))

thetas = inversed.dot(xT).dot(y)

return thetas

Обучим модель и выведем коэффициенты.

thetas = fit(X, y)

thetas[0], thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Примечание. Замечу, что не все матрицы обратимы, в этом случае они называются вырожденными (non-invertible, degenerate). В этом случае можно найти псевдообратную матрицу (pseudoinverse). Для этого в Numpy есть функция np.linalg.pinv().

Сделаем прогноз.

y_pred = h(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим код в класс.

class ols():

def __init__(self):

self.thetas = None

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def fit(self, x, y):

x = x.copy()

self.add_ones(x)

xT = x.T

inversed = np.linalg.inv(np.dot(xT, x))

self.thetas = inversed.dot(xT).dot(y)

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса и обучим модель.

model = ols()

model.fit(X, y)

Выведем коэффициенты.

model.thetas[0], model.thetas[1:]

(9.3718435789647e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]))

Сделаем прогноз.

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

Оценим качество через MAPE и $R^2$.

(0.7546883769637167, 0.7546883769637167)

Мы видим, что результаты аналогичны.

Метод градиентного спуска

В целом с этим методом мы уже хорошо знакомы. В качестве упражнения давайте реализуем этот алгоритм на Питоне для многомерных данных.

Нахождение градиента

Покажем расчет градиента на схеме.

В данном случае мы берем датасет из четырех наблюдений и двух признаков ($x_1$ и $x_2$) и соответственно используем три коэффициента ($theta_0, theta_1, theta_2$).

Пошаговое построение модели

Начнем с функции гипотезы.

$$ h_{theta}(x) = theta X $$

def h(x, thetas):

return np.dot(x, thetas)

Объявим функцию потерь.

$$ J({theta_j}) = frac{1}{2n} sum (y-theta X)^2 $$

def objective(x, y, thetas, n):

return np.sum((y — h(x, thetas)) ** 2) / (2 * n)

Объявим функцию для расчета градиента.

$$ frac{partial}{partial theta_j} J(theta) = -x_j(y — Xtheta) times frac{1}{n} $$

где j — индекс признака.

def gradient(x, y, thetas, n):

return np.dot(—x.T, (y — h(x, thetas))) / n

Напишем функцию для обучения модели.

$$ theta_j := theta_j-alpha frac{partial}{partial theta_j} J(theta) $$

Символ := означает, что левая часть равенства определяется правой. По сути, с каждой итерацией мы обновляем веса, умножая коэффициент скорости обучения на градиент.

def fit(x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

# функцию add_ones() мы написали раньше

add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

loss_history = []

for i in range(iter):

loss_history.append(objective(x, y, thetas, n))

grad = gradient(x, y, thetas, n)

thetas -= learning_rate * grad

return thetas, loss_history

Обучим модель, выведем коэффициенты и достигнутый (минимальный) уровень ошибки.

thetas, loss_history = fit(X, y, iter = 50000, learning_rate = 0.05)

thetas[0], thetas[1:], loss_history[—1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

Полученный результат очень близок к тому, что было найдено методом наименьших квадратов.

Прогноз

Сделаем прогноз.

def predict(x, thetas):

x = x.copy()

add_ones(x)

return np.dot(x, thetas)

y_pred = predict(X, thetas)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Создание класса

Объединим написанные функции в класс.

class gd():

def __init__(self):

self.thetas = None

self.loss_history = []

def add_ones(self, x):

return x.insert(0,‘x0’, np.ones(x.shape[0]))

def objective(self, x, y, thetas, n):

return np.sum((y — self.h(x, thetas)) ** 2) / (2 * n)

def h(self, x, thetas):

return np.dot(x, thetas)

def gradient(self, x, y, thetas, n):

return np.dot(—x.T, (y — self.h(x, thetas))) / n

def fit(self, x, y, iter = 20000, learning_rate = 0.05):

x, y = x.copy(), y.copy()

self.add_ones(x)

thetas, n = np.zeros(x.shape[1]), x.shape[0]

# объявляем переменную loss_history (отличается от self.loss_history (?))

loss_history = []

for i in range(iter):

loss_history.append(self.objective(x, y, thetas, n))

grad = self.gradient(x, y, thetas, n)

thetas -= learning_rate * grad

# записываем обратно во внутренние атрибуты, чтобы передать методу .predict()

self.thetas = thetas

self.loss_history = loss_history

def predict(self, x):

x = x.copy()

self.add_ones(x)

return np.dot(x, self.thetas)

Создадим объект класса, обучим модель, выведем коэффициенты и сделаем прогноз.

model = gd()

model.fit(X, y, iter = 50000, learning_rate = 0.05)

model.thetas[0], model.thetas[1:], model.loss_history[—1]

(9.493787734953824e-16,

array([-0.09989392, 0.03965441, 0.1069877 , 0.23172172, -0.05561128,

-0.16878987, -0.18057055, -0.49319274]),

0.1226558115181417)

y_pred = model.predict(X)

y_pred[:5]

array([1.24414666, 0.55999778, 1.48103299, 1.49481605, 1.21342788])

Оценка качества

(0.7546883769637167, 0.7546883769637167)

Теперь рассмотрим несколько дополнительных соображений, касающихся построения модели линейной регрессии.

Диагностика алгоритма

Работу алгоритма можно проверить с помощью кривой обучения (learning curve).

Ошибка постоянно снижается
Алгоритм остановится, после истечения заданного количества итераций
Можно задать пороговое значение, после которого он остановится (например, $10^{-1}$)

Построим кривую обучения.

plt.plot(loss_history)

plt.show()

plt.plot(loss_history[:100])

plt.show()

Она также позволяет выбрать адекватный коэффициент скорости обучения.

Подведем итог

Сегодня мы подробно рассмотрели модель множественной линейной регрессиии. В частности, мы поговорили про построение гипотезы, основные функции потерь, допущения модели линейной регрессии, метрики качества и диагностику модели.

Кроме того, мы узнали как изнутри устроены метод наименьших квадратов и метод градиентного спуска и построили соответствующие модели на Питоне.

Отдельно замечу, что, изучив скорректированный коэффициент детерминации, мы начали постепенно погружаться в способы усовершенствования базовых алгоритмов и метрик. На последующих занятиях мы продолжим этот путь в двух направлениях: познакомимся со способами регуляризации функции потерь и начнем создавать более сложные алгоритмы оптимизации.

Но прежде предлагаю в деталях изучить уже знакомый нам алгоритм логистической регрессии.

Дополнительные материалы к занятию.

В
идеале, когда все точки лежат на прямой
регрессии, все остатки равны нулю и
значения Y
полностью вычисляются или объясняются
линейной функцией от Х.

Используя
формулу отклонений и отнимая

от обеих частей равенства, имеем
следующее.

Несложными
алгебраическими преобразованиями можно
показать, что суммы квадратов
складываются:

или

где

Здесь
SS
обозначает «сумма квадратов» (Sum
of Squares), a T, R, Е— соответственно «общая»
(Total), «регрессионная» (Regression) и
«ошибки» (Error). С этими суммами
квадратов связаны следующие величины
степеней свободы.

Если
линейной связи нет, Y
не зависит от X
и дисперсия Y
оценивается значением выборочной
дисперсии.

Если
связь между X и Y
имеется, она может влиять на некоторые
разности значений Y.

Регрессионная
сумма квадратов, SSR, измеряет часть
дисперсии Y,
объясняемую линейной зависимостью.
Сумма квадратов ошибок, SSE
— это оставшаяся часть дисперсии Y,
или дисперсия Y,
не объясненная линейной зависимостью.

2.5 Коэффициент детерминации

Как
было указано в предыдущем разделе,
показатель SST измеряет общую вариацию
относительно Y,
а ее часть, объясненная изменением X,
соответствует SSR. Оставшаяся, или
необъясненная вариация, соответствует
SSE. Отношение объясненной вариации к
общей называется выборочным коэффициентом
детерминации и обозначается

Коэффициент
детерминации измеряет долю изменчивости
Y,
которую можно объяснить с помощью
информации об изменчивости (разнице
значений) независимой переменной X.

В
случае прямолинейной регрессии
коэффициент детерминации

равен квадрату коэффициента корреляции
.

В
регрессионном анализе коэффициенты

и

необходимо рассматривать отдельно, так
как они несут различную информацию.
Коэффициент корреляции выявляет не
только силу, но и направление линейной
связи. Следует отметить, что когда
коэффициент корреляции возводится в
квадрат, полученное значение всегда
будет положительным и информация о
характере взаимосвязи теряется.

Коэффициент
детерминации

измеряет силу взаимосвязи между Y и X
иначе, чем коэффициент корреляции
.
Значение

измеряет долю изменчивости Y, объясненную
разницей значений X. Эту полезную
интерпретацию можно обобщить на
взаимосвязь между Y и более чем одной
переменной X.

2.6 Проверка гипотез

Прямая
регрессии вычисляется по выборке пар
значений Х-Y. Статистическая модель
простой линейной регрессии предполагает,
что линейная связь величин X и Y имеет
место для всех возможных пар X-Y. Для
проверки гипотезы, что соотношение
истинно
для всех X и Y рассмотрим гипотезу:

Если
эта гипотеза справедлива, в генеральной
совокупности нет связи между значениями
X и Y. Если мы не можем опровергнуть
гипотезу, то, несмотря на ненулевое
значение вычисленного по выборке
углового коэффициента регрессионной
прямой, мы не имеем оснований гарантированно
утверждать, что значения X
и Y
взаимозависимы. Иными словами, нельзя
исключить возможность того, что
регрессионная прямая совокупности
горизонтальна.

Если
гипотеза

верна, проверочная статистика t со
значением

имеет t-распределение с количеством
степеней свободы df = n-2.
Здесь оценка стандартного отклонения
(или стандартная ошибка) равна

Для
выборки очень большого объема можно
отклонить гипотезу

и заключить, что между X и Y
есть линейная связь даже в тех случаях,
когда значение

мало (например, 10%). Аналогично для малых
выборок и очень большого значения

(например, 95%) можно сделать вывод, что
регрессионная зависимость имеет место.
Малое значение коэффициента детерминации

означает, что вычисленное уравнение
регрессии не имеет большого значения
для прогноза. С другой стороны, большое
значение

при очень малом объеме выборки не может
удовлетворить исследователя, и потребуются
дополнительные обоснования, чтобы
вычисленную функцию регрессии использовать
для целей прогноза. Такова разница между
статистической и практической значимостью.
В то же время вся собранная информация,
а также понимание сущности рассматриваемого
объекта будут необходимы, чтобы
определить, может ли вычисленная функция
регрессии быть подходящим средством
для прогноза.

Еще
один способ проверки гипотезы

возможен с помощью таблицы ANOVA. При
предположении, что статистическая
модель линейной регрессии правильна и
нулевая гипотеза

истинна, отношение

имеет
F-распределение со степенями свободы
df= 1, n-2.
Если гипотеза

истинна, каждая из величин MSR и MSE будет
оценкой
,
дисперсии слагаемого ошибки
в
статистической модели прямолинейной
регрессии. С другой стороны, если верна
гипотеза
,
числитель в отношении F стремится стать
большим, чем знаменатель. Большое
значение F согласуется с истинностью
альтернативной гипотезы.

Для
модели прямолинейной регрессии проверка
гипотезы

при альтернативе

основывается на отношении

с df= 1, n-2.
При уровне значимости

область отклонения гипотезы:.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Регрессивный анализ
Часть серии по

Модели
Линейная регрессия Простая регрессия Полиномиальная регрессия Общая линейная модель
Обобщенная линейная модель Дискретный выбор Биномиальная регрессия Бинарная регрессия Логистическая регрессия Полиномиальный логит Смешанный логит Пробит Полиномиальный пробит Заказал логит Заказал пробит Пуассон
Многоуровневая модель Фиксированные эффекты Случайные эффекты Линейная модель смешанных эффектов Нелинейная модель смешанных эффектов
Нелинейная регрессия Непараметрический Полупараметрический Крепкий Квантиль Изотонический Основные компоненты Наименьший угол Местный Сегментированный
Ошибки в переменных
Оценка
Наименьших квадратов Линейный Нелинейный
Обычный Взвешенный Обобщенный
Частичное Общий Неотрицательный Регрессия хребта Регулярный
Наименьшие абсолютные отклонения Итеративно переназначенный Байесовский Байесовский многомерный
Фон
Проверка регрессии Средний и прогнозируемый ответ Ошибки и остатки Доброту соответствия Студентизованный остаток Теорема Гаусса – Маркова
Математический портал

В статистике и оптимизации ошибки и остатки являются двумя тесно связанными и легко путаемыми мерами отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». В ошибка (или же беспокойство) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинный значение интересующей величины (например, среднее значение генеральной совокупности), и остаточный наблюдаемого значения — это разница между наблюдаемым значением и по оценкам значение интересующей величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибки регрессии и остатки регрессии и где они приводят к концепции стьюдентизированных остатков.

Вступление

Предположим, что есть серия наблюдений из одномерное распределение и мы хотим оценить иметь в виду этого распределения (так называемый модель местоположения ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.

А статистическая ошибка (или же беспокойство) — это величина, на которую наблюдение отличается от ожидаемое значение, последнее основано на численность населения из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся иметь в виду всего населения, обычно не наблюдается, и, следовательно, статистическая ошибка также не может быть обнаружена.

А остаточный (или подходящее отклонение), с другой стороны, является наблюдаемым оценивать ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка п люди. В выборочное среднее может служить хорошей оценкой численность населения иметь в виду. Тогда у нас есть:

Разница между ростом каждого человека в выборке и ненаблюдаемой численность населения означает это статистическая ошибка, в то время как
Разница между ростом каждого человека в выборке и наблюдаемым образец означает это остаточный.

Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, следовательно, остатки обязательно нет независимый. Статистические ошибки, с другой стороны, независимы, и их сумма в пределах случайной выборки равна почти наверняка не ноль.

Можно стандартизировать статистические ошибки (особенно нормальное распределение ) в z-оценка (или «стандартная оценка») и стандартизируйте остатки в т-статистический, или в более общем смысле стьюдентизированные остатки.

В одномерных распределениях

Если предположить нормально распределенный совокупность со средними μ и стандартное отклонение σ, и выбираем индивидуумов независимо, то имеем

X_1, точки, X_n sim N ( mu, sigma ^ 2) ,

и выборочное среднее

$overline {X} = {X_1 + cdots + X_n over n}$

случайная величина, распределенная таким образом, что:

${ displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).}$

В статистические ошибки тогда

$e_ {i} = X_ {i} - mu, ,$

с ожидал значения нуля,^[1] тогда как остатки находятся

$r_ {i} = X_ {i} - overline {X}.$

Сумма квадратов статистические ошибки, деленное на σ², имеет распределение хи-квадрат с п степени свободы:

${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.$

Однако это количество не наблюдается, так как среднее значение для населения неизвестно. Сумма квадратов остатки, с другой стороны, наблюдается. Частное этой суммы по σ² имеет распределение хи-квадрат только с п — 1 степень свободы:

${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} r_ {i} ^ {2} sim chi _ {{n-1}} ^ {2 }.$

Эта разница между п и п — 1 степень свободы дает Поправка Бесселя для оценки выборочная дисперсия популяции с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.

Примечательно, что сумма квадратов остатков и средние выборочные значения могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу расчетов, включающих t-статистика:

${ displaystyle T = { frac {{ overline {X}} _ {n} - mu _ {0}} {S_ {n} / { sqrt {n}}}},}$

куда ${ displaystyle { overline {X}} _ {n} - mu _ {0}}$ представляет ошибки, $S_ {n}$ представляет собой стандартное отклонение выборки для выборки размера п, и неизвестно σ, а член знаменателя учитывает стандартное отклонение ошибок согласно:^[2]

${ displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}}$

Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяется. Это удачно, потому что это означает, что даже если мы не знаемσ, мы знаем распределение вероятностей этого частного: оно имеет Распределение Стьюдента с п — 1 степень свободы. Поэтому мы можем использовать это частное, чтобы найти доверительный интервал заμ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».^[3]

Регрессии

В регрессивный анализ, различие между ошибки и остатки тонкий и важный, и ведет к концепции стьюдентизированные остатки. При наличии ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от приспособленный функции — остатки. Если применима линейная модель, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам.^[2] Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичность. Если все остатки равны или не разветвляются, они демонстрируют гомоскедастичность.

Однако возникает терминологическая разница в выражении среднеквадратичная ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатки, а не ненаблюдаемые ошибки. Если эту сумму квадратов разделить на п, количество наблюдений, результат — это среднее квадратов остатков. Поскольку это пристрастный Для оценки дисперсии ненаблюдаемых ошибок смещение устраняется путем деления суммы квадратов остатков на df = п − п — 1 вместо п, куда df это количество степени свободы (п минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует несмещенную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.^[4]

Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они такие же, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равны п − п — 1, где п — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать, разделив средний квадрат модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с).^[5]

Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) может отличаться даже если сами ошибки одинаково распределены. Конкретно в линейная регрессия где ошибки одинаково распределены, вариативность остатков входных данных в середине области будет выше чем изменчивость остатков на концах области:^[6] линейные регрессии лучше подходят для конечных точек, чем средние. Это также отражено в функции влияния различных точек данных на коэффициенты регрессии: конечные точки имеют большее влияние.

Таким образом, чтобы сравнить остатки на разных входах, необходимо скорректировать остатки на ожидаемую изменчивость остатки, который называется студенчество. Это особенно важно в случае обнаружения выбросы, где рассматриваемый случай чем-то отличается от другого случая в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.

Другое использование слова «ошибка» в статистике

Термин «ошибка», как обсуждалось в предыдущих разделах, используется в смысле отклонения значения от гипотетического ненаблюдаемого значения. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:

Средняя квадратичная ошибка или же среднеквадратичная ошибка (MSE) и Средняя квадратическая ошибка (RMSE) относятся к количеству, на которое значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).

Сумма квадратов ошибок (SSE или же SS_е), обычно сокращенно SSE или SS_е, относится к остаточная сумма квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой наименьших квадратов, когда коэффициенты регрессии выбираются таким образом, чтобы сумма квадратов была минимальной (т. Е. Ее производная равна нулю).

Точно так же сумма абсолютных ошибок (SAE) — сумма абсолютных значений остатков, которая минимизируется в наименьшие абсолютные отклонения подход к регрессу.

Смотрите также

Абсолютное отклонение
Консенсус-прогнозы
Обнаружение и исправление ошибок
Объясненная сумма квадратов
Инновации (обработка сигналов)
Неподходящая сумма квадратов
Допустимая погрешность
Средняя абсолютная ошибка
Ошибка наблюдения
Распространение ошибки
Вероятная ошибка
Случайные и систематические ошибки
Разбавление регрессии
Среднеквадратичное отклонение
Ошибка выборки
Стандартная ошибка
Студентизованный остаток
Ошибки типа I и типа II

внешняя ссылка

СМИ, связанные с Ошибки и остатки в Wikimedia Commons

В этой серии мы внимательно рассмотрим алгоритм машинного обучения и изучим плюсы и минусы каждого алгоритма. Мы рассмотрим алгоритмы вместе с математикой, лежащей в основе алгоритма.

Во-первых, давайте проясним некоторые основные термины, используемые в машинном обучении.

Контролируемый алгоритм ML: Те алгоритмы, которые используют помеченные данные, известны как контролируемые алгоритмы ml. Контролируемые алгоритмы ml широко используются для двух задач: классификации и регрессии.
Классификация: Когда задача состоит в том, чтобы классифицировать объекты выборки по определенным категориям (целевая переменная), тогда это называется классификацией. Например, определение того, является ли электронное письмо спамом или нет.
Регрессия: когда задача состоит в том, чтобы предсказать непрерывную переменную (целевую переменную), тогда это называется регрессией. Например, прогнозирование цен на жилье.
Неконтролируемый алгоритм ML: те алгоритмы, которые используют немаркированные данные, известны как неконтролируемые алгоритмы ml. Для кластеризации используется неконтролируемый алгоритм.
Кластеризация: задача поиска групп в заданных немаркированных данных известна как кластеризация.
Ошибка: разница между фактическим и прогнозируемым значением.
Градиентный спуск: механизм обновления параметров модели таким образом, чтобы генерировать минимальное значение функции ошибки.

Что такое линейная регрессия в машинном обучении?

Линейная регрессия — это тип контролируемого алгоритма машинного обучения, который используется для прогнозирования непрерывной числовой переменной, известной как цель. Это один из самых простых алгоритмов машинного обучения. Он называется «линейным», потому что алгоритм предполагает, что взаимосвязь между входными характеристиками (также известными как независимые переменные) и выходной переменной (также известной как зависимая или целевая переменная) является линейной. Другими словами, алгоритм пытается найти прямую линию (или гиперплоскость в случае нескольких входных объектов), которая наилучшим образом соответствует данным.

Типы линейной регрессии:

Простая линейная регрессия:

Линейная регрессия известна как простая линейная регрессия, когда прогнозирование выходного значения выполняется с использованием одной входной функции. Мы можем провести линию между зависимыми и независимыми переменными в 2D-пространстве, когда задан один входной признак. здесь b0 — точка пересечения, b1 — коэффициент, x1, x2,…, xn — входные признаки, а y — выходная переменная.

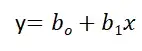
Множественная линейная регрессия:

Линейная регрессия известна как множественная линейная регрессия, когда прогнозирование выходной переменной выполняется с использованием нескольких входных признаков. Мы можем нарисовать плоскость между зависимой и независимой переменными в 3D-пространстве, когда заданы только два входных объекта. В более высоких измерениях визуализация становится затруднительной, но интуиция заключается в том, чтобы найти гиперплоскость в более высоких измерениях. здесь b0 — это перехват, а b1, b2, b3, ......., bn-1, bn известны как коэффициенты, а x1, x2,..., xn известны как входные характеристики, а y — переменная результата.

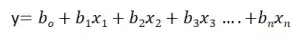
К этому моменту мы поняли, что линейная регрессия пытается построить линейную границу, но как она это делает?

Как он найдет идеальную линию, которая разделяет данные два класса?

Как указано в уравнении, b0 известен как перехват, а b1, b2,...., bn известны как коэффициенты линейной регрессии, и теперь цель состоит в том, чтобы найти ту линейную границу, которая минимизирует функцию ошибки. Функция ошибки представляет собой квадрат суммы разностей между прогнозируемыми и фактическими значениями целевой переменной. Если мы не сведем ошибку в квадрат, то положительные и отрицательные моменты будут компенсировать друг друга.

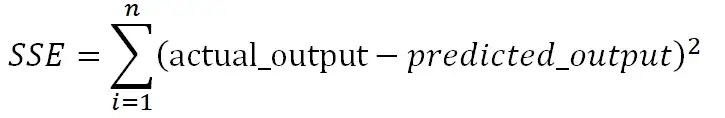
Нам нужно найти коэффициенты и перехваты для линейной регрессии таким образом, чтобы сумма квадратов ошибок (SSE) была минимизирована. Градиентный спуск — один из самых популярных методов, который используется для нахождения оптимальных коэффициентов для ml и алгоритмов глубокого обучения.

В приведенном ниже разделе мы обучим модель на базе данных страхования, где мы должны спрогнозировать расходы с учетом входных данных: возраст, пол, ИМТ, расходы на больницу, количество прошлых консультаций и т.д.

Реализация на Python:

Вы можете использовать библиотеку sklearn на python для обучения и тестирования модели линейной регрессии. Мы будем использовать набор данных insurance.csv для обучения модели линейной регрессии. Некоторые этапы предварительной обработки выполняются для описания данных, обработки пропущенных значений и проверки допущений линейной регрессии.

Шаг 1: Загрузите все необходимые библиотеки и наборы данных, используя библиотеку pandas.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.stats.outliers_influence import variance_inflation_factor as VIF
from sklearn.metrics import classification_report
insurance=pd.read_csv('new_insurance_data.csv') 
insurance.head()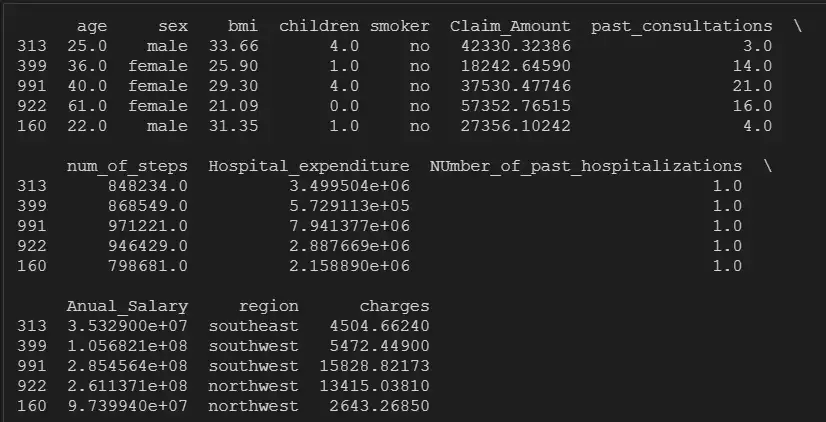

Случайно выбранные 5 записей из набора данных

Шаг 2: Проверьте нулевые значения, форму и тип данных переменных:

# checks for non-null entries, size and datatype
insurance.info()

Мы можем отдельно проверить количество нулей для каждой функции, используя df.isna().sum():

insurance.isnull().sum()
# helps me to check for null values

Шаг 3. Заполните пропущенные значения

Мы можем заполнить недостающие значения объектов объектного типа, используя режим, а объектов целочисленного типа — среднее значение или медиану.

# calculating mode for object data type features which will be used to fill missing values.
# We have 3 features which are of object type
print(f"mode of sex feature: {insurance['sex'].mode()[0]}")
print(f"mode of region feature: {insurance['region'].mode()[0]}")
print(f"mode of smoker feature: {insurance['smoker'].mode()[0]}")

# describe() function will give the descriptive statistics for all numerical features
insurance.describe().transpose()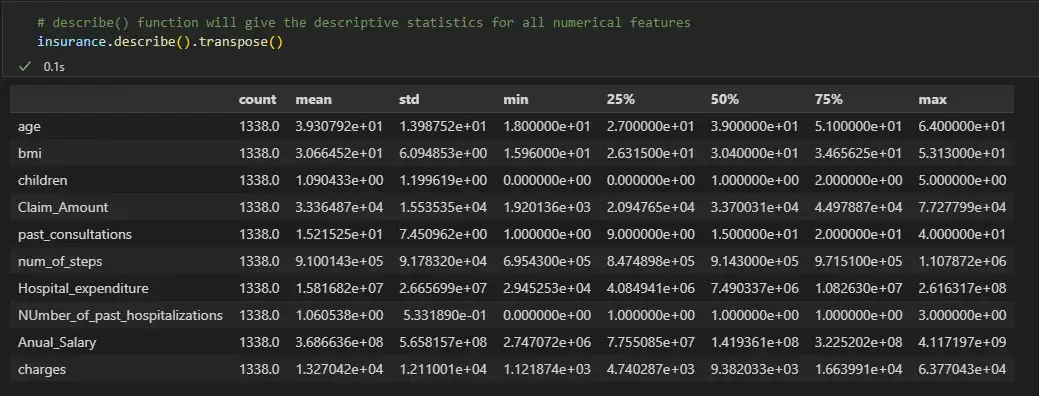

Мы видим, что для числовых признаков среднее и медиана почти одинаковы. Поэтому теперь мы заменим нулевые значения числовых признаков их медианой, а нулевые значения категориальных переменных — их режимом.

for col_name in list(insurance.columns):
    if insurance[col_name].dtypes=='object':
        # filling null values with mode for object type features
        insurance[col_name] = insurance[col_name].fillna(insurance[col_name].mode()[0])
    else:
        # filling null values with mean for numeric type features
        insurance[col_name] = insurance[col_name].fillna(insurance[col_name].median())
# Now the null count for each feature is zero
print("After filling null values:")
print(insurance.isna().sum())

Шаг 4: Анализ выбросов

Мы построим прямоугольную диаграмму для всех числовых характеристик, кроме целевых переменных зарядов.

i = 1
plt.figure(figsize=(16,15))
for col_name in list(insurance.columns):
    # total 9 box plots will be plotted, therefore 3*3 grid is taken
    if((insurance[col_name].dtypes=='int64' or insurance[col_name].dtypes=='float64') and col_name != 'charges'):
        plt.subplot(3,3, i)
        plt.boxplot(insurance[col_name])
        plt.xlabel(col_name)
        plt.ylabel('count')
        plt.title(f"Box plot for {col_name}")
        i += 1
plt.show()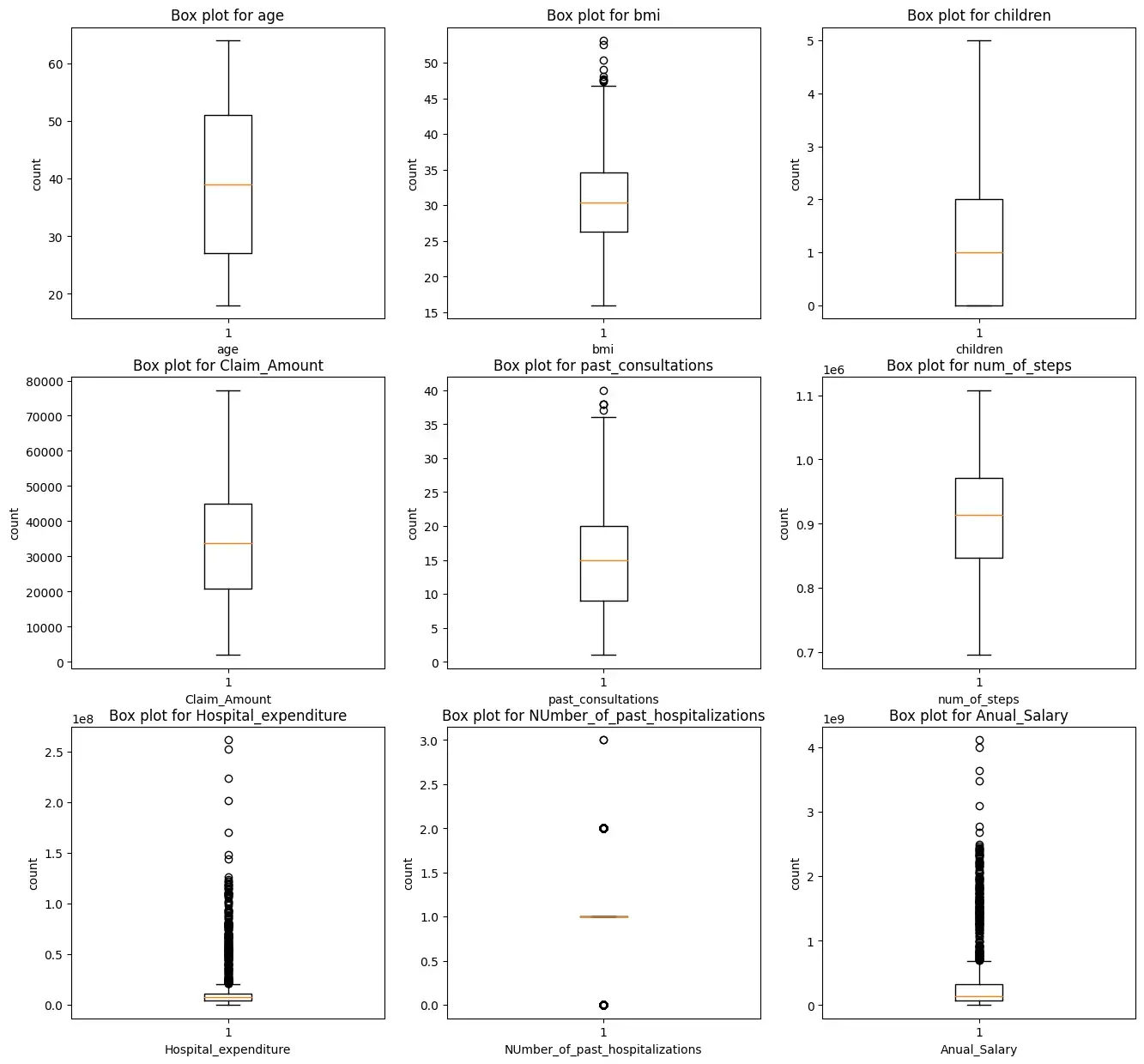

Мы видим, что характеристики ‘bmi’, ‘Hospital_expenditure’ и ‘Number_of_past_hospitalizations’ имеют выбросы. Мы удалим эти выбросы:

outliers_features = ['bmi', 'Hospital_expenditure', 'Anual_Salary', 'past_consultations']
for col_name in outliers_features:
    Q3 = insurance[col_name].quantile(0.75)
    Q1 = insurance[col_name].quantile(0.25)
    IQR = Q3 - Q1
    upper_limit = Q3 + 1.5*IQR
    lower_limit = Q1 - 1.5*IQR
    prev_size = len(insurance)
    insurance = insurance[(insurance[col_name] >= lower_limit) & (insurance[col_name] <= upper_limit)]
    cur_size = len(insurance)
    print(f"dropped {prev_size - cur_size} rows for {col_name}  due to presence of outliers")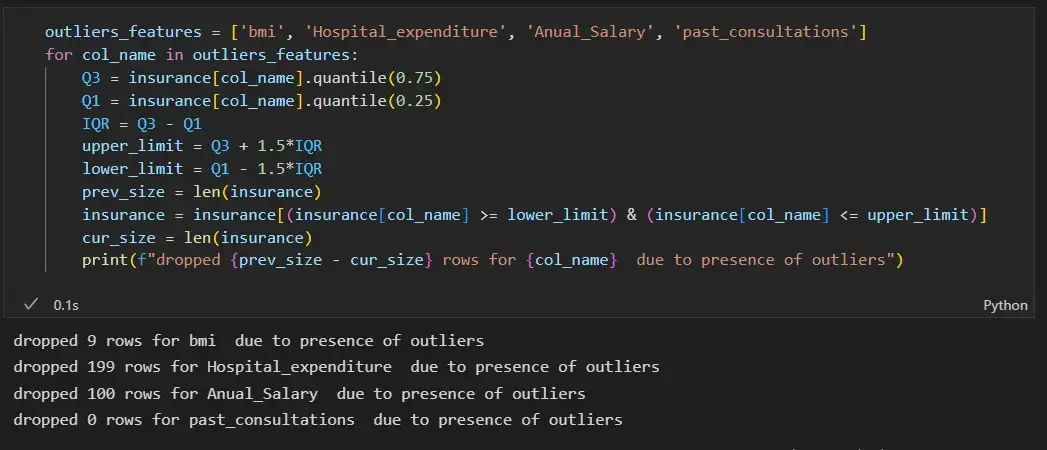

Шаг 5: Проверьте корреляцию:

Существует корреляция между age & charges, age & Anual_salary и т. д., поскольку их корреляция больше 0,5.

import seaborn as sns
sns.heatmap(insurance.corr(),cmap='gist_rainbow',annot=True)
plt.show()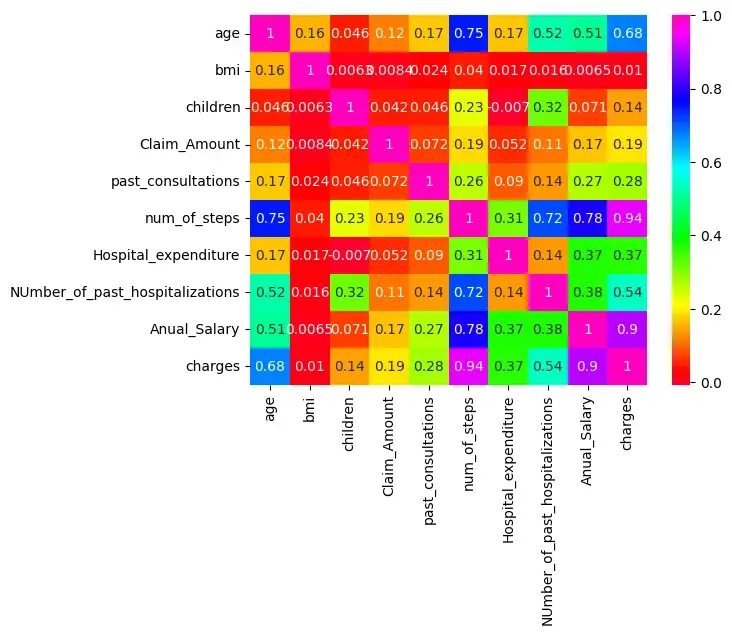

Мы проверим наличие мультиколлинеарности среди признаков:

from statsmodels.stats.outliers_influence import variance_inflation_factor 
col_list = []
for col in insurance.columns:
    if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
        col_list.append(col)

X = insurance[col_list]
vif_data = pd.DataFrame() 
vif_data["feature"] = X.columns 
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))] 
print(vif_data)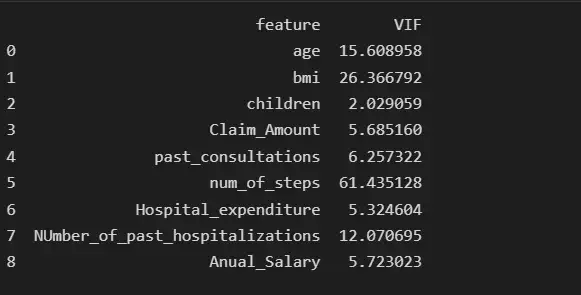

Мы видим, что функция num_of_steps имеет самую высокую коллинеарность, равную 61,43, поэтому мы удалим функцию num_of_steps и снова проверим оценку VIF.

# deleting num_of_steps feature
insurance.drop('num_of_steps', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor 
col_list = []
for col in insurance.columns:
    if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
        col_list.append(col)
X = insurance[col_list]

X = insurance[col_list]
vif_data = pd.DataFrame() 
vif_data["feature"] = X.columns 
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))] 
print(vif_data)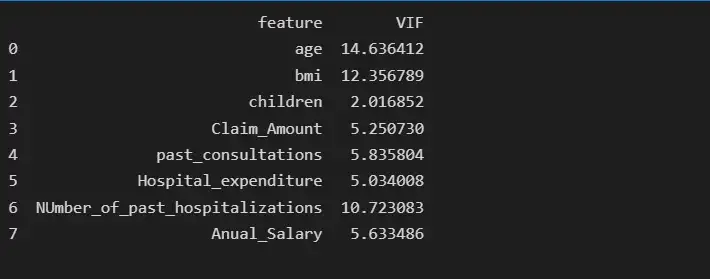

После удаления функции num_of_steps age имеет самую высокую коллинеарность, равную 14,63, поэтому мы удалим функцию age и снова проверим оценку VIF.

# deleting age feature
insurance.drop('age', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor 
col_list = []
for col in insurance.columns:
    if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
        col_list.append(col)
X = insurance[col_list]

X = insurance[col_list]
vif_data = pd.DataFrame() 
vif_data["feature"] = X.columns 
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))] 
print(vif_data)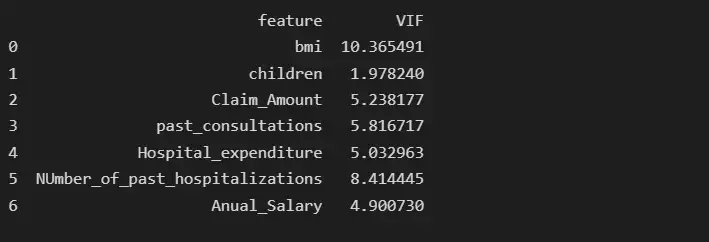

После удаления функции возраста BMI имеет самую высокую коллинеарность, равную 10,36, поэтому мы удалим BMI и снова проверим показатель VIF.

# deleting bmi feature
insurance.drop('bmi', axis = 1, inplace= True)
from statsmodels.stats.outliers_influence import variance_inflation_factor 
col_list = []
for col in insurance.columns:
    if ((insurance[col].dtype != 'object') & (col != 'charges') ):#only num cols except for the charges column
        col_list.append(col)
X = insurance[col_list]

X = insurance[col_list]
vif_data = pd.DataFrame() 
vif_data["feature"] = X.columns 
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))] 
print(vif_data)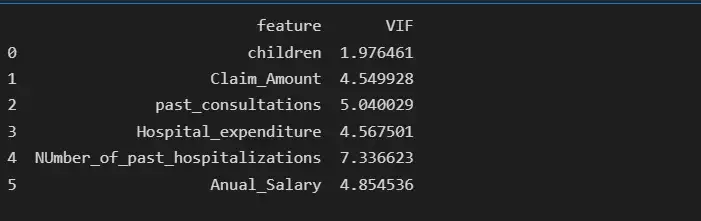

Шаг 6: Разделение входных функций и целевой переменной:

x=insurance.loc[:,['children','Claim_Amount','past_consultations','Hospital_expenditure','NUmber_of_past_hospitalizations','Anual_Salary']]
y=insurance.loc[:,'charges']
x_train, x_test, y_train, y_test=train_test_split(x,y,train_size=0.8, random_state=0)
print("length of train dataset: ",len(x_train) )
print("length of test dataset: ",len(x_test) )

Шаг 7: Обучение модели линейной регрессии на наборе поездов и ее оценка на тестовом наборе данных:

from sklearn.linear_model import LinearRegression
from sklearn.metrics import classification_report, recall_score, r2_score, f1_score, accuracy_score

model = LinearRegression()
# train the model
model.fit(x_train, y_train)
print("trained model coefficients:", model.coef_, " and intercept is: ", model.intercept_)
# model.intercept_ is b0 term in linear boundary equation, and model.coef_ is
#  the array of weights assigned to ['children','Claim_Amount','past_consultations','Hospital_expenditure',
#                    'NUmber_of_past_hospitalizations','Anual_Salary'] respectively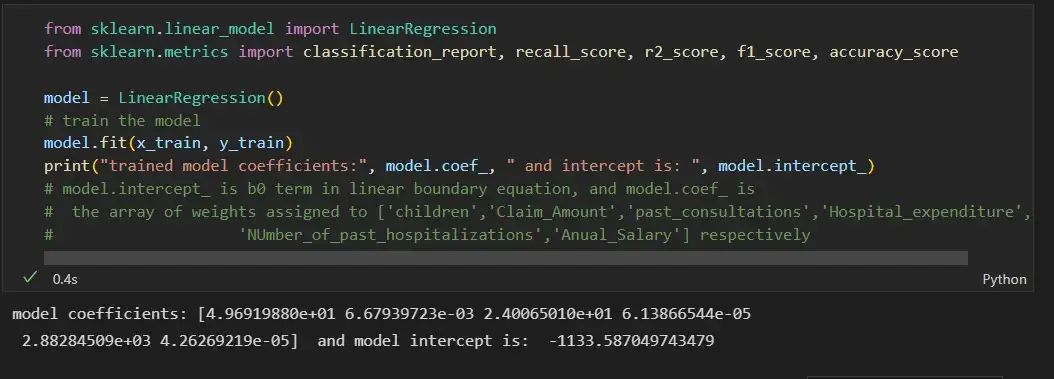

y_pred = model.predict(x_test)
error_pred=pd.DataFrame(columns={'Actual_data','Prediction_data'})
error_pred['Prediction_data'] = y_pred
error_pred['Actual_data'] = y_test
error_pred["error"] = y_test - y_pred
sns.distplot(error_pred['error'])
plt.show()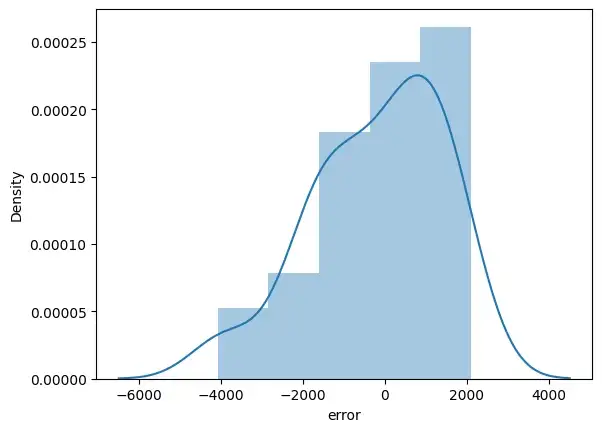

Мы можем построить остаточные графики между фактической целью и остатками или ошибками:

sns.scatterplot(x = y_test,y =  (y_test - y_pred), c = 'g', s = 40)
plt.hlines(y = 0, xmin = 0, xmax=20000)
plt.title("residual plot")
plt.xlabel("actural target")
plt.ylabel("residula error")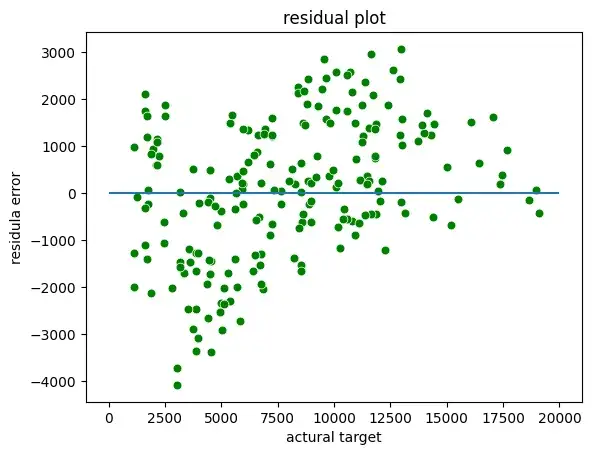

Оценка R-квадрата:

R-квадрат известен как коэффициент детерминации. R Squared — это статистическая мера, которая представляет долю дисперсии зависимой переменной, объясненную независимыми переменными в регрессии. Это значение находится в диапазоне от 0 до 1. Значение «1» указывает, что предиктор полностью учитывает все изменения в Y. Значение «0» указывает, что предиктор «x» не учитывает никаких изменений в «y». Значение R-Squared содержит три термина SSE, SSR и SST.

SSE — это сумма квадратов ошибок. Его также называют остаточной суммой квадратов (RSS).

SSR — это сумма квадратов регрессии.

SST (Сумма в квадрате) — это квадрат разницы между наблюдаемой зависимой переменной и ее средним значением.

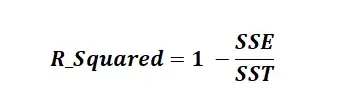
# check for model performance
print(f'r2 score of trained model: {r2_score(y_pred=y_pred, y_true= y_test)}')

Предположения линейной регрессии

Линейная связь: линейная регрессия предполагает линейную связь между прогнозируемой переменной и независимой переменной. Вы можете использовать точечную диаграмму, чтобы визуализировать взаимосвязь между независимой переменной и зависимой переменной в 2D-пространстве.
Небольшая мультиколлинеарность или отсутствие мультиколлинеарности между функциями: линейная регрессия предполагает, что функции должны быть независимыми друг от друга, т. Е. Никакой корреляции между функциями. Вы можете использовать функцию VIF, чтобы найти значение мультиколлинеарности признаков. Общее предположение гласит, что если значение признака VIF больше 5, то признаки сильно коррелированы.
Однородность: линейная регрессия предполагает, что члены ошибок имеют постоянную дисперсию, т. е. разброс членов ошибок должен быть постоянным. Это предположение можно проверить, построив остаточную диаграмму. Если предположение нарушается, то точки образуют форму воронки, в противном случае они будут постоянными.
Нормальность: линейная регрессия предполагает, что каждая функция данного набора данных следует нормальному распределению. Вы можете строить гистограммы и графики KDE для каждой функции, чтобы проверить, нормально ли они распределены или нет.
Ошибка: линейная регрессия предполагает, что условия ошибки также должны быть нормально распределены. Вы можете строить гистограммы, а KDE строит графики ошибок, чтобы проверить, нормально ли они распределены или нет.

Вот ссылка GitHub для кода и набора данных.

В статистике и оптимизации ошибки и остатки тесно связаны и легко запутанные меры отклонения наблюдаемого значения элемента статистической выборки от его «теоретического значения». ошибка (или возмущение ) наблюдаемого значения — это отклонение наблюдаемого значения от (ненаблюдаемого) истинного значения интересующей величины (например, среднего генерального значения), и остаток наблюдаемого значения представляет собой разность между наблюдаемым значением и оценочным значением представляющей интерес величины (например, выборочное среднее). Это различие наиболее важно в регрессионном анализе, где концепции иногда называют ошибками регрессии и остатками регрессии, и где они приводят к концепции студентизированных остатков.

Содержание

1 Введение
2 В одномерных распределениях
- 2.1 Замечание
3 Регрессии
4 Другие варианты использования слова «ошибка» в статистике
5 См. Также
6 Ссылки
7 Внешние ссылки

Введение

Предположим, есть серия наблюдений из одномерного распределения, и мы хотим оценить среднее этого распределения. (так называемая локационная модель ). В этом случае ошибки — это отклонения наблюдений от среднего по совокупности, а остатки — это отклонения наблюдений от среднего по выборке.

A статистическая ошибка (или нарушение ) — это величина, на которую наблюдение отличается от его ожидаемого значения, последнее основано на всей генеральной совокупности из которого статистическая единица была выбрана случайным образом. Например, если средний рост среди 21-летних мужчин составляет 1,75 метра, а рост одного случайно выбранного мужчины — 1,80 метра, то «ошибка» составляет 0,05 метра; если рост случайно выбранного мужчины составляет 1,70 метра, то «ошибка» составляет -0,05 метра. Ожидаемое значение, являющееся средним для всей генеральной совокупности, обычно ненаблюдаемо, и, следовательно, статистическая ошибка также не может быть обнаружена.

A невязка (или аппроксимирующее отклонение), с другой стороны, представляет собой наблюдаемую оценку ненаблюдаемой статистической ошибки. Рассмотрим предыдущий пример с ростом мужчин и предположим, что у нас есть случайная выборка из n человек. среднее значение выборки может служить хорошей оценкой среднего значения генеральной совокупности. Тогда у нас есть:

Разница между ростом каждого человека в выборке и ненаблюдаемым средним по совокупности является статистической ошибкой, тогда как
разница между ростом каждого человека в выборке и наблюдаемой выборкой среднее — это остаток.

Обратите внимание, что из-за определения выборочного среднего, сумма остатков в случайной выборке обязательно равна нулю, и, таким образом, остатки не обязательно независимы. Статистические ошибки, с другой стороны, независимы, и их сумма в случайной выборке почти наверняка не равна нулю.

Можно стандартизировать статистические ошибки (особенно нормального распределения ) в z-балле (или «стандартном балле») и стандартизировать остатки в t-статистика или, в более общем смысле, стьюдентизированные остатки.

в одномерном распределении

Если мы предположим нормально распределенную совокупность со средним μ и стандартным отклонением σ и независимо выбираем людей, тогда мы имеем

X 1,…, X n ∼ N (μ, σ 2) { displaystyle X_ {1}, dots, X_ {n} sim N ( mu, sigma ^ {2}) ,}

и выборочное среднее

X ¯ = X 1 + ⋯ + X nn { displaystyle { overline {X}} = {X_ { 1} + cdots + X_ {n} over n}} $overline {X} = {X_1 + cdots + X_n over n}$

— случайная величина, распределенная так, что:

X ¯ ∼ N (μ, σ 2 n). { displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).} ${ displaystyle { overline {X}} sim N left ( mu, { frac { sigma ^ {2}} {n}} right).}$

Тогда статистические ошибки

ei = X i — μ, { displaystyle e_ {i} = X_ {i} — mu, ,} $e_ {i} = X_ {i} - mu, ,$

с ожидаемыми значениями нуля, тогда как остатки равны

ri = X i — X ¯. { displaystyle r_ {i} = X_ {i} — { overline {X}}.} $r_ {i} = X_ {i} - overline {X}.$

Сумма квадратов статистических ошибок, деленная на σ, имеет хи -квадратное распределение с n степенями свободы :

1 σ 2 ∑ i = 1 nei 2 ∼ χ n 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.} ${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} e_ {i} ^ {2} sim chi _ {n} ^ {2}.$

Однако это количество не наблюдается, так как среднее значение для генеральной совокупности неизвестно. Сумма квадратов остатков, с другой стороны, является наблюдаемой. Частное этой суммы по σ имеет распределение хи-квадрат только с n — 1 степенями свободы:

1 σ 2 ∑ i = 1 n r i 2 ∼ χ n — 1 2. { displaystyle { frac {1} { sigma ^ {2}}} sum _ {i = 1} ^ {n} r_ {i} ^ {2} sim chi _ {n-1} ^ { 2}.} ${ frac 1 { sigma ^ {2}}} sum _ {{i = 1}} ^ {n} r_ {i} ^ {2} sim chi _ {{n-1}} ^ {2}.$

Эта разница между n и n — 1 степенями свободы приводит к поправке Бесселя для оценки выборочной дисперсии генеральной совокупности с неизвестным средним и неизвестной дисперсией. Коррекция не требуется, если известно среднее значение для генеральной совокупности.

Замечание

Примечательно, что сумма квадратов остатков и выборочного среднего могут быть показаны как независимые друг от друга, используя, например, Теорема Басу. Этот факт, а также приведенные выше нормальное распределение и распределение хи-квадрат составляют основу вычислений с использованием t-статистики :

T = X ¯ n — μ 0 S n / n, { displaystyle T = { frac {{ overline {X}} _ {n} — mu _ {0}} {S_ {n} / { sqrt {n}}}},} ${ displaystyle T = { frac {{ overline {X}} _ {n} - mu _ {0}} {S_ {n} / { sqrt {n}}}},}$

где X ¯ n — μ 0 { displaystyle { overline {X}} _ {n} — mu _ {0}} ${ displaystyle { overline {X}} _ {n} - mu _ {0}}$ представляет ошибки, S n { displaystyle S_ {n}} $S_ {n}$ представляет стандартное отклонение для выборки размера n и неизвестного σ, а член знаменателя S n / n { displaystyle S_ {n} / { sqrt {n}}}учитывает стандартное отклонение ошибок в соответствии с:

Var ⁡ (X ¯ n) = σ 2 n { displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}} ${ displaystyle operatorname {Var} ({ overline {X}} _ {n}) = { frac { sigma ^ {2}} {n}}}$

Распределения вероятностей числителя и знаменателя по отдельности зависят от значения ненаблюдаемого стандартного отклонения генеральной совокупности σ, но σ появляется как в числителе, так и в знаменателе и отменяет. Это удачно, потому что это означает, что, хотя мы не знаем σ, мы знаем распределение вероятностей этого частного: оно имеет t-распределение Стьюдента с n — 1 степенями свободы. Таким образом, мы можем использовать это частное, чтобы найти доверительный интервал для μ. Эту t-статистику можно интерпретировать как «количество стандартных ошибок от линии регрессии».

Регрессии

В регрессионном анализе различие между ошибками и остатками является тонким и важным, и приводит к концепции стьюдентизированных остатков. Для ненаблюдаемой функции, которая связывает независимую переменную с зависимой переменной — скажем, линии — отклонения наблюдений зависимой переменной от этой функции являются ненаблюдаемыми ошибками. Если запустить регрессию на некоторых данных, то отклонения наблюдений зависимой переменной от подобранной функции являются остатками. Если линейная модель применима, диаграмма рассеяния остатков, построенная против независимой переменной, должна быть случайной около нуля без тенденции к остаткам. Если данные демонстрируют тенденцию, регрессионная модель, вероятно, неверна; например, истинная функция может быть квадратичным полиномом или полиномом более высокого порядка. Если они случайны или не имеют тенденции, но «разветвляются» — они демонстрируют явление, называемое гетероскедастичностью. Если все остатки равны или не разветвляются, они проявляют гомоскедастичность.

Однако терминологическое различие возникает в выражении среднеквадратическая ошибка (MSE). Среднеквадратичная ошибка регрессии — это число, вычисляемое из суммы квадратов вычисленных остатков, а не ненаблюдаемых ошибок. Если эту сумму квадратов разделить на n, количество наблюдений, результатом будет среднее квадратов остатков. Поскольку это смещенная оценка дисперсии ненаблюдаемых ошибок, смещение устраняется путем деления суммы квадратов остатков на df = n — p — 1 вместо n, где df — число степеней свободы (n минус количество оцениваемых параметров (без учета точки пересечения) p — 1). Это формирует объективную оценку дисперсии ненаблюдаемых ошибок и называется среднеквадратической ошибкой.

Другой метод вычисления среднего квадрата ошибки при анализе дисперсии линейной регрессии с использованием техники, подобной той, что использовалась в ANOVA (они одинаковы, потому что ANOVA — это тип регрессии), сумма квадратов остатков (иначе говоря, сумма квадратов ошибки) делится на степени свободы (где степени свободы равно n — p — 1, где p — количество параметров, оцениваемых в модели (по одному для каждой переменной в уравнении регрессии, не включая точку пересечения). Затем можно также вычислить средний квадрат модели, разделив сумму квадратов модели за вычетом степеней свободы, которые представляют собой просто количество параметров. Затем значение F можно рассчитать путем деления среднего квадрата модели на средний квадрат ошибки, и затем мы можем определить значимость (вот почему вы хотите, чтобы средние квадраты начинались с.).

Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) могут различаться, даже если сами ошибки распределены одинаково. Конкретно, в линейной регрессии , где ошибки одинаково распределены, изменчивость остатков входных данных в середине области будет выше, чем изменчивость остатков на концах области: линейные регрессии соответствуют конечным точкам лучше среднего. Это также отражено в функциях влияния различных точек данных на коэффициенты регрессии : конечные точки имеют большее влияние.

Таким образом, чтобы сравнить остатки на разных входах, нужно скорректировать остатки на ожидаемую изменчивость остатков, что называется стьюдентизацией. Это особенно важно в случае обнаружения выбросов, когда рассматриваемый случай каким-то образом отличается от другого в наборе данных. Например, можно ожидать большой остаток в середине домена, но он будет считаться выбросом в конце домена.

Другое использование слова «ошибка» в статистике

Использование термина «ошибка», как обсуждалось в разделах выше, означает отклонение значения от гипотетического ненаблюдаемого значение. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:

Среднеквадратичная ошибка или Среднеквадратичная ошибка (MSE) и Среднеквадратичная ошибка (RMSE) относятся к величине, на которую значения, предсказанные оценщиком, отличаются от оцениваемых количеств (обычно за пределами выборки, на основе которой была оценена модель).

Сумма квадратов ошибок (SSE или SSe), обычно сокращенно SSE или SS e, относится к остаточной сумме квадратов (сумма квадратов остатков) регрессии; это сумма квадратов отклонений фактических значений от прогнозируемых значений в пределах выборки, используемой для оценки. Это также называется оценкой методом наименьших квадратов, где коэффициенты регрессии выбираются так, чтобы сумма квадратов минимально (т.е. его производная равна нулю).

Аналогично, сумма абсолютных ошибок (SAE) является суммой абсолютных значений остатков, которая минимизирована в наименьшие абсолютные отклонения подход к регрессии.

См. также

Портал математики

Абсолютное отклонение
Консенсус-прогнозы
Обнаружение и исправление ошибок
Объясненная сумма квадраты
Инновация (обработка сигналов)
Неподходящая сумма квадратов
Погрешность
Средняя абсолютная погрешность
Погрешность наблюдения
Распространение ошибки
Вероятная ошибка
Случайные и систематические ошибки
Разбавление регрессии
Среднеквадратичное отклонение
Ошибка выборки
Стандартная ошибка
Стьюдентизированная невязка
Ошибки типа I и типа II

Ссылки

Кук, Р. Деннис; Вайсберг, Сэнфорд (1982). Остатки и влияние на регресс (Отредактированный ред.). Нью-Йорк: Чепмен и Холл. ISBN 041224280X. Проверено 23 февраля 2013 г.
Кокс, Дэвид Р. ; Снелл, Э. Джойс (1968). «Общее определение остатков». Журнал Королевского статистического общества, серия B. 30(2): 248–275. JSTOR 2984505.
Вайсберг, Сэнфорд (1985). Прикладная линейная регрессия (2-е изд.). Нью-Йорк: Вили. ISBN 9780471879572. Проверено 23 февраля 2013 г.
, Энциклопедия математики, EMS Press, 2001 [1994]

Внешние ссылки

СМИ, связанные с ошибками и остатками на Викимедиа Commons

Источник

We often use three different sum of squares values to measure how well a regression line actually fits a dataset:

1. Sum of Squares Total (SST) – The sum of squared differences between individual data points (y_i) and the mean of the response variable (y).

SST = Σ(y_i – y)²

2. Sum of Squares Regression (SSR) – The sum of squared differences between predicted data points (ŷ_i) and the mean of the response variable(y).

SSR = Σ(ŷ_i – y)²

3. Sum of Squares Error (SSE) – The sum of squared differences between predicted data points (ŷ_i) and observed data points (y_i).

SSE = Σ(ŷ_i – y_i)²

The following step-by-step example shows how to calculate each of these metrics for a given regression model in Excel.

Step 1: Create the Data

First, let’s create a dataset that contains the number of hours studied and exam score received for 20 different students at a certain school:

Step 2: Fit a Regression Model

Along the top ribbon in Excel, click the Data tab and click on Data Analysis. If you don’t see this option, then you need to first install the free Analysis ToolPak.

Once you click on Data Analysis, a new window will pop up. Select Regression and click OK.

In the new window that appears, fill in the following information:

Once you click OK, the regression output will appear.

Step 3: Analyze the Output

The three sum of squares metrics – SST, SSR, and SSE – can be seen in the SS column of the ANOVA table:

The metrics turn out to be:

Sum of Squares Total (SST): 1248.55
Sum of Squares Regression (SSR): 917.4751
Sum of Squares Error (SSE): 331.0749

We can verify that SST = SSR + SSE:

SST = SSR + SSE
1248.55 = 917.4751 + 331.0749

We can also manually calculate the R-squared of the regression model:

R-squared = SSR / SST
R-squared = 917.4751 / 1248.55
R-squared = 0.7348

This tells us that 73.48% of the variation in exam scores can be explained by the number of hours studied.

Additional Resources

How to Perform Simple Linear Regression in Excel
How to Perform Multiple Linear Regression in Excel
How to Perform Polynomial Regression in Excel
How to Perform Exponential Regression in Excel

Источник

Основы линейной регрессии

Время на прочтение
13 мин

Количество просмотров 125K

Здравствуй, Хабр!

Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.

! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.

Содержание

Введение
Метод наименьших квадратов
- Математический анализ
- Статистика
- Теория вероятностей
Мультилинейная регрессия
- Линейная алгебра
Произвольный базис
Заключительные замечания
- Проблема выбора размерности
- Численные методы
Реклама и заключение

Введение

Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.

Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.

Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.

Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).

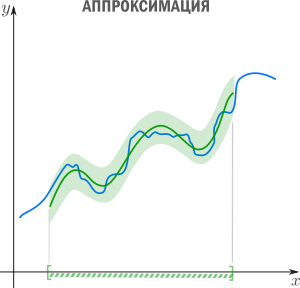
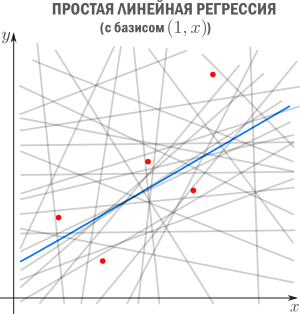
В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций

${f_i}$

Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию

$f$ (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).

Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.

Метод наименьших квадратов

Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости

${(x_1,y_1),cdots,(x_N,y_N)}$ и мы ищем такую аффинную функцию

чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной

Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого

$x_i,$ поэтому измерять нужно вдоль оси

$y$ .

Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц

. Простейший вариант — сумма модулей отклонений

приводит к Least Absolute Distance (LAD) регрессии.

Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)

$text{SSE}(a,b)=text{SS}_{res[iduals]}=sum_{i=1}^N{text{отклонение}_i}^2=sum_{i=1}^N(y_i-f(x_i))^2=sum_{i=1}^N(y_i-a-bcdot x_i)^2,$

Метод наименьших квадратов (по англ. OLS) — линейная регрессия c

в качестве функции потерь.

Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу

Математический анализ

Простейший способ найти

$text{argmin}_{a,b} , text{SSE}(a,b)$ — вычислить частные производные по

$ a $ и

$ b $ , приравнять их нулю и решить систему линейных уравнений

$begin{aligned} frac{partial}{partial a}text{SSE}(a,b)&=-2sum_{i=1}^N(y_i-a-bx_i), \ frac{partial}{partial b}text{SSE}(a,b)&=-2sum_{i=1}^N(y_i-a-bx_i)x_i. end{aligned}$

Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям

$begin{aligned} 0 &= -2sum_{i=1}^N(y_i-hat{a}-hat{b}x_i), \ 0 &= -2sum_{i=1}^N(y_i-hat{a}-hat{b}x_i)x_i, end{aligned}$

которые легко решить

$begin{aligned} hat{a}&=frac{sum_i y_i}{N}-hat{b}frac{sum_i x_i}{N},\ hat{b}&=frac{frac{sum_i x_i y_i}{N}-frac{sum_i x_isum_i y_i}{N^2}}{frac{sum_i x_i^2}{N}-left(frac{sum_i x_i^2}{N}right)^2}. end{aligned}$

Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.

Статистика

Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего

, вариации

$sigma_{cdot}$ (стандартного отклонения), ковариации

и корреляции

$begin{aligned} hat{a}&=langle{y}rangle-hat{b}langle{x}rangle, \ hat{b}&=frac{langle{xy}rangle-langle{x}ranglelangle{y}rangle}{langle{x^2}rangle-langle{x}rangle^2}. end{aligned}$

Перепишем

как

$hat{b} = frac{sigma(x,y)}{sigma_x^2},$

где

это нескорректированное (смещенное) стандартное выборочное отклонение, а

— ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)

$rho(x,y)=frac{sigma(x,y)}{sigma_x sigma_y}$

и запишем

$hat{b}=rho(x,y)frac{sigma_y}{sigma_x}.$

Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так

$boxed{y-langle {y} rangle = rho(x,y)frac{sigma_y}{sigma_x}(x-langle {x} rangle)}.$

Во-первых, это уравнение сразу указывает на два свойства регрессионной прямой:

Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения

$y$ отклоняется от своего среднего значения меньше чем

$x$ , потому что

. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.

Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации

. Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.

$R^2$ , равный

$1$ , означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что

$R^2$ показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения

$begin{aligned} text{Var}_{data} &= frac{1}{N}sum_i (y_i-langle y rangle)^2, \ text{Var}_{res} &= frac{1}{N} sum_i (y_i-text{модель}(x_i))^2, \ text{Var}_{reg} &= frac{1}{N} sum_i (text{модель}(x_i)-langle y rangle)^2. end{aligned}$

$text{Var}_{data}$ — вариация исходных данных (вариация точек

$y_i$ ).

$text{Var}_{res}$ — вариация остатков, то есть вариация отклонений от регрессионной модели — от

$y_i$ нужно отнять предсказание модели и найти вариацию.

$text{Var}_{reg}$ — вариация регрессии, то есть вариация предсказаний регрессионной модели в точках

$x_i$ (обратите внимание, что среднее предсказаний модели совпадает с

Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)

$boxed{{color{red}{text{Var}_{data}}} ={color{green}{text{Var}_{res}}}+ {color{blue}{text{Var}_{reg}}}.}$

или

$sigma^2_{data} =sigma^2_{res}+ sigma^2_{reg}.$

Как видим, стандартные отклонения образуют прямоугольный треугольник.

Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует

$R^2$ , равный единице минус доля вариации ошибок в суммарной вариации

$R^2=frac{text{Var}_{data}-text{Var}_{res}}{text{Var}_{data}}=1-frac{color{green}{text{Var}_{res}}}{color{red}{text{Var}_{data}}}$

или доле объясненной вариации (доля вариации регрессии в полной вариации)

$R^2=frac{color{blue}{text{Var}_{reg}}}{color{red}{text{Var}_{data}}}.$

$R$ равен косинусу угла в прямоугольном треугольнике

$(sigma_{data}, sigma_{reg}, sigma_{res})$ . Кстати, иногда вводят долю необъясненной вариации

и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.

Теория вероятностей

Ранее мы пришли к функции потерь

из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть

$N$ независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например

$mu$ и

$sigma$ ). Для этого нужно вычислить вероятность получить

$N$ датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.

Вернемся к задаче простой регрессии. Допустим, что значения

$x$ нам известны точно, а в измерении

$y$ присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда

где

— нормально распределенная случайная величина

$epsilon sim mathcal{N}(0,,sigma^{2}), qquad p(epsilon) = frac{1}{sqrt{2 pi sigma^2}} e^{-frac{epsilon^2}{2sigma^2}}.$

Исходя из предположений выше, запишем функцию правдоподобия

$begin{aligned} L(a,b|mathbf{y})&=P(mathbf{y}|a,b)=prod_i P(y_i|a,b)=prod_i p(y_i-a-bx|a,b)=\ &= prod_i frac{1}{sqrt{2 pi sigma^2}} e^{-frac{(y_i-a-bx)^2}{2sigma^2}}= frac{1}{sqrt{2 pi sigma^2}}e^{-frac{sum_i (y_i-a-bx)^2}{2 sigma^2}}=\ &= frac{1}{sqrt{2 pi sigma^2}}e^{-frac{text{SSE}(a,b)}{2 sigma^2}} end{aligned}$

и ее логарифм

Таким образом, максимум правдоподобия достигается при минимуме

$(hat{a},hat{b})=text{argmax}_{a,b} , l(a,b|mathbf{y}) = text{argmin}_{a,b} , text{SSE}(a,b),$

что дает основание принять ее в качестве функции потерь. Кстати, если

$begin{aligned} epsilon sim text{Laplace}(0, alpha), qquad p_{L}(epsilon; mu, alpha) =frac{alpha}{2}e^{-alpha |epsilon-mu|} end{aligned}$

мы получим функцию потерь LAD регрессии

$E_{LAD}(a,b)=sum_i |y_i-a-bx_i|,$

которую мы упоминали ранее.

Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.

Мультилинейная регрессия

До сих пор мы рассматривали задачу регрессии для одного скалярного признака

$x$ , однако обычно регрессор — это

$n$ -мерный вектор

. Другими словами, для каждого измерения мы регистрируем

$n$ фич, объединяя их в вектор. В этом случае логично принять модель с

$n+1$ независимыми базисными функциями векторного аргумента —

$n$ степеней свободы соответствуют

$n$ фичам и еще одна — регрессанту

$y$ . Простейший выбор — линейные базисные функции

. При

$n = 1$ получим уже знакомый нам базис

Итак, мы хотим найти такой вектор (набор коэффициентов)

, что

$sum_{j=0}^n w_j x_j^{(i)}= mathbf{w}^{top}mathbf{x}^{(i)} simeq y_i, qquad qquad qquad qquad i=1dots N.$

Знак «

$simeq$ » означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок

$hat{mathbf{w}}=text{argmin}_mathbf{w} , sum_{i=1}^N left({y_i - mathbf{w}^{top}mathbf{x}^{(i)}}right)^2$

Последнее уравнение можно переписать более удобным образом. Для этого расположим

$mathbf{x}^{(i)}$ в строках матрицы (матрицы информации)

$X= begin{pmatrix} - & mathbf{x}^{(1)top} & - \ cdots & cdots & cdots\ - & mathbf{x}^{(N)top} & - end{pmatrix} = begin{pmatrix} | & | & & | \ mathbf{x}_0 & mathbf{x}_1 & cdots & mathbf{x}_n \ | & | & & | end{pmatrix} = begin{pmatrix} 1 & x^{(1)}_{1} & cdots & x^{(1)}_{n} \ cdots & cdots & cdots & cdots\ 1 & x^{(N)}_{1} & cdots & x^{(N)}_{n} end{pmatrix}.$

Тогда столбцы матрицы

$mathbf{x}_{i}$ отвечают измерениям

$i$ -ой фичи. Здесь важно не запутаться:

$N$ — количество измерений,

$n$ — количество признаков (фич), которые мы регистрируем. Систему можно записать как

Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь

$text{SSE}(mathbf{w}) = {|mathbf{y}-X mathbf{w}|}^2, qquad qquad mathbf{w} in mathbb{R}^{n+1}; , mathbf{y} in mathbb{R}^{N},$

которую мы намерены минимизировать

$begin{aligned} hat{mathbf{w}}&=text{argmin}_mathbf{w} , text{SSE}(mathbf{w}) = text{argmin}_mathbf{w} , (mathbf{y}-X mathbf{w})^{top}(mathbf{y}-X mathbf{w})=\ &= text{argmin}_mathbf{w} ,(mathbf{y}^{top}mathbf{y}-2mathbf{w}^{top}X^{top}mathbf{y}+mathbf{w}^{top}X^{top}Xmathbf{w}). end{aligned}$

Продифференцируем финальное выражение по

(если забыли как это делается — загляните в Matrix cookbook)

$frac{partial , text{SSE}(mathbf{w})}{partial mathbf{w}}=-2 X^{top}mathbf{y}+2 X^{top}Xmathbf{w},$

приравняем производную к

и получим т.н. нормальные уравнения

$X^{top}X , hat{mathbf{w}}=X^{top}mathbf{y}.$

Если столбцы матрицы информации

$X$ линейно независимы (нет идеально скоррелированных фич), то матрица

$X^{top}X$ имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать

$boxed{hat{mathbf{w}} = (X^{top}X)^{-1}X^{top}mathbf{y}=X^{+}mathbf{y}},$

где

$X^{+}=(X^{top}X)^{-1}X^{top}$

псевдообратная к

$X$ . Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.

Напомню, что обратить

$X^{top}X$ и найти

$X^{+}$ можно только если столбцы

$X$ линейно независимы. Впрочем, если столбцы

$X$ близки к линейной зависимости, вычисление

$(X^{top}X)^{-1}$ уже становится численно нестабильным. Степень линейной зависимости признаков в

$X$ или, как говорят, мультиколлинеарности матрицы

$X^{top}X$ , можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе

$X^{top}X$ к вырожденной и неустойчивее вычисление псевдообратной.

Линейная алгебра

К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению

Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор

, образ которого

ближе остальных к

. Напомню, что множество образов или колоночное пространство

— это линейная комбинация вектор-столбцов матрицы

$X$

$begin{pmatrix} | & | & & | \ mathbf{x}_0 & mathbf{x}_1 & cdots & mathbf{x}_n \ | & | & & | end{pmatrix} mathbf{w} = w_0 mathbf{x}_0 + w_1 mathbf{x}_1 + cdots w_n mathbf{x}_n .$

—

$n+1$ -мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов

$X$ . Итак, если

принадлежит

, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.

Если в дополнение к векторам

мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из

$mathbb{R}^{N}$ разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай

$mathbf{v} in mathbb{R}^{N}$ , тогда

$X^top mathbf{v} = begin{pmatrix} - & mathbf{x}_0^{top} & - \ cdots & cdots & cdots\ - & mathbf{x}_n^{top} & - end{pmatrix} mathbf{v} = begin{pmatrix} mathbf{x}_0^{top} cdot mathbf{v} \ cdots \ mathbf{x}_n^{top} cdot mathbf{v} \ end{pmatrix}$

равен нулю в том и только в том случае, если

перпендикулярен всем

$mathbf{x}_i$ , а значит и целому

. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все

$mathbb{R}^N$ . Иногда это обозначают c помощью символа ортогональной прямой суммы

где

$text{ker}(X^{top})={mathbf{v}|X^{top}mathbf{v}=mathbf{0}}$ . В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.

Теперь представим

в виде разложения

$mathbf{y} = mathbf{y}_{text{proj}} + mathbf{y}_{perp}, qquad mathbf{y}_{text{proj}} in mathcal{C}(X), qquad mathbf{y}_{perp} in text{ker}(X^{top}).$

Если мы ищем решение

, то естественно потребовать, чтобы

была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора

$text{argmin}_mathbf{w} || mathbf{y} - Xmathbf{w} || = text{argmin}_mathbf{w} || mathbf{y}_{perp} + mathbf{y}_{text{proj}} - Xmathbf{w} || = text{argmin}_mathbf{w} sqrt{|| mathbf{y}_{perp} ||^2 + || mathbf{y}_{text{proj}} - Xmathbf{w} ||^2},$

но поскольку, выбрав подходящий

, я могу получить любой вектор колоночного пространства, то задача сводится к

$Xhat{mathbf{w}} = mathbf{y}_{text{proj}},$

$mathbf{y}_{perp}$ останется в качестве неустранимой ошибки. Любой другой выбор

сделает ошибку только больше.

Если теперь вспомнить, что

$X^{top} mathbf{y}_{perp} = mathbf{0}$ , то легко видеть

$X^top X mathbf{w} = X^{top} mathbf{y}_{text{proj}} = X^{top} mathbf{y}_{text{proj}} + X^{top} mathbf{y}_{perp} = X^{top} mathbf{y},$

что очень удобно, так как

$mathbf{y}_{text{proj}}$ у нас нет, а вот

— есть. Вспомним из предыдущего параграфа, что

$X^{top} X$ имеет обратную при условии линейной независимости признаков и запишем решение

$mathbf{w} = (X^top X)^{-1} X^top mathbf{y} = X^{+} mathbf{y},$

где

$X^{+}$ уже знакомая нам псевдообратная матрица. Если нам интересна проекция

$mathbf{y}_{text{proj}}$ , то можно записать

$mathbf{y}_{text{proj}} = X mathbf{w} = X X^{+} mathbf{y} = text{Proj}_X mathbf{y},$

где

$text{Proj}_X$ — оператор проекции на колоночное пространство.

Выясним геометрический смысл коэффициента детерминации.

Заметьте, что фиолетовый вектор

$bar{y} cdot boldsymbol{1}=bar{y} cdot (1,1,dots,1)^{top}$ пропорционален первому столбцу матрицы информации

$X$ , который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике

Так как этот треугольник прямоугольный, то по теореме Пифагора

${color{red}{|mathbf{y}-hat{y} cdot boldsymbol{1}|^2}}={color{green}{|mathbf{y}-bar{mathbf{y}}|^2}}+{color{blue}{|hat{mathbf{y}}-bar{y} cdot boldsymbol{1}|^2}}.$

Это геометрическая интерпретация уже известного нам факта, что

${color{red}{text{Var}_{data}}} = {color{green}{text{Var}_{res}}}+{color{blue}{text{Var}_{reg}}}.$

Мы знаем, что

$R^2=frac{color{blue}{text{Var}_{reg}}}{color{red}{text{Var}_{data}}},$

а значит

Красиво, не правда ли?

Произвольный базис

Как мы знаем, регрессия выполняется на базисных функциях

$f_i$ и её результатом есть модель

но до сих пор мы использовали простейшие

$f_i$ , которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей

$f_0(mathbf{x}) = 1$ . Как можно было заметить, на самом деле ни вид

$f_i$ , ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки

${(x_1,y_1),cdots,(x_N,y_N)}$ ложатся на параболу, а не на прямую, то стоит выбрать базис

. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.

Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации

$Phi = begin{pmatrix} - & boldsymbol{f}^{(1)top} & - \ cdots & cdots & cdots\ - & boldsymbol{f}^{(N)top} & - end{pmatrix} = begin{pmatrix} {f}_{0}left(mathbf{x}^{(1)}right) & {f}_{1}left(mathbf{x}^{(1)}right) & cdots & {f}_{n}left(mathbf{x}^{(1)}right) \ cdots & cdots & cdots & cdots\ {f}_{0}left(mathbf{x}^{(N)}right) & {f}_{1}left(mathbf{x}^{(N)}right) & cdots & {f}_{n}left(mathbf{x}^{(N)}right) end{pmatrix},$

записываем функцию потерь

$E(mathbf{w})={|{boldsymbol{epsilon}}(mathbf{w})|}^2={|mathbf{y}-Phi , mathbf{w}|}^2$

и находим её минимум, например с помощью псевдообратной матрицы

$hat{mathbf{w}} = text{argmin}_mathbf{w} ,E(mathbf{w}) = (Phi^{top}Phi)^{-1}Phi^{top}mathbf{y}=Phi^{+}mathbf{y}$

или другим методом.

Заключительные замечания

Проблема выбора размерности

На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).

Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что

$R^2$ монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент

$bar{R}^2=1-(1-R^2)left[frac{N-1}{N-(n+1)}right],$

где

$N$ — размер выборки,

$n$ — количество независимых переменных. Следя за

$bar{R}^2$ , мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.

Вторая группа подходов — регуляризации, самые известные из которых Ridge(

$L_2$ /гребневая/Тихоновская регуляризация), Lasso(

$L_1$ регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов

неограниченно расти и тем самым воспрепятствуют переобучению

$begin{aligned} E_{text{Ridge}}(mathbf{w})&=text{SSE}(mathbf{w})+alpha sum_i |w_i|^2 = text{SSE}(mathbf{w})+alpha | mathbf{w}|_{L_2}^2,\ E_{text{Lasso}}(mathbf{w})&=text{SSE}(mathbf{w})+beta sum_i |w_i| =text{SSE}(mathbf{w})+beta | mathbf{w}|_{L_1},\ E_{text{EN}}(mathbf{w})&=text{SSE}(mathbf{w})+alpha | mathbf{w}|_{L_2}^2+beta | mathbf{w}|_{L_1}, \ end{aligned}$

где

$alpha$ и

$beta$ — параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента

$b$

$y = a + bx + epsilon,qquad epsilon sim mathcal{N}(0,,sigma^{2}),qquad left{begin{aligned} &b sim mathcal{N}(0,,tau^{2})&leftarrowtext{Ridge},\ &b sim text{Laplace} (0,,alpha)&leftarrowtext{Lasso}. end{aligned}right.$

Численные методы

Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.

Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.

Реклама и заключение

Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:

все материалы должны быть доступны студентам с первой пары;
лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).

Если хотите посмотреть на результат — загляните на страничку курса на GitHub.

Надеюсь вам было интересно, спасибо за внимание.

Источник

You may be wondering what all of those sums of squares are all about. Maybe that’s what got you here in the first place. Well, they are the determinants of a good linear regression. This tutorial is based on the ANOVA framework you may have heard before.

Before reading it, though, make sure you are not mistaking regression for correlation. If you’ve got this checked, we can get straight into the action.

A quick side-note: Want to learn more about linear regression? Check out our explainer videos The Linear Regression Model. Geometrical Representation and The Simple Linear Regression Model.

SST, SSR, SSE: Definition and Formulas

There are three terms we must define. The sum of squares total, the sum of squares regression, and the sum of squares error.

What is the SST?

The sum of squares total, denoted SST, is the squared differences between the observed dependent variable and its mean. You can think of this as the dispersion of the observed variables around the mean – much like the variance in descriptive statistics.

It is a measure of the total variability of the dataset.

Side note: There is another notation for the SST. It is TSS or total sum of squares.

What is the SSR?

The second term is the sum of squares due to regression, or SSR. It is the sum of the differences between the predicted value and the mean of the dependent variable. Think of it as a measure that describes how well our line fits the data.

If this value of SSR is equal to the sum of squares total, it means our regression model captures all the observed variability and is perfect. Once again, we have to mention that another common notation is ESS or explained sum of squares.

What is the SSE?

The last term is the sum of squares error, or SSE. The error is the difference between the observed value and the predicted value.

We usually want to minimize the error. The smaller the error, the better the estimation power of the regression. Finally, I should add that it is also known as RSS or residual sum of squares. Residual as in: remaining or unexplained.

The Confusion between the Different Abbreviations

It becomes really confusing because some people denote it as SSR. This makes it unclear whether we are talking about the sum of squares due to regression or sum of squared residuals.

In any case, neither of these are universally adopted, so the confusion remains and we’ll have to live with it.

Simply remember that the two notations are SST, SSR, SSE, or TSS, ESS, RSS.

There’s a conflict regarding the abbreviations, but not about the concept and its application. So, let’s focus on that.

How Are They Related?

Mathematically, SST = SSR + SSE.

The rationale is the following: the total variability of the data set is equal to the variability explained by the regression line plus the unexplained variability, known as error.

Given a constant total variability, a lower error will cause a better regression. Conversely, a higher error will cause a less powerful regression. And that’s what you must remember, no matter the notation.

Next Step: The R-squared

Well, if you are not sure why we need all those sums of squares, we have just the right tool for you. The R-squared. Care to learn more? Just dive into the linked tutorial where you will understand how it measures the explanatory power of a linear regression!

***

Interested in learning more? You can take your skills from good to great with our statistics course.

Try statistics course for free

Next Tutorial: Measuring Variability with the R-squared

Источник

SSR, SST и R-квадрат

Расчет SST, SSR, SSE: пошаговый пример

Дополнительные ресурсы

SSR, SST и R-квадрат

Расчет SST, SSR, SSE: пошаговый пример

Дополнительные ресурсы

Сквозной пример

Данные и постановка задачи

Разделение выборки

Исследовательский анализ данных

Обработка данных

Пропущенные значения

Выбросы

Масштабирование признаков

Кодирование категориальных переменных

Построение модели

baseline-модель

Оценка качества

Диагностика модели, метрики качества и функции потерь

MSE, RMSE, MAE, MAPE

MSE и RMSE

MAE

MAPE

Коэффициент детерминации

Диагностика модели

Анализ остатков и прогнозных значений

Мультиколлинеарность

Дополнительная обработка данных

VIF

Преобразование данных

Отбор признаков

Повторное моделирование и диагностика

Повторное моделирование

Оценка качества и диагностика

Коэффициенты

Обучение модели

Векторизация уравнения

Функция потерь

Абсолютная ошибка, L1 loss

Квадрат ошибки, L2 loss

Функция Хьюбера

Метод наименьших квадратов

Нормальные уравнения

Код на Питоне

Создание класса

Оценка качества

Метод градиентного спуска

Нахождение градиента

Пошаговое построение модели

Прогноз

Создание класса

Оценка качества

Диагностика алгоритма

Подведем итог

2.5 Коэффициент детерминации

2.6 Проверка гипотез

Вступление

В одномерных распределениях

Регрессии

Другое использование слова «ошибка» в статистике

Смотрите также

Рекомендации

внешняя ссылка

Типы линейной регрессии:

Простая линейная регрессия:

Множественная линейная регрессия:

Реализация на Python:

Шаг 1: Загрузите все необходимые библиотеки и наборы данных, используя библиотеку pandas.

Шаг 2: Проверьте нулевые значения, форму и тип данных переменных:

Шаг 3. Заполните пропущенные значения

Шаг 4: Анализ выбросов

Шаг 5: Проверьте корреляцию:

Шаг 6: Разделение входных функций и целевой переменной:

Шаг 7: Обучение модели линейной регрессии на наборе поездов и ее оценка на тестовом наборе данных:

Оценка R-квадрата:

Предположения линейной регрессии

Содержание

Введение

в одномерном распределении

Замечание