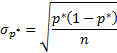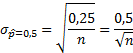Often in statistics we’re interested in estimating the proportion of individuals in a population with a certain characteristic.
For example, we might be interested in estimating the proportion of residents in a certain city who support a new law.
Instead of going around and asking every individual resident if they support the law, we would instead collect a simple random sample and find out how many residents in the sample support the law.
We would then calculate the sample proportion (p̂) as:
Sample Proportion Formula:
p̂ = x / n
where:
- x: The count of individuals in the sample with a certain characteristic.
- n: The total number of individuals in the sample.
We would then use this sample proportion to estimate the population proportion. For example, if 47 of the 300 residents in the sample supported the new law, the sample proportion would be calculated as 47 / 300 = 0.157.
This means our best estimate for the proportion of residents in the population who supported the law would be 0.157.
However, there’s no guarantee that this estimate will exactly match the true population proportion so we typically calculate the standard error of the proportion as well.
This is calculated as:
Standard Error of the Proportion Formula:
Standard Error = √p̂(1-p̂) / n
For example, if p̂ = 0.157 and n = 300, then we would calculate the standard error of the proportion as:
Standard error of the proportion = √.157(1-.157) / 300 = 0.021
We then typically use this standard error to calculate a confidence interval for the true proportion of residents who support the law.
This is calculated as:
Confidence Interval for a Population Proportion Formula:
Confidence Interval = p̂ +/- z*√p̂(1-p̂) / n
Looking at this formula, it’s easy to see that the larger the standard error of the proportion, the wider the confidence interval.
Note that the z in the formula is the z-value that corresponds to popular confidence level choices:
| Confidence Level | z-value |
|---|---|
| 0.90 | 1.645 |
| 0.95 | 1.96 |
| 0.99 | 2.58 |
For example, here’s how to calculate a 95% confidence interval for the true proportion of residents in the city who support the new law:
- 95% C.I. = p̂ +/- z*√p̂(1-p̂) / n
- 95% C.I. = .157 +/- 1.96*√.157(1-.157) / 300
- 95% C.I. = .157 +/- 1.96*(.021)
- 95% C.I. = [ .10884 , .19816]
Thus, we would say with 95% confidence that the true proportion of residents in the city who support the new law is between 10.884% and 19.816%.
Additional Resources
Standard Error of the Proportion Calculator
Confidence Interval for Proportion Calculator
What is a Population Proportion?
Стандартная ошибка пропорции Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Образец пропорции: 0.6 —> Конверсия не требуется
Размер образца: 10 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.154919333848297 —> Конверсия не требуется
7 Ошибки Калькуляторы
Стандартная ошибка пропорции формула
Стандартная ошибка пропорции = sqrt((Образец пропорции*(1-Образец пропорции))/Размер образца)
σp = sqrt((p*(1-p))/N)
Что такое стандартная ошибка и ее важность?
В статистике и анализе данных большое значение имеет стандартная ошибка. Термин «стандартная ошибка» используется для обозначения стандартного отклонения различных выборочных статистических данных, таких как среднее значение или медиана. Например, «стандартная ошибка среднего» относится к стандартному отклонению распределения выборочных средних, взятых из совокупности. Чем меньше стандартная ошибка, тем более репрезентативной будет выборка для генеральной совокупности. Соотношение между стандартной ошибкой и стандартным отклонением таково, что для данного размера выборки стандартная ошибка равна стандартному отклонению, деленному на квадратный корень размера выборки. Стандартная ошибка также обратно пропорциональна размеру выборки; чем больше размер выборки, тем меньше стандартная ошибка, потому что статистика будет приближаться к фактическому значению.
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
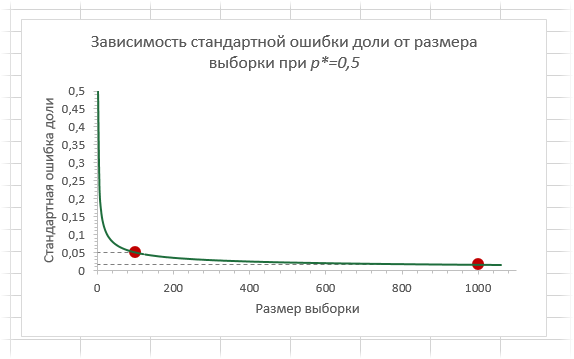
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.
Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.
Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:
Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы
Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Полное руководство по проверке гипотез для специалистов по данным, использующих Python
Ясно объяснен с примерами вопросов для исследования, шагами решения и полными кодами
Проверка гипотез — важная часть статистики и анализа данных. В большинстве случаев практически невозможно получить данные от всего населения. В этом случае мы берем образец и делаем оценки или утверждения относительно всего населения. Эти предположения или утверждения являются гипотезами. Проверка гипотез — это процесс проверки наличия доказательств для отклонения этой гипотезы.
Проверка гипотез обычно проводится по соотношению и среднему значению.
В этой статье мы собираемся охватить проверку гипотез о доле населения, разнице в доле населения, среднем по совокупности или выборке и разнице в среднем по выборке.
Я объясню процесс проверки гипотез шаг за шагом для всех четырех категорий индивидуально с примерами.
Для этого упражнения я использовал среду Jupyter Notebook. Если у вас его нет, вы можете использовать любой ноутбук или IDE по вашему выбору.
Блокнот Google Collab тоже подойдет. Google Collab — это умный блокнот. В нем предустановлены эти общие библиотеки.
Проверка гипотез для одной пропорции
Это самая основная проверка гипотез. В большинстве случаев у нас нет конкретного фиксированного значения для сравнения. Но если да, то это самая простая проверка гипотез. Я собираюсь начать с проверки гипотезы одной пропорции.
Для этой демонстрации я использовал набор данных Heart из Kaggle. Не стесняйтесь загрузить набор данных для своей практики. Здесь я импортирую пакеты и набор данных:
import pandas as pd
import numpy as np
import statsmodels.api as sm
import scipy.stats.distributions as distdf = pd.read_csv('Heart.csv')
df.head()
Последний столбец набора данных — «AHD». Это если у человека болезнь сердца. Вопрос исследования для этого раздела:
«Доля населения Ирландии, страдающего сердечными заболеваниями, составляет 42%. В США больше людей страдают сердечными заболеваниями »?
Теперь найдите ответ на этот исследовательский вопрос шаг за шагом.
Шаг 1: определите нулевую гипотезу и альтернативную гипотезу.
В этой задаче нулевая гипотеза состоит в том, что доля населения, страдающего сердечными заболеваниями, в США меньше или равна 42%. Но если мы проверим, что меньше, то будет автоматически. Итак, я делаю это только равным.
Альтернативная гипотеза состоит в том, что доля населения США, страдающего сердечными заболеваниями, составляет более 42%.
Ho: p0 = 0.42 #null hypothesis Ha: p > 0.42 #alternative hypothesis
Посмотрим, сможем ли мы найти доказательства, чтобы отвергнуть нулевую гипотезу.
Шаг 2: Предположим, что приведенный выше набор данных является репрезентативной выборкой из населения США. Итак, рассчитайте долю населения США, страдающую сердечными заболеваниями.
p_us = len(df[df['AHD']=='Yes'])/len(df)
Доля населения выборки, страдающая сердечными заболеваниями, составляет 0,46 или 46%. Этот процент превышает нулевую гипотезу. Это 42%.
Но вопрос в том, значительно ли больше 42%. Если мы возьмем другую простую случайную выборку, наблюдаемая в настоящее время доля населения (46%) может быть другой.
Чтобы выяснить, значительно ли превышает наблюдаемую долю населения нулевую гипотезу, выполните проверку гипотезы.
Шаг 3. Рассчитайте статистику теста:
Вот формула тестовой статистики:
Мы используем эту формулу для стандартной ошибки:
В этой формуле p0 составляет 0,42 (согласно нулевой гипотезе), а n — размер выборки. Теперь вычислите Стандартную ошибку и статистику теста:
se = np.sqrt(0.42 * (1-0.42) / len(df))
Найдите статистику теста, используя формулу для статистики теста выше:
#Best estimate be = p_us #hypothesized estimate he = 0.42test_stat = (be - he)/se
Статистика теста составила 1,3665.
Шаг 4: Рассчитайте p-значение
Эта статистика теста также называется z-оценкой. Вы можете найти p-значение из z_table или вы можете найти p-значение из этой формулы в python.
pvalue = 2*dist.norm.cdf(-np.abs(test_stat))
Значение p равно 0,1718. Это означает, что доля выборки (46% или 0,46) составляет 0,1718 нулевых стандартных ошибок выше нулевой гипотезы.
Шаг 5. Сделайте вывод по p-значению
Считайте, что уровень значимости альфа составляет 5% или 0,05. Уровень значимости 5% или меньше означает, что существует вероятность 95% или больше, что результаты не являются случайными.
Здесь p-значение больше, чем наш рассмотренный уровень значимости 0,05. Итак, мы не можем отвергнуть нулевую гипотезу. Это означает, что нет значительной разницы в доле населения, страдающего сердечными заболеваниями, в Ирландии и США.
Проверка гипотез о разнице в двух пропорциях
Сравнительные тесты проводятся гораздо чаще, чем одна проверка гипотезы о доле населения. Двухвыборочный тест пропорций выполняется для оценки того, различаются ли доли популяции некоторых признаков между двумя подгруппами.
Здесь мы собираемся проверить, отличается ли доля женщин с сердечными заболеваниями в популяции мужчин с сердечными заболеваниями.
Шаг 1. Установите нулевую гипотезу, альтернативную гипотезу и уровень значимости.
Здесь мы хотим проверить, есть ли разница между долей мужчин и женщин, страдающих сердечными заболеваниями. Начнем с предположения, что разницы нет.
Ho: p1 -p2 = 0
Это наша нулевая гипотеза. Здесь p1 — доля женщин с сердечными заболеваниями в популяции, а p2 — доля мужчин, страдающих сердечными заболеваниями.
Какая может быть альтернативная гипотеза?
Альтернативная гипотеза может быть, есть разница.
Ha: p1 - p2 != 0
Давайте воспользуемся уровнем значимости 0,1 или 10%.
Шаг 2. Подготовьте диаграмму, показывающую долю мужчин и женщин с сердечными заболеваниями в общей численности мужского и женского населения.
df['Gender'] = df.Sex.replace({1: "Male", 0: "Female"})
p = df.groupby("Gender")['AHD'].agg([lambda z: np.mean(z=='Yes'), "size"])
p.columns = ["HeartDisease", 'Total']
p
Шаг 3. Рассчитайте статистику теста.
Мы будем использовать ту же формулу для статистики теста, что и раньше. Наилучшая оценка — p1 — p2. Здесь p1 — доля женщин с сердечными заболеваниями в популяции, а p2 — доля мужчин с сердечными заболеваниями.
#Best estimate is p1 - p2. Get p1 and p2 from the chart p above p_fe = p.HeartDisease.Female p_male = p.HeartDisease.Male
Стандартная ошибка для двух пропорций населения рассчитывается по следующей формуле:
Здесь p — общая доля населения в выборке с сердечными заболеваниями. n1 и n2 — общее количество женского и мужского населения в выборке.
p = p_us #calculated in the beginning of the previous example n1 = p.Total.Female n2 = p.Total.Male se = np.sqrt(p_us*(1-p_us)*(1/n1 + 1/n2))
Теперь используйте эту стандартную ошибку и вычислите статистику теста.
#calculate the best estimate be = p_fe - p_male #Calculate the hypothesized estimate #Our null hypothesis is p1 - p2 = 0he = 0 #Calculate the test statistic test_statistic = (be - he)/se
Вычисленное значение test_statistic равно -0,296. Это означает, что наблюдаемая разница в пропорциях выборки на 0,296 расчетной стандартной ошибки ниже предполагаемого значения.
Шаг 4. Рассчитайте p-значение
pvalue = 2*dist.norm.cdf(-np.abs(test_statistic)
Значение p равно 0,7675. Это означает, что более 76% случаев мы увидим, что наблюдаемые нами результаты верны, учитывая, что нулевая гипотеза верна.
С другой стороны, p-значение больше, чем уровень значимости (0,1). Итак, у нас недостаточно доказательств, чтобы отвергнуть нулевую гипотезу.
Доля мужчин с сердечными заболеваниями существенно не отличается от доли женщин с сердечными заболеваниями.
Проверка гипотез для одного среднего
Это простой процесс проверки гипотез. Мы можем выполнить этот тест, если у нас есть конкретное фиксированное среднее значение для сравнения. Давайте поработаем на примере, чтобы понять процесс.
Это вопрос исследования:
«Проверьте, не превышает ли среднее значение RestBP 135». Здесь RestBP показывает артериальное давление в покое. У нас есть столбец RestBP в DataFrame. Решим эту задачу пошагово.
Шаг 1. Сформулируйте гипотезу.
Нам нужно выяснить, больше ли среднее значение RestBP 135. Предположим, что среднее значение RestBP меньше или равно 135.
Итак, нулевая гипотеза может заключаться в том, что среднее значение RestBP равно 135. Потому что, если мы можем доказать, что среднее значение RestBP больше 135, оно автоматически больше 134 или 130.
Если мы найдем достаточно доказательств, чтобы отклонить нулевую гипотезу, мы можем принять, что среднее значение RestBP больше 135. Это альтернативная гипотеза для данного примера.
Ho: mu = 135 Ha: mu > 135
Мы проверим, можем ли мы отклонить нулевую гипотезу, используя уровень значимости 0,05.
Шаг 2. Проверьте предположения.
Есть два предположения:
- Выборка должна быть простой случайной выборкой.
- Данные должны быть нормально распределены.
Я собрал этот набор данных из Kaggle. Я не участвовал в сборе данных. В целях демонстрации просто предположим, что это простая случайная выборка. Чтобы проверить второе предположение, постройте данные и посмотрите на распределение.
sns.distplot(df.RestBP)
Распределение не совсем нормальное. Но это близко к норме.
Хорошая новость в том, что нам не нужно беспокоиться о нормальности данных. Потому что у нас достаточно большой размер выборки (более 25 данных).
Шаг 3. Рассчитайте статистику теста.
Вот формула для расчета статистики теста:
Сначала вычислите стандартную ошибку, используя формулу ниже:
Здесь S — стандартное отклонение выборки, а n — количество выборок.
std= df.RestBP.std() n = len(df) se = std/np.sqrt(n)
Теперь используйте эту стандартную ошибку, чтобы найти статистику теста:
#Best estimate be = df.RestBP.mean() #Hypothesized estimatehe = 135 test_statistic = (be - he)/se
Статистика теста составила -3,27. Посмотрите на формулу тестовой статистики. Сверху он измеряет расстояние между исходным средним и предполагаемым средним. А внизу — стандартная ошибка.
Итак, этот test_statistic означает, что выборочное среднее на 3,27 стандартной ошибки ниже предполагаемого среднего.
Шаг 4. Сделайте вывод на основании статистики теста.
Преобразуйте этот test_statistic в значение вероятности, чтобы увидеть, является ли эта разница необычной или нет. Мы можем получить значение, используя эту формулу Python:
pvalue = 2*dist.norm.cdf(-np.abs(test_statistic))
Значение p равно 0,001, что меньше уровня значимости (0,05).
Итак, мы можем отвергнуть нулевую гипотезу.
Вероятность того, что наблюдаемый результат верен, составляет всего 0,1%, когда верна нулевая гипотеза. Вероятность 0,1% слишком низкая.
Итак, мы отвергаем нулевую гипотезу и принимаем альтернативную гипотезу, основанную на этих выборочных данных.
Проверка гипотез о разнице в средних значениях
В этом примере мы будем использовать те же данные, столбец RestBP. Но на этот раз, чтобы проверить, есть ли разница между средним RestBP самок и средним RestBP самцов.
Шаг 1. Сформулируйте гипотезу
В качестве нулевой гипотезы начните с утверждения, что среднее значение RestBP у женщин и среднее значение RestBP у мужчин одинаковы. Таким образом, разница между этими двумя средними будет равна нулю.
Альтернативная гипотеза состоит в том, что эти два средства не совпадают. Давайте проведем тест с 10% уровнем значимости.
Ho: mu_female - mu_male = 0 Ha: mu_female - mu_male != 0
И у мужского, и у женского населения есть достаточно большие данные в этих данных. Таким образом, проверка нормальности данных не требуется.
Шаг 2. Рассчитайте статистику теста.
Формула для статистики теста такая же, как и раньше. Но формула для стандартной ошибки другая.
Здесь s1 и s2 — стандартное отклонение выборки для женского и мужского населения соответственно. n1 и n2 — размер выборки женского и мужского населения. Теперь вычислите стандартную ошибку:
pop_fe = df[df.Gender=='Female'].dropna() pop_male = df[df.Gender=='Male'].dropna()std_fe = pop_fe.RestBP.std() std_male = pop_male.RestBP.std()se = np.sqrt(std_fe**2/len(pop_fe) + std_male**2/len(pop_male))
Используйте стандартную ошибку, чтобы получить статистику теста.
#calculate the best estimate mu_fe = pop_fe.RestBP.mean() #Mean RestBP for females mu_male = pop_male.RestBP.mean() #Mean RestBP for malesmu_diff = mu_fe - mu_male #hypothesized estimate mu_diff_hyp = 0 #null hypothesis: difference of two mean = zerotest_statistic = (be-he)/se
Test_statistic — 1.086. Для информации: наблюдаемая разница в средних значениях «mu_diff» составляет 2,52.
Поскольку мы проверяем, отличаются ли средние значения друг от друга, это двусторонний тест.
Значение p — это вероятность того, что статистика теста меньше 1,086 или больше 1,086.
Шаг 3. Сделайте выводы на основе статистики теста.
Рассчитайте p-значение из этой тестовой статистики в python:
pvalue = 2*dist.norm.cdf(-np.abs(test_statistic))
P-значения оказались равными 0,277. Поскольку это двусторонний тест,
p(z < -1.086) = 0.277
p(z > 1.086) = 0.277
p-значение = 0,277 + 0,277 = 0,554
Это означает, что существует приблизительно 55,4% вероятности того, что наблюдаемый результат или более экстремальный верен, когда верна нулевая гипотеза.
С другой стороны, p-значение намного больше, чем уровень значимости. Итак, мы не можем отвергнуть нулевую гипотезу.
Окончательный вывод, основанный на наблюдаемой разнице между средним RestBP женщин и средним RestBP мужчин, мы не можем поддержать идею о том, что существует значительная разница между двумя средними значениями.
Заключение
В этой статье я объяснил четыре наиболее распространенных типа исследовательских вопросов с рабочими примерами. Надеюсь, что с этого момента вы сможете использовать проверку гипотез при принятии решений.
Рекомендуемая литература
Что такое Стандартная формула ошибки?
Стандартная ошибка — это ошибка, которая возникает в распределении выборки при выполнении статистического анализа. Это вариант стандартного отклонения, так как оба понятия соответствуют мерам спреда. Высокая стандартная ошибка соответствует более высокому разбросу данных для взятой выборки. Вычисление формулы стандартной ошибки выполняется для выборки. В то же время стандартное отклонение определяет генеральную совокупность.
Оглавление
- Что такое Стандартная формула ошибки?
- Объяснение
- Пример формулы стандартной ошибки
- Калькулятор стандартной ошибки
- Актуальность и использование
- Стандартная формула ошибки в Excel
- Рекомендуемые статьи
Следовательно, стандартная ошибка среднего значения будет выражаться и определяться в соответствии с соотношением, описанным следующим образом:
σ͞x = σ/√n
Здесь,
- Стандартная ошибка, выраженная как σ͞x.
- Стандартное отклонение совокупности выражается как σ.
- Количество переменных в выборке, выраженное как n.
В статистическом анализе среднее значение, медиана и мода являются центральной тенденцией. Центральная тенденция Центральная тенденция — это статистическая мера, которая отображает центральную точку всего распределения данных, и вы можете найти ее с помощью 3 различных мер, т. е. среднего, медианы и моды.Подробнее меры. Стандартное отклонение, дисперсия и стандартная ошибка среднего классифицируются как меры изменчивости. Стандартная ошибка среднего для выборочных данных напрямую связана со стандартным отклонением большей совокупности и обратно пропорциональна или связана с квадратным корнем. число. Чтобы использовать эту функцию, введите термин =SQRT и нажмите клавишу табуляции, которая вызовет функцию SQRT. Более того, эта функция принимает один аргумент из нескольких переменных, используемых для создания выборки. Следовательно, если размер выборки Размер выборкиФормула размера выборки отображает соответствующий диапазон генеральной совокупности, в которой проводится эксперимент или опрос. Он измеряется с использованием размера генеральной совокупности, критического значения нормального распределения при требуемом доверительном уровне, доли выборки и предела погрешности. Если больше, то может быть равная вероятность того, что стандартная ошибка также будет большой.
Объяснение
Можно объяснить формулу для стандартной ошибки среднего, используя следующие шаги:
- Определите и организуйте выборку и определите количество переменных.
- Затем среднее значение выборки соответствует количеству переменных, присутствующих в выборке.
- Затем определите стандартное отклонение выборки.
- Затем определите квадратный корень из числа переменных, включенных в выборку.
- Теперь разделите стандартное отклонение, вычисленное на шаге 3, на полученное значение на шаге 4, чтобы получить стандартную ошибку.
Пример формулы стандартной ошибки
Ниже приведены примеры формул для расчета стандартной ошибки.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон стандартной формулы ошибки Excel здесь — Стандартная формула ошибки Шаблон Excel
Пример №1
Возьмем в качестве примера акции ABC. В течение 30 лет акции приносили средний долларовый доход в размере 45 долларов. Кроме того, было замечено, что акции приносят прибыль со стандартным отклонением в 2 доллара. Помогите инвестору рассчитать общую стандартную ошибку средней доходности, предлагаемой акцией ABC.
Решение:
- Стандартное отклонение (σ) = $2
- Количество лет (n) = 30
- Средняя доходность в долларах = 45 долларов.
Расчет стандартной ошибки выглядит следующим образом:
- σ͞x = σ/√n
- = 2 доллара США/√30
- = 2 доллара США / 5,4773
Стандартная ошибка,
- σx = 0,3651 доллара США
Таким образом, инвестиция предлагает инвестору стандартную долларовую ошибку в среднем 0,36515 доллара при удерживании позиции ABC в течение 30 лет. Однако, если бы акции сохранялись для более высокого инвестиционного горизонта, то стандартная ошибка среднего значения в долларах значительно уменьшилась бы.
Пример #2
Возьмем в качестве примера инвестора, который получил следующую доходность акций XYZ:
Год инвестиций Предлагаемая доходность120%225%35%410%
Помогите инвестору рассчитать общую стандартную ошибку средней доходности акций XYZ.
Решение:
Сначала определите среднее значение доходности, как показано ниже: –
- ͞X = (x1+x2+x3+x4)/количество лет
- = (20+25+5+10)/4
- =15%
Теперь определите стандартное отклонение доходности, как показано ниже: –
- σ = √ ((x1-͞X)2 + (x2-͞X)2 + (x3-͞X)2 + (x4-͞X)2) / √ (количество лет -1)
- = √ ((20-15) 2 + (25-15) 2 + (5-15) 2 + (10-15) 2) / √ (4-1)
- = (√ (5) 2 + (10) 2 + (-10) 2 + (-5) 2 ) / √ (3)
- = (√25+100+100+25)/ √ (3)
- =√250/√3
- =√83,3333
- «=» 9,1287%
Теперь вычисление стандартной ошибки выглядит следующим образом:
- σ͞x = σ/√n
- = 9,128709/√4
- = 9,128709/2
Стандартная ошибка,
- σx = 4,56%
Таким образом, инвестиции предлагают инвестору стандартную ошибку в долларах в среднем 4,56% при удержании позиции XYZ в течение 4 лет.
Калькулятор стандартной ошибки
Вы можете использовать следующий калькулятор.
.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } σnСтандартная формула ошибки
Формула стандартной ошибки =σ =√n 0 = 0√0
Актуальность и использование
Стандартная ошибка имеет тенденцию быть высокой, если размер выборки для анализа мал. Следовательно, выборка всегда берется из большей совокупности, которая включает больший размер переменных. Это всегда помогает статистику определить достоверность среднего значения выборки относительно среднего значения генеральной совокупности.
Большая стандартная ошибка говорит статистику, что выборка неоднородна в отношении среднего значения генеральной совокупности. Относительно населения наблюдается большой разброс в выборке. Точно так же небольшая стандартная ошибка говорит статистику, что выборка однородна относительно среднего значения генеральной совокупности. Отсутствуют или незначительные различия в выборке относительно населения.
Не следует смешивать его со стандартным отклонением. Вместо этого следует рассчитать стандартное отклонение для всей совокупности. Стандартная ошибкаСтандартная ошибкаСтандартная ошибка (SE) — это метрика, которая измеряет точность выборочного распределения, обозначающего совокупность, с использованием стандартного отклонения. Другими словами, это мера дисперсии среднего значения выборки, связанная со средним значением генеральной совокупности, а не стандартное отклонение. С другой стороны, оно определяется для среднего значения выборки.
Стандартная формула ошибки в Excel
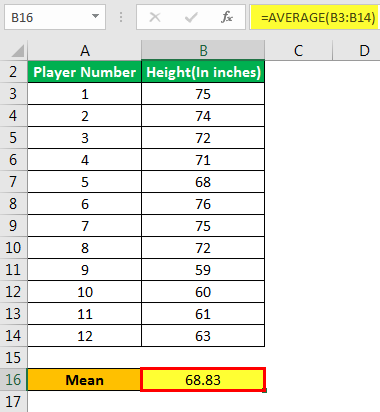
Теперь давайте возьмем пример Excel, чтобы проиллюстрировать концепцию стандартной формулы ошибки в шаблоне Excel ниже. Предположим, администрация школы хочет определить стандартную ошибку среднего значения роста футболистов.
Выборка состоит из следующих значений: –
Помогите администрации оценить стандартную ошибку среднего значения.
Шаг 1: Определите среднее значение, как показано ниже: –
Шаг 2: Определите стандартное отклонение, как показано ниже: –
Шаг 3: Определите стандартную ошибку среднего значения, как показано ниже: –
Следовательно, стандартная ошибка среднего значения для футболистов составляет 1,846 дюйма. Руководство должно заметить, что оно значительно велико. Таким образом, выборочные данные, взятые для анализа, неоднородны и имеют большую дисперсию.
Руководству следует либо исключить более мелких игроков, либо добавить игроков значительно выше, чтобы сбалансировать средний рост футбольной команды, заменив их людьми с меньшим ростом по сравнению с их сверстниками.
Рекомендуемые статьи
Эта статья была руководством по формуле стандартной ошибки. Здесь мы обсуждаем формулу для расчета среднего значения, стандартную ошибку, примеры и загружаемый лист Excel. Вы можете узнать больше из следующих статей: –
- Формула рентабельности EBITDA
- Формула валовой прибыли
- Формула относительного стандартного отклонения
- Формула погрешности

Всем привет! Я Ваня Касторнов, продуктовый аналитик Лиги Ставок. На сегодняшний день все вокруг говорят о необходимости проведения а/б тестирования, но зачастую оказывается, что их проводят, не проверяя статистическую значимость, или даже не знают, как их проводить. Здесь не будет абстрактного описания, зачем и как делать а/б тесты, вместо этого я постараюсь развеять туман над тем, какие статистические методы использовать в разных ситуациях, а также приведу примеры скриптов на python, чтобы вы могли сразу ими воспользоваться.
Для кого эта статья: для аналитиков, продактов или любого, кто сам планирует провести аб тест.
Как читать? Я старался учесть последовательность при написании, но на самом деле, это скорее шпаргалка — в любой момент, когда вам нужно провести аб тест, вы можете найти в ней кейс, который подходит для вас, и воспользоваться им, в конце есть ссылка на сводную схему.
Пара слов, и начнем. Пока я писал эту статью, я старался не использовать много научной терминологии, чтобы не распугать вас, но где‑то она встречается, извините за это…))
Что ж, начнем…
У нас есть две выборки, которые мы получили рандомным путем. Первое, что нам нужно сделать, чтобы начать эксперимент, это определить метрику (или метрики), на основании которой мы будем принимать решение: то, на основании чего, построена сама гипотеза. Выбор статистического метода в том числе зависит от типа метрики, на которую мы будем смотреть. Мы поделим метрики на три типа:
-
Количественные (количество ставок или заказов).
-
Пропорционные или качественные (конверсия в покупку, CTR)
-
Соотношения (рентабельность или отношение открытых продуктовых карточек к количеству покупок).
С каждым типом метрик — свой определенный подход, так как наибольшее количество А/Б тестов проводят с метриками пропорций, то с него и начнем, он же и самый простой.
Пропорции (качественные)
Тут все просто, наилучший метод чтобы проверить статистическую значимость изменения для пропорций это метод Хи‑Квадрат. Но перед тем, как его проводить, стоит проверить размер тестовой группы для желаемого минимального статистически значимого изменения. Это можно сделать, используя один из инструментов в интернете, например, этот или с помощью библиотеки statsmodels.stats через python, вот пример кода:
from statsmodels.stats.proportion import proportion_effectsize
from statsmodels.stats.power import TTestIndPower
baseline_cr = 0.2 # базовый уровень конверсии
min_effect = 0.05 # минимальный значимый результат
effect_size = proportion_effectsize(baseline_cr, baseline_cr + min_effect)
alpha = 0.05 # уровень значимости
power = 0.8 #уровень мощности
power_analysis = TTestIndPower()
sample_size = power_analysis.solve_power(effect_size, power=power, alpha=alpha, alternative='two-sided')
print(f"Необходимый размер выборки: {sample_size:.0f}")В обоих вариантах вам необходимо указать базовый уровень конверсии, минимальное значение для обнаружения изменения, уровень a (процент раз, когда разница будет обнаружена при условии, что ее нет) и уровень мощности (процент раз, когда будет обнаружено минимальное значение изменения, если оно существует).
Обнаружив необходимый размер выборки, мы можем приступать к самому тесту.
Опять же, в интернете полно сайтов с онлайн‑калькуляторами, которые позволят это сделать, например, вот этот. Если же вы решите провести тест используя python, то вот пример скрипта, который позволит это сделать.
import numpy as np
import scipy.stats as stats
# Загрузите данные в переменные
group_A = [50, 100]
group_B = [60, 90]
# Запустите тест
chi2, p, dof, ex = stats.chi2_contingency([group_A, group_B], correction=False)
# Рассчитайте доверительный интервал для изменения
lift = (group_B[0]/group_B[1])/(group_A[0]/group_A[1])
std_error = np.sqrt(1/group_B[0] + 1/group_B[1] + 1/group_A[0] + 1/group_A[1])
ci = stats.norm.interval(0.95, loc=lift, scale=std_error)
# Выводим результаты
print("Хи-квадрат p-value: ", p)
print("Доверительный интервал изменения: ", ci)
# Проверяем есть ли изменение
if p < 0.05 and ci[0] > 1:
print("Вариант лучше.")
else:
print("Разницы нет.")Количественные
Вторые по популярности аб тесты проходят с количественными метриками, примерами таких метрик могут быть: количество ставок, длина сессии и тд. При анализе количественных метрик важно выбрать правильный метод проверки статистической значимости. Так как мы выбрали рандомизированный метод сплитования, то скорее всего мы столкнемся с высоким уровнем дисперсии (разности) данных, что будет негативно влиять на определение значимости результатов, поэтому я рекомендую использовать CUPED (Controlled pre‑post experimental design) — это статистический метод, который все чаще используется в А/Б тестировании для повышения точности полученных результатов.
Таким образом, мы сможем нивелировать уровень дисперсии, сезонные изменения, маркетинговые акции и другие факторы. Подробнее про метод вы можете почитать тут или в оригинальной статье.
Для того, чтобы использовать cuped, нам потребуются набор данных со значением метрик в предтестовый период и само значение в момент теста. Для того, чтобы преобразовать данные, есть удобная библиотека ambrosia, вот пример скрипта:
import pandas as pd
def get_cuped_adjusted(A_before, B_before, A_after, B_after):
cv = cov([A_after + B_after, A_before + B_before])
theta = cv[0, 1] / cv[1, 1]
mean_before = mean(A_before + B_before)
A_after_adjusted = [after - (before - mean_before) * theta for after, before in zip(A_after, A_before)]
B_after_adjusted = [after - (before - mean_before) * theta for after, before in zip(B_after, B_before)]
return A_after_adjusted, B_after_adjustedПосле того, как мы получили данные, стоит оценить размер выборки, тут есть два варианта.
Если выборка большая…
То нужно посмотреть на нормальность распределения данных, в целом все просто, проверить нормальность распределения поможет вот этот скрипт, который использует тест Шапиро‑Уилка, он подойдет в большинстве случаев:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import shapiro, norm
data = pd.read_csv('adjusted_experiment_data.csv')
# Применяем тест Шапиро-Уилка
stat, p = shapiro(data)
alpha = 0.05
if p > alpha:
print("Нормальное распределение.")
else:
print("Не нормальное распределение.")
# График с расрпеделением
fig, ax = plt.subplots()
ax.hist(data, bins=5, density=True, alpha=0.5, label='Data')
mu, std = norm.fit(data)
xmin, xmax = ax.get_xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, std)
ax.plot(x, p, 'k', linewidth=2, label='Normal distribution')
Итак, распределение получилось нормальным, что же дальше..
Дальше мы можем провести самый используемый метод проверки отсутствия нулевой гипотезы, а именно t‑test, наиболее известным является т‑критерий стъюдента, он также подойдет, если же между группами осталась неравная дисперсия, то лучше подойдет т‑критерий Уэлча, в целом может использовать его всегда не будет ошибкой, но вы можете столкнуться с меньшим уровнем значимости. Оба теста удобно проводить, используя библиотеку scipy.stats, вот примеры запросов:
import pandas as pd
import scipy.stats as stats
data = pd.read_csv('adjusted_experiment_data.csv')
control = data[data['group_type'] == 'control']['experiment_data']
test = data[data['group_type'] == 'test']['experiment_data']
# т-критерий Уэлча
welch_t, welch_p = stats.ttest_ind(control, test, equal_var=False)
# т-критерий Стъюдента
student_t, student_p = stats.ttest_ind(control, test, equal_var=True)
print("Welch's t-test:")
print("t-statistic: ", welch_t)
print("p-value: ", welch_p)
print("nStudent's t-test:")
print("t-statistic: ", student_t)
print("p-value: ", student_p)Но бывает и так, что распределение данных не соответствует нормальному, что же тогда?
В этом случае лучше всего подходит U‑test Манна‑Уитни, В отличие от параметрических тестов, таких как t‑тест Стьюдента или t‑test Уэлча, U‑test Манна‑Уитни не делает никаких предположений о форме базового распределения. Для того, чтобы его провести, мы можем обратится к той же библиотеке scipy.stats:
u, p = stats.mannwhitneyu(control, test, alternative='two-sided')
print("Mann-Whitney U-test:")
print("U-statistic: ", u)
print("p-value: ", p)Что делать, если размер выборки нормальный, мы разобрались, но бывает, когда данных очень мало, тут на помощь приходит bootstrap. Основная идея bootstrap заключается в многократной выборке с заменой из исходных данных для создания большого количества «выборок». Каждая выборка похожа на исходную выборку, но имеет немного другие значения из‑за случайного подставления, подробнее можно узнать в этой статье, а пример скрипта выглядит так:
import pandas as pd
import numpy as np
import scipy.stats as stats
# Назначаем количество сэмплов
n_bootstrap = 10000
# генерирует сэмплы и расчитываем средние
bootstrap_diff = []
for i in range(n_bootstrap):
control_sample = np.random.choice(control, size=len(control), replace=True)
test_sample = np.random.choice(test, size=len(test), replace=True)
bootstrap_diff.append(np.mean(test_sample) - np.mean(control_sample))
bootstrap_diff = np.array(bootstrap_diff)
# считаем доверительный интервал
ci = np.percentile(bootstrap_diff, [2.5, 97.5])
# проводим т-тест
t, p = stats.ttest_1samp(bootstrap_diff, 0)
print("Bootstrap mean difference 95% CI: ({:.2f}, {:.2f})".format(ci[0], ci[1]))
print("t-statistic: ", t)
print("p-value: ", p)Фух, кажется с количественными метриками все…
Соотношения
В соотношениях два числовых значения, чаще всего числитель — это количество выполненных действий, а знаменатель — это количество пользователей, например, количество ставок на пользователей, которые открывали карточки событий, или же количество открытых карточек на количество просмотренных. Бывает, что суть гипотезы именно в изменении подобных метрик, что ж, тут мы будем ориентироваться на два варианта проверки статистической значимости, которые основываются на размерах выборки.
Перво‑наперво я рекомендую так же использовать один из вариантов сокращения дисперсии между данными, CUPED в данном случае не подойдет, так как это метод, который помогает уменьшить ошибки в данных, контролируя одну переменную, которая сильно связана с исследуемой переменной. Однако, если причина изменения исследуемой переменной является тем, имеет ли место какое‑то воздействие (например, показ обучающего баннера или получение фрибета (бесплатной ставки)), то CUPED не может использоваться, так как не существует других факторов, которые можно контролировать. В этом случае лучше использовать метод Diff‑in‑diff, который позволяет учитывать другие факторы, влияющие на результаты, и исследовать эффект воздействия на исследуемую переменную.
Чтобы использовать diff in diff, можно воспользоваться скриптом, который указан ниже, структура данных должна быть следующей: каждая строка соответствует одному участнику теста, а столбцы представляют различные переменные, например: ID участника, группа A/B‑теста, временной период, зависимая переменная:
import pandas as pd
# загрузка данных из csv файла в DataFrame
data = pd.read_csv('data.csv')
# фильтрация данных по группе и временному периоду
control = data[(data['group'] == 'control') & (data['time'] == 'before')]
treatment = data[(data['group'] == 'treatment') & (data['time'] == 'before')]
# вычисление среднего значения зависимой переменной для контрольной и экспериментальной групп до воздействия
control_before = control['dependent_variable'].mean()
treatment_before = treatment['dependent_variable'].mean()
# фильтрация данных по временному периоду после воздействия
control = data[(data['group'] == 'control') & (data['time'] == 'after')]
treatment = data[(data['group'] == 'treatment') & (data['time'] == 'after')]
# вычисление среднего значения зависимой переменной для контрольной и экспериментальной групп после воздействия
control_after = control['dependent_variable'].mean()
treatment_after = treatment['dependent_variable'].mean()
# вычисление разницы между средними значениями для контрольной и экспериментальной групп до и после воздействия
control_diff = control_after - control_before
treatment_diff = treatment_after - treatment_before
# вычисление оценки эффекта воздействия с помощью метода Diff-in-Diff
diff_in_diff = treatment_diff - control_diff
# сохранение преобраз
output_data = pd.DataFrame({'group': ['control', 'treatment'], 'before': [control_before, treatment_before], 'after': [control_after, treatment_after], 'diff': [control_diff, treatment_diff]})
output_data.to_csv('output.csv', index=False)Так, данные в порядке, переходим к проверке.
Большая выборка
Предположим, что выборка имеет внушительный размер, тогда нам нужно всего‑то провести t‑test, но сперва стоит взглянуть еще раз на дисперсию. Например, наша метрика это CTR, клики и просмотры являются случайными величинами, и когда мы объединяем их в одну метрику CTR, они будут иметь совместное распределение. Кроме того, если наша рандомизация основана на user_id, один пользователь может генерировать несколько просмотров, так что просмотры не являются независимыми друг от друга. Лучше использовать дельта‑метод для аппроксимации дисперсии соотношений и после этого проводить t‑test, в помощь приходит библиотека scipy.stats. Скрипт может выглядеть следующим образом.
import pandas as pd
import scipy.stats as stats
# загрузка преобразованных данных из CSV-файла
data = pd.read_csv('output.csv')
# вычисление стандартной ошибки разницы между средними значениями для контрольной и экспериментальной групп после воздействия с использованием дельта-метода
se_diff = ((data['after'][0] - data['after'][1]) ** 2 * control_var / 2 + (data['before'][0] - data['before'][1]) ** 2 * treatment_var / 2) ** 0.5 / pooled_var ** 0.5
# вычисление t-статистики и p-значения с использованием оценки стандартной ошибки, полученной из дельта-метода
t_stat = (data['after'][0] - data['after'][1]) / se_diff
df = len(data) - 2
p_val = stats.t.sf(abs(t_stat), df) * 2
# вывод результатов
print('Diff-in-Diff with Delta Method:')
print(f"Standard Error: {se_diff}")
print(f"t-statistic: {t_stat}")
print(f"p-value: {p_val}")
Маленькая выборка
Ну и последний метод, который мы рассмотрим, который стоит применять если размер выборки маленький. В таком случае bootstrap будет также актуален. Но так как мы пытаемся анализировать метрику, соотношения и наблюдения в данных могут быть независимыми, то больше подойдет блочный bootstrap. В обычном bootstrap данные берутся из исходной выборки с заменой, в блочном данные берутся группами (или блоками). Это нужно потому, что мы хотим учесть структуру зависимости в данных. В конце проведем уже известным нам t‑test.
Скрипт похож на обычный bootstrap:
import pandas as pd
import numpy as np
import scipy.stats as stats
data = pd.read_csv('output.csv')
control = data[data['group'] == 'control']
treatment = data[data['group'] == 'test']
observed_effect = treatment['after'].mean() - control['after'].mean()
# определяем количество блоков
num_blocks = 100
block_size = len(data) // num_blocks
bootstrap_samples = []
for i in range(num_blocks):
# вставляем данные в блоки
block_indices = np.random.choice(range(len(data)), size=block_size, replace=True)
bootstrap_sample = data.iloc[block_indices]
# сплитуем по группам
bootstrap_control = bootstrap_sample[bootstrap_sample['group'] == 'control']
bootstrap_test = bootstrap_sample[bootstrap_sample['group'] == 'test']
# считаем эффект через bootstrap
bootstrap_effect = bootstrap_test['after'].mean() - bootstrap_control['after'].mean()
bootstrap_samples.append(bootstrap_effect)
# стандартная ошибка bootstrap
bootstrap_std_err = np.std(bootstrap_samples)
# проводим t-test
t_statistic = observed_effect / bootstrap_std_err
p_value = stats.t.sf(np.abs(t_statistic), len(data) - 1) * 2
print("Observed treatment effect: ", observed_effect)
print("Bootstrap estimate of standard error: ", bootstrap_std_err)
print("t-statistic: ", t_statistic)
print("p-value: ", p_value)
Проверка Мощности
Важный критерий после проведения тестов статистической значимости — это проверка мощности. Эксперимент с низкой мощностью будет страдать от высокой частоты ложных отрицательных результатов (ошибка второго типа). Размер эффекта обычно представляет собой разницу в средних между контрольной и тестовой группами, деленную на стандартное отклонение. Чтобы проверить мощность после получения результатов, можно воспользоваться TTestIndPower из библиотеки statsmodels, а скрипт может выглядеть следующим образом:
import pandas as pd
import numpy as np
from statsmodels.stats.power import TTestIndPower
# загрузка данных из CSV-файла
data = pd.read_csv('output.csv')
# вычисление размера выборок на основе количества уникальных значений ID
n1 = len(data[data['group'] == 'control']['id'].unique())
n2 = len(data[data['group'] == 'test']['id'].unique())
# вычисление ожидаемого эффекта на основе наблюдаемого эффекта
observed_effect = data[data['group'] == 'test']['after'].mean() - data[data['group'] == 'control']['after'].mean()
effect_size = observed_effect / data['after'].std()
# задание параметров теста
alpha = 0.05 # уровень значимости
power = 0.8 # мощность теста
# вычисление мощности теста
power_analysis = TTestIndPower()
sample_size = power_analysis.solve_power(effect_size=effect_size, alpha=alpha, power=power, ratio=n2/n1)
power = power_analysis.power(effect_size=effect_size, nobs1=sample_size, alpha=alpha, ratio=n2/n1)
# вывод результатов
print("Sample size required: ", sample_size)
print("Power of the test: ", power)
Вывод
В итоге, чтобы провести успешный A/B тест, необходимо выбрать метод анализа, который подходит для конкретных метрик и размера выборки, а также учитывать все факторы, которые могут повлиять на результаты. Важно следить за мощностью эксперимента после его проведения, чтобы убедиться, что результаты являются значимыми.
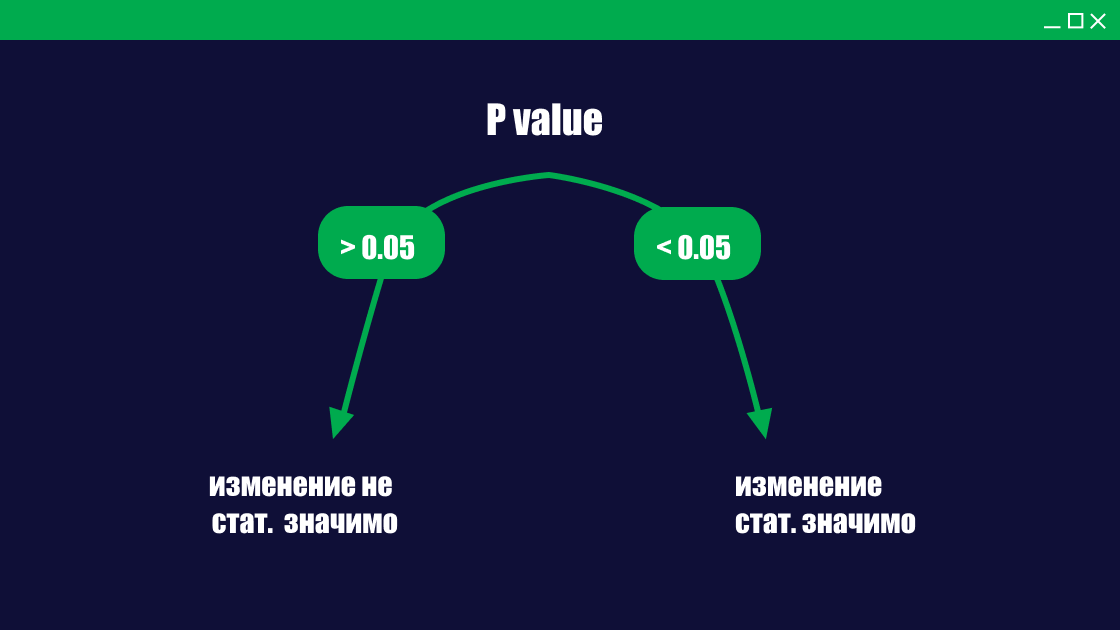
Для более простого восприятия я добавил в Miro общую схему, которая будет работать как навигатор выбора стат метода для вашего теста.
Я надеюсь, что эта статья поможет вам в проведении АБ тестов и увеличит значимость принимаемых решений, что положительно отразится на вашем продукте и личном прогрессе.
Подписывайтесь на мой телеграм канал, где я собираюсь рассказывать про развитие продуктов, аналитику и гедонизм, а также добавляйте статью в избранное, и до скорой встречи!
Все, что вам нужно знать о проверке гипотез — часть I
Перевод
Ссылка на автора
Статистика — это все о данных, но одни данные не интересны. Это интерпретация данных, которые нас интересуют …
Область Data Science развивается как никогда раньше. Многие компании в настоящее время ищут профессионалов, которые могут просеять свои данные о добыче золота и помочь им эффективно принимать быстрые бизнес-решения. Это также дает возможность многим работающим профессионалам переключить свою карьеру на область Data Science.
Имея этот ИИ, Data Science окружает многих студентов колледжей и хочет продолжить свою карьеру в области Data Science. И эта шумиха вокруг Data Science правильно провозглашена Томасом Х. Давенпортом и Д.Дж. Патил в одной из статей Harvard Business Review,
«Data Scientist: самая сексуальная работа XXI века»
В современном мире аналитики модели машинного обучения в строительстве стали сравнительно простыми (благодаря более надежным и гибким инструментам и алгоритмам), но фундаментальные концепции по-прежнему сбивают с толку. Одним из таких понятий является проверка гипотез.
В этом посте я пытаюсь прояснить основные понятия проверки гипотез с помощью иллюстраций.
Что такое проверка гипотез? Чего мы пытаемся достичь? Зачем нам нужно проверять гипотезы? Мы должны знать ответы на все эти вопросы, прежде чем мы продолжим.
Статистика это все о данных. Данные сами по себе не интересны. Это интерпретация данных, которые нас интересуют. ИспользованиеПроверка гипотезымы пытаемся интерпретировать или делать выводы о населении, используя выборочные данные.Проверка гипотезоценивает два взаимоисключающих утверждения о совокупности, чтобы определить, какое утверждение лучше всего подтверждается данными выборки. Всякий раз, когда мы хотим заявить о распределении данных или о том, отличается ли один набор результатов от другого набора результатов в прикладном машинном обучении, мы должны полагаться на статистические проверки гипотез.
Есть два возможных результата: если результат подтверждает гипотезу, то вы произвели измерение. Если результат противоречит гипотезе, то вы сделали открытие — Энрико Ферми
Давайте посмотрим на терминологию, которую мы должны знать вПроверка гипотезы
1. Параметр и статистика:
параметрявляется кратким описанием фиксированной характеристики или показателя целевой группы населения. Параметр обозначает истинное значение, которое будет получено при проведении переписи, а не выборки.
Пример:Среднее (μ), дисперсия (σ²), стандартное отклонение (σ), пропорция (π)
Население: Население — это совокупность объектов, которые мы хотим изучить / протестировать. Коллекция объектов может быть города, студенты, фабрики и т. Д. Это зависит от изучения под рукой.
В реальном мире сложно получить полную информацию о населении. Следовательно, мы выбираем выборку из этой совокупности и получаем те же статистические показатели, упомянутые выше. И эти меры называются выборочной статистикой. Другими словами,
статистикаявляется кратким описанием характеристики или меры выборки. Выборочная статистика используется в качестве оценки параметра совокупности.
Пример:Среднее значение выборки (x̄), дисперсия выборки (S²), стандартное отклонение выборки (S), пропорция выборки (п)
2. Распределение выборки:
Распределение выборки — это распределение вероятностей статистики, полученной с помощью большого числа выборок, взятых из определенной совокупности.
Пример:Предположим, что простая выборка из пяти больниц должна быть взята из населения 20 больниц. Возможны следующие варианты: (20, 19, 18, 17, 16) или (1,2,4,7,8) или любая из 15 504 (с использованием комбинаций 20C)) различных образцов размера 5.
В целом среднее значение распределения выборки будет приблизительно эквивалентно среднему значению для населения, т.е. E (x̄) = μ
Чтобы узнать больше о распределении выборки, пожалуйста, проверьте это ниже видео:
3. Стандартная ошибка (SE):
Стандартная ошибка (SE) очень похожа на стандартное отклонение. Оба являются мерами распространения. Чем выше число, тем больше разбросаны ваши данные. Проще говоря, два термина по сути равны, но есть одно важное отличие. Пока стандартная ошибка используетстатистика(пример данных) использование стандартного отклоненияпараметры(данные о населении)
Стандартная ошибка говорит вам, насколько далеко ваша выборочная статистика (например, среднее значение выборки) отклоняется от фактического среднего значения населения. Чем больше размер вашей выборки, тем меньше SE. Другими словами, чем больше размер выборки, тем ближе среднее значение выборки к среднему значению популяции.
Чтобы узнать больше о стандартной ошибке (SE), пожалуйста, смотрите видео ниже
Теперь давайте рассмотрим следующий пример, чтобы лучше понять остальные концепции.
4. (а) Нулевая гипотеза (H₀):
Заявление, в котором не ожидается никакой разницы или эффекта. Если нулевая гипотеза не отклонена, никакие изменения не будут внесены.
Слово «ноль» в данном контексте означает, что общепринятый факт, что исследователи аннулируют. Это не означает, что само утверждение является нулевым! (Возможно, этот термин следует называть «недействительной гипотезой», поскольку это может вызвать меньше путаницы)
4. (б). Альтернативная гипотеза (H₁):
Утверждение, что ожидается некоторое различие или эффект. Принятие альтернативной гипотезы приведет к изменению мнений или действий. Это противоположность нулевой гипотезы.
Чтобы узнать больше о нулевых и альтернативных гипотезах, пожалуйста, посмотрите это видео ниже
5. (а). Односторонний тест:
Односторонний тест — это тест статистической гипотезы, в котором критическая область распределения является односторонней, так что она либо превышает определенное значение, либо меньше, но не одновременно. Если тестируемый образец попадает в одностороннюю критическую область, альтернативная гипотеза будет принята вместо нулевой гипотезы.
Односторонний тест также известен как направленная гипотеза или направленный тест.
Критический регион:Критическая область — это область значений, которая соответствует отклонению нулевой гипотезы на некотором выбранном уровне вероятности.
5. (б). Двусторонний тест:
Двухсторонний тест — это метод, в котором критическая область распределения является двусторонней, и он проверяет, является ли выборка больше или меньше определенного диапазона значений. Если тестируемый образец попадает в одну из критических областей, альтернативная гипотеза принимается вместо нулевой гипотезы.
По соглашению, двусторонние тесты используются для определения значимости на уровне 5%, то есть каждая сторона распределения сокращается на 2,5%.
6. Тестовая статистика:
тестовая статистикаизмеряет, насколько близко образец пришел к нулевой гипотезе. Его наблюдаемое значение изменяется случайным образом от одной случайной выборки к другой выборке. Тестовая статистика содержит информацию о данных, которые имеют значение для принятия решения о том, следует ли отклонить нулевую гипотезу или нет.
Различные тесты гипотез используют разные статистические тесты, основанные на вероятностной модели, принятой в нулевой гипотезе. Общие тесты и их тестовая статистика включают в себя:
В общем, выборочные данные должны предоставить достаточные доказательства, чтобы отвергнуть нулевую гипотезу и сделать вывод, что эффект существует в популяции. В идеале, проверка гипотезы не позволяет отклонить нулевую гипотезу, когда эффект отсутствует в популяции, и отвергает нулевую гипотезу, когда эффект существует.
К настоящему времени мы понимаем, что вся проверка гипотез работает на основе имеющегося образца. Мы можем прийти к другому выводу, если образец будет изменен. Есть два типа ошибок, которые относятся к неверным выводам о нулевой гипотезе.
7. (а). Ошибка типа I:
Тип-IОшибка возникает, когда результаты выборки приводят к отклонению нулевой гипотезы, когда она на самом деле верна.Тип-Iошибки эквивалентны ложным срабатываниям.
Тип-Iошибки можно контролировать. Значение альфа, которое связано суровень значимостичто мы выбрали, имеет прямое отношение кТип-Iошибки.
7. (б). Ошибка типа II:
Тип-IIошибка возникает, когда на основании результатов выборки нулевая гипотеза не отклоняется, если она фактически ложна.Тип-IIошибки эквивалентны ложным негативам.
Уровень значимости (α):
Вероятность сделатьТип-Iошибка, и это обозначаетсяальфа (α), Альфа это максимальная вероятность того, что у нас естьТип-Iошибка. Для уровня достоверности 95% значение альфа составляет 0,05. Это означает, что существует 5% вероятность того, что мы отвергнем истинную нулевую гипотезу.
P-значение:
р-значениеиспользуется во всей статистике, от t-тестов до простого регрессионного анализа до моделей на основе дерева, почти во всех моделях машинного обучения. Мы все используемP-значениеопределить статистическую значимость в тесте гипотезы. Несмотря на то чтоР-значениескользкая концепция, которую люди часто неправильно интерпретируют.
P-значениеоцените, насколько хорошо выборочные данные подтверждают аргумент защитника дьявола о том, что нулевая гипотеза верна. Он измеряет, насколько совместимы ваши данные с нулевой гипотезой. Насколько вероятен эффект, наблюдаемый в ваших данных выборки, если нулевая гипотеза верна?
Другими словами, если нулевая гипотеза верна,Р-значениевероятность получения результата как экстремального или более экстремального, чем результат выборки, только по случайной случайности
Высокие значения P:Ваши данные, скорее всего, с истинным нулем
Низкие значения P:Ваши данные вряд ли с истинным нулем
Пример: Предположим, что вы проверяете следующую гипотезу на уровне значимости (α) 5%, и вы получаете значение p как 3%, и ваша выборочная статистикаИксзнак равно25
H₀: μ = 20
H₁: μ> 20
Интерпретация р-значения выглядит следующим образом:
Мы видели выше, чтоαтакже известен как совершениеТип-Iошибка. Когда мы говорим, αзнак равно5%, мы можем отклонить нашу нулевую гипотезу 5 из 100 раз, даже если это правда. Теперь, когда нашиР-значение3%, что меньшеα(мы определенно ниже порога совершенияТип-Iошибка),означает получение выборочной статистики как можно более экстремальной (x̄>знак равно25) учитывая, что H₀ истинно, очень меньше. Другими словами, мы не можем получить нашу выборочную статистику, если предположим, что H₀ истинно. Следовательно, мы отвергаем H₀ и принимаем H₁. Предположим, вы получаетеР-значениекак 6%, т. е. вероятность получения выборочной статистики как можно более экстремальной, тем выше, учитывая, что нулевая гипотеза верна. Таким образом, мы не можем отказаться от H₀, по сравнению сαмы не можем рисковатьТип-Iошибка больше, чем согласованный уровень значимости. Следовательно, мы не можем отвергнуть нулевую гипотезу и отвергнуть альтернативную гипотезу.
Теперь, когда мы поняли основную терминологию вПроверка гипотезы,Теперь давайте рассмотрим этапы проверки гипотез и приведем пример с примером.
Например, крупный универмаг рассматривает возможность введения услуги интернет-магазина. Новая услуга будет введена, если более 40 процентов интернет-пользователей совершают покупки через Интернет.
Шаг 1: сформулируйте гипотезы:
Подходящий способ сформулировать гипотезы:
H₀: π ≤ 0,40
H₁: π> 0,40
Если нулевая гипотеза H₀ отклонена, то будет принята альтернативная гипотеза H₁ и введена новая услуга интернет-покупок. С другой стороны, если мы не сможем отклонить H₀, то новая услуга не должна быть введена, пока не будут получены дополнительные доказательства. Этот тест нулевой гипотезы являетсяодин хвостТест, потому что альтернативная гипотеза выражается направленно: доля интернет-пользователей, которые используют Интернет для покупок, превышает 0,40.
Шаг 2: Выберите подходящий тест:
Чтобы проверить нулевую гипотезу, необходимо выбрать соответствующий статистический метод. Для этого примераZстатистика, которая соответствует стандартному нормальному распределению, будет уместной.
z = (p-π) / σₚ, где σₚ = sqrt (π (1-π) / n)
Шаг 3: Выберите уровень значимости, α:
Мы поняли чтоУровень значимостиотносится кТип-Iошибка. В нашем примере ошибка Типа I произошла бы, если бы мы пришли к выводу, основываясь на выборочных данных, что доля клиентов, предпочитающих новый тарифный план, была больше 0,40, тогда как на самом деле она была меньше или равна 0,40.
Ошибка типа II возникла бы, если бы мы пришли к выводу, основываясь на выборочных данных, что доля клиентов, предпочитающих новый тарифный план, была меньше или равна 0,40, тогда как фактически она была больше 0,40.
Необходимо сбалансировать два типа ошибок. В качестве компромисса α часто устанавливается на 0,05; иногда это 0,01; другие значения α редки. Мы рассмотрим 0,05 для нашего примера.
Шаг 4: Соберите данные и рассчитайте статистику теста:
Размер выборки определяется после учета требуемого значения α и других качественных соображений, таких как бюджетные ограничения для сбора данных выборки. Для нашего примера, скажем, 30 пользователей были опрошены, а 17 указали, что они использовали Интернет для покупок.
Таким образом, значение пропорции выборки составляетр = 17/30 = 0,567.
Значениеσₚ = SQRT ((0,40) (0,60) / 30) = 0,089.
Тестовая статистикаZможно рассчитать как
г = (р-π) / σₚ = (0.567-0.40) /0.089=1.88
Шаг 5: Определите вероятность (или критическое значение):
Используя стандартные нормальные таблицы из приведенного выше, вероятность полученияZзначение 1,88 составляет 0,96995, т.е.Р (z≤1.88) = 0,96995,Но мы хотели вычислить вероятность справа отz (потому что мы заинтересованы в получении значения вероятности, которое попадает в область отклонения или критическую область),то есть1-0.96995знак равно0,03005, Эта вероятность прямо сопоставима с(поскольку α совершает ошибку Типа I, а рассчитанное нами значение вероятности также попадает в критическую область)
Если вы хотите понять, как искать значения вероятностей для данных z-оценок, посмотрите видео ниже:
В качестве альтернативы, критическое значениег,который даст область справа от критического значения 0,05, находится между 1,64(при 1,64 вероятность составляет 0,94950)и 1,65(при 1,65 вероятность равна 0 95053)и равен 1,645(вероятность равна 0,95, то есть слева от нормального распределения, что означает, что справа она равна 0,05),
Обратите внимание, что при определении критического значения статистики теста, область в хвосте за критическим значением либоα или α / 2.этоαдля одностороннего теста иα / 2для двустороннего теста. Наш пример — односторонний тест.
Если вы хотите понять, как искать критическое значениеα,Пожалуйста, посмотрите видео ниже:
Шаг 6 и 7: сравните вероятность (или критическое значение) и примите решение:
Вероятность, связанная с вычисленным или наблюдаемым значением статистики теста, составляет 0,03005. Это вероятность полученияР-значение0,567 (доля образца =п)когда π = 0,40. Это меньше уровня значимости 0,05. Следовательно, нулевая гипотеза отвергается.
В качестве альтернативы рассчитывается значение тестовой статистикиг = 1,88лежит в области отклонения, за пределами значения 1,645. Снова, тот же самый вывод отклонить нулевую гипотезу сделан.
Обратите внимание, что два способа проверки нулевой гипотезы эквивалентны, но математически противоположны в направлении сравнения. Если вероятность, связанная с вычисленным или наблюдаемым значением тестовой статистики (TSCAL), равнаменьше, чемНа уровне значимости (α) нулевая гипотеза отвергается. Однако, если абсолютное значение рассчитанного значения статистики тестабольше чемабсолютное значение критического значения тестовой статистики (TSCR), нулевая гипотеза отклоняется. Причина этого смещения знака состоит в том, что чем больше абсолютное значение TSCAL, тем меньше вероятность получения более экстремального значения тестовой статистики при нулевой гипотезе.
если вероятность TSCAL <уровень значимости (α), то отклонить H₀.
Но, если | TSCAL | > | TSCR |, затем отклонить H₀
Шаг 8: Вывод:
В нашем примере мы заключаем, что есть свидетельства того, что доля интернет-пользователей, совершающих покупки через Интернет, значительно превышает 0,40. Следовательно, рекомендация для универмага будет заключаться в том, чтобы ввести новый сервис интернет-магазинов.
Этот пример относится к одному образцу теста пропорций. Тем не менее, существует несколько типов тестов, которые зависят от знаний о населении и рассматриваемой проблемы.
Например, у нас есть t-тест, Z-тест. Тест хи-квадрат, тест Манна-Уитни, тест Вилкоксона и т. Д.
На этом я хотел бы завершить часть I «Все, что вам нужно знать о проверке гипотез». Я буду обсуждать параметрические и непараметрические тесты и какой тест использовать в каком сценарии в части II. До тех порСчастливого обучения…
Спасибо за чтение!
Пожалуйста, поделитесь своим мнением в разделе комментариев ниже.
Ссылки:
- Маркетинговые исследования — прикладная ориентация Naresh K Malhotra и Satyabhushan Dash
- https://www.cliffsnotes.com/study-guides/statistics/sampling/populations-samples-parameters-and-statistics
- https://www.statisticshowto.datasciencecentral.com
- https://www.khanacademy.org
- https://blog.minitab.com