Стандартная ошибка точечного прогноза

Точечный прогноз
заключается в получении прогнозного
значения уp,
которое определяется путем подстановки
в уравнение регрессии соответствующего
(прогнозного) значения xp:

уp = a + b* xp

Интервальный
прогноз
заключается в построении доверительного
интервала прогноза, т. е. нижней и верхней
границ уpmin,
уpmax интервала,
содержащего точную величину для
прогнозного значения yp
(ypmin < yp <
ypmin) с заданной
вероятностью.

При построении
доверительного интервала прогноза
используется стандартная
ошибка прогноза:

,
где

Строится доверительный
интервал прогноза:

Множественный регрессионный анализ

(слайд
1)
Множественная регрессия применяется
в ситуациях, когда из множества факторов,
влияющих на результативный признак,
нельзя выделить один доминирующий
фактор и необходимо учитывать влияние
нескольких факторов. Например, объем
выпуска продукции определяется величиной
основных и оборотных средств, численностью
персонала, уровнем менеджмента и т. д.,
уровень спроса зависит не только от
цены, но и от имеющихся у населения
денежных средств.

Основная цель
множественной регрессии – построить
модель с несколькими факторами и
определить при этом влияние каждого
фактора в отдельности, а также их
совместное воздействие на изучаемый
показатель.

Таким образом,
множественная регрессия – это уравнение
связи с несколькими независимыми
переменными:

(слайд
2)
Построение уравнения множественной
регрессии

1. Постановка задачи

По имеющимся данным
n наблюдений
(табл. 3.1) за совместным изменением p+1
параметра y
и xj и
((yi,xj,i);
j=1,
2, …, p;
i=1,
2, …, n)
необходимо определить аналитическую
зависимость ŷ
= f(x1,x2,…,xp),
наилучшим образом описывающую данные
наблюдений.

Таблица 3.1

Данные наблюдений

	y	х1	х2	…	хр
1	y1	x11	х21	…	xp1
2	y2	х12	х22	…	xp2
…	…	…	…	…	…
n	yn	х1n	x2n	…	xpn

Каждая строка
таблицы представляет собой результат
одного наблюдения. Наблюдения различаются
условиями их проведения.

Вопрос о том, какую
зависимость следует считать наилучшей,
решается на основе какого-либо критерия.
В качестве такого критерия обычно
используется минимум суммы квадратов
отклонений расчетных значений
результативного показателя ŷi
от наблюдаемых
значений yi:

2. Спецификация модели

(слайд
3)
Спецификация модели включает в себя
решение двух задач:

– отбор факторов,
подлежащих включению в модель;

– выбор формы
уравнения регрессии.

2.1. Отбор факторов при построении множественной регрессии

Включение в
уравнение множественной регрессии того
или иного набора факторов связано прежде
всего с представлениями исследователя
о природе взаимосвязи моделируемого
показателя с другими экономическими
явлениями.

К факторам,
включаемым в модель, предъявляются
следующие требования:

1. Факторы должны
быть количественно измеримы.
Включение фактора в модель должно
приводить к существенному увеличению
доли объясненной части в общей вариации
зависимой переменной. Поскольку данная
величина характеризуется коэффициентом
детерминации,
включение нового фактора в модель должно
приводить к заметному изменению
коэффициента. Если этого не происходит,
то включаемый в анализ фактор не улучшает
модель и является лишним.

Например, если для
регрессии, включающей 5 факторов,
коэффициент детерминации составил
0,85, и включение шестого фактора дало
коэффициент детерминации 0,86, то вряд
ли целесообразно дополнять модель этим
фактором.

Если необходимо
включить в модель качественный фактор,
не имеющий количественной оценки, то
нужно придать ему количественную
определенность. В этом случае в модель
включается соответствующая ему
«фиктивная»
переменная,
имеющая конечное количество формально
численных значений, соответствующих
градациям качественного фактора (балл,
ранг).

Например, если
нужно учесть влияние уровня образования
(на размер заработной платы), то в
уравнение регрессии можно включить
переменную, принимающую значения: 0 –
при начальном образовании, 1 – при
среднем, 2 – при высшем.

Несмотря на то,
что теоретически регрессионная модель
позволяет учесть любое количество
факторов, на практике в этом нет
необходимости, т.к. неоправданное их
увеличение приводит к затруднениям в
интерпретации модели и снижению
достоверности результатов.

2. Факторы не
должны быть взаимно коррелированы
и, тем более, находиться в точной
функциональной связи. Наличие высокой
степени коррелированности между
факторами может привести к неустойчивости
и ненадежности оценок коэффициентов
регрессии, а также к невозможности
выделить изолированное влияние факторов
на результативный показатель. В результате
параметры регрессии оказываются
неинтерпретируемыми.

Пример.
Рассмотрим регрессию себестоимости
единицы продукции (у)
от заработной платы работника (х)
и производительности труда в час (z).

Коэффициент
регрессии при переменной z
показывает, что с ростом производительности
труда на 1 ед-цу в час себестоимость
единицы продукции снижается в среднем
на 10 руб. при постоянном уровне оплаты
труда.

А параметр при х
нельзя интерпретировать как снижение
себестоимости единицы продукции за
счет роста заработной платы. Отрицательное
значение коэффициента регрессии в
данном случае обусловлено высокой
корреляцией между х
и z
(0,95).

(слайд
4)
Считается, что две переменные явно
коллинеарны,
т.е. находятся между собой в линейной
зависимости, если коэффициент
интеркорреляции
(корреляции между двумя объясняющими
переменными) ≥ 0,7. Если факторы явно
коллинеарны, то они дублируют друг друга
и один из них рекомендуется исключить
из уравнения. Предпочтение при этом
отдается не тому фактору, который более
тесно связан с результатом, а тому,
который при достаточно тесной связи с
результатом имеет наименьшую тесноту
связи с другими факторами.

В этом требовании
проявляется специфика множественной
регрессии как метода исследования
комплексного воздействия факторов в
условиях их независимости друг от друга.

Наряду с парной
коллинеарностью может иметь место
линейная зависимость между более чем
двумя переменными – мультиколлинеарность,
т.е. совокупное воздействие факторов
друг на друга.

Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестанет
быть полностью независимой, что не
позволит оценить воздействие каждого
фактора в отдельности. Чем сильнее
мультиколлинеарность факторов, тем
менее надежна оценка распределения
суммы объясненной вариации по отдельным
факторам с помощью МНК.

(слайд
5) Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:

• затрудняется
  интерпретация параметров множественной
  регрессии; параметры линейной регрессии
  теряют экономический смысл;

• оценки параметров
  не надежны, имеют большие стандартные
  ошибки и меняются с изменением количества
  наблюдений (не только по величине, но
  и по знаку), что делает модель непригодной
  для анализа и прогнозирования.

(слайд
6) Для
оценки мультиколлинеарности используется
определитель
матрицы парных коэффициентов
интеркорреляции:

(!)
Если факторы не коррелируют между собой,
то матрица коэффициентов интеркорреляции
является единичной, поскольку в этом
случае все недиагональные элементы
равны 0. Например, для уравнения с тремя
переменными
матрица коэффициентов интеркорреляции
имела бы определитель, равный 1, посколькуи.

(слайд
7)

(!)
Если между факторами существует полная
линейная зависимость
и все коэффициенты корреляции равны 1,
то определитель такой матрицы равен 0
(Если
две строки матрицы совпадают, то её
определитель равен нулю).

Чем ближе к 0
определитель матрицы коэффициентов
интеркорреляции, тем сильнее
мультиколлинеарность и ненадежнее
результаты множественной регрессии.

Чем ближе к 1
определитель
матрицы коэффициентов интеркорреляции,
тем меньше мультиколлинеарность
факторов.

(слайд

Способы
преодоления мультиколлинеарности
факторов:

1)
исключение из модели одного или нескольких
факторов;

2)
переход к совмещенным уравнениям
регрессии, т.е. к уравнениям, которые
отражают не только влияние факторов,
но и их взаимодействие. Например, если
,
то можно построить следующее совмещенное
уравнение:;

3)
переход к уравнениям приведенной формы
(в уравнение регрессии подставляется
рассматриваемый фактор, выраженный из
другого уравнения).

(слайд
9)
2.2. Выбор формы уравнения регрессии

Различают следующие
виды уравнений
множественной регрессии:

• линейные,

• нелинейные,
  сводящиеся к линейным,

• нелинейные, не
  сводящиеся к линейным (внутренне
  нелинейные).

В первых двух
случаях для оценки параметров модели
применяются методы классического
линейного регрессионного анализа. В
случае внутренне нелинейных уравнений
для оценки параметров применяются
методы нелинейной оптимизации.

Основное требование,
предъявляемое к уравнениям регрессии,
заключается в наличии наглядной
экономической интерпретации модели и
ее параметров. Исходя из этих соображений,
наиболее часто используются линейная
и степенная зависимости.

Линейная
множественная регрессия имеет вид:

Параметры bi
при факторах хi
называются коэффициентами
«чистой» регрессии.
Они показывают, на сколько единиц в
среднем изменится результативный
признак за счет изменения соответствующего
фактора на единицу при неизмененном
значении других факторов, закрепленных
на среднем уровне.

(слайд
10)
Например, зависимость спроса на товар
(Qd) от цены (P) и дохода (I) характеризуется
следующим уравнением:

Qd = 2,5 — 0,12P + 0,23 I.

Коэффициенты
данного уравнения говорят о том, что
при увеличении цены на единицу, спрос
уменьшится в среднем на 0,12 единиц, а при
увеличении дохода на единицу, спрос
возрастет в среднем 0,23 единицы.

Параметр а
не всегда может быть содержательно
проинтерпретирован.

Степенная
множественная регрессия имеет вид:

Параметры bj
(степени факторов хi)
являются коэффициентами эластичности.
Они показывают, на сколько % в среднем
изменится результативный признак за
счет изменения соответствующего фактора
на 1% при неизмененном значении остальных
факторов.

Наиболее широкое
применение этот вид уравнения регрессии
получил в производственных функциях,
а также при исследовании спроса и
потребления.

Например, зависимость
выпуска продукции Y от затрат капитала
K и труда L:
говорит
о том, что увеличение затрат капитала
K на 1% при неизменных затратах труда
вызывает увеличение выпуска продукции
Y на 0,23%. Увеличение затрат труда L на 1%
при неизменных затратах капитала K
вызывает увеличение выпуска продукции
Y на 0,81 %.

Возможны и другие
линеаризуемые функции для построения
уравнения множественной регрессии:

• экспонента

  ;

• гипербола

  .

Чем сложнее функция,
тем менее интерпретируемы ее параметры.
Кроме того, необходимо помнить о
соотношении между количеством наблюдений
и количеством факторов в модели. Так,
для анализа трехфакторной модели должно
быть проведено не менее 21 наблюдения.

(слайд
11) 3.
Оценка параметров модели

Параметры уравнения
множественной регрессии оцениваются,
как и в парной регрессии, методом
наименьших квадратов,
согласно которому следует выбирать
такие значения
параметров а
и bi,
при которых сумма квадратов отклонений
фактических значений результативного
признака yi
от теоретических
значений ŷ
минимальна,
т. е.:

Если
,
тогдаS
является функцией неизвестных параметров
a,
bi:

Чтобы найти минимум
функции, нужно найти частные производные
по каждому из параметров и приравнять
их к 0:

Отсюда получаем
систему уравнений:

(слайд
12) Ее
решение может быть осуществлено методом
определителей:

,

где ∆
– определитель системы;

∆a,
∆b1,
∆bp
– частные определители (∆j).

–определитель
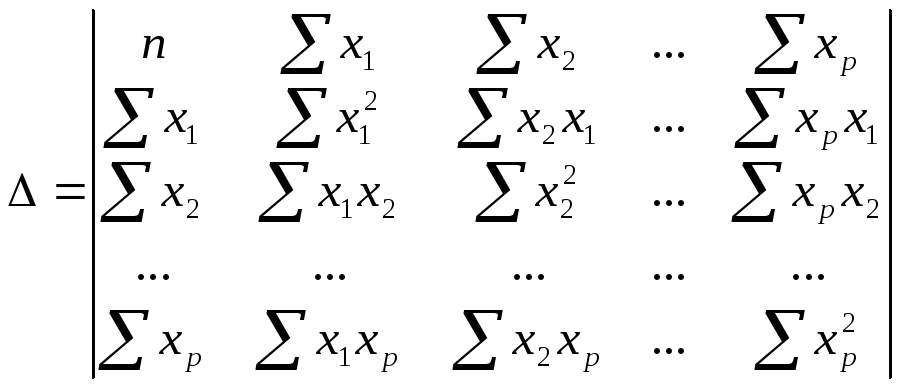
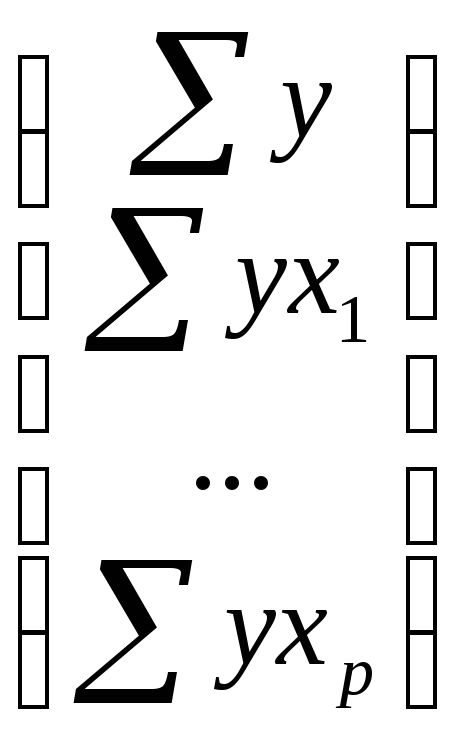
системы,

∆j
– частные
определители, которые получаются из
основного определителя путем замены
j-го столбца на столбец свободных членов
.

При использовании
данного метода возможно возникновение
следующих ситуаций:

1) если основной
определитель системы Δ равен
нулю и все определители Δj
также равны
нулю, то данная система имеет бесконечное
множество решений;

2) если основной
определитель системы Δ равен
нулю и хотя бы один из определителей Δj
также равен
нулю, то система решений не имеет.

(слайд
13) Помимо
классического МНК для определения
неизвестных параметров линейной модели
множественной регрессии используется
метод оценки параметров через 
β-коэффициенты
– стандартизованные коэффициенты
регрессии.

Построение
модели множественной регрессии в
стандартизированном, или нормированном,
масштабе
означает, что все переменные, включенные
в модель регрессии, стандартизируются
с помощью специальных формул.

Уравнение
регрессии
в стандартизованном масштабе:

,

где
,— стандартизованные переменные;

— стандартизованные
коэффициенты регрессии.

Т.е. посредством
процесса стандартизации точкой отсчета
для каждой нормированной переменной
устанавливается ее среднее значение
по выборочной совокупности. При этом в
качестве единицы измерения
стандартизированной переменной
принимается ее среднеквадратическое
отклонение σ.

β-коэффициенты
показывают,
на сколько сигм (средних квадратических
отклонений) изменится в среднем результат
за счет изменения соответствующего
фактора xi
на одну сигму при неизменном среднем
уровне других факторов.

Стандартизованные
коэффициенты регрессии βi
сравнимы
между собой, что позволяет ранжировать
факторы по силе их воздействия на
результат. Большее относительное влияние
на изменение результативной переменной
y оказывает
тот фактор, которому соответствует
большее по модулю значение коэффициента
βi.
В этом основное
достоинство стандартизованных
коэффициентов регрессии,
в отличие от коэффициентов «чистой»
регрессии, которые не сравнимы между
собой.

(слайд
14)
Связь коэффициентов «чистой» регрессии
bi
с коэффициентами βi
описывается соотношением:

,
или

Параметр a
определяется как
.

Коэффициенты
β определяются при помощи
МНК
из следующей системы уравнений
методом определителей:

Для оценки параметров
нелинейных
уравнений множественной регрессии
предварительно осуществляется
преобразование последних в линейную
форму (с помощью замены переменных) и
МНК применяется для нахождения параметров
линейного уравнения множественной
регрессии в преобразованных переменных.
В случае внутренне
нелинейных
зависимостей для оценки параметров
приходится применять методы нелинейной
оптимизации.

(слайд
1) 4.
Проверка качества уравнения регрессии

Практическая
значимость уравнения множественной
регрессии оценивается с помощью
показателя множественной корреляции
и его квадрата – коэффициента детерминации.

Показатель
множественной корреляции
характеризует тесноту связи рассматриваемого
набора факторов с исследуемым признаком,
т.е. оценивает тесноту совместного
влияния факторов на результат.

Независимо от
формы связи показатель
множественной корреляции
рассчитывается по формуле:

Коэффициент
множественной корреляции принимает
значения в диапазоне 0 ≤ R
≤ 1. Чем ближе
он к 1, тем теснее связь результативного
признака со всем набором исследуемых
факторов.

При линейной
зависимости признаков формулу индекса
множественной корреляции можно записать
в виде:

,

где
—
стандартизованные коэффициенты
регрессии,

—
парные коэффициенты корреляции результата
с каждым фактором.

Данная формула
получила название линейного
коэффициента множественной корреляции,
или совокупного
коэффициента корреляции.

Индекс детерминации
для нелинейных по оцениваемым параметрам
функций принято называть «квази-».Для его
определения по функциям, использующим
логарифмические преобразования
(степенная, экспонента), необходимо
сначала найти теоретические значения
ln
y,
затем трансформировать их через
антилогарифмы (антилогарифм ln
y
= y)
и далее определить индекс детерминации
как «квази-»
по формуле:

.

Величина «квази-»
не будет совпадать с совокупным
коэффициентом корреляции, который может
быть рассчитан для линейного в логарифмах
уравнения множественной регрессии,
потому что в последнем раскладывается
на факторную и остаточную суммы квадратов
не,
а.

(слайд
2)
Использование коэффициента множественной
детерминации

для оценки качества модели обладает
тем недостатком, что включение в модель
нового фактора (даже несущественного)
автоматически увеличивает величину.
Поэтому при большом количестве факторов
предпочтительней использовать так
называемый скорректированный
(улучшенный) коэффициент множественной
детерминации

,
определяемый соотношением:

,

где n
– число наблюдений,

m
– число параметров при переменных х
(чем больше величина m,
тем сильнее различия между к-том множ.
детерминации

и скорректированным к-том
).

При заданном объеме
наблюдений и при прочих равных условиях
с увеличением числа независимых
переменных (параметров) скорректированный
к-т множ. детерминации убывает. Его
величина может стать и отрицательной
при слабых связях результата с факторами.
При небольшом числе наблюдений
нескорректированная величина к-та
имеет
тенденцию переоценивать долю вариации
результативного признака, связанную с
влиянием факторов, включенных в
регрессионную модель. Чем
больше объем совокупности, по которой
исчислена регрессия, тем меньше
различаются
и
.

Отметим, что низкое
значение коэффициента множественной
корреляции и коэффициента множественной
детерминации может быть обусловлено
следующими причинами:

– в регрессионную
модель не включены существенные факторы;

– неверно выбрана
форма аналитической зависимости, не
отражающая реальные соотношения между
переменными, включенными в модель.

(слайд
3)
Значимость уравнения множественной
регрессии в целом оценивается с помощью
F—
критерия Фишера:

Выдвигаемая
«нулевая» гипотеза H0 о статистической
незначимости уравнения регрессии
отвергается при выполнении условия F
> Fкрит,
где Fкрит
определяется по таблицам F-критерия
Фишера по двум степеням свободы k1
= m,
k2=
n-m—1
и заданному уровню значимости α.

Значимость одного
и того же фактора может быть различной
в зависимости от последовательности
введения его в модель.

(слайд
4) Мерой
для оценки включения фактора в модель
служит частный
F-критерий
(оценивает статистическую значимость
присутствия каждого из факторов в
уравнении):

,

где
—
коэффициент множ. детерминации для
модели с полным

набором
факторов;

—
тот же показатель, но без включения в
модель фактора х1;

n
– число наблюдений;

m
– число параметров при переменных х.

Если фактическое
значение F
превышает табличное, то дополнительное
включение в модель фактора xi
статистически оправдано и коэффициент
чистой регрессии bi
при факторе xi
статистически значим.

Если же фактическое
значение F
меньше табличного, то нецелесообразно
включать в модель дополнительный фактор,
поскольку он не увеличивает существенно
долю объясненной вариации результата,
а коэффициент регрессии при данном
факторе статистически не значим.

(слайд
5) Частный
F-критерий
оценивает значимость коэффициентов
чистой регрессии. Зная величину
,
можно определить и t-критерий
Стьюдента:

или

где m_bi
– средняя квадратическая ошибка
коэффициента регрессии b_i,
она может быть определена по формуле:

.

Величина
стандартной ошибки совместно с
t-распределением Стьюдента при n-m-1
степенях свободы применяется для
проверки значимости коэффициента
регрессии и для расчета его доверительного
интервала.

Соседние файлы в папке Эконометрика

• #
• #
• #
• #
• #
• #
• #
• #

Вариант 1

Задание 1. Модель парной линейной регрессии.

Имеются данные о размере среднемесячных доходов в разных группах семей

Номер группы	Среднедушевой денежный доход в месяц, руб., X	Доля оплаты труда в структуре доходов семьи, %, Y
1	79,8	64,2
2	152,1	66,1
3	199,3	69,0
4	240,8	70,6
5	282,4	72,4
6	301,8	74,3
7	385,3	76,0
8	457,8	77,1
9	577,4	78,4

Задания:

1. Рассчитать линейный коэффициент парной корреляции, оценить его статистическую значимость и построить для него доверительный интервал с уровнем значимости a =0,05. Сделать выводы

2. Построить линейное уравнение парной регрессии Y на X и оценить статистическую значимость параметров регрессии. Сделать рисунок.

3. Оценить качество уравнения регрессии при помощи коэффициента детерминации. Сделать выводы. Проверить качество уравнения регрессии при помощи F-критерия Фишера.

4. Выполнить прогноз доли оплаты труда структуре доходов семьи Y при прогнозном значении среднедушевого денежного дохода X, составляющем 111% от среднего уровня. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал для уровня значимости a =0,05. Сделать выводы.

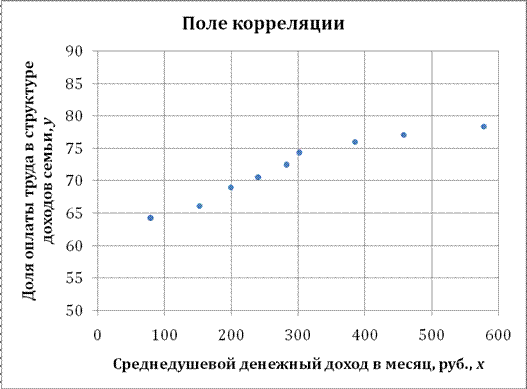
Решение: Построим поле корреляции зависимости доли оплаты труда в структуре доходов семьи от среднедушевого денежного дохода в месяц.

Точки на построенном графике размещаются вблизи кривой, напоминающей по форме Прямую, поэтому можно предположить, что между указанными величинами существует Линейная зависимость вида .

Для расчета линейного коэффициента парной корреляции и параметров линейной регрессии составим вспомогательную таблицу.

№ п/п	X	Y	X×Y	X2	Y2
1	79,8	64,2	5123,16	6368,04	4121,64
2	152,1	66,1	10053,81	23134,41	4369,21
3	199,3	69,0	13751,70	39720,49	4761,00
4	240,8	70,6	17000,48	57984,64	4984,36
5	282,4	72,4	20445,76	79749,76	5241,76
6	301,8	74,3	22423,74	91083,24	5520,49
7	385,3	76,0	29282,80	148456,09	5776,00
8	457,8	77,1	35296,38	209580,84	5944,41
9	577,4	78,4	45268,16	333390,76	6146,56
S	2676,7	648,1	198645,99	989468,27	46865,43
Среднее	297,41	72,01	22071,78	109940,92	5207,27

Вычислим коэффициент корреляции. Используем следующую формулу:

= 0,9568.

Можно сказать, что между рассматриваемыми признаками существует Прямая тесная Корреляционная связь.

Среднюю ошибку коэффициента корреляции определим по формуле:

= 0,032.

Найдем табличное значение TТабл по таблице распределения Стьюдента для
a = 0,05 и числе степеней свободы K = N – M – 1 = 9 – 1 – 1 = 7.

TТабл(0,05; 7) = 2,36.

Запишем доверительный интервал для коэффициента корреляции.

Доверительный интервал не включает число 0, поэтому при заданном уровне значимости коэффициент корреляции является статистически значимым.

Вычислим параметры уравнения регрессии.

= 0,03.

= 72,01 – 0,03×297,41 = 63,09.

Получим следующее уравнение: .

Для проверки статистической значимости (существенности) линейного коэффициента парной корреляции рассчитаем T-критерий Стьюдента по формуле:

= 23,04.

Фактическое значение по абсолютной величине больше табличного, что свидетельствует о значимости линейного коэффициента корреляции и существенности связи между рассматриваемыми признаками.

Проверим значимость оценок теоретических коэффициентов регрессии с помощью t-статистики Стьюдента и сделаем соответствующие выводы о значимости этих оценок.

Для определения статистической значимости коэффициентов A и B найдем T-статистики Стьюдента:

Рассчитаем по полученному уравнению теоретические значения. Составим вспомогательную таблицу.

№ п/п	X	Y
1	79,8	64,2	65,48	1,6384	47354,1
2	152,1	66,1	67,65	2,4025	21115,0
3	199,3	69,0	69,07	0,0049	9625,6
4	240,8	70,6	70,31	0,0841	3204,7
5	282,4	72,4	71,56	0,7056	225,3
6	301,8	74,3	72,14	4,6656	19,3
7	385,3	76,0	74,65	1,8225	7724,7
8	457,8	77,1	76,82	0,0784	25725,0
9	577,4	78,4	80,41	4,0401	78394,4
S	2676,7	648,1	648,09	15,4421	193388,1

Вычислим стандартные ошибки коэффициентов уравнения.

= 1,2.

= 0,003.

Вычислим T-статистики.

Сравнение расчетных и табличных величин критерия Стьюдента показывает, что и , т. е. оценки A и B теоретических коэффициентов регрессии статистически значимы.

Сделаем рисунок.

Рассчитаем коэффициент детерминации: = 0,95682= 0,915 = 91,5%.

Таким образом, вариация результата Y на 91,5% объясняется вариацией фактора X.

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

= 75,81.

Найдем табличное значение Fтабл по таблице критических точек Фишера для
a = 0,05; K1 = M = 1 (число факторов), K2 = N – M – 1 = 9 – 1 – 1 = 7.

Fтабл(0,05; 1; 7) = 5,59.

Поскольку F > FТабл, уравнение регрессии с вероятностью 0,95 в целом Является статистически значимым.

Выполним прогноз доли оплаты труда структуре доходов семьи y при прогнозном значении среднедушевого денежного дохода x, составляющем 111% от среднего уровня.

XP = 297,41 × 1,11 = 330,1.

Вычислим прогнозное значение Yp с помощью уравнения регрессии.

» 73%.

Доверительный интервал прогноза имеет вид

(УP – Tкр×My, УP + Tкр×My),

Где , M = 2 – число параметров уравнения.

= 1,695 » 1,7.

Запишем доверительный интервал прогноза:

Þ

Данный прогноз является надежным, поскольку доверительный интервал не включает число 0, точность прогноза составляет 4.

Задание 2. Модель парной нелинейной регрессии.

По территориям Центрального района известны данные за 1995 г.

Район	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб., X	Средний размер назначенных ежемесячных пенсий, тыс. руб., Y
Брянская обл.	178	240
Владимирская обл.	202	226
Ивановская обл.	197	221
Калужская обл.	201	226
Костромская обл.	189	220
Орловская обл.	166	232
Рязанская обл.	199	215
Смоленская обл.	180	220
Тверская обл.	181	222
Тульская обл.	186	231
Ярославская обл.	250	229

Задания:

1. Построить поле корреляции и сформулируйте гипотезу о форме связи. Рассчитать параметры уравнений полулогарифмической () и степенной () парной регрессии. Сделать рисунки.

2. Дать с помощью среднего коэффициента эластичности сравнительную оценку силы связи фактора с результатом для каждой модели. Сделать выводы. Оценить качество уравнений регрессии с помощью средней ошибки аппроксимации и коэффициента детерминации. Сделать выводы.

3. По значениям рассчитанных характеристик выбрать лучшее уравнение регрессии. Дать экономический смысл коэффициентов выбранного уравнения регрессии

4. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a =0,05. Сделать выводы.

Решение: Решение: Для предварительного определения вида связи между указанными признаками построим поле корреляции. Для этого построим в системе координат точки, у которых первая координата X, а вторая – Y.

Получим следующий рисунок.

По внешнему виду диаграммы рассеяния трудно предположить, какая зависимость существует между указанными показателями.

Построение полулогарифмической модели регрессии.

Уравнение логарифмической кривой: .

Обозначим:

Получим линейное уравнение регрессии:

Y = A + B×X.

Произведем линеаризацию модели путем замены . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Xy	X2	Y2				Ai
1	178	240	5,1818	1243,63	26,85	57600	226,40	206,314	184,904	6,006
2	202	226	5,3083	1199,67	28,18	51076	225,17	0,132	0,694	0,370
3	197	221	5,2832	1167,59	27,91	48841	225,41	21,496	19,464	1,957
4	201	226	5,3033	1198,55	28,13	51076	225,22	0,132	0,615	0,348
5	189	220	5,2417	1153,18	27,48	48400	225,82	31,769	33,833	2,576
6	166	232	5,1120	1185,98	26,13	53824	227,08	40,496	24,172	2,165
7	199	215	5,2933	1138,06	28,02	46225	225,31	113,132	106,362	4,577
8	180	220	5,1930	1142,45	26,97	48400	226,29	31,769	39,601	2,781
9	181	222	5,1985	1154,07	27,02	49284	226,24	13,223	17,968	1,874
10	186	231	5,2257	1207,15	27,31	53361	225,97	28,769	25,273	2,225
11	250	229	5,5215	1264,41	30,49	52441	223,09	11,314	34,980	2,651
Итого	2129	2482	57,862	13054,74	304,48	560528	2482,00	498,545	487,867	27,530
Среднее	193,5	225,6	5,260	1186,79	27,68	50957,091	225,636	45,322	44,352	2,503

= -9,76.

= 225,6 – (-9,76)×5,26 = 276,99.

Уравнение модели имеет вид:

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,14642= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Рассчитаем средний коэффициент эластичности по формуле:

= -0,04%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,04%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид: .

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

.

Произведем линеаризацию модели путем замены и . В результате получим линейное уравнение .

Рассчитаем его параметры, используя данные таблицы.

№ п/п	X	Y	X = ln(X)	Y = ln(Y)	XY	X2	Y2					Ai
1	178	240	5,1818	5,4806	28,3995	26,851	30,037	226,3	206,3	188,391	241,661	6,07
2	202	226	5,3083	5,4205	28,7737	28,178	29,382	225,1	0,132	0,835	71,479	0,406
3	197	221	5,2832	5,3982	28,5196	27,912	29,140	225,3	21,496	18,671	11,934	1,918
4	201	226	5,3033	5,4205	28,7467	28,125	29,382	225,1	0,132	0,753	55,570	0,385
5	189	220	5,2417	5,3936	28,2720	27,476	29,091	225,7	31,769	32,607	20,661	2,530
6	166	232	5,1120	5,4467	27,8437	26,132	29,667	226,9	40,496	25,675	758,752	2,233
7	199	215	5,2933	5,3706	28,4284	28,019	28,844	225,2	113,132	104,576	29,752	4,540
8	180	220	5,1930	5,3936	28,0089	26,967	29,091	226,2	31,769	38,059	183,479	2,728
9	181	222	5,1985	5,4027	28,0858	27,024	29,189	226,1	13,223	16,950	157,388	1,821
10	186	231	5,2257	5,4424	28,4407	27,308	29,620	225,9	28,769	26,413	56,934	2,275
11	250	229	5,5215	5,4337	30,0021	30,487	29,525	223,1	11,314	34,846	3187,116	2,646
Итого	2129	2482	57,862	59,603	313,521	304,479	322,969	2480,927	498,545	487,777	4774,727	27,548
Среднее	193,5	225,6	5,260	5,418	28,502	27,680	29,361	225,539	45,322	44,343	434,066	2,504

С учетом введенных обозначений уравнение примет вид: Y = A + BX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы.

= -0,042.

= 5,418 – 0,959×5,26 = 5,637.

Перейдем к исходным переменным X и Y, выполнив потенцирование данного уравнения.

A = eA = e5,637 = 280,76

Получим уравнение степенной модели регрессии: .

Определим индекс корреляции

Используя данные таблицы, получим:

.

Рассчитаем коэффициент детерминации: = 0,1472= 0,021 = 2,1%.

Вариация результата Y всего на 2,1% объясняется вариацией фактора X.

Сделаем рисунок.

Для степенной модели средний коэффициент эластичности равен коэффициенту B.

= -0,042%.

Коэффициент эластичности показывает, что при среднем росте признака X на 1% признак Y снижается на 0,042%.

Вычислим среднюю ошибку аппроксимации. Используя данные расчетной таблицы, получаем:

= 2,5%.

Сводная таблица вычислений

Параметры	Модель
Полулогарифмическая	Степенная
Уравнение связи
Индекс корреляции	0,1464	0,147
Коэффициент детерминации	0,021	0,021
Средняя ошибка аппроксимации, %	2,5	2,5

Для выявления формы связи между указанными признаками были построены полулогарифмическая и степенная модели регрессии. Анализ показателей корреляции, а также оценка качества моделей с использованием средней ошибки аппроксимации позволил предположить, что из перечисленных моделей более адекватной является степенная модель, поскольку для нее индекс корреляции принимает наибольшее значение R = 0,147, свидетельствующий о том, что между рассматриваемыми признаками наблюдается Слабая корреляционная связь.

Рассчитаем прогнозное значение результата по степенной модели регрессии, если прогнозируется увеличение значения фактора на 10% от среднего уровня.

Прогнозное значение составит:

= 193,5 × 1,1 = 212,9 тыс. р., тогда прогнозное значение Y составит:

= 224,6 тыс. р.

Определим доверительный интервал прогноза для уровня значимости a = 0,05.

Вычислим Среднюю стандартную ошибку прогноза По следующей формуле:

, где

Получаем: = 7,55.

Найдем предельную ошибку прогноза , где для доверительной вероятности 0,95 значение T составляет 1,96.

= 14,8.

Запишем доверительный интервал прогноза.

= 224,6 – 14,8 = 209,8 тыс. р.

= 224,6 + 14,8 = 239,4 тыс. р.

Таким образом, с вероятностью 0,95 можно утверждать, что прогнозное значение среднего размера назначенных ежемесячных пенсий будет находиться в пределах от 209,8 тыс. р. до 239,4 тыс. р.

Задание 3. Моделирование временных рядов

Имеются поквартальные данные по розничному товарообороту России в 1995-1999 гг.

Номер квартала	Товарооборот % к предыдущему периоду	Номер квартала	Товарооборот % к предыдущему периоду
1	100	11	98,8
2	93,9	12	101,9
3	96,5	13	113,1
4	101,8	14	98,4
5	107,8	15	97,3
6	96,3	16	112,1
7	95,7	17	97,6
8	98,2	18	93,7
9	104	19	114,3
10	99	20	108,4

Задания:

1. Построить график данного временного ряда. Охарактеризовать структуру этого ряда.

2. Рассчитать сезонную компоненты временного ряда и построить его Мультипликативную Модель.

3. Рассчитать трендовую компоненту временного ряда и построить его график

4. Оценить качество модели через показатели средней абсолютной ошибки и среднего относительного отклонения.

Решение: Пронумеруем указанные месяцы от 1 до 24 и построим график временного ряда.

Полученный график показывает, что а данном временном ряду присутствуют сезонные колебания.

Построим мультипликативную модель временного ряда.

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (T), сезонной (S) и случайной (E) компонент.

Построение мультипликативной моделей сведем к расчету значений T, S и E для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1)  Выравнивание исходного ряда методом скользящей средней.

2)  Расчет значений сезонной компоненты S.

3)  Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных T×E.

4)  Аналитическое выравнивание уровней T×E и расчет значений T с использованием полученного уравнения тренда.

5)  Расчет полученных по модели значений T×E.

6)  Расчет абсолютных и/или относительных ошибок.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1.1. Просуммируем уровни ряда последовательно за каждые четыре месяца со сдвигом на один момент времени и определим условные годовые уровни объема продаж (гр. 3 табл. 2.1).

1.2. Разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл. 2.1). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

1.3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние (гр. 5 табл. 2.1).

Таблица 2.1

№ месяца, T	Товарооборот, Yi	Итого за четыре месяца	Скользящая средняя за четыре месяца	Центрированная скользящая средняя	Оценка сезонной компоненты
1	2	3	4	5	6
1	100,0	–	–	–	–
2	93,9	392	98	–	–
3	96,5	400	100	99	0,975
4	101,8	402	100,5	100,25	1,015
5	107,8	402	100,5	100,5	1,073
6	96,3	398	99,5	100	0,963
7	95,7	394	98,5	99	0,967
8	98,2	397	99,25	98,875	0,993
9	104,0	400	100	99,625	1,044
10	99,0	404	101	100,5	0,985
11	98,8	413	103,25	102,125	0,967
12	101,9	412	103	103,125	0,988
13	113,1	411	102,75	102,875	1,099
14	98,4	309	77,25	90	1,093
15	97,3	196	49	63,125	1,541
16	112,1	303	75,75	62,375	1,797
17	97,6	418	104,5	90,125	1,083
18	93,7	414	103,5	104	0,901
19	114,3	–	–	–	–
20	108,4	–	–	–	–

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 2.1). Эти оценки используются для расчета сезонной компоненты S (табл. 2.2). Для этого найдем средние за каждый месяц оценки сезонной компоненты Si. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.

Таблица 2.2

Показатели	Год	№ квартала, I
I	II	III	IV
	1	–	–	0,975	1,015
	2	1,073	0,963	0,967	0,993
	3	1,044	0,985	0,967	0,988
	4	1,099	1,093	1,541	1,797
	5	1,083	0,901	–	–
Всего за I-й квартал		4,299	3,942	4,45	4,793
Средняя оценка сезонной компоненты для I-го квартала,		0,860	0,788	0,890	0,959
Скорректированная сезонная компонента,		0,984	0,901	1,018	1,097

Имеем: 0,860 + 0,788 + 0,890 + 0,959 = 3,497.

Определяем корректирующий коэффициент: K = 4 : 3,497 = 1,144.

Скорректированные значения сезонной компоненты получаются при умножении ее средней оценки на корректирующий коэффициент K.

Проверяем условие: равенство 4 суммы значений сезонной компоненты:

0,984 + 0,901 + 1,018 + 1,097 = 4.

Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины (гр. 4 табл. 2.3), которые содержат только тенденцию и случайную компоненту.

Таблица 2.3

T	Yt	St		T	T×S
1	2	3	4	5	6	7
1	100,0	0,984	101,6	100,02	98,42	1,016
2	93,9	0,901	104,2	100,19	90,27	1,040
3	96,5	1,018	94,8	100,36	102,17	0,945
4	101,8	1,097	92,8	100,53	110,28	0,923
5	107,8	0,984	109,6	100,7	99,09	1,088
6	96,3	0,901	106,9	100,87	90,88	1,060
7	95,7	1,018	94,0	101,04	102,86	0,930
8	98,2	1,097	89,5	101,21	111,03	0,884
9	104,0	0,984	105,7	101,38	99,76	1,043
10	99,0	0,901	109,9	101,55	91,50	1,082
11	98,8	1,018	97,1	101,72	103,55	0,954
12	101,9	1,097	92,9	101,89	111,77	0,912
13	113,1	0,984	114,9	102,06	100,43	1,126
14	98,4	0,901	109,2	102,23	92,11	1,068
15	97,3	1,018	95,6	102,4	104,24	0,933
16	112,1	1,097	102,2	102,57	112,52	0,996
17	97,6	0,984	99,2	102,74	101,10	0,965
18	93,7	0,901	104,0	102,91	92,72	1,011
19	114,3	1,018	112,3	103,08	104,94	1,089
20	108,4	1,097	98,8	103,25	113,27	0,957
Среднее	101,4					1,0011

Шаг 4. Определим компоненту T в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни T×E. Составим вспомогательную таблицу.

Таблица 2.4

	T		T2
	1	2	3	4	5	6	7
	1	101,6	1	101,6	2,5	1,58	2,0
	2	104,2	4	208,4	13,2	3,87	56,3
	3	94,8	9	284,4	32,1	5,88	24,0
	4	92,8	16	371,2	71,9	8,33	0,2
	5	109,6	25	548	75,9	8,08	41,0
	6	106,9	36	641,4	29,4	5,63	26,0
	7	94,0	49	658	51,3	7,48	32,5
	8	89,5	64	716	164,6	13,07	10,2
	9	105,7	81	951,3	18,0	4,08	6,8
	10	109,9	100	1099	56,3	7,58	5,8
	11	97,1	121	1068,1	22,6	4,81	6,8
	12	92,9	144	1114,8	97,4	9,69	0,3
	13	114,9	169	1493,7	160,5	11,20	136,9
	14	109,2	196	1528,8	39,6	6,39	9,0
	15	95,6	225	1434	48,2	7,13	16,8
	20	102,2	400	2044	0,2	0,37	114,5
	21	99,2	441	2083,2	12,3	3,59	14,4
	22	104,0	484	2288	1,0	1,05	59,3
	23	112,3	529	2582,9	87,6	8,19	166,4
	24	98,8	576	2371,2	23,7	4,49	49,0
Сумма	230	2035,2	3670	23588	1008,3	122,49	778,2
Среднее	11,5	101,8	183,5	1179,4	50,4	6,12	38,91

Вычислим параметры уравнения тренда.

= 0,17.

= 99,85.

В результате получим уравнение тренда:

T = 99,85 + 0,17×T.

Подставляя в это уравнение значения T = 1,2,…,16, найдем уровни T для каждого момента времени (гр. 5 табл. 2.3).

Шаг 5. Найдем уровни ряда, умножив значения T на соответствующие значения сезонной компоненты (гр. 6 табл. 2.3). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.

Расчет ошибки в мультипликативной модели произведем по формуле:

Средняя абсолютная ошибка составила 1,0011 (см. гр. 7 табл. 2.3).

Рассчитаем сумму квадратов абсолютных ошибок .

Используя 5-й столбец таблицы 2.4, получим:

= 7,099.

Рассчитаем среднюю относительную ошибку: .

Используя 6-й столбец таблицы 2.4, получим, что средняя относительная ошибка составила 6,12%, т. е. построенная модель достаточно точно описывает динамику данного явления.

< Предыдущая		Следующая >

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

---

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

1. Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
2. Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
3. Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

---

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
2. Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
3. Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

---

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

1. Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
2. Находится сумма всех фактов по всем позициям  (общий фактический объем)
3. Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

---

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

1. Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
2. Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
3. Извлекаем корень из полученного результат — RMSE
4. Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
   1. Разделить на разницу между максимальным и минимальным значением показателей
   2. Разделить на разницу между третьим и первым квартилем значений показателей
   3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

---

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

---

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU