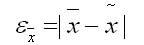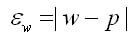Слайд 1 ЗИМНИЙ МАРШРУТНЫЙ
УЧЕТ
Инструкция
по проведению учета и расчету численности
учитываемых видов зверей и птиц на территории субъектов РФ

Слайд 2 Расчет нормативного объема учетных маршрутов
На исследуемой
территории площадью до 200 тыс. га определяется
не менее 35 учетных маршрутов общей протяженностью маршрутов не менее 350 км
На исследуемой территории площадью свыше 200 тыс. га определяется не менее 35 учетных маршрутов, общая протяженность которых определяется по следующей формуле:
D = 350 + (S – 200) * Ki
D – протяженность учетных маршрутов, км;
S – общая площадь исследуемой территории, тыс. га;
Кi – региональный коэффициент (1 или 0,1 для разных субъектов
определяется в соответствии с п.16 Методических указаний).

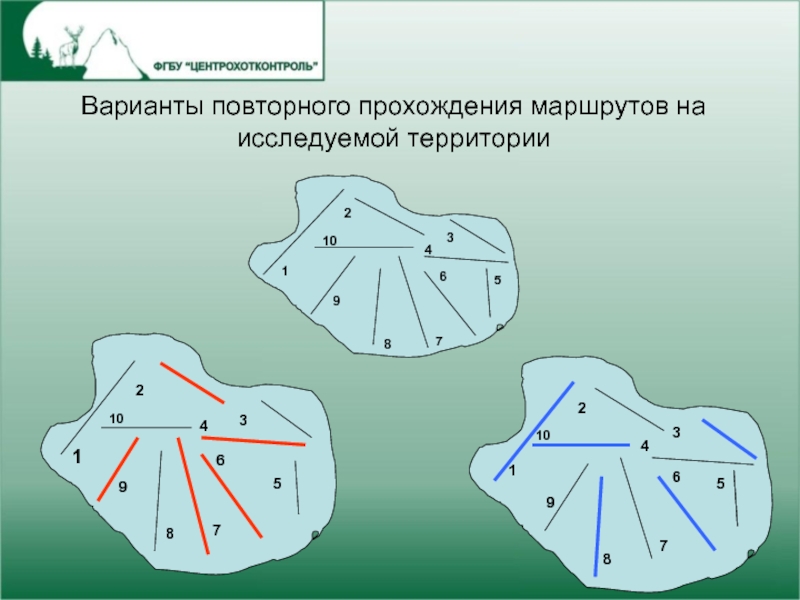
Слайд 3Варианты повторного прохождения маршрутов на исследуемой территории
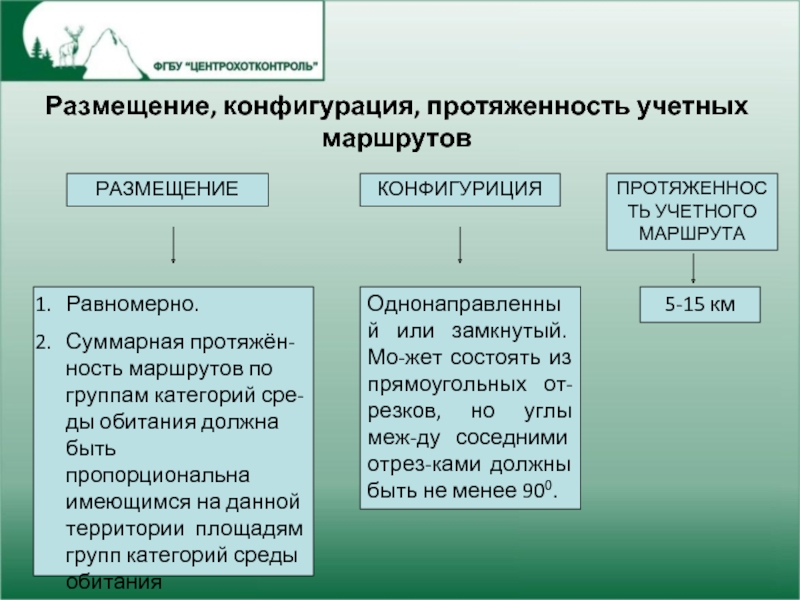
Слайд 4Размещение, конфигурация, протяженность учетных маршрутов
РАЗМЕЩЕНИЕ
КОНФИГУРИЦИЯ
ПРОТЯЖЕННОСТЬ УЧЕТНОГО МАРШРУТА
Равномерно.
Суммарная
протяжён-ность маршрутов по группам категорий сре-ды обитания
должна быть пропорциональна имеющимся на данной территории площадям групп категорий среды обитания
Однонаправленный или замкнутый. Мо-жет состоять из прямоугольных от-резков, но углы меж-ду соседними отрез-ками должны быть не менее 900.
5-15 км
Слайд 5 Составление экспликации площадей групп категорий среды
обитания
Категории распределяются в 3 группы
«лес»
«поле»
«болото»
Составление реестра
учётных маршрутов
В реестре учетных маршрутов указывается:
порядковый номер учетного маршрута,
общая протяженность и протяженность по группам категорий среды
обитания,
географические координаты начала, конца маршрута, а так же точек
поворота маршрута

Слайд 6Инструкция по проведению полевых учетных работ
Учет охотничьих
зверей
Учет проводится в один или в два
дня.
Обход препятствий не является отклонением от учетного маршрута.
Учет в один день (без затирки)
Проводится только в том случае, если накануне проведения учета выпал снег.
Между окончанием снегопада и началом учета должно пройти не менее 24 ± 4 часа.
Учёт на маршруте проводится на лыжах (пешком).
Для учета используется спутниковый навигатор, с помощью которого, фиксируются географические координаты начала, конца, точек поворота маршрута или записывается весь трек с указанием даты и времени создания координат маршрута.

Слайд 7Учет в два дня.
Первый день —
затирка следов.
Допускается затирка следов с использованием
транспортных средств (снегохода).
Второй день
Учет проводится на лыжах. Используется спутниковый навигатор
Фиксируются вновь появившиеся следы копытных и пушных животных.
Следы лося, благородного и пятнистого оленей, рыси, находящиеся на границе группы «ЛЕС» с другой группой категорий среды обитания на расстоянии порядка 100 м, относят к группе «ЛЕС».

Слайд 8
Учет охотничьих птиц ведется дважды:
в день затирки и в день учета.
Если затирка не проводилась, то один раз – в день учета следов.
При учете записываются:
вид птицы расстояние обнаружения
группу категорий среды обитания
Учету подлежат те птицы, которые:
выпорхнули из-под снега (спереди и (или) сбоку)
взлетели со снега,
слетели с дерева.
Птицы, взлетевшие сзади учетчика, а также обнаруженные летящими мимо, не регистрируются.
Учет охотничьих птиц

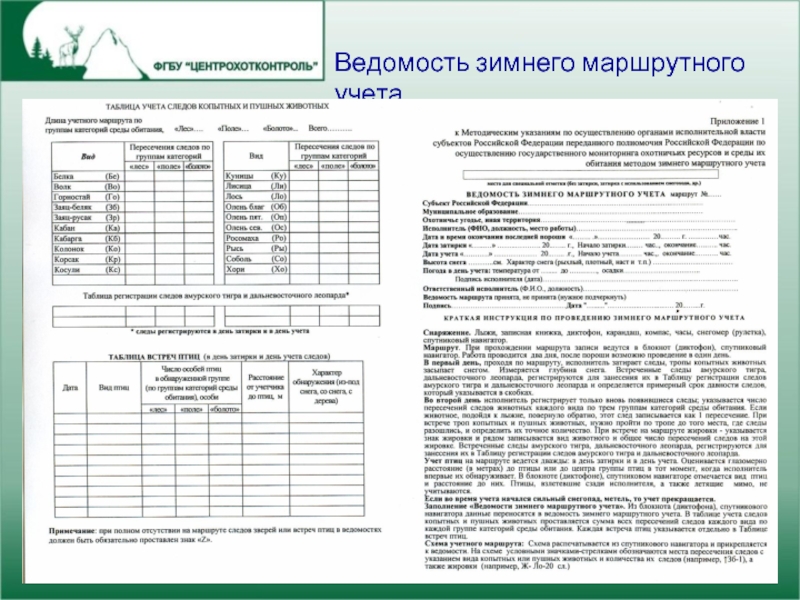
Слайд 9Ведомость зимнего маршрутного учета
Слайд 10Выбраковка (оценка качества) первичных материалов
и расчет численности
(по IV этапу)
Выбраковка проводится по следующим позициям:
«ведомость» заполнена с нарушениями требований, предусмотренными методикой,
учет проводился не через 24±4 часа после затирки (или окончания снега (пороши).
в «Ведомости» не все графы заполнены или в них содержатся ошибки.
в «Ведомости» отсутствует (не прилагается) схема учетного маршрута.
«Ведомости», в которых имеются исправления.

Слайд 11
Расчет численности
охотничьих животных
Полученные
результаты учета следов зверей и встреч птиц заносятся в ведомость расчета численности копытных и пушных животных и в ведомость расчета численности птиц.
Порядок расчета численности зверей
1. Показатель
учета
2.Плотность
населения
3.Численность
Статистическая
ошибка
показателя учета

Слайд 12Показатель учета
Расчет показателя учета данного вида по
данной группе категорий среды обитания производится по
формуле:
, где
Хru – суммарное число пересечений маршрутами следов зверей данного вида в данной группе категорий среды обитания, (количество следов);
Sru – суммарная протяженность маршрутов по данной группе категорий среды обитания, (км).

Слайд 13
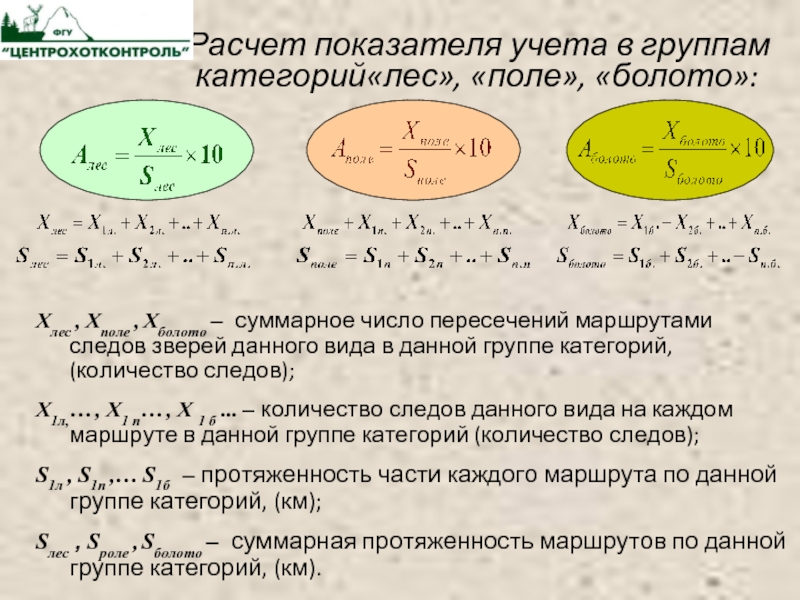
Расчет показателя учета в группам
категорий«лес», «поле», «болото»:
Хлес , Хполе , Хболото – суммарное число пересечений маршрутами следов зверей данного вида в данной группе категорий, (количество следов);
X1л,… , X1 п… , X 1 б … – количество следов данного вида на каждом маршруте в данной группе категорий (количество следов);
S1л , S1п ,… S1б – протяженность части каждого маршрута по данной группе категорий, (км);
Sлес , Sроле , Sболото – суммарная протяженность маршрутов по данной группе категорий, (км).
Слайд 14
Плотность населения
Расчет плотности населения данного
вида (особей/1000 га) в данной группе категорий
среды обитания
производится по формуле:
Dru= Aru×K , где
Аru – суммарное число пересечений маршрутами следов зверей данного вида в данной группе категорий среды обитания, (количество следов);
К – Пересчетный коэффициент для данного вида зверей выбирается из таблицы пересчетных коэффициентов Приложения Методики.

Слайд 15
Расчет плотности
населения данного вида в группе категорий «лес»:
Dлес = Aлес ×K , где
Aлес – показатель учета данного вида в «лесу»
Расчет плотности населения данного вида в группе категорий «поле»:
Dполе= Aполе×K , где
Aполе – показатель учета данного вида в «поле»
Расчет плотности населения данного вида в группе категорий «болото»:
Dболото= Aболото×K , где
Aболото – показатель учета данного вида по «болоту»

Слайд 16Численность населения
Расчет численности (особей) данного вида
охотничьих зверей в данной группе категорий среды
обитания:
Nru =Dru × Qru , где
Qru – площадь данной группы категорий среды обитания на исследуемой территории, (тыс.га).

Слайд 17
Расчет численности данного вида
в группе категорий:
«Лес»: Nлес=Dлес×Qлес ,
Qлес – площадь категории «лес»
«Поле»: Nполе=Dполе×Qполе ,
Qполе – площадь категории «поле»
«Болото»: Nболото=Dболото×Qболото ,
Qболото – площадь категории «болото»
Численность данного вида охотничьего ресурса на исследуемой территории складывается из показателей численности данного вида по «лесу», «полю», «болоту»: Nи = Nлес + Nполе + Nболото

Слайд 18Статистическая ошибка показателя учета
Статистическая ошибка показателя учета
рассчитывается для каждого вида зверя в каждой
категории среды обитания.
Расчет статистической ошибки показателя учета для данного вида зверя для данной группы категорий среды обитания.

Слайд 19Расчет статистической ошибки показателя учета
по«лесу»:
В развернутом виде формула расчета статистической ошибки
данного вида в данной группе категорий среды обитания «лесу» выглядит следующим образом:

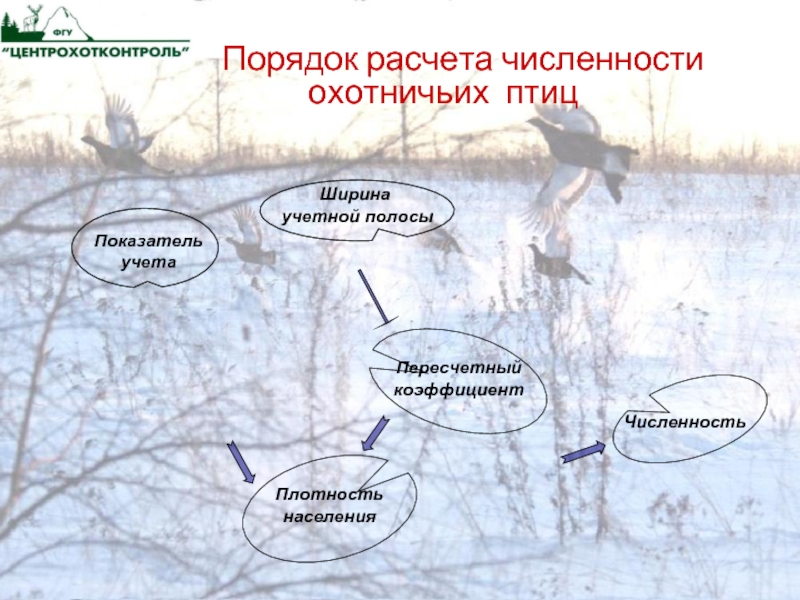
Слайд 20 Порядок расчета численности
охотничьих
птиц
Показатель
учета
Плотность
населения
Численность
Ширина
учетной полосы
Пересчетный
коэффициент
Слайд 21Показатель учета
Расчет показателя учета данного вида птиц
по данной группе категорий среды обитания производится
по формуле:
,
Yruj – число птиц, зарегистрированных на части данного маршрута, проходящей по данной группе категорий среды обитания, (особей).
Еruj – длина части маршрута, проходящего по данной группе категорий среды обитания (если учет проведен в два дня, т.е. учет проведен с затиркой, то соответствующая длина удваивается), (км).
Еru – суммарная длина частей всех маршрутов, проходящих по данной группе категорий среды обитания, (км).
Mr – количество учетных маршрутов на исследуемой территории (штук).

Слайд 22 Ширина учетной полосы
Для каждого вида птиц
в каждой группе категорий среды обитания ширина
учетной полосы (Bu) рассчитывается по формуле:
, где
Gu – общее число птиц одного вида, обнаруженное на всей обследуемой территории в данной группе категорий среды обитания, (особей);
Gui – число птиц при каждой встрече, (особей).
Rui –расстояние обнаружения каждой птицы (группы птиц) в данной группе категорий среды обитания, (м).
Gui1…Gui n – число птиц (одиночной или группы) данного вида в каждой встрече при учете или затирке на отрезке маршрута, проходящего по данной группе категорий среды обитания, (особей);
Rui1…Rui n — расстояние обнаружения каждой встреченной группы птиц или одиночной птицы при учете или затирки на отрезке маршрута, проходящего по данной группе категорий среды обитания, (м).
Т – количество маршрутов

Слайд 23
Пересчетный коэффициент
Пересчетный коэффициент для данного вида птиц
для данной группы категорий среды обитания можно рассчитать по формуле:
Ku=500 / Bu
Bu – ширина учетной полосы для данного вида птиц в данной категории среды обитания, м
Плотность населения птиц
Плотность населения птиц каждого вида (особей/1000 га) для каждой группы категорий среды обитания рассчитывается по формуле:
Dru=Aru× Kи

Слайд 24Численность
Численность данного вида птиц в данной группе
категорий среды обитания рассчитывается по формуле:
Nru=Dru×Qru ,
где
Qru – площадь данной группы категорий среды обитания, тыс.га.
Численность данного вида птицы на исследуемой территории получается суммированием показателей численности, рассчитанных по каждой группе категорий среды обитания («лес», «поле», «болото»):

Слайд 25ПРИМЕРЫ ПРИМЕНЕНИЯ ДАННЫХ,
ПОЛУЧЕННЫХ МЕТОДОМ
ЗМУ

Статистические ошибки
Использование
методов биометрии позволяет исследователю
на ограниченном по численности материале
делать заключения о проявлении признака,
его изменчивости и других параметрах
в генеральной совокупности. Но так
как выборочная совокупность — часть
генеральной и ее формируют методом
случайного отбора, то в выборку могут
попасть животные с более низкими
продуктивными качествами, или несколько
лучшие особи. В этом случае вычисленные
значения M, б, Cv и
других биометрических величин будут
отличаться от значений этих величин в
генеральной совокупности, то есть
выборка отражает генеральную совокупность
с ошибкой. Эти ошибки, связанные с
методом выборочности, называются
статистическими и устранить их нельзя.
Ошибки не будет лишь в том случае, когда
в обработку включаются все члены
генеральной совокупности. Величины
статистических ошибок зависят от
изменчивости признаков и объема выборки:
чем более изменчив признак, тем больше
ошибка, и чем больше объем выборки, тем
она меньше. Ошибки статистических
величин в биометрии принято обозначать
буквой m.
Ошибки
имеют все статистические величины.
Вычисляют их по формулам:
Все
ошибки измеряют в тех же единицах, что
и сами показатели, и записывают обычно
рядом с ними.
Статистические
ошибки указывают интервал, в котором
находится величина того или иного
статистического показателя в генеральной
совокупности. Зная среднее значение
признака (М) и его ошибку (m), можно
установить доверительные границы
средней величины в генеральной
совокупности по формуле: Мген.=Мв.
tm, где t — нормированное отклонение,
которое зависит от уровня вероятности
и объема выборки. Цифровое значение t
для каждого конкретного случая находят
с помощью специальной таблицы. Например,
нас интересует средняя частота пульса
у овец породы прекос. Для изучения этого
показателя была сформирована выборка
в количестве 50 голов и определена у
этих животных средняя частота пульса.
Оказалось, что этот показатель равен
75 ударов в минуту, изменчивость его б =
12 ударов. Ошибка средней арифметической
величины в этом случае составит:
б
12
m
= ──── = ──── = 1,7 (уд./мин).
n
50
Итоговая
запись будет иметь вид: М
m или 75
1,7, то есть частота пульса 75 ударов в
минуту — среднее значение для 50 голов.
Чтобы определить среднюю частоту пульса
в генеральной совокупности животных,
возьмем в качестве доверительной
вероятности P = 0,95. В этом случае, исходя
из таблицы, t = 2,01. Определим доверительные
границы частоты пульса в генеральной
совокупности M
tm.
75,0
+ 2,01 x 1,7 = 75,0 + 3,4 = 78,4 (уд./мин)
75,0
— 2,01 x 1,7 = 75,0 — 3,4 = 71,6 (уд./мин)
Таким
образом, средняя частота пульса для
генеральной совокупности будет в
пределах от 71,6 до 78,4 ударов в минуту.
Зная
величину статистических ошибок,
устанавливают также, правильно ли
выборочная совокупность отражает тот
или иной параметр генеральной, то есть
устанавливают критерий доверительности
выборочных величин.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статистическая погрешность — это та неопределенность в оценке истинного значения измеряемой величины, которая возникает из-за того, что несколько повторных измерений тем же самым инструментом дали различающиеся результаты. Возникает она, как правило, из-за того, что результаты измерения в микромире не фиксированы, а вероятностны. Она тесно связана с объемом статистики: обычно чем больше данных, тем меньше статистическая погрешность и тем точнее результат измерения. Среди всех типов погрешностей она, пожалуй, самая безобидная: понятно, как ее считать, и понятно, как с ней бороться.
Статистическая погрешность: чуть подробнее
Предположим, что ваш детектор может очень точно измерить какую-то величину в каждом конкретном столкновении. Это может быть энергия или импульс какой-то родившейся частицы, или дискретная величина (например, сколько мюонов родилось в событии), или вообще элементарный ответ «да» или «нет» на какой-то вопрос (например, родилась ли в этом событии хоть одна частица с импульсом больше 100 ГэВ).
Это конкретное число, полученное в одном столкновении, почти бессмысленно. Скажем, взяли вы одно событие и выяснили, что в нём хиггсовский бозон не родился. Никакой научной пользы от такого единичного факта нет. Законы микромира вероятностны, и если вы организуете абсолютно такое же столкновение протонов, то картина рождения частиц вовсе не обязана повторяться, она может оказаться совсем другой. Если бозон не родился сейчас, не родился в следующем столкновении, то это еще ничего не говорит о том, может ли он родиться вообще и как это соотносится с теоретическими предсказаниями. Для того, чтобы получить какое-то осмысленное число в экспериментах с элементарными частицами, надо повторить эксперимент много раз и набрать статистику одинаковых столкновений. Всё свое рабочее время коллайдеры именно этим и занимаются, они накапливают статистику, которую потом будут обрабатывать экспериментаторы.
В каждом конкретном столкновении результат измерения может быть разный. Наберем статистику столкновений и усредним по ней результат. Этот средний результат, конечно, тоже не фиксирован, он может меняться в зависимости от статистики, но он будет намного стабильнее, он не будет так сильно прыгать от одной статистической выборки к другой. У него тоже есть некая неопределенность (в статистическом анализе она так и называется: «неопределенность среднего»), но она обычно небольшая. Вот эта величина и называется статистической погрешностью измерения.
Итак, когда экспериментаторы предъявляют измерение какой-то величины, то они сообщают результат усреднения этой величины по всей набранной статистике столкновений и сопровождают его статистической погрешностью. Именно такие средние значения имеют физический смысл, только их может предсказывать теория.
Есть, конечно, и иной источник статистической погрешности: недостаточный контроль условий эксперимента при повторном измерении. Если в физике частиц этот источник можно попытаться устранить, по крайней мере, в принципе, то в других разделах естественных наук он выходит на первый план; например, в медицинских исследованиях каждый человек отличается от другого по большому числу параметров.
Как считать статистическую погрешность?
Существует теория расчета статистической погрешности, в которую мы, конечно, вдаваться не будем. Но есть одно очень простое правило, которое легко запомнить и которое срабатывает почти всегда. Пусть у вас есть статистическая выборка из N столкновений и в ней присутствует n событий какого-то определенного типа. Тогда в другой статистической выборке из N событий, набранной в тех же условиях, можно ожидать примерно n ± √n таких событий. Поделив это на N, мы получим среднюю вероятность встретить такое событие и погрешность среднего: n/N ± √n/N. Оценка истинного значения вероятности такого типа события примерно соответствует этому выражению.
Сразу же, впрочем, подчеркнем, что эта простая оценка начинает сильно «врать», когда количество событий очень мало. В науке обсчета маленькой статистики есть много дополнительных тонкостей.
Более серьезное (но умеренно краткое) введение в методы статистической обработки данных в применении к экспериментам на LHC см. в лекциях arXiv.1307.2487.
Именно поэтому эксперименты в физике элементарных частиц стараются оптимизировать не только по энергии, но и по светимости. Ведь чем больше светимость, тем больше столкновений будет произведено — значит, тем больше будет статистическая выборка. И уже это позволит сделать измерения более точными — даже без каких-либо улучшений в эксперименте. Примерная зависимость тут такая: если вы увеличите статистику в k раз, то относительные статистические погрешности уменьшатся примерно в √k раз.
Этот пример — некая симуляция того, как могло бы происходить измерение массы ρ-мезона свыше полувека назад, на заре адронной физики, если бы он был вначале обнаружен в процессе e+e– → π+π–. А теперь перенесемся в наше время.
Сейчас этот процесс изучен вдоль и поперек, статистика набрана огромная (миллионы событий), а значит, и масса ρ-мезона сейчас определена несравнимо точнее. На рис. 3 показано современное состояние дел в этой области масс. Если ранние эксперименты еще имели какие-то существенные погрешности, то сейчас они практически неразличимы глазом. Огромная статистика позволила не только измерить массу (примерно равна 775 МэВ с точностью в десятые доли МэВ), но и заметить очень странную форму этого пика. Такая форма получается потому, что практически в том же месте на шкале масс находится и другой мезон, ω(782), который «вмешивается» в процесс и искажает форму ρ-мезонного пика.
Другой, гораздо более реальный пример влияния статистики на процесс поиска и изучения хиггсовского бозона обсуждался в новости Анимации показывают, как в данных LHC зарождался хиггсовский сигнал.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
From Wikipedia, the free encyclopedia
«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.
Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.
Measurement errors can be divided into two components: random and systematic.[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.[citation needed]
Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.
Science and experiments[edit]
When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.
Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:
- Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
- Random error which may vary from observation to another.
Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.
Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.
Characterization[edit]
Measurement errors can be divided into two components: random error and systematic error.[2]
Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.
Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.
Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.
Sources[edit]
Sources of systematic error[edit]
Imperfect calibration[edit]
Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.
Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.
Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.
Quantity[edit]
Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.
Drift[edit]
Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.
If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.
Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.
Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.
Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.
Sources of random error[edit]
The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.
Surveys[edit]
The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).[4][5]
These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.[7][8]
Effect on regression analysis[edit]
If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R2 will be lower than it would be with perfect measurement.
However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.[9]: p. 187 This is known as attenuation bias.[10]
See also[edit]
- Bias (statistics)
- Cognitive bias
- Correction for measurement error (for Pearson correlations)
- Errors and residuals in statistics
- Error
- Replication (statistics)
- Statistical theory
- Metrology
- Regression dilution
- Test method
- Propagation of uncertainty
- Instrument error
- Measurement uncertainty
- Errors-in-variables models
- Systemic bias
References[edit]
- ^ a b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
- ^ a b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
- ^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
- ^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
- ^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
- ^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
- ^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
- ^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199.
The bias generated by this sort of measurement error in regressors is called attenuation bias.
Further reading[edit]
- Cochran, W. G. (1968). «Errors of Measurement in Statistics». Technometrics. 10 (4): 637–666. doi:10.2307/1267450. JSTOR 1267450.
Опираясь на статистику легко лгать,
но без статистики очень трудно выяснить истину.
В любом научном исследовании главное — это полученные результаты. Однако, для того чтобы из них можно было сделать выводы, требуется статистическая обработка полученных данных.
Для тех, кто хорошо разбирается в математике, статистика не вызывает серьезных затруднений. Тем не менее разнообразные исследования показывают, что значительная доля научных публикаций содержит те или иные статистические ошибки. Об ошибках при переводе научных работ читайте в статье.
В. Джонсон из Техасского университета считает, что плохая статистика является одной из главных причин недостаточной воспроизводимости результатов в психологических исследованиях.
В этой статье мы расскажем о часто встречающихся ошибках статистического анализа и о том, как их избежать. С полезными сервисами для авторов можно ознакомиться здесь.
Содержание статьи
- 1. Сколько вешать в граммах?
- 2. Разбивка непрерывных данных на группы.
- 3. Среднее и сигмальное отклонение, медиана и доверительный интервал.
- 4. p-критерий.
- 5. Адекватность модели.
- 6. Понятие нормы.
- 7. Учет сомнительных и неопределенных результатов.
- 8. Понятие объекта исследования.
- 9. Статистическая значимость полученных результатов.
- 10. Влияние факторов риска.
- Заключение
1. Сколько вешать в граммах?
Любой ученый дорожит полученными результатами. Каждая цифра представляется нам достаточно значимой, чтобы представить ее в том виде, в котором она была получена. Получили вес 60,245 кг — так и запишем. Часто кажется, что, округляя данные, мы обесцениваем собственный труд.
Однако, с точки зрения читателя излишняя точность скорее мешает. Цифры с длинными хвостами трудно воспринимать и оценивать. Если их можно округлить без ущерба для точности выводов, нужно это сделать. Например, ни для каких целей нет смысла указывать вес взрослого человека с точностью до грамма.
Учитывайте при округлении точность приборов. Если весы дают погрешность более 100 граммов, указывать десятые доли килограмма не стоит.
При округлении процентов в научных статьях рекомендуется использовать следующие правила: если выборка больше 1 000, результат округляется до сотых; от 100 до 1 000 – до десятых; от 20 до 100 – до целых значений процентов. Для выборки менее 20, лучше дать абсолютные значения. В маленьких группах проценты скорее запутывают читателя и часто выглядят курьезно: в результате лечения 33, 333% животных выздоровели; 33, 333% погибли; третья мышь убежала.
Количество знаков после запятой должно быть одинаковым во всей статье. Если все результаты округляются до сотых, а какой-то из них имеет вид целого числа, то его нужно записать так же, как все остальные цифры, например 24,00.
2. Разбивка непрерывных данных на группы.
Такие данные, как рост, вес или возраст часто делят на категории. Разбивка упрощает статистический анализ, но в любом случае необходимо обосновать принципы, по которым это сделано.
Деление на категории может приводить к некорректным выводам. Например, если выборку разделили на пациентов с нормальной массой тела, дефицитом и избытком массы, то различия между людьми с весом 80 и 150 килограммов могут быть больше, чем между людьми с весом 70 и 80 килограммов, хотя в первом случае они входят в одну группу (с избытком массы), а во втором — в разные.
3. Среднее и сигмальное отклонение, медиана и доверительный интервал.
Представление в статье только средних групповых значений без учета индивидуальных различий может приводить к неверным выводам. Пресловутая средняя температура по больнице не дает представления не только обо всех пациентах, но даже о большинстве из них.
Средняя величина и среднее квадратическое отклонение или сигмальное отклонение δ (standard deviation — sd) описывают вариабельность выборки.
Среднее квадратическое отклонение применяется только в случае нормального распределения данных, то есть когда 68% показателей находятся в пределах ±1δ, 95% в пределах ±2δ, и 99% в пределах ±3δ.
При асимметричном распределении данных среднее квадратическое отклонение не дает правильного представления о выборке. В этом случае используется медиана median и межквартильный диапазон interquartile range (IQR) (как правило, от 25 до 75 центиля).
Точечные данные характеризуют такие показатели, как стандартная ошибка среднего и доверительный интервал.
Стандартная ошибка среднего standard error of the mean (m) показывает отличие фактических данных от значений, полученных на модели. Она позволяет оценить точность модели.
Доверительный интервал confidence interval (CI) демонстрирует, насколько выборка отражает свойства генеральной совокупности. В медицинских исследованиях обычно указывают 95% доверительный интервал.
Средняя величина, указанная без доверительного интервала, не дает полного и правильного представления о полученном эффекте. Например, если среднее снижение артериального давления 20 мм. рт. ст., эффект может показаться клинически значимым. Однако при 95% доверительном интервале от 5 до 30 мм. рт. ст. целесообразность применяемой схемы лечения уже представляется сомнительной, так как снижение показателя на 5 мм. рт. ст. клинически несущественно. Окончательный вывод о целесообразности изучаемой схемы лечения из этих результатов сделать нельзя.
Важно: в медицинских исследованиях результаты, подчиняющиеся нормальному распределению, встречаются довольно редко. Кроме того, средняя величина и среднее квадратическое отклонение плохо работают на малых выборках.
4. p-критерий.
Критерий р недостаточно информативен в медицинских и биологических исследованиях.
Дело в том, что статистическая значимость не равна клиническому значению и целесообразности использования тех или иных выводов на практике. Решение о рациональности использования препарата не может опираться только на статистическую значимость полученного клинического эффекта. Например, статистически значимое снижение артериального давления на 10 мм. рт. ст. клинически можно расценивать как отсутствие эффекта.
р-критерий не может равняться нулю. Это значило бы, что между группами есть действительно достоверное различие. Однако, такое различие невозможно установить методами статистики. Обычно эта ошибка связана с тем, что программы для статистической обработки данных приводят очень малые значения как р=0,00000. На самом деле это означает p<0,000001, что и должно быть указано в статье.
р-критерий не применяется к генеральной совокупности. Он показывает, что имеющиеся различия не являются случайностью и такой же результат может быть получен на другой выборке. В случае генеральной совокупности этот показатель не имеет смысла, так как речь о случайности различий не идет.
Если в исследовании участвует несколько групп, определение нескольких p-критериев повышает вероятность принять случайное совпадение фактов за причинно-следственную связь. Существует несколько методов решения проблемы множественных сравнений, их использование должно быть обосновано и описано.
В рандомизированных клинических исследованиях р-критерий указывать необязательно, так как исходные различия между группами всегда имеют место в силу случайности выбора.
5. Адекватность модели.
Регрессионные модели не работают, если зависимость между переменными не имеет линейного характера.
Чтобы подтвердить или опровергнуть линейный характер связи между величинами, нужно изучить остатки residuals, то есть отклонение реальных данных от линии регрессии, построенной на основании модели.
Регрессионная модель хорошо объясняет реальное положение дел, если остатки:
- независимы
- подчиняются нормальному распределению
- имеют нулевое среднее
- в их величинах нет тренда
Дисперсия остатков variance of the residuals показывает те изменения полученных данных, которые не объясняются моделью. Чем меньше дисперсия, тем лучше работает модель.
6. Понятие нормы.
Отсутствие четкого понимания, что следует принять за норму является серьезным недостатком клинических исследований.
Для определения нормы существует несколько подходов:
- результат говорит о наличии или отсутствии заболевания
- является показанием к назначению лечения
- указывает на риск развития болезни
- встречается у здоровых лиц
- укладывается в определенный диапазон значений
Далеко не во всех случаях норма клинически значима. Например, несовпадение индивидуальных сроков прорезывания зубов с нормальными, как правило, ни о чем не говорит.
Причины, по которым тот или иной показатель принят за норму, должны быть обоснованы.
7. Учет сомнительных и неопределенных результатов.
В медицинских и клинических исследованиях не всегда ясно, как учитываются сомнительные результаты при определении чувствительности и специфичности тестов. При наличии значительного процента сомнительных результатов практическая значимость выводов снижается.
Результат нельзя однозначно оценить как отрицательный или положительный если:
- получены пограничные значения показателя;
- интенсивность окрашивания препарата недостаточная;
- ответы на вопросы психологических тестов неоднозначные;
- нарушены стандарты при проведении исследования.
Если в статистический анализ включены не все результаты и не все участники исследования, возникают вопросы:
- Данные пропустили по ошибке или сознательно исключили из анализа, поскольку они противоречат первоначальной гипотезе и выводам?
- Не приведет ли исключение некоторых данных к тому, что результаты не будут воспроизводиться на другой выборке или при повторном исследовании?
- Если данные не были представлены полностью, то можно ли доверять другим фактам, содержащимся в статье?
Все это не украшает автора и снижает ценность его работы в глазах читателя и редактора журнала. Поэтому в статье нужно указать наличие и количество сомнительных и неопределенных результатов; пояснить, включались ли они в статистический анализ и как были интерпретированы.
8. Понятие объекта исследования.
Неверное определение объекта исследования может приводить к ошибкам и неточностям.
В клинических исследованиях объектом принято считать пациента. Когда в работе о методах лечения переломов единицей учета является не пациент, а сломанная кость, возникает вопрос, сколько больных участвовали в исследовании. Тем более непонятно, что означает 50% эффективность.
Если объектом исследования является язвенная болезнь, то размер выборки будет соответствовать количеству выявленных случаев заболевания, а не количеству обследованных пациентов.
В работах, основанных на заключениях специалистов, может быть необходимым исследовать выборку специалистов, а не общий массив заключений.
9. Статистическая значимость полученных результатов.
Статистическая значимость Statistical significance не равна клиническому значению.
При сравнении больших выборок статистически значимыми могут оказаться различия, не имеющие никакой реальной важности. Например, при среднем сроке службы приборов 5 лет различия на 1-2 недели клинического значения не имеют.
Наоборот, в малых выборках статистически незначимые различия могут быть важными клинически. Например, если в группе из нескольких больных в терминальном состоянии выжил хотя бы один, это безусловно клинически значимо.
10. Влияние факторов риска.
Истинное влияние фактора риска показывает относительный риск relative risk (RR) — отношение риска наступления исхода у подвергавшихся воздействию фактора к риску в контрольной группе. Этот показатель можно рассчитать, если группы набираются по принципу наличия и отсутствия фактора риска.
Если же группы набираются по принципу наличия или отсутствия исхода, то влияние можно оценить только приблизительно, используя показатель отношения шансов odds ratio (OR), описывающий силу связи между факторами.
Заключение
Главный вывод из сказанного: методы статистического анализа должны соответствовать характеру данных. Выбор тех или иных методов анализа нужно обосновать. Во избежание ошибок учтите:
- Характер распределения данных. Нормальное и асимметричное распределение требует разных подходов к анализу.
- Для анализа независимых выборок и парных данных (относящихся к одному и тому же участнику исследования) используются разные методы.
- Характер связи между переменными. Линейный характер связи позволяет использовать регрессионные модели. Чтобы подтвердить или опровергнуть линейную зависимость, нужно проанализировать остатки.
- В медицинских исследованиях клиническая значимость имеет приоритет над статистической.
- Норма должна быть клинически значимой; а выбор значения, принимаемого за норму, нужно обосновать.
- При наличии сомнительных или неопределенных результатов следует объяснить, как они учитываются в статистическом анализе.
- Объектом исследования следует считать человека или животное, а не болезнь и не клинический случай, так как два и более клинических случая могут иметь отношение к одному пациенту.
Статистические показатели в любом случае можно улучшить увеличением числа участников. По мнению В. Джонсона, принимая эталонное значение р-критерия в медицинских и биологических исследованиях на уровне <0.0005, можно существенно повысить качество статистики.
Часто ошибки статистического анализа вытекают из того, что эксперимент или исследование было изначально неправильно спланировано. В сомнительных случаях стоит обратиться к специалистам по статистике, однако делать это нужно на этапе подготовки, а не тогда, когда все работы уже завершены и возник вопрос, что же теперь делать с этими цифрами.
Современные программы для статистической обработки данных сильно облегчают вычисления, однако они не решают проблему выбора адекватных методов анализа и соответствия их характеру полученных данных. Поэтому залог успеха — тщательная подготовка исследования. Убедитесь, что материалы и методы, статистический анализ результатов и выводы соответствуют цели исследования.
Присоединяйтесь, чтобы моментально узнавать о новых статьях в нашем научном блоге, акциях и получать только полезные материалы!
Ошибки в статистике
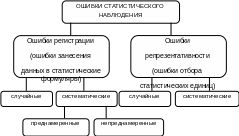
Ошибки в статистике (сплошных и выборочных) могут возникнуть ошибки двух видов: репрезентативности и регистрации.
Ошибки репрезентативности характерны только для выборочного наблюдения и возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Они определяются как расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном сплошном наблюдении с одинаковой степенью точности.
Ошибки регистрации могут иметь случайный, систематический и непреднамеренный характер.
Случайные ошибки часто уравновешивают друг друга, так как они не имеют преимущественного направления в сторону преувеличения (преуменьшении) значения изучаемого показателя. Данные ошибки имеют объективный характер и возникают в следствии случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности. В результате и структуры этих совокупностей чаще всего не совпадают. Научным обоснованием случайных ошибок являются теория вероятностей и ее предельные теоремы.
Систематические ошибки направлены в одну сторону в результате предумышленного нарушения правил отбора. Их можно избежать при правильной организации и проведении наблюдения.
Ошибка выборки в статистике
Ошибка выборки или ошибка репрезентативности определяется как разница между значением показателя, который был получен по выборке, и генеральным параметром. Она характерна только для выборочных наблюдений. Чем больше значение этой ошибки, тем в большей степени выборочные показатели отличаются от соответствующих им генеральных показателей.
Ошибку выборки часто определяют по формулам:
1. Для среднего количественного признака:
где первое — среднее значение признака в генеральной совокупности или генеральная средняя;
второе — выборочная средняя.
2. Для доли (альтернативного признака):
где w — выборочная доля;
р — генеральная доля, или доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности.
Ошибки выборки возникают вследствие двух причин из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки) и в результате случайного отбора (случайные ошибки). Выборки являются случайными величинами и могут принимать разные значения.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Ошибки, встроенные в систему: их роль в статистике
В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.
Ошибка и некорректное применение: в чем разница?
В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.
И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.
То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.
Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.
Ошибки первого и второго рода
Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.
Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:
До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.
Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.
Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.
Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?
ROC-анализ
ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.
Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
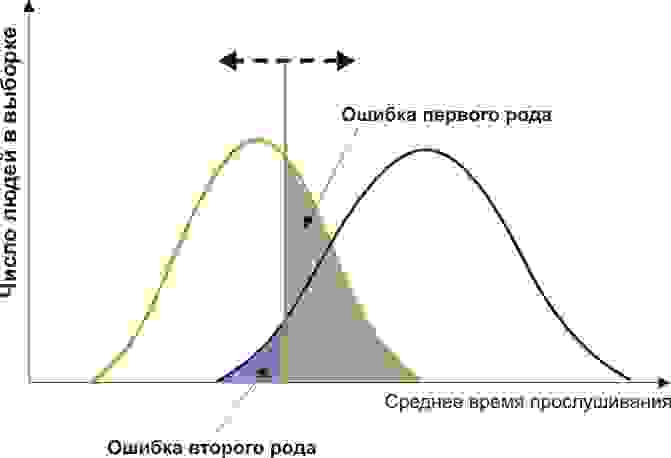
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):
Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:
Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).
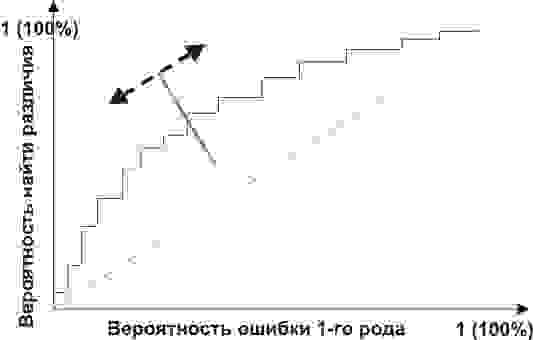
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):
А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.
С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.
Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.
С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.
Ошибки в статистике
Ошибки в статистике (сплошных и выборочных) могут возникнуть ошибки двух видов: репрезентативности и регистрации.
Ошибки репрезентативности характерны только для выборочного наблюдения и возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Они определяются как расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном сплошном наблюдении с одинаковой степенью точности.
Ошибки регистрации могут иметь случайный, систематический и непреднамеренный характер.
Случайные ошибки часто уравновешивают друг друга, так как они не имеют преимущественного направления в сторону преувеличения (преуменьшении) значения изучаемого показателя. Данные ошибки имеют объективный характер и возникают в следствии случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности. В результате и структуры этих совокупностей чаще всего не совпадают. Научным обоснованием случайных ошибок являются теория вероятностей и ее предельные теоремы.
Систематические ошибки направлены в одну сторону в результате предумышленного нарушения правил отбора. Их можно избежать при правильной организации и проведении наблюдения.
Ошибка выборки в статистике
Ошибка выборки или ошибка репрезентативности определяется как разница между значением показателя, который был получен по выборке, и генеральным параметром. Она характерна только для выборочных наблюдений. Чем больше значение этой ошибки, тем в большей степени выборочные показатели отличаются от соответствующих им генеральных показателей.
Ошибку выборки часто определяют по формулам:
1. Для среднего количественного признака:
где первое — среднее значение признака в генеральной совокупности или генеральная средняя;
второе — выборочная средняя.
2. Для доли (альтернативного признака):
где w — выборочная доля;
р — генеральная доля, или доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности.
Ошибки выборки возникают вследствие двух причин из-за нарушения принципа случайности как основного принципа выборки (систематические ошибки) и в результате случайного отбора (случайные ошибки). Выборки являются случайными величинами и могут принимать разные значения.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
From Wikipedia, the free encyclopedia
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its «true value» (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the estimated value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals.
In econometrics, «errors» are also called disturbances.[1][2][3]
Introduction[edit]
Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors are the deviations of the observations from the population mean, while the residuals are the deviations of the observations from the sample mean.
A statistical error (or disturbance) is the amount by which an observation differs from its expected value, the latter being based on the whole population from which the statistical unit was chosen randomly. For example, if the mean height in a population of 21-year-old men is 1.75 meters, and one randomly chosen man is 1.80 meters tall, then the «error» is 0.05 meters; if the randomly chosen man is 1.70 meters tall, then the «error» is −0.05 meters. The expected value, being the mean of the entire population, is typically unobservable, and hence the statistical error cannot be observed either.
A residual (or fitting deviation), on the other hand, is an observable estimate of the unobservable statistical error. Consider the previous example with men’s heights and suppose we have a random sample of n people. The sample mean could serve as a good estimator of the population mean. Then we have:
- The difference between the height of each man in the sample and the unobservable population mean is a statistical error, whereas
- The difference between the height of each man in the sample and the observable sample mean is a residual.
Note that, because of the definition of the sample mean, the sum of the residuals within a random sample is necessarily zero, and thus the residuals are necessarily not independent. The statistical errors, on the other hand, are independent, and their sum within the random sample is almost surely not zero.
One can standardize statistical errors (especially of a normal distribution) in a z-score (or «standard score»), and standardize residuals in a t-statistic, or more generally studentized residuals.
In univariate distributions[edit]
If we assume a normally distributed population with mean μ and standard deviation σ, and choose individuals independently, then we have
and the sample mean
is a random variable distributed such that:
The statistical errors are then
with expected values of zero,[4] whereas the residuals are
The sum of squares of the statistical errors, divided by σ2, has a chi-squared distribution with n degrees of freedom:
However, this quantity is not observable as the population mean is unknown. The sum of squares of the residuals, on the other hand, is observable. The quotient of that sum by σ2 has a chi-squared distribution with only n − 1 degrees of freedom:
This difference between n and n − 1 degrees of freedom results in Bessel’s correction for the estimation of sample variance of a population with unknown mean and unknown variance. No correction is necessary if the population mean is known.
[edit]
It is remarkable that the sum of squares of the residuals and the sample mean can be shown to be independent of each other, using, e.g. Basu’s theorem. That fact, and the normal and chi-squared distributions given above form the basis of calculations involving the t-statistic:
where 


The probability distributions of the numerator and the denominator separately depend on the value of the unobservable population standard deviation σ, but σ appears in both the numerator and the denominator and cancels. That is fortunate because it means that even though we do not know σ, we know the probability distribution of this quotient: it has a Student’s t-distribution with n − 1 degrees of freedom. We can therefore use this quotient to find a confidence interval for μ. This t-statistic can be interpreted as «the number of standard errors away from the regression line.»[6]
Regressions[edit]
In regression analysis, the distinction between errors and residuals is subtle and important, and leads to the concept of studentized residuals. Given an unobservable function that relates the independent variable to the dependent variable – say, a line – the deviations of the dependent variable observations from this function are the unobservable errors. If one runs a regression on some data, then the deviations of the dependent variable observations from the fitted function are the residuals. If the linear model is applicable, a scatterplot of residuals plotted against the independent variable should be random about zero with no trend to the residuals.[5] If the data exhibit a trend, the regression model is likely incorrect; for example, the true function may be a quadratic or higher order polynomial. If they are random, or have no trend, but «fan out» — they exhibit a phenomenon called heteroscedasticity. If all of the residuals are equal, or do not fan out, they exhibit homoscedasticity.
However, a terminological difference arises in the expression mean squared error (MSE). The mean squared error of a regression is a number computed from the sum of squares of the computed residuals, and not of the unobservable errors. If that sum of squares is divided by n, the number of observations, the result is the mean of the squared residuals. Since this is a biased estimate of the variance of the unobserved errors, the bias is removed by dividing the sum of the squared residuals by df = n − p − 1, instead of n, where df is the number of degrees of freedom (n minus the number of parameters (excluding the intercept) p being estimated — 1). This forms an unbiased estimate of the variance of the unobserved errors, and is called the mean squared error.[7]
Another method to calculate the mean square of error when analyzing the variance of linear regression using a technique like that used in ANOVA (they are the same because ANOVA is a type of regression), the sum of squares of the residuals (aka sum of squares of the error) is divided by the degrees of freedom (where the degrees of freedom equal n − p − 1, where p is the number of parameters estimated in the model (one for each variable in the regression equation, not including the intercept)). One can then also calculate the mean square of the model by dividing the sum of squares of the model minus the degrees of freedom, which is just the number of parameters. Then the F value can be calculated by dividing the mean square of the model by the mean square of the error, and we can then determine significance (which is why you want the mean squares to begin with.).[8]
However, because of the behavior of the process of regression, the distributions of residuals at different data points (of the input variable) may vary even if the errors themselves are identically distributed. Concretely, in a linear regression where the errors are identically distributed, the variability of residuals of inputs in the middle of the domain will be higher than the variability of residuals at the ends of the domain:[9] linear regressions fit endpoints better than the middle. This is also reflected in the influence functions of various data points on the regression coefficients: endpoints have more influence.
Thus to compare residuals at different inputs, one needs to adjust the residuals by the expected variability of residuals, which is called studentizing. This is particularly important in the case of detecting outliers, where the case in question is somehow different from the others in a dataset. For example, a large residual may be expected in the middle of the domain, but considered an outlier at the end of the domain.
Other uses of the word «error» in statistics[edit]
The use of the term «error» as discussed in the sections above is in the sense of a deviation of a value from a hypothetical unobserved value. At least two other uses also occur in statistics, both referring to observable prediction errors:
The mean squared error (MSE) refers to the amount by which the values predicted by an estimator differ from the quantities being estimated (typically outside the sample from which the model was estimated).
The root mean square error (RMSE) is the square-root of MSE.
The sum of squares of errors (SSE) is the MSE multiplied by the sample size.
Sum of squares of residuals (SSR) is the sum of the squares of the deviations of the actual values from the predicted values, within the sample used for estimation. This is the basis for the least squares estimate, where the regression coefficients are chosen such that the SSR is minimal (i.e. its derivative is zero).
Likewise, the sum of absolute errors (SAE) is the sum of the absolute values of the residuals, which is minimized in the least absolute deviations approach to regression.
The mean error (ME) is the bias.
The mean residual (MR) is always zero for least-squares estimators.
See also[edit]
- Absolute deviation
- Consensus forecasts
- Error detection and correction
- Explained sum of squares
- Innovation (signal processing)
- Lack-of-fit sum of squares
- Margin of error
- Mean absolute error
- Observational error
- Propagation of error
- Probable error
- Random and systematic errors
- Reduced chi-squared statistic
- Regression dilution
- Root mean square deviation
- Sampling error
- Standard error
- Studentized residual
- Type I and type II errors
References[edit]
- ^ Kennedy, P. (2008). A Guide to Econometrics. Wiley. p. 576. ISBN 978-1-4051-8257-7. Retrieved 2022-05-13.
- ^ Wooldridge, J.M. (2019). Introductory Econometrics: A Modern Approach. Cengage Learning. p. 57. ISBN 978-1-337-67133-0. Retrieved 2022-05-13.
- ^ Das, P. (2019). Econometrics in Theory and Practice: Analysis of Cross Section, Time Series and Panel Data with Stata 15.1. Springer Singapore. p. 7. ISBN 978-981-329-019-8. Retrieved 2022-05-13.
- ^ Wetherill, G. Barrie. (1981). Intermediate statistical methods. London: Chapman and Hall. ISBN 0-412-16440-X. OCLC 7779780.
- ^ a b Frederik Michel Dekking; Cornelis Kraaikamp; Hendrik Paul Lopuhaä; Ludolf Erwin Meester (2005-06-15). A modern introduction to probability and statistics : understanding why and how. London: Springer London. ISBN 978-1-85233-896-1. OCLC 262680588.
- ^ Peter Bruce; Andrew Bruce (2017-05-10). Practical statistics for data scientists : 50 essential concepts (First ed.). Sebastopol, CA: O’Reilly Media Inc. ISBN 978-1-4919-5296-2. OCLC 987251007.
- ^ Steel, Robert G. D.; Torrie, James H. (1960). Principles and Procedures of Statistics, with Special Reference to Biological Sciences. McGraw-Hill. p. 288.
- ^ Zelterman, Daniel (2010). Applied linear models with SAS ([Online-Ausg.]. ed.). Cambridge: Cambridge University Press. ISBN 9780521761598.
- ^ «7.3: Types of Outliers in Linear Regression». Statistics LibreTexts. 2013-11-21. Retrieved 2019-11-22.
- Cook, R. Dennis; Weisberg, Sanford (1982). Residuals and Influence in Regression (Repr. ed.). New York: Chapman and Hall. ISBN 041224280X. Retrieved 23 February 2013.
- Cox, David R.; Snell, E. Joyce (1968). «A general definition of residuals». Journal of the Royal Statistical Society, Series B. 30 (2): 248–275. JSTOR 2984505.
- Weisberg, Sanford (1985). Applied Linear Regression (2nd ed.). New York: Wiley. ISBN 9780471879572. Retrieved 23 February 2013.
- «Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
External links[edit]
Media related to Errors and residuals at Wikimedia Commons
Ошибка
статистического наблюдения – это
отклонение расчетных значений показателей
от фактических. Классификация различных
видов ошибок представлена на схеме 2.1.
Ошибки
регистрации
– это просто ошибки записей при заполнении
статистических формуляров. Такие ошибки
встречаются при любых видах наблюдений.
Ошибки
репрезентативности
(то есть представительности)1
характерны только для так называемых
выборочных
наблюдений (которые более подробно
будут изучаться в дальнейшем). Их суть
заключается в том, что статистические
единицы, отобранные для проведения
наблюдения (включенные в выборочную
совокупность или «выборку») недостаточно
полно представляют всю (генеральную)
статистическую совокупность. Например,
при проведении социологического опроса
были собраны данные о среднедушевом
доходе только у лиц в возрасте от 30 до
50 лет, и не были охвачены другие категории
населения.
Случайные
ошибки
бывают всегда,
а процент систематических
ошибок
можно уменьшить
за счет улучшения организации самого
наблюдения. Однако, если эти ошибки
являются преднамеренными
(например, скрываются данные о доходах,
чтобы снизить величину налоговых
отчислений), то снизить процент таких
ошибок можно, только выходя за рамки
компетенции статистических органов.
Схема
2.1
Классификация ошибок статистического наблюдения
3. Организационные формы, виды и способы статистического наблюдения
Существует
три основных организационных формы
статистического наблюдения:
-
Официальная
статистическая отчетность; -
Специально
организованные наблюдения; -
Регистры
(регистрационная форма наблюдения)
Роль
официальной статистической отчетности
для статистических исследований в том,
что она позволяет в течение длительного
промежутка времени накапливать
статистические данные, представленные
в виде единообразного, официально
утвержденного перечня показателей. Эти
показатели обычно комплексно характеризуют
развитие отдельных социально-экономических
процессов во времени. Однако с переходом
к рыночной экономике в нашей стране
существенно изменились многие формы
статистической отчетности. Поэтому,
как правило, статистические ряды данных,
сформированные в период до начала 1990-х
годов, фактически несопоставимы с той
статистической информацией, которая
была накоплена в течение последнего
десятилетия.
Официальная
статистическая отчетность является
обязательной,
документально обоснованной, периодической.
Все
сведения в отчетности должны быть
юридически заверены подписью руководителя
предприятия.
Официальная
статистическая отчетность делится на:
1)
типовую (обязательную для всех
предприятий),
2) специальную
(заполняют только предприятия одной
отрасли).
Специально
организованные наблюдения –
это те, для которых всякий раз, независимо
от их периодичности и сроков проведения,
разрабатывается специальная программа
(например, к таким наблюдениям относится
перепись, опросы общественного мнения
и т.д.)
Регистр
– это особая форма непрерывного
наблюдения за социально-экономическими
процессами, имеющими фиксированное
начало и фиксированный конец. Проще
говоря, регистр – это список, в который
заносятся статистические единицы с
определенными признаками, некоторые
из которых имеют постоянное значение,
а другие изменяются. Все эти изменения
фиксируются и также заносятся в регистр.
Примером такого наблюдения является
регистрация актов гражданского состояния
или регистрация всех предприятий,
создаваемых на территории Российской
Федерации.
Кроме
того, все статистические наблюдения
разделяют на различные виды, в зависимости
от периодичности их проведения:
-
Периодические
(которые проводятся через равные
промежутки времени, например, через
год, месяц, квартал): примером такого
наблюдения является официальная
статистическая отчетность); -
Непрерывные
(или текущие),
которые фиксируют все факты, имеющие
отношения к данному социально-экономическому
явлению, независимо от момента времени,
когда происходят соответствующие
события: примером такого наблюдения
является регистрация дорожно-транспортных
происшествий; -
Разовые
или единовременные,
которые могут больше не повториться:
например, опрос общественного мнения
перед выборами.
В
зависимости от степени охвата
статистических единиц, статистические
наблюдения также разделяют на сплошные
и несплошные
наблюдения. В свою очередь, несплошные
наблюдения разделяют на выборочные,
обследования
основного массива
и монографические
исследования.
Нередко
всякие наблюдения, не являющиеся
сплошными, называют выборочными. Однако
выборочные
наблюдения
– это только одна
из нескольких возможных разновидностей
несплошных наблюдений. При выборочных
наблюдениях
отбор обследуемых единиц осуществляется
с помощью особых, научно обоснованных
способов формирования выборочной
совокупности единиц. Другой формой
несплошных наблюдений являются
обследования основного
массива, при которых
отбирается такая часть статистических
единиц, которая дает наибольший вклад
в итоговый показатель. (Например,
отбираются предприятия с наибольшим
объемом реализованной продукции или
магазины с наибольшим объемом
товарооборота). Наконец, при монографических
исследованиях обычно обследуется совсем
немного статистических единиц, но очень
детально, по чрезвычайно широкому
перечню признаков. Например, изучаются
только те предприятия, где внедрена
совершенно новая форма оплаты труда,
но необходимо очень тщательно изучить
влияние этой новой формы на результаты
работы предприятия (с привлечением
большого числа показателей, характеризующих
деятельность предприятия).
В
зависимости от способа проведения
статистического наблюдения выделяют:
-
непосредственное
наблюдение (подсчет, измерение,
взвешивание); -
наблюдение
на основе документальных источников
первичной информации (например, на
основе форм бухгалтерского учета и
отчетности); -
опрос
(письменный или устный).
Таблица 2.1
Классификация форм, видов и способов
статистических наблюдений
|
Признаки классификации |
|||||
|
Организацион-ная наблюдения |
Вид |
Способ |
|||
|
По времени регистрации актов |
По степени |
Непосредственное |
Документальный |
Опрос (письменный или устный) |
|
|
Официальная |
Периоди-ческие |
Сплошные |
Саморе-гистрация |
||
|
Специально организован-ные |
Разовые |
Выбороч-ные |
Экспеди-ционный |
||
|
Регистры |
Непрерыв-ные |
Основного массива |
Корреспон-дентский |
||
|
Моногра-фические |
Лекция
№3.
Сводка
и группировка статистических материалов
Введение
На
предыдущих лекциях мы изучили
содержание
трех этапов статистического исследования
и
более подробно ознакомились
с
основным
методом сбора информации на первом
этапе исследования, то есть со
статистическим наблюдением, его основными
видами и формами.
На
втором этапе статистического исследования
основную
роль играют такие методы обработки
статистической информации, как сводка
и группировка. Это давно известные в
статистике методы, исторически
сформировавшиеся еще в позапрошлом
веке.
Но
раньше эти методы использовались для
сложного и трудоемкого процесса обработки
данных вручную. В настоящее время те же
самые процессы осуществляются с
использованием современных компьютерных
программ.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #