Задана система
точек (узлы интерполяции)
xi ,
i=1,2,…,N; a
xi
b, и значения
fi,
i = 1,2,….,N.
Требуется построить полиномы:
-
1-ой степени
P1(x)=a1+a2x, -
2-ой
степени
P2(x)=a1+a2x+a3x2, -
3-ой
степени
P3(x)=a1+a2x+a3x2+a4x3,
имеющие в узлах
интерполяции минимальное отклонение
от заданных значений fi.
Искомыми величинами являются коэффициенты
полинома (ai).
Полиномы
должны быть самым близким к заданным
точкам из всех возможных полиномов,
соответствующей степени в смысле МНК,
т.е. сумма квадратов отклонений
должна быть минимальной.
-
Получить систему
нормальных уравнений для каждого
полинома. -
Вычислить
коэффициенты ai
. -
Определить какой
из полиномов имеет минимальную сумму
квадратов отклонений.
|
x |
-10 |
-8,3 |
-6,7 |
-5 |
-3 |
-1,67 |
|
Вар.9 |
-100 |
-60 |
-33 |
-16 |
-7 |
-2,08 |
|
0 |
1,67 |
3,33 |
5 |
6,7 |
8,33 |
10 |
|
0 |
2,08 |
6,67 |
16 |
33 |
60,4 |
100 |
-
Полином 1-ой степени.
|
xi |
Xi^2 |
fi |
fi xi |
|
0,36 |
503,7256 |
0,07 |
3653,4903 |
|
S |
|
|
13 |
0,36 |
|
0,36 |
503,7256 |
|
S(-1) |
0,076924599 |
-5,49761E-05 |
|
-5,49761E-05 |
0,001985247 |
|
z |
|
0,07 |
|
3653,49 |
|
a |
-0,19546983 |
|
7,253077209 |
Ф(x)=-0,19547+7,25308x
Сумма квадратов
отклонений:
|
G1= |
3541,268153 |
-
Полином 2-ой степени.
|
xi |
Xi^2 |
Xi^3 |
Xi^4 |
fi |
fi xi |
fi xi^2 |
|
0,36 |
503,7256 |
16,148574 |
35060,3954 |
0,07 |
3653,4903 |
68,652523 |
|
S |
13 |
0,36 |
503,7256 |
|
0,36 |
503,7256 |
16,14857 |
|
|
503,7256 |
16,14857 |
35060,3954 |
|
S(-1) |
0,173528 |
-4,4091E-05 |
-0,00249312 |
|
-4,4E-05 |
0,001985248 |
-2,8092E-07 |
|
|
-0,00249 |
-2,8092E-07 |
6,43419E-05 |
|
z |
0,07 |
|
3653,49 |
|
|
68,65252 |
|
a |
-0,32009809 |
|
7,253062571 |
|
|
0,003216379 |
Ф(х)=-0,32009809+7,253062571*х+0,003216379*х^2
Сумма квадратов
отклонений:
|
G2 |
3541,10737 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Решения задач: метод наименьших квадратов
Метод наименьших квадратов применяется для решения различных математических задач и основан на минимизации суммы квадратов отклонений функций от исходных переменных. Мы рассмотриваем его приложение к математической статистике в простейшем случае, когда нужно найти зависимость (парную линейную регрессию) между двумя переменными, заданными выборочными данным. В этом случае речь идет об отклонениях теоретических значений от экспериментальных.
Краткая инструкция по методу наименьших квадратов для чайников: определяем вид предполагаемой зависимости (чаще всего берется линейная регрессия вида $y(x)=ax+b$), выписываем систему уравнений для нахождения параметров $a, b$. По экспериментальным данным проводим вычисления и подставляем значения в систему, решаем систему любым удобным методом (для размерности 2-3 можно и вручную). Получается искомое уравнение.
Иногда дополнительно к нахождению уравнения регрессии требуется: найти остаточную дисперсию, сделать прогноз значений, найти значение коэффициента корреляции, проверить качество аппроксимации и значимость модели. Примеры решений вы найдете ниже. Удачи в изучении!
Примеры решений МНК
Пример 1. Методом наименьших квадратов для данных, представленных в таблице, найти линейную зависимость
Пример 2. Прибыль фирмы за некоторый период деятельности по годам приведена ниже:
Год 1 2 3 4 5
Прибыль 3,9 4,9 3,4 1,4 1,9
1) Составьте линейную зависимость прибыли по годам деятельности фирмы.
2) Определите ожидаемую прибыль для 6-го года деятельности. Сделайте чертеж.
Пример 3. Экспериментальные данные о значениях переменных х и y приведены в таблице:
1 2 4 6 8
3 2 1 0,5 0
В результате их выравнивания получена функция Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.
Пример 4. Данные наблюдений над случайной двумерной величиной (Х, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X.
Пример 5. Считая, что зависимость между переменными x и y имеет вид $y=ax^2+bx+c$, найти оценки параметров a, b и c методом наименьших квадратов по выборке:
x 7 31 61 99 129 178 209
y 13 10 9 10 12 20 26
Пример 6. Проводится анализ взаимосвязи количества населения (X) и количества практикующих врачей (Y) в регионе.
Годы 81 82 83 84 85 86 87 88 89 90
X, млн. чел. 10 10,3 10,4 10,55 10,6 10,7 10,75 10,9 10,9 11
Y, тыс. чел. 12,1 12,6 13 13,8 14,9 16 18 20 21 22
Оцените по МНК коэффициенты линейного уравнения регрессии $y=b_0+b_1x$.
Существенно ли отличаются от нуля найденные коэффициенты?
Проверьте значимость полученного уравнения при $alpha = 0,01$.
Если количество населения в 1995 году составит 11,5 млн. чел., каково ожидаемое количество врачей? Рассчитайте 99%-й доверительный интервал для данного прогноза.
Рассчитайте коэффициент детерминации
Основы линейной регрессии
Что такое регрессия?
Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.
Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.
Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).
Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).
Линия регрессии
Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:
x называется независимой переменной или предиктором.
Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»
- a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
- b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
- a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.
Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)
Метод наименьших квадратов
Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).
Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).
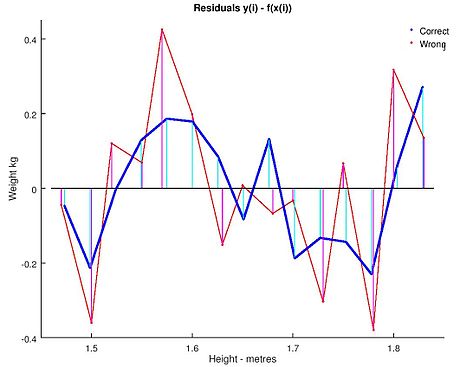
Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).
Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.
Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.
Предположения линейной регрессии
Итак, для каждой наблюдаемой величины остаток равен разнице
и соответствующего предсказанного
Каждый остаток может быть положительным или отрицательным.
Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:
- Остатки нормально распределены с нулевым средним значением;
Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или
и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).
Аномальные значения (выбросы) и точки влияния
«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).
Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.
И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).
При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.
Гипотеза линейной регрессии
При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.
Если угловой коэффициент линии равен нулю, между и
нет линейного соотношения: изменение
не влияет на
Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:
Вычислить статистику критерия, равную отношению , которая подчиняется
распределению с
степенями свободы, где
стандартная ошибка коэффициента
,
— оценка дисперсии остатков.
Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.
Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :
где процентная точка
распределения со степенями свободы
что дает вероятность двустороннего критерия
Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.
Для больших выборок, скажем, мы можем аппроксимировать
значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)
Оценка качества линейной регрессии: коэффициент детерминации R 2
Из-за линейного соотношения и
мы ожидаем, что
изменяется, по мере того как изменяется
, и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.
Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.
Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.
Разность представляет собой процент дисперсии который нельзя объяснить регрессией.
Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.
Применение линии регрессии для прогноза
Можно применять регрессионную линию для прогнозирования значения по значению
в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).
Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение
путем подстановки этого значения
в уравнение линии регрессии.
Итак, если прогнозируем
как
Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины
в популяции.
Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.
Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.
Простые регрессионные планы
Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид
а регрессионное уравнение с использованием P для X1 выглядит как
Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:
а уравнение примет вид
Y = b 0 + b 1 P 2
Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.
Пример: простой регрессионный анализ
Этот пример использует данные, представленные в таблице:
Рис. 3. Таблица исходных данных.
Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:
Рис. 4. Таблица спецификаций переменных.
Задача исследования
Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.
Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.
Просмотр результатов
Коэффициенты регрессии
Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.
На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.
Распределение переменных
Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .
Рис. 6. Гистограмма переменной Pt_Poor.
Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»
Рис. 7. Гистограмма переменной Pt_Poor.
Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.
Диаграмма рассеяния
Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.
Рис. 8. Диаграмма рассеяния.
Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.
Критерии значимости
Рис. 9. Таблица, содержащая критерии значимости.
Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .
На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.
источники:
http://www.matburo.ru/ex_ms.php?p1=msmnk
http://statistica.ru/theory/osnovy-lineynoy-regressii/
На этом занятии
мы с вами рассмотрим алгоритм, который носит название метод наименьших
квадратов. Для начала немного теории. Чтобы ее хорошо понимать нужны
базовые знания по теории вероятностей, в частности понимание ПРВ, а также
знать, что такое производная и как она вычисляется. Остальное я сейчас
расскажу.
На практике
встречаются задачи, когда производились измерения некоторой функциональной
зависимости, но из-за погрешностей приборов, или неточных сведений или еще по
какой-либо причине, измерения немного отстоят от истинных значений функции и
образуют некий разброс:
Наша задача:
зная характер функциональной зависимости, подобрать ее параметры так, чтобы она
наилучшим образом описывала экспериментальные данные Например, на
рисунке явно прослеживается линейная зависимость. Мы это можем определить либо
чисто визуально, либо заранее знать о характере функции. Но, в любом случае
предполагается, что ее общий вид нам известен. Так вот, для линейной функции
достаточно определить два параметра k и b:
чтобы построить
аппроксимацию (приближение) линейного графика к экспериментальным зависимостям.
Конечно, вид функциональной зависимости может быть и другим, например,
квадратической (парабола), синусоидальной, или даже определяться суммой
известных функций, но для простоты понимания, мы для начала рассмотрим именно
линейный график с двумя неизвестными коэффициентами.
Итак, будем
считать, что на первый вопрос о характере функциональной зависимости
экспериментальных данных ответ дан. Следующий вопрос: как измерить качество
аппроксимации измерений функцией
? Вообще, таких
критериев можно придумать множество, например:
— сумма квадратов
ошибок отклонений:
— сумма модулей
ошибок отклонений:
— минимум
максимальной по модулю ошибки:
и так далее. Каждый
из критериев может приводить к своему алгоритму обработки экспериментальных
значений. Так вот, в методе наименьших квадратов используется минимум суммы
квадратов ошибок. И этому есть математическое обоснование. Часто результаты
реальных измерений имеют стандартное (гауссовское) отклонение относительно
измеряемого параметра:
Здесь σ –
стандартное отклонение (СКО) наблюдаемых значений от функции
. Отсюда хорошо
видно, что чем ближе измерение к истинному значению параметра, тем больше
значение функции плотности распределения условной вероятности. И, так для всех
точек измерения. Учитывая, что они выполняются независимо друг от друга, то
можно записать следующее функциональное выражение:
Получается, что лучшее
описание экспериментальных данных с помощью функции должно проходить по
точкам, в которых достигается максимум этого выражения. Очевидно, что при
поиске максимума можно не учитывать множитель 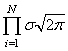
принимать максимальное значение при минимуме ее отрицательной степени:
Здесь также
множитель можно не учитывать, получаем критерий качества минимум суммы квадрата
ошибок:
Как мы помним,
наша цель – подобрать параметры функции
которые как раз
и обеспечивают минимум этого критерия, то есть, величина E зависит от этих
подбираемых величин:
И ее можно
рассматривать как квадратическую функцию от аргументов Из школьного курса
математики мы знаем как находится точка экстремума функции – это точка, в
которой производная равна нулю:
Здесь все также,
нужно взять частные производные по каждому параметру и приравнять результат
нулю, получим систему линейных уравнений:
Чтобы наполнить
конкретикой эту систему, нам нужно вернуться к исходному примеру с линейной
функцией:
Эта функция
зависит от двух параметров: k и b с частными
производными:
Подставляем все
в систему, имеем:
или, в виде:
Разделим все на N:
Смотрите, что в
итоге получилось. Формулы с суммами представляют собой первые и вторые
начальные моменты, а также один смешанный момент:
Здесь * означает
экспериментальные моменты. В этих обозначениях, получаем:
Отсюда находим,
что
Все, мы получили
оценки параметров k и b для линейной
аппроксимации экспериментальных данных по методу наименьших квадратов. По
аналогии можно вычислять параметры для других функциональных зависимостей,
например, квадратической:
Здесь будет уже
три свободных параметра и три уравнения, решая которые будем получать лучшую
аппроксимацию по критерию минимума суммарной квадратической ошибки отклонений.
Реализация на Python
В заключение
этого занятия реализуем метод наименьших квадратов на Python. Для этого нам
понадобятся две довольно популярные библиотеки numpy и matplotlib. Если они у вас
не установлены, то делается это просто – через команды:
pip install numpy
pip install matplotlib
После этого, мы
можем их импортировать и использовать в программе:
import numpy as np import matplotlib.pyplot as plt
Первая довольно
эффективная для выполнения различных математических операций, включая векторные
и матричные. Вторая служит для построения графиков.
Итак, вначале
определим необходимые начальные величины:
N = 100 # число экспериментов sigma = 3 # стандартное отклонение наблюдаемых значений k = 0.5 # теоретическое значение параметра k b = 2 # теоретическое значение параметра b
Формируем
вспомогательный вектор
с помощью метода
array, который
возвращает объект-вектор на основе итерируемой функции range:
Затем, вычисляем
значения теоретической функции:
f = np.array([k*z+b for z in range(N)])
и добавляем к
ней случайные отклонения для моделирования результатов наблюдений:
y = f + np.random.normal(0, sigma, N)
Если сейчас
отобразить наборы точек y, то они будут выглядеть следующим
образом:
plt.scatter(x, y, s=2, c='red') plt.grid(True) plt.show()
Теперь у нас все
есть для вычисления коэффициентов k и b по экспериментальным
данным:
# вычисляем коэффициенты mx = x.sum()/N my = y.sum()/N a2 = np.dot(x.T, x)/N a11 = np.dot(x.T, y)/N kk = (a11 - mx*my)/(a2 - mx**2) bb = my - kk*mx
Здесь выражение x.T*x – это
произведение:
Далее, построим
точки полученной аппроксимации:
ff = np.array([kk*z+bb for z in range(N)])
и отобразим оба
линейных графика:
plt.plot(f) plt.plot(ff, c='red')
Как видите
результат аппроксимации довольно близок начальному, теоретическому графику. Вот
так работает метод наименьших квадратов.
Реализация алгоритма на Python (файл mnsq.py)
Видео по теме
Цель любого физического эксперимента — проверить, выполняется ли некоторая
теоретическая закономерность (модель), а также получить или уточнить
её параметры. Поскольку набор экспериментальных данных неизбежно ограничен,
а каждое отдельное измерение имеет погрешность, можно говорить лишь
об оценке этих параметров. В большинстве случаев измеряется не одна
величина, а некоторая функциональная зависимость величин друг от друга.
В таком случае возникает необходимость построить оценку параметров этой зависимости.
Пример. Рассмотрим процедуру измерения сопротивления некоторого резистора.
Простейшая теоретическая модель для резистора — закон Ома U=RI,
где сопротивление R — единственный параметр модели. Часто при измерениях
возможно возникновение систематической ошибки — смещение нуля напряжения или тока.
Тогда для получения более корректной оценки сопротивления стоит использовать
модель с двумя параметрами: U=RI+U0.
Для построения оценки нужны следующие компоненты
- •
данные — результаты измерений {xi,yi}
и их погрешности {σi}
(экспериментальная погрешность является неотъемлемой
частью набора данных!); - •
модель y=f(x|θ1,θ2,…) —
параметрическое описание исследуемой зависимости
(θ — набор параметров модели, например,
коэффициенты {k,b} прямой f(x)=kx+b); - •
процедура построения оценки параметров по
измеренным данным («оценщик»):
Рассмотрим самые распространенные способы построения оценки.
3.1 Метод минимума хи-квадрат
Обозначим отклонения результатов некоторой серии измерений от теоретической
модели y=f(x|θ) как
| Δyi=yi-f(xi|θ),i=1…n, |
где θ — некоторый параметр (или набор параметров),
для которого требуется построить наилучшую оценку. Нормируем Δyi
на стандартные отклонения σi и построим сумму
которую принято называть суммой хи-квадрат.
Метод минимума хи-квадрат (метод Пирсона) заключается в подборе такого
θ, при котором сумма квадратов отклонений от теоретической
модели, нормированных на ошибки измерений, достигает минимума:
Замечание. Подразумевается, что погрешность измерений σi указана только для
вертикальной оси y. Поэтому, при использовании метода следует выбирать оcи
таким образом, чтобы относительная ошибка по оси абсцисс была значительно меньше,
чем по оси ординат.
Данный метод вполне соответствует нашему интуитивному представлению
о том, как теоретическая зависимость должна проходить через экспериментальные
точки. Ясно, что чем ближе данные к модельной кривой, тем
меньше будет сумма χ2. При этом, чем больше погрешность точки, тем
в большей степени дозволено результатам измерений отклоняться от модели.
Метода минимума χ2 является частным случаем
более общего метода максимума правдоподобия (см. ниже),
реализующийся при нормальном (гауссовом) распределении ошибок.
Можно показать (см. [5]), что оценка по методу хи-квадрат является состоятельной,
несмещенной и, если данные распределены нормально,
имеет максимальную эффективность (см. приложение 5.2).
Замечание. Простые аналитические выражения для оценки методом хи-квадрат существуют
(см. п. 3.6.1, 3.6.4) только в случае линейной
зависимости f(x)=kx+b (впрочем, нелинейную зависимость часто можно
заменой переменных свести к линейной). В общем случае задача поиска
минимума χ2(θ) решается численно, а соответствующая процедура
реализована в большинстве специализированных программных пакетов
по обработке данных.
3.2 Метод максимального правдоподобия.
Рассмотрим кратко один
из наиболее общих методов оценки параметров зависимостей —
метод максимума правдоподобия.
Сделаем два ключевых предположения:
- •
зависимость между измеряемыми величинами действительно может
быть описана функцией y=f(x|θ) при некотором θ; - •
все отклонения Δyi результатов измерений от теоретической модели
являются независимыми и имеют случайный (не систематический!) характер.
Пусть P(Δyi) — вероятность обнаружить отклонение Δyi
при фиксированных {xi}, погрешностях {σi} и параметрах модели θ.
Построим функцию, равную вероятности обнаружить
весь набор отклонений {Δy1,…,Δyn}. Ввиду независимости
измерений она равна произведению вероятностей:
Функцию L называют функцией правдоподобия.
Метод максимума правдоподобия заключается в поиске такого θ,
при котором наблюдаемое отклонение от модели будет иметь
наибольшую вероятность, то есть
Замечание. Поскольку с суммой работать удобнее, чем с произведениями, чаще
используют не саму функцию L, а её логарифм:
Пусть теперь ошибки измерений имеют нормальное распределение
(напомним, что согласно центральной предельной теореме нормальное распределение
применимо, если отклонения возникают из-за большого
числа независимых факторов, что на практике реализуется довольно часто).
Согласно (2.5), вероятность обнаружить в i-м измерении
отклонение Δyi пропорциональна величине
где σi — стандартная ошибка измерения величины yi. Тогда
логарифм функции правдоподобия (3.2) будет равен (с точностью до константы)
| lnL=-∑iΔyi22σi2=-12χ2. |
Таким образом, максимум правдоподобия действительно будет соответствовать
минимуму χ2.
3.3 Метод наименьших квадратов (МНК).
Рассмотрим случай, когда все погрешности измерений одинаковы,
σi=const. Тогда множитель 1/σ2 в сумме χ2
выносится за скобки, и оценка параметра сводится к нахождению минимума суммы
квадратов отклонений:
| S(θ)=∑i=1n(yi-f(xi|θ))2→min. | (3.3) |
Оценка по методу наименьших квадратов (МНК) удобна в том случае,
когда не известны погрешности отдельных измерений. Однако тот факт, что
метод МНК игнорирует информацию о погрешностях, является и его основным
недостатком. В частности, это не позволяет определить точность оценки
(например, погрешности коэффициентов прямой σk и
σb) без привлечения дополнительных предположений
(см. п. 3.6.2 и 3.6.3).
3.4 Проверка качества аппроксимации
Значение суммы χ2 позволяет оценить, насколько хорошо данные описываются
предлагаемой моделью y=f(x|θ).
Предположим, что распределение ошибок при измерениях нормальное.
Тогда можно ожидать, что большая часть отклонений данных от модели будет
порядка одной среднеквадратичной ошибки: Δyi∼σi.
Следовательно, сумма хи-квадрат (3.1) окажется по порядку
величины равна числу входящих в неё слагаемых: χ2∼n.
Замечание. Точнее, если функция f(x|θ1,…,θp)
содержит p подгоночных параметров
(например, p=2 для линейной зависимости f(x)=kx+b),
то при заданных θ лишь n-p слагаемых в сумме хи-квадрат будут независимы.
Иными словами, когда параметры θ определены
из условия минимума хи-квадрат, сумму χ2 можно рассматривать как функцию
n-p переменных. Величину n-p называют числом степеней свободы задачи.
В теории вероятностей доказывается (см. [4] или [5]),
что ожидаемое среднее значение (математическое ожидание) суммы χ2
в точности равно числу степеней свободы:
Таким образом, при хорошем соответствии модели и данных,
величина χ2/(n-p) должна в среднем быть равна единице.
Значения существенно большие (2 и выше) свидетельствуют либо о
плохом соответствии теории и результатов измерений,
либо о заниженных погрешностях.
Значения меньше 0,5 как правило свидетельствуют о завышенных погрешностях.
Замечание. Чтобы дать строгий количественный критерий, с какой долей вероятности
гипотезу y=f(x) можно считать подтверждённой или опровергнутой,
нужно знать вероятностный закон, которому подчиняется функция χ2.
Если ошибки измерений распределены нормально, величина хи-квадрат подчинятся
одноимённому распределению (с n-p степенями свободы).
В элементарных функциях распределение хи-квадрат не выражается,
но может быть легко найдено численно: функция встроена во все основные
статистические пакеты, либо может быть вычислена по таблицам.
3.5 Оценка погрешности параметров
Важным свойством метода хи-квадрат является «встроенная» возможность
нахождения погрешности вычисленных параметров σθ.
Пусть функция L(θ) имеет максимум при θ=θ^, то есть
θ^ — решение задачи о максимуме правдоподобия. Согласно центральной предельной теореме мы ожидаем, что функция правдоподобия будем близка к нормальному распределению: L(θ)∝exp(-(θ-θ^)22σθ2),
где σθ — искомая погрешность параметра. Тогда в окрестности θ^ функция χ2(θ)=-2ln(L(θ)) имеет вид параболы:
Легко убедиться, что:
Иными словами, при отклонении параметра θ на одну ошибку σθ от значения
θ^,
минимизирующего χ2, функция χ2(θ) изменится на единицу. Таким образом для нахождения интервальной оценки для искомого параметра достаточно графическим или численным образом решить уравнение
Вероятностное содержание этого интервала будет равно 68% (его еще называют 1–σ интервалом).
Отклонение χ2 на 2 будет соответствовать уже 95% доверительному интервалу.
Замечание.
Приведенное решение просто использовать только в случае одного параметра. Впрочем, все приведенные рассуждения верны и в много-параметрическом случае. Просто решением уравнения 3.4 будет не отрезок, а некоторая многомерная фигура (эллипс в двумерном случае и гипер-эллипс при больших размерностях пространства параметров). Вероятностное содержание области, ограниченной такой фигурой будет уже не равно 68%, но может быть вычислено по соответствующим таблицам. Подробнее о многомерном случае в разделе 5.5.
3.6 Методы построения наилучшей прямой
Применим перечисленные выше методы к задаче о построении наилучшей прямой
y=kx+b по экспериментальным точкам {xi,yi}.
Линейность функции позволяет записать решение в относительно
простом аналитическом виде.
Обозначим расстояние от i-й экспериментальной точки до искомой прямой,
измеренное по вертикали, как
и найдём такие параметры {k,b}, чтобы «совокупное» отклонение
результатов от линейной зависимости было в некотором смысле минимально.
3.6.1 Метод наименьших квадратов
Пусть сумма квадратов расстояний от точек до прямой минимальна:
| S(k,b)=∑i=1n(yi-(kxi+b))2→min. | (3.5) |
Данный метод построения наилучшей прямой называют методом наименьших
квадратов (МНК).
Рассмотрим сперва более простой частный случай, когда искомая прямая
заведомо проходит через «ноль», то есть b=0 и y=kx.
Необходимое условие минимума функции S(k), как известно,
есть равенство нулю её производной. Дифференцируя сумму (3.5)
по k, считая все величины {xi,yi} константами,
найдём
| dSdk=-∑i=1n2xi(yi-kxi)=0. |
Решая относительно k, находим
Поделив числитель и знаменатель на n, этот результат можно записать
более компактно:
Напомним, что угловые скобки означают усреднение по всем экспериментальным точкам:
В общем случае при b≠0 функция S(k,b) должна иметь
минимум как по k, так и по b. Поэтому имеем систему из двух
уравнений ∂S/∂k=0, ∂S/∂b=0,
решая которую, можно получить (получите самостоятельно):
| k=⟨xy⟩-⟨x⟩⟨y⟩⟨x2⟩-⟨x⟩2,b=⟨y⟩-k⟨x⟩. | (3.7) |
Эти соотношения и есть решение задачи о построении наилучшей прямой
методом наименьших квадратов.
Замечание. Совсем кратко формулу (3.7) можно записать, если ввести обозначение
Dxy≡⟨xy⟩-⟨x⟩⟨y⟩=⟨x-⟨x⟩⟩⋅⟨y-⟨y⟩⟩.
(3.8)
В математической статистике величину Dxy называют ковариацией.
При x≡y имеем дисперсию
Dxx=⟨(x-⟨x⟩)2⟩.
Тогда
k=DxyDxx,b=⟨y⟩-k⟨x⟩.
(3.9)
3.6.2 Погрешность МНК в линейной модели
Погрешности σk и σb коэффициентов, вычисленных
по формуле (3.7) (или (3.6)), можно оценить в
следующих предположениях.
Пусть погрешность измерений величины x пренебрежимо мала: σx≈0,
а погрешности по y одинаковы для всех экспериментальных точек
σy=const, независимы и имеют случайный характер
(систематическая погрешность отсутствует).
Пользуясь в этих предположениях формулами для погрешностей косвенных
измерений (см. раздел (2.6)) можно получить следующие
соотношения:
| σk=1n-2(DyyDxx-k2), | (3.10) |
где использованы введённые выше сокращённые обозначения (3.8).
Коэффициент n-2 отражает число независимых <<степеней
свободы>>: n экспериментальных точек за вычетом двух
условий связи (3.7).
В частном случае y=kx:
| σk=1n-1(⟨y2⟩⟨x2⟩-k2). | (3.12) |
3.6.3 Недостатки и условия применимости МНК
Формулы (3.7) (или (3.6)) позволяют провести
прямую по любому набору экспериментальных данных, а полученные
выше соотношения — вычислить
соответствующую среднеквадратичную ошибку для её коэффициентов. Однако
далеко не всегда результат будет иметь физический смысл. Перечислим
ограничения применимости данного метода.
В первую очередь метод наименьших квадратов — статистический,
и поэтому он предполагает использование достаточно большого количества
экспериментальных точек (желательно n>10).
Поскольку метод предполагает наличие погрешностей только по y,
оси следует выбирать так, чтобы погрешность σx откладываемой
по оси абсцисс величины была минимальна.
Кроме того, метод предполагает, что все погрешности в опыте —
случайны. Соответственно, формулы (3.10)–(3.12)
применимы только для оценки случайной составляющей ошибки k
или b. Если в опыте предполагаются достаточно большие систематические
ошибки, они должны быть оценены отдельно. Отметим, что для
оценки систематических ошибок не существует строгих математических
методов, поэтому в таком случае проще и разумнее всего воспользоваться
графическим методом.
Одна из основных проблем, связанных с определением погрешностей методом
наименьших квадратов заключается в том, что он дает разумные погрешности даже в
том случае, когда данные вообще не соответствуют модели.
Если погрешности измерений известны, предпочтительно использовать
метод минимума χ2.
Наконец, стоит предостеречь от использования любых аналитических
методов «вслепую», без построения графиков. В частности, МНК не способен
выявить такие «аномалии», как отклонения от линейной зависимости,
немонотонность, случайные всплески и т.п. Все эти случаи требуют особого
рассмотрения и могут быть легко обнаружены визуально при построении графика.
3.6.4 Метод хи-квадрат построения прямой
Пусть справедливы те же предположения, что и для метода наименьших квадратов,
но погрешности σi экспериментальных точек различны. Метод
минимума хи-квадрат сводится к минимизации суммы квадратов отклонений,
где каждое слагаемое взято с весом wi=1/σi2:
| χ2(k,b)=∑i=1nwi(yi-(kxi+b))2→min. |
Этот метод также называют взвешенным методом наименьших квадратов.
Определим взвешенное среднее от
некоторого набора значений {xi} как
где W=∑iwi — нормировочная константа.
Повторяя процедуру, использованную при выводе (3.7), нетрудно
получить (получите) совершенно аналогичные формулы для искомых коэффициентов:
| k=⟨xy⟩′-⟨x⟩′⟨y⟩′⟨x2⟩′-⟨x⟩′2,b=⟨y⟩′-k⟨x⟩′, | (3.13) |
с тем отличием от (3.7), что под угловыми скобками
⟨…⟩′
теперь надо понимать усреднение с весами wi=1/σi2.
Записанные формулы позволяют вычислить коэффициенты прямой,
если известны погрешности σyi. Значения σyi
могут быть получены либо из некоторой теории, либо измерены непосредственно
(многократным повторением измерений при каждом xi), либо оценены из
каких-то дополнительных соображений (например, как инструментальная погрешность).
Материал из MachineLearning.
Перейти к: навигация, поиск
Метод наименьших квадратов — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации евклидова расстояния между двумя векторами — вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.
Содержание
- 1 Постановка задачи
- 2 Пример построения линейной регрессии
- 3 Смотри также
- 4 Литература
- 5 Внешние ссылки
Постановка задачи
Задача метода наименьших квадратов состоит в выборе вектора , минимизирующего ошибку
.
Эта ошибка есть расстояние от вектора до вектора
.
Вектор лежит в простанстве столбцов матрицы
,
так как есть линейная комбинация столбцов этой матрицы с коэффициентами
.
Отыскание решения по методу наименьших квадратов эквивалентно задаче отыскания такой точки
,
которая лежит ближе всего к и находится при этом в пространстве столбцов матрицы
.
Таким образом, вектор должен быть проекцией
на пространство столбцов и вектор невязки
должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов
есть линейная комбинация столбцов с некоторыми коэффициентами , то есть это вектор
.
Для всех в пространстве
, эти векторы должны быть перпендикулярны невязке
:
Так как это равенство должно быть справедливо для произвольного вектора , то
Решение по методу наименьших квадратов несовместной системы ,
состоящей из уравнений с
неизвестными, есть уравнение
которое называется нормальным уравнением.
Если столбцы матрицы линейно независимы, то матрица
обратима
и единственное решение
Проекция вектора на пространство столбцов матрицы имеет вид
Матрица называется матрицей проектирования вектора
на пространство столбцов матрицы
.
Эта матрица имеет два основных свойства: она идемпотентна, , и симметрична,
.
Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов.
Пример построения линейной регрессии
Задана выборка — таблица
Задана регрессионная модель — квадратичный полином
Назначенная модель является линейной. Для нахождения оптимального
значения вектора параметров выполняется следующая подстановка:
Тогда матрица значений подстановок свободной переменной
будет иметь вид
Задан критерий качества модели: функция ошибки
Здесь вектор . Требуется найти такие параметры
, которые бы доставляли
минимум этому функционалу,
Требуется найти такие параметры , которые доставляют минимум
— норме вектора
невязок .
Для того, чтобы найти минимум функции невязки, требуется
приравнять ее производные к нулю. Производные данной функции
по составляют
Это выражение совпадает с нормальным уравнением. Решение
этой задачи должно удовлетворять системе линейных уравнений
то есть,
После получения весов можно построить график найденной функции.
При обращении матрицы предполагается, что эта
матрица невырождена и не плохо обусловлена. О том, как работать с плохо обусловленными матрицами см. в статье Сингулярное разложение.
Смотри также
- Линейная регрессия (пример)
- Нелинейная регрессия и метод наименьших квадратов
- Регрессионный анализ
- Анализ регрессионных остатков
- Сингулярное разложение
Литература
- Стренг Г. Линейная алгебра и ее применения. М.: Мир. 1980.
- Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. М.: Мир. 1998.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
Внешние ссылки
Wikipedia.org, Least squares

Метод наименьших квадратов (МНК) — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от экспериментальных входных данных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа (b) для оценки неизвестных параметров регрессионных моделей по выборочным данным.
История
До начала XIX в. учёные не имели определённых правил для решения системы уравнений (b) , в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (b) (1795) принадлежит первое применение метода, а Лежандр (b) (1805) независимо открыл и опубликовал его под современным названием (фр. (b) Méthode des moindres quarrés)[1]. Лаплас (b) связал метод с теорией вероятностей (b) , а американский математик Эдрейнru (b) en (1808) рассмотрел его теоретико-вероятностные приложения[2]. Метод распространён и усовершенствован дальнейшими изысканиями Энке (b) , Бесселя (b) , Ганзена и других.
Работы А. А. Маркова (b) в начале XX века позволили включить метод наименьших квадратов в теорию оценивания (b) математической статистики, в которой он является важной и естественной частью. Усилиями Ю. Неймана, Ф. Дэвида, А. Эйткена, С. Рао было получено множество немаловажных результатов в этой области[3].
Суть метода наименьших квадратов
Пусть , набор скалярных экспериментальных данных, , набор векторных экспериментальных данных и предполагается, что зависит от .
Вводится некоторая (в простейшем случае линейная) скалярная функция , которая определяется вектором неизвестных параметров .
Ставится задача найти вектор такой, чтобы совокупность погрешностей была в некотором смысле минимальной.
Согласно методу наименьших квадратов решением этой задачи является вектор , который минимизирует функцию
В простейшем случае , и тогда результатом МНК будет среднее арифметическое (b) входных данных.
Преимущество МНК перед минимизацией других видов ошибок состоит в том, что если дифференцируема по , то тоже дифференцируема. Приравнивание частных производных к нулю сводит задачу к решению системы уравнений, причём если зависит от линейно, то и система уравнений будет линейной.
Пример — система линейных уравнений
В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений
- ,
где прямоугольная матрица размера (то есть число строк матрицы A больше количества искомых переменных).
Такая система уравнений в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора , чтобы минимизировать «расстояние» между векторами и . Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть . Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений
- .
Используя оператор псевдоинверсии (b) , решение можно переписать так:
- ,
где — псевдообратная матрица для .
Эту задачу также можно «решить», используя так называемый взвешенный МНК (см. ниже), когда разные уравнения системы получают разный вес из теоретических соображений.
Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым (b) и А. Н. Колмогоровым (b) .
МНК в регрессионном анализе (аппроксимация данных)
Пусть имеется значений некоторой переменной (это могут быть результаты наблюдений, экспериментов и т. д.) и соответствующих переменных . Задача заключается в том, чтобы взаимосвязь между и аппроксимировать некоторой функцией , известной с точностью до некоторых неизвестных параметров , то есть фактически найти наилучшие значения параметров , максимально приближающие значения к фактическим значениям . Фактически это сводится к случаю «решения» переопределенной системы уравнений относительно :
.
В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными
,
где — так называемые случайные ошибки модели.
Соответственно, отклонения наблюдаемых значений от модельных предполагается уже в самой модели. Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры , при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) будет минимальной:
- ,
где — англ. (b) Residual Sum of Squares[4] определяется как:
- .
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. (b) Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции , продифференцировав её по неизвестным параметрам , приравняв производные к нулю и решив полученную систему уравнений:
- .
МНК в случае линейной регрессии
Пусть регрессионная зависимость является линейной (b) :
- .
Пусть y — вектор-столбец наблюдений объясняемой переменной, а — это -матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:
- .
Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны
- .
соответственно сумма квадратов остатков регрессии будет равна
- .
Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):
- .
В расшифрованной матричной форме эта система уравнений выглядит следующим образом:
где все суммы берутся по всем допустимым значениям .
Если в модель включена константа (как обычно), то при всех , поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений , а в остальных элементах первой строки и первого столбца — просто суммы значений переменных: и первый элемент правой части системы — .
Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:
- .
Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.
Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:
- .
В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.
Простейшие частные случаи
В случае парной линейной регрессии , когда оценивается линейная зависимость одной переменной от другой, формулы расчёта упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:
- .
Отсюда несложно найти оценки коэффициентов:
Несмотря на то, что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид ; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели . В этом случае вместо системы уравнений имеем единственное уравнение
.
Следовательно, формула оценки единственного коэффициента имеет вид
.
Случай полиномиальной модели
Если данные аппроксимируются полиномиальной функцией регрессии одной переменной , то, воспринимая степени как независимые факторы для каждого можно оценить параметры модели исходя из общей формулы оценки параметров линейной модели. Для этого в общей формуле достаточно учесть, что при такой интерпретации и . Следовательно, матричные уравнения в данном случае примут вид:
Статистические свойства МНК-оценок
В первую очередь отметим, что для линейных моделей МНК-оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещённости (b) МНК-оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа (b) : условное по факторам математическое ожидание (b) случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если
- математическое ожидание случайных ошибок равно нулю и
- факторы и случайные ошибки — независимые случайные величины (b) .
Первое условие для моделей с константой можно считать выполненным всегда, так как константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).
Второе условие — условие экзогенности (b) факторов — принципиальное. Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (b) (то есть даже очень большой объём данных не позволяет в этом случае получить качественные оценки). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.
Для того, чтобы кроме состоятельности и несмещённости (b) , оценки (обычного) МНК были ещё и эффективными (наилучшими в классе линейных несмещённых оценок), необходимо выполнение дополнительных свойств случайной ошибки:
- Постоянная (одинаковая) дисперсия случайных ошибок во всех наблюдениях (отсутствие гетероскедастичности (b) ): .
- Отсутствие корреляции (автокорреляции (b) ) случайных ошибок в разных наблюдениях между собой .
Данные предположения можно сформулировать для ковариационной матрицы (b) вектора случайных ошибок .
Линейная модель, удовлетворяющая таким условиям, называется классической. МНК-оценки для классической линейной регрессии являются несмещёнными (b) , состоятельными (b) и наиболее эффективными (b) оценками в классе всех линейных несмещённых оценок (в англоязычной литературе иногда употребляют аббревиатуру BLUE (Best Linear Unbiased Estimator) — наилучшая линейная несмещённая оценка; в отечественной литературе чаще приводится теорема Гаусса — Маркова (b) ). Как нетрудно показать, ковариационная матрица вектора оценок коэффициентов будет равна:
.
Эффективность (b) означает, что эта ковариационная матрица является «минимальной» (любая линейная комбинация оценок коэффициентов, и в частности сами оценки коэффициентов имеют минимальную дисперсию), то есть в классе линейных несмещённых оценок оценки МНК-наилучшие. Диагональные элементы этой матрицы — дисперсии оценок коэффициентов — важные параметры качества полученных оценок. Однако рассчитать ковариационную матрицу невозможно, поскольку дисперсия случайных ошибок неизвестна. Можно доказать, что несмещённой и состоятельной (для классической линейной модели) оценкой дисперсии случайных ошибок является величина:
.
Подставив данное значение в формулу для ковариационной матрицы, получим оценку ковариационной матрицы. Полученные оценки также являются несмещёнными (b) и состоятельными (b) . Важно также то, что оценка дисперсии ошибок (а значит и дисперсий коэффициентов) и оценки параметров модели являются независимыми случайными величинами, что позволяет получить тестовые статистики для проверки гипотез о коэффициентах модели.
Необходимо отметить, что если классические предположения не выполнены, МНК-оценки параметров не являются наиболее эффективными (b) оценками (оставаясь несмещёнными (b) и состоятельными (b) ). Однако ещё более ухудшается оценка ковариационной матрицы: она становится смещённой (b) и несостоятельной (b) . Это означает, что статистические выводы о качестве построенной модели в таком случае могут быть крайне недостоверными. Одним из вариантов решения этой проблемы является применение специальных оценок ковариационной матрицы, которые являются состоятельными при нарушениях классических предположений (стандартные ошибки в форме Уайта (b) и стандартные ошибки в форме Ньюи-Уеста (b) ). Другой подход заключается в применении так называемого обобщённого МНК (b) .
Обобщённый МНК
Метод наименьших квадратов допускает широкое обобщение. Вместо минимизации суммы квадратов остатков можно минимизировать некоторую положительно определённую квадратичную форму (b) от вектора остатков , где — некоторая симметрическая положительно определённая весовая матрица. Обычный МНК является частным случаем данного подхода, когда весовая матрица пропорциональна единичной матрице. Как известно, для симметрических матриц (или операторов) существует разложение . Следовательно, указанный функционал можно представить следующим образом: , то есть этот функционал можно представить как сумму квадратов некоторых преобразованных «остатков». Таким образом, можно выделить класс методов наименьших квадратов — LS-методы (Least Squares).
Доказано (теорема Айткена), что для обобщённой линейной регрессионной модели (в которой на ковариационную матрицу случайных ошибок не налагается никаких ограничений) наиболее эффективными (в классе линейных несмещённых оценок) являются оценки т. н. обобщённого МНК (ОМНК, GLS — Generalized Least Squares) — LS-метода с весовой матрицей, равной обратной ковариационной матрице случайных ошибок: .
Можно показать, что формула ОМНК-оценок параметров линейной модели имеет вид
.
Ковариационная матрица этих оценок соответственно будет равна
.
Фактически сущность ОМНК заключается в определённом (линейном) преобразовании (P) исходных данных и применении обычного МНК к преобразованным данным. Цель этого преобразования — для преобразованных данных случайные ошибки уже удовлетворяют классическим предположениям.
Взвешенный МНК
В случае диагональной весовой матрицы (а значит и ковариационной матрицы случайных ошибок) имеем так называемый взвешенный МНК. В данном случае минимизируется взвешенная сумма квадратов остатков модели, то есть каждое наблюдение получает «вес», обратно пропорциональный дисперсии случайной ошибки в данном наблюдении: . Фактически данные преобразуются взвешиванием наблюдений (делением на величину, пропорциональную предполагаемому стандартному отклонению случайных ошибок), а к взвешенным данным применяется обычный МНК.
См. также
- Обобщенный метод наименьших квадратов (b)
- Двухшаговый метод наименьших квадратов (b)
- Рекурсивный МНК (b)
- Алгоритм Гаусса — Ньютона (b)
Примечания
- ↑ Legendre, On Least Squares. Translated from the French by Professor Henry A. Ruger and Professor Helen M. Walker, Teachers College, Columbia University, New York City.Архивная копия от 7 января 2011 на Wayback Machine (b) (англ.)
- ↑ Александрова, 2008, с. 102.
- ↑ Линник, 1962, с. 21.
- ↑ Магнус, Катышев, Пересецкий, 2007, Обозначение RSS не унифицировано. RSS может быть сокращением от regression sum of squares, а ESS — error sum of squares, то есть, RSS и ESS будут иметь обратный смысл. с. 52. Издания 2004 года..
Литература
- Линник Ю. В (b) . Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд. — М., 1962. (математическая теория)
- Айвазян С. А. (b) Прикладная статистика. Основы эконометрики. Том 2. — М.: Юнити-Дана, 2001. — 432 с. — ISBN 5-238-00305-6.
- Доугерти К. Введение в эконометрику: Пер. с англ. — М.: ИНФРА-М, 1999. — 402 с. — ISBN 8-86225-458-7.
- Кремер Н. Ш., Путко Б. А. Эконометрика. — М.: Юнити-Дана, 2003—2004. — 311 с. — ISBN 8-86225-458-7.
- Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с. — ISBN 978-5-7749-0473-0.
- Эконометрика. Учебник / Под ред. Елисеевой И. И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с. — ISBN 5-279-02786-3.
- Александрова Н. В. История математических терминов, понятий, обозначений: словарь-справочник. — 3-е изд.. — М.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
- Витковский В. В. (b) Наименьшие квадраты // Энциклопедический словарь Брокгауза и Ефрона (b) : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Митин И. В., Русаков В. С. Анализ и обработка экспериментальных данных. — 5-е издание. — 24 с.
Ссылки
- Метод наименьших квадратов онлайн для зависимости y = a + bx с вычислением погрешностей коэффициентов и оцениванием автокорреляции.
На этом занятии
мы с вами рассмотрим алгоритм, который носит название метод наименьших
квадратов. Для начала немного теории. Чтобы ее хорошо понимать нужны
базовые знания по теории вероятностей, в частности понимание ПРВ, а также
знать, что такое производная и как она вычисляется. Остальное я сейчас
расскажу.
На практике
встречаются задачи, когда производились измерения некоторой функциональной
зависимости, но из-за погрешностей приборов, или неточных сведений или еще по
какой-либо причине, измерения немного отстоят от истинных значений функции и
образуют некий разброс:
Наша задача:
зная характер функциональной зависимости, подобрать ее параметры так, чтобы она
наилучшим образом описывала экспериментальные данные Например, на
рисунке явно прослеживается линейная зависимость. Мы это можем определить либо
чисто визуально, либо заранее знать о характере функции. Но, в любом случае
предполагается, что ее общий вид нам известен. Так вот, для линейной функции
достаточно определить два параметра k и b:
чтобы построить
аппроксимацию (приближение) линейного графика к экспериментальным зависимостям.
Конечно, вид функциональной зависимости может быть и другим, например,
квадратической (парабола), синусоидальной, или даже определяться суммой
известных функций, но для простоты понимания, мы для начала рассмотрим именно
линейный график с двумя неизвестными коэффициентами.
Итак, будем
считать, что на первый вопрос о характере функциональной зависимости
экспериментальных данных ответ дан. Следующий вопрос: как измерить качество
аппроксимации измерений функцией
? Вообще, таких
критериев можно придумать множество, например:
— сумма квадратов
ошибок отклонений:
— сумма модулей
ошибок отклонений:
— минимум
максимальной по модулю ошибки:
и так далее. Каждый
из критериев может приводить к своему алгоритму обработки экспериментальных
значений. Так вот, в методе наименьших квадратов используется минимум суммы
квадратов ошибок. И этому есть математическое обоснование. Часто результаты
реальных измерений имеют стандартное (гауссовское) отклонение относительно
измеряемого параметра:
Здесь σ –
стандартное отклонение (СКО) наблюдаемых значений от функции
. Отсюда хорошо
видно, что чем ближе измерение к истинному значению параметра, тем больше
значение функции плотности распределения условной вероятности. И, так для всех
точек измерения. Учитывая, что они выполняются независимо друг от друга, то
можно записать следующее функциональное выражение:
Получается, что лучшее
описание экспериментальных данных с помощью функции должно проходить по
точкам, в которых достигается максимум этого выражения. Очевидно, что при
поиске максимума можно не учитывать множитель 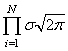
принимать максимальное значение при минимуме ее отрицательной степени:
Здесь также
множитель можно не учитывать, получаем критерий качества минимум суммы квадрата
ошибок:
Как мы помним,
наша цель – подобрать параметры функции
которые как раз
и обеспечивают минимум этого критерия, то есть, величина E зависит от этих
подбираемых величин:
И ее можно
рассматривать как квадратическую функцию от аргументов Из школьного курса
математики мы знаем как находится точка экстремума функции – это точка, в
которой производная равна нулю:
Здесь все также,
нужно взять частные производные по каждому параметру и приравнять результат
нулю, получим систему линейных уравнений:
Чтобы наполнить
конкретикой эту систему, нам нужно вернуться к исходному примеру с линейной
функцией:
Эта функция
зависит от двух параметров: k и b с частными
производными:
Подставляем все
в систему, имеем:
или, в виде:
Разделим все на N:
Смотрите, что в
итоге получилось. Формулы с суммами представляют собой первые и вторые
начальные моменты, а также один смешанный момент:
Здесь * означает
экспериментальные моменты. В этих обозначениях, получаем:
Отсюда находим,
что
Все, мы получили
оценки параметров k и b для линейной
аппроксимации экспериментальных данных по методу наименьших квадратов. По
аналогии можно вычислять параметры для других функциональных зависимостей,
например, квадратической:
Здесь будет уже
три свободных параметра и три уравнения, решая которые будем получать лучшую
аппроксимацию по критерию минимума суммарной квадратической ошибки отклонений.
Реализация на Python
В заключение
этого занятия реализуем метод наименьших квадратов на Python. Для этого нам
понадобятся две довольно популярные библиотеки numpy и matplotlib. Если они у вас
не установлены, то делается это просто – через команды:
pip install numpy
pip install matplotlib
После этого, мы
можем их импортировать и использовать в программе:
import numpy as np import matplotlib.pyplot as plt
Первая довольно
эффективная для выполнения различных математических операций, включая векторные
и матричные. Вторая служит для построения графиков.
Итак, вначале
определим необходимые начальные величины:
N = 100 # число экспериментов sigma = 3 # стандартное отклонение наблюдаемых значений k = 0.5 # теоретическое значение параметра k b = 2 # теоретическое значение параметра b
Формируем
вспомогательный вектор
с помощью метода
array, который
возвращает объект-вектор на основе итерируемой функции range:
Затем, вычисляем
значения теоретической функции:
f = np.array([k*z+b for z in range(N)])
и добавляем к
ней случайные отклонения для моделирования результатов наблюдений:
y = f + np.random.normal(0, sigma, N)
Если сейчас
отобразить наборы точек y, то они будут выглядеть следующим
образом:
plt.scatter(x, y, s=2, c='red') plt.grid(True) plt.show()
Теперь у нас все
есть для вычисления коэффициентов k и b по экспериментальным
данным:
# вычисляем коэффициенты mx = x.sum()/N my = y.sum()/N a2 = np.dot(x.T, x)/N a11 = np.dot(x.T, y)/N kk = (a11 - mx*my)/(a2 - mx**2) bb = my - kk*mx
Здесь выражение x.T*x – это
произведение:
Далее, построим
точки полученной аппроксимации:
ff = np.array([kk*z+bb for z in range(N)])
и отобразим оба
линейных графика:
plt.plot(f) plt.plot(ff, c='red')
Как видите
результат аппроксимации довольно близок начальному, теоретическому графику. Вот
так работает метод наименьших квадратов.
Реализация алгоритма на Python (файл mnsq.py)
Видео по теме
Метод наименьших квадратов регрессия
Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид
y=ax+b
a, b – коэффициенты линейного уравнения регрессии;
x – независимая переменная;
y – зависимая переменная.
Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов:
частные производные функции приравниваем к нулю
отсюда получаем систему линейных уравнений
Формулы определения коэффициентов уравнения линейной регрессии:
Также запишем уравнение регрессии для квадратной нелинейной функции:
Система линейных уравнений регрессии полинома n-ого порядка:
Формула коэффициента детерминации R 2 :
Формула средней ошибки аппроксимации для уравнения линейной регрессии (оценка качества модели):
Чем меньше ε, тем лучше. Рекомендованный показатель ε
Формула среднеквадратической погрешности:
Для примера, проведём расчет для получения линейного уравнения регрессии аппроксимации функции, заданной в табличном виде:
| x | y |
| 3 | 4 |
| 4 | 7 |
| 6 | 11 |
| 7 | 16 |
| 9 | 18 |
| 11 | 22 |
| 13 | 24 |
| 15 | 27 |
| 16 | 30 |
| 19 | 33 |
Решение
Расчеты значений суммы, произведения x и у приведены в таблицы.
Расчет коэффициентов линейной регрессии:
при этом средняя ошибка аппроксимации равна:
ε=11,168%
Получаем уравнение линейной регрессии с помощью метода наименьших квадратов:
y=1,7871x+0,79
График функции линейной зависимости y=1,7871x+0,79 и табличные значения, в виде точек
Коэффициент корреляции равен 0,988
Коэффициента детерминации равен 0,976
Метод наименьших квадратов
Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | |
| x i | 0 | 1 | 2 | 4 | 5 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 , 0 |
После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .
Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.
В чем именно заключается МНК (метод наименьших квадратов)
Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.
Как вывести формулы для вычисления коэффициентов
Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .
δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i
Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n
Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.
Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .
Обратимся вновь к исходному примеру.
Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | ∑ i = 1 5 | |
| x i | 0 | 1 | 2 | 4 | 5 | 12 |
| y i | 2 , 1 | 2 , 4 | 2 , 6 | 2 , 8 | 3 | 12 , 9 |
| x i y i | 0 | 2 , 4 | 5 , 2 | 11 , 2 | 15 | 33 , 8 |
| x i 2 | 0 | 1 | 4 | 16 | 25 | 46 |
Решение
Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.
Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:
n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184
У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.
Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.
σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096
Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .
Как изобразить МНК на графике функций
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.
Поясним, для чего именно нужны приближения подобного вида.
Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.
Доказательство метода МНК
Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.
У нас есть дифференциал второго порядка следующего вида:
d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b
Решение
δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n
Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .
Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .
В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.
Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.
Вычисляем угловой минор второго порядка:
d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2
После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.
- Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:
2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0
У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).
- Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
- Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .
( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0
Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.
Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).
Математика на пальцах: методы наименьших квадратов
Я математик-программист. Самый большой скачок в своей карьере я совершил, когда научился говорить:«Я ничего не понимаю!» Сейчас мне не стыдно сказать светилу науки, что мне читает лекцию, что я не понимаю, о чём оно, светило, мне говорит. И это очень сложно. Да, признаться в своём неведении сложно и стыдно. Кому понравится признаваться в том, что он не знает азов чего-то-там. В силу своей профессии я должен присутствовать на большом количестве презентаций и лекций, где, признаюсь, в подавляющем большинстве случаев мне хочется спать, потому что я ничего не понимаю. А не понимаю я потому, что огромная проблема текущей ситуации в науке кроется в математике. Она предполагает, что все слушатели знакомы с абсолютно всеми областями математики (что абсурдно). Признаться в том, что вы не знаете, что такое производная (о том, что это — чуть позже) — стыдно.
Но я научился говорить, что я не знаю, что такое умножение. Да, я не знаю, что такое подалгебра над алгеброй Ли. Да, я не знаю, зачем нужны в жизни квадратные уравнения. К слову, если вы уверены, что вы знаете, то нам есть над чем поговорить! Математика — это серия фокусов. Математики стараются запутать и запугать публику; там, где нет замешательства, нет репутации, нет авторитета. Да, это престижно говорить как можно более абстрактным языком, что есть по себе полная чушь.
Знаете ли вы, что такое производная? Вероятнее всего вы мне скажете про предел разностного отношения. На первом курсе матмеха СПбГУ Виктор Петрович Хавин мне определил производную как коэффициент первого члена ряда Тейлора функции в точке (это была отдельная гимнастика, чтобы определить ряд Тейлора без производных). Я долго смеялся над таким определением, покуда в итоге не понял, о чём оно. Производная не что иное, как просто мера того, насколько функция, которую мы дифференцируем, похожа на функцию y=x, y=x^2, y=x^3.
Я сейчас имею честь читать лекции студентам, которые боятся математики. Если вы боитесь математики — нам с вами по пути. Как только вы пытаетесь прочитать какой-то текст, и вам кажется, что он чрезмерно сложен, то знайте, что он хреново написан. Я утверждаю, что нет ни одной области математики, о которой нельзя говорить «на пальцах», не теряя при этом точности.
Задача на ближайшее время: я поручил своим студентам понять, что такое линейно-квадратичный регулятор. Не постесняйтесь, потратьте три минуты своей жизни, сходите по ссылке. Если вы ничего не поняли, то нам с вами по пути. Я (профессиональный математик-программист) тоже ничего не понял. И я уверяю, в этом можно разобраться «на пальцах». На данный момент я не знаю, что это такое, но я уверяю, что мы сумеем разобраться.
Итак, первая лекция, которую я собираюсь прочитать своим студентам после того, как они в ужасе прибегут ко мне со словами, что линейно-квадратичный регулятор — это страшная бяка, которую никогда в жизни не осилить, это методы наименьших квадратов. Умеете ли вы решать линейные уравнения? Если вы читаете этот текст, то скорее всего нет.
Итак, даны две точки (x0, y0), (x1, y1), например, (1,1) и (3,2), задача найти уравнение прямой, проходящей через эти две точки:
Эта прямая должна иметь уравнение типа следующего:
Здесь альфа и бета нам неизвестны, но известны две точки этой прямой:
Можно записать это уравнение в матричном виде:
Тут следует сделать лирическое отступление: что такое матрица? Матрица это не что иное, как двумерный массив. Это способ хранения данных, более никаких значений ему придавать не стоит. Это зависит от нас, как именно интерпретировать некую матрицу. Периодически я буду её интерпретировать как линейное отображение, периодически как квадратичную форму, а ещё иногда просто как набор векторов. Это всё будет уточнено в контексте.
Давайте заменим конкретные матрицы на их символьное представление:
Тогда (alpha, beta) может быть легко найдено:
Более конкретно для наших предыдущих данных:
Что ведёт к следующему уравнению прямой, проходящей через точки (1,1) и (3,2):
Окей, тут всё понятно. А давайте найдём уравнение прямой, проходящей через три точки: (x0,y0), (x1,y1) и (x2,y2):
Ой-ой-ой, а ведь у нас три уравнения на две неизвестных! Стандартный математик скажет, что решения не существует. А что скажет программист? А он для начала перепишет предыдующую систему уравнений в следующем виде:
И дальше постарается найти решение, которое меньше всего отклонится от заданных равенств. Давайте назовём вектор (x0,x1,x2) вектором i, (1,1,1) вектором j, а (y0,y1,y2) вектором b:
В нашем случае векторы i,j,b трёхмерны, следовательно, (в общем случае) решения этой системы не существует. Любой вектор (alpha*i + beta*j) лежит в плоскости, натянутой на векторы (i, j). Если b не принадлежит этой плоскости, то решения не существует (равенства в уравнении не достичь). Что делать? Давайте искать компромисс. Давайте обозначим через e(alpha, beta) насколько именно мы не достигли равенства:
И будем стараться минимизировать эту ошибку:
Очевидно, что ошибка минимизируется, когда вектор e ортогонален плоскости, натянутой на векторы i и j.
Иными словами: мы ищем такую прямую, что сумма квадратов длин расстояний от всех точек до этой прямой минимальна:
UPDATE: тут у меня косяк, расстояние до прямой должно измеряться по вертикали, а не ортогональной проекцией. Вот этот комментатор прав.
Совсеми иными словами (осторожно, плохо формализовано, но на пальцах должно быть ясно): мы берём все возможные прямые между всеми парами точек и ищем среднюю прямую между всеми:
Иное объяснение на пальцах: мы прикрепляем пружинку между всеми точками данных (тут у нас три) и прямой, что мы ищем, и прямая равновесного состояния есть именно то, что мы ищем.
Минимум квадратичной формы
Итак, имея данный вектор b и плоскость, натянутую на столбцы-векторы матрицы A (в данном случае (x0,x1,x2) и (1,1,1)), мы ищем вектор e с минимум квадрата длины. Очевидно, что минимум достижим только для вектора e, ортогонального плоскости, натянутой на столбцы-векторы матрицы A:
Иначе говоря, мы ищем такой вектор x=(alpha, beta), что:
Напоминаю, что этот вектор x=(alpha, beta) является минимумом квадратичной функции ||e(alpha, beta)||^2:
Тут нелишним будет вспомнить, что матрицу можно интерпретирвать в том числе как и квадратичную форму, например, единичная матрица ((1,0),(0,1)) может быть интерпретирована как функция x^2 + y^2:
Вся эта гимнастика известна под именем линейной регрессии.
Уравнение Лапласа с граничным условием Дирихле
Теперь простейшая реальная задача: имеется некая триангулированная поверхность, необходимо её сгладить. Например, давайте загрузим модель моего лица:
Изначальный коммит доступен здесь. Для минимизации внешних зависимостей я взял код своего софтверного рендерера, уже подробно описанного на хабре. Для решения линейной системы я пользуюсь OpenNL, это отличный солвер, который, правда, очень сложно установить: нужно скопировать два файла (.h+.c) в папку с вашим проектом. Всё сглаживание делается следующим кодом:
X, Y и Z координаты отделимы, я их сглаживаю по отдельности. То есть, я решаю три системы линейных уравнений, каждое имеет количество переменных равным количеству вершин в моей модели. Первые n строк матрицы A имеют только одну единицу на строку, а первые n строк вектора b имеют оригинальные координаты модели. То есть, я привязываю по пружинке между новым положением вершины и старым положением вершины — новые не должны слишком далеко уходить от старых.
Все последующие строки матрицы A (faces.size()*3 = количеству рёбер всех треугольников в сетке) имеют одно вхождение 1 и одно вхождение -1, причём вектор b имеет нулевые компоненты напротив. Это значит, я вешаю пружинку на каждое ребро нашей треугольной сетки: все рёбра стараются получить одну и ту же вершину в качестве отправной и финальной точки.
Ещё раз: переменными являются все вершины, причём они не могут далеко отходить от изначального положения, но при этом стараются стать похожими друг на друга.
Всё бы было хорошо, модель действительно сглажена, но она отошла от своего изначального края. Давайте чуть-чуть изменим код:
В нашей матрице A я для вершин, что находятся на краю, добавляю не строку из разряда v_i = verts[i][d], а 1000*v_i = 1000*verts[i][d]. Что это меняет? А меняет это нашу квадратичную форму ошибки. Теперь единичное отклонение от вершины на краю будет стоить не одну единицу, как раньше, а 1000*1000 единиц. То есть, мы повесили более сильную пружинку на крайние вершины, решение предпочтёт сильнее растянуть другие. Вот результат:
Давайте вдвое усилим пружинки между вершинами:
Логично, что поверхность стала более гладкой:
А теперь ещё в сто раз сильнее:
Что это? Представьте, что мы обмакнули проволочное кольцо в мыльную воду. В итоге образовавшаяся мыльная плёнка будет стараться иметь наименьшую кривизну, насколько это возможно, касаясь-таки границы — нашего проволочного кольца. Именно это мы и получили, зафиксировав границу и попросив получить гладкую поверхность внутри. Поздравляю вас, мы только что решили уравнение Лапласа с граничными условиями Дирихле. Круто звучит? А на деле всего-навсего одну систему линейных уравнений решить.
Уравнение Пуассона
Давайте ещё крутое имя вспомним.
Предположим, что у меня есть такая картинка:
Всем хороша, только стул мне не нравится.
Разрежу картинку пополам:
И выделю руками стул:
Затем всё, что белое в маске, притяну к левой части картинки, а заодно по всей картинке скажу, что разница между двумя соседними пикселями должна равняться разнице между двумя соседними пикселями правой картинки:
Код и картинки доступны здесь.
Пример из жизни
Я специально не стал делать вылизанные результаты, т.к. мне хотелось всего-навсего показать, как именно можно применять методы наименьших квадратов, это обучающий код. Давайте я теперь дам пример из жизни:
У меня есть некоторое количество фотографий образцов ткани типа вот такой:
Моя задача сделать бесшовные текстуры из фотографий вот такого качества. Для начала я (автоматически) ищу повторяющийся паттерн:
Если я вырежу прямо вот этот четырёхугольник, то из-за искажений у меня края не сойдутся, вот пример четыре раза повторённого паттерна:
Вот фрагмент, где чётко видно шов:
Поэтому я вырезать буду не по ровной линии, вот линия разреза:
А вот повторённый четыре раза паттерн:
И его фрагмент, чтобы было виднее:
Уже лучше, рез шёл не по прямой линии, обойдя всякие завитушки, но всё же шов виден из-за неравномерности освещения на оригинальной фотографии. Вот тут-то и приходит на помощь метод наименьших квадратов для уравнения Пуассона. Вот конечный результат после выравнивания освещения:
Текстура получилась отлично бесшовной, и всё это автоматически из фотографии весьма посредственного качества. Не бойтесь математики, ищите простые объяснения, и будет вам инженерное счастье.
http://zaochnik.com/spravochnik/matematika/stati/metod-naimenshih-kvadratov/
http://habr.com/ru/post/277275/
Материал из MachineLearning.
(Перенаправлено с МНК)
Перейти к: навигация, поиск
Метод наименьших квадратов — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации евклидова расстояния между двумя векторами — вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.
Содержание
- 1 Постановка задачи
- 2 Пример построения линейной регрессии
- 3 Смотри также
- 4 Литература
- 5 Внешние ссылки
Постановка задачи
Задача метода наименьших квадратов состоит в выборе вектора , минимизирующего ошибку
.
Эта ошибка есть расстояние от вектора до вектора
.
Вектор лежит в простанстве столбцов матрицы
,
так как есть линейная комбинация столбцов этой матрицы с коэффициентами
.
Отыскание решения по методу наименьших квадратов эквивалентно задаче отыскания такой точки
,
которая лежит ближе всего к и находится при этом в пространстве столбцов матрицы
.
Таким образом, вектор должен быть проекцией
на пространство столбцов и вектор невязки
должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов
есть линейная комбинация столбцов с некоторыми коэффициентами , то есть это вектор
.
Для всех в пространстве
, эти векторы должны быть перпендикулярны невязке
:
Так как это равенство должно быть справедливо для произвольного вектора , то
Решение по методу наименьших квадратов несовместной системы ,
состоящей из уравнений с
неизвестными, есть уравнение
которое называется нормальным уравнением.
Если столбцы матрицы линейно независимы, то матрица
обратима
и единственное решение
Проекция вектора на пространство столбцов матрицы имеет вид
Матрица называется матрицей проектирования вектора
на пространство столбцов матрицы
.
Эта матрица имеет два основных свойства: она идемпотентна, , и симметрична,
.
Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов.
Пример построения линейной регрессии
Задана выборка — таблица
Задана регрессионная модель — квадратичный полином
Назначенная модель является линейной. Для нахождения оптимального
значения вектора параметров выполняется следующая подстановка:
Тогда матрица значений подстановок свободной переменной
будет иметь вид
Задан критерий качества модели: функция ошибки
Здесь вектор . Требуется найти такие параметры
, которые бы доставляли
минимум этому функционалу,
Требуется найти такие параметры , которые доставляют минимум
— норме вектора
невязок .
Для того, чтобы найти минимум функции невязки, требуется
приравнять ее производные к нулю. Производные данной функции
по составляют
Это выражение совпадает с нормальным уравнением. Решение
этой задачи должно удовлетворять системе линейных уравнений
то есть,
После получения весов можно построить график найденной функции.
При обращении матрицы предполагается, что эта
матрица невырождена и не плохо обусловлена. О том, как работать с плохо обусловленными матрицами см. в статье Сингулярное разложение.
Смотри также
- Линейная регрессия (пример)
- Нелинейная регрессия и метод наименьших квадратов
- Регрессионный анализ
- Анализ регрессионных остатков
- Сингулярное разложение
Литература
- Стренг Г. Линейная алгебра и ее применения. М.: Мир. 1980.
- Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. М.: Мир. 1998.
- Стрижов В. В. Методы индуктивного порождения регрессионных моделей. М.: ВЦ РАН. 2008. 55 с. Брошюра, PDF.
Внешние ссылки
Wikipedia.org, Least squares
В статистике , обычный метод наименьших квадратов ( МНК ) представляет собой тип линейной наименьших квадратов метода оценки неизвестных параметров в линейной регрессии модели. OLS выбирает параметры линейной функции набора объясняющих переменных по принципу наименьших квадратов : минимизируя сумму квадратов различий между наблюдаемой зависимой переменной (значения наблюдаемой переменной) в данном наборе данных и предсказанными линейной функцией независимой переменной .
Геометрически это рассматривается как сумма квадратов расстояний, параллельных оси зависимой переменной, между каждой точкой данных в наборе и соответствующей точкой на поверхности регрессии — чем меньше различия, тем лучше модель соответствует данным. . Результирующая оценка может быть выражена простой формулой, особенно в случае простой линейной регрессии , в которой в правой части уравнения регрессии есть единственный регрессор .
МНК — оценка является последовательным , когда регрессоры экзогенные , и по- Гаусс-Марков теоремы — оптимальным в классе линейных несмещенных оценок , когда ошибки являются гомоскедастичными и последовательно коррелированны . В этих условиях метод OLS обеспечивает несмещенную оценку с минимальной дисперсией, когда ошибки имеют конечную дисперсию . При дополнительном предположении, что ошибки имеют нормальное распределение , OLS является оценкой максимального правдоподобия .
Линейная модель
Закон Окуня в макроэкономике гласит, что в экономике рост ВВП должен линейно зависеть от изменений уровня безработицы. Здесь для построения линии регрессии, описывающей этот закон, используется обычный метод наименьших квадратов.
Предположим, что данные состоят из наблюдений . Каждое наблюдение включает в себя скалярный ответ и вектор — столбец из параметров (регрессор), то есть . В модели линейной регрессии переменная отклика является линейной функцией регрессоров:

или в векторной форме,
где , как было введено ранее, — вектор-столбец -го наблюдения всех независимых переменных; — вектор неизвестных параметров; а скаляр представляет ненаблюдаемые случайные величины ( ошибки ) -го наблюдения. учитывает влияние на ответы источников, отличных от поясняющих . Эта модель также может быть записана в матричных обозначениях как
где и — векторы переменных отклика и ошибок наблюдений, а — матрица регрессоров, также иногда называемая матрицей плана , строка которой является и содержит -е наблюдение по всем независимым переменным.
Как правило, постоянный член всегда входит в набор регрессоров , например, принимая для всех . Коэффициент , соответствующий этому регрессора называется перехватывают .
Регрессоры не обязательно должны быть независимыми: между регрессорами может быть любое желаемое отношение (при условии, что оно не является линейным). Например, мы можем подозревать, что ответ линейно зависит как от значения, так и от его квадрата; в этом случае мы должны включить один регрессор, значение которого является просто квадратом другого регрессора. В этом случае модель будет квадратичной во втором регрессоре, но, тем не менее, по-прежнему считается линейной моделью, потому что модель по- прежнему линейна по параметрам ( ).
Матричная / векторная формулировка
Рассмотрим переопределенную систему
из линейных уравнений в неизвестных коэффициентов , с . (Примечание: для линейной модели, как указано выше, не все элементы содержат информацию о точках данных. Первый столбец заполнен единицами . Только другие столбцы содержат фактические данные. Таким образом, здесь количество регрессоров равно количеству регрессоров плюс один. ) Это можно записать в матричной форме как

куда
Такая система , как правило , не имеет точного решения, поэтому цель вместо того, чтобы найти коэффициенты , которые соответствуют уравнениям «лучшие», в смысле решения квадратичной минимизации проблемы

где целевая функция определяется выражением
Обоснование выбора этого критерия приведено в разделе «Свойства» ниже. Эта задача минимизации имеет единственное решение, при условии , что столбцы матрицы являются линейно независимыми , данным решением нормальных уравнений
Матрица известна как матрица Грама, а матрица известна как матрица регрессии моментов и регрессоров. Наконец, — вектор коэффициентов гиперплоскости наименьших квадратов , выраженный как
или
Предварительный расчет
Предположим, что b — значение «кандидата» для вектора параметров β . Величина y i — x i T b , называемая остатком для i -го наблюдения, измеряет расстояние по вертикали между точкой данных ( x i , y i ) и гиперплоскостью y = x T b , и, таким образом, оценивает степень отклонения. соответствие между фактическими данными и моделью. Сумма квадратов остатков ( SSR ) (также называется сумма ошибки квадратов ( ESS ) или остаточной суммы квадратов ( RSS )) является мерой общей модели , пригодной:
где Т обозначает матрицу транспонирование , а строки X , обозначая значения всех независимых переменных , связанных с конкретным значением зависимой переменной, являются Х я = х я Т . Значение b, которое минимизирует эту сумму, называется оценкой МНК для β . Функция S ( b ) квадратична по b с положительно определенным гессианом , и поэтому эта функция обладает единственным глобальным минимумом в точке , который может быть задан явной формулой: [доказательство]
Продукт Н = Х Т Х является матрицей Грама и обратное, Q = N -1 , является кофактором матрицы из р , тесно связано с его ковариационной матрицей , C р . Матрица ( X T X ) –1 X T = Q X T называется псевдообратной матрицей Мура – Пенроуза для X. Эта формулировка подчеркивает, что оценка может быть проведена тогда и только тогда, когда нет идеальной мультиколлинеарности между независимые переменные (которые заставили бы матрицу грамма не иметь инверсии).
После того, как мы оценили β , подогнанные значения (или предсказанные значения ) из регрессии будут
где Р = Х ( Х Т Х ) -1 Х Т является матрица проекции на пространство V , натянутого на столбцы X . Эту матрицу P также иногда называют матрицей шляпы, потому что она «накладывает шляпу» на переменную y . Другая матрица, тесно связанная с P, — это аннигиляторная матрица M = I n — P ; это матрица проекции на пространство , ортогональное V . Обе матрицы P и M являются симметричными и идемпотентная ( что означает , что Р 2 = Р и М 2 = М ), и относятся к данным матрицы X с помощью тождеств PX = Х и МХ = 0 . Матрица M создает остатки из регрессии:
Используя эти остатки, мы можем оценить значение σ 2, используя приведенную статистику хи-квадрат :
Знаменатель n — p — это статистические степени свободы . Первая величина s 2 является оценкой OLS для σ 2 , а вторая — оценкой MLE для σ 2 . Эти две оценки очень похожи в больших выборках; первый оценщик всегда несмещен , а второй оценщик смещен, но имеет меньшую среднеквадратичную ошибку . На практике s 2 используется чаще, так как это более удобно для проверки гипотез. Квадратный корень из s 2 называется стандартной ошибкой регрессии , стандартной ошибкой регрессии или стандартной ошибкой уравнения .
Обычно для оценки благость-о-приступе регрессии методом наименьших квадратов, сравнивая , сколько начальное изменение в образце может быть уменьшено регресс на X . Коэффициент детерминации R 2 определена как отношение «объяснено» дисперсии к «общему» дисперсии зависимой переменной у , в тех случаях , когда сумма квадратов регрессии равна сумме квадратов остатков:
где ТСС является общая сумма квадратов для зависимой переменной, и является п × п матрица из них. ( представляет собой центрирующую матрицу, которая эквивалентна регрессии по константе; она просто вычитает среднее значение из переменной.) Для того, чтобы R 2 был значимым, матрица X данных в регрессорах должна содержать вектор-столбец из единиц для представления константа, коэффициент которой является отрезком регрессии. В этом случае R 2 всегда будет числом от 0 до 1, а значения, близкие к 1, указывают на хорошую степень соответствия.
Дисперсия предсказания независимой переменной как функции зависимой переменной приведена в статье Полиномиальные наименьшие квадраты .
Модель простой линейной регрессии
Если матрица данных X содержит только две переменные, константу и скалярный регрессор x i , то это называется «моделью простой регрессии». Этот случай часто рассматривается в классах статистики для начинающих, поскольку он предоставляет гораздо более простые формулы, подходящие даже для ручного расчета. Параметры обычно обозначаются как ( α , β ) :
Оценки наименьших квадратов в этом случае даются простыми формулами
Альтернативные производные
В предыдущем разделе оценка методом наименьших квадратов была получена как значение, которое минимизирует сумму квадратов остатков модели. Однако можно получить такую же оценку и из других подходов. Во всех случаях формула для оценки OLS остается той же: ^ β = ( X T X ) −1 X T y ; единственная разница в том, как мы интерпретируем этот результат.
Проекция
МНК-оценку можно рассматривать как проекцию на линейное пространство, охватываемое регрессорами. (Здесь каждый из и относится к столбцу матрицы данных.)
Для математиков OLS — это приближенное решение переопределенной системы линейных уравнений Xβ ≈ y , где β — неизвестное. Предполагая, что система не может быть решена точно (количество уравнений n намного больше, чем количество неизвестных p ), мы ищем решение, которое могло бы обеспечить наименьшее расхождение между правой и левой частями. Другими словами, мы ищем решение, удовлетворяющее
где || · || является стандартом L 2 норма в п — мерном евклидовом пространстве R п . Прогнозируемая величина Xβ — это просто некоторая линейная комбинация векторов регрессоров. Таким образом, остаточный вектор у — хр будет иметь наименьшую длину , когда у является прогнозируемое ортогонально на линейное подпространство , натянутое на столбцы X . МНК — оценка в этом случае можно интерпретировать как коэффициенты вектора разложения по ^ у = Py вдоль основе X .
Другими словами, уравнения градиента в минимуме можно записать как:
Геометрическая интерпретация этих уравнений является то , что вектор невязок, ортогональна к колонке пространства в X , так как скалярное произведение равно нулю для любого конформного вектора, об . Это означает, что это самый короткий из всех возможных векторов , то есть дисперсия остатков минимально возможна. Это показано справа.
Вводя матрицу K в предположении, что матрица невырожденная и K T X = 0 (см. Ортогональные проекции ), остаточный вектор должен удовлетворять следующему уравнению:
![[X K]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0c7583e31f8e4111806d1612b81b39d3f76af01)
Таким образом, уравнение и решение линейных наименьших квадратов описываются следующим образом:
Другой способ взглянуть на это — рассматривать линию регрессии как средневзвешенное значение линий, проходящих через комбинацию любых двух точек в наборе данных. Хотя этот способ вычисления более затратен с точки зрения вычислений, он обеспечивает лучшую интуицию на OLS.
Максимальная вероятность
Оценщик OLS идентичен оценщику максимального правдоподобия (MLE) в предположении нормальности для членов ошибки. [доказательство] Это предположение о нормальности имеет историческое значение, поскольку оно легло в основу ранних работ Юла и Пирсона по линейному регрессионному анализу . Из свойств MLE мы можем сделать вывод, что оценка OLS асимптотически эффективна (в смысле достижения границы Крамера – Рао для дисперсии), если выполняется предположение нормальности.
Обобщенный метод моментов
В iid случае оценщик МНК можно также рассматривать как ОММ оценщик, возникающий из моментных условий
Эти моментные условия утверждают, что регрессоры не должны коррелировать с ошибками. Поскольку x i является p -вектором, количество моментов равно размерности вектора параметров β , и, таким образом, система точно идентифицируется. Это так называемый классический случай GMM, когда оценка не зависит от выбора весовой матрицы.
Отметим, что исходное предположение строгой экзогенности E [ ε i | x i ] = 0 подразумевает гораздо более богатый набор моментных условий, чем указано выше. В частности, из этого предположения следует, что для любой вектор-функции ƒ будет выполнено моментное условие E [ ƒ ( x i ) · ε i ] = 0 . Однако с помощью теоремы Гаусса – Маркова можно показать, что оптимальный выбор функции ƒ состоит в том, чтобы взять ƒ ( x ) = x , что приводит к уравнению моментов, опубликованному выше.
Характеристики
Предположения
Существует несколько различных структур, в которых можно применить модель линейной регрессии , чтобы применить метод OLS. Каждый из этих параметров дает одинаковые формулы и одинаковые результаты. Единственная разница заключается в интерпретации и допущениях, которые должны быть наложены, чтобы метод давал значимые результаты. Выбор применяемой структуры зависит главным образом от природы имеющихся данных и от задачи вывода, которую необходимо выполнить.
Одна из линий разницы в интерпретации заключается в том, следует ли рассматривать регрессоры как случайные величины или как предопределенные константы. В первом случае ( случайный план ) регрессоры x i являются случайными и отбираются вместе с y i из некоторой совокупности , как в наблюдательном исследовании . Такой подход позволяет более естественно изучить асимптотические свойства оценок. В другой интерпретации ( фиксированный план ) регрессоры X рассматриваются как известные константы, установленные планом , а y выбирается условно на основе значений X, как в эксперименте . Для практических целей это различие часто несущественно, так как оценка и вывод осуществляется в то время кондиционирования на X . Все результаты, изложенные в этой статье, находятся в рамках случайного проектирования.
Классическая модель линейной регрессии
Классическая модель фокусируется на оценке и выводе «конечной выборки», что означает, что количество наблюдений n фиксировано. Это контрастирует с другими подходами, которые изучают асимптотическое поведение OLS и в которых количество наблюдений может расти до бесконечности.
- Правильная спецификация . Линейная функциональная форма должна совпадать с формой фактического процесса генерации данных.
-
Строгая экзогенность . Ошибки в регрессии должны иметь условное среднее значение ноль:
- Непосредственным следствием предположения об экзогенности является то, что ошибки имеют нулевое среднее значение: E [ ε ] = 0 , и что регрессоры не коррелируют с ошибками: E [ X T ε ] = 0 .
- Предположение экзогенности имеет решающее значение для теории OLS. Если это так, то переменные регрессора называются экзогенными . В противном случае те регрессоры, которые коррелируют с ошибкой, называются эндогенными , и тогда оценки OLS становятся недействительными. В таком случае для вывода можно использовать метод инструментальных переменных .
-
Нет линейной зависимости . Все регрессоры в X должны быть линейно независимыми . Математически это означает, что матрица X почти наверняка должна иметь полный ранг столбца :
- Обычно также предполагается, что регрессоры имеют конечные моменты, по крайней мере, до второго момента. Тогда матрица Q xx = E [ X T X / n ] конечна и положительно полуопределена.
- Когда это предположение нарушается, регрессоры называют линейно зависимыми или полностью мультиколлинеарными . В таком случае значение коэффициента регрессии β невозможно узнать, хотя предсказание значений y все еще возможно для новых значений регрессоров, которые лежат в том же линейно зависимом подпространстве.
-
Сферические ошибки :
- где I n — единичная матрица в размерности n , а σ 2 — параметр, определяющий дисперсию каждого наблюдения. Этот параметр σ 2 считается мешающим параметром в модели, хотя обычно он также оценивается. Если это предположение нарушается, то оценки OLS по-прежнему действительны, но уже неэффективны.
- Это предположение принято разделять на две части:
- Гомоскедастичность : E [ ε i 2 | X ] = σ 2 , что означает, что член ошибки имеет одинаковую дисперсию σ 2 в каждом наблюдении. Когда это требование нарушается, это называется гетероскедастичностью , в этом случае более эффективной оценкой будет взвешенный метод наименьших квадратов . Если ошибки имеют бесконечную дисперсию, тогда оценки OLS также будут иметь бесконечную дисперсию (хотя по закону больших чисел они, тем не менее, будут стремиться к истинным значениям, пока ошибки имеют нулевое среднее). В этом случаерекомендуются надежные методы оценки .
- Нет автокорреляции : ошибки между наблюдениями не коррелированы : E [ ε i ε j | X ] = 0 для i ≠ j . Это предположение может быть нарушено в контексте данных временных рядов , панельных данных , кластерных выборок, иерархических данных, данных повторных измерений, продольных данных и других данных с зависимостями. В таких случаях обобщенный метод наименьших квадратов является лучшей альтернативой, чем МНК. Еще одно выражение автокорреляции — это серийная корреляция .
-
Нормальность . Иногда дополнительно предполагается, что ошибки имеют нормальное распределение, обусловленное регрессорами:
- Это предположение не требуется для достоверности метода OLS, хотя некоторые дополнительные свойства конечной выборки могут быть установлены в том случае, если это произойдет (особенно в области проверки гипотез). Также, когда ошибки являются нормальными, оценщик OLS эквивалентен оценщику максимального правдоподобия (MLE), и, следовательно, он асимптотически эффективен в классе всех обычных оценщиков . Важно отметить, что предположение о нормальности применимо только к ошибочным членам; Вопреки распространенному заблуждению, не требуется, чтобы переменная ответа (зависимая) имела нормальное распределение.
Независимые и идентично распределенные (iid)
В некоторых приложениях, особенно с данными поперечного сечения , накладывается дополнительное предположение — что все наблюдения независимы и одинаково распределены. Это означает, что все наблюдения берутся из случайной выборки, что упрощает все перечисленные ранее допущения и упрощает их интерпретацию. Также эта структура позволяет сформулировать асимптотические результаты (размер выборки n → ∞ ), которые понимаются как теоретическая возможность получения новых независимых наблюдений из процесса генерации данных . Список предположений в этом случае:
- iid наблюдений : ( x i , y i ) не зависит от, и имеет то же распределение, что и, ( x j , y j ) для всех i ≠ j ;
- нет идеальной мультиколлинеарности : Q xx = E [ x i x i T ] — положительно определенная матрица ;
- экзогенность : E [ ε i | x i ] = 0;
- гомоскедастичность : Var [ ε i | х i ] = σ 2 .
Модель временного ряда
- Случайный процесс { х я , у я } является стационарным и эргодическая ; если { x i , y i } нестационарен, результаты OLS часто бывают ложными, если только { x i , y i } не совмещает .
- Регрессоры предопределены : E [ x i ε i ] = 0 для всех i = 1, …, n ;
- Р × р матрица Q хх = Е [ х я х я Т ] имеет полный ранг, и , следовательно , положительно определена ;
- { x i ε i } — разностная последовательность мартингалов с конечной матрицей вторых моментов Q xxε ² = E [ ε i 2 x i x i T ] .
Свойства конечного образца
Прежде всего, под строгой Экзогенностью предположению МНКА оценки и S 2 являются беспристрастными , а это означает , что их ожидаемые значения совпадают с истинными значениями параметров: [доказательством]
Если строгая экзогенность не соблюдается (как в случае со многими моделями временных рядов , где экзогенность предполагается только в отношении прошлых шоков, но не будущих), то эти оценки будут смещены в конечных выборках.
Матрица ковариационной (или просто ковариационная матрица ) из равна
В частности, стандартная ошибка каждого коэффициента равна квадратному корню из j-го диагонального элемента этой матрицы. Оценка этой стандартной ошибки получается заменой неизвестной величины σ 2 ее оценкой s 2 . Таким образом,
Также легко показать, что оценка не коррелирует с остатками модели:
Теорема Гаусса – Маркова утверждает, что в предположении сферических ошибок (то есть ошибки должны быть некоррелированными и гомоскедастическими ) оценка эффективна в классе линейных несмещенных оценок. Это называется лучшей линейной несмещенной оценкой (СИНИЙ). Эффективность следует понимать так, как если бы мы должны были найти какую-то другую оценку, которая была бы линейной по y и несмещенной, тогда
в том смысле, что это неотрицательно определенная матрица . Эта теорема устанавливает оптимальность только в классе линейных несмещенных оценок, что весьма ограничительно. В зависимости от распределения членов ошибки ε другие, нелинейные оценки могут дать лучшие результаты, чем OLS.
Предполагая нормальность
Все перечисленные до сих пор свойства действительны независимо от основного распределения условий ошибки. Однако, если вы готовы предположить, что выполняется предположение нормальности (то есть, что ε ~ N (0, σ 2 I n ) ), тогда можно указать дополнительные свойства оценок МНК.
Оценщик имеет нормальное распределение со средним значением и дисперсией, как указано выше:
где Q — матрица сомножителей . Эта оценка достигает границы Крамера – Рао для модели и, таким образом, является оптимальной в классе всех несмещенных оценок. Обратите внимание, что в отличие от теоремы Гаусса – Маркова , этот результат устанавливает оптимальность как линейных, так и нелинейных оценок, но только в случае нормально распределенных членов ошибки.
Оценщик s 2 будет пропорционален распределению хи-квадрат :
Дисперсия этой оценки равна 2 σ 4 / ( п - р ) , который не достигает Крамера-Рао из 2 сг 4 / п . Однако было показано, что не существует несмещенных оценок σ 2 с дисперсией меньше, чем у оценки s 2 . Если мы готовы допустить предвзятые оценки и рассмотреть класс оценок, которые пропорциональны сумме квадратов остатков (SSR) модели, то лучшей (в смысле среднеквадратичной ошибки ) оценкой в этом классе будет ~ σ 2 = SSR / ( n - p + 2) , что даже превосходит границу Крамера – Рао в случае, когда имеется только один регрессор ( p = 1 ).
Кроме того, оценщики и s 2 являются независимыми , факт , который приходит в полезно при построении t- и F-тесты для регрессии.
Влиятельные наблюдения
Как упоминалось ранее, оценка линейна по y , что означает, что она представляет собой линейную комбинацию зависимых переменных y i . Веса в этой линейной комбинации являются функциями регрессоров X и обычно не равны. Наблюдения с большим весом называются влиятельными, потому что они оказывают более выраженное влияние на значение оценки.
Чтобы проанализировать, какие наблюдения имеют влияние, мы удаляем конкретное j-е наблюдение и рассматриваем, насколько предполагаемые количества изменятся (аналогично методу складного ножа ). Можно показать, что изменение МНК-оценки для β будет равно
где h j = x j T ( X T X ) −1 x j — j-й диагональный элемент матрицы P , а x j — вектор регрессоров, соответствующих j- му наблюдению. Точно так же изменение прогнозируемого значения для j -го наблюдения в результате исключения этого наблюдения из набора данных будет равно
Из свойств матрицы шляпы 0 ≤ h j ≤ 1 , и они в сумме дают p , так что в среднем h j ≈ p / n . Эти величины h j называются рычагами , а наблюдения с высокими h j называются точками рычагов . Обычно наблюдения с большим кредитным плечом должны быть изучены более тщательно, на случай, если они ошибочны, выбросы или иным образом нетипичны для остальной части набора данных.
Разделенная регрессия
Иногда переменные и соответствующие параметры в регрессии можно логически разделить на две группы, так что регрессия принимает вид
где X 1 и X 2 имеют размерности n × p 1 , n × p 2 и β 1 , β 2 — векторы p 1 × 1 и p 2 × 1, причем p 1 + p 2 = p .
Теорема Фриша – Во – Ловелла утверждает, что в этой регрессии остатки и оценка МНК будут численно идентичны остаткам и оценке МНК для β 2 в следующей регрессии:
где M 1 — матрица аннигилятора для регрессоров X 1 .
Теорема может быть использована для получения ряда теоретических результатов. Например, наличие регрессии с константой и другим регрессором эквивалентно вычитанию средних значений из зависимой переменной и регрессора и последующему запуску регрессии для переменных, не имеющих значения, но без постоянного члена.
Ограниченная оценка
Предположим, известно, что коэффициенты регрессии удовлетворяют системе линейных уравнений
где Q — это матрица полного ранга размера p × q , а c — вектор известных констант размером q × 1, где q <p . В этом случае оценка по методу наименьших квадратов эквивалентно минимизации суммы квадратов остатков модели при условии ограничения А . Оценка методом наименьших квадратов с ограничениями (CLS) может быть задана явной формулой:
Это выражение для оценки с ограничениями действительно до тех пор, пока матрица X T X обратима. С самого начала этой статьи предполагалось, что эта матрица имеет полный ранг, и было отмечено, что, когда условие ранга не выполняется, β не будет идентифицироваться. Однако может случиться так, что добавление ограничения A сделает β идентифицируемым, и в этом случае нужно будет найти формулу для оценки. Оценщик равен
где R — матрица размера p × ( p — q ) такая, что матрица [ QR ] неособая, и R T Q = 0 . Такую матрицу всегда можно найти, хотя в целом она не уникальна. Вторая формула совпадает с первой в случае обратимости
X T X.
Свойства большого образца
Оценщики наименьших квадратов представляют собой точечные оценки параметров модели линейной регрессии β . Однако обычно мы также хотим знать, насколько близки эти оценки к истинным значениям параметров. Другими словами, мы хотим построить интервальные оценки .
Поскольку мы не делали никаких предположений о распределении члена ошибки ε i , невозможно вывести распределение оценок и . Тем не менее, мы можем применить центральную предельную теорему для вывода их асимптотических свойств, когда размер выборки n стремится к бесконечности. Хотя размер выборки обязательно конечен, принято считать, что n «достаточно велико», так что истинное распределение оценки OLS близко к его асимптотическому пределу.
Можно показать , что в модельных предположениях, оценка наименьших квадратов для р является последовательным (т.е. сходится по вероятности к р ) и асимптотически нормальна: [доказательство]
куда 
Интервалы
Используя это асимптотическое распределение, приближенные двусторонние доверительные интервалы для j -го компонента вектора могут быть построены как
-
на уровне достоверности 1 — α ,
где q обозначает функцию квантиля стандартного нормального распределения, а [·] jj — j-й диагональный элемент матрицы.
Точно так же оценка наименьших квадратов для σ 2 также согласована и асимптотически нормальна (при условии, что существует четвертый момент ε i ) с предельным распределением
Эти асимптотические распределения можно использовать для прогнозирования, проверки гипотез, построения других оценок и т. Д. В качестве примера рассмотрим проблему прогнозирования. Предположим, есть некоторая точка в области распределения регрессоров, и кто-то хочет знать, какой была бы переменная ответа в этой точке. Средний ответ является количество , в то время как предсказывал реакция является . Очевидно, что прогнозируемый ответ является случайной величиной, его распределение может быть получено из следующего :
что позволяет построить доверительные интервалы для построения среднего отклика :
-
на уровне достоверности 1 — α .
Проверка гипотезы
Особенно широко используются две проверки гипотез. Во-первых, кто-то хочет знать, лучше ли оценочное уравнение регрессии, чем простое предсказание, что все значения переменной ответа равны ее выборочному среднему (в противном случае, говорят, что оно не имеет объяснительной силы). Нулевая гипотеза не имеет объяснительного значения расчетной регрессии тестировалась с помощью F-тест . Если вычисленное F-значение оказывается достаточно большим, чтобы превышать его критическое значение для предварительно выбранного уровня значимости, нулевая гипотеза отклоняется и принимается альтернативная гипотеза о том , что регрессия обладает объяснительной силой. В противном случае принимается нулевая гипотеза об отсутствии объяснительной силы.
Во-вторых, для каждой представляющей интерес объясняющей переменной нужно знать, существенно ли отличается ее оценочный коэффициент от нуля, то есть действительно ли эта конкретная независимая переменная имеет объяснительную силу при прогнозировании переменной отклика. Здесь нулевая гипотеза состоит в том, что истинный коэффициент равен нулю. Эта гипотеза проверяется путем вычисления t-статистики коэффициента как отношения оценки коэффициента к его стандартной ошибке . Если t-статистика больше заданного значения, нулевая гипотеза отклоняется, и выясняется, что переменная имеет объяснительную силу, а ее коэффициент значительно отличается от нуля. В противном случае принимается нулевая гипотеза о нулевом значении истинного коэффициента.
Кроме того, тест Чоу используется для проверки того, имеют ли две подвыборки одинаковые основные истинные значения коэффициентов. Сумма квадратов остатков регрессий для каждого из подмножеств и для комбинированного набора данных сравнивается путем вычисления F-статистики; если это превышает критическое значение, нулевая гипотеза об отсутствии разницы между двумя подмножествами отклоняется; в противном случае принимается.
Пример с реальными данными
Следующий набор данных дает средние показатели роста и веса для американских женщин в возрасте 30–39 лет (источник: The World Almanac and Book of Facts, 1975 ).
-
Высота (м) 1,47 1,50 1,52 1,55 1,57 1,60 1,63 1,65 1,68 1,70 1,73 1,75 1,78 1,80 1,83 Вес (кг) 52,21 53,12 54,48 55,84 57,20 58,57 59,93 61,29 63,11 64,47 66,28 68,10 69,92 72,19 74,46
Когда моделируется только одна зависимая переменная, диаграмма рассеяния предложит форму и силу связи между зависимой переменной и регрессорами. Он также может выявить выбросы, гетероскедастичность и другие аспекты данных, которые могут усложнить интерпретацию подобранной регрессионной модели. Диаграмма рассеяния предполагает, что связь сильная и может быть аппроксимирована квадратичной функцией. OLS может обрабатывать нелинейные отношения, вводя регрессор HEIGHT 2 . Затем регрессионная модель становится множественной линейной моделью:
Результаты наиболее популярных статистических пакетов будут выглядеть примерно так:
-
Метод Наименьших квадратов Зависимая переменная МАССА Наблюдения 15
Параметр Ценить Стандартная ошибка t-статистика p-значение
128,8128 16.3083 7,8986 0,0000 –143,1620 19,8332 –7,2183 0,0000 61,9603 6,0084 10,3122 0,0000
R 2 0,9989 SE регрессии 0,2516 Скорректированный R 2 0,9987 Сумма кв. 692,61 Логарифмическая вероятность 1.0890 Остаточная кв. 0,7595 Стат. Дурбина – Ватсона. 2,1013 Общая сумма кв. 693,37 Критерий Акаике 0,2548 F-статистика 5471,2 Критерий Шварца 0,3964 p-значение (F-stat) 0,0000
В этой таблице:
- В столбце « Значение» приведены оценки параметров β j по методу наименьших квадратов.
- Std ошибка колонка показывает стандартные ошибки каждого коэффициента оценки:
- В т-статистические и р-значение колонки тестируют ли какой — либо из коэффициентов может быть равна нулю. Т -статистики рассчитывается просто как . Если ошибки ε подчиняются нормальному распределению, t следует распределению Стьюдента-t. В более слабых условиях t асимптотически нормально. Большие значения t указывают на то, что нулевая гипотеза может быть отклонена и соответствующий коэффициент не равен нулю. Второй столбец, p -значение , выражает результаты проверки гипотезы в виде уровня значимости . Обычно p-значения меньше 0,05 принимаются как свидетельство того, что коэффициент совокупности отличен от нуля.
- R-квадрат — это коэффициент детерминации, указывающий на соответствие регрессии. Эта статистика будет равна единице, если соответствие идеально, и нулю, если регрессоры X вообще не обладают объяснительной силой. Это смещенная оценка R-квадрата популяции , и она никогда не уменьшится при добавлении дополнительных регрессоров, даже если они не имеют отношения к делу.
-
Скорректированный R-квадрат — это слегка измененная версия , предназначенная для наказания за избыточное количество регрессоров, которые не увеличивают объяснительную силу регрессии. Эта статистика всегда меньше , может уменьшаться при добавлении новых регрессоров и даже быть отрицательной для плохо подходящих моделей:
- Логарифмическое правдоподобие рассчитывается в предположении, что ошибки подчиняются нормальному распределению. Несмотря на то, что это предположение не очень разумно, эта статистика все же может найти свое применение при проведении тестов LR.
- Статистика Дарбина-Ватсона проверяет, есть ли какие-либо доказательства серийной корреляции между остатками. Как показывает опыт, значение меньше 2 свидетельствует о положительной корреляции.
- Для выбора модели используются информационный критерий Акаике и критерий Шварца . Обычно при сравнении двух альтернативных моделей меньшие значения одного из этих критериев указывают на лучшую модель.
- Стандартная ошибка регрессии — это оценка σ , стандартная ошибка члена ошибки.
- Общая сумма квадратов , модельная сумма квадратов и остаточная сумма квадратов говорят нам, какая часть начальных вариаций в выборке была объяснена регрессией.
- F-статистика пытается проверить гипотезу о том, что все коэффициенты (кроме точки пересечения) равны нулю. Эта статистика имеет распределение F ( p – 1 , n – p ) при нулевой гипотезе и предположении нормальности, а ее значение p указывает вероятность того, что гипотеза действительно верна. Обратите внимание, что если ошибки не являются нормальными, эта статистика становится недействительной, и следует использовать другие тесты, такие как тест Вальда или тест LR .
Обычный анализ методом наименьших квадратов часто включает использование диагностических графиков, предназначенных для обнаружения отклонений данных от предполагаемой формы модели. Вот некоторые из распространенных диагностических графиков:
- Остатки против независимых переменных в модели. Нелинейная связь между этими переменными предполагает, что линейность функции условного среднего может не соблюдаться. Различные уровни изменчивости остатков для разных уровней объясняющих переменных предполагают возможную гетероскедастичность.
- Остатки против объясняющих переменных, которых нет в модели. Любая связь остатков с этими переменными предполагает рассмотрение этих переменных для включения в модель.
- Остаточные против подобранных значений, .
- Остатки против предыдущего остатка. Этот график может выявить серийные корреляции в остатках.
Важным моментом при выполнении статистического вывода с использованием регрессионных моделей является выборка данных. В этом примере это средние данные, а не измерения по отдельным женщинам. Подгонка модели очень хорошая, но это не означает, что вес отдельной женщины можно предсказать с высокой точностью только на основе ее роста.
Чувствительность к округлению
Этот пример также демонстрирует, что коэффициенты, определяемые этими вычислениями, чувствительны к тому, как подготовлены данные. Первоначально высота была округлена до ближайшего дюйма, а затем была преобразована и округлена до ближайшего сантиметра. Поскольку коэффициент преобразования составляет от одного дюйма до 2,54 см, это не точное преобразование. Исходные дюймы можно восстановить с помощью функции Round (x / 0,0254), а затем преобразовать в метрическую систему без округления. Если это будет сделано, результаты станут:
| Const | Рост | Высота 2 | |
|---|---|---|---|
| Преобразовано в метрическую систему с округлением. | 128,8128 | -143,162 | 61,96033 |
| Преобразуется в метрическую систему без округления. | 119,0205 | -131,5076 | 58,5046 |
Невязки к квадратичной аппроксимации для правильно и неправильно преобразованных данных.
Использование любого из этих уравнений для прогнозирования веса женщины ростом 5 футов 6 дюймов (1,6764 м) дает аналогичные значения: 62,94 кг с округлением по сравнению с 62,98 кг без округления. Таким образом, кажущиеся незначительными отклонения в данных реально влияют на коэффициенты. но небольшое влияние на результаты уравнения.
Хотя это может выглядеть безобидным в середине диапазона данных, оно может стать значимым в крайних случаях или в случае, когда подобранная модель используется для проецирования за пределы диапазона данных ( экстраполяция ).
Это подчеркивает общую ошибку: этот пример представляет собой злоупотребление OLS, которое по своей сути требует, чтобы ошибки в независимой переменной (в данном случае высоте) были равны нулю или, по крайней мере, незначительны. Первоначальное округление до ближайшего дюйма плюс любые фактические ошибки измерения составляют конечную погрешность, которой нельзя пренебречь. В результате подобранные параметры не являются лучшими оценками, как предполагалось. Хотя это и не является полностью ложным, ошибка в оценке будет зависеть от относительного размера ошибок x и y .
Другой пример с менее реальными данными
Постановка задачи
Мы можем использовать механизм наименьших квадратов, чтобы выяснить уравнение орбиты двух тел в полярных координатах. Обычно используется уравнение: где — радиус расстояния от объекта до одного из тел. В уравнении параметры и используются для определения траектории орбиты. Мы измерили следующие данные.
 (в градусах) (в градусах)
|
43 год | 45 | 52 | 93 | 108 | 116 |
|---|---|---|---|---|---|---|

|
4,7126 | 4,5542 | 4,0419 | 2,2187 | 1,8910 | 1,7599 |
Нам нужно найти приближение по методу наименьших квадратов и для приведенных данных.
Решение
Сначала нам нужно представить e и p в линейной форме. Итак, мы собираемся переписать уравнение как . Теперь мы можем использовать эту форму для представления наших данных наблюдений как:


При решении получаем 
так и
Смотрите также
- Байесовский метод наименьших квадратов
- Регрессия Фамы – Макбета
- Нелинейный метод наименьших квадратов
- Численные методы линейных наименьших квадратов
- Идентификация нелинейной системы
использованная литература
дальнейшее чтение
- Догерти, Кристофер (2002). Введение в эконометрику (2-е изд.). Нью-Йорк: Издательство Оксфордского университета. С. 48–113. ISBN 0-19-877643-8.
- Гуджарати, Дамодар Н .; Портер, Дон С. (2009). Основы эконометики (Пятое изд.). Бостон: Макгроу-Хилл Ирвин. С. 55–96. ISBN 978-0-07-337577-9.
- Хейдж, христианский; Бур, Пол; Franses, Philip H .; Клок, Теун; ван Дейк, Герман К. (2004). Эконометрические методы с приложениями в бизнесе и экономике (1-е изд.). Оксфорд: Издательство Оксфордского университета. С. 76–115. ISBN 978-0-19-926801-6.
- Хилл, Р. Картер; Гриффитс, Уильям Э .; Лим, Гуай С. (2008). Принципы эконометрики (3-е изд.). Хобокен, Нью-Джерси: Джон Уайли и сыновья. С. 8–47. ISBN 978-0-471-72360-8.
- Вулдридж, Джеффри (2008). «Модель простой регрессии» . Вводная эконометрика: современный подход (4-е изд.). Мейсон, Огайо: Обучение Cengage. С. 22–67. ISBN 978-0-324-58162-1.

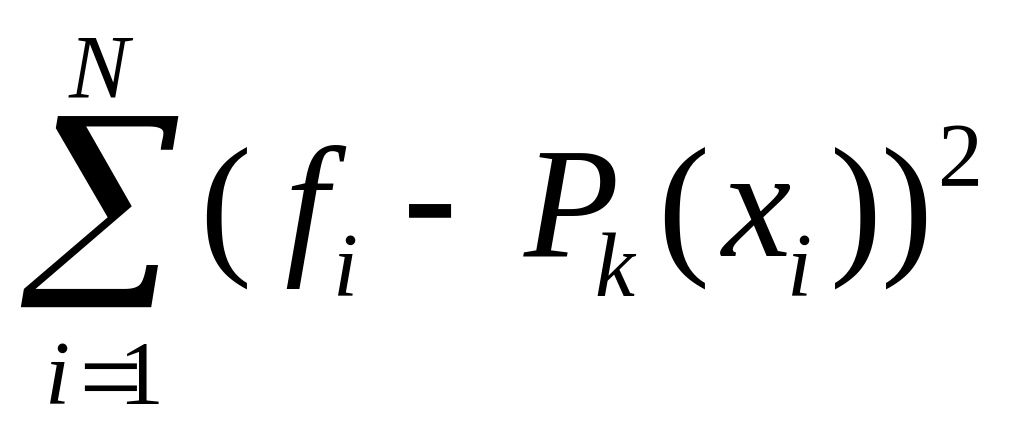
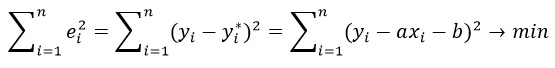
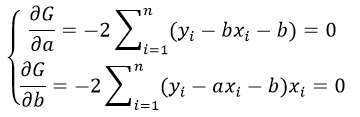
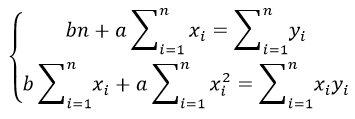
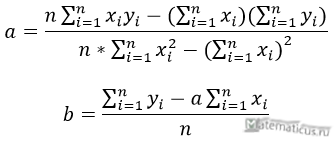
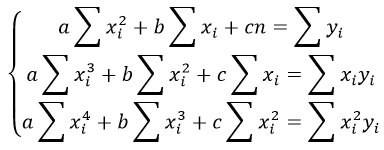
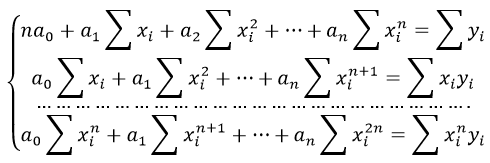
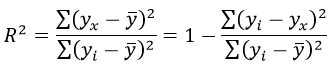
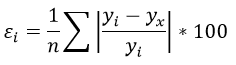
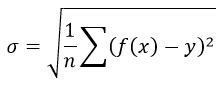
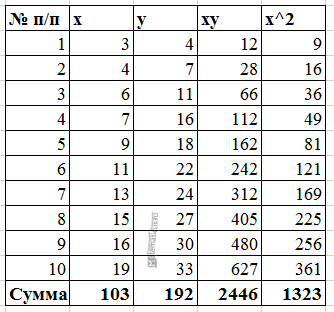
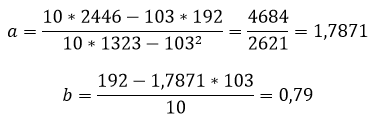
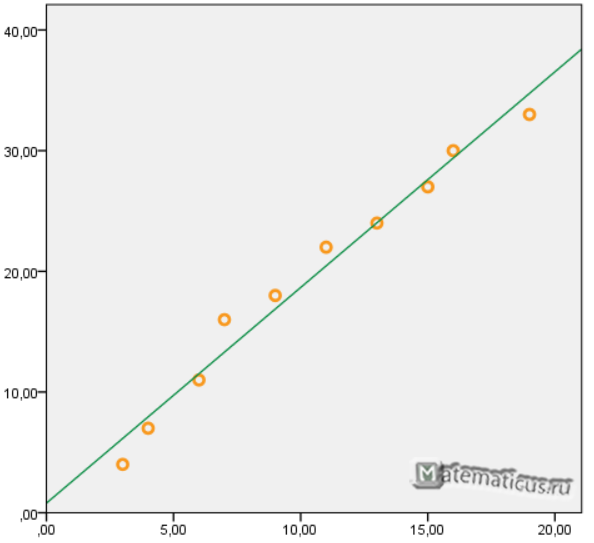







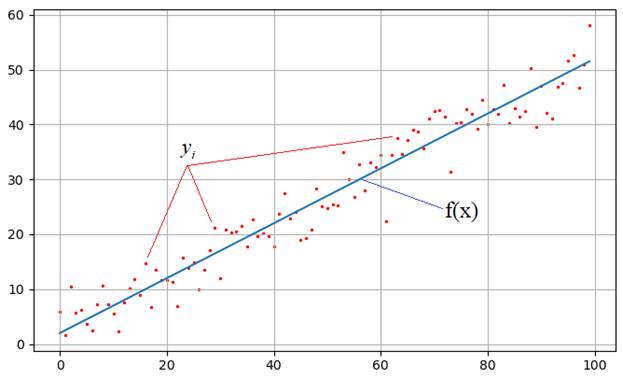
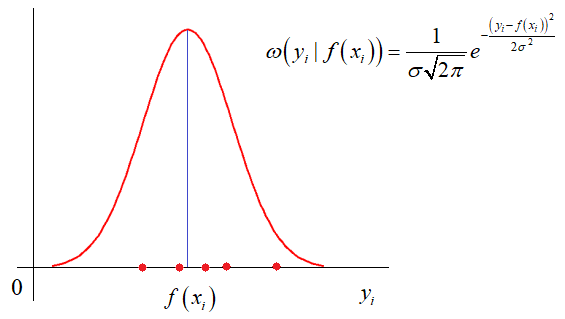
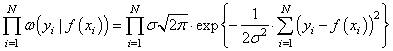
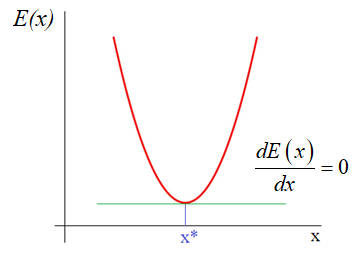
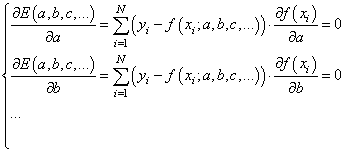
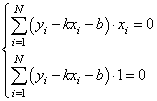
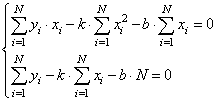
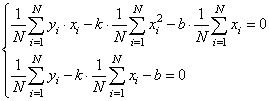
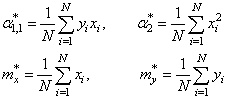
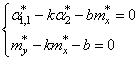
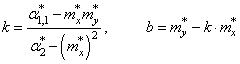
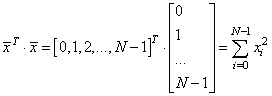
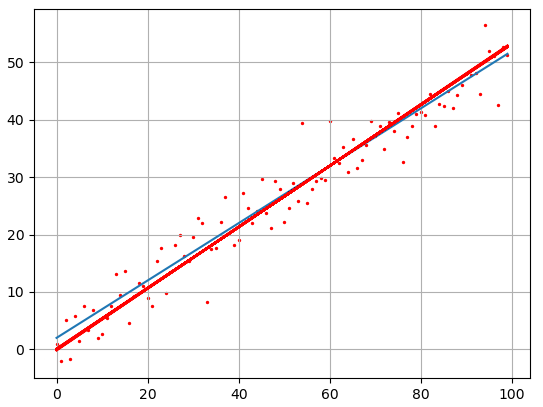
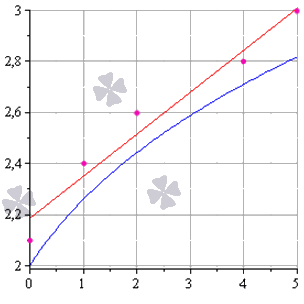

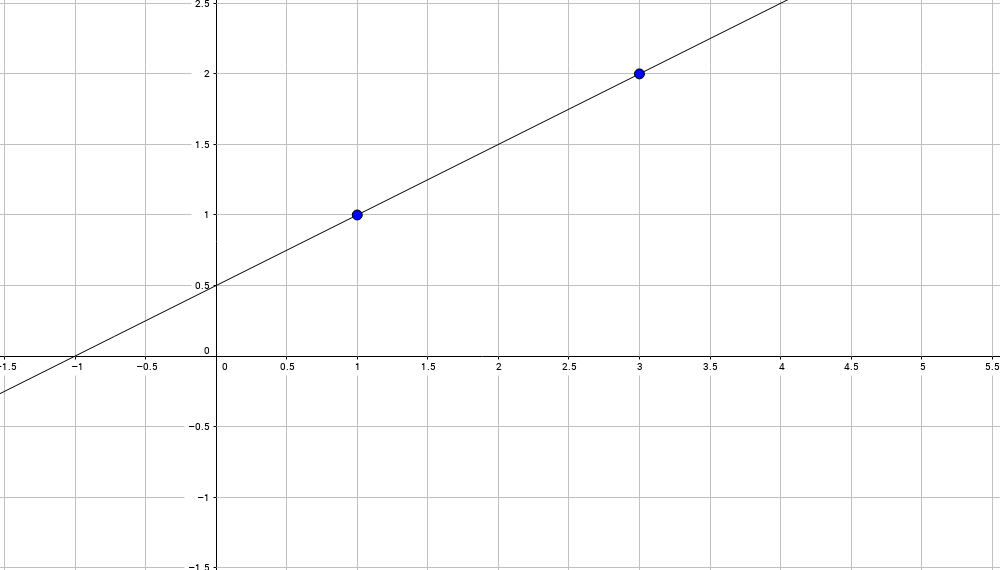
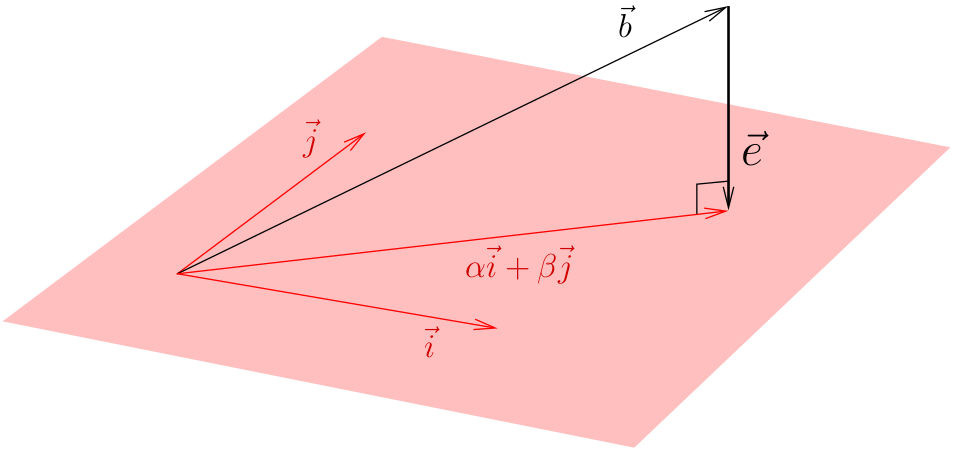
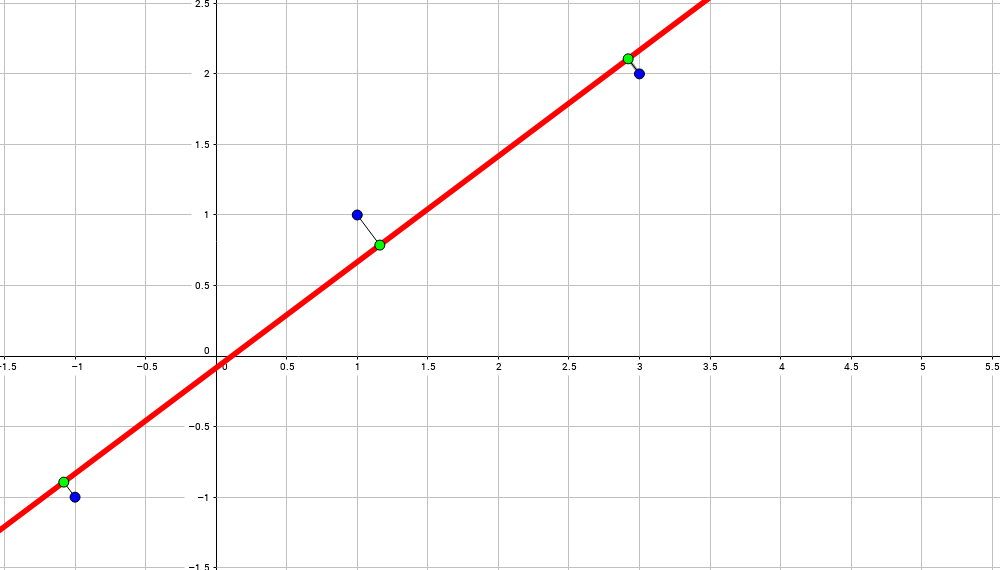
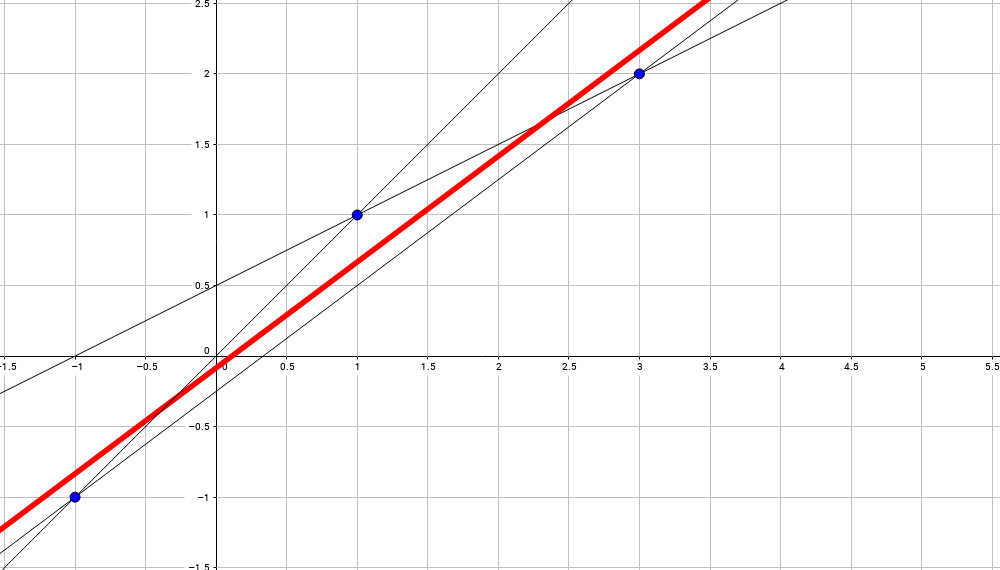
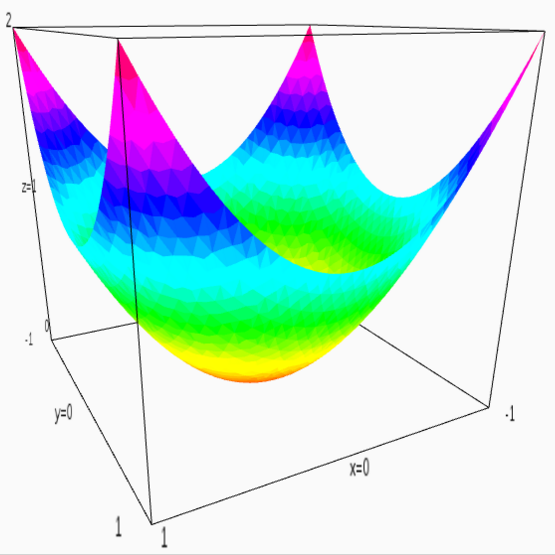







![{ displaystyle mathbf {x} _ {i} = left [x_ {i1}, x_ {i2}, dots, x_ {ip} right] ^ { mathsf {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/daad19b2eabb379c5fce21e00f9e77f64b7a2808)





















































![mathrm {E} { big [} , x_ {i} (y_ {i} -x_ {i} ^ {T} beta) , { big]} = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb1a1f1cb2be7e80f44761892bf788fe2b2af548)
![{ Displaystyle OperatorName {E} [, varepsilon mid X ,] = 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcdfa07f07180573874658708bc2a889d5416199)
![Pr ! { Big [} , operatorname {rank} (X) = p , { big]} = 1.](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a11be3b89ce51c6441155fddbe512a991132fbf)
![operatorname {Var} [, varepsilon mid X ,] = sigma ^ {2} I_ {n},](https://wikimedia.org/api/rest_v1/media/math/render/svg/0df70427bd7e0b69175caf9150b2d465dd152474)

![operatorname {E} [, { hat { beta}} mid X ,] = beta, quad operatorname {E} [, s ^ {2} mid X ,] = sigma ^ {2}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/67bc2fd0f90c46da207712893fdcea01e729026c)
![{ displaystyle operatorname {Var} [, { hat { beta}} mid X ,] = sigma ^ {2} (X ^ {T} X) ^ {- 1} = sigma ^ { 2} Q.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f96b58e87986e32ad2375a1db34fb64a7a16e2f)


![operatorname {Cov} [, { hat { beta}}, { hat { varepsilon}} mid X ,] = 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/664c1a5e37957a1aa2ae381b9bcb07350c2c816c)

![operatorname {Var} [, { tilde { beta}} mid X ,] - operatorname {Var} [, { hat { beta}} mid X ,] geq 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/53796c9205889cc4d675b9749a58eb97fcd998f1)













![{ displaystyle beta _ {j} in { bigg [} { hat { beta}} _ {j} pm q_ {1 - { frac { alpha} {2}}} ^ {{{ mathcal {N}} (0,1)} ! { sqrt {{ hat { sigma}} ^ {2} left [Q_ {xx} ^ {- 1} right] _ {jj}} } { bigg]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf79688aac9f662ff39253fbfb0d234246d370e5)
![{ displaystyle ({ hat { sigma}} ^ {2} - sigma ^ {2}) { xrightarrow {d}} { mathcal {N}} left (0, ; operatorname { E} left [ varepsilon _ {i} ^ {4} right] - sigma ^ {4} right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c909dea2a4f0bf40e253680b953d1bfbb66298f)





![{ displaystyle y_ {0} in left [ x_ {0} ^ { mathrm {T}} { hat { beta}} pm q_ {1 - { frac { alpha} {2}} } ^ {{ mathcal {N}} (0,1)} ! { sqrt {{ hat { sigma}} ^ {2} x_ {0} ^ { mathrm {T}} Q_ {xx} ^ {- 1} x_ {0}}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf86d7a311c97d35fb6e039c3cd74bc9f3e752bf)
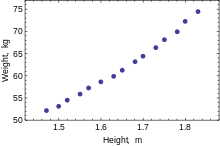

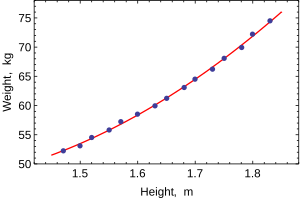


![{ displaystyle { hat { sigma}} _ {j} = left ({ hat { sigma}} ^ {2} left [Q_ {xx} ^ {- 1} right] _ {jj} right) ^ { frac {1} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5087e66171bf3ef9ad3ac75decdd715274919669)