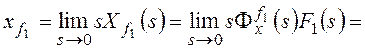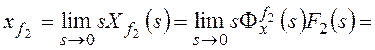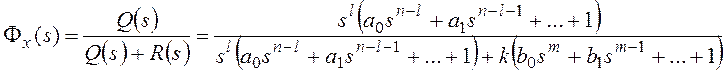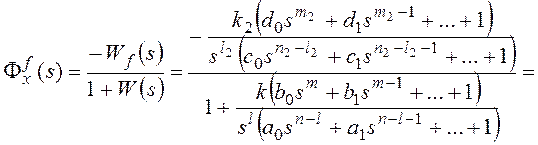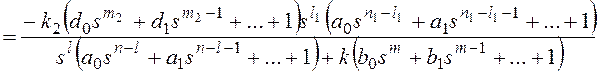Тау статистическая ошибка

Точность системы автоматического управления Статическая ошибка системы

В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:

.

Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.

Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать

,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.

Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов

.

Поскольку

,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:

,
где.

Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку

.

Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:

,
гдеK– коэффициент
усиления системы,A^*(p),B^*(p)
– нормированные полиномыA(p)
иB(p).
При этоми.
Тогдаи статическая ошибка в статической
системе

.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.

Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы

и передаточная функция замкнутой системы
по ошибке

.

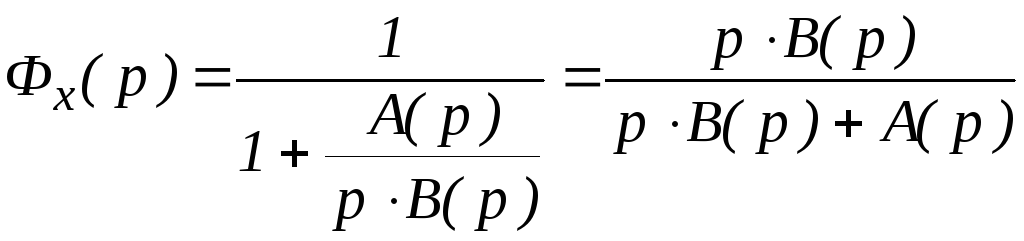
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.

Вынужденная ошибка системы

Процесс в
системе складывается из свободного
процесса и вынужденного процесса:

.
Для
устойчивой системы свободный процесс
по истечении времениt_пзатухает и в системе устанавливается
вынужденный процесс

Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы

.

Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.

Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки

.

В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда

и
выражение для вынужденной ошибки системы
примет вид

гдепостоянные
коэффициенты.

Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки

где
,,…коэффициенты
ошибок, полученные выше (C₀– коэффициент статической ошибки,C₁
– коэффициент скоростной ошибки и
т. д.).

Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.

Соседние файлы в папке ТАУ

• #
• #
• #

Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма

Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.

Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:

,  ,   и так
далее.

При наличии нескольких воздействий на линейную систему
для определения x_уст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:

, где
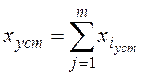
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.

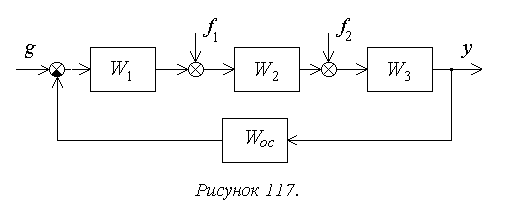
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).

В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .

Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке  при известном изображении задающего
воздействия G(s):

, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117

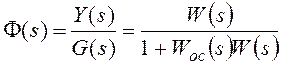
, где  — передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.

Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:

В результате:

.

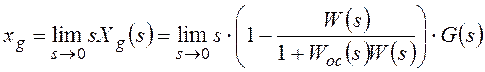
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения  при известном изображении возмущающего
воздействия F(s):

, где
F_f(s) –передаточная функция замкнутой системы по
возмущающему воздействию,

;

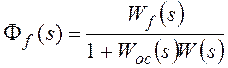
W_f(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).

Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.

Для f₁:                             
,

,

.

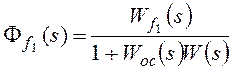
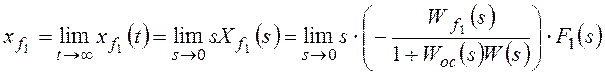
Для f₂:                                
,

,

.

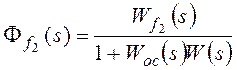
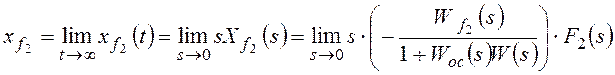
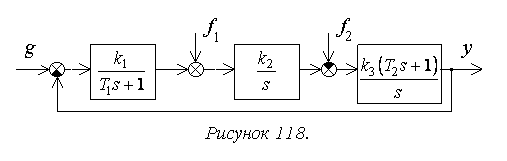
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):

,

, где k=k₁k₂k₃ – коэффициент передачи
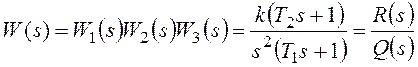
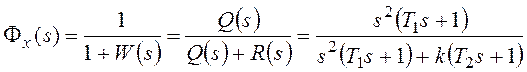
разомкнутой системы.

Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.

При  получим:

.

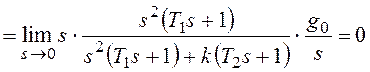
При  получим:

.

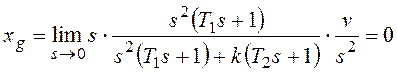
При  получим:

.

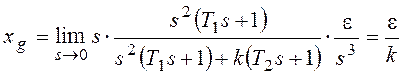
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.

Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.

Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.

Рассмотрим установившуюся
ошибку от возмущения f₁:

,

, где  –
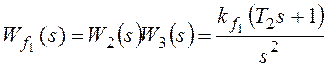
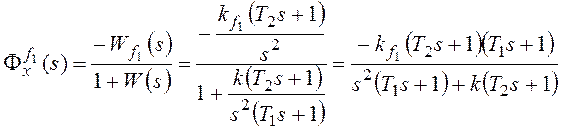
коэффициент передачи разомкнутой системы по возмущению f₁.

При  получим:

.

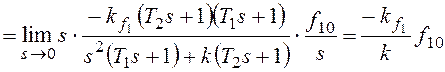
При  получим:

.

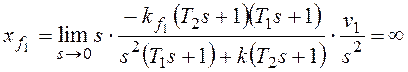
При 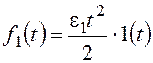 получим
тот же результат.

Отметим, что по возмущению f₁ рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.

Рассмотрим установившуюся
ошибку от возмущения f₂:

,

, где  –
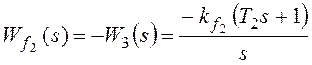
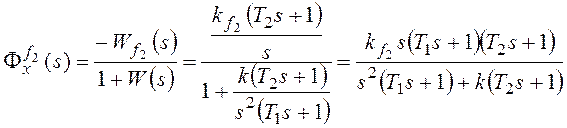
коэффициент передачи разомкнутой системы по возмущению f₂.

При  получим:

.

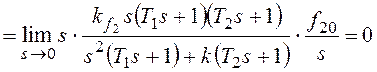
При  получим:

.

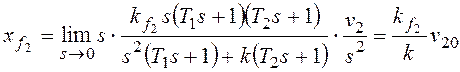
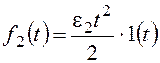
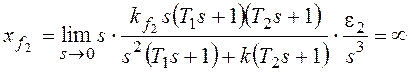
При  получим:

.

По возмущению f₂ рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.

Подведем некоторые итоги:

1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.

2. Постоянные времени
звеньев системы не влияют на ее точность.

3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.

Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.

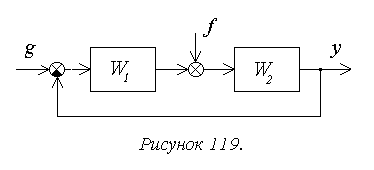
Рассмотрим структуру,
показанную на рисунке 119.

В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:

, где l³0.

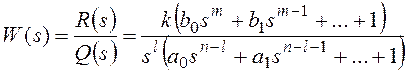
Тогда получим:

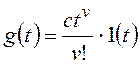
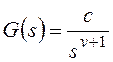
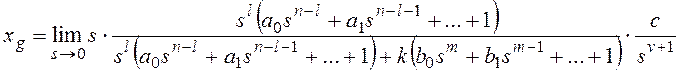
и для общего вида задающего воздействия , которому соответствует изображение ,

.

Результат нахождения этого
предела зависит от соотношения показателей степени:

— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;

— при l=v получаем
константу;

— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.

Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.

Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.

Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.

Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:

,

, где l₁+l₂=l,
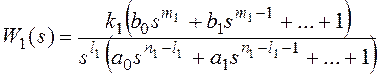
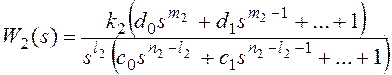
k₁k₂=k, m₁+m₂=m,
n₁+n₂=n,
причем  и .

Тогда получим:

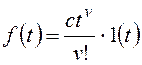
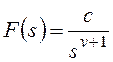
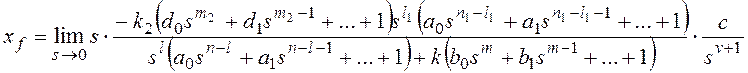
и для общего вида возмущающего воздействия , которому соответствует изображение ,

.

Все вышеприведенные выводы
можно повторить для показателя степени l₁.

Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.

Точность систем автоматического управления

1. Точность САУ

Точность САУ оценивается в установившемся режиме по величине установившейся ошибки при типовых воздействиях. При анализе точности систем рассматривается установившийся режим, так как текущее значение ошибки резко меняется вследствие наличия переходных процессов и не может быть мерой точности.

Рассмотрим систему представленную на рис. 1.

На схеме приняты следующие обозначения: K_у(p) – передаточная функция устройства управления; K₀(p) – передаточная функция объекта управления; f – возмущающее воздействие; x – задающее воздействие; y – регулируемая величина.

Ошибка по задающему воздействию равна (t) = x(t) – y(t).

Изображение ошибки равно

(1)

Установившееся значение ошибки определяется с помощью теоремы о конечном значении функции

(2)

Ошибка по возмущению воздействию равна (t) = – y(t), т.е. равна изменению регулируемой величины под действием возмущения при отсутствии входного воздействия.

В общем случае как задающее, так и возмущающее воздействия являются сложными функциями времени. При определении ошибок пользуются типовыми воздействиями, которые с одной стороны соответствуют наиболее тяжелым режимам работы системы и, вместе с тем, достаточно просты для аналитических исследований.

Кроме того, типовые воздействия удобны для сравнительного анализа различных систем, и соответствуют наиболее часто применяемым законам изменения управляющих и возмущающих воздействий.

2. Типы ошибок

Различают следующие типы ошибок:

– статическая ошибка (ошибка по положению) – ошибка, возникающая в системе при отработке единичного воздействия;

– кинетическая ошибка (ошибка по скорости) – ошибка, возникающая в системе при отработке линейно – возрастающего воздействия;

– инерционная ошибка (ошибка по ускорению) – ошибка, возникающая в системе при отработке квадратичного воздействия.

С точки зрения ошибок, системы можно классифицировать на статические и астатические.

Передаточная функция статической системы имеет вид

(3)

Передаточная функция астатической системы имеет вид

(4)

где K*(p) – передаточная функция, не содержащая интегрирующих звеньев а s – порядок астатизма.

Рассмотрим статическую систему (s = 0). Определим выражения для соответствующих ошибок.

1. Статическая ошибка определяется следующим соотношением

(5)

2. Кинетическая ошибка определяется следующим соотношением

(6)

3. Инерционная ошибка определяется следующим соотношением

(7)

Эта система не может быть использована как синхронно – следящая, так как кинетическая ошибка стремится к бесконечности.

Пример 1. Для заданной системы (рис. 2) определить установившиеся ошибки

x y

—

Рис. 2

Решение: Определим установившиеся ошибки.

1. Статическая ошибка определяется следующим соотношением

1. Кинетическая ошибка определяется следующим соотношением

1. Инерционная ошибка определяется следующим соотношением

На графиках это можно изобразить следующим образом (рис. 3)

Рассмотрим астатическую систему первого порядка (s = 1).

Определим выражения для установившихся ошибок.

1. Статическая ошибка определяется следующим соотношением

(8)

1. Кинетическая ошибка определяется следующим соотношением

(9)

1. Инерционная ошибка определяется следующим соотношением

(10)

Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 2. Для заданной системы (рис. 4) определить ошибки

Решение: Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

2. Кинетическая ошибка определяется следующим соотношением

Т.е. ошибка является функцией скорости изменения входного воздействия и коэффициента усиления системы.

3. Инерционная ошибка определяется следующим соотношением

Графики изменения ошибок приведены на рис. 5.

Р

а) b) c)

Рис. 5

ассмотрим астатическую систему второго порядка (s = 2).

Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

(11)

1. Кинетическая ошибка определяется следующим соотношением

(12)

1. Инерционная ошибка определяется следующим соотношением

(13)

Инерционная ошибка является функцией ускорения изменения входного воздействия и коэффициента усиления системы.

Эта система может быть использована как синхронно – следящая, так как кинетическая ошибка равна нулю.

Пример 3. Для заданной системы (рис. 6) определить установившиеся ошибки

x y

—

Рис. 6

Решение: Определим выражения для ошибок.

1. Статическая ошибка определяется следующим соотношением

1. Кинетическая ошибка определяется следующим соотношением

3. Инерционная ошибка определяется следующим соотношением

На графиках это можно изобразить следующим образом (рис. 7)

1. b) c)

Рис. 7

Для повышения точности САУ необходимо увеличивать коэффициент усиления системы и порядок астатизма, но это может привести к неустойчивости, т.е. требования по точности и устойчивости противоречивы.

Определение ошибок по виду частотных характеристик САУ

О характере ошибок можно судить по низкочастотной ветви любой частотной характеристики (АФХ, ЛАЧХ, ФЧХ), так как низкочастотная ветвь характеризует статику системы. Частотные характеристики систем с различным порядком астатизма приведены в таблице 1.

Таблица 1

	АФХ	ЛАЧХ	ФЧХ
s = 0; c = x0/(1+k); к = ; и = .	+j -1 +
s = 1; c = 0; к = v/kv; и = .	+j -1 +
s = 1; c = 0; к = 0; и = /k.	+j -1 +

3. Ошибки по возмущению

Установившаяся ошибка по возмущению равна

(14)

Рассмотрим примеры

Пример 4. Для заданной системы (рис. 9) со статическим регулятором определить ошибку по возмущению.

Решение: Пусть f(p) = f₀ /p, при этом ошибка равна

При статическом регуляторе установившаяся ошибка по возмущению зависит от амплитуды воздействия и коэффициента усиления регулятора т.е. _f = f(f₀, k₁).

Пример 5. Для заданной системы (рис. 10) с астатическим регулятором, определить ошибку по возмущению.

Решение: Пусть f(p) = f₀ /p, при этом ошибка равна

При астатическом регуляторе ошибка по возмущению равна нулю.

Литература

1. Вероятностные методы в вычислительной технике. Под ред. А.Н. Лебедева и Е.А. Чернявского – М.: Высш. Шк., 1986. -312 с.

2. Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., перераб. и доп. Киев, Издательство Выща школа Головное издательство, 198

3. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.

4. Теория автоматического управления: Учебник для вузов. Ч1 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. – 367 с.

5. Теория автоматического управления: Учебник для вузов. Ч2 / Под ред. А.А. Воронова – М.: Высш. Шк., 1986. -504 с.

6. Шандров Б.В. Технические средства автоматизации: учебник для студентов высших учебных заведений. Москва, Издательский центр «Академия», 2007.