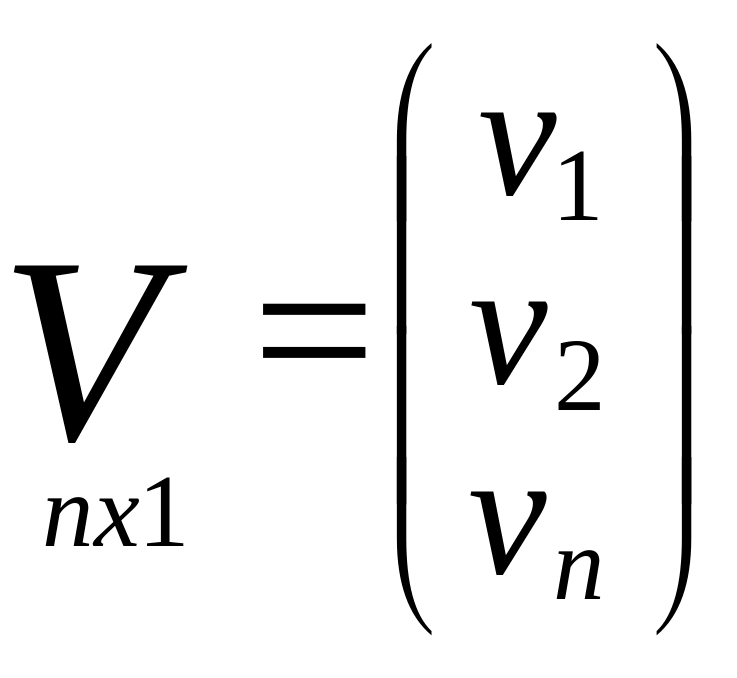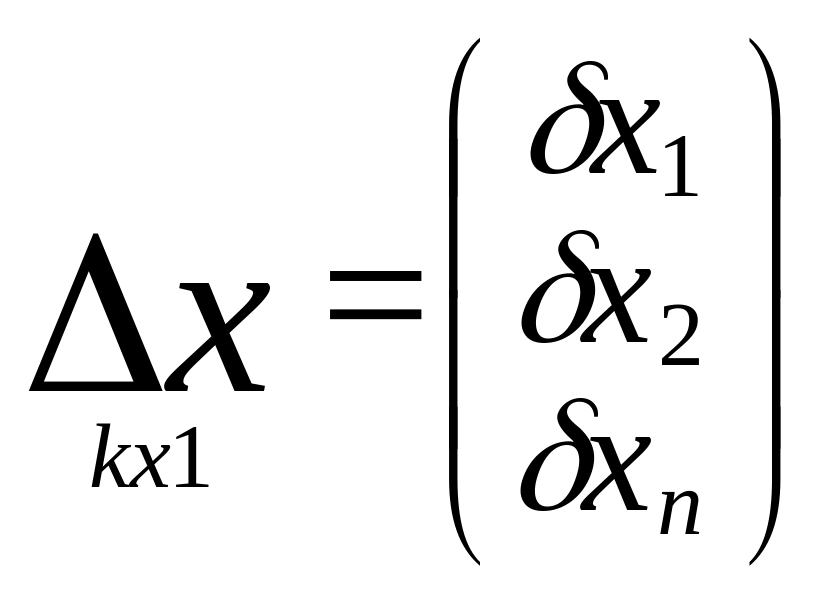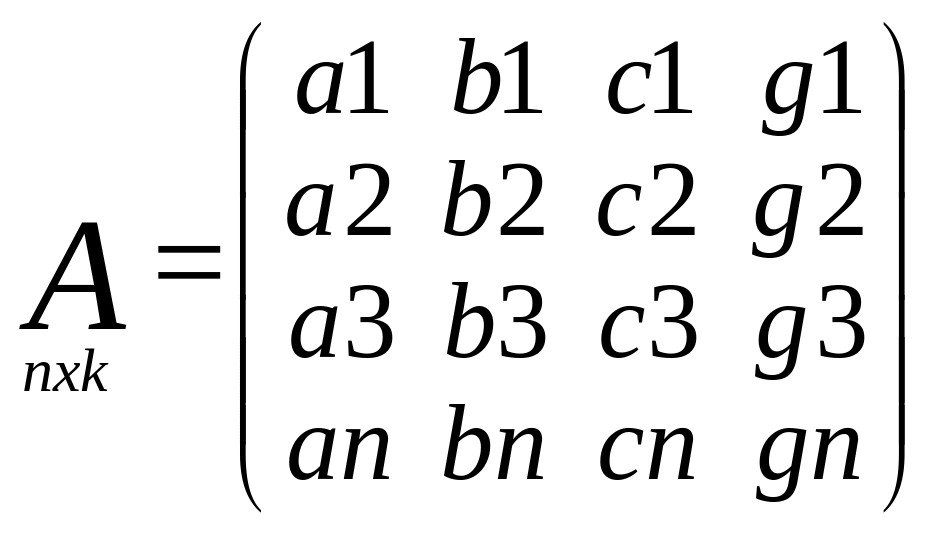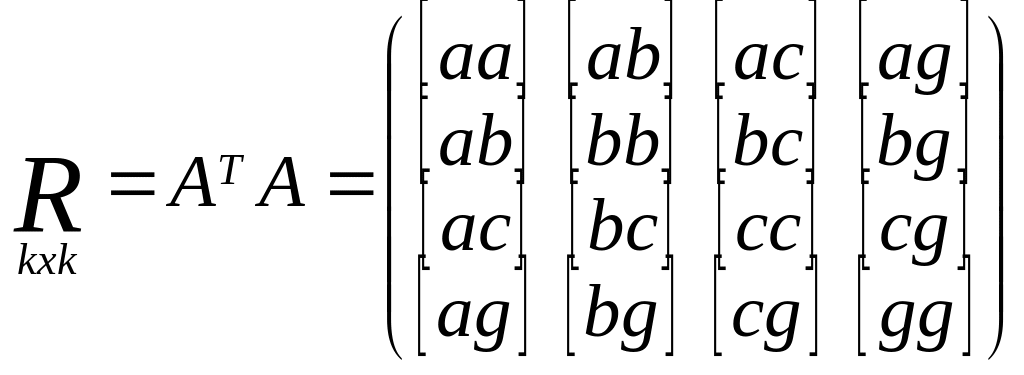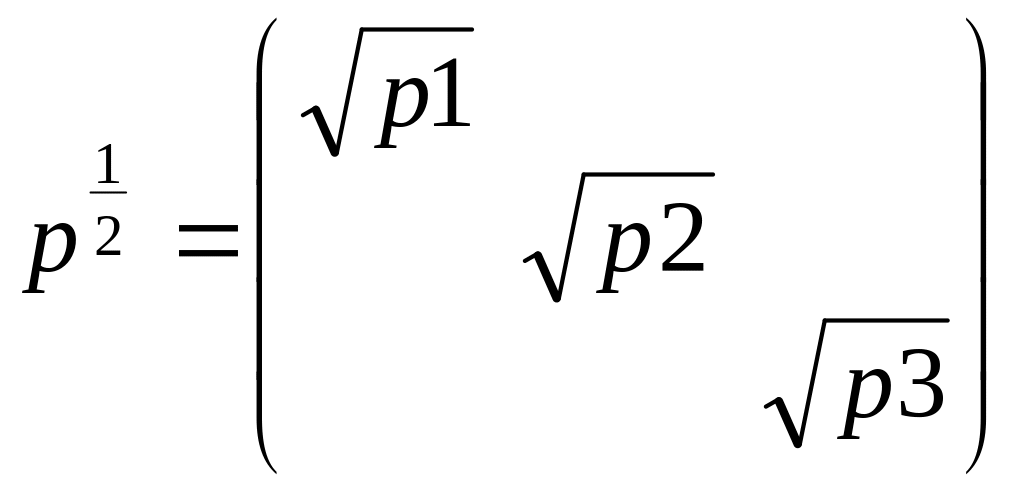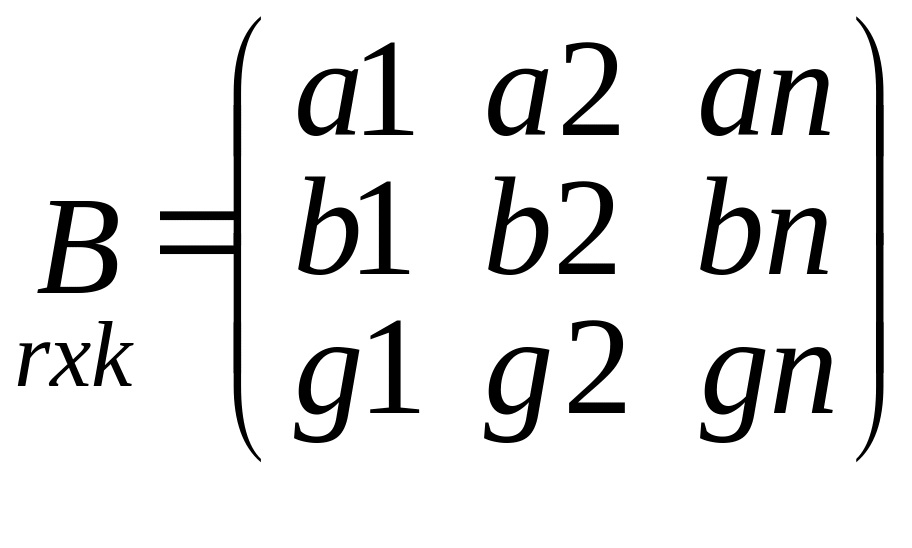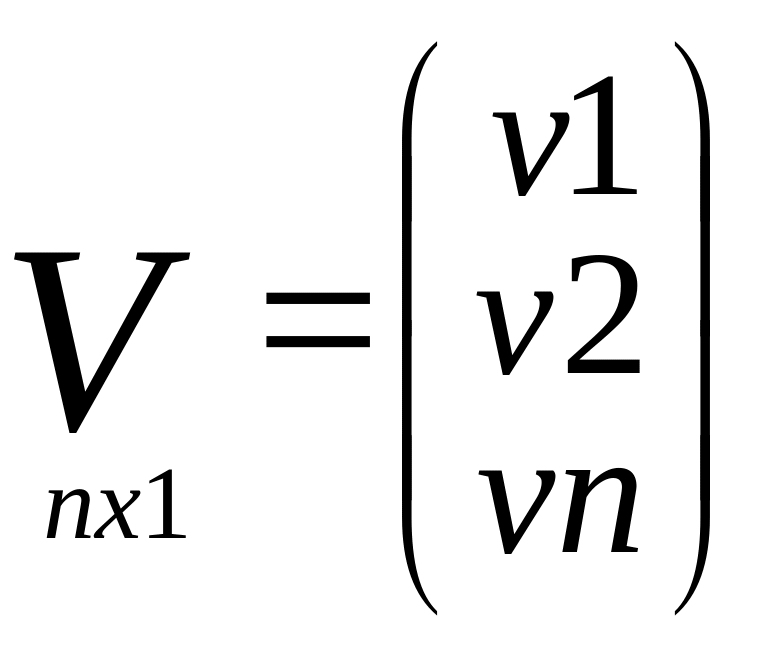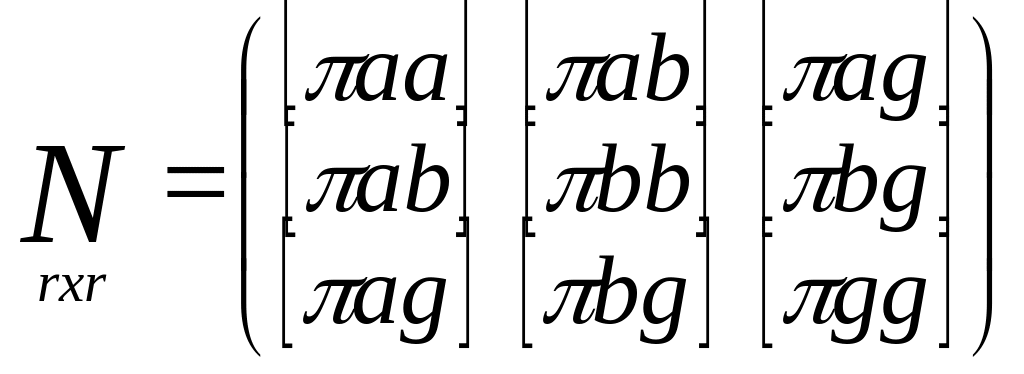ОШИБКИ ТЕОРЕТИЧЕСКИЕ
- ОШИБКИ ТЕОРЕТИЧЕСКИЕ
- — англ. error/mistake, theoretical; нем. Fehler, theoretische. Ошибки, связанные с несовершенством теории, положенной в основу исследования, неверностью предположений, неправильным выбором логической модели изучаемого соц. явления.
Толковый словарь по социологии.
2013.
Смотреть что такое «ОШИБКИ ТЕОРЕТИЧЕСКИЕ» в других словарях:
-
ОШИБКИ ТЕОРЕТИЧЕСКИЕ — англ. error/mistake, theoretical; нем. Fehler, theoretische. Ошибки, связанные с несовершенством теории, положенной в основу исследования, неверностью предположений, неправильным выбором логической модели изучаемого соц. явления. Antinazi.… … Энциклопедия социологии
-
Ошибки в сложных предложениях — 1. Р а з н о т и п н о с т ь ч а с т е й с л о ж н о г о п р е д л о ж е н и я проявляется в различной форме: а) в качестве однородных конструкций употребляются придаточное предложение и член простого предложения, например: «На… … Справочник по правописанию и стилистике
-
Ошибки в сложных предложениях — 1. Р а з н о т и п н о с т ь ч а с т е й с л о ж н о г о п р е д л о ж е н и я проявляется в различной форме: а) в качестве однородных конструкций употребляются придаточное предложение и член простого предложения, например: «На… … Справочник по правописанию и стилистике
-
ВЫБОРКИ ОШИБКИ — – вызванные различн. причинами отклонения выбороч. оценок признаков от их значений по генеральной совокупности. По происхождению В.о. можно подразделить на теоретические, возникающие до процесса отбора на стадии формирования концептуального… … Российская социологическая энциклопедия
-
ВРАЧЕБНЫЕ ОШИБКИ — ВРАЧЕБНЫЕ ОШИБКИ, род добросовестных заблуждений врача в его суждениях и действиях при исполнении им тех или иных спец. врачебных обязанностей. Отсутствие в этих суждениях и действиях элементов преступления, как то: явной небрежности,… … Большая медицинская энциклопедия
-
СССР. Общественные науки — Философия Будучи неотъемлемой составной частью мировой философии, философская мысль народов СССР прошла большой и сложный исторический путь. В духовной жизни первобытных и раннефеодальных обществ на землях предков современных… … Большая советская энциклопедия
-
Медицина — I Медицина Медицина система научных знаний и практической деятельности, целями которой являются укрепление и сохранение здоровья, продление жизни людей, предупреждение и лечение болезней человека. Для выполнения этих задач М. изучает строение и… … Медицинская энциклопедия
-
Сковородников, Александр Петрович — Александр Петрович Сковородников Дата рождения: 30 ноября 1929(1929 11 30) (83 года) Место рождения: Харбин, Китай Страна … Википедия
-
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
-
Астрономия — (от греческих слов άστρον, светило, и νόμος, закон) наука о небесных светилах. В обширном значении этого слова А. включает в себе исследование всего того, что можно знать о небесных светилах: солнце, луне, планетах, кометах, падающих звездах,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Какие бывают погрешности
Любое число, которое выдает нам эксперимент, это результат измерения. Измерение производится прибором, и это либо непосредственные показания прибора, либо результат обработки этих показаний. И в том, и в другом случае полученный результат измерения неидеален, он содержит погрешности. И потому любой грамотный физик должен не только предъявить численный результат измерения, но и обязан указать все сопутствующие погрешности. Не будет преувеличением сказать, что численный экспериментальный результат, предъявленный без указания каких-либо погрешностей, бессмыслен.
В физике элементарных частиц к указанию погрешностей относятся исключительно ответственно. Экспериментаторы не только сообщают погрешности, но и разделяют их на разные группы. Три основных погрешности, которые встречаются чаще всего, это статистическая, систематическая и теоретическая (или модельная) погрешности. Цель такого разделения — дать четкое понимание того, что именно ограничивает точность этого конкретного измерения, а значит, за счет чего эту точность можно улучшить в будущем.
Статистическая погрешность связана с разбросом значений, которые выдает эксперимент после каждой попытки измерить величину.
(Подробнее о статистической погрешности)
Систематическая погрешность характеризует несовершенство самого измерительного инструмента или методики обработки данных, а точнее, недостаточное знание того, насколько «сбоит» инструмент или методика.
(Подробнее о систематической погрешности)
Теоретическая/модельная погрешность — это неопределенность результата измерения, которая возникла потому, что методика обработки данных была сложная и в чем-то опиралась на теоретические предположения или результаты моделирования, которые тоже несовершенны. Впрочем, иногда эту погрешность считают просто разновидностью систематических погрешностей.
(Подробнее о погрешности теории и моделирования)
Наконец, в отдельный класс, видимо, можно отнести возможные человеческие ошибки, прежде всего психологического свойства (предвзятость при анализе данных, ленность при проверке того, как результаты зависят от методики анализа). Строго говоря, они не являются погрешностью измерения, поскольку могут и должны быть устранены. Зачастую это избавление от человеческих ошибок может быть вполне формализовано. Так называемый дважды слепой эксперимент в биомедицинских науках — один тому пример. В физике частиц есть похожие приемы (см. заметку Что означает «слепой анализ» при поиске новых частиц?).
Что означает погрешность
Стандартный вид записи измеренной величины с погрешностью знаком всем. Например, результат взвешивания какого-то предмета может быть 100 ± 5 грамм. Это означает, что мы не знаем абсолютно точно массу, она может быть и 101 грамм, и 96 грамм, а может быть и все 108 грамм. Но уж точно не 60 и не 160 грамм. Мы говорим лишь, сколько нам показывают весы, и из каких-то соображений определяем тот примерный разброс, который измерение вполне могло бы дать.
Тут надо подчеркнуть две вещи. Во-первых, в бытовой ситуации значение 100 ± 5 грамм часто интерпретируется так, словно истинная масса гарантированно лежит в этом диапазоне и ни в коей мере не может быть 94 или 106 грамм. Научная запись подразумевает не это. Она означает, что истинная масса скорее всего лежит в этом интервале, но в принципе может случиться и так, что она немножко выходит за его пределы. Это становится наиболее четко, когда речь идет о статистических погрешностях; см. подробности на страничке Что такое «сигма»?.
Во-вторых, надо четко понимать, что погрешности — это не ошибки эксперимента. Наоборот, они являются показателем качества эксперимента. Погрешности характеризуют объективный уровень несовершенства прибора или неидеальности методики обработки. Их нельзя полностью устранить, но зато можно сказать, в каких рамках результату можно доверять.
Некоторые дополнительные тонкости, связанные с тем, что именно означают погрешности, описаны на странице Тонкости анализа данных.
Как записывают погрешности
Указанный выше способ записи не уточняет, что это за погрешность перед нами. В физике элементарных частиц при предъявлении результатов источники погрешностей принято уточнять. В результате запись результата может иногда принять пугающий своей сложностью вид. Таких выражений не надо бояться, просто нужно внимательно посмотреть, что там указано.
В самом простом случае экспериментально измеренное число записывается так: результат и две погрешности одна за другой:
μ = 1,33 ± 0,14 ± 0,15.
Тут вначале всегда идет статистическая, а за ней — систематическая погрешность. Если же измерение не прямое, а в чем-то опирается на теорию, которая тоже не идеально точна, то следом за ними приписывается теоретическая погрешность, например:
μ = 1,33 ± 0,14 ± 0,15 ± 0,11.
Иногда для пущей понятности явно указывают, что есть что, и тогда погрешностей может быть даже больше. Это делается вовсе не для того, чтобы запутать читателя, а с простой целью: упростить в будущем расчет уточенного результата, если какой-то один из источников погрешностей будет уменьшен. Вот пример из статьи arXiv:1205.0934 коллаборации LHCb:
Означает эта длинная строка следующее. Тут записана измеренная детектором вероятность выписанного распада Bs-мезона, которая равна [1,83 ± четыре вида погрешностей] · 10–5. В перечислении погрешностей вначале идет статистическая погрешность, потом систематическая погрешность, затем погрешность, связанная с плохим знанием некоторой величины fs/fd (неважно, что это такое), и наконец, погрешность, связанная с плохим знанием вероятности распада B0-мезона (потому что измерение Bs-распада косвенно опирается на B0-распад).
Нередки также случаи, когда погрешности в сторону увеличения и уменьшения разные. Тогда это тоже указывается явно (пример из статьи hep-ex/0403004):
И наконец, совсем экзотический случай: когда величина настолько плохо определена, что погрешность пишут не к самому числу, а к показателю степени. Например, 1012 ± 2 означает, что величина вполне может лежать где-то между 10 миллиардами и 100 триллионами. В этом случае обычно нет большого смысла разделять погрешности на разные типы.
Величина со всеми явно указанными погрешностями часто не очень удобна для работы, например при сравнении теории и эксперимента. В этом случае погрешности суммируют. Эти слова ни в коем случае нельзя воспринимать как простое сложение! Как правило, речь идет о сложении в квадратах: если все три типа погрешностей обозначить как Δxstat., Δxsys., Δxtheor., то глобальная погрешность обычно вычисляется по формуле
Стоит еще добавить, что в других разделах физики нередко используют иную запись: вместо символа «±» погрешность просто помещают в скобках. Тогда ее понимают так: это погрешность, выраженная в единицах последней значащей цифры. Например, 100(5) означает 100 ± 5, а 1,230(15) означает 1,230 ± 0,015. В этом случае принципиально важно писать правильное число нулей в результате измерения, ведь запись 1,23(15) уже будет означать вдесятеро большую погрешность: 1,23 ± 0,15.
Как изображают погрешности
Когда экспериментально измеренные значения наносятся на график, погрешности тоже приходится указывать. Это обычно делают в виде «усов», как на рисунке слева. Такие «усы» с засечками относятся к глобальной погрешности. Если же хочется разделить статистические и систематические погрешности, то делают так, как показано на рисунке справа. Здесь засечки показывают только статистические погрешности, а полные усы во всю длину отвечают глобальным погрешностям. Другой вариант: выделение полных погрешностей цветом, как это показано, например, на рисунке с данными ATLAS по хиггсовскому бозону.
Наконец, когда экспериментальная точка имеет отдельные погрешности по обеим осям, то их тоже наносят, и результат выглядит в виде крестика.
Предложения со словосочетанием «теоретическая ошибка»

Пусть грамотный марксист просмотрит их и поможет в редактировании этих текстов, с тем чтобы не допустить каких-либо теоретических ошибок.
Но эта путаница предопределила также и другую огромную теоретическую ошибку классической школы.
Поэтому перенесение эстетических задач чтения литературных произведений с листа на устное исполнение литературных произведений не только художественно ограничивает эстетические принципы данного искусства, но и приводит к серьёзным теоретическим ошибкам.
Опыты такого рода невольно вызывали сомнение в том, действительно ли теория так непогрешима, как она заявляет, действительно ли практика настолько бессмысленна, как то утверждает теория, – они возбудили опасения, чтобы наша национальность в конце концов не подверглась опасности погибнуть вследствие какой-нибудь теоретической ошибки, подобно пациенту, который, следуя данному ему рецепту, умирает вследствие вкравшейся в него описки, – они возбудили, наконец, подозрение, не для того ли, собственно, эта теория воздвигнута так широко и так высоко, чтобы, наподобие известного греческого коня, скрыть оружие и людей и тем принудить нас своими собственными руками разрушить защищающие нас стены.
Здесь была допущена грубая теоретическая ошибка.
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: аболиционистский — это что-то нейтральное, положительное или отрицательное?
Но теоретические ошибки часто бывают менее вредны, чем практические выводы, на которые они наводят.
Растущее во всём мире пролетарское революционное движение вообще, коммунистическое в особенности не может обойтись без анализа и разоблачения теоретических ошибок «каутскианства».
Вот ключевая теоретическая ошибка или сознательное «передёргивание», «шулерство» экономистов, пытающихся доказать якобызаконность разделения стоимости, созданной трудом наёмного рабочего на заработную плату и прибавочную стоимость.
Ассоциации к слову «теоретический»
Ассоциации к слову «ошибка»
Синонимы к слову «теоретический»
Синонимы к слову «ошибка»
Цитаты из русской классики со словосочетанием «теоретическая ошибка»
- Учение об естественном праве, которое признавало права человека независимо от политических прав, установленных государством, делало теоретическую ошибку, которая свойственна незрелой метафизике того времени.
- (все
цитаты из русской классики)
Сочетаемость слова «ошибка»
- большая ошибка
роковая ошибка
подобная ошибка - ошибки прошлого
ошибка природы
ошибки молодости - исправление ошибок
множество ошибок
цена ошибки - ошибка вышла
ошибки случаются
ошибка произошла - совершать ошибку
допустить ошибку
исправить ошибку - (полная таблица сочетаемости)
Значение слова «теоретический»
-
ТЕОРЕТИ́ЧЕСКИЙ, —ая, —ое. 1. Прил. к теория; основанный на теории, связанный с ней. Теоретическая подготовка. Теоретические исследования. (Малый академический словарь, МАС)
Все значения слова ТЕОРЕТИЧЕСКИЙ
Значение слова «ошибка»
-
ОШИ́БКА, -и, род. мн. —бок, дат. —бкам, ж. 1. Неправильность в какой-л. работе, вычислении, написании и т. п. Допустить ошибку. Грамматическая ошибка. (Малый академический словарь, МАС)
Все значения слова ОШИБКА
Афоризмы русских писателей со словом «теоретический»
- Множество стихов Крылова обратилось в пословицы и поговорки, которыми часто можно окончить спор и доказать свою мысль лучше, нежели какими-нибудь теоретическими доводами.
- Нет никакого сомнения, что когда к инстинктивной способности хорошо говорить или писать, присоединяется теоретическое знание языка, — сила способности удвояется, утрояется…
- (все афоризмы русских писателей)
Отправить комментарий
Дополнительно
И. М. Кольтгоф, В. А. Стенгер. Объемный анализ. Госхимиздат, 1950, (т. I. 376 стр.) и 1952, (т. И, 444 стр.). В т. I рассматриваются теоретические основы объемного анализа. Изложена теория методов нейтрализации и соединения ионов, приведены кривые титрования для различных случаев метода нейтрализации. Отдельные главы содержат материал ио теории методов окисления-восстановления, теории индикаторов, по ошибкам титрования. Рассмотрены явления адсорбции и соосаждения, катализа и индукции, применение объемных методов в органическом анализе описаны теоретические положения, касающиеся применения физико-химических методов для определения точки эквивалентности. В т. 11 книги изложено практическое применение методов нейтрализации, осаждения и комплексообразования. В томе 111 (840 стр., 1961 г.) описано применение окислительно-восстановительных методов объемного анализа. [c.486]
Отсюда 1 — Х = 2,9 10″ , что соответствует ошибке определения 0,29%. В разобранном примере гидролиз цианида в значительной степени подавляется благодаря гидроксильным ионам, доставляемым раствором аммиака. Если исходная концентрация цианида составляет 0,02 М и титрование ведется 0,01 М раствором соли серебра, конечная концентрация Ag (СК) равна 0,005 М и теоретическая ошибка составляет 0,9%. [c.254]
Теоретическая ошибка титрования (А, % определяется величиной Ркк, начальной концентрацией титруемого иона См и разностью величин рМ в конечной точке титрования (рМ ер) и в точке эквивалентности (рМз) [c.190]
Какая концентрация хромата теоретически необходима при титровании бромида методом Мора, чтобы осаждение хромата серебра как раз началось в точке эквивалентности Какова относительная ошибка титрования 0,01 М бромида, если концентрация хромата райна 0,002 М. [c.246]
Для СДа> 0 теоретическая ошибка титрования ничтожно мала, поэтому ее следует учитывать в относительно небольшом интервале значений СКа- [c.55]
Конечная точка титрования железа (П) в сернокислой среде церием (IV) наблюдается при = 0,88 в. Кокова теоретическая ошибка титрования, если реальные потенциалы пар — Ре и Се —Се составляют соответственно 0,68 и 1,44 е [c.374]
А минимальная теоретическая ошибка титрования, % и Эмк — ориентировочная концентрация и условная константа устойчивости комплекса определяемого металла 7 — коэффициент разбавления раствора при титровании. [c.190]
Теоретическая ошибка прямого титрования [c.292]
Относительная теоретическая ошибка титрования Да представляет собой разность между значением а для найденной конечной [c.292]
Зависимость теоретической ошибки титрования Да (%) от условий эксперимента [c.294]
Теоретическая ошибка титрования при определении М в присутствии N описывается выражением [c.297]
Теоретическая ошибка при обратном титровании [c.301]
Кривые титрования хлоридов нитратом серебра в расплавленных солях получаются такими же, как кривые титрования в водных растворах для экзотермических процессов. Относительная ошибка титрования для указанных выше концентраций приближалась к 4%. Применение метода ограничено в связи с трудностью достаточно точного измерения повышения температуры, происходящего в результате реакции. Необходимо, чтобы изменение температуры окружающей среды было на несколько порядков меньше, чем изменение температуры, происходящее в результате рассматриваемой реакции. Теоретически в среде расплавленных солей возможно проводить любые реакции осаждения, комплексообразования или окислительно-восстановительные реакции, однако практически сложность прибора, который требуется для этого, ограничивает применимость расплавленных солей в качестве растворителей. [c.110]
Если рмь >рму, то уравнение (4.78) упрощается, принимая вид См, е= (сь/Рму ) в этом случае присутствие очень устойчивого комплекса МЬ не влияет на обратное титрование [ср. уравнения (4.53) и (4.56)]. Теоретическая ошибка титрования определяется выражением [c.303]
Дифференцируя дважды уравнение кривой титрования и приравнивая вторую производную нулю, можно легко показать [1], что на симметричной кривой титрования tii = П2) точка максимума теоретически совпадает с точкой эквивалентности. Это положение лежит в основе потенциометрических методов определения конечной точки. Вместе с тем при /ii 2 и асимметричности кривой титрования вблизи точки эквивалентности в случае, если точку перегиба принимают за конечную точку, наблюдается небольшая теоретическая ошибка. Однако эта ошибка не имеет никакого практического значения, так как она очень незначительна в сравнении с ошибками, связанными с неточностью стехиометрических соотношений, медленным течением реакции при титровании, длительностью установления электродного равновесия и т. д. [c.312]
Следует заметить, что объем нитрата серебра, необходимый для достижения первой точки эквивалентности, обычно несколько выше теоретического, но общий объем приближается к правильному значению. Это объясняется тем, что более растворимый галогенид серебра осаждается во время образования менее растворимого соединения. Поэтому наблюдается перерасход реагента в первой части титрования. Несмотря на ошибки, возникающие в результате соосаждения, потенциометрический метод широко применяется для анализа смеси галогенид-ионов. Если галогениды присутствуют в приблизительно равных концентрациях, относительная ошибка не превышает 1-2%. [c.242]
Ниже приводятся теоретические относительные ошибки (в %) титрования слабых кислот для иных значений СКа- [c.55]
В книге на современном уровне кратко изложены теоретические основы гравиметрии и титриметрии — образование и свойства осадков, типы химических равновесий в гомогенных и гетерогенных растворах описаны кривые титрования проанализированы ошибки в кислотно-основном, осацительном, комплексимет-рическом и окислительно-восстановительном титровании. Подробно рассмотрены аппаратура и техника проведения всех операций в количественном химическом анализе. Все расчеты проведены с учетом новых данных о величинах констант, стандартных потенциалов и т.п. [c.2]
Ошибка, вычисленная более точно и с учетом гидролиза цианида составляет 0,018%. Конечно, такая ошибка теоретически кажется вполне допустимой, однако на практике титрование занимает очень много времени, так как цианид серебра местами осаждается до наступления конечной точки, а затем растворяется очень медленно. [c.254]
Обычно раствор дитизона добавляют следующими порциями 1) —% всего предполагаемого количества 2) /г—оставшегося количества и т. д., пока почти весь раствор не будет добавлен, затем добавляют избыток 0,05 мл. Так как при титровании I мкг Ад+ в 50 мл водного раствора 5 мкМ раствором дитизона теоретическая погрешность равна 5%, то при содержании 100 мкг Ag+ эта погрешность должна равняться 0,05% от этой величины. Обычно к этой погрешности еще прибавляются ошибки, возможные при отсчете объема, потери и др., так что практически точность определения составляет 0,2%. [c.98]
Экспериментальное определение эквивалентной точки титрования, которая соответствует точно стехиометрическим количествам реагентов, — один из наиболее существенных вопросов объемного анализа. Точка, определяемая экспериментально с использованием цветных индикаторов, по появлению осадка или электрометрически, называется конечной. Эквивалентная точка является теоретической, а конечная — экспериментальным приближением к ней последняя поэтому зависит от метода определения. Разница между этими двумя величинами дает ошибку титрования. [c.96]
Кривые титрования этого типа также можно теоретически вычислить. Скачок у первой точки эквивалентности будет тем больше ( и ошибка титрования будет тем меньше ), чем меньше величина [А [ ] и чем меньше отношение произведений растворимости обеих солей. [c.89]
I п-ПАК [95], ПАР [323, 494], ПАН-2 [494, 584, 589, 604], комплек-I сонат меди—ПАН-2 [625], ПАФЕН [565] и МАН-1 [16]. Сопостав-I лены теоретические ошибки титрования различных количеств кад- [c.167]
Для осадков несимметричного зарядового типа, например МАг МгА и т. п., кривая титрования несимметрична, и выражение для относительной точности намного сложнее. Следует помнить, что точка максимальной кривизны (точка перегиба) не совпадает с точкой эквивалеитности на несимметричной кривой титрования. Поэтому, если считать конечной точкой точку перегиба, как это обычно практикуется нри потенциометрических титрованиях, то, как правило, имеет место теоретическая ошибка титрования. Величина ошибки увеличивается с повышением растворимости соединения и при увеличении разбавления. [c.231]
Пример 12-2. Найдите теоретическую ошибку титрования 0,1 М раствора АеЫОз 0,05 Л1 раствором К2СГО4, если произведение растворимости А2аСг04 равно 2 10″ 2. [c.232]
Пример 12-3. Рассчитайте теоретическую ошибку титрования иодида и бромида нитратом серебра, если указанные ионы определяются в смеси, содержащей 10- М иодида и 10 М бромида разбавление не учитывать. Хвр для А 1 и AgBr соответственно равны 10- и 4- 10 . [c.233]
Пример 12-4. Найдите теоретическую ошибку титрования при определении 0,1 М Вг в присутствии 0,01 Л1 I» и С1 соосаждение не учитывать. /(бр, АвС1=2- Ю- о. [c.233]
Какова теоретическая ошибка титрования, если 0,01 М раствор хлорида с pH 11,3 титруют ионами серебра до появления окиси серебра sp, Ae.o = fAe +] [0Н ] = 5 Ю» / sp, Ag i=2 10″ ° разбавление не учитывать. Ответ. 0,17%, [c.246]
Пример 13-5. Найдите теоретическую ошибку титрования 10 М раствора магния при pH 10 в присутствии ЭЧТ в качестве индикатора, предполагая два случая констатации конечной точки а) 9% и б) 91% индикатора превратились из Мк1п в Н1п2 . Разбавление и гидролиз ионов магния не учитывать. [c.263]
Если берется большой избыток титранта, так что суммарная концентрация N (главным образом в виде НУ) в точке эквивалентности также оказывается высокой, то количество не вступившего в реакцию М, выражаемое через См.е, тоже становится большим, особенно в тех случаях, когда комплекс ЫУ облада1ет низкой устойчивостью. Этот фактор уменьшает воспроизводимость определения конечной точки титрования, поскольку наклон кривой титрования обратно пропорционален значению см,е [см. уравнение (4.56)]. Большой избыток хелона уменьшает и точность обратного титрования, как это можно видеть из данных табл. 4.6, которые были вычислены по уравнениям (4.72) и (4.77) для простой системы, состоящей из двух комплексов с одинаковой устойчивостью. Из данных табл. 4.6 следует, что теоретическая ошибка титрования, соответствующая определенной погрешности в определении рМе (предполагается, что АрМ= 0,5), минимальна для умеренного избытка (около 10%) хелона. На практике такой избыток обычно не достаточен для обеспечения полноты реакции илй предотвращения образования осадка. Однако в интервале Сы См=0,1—1,0 не наблюдается значительного возрастания погрешности, так что 100%-ный избыток хелона мало влияет на точность обратного титрования. [c.300]
Эти данные можно использовать как для внесения соответствующих поправок, так и для вычисления минимального количества титруемого вещества при заданной точности определения. Если, например, на некоторое титрование теоретически необходимо затратить а миллиграмм-эквивалентов КМПО4, то в действительности затрачивается а -т миллиграмм-эквивалентов. Отсюда индикаторная ошибка О в процентах равна [c.149]
Теоретическая ошибка титрования (А, %) определяется константой Рмк, начальной концентрацией титруемого иона С м и разностью значений рМ в конечной точке титрования (рМцер) и в точке эквивалентности (рМэ) [c.225]
Для определения кадмия в качестве индикаторов предложены п-ПАК [95], ПАР [323, 494], ПАН-2 [494, 584, 589, 604], комплексонат меди—ПАН-2 [625], ПАФЕН [565] и МАН-1 [16]. Сопоставлены теоретические ошибки титрования различных количеств кадмия в присутствии ПАР и ПАН-2 (%) [494] [c.167]
Для определения степени разложения фосфата по этому методу периодически (например, каждые 15—30 мин) отбирают из реакционного сосуда пробу пульпы и определяют в ней отношение азотной и фосфорной кислот таким же способом, как это описано на стр, 147 для суперфосфат юй пульпы, т, е, титрованием с двумя индикаторами — метиловым оранжевым (или бромкрезоловым синим) и фенолфталеином. При этом количество оксалата калия или натрия, вводимых в раствор перед титрованием, должно быть достаточным для осаждения всего кальция во избежание ошибки при титровании. Теоретически для этого достаточно количеств К2С2О4 или Ма2С20.1, указанных на стр, 148, Однако для большей надежности следует эти количества увеличить в 1,5—2 раза. [c.348]
При выполнении титрования главное состоит в определении того момента, когда реактив добавлен точно в требуемом количестве. Если количество прибавленного реактива химически эквивалентно количеству определяемого вещества, то мы говорим, что смесь находится в своей точке эквивалентности. Для опознания точки эквивалентности может быть использовано любое свойство смеси, которое в этой точке или очень близко от нее резко изменяется. Чаще всего прибавляют индикатор, который у точки эквивалентности изменяет цвет или мутность раствора. Точка, при которой индикатор показывает заметное изменение, называется точкой конца титрования. В идеальном случае эта точка должна совпадать с точкой эквивалентности или с теоретическим концом титрования. На практике, однако, конец титрования несколько отклоняется от точки эквивалентности на величину, которая зависит от химических свойств всей системы. Эта разность называется ошибкой гитрования она имеет большое значение и будет рас-шотрена нами в гл. VI. [c.9]
Точные математические выражения величины ошибки титрования в методе нейтрализации даны Р. S. Roller [J. Аш. hem. So . 54, 3485 (1932)]. Вычисления эти в теоретическом отношении очень интересны, но они слишком сложны для практического их использования, тем более, что и на ионизационные константы слабых электролитов (включая индикаторы) и на коэфициенты активности ионов влияют различные факторы. [c.175]
Теория ошибок
Теория ошибок
– дисциплина, которая изучает законы
возникновения и распределения ошибок
измерений, а также методы их обработки.
Виды измерений: 1)полученные непосредственно
из измерения (длина линии при изм. мерной
летной) и косвенным путем (неприступные
расстояния); 2) необходимые
(назыв.минимальное
кол-во измерений, которое нужно выполнить
для определения искомой величины) и
избыточные
(назыв измерения в которых для контроля
всегда выполняются дополнительные
измерения) вычисл. по формуле : r=n-k,
где n
– общее число изм., k
– необходим число изм.; 3) равноточные
(измерения выполненные одним и тем же
инструментом, при одинаковых внешних
условиях, по одной и той же методике,
наблюдателями одинаковой опытности) и
неравноточные (если хотя бы одно из
условий равноточности нарушается это
приводит к неравноточности).
Ошибки измерений
Теория ошибок делит
ошибки на: грубые(возникают
при просчетах и промахах, теор.ош. их не
изучает), систематические
( назыв ошибки МО которых отлично от
нуля. Н.ошибка компарирования), случайные
(ошибки
измерений которых имеют различные знаки
и их МО равно 0). Св-ва случайных ошибок:
1) их МО равно нулю; 2) Положит и отриц
ошибки появляются равновозможно; 3)
Малые по абсолютной величине ошибки
появляются чаще чем большие; 4) Ошибки
не превосходят определенной величины
равной 3m.
Истинная
ошибка
измерения: Δi=xi-X,
где xi
– результат измерения, Х – истинное
значение измеренной величины. Истинное
значение практически никогда не известно.
Средняя
квадратическая ошибка
Это МО квадрата
истинной ошибки, т.е. нач момент второго
порядка:
.
Истинная ошибка состоит из: Δ=Θ+с;
.
Т.е. любая СКО содержит случайную и
систематическую составляющую.
Систематической ошибкой можно пренебречь
если ее величина равна:
,
Θ – случайная ошибка.
Равноточные
измерения
Условие: измерения
выполненные одним и тем же инструментом,
при одинаковых внешних условиях, по
одной и той же методике, наблюдателями
одинаковой опытности. Т.к. равноточность
подразумевает одинаковую точность
каждого измерения для хар-ки точности
любого одного измерения используют СКО
одного измерения. Наиболее надежным
значением из ряда равноточных измерений
будет среднее арифметическое, которое
вычисляется по формуле:
,
где х – результат измерения, n
– число изм.
Оценка точности
равноточных измерений
1) СКО одного
измерения.
Если известна истинная ошибка измерения
Δ, которая находиться по формуле: Δi=xi-X,
где xi
– результат измерения, Х – истинное
значение измеренной величины.
.СКО
одного измерения находим как: а) n>=30.
Формула Гаусса:
,
где
;
б) n<30.
Формула Бесселя:
.
2) При вычислении СКО удерживают две
значащих цифры. Для того чтобы убедиться
что этого достаточно вычислим СКО самой
СКО:
— если СКО вычислено по формулам Гаусса,
— -«»- по формулам Бесселя; 3) СКО среднего
арифметического: вычисляется по формулам:
,
где m
– CКО
одного измерения, n
– число измерений. 4) Кроме СКО для хар-ки
точности равн.измерний используют
среднюю и вероятную ошибку: Средняя
ошибка —
,
ν – уклонение ср.кв.значения. Для
вычисления вероятной ошибки r,
которая хар-ет середину ряда используют
или ряд истинных значений Δ, или уклонения
от среднего ν.
Эти величины берут по абсолютной величине
и выстраивают в порядке возвр. Вероятная
ошибка r
будет равна центральному значению из
полученного ряда если число измерений
нечетное или среднему из двух центральных
знач. при четном числе измерений.
Относительные
ошибки измерений Абсолютные
Абсолютными ошибками
назыв СКО, среднюю v,
вероятную r,
истинную Θ. Относительной ошибкой –
назыв. величину получаемую как отношение
ошибки измерения к результату измерения:
mx/x.
В геодезии принято представлять
относительную ошибку в виде простой
дроби: 1/(х/mx)
И округлять
до целых сотых. В зависимости от того
какую точечную оценку использовали для
хар-ки точности различают относит.
истинная ош. – Δ/х, относит ср.кв.ош –
ν/х, относит вер-я ош – r/x.
СКО функции.
Принцип равного влияния
Если представить
ф-ю F(x)=F(x1,
x2…xn),
которую оцениваем как ф-ю измеренных
величин, то СКО ф-ии для некоррелированных
измерений
будет найдена как:
,
где
— частная производная оцениваемой ф-ии
по i-му
измерению. Если измерения коллерированы:
,
mxi
mxj
– коэф.кореляц между i-м
j-м
измерениями. Для определения СКО
отдельных аргументов применяют принцип
равного влияния. Суть принципа в том
что влияние каждого источника ошибок
на конечный результат применяют
одинаковым:
1)СКО алгебраической
суммы: F=x1±x2±..±xn,
— для неравноточных. Частный случай
когда измерения равноточны:
.
В этом случае формула приобретает вид:
2)Как СКО ф-ии
получают и СКО арифметической середины:
,
Неравноточные
измерения
Неравноточными
назыв измерения в которых каждое
измерение будет иметь свою отличную от
других СКО. Вычислить ошибку каждого
неравноточного измерения сложно, поэтому
для хар-ки неравноточ измерений применяют
относительную меру точности, которую
назыв.весом. Веса измерений обратны
квадратам СКО:
,
mi
– ско соотв измерения, с – произвольная
постоянная для данного ряда измерений.
При выборе с стараются чтобы вычисленные
веса измерений были близки к 1.Зная вес
всегда можно определить величину СКО
измерения:
.
При оценке точности заменяют с=μ2.
Ошибка единицы
веса для ряда неравноточных измерений
играет ту же роль что и СКО одного
измерения для ряда равноточных:
.
Для вычисления ошибки единицы веса
используют формулу Гаусса:
— когда известно истинное значение,
— при n<30,
— при n>30.
Наиболее надежное
значение из ряда неравноточных измерений
и его оценка точности:
Наиболее надежным
будет ср.весовое
.
Эту величину так же назыв.общая
арифметич.середина. СКО среднего
весового:
.
Вес функции:
Формулы для
вычисления весов ф-ии получают из формул
для вычисления весов ф-ий разделив их
на μ2.
Для некоррелированных
измерений:
.
Для коррелированных:
Задача уравнивания
Наличие в сети
избыточных измерений приводит к
неоднозначности определения неизвестных,
а значит возникает задача ур-я, которая
Состоит в определении наиболее надежных
значений неизвестных параметров и их
оценки точности. Мы решали такую задачу
при обработке измерения одной величины
в теории ошибок. Принципиальное отличие
задачи в том что в обработку включаются
разнородные величины. Существует два
вида ур-я: параметрический и корелантный.
Параметрический
способ ур-я
Х – истинное
значение неизвестного параметра, У –
истинное значение измеренной величины,
у – измеренное значение. Результаты
измерений всегда можно связать с какой
то ф-ей. Т.к. в общем случае ур-е (1) нелинейно
приведем его у линейному виду разложив
в ряд Тейлора
Порядок уравнивания
параметрическим способом
1) Выберем неизвестные
и обозначим их xj.
2)Составим у-е связей между измеренными
значениями и неизвестными У=φ(х).
3) Составим параметрическое у-е поправок
А∆х+L=V.
4)Находим приближенное значение
неизвестных и вычисляем свободные члены
параметрических у-ий поправок: φ(х(0))-у=L.
5) Составим нормальное у-е R∆x+B=0,
R=ATA,
b=ATL.
6) Получим поправки из уравнивания
приближенным значением неизвестных
∆х=-R-1b.
7) Вычислим уравненные значения неизвестных
.
Выполним оценку точности.
Запись матричных
выражений в параметрич.способе
Параметрич.у-е
поправок
V=A∆x+L
Для каждого измерения
Матрица поправок
изм.знач.
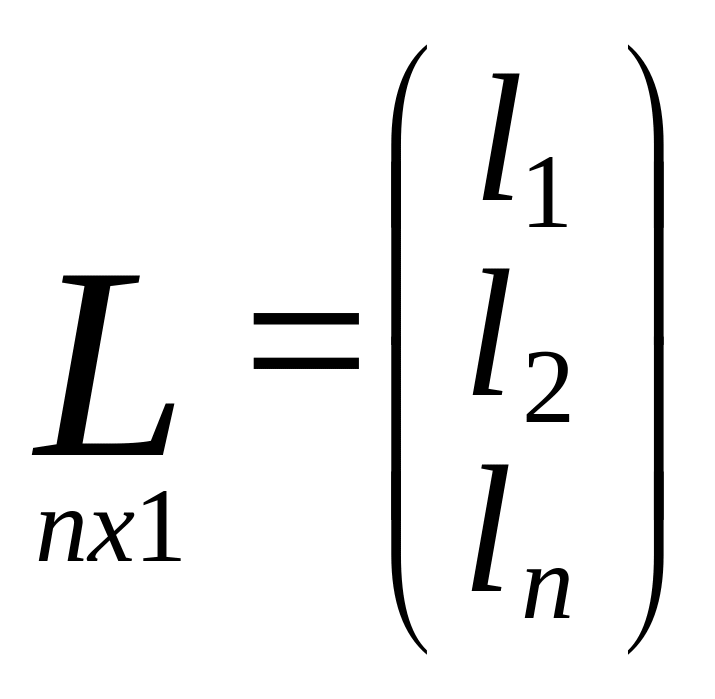
Матрица частных
произв.
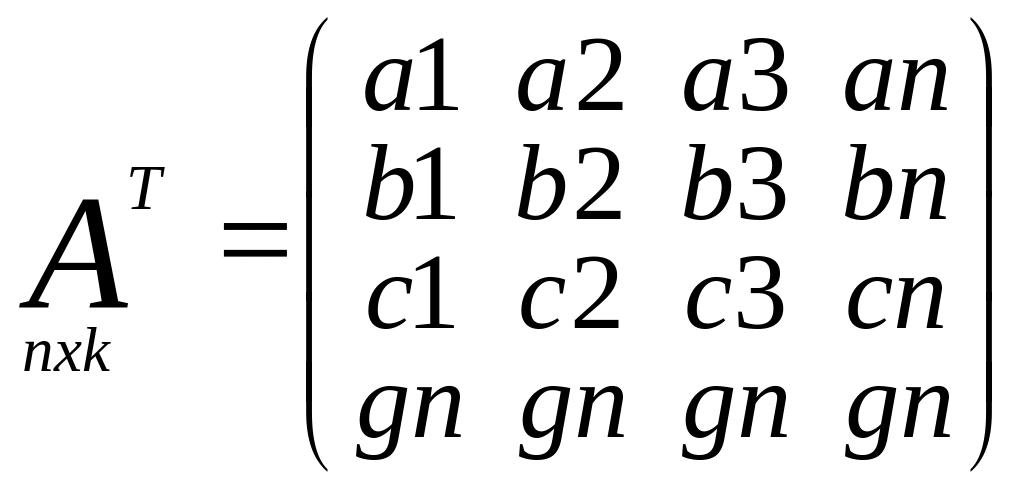
Матрица коэфиц.
норм.ур-й. Св-ва:
1) по диагонали стоят квадратичные коэф.,
они всегда положит. 2) не лиагональные
элементы симметричны относительно
главной диагонали.
Матрица свободных
членов нормальных ур-ий
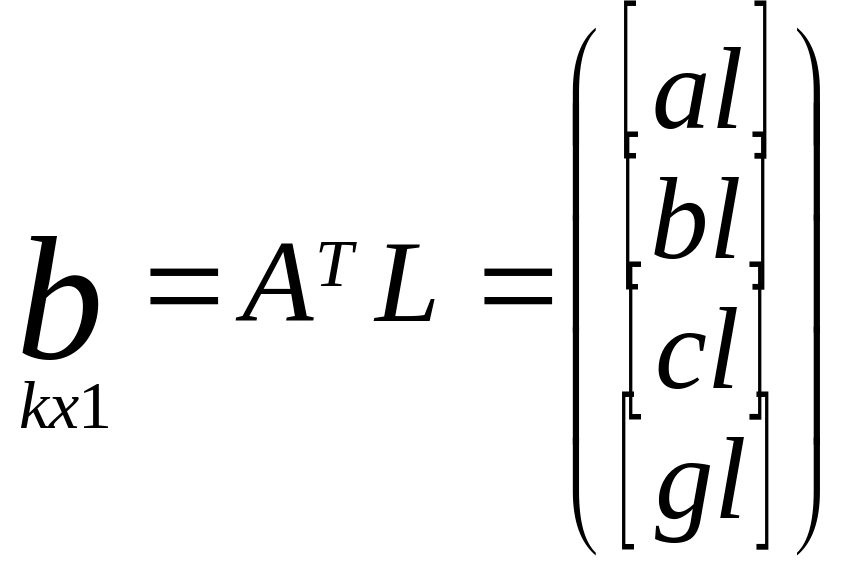
Номальные у-я для
4 неизвестных
R∆х+b=0
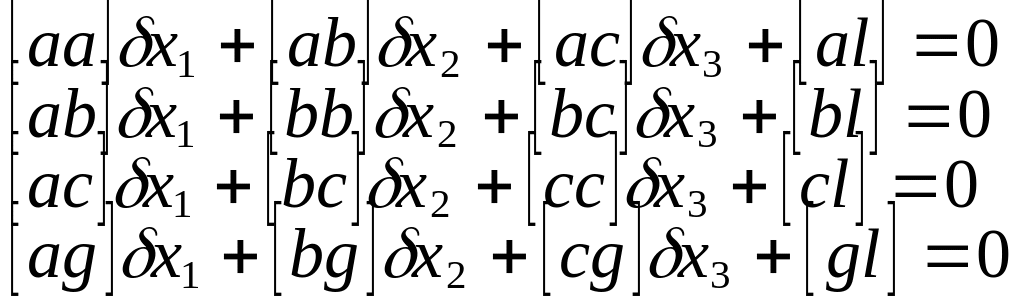
Способы решения
нормальных ур-ий
Прямой способ,
когда решения получают в виде: ax=b,
x=b/a.
При прямых способах мы можем заранее
указать кол-во операций. Приближенный
способ, когда решения получаем в виде:
ax+x-x-b=0,
xi=(1-a)xi-1-b,
т.е. в каждом последующем приближении
I
используется значение неизвестного
xi-1
полученное
в предыдущем приближении. В этом способе
мы заранее не можем описать кол-во
операций, но этот способ занимает меньше
памяти в ЭВМ.
Оценка точности
при параметрическом способе
а) оценка точности
неизвестных. Обратный вес уравненного
значения каждого неизвестного будет
равен соотв.диагональному элементу
обратной матрицы коэф.норм. ур-й
.В
матрице Q
по диагонали стоят обратные веса
неизвестных ее так же назыв. весовой
матрицей.
б) вычисление ошибки
единицы веса. При параметр. способе
ошибки единицы веса вычисляются по
формуле:
,
здесь v
может быть вычислено по формуле:
,
где n
– общее число изм., k
– число необходим изм., равное числу
определяемых неизвестных.
Ур-ие неравноточных
измерений
1)пусть измерения
неравноточны, чтобы привести их к
равноточному виду мы умножим их на
матрицу:
.
Получим у-е:
.
Решаем задачу также как и для равноточных
изм.: получим нормальное у-е и вектор
решения:
;
.
Из ур-я мы получим
,
чтобы получить величину V.
После ур-я разделим поправки:
2) для учета
неравноточных измерений во все алгоритмы
Гаусса ввести веса измерений и получит
алгоритмы в виде:
;
Коррелатный
способ ур-я
Сущность ур-я
коррелатным способом заключается в том
чт задачу нахождения минимума ф-ии
зависимых переменных [pv2]
решают способом Лагранжа, вводя
вспомогательные множители независимых
условных ур-ий. Приводит к тем же
результатам что и параметрический, но
иногда более выгоден.
Порядок ур-я
корелатным способом
1) Подсчитываем
число избыточных измерений в геод.сети.
Каждое избыточное измерение приводит
к возникновению независимого ксловного
у-я поправок. 2) Составляем у-е связей
между измеренными величинами которые
выражают какое-то математическое
соотношение: φ(У)=0;
3) Составляем условное у-е поправок:
BV+w=0;
4) Составляем нормальные у-я: Nk+w=0;
5)Получаем корелаты решив у-е любым
известным споcобом:
k=-N-1w;
6) вычисляем поправки к измеренным
величинам: V=p-1BTk;
7)Вычисляем уравненные значения измеренных
величин
;
По уравненным значениям измерений
вычисляем значения неизвестных; 9) Оценка
точности.
Подробная запись
матричных выражений
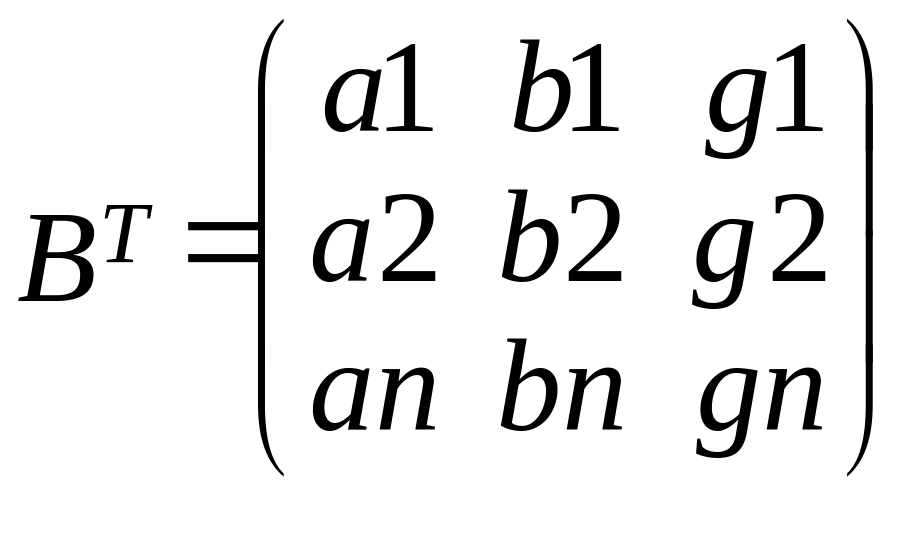
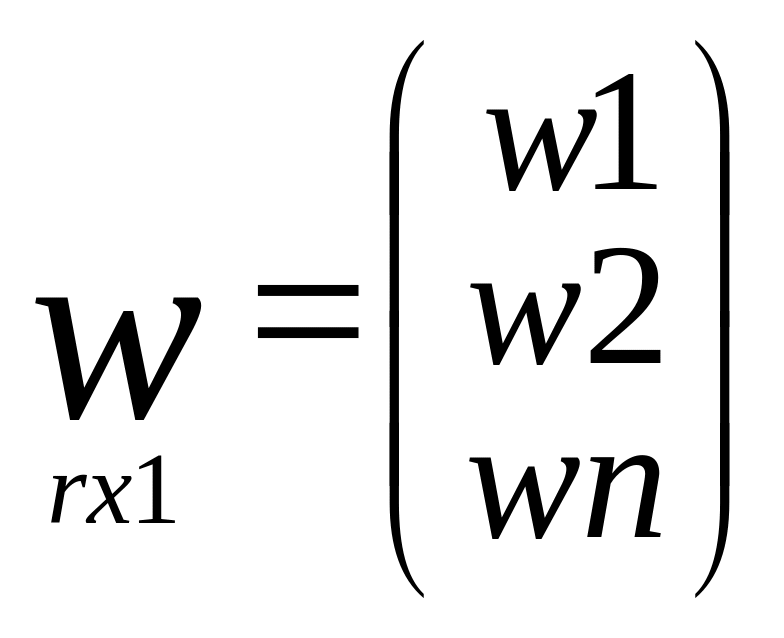
C
учетом у-я поправок:
Нормальные у-я в
подробной записи:
,
где
— обратный вес
Порядок обработки
ряда неравноточных измерений
1) Вычисляем общую
арифметич. середину:
,
где εi=xi-x’,
x’=minxi
. 2)
Вычисялем уклонения vi=хо-хточн
и выполняем контроль
,
где ошибка округления при вычислении
будет
.
3)Вычисляем [pv2]
с контролем:
.
4) Вычисляем μ, M,
mμ,
mM
b
и строим
доверительные интервалы
Порядок обработки
ряда равноточных измерений
1.Вычисляем простую
арифметич. середину:
,
где εi=xi-x’,
x’-
приближенное значение х (обычно
минимальное значение xi).
2) Вычисляем отклонения vi=
хi-xокр,
и выполняем контроль
,
где β – ошиюка округления х —
.
3) Вычисляем [v2]
с контролем:
.
4) Вычисляем m,
M,
mm.
5)Cтроим
доверительные интервалы
;
;
Число нормальных
ур-й в параметрическом и корелатном
способе
В параметрическом
способе: это определенная система из k
линейных уравнений с k
неизвестными: R∆х+b=0.
В корелатном: в системе нормальных
уравнений число уравнений r
равно числу неизвестных.
Алгоритм гаусса.
Эквивалентные ур-я.
Система эквивалентных
у-й имеет вид:
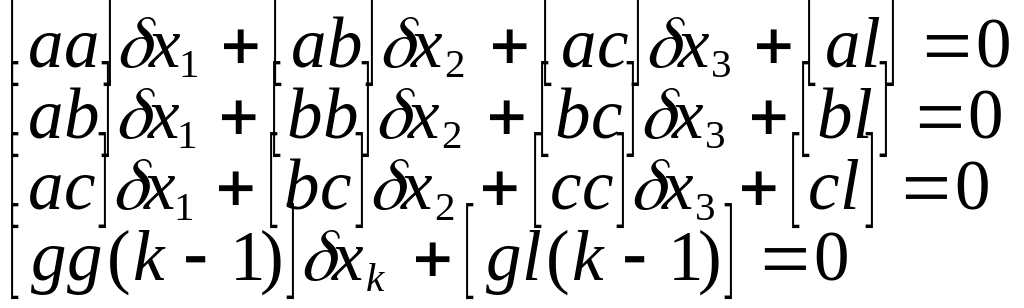
Алгоритм полученный
для вычисления коэффициентов в
экквивалентной системе, назыв алгоритмом
Гаусса. Первый сомножитель получается
как произведение первой буквы знаменателя
на первую букву раскрываемого алгоритма,
а второй как произведение второй буквы
знаменателя на его вторую букву
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
появления события |
обстоятельства, |
то ( ) |
|
b или не—b |
когда ( ) |
|
|
1 |
afcd |
b |
|
2 |
hsp |
не—b |
|
3 |
gtu |
не—b |
|
. . . . |
. . . . |
. . . . |
Вероятно, если (а), то(b).
Заключение по сопутствующим изменениям. Данный вид заключений осуществляется на основе эмпирической таблицы наблюдений, в которой обстоятельство a, выступающее причиной явления b, изменяется, в то время как другие обстоятельства остаются неизменными (см. табл. 3.5.3).
Таблица 3.5.3.
|
Случаи (k) |
Предшествующие |
Наблюдаемое явление, |
|
обстоятельства, |
то ( ) |
|
|
когда ( ) |
||
|
1 |
afcd |
b |
|
2 |
fcd |
не—b |
Вероятно, если (а), то(b).
В общем случае вероятностное заключение основывается на совокупности наблюдений, в которой представлены все рассмотренные случаи. Так как заключение вероятностное, то полученное правило «если (а), то(b)» может выполняться не для всех наблюдений. Здесь возможны следующие ошибки правила вывода:
—обстоятельство а присутствует, однако явление b в наблюдении отсутствует;
—обстоятельство а отсутствует, однако явление b в наблюдении
присутствует.
70. Предположим, что совокупность наблюдений представляет собой генеральную выборку данных, т.е. представляет собой набор всех возможных данных по исследуемому явлению. Тогда можно подсчитать относительную частоту правильных выводов на основе полученного правила:
|
пр = 1 — ош , |
ош = |
Nош |
. |
|
N |
Здесь N – общее число наблюдений в генеральной совокупности; Nош – число наблюдений, на которых полученное правило дает ошибочные выводы; ош – относительная частота ошибочных выводов.
80. Необходимо отметить, что относительная частота ошибочных выводов образуется из ошибок двух видов. Ошибка ложного вывода состоит в том, что согласно полученному правилу мы делаем утвердительный теоретический вывод, однако эксперимент его не
254

подтверждает. Другой вид ошибки состоит в том, что согласно полученному правилу мы делаем отрицательный теоретический вывод, однако эксперимент свидетельствует обратное. Зная частоту указанных ошибок можно подсчитать относительную частоту ложного вывода и относительную частоту пропуска вывода для найденного правила.
90. Если совокупность наблюдений не представляет собой генеральной совокупности, то всю выборку данных необходимо разделить на две выборки: обучающую и поверочную. На обучающей выборке находится искомое правило, на поверочной выборке определяется относительная частота его выполнения. Этот подход следует из общего принципа проверки знаний: знания приобретаются на обучающих примерах, а проверяются на других — поверочных примерах.
В результате проверки найденного правила «если (а), то (b)» принимается решение о его достоверности.
100. В итоге, после проведения серии экспериментальных исследований в дальнейших теоретических исследованиях может быть принята в качестве исходной посылки теории причинно-следственная связь
x f y ,
содержание которой раскрывается в серии суждений:
если (аi(1)) то (bj(1)); если(аi(2)) то (bj(2));
. . . .
если (аi(k)) то (bj(k));
. . . .
С математической точки зрения совокупность данных суждений представляет собой функцию общего вида y f (x) .
3.5.2. Построение факторных зависимостей
110. Рассмотрим задачу построения зависимости выходных эффектов объекта исследования от значений действующих факторов на его входах
(рис. 3.5.1).
x1
xn
Рис. 3.5.1. Факторное представление объекта исследования.
255
Здесь x1 , x2 , …, xn — входные факторы, y — выходной эффект. Так как зависимость F a priori неизвестна, то рассматриваемую задачу называют также задачей о «черном ящике». К указанному представлению сводится широкий класс задач исследования как статических, так и динамических зависимостей.
Так, например, рекуррентная зависимость
|
n |
m |
|
yk ar yk r bluk l , |
|
|
r 1 |
l 0 |
описывающая динамику линейных стационарных процессов, а также модель линейных динамических систем в пространстве состояний
|
n |
m |
|
xi, k 1 air xr , k bilul , k , |
|
|
r 1 |
l 1 |
|
n |
m |
|
y j, k cir xr , k dilul , k ; |
|
|
r 1 |
l 1 |
путем замены переменных приводятся к указанному базовому представлению.
120. Предположим вначале, что нам известна общая структура зависимости F в виде линейной композиции функций общего вида:
|
n |
|||||
|
y ai i (x) , |
(2.1) |
||||
|
i 0 |
|||||
|
где x — вектор ( x |
, x |
, …, |
x |
)т входных факторов; |
( ) — некоторые известные |
|
1 |
2 |
n |
i |
функции; ai — неизвестные коэффициенты.
Изложение материала будем вести на высоком уровне абстракции, предполагая, что значения входных факторов представляют собой элементы произвольной природы. Значения функций i ( ) и y будем также полагать
элементами произвольной природы, однако будем дополнительно считать, что они являются элементами абстрактного линейного пространства. В этом случае для них определены абстрактные алгебраические операции умножения на число и сложения. Соответствующее линейное пространство будем полагать эвклидовым. Кроме того функции i ( ) могут иметь
различные частные виды, например: зависеть лишь от одной переменнойi (xi ) , отождествляться с переменной xi , представлять произведение
i
переменных xr и др.
r 1
130. Предположим, что в результате экспериментальных наблюдений за поведением объекта исследования получено множество экспериментальных данных
|
{(xs , ys ) : s 1, 2, . . . , N}, |
(2.2) |
|
256 |
где s — индекс экспериментального наблюдения, N — общее число наблюдений.
140. Для того чтобы адекватно отражать действительность, зависимость (2.1) должна теоретически предсказывать значения ys по заданным
значениям xs . Так как в общем случае это не происходит, то ошибку предсказания можно определить соотношением
|
n |
||
|
es ys ai i (xs ) , |
s 1, 2, . . . , N . |
(2.3) |
i 0
Среднюю норму ошибок определим с использованием соотношения
|
1 |
N |
||||||||||
|
E2 |
es |
2 . |
(2.4) |
||||||||
|
N s 1 |
150. Ставится задача: определить неизвестные значения коэффициентов ai зависимости (2.1), исходя их условия минимума средней
нормы ошибок (2.4)
Определим норму ошибки на основе скалярного произведения в некотором эвклидовом пространстве
|
e |
2 e , |
e |
, |
(2.6) |
|
|
s |
s |
s |
где 

эвклидовом пространстве.
С учетом (2.3), (2.4), (2.6) средняя норма ошибок определится соотношением
|
1 |
N |
n |
n |
|||
|
E2 |
ys |
a j j (xs ), ys |
ak k (xs ) . |
(2.7) |
||
|
N s 1 |
j 0 |
k 0 |
Выражение (2.7) есть числовая квадратичная функция относительно
|
коэффициентов ai |
и называется квадрат среднеквадратической ошибки. |
||||||||||||
|
Сама |
среднеквадратическая |
ошибка, |
естественно, |
определяется |
|||||||||
|
соотношением E |
|||||||||||||
|
E2 . |
|||||||||||||
|
160. Необходимым условием минимума квадратичной функции (2.7) |
|||||||||||||
|
является равенство нулю всех ее частных производных |
|||||||||||||
|
E |
2 |
1 |
N |
n |
1 |
N |
n |
||||||
|
i (xs ), ys ak k |
(xs ) |
ys a j j (xs ), i (xs )) 0 , |
|||||||||||
|
a |
N |
N |
|||||||||||
|
s 1 |
k 0 |
s 1 |
j 0 |
||||||||||
|
i |
i 0, 1, . . . , n .
Полученные соотношения представляют собой систему линейных алгебраических уравнений относительно неизвестных ai . На основе
эквивалентных преобразований данную систему уравнений можно привести к нормальному виду
257

|
n |
|||||
|
cij a j di , |
|||||
|
j 0 |
|||||
|
N |
1 |
||||
|
i |
(xs ), j (xs ) |
||||
|
s 1 |
N |
||||
|
1 |
N |
1 |
|||
|
i (xs ), ys |
|||||
|
N |
|||||
|
N s 1 |
|
i, j 0, 1, . . . , n . |
(2.8) |
||
|
N |
|||
|
j (xs ), i (xs ) |
; i, j 0, 1, . . . , n ; |
(2.9) |
|
|
s 1 |
|||
|
N |
|||
|
ys , |
i (xs ) ; |
i 0, 1, . . . , n . |
(2.10) |
s 1
170. Таким образом, на основе экспериментальных данных (2.2) можно построить аналитическую зависимость (2.1), неизвестные коэффициенты которой определяются на основе решения системы линейных алгебраических уравнений (2.8). Полученное решение будет оптимальным по критерию минимума квадрата среднеквадратической ошибки (2.5). Изложенный метод решения называется методом наименьших квадратов31. Метод наименьших квадратов является одним из наиболее распространенных методов построения зависимостей по экспериментальным данным.
180. Рассмотрим далее вопрос оценки точности решения рассматриваемой задачи. Прежде всего, необходимо обратить внимание, что оценку точности решения задачи (2.5) не следует проводить на экспериментальных данных, которые непосредственно использовались для решения задачи. Эти данные представляют собой обучающую выборку. Оценку точности необходимо осуществлять на дополнительных данных – поверочной выборке, которые не участвовали в решении задачи. Данное требование составляет общее правило для процессов обучения.
В нашем случае разрешимость задачи (2.5) непосредственно определяется разрешимостью системы линейных алгебраических уравнений (2.8). Из теории линейных алгебраических уравнений известно, что необходимым и достаточным условием разрешимости системы уравнений (2.8) является неравенство нулю определителя системы уравнений: 0 . Это условие эквивалентно требованию линейной независимости каждой i -ой строки системы уравнений (2.8). В свою очередь данное требование эквивалентно требованию линейной независимости результатов наблюдений, составляющих обучающую выборку (2.1). Минимальное число линейно независимых результатов наблюдений равняется числу неизвестных в системе уравнений (2.8). Таким образом, для разрешимости задачи (2.8) минимальное число линейно независимых результатов наблюдений
31 Задачу построения неизвестной зависимости на основе метода наименьших квадратов впервые поставил и решил немецкий математик К. Гаусс. Гаусс решал астрономическую задачу оценки траектории движения планет при наличии возмущений.
258

|
N об |
n 1. |
(2.11) |
|
|
min |
|||
|
При общем числе экспериментальных наблюдений — |
N , объем поверочной |
||
|
выборки составит |
|||
|
N пов N N об |
N (n 1) . |
(2.12) |
|
|
min |
Поверочная выборка должна представлять собой линейно независимые результаты наблюдений.
С учетом сказанного, квадрат среднеквадратической ошибки решения задачи (2.5) определится выражением
|
1 |
N |
||||||||||
|
E2 |
es |
2 . |
(2.13) |
||||||||
|
N (n 1) |
|||||||||||
|
s 1 |
190. Точность (2.13) решения задачи (2.5) непосредственно связана со сложностью представления искомой зависимости (2.1).
Сложность искомой зависимости (2.1) будем оценивать числом ее неизвестных, другими словами, числом ее степеней свободы. В нашем
|
случае число степеней свободы |
|
|
Nсв n 1. |
(2.14) |
Число степеней свободы искомой зависимости должно соответствовать реальной сложности функциональных свойств исследуемого объекта. Если число степеней свободы искомой зависимости меньше реальной сложности функциональных свойств исследуемого объекта, то точность решения задачи (2.5) будет низкой. Аналогично в противоположном случае, если число степеней свободы искомой зависимости больше реальной сложности функциональных свойств исследуемого объекта, то точность решения задачи (2.5) также будет низкой. Общий характер связи точности решения задачи (2.5) от числа степеней свободы искомой зависимости представлен на рис. 3.5.2.
E2
Nсв
Nсвopt
Рис. 3.5.2. Связь точности построения зависимости от числа ее степеней свободы.
Из рисунка 3.5.2 следует, что существует оптимальное число степеней свободы искомой зависимости, обеспечивающее максимальную
259
точность представления функциональных свойств конкретного объекта исследования.
200. Другой проблемой является возможность информационной неполноты статистики, которая используется для построения эмпирических формул. В этом случае постановка задачи построения эмпирической формулы будет некорректной и необходимо использовать методы регуляризации.
С практической точки зрения здесь можно рекомендовать использовать в качестве регуляризующей функции оценку нормы уклонения искомого решения от некоторого номинального, имеющего регуляризующий эффект
|
1 |
n |
|||||||||
|
R2 |
ai aiр |
2 . |
(2.15) |
|||||||
|
n 1 i 0 |
||||||||||
В итоге задача построения эмпирической зависимости сведется к задаче минимизации функции Лагранжа
|
min L(a), |
L(a) E2 (a) |
R |
R2 (a) ; |
(2.16) |
|||
|
(a) |
|||||||
|
где R |
– параметр регуляризации. |
||||||
|
В этом случае система уравнений (2.8) преобразуется к виду |
|||||||
|
n |
|||||||
|
(cij ij R )a j di |
Raiр , |
i, |
j 0, 1, . . . , n ; |
(2.17) |
|||
|
j 0 |
|||||||
|
где ij |
– символ Кронекера: |
ij |
1, при i j; |
ij 0, при i j. |
Постановка задачи (2.16) формально сводит задачу построения эмпирических формул к задаче управления. Здесь степень отклонения искомой зависимости от номинальной зависит от величины параметра регуляризации. При малых значениях параметра регуляризации точность определения искомой зависимости повышается, однако снижается устойчивость решения задачи к воздействию различных возмущений. При больших значениях параметра регуляризации точность определения искомой зависимости падает, однако повышается устойчивость решения к возмущениям, и само решение задачи стремится к номинальному.
3.5.3. Построение эмпирических зависимостей в нелинейном случае
210. В нелинейном случае исходная эмпирическая формула имеет
|
общий вид |
|
|
y F[a](x) , |
(3.1) |
где a — вектор структурных параметров формулы, x — вектор переменных. 220. Предположим, что известно начальное приближение значения вектора
a a0 . Тогда в окрестности точки a0 формулу (3.1) можно разложить в линейный ряд
260

|
n |
||
|
y F[a](x) F[a0 ](x) ai i (x) , где |
ai ai ai 0 . |
(3.2) |
i 1
Линейный ряд (3.2) соответствует линейной эмпирической формуле (2.1), для которой был изложен метод наименьших квадратов определения неизвестных коэффициентов зависимости по экспериментальным данным. Данный метод можно применить и к определению неизвестных коэффициентов ai зависимости (3.2). В результате будут получены
искомые значения коэффициентов ai . Зная значения ai можно уточнить искомые значения структурных параметров зависимости (3.1)
|
ai1 ai 0 ai |
; i 0, 1, . . . , n . |
(3.3) |
|
Далее, рассматривая параметры |
{ai1} как начальное приближение |
для |
следующего шага решения, процедуру решения задачи можно повторить. В результате будет получено следующее приближение решения {ai 2 }.
Рекуррентно повторяя указанную процедуру решения, получим последовательность решений
|
a0 , a1 , a2 , . . . |
(3.4) |
||||||||
|
Если последовательность (3.4) сходится: |
|||||||||
|
lim |
ak ak 1 |
0 , |
|||||||
|
k |
то она сходится к искомому решению.
Изложенный метод позволяет строить нелинейные эмпирические формулы на множестве экспериментальных данных. Он реализует метод Ньютона решения нелинейных уравнений.
3.5.4. Планирование экспериментов
230. Рассмотрим вопросы планирования экспериментов. При планировании экспериментов, прежде всего, необходимо определить критерий планирования. Одним из естественных критериев планирования является, например, разрешимость задачи построения искомой зависимости при минимальной сложности решения.
Как было показано ранее, разрешимость задачи (2.5) связана с разрешимостью системы линейных алгебраических уравнений (2.8) – (2.10). При этом решение задачи предельно упрощается, если данные
|
экспериментов удовлетворяют условиям |
|
|
cij 0 , для всех i j . |
(4.1) |
Тогда решение задачи
ai di ,
cii
при использовании регуляризации
261

|
a |
di R aiр |
; |
i 0, 1, …, n . |
(4.2) |
|||||
|
i |
cii R |
||||||||
|
В соответствии с соотношением (2.9) условия (4.1) выражаются в виде |
|||||||||
|
1 |
N |
1 |
N |
||||||
|
cij |
i (xs ), j (xs ) |
j (xs ), i (xs ) 0 ; i, j 0, 1, …, n ; i j |
|||||||
|
N s 1 |
N s 1 |
||||||||
|
.(4.3) |
Условия (4.3) представляют собой условия ортогональности для плана эксперимента
|
э {xs : s 1, 2, …, N}. |
(4.4) |
|
|
240. В качестве примера рассмотрим случай, когда |
||
|
i (xs ) xis , i 0, 1, …, n ; |
(4.5) |
|
|
где xis – числовая переменная. Тогда зависимость (2.1) имеет вид |
||
|
N |
||
|
y ai xi , |
x0 1. |
(4.6) |
i 0
Предположим, что в процессе эксперимента значения переменных xi изменяются только на двух уровнях: максимальное значение — ximax и минимальное значение — ximin . Тогда на основе замены переменных можно перейти к безразмерным нормированным величинам
|
i |
x 0,5(xmax xmin ) |
, |
i 0, 1, . . . , n . |
(4.7) |
||||
|
i |
i |
i |
||||||
|
xmax 0,5(xmax xmin ) |
||||||||
|
i |
i |
i |
||||||
|
При x xmax , переменная |
i |
1 |
, при x xmin , переменная |
1. |
||||
|
i i |
i |
i |
i |
Для нормированных переменных в качестве примера ортогонального плана эксперимента можно привести полный факторный эксперимент. Полный факторный эксперимент содержит все возможные сочетания значений нормированных переменных i . В таблице 3.5.4
приведен план полного факторного эксперимента для числа переменных n 3. Здесь при составлении таблицы положительное значение факторов «+1» условно обозначено знаком «+», аналогично значение «-1» обозначено как «-». Базовая часть плана эксперимента выделена рамкой. Вне рамки приводятся так называемые взаимодействия, представляющие собой произведения факторов.
Таблица 3.5.4
|
s |
0 |
1 |
2 |
3 |
1 2 |
1 3 |
2 3 |
1 2 3 |
y |
|
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
||
|
2 |
+ |
+ |
+ |
— |
+ |
— |
— |
— |
||
|
3 |
+ |
+ |
— |
+ |
— |
+ |
— |
— |
||
|
262 |
|
4 |
+ |
+ |
— |
— |
— |
— |
+ |
+ |
|
|
5 |
+ |
— |
+ |
+ |
— |
— |
+ |
— |
|
|
6 |
+ |
— |
+ |
— |
— |
+ |
— |
+ |
|
|
7 |
+ |
— |
— |
+ |
+ |
— |
— |
+ |
|
|
8 |
+ |
— |
— |
— |
+ |
+ |
+ |
— |
Базовая часть приведенного выше плана эксперимента, а также план взаимодействий являются ортогональными. В этом легко убедиться на основе подстановки значений факторов из плана эксперимента в формулу, выражающую условие ортогональности для плана (таб. 3.5.4)
|
1 |
N |
||||||
|
cij |
is js 0 |
, |
i, j 0, 1, …, n ; |
i j . |
(4.8) |
||
|
N s 1 |
|||||||
|
Формула (4.8) непосредственно следует из формулы (4.3). |
|||||||
|
Предположим, что искомая зависимость имеет вид |
|||||||
|
N |
|||||||
|
y ai i , |
0 |
1. |
(4.9) |
i 0
Тогда, для ортогонального плана вида (таб. 3.5.4) неизвестные коэффициенты ai зависимости (4.9) определятся по соотношениям
|
1 |
N |
|||||
|
ai |
is ys , |
i 0, |
1, …, n . |
(4.10) |
||
|
N s 1 |
||||||
|
Формулы (4.10) являются частными случаями формул (4.2). |
||||||
|
Необходимо отметить, |
что формулы |
(4.10) справедливы |
и для |
взаимодействий. Так, если для таблицы 3.5.4 ввести обозначения
4 1 2 , 5 1 3 , 6 2 3 , 7 1 2 3 , (4.11)
то для расширенного состава переменных (4.11) формулы (4.10) останутся справедливыми.
250. Ортогональный план эксперимента вида (таб. 3.5.4) называется полным факторным экспериментом. Называется он так по той причине, что содержит полный перебор значений факторов. Для полного факторного эксперимента общее число экспериментов
При большом числе переменных n число экспериментов (4.12) становится большим, что является недостатком полного факторного эксперимента.
Для снижения числа экспериментов используют так называемые дробные реплики. Дробными репликами называют ортогональные планы экспериментов типа (таб. 3.5.4), в которых часть переменных рассматриваются как взаимодействия, при этом размерность таблицы экспериментов снижается.
260. Например, необходимо определить зависимость
263
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вы перелопатили тонну научных трудов, потратили несколько недель, а то и месяцев на сбор материалов, сутками сидели над теоретической главой своего диплома… Почему же преподаватель раз за разом отправляет её на доработку?
О том, какие требования предъявляются к дипломнику при написании этой главы, мы подробно рассмотрели в статье «Как написать теоретическую часть дипломной работы». Ну а здесь мы сконцентрируемся на типичных ошибках дипломников, выделив основные проблемы и представив их в тезисах:
Ошибка 1. Недостаточно полное раскрытие тех или иных вопросов. Одна из причин – в нехватке материала: глава получается маленькой, объём приходится натягивать, лить воду. Проблема решается сбором дополнительных материалов или коррекцией темы (если с материалами совсем уж швах). Другой причиной может быть непонимание необходимости осветить определённые аспекты изучаемой темы. С этой проблемой справиться проще, так как на упущения укажет преподаватель, вернув диплом на доработку. Нужно учесть его замечания и восполнить пробелы.
Ошибка 2. Использование 2 – 3 научных источников. Для диплома это очень мало. Даже если вы почерпнули основной материал именно из них, его нужно разбавить вставками из 20 – 30 других источников. Хотя бы для вида.
Ошибка 3. Компилятивный характер, злоупотребление цитатами. Чем диплом отличается от курсовой и тем более реферата? Высокой степенью самостоятельного осмысления проблемы. Если вы просто «сшиваете» куски чужих текстов, получается не диплом, а большой-пребольшой реферат. Даже если вы накомпилируете сто страниц, всё равно это будет реферат.
Кстати, эту ошибку часто допускают влюблённые в тему студенты, которым хочется всунуть в диплом как можно больше информации по теме. Не нужно этого делать, информация в дипломе – не самоцель, а опора для выводов.
Ошибка 4. Отклонение от генеральной линии. Как в советском анекдоте: «Может ли змея сломать себе хребет? – Да, если будет ползти по генеральной линии партии». То есть вы сначала начали писать по теме, потом зацепились за какой-то аспект проблемы и увели линию в сторону. Эта ошибка тоже часто встречается у увлечённых наукой отличников, которым тесно в узкоспециальной теме и хочется объять необъятное.
Как решить проблему? Проработайте структуру дипломной работы и опирайтесь на план, не позволяя себе от него отклоняться.
Представьте, что вы канатоходец Филипп Пети, шагающий по тросу, натянутому между башен-близнецов в Нью-Йорке. Без страховки. Для вдохновения можно посмотреть вышедший недавно на экраны фильм «Прогулка».
Ошибка 5. Отсутствие логики в изложении. Сначала про Фому, потом про Ерёму. Это крайний вариант ошибки №4. Генеральной линии вообще не видно. Теоретическая глава похожа на свалку, где встречаются ценные вещи, но царящий хаос превращает всё вами вываленное в картину Малевича «Дама на остановке трамвая». Но вы не Малевич, вы диплом пишете.
Ошибка 6. Недостаточный уровень самостоятельного осмысления проблемы. Вы неплохо поработали над сбором теоретического материала, а может даже, собрали всё, что написано предшественниками по этой теме. Вклад предшественников в разработку проблемы понятен. А ваш?
Ошибка 7. Отсутствие выводов. Эта проблема часто совмещается с ошибкой №3 (компилятивным характером диплома), но встречается и в самостоятельном виде. Все главы и все пункты исследования должны завершаться выводами. Мало разобрать тему по полочкам и напичкать текст собственными размышлениями. В конце каждого пункта нужно подытожить свои размышления.
Ошибка 8. Отсутствие или малое количество ссылок. Теоретическая часть на то и теоретическая, чтобы в ней проработать материалы по теме и собрать мнения предшественников. Среднее количество ссылок на страницу – три штуки. Разумеется, это не абсолютное правило, но 2 – 3 ссылки на листе надо бы поставить. Кроме того, в ссылках нужно упомянуть все источники, указанные в списке литературы – а вот это уже правило, которое нельзя игнорировать.
Ошибка 9. Отсутствие связи с практической главой дипломной работы. Если теория представляет собой Ding an sich, «вещь в себе», лавры Канта вам не светят. Выражаясь по-русски и без философствований – теория не должна болтаться сама по себе, как нечто в проруби. Теоретическая глава должна быть базисом для практической.
Ошибка 10. Малый или большой объём, несбалансированность частей. Это ещё одна причина, по которой научный руководитель может потребовать переработки теоретической главы. Интересно, что чрезмерно большой объём теории у дипломников встречается, пожалуй, чаще, чем слишком маленький. Основные причины – ошибки №3 и №4. Кто-то допускает несбалансированность частей из-за того, что лень вычленять главное, а кто-то – из-за высокого градуса энтузиазма. Безумно жалко резать теорию, в которой вы расписались, как в монографии, но придётся!
Ошибка 11. Ненаучный стиль, безграмотность. Обычно к моменту написания диплома студент худо-бедно набивает руку на курсовиках и рефератах, овладевая искусством изъясняться научно-респектабельно – копируя стиль монографий и научных статей. Но если наука – не страсть студента, да ещё и языкового чутья не имеется, косноязычие в тексте дипломной работы может достигать уровня facepalm. Особенно в тех местах, где студент высказывает личные выводы. Что делать? Обратитесь за помощью к человеку, владеющему научным стилем – например, закажите редактуру вашего диплома у студлансера. И обязательно вычитайте текст на предмет опечаток: Word не всесилен.
Ошибка 12. Антиплагиат ругается. Возможно, у вас и не было злого умысла, вы и не собирались обманывать научное сообщество в целом и вашего научного руководителя лично, но… уникальность низковата, и надо садиться и корпеть над текстом, доводя его до нужного процента уникальности различными методами. Ну а если вы использовали мошеннические, да ещё и неработающие методы борьбы с антиплагиатом – кто ж вам виноват? Вы нарушили главное правило: «Не попадайся!».
Устранение этих недочётов позволит вам получить «одобрямс» от научного руководителя, прочитавшего вашу теоретическую главу. Правда, этот факт сам по себе не гарантирует пятёрки, ведь преподавателю предстоит ещё прочитать практическую главу, введение и заключение. О том, как избежать типичных проблем при написании этих структурных частей диплома, читайте в статьях:
— 10 ошибок при написании практической части диплома
— 10 ошибок при написании введения
— 10 ошибок при написании заключения
— 10 распространнённых ошибок в оформлении дипломной работы
Дипломная работа – один из важных проектов каждого выпускника. На данном этапе молодому ученому предстоит провести собственное «расследование», в ходе которого необходимо применить теоретические аспекты по теме, имеющиеся знания и опыт.
Конечно, ни один студент не может предоставить комиссии качественно и правильно написанный проект с первого раза. Поэтому на его создание дается около 4-6 месяцев, в течение которых он может его доработать в соответствии с требованиями научного руководителя, замечаниями, полученными на предзащите и пр.
Рассмотрим самые распространенные ошибки, которые дипломанты допускают при написании теоретической части диплома.
Неполное освещение отдельных элементов работы, вопросов
Зачастую студенты подробно описывают второстепенный элемент, вторичную гипотезу, а главный вопрос остается рассмотренным не полностью. Эта ошибка возникает чаще всего вследствие дефицита материалов, источников информации.
Решить проблему можно путем дополнительного сбора информации, исследования трудов по данной или подобной теме. В крайних случаях допускается смена темы исследования. Порой достаточно устранить выявленные куратором замечания.
Студент опирается на 2-3 источника
Дипломная работа – это довольно серьезный и крупный проект, который требует изучения большого количества информации, литературы. В списке использованных источников, как правило, следует указать не менее 25-30 трудов. Если при написании ВКР дипломант опирался только на 2-3 источника, то необходимо разбавить утверждения и выводы дополнительными ссылками на иные труды.
Злоупотребление цитатами
В хорошем дипломе объема цитирования не превосходит 20-30% от общего объема исследования. Злоупотребление цитатами чревато снижением уникальности работы. Более того, автор должен продемонстрировать не только мнение профессионалов, но и собственную точку зрения, провести качественный анализ, разработать план мероприятий на перспективу с доказательством эффективности предложенных действий.
Если каждый второй абзац будет цитирован, то получится не диплом, а большой реферат. Не стоит включать в диплом всю информацию, которую удалось найти. Важно ее обработать, отсортировать и правильно скомпоновать, изложить.
Отклонение от основной проблемы и темы исследования
Важно соблюдать план работы, структуру. Не стоит отвлекаться на второстепенные элементы, подробно расписывая их, ущемляя при этом основную проблему исследования. Все отклонения от гипотезы, темы должны быть незначительными, тесным образом соприкасаться с главным вопросом и дополнять его.
Возникли сложности?
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Несоблюдение принципа логики, грамотности
Данная ошибка возникает, когда студент старается рассмотреть как можно больше вопросов в одной теме, перепрыгивая с одного момента на другой. Весь ход исследования должен быть последовательным, логически связанным между собой: одно вытекает из другого и объясняет это явление. Важно не отклоняться от главного ориентира, поэтапно добиваясь цели.
Помимо этого, следите за тем, чтобы текст был грамотно изложен, без ошибок, на научном языке, с учетом требований к оформлению.
Малый объем собственных выводов
Собрать материал, скомпоновать и изложить его – недостаточно. Дипломант должен проанализировать все источники, весь материал, изложить собственное мнение по теме в выводах по параграфам, главе и диплому в целом. Опираясь на труды других ученых, автор должен сделать выводы аргументированными.
Дефицит ссылок или их отсутствие
В теоретической части автор приводит результаты трудов свои предшественников, поэтому указание ссылок в этом разделе неизбежно. Как правило, на каждой странице теоретической главы должно присутствовать около 1-3 ссылок. Если автор пренебрегает сносками, ссылками, то это создает впечатление, что он самостоятельно «изобрел велосипед» без чьей –либо помощи, а, значит, присвоил часть «чужого успеха» себе.
Учтите, литература, указанная в списке использованных источников, должна быть полностью отражена в ссылках. Это доказывает, что каждый из материалов был использован в исследовании.
Несоответствие теории и практики
В первой главе необходимо осветить именно те постулаты, которые автор будет применять в дальнейшем при написании практической части: формулы, методики, алгоритмы и пр. Не стоит применять в следующих разделах диплома то, что не указано в первой главе, или прописывать в теории ненужное, что не пригодится. Это противоречит принципам логики, структуре работы и фактически порождает противоречия, ошибки.
Недостаточный или избыточный объем
В методических рекомендациях всегда дается совет относительно минимального объема дипломного проекта, реже – максимальный.
Из-за большого объема цитирования, отвлечений от основной темы диплом «раздувается», присутствует лишний материал, который неважен, не нужен. На фоне дефицита источников информации наблюдается слишком сжатое раскрытие темы, которое не может полностью отразить важность, значимость проекта, его эффективность.
Исправить эту ошибку можно при очередной доработке проекта. Для этого придется вновь переписать теорию с учетом выявленных замечаний.
Несоответствие требованиям плагиата
Каждый дипломный проект проверяется на уникальность. Минимальные требования к плагиату указываются в методических рекомендациях, утвержденных в ВУЗе. Конечно, никто не станет требовать от дипломанта 100% уникальности, ведь он должен опираться на труды ученых.
Чтобы не допустить эту ошибку, необходимо изначально хорошо обрабатывать собранный материал, а перед проверкой самостоятельно на бесплатных сервисах проверить уникальность текста. Несоблюдение требований к плагиату демонстрирует халатное отношение дипломанта к своей работе, понижает его репутацию в глазах преподавателей.
Наличие этой ошибки может стать серьезной преградой для получения диплома. При низкой уникальности текста проект не будет допущен до защиты.
Содержание
- Как написать вывод в курсовой работе: пример удачного заключения
- Как писать вывод в курсовой работе
- Как написать вывод по главе в курсовой работе
- Подходящие вводные слова для вывода в курсовой
- Образец вывода в курсовой работе
- теоретический вывод
- Смотреть что такое «теоретический вывод» в других словарях:
- теоретический вывод
- Смотреть что такое «теоретический вывод» в других словарях:
- Теоретическая и практическая значимость курсовой работы с примерами
- Теоретическая значимость курсовой работы
- Как описать теоретическую значимость исследования
- Пример написания теоретической значимости
- Практическая значимость курсовой работы
- Как описать практическую значимость исследования
- Пример написания практической значимости
Как написать вывод в курсовой работе: пример удачного заключения
Вывод в курсовой работе – важный и неотъемлемый элемент подобного исследования. Однако написание часто вызывает затруднения по сравнению с подготовкой того же реферата. Важно, чтобы они были согласованы с целями и задачами, озвученными в начале труда. Это покажет научному руководителю, что студент справился с поставленной задачей, а также позволит составить хорошее впечатление о проведенном исследовании.
Как писать вывод в курсовой работе
Все сделанные по итогам написания проекта выводы, как правило, размещаются в заключении. И главное правило, которому стоит обязательно следовать, – не пытаться уместить всю курсовую в эту часть. Необходимо сформулировать основные тезисы, остановиться на ценности исследования с точки зрения теории и практики. Нелишним является озвучить те проблемы, с которыми вы столкнулись при подготовке, отметить плюсы изучения материала по теме.
Заявка на курсовую
Для упрощения подобной работы следуйте следующему плану:
Заново прочитайте введение, сделайте упор на цели и задачи проекта. Ведь выводы делаются именно на их основе. Остановитесь на степени их проработки и достижении.
Если вы давали в конце каждого раздела мини-выводы, это станет хорошим подспорьем при составлении заключения. Обобщите и упорядочите их. Важно, чтобы каждая новая мысль была связана с предыдущей. Поэтому при необходимости пишутся связующие предложения и абзацы.
После того, как были подведены итоги по теоретической части, стоит перейти к учебно-практическому разделу. Расскажите обо всех проведенных расчетах, внесите предложения или рекомендации, опишите используемые методы. Главное одно – показать, что вы проявили самостоятельность при принятии решений.
Высказывайте личное мнение о теме и тех проблемах, которые были рассмотрены, особенностях изучения, расставляйте акценты. Это позволит сделать ваши выводы интересными и полезными.
Если вы сделали все возможные выводы, прочитайте текст повторно и удалите подробные описания. Как правило, они уже присутствуют в основном разделе. Повествование должно отличаться краткостью и лаконичностью.
Структура заключения
Чтобы грамотно составить заключение в курсовой работе, потребуется выделить важные моменты. Этот раздел должен включать в себя краткие тезисы:
из введения – акцент делается на актуальности темы, целях, задачах и проблематике;
основных глав – теории и практики.
Помогут также в этом мини-выводы, которые были сделаны по итогам написания отдельных подразделов, и перспективы проекта. В среднем объем заключения достигает 3 страниц. Выходить за эти рамки не рекомендуется.
Помните, что все озвученное должно подкрепляться доказательствами, в роли которых могут выступать приложения и различные ссылки.
Не стоит приводить общеизвестные факты, это испортит общее впечатление: только уникальные выводы, к которым вы пришли в ходе изучения материала.
В общем виде структура заключения будет выглядеть следующим образом:
Вступление. Расскажите о теме исследования и важности ее изучения. Опишите все проблемы, связанные с ней. Отведите данной информации несколько абзацев.
Основная часть. Описываются решенные задачи, результаты исследования. Дайте исчерпывающие ответы на те вопросы, которые были поставлены во введении к курсовой. Старайтесь соблюдать последовательность изложения. В конце стоит подвести итог о том, достигнута ли изначальная цель проекта.
Заключение. Озвучьте ценность исследования, рекомендации по улучшению объекта и внедрению итогов в деятельность общества. Обязательно сделайте акцент на ваших успехах, достигнутых по мере изучения темы.
Теперь вы знаете, как правильно написать вывод в курсовой работе. Заключение станет лицом вашего исследования, поэтому стоит ответственно подойти к его созданию. Именно по такому разделу преподаватель судит о глубине изучения и вовлеченности самого студента в процесс, его заинтересованности.
Как написать вывод по главе в курсовой работе
Первое и главное правило – выводы не должны включать в себя лишнюю информацию, которая не связана с темой работы. Поэтому прежде чем делать их по каждому разделу, стоит еще раз внимательно ознакомиться с введением. Объем не должен превышать 1-2 абзацев. Это краткая выжимка по размещенной в них информации.
Выводы по первой, теоретической, части составляются на основе использованных источников, которые соответствовали выбранной теме. Можно кратко остановиться на противоречивости или общности научных точек зрения разных авторов. Обязательно отразить личное мнение и научно обосновать значимость темы в современном мире.
По итогам написания второй, практической, главы уместно подчеркнуть новизну и важность разработок. Укажите на возможность применения результатов исследования на практике. Обязательно подкрепите это фактами и проведенными расчетами.
Подходящие вводные слова для вывода в курсовой
Как начать писать заключение? Какие слова подобрать, чтобы сразу перейти к сути дела? Эти вопросы часто задают многие студенты.
Оптимально начинать заключение со следующих вводных слов и словосочетаний:
резюмируя все вышесказанное;
в заключение можно отметить, что;
результаты изучения материала показали, что;
исходя из выполненных исследований, мы приходим к таким выводам;
написав работу, я пришел (-а) к следующему выводу;
актуальность данного курсового проекта заключается;
констатируем следующие особенности исследования.
Помимо этого, написать заключение в курсовой помогут следующие стандартные предложения и фразы:
на основании изложенного выше;
из этого следует;
в ходе анализа выявлены следующие закономерности;
мы убеждаемся в том, что;
Но даже используя общий алгоритм, учесть особенности конкретного проекта невозможно. Так, курсовые по гуманитарным и техническим дисциплинам будут иметь совершенно разные выводы.
Главное – не забывать, что представление о вашей работе будет составлено по большей части по введению и заключению
Образец вывода в курсовой работе
Ниже вы сможете подробно изучить примеры выводов в курсовой работе, которые были составлены студентами различных специальностей. Это поможет закрепить весь теоретический материал и иметь перед глазами образец, как делать хорошее и правильное заключение.


Источник
теоретический вывод
Большой англо-русский и русско-английский словарь . 2001 .
Смотреть что такое «теоретический вывод» в других словарях:
ТЕОРЕТИЧЕСКИЙ — ТЕОРЕТИЧЕСКИЙ, теоретическая, теоретическое. 1. прил. к теория. Теоретическое построение. Теоретический вывод. || Склонный к занятиями теорией. Теоретический ум. Теоретический талант. У него теоретическая складка. || Представляющий собой тот… … Толковый словарь Ушакова
ТЕОРЕТИЧЕСКИЙ — ТЕОРЕТИЧЕСКИЙ, ая, ое. 1. см. теория. 2. Основанный на теории, относящийся к вопросам теории. Т. вывод. Теоретическая конференция. Рассуждать теоретически (нареч.). 3. О складе мышления: склонный к обобщениям, к теоретизированию. Т. ум. 4. Не… … Толковый словарь Ожегова
вывод — Логически выведенное положение, умозаключение. Важный, верный, глубокий, единогласный, закономерный, значимый, категорический, категоричный, конкретный, логический, логичный, ложный, малообоснованный, мудрый, научный, неверный, необоснованный,… … Словарь эпитетов
Гидродинамика — Т. наз. та часть теоретической механики, которая имеет целью нахождение общих законов движения жидкостей. первыми исследованиями относительно движения жидкостей были опытные исследования Торичелли, которые привели его к открытию известного закона … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Платежный баланс — (Balance of payments) Платежный баланс это статистический документ, отражающий все внешнеэкономические операции данной страны Платежный баланс страны, методы и структура составления платежного баланса, отрицательное и положительное сальдо… … Энциклопедия инвестора
Марксизм-ленинизм — научная система философских, экономических и социально политических взглядов, составляющих мировоззрение рабочего класса; наука о познании и революционном преобразовании мира, о законах развития общества, природы и человеческого мышления … Большая советская энциклопедия
История квантовой механики — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
Поляризация света — одно из фундаментальных свойств оптического излучения (См. Оптическое излучение) (света), состоящее в неравноправии различных направлений в плоскости, перпендикулярной световому лучу (направлению распространения световой волны). П. с.… … Большая советская энциклопедия
Сатурн — I Сатурн в древнеримской религии и мифологии бог посевов. Отождествлялся с древнегреческим богом Кроносом. В честь С. устраивались ежегодные празднества (см. Сатурналии). II Сатурн шестая по расстоянию от Солнца большая планета… … Большая советская энциклопедия
Сатурн (планета) — Сатурн, шестая по расстоянию от Солнца большая планета Солнечной системы; астрономический знак · С. относится к числу планет гигантов. Большая полуось орбиты С. (его среднее расстояние от Солнца) составляет 9,54 а. е., или 1,43 млрд. км.… … Большая советская энциклопедия
Градусные измерения — Градусным измерением называется измерение дуги на земной поверхности, имеющее целью найти фигуру и размеры обитаемой нами планеты. Каждое градусное измерение состоит из двух существенно различных действий: из определении линейной длины какой либо … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Источник
теоретический вывод
Русско-английский научно-технический словарь переводчика . 2013 .
Смотреть что такое «теоретический вывод» в других словарях:
ТЕОРЕТИЧЕСКИЙ — ТЕОРЕТИЧЕСКИЙ, теоретическая, теоретическое. 1. прил. к теория. Теоретическое построение. Теоретический вывод. || Склонный к занятиями теорией. Теоретический ум. Теоретический талант. У него теоретическая складка. || Представляющий собой тот… … Толковый словарь Ушакова
ТЕОРЕТИЧЕСКИЙ — ТЕОРЕТИЧЕСКИЙ, ая, ое. 1. см. теория. 2. Основанный на теории, относящийся к вопросам теории. Т. вывод. Теоретическая конференция. Рассуждать теоретически (нареч.). 3. О складе мышления: склонный к обобщениям, к теоретизированию. Т. ум. 4. Не… … Толковый словарь Ожегова
вывод — Логически выведенное положение, умозаключение. Важный, верный, глубокий, единогласный, закономерный, значимый, категорический, категоричный, конкретный, логический, логичный, ложный, малообоснованный, мудрый, научный, неверный, необоснованный,… … Словарь эпитетов
Гидродинамика — Т. наз. та часть теоретической механики, которая имеет целью нахождение общих законов движения жидкостей. первыми исследованиями относительно движения жидкостей были опытные исследования Торичелли, которые привели его к открытию известного закона … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Платежный баланс — (Balance of payments) Платежный баланс это статистический документ, отражающий все внешнеэкономические операции данной страны Платежный баланс страны, методы и структура составления платежного баланса, отрицательное и положительное сальдо… … Энциклопедия инвестора
Марксизм-ленинизм — научная система философских, экономических и социально политических взглядов, составляющих мировоззрение рабочего класса; наука о познании и революционном преобразовании мира, о законах развития общества, природы и человеческого мышления … Большая советская энциклопедия
История квантовой механики — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
Поляризация света — одно из фундаментальных свойств оптического излучения (См. Оптическое излучение) (света), состоящее в неравноправии различных направлений в плоскости, перпендикулярной световому лучу (направлению распространения световой волны). П. с.… … Большая советская энциклопедия
Сатурн — I Сатурн в древнеримской религии и мифологии бог посевов. Отождествлялся с древнегреческим богом Кроносом. В честь С. устраивались ежегодные празднества (см. Сатурналии). II Сатурн шестая по расстоянию от Солнца большая планета… … Большая советская энциклопедия
Сатурн (планета) — Сатурн, шестая по расстоянию от Солнца большая планета Солнечной системы; астрономический знак · С. относится к числу планет гигантов. Большая полуось орбиты С. (его среднее расстояние от Солнца) составляет 9,54 а. е., или 1,43 млрд. км.… … Большая советская энциклопедия
Градусные измерения — Градусным измерением называется измерение дуги на земной поверхности, имеющее целью найти фигуру и размеры обитаемой нами планеты. Каждое градусное измерение состоит из двух существенно различных действий: из определении линейной длины какой либо … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Источник
Теоретическая и практическая значимость курсовой работы с примерами
Практическая значимость курсовой работы, наряду с теоретической, является одним из главных требований, выдвигаемых к исследованию ГОСТами. Этим обуславливается польза и актуальность подготовленного материала для общества и научного мира.
Данные параметры должны присутствовать во введении, а также в основной части учебного труда
Понятия основываются на новизне полученных в ходе анализа результатов.
Теоретическая значимость курсовой работы
Теоретическая значимость призвана доказать пользу работы, применимость ее результатов на практике для решения определенных вопросов или улучшения ситуации в некой сфере. Понятие является близким к научной новизне. Однако они будут тождественными только в том случае, если исследование привело к серьезным достижениям и превзошло прежний уровень изученности вопроса. В итоге теоретическая значимость будет полностью заключаться в новизне.

Но совершать действительно важные открытия могут не все. Поэтому чаще всего теоретическая значимость сводится к некоторым деталям проекта. Указание на данный параметр является обязательным и позволяет повысить ценность труда, что в свою очередь говорит о грамотном и самостоятельном проведении всех рассуждений.
Кратко говоря, в данной части студент должен написать ответ, с какой целью был подобран и составлен весь материал. Теоретическая обоснованность также дает возможность:
рассматривать все итоги в практическом аспекте;
выдвигать доказательства сделанных в ходе анализа выводов;
вести дискуссию о гипотезе проекта, различных мнениях и взглядах.
Чем более проработанной и информативной будет теоретическая значимость, тем сильнее возрастает значение практической части
Например, курсовой проект касается темы конфликтов родителей и детей и способа их решения. Если ваша учебная работа сделана по всем правилам, она даст новые идеи для практикующих психологов, которые занимаются данным вопросом.

Как описать теоретическую значимость исследования
Чтобы грамотно составить описание этой части введения, следует начинать со следующих слов: «Теоретическая значимость проведенного исследования заключается в том, что полученные результаты могут быть применимы в… для…». Сразу пишем о пользе материала для человека, общества. Так вы сможете обобщить всю информацию и акцентировать внимание на наиболее важных моментах.
Так, например, теоретическая обоснованность может быть:
в глубоком изучении проблемы;
стимулировании развития базы данных в определенной сфере;
выявлении новых аспектов исследуемого вопроса;
подтверждении теории с помощью экспериментов;
возможности внедрения выводов для оптимизации практического раздела;
научном вкладе в конкретную сферу для расширения ее теоретической основы.
Пример написания теоретической значимости
Чтобы до конца понимать, что же представляет собой теоретическая значимость в курсовой работе, можно ознакомиться с ниже размещенными образцами.
Курсовая работа по экономике
Теоретическая значимость данного исследования состоит в успешно осуществленном анализе экономических отношений при создании и развитии СЭЗ на базе развивающегося государства с экономикой рыночно-трансформируемого типа. Полученные сведения могут быть использованы для дальнейшего изучения проблемного вопроса, как для рассматриваемой страны, так и в сходных по типу экономики государствах
Курсовая работа по педагогике
Теоретическая значимость исследования:
Получено более обширное представление о характере предрасположенности дошкольников к дисграфии из числа тех, что имеют недоразвитие речи или не имеют речевых патологий.
Полученные сведения отражают готовность таких детей к освоению письма.
Практическая значимость курсовой работы
Данный элемент не является обязательным в структуре курсовой. Однако большинство вузов считают разработку и наличие такой информации важнейшим качеством грамотно построенного проекта. Это повышает итоговую оценку на защите и позволяет продемонстрировать комиссии заинтересованность в теме и дальнейшем ее изучении.
Определение практической значимости – достаточно сложный этап всего процесса подготовки курсовой. Именно здесь проводится обоснование возможности применения всех результатов в научной деятельности или сфере производства.

Содержание этой части во многом определяется особенностью проекта:
завершение ранее незаконченного труда;
работа над новой методологией;
наполнение базы данных определенного вопроса совершенно новыми знаниями;
обоснование перспектив развития в конкретной отрасли;
составление базы для дальнейшего рассмотрения проблем в уже более широких масштабах;
решение четко поставленной задачи.
Так, например, в случае гуманитарных дисциплин чаще всего разрабатываются методы и способы для внедрения в деятельность различных организаций.
Чтобы подтвердить практическую значимость, можно приложить акты внедрения, а также разного рода справки, заключения, методические указания и пр.
Эти документы выдаются государственными органами либо же результаты оформляются в виде нормативной документации, инструкций. Дополнить их можно информацией об эффективном использовании выводов. Таким образом, на руках у студента будет не только подтверждение о применении, но и материал с описанием получения результата.
Как описать практическую значимость исследования
Чтобы действительно успешно сформулировать этот параметр, нужно:
понимание реальных преимуществ исследования;
умение лаконично подводить итоги;
Заявка на курсовую
наличие настоящих практических наработок.
Начинать эту часть курсовой стоит со следующих слов: «Практическая значимость научной работы состоит в том, что результаты могут быть применимы в … для …». Обоснуйте пользу от внедрения результатов с помощью:
включения различных документов и справок, подтверждающих эффективность;
учебно-методических источников, использованных во время работы.
Также можно остановиться на научной, социальной и экономической эффективности, заключающейся в проекте. Под первым понятием подразумеваются новейшие полезные знания о мышлении или обществе, которые помогли найти ранее неизвестные факты и закономерности.
Экономическая эффективность позволяет обосновать возможность экономии различных ресурсов: финансовых, людских или материальных. Третий, социальный, аспект может быть рассмотрен в плане улучшения условий жизни и труда людей, повышения уровня образования и системы здравоохранения.
В итоге верно обоснованная практическая значимость может послужить в будущем:
для преподавания специальности или ведения курсов;
осуществления новых проектов;
разрешения загадок исследований, которые по тем или иным причинам не были завершены;
в качестве основы для диссертаций.
Пример написания практической значимости
Если вы затрудняетесь при определении практической значимости курсовой работы, ознакомьтесь с примерами, представленными ниже. Это упростит последующую работу и поможет прийти к собственным умозаключениям.
Курсовая работа по психологии
Практическая значимость исследования отражается в возможности использования полученных результатов дипломированными специалистами, работающими, к примеру, в семейной консультации.
Курсовая работа по банковскому делу
Практическая значимость разработанного алгоритма может быть подтверждена путём его внедрения в деятельность государственных органов и прочих организаций, предоставляющих населению консультационные услуги, а также тех, что осуществляют функциональные мероприятия по оптимизации системы ИЖК.

Источник