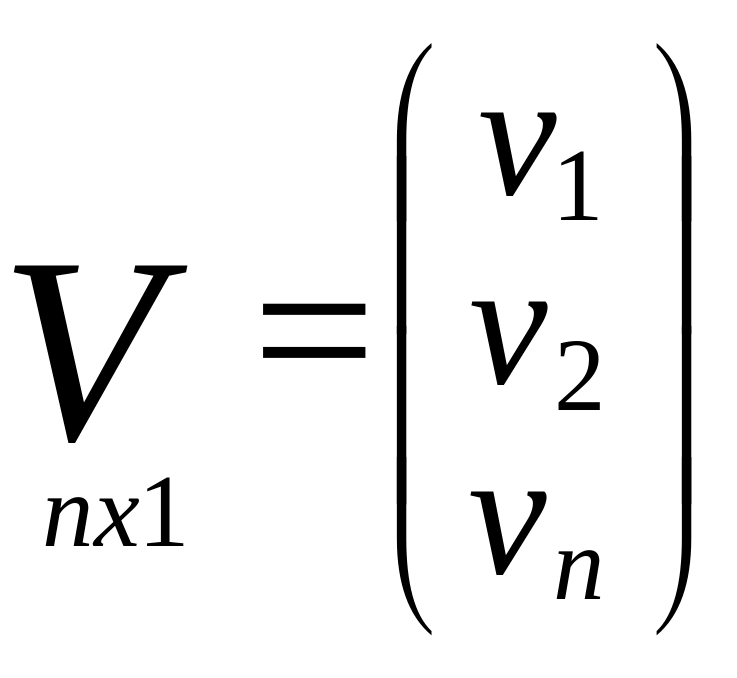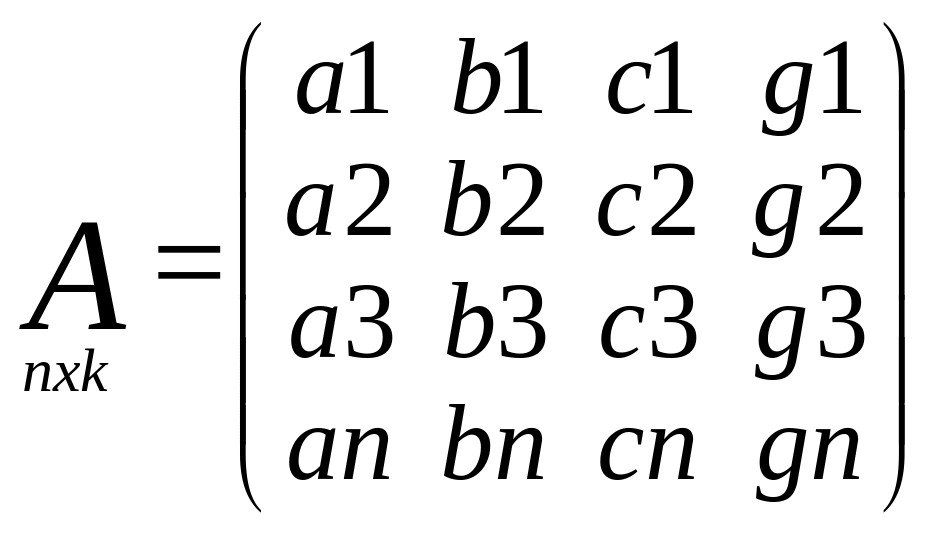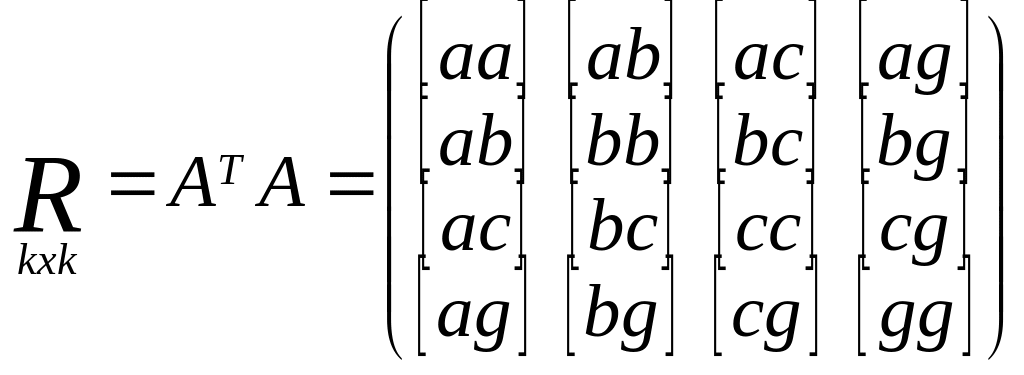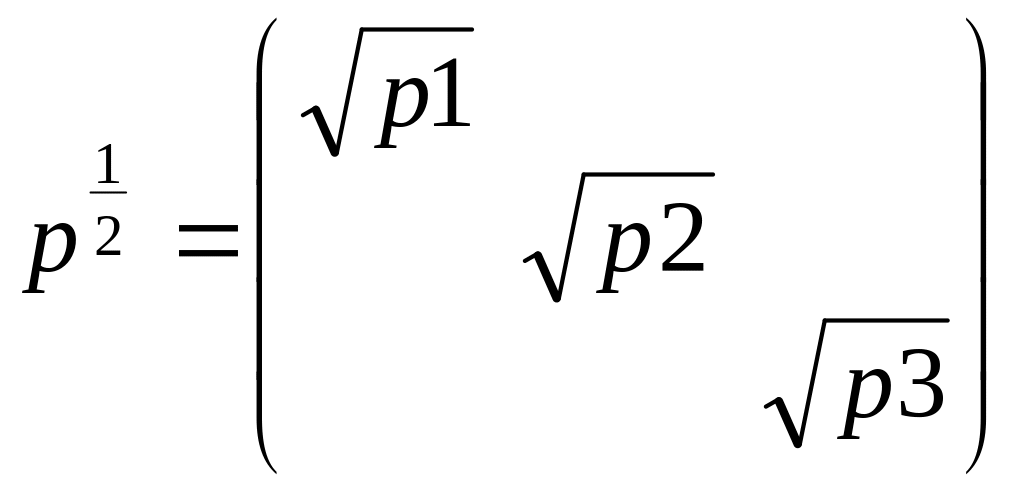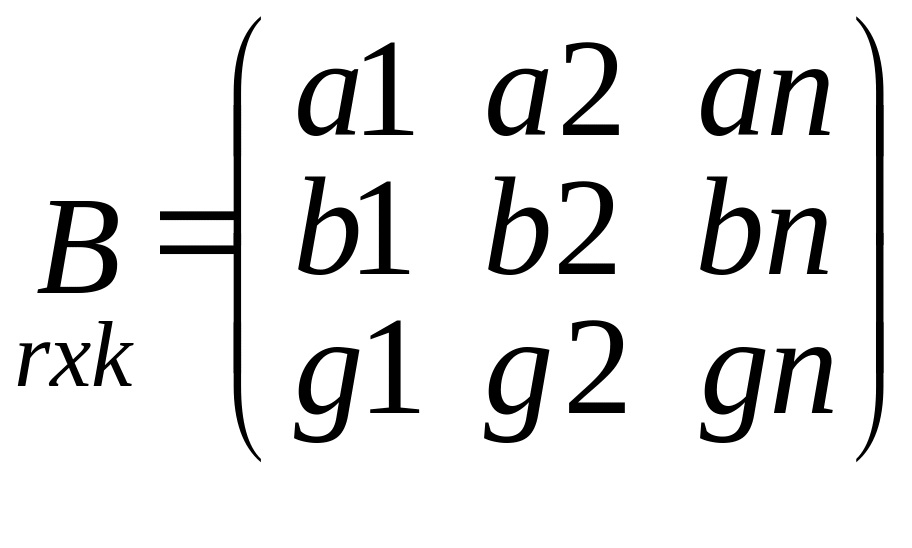Теория ошибок реферат

Обновлено: 05.06.2023

погрешность гейзенберг измерение неопределенность

Измерить какую-нибудь величину — значит узнать, сколько раз в ней заключается однородная величина, принимаемая за единицу меры.

Произвести измерения физических величин абсолютно точно невозможно, так как всякое измерение сопровождается той или иной ошибкой или погрешностью. Другими словами, измеренное значение величины всегда отличается от истинного ее значения. Задачей экспериментатора является не только нахождение самой величины, но и оценка допущенной при измерении погрешности.

Результат любого измерения отличается от истинного значения измеряемой величины на некоторое значение, зависящее от точности средств и метода измерения, квалификации оператора, условий, при которых производится измерение. Отклонение результата измерения от истинного значения измеряемой величины называется погрешностью измерения.

1. Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

· Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

· Средняя квадратическая погрешность:

· Средняя квадратическая погрешность среднего арифметического:

. Классификация погрешностей по форме представления

·Абсолютная погрешность — ?X является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas . При этом неравенство: ?X > | Xmeas ? Xtrue |, где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

·Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины (РМГ 29-99):

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

·Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке: — если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений; — если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора. Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

3. Классификация погрешностей по причине возникновения

·Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.

·Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.

·Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определённой заранее заданной точностью — основной погрешностью, допускаемой в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°C, за нормальное атмосферное давление 101,325 кПа.

Обобщённой характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведённых основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10 n , где показатель степени n = 1; 0; ?1; ?2 и т.д.

. Классификация погрешностей по характеру проявления

·Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).

·Систематическая погрешность — погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.

·Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.

·Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).

5. Классификация погрешностей по способу измерения

·Погрешность прямых измерений — вычисляются по формуле

где: t = Sx?s; Sx — средняя квадратическая погрешность, а ?s — коэффициент Стьюдента, а А — число, численно равное половине цены деления измерительного прибора.

·Погрешность косвенных воспроизводимых измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если F = F (x 1 , x 2 …xn ), где xi — непосредственно измеряемые независимые величины, имеющие погрешность ?xi , тогда:

·Погрешность косвенных невоспроизводимых измерений — вычисляется по принципу прямой погрешности , но вместо xi ставится значение полученное в процессе расчётов.

. Погрешность измерения и принцип неопределенности Гейзенберга

Очень важно при измерениях рассчитывать погрешность, чтобы получить более точный результат. Важно также знать причины возникновения погрешностей. Причинами возникновения погрешностей являются: несовершенство методов измерений, технических средств, применяемых при измерениях, и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений. Последние проявляются двояко. С одной стороны, все физические величины, играющие какую-либо роль при проведении измерений, в той или иной степени зависят друг от друга. Поэтому с изменением внешних условий изменяются истинные значения измеряемых величин. С другой стороны, условия проведения измерений влияют и на характеристики средств измерений и физиологические свойства органов чувств наблюдателя и через их посредство становятся источником погрешностей измерения.

Использованная литература

1. Лабораторные занятия по физике. Учебное пособие / Гольдин Л.Л., Игошин Ф.Ф., Козел С.М. и др.; под ред. Гольдина Л.Л. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 704 с.

. Назаров Н.Г. Метрология. Основные понятия и математические модели. — М.: Высшая школа, 2002. — 348 с.

Проблема создания удобной практически, всеохватной с точки зрения негативного речевого материала классификации основных речевых ошибок остается открытой [1]. Ю.В. Фоменко справедливо отмечает, что «вопрос о классификации ошибок в речи школьников продолжает оставаться одной из болевых точек преподавания русского языка в школе» [2]. Данная проблема является болезненной не только для учителей, методистов, специалистов по культуре речи, она актуальна и для всех людей, пишущих и читающих по-русски.

Возвращаться к попыткам классификации речевых нарушений заставляет ряд причин. Во-первых, нечеткое разграничение основных видов ошибок в существующих классификациях (это касается разделов грамматических, лексических, синтаксических ошибок); во-вторых, выведение из классификаций логических ошибок (традиционно они считаются неречевыми); в-третьих, отсутствие в классификациях целого ряда коммуникативно значимых нарушений, существенно ухудшающих восприятие и понимание речи или отдельного высказывания; в-четвертых, осознание необходимости создания классификации, отвечающей современному пониманию теории коммуникации [3].

Было бы логичным, с нашей точки зрения, основополагающим принципом классификации считать единицу языкового яруса, нормы образования, написания, функционирования которой нарушаются. Предлагаемая классификация ошибок имеет следующий вид:

Речевые ошибки на уровне слова

1. ОРФОГРАФИЧЕСКИЕ ОШИБКИ (нарушение существующих в русском языке орфограмм).

Перечень таких нарушений известен.

2. СЛОВООБРАЗОВАТЕЛЬНЫЕ ОШИБКИ (нарушение норм русского литературного словообразования ): а) неправильное прямое словообразование, например, зайцата (вместо зайчата), раздумчивый взгляд (вместо задумчивый взгляд) и т.п.; б) неправильное обратное словообразование: кудряха (от кудряшка), лога (от ложка) и т.п. Такого рода словообразование присуще детям дошкольного и младшего школьного возраста; в) заменительное словообразование, проявляющееся в замене какой-либо морфемы: укидываться (вместо раскидываться), отвесить (от повесить); г) словосочинительство (создание несуществующей производной единицы, которую нельзя рассматривать как окказиональную): мотовщик, рецензист.

3. ГРАММАТИЧЕСКИЕ ОШИБКИ (неправильное формообразование, нарушение системных свойств формообразовательной системы у разных частей речи ): а) нарушение норм формообразования имен существительных : 1) образование формы В.п. неодушевленного существительного, как у одушевленного — «Я попросила ветерка» (вместо: ветерок); 2) образование формы В.п. одушевленного существительного, как у неодушевленного — «Запрягли в сани два медведя» (вместо: двух медведей); 3) изменение рода при образовании падежных форм: «пирожок с повидлой», «февральский лазурь»; 4) склонение несклоняемых существительных: «играть на пианине», «ехать на метре»; 5) образование форм множественного числа у существительных, имеющих только единственное, и наоборот: «поднос чаев», «Небо затянулось облаком»; б) нарушение норм формообразования имен прилагательных : 1) неправильный выбор полной и краткой форм: «Шляпка была полная воды», «Мальчик был очень полон»; 2) неправильное образование форм степеней сравнения: «Новенькие становятся боевее», «Она была послабже Пети»; 3) нарушение норм формообразования глагола: «Человек метается по комнате»; 4) нарушение образования деепричастий и причастий: «Ехавши в автобусе», «Охотник шел, озирая по сторонам»; 5) нарушение норм образования форм местоимений: «Ихний вклад в победу», «Не хотелось от ее (книги) оторваться» и т.п.

4. ЛЕКСИЧЕСКИЕ ОШИБКИ (нарушение лексических норм, т.е. норм словоупотребления и лексико-семантической сочетаемости слова). Лексические ошибки проявляются в нарушении сочетаемости (т.е. на уровне семантики словосочетания, реже — предложения): а) употребление слова в несвойственном ему значении: «Все стены класса были покрыты панелями». «Троекуров был роскошный (т.е. живущий в роскоши) помещик»; б) нарушение лексико-семантической сочетаемости слова: «Небо стояло светлое» («стоять» в зн. «иметь место» может только погода, жара), «На поляне лежали лучи солнца» ( лучи солнца освещали поляну). Данный тип ошибок затрагивает в первую очередь глагол, поэтому частотным оказывается нарушение субъектных и объектных лексико-семантических сочетаемостных связей (другие семантические связи глагола, например локативные, нарушаются крайне редко); в) приписывание переносного значения слову, не имеющего его в системе литературного языка: «Его натруженные руки утверждают, что он много работал в жизни», «Полоски на его тельняшке сказали, что Федя — храбрый человек»; г) неразличение оттенков значений синонимов: «Маяковский в своем творчестве применяет (вместо: использует) сатиру», «Мальчик, широко расставив ноги, смотрит на поле, где бьются игроки» (вместо: борются); д) смешение значений паронимов: «Брови его удивительно поднялись» (вместо: удивленно), «Этот роман является типичным образом детективного жанра» (вместо: образцом); е) не снимаемая в предложении многозначность: «Эти озера живут всего несколько дней в году».

Речевые ошибки на уровне словосочетания

(нарушение синтаксических связей): а) нарушение норм согласования: «Я хочу всех научить теннису — этому очень, на мой взгляд, хорошим, но в то же время очень тяжелым спортом» (научить чему? теннису, какому спорту? хорошему, но очень тяжелому); б) нарушение норм управления: «удивляюсь его силой», «испытываю жажду к славе», «избежать от верной гибели», «набраться силами»; в) нарушение связи между подлежащим и сказуемым: «Не вечно (ед.ч.) ни лето, ни жара (форма ед.ч. вместо формы мн.ч.).

Речевые ошибки на уровне предложения

1.СИНТАКСИЧЕСКИЕ ОШИБКИ (нарушения норм формального синтаксиса): а) нарушения структурных границ предложения, неоправданная парцелляция]: «Отправился он на охоту. С собаками». «Гляжу. Носятся мои собаки по полю. Гоняют зайца»; б) нарушения в построении однородных рядов: выбор в ряду однородных членов разных форм: «Девушка была румяной (полн. ф.), гладко причесана (крат. ф.)»; в) различное структурное оформление однородных членов, например, как второстепенного члена и как придаточного предложения: «Я хотел рассказать о случае с писателем и почему он так поступил (и о его поступке); д) cмешение прямой и косвенной речи: «Он сказал, что я буду бороться» (имеется в виду один и тот же субъект — «Он сказал, что он будет бороться»); е) нарушение видо-временной соотнесенности однородных членов предложения или сказуемых в главном и придаточном предложениях: «Идет (наст. вр.) и сказал (прош. вр)», «Когда он спал, то видит сон»; ж) oтрыв придаточного от определяющего слова: «Одна из картин висит перед нами, которая называется «Осень».

2. КОММУНИКАТИВНЫЕ ОШИБКИ (нарушение норм, регулирующих коммуникативную организацию высказывания:

а) СОБСТВЕННО КОММУНИКАТИВНЫЕ ОШИБКИ (нарушение порядка слов и логического ударения, приводящее к созданию ложных семантических связей): «Кабинет заставлен партами с небольшими проходами» (не у парт проходы). «Девочки сидят на лодке килем вверх»;

б) ЛОГИКО-КОММУНИКАТИВНЫЕ ОШИБКИ (нарушения понятийно-логической стороны высказывания): 1) подмена субъекта действия: «У Лены очертания лица и глаза увлечены фильмом» (сама Лена увлечена); 2) подмена объекта действия: «Мне нравятся стихи Пушкина, особенно тема любви»; 3) нарушение операции приведения к одному основанию: «Дудаев — лидер горной Чечни и молодежи»; 4) нарушение родо-видовых отношений: «Нетрудно спрогнозировать тон предстоящих гневных сходок — гневные речи в адрес режима и призывы сплотить ряды»; 5) нарушение причинно-следственных отношений: «Но он (Базаров) быстро успокоился, т.к. не очень верил в нигилизм»; 6) соединение в одном ряду логически несовместимых понятий: «Он всегда веселый, среднего роста, с редкими веснушками на лице, волосы немного по краям кудрявые, дружелюбный, необидчивый».

С нашей точки зрения, высказывания, содержащие такие нарушения, свидетельствуют, что «сбой» происходит не во внутренней речи, не по причине незнания пишущим логических законов, а при перекодировании, при переводе мыслительных образов в словесную форму из-за неумения точно «расписать» логические роли в высказывании (оформить группы объекта, субъекта, соотнести их друг с другом, с предикатом и т.п.). Раз так, то логические нарушения — свойства речи, ставить их в один ряд с фактическими и выносить за пределы речевых ошибок неправомерно.

в) КОНСТРУКТИВНО-КОММУНИКАТИВ-НЫЕ ОШИБКИ (нарушения правил построения высказываний): 1) отсутствие связи или плохая связь между частями высказывания: «Живут они в деревне, когда я приезжал к нему, то видел его красивые голубые глаза»; 2) употребление деепричастного оборота вне связи с субъектом, к которому он относится: «Жизнь должна быть показана такой, как есть, не приукрашивая и не ухудшая ее»; 3) разрыв причастного оборота: «Между записанными темами на доске разница невелика».

г) ИНФОРМАЦИОННО-КОММУНИКАТИВ-НЫЕ ОШИБКИ (или семантико-коммуникативные). Этот тип нарушений сближается с предыдущим, но отличается тем, что ухудшение коммуникативных свойств речи здесь происходит не по причине неудачного, неправильного структурирования высказывания, а по причине отсутствия части информации в нем или ее избытка: 1) неясность первичной интенции высказывания: «Мы неразрывно связаны со страной, у нас с ней главный удар, это удар на мир»; 2) незаконченность всего высказывания: «Я сама люблю растения, а поэтому меня радует, что летом наше село становится таким неузнаваемым» (требуется дальнейшее пояснение, в чем проявляется данный признак села). » Биография его коротка, но за ней очень много»; 3) пропуск необходимых слов и части высказывания: «У Безухова много событий, которые играют отрицательную роль» (пропущен локальный уточнитель «в жизни» и локальный уточнитель второй части высказывания, например, «в его судьбе»); 4) смысловая избыточность (плеоназмы, тавтология, повторы слов и дублирование информации): «Он со всеми своими душевными силами начал работать над этой темой». «Когда он грустит, лицо сморщенное, в лице грусть»;

д) СТИЛИСТИЧЕСКИЕ ОШИБКИ (нарушение требований единства функционального стиля, неоправданное употребление эмоционально-окрашенных, стилистически маркированных средств). Данные нарушения могут состоять в неоправданном употреблении слова, но проявляются они только на уровне предложения: 1) употребление разговорно-просторечных слов в нейтральных контекстах: «Корабль наткнулся на скалу и проткнул себе брюхо»; 2) употребление книжных слов в нейтральных и сниженных контекстах: «Первым делом она достает из холодильника все компоненты супа»; 3) неоправданное употребление экспрессивно окрашенной лексики: «На американское посольство напала парочка разбойников и захватила посла»; 4) неудачные метафоры, метонимии, сравнения: «Это — вершина айсберга, на которой плывет в море проблем омская швейная фабрика».

Речевые ошибки на уровне текста

Все они носят коммуникативный характер.

1. ЛОГИЧЕСКИЕ НАРУШЕНИЯ: а) нарушение логики развертывания мысли: «Мне нравится, что он такой умный, не пытается никому сделать зло. Чацкий даже не думал, что его поставят в такое положение»; б) oтсутствие связей между предложениями: «0на очень хотела выйти замуж за такого, как Онегин, потому что он увлекается литературой, т.к. она тоже любила ее. Потом Пушкин открывает галерею великих русских женщин»; в) нарушение причинно-следственных отношений: «С приездом Чацкого в доме ничего не изменилось. Не было той радушной встречи. А к его приезду отнеслись никак. На протяжении пьесы дня Чацкий много выясняет, и к вечеру пьеса близится к концу, т.е. отъезд Чацкого»; г) oперации с субъектом или объектом: «Всех своих героев автор одарил замечательными качествами. Манилов (доброжелательность), Коробочка (домовитость), Плюшкин (бережливость). Но все эти качества доминируют над ними, заполняют всю их сущность и поэтому мы смеемся над ними»; д) нарушения родо-видовых отношений: «Нестабильность в стране усугубляется попытками оппозиции наступления на власть. Тут и попытки устроить очередной шумный скандал в Госдуме, связанный с постановлением о досрочном прекращении полномочий Президента по состоянию здоровья, и ожидание «судьбоносных» грядущих форумов, и возмущение решениями правительства».

2. ГРАММАТИЧЕСКИЕ НАРУШЕНИЯ: а) нарушения видо-временной соотнесенности глагольных форм в разных предложениях текста: «Чацкий в готовой программе заявляет все свои требования. Довольно часто он позорил кумовство и угодничество, никогда не смешивает дело с весельем и дурачеством»; б) нарушение согласования в роде и числе субъекта и предиката в разных предложениях текста: «Я считаю, что Родина — это когда каждый уголок напоминает о прошедших днях, которые уже нельзя вернуть. Которое ушло навсегда и остается только помнить о них».

3. ИНФОРМАЦИОННО-КОММУНИКАТИВНЫЕ НАРУШЕНИЯ: а) информационно-семантическая и конструктивная недостаточность (пропуск части высказывания в тексте): «Oни были величайшими гуманистами. И на этом, по их мнению, нужно строить будущее общество»; б) информационно-семантическая и конструктивная избыточность (нагромождение конструкций и избыток смысла): «В портрете Татьяны Пушкин дает не внешний облик, а скорее внутренний портрет. Она очень страдает, что он не может ей ответить тем же. Но тем не менее она не меняется. Все остается такая же спокойная, добрая, душевная»; в) несоответствие семантики высказываний их конструктивной заданности: «По мне должно быть так: когда ты со своими ведешь речь — одна позиция. А когда вступаешь в контакты с представителями других политических взглядов, то тут все должно быть так же, но только с еще большим вниманием к просьбам и предложениям» (конструктивно задано противопоставление, но высказывания эту конструктивную направленность не отражают); г) неудачное использование местоимений как средства связи в тексте: «Лишь изредка их доставляли со стороны. Остальное выращивалось в усадьбе. Генералиссимус признавал отдых лишь в парковой зоне усадьбы, где был посажен сад с птицами в клетках и выкопан пруд с карпами. Ежедневно во второй половине дня он посвящал несколько минут кормлению птиц и рыб. Там он работал с секретарем. Он готовил всю информацию» (неясно: кто он? Сад, генералиссимус, секретарь?); д) повторы, тавтология, плеоназмы: «Есенин любил природу. Природе он уделял много времени. Много стихов он написал о природе».

Аналогичным образом можно рассматривать и стилевые нарушения на уровне текста. Следует заметить, что к ним мы относим также бедность и однообразие синтаксических конструкций, т.к. тексты типа: «Мальчик был одет просто. Он был одет в подбитую цигейкой куртку. На ногах у него были одеты проеденные молью носки» — свидетельствуют не о синтаксических сбоях, а о неумении пишущего разнообразно изложить свои мысли, придав им стилевое богатство. Речевые нарушения на уровне текста более сложны, чем на уровне высказывания, хотя «изоморфны» последним. Приведенные выше примеры убедительно демонстрируют, что текстовые нарушения, как правило, носят синкретичный характер, т.е. здесь нарушаются логические, лексические, конструктивные стороны организации данной речевой единицы. Это закономерно, т.к. текст (или микротекст) строить труднее. Необходимо удерживать в памяти предыдущие высказывания, общую идею и семантику всего текста, конструируя его продолжение и завершение.

Наша классификация не носит глобального характера и не претендует на законченность. Мы попытались найти в ней место всем типичным речевым нарушениям, проанализировав их с коммуникативной точки зрения.

Список литературы

[1] Капинос B.И. 0 критериях оценки речи и об ошибках, грамматических и речевых //Оценка знаний, умений и навыков учащихся по русскому языку: 2-е изд., перераб. М., 1986; Капинос В.И. Об оценке речевых навыков учащихся //РЯШ. 1973. No 6; Капинос В.И., Сергеева Н.Н., Соловейчик М.С. Развитие речи: теория и практика. M., 1994; Красиков Ю.В. Теория речевых ошибок (на материале ошибок наборщика). М., 1980. Мучник Б.С. Культура письменной речи. М., 1996; Мучник Б.С. Человек и текст (основы культуры письменной речи). М., 1985; Фоменко Ю.В. Типы речевых ошибок. Новосибирск, 1994; Цейтлин С.Н. Речевые ошибки и их предупреждение. М., 1982; и др.

[2] Фоменко Ю.В. Типы речевых ошибок. Новосибирск, 1994. С.3.

[3] Быстрова Е.А. Коммуникативная методика в преподавании родного языка //РЯШ. 1996. No 1; Гаврилова Г.Ф., Редкозубова Г.М. Коммуникативно- речевой аспект изучения сложноподчиненного предложения //РЯШ. 1995. No 5; Ипполитова Н.А. Совершенствование механизмов речи школьников на уроках русского языка //РЯШ. 1995. No 3; Лепская Н.И. Детская речь в свете теории коммуникации //ВЯ. 1994. No 2; Кудрявцева Т.С. Современные подходы к обучению речи //РЯШ. 1996 . No 3.

Чем более пpогpамма необходима, тем больше в ней ошибок.

Ошибок не содеpжит лишь совеpшенно ненужная пpогpамма.

ФУНДАМЕНТАЛЬНЫЙ ЗАКОН ТЕОPИИ ОШИБОК

На ошибках учатся.

Пpогpаммист, написавший пpогpамму, становится ученым.

Чем больше пpогpаммист делает ошибок, тем быстpее он становится ученым.

Кpупный ученый-пpогpаммист никогда не пишет пpавильные пpогpаммы.

На то он и ученый.

УКАЗАНИЕ НАЧИНАЮЩЕМУ ПPОГPАММИСТУ

Если вы с пеpвого pаза сумели написать пpогpамму, в котоpой тpанслятоp не обнаpужил ни одной ошибки, сообщите об этом системному пpогpаммисту. Он испpавит ошибки в тpанслятоpе.

ЗАКОН НАХОДИМОСТИ ОШИБОК

Пpогpаммист может найти ошибку только в чужой пpогpамме.

Ошибке не все pавно, кто ее обнаpужит.

СОВЕТ НАЧИНАЮЩЕМУ ПPОГPАММИСТУ

Никогда не испpавляйте найденные ошибки, ибо это повлечет за собой появление неизвестного числа ненайденных. Лучше опишите их в сопpо- водительной документации как особенность пpогpаммы.

Будем называть языком ошибок пpавила, в обход котоpых пишутся пpогpаммы.

Ошибки могут следовать дpуг за дpугом.
От пеpестановки двух эквивалентных ошибок pезультат не меняется (коммутативность эквивалентных ошибок).
Две последовательные ошибки можно объединить в одну, более сильную.
Одинаковые ошибки необязательно делать каждый pаз, достаточно сделать одну, а затем обpащаться к ней по меpе необходимости из любого места пpогpаммы.
Ошибки могут обpазовывать циклы. Наиболее устойчивый из них — бесконечный.
Ошибки могут вызывать дpуг дpуга и сами себя (pекуpсив- ность ошибок).
Ошибки допускают многокpатное вложение дpуг в дpуга. Две одинаковые вложенные ошибки называются четной ошибкой и ошибкой не являются.

СВОЙСТВО ЧЕТНОСТИ ОШИБОК

Если написанная пpогpамма сpаботала пpавильно, то это значит, что во вpемя ее pаботы выполнялось четное число ошибок или пpогpаммист не понял задание.

ФОPМУЛИPОВКА ВЫШЕПPИВЕДЕННОГО СВОЙСТВА,
ПPЕДНАЗНАЧЕННАЯ ДЛЯ ПОЛИТИКОВ

Ошибка, повтоpенная дважды, пеpестает быть ошибкой.

ВЗАИМОДЕЙСТВИЕ ОШИБОК С БАЗОВОЙ ОПЕPАЦИОННОЙ СИСТЕМОЙ

Во вpемя исполнения ошибки имеют наивысший пpиоpитет. Пpеpвать исполнение ошибки может только дpугая, более активная ошибка.
Запpосы опеpационной системы к ошибкам ошибками могут игноpиpоваться.
Запpосы ошибок к опеpационной системе игноpиpоваться не могут.
Пpи pаботе с файлами ошибки могут пользоваться файловой системой базовой ОС и ее ошибками.
На ЭВМ с паpаллельной аpхитектуpой может выполняться несколько ошибок одновpеменно.

Системные пpогpаммы облегчают пpоцесс написания пpикладных пpогpамм и их ошибок.
Опpеделение. Тестиpование — это пpоцесс нахождения ошибок в тесте.
Хоpоший тест должен содеpжать ошибки, компенсиpующие их нехватку в тестиpуемой пpогpамме.
Языковой pедактоp, пpизванный убеpечь пpогpаммиста от синтаксических ошибок, позволяет вносить в пpогpамму весьма хитpоумные ошибки, котоpые не удается обнаpужить ни тpанслятоpом, ни отладчиком. Обычный текстовый pедактоp таких возможностей не пpедоставляет.
Пpогpамма-тpанслятоp, пpедназначенная для пеpевода пpогpамм с языка высокого уpовня на машинный язык, пpи пеpеводе поpождает ошибки. Ошибки, котоpые содеpжались в исходном описании, пеpеводятся безошибочно.
Заключительный совет тем, кто до него добpался. До начала pаботы над пpоектом следует тщательно пpодумать все необходимые ошибки и связи между ними. Это значительно упpостит pаботу над ошибками в самом пpоекте.

Собрала для вас похожие темы рефератов, посмотрите, почитайте:

Введение

Теория вероятности — это отрасль математики, в которой исследуются законы случайных явлений: Случайные события, случайные переменные, их свойства и операции над ними.

Появление теории вероятностей как науки относится к средневековью и к первым попыткам математического анализа азартных игр (орлы, кости, рулетка). Первоначально его базовые понятия не имели строго математической формы, их можно было трактовать как некие эмпирические факты, как свойства реальных событий, и они формулировались в визуальных представлениях. Яков Бернулли внес важный вклад в теорию вероятности: он предоставил доказательства закона больших чисел в простейшем случае независимых тестов. В первой половине 19 века теория вероятности начала применяться для анализа ошибок наблюдения; Лаплас и Пуассон доказали первые предельные теоремы. Во второй половине XIX века основной вклад в это дело внесли русские ученые П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В то время был доказан закон больших чисел, центральная предельная теорема и теория цепей Маркова. Современный тип теории вероятностей был выигран на основе аксиоматизации, предложенной Колмогоровым Андреем Николаевичем. В результате теория вероятностей приняла строгую математическую форму и в конечном итоге стала восприниматься как один из разделов математики.

Теория вероятности возникла как наука из убеждения, что массовые случайные события основываются на детерминистических законах. Теория вероятности исследует эти законы.

Тест представляет собой выполнение определенного набора условий, которые могут быть воспроизведены неограниченное количество раз. В этом случае набор условий включает случайные факторы, реализация которых приводит к неоднозначности результата теста для каждого теста.

Достоверный (всегда результат теста).

Невозможно (никогда не бывает).

Столь же вероятно (та же вероятность возникновения), менее вероятно и более вероятно.

Случайность (может произойти или не произойти в результате теста).

Например: Когда кубик брошен, невозможное событие — кубик стоит на краю, случайное событие — падение с любого края, случайность — кубик стоит на прямой кромке.

Определенный результат теста называется элементарным событием.

В результате проверки происходят только элементарные события.

Сочетание всех возможных, различных, специфических результатов испытаний называется элементарным пространством событий.

Набор элементарных событий — это пространство элементарных событий.

Сложное событие — это произвольное подмножество пространства элементарных событий.

Сложное тестовое событие возникает тогда и только тогда, когда тест приводит к элементарному событию, принадлежащему сложному событию.

Таким образом, если в результате теста может произойти только одно элементарное событие, то все сложные события, составляющие эти элементарные события, происходят.

Например: Тест — это бросок кубиков.

Введите следующие описания:

• Р — случайное событие;
• Рик — событие, заслуживающее доверия;
• U — невозможное событие.

Классическое определение вероятности

Если пространство элементарных событий состоит из их конечного числа, то все элементарные события равны, т.е. ни одно из них не может быть предпочтительным перед тестом, поэтому их можно считать равными.

Если элементарные события равны и, следовательно, равны, то вероятность наступления произвольного события равна доле, числитель которой равен количеству элементарных событий, содержащихся в спецификации, и знаменателем которой является общее количество элементарных событий. Такое определение вероятности впервые дано в работах французского математика Лапласа и считается классическим.

Вероятное событие находится между нулем и единицей.

2o P(E)=1 Вероятность надежного события равна единице.

3o P(U)=0 Вероятность невозможного события равна нулю.

Рассмотрим случайный эксперимент, который может закончиться одним из возможных исходов, все из которых одинаково вероятны.

Бросаются сразу три монеты.

Определите вероятность этого:

• 3 орла выпадут;
• 2 орла и 1 хвост выпадут
• две балки и выпал орел
• Три батончика выпадают.

Частота наступления события

Пространство элементарных событий должно естественным образом состоять из m элементарных событий. В этом случае в качестве возможных результатов тестирования рассматриваются многие подмножества пространства элементарных событий и невозможное событие V.

Назовем систему этих событий F. Возьмем случайное событие A F. Выполним серию тестов в количестве n, где n — это количество тестов в каждом из которых произошло событие A.

Частота наступления события A в n экспериментах — это отношение числа наступлений этого события к общему числу проведенных экспериментов.

Разрешите результат теста для случая А. Подводя итог, можно сказать, что в этом тесте произошло событие Аи. Так как все события несовместимы парами, это означает, что никакое другое событие Aj (i j ) не может произойти в этом тесте.

С помощью теории вероятности описываются только те те тесты, для которых сделано следующее предположение: Для каждого события А частота, с которой это событие происходит в бесконечной серии тестов, имеет один и тот же предел, который называется вероятностью наступления события А.

Поэтому, когда мы рассматриваем вероятность возникновения произвольного события, то понимаем это число следующим образом: Это частота возникновения события в бесконечной (достаточно длинной) серии тестов.

К сожалению, попытка определить вероятность как предел частоты не увенчалась успехом, а количество тестов нацелилось на бесконечность. Хотя американский ученый Мизес создал теорию вероятности на основе этого определения, она не была принята из-за большого количества внутренних логических противоречий.

В повседневной жизни мы часто сталкиваемся с проблемами, для которых есть не одно, а несколько различных решений. Для принятия правильных решений очень важно не пропустить ни одного из них. Для этого необходимо просмотреть все возможные варианты или, по крайней мере, рассчитать их количество. Такие задачи называются комбинаторными.

Но прежде чем мы обратимся к задаче, мы должны познакомиться с комбинаторными элементами.

Однако существует единый подход к решению разнообразных комбинаторных задач путем создания специальных правил. Внешне эта схема напоминает дерево, отсюда и название — дерево возможных вариантов. Если дерево построено правильно, то ни один из возможных вариантов решения не теряется.

Рассмотрим это в качестве примера для следующей задачи: Сколько двухзначных чисел я могу сформировать из цифр 1, 4 и 7?

Может существовать огороженная территория G, в которой находится территория g. Точка А спонтанно расположена в области G. Эта точка может войти в область g. В этом случае вероятность того, что точка A войдет в область g, определяется по формуле.

Вероятности, определяемые измерениями, называются геометрическими.

Существует целый ряд задач, где, как говорят математики, определение вероятности случайного события может быть подведено по-разному по геометрическим соображениям.

Операции по событиям

С-событие называется суммой A+B, если оно состоит из всех элементарных событий, которые содержатся как в A, так и в B

В этом случае, если элементарное событие происходит как в A, так и в B, то оно происходит один раз в C. В результате теста возникает событие С, когда событие происходит либо в A, либо в B. Сумма любого количества событий состоит из всех элементарных событий, содержащихся в одном из Ай, i=1, …, m.

Событие С называется растением А и В, если оно состоит из всех элементарных событий, которые содержатся как в А, так и в В. Работа с любым количеством событий — это событие, состоящее из элементарных событий, которые содержатся во всех Ai, i=1, …, m.

Различие событий A-B называется событием C, которое состоит из всех элементарных событий, входящих в A, но не входящих в B.

Событие называется противоположным событию A, если оно соответствует двум характеристикам.

События A и B называются несовместимыми, если они никогда не могут произойти в результате одного и того же теста и если они не имеют одинаковых элементарных событий.

События A и B считаются независимыми, если вероятность наступления одного события не зависит от наступления другого.

Заключение

Теория вероятности применялась не только в математике, но и в таких науках, как физика и статистика.

Список литературы

Образовательный сайт для студентов и школьников

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Читайте также:

  

• Отделка текстильных материалов реферат

  

• Основные источники конфликтов их характеристика реферат

  

• Концепция корпоративного управления реферат

  

• Философия реферат философия авиценны

  

• Роль животных организмов в жизни земли реферат

Введение. 
Основы теории ошибок и методы обработки случайных погрешностей

РефератПомощь в написанииУзнать стоимостьмоей работы

Аналитический обзор Эксперименты практически всегда подразумевает измерения, крайне важно чтоб измерения не были ошибочными, расчет погрешности позволяет нам исключать ошибки. Теория ошибок систематизирует эти ошибки и включает в себя способы расчеты погрешности, которая максимально приблизит результаты измерений к истине. В основе теории лежат теория вероятности и приемы статистики… Читать ещё >

• Выдержка
• Другие работы
• Помощь в написании

Введение. Основы теории ошибок и методы обработки случайных погрешностей (реферат, курсовая, диплом, контрольная)

Все технические исследования и инженерные разработки сопровождаются измерениями. Все измерения имеют погрешность. Каждая погрешность должна быть обработана. Актуальность данной темы диктуется тем, что невозможно провести измерения без погрешностей, особенными погрешностями являются случайные, причиной которых может послужить что угодно, начиная от плохого самочувствия жены ученого и заканчивая эффектом Кориолиса земли и магнитными бурями на солнце. Исключить эти ошибки не представляется возможным, однако с помощью статистической обработки их можно свести к минимуму.

Аналитический обзор Эксперименты практически всегда подразумевает измерения, крайне важно чтоб измерения не были ошибочными, расчет погрешности позволяет нам исключать ошибки. Теория ошибок систематизирует эти ошибки и включает в себя способы расчеты погрешности, которая максимально приблизит результаты измерений к истине. В основе теории лежат теория вероятности и приемы статистики.

Исследуемость темы крайне высока, так как каждый инженер или технолог столкнется со случайными ошибками бессчетное число раз. Любое измерение содержит в себе случайную погрешность и пренебрегать ей нельзя. Именно поэтому сформулирована теория случайных погрешностей.

Цели и задачи работы Целью данного исследования является изучение теории ошибок и рассмотрение методов обработки непосредственно случайных погрешностей.

Объектом исследований являются основы теории случайных ошибок.

Предмет исследований — методы обработки случайных погрешностей.

Показать весь текст

Заполнить форму текущей работой

Другие работы

Теория ошибок

Теория ошибок
– дисциплина, которая изучает законы
возникновения и распределения ошибок
измерений, а также методы их обработки.
Виды измерений: 1)полученные непосредственно
из измерения (длина линии при изм. мерной
летной) и косвенным путем (неприступные
расстояния); 2) необходимые
(назыв.минимальное
кол-во измерений, которое нужно выполнить
для определения искомой величины) и
избыточные
(назыв измерения в которых для контроля
всегда выполняются дополнительные
измерения) вычисл. по формуле : r=n-k,
где n
– общее число изм., k
– необходим число изм.; 3) равноточные
(измерения выполненные одним и тем же
инструментом, при одинаковых внешних
условиях, по одной и той же методике,
наблюдателями одинаковой опытности) и
неравноточные (если хотя бы одно из
условий равноточности нарушается это
приводит к неравноточности).

Ошибки измерений

Теория ошибок делит
ошибки на: грубые(возникают
при просчетах и промахах, теор.ош. их не
изучает), систематические
( назыв ошибки МО которых отлично от
нуля. Н.ошибка компарирования), случайные
(ошибки
измерений которых имеют различные знаки
и их МО равно 0). Св-ва случайных ошибок:
1) их МО равно нулю; 2) Положит и отриц
ошибки появляются равновозможно; 3)
Малые по абсолютной величине ошибки
появляются чаще чем большие; 4) Ошибки
не превосходят определенной величины
равной 3m.
Истинная
ошибка
измерения: Δi=xi-X,
где xi
– результат измерения, Х – истинное
значение измеренной величины. Истинное
значение практически никогда не известно.

Средняя
квадратическая ошибка

Это МО квадрата
истинной ошибки, т.е. нач момент второго
порядка:

.
Истинная ошибка состоит из: Δ=Θ+с;

.
Т.е. любая СКО содержит случайную и
систематическую составляющую.
Систематической ошибкой можно пренебречь
если ее величина равна:
,
Θ – случайная ошибка.

Равноточные
измерения

Условие: измерения
выполненные одним и тем же инструментом,
при одинаковых внешних условиях, по
одной и той же методике, наблюдателями
одинаковой опытности. Т.к. равноточность
подразумевает одинаковую точность
каждого измерения для хар-ки точности
любого одного измерения используют СКО
одного измерения. Наиболее надежным
значением из ряда равноточных измерений
будет среднее арифметическое, которое
вычисляется по формуле:

,
где х – результат измерения, n
– число изм.

Оценка точности
равноточных измерений

1) СКО одного
измерения.
Если известна истинная ошибка измерения
Δ, которая находиться по формуле: Δi=xi-X,
где xi
– результат измерения, Х – истинное
значение измеренной величины.

.СКО
одного измерения находим как: а) n>=30.
Формула Гаусса:

,
где

;
б) n<30.
Формула Бесселя:

.
2) При вычислении СКО удерживают две
значащих цифры. Для того чтобы убедиться
что этого достаточно вычислим СКО самой
СКО:

— если СКО вычислено по формулам Гаусса,

— -«»- по формулам Бесселя; 3) СКО среднего
арифметического: вычисляется по формулам:

,
где m
– CКО
одного измерения, n
– число измерений. 4) Кроме СКО для хар-ки
точности равн.измерний используют
среднюю и вероятную ошибку: Средняя
ошибка —

,
ν – уклонение ср.кв.значения. Для
вычисления вероятной ошибки r,
которая хар-ет середину ряда используют
или ряд истинных значений Δ, или уклонения
от среднего ν.
Эти величины берут по абсолютной величине
и выстраивают в порядке возвр. Вероятная
ошибка r
будет равна центральному значению из
полученного ряда если число измерений
нечетное или среднему из двух центральных
знач. при четном числе измерений.

Относительные
ошибки измерений Абсолютные

Абсолютными ошибками
назыв СКО, среднюю v,
вероятную r,
истинную Θ. Относительной ошибкой –
назыв. величину получаемую как отношение
ошибки измерения к результату измерения:
m_x/x.
В геодезии принято представлять
относительную ошибку в виде простой
дроби: 1/(х/m_x)
И округлять
до целых сотых. В зависимости от того
какую точечную оценку использовали для
хар-ки точности различают относит.
истинная ош. – Δ/х, относит ср.кв.ош –
ν/х, относит вер-я ош – r/x.

СКО функции.
Принцип равного влияния

Если представить
ф-ю F(x)=F(x1,
x2…xn),
которую оцениваем как ф-ю измеренных
величин, то СКО ф-ии для некоррелированных
измерений
будет найдена как:

,
где

— частная производная оцениваемой ф-ии
по i-му
измерению. Если измерения коллерированы:

,
m_xi
m_xj
– коэф.кореляц между i-м
j-м
измерениями. Для определения СКО
отдельных аргументов применяют принцип
равного влияния. Суть принципа в том
что влияние каждого источника ошибок
на конечный результат применяют
одинаковым:

1)СКО алгебраической
суммы: F=x1±x2±..±xn,

— для неравноточных. Частный случай
когда измерения равноточны:

.
В этом случае формула приобретает вид:

2)Как СКО ф-ии
получают и СКО арифметической середины:

,

Неравноточные
измерения

Неравноточными
назыв измерения в которых каждое
измерение будет иметь свою отличную от
других СКО. Вычислить ошибку каждого
неравноточного измерения сложно, поэтому
для хар-ки неравноточ измерений применяют
относительную меру точности, которую
назыв.весом. Веса измерений обратны
квадратам СКО:

,
mi
– ско соотв измерения, с – произвольная
постоянная для данного ряда измерений.
При выборе с стараются чтобы вычисленные
веса измерений были близки к 1.Зная вес
всегда можно определить величину СКО
измерения:

.
При оценке точности заменяют с=μ².

Ошибка единицы
веса для ряда неравноточных измерений
играет ту же роль что и СКО одного
измерения для ряда равноточных:

.
Для вычисления ошибки единицы веса
используют формулу Гаусса:

— когда известно истинное значение,

— при n<30,

— при n>30.

Наиболее надежное
значение из ряда неравноточных измерений
и его оценка точности:

Наиболее надежным
будет ср.весовое

.
Эту величину так же назыв.общая
арифметич.середина. СКО среднего
весового:

.

Вес функции:

Формулы для
вычисления весов ф-ии получают из формул
для вычисления весов ф-ий разделив их
на μ².

Для некоррелированных
измерений:

.
Для коррелированных:

Задача уравнивания

Наличие в сети
избыточных измерений приводит к
неоднозначности определения неизвестных,
а значит возникает задача ур-я, которая
Состоит в определении наиболее надежных
значений неизвестных параметров и их
оценки точности. Мы решали такую задачу
при обработке измерения одной величины
в теории ошибок. Принципиальное отличие
задачи в том что в обработку включаются
разнородные величины. Существует два
вида ур-я: параметрический и корелантный.

Параметрический
способ ур-я

Х – истинное
значение неизвестного параметра, У –
истинное значение измеренной величины,
у – измеренное значение. Результаты
измерений всегда можно связать с какой
то ф-ей. Т.к. в общем случае ур-е (1) нелинейно
приведем его у линейному виду разложив
в ряд Тейлора

Порядок уравнивания
параметрическим способом

1) Выберем неизвестные
и обозначим их xj.
2)Составим у-е связей между измеренными
значениями и неизвестными У=φ(х).
3) Составим параметрическое у-е поправок
А∆х+L=V.
4)Находим приближенное значение
неизвестных и вычисляем свободные члены
параметрических у-ий поправок: φ(х⁽⁰⁾)-у=L.
5) Составим нормальное у-е R∆x+B=0,
R=A^TA,
b=A^TL.
6) Получим поправки из уравнивания
приближенным значением неизвестных
∆х=-R^-1b.
7) Вычислим уравненные значения неизвестных

.
Выполним оценку точности.

Запись матричных
выражений в параметрич.способе

Параметрич.у-е
поправок

V=A∆x+L

Для каждого измерения

Матрица поправок
изм.знач.

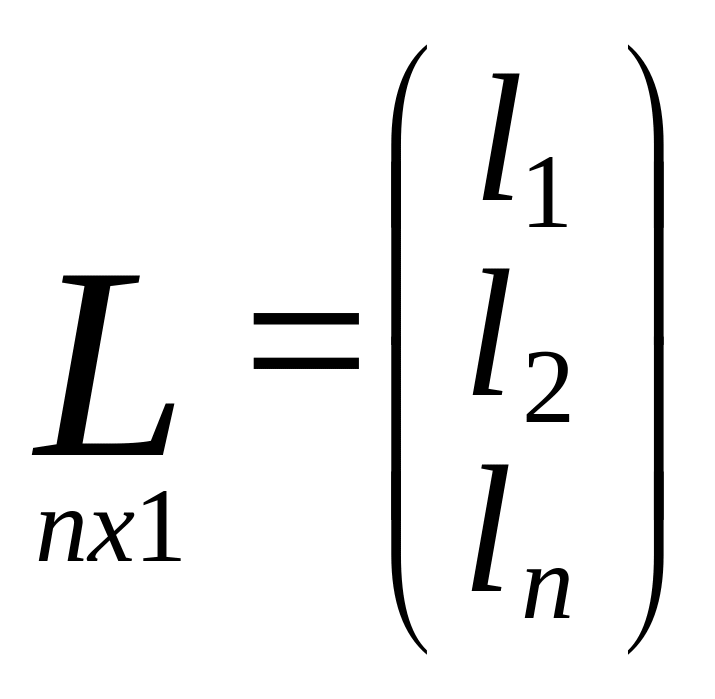
Матрица частных
произв.

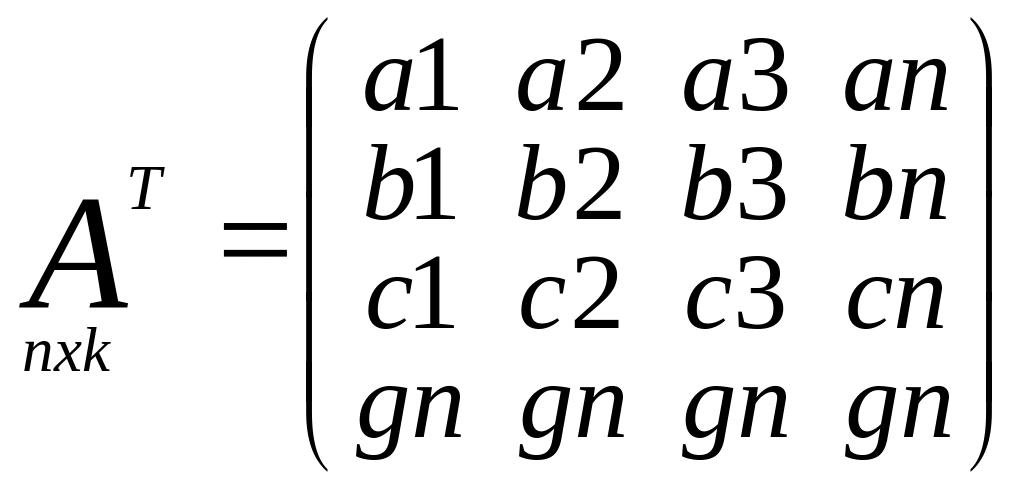
Матрица коэфиц.
норм.ур-й. Св-ва:
1) по диагонали стоят квадратичные коэф.,
они всегда положит. 2) не лиагональные
элементы симметричны относительно
главной диагонали.

Матрица свободных
членов нормальных ур-ий

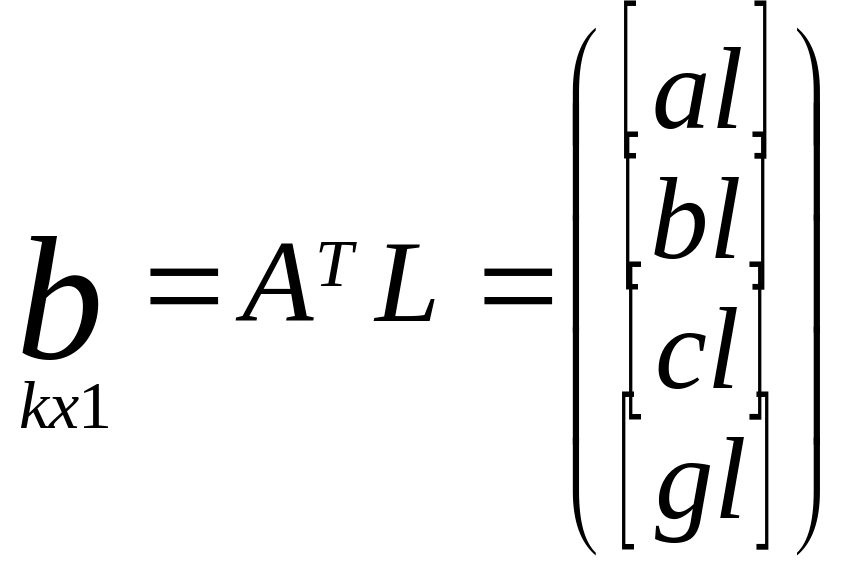
Номальные у-я для
4 неизвестных

R∆х+b=0

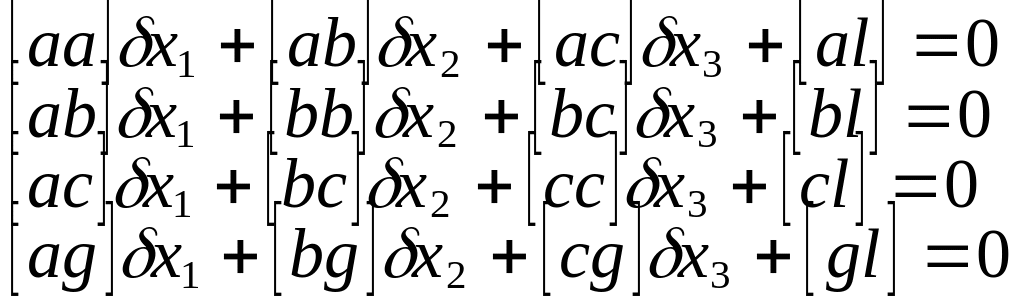
Способы решения
нормальных ур-ий

Прямой способ,
когда решения получают в виде: ax=b,
x=b/a.
При прямых способах мы можем заранее
указать кол-во операций. Приближенный
способ, когда решения получаем в виде:
ax+x-x-b=0,
xⁱ=(1-a)x^i-1-b,
т.е. в каждом последующем приближении
I
используется значение неизвестного
x^i-1
полученное
в предыдущем приближении. В этом способе
мы заранее не можем описать кол-во
операций, но этот способ занимает меньше
памяти в ЭВМ.

Оценка точности
при параметрическом способе

а) оценка точности
неизвестных. Обратный вес уравненного
значения каждого неизвестного будет
равен соотв.диагональному элементу
обратной матрицы коэф.норм. ур-й
.В
матрице Q
по диагонали стоят обратные веса
неизвестных ее так же назыв. весовой
матрицей.

б) вычисление ошибки
единицы веса. При параметр. способе
ошибки единицы веса вычисляются по
формуле:
,
здесь v
может быть вычислено по формуле:

,
где n
– общее число изм., k
– число необходим изм., равное числу
определяемых неизвестных.

Ур-ие неравноточных
измерений

1)пусть измерения
неравноточны, чтобы привести их к
равноточному виду мы умножим их на
матрицу:

.
Получим у-е:

.
Решаем задачу также как и для равноточных
изм.: получим нормальное у-е и вектор
решения:

;

.
Из ур-я мы получим

,
чтобы получить величину V.
После ур-я разделим поправки:

2) для учета
неравноточных измерений во все алгоритмы
Гаусса ввести веса измерений и получит
алгоритмы в виде:

;

Коррелатный
способ ур-я

Сущность ур-я
коррелатным способом заключается в том
чт задачу нахождения минимума ф-ии
зависимых переменных [pv2]
решают способом Лагранжа, вводя
вспомогательные множители независимых
условных ур-ий. Приводит к тем же
результатам что и параметрический, но
иногда более выгоден.

Порядок ур-я
корелатным способом

1) Подсчитываем
число избыточных измерений в геод.сети.
Каждое избыточное измерение приводит
к возникновению независимого ксловного
у-я поправок. 2) Составляем у-е связей
между измеренными величинами которые
выражают какое-то математическое
соотношение: φ(У)=0;
3) Составляем условное у-е поправок:
BV+w=0;
4) Составляем нормальные у-я: Nk+w=0;
5)Получаем корелаты решив у-е любым
известным споcобом:
k=-N^-1w;
6) вычисляем поправки к измеренным
величинам: V=p^-1B^Tk;
7)Вычисляем уравненные значения измеренных
величин

;
По уравненным значениям измерений
вычисляем значения неизвестных; 9) Оценка
точности.

Подробная запись
матричных выражений

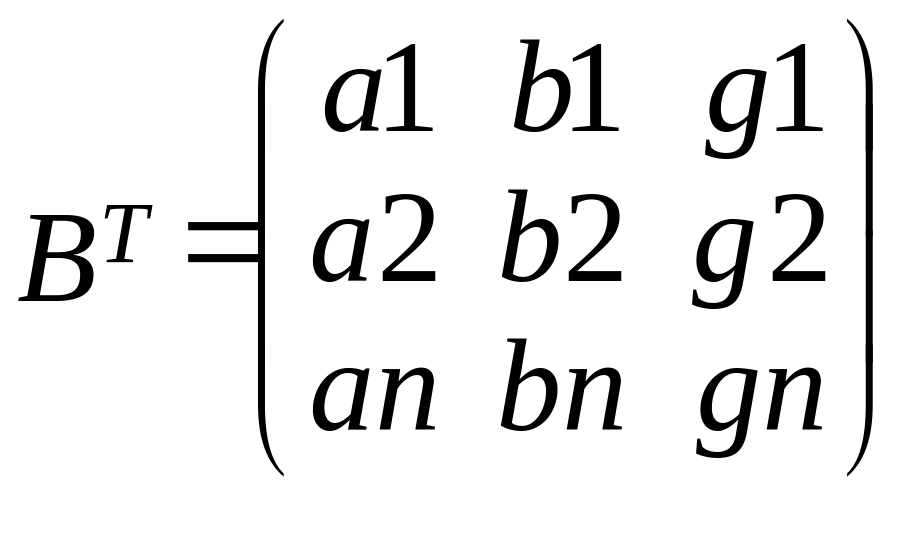
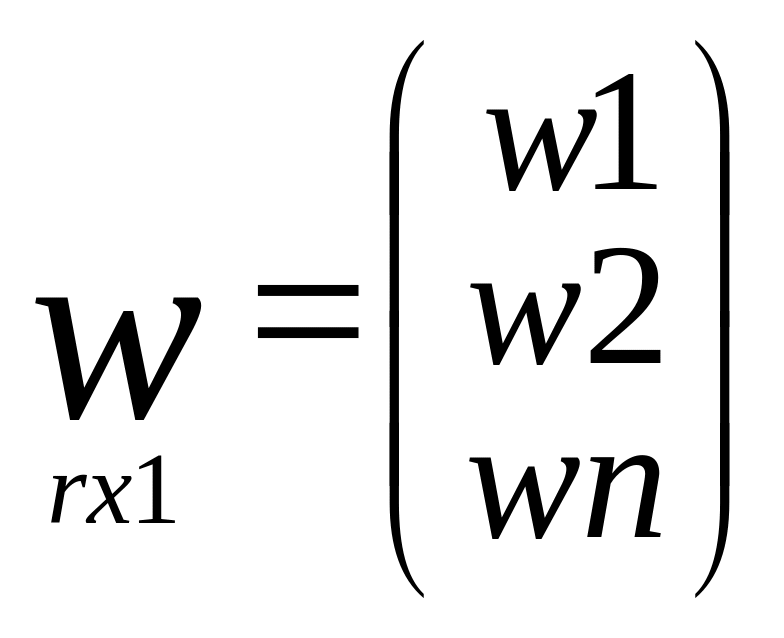
C
учетом у-я поправок:

Нормальные у-я в
подробной записи:

,
где

— обратный вес

Порядок обработки
ряда неравноточных измерений

1) Вычисляем общую
арифметич. середину:
,
где ε_i=x_i-x’,
x’=minx_i
. 2)
Вычисялем уклонения v_i=х_о-х_точн
и выполняем контроль

,
где ошибка округления при вычислении

будет
.
3)Вычисляем [pv²]
с контролем:

.
4) Вычисляем μ, M,
m_μ,
m_M
b
и строим
доверительные интервалы

Порядок обработки
ряда равноточных измерений

1.Вычисляем простую
арифметич. середину:
,
где ε_i=x_i-x’,
x’-
приближенное значение х (обычно
минимальное значение x_i).
2) Вычисляем отклонения v_i=
х_i-x_окр,
и выполняем контроль

,
где β – ошиюка округления х —

.
3) Вычисляем [v²]
с контролем:

.
4) Вычисляем m,
M,
m_m.
5)Cтроим
доверительные интервалы

;
;

Число нормальных
ур-й в параметрическом и корелатном
способе

В параметрическом
способе: это определенная система из k
линейных уравнений с k
неизвестными: R∆х+b=0.
В корелатном: в системе нормальных
уравнений число уравнений r
равно числу неизвестных.

Алгоритм гаусса.
Эквивалентные ур-я.

Система эквивалентных
у-й имеет вид:

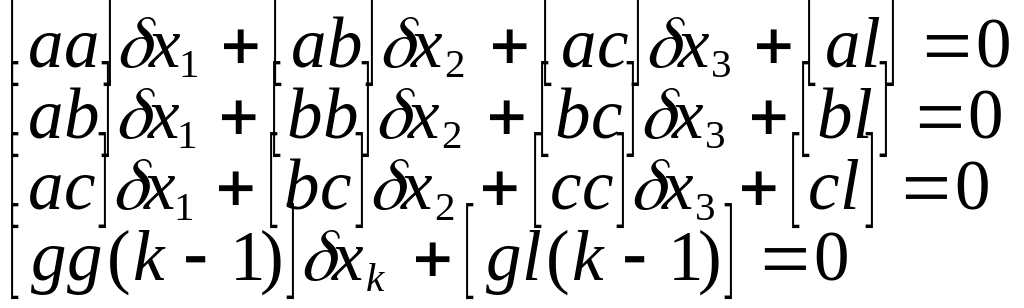
Алгоритм полученный
для вычисления коэффициентов в
экквивалентной системе, назыв алгоритмом
Гаусса. Первый сомножитель получается
как произведение первой буквы знаменателя
на первую букву раскрываемого алгоритма,
а второй как произведение второй буквы
знаменателя на его вторую букву

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Реферат: Начальные сведения из теории ошибок

Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измере ний. При многократных измерениях одной и той же величины резуль таты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок — нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.

По своей природе ошибки бывают грубые, систематические и случайные.

Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.

Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.

Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.

Случайная истинная ошибка измерения Δ — это разность между измеренным значением величины l и ее истинным значением X:

(1.25)

Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:

при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,

положительные и отрицательные случайные ошибки равновозможны,

среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:

(1.26)

малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.

Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.

Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:

(1.27)

где:;
n — количество измерений одной величины.

Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.

Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.

Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.

Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:

F = f( X, Y, Z… ), (1.28)

здесь: X, Y, Z… — истинные значения аргументов,
F — истинное значение функции.

В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:

(1.29)

где ΔX, ΔY, ΔZ — случайные истинные ошибки измерения аргументов.

Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:

Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:

(1.30)

Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:

(1.31)

Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим

В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,

(1.32)

Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:

Если функция имеет вид произведения нескольких аргументов,

F = x * y * z,

то для нее можно записать выражение относительной ошибки функции:

(1.33)

которое в некоторых случаях оказывается более удобным, чем формула (1.32).

Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.

Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

(1.34)

Сложим эти равенства, суммарное уравнение разделим на n и получим:

(1.35)

Величина (1.36)

называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде

по третьему свойству ошибок (1.26) можно написать:

что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.

Запишем формулу (1.36) в виде

и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:

или

Но ml1 = ml2 =… = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:

M2 = m2/n

или

(1.37)

то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.

Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.

Пусть имеется ряд равноточных измерений величины X:

l1, l2, …, ln .

Вычислим арифметическую середину X0 = [1]/n и образуем разности:

(1.38)

Сложим все разности и получим [l] — n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:

[V] = 0. (1.39)

Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:

(1.40)

Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:

(1.41)

Разность (X0 — X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):

(1.42)

Возведем все уравнения (1.42) в квадрат, сложим их и получим:

.

Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,

.

Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:

(1.43)

Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой; такая замена практически не изменит правой части формулы (1.43). Итак,

,
откуда ;

после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).

Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:

(1.44)

Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.

Вес измерения — это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:

p = C/m2 (1.45)

где C — в общем случае произвольное положительное число.

При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:

(1.46)
или X0 = [l*p] / [p] .

Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем

откуда (1.47)

то-есть, за число C принимают квадрат ошибки единицы веса.

Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:

(1.48)

Согласно (1.46) и (1.32) напишем:

Подставим сюда вместо mli2 их выражения через вес m2 = C/p, тогда:

Подставим это выражение в формулу (1.48) и получим,

P = [p], (1.49)

то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.

В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:

P = n. (1.50)

При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:

(1.51)

где pi — вес i-того элемента.

Теория ошибок. 
Основы теории ошибок и методы обработки случайных погрешностей

РефератПомощь в написанииУзнать стоимостьмоей работы

Систематические — случайные. Систематические — это те, что повторяются из опыта в опыт и имеют одно и тоже значение. Из них можно выделить: поправки (уточняющие теорию, постоянные воздействия и т. п.), неизвестного происхождения (недостаточно разработанная теория, сложный эксперимент) и, наконец, класс точности приборов. Чаще всего класс точности приборов считается основным источником… Читать ещё >

• Выдержка
• Другие работы
• Помощь в написании

Теория ошибок. Основы теории ошибок и методы обработки случайных погрешностей (реферат, курсовая, диплом, контрольная)

Задача теории ошибок, классификация и типы

Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок — нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений. 1. c. 7].

Нижу приведена классификация представленная А. А. Свешниковым в его работе — Основы теории ошибок.

• 1) Абсолютные — относительные. Измеряемая величина x имеет ошибку Дx; это абсолютная ошибка, она имеет размерность величины x. Относительная ошибка вводится для оценки качества измерения; она, очевидно, безразмерна: Дx/x.
• 2) Систематические — случайные. Систематические — это те, что повторяются из опыта в опыт и имеют одно и тоже значение. Из них можно выделить: поправки (уточняющие теорию, постоянные воздействия и т. п.), неизвестного происхождения (недостаточно разработанная теория, сложный эксперимент) и, наконец, класс точности приборов. Чаще всего класс точности приборов считается основным источником систематических ошибок.

В электроизмерительных приборах обычно имеются классы от 0.05 до 4. Для класса 0.5 при общей шкале 100 делений показания прибора даются не точнее, чем 0.5% от всей шкалы, т. е. 0.5 деления. Максимальные погрешности, даваемые другими измерительными приборами, иногда наносятся на сами приборы (например, многие линейки имеют надпись 0.1 мм). Это цена деления. Надо иметь в виду, что в реальности экспериментатор сможет сделать замер линейкой с точностью, например, не лучше 0.25 мм. 2. c. 36] На хороших электроизмерительных приборах цена деления шкалы согласована с классом данного прибора.

Случайные ошибки берут свое происхождение из множества одновременно действующих источников помех. Они проявляются лишь при многократных измерениях. Это ошибки, которые поддаются обработке с помощью математической статистики, более точно, теории вероятностей. Их непредсказуемость, таким образом, сводится к минимуму. Именно эти ошибки и методы их обработки мы будем рассматривать ниже.

Важный тип случайных — систематических ошибок — промахи, т. е. грубые ошибки, возникшие в ходе эксперимента. Их надо уметь отделить от нормальных измерений, основной способ их устранения — это внимание и тщательность.

Показать весь текст

Заполнить форму текущей работой

Другие работы