Термин ошибка ii го рода означает - Не ошибается лишь тот, кто ничего не делает!

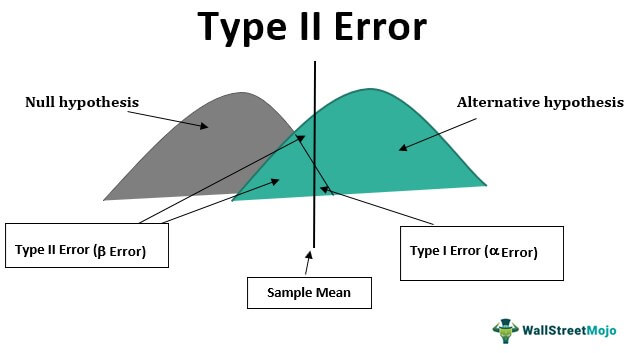
Ошибки первого и второго рода

Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.

Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.

Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.

Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.

Замечание 1.
Правильное решение может быть принято
также в двух случаях:

гипотеза принимается,
причём и в действительности она
правильная;
гипотеза отвергается,
причём и в действительности она неверна.

Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).

Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия

Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.

Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.

Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:.

Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.

Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.

Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии,
то наблюдаемое значение критерия.

Критическая
область. Область принятия гипотезы.
Критические точки

После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.

Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.

Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.

Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.

Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.

Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.

Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.

Правосторонней
называют критическую область, определяемую
неравенством
>,
где— положительное число.

Левосторонней
называют критическую область, определяемую
неравенством
<,
где— отрицательное число.

Односторонней
называют правостороннюю или левостороннюю
критическую область.

Двусторонней
называют критическую область, определяемую
неравенствами
где.

В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):

,
или равносильным неравенством
.

Отыскание
правосторонней критической области

Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?

Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее,
была равна принятому уровню значимости:
Р(>)=.

Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.

Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>,
то нулевую гипотезу отвергают; если же<,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.

Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение

Р(>)=?
(*)

Поскольку вероятность
события
>мала (— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.

Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.

Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».

На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.

Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.

Отыскание
левосторонней и двусторонней критических
областей***

Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<(<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<)=.

Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее,
была равна принятому уровню значимости:

.
(*)

Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и(>0),
то

Учитывая (*), получим
.

Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.

Дополнительные
сведения о выборе критической области.
Мощность критерия

Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.

Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.

Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.

Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.

Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.

Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.

Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
иневозможно; если уменьшить,
тобудет возрастать. Например, если принять=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.

Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.

Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.

Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.

Источник

Что такое ошибка второго рода?

Ошибка типа II, обычно называемая ошибкой «β», представляет собой вероятность сохранения неверного фактического утверждения. Это ошибка ложного срабатывания, т. е. утверждение фактически ложно, и мы уверены в этом.

Оглавление

Что такое ошибка второго рода?
- Объяснение
- Пример ошибки типа II
- Как возникает ошибка типа II?
- Можно ли избежать ошибок типа II?
- Важность
- Ошибка типа I против ошибки типа II
- Заключение
- Рекомендуемые статьи

Объяснение

Ошибки типа обычно используются для создания гипотезы, определения решения на основе вероятности их появления и определения фактической корректировки данных, которые структурировали гипотезу.

На диаграмме показано создание нулевой гипотезыНулевая гипотезаНулевая гипотеза предполагает, что данные выборки и данные населения не имеют различий, или, говоря простыми словами, она предполагает, что утверждение, сделанное человеком в отношении данных или населения, является абсолютной истиной и всегда верно . Таким образом, даже если выборка берется из населения, результат, полученный в результате изучения выборки, будет таким же, как и предположение. Читать далее, альтернативная гипотеза, среднее значение выборки и вероятность ошибки.

Каждый тест, который мы проводим, всегда имеет вероятность ошибки при принятии решения, и такое решение может быть ошибкой типа I или типа II. Проще говоря, принимая решения, мы можем отвергать правильные факты или принимать неправильные. Отвержение правильных фактов — это ошибка первого рода, а принятие неверных фактов — ошибка второго рода. Эта ошибка может быть очень опасной в корпоративном мире, поскольку полный анализ и эксперимент могут быть ошибочными, если сама база неверна.

Ниже приведена матрица того, какой тип ошибки можно совершить, если факты будут приняты неправильно:

Было принято решение сохранитьПринято решение об отказе (Положительный) (Отрицательный) Нулевая гипотеза верна Истинно положительная Истинно отрицательная (1-a) = ошибка типа I Нулевая гипотеза ложная Ложноположительная ложноотрицательная (β) = ошибка типа II (1 – β) популяция сравнительно очень мала, чтобы обнаружить

Если тенденция к изменению не видна в самой популяции, то любая проверка гипотез Проверка гипотез Проверка гипотез является статистическим инструментом, который помогает измерить вероятность правильности результата гипотезы, полученного после выполнения гипотезы на выборочных данных. Это подтверждает правильность полученных результатов первичной гипотезы. Такой сценарий приведет к принятию неверных фактов, что приведет к ошибкам второго рода.

№ 2. Размер выборки охватывает очень небольшую часть населения.

Выборка должна представлять всю совокупность. Таким образом, если выборка не является идеальным представлением генеральной совокупности, маловероятно, что она даст правильный анализ. Аналитик не сможет определить правильные факты. В результате они будут полагаться на неправильные факты, что приведет к ошибке типа II.

#3 – Неправильный выбор образца

Как правило, во всем мире используется случайная выборка, поскольку она считается одним из самых объективных методов отбора выборки. Однако во многих случаях это приводит к неправильному выбору образцов. В результате это приводит к неправильному охвату населения и приводит к ошибке второго рода.

Можно ли избежать ошибок типа II?

# 1 — Повторяйте анализ, пока не достигнете требуемой значимости

Значимость указывает, является ли нулевая гипотеза фактически верной или нет. В конце всех анализов принимается нулевая гипотеза и проверяется правильность фактов. Однако часто только один анализ не может достичь такой значимости. Такой односторонний анализ может привести к ошибкам типа I или типа II. С другой стороны, если при повторном анализе будут получены одни и те же выходные данные, можно гарантировать отсутствие ошибок.

#2 – При каждом повторении анализа меняйте размер критерия значимости

Как обсуждалось в пункте 1, значимость показывает правильность нулевой гипотезы. Если обнаруживается, что выборка недостаточно охвачена, можно повторить, что размер значимости увеличивается. Это поможет понять поведение и избежать ошибки типа II.

№ 3. Уровень альфа около 0,1 является идеальным.

Как правило, альфа около 0,1 приводит к отклонению гипотезы. Любой отказ позволит несколько проверок. В результате вероятность возникновения ошибок снижается. Ошибка типа II возникает, когда что-то принимается неправильно. Если возможности для принятия нет, такой ошибки не произойдет.

Важность

Это более опасно по сравнению с ошибками первого рода.
Любой анализ может быть разработан на основе нескольких необходимых деталей и основных предположений. В конце гипотезы можно определить, соответствует ли тестовая статистика данному факту или нет. Такие особенности теста будут отображать, эквивалентны ли выборочные средние среднему значению генеральной совокупности.
Если кажется, что нулевая гипотеза достигает значимости из-за какой-то ошибки в анализе, можно принять этот факт в нулевой гипотезе.
Однако в действительности такая нулевая гипотеза должна быть неприемлемой. В результате нужно быть очень уверенным, принимая утверждение нулевой гипотезы. Повторно проверяя его, можно получить большее значение, чтобы повысить правильность факта.

Ошибка типа I против ошибки типа II

Ниже приведены основные различия между двумя типами ошибок:

старший нетОшибка I типаОшибка второго рода1 Это происходит, когда правильная нулевая гипотеза не принимается. Это происходит, когда принимается неверная нулевая гипотеза.2 Такие ошибки действительно отрицательные. Такие ошибки являются ложноположительными.3Обозначается альфа. Обозначается бета4Нулевая гипотеза и ошибка 1-го рода Альтернативная гипотеза и ошибка 2-го рода5Если результирующий эффект этой ошибки хуже, чем ошибка типа I, следует рассматривать альфа со значением выше 0,10. Если результирующий эффект ошибки типа I хуже, следует установить альфа со значением ниже 0,01.

Заключение

Ошибка II рода — это ложноотрицательный результат, возникающий в результате принятия неверной нулевой гипотезы. В практическом мире такие ошибки приводят к провалу всего проекта, поскольку база неточна. Более того, такой базой могут быть как детали, факты или предположения, ставящие под угрозу полноту анализа.

Ошибки первого и второго рода

Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.

Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.

Замечание 1.
Правильное решение может быть принято
также в двух случаях:

гипотеза принимается,
причём и в действительности она
правильная;
гипотеза отвергается,
причём и в действительности она неверна.