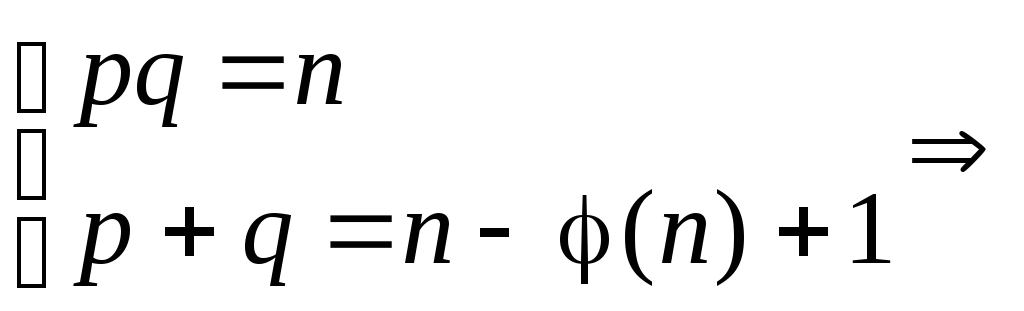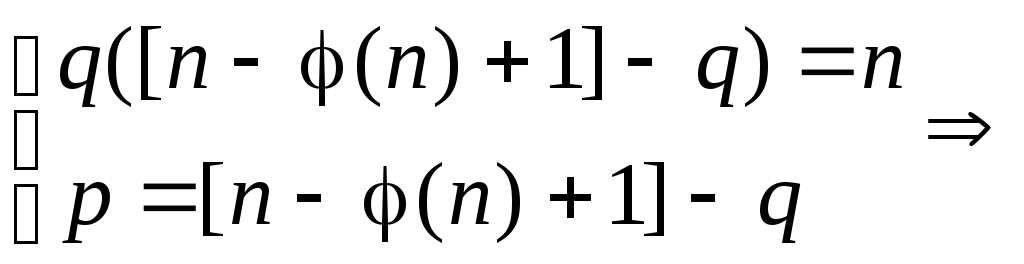The Miller–Rabin primality test or Rabin–Miller primality test is a probabilistic primality test: an algorithm which determines whether a given number is likely to be prime, similar to the Fermat primality test and the Solovay–Strassen primality test.
It is of historical significance in the search for a polynomial-time deterministic primality test. Its probabilistic variant remains widely used in practice, as one of the simplest and fastest tests known.
Gary L. Miller discovered the test in 1976; Miller’s version of the test is deterministic, but its correctness relies on the unproven extended Riemann hypothesis.[1] Michael O. Rabin modified it to obtain an unconditional probabilistic algorithm in 1980.[2][a]
Mathematical concepts[edit]
Similarly to the Fermat and Solovay–Strassen tests, the Miller–Rabin primality test checks whether a specific property, which is known to hold for prime values, holds for the number under testing.
Strong probable primes[edit]
The property is the following. For a given odd integer n > 2, let’s write n − 1 as 2sd where s is a positive integer and d is an odd positive integer. Let’s consider an integer a, called a base, which is coprime to n.
Then, n is said to be a strong probable prime to base a if one of these congruence relations holds:
The idea beneath this test is that when n is an odd prime, it passes the test because of two facts:
- by Fermat’s little theorem,
(this property alone defines the weaker notion of probable prime to base a, on which the Fermat test is based);
- the only square roots of 1 modulo n are 1 and −1.
Hence, by contraposition, if n is not a strong probable prime to base a, then n is definitely composite, and a is called a witness for the compositeness of n.
However, this property is not an exact characterization of prime numbers. If n is composite, it may nonetheless be a strong probable prime to base a, in which case it is called a strong pseudoprime, and a is a strong liar.
Choices of bases[edit]
Thankfully, no composite number is a strong pseudoprime to all bases at the same time (contrary to the Fermat primality test for which Fermat pseudoprimes to all bases exist: the Carmichael numbers). However no simple way of finding a witness is known. A naïve solution is to try all possible bases, which yields an inefficient deterministic algorithm. The Miller test is a more efficient variant of this (see section Miller test below).
Another solution is to pick a base at random. This yields a fast probabilistic test. When n is composite, most bases are witnesses, so the test will detect n as composite with a reasonably high probability (see section Accuracy below). We can quickly reduce the probability of a false positive to an arbitrarily small rate, by combining the outcome of as many independently chosen bases as necessary to achieve the said rate. This is the Miller–Rabin test. The number of bases to try does not depend on n. There seems to be diminishing returns in trying many bases, because if n is a pseudoprime to some base, then it seems more likely to be a pseudoprime to another base.[4]: §8
Note that ad ≡ 1 (mod n) holds trivially for a ≡ 1 (mod n), because the congruence relation is compatible with exponentiation. And ad = a20d ≡ −1 (mod n) holds trivially for a ≡ −1 (mod n) since d is odd, for the same reason. That is why random a are usually chosen in the interval 1 < a < n − 1.
For testing arbitrarily large n, choosing bases at random is essential, as we don’t know the distribution of witnesses and strong liars among the numbers 2, 3, …, n − 2.[b]
However, a pre-selected set of a few small bases guarantees the identification of all composites up to a pre-computed maximum. This maximum is generally quite large compared to the bases. This gives very fast deterministic tests for small enough n (see section Testing against small sets of bases below).
Proofs[edit]
Here is a proof that, if n is a prime, then the only square roots of 1 modulo n are 1 and −1.
Proof
Certainly 1 and −1, when squared modulo n, always yield 1. It remains to show that there are no other square roots of 1 modulo n. This is a special case, here applied with the polynomial X2 − 1 over the finite field Z/nZ, of the more general fact that a polynomial over some field has no more roots than its degree (this theorem follows from the existence of an Euclidean division for polynomials). Here follows a more elementary proof. Suppose that x is a square root of 1 modulo n. Then:
In other words, n divides the product (x − 1)(x + 1). By Euclid’s lemma, since n is prime, it divides one of the factors x − 1 or x + 1, implying that x is congruent to either 1 or −1 modulo n.
Here is a proof that, if n is an odd prime, then it is a strong probable prime to base a.
Proof
If n is an odd prime and we write n − 1= 2sd where s is a positive integer and d is an odd positive integer, by Fermat’s little theorem:
Each term of the sequence 
Example[edit]
Suppose we wish to determine if n = 221 is prime. We write n − 1 as 22 × 55, so that we have s = 2 and d = 55. We randomly select a number a such that 2 ≤ a ≤ n−2, say a = 174. We proceed to compute:
- a20d mod n = 17455 mod 221 = 47 ≠ 1, n − 1
- a21d mod n = 174110 mod 221 = 220 = n − 1.
Since 220 ≡ −1 mod n, either 221 is prime, or 174 is a strong liar for 221. We try another random a, this time choosing a = 137:
- a20d mod n = 13755 mod 221 = 188 ≠ 1, n − 1
- a21d mod n = 137110 mod 221 = 205 ≠ n − 1.
Hence 137 is a witness for the compositeness of 221, and 174 was in fact a strong liar. Note that this tells us nothing about the factors of 221 (which are 13 and 17). However, the example with 341 in a later section shows how these calculations can sometimes produce a factor of n.
Miller–Rabin test[edit]
The algorithm can be written in pseudocode as follows. The parameter k determines the accuracy of the test. The greater the number of rounds, the more accurate the result.[6]
Input #1: n > 2, an odd integer to be tested for primality
Input #2: k, the number of rounds of testing to perform
Output: “composite” if n is found to be composite, “probably prime” otherwise
let s > 0 and d odd > 0 such that n − 1 = 2sd # by factoring out powers of 2 from n − 1
repeat k times:
a ← random(2, n − 2) # n is always a probable prime to base 1 and n − 1
x ← ad mod n
repeat s times:
y ← x2 mod n
if y = 1 and x ≠ 1 and x ≠ n − 1 then # nontrivial square root of 1 modulo n
return “composite”
x ← y
if y ≠ 1 then
return “composite”
return “probably prime”
Complexity[edit]
Using repeated squaring, the running time of this algorithm is O(k log3 n), where n is the number tested for primality, and k is the number of rounds performed; thus this is an efficient, polynomial-time algorithm. FFT-based multiplication (Harvey-Hoeven algorithm) can decrease the running time to O(k log2 n log log n) = Õ(k log2 n).
Accuracy[edit]
The error made by the primality test is measured by the probability that a composite number is declared probably prime. The more bases a are tried, the better the accuracy of the test. It can be shown that if n is composite, then at most 1/4 of the bases a are strong liars for n.[2][7] As a consequence, if n is composite then running k iterations of the Miller–Rabin test will declare n probably prime with a probability at most 4−k.
This is an improvement over the Solovay–Strassen test, whose worst‐case error bound is 2−k. Moreover, the Miller–Rabin test is strictly stronger than the Solovay–Strassen test in the sense that for every composite n, the set of strong liars for n is a subset of the set of Euler liars for n, and for many n, the subset is proper.
In addition, for large values of n, the probability for a composite number to be declared probably prime is often significantly smaller than 4−k. For instance, for most numbers n, this probability is bounded by 8−k; the proportion of numbers n which invalidate this upper bound vanishes as we consider larger values of n.[8] Hence the average case has a much better accuracy than 4−k, a fact which can be exploited for generating probable primes (see below). However, such improved error bounds should not be relied upon to verify primes whose probability distribution is not controlled, since a cryptographic adversary might send a carefully chosen pseudoprime in order to defeat the primality test.[c]
In such contexts, only the worst‐case error bound of 4−k can be relied upon.
The above error measure is the probability for a composite number to be declared as a strong probable prime after k rounds of testing; in mathematical words, it is the conditional probability
where P is the event that the number being tested is prime, and MRk is the event that it passes the Miller–Rabin test with k rounds. We are often interested instead in the inverse conditional probability 
In the last equation, we simplified the expression using the fact that all prime numbers are correctly reported as strong probable primes (the test has no false negative). By dropping the left part of the denominator, we derive a simple upper bound:
Hence this conditional probability is related not only to the error measure discussed above — which is bounded by 4−k — but also to the probability distribution of the input number. In the general case, as said earlier, this distribution is controlled by a cryptographic adversary, thus unknown, so we cannot deduce much about 
Deterministic variants[edit]
Miller test[edit]
The Miller–Rabin algorithm can be made deterministic by trying all possible a below a certain limit. Taking n as the limit would imply O(n) trials, hence the running time would be exponential with respect to the size log n of the input. To improve the running time, the challenge is then to lower the limit as much as possible while keeping the test reliable.
If the tested number n is composite, the strong liars a coprime to n are contained in a proper subgroup of the group (Z/nZ)*, which means that if we test all a from a set which generates (Z/nZ)*, one of them must lie outside the said subgroup, hence must be a witness for the compositeness of n. Assuming the truth of the generalized Riemann hypothesis (GRH), it is known that the group is generated by its elements smaller than O((ln n)2), which was already noted by Miller.[1] The constant involved in the Big O notation was reduced to 2 by Eric Bach.[10] This leads to the following deterministic primality testing algorithm, known as the Miller test:
Input: n > 2, an odd integer to be tested for primality
Output: “composite” if n is composite, “prime” otherwise
let s > 0 and d odd > 0 such that n − 1 = 2sd # by factoring out powers of 2 from n − 1
for all a in the range [2, min(n − 2, ⌊2(ln n)2⌋)]:
x ← ad mod n
repeat s times:
y ← x2 mod n
if y = 1 and x ≠ 1 and x ≠ n − 1 then # nontrivial square root of 1 modulo n
return “composite”
x ← y
if y ≠ 1 then
return “composite”
return “prime”
The full power of the generalized Riemann hypothesis is not needed to ensure the correctness of the test: as we deal with subgroups of even index, it suffices to assume the validity of GRH for quadratic Dirichlet characters.[7]
The running time of the algorithm is, in the soft-O notation, Õ((log n)4) (using FFT‐based multiplication).
The Miller test is not used in practice. For most purposes, proper use of the probabilistic Miller–Rabin test or the Baillie–PSW primality test gives sufficient confidence while running much faster. It is also slower in practice than commonly used proof methods such as APR-CL and ECPP which give results that do not rely on unproven assumptions. For theoretical purposes requiring a deterministic polynomial time algorithm, it was superseded by the AKS primality test, which also does not rely on unproven assumptions.
Testing against small sets of bases[edit]
When the number n to be tested is small, trying all a < 2(ln n)2 is not necessary, as much smaller sets of potential witnesses are known to suffice. For example, Pomerance, Selfridge, Wagstaff[4] and Jaeschke[11] have verified that
- if n < 2,047, it is enough to test a = 2;
- if n < 1,373,653, it is enough to test a = 2 and 3;
- if n < 9,080,191, it is enough to test a = 31 and 73;
- if n < 25,326,001, it is enough to test a = 2, 3, and 5;
- if n < 3,215,031,751, it is enough to test a = 2, 3, 5, and 7;
- if n < 4,759,123,141, it is enough to test a = 2, 7, and 61;
- if n < 1,122,004,669,633, it is enough to test a = 2, 13, 23, and 1662803;
- if n < 2,152,302,898,747, it is enough to test a = 2, 3, 5, 7, and 11;
- if n < 3,474,749,660,383, it is enough to test a = 2, 3, 5, 7, 11, and 13;
- if n < 341,550,071,728,321, it is enough to test a = 2, 3, 5, 7, 11, 13, and 17.
Using the work of Feitsma and Galway enumerating all base 2 pseudoprimes in 2010, this was extended (see OEIS: A014233), with the first result later shown using different methods in Jiang and Deng:[12]
- if n < 3,825,123,056,546,413,051, it is enough to test a = 2, 3, 5, 7, 11, 13, 17, 19, and 23.
- if n < 18,446,744,073,709,551,616 = 264, it is enough to test a = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and 37.
Sorenson and Webster[13] verify the above and calculate precise results for these larger than 64‐bit results:
- if n < 318,665,857,834,031,151,167,461, it is enough to test a = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and 37.
- if n < 3,317,044,064,679,887,385,961,981, it is enough to test a = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, and 41.
Other criteria of this sort, often more efficient (fewer bases required) than those shown above, exist.[14][15][16][17] They give very fast deterministic primality tests for numbers in the appropriate range, without any assumptions.
There is a small list of potential witnesses for every possible input size (at most b values for b‐bit numbers). However, no finite set of bases is sufficient for all composite numbers. Alford, Granville, and Pomerance have shown that there exist infinitely many composite numbers n whose smallest compositeness witness is at least (ln n)1/(3ln ln ln n).[18] They also argue heuristically that the smallest number w such that every composite number below n has a compositeness witness less than w should be of order Θ(log n log log n).
Variants for finding factors[edit]
By inserting greatest common divisor calculations into the above algorithm, we can sometimes obtain a factor of n instead of merely determining that n is composite. This occurs for example when n is a probable prime to base a but not a strong probable prime to base a.[19]: 1402
If x is a nontrivial square root of 1 modulo n,
- since x2 ≡ 1 (mod n), we know that n divides x2 − 1 = (x − 1)(x + 1);
- since x ≢ ±1 (mod n), we know that n does not divide x − 1 nor x + 1.
From this we deduce that A = gcd(x − 1, n) and B = gcd(x + 1, n) are nontrivial (not necessarily prime) factors of n (in fact, since n is odd, these factors are coprime and n = AB). Hence, if factoring is a goal, these gcd calculations can be inserted into the algorithm at little additional computational cost. This leads to the following pseudocode, where the added or changed code is highlighted:
Input #1: n > 2, an odd integer to be tested for primality Input #2: k, the number of rounds of testing to perform Output: (“multiple of”, m) if a nontrivial factor m of n is found, “composite” if n is otherwise found to be composite, “probably prime” otherwise let s > 0 and d odd > 0 such that n − 1 = 2sd # by factoring out powers of 2 from n − 1 repeat k times: a ← random(2, n − 2) # n is always a probable prime to base 1 and n − 1 x ← ad mod n repeat s times: y ← x2 mod n if y = 1 and x ≠ 1 and x ≠ n − 1 then # nontrivial square root of 1 modulo n return (“multiple of”, gcd(x − 1, n)) x ← y if y ≠ 1 then return “composite” return “probably prime”
This is not a probabilistic factorization algorithm because it is only able to find factors for numbers n which are pseudoprime to base a (in other words, for numbers n such that an−1 ≡ 1 mod n). For other numbers, the algorithm only returns “composite” with no further information.
For example, consider n = 341 and a = 2. We have n − 1 = 85 × 4. Then 285 mod 341 = 32 and 322 mod 341 = 1. This tells us that n is a pseudoprime base 2, but not a strong pseudoprime base 2. By computing a gcd at this stage, we find a factor of 341: gcd(32 − 1, 341) = 31. Indeed, 341 = 11 × 31.
In order to find factors more often, the same ideas can also be applied to the square roots of −1 (or any other number).
This strategy can be implemented by exploiting knowledge from previous rounds of the Miller–Rabin test. In those rounds we may have identified a square root modulo n of −1, say R. Then, when x2 mod n = n − 1, we can compare the value of x against R: if x is neither R nor n−R, then gcd(x − R, n) and gcd(x + R, n) are nontrivial factors of n.[14]
Generation of probable primes[edit]
The Miller–Rabin test can be used to generate strong probable primes, simply by drawing integers at random until one passes the test. This algorithm terminates almost surely (since at each iteration there is a chance to draw a prime number). The pseudocode for generating b‐bit strong probable primes (with the most significant bit set) is as follows:
Input #1: b, the number of bits of the result
Input #2: k, the number of rounds of testing to perform
Output: a strong probable prime n
while True:
pick a random odd integer n in the range [2b−1, 2b−1]
if the Miller–Rabin test with inputs n and k returns “probably prime” then
return n
Complexity[edit]
Of course the worst-case running time is infinite, since the outer loop may never terminate, but that happens with probability zero. As per the geometric distribution, the expected number of draws is 
As any prime number passes the test, the probability of being prime gives a coarse lower bound to the probability of passing the test. If we draw odd integers uniformly in the range [2b−1, 2b−1], then we get:
where π is the prime-counting function. Using an asymptotic expansion of π (an extension of the prime number theorem), we can approximate this probability when b grows towards infinity. We find:
Hence we can expect the generator to run no more Miller–Rabin tests than a number proportional to b. Taking into account the worst-case complexity of each Miller–Rabin test (see earlier), the expected running time of the generator with inputs b and k is then bounded by O(k b4) (or Õ(k b3) using FFT-based multiplication).
Accuracy[edit]
The error measure of this generator is the probability that it outputs a composite number.
Using the relation between conditional probabilities (shown in an earlier section) and the asymptotic behavior of 
Hence, for large enough b, this error measure is less than 
Using the fact that the Miller–Rabin test itself often has an error bound much smaller than 4−k (see earlier), Damgård, Landrock and Pomerance derived several error bounds for the generator, with various classes of parameters b and k.[8] These error bounds allow an implementor to choose a reasonable k for a desired accuracy.
One of these error bounds is 4−k, which holds for all b ≥ 2 (the authors only showed it for b ≥ 51, while Ronald Burthe Jr. completed the proof with the remaining values 2 ≤ b ≤ 50[20]). Again this simple bound can be improved for large values of b. For instance, another bound derived by the same authors is:
which holds for all b ≥ 21 and k ≥ b/4. This bound is smaller than 4−k as soon as b ≥ 32.
Notes[edit]
- ^
The Miller–Rabin test is often incorrectly said to have been discovered by M. M. Artjuhov as soon as 1967; a reading of Artjuhov’s paper[3]
(particularly his Theorem E) shows that he actually discovered the Solovay–Strassen test. - ^
For instance, in 1995, Arnault gives a 397-digit composite number for which all bases less than 307 are strong liars; this number was reported to be prime by the Mapleisprime()function, because it implemented the Miller–Rabin test with the specific bases 2, 3, 5, 7 and 11.[5] - ^
For instance, in 2018, Albrecht et al. were able to construct, for many cryptographic libraries such as OpenSSL and GNU GMP, composite numbers that these libraries declared prime, thus demonstrating that they were not implemented with an adversarial context in mind.[9]
References[edit]
- ^ a b Miller, Gary L. (1976), «Riemann’s Hypothesis and Tests for Primality», Journal of Computer and System Sciences, 13 (3): 300–317, doi:10.1145/800116.803773, S2CID 10690396
- ^ a b Rabin, Michael O. (1980), «Probabilistic algorithm for testing primality», Journal of Number Theory, 12 (1): 128–138, doi:10.1016/0022-314X(80)90084-0
- ^ Artjuhov, M. M. (1966–1967), «Certain criteria for primality of numbers connected with the little Fermat theorem», Acta Arithmetica, 12: 355–364, MR 0213289
- ^ a b Carl Pomerance; John L. Selfridge; Samuel S. Wagstaff, Jr. (July 1980). «The pseudoprimes to 25 ⋅ 109» (PDF). Mathematics of Computation. 35 (151): 1003–1026. doi:10.1090/S0025-5718-1980-0572872-7.
- ^ F. Arnault (August 1995). «Constructing Carmichael Numbers Which Are Strong Pseudoprimes to Several Bases». Journal of Symbolic Computation. 20 (2): 151–161. doi:10.1006/jsco.1995.1042.
- ^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. «31». Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. pp. 968–971. ISBN 0-262-03384-4.
- ^ a b Schoof, René (2004), «Four primality testing algorithms» (PDF), Algorithmic Number Theory: Lattices, Number Fields, Curves and Cryptography, Cambridge University Press, ISBN 978-0-521-80854-5
- ^ a b Damgård, I.; Landrock, P. & Pomerance, C. (1993), «Average case error estimates for the strong probable prime test» (PDF), Mathematics of Computation, 61 (203): 177–194, Bibcode:1993MaCom..61..177D, doi:10.2307/2152945, JSTOR 2152945
- ^ Martin R. Albrecht; Jake Massimo; Kenneth G. Paterson; Juraj Somorovsky (15 October 2018). Prime and Prejudice: Primality Testing Under Adversarial Conditions (PDF). ACM SIGSAC Conference on Computer and Communications Security 2018. Toronto: Association for Computing Machinery. pp. 281–298. doi:10.1145/3243734.3243787.
- ^ Bach, Eric (1990), «Explicit bounds for primality testing and related problems», Mathematics of Computation, 55 (191): 355–380, Bibcode:1990MaCom..55..355B, doi:10.2307/2008811, JSTOR 2008811
- ^ Jaeschke, Gerhard (1993), «On strong pseudoprimes to several bases», Mathematics of Computation, 61 (204): 915–926, doi:10.2307/2153262, JSTOR 2153262
- ^ Jiang, Yupeng; Deng, Yingpu (2014). «Strong pseudoprimes to the first eight prime bases». Mathematics of Computation. 83 (290): 2915–2924. doi:10.1090/S0025-5718-2014-02830-5.
- ^ Sorenson, Jonathan; Webster, Jonathan (2015). «Strong Pseudoprimes to Twelve Prime Bases». Mathematics of Computation. 86 (304): 985–1003. arXiv:1509.00864. Bibcode:2015arXiv150900864S. doi:10.1090/mcom/3134. S2CID 6955806.
- ^ a b Caldwell, Chris. «Finding primes & proving primality — 2.3: Strong probable-primality and a practical test». The Prime Pages. Retrieved February 24, 2019.
- ^ Zhang, Zhenxiang & Tang, Min (2003), «Finding strong pseudoprimes to several bases. II», Mathematics of Computation, 72 (44): 2085–2097, Bibcode:2003MaCom..72.2085Z, doi:10.1090/S0025-5718-03-01545-X
- ^ Sloane, N. J. A. (ed.). «Sequence A014233 (Smallest odd number for which Miller–Rabin primality test on bases <= n-th prime does not reveal compositeness)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Izykowski, Wojciech. «Deterministic variants of the Miller–Rabin primality test». Retrieved February 24, 2019.
- ^ Alford, W. R.; Granville, A.; Pomerance, C. (1994), «On the difficulty of finding reliable witnesses» (PDF), Lecture Notes in Computer Science, Springer-Verlag, 877: 1–16, doi:10.1007/3-540-58691-1_36, ISBN 978-3-540-58691-3
- ^ Robert Baillie; Samuel S. Wagstaff, Jr. (October 1980). «Lucas Pseudoprimes» (PDF). Mathematics of Computation. 35 (152): 1391–1417. doi:10.1090/S0025-5718-1980-0583518-6. MR 0583518.
- ^ Burthe Jr., Ronald J. (1996), «Further investigations with the strong probable prime test» (PDF), Mathematics of Computation, 65 (213): 373–381, Bibcode:1996MaCom..65..373B, doi:10.1090/S0025-5718-96-00695-3
External links[edit]
- Weisstein, Eric W. «Rabin-Miller Strong Pseudoprime Test». MathWorld.
- Interactive Online Implementation of the Deterministic Variant (stepping through the algorithm step-by-step)
- Applet (German)
- Miller–Rabin primality test in C#
- Miller–Rabin primality test in JavaScript using arbitrary precision arithmetic
Тесты Ферма и Миллера-Рабина на простоту
Время на прочтение
3 мин
Количество просмотров 19K
Салют хабровчане! Сегодня мы продолжаем делиться полезным материалом, перевод которого подготовлен специально для студентов курса «Алгоритмы для разработчиков».
Дано некоторое число n, как понять, что это число простое? Предположим, что n изначально нечетное, поскольку в противном случае задача совсем простая.
Самой очевидной идеей было бы искать все делители числа n, однако до сих пор основная проблема заключается в том, чтобы найти эффективный алгоритм.
Тест Ферма
По Теореме Ферма, если n – простое число, тогда для любого a справедливо следующее равенство an−1=1 (mod n). Отсюда мы можем вывести правило теста Ферма на проверку простоты числа: возьмем случайное a ∈ {1, ..., n−1} и проверим будет ли соблюдаться равенство an−1=1 (mod n). Если равенство не соблюдается, значит скорее всего n – составное.
Тем не менее, условие равенства может быть соблюдено, даже если n – не простое. Например, возьмем n = 561 = 3 × 11 × 17
Z561 = Z3 × Z11 × Z17
, где каждое a ∈ Z∗561 отвечает следующему:
(x,y,z) ∈ Z∗3×Z∗1111×Z∗17.
По теореме Ферма, x2=1, y10=1, и z16=1. Поскольку 2, 10 и 16 все являются делителями 560, это значит, что (x,y,z)560 = (1, 1, 1), другими словами a560 = 1 для любого a ∈ Z∗561.
Не имеет значения какое a мы выберем, 561 всегда будет проходить тест Ферма несмотря на то, что оно составное, до тех пор, пока a является взаимно простым с n. Такие числа называются числами Кармайкла и оказывается, что их существует бесконечное множество.
Если a не взаимно простое с n, то оно тест Ферма не проходит, но в этом случае мы можем отказаться от тестов и продолжить искать делители n, вычисляя НОД(a,n).
Тест Миллера-Рабина
Мы можем усовершенствовать тест, сказав, что n — простое тогда и только тогда, когда решениями x2 = 1 (mod n) являются x = ±1.
Таким образом, если n проходит тест Ферма, то есть an−1 = 1, тогда мы проверяем еще чтобы a(n−1)/2 = ±1, поскольку a(n−1)/2 это квадратный корень 1.
К сожалению, такие числа, как, например 1729 — третье число Кармайкла до сих пор могут обмануть этот улучшенный тест. Что если мы будем проводить итерации? То есть пока это будет возможно, мы будем уменьшать экспоненту вдвое, до тех пор, пока не дойдем до какого-либо числа, помимо 1. Если мы получим в итоге что-то, кроме -1, тогда n будет составным.
Если говорить более формально, то пускай 2S будет самой большой степенью 2, делящейся на n-1, то есть n−1=2Sq для какого-то нечетного числа q. Каждое число из последовательности
an−1 = a(2^S)q, a(2^S-1)q,…, aq.
Это квадратный корень предшествующего члена последовательности.
Тогда если n – простое число, то последовательность должна начинаться с 1 и каждое последующее число тоже должно быть 1, или же первый член последовательность может быть не равен 1, но тогда он равен -1.
Тест Миллера-Рабина берет случайное a∈ Zn. Если вышеуказанная последовательность не начинается с 1, либо же первый член последовательности не равен 1 или -1, тогда n – не простое.
Оказывается, что для любого составного n, включая числа Кармайкла, вероятность пройти тест Миллера-Рабина равна примерно 1/4. (В среднем значительно меньше.) Таким образом, вероятность того, что n пройдет несколько прогонов теста, уменьшается экспоненциально.
Если n не проходит тест Миллера-Рабина с последовательностью начинающейся с 1, тогда у нас появляется нетривиальный квадратный корень из 1 по модулю n, и мы можем эффективно находить делители n. Поэтому числа Кармайкла всегда удобно раскладывать на множители.
Когда тест применяется к числам вида pq, где p и q – большие простые числа, они не проходят тест Миллера-Рабина практически во всех случаях, поскольку последовательность не начинается с 1. Итого, так мы RSA сломать не сможем.
На практике тест Миллера-Рабина реализуется следующим образом:
- Дано
n, нужно найтиs, такое чтоn – 1 = 2Sqдля некоторого нечетногоq. - Возьмем случайное
a ∈ {1,...,n−1} - Если aq = 1, то
nпроходит тест и мы прекращаем выполнение. - Для
i= 0, ... , s−1проверить равенствоa(2^i)q = −1. Если равенство выполняется, тоnпроходит тест (прекращаем выполнение). - Если ни одно из вышеприведенных условий не выполнено, то
n– составное.
Перед выполнением теста Миллера-Рабина стоит провести еще несколько тривиальных делений на маленькие простые числа.
Строго говоря эти тесты являются тестами на то считается ли число составным, поскольку они не доказывают по сути, что проверяемое число простое, но точно доказывают, что оно может оказаться составным.
Существуют еще детерминированные алгоритма работающие за полиномиальное время для определения простоты (Agrawal, Kayal и Saxena), однако на сегодняшний день они считаются непрактичными.
Тесты Ферма и Миллера-Рабина на простоту
Салют хабровчане! Сегодня мы продолжаем делиться полезным материалом, перевод которого подготовлен специально для студентов курса «Алгоритмы для разработчиков».
Дано некоторое число n, как понять, что это число простое? Предположим, что n изначально нечетное, поскольку в противном случае задача совсем простая.
Самой очевидной идеей было бы искать все делители числа n, однако до сих пор основная проблема заключается в том, чтобы найти эффективный алгоритм.
Тест Ферма
По Теореме Ферма, если n – простое число, тогда для любого a справедливо следующее равенство an−1=1 (mod n). Отсюда мы можем вывести правило теста Ферма на проверку простоты числа: возьмем случайное a ∈ {1, ..., n−1} и проверим будет ли соблюдаться равенство an−1=1 (mod n). Если равенство не соблюдается, значит скорее всего n – составное.
Тем не менее, условие равенства может быть соблюдено, даже если n – не простое. Например, возьмем n = 561 = 3 × 11 × 17
Z561 = Z3 × Z11 × Z17
, где каждое a ∈ Z∗561 отвечает следующему:
(x,y,z) ∈ Z∗3×Z∗1111×Z∗17.
По теореме Ферма, x2=1, y10=1, и z16=1. Поскольку 2, 10 и 16 все являются делителями 560, это значит, что (x,y,z)560 = (1, 1, 1), другими словами a560 = 1 для любого a ∈ Z∗561.
Не имеет значения какое a мы выберем, 561 всегда будет проходить тест Ферма несмотря на то, что оно составное, до тех пор, пока a является взаимно простым с n. Такие числа называются числами Кармайкла и оказывается, что их существует бесконечное множество.
Если a не взаимно простое с n, то оно тест Ферма не проходит, но в этом случае мы можем отказаться от тестов и продолжить искать делители n, вычисляя НОД(a,n).
Тест Миллера-Рабина
Мы можем усовершенствовать тест, сказав, что n — простое тогда и только тогда, когда решениями x2 = 1 (mod n) являются x = ±1.
Таким образом, если n проходит тест Ферма, то есть an−1 = 1, тогда мы проверяем еще чтобы a(n−1)/2 = ±1, поскольку a(n−1)/2 это квадратный корень 1.
К сожалению, такие числа, как, например 1729 — третье число Кармайкла до сих пор могут обмануть этот улучшенный тест. Что если мы будем проводить итерации? То есть пока это будет возможно, мы будем уменьшать экспоненту вдвое, до тех пор, пока не дойдем до какого-либо числа, помимо 1. Если мы получим в итоге что-то, кроме -1, тогда n будет составным.
Если говорить более формально, то пускай 2S будет самой большой степенью 2, делящейся на n-1, то есть n−1=2Sq для какого-то нечетного числа q. Каждое число из последовательности
an−1 = a(2^S)q, a(2^S-1)q,…, aq.
Это квадратный корень предшествующего члена последовательности.
Тогда если n – простое число, то последовательность должна начинаться с 1 и каждое последующее число тоже должно быть 1, или же первый член последовательность может быть не равен 1, но тогда он равен -1.
Тест Миллера-Рабина берет случайное a∈ Zn. Если вышеуказанная последовательность не начинается с 1, либо же первый член последовательности не равен 1 или -1, тогда n – не простое.
Оказывается, что для любого составного n, включая числа Кармайкла, вероятность пройти тест Миллера-Рабина равна примерно 1/4. (В среднем значительно меньше.) Таким образом, вероятность того, что n пройдет несколько прогонов теста, уменьшается экспоненциально.
Если n не проходит тест Миллера-Рабина с последовательностью начинающейся с 1, тогда у нас появляется нетривиальный квадратный корень из 1 по модулю n, и мы можем эффективно находить делители n. Поэтому числа Кармайкла всегда удобно раскладывать на множители.
Когда тест применяется к числам вида pq, где p и q – большие простые числа, они не проходят тест Миллера-Рабина практически во всех случаях, поскольку последовательность не начинается с 1. Итого, так мы RSA сломать не сможем.
На практике тест Миллера-Рабина реализуется следующим образом:
- Дано
n, нужно найтиs, такое чтоn – 1 = 2Sqдля некоторого нечетногоq. - Возьмем случайное
a ∈ {1,...,n−1} - Если aq = 1, то
nпроходит тест и мы прекращаем выполнение. - Для
i= 0, ... , s−1проверить равенствоa(2^i)q = −1. Если равенство выполняется, тоnпроходит тест (прекращаем выполнение). - Если ни одно из вышеприведенных условий не выполнено, то
n– составное.
Перед выполнением теста Миллера-Рабина стоит провести еще несколько тривиальных делений на маленькие простые числа.
Строго говоря эти тесты являются тестами на то считается ли число составным, поскольку они не доказывают по сути, что проверяемое число простое, но точно доказывают, что оно может оказаться составным.
Существуют еще детерминированные алгоритма работающие за полиномиальное время для определения простоты (Agrawal, Kayal и Saxena), однако на сегодняшний день они считаются непрактичными.
Аннотация: Для построения многих систем защиты информации требуются простые числа большой разрядности. В связи с этим актуальной является задача тестирования на простоту натуральных чисел. В лекции 2 рассматриваются тесты техника компьютерных вычислений с многоразрядными числами.
Определение 2.1 Время работы алгоритма 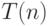




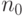


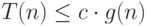
Пример 2.1 Докажем, что функция 

Действительно, положим 




Оценка сложности алгоритма — важнейший вопрос для криптографии, поскольку от оценки сложности решающим образом зависит стойкость соответствующей криптосистемы.
Далее мы будем рассматривать алгоритмы (в основном теоретико-числовые) и в большинстве случаев будем приводить оценку сложности представленного алгоритма.
2.1 Тестирование на простоту
Существует два типа критериев простоты: детерминированные и вероятностные. Детерминированные тесты позволяют доказать, что тестируемое число — простое. Практически применимые детерминированные тесты способны дать положительный ответ не для каждого простого числа, поскольку используют лишь достаточные условия простоты.
Детерминированные тесты более полезны, когда необходимо построить большое простое число, а не проверить простоту, скажем, некоторого единственного числа.
В отличие от детерминированных, вероятностные тесты можно эффективно использовать для тестирования отдельных чисел, однако их результаты, с некоторой вероятностью, могут быть неверными. К счастью, ценой количества повторений теста с модифицированными исходными данными вероятность ошибки можно сделать как угодно малой.
На сегодня известно достаточно много алгоритмов проверки чисел на простоту. Несмотря на то, что большинство из таких алгоритмов имеет субэкспоненциальную оценку сложности, на практике они показывают вполне приемлемую скорость работы.
На практике рассмотренные алгоритмы чаще всего по отдельности не применяются. Для проверки числа на простоту используют либо их комбинации, либо детерминированные тесты на простоту.
Детерминированный алгоритм всегда действует по одной и той же схеме и гарантированно решает поставленную задачу. Вероятностный алгоритм использует генератор случайных чисел и дает не гарантированно точный ответ. Вероятностные алгоритмы в общем случае не менее эффективны, чем детерминированные (если используемый генератор случайных чисел всегда дает набор одних и тех же чисел, возможно, зависящих от входных данных, то вероятностный алгоритм становится детерминированным).
2.1.1 Вероятностные тесты простоты
Для того чтобы проверить вероятностным алгоритмом, является ли целое число 






Если же 








рис.
1.1}).
2.1.2 Тест Ферма
Согласно малой теореме Ферма для простого числа 


Следовательно, если для нечетного 



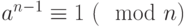

Вход: нечетное целое число 
Выход: «Число 

- Выбрать случайное целое число
,
.
- Вычислить
.
- При
результат: «Число
, вероятно, простое». В противном случае результат: «Число
составное».
На шаге 1 алгоритма мы не рассматриваем числа 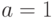





Сложность теста Ферма равна: 
Тест имеет существенный недостаток в виде наличия чисел Кармайкла. Это нечетные составные числа, для которых сравнение из формулы выполняется при любом 




Числа Кармайкла являются достаточно редкими. В пределах до 100000 существует лишь 16 чисел Кармайкла: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973, 75361.
2.1.3 Тест Леманна
Если для какого-либо целого числа 

то число 

Таким образом, получаем следующий вероятностный алгоритм проверки числа на простоту:
Вход: нечетное целое число 
Выход: «Число 

- Выбрать случайное целое число
,
.
- Вычислить
.
- При
и
результат: «Число
составное». В противном случае результат: «Число
, вероятно, простое».
Сложность теста Леманна равна 
2.1.4 Тест Соловея-Штрассена
В основе этого теста лежит следующая теорема:
Теорема 1.28 (критерий Эйлера) Нечетное число 



 |
( 2.1) |
где 


Критерий Эйлера лежит в основе следующего вероятностного теста числа на простоту:
Вход: нечетное целое число 
Выход: «Число 

- Выбрать случайное целое число
,
.
- Вычислить
.
- При
и
результат: «Число
составное».
- Вычислить символ Якоби
.
- При
результат: «Число
составное». В противном случае результат: «Число
, вероятно, простое».
На шаге 1 мы снова не рассматриваем числа 






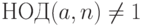
Сложность теста Соловэя-Штрассена определяется сложностью вычисления символа Якоби и равна 
Для теста Соловея-Штрассена не существует чисел, подобных числам Кармайкла, то есть составных чисел, которые были бы эйлеровыми псевдопростыми по всем основаниям 
2.1.5 Тест Миллера-Рабина
На сегодняшний день для проверки чисел на простоту чаще всего используется тест Миллера-Рабина, основанный на следующем наблюдении. Если 

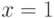

Пусть число 





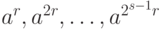




Это свойства лежит в основе следующего теста:
Вход: нечетное целое число 
Выход: «Число 

- Представить
в виде
, где число
— нечетное.
- Выбрать случайное целое число
,
, взаимно простое с
.
- Вычислить
.
- При
и
выполнить следующие действия.
- Результат: «Число
, вероятно, простое».
В результате выполнения теста для простого числа 
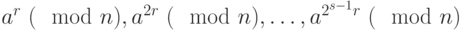







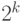

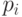


Поэтому 
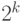
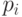

Сложность теста Миллера-Рабина равна 
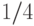
2.1.6 N — 1-алгоритмы генерации простых чисел
Перечислим некоторые теоремы, которые могут быть использованы для генерации доказуемо простых чисел [1].
Теорема 2.1 (Прот, 1878) Пусть 





 |
( 2.2) |
Для генерации простого числа нужно перебирать числа 


Недостатком этого подхода является плохое распределение генерируемых простых чисел: все они будут иметь вид 




Теорема 2.2 (Диемитко, 1988) Пусть 




то 
С помощью этой теоремы генерировать простые числа можно итерационно. На вход каждой итерации подаётся какое-либо простое число 




На заключительной итерации желательно выбирать как можно меньшее число 




Эта теорема лежала в основе алгоритма генерации простых чисел для алгоритма цифровой подписи ГОСТ 34.10-94, пока этот алгоритм не был заменён на новый, основанный на группе точек эллиптической кривой.
В этом пункте
будут доказаны важнейшие теоремы теории
чисел и показаны их приложения к задачам
криптографии.
Теорема Эйлера.
При m
> 1, (a,
m)
= 1
aφ(m)
≡ 1 (mod
m).
Доказательство:
Если x
пробегает приведенную систему вычетов
x
= r1,
r2,…,rc
(c
= φ(m)),
составленную из наименьших неотрицательных
вычетов, то в силу того, что (a,m)=1,
наименьшие неотрицательные вычеты
чисел ax
= ρ1,
ρ2,…,
ρc
будут
пробегать ту же систему, но, возможно,
в другом порядке (это следует из
утверждения 2 пункт 3). Тогда, очевидно,
r1·…·rc
= ρ1·…
·ρc
*
Кроме того,
справедливы сравнения
ar1
≡ ρ1(mod
m),
ar2
≡ ρ2(mod
m),
… , arc
≡ ρc(mod
m).
Перемножая данные
сравнения почленно, получим
ac
·r1
·r2
·…·rc
≡ ρ
1·…· ρ
c(mod
m)
Откуда в силу (*)
получаем
ac
≡ 1 (mod
m)
А поскольку
количество чисел в приведенной системе
вычетов по модулю m
есть φ(m),
то есть c
= φ(m),
то
aφ(m)
≡ 1 (mod
m).
□
Теорема Ферма
(малая)
р
– простое, p
не делит
a
ap–1
≡ 1 (mod
m)
Доказательство:
по теореме Эйлера при m=p.
Важное следствие:
ap
≡ a
(mod
p)
a,
в том числе и для случая pa.
Теорема Эйлера
применяется для понижения степени в
модулярных вычислениях.
Пример:
10100
mod
11 = 109∙11+1
= 109+1
mod
11 = (–1)10
mod
11 = 1.
Следствие:
Если
a:
0 < a
< p,
для которого ap–1
1
(mod
p)
p
– составное.
Отсюда –
Тест Ферма на простоту
Вход: число n
– для проверки на простоту, t
– параметр надежности.
-
Повторяем t
раз:
а) Случайно выбираем
a
[2, n-2]
б) Если an–1
1
(mod
n)
«n
– составное». Выход.
-
«n
– простое с вероятностью 1–
εt
»
Этот тест может
принять составное число за простое, но
не наоборот.
Вероятность ошибки
есть εt,
где ε
В случае составного
числа n,
имеющего только большие делители, ε,
то есть существуют числа, для которых
вероятность ошибки при проверке их на
простоту тестом Ферма близка к 1.
Для теста Ферма
существуют так называемые числа
Кармайкла
– такие составные числа, что
a:
(a,n)
= 1
an–1
≡ 1(mod
n).
То есть числа Кармайкла – это такие
составные числа, которые всегда
принимаются тестом Ферма за простые,
несмотря на то, как велико число t
– параметр надежности теста.
Теорема
Кармайкла
n
– число Кармайкла
1)n
свободно от квадратов (т.е. n
= p1∙p2∙…∙pk);
2) (pi
– 1)(n
– 1), i
= 1,…,k
;
3) k
.
Наименьшее
известное число Кармайкла
n=561
= 3∙11·17
3.7. Применение теоремы Эйлера в rsa:
Если известно
разложение числа на простые сомножители
a
= p1p2
…
pn,
то легко вычислить функцию Эйлера φ(a).
Отсюда вывод:
сложность вычисления функции Эйлера
не выше сложности задачи факторизации
.
Покажем, что в
случае n=pq
(p,q
– простые числа, pq)
задачи нахождения функции Эйлера и
факторизации эквивалентны. (то есть в
случае, когда n
– модуль RSA).
Учтем, что φ(n)
= (p
– 1)(q
– 1). Тогда имеем систему
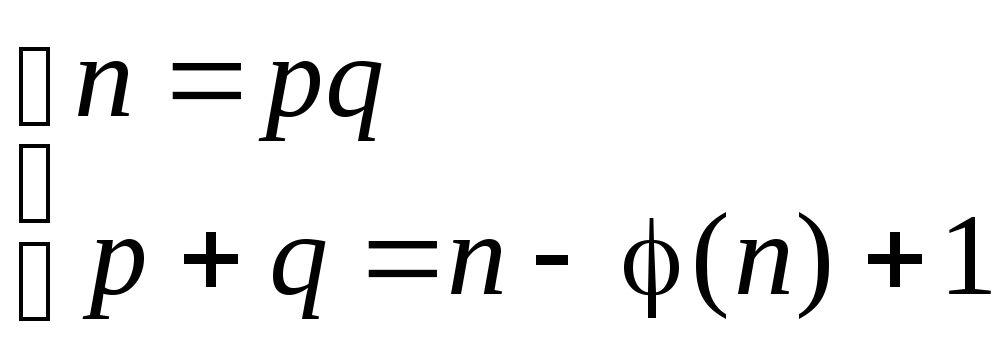
Зная n
и φ(n),
находим p
и q
из системы, приведенной выше, следующим
образом:
Первое уравнение
системы является квадратным уравнением
относительно q,
q
=
, где Dq
= [n–
φ(n)+1]2
– 4n.
Подставляя
полученное q
во второе уравнение системы, находим
p.
Видим, что при
нахождении чисел p,
q
по известным n,
φ(n)
применяются только «дешевые» в смысле
времени операции – сложение, деление
на 2. Только при вычислении дискриминанта
приходится применять возведение в
степень, а при вычислении q
– извлечение квадратного корня. Однако
эти операции производятся однократно,
поэтому временные затраты не столь
существенны.
Итак, для модуля
RSA
задачи нахождения функции Эйлера и
факторизации равносложны.
Формулировка
теоремы Эйлера для RSA:
n
= pq;
p≠q;
p,
q
– простые числа
a
выполняется akφ(n)+1≡
a
(mod
n).
(на самом деле n
может быть просто свободно от квадратов,
то есть произведением произвольного
количества различных простых чисел)
Доказательство:
Возможны два
случая:
-
(a,
n)
= 1
по теореме Эйлера aφ(n)
≡ 1 (mod
n)
akφ(n)+1
= 1k
∙a
≡ a
(mod n).
-
(a,
n)
≠ 1, n
не делит a
в силу основного свойства простых
чисел, либо p
a,
либо q
a.
Не нарушая общности,
предположим, что pa,
q
не делит a.
Тогда по теореме
Ферма, akφ(n)+1≡a(mod
p),
qq–1≡1
(mod q)
akφ(n)+1≡1k(p–1)·a
≡ a
(mod q).
Итак,
akφ(n)+1
≡ a
(mod p),
akφ(n)+1≡
a
(mod q).
Отсюда по
св-ву сравнений №12, akφ(n)+1≡
a(mod
НОК(p,q)).
В силу простоты p
и q,
НОК(p,q)=pq=n,
значит
akφ(n)+1≡
a
(mod n).
-
na
a≡0(mod
n)
akφ(n)+1≡0≡a(mod
n).
□
Примечание:
Если вместо φ(n)
в теореме Эйлера для RSA
взять НОК(p–1,
q–1),
теорема все равно будет верна.
Применение
теоремы Эйлера в RSA:
Напомним, что
криптосистема RSA
является системой с открытым ключом.
В качестве параметров системы выбираются
различные большие простые числа p
и
q,
вычисляется n=pq,
φ(n)=(p–1)(q–1),
выбирается число e:
2<e<n,
(e,
φ(n))=1
и вычисляется d=e-1(mod
φ(n)).
В качестве открытого ключа берется
пара (n,
e),
в качестве закрытого, хранимого в
секрете, четверка (p,
q,
φ(n),
d).
Для того, чтобы
зашифровать открытый текст x,
абонент, пользуясь открытым ключом,
вычисляет зашифрованный текст y
по следующей формуле:
y
= xe
mod
n.
Для того, чтобы
осуществить расшифрование, владелец
секретного ключа вычисляет
x
= yd
mod
n.
В результате
такого расшифрования действительно
получится открытый текст, поскольку
yd
mod
n=xed
mod
n=xed
mod
φ(n)mod
n
=x1
mod
n=x.
Без знания простых
сомножителей p
и q
сложно вычислить значение функции
Эйлера φ(n),
а значит, и степень d,
в которую следует возводить зашифрованный
текст, чтобы получить открытый.
Более того, знание
простых сомножителей p
и q
может
значительно облегчить
процедуру возведения шифрованного
текста y
в степень d.
Действительно, пользуясь теоремой
Эйлера для RSA,
можем понизить степень d.
Разделим d
на φ(n)
с остатком:
d=kφ(n)+r
x=yd
mod
n=
ykφ(n)+r
mod
n=
yr
mod n.
Еще более можно
понизить степень, используя НОК(p–1,q–1)=
вместо φ(n).
Пример:
n=19∙23=,
φ(n)=18∙22=396,
d=439.
НОК(18,22)=18∙22/2=198.
d
mod
φ(n)=43.
d
mod
НОК(p–1,q–1)=43.
Число d=439
в двоичном представлении есть 110110111.
Поэтому возведение в степень d
c
применением дихтономического алгоритма
(см. гл.2) требует 8 возведений в квадрат
и 6 умножений чисел.
Число 43 в двоичном
представлении есть 101011. Возведение в
степень 43 требует 5 возведений в квадрат
и 3 умножения чисел. Кроме того, для
вычисления φ(n)
требуется 1 операция умножения.
Таким образом,
для данного примера экономия времени
составляет 2 сложные операции.
В случае больших
простых делителей числа n
экономия оказывается более существенной.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тест простоты — алгоритм, который по заданному натуральному числу определяет, простое ли это число. Различают детерминированные и вероятностные тесты.
Определение простоты заданного числа в общем случае не такая уж тривиальная задача. Только в 2002 году было доказано, что она полиномиально разрешима. Тем не менее, тестирование простоты значительно легче факторизации заданного числа.
*-Нравится статья? Кликни по рекламе!
Мы уже разобрали методы выбора всех простых чисел, до определенного, в статье Простые числа. Пришло время рассмотреть ряд алгоритмов, под общим названием — «Тесты простоты»:
1.) Перебор делителей:
Перебор делителей — алгоритм факторизации или тестирования простоты числа путем полного перебора всех возможных потенциальных делителей.
Описание алгоритма:
Обычно перебор делителей заключается в переборе всех целых (как вариант: простых) чисел от 2 до квадратного корня из факторизуемого числа n и в вычислении остатка от деления n на каждое из этих чисел. Если остаток от деления на некоторое число m равен нулю, то m является делителем n. В этом случае либо n объявляется составным, и алгоритм заканчивает работу (если тестируется простота n), либо n сокращается на m и процедура повторяется (если осуществляется факторизация n). По достижении квадратного корня из n и невозможности сократить n ни на одно из меньших чисел, n объявляется простым.
Примечание: если у n есть некоторый делитель p, то n/p так же будет делителем, причем одно из этих чисел не превосходит .
Реализация на Python:
def divider(n):
i = 2
j = 0 # флаг
while i**2 <= n and j != 1:
if n%i == 0:
j = 1
i += 1
if j == 1:
print ("Это составное число")
else:
print ("Это простое число")
2.) Теорема Вильсона
Теорема теории чисел, которая утверждает, что
p — простое число тогда и только тогда, когда (p − 1)! + 1 делится на p
Практическое использование теоремы Вильсона для определения простоты числа нецелесообразно из-за сложности вычисления факториала. Таким образом, время выполнения данного алгоритма = поиску факториала. Алгоритм поиска факториала мы уже рассматривали.
Реализация:
def prime(n):
if (math.factorial(n-1)+1) % n!=0:
print ("Это составное число")
else:
print ("Это простое число")
3.) Тест простоты Ферма
Первый вероятностный метод, который мы обсуждаем, — испытание простоты чисел тестом Ферма.
Если n — простое число, то an-1 1 mod n.
Обратите внимание, что если n — простое число, то сравнение справедливо. Это не означает, что если сравнение справедливо, то n — простое число. Целое число может быть простым числом или составным объектом. Мы можем определить следующие положения как тест Ферма:
Простое число удовлетворяет тесту Ферма. Составной объект может пройти тест Ферма с вероятностью . Сложность разрядной операции испытания Ферма равна сложности алгоритма, который вычисляет возведение в степень.Поскольку вычисление
(mod N) довольно быстрая операция, у нас возникает быстрый тест, проверяющий, является ли данное число составным. Его называют тестом Ферма по основанию а. Заметим, что тест Ферма может лишь убедить нас в том, что число N имеет делители, но не в состоянии доказать его простоту. Действительно, рассмотрим составное число N = 11 · 13 = 341, а основание в тесте Ферма выберем равным 2. Тогда
= 1 mod 341, в то время как число 341 не простое. В этом случае говорят, что N — псевдопростое число (в смысле Ферма) по основанию 2. Существует бесконечно много псевдопростых чисел по фиксированному основанию, хотя они встречаются реже, чем простые. Можно показать, что для составного N вероятность неравенства
≠ 1 (mod N).
больше 1/2. Подводя итог сказанному, выпишем алгоритм теста Ферма.
def primFerma(a,n):
if a**(n-1)%n==1:
print "правдоподобно простое"
else:
print "составное"
Если на выходе этого алгоритма напечатано «составное, а», то мы с определенностью можем заявить, что число n не является простым, и что а свидетельствует об этом факте, т. е. чтобы убедиться в истинности высказывания, нам достаточно провести тест Ферма по основанию а. Такое а называют свидетелем того, что n составное.
Если же в результате работы теста мы получим сообщение: «правдоподобно простое», то можно заключить: n — составное с вероятностью ≤ существуют составные числа, относительно которых тест Ферма выдаст ответ правдоподобно простое, для всех взаимно простых с n оснований а. Такие числа называются числами Кармайкла. К сожалению, их бесконечно много. Первые из них — это 561, 1105 и 1729. Числа Кармайкла обладают следующими свойствами:
- они нечетны,
- имеют по крайней мере три простых делителя,
- свободны от квадратов1,
- если р делит число Кармайкла N, то р — 1 делит N — 1.
Чтобы получить представление об их распределении, посмотрим на числа, не превосходящие. Среди них окажется примерно 2, 7 •
простых чисел, но только 246 683 ≈ 2,4 •
чисел Кармайкла. Следовательно, они встречаются не очень часто, но и не настолько редко, чтобы их можно было игнорировать.
4.)Тест Миллера — Рабина
Вероятностный полиномиальный тест простоты. Тест Миллера — Рабина позволяет эффективно определять, является ли данное число составным. Однако, с его помощью нельзя строго доказать простоту числа. Тем не менее тест Миллера — Рабина часто используется в криптографии для получения больших случайных простых чисел.
Алгоритм был разработан Гари Миллером в 1976 году и модифицирован Майклом Рабином в 1980 году.
Пусть — нечётное число большее 1. Число
однозначно представляется в виде
, где
нечётно. Целое число
,
, называется свидетелем простоты числа
, если выполняется одно из условий:
или
Теорема Рабина утверждает, что составное нечётное число m имеет не более различных свидетелей простоты, где
— функция Эйлера.
Алгоритм Миллера — Рабина параметризуется количеством раундов r. Рекомендуется брать r порядка величины log2(m), где m — проверяемое число.
Для данного m находятся такие целое число s и целое нечётное число t, что m − 1 = 2st. Выбирается случайное число a, 1 < a < m. Если a не является свидетелем простоты числа m, то выдается ответ «m составное», и алгоритм завершается. Иначе, выбирается новое случайное число a и процедура проверки повторяется. После нахождения r свидетелей простоты, выдается ответ «m, вероятно, простое», и алгоритм завершается. Как и для теста Ферма, все числа n > 1, которые не проходят этот тест – составные, а числа, которые проходят, могут быть простыми. И, что важно, для этого теста нет аналогов чисел Кармайкла.
В 1980 году было доказано, что вероятность ошибки теста Рабина-Миллера не превышает 1/4. Таким образом, применяя тест Рабина-Миллера t раз для разных оснований, мы получаем вероятность ошибки 2-2t.
def toBinary(n):
r = []
while (n > 0):
r.append(n % 2)
n = n / 2
return r
def MillerRabin(n, s = 50):
for j in xrange(1, s + 1):
a = random.randint(1, n - 1)
b = toBinary(n - 1)
d = 1
for i in xrange(len(b) - 1, -1, -1):
x = d
d = (d * d) % n
if d == 1 and x != 1 and x != n - 1:
return True # Составное
if b[i] == 1:
d = (d * a) % n
if d != 1:
return True # Составное
return False # Простое
Ещё реализации:
- http://en.literateprograms.org/Miller-Rabin_primality_test_%28Python%29
- http://code.activestate.com/recipes/410681-rabin-miller-probabilistic-prime-test/
- http://code.activestate.com/recipes/511459-miller-rabin-primality-test/
UPD:На сладкое, нашел на Хабре статейку, где предлагали следующее регулярное выражение для определения простоты числа:
/^1?$|^(11+?)1+$/
Применять его следует не к самому целому числу. Вместо этого, нужно создать строку из единиц, где количество единиц соответствует самому числу и уже к этой строке применить регулярное выражение. Если совпадения нет — число простое. Так как же оно работает? Подвыражение (11+?) совпадает со строками вроде 11, 111, и т.д… Часть «1+» будет искать далее по строке совпадения с результатами поиска первого подвыражения. В первый раз совпадение произойдет по строке «11» и потом поиск строки «11» будет произведен снова, а затем снова до конца строки. Если поиск завершится успешно, число не является простым. Почему? Потому, что будет доказано, что длина строки делится на 2 и, соответственно, само число тоже делится на два. Если совпадения не произойдет, движок регулярных выражений начнет искать строку «111» и ее повторения. Если первое подвыражение становится достаточно длинным (n/2) и совпадений по-прежнему не будет обнаружено, число будет являться простым.
Реализовывать я его не стал, не люблю регулярки(если кто напишет, жду в комменты, добавлю).
Используемая литература:
- http://younglinux.info/algorithm/divider
- Тест простоты
- http://masteroid.ru/content/view/1292/49/
- http://www.intuit.ru/department/security/mathcryptet/
- http://www.re.mipt.ru/infsec/2005/essay/2005_Primality_tests_survey__Kuchin.htm
- http://algolist.manual.ru/maths/teornum/rabmil.php
Проверка простых чисел
Общее
В данной статье вы увидите обзор известных алгоритмов проверки чисел на простоту. На сегодня не существует единого алгоритма для определения всех простых чисел. Все методы проверки делят на две группы: вероятностные проверки и детерминированные. Детерминированные методы определяют точно, является ли число простым. Вероятностные проверки определяют число на простоту с некой вероятностью ошибки. Многократное повторение для одного числа, но с разными переменными, разрешает сделать вероятность ошибки сколь угодно малой величины.
Быстрые тесты для малых чисел и вероятно простые числа
Малые простые числа
Пока не было нужды в генерации больших простых чисел, можно было реализовывать методы проверки без применения вычислительной техники. Первым из таких методов является полный перебор всех возможных делителей. Есть модификация, которая не хуже всего перебора, называется — пробное деление. Он заключается в делении на предыдущие простые числа либо равные корню из этого числа. Для такого метода можно использовать решето Эратосфена.
Малая теорема Ферма
Французский математик Пьер Ферма в 17 веке выдал закономерность, которая лежит в основе почти всех методов проверки на простоту.
Малая теорема Ферма — Если P простое и A — любое целое, то AP = A (mod P). Если P не делит А, то АP-1 = 1 (mod P). На основе такой теоремы, можно создать мощный алгоритм на простоту:
- Тест Ферма: Для n > 1 выбираем a > и вычисляем An-1 mod n, если результат не 1, то n составное число, если 1, то n — слабо возможно простое по основанию a (a-PRP)
Часть чисел проходящие Тест Ферма являются составными, и их называют псевдопростыми.
Тест Рабина-Миллера
Можно улучшить тест Ферма, заметив, что если n — простое нечетное, то для 1 есть только два квадратных корня по модулю n: 1 и -1. По этому квадратный корень из An-1, A(n-1)/2 равен минус или плюс еденице. Если (n-1)/2 опять нечетно, то можно снова извлечь корень и тд. Первый вариант алгоритма определяет только одно деление:
- Тест Леманна: Если для любого целого числа А меньшего n не выполняется условие A(n-1)/2 = ± 1 (mod n), то число n — составное. Если это условие выполнено, то число n — возможно простое с вероятностью ошибки не больше 50%.
- Тест Рабина-Миллера: Запишем (n-1) в виде 2sd, где d нечетно, а s — неотрицательно: n называют сильно возможно простым по основанию A (A-SPRP), если реализуется одно из двух условий:
- Ad = 1 (mod n)
- (Ad)2r = -1 (mod n), для любого неотрицательного r < s
В 1980 году была доказана вероятность ошибки теста Рабина-Миллера не превышающая 1/4. Реализуя этот тест T раз для разных оснований, мы получим вероятность ошибки 2-2t
Объединение тестов
Классические тесты
Проверки чисел вида n + 1
Тест заключается в том, что мы должны знать частичное или полное разложение на множители числа n — 1. Разложение на множители n — 1 просто найти, если n имеет определенный вид.
- Тест Лукаса: N ≥ 3. Если для каждого простого q, делящего n — 1 есть целое А такое что:
- An-1 = 1 (mod n) и
- A(n-1)/q ≠ 1 (mod n), то n — простое
Для такой проверки нужно знать полное разложение n — 1 на простые множители. Более мощная версия определяет знание не полного, а частичного разложения n — 1 на простые множители. Такой вариант алгоритма был выдан Поклингтоном в 1914 году.
- Тест Поклингтона: N ≥ 3 и n = FR + 1 (F делит n-1), причем F > R, НОД (F,R) = 1 и известно разложение F на простые множители. Тогда, если для любого простого q, делящего F есть такое целое A > 1, что:
- An-1 = 1 (mod n) и
- НОД (A(n-1)/q — 1, n) = 1
- Теорема Пепина: пусть Fn это n-е число Ферма и n > 1, тогда Fn — простое тогда и только тогда, когда 3(Fn — 1)/2 = 1 (mod Fn
- Теорема Прота: Пусть n = h × 2k + 1, причем 2k > h. Если есть такое целое A, что A(n-1)/2 = -1 (mod n), то n — простое
На основе теоремы Прота было найдено пятое по величине из известных простых чисел — 28433 × 27830457
Проверки чисел вида n — 1
Здесь рассмотрим числа только определенного вида. 7 из первых 10 позиций по самым большим известным простым числам были найдены с помощью чисел Мерсенна. Числа Мерсенна называют числа вида 2s -1.
Лукасом и Лемером в 1930 году было создано следующее утверждение: пусть s — простое, тогда число Мерсенна n = 2s — 1 является простым тогда, когда S (n — 2) = 0, где S(0) = 4 и S(k+1) = S(k)2 — 2 (mod n). На основе такого факта можно создать проверку на простоту, которая точно скажет нам, является ли для заданного s число Мерсенна простым.
- Тест Лукаса-Лемера:
- С помощью пробного деления проверяем, является ли данное s простым, если нет, то получившееся число Мерсенна — составное
- Задаем S(0) = 4
- Для k от 1 до s — 2 вычисляем S(k) = S(k-1)2 — 2 (mod n)
- Если в результате получился 0, то число Мерсенна простое
Неоклассические алгоритмы ARP и ARP-CL
Можно рассматривать числа в виде n2 + n + 1 или n2 — n + 1. А можно рассмотреть число вида nm — 1 для больших m. Тогда любое просто число q такое, что q — 1 делит m, по малой теореме Ферма будет делить nm — 1.
Было представлено, что всегда существует целое число m:
- m < (log n)log log log n
Эллиптические кривые: ECPP
Современные вариант проверок на простоту основан на теореме Поклингтона, но для эллиптических кривых. Смысл алгоритма заключается в переходе от групп порядка n — 1 и n + 1 к достаточно большему диапазону размеров групп.
AKS
В 2002 году летом индийские математики Аграавал, Саксен и Кайал нашли полиномиальный детерминированный алгоритм проверки числа на простоту. Их метод основан на версии малой теоремы Ферма:
- Теорема: Пусть A и P взаимно простые целые числа и P > 1. Число P является простым, когда (x — a)p = (xp — a) (mod p)
- Доказательство: Если p — простое, то p делит биномиальные коэффициенты pCr для r = 1,2 ..p-1. Пусть p — составное, и пусть q — простой делитель p. Пусть qk максимальная степень q которая делит p. Тогда qk не делит pCr и взаимно просто с Ap-q. Отсюда, коэффициент перед xq в левой части требуемого равенства не равен нулю, а в правой равен. Алгоритм для числа n ≥ 23 (странное число получается из одного из требований для корректной работы алгоритма)
if (n is has the form ab with b > 1) then output COMPOSITE
r := 2
while (r < n) {
if (gcd(n,r) is not 1) then output COMPOSITE
if (r is prime greater than 2) then {
let q be the largest factor of r-1
if (q > 4sqrt(r)log n) and (n(r-1)/q is not 1 (mod r)) then
break
}
r := r+1
}
for a = 1 to 2sqrt(r)log n {
if ( (x-a)n is not (xn-a) (mod xr-1,n) ) then output COMPOSITE
}
output PRIME;
Итоги
| Тест | Тип теста | Где используется |
|---|---|---|
| Пробное деление | детерминированный | Из-за большой вычислительной сложности в чистом виде не используется. Пробное деление на маленькие простые числа реализуется во многих тестах как один из шагов |
| Ферма | вероятностный | В чистом виде не реализуется. Может быть одним из первых шагов на проверку простоты для очень больших чисел |
| Леманна | верляьнлсьный | Не используется |
| Рабина-Миллера | вероятностный | В чистом виде может реализовываться в криптосистемах с открытым ключом для реализации простых ключей длиной 512, 1024 и 2048 бит. |
| Миллера | детерминированный | На практике не используется, так как пока не доказана расширенная гипотеза Римана |
| Лукаса | детерминированный | Для получения больших простых чисел определенного вида |
| Поклингтона | детерминированный | Для получения больших чисел с частично известной факторизацией n — 1 |
| Петина | детерминированный | Для получения больших простых чисел Ферма |
| Прота | детерминированный | Для получения больших простых чисел определенного вида |
| Лукаса-Лемера | детерминированный | Для получения больших простых чисел Мерсенна |
| APR | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| ECPP | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| AKS | детерминированный | В качестве детерминированной полиномиальной проверки на простоту |
Из таблицы видно, что разные методы проверки на простоту служат для двух целей:
- для получения очень больших целый чисел
- для генерации простых чисел определенного размера для реализации в криптографии
Аналитическую работу провел студент (ГУ МФТИ) кафедры радиотехники Кучин Борис.
Калькулятор выполняет тест простоты Миллера-Рабина и выясняет может ли заданное число быть простым или нет. Если ответ отрицательный — число составное, если ответ положительный, то число с большой вероятностью простое. Тест использует заданное число оснований (пробных свидетелей простоты), которые вводятся списком или генерируются случайным образом в диапазоне от 2 до n-1, где n — проверяемое число. Калькулятор может выдавать пошаговую детализацию работы теста. Информацию по алгоритму Миллера-Рабина можно найти сразу за калькулятором.
Тест простоты Миллера-Рабина
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Алгоритм теста простоты Миллера-Рабина
Для проверки на простоту числа алгоритмом Миллера-Рабина мы должны привести четное число n-1 число к виду 2sd, где n-тестируемое число, d — нечетное число, s — степень двойки. Числа s и d можно получить последовательным делением n-1 на 2.
Тогда мы проверяем, что для любого целого a, в диапазоне [2..n-1], справедливо хотя бы одно из условий:
В условии 2. r берется в диапазоне [0..s).
Если хотя бы одно условие выполняется — значит выбранное a — является свидетелем простоты числа n, и число n с большой вероятностью может быть простым. Для увеличения этой вероятности мы повторяем тест для другого случайно выбранного основания.
Если оба условия не выполняются, то число n — составное и дальнейшее тестирование можно прекратить.
Тест Миллера-Рабина успешно справляется с числами Кармайкла, которые не поддаются тесту Ферма. К примеру число 29341, ошибочно определяемое тестом Ферма, как возможно простое, определяется как составное тестом Миллера-Рабина, уже по основанию 3.
В отличие от теста Ферма, для теста Миллера-Рабина нет плохих тестируемых чисел. Для любого числа тест дает правильный ответ с большой вероятностью. Неверный результат работы определяется лишь случайным выбором пробных свидетелей, вероятность чего мала 1.
Согласно исследованию Рабина не более четверти чисел в диапазоне [1..n) не являются свидетелями2 (т.е. дают ошибочный результат в тесте Миллера-Рабина), поэтому, получая потенциальных свидетелей случайным образом k раз, вероятность ошибки теста будет не более 1/4k.
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А.
БОНЧ-БРУЕВИЧА»
(СПбГУТ)

Факультет
Инфокоммуникационных
сетей и систем
Кафедра
Защищенных
систем связи
ОТЧЕТ
ПО ЛАБОРТОРНОЙ РАБОТЕ №9
Проверка
заданного числа
(тема
отчета)
Направление/специальность
подготовки
10.03.01
Информационная безопасность
(код
и наименование направления/специальности)
Студенты:
(Ф.И.О.,
№ группы) (подпись)
Преподаватель:
Кушнир
Д.В.
(уч.
степень, уч. звание, Ф.И.О.) (подпись)
Оглавление
Теория…………………………………………………………………………….3
Ход
работы……………………………………………………………………….5
Теория
Тест Рабина-Миллера
Тест Миллера — Рабина —
вероятностный полиномиальный тест
простоты. Тест Миллера — Рабина позволяет
эффективно определять, является ли
данное число составным. Однако, с его
помощью нельзя строго доказать простоту
числа. Тем не менее тест Миллера — Рабина
часто используется в криптографии для
получения больших случайных простых
чисел.
Алгоритм был разработан Гари
Миллером в 1976 году и модифицирован
Майклом Рабином в 1980 году.
Как и для теста Ферма, все
числа m>1,
которые не проходят этот тест – составные,
а числа, которые проходят, могут быть
простыми. Для этого теста нет аналогов
чисел Кармайкла. В 1980 году было доказано,
что вероятность ошибки теста Рабина-Миллера
не превышает 1/4. Таким образом, применяя
тест Рабина-Миллера r
раз для разных
оснований, мы получаем вероятность
ошибки 2−2r.
Число m — 1 однозначно представляется в виде m — 1=2s∙t,
где t
нечётно.
Целое число a,
1< a < m,
называется свидетелем
простоты числа
m,
если выполняются два условия:
-
m
не
делится на a; -
at ≡ 1
mod m
или существует целое k,
0≤ k < s,
такое, что:
Теорема Рабина утверждает, что составное нечётное число m имеет не более
φ(m)/4
различных свидетелей простоты, где φ(m)
–
функция Эйлера.
Алгоритм теста Рабина-Миллера
Алгоритм
параметризуется
количеством
раундов
r.
Рекомендуется
брать
r
порядка
величины log2(m),
где
m
—
проверяемое
число.
Для
данного
m
находят
такое
целое
число
s
и
целое
нечётное
число
t,
что
m
−
1
= 2s∙t.
Выбирается
случайное
число
a,1
< a
< m.
Если
a
не
является
свидетелем
простоты
числа
m,
то
выдается
ответ
«m
— составное»,
и
алгоритм
завершается.
Иначе,
выбирается
новое
случайное
число
a
и
процедура
проверки
повторяется.
После
нахождения
r
свидетелей
простоты,
выдается
ответ
«m,
вероятно,
простое»,
и
алгоритм
завершается.
Алгоритм
может
быть
записан
на
псевдокоде
следующим
образом:
Ввод:
число
проверяемое на простоту:
m
> 2
(нечётное
натуральное);
параметр,
определяющий
вероятность
ошибки теста r.
Вывод:
составное,
означает,
что
m
точно
составное;
или
вероятно
простое,
т.е. m
с
высокой
вероятностью
является
простым.
Представить
m
−
1
в
виде
2s·t,
где
t
нечётно,
можно
сделать
последовательным
делением
m
— 1
на
2.
цикл
А:
повторить
r
раз:
Выбрать
случайное
a
в
диапазоне
[2,
m
−
2]
x
← at
mod
m
если
x
= 1
или
x
= m
−
1
то
перейти
на
следующую
итерацию
цикла
А
для
r
= 1
.. s
−
1
x
← x2
mod
m
если
x
= 1
то
вернуть
составное
если
x
= m
−
1
то
перейти
на
следующую
итерацию
цикла
А
вернуть
составное
вернуть
вероятно
простое
Из
теоремы
Рабина
следует,
что
если
r
случайно
выбранных
чисел
оказались
свидетелями
простоты
числа
m,
то
вероятность
того,
что
m
составное,
не
превосходит
4
—
r.
Пример
выполнения проверки:
Проверяем
число m = 221.
Запишем
m − 1 = 220 как (2^2)·55, таким образом s = 2 и t
= 55.
Произвольно
выберем число a такое, что 1 < a < m-1,
допустим a = 174. Переходим к вычислениям:
Шаг
1. a^((2^0)·t) mod m = 174^55 mod 221 = 47 ≠ 1, или
m − 1
Шаг
2. a^((2^1)·t) mod m = 174^110 mod 221 = 220 = m − 1.
Так как
220 ≡ −1 mod m,
число 221 или простое (174 —свидетель
простоты числа 221)
или составное,
(тогда 174 ложный свидетель простоты).
Возьмём
другое произвольное «a», на этот раз
выбрав a = 137:
Шаг
1. a^((2^0)·t) mod n = 137^55 mod 221 = 188 ≠ 1, m − 1
Шаг
2. a^((2^1)·t) mod n = 137^110 mod 221 = 205 ≠ m − 1.
Т.е. 221
– составное.
Так как
137 свидетель того, что 221 составное, число
174 на самом деле было ложным свидетелем
простоты.
Задание
Выбрать два простых и два
составных нечетных числа (не кратных 3
и 5) и еще одно составное число Кармайкла.
Выбирать числа для выполнения задания
по следующей формуле:
1. Вычисляем:
X=((№ студента в
группе)+110)*23. Далее произвольно в диапазоне
X±20 выбрать нужные числа
(если в группе один студент, то проверяем
4-ые числа, если два, то 8, если три то 12).
Число Кармайкла выбирать по следующему
алгоритму:
студент в группе с номером
1. Берёт число 1105
студент в группе с
номером 2. Берёт число 1729
студент в
группе с номером 3. Берёт число 2465
студент
в группе с номером 4. Берёт число
2821
студент в группе с номером 5. Берёт
число 6601
студент в группе с номером
6. Берёт число 8911
для студентов с
большими номерами выбирать число
Кармайкла циклически, 7-й берёт опять
число 1105 и т.п. Сколько человек в бригаде,
столько разных чисел Кармайкла должно
быть проверено.
-
Проверить каждое из чисел
тестом Рабина-Миллера. При выполнении
задания в EXCEL выбирать k
таком образом, чтоб вероятность принять
составное за простое была не более
0,0625. При программировании алгоритма
выбирать k таком образом,
чтоб вероятность принять составное за
простое была не более 10-3.
Ход
работы
X
= (25+110)*23= 3105
Простые
числа – 3119, 3121
Составные
числа – 3097, 3113
Число
Кармайкла – 1105
Алгоритм
проверки, реализованный на языке Python3
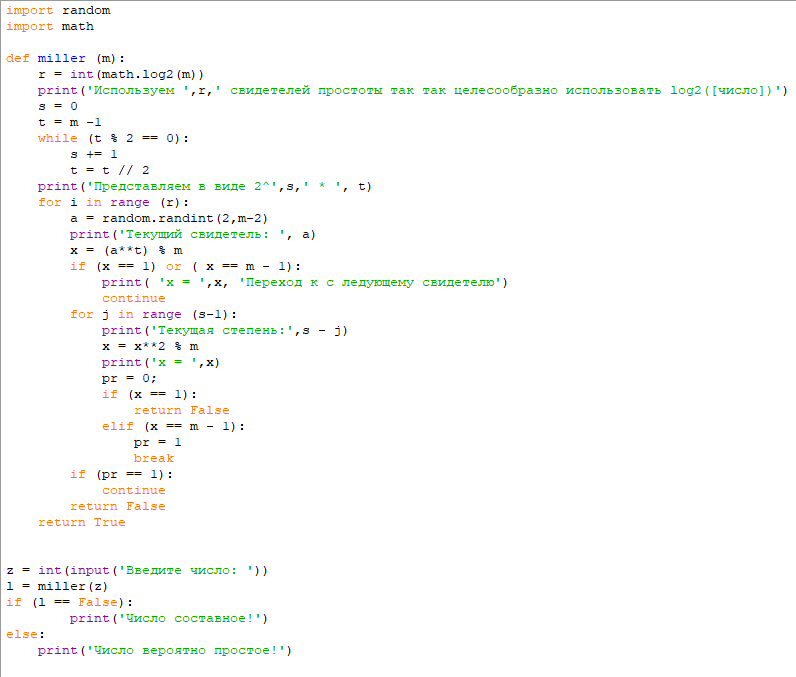
Результат
проверки чисел:
3119:
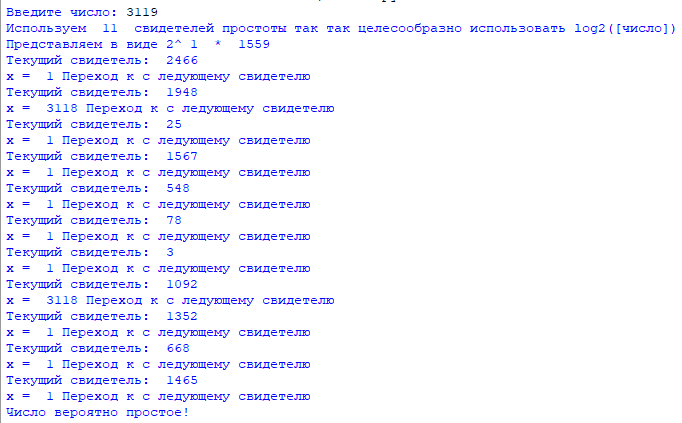
3121:

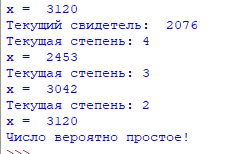
3097:
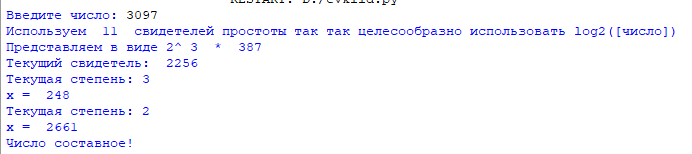
3113:
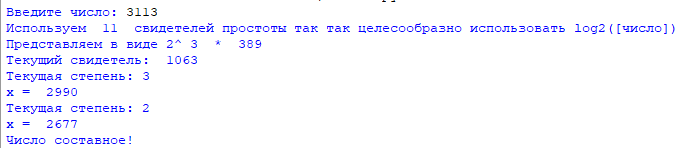
1105:
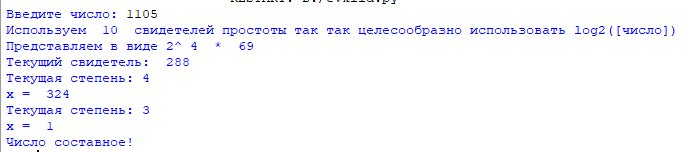
Санкт-Петербург
2021
Соседние файлы в предмете Математические основы защиты информации
- #
- #
09.04.20231.28 Кб4Lab_09.py
- #
- #
- #
- #
- #
- #
09.04.202311.87 Кб3Лаба 3.xlsx















 .
. .
. результат: «Число
результат: «Число 
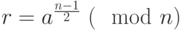 .
.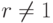 и
и  результат: «Число
результат: «Число 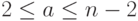 .
. .
. и
и  результат: «Число
результат: «Число  .
. результат: «Число
результат: «Число  .
. и
и  выполнить следующие действия.
выполнить следующие действия.