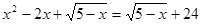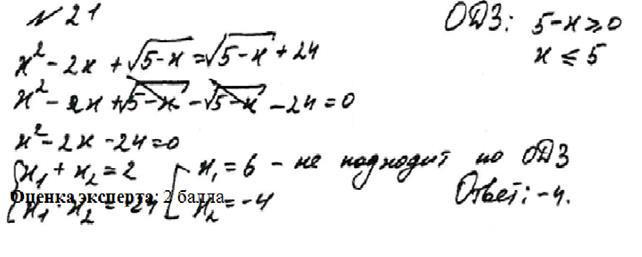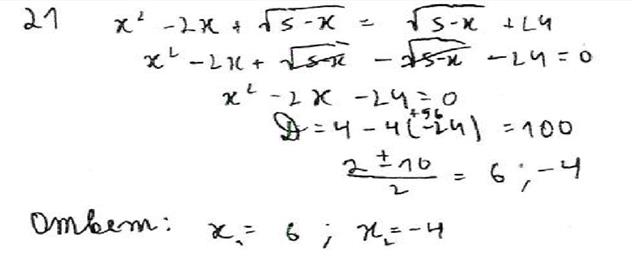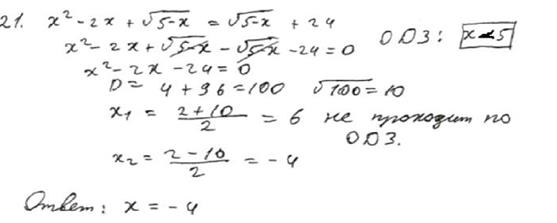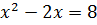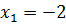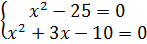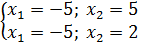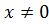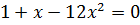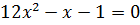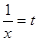Галсанова Людмила Баторовна
Магистрант, Бурятский государственный университет имени Доржи Банзарова (г. Улан-Удэ)
Учитель математики МБОУ Иройская СОШ Селенгинского района
ОГЭ по математике: типичные ошибки учащихся и пути их преодоления.
В данной статье говориться об ошибках учащихся, которые наиболее часто допускаются на ОГЭ по математике. Также рассматриваются пути решения данной проблемы для успешной сдачи экзамена.
Итоговая аттестация – первая серьёзная проверка освоения основной образовательной программы основного общего образования. Результаты, полученные выпускниками на ГИА – это и результат освоения ими школьной программы, и оценка работы учителя.
Специфика математики как школьного предмета состоит в том, что ее изучение в значительной степени строится на системе опорных знаний, без овладения которыми невозможно дальнейшее продвижение по курсу. В ходе ОГЭ учащийся должен продемонстрировать наличие у него опорных знаний, позволяющих изучать математику в старшей школе.
ОГЭ проверяет не только знания по предмету, но и умение читать и понимать прочитанное, внимательность и аккуратность в оформлении решений (запись ответов в бланк), умение проверять свои решения.
Можно утверждать, что полученные учащимися баллы в большинстве случаев могли бы быть значительно выше. Это возможно в случае, если школьники более критично отнеслись бы как к приводимым ими ответам, так и к заполнению бланков и записи решения задач с развернутым ответом.
Ошибки, которые допускают обучающиеся в 1 части экзаменационной работы, можно условно делить на три группы: технические, содержательные, связанные с невнимательным чтением условия задачи.
Технические ошибки – это, во-первых, неграмотное заполнение бланка с кратким ответом.
Рассмотрим примеры:
1) К заданиям, где требуется установить соответствие, а это соответствие в КИМах предлагается привести в форме таблицы, учащиеся нередко переносят в бланк ответов как «А2Б4В3», или «2,4,3», или «2;4;3», или «2 4 3» вместо верного «243».
2) Запятую или точку с запятой ученики также часто приводят и в ответах к заданиям, где требуется указать номера верных (неверных) утверждений, в то время как имеется указание на то, что ответом к этим заданиям является последовательность цифр, записанных в любом порядке без пробелов и использования других символов.
3) Нередко ученики в бланк ответов вписывают единицы измерения, что нельзя делать, – если единицы длины, веса и т.п. еще можно верифицировать вручную, то знак градусов компьютер может принять и за ноль.
4) Случается, что задача учащимся решена неверно и в неверном ответе содержится знак радикала – в этом случае следовало бы пересмотреть решение, но школьники упорно пытаются вписать знак арифметического квадратного корня в клетки бланка ответов.
5) В некоторых работах встречается, что числа написаны небрежно, иногда бывает невозможно понять, что написано 6 или 0, 5 или 6, 1 или 7, 3 или 9.
Далее – содержательные ошибки.
Все задания, которые имеют жизненные формулировки, имеют реальные числовые данные, поэтому следует сопоставлять ответ с реальной ситуацией, делать проверку, прикидку результата. Это относится и к «чисто математическим» задачам. Между тем, можно нередко встретить неверные ответы, для которых даже грубая прикидка говорит об их ошибочности.
Покажем это на нескольких примерах:
В задаче требуется найти высоту равностороннего треугольника со стороной 54√3. Приводимые иногда ответы «9» или «162» значительно меньше или больше верного – для исключения таких ответов достаточно попробовать привести геометрическую конструкцию с данными, которые известны в условии и получены в ответе.
Дана задача: «Найдите корень уравнения 
Дано задание: «27 выпускников школы собираются учиться в технических вузах. Они составляют 30% от числа выпускников. Сколько в школе выпускников?». Встречаются работы, в которых ответом к данной задаче указывалось число 8,1, что явно противоречит здравому смыслу.
Следующая группа ошибок в заданиях с кратким ответом связана с невнимательным чтением условия задачи.
Вот некоторые примеры:
В одном задании требовалось полученный ответ округлить до целого числа, чего не сделали некоторые учащиеся, записывая верный точный ответ с дробной его частью.
В задании требовалось указать номер первого отрицательного члена заданной последовательности. Видится, что приводимый иногда ответ «–3» явно не есть номер члена прогрессии, а сам этот член заданной прогрессии.
В задании на чтение графиков требовалось по заданной диаграмме указать число стран, а которых средний балл тестирования отличается от среднего балла российских участников не меньше, чем на 15. Учащиеся представляют ошибочный ответ — перечисляют названия стран, а не их количество.
Анализ выполнения заданий с развернутым ответом показывает, что одной из самых больших проблем выпускников 9 класса является прочтение условия задачи и его содержательная интерпретация на математический язык.
Задание № 20 – Алгебраические выражения, уравнения, неравенства и их системы.
Типичные ошибки:
— потеря корня;
— неправильно сформированный ответ;
— к нулю или между собой приравнены два абсолютно разных по значению выражения;
— содержательные ошибки, наличие которых не позволяло засчитать это задание;
— логически незавершенные решения при полученном верном ответе, что свидетельствует о несформированном навыке логически верно записывать интуитивно понятное решение;
— вычислительные ошибки.
Задание № 21 — Текстовая задача.
Типичные ошибки:
— перевод содержания задачи на математический язык;
— составление уравнений, связывающих данные величины и переменные, которые вводит учащийся;
— вычислительные ошибки при решении уравнения;
— наличие неправильно сформированного ответа в части отсутствия именованных величин.
Задание № 22 – Функции и их свойства. Графики функций.
Типичные ошибки:
— неправильно построен график;
— записано верное значение параметра, но не указано, как оно получено;
— отсутствуют единичный отрезок на координатных осях, направления координатных осей.
Задание № 23 — Уметь выполнять действия с геометрическими фигурами. Проводить доказательные рассуждения при решении задач.
Типичные ошибки:
— неверное построение чертежа к задаче;
— решают частную задачу, изменяя фактически ее смысл;
— неправильно указан признак подобия треугольников;
— неверно найдены сходственные стороны;
— неверно решена пропорция;
— вычислительные ошибки.
Задание № 24 — Проводить доказательные рассуждения при решении задач.
Типичные ошибки:
— неверное построение чертежа к задаче
— неполное доказательство;
— путают свойства и признаки параллелограмма;
— интуитивно понятные факты не доказывают, считая их очевидными, а также не умеют математически грамотно и ясно записывать решение, приводя при этом необходимые пояснения и обоснования.
Задание № 25 — Уметь выполнять действия с геометрическими фигурами. Решать планиметрические задачи на нахождение геометрических величин. Различать взаимное расположение геометрических фигур на плоскости, изображать геометрические фигуры; выполнять чертежи по условию задачи. Проводить доказательные рассуждения при решении задач.
Типичные ошибки:
-доказательство верное, но записи неаккуратные, иногда просто невозможно понять, что написано учеником;
— присутствуют только отдельные факты, по сути, не связанные с тем, что необходимо доказать;
— неправильно понимают условие задания;
— использовали неверные методы решения.
Выводы:
Основные проблемы, возникающие при написании выпускниками экзаменационной работы:
- неумение понять суть вопроса, содержание задания, приводящее к построению неверного хода решения;
- недостаточно развитые умения смыслового чтения, не позволяющие построить адекватную математическую модель по условию задания;
- вычислительные навыки слабо сформированы;
- неспособность грамотно сформулировать решение в письменном виде, небрежное оформлении письменного решения задачи;
- недостаточные геометрические знания, слабая графическая культура;
- неумение проводить анализ условия задания при решении практических и ситуационных задач, неумение применять известный алгоритм в нестандартной ситуации;
- недостаточно развиты аналитические навыки.
Пути преодоления:
1. Рабочая программа должна не только эффективно использовать учебное время при изучении текущего материала, организации повторения и подготовки выпускников к итоговой аттестации, но и составлять часть целостной системы, позволяющей учитывать освоение проблемных тем в каждом классе, а также ликвидировать пробелы в знаниях и умениях учащихся.
2. Необходимо проводить диагностические работы, направленные на выявление уровня подготовки учащихся по отдельным темам, что позволит спланировать индивидуальную и групповую работу обучающихся.
3. При изучении нового материала и его отработке необходимо сочетать различные методы обучения: традиционные и интерактивные, направленные на организацию самостоятельной работы каждого ученика, что также позволит устранить пробелы в знаниях и умениях, и поможет проводить подготовку к аттестации дифференцированно для слабых и сильных учеников.
4. Особое внимание следует уделять формированию навыков самоконтроля и самопроверки выполненных заданий.
5. Необходимо повышать уровень вычислительных навыков, развивать умение пользоваться справочными материалами, читать условие и вопрос задачи, записывать математически верно решение задачи, применять знания в нестандартных ситуациях.
6. Со слабоуспевающими школьниками необходимо выделить круг доступных ему заданий, помочь освоить основные математические факты, позволяющие их решать и сформировать уверенные навыки их решения. Для «средних» учеников необходимо использовать методику, при которой они смогут перейти от теоретических знаний к практическим навыкам, от решения стандартных алгоритмических задач к решению задач похожего содержания, но иной формулировки и применению уже отработанных навыков в новой ситуации. Для сильных учеников требуется создание условия для продвижения: дифференцированные по уровню сложности задания, возможность саморазвития, помощь в решении заданий второй части.
7. «Нарешивание» заданий Открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у учащихся общие учебные действия, способствующие более эффективному усвоению изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки.
8. В процессе подготовки к ОГЭ должны участвовать все стороны: дети, школа и родители, поэтому необходимо своевременно знакомить родителей с нормативными документами по подготовке к экзаменам, информировать их о процедуре итоговой аттестации, о всевозможных методических рекомендациях и ресурсах, о результатах пробных испытаний и текущей успеваемости.
ОГЭ -2021 по математике: типичные ошибки и пути их
преодоления
Воротницкая А.И.,
учитель математики
МБОУ «Мужевская
СОШ имени Н.В.Архангельского
Специфика математики как школьного предмета
состоит в том, что ее изучение в значительной степени строится на системе
опорных знаний, без овладения которыми невозможно дальнейшее продвижение по
курсу. В ходе ОГЭ учащийся должен продемонстрировать наличие у него
опорных знаний, позволяющих изучать математику в старшей школе.
Результаты ОГЭ по математике в этом году не
очень хорошие. Эти результаты уже привлекли внимание общественности всей
страны. Поэтому предлагаю поговорить о типичных ошибках учащихся и путях их
преодоления.
ОГЭ представляет собой форму государственной
итоговой аттестации, цель которой определить соответствие результатов освоения
ООП ООО соответствующим требованиям ФГОС
Результатом
освоения ООП ООО должна стать математическая компетентность выпускников.
Выпускники
должны:
·
овладеть
специфическими для математики знаниями и видами деятельности;
·
научиться
преобразованию знания и его применению в учебных и внеучебных ситуациях;
·
сформировать
качества, присущие математическому мышлению;
·
овладеть
математической терминологией, ключевыми понятиями, методами и приёмами.
Работа по математике состоит
из двух частей.
Часть 1, нацеленная на проверку овладения курсом на базовом уровне, содержит 19 заданий, в совокупности охватывающих все разделы курса и предусматривающих три формы ответа: задания с выбором ответа из четырех предложенных вариантов, задания с кратким ответом, задание на соотнесение
Часть 2 состоит из заданий повышенного и высокого
уровней сложности и
включает 6 заданий с развернутым ответом. Их назначение – дифференцировать хорошо успевающих обучающихся по уровням подготовки, выявить наиболее подготовленную часть выпускников. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности.
При проверке базовой
математической компетентности обучающиеся должны продемонстрировать:
— владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических
понятий, их свойств, приемов
решения задач и прочее);
— умение пользоваться математической записью;
— умение
применять знания в решении
математических задач, не сводящихся к прямому применению алгоритма;
— умение применять математические
знания в простейших практических ситуациях.
ОГЭ
проверяет не только знания по предмету, но и умение читать и понимать
прочитанное, внимательность и аккуратность в оформлении решений (запись ответов
в бланк), умение проверять свои решения.
Виды
типичных ошибок обучающихся на ОГЭ по математике:
1)
языковые
;
2) технические;
3) содержательные.
Для
преодоления языковых ошибок я применяю групповую, парную формы работы на
уроке, постоянно прошу обучающихся аргументировать свои ответы, часто провожу
устные диктанты и тематические зачеты (особенно по геометрии).
Для преодоления технических ошибок я систематически (ежемесячно) провожу
диагностические работы, которые помогают обучающимся вырабатывать
внимательность и приучают детей делать проверку в каждом задании.
Вероятные
причины затруднений и типичных ошибок в 2021 году:
·
Сложная
эпидемиологическая обстановка в 2019-2021 уч.годах: переход на дистанционное
обучение, что привело к сокращению времени на отработку материала.
·
Низкие
проценты выполнения заданий 3-5, 11-14 можно объяснить тем, что они
соответствуют трудно формируемым умениям у многих школьников: выполнять
преобразования со степенями, решение квадратных и линейных неравенств и их
систем, применение знаний в практических ситуациях, построение математической
модели, вычисление числовых характеристик прогрессии.
·
Геометрические
задачи также традиционно вызывают трудности у обучающихся.
·
Отсутствие
у обучающихся должного уровня развития логического мышления – одна из основных
причин затруднений в выполнении геометрических заданий.
Традиционно
основными направлениями подготовки обучающихся к ГИА по математике
являются:
1) Информационная
работа;
2) Психологическая
поддержка;
3) Предметная
работа.
Важно заранее
познакомить обучающихся с особенностями структуры КИМ и технологией проведения
экзамена. Используя образовательные сайты ФИПИ или ОБРНАДЗОР ознакомиться
самому и ознакомить родителей с нормативной базой ГИА. Настроить
ребят на то, что экзамен-это
возможность показать свои знания, поэтому не следует бояться и переживать.
Выработке психологической готовности помогает апробирование и отработка
формы проведения экзамена в формате и по материалам ОГЭ.
В
организации предметной подготовки необходимо обращать внимание на опорные
алгоритмы (формирование вычислительных навыков), на теоретическую подготовку
по геометрии (зачеты), учить составлять план решения задачи, решать геометрические
задач разного вида на применение теоретических знаний. Необходимо готовить
учащихся к использованию справочных материалов, усилить работу по формированию
языковых умений ( учить четко и лаконично выражать свои мысли при развернутом ответе),
«нарешивать» задачи с практическим содержанием, использовать различные формы (устный
счет, математический диктант) формирования алгоритмов и вычислительных навыков.
Итак,
считаю эффективными следующие пути преодоления типичных ошибок:
— необходимо
достаточно часто проводить диагностические работы, направленные на выявление
уровня подготовки обучающихся по отдельным темам, что позволит спланировать
индивидуальную и групповую работу обучающихся;
— при изучении
нового материала и его отработке необходимо сочетать различные методы обучения:
традиционные и интерактивные, направленные на организацию самостоятельной
работы каждого ученика, что также позволит устранить пробелы в знаниях и
умениях, и поможет проводить подготовку к аттестации дифференцированно для
слабых и сильных учеников;
— особое внимание
следует уделять формированию навыков самоконтроля и самопроверки выполненных
заданий;
— необходимо повышать
уровень вычислительных навыков, развивать умение пользоваться справочными
материалами, читать условие и вопрос задачи, записывать математически верно
решение задачи, применять знания в нестандартных ситуациях;
— со слабо
успевающими обучающимися необходимо выделить круг доступных ему заданий,
помочь освоить основные математические факты, позволяющие их решать и
сформировать уверенные навыки их решения;
— для «средних»
учеников необходимо использовать методику, при которой они смогут перейти
от теоретических знаний к практическим навыкам, от решения стандартных
алгоритмических задач к решению задач похожего содержания, но иной формулировки
и применению уже отработанных навыков в новой ситуации;
— для сильных
учеников требуется
создание условия для продвижения: дифференцированные по уровню сложности
задания, возможность саморазвития, помощь в решении заданий второй части;
— «нарешивание» заданий
открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но
его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у
учащихся общие учебные действия, способствующие более эффективному усвоению
изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки;
— учителю следует ставить
перед каждым учащимся ту цель, которую он может реализовать в соответствии с
уровнем его подготовки, при этом опираясь на самооценку и устремления каждого
учащегося
— наряду с более
тщательным изучением тем «Уравнения, неравенства и их системы» (более сложные
виды), «Решение текстовых задач», «Решение планиметрических задач, содержащих
комбинацию фигур», «Решение задач на доказательство» (причем как по геометрии,
так и по алгебре) необходимо уделять внимание и остальным темам с тем, чтобы
поддерживать и повышать достигнутый уровень их освоения;
— для успешного
выполнения заданий второй части необходимо овладение отдельными элементами
знаний и умений переводить на овладение навыками решения комплексных,
многошаговых заданий;
— в процессе
подготовки к ОГЭ должны участвовать все стороны: обучающийся, школа и родители,
поэтому необходимо своевременно знакомить родителей с нормативными документами
по подготовке к экзаменам, информировать их о процедуре итоговой аттестации,
особенностях подготовки к тестовой форме сдачи экзаменов, о всевозможных
методических рекомендациях и ресурсах, о результатах пробных испытаний и
текущей успеваемости;
— необходимо
использовать имеющиеся в достаточном количестве дополнительные материалы,
уделять внимание различным способам решения задач, их сопоставлению и выбору
лучшего; учить использовать логические цепочки не только при доказательстве, но
и при решении задач, стараться достичь осознанности знаний учащихся,
сформированности умения применять полученные знания в практической
деятельности, умения анализировать, сопоставлять, делать выводы в нестандартных
ситуациях.
Таким
образом, необходимым условием успешной подготовки обучающихся к сдаче ГИА
является освоение учителем материалов, публикуемых ФИПИ:
демонстрационного варианта, кодификатора элементов содержания и кодификатора
требований к уровню подготовки, спецификации КИМ по математике, учебно-методических
материалов для председателей и членов региональных предметных комиссий по
проверке выполнения заданий с развернутым ответом экзаменационных работ ОГЭ и,
конечно, изучение заданий открытого банка, их систематизация, выделение
основных способов решения различных классов заданий. А также, изучить
разнообразные методические пособия, учебно-тренировочные материалы,
представленные на сайтах и различными издательствами.
Для
успешного выполнения заданий второй части КИМ необходим особый подход в работе
с наиболее подготовленными учащимися.
В целом,
для успешного прохождения ГИА необходима дифференцированная работа с учащимися
класса и на уроке, и при составлении домашних заданий и заданий, предлагающихся
обучающимся на контрольных, проверочных, диагностических работах. Необходимо
обратить серьёзное внимание на решение прикладных и ситуационных задач, а также
на формирование уверенных вычислительных навыков
Список
используемой литературы:
1.
Документы,
определяющие структуру и содержание КИМ ) ОГЭ 2021 г.;
2.
Учебно-методические
материалы для председателей и членов региональных предметных комиссий по
проверке выполнения заданий с развёрнутым ответом экзаменационных работ ОГЭ;
3.
Методические
рекомендации на основе анализа типичных ошибок участников ОГЭ прошлых лет
(2019, 2020 гг.);
4.
Методические
рекомендации для учителей школ с высокой долей обучающихся с рисками учебной
неуспешности (fipi.ru);
5.
журнал
«Педагогические измерения»;
6.
Youtube-канал
Рособрнадзора.
Приложение
1
Анализ
типичных ошибок обучающихся на ОГЭ 2021
по
математике в МБОУ «Мужевская МОШ имени Н.В. Архангельского»
Таблица1
|
№ |
Содержание задания в |
Содержательные ошибки |
|
|
№ 1. |
Выделять из текста нужную информацию, преобразование информации |
Задание выполнено на ожидаемом уровне. |
|
|
№ 2. |
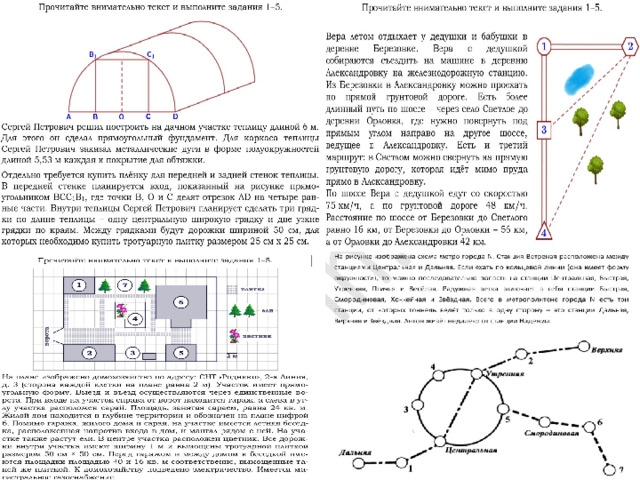
Решить задачу на нахождение расстояния по шоссе между селами, используя |
не обращают внимание на единицы измерения, не учитывают масштаб, |
|
|
№ 3. |
Решить задачу на нахождение расстояния по прямой с помощью |
невнимательное прочтение текста, работа с формулой, вычисления. |
|
|
№ 4. |
Решить задачу на нахождение времени движения, используя информацию |
невнимательное прочтение текста, неверное построение |
|
|
№ 5. |
Задание на определение |
вычислительные, невнимательное прочтение вопроса к заданию, в |
|
|
№ 6. |
Задание направлено на проверку умения выполнять арифметические |
в применении правил выполнения арифметических действий с |
|
|
№ 7. |
Задание направлено на проверку умений выполнять вычисления и |
Задание выполнено на ожидаемом уровне. |
|
|
№ 8. |
Задание на умение выполнять преобразования алгебраических |
в применении свойств степени или корня, вычислительная ошибка. |
|
|
№ 9. |
Задание проверяет умения решать линейные уравнения или неполное |
в алгоритме решения уравнений, вычислительная. |
|
|
№ 10. |
Задание проверяет умения решать практическую расчетную задачу на |
невнимательное чтение условия, неумение определять число |
|
|
№ 11. |
Задание направлено на проверку умений чтения графиков функций, содержащие |
Неверное установление соответствия между знаками |
|
|
№ 12. |
Задание представляет собой задачу на умение осуществлять |
Данное задание некоторые учащиеся пропускают, это говорит о том, |
|
|
№13 |
Задание представляет собой квадратное неравенство или линейное |
Ошибки связаны с незнанием свойств неравенств и алгоритма |
|
|
№ 14. |
Задание с практическим содержанием, направленное на проверку |
неверное установление вида прогрессии, вычислительные ошибки, |
|
|
№ 15. |
Несложная планиметрическая задача в одно действие, проверяющая |
Неверное нахождение острого угла прямоугольного треугольника и Незнание теоремы о сумме углов тр-ка |
|
|
№ 16. |
Представляет собой задачу, связанную с окружностью . Для решения |
вычислительная, незнание нужной теоремы, определения |
|
|
№ 17. |
Представляет собой задачу по теме «Четырехугольники». Решение |
вычислительная, по причине невнимательности учащихся, незнание |
|
|
№ 18. |
Представляет собой задачу по планиметрии на вычисление В данном случае на клетчатой бумаге была изображена фигура, |
невнимательность при подсчете клеток, незнание способа |
|
|
№19 |
Задание на умение оценивать логическую правильность рассуждений, |
не владеют достаточными знаниями точных определений и |
|
|
№ 20 |
требовалось решить иррационального алгебраическое уравнение, 1) преобразование уравнения к виду квадратного уравнения, 2)Найти область определения ; 3)Определить посторонний корень |
ошибки в действиях: 1) Вычеркивание квадратного корня из обеих частей уравнения без 2) перенос слагаемых из одной части уравнения в другую; 3) решение квадратного уравнения. Данное обстоятельство свидетельствует о недостаточном уровне 4) не содержит записи ответа, хотя данный шаг является В связи с чем, учителям следует обратить внимание на обеспечение |
|
|
№ 21 |
требовалось решить текстовую задачу на нахождение количества Для верного и полного решения обучающимися должны быть выполнены |
Самая распространённая ошибка при решении задачи на нахождение у большинства обучающихся возникают серьезные затруднения при |
|
|
№ 22 |
В задании предусмотрено построение графика функции, содержащей Задания, предполагающие построение графиков функций и их анализ, |
1) неправильное преобразование формулы, задающей функцию; 2) отсутствие обоснований построения графика функции; 3) вычислительные ошибки при определении координат точек; 4) несоблюдение масштаба при построении системы координат, 5) отсутствие вычислений координат точек «стыка», и как 6) не определено значение параметра в соответствие с 7) ограничение графика (кривой или прямой) точкой, когда Самой распространённой ошибкой при решении задания № 22 является Достаточно большое количество работ, в которых представлено |
|
|
№ 23 |
В задании предложена планиметрическая задача на нахождение |
обучающийся должен показать все шаги решения, хотя его Встречаются ошибки, связанные с некорректным использованием |
|
|
№24 |
При выполнении задания требовалось доказать подобие Задания на применение признаков подобия треугольников Решение проблемы освоения темы «Подобные треугольники» возможно |
К сожалению, оказалось, что обучающиеся недостаточно глубоко При выполнении задания № 24 обучающиеся допускали неверное Встречаются ошибки, связанные с некорректным использованием . Это серьезная проблема в целом, источником которой может быть: |
|
|
№25 |
Выполнение задания традиционно остается низким, так как это задача высокого уровня. |
— обучающимся не известны стратегии поиска решения задач — недостаточно опыта применения разных методов решения одной — недостаточно опыта конструирования задач (опыт — недостаточно опыта самостоятельного поиска решения задачи |
|
ОГЭ по математике :
изменения в 2022 году, типичные ошибки обучающихся и пути их преодоления
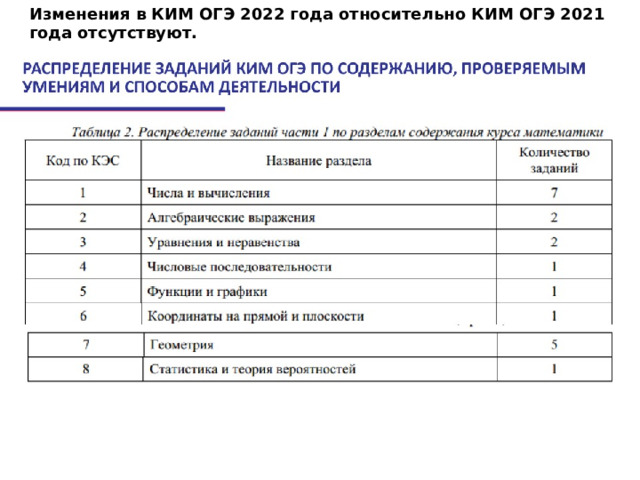
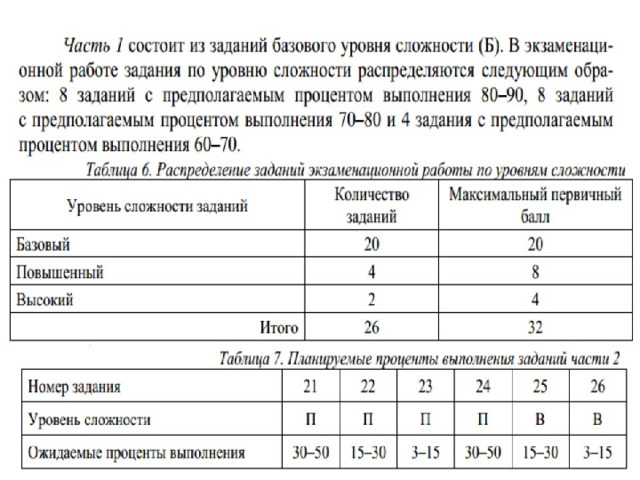
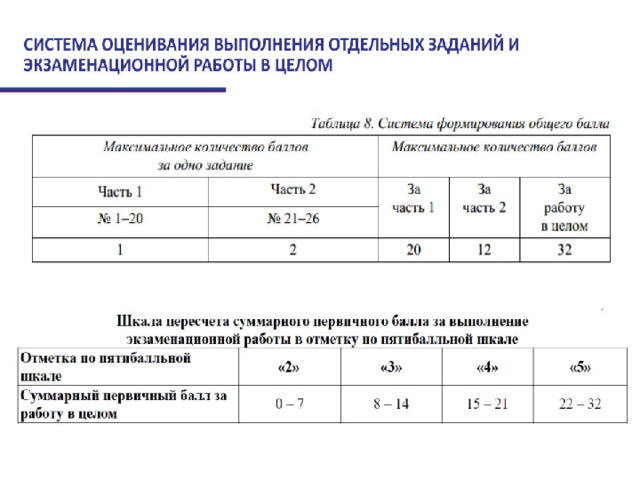
Изменения в КИМ ОГЭ 2022 года относительно КИМ ОГЭ 2021 года отсутствуют.
- В 2021-2022 учебном году 9 класс заканчивают ученики, программа обучения которых с 1-го класса была построена с учетом требований ФГОС.
- В сравнении с экзаменационными моделями 2019 г. в проектах КИМ ОГЭ 2022 г. усилены деятельностная составляющая, практический характер заданий.
- Проверяться будут не только знания, но и метапредметные навыки. Это смысловое чтение, коммуникационная грамотность, умение пользоваться справочной информацией и многое другое.
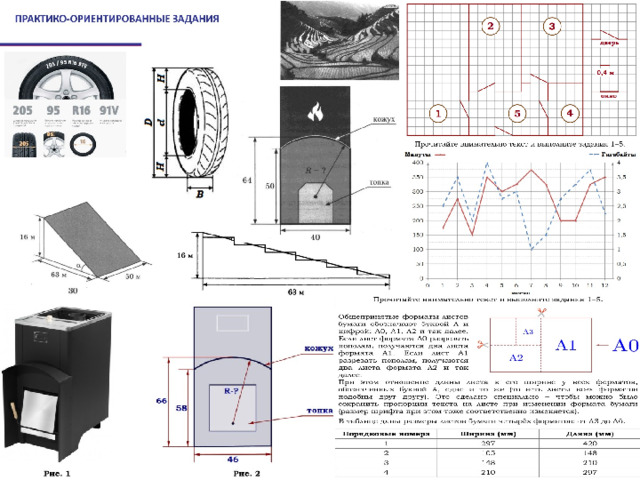
В КИМ включён новый блок практико-ориентированных заданий 1-5
Раньше реальная математика представляла несколько разрозненных задач, теперь — это первый блок экзамена.
Разделение на модули «Алгебра» и «Геометрия» условно отсутствует.
№ 1
Часть 1
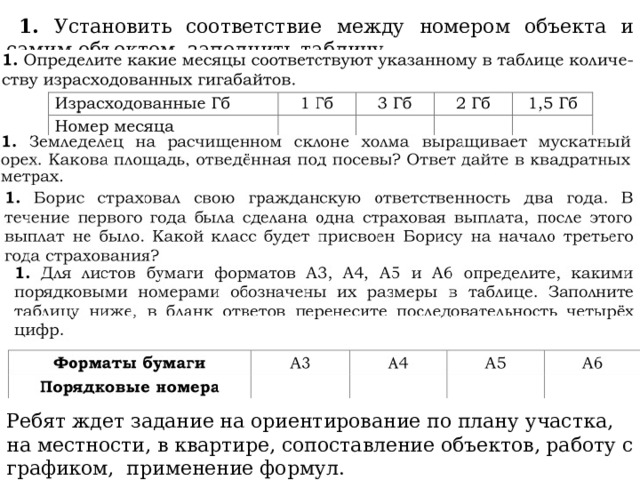
1. Установить соответствие между номером объекта и самим объектом, заполнить таблицу.
Ребят ждет задание на ориентирование по плану участка, на местности, в квартире, сопоставление объектов, работу с графиком, применение формул.
№ 2
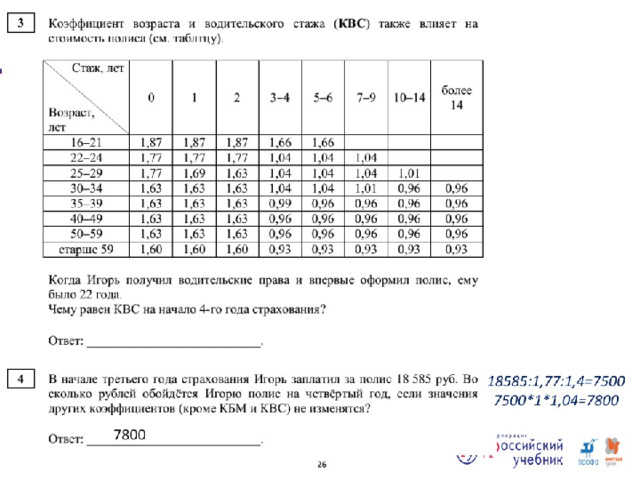
№ 2 — рассчитать количество плиток для тротуара, посчитать количество листов бумаги при разрезании пополам, найти ширину окна, определить по графику затраты на услуги связи в определенный месяц, найти диаметр колеса, вычислить угол склона террасы (в процентах), найти КВМ в зависимости от класса водителя, посчитать время, затраченное на ремонт участка и т.д.
№ 2. Прежде, чем решить задачу, необходимо посчитать количество плиток.
- Можно сэкономить время при подсчёте, т.к. дана площадь площадки (64 кв.м) и размер плитки 1×1м, но нужно уметь извлекать из указанных данных информацию, что площадь одной плитки 1 кв.м;
- При подсчёте нужно учесть, что дорожки пересекаются.
- Задача решается в два действия и предполагает внимательное прочтение текста, его смысловое восприятие, знание формул площади, объема, умение округлять.
№ 3
№ 3 . Можно посчитать количество клеток, не пользуясь формулой площади, но не забыть, что площадь одной клетки 4 кв.м (2×2м).
- Задача решается в два действия и предполагает внимательное прочтение текста, его смысловое восприятие, знание формул площади, объема, понятие процента, умение переводить одни единицы измерения в другие.
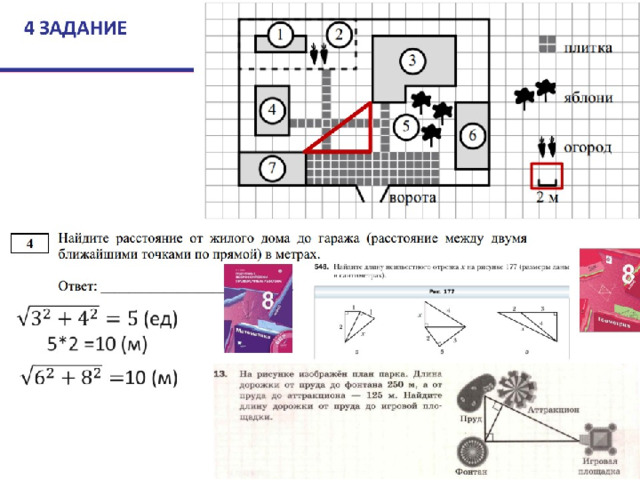
№ 4
№ 4. Для определения расстояния простого подсчёта клеток недостаточно, нужно построить прямоугольный треугольник, применить теорему Пифагора и снова не забыть о том, что сторона клетки 2м.
№ 5. Мы уже знаем по результатам предыдущих экзаменов , что для учащихся это задание вызывает затруднения.
- Различные единицы измерения, а именно тыс. рублей и рубли;
- Задача решается в 7 действий;
- Много времени займут вычисления.
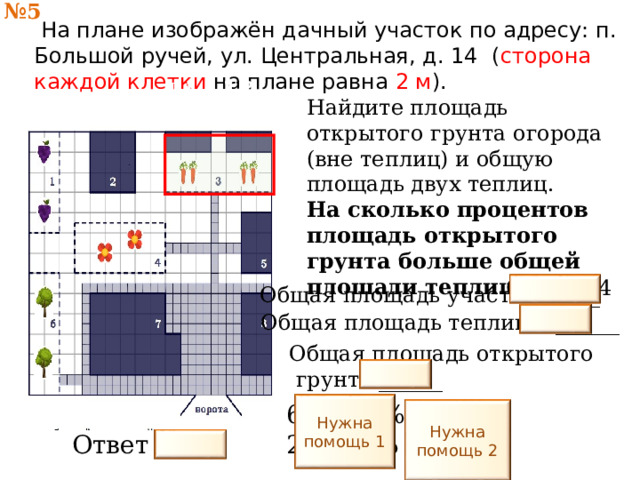
На плане изображён дачный участок по адресу: п. Большой ручей, ул. Центральная, д. 14 ( сторона
каждой клетки на плане равна 2 м ).
№ 5
Т 2
Т 1
Найдите площадь открытого грунта огорода (вне теплиц) и общую площадь двух теплиц.
На сколько процентов площадь открытого грунта больше общей площади теплиц ?
6·14= 84
Общая площадь участка______
24
Общая площадь теплиц ______
Общая площадь открытого
грунта ______
60
60- 100%
24- Х%
Нужна помощь 1
Нужна помощь 2
Ответ 60
№ 5
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели ? В каждой пачке 25 пакетиков
8·3 · 14 = 336
336 : 25=
проверка
Ответ 14
Плата за телефон составляет 400 рублей в месяц. В следующем году она увеличится на 9 % .Сколько рублей придётся платить ежемесячно за телефон в следующем году?
Ответ 436
Дальше видим, что задачи с 6 по 19 (1 часть) были и раньше
- № 6. — №1 в ОГЭ-2019 №7. — №3 в ОГЭ-2019
- № 8. — №4 в ОГЭ-2019 №9. — №6 в ОГЭ-2019
- № 10. — №9 в ОГЭ-2019 №11. — №10 в ОГЭ-2019
- № 12. — №11 в ОГЭ-2019 №13. — №12 в ОГЭ-2019
- № 14. — №13 в ОГЭ-2019 №15. — №14 в ОГЭ-2019
- № 16 — №20 — №16 — №19 в ОГЭ-2022
Ведущий методист по математике корпорации «Российский учебник» Сунцова Светлана Владимировна, принимая участие в вебинаре по теме «Новая модель ОГЭ по математике: как не допустить ошибок» постоянно обращается к учебникам линии Мерзляка А.Г., Полонского В.Б., ЯкираМ.С. Сравнивая формулировки заданий ОГЭ и задач из учебников данных авторов, невольно делаешь вывод, что и разработчики КИМ ОГЭ опираются на эти учебники (любой сборник «ОГЭ 2022. Математика. Типовые варианты экзаменационных заданий от разработчиков ОГЭ»
Блок второй части не претерпел изменения. Всё те же 6 задач: №21 — №26 — №20- №25 в ОГЭ-2022
По-прежнему остаются в качестве 20-го задания: уравнения, неравенства, их системы, действия с алгебраическими выражениями. 21 задача как всегда текстовая (движение, работа, сплавы, смеси). 22 задача на построение графика функции. 23, 24 и 25 задачи остаются по-прежнему геометрическими.
Сама система оценивания ГИА-9 в 2021-2022 учебном году останется неизменной. Первый блок будут проверять через компьютер, оцифровывая бланк ответов. Проверку второго блока традиционно доверят экспертам.
Для каждой работы обязательной будет проверка двумя независимыми экспертами. Третий эксперт будет перепроверять работу, если: расхождение в оценивании какого-либо задания будет более 2-х баллов; мнение экспертов не сойдется при оценивании 2-х и более задач.
Решение задания второй части должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений учащегося. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, рассматривается как решение без недочетов и оценивается в 2 балла
Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного, что и отражено в критериях оценивания заданий с развернутым ответом.
Типичные ошибки учащихся и пути их преодоления
Ошибки , которые допускают обучающиеся в 1 части ГИА, можно условно делить на три группы:
- технические ,
- содержательные,
- невнимательное чтение условия задачи.
1. Технические ошибки
1) К заданиям, где требуется установить соответствие , а это соответствие в КИМах предлагается привести в форме таблицы, учащиеся нередко переносят в бланк ответов как «А2Б4В3», или «2,4,3», или «2;4;3», или «2 4 3» вместо верного «243».
2) Запятую или точку с запятой ученики также часто приводят и в ответах к заданиям, где требуется указать номера верных (неверных) утверждений, в то время, как имеется указание на то, что ответом к этим заданиям является последовательность цифр, записанных в любом порядке без пробелов и использования других символов.
3) Нередко ученики в бланк ответов вписывают единицы измерения , что нельзя делать, – если единицы длины, веса и т.п. еще можно верифицировать вручную, то знак градусов компьютер может принять и за ноль.
4) Случается, что задача учащимся решена неверно и в неверном ответе содержится знак радикала – в этом случае следовало бы пересмотреть решение, но школьники упорно пытаются вписать знак арифметического квадратного корня в клетки бланка ответов.
5) В некоторых работах встречается, что числа написаны небрежно, иногда бывает невозможно понять, что написано 6 или 0, 5 или 6, 1 или 7, 3 или 9
2. С одержательные ошибки
Например, дано задание: «27 выпускников школы собираются учиться в технических вузах. Они составляют 30% от числа выпускников. Сколько в школе выпускников?». Встречаются работы, в которых ответом к данной задаче указывалось число 8,1, что явно противоречит здравому смыслу
3. Н евнимательн ое чтение условия задачи
- В одном задании требовалось полученный ответ округлить до целого числа, чего не сделали некоторые учащиеся, записывая верный точный ответ с дробной его частью.
- В задании требовалось указать номер первого отрицательного члена заданной последовательности. Видится, что приводимый иногда ответ «–3» явно не есть номер члена прогрессии, а сам этот член заданной прогрессии.
Ошибки во второй части экзаменационной работы
- Анализ выполнения заданий с развернутыми ответом показывает, что одной из самых больших проблем выпускников 9 класса является прочтение условия задачи и его содержательная интерпретация на математический язык.
Задание № 20 Типичные ошибки:
- потеря корня,
- неправильно сформированный ответ,
- к нулю или между собой приравнены два абсолютно разных по значению выражения ,
- содержательные ошибки, наличие которых не позволяло засчитать это задание.
- логически незавершенные решения при полученном верном ответе, что свидетельствует о несформированности навыка логически верно записывать интуитивно понятное решение.
- вычислительные ошибки.
Задание № 21 Типичные ошибки:
- перевод содержания задачи на математический язык,
- составление уравнений, связывающих данные величины и переменные, которые вводит учащийся.
- вычислительные ошибки при решении уравнения,
- наличие неправильно сформированного ответа в части отсутствия именованных величин.
Задание № 22 Типичные ошибки
- неправильно построен график,
- записано верное значение параметра, но не указано, как оно получено,
- отсутствуют единичный отрезок на координатных осях, направления координатных осей.
Задание № 23 Типичные ошибки
- неверное построение чертежа к задаче;
- решают частную задачу, изменяя фактически ее смысл;
- неправильно указан признак подобия треугольников;
- неверно найдены сходственные стороны;
- неверно решена пропорция;
- вычислительные ошибки.
Задание № 24 Типичные ошибки
- неверное построение чертежа к задаче
- неполное доказательство;
- путают свойства и признаки параллелограмма;
- интуитивно понятные факты не доказывают, считая их очевидными, а также не умеют математически грамотно и ясно записывать решение, приводя при этом необходимые пояснения и обоснования.
Задание № 25 Типичные ошибки
- доказательсво верное, но записи неаккуратные, иногда просто невозможно понять, что написано учеником ;
- присутствуют только отдельные факты, по сути не связанные с тем, что необходимо доказать;
- неправильно понимают условие задания;
используют неверные методы решения.
Основные проблемы , возникающие при написании выпускниками экзаменационной работы:
- неумение понять суть вопроса, содержания задания, приводящее к построению неверного хода решения;
- недостаточно развитые умения смыслового чтения, не позволяющие построить адекватную математическую модель по условию задания;
- неумение пользоваться справочными материалами.
Пути преодоления:
1. Рабочая программа должна не только эффективно использовать учебное время при изучении текущего материала, организации повторения и подготовки выпускников к итоговой аттестации, но и составлять часть целостной системы, позволяющей учитывать освоение проблемных тем в каждом классе , а также ликвидировать пробелы в знаниях и умениях учащихся.
2. Необходимо проводить диагностические работы , направленные на выявление уровня подготовки обучающихся по отдельным темам, что позволит спланировать индивидуальную и групповую работу обучающихся.
3. При изучении нового материала и его отработке необходимо сочетать различные методы обучения: традиционные и интерактивные, направленные на организацию самостоятельной работы каждого ученика, что также позволит устранить пробелы в знаниях и умениях, и поможет проводить подготовку к аттестации дифференцированно для слабых и сильных учеников
4. Особое внимание следует уделять формированию навыков самоконтроля и самопроверки выполненных заданий.
5. Необходимо повышать уровень вычислительных навыков , развивать умение пользоваться справочными материалами , читать условие и вопрос задачи, записывать математически верно решение задачи, учить применять знания в нестандартных ситуациях .
6. Со слабоуспевающими обучающимися необходимо выделить круг доступных ему заданий, помочь освоить основные математические факты, позволяющие их решать и сформировать уверенные навыки их решения. Для «средних» учеников необходимо использовать методику, при которой они смогут перейти от теоретических знаний к практическим навыкам, от решения стандартных алгоритмических задач к решению задач похожего содержания, но иной формулировки и применению уже отработанных навыков в новой ситуации. Для сильных учеников требуется создание условия для продвижения: дифференцированные по уровню сложности задания, возможность саморазвития, помощь в решении заданий второй части.
7. «Нарешивание» заданий Открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у учащихся общие учебные действия, способствующие более эффективному усвоению изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки
8. В процессе подготовки к ОГЭ должны участвовать все стороны : обучающийся, школа, родители, поэтому необходимо своевременно знакомить родителей с нормативными документами по подготовке к экзаменам, информировать их о процедуре итоговой аттестации, о всевозможных методических рекомендациях и ресурсах, о результатах пробных испытаний и текущей успеваемости.
Ответственность учителя (тезисы А.В.Семенова)
- «Экзамен сдаёт ребенок, а не вы. Не берите на себя чужого! Коллективная ответственность не даёт нужного результата».
- «Учитель не должен формировать иллюзию, что ребёнок всё знает. Эксперт так не считает!»
- «Мы решаем не конкретную задачу, а задачу, которая может пригодиться!».
- «Не учите детей выпендриваться!».
- «Задания с развёрнутым ответом не проверяют скорость решения, как учил конкретный учитель. Эти задания проверяют логику и обоснованность!».
- «На экзамене хватит времени именно на то, на что должно хватить!».
Спасибо за внимание!
Проблем на экзамене может быть гораздо меньше, если заранее отработать все типичные ошибки ЕГЭ по математике, с которыми сталкиваются ученики из года в год. За все время проведения ОГЭ набралось достаточно информации о них, поэтому мы решили рассказать обо всех в одной статье.
Невнимательное чтение условия задачи
Все типичные ошибки ЕГЭ по математике начинаются с невнимательности. Сваливать всю вину на учеников нет смысла, ведь многое играет уровень стресса, который испытывают выпускники. Однако, с этим можно бороться с помощью разных практик:
- Чаще ставьте себя в условия экзамена. Записывайтесь на платные пробники, пишите больше полных вариантов, чтобы привыкнуть к долгой сфокусированной работе. Засекайте время, на которое вы не будете трогать свой телефон и сосредоточитесь на задачах.
- Заранее подготовьтесь к возможным ловушкам в тексте заданий. Прорешивайте как можно больше заданий, чтобы со временем у вас отложилось в памяти все тонкости каждого номера. Где-то есть акцент на слове «НЕТ», где-то нужно округлить цифры и так далее.
- После решения сверяйтесь с текстом задания. Приучите себя каждый раз после получения ответа перечитывать задание, мысленно отвечая на него. Таким образом, на экзамене вы сделаете это «на автомате», сделав работу над ошибками.
В остальном типичные ошибки ЕГЭ по математике можно не совершать, если просто проверять ответы перед сдачей бланка.
Устный счет
В мире технологий все ученики привыкли складывать, умножать и делить на калькуляторе, из-за чего типичные ошибки ЕГЭ по математике стали совершать чаще. На экзамене доступа к нему не будет, поэтому в процессе подготовки стоит придерживаться правил:
- Выучить таблицу умножения, если вы еще этого не сделали;
- Не считать на калькуляторе;
- Практиковаться в устном счете с помощью различных приложений;
- Посмотреть различные техники устного счета.
Это поможет вам быстрее освоить устный счет, но закрепить знания поможет только практика.
Ошибки в основных формулах и утверждениях
Чтобы прийти на ОГЭ в полной готовности и не совершить типичные ошибки ЕГЭ по математике, нужно выучить формулы по темам:
- Степени;
- Формулы сокращенного умножения;
- Последовательности и прогрессии;
- Таблица квадратов;
- Синусы и косинусы;
- Площадь фигур.
Знание этих формул — большой вклад не только в ОГЭ, но и ЕГЭ по математике, готовиться к которому будет намного легче.
Проверка ответа подстановкой
Заданиям, в которых можно проверить свой ответ данным методом, лучше уделить чуть больше времени и убедиться в правильности решения. При хорошем знании всех формул, описанных выше, у вас как раз освободится время для проверки задач. Делать это можно:
- Сразу, когда вы в фокусе на конкретную задачу и можете быстро вникнуть в то, что вам нужно сделать;
- После решения задач, чтобы пройтись целиком по работе и сделать работу над ошибками.
Каждый выбирает удобный способ для себя. Второй способ хорош тем, что вы отдохнете от конкретной задачи и сможете посмотреть на нее свежим взглядом. Но есть и минус — это требует больше времени, так как нужно заново погружаться в задачу.
Вписывание в бланк ответов единиц измерения
В какой-то степени это относится к первой распространенной проблеме, почему совершают типичные ошибки в ЕГЭ по математике — невнимательности. Но из-за частоты вписывания единиц измерения мы выделили ее в отдельную главу.
Запомните, в заданиях часто прямым текстом пишут, какой ответ от вас хотят. Например:
- «Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке»;
- «В ответе укажите номер правильного варианта»;
- «В ответе укажите полученное число» и так далее.
Читайте текст задания как до его решения, так и после, чтобы записать правильный ответ.
Знак радикала в ответе
Эту ошибку тоже совершают многие, не понимая, что правило само подсказывает о том, правильно вы решили задачу или нет: в бланк не пишут радикалы. Если у вас получился ответ с радикалом, вы либо:
- Неправильно решили задачу;
- Неправильно прочитали текст задания;
- Неправильно поняли, что именно нужно писать в ответе.
Решайте больше заданий с корнями, чтобы не совершать типичные ошибки в ЕГЭ по математике.
Итог
Мы рассказали вам о самых распространенных ошибках, на которых теряют баллы выпускники девятых классов. Но знать о них — это только малая часть успеха. Уметь преодолевать эти ошибки намного сложнее, а для этого нужно практиковаться. От этого зависят ваши баллы, поэтому не сидите сложа руки, а действуйте!
Галсанова Людмила Баторовна
Магистрант, Бурятский государственный университет имени Доржи Банзарова (г. Улан-Удэ)
Учитель математики МБОУ Иройская СОШ Селенгинского района
ОГЭ по математике: типичные ошибки учащихся и пути их преодоления.
В данной статье говориться об ошибках учащихся, которые наиболее часто допускаются на ОГЭ по математике. Также рассматриваются пути решения данной проблемы для успешной сдачи экзамена.
Итоговая аттестация – первая серьёзная проверка освоения основной образовательной программы основного общего образования. Результаты, полученные выпускниками на ГИА – это и результат освоения ими школьной программы, и оценка работы учителя.
Специфика математики как школьного предмета состоит в том, что ее изучение в значительной степени строится на системе опорных знаний, без овладения которыми невозможно дальнейшее продвижение по курсу. В ходе ОГЭ учащийся должен продемонстрировать наличие у него опорных знаний, позволяющих изучать математику в старшей школе.
ОГЭ проверяет не только знания по предмету, но и умение читать и понимать прочитанное, внимательность и аккуратность в оформлении решений (запись ответов в бланк), умение проверять свои решения.
Можно утверждать, что полученные учащимися баллы в большинстве случаев могли бы быть значительно выше. Это возможно в случае, если школьники более критично отнеслись бы как к приводимым ими ответам, так и к заполнению бланков и записи решения задач с развернутым ответом.
Ошибки, которые допускают обучающиеся в 1 части экзаменационной работы, можно условно делить на три группы: технические, содержательные, связанные с невнимательным чтением условия задачи.
Технические ошибки – это, во-первых, неграмотное заполнение бланка с кратким ответом.
Рассмотрим примеры:
1) К заданиям, где требуется установить соответствие, а это соответствие в КИМах предлагается привести в форме таблицы, учащиеся нередко переносят в бланк ответов как «А2Б4В3», или «2,4,3», или «2;4;3», или «2 4 3» вместо верного «243».
2) Запятую или точку с запятой ученики также часто приводят и в ответах к заданиям, где требуется указать номера верных (неверных) утверждений, в то время как имеется указание на то, что ответом к этим заданиям является последовательность цифр, записанных в любом порядке без пробелов и использования других символов.
3) Нередко ученики в бланк ответов вписывают единицы измерения, что нельзя делать, – если единицы длины, веса и т.п. еще можно верифицировать вручную, то знак градусов компьютер может принять и за ноль.
4) Случается, что задача учащимся решена неверно и в неверном ответе содержится знак радикала – в этом случае следовало бы пересмотреть решение, но школьники упорно пытаются вписать знак арифметического квадратного корня в клетки бланка ответов.
5) В некоторых работах встречается, что числа написаны небрежно, иногда бывает невозможно понять, что написано 6 или 0, 5 или 6, 1 или 7, 3 или 9.
Далее – содержательные ошибки.
Все задания, которые имеют жизненные формулировки, имеют реальные числовые данные, поэтому следует сопоставлять ответ с реальной ситуацией, делать проверку, прикидку результата. Это относится и к «чисто математическим» задачам. Между тем, можно нередко встретить неверные ответы, для которых даже грубая прикидка говорит об их ошибочности.
Покажем это на нескольких примерах:
В задаче требуется найти высоту равностороннего треугольника со стороной 54√3. Приводимые иногда ответы «9» или «162» значительно меньше или больше верного – для исключения таких ответов достаточно попробовать привести геометрическую конструкцию с данными, которые известны в условии и получены в ответе.
Дана задача: «Найдите корень уравнения 
Дано задание: «27 выпускников школы собираются учиться в технических вузах. Они составляют 30% от числа выпускников. Сколько в школе выпускников?». Встречаются работы, в которых ответом к данной задаче указывалось число 8,1, что явно противоречит здравому смыслу.
Следующая группа ошибок в заданиях с кратким ответом связана с невнимательным чтением условия задачи.
Вот некоторые примеры:
В одном задании требовалось полученный ответ округлить до целого числа, чего не сделали некоторые учащиеся, записывая верный точный ответ с дробной его частью.
В задании требовалось указать номер первого отрицательного члена заданной последовательности. Видится, что приводимый иногда ответ «–3» явно не есть номер члена прогрессии, а сам этот член заданной прогрессии.
В задании на чтение графиков требовалось по заданной диаграмме указать число стран, а которых средний балл тестирования отличается от среднего балла российских участников не меньше, чем на 15. Учащиеся представляют ошибочный ответ — перечисляют названия стран, а не их количество.
Анализ выполнения заданий с развернутым ответом показывает, что одной из самых больших проблем выпускников 9 класса является прочтение условия задачи и его содержательная интерпретация на математический язык.
Задание № 20 – Алгебраические выражения, уравнения, неравенства и их системы.
Типичные ошибки:
— потеря корня;
— неправильно сформированный ответ;
— к нулю или между собой приравнены два абсолютно разных по значению выражения;
— содержательные ошибки, наличие которых не позволяло засчитать это задание;
— логически незавершенные решения при полученном верном ответе, что свидетельствует о несформированном навыке логически верно записывать интуитивно понятное решение;
— вычислительные ошибки.
Задание № 21 — Текстовая задача.
Типичные ошибки:
— перевод содержания задачи на математический язык;
— составление уравнений, связывающих данные величины и переменные, которые вводит учащийся;
— вычислительные ошибки при решении уравнения;
— наличие неправильно сформированного ответа в части отсутствия именованных величин.
Задание № 22 – Функции и их свойства. Графики функций.
Типичные ошибки:
— неправильно построен график;
— записано верное значение параметра, но не указано, как оно получено;
— отсутствуют единичный отрезок на координатных осях, направления координатных осей.
Задание № 23 — Уметь выполнять действия с геометрическими фигурами. Проводить доказательные рассуждения при решении задач.
Типичные ошибки:
— неверное построение чертежа к задаче;
— решают частную задачу, изменяя фактически ее смысл;
— неправильно указан признак подобия треугольников;
— неверно найдены сходственные стороны;
— неверно решена пропорция;
— вычислительные ошибки.
Задание № 24 — Проводить доказательные рассуждения при решении задач.
Типичные ошибки:
— неверное построение чертежа к задаче
— неполное доказательство;
— путают свойства и признаки параллелограмма;
— интуитивно понятные факты не доказывают, считая их очевидными, а также не умеют математически грамотно и ясно записывать решение, приводя при этом необходимые пояснения и обоснования.
Задание № 25 — Уметь выполнять действия с геометрическими фигурами. Решать планиметрические задачи на нахождение геометрических величин. Различать взаимное расположение геометрических фигур на плоскости, изображать геометрические фигуры; выполнять чертежи по условию задачи. Проводить доказательные рассуждения при решении задач.
Типичные ошибки:
-доказательство верное, но записи неаккуратные, иногда просто невозможно понять, что написано учеником;
— присутствуют только отдельные факты, по сути, не связанные с тем, что необходимо доказать;
— неправильно понимают условие задания;
— использовали неверные методы решения.
Выводы:
Основные проблемы, возникающие при написании выпускниками экзаменационной работы:
- неумение понять суть вопроса, содержание задания, приводящее к построению неверного хода решения;
- недостаточно развитые умения смыслового чтения, не позволяющие построить адекватную математическую модель по условию задания;
- вычислительные навыки слабо сформированы;
- неспособность грамотно сформулировать решение в письменном виде, небрежное оформлении письменного решения задачи;
- недостаточные геометрические знания, слабая графическая культура;
- неумение проводить анализ условия задания при решении практических и ситуационных задач, неумение применять известный алгоритм в нестандартной ситуации;
- недостаточно развиты аналитические навыки.
Пути преодоления:
1. Рабочая программа должна не только эффективно использовать учебное время при изучении текущего материала, организации повторения и подготовки выпускников к итоговой аттестации, но и составлять часть целостной системы, позволяющей учитывать освоение проблемных тем в каждом классе, а также ликвидировать пробелы в знаниях и умениях учащихся.
2. Необходимо проводить диагностические работы, направленные на выявление уровня подготовки учащихся по отдельным темам, что позволит спланировать индивидуальную и групповую работу обучающихся.
3. При изучении нового материала и его отработке необходимо сочетать различные методы обучения: традиционные и интерактивные, направленные на организацию самостоятельной работы каждого ученика, что также позволит устранить пробелы в знаниях и умениях, и поможет проводить подготовку к аттестации дифференцированно для слабых и сильных учеников.
4. Особое внимание следует уделять формированию навыков самоконтроля и самопроверки выполненных заданий.
5. Необходимо повышать уровень вычислительных навыков, развивать умение пользоваться справочными материалами, читать условие и вопрос задачи, записывать математически верно решение задачи, применять знания в нестандартных ситуациях.
6. Со слабоуспевающими школьниками необходимо выделить круг доступных ему заданий, помочь освоить основные математические факты, позволяющие их решать и сформировать уверенные навыки их решения. Для «средних» учеников необходимо использовать методику, при которой они смогут перейти от теоретических знаний к практическим навыкам, от решения стандартных алгоритмических задач к решению задач похожего содержания, но иной формулировки и применению уже отработанных навыков в новой ситуации. Для сильных учеников требуется создание условия для продвижения: дифференцированные по уровню сложности задания, возможность саморазвития, помощь в решении заданий второй части.
7. «Нарешивание» заданий Открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у учащихся общие учебные действия, способствующие более эффективному усвоению изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки.
8. В процессе подготовки к ОГЭ должны участвовать все стороны: дети, школа и родители, поэтому необходимо своевременно знакомить родителей с нормативными документами по подготовке к экзаменам, информировать их о процедуре итоговой аттестации, о всевозможных методических рекомендациях и ресурсах, о результатах пробных испытаний и текущей успеваемости.
ОГЭ -2021 по математике: типичные ошибки и пути их
преодоления
Воротницкая А.И.,
учитель математики
МБОУ «Мужевская
СОШ имени Н.В.Архангельского
Специфика математики как школьного предмета
состоит в том, что ее изучение в значительной степени строится на системе
опорных знаний, без овладения которыми невозможно дальнейшее продвижение по
курсу. В ходе ОГЭ учащийся должен продемонстрировать наличие у него
опорных знаний, позволяющих изучать математику в старшей школе.
Результаты ОГЭ по математике в этом году не
очень хорошие. Эти результаты уже привлекли внимание общественности всей
страны. Поэтому предлагаю поговорить о типичных ошибках учащихся и путях их
преодоления.
ОГЭ представляет собой форму государственной
итоговой аттестации, цель которой определить соответствие результатов освоения
ООП ООО соответствующим требованиям ФГОС
Результатом
освоения ООП ООО должна стать математическая компетентность выпускников.
Выпускники
должны:
·
овладеть
специфическими для математики знаниями и видами деятельности;
·
научиться
преобразованию знания и его применению в учебных и внеучебных ситуациях;
·
сформировать
качества, присущие математическому мышлению;
·
овладеть
математической терминологией, ключевыми понятиями, методами и приёмами.
Работа по математике состоит
из двух частей.
Часть 1, нацеленная на проверку овладения курсом на базовом уровне, содержит 19 заданий, в совокупности охватывающих все разделы курса и предусматривающих три формы ответа: задания с выбором ответа из четырех предложенных вариантов, задания с кратким ответом, задание на соотнесение
Часть 2 состоит из заданий повышенного и высокого
уровней сложности и
включает 6 заданий с развернутым ответом. Их назначение – дифференцировать хорошо успевающих обучающихся по уровням подготовки, выявить наиболее подготовленную часть выпускников. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности.
При проверке базовой
математической компетентности обучающиеся должны продемонстрировать:
— владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических
понятий, их свойств, приемов
решения задач и прочее);
— умение пользоваться математической записью;
— умение
применять знания в решении
математических задач, не сводящихся к прямому применению алгоритма;
— умение применять математические
знания в простейших практических ситуациях.
ОГЭ
проверяет не только знания по предмету, но и умение читать и понимать
прочитанное, внимательность и аккуратность в оформлении решений (запись ответов
в бланк), умение проверять свои решения.
Виды
типичных ошибок обучающихся на ОГЭ по математике:
1)
языковые
;
2) технические;
3) содержательные.
Для
преодоления языковых ошибок я применяю групповую, парную формы работы на
уроке, постоянно прошу обучающихся аргументировать свои ответы, часто провожу
устные диктанты и тематические зачеты (особенно по геометрии).
Для преодоления технических ошибок я систематически (ежемесячно) провожу
диагностические работы, которые помогают обучающимся вырабатывать
внимательность и приучают детей делать проверку в каждом задании.
Вероятные
причины затруднений и типичных ошибок в 2021 году:
·
Сложная
эпидемиологическая обстановка в 2019-2021 уч.годах: переход на дистанционное
обучение, что привело к сокращению времени на отработку материала.
·
Низкие
проценты выполнения заданий 3-5, 11-14 можно объяснить тем, что они
соответствуют трудно формируемым умениям у многих школьников: выполнять
преобразования со степенями, решение квадратных и линейных неравенств и их
систем, применение знаний в практических ситуациях, построение математической
модели, вычисление числовых характеристик прогрессии.
·
Геометрические
задачи также традиционно вызывают трудности у обучающихся.
·
Отсутствие
у обучающихся должного уровня развития логического мышления – одна из основных
причин затруднений в выполнении геометрических заданий.
Традиционно
основными направлениями подготовки обучающихся к ГИА по математике
являются:
1) Информационная
работа;
2) Психологическая
поддержка;
3) Предметная
работа.
Важно заранее
познакомить обучающихся с особенностями структуры КИМ и технологией проведения
экзамена. Используя образовательные сайты ФИПИ или ОБРНАДЗОР ознакомиться
самому и ознакомить родителей с нормативной базой ГИА. Настроить
ребят на то, что экзамен-это
возможность показать свои знания, поэтому не следует бояться и переживать.
Выработке психологической готовности помогает апробирование и отработка
формы проведения экзамена в формате и по материалам ОГЭ.
В
организации предметной подготовки необходимо обращать внимание на опорные
алгоритмы (формирование вычислительных навыков), на теоретическую подготовку
по геометрии (зачеты), учить составлять план решения задачи, решать геометрические
задач разного вида на применение теоретических знаний. Необходимо готовить
учащихся к использованию справочных материалов, усилить работу по формированию
языковых умений ( учить четко и лаконично выражать свои мысли при развернутом ответе),
«нарешивать» задачи с практическим содержанием, использовать различные формы (устный
счет, математический диктант) формирования алгоритмов и вычислительных навыков.
Итак,
считаю эффективными следующие пути преодоления типичных ошибок:
— необходимо
достаточно часто проводить диагностические работы, направленные на выявление
уровня подготовки обучающихся по отдельным темам, что позволит спланировать
индивидуальную и групповую работу обучающихся;
— при изучении
нового материала и его отработке необходимо сочетать различные методы обучения:
традиционные и интерактивные, направленные на организацию самостоятельной
работы каждого ученика, что также позволит устранить пробелы в знаниях и
умениях, и поможет проводить подготовку к аттестации дифференцированно для
слабых и сильных учеников;
— особое внимание
следует уделять формированию навыков самоконтроля и самопроверки выполненных
заданий;
— необходимо повышать
уровень вычислительных навыков, развивать умение пользоваться справочными
материалами, читать условие и вопрос задачи, записывать математически верно
решение задачи, применять знания в нестандартных ситуациях;
— со слабо
успевающими обучающимися необходимо выделить круг доступных ему заданий,
помочь освоить основные математические факты, позволяющие их решать и
сформировать уверенные навыки их решения;
— для «средних»
учеников необходимо использовать методику, при которой они смогут перейти
от теоретических знаний к практическим навыкам, от решения стандартных
алгоритмических задач к решению задач похожего содержания, но иной формулировки
и применению уже отработанных навыков в новой ситуации;
— для сильных
учеников требуется
создание условия для продвижения: дифференцированные по уровню сложности
задания, возможность саморазвития, помощь в решении заданий второй части;
— «нарешивание» заданий
открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но
его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у
учащихся общие учебные действия, способствующие более эффективному усвоению
изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки;
— учителю следует ставить
перед каждым учащимся ту цель, которую он может реализовать в соответствии с
уровнем его подготовки, при этом опираясь на самооценку и устремления каждого
учащегося
— наряду с более
тщательным изучением тем «Уравнения, неравенства и их системы» (более сложные
виды), «Решение текстовых задач», «Решение планиметрических задач, содержащих
комбинацию фигур», «Решение задач на доказательство» (причем как по геометрии,
так и по алгебре) необходимо уделять внимание и остальным темам с тем, чтобы
поддерживать и повышать достигнутый уровень их освоения;
— для успешного
выполнения заданий второй части необходимо овладение отдельными элементами
знаний и умений переводить на овладение навыками решения комплексных,
многошаговых заданий;
— в процессе
подготовки к ОГЭ должны участвовать все стороны: обучающийся, школа и родители,
поэтому необходимо своевременно знакомить родителей с нормативными документами
по подготовке к экзаменам, информировать их о процедуре итоговой аттестации,
особенностях подготовки к тестовой форме сдачи экзаменов, о всевозможных
методических рекомендациях и ресурсах, о результатах пробных испытаний и
текущей успеваемости;
— необходимо
использовать имеющиеся в достаточном количестве дополнительные материалы,
уделять внимание различным способам решения задач, их сопоставлению и выбору
лучшего; учить использовать логические цепочки не только при доказательстве, но
и при решении задач, стараться достичь осознанности знаний учащихся,
сформированности умения применять полученные знания в практической
деятельности, умения анализировать, сопоставлять, делать выводы в нестандартных
ситуациях.
Таким
образом, необходимым условием успешной подготовки обучающихся к сдаче ГИА
является освоение учителем материалов, публикуемых ФИПИ:
демонстрационного варианта, кодификатора элементов содержания и кодификатора
требований к уровню подготовки, спецификации КИМ по математике, учебно-методических
материалов для председателей и членов региональных предметных комиссий по
проверке выполнения заданий с развернутым ответом экзаменационных работ ОГЭ и,
конечно, изучение заданий открытого банка, их систематизация, выделение
основных способов решения различных классов заданий. А также, изучить
разнообразные методические пособия, учебно-тренировочные материалы,
представленные на сайтах и различными издательствами.
Для
успешного выполнения заданий второй части КИМ необходим особый подход в работе
с наиболее подготовленными учащимися.
В целом,
для успешного прохождения ГИА необходима дифференцированная работа с учащимися
класса и на уроке, и при составлении домашних заданий и заданий, предлагающихся
обучающимся на контрольных, проверочных, диагностических работах. Необходимо
обратить серьёзное внимание на решение прикладных и ситуационных задач, а также
на формирование уверенных вычислительных навыков
Список
используемой литературы:
1.
Документы,
определяющие структуру и содержание КИМ ) ОГЭ 2021 г.;
2.
Учебно-методические
материалы для председателей и членов региональных предметных комиссий по
проверке выполнения заданий с развёрнутым ответом экзаменационных работ ОГЭ;
3.
Методические
рекомендации на основе анализа типичных ошибок участников ОГЭ прошлых лет
(2019, 2020 гг.);
4.
Методические
рекомендации для учителей школ с высокой долей обучающихся с рисками учебной
неуспешности (fipi.ru);
5.
журнал
«Педагогические измерения»;
6.
Youtube-канал
Рособрнадзора.
Приложение
1
Анализ
типичных ошибок обучающихся на ОГЭ 2021
по
математике в МБОУ «Мужевская МОШ имени Н.В. Архангельского»
Таблица1
|
№ |
Содержание задания в |
Содержательные ошибки |
|
|
№ 1. |
Выделять из текста нужную информацию, преобразование информации |
Задание выполнено на ожидаемом уровне. |
|
|
№ 2. |
Решить задачу на нахождение расстояния по шоссе между селами, используя |
не обращают внимание на единицы измерения, не учитывают масштаб, |
|
|
№ 3. |
Решить задачу на нахождение расстояния по прямой с помощью |
невнимательное прочтение текста, работа с формулой, вычисления. |
|
|
№ 4. |
Решить задачу на нахождение времени движения, используя информацию |
невнимательное прочтение текста, неверное построение |
|
|
№ 5. |
Задание на определение |
вычислительные, невнимательное прочтение вопроса к заданию, в |
|
|
№ 6. |
Задание направлено на проверку умения выполнять арифметические |
в применении правил выполнения арифметических действий с |
|
|
№ 7. |
Задание направлено на проверку умений выполнять вычисления и |
Задание выполнено на ожидаемом уровне. |
|
|
№ 8. |
Задание на умение выполнять преобразования алгебраических |
в применении свойств степени или корня, вычислительная ошибка. |
|
|
№ 9. |
Задание проверяет умения решать линейные уравнения или неполное |
в алгоритме решения уравнений, вычислительная. |
|
|
№ 10. |
Задание проверяет умения решать практическую расчетную задачу на |
невнимательное чтение условия, неумение определять число |
|
|
№ 11. |
Задание направлено на проверку умений чтения графиков функций, содержащие |
Неверное установление соответствия между знаками |
|
|
№ 12. |
Задание представляет собой задачу на умение осуществлять |
Данное задание некоторые учащиеся пропускают, это говорит о том, |
|
|
№13 |
Задание представляет собой квадратное неравенство или линейное |
Ошибки связаны с незнанием свойств неравенств и алгоритма |
|
|
№ 14. |
Задание с практическим содержанием, направленное на проверку |
неверное установление вида прогрессии, вычислительные ошибки, |
|
|
№ 15. |
Несложная планиметрическая задача в одно действие, проверяющая |
Неверное нахождение острого угла прямоугольного треугольника и Незнание теоремы о сумме углов тр-ка |
|
|
№ 16. |
Представляет собой задачу, связанную с окружностью . Для решения |
вычислительная, незнание нужной теоремы, определения |
|
|
№ 17. |
Представляет собой задачу по теме «Четырехугольники». Решение |
вычислительная, по причине невнимательности учащихся, незнание |
|
|
№ 18. |
Представляет собой задачу по планиметрии на вычисление В данном случае на клетчатой бумаге была изображена фигура, |
невнимательность при подсчете клеток, незнание способа |
|
|
№19 |
Задание на умение оценивать логическую правильность рассуждений, |
не владеют достаточными знаниями точных определений и |
|
|
№ 20 |
требовалось решить иррационального алгебраическое уравнение, 1) преобразование уравнения к виду квадратного уравнения, 2)Найти область определения ; 3)Определить посторонний корень |
ошибки в действиях: 1) Вычеркивание квадратного корня из обеих частей уравнения без 2) перенос слагаемых из одной части уравнения в другую; 3) решение квадратного уравнения. Данное обстоятельство свидетельствует о недостаточном уровне 4) не содержит записи ответа, хотя данный шаг является В связи с чем, учителям следует обратить внимание на обеспечение |
|
|
№ 21 |
требовалось решить текстовую задачу на нахождение количества Для верного и полного решения обучающимися должны быть выполнены |
Самая распространённая ошибка при решении задачи на нахождение у большинства обучающихся возникают серьезные затруднения при |
|
|
№ 22 |
В задании предусмотрено построение графика функции, содержащей Задания, предполагающие построение графиков функций и их анализ, |
1) неправильное преобразование формулы, задающей функцию; 2) отсутствие обоснований построения графика функции; 3) вычислительные ошибки при определении координат точек; 4) несоблюдение масштаба при построении системы координат, 5) отсутствие вычислений координат точек «стыка», и как 6) не определено значение параметра в соответствие с 7) ограничение графика (кривой или прямой) точкой, когда Самой распространённой ошибкой при решении задания № 22 является Достаточно большое количество работ, в которых представлено |
|
|
№ 23 |
В задании предложена планиметрическая задача на нахождение |
обучающийся должен показать все шаги решения, хотя его Встречаются ошибки, связанные с некорректным использованием |
|
|
№24 |
При выполнении задания требовалось доказать подобие Задания на применение признаков подобия треугольников Решение проблемы освоения темы «Подобные треугольники» возможно |
К сожалению, оказалось, что обучающиеся недостаточно глубоко При выполнении задания № 24 обучающиеся допускали неверное Встречаются ошибки, связанные с некорректным использованием . Это серьезная проблема в целом, источником которой может быть: |
|
|
№25 |
Выполнение задания традиционно остается низким, так как это задача высокого уровня. |
— обучающимся не известны стратегии поиска решения задач — недостаточно опыта применения разных методов решения одной — недостаточно опыта конструирования задач (опыт — недостаточно опыта самостоятельного поиска решения задачи |
|
Проблем на экзамене может быть гораздо меньше, если заранее отработать все типичные ошибки ЕГЭ по математике, с которыми сталкиваются ученики из года в год. За все время проведения ОГЭ набралось достаточно информации о них, поэтому мы решили рассказать обо всех в одной статье.
Невнимательное чтение условия задачи
Все типичные ошибки ЕГЭ по математике начинаются с невнимательности. Сваливать всю вину на учеников нет смысла, ведь многое играет уровень стресса, который испытывают выпускники. Однако, с этим можно бороться с помощью разных практик:
- Чаще ставьте себя в условия экзамена. Записывайтесь на платные пробники, пишите больше полных вариантов, чтобы привыкнуть к долгой сфокусированной работе. Засекайте время, на которое вы не будете трогать свой телефон и сосредоточитесь на задачах.
- Заранее подготовьтесь к возможным ловушкам в тексте заданий. Прорешивайте как можно больше заданий, чтобы со временем у вас отложилось в памяти все тонкости каждого номера. Где-то есть акцент на слове «НЕТ», где-то нужно округлить цифры и так далее.
- После решения сверяйтесь с текстом задания. Приучите себя каждый раз после получения ответа перечитывать задание, мысленно отвечая на него. Таким образом, на экзамене вы сделаете это «на автомате», сделав работу над ошибками.
В остальном типичные ошибки ЕГЭ по математике можно не совершать, если просто проверять ответы перед сдачей бланка.
Устный счет
В мире технологий все ученики привыкли складывать, умножать и делить на калькуляторе, из-за чего типичные ошибки ЕГЭ по математике стали совершать чаще. На экзамене доступа к нему не будет, поэтому в процессе подготовки стоит придерживаться правил:
- Выучить таблицу умножения, если вы еще этого не сделали;
- Не считать на калькуляторе;
- Практиковаться в устном счете с помощью различных приложений;
- Посмотреть различные техники устного счета.
Это поможет вам быстрее освоить устный счет, но закрепить знания поможет только практика.
Ошибки в основных формулах и утверждениях
Чтобы прийти на ОГЭ в полной готовности и не совершить типичные ошибки ЕГЭ по математике, нужно выучить формулы по темам:
- Степени;
- Формулы сокращенного умножения;
- Последовательности и прогрессии;
- Таблица квадратов;
- Синусы и косинусы;
- Площадь фигур.
Знание этих формул — большой вклад не только в ОГЭ, но и ЕГЭ по математике, готовиться к которому будет намного легче.
Проверка ответа подстановкой
Заданиям, в которых можно проверить свой ответ данным методом, лучше уделить чуть больше времени и убедиться в правильности решения. При хорошем знании всех формул, описанных выше, у вас как раз освободится время для проверки задач. Делать это можно:
- Сразу, когда вы в фокусе на конкретную задачу и можете быстро вникнуть в то, что вам нужно сделать;
- После решения задач, чтобы пройтись целиком по работе и сделать работу над ошибками.
Каждый выбирает удобный способ для себя. Второй способ хорош тем, что вы отдохнете от конкретной задачи и сможете посмотреть на нее свежим взглядом. Но есть и минус — это требует больше времени, так как нужно заново погружаться в задачу.
Вписывание в бланк ответов единиц измерения
В какой-то степени это относится к первой распространенной проблеме, почему совершают типичные ошибки в ЕГЭ по математике — невнимательности. Но из-за частоты вписывания единиц измерения мы выделили ее в отдельную главу.
Запомните, в заданиях часто прямым текстом пишут, какой ответ от вас хотят. Например:
- «Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке»;
- «В ответе укажите номер правильного варианта»;
- «В ответе укажите полученное число» и так далее.
Читайте текст задания как до его решения, так и после, чтобы записать правильный ответ.
Знак радикала в ответе
Эту ошибку тоже совершают многие, не понимая, что правило само подсказывает о том, правильно вы решили задачу или нет: в бланк не пишут радикалы. Если у вас получился ответ с радикалом, вы либо:
- Неправильно решили задачу;
- Неправильно прочитали текст задания;
- Неправильно поняли, что именно нужно писать в ответе.
Решайте больше заданий с корнями, чтобы не совершать типичные ошибки в ЕГЭ по математике.
Итог
Мы рассказали вам о самых распространенных ошибках, на которых теряют баллы выпускники девятых классов. Но знать о них — это только малая часть успеха. Уметь преодолевать эти ошибки намного сложнее, а для этого нужно практиковаться. От этого зависят ваши баллы, поэтому не сидите сложа руки, а действуйте!
ОГЭ по математике :
изменения в 2022 году, типичные ошибки обучающихся и пути их преодоления
Изменения в КИМ ОГЭ 2022 года относительно КИМ ОГЭ 2021 года отсутствуют.
- В 2021-2022 учебном году 9 класс заканчивают ученики, программа обучения которых с 1-го класса была построена с учетом требований ФГОС.
- В сравнении с экзаменационными моделями 2019 г. в проектах КИМ ОГЭ 2022 г. усилены деятельностная составляющая, практический характер заданий.
- Проверяться будут не только знания, но и метапредметные навыки. Это смысловое чтение, коммуникационная грамотность, умение пользоваться справочной информацией и многое другое.
В КИМ включён новый блок практико-ориентированных заданий 1-5
Раньше реальная математика представляла несколько разрозненных задач, теперь — это первый блок экзамена.
Разделение на модули «Алгебра» и «Геометрия» условно отсутствует.
№ 1
Часть 1
1. Установить соответствие между номером объекта и самим объектом, заполнить таблицу.
Ребят ждет задание на ориентирование по плану участка, на местности, в квартире, сопоставление объектов, работу с графиком, применение формул.
№ 2
№ 2 — рассчитать количество плиток для тротуара, посчитать количество листов бумаги при разрезании пополам, найти ширину окна, определить по графику затраты на услуги связи в определенный месяц, найти диаметр колеса, вычислить угол склона террасы (в процентах), найти КВМ в зависимости от класса водителя, посчитать время, затраченное на ремонт участка и т.д.
№ 2. Прежде, чем решить задачу, необходимо посчитать количество плиток.
- Можно сэкономить время при подсчёте, т.к. дана площадь площадки (64 кв.м) и размер плитки 1×1м, но нужно уметь извлекать из указанных данных информацию, что площадь одной плитки 1 кв.м;
- При подсчёте нужно учесть, что дорожки пересекаются.
- Задача решается в два действия и предполагает внимательное прочтение текста, его смысловое восприятие, знание формул площади, объема, умение округлять.
№ 3
№ 3 . Можно посчитать количество клеток, не пользуясь формулой площади, но не забыть, что площадь одной клетки 4 кв.м (2×2м).
- Задача решается в два действия и предполагает внимательное прочтение текста, его смысловое восприятие, знание формул площади, объема, понятие процента, умение переводить одни единицы измерения в другие.
№ 4
№ 4. Для определения расстояния простого подсчёта клеток недостаточно, нужно построить прямоугольный треугольник, применить теорему Пифагора и снова не забыть о том, что сторона клетки 2м.
№ 5. Мы уже знаем по результатам предыдущих экзаменов , что для учащихся это задание вызывает затруднения.
- Различные единицы измерения, а именно тыс. рублей и рубли;
- Задача решается в 7 действий;
- Много времени займут вычисления.
На плане изображён дачный участок по адресу: п. Большой ручей, ул. Центральная, д. 14 ( сторона
каждой клетки на плане равна 2 м ).
№ 5
Т 2
Т 1
Найдите площадь открытого грунта огорода (вне теплиц) и общую площадь двух теплиц.
На сколько процентов площадь открытого грунта больше общей площади теплиц ?
6·14= 84
Общая площадь участка______
24
Общая площадь теплиц ______
Общая площадь открытого
грунта ______
60
60- 100%
24- Х%
Нужна помощь 1
Нужна помощь 2
Ответ 60
№ 5
Ребята решили, что нужно взять в поездку чай в пакетиках определённого сорта. Оксане поручили купить чай на всех. Сколько пачек чая должна купить Оксана, если в компании 8 человек, в день они выпивают в среднем 3 пакетика на одного человека и поездка продлится две недели ? В каждой пачке 25 пакетиков
8·3 · 14 = 336
336 : 25=
проверка
Ответ 14
Плата за телефон составляет 400 рублей в месяц. В следующем году она увеличится на 9 % .Сколько рублей придётся платить ежемесячно за телефон в следующем году?
Ответ 436
Дальше видим, что задачи с 6 по 19 (1 часть) были и раньше
- № 6. — №1 в ОГЭ-2019 №7. — №3 в ОГЭ-2019
- № 8. — №4 в ОГЭ-2019 №9. — №6 в ОГЭ-2019
- № 10. — №9 в ОГЭ-2019 №11. — №10 в ОГЭ-2019
- № 12. — №11 в ОГЭ-2019 №13. — №12 в ОГЭ-2019
- № 14. — №13 в ОГЭ-2019 №15. — №14 в ОГЭ-2019
- № 16 — №20 — №16 — №19 в ОГЭ-2022
Ведущий методист по математике корпорации «Российский учебник» Сунцова Светлана Владимировна, принимая участие в вебинаре по теме «Новая модель ОГЭ по математике: как не допустить ошибок» постоянно обращается к учебникам линии Мерзляка А.Г., Полонского В.Б., ЯкираМ.С. Сравнивая формулировки заданий ОГЭ и задач из учебников данных авторов, невольно делаешь вывод, что и разработчики КИМ ОГЭ опираются на эти учебники (любой сборник «ОГЭ 2022. Математика. Типовые варианты экзаменационных заданий от разработчиков ОГЭ»
Блок второй части не претерпел изменения. Всё те же 6 задач: №21 — №26 — №20- №25 в ОГЭ-2022
По-прежнему остаются в качестве 20-го задания: уравнения, неравенства, их системы, действия с алгебраическими выражениями. 21 задача как всегда текстовая (движение, работа, сплавы, смеси). 22 задача на построение графика функции. 23, 24 и 25 задачи остаются по-прежнему геометрическими.
Сама система оценивания ГИА-9 в 2021-2022 учебном году останется неизменной. Первый блок будут проверять через компьютер, оцифровывая бланк ответов. Проверку второго блока традиционно доверят экспертам.
Для каждой работы обязательной будет проверка двумя независимыми экспертами. Третий эксперт будет перепроверять работу, если: расхождение в оценивании какого-либо задания будет более 2-х баллов; мнение экспертов не сойдется при оценивании 2-х и более задач.
Решение задания второй части должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений учащегося. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, рассматривается как решение без недочетов и оценивается в 2 балла
Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного, что и отражено в критериях оценивания заданий с развернутым ответом.
Типичные ошибки учащихся и пути их преодоления
Ошибки , которые допускают обучающиеся в 1 части ГИА, можно условно делить на три группы:
- технические ,
- содержательные,
- невнимательное чтение условия задачи.
1. Технические ошибки
1) К заданиям, где требуется установить соответствие , а это соответствие в КИМах предлагается привести в форме таблицы, учащиеся нередко переносят в бланк ответов как «А2Б4В3», или «2,4,3», или «2;4;3», или «2 4 3» вместо верного «243».
2) Запятую или точку с запятой ученики также часто приводят и в ответах к заданиям, где требуется указать номера верных (неверных) утверждений, в то время, как имеется указание на то, что ответом к этим заданиям является последовательность цифр, записанных в любом порядке без пробелов и использования других символов.
3) Нередко ученики в бланк ответов вписывают единицы измерения , что нельзя делать, – если единицы длины, веса и т.п. еще можно верифицировать вручную, то знак градусов компьютер может принять и за ноль.
4) Случается, что задача учащимся решена неверно и в неверном ответе содержится знак радикала – в этом случае следовало бы пересмотреть решение, но школьники упорно пытаются вписать знак арифметического квадратного корня в клетки бланка ответов.
5) В некоторых работах встречается, что числа написаны небрежно, иногда бывает невозможно понять, что написано 6 или 0, 5 или 6, 1 или 7, 3 или 9
2. С одержательные ошибки
Например, дано задание: «27 выпускников школы собираются учиться в технических вузах. Они составляют 30% от числа выпускников. Сколько в школе выпускников?». Встречаются работы, в которых ответом к данной задаче указывалось число 8,1, что явно противоречит здравому смыслу
3. Н евнимательн ое чтение условия задачи
- В одном задании требовалось полученный ответ округлить до целого числа, чего не сделали некоторые учащиеся, записывая верный точный ответ с дробной его частью.
- В задании требовалось указать номер первого отрицательного члена заданной последовательности. Видится, что приводимый иногда ответ «–3» явно не есть номер члена прогрессии, а сам этот член заданной прогрессии.
Ошибки во второй части экзаменационной работы
- Анализ выполнения заданий с развернутыми ответом показывает, что одной из самых больших проблем выпускников 9 класса является прочтение условия задачи и его содержательная интерпретация на математический язык.
Задание № 20 Типичные ошибки:
- потеря корня,
- неправильно сформированный ответ,
- к нулю или между собой приравнены два абсолютно разных по значению выражения ,
- содержательные ошибки, наличие которых не позволяло засчитать это задание.
- логически незавершенные решения при полученном верном ответе, что свидетельствует о несформированности навыка логически верно записывать интуитивно понятное решение.
- вычислительные ошибки.
Задание № 21 Типичные ошибки:
- перевод содержания задачи на математический язык,
- составление уравнений, связывающих данные величины и переменные, которые вводит учащийся.
- вычислительные ошибки при решении уравнения,
- наличие неправильно сформированного ответа в части отсутствия именованных величин.
Задание № 22 Типичные ошибки
- неправильно построен график,
- записано верное значение параметра, но не указано, как оно получено,
- отсутствуют единичный отрезок на координатных осях, направления координатных осей.
Задание № 23 Типичные ошибки
- неверное построение чертежа к задаче;
- решают частную задачу, изменяя фактически ее смысл;
- неправильно указан признак подобия треугольников;
- неверно найдены сходственные стороны;
- неверно решена пропорция;
- вычислительные ошибки.
Задание № 24 Типичные ошибки
- неверное построение чертежа к задаче
- неполное доказательство;
- путают свойства и признаки параллелограмма;
- интуитивно понятные факты не доказывают, считая их очевидными, а также не умеют математически грамотно и ясно записывать решение, приводя при этом необходимые пояснения и обоснования.
Задание № 25 Типичные ошибки
- доказательсво верное, но записи неаккуратные, иногда просто невозможно понять, что написано учеником ;
- присутствуют только отдельные факты, по сути не связанные с тем, что необходимо доказать;
- неправильно понимают условие задания;
используют неверные методы решения.
Основные проблемы , возникающие при написании выпускниками экзаменационной работы:
- неумение понять суть вопроса, содержания задания, приводящее к построению неверного хода решения;
- недостаточно развитые умения смыслового чтения, не позволяющие построить адекватную математическую модель по условию задания;
- неумение пользоваться справочными материалами.
Пути преодоления:
1. Рабочая программа должна не только эффективно использовать учебное время при изучении текущего материала, организации повторения и подготовки выпускников к итоговой аттестации, но и составлять часть целостной системы, позволяющей учитывать освоение проблемных тем в каждом классе , а также ликвидировать пробелы в знаниях и умениях учащихся.
2. Необходимо проводить диагностические работы , направленные на выявление уровня подготовки обучающихся по отдельным темам, что позволит спланировать индивидуальную и групповую работу обучающихся.
3. При изучении нового материала и его отработке необходимо сочетать различные методы обучения: традиционные и интерактивные, направленные на организацию самостоятельной работы каждого ученика, что также позволит устранить пробелы в знаниях и умениях, и поможет проводить подготовку к аттестации дифференцированно для слабых и сильных учеников
4. Особое внимание следует уделять формированию навыков самоконтроля и самопроверки выполненных заданий.
5. Необходимо повышать уровень вычислительных навыков , развивать умение пользоваться справочными материалами , читать условие и вопрос задачи, записывать математически верно решение задачи, учить применять знания в нестандартных ситуациях .
6. Со слабоуспевающими обучающимися необходимо выделить круг доступных ему заданий, помочь освоить основные математические факты, позволяющие их решать и сформировать уверенные навыки их решения. Для «средних» учеников необходимо использовать методику, при которой они смогут перейти от теоретических знаний к практическим навыкам, от решения стандартных алгоритмических задач к решению задач похожего содержания, но иной формулировки и применению уже отработанных навыков в новой ситуации. Для сильных учеников требуется создание условия для продвижения: дифференцированные по уровню сложности задания, возможность саморазвития, помощь в решении заданий второй части.
7. «Нарешивание» заданий Открытого банка ОГЭ необходимо для формирования устойчивых навыков решения, но его нужно сочетать с фундаментальной подготовкой, позволяющей сформировать у учащихся общие учебные действия, способствующие более эффективному усвоению изучаемых вопросов, а также дифференциации обучающихся по уровню подготовки
8. В процессе подготовки к ОГЭ должны участвовать все стороны : обучающийся, школа, родители, поэтому необходимо своевременно знакомить родителей с нормативными документами по подготовке к экзаменам, информировать их о процедуре итоговой аттестации, о всевозможных методических рекомендациях и ресурсах, о результатах пробных испытаний и текущей успеваемости.
Ответственность учителя (тезисы А.В.Семенова)
- «Экзамен сдаёт ребенок, а не вы. Не берите на себя чужого! Коллективная ответственность не даёт нужного результата».
- «Учитель не должен формировать иллюзию, что ребёнок всё знает. Эксперт так не считает!»
- «Мы решаем не конкретную задачу, а задачу, которая может пригодиться!».
- «Не учите детей выпендриваться!».
- «Задания с развёрнутым ответом не проверяют скорость решения, как учил конкретный учитель. Эти задания проверяют логику и обоснованность!».
- «На экзамене хватит времени именно на то, на что должно хватить!».
Спасибо за внимание!
1
ОГЭ —2021 по математике: типичные ошибки и пути их преодоления
Воротницкая А.И., учитель математики
МБОУ «Мужевская СОШ имени Н.В.Архангельского
Специфика математики как школьного предмета состоит в том, что ее
изучение в значительной степени строится на системе опорных знаний, без
овладения которыми невозможно дальнейшее продвижение по курсу. В ходе
ОГЭ учащийся должен продемонстрировать наличие у него опорных знаний,
позволяющих изучать математику в старшей школе.
Результаты ОГЭ по математике в этом году не очень хорошие. Эти
результаты уже привлекли внимание общественности всей страны. Поэтому
предлагаю поговорить о типичных ошибках учащихся и путях их
преодоления.
ОГЭ представляет собой форму государственной итоговой аттестации,
цель которой определить соответствие результатов освоения ООП ООО
соответствующим требованиям ФГОС
Результатом освоения ООП ООО должна стать математическая
компетентность выпускников. Выпускники должны:
• овладеть специфическими для математики знаниями и видами
деятельности;
• научиться преобразованию знания и его применению в учебных и
внеучебных ситуациях;
• сформировать качества, присущие математическому мышлению;
• овладеть математической терминологией, ключевыми понятиями,
методами и приёмами.
Р
аб
от
а по математике с
о
с
тоит
из
д
вух
час
т
е
й.
Час
ть
1,
н
а
ц
е
л
е
нн
ая
н
а
пров
е
р
к
у
овл
аде
ни
я к
ур
с
о
м
н
а ба
зово
м
уровн
е
,
с
о
де
р
ж
ит
19
з
ада
ний,
в
с
ово
к
упно
с
ти
охв
а
т
ы
в
а
ющих
в
се
р
а
з
де
л
ы
к
ур
са
и
пр
ед
у
сма
трив
а
ющих
три
ф
ор
мы
отв
е
т
а:
з
ада
ни
я с
в
ыб
оро
м
отв
е
т
а
из
че
т
ы
р
е
х
пр
ед
ло
же
нн
ы
х
в
а
ри
а
нтов,
з
ада
ни
я с к
р
а
т
к
и
м
отв
е
то
м
,
з
ада
ни
е
н
а с
оотн
есе
ни
е
Час
ть
2
с
о
с
тоит
из
з
ада
ний
пов
ы
ш
е
нного
и
в
ыс
о
к
ого
уровн
е
й
с
ло
ж
но
с
ти
и
в
к
лю
чае
т
6
з
ада
ний
с
р
а
зв
е
рнут
ым
отв
е
то
м
.
Их
н
а
зн
аче
ни
е
–
д
и
ффе
р
е
нциров
а
ть
хорошо
у
с
п
е
в
а
ющих
о
б
у
ча
ющих
ся
по
уровн
ям
по
д
готов
к
и,
в
ыя
вить
н
а
и
б
ол
ее
по
д
готовл
е
нную
час
ть
в
ы
пу
ск
ни
к
ов.
Все
з
ада
ни
я
тр
еб
уют
з
а
пи
с
и
р
е
ш
е
ний
и
отв
е
т
а
.
Зада
ни
я
р
ас
поло
же
н
ы
по
н
а
р
ас
т
а
нию
тру
д
но
с
ти.
При
пров
е
р
ке ба
зовой
ма
т
ема
ти
ческ
ой
к
о
м
п
е
т
е
нтно
с
ти
о
б
у
ча
ющи
еся
д
ол
ж
н
ы
про
дем
он
с
триров
а
ть
:
2
—
вл
аде
ни
е
о
с
новн
ым
и
а
лгорит
мам
и,
зн
а
ни
е
и
пони
ма
ни
е
к
лю
че
в
ы
х
эл
еме
нтов
с
о
де
р
жа
ни
я
(
ма
т
ема
ти
ческ
их
пон
я
тий,
их
с
вой
с
тв,
при
ем
ов
р
е
ш
е
ни
я
з
адач
и
про
чее
)
;
—
у
ме
ни
е
пользов
а
ть
ся ма
т
ема
ти
ческ
ой
з
а
пи
с
ью;
—
умение
при
ме
н
я
ть
зн
а
ни
я
в
р
е
ш
е
нии
ма
т
ема
ти
ческ
их
з
адач
,
н
е
с
во
дя
щих
ся к
пр
ям
о
м
у
при
ме
н
е
нию
а
лгорит
ма
;
—
у м е н и е
при
ме
н
я
ть
ма
т
ема
ти
ческ
и
е
зн
а
ни
я
в
про
с
т
е
йших
пр
ак
ти
ческ
их
с
иту
а
ци
я
х.
ОГЭ проверяет не только знания по предмету, но и умение читать и
понимать прочитанное, внимательность и аккуратность в оформлении
решений (запись ответов в бланк), умение проверять свои решения.
Виды типичных ошибок обучающихся на ОГЭ по математике:
1) языковые ;
2) технические;
3) содержательные.
Для преодоления языковых ошибок я применяю групповую, парную
формы работы на уроке, постоянно прошу обучающихся аргументировать
свои ответы, часто провожу устные диктанты и тематические зачеты
(особенно по геометрии).
Для преодоления технических ошибок я систематически (ежемесячно)
провожу диагностические работы, которые помогают обучающимся
вырабатывать внимательность и приучают детей делать проверку в каждом
задании.
Вероятные причины затруднений и типичных ошибок в 2021 году:
• Сложная эпидемиологическая обстановка в 2019—2021 уч.годах:
переход на дистанционное обучение, что привело к сокращению
времени на отработку материала.
• Низкие проценты выполнения заданий 3-5, 11-14 можно объяснить тем,
что они соответствуют трудно формируемым умениям у многих
школьников: выполнять преобразования со степенями, решение
квадратных и линейных неравенств и их систем, применение знаний в
практических ситуациях, построение математической модели,
вычисление числовых характеристик прогрессии.
• Геометрические задачи также традиционно вызывают трудности у
обучающихся.
• Отсутствие у обучающихся должного уровня развития логического
мышления – одна из основных причин затруднений в выполнении
геометрических заданий.
Традиционно основными направлениями подготовки обучающихся к
ГИА по математике являются:
1) Информационная работа;
2) Психологическая поддержка;
3) Предметная работа.
3
Важно заранее познакомить обучающихся с особенностями структуры
КИМ и технологией проведения экзамена. Используя образовательные
сайты ФИПИ или ОБРНАДЗОР ознакомиться самому и ознакомить
родителей с нормативной базой ГИА. Настроить ребят на то, что экзамен—это
возможность показать свои знания, поэтому не следует бояться и
переживать. Выработке психологической готовности помогает
апробирование и отработка формы проведения экзамена в формате и по
материалам ОГЭ.
В организации предметной подготовки необходимо обращать внимание
на опорные алгоритмы (формирование вычислительных навыков), на
теоретическую подготовку по геометрии (зачеты), учить составлять план
решения задачи, решать геометрические задач разного вида на применение
теоретических знаний. Необходимо готовить учащихся к использованию
справочных материалов, усилить работу по формированию языковых
умений ( учить четко и лаконично выражать свои мысли при развернутом
ответе), «нарешивать» задачи с практическим содержанием, использовать
различные формы (устный счет, математический диктант) формирования
алгоритмов и вычислительных навыков.
Итак, считаю эффективными следующие пути преодоления типичных
ошибок:
— необходимо достаточно часто проводить диагностические работы,
направленные на выявление уровня подготовки обучающихся по отдельным
темам, что позволит спланировать индивидуальную и групповую работу
обучающихся;
— при изучении нового материала и его отработке необходимо сочетать
различные методы обучения: традиционные и интерактивные, направленные
на организацию самостоятельной работы каждого ученика, что также
позволит устранить пробелы в знаниях и умениях, и поможет проводить
подготовку к аттестации дифференцированно для слабых и сильных
учеников;
— особое внимание следует уделять формированию навыков самоконтроля и
самопроверки выполненных заданий;
— необходимо повышать уровень вычислительных навыков, развивать умение
пользоваться справочными материалами, читать условие и вопрос задачи,
записывать математически верно решение задачи, применять знания в
нестандартных ситуациях;
— со слабо успевающими обучающимися необходимо выделить круг
доступных ему заданий, помочь освоить основные математические факты,
позволяющие их решать и сформировать уверенные навыки их решения;
— для «средних» учеников необходимо использовать методику, при которой
они смогут перейти от теоретических знаний к практическим навыкам, от
решения стандартных алгоритмических задач к решению задач похожего
содержания, но иной формулировки и применению уже отработанных
навыков в новой ситуации;
4
— для сильных учеников требуется создание условия для продвижения:
дифференцированные по уровню сложности задания, возможность
саморазвития, помощь в решении заданий второй части;
— «нарешивание» заданий открытого банка ОГЭ необходимо для
формирования устойчивых навыков решения, но его нужно сочетать с
фундаментальной подготовкой, позволяющей сформировать у учащихся
общие учебные действия, способствующие более эффективному усвоению
изучаемых вопросов, а также дифференциации обучающихся по уровню
подготовки;
— учителю следует ставить перед каждым учащимся ту цель, которую он
может реализовать в соответствии с уровнем его подготовки, при этом
опираясь на самооценку и устремления каждого учащегося
— наряду с более тщательным изучением тем «Уравнения, неравенства и их
системы» (более сложные виды), «Решение текстовых задач», «Решение
планиметрических задач, содержащих комбинацию фигур», «Решение задач
на доказательство» (причем как по геометрии, так и по алгебре) необходимо
уделять внимание и остальным темам с тем, чтобы поддерживать и повышать
достигнутый уровень их освоения;
— для успешного выполнения заданий второй части необходимо овладение
отдельными элементами знаний и умений переводить на овладение навыками
решения комплексных, многошаговых заданий;
— в процессе подготовки к ОГЭ должны участвовать все стороны:
обучающийся, школа и родители, поэтому необходимо своевременно
знакомить родителей с нормативными документами по подготовке к
экзаменам, информировать их о процедуре итоговой аттестации,
особенностях подготовки к тестовой форме сдачи экзаменов, о
всевозможных методических рекомендациях и ресурсах, о результатах
пробных испытаний и текущей успеваемости;
— необходимо использовать имеющиеся в достаточном количестве
дополнительные материалы, уделять внимание различным способам решения
задач, их сопоставлению и выбору лучшего; учить использовать логические
цепочки не только при доказательстве, но и при решении задач, стараться
достичь осознанности знаний учащихся, сформированности умения
применять полученные знания в практической деятельности, умения
анализировать, сопоставлять, делать выводы в нестандартных ситуациях.
Таким образом, необходимым условием успешной подготовки
обучающихся к сдаче ГИА является освоение учителем материалов,
публикуемых ФИПИ: демонстрационного варианта, кодификатора элементов
содержания и кодификатора требований к уровню подготовки, спецификации
КИМ по математике, учебно—методических материалов для председателей и
членов региональных предметных комиссий по проверке выполнения
заданий с развернутым ответом экзаменационных работ ОГЭ и, конечно,
изучение заданий открытого банка, их систематизация, выделение основных
способов решения различных классов заданий. А также, изучить
5
разнообразные методические пособия, учебно—тренировочные материалы,
представленные на сайтах и различными издательствами.
Для успешного выполнения заданий второй части КИМ необходим
особый подход в работе с наиболее подготовленными учащимися.
В целом, для успешного прохождения ГИА необходима
дифференцированная работа с учащимися класса и на уроке, и при
составлении домашних заданий и заданий, предлагающихся обучающимся на
контрольных, проверочных, диагностических работах. Необходимо обратить
серьёзное внимание на решение прикладных и ситуационных задач, а также
на формирование уверенных вычислительных навыков
Список используемой литературы:
1. Документы, определяющие структуру и содержание КИМ ) ОГЭ 2021
г.;
2. Учебно—методические материалы для председателей и членов
региональных предметных комиссий по проверке выполнения заданий с
развёрнутым ответом экзаменационных работ ОГЭ;
3. Методические рекомендации на основе анализа типичных ошибок
участников ОГЭ прошлых лет (2019, 2020 гг.);
4. Методические рекомендации для учителей школ с высокой долей
обучающихся с рисками учебной неуспешности (fipi.ru);
5. журнал «Педагогические измерения»;
6. Youtube-канал Рособрнадзора.
Приложение 1
Анализ типичных ошибок обучающихся на ОГЭ 2021
по математике в МБОУ «Мужевская МОШ имени Н.В.
Архангельского»
Таблица1
Содержание
задания в КИМ ОГЭ
Выделять из текста нужную
информацию, преобразование
информации из одного вида в другой,
сопоставлять информацию,
представленную в таблице с
текстовой, отвечать на поставленный
вопрос.
Задание выполнено на ожидаемом
уровне.
Решить задачу на нахождение
расстояния по шоссе
между селами,
используя информацию из текста,
картинки, масштаб
не обращают внимание на единицы
измерения, не учитывают масштаб,
вычислительные ошибки.
Решить задачу на нахождение
расстояния по прямой с помощью
теоремы Пифагора, используя
информацию из текста, таблицы.
невнимательное прочтение текста,
работа с формулой, вычисления.
Решить задачу на нахождение
времени движения, используя
информацию из текста
и данные
задачи 2
.
невнимательное прочтение текста,
неверное построение математической
модели, вычислительная ошибка,
не
знание формул
Задание на определение
наиболее
дешевого набора продуктов,
используя информацию из таблицы
вычислительные, невнимательное
прочтение вопроса к заданию, в
построении математической модели.
Задание направлено на проверку
умения выполнять арифметические
действия с десятичными дробями.
в применении правил выполнения
арифметических действий с
десятичными дробями.
Задание направлено на проверку
умений выполнять вычисления и
преобразования на координатной
прямой.
Задание выполнено на ожидаемом
уровне.
Задание на умение выполнять
преобразования алгебраических
выражений, содержащих степень или
корень, и находить значение данного
выражения при заданном
неизвестном.
в применении свойств степени или
корня, вычислительная ошибка.
Задание проверяет умения решать
линейные уравнения или неполное
квадратное уравнение
в алгоритме решения уравнений,
вычислительная.
Задание проверяет умения решать
практическую расчетную задачу на
вычисление вероятности события.
Для решения таких задач необходимо
знать определение вероятности
события и, что общая вероятность
несовместных событий равна 1;
достаточно уметь находить
отношение числа благоприятных для
наступления некоторого события
исходов к числу всех
равновозможных исходов. Иногда это
требует определённых
невнимательное чтение условия,
неумение определять число
благоприятных исходов, кроме того,
часть учеников вероятности события
записали в процентах.
Задание направлено на проверку
умений чтения графиков функций,
содержащие задания, в которых
требуется установить соответствие
между знаками коэффициентов
квадратичной функции
Неверное установление соответствия
между знаками
коэффициентов, неумение читать
графики.
Задание представляет собой задачу
на умение осуществлять
практические расчёты по формулам;
составлять несложные формулы,
выражающие зависимости между
величинами. В условиях таких задач
даются формулы из разных областей
знаний, причём значения всех
величин за исключением одной в
этих формулах известны. Требуется
найти значение именно этой
величины.
Данное задание некоторые учащиеся
пропускают, это говорит о том, что
девятиклассники не умеют работать с
математической моделью.
Вычислительные ошибки
Задание представляет собой
квадратное неравенство или
линейное неравенство. Необходимо
было решить неполное квадратное
неравенство
Ошибки связаны с незнанием
свойств неравенств и алгоритма
решения квадратных неравенств,
неумением определить знак
соответствующей функции (или
многочлена) на интервале.
Задание с практическим
содержанием, направленное на
проверку умения применять знания
об арифметической и геометрической
прогрессиях в прикладных задачах.
неверное установление вида
прогрессии, вычислительные
ошибки, непонимание прочитанного
текста
Несложная планиметрическая задача
в одно действие, проверяющая
владение базовыми знаниями по теме
«Треугольники». Для успешного
решения задачи достаточно знать
теорему о сумме углов треугольника
Неверное нахождение острого угла
прямоугольного треугольника и
вычислительные ошибки.
Незнание теоремы о сумме углов тр—
ка
Представляет собой задачу,
связанную с окружностью . Для
решения данной задачи необходимо
знать теорему об угле между хордой
и касательной к окружности
вычислительная, незнание нужной
теоремы, определения касательной
Представляет собой задачу по теме
«Четырехугольники». Решение
задачи сводилось к применению
формулы площади параллелограмма.
вычислительная, по причине
невнимательности учащихся,
незнание формулы площади
Представляет собой задачу по
планиметрии на вычисление
геометрических величин по готовому
чертежу, изображённому на
клетчатой бумаге. В таких задачах
данные представлены в виде чертежа
на бумаге в клетку, причём размеры
клеток одинаковы и заданы
условием.
В данном случае на клетчатой бумаге
была изображена фигура, необходимо
было найти площадь, посчитав к—во
клеток треугольник или трапеция,
требовалось найти их площади.
невнимательность при подсчете
клеток, незнание способа
нахождения площади по клеткам
Задание на умение оценивать
логическую правильность
рассуждений, распознавать
ошибочные заключения, требующее
выбрать одно или несколько верных
утверждений из множества данных (в
настоящее время – из трёх данных).
В большинстве случаев правильный
ответ на вопрос задачи связан со
знанием простейших геометрических
фактов и утверждений.
не владеют достаточными знаниями
точных определений и формулировок
теорем, свойств геометрических
фигур.
требовалось решить
иррационального алгебраическое
уравнение, применив один из
основных методов решения:
1) преобразование уравнения к виду
квадратного уравнения,
2)Найти область определения ;
3)Определить посторонний корень
ошибки в действиях:
1) Вычеркивание квадратного корня
из обеих частей уравнения без учёта
условий выполнимости данного
действия и равносильности
преобразования (рассматривание
одного случая из возможных);
2) перенос слагаемых из одной части
уравнения в другую;
3) решение квадратного уравнения.
Данное обстоятельство
свидетельствует о недостаточном
уровне освоения методов решения
алгебраических уравнений,
формальном, не осмысленном
выполнении шагов алгоритмов
решения уравнений тем или иным
методом.
4) не содержит записи ответа, хотя
данный шаг является обязательным
при решении уравнений, кроме того,
перед заданиями второй части в
прямоугольной рамке фиксируется
инструкция: «…запишите его
решение и ответ».
В связи с чем, учителям следует
обратить внимание на обеспечение
условий для качественной
реализации этапов осмысления и
применения методов решения
алгебраических уравнений на уроках
математики в школе.
требовалось решить текстовую
задачу на нахождение количества
свежих фруктов из определенного
количества высушенных.
Для верного и полного решения
обучающимися должны быть
выполнены следующие этапы работы
с задачей: составление
математической модели,
преобразование составленной
модели, интерпретация полученных
результатов и запись ответа. Все
этапы должны быть зафиксированы в
представленном решении.
Самая распространённая ошибка при
решении задачи на нахождение
количества свежих фруктов из
определенного количества
высушенных. В неумении составить
модель задачи.
у большинства обучающихся
возникают серьезные затруднения
при решении этих задач. Это
свидетельствует о необходимости
изменения подходов к обучению по
решению текстовых задач, в
частности, обучению деятельности
по реализации основных этапов
решения
задачи: анализу условия задачи,
составлению математической модели,
преобразованию составленной
модели, интерпретации полученных
результатов и записи ответа.
В задании предусмотрено
построение графика функции,
содержащей переменную в
знаменателе дроби,
Задания, предполагающие
построение графиков функций и их
анализ, всегда вызывают у
обучающихся трудности. Такие
задачи рассчитаны на более
серьёзную, выходящую за рамки
пятичасового курса алгебры,
математическую подготовку
выпускников.
1) неправильное преобразование
формулы, задающей функцию;
2) отсутствие обоснований
построения графика функции;
3) вычислительные ошибки при
определении координат точек;
4) несоблюдение масштаба при
построении системы координат,
графика;
5) отсутствие вычислений координат
точек «стыка», и как следствие, –
неверное построение графика;
6) не определено значение параметра
в соответствие с требованиями
задачи или нет пояснений, как этот
параметр определен;
7) ограничение графика (кривой или
прямой) точкой, когда
рассматриваемая функция не
является ограниченной.
Самой распространённой ошибкой
при решении задания № 22 является
неграмотное обоснование
построения графика функции.
Достаточно большое количество
работ, в которых представлено
решение задания 22, ежегодно не
содержит описание построения
графика функции, хотя развернутый
ответ, который требуется в этом
задании, предполагает описание
рассуждений.
В задании предложена
планиметрическая задача на
нахождение высоты прямоугольного
треугольника, если известны длины
двух катетов
обучающийся должен показать все
шаги решения, хотя его объяснения
могут быть неполными или может
быть допущена одна вычислительная
ошибка.
Встречаются ошибки, связанные с
некорректным использованием
чертежа, приводящим к решению
другой задачи. В этом случае задача
не считается решенной. Требуется
знание теоремы о высоте
прямоугольного треугольника
При выполнении задания
требовалось доказать
подобие треугольников,
применив два признака
подобия. Для того чтобы
получить 1 балл за решение
этой задачи достаточно было
составить верно пропорцию
без обоснования подобия
треугольников.
Задания на применение
признаков подобия
треугольников по—прежнему
являются для большинства
девятиклассников сложным
Решение проблемы освоения
темы «Подобные
треугольники» возможно при
К сожалению, оказалось, что обучающиеся
недостаточно глубоко владеют темой
«Признаки подобия треугольников».
Несмотря на стандартную формулировку
задачи, наличие в учебниках геометрии
большого количества подобных задач,
незначителен процент участников экзамена,
верно ее решивших.
При выполнении задания № 24 обучающиеся
допускали неверное использование терминов,
При обосновании подобия треугольников
использовались неверные формулировки
признаков, неверные посылки для суждения о
подобии треугольников, например, подобие
следует из равенства углов и параллельности
сторон. Данные факты говорят о
недостаточном уровне сформированности
понятийного и логического мышления,
условии целенаправленной
подготовительной работы к
изучению данной темы,
связанной с развитием
понятийного, логического
мышления обучающихся в
процессе обучения
математике с 5 по 8 класс и
выполнением условия: опора
на личный опыт ученика при
введении в тему, изучении
темы.
действия «построение логических
рассуждений».
Встречаются ошибки, связанные с
некорректным использованием чертежа,
приводящим к решению другой задачи, не
соответствующей заданному условию, в
таком случае задание нельзя считать
выполненным верно.
. Это серьезная проблема в целом,
источником которой может быть:
несформированность понятий
«пропорциональность» (5 – 6 классы),
«соответствие» (5 – 9 классы),
«пропорциональные отрезки», «сходственные
стороны» (8 класс), недостаточный уровень
развития понятийного мышления,
несформированность умений составлять и
преобразовывать пропорцию (6 класс),
несформированность познавательного
действия «построение логических
рассуждений» (5 – 9 классы),
недостаточность опыта доказательства
подобия треугольников с помощью признаков
подобия, недостаточность опыта составления
пропорции из сходственных сторон подобных
треугольников (8 класс), и др.
Выполнение задания
традиционно остается
низким, так как это
геометрическая
задача высокого уровня.
— обучающимся не известны стратегии поиска
решения задач (принципы отбора
математических предложений (теорем,
аксиом, др. из большого набора
теоретических фактов) методов решения (из
перечня методов);
— недостаточно опыта применения разных
методов решения одной задачи;
— недостаточно опыта конструирования задач
(опыт переформулирования задачи,
конструирования задачи, решаемой с
помощью заданного математического
предложения (теорем, аксиом, др.)), заданным
методом);
— недостаточно опыта самостоятельного
поиска решения задачи (опыт, основанный на
планировании решения, использовании
различных способов решения одной задачи,
анализа и сравнения этих способов решения,
опыт самостоятельного поиска решения
трудных задач).
ОГЭ. Ошибки в оформлении 2 части 20-25 задания
ОГЭ.
Ошибки в оформлении 2 части
20-25 задания
Контрольные измерительные материалы (далее
Контрольные измерительные материалы (далее КИМ) разработаны с учётом положения, что результатом освоения основной образовательной программы основного общего образования должна стать математическая компетентность выпускников, т.е. они должны:
овладеть специфическими для математики знаниями и видами деятельности;
научиться преобразованию знания и его применению в учебных и внеучебных ситуациях;
сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приёмами.
Работа состоит из двух частей, соответствующих проверке на базовом, повышенном и высоком уровнях.
Нумерация заданий Общ. балл 2021 (6 заданий) №20 №21 №22 №23 №24 № 25
|
Нумерация заданий |
Общ. балл |
||||||
|
2021 |
№20 |
№21 |
№22 |
№23 |
№24 |
№ |
|
|
Максим. балл |
2 |
12 |
Каждое задание второй части КИМ ОГЭ по математике оценивается в два балла.
Тематическая принадлежность заданий осталась в основном неизменной.
А именно, в 2021 году,
задание №20 – упрощение алгебраических выражений, решение уравнений, решение систем уравнений,
№21 – решение текстовой задачи,
№22 – построение графика функции,
№23 – задача на вычисление по геометрии,
№24 – задача по геометрии на доказательство,
№25 – геометрическая задача по геометрии высокого уровня сложности.
Общие подходы к проверке и оценке выполнения заданий с развернутым ответом
Общие подходы к проверке и оценке выполнения заданий с развернутым ответом
Решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений обучающегося. Эксперты не оценивают положительными баллами частично решенное;
Решение в демоверсии и критериях, это не эталон, это для эксперта, а ученик должен решать подробно, чтобы был виден ход его мыслей. Мы не должны ни о чем догадываться;
Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Не следует требовать от учащихся слишком подробных комментариев (например, описания алгоритмов). Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, следует рассматривать как решение без недочетов.
Если решение заданий 20–25 удовлетворяет этим требованиям, то выставляется полный балл – 2 балла за каждое задание
Если решение заданий 20–25 удовлетворяет этим требованиям, то выставляется полный балл – 2 балла за каждое задание. Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного, что и отражено в критериях оценивания заданий с развернутым ответом. В критериях исчезло слово ОПИСКА, значит, если в системе ученик между скобками с ответом поставит знак объединение, то эксперт имеет право поставить 0 баллов, даже если пример решен верно.
Результаты оценивания заданий фиксируются в протоколе проверки развернутых ответов.
Задание № 20 из второй части ОГЭ по математике включает в себя следующие разделы: 1
1. Алгебраические выражения;
2. Неравенства;
3. Системы неравенств;
4. Уравнения;
5. Системы уравнений.
Основные проверяемые требования к математической подготовке:
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы.
Уравнения
Уравнения
1. Алгебраические выражения
1. Алгебраические выражения
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Типичные ошибки Пропускают шаги (нет обоснований перехода от одного действия к последующему); записывают необоснованные алгебраические преобразования; -Подбирают ответ, не показывая, откуда он получается;
Типичные ошибки
Пропускают шаги (нет обоснований перехода от одного действия к последующему); записывают необоснованные алгебраические преобразования;
-Подбирают ответ, не показывая, откуда он получается;
Допускают вычислительные ошибки
-Допускают ошибки при сравнении двух выражений, нарушают основное математическое понятие «равенство», ошибки вида: 0=15, то есть приравнивают разные по числовым значениям буквенные выражения;
-Неверное оформление решения;
— неверное использование математической терминологии: вместо слова «выражение» записывают «уравнение» и т. д.;
-Приравнивают к нулю буквенное выражение, значение которого необходимо найти;
-Делают ссылки на основное свойство пропорции или дроби, а в дальнейшем этими свойствами не пользуются, или пользуются неверно;
-Невнимательно читают задание, не доводят решение до конца.
Системы уравнений
Типичные ошибки Ошибки при раскрытии скобок, используя формулы сокращенного умножения
Типичные ошибки
Ошибки при раскрытии скобок, используя формулы сокращенного умножения.
Отсутствие ОДЗ, либо проверки корней.
Ошибки при решении квадратных уравнений (желательно всегда писать формулу)
Использование символики (уравнения объединяют системой и в ответ записывают как для системы, а не уравнения)
При введении новой переменной забывают вернуться к исходным неизвестным.
Вычислительные ошибки.
Отсутствие ответа.
Типичные ошибки на ОГЭ
Ошибки при нарушении алгоритма решения неравенства
Ошибки при нарушении алгоритма решения неравенства
Невнимательное чтение условия (неправильный выбор интервала)
Неправильно записанный ответ (скобки)
Арифметические ошибки с отрицательными числами
Типичные ошибки
Типичные ошибки на ОГЭ
Задание 21 Текстовые задачи 1.
Задание 21
Текстовые задачи
1. Задачи на движение по воде;
2. Задачи на проценты, сплавы и смеси;
3. Задачи на совместную работу;
4. Разные задачи;
5. Движение по прямой.
Решение. Скорость обгона пешехода поездом, равна v = 141 — 6 = 135 км/ч
Решение.
Скорость обгона пешехода поездом, равна
v = 141 — 6 = 135 км/ч.
С этой скоростью поезд обгонял пешехода в течении 12 секунд, то есть в течении t = 12/3600 = 1/300 часа. Следовательно, длина поезда есть
l = v• t = 135/300 = 0,45 км
что составляет 450 метров.
Ответ: 450.
Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 12 секунд. Найдите длину поезда в метрах.
Игорь и Паша могут покрасить забор за 14 часов,
Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 700 минут
Первую половину пути автомобиль проехал со скоростью 60км/ч, а вторую – 90км/ч
Первую половину пути автомобиль проехал со скоростью 60км/ч, а вторую – 90км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Ответ:72 км/ч
Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления
Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде , если скорость течения равна 4 км/ч , стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него
Типичные ошибки на ОГЭ
Перед началом решения обсудим следующее-
Перед началом решения обсудим следующее- ПРИ СУШКЕ ИЗ ФРУКТОВ ИСПАРЯЕТСЯ ВОДА, НО СУХОЕ ВЕЩЕСТВО (МЯКОТЬ) НЕ МЕНЯЕТСЯ ПО МАССЕ.
Данные задачи представлю в небольшой, но, на мой взгляд, наглядной таблице:
Найдем массу сухого вещества в высущенных фруктах, используя следующее:
78%=0,78.
5%=0,05
Чтобы найти дробь от числа, нужно дробь умножить на это число.
1) 55*0,78=42,9 (кг) — масса сухого вещества в высушенных фруктах.
Помним, что именно столько же (42,9 кг) сухого вещества в еще свежих фруктах, массу которых и нужно найти.
2) 0,05х (кг) — масса сухого вещества в свежих фруктах.
Приравниваем массы:
3) 0,05х=42,9 (линейное уравнение с неизвестным множителем)
х=42,9/0,05
х=858 (кг) — необходимая масса свежих фруктов для получения 55 кг высушенных.
Ответ: 585 кг.
Типичные ошибки -Находят среднюю скорость движения как среднее арифметическое двух скоростей (
Типичные ошибки
-Находят среднюю скорость движения как среднее арифметическое двух скоростей ( Vср. = 𝑉1+𝑉2 2 𝑉𝑉1+𝑉𝑉2 𝑉1+𝑉2 2 2 𝑉1+𝑉2 2 );
-Решают задачу, рассматривая только частные случаи (придают величине пути всевозможные значения- 1 км., или 108 км.);
-Приписывают единицы измерения не соответствующие данным величинам;
-Забывают записывать единицы измерения к введенным значениям;
-Допускают записи вида: составим уравнение, а сами составляют выражения и их преобразования, неоднократно используют при этом знак равенства;
-Не вводят переменные величины, а используют при составлении уравнений;
Не показано как составлено уравнение (формула)
-Путают понятия скорости и времени движения;
-Допускают вычислительные ошибки;
-Записывают ответ, используя приближения (≈);
-Используют формулу для нахождения средней скорости без ее вывода;
-Отсутствие краткой записи к решению задачи, и таблицы, и обоснований, решение задачи выглядит как столбик примеров без каких бы то ни было пояснений;
-Использование неравносильных преобразований при решении уравнений.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Задание 23 Комментарий . Форма графика соблюдена, выколотая точка обозначена верно
Задание 23
Комментарий. Форма графика соблюдена, выколотая точка обозначена верно. Вторая часть задания выполнена верно.
Оценка эксперта: 2 балла.
Комментарий Несмотря на описание, по данному рисунку нельзя судить о верности графика
Комментарий
Несмотря на описание, по данному рисунку нельзя судить о верности графика.
Оценка эксперта: 0 баллов.
Комментарий . График построен верно
Комментарий.
График построен верно. Наличие некоторой прямой на графике не может быть поводом для снижения баллов.
Оценка эксперта: 1 балл.
Типичные ошибки: -Вместо области определения записывают
Типичные ошибки:
-Вместо области определения записывают ОДЗ
— Не показывают нахождение значений параметра m графическим способом (не чертят прямые, заданные уравнением у=m, или не описывают их построение);
-Отсутствуют деления на координатных осях, в результате чего график построен схематично и не проходит через точки, взятые в таблице значений;
-Запись не соответствует построению, например, пишут: построим параболу, а строят ее часть и т.д.;
-Путают линейную функцию с функцией прямой пропорциональной зависимости;
Отсутствие таблиц значений для построения графиков, либо значения переменной(ых) найдены с ошибкой;
Построение части графика функции, не являющейся линейной, по двум точкам и наоборот, построение части графика линейной функции по трем и более точкам;
Ошибки при словесном описании функции, например, при нахождении вершины параболы, значение абсциссы и ординаты называют средними точками; -При вычислении координат вершины параболы используют несуществующие формулы:
-Ошибки при словесном описании функции, например, при нахождении вершины параболы, значение абсциссы и ординаты называют средними точками;
-При вычислении координат вершины параболы используют несуществующие формулы: Д= в а в в а а в а ;
-Неверная запись параметра в виде двойного неравенства или промежутка (допускали записи вида:-1<м<-2, или (-1;-2));
-Выписывают не все значения параметра;
— Неверное название или отсутствие названия функции, ее графика;
-Отсутствует проверка граничной (критической) точки;
-Подписывают построенный график исходной функции без учета промежутков построения;
-Допускают небрежность в написании функции, например функцию вида y=-x-2 записывают как -x-2, выражение называют функцией;
-Вычислительные ошибки при нахождении значений ординат, при нахождении точек пересечения с осями координат: Д=4+4=16.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Задание 23 Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла
Задание 23
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
Комментарий.
Арифметическая ошибка под знаком корня.
Оценка эксперта: 1 балл.
Комментарий . Задача выполнена верно, несмотря на изображение перпендикуляра
Комментарий.
Задача выполнена верно, несмотря на изображение перпендикуляра AH.
Оценка эксперта: 2 балла.
Пример 2
Пример 3 Комментарий . Учащийся решает свою задачу: не учтен порядок расположения отрезков
Пример 3
Комментарий. Учащийся решает свою задачу: не учтен порядок расположения отрезков.
Оценка эксперта: 0 баллов.
Типичные ошибки -Чертеж не соответствует условию задачи; -Допускают ошибки в чертежах, обозначение разных углов одинаковыми дугами, «пустые» чертежи…; -Отсутствие чертежа при решении геометрической задачи; -На…
Типичные ошибки
-Чертеж не соответствует условию задачи;
-Допускают ошибки в чертежах, обозначение разных углов одинаковыми дугами, «пустые» чертежи…;
-Отсутствие чертежа при решении геометрической задачи;
-На чертеже неверно определяют центр описанной окружности;
— Не записывают обоснования к действиям геометрической задачи, отсутствуют ссылки на свойства, признаки, теоремы;
-Допускают ошибки в пояснениях, например, используют признак равностороннего треугольника, а записывают по определению (в треугольнике все углы по 60 градусов, значит треугольник равносторонний по определению);
Обозначают накрест лежащие углы одной заглавной буквой; -необоснованный вывод равенства двух отрезков, имеющих общую точку, которая является так же точкой пересечения диагоналей параллелограмма (частный случай…
-Обозначают накрест лежащие углы одной заглавной буквой;
-необоснованный вывод равенства двух отрезков, имеющих общую точку, которая является так же точкой пересечения диагоналей параллелограмма (частный случай переносится на решение общей задачи);
-Точку пересечения диагоналей параллелограмма называют центром или серединой параллелограмма;
-Применяют ошибочное утверждение о том, что точка пересечения диагоналей параллелограмма равноудалена от сторон параллелограмма;
-Из доказательства равенства определенной пары треугольников делают вывод о равенстве отрезков, не являющихся элементами этих треугольников.
-применяют факты, которые требуют доказательства, без таковых;
— путают названия углов, например, вместо накрест лежащего- смежный, или вместо вертикальных- односторонние…;
-ошибки в использовании свойств параллелограмма.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Задание 24 Две окружности с центрами
Задание 24
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Комментарий. Классическое доказательство данного факта.
Оценка эксперта: 2 балла.
Пример 2 Комментарий Неточность в обосновании (см
Пример 2
Комментарий
Неточность в обосновании (см. пункт 5)
Оценка эксперта: 1 балл.
Пример 3 Комментарий . Не доказано, почему
Пример 3
Комментарий. Не доказано, почему FH делит CD пополам. Оценка эксперта: 0 баллов.
Типичные ошибки -Ошибки при выполнении чертежа: изображение трапеции вместо параллелограмма; -Применение свойств несуществующей средней линии параллелограмма; -Путают признаки равенства треугольников с признаками подобия треугольников; -Используют…
Типичные ошибки
-Ошибки при выполнении чертежа: изображение трапеции вместо параллелограмма;
-Применение свойств несуществующей средней линии параллелограмма;
-Путают признаки равенства треугольников с признаками подобия треугольников;
-Используют не существующий признак равенства треугольников по трем углам, либо признак формулируют неверно, например, по двум углам и стороне между ними;
-При доказательстве равенства элементов записывают неграмотные обоснования;
-Не указывают признак по которому доказывают равенство треугольников;
-Производят подмену геометрических понятий: путают отрезок и прямую;
— Не указаны параллельные прямые при которых накрест лежащие углы равны, либо секущая при которой накрест лежащие углы образованы, либо неверное указание пары накрест лежащих углов (нет обоснования параллельности прямых);
Совмещают теорему синусов и обобщенную теорему синусов, а ссылку делают только на одну из теорем; -Сторону треугольника, вписанного в окружность, называют диаметром, а по условию…
Совмещают теорему синусов и обобщенную теорему синусов, а ссылку делают только на одну из теорем;
-Сторону треугольника, вписанного в окружность, называют диаметром, а по условию задачи треугольник не содержит прямой угол;
-Алгебраические преобразования выполняют с ошибками, например: вс sin А вс вс sin А sin А sin sin А А sin А вс sin А = 2R, ВС= 2𝑅 sin А 2𝑅𝑅 2𝑅 sin А sin А sin sin А А sin А 2𝑅 sin А ;
-Допускают ошибки при нахождении sin 30 sin sin 30 30 sin 30 ;
-При словесном обосновании действий недопустимы фразы вида: 2 угла лежат на одной стороне;
-При введении обозначений их не описывают;
-Решение задачи с другими данными;
-Использование формулы для нахождения радиуса равностороннего треугольника, вместо произвольного, в случае когда равносторонний треугольник является частью данного.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Биссектриса угла A , треугольника
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Пример 4. Биссектриса A , треугольника
Пример 4. Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. BC равно 14. Найдите радиус описанной окружности. Ответ: 25.
.
Комментарий. Арифметическая ошибка.
Оценка эксперта: 1 балл.
Биссектриса угла A , треугольника
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Комментарий. Решение незаконченное: формула для нахождения радиуса выписана, все компоненты найдены, но не получен итоговый результат. Оценка эксперта: 1 балл.
Биссектриса A , треугольника
Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. Длина BC равна 14. Найдите радиус описанной окружности.
Ответ: 25.
Пример 2 Комментарий . Логическая ошибка, неверно применено свойство биссектрисы
Пример 2
Комментарий. Логическая ошибка, неверно применено свойство биссектрисы.Оценка эксперта: 0 баллов.
Типичные ошибки -Неверно построенный чертеж -Отсутствие доказательства геометрических фактов; -Отсутствие введения переменной (в случаях, когда величину отрезка обозначали переменной); -Арифметические ошибки при вычислениях
Типичные ошибки
-Неверно построенный чертеж
-Отсутствие доказательства геометрических фактов;
-Отсутствие введения переменной (в случаях, когда величину отрезка обозначали переменной);
-Арифметические ошибки при вычислениях
Спасибо за внимание!
Спасибо за внимание!
- Авторы
- Файлы
- Ключевые слова
- Литература
Беляева Е.Р.
1
1 МБОУ ШР «СОШ №2»
подготовка к огэ по математике
анализ ошибок
уравнения
1. Марков С.Н., Осипенко Л.А., Лапшина Е.С. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2017 году. Методические рекомендации. – И: ГАУ ДПО ИРО, 2017. – 23с.
2. Лапшина Е. С., Марков С. Н., Осипенко Л. А. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2018 году. Методические рекомендации.– И: ГАУ ДПО ИРО, 2018. – 42 с.
3. Гаер М. А., Лапшина Е. С., Марков С. Н. Результаты государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области в 2019 году. Методические рекомендации. – И: ГАУ ДПО ИРО, 2019. – 38 с.
Введение
Структура Контрольно-измерительных материалов ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе. Дифференциация обучения направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и одновременного создания условий, способствующих получению частью обучающихся подготовки повышенного уровня, достаточной для активного использования математики во время дальнейшего обучения, прежде всего при изучении её в средней школе на профильном уровне.
Чтобы быть зачисленным в профильный 10 класс на базе нашего учебного учреждения, необходимо сдать успешно экзамены по итогу 9-го класса. Успешно для меня – это значит на «отлично». Критерии оценивания экзамена по математике таковы: чтобы получить отметку «отлично», необходимо набрать минимум 22 балла. Это становится возможным лишь тогда, когда выпускник приступает к решению заданий с развёрнутым ответом с №20 — №25.
Со слов сверстников, я знаю, что не все педагоги, работающие в общеобразовательных школах, рассматривают с обучающимися задания повышенного уровня сложности, анализ типичных ошибок, которые допускают выпускники прошлых лет.
Мой вклад в решение данного проблемного вопроса заключается в том, что я предлагаю своим ровесникам, на основании моей работы, рассмотреть типичные ошибки выпускников, и самостоятельно закрепить материал, подготовиться к экзамену с помощью предложенных заданий. Мной были проанализированы КИМы с 2016-2019 годы.
Обзор литературы
Вопрос типичных ошибок, которые допускают выпускники, в тех или иных заданиях, особенно 2 части, рассматривается педагогами на совещаниях по итогам ГИА. Я не нашла ни одной исследовательской работы по данному направлению, которая была бы предложена учащимися. В основном данный проблемный вопрос представлен в виде педагогических статей.
По рекомендации своего руководителя основным источником исследования стали «Методические рекомендации результатов государственной итоговой аттестации в форме основного государственного экзамена по математике в Иркутской области», которые издаются Государственным автономным учреждением дополнительного профессионального образования Иркутской области «Институт развития образования Иркутской области».
Цель
Анализ типичных ошибок выпускников в решении задания №20 (2 часть) по теме «Уравнения».
Методы исследования
1.Поисковый.
2. Анализ, синтез (отбор необходимой информации, обобщение)
3.Практический
Результаты исследования
Спецификация контрольно измерительных материалов ОГЭ по математике.
Я рассмотрела спецификацию контрольных измерительных материалов для проведения ОГЭ. И сделала вывод, что задание №20 проверяет умение учащегося выполнять преобразования алгебраических выражений, решать уравнения. Задание №20 относится к повышенному уровню сложности и оценивается на 2 балла. Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.
Задание №20 подразделяется на:
-алгебраические выражения;
-уравнения;
-неравенства;
-системы неравенств;
-системы уравнений.
На данном этапе мной рассмотрены и представлены в работе:
Уравнения:
· Иррациональные.
· Дробно-рациональные.
· Уравнения, приводимые к квадратным.
· Применение свойств при решении уравнений.
Таблица 1
Основная статистика по выполнению задания №20 учащимися 9-х классов Иркутской области.
|
№ задания |
Содержание задания |
Процент участников, набравших максимальный балл по заданию |
|||
|
2016 |
2017 |
2018 |
2019 |
||
|
21 * |
Решить уравнение или систему уравнений |
6,4 |
21,1 |
10,6 |
14,8 |
*До 2020 года задание №20 значилось под №21. Изменения произошли в контрольно-измерительных материалах в 2020-2021 учебном году.
Приведённая статистика говорит о том, что в среднем лишь 13% выпускников справляются с заданием №20. [3:19]
Содержание задания №20 по годам. Типичные ошибки выпускников.
2016 год
Решите уравнение:
Поскольку приём использования в решении уравнений свойств отрабатывается в школе редко, с заданием справились лишь 6,4% учащихся Иркутской области.
2017 год
Решите уравнение:
Типичные ошибки выпускников:
1.Вычислительные ошибки
2.Ошибки в формуле нахождения корней квадратного уравнения
3.Распостранённая ошибка в представлении ответа. Множество из двух корней уравнения описывалось как упорядоченная пара 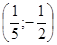
4.Обучающиеся записывали корни в виде десятичных дробей и отбрасывали из ответа те из них, которые имели ненулевой период.
О критериях оценивания:
Решение, в котором была допущена вычислительная ошибка, но с ее учетом доведенное до конца, оценивалось в 1 балл.
Подчеркну, что ошибка в формуле нахождения корней квадратного уравнения не является вычислительной, и за ее допущение ставится 0 баллов.
Правильное решение с ошибкой в форме представления ответа – 1 балл.
Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов.[1:15]
2018 год
Решите уравнение:
Типичные ошибки выпускников:
1) Основные ошибки в решении задачи 21 связаны с областью допустимых значений переменной, входящей в уравнение. Ошибка, как правило, заключалась либо в неэквивалентном преобразовании уравнения, произведенном без учета ограничения на область допустимых значений переменной, либо в неправильном определении (возможно, описании) области допустимых значений. Ошибки такого рода не относятся к вычислительным. Решение в таком случае оценивается в 0 баллов.
2) Вычислительные ошибки.
О критериях оценивания:
Решение, в котором была допущена вычислительная ошибка, но с ее
учетом доведенное до конца, оценивалось в 1 балл.
Подчеркну, что ошибка в определении области допустимых значений переменной не является вычислительной и за ее допущение ставится 0 баллов.
Появление лишних корней в ответе в результате логической (не вычислительной) ошибки – 0 баллов. [2:15]
Рисунок 1
Вывод: данное уравнение решено верно. Обучающийся получил максимальное количество баллов.
Рисунок 2
Вывод: в данном примере решения уравнения учащийся не определил ОДЗ и не учёл его при ответе. Оценка эксперта 0 баллов.
Рисунок 3
Вывод: здесь учащимся определена область допустимых значений, но неправильно: упущен случай равенства 5. Оценка эксперта 0 баллов.
2019 год
Решите уравнение:
Типичные ошибки выпускников:
1.Вычислительные ошибки
2.Второй класс ошибок касается применения метода введения вспомогательной неизвестной при решении уравнения. [3:20]
Рисунок 4
Вывод: уравнение выпускником решено верно. Оценка эксперта 2 балла.
Банк заданий №20
Тщательно разобравшись в решении новых для меня уравнений, сделав анализ типичных ошибок выпускников, предлагаю небольшой банк заданий, который поможет моим сверстникам отработать задание №20.
Иррациональные уравнения (2019 год)
Решите уравнение:
Решение:
Поскольку подкоренное выражение не может быть меньше нуля, по свойству арифметического корня, область допустимых значений ограничивается выражением 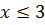
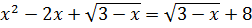
при уничтожении корней получаем:
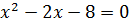
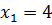
Решением искомого уравнения является только 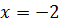
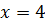
Ответ: 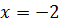
Решите уравнения самостоятельно:
a) 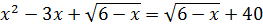
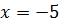
b)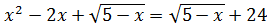
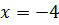
c) 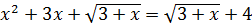
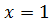
d) 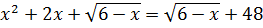
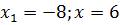
Применение свойств при решении уравнений (2016 год)
Решите уравнение: 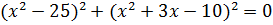
Решение:
Квадрат любого числа неотрицателен. Сумма двух неотрицательных чисел равна нулю, только если они оба равны нулю. Получаем систему уравнений:
Так как системе удовлетворяет только 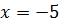
Ответ: 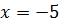
Решите уравнения самостоятельно:
a) 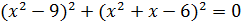
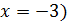
b) 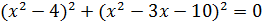
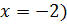
c) 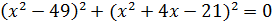
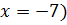
d) 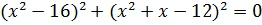
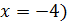
Дробно-рациональные уравнения (2017 год)
Решите уравнение:
Решение:
Так как на ноль делить нельзя, обозначаем область допустимых значений 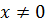
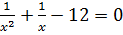
Решением через дискриминант получаем:
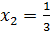
Сверим корни с ОДЗ, не входят. Соответственно в ответе записываем оба корня.
Ответ: 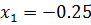
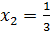
Второй способ: замена переменной
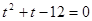
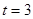
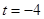
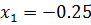
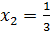
Второй способ решения был предложен составителями экзаменационных материалов. Его применяет подавляющее большинство обучающихся.
Решите уравнения самостоятельно:
a) 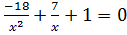
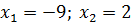
b) 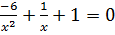
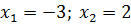
c) 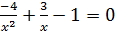
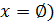
d) 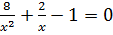
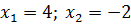
Библиографическая ссылка
Беляева Е.Р. АНАЛИЗ ТИПИЧНЫХ ОШИБОК В РЕШЕНИИ УРАВНЕНИЙ, ПРЕДЛАГАЕМЫХ В КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛАХ ОГЭ. ЗАДАНИЕ №20. МАТЕМАТИКА // Международный школьный научный вестник. – 2021. – № 2.
;
URL: https://school-herald.ru/ru/article/view?id=1423 (дата обращения: 31.01.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
1
ОГЭ —2021 по математике: типичные ошибки и пути их преодоления
Воротницкая А.И., учитель математики
МБОУ «Мужевская СОШ имени Н.В.Архангельского
Специфика математики как школьного предмета состоит в том, что ее
изучение в значительной степени строится на системе опорных знаний, без
овладения которыми невозможно дальнейшее продвижение по курсу. В ходе
ОГЭ учащийся должен продемонстрировать наличие у него опорных знаний,
позволяющих изучать математику в старшей школе.
Результаты ОГЭ по математике в этом году не очень хорошие. Эти
результаты уже привлекли внимание общественности всей страны. Поэтому
предлагаю поговорить о типичных ошибках учащихся и путях их
преодоления.
ОГЭ представляет собой форму государственной итоговой аттестации,
цель которой определить соответствие результатов освоения ООП ООО
соответствующим требованиям ФГОС
Результатом освоения ООП ООО должна стать математическая
компетентность выпускников. Выпускники должны:
• овладеть специфическими для математики знаниями и видами
деятельности;
• научиться преобразованию знания и его применению в учебных и
внеучебных ситуациях;
• сформировать качества, присущие математическому мышлению;
• овладеть математической терминологией, ключевыми понятиями,
методами и приёмами.
Р
аб
от
а по математике с
о
с
тоит
из
д
вух
час
т
е
й.
Час
ть
1,
н
а
ц
е
л
е
нн
ая
н
а
пров
е
р
к
у
овл
аде
ни
я к
ур
с
о
м
н
а ба
зово
м
уровн
е
,
с
о
де
р
ж
ит
19
з
ада
ний,
в
с
ово
к
упно
с
ти
охв
а
т
ы
в
а
ющих
в
се
р
а
з
де
л
ы
к
ур
са
и
пр
ед
у
сма
трив
а
ющих
три
ф
ор
мы
отв
е
т
а:
з
ада
ни
я с
в
ыб
оро
м
отв
е
т
а
из
че
т
ы
р
е
х
пр
ед
ло
же
нн
ы
х
в
а
ри
а
нтов,
з
ада
ни
я с к
р
а
т
к
и
м
отв
е
то
м
,
з
ада
ни
е
н
а с
оотн
есе
ни
е
Час
ть
2
с
о
с
тоит
из
з
ада
ний
пов
ы
ш
е
нного
и
в
ыс
о
к
ого
уровн
е
й
с
ло
ж
но
с
ти
и
в
к
лю
чае
т
6
з
ада
ний
с
р
а
зв
е
рнут
ым
отв
е
то
м
.
Их
н
а
зн
аче
ни
е
–
д
и
ффе
р
е
нциров
а
ть
хорошо
у
с
п
е
в
а
ющих
о
б
у
ча
ющих
ся
по
уровн
ям
по
д
готов
к
и,
в
ыя
вить
н
а
и
б
ол
ее
по
д
готовл
е
нную
час
ть
в
ы
пу
ск
ни
к
ов.
Все
з
ада
ни
я
тр
еб
уют
з
а
пи
с
и
р
е
ш
е
ний
и
отв
е
т
а
.
Зада
ни
я
р
ас
поло
же
н
ы
по
н
а
р
ас
т
а
нию
тру
д
но
с
ти.
При
пров
е
р
ке ба
зовой
ма
т
ема
ти
ческ
ой
к
о
м
п
е
т
е
нтно
с
ти
о
б
у
ча
ющи
еся
д
ол
ж
н
ы
про
дем
он
с
триров
а
ть
:
2
—
вл
аде
ни
е
о
с
новн
ым
и
а
лгорит
мам
и,
зн
а
ни
е
и
пони
ма
ни
е
к
лю
че
в
ы
х
эл
еме
нтов
с
о
де
р
жа
ни
я
(
ма
т
ема
ти
ческ
их
пон
я
тий,
их
с
вой
с
тв,
при
ем
ов
р
е
ш
е
ни
я
з
адач
и
про
чее
)
;
—
у
ме
ни
е
пользов
а
ть
ся ма
т
ема
ти
ческ
ой
з
а
пи
с
ью;
—
умение
при
ме
н
я
ть
зн
а
ни
я
в
р
е
ш
е
нии
ма
т
ема
ти
ческ
их
з
адач
,
н
е
с
во
дя
щих
ся к
пр
ям
о
м
у
при
ме
н
е
нию
а
лгорит
ма
;
—
у м е н и е
при
ме
н
я
ть
ма
т
ема
ти
ческ
и
е
зн
а
ни
я
в
про
с
т
е
йших
пр
ак
ти
ческ
их
с
иту
а
ци
я
х.
ОГЭ проверяет не только знания по предмету, но и умение читать и
понимать прочитанное, внимательность и аккуратность в оформлении
решений (запись ответов в бланк), умение проверять свои решения.
Виды типичных ошибок обучающихся на ОГЭ по математике:
1) языковые ;
2) технические;
3) содержательные.
Для преодоления языковых ошибок я применяю групповую, парную
формы работы на уроке, постоянно прошу обучающихся аргументировать
свои ответы, часто провожу устные диктанты и тематические зачеты
(особенно по геометрии).
Для преодоления технических ошибок я систематически (ежемесячно)
провожу диагностические работы, которые помогают обучающимся
вырабатывать внимательность и приучают детей делать проверку в каждом
задании.
Вероятные причины затруднений и типичных ошибок в 2021 году:
• Сложная эпидемиологическая обстановка в 2019—2021 уч.годах:
переход на дистанционное обучение, что привело к сокращению
времени на отработку материала.
• Низкие проценты выполнения заданий 3-5, 11-14 можно объяснить тем,
что они соответствуют трудно формируемым умениям у многих
школьников: выполнять преобразования со степенями, решение
квадратных и линейных неравенств и их систем, применение знаний в
практических ситуациях, построение математической модели,
вычисление числовых характеристик прогрессии.
• Геометрические задачи также традиционно вызывают трудности у
обучающихся.
• Отсутствие у обучающихся должного уровня развития логического
мышления – одна из основных причин затруднений в выполнении
геометрических заданий.
Традиционно основными направлениями подготовки обучающихся к
ГИА по математике являются:
1) Информационная работа;
2) Психологическая поддержка;
3) Предметная работа.
3
Важно заранее познакомить обучающихся с особенностями структуры
КИМ и технологией проведения экзамена. Используя образовательные
сайты ФИПИ или ОБРНАДЗОР ознакомиться самому и ознакомить
родителей с нормативной базой ГИА. Настроить ребят на то, что экзамен—это
возможность показать свои знания, поэтому не следует бояться и
переживать. Выработке психологической готовности помогает
апробирование и отработка формы проведения экзамена в формате и по
материалам ОГЭ.
В организации предметной подготовки необходимо обращать внимание
на опорные алгоритмы (формирование вычислительных навыков), на
теоретическую подготовку по геометрии (зачеты), учить составлять план
решения задачи, решать геометрические задач разного вида на применение
теоретических знаний. Необходимо готовить учащихся к использованию
справочных материалов, усилить работу по формированию языковых
умений ( учить четко и лаконично выражать свои мысли при развернутом
ответе), «нарешивать» задачи с практическим содержанием, использовать
различные формы (устный счет, математический диктант) формирования
алгоритмов и вычислительных навыков.
Итак, считаю эффективными следующие пути преодоления типичных
ошибок:
— необходимо достаточно часто проводить диагностические работы,
направленные на выявление уровня подготовки обучающихся по отдельным
темам, что позволит спланировать индивидуальную и групповую работу
обучающихся;
— при изучении нового материала и его отработке необходимо сочетать
различные методы обучения: традиционные и интерактивные, направленные
на организацию самостоятельной работы каждого ученика, что также
позволит устранить пробелы в знаниях и умениях, и поможет проводить
подготовку к аттестации дифференцированно для слабых и сильных
учеников;
— особое внимание следует уделять формированию навыков самоконтроля и
самопроверки выполненных заданий;
— необходимо повышать уровень вычислительных навыков, развивать умение
пользоваться справочными материалами, читать условие и вопрос задачи,
записывать математически верно решение задачи, применять знания в
нестандартных ситуациях;
— со слабо успевающими обучающимися необходимо выделить круг
доступных ему заданий, помочь освоить основные математические факты,
позволяющие их решать и сформировать уверенные навыки их решения;
— для «средних» учеников необходимо использовать методику, при которой
они смогут перейти от теоретических знаний к практическим навыкам, от
решения стандартных алгоритмических задач к решению задач похожего
содержания, но иной формулировки и применению уже отработанных
навыков в новой ситуации;
4
— для сильных учеников требуется создание условия для продвижения:
дифференцированные по уровню сложности задания, возможность
саморазвития, помощь в решении заданий второй части;
— «нарешивание» заданий открытого банка ОГЭ необходимо для
формирования устойчивых навыков решения, но его нужно сочетать с
фундаментальной подготовкой, позволяющей сформировать у учащихся
общие учебные действия, способствующие более эффективному усвоению
изучаемых вопросов, а также дифференциации обучающихся по уровню
подготовки;
— учителю следует ставить перед каждым учащимся ту цель, которую он
может реализовать в соответствии с уровнем его подготовки, при этом
опираясь на самооценку и устремления каждого учащегося
— наряду с более тщательным изучением тем «Уравнения, неравенства и их
системы» (более сложные виды), «Решение текстовых задач», «Решение
планиметрических задач, содержащих комбинацию фигур», «Решение задач
на доказательство» (причем как по геометрии, так и по алгебре) необходимо
уделять внимание и остальным темам с тем, чтобы поддерживать и повышать
достигнутый уровень их освоения;
— для успешного выполнения заданий второй части необходимо овладение
отдельными элементами знаний и умений переводить на овладение навыками
решения комплексных, многошаговых заданий;
— в процессе подготовки к ОГЭ должны участвовать все стороны:
обучающийся, школа и родители, поэтому необходимо своевременно
знакомить родителей с нормативными документами по подготовке к
экзаменам, информировать их о процедуре итоговой аттестации,
особенностях подготовки к тестовой форме сдачи экзаменов, о
всевозможных методических рекомендациях и ресурсах, о результатах
пробных испытаний и текущей успеваемости;
— необходимо использовать имеющиеся в достаточном количестве
дополнительные материалы, уделять внимание различным способам решения
задач, их сопоставлению и выбору лучшего; учить использовать логические
цепочки не только при доказательстве, но и при решении задач, стараться
достичь осознанности знаний учащихся, сформированности умения
применять полученные знания в практической деятельности, умения
анализировать, сопоставлять, делать выводы в нестандартных ситуациях.
Таким образом, необходимым условием успешной подготовки
обучающихся к сдаче ГИА является освоение учителем материалов,
публикуемых ФИПИ: демонстрационного варианта, кодификатора элементов
содержания и кодификатора требований к уровню подготовки, спецификации
КИМ по математике, учебно—методических материалов для председателей и
членов региональных предметных комиссий по проверке выполнения
заданий с развернутым ответом экзаменационных работ ОГЭ и, конечно,
изучение заданий открытого банка, их систематизация, выделение основных
способов решения различных классов заданий. А также, изучить
5
разнообразные методические пособия, учебно—тренировочные материалы,
представленные на сайтах и различными издательствами.
Для успешного выполнения заданий второй части КИМ необходим
особый подход в работе с наиболее подготовленными учащимися.
В целом, для успешного прохождения ГИА необходима
дифференцированная работа с учащимися класса и на уроке, и при
составлении домашних заданий и заданий, предлагающихся обучающимся на
контрольных, проверочных, диагностических работах. Необходимо обратить
серьёзное внимание на решение прикладных и ситуационных задач, а также
на формирование уверенных вычислительных навыков
Список используемой литературы:
1. Документы, определяющие структуру и содержание КИМ ) ОГЭ 2021
г.;
2. Учебно—методические материалы для председателей и членов
региональных предметных комиссий по проверке выполнения заданий с
развёрнутым ответом экзаменационных работ ОГЭ;
3. Методические рекомендации на основе анализа типичных ошибок
участников ОГЭ прошлых лет (2019, 2020 гг.);
4. Методические рекомендации для учителей школ с высокой долей
обучающихся с рисками учебной неуспешности (fipi.ru);
5. журнал «Педагогические измерения»;
6. Youtube-канал Рособрнадзора.
Приложение 1
Анализ типичных ошибок обучающихся на ОГЭ 2021
по математике в МБОУ «Мужевская МОШ имени Н.В.
Архангельского»
Таблица1
Содержание
задания в КИМ ОГЭ
Выделять из текста нужную
информацию, преобразование
информации из одного вида в другой,
сопоставлять информацию,
представленную в таблице с
текстовой, отвечать на поставленный
вопрос.
Задание выполнено на ожидаемом
уровне.
Решить задачу на нахождение
расстояния по шоссе
между селами,
используя информацию из текста,
картинки, масштаб
не обращают внимание на единицы
измерения, не учитывают масштаб,
вычислительные ошибки.
Решить задачу на нахождение
расстояния по прямой с помощью
теоремы Пифагора, используя
информацию из текста, таблицы.
невнимательное прочтение текста,
работа с формулой, вычисления.
Решить задачу на нахождение
времени движения, используя
информацию из текста
и данные
задачи 2
.
невнимательное прочтение текста,
неверное построение математической
модели, вычислительная ошибка,
не
знание формул
Задание на определение
наиболее
дешевого набора продуктов,
используя информацию из таблицы
вычислительные, невнимательное
прочтение вопроса к заданию, в
построении математической модели.
Задание направлено на проверку
умения выполнять арифметические
действия с десятичными дробями.
в применении правил выполнения
арифметических действий с
десятичными дробями.
Задание направлено на проверку
умений выполнять вычисления и
преобразования на координатной
прямой.
Задание выполнено на ожидаемом
уровне.
Задание на умение выполнять
преобразования алгебраических
выражений, содержащих степень или
корень, и находить значение данного
выражения при заданном
неизвестном.
в применении свойств степени или
корня, вычислительная ошибка.
Задание проверяет умения решать
линейные уравнения или неполное
квадратное уравнение
в алгоритме решения уравнений,
вычислительная.
Задание проверяет умения решать
практическую расчетную задачу на
вычисление вероятности события.
Для решения таких задач необходимо
знать определение вероятности
события и, что общая вероятность
несовместных событий равна 1;
достаточно уметь находить
отношение числа благоприятных для
наступления некоторого события
исходов к числу всех
равновозможных исходов. Иногда это
требует определённых
невнимательное чтение условия,
неумение определять число
благоприятных исходов, кроме того,
часть учеников вероятности события
записали в процентах.
Задание направлено на проверку
умений чтения графиков функций,
содержащие задания, в которых
требуется установить соответствие
между знаками коэффициентов
квадратичной функции
Неверное установление соответствия
между знаками
коэффициентов, неумение читать
графики.
Задание представляет собой задачу
на умение осуществлять
практические расчёты по формулам;
составлять несложные формулы,
выражающие зависимости между
величинами. В условиях таких задач
даются формулы из разных областей
знаний, причём значения всех
величин за исключением одной в
этих формулах известны. Требуется
найти значение именно этой
величины.
Данное задание некоторые учащиеся
пропускают, это говорит о том, что
девятиклассники не умеют работать с
математической моделью.
Вычислительные ошибки
Задание представляет собой
квадратное неравенство или
линейное неравенство. Необходимо
было решить неполное квадратное
неравенство
Ошибки связаны с незнанием
свойств неравенств и алгоритма
решения квадратных неравенств,
неумением определить знак
соответствующей функции (или
многочлена) на интервале.
Задание с практическим
содержанием, направленное на
проверку умения применять знания
об арифметической и геометрической
прогрессиях в прикладных задачах.
неверное установление вида
прогрессии, вычислительные
ошибки, непонимание прочитанного
текста
Несложная планиметрическая задача
в одно действие, проверяющая
владение базовыми знаниями по теме
«Треугольники». Для успешного
решения задачи достаточно знать
теорему о сумме углов треугольника
Неверное нахождение острого угла
прямоугольного треугольника и
вычислительные ошибки.
Незнание теоремы о сумме углов тр—
ка
Представляет собой задачу,
связанную с окружностью . Для
решения данной задачи необходимо
знать теорему об угле между хордой
и касательной к окружности
вычислительная, незнание нужной
теоремы, определения касательной
Представляет собой задачу по теме
«Четырехугольники». Решение
задачи сводилось к применению
формулы площади параллелограмма.
вычислительная, по причине
невнимательности учащихся,
незнание формулы площади
Представляет собой задачу по
планиметрии на вычисление
геометрических величин по готовому
чертежу, изображённому на
клетчатой бумаге. В таких задачах
данные представлены в виде чертежа
на бумаге в клетку, причём размеры
клеток одинаковы и заданы
условием.
В данном случае на клетчатой бумаге
была изображена фигура, необходимо
было найти площадь, посчитав к—во
клеток треугольник или трапеция,
требовалось найти их площади.
невнимательность при подсчете
клеток, незнание способа
нахождения площади по клеткам
Задание на умение оценивать
логическую правильность
рассуждений, распознавать
ошибочные заключения, требующее
выбрать одно или несколько верных
утверждений из множества данных (в
настоящее время – из трёх данных).
В большинстве случаев правильный
ответ на вопрос задачи связан со
знанием простейших геометрических
фактов и утверждений.
не владеют достаточными знаниями
точных определений и формулировок
теорем, свойств геометрических
фигур.
требовалось решить
иррационального алгебраическое
уравнение, применив один из
основных методов решения:
1) преобразование уравнения к виду
квадратного уравнения,
2)Найти область определения ;
3)Определить посторонний корень
ошибки в действиях:
1) Вычеркивание квадратного корня
из обеих частей уравнения без учёта
условий выполнимости данного
действия и равносильности
преобразования (рассматривание
одного случая из возможных);
2) перенос слагаемых из одной части
уравнения в другую;
3) решение квадратного уравнения.
Данное обстоятельство
свидетельствует о недостаточном
уровне освоения методов решения
алгебраических уравнений,
формальном, не осмысленном
выполнении шагов алгоритмов
решения уравнений тем или иным
методом.
4) не содержит записи ответа, хотя
данный шаг является обязательным
при решении уравнений, кроме того,
перед заданиями второй части в
прямоугольной рамке фиксируется
инструкция: «…запишите его
решение и ответ».
В связи с чем, учителям следует
обратить внимание на обеспечение
условий для качественной
реализации этапов осмысления и
применения методов решения
алгебраических уравнений на уроках
математики в школе.
требовалось решить текстовую
задачу на нахождение количества
свежих фруктов из определенного
количества высушенных.
Для верного и полного решения
обучающимися должны быть
выполнены следующие этапы работы
с задачей: составление
математической модели,
преобразование составленной
модели, интерпретация полученных
результатов и запись ответа. Все
этапы должны быть зафиксированы в
представленном решении.
Самая распространённая ошибка при
решении задачи на нахождение
количества свежих фруктов из
определенного количества
высушенных. В неумении составить
модель задачи.
у большинства обучающихся
возникают серьезные затруднения
при решении этих задач. Это
свидетельствует о необходимости
изменения подходов к обучению по
решению текстовых задач, в
частности, обучению деятельности
по реализации основных этапов
решения
задачи: анализу условия задачи,
составлению математической модели,
преобразованию составленной
модели, интерпретации полученных
результатов и записи ответа.
В задании предусмотрено
построение графика функции,
содержащей переменную в
знаменателе дроби,
Задания, предполагающие
построение графиков функций и их
анализ, всегда вызывают у
обучающихся трудности. Такие
задачи рассчитаны на более
серьёзную, выходящую за рамки
пятичасового курса алгебры,
математическую подготовку
выпускников.
1) неправильное преобразование
формулы, задающей функцию;
2) отсутствие обоснований
построения графика функции;
3) вычислительные ошибки при
определении координат точек;
4) несоблюдение масштаба при
построении системы координат,
графика;
5) отсутствие вычислений координат
точек «стыка», и как следствие, –
неверное построение графика;
6) не определено значение параметра
в соответствие с требованиями
задачи или нет пояснений, как этот
параметр определен;
7) ограничение графика (кривой или
прямой) точкой, когда
рассматриваемая функция не
является ограниченной.
Самой распространённой ошибкой
при решении задания № 22 является
неграмотное обоснование
построения графика функции.
Достаточно большое количество
работ, в которых представлено
решение задания 22, ежегодно не
содержит описание построения
графика функции, хотя развернутый
ответ, который требуется в этом
задании, предполагает описание
рассуждений.
В задании предложена
планиметрическая задача на
нахождение высоты прямоугольного
треугольника, если известны длины
двух катетов
обучающийся должен показать все
шаги решения, хотя его объяснения
могут быть неполными или может
быть допущена одна вычислительная
ошибка.
Встречаются ошибки, связанные с
некорректным использованием
чертежа, приводящим к решению
другой задачи. В этом случае задача
не считается решенной. Требуется
знание теоремы о высоте
прямоугольного треугольника
При выполнении задания
требовалось доказать
подобие треугольников,
применив два признака
подобия. Для того чтобы
получить 1 балл за решение
этой задачи достаточно было
составить верно пропорцию
без обоснования подобия
треугольников.
Задания на применение
признаков подобия
треугольников по—прежнему
являются для большинства
девятиклассников сложным
Решение проблемы освоения
темы «Подобные
треугольники» возможно при
К сожалению, оказалось, что обучающиеся
недостаточно глубоко владеют темой
«Признаки подобия треугольников».
Несмотря на стандартную формулировку
задачи, наличие в учебниках геометрии
большого количества подобных задач,
незначителен процент участников экзамена,
верно ее решивших.
При выполнении задания № 24 обучающиеся
допускали неверное использование терминов,
При обосновании подобия треугольников
использовались неверные формулировки
признаков, неверные посылки для суждения о
подобии треугольников, например, подобие
следует из равенства углов и параллельности
сторон. Данные факты говорят о
недостаточном уровне сформированности
понятийного и логического мышления,
условии целенаправленной
подготовительной работы к
изучению данной темы,
связанной с развитием
понятийного, логического
мышления обучающихся в
процессе обучения
математике с 5 по 8 класс и
выполнением условия: опора
на личный опыт ученика при
введении в тему, изучении
темы.
действия «построение логических
рассуждений».
Встречаются ошибки, связанные с
некорректным использованием чертежа,
приводящим к решению другой задачи, не
соответствующей заданному условию, в
таком случае задание нельзя считать
выполненным верно.
. Это серьезная проблема в целом,
источником которой может быть:
несформированность понятий
«пропорциональность» (5 – 6 классы),
«соответствие» (5 – 9 классы),
«пропорциональные отрезки», «сходственные
стороны» (8 класс), недостаточный уровень
развития понятийного мышления,
несформированность умений составлять и
преобразовывать пропорцию (6 класс),
несформированность познавательного
действия «построение логических
рассуждений» (5 – 9 классы),
недостаточность опыта доказательства
подобия треугольников с помощью признаков
подобия, недостаточность опыта составления
пропорции из сходственных сторон подобных
треугольников (8 класс), и др.
Выполнение задания
традиционно остается
низким, так как это
геометрическая
задача высокого уровня.
— обучающимся не известны стратегии поиска
решения задач (принципы отбора
математических предложений (теорем,
аксиом, др. из большого набора
теоретических фактов) методов решения (из
перечня методов);
— недостаточно опыта применения разных
методов решения одной задачи;
— недостаточно опыта конструирования задач
(опыт переформулирования задачи,
конструирования задачи, решаемой с
помощью заданного математического
предложения (теорем, аксиом, др.)), заданным
методом);
— недостаточно опыта самостоятельного
поиска решения задачи (опыт, основанный на
планировании решения, использовании
различных способов решения одной задачи,
анализа и сравнения этих способов решения,
опыт самостоятельного поиска решения
трудных задач).
ОГЭ. Ошибки в оформлении 2 части 20-25 задания
ОГЭ.
Ошибки в оформлении 2 части
20-25 задания
Контрольные измерительные материалы (далее
Контрольные измерительные материалы (далее КИМ) разработаны с учётом положения, что результатом освоения основной образовательной программы основного общего образования должна стать математическая компетентность выпускников, т.е. они должны:
овладеть специфическими для математики знаниями и видами деятельности;
научиться преобразованию знания и его применению в учебных и внеучебных ситуациях;
сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приёмами.
Работа состоит из двух частей, соответствующих проверке на базовом, повышенном и высоком уровнях.
Нумерация заданий Общ. балл 2021 (6 заданий) №20 №21 №22 №23 №24 № 25
|
Нумерация заданий |
Общ. балл |
||||||
|
2021 |
№20 |
№21 |
№22 |
№23 |
№24 |
№ |
|
|
Максим. балл |
2 |
12 |
Каждое задание второй части КИМ ОГЭ по математике оценивается в два балла.
Тематическая принадлежность заданий осталась в основном неизменной.
А именно, в 2021 году,
задание №20 – упрощение алгебраических выражений, решение уравнений, решение систем уравнений,
№21 – решение текстовой задачи,
№22 – построение графика функции,
№23 – задача на вычисление по геометрии,
№24 – задача по геометрии на доказательство,
№25 – геометрическая задача по геометрии высокого уровня сложности.
Общие подходы к проверке и оценке выполнения заданий с развернутым ответом
Общие подходы к проверке и оценке выполнения заданий с развернутым ответом
Решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений обучающегося. Эксперты не оценивают положительными баллами частично решенное;
Решение в демоверсии и критериях, это не эталон, это для эксперта, а ученик должен решать подробно, чтобы был виден ход его мыслей. Мы не должны ни о чем догадываться;
Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Не следует требовать от учащихся слишком подробных комментариев (например, описания алгоритмов). Лаконичное решение, не содержащее неверных утверждений, все выкладки которого правильны, следует рассматривать как решение без недочетов.
Если решение заданий 20–25 удовлетворяет этим требованиям, то выставляется полный балл – 2 балла за каждое задание
Если решение заданий 20–25 удовлетворяет этим требованиям, то выставляется полный балл – 2 балла за каждое задание. Если в решении допущена ошибка непринципиального характера (вычислительная, погрешность в терминологии или символике и др.), не влияющая на правильность общего хода решения (даже при неверном ответе) и позволяющая, несмотря на ее наличие, сделать вывод о владении материалом, то учащемуся засчитывается балл, на 1 меньший указанного, что и отражено в критериях оценивания заданий с развернутым ответом. В критериях исчезло слово ОПИСКА, значит, если в системе ученик между скобками с ответом поставит знак объединение, то эксперт имеет право поставить 0 баллов, даже если пример решен верно.
Результаты оценивания заданий фиксируются в протоколе проверки развернутых ответов.
Задание № 20 из второй части ОГЭ по математике включает в себя следующие разделы: 1
1. Алгебраические выражения;
2. Неравенства;
3. Системы неравенств;
4. Уравнения;
5. Системы уравнений.
Основные проверяемые требования к математической подготовке:
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы.
Уравнения
Уравнения
1. Алгебраические выражения
1. Алгебраические выражения
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Типичные ошибки Пропускают шаги (нет обоснований перехода от одного действия к последующему); записывают необоснованные алгебраические преобразования; -Подбирают ответ, не показывая, откуда он получается;
Типичные ошибки
Пропускают шаги (нет обоснований перехода от одного действия к последующему); записывают необоснованные алгебраические преобразования;
-Подбирают ответ, не показывая, откуда он получается;
Допускают вычислительные ошибки
-Допускают ошибки при сравнении двух выражений, нарушают основное математическое понятие «равенство», ошибки вида: 0=15, то есть приравнивают разные по числовым значениям буквенные выражения;
-Неверное оформление решения;
— неверное использование математической терминологии: вместо слова «выражение» записывают «уравнение» и т. д.;
-Приравнивают к нулю буквенное выражение, значение которого необходимо найти;
-Делают ссылки на основное свойство пропорции или дроби, а в дальнейшем этими свойствами не пользуются, или пользуются неверно;
-Невнимательно читают задание, не доводят решение до конца.
Системы уравнений
Типичные ошибки Ошибки при раскрытии скобок, используя формулы сокращенного умножения
Типичные ошибки
Ошибки при раскрытии скобок, используя формулы сокращенного умножения.
Отсутствие ОДЗ, либо проверки корней.
Ошибки при решении квадратных уравнений (желательно всегда писать формулу)
Использование символики (уравнения объединяют системой и в ответ записывают как для системы, а не уравнения)
При введении новой переменной забывают вернуться к исходным неизвестным.
Вычислительные ошибки.
Отсутствие ответа.
Неравенства (х – 8)2 < 3 3 3 3 (х –  (х – 8)2 — 3 3 3 3 (х –
(х – 8)2 — 3 3 3 3 (х –  < 0…
< 0…
Неравенства
(х – 8)2 < 3 3 3 3 (х – 
(х – 8)2 — 3 3 3 3 (х – 
(х – 
у = (х – 
Найдем нули функции: х = 8 и х = 8 + 3 3 3 3
+ — +
8 8+ 3 3 3 3
Если х = 9 , то (9-8)(9-8- 3 3 3 3 ) < 0
Ответ: (8;8+ 3 3 3 3 )
Типичные ошибки на ОГЭ
Ошибки при нарушении алгоритма решения неравенства
Ошибки при нарушении алгоритма решения неравенства
Невнимательное чтение условия (неправильный выбор интервала)
Неправильно записанный ответ (скобки)
Арифметические ошибки с отрицательными числами
Типичные ошибки
Типичные ошибки на ОГЭ
Задание 21 Текстовые задачи 1.
Задание 21
Текстовые задачи
1. Задачи на движение по воде;
2. Задачи на проценты, сплавы и смеси;
3. Задачи на совместную работу;
4. Разные задачи;
5. Движение по прямой.
Решение. Скорость обгона пешехода поездом, равна v = 141 — 6 = 135 км/ч
Решение.
Скорость обгона пешехода поездом, равна
v = 141 — 6 = 135 км/ч.
С этой скоростью поезд обгонял пешехода в течении 12 секунд, то есть в течении t = 12/3600 = 1/300 часа. Следовательно, длина поезда есть
l = v• t = 135/300 = 0,45 км
что составляет 450 метров.
Ответ: 450.
Поезд, двигаясь равномерно со скоростью 141 км/ч, проезжает мимо пешехода, идущего в том же направлении параллельно путям со скоростью 6 км/ч, за 12 секунд. Найдите длину поезда в метрах.
Игорь и Паша могут покрасить забор за 14 часов,
Игорь и Паша могут покрасить забор за 14 часов, Паша и Володя – за 15 часов, а Володя и Игорь за 30 часов. За какое время покрасят забор мальчики, работая втроем. Ответ дайте в минутах.
Ответ: 700 минут
Первую половину пути автомобиль проехал со скоростью 60км/ч, а вторую – 90км/ч
Первую половину пути автомобиль проехал со скоростью 60км/ч, а вторую – 90км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Ответ:72 км/ч
Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления
Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде , если скорость течения равна 4 км/ч , стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него
Типичные ошибки на ОГЭ
Перед началом решения обсудим следующее-
Перед началом решения обсудим следующее- ПРИ СУШКЕ ИЗ ФРУКТОВ ИСПАРЯЕТСЯ ВОДА, НО СУХОЕ ВЕЩЕСТВО (МЯКОТЬ) НЕ МЕНЯЕТСЯ ПО МАССЕ.
Данные задачи представлю в небольшой, но, на мой взгляд, наглядной таблице:
Найдем массу сухого вещества в высущенных фруктах, используя следующее:
78%=0,78.
5%=0,05
Чтобы найти дробь от числа, нужно дробь умножить на это число.
1) 55*0,78=42,9 (кг) — масса сухого вещества в высушенных фруктах.
Помним, что именно столько же (42,9 кг) сухого вещества в еще свежих фруктах, массу которых и нужно найти.
2) 0,05х (кг) — масса сухого вещества в свежих фруктах.
Приравниваем массы:
3) 0,05х=42,9 (линейное уравнение с неизвестным множителем)
х=42,9/0,05
х=858 (кг) — необходимая масса свежих фруктов для получения 55 кг высушенных.
Ответ: 585 кг.
Типичные ошибки -Находят среднюю скорость движения как среднее арифметическое двух скоростей (
Типичные ошибки
-Находят среднюю скорость движения как среднее арифметическое двух скоростей ( Vср. = 𝑉1+𝑉2 2 𝑉𝑉1+𝑉𝑉2 𝑉1+𝑉2 2 2 𝑉1+𝑉2 2 );
-Решают задачу, рассматривая только частные случаи (придают величине пути всевозможные значения- 1 км., или 108 км.);
-Приписывают единицы измерения не соответствующие данным величинам;
-Забывают записывать единицы измерения к введенным значениям;
-Допускают записи вида: составим уравнение, а сами составляют выражения и их преобразования, неоднократно используют при этом знак равенства;
-Не вводят переменные величины, а используют при составлении уравнений;
Не показано как составлено уравнение (формула)
-Путают понятия скорости и времени движения;
-Допускают вычислительные ошибки;
-Записывают ответ, используя приближения (≈);
-Используют формулу для нахождения средней скорости без ее вывода;
-Отсутствие краткой записи к решению задачи, и таблицы, и обоснований, решение задачи выглядит как столбик примеров без каких бы то ни было пояснений;
-Использование неравносильных преобразований при решении уравнений.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Задание 23 Комментарий . Форма графика соблюдена, выколотая точка обозначена верно
Задание 23
Комментарий. Форма графика соблюдена, выколотая точка обозначена верно. Вторая часть задания выполнена верно.
Оценка эксперта: 2 балла.
Комментарий Несмотря на описание, по данному рисунку нельзя судить о верности графика
Комментарий
Несмотря на описание, по данному рисунку нельзя судить о верности графика.
Оценка эксперта: 0 баллов.
Комментарий . График построен верно
Комментарий.
График построен верно. Наличие некоторой прямой на графике не может быть поводом для снижения баллов.
Оценка эксперта: 1 балл.
Типичные ошибки: -Вместо области определения записывают
Типичные ошибки:
-Вместо области определения записывают ОДЗ
— Не показывают нахождение значений параметра m графическим способом (не чертят прямые, заданные уравнением у=m, или не описывают их построение);
-Отсутствуют деления на координатных осях, в результате чего график построен схематично и не проходит через точки, взятые в таблице значений;
-Запись не соответствует построению, например, пишут: построим параболу, а строят ее часть и т.д.;
-Путают линейную функцию с функцией прямой пропорциональной зависимости;
Отсутствие таблиц значений для построения графиков, либо значения переменной(ых) найдены с ошибкой;
Построение части графика функции, не являющейся линейной, по двум точкам и наоборот, построение части графика линейной функции по трем и более точкам;
Ошибки при словесном описании функции, например, при нахождении вершины параболы, значение абсциссы и ординаты называют средними точками; -При вычислении координат вершины параболы используют несуществующие формулы:
-Ошибки при словесном описании функции, например, при нахождении вершины параболы, значение абсциссы и ординаты называют средними точками;
-При вычислении координат вершины параболы используют несуществующие формулы: Д= в а в в а а в а ;
-Неверная запись параметра в виде двойного неравенства или промежутка (допускали записи вида:-1<м<-2, или (-1;-2));
-Выписывают не все значения параметра;
— Неверное название или отсутствие названия функции, ее графика;
-Отсутствует проверка граничной (критической) точки;
-Подписывают построенный график исходной функции без учета промежутков построения;
-Допускают небрежность в написании функции, например функцию вида y=-x-2 записывают как -x-2, выражение называют функцией;
-Вычислительные ошибки при нахождении значений ординат, при нахождении точек пересечения с осями координат: Д=4+4=16.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Задание 23 Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла
Задание 23
Высота, опущенная из вершины ромба, делит противоположную сторону на отрезки равные 24 и 2, считая от вершины острого угла. Вычислите длину высоты ромба. Ответ: 10.
Комментарий.
Арифметическая ошибка под знаком корня.
Оценка эксперта: 1 балл.
Комментарий . Задача выполнена верно, несмотря на изображение перпендикуляра
Комментарий.
Задача выполнена верно, несмотря на изображение перпендикуляра AH.
Оценка эксперта: 2 балла.
Пример 2
Пример 3 Комментарий . Учащийся решает свою задачу: не учтен порядок расположения отрезков
Пример 3
Комментарий. Учащийся решает свою задачу: не учтен порядок расположения отрезков.
Оценка эксперта: 0 баллов.
Типичные ошибки -Чертеж не соответствует условию задачи; -Допускают ошибки в чертежах, обозначение разных углов одинаковыми дугами, «пустые» чертежи…; -Отсутствие чертежа при решении геометрической задачи; -На…
Типичные ошибки
-Чертеж не соответствует условию задачи;
-Допускают ошибки в чертежах, обозначение разных углов одинаковыми дугами, «пустые» чертежи…;
-Отсутствие чертежа при решении геометрической задачи;
-На чертеже неверно определяют центр описанной окружности;
— Не записывают обоснования к действиям геометрической задачи, отсутствуют ссылки на свойства, признаки, теоремы;
-Допускают ошибки в пояснениях, например, используют признак равностороннего треугольника, а записывают по определению (в треугольнике все углы по 60 градусов, значит треугольник равносторонний по определению);
Обозначают накрест лежащие углы одной заглавной буквой; -необоснованный вывод равенства двух отрезков, имеющих общую точку, которая является так же точкой пересечения диагоналей параллелограмма (частный случай…
-Обозначают накрест лежащие углы одной заглавной буквой;
-необоснованный вывод равенства двух отрезков, имеющих общую точку, которая является так же точкой пересечения диагоналей параллелограмма (частный случай переносится на решение общей задачи);
-Точку пересечения диагоналей параллелограмма называют центром или серединой параллелограмма;
-Применяют ошибочное утверждение о том, что точка пересечения диагоналей параллелограмма равноудалена от сторон параллелограмма;
-Из доказательства равенства определенной пары треугольников делают вывод о равенстве отрезков, не являющихся элементами этих треугольников.
-применяют факты, которые требуют доказательства, без таковых;
— путают названия углов, например, вместо накрест лежащего- смежный, или вместо вертикальных- односторонние…;
-ошибки в использовании свойств параллелограмма.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Задание 24 Две окружности с центрами
Задание 24
Две окружности с центрами E и F пересекаются в точках C и D, центры E и F лежат по одну сторону относительно прямой CD. Докажите, что прямая CD перпендикулярна прямой EF.
Комментарий. Классическое доказательство данного факта.
Оценка эксперта: 2 балла.
Пример 2 Комментарий Неточность в обосновании (см
Пример 2
Комментарий
Неточность в обосновании (см. пункт 5)
Оценка эксперта: 1 балл.
Пример 3 Комментарий . Не доказано, почему
Пример 3
Комментарий. Не доказано, почему FH делит CD пополам. Оценка эксперта: 0 баллов.
Типичные ошибки -Ошибки при выполнении чертежа: изображение трапеции вместо параллелограмма; -Применение свойств несуществующей средней линии параллелограмма; -Путают признаки равенства треугольников с признаками подобия треугольников; -Используют…
Типичные ошибки
-Ошибки при выполнении чертежа: изображение трапеции вместо параллелограмма;
-Применение свойств несуществующей средней линии параллелограмма;
-Путают признаки равенства треугольников с признаками подобия треугольников;
-Используют не существующий признак равенства треугольников по трем углам, либо признак формулируют неверно, например, по двум углам и стороне между ними;
-При доказательстве равенства элементов записывают неграмотные обоснования;
-Не указывают признак по которому доказывают равенство треугольников;
-Производят подмену геометрических понятий: путают отрезок и прямую;
— Не указаны параллельные прямые при которых накрест лежащие углы равны, либо секущая при которой накрест лежащие углы образованы, либо неверное указание пары накрест лежащих углов (нет обоснования параллельности прямых);
Совмещают теорему синусов и обобщенную теорему синусов, а ссылку делают только на одну из теорем; -Сторону треугольника, вписанного в окружность, называют диаметром, а по условию…
Совмещают теорему синусов и обобщенную теорему синусов, а ссылку делают только на одну из теорем;
-Сторону треугольника, вписанного в окружность, называют диаметром, а по условию задачи треугольник не содержит прямой угол;
-Алгебраические преобразования выполняют с ошибками, например: вс sin А вс вс sin А sin А sin sin А А sin А вс sin А = 2R, ВС= 2𝑅 sin А 2𝑅𝑅 2𝑅 sin А sin А sin sin А А sin А 2𝑅 sin А ;
-Допускают ошибки при нахождении sin 30 sin sin 30 30 sin 30 ;
-При словесном обосновании действий недопустимы фразы вида: 2 угла лежат на одной стороне;
-При введении обозначений их не описывают;
-Решение задачи с другими данными;
-Использование формулы для нахождения радиуса равностороннего треугольника, вместо произвольного, в случае когда равносторонний треугольник является частью данного.
Типичные ошибки на ОГЭ
Типичные ошибки на ОГЭ
Биссектриса угла A , треугольника
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Пример 4. Биссектриса A , треугольника
Пример 4. Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. BC равно 14. Найдите радиус описанной окружности. Ответ: 25.
.
Комментарий. Арифметическая ошибка.
Оценка эксперта: 1 балл.
Биссектриса угла A , треугольника
Биссектриса угла A, треугольника ABC делит высоту BH в отношении 5:4, считая от вершины. BC равно 6. Найдите радиус описанной окружности. Ответ: 5.
Комментарий. Решение незаконченное: формула для нахождения радиуса выписана, все компоненты найдены, но не получен итоговый результат. Оценка эксперта: 1 балл.
Биссектриса A , треугольника
Биссектриса A, треугольника ABC делит высоту BH в отношении 25:24, считая от вершины. Длина BC равна 14. Найдите радиус описанной окружности.
Ответ: 25.
Пример 2 Комментарий . Логическая ошибка, неверно применено свойство биссектрисы
Пример 2
Комментарий. Логическая ошибка, неверно применено свойство биссектрисы.Оценка эксперта: 0 баллов.
Типичные ошибки -Неверно построенный чертеж -Отсутствие доказательства геометрических фактов; -Отсутствие введения переменной (в случаях, когда величину отрезка обозначали переменной); -Арифметические ошибки при вычислениях
Типичные ошибки
-Неверно построенный чертеж
-Отсутствие доказательства геометрических фактов;
-Отсутствие введения переменной (в случаях, когда величину отрезка обозначали переменной);
-Арифметические ошибки при вычислениях
Спасибо за внимание!
Спасибо за внимание!
02.03.2020
Статья: «Государственная итоговая аттестация по математике. Типичные ошибки и методические приемы их устранения»
В данной статье рассматриваются типичные ошибки, которые допускают учащиеся на ОГЭ по математике. На конкретных примерах разобраны возможные ошибки и рассмотрены пути их предупреждения. Автор делится со своими методическими приемами в работе со слабоуспевающими учащимися. Материал может заинтересовать учителей математики.
Оценить
1375
Содержимое разработки
Статья: «Государственная итоговая аттестация по математике. Типичные ошибки и методические приемы их устранения»
Бушкова Марина Григорьевна
Муниципальное общеобразовательное учреждение
Школа с. Белоярск
учитель математики
В математике приходится учиться в основном на собственных ошибках. Не ошибается тот, кто ничего не делает. Ошибка – вещь необходимая и полезная. Необходимая и полезная, но не на экзамене. На экзамене ученик должен показать хорошие результаты, чтобы затем продолжить образование на следующей ступени обучения. Задача учителя — в процессе обучения математике целенаправленно и систематически организовывать работу учащихся над типичными ошибками, что будет способствовать повышению качества математической подготовки учащихся. Я.А. Коменский писал: «Любая ошибка превращается из маленького снежка в большой снежный ком, если на эту ошибку сразу не реагировал учитель при непременном привлечении самого учащегося к ее осознанию и последующему труду, направленному на ее полное преодоление».
Типичные ошибки учащихся:
незнание правил, определений, формул;
непонимание правил, определений, формул;
неумение применять правила, определения, формулы;
неверное применение формул;
невнимательное чтение условия и вопроса задания;
вычислительные ошибки;
неиспользование свойств фигур при решении геометрических задач;
логические ошибки при решении текстовых задач;
раскрытие скобок и применение формул сокращенного умножения.
Причины ошибок по математике:
пропуски занятий приводят к незнанию материала, пробелам в знаниях;
поверхностное, невдумчивое восприятие нового материала приводят к непониманию его;
недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы;
неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам (учащиеся не всегда сами понимают, что именно они написали);
усталость, чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам;
кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала;
низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки;
«зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается ошибка.
низкая мотивация: следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые учениками на экзамене по математике, я бы условно разделила на три категории: технические; глупые, обидные, сделанные на ровном месте; содержательные.
Технические ошибки связаны с неправильным заполнением бланков ответов. При проверке пробных диагностических и тренировочных работ, первое, что бросается в глаза, – это неграмотное заполнение бланка с кратким ответом.
Есть смысл показать ученикам презентацию, в которой показано то, как нельзя заполнять бланки.
К заданиям, где требуется установить соответствие, а это соответствие в КИМах предлагается привести в форме таблицы, учащиеся нередко переносят в бланк ответов как «А2Б1В3», или «2,1,3», или «2;1;3», или «2 1 3» вместо верного «213».
Нередко ученики в бланк ответов вписывают единицы измерения, что нельзя делать (единицы длины, веса, градус).
Случается, что задача учащимся решена неверно и в неверном ответе содержится знак радикала – в этом случае следовало бы пересмотреть решение, но школьники упорно пытаются вписать знак арифметического квадратного корня в клетки бланка ответов.
В некоторых работах наблюдаем, как числа написаны небрежно: иногда бывает невозможно понять, что написано 6 или 0, 5 или 6, 1 или 7, 3 или 9. Данное замечание относится и к записи решения задач с развернутым ответом – иногда просто невозможно понять, что написано учеником.
Некоторые ученики в черновиках пишут настолько неаккуратно, что из-за этого на пустом месте теряют знаки или числа. Почему-то вычисления в столбик и деление уголком многие выполняют в черновиках стыдливо мелким шрифтом где-то сбоку, будто боятся, что кто-то заметит их за этим постыдным занятием. Приучайте работать учеников в своих черновиках разумно. Это поможет избежать ненужных, досадных ошибок.
Самые частые и обидные ошибки дети совершают в том, что, как им кажется, они знают.
Во избежание обидных ошибок следует обращать внимание учащихся на указания, написанные курсивом или записанные в скобках.
Пример. Найдите корни уравнения х2 + 7х – 8 = 0
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
В этом примере формирование ответа у многих учеников может вызвать затруднение. Полученные корни: -9 и 2. В соответствии с указанием ученики должны записать -92.
Отрабатываем материал с опорой на теорию. Рассмотрим задание на числовые неравенства.
Какие из следующих утверждений верны при любых значениях a и b, удовлетворяющих условию а > b?
a – 3 > b – 2
a2 > b2
5a > 5b
a – b>—2
Как чаще всего решают такие задачи? Выбирают какие-то конкретные значения a и b, а затем начинают подставлять их в утверждения. В большинстве случаев такой способ годится, но не всегда. Надежнее пользоваться свойствами неравенств.
Давайте подставим значения а = 6, b =2, ведь 6 >2. Проверим первое утверждение:
6 – 3 > 2-2; 3 > 0. Получили верное неравенство. Ученики в таком случае поставят «+» и будут уверены в своей правоте.
Однако, если взять пару чисел а = 3,5 и b =3, то получится неверное равенство: 3,5 — 3 > 3-2; 0,5 > 1.
Оказывается, это неравенство верно, но не при любых значениях а и b. Поэтому ставим «- «.
Как нужно действовать, чтобы избежать ошибки?
Из того, что а > b, следует а – b > 0. Неравенство а – 3 > b – 2 преобразуем: а – b > 1. Думаем: всегда ли верно это неравенство? Этого гарантировать мы не можем, так как нельзя же утверждать, что, если а > b , то разность этих чисел всегда > 1. Например, при а = 1,2 и b = 1 разность а – b = 1,2 — 1 = 0,2 < 1.
Проверим второе утверждение. 62 > 22, 36 > 4. Но если взять а = — 6, b = — 10, то получим неверное равенство: 36 > 10. Когда мы взяли отрицательные числа, то все сломалось. Это утверждение верно, но не при любых значениях. В этом утверждении мы также вынуждены поставить «- «.
Третье утверждение верно всегда, так как, если обе части неравенства умножить на положительное число, то получится равносильное неравенство.
Четвертое утверждение верно всегда. По условию а – b > 0, но 0 > — 2. Следовательно, тем более, а – b > -2.
Как наши дети применяют формулы сокращенного умножения? Можно встретить такие решения: (а + b)2 = а2 + b2; (а – b)2 = а2 — b2. Удвоенное произведение членов пропускают. Придумывают несуществующие формулы, например, а2 + b2 = (а – b)(a+b).
Что с этим делать? Учить, доводить до автоматизма, учить применять эти формулы в 7 классе, продолжать работу в 8-9 классах. Включать упражнения на применение этих формул на этапе повторение пройденных материалов на уроках.
Самые глупые и обидные ошибки связаны с банальной невнимательностью. Во многих случаях учащиеся невнимательно или не до конца читают текст задачи, отвечают не на поставленный вопрос. Чаще всего это задачи на чтение графиков, теорию вероятности.
Пример. На экзамене 25 билетов, Иван не выучил 7 из них. Найдите вероятность того, что ему попадется выученный билет.
Ответ: 0,28.
Этот ошибочный ответ объясняется тем, что ученик невнимательно прочитал вопрос задачи.
Необходимо приучать учеников проверять, отвечает ли полученный ответ на вопрос, поставленный в задаче. Можно пару раз самому учителю допустить ошибку и спровоцировать их на обсуждение данной проблемы.
Итак, добиваемся от учеников внимательного чтения условия задачи
Необходимо приучать учеников детально прорабатывать каждое задание, делать проверки. Некоторые ученики стараются перескакивать через несколько шагов вычислений, делая их в уме. Но в условиях экзамена лучше посчитать надежнее, расписав несколько лишних действий, чем провести их в уме, рискуя сделать ошибку. Если ученик все сделает верно, это сэкономит 5 с из 4 часов. Если ученик приучен делать проверки в вычислениях, это поможет ему избежать на экзамене досадных ошибок. Цена ошибки – драгоценные баллы.
Ошибки нужно изучать, выявлять наиболее устойчивые, вести учет. Работать над формированием навыков самоконтроля, приучая учащихся к проверке вычислений и преобразований путем обратного действия, к оценке результата решения задачи с точки зрения здравого смысла.
Пример. Решить уравнение 58 – 11х – 8 = 0
58 – 11х – 8 = 0
-11х = 58 + 8
-11х = 58 + 8
-11х = 66
х = 66 : (-11)
х = -6
Приучаем детей делать проверку:
-58 — 11(-6) – 8 = 0
-58 + 66 -8 = 0
0 = 0
При упрощении дробно-рациональных выражений зачастую подводит «коварный» минус. При вычитании многочлена ученики не меняют знаки членов, тем самым приводят решение в тупик, теряют время и получают неверный ответ.
Пример. Найти значение выражения при а = 78, с = 21.
Приведем пример неверного решения:
Как избежать ошибку?
После «минуса» многочлен сначала лучше записать в скобках, а затем эти скобки раскрыть:
Задания по геометрии учащимися решаются с меньшей успешностью.
Определение сosα, sinα, tgα, ctgα- больная тема. Ученики плохо запоминают определение, а в стрессовой ситуации путают эти определения. Можно применить секреты для запоминания.
Начнем с определения сosα. Слово «косинус» созвучно со словом «коснуться». Значит, в определении косинуса фигурирует катет, который касается угла, то есть сosα — это отношение катета, прилежащего к углу, к гипотенузе. Для sinα остается отношение противоположного катета к гипотенузе.
Слово «тангенс» созвучно со словом «там» (далеко), то есть – это отношение противоположного (дальнего) катета к прилежащему катету.
Таких секретов для лучшего запоминания в математике много, и мы, учителя, щедро делимся с учениками этими секретами.
В задачах по геометрии в работе со слабоуспевающими при отработке конкретного задания не стоит показывать все вариации решений. На мой взгляд, лучше выбрать самый оптимальный способ решения, сформулировать его на этапе изучения нового материала с учениками и пользоваться этим способом вплоть до сдачи экзамена. Дело в том, что малейшее отступление от алгоритма сбивает слабых учеников с толку, они теряют уверенность, допускают ошибки.
Пример. Тема «Теорема Пифагора» применяется на ОГЭ в практических геометрических задачах. В этом году эта теорема может быть использована в одном из практико-ориентированных заданий №№ 1-5.
В работе со слабоуспевающими детьми отрабатываю следующую схему применения теоремы Пифагора:
|
Записать формулу: |
с2 = а2 + b2 |
|
Подставить числовые значения: |
172 = 152 + b2 |
|
Вычислить квадраты чисел: |
289 = 225 + b2 |
|
Поменять левую и правую части уравнения местами, чтобы переменная оказалась в левой части уравнения: |
225 + b2 = 289 |
|
Выразитьb2: |
b2 = 289 – 225 |
|
Вычислить значение выражения в правой части уравнения: |
b2 = 64 |
|
Вычислитьb: |
b= = 8 |
Многократное использование одной и той же схемы позволит даже самым слабым ученикам справиться с заданием. Пусть будет один способ, но надежный.
Самые частые ошибки в ГИА по математике связаны с дробями и отрицательными числами — такие результаты из года в год отмечают специалисты из федеральной группы разработчиков ГИА по математике. То есть «слабым местом» оказались темы, которые ученики проходят в 5-7 классах.
Чтобы перед экзаменом не терять время на ликбез, необходимо отрабатывать материал на этапе его изучения. Много сил и энергии учитель тратит на работу со слабоуспевающими учениками. В работе с ними помимо математических правил необходимы особые приемы, личные придумки, и у каждого учителя их немало.
Даю совет слабоуспевающим ученикам: перед тем как начать работу, напишите таблицу умножения. Пусть она будет перед глазами.
Но даже написание таблицы в черновике нужно отрабатывать с учеником при подготовке к экзамену. Пусть он на консультации вам несколько раз продемонстрирует умение составления таблицы умножения.
Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Пример. Расположить числа 0,66; 0,066; 0,606; 0,0606 в порядке возрастания.
Очень важно, как ученики оформляют решение в черновиках. Сильные ученики буквально устно могут выполнить это задание. А вот слабых и невнимательных учеников желательно приучать к строгим схемам.
Одна из схем может выглядеть следующим образом:
|
Записать числа столбиком: |
0,66 0,066 0,606 0,0606 |
|
Уравнять количество знаков после запятой: |
0,66 = 0,6600 0,066 = 0,0660 0,606 = 0,6060 0,0606 = 0,0606 |
|
Сравнить числа, невзирая на запятые, и присвоить каждому числу порядковый номер (в порядке возрастания): |
0,66 = 0,6600 6600 (4) 0,066 = 0,0660 660 (2) 0,606 = 0,6060 6060 ( 3) 0,0606 = 0,0606 606 (4) |
|
С новой строки записать числа в их первоначальном виде в этом порядке: |
0,606; 0,066; 0,606; 0,66. |
|
Выбрать правильный вариант ответа: |
Ответ: |
Тщательное прорабатывание решения – залог успеха.
Лучшему усвоению математического материала помогут некоторые ассоциативные картинки. Математика должна ожить в образах.
В работе со слабоуспевающими учениками необходимо использовать универсальные способы решения. Например, у них возникают большие проблемы при нахождении НОЗ, при сокращении дробей, при внесении множителя за знак корня. Во всех перечисленных случаях поможет разложение на простые множители.
Пример: Найти значение выражения .
Пример .
Итак, учащиеся с низким уровнем обученности:
•выполняют задания по образцу;
•с проработкой;
•многократным повторением правил и формул;
• методы и приемы отрабатывают до автоматизма.
Разберем некоторые ошибки в заданиях ОГЭ с развернутым решением.
В задачах на проценты необходимо акцентировать внимание на необходимости определить стопроцентную величину, только после этого выбирать способ решения.
Пример. Вишня стоит 120 рублей за килограмм, а черешня – 150 рублей за килограмм. На сколько процентов черешня дороже вишни?
Как могут дети решить такую задачу? Некоторым учащимся кажется, что 150 руб. – 100%, что неверно. Ключевое утверждение к таким задачам: за 100% принимают ту величину, с которой сравнивают другие величины.
В нашей задаче стоимость черешни сравнивается со стоимостью вишни. Следовательно, 100% — 120 руб.
Полезно разобрать эту же задачу с другим вопросом.
Пример. Вишня стоит 120 рублей за килограмм, а черешня – 150 рублей за килограмм. На сколько процентов вишня дешевле черешни?
Решение. В этой задаче стоимость вишни сравнивается со стоимостью черешни. Следовательно, 150 руб. – 100%.
В качестве еще одного примера рассмотрим задачу, предлагаемую в 9-ом классе для развернутого ответа
Задача: «На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей за час делает первый рабочий?».
Решение одного из учеников: ; х = 25; х = -9,5 (не подходит).
Ответ: 25 деталей.
Комментарий. Приведенный ответ совпадает с верным. Уравнение по условию задачи составлено верно, если принять, что x – это число деталей, которые изготавливает за час первый рабочий. Но если учащийся не говорит, что принимается за x, то проверить правильность составления уравнения невозможно: в зависимости от того, какую величину приняли за x, получим различные уравнения. К сожалению, эксперт вынужден будет поставить 0 баллов. Заметим, что при арифметической ошибке при решении верно составленного уравнения решение оценивается неполным баллом.
Иногда ученики приводят пояснение к составлению уравнения в форме таблицы – это выбор учащегося, но при этом сам учащийся должен понимать, что его запись должна быть понятна не только ему, но и проверяющему. Думаем, размышляющий ученик здесь согласится, что запись решения текстовой задачи с помощью составления уравнения следует начинать словами: «Пусть x – это…».
В случае арифметического решения задачи (по действиям) необходимо давать пояснения каждому действию. Иначе получаем, что ученик складывает, вычитает, умножает, делит числа, в итоге получает некоторое число, которое записывает в ответ. Это число, конечно, может и совпадать с верным ответом, но верны ли при этом размышления? Подчеркнем, эксперт не должен додумывать за ученика, он проверяет верность решения.
Кроме того, если составленное уравнение – дробно-рациональное, необходимо указать О.Д.З.
Задание 23. Основным условием положительной оценки за решение задания № 23 является верное построение графика. Верное построение графика включает в себя: масштаб, содержательная таблица значений или объяснение построения, выколотая точка обозначена в соответствии с ее координатами.
Комментарий: график построен неверно – отсутствует выколотая точка. В соответствии с критериями – 0 баллов.
Оценка эксперта: 0 баллов.
При проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.
Перед учителем математики стоит задача: научить всех учащихся, подготовить их к прохождению ГИА, создать базу для дальнейшего образования. Но его терпение, тактичные и доброжелательные отношения ко всем ученикам, искренняя заинтересованность в их успехах является основой выполнения этой нелегкой задачи.
Чем ученики больше знают — тем меньше стресс и больше уверенность в себе и своих силах. Очень важна аксиома: больше знаешь – меньше боишься, меньше боишься — больше веришь в победу, веришь в победу — значит победишь. Задача педагогов и родителей заставить поверить в это учеников.
Список литературы:
Дука Н. И. Методическая разработка. Ошибки учащихся при изучении математики, их предупреждение и объяснение. // сайт Социальная сеть работников образования.nsportal.ru/20.08.2013.
Сайт Сдам ГИА: Решу ОГЭ. математика
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/399296-statja-gosudarstvennaja-itogovaja-attestacija

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!