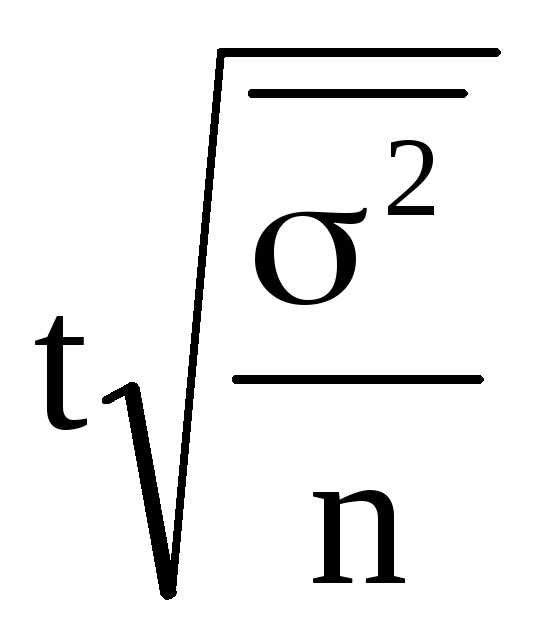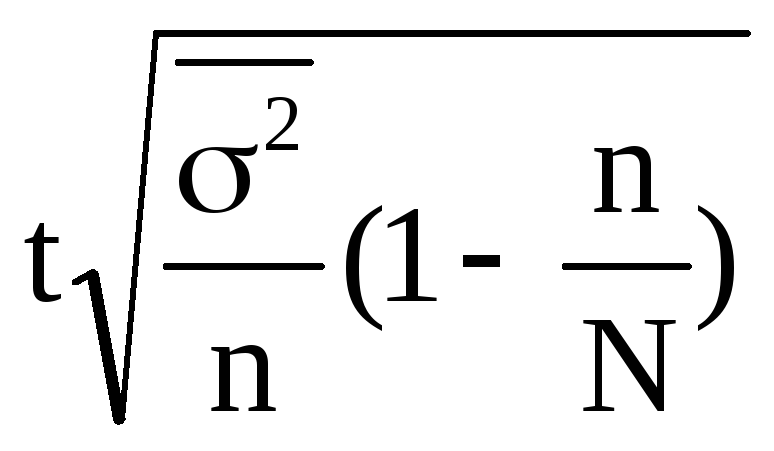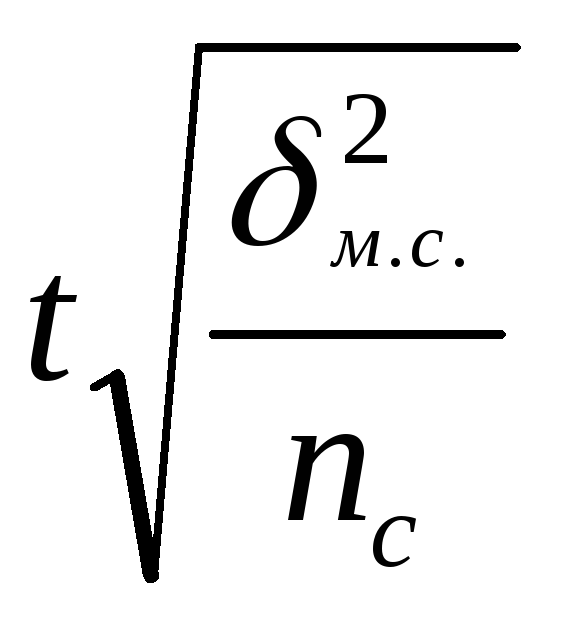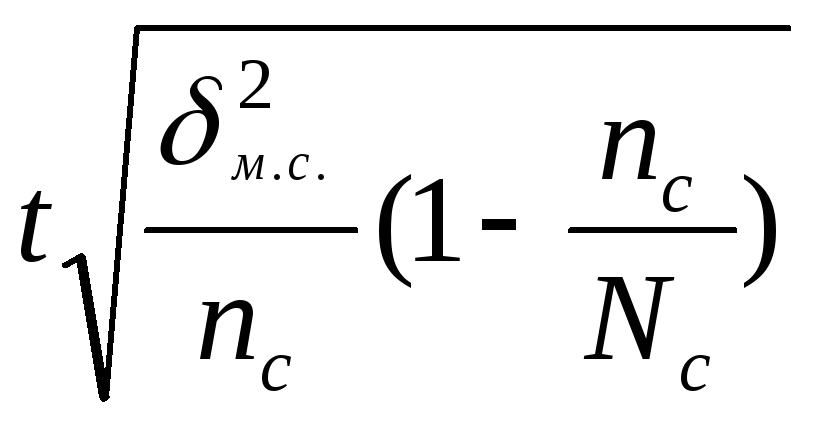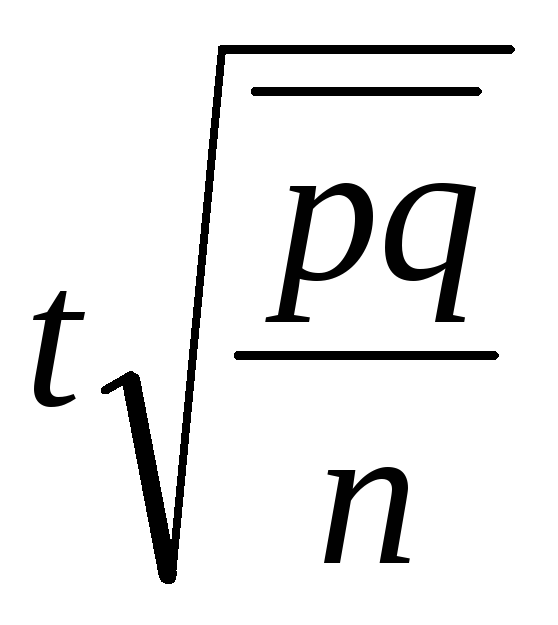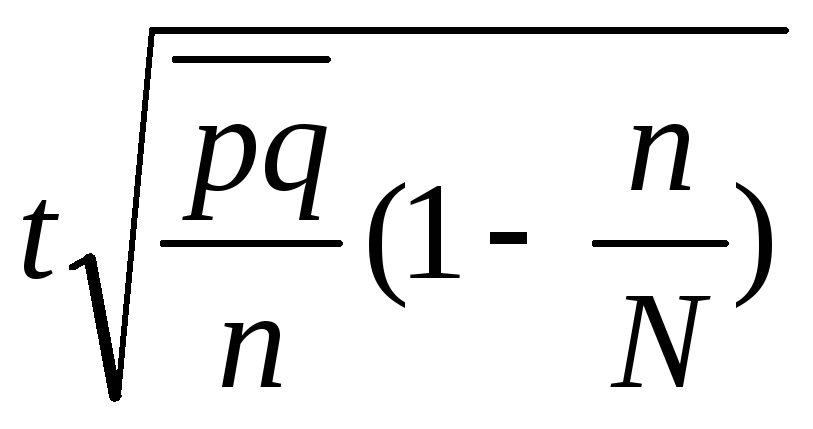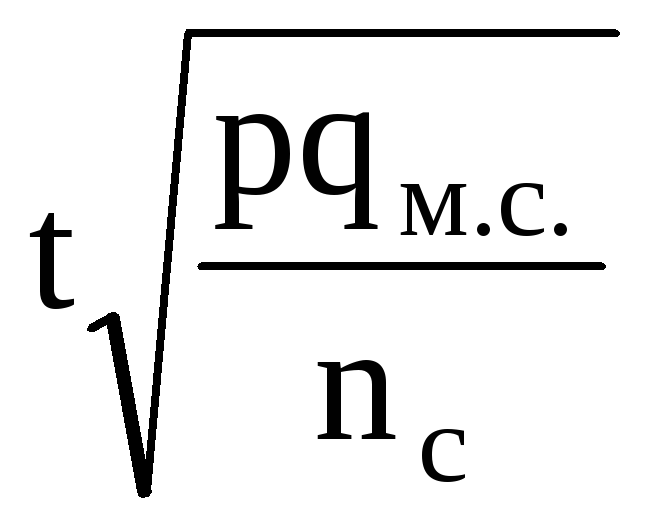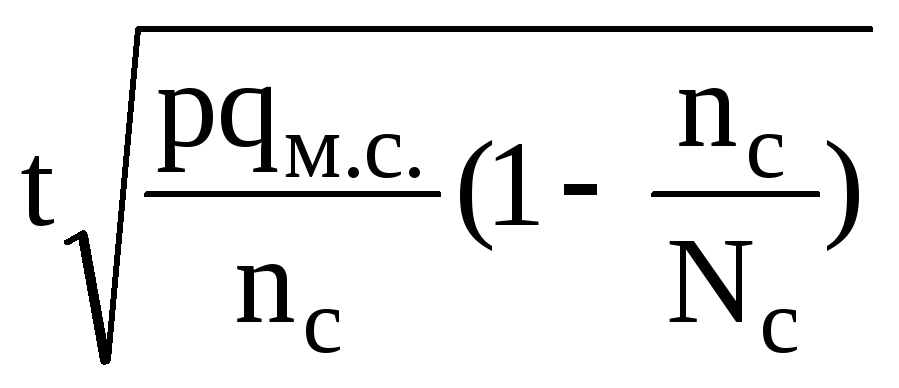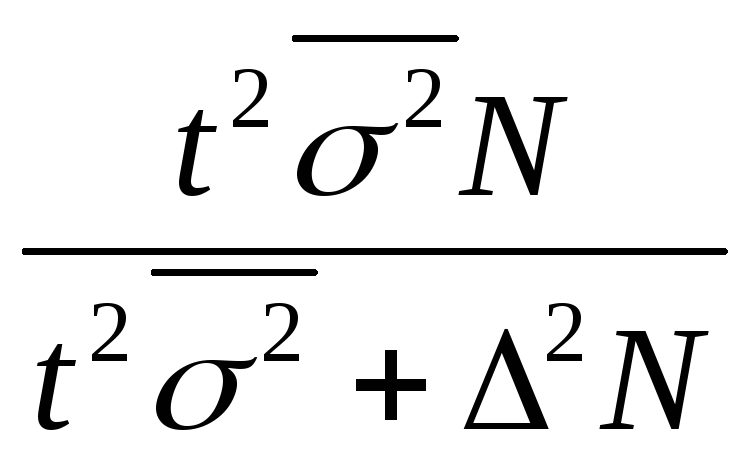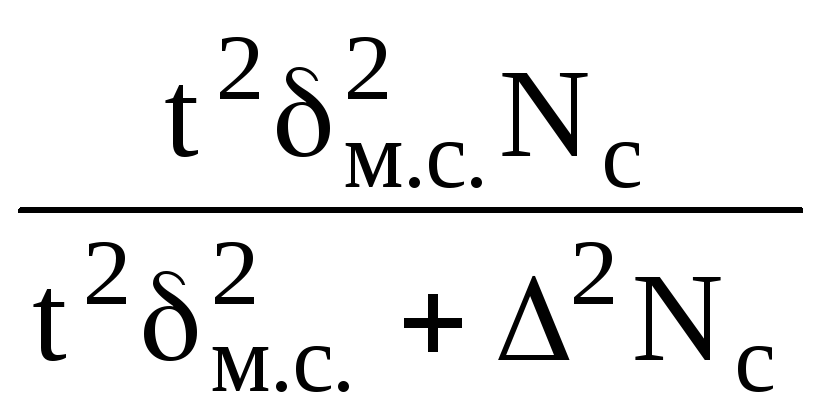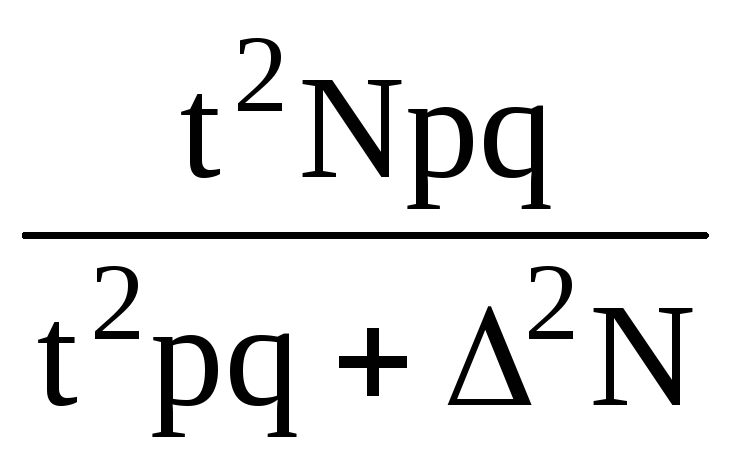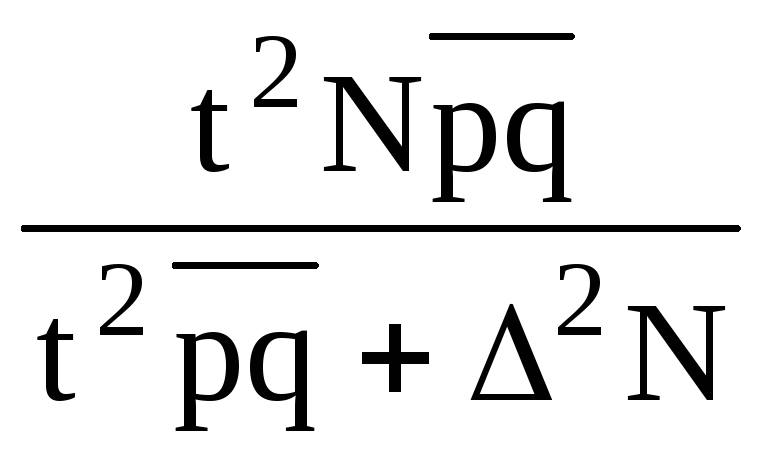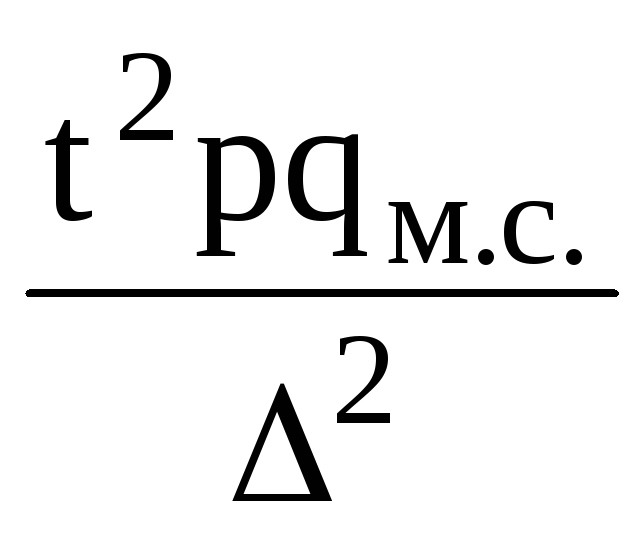Точечная и интервальная оценка ошибки выборки

Различают
точечные и интервальные оценки.

Точечная
оценка характеристики генеральной
совокупности — это число, определяемое
по выборке. Точечные оценки получают
обычно с помощью метода моментов и
метода максимального правдоподобия.

Интервальной
называют оценку, которая определяется
двумя числами- границами интервала. Она
позволяет ответить на вопрос: внутри
какого интервала и с какой вероятностью
находится неизвестное значение
оцениваемого параметра
генеральной
совокупности.

Пусть
точечная
оценка параметраЧем
меньше разностьитем точнее и лучше оценка. Обычно говорят
о доверительной вероятности (надежности
оценки)p=1-,
с которойбудет находиться в интервале,
где: Δ(Δ >0) –предельная ошибка выборки,
которая может быть либо задана наперёд,
либо вычислена; α — риск или уровень
значимости (вероятность того, что
неравенство будет неверным). Оценка
указанного доверительного интервала
может быть получена (с наименьшей
вероятностью) с помощью неравенства
Чебышева (при).
В качествепринимают значения 0,90; 0,95; 0,99; 0,999.
Доверительная вероятность показывает,
что в

(1-α)100%
случаев оценка
будет накрываться указанным интервалом.

Точечная
оценка математического ожидания M(X)=aопределяется как средняя арифметическая:

(10.3)

Точечная
оценка вероятности p_iопределяется
как относительная частота:

.
(10.4)

Лекция
2. Вопросы

Определение
доверительного интервала для средней
и доли при случайном и типическом отборе.

Определение
необходимой численности выборки.

Для
построения доверительного интервала
параметра a – математического ожидания
нормального распределения составляют
выборочную характеристику (статистику),
функционально зависимую от наблюдений
и связанную с a, например,
для повторного отбора:

.
(10.5)

Статистика
u распределена по нормальному закону
распределения с математическим ожиданием
a= 0 и средним квадратическим
отклонением=1.
Отсюда,

где
Ф − функция Лапласа, u_α/2− квантиль нормального закона
распределения, соответствующая уровню
значимости.
Доверительный интервал для параметра
а:

<
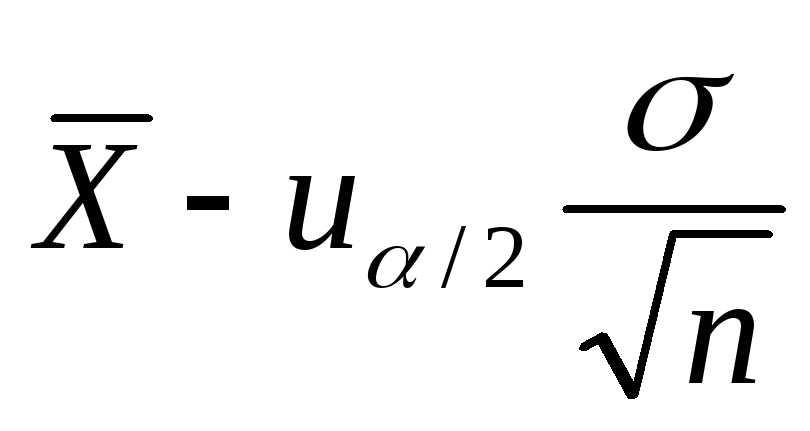
a<, (10.6)

где
—
предельная ошибка выборочной средней.

Формулы
предельной ошибки и необходимого объема
выборки

для
различных способов отбора В таблице:

1)
t – квантиль распределения, соответствующая
уровню значимости ,

а) при
n30 t=u_/2— квантиль нормального закона распределения
(прил.1),

б)
при n<30 t — квантиль распределения
Стьюдента с ν=n-1
степенями свободы для двусторонней
области (прил.3);

2)
²– выборочная
дисперсия,

а)
при n30,

б)
при n<30 вместо ²берут;

3)
pq — дисперсия относительной частоты в
схеме повторных независимых испытаний;

4)
N — объем генеральной совокупности;

5)
n — объем выборки;

6)
—
средняя арифметическая групповых
дисперсий (внутригрупповая дисперсия);

Выборка	Собственно-случайная	Типическая	Серийная
повторная	бесповторная	повторная	бесповторная	повторная	Бесповторная
Предельная ошибка, 	средней,
доли,
Необходимая численность, n	средней,
доли,

7)
—
средняя арифметическая дисперсий
групповых долей;

²_м.с. —
межсерийная дисперсия;

9)
pq_м.с.— межсерийная дисперсия доли;

10)
N_c— число серий в генеральной
совокупности;11) n_c— число отобранных
серий (объем выборки);12)- предельная ошибка выборки (или).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Точечное и интервальное оценивание числовых характеристик

Точечной оценкой числовой характеристики называют оценку, которая определяется одним числом. К точечным оценкам относятся: среднее арифметическое, дисперсия или стандартное отклонение.

Например, среднее арифметическое пробегания 100 м равно 15,38 с.

Если выборка небольшого объёма, то точечная оценка может значительно отличаться от оцениваемого параметра генеральной совокупности, в данном случае от среднего арифметического генеральной совокупности (обозначается μ) и её использование может привести к грубым ошибкам. Поэтому при небольшом объёме выборки в математической статистике используют другого типа оценки характеристик генеральной совокупности – интервальные.

Интервальной оценкой числовой характеристики называется интервал[1], который с доверительной вероятностью P (задаваемой заранее) накрывает истинное значение числовой характеристики генеральной совокупности.

Как правило, в научных исследованиях в области физической культуры и спорта считается достаточной доверительная вероятность Р=0,95. В некоторых случаях, связанных с большой ответственностью при принятии решений, принимают P равной 0,99 или 0,999. Таким образом, доверительная вероятность – это уровень гарантии суждения о значениях генеральной характеристики на основании выборочных данных.

Вероятность α=1-Р того, что построенный доверительный интервал не накроет значение генеральной характеристики, называется уровнем значимости; другими словами, α — вероятность ошибки.

В литературе часто обе вероятности α и P выражают в процентах, т.е. 100α% и 100P%.

Для определения доверительного интервала необходимо знать значение параметра t. Он зависит от объема выборки (n) и доверительной вероятности P (таблица 1).

Таблица 1 — Значения t в зависимости от объёма выборки и доверительной вероятности Р.

n	Р
0,95	0,99	0,999
10	2,265	3,250	4,781
15	2,145	2,977	4,140
20	2,093	2,861	3,883
30	2,042	2,750	3,646
40	2,021	2,704	3,551
50	2,009	2,678	3,505
60	2,000	2,660	3,505
80	1,990	2,639	3,416

Покажем на примере, как определить границы 95% доверительного интервала для среднего результата в беге на 100 м (n = 50), если: среднее арифметическое равно 15,38 с, а ошибка среднего арифметического равна 0,13 с.

Из таблицы 1 для n = 50 и P= 0,95 находим значение t. Оно равно t=2,009. Следовательно, доверительный интервал будет следующим: 15,38 — 2,009·0,13<μ<15,38+2,009·0,13

или 15,12<μ<15,64 с

После округления получим итоговый результат: 15,1<μ<15,6 c

Таким образом, с доверительной вероятностью  Р=0,95 можно утверждать, что генеральное среднее μ заключено в границах от 15,1 до 15,6 с.

Если мы хотим с большей вероятность (например, Р=0,99) утверждать, что генеральное среднее заключено в определенном интервале, необходимо из таблицы 1 найти значение t для n = 50 и P= 0,99. Оно равно t=2,678.

Тогда доверительный интервал для генерального среднего арифметического будет следующим:

15,38 — 2,678·0,13<μ<15,38+2,678·0,13

или 15,03<μ<15,73 с.

После округления получим итоговый результат: 15,0<μ<15,7 c.

Таким образом, с доверительной вероятностью  Р=0,99 можно утверждать, что генеральное среднее μ заключено в границах от 15,0 до 15,7 с. То есть утверждение с большей вероятностью увеличивает интервал, в котором заключено генеральное среднее арифметическое.

[1] Интервал – множество всех чисел, удовлетворяющих строгому неравенству a < x < b

Содержание:

1. Точечные и интервальные оценки параметров распределения
2. Примеры решения задач

Точечные и интервальные оценки параметров распределения

Оценка параметра распределения совокупности в общем случае является случайной величиной, которая определяется по данным выборки и используется вместо неизвестного значения параметра, который нужно оценить.

Оценка называется обоснованной, если она совпадает по вероятности с соответствующим параметром при 

Оценка называется несмещенной, если ее математическое ожидание совпадает со значением параметра.

В случае выбора из всех известных несмещенных обоснованных оценок определенной оценки, необходимо указать критерий, по которому сделан выбор.

Чаще всего используется критерий, который состоит в выборе оценки, имеющей наименьшую возможную дисперсию. Такая оценка называется эффективной. Нижняя граница дисперсии несмещенной оценки параметра (которую будем обозначать ) определяется по формуле:

где — плотность распределения случайной величины (для дискретной случайной величины ).

Оценки параметров распределения находят методами максимальной правдоподобности и моментов. Метод максимальной правдоподобности состоит вот в чем. Пусть закон распределения случайной величины определяется через параметр  который в общем случае -мерный. Тогда для выборки общий закон распределения представляется функцией правдоподобности (запишем, например, для непрерывных величин):

За оценки максимальной правдоподобности параметров  берутся выборочные функции, которые является решением системы уравнений:

Использование метода моментов основывается на сходстве (по вероятности) статистических моментов распределения с соответствующими теоретическими моментами распределения, которые в этом случае должны существовать. Как известно, теоретические моменты распределения выражаются через параметры распределения. Составим систему уравнений, в которой попарно приравняем соответствующие теоретические и статистические моменты. Решением этой системы являются оценки для параметров распределения.

Пусть есть точечная оценка параметра  Найдем для параметра интервальную оценку, воспользовавшись условием  В этом случае  называется точностью оценки, а — ее надежностью. Тогда интервальная оценка (доверительный интервал) для параметра  принимает вид  Параметр  — не случайная величина, надежность  можно рассматривать как вероятность того, что случайный интервал покрывает действительное значение параметра. Величины  и  тесно связаны с объемом выборки  Если задать две из этих величин, то модно найти третью. Для этого нужно знать закон распределения для 

Примеры решения задач

Пример 1. Выборка объемом  сделана из совокупности, распределенной по закону Релея 

Найти оценку для параметра  и преобразовать ее в  несмещенность, обоснованность и эффективность.

Решение. Применим метод максимальной правдоподобности. Построим функцию правдоподобности, составим и решим уравнение для определения оценки:

Проверим оценку на несмещенность, найдя ее математическое ожидание:

Преобразование выполнено согласно свойствам математического ожидания и с учетом того, что результаты выборки являются независимыми одинаково распределенными случайными величинами. Найдем  случайной величины, распределенной по закону Релея:

Тогда  то есть оценка несмещенная.

Проверку обоснованности оценки выполним, второй формой неравенства Чебышева, то есть оценим вероятность  Чтобы найти дисперсию оценки, выполним вычисления:

(Последний интервал, который является математическим ожиданием квадрата случайной величины, равен и вычислялся ранее). Тогда  Следовательно, получим:

Подставляя дисперсию оценки в неравенство Чебышева, получим:

 если 

Следовательно, оценка обоснованная.

Находим дисперсию эффективной оценки:

Дисперсия эффективной оценки совпадает с дисперсией найденной оценки для  а это означает, что оценка эффективная.

Пример 2. Методом моментов найти оценку параметра  геометрического распределения поп данным выборки объемом 

Решение. Геометрический закон распределения определяется формулой Поскольку нужно найти оценку одного параметра, сравниваем теоретические и статистические начальные моменты первого порядка:

Пример 3. По данным выборки объемом  из нормально распределенной совокупности, дисперсия которой а надежность  найти интервальную оценку для математического ожидания этой совокупности.

Решение. Интервальная оценка для математического ожидания, если дисперсия совокупности известна, представляется в виде  где где  — функция Лапласа.

Для построения оценки рассматривалась выборочная функция  которая имеет нормальный закон распределения с нулевым математически ожиданием и единичной дисперсией. 

Пример 4. Решить предыдущую задачу для случая, когда дисперсия совокупности неизвестна.

Решение. В этом случае интервальную оценку построим с помощью выборочной функции  которая распределена по закону Стьюдента с  степенями свободы. Доверительный интервал где  где — функция распределения Стьюдента с  степенями свободы. Если количество степеней свободы превышает 20, то распределение Стьюдента практически не отличается от нормального закона распределения с нулевым математическим ожиданием и единичной дисперсией. 

Пример 5. По результатам выборки объемом из нормально распределенной совокупности с надежностью  найти доверительный интервал для дисперсии совокупности.

Решение. Для определения доверительного интервала берем выборочную функцию  которая имеет распределение с  степенями свободы. Доверительный интервал представляется в виде Значения и  определяются с помощью таблиц распределения  с соответствующим количеством степеней свободы: 

Пример 6. Найти с надежностью  интервальную оценку для вероятности наступления события в каждом из независимых повторных испытаний, если событие произошло  раз.

Решение. Для определения доверительного интервала берем выборочную функцию  которая имеет закон распределения близкий к нормальному, с нулевым математическим ожиданием и единичной дисперсией. Доверительный интервал:

где — значение найдено по таблицам функции Лапласа. Вычислим  и  — левую и правую границы доверительного интервала:

Получим интервал 

Пример 7. Определить минимальный объем выборки  для того, чтобы с надежностью  можно было получить оценку математического ожидания нормально распределенной совокупности  если среднее квадратическое отклонение в генеральной совокупности и оценка находится с помощью выборочной средней величины.

Решение. Воспользовавшись формулой получаем Найдем  из формулы  По таблицам функции Лапласа  следовательно, 

Пример 8. Из партии однотипных высокоомных сопротивлений взяли для контроля 10 штук. Измерения показали такие отклонения от номинала, кОм:

Найти выборочную среднюю и дисперсию отклонения фактического значения сопротивления от номинала в этой партии и определить точность оценки математического ожидания выборочной средней величиной с надежностью (использовать распределение Стьюдента).

Решение. Считаем, что отклонение  имеет нормальный закон распределения с неизвестными параметрами и  Находим числовые характеристики  и  выборочной совокупности: Точность оценки определяем по формуле  Значение  ищем по таблицам функции распределения Стьюдента с 9 степенями свободы: 

Следовательно, получим такой доверительный интервал для математического ожидания: 

Пример 9. В ВТК были измерены диаметры 200 валов, изготовленных на станке-автомате. Отклонения измеренных диаметров от номинала, мкм, приведены в таблице.

Считая, что выборка сделана из нормально распределенной совокупности, определить с надежностью  точность оценки дисперсии выборочной дисперсией 

Решение. С помощью условных моментов распределения, вычислим выборочную дисперсию  составив таблицу:

найдем условные моменты распределения и выборочную дисперсию на основании расчетов в таблице:

Точность оценки равна половине длины доверительного интервала Значения и вычислим с помощью таблиц распределения  с  степенями свободы. Но в этой задаче объем выборки тогда как таблицы составлены для значений  которые не превышают 30. Поэтому воспользуемся тем, что при распределение  приближается к нормальному закону распределения с соответствующими математическим ожиданием и дисперсией. Выборочная функция  имеет распределение  с  степенями свободы. Поэтому 

Выборочная функция распределена нормально с нулевым математическим ожиданием и единичной дисперсией. Доверительный интервал найдем из условия:

Выполним преобразование для определения границ доверительного интервала:

Следовательно, доверительный интервал для дисперсии такой: 

Найдем точность оценки как половину длины доверительного интервала:

Согласно значению по таблицам функции Лапласа 

Окончательно получим: