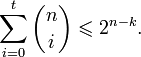Упреждающая коррекция ошибок FEC (Forward Error Correction) нашла широкое применение в технике оптической связи последнего поколения. Её использование предусмотрено стандартами передачи SDH, OTH, Ethernet.
Для обнаружения и исправления ошибок чаще всего используются циклические блочные коды (коды Хэмминга, коды Боуза-Чоудхури-Хоквенгема (БХЧ), коды Рида-Соломона (RS). Подробные сведения о этих кодах приведены в ряде изданий [115, 116,117].
В технике оптических систем нашли широкое применение коды Рида-Соломона (Reed-Solomon – RS). При использовании этих кодов данные обрабатываются порциями по m-бит, которые именуют символами. Код RS(n, k) характеризуется следующими параметрами:
- длина символа m бит;
- длина блока n = (2m – 1) символов = m(2m – 1) бит;
- длина блока данных k символов;
- n – k = 2t символов = m(2t) бит;
- минимальное расстояние Хэмминга dmin = (2t + 1);
- число ошибок, требующих исправления t.
Алгоритм кодирования RS(n, k) расширяет блок k символов до размера n, добавляя (n – k) избыточных контрольных символов. Как правило, длина символа является степенью 2 и широко используется значение m = 8, т.е. символ равен одному байту. Для исправления всех 1 и 3 битовых ошибок в символах требуется выполнение неравенства:
. (8.22)
Рисунок 8.33. Образование строки с блоком контроля FEC
Для исправления ошибок применяется 16-символьный код RS(255, 239), который относится к классу линейных циклических блочных кодов.Каждый цикл передачи, например, STM-N или OTUk разбивается на блоки символов данных по 239 байт. Каждому такому блоку вычисляется контрольный блок из 16 символов – байт и присоединяется к 239 байтам, 240-255 байты. Т.о. n = 255, k = 239, т.е. RS(255, 239). Объединенный блок k и n – k образуют подстроку цикла. Синхронное побайтовое мультиплексирование подстрок образует одну строку цикла (рисунок 8.33).Порядок передачи строки слева направо. При формировании блока (n – k) блок данных k сдвигается на n – k и делится на производящий полином:
Р = х8 + х4 + х3 + х2 + 1. (8.23)
В результате получается частное от деления и остаток деления длиной n – k. Блок данных k и остаток деления объединяются, образуя подстроку. После передачи подстроки на приемной стороне производится ее деление на производящий полином Р, аналогичный тому что был на передаче. если после деления остаток ноль, то передача прошла без ошибок. Если после деления остаток не равен нулю, то это признак ошибки. Место положения ошибки в блоке k обнаруживается по остатку, например табличным методом.
Исправлению подлежит заданное количество ошибок в символе (1, 2 или более в байте). Благодаря тому, что RS(255, 239) имеет расстояние Хэмминга dmin = 17 можно корректировать до 8 символьных ошибок.
Таблица 8.6 Пример результата расчета коэффициента ошибок на выходе декодера FEC RS(255, 239)
При этом число обнаруживаемых ошибок составляет 16 в подстроке с FEC. В таблице 8.6 приведен пример теоретически рассчитанного коэффициента ошибок на выходе декодера FEC RS(255, 239) [117].Практическая эффективность кодирования RS(255, 239) может составить от 5 до 8 дБ, т.е. FEC позволяет увеличивать длины участков передачи по сравнению с системами без FEC. Это особенно актуально на протяженных линиях оптической передачи и при реконструкции, когда производится переход на высокие скоростные режимы, например, с 2.5Гбит/с на 10Гбит/с. При этом очень важно сохранить длины участков передачи существующей сети и не строить дополнительных промежуточных станций.
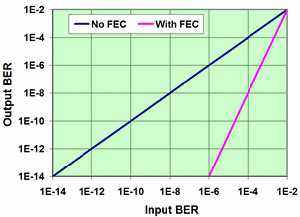
Пример оценки эффективности применения упреждающей коррекции при цифровой передаче приведен на рисунке 8.34.
Рисунок 8.34. Эффективность использования FEC
Упреждающая
коррекция ошибок FEC (Forward Error Correction) нашла
широкое применение в технике оптической
связи последнего поколения. Её
использование предусмотрено стандартами
передачи SDH, OTH, Ethernet.
Для
обнаружения и исправления ошибок чаще
всего используются циклические блочные
коды (коды Хэмминга, коды
Боуза-Чоудхури-Хоквенгема (БХЧ), коды
Рида-Соломона (RS). Подробные сведения о
этих кодах приведены в ряде изданий
[115, 116,117].
В
технике оптических систем нашли широкое
применение коды Рида-Соломона (Reed-Solomon
– RS). При использовании этих кодов данные
обрабатываются порциями поm-бит,
которые именуют символами. Код RS(n, k)
характеризуется следующими параметрами:
-
длина
символа m бит; -
длина
блока n =
(2m –
1) символов = m(2m –
1) бит; -
длина
блока данных k символов; -
n – k =
2t символов
= m(2t)
бит; -
минимальное
расстояние Хэмминга dmin =
(2t +
1); -
число
ошибок, требующих исправления t.
Алгоритм
кодирования RS(n, k)
расширяет блок k символов
до размера n,
добавляя (n – k)
избыточных контрольных символов. Как
правило, длина символа является степенью
2 и широко используется значение m =
8, т.е. символ равен одному байту. Для
исправления всех 1 и 3 битовых ошибок в
символах требуется выполнение неравенства:
. (8.22)
Рисунок
8.33 Образование строки с блоком контроля
FEC
Для
исправления ошибок применяется
16-символьный код RS(255, 239), который относится
к классу линейных циклических блочных
кодов.Каждый цикл передачи, например,
STM-N или OTUk разбивается на блоки символов
данных по 239 байт. Каждому такому блоку
вычисляется контрольный блок из 16
символов – байт и присоединяется к 239
байтам, 240-255 байты. Т.о. n =
255, k =
239, т.е. RS(255, 239). Объединенный
блок k и n – k образуют
подстроку цикла. Синхронное побайтовое
мультиплексирование подстрок образует
одну строку цикла (рисунок 8.33).Порядок
передачи строки слева направо. При
формировании блока (n – k)
блок данных k сдвигается
на n – k и
делится на производящий полином:
Р
= х8 +
х4 +
х3 +
х2 +
1. (8.23)
В
результате получается частное от деления
и остаток деления длиной n – k.
Блок данных k и
остаток деления объединяются, образуя
подстроку. После передачи подстроки на
приемной стороне производится ее деление
на производящий полином Р,
аналогичный тому что был на передаче.
если после деления остаток ноль, то
передача прошла без ошибок. Если после
деления остаток не равен нулю, то это
признак ошибки. Место положения ошибки
в блоке k обнаруживается
по остатку, например табличным методом.
Исправлению
подлежит заданное количество ошибок в
символе (1, 2 или более в байте). Благодаря
тому, что RS(255, 239) имеет расстояние
Хэмминга dmin =
17 можно корректировать до 8 символьных
ошибок.
Таблица
8.6 Пример результата расчета коэффициента
ошибок на выходе декодера FEC RS(255, 239)
При
этом число обнаруживаемых ошибок
составляет 16 в подстроке с FEC. В таблице
8.6 приведен пример теоретически
рассчитанного коэффициента ошибок на
выходе декодера FEC RS(255, 239) [117].Практическая
эффективность кодирования RS(255, 239) может
составить от 5 до 8 дБ, т.е. FEC позволяет
увеличивать длины участков передачи
по сравнению с системами без FEC. Это
особенно актуально на протяженных
линиях оптической передачи и при
реконструкции, когда производится
переход на высокие скоростные режимы,
например, с 2.5Гбит/с на 10Гбит/с. При этом
очень важно сохранить длины участков
передачи существующей сети и не строить
дополнительных промежуточных станций.
Пример
оценки эффективности применения
упреждающей коррекции при цифровой
передаче приведен на рисунке 8.34.
Рисунок
8.34 Эффективность использования FEC
Таблица
8.7 Характеристики используемых кодов
упреждающей коррекции ошибок FEC для
ВОСП
В
таблице обозначено и имеет смысл: RS код
Рида –Соломона; минимальное допустимое
отношение сигнал/помеха Qмин=18дБ для
допустимого коэффициента ошибок
BER=10-9.
Можно
считать одиночный RS улучшающим
чувствительность приемника на 6.5дБ, а
кратный RS на 9.5дБ.
Другую
дополнительную информацию по проектированию
участков оптической передачи WDM можно
найти в добавление 39 к Рекомендациям
МСЭ-Т серии G «Рассмотрение вопросов
расчета и проектирования оптических
систем».
|
9. |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Время на прочтение
4 мин
Количество просмотров 20K
Одним из основных ограничений при проектировании протяженных оптических транспортных сетей является соотношение сигнал-шум (OSNR). WDM-сети должны функционировать в допустимых пределах OSNR, чтобы обеспечить корректную работу систем.
Пороговое значение OSNR является одним из ключевых параметров, определяющих как далеко могут передаваться сигналы без необходимости в 3R-регенерации.
Для формирования каналов передачи данных со скоростью выше 10 Гбит используются сложные механизмы модуляции оптических сигналов для достижения аналогичной дальности передачи каналов связи 1-10 Гбит. Данные форматы модуляции необходимы для минимизации последствий таких оптических явлений, как хроматическая и поляризационная модовая дисперсии, а также для формирования оптического сигнала, соответствующего стандартам ITU 100/50-GHz, который используется в современных DWDM-системах. Недостатком высокоскоростных каналов передачи данных является тот факт, что они требуют существенно более высокого соотношения OSNR, чем обычные системы передачи (1-10 Гбит).
В системах 100 Гбит минимальное значение OSNR должно быть на 10 дБ выше, чем для сигналов в системах 10 Гбит. Без определенной коррекции или компенсации OSNR ограничивает 100G передачу данных до очень коротких расстояний, на данный момент максимальная дальность передачи составляет 40 км по стандартному одномодовому оптоволокну. Однако благодаря современным методам коррекции ошибок ( Forward Error Correction — FEC), особенно алгоритму Soft decision FEC, возможно расширение передачи высокоскоростных сигналов на протяженные расстояния.
Forward Error Correction (FEC) является техникой кодирования/декодирования сигнала с возможностью обнаружения ошибок и коррекцией информации методом упреждения. Таким образом, приемное оборудование может выявлять и исправлять ошибки, возникающие в канале передачи. FEC резко снижает количество битовых ошибок (BER), что позволяет увеличить расстояние передачи сигнала без регенерации.
Существует несколько FEC-алгоритмов кодирования, которые различаются по сложности и производительности. Одним из наиболее распространенных кодов первого поколения FEC является код «Рида-Соломона» (255, 239). Данный код добавляет немного — 7% проверочных байтов и около 6 дБ дополнительного запаса OSNR, но для высокоскоростных оптических сетей увеличение на 6 дБ является улучшенным показателем производительности, увеличивая расстояние между регенераторами примерно в четыре раза.
Некоторые производители предлагают в дополнение к коду «Рида-Соломона» более сложные схемы кодирования второго поколения FEC, например, превентивный параметр для оптических интерфейсов 10G и 40G. Данные алгоритмы, называемые «ультра» FEC или «усиленный» FEC (EFEC), также используют не более 7% объема передаваемого кадра, но в них заложены более сложные алгоритмы кодирования/декодирования, которые и обеспечивают бОльший выигрыш по OSNR — от 2 до 3 дБ, нежели код «Рида-Соломона».
Наряду с разработками первого поколения — «Рида-Соломона FEC» и второго поколения — «EFEC», которые позволили существенно улучшить производительность для 10G- и 40G-сигналов, было разработано более производительное FEC-решение третьего поколения, обеспечивающее увеличенную дальность и оптимальную производительность для высокоскоростных каналов передачи данных 100G.
FEC-решение третьего поколения основано на еще более мощных алгоритмах кодирования/декодирования и итеративного кодирования. В hard decision FEC —блок декодирования определяет «твердое» решение на основе входящего сигнала и иницилизирует один бит информации как «1» или «0» путем сравнения с пороговым значением. Значения выше установленного порога определяются «1», а значения ниже определяются как «0». В декодере используются дополнительные биты для обеспечения более детальной и точной индикации входящего сигнала. Иными словами, декодер не только определяет на основе порогового значения — является ли входящий сигнал «1» или «0», но и обеспечивает фактор надежности «принятия решения». Коэффициент надежности определяется индикатором, показывающим насколько сигнал выше или ниже порогового значения.
Использование коэффициента надежности или «вероятности» битов вместе с более сложными алгоритмами FEC-кодирования третьего поколения позволяет декодеру SD-FEC обеспечить дополнительное повышение OSNR на 1-2 дБ. В то время как увеличение OSNR на 1-2 дБ не звучит внушительно, оно может интерпретироваться как возможное увеличение расстояния на 20-40%, что является существенным показателем для 100G.
Одним из недостатков soft decision FEC является тот факт, что для него требуется ~20 % объема передаваемого кадра, а это более чем в два раза больше, чем занимаемый объем FEC первого и второго поколения.
С увеличением скорости в канале передачи данных с 10G до 100G, требование к OSNR увеличилось на 10 дБ. Без определенного вида компенсации или коррекции протяженность трасс с канальной скоростью 100G будет весьма ограниченной и неэкономичной.
Алгоритмы FEC первого и второго поколения были использованы на 10G и 40G для снижения BER и увеличения расстояния. SD-FEC является алгоритмом кодирования третьего поколения, обеспечивая передачу данных для оптических сетей 100G на бо́льшие расстояния и с бо́льшим ретрансляционным участком.
Поскольку требования к полосе пропускания увеличиваются, а допуск на ошибки и задержку уменьшаются, разработчики систем передачи данных искали новые способы расширения доступной полосы пропускания и повышения качества передачи. Одно из решений на самом деле не ново, но оказалось весьма полезным. Это называется прямым исправлением ошибок (FEC), в течение многих лет этот метод использовался для обеспечения эффективной высококачественной передачи данных по шумным каналам. Сегодня с увеличением пропускной способности передачи данных и увеличением расстояния, давайте узнаем больше о методике FEC в оптических сетях.
Что такое FEC?
Прямая коррекция ошибок (FEC) — это метод цифровой обработки сигналов, используемый для повышения надежности данных. Это делается путем введения избыточных данных, называемых кодом с исправлением ошибок, перед передачей или хранением данных. FEC предоставляет приемнику возможность исправления ошибок без обратного канала для запроса повторной передачи данных. Как мы знаем, иногда оптические сигналы могут ухудшаться из-за некоторых факторов во время передачи, что может привести к неправильной оценке на стороне приемника, возможно, принятию сигнала «1» за сигнал «0» или сигнала «0» за сигнал «1». Если количество ошибок при передаче находится в пределах корректирующей способности (прерывистые ошибки), канальный декодер обнаружит и исправит ложные “0” или “1” для улучшения качества сигнала.
Рисунок 1. Принцип работы FEC
Развитие прямого исправления ошибок в оптической связи можно разделить на три поколения. FEC первого поколения представляет собой первое, которое будет успешно использоваться в подводных системах и наземных системах. По мере развития систем WDM в коммерческих системах был установлен более мощный FEC второго поколения. Появление FEC третьего поколения открыло новые перспективы для следующего поколения систем оптической связи.
Каковы типы и особенности FEC?
Типы
В настоящее время практические технологии FEC для SDH (синхронная цифровая иерархия) и DWDM (плотное мультиплексирование с разделением по длине волны) в основном следующие:
In-band FEC. In-band FEC поддерживается стандартом ITU-T G.707. Контролируемые символы кода FEC загружаются с использованием части служебных байтов в кадре SDH. Усиление кодирования невелико (3-4 дБ).Внеполосный FEC. Внеполосный FEC поддерживается стандартом ITU-T G.975/709.
Out-of-band FEC обладает большой избыточностью кодирования, возможностью исправления ошибок, высокой гибкостью и высоким коэффициентом усиления кодирования (5-6 дБ).
Enhanced FEC (EFEC). Enhanced FEC в основном используется в системах оптической связи, где требования к задержке не являются строгими, а требования по усилению кодирования особенно высоки. Хотя процесс кодирования и декодирования EFEC является более сложным и менее применимым в настоящее время, благодаря его преимуществам в производительности, он превратится в практическую технологию и станет основным направлением следующего поколения out-of-band FEC.
Характеристики
FEC уменьшает количество ошибок передачи, расширяет рабочий диапазон и снижает требования к питанию для систем связи. FEC также увеличивает эффективную пропускную способность системы, даже с дополнительными контрольными битами, добавленными к битам данных, устраняя необходимость повторной передачи данных, искаженных случайным шумом.
FEC самостоятельно повышает достоверность данных на приемнике. В рамках системного контекста FEC становится технологией, которую разработчик системы может использовать несколькими способами. Наиболее очевидным преимуществом использования FEC является использование систем с ограниченной мощностью. Однако посредством использования сигнализации более высокого порядка ограничения полосы пропускания также могут быть устранены. Во многих беспроводных системах допустимая мощность передатчика ограничена. Эти ограничения могут быть вызваны соблюдением стандарта или практическими соображениями. FEC позволяет передавать с гораздо более высокими скоростями передачи данных, если доступна дополнительная полоса пропускания.
Применение FEC в 100G сетях
В контексте оптоволоконных сетей FEC используется для определения оптического SNR (OSNR) — одного из ключевых параметров, определяющих, как далеко может пройти длина волны, прежде чем она нуждается в регенерации. FEC особенно важен при скоростях высокоскоростной передачи данных, где требуются усовершенствованные схемы модуляции, чтобы минимизировать дисперсию и соответствие сигнала с частотной сеткой. Без включения FEC транспорт 100G был бы ограничен чрезвычайно короткими расстояниями. Для реализации передачи на большие расстояния (> 2500 км) усиление системы должно быть дополнительно улучшено примерно на 2 дБ. Переход FEC с жесткого решения на мягкое решение восполняет этот пробел в производительности.
Поскольку стремление к все более высоким скоростям передачи продолжается, схемы прямого исправления ошибок (SD-FEC) становятся все более популярными. Хотя для этого может потребоваться около 20% байтов — почти в три раза больше, чем в исходной схеме кодирования RS — выгоды, которые они получают в контексте высокоскоростных сетей, значительны. Например, FEC, который приводит к усилению от 1 до 2 дБ в сети 100G, означает увеличение охвата на 20-40%.
Замечания для FEC в сетях 100G
Что следует учитывать при настройке FEC в 100G сетях? Предлагается обратить внимание на следующие советы.
Метод реализации
Некоторые специальные модули имеют свои собственные функции FEC, такие как FS 100G CFP конвертеры интерфейсов. В то время как 100G QSFP28 оптический модуль в основном полагается на конфигурацию функции FEC на устройстве для реализации исправления ошибок, таких как 100G коммутаторы.
Поддерживает ли коммутатор FEC
Конфигурирование FEC на 100G коммутаторах может быть достигнуто только в том случае, если коммутатор поддерживает его, и не все коммутаторы поддерживают это. В то время как все 100G коммутаторы поддерживают FEC, предоставляемые FS.
| Тип коммутатора | Тип порта | Поддержка FEC или нет |
| S5850-48S2Q4C | 48*10Gb, 2*40Gb, 4*100Gb | Да (для оба 40Gb и 100Gb порты) |
| S8050-20Q4C | 20*40Gb, 4*100Gb | Да (для оба 40Gb и 100Gb порты) |
| N8500-48B6C | 40*25Gb, 6*100Gb | Да (для оба 25Gb и 100Gb порты) |
| N8500-32C | 32*100Gb | Да |
Таблица 1. Технические характеристики FS 100G коммутаторов
Внимание: для FS 100G коммутаторов функция FEC включена по умолчанию. Если требуется включить его после выключения, можно настроить команду FEC.
Включить ли FEC на QSFP28 100G модулях
Функция FEC — это не просто преимущество, процесс исправления кода ошибки неизбежно приведет к некоторой задержке пакета данных. Поэтому не все QSFP28 100G модули нуждаются в этом. Согласно стандартному протоколу IEEE не рекомендуется включать FEC при использовании QSFP28-LR4-100G модулей, за исключением того, что рекомендуется включать его. Поскольку технология QSFP28 100G модулей варьируется от компании к компании, поэтому ситуация не совсем одинакова. В следующей таблице объясняется, рекомендуется ли включать FEC при использовании FS 100G QSFP28 модулей.
| Тип модуля | Описание | с FEC |
| QSFP28-SR4-100G | 850nm 100m MTP/MPO Модуль для SMF | Нет |
| QSFP28-LR4-100G | 1310nm 10km Модуль для SMF | Нет |
| QSFP28-PIR4-100G | 1310nm 500m Модуль для SMF | Нет |
| QSFP28-IR4-100G | 1310nm 2km Модуль для SMF | Да |
| QSFP28-EIR4-100G | 1310nm 10km Модуль для SMF | Да |
| QSFP28-ER4-100G | 1310nm 40km Модуль для SMF | Да |
Таблица 2. Технические характеристики FS 100G QSFP28 модулей
Согласованность функций FEC на обоих концах канала
Функция FEC порта является частью автосогласования. Когда автоматическое согласование порта включено, функция FEC определяется согласованием на обоих концах канала. Если функция FEC включена на одном конце, другой конец должен также включить ее, в противном случае порт не работает.
Стекирование & FEC
Настройка команды FEC не поддерживается, если порт уже настроен как физически стековый порт.Наоборот, порты, которые были настроены с помощью команд FEC, не поддерживают настройку в качестве физического стекового члена.
Заключение
FEC стал критически важной в волоконно-оптической связи, так как магистральные сети увеличиваются в скорости до 40 и 100G, особенно в условиях плохой связи оптического сигнала с шумом. Такие среды становятся более распространенными в высокоскоростных средах, поскольку в сетях используется больше оптических усилителей. Со всеми этими событиями, FEC будет продолжать играть роль в будущих сетях. Для обеспечения нормальной работы сети рекомендуется обратить особое внимание на функцию FEC на оптических модулях, которая поможет вам повысить производительность при передаче данных.

В качестве примера, рассмотрим работу вашего мобильного телефона в условиях слабого сигнала сотовой сети. Допустим, вы хотели сказать человеку на другом конце линии некую последовательность чисел. Есть несколько методов, которые можно использовать для повышения точности. Предположим, что список чисел, которые вы хотите передать, это 7, 3, 8, 10, 12 и 21. Одним из способов может быть повтор списка чисел два раза. Запишите каждый список и сравните их, если они совпадают, передача данных, вероятно, корректна. Основным недостатком такого метода является то, что, поскольку данные передаются дважды, пропускная способность системы делится пополам и, если списки не совпадают, у вас не будет ни малейшего представления, который из них верный. Используя этот метод, для того, чтобы убедиться в хорошем качестве передачи и исправить некоторые ошибки, вам придется отправить данные три раза и проверить, что два из трех списков полностью совпадают. Второй способ будет выглядеть примерно так: в первую очередь, вы будете отправлять количество чисел, которые необходимо принять, затем саму последовательно, и в конце последует передача числа, являющегося суммой последовательности. Передаваемое сообщение при этом примет следующий вид: 6, 7, 3, 8, 10, 12, 21, и 67. Человек, принимающий сообщение, будет смотреть на первое число, чтобы затем убедится, что будет получено правильное количество чисел в сообщении, а затем проверит, что число в конце последовательности, действительно является суммой переданных чисел. Этот метод требует отправки значительно меньшего количества дополнительных данных. Если любое полученное число неверно или пропущено, то число контрольной суммы в конце передачи не будет соответствовать сумме, передаваемых чисел. Показанные выше методы представляют собой примеры кода обнаружения ошибок. Они позволяют определить, была ли передача точной, но не позволяют исправлять ошибки.
Примечание: Термин «Forward» в аббревиатуре FEC означает, что исправление ошибок осуществляется путем передачи некоторой информации вместе с передачей данных.
Код исправления ошибок считаются более сложными, в сравнении с кодом обнаружения ошибок и используются почти в каждом современном коммуникационном приложении. Также, коды исправления ошибок нашли широкое применение в CD и DVD проигрывателях. Для того, чтобы привести пример кода исправления ошибок, нужно ввести и объяснить два термина: двоичность и чётность. В предыдущих примерах кода обнаружения ошибок, мы использовали такие числа, как 7, 3, 8, и т.д. Это базовые числа системы исчисления, знакомой нам в повседневной жизни. Двоичные числа в основе имеют два числа, которые могут иметь только два возможных значения – 0 или 1. Бинарная система используется почти во всех коммуникационных и компьютерных системах. Второе определение, которое необходимо разобрать, называется четность. Чётность — термин, который используется в двоичных системах связи, чтобы указать, является ли число единиц в передаче четным или же нет. Если число единиц является четным, то чётность совпадает и наоборот.
Код Хэмминга
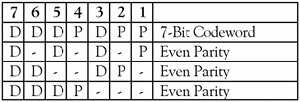
Рассмотрим сообщение, имеющее четыре бита данных (D), которое должно быть передано в 7-битной кодировке с добавлением трёх битов данных для поиска и устранения ошибок. Этот код будет называться (7, 4). Это означает, что общая длина кода составляет семь битов, но только четыре из них на самом деле данные. Три добавленных бита — это три бита проверки на четность (Р), где чётность каждого вычисляется в разных группах битов сообщения, как показано на рисунке 1.
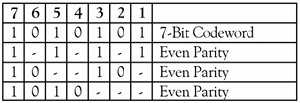
Например, сообщение 1011 будут направлено, как 1010101, как показано на рисунке 2.
Можно заметить, что в случае возникновения ошибки в любом из семи битов, эта ошибка оказывает влияние на различные комбинации трех битов четности в зависимости от битовой позиции.
Например, предположим, что вышеупомянутое сообщение 1010101 передаётся и возникает один бит ошибки, так что получено кодовое слово 1110101:
Передача Приём
Сообщение Сообщение
1 0 1 0 1 0 1 ————> 1 1 1 0 1 0 1
Эта ошибка может быть исправлена путем определения, какой из трех битов четности пострадал, как показано на рисунке ниже:
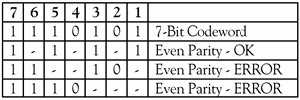
Характер ошибок четности битов указывает, какой бит в кодовом слове с ошибкой, таким образом, он может быть исправлен.
Основные функции кода Хэмминга можно резюмировать:
- Обнаружение 2-битовых ошибок (при условии отсутствия ошибок корректировка не выполняется)
- Коррекция единичных ошибочных битов
- 3 проверочных бита добавляется к 4-битовому сообщению
Способность корректировать одиночные ошибочные биты приводит к снижению себестоимости передачи, которая получается меньше, чем в случае отправки сообщения дважды целиком. (Напомним, что, просто отправив сообщение дважды коррекция ошибок не выполняется.) К тому же, при увеличении размера кодового слова, дополнительная нагрузка исправления ошибочных битов уменьшается. Например, одним из возможных вариантов кода Хэмминга для передачи по морским подводным оптоволоконным системам является код (18880, 18865). Это означает, что кодовое слово 18880 в действительности содержит 18,865 бит данных и 15 бит коррекции ошибок. Более надежные методы прямой коррекции ошибок (FEC) могут содержать гораздо больше битов коррекции ошибок, так что несколько ошибочных битов могут быть обнаружены и исправлены в каждом кодовом слове.
Таким образом, интеграция прямой коррекции ошибок в систему позволяет разработчику увеличивать расстояние и скорости передачи данных значительнее, чем при использовании любой другой технологии, а также увеличит срок службы системы.
Forward Error Correction (FEC) is a technique used to minimize errors in data transmission over communication channels. In real-time multimedia transmission, re-transmission of corrupted and lost packets is not useful because it creates an unacceptable delay in reproducing : one needs to wait until the lost or corrupted packet is resent. Thus, there must be some technique which could correct the error or reproduce the packet immediately and give the receiver the ability to correct errors without needing a reverse channel to request re-transmission of data. There are various FEC techniques designed for this purpose.
These are as follows :
1. Using Hamming Distance :
For error correction, the minimum hamming distance required to correct t errors is:
For example, if 20 errors are to be corrected then the minimum hamming distance has to be 2*20+1= 41 bits. This means, lots of redundant bits need to be sent with the data. This technique is very rarely used as we have large amount of data to be sent over the networks, and such a high redundancy cannot be afforded most of the time.
2. Using XOR :
The exclusive OR technique is quite useful as the data items can be recreated by this technique. The XOR property is used as follows –
If the XOR property is applied on N data items, we can recreate any of the data items P1 to PN by exclusive-Oring all of the items, replacing the one to be created by the result of the previous operation(R). In this technique, a packet is divided into N chunks, and then the exclusive OR of all the chunks is created and then, N+1 chunks are sent. If any chunk is lost or corrupted, it can be recreated at the receiver side.
Practically, if N=4, it means that 25 percent extra data has to be sent and the data can be corrected if only one out of the four chunks is lost.
3. Chunk Interleaving :
In this technique, each data packet is divided into chunks. The data is then created chunk by chunk(horizontally) but the chunks are combined into packets vertically. This is done because by doing so, each packet sent carries a chunk from several original packets. If the packet is lost, we miss only one chunk in each packet, which is normally acceptable in multimedia communication. Some small chunks are allowed to be missing at the receiver. One chunk can be afforded to be missing in each packet as all the chunks from the same packet cannot be allowed to miss.
Forward Error Correction (FEC) is a technique used to minimize errors in data transmission over communication channels. In real-time multimedia transmission, re-transmission of corrupted and lost packets is not useful because it creates an unacceptable delay in reproducing : one needs to wait until the lost or corrupted packet is resent. Thus, there must be some technique which could correct the error or reproduce the packet immediately and give the receiver the ability to correct errors without needing a reverse channel to request re-transmission of data. There are various FEC techniques designed for this purpose.
These are as follows :
1. Using Hamming Distance :
For error correction, the minimum hamming distance required to correct t errors is:
For example, if 20 errors are to be corrected then the minimum hamming distance has to be 2*20+1= 41 bits. This means, lots of redundant bits need to be sent with the data. This technique is very rarely used as we have large amount of data to be sent over the networks, and such a high redundancy cannot be afforded most of the time.
2. Using XOR :
The exclusive OR technique is quite useful as the data items can be recreated by this technique. The XOR property is used as follows –
If the XOR property is applied on N data items, we can recreate any of the data items P1 to PN by exclusive-Oring all of the items, replacing the one to be created by the result of the previous operation(R). In this technique, a packet is divided into N chunks, and then the exclusive OR of all the chunks is created and then, N+1 chunks are sent. If any chunk is lost or corrupted, it can be recreated at the receiver side.
Practically, if N=4, it means that 25 percent extra data has to be sent and the data can be corrected if only one out of the four chunks is lost.
3. Chunk Interleaving :
In this technique, each data packet is divided into chunks. The data is then created chunk by chunk(horizontally) but the chunks are combined into packets vertically. This is done because by doing so, each packet sent carries a chunk from several original packets. If the packet is lost, we miss only one chunk in each packet, which is normally acceptable in multimedia communication. Some small chunks are allowed to be missing at the receiver. One chunk can be afforded to be missing in each packet as all the chunks from the same packet cannot be allowed to miss.
|
|
Прямая коррекция ошибок (англ. Forward Error Correction, FEC, помехоустойчивое кодирование) — техника кодирования/декодирования, позволяющая исправлять ошибки методом упреждения. Применяется для исправления сбоев и ошибок при передаче данных, путём передачи избыточной служебной информации, на основе которой может быть восстановлена первоначальное содержание посылки. На практике широко используется в компьютерных ЛВС, LAN и различных телекоммуникационных сетях. Коды, обеспечивающие прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, которые только обнаруживают ошибки.
В спутниковом телевидении при передаче цифрового сигнала, к примеру, с FEC 7/8, будет передаваться восемь бита информации: 7 бит полезной информации и 1 контрольный бит.[1]
На практике в DVB-S используется всего 5 видов:
- 1/2
- 2/3
- 3/4 (наиболее популярен)
- 5/6
- 7/8
При прочих равных условиях, можно утверждать, что чем выше значение FEC, тем меньше пакетов допустимо потерять, и, следовательно, выше требуемое качество сигнала.
См. также
- ECC
Литература
- Clark, George C., Jr., and J. Bibb Cain. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981. ISBN 0-306-40615-2.
- Lin, Shu, and Daniel J. Costello, Jr. «Error Control Coding: Fundamentals and Applications». Englewood Cliffs, N.J.: Prentice-Hall, 1983. ISBN 0-13-283796-X.
- Mackenzie, Dana. «Communication speed nears terminal velocity». New Scientist 187.2507 (9 июля 2005): 38-41. ISSN 0262-4079.
- Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Englewood Cliffs, N.J.: Prentice-Hall, 1995. ISBN 0-13-200809-2.
- Wilson, Stephen G. Digital Modulation and Coding, Englewood Cliffs, N.J.: Prentice-Hall, 1996. ISBN 0-13-210071-1.
- United States Patent 6041001 «Method of increasing data reliability of a flash memory device without compromising compatibility»
- United States Patent 7187583 «Method for reducing data error when flash memory storage device using copy back command»
Примечания
- ↑ Understanding Digital Television: An Introduction to Dvb Systems With … — Lars-Ingemar Lundström — Google Книги
Ссылки
- Forward Error-Correction Coding. Статья в журнале Aerospace Corporation. The Aerospace Corporation (Volume 3, Number 1 (Winter 2001/2002)). Архивировано из первоисточника 25 февраля 2012. Проверено 24 мая 2009. (англ.)
- How Forward Error-Correcting Codes Work. Еще одна статья в журнале Aerospace Corporation. The Aerospace Corporation. Архивировано из первоисточника 25 февраля 2012. Проверено 24 мая 2009. (англ.)
- Morelos-Zaragoza, Robert The Error Correcting Codes (ECC) Page (2004). Архивировано из первоисточника 25 февраля 2012. Проверено 24 мая 2009. (англ.)
-
Методы коррекции ошибок
Техника
кодирования,
которая
позволяет
приемнику
не только
понять,
что
присланные
данные
содержат
ошибки, но
и исправить
их, называется
прямой
коррекцией
ошибок (Forward Error Correction, FEC).
Коды,
которые
обеспечивают
прямую
коррекцию
ошибок,
требуют
введения
большей
избыточности
в
передаваемые
данные,
чем
коды,
которые
только
обнаруживают
ошибки.
При
применении
любого
избыточного
кода не
все
комбинации
кодов являются разрешенными.
Например,
контроль по паритету
делает
разрешенными
только
половину кодов. Если мы
контролируем
три
информационных
бита,
то разрешенными 4-битными кодами
с дополнением
до нечетного
количества
единиц
будут:
000
1,
001
0,
010
0,
011
1,
100
0,
101
1,
110
1,
111
0,
то
есть
всего
8
кодов
из
16
возможных.
Для
того
чтобы
оценить
количество
дополнительных
битов,
требуемых
для
исправления
ошибок,
нужно
знать так
называемое
расстояние
Хемминга
между
разрешенными
комбинациями
кода.
Расстоянием
Хемминга
называется
минимальное
число
битовых
разрядов,
в
которых
отличается
любая
пара
разрешенных
кодов.
Для схем
контроля
по паритету
расстояние
Хемминга
равно
2.
Можно
доказать,
что
если мы
сконструировали
избыточный
код
с
расстоянием
Хемминга,
равным
n,
то
такой
код
будет
в
состоянии
распознавать
(n-
1)-кратные
ошибки и
исправлять (n-1)/2-кратные
ошибки.
Так
как коды
с
контролем
по паритету
имеют
расстояние
Хемминга,
равное
2,
то
они
могут
только
обнаруживать
однократные
ошибки и
не могут
исправлять
ошибки.
Коды
Хемминга
эффективно
обнаруживают
и
исправляют
изолированные
ошибки,
то есть отдельные
искаженные
биты,
которые
разделены
большим
количеством
корректных битов. Однако при появлении
длинной последовательности искаженных
битов (пульсации
ошибок)
коды Хемминга
не
работают.
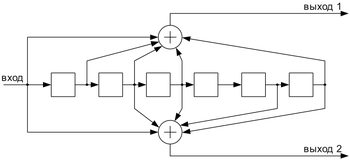
Наиболее
часто
в современных
системах
связи применяется тип кодирования,
реализуемый
сверточным
кодирующим
устройством
(Сonvolutional
coder),
потому
что такое
кодирование
может быть
довольно
просто
реализовано
аппаратно
с
использованием
линий задержки
(delay)
и сумматоров.
В
отличие
от
рассмотренного
выше
кода,
который относится
к
блочным
кодам
без памяти,
сверточпый
код
относится
к
кодам
с
конечной
памятью (Finite memory
code);
это
означает,
что выходная
последовательность кодера является
функцией
не только
текущего
входного
сигнала,
но также
нескольких
из числа
последних предшествующих
битов.
Длина
кодового
ограничения
(Constraint
length of a code) показывает,
как
много
выходных
элементов
выходит
из системы
в пересчете
на
один
входной.
Коды
часто
характеризуются
их
эффективной
степенью
(или
коэффициентом)
кодирования (Code rate).
Вам
может встретиться
сверточный
код с коэффициентом кодирования
1/2.
Этот
коэффициент
указывает,
что
на
каждый
входной
бит
приходятся
два
выходных.
При
сравнении
кодов
обращайте
внимание
на
то,
что,
хотя
коды
с
более
высокой
эффективной
степенью
кодирования
позволяют
передавать
данные
с более высокой
скоростью,
они
соответственно
более
чувствительны
к
шуму.
В беспроводных
системах
с блочными
кодами
широко
используется
метод
чередования
блоков.
Преимущество
чередования
состоит
в том,
что приемник
распределяет
пакет ошибок, исказивший некоторую
последовательность
битов, по большому
числу
блоков,
благодаря
чему
становится
возможным
исправление
ошибок.
Чередование
выполняется
с
помощью
чтения
и
записи
данных
в
различном
порядке.
Если
во
время
передачи
пакет
помех
воздействует
на
некоторую
последовательность
битов,
то все
эти
биты
оказываются
разнесенными
по
различным
блокам.
Следовательно,
от
любой
контрольной
последовательности
требуется
возможность
исправления
лишь
небольшой
части
от
общего
количества
инвертированных
битов.
Соседние файлы в папке Методические материалы
- #
- #
- #
- #
16.03.2016785.94 Кб14305 — Презентации лекций(Беспроводные технологии)_часть 2.1.1_СОС.ppsx
- #
16.03.2016842.38 Кб11305 — Презентации лекций(Беспроводные технологии)_часть 2.1.2_СОС.ppsx
- #
16.03.2016244.08 Кб9805 — Презентации лекций(Беспроводные технологии)_часть 2.1.3_СОС.ppsx
- #
16.03.2016237.31 Кб8905 — Презентации лекций(Беспроводные технологии)_часть 2.2.1_СОС.ppsx
- #
16.03.2016297.49 Кб8905 — Презентации лекций(Беспроводные технологии)_часть 2.2.2_СОС.ppsx
Контроль ошибок — комплекс методов обнаружения и исправления ошибок в данных (b) при их записи и воспроизведении или передаче по линиям связи.
Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом (b) , канальном (b) , транспортном (b) уровнях сетевой модели OSI (b) ) в связи с тем, что в процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Различные области применения контроля ошибок диктуют различные требования к используемым стратегиям и кодам.
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи[⇨] повреждённых блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- упреждающая коррекция ошибок добавляет к передаваемой информации такие дополнительные данные, которые позволяют исправить ошибки без дополнительного запроса.
В контроле ошибок, как правило, используется помехоустойчивое кодирование (b) — кодирование данных при записи или передаче и декодирование (b) при считывании или получении при помощи корректирующих кодов (b) , которые и позволяют обнаружить и, возможно, исправить ошибки в данных. Алгоритмы помехоустойчивого кодирования в различных приложениях могут быть реализованы как программно, так и аппаратно.
Современное развитие корректирующих кодов (b) приписывают Ричарду Хэммингу (b) с 1947 года (b) [1]. Описание кода Хэмминга (b) появилось в статье Клода Шеннона (b) «Математическая теория связи (b) »[2] и было обобщено Марселем Голеем (b) [3].
Стратегии исправления ошибок
Упреждающая коррекция ошибок
Упреждающая коррекция ошибок (также прямая коррекция ошибок, англ. (b) Forward Error Correction, FEC) — техника помехоустойчивого кодирования и декодирования (b) , позволяющая исправлять ошибки методом упреждения. Применяется для исправления сбоев и ошибок при передаче данных путём передачи избыточной служебной информации, на основе которой может быть восстановлено первоначальное содержание. На практике широко используется в сетях передачи данных (b) , телекоммуникационных технологиях. Коды, обеспечивающие прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, которые только обнаруживают ошибки.
Например, в спутниковом телевидении (b) при передаче цифрового сигнала с FEC 7/8 передаётся восемь бит информации: 7 бит полезной информации и 1 контрольный бит[4]; в DVB-S (b) используется всего 5 видов: 1/2, 2/3, 3/4 (наиболее популярен), 5/6 и 7/8. При прочих равных условиях, можно утверждать, что чем ниже значение FEC, тем меньше пакетов допустимо потерять, и, следовательно, выше требуемое качество сигнала.
Техника прямой коррекции ошибок широко применяется в различных устройствах хранения данных — жёстких дисках, флеш-памяти, оперативной памяти. В частности, в серверных приложениях применяется ECC-память (b) — оперативная память, способная распознавать и исправлять спонтанно возникшие ошибки.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (b) (англ. (b) Automatic Repeat Request, ARQ) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Идея запроса ARQ с остановками (англ. (b) stop-and-wait ARQ) заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем, как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного (b) канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Для метода непрерывного запроса ARQ с возвратом (continuous ARQ with pullback) необходим полнодуплексный (b) канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть передается ошибочный блок и все последующие).
При использовании метода непрерывного запроса ARQ с выборочным повторении (continuous ARQ with selective repeat) осуществляется передача только ошибочно принятых блоков данных.
Сетевое кодирование
Раздел теории информации (b) , изучающий вопрос оптимизации передачи данных по сети с использованием техник изменения пакетов данных на промежуточных узлах называют сетевым кодированием (b) . Для объяснения принципов сетевого кодирования используют пример сети «бабочка», предложенной в первой работе по сетевому кодированию «Network information flow»[5]. В отличие от статического сетевого кодирования, когда получателю известны все манипуляции, производимые с пакетом, также рассматривается вопрос о случайном сетевом кодировании, когда данная информация неизвестна. Авторство первых работ по данной тематике принадлежит Кёттеру, Кшишангу и Силве[6]. Также данный подход называют сетевым кодированием со случайными коэффициентами — когда коэффициенты, под которыми начальные пакеты, передаваемые источником, войдут в результирующие пакеты, принимаемые получателем, с неизвестными коэффициентами, которые могут зависеть от текущей структуры сети и даже от случайных решений, принимаемых на промежуточных узлах. Для неслучайного сетевого кодирования можно использовать стандартные способы защиты от помех и искажений, используемых для простой передачи информации по сети.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум (b) на входе демодулятора, таким образом, при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Примечания
- ↑ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, с. vii, ISBN 0-88385-023-0
- ↑ Shannon, C.E. (1948), A Mathematical Theory of Communication, Bell System Technical Journal (p. 418) Т. 27 (3): 379–423, PMID 9230594, DOI 10.1002/j.1538-7305.1948.tb01338.x
- ↑ Golay, Marcel J. E. (1949), Notes on Digital Coding, Proc.I.R.E. (I.E.E.E.) (p. 657) Т. 37
- ↑ Understanding Digital Television: An Introduction to Dvb Systems With … — Lars-Ingemar Lundström — Google Книги. Дата обращения: 19 мая 2020. Архивировано 11 ноября 2021 года.
- ↑ Ahlswede, R.; Ning Cai; Li, S.-Y.R.; Yeung, R.W., «Network information flow», Information Theory, IEEE Transactions on, vol.46, no.4, pp.1204-1216, Jul 2000
- ↑ Статьи:
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding// IEEE International Symposium on Information Theory. Proc.ISIT-07.-2007.- P. 791—795.
- Silva D., Kschischang F.R. Using rank-metric codes for error correction in random network coding // IEEE International Symposium on Information Theory. Proc. ISIT-07. — 2007.
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding // IEEE Transactions on Information Theory. — 2008- V. IT-54, N.8. — P. 3579-3591.
- Silva D., Kschischang F.R., Koetter R. A Rank-Metric Approach to Error Control in Random Network Coding // IEEE Transactions on Information Theory.- 2008- V. IT-54, N. 9.- P.3951-3967.
Литература
| Имеется викиучебник (b) по теме «Помехоустойчивое кодирование» |
- Блейхут Р. (b) Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир (b) , 1986. — 576 с.
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Морелос-Сарагоса Р. (b) Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева (b) . — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
- Clark, George C., Jr., and J. Bibb Cain. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981. ISBN 0-306-40615-2.
- Lin, Shu, and Daniel J. Costello, Jr. «Error Control Coding: Fundamentals and Applications». Englewood Cliffs, N.J.: Prentice-Hall, 1983. ISBN 0-13-283796-X.
- Mackenzie, Dana. «Communication speed nears terminal velocity». New Scientist 187.2507 (9 июля (b) 2005 (b) ): 38-41. ISSN 0262-4079.
- Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Englewood Cliffs, N.J.: Prentice-Hall, 1995. ISBN 0-13-200809-2.
- Wilson, Stephen G. Digital Modulation and Coding, Englewood Cliffs, N.J.: Prentice-Hall, 1996. ISBN 0-13-210071-1.
Ссылки
- Charles Wang, Dean Sklar, and Diana Johnson. Forward Error-Correction Coding. The Aerospace Corporation. — Volume 3, Number 1 (Winter 2001/2002). Дата обращения: 24 мая 2009. Архивировано из оригинала 20 февраля 2005 года. (англ.)
- Charles Wang, Dean Sklar, and Diana Johnson. How Forward Error-Correcting Codes Work (недоступная ссылка — история). The Aerospace Corporation. Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
- Morelos-Zaragoza, Robert The Error Correcting Codes (ECC) Page (недоступная ссылка — история) (2004). Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
Прямая коррекция ошибок
Пряма́я корре́кция оши́бок (англ. Forward Error Correction, FEC, помехоустойчивое кодирование) — техника кодирования/декодирования, позволяющая исправлять ошибки методом упреждения. Применяется для исправления сбоев и ошибок при передаче данных путём передачи избыточной служебной информации, на основе которой может быть восстановлена первоначальное содержание посылки. На практике широко используется в компьютерных ЛВС, LAN и различных телекоммуникационных сетях. Коды, обеспечивающие прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, которые только обнаруживают ошибки.
В спутниковом телевидении при передаче цифрового сигнала, к примеру, с FEC 7/8, будет передаваться восемь бит информации: 7 бит полезной информации и 1 контрольный бит[1].
На практике в DVB-S используется всего 5 видов:
- 1/2
- 2/3
- 3/4 (наиболее популярен)
- 5/6
- 7/8
При прочих равных условиях, можно утверждать, что чем ниже значение FEC, тем меньше пакетов допустимо потерять, и, следовательно, выше требуемое качество сигнала.
См. также
- ECC
- Код Хемминга
- Код Рида-Соломона
- Циклический код
- Помехоустойчивое кодирование
- Избыточность информации
Литература
- Clark, George C., Jr., and J. Bibb Cain. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981. ISBN 0-306-40615-2.
- Lin, Shu, and Daniel J. Costello, Jr. «Error Control Coding: Fundamentals and Applications». Englewood Cliffs, N.J.: Prentice-Hall, 1983. ISBN 0-13-283796-X.
- Mackenzie, Dana. «Communication speed nears terminal velocity». New Scientist 187.2507 (9 июля 2005): 38-41. ISSN 0262-4079.
- Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Englewood Cliffs, N.J.: Prentice-Hall, 1995. ISBN 0-13-200809-2.
- Wilson, Stephen G. Digital Modulation and Coding, Englewood Cliffs, N.J.: Prentice-Hall, 1996. ISBN 0-13-210071-1.
- United States Patent 6041001 «Method of increasing data reliability of a flash memory device without compromising compatibility»
- United States Patent 7187583 «Method for reducing data error when flash memory storage device using copy back command»
Примечания
- ↑ Understanding Digital Television: An Introduction to Dvb Systems With … — Lars-Ingemar Lundström — Google Книги
Ссылки
- Forward Error-Correction Coding. Статья в журнале Aerospace Corporation. The Aerospace Corporation (Volume 3, Number 1 (Winter 2001/2002)). Проверено 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
- How Forward Error-Correcting Codes Work. Еще одна статья в журнале Aerospace Corporation. The Aerospace Corporation. Проверено 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
- Morelos-Zaragoza, Robert The Error Correcting Codes (ECC) Page (2004). Проверено 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи. Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.
Для обнаружения ошибок используют коды обнаружения ошибок, для исправления — корректирующие коды (коды, исправляющие ошибки, коды с коррекцией ошибок, помехоустойчивые коды).
Содержание
- 1 Способы борьбы с ошибками
- 2 Коды обнаружения и исправления ошибок
- 2.1 Блоковые коды
- 2.1.1 Линейные коды общего вида
- 2.1.1.1 Минимальное расстояние и корректирующая способность
- 2.1.1.2 Коды Хемминга
- 2.1.1.3 Общий метод декодирования линейных кодов
- 2.1.2 Линейные циклические коды
- 2.1.2.1 Порождающий (генераторный) полином
- 2.1.2.2 Коды CRC
- 2.1.2.3 Коды БЧХ
- 2.1.2.4 Коды коррекции ошибок Рида — Соломона
- 2.1.3 Преимущества и недостатки блоковых кодов
- 2.1.1 Линейные коды общего вида
- 2.2 Свёрточные коды
- 2.2.1 Преимущества и недостатки свёрточных кодов
- 2.3 Каскадное кодирование. Итеративное декодирование
- 2.4 Оценка эффективности кодов
- 2.4.1 Граница Хемминга и совершенные коды
- 2.4.2 Энергетический выигрыш
- 2.5 Применение кодов, исправляющих ошибки
- 2.1 Блоковые коды
- 3 Автоматический запрос повторной передачи
- 3.1 Запрос ARQ с остановками (stop-and-wait ARQ)
- 3.2 Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
- 3.3 Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
- 4 См. также
- 5 Литература
- 6 Ссылки
Способы борьбы с ошибками
В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков — этот подход применяется в основном на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- исправление ошибок (forward error correction) применяется на физическом уровне.
Коды обнаружения и исправления ошибок
Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении.
Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.
С кодами, исправляющими ошибки, тесно связаны коды обнаружения ошибок. В отличие от первых, последние могут только установить факт наличия ошибки в переданных данных, но не исправить её.
В действительности, используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).
По способу работы с данными коды, исправляющие ошибки делятся на блоковые, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности, и свёрточные, работающие с данными как с непрерывным потоком.
Блоковые коды
Пусть кодируемая информация делится на фрагменты длиной k бит, которые преобразуются в кодовые слова длиной n бит. Тогда соответствующий блоковый код обычно обозначают 
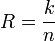
Если исходные k бит код оставляет неизменными, и добавляет n − k проверочных, такой код называется систематическим, иначе несистематическим.
Задать блоковый код можно по-разному, в том числе таблицей, где каждой совокупности из k информационных бит сопоставляется n бит кодового слова. Однако, хороший код должен удовлетворять, как минимум, следующим критериям:
- способность исправлять как можно большее число ошибок,
- как можно меньшая избыточность,
- простота кодирования и декодирования.
Нетрудно видеть, что приведённые требования противоречат друг другу. Именно поэтому существует большое количество кодов, каждый из которых пригоден для своего круга задач.
Практически все используемые коды являются линейными. Это связано с тем, что нелинейные коды значительно сложнее исследовать, и для них трудно обеспечить приемлемую лёгкость кодирования и декодирования.
Линейные коды общего вида
Линейный блоковый код — такой код, что множество его кодовых слов образует k-мерное линейное подпространство (назовём его C) в n-мерном линейном пространстве, изоморфное пространству k-битных векторов.
Это значит, что операция кодирования соответствует умножению исходного k-битного вектора на невырожденную матрицу G, называемую порождающей матрицей.
Пусть 
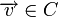
Минимальное расстояние и корректирующая способность
Расстоянием Хемминга (метрикой Хемминга) между двумя кодовыми словами 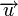

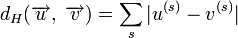
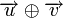
Минимальное расстояние Хемминга 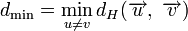
, округляем «вниз», так чтобы 2t < dmin.
Корректирующая способность определяет, сколько ошибок передачи кода (типа 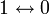
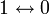

Таким образом получив искажённый код из At декодер принимает решение, что был исходный код A, исправляя тем самым не более t ошибок.
Поясним на примере. Предположим, что есть два кодовых слова A и B, расстояние Хемминга между ними равно 3. Если было передано слово A, и канал внёс ошибку в одном бите, она может быть исправлена, так как даже в этом случае принятое слово ближе к кодовому слову A, чем к любому другому, и в частности к B. Но если каналом были внесены ошибки в двух битах (в которых A отличалось от B) то результат ошибочной передачи A окажется ближе к B, чем A, и декодер примет решение что передавалось слово B.
Коды Хемминга
Коды Хемминга — простейшие линейные коды с минимальным расстоянием 3, то есть способные исправить одну ошибку. Код Хемминга может быть представлен в таком виде, что синдром
, где
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
Общий метод декодирования линейных кодов
Любой код (в том числе нелинейный) можно декодировать с помощью обычной таблицы, где каждому значению принятого слова 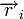

Для линейных кодов этот метод можно существенно упростить. При этом для каждого принятого вектора 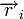
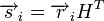
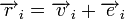
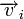
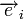

Линейные циклические коды
Несмотря на то, что декодирование линейных кодов уже значительно проще декодирования большинства нелинейных, для большинства кодов этот процесс всё ещё достаточно сложен. Циклические коды, кроме более простого декодирования, обладают и другими важными свойствами.
Циклическим кодом является линейный код, обладающий следующим свойством: если 
Слова циклического кода удобно представлять в виде многочленов. Например, кодовое слово 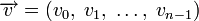
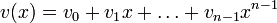
В дальнейшем, если не указано иное, мы будем считать, что циклический код является двоичным, то есть 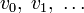
Порождающий (генераторный) полином
Можно показать, что все кодовые слова конкретного циклического кода кратны определённому порождающему полиному g(x). Порождающий полином является делителем xn − 1.
С помощью порождающего полинома осуществляется кодирование циклическим кодом. В частности:
- несистематическое кодирование осуществляется путём умножения кодируемого вектора на g(x): v(x) = u(x)g(x);
- систематическое кодирование осуществляется путём «дописывания» к кодируемому слову остатка от деления xn − ku(x) на g(x), то есть
.
Коды CRC
Коды CRC (cyclic redundancy check — циклическая избыточная проверка) являются систематическими кодами, предназначенными не для исправления ошибок, а для их обнаружения. Они используют способ систематического кодирования, изложенный выше: «контрольная сумма» вычисляется путем деления xn − ku(x) на g(x). Ввиду того, что исправление ошибок не требуется, проверка правильности передачи может производиться точно так же.
Таким образом, вид полинома g(x) задаёт конкретный код CRC. Примеры наиболее популярных полиномов:
| название кода | степень | полином |
|---|---|---|
| CRC-12 | 12 | x12 + x11 + x3 + x2 + x + 1 |
| CRC-16 | 16 | x16 + x15 + x2 + 1 |
| CRC-x16 + x12 + x5 + 1 | ||
| CRC-32 | 32 | x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1 |
Коды БЧХ
Коды Боуза — Чоудхури — Хоквингема (БЧХ) являются подклассом циклических кодов. Их отличительное свойство — возможность построения кода БЧХ с минимальным расстоянием не меньше заданного. Это важно, потому что, вообще говоря, определение минимального расстояния кода есть очень сложная задача.
Математически полинома g(x) на множители в поле Галуа.
Коды коррекции ошибок Рида — Соломона
Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида-Соломона, работающие с байтами (октетами).
Математически коды Рида — Соломона являются кодами БЧХ.
Преимущества и недостатки блоковых кодов
Хотя блоковые коды, как правило, хорошо справляются с редкими, но большими пачками ошибок, их эффективность при частых, но небольших ошибках (например, в канале с АБГШ), менее высока.
Свёрточные коды
Свёрточный кодер (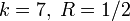
Свёрточные коды, в отличие от блоковых, не делят информацию на фрагменты и работают с ней как со сплошным потоком данных.
Свёрточные коды, как правило, порождаются дискретной линейной инвариантной во времени системой. Поэтому, в отличие от большинства блоковых кодов, свёрточное кодирование — очень простая операция, чего нельзя сказать о декодировании.
Кодирование свёрточным кодом производится с помощью регистра сдвига, отводы от которого суммируются по модулю два. Таких сумм может быть две (чаще всего) или больше.
Декодирование свёрточных кодов, как правило, производится по алгоритму Витерби, который пытается восстановить переданную последовательность согласно критерию максимального правдоподобия.
Преимущества и недостатки свёрточных кодов
Свёрточные коды эффективно работают в канале с белым шумом, но плохо справляются с пакетами ошибок. Более того, если декодер ошибается, на его выходе всегда возникает пакет ошибок.
Каскадное кодирование. Итеративное декодирование
Преимущества разных способов кодирования можно объединить, применив каскадное кодирование. При этом информация сначала кодируется одним кодом, а затем другим, в результате получается код-произведение.
Например, популярной является следующая конструкция: данные кодируются кодом Рида-Соломона, затем перемежаются (при этом символы, расположенные близко, помещаются далеко друг от друга) и кодируются свёрточным кодом. На приёмнике сначала декодируется свёрточный код, затем осуществляется обратное перемежение (при этом пачки ошибок на выходе свёрточного декодера попадают в разные кодовые слова кода Рида — Соломона), и затем осуществляется декодирование кода Рида — Соломона.
Некоторые коды-произведения специально сконструированы для итеративного декодирования, при котором декодирование осуществляется в несколько проходов, каждый из которых использует информацию от предыдущего. Это позволяет добиться большой эффективности, однако, декодирование требует больших ресурсов. К таким кодам относят турбо-коды и LDPC-коды (коды Галлагера).
Оценка эффективности кодов
Эффективность кодов определяется количеством ошибок, которые тот может исправить, количеством избыточной информации, добавление которой требуется, а также сложностью реализации кодирования и декодирования (как аппаратной, так и в виде программы для ЭВМ).
Граница Хемминга и совершенные коды
Пусть имеется двоичный блоковый (n,k) код с корректирующей способностью t. Тогда справедливо неравенство (называемое границей Хемминга):
Коды, удовлетворяющие этой границе с равенством, называются совершенными. К совершенным кодам относятся, например, коды Хемминга. Часто применяемые на практике коды с большой корректирующей способностью (такие, как коды Рида — Соломона) не являются совершенными.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Применение кодов, исправляющих ошибки
Коды, исправляющие ошибки, применяются:
- в системах цифровой связи, в том числе: спутниковой, радиорелейной, сотовой, передаче данных по телефонным каналам.
- в системах хранения информации, в том числе магнитных и оптических.
Коды, обнаруживающие ошибки, применяются в сетевых протоколах различных уровней.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (ARQ — Automatic Repeat reQuest) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Запрос ARQ с остановками (stop-and-wait ARQ)
Идея этого метода заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Непрерывный запрос ARQ с возвратом (continuous ARQ with pullback)
Для этого метода необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть, передается ошибочный блок и все последующие).
Непрерывный запрос ARQ с выборочным повторением (continuous ARQ with selective repeat)
При этом подходе осуществляется передача только ошибочно принятых блоков данных.
См. также
- Цифровая связь
- Линейный код
- Циклический код
- Код Боуза — Чоудхури — Хоквингема
- Код Рида — Соломона
- LDPC
- Свёрточный код
- Турбо-код
Литература
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир, 1986.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. — ISBN 5-94836-035-0
Ссылки
- Помехоустойчивое кодирование (11 ноября 2001). — реферат по проблеме кодирования сообщений с исправлением ошибок. Проверено 25 декабря 2006.
Wikimedia Foundation.
2010.
Эта статья — о работе с ошибками в данных при их хранении или передаче. О контроле фактических ошибок в текстах см. Проверка фактов; о проверке знаний и навыков при обучении см. Педагогическое тестирование; о методе обучения нейросети см. Метод коррекции ошибки.
Контроль ошибок — комплекс методов обнаружения и исправления ошибок в данных при их записи и воспроизведении или передаче по линиям связи.
Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях сетевой модели OSI) в связи с тем, что в процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Различные области применения контроля ошибок диктуют различные требования к используемым стратегиям и кодам.
В системах связи возможны несколько стратегий борьбы с ошибками:
- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи[⇨] повреждённых блоков — этот подход применяется, в основном, на канальном и транспортном уровнях;
- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков — такой подход иногда применяется в системах потокового мультимедиа, где важна задержка передачи и нет времени на повторную передачу;
- упреждающая коррекция ошибок добавляет к передаваемой информации такие дополнительные данные, которые позволяют исправить ошибки без дополнительного запроса.
В контроле ошибок, как правило, используется помехоустойчивое кодирование — кодирование данных при записи или передаче и декодирование при считывании или получении при помощи корректирующих кодов, которые и позволяют обнаружить и, возможно, исправить ошибки в данных. Алгоритмы помехоустойчивого кодирования в различных приложениях могут быть реализованы как программно, так и аппаратно.
Современное развитие корректирующих кодов приписывают Ричарду Хэммингу с 1947 года[1]. Описание кода Хэмминга появилось в статье Клода Шеннона «Математическая теория связи»[2] и было обобщено Марселем Голеем[3].
Стратегии исправления ошибок
Упреждающая коррекция ошибок
Упреждающая коррекция ошибок (также прямая коррекция ошибок, англ. Forward Error Correction, FEC) — техника помехоустойчивого кодирования и декодирования, позволяющая исправлять ошибки методом упреждения. Применяется для исправления сбоев и ошибок при передаче данных путём передачи избыточной служебной информации, на основе которой может быть восстановлено первоначальное содержание. На практике широко используется в сетях передачи данных, телекоммуникационных технологиях. Коды, обеспечивающие прямую коррекцию ошибок, требуют введения большей избыточности в передаваемые данные, чем коды, которые только обнаруживают ошибки.
Например, в спутниковом телевидении при передаче цифрового сигнала с FEC 7/8 передаётся восемь бит информации: 7 бит полезной информации и 1 контрольный бит[4]; в DVB-S используется всего 5 видов: 1/2, 2/3, 3/4 (наиболее популярен), 5/6 и 7/8. При прочих равных условиях, можно утверждать, что чем ниже значение FEC, тем меньше пакетов допустимо потерять, и, следовательно, выше требуемое качество сигнала.
Техника прямой коррекции ошибок широко применяется в различных устройствах хранения данных — жёстких дисках, флеш-памяти, оперативной памяти. В частности, в серверных приложениях применяется ECC-память — оперативная память, способная распознавать и исправлять спонтанно возникшие ошибки.
Автоматический запрос повторной передачи
Системы с автоматическим запросом повторной передачи (англ. Automatic Repeat Request, ARQ) основаны на технологии обнаружения ошибок. Распространены следующие методы автоматического запроса:
Идея запроса ARQ с остановками (англ. stop-and-wait ARQ) заключается в том, что передатчик ожидает от приемника подтверждения успешного приема предыдущего блока данных перед тем, как начать передачу следующего. В случае, если блок данных был принят с ошибкой, приемник передает отрицательное подтверждение (negative acknowledgement, NAK), и передатчик повторяет передачу блока. Данный метод подходит для полудуплексного канала связи. Его недостатком является низкая скорость из-за высоких накладных расходов на ожидание.
Для метода непрерывного запроса ARQ с возвратом (continuous ARQ with pullback) необходим полнодуплексный канал. Передача данных от передатчика к приемнику производится одновременно. В случае ошибки передача возобновляется, начиная с ошибочного блока (то есть передается ошибочный блок и все последующие).
При использовании метода непрерывного запроса ARQ с выборочным повторении (continuous ARQ with selective repeat) осуществляется передача только ошибочно принятых блоков данных.
Сетевое кодирование
Раздел теории информации, изучающий вопрос оптимизации передачи данных по сети с использованием техник изменения пакетов данных на промежуточных узлах называют сетевым кодированием. Для объяснения принципов сетевого кодирования используют пример сети «бабочка», предложенной в первой работе по сетевому кодированию «Network information flow»[5]. В отличие от статического сетевого кодирования, когда получателю известны все манипуляции, производимые с пакетом, также рассматривается вопрос о случайном сетевом кодировании, когда данная информация неизвестна. Авторство первых работ по данной тематике принадлежит Кёттеру, Кшишангу и Силве[6]. Также данный подход называют сетевым кодированием со случайными коэффициентами — когда коэффициенты, под которыми начальные пакеты, передаваемые источником, войдут в результирующие пакеты, принимаемые получателем, с неизвестными коэффициентами, которые могут зависеть от текущей структуры сети и даже от случайных решений, принимаемых на промежуточных узлах. Для неслучайного сетевого кодирования можно использовать стандартные способы защиты от помех и искажений, используемых для простой передачи информации по сети.
Энергетический выигрыш
При передаче информации по каналу связи вероятность ошибки зависит от отношения сигнал/шум на входе демодулятора, таким образом, при постоянном уровне шума решающее значение имеет мощность передатчика. В системах спутниковой и мобильной, а также других типов связи остро стоит вопрос экономии энергии. Кроме того, в определённых системах связи (например, телефонной) неограниченно повышать мощность сигнала не дают технические ограничения.
Поскольку помехоустойчивое кодирование позволяет исправлять ошибки, при его применении мощность передатчика можно снизить, оставляя скорость передачи информации неизменной. Энергетический выигрыш определяется как разница отношений с/ш при наличии и отсутствии кодирования.
Примечания
- ↑ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), The Mathematical Association of America, с. vii, ISBN 0-88385-023-0
- ↑ Shannon, C.E. (1948), A Mathematical Theory of Communication, Bell System Technical Journal (p. 418) Т. 27 (3): 379–423, PMID 9230594, DOI 10.1002/j.1538-7305.1948.tb01338.x
- ↑ Golay, Marcel J. E. (1949), Notes on Digital Coding, Proc.I.R.E. (I.E.E.E.) (p. 657) Т. 37
- ↑ Understanding Digital Television: An Introduction to Dvb Systems With … — Lars-Ingemar Lundström — Google Книги. Дата обращения: 19 мая 2020. Архивировано 11 ноября 2021 года.
- ↑ Ahlswede, R.; Ning Cai; Li, S.-Y.R.; Yeung, R.W., «Network information flow», Information Theory, IEEE Transactions on, vol.46, no.4, pp.1204-1216, Jul 2000
- ↑ Статьи:
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding// IEEE International Symposium on Information Theory. Proc.ISIT-07.-2007.- P. 791—795.
- Silva D., Kschischang F.R. Using rank-metric codes for error correction in random network coding // IEEE International Symposium on Information Theory. Proc. ISIT-07. — 2007.
- Koetter R., Kschischang F.R. Coding for errors and erasures in random network coding // IEEE Transactions on Information Theory. — 2008- V. IT-54, N.8. — P. 3579-3591.
- Silva D., Kschischang F.R., Koetter R. A Rank-Metric Approach to Error Control in Random Network Coding // IEEE Transactions on Information Theory.- 2008- V. IT-54, N. 9.- P.3951-3967.
Литература
- Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.
- Мак-Вильямс Ф. Дж., Слоэн Н. Дж. А. Теория кодов, исправляющих ошибки. М.: Радио и связь, 1979.
- Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева. — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.
- Clark, George C., Jr., and J. Bibb Cain. Error-Correction Coding for Digital Communications. New York: Plenum Press, 1981. ISBN 0-306-40615-2.
- Lin, Shu, and Daniel J. Costello, Jr. «Error Control Coding: Fundamentals and Applications». Englewood Cliffs, N.J.: Prentice-Hall, 1983. ISBN 0-13-283796-X.
- Mackenzie, Dana. «Communication speed nears terminal velocity». New Scientist 187.2507 (9 июля 2005): 38-41. ISSN 0262-4079.
- Wicker, Stephen B. Error Control Systems for Digital Communication and Storage. Englewood Cliffs, N.J.: Prentice-Hall, 1995. ISBN 0-13-200809-2.
- Wilson, Stephen G. Digital Modulation and Coding, Englewood Cliffs, N.J.: Prentice-Hall, 1996. ISBN 0-13-210071-1.
Ссылки
- Charles Wang, Dean Sklar, and Diana Johnson. Forward Error-Correction Coding. The Aerospace Corporation. — Volume 3, Number 1 (Winter 2001/2002). Дата обращения: 24 мая 2009. Архивировано из оригинала 20 февраля 2005 года. (англ.)
- Charles Wang, Dean Sklar, and Diana Johnson. How Forward Error-Correcting Codes Work (недоступная ссылка — история). The Aerospace Corporation. Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
- Morelos-Zaragoza, Robert The Error Correcting Codes (ECC) Page (недоступная ссылка — история) (2004). Дата обращения: 24 мая 2009. Архивировано 25 февраля 2012 года. (англ.)
Эта страница в последний раз была отредактирована 17 октября 2022 в 07:46.
Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.

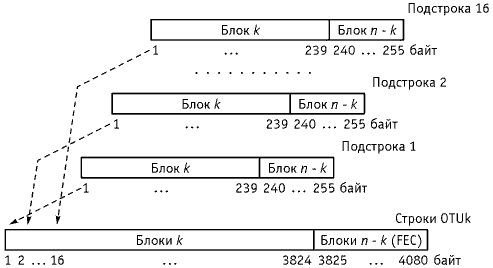
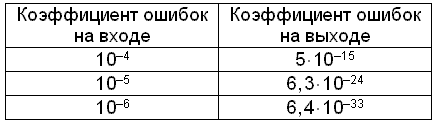
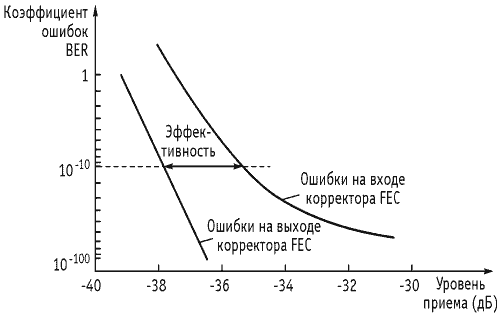
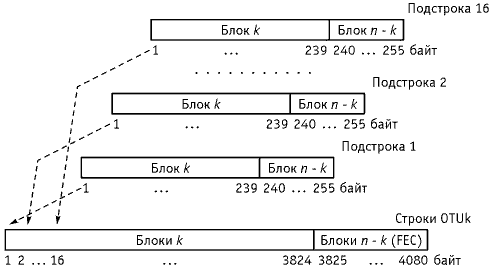

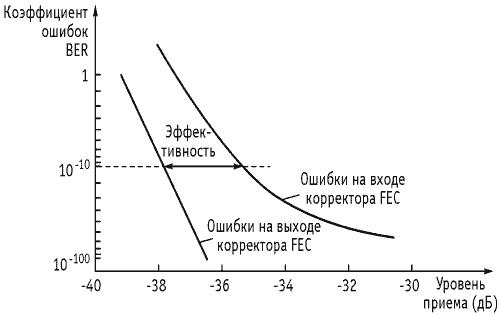

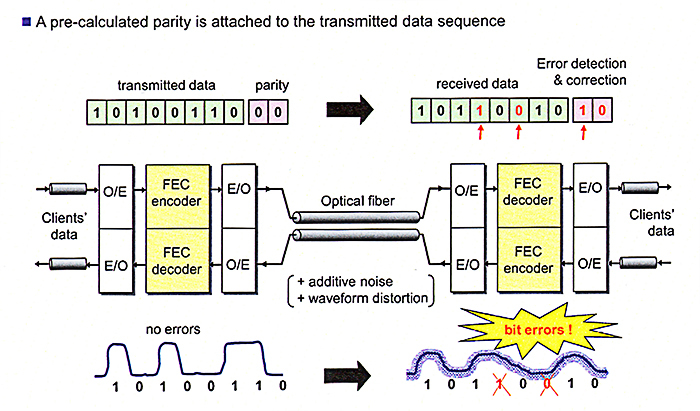
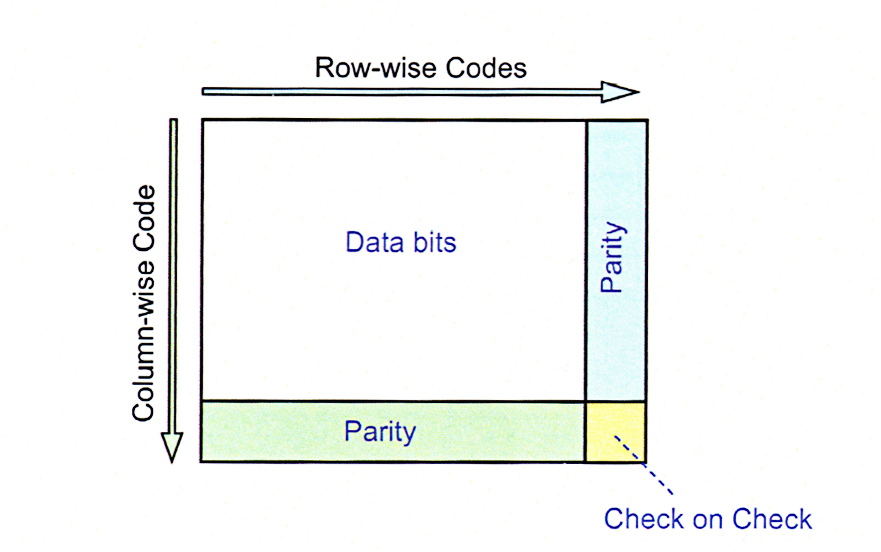
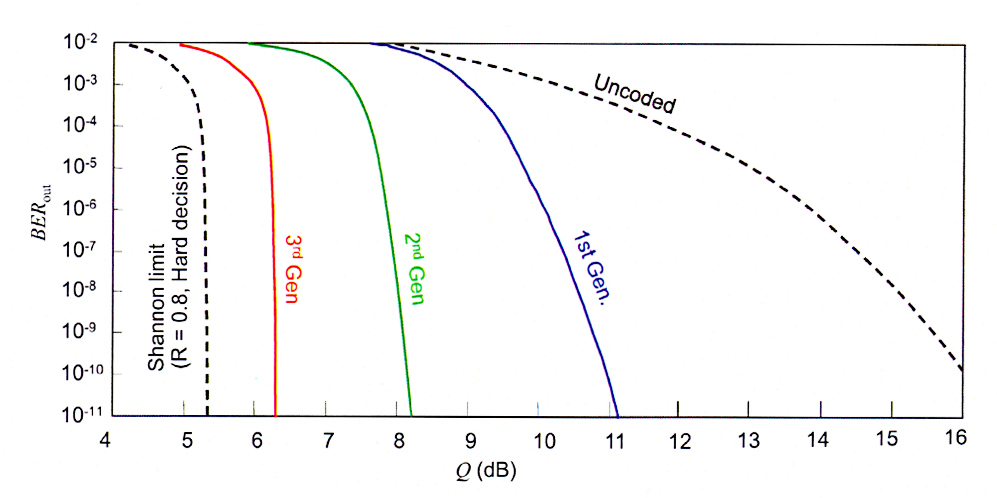
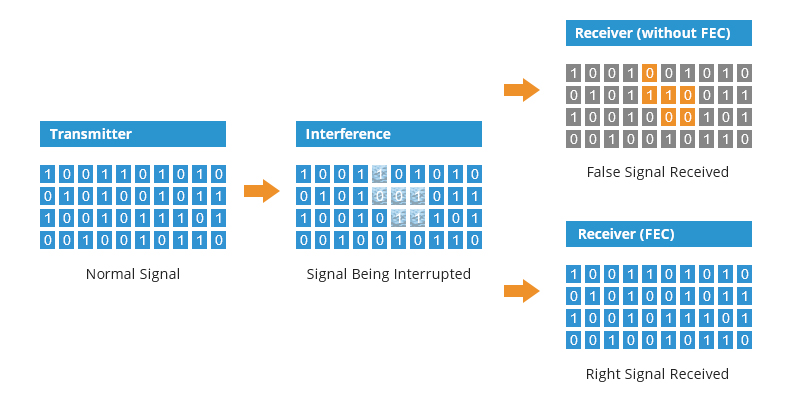

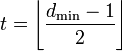 , округляем «вниз», так чтобы
, округляем «вниз», так чтобы  , где
, где 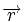 — принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.
— принятый вектор, будет равен номеру позиции, в которой произошла ошибка. Это свойство позволяет сделать декодирование очень простым.![v(x)=x^{n-k}u(x)+[x^{n-k}u(x),bmod,g(x)]](https://dic.academic.ru/pictures/wiki/files/97/ab852c2832864dffc1acf3cbd9eff59e.png) .
.