Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Проверка корректности А/Б тестов
Время на прочтение
8 мин
Количество просмотров 7.7K
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
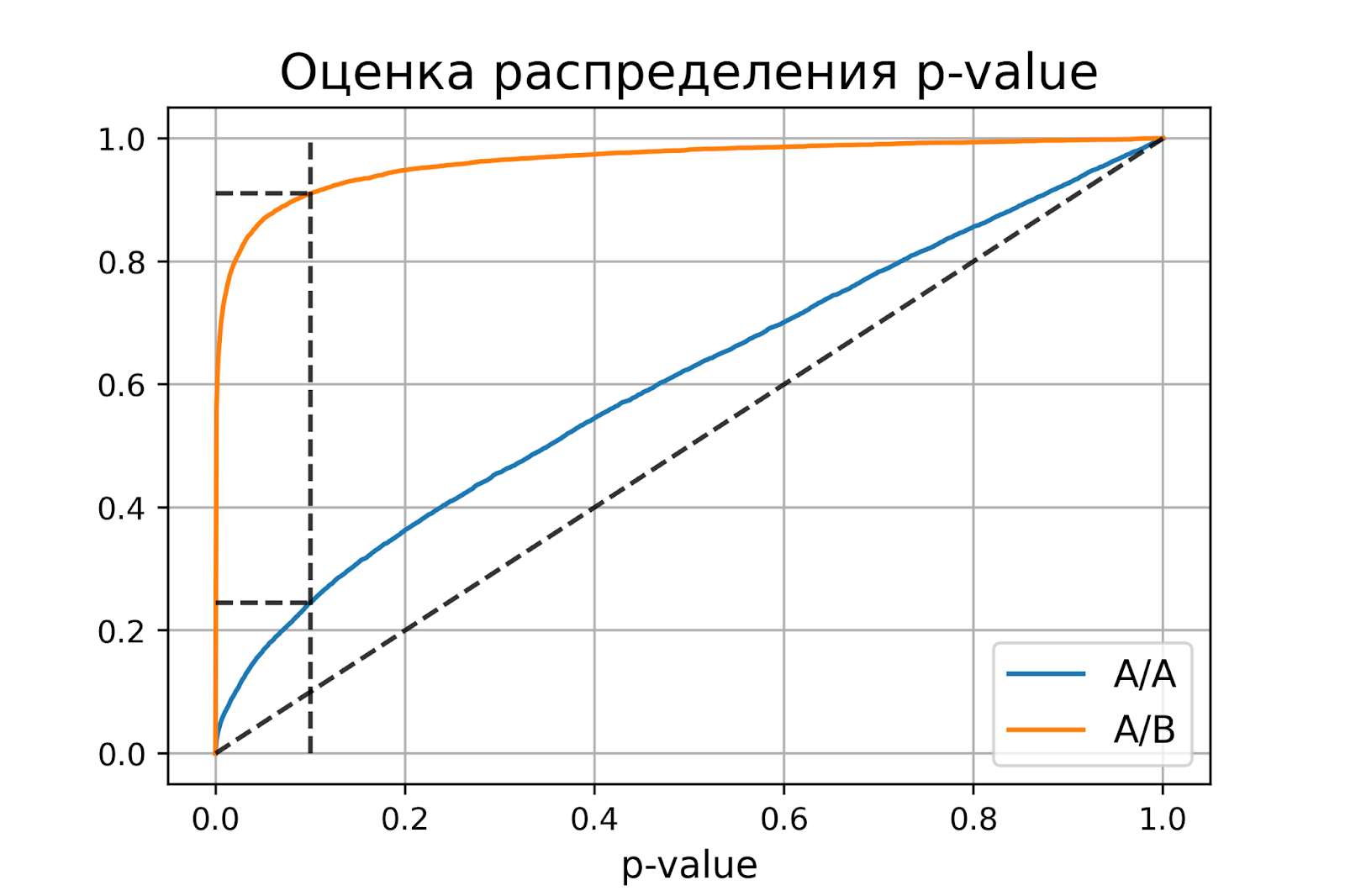
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
5.3. Ошибки первого и второго рода
Ошибка первого рода состоит в том, что гипотеза будет отвергнута, хотя на самом деле она правильная. Вероятность
допустить такую ошибку называют уровнем значимости и обозначают буквой («альфа»).
Ошибка второго рода состоит в том, что гипотеза будет принята, но на самом деле она неправильная. Вероятность
совершить эту ошибку обозначают буквой («бета»). Значение
называют мощностью критерия – это вероятность отвержения неправильной
гипотезы.
В практических задачах, как правило, задают уровень значимости, наиболее часто выбирают значения .
И тут возникает мысль, что чем меньше «альфа», тем вроде бы лучше. Но это только вроде: при уменьшении
вероятности —
отвергнуть правильную гипотезу растёт вероятность — принять неверную гипотезу (при прочих равных условиях).
Поэтому перед исследователем стоит задача грамотно подобрать соотношение вероятностей и
, при этом учитывается тяжесть последствий, которые
повлекут за собой та и другая ошибки.
Понятие ошибок 1-го и 2-го рода используется не только в статистике, и для лучшего понимания я приведу пару
нестатистических примеров.
Петя зарегистрировался в почтовике. По умолчанию, – он считается добропорядочным пользователем. Так считает антиспам
фильтр. И вот Петя отправляет письмо. В большинстве случаев всё произойдёт, как должно произойти – нормальное письмо дойдёт до
адресата (правильное принятие нулевой гипотезы), а спамное – попадёт в спам (правильное отвержение). Однако фильтр может
совершить ошибку двух типов:
1) с вероятностью ошибочно отклонить нулевую гипотезу (счесть нормальное письмо
за спам и Петю за спаммера) или
2) с вероятностью ошибочно принять нулевую гипотезу (хотя Петя редиска).
Какая ошибка более «тяжелая»? Петино письмо может быть ОЧЕНЬ важным для адресата, и поэтому при настройке фильтра
целесообразно уменьшить уровень значимости , «пожертвовав» вероятностью
(увеличив её). В результате в основной ящик будут попадать все
«подозрительные» письма, в том числе особо талантливых спаммеров. …Такое и почитать даже можно, ведь сделано с любовью 
Существует примеры, где наоборот – более тяжкие последствия влечёт ошибка 2-го рода, и вероятность следует увеличить (в пользу уменьшения
вероятности ). Не хотел я
приводить подобные примеры, и даже отшутился на сайте, но по какой-то мистике через пару месяцев сам столкнулся с непростой
дилеммой. Видимо, таки, надо рассказать:
У человека появилась серьёзная болячка. В медицинской практике её принято лечить (основное «нулевое» решение). Лечение
достаточно эффективно, однако не гарантирует результата и более того опасно (иногда приводит к серьёзному пожизненному
увечью). С другой стороны, если не лечить, то возможны осложнения и долговременные функциональные нарушения.
Вопрос: что делать? И ответ не так-то прост – в разных ситуациях разные люди могут принять разные
решения (упаси вас).
Если болезнь не особо «мешает жить», то более тяжёлые последствия повлечёт ошибка 2-го рода – когда человек соглашается
на лечение, но получает фатальный результат (принимает, как оказалось, неверное «нулевое» решение). Если же…, нет, пожалуй,
достаточно, возвращаемся к теме:


| Оглавление |
Проверка статистических гипотез
- Понятие о статистической гипотезе
- Уровень значимости при проверке гипотезы
- Критическая область
- Простая гипотеза и критерии согласия
- Критерий согласия (X^2) Пирсона
- Примеры
п.1. Понятие о статистической гипотезе
Статистическая гипотеза – это предположение о виде распределения и свойствах случайной величины в наблюдаемой выборке данных.
Прежде всего, мы формулируем «рабочую» гипотезу. Желательно это делать не на основе полученных данных, а исходя из природы и свойств исследуемого явления.
Затем формулируется нулевая гипотеза (H_0), отвергающая нашу рабочую гипотезу.
Наша рабочая гипотеза при этом называется альтернативной гипотезой (H_1).
Получаем, что (H_0=overline{H_1}), т.е. нулевая и альтернативная гипотеза вместе составляют полную группу несовместных событий.
Основной принцип проверки гипотезы – доказательство «от противного», т.е. опровергнуть гипотезу (H_0) и тем самым доказать гипотезу (H_1).
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| (H_0) | (H_1) | ||
| Принятая гипотеза | (H_0) | True Negative (H_0) принята верно |
False Negative (H_0) принята неверно Ошибка 2-го рода |
| (H_1) | False Positive (H_0) отвергнута неверно (H_1) принята неверно Ошибка 1-го рода |
True Positive (H_0) отвергнута верно (H_1) принята верно |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Например:
К врачу обращается человек с некоторой жалобой.
Гипотеза (H_1) — человек болен, гипотеза (H_0) — человек здоров.
True Negative – здорового человека признают здоровым
True Positive – больного человека признают больным
False Positive – здорового человека признают больным – «ложная тревога»
False Negative – больного человека признают здоровым – «пропуск события»
Уровень значимости при проверке гипотезы
Статистический тест (статистический критерий) – это строгое математическое правило, по которому гипотеза принимается или отвергается.
В статистике разработано множество критериев: критерии согласия, критерии нормальности, критерии сдвига, критерии выбросов и т.д.
Уровень значимости – это пороговая (критическая) вероятность ошибки 1-го рода, т.е. непринятия гипотезы (H_0), когда она верна («ложная тревога»).
Требуемый уровень значимости α задает критическое значение для статистического теста.
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
В результате статистического теста на конкретных данных получают эмпирический уровень значимости p. Чем меньше значение p, тем сильнее аргументы против гипотезы (H_0).
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости (p) |
Решение о гипотезе (H_0) | Вывод для гипотезы (H_1) |
| (pgt 0,1) | (H_0) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| (0,5lt pleq 0,1) | Истинность (H_0) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| (0,01lt pleq 0,05) | Отклонение (H_0), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| (pleq 0,01) | Отклонение (H_0), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы (H_1).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с (ngeq 100) критический уровень снижают до α=0,01.
п.3. Критическая область
Критическая область – область выборочного пространства, при попадании в которую нулевая гипотеза отклоняется.
Требуемый уровень значимости α, который задается исследователем, определяет границу попадания в критическую область при верной нулевой гипотезе.
Различают 3 вида критических областей
Критическая область на чертежах заштрихована.
(K_{кр}=chi_{f(alpha)}) определяют границы критической области в зависимости от α.
Если эмпирическое значение критерия попадает в критическую область, гипотезу (H_0) отклоняют.
Пусть (K*) — эмпирическое значение критерия. Тогда:
(|K|gt K_{кр}) – гипотеза (H_0) отклоняется
(|K|leq K_{кр}) – гипотеза (H_0) не отклоняется
п.4. Простая гипотеза и критерии согласия
Пусть (x=left{x_1,x_2,…,x_nright}) – случайная выборка n объектов из множества (X), соответствующая неизвестной функции распределения (F(t)).
Простая гипотеза состоит в предположении, что неизвестная функция (F(t)) является совершенно конкретным вероятностным распределением на множестве (X).
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
(H_0): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
К критериям согласия относятся:
- Критерий Колмогорова-Смирнова;
- Критерий (X^2) Пирсона;
- Критерий (omega^2) Смирнова-Крамера-фон Мизеса
п.5. Критерий согласия (X^2) Пирсона
Пусть (left{t_1,t_2,…,t_nright}) — независимые случайные величины, подчиняющиеся стандартному нормальному распределению N(0;1) (см. §63 данного справочника)
Тогда сумма квадратов этих величин: $$ x=t_1^2+t_2^2+⋯+t_n^2 $$ является случайной величиной, которая имеет распределение (X^2) с n степенями свободы.
График плотности распределения (X^2) при разных n имеет вид:
С увеличением n распределение (X^2) стремится к нормальному (согласно центральной предельной теореме – см. §64 данного справочника).
Если мы:
1) выдвигаем простую гипотезу (H_0) о том, что полученные данные являются выборкой из некоторого закона распределения (f(x));
2) выбираем в качестве теста проверки гипотезы (H_0) критерий Пирсона, —
тогда определение критической области будет основано на распределении (X^2).
Заметим, что выдвижение основной гипотезы в качестве (H_0) при проведении этого теста исторически сложилось.
В этом случае критическая область правосторонняя.
Мы задаем уровень значимости α и находим критическое значение
(X_{кр}^2=X^2(alpha,k-r-1)), где k — число вариант в исследуемом ряду, r – число параметров предполагаемого распределения.
Для этого есть специальные таблицы.
Или используем функцию ХИ2ОБР(α,k-r-1) в MS Excel (она сразу считает нужный нам правый хвост). Например, при r=0 (для равномерного распределения):
Пусть нам дан вариационный ряд с экспериментальными частотами (f_i, i=overline{1,k}).
Пусть наша гипотеза (H_0) –данные являются выборкой из закона распределения с известной плотностью распределения (p(x)).
Тогда соответствующие «теоретические частоты» (m_i=Ap(x_i)), где (x_i) – значения вариант данного ряда, A – коэффициент, который в общем случае зависит от ряда (дискретный или непрерывный).
Находим значение статистического теста: $$ X_e^2=sum_{j=1}^kfrac{(f_i-m_i)^2}{m_i} $$ Если эмпирическое значение (X_e^2) окажется в критической области, гипотеза (H_0) отвергается.
(X_e^2geq X_{кр}^2) — закон распределения не подходит (гипотеза (H_0) не принимается)
(X_e^2lt X_{кр}^2) — закон распределения подходит (гипотеза (H_0) принимается)
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 12 | 8 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=60 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 60=10 $$ по 10 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| (m_i) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| (f_i-m_i) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
Значение теста: $$ X_e^2=3,4 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик не фальшивый.
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
| Очки, (x_i) | 1 | 2 | 3 | 4 | 5 | 6 |
| Частота, (f_i) | 8 | 12 | 13 | 7 | 10 | 22 |
Не является ли кубик фальшивым?
Если кубик не фальшивый, то справедлива гипотеза (H_0) — частота выпадений очков подчиняется равномерному распределению: $$ p_i=frac16, i=overline{1,6} $$ При N=72 экспериментах каждая сторона теоретически должна выпасть: $$ m_i=p_icdot N=frac16cdot 72=12 $$ по 12 раз.
Строим расчетную таблицу:
| (x_i) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| (f_i) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| (m_i) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| (f_i-m_i) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Значение теста: $$ X_e^2=12,167 $$ Для уровня значимости α=0,05, k=6 и r=0 находим критическое значение:
Значит, с вероятностью 95% кубик фальшивый.
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
Проверялась гипотеза (H_0) — стрельба случайна.
Если стрельба случайна, то попадание на участок должно иметь распределение, подчиняющееся «закону редких событий» — закону Пуассона с плотностью вероятности: $$ p(k)=frac{lambda^k}{k!}e^{-lambda} $$ где (k) — число попаданий. Чтобы получить значение (lambda), нужно посчитать математическое ожидание данного распределения.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Тогда теоретические частоты будут равны: $$ m_i=Ncdot p(k) $$ Получаем:
| (x_i) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| (p_i) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) (результат) | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: (X_e^2=36,84)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для (X_{кр}^2=X^2(alpha,k-2)).
Для уровня значимости α=0,05 и k=8, r=1 находим:
(X_{кр}^2approx 12,59)
Получается, что: (X_e^2gt X_{кр}^2)
Гипотеза (H_0) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x={4;5;6;7} с редким числом попаданий:
| Число попаданий, (x_i) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, (f_i) | 229 | 211 | 93 | 35 | 8 |
Проверялась гипотеза (H_0) — стрельба случайна.
Для последней объединенной варианты находим среднюю взвешенную: $$ x_5=frac{4cdot 7+5cdot 0+6cdot 0+7cdot 1}{7+1}=4,375 $$ Найдем оценку λ.
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (x_if_i) | 0 | 211 | 186 | 105 | 35 | 537 |
$$ lambdaapprox M(x)=frac{sum x_if_i}{N}=frac{537}{576}approx 0,932 $$ Оценка не изменилась, что указывает на правильное определение средней для (x_5).
Строим расчетную таблицу для подсчета статистики:
| (x_i) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| (f_i) | 229 | 211 | 93 | 35 | 8 | 576 |
| (p_i) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| (m_i) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| (f_i-m_i) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| (frac{(f_i-m_i)^2}{m_i}) | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: (X_e^2=1,12)
Критическое значение статистики ищем в виде (X_{кр}^2=X^2(alpha,k-2)), где α=0,05 и k=5, r=1
(X_{кр}^2approx 7,81)
Получается, что: (X_e^2lt X_{кр}^2)
Гипотеза (H_0) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики (X_e^2) в Примере 2, основной вклад внесло слагаемое для (x_i=7). Оно равно 34,34 и поэтому сумма (X_e^2=36,84) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты (x_i=4,375) слагаемое статистики равно 0,16 и сумма (X_e^2=1,12) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.