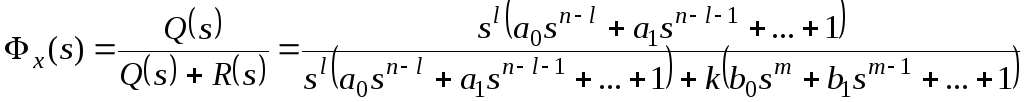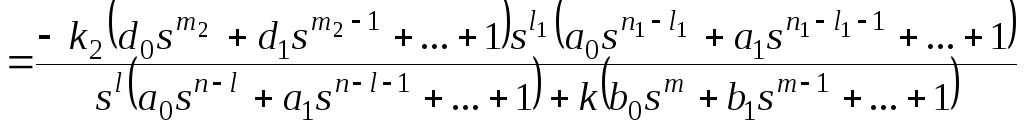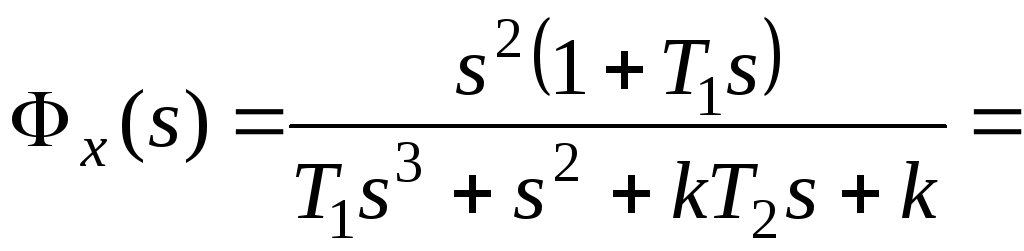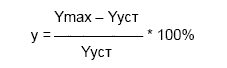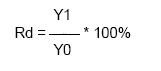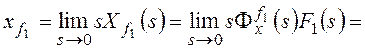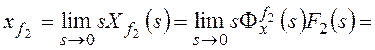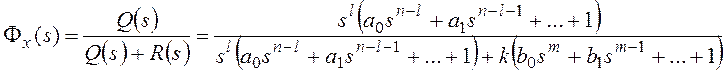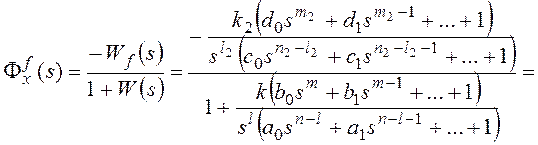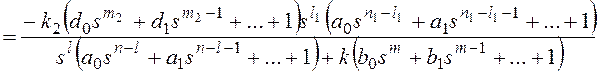Лекция 17.
Расчет
установившейся ошибки в системах
управления. Структурные признаки
астатизма. Коэффициенты ошибок
Установившейся
(статической) ошибкой называют постоянное
значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании
переходного процесса:
,
рисунок 116.
Очевидно,
установившаяся ошибка зависит от законов
изменения и численных характеристик
входных сигналов системы. Поэтому при
ее определении принято рассматривать
так называемые типовые входные сигналы,
законы изменения которых составляют
степенной ряд относительно времени.
Например, для задающего воздействия:
,
,
и так далее.
При наличии
нескольких воздействий на линейную
систему для определения xуст
используется принцип суперпозиции –
реакция линейной системы на совокупность
входных сигналов совпадает с алгебраической
суммой ее реакций на каждый из сигналов
в отдельности:
,
где каждое слагаемое,
или составляющая сигнала ошибки,
определяется
для i-го
входного сигнала при условии, что
остальные тождественно равны нулю.
Такой подход полностью соответствует
определению передаточной функции и
позволяет выполнять расчет установившейся
ошибки на основе структурной схемы
системы.
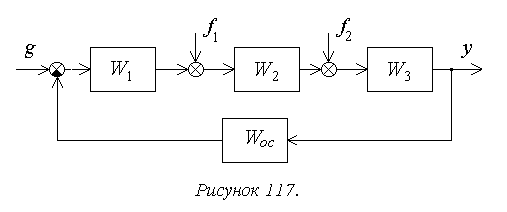
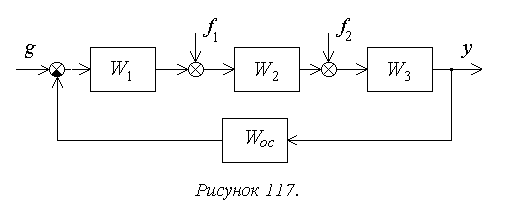
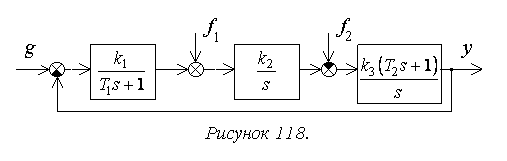
Рассмотрим порядок
расчета установившейся ошибки на
следующем достаточно общем примере
(рисунок 117).
В соответствии с
принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде
суммы трех составляющих
.
Изображение по
Лапласу ошибки от задающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке
при известном изображении задающего
воздействия G(s):
,
где (s)
– основная передаточная функция
замкнутой системы. Для структурной
схемы на рисунке 117
,
где
— передаточная функция разомкнутой
системы, или прямой цепи системы, для
рассматриваемого примера.
Непосредственно
для расчета установившегося значения
ошибки от задающего воздействия
используют теорему о конечном значении
для преобразования Лапласа:
В результате:
.
Изображение по
Лапласу ошибки от возмущающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке от возмущения
при известном изображении возмущающего
воздействия F(s):
,
где f(s)
–передаточная функция замкнутой системы
по возмущающему воздействию,
;
Wf(s)
– передаточная функция разомкнутой
системы по возмущению (передаточная
функция участка прямой цепи системы от
точки приложения возмущающего воздействия
до выхода системы).
Для структурной
схемы на рисунке 8 необходимо учитывать
два возмущающих воздействия, приложенные
в различные точки системы.
Для f1:
,
,

Для f2:
,
,

Расчет упрощается
для системы с единичной отрицательной
обратной связью (рисунок 118):


где k=k1k2k3
– коэффициент передачи разомкнутой
системы.
Найдем установившуюся
ошибку для некоторых типовых вариантов
задающего воздействия.
При
получим:

При
получим:

При
получим:
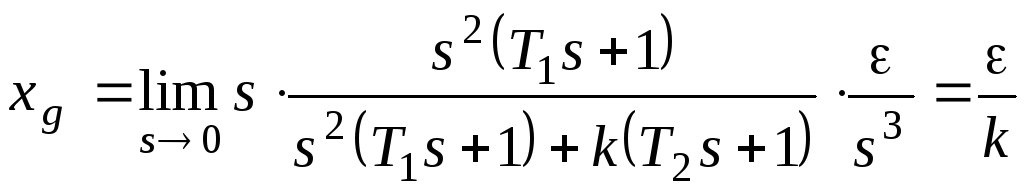
Если установившаяся
ошибка тождественно равна нулю при
каком-либо типовом варианте входного
сигнала, независимо от его численных
характеристик, систему называют
астатической по рассматриваемому
входному сигналу.
Количество типовых
вариантов входного сигнала – членов
степенного ряда, при которых установившаяся
ошибка тождественно равна нулю, определяет
порядок астатизма.
Рассматриваемая
система обладает свойством астатизма
второго порядка по задающему воздействию.
Рассмотрим
установившуюся ошибку от возмущения
f1:
,

где
– коэффициент передачи разомкнутой
системы по возмущению f1.
При
получим:

При
получим:

При
получим тот же результат.
Отметим, что по
возмущению f1
рассматриваемая система не является
астатической. Кроме того, она не в
состоянии отработать два последних
варианта входного сигнала.
Рассмотрим
установившуюся ошибку от возмущения
f2:
,
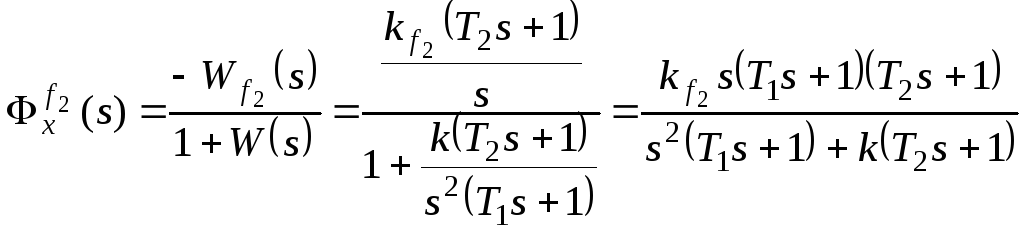
где
– коэффициент передачи разомкнутой
системы по возмущению f2.
При
получим:

При
получим:

При
получим:

По возмущению f2
рассматриваемая система имеет астатизм
первого порядка. Она не в состоянии
отработать возмущающее воздействие,
изменяющееся во времени с постоянным
ускорением.
Подведем некоторые
итоги:
1. Наличие и глубина
свойства астатизма зависят от точки
приложения входного сигнала.
2. Постоянные
времени звеньев системы не влияют на
ее точность.
3. Увеличение
значения коэффициента передачи
разомкнутой системы приводит к снижению
величины установившейся ошибки.
Для систем с
единичной отрицательной обратной связью
существуют достаточно простые структурные
признаки астатизма.
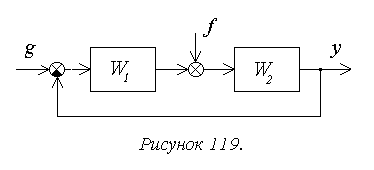
Рассмотрим
структуру, показанную на рисунке 119.
В общем случае
передаточная функция разомкнутой
системы может быть представлена в
следующей форме:

где l0.
Тогда получим:
и для общего вида
задающего воздействия
,
которому соответствует изображение
,

Результат нахождения
этого предела зависит от соотношения
показателей степени:
— при l>v
установившаяся ошибка равна нулю
независимо от остальных параметров, то
есть имеет место астатизм;
— при l=v
получаем константу;
— при l<v
установившаяся ошибка стремится к
бесконечности, то есть система не в
состоянии отработать входной сигнал.
Учитывая, что
минимальное значение v
нулевое, получаем условие астатизма по
задающему воздействию: l>0.
Таким образом,
структурный признак астатизма по
задающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
разомкнутой системы, или интегрирующих
звеньев в прямой цепи системы.
Нетрудно также
убедиться, что положительное значение
l
совпадает с порядком астатизма.
Для получения
признака астатизма по возмущающему
воздействию представим передаточные
функции на рисунке 10 в форме:


где l1+l2=l,
k1k2=k,
m1+m2=m,
n1+n2=n,
причем
и
.
Тогда получим:
и для общего вида
возмущающего воздействия
,
которому соответствует изображение
,

Все вышеприведенные
выводы можно повторить для показателя
степени l1.
Таким образом,
структурный признак астатизма по
возмущающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
участка системы до точки приложения
воздействия, или интегрирующих звеньев
на том же участке.
Более общий подход
к оценке точности линейных систем
управления основан на получении и
использовании коэффициентов ошибок.
Рассмотрим его на примере анализа
реакции системы на задающее воздействие.
Если рассматривать
произвольный закон изменения задающего
воздействия g(t),
то эта функция времени может быть
разложена в степенной ряд относительно
аргумента t.
Члены степенного ряда, как известно,
находятся через производные
,
,
…,
,
…
В общем случае ряд
бесконечен. Поэтому с практической
точки зрения рассматривать такое
представление сигнала целесообразно
только при достаточно плавном его
изменении, когда можно ограничиться
конечным числом членов ряда, имея в
виду, что при n
большем некоторого m
можно принять
,
n>m.
Для задачи оценки
установившейся ошибки при
с формулированное допущение вполне
корректно, так как в противном случае
эта задача не имеет смысла.
Коэффициенты
ошибки получают разложением передаточной
функции замкнутой системы по ошибке в
степенной ряд (ряд Тейлора) относительно
аргумента s:
,
где коэффициенты
разложения в общем случае находят как
значения производных в точке s=0:

Передаточные
функции, представляющие собой отношения
полиномов, при достаточно высоком
порядке системы могут оказаться слишком
сложными для дифференцирования. Поэтому
на практике коэффициенты их разложения
в ряд чаще находят путем деления полиномов
– числителя на знаменатель.
С учетом разложения
передаточной функции в ряд можно записать
изображение по Лапласу сигнала ошибки
в следующей форме:
.
Отметим, что с
учетом сформулированного выше допущения
такое представление сигнала ошибки
соответствует
или
.
Перейдя к оригиналу
с учетом теоремы дифференцирования
получим:
.
Вернемся к
рассмотренному выше примеру и предположим,
что задающее воздействие изменяется
по произвольному закону, но при достаточно
больших значениях времени этот закон
аппроксимируется выражением
.
Найдем коэффициенты
разложения передаточной функции по
ошибке
в степенной ряд.
Здесь сразу можно
отметить, что номер первого ненулевого
члена ряда определяется низшей степенью
аргумента s
в числителе дроби, то есть первые два
коэффициента c0
и c1
здесь получаем тождественно равными
нулю.
Далее получим:
В результате
получаем
,
,
,
и так далее.
Найдем производные
задающего воздействия:
,
,
.
Ясно, что для
определения установившейся ошибки
достаточно первых трех коэффициентов:
.
В заключение
отметим, что порядок астатизма системы
по какому-либо входному сигналу совпадает
с количеством нулевых коэффициентов
ошибки, получаемых в разложении в ряд
передаточной функции по ошибке от
данного входного сигнала.
Соседние файлы в папке Конспект ТАУ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Установившаяся ошибка
Система с обратной связью предоставляет инженеру возможность влиять на вид переходной характеристики. Кроме того, как мы уже видели, такая система позволяет значительно уменьшить ее чувствительность к изменению параметров и ослабить влияние возмущений. Однако имеет также смысл исследовать и сравнить установившуюся ошибку в разомкнутой и в замкнутой системах. Установившаяся ошибка — это ошибка, остающаяся после окончания переходного процесса, вызванного внешним воздействием.
+ ~ я»
-R(s) —— *~С>——- *
-Y(s)
G(s)
H(s)
Рис. 4.18. Разомкнутая система управления
Рис. 4.19. Замкнутая система управления В разомкнутой системе, изображенной на рис. 4.18, ошибка равна
ад=ад — ад=[і — стт. (4.48)
В замкнутой системе на рис. 4.19 при H(s) = 1 согласно (4.3)* ошибка равна
Для вычисления установившейся ошибки используется теорема о конечном значении:
lim e(t)= lims£(s). (4.50)
_ 1 —КО А—>0
Приняв для сравнения входной сигнал в виде единичной ступенчатой функции, в разомкнутой системе мы получим:
е0 (о°) = limaf 1 — G(s)] ■ — = lim[l — G(s)] = 1 — G(0).
■v-»0 s -‘->0
В замкнутой системе при H(s) = 1 имеем:
Случай неединичной обратной связи рассматривается в разд. 5.8.
4.5. Установившаяся ошибка
Значение G(s) при 5 = 0 часто называют коэффициентом усиления на нулевой частоте (по постоянному току), и это значение обычно больше единицы. Следовательно, в разомкнутой системе мы получим большую установившуюся ошибку, а в замкнутой системе она будет незначительной.
Анализ выражения (4.51) показывает, что в разомкнутой системе установившаяся ошибка может равняться нулю, если обеспечить выполнение условия 6′(0) = 1. Тогда возникает естественный вопрос: а в чем же заключается преимущество замкнутой системы? Чтобы ответить на этот вопрос, нам придется вернуться к понятию чувствительности. Действительно, в разомкнутой системе можно так подобрать ее параметры, чтобы выполнялось условие С(0) = 1. Однако в процессе эксплуатации системы ее параметры наверняка будут изменяться под влиянием внешних факторов, что приведет к отклонению коэффициента усиления G(0) от единицы. Значит, появится отличная от нуля установившаяся ошибка, устранить которую можно только перенастроив систему. Напротив, в замкнутой системе происходит непрерывное измерение ошибки и вырабатывается сигнал, приводящий к уменьшению ее установившегося значения. Таким образом, мы приходим к выводу, что побудительным мотивом к введению отрицательной обратной связи является снижение чувствительности системы к дрейфу ее параметров, неточности их настройки и внешним возмущающим факторам. Пример оригинальной системы с обратной связью приведен на рис. 4.20.
Рис. 4.20
Грип-11 — это искусственная рука в виде протеза, управляемая с помощью троса. Она может быть использована для переключения скоростей автомобиля, забивания гвоздей, нарезания помидоров и выполнения других несложных задач, требующих двух рук. Ее действие основано на тяговом усилии троса, а сила захвата изменяется в диапазоне от 0 до 110 фунтов. Рука воспроизводит движение большого и указательного пальцев и осуществляет захват, когда на трос воздействуют спинные мышцы человека. Обратная связь осуществляется человеком визуально, но он не испытывает нормального ощущения прикосновения, присущего большинству людей при осторожных действиях с предметом
Способность замкнутой системы уменьшать установившуюся ошибку, вызванную изменениями параметров и неточностью их настройки, мы проиллюстрируем следующим примером. Рассмотрим систему, в которой объект управления имеет передаточную функцию
G(s) = —. (4.53)
TS+ 1
Такая передаточная функция характерна для тепловых объектов, регуляторов напряжения или емкостей с жидкостью при регулировании уровня. При задании входной переменной в
виде единичной ступенчатой функции мы имеем R(s) = 1/5. Тогда в соответствии с (4.51) в разомкнутой системе установившаяся ошибка будет равна
е0(со) = 1 — 6X0) = 1 — К (4.54)
при согласованных единицах измерения R(s) и К. В замкнутой системе (рис. 4.19) мы имеем:
Ec(s) = R(s)-ns)R(s), где T(s) = (7(,v)/[ 1 + GH{s). Установившаяся ошибка равна
ес(оэ)= lim 41 — 7X5)] — = 1 — 7X0).
.v->0 s
Если H(s) = 1/(Т[Л + 1), то Я(0) =1 и G(0) = К. Следовательно,
ес(со) = 1 J! Le_L. (4.55)
1+ К 1+ К
В разомкнутой системе можно было бы, к примеру, задать К= 1, тогда установившаяся ошибка будет равна нулю. В замкнутой системе можно задать большое значение К, например, К = 100. Тогда установившаяся ошибка в ней составит ес(со) = 1/101.
Если теперь в силу каких-то факторов начальное значение К изменится на 10%, т. е. АК/К = 0,1, то в разомкнутой системе появится абсолютное приращение установившейся ошибки Де0(со) = 0,1, а относительное приращение составит
Ае0(со) 0,1
(4.56)
IKOI 1
т. е. также 10%. При таком же приращении АК/К = 0,1 в замкнутой системе установившаяся ошибка составит ес(со) =1/91 (при отрицательном приращении К). Следовательно, абсолютное изменение установившейся ошибки будет равно
Аес (оо ) = ——(4.57) 91 101
а относительное приращение составит
Аес (оо)
= 0,0011, (4.58)
IKOI
или 0,11%. Как говорится, результат в комментариях не нуждается.
Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …
Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …
К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.
Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).
Классификация показателей качества состоит из нескольких групп:
- прямые — определяемые непосредственно по переходной характеристике процесса,
- корневые — определяемые по корням характеристического полинома,
- частотные — по частотным характеристикам,
- интегральные — получаемые путем интегрирования функций.
Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:
- Установившееся значение выходной величины Yуст,
- Степень затухания ?,
- Время достижения первого максимума tmax,
- Время регулирования tp,
- Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
- Перерегулирование у,
- Динамический коэффициент регулирования Rd,
- Показатель колебательности М.
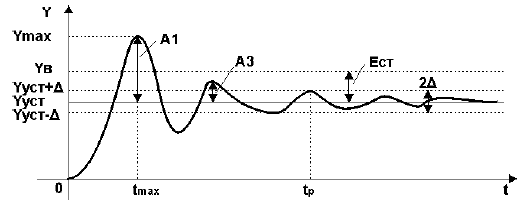
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.
Рисунок 1 — Определение показателей качества по переходной характеристике
Установившееся значение выходной величины Yуст
Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.
Степень затухания ?
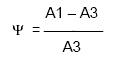
Степень затухания ? определяется по формуле:
где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.
Время достижения первого максимума tmax
Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.
Время регулирования tp
Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.
В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.
Ошибка регулирования Ест
Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.
Перерегулирование у
Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:
где значения величин Ymax и Yуст определяются согласно рис.1.
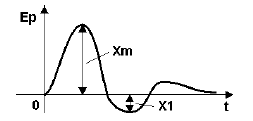
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:
где значения величин Xm и X1 определяются согласно рис. 2.
Рисунок 2 — График переходного процесса при отработке возмущения
Динамический коэффициент регулирования Rd
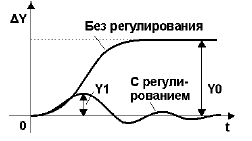
Динамический коэффициент регулирования Rd определяется из формулы:
где значения величин Y1 и Y0 определяются согласно рис. 3.
Рисунок 3 — К понятию динамического коэффициента регулирования
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.
Показатель колебательности М
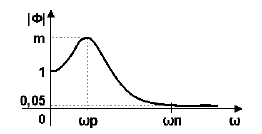
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.
Рисунок 4 — График модуля частотной передаточной функции замкнутой системы
Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.
В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.
Демьян Бондарь
Эксперт по предмету «Автоматизация технологических процессов»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Качество систем управления в переходном режиме
Определение 1
Качество системы управления – это комплексная оценка работы системы управления в зависимости от ее назначения.
Самыми распространенными показателями качества системы в переходном процессе являются:
- Интегральные критерии.
- Статическая ошибка регулирования.
- Степень колебательности.
- Динамическая ошибка регулирования.
- Время регулирования.
- Степень устойчивости.
Статическая ошибка регулирования представляет собой разность между установившемся значением регулируемого параметра и его заданным значением. Динамическая ошибка регулирования равняется наибольшему отклонению регулируемой величины от ее установившегося значения. Время регулирования определяется, как время, за которое разность между текущим значением регулируемого параметра и его заданным значением становится меньше допустимого отклонения. Степень устойчивости автоматической системы управления характеризует запас устойчивости в плоскости корней характеристического уравнения и равняется расстоянию до оси ближайшего корня. Данный критерий характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса.

Тренируй мозг с удовольствием
Развивай память, внимание и мышление c помощью онлайн-тренажеров
Выбрать программу
Степень колебательности равняется минимальному модулю отношения действительной и мнимой частей корня, то есть:
Рисунок 1.
Если в плоскости корней характеристического уравнения устойчивой системы провести из начала координат два луча (как показано на рисунке ниже) таким образом, чтобы одна пара корней находилась на данных лучах, а остальные лежали слева от них, то тангенс угла, который заключен между лучами и мнимой осью, равный отношению действительной и мнимой частей корней, лежащих на лучах АОВ, является степенью колебательности системы.
Рисунок 2. График. Автор24 — интернет-биржа студенческих работ
«Качество систем управления в установившемся и переходном режимах» 👇
Степень затухания является количественной оценкой интенсивности затухания колебательного процесса:
Рисунок 3.
Между степенью затухания и степенью колебательности существует однозначная зависимость:
Рисунок 4.
Степень затухания может изменяться в пределах от 0,1 до 1, а степень колебательности от 0 до бесконечности. В отличии от прямых показателей интегральные критерии дают обобщенную оценку качества системы, они делятся на:
- линейный интегральный критерий,
- модульные интегральные критерии,
- квадратичный интегральный критерий,
- обобщенные интегральные критерии.
Качество системы управления в установившемся режиме
Определение 2
Установившийся режим – это режим, параметры которого не изменяются во времени или меняются в соответствии с периодическим законом.
Рассмотрим схему одноконтурной системы, которая представлена на рисунке ниже.
Рисунок 5. Схема одноконтурной системы. Автор24 — интернет-биржа студенческих работ
Рассматриваемая схема может быть упрощена следующим образом.
Рисунок 6. Упрощенная схема. Автор24 — интернет-биржа студенческих работ
Для того, чтобы согласовать сигналы u3(t) и uoc(t) надо подобрать одинаковые передаточные функции Wбз(р) и Wби(р), поэтому должно выполняться следующее равенство:
$Wбз(р) = Wби(р)$
С учетом представленного выше равенства схему рассматриваемой системы можно представить в следующем виде.
Рисунок 7. Схема системы. Автор24 — интернет-биржа студенческих работ
В этом случае ошибка регулирования входит в формулу для определения сигнала рассогласования:
$ΔU(р) = Δ(р) WБИ(р)$
Ошибка δ(t) зависит от величины параметров, задающего и возмущающего воздействия, таким образом ее значение может быть выражено как сумма ошибок данных воздействий:
$δ(t) =δy(t) + δf(t)$
Передаточные функции выражаются следующим образом:
Рисунок 8.
Рисунок 9.
Передаточная функция разомкнутого контура выражается следующим образом
$Wрк (р) =WБИ(р) WБУ (р) WОУ(р)$
Исходя из представленных выше выражений величина изображения ошибки определяется следующим образом:
Рисунок 10.
Существую типовые законы оценки установившегося режима, установленные условиями:
- Возмущающее и задающее воздействия не изменяются во времени и постоянны, то есть — yз(t), f (t) = const.
- Изменения в системе происходят с постоянной скоростью, то есть — yз (t) = a t и f (t) = const.
- Изменения в системе происходят с постоянным ускорением, то есть — y(t) = b t2/2и f (t) = const.
- Изменения в системе происходят по гармоническому закону, то есть — yз (t) = y0 sin(ω t) и f (t) = const.
Определение 3
Статическая ошибка – это значение ошибки регулирования при постоянной величине входного воздействия.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Установившаяся ошибка
Cтраница 1
Установившаяся ошибка в данной системе при ступенчатом входном сигнале равна нулю, ( а) Изобразите графически частотные характеристики данной системы и обратите внимание на наличие двух всплесков на амплитудной характеристике, ( б) Предскажите вид переходной характеристики системы с учетом того, что она имеет 4 полюса и не может быть аппроксимирована моделью второго порядка, предполагающей наличие доминирующих полюсов, ( в) Получите график переходной характеристики.
[1]
Установившаяся ошибка характеризует точность регулирования в установившемся режиме.
[3]
Установившаяся ошибка при этом оказывается равной нулю, и система действует подобно линейной системе с однократным астатизмом в контуре ошибки. Фактически регулятор получается двухконтурным, причем пропускание низких частот регулируется параметрическим управляющим контуром, а высоких — релейным контуром.
[5]
Установившаяся ошибка ( в силу рабочего движения) при таком законе управления, очевидно, равна нулю.
[6]
Установившаяся ошибка по положению уменьшается при увеличении статического коэффициента усиления разомкнутой цепи.
[7]
Установившаяся ошибка по положению ликвидируется введением интегратора2 в разомкнутую цепь.
[8]
Установившаяся ошибка при постоянных внешних воздействиях называется статической.
[9]
Установившаяся ошибка характеризует точность регулирования в установившемся режиме.
[10]
Установившаяся ошибка при постоянных внешних воздействиях называется статической. Поэтому статические и астатические системы можно определить следующим образом: система называется статической, если статическая ошибка отлична от нуля, и астатической, если она равна нулю.
[11]
Установившаяся ошибка является ошибкой, которая остается после окончания переходного процесса.
[12]
Установившаяся ошибка равняется сумме статической, ошибки, вызванной действием Мот и скоростной ошибки, обусловленной заданной скоростью изменения входного сигнала.
[13]
Установившаяся ошибка является ошибкой, которая остается после окончания переходного процесса.
[14]
Страницы:
1
2
3
4
-
Виды ошибок регулирования и методы их снижения.
Прямые показатели качества подразделяются
на показатели качества динамического
и установившегося режимов.
Показателями качества динамических
режимов определяются из графика
переходного процесса и основными из
них являются (рис.1.42):
—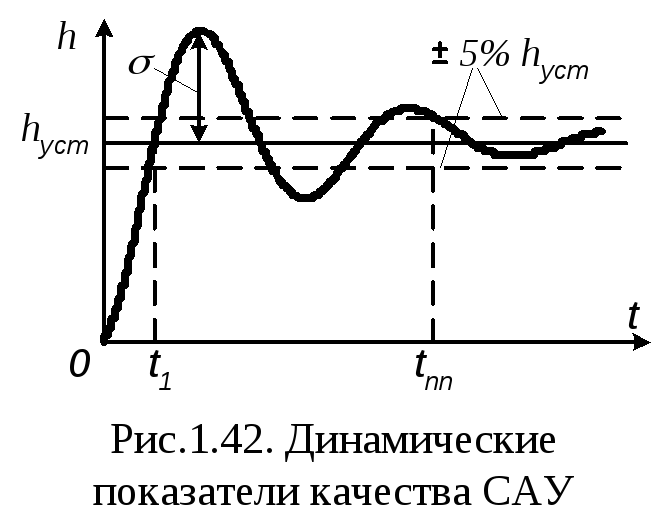
равный максимуму отклонения значения
переходного процесса относительно
установившегося значения процессаhycm;
— время первой установки t1,
определяемое моментом первого пересечения
графиком переходного процесса
установившегося значенияhycm;
— время переходного процесса tПП,
определяемое момент окончательного
входа графика переходного процесса в
зону допуска, равную±5%от
установившегося значения процессаhycm.
Для всех названных динамических
показателей качества невозможно в общем
случае получить формулы для их расчета.
Это является существенным препятствием
для решения задач анализа и синтеза
САУ.
Показателями качества установившихся
режимов являются ошибки регулирования,
равные абсолютной величине разности
между заданным и фактическим значениями
сигналов САУ и которые в зависимости
от вида входного сигнала САУ подразделяются
на статические (εСТ) и
скоростные ошибки (εСК) и
ошибки (εm)
при отработке гармонического входного
сигнала.
Д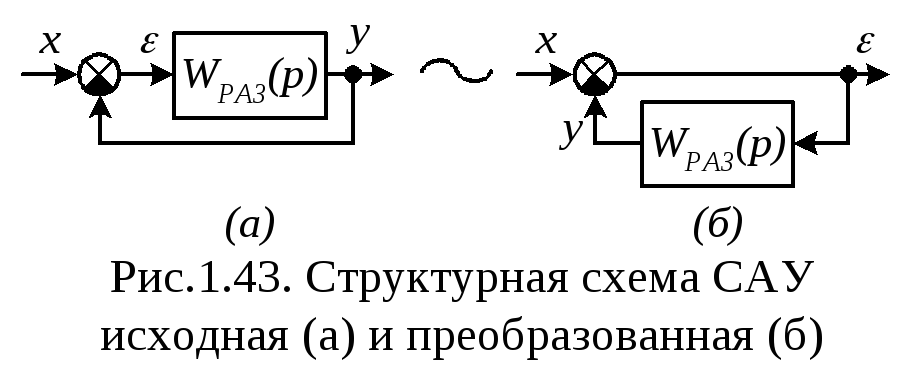
всех названных ошибок регулирования
можно в общем случае получить формулы
их расчета.
Из структурной схемы замкнутой САУ
(рис.1.43) следуют выражения передаточной
функции САУ Wε(p)по ошибке и изображенияε(р)ошибки
регулирования:
Расчет ошибки εmотработки гармонического входного
сигналаx=Xmsinωt
производится по формуле
где
— модуль комплексного числа
.
Статическая (εСТ) и
скоростная (εСК) ошибки
равны установившимся значениям оригиналаи
,
или в общем виде, по формуле.
Значениевычисляют через изображениеε(р)
по доказываемой в теории операционного
исчисления формуле предельного перехода,
(1.54)
Выражение передаточной функции
разомкнутой САУ в общем случае может
быть приведено к виду:
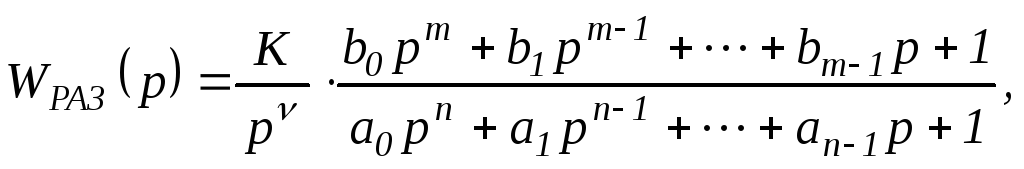
где К– общий коэффициент усиления
разомкнутой САУ:
ν— порядок астатизма САУ, причемνявляется целым неотрицательным
числом.
Для удобства вычислений по формуле
(1.54) подставим в нее выражение WРАЗ(р)из (1.55) и выполним предельный переход:
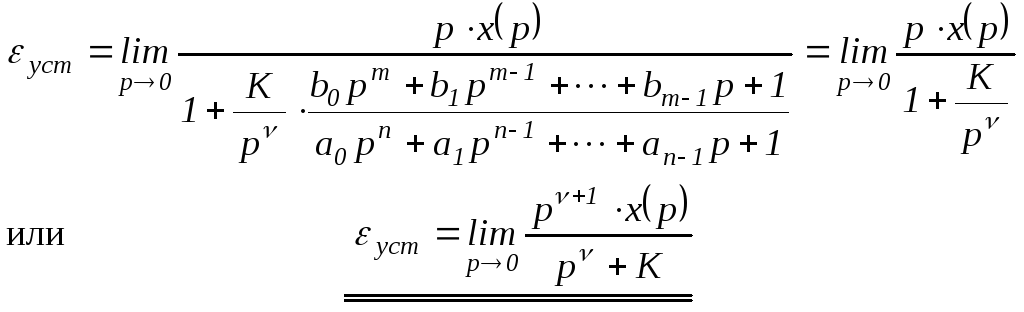
Статическая ошибка регулирования εСТрассчитывается при постоянном входном
сигналеx(t)=X=const,
а скоростнаяεСК— при
входном сигналеx=Vt,
изменяющемуся во времени с постоянной
скоростьюV=const.
Далее расчеты статической (εСТ)
и скоростной (εСК) ошибок
выполним раздельно.
Расчеты статической ошибки εСт регулирования
Входной сигнал x(t)=X=constи изображением его является.
В соответствии с (1.56) статическую ошибкуεСТследует вычислять по
формуле
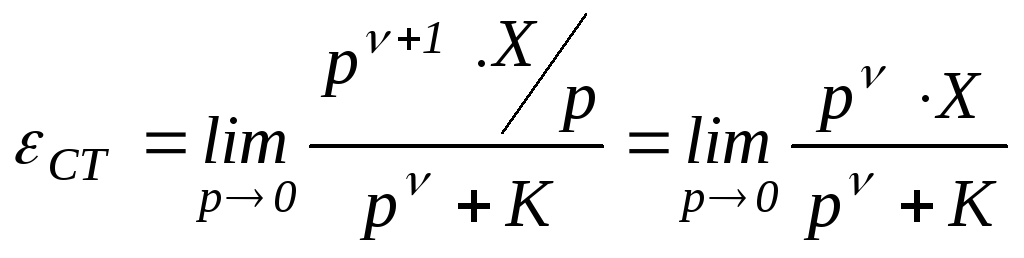
1). Пусть в (1.57) значение порядка νастатизма САУ равно нулю:ν=0. Такая
САУ называется статической. Тогда
статическая ошибкаεСТбудет равна
В статической САУ имеется статическая
ошибка εСТ, которую можно
только уменьшить путем увеличения
общего коэффициента усиленияКразомкнутой САУ, но обратить в ноль ее
нельзя.
2). Пусть в (1.57) значение порядка νастатизма САУ равно 1:ν=1. Такая САУ
называется астатической 1-го порядка.
Тогда статическая ошибкаεСТбудет равна
В астатической САУ 1-го порядка статическая
ошибка εСТравна нулю,
т.е САУ является абсолютно точной. Можно
проверить, что при астатизме САУ выше1, статическая ошибка регулирования
всегда будет нулевой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: , рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
,
,

далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
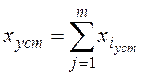
каждое слагаемое, или составляющая сигнала ошибки, определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих .
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
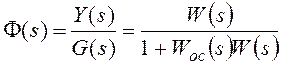
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
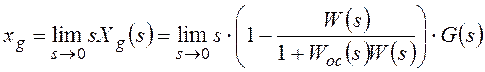
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
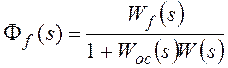
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
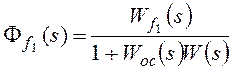
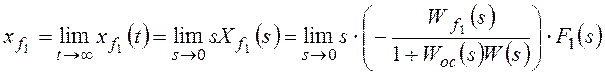
Для f2:
,
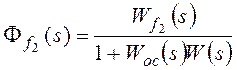
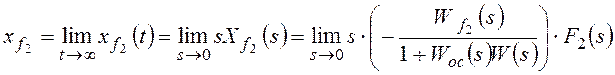
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
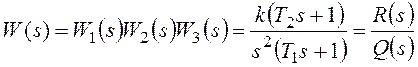
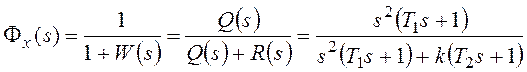
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
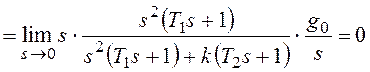
При получим:
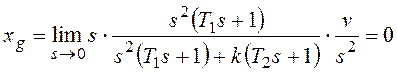
При 
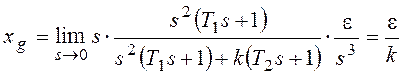
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
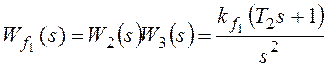
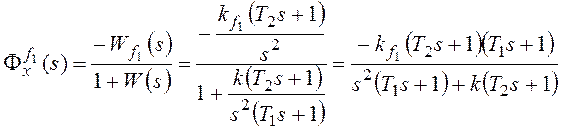
–
коэффициент передачи разомкнутой системы по возмущению f1.
При получим:
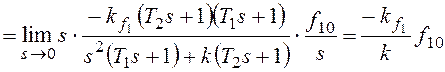
При получим:
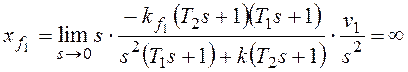
При 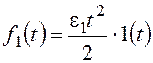
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
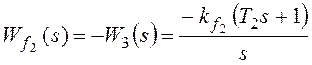
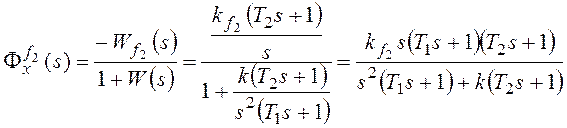
–
коэффициент передачи разомкнутой системы по возмущению f2.
При получим:
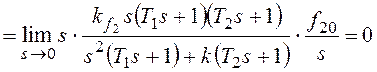
При получим:
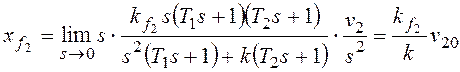
При 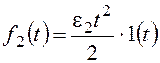
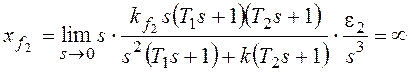
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
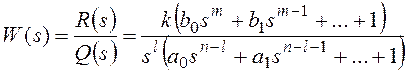
Тогда получим:
и для общего вида задающего воздействия 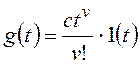
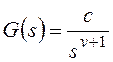
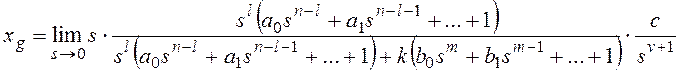
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
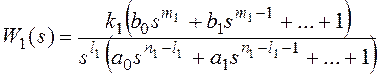
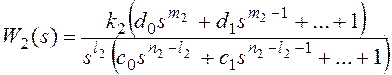
k1k2=k, m1+m2=m,
n1+n2=n,
причем и
.
Тогда получим:
и для общего вида возмущающего воздействия 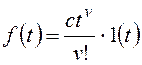
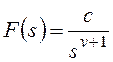
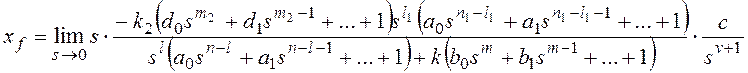
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
К системам автоматического регулирования (САР) предъявляются требования не только
устойчивости процессов регулирования. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных показателей качества процесса управления.
Если исследуемая САР является устойчивой, возникает вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям обьекта управления.На практике качество регулирования определяется визуально по графику переходной характеристики. Однако, имеются точные но более сложные математические методы, дающие конкретные числовые значения (которые не рассматриваются в данной методике).
Классификация показателей качества состоит из нескольких групп:
- прямые — определяемые непосредственно по переходной характеристике процесса,
- корневые — определяемые по корням характеристического полинома,
- частотные — по частотным характеристикам,
- интегральные — получаемые путем интегрирования функций.
Прямыми показателями качества процесса управления, определяемые непосредственно по
переходной характеристике являются:
- Установившееся значение выходной величины Yуст,
- Степень затухания ?,
- Время достижения первого максимума tmax,
- Время регулирования tp,
- Ошибка регулирования Ест (статистическая или среднеквадратическая составляющие),
- Перерегулирование у,
- Динамический коэффициент регулирования Rd,
- Показатель колебательности М.
Например, переходная характеристика, снятая на объекте управления при отработке ступенчатого воздействия, имеет колебательный вид и представлена на рис.1.
Рисунок 1 — Определение показателей качества по переходной характеристике
Установившееся значение выходной величины Yуст
Установившееся значение выходной величины Yуст определяется по переходной характеристике,представленной на рис.1.
Степень затухания ?
Степень затухания ? определяется по формуле:
где А1 и А3 — соответственно 1-я и 3-я амплитуды переходной характеристики рис.1.
Время достижения первого максимума tmax
Время достижения первого максимума tmax определяется по переходной характеристике,представленной на рис.1.
Время регулирования tp
Время регулирования tp определяется согласно рис.1 следующим образом:Находится допустимое отклонение Д, например, задано Д = 5%Yуст и строится «зона» толщиной 2 Д(см. рис.1). Время tp соответствует последней точке пересечения Y(t) с данной границей. То есть время,когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.
Настройки регулятора необходимо выбирать так, чтобы обеспечить минимально возможное значение общего времени регулирования, либо минимальное значение первой полуволны переходного процесса.
В непрерывных системах с типовыми регуляторами это время бывает минимальным при так называемых оптимальных апериодических переходных процессах. Дальнейшего уменьшения времени регулирования до абсолютного минимума можно достичь при использовании специальных оптимальных по быстродействию систем регулирования.
Ошибка регулирования Ест
Статическая ошибка регулирования Ест = Ув — Ууст, где Ув — входная величина (см. рис.1).В некоторых САР наблюдается ошибка, которая не исчезает даже по истечении длительногоинтервала времени — это статическая ошибка регулирования Ест. Данная ошибка не должна превышатьнекоторой наперед заданной величины. У регуляторов с интегральной составляющей ошибки в установившемся состоянии теоретическиравны нулю, но практически незначительные ошибки могут существовать из-за наличия зоннечувствительности в элементах системы.
Перерегулирование у
Величина перерегулирования у зависит от вида отрабатываемого сигнала.При отработке ступенчатого воздействия (по сигналу задания) – см. рис.1 величина перерегулирования у определяется по формуле:
где значения величин Ymax и Yуст определяются согласно рис.1.
При отработке возмущающего воздействия, величина перерегулирования у определяется изсоотношения:
где значения величин Xm и X1 определяются согласно рис. 2.
Рисунок 2 — График переходного процесса при отработке возмущения
Динамический коэффициент регулирования Rd
Динамический коэффициент регулирования Rd определяется из формулы:
где значения величин Y1 и Y0 определяются согласно рис. 3.
Рисунок 3 — К понятию динамического коэффициента регулирования
Величина динамического коэффициента Rd характеризует степень воздействия регулятора напроцесс, т.е. степень понижения динамического отклонения в системе с регулятором и без него.
Показатель колебательности М
Показатель колебательности M характеризует величину максимума модуля частотной передаточной функции замкнутой системы (на частоте резонанса) и, тем самым, характеризует колебательные свойства системы. Показатель колебательности наглядно иллюстрируется на рисунке 4.
Рисунок 4 — График модуля частотной передаточной функции замкнутой системы
Условно считается, что значение М=1,5-1,6 является оптимальным для промышленных САР, т.к. вэтом случае у обеспечивается в районе от 20% до 40%. При увеличении значения M колебательность всистеме возрастает.
В некоторых случаях нормируется полоса пропускания системы щп, которая соответствует уровню усиления в замкнутой системе 0,05. Чем больше полоса пропускания, тем больше быстродействие замкнутой системы. Однако при этом повышается чувствительность системы к шумам в канале измерения и возрастает дисперсия ошибки регулирования.
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Установившаяся ошибка
Система с обратной связью предоставляет инженеру возможность влиять на вид переходной характеристики. Кроме того, как мы уже видели, такая система позволяет значительно уменьшить ее чувствительность к изменению параметров и ослабить влияние возмущений. Однако имеет также смысл исследовать и сравнить установившуюся ошибку в разомкнутой и в замкнутой системах. Установившаяся ошибка — это ошибка, остающаяся после окончания переходного процесса, вызванного внешним воздействием.
+ ~ я»
-R(s) —— *~С>——- *
-Y(s)
G(s)
H(s)
Рис. 4.18. Разомкнутая система управления
Рис. 4.19. Замкнутая система управления В разомкнутой системе, изображенной на рис. 4.18, ошибка равна
ад=ад — ад=[і — стт. (4.48)
В замкнутой системе на рис. 4.19 при H(s) = 1 согласно (4.3)* ошибка равна
Для вычисления установившейся ошибки используется теорема о конечном значении:
lim e(t)= lims£(s). (4.50)
_ 1 —КО А—>0
Приняв для сравнения входной сигнал в виде единичной ступенчатой функции, в разомкнутой системе мы получим:
е0 (о°) = limaf 1 — G(s)] ■ — = lim[l — G(s)] = 1 — G(0).
■v-»0 s -‘->0
В замкнутой системе при H(s) = 1 имеем:
Случай неединичной обратной связи рассматривается в разд. 5.8.
4.5. Установившаяся ошибка
Значение G(s) при 5 = 0 часто называют коэффициентом усиления на нулевой частоте (по постоянному току), и это значение обычно больше единицы. Следовательно, в разомкнутой системе мы получим большую установившуюся ошибку, а в замкнутой системе она будет незначительной.
Анализ выражения (4.51) показывает, что в разомкнутой системе установившаяся ошибка может равняться нулю, если обеспечить выполнение условия 6′(0) = 1. Тогда возникает естественный вопрос: а в чем же заключается преимущество замкнутой системы? Чтобы ответить на этот вопрос, нам придется вернуться к понятию чувствительности. Действительно, в разомкнутой системе можно так подобрать ее параметры, чтобы выполнялось условие С(0) = 1. Однако в процессе эксплуатации системы ее параметры наверняка будут изменяться под влиянием внешних факторов, что приведет к отклонению коэффициента усиления G(0) от единицы. Значит, появится отличная от нуля установившаяся ошибка, устранить которую можно только перенастроив систему. Напротив, в замкнутой системе происходит непрерывное измерение ошибки и вырабатывается сигнал, приводящий к уменьшению ее установившегося значения. Таким образом, мы приходим к выводу, что побудительным мотивом к введению отрицательной обратной связи является снижение чувствительности системы к дрейфу ее параметров, неточности их настройки и внешним возмущающим факторам. Пример оригинальной системы с обратной связью приведен на рис. 4.20.
Рис. 4.20
Грип-11 — это искусственная рука в виде протеза, управляемая с помощью троса. Она может быть использована для переключения скоростей автомобиля, забивания гвоздей, нарезания помидоров и выполнения других несложных задач, требующих двух рук. Ее действие основано на тяговом усилии троса, а сила захвата изменяется в диапазоне от 0 до 110 фунтов. Рука воспроизводит движение большого и указательного пальцев и осуществляет захват, когда на трос воздействуют спинные мышцы человека. Обратная связь осуществляется человеком визуально, но он не испытывает нормального ощущения прикосновения, присущего большинству людей при осторожных действиях с предметом
Способность замкнутой системы уменьшать установившуюся ошибку, вызванную изменениями параметров и неточностью их настройки, мы проиллюстрируем следующим примером. Рассмотрим систему, в которой объект управления имеет передаточную функцию
G(s) = —. (4.53)
TS+ 1
Такая передаточная функция характерна для тепловых объектов, регуляторов напряжения или емкостей с жидкостью при регулировании уровня. При задании входной переменной в
виде единичной ступенчатой функции мы имеем R(s) = 1/5. Тогда в соответствии с (4.51) в разомкнутой системе установившаяся ошибка будет равна
е0(со) = 1 — 6X0) = 1 — К (4.54)
при согласованных единицах измерения R(s) и К. В замкнутой системе (рис. 4.19) мы имеем:
Ec(s) = R(s)-ns)R(s), где T(s) = (7(,v)/[ 1 + GH{s). Установившаяся ошибка равна
ес(оэ)= lim 41 — 7X5)] — = 1 — 7X0).
.v->0 s
Если H(s) = 1/(Т[Л + 1), то Я(0) =1 и G(0) = К. Следовательно,
ес(со) = 1 J! Le_L. (4.55)
1+ К 1+ К
В разомкнутой системе можно было бы, к примеру, задать К= 1, тогда установившаяся ошибка будет равна нулю. В замкнутой системе можно задать большое значение К, например, К = 100. Тогда установившаяся ошибка в ней составит ес(со) = 1/101.
Если теперь в силу каких-то факторов начальное значение К изменится на 10%, т. е. АК/К = 0,1, то в разомкнутой системе появится абсолютное приращение установившейся ошибки Де0(со) = 0,1, а относительное приращение составит
Ае0(со) 0,1
(4.56)
IKOI 1
т. е. также 10%. При таком же приращении АК/К = 0,1 в замкнутой системе установившаяся ошибка составит ес(со) =1/91 (при отрицательном приращении К). Следовательно, абсолютное изменение установившейся ошибки будет равно
Аес (оо ) = ——(4.57) 91 101
а относительное приращение составит
Аес (оо)
= 0,0011, (4.58)
IKOI
или 0,11%. Как говорится, результат в комментариях не нуждается.
Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …
Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …
Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …