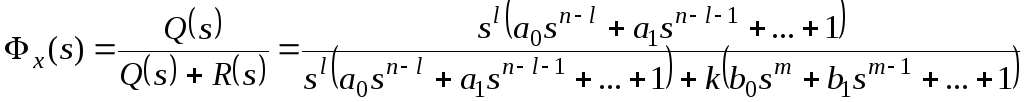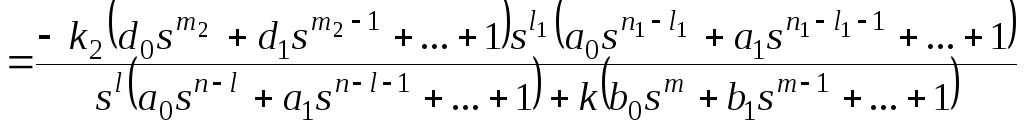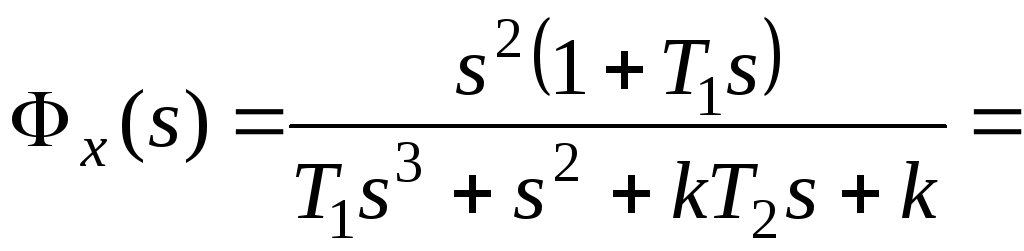Лабораторная
работа №3
Исследование
законов управления САУ
Цель работы:
исследование пропорционального,
интегрального и дифференциального
закона управления и влияния его на
точность САУ.
Общие сведения
При законном
управления понимается алгоритм
управления, в соответствии которым
регулятор форматирует управляющее
воздействие u(t).
Эта зависимость может быть представлена
в виде:
,
где х3
– задающее воздействие;
— ошибка управления;
— возмущающее воздействие.
Существует три
основных закона управления автоматической
системы: пропорциональный, интегральный
и дифференциальный.
1. Пропорциональный
закон управления ( этот закон характерен
для так называемых статических САУ).
Передаточная функция П – регулятора в
этом случае равна:
;
В установившемся
режиме, т.е. при t→∞
(s→0)
;
Пропорциональное
управление используется только для
систем стабилизации (х3
= const)
Статическая ошибка
управления в отсутствие возмущения (f
= 0) определяется так
,
где К1
– коэффициент передачи регулятора;
К0
– коэффициент передачи объекта управления
2. Интегральный
закон управления (система, у которых
используется данный закон называется
астатической САУ).
Передаточная
функция И – регулятора равна
Существует два
режима работы данной САУ в зависимости
от задающего воздействия Хз.
При работе САУ
режиме стабилизации (х3
= const)
статическая ошибка
равна нулю, так как
В случае следующей
системы, когда
,
т.е. входное воздействие меняется по
линейной зависимости, так называемая
скоростная ошибка
равна
,
В этой формуле Д
= К2К0
называется добротностью САУ следящей
САУ по скорости
3.
Пропорционально-интегральное уравнение
Передаточная
функция ПИ – регулятора равна:
4.
Пропорционально-интегрально-дифференциальное
уравнение
Передаточная
функция ПИД – регулятор равна:
2.1.
Моделирование передаточных функций в
MatLab
В
пакете
MatLab
имеется два основных варианта для
исследования
передаточных функций и моделирования
САУ:
-
использование
команд пакета расширения Control
System
Toolbox; -
использование
пакета Simulink.
Control
System
Toolbox
предназначен для работы с LTI-моделями
(Linear
Time
Invariant
Models
– линейные модели с постоянными
параметрами) систем управления.
Команда,
создающая LTI-систему
с одним входом и одним выходом в виде
передаточной функции, имеет следующий
синтаксис:
где
и
–
значения
коэффициентов полиномов В
и
А
в (3).
Например, если
требуется описать ПФ вида
и
узнать значения ее нулей и полюсов, то
нужно ввести в окне команд MatLab
следующие команды:
>>
w=tf([1 1],[2 8 5])
>>
zero(w)
>>
pole(w)
Исследовать
реакцию LTI-модели
на типовые входные воздействия можно
с помощью команд
>>
step(w)
>>
impulse(w)
Можно
получить на одном графике реакцию сразу
нескольких динамических
звеньев, если использовать команды
вида:
>>
step(w,w1,w2)
>>
impulse(w, w1 ,w2)
В
приведенных примерах время моделирования
выбирается автоматически.
При необходимости его можно явно указать
в команде
>>step(w,
w1,
w2,t),
где t
— время
моделирования в секундах.
Рис. 1. Исследование
реакции колебательного звена
На
рис. 1 показан пример моделирования
динамики колебательного
звена при различных параметрах:
>>
w=tf([1],[2 0.3 1]);
>>
w1=tf([1],[2 0.5 1]);
>>
w2=tf([1],[2 0.1 1]);
>>
step(w,w1,w2,50).
В
Simulink
ПФ можно описать с помощью блока Transfer
Fcn
в разделе библиотеки Continuous.
Для подачи типовых воздействий
надо использовать блок Step
из раздела Sources.
Импульсную переходную
характеристику звена можно получить,
подавая на вход импульс
маленькой длительности и большой
амплитуды (приближение
δ-функции) при нулевых начальных условиях.
Порядок выполнения
работы
1
.
С помощью программы MATLAB создать модель
САУ с П-регулятором.
Созданная модель
САУ с П-регулятором с помощью программы
MATLAB
2. Задавая значения
К = 1, 10, 60 построить переходные процессы
и
при единичном ступенчатом воздействии.
3. Определить
значения ошибки управления
расчетным путем и сравнить их с
экспериментальными.
4. Создать модель
САУ с И – регулятором.
5. Задаваясь
значениями К2
= 1, 10, 60 построить переходные процессы
и
.
6. Определить
установившуюся величину статической
ошибки
.
7
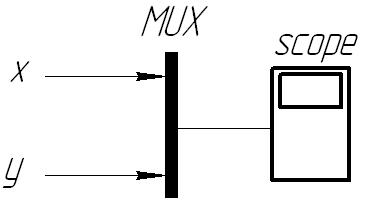
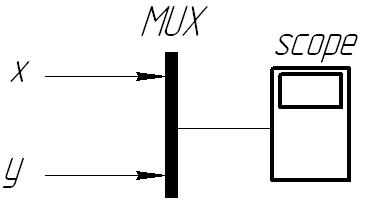
.
Теперь после источника STEP
поместить интегрирующее звено
,
а перед осциллографом scope
поместить
мультиплексор и приняв значение К2
= 10 построить
и
при следующих значениях К = 1, 10;
8. Рассчитать
скоростные ошибки
для этих значений и сравнить их с
экспериментальными.
9. Создать САУ с ПИ
– регулятором.
1
Построить зависимости
,
.
11. Заменить источник
STEP на
источник RAMP
и определить величину скоростной ошибки
,
на вход scope
поставить
мультиплексор MUX.
12. Создать САУ с
ПИД – регулятором.
13. Построить
зависимости
и
14. Заменить источник
STEP
на источник RAMP
и определить скоростную ошибку
,
на вход scope
поставить
мультиплексор MUX.
Содержание отчета
Отчет должен
содержать название, цель работы, расчеты.
графики и выводы по работе.
Контрольные
вопросы
-
Как зависит
статическая ошибка от коэффициента
передачи разомкнутой системы? -
Чему равна
статистическая ошибка в астатической
системе при воздействии – 1(t)? -
Что такое добротность
по скорости? -
В чем преимущество
П-регулятора по сравнению с И-регулятором?
3.
Порядок выполнения работы
1. Получить у
преподавателя вариант выполнения
работы.
2. С
помощью пакета MatLab
построить реакцию каждого типового
звена
с параметрами своего варианта (см.
таблицу 2) на ступенчатое и импульсное
входное воздействие. Определить
влияние коэффициентов, входящих в
описание каждого звена на параметры
переходного процесса.
Таблица 2
|
№ |
Апериод |
Апериодич. |
Интегр звено |
Изодр. |
Реальное диф. звено |
Инерц.-форс Звено |
|||||||
|
K |
T,[с] |
K |
T,[с] |
ξ |
K |
K1 |
K2 |
K |
τ [с] |
K |
T0 [с] |
T |
|
|
1,9,17 |
2 |
0,2 |
1 |
0,2 |
2,0 (0,2) |
2 |
2 |
0,5 |
2 |
0,4 |
2 |
2 |
0,8 |
|
2,10,18 |
3 |
0,3 |
2 |
0,3 |
1,5 (0,15) |
3 |
3 |
1 |
3 |
0,3 |
3 |
3 |
1,2 |
|
3,11,19 |
4 |
0,4 |
3 |
0,4 |
2,5 (0,25) |
4 |
4 |
0,8 |
4 |
0,5 |
4 |
4 |
1,5 |
|
4,12,20 |
5 |
0,5 |
4 |
0,5 |
1,6 (0,3) |
5 |
5 |
2 |
5 |
1,0 |
5 |
5 |
2,0 |
|
5,13,21 |
6 |
0,6 |
5 |
0,6 |
2,8 (0,2) |
6 |
6 |
3 |
6 |
0,8 |
6 |
6 |
2,0 |
|
6,14,22 |
7 |
0,7 |
6 |
0,7 |
2,2 (0,08) |
7 |
7 |
3,5 |
7 |
1,0 |
7 |
7 |
2,0 |
|
7,15,23 |
8 |
0,8 |
7 |
0,8 |
2,1 (0,07) |
8 |
8 |
1 |
8 |
0,9 |
8 |
8 |
3,0 |
|
8,16,24 |
10 |
1,0 |
8 |
1,0 |
3,0 (0,1) |
10 |
10 |
2,0 |
10 |
2,0 |
1,0 |
10 |
4,0 |
Соседние файлы в папке молодой сазаннннн2
- #
- #
- #
a=feedback(sys1,sys2,1)
OL=-1*a
[y,t]=step(OL)
The output of the closed loop system is negated before it is supplied to the step function.
So even though the output of the original system a is going to 0.66 (steady state error 0.33), due to the negation of the output in OL, the calculation returns 1.66 > 1.
What is the reason / logic for doing OL = -1 * a ?
Note
There is one logical error also.
[y,t]=step(OL) % SP is NOT the input given here!
SP=1 % the set point has NO effect on y !
sserror=abs(SP-y(end)) % this calculation is hence invalid
Since the step function is called before setting the setpoint SP, the calculation SP - y(end) is invalid since SP was not the input actually supplied to the system.
The code in the link you provided in the question has the correct order of operations.
SP=5; %input value, if you put 1 then is the same as step(sys)
[y,t]=step(SP*sys); %get the response of the system to a step with amplitude SP
sserror=abs(SP-y(end)) %get the steady state error
Лекция 17.
Расчет
установившейся ошибки в системах
управления. Структурные признаки
астатизма. Коэффициенты ошибок
Установившейся
(статической) ошибкой называют постоянное
значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании
переходного процесса:
,
рисунок 116.
Очевидно,
установившаяся ошибка зависит от законов
изменения и численных характеристик
входных сигналов системы. Поэтому при
ее определении принято рассматривать
так называемые типовые входные сигналы,
законы изменения которых составляют
степенной ряд относительно времени.
Например, для задающего воздействия:
,
,
и так далее.
При наличии
нескольких воздействий на линейную
систему для определения xуст
используется принцип суперпозиции –
реакция линейной системы на совокупность
входных сигналов совпадает с алгебраической
суммой ее реакций на каждый из сигналов
в отдельности:
,
где каждое слагаемое,
или составляющая сигнала ошибки,
определяется
для i-го
входного сигнала при условии, что
остальные тождественно равны нулю.
Такой подход полностью соответствует
определению передаточной функции и
позволяет выполнять расчет установившейся
ошибки на основе структурной схемы
системы.
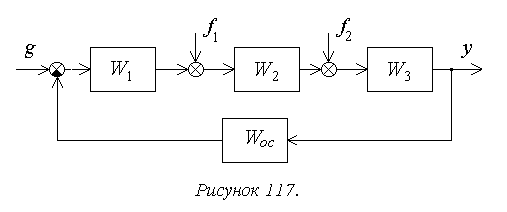
Рассмотрим порядок
расчета установившейся ошибки на
следующем достаточно общем примере
(рисунок 117).
В соответствии с
принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде
суммы трех составляющих
.
Изображение по
Лапласу ошибки от задающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке
при известном изображении задающего
воздействия G(s):
,
где (s)
– основная передаточная функция
замкнутой системы. Для структурной
схемы на рисунке 117
,
где
— передаточная функция разомкнутой
системы, или прямой цепи системы, для
рассматриваемого примера.
Непосредственно
для расчета установившегося значения
ошибки от задающего воздействия
используют теорему о конечном значении
для преобразования Лапласа:
В результате:
.
Изображение по
Лапласу ошибки от возмущающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке от возмущения
при известном изображении возмущающего
воздействия F(s):
,
где f(s)
–передаточная функция замкнутой системы
по возмущающему воздействию,
;
Wf(s)
– передаточная функция разомкнутой
системы по возмущению (передаточная
функция участка прямой цепи системы от
точки приложения возмущающего воздействия
до выхода системы).
Для структурной
схемы на рисунке 8 необходимо учитывать
два возмущающих воздействия, приложенные
в различные точки системы.
Для f1:
,
,

Для f2:
,
,

Расчет упрощается
для системы с единичной отрицательной
обратной связью (рисунок 118):


где k=k1k2k3
– коэффициент передачи разомкнутой
системы.
Найдем установившуюся
ошибку для некоторых типовых вариантов
задающего воздействия.
При
получим:

При
получим:

При
получим:
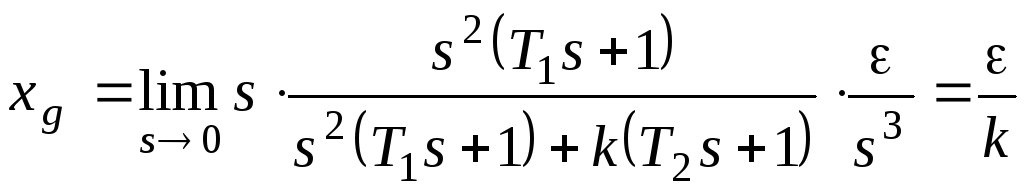
Если установившаяся
ошибка тождественно равна нулю при
каком-либо типовом варианте входного
сигнала, независимо от его численных
характеристик, систему называют
астатической по рассматриваемому
входному сигналу.
Количество типовых
вариантов входного сигнала – членов
степенного ряда, при которых установившаяся
ошибка тождественно равна нулю, определяет
порядок астатизма.
Рассматриваемая
система обладает свойством астатизма
второго порядка по задающему воздействию.
Рассмотрим
установившуюся ошибку от возмущения
f1:
,

где
– коэффициент передачи разомкнутой
системы по возмущению f1.
При
получим:

При
получим:

При
получим тот же результат.
Отметим, что по
возмущению f1
рассматриваемая система не является
астатической. Кроме того, она не в
состоянии отработать два последних
варианта входного сигнала.
Рассмотрим
установившуюся ошибку от возмущения
f2:
,
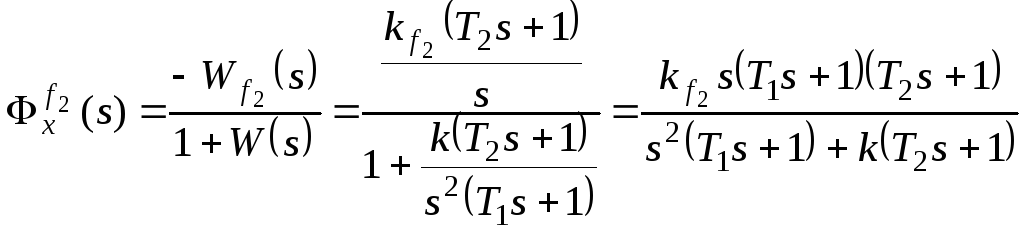
где
– коэффициент передачи разомкнутой
системы по возмущению f2.
При
получим:

При
получим:

При
получим:

По возмущению f2
рассматриваемая система имеет астатизм
первого порядка. Она не в состоянии
отработать возмущающее воздействие,
изменяющееся во времени с постоянным
ускорением.
Подведем некоторые
итоги:
1. Наличие и глубина
свойства астатизма зависят от точки
приложения входного сигнала.
2. Постоянные
времени звеньев системы не влияют на
ее точность.
3. Увеличение
значения коэффициента передачи
разомкнутой системы приводит к снижению
величины установившейся ошибки.
Для систем с
единичной отрицательной обратной связью
существуют достаточно простые структурные
признаки астатизма.
Рассмотрим
структуру, показанную на рисунке 119.
В общем случае
передаточная функция разомкнутой
системы может быть представлена в
следующей форме:

где l0.
Тогда получим:
и для общего вида
задающего воздействия
,
которому соответствует изображение
,

Результат нахождения
этого предела зависит от соотношения
показателей степени:
— при l>v
установившаяся ошибка равна нулю
независимо от остальных параметров, то
есть имеет место астатизм;
— при l=v
получаем константу;
— при l<v
установившаяся ошибка стремится к
бесконечности, то есть система не в
состоянии отработать входной сигнал.
Учитывая, что
минимальное значение v
нулевое, получаем условие астатизма по
задающему воздействию: l>0.
Таким образом,
структурный признак астатизма по
задающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
разомкнутой системы, или интегрирующих
звеньев в прямой цепи системы.
Нетрудно также
убедиться, что положительное значение
l
совпадает с порядком астатизма.
Для получения
признака астатизма по возмущающему
воздействию представим передаточные
функции на рисунке 10 в форме:


где l1+l2=l,
k1k2=k,
m1+m2=m,
n1+n2=n,
причем
и
.
Тогда получим:
и для общего вида
возмущающего воздействия
,
которому соответствует изображение
,

Все вышеприведенные
выводы можно повторить для показателя
степени l1.
Таким образом,
структурный признак астатизма по
возмущающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
участка системы до точки приложения
воздействия, или интегрирующих звеньев
на том же участке.
Более общий подход
к оценке точности линейных систем
управления основан на получении и
использовании коэффициентов ошибок.
Рассмотрим его на примере анализа
реакции системы на задающее воздействие.
Если рассматривать
произвольный закон изменения задающего
воздействия g(t),
то эта функция времени может быть
разложена в степенной ряд относительно
аргумента t.
Члены степенного ряда, как известно,
находятся через производные
,
,
…,
,
…
В общем случае ряд
бесконечен. Поэтому с практической
точки зрения рассматривать такое
представление сигнала целесообразно
только при достаточно плавном его
изменении, когда можно ограничиться
конечным числом членов ряда, имея в
виду, что при n
большем некоторого m
можно принять
,
n>m.
Для задачи оценки
установившейся ошибки при
с формулированное допущение вполне
корректно, так как в противном случае
эта задача не имеет смысла.
Коэффициенты
ошибки получают разложением передаточной
функции замкнутой системы по ошибке в
степенной ряд (ряд Тейлора) относительно
аргумента s:
,
где коэффициенты
разложения в общем случае находят как
значения производных в точке s=0:

Передаточные
функции, представляющие собой отношения
полиномов, при достаточно высоком
порядке системы могут оказаться слишком
сложными для дифференцирования. Поэтому
на практике коэффициенты их разложения
в ряд чаще находят путем деления полиномов
– числителя на знаменатель.
С учетом разложения
передаточной функции в ряд можно записать
изображение по Лапласу сигнала ошибки
в следующей форме:
.
Отметим, что с
учетом сформулированного выше допущения
такое представление сигнала ошибки
соответствует
или
.
Перейдя к оригиналу
с учетом теоремы дифференцирования
получим:
.
Вернемся к
рассмотренному выше примеру и предположим,
что задающее воздействие изменяется
по произвольному закону, но при достаточно
больших значениях времени этот закон
аппроксимируется выражением
.
Найдем коэффициенты
разложения передаточной функции по
ошибке
в степенной ряд.
Здесь сразу можно
отметить, что номер первого ненулевого
члена ряда определяется низшей степенью
аргумента s
в числителе дроби, то есть первые два
коэффициента c0
и c1
здесь получаем тождественно равными
нулю.
Далее получим:
В результате
получаем
,
,
,
и так далее.
Найдем производные
задающего воздействия:
,
,
.
Ясно, что для
определения установившейся ошибки
достаточно первых трех коэффициентов:
.
В заключение
отметим, что порядок астатизма системы
по какому-либо входному сигналу совпадает
с количеством нулевых коэффициентов
ошибки, получаемых в разложении в ряд
передаточной функции по ошибке от
данного входного сигнала.
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5