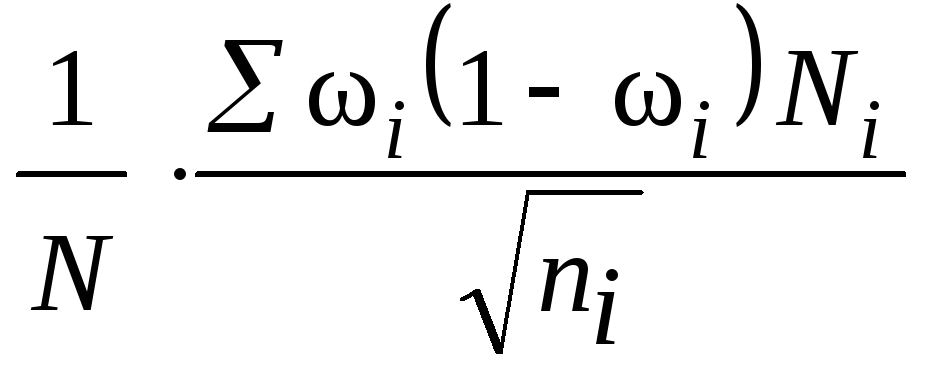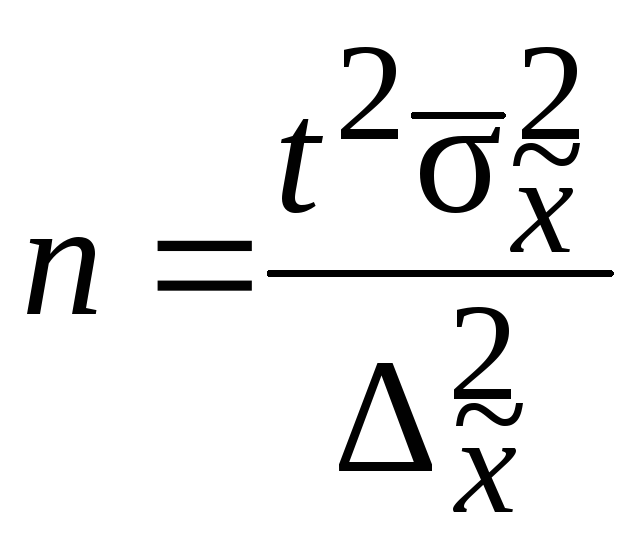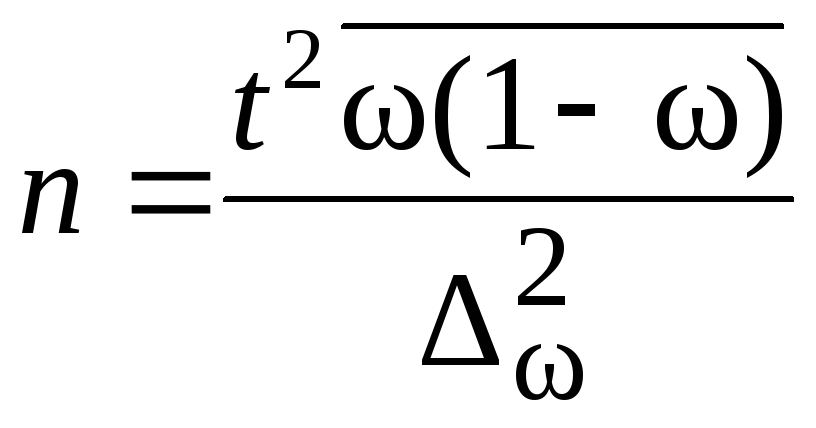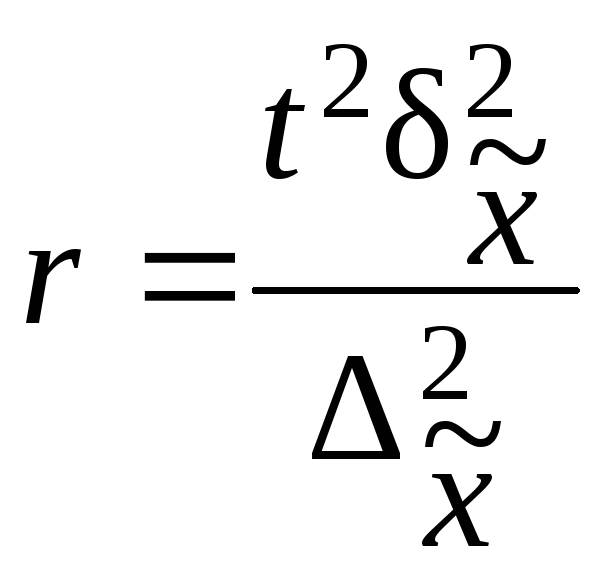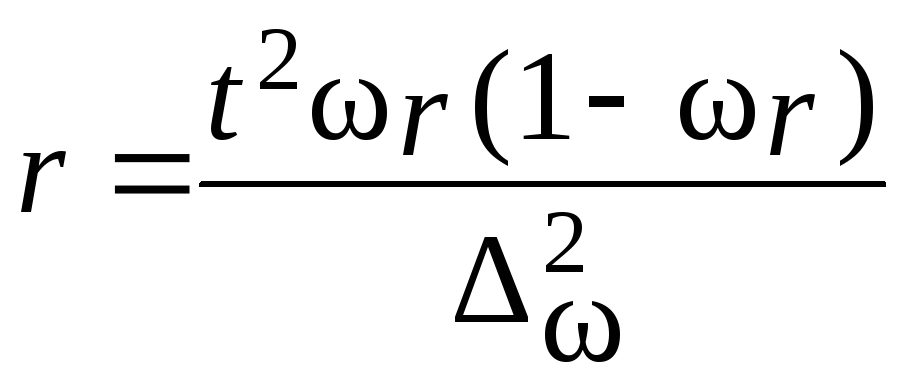Величина допустимой ошибки выборки зависит от чего - Не ошибается лишь тот, кто ничего не делает!

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Размер
выборки
– это количество элементов, которые
необходимо отобрать из генеральной
совокупности для проведения выборочного
исследования.

Определение
размера выборки для вероятностного
метода отбора представляет собой сложный
процесс, включающий ряд этапов: 1) оценка
факторов, влияющих на объем выборки; 2)
выбор метода расчета размера выборки;
3) расчет размера выборки; 4) оценка
стандартного отклонения среднего в
выборочной совокупности; 5) расчет
предельной ошибки выборки; 6) оценка
среднего значения признака в генеральной
совокупности (см. рис. 4.8).

В
случае применения детерминированного
метода отбора используются только
приблизительные методы расчета размера
выборки и оценить объективно точность
результатов исследования не представляется
возможным.

1.
Оценка факторов, влияющих на размер
выборки.
К наиболее важным факторам, определяющим
объем выборки, относятся следующие:
важность принимаемого решения, характер
исследования, бюджет исследования,
стоимость сбора информации, число групп
и подгрупп в генеральной совокупности,
коэффициенты охвата и завершенности,
размер генеральной совокупности и
требуемая точность исследования (см.
рис. 4.9). На размер ошибки выборки и,
соответственно, точность результатов
исследования влияют применяемая
процедура отбора и степень вариации
признака в совокупности.

Как
правило, для
принятия важных решений
необходима детальная, максимально
точная информация. Ее получение
предусматривает создание больших
выборок, но при увеличении объема выборки
возрастает и стоимость каждой
дополнительной единицы информации.

На
величину объема выборки влияет также
характер
исследования.
В поисковых исследованиях, изучающих
качественные характеристики, объем
выборки, как правило, невелик. Для
исследований, предусматривающих
статистическое заключение, таких как
дескриптивные, необходим больший объем
выборки. Кроме того, большие выборки
нужны, когда информация собирается
с учетом большого количества переменных.
Большой объем выборки позволяет снизить
общий эффект от ошибок выборки по всем
переменным.

Принимая
решения об объеме выборки, нужно учитывать
фактор ограниченности ресурсов или
располагаемый
бюджет исследования.
В любом исследовательском проекте
существуют временные и финансовые
ограничения. При жестких бюджетных
ограничениях исследователь будет стоять
перед выбором: использовать более
дешевые методы сбора информации или
ограничить размер выборки, допуская
снижение точности результатов.

Р
исунок
4.8.
Этапы расчета необходимого размера
выборки и оценки значения признака в
генеральной совокупности

Р
исунок
4.9.
Факторы, учитываемые при определении
размера выборки и взаимосвязи между
ними

Чем
больше размер выборки
(чем
он ближе к размерам генеральной
совокупности в целом), тем надежнее и
достовернее полученные данные, однако
стоимость
сбора информации
(включающая в себя расходы на размножение
инструментария, оплату труда интервьюеров,
супервайзеров и операторов компьютерного
набора данных) при этом значительно
возрастает;

При
проведении углубленного анализа данных
с использованием разнообразных
методов многомерного статистического
анализа необходим большой объем выборки.
Это же касается данных, которые
анализируются с особой точностью. Таким
образом, для
анализа данных на уровне группы или
подгруппы
потребуется больший объем выборки, чем
для анализа общей или генеральной
совокупности.

К примеру, мы хотим
исследовать потребительское поведение
населения города. Перед нами – структура
генеральной совокупности, которая
представляет распределение в целом
населения города и по трем квотным
признакам: район города, пол, возраст.
Совершенно очевидно, что если в
исследовании ставится задача изучить
мнения населения города в целом — это
одна ситуация; если в том числе и по
возрастным группам – это другая (здесь
мы имеем 3 группы); если необходимо
выявить распределения мнений по
возрастным и половым группам — это третья
ситуация (здесь мы имеем уже шесть
групп); наконец, если в исследовании нас
интересует распределение информации
по возрастным, половым группам и районам
города (к примеру, мы хотим определить,
как к покупкам того или иного товара
относятся молодые женщины, проживающие
во Фрунзенском районе г. Минска), то
здесь мы имеем дело уже с четвертой
ситуацией (54 группы). Для получения
репрезентативной информации в последним
случае необходимо обеспечить
представительство в минимальной из
этих пятидесяти четырех групп 25-30 чел.
Следовательно, минимальный объем
выборочной совокупности здесь будет
находиться в пределах 1600 чел.

Статистически
определенный объем выборки представляет
собой конечный, или чистый объем выборки,
который необходимо получить, чтобы
обеспечить расчет параметров с желательной
степенью точности и заданным уровнем
достоверности. При проведении опросов
он выражается в количестве завершенных
интервью. Для получения конечного объема
выборки необходимо связаться с большим
количеством потенциальных респондентов.
Другими словами, начальный объем выборки
должен намного превышать конечный,
поскольку коэффициенты охвата и
завершенности обычно составляют меньше
100%.

Коэффициентом
охвата
называется степень наличия или процент
людей, подходящих для участия в
исследовании. Коэффициент охвата
определяет, какое количество контактов
с людьми необходимо осуществить, чтобы
в итоге получить объем выборки,
соответствующий заданным критериям.

Предположим,
что для исследования характеристик
моющих средств необходимо создать
выборку из женщин – глав семьи в возрасте
от 25 до 55 лет. Приблизительно 75% женщин
в возрасте от 20 до 60 лет, к которым можно
обратиться, – это женщины – главы семьи
в возрасте от 25 до 55 лет. Это означает,
что, в среднем, необходимо обратиться
к 1,33 женщин, чтобы получить одного
подходящего респондента. Дополнительные
критерии для отбора респондентов
(например, каким образом использовался
продукт) увеличивают необходимое
количество контактов. Предположим, что
дополнительным критерием является
использование женщиной моющего средства
для пола в течение последних двух
месяцев. Предполагается, что 60% женщин,
к которым обратятся исследователи,
будут соответствовать этому критерию.
Тогда коэффициент охвата составит 0,75
х 0,60 = 0,45. Таким образом, конечный объем
выборки следует увеличить на 2,22 (1/0,45).

Точно
так же при определении объема выборки
необходимо учитывать ожидаемые отказы
людей, соответствующих критериям
исследования. Коэффициент
завершенности
указывает на процент респондентов,
соответствующих критериям отбора,
которые полностью прошли интервью.
Например, если исследователь предполагает,
что коэффициент завершенности интервью
составит 80% от числа подходящих
респондентов, необходимое количество
контактов следует умножить на коэффициент
1,25. Применение коэффициентов охвата и
завершенности означает, что число
контактов с потенциальными респондентами,
т.е. начальный объем выборки, должно
быть в 2,22 х 1,25 (или 2,77) раз больше
необходимого объема выборки.

Заранее
заданная точность
результатов исследования или допустимая
ошибка выборки
позволяют рассчитать необходимый размер
выборочной совокупности, используя
статистические методы, которые будут
рассмотрены далее.

Ошибкой
выборочного исследования
называется
любая ошибка, возникающая в результате
опроса или наблюдения и являющаяся
следствием использования выборки, а не
всей генеральной совокупности. Ошибки
выборочного исследования обусловлены
процедурой формирования выборки и
объемом выборки. Крупные выборки
порождают меньшую ошибку выборочного
исследования, чем малые.

Чтобы
извлечь выборку, как уже отмечалось в
предыдущем параграфе, сначала необходимо
определит: основу
выборки,
представляющую собой сводный список
все членов генеральной совокупности.
Как известно, списки не всегда полно
представляют генеральную совокупность,
поскольку в ней постоянно происходят
изменения: одни члены появляются, другие
– уходят. Кроме того, списки не застрахованы
от ошибок и опечаток. Таким образом,
ошибка
основы выборки
выражается
в неправильном описании всей генеральной
совокупности. Независимо от способа
формирования выборки, исследователь
должен учитывать ошибку основы. Иногда
в распоряжении исследователя оказывается
основа, лишь приблизительно описывающая
всю генеральную совокупность, однако,
если альтернативы нет, приходится
использовать и такие списки. Исследователь
должен тщательно выбирать основу
выборки, стремясь минимизировать
ошибки. Кроме того, исследователь должен
предупредить клиента о том, что
используемая основа выборки может
содержать ошибки.

Далее
будет идти речь только о случайных
ошибках выборочного
исследования, которые не связанны с
основой выборки и могут быть оценены
статистически. Иначе говоря, будем
предполагать, что основа выборки является
достаточно качественной и обеспечивает
низкий уровень ошибок, так что мы можем
извлечь из нее репрезентативную выборку.

Ошибка
выборки
зависит
не
только от ее величины, но и от
степени различий между отдельными
единицами внутри данной генеральной
совокупности.
Например, если нужно узнать, средний
размер потребления пива молодежью г.
Минска в возрасте 18-25 лет, то обнаружится,
что внутри имеющейся генеральной
совокупности нормы потребления у
различных людей существенно различны
(гетерогенная
генеральная
совокупность). Если же необходимо узнать
размер потребления хлеба в той же
генеральной совокупности, то он будет
различаться значительно меньше
(гомогенная
генеральная
совокупность). Чем больше различия
(гетерогенность) внутри генеральной
совокупности, тем больше возможная
ошибка выборки.

Некоторые
методы выборочного исследования
минимизируют ошибку выборки, другие –
никак на нее не влияют.
Например, использование стратифицированного
отбора может дать выигрыш в точности
при оценивании характеристик всей
совокупности. Часто неоднородную
совокупность удается расслоить на
подсовокупности (страты), каждая из
которых внутренне однородна. Если каждая
страта однородна в том смысле, что
результаты измерений в ней мало изменяются
от единицы к единице, то можно получить
точную оценку среднего значения для
любой страты по небольшой выборке в
этой страте. Затем эти оценки можно
объединить в одну точную оценку для
всей совокупности.

2. Выбор метода
расчета размера выборки.
Если специалист из опыта знает, какой
размер выборки следует использовать,
или же существуют различные ограничения
(например, связанные с бюджетом),
используют приблизительные
методы расчета размера выборки,
к которым относятся следующие:

— произвольный
метод расчета.
В этом случае объем выборки определяется
на уровне 5-10 % от генеральной совокупности.

— по
эмпирическим правилам.
Рекомендуется
выбирать размер выборки таким образом,
чтобы при ее разделении на группы в
каждой группе было не меньше 100 элементов.
Кроме сопоставления основных групп
анализ часто может потребовать
использования подгрупп. Размеры таких
подгрупп должны составлять от 20 до 50
человек. Это основано на том, что для
подгрупп требуется меньшая точность.

Если
одна из групп или подгрупп составляет
сравнительно небольшой процент
совокупности, то будет разумно использовать
непропорциональную выборку. Допустим,
что только 10% совокупности смотрит
образовательные телепередачи, и мнения
представителей этой группы требуется
сопоставить с мнениями других членов
совокупности. Если используются
телефонные интервью, контакты с жителями
могут устанавливаться случайно до тех
пор, пока не будут набраны 100 человек,
которые не смотрят образовательные
телепередачи. Далее опрос продолжается,
однако уже опрашиваются лишь те
респонденты, кто образовательные
телепередачи смотрит. В результате
будет получена выборка из 200 человек,
половина из которых смотрят образовательные
телепередачи.

— традиционный
метод расчета
связан с проведением периодических
ежегодных исследований, охватывающих,
например, 500, 1000 или 1500 респондентов.

— на
основе опыта сопоставимых исследований.
Таблица
4.7 дает представление об объемах выборок,
используемых в различных маркетинговых
исследованиях. Эти величины установлены
опытным путем и могут использоваться
в качестве ориентировочных данных,
особенно при детерминированных методах
формирования выборки.

— затратный
метод основан
на размере расходов, которые допустимо
затратить на проведение исследования.

Статистический
метод определения объема выборки
основан на традиционном статистическом
заключении. В соответствии с этим методом
заранее определяется уровень (степень)
точности.

Рассмотрение
данного метода начнем с краткой
характеристики базовых
понятий математической статистики.

Наиболее
важным понятием, позволяющим делать
заключения о свойствах генеральной
совокупности на основе выборочных
методов является кривая нормального
распределения.

Таблица
4.7.
Объемы выборок, используемых в
маркетинговых исследованиях

Вид исследования	Минимальный объем	Обычный диапазон
Исследование, цель которого – определить проблему (например, изучение потенциала рынка)	500	1000-2500
Исследование, цель которого – решить проблему (например, определить цену)	200	300-500
Тестирование товара	200	300-500
Пробный маркетинг	200	300-500
Теле- радио- и печатная реклама (в расчете на одно рекламное объявление, эффективность которого исследуется)	150	200-300
Аудит на пробном рынке	10 магазинов	10-20 магазинов
Фокус-группы	2 группы	10-15 групп

Кривая нормального
распределения
– это теоретическая модель, представляющая
собой абсолютно симметричный и гладкий
вид полигона частот. Она имеет форму
колокола и одну вершину, а ее концы
уходят в бесконечность в обоих
направлениях. Важнейшим свойством,
которым обладает кривая нормального
распределения, является то, что расстояние
по абсциссе (горизонтальная ось)
распределения, измеренное в единицах
стандартного отклонения от среднего
арифметического распределения, всегда
дает одинаковую общую площадь под
кривой: между ±1 стандартным отклонением
находится 68,3% площади; между ±2 стандартными
отклонениями – 95,4% площади; между ±3
стандартными отклонениями – 99,7% площади
(см. рис. 4.10).

Рисунок
4.10. Области
под теоретической кривой нормального
распределения

C
понятием кривой нормального распределения
связана центральная
предельная теорема, которая
гласит:
«Если
из генеральной совокупности, имеющей
любое распределение со средним μ
и
стандартным отклонением σ,
многократно извлекать случайные выборки
объема n,
то
при большом n
распределение всех возможных выборочных
средних будет стремиться к нормальному
распределению со средним μ
и
стандартным
отклонением σ
/
».

Таким
образом, центральная предельная теорема
позволяет распространять данные,
полученные в результате выборочного
исследования на всю генеральную
совокупность с определенной степенью
допущения при условии достаточно
большого объема выборки.

Конечно,
остается вопрос о том, что же такое
большой объем выборки. Полезное
эмпирическое правило гласит: если объем
выборки (n)
равен
100 или более, то применима центральная
предельная теорема и вы можете принять
допущение о нормальности распределения
всех возможных выборочных средних. Если
же n
меньше
100, то вы должны иметь веские доказательства
нормальности распределения генеральной
совокупности, и только после этого вы
можете полагать, что распределение,
которому подчиняются выборочные
статистики, является нормальным.
Следовательно, нормальность распределения
выборочных статистик гарантируется
путем использования довольно больших
выборок.

3.
Выбор требуемой степени точности и
достоверности результатов исследования.
При проведении любого выборочного
опроса или наблюдения перед исследователем
ставится задача оценить, каково истинное
значение во всей генеральной совокупности
либо среднего
значения
абсолютного
признака (доход
потребителей, размер потребления
конкретного товара), либо доли
единиц в совокупности, обладающих
каким-либо
признаком
(доля постоянных потребителей конкретного
товара; доля потребителей, удовлетворенных
уровнем обслуживания). Точность
выборки
в первом случае будет представлена в
виде абсолютной величины со знаком ±
(например, ±100 тыс. руб.; ±1 кг), или в виде
процента, во втором случае – только в
виде процента с тем же знаком (например,
±1% или ±5%).

Интерпретация
точности выборки подчиняется следующей
логике: если объем выборки обеспечивает
точность ±5%, то результаты опроса или
наблюдения, полученные с помощью выборки,
отличаются от результатов полной
переписи не более чем на 5%.

Еще одним фактором,
влияющим на объем выборки является
заданная исследователем степень
достоверности
(надежности)
оценки,
то есть степень
уверенности в том, что оценка близка к
истинному значению.

Для выборки
фиксированного объема степень точности
и степень достоверности являются
связанными величинами. На деле определение
объема выборки предполагает достижение
известного баланса между двумя этими
принципами.

Зависимость
точности выборки от ее объема для 95,4% и
99,7% уровня надежности представлена на
рисунке 4.11. Объем выборок на графике
колеблется от 50 до 2000. График демонстрирует,
что при увеличении объема выборки
ее ошибка уменьшается. Однако, как видим,
зависимость ошибки выборки от ее объема
не является прямолинейной. Иначе говоря,
удвоение объема выборки, не приводит к
существенному уменьшению ошибки.

исунок
4.11. Зависимость
точности и достоверности от объема
выборки

Если
объем выборки превышает 500, ошибка
выборки для 95,4% надежности падает ниже
±4% и продолжает очень медленно снижаться.
С другой стороны, анализ графика в
области малых выборок показывает, что
относительно небольшое изменение объема
выборки позволяет значительно повысить
их точность. Например, если объем выборки
равен 50, то ее уровень точности равен
±13,9%, а увеличение их объема до 250 позволяет
уменьшить ошибку выборки до ±6,2%. Иными
словами, точность выборки, объем которой
равен 25 примерно вдвое выше, чем точность
выборки, объем которой равен 50. Однако
в области крупных выборок это правило
не выполняется.

4. Определение
t
параметра, связанного с уровнем
надежности.
Определить значение t,
связанное с уровнем надежности можно
воспользовавшись таблицей 1 приложения.
Как видно по данным таблицы, при объеме
выборки больше 100 для 95,4% надежности
t≈2,
для 99,7% надежности t≈3.

5. Поиск информации
об уровне стандартного отклонения
среднего значения признака в генеральной
совокупности.
Здесь возможны
две различные ситуации: 1) стандартное
отклонение среднего значения признака
(σ)
в генеральной совокупности известно и
2) стандартное отклонение среднего
значения признака в генеральной
совокупности неизвестно.

В
первом случае можно приступить к расчету
объема
выборки с помощью формулы стандартной
ошибки выборки.

6.
Определение
объема выборки с помощью формулы
стандартной ошибки с учетом корректировки
на охват и завершенность.

Принято различать
среднюю и предельную ошибки выборки.
Предельная ошибка выборки определяется
следующим образом:

где
∆
— предельная ошибка выборки;

t
– параметр, связанный с уровнем
надежности;

μ
– средняя ошибка выборки.

Формулы расчета
средней ошибки
выборки для средней и для доли с учетом
способа отбора приведены в таблице 4.8.

Доверительные
интервалы для генеральной средней
можно установить на основе соотношений

Доверительные
интервалы для генеральной доли
устанавливаются на основе соотношений

Далее
для вычисления объема выборки применяется
формула
вычисление объема выборки по заданному
доверительному интервалу.
Формулы
расчета численности выборки
для определения средней и доли с учетом
способа отбора приведены в таблице 4.9.

Например,
для обследования, преследующего цель
выявить мнение потребителей о новом
товаре, в регионе, насчитывающем 10 тыс.
семей, необходимо провести анкетирование.
Условно принимается, что в каждой
квартире проживает одна семья и на нее
будет выделена одна анкета. Предварительные
исследования установили, что дисперсия
среднего размера покупки составляет
24 тыс. руб.; σ²
= 2; предельная ошибка не должна превышать
0,5 тыс. руб. Отсюда численность выборки
(п)
составит:

Эта
величина округляется до 400 семей
(квартир), т.е. установлена 4%-я выборка.
Однако практика показывает, что некоторая
часть анкет не возвращается (предположим
каждая пятая), поэтому увеличиваем число
анкет до 500. Следовательно, необходимо
включить в выборку каждую 20-ю квартиру
(10000 : 500).

Все
вышеприведенные формулы применимы для
большой выборки.
Кроме большой выборки используются так
называемые малые
выборки (n
< 30), которые могут иметь место в случаях
нецелесообразности использования
больших выборок.

При
расчете ошибок малой
выборки
необходимо учесть два момента:

1) формула средней
ошибки имеет вид

2)
при определении доверительных интервалов
исследуемого показателя в генеральной
совокупности или при нахождении
вероятности допуска той или иной ошибки
необходимо использовать таблицы
вероятности Стьюдента. При этом
вероятность
определяется
в зависимости от объема выборки и t
(см. табл.
прил. 1).

Таблица 4.8.
Формулы определения стандартной ошибки
выборки при различных способах отбора

Виды выборки Способы отбора	Повторная выборка	Бесповторная выборка
	Для средней
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—
	Для доли
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—	—

В
таблице используются следующие условные
обозначения:

N
– объем генеральной совокупности;

п
– объем выборочной совокупности;

– средняя в
генеральной совокупности;

–
средняя в выборочной
совокупности;

р
– доля единиц в генеральной совокупности;

w
– доля единиц в выборочной совокупности;

– генеральная
дисперсия (заменяется на выборочную
(S²) в случае, если она
не известна);

– межсерийная
дисперсия

;

r
— число отобранных серий;

R—
число серий в генеральной совокупности.

Таблица 4.9.
Формулы определения численности выборки
(n)
при различных способах отбора

Виды выборки Способы отбора	Повторная выборка	Бесповторная выборка
	Для средней
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—
	Для доли
Простая случайная выборка
Стратифицированная или типическая выборка
Кластерная, гнездовая или серийная выборка	—	—

Например, для
разработки бизнес-плана нового ресторана,
который открывается в центральной части
г. Минска необходимо узнать ожидаемый
диапазон расходов одного посетителя в
вечернее время. Удалось получить
информацию о том, что стандартное
отклонение расходов посетителей близкого
по уровню и месту расположения ресторана
составляет 30$. Существует возможность
опросить около 26 посетителей ресторана.
С какой достоверностью можно получить
результат при заданной точности ±10$?

Рассчитаем среднюю
ошибку выборки:

Тогда

Из
таблицы приложения 1 для n=26
и t=1,66
можно определить, что при допуске ошибки
±10$ достоверность
результатов составит менее 90%. Более
точное значение достоверности для тех
же параметров можно получить, например,
при помощи функции СТЬЮДРАСП в Microsoft
Excel
— 89,2%.

С 95,4% надежностью
будет обеспечена меньшая точность:

7. Отбор
произвольной пробной выборки.
В случае если стандартное
отклонение среднего значения признака
в генеральной совокупности неизвестно,
необходимо сформировать произвольную
пробную выборку.

8. Расчет
стандартного отклонения средней в
выборочной совокупности.
На основе полученных данных рассчитывается
стандартное отклонение признака в
выборочной совокупности и, затем –
необходимый размер выборки по приведенным
выше формулам.

9. Расчет точности
полученных результатов по формуле
предельной ошибки выборки.По
данным, собранным в ходе проведенного
выборочного исследования, рассчитывается
точность результатов. Если полученная
точность не устраивает исследователя,
может возникнуть необходимость увеличить
размер выборки с учетом рассчитанного
стандартного отклонения и коэффициентов
отклика и завершенности.

Предположим, что
в предыдущем примере не было возможности
узнать стандартное отклонение расходов
посетителей ресторана. По данным опроса
30 случайно отобранных респондентов
получены следующие данные: 25$ – 2 чел.;
30$ – 3 чел.; 45$ – 7 чел.; 55$ – 6 чел.; 70$ – 3
чел.; 85$ – 5 чел.; 110$ – 2 чел.; 150$ – 2 чел.

Определяем среднее
значение по формуле средней взвешенной:

Далее
рассчитываем дисперсию (квадрат
стандартного отклонения) расходов
посетителей ресторана по выборочной
совокупности.

Тогда
точность полученных результатов с
достоверностью 95,4%:

Для
того, чтобы обеспечить заданную точность
(±10$) рассчитываем
необходимый размер выборки:

В
целом, для принятия взвешенного решения
по размеру выборки наряду со статистическими
методами расчета следует применить
рассмотренные ранее приблизительные
методы и сравнить полученные результаты.

10. Оценка значения
признака в генеральной совокупности.
Основными
методами распространения выборочного
наблюдения на генеральную совокупность
являются прямой пересчет и способ
коэффициентов.

Прямой
пересчет есть
произведение среднего значения признака
на объем генеральной совокупности.
Однако большое число факторов не
позволяет в полной мере использовать
точечную оценку прямого пересчета при
распространении результатов выборки
на генеральную совокупность. На практике
чаще пользуются интервальной оценкой,
которая дает возможность учитывать
размер предельной ошибки выборки,
которая рассчитана для средней или для
доли признака.

Оценка
среднего по совокупности при использовании
стратифицированной выборки является
взвешенным средним средних значений
по каждой страте выборки.

Например,
производителю пива для оценки емкости
внутреннего рынка в частности необходимо
определить долю потребителей пива в
общей численности населения региона в
возрасте от 20 до 60 лет с точностью ±5%.
Можно предположить, что данный показатель
будет варьировать по полу и возрасту.
В таблице 4.10 представлена информация
о численности и структуре населения
региона в возрасте от 20 до 60 лет.

Таблица
4.10. Численность
населения региона в возрасте от 20 до 60
лет

Возрастные категории населения	Всего, тыс. чел.	В том числе
мужчины	женщины
20-29	1576,0	802,0	774,0
30-39	1357,3	671,4	685,9
40-49	1559,6	751,9	807,7
50-59	1276,1	582,7	693,4
Всего	5769,0	2807,9	2961,1

Ранее
проведенный опрос 200 респондентов в
возрасте от 20 до 60 лет показал, что доля
потребителей пива в общей численности
населения региона составляет 83%. По
имеющейся информации был рассчитан
необходимый объем выборки:

С
учетом необходимости обеспечить
необходимый минимальный размер подгрупп
округляем полученный результат до 300
человек и рассчитываем объем выборки
для каждой из страт по полу и возрасту
пропорционально соответствующей
численности населения. Результаты
расчета представлены в таблице 4.11.

Таблица
4.11. Структура
населения региона в возрасте от 20 до 60
лет и численность выборки.

Возрастные категории населения	В % к общей численности населения	Численность выборки
всего	мужчины	женщины	мужчины	женщины
20-29	27,3	13,9	13,4	42	40
30-39	23,6	11,7	11,9	35	36
40-49	27,0	13,0	14,0	39	42
50-59	22,1	10,1	12,0	30	36
Всего	100,0	48,7	51,3	146	154

В
результате опроса получены данные,
представленные в таблице 4.12.

Таблица
4.12. Доля
потребителей пива в общей численности
населения в разрезе возрастных категорий
по данным выборочного опроса.

Возрастные категории населения	Доля потребителей пива
мужчины	женщины
20-29	0,812	0,795
30-39	0,855	0,743
40-49	0,848	0,683
50-59	0,867	0,542

Определяем долю
потребителей пива по формуле средней
взвешенной:

Средняя
ошибка выборки:

Предельная ошибка
выборки для 95,4% надежности составит:

Таким
образом, с 95,4% надежностью можно
утверждать, что доля потребителей пива
в общей численности населения региона
в возрасте от 20 до 60 лет находится в
интервале от 71,8% (76,6% — 4,8%) до 81,4% (76,6% +
4,8%).

Опрос
обычно не ограничивается одним вопросом
–
иногда их сотни. Поэтому повторять
подобный процесс для каждого вопроса
смысла не имеет. Разумный подход –
выбрать несколько репрезентативных
вопросов и по ним определить размер. В
этот набор следует включить наиболее
критичные вопросы с максимальным уровнем
ожидаемой дисперсии.

В таком случае
может оказаться полезным подход
к расчету объема выборки, основанный
на сценарии максимально возможной
вариации признака в совокупности. Как
видно на рисунке 6, вариант,
когда w=
0,5 (50%) является наиболее консервативным,
поскольку он порождает максимальный
размер ошибки и, соответственно,
максимальный объем выборки. Следовательно,
его следует выбирать, когда изменчивость
не известна. Тогда формула размера
выборки упрощается:

Для 95% уровня
надежности и 5% уровня точности:

Р
исунок
4.12.
График

Использование
номограмм для
расчета
объема выборки. Стремление
упростить процедуру расчета объема
выборки приводит к созданию таблиц,
шкал или программ, которые ориентированы
на обеспечение статистической
надежности информации, но при этом не
обременяют пользователя знаниями
специальных формул из области статистики.
Например, существует калькулятор выборки
(www.
shortway.
to/few/calculator,
htm).

Номограмма является
графическим способом определения
размера выборки. Номограмма включает
три шкалы (рис. 7). На шкале слева
устанавливается разметка показателя
среднеквадратического отклонения
или распределения доли признака. На
правой шкале наносится разметка точности
измерения в виде допустимой ошибки при
заданной доверительной вероятности
95,4% или 99,7%. На средней шкале делается
разметка, соответствующая требуемому
объему выборки. На правой и левой
шкалах делаются отметки на уровне
желаемых значений показателей (доли
признака и допустимой ошибки). Линейкой
эти две отметки соединяются, на пересечении
линейки со средней шкалой делается
отметка, соответствующая тому объему
выборки, который отвечает пожеланиям
исследователя.

Как мы уже знаем, репрезентативность — свойство выборочной совокупности представлять характеристику генеральной. Если совпадения нет, говорят об ошибке репрезентативности — мере отклонения статистической структуры выборки от структуры соответствующей генеральной совокупности. Предположим, что средний ежемесячный семейный доход пенсионеров в генеральной совокупности составляет 2 тыс. руб., а в выборочной — 6 тыс. руб. Это означает, что социолог опрашивал только зажиточную часть пенсионеров, а в его исследование вкралась ошибка репрезентативности. Иными словами, ошибкой репрезентативности называется расхождение между двумя совокупностями — генеральной, на которую направлен теоретический интерес социолога и представление о свойствах которой он хочет получить в конечном итоге, и выборочной, на которую направлен практический интерес социолога, которая выступает одновременно как объект обследования и средство получения информации о генеральной совокупности.

Наряду с термином «ошибка репрезентативности» в отечественной литературе можно встретить другой — «ошибка выборки». Иногда они употребляются как синонимы, а иногда «ошибка выборки» используется вместо «ошибки репрезентативности» как количественно более точное понятие.

Ошибка выборки — отклонение средних характеристик выборочной совокупности от средних характеристик генеральной совокупности.

На практике ошибка выборки определяется путем сравнения известных характеристик генеральной совокупности с выборочными средними. В социологии при обследованиях взрослого населения чаще всего используют данные переписей населения, текущего статистического учета, результаты предшествующих опросов. В качестве контрольных параметров обычно применяются социально-демографические признаки. Сравнение средних генеральной и выборочной совокупностей, на основе этого определение ошибки выборки и ее уменьшение называется контролированием репрезентативности. Поскольку сравнение своих и чужих данных можно сделать по завершении исследования, такой способ контроля называется апостериорным, т.е. осуществляемым после опыта.

В опросах Института Дж. Гэллапа репрезентативность контролируется по имеющимся в национальных переписях данным о распределении населения по полу, возрасту, образованию, доходу, профессии, расовой принадлежности, месту проживания, величине населенного пункта. Всероссийский центр изучения общественного мнения (ВЦИОМ) использует для подобных целей такие показатели, как пол, возраст, образование, тип поселения, семейное положение, сфера занятости, должностной статус респондента, которые заимствуются в Государственном комитете по статистике РФ. В том и другом случае генеральная совокупность известна. Ошибку выборки невозможно установить, если неизвестны значения переменной в выборочной и генеральной совокупностях.

Специалисты ВЦИОМ обеспечивают при анализе данных тщательный ремонт выборки, чтобы минимизировать отклонения, возникшие на этапе полевых работ. Особенно сильные смещения наблюдаются по параметрам пола и возраста. Объясняется это тем, что женщины и люди с высшим образованием больше времени проводят дома и легче идут на контакт с интервьюером, т.е. являются легко достижимой группой по сравнению с мужчинами и людьми «необразованными»35.

Ошибка выборки обусловливается двумя факторами: методом формирования выборки и размером выборки.

Ошибки выборки подразделяются на два типа — случайные и систематические. Случайная ошибка — это вероятность того, что выборочная средняя выйдет (или не выйдет) за пределы заданного интервала. К случайным ошибкам относят статистические погрешности, присущие самому выборочному методу. Они уменьшаются при возрастании объема выборочной совокупности.

Второй тип ошибок выборки — систематические ошибки. Если социолог решил узнать мнение всех жителей города о проводимой местными органами власти социальной политике, а опросил только тех, у кого есть телефон, то возникает предумышленное смещение выборки в пользу зажиточных слоев, т.е. систематическая ошибка.

Таким образом, систематические ошибки — результат деятельности самого исследователя. Они наиболее опасны, поскольку приводят к довольно значительным смещениям результатов исследования. Систематические ошибки считаются страшнее случайных еще и потому, что они не поддаются контролю и измерению.

Они возникают, когда, например:

выборка не соответствует задачам исследования (социолог решил изучить только работающих пенсионеров, а опросил всех подряд);
налицо незнание характера генеральной совокупности (социолог думал, что 70% всех пенсионеров не работает, а оказалось, что не работает только 10%);
отбираются только «выигрышные» элементы генеральной совокупности (например, только обеспеченные пенсионеры).

Внимание! В отличие от случайных ошибок систематические ошибки при возрастании объема выборки не уменьшаются.

Обобщив все случаи, когда происходят систематические ошибки, методисты составили их реестр. Они полагают, что источником неконтролируемых перекосов в распределении выборочных наблюдений могут быть следующие факторы:

нарушены методические и методологические правила проведения социологического исследования;
выбраны неадекватные способы формирования выборочной совокупности, методы сбора и расчета данных;
произошла замена требуемых единиц наблюдения другими, более доступными;
отмечен неполный охват выборочной совокупности (недополучение анкет, неполное их заполнение, труднодоступность единиц наблюдения).

Намеренные ошибки социолог допускает редко. Чаще ошибки возникают из-за того, что социологу плохо известна структура генеральной совокупности: распределение людей по возрасту, профессии, доходам и т.д.

Систематические ошибки легче предупредить (по сравнению со случайными), но их очень трудно устранить. Предупреждать систематические ошибки, точно предвидя их источники, лучше всего заранее — в самом начале исследования.

Вот некоторые способы избежать ошибок выборки:

каждая единица генеральной совокупности должна иметь равную вероятность попасть в выборку;
отбор желательно производить из однородных совокупностей;
надо знать характеристики генеральной совокупности;
при составлении выборочной совокупности надо учитывать случайные и систематические ошибки.

Если выборочная совокупность (или просто выборка) составлена правильно, то социолог получает надежные результаты, харастеризующие всю генеральную совокупность. Если она составлена неправильно, то ошибка, возникшая на этапе составления выборки, на каждом следующем этапе проведения социологического исследования приумножается и достигает в конечном счете такой величины, которая перевешивает ценность проведенного исследования. Говорят, что от такого исследования больше вреда, нежели пользы.

Подобные ошибки могут произойти только с выборочной совокупностыо. Чтобы избежать или уменьшить вероятность ошибки, самый простой способ — увеличивать размеры выборки (в идеале до объема генеральной: когда обе совокупности совпадут, ошибка выборки вообще исчезнет). Экономически такой метод невозможен. Остается другой путь — совершенствовать математические методы составления выборки. Они то и применяются на практике. Таков первый канал проникновения в социологию математики. Второй канал — математическая обработка данных.

Особенно важной проблема ошибок становится в маркетинговых исследованиях, где используются не очень большие выборки. Обычно они составляют несколько сотен, реже — тысячу респондентов. Здесь исходным пунктом расчета выборки выступает вопрос об определении размеров выборочной совокупности. Численность выборочной совокупности зависит от двух факторов:

стоимости сбора информации,
стремления к определенной степени статистической достоверности результатов, которую надеется получить исследователь.

Конечно, даже не искушенные в статистике и социологии люди интуитивно понимают, что чем больше размеры выборки, т.е. чем ближе они к размерам генеральной совокупности в целом, тем более надежны и достоверны полученные данные. Однако выше мы уже говорили о практической невозможности сплошных опросов в тех случаях, когда они проводятся на объектах, численность которых превышает десятки, сотни тысяч и даже миллионы. Понятно, что стоимость сбора информации (включающая оплату тиражирования инструментария, труда анкетеров, полевых менеджеров и операторов по компьютерному вводу) зависит от той суммы, которую готов выделить заказчик, и слабо зависит от исследователей. Что же касается второго фактора, то мы остановимся на нем чуть подробнее.

Итак, чем больше величина выборки, тем меньше возможная ошибка. Хотя необходимо отметить, что при желании увеличить точность вдвое вам придется увеличить выборку не в два, а в четыре раза. Например, чтобы сделать в два раза более точной оценку данных, полученных путем опроса 400 человек, вам потребуется опросить не 800, а 1600 человек. Впрочем, вряд ли маркетинговое исследование испытывает нужду в стопроцентной точности. Если пивовару необходимо узнать, какая часть потребителей пива предпочитает именно его марку, а не сорт его конкурента, — 60% или 40%, то на его планы никак не повлияет разница между 57%, 60 или 63%.

Ошибка выборки может зависеть не только от ее величины, но и от степени различий между отдельными единицами внутри генеральной совокупности, которую мы исследуем. Например, если нам нужно узнать, какое количество пива потребляется, то мы обнаружим, что внутри нашей генеральной совокупности нормы потребления у различных людей существенно различаются (гетерогенная генеральная совокупность). В другом случае мы будем изучать потребление хлеба и установим, что у разных людей оно различается гораздо менее существенно {гомогенная генеральная совокупность). Чем больше различия (или гетерогенность) внутри генеральной совокупности, тем больше величина возможной ошибки выборки. Указанная закономерность лишь подтверждает то, что нам подсказывает простой здравый смысл. Таким образом, как справедливо утверждает В. Ядов, «численность (объем) выборки зависит от уровня однородности или разнородности изучаемых объектов. Чем более они однородны, тем меньшая численность может обеспечить статистически достоверные выводы».

Определение объема выборки зависит также от уровня доверительного интервала допустимой статистической ошибки. Здесь имеются в виду так называемые случайные ошибки, которые связаны с природой любых статистических погрешностей. В.И. Паниотто приводит следующие расчеты репрезентативной выборки с допущением 5%-ной ошибки:
Это означает,что если вы, опросив, предположим, 400 человек в районном городе, где численность взрослого платежеспособного населения составляет 100 тыс. человек, выявили, что 33% опрошенных покупателей предпочитают продукцию местного мясокомбината, то с 95%-ной вероятностью можете утверждать, что постоянными покупателями этой продукции являются 33+5% (т.е. от 28 до 38%) жителей этого города.

Можно также воспользоваться расчетами института Гэллапа для оценки соотношения размеров выборки и ошибки выборки.

Источник

Расхождения
между величиной какого-либо показателя,
найденного посредством статистического
наблюдения, и действительными его
размерами называются ошибками
наблюдения.В зависимости от
причин возникновения различают ошибки
регистрации и ошибки репрезентативности.

Ошибки
регистрациивозникают в результате
неправильного установления фактов или
ошибочной записи в процессе наблюдения
или опроса. Они бывают случайными или
систематическими. Случайные ошибки
регистрации могут быть допущены как
опрашиваемыми в их ответах, так и
регистраторами. Систематические ошибки
могут быть и преднамеренными, и
непреднамеренными. Преднамеренные –
сознательные, тенденциозные искажения
действительного положения дела.
Непреднамеренные вызываются различными
случайными причинами (небрежность,
невнимательность).

Ошибки
репрезентативности(представительности)
возникают в результате неполного
обследования и в случае, если обследуемая
совокупность недостаточно полно
воспроизводит генеральную совокупность.
Они могут быть случайными и систематическими.
Случайные ошибки репрезентативности
– это отклонения, возникающие при
несплошном наблюдении из-за того, что
совокупность отобранных единиц наблюдения
(выборка) неполно воспроизводит всю
совокупность в целом. Систематические
ошибки репрезентативности – это
отклонения, возникающие вследствие
нарушения принципов случайного отбора
единиц. Ошибки репрезентативности
органически присущи выборочному
наблюдению и возникают в силу того, что
выборочная совокупность не полностью
воспроизводит генеральную. Избежать
ошибок репрезентативности нельзя,
однако, пользуясь методами теории
вероятностей, основанными на использовании
предельных теорем закона больших чисел,
эти ошибки можно свести к минимальным
значениям, границы которых устанавливаются
с достаточно большой точностью.

Ошибки
выборки –разность между
характеристиками выборочной и генеральной
совокупности. Для среднего значения
ошибка будет определяться по формуле

(7.1)

где

Величина
называетсяпредельной ошибкойвыборки.

Предельная
ошибка выборки – величина случайная.
Исследованию закономерностей случайных
ошибок выборки посвящены предельные
теоремы закона больших чисел. Наиболее
полно эти закономерности раскрыты в
теоремах П. Л. Чебышева и А. М. Ляпунова.

Теорему П.
Л. Чебышева применительно к
рассматриваемому методу можно
сформулировать следующим образом: при
достаточно большом числе независимых
наблюдений можно с вероятностью, близкой
к единице (т. е. почти с достоверностью),
утверждать, что отклонение выборочной
средней от генеральной будет сколько
угодно малым. В теореме П. Л. Чебышева
доказано, что величина ошибки не должна
превышать.
В свою очередь величина,
выражающая среднее квадратическое
отклонение выборочной средней от
генеральной средней, зависит от
колеблемости признака в генеральной
совокупностии числа отобранных единицn. Эта
зависимость выражается формулой

,
(7.2)

где
зависит также от способа производства
выборки.

Величину
=называютсредней ошибкой выборки. В
этом выражении– генеральная дисперсия,n– объем
выборочной совокупности.

Рассмотрим, как
влияет на величину средней ошибки число
отбираемых единиц n. Логически
нетрудно убедиться, что при отборе
большого числа единиц расхождения между
средними будут меньше, т. е. существует
обратная связь между средней ошибкой
выборки и числом отобранных единиц. При
этом здесь образуется не просто обратная
математическая зависимость, а такая
зависимость, которая показывает, что
квадрат расхождения между средними
обратно пропорционален числу отобранных
единиц.

Увеличение
колеблемости признака влечет за собой
увеличение среднего квадратического
отклонения, а следовательно, и ошибки.
Если предположить, что все единицы будут
иметь одинаковую величину признака, то
среднее квадратическое отклонение
станет равно нулю и ошибка выборки
также исчезнет. Тогда нет необходимости
применять выборку. Однако следует иметь
в виду, что величина колеблемости
признака в генеральной совокупности
неизвестна, поскольку неизвестны размеры
единиц в ней. Можно рассчитать лишь
колеблемость признака в выборочной
совокупности. Соотношение между
дисперсиями генеральной и выборочной
совокупности выражается формулой

Поскольку
величина
при достаточно большихnблизка к
единице, можно приближенно считать, что
выборочная дисперсия равна генеральной
дисперсии, т. е.

Следовательно,
средняя ошибка выборки показывает,
какие возможны отклонения характеристик
выборочной совокупности от соответствующих
характеристик генеральной совокупности.
Однако о величине этой ошибки можно
судить с определенной вероятностью. На
величину вероятности указывает множитель

Теорема А.
М. Ляпунова. А. М. Ляпунов доказал,
что распределение выборочных средних
(следовательно, и их отклонений от
генеральной средней) при достаточно
большом числе независимых наблюдений
приближенно нормально при условии, что
генеральная совокупность обладает
конечной средней и ограниченной
дисперсией.

Математически
теорему Ляпуноваможно записать
так:

(7.3)

где

,
(7.4)

где – математическая постоянная;

–предельная ошибка выборки,которая дает возможность выяснить, в
каких пределах находится величина
генеральной средней.

Значения этого
интеграла для различных значений
коэффициента доверия tвычислены и
приводятся в специальных математических
таблицах. В частности, при:

Поскольку tуказывает на вероятность расхождения,
т. е. на вероятность того, на какую
величину генеральная средняя будет
отличаться от выборочной средней, то
это может быть прочитано так: с вероятностью
0,683 можно утверждать, что разность между
выборочной и генеральной средними не
превышает одной величины средней ошибки
выборки. Другими словами, в 68,3 % случаев
ошибка репрезентативности не выйдет
за пределыС вероятностью 0,954 можно утверждать,
что ошибка репрезентативности не
превышает(т. е. в 95 % случаев). С вероятностью
0,997, т. е. довольно близкой к единице,
можно ожидать, что разность между
выборочной и генеральной средней не
превзойдет трехкратной средней ошибки
выборки и т. д.

Логически связь
здесь выглядит довольно ясно: чем больше
пределы, в которых допускается
возможная ошибка, тем с большей
вероятностью судят о ее величине.

Зная выборочную
среднюю величину признака
и предельную ошибку выборки,
можно определить границы (пределы),
в которых заключена генеральная
средняя

(7.5)

1.
Собственно-случайная выборка–
этот способ ориентирован на выборку
единиц из генеральной совокупности без
всякого расчленения на части или группы.
При этом для соблюдения основного
принципа выборки – равной возможности
всем единицам генеральной совокупности
быть отобранным – используются схема
случайного извлечения единиц путем
жеребьевки (лотереи) или таблицы случайных
чисел. Возможен повторный и бесповторный
отбор единиц

Средняя ошибка
собственно-случайной выборки
представляет собой среднеквадратическое
отклонение возможных значений выборочной
средней от генеральной средней. Средние
ошибки выборки при собственно-случайном
методе отбора представлены в табл. 7.2.

Таблица 7.2

Средняя ошибка выборки μ	При отборе
повторном	бесповторном
Для средней
Для доли

В таблице
использованы следующие обозначения:

– дисперсия выборочной совокупности;

– численность выборки;

– численность генеральной совокупности;

– выборочная доля единиц, обладающих
изучаемым признаком;

– число единиц, обладающих изучаемым
признаком;

– численность выборки.

Для увеличения
точности вместо множителя
следует
брать множитель
,
но при большой численностиNразличие
между этими выражениями практического
значения не имеет.

Предельная
ошибка собственно-случайной выборки
рассчитывается по формуле

,
(7.6)

где t
– коэффициент доверия зависит от
значения вероятности.

Пример.При
обследовании ста образцов изделий,
отобранных из партии в случайном порядке,
20 оказалось нестандартными. С вероятностью
0,954 определите пределы, в которых
находится доля нестандартной продукции
в партии.

Решение.
Вычислим генеральную долю (Р):
.

Доля нестандартной
продукции:
.

Предельная
ошибка выборочной доли с вероятностью
0,954 рассчитывается по формуле (7.6) с
применением формулы табл. 7.2 для доли:

С вероятностью
0,954 можно утверждать, что доля нестандартной
продукции в партии товара находится в
пределах 12 % ≤ P≤ 28 %.

В практике
проектирования выборочного наблюдения
возникает потребность определения
численности выборки, которая необходима
для обеспечения определенной точности
расчета генеральных средних. Предельная
ошибка выборки и ее вероятность при
этом являются заданными. Из формулы
и формул средних ошибок выборки
устанавливается необходимая численность
выборки. Формулы для определения
численности выборки (n) зависят от
способа отбора. Расчет численности
выборки для собственно-случайной выборки
приведен в табл. 7.3.

Таблица 7.3

Предполагаемый отбор	Формулы
для средней	для доли
Повторный
Бесповторный

2.
Механическая выборка– при этом
методе исходят из учета некоторых
особенностей расположения объектов в
генеральной совокупности, их упорядоченности
(по списку, номеру, алфавиту). Механическая
выборка осуществляется путем отбора
отдельных объектов генеральной
совокупности через определенный интервал
(каждый 10-й или 20-й). Интервал рассчитывается
по отношению,
гдеn– численность выборки,N–
численность генеральной совокупности.
Так, если из совокупности в 500 000 единиц
предполагается получить 2 %-ную выборку,
т. е. отобрать 10 000
единиц, то пропорция отбора составитОтбор
единиц осуществляется в соответствии
с установленной пропорцией через равные
интервалы. Если расположение объектов
в генеральной совокупности носит
случайный характер, то механическая
выборка по содержанию аналогична
случайному отбору. При механическом
отборе применяется только бесповторная
выборка [1, 5–10].

Средняя ошибка
и численность выборки при механическом
отборе подсчитывается по формулам
собственно-случайной выборки (см.
табл. 7.2 и 7.3).

3.
Типическая выборка, при котрой
генеральная совокупность делится по
некоторым существенным признакам на
типические группы; отбор единиц
производится из типических групп. При
этом способе отбора генеральная
совокупность расчленяется на однородные
в некотором отношении группы, которые
имеют свои характеристики, и вопрос
сводится к определению объема выборок
из каждой группы. Может бытьравномерная
выборка– при этом способе из каждой
типической группы отбирается одинаковое
число единицТакой подход оправдан лишь при равенстве
численностей исходных типических групп.
При типическом отборе, непропорциональном
объему групп, общее число отбираемых
единиц делится на число типических
групп, полученная величина дает
численность отбора из каждой типической
группы.

Более совершенной
формой отбора является пропорциональная
выборка. Пропорциональной называется
такая схема формирования выборочной
совокупности, когда численность выборок,
взятых из каждой типической группы в
генеральной совокупности, пропорциональна
численностям, дисперсиям (или комбинированно
и численностям, и дисперсиям). Условно
определяем численность выборки в 100
единиц и отбираем единицы из групп:

– пропорционально
численности их генеральной совокупности
(табл. 7.4). В таблице
обозначено:

N_i– численность типической группы;

d_j– доля (N_i/N);

N– численность
генеральной совокупности;

n_i– численность выборки из типической
группы вычисляется:

, (7.7)

n – численность выборки из генеральной
совокупности.

Таблица
7.4

Группы	N_i	d_j	n_i
1	300	0,3	30
2	500	0,5	50
3	200	0,2	20
	1000	1,0	100

–
пропорционально среднему квадратическому
отклонению(табл. 7.5).

здесь
_i– среднее
квадратическое отклонение типических
групп;

n_i
– численность выборки из типической
группы вычисляется по формуле

(7.8)

Таблица
7.5

N_i	_i		n_i
300	5	0,25	25
500	7	0,35	35
200	8	0,40	40
1000	20	1,0	100

–
комбинированно (табл. 7.6).

Численность
выборки вычисляется по формуле

. (7.9)

Таблица 7.6

	_i	_iN_i
300	5	1500	0,23	23
500	7	2100	0,53	53
200	8	1600	0.24	24
1000	20	6600	1,0	100

При проведении
типической выборки непосредственный
отбор из каждой группы проводится
методом случайного отбора.

Средние ошибки
выборки рассчитываются по формулам
табл. 7.7 в зависимости от способа отбора
из типических групп.

Таблица 7.7

Способ отбора	Повторный	Бесповторный
для средней	для доли	для средней	для доли
Непропорциональный объему групп
Пропорциональный объему групп
Пропорциональный колеблемости в группах (является наивыгоднейшим)

здесь
– средняя из внутригрупповых дисперсий
типических групп;

– доля единиц, обладающих изучаемым
признаком;

– средняя из внутригрупповых дисперсий
для доли;

– среднее квадратическое отклонение
в выборке изi-й типической группы;

– объем выборки из типической группы;

– общий объем выборки;

–
объем типической группы;

– объем генеральной совокупности.

Численность
выборки из каждой типической группы
должна быть пропорциональна среднему
квадратическому отклонению в этой
группе
.Расчет численности
производится по формулам, приведенным
в табл. 7.8.

Таблица 7.8

	Повторный	Бесповторный
Для определения средней
Для определения доли

4. Серийная
выборка– удобена в тех случаях,
когда единицы совокупности объединены
в небольшие группы или серии. При серийной
выборке генеральную совокупность делят
на одинаковые по объему группы – серии.
В выборочную совокупность отбираются
серии. Сущность серийной выборки
заключается в случайном или механическом
отборе серий, внутри которых производится
сплошное обследование единиц. Средняя
ошибка серийной выборки с равновеликими
сериями зависит от величины только
межгрупповой дисперсии. Средние ошибки
сведены в табл. 7.9.

Таблица 7.9

Способ отбора серии	Формулы
для средней	для доли
Повторный
Бесповторный

Здесь
R– число серий в генеральной
совокупности;

r – число
отобранных серий;

– межсерийная (межгрупповая) дисперсия
средних;

– межсерийная (межгрупповая) дисперсия
доли.

При серийном
отборе необходимую численность отбираемых
серий определяют так же, как и при
собственно-случайном методе отбора.

Расчет численности
серийной выборки производится по
формулам, приведенным в табл. 7.10.

Таблица 7.10

	Повторный	Бесповторный
Для определения среднего признака
Для определения доли

Пример.В
механическом цехе завода в десяти
бригадах работает 100 рабочих. В целях
изучения квалификации рабочих была
произведена 20 %-ная серийная бесповторная
выборка, в которую вошли две бригады.
Получено следующее распределение
обследованных рабочих по разрядам:

Рабочие

Разряды

рабочих
в бригаде 1

Разряды

рабочих
в бригаде 2

Рабочие

Разряды
рабочих
в бригаде 1

Разряды
рабочих
в бригаде 2

Необходимо
определить с вероятностью 0,997 пределы,
в которых находится средний разряд
рабочих механического цеха.

Решение.
Определим выборочные средние по
бригадам и общую среднюю как среднюю
взвешенную из групповых средних:

Определим
межсерийную дисперсию по формулам
(5.25):

Рассчитаем
среднюю ошибку выборки по формуле табл.
7.9:

Вычислим
предельную ошибку выборки с вероятностью
0,997:

С вероятностью
0,997 можно утверждать, что средний разряд
рабочих механического цеха находится
в пределах

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Краткий
курс лекции

Понятие и методы
обоснования аудиторской выборки. Критерии аудиторской выборки.

Международный стандарт аудита 530 «Аудиторская выборка» введен в
действие на территории Российской Федерации приказом Минфина России от
09.01.2019 № 2н

Аудиторская
выборка – это перечень
определенным образом отобранных элементов проверяемой совокупности с целью на
основе их изучения сделать вывод обо всей проверяемой совокупности.

Аудиторская выборка — это применение аудиторских процедур
менее чем ко всем элементам одной статьи отчетности или группы однотипных
операций.

Она дает возможность аудитору получить и оценить аудиторские доказательства в отношении некоторых характеристик
элементов, отобранных для того, чтобы сформировать или помочь сформировать
выводы, касающиеся генеральной совокупности, из которой произведена выборка.

Выборка может быть нестатистической
(произвольной) и статистической.

Нестатистический
выборочный метод – это анализ
по качественным признакам в зонах повышенного аудиторского риска. Как правило,
его применяют при невозможности использовать метод статистической выборки.

Например – проверяемая совокупность неоднородна, разный
уровень эффективности внутреннего контроля в структурных подразделениях
предприятия, небольшое количество хозяйственных операций, имеющих высокий
уровень существенности.

Наиболее распространенными методами нестатистической
(произвольной) выборки являются: блочный отбор (выбор первого элемента
определяет все остальные элементы проверяемого блока), беспорядочный отбор,
оценочные методы.

Статистический
выборочный метод может
применяться для достижения следующих целей:

· обнаружения повторяющихся ошибок, искажений,
проявляющихся с определенной частотой и в определенном количестве;

· оценка масштабов распространения обнаруженных ошибок.

Основными методами статистической выборки при аудите
являются:

— возвратная выборка – не исключаются из процесса отбора
ранее проверенные элементы;

— безвозвратная выборка — исключаются из процесса отбора
ранее проверенные элементы;

— механическая выборка – предполагает предварительное
ранжирование единиц проверяемой совокупности;

— серийная выборка – отбор элементов для проверки
осуществляется не единицами, а сериями и другие методы.

Риск выборки возникает,
когда вывод аудитора, сделанный на основе отобранной совокупности, отличается
от вывода при применении идентичных процедур аудита к генеральной совокупности
в целом.

В аудите различают два типа рисков выборки. Риск
первого типа представляет собой риск того, что аудитор сделает следующие
заключения:

риск средств внутреннего контроля ниже, чем в
действительности (при выполнении тестов средств внутреннего контроля);

существенной ошибки не существует, вопреки тому,
что в действительности она есть (при выполнении аудиторских процедур проверки
по существу).

Риск данного типа
оказывает влияние на надежность аудита и с большой степенью вероятности может
привести к ненадлежащему аудиторскому мнению.

Риск второго типа
представляет собой риск того, что аудитор придет к следующим выводам:

риск средств внутреннего контроля выше, чем в
действительности (при выполнении тестов средств внутреннего контроля);

имеет место существенная ошибка, тогда как в
действительности ее не существует (при выполнении аудиторских процедур проверки
по существу).

Риск такого типа
оказывает влияние на эффективность аудита, поскольку он обычно приводит к
дополнительной работе по установлению того, что первоначальные выводы были
неверны.

Риск, не зависящий от
аудиторской выборки, является следствием факторов, которые приводят аудитора к
ошибочному выводу по любым причинам, кроме тех, которые связаны с объемом
выборки (т.е. числом отбираемых для проверки элементов). Риск, связанный с
выборкой, может быть снижен путем увеличения объема отбираемой совокупности, а
не связанный — путем надлежащего планирования задания, текущего контроля за
работой аудиторов и проверки выполнения процедур.

Различают следующие
виды выборки:

представительная (репрезентативная) — элементы ее
генеральной совокупности имеют равную вероятность быть отобранными;

непредставительная (нерепрезентативная) — элементы ее
генеральной совокупности не имеют равную вероятность быть отобранными. Аудитор
полагается на свое профессиональное суждение при отборе элементов.

Элементами выборки могут
быть натуральные объекты (например, первичные учетные документы) или показатели
в денежном выражении. Аудитор должен стараться сформировать репрезентативную совокупность
путем отбора элементов выборки, которые обладают характеристиками, типичными
для генеральной совокупности, так как целью выборки является получение выводов
по всей генеральной совокупности. При формировании проверяемой совокупности
необходимо исключать предвзятость.

Для построения выборки
аудитор определяет метод отбора элементов, который будет использоваться при
тестировании с целью получения аудиторских доказательств. Различают следующие
методы отбора элементов:

отбор всех элементов (сплошная проверка);

отбор специфических (определенных) элементов;

отбор отдельных элементов (формирование
аудиторской выборки).

Первый метод отбора не
применяют при проведении тестов средств внутреннего контроля, его используют в
отношении аудиторских процедур проверок по существу. Сплошная проверка
целесообразна в следующих случаях:

генеральная совокупность состоит из небольшого
числа элементов наибольшей стоимости;

неотъемлемый риск и риск средств контроля
являются высокими, а другие средства не позволяют получить достаточные
надлежащие аудиторские доказательства;

повторяющийся характер расчетов или иных
процессов, осуществляемых с помощью компьютерной системы бухгалтерского учета,
делает сплошную проверку эффективной с точки зрения соотношения затрат и результатов.

Второй метод
предполагает отбор специфических элементов. Различают специфические элементы
наибольшей стоимости и ключевые элементы. К элементам наибольшей стоимости
относят суммы сальдо счетов, которые превышают планируемую степень точности, т.е.
уровень существенности. При определении ключевых элементов аудитор отбирает
сальдо счетов, существенных качественно, т.е. элементы, по которым возможна
наибольшая вероятность наличия ошибки или искажения, и элементы существенные
количественно, т.е. элементы (например, месяцы), имеющие наибольший оборот по
данному счету в отчетном периоде. При использовании данного метода
осуществляется построение непредставительной выборки, в связи с чем результаты,
полученные по отобранным элементам, не могут быть экстраполированы на всю
совокупность.

Третий метод
представляет собой отбор элементов для построения представительной выборки.
Прежде чем отобрать элементы, необходимо определить объем выборки.

Организация выборочного исследования включает в себя определение:

— величины
выборки (массива, поля проверяемой и генеральной совокупности);

— единицы
наблюдения;

— единицы
отбора;

— методов
отбора;

— объема
выборки;

— проверки
представительности (репрезентативности) выборки;

— порядка
распространения выборочных данных на проверяемую совокупность.

Для достижения
поставленных целей проверки необходимо определение соответствующей проверяемой
совокупности, поскольку именно к ней относится заключение, сделанное на основе
выборки.

В аудите в
качестве элементов могут выступать бухгалтерские записи (проводки), статьи,
записи, из которых делается выборка.

Для составления
проверяемой совокупности вся документация клиента разбивается на однородные
массивы данных по различным признакам (характеру документов, материально ответственным
лицам, временной последовательности и др.).

Например, аудитор
собирает информацию о дебиторской задолженности свыше 600 тыс. руб.,
исследуемой совокупностью будет совокупность всех бухгалтерских документов,
записей, затрагивающих расчеты с дебиторами, но не менее чем на 600 тыс. руб.

Единица отбора
при таком типе выборок совпадает с единицей наблюдения (документом).

Единица
наблюдения при аудиторской проверке объективно обусловлена. Ею может быть
какой-либо раздел или участок бухучета, тип хозяйственных операций. В рамках
одной и той же единицы наблюдения единицы отбора могут быть различными.

Осуществляя
выборку, аудитор может разбить всю изучаемую
совокупность на отдельные группы, элементы, каждый из которых имеет сходные
характеристики. Эта процедура называется стратификацией, она позволяет снизить
разброс (вариацию) данных.

Обычно выборка
должна быть репрезентативной. Это предполагает, что все элементы изучаемой
совокупности имеют равную вероятность быть
отобранными в выборку. Репрезентативность
выборки обеспечивается одним из способов отбора:

— случайный – может проводиться по таблице случайных чисел;

— систематический – предполагает, что элементы отбираются через постоянный
интервал, начиная со случайно выбранного числа.

Интервал строится
либо на определенном числе элементов совокупности (например, изучение каждого
20-го документа из всех документов данной категории), либо на стоимостной их
оценке (например, отбирается тот элемент, на который приходится каждый
следующий миллион рублей в совокупной стоимости элементов);

— комбинированный – представляет собой комбинацию различных методов
случайного и систематического отбора.

Аудитор имеет право
прибегать к нерепрезентативной (непредставительной)
выборке только тогда, когда профессиональное суждение аудитора по итогам
проведения выборки не должно касаться всей совокупности в целом.

Например,
когда аудитор проверяет отдельно взятую группу операций либо класс операций, по
которым установлены возможные ошибки.

Для
любой выборки аудитор обязан:

— анализировать
каждую ошибку, попавшую в выборку;

— экстраполировать
полученные при выборке результаты на всю проверяемую совокупность;

— оценить
риски выборки.

При
анализе ошибок, попавших в выборку, аудитор должен в первую очередь установить
их характер. Формируя выборку, следует описать, для достижения каких целей она
проводится, и применительно к ним оценить найденные в выборке ошибки.

Если поставленные цели проверки не
были достигнуты с помощью выборочного исследования, то аудитор может провести
альтернативные аудиторские процедуры.

Аудитор может оценить качественный
аспект ошибок (их сущность и вызвавшую их причину), а также установить их
влияние на другие участки аудита.

Аудитор должен убедиться, что ошибка
в проверяемой совокупности не превышает допустимую величину. Для этого он
сравнивает ошибку совокупности, полученную посредством распространения, с
допустимой ошибкой.

Если первая ошибка оказалась больше
допустимой, аудитор должен повторно оценить риски выборки, и если сочтет их
неприемлемыми, то ему следует расширить круг аудиторских процедур или применять
аудиторские процедуры, альтернативные уже проведенным.

При определении объема выборки
аудитор должен установить риск выборки, допустимую и ожидаемую ошибки.

Риск выборки заключается в том, что
мнение аудитора по определенному
вопросу, составленное на основе выборочных данных, может отличаться от мнения
по данному вопросу, составленному на основании изучения всей совокупности. Риск
выборки имеется как при тестировании средств системы контроля, так и при
проведении детальной проверки верности отражения в бухучете оборотов и сальдо
по счетам. Различают риски первого и второго рода.

При тестировании средств контроля различают
следующие риски выборки:

— риск первого рода – риск отклонить верную гипотезу,
когда результат выборки свидетельствует
о ненадежности системы контроля, в то время как в действительности система
надежна;

—риск второго рода – риск принять неверную гипотезу,
когда результат выборки свидетельствует о надежности системы, в то время как в действительности
система контроля не обладает необходимой надежностью.

При проведении детальной проверки
верности отражения в учете оборотов и сальдо по счетам выделяют следующие риски
выборки:

— риск первого
рода – риск отклонить верную гипотезу, когда результат выборки свидетельствует,
что проверяемая совокупность содержит существенную ошибку, в то время как
совокупность свободна от такой ошибки;

— риск второго рода – риск принять неверную гипотезу,
когда результат выборки свидетельствует, что проверяемая совокупность не

существенную ошибку.

Риск
отклонения верной гипотезы требует проведения дополнительной работы со стороны
аудиторской организации или экономического субъекта.

Риск
принятия неверной гипотезы ставит под сомнение сами результаты работы аудитора.

Размер
выборки определяется величиной ошибки, которую аудитор считает допустимой.

Допустимая
ошибка устанавливается на стадии планирования аудита. Чем меньше размер
допустимой ошибки, тем больше должен быть объем аудиторской выборки.

Пример 1.

Аудитор располагает информацией по ООО «Контакт»: аудиту подлежат
материально-производственные запасы, общий объем проверяемой совокупности
составляет 500 тыс. руб., уровень существенности – 10 тыс. руб., номера
документов – с 50-го по 1050-й, система внутреннего контроля эффективна, в
бухгалтерском учёте по данным предыдущих проверок нет существенных искажений.

Необходимо построить выборку, указав
первые семь элементов методом случайного отбора (используя таблицу случайных
чисел и соответствующий коэффициент проверки).

Решение задачи:

Для построения выборки необходимо
определить ее элементы:

ЭВ = (ГС ∗ к)/УС,

ЭВ – элементы выборки;

ГС – генеральная совокупность;

к – коэффициент проверки;

УС – уровень существенности.

Из
генеральной совокупности исключаются элементы наибольших значений и ключевые
значения. По условию задачи они отсутствуют. Тогда:

ЭВ
= (500000 ∗ 0,7)/1000 =
35.

Коэффициент
проверки равен 0,7, так как система внутреннего контроля эффективна, в
бухгалтерском учете по данным предыдущих проверок нет существенных искажений.

Далее
определяются элементы выборки методом случайного отбора по формуле:

(ЗК
– ЗН) ∗ СЧ + ЗН,

ЗК – значение конечное;

ЗН – значение начальное;

СЧ – случайное число, взятое из таблицы
случайных чисел случайным образом.

Подставив ЗН, ЗК, имеем:

(1050
– 50) ∗ СЧ + 50.

Используя данный алгоритм, находим семь
первых значений выборки:

1000*0,4877+50=538;

1000*0,0441+50=94;

1000*0,2017+50=252;

1000*0,1797+50=230;

1000*0,7575+50=808;

1000*0,9374+50=987;

1000*0,3228+50=373.

Пример 2.

Аудитор
выборочно изучил 120 документов из 1250. При этом выявленная величина ошибок
(искажений) составила 1850 руб. Определить величину суммарной ошибки во всей
совокупности документов. Какими должны быть выводы и действия аудитора, если
приемлемой считается величина ошибки 17800 руб.?

Решение:
Суммарная
ошибка совокупности рассчитывается по формуле:
Ос=Ов*С/В,
где Ос – ошибка совокупности;

ОВ – ошибка выборки;

С – объем совокупности в целом;

В – объем исследуемой выборки.

Ос=1850*1250/120=19271
руб.
Суммарная
ошибка совокупности (19271 руб.) больше приемлемой величины ошибки (17800
руб.). Поскольку исчисленная суммарная ошибка выше приемлемой величины ошибки,
то финансовая отчетность считается неприемлемой. Аудитор может либо определить,
действительно ли завышенное показание превышает 17800 руб., либо представить заключение
с оговоркой или отрицательное заключение.

Практическое задание

Задание 1

Тест

	1. Величина допустимой ошибки выборки зависит от:
А)	Показателя оценки системы внутреннего контроля
Б)	Уровня существенности
В)	Риска необнаружения
	2. Допустимая ошибка в процессе аудита должна определяться в стадии:
А)	Планирования
Б)	Ознакомления с деятельностью экономического субъекта
В)	Проведения проверки
	3. Если ошибка в проверяемой совокупности больше допустимой, аудитор должен:
А)	Расширить круг применяемых аудиторских процедур и проверить другие элементы совокупности
Б)	Отказаться от выражения мнения по поводу достоверности бухгалтерской отчетности
В)	Сообщить о данном факте в письменной информации руководству экономического субъекта
	4. Методы распространения результатов выборки на всю совокупность:
А)	Четко регламентированы внутренними стандартами аудиторских организаций
Б)	Определяется законодательно
В)	Устанавливаются аудиторской организацией в зависимости от методов построения выборки
	5. Выбор метода построения выборки определяется:
А)	Аудитором в каждой конкретной ситуации
Б)	Внутренними правилами аудиторской организации
В)	Стандартами аккредитованных профессиональных аудиторских объединений
	6. Основная цель стратификации генеральной совокупности:
А)	Распределить обязанности между аудиторами при проверке
Б)	Уменьшить риск выборки за счет снижения вариации данных
В)	Увеличить допустимую ошибку выборки
	7. Преднамеренными искажениями бухгалтерской отчетности являются:
А)	Ошибки в расчетах
Б)	Арифметические ошибки
В)	Действия, совершенные в корыстных целях для введения в заблуждение пользователей финансовой отчетности
	8. Недостаточность или неадекватность описания учетной политики, когда существует вероятность того, что пользователи финансовой отчетности будут введены в заблуждение, являются примером:
А)	Количественных искажений
Б)	Качественных искажений
В)	Не являются искажениями
	9.Максимальный размер ошибки генеральной совокупности, которую аудитор считает приемлемой, — это:
А)	Общая ошибка выборки
Б)	Аномальная ошибка
В)	Допустимая ошибка
	10. Если элементы генеральной совокупности не имеют равную вероятность быть отобранными, то речь идет о:
А)	Репрезентативной выборке
Б)	Нерепрезентативной выборке
В)	Случайной выборке
	11.Аудиторская организация может применять нерепрезентативную выборку в случае:
А)	Если не следует распространить результаты исследования на всю совокупность
Б)	Большого объема проверяемой совокупности
В)	Неоднородности элементов генеральной совокупности
	12.Полный набор элементов, из которых аудитор проводит выборку для того, чтобы сделать выводы, — это:
А)	Генеральная совокупность
Б)	Выборочная совокупность
В)	Стратифицированная совокупность
	13. Аудиторская выборка – это:
А)	Полный набор элементов, из которых аудитор проводит выборку для того, чтобы сделать выводы
Б)	Индивидуальные элементы, отражаемые в учете и составляющие генеральную совокупность
В)	Применение аудиторских процедур менее чем ко всем элементам одной статьи отчетности или группы однотипных операций
	14. К методам отбора элементов для построения выборки не относится:
А)	Систематический
Б)	Бессистемный
В)	Систематизированный
	15. Аудиторская выборка это: а) один из методов аудиторской проверки; б) определенным образом отобранные элементы с целью распространения полученных результатов на всю проверяемую совокупность; в) способ группировки данных по определенным признакам:
А)	а, б
Б)	а, б, в
В)	а, в
	16. Отбор элементов из генеральной совокупности через определенный интервал – это:
А)	Статистический отбор
Б)	Систематический отбор
В)	Бессистемный отбор

Задание 2

Задача 2.1

Аудитор должен подтвердить оценку товарных
запасов. По данным бухгалтерского учета стоимость материальных ценностей на
складе составляет 600 000 руб., стоимость выборки — 195 000
руб., обнаруженная ошибка— 3000 руб.

Следует определить планируемую ожидаемую ошибку в
генеральной совокупности.

Задача 2.2.

Размер выборочной
совокупности —250 документов, размер
генеральной совокупности — 2500

Необходимо установить
выборочный интервал и порядок проведения случайной выборки.

Задание 3.

Составить кроссворд

Ключевые слова —

хх

Аудитор

Существенность

Репрезентативность

Стратификация

Компиляция

Независимость

Планирование

Конфидициальность

Достаточность (в аудите)

Программа (аудита)

Рекомендованная
литература:

1.
ЭБС
«Юрайт»: Аудит: учебник для СПО/ Н.А.Казакова и др. ; под ред. Н.А.Казаковой — 3-е изд., перераб. и доп. — М.:Изд-во Юрайт,
2018. — 409 с. — (Серия: Профессиональное образование). — ISBN
978-5-534-09320-9/

2. Парушина, Н. В. Аудит: практикум : учеб. пособие /
Н.В. Парушина, С.П. Суворова, Е.В. Галкина. — 3-е изд., перераб. и доп. —
Москва : ИД «ФОРУМ» : ИНФРА-М, 2017. — 286 с. — (Профессиональное образование).
— ISBN 978-5-16-102859-9. — Текст : электронный. — URL:
https://znanium.com/catalog/product/773992

3. Парушина, Н. В.
Аудит: практикум : учеб. пособие / Н.В. Парушина, С.П. Суворова, Е.В. Галкина.
— 3-е изд., перераб. и доп. — Москва : ИД «ФОРУМ» : ИНФРА-М, 2017. — 286 с. —
(Профессиональное образование). — ISBN 978-5-16-102859-9. — Текст :
электронный. — URL: https://znanium.com/catalog/product/773992

Источник

Ошибка выборки обусловливается двумя факторами: методом формирования выборки и размером выборки.

Они возникают, когда, например:

выборка не соответствует задачам исследования (социолог решил изучить только работающих пенсионеров, а опросил всех подряд);
налицо незнание характера генеральной совокупности (социолог думал, что 70% всех пенсионеров не работает, а оказалось, что не работает только 10%);
отбираются только «выигрышные» элементы генеральной совокупности (например, только обеспеченные пенсионеры).

нарушены методические и методологические правила проведения социологического исследования;
выбраны неадекватные способы формирования выборочной совокупности, методы сбора и расчета данных;
произошла замена требуемых единиц наблюдения другими, более доступными;
отмечен неполный охват выборочной совокупности (недополучение анкет, неполное их заполнение, труднодоступность единиц наблюдения).

Вот некоторые способы избежать ошибок выборки:

каждая единица генеральной совокупности должна иметь равную вероятность попасть в выборку;
отбор желательно производить из однородных совокупностей;
надо знать характеристики генеральной совокупности;
при составлении выборочной совокупности надо учитывать случайные и систематические ошибки.

стоимости сбора информации,
стремления к определенной степени статистической достоверности результатов, которую надеется получить исследователь.

Источник

Аудит

Ответ на вопрос «величина допустимой ошибки выборки зависит от …»

показателя оценки системы внутреннего контроля (СВК)
риска необнаружения
уровня существенности

Источник

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

Международный стандарт аудита 530 «Аудиторская выборка» введен в действие на территории Российской Федерации приказом Минфина России от 09.01.2019 № 2н

Аудит Ответ на вопрос «величина допустимой ошибки выборки зависит от …»

Международный стандарт аудита 530 «Аудиторская выборка» введен в
действие на территории Российской Федерации приказом Минфина России от
09.01.2019 № 2н

Аудит

Ответ на вопрос «величина допустимой ошибки выборки зависит от …»