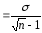-
Значение и применение ошибки средней арифметической величины и относительного показателя.
Определение
ошибок репрезентативности: Возникает
в тех случаях, когда требуется по частям
охарактеризовать явление в целом.
Генеральная совокупность может быть
охарактеризована по выборочной только
с определенными погрешностями,
измеряемыми ошибкой репрезентативности.
По величине ошибки репрезентативности
определяют, на сколько результаты,
полученные при выборочном наблюдении,
отличаются от результатов, которые
могли бы быть получены при проведении
сплошного исследования.
-
Средняя ошибка
средней арифметической, при числе
наблюдений
п
30: тм
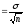
при п
30; тм
где: т
– ошибка репрезентативности средней
арифметической величины;
п – число
наблюдений;
σ- среднее
квадратическое отклонение.
Из формул видно,
что средняя ошибка средней арифметической
прямо пропорциональна степени
разнообразия признака и обратно
пропорциональна корню квадратному из
числа наблюдений, следовательно, для
уменьшения этой ошибки нужно увеличить
число наблюдений.
В) Ошибка относительных
показателей при числе наблюдений
п 30:
тр

при п
30 тр

– mp –
ошибка относительных показателей
P
– показатель, выраженный в %, ‰ и.т.д.
g
– (100-Р) при Р=%; (1000-Р) при Р=‰
n
– число наблюдений.
-
Метод стандартизации, его значение и применение.
Условие для
применения метода стандартизации:
Метод стандартизации
применяется при сравнении интенсивных
показателей, рассчитанных для
совокупностей, отличающихся по своему
составу.
Сущность метода
стандартизации состоит в том, что он
позволяет устранить возможное внешнее
различие в составе совокупностей по
какому-либо признаку на величину
сравниваемых интенсивных показателей.
Это достигается путём условного
уравнивания составов этих совокупностей
по данному признаку.
Характеристика
стандартизированных показателей:
—- — это условные
величины, не дающие представление об
истинном размере явления, а указывающие
лишь на то, какова была бы величина
сравниваемых интенсивных показателей,
если бы они были бы вписаны для однородных
по своему составу совокупностей.
Назначение метода
стандартизации:
Метод стандартизации
применяется для того, чтобы установить,
повлияла ли неоднородность составов
совокупностей по какому-либо признаку
на различия сравниваемых интенсивных
показателей
Этапы расчёта
стандартизированных показателей:
I
этап. Расчёт интенсивных показателей
в отдельных группах, по признаку различия
и по совокупности в целом
II
этап. Определение стандарта, то есть
одинакового для сравниваемых совокупностей
численного состава по данному признаку.
Как правило за стандарт принимается
сумма или полу сумма численностей
соответствующих групп.
III
этап. Вычисление ожидаемых абсолютных
величин в группах стандарта на основе
групповых интенсивных показателей,
получение итоговых чисел по сравниваемым
совокупностям путём суммирования
ожидаемых величин
IV
этап. Вычисление стандартизированных
показателей для сравнивания совокупностей
V
этап. Сопоставление соотношений
стандартизированных и интенсивных
показателей. Формулировка вывода.
Концепция репрезентативности часто встречается в статистических отчетах и при подготовке выступлений и отчетов. Пожалуй, без него сложно представить какое-либо представление информации для ознакомления.
Содержание
- 1 Репрезентативность — что это?
- 2 Другие определения
- 3 Репрезентативная выборка
- 4 Вероятностная выборка
- 5 Вероятностные выборки
- 6 Выборка потребителей
- 7 Размер выборки
- 8 Понятие ошибки репрезентативности
- 9 Виды ошибок
- 10 Преднамеренные и непреднамеренные ошибки репрезентативности
- 11 Валидность, надежность, репрезентативность. Расчет ошибок
- 12 Репрезентативные системы
Репрезентативность — что это?
Репрезентативность отражает степень, в которой выбранные объекты или части соответствуют содержанию и значению набора данных, из которого они были выбраны.
Другие определения
Репрезентативность можно понимать в разных контекстах. Но по своему смыслу репрезентативность — это соответствие характеристик и свойств выбранных единиц генеральной совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Кроме того, репрезентативность информации определяется как способность данных выборки представлять параметры и свойства совокупности, которые важны с точки зрения проводимых исследований.
Репрезентативная выборка
Принцип выборки заключается в выборе наиболее важных свойств, которые точно отражают общую совокупность данных. Для этого используются различные методы, позволяющие получить точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качество всех данных.
Таким образом, нет необходимости изучать весь материал, но достаточно учесть выборочную репрезентативность. Что это? Это набор отдельных данных, чтобы получить представление об общей массе информации.
В зависимости от метода они делятся на вероятностные и маловероятные. Вероятностный — это выборка, которая создается путем вычисления наиболее важных и интересных данных, которые в будущем будут репрезентативными для генеральной совокупности. Это осознанный выбор или случайная выборка, однако оправданная своим содержанием.
Маловероятно — это одна из разновидностей случайной выборки, составленной по принципу обычной лотереи. В этом случае мнение лица, взявшего такую пробу, не принимается во внимание. Используется только слепая жребий.
Вероятностная выборка
Вероятностные выборки также можно разделить на несколько типов:
- Один из самых простых и понятных принципов — нерепрезентативная выборка. Например, этот метод часто используется при проведении социальных опросов. При этом участники опроса не выбираются из общей массы по каким-либо конкретным критериям, а информация берется от первых 50 человек, принявших участие.
- Выборка вероятностей — это еще одна разновидность выборки невероятности, которая часто используется для исследования больших наборов данных. Для этого используется множество условий и правил. Выбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что будет опрошено 100 человек, но при составлении статистического отчета будет учитываться только мнение определенного количества людей, которые будут соответствовать установленным требованиям.
- Преднамеренные выборки отличаются тем, что они имеют ряд требований и условий для отбора, но все же полагаются на совпадения, не преследуя цели получения хорошей статистики.
Вероятностные выборки
Для вероятностных выборок рассчитывается ряд параметров, которым будут соответствовать объекты в выборке, и среди них различными способами могут быть выбраны именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Эти методы расчета требуемых данных могут быть:
- Простая случайная выборка. Он заключается в том, что среди выделенного сегмента методом полностью случайной лотереи выбирается необходимый объем данных, который будет репрезентативной выборкой.
- Систематическая и случайная выборка позволяет составить систему расчета необходимых данных на основе случайно выбранного сегмента. Итак, если первое случайное число, указывающее порядковый номер данных, выбранных из общей совокупности, равно 5, следующими данными для выбора могут быть, например, 15, 25, 35 и так далее. Этот пример ясно объясняет, что даже случайный выбор может быть основан на систематических вычислениях требуемых входных данных.
Выборка потребителей
Осмысленная выборка — это способ взглянуть на каждый отдельный сегмент, и на основе его оценки составляется генеральная совокупность, отражающая характеристики и свойства всей базы данных. Таким образом, собирается больше данных, отвечающих требованиям репрезентативной выборки. Легко выбрать набор параметров, которые не будут включены в общее количество, без потери качества выбранных данных, представляющих генеральную совокупность. Таким образом определяется репрезентативность результатов исследования.
Размер выборки
Не последняя проблема, которую необходимо решить, — это размер выборки для репрезентативной репрезентативности населения. Размер выборки не всегда зависит от количества источников в генеральной совокупности. Однако репрезентативность выборки напрямую зависит от того, на сколько сегментов в конечном итоге следует разделить результат. Чем больше таких сегментов, тем больше данных включается в итоговую выборку. Если результаты требуют общих обозначений и не требуют конкретики, то в результате выборка становится меньше, поскольку, не вдаваясь в детали, информация представлена более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Репрезентативная систематическая ошибка — это конкретное несоответствие между характеристиками населения и данными выборки. При проведении выборочного исследования невозможно получить абсолютно точные данные, как при полном изучении генеральных популяций и выборки, представленной только частью информации и параметров, в то время как более детальное изучение возможно только при изучении всей совокупности численность населения. Поэтому некоторые ошибки и ошибки неизбежны.
Виды ошибок
При составлении репрезентативной выборки возникают некоторые ошибки:
- Случайный.
- Стандарт.
- Не намеренно.
- Систематический.
- Предел.
- Умышленное.
Причиной появления случайных ошибок может быть прерывистый характер исследования генеральной совокупности. Обычно ошибка случайной репрезентативности незначительна по величине и характеру.
Между тем систематические ошибки возникают, когда нарушаются правила отбора данных из генеральной совокупности.
Средняя ошибка — это разница между средним значением выборки и основной совокупностью. Это не зависит от количества единиц в выборке. Он обратно пропорционален размеру выборки. Таким образом, чем больше объем, тем меньше среднее значение ошибки.
Предельная ошибка — это наибольшая возможная разница между средним значением выполненной выборки и всей генеральной совокупностью. Эта ошибка характеризуется как максимум возможных ошибок в данных условиях их возникновения.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки искажения данных могут быть преднамеренными или непреднамеренными.
Итак, причины появления преднамеренных ошибок — это подход к отбору данных с использованием метода выявления трендов. Непреднамеренные ошибки возникают и на этапе подготовки выборочного наблюдения, формирования репрезентативной выборки. Чтобы избежать таких ошибок, необходимо создать хорошую основу выборки для списков единиц выборки. Он должен полностью соответствовать целям выборки, быть надежным и охватывать все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Mm) среднего арифметического (M).
Стандартное отклонение: размер выборки (> 30).
Репрезентативная ошибка (Мр) и относительная величина (Р): размер выборки (n> 30).
В случае, если необходимо изучить совокупность, где размер выборки невелик и менее 30 единиц, количество наблюдений уменьшится на одну единицу.
Величина ошибки прямо пропорциональна размеру выборки. Репрезентативность информации и расчет степени возможности составления точного прогноза отражает определенное значение предельной погрешности.
Репрезентативные системы
В процессе оценки представления информации используется не только репрезентативная выборка, но и лицо, получающее информацию, также использует репрезентативные системы. Таким образом, мозг обрабатывает определенный объем информации, создавая репрезентативную выборку всего потока информации, чтобы качественно и быстро оценить предоставленные данные и понять суть проблемы. Ответьте на вопрос: «Представление — что это?» — В масштабе человеческого сознания это довольно просто. Для этого мозг использует все подчиненные органы чувств, в зависимости от типа информации, которую необходимо изолировать от общего потока. Поэтому проводится различие между:
- Система визуального представления, в которой задействованы органы зрительного восприятия глаза. Людей, которые часто используют эту систему, называют визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Система кинестетической репрезентации — это обработка потока информации путем ее восприятия через обонятельные и тактильные каналы.
- Система слухового представления. Основной используемый орган — слух. Информация, предоставленная в виде аудио- или голосового файла, обрабатывается именно этой системой. Людей, которые лучше всего воспринимают информацию на слух, называют аудиалами.
- Система цифрового представления используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и понимание полученных данных.
Так что же такое репрезентативность? Простая выборка из набора или целостная процедура обработки информации? Мы можем однозначно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая выделить самые тяжелые и наиболее важные из них.
В
статистике выделяют два основных метода
исследования — сплошной и выборочный.
При проведении выборочного исследования
обязательным является соблюдение
следующих требований: репрезентативность
выборочной совокупности и достаточное
число единиц наблюдений. При выборе
единиц наблюдения возможны ошибки
смещения,
т.е. такие события, появление которых
не может быть точно предсказуемым. Эти
ошибки являются объективными и
закономерными. При определении степени
точности выборочного исследования
оценивается величина ошибки, которая
может произойти в процессе выборки
— случайная
ошибка репрезентативности (m)
— является
фактической разностью между средними
или относительными величинами, полученными
при проведении выборочного исследования
и аналогичными величинами, которые были
бы получены при проведении исследования
на генеральной совокупности.
Оценка
достоверности результатов исследования
предусматривает определение:
1.
ошибки репрезентативности
2.
доверительных границ средних (или
относительных) величин в генеральной
совокупности
3.
достоверности разности средних (или
относительных) величин (по критерию t)
Расчет
ошибки репрезентативности
(mм)
средней арифметической величины
(М):
,
где σ
— среднее квадратическое отклонение; n
— численность выборки (>30).
Расчет
ошибки репрезентативности (mР)
относительной величины (Р):
,
где Р — соответствующая относительная
величина (рассчитанная, например, в %);
q
=100 — Ρ%
— величина, обратная Р; n
— численность выборки (n>30)
В
клинических и экспериментальных работах
довольно часто приходится использовать
малую
выборку, когда
число наблюдений меньше или равно 30.
При малой выборке для расчета ошибок
репрезентативности, как средних, так
и относительных величин,
число
наблюдений уменьшается на единицу,
т.е.
;
.
Величина
ошибки репрезентативности зависит от
объема выборки: чем больше число
наблюдений, тем меньше ошибка. Для оценки
достоверности выборочного показателя
принят следующий подход: показатель
(или средняя величина) должен в 3 раза
превышать свою ошибку, в этом случае он
считается достоверным.
83. Определение доверительных границ средних и относительных величин.
Знание
величины ошибки недостаточно для того,
чтобы быть уверенным в результатах
выборочного исследования, так как
конкретная ошибка выборочного
исследования может быть значительно
больше (или меньше) величины средней
ошибки репрезентативности. Для
определения точности, с которой
исследователь желает получить результат,
в статистике используется такое понятие,
как вероятность безошибочного
прогноза, которая является характеристикой
надежности результатов выборочных
медико-биологических статистических
исследований. Обычно, при проведении
медико-биологических статистических
исследований используют вероятность
безошибочного прогноза 95% или 99%. В
наиболее ответственных случаях, когда
необходимо сделать особенно важные
выводы в теоретическом или практическом
отношении, используют вероятность
безошибочного прогноза 99,7%
Определенной
степени вероятности безошибочного
прогноза соответствует определенная
величина предельной
ошибки случайной выборки (Δ
— дельта),
которая определяется по формуле:
Δ=t
* m
, где t
— доверительный коэффициент, который
при большой выборке при вероятности
безошибочного прогноза 95% равен 2,6;
при вероятности безошибочного
прогноза 99% — 3,0; при вероятности
безошибочного прогноза 99,7% — 3,3, а при
малой выборке определяется по специальной
таблице значений t
Стьюдента.
Используя
предельную ошибку выборки (Δ),
можно определить доверительные
границы,
в которых с определенной вероятностью
безошибочного прогноза заключено
действительное значение статистической
величины,
характеризующей
всю генеральную совокупность (средней
или относительной).
Для
определения доверительных границ
используются следующие формулы:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ ГОРОДА МОСКВЫ
Государственное бюджетное профессиональное образовательное учреждение города Москвы
«ЮРИДИЧЕСКИЙ КОЛЛЕДЖ»
(ГБПОУ Юридический колледж)
ПЛАН-КОНСПЕКТ учебного занятия
по ОП.11 Статистика
учебной дисциплине/междисциплинарному курсу
для обучающихся 2 курса
специальность 40.02.01 Право и организация социального обеспечения
(набор 2016 г.)
(углубленная подготовка)
дата проведения занятия по расписанию
Тема 3.1. Выборочное наблюдение
Занятие 15. ПЗ №8 Определение ошибки репрезентативности.
Определение объема выборочной совокупности
Цель занятия: отработать практические навыки по определению доверительных пределов и исчислению ошибок выборки
Задачи занятия:
Обучающая: Обеспечить усвоение обучающимися материала о понятиях: ошибки репрезентативности, выборка, выборочная совокупность;
Воспитательная: воспитывать навыки самостоятельной работы, чувство ответственности за порученный участок работы, дисциплину умственного труда, уверенность в своих силах, стремление к достижению результата;
Развивающая: создавать условия для развития самостоятельности мышления, способности высказывания собственной точки зрения, систематизировать необходимую информацию, анализировать, сравнивать и обобщать информацию, развивать монологическую речь.
Основная литература:
Глава 11. Выборочное наблюдение. (211-220) Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Дополнительная литература:
Савюк Л.К. Правовая статистика: Учебник. — М.: Юрист, 2016
Интернет-ресурсы:
- Информационно-издательский центр «Статистика России» http://www.statbook.ru
- Электронный фонд правовой и технической документации http://docs.cntd.ru
- Информационно правовой портал http://www.garant.ru/
Междисциплинарные связи: Право социальное обеспечение
Внутридисциплинарные связи: Тема 2.1. Сводка и группировка статистических данных
1. Актуализация знаний по ранее пройденному материалу учебного курса
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 1.
|
Вопрос (тестовое задание) |
Ответ |
|
|
|
|
|
|
|
|
|
2. Изучаемые вопросы занятия
|
1. Определение ошибки репрезентативности. |
|
2. Определение объема выборочной совокупности. |
Вопрос 1. Определение ошибки репрезентативности
В статистике выделяют два основных метода исследования – сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны Ошибки смещения, т. е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объективными и закономерными. При определении степени точности выборочного исследования оценивается величина ошибки, которая может произойти в процессе выборки – Случайная ошибка репрезентативности (M) – Является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на генеральной совокупности.
Оценка достоверности результатов исследования предусматривает определение:
1. ошибки репрезентативности
2. доверительных границ средних (или относительных) величин в генеральной совокупности
3. достоверности разности средних (или относительных) величин (по критерию t)
Расчет ошибки репрезентативности (mм) средней арифметической величины (М):

Расчет ошибки репрезентативности (mР) относительной величины (Р):

Q =100 – Ρ% – величина, обратная Р; n – численность выборки (n>30)
В клинических и экспериментальных работах довольно часто приходится использовать Малую выборку, Когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентативности, как средних, так и относительных величин, Число наблюдений уменьшается на единицу, т. е.


Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.
Знание величины ошибки недостаточно для того, чтобы быть уверенным в результатах выборочного исследования, так как конкретная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для определения точности, с которой исследователь желает получить результат, в статистике используется такое понятие, как вероятность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%
Определенной степени вероятности безошибочного прогноза соответствует определенная величина Предельной ошибки случайной выборки (Δ – дельта), которая определяется по формуле:
Δ=t * m, где t – доверительный коэффициент, который при большой выборке при вероятности безошибочного прогноза 95% равен 2,6; при вероятности безошибочного прогноза 99% – 3,0; при вероятности безошибочного прогноза 99,7% – 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента.
Используя предельную ошибку выборки (Δ), можно определить Доверительные границы, в которых с определенной вероятностью безошибочного прогноза заключено действительное значение статистической величины, Характеризующей всю генеральную совокупность (средней или относительной).
Для определения доверительных границ используются следующие формулы:
- для средних величин:

Мвыб – средняя величина, Полученная при проведении исследования на выборочной совокупности; t – доверительный коэффициент, значение которого определяется степенью вероятности безошибочного прогноза, с которой исследователь желает получить результат; mM – ошибка репрезентативности средней величины.
2) для относительных величин:

Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.
При малом числе наблюдений (n<30), для вычисления доверительных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, Указывающей на имеющееся число степеней свободы (n), Которое равно n-1.
на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген) при числе наблюдений больше 30
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80 ударов в 1 минуту; σ = ± 6 ударов в минуту.
Задание: определить ошибку репрезентативности (mM) и доверительные границы средней величины генеральной совокупности (Мген).
Решение.
- Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m): m = σ / √n = 6 / √36 = ±1 удар в минуту
- Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо:
- а) задать степень вероятности безошибочного прогноза (Р = 95 %);
- б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t, определяемого по таблице, равна 2 (t = 2). Тогда Мген = Мвыб ± tm = 80 ± 2×1 = 80 ± 2 удара в минуту.
Вывод. Установлено с вероятностью безошибочного прогноза Р = 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген)
Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18% случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген).
Решение.
- Вычисление ошибки репрезентативности относительного показателя: m = √P x q / n = √18 x (100 — 18) / 164 = ± 3%
- Вычисление доверительных границ средней величины генеральной совокупности (Рген) производится следующим образом:
- необходимо задать степень вероятности безошибочного прогноза (Р=95%);
- при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2). Тогда Рген = Рвыб± tm = 18% ± 2 х 3 = 18% ± 6%.
Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
на оценку достоверности разности средних величин
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у водителей сельскохозяйственных машин через 1 ч после начала работы составила 80 ударов в минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы водителей до начала работы равнялась 75 ударам в минуту; m = ± 1 удар в минуту.
Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч работы.
Решение.
Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24% (m = ± 2,64%).
Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.
Решение.
Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено влиянием возраста детей.
|
Источники информации по 1 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 1
- Записать в тетрадь конспект (1-2 стр.)
Вопрос 2. Определение объема выборочной совокупности
Социологические исследования редко бывают сплошными, как, например, перепись населения. Обычно сплошное исследование проводится при небольшой генеральной совокупности.
Чаще всего исследования носят выборочный характер, при котором наиболее важным основанием является возможность распространения полученных результатов и выводов на всю генеральную совокупность. В таком случае сплошное исследование нецелесообразно. Обеспечение этой нецелесообразности — вопрос о репрезентативности выборки, т.е. достаточной количественной и качественной представительности генеральной совокупности в выборке.
Условиями соблюдения репрезентативности выборки являются:
1) равная возможность каждого члена генеральной совокупности попасть в выборку;
2) отбор необходимо проводить независимо от изучаемого признака (иначе в выборку могут попасть, например, только спортсмены);
3) отбор по возможности должен производиться из однородных совокупностей;
4) величина выборки должна быть достаточно большой.
Далее возникает вопрос: как определить достаточный объем выборки? Для этого необходимо иметь характеристики генеральной совокупности по важнейшим (с точки зрения исследования) признакам. К ним, например, можно отнести сведения о количестве желающих заниматься физической культурой и спортом, о числе занимающихся и т.д. Но, как правило, такие характеристики (или многие из них) не известны. Пилотажные исследования как раз и направлены на их выявление.
Приведем пример определения объема выборочной совокупности. В ходе подготовки к проведению конкретно-социологического исследования на основании теоретических посылок были выделены характеристики и признаки, подлежащие изучению. Например, желание заниматься физической культурой, спортом, величина потребности, участие в видах деятельности и др.
На основании результатов изучения этих признаков в пробном исследовании (30 и более респондентов) определяется объем выборки.
Предположим, что в пробном исследовании опрошено 147 студентов 4-х курсов в четырех вузах Республики Беларусь.
Для желания заниматься физической культурой получены следующие распределения:
1.«Нет, не хочу» — 5 человек;
2.«Скорее не хочу, чем хочу» — 3 человека;
3.«Безразлично» — 11 человек;
4.«Скорее хочу, чем не хочу» — 34 человека;
5.«Да, хочу» — 72 человека.
Для расчета объема выборки используются формулы:
t — 1,96 — распределение Стьюдента для вероятности 0,95 или 95% (т.е., если требуемая вероятность соответствия характеристик выборки и характеристик генеральной совокупности 95%, всегда = 1,96. Их соответствие на 95% — общепринятое требование в социологических исследованиях.
Для нашего распределения:
При условии, что выборка в пробном исследовании представляла бы собой модель генеральной совокупности, величина выборочной совокупности для изучения желания заниматься физической культурой должна быть не меньше 147 человек. Тогда с вероятностью 95% можно утверждать, что генеральное среднее лежит в пределах 4,39+0,155.
Поскольку модель выборки в пробном исследовании во вузам не представляет собой модели генеральной совокупности (опрос был в четырех вузах из 30), то увеличиваем полученное n (30/4) в 7,5 раза. Тогда необходимый объем выборки — 1102 респондента.
Качественная представительность полученной выборки оценивается сравнением существенных характеристик (либо связанных с существенными) генеральной совокупности и выборки. Для студенчества, например, такими характеристиками являются: соотношение по полу, охват учебными занятиями по физическому воспитанию, соотношение форм занятий и др.
Когда информация о признаках элементов генеральной совокупности отсутствует, исключается возможность определения объема выборочной совокупности при помощи формул. В этом случае можно опереться на многолетний опыт социологов — практиков, свидетельствующий о том, что для пробных опросов достаточна выборка объемом 100-250 человек. При массовых опросах, если величина генеральной совокупности 5000 человек, достаточный объем выборочной совокупности — не менее 500 человек, если же величина генеральной совокупности 5000 человек и более, то — 10% ее состава (но не более 2000-2500 человек). Это характеризует достаточно достоверные результаты исследования.
ПРИМЕР 1
При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.
Решение.
В данном примере – случайный повторный отбор.
n=200


p=0,997, тогда t=3
Формула средней ошибки для случайного повторного отбора:


Определяем величину средней ошибки.
Ответ: пределы в которых находится средний вес изделий:
ПРИМЕР 2
В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:
P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.
|
Число детей в семье, xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кол-во детей в семье |
1000 |
2000 |
1200 |
400 |
200 |
200 |
Решение
2%-я выборка означает: n=250000*0,02= 5000 семей было исследовано.
Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:
Найдем среднее число детей в выборочной совокупности:

Определим дисперсию

Т.к p = 0,954, то t = 2


Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.
|
Источники информации по 2 вопросу |
Автор и наименование |
Страницы (форма доступа для Интернет-ресурсов) |
|
Основная литература |
Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 3-е издание, стер. – М.: КНОРУС, 2019. – 232 с. – СПО |
стр. 211-220 |
|
Интернет ресурсы |
|
http://www.statbook.ru |
|
http://docs.cntd.ru |
|
|
http://www.garant.ru/ |
Контрольное задание по Вопросу 2
- Записать в тетрадь конспект (1-2 стр.)
3. Подведение итогов учебного занятия
(ответить на вопросы (тестовые задания) и провести самооценку усвоенного материала)
Таблица 2.
|
Наименование изученного вопроса учебного занятия |
Контрольное задание по изученному вопросу |
Ответ |
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 1 Условие задачи: при медицинском осмотре 126 детей 6 летнего возраста, проживающих в одном из районов городе А., в 12% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген). |
|
|
Определение ошибки репрезентативности. |
ЗАДАНИЕ 2. Условие задачи: при медицинском осмотре детей 6 летнего возраста в 15% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 7-летнего возраста составила 24% (m = ± 2,64%). Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп. |
|
|
Определение объема выборочной совокупности |
ЗАДАНИЕ 3. В городе проживает 300 тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей: P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Сформулируйте понятие генеральной совокупности |
|
|
Определение объема выборочной совокупности |
Перечислите способы отбора единиц для выборочного наблюдения |
- Домашнее задание на следующее занятие
- Выучить основные понятия. Глава 11. Выборочное наблюдение. Статистика: учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО (стр. 211-220)
- Выполнить задание 11.1. в тетради (стр. 224) учебник / И.В. Гладун. – 2-е издание, стер. – М.: КНОРУС, 2014. – 232 с. – СПО
Преподаватель Ю.В. Древаль
|
СОГЛАСОВАНО Протокол заседания ЦК дисциплин профессионального цикла специальности «Право и организация социального обеспечения» ГБПОУ Юридический колледж от ____________ 2017 г. № ___ |